
Pilot
TNC 426
NC-Software
280 462 xx
280 463 xx
1/97


The Pilot
Contents
... is your concise programming guide for the HEIDENHAIN
TNC 426 CA and TNC 426 PA contouring controls. For more
comprehensive information on programming and operating,
refer to the TNC User's Manual. There you will find complete information on:
the SL cycle group I (Cycles 6, 14, 15, 16)
Q-parameter programming
the central tool file
3D tool compensation
tool measurement
Certain symbols are used in the Pilot to denote specific types
of information:
Important note
Warning: danger for the user or the machine!
The TNC and the machine tool must be prepared by
the machine tool builder to perform these functions!
Chapter in User's Manual where you will find more
detailed information on the current topic.
The information in this Pilot applies to TNCs with the following
software numbers:
Control NC Software Number
Fundamentals ................................................................... 4
Contour Approach and Departure..................................... 13
Path Functions .................................................................. 18
FK Free Contour Programming ......................................... 25
Subprograms and Program Section Repeats ................... 33
Working with Cycles......................................................... 36
Drilling Cycles ................................................................... 39
Pockets, Studs, and Slots ................................................. 46
Point Patterns ................................................................... 55
SL Cycles .......................................................................... 57
Multipass Milling ............................................................... 64
Coordinate Transformation Cycles ................................... 67
Special Cycles ................................................................... 73
Digitizing 3D Surfaces....................................................... 75
Graphics and Status Displays ........................................... 81
ISO Programming ............................................................. 84
Miscellaneous Functions M.............................................. 88
Contents
TNC 426 CA, TNC 426 PA 280 462 01
TNC 426 CE*, TNC 426 PE* 280 463 01
*) Export version
3
Fundamentals
Files in the TNC
File type
Programs/Files
See Introduction, File Management
The TNC keeps its programs, tables and texts in files.
A file designation consists of two components:
THREAD2.H
Fundamentals
File name File type
Maximum length: see table at right
8 characters
Creating a New Part Program
PGM
MGT
1 BLK FORM 0.1 Z X+0 Y+0 Z-50
2 BLK FORM 0.2 X+100 Y+100 Z+0
Select the directory in which the program is stored
Enter a new file name with file type
Select unit of measure for dimensions (mm or inches)
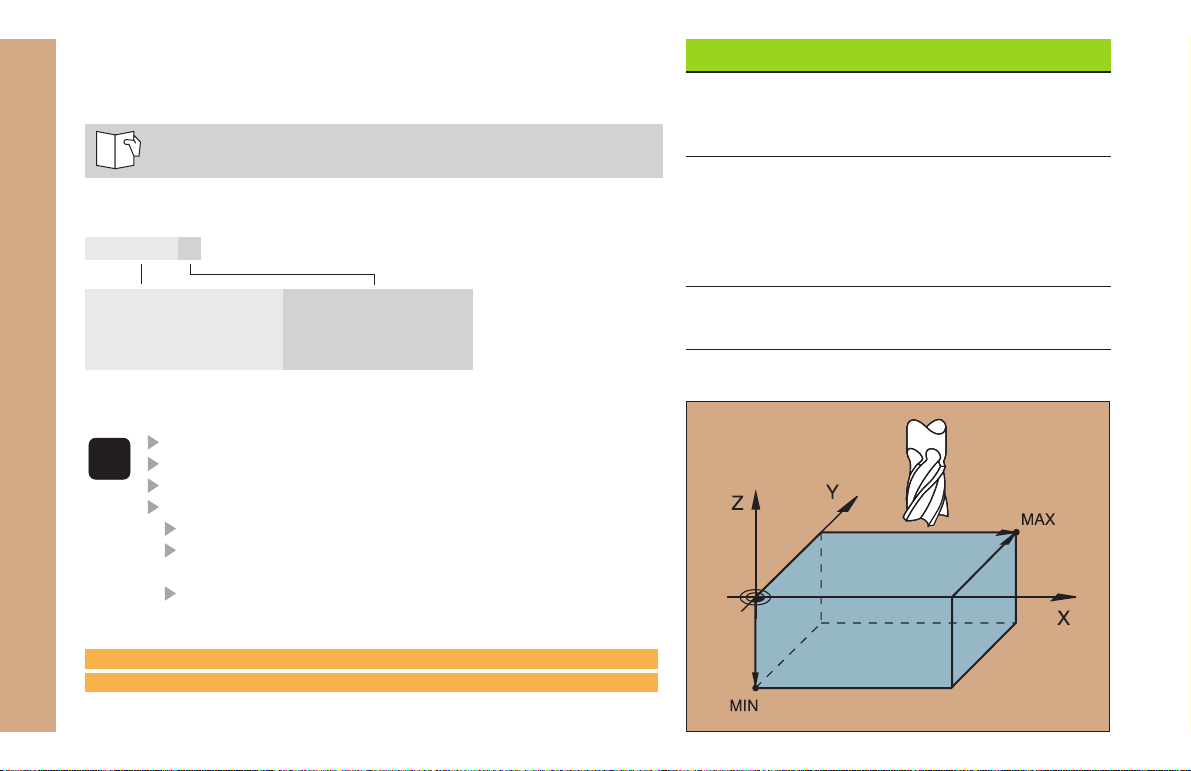
Define the blank form (BLK) for graphics:
Enter the spindle axis
Enter coordinates of the MIN point:
the smallest X, Y and Z coordinates
Enter coordinates of the MAX point:
the greatest X, Y and Z coordinates
4
Programs
in HEIDENHAIN format
in ISO format
Tables for
Tools
Datums
Pallets
Points
Texts as
ASCII files
.H
.I
.T
.D
.P
.PNT
.A
Choosing the Screen Layout
See Introduction, the TNC 426
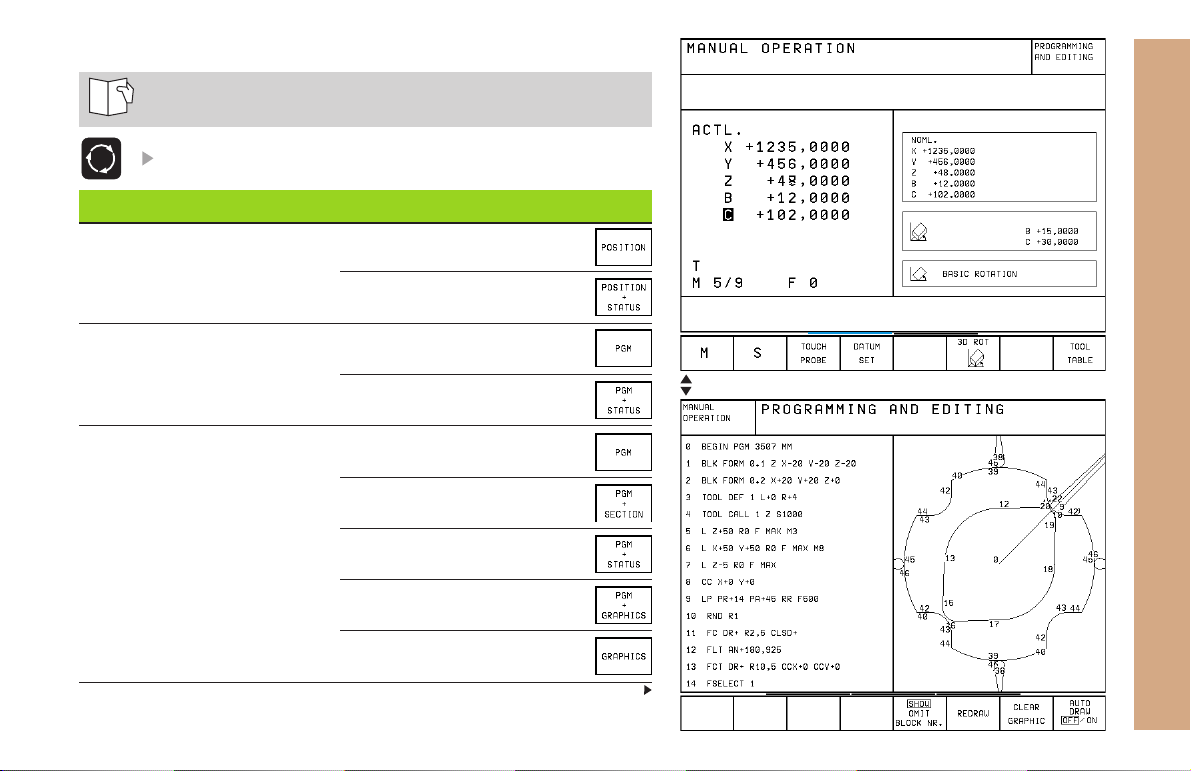
Show soft keys for setting the screen layout
Mode of operation Screen contents
MANUAL OPERATION
ELECTRONIC HANDWHEEL
POSITIONING WITH
MANUAL DATA INPUT
PROGRAM RUN,
FULL SEQUENCE
PROGRAM RUN,
SINGLE BLOCK TEST RUN
Positions
Positions at left
Status at right
Program
Program at left
Status at right
Program
Program at left
Program structure at right
Program at left
Status at right
Program at left
Graphics at right
Graphics
Positions at left, status at right
Program at left, graphics at right
Fundamentals
Continued
5
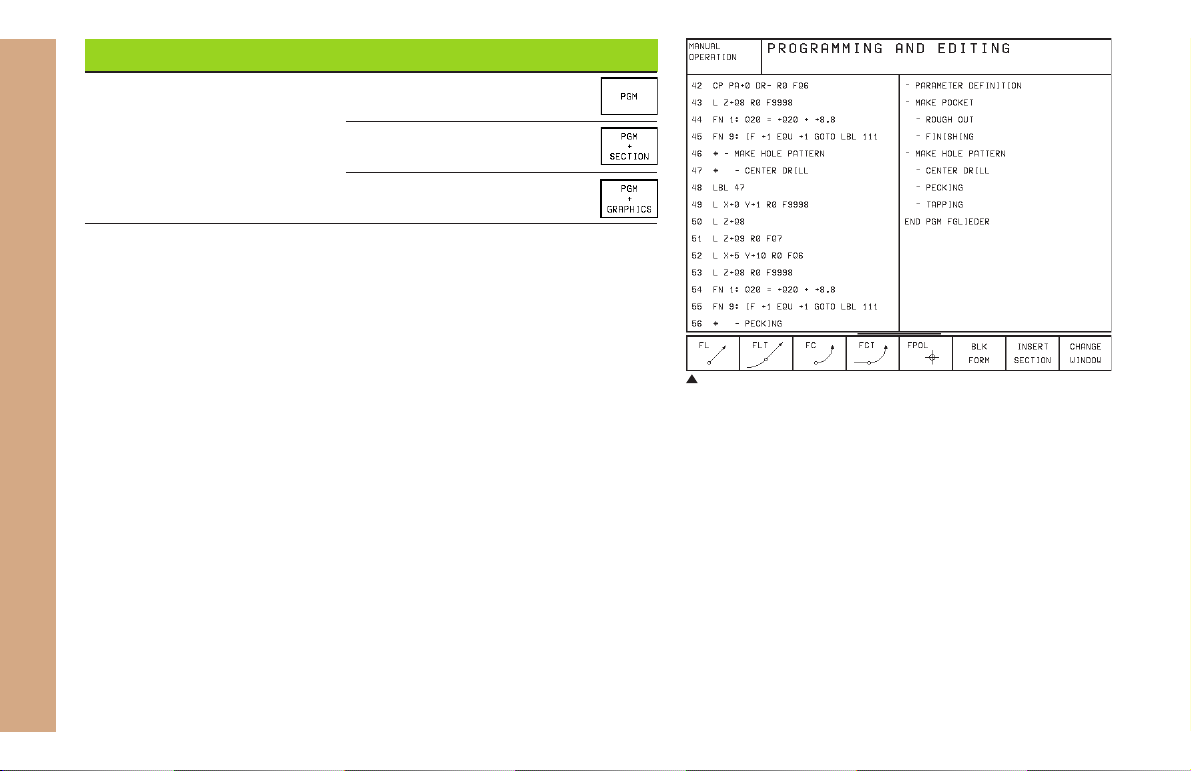
Mode of operation Screen contents
PROGRAMMING AND EDITING
Program
Program at left
Program structure at right
Program at left
Programming graphics at right
Fundamentals
Program at left, program structure at right
6
Absolute Cartesian Coordinates
The dimensions are measured from the current datum.
The tool moves to the absolute coordinates.
Programmable axes in an NC block
Linear motion: 3 or 5 axes (depending on machine or control)
Circular motion: 2 linear axes in a plane or
3 linear axes with cycle 19
WORKING PLANE
Incremental Cartesian Coordinates
The dimensions are measured from the last programmed position of
the tool.
The tool moves by the incremental coordinates.
Fundamentals
7
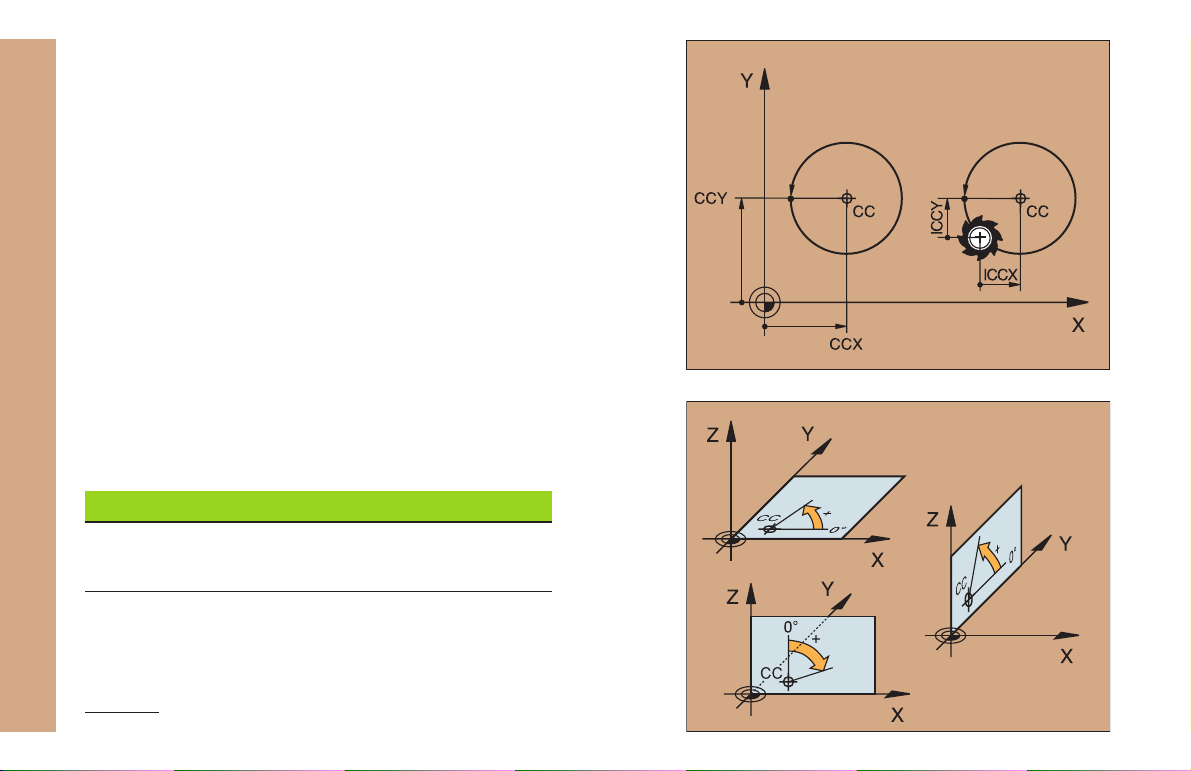
Circle Center and Pole: CC
The circle center (CC) must be entered to program circular tool
movements with the path function C (see page 21). CC is also needed
to define the pole for polar coordinates.
CC is entered in Cartesian coordinates*.
An absolutely defined circle center or pole is always measured from
the workpiece datum.
Fundamentals
An incrementally defined circle center or pole is always measured
from the last programmed position of the workpiece.
Angle Reference Axis
Angles such as a polar coordinate angle PA or an angle of rotation
ROT are measured from the angle reference axis.
Working plane Ref. axis and 0° direction
X/Y X
Y/Z Y
Z/X Z
8
*Circle center in polar coordinates: See FK programming
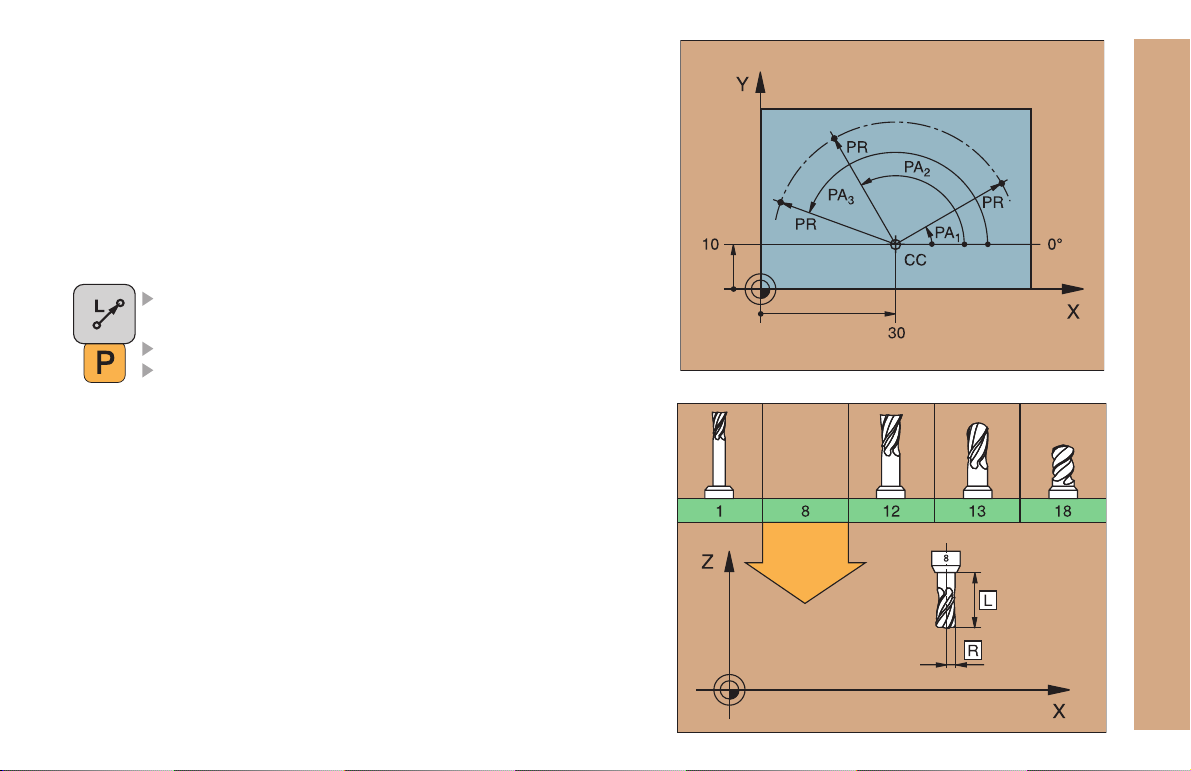
Polar Coordinates
Dimensions in polar coordinates are referenced to the pole (CC).
A position in the working plane is defined by
Polar coordinate radius PR = Distance of the position from the pole
Polar coordinate angle PA = Angle from the angle reference axis to
the straight line CC PR
Incremental dimensions
Incremental dimensions in polar coordinates are measured from the
last programmed position.
Programming polar coordinates
Select the path function
Press the P key
Answer the dialog prompts
Defining Tools
Tool data
Every tool is designated by a tool number between 1 and 254 or, if
you are using tool tables, by a tool name.
Entering tool data
You can enter the tool data (length L and radius R)
in a tool table (centrally, Program TOOL.T)
or
within the part program in TOOL DEF blocks (locally)
Fundamentals
9
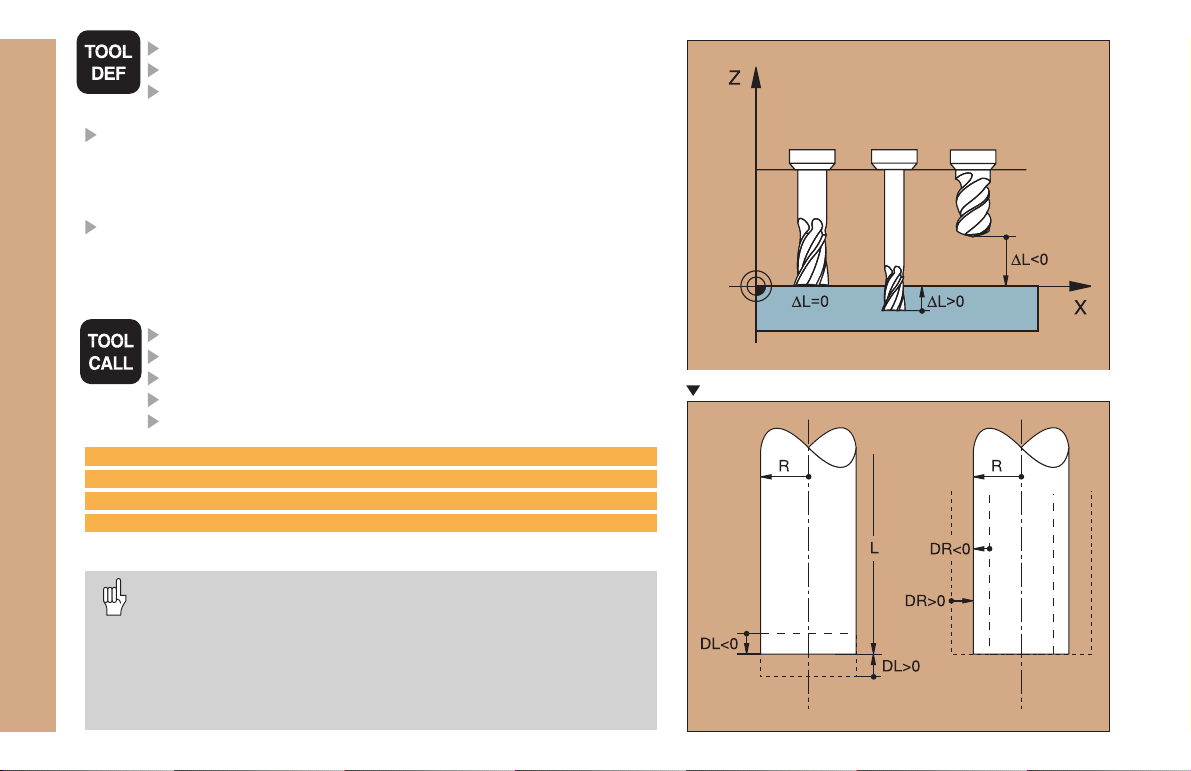
TOOL NUMBER
TOOL LENGTH L
TOOL RADIUS R
Program the tool length as its difference ∆L to the zero tool:
∆L>0: The tool is longer than the zero tool
∆L<0: The tool is shorter than the zero tool
With a tool presetter you can measure the actual tool length, then
Fundamentals
program that length.
Calling the tool data
TOOL NUMBER or name
WORKING SPINDLE AXIS: tool axis
SPINDLE SPEED S
TOOL LENGTH OVERSIZE DL (e.g. to compensate wear)
TOOL RADIUS OVERSIZE DR (e.g. to compensate wear)
3 TOOL DEF 6 L+7.5 R+3
4 TOOL CALL 6 Z S2000 DL+1 DR+0.5
5 L Z+100 R0 FMAX
6 L X-10 Y-10 R0 FMAX M6
Tool change
Beware of tool collision when moving to the tool change
position!
The direction of spindle rotation is defined by M function:
The maximum permissible oversize for tool radius or length
10
is ±99.999mm!
Oversizes on an end mill
M3: Clockwise
M4: Counterclockwise
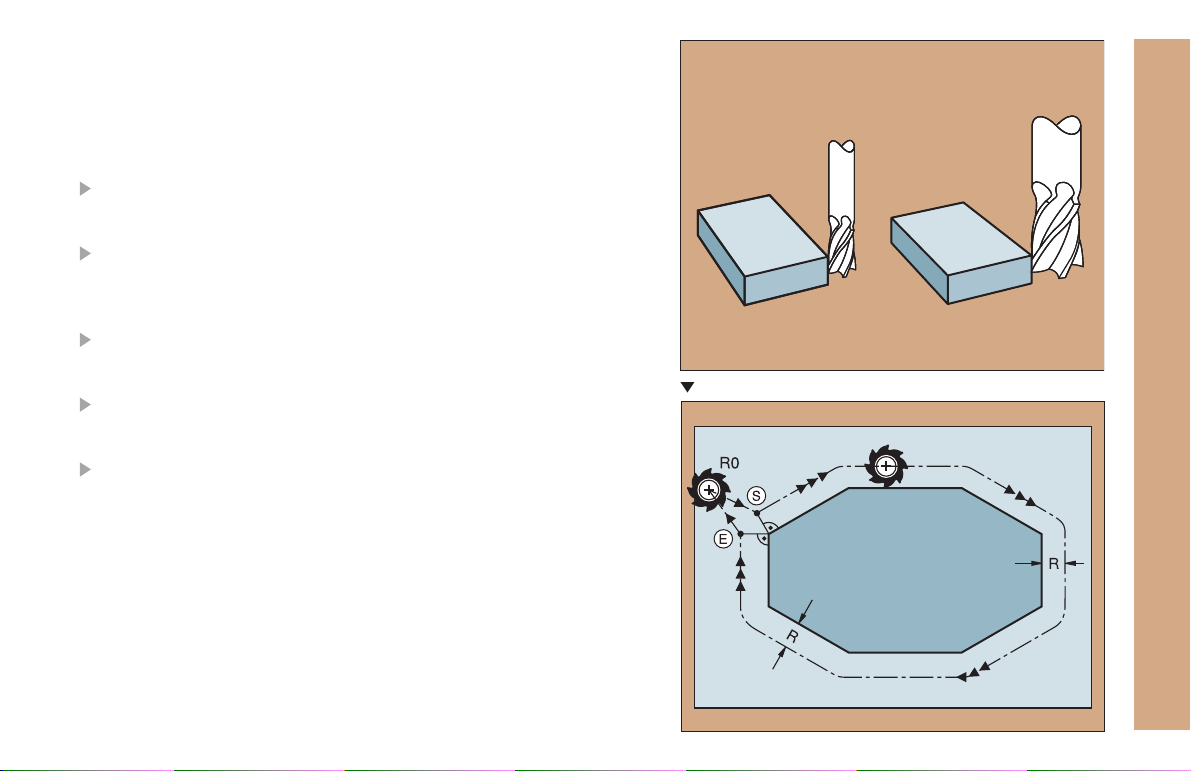
Tool Compensation
The TNC compensates the length L and radius R of the tool during
machining.
Length compensation
Beginning of effect:
Tool movement in the spindle axis
End of effect:
Tool exchange or tool with the length L=0
Radius compensation
Beginning of effect:
Tool movement in the working plane with RR or RL
Fundamentals
End of effect:
Execution of a positioning block with R0
Working without radius compensation (e.g. drilling):
Tool movement with R0
S = Start; E = End
11
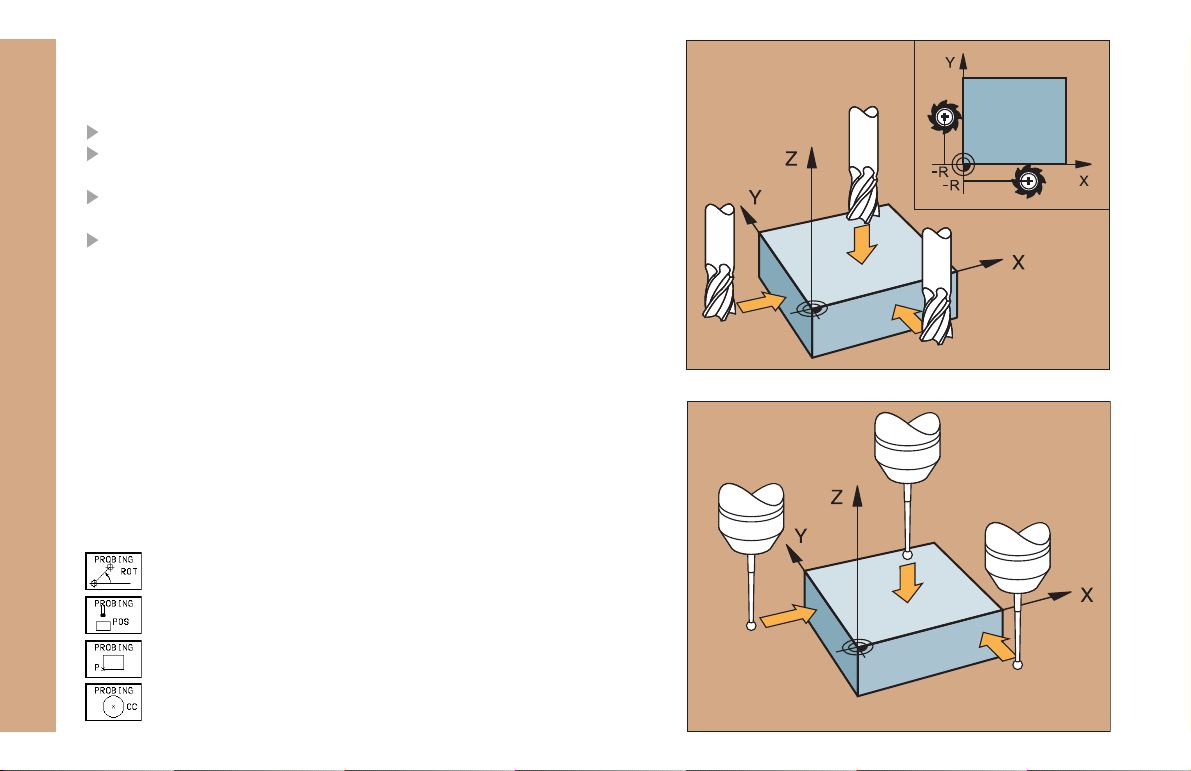
Datum Setting Without a 3D Touch Probe
During datum setting you set the TNC display to the coordinates of a
known position on the workpiece:
Insert a zero tool with known radius
Select the MANUAL OPERATION or
ELECTRONIC HANDWHEEL mode
Touch the reference surface in the tool axis with the tool and enter
its length
Fundamentals
Touch the reference surface in the working plane with the tool and
enter the position of the tool center
Datum Setting with a 3D Touch Probe
The fastest, simplest and most accurate way to set a datum is to use
a HEIDENHAIN 3D touch probe.
The following probe functions are provided by the MANUAL OPERATION and ELECTRONIC HANDWHEEL modes of operation:
Basic rotation
Datum setting in one axis
12
Datum setting at a corner
Datum setting at a circle center
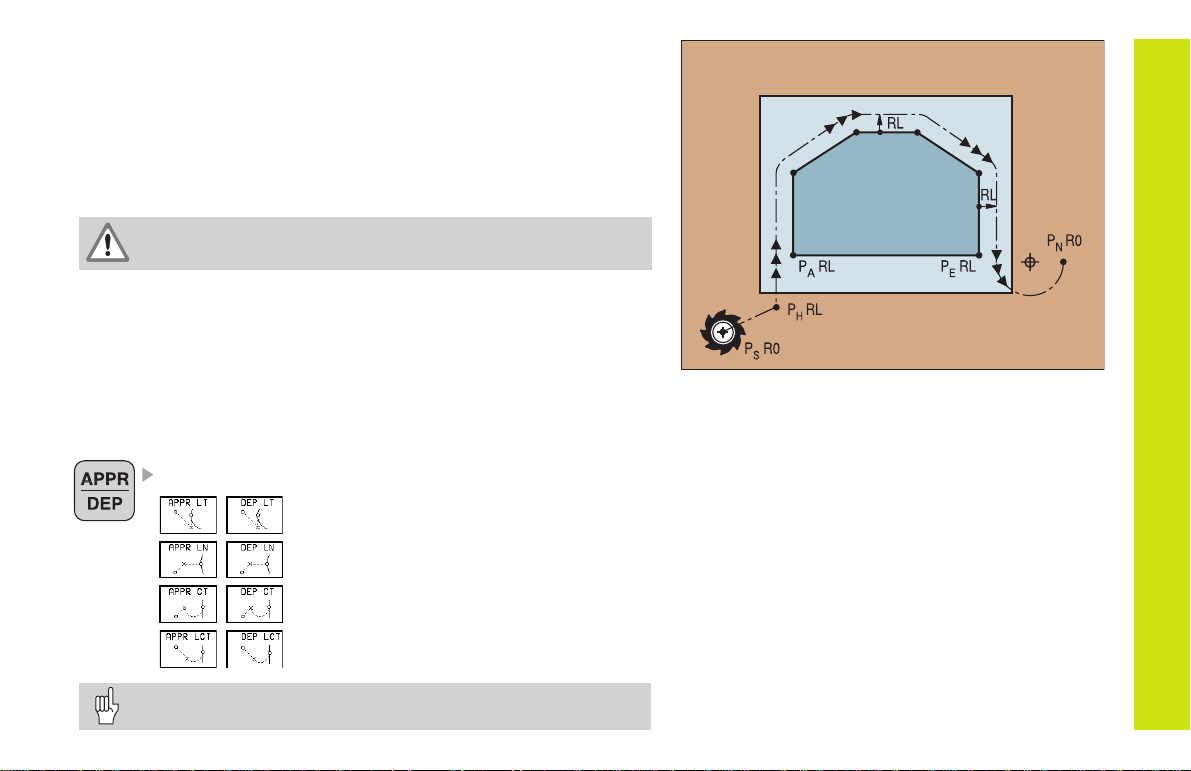
Contour Approach and Departure
Starting point P
PS lies outside of the contour and must be approached without radius
S
compensation.
Auxiliary point P
PH lies outside of the contour and is calculated by the TNC.
The tool moves from the starting point P
P
at the feed rate last programmed feed rate!
H
First contour point P
The first contour point PA is programmed in the APPR (approach) block.
H
and last contour point P
A
to the auxiliary point
S
E
The last contour point is programmed as usual.
End point P
PN lies outside of the contour and results from the DEP (departure)
block. P
N
is automatically approached with R0.
N
Path Functions for Approach and Departure
Press the soft key with the desired path function:
Straight line with tangential connection
Straight line perpendicular to the
contour point
Circular arc with tangential connection
Straight line segment tangentially connected
to the contour through an arc
Contour Approach and Departure
Program a radius compensation in the APPR block!
DEP blocks set the radius compensation to 0!
13
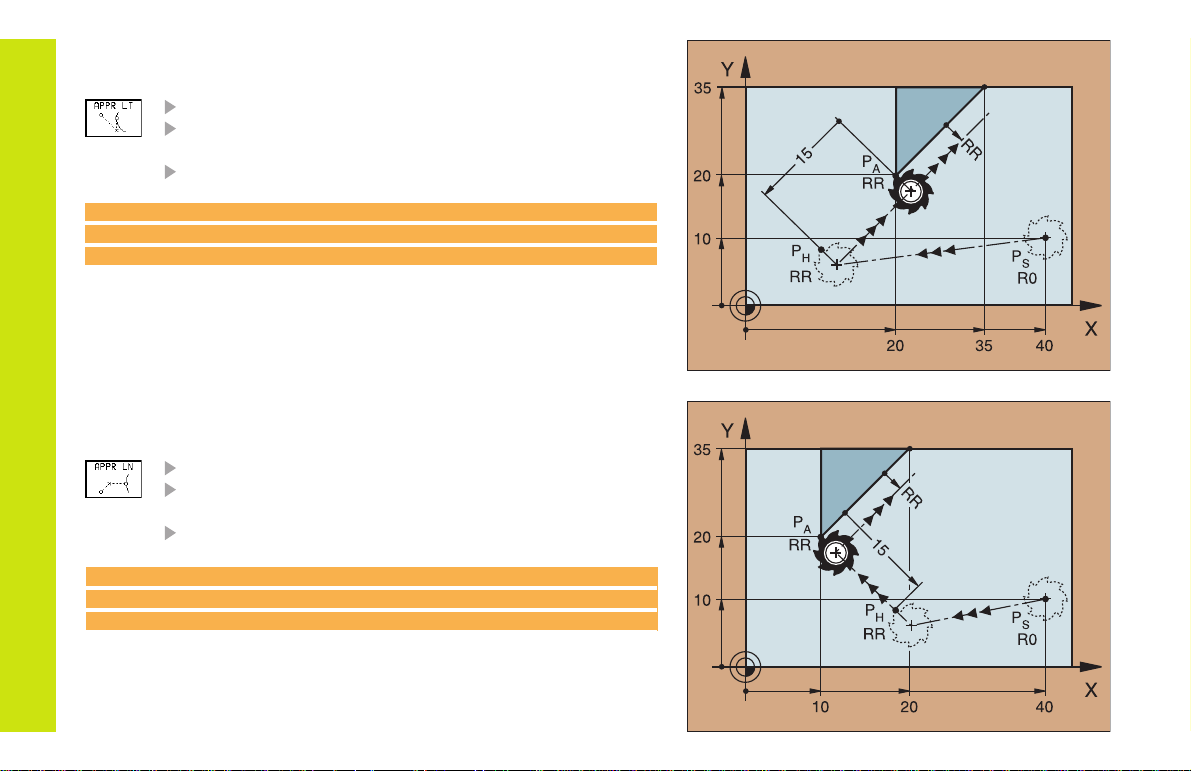
Approaching on a Straight Line with
Tangential Connection
COORDINATES for the first contour point P
Distance LEN (length) from PH to P
Enter a length LEN > 0
TOOL RADIUS COMPENSATION RR/RL
A
7 L X+40 Y+10 R0 FMAX M3
8 APPR LT X+20 Y+20 LEN 15 RR F100
9 L X+35 Y+35
A
Approaching on a Straight Line Perpendicular to
the First Contour Element
COORDINATES for the first contour point P
Distance LEN (length) from PH to P
Enter a length LEN > 0
Contour Approach and Departure
RADIUS COMPENSATION RR/RL
A
7 L X+40 Y+10 R0 FMAX M3
8 APPR LN X+10 Y+20 LEN 15 RR F100
9 L X+20 Y+35
A
14
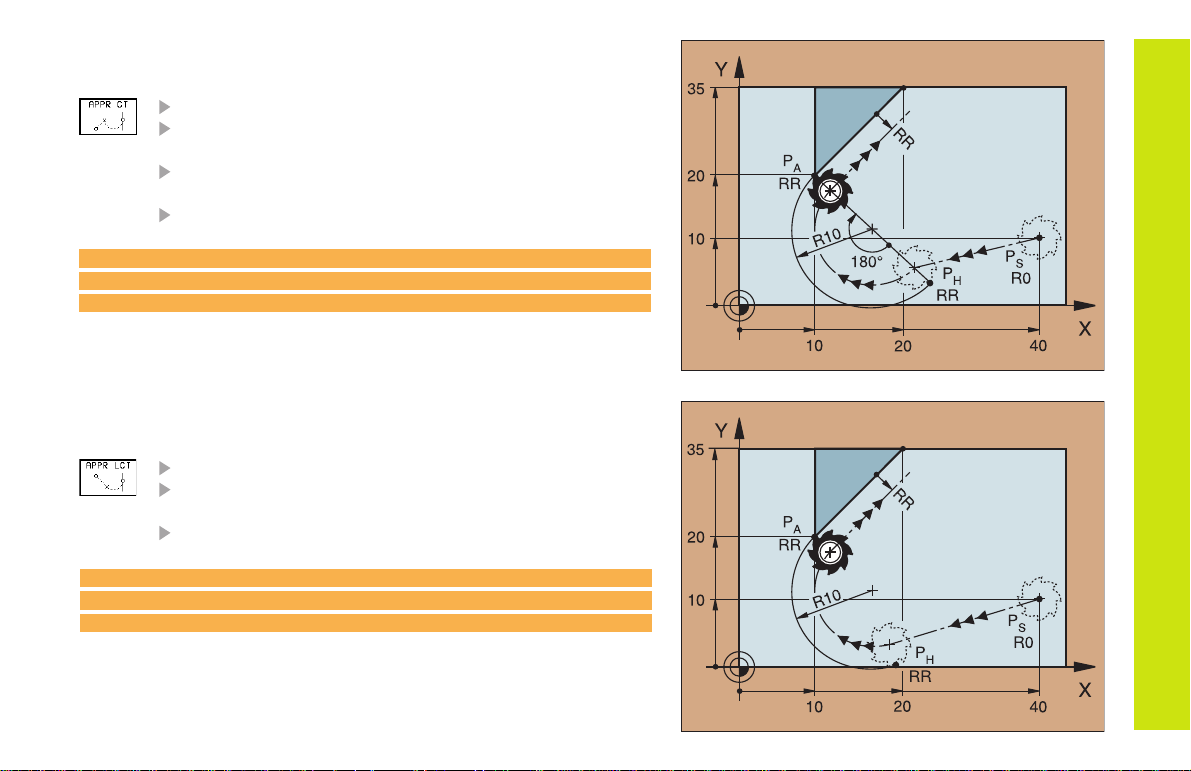
Approaching Tangentially on an Arc
COORDINATES for the first contour point P
RADIUS R
Enter a radius R > 0
CIRCLE CENTER ANGLE (CCA)
Enter a CCA > 0
TOOL RADIUS COMPENSATION RR/RL
7 L X+40 Y+10 R0 FMAX M3
8 APPR CT X+10 Y+20 CCA 180 R10 RR F100
9 L X+20 Y+35
Approaching Tangentially on an Arc
and a Straight Line
COORDINATES for the first contour point P
RADIUS R
Enter a radius R > 0
TOOL RADIUS COMPENSATION RR/RL
7 L X+40 Y+10 R0 FMAX M3
8 APPR LCT X+10 Y+20 R10 RR F100
9 L X+20 Y+35
A
A
Contour Approach and Departure
15
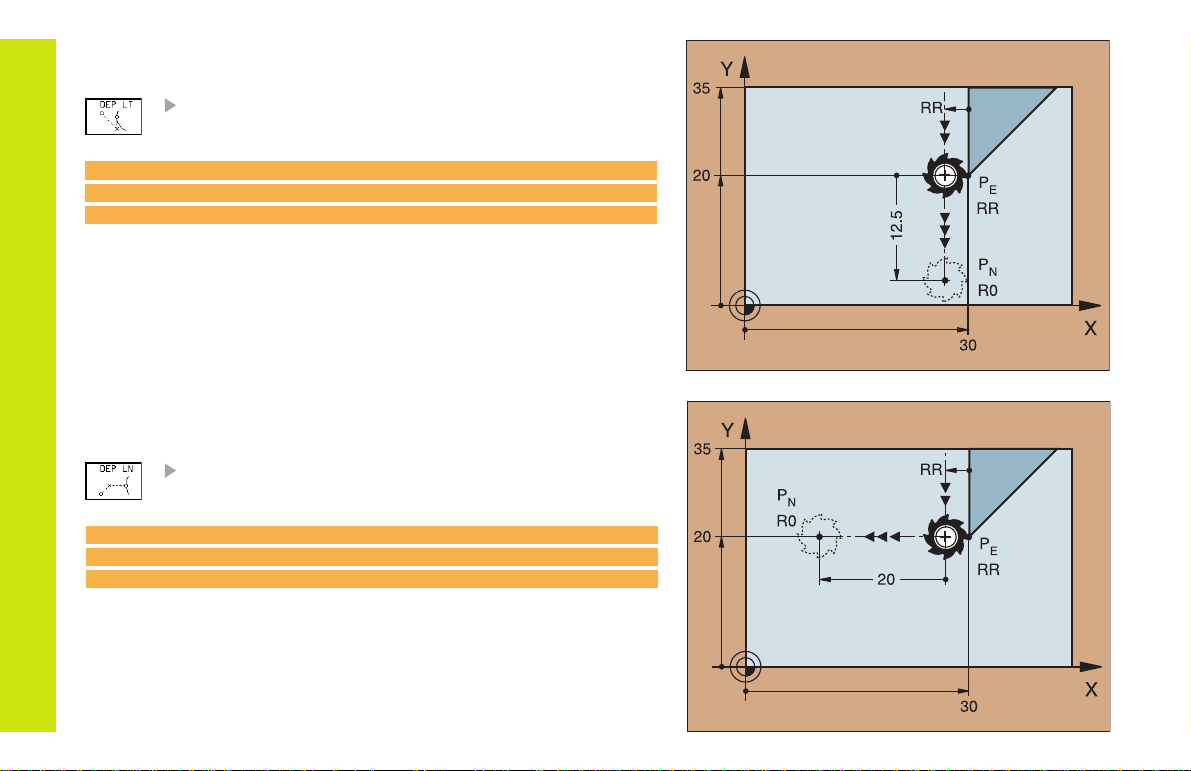
Departing Tangentially on a Straight Line
Distance LEN (length) from PE to P
Enter a length LEN > 0
N
23 L X+30 Y+35 RR F100
24 L Y+20 RR F100
25 DEP LT LEN 12.5 F100 M2
Departing on a Straight Line
Perpendicular to the Last Contour Element
Distance LEN (length) from PE to P
Enter a length LEN > 0
Contour Approach and Departure
23 L X+30 Y+35 RR F100
24 L Y+20 RR F100
25 DEP LN LEN+20 F100 M2
N
16
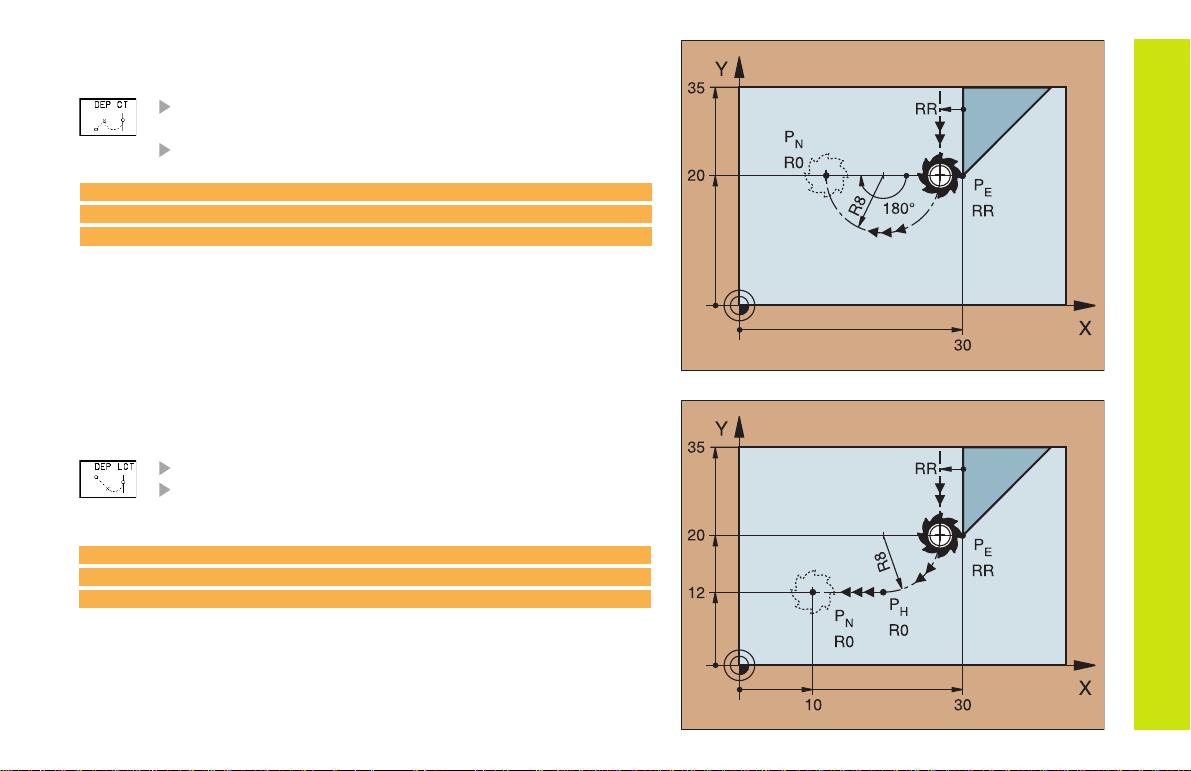
Departing Tangentially on an Arc
RADIUS R
Enter a radius R > 0
CIRCLE CENTER ANGLE (CCA)
23 L X+30 Y+35 RR F100
24 L Y+20 RR F10
25 DEP CT CCA 180 R+8 F100 M2
Departing on an Arc Tangentially Connecting
the Contour and a Straight Line
COORDINATES of the end point P
RADIUS R
Enter a radius R > 0
N
23 L X+30 Y+35 RR F100
24 L Y+20 RR F100
25 DEP LCT X+10 Y+12 R8 F100 M2
Contour Approach and Departure
17

Path Functions for Positioning Blocks
Path functions
See Programming Tool Movements.
Programming the Direction of Traverse
Regardless of whether the tool or the workpiece is actually moving,
you always program as if the tool is moving and the workpiece is
stationary.
Entering the Target Positions
Target positions can be entered in Cartesian or polar coordinates
Path Functions
either as absolute or incremental values, or with both absolute and
incremental values in the same block.
Entries in the Positioning Block
A complete positioning block contains the following data:
Path function
Coordinates of the contour element end points (target position)
Radius compensation RR/RL/R0
Feed rate F
Miscellaneous function M
Before you execute a part program, always pre-position the tool
to prevent the possibility of damaging the tool or workpiece!
Straight line
Chamfer between two
straight lines
Corner rounding
Circle center or pole for
polar coordinates
Circular path aroundthe
circle center CC
Circular path with
known radius
Circular path with
tangential connection to
previous contour
Page 19
Page 20
Page 20
Page 21
Page 21
Page 22
Page 23
18
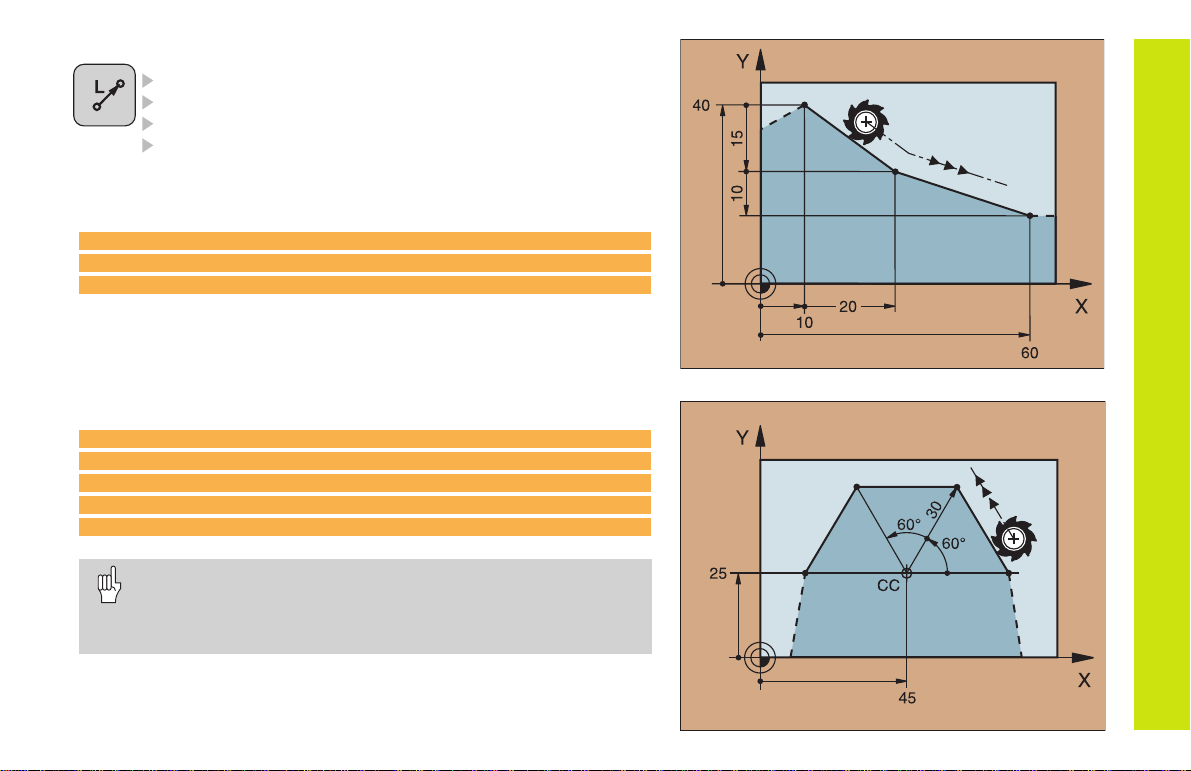
Straight Line
COORDINATES of the straight line end point
TOOL RADIUS COMPENSATION RR/RL/R0
FEED RATE F
MISCELLANEOUS FUNCTION M
With Cartesian coordinates:
7 L X+10 Y+40 RL F200 M3
8 L IX+20 IY-15
9 L X+60 IY-10
With polar coordinates:
12 CC X+45 Y+25
13 LP PR+30 PA+0 RR F300 M3
14 LP PA+60
15 LP IPA+60
16 LP PA+180
You must first define the pole CC before you can program
polar coordinates!
Program the pole CC only in Cartesian coordinates!
The pole CC remains effective until you define a new one!
Path Functions
19
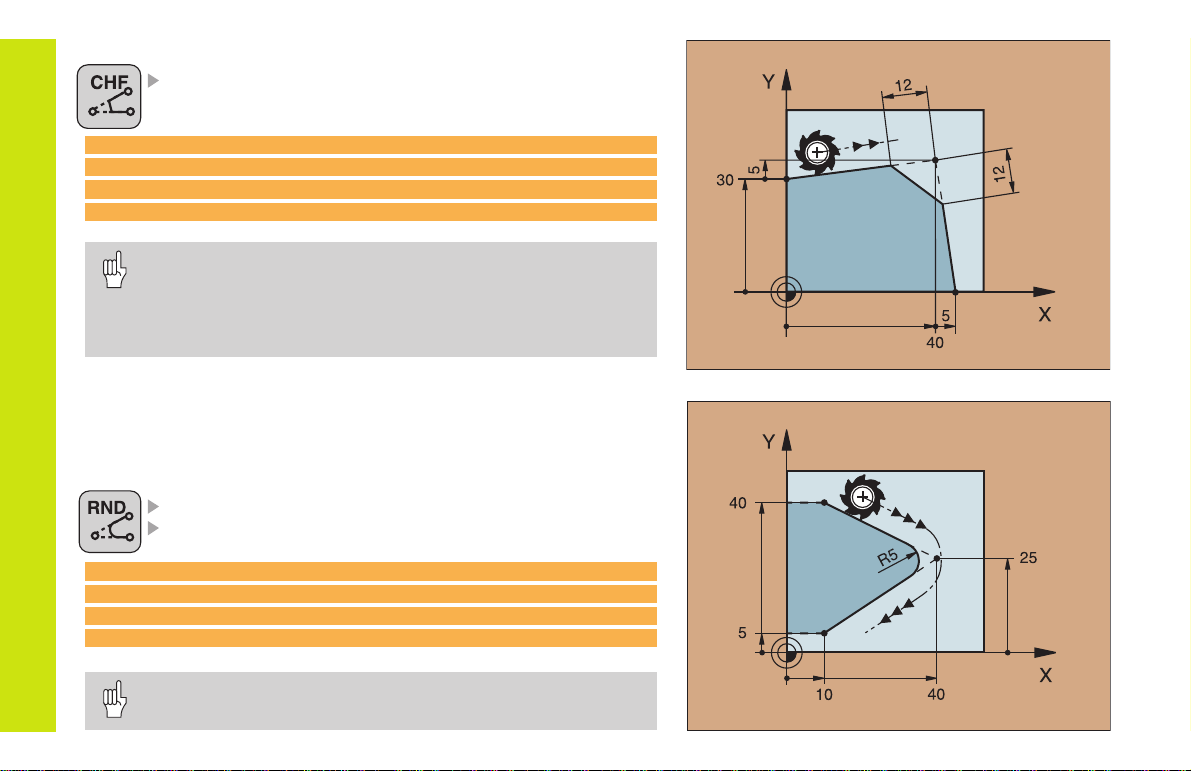
Inserting a Chamfer Between Two Straight Lines
CHAMFER SIDE LENGTH
7 L X+0 Y+30 RL F300 M3
8 L X+40 IY+5
9 CHF 12
10 L IX+5 Y+0
Path Functions
You cannot start a contour with a CHF block!
The radius compensation before and after the CHF block
must be the same!
An inside chamfer must be large enough to accommodate
the current tool!
Corner Rounding
The beginning and end of the arc extend tangentially from the previous and subsequent contour elements.
RADIUS R of the circular arc
FEED RATE F for corner rounding
5 L X+10 Y+40 RL F300 M3
6 L X+40 Y+25
7 RND R5 F100
8 L X+10 Y+5
An inside arc must be large enough to accommodate the
20
current tool!
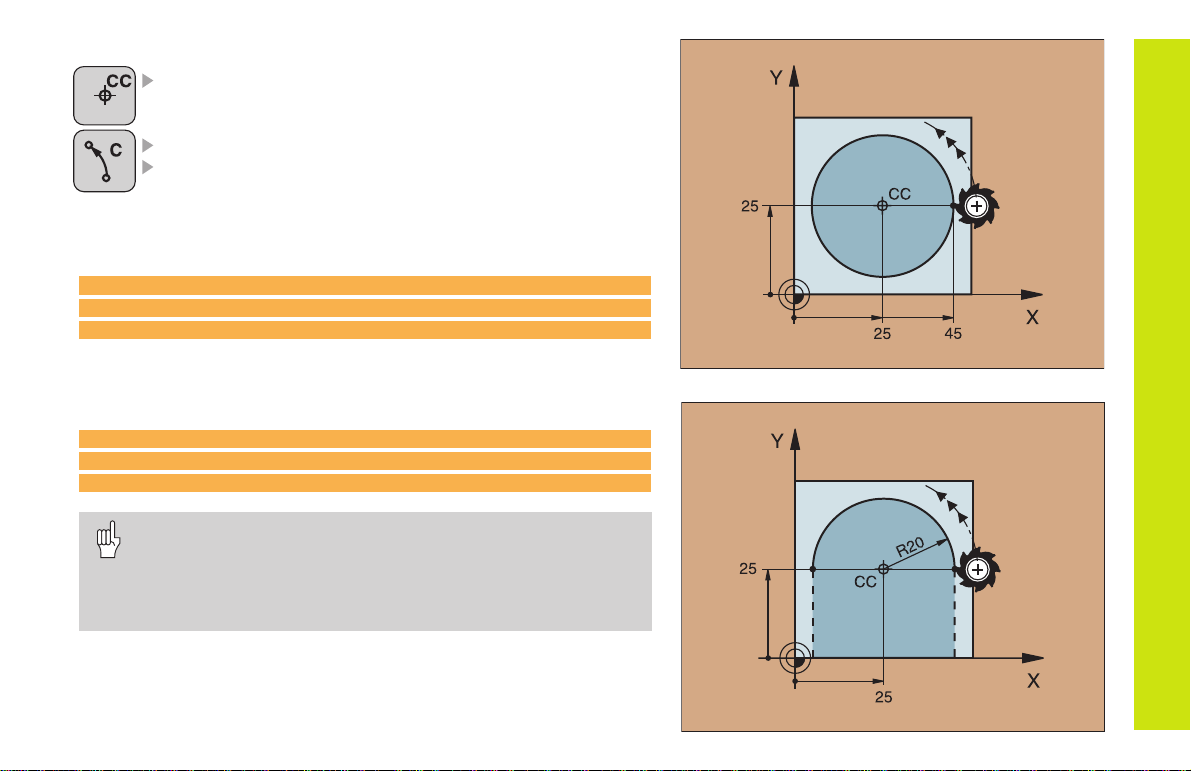
Circular Path Around the Circle Center CC
COORDINATES of the circle center CC
COORDINATES of the arc end point
DIRECTION OF ROTATION DR
C and CP enable you to program a complete circle in one block.
With Cartesian coordinates:
5 CC X+25 Y+25
6 L X+45 Y+25 RR F200 M3
7 C X+45 Y+25 DR+
With polar coordinates:
18 CC X+25 Y+25
19 LP PR+20 PA+0 RR F250 M3
20 CP PA+180 DR+
Define the pole CC before programming polar coordinates!
Program the pole CC only in Cartesian coordinates!
The pole CC remains effective until you define a new one!
The arc end point can be defined only with the polar
coordinate angle (PA)!
Path Functions
21
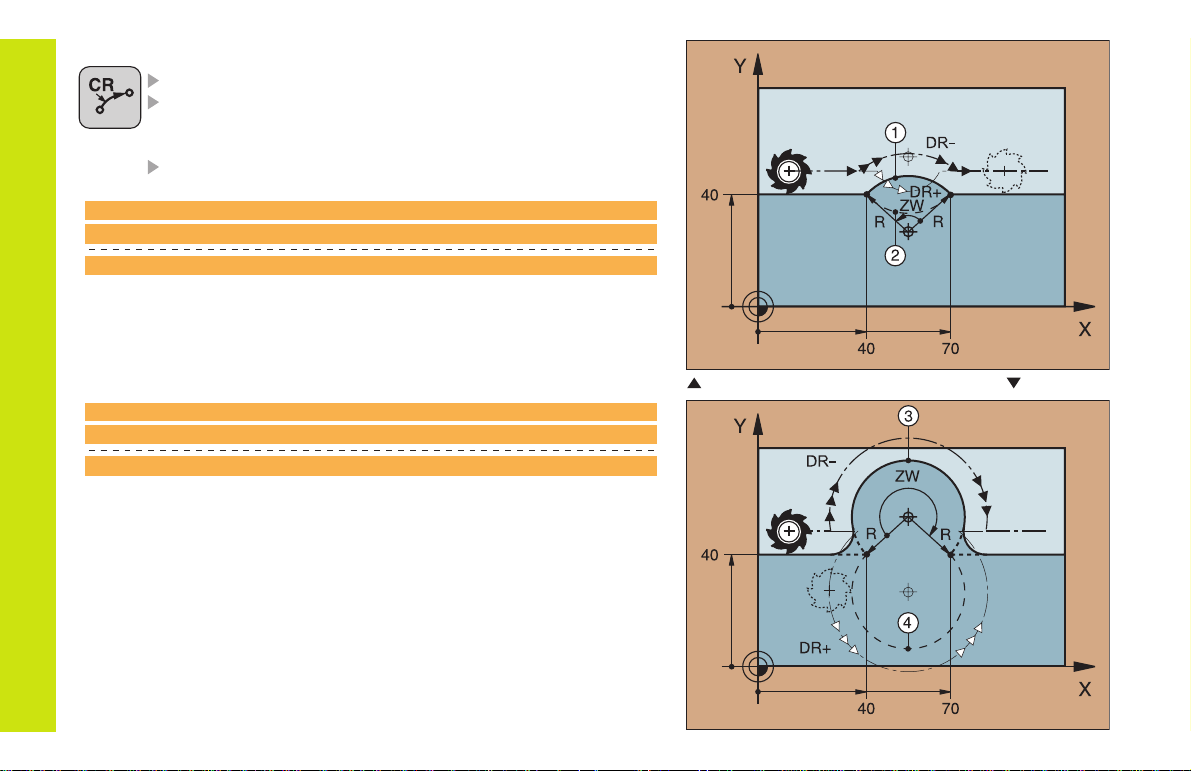
Circular Path with Known Radius (CR)
COORDINATES of the arc end point
RADIUS R
If the central angle ZW > 180, R is negative.
If the central angle ZW < 180, R is positive.
DIRECTION OF ROTATION DR
10 L X+40 Y+40 RL F200 M3 Arc starting point
11 CR X+70 Y+40 R+20 DR- Arc
11 CR X+70 Y+40 R+20 DR+ Arc
Path Functions
10 L X+40 Y+40 RL F200 M3 Arc starting point
11 CR X+70 Y+40 R-20 DR- Arc
11 CR X+70 Y+40 R-20 DR+ Arc
or
1
2
Arcs
and
1
2
or
3
Arcs 3 and
4
4
22
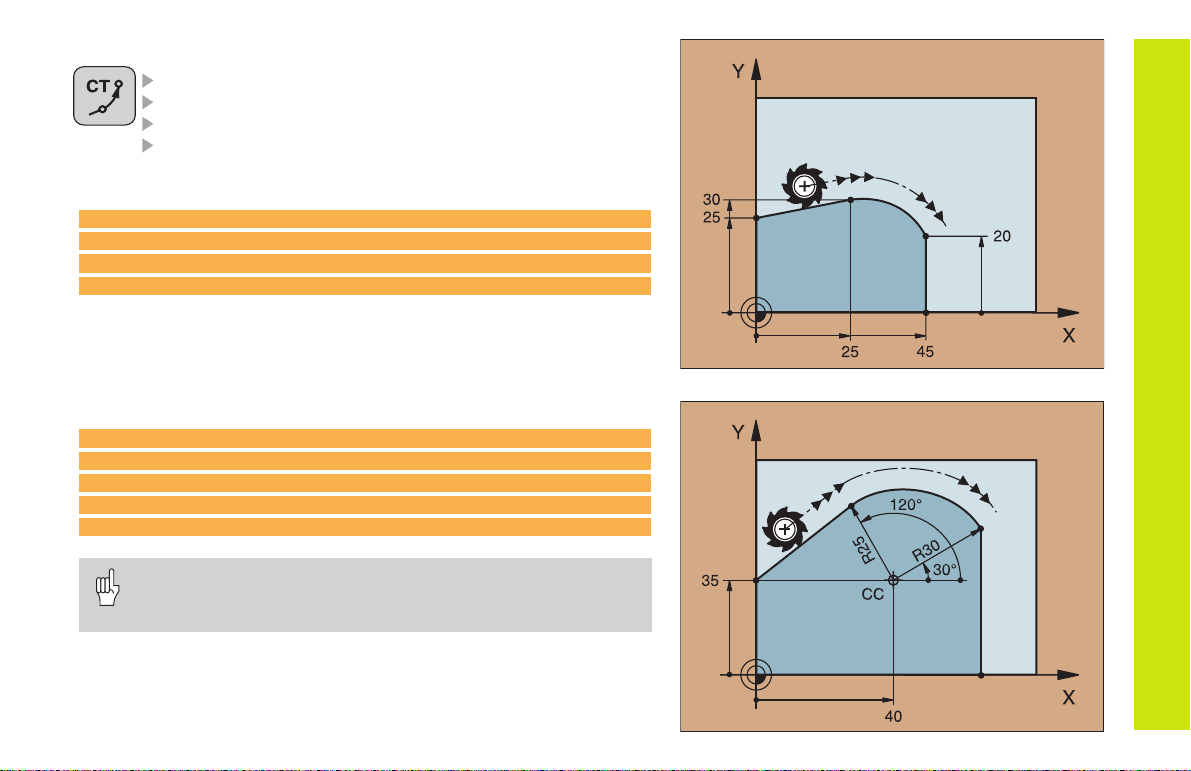
Circular Path CT with Tangential Connection
COORDINATES of the arc end point
RADIUS COMPENSATION RR/RL/R0
FEED RATE F
MISCELLANEOUS FUNCTION M
With Cartesian coordinates:
5 L X+0 Y+25 RL F250 M3
6 L X+25 Y+30
7 CT X+45 Y+20
8 L Y+0
With polar coordinates:
12 CC X+40 Y+35
13 L X+0 Y+35 RL F250 M3
14 LP PR+25 PA+120
15 CTP PR+30 PA+30
16 L Y+0
Define the pole CC before programming polar coordinates!
Program the pole CC only in Cartesian coordinates!
The pole CC remains effective until you define a new one!
Path Functions
23
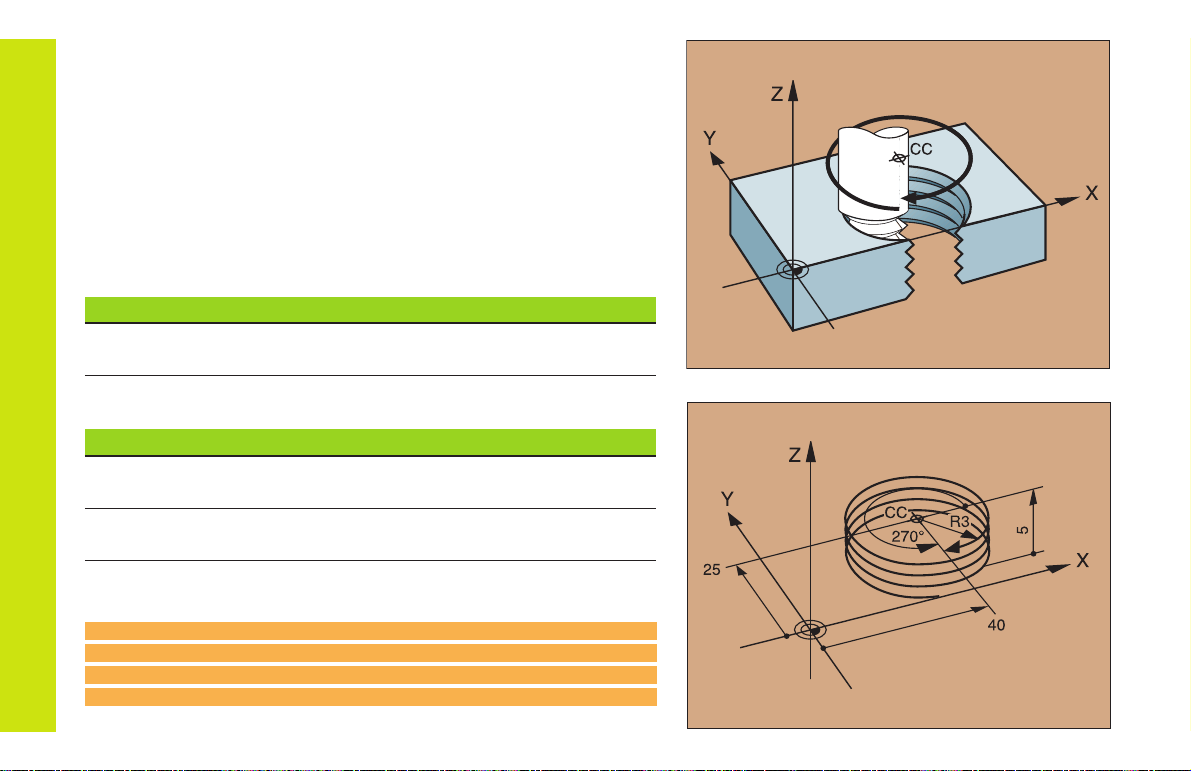
Helix (Only in Polar Coordinates)
Calculations (upward milling direction)
Path revolutions: n = Thread revolutions + overrun at start and
end of thread
Total height: h = Pitch P x path revolutions n
Incr. coord. angle: IPA = Path revolutions n x 360°
Start angle: PA = Angle at start of thread + angle for
overrun
Start coordinate: Z = Pitch P x (thread revolutions + thread
overrun at start of thread)
Path Functions
Shape of helix
Internal thread Work direction Direction Radius comp.
Right-hand Z+ DR+ RL
Left-hand Z+ DR RR
Right-hand Z DR RR
Left-hand Z DR+ RL
External thread
Right-hand Z+ DR+ RR
Left-hand Z+ DR RL
Right-hand Z DR RL
Left-hand Z DR+ RR
24
M6 x 1 mm thread with 5 revolutions
12 CC X+40 Y+25
13 L Z+0 F100 M3
14 LP PR+3 PA+270 RL
15 CP IPA-1800 IZ+5 DR- RL F50
:
FK Free Contour Programming
See Programming Tool Movements FK Free Contour
Programming
If the end point coordinates are not given in the workpiece drawing
or if the drawing gives dimensions that cannot be entered with the
gray path function keys, you can still program the part by using the
FK Free Contour Programming.
Possible data on a contour element:
Known coordinates of the end point
Auxiliary points on the contour element
Auxiliary points near the contour element
A reference to another contour element
Directional data (angle) / position data
Data regarding the course of the contour
To use FK programming properly:
All contour elements must lie in the working plane.
Enter all available data on each contour element.
If a program contains both FK and conventional blocks, the FK
contour must be fully defined before you can return to conventional
programming.
These dimensions can be programmed with FK
FK Free Contour Programming
25

Working with the Interactive Graphics
Select the PGM+GRAPHICS screen layout!
The interactive graphics show the contour as you are programming it.
If the data you enter can apply to more than one solution, the following soft keys will appear:
To show the possible solutions
To enter the displayed solution in the part program
To enter data for subsequent contour elements
To graphically display the next programmed block
Standard colors of the interactive graphics
Fully defined contour element
The displayed element is one of a limited number of
FK Free Contour Programming
possible solutions
The element is one of an infinite number of solutions
Contour element from a subprogram
26
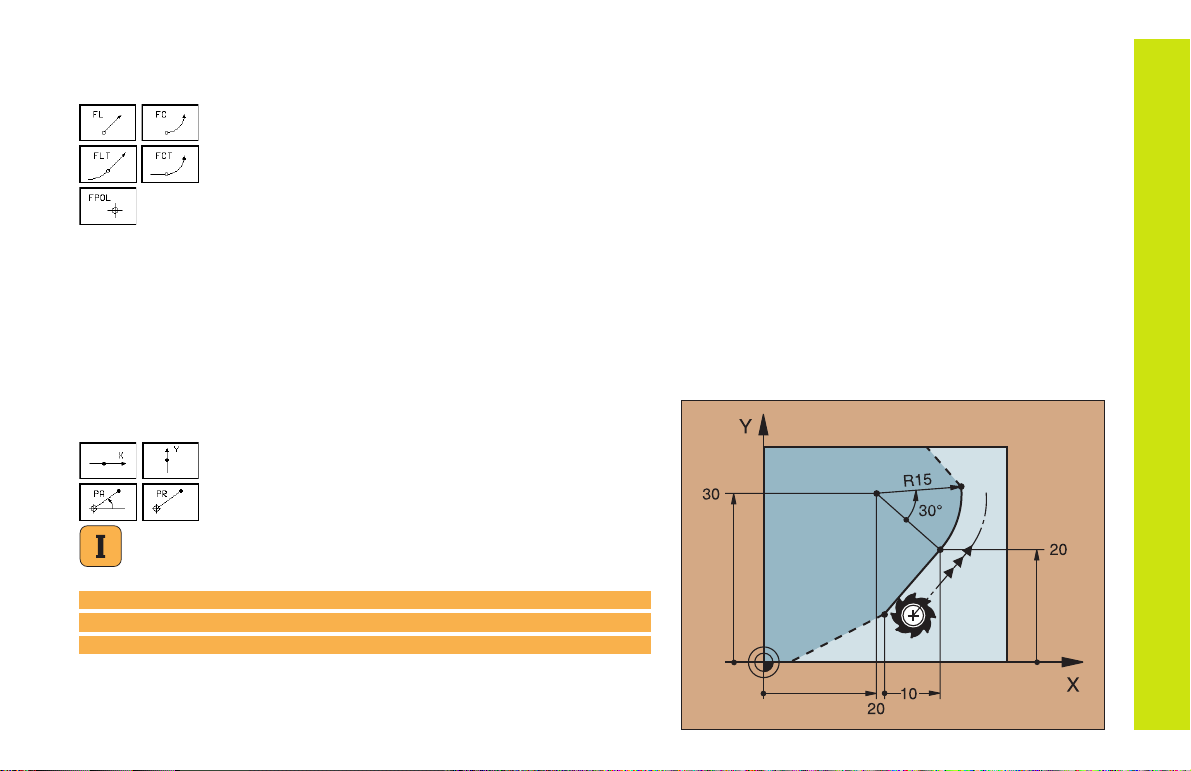
Initiating the FK Dialog
Straight Circular
Contour element without tangential connection
Contour element with tangential connection
Pole for FK programming
End Point Coordinates X, Y or PA, PR
Cartesian coordinates X and Y
Polar coordinates referenced to FPOL
Incremental input
7 FPOL X+20 Y+30
8 FL IX+10 Y+20 RR F100
9 FCT PR+15 IPA+30 DR+ R15
FK Free Contour Programming
27
 Loading...
Loading...