
Matrices
TI
for the TI-73
Getting Started
Start here
How To…
Find Installation Instructions
Move Between Matrix Application Screens
View and Edit a Matrix
Use Matrices with Expressions
Display and Copy Matrices
Use Math Functions with Matrices
Use the Matrix MTH Operations
Delete a Matrix
More Infor m a t ion
Uninstalling the Application from the TI-73
Error Recovery
Customer Support
6/26/01 © 1999, 2001 Texas Instruments

Important Information
Texas Instruments makes no warranty, either expressed or
implied, including but not limited to any implied warranties of
merchantability and fitness for a particular purpose, regarding
any programs or book materials and makes such materials
available solely on an “as-is” basis.
In no event shall Texas Instruments be liable to anyone for
special, collateral, incidental, or consequential damages in
connection with or arising out of the purchase or use of these
materials, and the sole and exclusive liability of Texas
Instruments, regardless of the form of action, shall not exceed
the purchase price of this product. Moreover, Texas Instruments
shall not be liable for any claim of any kind whatsoever against
the use of these materials by any other party.
This graphing product application (APP) is licensed. See the
terms of the license agreement
.
Copyright © 1999, 2001 Texas Instruments Incorporated.
Matrices for the TI-73 Page 2

Where to Find Installation Instructions
You can find detailed instructions on installing Flash applications
at education.ti.com/guides
.
Matrices for the TI-73 Page 3

Getting Started: Systems of Linear Equations
Steps
Keystrokes
Display
1. Run the Matrices
application.
9
, highlight
MATRICES
and press
b
, then
press any key
2. Display the
MATRIX EDT
menu, and select the
[A]
matrix.
" "
1
Use the Matrices application to solve the system of linear
equations:
X + 2Y + 3Z = 3
2X + 3Y + 4Z = 3
Enter the coefficients as elements in a matrix, and then use
to find the reduced row-echelon form.
Matrices for the TI-73 Page 4
rref(

Steps
Keystrokes
Display
3. Define a 2×4 matrix. The
rectangular cursor
indicates the current
element. Ellipses (
...
)
indicate additional
columns beyond the
screen.
2
b
4
b
4. Enter 1for the first
element. The rectangular
cursor moves to the
second column of the
first row.
1
b
5. Complete the first row
for X + 2Y + 3Z = 3.
6. Enter the second row for
2X + 3Y + 4Z = 3.
2
b
3
b
3
b
2
b
3
b
4
b
3
b
7. Display the
Matrix Home
screen.
9 :
Matrices for the TI-73 Page 5

Steps
Keystrokes
Display
8. Clear the screen, if
necessary.
9. Display the
MATRIX MTH
menu. Press $to wrap
to the end of the menu,
and then select
B:rref(
.
:
9 "
$
$$$$$$
b
10. Display the
MATRIX NAME
menu and select matrix
[A]
. Then complete the
calculation. The reduced
row-echelon form of the
matrix is:
1X + 0Y
N
1Z =L3 so
X =L3 + Z
0X + 1Y + 2Z = 3 so
Y = 3N2Z
9
1
E b
Matrices for the TI-73 Page 6

Running or Quitting the Application
After installing the application:
1. Press
9
.
2. Select the
Matrices
application. An
informational screen appears.
Note
If you ever need technical support, you may need the version
number shown on this screen.
3. Press any key to display the
Matrix Menu
screen.
Running the Application
Matrices for the TI-73 Page 7

Quitting the Application
•
Press
- l
.
– or –
•
On the
Matrix Menu
screen, highlight
HLP
. Then select
2:Quit
.
To exit the Matrices application and return to the TI-73 Home
screen, either:
Any matrices or other variables that you stored while using the
Matrices application are retained in memory. Matrices are stored
as application variables (App vars). After quitting the application,
you cannot use a stored matrix from the TI-73 Home screen; you
must run the Matrices application to access a matrix or perform a
matrix calculation.
Matrices for the TI-73 Page 8

Matrices Application Screens and How to
The Matrices application
starts on this screen.
The
Matrix Home
screen replaces the
normal TI.73 Home
screen. Use this
screen to perform all
calculations while
running the Matrices
application. From this
screen, you can also
access most of the
normal TI.73 menus.
The
Matrix Edit
screen lets you edit an
existing matrix or
create a new one.
The
Matrix Menu
screen lets you access
menus to:
•
Select matrix names
for use in a
calculation
•
Select matrix math
operations.
•
Edit or create a
matrix.
•
View online Help.
9
:
Select from
EDT menu
9
Move Between Them
The three primary screens used in the Matrices application are
shown below. Notice the keys used to move from one screen to
another.
Matrices for the TI-73 Page 9

Viewing Online Help
At any time, press
- l
to
exit Help and return to the
Matrix Menu screen.
Press "(next) and !(back) to
move through the Help, one page
at a time. On the last page,
"
returns to the Matrix Menu screen.
To view online Help, highlight
Then select
1:Help
.
HLP
on the
Matrix Menu
screen.
Matrices for the TI-73 Page 10

Defining a Matrix
NAME lets you select the
name of an existing matrix
for use in a calculation,
not for creating or editing.
(You can perform a matrix
calculation only on the
Matrix Home screen.)
Matrix [C] is already
defined as a 2x4 matrix.
EDT lets you select
a matrix to create or
edit.
What Is a Matrix?
A matrix is a two-dimensional array. You can define, display, or
edit a matrix using the
matrix directly in an expression. The Matrices application for the
TI-73 has six matrix variables,
depending on available memory, can have up to 100 elements in
any arrangement of rows and columns (with a maximum of 99
individual rows or columns). You can store only real numbers in
a matrix.
Defining a New Matrix
Before you can define or edit a matrix in the editor, you must
select the matrix name. From the
Matrix Edit
screen. You can also define a
through
[A]
Matrix Home
. A matrix,
[F]
screen:
1. Press
NAME
Matrices for the TI-73 Page 11
9 " "
).
to display the
MATRIX EDT
menu (not
MATRIX

2. Select the matrix you want to define. Use #or $to highlight
Sets the number of
rows, up to 99.
Sets the number of
columns, up to 99.
the corresponding number and then press
that number key. The
Matrix Edit
screen is displayed.
b
, or press
When you edit or create a matrix, the cursor highlights the
number of rows.
3. Accept or change the number of rows.
To accept the value, press
•
To change the value, type the number of rows and then
•
press
b
.
b
.
The cursor moves to the number of columns.
Matrices for the TI-73 Page 12

4. Accept or change the number of columns. When you press
To change a value, use !, ", #,
and $to highlight that element
and then enter a new value (or
press
b
and then edit the
current value).
In a new matrix, all
elements are zero.
b
, the cursor moves to the first matrix element.
5. Type the value (or an expression) for each element and
press
b
, one row at a time. Each time you press
b
the cursor moves to the next element in the row. At the end
of a row, the cursor moves to the next row.
,
6. After entering the last element, press
Matrix Menu
Matrix Home
Matrices for the TI-73 Page 13
screen. You can then press
screen.
9
:
to return to the
to display the

Viewing and Editing a Matrix on the Matrix
Key
Description
!
or
"
Moves the cursor within the current row.
#
or
$
Moves the cursor within the current column.
•
On the first row, $moves the cursor to the number of columns
•
On the number of columns, $or !moves the cursor to the
number of rows.
Dimensions of the matrix.
Ellipses (...) in the left or right column indicate
additional columns.
#
or $in the right column indicates additional rows
The full value of the highlighted element is shown
on the bottom line.
Edit Screen
Viewing an Existing Matrix
On the
Matrix Edit
screen, select the matrix. As necessary, use the
cursor keys to move the rectangular cursor from one matrix
element to the next.
When the rectangular cursor highlights an element (and an edit
cursor is not shown on the bottom line), you can use the
following keys:
Matrices for the TI-73 Page 14

Key
Description
b
or
:
or
any entry
character
Lets you edit the highlighted element, and activates the edit cursor
on the bottom line of the screen.
•
b
retains the current value in the bottom line so that you
can modify it.
•
:
clears the bottom line so you can enter a new value.
•
Any entry character clears the bottom line and places that
character on the line.
Note
If you edit a value by mistake and want to restore the original
value, press
: b
.
Editing a Matrix Element
To edit a matrix element, you must first activate the edit cursor.
1. Select the matrix from the
Matrix Edit
menu, and then enter or
accept the number of rows and columns.
2. Press !, $, ", and #to highlight the element.
3. Press either
b, :
, or an entry key to activate the
edit cursor on the bottom line.
4. Change the value of the matrix element using the editing
keys described below. You can enter an expression, which is
evaluated when you move the cursor to another element.
Matrices for the TI-73 Page 15

5. Press
Key
Description
!
or
"
Moves the edit cursor within the value.
#
or
$
Stores the value displayed on the bottom line to the matrix element;
deactivates the edit cursor and moves the rectangular cursor within
the column.
b
Stores the value displayed on the bottom line to the matrix element;
deactivates the edit cursor and moves the rectangular cursor to the
next row element.
:
Clears the value on the bottom line.
Any entry
character
Places that character at the location of the edit cursor.
- m
Activates the insert cursor.
/
Deletes the character under the edit cursor.
b, $
, or #to move to another element.
When the edit cursor is shown on the bottom line, use the
following keys to edit the value:
Matrices for the TI-73 Page 16

Using Matrices with Expressions on the Matrix Home Screen
Using a Matrix in an Expression
To use a matrix in an expression, either:
Copy the name of an existing matrix from the
•
MATRIX NAME
menu.
Type the matrix elements directly from the keyboard.
•
An expression can perform a maximum of two operations that
create or return a matrix. For example:
[ [1,2] [3,4] ] Ü[A]
and
[ [1,2] [3,4] ] ¦3
are valid because they contain two matrix operations (the input
matrix is created in the calculator’s memory, and so is the
resulting output matrix).
Matrices for the TI-73 Page 17

If an expression has three or more such operations, an error
An error occurs for:
Instead, enter:
[ [1,2] [3,4] ] + [ [5,6] [7,8] ]
[ [1,2] [3,4] ] Ü[A]
[ [5,6] [7,8] ] Ü[B]
[A] +[B]
augment([ [1,2] [3,4] ] , [ [5,6] [7,8] ])
[ [1,2] [3,4] ] Ü[A]
[ [5,6] [7,8] ] Ü[B]
augment( [A] , [B] )
identity(3) * randM(3,3)
identity(3) Ü[A]
randM(3,3) Ü[B]
[A] * [B]
Note
These expressions cause an error because they contain three
matrix operations (two input matrices and one result matrix).
occurs. In most cases, however, you can perform the operations
successfully by breaking them into separate pieces. For
example:
Matrices for the TI-73 Page 18

Typing a Matrix Directly from the Keyboard
Use [(press &) to
begin the matrix.
Use ](press
'
) to
end the matrix.
Note:
The closing
] ]
are
not necessary at the end of
an expression or preceding
Ü
(
X
).
Use
[ ]
to enclose the elements for each
row. Use commas to separate the
elements. An element can be an
expression.
Note:
At the start,
[ [
begins the matrix
and then begins the first row.
The commas that you
must enter to separate
elements are not
displayed on output.
Select the matrix from the
Matrix NAME menu or type it
directly. Press &and
'
to type [and ].
On the
element
[ [
Matrix Home
...,element
,
1,1
Any expressions are evaluated when you press
screen, use the syntax:
...,[element
],
1,n
...,element
,
m,1
b
example:
To store a matrix directly to a matrix variable, use
example:
] ]
m,n
X
. For
. For
Matrices for the TI-73 Page 19

Accessing a Specified Matrix Element
On the
Matrix Home
screen, you can store a value to, or recall a
value from, a specified matrix element. The element must be
within the defined matrix dimensions. Use the syntax:
matrix
[
row,column
] (
)
Matrices for the TI-73 Page 20

Displaying and Copying Matrices on the Matrix
#
or $in the right column
indicates additional rows.
Ellipses (...) in the left or right
column indicate additional
columns.
Home Screen
Displaying a Matrix
To display the contents of a matrix on the
select the matrix from the
b
.
If the matrix is too large to be displayed on the screen, press ",
!, #
, and $to scroll the matrix.
MATRIX NAME
Matrix Home
screen,
menu and then press
Matrices for the TI-73 Page 21

Copying One Matrix to Another
To copy a matrix:
1. Press
9
to display the
MATRIX NAME
menu.
2. Select the name of the matrix you want to copy. You can
either use #and $to highlight the number to the left of the
matrix name and then press
b
, or simply press the
corresponding number key.
3. Press
4. Press
X
9
.
again and select the name of the new matrix to
which you want to copy the existing matrix.
5. Press
b
to copy the matrix.
Matrices for the TI-73 Page 22

Using Math Functions with Matrices
You can use matrices with many of the math functions on the TI-73
keyboard, the
MATH
menu, the
relational operations available from the Text Editor. However, the
dimensions must be appropriate. Each of the functions below
creates a new matrix; the original matrix remains the same.
+ (Add), – (Subtract), * (Multiply)
To add (\) or subtract (T) matrices, the dimensions must be
the same. The answer is a matrix in which the elements are the
sum or difference of the individual corresponding elements.
MATH NUM
menu, and the = and
ƒ
matrixA+matrixB
matrixANmatrixB
To multiply (M) two matrices, the column dimension of
must match the row dimension of
matrixA¦matrixB
Matrices for the TI-73 Page 23
matrixB
matrixA
.

Multiplying a
matrix
matrix in which each element of
matrix¦value
value¦matrix
–
(Negation)
by a
value
or a
matrix
by a
value
matrix
is multiplied by
returns a
.
value
a
Returns a matrix in which the sign of every element is changed
(reversed).
matrix
L
Matrices for the TI-73 Page 24

abs( MATH NUM menu
Returns a matrix containing the absolute value of each element
of
matrix
abs(
.
matrix
)
round( MATH NUM menu
Returns a matrix in which every element in
#
decimals
(
9). If
#decimals
is omitted, the elements are rounded
matrix
is rounded to
to 10 digits.
round(
round(
Matrices for the TI-73 Page 25
matrix
)
matrix,#decimals
)
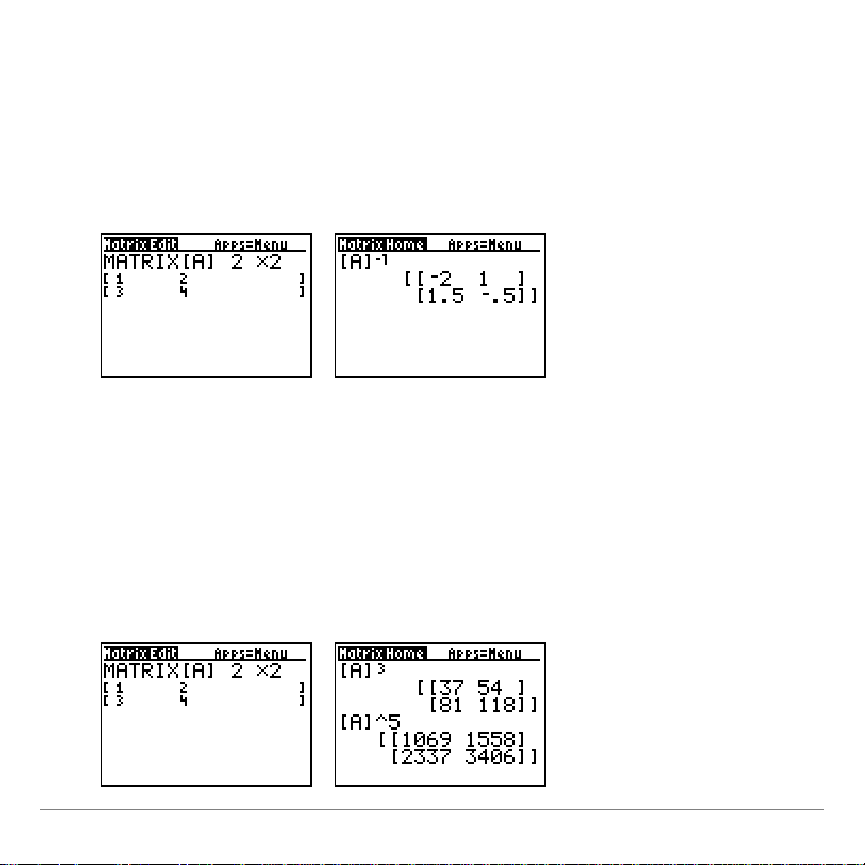
–
1 (Inverse)
- ƒ
Inverts a square
matrix
(^L1 is not valid). The determinant cannot
equal zero.
1
matrix
L
Powers
To raise a matrix to a power,
square (6), cube (
integer
matrix
matrix
power
2
3
matrix^power
7
(
power
3
MATH
from
) between 0 and 255.
matrix
must be square. You can
menu), or raise a matrix to any
Matrices for the TI-73 Page 26

Relational Operations
False
True
- t
To compare two matrices using the relational operations
(available from the Text Editor), they must have the same
dimensions. The
element comparison between
and ≠≠operations perform an element-by-
=
matrixA
and
matrixB
. Other
relational operations are not valid with matrices.
matrixA=matrixB
returns 1 if every comparison is true, or 0 if any
comparison is false.
matrixA≠≠matrixB
returns 1 if at least one comparison is false, or 0
if no comparison is false.
=
and
≠≠
Matrices for the TI-73 Page 27
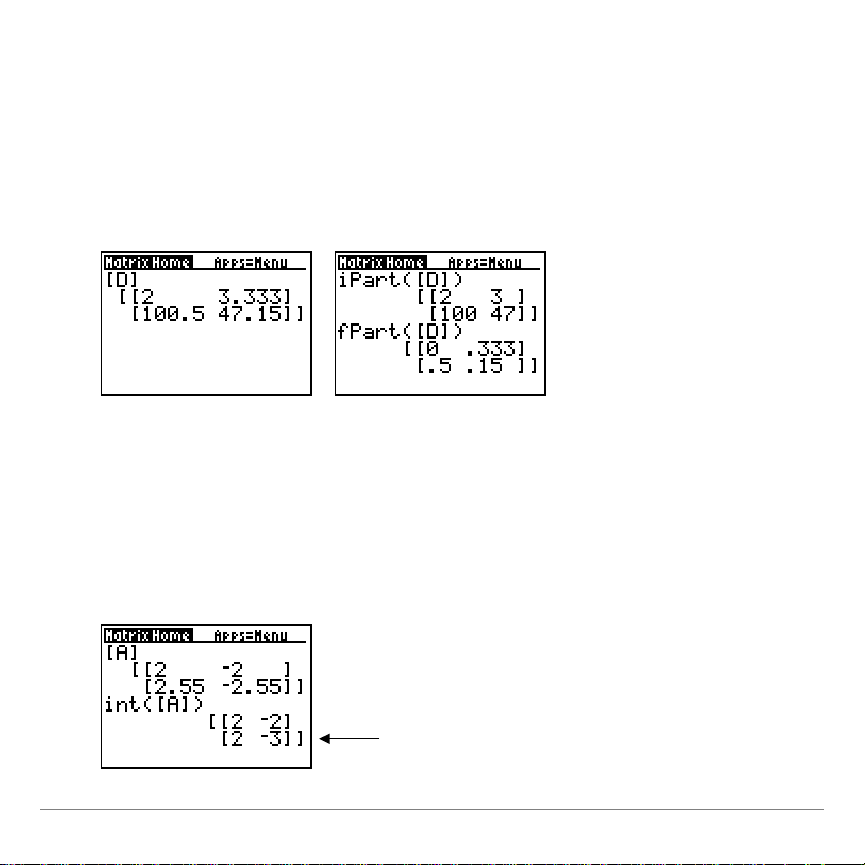
iPart(, fPart( MATH NUM menu
For a negative non-integer,
int(
returns the integer that is one less
than the integer part of the number.
To return the exact integer part, use
iPart(
instead.
and
iPart(
the fractional part, respectively, of each element of
matrix
iPart(
matrix
fPart(
return a matrix containing the integer part and
fPart(
)
)
matrix
.
int( CATALOG
Returns a matrix containing the greatest integer of each element
of
int(
matrix
matrix
.
)
Matrices for the TI-73 Page 28

Using the Matrix MTH Operations
NAME
MTH
EDT
HLP
1:
det(
Calculates the determinant.
2:
T
Transposes the matrix.
3:
dim(
Returns the matrix dimensions.
4:
Fill(
Fills all elements with a constant.
5:
identity(
Returns the identity matrix.
6:
randM(
Returns a random matrix.
7:
augment(
Appends two matrices.
8:
Matr4list(
Stores a matrix to a list.
9:
List4matr(
Stores a list to a matrix.
0:
cumSum(
Returns the cumulative sums of a matrix.
A:
ref(
Returns the row-echelon form of a matrix.
B:
rref(
Returns the reduced row-echelon form.
C:
rowSwap(
Swaps two rows of a matrix.
D:
row+(
Adds two rows; stores in the second row.
E:¦row(
Multiplies the row by a number.
F:¦row+(
Multiplies the row, adds to the second row.
G:
[
Defines the beginning of a matrix and row.
H:
]
Defines the end of a matrix and row.
To display the
Matrix MTH
menu, press
9 "
.
Matrices for the TI-73 Page 29

det( 1: Determinant
Returns the determinant (a real number) of
matrixname
. The
matrix must be square.
matrixname
det(
)
T 2: Transpose
Returns a matrix in which each element (row, column) is
swapped with the corresponding element (column, row) of
matrixname
matrixname
.
T
Matrices for the TI-73 Page 30

dim( 3: Matrix Dimensions
Note
If
dim
(
matrix
)
Ü
L
1
, then
L1(1)
returns the number of rows and
L1(2)
returns the number of columns.
You can press
- v
and then
select L1.
lets you perform three separate operations.
dim(
To find the dimensions of a matrix:
•
Use
dim(
(
rows columns
{
matrix
dim(
to return a list containing the dimensions
) of
matrix
}
)
.
Matrices for the TI-73 Page 31

To create a new matrix:
{ and } are available
from the Text Editor
or the
CATALOG
.
•
Use
dim(
×
rows
rows,columns
{
To change the dimensions of a matrix:
♦
Use
columns
dim(
with
dimensions
X
with
to create a new
with 0 as each element.
}Üdim(
X
rows × columns
matrixname
to redimension an existing
. The elements in the old
matrixname
)
of dimensions
matrixname
matrixname
that are within the new dimensions are not changed.
Additional created elements are zeros. Matrix elements that
are outside the new dimensions are deleted.
rows,columns
{
}Üdim(
matrixname
)
to
Matrices for the TI-73 Page 32

Fill( 4: Fill Matrix Elements
Stores
value,matrixname
Fill(
to every element in
value
)
identity( 5: Identity Matrix
Returns the identity matrix of
identity(
dimension
)
dimension
matrixname
rows ×
.
dimension
columns.
Matrices for the TI-73 Page 33

randM( 6: Random Matrix
Returns a
rows
×
columns
random matrix of integers
The seed value stored to the
function controls the values
rand
L
9 and 9.
‚
(Chapter 2 in the TI-73 Guidebook at education.ti.com/guides
randM(
rows,columns
)
augment( 7: Append Matrices
Appends
matrixnameA
matrixnameA
and
matrixnameB
to
matrixnameB
both must have the same number
as new columns.
of rows.
augment(
matrixnameA,matrixnameB
)
).
Matrices for the TI-73 Page 34

Matr4list( 8: Store Matrix to List
You can press
- v
and then
select L1, L2, and L3.
Matr4list(
•
has two variations.
To fill each
matrixname
listname
:
Use the syntax:
Matr4list(
matrixname,listnameA
If you specify more
columns, the additional
specify fewer
matrixname
listnames
are ignored.
with elements from each column in
...
listname n
,
listnames
listnames
,
than the
are ignored. Likewise, if you
)
matrixname
has
, the additional columns in the
Matrices for the TI-73 Page 35

To fill a
2nd column is filled with a 0.
3rd column in
matrix [A].
•
matrixname
Use the syntax:
listname
:
with elements from a specified
column
in
#
Matr4list(
matrixname,column
#
listname
,
List4matr( 9: Store List to Matrix
Fills
matrixname
. If dimensions of all
list
matrixname
List4matr(
listA
column by column with the elements from each
are not equal,
lists
row with 0.
...
listN,matrixname
,
,
)
)
List4matr(
fills each extra
Matrices for the TI-73 Page 36

cumSum( 0: Cumulative Sums
2, 2+4, 2+4+6
1, 1+3, 1+3+5
Returns cumulative sums of the elements in
matrixname
, starting
with the first element. Each element is the cumulative sum of the
column from top to bottom.
cumSum(
matrixname
)
Note About Row Operations
MATRIX MTH
menu items Athrough F, as described in the
remaining part of this section, are row operations. You can use a
row operation in an expression. Row operations do not change
the matrix in memory. You can enter all row numbers and values
as expressions. You can select the matrix from the
MATRIX NAME
menu.
Matrices for the TI-73 Page 37
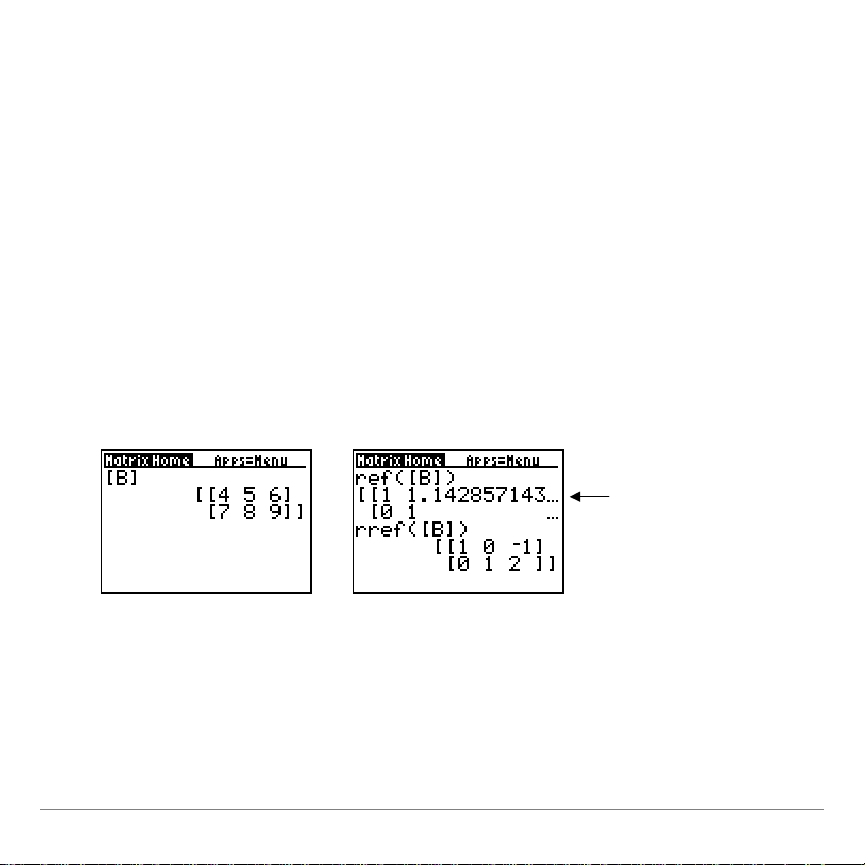
ref(, rref( A: and B: Row-echelon and Reduced
... indicates that the
result extends beyond
the screen. To scroll the
result right or left, press
"
or !at any time
before you perform the
next calculation.
Row-echelon Forms
returns the row-echelon form of a real
ref(
matrixname
. The
number of columns must be greater than or equal to the number
of rows.
matrixname
ref(
returns the reduced row-echelon form of a real
rref(
)
matrixname
The number of columns must be greater than or equal to the
number of rows.
matrixname
rref(
Matrices for the TI-73 Page 38
)
.

rowSwap( C: Row Swap
From the original
matrix, rows 2
and 4 are
swapped.
From the original
matrix, rows 1
and 2 are added
to create this
new row 2.
Swaps
rowSwap(
rowA
and
matrixname,rowA,rowB
rowB
of
matrixname
row+( D: Row Addition
Adds
rowA
and
rowB
of
matrixname
returns the new matrix.
row+(
matrixname,rowA,rowB
, and returns the new matrix.
)
, stores the sum in
)
rowB
, and
Matrices for the TI-73 Page 39

row( E: Row Multiplication
From the original matrix,
row 1 is multiplied by 2 to
create this new row 1.
From the original
matrix, row 1 is
multiplied by 3 to
produce [3 6 9], which
is then added to row 2.
*
Multiplies a specified
in
¦
*
Multiplies
results in
¦
, and returns the new matrix.
row
value,matrixname,row
row(
row+( F: Row Multiplication and Addition
of
rowA
rowB
value,matrixname,rowA,rowB
row+(
matrixname
, and returns the new matrix.
row
of
matrixname
)
by
value
by
, adds it to
)
value
, stores the result
, stores the
rowB
Matrices for the TI-73 Page 40

[ , ] G: and H: Direct Matrix Entry
For Ü, press
X
.
Let you enter a matrix directly from the
example:
[ [1, 2, 3] [3, 2, 1] ] Ü[B]
You can also press &and
'
to type [and ]directly from
the keyboard.
Matrix Home
screen. For
Matrices for the TI-73 Page 41

Deleting a Matrix
Note
On this calculator screen, matrix names are shown as
MATA
and
MATB
instead of
[A]
and
[B]
.
From the Matrix Home Screen
Use the
DelVar
instruction available from the
From the MEMORY Menu
1. Quit the Matrices application (
2. Press
3. Select
4. Select
- Ÿ
4:Delete
9:AppVars
.
.
. (Because matrices are not standard
variables on a TI.73, they are stored as application variables.)
5. Use #and $to move the 4pointer to the applicable matrix
name.
6. Press
b
to delete the matrix.
- l
CATALOG
).
.
7. Continue deleting matrices as necessary.
Matrices for the TI-73 Page 42

Uninstalling the Application from Your TI-73
To uninstall the application and delete it from the calculator’s
memory:
1. Quit the Matrices application (
2. Press
3. Select
4. Select
5. Select
6. Select
- Ÿ
4:Delete
8:Apps
Matrices
2:Yes
.
to confirm that you want to delete the
.
.
and press
- l
b
).
.
application.
If you retained the application file on your computer, you can
reinstall it later.
Matrices for the TI-73 Page 43

Error Recovery Instructions
Low Battery Condition
Do not attempt a Flash download if the low-battery message
appears on the calculator. Low battery indication is shown on the
initial screen. If you receive this error during an installation,
change the batteries before trying again.
Check Amount of Flash Application Free Space
On the TI-73, select
the right of
Spaces Free:
- Ÿ
3:Check APPs…
. The number to
indicates the number of spaces
available for applications. The Matrices application requires one
space. There are a maximum of four spaces.
Communication Error
This error indicates the Flash installer is unable to communicate
with the TI-73. The problem is usually associated with the
TI-GRAPH LINK™ cable and its connection to the TI-73 and/or
to the computer. Make sure the cable is firmly pushed in to the
calculator and the computer.
Matrices for the TI-73 Page 44

If this does not correct the problem, try a different
TI-GRAPH LINK
to get this error, please contact TI-Cares
cable and reboot your computer. If you continue
Customer Support for
é
assistance.
Memory is Full
This download error appears when the TI-73 contains one to four
applications that occupy the available 64K of space. To make
room for another application, you must delete one from the
TI-73. Before deleting an application, you can back it up to your
computer so that you can reload it later as necessary.
Syntax Error
QUIT
ignores the last transaction and displays the last results.
GOTO
displays the screen with the error highlighted. Make any
necessary correction and press
b
.
Singular Mat
A singular matrix (determinant=0) is not valid as an argument
-1
for
.
Matrices for the TI-73 Page 45

Invalid Dim
You specified a matrix dimension as something other than an
integer between 1 and 99.
You attempted to invert a non-square matrix.
You attempted to access an invalid row or column value
referencing an existing matrix (e.g. [A] (1,2) when [A]=1Q1).
Memory
You specified a matrix with more than 100 elements.
Dim Mismatch
You attempted to perform an operation that references more
than one matrix, but the dimensions do not match.
Miscellaneous Error Received
Write down the error code displayed in the dialog box and
contact TI-CARES
.
Checksum Error
Exit the installation and try it again. If this problem persists,
contact TI-CARES
Matrices for the TI-73 Page 46
.

Miscellaneous
If you obtain new or upgraded software for your TI-73, you may
need to provide your current software version and/or the serial
number of your unit. It is also good to know your version number
in case you have difficulties with your TI-73 and need to contact
technical support. Knowing the software version may make it
easier to diagnose the problem.
Knowing the available number of application spaces in advance
helps you better manage your application downloads.
Verify Maintenance Upgrade Version
On the TI-73, enter
- Ÿ
1:About
. The version number has
the format x.yy or x.yyyy.
Verify Flash Application Version
On the TI-73, select
press
b
. The version number of the application appears on
9
. Select the appropriate application and
the initial screen.
Verify Serial Number
On the TI-73, enter
- Ÿ
1:About
. The serial number
appears on the line beneath the product ID number.
Matrices for the TI-73 Page 47

Texas Instruments (TI) Support and Service Information
For general information
E-mail:
Phone:
ti-cares@ti.com
1-800-TI-CARES (1-800-842-2737)
For US, Canada, Mexico, Puerto Rico, and
Virgin Islands only
Home page:
education.ti.com
For technical questions
Phone
: 1-972-917-8324
For product (hardware) service
Customers in the US, Canada, Mexico, Puerto Rico, and Virgin
Islands:
Always contact TI Customer Support before
returning a product for service.
All other customers:
Refer to the leaflet enclosed with your
product (hardware) or contact your local TI
retailer/distributor.
Matrices for the TI-73 Page 48

End-User License Agreement
BY INSTALLING THIS SOFTWARE YOU AGREE TO ABIDE BY THE FOLL OW ING PROVISIONS.
1.
LICENSE:
software program(s) (“License Mat eri al s”) contained on this diskette/CD/web site. You, and any
subsequent user, may only use the Licensed Materials on T exas Instruments cal culator
products.
2.
RESTRICTIONS:
You may not sell, rent, or lease copies that you make.
3.
COPYRIGHT:
If you make copies, do not delete the copyright noti ce, trademark, or protecti ve notices from the
copies.
4.
WARRANTY:
from errors or that they will m eet your specific requirement s.
ARE PROVIDED “AS IS” TO YOU OR ANY SUBSEQUENT USER.
5.
LIMITATIONS:
limited to any implied warrant ies of merchantability and fitness for a particular purpos e,
regarding the Licensed Materials.
IN NO EVENT SHALL T I OR ITS SUPPLI ERS BE LIABLE FOR ANY I NDIRECT,
INCIDENTAL, OR CONSEQUENTIAL DAMAGES, L O SS OF PROFITS, LOSS OF USE OR
DATA, OR INTERRUPTIO N O F BUSINESS, WHETHE R T HE ALLEGED DAMAGES ARE
LABELED IN TORT, CO NT RACT , OR INDEMNITY.
SOME STATES O R JURISDICTIONS DO NOT ALL O W T HE EXCLUSION OR LIM ITATION
OF INCIDENTAL OR CONSEQUENTIAL DAMAGES, SO THE ABOVE LIMI T AT ION MAY
NOT APPLY.
IF YOU AGREE TO BE BO UND BY THIS LICENSE, CL ICK ON THE “ACCEPT” BUTT O N; IF YOU
DO NOT AGREE TO BE BOUND BY THIS LICENSE, CL ICK ON THE “DECLINE” BUTTON TO
EXIT THE INSTALLATION.
Texas Instruments Incorporated (“TI”) grants you a license to use and copy the
You may not reverse-assem ble or reverse-compile the Licensed Materials.
The Licensed Materials and any accompanying documentation are c opyrighted.
TI does not warrant that the Li censed Materials or documentat i on wi l l be free
THE LICENSED MAT ERIALS
TI makes no warranty or condition, either expressed or impli ed, including but not
Matrices for the TI-73 Page 49

Page Reference
This PDF document contains electronic bookmar ks designed for easy onscreen navigation. If you decide to print this doc um ent, please use the
page numbers below to find specific topics.
Important Information...............................................................................2
Where to Find Installation Instructions.....................................................3
Getting Started: Systems of Linear Equations .........................................4
Running or Quitting the Application..........................................................7
Matrices Application Screens and How to Move Between Them.... .......... 9
Viewing Online Help...............................................................................10
Defining a Matrix....................................................................................11
Viewing and Editing a Matrix on the Matrix Edit Screen.........................14
Using Matrices with Expressions on the Matrix Home Screen...... . ......... 17
Displaying and Copying Matrices on the Matrix Home Screen............... 21
Using Math Functions with Matrices.......................................................23
Using the Matrix MTH Operations..........................................................29
Deleting a Matrix....................................................................................42
Uninstalling the Application from Your TI-73..........................................43
Error Recovery Instructions....................................................................44
Miscellaneous........................................................................................47
Texas Instruments (TI) Support and Service Information.......................48
End-User License Agreement ................................................................ 49
Matrices for the TI-73 Page 50
 Loading...
Loading...