Page 1
TI-83
Manuel d'utilisation
Page 2

Page 3

TI-83
CALCULATRICE GRAPHIQUE
MANUEL
D’UTILISATION
Remerciements à :
Gloria Barrett North Carolina School of Science and Math, Durham, NC
Allan Bellman Watkins Mill High School Gaithersburg, MD
Chris Brueningsen The Brunswick School, Greenwich, CT
Larry Morgan Montgomery County Community College, Blue Bell, PA
David S. Moore Purdue University, West Lafayette, IN
Chuck Vonder Embse Central Michigan University, Mount Pleasant, MI
Bert K. Waits The Ohio State University, Columbus, OH
Participants pour Texas Instruments :
Randy Ahlfinger, Charlotte Andreini, Nina Bayer, Dave Caldwell, Viet Dinh,
Rob Egemo, Doug Feltz, Eric Ho, Sallie Huffman, Paul Leighton, Stuart Manning,
Chris McLean, Pat Milheron, Alton Ryan, Charley Scarborough, Danny Srader,
Dianna Tidwell.
Copyright © 1996 par Texas Instruments Incorporated.
è Marque de Texas Instruments Incorporated.
IBM est une marque déposée de International Business Machines Corporation
Macintosh est une marque déposée de Apple Computer, Inc.
Page 4

Important
Texas Instruments n’offre aucune garantie, expresse ou tacite,
concernant notamment, mais pas exclusivement, la qualité de ses
produits ou leur capacité à remplir quelque application que ce soit,
qu’il s’agisse de programmes ou de documentation imprimée. Ces
produits sont en conséquence vendus “tels quels”.
En aucun cas Texas Instruments ne pourra être tenu pour
responsable des préjudices directs ou indirects, de quelque nature
que ce soit, qui pourraient être liés ou dûs à l’achat ou à
l’utilisation de ces produits. La responsabilité unique et exclusive
de Texas Instruments, quelle que soit la nature de l’action, ne
devra pas excéder le prix d’achat du présent équipement. En outre,
Texas Instruments décline toute responsabilité en ce qui concerne
les plaintes d’utilisateurs tiers.
Page 5

Table des matières
Ce manuel explique comment vous devez utiliser la calculatrice graphique
TI-83. L’introduction “Vos débuts” présente rapidement ses principales
fonctions et le chapitre 1 fournit des directives générales d’utilisation. Les
autres chapitres décrivent les fonctions interactives de la TI.83. Vous
trouverez des exemples pratiques d’application et de combinaison de ces
fonctions dans le chapitre 17.
Vos débuts :
Commencez
ici !
Clavier de la TI.83.................................................................... 2
Menus de la TI.83..................................................................... 4
Etapes préliminaires................................................................ 6
Saisie d’un calcul : formule quadratique................................ 7
Définition d’une fonction : boîte avec couvercle................ 10
Définition d’une table de valeurs.......................................... 11
Zoom sur une table................................................................. 12
Configuration de la fenêtre d’affichage ............................... 13
Affichage et parcours d’un graphe ....................................... 14
Zoom sur un graphe ............................................................... 16
Trouver le maximum calculé ................................................ 17
Autres caractéristiques de la TI-83....................................... 19
Chapitre 1:
Utilisation de
la TI-83
Chapitre 2 :
Opérations
mathématiques,
angles et tests
Mise en marche et arrêt de la TI-83........................................ 2
Réglage du contraste ............................................................... 3
Ecran.......................................................................................... 5
Saisie des expressions et instructions................................... 7
Touches d’édition de la TI-83................................................10
Sélection des modes .............................................................. 11
Noms des variables de la TI-83............................................. 15
Mémorisation de variables.................................................... 17
Rappel de variables................................................................ 18
Zone de mémoire ENTRY (Dernière entrée) ......................19
Zone de mémoire Last Answer (Ans) .................................. 21
Menus de la TI-83 ...................................................................22
Menus VARS et VARS Y-VARS.............................................. 24
Système EOS de saisie d’équations......................................26
Conditions d’erreur ................................................................ 28
Pour commencer : Pile ou Face ?...........................................2
Opérations mathématiques au clavier ...................................3
Opérations MATH..................................................................... 6
Résolution d’équation .............................................................. 9
Utilisation de la résolution d’équation.................................13
Opérations MATH NUM (Nombre) ......................................14
Saisie et utilisation de nombres complexes........................17
Opérations MATH CPX (Complexe).................................... 19
Opérations MATH PRB (Probabilité) .................................. 21
Opérations sur les ANGLES.................................................. 24
Tests de comparaison............................................................ 27
Tests booléens........................................................................ 28
Introduction iii
Page 6

Table des matières (suite)
Chapitre 3 :
Graphes de
fonctions
Chapitre 4 :
Courbes
paramétrées
Chapitre 5 :
Courbes
polaires
Chapitre 6 :
Représentation
graphique
d’une suite
Pour commencer : tracer un cercle........................................ 2
Définir un graphe ..................................................................... 3
Choix du mode graphique .......................................................4
Définir une fonction dans l’éditeur Y=................................... 5
Sélectionner et désactiver les fonctions................................ 7
Définir les styles de graphes pour représenter
les fonctions.............................................................................. 9
Définir les variables de la fenêtre d’affichage..................... 12
Définir le format d’un graphe................................................ 14
Afficher un graphe ................................................................. 16
Parcourir un graphe à l’aide du curseur libre ..................... 18
Parcourir un graphe à l’aide de TRACE............................... 19
Parcourir un graphe à l’aide de ZOOM ................................21
Utilisation de ZOOM MEMORY ............................................24
Utiliser les opérations CALC (Calcul) ................................. 26
Pour commencer : trajectoire d’un ballon............................. 2
Définition et affichage d’une courbe paramétrée................. 4
Parcourir une courbe paramétrée.......................................... 7
Pour commencer : la rose polaire ..........................................2
Définition et affichage d’une courbe polaire......................... 3
Parcourir une courbe polaire.................................................. 6
Pour commencer : les arbres d’une forêt ..............................2
Définition et représentation du graphique d’une
suite finie...................................................................................4
Choix du type de tracé............................................................. 9
Parcourir un graphe de suite ................................................ 10
Tracés en format Web............................................................ 12
Utilisation des diagrammes de phase ..................................15
Comparaison des fonctions de suite de la TI-83 et
de la TI-82................................................................................18
Chapitre 7 :
Tables
iv Introduction
Pour commencer : racines d’une fonction ............................ 2
Définir des variables ................................................................ 3
Définir des fonctions................................................................ 4
Afficher une table..................................................................... 5
Page 7

Chapitre 8 :
Opérations
DRAW
Pour commencer : dessiner une tangente............................. 2
Utilisation du menu DRAW ..................................................... 3
Effacer un dessin...................................................................... 5
Tracer des segments ................................................................ 6
Tracer des droites horizontales et verticales........................ 7
Tracer des tangentes................................................................ 8
Tracer des fonctions et des réciproques ...............................9
Zones ombrées sur un graphe............................................... 10
Tracer des cercles.................................................................. 11
Annotation d’un graphe ......................................................... 12
Utilisation de Pen pour dessiner sur un graphe ................. 13
Dessiner des points................................................................ 14
Dessiner des pixels ................................................................15
Mémoriser des images........................................................... 17
Rappeler des images .............................................................. 18
Mémoriser les bases de données des graphes .................... 19
Rappeler les bases de données des graphes ....................... 20
Chapitre 9 :
Partage de
l’écran
Chapitre 10 :
Matrices
Chapitre 11 :
Listes
Pour commencer : exploration du cercle unitaire ............... 2
Utilisation de l’écran partagé.................................................. 3
Ecran partagé en mode Horiz (horizontal) ........................... 4
Ecran partagé en mode G-T (Graphe-Table) ........................ 5
Pixels de la TI-83 en mode Horiz et en mode G-T ................ 6
Pour commencer : systèmes d’équations linéaires .............. 2
Définir une matrice .................................................................. 3
Visualisation des éléments d’une matrice .............................4
Edition des éléments d’une matrice....................................... 5
Utiliser une matrice dans une expression............................. 7
Afficher et copier des matrices .............................................. 8
Fonctions mathématiques matricielles................................ 10
Opérations MATRX MATH....................................................13
Opérations ligne .....................................................................17
Pour commencer : générer une suite..................................... 2
Nommer une liste..................................................................... 4
Mémorisation et affichage des listes...................................... 5
Saisie des noms de liste...........................................................7
Formules jointes aux noms de liste ....................................... 9
Utilisation de listes dans les expressions............................ 11
Menu LIST OPS....................................................................... 13
Menu LIST MATH................................................................... 21
Introduction v
Page 8

Table des matières (suite)
Chapitre 12 :
Statistiques
Chapitre 13 :
Estimations et
distributions
Chapitre 14 :
Fonctions
financières
Pour commencer : longueur et période d’un pendule.......... 2
Définition d’une analyse statistique ..................................... 10
Utilisation de l’éditeur de listes statistiques ....................... 11
Formules jointes aux noms de liste ..................................... 15
Suppression du lien entre formule et nom de liste............. 18
Contextes de l’éditeur de listes statistiques........................ 19
Menu STAT EDIT ...................................................................22
Modèles de régression........................................................... 24
Menu STAT CALC .................................................................. 27
Variables statistiques ............................................................. 33
L’analyse statistique dans un programme ...........................34
Graphes statistiques............................................................... 35
Les graphes statistiques dans un programme..................... 41
Pour commencer : taille moyenne d’une population ...........2
Ecrans d’édition pour les estimations ................................... 6
Menu STAT TESTS................................................................... 9
Variables de sortie des tests et des intervalles................... 27
Description des données d’entrée d’une estimation .......... 28
Distributions ...........................................................................30
Ombrage de la zone de distribution ..................................... 37
Pour commencer : financement d’une voiture...................... 2
Pour commencer : calcul de l’intérêt composé ....................3
Utilisation de Solve TVM......................................................... 4
Utilisation des fonctions financières .....................................5
Calculs TVM.............................................................................. 6
Calcul des mouvements de trésorerie ................................... 7
Calcul de l’amortissement d’un emprunt............................... 9
Exemple : Déterminer les échéances d’un prêt.................. 10
Calcul de conversion d’intérêts ............................................ 12
Nombre de jours entre deux dates / Modes de paiement ....... 13
Utilisation des variables TVM............................................... 14
Chapitre 15 :
CATALOGUE
vi Introduction
Opérations de la TI-83 répertoriées dans le catalogue ........2
Introduction et utilisation des chaînes .................................. 4
Stockage d’une chaîne dans une variable chaîne................. 5
Fonctions et instructions de chaîne du catalogue................ 7
Fonctions hyperboliques du catalogue................................10
Page 9

Chapitre 16 :
Programmation
Pour commencer : volume d’un cylindre............................... 2
Création et suppression de programmes............................... 4
Introduction des commandes ................................................. 5
Exécution du programme........................................................ 6
Edition de programmes ........................................................... 7
Copier et renommer des programmes................................... 8
Instructions PRGM CTL (Contrôle) ....................................... 9
Instructions PRGM I/O (Entrées/Sorties)............................ 17
Appel de programmes en tant que sous-routines ............... 23
Chapitre 17 :
Applications
Chapitre 18 :
Gestion de la
mémoire
Chapitre 19 : La
liaison de
communication
Boîte à moustache : résultats comparés d’un test................ 2
Graphe d’une fonction définie par intervalles ......................5
Représentation graphique d’une inéquation ......................... 7
Résolution d’un système d’équations non linéaires .............9
Programme : Le triangle de Sierpinski................................. 11
La toile d’araignée .................................................................. 12
Programme : deviner les coefficients .................................. 13
Le cercle trigonométrique et les courbes
trigonométriques .................................................................... 14
Calcul de la surface entre deux courbes ............................. 15
Equations paramétriques : la Grande Roue......................... 16
Illustration du théorème de base du calcul intégral........... 19
Calcul de la surface d’un polygone régulier à N côtés....... 21
Calcul et graphe d’un remboursement d’hypothèque ........ 24
Vérifier la quantité de mémoire disponible........................... 2
Effacer des informations de la mémoire ............................... 3
Effacer des entrées et des éléments de liste.........................4
Réinitialiser la TI-83................................................................. 5
Pour commencer : Envoi de variables................................... 2
TI-83 LINK ................................................................................. 4
Sélection des informations à envoyer.................................... 5
Réception des informations.................................................... 7
Transmission des informations ..............................................9
Transmission de listes à une TI-82....................................... 12
Transmission de TI-82 à TI-83............................................... 13
Copie de mémoire .................................................................. 15
Annexe A
Tableau des fonctions et instructions................................ A-2
Hiérarchie des menus de la TI.83..................................... A-49
Variables.............................................................................. A-59
Formules statistiques......................................................... A-61
Formules financières ......................................................... A-65
Introduction vii
Page 10

Table des matières
(suite)
Annexe B
Index
Piles ................................................................................ B-2
En cas de problème ...................................................... B-4
Conditions d’erreur....................................................... B-5
Considérations relatives à la précision .................... B-11
Informations sur les services et la garantie TI ........ B-13
viii Introduction
Page 11

0 0 Vos débuts : Commencez ici !
Contenu du
chapitre
Clavier de la TI-83.................................................................. 2
Menus de la TI-83................................................................... 4
Etapes préliminaires .............................................................6
Saisie d’un calcul : équation du 2ème degré.......................7
Définition d’une fonction : boîte avec couvercle.............10
Définition d’une table de valeurs.......................................11
Zoom sur une table..............................................................12
Configuration de la fenêtre d’affichage.............................13
Affichage et parcours d’un graphe.....................................14
Zoom sur un graphe.............................................................16
Calculer le maximum ..........................................................17
Autres caractéristiques de la TI-83....................................19
Vos débuts 1
Page 12
Clavier de la TI-83
Utilisation du
clavier à code
de couleur
Touches
2nd et Alpha
La touche
permet d’accéder
à la seconde
fonction indiquée
en jaune au-dessus
de chaque touche.
y
Les touches de la TI-83 présentent un code de couleur
pour vous permettre de repérer plus facilement la touche
que vous devez presser.
Les touches grises sont les touches numériques. Les
touches bleues à droite du clavier correspondent aux
fonctions mathématiques courantes. Les touches bleues
situées en haut du clavier servent à la configuration et à
l’affichage des graphes.
La fonction principale de chaque touche est indiquée en
blanc sur le plateau de la touche. Par exemple, lorsque
vous appuyez sur , le menu
MATH s’affiche.
La fonction secondaire des touches est indiquée en jaune
au-dessus de chaque touche. Lorsque vous appuyez sur la
touche jaune y, le caractère, l’abréviation ou le mot
imprimé en jaune devient la fonction active de la touche
que vous pressez ensuite.
Par exemple, si vous appuyez sur y puis sur , le
TEST s’affiche. Le présent manuel d’utilisation
menu
identifie cette combinaison de touches sous la forme y
TEST].
[
La fonction Alpha des touches est imprimée en vert au-
dessus de chaque touche. Lorsque vous appuyez sur la
touche verte ƒ, le caractère alphanumérique en vert
devient la fonction active de la touche que vous pressez
ensuite.
Par exemple, si vous appuyez sur ƒ puis sur ,
vous tapez la lettre
A. Le présent manuel d’utilisation
identifie cette combinaison de touches sous la forme
ƒ [
A].
La touche
permet d’accéder
à la fonction
indiquée en vert
au-dessus de
chaque touche.
ƒ
2 Vos débuts
Page 13
En général, le clavier est divisé en quatre zones : touches graphiques, touches
d’édition, touches de fonctions avancées et touches de calcul scientifique.
Touches
graphiques
Touches d'édtion
Touches de
fonctions avancées
Touches de calcul
scientifique
Touches
graphiques
Touches
d’édition
Touches de
fonctions
avancées
Touches de
calcul
scientifique
Ces touches sont surtout utilisées pour accéder aux
fonctions graphiques interactives de la TI-83.
Ces touches sont surtout utilisées pour modifier des
expressions et des valeurs.
Ces touches sont surtout utilisées pour accéder aux
fonctions avancées de la TI-83.
Ces touches sont surtout utilisées pour accéder aux
fonctions d’une calculatrice scientifique standard.
Vos débuts 3
Page 14

Menus de la TI-83
La TI-83 met en oeuvre des menus en plein écran permettant d’accéder à de
nombreuses opérations. Les différents menus sont décrits dans les autres
chapitres.
Afficher un menu
Lorsque vous appuyez sur une touche qui
affiche un menu, ce dernier remplace
temporairement l’écran où vous travaillez.
Par exemple, si vous appuyez sur , le
menu
Une fois que vous avez sélectionné une
option dans un menu, vous retournez
normalement à votre écran de travail.
Passer d’un menu à l’autre
Certaines touches permettent d’accéder à
plusieurs menus. Lorsque vous appuyez sur
l’une de ces touches, les noms de tous les
menus accessibles s’affichent sur la
première ligne de l’écran. Si vous mettez en
surbrillance un nom de menu, les options
qu’il contient s’affichent. Utilisez les touches
~ et | pour mettre en surbrillance tour à
tour tous les noms de menus.
s’affiche en plein écran.
MATH
4 Vos débuts
Page 15
Sélectionner une option dans un menu
Le chiffre ou la lettre situé(e) en regard de
l’option de menu sélectionnée est en
surbrillance. Si le menu se poursuit au-delà
de l’écran, une flèche dirigée vers le bas ( $ )
remplace le signe deux-points (
: ) dans la
dernière option affichée. Si vous faites
défiler le menu vers le bas, une flèche
dirigée vers le haut ( # ) remplace les deuxpoints dans la première option affichée.
Il existe deux manières de sélectionner une
option dans un menu.
¦ Utilisez la touche † or } pour amener le
curseur jusqu’au chiffre ou à la lettre
identifiant l’option choisie, puis appuyez
sur Í.
¦ Appuyez sur la touche ou combinaison de
touches correspondant au chiffre ou à la
lettre affichée en regard de l’option
choisie.
Quitter un menu sans choisir d’option
Il existe trois manières de quitter un menu
sans sélectionner d’option.
¦ Appuyez sur ‘ pour retourner à
l’écran où vous travailliez précédemment.
¦ Appuyez sur y [
QUIT] pour retourner à
l’écran principal.
¦ Appuyez sur la touche d’accès à un autre
menu ou écran.
Vos débuts 5
Page 16

Etapes préliminaires
Avant de passer aux exercices proposés dans ce chapitre, suivez les étapes
décrites sur cette page pour réinitialiser la TI-83 selon les réglages d’usine
et effacer toutes les données en mémoire. Cette opération vise à garantir
que vous obteniez les effets décrits dans les illustrations lorsque vous
appuyez sur les touches indiquées.
Procédez de la manière suivante pour réinitialiser la TI-83.
1. Appuyez sur É pour mettre la
calculatrice en marche.
2. Enfoncez et relâchez la touche y puis
appuyez sur [
Lorsque vous appuyez sur y, vous
accédez à l’action imprimée en jaune audessus de la touche que vous pressez
ensuite.
touche Ã. Le menu
3. Tapez 5 pour sélectionner 5:Reset. Le
menu
MEM] (au-dessus de Ã).
MEM est l’opération y de la
MEMORY s’affiche.
RESET s’affiche.
4. Tapez 1 pour sélectionner 1:All Memory.
Le menu
5. Tapez 2 pour sélectionner 2:Reset. Tout
le contenu de la mémoire est effacé et la
calculatrice est réinitialisée selon les
réglages par défaut.
Lorsque vous réinitialisez la TI-83, le
contraste de l’écran revient à son réglage
usine.
¦ Si l’écran est très sombre, enfoncez et
¦ Si l’écran est très clair ou blanc, enfoncez
6 Vos débuts
RESET MEMORY s’affiche.
relâchez y, puis maintenez la touche †
enfoncée pour éclaircir l’affichage.
et relâchez y, puis maintenez enfoncée
la touche } pour assombrir l’affichage).
Page 17
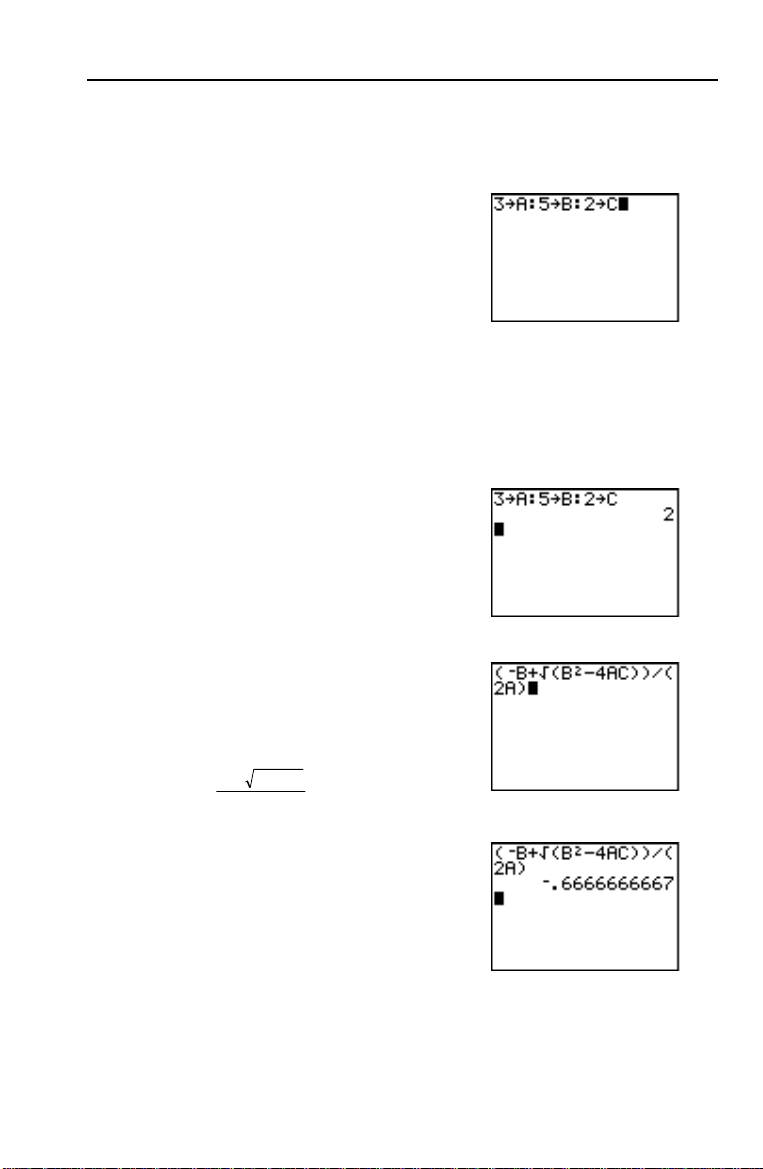
Saisie d’un calcul : équation du 2ème degré
Utilisez le théorème donnant les solutions des équations du 2ème degré
pour résoudre : 3X
1. Appuyez sur
dessus de ) pour mémoriser le
coefficient du terme X
2. Appuyez sur ƒ [
2
+ 5X + 2 = 0 et 2X2 N X + 3 = 0.
3 ¿ ƒ [A] (au-
2
.
: ]. Le signe deux-
points vous permet de saisir plusieurs
instructions sur la même ligne.
3. Appuyez sur
5 ¿ ƒ [B] (au-
dessus de ) pour mémoriser le
coefficient du terme X. Appuyez sur
ƒ [
: ] pour saisir une nouvelle
instruction sur la même ligne. Appuyez
2 ¿ ƒ [C] (au-dessus de
sur
) pour mémoriser la constante.
4. Appuyez sur Í pour mémoriser les
valeurs dans les variables A, B et C.
5. Appuyez sur £ Ì ƒ [B] Ã y [‡]
ƒ [
¤ ¤ ¥ £
B] ¡ ¹ 4 ƒ [A] ƒ [C]
2 ƒ [A] ¤ pour saisir
l’expression correspondant à l’une des
solutions.
2
bb ac
a
2
4
−+ −
6. Appuyez sur Í pour trouver une
solution à l’équation 3X
2
+ 5X + 2 = 0.
La réponse s’affiche à droite de l’écran.
Le curseur passe à la ligne suivante pour
vous permettre de saisir l’expression
suivante.
Vos débuts 7
Page 18

Saisie d’un calcul : équation du 2ème degré (suite)
Vous pouvez afficher la solution sous
forme de fraction.
7. Appuyez sur pour afficher le menu
MATH.
8. Tapez 1 pour sélectionner 1:4Frac dans
le menu
Lorsque vous tapez
MATH.
1, Ans4Frac
s’affiche. Ans est une variable qui
contient la dernière réponse calculée.
9. Appuyez sur Í pour convertir le
résultat en une fraction.
Pour ne pas tout retaper, vous pouvez
rappeler la dernière expression saisie et
la modifier pour le nouveau calcul.
10. Appuyez sur y [
ENTRY] (au-dessus de
Í) pour sauter la ligne de
conversion en fraction, puis appuyez à
nouveau sur y [
ENTRY] pour rappeler
l’expression de la solution.
2
bb ac
a
2
4
−+ −
11. Utilisez la touche } pour placer le
curseur sur le signe
+ dans la formule.
Appuyez sur ¹ pour modifier
l’expression qui doit devenir :
2
−− −bb ac
12. Appuyez sur Í pour trouver l’autre
solution de l’équation 3X
Remarque : Une autre méthode consiste à utiliser l’outil intégré Solver (menu
MATH) et à saisir directement Ax
Solver, consultez le chapitre 2.
a
2
4
2
+ 5X + 2 = 0.
2
+ Bx + C. Pour plus d’informations sur l’outil
8 Vos débuts
Page 19

2
Il reste à résoudre l’équation 2X
N X + 3 = 0. Pour permettre à la TI-83
d’afficher des résultats complexes, nous allons définir le mode autorisant
les nombres complexes
a+bi.
13. Appuyez sur z † † † † † † (6
fois) puis sur ~ pour positionner le
curseur sur
a+bi. Appuyez sur Í
pour sélectionner le mode des nombres
complexes
a+bi.
14. Appuyez sur y [QUIT] (au-dessus de
z) pour retourner à l’écran principal,
puis sur ‘ pour effacer cet écran.
15. Appuyez sur
: ] Ì 1 ¿ ƒ [B] ƒ [ : ] 3
[
2 ¿ ƒ [A] ƒ
¿ ƒ [C] Í.
2
Le coefficient du terme X
, celui du
terme X et la constante de la nouvelle
équation sont mémorisés dans les
variables A, B et C respectivement.
16. Appuyez sur y [ENTRY] pour sauter
l’instruction de mémorisation, puis à
nouveau sur y [
ENTRY] pour rappeler
l’expression de la solution.
2
bb ac
−− −
a
2
4
17. Appuyez sur Í pour trouver une
solution de l’équation 2X
2
-X+3=0.
18. Appuyez sur y [ENTRY] jusqu’à ce que
l’expression de la solution s’affiche.
2
bb ac
−+ −
a
2
4
19. Appuyez sur Í pour trouver l’autre
solution de l’équation du second degré
2
-X+3=0.
2X
Vos débuts 9
Page 20
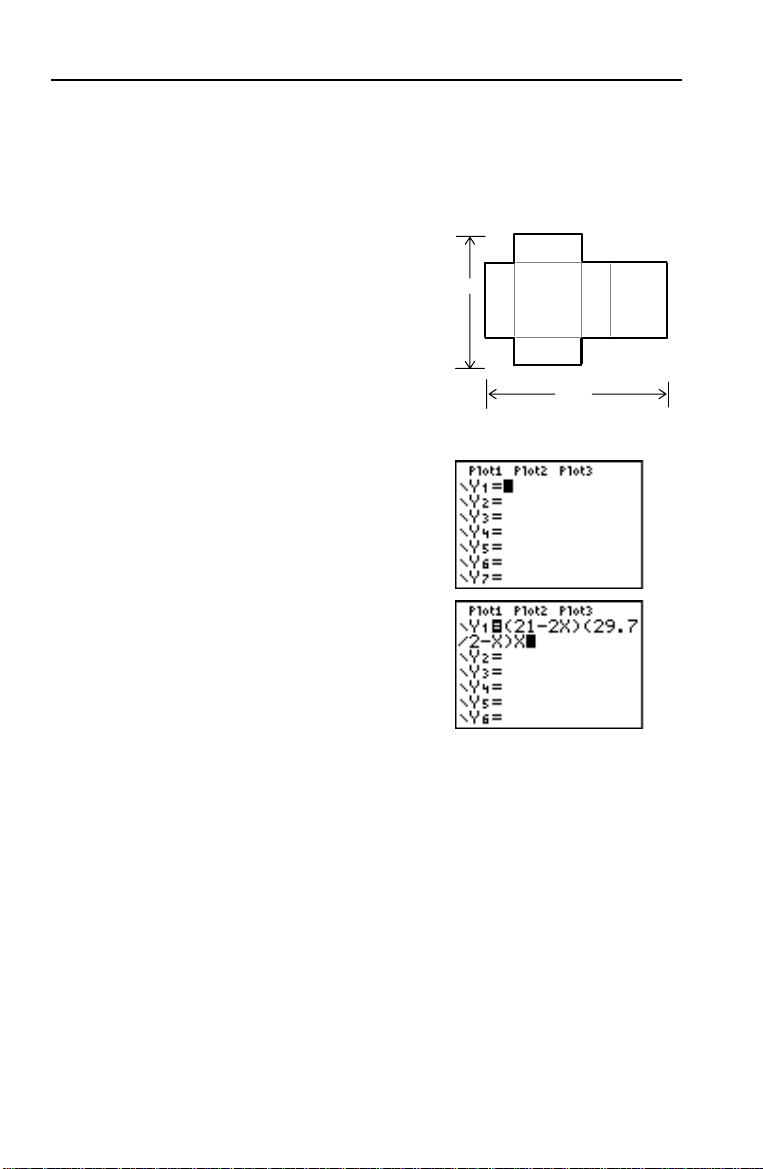
V
Définition d’une fonction : boîte avec couvercle
X
Prenez une feuille de papier de format 21 x 29,7 cm. Découpez des carrés
de X x X dans deux coins et des rectangles de X × 14 cm dans les deux
autres coins selon le schéma ci-dessous. Pliez la feuille pour former une
boîte avec couvercle. Quelle valeur de X donnera le volume V maximum de
la boîte ? Utilisez des graphes et la table pour arriver à la solution.
Commencez par définir la fonction qui
décrit le volume de la boîte.
En partant du schéma : 2X + A = 21
2X + 2B = 29.7
V = ABX
Remplaçons A et B:
= (21 N 2X) (29.7à 2 N X)X
1. Appuyez sur ‘ pour effacer l’écran
principal.
2. Appuyez sur o pour afficher l’écran
d’édition
Y= où vous définissez les
fonctions générant les tables et les
graphes.
3. Appuyez sur £ 21 ¹ 2 „ ¤ £ 29
Ë 7
¥ 2 ¹ „ ¤ „ Í pour
définir le volume sous le nom
fonction de
X.
„ permet de saisir
sans appuyer sur ƒ. Le signe
Y1 en
X rapidement,
= est
en surbrillance pour indiquer que la
fonction
Y1 est sélectionnée.
21
X
XB
29.7
10 Vos débuts
Page 21
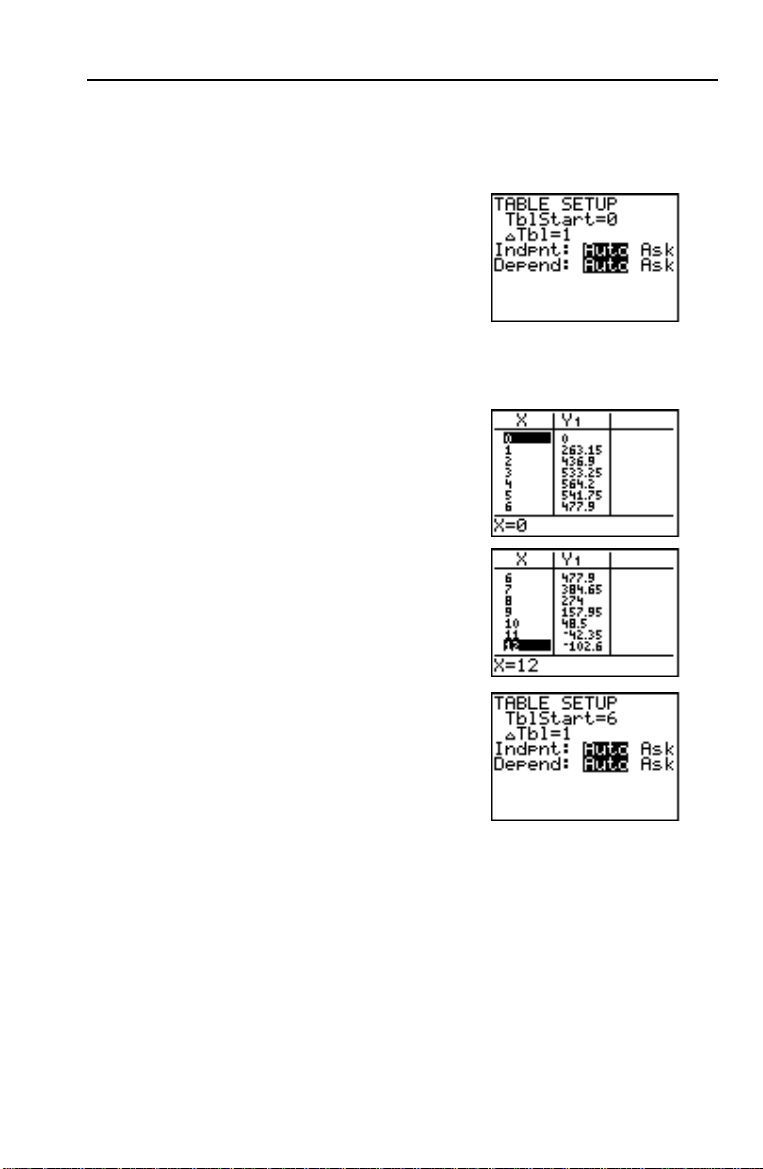
Définition d’une table de valeurs
La fonction table de la TI-83 affiche des informations chiffrées sur une
fonction. Vous pouvez utiliser une table de valeurs de la fonction définie
précédemment pour estimer une solution au problème.
1. Appuyez sur y [
de p) pour afficher le menu
SETUP
.
2. Appuyez sur Í pour valider
TblStart=0.
3. Tapez
1 Í pour définir le pas de la
@Tbl=1. Conservez les paramètres
table
Indpnt: Auto et Depend: Auto pour que
la table soit générée automatiquement.
4. Appuyez sur y [TABLE] (au-dessus de
s) pour afficher la table.
Vous remarquez que la valeur maximum
Y1 est atteinte lorsque X est aux
de
alentours de
5. Maintenez la touche † enfoncée pour
faire défiler la table jusqu’à ce
qu’apparaisse une valeur négative de
Vous remarquez que la valeur maximum
X s’obtient lorsque le signe de Y1
de
(volume) devient négatif.
6. Appuyez sur y [TBLSET].
Vous remarquez que
6 pour tenir compte de la dernière ligne
affichée. Dans l’étape 5, le premier
élément
X affiché dans la table est 6.
TBLSET] (au-dessus
4, entre 3 et 5.
TblStart est passé à
TABLE
Y
1.
Vos débuts 11
Page 22

Zoom sur une table
Vous avez la possibilité de faire varier l’affichage d’une table pour obtenir
des informations plus détaillées sur une fonction en particulier. En
affectant des valeurs plus petites à
ou zoom de la table.
1. Faites varier les paramètres de la table
afin d’obtenir une estimation plus
précise de
X pour un volume Y1
maximum. Tapez 3 Í pour définir
TblStart. Tapez Ë 1 Í pour définir
@Tbl.
2. Appuyez sur y [TABLE].
3. Utilisez † et } pour faire défiler la
table. Vous remarquez que la valeur
maximum de
obtenue avec
Y1 est 564.2 et qu’elle est
X=4. A 1 mm près, le
volume maximum est obtenu pour
3.9<X<4.1.
4. Appuyez sur y [TBLSET]. Tapez 3 Ë 9
Í pour définir TblStart. Tapez Ë 01
Í pour définir @Tbl.
5. Appuyez sur y [TABLE], puis utilisez
† et } pour faire défiler la table.
La valeur maximum de
Y1 , soit 564.25,
s’obtient pour deux valeurs différentes
X : X=4.04 et X=4.05.
de
@Tbl, vous obtenez une vue rapprochée
6. Utilisez † et } pour placer le curseur
4.04. Appuyez sur ~ pour le placer
sur
dans la colonne
Y1.
La ligne du bas indique plus précisément
la valeur de
Y1 pour X=4.04 : 564.247408.
7. Tapez † pour afficher l’autre valeur
maximum. Pour
X=4.05, la valeur de Y1
est 564.246. Ce serait le volume
maximum de la boîte si vous pouviez
couper la feuille de papier avec une
précision d’un dixième de millimètre.
12 Vos débuts
Page 23
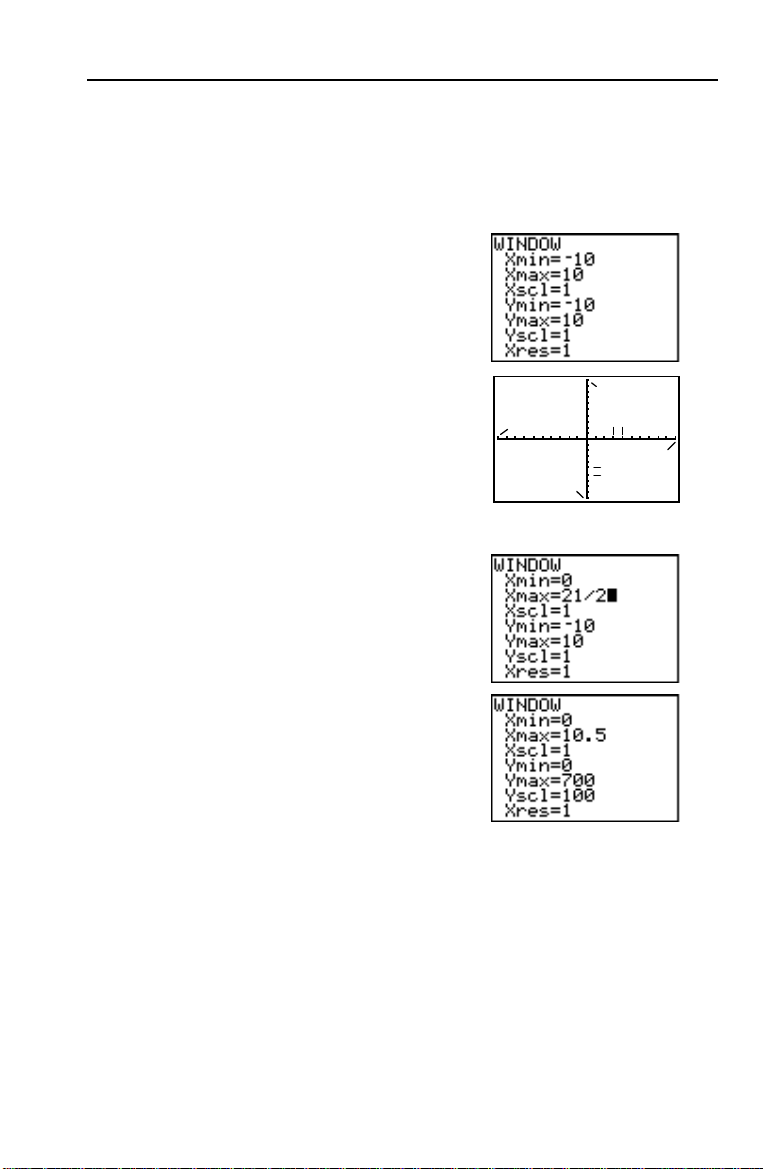
Xmax
Ymin
Ymax
Xscl
Yscl
Xmin
Configuration de la fenêtre d’affichage
Vous pouvez utiliser les fonctions graphiques de la TI-83 pour trouver la
valeur maximum d’une fonction définie précédemment. Lorsque le graphe
est activé, la fenêtre d’affichage définit la partie du plan qui apparaît dans
l’écran. Les valeurs des variables
fenêtre.
1. Appuyez sur p pour afficher
l’écran d’édition des variables
où vous pouvez visualiser et modifier la
valeur de ces variables.
Les variables WINDOW par défaut
définissent la fenêtre d’affichage
standard.
Xmin, Xmax, Ymin et Ymax
définissent les limites de l’affichage.
Xscl et Yscl déterminent la distance
entre les marques de graduation sur les
X et Y axes. Xres contrôle la
axes
résolution.
2. Tapez 0 Í pour définir Xmin.
WINDOW déterminent la taille de cette
WINDOW
3. Tapez
21 ¥ 2 pour définir Xmax à l’aide
d’une expression.
4. Appuyez sur Í. L’expression est
calculée et la valeur
Xmax. Appuyez sur Í pour
dans
valider la valeur
5. Tapez
0 Í 700 Í 100 Í 1
10.5 est mémorisée
1 de Xscl.
Í pour définir les autres variables
WINDOW.
Vos débuts 13
Page 24

Affichage et parcours d’un graphe
Vous avez défini la fonction à représenter et la fenêtre dans laquelle
afficher le graphe. Vous pouvez maintenant afficher et explorer le graphe.
Pour parcourir le graphe d’une fonction, utilisez la fonction
1. Appuyez sur s pour tracer le
graphe de la fonction sélectionnée dans
la fenêtre d’affichage. Le graphe de
Y1=(21N2X)(29.7 à 2NX)X s’affiche.
2. Appuyez sur ~ pour activer le curseur
graphique libre.
La ligne du bas indique les valeurs des
coordonnées
position du curseur graphique.
3. Appuyez sur |, ~, } et † pour
positionner le curseur libre sur le
maximum apparent de la fonction.
Lorsque le curseur se déplace, les
valeurs des coordonnées
actualisées en permanence pour refléter
la position courante.
X et Y correspondant à la
X et Y sont
TRACE.
14 Vos débuts
Page 25
4. Appuyez sur r. Le curseur
TRACE
apparaît sur le graphe de la fonction Y1.
La fonction que vous parcourez est
affichée dans le coin supérieur gauche.
Utilisez | et ~ pour parcourir le graphe
d’un point
X à un autre et calculer Y1
pour chaque valeur de X.
Vous pouvez également taper une
estimation de la valeur maximum de
Tapez 4 Ë
une touche numérique en mode
l’invite
1. Lorsque vous appuyez sur
TRACE,
X= s’affiche dans le coin inférieur
gauche du graphe.
5. Appuyez sur Í. Le curseur TRACE
se positionne sur le point Y1 calculé pour
la valeur de
X que vous avez spécifiée.
6. Appuyez sur | et ~ jusqu’à ce que le
curseur atteigne la valeur maximum de
Y.
Il s’agit de la valeur maximum de la
fonction
Y1(X) pour les pixels X. La
valeur maximum exacte peut se trouver
entre deux pixels.
X.
Vos débuts 15
Page 26
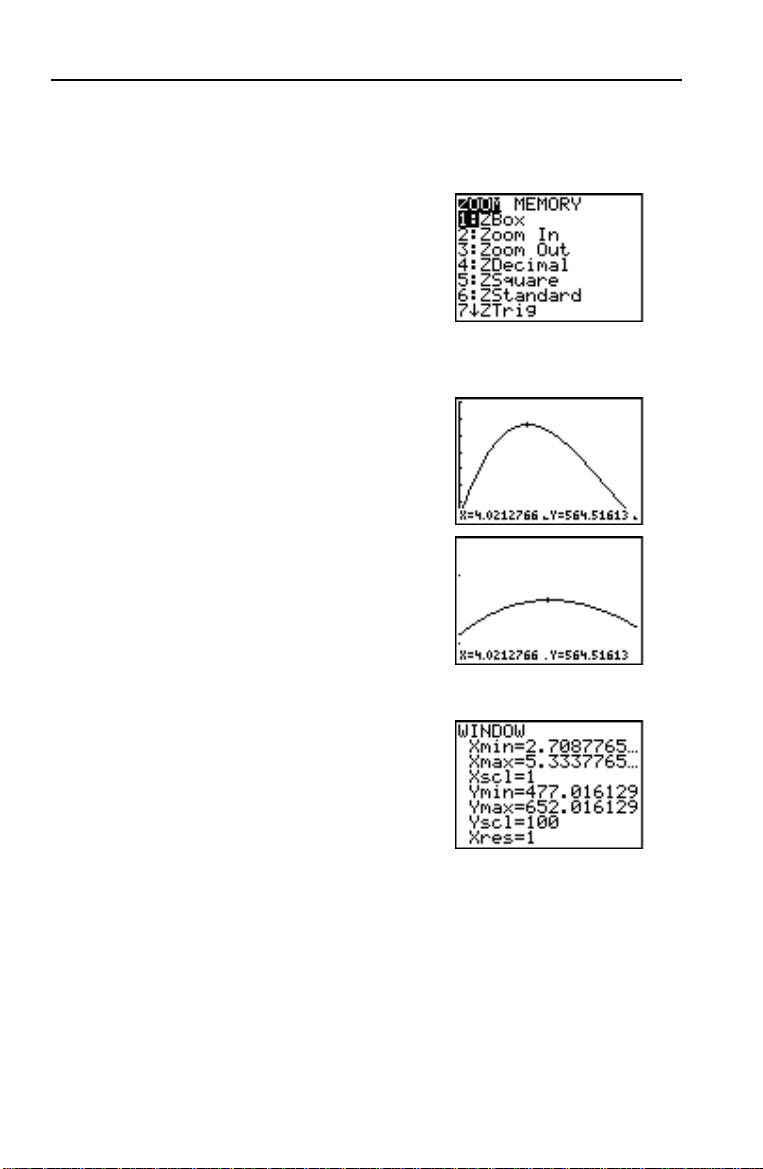
Zoom sur un graphe
Pour identifier plus facilement les valeurs maximum et minimum, le zéro et
les intersections des fonctions, vous pouvez agrandir la fenêtre d’affichage
autour d’un endroit précis à l’aide des instructions du menu
1. Appuyez sur q pour afficher le menu
ZOOM.
Ce menu est typique de la TI-83. Pour
sélectionner une option, vous pouvez
taper le numéro ou la lettre située en
regard de l’option choisie ou appuyer sur
† jusqu’à ce que ce numéro ou cette
lettre apparaisse en surbrillance.
Ensuite, appuyez sur Í.
2. Tapez 2 pour sélectionner 2:Zoom In.
Le graphe s’affiche à nouveau. Le
curseur a changé d’aspect pour indiquer
que vous utilisez une instruction
3. Positionnez le curseur près de la valeur
maximum de la fonction (comme vous
l’avez fait à l’étape 6 de la page 12) et
appuyez sur Í.
La nouvelle fenêtre d’affichage apparaît.
Les valeurs
ont été divisées par 4, la valeur par
défaut du facteur de zoom.
4. Appuyez sur p pour afficher les
nouvelles valeurs
XmaxNXmin et YmaxNYmin
WINDOW.
ZOOM.
ZOOM.
16 Vos débuts
Page 27
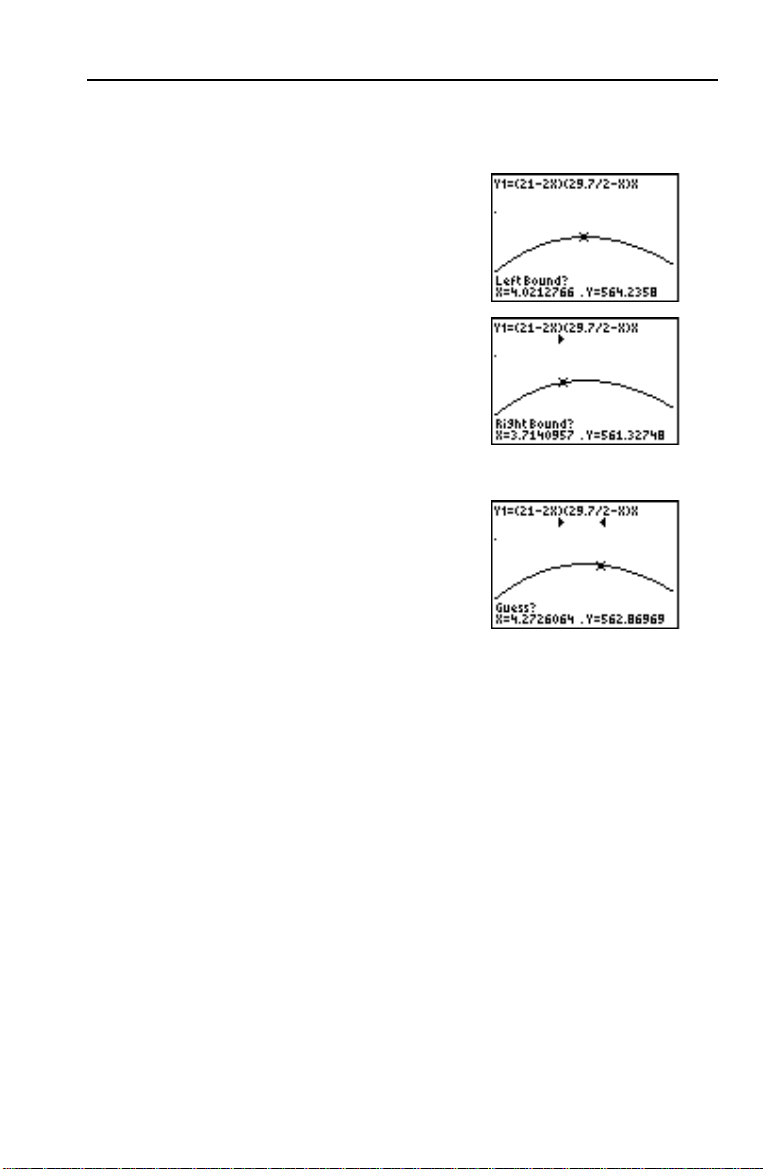
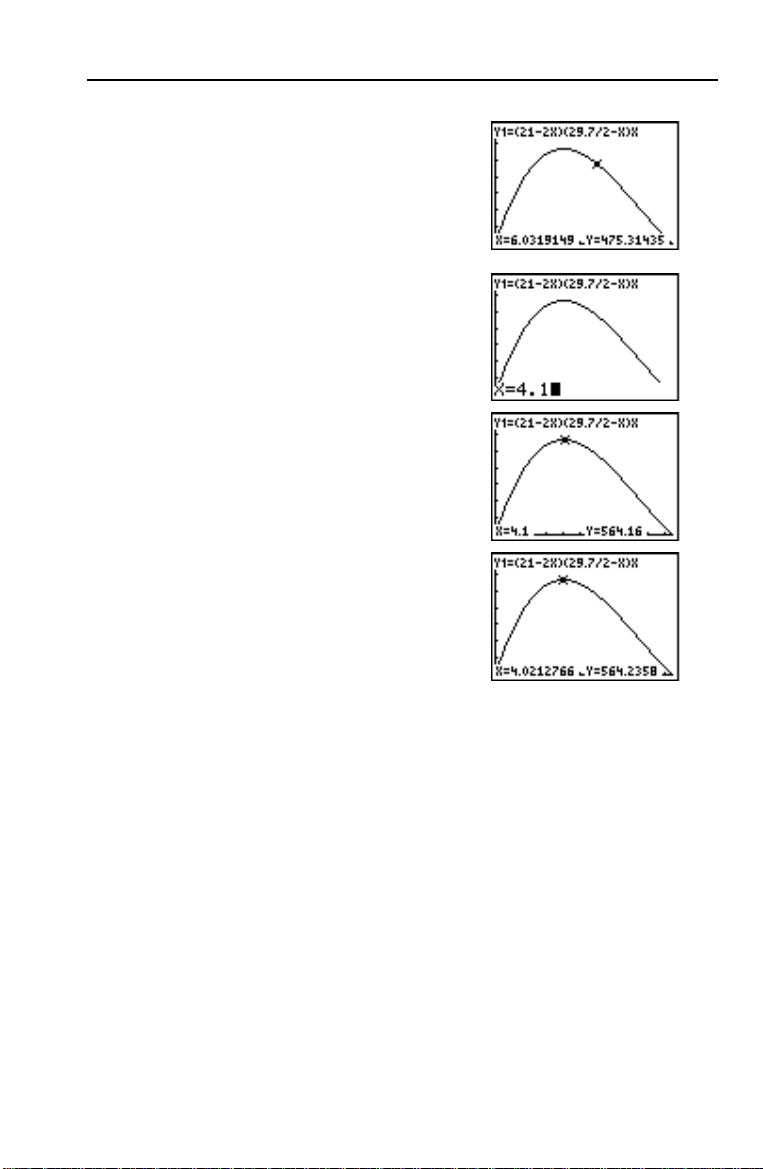
Calculer le maximum
Vous pouvez une opération du menu
CALCULATE pour calculer le
maximum local d’une fonction.
1. Appuyez sur y [
CALCULATE. Tapez 4 pour
menu
sélectionner
CALC] pour afficher le
4:maximum.
Le graphe réapparaît, accompagné d’une
invite à indiquer la limite inférieure
Left Bound?).
(
2. Utilisez | pour déplacer le curseur le
long de la courbe jusqu’à un point situé à
gauche du maximum, puis appuyez sur
Í.
Le symbole 4 s’affiche en haut de l’écran
pour indiquer la limite choisie. Une
nouvelle invite apparaît pour la limite
supérieure (
Right Bound?).
3. Utilisez ~ pour déplacer le curseur le
long de la courbe jusqu’à un point situé à
droite du maximum, puis appuyez sur
Í.
Le symbole 3 s’affiche en haut de l’écran
pour indiquer la fin du tronçon choisi.
L’invite
Guess? apparaît pour vous
permettre de fournir une approximation.
Vos débuts 17
Page 28

Calculer le maximum (suite)
4. Utilisez | pour déplacer le curseur
jusqu’à un point situé près du maximum,
puis appuyez sur Í.
Vous avez également la possibilité de
taper une approximation du maximum.
4 Ë 1 et appuyez sur Í.
Tapez
Lorsque vous appuyez sur une touche
numérique en mode
s’affiche dans le coin inférieur gauche de
l’écran.
Vous remarquez que les valeurs
calculées du maximum sont
comparables à celles obtenues à l’aide
du curseur libre, de la fonction
et de la table.
Remarque : Aux étapes 2 et 3 ci-dessus,
vous pouvez taper directement les valeurs
des limites inférieure et supérieure de la
même façon qu’à l’étape 4.
TRACE, l’invite X=
TRACE
18 Vos débuts
Page 29

Autres caractéristiques de la TI-83
Le chapitre “Vos débuts” vous a présenté le fonctionnement de base de la
calculatrice TI-83. Les chapitres suivants du manuel développent les
fonctions que vous venez de découvrir et abordent d’autres caractéristiques
de la TI-83.
Graphes
Suites
numériques
Tables
Ecran partagé
Matrices
Listes
Vous pouvez mémoriser, représenter graphiquement et
analyser jusqu’à dix fonctions (chapitre 3), jusqu’à six
fonctions paramétriques (chapitre 4), jusqu’à six
fonctions polaires (chapitre 5) et jusqu’à trois suites
numériques (chapitre 6). Les opérations
DRAW vous
permettent d’annoter vos graphes (chapitre 8).
Vous pouvez générer des suites numériques et les
représenter graphiquement, dans le temps ou sous forme
de réseaux de points ou de diagrammes de phase
(chapitre 6).
Vous pouvez créer des tables de calcul des fonctions
pour analyser plusieurs fonctions simultanément
(chapitre 7).
Vous pouvez diviser l’écran horizontalement pour
afficher en plus du graphe l’écran d’édition associé (par
exemple
Y=), la table, l’éditeur de liste statistique ou
l’écran principal. En partageant l’écran verticalement,
vous affichez un graphe et la table associée (chapitre 9).
Vous pouvez saisir et mémoriser jusqu’à dix matrices et
effectuer sur celles-ci les opérations matricielles usuelles
(chapitre 10).
Vous pouvez saisir et mémoriser autant de listes que
l’espace mémoire vous le permet en vue de les utiliser
dans les analyses statistiques. Il est possible d’associer
des formules aux listes pour permettre un calcul
automatique. Il est possible d’utiliser les listes dans
l’évaluation d’expressions ou pour tracer le graphe d’une
famille de fonctions (chapitre 11).
Vos débuts 19
Page 30

Autres caractéristiques de la TI-83 (suite)
Statistiques
Estimations
Fonctions
financières
CATALOG
Programmation
Vous pouvez effectuer des analyses statistiques à une et à
deux variables sur la base de listes, par exemple des
analyses logistiques et de régression. Les graphes
correspondant peuvent se présenter sous forme
d’histogrammes, courbes xy, nuages de points, boîtes à
moustaches normales ou modifiées. Vous pouvez définir
et mémoriser jusqu’à trois définitions de tracé statistique
(chapitre 12)
La TI-83 dispose de 16 fonctions “Test” et “Intervalle de
confiance” et de 15 fonctions associées aux lois de
probabilité usuelles. Il est possible d’afficher les résultats
des tests d’hypothèses sous forme graphique ou
numérique (chapitre 13).
Vous pouvez utiliser les fonctions financières (TVM) pour
analyser des instruments financiers tels que des annuités,
un prêt, une hypothèque, un crédit ou une épargne
(chapitre 14).
Le menu
CATALOG est une liste alphabétique de toutes
les fonctions et instructions disponibles sur la TI-83. Vous
pouvez insérer à l’emplacement du curseur n’importe
quelle fonction ou instruction copiée dans le
CATALOG
(chapitre 15).
Vous pouvez saisir et mémoriser des programmes
comprenant un contrôle étendu et des instructions
d’entrée/sortie (chapitre 16).
20 Vos débuts
Page 31

Chapitre 1: Utilisation de la TI-83
Contenu du
chapitre
Mise en marche et arrêt de la TI-83.....................................2
Réglage du contraste.............................................................3
Ecran.......................................................................................5
Saisie des expressions et instructions ................................7
Touches d’édition de la TI-83 ............................................. 10
Sélection des modes............................................................ 11
Noms des variables de la TI-83 ..........................................15
Mémorisation de variables .................................................17
Rappel de variables .............................................................18
Zone de mémoire ENTRY (Dernière entrée).................... 19
Zone de mémoire Last Answer (Ans)................................21
Menus de la TI-83................................................................. 22
Menus VARS et VARS Y-VARS ...........................................24
Système EOS de saisie d’équations ................................... 26
Conditions d’erreur .............................................................28
Utilisation de la TI-83 1–1
Page 32

Mise en marche et arrêt de la TI-83
Mise en marche
de la
calculatrice
Arrêt de la
calculatrice
Piles
Pour allumer la TI-83, appuyez sur la touche É.
¦ Si vous avez éteint la calculatrice en appuyant sur la
touche y [
OFF], l’écran initial de la TI-83 s’affiche
dans l’état où il se trouvait lors de sa dernière
utilisation et les conditions d’erreur sont effacées.
¦ Si la calculatrice a été précédemment éteinte par le
dispositif automatique de mise hors tension
(Automatic Power Down, APD
TM
), la TI-83 se retrouve
dans la situation antérieure: l’écran, le curseur et les
conditions d’erreur sont restitués intégralement.
Afin de prolonger la durée des piles, le dispositif APD
éteint automatiquement la TI-83 après cinq minutes
environ de non utilisation.
Pour éteindre la TI-83 manuellement, appuyez sur la
touche y [
¦ La fonction de mémoire permanente (Constant
Memory
OFF].
TM)
conserve tous les paramètres de réglage
choisis et l’intégralité du contenu de la mémoire.
¦ Toute condition d’erreur est effacée.
La TI-83 utilise quatre piles alcalines AAA et une pile de
sauvegarde au lithium (CR1616 ou CR1620). Pour
remplacer ces piles sans perdre de données stockées
dans la mémoire, suivez les instructions de l’annexe B.
1–2 Utilisation de la TI-83
Page 33

Réglage du contraste
Réglage du
contraste
Vous pouvez à tout moment adapter le contraste de
l’écran à votre angle de vision et à l’éclairage. Le degré de
contraste que vous choisissez s’affiche dans le coin
supérieur droit de l’écran, de
0 (le plus clair) à 9 (le plus
sombre). Il est possible que vous puissiez ne pas voir le
chiffre si le contraste est trop important, ou au contraire
pas assez.
Note: La TI-83 comprend quarante réglages de contraste, ainsi
chaque nombre de 0 à 9 représente quatre réglages.
Une fois éteinte, la TI-83 conserve en mémoire les
réglages de contraste.
Pour régler le contraste, procédez de la manière suivante:
1. Pressez puis relâchez la touche y.
2. Pressez et maintenez enfoncée la touche † ou la
touche }, situées au-dessus ou en-dessous du
symbole de contraste (cercle jaune à demi ombré).
¦ † pour éclairer l’écran.
¦ } pour assombrir l’écran.
Remarque: Un degré de contraste réglé à 0 peut faire
disparaître tout affichage. Pour rétablir le contraste original,
pressez puis relâchez la touche y, avant de presser et de
maintenir enfoncée la touche } jusqu’à ce que l’affichage
réapparaisse.
Utilisation de la TI-83 1–3
Page 34

Réglage du contraste (suite)
Quand
remplacer les
piles ?
Lorsque les batteries s’usent, un message vous en avertit
lorsque vous mettez la calculatrice en marche.
Pour remplacer ces piles sans perdre de données
stockées dans la mémoire, suivez les instructions de
l’annexe B.
La calculatrice continuera généralement à fonctionner
pendant une à deux semaines après la première
apparition du message. Au delà de cette période, la TI-83
s’éteindra automatiquement et ne sera plus
opérationnelle. Les piles doivent être remplacées. Le
contenu de la mémoire est intégralement préservé.
Remarque: La durée de fonctionnement après l’apparition du
premier message sur l’utilisation des piles peut dépasser deux
semaines si vous n’utilisez pas la calculatrice fréquemment.
1–4 Utilisation de la TI-83
Page 35

Ecran
Types d’écrans
Ecran principal
Affichage des
expressions et
des résultats
La TI-83 affiche du texte et des graphes. Les graphes sont
décrits au chapitre 3. Le chapitre 9 décrit comment
l’écran de la TI-83 peut aussi être partagé
horizontalement ou verticalement et afficher
simultanément du texte et des graphes.
L’écran principal apparaît lors de la mise en fonction de
la TI-83. Il sert à saisir les instructions à exécuter et les
expressions à évaluer. Les réponses sont affichées sur le
même écran.
L’écran de la TI-83 peut afficher jusqu’à 8 lignes de 16
caractères. Lorsque l’écran est plein, le texte défile vers
le haut, chaque nouvelle ligne au bas de l’écran efface la
première ligne. Si une expression dans l’écran principal,
l’éditeur
Y= (voir chapitre 3), ou l’éditeur de programme
(voir chapitre 16) dépasse la longueur d’une ligne, la suite
s’affiche au début de la ligne suivante. Pour les éditeurs
numériques comme l’écran WINDOW (voir chapitre 3),
une expression longue peut défiler à gauche comme à
droite.
Lorsqu’une entrée est calculée sur l’écran principal, le
résultat s’affiche à la ligne suivante, du côté droit.
Entrée
Résultat
Les paramètres de mode commandent la manière dont la
TI-83 interprète les expressions et affiche les résultats
(voir page 1-11).
Si un résultat, liste ou matrice, est trop long pour
s’afficher entièrement, des points de suspension (
...)
apparaissent à gauche ou à droite. Utilisez les touches ~
et | pour faire défiler le résultat.
Entrée
Résultat
Retour à l’écran
principal
Indicateur de
calcul en cours
Pour retourner à l’écran principal depuis un autre écran,
appuyez sur y [
QUIT].
Lorsque la TI-83 effectue des calculs ou des dessins, une
barre verticale mobile s’affiche dans le coin supérieur
droit de l’écran, indiquant un travail en cours. Si vous
interrompez un graphe ou un programme, l’indicateur de
calcul en cours prend la forme d’une barre pointillée.
Utilisation de la TI-83 1–5
Page 36

j
A
Ecran (suite)
Curseurs
La forme du curseur indique le plus souvent l’effet obtenu
en pressant la touche suivante ou en sélectionnant la
prochaine option de menu.
Curseur Forme Effet de la prochaine
Curseur de
saisie
Rectangle
clignotant
$
touche pressée
Le caractère sera tapé à
l’emplacement du
curseur, écrasant tout
caractère existant
Curseur
d’insertion
Tiret clignotant__Le caractère sera tapé à
l’emplacement du
curseur
Curseur 2nd
de fonction
auxiliaire
Flèche
clignotante
Þ
Un caractère 2nd (en
aune sur le clavier) est
saisi ou une opération
du deuxième groupe est
exécutée
Curseur
LPHA
A
clignotant
Ø
Un caractère
alphabétique (en vert
sur le clavier) est saisi
ou SOLVE est exécuté
Curseur de
saturation
Motif à
damiers
#
Aucune saisie n’est
possible; le nombre
maximum de caractères
admis est atteint ou la
mémoire est saturée
1–6 Utilisation de la TI-83
Si vous appuyez sur ƒ pendant une insertion, le
) Si vous appuyez sur
curseur devient un A souligné (
A
y pendant une insertion, le curseur souligné devient un
# souligné (
# ).
Les graphes et les éditeurs affichent parfois des curseurs
différents, décrits dans d’autres chapitres.
Page 37

Saisie des expressions et instructions
Qu’est-ce
qu’une
expression?
Saisie d’une
expression
Une expression est une suite de nombres, de variables,
de fonctions et leurs arguments. Cette suite permet
d’obtenir un résultat unique. L’utilisateur de la TI-83
introduit les opérations comme s’il les écrivait sur papier.
Par exemple, p
On peut utiliser les expressions comme commandes sur
l’écran principal pour calculer un résultat. En général,
lorsqu’une valeur est requise, il est possible d’utiliser une
expression.
Le clavier et les menus permettent de saisir les nombres,
variables et fonctions nécessaires pour créer une
expression. La touche Í clôture l’expression, quelle
que soit la position du curseur. La calculatrice calcule
l’expression selon les règles du système Equation
Operation System (EOSè) (voir page 1-26), puis affiche
le résultat.
La majorité des fonctions et des opérations de la TI-83
sont constituées de symboles de plusieurs caractères.
Vous devez saisir le symbole à l’aide du clavier ou du
menu ; il ne faut pas l’entrer lettre par lettre. Par
exemple, pour calculer le logarithme de 45, vous devez
appuyer sur «
L, O, et G. Si vous tapez LOG, la TI-83
lettres
interpréterait cette saisie comme la multiplication
implicite des variables
2
R
est une expression.
45. Vous ne pouvez pas frapper les
L, O, et G.
Saisie de plus
d’une
commande sur
une ligne
Calculez 3.76 ÷ (L7.9 + ‡5) + 2 log 45.
3.76 ¥ £ Ì 7.9 à y ã‡ä
5 ¤ ¤ Ã 2 « 45 ¤
Í
Pour saisir plus d’une expression ou instruction sur une
ligne séparez-les par (ƒ [ : ]). Toutes les instructions
sont mémorisées simultanément dans
1-19).
Utilisation de la TI-83 1–7
ENTRY (voir page
Page 38

Saisie des expressions et instructions (suite)
Saisie d’un
nombre en
notation
scientifique
Fonctions
Instructions
Pour saisir un nombre en notation scientifique, procédez
comme suit :
1. Tapez la partie du nombre qui précède l’exposant.
Cette valeur peut être une expression.
2. Appuyez sur y [
EE]. åå apparaît sur l’écran, à
l’emplacement du curseur.
3. Si l’exposant est négatif, appuyez sur Ì. Tapez
ensuite l’exposant qui peut comporter un ou deux
chiffres.
La saisie d’un nombre en notation scientifique n’induit
pas l’affichage du résultat sur la TI-83 en notation
scientifique ou ingénieur. Le style d’affichage est
déterminé par les paramètres de mode (voir page 1-11) et
la taille du nombre.
Une fonction fournit une valeur. Ainsi dans les exemples
de la page 1-7,
÷, L, +, ‡(, et log( sont des fonctions. En
général, sur la TI-83, les noms des fonctions commencent
par une lettre minuscule. La plupart des fonctions
nécessitent au moins un paramètre, c’est ce qu’indique la
parenthèse ouvrante (
sin( nécessite un paramètre, sin(valeur).
( ) à la suite du nom. Par exemple,
Toute instruction déclenche une action. Par exemple,
ClrDraw est une instruction qui efface tout élément
dessiné d’un graphe. Les instructions ne peuvent pas être
utilisées dans des expressions. En général, le nom d’une
instruction commence par une majuscule. Certaines
instructions nécessitent plusieurs paramètres, ce
qu’indique une parenthèse ouverte (
Par exemple,
Circle(X,Y,radius).
Circle( exige trois paramètres,
( ) à la suite du nom.
1–8 Utilisation de la TI-83
Page 39

Utilisation de la TI-83 1–9
Lorsque la TI-83 effectue un calcul ou trace un graphe,
l’indicateur “calcul en cours” s’allume. Pour interrompre
la calcul ou le tracé du graphique, pressez la touche É.
L’écran ERR:BREAK s’affiche.
¦ Pour retourner à l’écran principal, sélectionnez 1:Quit.
¦ Pour retourner à l’emplacement de l’interruption,
sélectionnez 2:Goto.
Remarque : Pour interrompre le tracé d’un graphique sur la
TI-83, appuyez sur la touche É. Pour retourner à l’écran
principal, appuyez sur la touche ‘ ou une autre touche.
Interruption
d’un calcul
Page 40

Touches d’édition de la TI-83
Touches Résultat
~ ou | Déplace le curseur dans une expression. Ces touches sont
} ou † Déplace le curseur d’une ligne à l’autre au sein d’une
y | Place le curseur au début d’une expression
y ~ Place le curseur à la fin d’une expression
Í Calcule une expression ou exécute une instruction
‘
{ Supprime le caractère sur lequel se trouve le curseur.
y [INS] Transforme le curseur en __ ; insère des caractères à
y Transforme le curseur en Þ; la frappe suivante sur une
ƒ Transforme le curseur en Ø; la frappe qui va suivre sera
y [A-LOCK] Transforme le curseur en Ø; introduit un alpha-lock.
„ Permet d’entrer un X en mode Func, un T en mode Par, un
répétitives
expression qui comprend plus d’une ligne. Ces touches
sont répétitives
¦ Sur la ligne supérieure d’une expression dans l’écran
principal, } place le curseur au début de l’expression
¦ Sur la ligne inférieure d’une expression dans l’écran
principal, † place le curseur à la fin de l’expression
¦ Sur une ligne de texte de l’écran principal, efface la
ligne de commande présente
¦ Sur une ligne vide de l’écran principal, efface la totalité
de l’écran principal
¦ Dans un éditeur, efface l’expression ou la valeur sur
laquelle le curseur est placé ; ne mémorise pas un zéro
Cette touche est répétitive
l’emplacement du curseur. Pour terminer l’insertion,
appuyez sur y [
INS] sur |, }, ~, ou sur †
touche déclenche une opération auxiliaire (une opération
marquée en jaune à gauche au-dessus d’une touche). Pour
supprimer 2nd, appuyez à nouveau sur la touche y
un caractère alpha (caractère marqué en vert à droite audessus de la touche) ou l’exécution de
SOLVE (Voir
chapitres 10 et 11). Pour annuler ƒ, appuyez sur
ƒ |, }, ~, ou †
Toute frappe ultérieure (sur une touche alpha) ajoute un
caractère alpha. Pour annuler alpha-lock, appuyez sur
ƒ; les invites de noms mettent automatiquement le
clavier en mode alpha-lock
q en mode Pol, ou un
n
en mode Seq en appuyant sur une
seule touche
1–10 Utilisation de la TI-83
Page 41

Sélection des modes
Visualisation
des options du
menu MODE
Modification
des paramètres
de la
commande
MODE
Sélection d’un
MODE à partir
d’un
programme
La commande MODE définit le type d’affichage et le
mode d’interprétation des nombres et des graphes sur la
TI-83. En cas d’arrêt de la calculatrice TI-83, les
paramètres définis dans le menu MODE sont mémorisés
automatiquement par la fonction brevetée de Mémoire
Permanente. Tous les nombres, y compris les éléments
des matrices et des listes, sont affichés suivant les
paramètres de la commande MODE.
Appuyez sur z pour afficher les options du menu
MODE. Les paramètres courants sont mis en surbrillance.
Les valeurs par défaut sont mises en surbrillance cidessous. Les paramètres spécifiques de la commande
MODE sont décrits dans les pages suivantes.
Normal Sci Eng Notation numérique
Float 0123456789 Nombre de décimales
Radian Degree Unité de mesure angulaire
Func Par Pol Seq Type de représentation graphique
Connected Dot Relier éventuellement les points
d’un graphe
Sequential Simul Tracé simultané éventuel
Real a+bi re^qi Réel, forme algébrique, forme
exponentielle
Full Horiz G-T Ecran entier, deux modes d’écrans
partagés
Pour modifier les paramètres de la commande MODE,
procédez comme suit :
1. Appuyez sur † ou } pour placer le curseur sur la
ligne du paramètre à modifier.
2. Appuyez sur ~ ou | pour atteindre le paramètre
souhaité.
3. Appuyez sur Í.
Vous pouvez choisir un MODE à l’aide d’un programme
en introduisant le nom du MODE comme s’il s’agissait
d’une instruction; par exemple,
Func ou Float. Dans une
ligne de commande vide, choisissez le nom dans l’écran
de sélection MODE interactif; le nom vient se placer à
l’emplacement du curseur.
Utilisation de la TI-83 1–11
Page 42

Sélection des modes (suite)
Notation
normale
scientifique
ingénieur
Virgule flottante
ou fixe
Le choix de la notation influence uniquement l’affichage
d’un résultat sur l’écran principal. Les résultats chiffrés
peuvent atteindre un maximum de 10 chiffres et un
exposant à deux chiffres. La saisie d’un nombre est
possible dans tous les systèmes de notation.
Le format d’affichage
Normal correspond à celui que l’on
emploie généralement pour exprimer les nombres, c’està-dire en plaçant les chiffres à gauche et à droite du point
décimal, par exemple
La notation
Sci (scientifique) exprime les nombres en
123456.67.
deux parties. Les chiffres significatifs s’affichent avec un
chiffre à gauche du point décimal. La puissance de 10 se
met à droite de
La notation
E, comme dans 1.234667E4.
Eng (ingénieur) est semblable à la notation
scientifique. Cependant, le nombre peut posséder un,
deux ou trois chiffres avant le point décimal. La
puissance de 10 est un multiple de 3, part exemple
12.34667E3.
Remarque : Si vous avez sélectionné la notation Normal alors
que le résultat ne peut être affiché avec 10 chiffres (ou si la
valeur absolue est inférieure à .001), seul ce dernier résultat est
affiché en mode scientifique.
La représentation Float (virgule flottante) affiche un
maximum de 10 chiffres plus le signe et le point décimal.
La représentation en virgule fixe affiche le nombre de
chiffres sélectionné (
0 à 9) à droite de la décimale. Placez
le curseur sur le nombre de chiffre décimaux souhaité et
appuyez sur Í.
Le mode décimal s’applique aux trois modes de notation.
Le mode décimal s’applique aux nombres suivants :
¦ Un résultat affiché sur l’écran principal.
¦ Les coordonnées d’un graphique (Voir chapitres 3, 4, 5
et 6)
¦ Les coéfficients, dans DRAW, de l’équation de la
tangente, et les valeurs
¦ Les résultats d’opérations
dy/dx (Voir chapitre 8)
CALCULATE (Voir chapitres
3, 4, 5 et 6)
¦ Eléments d’une équation de régression stockés après
l’exécution d’un modèle de régression (Voir
chapitre 12)
1–12 Utilisation de la TI-83
Page 43

Radian
Degree
Func
Par
Pol
Seq
Connected
Dot
L’unité d’angle commande l’interprétation des valeurs
d’angle par la TI-83 dans les fonctions trigonométriques
et dans les conversions de coordonnées
polaires/rectangulaires.
Si vous choisissez
Radian comme unité d’angle, les
arguments sont transcrits en radians. Les résultats
s’affichent en radians.
Si vous choisissez
Degree comme unité d’angle, les
arguments sont transcrits en degrés. Les résultats
s’affichent en degrés.
Les modes de représentation graphique définissent les
paramètres graphiques. Les chapitres 3, 4, 5 et 6
décrivent ces modes en détail.
La fonction graphique
représentation graphique des fonctions où
en fonction de
La fonction graphique
représentation graphique des fonctions où
chacun exprimés en fonction de
La fonction graphique
représentation graphique des fonctions où
Func (fonction) permet la
Y est exprimé
X (Voir chapitre 3).
Par (paramétrique) permet la
X et Y sont
T (Voir chapitre 4).
Pol (polaire) permet la
r est exprimé
en fonction de q (Voir chapitre 5).
La fonction graphique
Seq (séquence) permet la
représentation graphique des suites numériques (Voir
chapitre 6).
Connected trace une ligne entre les points calculés pour
les fonctions choisies.
Dot se limite à marquer les points calculés des fonctions
choisies.
Utilisation de la TI-83 1–13
Page 44

Sélection des modes (suite)
Sequential
Simul
Real
a+bi
re^qi
Full
Horiz
G-T
Sequential (séquentiel) calcule et représente
complètement une fonction avant calcul et
représentation de la fonction suivante.
Simul (simultané) calcule et représente toutes les
fonctions choisies pour une seule valeur de
et trace le graphe pour la valeur suivante de
Remarque : Quel que soit le mode de représentation graphique
choisi, la TI-83 représente séquentiellement tous les points
calculés avant de représenter une fonction.
X puis calcule
X.
Le mode Real n’affiche pas de résultats complexes mais
permet la saisie de nombres complexes en entrée.
Deux modes complexes affichent des résultats
complexes.
a+bi (mode complexe algébrique) affiche les nombres
¦
complexes sous la forme a+bi.
¦
re^qi (mode complexe exponentiel) affiche les
nombres complexes sous la forme re^qi.
Le mode écran
Full utilise la totalité de l’écran pour
afficher un graphe ou un écran d’édition.
Chacun des modes écran partagé affiche deux écrans
simultanément.
Horiz (horizontal) affiche le graphe en cours dans la
¦
partie supérieure de l’écran et l’écran principal ou un
éditeur dans la partie inférieure (Voir chapitre 9).
¦
G-T (table graphique) affiche le graphe en cours dans
la moitié gauche de l’écran et l’écran table dans la
moitié droite (Voir chapitre 9).
1–14 Utilisation de la TI-83
Page 45

V
Noms des variables de la TI-83
Variables et
éléments
définis
La TI-83 accepte plusieurs types de données, dont les
nombres réels et complexes, les matrices, les listes, les
fonctions, les tracés statistiques, les bases de données
graphiques, les images graphiques et les chaînes.
La TI-83 utilise des noms prédéfinis pour les variables et
autres éléments stockés dans la mémoire. En ce qui
concerne les listes, vous pouvez également créer vos
noms à cinq caractères.
Type de variable Désignation
Nombres réels A, B, . . ., Z, q
Nombres complexes A, B, . . ., Z, q
Matrices ãAä, ãBä, ãCä, . . . , ãJä
Listes L1, L2, L3, L4, L5, L6 et
noms définis par l’utilisateur
Fonctions Y1, Y2, . . . , Y9, Y0
Equations
X1T and Y1T, . . . , X6T et Y6T
paramétriques
Fonctions polaires r1, r2, r3, r4, r5, r6
Fonctions de suites u, v, w
Représentation de
Plot1, Plot2, Plot3
statistiques
Bases de données
GDB1, GDB2, . . . , GDB9, GDB0
graphiques
Images graphiques Pic1, Pic2, . . . , Pic9, Pic0
Chaînes Str1, Str2, . . . , Str9, Str0
ariables système Xmin, Xmax et autres
Utilisation de la TI-83 1–15
Page 46

Noms des variables de la TI-83 (suite)
Notes sur les
variables
¦ Vous pouvez créer autant de noms de listes que la
mémoire vous le permet (Voir chapitre 11).
¦ Les programmes ont des noms définis par l’utilisateur
et se partagent la mémoire avec les variables (Voir
chapitre 16).
¦ A partir de l’écran principal ou d’un programme, vous
pouvez mémoriser des matrices (Voir chapitre 10), des
listes (Voir chapitre 11), des chaînes (Voir chapitre
15), des variables système telles que
chapitre 1),
fonctions
TblStart (Voir chapitre 7), et toutes les
Y= (Voir chapitres 3, 4, 5 et 6).
Xmax (Voir
¦ A partir d’un éditeur, vous pouvez mémoriser des
matrices, des listes et des fonctions
Y= (Voir
chapitre 3).
¦ Vous pouvez également, à partir de l’écran principal,
d’un programme ou d’un éditeur, mémoriser un
élément de matrice ou de liste.
¦ Les bases de données et les images graphiques sont
mémorisées et rappelées à l’aide des instructions du
DRAW STO (Voir chapitre 8).
menu
1–16 Utilisation de la TI-83
Page 47

Mémorisation de variables
Mémorisation
de valeurs dans
une variable
Affichage d’une
valeur de
variable
Les valeurs sont mises en mémoire et rappelées à l’aide
des noms des variables. Lorsqu’une expression contenant
une variable est calculée, la calculatrice utilise la valeur
contenue dans la variable à ce moment-là.
Pour mémoriser une valeur dans une variable à partir de
l’écran principal ou d’un programme en utilisant la
touche ¿, commencez à une ligne vide et procédez
comme suit :
1. Saisissez la valeur que vous désirez mémoriser, et qui
peut être une expression.
2. Appuyez sur ¿. Le symbole ! se place à
l’emplacement du curseur.
3. Appuyez sur ƒ, puis sur la lettre de la variable
sous laquelle vous désirez stocker la valeur.
4. Appuyez sur Í. Si vous avez entré une expression,
elle est calculée. La valeur est mémorisée dans la
variable.
Pour afficher le nom d’une variable, entrez son nom sur
une ligne de commande vierge de l’écran principal puis
appuyez sur Í.
Utilisation de la TI-83 1–17
Page 48
Rappel de variables
Utilisation de
RCL (Rappel)
Pour rappeler et copier le contenu de variables à
l’emplacement du curseur, procédez comme suit. (Pour
RCL, appuyez sur ‘.)
quitter
1. Appuyez sur y ã
RCLä. Rcl et le curseur d’édition
sont affichés sur la dernière ligne de l’écran.
2. Entrez le nom de la variable de l’une des manières
suivantes.
¦ Appuyez sur ƒ et sur la lettre de la variable.
¦ Appuyez sur y ã
de la liste ou appuyez sur y [
LISTä, puis sélectionnez le nom
Ln].
¦ Appuyez sur et choisissez le nom de la
matrice.
¦ Appuyez sur pour afficher le menu
sur ~ pour afficher le menu
VARS ou
VARS Y-VARS ;
puis sélectionnez le type et le nom de la variable ou
de la fonction.
¦ Appuyez sur | et choisissez le nom du
programme (dans l’éditeur de programme
uniquement).
Le nom de la variable que vous avez sélectionnée est
affiché sur la dernière ligne et le curseur disparaît.
3. Appuyez sur Í. Le contenu de la variable est
inséré à l’endroit où se trouvait le curseur avant de
commencer ces étapes. Vous pouvez modifier les
caractères copiés dans l’expression sans affecter la
valeur en mémoire.
1–18 Utilisation de la TI-83
Page 49

Zone de mémoire ENTRY (Dernière entrée)
Utilisation de la
fonction ENTRY
(Dernière
entrée)
Accès à une
saisie
précédente
Lorsque vous appuyez sur Í dans l’écran principal
pour calculer une expression ou exécuter une
instruction, l’expression ou l’instruction est mémorisée
dans une zone de mémoire spéciale appelée
(dernière entrée). La dernière entrée est mémorisée
lorsque vous arrêtez la TI-83.
Pour rappeler
dernière entrée vient s’insérer à l’emplacement du
curseur, où vous pouvez la modifier et l’exécuter. Sur
l’écran principal ou dans un éditeur la ligne en cours est
effacée et la dernière entrée est insérée sur la ligne.
La TI-83 met à jour
appuyez sur la touche Í, il est donc possible de
rappeler la dernière expression, même si l’expression
suivante est en cours de saisie. Lorsque vous rappelez la
dernière expression via
que vous avez tapé.
5 Ã 7
Í
y [ENTRY]
La TI-83 mémorise un nombre d’entrées correspondant à
la taille de sa mémoire
consulter ces saisies, appuyez sur y [
plusieurs reprises. Si une seule entrée occupe plus de 128
octets, elle est considérée comme
pas trouver place dans la mémoire
ENTRY, appuyez sur y [ENTRY]. La
ENTRY uniquement lorsque vous
ENTRY, celle-ci se substitue à ce
ENTRY (jusqu’à 128 octets). Pour
ENTRY, mais ne peut
ENTRY.
ENTRY
ENTRY] à
1 ¿ ƒ A
Í
2 ¿ ƒ B
Í
y ã
ENTRYä
A chaque pression sur y [ENTRY], la ligne de
commande utilisée est écrasée. Si vous appuyez sur y
ENTRY] après affichage du plus ancien élément,
[
l’élément le plus récent s’affiche.
y ãENTRYä
Utilisation de la TI-83 1–19
Page 50

Zone de mémoire ENTRY (Dernière entrée) (suite)
Recalcul de la
dernière saisie
ENTRY
Entrées
contenant
plusieurs
commandes
Après avoir inséré la dernière saisie sur l’écran principal
et l’avoir modifiée (si vous décidez de la modifier), vous
pouvez exécuter l’expression saisie. Pour ce faire,
appuyez sur Í.
Pour exécuter à nouveau l’entrée affichée, appuyez sur
Í à nouveau. Chaque nouveau calcul affiche un
résultat sur le côté droit de la ligne suivante, l’entrée ne
réapparaît pas.
0 ¿ ƒ N
Í
ƒ N Ã 1 ¿ ƒ N
ƒã:ä ƒ N ¡ Í
Í
Í
Pour mémoriser dans ENTRY deux ou plusieurs
expressions ou instructions sur une ligne, séparez deux
expressions ou instructions par deux points ( : ), puis
appuyez sur Í. Toutes les expressions et instructions
séparées par deux points sont mémorisées dans
Lorsque vous appuyez sur y [
expressions et instructions séparées par deux points sont
insérées à l’emplacement du curseur. Vous pouvez
modifier toutes les commandes, puis les exécuter lorsque
vous appuyez sur Í.
A l’aide de l’équation A=pr
rayon d’un disque qui couvre 200 cm2. Utilisez 8 comme
première supposition.
ENTRY], toutes les
2
, trouvez par tâtonnements le
ENTRY.
8 ¿ ƒ R ƒ ã:ä
y ãpä ƒ R ¡ Í
y[ENTRY]
y | 7 y ãINSä Ë 95
Í
Continuez jusqu’à ce que le résultat atteigne la précision
recherchée.
Annulation de
ENTRY
1–20 Utilisation de la TI-83
Clear Entries (Voir chapitre 18) efface toutes les données
contenues dans la zone de mémorisation
TI-83.
ENTRY de la
Page 51

Zone de mémoire Last Answer (Ans)
Utilisation de la
variable Ans
dans une
Expression
Continuation du
calcul d’une
expression
A chaque calcul d’une expression à partir de l’écran
principal ou d’un programme, la TI-83 mémorise le
résultat dans une zone de mémoire appelée
answer, dernier résultat).
ou complexe, une liste, une matrice ou une chaîne.
Lorsque vous arrêtez la TI-83, la valeur contenue dans
Ans est mémorisée.
Vous pouvez utiliser la variable
expressions où ce type de données est correct. Appuyez
sur y [
l’emplacement du curseur. Lorsque l’expression est
calculée, la TI-83 utilise la valeur de
Calculez la superficie d’une parcelle de jardin de 1,7
mètres sur 4,2 mètres. Calculez ensuite le rendement par
are sachant que la parcelle a produit un total de 147
tomates.
1.7 ¯ 4.2
Í
147 ¥
Í
Vous pouvez utiliser la valeur Ans comme première
entrée de l’expression suivante, sans avoir à ressaisir la
valeur ou presser y [
ligne vierge de l’écran principal. La TI-83 insère la
variable
ANS] et le nom de la variable Ans sera copié à
y [ANS]
Ans à l’écran, suivi de la fonction.
Ans peut être un nombre réel
Ans dans la plupart des
ANS]. Entrez la fonction sur la
Ans (last
Ans dans le calcul.
Mémorisation
d’un résultat
5 ¥ 2
Í
¯ 9.9
Í
Pour mémoriser un résultat, mémorisez d’abord Ans dans
une variable avant de calculer une autre expression.
Calculez l’aire d’un cercle d’un rayon de 5 mètres.
Calculez ensuite le volume d’un cylindre de 5 mètres de
rayon et de 3,3 mètres de hauteur, puis mémorisez dans
la variable V.
y ãpä 5 ¡
Í
¯ 3.3
Í
¿ ƒ V
Í
Utilisation de la TI-83 1–21
Page 52

Menus de la TI-83
Utilisation d’un
menu de la
TI-83
Défilement à
l’intérieur d’un
menu
La plupart des opérations de la TI-83 sont accessibles à
partir de menus. Lorsque vous appuyez sur une touche ou
une combinaison de touches pour afficher un menu, un
ou plusieurs noms de menu apparaissent sur la ligne
supérieure de l’écran.
¦ Le nom du menu, situé à gauche de la ligne, est mis en
surbrillance. Chaque menu peut afficher jusqu’à sept
options à partir de l’élément
1 qui est également mis
en surbrillance.
¦ Un numéro ou une lettre identifie l’emplacement de
chaque option dans le menu. L’ordre normal est
0, puis A, B, C et ainsi de suite. Les menus LIST
puis
NAMES
uniquement les éléments
, PRGM EXEC et PRGM EDIT identifient
1 à 9 et 0.
1 à 9,
¦ Lorsque le menu continue au-delà des options
affichées, une flèche descendante ( $ ) remplace les
deux-points en regard de la dernière option affichée.
¦ Lorsqu’une option de menu se termine par des points
de suspension, cette option affiche un menu
secondaire ou un écran d’édition lorsque vous la
sélectionnez.
Pour afficher tout autre menu mentionné sur la ligne
supérieure, appuyez sur ~ ou | jusqu’à ce que le nom du
menu souhaité soit mis en surbrillance. Quelle que soit la
position du curseur dans le menu précédent, il apparaît
au niveau de la première option du nouveau menu
affiché.
Remarque : La Hiérarchie des menus présentée dans l’Annexe
A montre chaque menu avec toutes les opérations qu’il propose
et la touche ou la combinaison de touches à utiliser pour
l’afficher.
Pour faire défiler les options de menu vers le bas,
appuyez sur †. Pour faire défiler les options de menu
vers le haut, appuyez sur }.
Pour descendre de six options de menu à la fois, appuyez
sur ƒ †. Pour remonter de six options de menu à la
fois, appuyez sur ƒ }.
Les flèches vertes entre † et } correspondent aux
symboles écran suivant et écran précédent.
Pour passer directement de la première à la dernière
option de menu, appuyez sur }. Pour passer directement
de la dernière à la première option de menu, appuyez sur
†. Certains menus ne sont cependant pas circulaires.
1–22 Utilisation de la TI-83
Page 53

Sélection d’une
option de menu
Quitter un
menu sans faire
de sélection
Il existe deux méthodes de sélection d’une option dans
un menu :
¦ Taper le numéro ou la lettre de l’option choisie. Le
curseur peut se trouver à n’importe quel endroit du
menu et l’option à sélectionner peut ne pas être
affichée à l’écran.
¦ Appuyer sur † ou sur } pour placer le curseur sur
l’option choisie, puis presser Í.
Après avoir fait une sélection, vous revenez en général à
l’écran que vous utilisiez.
Remarque : Dans les menus LIST NAMES, PRGM EXEC et
PRGM EDIT, vous ne pouvez sélectionner que l’une des dix
premières options en tapant un chiffre entre 1 et 9 ou 0.
Appuyez sur un caractère alphabétique ou sur q pour placer le
curseur sur la première option commençant par ce caractère.
S’il n’en existe aucune, le curseur passe tout simplement à
l’option suivante.
Vous pouvez quitter un menu sans faire de sélection de
l’une des façons suivantes :
¦ Appuyez sur y [
QUIT] pour retourner à l’écran
principal.
¦ Appuyez sur ‘ pour retourner à l’écran
précédent.
¦ Appuyez sur la touche ou combinaison de touches
correspondant à un autre menu tel que ou y
LIST].
[
¦ Appuyez sur la touche ou combinaison de touches
permettant d’accéder à un autre écran, par exemple
o ou y [
TABLE].
Calculez
† † † Í
27 ¤ Í
3
‡27.
Utilisation de la TI-83 1–23
Page 54

Menus VARS et VARS Y-VARS
Menu VARS
Menu VARS
Y-VARS
Vous pouvez saisir le nom des fonctions et des variables
système dans une expression ou les mémoriser
directement.
Pour afficher le menu
VARS menu, appuyez sur .
Toutes les options de ce menu permettent d’accéder à
des menus secondaires qui affichent les noms des
variables système. Les options
5:Statistics permettent d’accéder à plus d’un menu
1:Window, 2:Zoom et
secondaire.
VARS Y-VARS
1: Window... Variables X/Y, T/q et U/V/W
2: Zoom
3: GDB
4: Picture
5: Statistics
6: Table
7: String... Variables STRING
... Variables ZX/ZY, ZT/Zq et ZU
... Variables GRAPH DATABASE
... Variables PICTURE
... Variables XY, G, EQ, TEST et PTS
... Variables TABLE
Pour afficher les menus VARS Y-VARS, appuyez sur
~.
l’affichage des noms des fonctions définies dans
VARS Y-VARS
1: Function... Fonctions Yn
2: Parametric... Fonctions XnT, YnT
3: Polar... Fonctions rn
4: On/Off... Permet de sélectionner ou désactiver
1:Function, 2:Parametric et 3:Polar permettent
Y=.
des fonctions
Remarque : Les noms de suite (u, v, w) sont situées sur le
clavier comme fonctions secondaires de ¬, − et ®.
1–24 Utilisation de la TI-83
Page 55

Sélection d’un
nom par le
menu VARS ou
Y-VARS
Pour sélectionner une variable ou un nom de fonction à
partir du menu
VARS ou Y-VARS, procédez de la
manière suivante :
1. Sélectionnez le menu
¦ Appuyez sur pour afficher le menu
¦ Appuyez sur ~ pour afficher le menu
Y-VARS
.
VARS ou Y-VARS.
VARS
VARS
.
2. Sélectionnez le type de nom de variable, comme
2:Zoom dans le menu VARS ou 3:Polar dans le menu
VARS Y-VARS. Un menu secondaire s’affiche.
3. Si vous avez sélectionné
5:Statistics dans le menu VARS, vous pouvez appuyer
1:Window, 2:Zoom ou
sur ~ ou | pour afficher d’autres menus secondaires.
4. Sélectionnez un autre nom de variable dans ce menu.
Il est inséré à l’emplacement du curseur.
Utilisation de la TI-83 1–25
Page 56

Système EOS de saisie d’équations
Ordre de calcul
Multiplication
implicite
Le système breveté de saisie d’équations EOS de la TI-83
définit l’ordre dans lequel les fonctions sont saisies dans
les expressions puis calculées. Il vous permet de saisir
des nombres et fonctions dans un ordre simple et direct.
EOS calcule les fonctions d’une expression dans l’ordre
suivant :
1 Fonctions introduites après l’argument, telles que
2 Puissances et racines, telles que 2^5 ou 5
2, M1
, !, ¡, r, et conversions
x
‡32
3 Fonctions simples précédant l’argument, telles
‡( , sin( ou log(
que
4 Permutations (nPr) et combinaisons (nCr)
5 Multiplications, multiplications implicites et
divisions
6 Additions et soustractions
7 Fonctions relationnelles, telles que > ou
8 Opérateur booléen and
9 Opérateurs booléens or et xor
Les fonctions d’un même groupe de priorité sont évaluées
de gauche à droite par EOS.
Les calculs inclus dans des parenthèses sont effectués en
priorité.
Les fonctions multi-arguments, telles que
nDeriv(A
2
,A,6)
sont évaluées dans l’ordre où elles sont rencontrées.
La TI-83 reconnaît la multiplication implicite, il n’est donc
pas toujours nécessaire d’appuyer sur ¯ pour exprimer la
multiplications. Par exemple, la TI-83 interprète
sin(46)
, 5(1+2) et (2ää5)7 comme multiplications implicites.
Remarque : Les règles de multiplication implicite de la TI-83
diffèrent de celles de la TI-82. Par exemple, la TI-83 interprète 1/2X
comme (1/2)ääX, alors que la TI-82 interprète 1/2X comme 1/(2ääX).
2p, 4
1–26 Utilisation de la TI-83
Page 57

Parenthèses
Opposée
Tous les calculs entre parenthèses sont exécutés en
priorité. Par exemple, dans l’expression
4(1+2), EOS
calcule d’abord la partie de l’expression entre parenthèses,
c’est-à-dire
1+2, puis multiplie le résultat, 3, par 4.
Il n’est pas nécessaire d’ajouter la parenthèse fermante
) ) à la fin d’une expression. Tous les éléments de
(
parenthèse “ouverts” sont fermés automatiquement à la
fin de l’expression. C’est également le cas pour les
éléments suivant une parenthèse ouverte qui précédent la
mémorisation ou l’affichage d’instructions de conversion.
Remarque : Si le nom d’une liste, d’une matrice ou d’une
fonction Y= est suivi d’une parenthèse ouverte, cela n’indique
pas une multiplication implicite. La parenthèse est utilisée pour
accéder à des éléments spécifiques de la liste (Voir chapitre 11)
ou de la matrice (Voir chapitre 10) et précise une valeur pour
laquelle on veut la valeur de la fonction Y=.
Pour saisir un nombre négatif, utilisez la touche
“opposée”. Appuyez sur Ì et saisissez ensuite le nombre.
Sur la TI-83, l’opposé se trouve dans le troisième groupe
hiérarchique EOS. Les fonctions du premier groupe,
comme la mise au carré, sont calculées avant l’opposé.
2
X
Par exemple, le résultat de M
est un nombre négatif
(ou 0). Utilisez les parenthèses pour mettre un nombre
négatif au carré.
Remarque : Utilisez la touche ¹ pour la soustraction et la
touche Ì pour l’opposé.
Utilisation de la TI-83 1–27
Page 58

Conditions d’erreur
Diagnostic
d’erreur
Correction
d’une erreur
La TI-83 détecte les erreurs survenant lors :
¦ du calcul d’une expression.
¦ de l’exécution d’une instruction.
¦ du tracé d’une courbe.
¦ de la mémorisation d’une valeur.
Lorsque la TI-83 détecte une erreur, elle retourne un
message d’erreur avec menu, comme
ERR:DOMAIN. Les codes et situations d’erreur sont
ERR:SYNTAX. ou
décrits en détail dans l’Annexe B.
¦ Si vous sélectionnez 1:Quit (ou si vous appuyez sur
QUIT] ou ‘), vous retournez à l’écran initial.
y [
¦ Si vous sélectionnez
2:Goto, l’écran précédent est
affiché et le curseur se place à l’endroit où l’erreur a
été détectée.
Remarque : Si une erreur de syntaxe a été détectée dans le
contenu d’une fonction Y= pendant l’exécution d’un programme,
l’option Goto renvoie l’utilisateur à l’éditeur Y= et non au
programme.
Pour corriger une erreur, procédez de la manière
suivante :
1. Notez le type d’erreur (
2. Sélectionnez
2:Goto, si cette option est disponible.
ERR:error type).
L’écran précédent est affiché et le curseur se place à
l’endroit où l’erreur a été détectée.
3. Déterminez la nature de l’erreur. Si vous n’y parvenez
pas, reportez-vous à l’annexe B.
4. Corrigez l’expression.
1–28 Utilisation de la TI-83
Page 59

Chapitre 2 : Opérations mathématiques, angles et tests
Contenu du
chapitre
Pour commencer : Pile ou Face ? ........................................ 2
Opérations mathématiques au clavier................................. 3
Opérations MATH..................................................................6
Résolution d’équation............................................................9
Utilisation de la résolution d’équation .............................. 13
Opérations MATH NUM (Nombre)....................................14
Saisie et utilisation de nombres complexes .....................17
Opérations MATH CPX (Complexe) .................................19
Opérations MATH PRB (Probabilité)................................21
Opérations sur les ANGLES ...............................................24
Tests de comparaison .........................................................27
Tests booléens .....................................................................28
Opérations mathématiques, angles et tests 2–1
Page 60

Pour commencer : Pile ou Face ?
“Pour commencer” est une présentation rapide. Tous les détails figurent
dans la suite du chapitre.
Supposons que vous vouliez modéliser 10 lancers de pièce à “pile ou face”
et mettre en évidence le nombre de résultats “face”. Vous allez effectuer
cette simulation 40 fois. La pièce n’est pas truquée : la probabilité d’obtenir
face est la même que celle d’obtenir pile, soit 0,5.
1. Sur l’écran principal, tapez | pour
afficher le menu
pour sélectionner
aléatoire en simulant une loi binomiale).
L’instruction
l’écran principal. Tapez
nombre de lancers. Tapez ¢. Tapez
pour entrer la probabilité de “face”.
Tapez ¢. Tapez
nombre de simulations. Appuyez sur ¤.
2. Appuyez sur Í pour calculer
l’expression. Une liste de 40 éléments
s’affiche. Il s’agit du nombre de résultats
“face” dans chaque série de 10 lancers.
La liste comprend 40 éléments car la
simulation a été effectuée 40 fois. Dans
cet exemple, “face” est sorti cinq fois
dans la première série de 10 lancers, cinq
fois dans la deuxième série de 10 lancers,
et ainsi de suite.
3. Appuyez surs ¿ y ãL1ä Í pour
enregistrer ces données dans une liste
nommée
L1. Vous pourrez les utiliser
ultérieurement, par exemple pour tracer
un histogramme (Voir chapitre 12).
MATH PRB. Tapez 7
7:randBin(
randBin( apparaît dans
40 pour spécifier le
(tirage
10 pour entrer le
Ë 5
4. Tapez ~ ou | pour visualiser les autres
résultats de la liste. Les points de
suspension (
...) indiquent que la liste
continue au-delà de l’écran.
Remarque : Dans la mesure où l’opération
randBin( génère des nombres aléatoires,
vous n’obtiendrez pas forcément les mêmes
résultats que dans cet exemple.
2–2 Opérations mathématiques, angles et tests
Page 61

Opérations mathématiques au clavier
Utilisation des
listes avec les
fonctions
mathématiques
+ (Addition)
N (Soustraction)
ää (Multiplication)
à (Division)
Fonctions
trigonométriques
Les opérations mathématiques autorisées pour des listes
donnent une liste calculée terme par terme. Si deux listes
interviennent dans la même expression, elles doivent
avoir la même longueur.
+ (addition, Ã), N (soustraction, ¹),
ää (multiplication, ¯) et à (division, ¥) peuvent être
utilisés avec des nombres réels ou complexes, des
expressions, des listes et des matrices. Il est impossible
d’utiliser
valeurA
valeurA
à avec des matrices.
+valeurB valeurANvaleurB
äävaleurB valeurAàvaleurB
Les fonctions trigonométriques (sinus, ˜; cosinus, ™;
et tangente, š) peuvent être utilisées avec des nombres
réels, des expressions et des listes. Les paramètres du
mode angle courant affectent l’interprétation. Par
exemple,
mode
sin(valeur) cos(valeur) tan(valeur)
Vous pouvez utiliser les fonctions trigonométriques
inverses (arcsinus, y [
et arctangente, y [
sin(30) en mode Radian donne L.9880316241; en
Degré le résultat est .5.
L1
SIN
]; arccosinus, y [COSL1];
L1
TAN
]) avec des nombres réels, des
expressions et des listes. Les paramètres du mode angle
courant affectent l’interprétation.
sinL1(valeur) cosL1(valeur) tanL1(valeur)
Remarque : Les fonctions trigonométriques ne sont pas
définies avec des nombres complexes.
Opérations mathématiques, angles et tests 2–3
Page 62

Opérations mathématiques au clavier (suite)
2
^ (Puissance)
2
(Carré)
‡( (Racine
carrée)
L1
(Inverse)
Vous pouvez utiliser ^ (puissance, ›),
(racine carrée, y [‡]) avec des nombres réels et
complexes, des expressions, des listes et des matrices. Il
est impossible d’utiliser
valeur^puissance valeur
L1
(inverse, —) peut être utilisé avec des nombres réels
et complexes, des expressions, des listes et des matrices.
L1
et 1/x donnent le même résultat.
x
L1
valeur
‡( avec des matrices.
2
(carré, ¡), et ‡(
‡(valeur)
log(
10^(
ln(
e^(
(Exponentielle)
e (Constante)
log( (logarithme, «), 10^( (puissance de 10, y
x
10
]), et ln( (logarithme népérien, µ) peuvent être
[
utilisés avec des nombres réels et complexes, des
expressions ou des listes.
log(valeur) 10^(puissance) ln(valeur)
e^(
(exponentielle, y ãex]) donne une constante e
élevée à une puissance. Vous pouvez utiliser
e^( avec
des nombres complexes ou réels, des expressions et des
listes.
e^(puissance)
e (constante, y [e]) est mémorisée comme constante
sur la TI-83. Appuyez sur y [
e] pour copier e à
l’emplacement du curseur. Lors des calculs, la TI-83
utilise 2.718281828459 pour
e.
2–4 Opérations mathématiques, angles et tests
Page 63

L (opposée)
p (Pi)
L (opposée, Ì) donne l’opposé d’un nombre réel ou
complexe, d’une expression, d’une liste ou d’une matrice.
Lvaleur
Les règles EOS (Voir chapitre 1) déterminent les cas où
l’opposée est calculée. Par exemple,
2
LA
donne un
nombre négatif, car le carré est calculé avant l’opposée
selon les règles EOS. Il faut utiliser des parenthèses pour
élever un nombre négatif au carré, comme dans
Remarque : sur la TI-83, le symbole de négation (M) est plus
court et positionné plus haut que le signe de la soustraction (N).
Il s’affiche quand vous appuyez sur ¹.
p (Pi) est mémorisé en tant que constante par la TI-83.
Appuyez sur y [p] pour copier le symbole
p à
(LA)
2
.
l’emplacement du curseur. Dans les calculs, la TI-83
utilise la valeur 3.1415926535898 pour
p.
Opérations mathématiques, angles et tests 2–5
Page 64

Opérations MATH
Le menu MATH
4Frac
4Dec
Pour afficher le menu
MATH NUM CPX PRB
1:
4Frac
2:
4Dec
3
3:
4:3‡( Calcule la racine cubique
5:x‡ Calcule la racine x
6:fMin( Trouve le minimum d’une fonction
7:fMax( Trouve le maximum d’une fonction
8:nDeriv( Calcule le nombre dérivé
9:fnInt( Calcul d’intégrales
0:Solver... Résolution d’équation
4Frac (afficher sous forme de fraction) affiche le résultat
MATH, appuyez sur .
Affiche le résultat sous forme de fraction
Affiche le résultat sous forme décimale
Calcule le cube
ième
sous forme de son équivalent rationnel. valeur peut être
un nombre réel ou complexe, une expression, une liste
ou une matrice. Si le résultat n’est pas rationnel ou si le
dénominateur compte plus de trois chiffres, on obtient
l’équivalent décimal. 4
Frac n’est autorisé qu’à la suite de
valeur.
Frac
valeur4
4Dec
(afficher sous forme décimale) affiche le résultat
sous forme décimale. La valeur peut être un nombre réel
ou complexe, une expression, une liste ou une matrice.
4Dec n’est autorisé qu’à la suite de valeur.
4Dec
valeur
2–6 Opérations mathématiques, angles et tests
Page 65

3
(Cube)
3
‡( (Racine
cubique)
3
(cube) donne le cube d’un nombre réel ou complexe,
d’une expression, d’une liste ou d’une matrice carrée.
3
valeur
3
‡( (racine cubique) donne la racine cubique d’un
nombre réel ou complexe, d’une expression ou d’une
liste.
3
‡(valeur)
x
‡ (Racine)
fMin(
fMax(
x
‡ (racine) donne la racine x
ième
d’un nombre réel ou
complexe, d’une expression ou d’une liste.
ièmex
racine x
‡valeur
fMin( (minimum fonction) et fMax( (maximum fonction)
donne la valeur de la variable (entre valeur inférieure et
supérieure) pour laquelle le minimum ou le maximum
d’une expression est atteint.
fMin(
et
fMax(
ne sont pas
autorisés dans expression. La précision est définie à
partir de tolérance (si pas déterminée, la valeur par
défaut est 1â
N5).
fMin(expression,variable,inférieure,supérieure[,tolérance])
fMax(
expression,variable,inférieure,supérieure[,tolérance])
Remarque : Dans ce manuel, les paramètres facultatifs et les
virgules qui les séparent sont placés entre crochets ([ ]).
Opérations mathématiques, angles et tests 2–7
Page 66

Opérations MATH (suite)
nDeriv(
fnInt(
nDeriv( (nombre dérivé) donne une valeur
approximative de la dérivée de l’expression par rapport à
la variable, au point valeur ; la précision est liée à H (si
pas déterminé, la valeur par défaut est 1â
nDeriv(expression,variable,valeur[,H])
nDeriv(
fait appel à la méthode de la dérivée symétrique
N3).
qui donne une approximation du nombre dérivé par la
pente d’une sécante.
f(
X+H)Nf(XNH)
f¢(
x) =
2H
A mesure que H diminue, l’approximation devient plus
précise.
nDeriv( ne peut être utilisée qu’une seule fois dans une
expression. En raison de la méthode appliquée pour
calculer
nDeriv( , la TI-83 peut donner une valeur dérivée
fausse en un point où t n’est pas dérivable.
fnInt( (fonction intégrale) donne une valeur numérique
de l’intégrale (méthode Gauss-Kronrod) de l’expression
par rapport à la variable, entre une limite inférieure et
une limite supérieure avec une précision liée à tolérance
(si pas déterminée, la valeur par défaut est 1â
fnInt(expression,variable,inférieure,supérieure[,tolérance])
N5).
Conseil : Pour accélérer le tracé des graphes d’intégration
(lorsque fnInt( est utilisé dans une équation Y=), augmentez la
valeur de la variable WINDOW Xres avant d’appuyer sur s.
2–8 Opérations mathématiques, angles et tests
Page 67

Résolution d’équation
Solver
Saisie d’une
expression
dans l’éditeur
de résolution
Solver permet la résolution d’équations ; toute variable
peut être considérée comme inconnue, c’est toujours une
équation du type expression = 0.
Lorsque vous sélectionnez
Solver, l’un des deux écrans
suivants s’affiche.
¦ L’éditeur d’équation (voir l’image de l’étape 1 ci-
dessous) est affiché lorsque la variable d’équation
eqn
est vide.
¦ L’éditeur de résolution interactif (voir l’image de
l’étape 3 à la page 2-10) est affiché lorsqu’une équation
est mémorisée dans
eqn.
Pour saisir une expression dans l’éditeur de résolution,
ce qui suppose que la variable
eqn est vide, procédez de
la manière suivante :
1. Sélectionnez
0:Solver dans le menu MATH pour
afficher l’éditeur d’équation.
2. Saisissez l’expression de l’une des trois façons
suivantes :
¦ Saisissez l’équation directement dans l’éditeur de
résolution.
¦ Insérer un nom de variable
VARS Y-VARS dans l’éditeur de résolution.
¦ Appuyer sur y [
Y= du menu VARS Y-VARS, et appuyer sur Í.
RCL], insérer un nom de variable
Y= du menu
L’expression est insérée dans l’éditeur de
résolution.
L’expression est mémorisée dans la variable
eqn dès
sa saisie.
Opérations mathématiques, angles et tests 2–9
Page 68

Résolution d’équation (suite)
Saisie d’une
expression
dans l’éditeur
de résolution
(suite)
Saisie et
modification de
valeurs de
variables
3. Appuyez sur Í ou †. L’éditeur de résolution
interactif est affiché.
¦ L’équation mémorisée dans eqn est affichée sur la
première ligne.
¦ Les variables de l’équation sont répertoriées dans
l’ordre où elles apparaissent dans l’équation. Toutes
les valeurs mémorisées dans les variables sont
également affichées.
¦ Les limites inférieures et supérieures par défaut
apparaissent à la dernière ligne de l’éditeur
bound={L1å99,1å99}).
(
¦ Un $ est affiché dans la première colonne de la
dernière ligne si l’éditeur continue au delà de l’écran.
Conseil : Pour utiliser l’éditeur de résolution avec une équation
telle que K=.5MV
d’équation.
2
, tapez eqn:0=KN.5MV2 dans l’éditeur
Lorsque vous saisissez une valeur de variable dans
l’éditeur de résolution interactif, la nouvelle valeur est
mémorisée dans cette variable.
Cette valeur de variable peut être une expression. Elle est
évaluée lorsque vous passez à la variable suivante. Les
expressions sont calculées à chaque étape de l’itération.
Il est possible de mémoriser des équations dans
n’importe quelle variable de fonction
comme
Y1 ou r6, puis d’utiliser ces variables Y= dans
VARS Y-VARS,
l’équation. L’éditeur de résolution interactif affiche toutes
les variables de toutes les fonctions
Y= utilisées dans
l’équation.
2–10 Opérations mathématiques, angles et tests
Page 69

Résolution
d’une variable
dans l’éditeur
de résolution
Pour résoudre une équation mémorisée dans
eqn en
utilisant l’éditeur de résolution, procédez comme suit :
1. Sélectionnez
0:Solver dans le menu MATH pour
afficher l’éditeur de résolution interactif, s’il n’est pas
déjà affiché.
2. Entrez ou modifiez la valeur de chacune des variables
connues. Toutes les variables, à l’exception de la
variable inconnue, doivent contenir une valeur. Pour
déplacer le curseur sur la prochaine variable, appuyez
sur Í ou †.
3. Entrez une valeur approchée de la solution, dans
l’intervalle d’étude. Cette étape est facultative mais
peut accélérer la recherche de la solution. De plus,
dans le cas d’équations à racines multiples, la TI-83
essaiera d’afficher la solution la plus proche de votre
approximation.
L’approximation par défaut est
(upperNlower)
2
.
Opérations mathématiques, angles et tests 2–11
Page 70

Résolution d’équation (suite)
Résolution
d’une équation
dans l’éditeur
de résolution
(suite)
Modifier une
équation
mémorisée
dans eqn
Equations à
racines
multiples
4. Modifiez
bound={inférieure,supérieure}. inférieure
et supérieure sont les bornes de l’intervalle dans
lequel la TI-83 cherche une solution. Cette étape est
également facultative, mais accélérer la recherche. La
valeur par défaut est
bound={L1å99,1å99}.
5. Déplacez votre curseur sur l’inconnue et appuyez sur
ƒ [
SOLVE].
¦ La solution est affichée à côté du nom de
l’inconnue. Un carré plein dans la première
colonne marque l’inconnue et indique que
l’équation est résolue. Les points de suspension
indiquent que la valeur continue au delà de l’écran.
¦ Les valeurs des variables sont mises à jour en
mémoire.
leftNrt=diff est affiché dans la dernière ligne de
¦
l’éditeur. diff est à la différence entre zéro et la
valeur calculée. Un carré plein dans la première
colonne à côté de
leftNrt= indique qu’elle a été
évaluée avec la solution obtenue.
Pour modifier ou remplacer une équation mémorisée
eqn alors que l’éditeur de résolution est affiché,
dans
appuyez sur } jusqu’à ce que l’éditeur d’équation
s’affiche. Modifiez alors l’équation.
Certaines équations possèdent plus d’une solution. Vous
pouvez saisir une nouvelle première approximation (Voir
page 2-9) ou un nouvel intervalle (Voir page 2-10) pour
rechercher des solutions supplémentaires.
2–12 Opérations mathématiques, angles et tests
Page 71

Utilisation de la résolution d’équation
D’autres
solutions
Contrôle de la
solution pour
Solver ou
solve(
Utilisation de
solve( à partir
de l’écran
principal ou
d’un
programme
Après avoir résolu une équation, vous pouvez changer
d’inconnue à l’aide de l’éditeur de résolution interactif.
Modifiez les valeurs d’une ou plusieurs variables. Lorsque
vous modifiez une valeur de variable, les carrés pleins
situés à côté de la solution précédente et de
leftNrt=diff
disparaissent. Déplacez le curseur sur la variable que
considérez comme inconnue et appuyez sur ƒ
SOLVE].
[
La TI-83 résout les équations selon un processus itératif.
Pour maîtriser ce processus, vous devez donner des
bornes relativement proches de la solution et une
approximation initiale qui doit être dans l’intervalle. Cela
permettra d’obtenir plus rapidement la solution. De plus,
cela définit de la solution recherchée pour des équations
à solutions multiples.
solve( n’est disponible qu’à partir de CATALOG ou d’un
programme. Il donne une solution (racine) d’expression
pour la variable, en tenant compte d’une approximation
initiale, et de limites inférieure et supérieure entre
lesquelles la solution est recherchée. La valeur par défaut
de inférieure est L1â99. La valeur par défaut de
supérieure est 1â99.
solve(expression,variable,approximation[,{inférieure,
supérieure
}])
expression est supposé égal à zéro. La valeur de la
variable ne sera pas mise à jour en mémoire.
approximation peut être une valeur ou une liste de deux
valeurs. Dans expression, chaque argument sauf variable
doit être initialisé avant que expression ne soit évaluée.
inférieure et supérieure doivent être saisies en format
liste.
Opérations mathématiques, angles et tests 2–13
Page 72

Opérations MATH NUM (Nombre)
Menu MATH
NUM
abs(
round(
Pour afficher le menu
MATH NUM CPX PRB
1:abs( Valeur absolue
2:round( Arrondi
3:iPart( Nombre - partie fractionnaire
4:fPart( Partie fractionnaire
5:int( Partie entière
6:min( Valeur minimum
7:max( Valeur maximum
8:lcm( Plus petit commun multiple
9:gcd( Plus grand commun diviseur
abs( (valeur absolue) donne la valeur absolue d’un
MATH NUM, appuyez sur ~.
nombre réel ou le module d’un complexe, d’une
expression, d’une liste ou d’une matrice.
abs(valeur)
Remarque : abs( est également disponible dans le menu
MATH CPX.
round( donne un nombre, une expression, une liste ou
une matrice arrondie à #decimales (9). Si #decimales
n’est pas mentionné, valeur est arrondi aux chiffres
affichés, soit jusqu’à 10 chiffres.
round(valeur[,#decimales])
2–14 Opérations mathématiques, angles et tests
Page 73

iPart(
fPart(
(x) = x - fPart(x) où x peut être un nombre réel ou
iPart
complexe, une expression, une liste ou une matrice.
iPart(valeur)
(partie fractionnée) donne la ou les partie(s)
fPart(
fractionnée(s) d’un nombre réel ou complexe, d’une
expression, d’une liste ou d’une matrice.
fPart(valeur)
int(
min(
max(
int( (partie entière) donne la partie entière d’un nombre
réel, d’une expression, d’une liste ou d’une matrice.
int(valeur)
Remarque : Pour une
égal à celui de iPart( pour les nombres non négatifs et les
entiers négatifs. Il est inférieur de 1 au résultat de iPart( pour
les nombres négatifs non entiers.
min( (valeur minimum) donne la plus petite des valeurs
valeur
donnée, le résultat de int( est
valeurA et valeurB ou le plus petit élément d’une liste. Si
listeA et listeB sont comparées,
min( donne la liste des
plus petits de chaque paire de termes. Si liste et valeur
sont comparées,
min( compare chaque élément de liste
avec valeur.
max( (valeur maximum) donne la plus grande des
valeurs valeurA et valeurB ou le plus grand élément
d’une liste. Si listeA et listeB sont comparées,
max(
donne la liste des plus grands de chaque paire de termes.
Si liste et valeur sont comparées,
max( compare chaque
élément de liste avec valeur.
min(valeurA,valeurB) max(valeurA,valeurB)
min(
liste) max(liste)
min(
listeA,listeB) max(listeA,listeB )
min(
liste,valeur) max(liste,valeur)
Opérations mathématiques, angles et tests 2–15
Page 74

Opérations MATH NUM (Nombre) (suite)
lcm(
gcd(
lcm( donne le plus petit commun multiple de valeurA et
valeurB, qui sont tous les deux des entiers non-négatifs.
Si on utilise listeA et listeB,
lcm( donne la liste de lcm
pour chaque paire d’éléments. Si on utilise liste et valeur,
lcm( donne la liste des plus petits multiples communs de
chaque élément de liste et valeur.
gcd( donne le plus grand commun diviseur de valeurA et
valeurB, qui sont tous les deux des entiers non-négatifs.
Si on utilise listeA et listeB,
gcd( donne la liste des gcd
de chaque paire d’éléments. Si on utilise liste et valeur,
gcd( donne la liste des plus grand diviseurs communs de
chaque élément de liste et valeur.
lcm(valeurA,valeurB) gcd(valeurA,valeurB )
lcm(
listeA,listeB) gcd(listeA,listeB )
lcm(
liste,valeur) gcd(liste,valeur)
2–16 Opérations mathématiques, angles et tests
Page 75

Saisie et utilisation de nombres complexes
Modes des
nombres
complexes
La TI-83 affiche les nombres complexes sous forme
rectangulaire ou polaire. Pour sélectionner l’un des modes
des nombres complexes, appuyez sur z, et optez soit
pour:
i
¦
¦
La TI-83, vous permet de mémoriser des nombres complexes
dans variables. Ces nombres sont également des éléments de
liste valides.
En mode
présentent toujours des erreurs si vous ne spécifiez pas
directement un nombre complexe en tant qu’entrée. Par
exemple, en mode
réponse est retournée en mode
Mode Real
(mode rectangulaire) soit pour
a+b
i
(mode polaire)
re^q
, les résultats exprimés en nombres complexes
Real
Real, ln(L1)
présente une erreur et une
i
a+b
ln(L1) :
i
a+b
Mode
$$
Saisie des
nombres
complexes
Remarques sur
le mode Radian
et le mode
Degree
Les nombres complexes sont mémorisés sous forme
rectangulaire, mais vous pouvez les saisir sous forme
rectangulaire ou polaire indépendamment du mode
actuellement en cours. Les composants des nombres
complexes peuvent être des nombres réels ou des
expressions à évaluer en nombre réels. En effet, les
expressions sont évaluées lors de l’exécution de la
commande.
Nous recommandons d’utiliser le mode Radian pour le calcul
des nombres complexes. En effet, la TI-83 convertit,
internement, toute valeur trigonométrique saisie en radians
mais il n’en est pas de même des valeurs des fonctions
exponentielles, logarithmiques ou hyperboliques.
En mode degree, les identités complexes telles que
iq) = cos(q) + i sin(q) ne sont pas vraies en général car
e^(
les valeurs de cos et sin sont converties en radians tandis
que celles de e^( ) ne le sont pas. Par exemple,
e^(i45) = cos(45) + i sin(45) est traité internement comme
e^(i45) = cos(p/4) + i sin(p/4). Les identités complexes sont
toujours vraies en mode radian.
Opérations mathématiques, angles et tests 2–17
Page 76

Saisie et utilisation de nombres complexes (suite)
Interprétation
de résultats
complexes
Mode
algébrique
Mode
exponentiel
Les résultats comportant des nombres complexes, ycompris les éléments de listes, sont affichés sous forme
algébrique ou polaire, selon le réglage de mode ou
l’instruction de conversion d’affichage (Voir page 2-20).
Dans l’exemple ci-dessous, les modes
re^qi et Degree
sont définis.
Le mode algébrique reconnaît et affiche un nombre
complexe sous la forme a+b
partie imaginaire, et
i une constante telle que i² = -1.
i, où a est la partie réelle, b la
Pour saisir un nombre complexe sous forme algébrique,
saisissez la valeur de a (partie réelle), appuyez sur à ou
¹, saisissez la valeur de b (partie imaginaire), et
appuyez sur y [
partie réelle(
i] (constante).
+ ou N)partie imaginaire i
Le mode exponentiel reconnaît et affiche un nombre
complexe sous la forme re^
du logarithme népérien,
qi, où r est le module, e la base
q un argument et i est une
constante telle que i² = -1.
Pour saisir un nombre complexe sous forme
exponentielle, tapez la valeur de r (module), appuyez sur
x
e
] (fonction exponentielle), tapez la valeur de q
y [
(argument), et appuyez sur y [i] (constante).
e^(argumenti)
module
2–18 Opérations mathématiques, angles et tests
Page 77

Opérations MATH CPX (Complexe)
Menu MATH
CPX
conj(
real(
imag(
Pour afficher le menu
MATH CPX appuyez sur ~
~.
MATH NUM CPX PRB
1:conj( Donne le conjugué complexe
2:real( Donne la partie réelle
3:imag( Donne la partie imaginaire
4;angle( Donne un argument
5:abs( Donne le module
6:4Rect Affiche le résultat sous forme algébrique
7:4Polar Affiche le résultat en forme exponentielle
conj( (conjugué ) donne le conjugué complexe d’un
nombre complexe ou d’une liste de nombres complexes.
conj(a+bi) donne aNbi en mode a+bi.
conj(re^(qi)) donne re^(Mqi) en mode re^qi.
real( (partie réelle) donne la partie réelle d’un nombre
complexe ou d’une liste de nombres complexes.
real(a+bi) donne a.
real(re^(qi)) donne räcos(q).
imag( (partie imaginaire) donne la partie imaginaire
(non-vraie) d’un nombre complexe ou d’une liste de
nombres complexes.
imag(a+bi) donne b.
imag(re^(qi)) donne räsin(q).
Opérations mathématiques, angles et tests 2–19
Page 78

Opérations MATH CPX (Complexe) (suite)
angle(
abs(
4Rect
8Polar
angle( donne la valeur d’un argument d’un nombre
complexe ou d’une liste de nombres complexes, calculés
en par tan
L1
(b/a), où b est la partie imaginaire et a est la
partie réelle. Si on est dans le deuxième quadrant on
ajoute p, dans le troisième quadrant on enlève p..
angle(a+bi) donne une valeur pour tan
L1
(b/a).
angle(re^(qi)) donne une valeur pour q, où Lp<q<p.
2
abs( (valeur absolue) donne le module,
(real
+
imag
2
)
d’un nombre complexe ou d’une liste de nombres
complexes.
2+b2
a
abs(a+bi) donne
)
(
.
abs(re^(qi)) donne r (module).
4Rect (affichage algébrique) affiche un résultat complexe
sous forme algébrique. Cela n’est valable qu’à la fin d’une
expression. Inutilisable si le résultat est réel.
résultat complexe
8Rect donne une valeur pour a+bi
8Polar (affichage exponentiel) affiche un résultat
complexe sous forme exponentielle. Cela n’est valable
qu’à la fin d’une expression. Inutilisable si le résultat est
réel.
résultat complexe
8Polar donne re^(qi)
,
2–20 Opérations mathématiques, angles et tests
Page 79

Opérations MATH PRB (Probabilité)
Menu MATH
PRB
Utilisation de
rand pour
générer un
nombre
aléatoire
Utilisation de
rand pour
générer une
liste de
nombres
aléatoires
Pour afficher le menu
MATH NUM CPX PRB
1:rand Générateur de nombre aléatoire
2:nPr Nombre de permutations
3:nCr Nombre de combinaisons
4:! Factorielle
5:randInt( Générateur d’entier aléatoire
6:randNorm( Aléatoire # distribution normale
7:randBin( Aléatoire # distribution binomiale
rand (nombre aléatoire) génère et donne un ou plusieurs
MATH PRB, appuyez sur |.
nombres aléatoires ‚ 0 et 1. Pour générer une suite de
nombres aléatoires, appuyez sur Í à plusieurs
reprises.
rand[(numtrials)]
Conseil : Pour générer des nombres aléatoires au delà de la
plage 0 à 1, vous pouvez entrer une expression dans rand. Par
exemple, rand 5 génère un nombre aléatoire supérieur à 0 mais
inférieur à 5.
A chaque exécution de rand, la TI-83 génère la même
suite de nombres aléatoires pour une valeur de départ. La
valeur de départ de la TI-83 réglée en usine pour
0. Pour générer une suite de nombre aléatoires différente,
rand est
mémorisez une valeur de départ différente de zéro dans
rand. Pour restaurer la valeur de départ configurée en
usine, mémorisez
0 dans rand ou réinitialisez les valeurs
par défaut (Voir chapitre 18).
Remarque : La valeur de départ a également une incidence sur
les instructions randInt( , randNorm( et randBin( (voir pages
2-22 et 2-23).
Pour générer une suite de nombres aléatoires affichés
sous forme de liste, spécifiez un nombre entier > 1 pour
numtrials (nombre d’essais) La valeur par défaut de
numtrials est 1).
Opérations mathématiques, angles et tests 2–21
Page 80

Opérations MATH PRB (Probabilité) (suite)
nPr
nCr
! (Factorielle)
randInt(
nPr (nombre de permutations) donne le nombre
d’arrangements de nombre éléments parmi termes
éléments. termes et nombre doivent être des entiers
positifs. termes et nombres peuvent être des listes.
termes
nPr nombre
nCr (nombre de combinaisons) donne le nombre de
parties à nombre éléments parmi termes éléments.
termes et nombre doivent être des entiers positifs.
termes et nombres peuvent être des listes.
termes
nCr nombre
! (factorielle) donne la factorielle d’un entier ou d’un multiple
de .5. Pour une liste, il donne les factorielles de chaque entier
ou multiple de .5. valeur doit être ‚ L.5 et 69.
valeur
!
Remarque : La factorielle est calculée de façon récursive en
utilisant la relation (n+1)! = nän!, jusqu’à ce que n soit réduit à 0
ou à L1/2. A ce stade, la définition 0!=1 ou (L1/2)!=‡p est
utilisée pour terminer le calcul. Donc :
n!=nä(nN1)ä(n-2)ä ... ä2ä1, si n est un entier ‚ 0
n!= nä(nN1)ä(n-2)ä ... ä1/2ä‡p, si n+1/2 est un entier ‚ 0
n! est erroné si ni n ni n+1/2 n’est un entier ‚ 0.
(La variable n est représentée par
plus haut).
randInt( (entier aléatoire) génère et affiche un entier
valeur
dans la syntaxe décrite
aléatoire d’une taille délimitée par les limites inférieure
et supérieure. Pour générer une suite d’entiers aléatoires,
appuyez sur Í à plusieurs reprises. Pour générer une
liste d’entiers aléatoires, précisez un entier > 1 pour
numtrials (nombre d’essais) ; si cette valeur n’est pas
définie, la valeur par défaut est 1).
randInt(inférieure,supérieure[,numtrials])
2–22 Opérations mathématiques, angles et tests
Page 81

Opérations mathématiques, angles et tests 2–23
randNorm( (aléatoire normal) génère et affiche un
nombre aléatoire réel tiré d’une distribution normale
spécifiée. Chaque valeur générée peut être n’importe quel
nombre réel, mais la majorité se situera dans l’intervalle
[mN3(s), m+3(s)]. Pour générer une liste de nombres
aléatoires, spécifiez un entier > 1 pour numtrials
(nombre d’essais) ; si cette valeur n’est pas définie, la
valeur par défaut est 1).
randNorm(m,s[,numtrials])
randBin( (aléatoire binomiale) génère et affiche un
entier aléatoire tiré d’une distribution binomiale
spécifiée.
numtrials
(nombre d’essais) doit être ‚ 1.
prob
(probabilité de réussite) doit être ‚ 0 et 1. Pour générer
une liste de nombres aléatoires, spécifiez un entier > 1
pour numsimulations (nombre de simulations; si cette
valeur n’est pas définie, la valeur par défaut est 1).
randBin(numtrials,prob[,numsimulations])
Remarque : La valeur de départ a également une incidence sur
les instructions randInt( , randNorm( et randBin( .
randNorm(
randBin(
Page 82

Opérations sur les ANGLES
Menu ANGLE
Notation DMS
Pour afficher le menu
Le menu
ANGLE affiche les indicateurs et les instructions
ANGLE, appuyez sur y[ANGLE].
d’angles. Les saisies d’angles sont interprétées selon les
paramètres du mode
ANGLE
1:
¡
2:' Notation des minutes
r
3:
4:
8DMS
5:R8Pr( Donne r, connaissant X et Y
6:R8Pq(
7:P8Rx(
8:P8Ry( Donne y, connaissant R et q
Radian/Degree.
Notation en degrés
Notation des radians
Affichage en degrés/minutes/secondes
Donne q, connaissant X et Y
Donne x, connaissant R et q
La notation DMS (affichage en degrés/minutes/secondes)
comprend le symbole des degrés (
minutes (
' ) et le symbole des secondes ( " ). degrés doit
¡ ), le symbole des
être un nombre réel; minutes et secondes doivent être
des nombres réels ‚ 0.
¡minutes'secondes"
degrés
Par exemple, tapez 30¡1'23'' pour 30 degrés, 1 minute,
23 secondes. Si
d’angle, vous devez utiliser
Degré n’est pas sélectionné dans le mode
¡ pour que la TI-83 puisse
interpréter l’argument en degrés, minutes et secondes.
Mode Degré Mode Radian
2–24 Opérations mathématiques, angles et tests
Page 83

¡ (Degrés)
' (Minutes)
" (Secondes)
r
(Radians)
¡ (degrés) désigne un angle ou une liste d’angles en
degrés, quel que soit le paramètre de mode choisi. En
Radian, vous pouvez utiliser ¡ pour convertir les
mode
degrés en radians.
¡
valeur
{
valeur1,valeur2,valeur3,valeur4,...,valeur n}¡
désigne également les degrés (D) en format DMS.
¡
' (minutes) désigne les minutes (M) en format DMS.
" (secondes) désigne les secondes (S) en format DMS.
Remarque : " n’est pas dans le menu ANGLE. Pour saisir " ,
appuyez sur ƒ [ã].
r
(radians) désigne un angle ou une liste d’angles en
radians, quel que soit le paramètre MODE choisi. En
Degré, vous pouvez utiliser
mode
r
pour convertir les
radians en degrés.
r
valeur
Degree mode
8DMS
8DMS (degré/minute/seconde) affiche le résultat en
format DMS (Voir page 2-24). Le paramètre de mode doit
Degré pour que le résultat soit interprété en degrés,
être
minutes et secondes. 8
DMS n’est autorisé qu’à la fin
d’une ligne.
résultat8
DMS
Opérations mathématiques, angles et tests 2–25
Page 84

Opérations sur les ANGLES (suite)
R8Pr(
R8Pq(
P8Rx(
P8Ry(
R8Pr( convertit le format algébrique en format
exponentiel et donne une valeur pour
r. R8Pq( convertit
le format algébrique en format exponentiel et donne une
valeur à
R8Pr(x,y )
R8Pq(
P8Rx( convertit le format exponentiel en format
algébrique et donne une valeur à
q. xet ypeuvent être des listes.
x,y)
Remarque : le mode Radian
est paramétré.
x. P8Ry( convertit le
format exponentiel en format algébrique et donne une
valeur à
P8Rx(r,q)
P8Ry(
y. r et q peuvent être des listes.
r,q)
Remarque : le mode Radian
est paramétré.
2–26 Opérations mathématiques, angles et tests
Page 85

Tests de comparaison
Menu TEST
=
ƒ
>
‚
<
Pour afficher le menu
Cet opérateur... Donne 1 (vrai) si...
TEST LOGIC
1:= Egal
2:ƒ Différent de
3:> Supérieur à
4:‚ Supérieur ou égal à
5:< Inférieur à
6: Inférieur ou égal à
TEST, appuyez sur y [TEST].
Les opérateurs relationnels comparent les valeurA et
valeurB et donnent
1 si la condition est vérifiée, 0 sinon.
valeurA et valeurB peuvent être des nombres réels ou
complexes, des expressions ou des listes. Seuls
= et ƒ
fonctionnent avec des matrices. Si valeurA et valeurB
sont des matrices, elles doivent avoir la même dimension.
On utilise souvent les opérateurs relationnels pour
commander le déroulement d’un programme et dans les
graphes pour commander la représentation d’une
fonction pour des valeurs déterminées.
valeurA
valeurA
valeurA
=valeurB valeurAƒvaleurB
>valeurB valeurA‚valeurB
<valeurB valeurAvaleurB
Utilisation des
tests
Les opérateurs relationnels sont évalués après les
fonctions mathématiques selon les règles EOS (Voir
chapitre 1).
¦ L’expression
2+2=2+3 donne 0. La TI-83 commence
par additionner en raison des règles EOS, puis elle
compare 4 à 5.
¦ L’expression
2+(2=2)+3 donne 6. La TI-83 effectue
d’abord le test relationnel car il est entre parenthèses,
puis elle ajoute 2, 1 et 3.
Opérations mathématiques, angles et tests 2–27
Page 86

1
0
0
0
Tests booléens
Menu TEST
LOGIC
Opérateurs
Booléens
and
or
xor
Pour afficher le menu
TESTä ~.
ã
Cet opérateur... Donne 1 (vrai) si...
TEST LOGIC
1:and Les deux valeurs sont différentes de zéro (vrai)
2:or Une valeur au moins est différente de zéro (vrai)
3:xor Une seule valeur est égale à zéro (faux)
4:not( La valeur est égale à zéro (faux)
TEST LOGIC, appuyez sur y
On utilise souvent les opérateurs Booléens dans les
programmes pour en commander le déroulement et dans
les graphiques pour commander la représentation d’une
fonction pour des valeurs déterminées. Les valeurs sont
interprétées comme égales à zéro (faux) ou différentes
de zéro (vrai).
and, or et xor (or exclusif) donnent une valeur de 1 si une
expression est vraie ou
0 si une expression est fausse,
selon la table ci-dessous. valeurA et valeurB peuvent être
des nombres réels, des expressions ou des listes.
valeurA
valeurA
valeurA
and valeurB
or valeurB
valeurB
xor
valeurA valeurB and or xor
ƒ0 ƒ0 donne
ƒ0 0 donne
0ƒ0 donne
0 0 donne
10
11
11
0 0
donne 1 si la valeur (qui peut être une expression)
not(
Utilisation des
opérations
Booléennes
not(
est égale à
not(valeur)
0.
On utilise souvent la logique Booléenne dans les tests
relationnels. Dans ce programme, les instructions
mémorisent
4 dans C.
2–28 Opérations mathématiques, angles et tests
Page 87

Chapitre 3 : Graphes de fonctions
Contenu du
chapitre
Pour commencer : tracer un cercle.....................................2
Définir un graphe...................................................................3
Choix du mode graphique..................................................... 4
Définir une fonction dans l’éditeur Y=................................5
Sélectionner et désactiver les fonctions.............................7
Définir les styles de graphes pour représenter les
fonctions.................................................................................9
Définir les variables de la fenêtre d’affichage..................12
Définir le format d’un graphe.............................................14
Afficher un graphe...............................................................16
Parcourir un graphe à l’aide du curseur libre...................18
Parcourir un graphe à l’aide de TRACE............................19
Parcourir un graphe à l’aide de ZOOM.............................. 21
Utilisation de ZOOM MEMORY..........................................24
Utiliser les opérations CALC (Calcul)...............................26
Graphes de fonctions 3–1
Page 88

Pour commencer : tracer un cercle
“Pour commencer” est une introduction rapide. Tous les détails nécessaires
figurent dans la suite du chapitre.
Tracez un cercle de rayon 10 dont le centre est le centre de la fenêtre
d’affichage. Pour tracer ce cercle, il faut entrer deux formules séparées,
pour la partie supérieure et la partie inférieure du cercle. Adaptez ensuite
l’affichage à l’aide de
cercle.
1. En mode
Func, appuyez sur o pour
afficher l’écran d’édition
y ã‡ä
100 ¹ „ ¡ ¤ Í pour
entrer l’expression Y=‡(100NX
définit la moitié supérieure du cercle.
L’expression Y=L‡(100NX
moitié inférieure du cercle. Sur la
TI-83 vous pouvez définir une fonction
par rapport à une autre. Ainsi pour
Y2=LY1, appuyez sur Ì pour
définir
saisir le signe de l’opposée. Appuyez sur
~ pour afficher le menu
Y-VARS
. Appuyez ensuite sur Í pour
sélectionner
secondaire
Appuyez sur
2. Appuyez sur q 6 pour sélectionner
6:ZStandard. Cette méthode permet de
régler rapidement les variables WINDOW
à leur valeur standard et de tracer le
graphe de la fonction ; il n’est donc pas
nécessaire de taper s.
Notez que le graphe est “elliptique”.
ZSquare (zoom square), afin que le graphe soit un
Y=. Appuyez sur
2
), qui
2
) définit la
VARS
1:Function. Le menu
FUNCTION est affiché.
1 pour sélectionner 1:Y1.
3. Il faut à présent ajuster l’affichage pour
avoir un repère orthonormé. A cet effet,
tapez q
5:ZSquare. Le graphe est retracé ; c’est
5 pour sélectionner
un cercle.
4. Pour visualiser l’effet de ZSquare sur les
variables WINDOW, appuyez sur p
et observez les nouvelles valeurs de
Xmin, Xmax, Ymin et Ymax.
3–2 Graphes de fonctions
Page 89

Définir un graphe
Similitudes
entre les modes
graphiques de
la TI-83
Définir un
graphe : les
étapes
Afficher et
observer un
graphe
Sauvegarder un
graphe pour
usage ultérieur
Le chapitre 3 est consacré à la représentation graphique
des fonctions, mais les procédures sont similaires dans
tous les modes graphiques de la TI-83. Les chapitres 4, 5
et 6 présentent les particularités propres aux graphes
paramétriques, aux graphes polaires et aux graphes de
suites.
Quel que soit le mode graphique utilisé, la définition d’un
graphe comporte les étapes décrites ci-dessous. Toutes
ne sont pas nécessaires pour certains graphes.
1. Appuyez sur z et définissez le mode graphique
approprié (voir page 3-4).
2. Appuyez sur o et entrez, éditez ou sélectionnez une ou
plusieurs fonctions dans l’éditeur
Y= (voir page 3-5).
3. Désactivez l’affichage des graphes statistiques (stat
plots) si nécessaire (voir page 3-7).
4. Définissez le style de graphe associé à chaque
fonction (voir page 3-9).
5. Appuyez sur p et définissez les variables de la
fenêtre d’affichage (voir page 3-12).
6. Appuyez sur y [
FORMAT] et sélectionnez les
paramètres du format graphique (voir page 3-14).
Après avoir défini un graphe, appuyez sur s pour
l’afficher. Observez le comportement de la ou des
fonctions représentées à l’aide des divers outils de la
TI-83 décrits dans ce chapitre.
Il est possible de mémoriser les éléments qui définissent
le graphe en cours dans l’une des 10 variables de base de
données graphiques (
GDB1 à GDB9, plus GDB0 ; voir le
chapitre 8). Vous pourrez ultérieurement rappeler la base
de données pour recréer ce graphe.
Une base de données de graphes (
GDB) contient les
types d’informations suivants :
¦ Fonctions
Y=
¦ Paramètres de modes graphiques
¦ Paramètres de fenêtre
¦ Paramètres de format
Il est aussi possible de mémoriser l’image du graphe
affiché dans l’une des 10 variables d’images de graphes
Pic1 à Pic9 et Pic0; Voir chapitre 8). Vous pourrez
(
ultérieurement superposer une ou plusieurs images
mémorisées au graphe affiché.
Graphes de fonctions 3–3
Page 90

Choix du mode graphique
Vérifier et
changer les
modes
graphiques
Choisir le mode
à partir d’un
programme
Pour afficher les paramètres de mode, appuyez sur z.
Les valeurs par défaut sont mises en exergue ci-dessous.
Pour tracer le graphe d’une fonction, vous devez
sélectionner le mode
Func avant d’entrer les valeurs des
variables WINDOW ainsi que les fonctions à représenter.
La TI-83 dispose de quatre modes graphiques :
¦
Func (graphes de fonctions)
¦
Par (graphes paramétriques ; voir chapitre 4)
¦
Pol (graphes polaires ; voir chapitre 5)
¦
Seq (graphes de suites ; voir chapitre 6)
D’autres paramètres de mode affectent le graphe en
cours. Ils sont décrits en détail dans le chapitre 1.
Float ou 0123456789 (fixe) : notation décimale en
¦
virgule flottante ou fixe, qui affecte l’affichage des
coordonnées des points du graphe.
Radian ou Degree : unité d’angle (radians ou degrés)
¦
affectant l’interprétation de certaines fonctions.
Connected ou Dot affecte le tracé des fonctions
¦
sélectionnées : ligne continue ou affichage de points
non reliés.
Sequential ou Simul : affecte ordre de calcul et de
¦
représentation des points lorsque plusieurs fonctions
sont sélectionnées.
Pour définir le mode graphique ou d’autres modes à
partir d’un programme, placez-vous sur une ligne vierge
dans l’éditeur de programme et suivez la procédure cidessous.
1. Appuyez sur z pour afficher les paramètres de
MODE.
2. Appuyez sur †, ~, | et } pour placer le curseur sur
le mode que vous désirez sélectionner.
3. Appuyez sur Í pour insérer le nom du mode à
l’emplacement du curseur.
Le mode est modifié lorsque le programme est exécuté.
3–4 Graphes de fonctions
Page 91

Définir une fonction dans l’éditeur Y=
Afficher des
fonctions dans
l’éditeur Y=
Définir ou
modifier une
fonction
Pour afficher l’éditeur
Y=, appuyez sur o. Il est possible
de mémoriser jusqu’à 10 fonctions dans des variables de
fonction (
Y1 à Y9, et Y0). Vous pouvez tracer
simultanément les graphes de plusieurs de ces fonctions.
Dans l’exemple ci-dessous, les fonctions
Y1 et Y2 sont
définies et sélectionnées.
Procédez comme suit pour définir ou modifier une
fonction.
1. Appuyez sur o pour afficher l’éditeur
Y=.
2. Appuyez sur † pour placer le curseur sur la fonction
que vous souhaitez définir ou modifier. Pour effacer la
fonction sélectionnée, appuyez sur ‘.
3. Tapez ou modifiez l’expression définissant la
fonction.
¦ Cette expression peut comprendre des fonctions et
des variables (y compris des matrices et des listes).
Si le résultat de l’expression est une valeur autre
qu’un nombre réel, le point n’est pas tracé ; aucune
erreur n’est signalée.
¦ La variable est
comme étant
ƒ [
X. Le mode Func définit „
X. Pour entrer X, tapez „ ou
X].
¦ Lorsque vous saisissez le premier caractère, le
= est mis en exergue pour indiquer que la
signe
fonction est sélectionnée.
A mesure que vous tapez l’expression, elle est mémorisée
dans la variable
Yn de l’éditeur Y=.
4. Appuyez sur Í ou sur † pour placer le curseur
sur la fonction suivante
Graphes de fonctions 3–5
Page 92

Définir une fonction dans l’éditeur Y= (suite)
Définir une
fonction à partir
de l’écran initial
ou d’un
programme
Evaluer des
fonctions Y=
dans des
expressions
Pour définir une fonction à partir de l’écran initial ou d’un
programme, placez le curseur sur une ligne vierge et
suivez les étapes ci-dessous.
1. Appuyez sur ƒ [
ã], entrez l’expression, puis
appuyez de nouveau sur ƒ [ã].
2. Appuyez sur ¿.
3. Tapez ~
VARS Y-VARS.
menu
1 pour sélectionner 1 Function dans le
4. Sélectionnez le nom de la fonction pour l’insérer à
l’emplacement du curseur dans l’écran initial ou
l’éditeur de programme.
5. Appuyez sur Í pour terminer l’instruction.
"expression"!!Yn
Lorsque cette instruction s’exécute, la TI-83 mémorise
l’expression dans la variable
fonction et affiche le message
Vous pouvez calculer la valeur d’une fonction
Yn pour une valeur donnée de X. Une liste de valeurs
Yn désignée, sélectionne la
Done (terminé).
Y= appelée
renvoie une liste.
Yn(valeur)
Y
n({valeur1,valeur2,valeur3, . . .,valeur n})
3–6 Graphes de fonctions
Page 93

Sélectionner et désactiver les fonctions
Sélectionner et
désactiver une
fonction
Activer ou
désactiver un
traçage
statistique dans
l’éditeur Y=
Vous pouvez sélectionner (“On”) et désactiver (“Off”) les
fonctions de l’écran d’édition
sélectionnée si le signe
Y=. Une fonction est
= est mis en exergue. La TI-83
trace uniquement les graphes des fonctions
sélectionnées. Vous pouvez sélectionner n’importe
quelle(s) fonction(s) de votre choix ou toutes, soit
Y9, et Y0.
Y1 à
Pour sélectionner ou désactiver une fonction dans
l’éditeur
1. Appuyez sur o pour afficher l’éditeur
Y=, procédez comme suit :
Y=
.
2. Placez le curseur sur la fonction que vous souhaitez
sélectionner ou désactiver.
3. Appuyez sur | pour placer le curseur sur le signe
= de
la fonction.
4. Appuyez sur Í pour modifier le statut de
sélection.
Si vous entrez ou modifiez une fonction, elle est
automatiquement sélectionnée. Si vous effacez une
fonction, elle est désactivée.
Pour visualiser et modifier l’état actif (“on”) ou inactif
(“off”) des graphiques statistiques dans l’écran d’édition
Y=, utilisez Plot1 Plot2 Plot3 (ligne du haut de l’écran
d’édition). Lorsqu’un tracé est actif, son nom est mis en
exergue sur cette ligne.
Pour changer l’état actif/inactif d’un graphique statistique
dans l’écran d’édition
placer le curseur sur
Y=, appuyez sur } et ~ pour
Plot1, Plot2 ou Plot3, puis appuyez
sur Í.
Le tracé Plot1 est
activé, les tracés Plot2
et Plot3 sont
désactivés.
Graphes de fonctions 3–7
Page 94

Sélectionner et désactiver les fonctions (suite)
Sélectionner les
fonctions à
partir de l’écran
initial ou d’un
programme
Pour sélectionner une fonction à partir de l’écran initial
ou d’un programme, placez le curseur sur une ligne
vierge et suivez la procédure ci-dessous.
1. Appuyez sur ~ pour afficher le menu
Y-VARS
2. Sélectionnez
secondaire
3. Sélectionnez
fonctions ou sélectionnez
.
4:On/Off pour afficher le menu
ON/OFF.
1:FnOn pour activer une ou plusieurs
2:FnOff pour désactiver une
VARS
ou plusieurs fonctions. L’instruction choisie vient se
placer à l’endroit du curseur.
4. Tapez le numéro (
1 à 9 ou 0 ; pas la variable Yn) de
chaque fonction à activer ou désactiver.
¦ Si vous tapez deux ou plusieurs numéros, séparez-
les par des virgules.
¦ Pour activer ou désactiver toutes les fonctions à la
fois, ne tapez aucun numéro après l’instruction
FnOn
FnOn[fonction#,fonction#, . . .,fonction n]
FnOff[fonction#,fonction#, . . .,fonction n]
ou
FnOff
.
5. Appuyez sur Í. Après exécution de cette
instruction, l’état de chaque fonction dans le mode en
cours est défini et le message
Done (terminé)
s’affiche.
Par exemple, en mode
1,3
désactive toutes les fonctions de l’écran d’édition Y=,
puis active
Y1 et Y3.
Func, l’instruction FnOff :FnOn
3–8 Graphes de fonctions
Page 95

Définir les styles de graphes pour représenter les fonctions
Icônes des
styles de
graphes dans
l’éditeur Y=
Le tableau suivant décrit les styles de graphes
disponibles pour représenter des fonctions. Utilisez
différents styles pour distinguer visuellement les diverses
fonctions à représenter en même temps. Par exemple,
vous pouvez définir une ligne continue pour représenter
Y1, une ligne en pointillés pour représenter Y2, et un trait
plus épais pour
Y3.
IcôneStyle Description
ç Line Une ligne continue relie les différents
points tracés ; c’est le style par défaut en
Connected
mode
è Thick Une ligne continue épaisse relie les
différents points tracés
é Above Un ombrage couvre la zone située au-
dessus de la courbe
ê Below Un ombrage couvre la zone située au-
dessous de la courbe
ë Path Un curseur circulaire parcourt la courbe
en laissant une trace
ì Animate Un curseur circulaire parcourt la courbe
sans laisser de trace
í Dot Chaque valeur calculée est représentée
par un petit point ; c’est le style par
défaut en mode
Remarque : Certains styles de graphes ne sont pas disponibles
dans tous les modes graphiques. Les chapitres 4, 5 et 6
répertorient les styles possibles en mode Par (graphes
paramétriques), Pol (graphes polaires) et Seq (graphes de
suites).
Dot
Graphes de fonctions 3–9
Page 96

Définir les styles de graphes pour représenter les fonctions (suite)
Définir le style
de graphe
Ombrage du
graphe
Pour définir le style du graphe représentant une fonction,
procédez comme suit :
1. Appuyez sur o pour afficher l’écran d’édition
Y=.
2. Tapez † et } pour placer le curseur sur la fonction à
représenter.
3. Appuyez sur | | pour faire reculer le curseur de
l’autre côté du signe
= jusqu’à l’icône de style
graphique située dans la première colonne. Le curseur
d’insertion s’affiche. (Les étapes 2 et 3 sont
interchangeables).
4. Appuyez plusieurs fois sur Í pour faire défiler les
styles. Les sept styles se succèdent dans l’ordre où ils
sont répertoriés ci-dessus.
5. Lorsque le style de votre choix s’affiche, appuyez sur
~, }, ou † pour le sélectionner.
Lorsque vous sélectionnez é ou ê pour deux ou plusieurs
fonctions, la TI-83 utilise tour à tour quatre motifs
d’ombrage.
¦ Ombrage par lignes verticales pour la première
fonction associée au style de graphe é ou ê.
¦ Ombrage par lignes horizontales pour la deuxième
fonction.
¦ Ombrage par lignes obliques descendantes pour la
troisième fonction.
¦ Ombrage par lignes obliques montantes pour la
quatrième fonction.
¦ Pour la cinquième fonction associée au style de
graphe é ou ê, on revient au motif des lignes
verticales, et ainsi de suite.
3–10 Graphes de fonctions
Page 97

Ombrage du
graphe (suite)
Définir un style
de graphe à
partir d’un
programme
Lorsque des zones ombrées se croisent, les motifs se
superposent.
Remarque : Lorsque le style é ou ê est sélectionné pour une
famille de fonctions, par exemple Y1={1,2,3}X, la rotation des
quatre motifs d’ombrage se fait à l’intérieur de la famille.
Pour définir le style de graphe à partir d’un programme,
sélectionnez
H:GraphStyle( dans le menu PRGM CTL. Ce
menu s’affiche lorsque vous appuyez sur dans
l’éditeur de programme. fonction# représente le numéro
associé au nom de la fonction
en cours. style# est un entier de
Y= dans le mode graphique
1 à 7 qui correspond à un
style de graphe :
1 = ç (ligne) 5 = ë (chemin)
2 = è (trait épais) 6 = ì (animation)
3 = é (ombrage au-dessus) 7 = í (pointillés)
4 = ê (ombrage au-dessous)
GraphStyle(fonction#,style#)
Par exemple, lorsque le programme suivant s’exécute en
Func, GraphStyle(1,3) affecte à Y1 le style é.
mode
Graphes de fonctions 3–11
Page 98

Définir les variables de la fenêtre d’affichage
Fenêtre
d’affichage de
la TI-83
Afficher les
variables
WINDOW
Changer la
valeur d’une
variable
WINDOW
La fenêtre d’affichage est la partie du plan définie par les
coordonnées
entre les graduations est définie par
horizontal et par
les marques de graduation, posez
Xmin
Xmin, Xmax, Ymin et Ymax. La distance
Xscl pour l’axe
Yscl pour l’axe vertical. Pour désactiver
Xscl=0 et Yscl=0.
Ymax
Xscl
Xmax
Yscl
Ymin
Pour afficher les valeurs en cours des variables WINDOW
(fenêtre), appuyez sur p. Les écrans d’édition cidessus indiquent les valeurs par défaut de ces variables
en mode graphique
Func et en unité d’angle Radian. Les
variables WINDOW sont différentes d’un mode graphique
à l’autre.
Xres définit la résolution de l’affichage (1 à 8) des
graphes de fonctions uniquement. Sa valeur par défaut
1.
est
¦ Pour
Xres=1, les fonctions sont calculées et tracées
pour chaque point de l’axe des x (horizontal)..
¦ Pour
Xres=8, les fonctions sont calculées et tracées
tous les huit points.
Conseil : Les petites valeurs de Xres fournissent des graphes
de meilleure résolution mais peuvent ralentir le tracé par la
TI-83.
Pour modifier la valeur d’une variable WINDOW à partir
de l’écran d’édition WINDOW, suivez la procédure cidessous.
1. Appuyez sur † ou sur } pour amener le curseur sur
la variable WINDOW que vous souhaitez modifier.
2. Changez sa valeur. Il peut s’agir d’une expression.
¦ Tapez la nouvelle valeur, ce qui efface
automatiquement l’ancienne.
¦ Placez le curseur sur une position particulière et
effectuez la modification voulue.
3. Appuyez sur Í, †, ou }. Si vous avez entré une
expression, elle est évaluée par la TI-83 et la nouvelle
valeur est enregistrée.
3–12 Graphes de fonctions
Page 99

Enregistrer une
variable
WINDOW à
partir de l’écran
initial ou d’un
programme
Pour enregistrer une valeur (qui peut être une
expression) dans une variable WINDOW, placez le
curseur sur une ligne vierge et suivez la procédure cidessous.
1. Entrez la valeur que vous désirez mémoriser.
2. Appuyez sur ¿.
3. Appuyez sur pour afficher le menu
4. Sélectionnez
WINDOW en mode graphique
X/Y).
1:Window pour afficher les variables
Func ( menu secondaire
VARS.
¦ Appuyez sur ~ pour afficher les variables
WINDOW en mode graphique
secondaire
T/q).
Par et Pol (menu
¦ Appuyez sur ~ ~ pour afficher les variables
WINDOW en mode graphique
secondaire
U/V/W).
Seq (menu
5. Sélectionnez la variable WINDOW dans laquelle vous
souhaitez enregistrer une valeur. Le nom de cette
variable apparaît à l’emplacement actuel du curseur.
6. Pour terminer l’instruction, appuyez sur Í.
Après exécution de l’instruction, la TI-83 mémorise la
valeur dans la variable WINDOW et l’affiche.
@X et @Y
Les variables @X et @Y (options 8 et 9 du menu secondaire
X/Y de VARS (1:Window) définissent la distance qui
sépare le centre de deux pixels adjacents d’un graphe
(résolution graphique).
Xmin, Xmax, Ymin et Ymax lorsqu’un graphe est affiché.
(Xmax - Xmin)
@X =
94
@X et @Y sont calculées à partir de
@Y =
(Ymax - Ymin)
62
Vous pouvez mémoriser des valeurs dans @X et @Y, auquel
Xmax et Ymax sont calculées à partir de @X, Xmin, @Y
cas
et Ymin.
Graphes de fonctions 3–13
Page 100

Définir le format d’un graphe
Afficher les
paramètres de
format
Modifier un
paramètre de
format
RectGC
PolarGC
Pour afficher les paramètres de format, appuyez sur y
FORMAT]. Les paramètres par défaut sont mis en
[
exergue dans le tableau ci-dessous.
RectGC PolarGC Sélectionne le curseur rectangulaire
ou polaire
CoordOn CoordOff Active et désactive l’affichage des
coordonnées
GridOff GridOn Active et désactive le quadrillage
AxesOn AxesOff Active et désactive les axes
LabelOff LabelOn Active et désactive les noms des
axes
ExprOn ExprOff Active et désactive l’affichage des
expressions
Les paramètres de format définissent l’aspect du graphe à
l’affichage. Ils s’appliquent à tous les modes graphiques.
Le mode graphique
Seq dispose d’un paramètre de
format supplémentaire (voir chapitre 6).
Pour modifier un paramètre de format, procédez comme
suit.
1. Appuyez sur †, ~, }, et sur | si nécessaire pour
amener le curseur sur le paramètre que vous désirez
sélectionner.
2. Appuyez sur Í pour sélectionner le paramètre mis
en exergue.
RectGC (coordonnées graphiques rectangulaires) affiche
les coordonnées rectangulaires
X et Y de l’emplacement
du curseur.
PolarGC (coordonnées graphiques polaires) affiche les
coordonnées polaires
R et q de l’emplacement du
curseur.
Le paramètre
RectGC/PolarGC détermine les variables
qui sont actualisées lorsque vous tracez le graphe,
déplacez le curseur libre ou effectuez une trace.
¦ En format
paramètre
RectGC, X et Y sont actualisés ; si le
CoordOn est défini, X et Y sont aussi
affichés.
¦ En format
paramètre
PolarGC, X, Y, R et q sont actualisés ; si le
CoordOn est défini, R et q sont aussi
affichés.
3–14 Graphes de fonctions
 Loading...
Loading...