Texas Instruments TI-83 User Manual

TI-83

GRAPHING CALCULATOR

GUIDEBOOK

TI-GRAPH LINK, Calculator-Based Laboratory, CBL, CBL 2, Calculator-Based Ranger, CBR, Constant Memory, Automatic Power Down, APD, and EOS are trademarks of Texas Instruments Incorporated.

IBM is a registered trademark of International Business Machines Corporation. Macintosh is a registered trademark of Apple Computer, Inc. Windows is a registered trademark of Microsoft Corporation.

Important

US FCC Information Concerning Radio Frequency Interference

Texas Instruments makes no warranty, either expressed or implied, including but not limited to any implied warranties of merchantability and fitness for a particular purpose, regarding any programs or book materials and makes such materials available solely on an “as-is” basis.

In no event shall Texas Instruments be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the purchase or use of these materials, and the sole and exclusive liability of Texas Instruments, regardless of the form of action, shall not exceed the purchase price of this equipment. Moreover, Texas Instruments shall not be liable for any claim of any kind whatsoever against the use of these materials by any other party.

This equipment has been tested and found to comply with the limits for a Class B digital device, pursuant to Part 15 of the FCC rules. These limits are designed to provide reasonable protection against harmful interference in a residential installation. This equipment generates, uses, and can radiate radio frequency energy and, if not installed and used in accordance with the instructions, may cause harmful interference with radio communications. However, there is no guarantee that interference will not occur in a particular installation.

If this equipment does cause harmful interference to radio or television reception, which can be determined by turning the equipment off and on, you can try to correct the interference by one or more of the following measures:

• Reorient or relocate the receiving antenna.

• Increase the separation between the equipment and receiver.

• Connect the equipment into an outlet on a circuit different

from that to which the receiver is connected.

• Consult the dealer or an experienced radio/television

technician for help.

Caution: Any changes or modifications to this equipment not expressly approved by Texas Instruments may void your authority to operate the equipment.

This manual describes how to use the TI.83 Graphing Calculator. Getting Started is an overview of TI.83 features. Chapter 1 describes how the TI.83 operates. Other chapters describe various interactive features. Chapter 17 shows how to combine these features to solve problems.

Getting Started: Do This First!

TI-83 Keyboard TI-83 Menus First Steps Entering a Calculation: The Quadratic Formula Converting to a Fraction: The Quadratic Formula Displaying Complex Results: The Quadratic Formula Defining a Function: Box with Lid Defining a Table of Values: Box with Lid Zooming In on the Table: Box with Lid Setting the Viewing Window: Box with Lid Displaying and Tracing the Graph: Box with Lid Zooming In on the Graph: Box with Lid Finding the Calculated Maximum: Box with Lid Other TI-83 Features

..........................................

.............................................

...............................................

..........

........

....

.......................

.................

...................

...............

.........

..................

..........

.....................................

2 4 5 6 7 8

9 10 11 12 13 15 16 17

Chapter 1: Operating the TI-83

Turning On and Turning Off the TI-83 Setting the Display Contrast The Display

..............................................

.............................

Entering Expressions and Instructions TI-83 Edit Keys Setting Modes Using TI-83 Variable Names Storing Variable Values Recalling Variable Values

(Last Entry) Storage Area

ENTRY

(Last Answer) Storage Area

Ans

TI-83 Menus

and

VARS

..........................................

...........................................

.............................

..................................

................................

........................

.........................

.............................................

Menus

VARS Y.VARS

.........................

Equation Operating System (EOSé) Error Conditions

.........................................

....................

...................

.....................

1-2 1-3 1-4 1-6 1-8

1-9 1-13 1-14 1-15 1-16 1-18 1-19 1-21 1-22 1-24

Introduction iii

Chapter 2: Math, Angle, and Test Operations

Getting Started: Coin Flip Keyboard Math Operations

Operations

MATH

Using the Equation Solver

MATH NUM

(Number) Operations

................................

..............................

........................................

...............................

........................

Entering and Using Complex Numbers

MATH CPX MATH PRB ANGLE TEST TEST LOGIC

(Complex) Operations (Probability) Operations

Operations

(Relational) Operations

(Boolean) Operations

.......................................

.......................

............................

......................

...................

.....................

2-2

2-3

2-5

2-8 2-13 2-16 2-18 2-20 2-23 2-25 2-26

Chapter 3: Function Graphing

Chapter 4: Parametric Graphing

Chapter 5: Polar Graphing

Getting Started: Graphing a Circle Defining Graphs Setting the Graph Modes Defining Functions

.........................................

.................................

......................................

Selecting and Deselecting Functions Setting Graph Styles for Functions Setting the Viewing Window Variables Setting the Graph Format Displaying Graphs

................................

.......................................

.......................

.....................

.......................

...................

Exploring Graphs with the Free-Moving Cursor Exploring Graphs with Exploring Graphs with the Using

ZOOM MEMORY

Using the

(Calculate) Operations

CALC

Getting Started: Path of a Ball Defining and Displaying Parametric Graphs Exploring Parametric Graphs

Getting Started: Polar Rose Defining and Displaying Polar Graphs Exploring Polar Graphs

...........................

TRACE

..................................

Instructions

ZOOM

..................

...........................

..............

............................

..............................

...................

..........

...........

3-2

3-3

3-4

3-5

3-7

3-9 3-11 3-13 3-15 3-17 3-18 3-20 3-23 3-25

4-2

4-4

4-7

5-2

5-3

5-6

iv Introduction

Chapter 6: Sequence Graphing

Getting Started: Forest and Trees Defining and Displaying Sequence Graphs Selecting Axes Combinations Exploring Sequence Graphs Graphing Web Plots

......................................

Using Web Plots to Illustrate Convergence Graphing Phase Plots

....................................

........................

...............

............................

..............................

...............

Comparing TI-83 and TI.82 Sequence Variables Keystroke Differences Between TI-83 and TI-82

..........

.........

6-2

6-3

6-8

6-9 6-11 6-12 6-13 6-15 6-16

Chapter 7: Tables

Chapter 8: DRAW Operations

Chapter 9: Split Screen

Getting Started: Roots of a Function Setting Up the Table

.....................................

Defining the Dependent Variables Displaying the Table

.....................................

.....................

........................

Getting Started: Drawing a Tangent Line Using the

DRAW

Clearing Drawings Drawing Line Segments Drawing Horizontal and Vertical Lines Drawing Tangent Lines Drawing Functions and Inverses Shading Areas on a Graph Drawing Circles Placing Text on a Graph Using Pen to Draw on a Graph Drawing Points on a Graph Drawing Pixels Storing Graph Pictures ( Recalling Graph Pictures ( Storing Graph Databases ( Recalling Graph Databases (

...................................

.......................................

..................................

...................

..................................

.........................

...............................

..........................................

.................................

...........................

..............................

..........................................

.............................

)

Pic

...........................

)

Pic

.........................

)

GDB

.......................

)

GDB

Getting Started: Exploring the Unit Circle Using Split Screen

(Horizontal) Split Screen

Horiz

(Graph-Table) Split Screen

G-T

TI.83 Pixels in

.......................................

...........................

..........................

Horiz

and

G-T

.....................

Modes

.................

................

7-2

7-3

7-4

7-5

8-2

8-3

8-4

8-5

8-6

8-8

8-9 8-10 8-11 8-12 8-13 8-14 8-16 8-17 8-18 8-19 8-20

9-2

9-3

9-4

9-5

9-6

Introduction v

Chapter 10: Matrices

Getting Started: Systems of Linear Equations Defining a Matrix Viewing and Editing Matrix Elements Using Matrices with Expressions Displaying and Copying Matrices Using Math Functions with Matrices Using the

........................................

....................

........................

.....................

MATRX MATH

Operations

.....................

............

10-2 10-3 10-4 10-7 10-8 10-9

10-12

Chapter 11: Lists

Chapter 12: Statistics

Chapter 13: Inferential Statistics and Distributions

Getting Started: Generating a Sequence Naming Lists Storing and Displaying Lists Entering List Names

.............................................

.............................

.....................................

Attaching Formulas to List Names Using Lists in Expressions

LIST OPS LIST MATH

..........................................

........................................

...............................

..................

.......................

Getting Started: Pendulum Lengths and Periods Setting up Statistical Analyses Using the Stat List Editor Attaching Formulas to List Names Detaching Formulas from List Names Switching Stat List Editor Contexts Stat List Editor Contexts

STAT EDIT

........................................

Regression Model Features

STAT CALC

Statistical Variables

........................................

......................................

Statistical Analysis in a Program Statistical Plotting

.......................................

Statistical Plotting in a Program

...........................

................................

.......................

....................

......................

.................................

..............................

.........................

Getting Started: Mean Height of a Population Inferential Stat Editors

STAT TESTS

Menu Inferential Statistics Input Descriptions Test and Interval Output Variables Distribution Functions Distribution Shading

...................................

......................................

..................

.......................

...................................

.....................................

.........

............

11-2 11-3 11-4 11-6 11-7

11-9 11-10 11-17

12-2 12-10 12-11 12-14 12-16 12-17 12-18 12-20 12-22 12-24 12-29 12-30 12-31 12-37

13-2

13-6

13-9 13-26 13-28 13-29 13-35

vi Introduction

Chapter 14: Financial Functions

Getting Started: Financing a Car Getting Started: Computing Compound Interest Using the

TVM Solver

....................................

Using the Financial Functions Calculating Time Value of Money ( Calculating Cash Flows

..................................

Calculating Amortization Calculating Interest Conversion

.........................

..........

...........................

.................

)

TVM

................................

..........................

Finding Days between Dates/Defining Payment Method Using the

TVM

Variables

.................................

.....

14-2

14-3

14-4

14-5

14-6

14-8

14-9 14-12 14-13 14-14

Chapter 15: CATALOG, Strings, Hyperbolic Functions

Chapter 16: Programming

Chapter 17: Applications

Browsing the TI-83

CATALOG

Entering and Using Strings Storing Strings to String Variables String Functions and Instructions in the Hyperbolic Functions in the

Getting Started: Volume of a Cylinder Creating and Deleting Programs Entering Command Lines and Executing Programs Editing Programs

........................................

Copying and Renaming Programs

PRGM CTL PRGM I/O

(Control) Instructions

(Input/Output) Instructions

Calling Other Programs as Subroutines

Comparing Test Results Using Box Plots Graphing Piecewise Functions Graphing Inequalities

....................................

Solving a System of Nonlinear Equations Using a Program to Create the Sierpinski Triangle Graphing Cobweb Attractors Using a Program to Guess the Coefficients Graphing the Unit Circle and Trigonometric Curves Finding the Area between Curves Using Parametric Equations: Ferris Wheel Problem

...........................

...............................

.......................

CATALOG

...........................

............................

..................

....................

.........................

........................

.......................

...................

..................

................

...............

........................

......

.......

......

Demonstrating the Fundamental Theorem of Calculus Computing Areas of Regular N-Sided Polygons Computing and Graphing Mortgage Payments

..........

...........

...

15-2

15-3

15-4

15-6 15-10

16-2

16-4

16-5

16-6

16-7

16-8 16-16 16-22

17-2

17-4

17-5

17-6

17-7

17-8

17-9 17-10 17-11 17-12 17-14 17-16 17-18

Introduction vii

Chapter 18: Memory Management

Checking Available Memory Deleting Items from Memory

.............................

............................

Clearing Entries and List Elements Resetting the TI.83

......................................

......................

18-2

18-3

18-4

18-5

Chapter 19: Communication Link

Appendix A: Tables and Reference Information

Appendix B: General Information

Index

Getting Started: Sending Variables TI-83 Selecting Items to Send Receiving Items Transmitting Items Transmitting Lists to a TI-82

...............................................

LINK

..................................

..........................................

.......................................

.............................

Transmitting from a TI-82 to a TI-83 Backing Up Memory

.....................................

Table of Functions and Instructions Menu Map Variables Statistical Formulas Financial Formulas

Battery Information In Case of Difficulty Error Conditions Accuracy Information Support and Service Information Warranty Information

...............................................

................................................

.....................................

......................................

.....................................

.........................................

....................................

.........................

....................................

.......................

.....................

19-2

19-3

19-4

19-5

19-6

19-8

19-9 19-10

A-2 A-39 A-49 A-50 A-54

B-2

B-4

B-5 B-10 B-12 B-13

viii Introduction

Getting Started: Do This First!

Contents

TI-83 Keyboard TI-83 Menus First Steps Entering a Calculation: The Quadratic Formula Converting to a Fraction: The Quadratic Formula

..........................................

.............................................

...............................................

..........

........

Displaying Complex Results: The Quadratic Formula Defining a Function: Box with Lid Defining a Table of Values: Box with Lid Zooming In on the Table: Box with Lid Setting the Viewing Window: Box with Lid Displaying and Tracing the Graph: Box with Lid Zooming In on the Graph: Box with Lid Finding the Calculated Maximum: Box with Lid Other TI.83 Features

.....................................

.......................

.................

...................

...............

.........

..................

..........

....

2 4 5 6 7 8

9 10 11 12 13 15 16 17

Getting Started 1

TI-83 Keyboard

Generally, the keyboard is divided into these zones: graphing keys, editing keys, advanced function keys, and scientific calculator keys.

Keyboard Zones

Graphing Keys

Graphing keys access the interactive graphing features.

Editing keys allow you to edit expressions and values.

Advanced function keys display menus that access the advanced functions.

Scientific calculator keys access the capabilities of a standard scientific calculator.

Editing Keys

Advanced Function Keys

Scientific Calculator Keys

2 Getting Started

Using the Color-Coded Keyboard

The keys on the TI.83 are color-coded to help you easily locate the key you need.

The gray keys are the number keys. The blue keys along the right side of the keyboard are the common math functions. The blue keys across the top set up and display graphs.

The primary function of each key is printed in white on the key. For example, when you press



, the

MATH

menu is

displayed.

Using the and

Keys

The y key accesses the second function printed in yellow above each key.

The secondary function of each key is printed in yellow above the key. When you press the yellow y key, the character, abbreviation, or word printed in yellow above the other keys becomes active for the next keystroke. For example, when you press y and then



, the

TEST

menu is displayed. This guidebook describes this keystroke combination as y [

TEST

The alpha function of each key is printed in green above the key. When you press the green

key, the alpha character printed in green above the other keys becomes active for the next keystroke. For example, when you press

and then

guidebook describes this keystroke combination as

[



, the letter

A is entered. This

The ƒ key accesses the alpha function printed in green above each key.

Getting Started 3

TI-83 Menus

Displaying a Menu

While using your TI.83, you often will need to access items from its menus.

When you press a key that displays a menu, that menu temporarily replaces the screen where you are working. For example, when you press as a full screen.

fter you select an item from a menu, the screen where you are working usually is displayed again.

Moving from One Menu to Another

Some keys access more than one menu. When you press such a key, the names of all accessible menus are displayed on the top line. When you highlight a menu name, the items in that menu are displayed. Press ~ and

to highlight each menu name.

Selecting an Item from a Menu

The number or letter next to the current menu item is highlighted. If the menu continues beyond the screen, a down arrow ( replaces the colon ( item. If you scroll beyond the last displayed item, an up arrow ( the first item displayed.You can select an item in either of two ways.

Press † or } to move the cursor to the number or letter of the item; press

Press the key or key combination for the number or letter next to the item.



, the

menu is displayed

MATH

) in the last displayed

) replaces the colon in

)

Leaving a Menu without Making a Selection

You can leave a menu without making a selection in any of three ways.

Press

‘

to return to the screen

where you were.

Press y [

QUIT

] to return to the home

screen.

Press a key for another menu or screen.

4 Getting Started

First Steps

Before starting the sample problems in this chapter, follow the steps on this page to reset the TI.83 to its factory settings and clear all memory. This ensures that the keystrokes in this chapter will produce the illustrated results.

To reset the TI.83, follow these steps.

1. Press É to turn on the calculator.

2. Press and release y, and then press

MEM

[

] (above Ã).

When you press y, you access the operation printed in yellow above the next key that you press. [

operation of the Ã key.

The

MEMORY

3. Press 5 to select 5:Reset.

The

menu is displayed.

RESET

4. Press 1 to select 1:All Memory.

The

RESET MEMORY

MEM

] is the

menu is displayed.

5. Press 2 to select 2:Reset.

All memory is cleared, and the calculator is reset to the factory default settings.

When you reset the TI.83, the display contrast is reset.

If the screen is very light or blank, press and release y, and then press and hold } to darken the screen.

If the screen is very dark, press and release y, and then press and hold to lighten the screen.

†

Getting Started 5

Entering a Calculation: The Quadratic Formula

Use the quadratic formula to solve the quadratic equations 3X2 + 5X + 2 = 0

and 2X

1. Press

2. Press

3. Press

4. Press

N X + 3 = 0. Begin with the equation 3X2 + 5X + 2 = 0.

¿ ƒ

[A] (above

store the coefficient of the X

] (above Ë). The colon

[



term.

) to

allows you to enter more than one instruction on a line.

¿ ƒ

[B] (above

store the coefficient of the X

the same line. Press (above

[

] to enter a new instruction on

¿ ƒ



) to store the constant.

to store the values to the



term. Press

[C]

) to

variables A, B, and C.

The last value you stored is shown on the right side of the display. The cursor moves to the next line, ready for your next entry.

5. Press £ Ì

¡ ¹ ƒ

[B] Ã y [‡]

[

] ¤ to enter the expression for

[A]

[C] ¤ ¤ ¥ £ 2

one of the solutions for the quadratic formula,

−

6. Press

equation 3X

+−

bb ac

to find one solution for the

+ 5X + 2 = 0.

The answer is shown on the right side of the display. The cursor moves to the next line, ready for you to enter the next expression.

6 Getting Started

[B]

Converting to a Fraction: The Quadratic Formula

You can show the solution as a fraction.

1. Press



to display the

MATH

menu.

2. Press 1 to select 1:

Frac from the

MATH

menu.

When you press the home screen.

1, Ans4Frac is displayed on

Ans is a variable that

contains the last calculated answer.

3. Press

to convert the result to a

fraction.

To save keystrokes, you can recall the last expression you entered, and then edit it for a new calculation.

4. Press y [

ENTRY

] (above

) to recall the fraction conversion entry, and then press y [

ENTRY

] again to recall the

quadratic-formula expression,

−

bb ac

+−

5. Press } to move the cursor onto the + sign in the formula. Press ¹ to edit the quadratic-formula expression to become:

−

6. Press the quadratic equation 3X

−−

bb ac

to find the other solution for

+ 5X + 2 = 0.

Getting Started 7

Displaying Complex Results: The Quadratic Formula

Now solve the equation 2X2 N X + 3 = 0. When you set a+b mode, the TI.83 displays complex results.

1. Press

z † † † † † †

(6 times), and

then press ~ to position the cursor over

a+b

. Press

to select

a+b

complex-

number mode.

QUIT

2. Press y [

] (above

the home screen, and then press

) to return to

‘

clear it.

]

¿ ƒ

[

3. Press 2

¿ ƒ

[

The coefficient of the X

]

[A]

[ : ] 3

[ : ] Ì 1

¿ ƒ

term, the coefficient of the X term, and the constant for the new equation are stored to A, B, and C, respectively.

4. Press y [ instruction, and then press y [

ENTRY

] to recall the store

ENTRY

] again to recall the quadratic-formula expression,

−

5. Press equation 2X

−−

bb ac

to find one solution for the

N X + 3 = 0.

complex number

6. Press y [

ENTRY

] repeatedly until this

quadratic-formula expression is displayed:

−

7. Press the quadratic equation: 2X

Note:

Solver (Chapter 2).

bb ac

+−

to find the other solution for

An alternative for solving equations for real numbers is to use the built-in Equation

N X + 3 = 0.

8 Getting Started

Defining a Function: Box with Lid

Take a 20 cm. × 25 cm. sheet of paper and cut X × X squares from two corners. Cut X × 12.5 cm. rectangles from the other two corners as shown in the diagram below. Fold the paper into a box with a lid. What value of X would give your box the maximum volume V? Use the table and graphs to determine the solution.

Begin by defining a function that describes the

olume of the box.

From the diagram: 2X + A = 20

2X + 2B = 25 V = A B X

Substituting: V = (20 N 2X) (25à2 N X) X

1. Press o to display the Y= editor, which is where you define functions for tables and graphing.

2. Press £ 20 ¹ 2

„ ¤ „ Í

volume function as

„

lets you enter

having to press

„ ¤ £

to define the

in terms of X.

X quickly, without

. The highlighted

25 ¥ 2

sign indicates that Y1 is selected.

X B X B

Getting Started 9

Defining a Table of Values: Box with Lid

The table feature of the TI.83 displays numeric information about a function. You can use a table of values from the function defined on page 9 to estimate an answer to the problem.

1. Press y [ display the

2. Press

3. Press

Tbl=1

Depend: Auto so that the table will be

TBLSET

] (above

TABLE SETUP

to accept

to define the table increment

. Leave Indpnt: Auto and

generated automatically.

4. Press y [

TABLE

] (above

the table.

Notice that the maximum value for (box’s volume) occurs when X is about 4, between

3 and 5.

5. Press and hold † to scroll the table until a negative result for

Notice that the maximum length of this problem occurs where the sign of (box’s volume) changes from positive to negative, between

6. Press y [

Notice that

TBLSET

10 and 11.

TblStart has changed to 6 to

reflect the first line of the table as it was last displayed. (In step 5, the first value of

X displayed in the table is 6.)

menu.

TblStart=0.

is displayed.

) to

) to display

X for

10 Getting Started

Zooming In on the Table: Box with Lid

You can adjust the way a table is displayed to get more information about a

defined function. With smaller values for

1. Press

to set

to set TblStart. Press Ë 1

Tbl

This adjusts the table setup to get a more accurate estimate of volume

X for maximum

Tbl

, you can zoom in on the table.

2. Press y [

TABLE

3. Press † and } to scroll the table.

Tbl

Notice that the maximum value for

410.26, which occurs at X=3.7. Therefore,

the maximum occurs where

4. Press y [ set

5. Press y [

TBLSET

TblStart. Press

TABLE

]. Press 3

], and then press † and

3.6<X<3.8.

to set

to scroll the table.

Four equivalent maximum values are shown,

3.70.

410.60 at X=3.67, 3.68, 3.69, and

6. Press † and } to move the cursor to 3.67. Press ~ to move the cursor into the

column.

The value of

at X=3.67 is displayed on

the bottom line in full precision as

410.261226.

7. Press † to display the other maximums.

The value of

410.264064, at X=3.69 is 410.262318, and at X=3.7 is 410.256.

at X=3.68 in full precision is

The maximum volume of the box would occur at

3.68 if you could measure and cut

the paper at .01-cm. increments.

}

Getting Started 11

Setting the Viewing Window: Box with Lid

You also can use the graphing features of the TI.83 to find the maximum value of a previously defined function. When the graph is activated, the viewing window defines the displayed portion of the coordinate plane. The values of the window variables determine the size of the viewing window.

1. Press

to display the window editor, where you can view and edit the values of the window variables.

The standard window variables define the viewing window as shown.

Ymin, and Ymax define the boundaries of

the display.

Xscl and Yscl define the

Xmin, Xmax,

distance between tick marks on the

Y axes. Xres controls resolution.

2. Press 0

3. Press

to define Xmin.

2 to define Xmax using an

expression.

4. Press

5. Press

. The expression is evaluated,

and

10 is stored in Xmax. Press

Xscl as 1.

500

100

to define the remaining window variables.

X and

Xmin

Ymax

Xscl

Xmax

Yscl

Ymin

12 Getting Started

Displaying and Tracing the Graph: Box with Lid

Now that you have defined the function to be graphed and the window in which to graph it, you can display and explore the graph. You can trace along a function using the

1. Press

to graph the selected function

in the viewing window.

The graph of

Y1=(20N2X)(25à2NX)X is

displayed.

2. Press ~ to activate the free-moving graph cursor.

The

X and Y coordinate values for the

position of the graph cursor are displayed on the bottom line.

3. Press |, ~, }, and † to move the freemoving cursor to the apparent maximum of the function.

As you move the cursor, the coordinate values are updated continually.

TRACE

feature.

X and Y

Getting Started 13

on the

. The trace cursor is displayed

function.

4. Press

The function that you are tracing is displayed in the top-left corner.

5. Press | and ~ to trace along at a time, evaluating

at each X.

You also can enter your estimate for the maximum value of

6. Press while in

8. When you press a number key

TRACE

, the X= prompt is displayed

in the bottom-left corner.

, one X dot

7. Press

The trace cursor jumps to the point on the

function evaluated at X=3.8.

8. Press | and ~ until you are on the maximum

This is the maximum of

Y value.

Y1(X) for the X

pixel values. The actual, precise maximum may lie between pixel values.

14 Getting Started

Zooming In on the Graph: Box with Lid

To help identify maximums, minimums, roots, and intersections of functions, you can magnify the viewing window at a specific location using the instructions.

1. Press

to display the

ZOOM

menu.

This menu is a typical TI.83 menu. To select an item, you can either press the number or letter next to the item, or you can press † until the item number or letter is highlighted, and then press

2. Press 2 to select 2:Zoom In.

The graph is displayed again. The cursor has changed to indicate that you are using a

ZOOM

instruction.

3. With the cursor near the maximum value of the function (as in step 8 on page 14),

press

The new viewing window is displayed. Both

XmaxNXmin and YmaxNYmin have

been adjusted by factors of 4, the default values for the zoom factors.

4. Press

to display the new window

settings.

ZOOM

Getting Started 15

Finding the Calculated Maximum: Box with Lid

You can use a

CALCULATE

menu operation to calculate a local maximum of a

function.

1. Press y [ the

CALCULATE

4:maximum.

CALC

] (above menu. Press 4 to select

) to display

The graph is displayed again with a

Left Bound? prompt.

2. Press | to trace along the curve to a point to the left of the maximum, and then press

at the top of the screen indicates the

selected bound.

Right Bound? prompt is displayed.

3. Press ~ to trace along the curve to a point to the right of the maximum, and then

press

at the top of the screen indicates the

selected bound.

Guess? prompt is displayed.

4. Press | to trace to a point near the maximum, and then press

Or, press

8, and then press

enter a guess for the maximum.

When you press a number key in the

X= prompt is displayed in the bottom-

TRACE

left corner.

Notice how the values for the calculated maximum compare with the maximums found with the free-moving cursor, the trace cursor, and the table.

Note:

In steps 2 and 3 above, you can enter values directly for Left Bound and Right Bound, in the same way as described in step 4.

16 Getting Started

Other TI-83 Features

Getting Started has introduced you to basic TI.83 operation. This guidebook describes in detail the features you used in Getting Started. It also covers the other features and capabilities of the TI.83.

Graphing

You can store, graph, and analyze up to 10 functions (Chapter 3), up to six parametric functions (Chapter 4), up to six polar functions (Chapter 5), and up to three sequences (Chapter 6). You can use

DRAW

operations to

annotate graphs (Chapter 8).

Sequences

Tables

Split Screen

Matrices

Lists

Statistics

You can generate sequences and graph them over time. Or, you can graph them as web plots or as phase plots (Chapter 6).

You can create function evaluation tables to analyze many functions simultaneously (Chapter 7).

You can split the screen horizontally to display both a graph and a related editor (such as the

editor), the

table, the stat list editor, or the home screen. Also, you can split the screen vertically to display a graph and its table simultaneously (Chapter 9).

You can enter and save up to 10 matrices and perform standard matrix operations on them (Chapter 10).

You can enter and save as many lists as memory allows for use in statistical analyses. You can attach formulas to lists for automatic computation. You can use lists to evaluate expressions at multiple values simultaneously and to graph a family of curves (Chapter 11).

You can perform one- and two-variable, list-based statistical analyses, including logistic and sine regression analysis. You can plot the data as a histogram, xyLine, scatter plot, modified or regular box-and-whisker plot, or normal probability plot. You can define and store up to three stat plot definitions (Chapter 12).

Getting Started 17

Inferential Statistics

You can perform 16 hypothesis tests and confidence intervals and 15 distribution functions. You can display hypothesis test results graphically or numerically (Chapter 13).

Financial Functions

CATALOG

Programming

Communication Link

You can use time-value-of-money (

) functions to

TVM

analyze financial instruments such as annuities, loans, mortgages, leases, and savings. You can analyze the value of money over equal time periods using cash flow functions. You can amortize loans with the amortization functions (Chapter 14).

The

CATALOG

is a convenient, alphabetical list of all functions and instructions on the TI.83. You can paste any function or instruction from the

CATALOG

to the current

cursor location (Chapter 15).

You can enter and store programs that include extensive control and input/output instructions (Chapter 16).

The TI.83 has a port to connect and communicate with another TI.83, a TI.82, the Calculator-Based Laboratory (CBL 2é, CBLé) System, a Calculator-Based Ranger

(CBRé), or a personal computer. The unit-to-unit link cable is included with the TI.83 (Chapter 19).

18 Getting Started

Operatin

Contents

the TI-83

Turning On and Turning Off the TI.83 Setting the Display Contrast The Display Entering Expressions and Instructions TI.83 Edit Keys Setting Modes Using TI.83 Variable Names Storing Variable Values Recalling Variable Values

ENTRY

(Last Answer) Storage Area

Ans

TI.83 Menus

VARS

Equation Operating System (EOSé) Error Conditions

..............................................

..........................................

...........................................

(Last Entry) Storage Area

.............................................

and

VARS Y.VARS

.........................................

.............................

..................................

................................

........................

.........................

Menus

....................

...................

.....................

1-2 1-3 1-4 1-6 1-8

1-9 1-13 1-14 1-15 1-16 1-18 1-19 1-21 1-22 1-24

Operating the TI-83 1-1

Turning On and Turning Off the TI-83

Turning On the Calculator

Turning Off the Calculator

Batteries

To turn on the TI.83, press É.

•

If you previously had turned off the calculator by pressing y [

OFF

], the TI.83 displays the home screen

as it was when you last used it and clears any error.

•

If Automatic Power Down™ (APDé) had previously turned off the calculator, the TI.83 will return exactly as you left it, including the display, cursor, and any error.

To prolong the life of the batteries, APD turns off the TI.83 automatically after about five minutes without any activity.

OFF

To turn off the TI.83 manually, press y [

•

All settings and memory contents are retained by

Constant Memoryé.

•

Any error condition is cleared.

The TI.83 uses four AAA alkaline batteries and has a userreplaceable backup lithium battery (CR1616 or CR1620). To replace batteries without losing any information stored in memory, follow the steps in Appendix B.

1-2 Operating the TI-83

Setting the Display Contrast

Adjusting the Display Contrast

When to Replace Batteries

You can adjust the display contrast to suit your viewing angle and lighting conditions. As you change the contrast setting, a number from

0 (lightest) to 9 (darkest) in the

top-right corner indicates the current level. You may not be able to see the number if contrast is too light or too dark.

Note:

The TI.83 has 40 contrast settings, so each number

represents four settings.

through

The TI.83 retains the contrast setting in memory when it is turned off.

To adjust the contrast, follow these steps.

1. Press and release the y key.

2. Press and hold † or }, which are below and above the contrast symbol (yellow, half-shaded circle).

•

†

lightens the screen.

•

}

darkens the screen.

Note:

If you adjust the contrast setting to completely blank. To restore the screen, press and release y, and then press and hold } until the display reappears.

, the display may become

When the batteries are low, a low-battery message is displayed when you turn on the calculator.

To replace the batteries without losing any information in memory, follow the steps in Appendix B.

Generally, the calculator will continue to operate for one or two weeks after the low-battery message is first displayed. After this period, the TI.83 will turn off automatically and the unit will not operate. Batteries must be replaced. All memory is retained.

Note:

The operating period following the first low-battery message could be longer than two weeks if you use the calculator infrequently.

Operating the TI-83 1-3

The Display

Types of Displays

Home Screen

Displaying Entries and Answers

The TI.83 displays both text and graphs. Chapter 3 describes graphs. Chapter 9 describes how the TI.83 can display a horizontally or vertically split screen to show graphs and text simultaneously.

The home screen is the primary screen of the TI.83. On this screen, enter instructions to execute and expressions to evaluate. The answers are displayed on the same screen.

When text is displayed, the TI.83 screen can display a maximum of eight lines with a maximum of 16 characters per line. If all lines of the display are full, text scrolls off the top of the display. If an expression on the home screen, the

editor (Chapter 3), or the program editor

(Chapter 16) is longer than one line, it wraps to the beginning of the next line. In numeric editors such as the window screen (Chapter 3), a long expression scrolls to the right and left.

When an entry is executed on the home screen, the answer is displayed on the right side of the next line.

Entry Answer

The mode settings control the way the TI.83 interprets expressions and displays answers (page 1.9).

If an answer, such as a list or matrix, is too long to display entirely on one line, an ellipsis (

...) is displayed to the right

or left. Press ~ and | to scroll the answer.

Entry Answer

Returning to the Home Screen

Busy Indicator

To return to the home screen from any other screen, press

QUIT

[

When the TI.83 is calculating or graphing, a vertical moving line is displayed as a busy indicator in the top-right corner of the screen. When you pause a graph or a program, the busy indicator becomes a vertical moving dotted line.

1-4 Operating the TI-83

Display Cursors

In most cases, the appearance of the cursor indicates what will happen when you press the next key or select the next menu item to be pasted as a character.

Cursor Appearance Effect of Next Keystroke

Entry Solid rectangle$A character is entered at the

cursor; any existing character is overwritten

Insert Underline

A character is inserted in front of the cursor location

Second Reverse arrowÞA 2nd character (yellow on the

keyboard) is entered or a 2nd operation is executed

lpha Reverse A

An alpha character (green on the keyboard) is entered or

SOLVE

executed

Full Checkerboard

rectangle

No entry; the maximum characters are entered at a prompt or memory is full

If you press an underlined underline cursor becomes an underlined # (

during an insertion, the cursor becomes

(A) If you press y during an insertion, the

Graphs and editors sometimes display additional cursors, which are described in other chapters.

Operating the TI-83 1-5

Entering Expressions and Instructions

What Is an Expression?

Entering an Expression

An expression is a group of numbers, variables, functions and their arguments, or a combination of these elements. An expression evaluates to a single answer. On the TI.83, you enter an expression in the same order as you would write it on paper. For example, pR

is an expression.

You can use an expression on the home screen to calculate an answer. In most places where a value is required, you can use an expression to enter a value.

To create an expression, you enter numbers, variables, and functions from the keyboard and menus. An expression is completed when you press

, regardless of the cursor location. The entire expression is evaluated according to Equation Operating System (EOSé) rules (page 1.22), and the answer is displayed.

Most TI.83 functions and operations are symbols comprising several characters. You must enter the symbol from the keyboard or a menu; do not spell it out. For example, to calculate the log of 45, you must press « Do not enter the letters

L, O, and G. If you enter LOG, the

45.

TI.83 interprets the entry as implied multiplication of the variables

Calculate 3.76 ÷ (L7.9 + ‡5) + 2 log 45.

L, O, and G.

76 ¥ £ Ì 7 Ë 9

[‡] 5 ¤

2 « 45

Multiple Entries on a Line

To enter two or more expressions or instructions on a line, separate them with colons ( stored together in last entry (

1-6 Operating the TI-83

¤ ¤

ENTRY

[

]). All instructions are ; page 1.16).

Entering a Number in Scientific Notation

Functions

To enter a number in scientific notation, follow these steps.

1. Enter the part of the number that precedes the

exponent. This value can be an expression.

2. Press y [

]. å is pasted to the cursor location.

3. If the exponent is negative, press Ì, and then enter the

exponent, which can be one or two digits.

When you enter a number in scientific notation, the TI.83 does not automatically display answers in scientific or engineering notation. The mode settings (page 1.9) and the size of the number determine the display format.

A function returns a value. For example,

÷,

, +,

‡

(

, and log(

are the functions in the example on page 1.6. In general, the first letter of each function is lowercase on the TI.83. Most functions take at least one argument, as indicated by an open parenthesis ( requires one argument, sin(

( ) following the name. For example, sin(

value

Instructions

Interrupting a Calculation

An instruction initiates an action. For example,

ClrDraw is

an instruction that clears any drawn elements from a graph. Instructions cannot be used in expressions. In general, the first letter of each instruction name is uppercase. Some instructions take more than one argument, as indicated by an open parenthesis ( end of the name. For example, arguments,

Circle(X,Y,

radius

Circle( requires three

( ) at the

To interrupt a calculation or graph in progress, which would be indicated by the busy indicator, press É.

When you interrupt a calculation, the menu is displayed.

•

To return to the home screen, select

•

To go to the location of the interruption, select

1:Quit.

2:Goto.

When you interrupt a graph, a partial graph is displayed.

•

To return to the home screen, press

‘

or any

nongraphing key.

•

To restart graphing, press a graphing key or select a graphing instruction.

Operating the TI-83 1-7

(

TI-83 Edit Keys

Keystrokes Result

}

y |

y ~

‘

{

[

„

†

INS

A.LOCK

Moves the cursor within an expression; these keys repeat.

Moves the cursor from line to line within an expression that occupies more than one line; these keys repeat.

On the top line of an expression on the home screen, } moves the cursor to the beginning of the expression.

On the bottom line of an expression on the home screen, moves the cursor to the end of the expression.

Moves the cursor to the beginning of an expression.

Moves the cursor to the end of an expression.

Evaluates an expression or executes an instruction.

On a line with text on the home screen, clears the current line.

On a blank line on the home screen, clears everythin home screen.

In an editor, clears the expression or value where the cursor is located; it does not store a zero.

Deletes a character at the cursor; this key repeats.

] Changes the cursor to __ ; inserts characters in front of the

underline cursor; to end insertion, press y [

, or †.

Chan operation (an operation in yellow above a key and to the left); to cancel

Chan character (a character in green above a key and to the right) or executes

] Changes the cursor to Ø; sets alpha-lock; subsequent keystrokes

on an alpha key) paste alpha characters; to cancel alpha-lock,

press

Pastes an

Seq

†

on the

INS

] or press |, },

es the cursor to Þ; the next keystroke performs a

, press y again.

2nd

es the cursor to Ø; the next keystroke pastes an alpha

(Chapters 10 and 11); to cancel

SOLVE

, press

or press |, }, ~, or †.

; name prompts set alpha-lock automatically.

Func

mode, a T in

Par

mode, a q in

Pol

mode, or an

mode with one keystroke.

1-8 Operating the TI-83

Setting Modes

Checking Mode Settings

Changing Mode Settings

Setting a Mode from a Program

Mode settings control how the TI.83 displays and interprets numbers and graphs. Mode settings are retained by the Constant Memory feature when the TI.83 is turned off. All numbers, including elements of matrices and lists, are displayed according to the current mode settings.

To display the mode settings, press

. The current settings are highlighted. Defaults are highlighted below. The following pages describe the mode settings in detail.

Normal Sci Eng Float 0123456789 Radian Degree Func Par Pol Seq Connected Dot Sequential Simul Real a+bi re^qi Full Horiz G-T

Numeric notation Number of decimal places Unit of angle measure Type of graphing Whether to connect graph points Whether to plot simultaneously Real, rectangular cplx, or polar cplx Full screen, two split-screen modes

To change mode settings, follow these steps.

1. Press † or } to move the cursor to the line of the

setting that you want to change.

2. Press ~ or | to move the cursor to the setting you

want.

3. Press

You can set a mode from a program by entering the name of the mode as an instruction; for example,

Func or Float.

From a blank command line, select the mode setting from the mode screen; the instruction is pasted to the cursor location.

Operating the TI-83 1-9

Normal, Sci, Eng

Notation modes only affect the way an answer is displayed on the home screen. Numeric answers can be displayed with up to 10 digits and a two-digit exponent. You can enter a number in any format.

Normal notation mode is the usual way we express

numbers, with digits to the left and right of the decimal, as in

12345.67.

Sci (scientific) notation mode expresses numbers in two

parts. The significant digits display with one digit to the left of the decimal. The appropriate power of 10 displays to the right of

Eng (engineering) notation mode is similar to scientific

, as in 1.234567

notation. However, the number can have one, two, or three digits before the decimal; and the power-of-10 exponent is a multiple of three, as in

Note

: If you select 10 digits (or the absolute value is less than .001), the TI.83 expresses the answer in scientific notation.

Normal

12.34567E3.

notation, but the answer cannot display in

Float, 0123456789

Float (floating) decimal mode displays up to 10 digits, plus

the sign and decimal.

0123456789 (fixed) decimal mode specifies the number of

digits ( Place the cursor on the desired number of decimal digits, and then press

The decimal setting applies to notation modes.

The decimal setting applies to these numbers:

•

An answer displayed on the home screen

•

Coordinates on a graph (Chapters 3, 4, 5, and 6)

•

The and dy/dx values (Chapter 8)

•

Results of and 6)

•

The regression equation stored after the execution of a regression model (Chapter 12)

1-10 Operating the TI-83

0 through 9) to display to the right of the decimal.

Normal, Sci, and Eng

Tangent(

CALCULATE

instruction equation of the line, x,

DRAW

operations (Chapters 3, 4, 5,

Radian, Degree

Angle modes control how the TI.83 interprets angle values in trigonometric functions and polar/rectangular conversions.

Radian mode interprets angle values as radians. Answers

display in radians.

Degree mode interprets angle values as degrees. Answers

display in degrees.

Func, Par, Pol, Seq

Connected, Dot

Graphing modes define the graphing parameters. Chapters 3, 4, 5, and 6 describe these modes in detail.

Func (function) graphing mode plots functions, where Y is

a function of

Par (parametric) graphing mode plots relations, where X

X (Chapter 3).

and Y are functions of T (Chapter 4).

Pol (polar) graphing mode plots functions, where r is a

function of

Seq (sequence) graphing mode plots sequences (Chapter 6).

Connected plotting mode draws a line connecting each

(Chapter 5).

point calculated for the selected functions.

Dot plotting mode plots only the calculated points of the

selected functions.

Operating the TI-83 1-11

Sequential, Simul

Real, a+bi, re^

Sequential graphing-order mode evaluates and plots one

function completely before the next function is evaluated and plotted.

Simul (simultaneous) graphing-order mode evaluates and

plots all selected functions for a single value of evaluates and plots them for the next value of

Note:

Regardless of which graphing mode is selected, the TI.83 will

sequentially graph all stat plots before it graphs any functions.

Real mode does not display complex results unless

X and then

complex numbers are entered as input.

Two complex modes display complex results.

•

(rectangular complex mode) displays complex

a+b

numbers in the form a+bi.

•

(polar complex mode) displays complex numbers

re^

in the form re^

Full, Horiz, G.T

Full screen mode uses the entire screen to display a graph

or edit screen.

Each split-screen mode displays two screens simultaneously.

•

Horiz (horizontal) mode displays the current graph on

the top half of the screen; it displays the home screen or an editor on the bottom half (Chapter 9).

•

G.T (graph-table) mode displays the current graph on

the left half of the screen; it displays the table screen on the right half (Chapter 9).

1-12 Operating the TI-83

Using TI-83 Variable Names

Variables and Defined Items

On the TI.83 you can enter and use several types of data, including real and complex numbers, matrices, lists, functions, stat plots, graph databases, graph pictures, and strings.

The TI.83 uses assigned names for variables and other items saved in memory. For lists, you also can create your own five-character names.

Variable Type Names

Real numbers

Complex numbers

Matrices

Lists

A, B

, . . . , Z,

A, B

, . . . , Z,

ãAä, ãBä, ãCä

ãJä

, . . . ,

, and user-

defined names

Functions

Parametric equations

Polar functions

Sequence functions

Stat plots

Graph databases

Graph pictures

Strings

System variables

and

u, v, w Plot1, Plot2, Plot3 GDB1, GDB2 Pic1, Pic2 Str1, Str2 Xmin, Xmax

, . . . ,

, and others

GDB9, GDB0

Pic9, Pic0

Str9, Str0

and

Notes about Variables

•

You can create as many list names as memory will allow (Chapter 11).

•

Programs have user-defined names and share memory with variables (Chapter 16).

•

From the home screen or from a program, you can store to matrices (Chapter 10), lists (Chapter 11), strings

Xmax

(Chapter 15), system variables such as

TblStart

1),

(Chapter 7), and all Y= functions (Chapters

(Chapter

3, 4, 5, and 6).

•

From an editor, you can store to matrices, lists, and

functions (Chapter 3).

•

From the home screen, a program, or an editor, you can store a value to a matrix element or a list element.

•

You can use

DRAW STO

menu items to store and recall

graph databases and pictures (Chapter 8).

Operating the TI-83 1-13

Storing Variable Values

Storing Values in a Variable

Displaying a Variable Value

Values are stored to and recalled from memory using variable names. When an expression containing the name of a variable is evaluated, the value of the variable at that time is used.

To store a value to a variable from the home screen or a program using the follow these steps.

1. Enter the value you want to store. The value can be an

expression.

2. Press

3. Press

4. Press

To display the value of a variable, enter the name on a blank line on the home screen, and then press

¿. !

you want to store the value.

evaluated. The value is stored to the variable.

key, begin on a blank line and

is copied to the cursor location.

and then the letter of the variable to which

. If you entered an expression, it is

1-14 Operating the TI-83

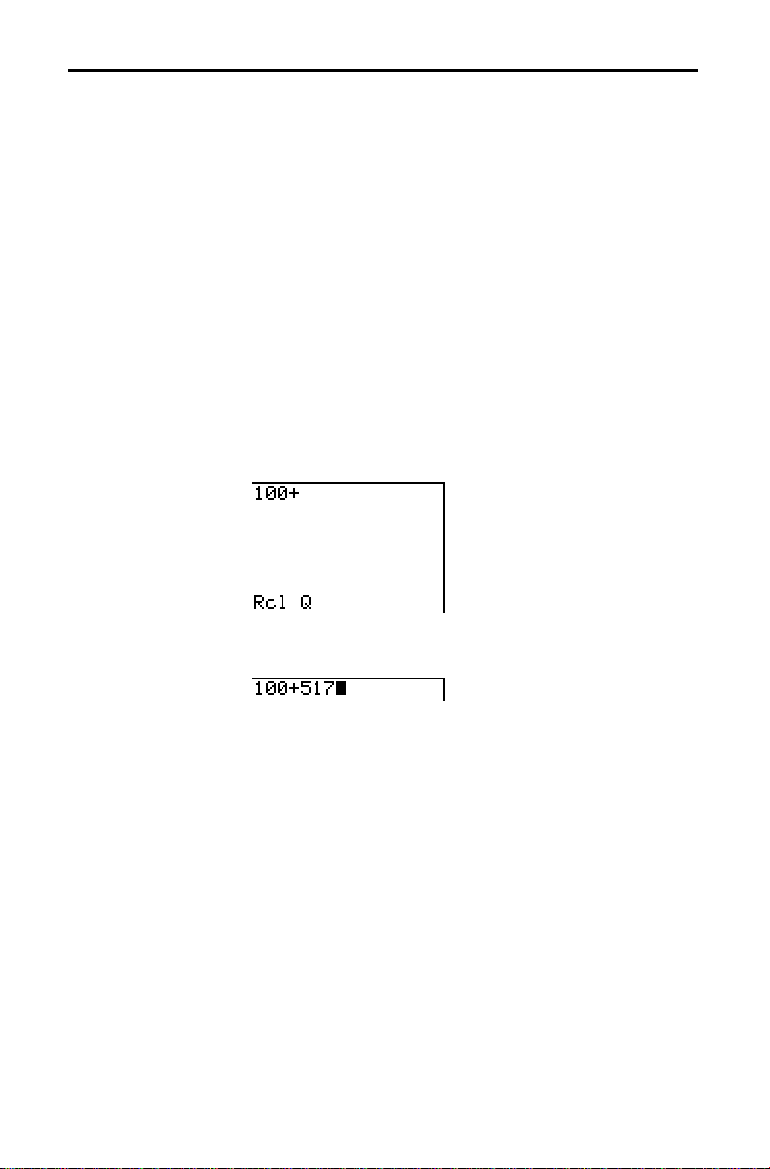
Recalling Variable Values

Using Recall (RCL)

To recall and copy variable contents to the current cursor location, follow these steps. To leave

RCLä

1. Press y

Rcl and the edit cursor are displayed on

RCL

, press

‘

the bottom line of the screen.

2. Enter the name of the variable in any of five ways.

•

Press Press y

and then the letter of the variable.

LISTä

, and then select the name of the list,

or press y [Ln].

•



Press



Press display the

, and then select the name of the matrix.

to display the

VARS Y.VARS

menu or

VARS

menu; then select the type

 ~

and then the name of the variable or function.

•

Press

 |

, and then select the name of the

program (in the program editor only).

The variable name you selected is displayed on the bottom line and the cursor disappears.

3. Press

. The variable contents are inserted where

the cursor was located before you began these steps.

Note:

You can edit the characters pasted to the expression without

affecting the value in memory.

Operating the TI-83 1-15

ENTRY (Last Entry) Storage Area

Using ENTRY (Last Entry)

Accessing a Previous Entry

When you press

on the home screen to evaluate an expression or execute an instruction, the expression or instruction is placed in a storage area called entry). When you turn off the TI.83,

ENTRY

is retained in

ENTRY

(last

memory.

To recall

ENTRY

, press y [

ENTRY

]. The last entry is pasted to the current cursor location, where you can edit and execute it. On the home screen or in an editor, the current line is cleared and the last entry is pasted to the line.

Because the TI.83 updates

, you can recall the previous entry even if you have

only when you press

ENTRY

begun to enter the next expression.

ENTRY

[

]

The TI.83 retains as many previous entries as possible in

, up to a capacity of 128 bytes. To scroll those

ENTRY

entries, press y [ more than 128 bytes, it is retained for be placed in the

¿ ƒ

ENTRY

] repeatedly. If a single entry is

, but it cannot

ENTRY

storage area.

¿ ƒ

ENTRY

[

]

If you press y [ entry, the newest stored entry is displayed again, then the next-newest entry, and so on.

ENTRY

[

1-16 Operating the TI-83

ENTRY

] after displaying the oldest stored

]

Reexecuting the Previous Entry

After you have pasted the last entry to the home screen and edited it (if you chose to edit it), you can execute the entry. To execute the last entry, press

To reexecute the displayed entry, press

again. Each reexecution displays an answer on the right side of the next line; the entry itself is not redisplayed.

¿ ƒ

Í ƒ ƒ

ã:ä

¿ ƒ

¡ Í

Í Í

Multiple Entry Values on a Line

Clearing ENTRY

To store to

two or more expressions or

ENTRY

instructions, separate each expression or instruction with a colon, then press separated by colons are stored in

When you press y [

. All expressions and instructions

ENTRY

], all the expressions and instructions separated by colons are pasted to the current cursor location. You can edit any of the entries, and then execute all of them when you press

For the equation A=pr2, use trial and error to find the radius of a circle that covers 200 square centimeters. Use 8 as your first guess.

¿ ƒ

[:] y [p]

ENTRY

[

y |

]

INS

[

R ¡

] Ë 95

Continue until the answer is as accurate as you want.

Clear Entries (Chapter 18) clears all data that the TI

holding in the

ENTRY

storage area.

83 is

Operating the TI-83 1-17

Ans (Last Answer) Storage Area

Using Ans in an Expression

Continuing an Expression

When an expression is evaluated successfully from the home screen or from a program, the TI.83 stores the answer to a storage area called

Ans (last answer). Ans may

be a real or complex number, a list, a matrix, or a string. When you turn off the TI.83, the value in

Ans is retained in

memory.

You can use the variable most places. Press y [

Ans to represent the last answer in

ANS

] to copy the variable name Ans

to the cursor location. When the expression is evaluated, the TI.83 uses the value of

Calculate the area of a garden plot 1.7 meters by 4.2 meters. Then calculate the yield per square meter if the plot produces a total of 147 tomatoes.

7 ¯ 4 Ë 2

Ans in the calculation.

147

¥ y

[

ANS

]

You can use Ans as the first entry in the next expression without entering the value again or pressing y [

ANS

]. On a blank line on the home screen, enter the function. The TI.83 pastes the variable name

Ans to the screen, then the

function.

Í ¯

Storing Answers

To store an answer, store Ans to a variable before you evaluate another expression.

Calculate the area of a circle of radius 5 meters. Next, calculate the volume of a cylinder of radius 5 meters and height 3.3 meters, and then store the result in the variable V.

[

] 5

Í ¯

3 Ë 3

Í ¿ ƒ Í

1-18 Operating the TI-83

TI-83 Menus

Using a TI-83 Menu

Scrolling a Menu

You can access most TI.83 operations using menus. When you press a key or key combination to display a menu, one or more menu names appear on the top line of the screen.

•

The menu name on the left side of the top line is highlighted. Up to seven items in that menu are displayed, beginning with item

1, which also is

highlighted.

•

A number or letter identifies each menu item’s place in the menu. The order is and so on. The

menus only label items 1 through 9 and 0.

EDIT

•

When the menu continues beyond the displayed items, a

LIST NAMES, PRGM EXEC

1 through 9, then 0, then A, B, C,

, and

PRGM

down arrow ( $ ) replaces the colon next to the last displayed item.

•

When a menu item ends in an ellipsis, the item displays a secondary menu or editor when you select it.

To display any other menu listed on the top line, press

or | until that menu name is highlighted. The cursor location within the initial menu is irrelevant. The menu is displayed with the cursor on the first item.

Note:

The Menu Map in Appendix A shows each menu, each operation under each menu, and the key or key combination you press to display each menu.

To scroll down the menu items, press †. To scroll up the menu items, press }.

To page down six menu items at a time, press page up six menu items at a time, press

ƒ †

ƒ }

. To

. The green arrows on the calculator, between † and }, are the page-down and page-up symbols.

To wrap to the last menu item directly from the first menu item, press }. To wrap to the first menu item directly from the last menu item, press †.

Operating the TI-83 1-19

Selecting an Item from a Menu

You can select an item from a menu in either of two ways.

•

Press the number or letter of the item you want to select. The cursor can be anywhere on the menu, and the item you select need not be displayed on the screen.

•

Press † or } to move the cursor to the item you want, and then press

After you select an item from a menu, the TI.83 typically displays the previous screen.

Note:

On the menus, only items 1 through 9 and 0 are labeled in such a way that you can select them by pressing the appropriate number key. To move the cursor to the first item beginning with any alpha character or q, press the key combination for that alpha character or q. If no items begin with that character, then the cursor moves beyond it to the next item.

Calculate

LIST NAMES, PRGM EXEC

‡

27.

, and

PRGM EDIT

 † † † Í

Leaving a Menu without Making a Selection

You can leave a menu without making a selection in any of four ways.

•

Press y [

•

Press

•

Press a key or key combination for a different menu, such as

•

Press a key or key combination for a different screen, such as o or y [

QUIT

] to return to the home screen.

‘

to return to the previous screen.



or y [

LIST

TABLE

1-20 Operating the TI-83

VARS and VARS Y-VARS Menus

VARS Menu

Selecting a Variable from the VARS Menu or VARS Y-VARS Menu

You can enter the names of functions and system variables in an expression or store to them directly.

To display the

menu, press

VARS



. All

VARS

menu items display secondary menus, which show the names of the system variables.

1:Window, 2:Zoom, and 5:Statistics

each access more than one secondary menu.

VARS Y-VARS 1: Window 2: Zoom 3: GDB 4: Picture 5: Statistics 6: Table 7: String

To display the

1:Function, 2:Parametric, and 3:Polar display secondary

menus of the

VARS Y-VARS 1: Function 2: Parametric 3: Polar 4: On/Off

Note:

as the second functions of ¬, −, and ®.

...

VARS Y.VARS

function variables.

...

The sequence variables (

Y X

...

Lets you select/deselect functions

To select a variable from the

, and

X/Y, T/ ZX/ZY, ZT/Z Graph database Picture

, G, EQ,

XY TABLE String

variables

TEST

variables

menu, press

functions

, Y

functions

u, v, w

) are located on the keyboard

VARS

variables

U/V/W

, and ZU variables

variables

, and

PTS

variables

 ~

VARS Y.VARS

menu,

follow these steps.

1. Display the

•

Press Press

  ~

2. Select the type of variable, such as

menu or 3:Polar from the

VARS

VARS Y.VARS

to display the

menu.

VARS

VARS Y.VARS

2:Zoom from the

VARS Y.VARS

menu.

menu. A

secondary menu is displayed.

3. If you selected

the

VARS

1:Window, 2:Zoom, or 5:Statistics from

menu, you can press ~ or | to display other

secondary menus.

4. Select a variable name from the menu. It is pasted to the

cursor location.

Operating the TI-83 1-21

Equation Operating System (EOS™)

Order of Evaluation

The Equation Operating System (EOSé) defines the order in which functions in expressions are entered and evaluated on the TI.83. EOS lets you enter numbers and functions in a simple, straightforward sequence.

EOS evaluates the functions in an expression in this order:

1 Single-argument functions that precede the

‡

argument, such as

2 Functions that are entered after the argument,

such as

, !, ¡, r, and conversions

3 Powers and roots, such as 2^5 or 5

(

, sin(, or log(

‡

4 Permutations (nPr) and combinations (nCr)

5 Multiplication, implied multiplication, and

division

6 Addition and subtraction 7 Relational functions, such as > or



8 Logic operator and 9 Logic operators or and xor

Within a priority level, EOS evaluates functions from left to right.

Calculations within parentheses are evaluated first. Multiargument functions, such as

nDeriv(A2,A,6), are

evaluated as they are encountered.

1-22 Operating the TI-83

Implied Multiplication

The TI.83 recognizes implied multiplication, so you need not press ¯ to express multiplication in all cases. For example, the TI.83 interprets

, 4sin(46), 5(1+2), and (2

as implied multiplication.

Note:

TI.83 implied multiplication rules differ from those of the TI.82. For example, the TI.83 evaluates evaluates

1à2X

1/(2äX)

1à2X

(Chapter 2).

(1à2)äX

, while the TI.82

5)7

Parentheses

Negation

All calculations inside a pair of parentheses are completed first. For example, in the expression evaluates the portion inside the parentheses, multiplies the answer,

3, by 4.

4(1+2), EOS first

1+2, and then

You can omit the close parenthesis ( ) ) at the end of an expression. All open parenthetical elements are closed automatically at the end of an expression. This is also true for open parenthetical elements that precede the store or display-conversion instructions.

Note:

An open parenthesis following a list name, matrix name, or function name does not indicate implied multiplication. It specifies elements in the list (Chapter 11) or matrix (Chapter 10) and specifies a value for which to solve the

function.

To enter a negative number, use the negation key. Press

and then enter the number. On the TI.83, negation is in the third level in the EOS hierarchy. Functions in the first level, such as squaring, are evaluated before negation.

For example,

, evaluates to a negative number (or 0).

Use parentheses to square a negative number.

Note:

Use the ¹ key for subtraction and the Ì key for negation. If you press ¹ to enter a negative number, as in press Ì to indicate subtraction, as in press

(

B, it is interpreted as implied multiplication

¯ ¹ 7, or if you

Ì 7, an error occurs. If you

Operating the TI-83 1-23

Error Conditions

Diagnosing an Error

Correcting an Error

The TI.83 detects errors while performing these tasks.

•

Evaluating an expression

•

Executing an instruction

•

Plotting a graph

•

Storing a value

When the TI.83 detects an error, it returns an error message as a menu title, such as

ERR:DOMAIN

. Appendix B describes each error type and

ERR:SYNTAX

possible reasons for the error.

•

If you select

1:Quit (or press

[

QUIT

] or

‘

), then

the home screen is displayed.

•

If you select

2:Goto, then the previous screen is

displayed with the cursor at or near the error location.

Note

: If a syntax error occurs in the contents of a Y= function during program execution, then the to the program.

Goto

option returns to the Y= editor, not

To correct an error, follow these steps.

1. Note the error type (

2. Select

2:Goto, if it is available. The previous screen is

ERR:

error type

displayed with the cursor at or near the error location.

3. Determine the error. If you cannot recognize the error,

refer to Appendix B.

4. Correct the expression.

1-24 Operating the TI-83

Math, Angle, and Test

Contents

Operations

Getting Started: Coin Flip Keyboard Math Operations

MATH

Operations

Using the Equation Solver

MATH NUM

Entering and Using Complex Numbers

MATH CPX MATH PRB ANGLE TEST TEST LOGIC

(Number) Operations

(Complex) Operations (Probability) Operations

Operations

(Relational) Operations

(Boolean) Operations

................................

..............................

........................................

...............................

........................

.......................

.......................................

............................

......................

...................

.....................

2-2 2-3 2-5

2-8 2-13 2-16 2-18 2-20 2-23 2-24 2-26

Math, Angle, and Test Operations 2-1

Getting Started: Coin Flip

Getting Started is a fast-paced introduction. Read the chapter for details.

Suppose you want to model flipping a fair coin 10 times. You want to track how many of those 10 coin flips result in heads. You want to perform this simulation 40 times. With a fair coin, the probability of a coin flip resulting in heads is 0.5 and the probability of a coin flip resulting in tails is 0.5.

1. Begin on the home screen. Press display the select

randBin( is pasted to the home screen. Press 10 to enter the number of coin flips. Press

. Press

MATH PRB

7:randBin( (random Binomial).

5 to enter the probability of

heads. Press ¢. Press

menu. Press 7 to

40 to enter the

 |

number of simulations. Press ¤.

2. Press

to evaluate the expression. A list of 40 elements is displayed. The list contains the count of heads resulting from each set of 10 coin flips. The list has 40 elements because this simulation was performed 40 times. In this example, the coin came up heads five times in the first set of 10 coin flips, five times in the second set of 10 coin flips, and so on.

L1ä

3. Press

¿ y

to the list name

. You then can use the

to store the data

data for another activity, such as plotting a histogram (Chapter 12).

4. Press ~ or | to view the additional counts in the list. Ellipses (

...) indicate that the list

continues beyond the screen.

Note:

numbers, your list elements may differ from those in the example.

Since

randBin(

generates random

2-2 Math, Angle, and Test Operations

Keyboard Math Operations

Using Lists with Math Operations

+ (Addition),

(Subtraction),

(Multiplication),

(Division)

Trigonometric Functions

Math operations that are valid for lists return a list calculated element by element. If you use two lists in the same expression, they must be the same length.

You can use + (addition, Ã), N (subtraction, ¹),

(multiplication, ¯), and à (division, ¥) with real and complex numbers, expressions, lists, and matrices. You cannot use

valueA valueA

with matrices.

valueB valueA

N à

valueB valueB

You can use the trigonometric (trig) functions (sine, ˜; cosine, ™; and tangent, š) with real numbers, expressions, and lists. The current angle mode setting affects interpretation. For example,

returns

sin(

You can use the inverse trig functions (arcsine, y [ arccosine, y [

.9880316241

value

) cos(

; in Degree mode it returns .5.

value

COS

]; and arctangent, y [

sin(30) in Radian mode

) tan(

TAN

value

]) with

)

SIN

real numbers, expressions, and lists. The current angle mode setting affects interpretation.

value

sin

(

) cos

Note:

The trig functions do not operate on complex numbers.

value

(

) tan

value

(

];

)

^ (Power),

(Square),

‡

( (Square Root)

(Inverse)

‡

You can use ^ (power, ›), 2 (square, ¡), and root, y [ lists, and matrices. You cannot use

value

You can use

‡

]) with real and complex numbers, expressions,

‡

(

with matrices.

power value

(inverse,

—

) with real and complex

(

(square

value

‡

(

numbers, expressions, lists, and matrices. The multiplicative inverse is equivalent to the reciprocal, 1

value

Math, Angle, and Test Operations 2-3

)

log(, 10^(, ln(

e^( (Exponential)

You can use log( (logarithm, «), 10^( (power of 10,

]), and ln( (natural log, µ) with real or complex

[ numbers, expressions, and lists.

log(

e^(

a power. You can use

) 10^(

value

(exponential, y

)ln(

power

]) returns the constant e raised to

e^( with real or complex numbers,

value

expressions, and lists.

e^(

power

)

e (Constant)

(Negation)

(Pi)

e (constant,

Press y [ calculations, the TI-83 uses 2.718281828459 for

(negation, Ì) returns the negative of

[e]) is stored as a constant on the TI-83.

] to copy e to the cursor location. In

value

. You can use with real or complex numbers, expressions, lists, and matrices.

value

EOS rules (Chapter 1) determine when negation is evaluated. For example, because squaring is evaluated before negation. Use parentheses to square a negated number, as in

Note:

On the TI-83, the negation symbol (

the subtraction sign (

(Pi, y [p]) is stored as a constant in the TI-83. In

), which is displayed when you press ¹.

calculations, the TI-83 uses 3.1415926535898 for

returns a negative number,

(LA)

) is shorter and higher than

2-4 Math, Angle, and Test Operations

MATH Operations

MATH Menu

Frac,

Dec

MATH

To display the

MATH NUM CPX PRB 1:4Frac 2:4Dec

‡

(

‡

5: 6: fMin( 7: fMax( 8: nDeriv( 9: fnInt( 0: Solver

Frac

...

(display as a fraction) displays an answer as its

menu, press

Displays the answer as a fraction. Displays the answer as a decimal. Calculates the cube. Calculates the cube root. Calculates the Finds the minimum of a function. Finds the maximum of a function. Computes the numerical derivative. Computes the function integral. Displays the equation solver.

rational equivalent. You can use



root.

Frac

with real or complex numbers, expressions, lists, and matrices. If the answer cannot be simplified or the resulting denominator is more than three digits, the decimal equivalent is returned. You

Frac

following

Dec

can only use

value

Dec

(display as a decimal) displays an answer in decimal form. You can use expressions, lists, and matrices. You can only use

Dec

value

following

value

with real or complex numbers,

Dec

Math, Angle, and Test Operations 2-5

(Cube),

‡

( (Cube Root)

(cube) returns the cube of

value

. You can use 3 with real or complex numbers, expressions, lists, and square matrices.

value

‡

(

(cube root) returns the cube root of

‡

(

with real or complex numbers, expressions, and lists.

value

‡

(

)

value

. You can use

‡

(Root)

fMin(, fMax(

‡

(

root) returns the

root

value

. You can use

‡

with real or complex numbers, expressions, and lists.

root

fMin( (function minimum) and fMax( (function maximum)

value

‡

return the value at which the local minimum or local maximum value of occurs, between and fMax( are not valid in controlled by

5).

expression,variable,lower,upper

fMin(

expression,variable,lower,upper

fMax(

Note:

In this guidebook, optional arguments and the commas that

accompany them are enclosed in brackets ([ ]).

expression

lower

tolerance

with respect to

upper

and

expression

values for

. The accuracy is

(if not specified, the default is

[

variable

tolerance

variable

]

)

]

)

fMin(

2-6 Math, Angle, and Test Operations

nDeriv(

nDeriv( (numerical derivative) returns an approximate

derivative of

value

at which to calculate the derivative and H (if not

specified, the default is 1

expression

with respect to

3). nDeriv( is valid only for real

variable

, given the

numbers.

expression,variable,value

nDeriv( nDeriv( uses the symmetric difference quotient method,

[

]

)

which approximates the numerical derivative value as the slope of the secant line through these points.

(

f¢(

) =

+H)Nf(

)

As H becomes smaller, the approximation usually becomes more accurate.

fnInt(

You can use nDeriv( once in method used to calculate

expression

nDeriv(, the TI

. Because of the

83 can return a

false derivative value at a nondifferentiable point.

fnInt( (function integral) returns the numerical integral

limit,

expression

upper

5). fnInt( is valid only for real

with respect to

limit, and a

tolerance

(Gauss-Kronrod method) of

variable

, given

lower

not specified, the default is 1 numbers.

expression,variable,lower,upper

fnInt(

To speed the drawing of integration graphs (when

Tip:

in a Y= equation), increase the value of the before you press

tolerance

[

window variable

Xres

]

)

fnInt(

is used

Math, Angle, and Test Operations 2-7

(if

Using the Equation Solver

Solver

Entering an Expression in the Equation Solver

Solver displays the equation solver, in which you can solve

for any variable in an equation. The equation is assumed to be equal to zero.

When you select

•

The equation editor (see step 1 picture below) is displayed when the equation variable

•

The interactive solver editor (see step 3 picture on page

2.9) is displayed when an equation is stored in

Solver is valid only for real numbers. Solver, one of two screens is displayed.

eqn is empty.

eqn.

To enter an expression in the equation solver, assuming that the variable

1. Select

eqn is empty, follow these steps.

0:Solver from the

MATH

menu to display the

equation editor.

2. Enter the expression in any of three ways.

•

Enter the expression directly into the equation solver.

•

Paste a

variable name from the

VARS Y.VARS

menu to the equation solver.

•

Press y [

VARS Y.VARS

RCL

], paste a Y= variable name from the

menu, and press

. The

expression is pasted to the equation solver.

The expression is stored to the variable

eqn as you

enter it.

2-8 Math, Angle, and Test Operations

3. Press

displayed.

or †. The interactive solver editor is

Entering and Editing Variable Values

•

The equation stored in

eqn is set equal to zero and

displayed on the top line.

•

Variables in the equation are listed in the order in which they appear in the equation. Any values stored to the listed variables also are displayed.

•

The default lower and upper bounds appear in the last line of the editor (

•

is displayed in the first column of the bottom line

bound={L1å99,1å99}).

if the editor continues beyond the screen.

To use the solver to solve an equation such as

Tip:

eqn:0=KN.5MV

in the equation editor.

K=.5MV

, enter

When you enter or edit a value for a variable in the interactive solver editor, the new value is stored in memory to that variable.

You can enter an expression for a variable value. It is evaluated when you move to the next variable. Expressions must resolve to real numbers at each step during the iteration.

You can store equations to any such as

or r6, and then reference the variables in the

VARS Y.VARS

variables,

equation. The interactive solver editor displays all variables of all

functions referenced in the equation.

Math, Angle, and Test Operations 2-9

Solving for a Variable in the Equation Solver

To solve for a variable using the equation solver after an equation has been stored to

1. Select

0:Solver from the

eqn, follow these steps.

menu to display the

MATH

interactive solver editor, if not already displayed.

2. Enter or edit the value of each known variable. All

variables, except the unknown variable, must contain a value. To move the cursor to the next variable, press

or †.

3. Enter an initial guess for the variable for which you are

solving. This is optional, but it may help find the solution more quickly. Also, for equations with multiple roots, the TI-83 will attempt to display the solution that is closest to your guess.

upper + lower

The default guess is calculated as

(

)

2-10 Math, Angle, and Test Operations

4. Edit

bound={

lower,upper

lower

and

upper

are the bounds between which the TI-83 searches for a solution. This is optional, but it may help find the solution more quickly. The default is

bound={L1å99,1å99}.

5. Move the cursor to the variable for which you want to solve and press

•

The solution is displayed next to the variable for

SOLVE

[

] (above the

key).

which you solved. A solid square in the first column marks the variable for which you solved and indicates that the equation is balanced. An ellipsis shows that the value continues beyond the screen.

Note:

When a number continues beyond the screen, be sure to press ~ to scroll to the end of the number to see whether it ends with a negative or positive exponent. A very small number may appear to be a large number until you scroll right to see the exponent.

•

The values of the variables are updated in memory.

•

diff

leftNrt=

diff

is displayed in the last line of the editor.

is the difference between the left and right sides of the equation. A solid square in the first column next to

leftNrt= indicates that the equation has been

evaluated at the new value of the variable for which you solved.

Math, Angle, and Test Operations 2-11

Editing an Equation Stored to eqn

To edit or replace an equation stored to eqn when the interactive equation solver is displayed, press } until the equation editor is displayed. Then edit the equation.

Equations with Multiple Roots

Further Solutions

Controlling the Solution for Solver or solve(

Using solve( on the Home Screen or from a Program

Some equations have more than one solution. You can enter a new initial guess (page 2.10) or new bounds (page 2.11) to look for additional solutions.

After you solve for a variable, you can continue to explore solutions from the interactive solver editor. Edit the values of one or more variables. When you edit any variable value, the solid squares next to the previous solution and

diff

leftNrt=

which you now want to solve and press

disappear. Move the cursor to the variable for

SOLVE

[

The TI-83 solves equations through an iterative process. To control that process, enter bounds that are relatively close to the solution and enter an initial guess within those bounds. This will help to find a solution more quickly. Also, it will define which solution you want for equations with multiple solutions.

The function

solve( is available only from

CATALOG

from within a program. It returns a solution (root) of

expression

upper

and default for

solve( is valid only for real numbers.

expression,variable,guess

solve(

expression

will not be updated in memory.

for

variable

, given an initial

guess

, and

lower

bounds within which the solution is sought. The

lower

is L1â99. The default for

[

is assumed equal to zero. The value of

guess

upper

is 1â99.

lower,upper

}])

may be a value or a

variable

list of two values. Values must be stored for every variable

expression

in evaluated.

, except

lower

and

variable

upper

, before

must be entered in list format.

expression

2-12 Math, Angle, and Test Operations

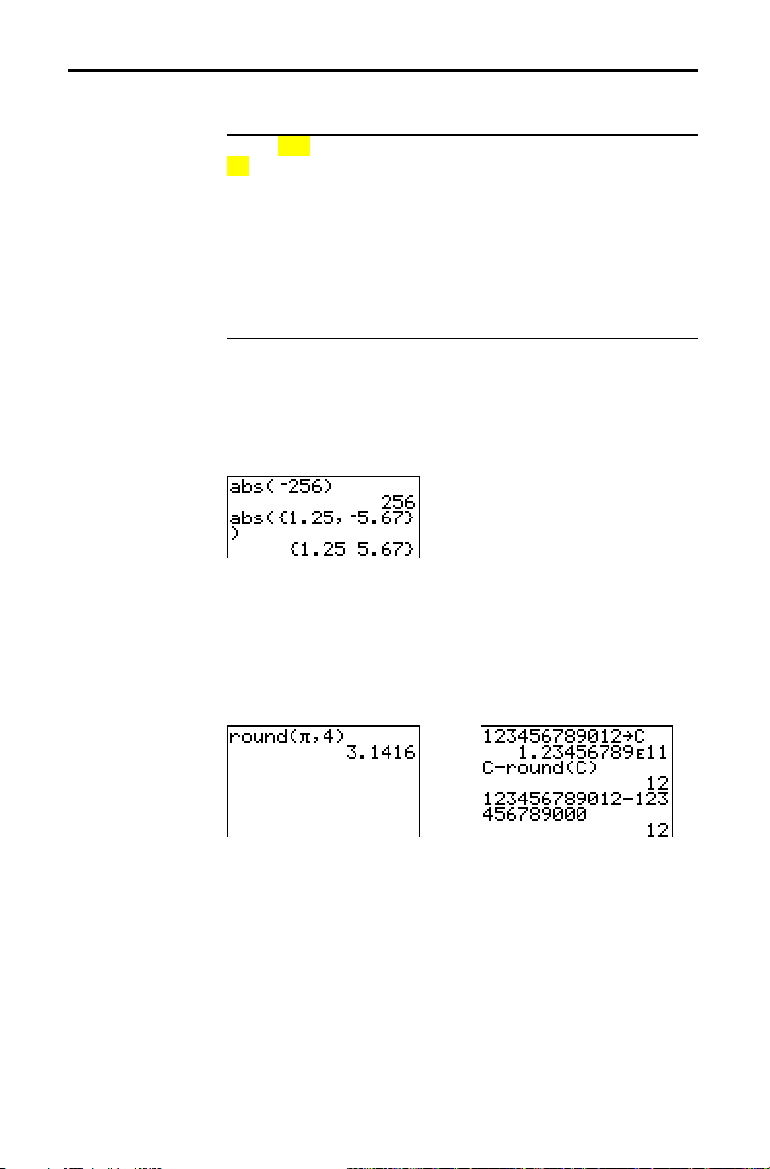
MATH NUM (Number) Operations

MATH NUM Menu

abs(

round(

To display the

MATH NUM CPX PRB 1: abs( 2: round( 3: iPart( 4: fPart( 5: int( 6: min( 7: max( 8: lcm( 9: gcd(

abs( (absolute value) returns the absolute value of real or

MATH NUM

menu, press

Absolute value Round Integer part Fractional part Greatest integer Minimum value Maximum value Least common multiple Greatest common divisor

 ~

complex (modulus) numbers, expressions, lists, and matrices.

value

abs(

Note:

round( returns a number, expression, list, or matrix

rounded to

)

is also available on the

abs(

#decimals (

9). If

MATH CPX

#decimals

menu.

is omitted,

value

is rounded to the digits that are displayed, up to 10 digits.

value

#decimals

round(

[

]

)

Math, Angle, and Test Operations 2-13

iPart(, fPart(

iPart( (integer part) returns the integer part or parts of real

or complex numbers, expressions, lists, and matrices.

value

iPart( fPart( (fractional part) returns the fractional part or parts of

)

real or complex numbers, expressions, lists, and matrices.

value

fPart(

)

int(

int( (greatest integer) returns the largest integer



complex numbers, expressions, lists, and matrices.

value

int(

Note:

iPart(

less than the result of

)

value

For a given

for nonnegative numbers and negative integers, but one integer

, the result of

iPart(

int(

is the same as the result of

for negative noninteger numbers.

real or

2-14 Math, Angle, and Test Operations

min(, max(

min( (minimum value) returns the smaller of

valueB

or the smallest element in compared, elements. If each element in

max( (maximum value) returns the larger of

valueB

compared, elements. If each element in

min( min( min( min(

min( returns a list of the smaller of each pair of

list

and

list

value

are compared,

value

with

or the largest element in

max( returns a list of the larger of each pair of

list

valueA,valueB list

) max(

listA,listB list,value

value

and

list

) max(

value

with

) max(

are compared,

list

. If

list

listA

. If

valueA,valueB list

)

listA,listB list,value

)

listA

min( compares

max( compares

)

valueA

and

valueA

and

listB

and

listB

and

are

lcm(, gcd(

and

min(

Note:

lcm( returns the least common multiple of

valueB

, both of which must be nonnegative integers. When

listA

and

listB

of each pair of elements. If

lcm( finds the lcm of each element in gcd( returns the greatest common divisor of

valueB

, both of which must be nonnegative integers. When

listA

and

listB

of each pair of elements. If

gcd( finds the gcd of each element in

valueA,valueB

lcm(

listA,listB

lcm(

list,value

lcm(

also are available on the

max(

are specified,

lcm( returns a list of the lcm

list

are specified,

gcd( returns a list of the gcd

list

) gcd(

LIST MATH

value

and

are specified,

list

and

value

are specified,

list

and

valueA,valueB listA,listB list,value

)

valueA

)

and

value

valueA

value

)

menu.

and

Math, Angle, and Test Operations 2-15

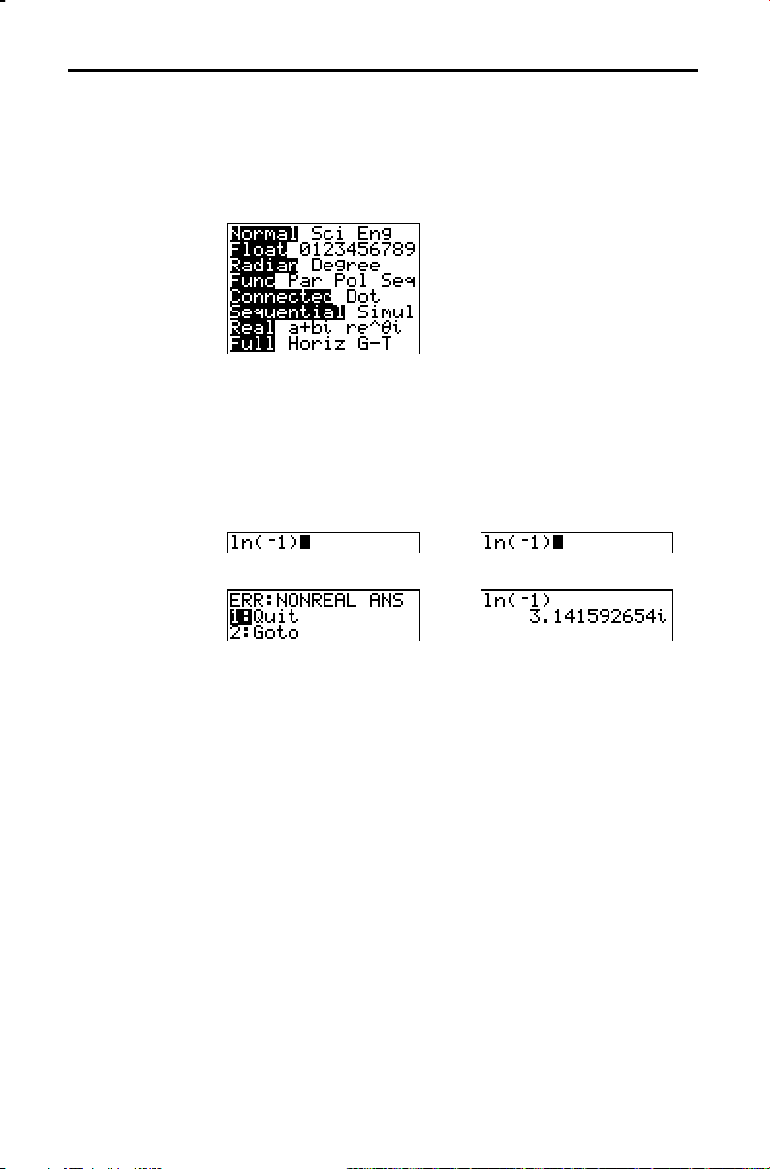
Entering and Using Complex Numbers

Complex-Number Modes

Entering Complex Numbers

The TI-83 displays complex numbers in rectangular form and polar form. To select a complex-number mode, press

, and then select either of the two modes.

•

a+b

•

(rectangular-complex mode)

re^

(polar-complex mode)

On the TI-83, complex numbers can be stored to variables. Also, complex numbers are valid list elements.

Real mode, complex-number results return an error,

unless you entered a complex number as input. For example, in

ln(L1) returns an answer. Real mode a+b

Real mode ln(L1) returns an error; in a+b

mode

Complex numbers are stored in rectangular form, but you can enter a complex number in rectangular form or polar form, regardless of the mode setting. The components of complex numbers can be real numbers or expressions that evaluate to real numbers; expressions are evaluated when the command is executed.

Note about Radian versus Degree Mode

Radian mode is recommended for complex number calculations. Internally, the TI-83 converts all entered trig values to radians, but it does not convert values for exponential, logarithmic, or hyperbolic functions.

In degree mode, complex identities such as

) = cos(q) + i sin(q) are not generally true because the values for cos and sin are converted to radians, while those for e^() are not. For example,

^(i45) = cos(45) + i sin(45) is treated internally as

^(i45) = cos(p/4) + i sin(p/4). Complex identities are

always true in radian mode.

2-16 Math, Angle, and Test Operations

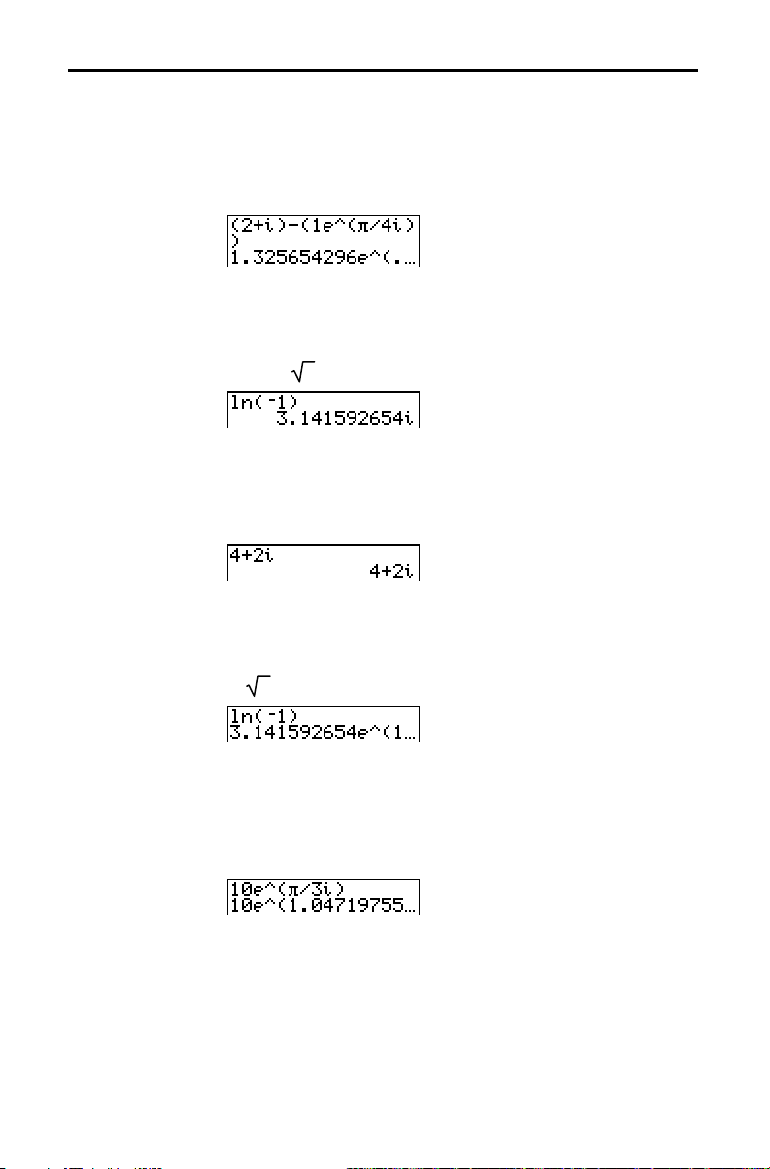
Interpreting Complex Results

Complex numbers in results, including list elements, are displayed in either rectangular or polar form, as specified by the mode setting or by a display conversion instruction

(page 2.19). In the example below,

re^

and

Radian modes

are set.

RectangularComplex Mode

Polar-Complex Mode

Rectangular-complex mode recognizes and displays a complex number in the form component, equal to

is the imaginary component, and i is a constant

-1

a+b

, where

is the real

To enter a complex number in rectangular form, enter the value of a ( of b (

real component

imaginary component

imaginary componenti

(

+ or

)

), press Ã or ¹, enter the value

), and press y [i] (constant).

Polar-complex mode recognizes and displays a complex

number in the form base of the natural log, to

-1

To enter a complex number in polar form, enter the value

magnitude

of r ( enter the value of

re^

, where r is the magnitude, e is the

is the angle, and i is a constant equal

), press y [

angle

(

] (exponential function),

), press y [i] (constant), and

then press ¤.

magnitude

e^(

angle

)

Math, Angle, and Test Operations 2-17

MATH CPX (Complex) Operations

MATH CPX Menu

conj(

real(

imag(

To display the

MATH NUM CPX PRB 1: conj( 2: real( 3: imag( 4: angle( 5: abs( 6:4Rect 7:4Polar

conj( (conjugate) returns the complex conjugate of a

MATH CPX

menu, press

Returns the complex conjugate. Returns the real part. Returns the imaginary part. Returns the polar angle. Returns the magnitude (modulus). Displays the result in rectangular form. Displays the result in polar form.

 ~ ~

complex number or list of complex numbers.

conj(a+ conj(re^(

real( (real part) returns the real part of a complex number

) returns

)) returns re^(

aNb

in a+b

mode.

) in re^

mode.

or list of complex numbers.

real(a+ real(re^(

imag( (imaginary part) returns the imaginary (nonreal) part

) returns

)) returns

cos

(

of a complex number or list of complex numbers.

imag(a+ imag(re^(

) returns

)) returns

sin(q)

2-18 Math, Angle, and Test Operations

angle(

angle( returns the polar angle of a complex number or list

of complex numbers, calculated as tan

(b/a), where b is the imaginary part and a is the real part. The calculation is adjusted by +p in the second quadrant or Np in the third quadrant.

(b/a)

angle(a+bi) returns

angle(re^(

)) returns

tan

, where Lp<q<p.

abs(

Rect

Polar

abs( (absolute value) returns the magnitude (modulus),

(real2+imag2)

, of a complex number or list of complex

numbers.

abs(a+bi) returns

abs(re^(

Rect

)) returns

(display as rectangular) displays a complex result in

(a2+b2)

(magnitude).

rectangular form. It is valid only at the end of an expression. It is not valid if the result is real.

complex result

Polar

(display as polar) displays a complex result in polar

Rect

returns a+bi.

form. It is valid only at the end of an expression. It is not valid if the result is real.

complex result

Polar

returns

e^(

Math, Angle, and Test Operations 2-19

MATH PRB (Probability) Operations

MATH PRB Menu

rand

To display the

MATH NUM CPX PRB 1: rand 2: nPr 3: nCr 4: ! 5: randInt( 6: randNorm( 7: randBin(

rand (random number) generates and returns one or more

MATH PRB

menu, press

Random-number generator Number of permutations Number of combinations Factorial Random-integer generator Random # from Normal distribution Random # from Binomial distribution

 |

random numbers > 0 and < 1. To generate a list of randomnumbers, specify an integer > 1 for trials). The default for

numtrials

rand[(

Tip:

To generate random numbers beyond the range of 0 to 1, you can include random number > 0 and < 5.

rand

in an expression. For example,

numtrials

)]

numtrials

is 1.

(number of

randä5

generates a

With each rand execution, the TI-83 generates the same random-number sequence for a given seed value. The TI-83 factory-set seed value for

rand is 0. To generate a different

random-number sequence, store any nonzero seed value to

rand. To restore the factory-set seed value, store 0 to rand

or reset the defaults (Chapter 18).

Note:

The seed value also affects

randBin(

instructions (page 2.22).

randInt(, randNorm(

, and

2-20 Math, Angle, and Test Operations

nPr, nCr

nPr (number of permutations) returns the number of

permutations of

number number

items

nCr (number of combinations) returns the number of

must be nonnegative integers. Both can be lists.

nPr

combinations of

number number

items

must be nonnegative integers. Both can be lists.

nCr

items

number

items

number

taken

number

at a time.

items

at a time.

items

and

items

and

! (Factorial)

! (factorial) returns the factorial of either an integer or a

multiple of .5. For a list, it returns factorials for each integer or multiple of .5.

value

The factorial is computed recursively using the relationship

Note:

(n+1)! = nän!, until n is reduced to either 0 or L1/2. At that point, the definition 0!=1 or the definition (L1à2)!=‡p is used to complete the calculation. Hence:

n!=nä(nN1)ä(nN2)ä ... ä2ä1, if n is an integer ‚0 n!= nä(nN1)ä(nN2)ä ... ä1à2 n! is an error, if neither n nor n+1à2 is an integer ‚0.

(The variable n equals

value

must be ‚L.5 and 69.

‡p

, if n+1à2 is an integer ‚0

value

in the syntax description above.)

Math, Angle, and Test Operations 2-21

randInt(

randInt( (random integer) generates and displays a random

integer within a range specified by

lower

and

upper

integer bounds. To generate a list of random numbers, specify an integer >1 for

numtrials

(number of trials); if not

specified, the default is 1.

randInt(

lower,upper

numtrials

[

]

)

randNorm(

randBin(

randNorm( (random Normal) generates and displays a

random real number from a specified Normal distribution. Each generated value could be any real number, but most will be within the interval [mN3(s), m+3(s)]. To generate a list of random numbers, specify an integer > 1 for

numtrials

(number of trials); if not specified, the default

is 1.

randNorm(m,

randBin( (random Binomial) generates and displays a

numtrials

]

)

random integer from a specified Binomial distribution.

numtrials

(number of trials) must be ‚ 1.

prob

(probability of success) must be ‚ 0 and  1. To generate a list of random numbers, specify an integer > 1 for

numsimulations

(number of simulations); if not specified,

the default is 1.

randBin(

numtrials,prob

numsimulations

[

]

)

Note:

The seed value stored to

randNorm(

, and

randBin(

2-22 Math, Angle, and Test Operations

rand

instructions (page 2-20).

also affects

randInt(

ANGLE Operations

ANGLE Menu

DMS Entry Notation

To display the

ANGLE

menu, press y [

ANGLE

]. The

ANGLE

menu displays angle indicators and instructions. The

Radian/Degree mode setting affects the TI

interpretation of

ANGLE

1: 2: '

3: 4:8DMS 5: R8Pr( 6: R8Pq( 7: P8Rx( 8: P8Ry(

ANGLE

menu entries.

Degree notation DMS minute notation Radian notation Displays as degree/minute/second Returns r, given X and Returns q, given X and Returns x, given R and Returns y, given R and

83’s

q q

DMS (degrees/minutes/seconds) entry notation comprises the degree symbol ( second symbol (

minutes

degrees

and

minutes'seconds

), the minute symbol ('), and the

degrees

").

seconds

must be a real number;

must be real numbers ‚ 0.

For example, enter for 30 degrees, 1 minute, 23 seconds. If the angle mode is not set to

Degree, you must use

so that the TI-83 can interpret the argument as degrees, minutes, and seconds.

Degree mode Radian mode

(Degree)

(degree) designates an angle or list of angles as degrees,

regardless of the current angle mode setting. In

Radian

mode, you can use ¡ to convert degrees to radians.

value

value1,value2,value3,value4

{

also designates

' (minutes) designates " (seconds) designates

is not on the

Note:

degrees

(D) in DMS format.

minutes

seconds

menu. To enter ", press

ANGLE

,...,

value n

}

(M) in DMS format. (S) in DMS format.

[ã].

Math, Angle, and Test Operations 2-23

(Radians)

(radians) designates an angle or list of angles as radians,

regardless of the current angle mode setting. In

Degree

mode, you can use r to convert radians to degrees.

value

Degree mode

DMS

R8Pr(, R8Pq(, P8Rx(, P8Ry(

DMS

(degree/minute/second) displays

format (page 2.23). The mode setting must be

answer

R8Pr( converts rectangular coordinates to polar

coordinates and returns

to be interpreted as degrees, minutes, and seconds.

DMS

is valid only at the end of a line.

DMS

r. R8Pq( converts rectangular

coordinates to polar coordinates and returns

answer

in DMS

Degree for

. x and y can

be lists.

R8Pr(x,y), R8Pq(x,y)

Note: Radian

converts polar coordinates to rectangular

P8Rx(

coordinates and returns

x. P8Ry( converts polar

mode is set.

coordinates to rectangular coordinates and returns

can be lists.

P8Rx(r,q), P8Ry(r,q)

Note: Radian

mode is set.

and

2-24 Math, Angle, and Test Operations

TEST (Relational) Operations

TEST Menu

=, ƒ, >, ‚, <,



TEST

To display the

This operator... Returns 1 (true) if...

TEST LOGIC

‚



Relational operators compare

return

valueB

and ƒ only,

if the test is true or 0 if the test is false.

can be real numbers, expressions, or lists. For

valueA

complex numbers. If

menu, press y [

Equal Not equal to Greater than Greater than or equal to Less than Less than or equal to

valueA

valueB

and

valueA

also can be matrices or

and

TEST

valueB

and

valueB

are matrices, both

and

valueA

and

must have the same dimensions.

Relational operators are often used in programs to control program flow and in graphing to control the graph of a function over specific values.

valueA valueA valueA

valueB valueAƒvalueB

valueB valueA‚valueB

valueB valueAvalueB

Using Tests

Relational operators are evaluated after mathematical functions according to EOS rules (Chapter 1).

•

The expression

2+2=2+3

returns 0. The TI-83 performs the addition first because of EOS rules, and then it compares 4 to 5.

•

The expression

2+(2=2)+3

returns 6. The TI-83 performs the relational test first because it is in parentheses, and then it adds 2, 1, and 3.

Math, Angle, and Test Operations 2-25

TEST LOGIC (Boolean) Operations

TEST LOGIC Menu

To display the

This operator... Returns a 1 (true) if...

TEST LOGIC 1: and 2: or 3: xor 4: not(

TEST LOGIC

menu, press y

Both values are nonzero (true). At least one value is nonzero (true). Only one value is zero (false). The value is zero (false).

TESTä

Boolean Operators

and, or, xor

not(

Using Boolean Operations

Boolean operators are often used in programs to control program flow and in graphing to control the graph of the function over specific values. Values are interpreted as zero (false) or nonzero (true).

and, or

expression is true or to the table below.

, and

xor

(exclusive or) return a value of 1 if an

if an expression is false, according

valueA

and

valueB

can be real

numbers, expressions, or lists.

valueA valueA valueA

not( not(

and

valueB

xor

valueB

valueA valueB and or xor

0 0 returns

0 returns

0 0 returns

returns 1 if

value

(which can be an expression) is 0.

)

110 011 011 000

Boolean logic is often used with relational tests. In the following program, the instructions store

into C.

2-26 Math, Angle, and Test Operations

Function

Contents

Graphin

Getting Started: Graphing a Circle Defining Graphs Setting the Graph Modes Defining Functions Selecting and Deselecting Functions Setting Graph Styles for Functions Setting the Viewing Window Variables Setting the Graph Format Displaying Graphs Exploring Graphs with the Free-Moving Cursor Exploring Graphs with Exploring Graphs with the Using

ZOOM MEMORY

Using the

.........................................

.................................

......................................

................................

.......................................

TRACE

..................................

(Calculate) Operations

CALC

.......................

.....................

.......................

...................

...........................

Instructions

ZOOM

..................

..........

...........

3-2 3-3 3-4 3-5 3-7

3-9 3-11 3-13 3-15 3-17 3-18 3-20 3-23 3-25

Function Graphing 3-1

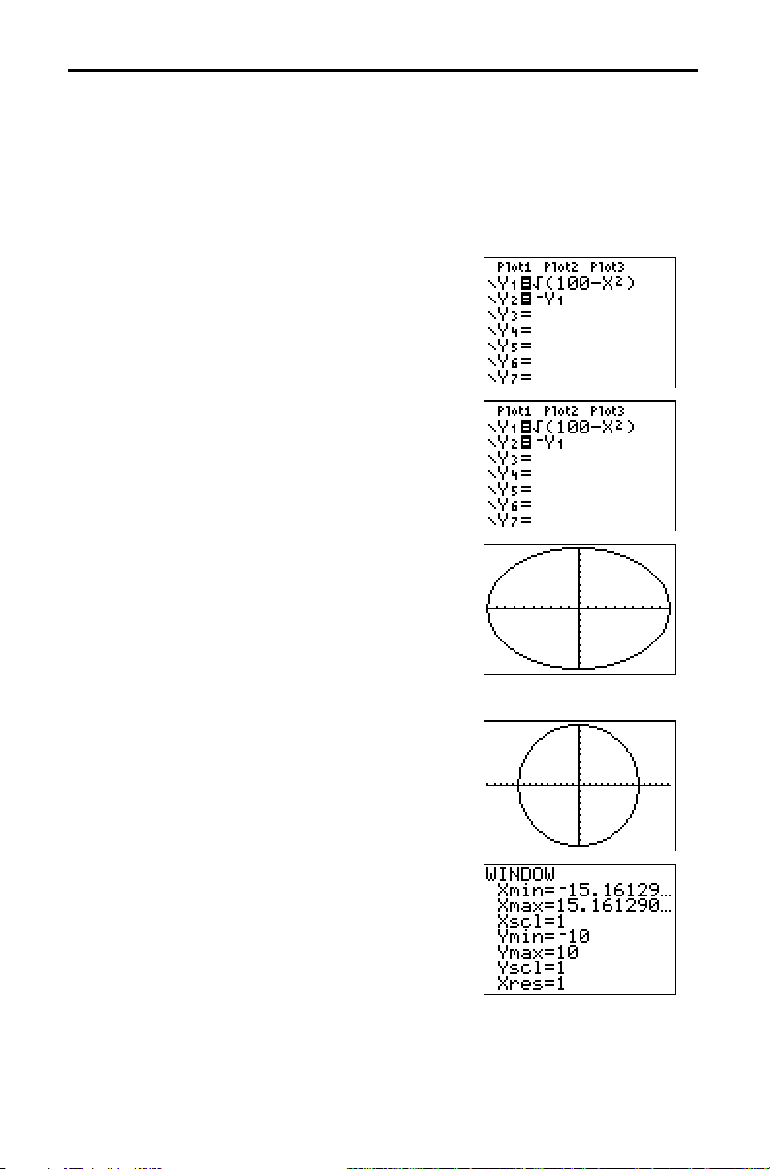
Getting Started: Graphing a Circle

Getting Started is a fast-paced introduction. Read the chapter for details.

Graph a circle of radius 10, centered on the origin in the standard viewing window. To graph this circle, you must enter separate formulas for the upper and lower portions of the circle. Then use display and make the functions appear as a circle.

ZSquare (zoom square) to adjust the

Func mode, press

1. In editor. Press y

to enter the expression Y=‡(100NX

to display the

‡

¹ „ ¡ ¤

100

which defines the top half of the circle.

The expression Y=L‡(100NX

) defines the bottom half of the circle. On the TI-83, you can define one function in terms of another. To define negation sign. Press

VARS Y.VARS

select

1:Function. The

menu is displayed. Press

2. Press

Y2=LY

, press Ì to enter the

 ~

menu. Then press

to display the

FUNCTION

1 to select 1:Y

secondary

6 to select 6:ZStandard. This is a

quick way to reset the window variables to the standard values. It also graphs the functions; you do not need to press

Notice that the functions appear as an ellipse in the standard viewing window.

3. To adjust the display so that each pixel represents an equal width and height, press

5 to select 5:ZSquare. The functions

are replotted and now appear as a circle on the display.

4. To see the ZSquare window variables, press

and notice the new values for

Xmax, Ymin, and Ymax.

Xmin,

3-2 Function Graphing

Defining Graphs

TI-83—Graphing Mode Similarities

Defining a Graph

Displaying and Exploring a Graph

Saving a Graph for Later Use

Chapter 3 specifically describes function graphing, but the steps shown here are similar for each TI-83 graphing mode. Chapters 4, 5, and 6 describe aspects that are unique to parametric graphing, polar graphing, and sequence graphing.

To define a graph in any graphing mode, follow these steps. Some steps are not always necessary.

1. Press

and set the appropriate graph mode

(page 3.4).

2. Press o and enter, edit, or select one or more functions in the

editor (page 3.5 and 3.7).

3. Deselect stat plots, if necessary (page 3.7).

4. Set the graph style for each function (page 3.9).

5. Press

and define the viewing window variables

(page 3.11).

FORMAT

6. Press y [

] and select the graph format settings

(page 3.13).

After you have defined a graph, press

to display it. Explore the behavior of the function or functions using the TI-83 tools described in this chapter.

You can store the elements that define the current graph to any of 10 graph database variables ( and

GDB0; Chapter 8). To recreate the current graph later,

GDB1 through GDB9,

simply recall the graph database to which you stored the original graph.

These types of information are stored in a

•

functions

•

Graph style settings

•

Window settings

•

Format settings

GDB.

You can store a picture of the current graph display to any of 10 graph picture variables (

Pic1 through Pic9, and Pic0;

Chapter 8). Then you can superimpose one or more stored pictures onto the current graph.

Function Graphing 3-3

Setting the Graph Modes

Checking and Changing the Graphing Mode

To display the mode screen, press

. The default settings are highlighted below. To graph functions, you must select

Func mode before you enter values for the

window variables and before you enter the functions.

The TI-83 has four graphing modes.

•

Func (function graphing)

•

Par (parametric graphing; Chapter 4)

•

Pol (polar graphing; Chapter 5)

•

Seq (sequence graphing; Chapter 6)

Other mode settings affect graphing results. Chapter 1 describes each mode setting.

•

Float or 0123456789 (fixed) decimal mode affects

displayed graph coordinates.

•

Radian or Degree angle mode affects interpretation of

some functions.

•

Connected or Dot plotting mode affects plotting of

selected functions.

•

Sequential or Simul graphing-order mode affects

function plotting when more than one function is selected.

Setting Modes from a Program

To set the graphing mode and other modes from a program, begin on a blank line in the program editor and follow these steps.

1. Press

2. Press †, ~, |, and } to place the cursor on the mode

that you want to select.

3. Press

location.

The mode is changed when the program is executed.

3-4 Function Graphing

to display the mode settings.

to paste the mode name to the cursor

Defining Functions

Displaying Functions in the Y= Editor

Defining or Editing a Function

To display the Y= editor, press o. You can store up to 10 functions to the function variables

through Y9, and Y0.

You can graph one or more defined functions at once. In this example, functions

and Y2 are defined and selected.

To define or edit a function, follow these steps.

1. Press o to display the

editor.

2. Press † to move the cursor to the function you want to

define or edit. To erase a function, press

‘

3. Enter or edit the expression to define the function.

•

You may use functions and variables (including matrices and lists) in the expression. When the expression evaluates to a nonreal number, the value is not plotted; no error is returned.

•

The independent variable in the function is mode defines or press

•

When you enter the first character, the

„

as X. To enter X, press

[X].

X. Func

„

= is

highlighted, indicating that the function is selected.

As you enter the expression, it is stored to the variable

as a user-defined function in the Y= editor.

4. Press

or † to move the cursor to the next

function.

Function Graphing 3-5

Defining a Function from the Home Screen or a Program

To define a function from the home screen or a program, begin on a blank line and follow these steps.

[

] again.

[

], enter the expression, and then press

1 to select 1:Function from the

menu.

1. Press

2. Press

3. Press

VARS Y.VARS

 ~

4. Select the function name, which pastes the name to the

cursor location on the home screen or program editor.

5. Press

to complete the instruction.

Evaluating Y= Functions in Expressions

expression

"!Y

When the instruction is executed, the TI-83 stores the

expression to the designated variable function, and displays the message

You can calculate the value of a

value

)

X. A list of

specified

Yn(

n({value1,value2,value3, . . .,value n

values

, selects the

Done.

function Y

returns a list.

})

at a

3-6 Function Graphing

Selecting and Deselecting Functions

Selecting and Deselecting a Function

Turning On or Turning Off a Stat Plot in the Y= Editor

You can select and deselect (turn on and turn off) a function in the

editor. A function is selected when the =

sign is highlighted. The TI-83 graphs only the selected functions. You can select any or all functions

, and Y0.

To select or deselect a function in the

through

editor, follow

these steps.

1. Press o to display the

editor.

2. Move the cursor to the function you want to select or

deselect.

3. Press | to place the cursor on the function’s

4. Press

to change the selection status.

= sign.

When you enter or edit a function, it is selected automatically. When you clear a function, it is deselected.

To view and change the on/off status of a stat plot in the

editor, use Plot1 Plot2 Plot3 (the top line of the

editor). When a plot is on, its name is highlighted on this

line.

To change the on/off status of a stat plot from the

editor, press } and ~ to place the cursor on Plot1,

Plot2, or Plot3, and then press

Plot1 Plot2

is turned on. and

Plot3

are turned off.

Function Graphing 3-7

Selecting and Deselecting Functions from the Home Screen or a Program

To select or deselect a function from the home screen or a program, begin on a blank line and follow these steps.

1. Press

2. Select

3. Select

 ~

4:On/Off to display the 1:FnOn to turn on one or more functions or

2:FnOff to turn off one or more functions. The

to display the

VARS Y.VARS

ON/OFF

secondary menu.

menu.

instruction you select is copied to the cursor location.

4. Enter the number (

) of each function you want to turn on or turn off.

•

If you enter two or more numbers, separate them

1 through 9, or 0; not the variable

with commas.

•

To turn on or turn off all functions, do not enter a number after

function#

FnOn[

function#

FnOff[

5. Press

FnOn or FnOff.

function#

, . . .,

function n function n

]

. When the instruction is executed, the

status of each function in the current mode is set and

Done is displayed.

For example, in functions in the

Func mode, FnOff :FnOn 1,3 turns off all

editor, and then turns on Y1 and Y3.

3-8 Function Graphing

Setting Graph Styles for Functions

Graph Style Icons in the Y= Editor

Setting the Graph Style

This table describes the graph styles available for function graphing. Use the styles to visually differentiate functions to be graphed together. For example, you can set solid line,

Icon Style Description

è é ê ë

as a dotted line, and Y3 as a thick line.

Line A solid line connects plotted points; this is

the default in

Connected mode

Thick A thick solid line connects plotted points

Above Shading covers the area a*bove the graph

Below Shading covers the area below the graph

Path A circular cursor traces the leadin

as a

edge of

the graph and draws a path

Animate A circular cursor traces the leadin

edge of

the graph without drawing a path

Dot A small dot represents each plotted point;

Note:

Some graph styles are not available in all graphing modes.

Chapters 4, 5, and 6 list the styles for

this is the default in

Par, Pol

Dot mode

, and

Seq

modes.

To set the graph style for a function, follow these steps.

1. Press o to display the

editor.

2. Press † and } to move the cursor to the function.

3. Press | | to move the cursor left, past the

= sign, to

the graph style icon in the first column. The insert cursor is displayed. (Steps 2 and 3 are interchangeable.)

4. Press

repeatedly to rotate through the graph styles. The seven styles rotate in the same order in which they are listed in the table above.

5. Press ~, }, or † when you have selected a style.

Function Graphing 3-9

Shading Above and Below

When you select é or ê for two or more functions, the TI-83 rotates through four shading patterns.

•

Vertical lines shade the first function with a é or graph style.

•

Horizontal lines shade the second.

•

Negatively sloping diagonal lines shade the third.

•

Positively sloping diagonal lines shade the fourth.

•

The rotation returns to vertical lines for the fifth é or function, repeating the order described above.

When shaded areas intersect, the patterns overlap.

Note:

When é or ê is selected for a Y= function that graphs a family of curves, such as each member of the family of curves.

Y1={1,2,3}X

, the four shading patterns rotate for

Setting a Graph Style from a Program

To set the graph style from a program, select from the



of the

graphstyle#

the graph style, as shown below.

= ç (line)

= ê (below)

(animate)

GraphStyle(

For example, when this program is executed in

GraphStyle(1,3)

3-10 Function Graphing

H:GraphStyle(

PRGM CTL

while in the program editor.

function name in the current graphing mode.

is an integer from

function#,graphstyle#

menu. To display this menu, press

function#

to 7 that corresponds to

= è (thick)

= ë (path)

= í (dot)

)

sets

to é (above).

is the number

3 6

= é (above)

Func

mode,

Setting the Viewing Window Variables

The TI-83 Viewing Window

Displaying the Window Variables

The viewing window is the portion of the coordinate plane defined by defines the distance between tick marks on the x-axis.

Xmin, Xmax, Ymin, and Ymax. Xscl (X scale)

Yscl

(Y scale) defines the distance between tick marks on the y-axis. To turn off tick marks, set

Ymax

Xmin

Xscl

Xmax

Yscl

Ymin

Xscl=0 and Yscl=0.

To display the current window variable values, press

the default values in

. The window editor above and to the right shows

Func graphing mode and Radian angle

mode. The window variables differ from one graphing mode to another.

Xres sets pixel resolution (1 through 8) for function graphs

only. The default is

•

Xres=1, functions are evaluated and graphed at each

pixel on the x-axis.

•

Xres=8, functions are evaluated and graphed at every

At eighth pixel along the x-axis.

Tip:

TI-83 to draw graphs more slowly.

Small

Xres

values improve graph resolution but may cause the

Changing a Window Variable Value

To change a window variable value from the window editor, follow these steps.

1. Press † or } to move the cursor to the window

variable you want to change.

2. Edit the value, which can be an expression.

•

Enter a new value, which clears the original value.

•

Move the cursor to a specific digit, and then edit it.

3. Press

Í, †

, or }. If you entered an expression, the

TI-83 evaluates it. The new value is stored.

Note:

Xmin<Xmax

Ymin<Ymax

and

must be true in order to graph.

Function Graphing 3-11

Storing to a Window Variable from the Home Screen or a Program

X and @Y

To store a value, which can be an expression, to a window variable, begin on a blank line and follow these steps.

1. Enter the value you want to store.

2. Press

3. Press

4. Select



to display the

1:Window to display the Func window variables

(

secondary menu).

X/Y

•

Press ~ to display the

(

secondary menu).

•

Press ~ ~ to display the (

secondary menu).

U/V/W

menu.

VARS

Par and Pol window variables

Seq window variables

5. Select the window variable to which you want to store a

value. The name of the variable is pasted to the current cursor location.

6. Press

to complete the instruction.

When the instruction is executed, the TI-83 stores the value to the window variable and displays the value.

The variables (1:Window)

X/Y

and

(items 8 and 9 on the

VARS

secondary menu) define the distance from the center of one pixel to the center of any adjacent pixel on a graph (graphing accuracy). from

Xmin, Xmax, Ymin, and Ymax when you display a

X and @Y are calculated

graph.

(Xmax N Xmin)

You can store values to

Ymax are calculated from

3-12 Function Graphing

@Y =

(Ymax N Ymin)

and

. If you do, Xmax and

, Xmin,

, and Ymin.

Setting the Graph Format

Displaying the Format Settings

Changing a Format Setting

RectGC, PolarGC

To display the format settings, press y [

FORMAT

]. The

default settings are highlighted below.

RectGC PolarGC CoordOn CoordOff GridOff GridOn AxesOn AxesOff LabelOff LabelOn ExprOn ExprOff

Sets cursor coordinates. Sets coordinates display on or off. Sets grid off or on. Sets axes on or off. Sets axes label off or on. Sets expression display on or off.

Format settings define a graph’s appearance on the display. Format settings apply to all graphing modes.

Seq graphing

mode has an additional mode setting (Chapter 6).

To change a format setting, follow these steps.

1. Press †, ~, }, and | as necessary to move the cursor

to the setting you want to select.

2. Press

RectGC (rectangular graphing coordinates) displays the

cursor location as rectangular coordinates

PolarGC (polar graphing coordinates) displays the cursor

location as polar coordinates

The

to select the highlighted setting.

X and Y.

R and

RectGC/PolarGC setting determines which variables

are updated when you plot the graph, move the freemoving cursor, or trace.

•

RectGC updates X and Y; if CoordOn format is selected, X and Y are displayed.

•

PolarGC updates X, Y, R, and

; if CoordOn format is

selected, R and q are displayed.

Function Graphing 3-13

CoordOn, CoordOff

CoordOn (coordinates on) displays the cursor coordinates

at the bottom of the graph. If

ExprOff format is selected,

the function number is displayed in the top-right corner.

CoordOff (coordinates off) does not display the function

number or coordinates.

GridOff, GridOn

AxesOn, AxesOff

LabelOff, LabelOn

ExprOn, ExprOff

Grid points cover the viewing window in rows that correspond to the tick marks (page 3.11) on each axis.

GridOff does not display grid points. GridOn displays grid points.

AxesOn displays the axes. AxesOff does not display the axes.

This overrides the

LabelOff and LabelOn determine whether to display labels

for the axes (

ExprOn and ExprOff determine whether to display the

expression when the trace cursor is active. This format

LabelOff/LabelOn format setting.

X and Y), if AxesOn format is also selected.

setting also applies to stat plots.

When

ExprOn is selected, the expression is displayed in the

top-left corner of the graph screen.

When

ExprOff and CoordOn both are selected, the number

in the top-right corner specifies which function is being traced.

3-14 Function Graphing

Displaying Graphs

Displaying a New Graph

Pausing or Stopping a Graph

Smart Graph

To display the graph of the selected function or functions,

press

TRACE, ZOOM

instructions, and

CALC

operations display the graph automatically. As the TI-83 plots the graph, the busy indicator is on. As the graph is plotted,

X and Y are updated.

While plotting a graph, you can pause or stop graphing.

•

Press

to pause; then press

Press É to stop; then press

to resume.

to redraw.

Smart Graph is a TI-83 feature that redisplays the last graph immediately when you press

, but only if all graphing factors that would cause replotting have remained the same since the graph was last displayed.

If you performed any of these actions since the graph was last displayed, the TI-83 will replot the graph based on new values when you press

•

Changed a mode setting that affects graphs

•

Changed a function in the current picture

•

Selected or deselected a function or stat plot

•

Changed the value of a variable in a selected function

•

Changed a window variable or graph format setting

•

Cleared drawings by selecting

•

Changed a stat plot definition

ClrDraw

Function Graphing 3-15

Overlaying Functions on a Graph

On the TI-83, you can graph one or more new functions without replotting existing functions. For example, store

sin(X) to Y cos(X) to Y

in the Y= editor and press

and press

graphed on top of

again. The function Y2 is

, the original function.

. Then store

Graphing a Family of Curves

If you enter a list (Chapter 11) as an element in an expression, the TI-83 plots the function for each value in the list, thereby graphing a family of curves. In

Simul

graphing-order mode, it graphs all functions sequentially for the first element in each list, and then for the second, and so on.

{2,4,6}sin(X) graphs three functions: 2 sin(X), 4 sin(X), and 6 sin(X).

{2,4,6}sin({1,2,3}X) graphs 2 sin(X), 4 sin(2X), and 6 sin(3X).

Note:

When using more than one list, the lists must have the same

dimensions.

3-16 Function Graphing

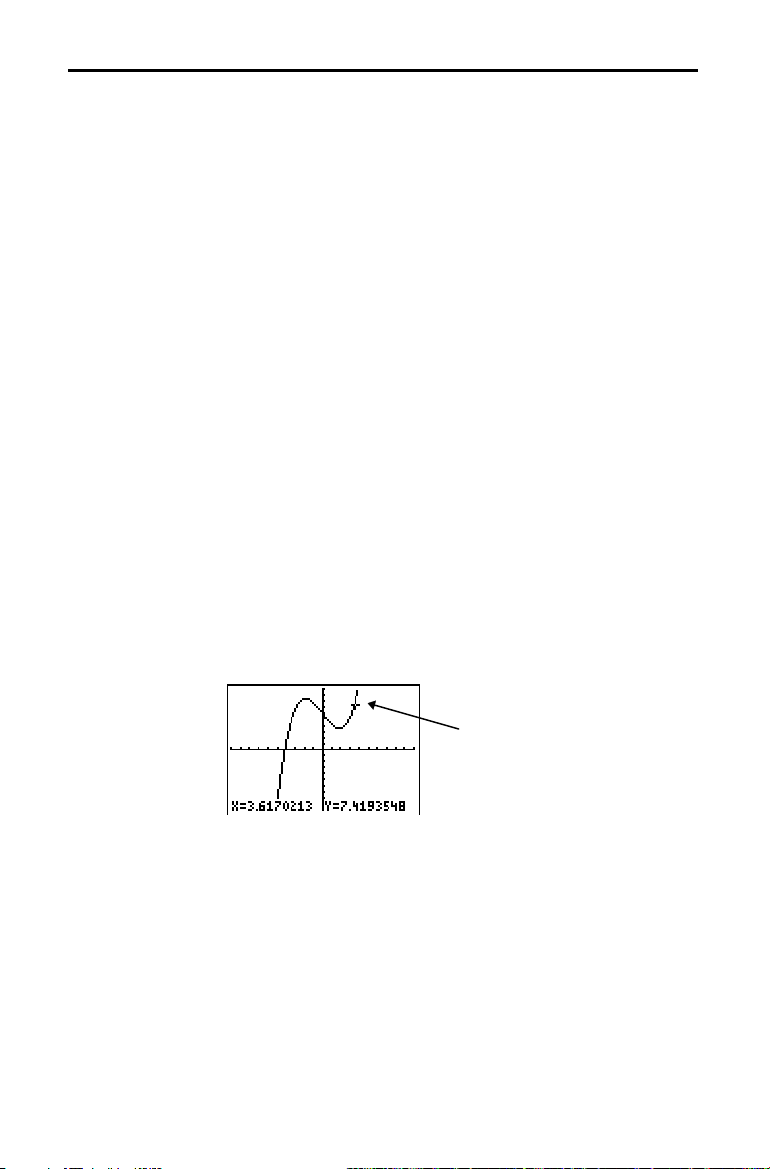
Exploring Graphs with the Free-Moving Cursor

Free-Moving Cursor

Graphing Accuracy

When a graph is displayed, press |, ~, }, or † to move the cursor around the graph. When you first display the graph, no cursor is visible. When you press |, ~, }, or †, the cursor moves from the center of the viewing window.

As you move the cursor around the graph, the coordinate values of the cursor location are displayed at the bottom of the screen if

CoordOn format is selected. The Float/Fix

decimal mode setting determines the number of decimal digits displayed for the coordinate values.

To display the graph with no cursor and no coordinate values, press

†

, the cursor moves from the same position.

‘

. When you press |, ~, }, or

The free-moving cursor moves from pixel to pixel on the screen. When you move the cursor to a pixel that appears to be on the function, the cursor may be near, but not actually on, the function. The coordinate value displayed at the bottom of the screen actually may not be a point on the function. To move the cursor along a function, use

(page 3.18).

The coordinate values displayed as you move the cursor approximate actual math coordinates, *accurate to within the width and height of the pixel. As

Ymax get closer together (as in a ZoomIn) graphing

Xmin, Xmax, Ymin, and

accuracy increases, and the coordinate values more closely approximate the math coordinates.

Free-moving cursor “on” the curve

Function Graphing 3-17

Exploring Graphs with TRACE

Beginning a Trace

Moving the Trace Cursor

Use the next along a function. To begin a trace, press the graph is not displayed already, press

to move the cursor from one plotted point to

TRACE

to display

it. The trace cursor is on the first selected function in the

editor, at the middle X value on the screen. The cursor

coordinates are displayed at the bottom of the screen if

CoordOn format is selected. The

in the top-left corner of the screen, if

expression is displayed

ExprOn format is

selected.

To move the TRACE cursor . . . do this:

. . . to the previous or next plotted

press | or ~.

point,

. . . five plotted points on a function (Xres affects this),

press y | or

. . . to any valid X value on a function, enter a value, and

then press

. . . from one function to another, press } or †.

When the trace cursor moves along a function, the is calculated from the function is undefined at an

X value; that is, Y=Yn(X). If the

X value, the Y value is blank.

Trace cursor on the curve

Y value

. If

If you move the trace cursor beyond the top or bottom of the screen, the coordinate values at the bottom of the screen continue to change appropriately.

Moving the Trace Cursor from Function to Function

To move the trace cursor from function to function, press

†

and }. The cursor follows the order of the selected functions in the function at the same the expression is updated.

3-18 Function Graphing

editor. The trace cursor moves to each

X value. If ExprOn format is selected,

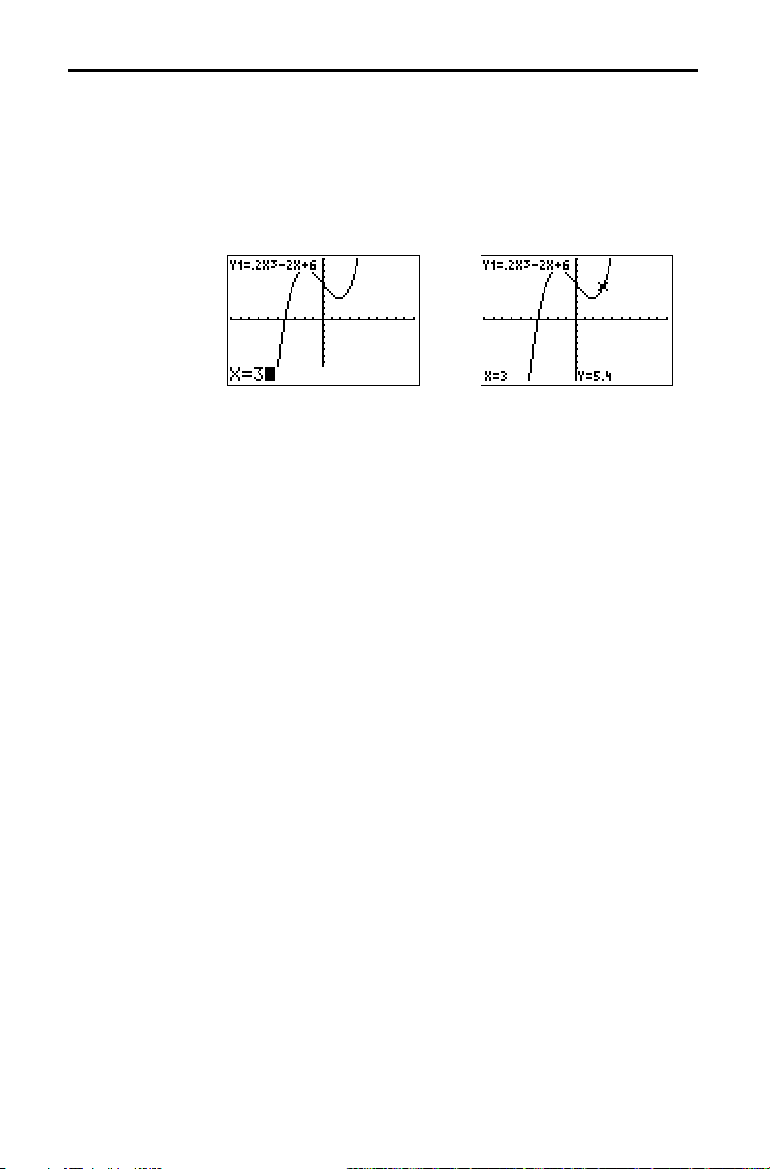
Moving the Trace Cursor to Any Valid X Value

To move the trace cursor to any valid X value on the current function, enter the value. When you enter the first digit, an

X= prompt and the number you entered are

displayed in the bottom-left corner of the screen. You can enter an expression at the

X= prompt. The value must be

valid for the current viewing window. When you have completed the entry, press

Note:

This feature does not apply to stat plots.

to move the cursor.

Panning to the Left or Right

Quick Zoom

Leaving and Returning to TRACE

Using TRACE in a Program

If you trace a function beyond the left or right side of the screen, the viewing window automatically pans to the left or right.

Xmin and Xmax are updated to correspond to the

new viewing window.

While tracing, you can press

to adjust the viewing window so that the cursor location becomes the center of the new viewing window, even if the cursor is above or below the display. This allows panning up and down. After Quick Zoom, the cursor remains in

When you leave and return to

TRACE

, the trace cursor is

displayed in the same location it was in when you left

, unless Smart Graph has replotted the graph

TRACE

(page 3.15).

On a blank line in the program editor, press instruction

Trace is pasted to the cursor location. When the

. The

instruction is encountered during program execution, the graph is displayed with the trace cursor on the first selected function. As you trace, the cursor coordinate values are updated. When you finish tracing the functions,

press

to resume program execution.

Function Graphing 3-19

Exploring Graphs with the ZOOM Instructions

ZOOM Menu

Zoom Cursor

ZBox

To display the

ZOOM

menu, press

. You can adjust the

viewing window of the graph quickly in several ways. All

instructions are accessible from programs.

ZOOM

ZOOM MEMORY 1: ZBox 2: Zoom In 3: Zoom Out 4: ZDecimal 5: ZSquare 6: ZStandard 7: ZTrig 8: ZInteger 9: ZoomStat 0: ZoomFit

When you select cursor on the graph becomes the zoom cursor ( smaller version of the free-moving cursor (

To define a new viewing window using

Draws a box to define the viewing window. Magnifies the graph around the cursor. Views more of a graph around the cursor.

Sets

X and @Y to 0.1.

Sets equal-size pixels on the X and Y axes. Sets the standard window variables. Sets the built-in trig window variables. Sets integer values on the X and Y axes. Sets the values for current stat lists. Fits YMin and YMax between XMin and XMax.

1:ZBox, 2:Zoom In, or 3:Zoom Out, the

), a

+).

ZBox, follow these

steps.

1. Select

1:ZBox from the

menu. The zoom cursor is

ZOOM

displayed at the center of the screen.

2. Move the zoom cursor to any spot you want to define as

a corner of the box, and then press

. When you move the cursor away from the first defined corner, a small, square dot indicates the spot.

3. Press |, }, ~, or †. As you move the cursor, the sides of the box lengthen or shorten proportionately on the screen.

Note:

To cancel

ZBox

before you press

4. When you have defined the box, press

, press

‘

to replot

the graph.

To use ZBox to define another box within the new graph, repeat steps 2 through 4. To cancel

3-20 Function Graphing

ZBox, press

‘

Zoom In, Zoom Out

Zoom In magnifies the part of the graph that surrounds the

cursor location. graph, centered on the cursor location. The

YFact settings determine the extent of the zoom.

Zoom Out displays a greater portion of the

XFact and

To zoom in on a graph, follow these steps.

1. Check

2. Select

XFact and YFact (page 3

2:Zoom In from the

24); change as needed.

menu. The zoom

ZOOM

cursor is displayed.

3. Move the zoom cursor to the point that is to be the center of the new viewing window.

4. Press

. The TI-83 adjusts the viewing window by

XFact and YFact; updates the window variables; and

replots the selected functions, centered on the cursor location.

5. Zoom in on the graph again in either of two ways.

•

To zoom in at the same point, press

•

To zoom in at a new point, move the cursor to the

point that you want as the center of the new viewing window, and then press

To zoom out on a graph, select

3:Zoom Out and repeat

steps 3 through 5.

To cancel

Zoom In or Zoom Out, press

‘

ZDecimal

ZSquare

ZDecimal replots the functions immediately. It updates the

window variables to preset values, as shown below. These values set

X and @Y equal to 0.1 and set the X and Y value

of each pixel to one decimal place.

Xmin=L4.7 Ymin=L3.1 Xmax=4.7 Ymax=3.1 Xscl=1 Yscl=1

ZSquare

replots the functions immediately. It redefines the viewing window based on the current values of the window variables. It adjusts in only one direction so that

@X=@

, which makes the graph of a circle look like a circle.

Xscl and Yscl remain unchanged. The midpoint of the

current graph (not the intersection of the axes) becomes the midpoint of the new graph.

Function Graphing 3-21

ZStandard

ZTrig

ZStandard replots the functions immediately. It updates the

window variables to the standard values shown below.

Xmin=L10 Ymin=L10 Xres=1 Xmax=10 Ymax=10 Xscl=1 Yscl=1

ZTrig

replots the functions immediately. It updates the window variables to preset values that are appropriate for plotting trig functions. Those preset values in

Radian mode

are shown below.

Xmin=L(47à24) Xmax=(47à24) Xscl=p/2 Yscl=1

Ymin=L4 Ymax=4

ZInteger

ZoomStat

ZoomFit

ZInteger

shown below. To use

redefines the viewing window to the dimensions

ZInteger, move the cursor to the point

that you want to be the center of the new window, and then press

X=1 Xscl=10

Y=1 Yscl=10

ZoomStat

;

ZInteger replots the functions.

redefines the viewing window so that all statistical data points are displayed. For regular and modified box plots, only

ZoomFit replots the functions immediately. ZoomFit

Xmin and Xmax are adjusted.

recalculates YMin and YMax to include the minimum and maximum current

Y values of the selected functions between the

XMin and XMax. XMin and XMax are not changed.

3-22 Function Graphing

Using ZOOM MEMORY

ZOOM MEMORY Menu

ZPrevious

ZoomSto

ZoomRcl

To display the

ZOOM MEMORY 1:ZPrevious 2:ZoomSto 3:ZoomRcl 4:SetFactors

ZPrevious

replots the graph using the window variables of

ZOOM MEMORY

menu, press

Uses the previous viewing window. Stores the user-defined window. Recalls the user-defined window.

...

Changes

Zoom In

and

q ~

Zoom Out

factors.

the graph that was displayed before you executed the last

instruction.

ZOOM

ZoomSto

immediately stores the current viewing window. The graph is displayed, and the values of the current window variables are stored in the user-defined variables

ZXres

ZXmin, ZXmax, ZXscl, ZYmin, ZYmax, ZYscl

ZOOM

, and

These variables apply to all graphing modes. For example, changing the value of

Par

mode.

ZoomRcl

graphs the selected functions in a user-defined

ZXmin

Func

mode also changes it

viewing window. The user-defined viewing window is determined by the values stored with the

ZoomSto

instruction. The window variables are updated with the user-defined values, and the graph is plotted.

Function Graphing 3-23

ZOOM FACTORS

The zoom factors, XFact and YFact, are positive numbers (not necessarily integers) greater than or equal to 1. They define the magnification or reduction factor used to

or Zoom Out around a point.

Zoom

Checking XFact and YFact

Changing XFact and YFact

Using ZOOM MEMORY Menu Items from the Home Screen or a Program

To display the

ZOOM FACTORS

review the current values for

4:SetFactors from the

ZOOM MEMORY

screen, where you can

XFact and YFact, select

menu. The values

shown are the defaults.

You can change XFact and YFact in either of two ways.

•

Enter a new value. The original value is cleared automatically when you enter the first digit.

•

Place the cursor on the digit you want to change, and then enter a value or press { to delete it.

From the home screen or a program, you can store directly to any of the user-defined

ZOOM

variables.

From a program, you can select the ZoomSto and ZoomRcl instructions from the

ZOOM MEMORY

menu.

3-24 Function Graphing

Texas Instruments TI-83 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Table of Contents

Getting Started: Do This First!

Chapter 1: Operating the TI-83

Chapter 2: Math, Angle, and Test Operations

Chapter 3: Function Graphing

Chapter 4: Parametric Graphing

Chapter 5: Polar Graphing

Chapter 6: Sequence Graphing

Chapter 7: Tables

Chapter 8: DRAW Operations

Chapter 9: Split Screen

Chapter 10: Matrices

Chapter 11: Lists

Chapter 12: Statistics

Chapter 13: Inferential Statistics and Distributions

Chapter 14: Financial Functions

Chapter 15: CATALOG, Strings, Hyperbolic Functions

Chapter 16: Programming

Chapter 17: Applications

Chapter 18: Memory Management

Chapter 19: Communication Link

Appendix A: Tables and Reference Information

Appendix B: General Information

Index

Getting Started: Do This First!

TI-83 Keyboard

Keyboard Zones

Using the Color-Coded Keyboard

TI-83 Menus

Displaying a Menu

Moving from One Menu to Another

Selecting an Item from a Menu

Leaving a Menu without Making a Selection

First Steps

Other TI-83 Features

Graphing

Sequences

Tables

Split Screen

Matrices

Lists

Statistics

Inferential Statistics

Financial Functions

CATALOG

Programming

Communication Link

Turning On and Turning Off the TI-83

Turning On the Calculator

Turning Off the Calculator

Batteries

Setting the Display Contrast

Adjusting the Display Contrast

When to Replace Batteries

The Display

Types of Displays

Home Screen

Displaying Entries and Answers

Returning to the Home Screen

Busy Indicator

Display Cursors

Entering Expressions and Instructions

What Is an Expression?

Entering an Expression

Multiple Entries on a Line

Entering a Number in Scientific Notation

Functions

Instructions

Interrupting a Calculation

TI-83 Edit Keys

Setting Modes

Checking Mode Settings

Changing Mode Settings

Setting a Mode from a Program

Normal, Sci, Eng

Float, 0123456789