Texas instruments TI-83 User Manual [pt]

Download

TI-83

GUIA

DA CALCULADORA GRÁFICA

TI-83

Marca comercial da Texas Instruments Incorporated.

IBM é uma marca comercial registada da International Business Machines Corporation Macintosh é uma marca comercial registada da Apple Computer, Inc.

Importante

A Texas Instruments não dá qualquer garantia, expressa ou implícita, incluindo mas não se limitando a quaisquer garantias de negociabilidade e adaptabilidade a qualquer objectivo específico, no que respeita a quaisquer programas ou materiais de livros e só disponibiliza tais matérias numa base de “tal como está”.

A Texas Instruments, seja em que evento for, não poderá responsabilizar-se perante ninguém por danos especiais, colaterais, acidentais ou consequenciais, que tenham qualquer ligação ou que resultem da compra ou utilização destes materiais, e a única e exclusiva responsabilidade da Texas Instruments, independentemente da forma de actuação, não deve exceder o preço de compra deste equipamento. Além disso, a Texas Instruments não pode ser responsabilizada por qualquer reclamação, seja de que espécie for, relativamente à utilização destes materiais por qualquer outra parte.

Índice

Este manual descreve a utilização da Calculadora Gráfica TI.83. Como Começar contém uma descrição geral das suas funções. O Capítulo 1 descreve o seu funcionamento. Outros capítulos descrevem várias funções interactivas. O Capítulo 17 mostra a conjugação destas funções para resolver problemas.

Como Começar: O que fazer primeiro!

Teclado da TI.83 Menus da TI.83 Primeiros Passos Introduzir um Cálculo: A Fórmula Quadrática Definir uma Função: Caixa com Tampa Definir uma Tabela de Valores: Caixa com Tampa Ampliar a Tabela: Caixa com Tampa Definir a Janela de Visualização: Caixa com Tampa Ver e Traçar o Gráfico: Caixa com Tampa Ampliar o Gráfico: Caixa com Tampa Achar o Máximo Calculado: Caixa com Tampa Outras Funções da TI.83

...................................

....................................

..................................

...........

................

........

...................

......

..............

..................

..........

............................

2 4 6

7 10 11 12 13 14 16 17 19

Capítulo 1: Utilização da TI-83

Capítulo 2: Operações Math, Angle e Test

Ligar e Desligar a TI-83 Definir o Contraste do Visor O Visor

..........................................

Introduzir Expressões e Instruções Teclas de Edição da TI-83 *Definir Modos Utilizar Nomes de Variáveis da TI-83 Armazenar Valores de Variáveis Recuperar Valores de Variáveis

.............................

.........................

....................

...........................

....................................

..................

......................

.......................

Área de Armazenamento ENTRY (Última Entrada) Área de Armazenamento Ans (Última Resposta) Menus da TI-83 Menus VARS e VARS Y-VARS Equation Operating System (EOSé) Condições de Erro

Como Começar: Moeda ao Ar Operações Matemáticas no Teclado Operações MATH Utilizar o Equation Solver Operações MATH NUM (Numéricas)

....................................

........................

...................

.................................

........................

...................

..................................

...........................

.................

Introduzir e Utilizar Números Complexos Operações MATH CPX (Complexas)

.................

Operações MATH PRB (Probabilidades) Operações ANGLE Operações TEST (Relacionais) Operações TEST LOGIC (Booleanas)

.................................

......................

.................

........

..............

......

1-2 1-3 1-5

1-7 1-10 1-11 1-15 1-17 1-18 1-19 1-21 1-22 1-24 1-26 1-28

2-2

2-3

2-6

2-9 2-14 2-17 2-19 2-21 2-24 2-27 2-28

Introdução iii

Índice

(cont.)

Capítulo 3: Elaboração de Gráficos de Funções

Capítulo 4: Elaboração de Gráficos Paramétricos

Capítulo 5: Elaboração de Gráficos Polares

Capítulo 6: Elaboração de Gráficos de Sucessões

Como Começar: Elaborar um Gráfico de Círculo Definir Gráficos Definir os Modos de Gráficos Definir Funções

...................................

........................

...................................

Seleccionar e Anular Selecção de Funções Definir Estilos de Gráficos para Funções Definir as Variáveis da Janela de Visualização Definir o Formato do Gráfico Ver Gráficos

......................................

........................

.........

.............

...............

...........

Explorar Gráficos com o Cursor de Movimento Livre Explorar Gráficos com TRACE Explorar Gráficos com as Instruções ZOOM Utilizar ZOOM MEMORY Utilizar as Operações CALC (Cálculo)

Como Começar: A Trajectória de uma Bola Definir e Ver Gráficos Paramétricos Explorar Gráficos Paramétricos

Como Começar: A Rosa Polar Definir e Ver Gráficos Polares Explorar Gráficos Polares

Como Começar: Floresta e Árvores Definir e Ver Gráficos de Sucessões Seleccionar Combinações de Eixos Explorar Gráficos de Sucessões Elaborar Gráficos de Traçados de Teia

.......................

............

............................

................

.............

..................

......................

........................

...........................

...................

......................

.................

Utilizar Traçados de Teia para Ilustrar Convergências Elaborar Gráficos de Traçados de Fase Comparar Variáveis de Sucessões da TI-83 e TI-82

................

.......

.....

....

3-2

3-3

3-4

3-5

3-7

3-9 3-12 3-14 3-16 3-18 3-19 3-21 3-24 3-26

4-2

4-4

4-7

5-2

5-3

5-6

6-2

6-4

6-9 6-10 6-12 6-13 6-15 6-18

Capítulo 7: Tabelas

iv Introdução

Como Começar: Raízes de uma Função Configurar a Tabela Definir as Variáveis Dependentes Ver a Tabela

................................

.....................

......................................

................

7-2

7-3

7-4

7-5

Capítulo 8: Operações DRAW

Como Começar: Desenhar uma Recta Tangente Utilizar o Menu DRAW Limpar Desenhos Desenhar Segmentos de Recta Desenhar Rectas Horizontais e Verticais Desenhar Rectas Tangentes Desenhar Funções e os Seus Inversos Sombrear Áreas num Gráfico Desenhar Círculos Colocar Texto num Gráfico

.............................

..................................

.......................

...............

..........................

.................

........................

.................................

..........................

Utilizar “Caneta” para Desenhar num Gráfico Desenhar Pontos num Gráfico Desenhar Pixels

...................................

Armazenar Imagens de Gráficos (Pics) Recuperar Imagens de Gráficos (Pics)

........................

................

Armazenar Bases de Dados de Gráficos (GDBs) Recuperar Bases de Dados de Gráficos (GDBs)

.........

...........

........

8-2

8-3

8-5

8-6

8-7

8-8

8-9 8-10 8-11 8-12 8-13 8-14 8-16 8-17 8-18 8-19 8-20

Capítulo 9: Dividir o Ecrã

Capítulo 10: Matrizes

Capítulo 11: Listas

Como Começar: Explorar o Círculo Trigonométrico Utilizar Dividir o Ecrã Dividir o Ecrã Horiz (Horizontal) Dividir o Ecrã G-T (Gráfico-Tabela) Pixels da TI-83 nos Modos Horiz e G-T

Como Começar: Sistemas de Equações Lineares Definir uma Matriz Visualizar e Editar Elementos de Matriz Utilizar Matrizes com Expressões Ver e Copiar Matrizes Utilizar Funções Matemáticas com Matrizes Utilizar as Operações MATRX MATH

Como Começar: Gerar uma Sequência Atribuir Nomes a Listas Armazenar e Ver Listas Introduzir Nomes de Listas Anexar Fórmulas a Nomes de Listas Utilizar Listas em Expressões Menu LIST OPS Menu LIST MATH

..............................

....................

..................

.................

.........

.................................

................

.....................

...............................

............

..................

.................

.............................

..........................

...................

........................

...................................

..................................

......

9-2 9-3 9-4 9-5 9-6

10-2 10-3 10-4 10-7

10-8 10-10 10-13

11-2

11-4

11-5

11-7

11-9 11-11 11-13 11-21

Introdução v

Índice

(cont.)

Capítulo 12: Estatísticas

Capítulo 13: Estatísticas e Distribuições Inferenciais

Capítulo 14: Funções Financeiras

Como Começar: Comprimentos e Períodos do

Pêndulo Configurar Análises Estatísticas Utilizar o Editor de Listas Estatísticas Anexar Fórmulas a Nomes de Listas Separar Fórmulas de Nomes de Listas

.......................................

......................

.................

...................

.................

Alternar Entre Contextos do Editor de Listas

Estatísticas Contextos do Editor de Listas Estatísticas Menu STAT EDIT Funções de Modelos de Regressão Menu STAT CALC Variáveis Estatísticas Análise Estatística num Programa Representação de Gráficos Estatísticos

.....................................

..............

..................................

....................

..................................

...............................

....................

................

Representação de Gráficos Estatísticos num

Programa

Como Começar: Altura Média de um Universo Editores de Estatísticas Inferenciais Menu STAT TESTS Variáveis de Saída e de Teste de Intervalo Descrições de Entrada de Estatísticas Inferenciais Funções de Distribuição Sombreado de Distribuição

Como Começar: Financiar um Carro Como Começar: Calcular um Juro Composto Utilizar o TVM Solver Utilizar as Funções Financeiras

......................................

..........

...................

.................................

..............

.......

............................

..........................

..................

...........

...............................

......................

Calcular Valor do Dinheiro ao Longo do Tempo (TVM) Calcular Fluxos de Caixa Calcular Amortização Calcular Conversão de Juros

............................

...............................

.........................

Achar Dias entre Datas /Definir Método de Pagamento Utilizar as Variáveis TVM

............................

...

....

12-2 12-10 12-11 12-15 12-18

12-19 12-20 12-22 12-24 12-27 12-33 12-34 12-35

12-41

13-2

13-6

13-9 13-28 13-29 13-30 13-37

14-2

14-3

14-4

14-5

14-6

14-7

14-9 14-12 14-13 14-14

Capítulo 15: CATALOG, Cadeias, Funções Hiperbólicas

vi Introdução

O CATALOG da TI-83 Introduzir e Utilizar Cadeias Armazenar Cadeias em Variáveis de Cadeia

...............................

.........................

.............

Funções e Instruções de Cadeia no CATALOG Funções Hiperbólicas no CATALOG

...................

..........

15-2

15-4

15-5

15-7 15-10

Capítulo 16: Programação

Como Começar: Volume de um Cilindro Criar e Eliminar Programas

..........................

................

Introduzir Linhas de Comandos e Executar Programas Editar Programas Copiar e Mudar o Nome dos Programas Instruções PRGM CTL (Controlo) Instruções PRGM I/O (Entrada/Saída) Chamar Outros Programas como Sub-rotinas

..................................

................

....................

................

...........

...

16-2

16-4

16-5

16-7

16-8

16-9 16-17 16-23

Capítulo 17: Aplicações

Capítulo 18: Gestão da Memória

Capítulo 19: Ligação de Comunicações

Comparar Resultados de Testes Utilizando Diagramas

de Extremos e Quartis

............................

Elaborar Gráficos de Funções Definidas por Partes Elaborar Gráficos de Inequações Resolver um Sistema de Equações Não Lineares

.....................

.........

Utilizar um Programa para Criar o Triângulo

de Sierpinski

Elaborar Gráficos dos Pontos de Atracção

...................................

..............

Utilizar um Programa para Calcular os Coeficientes Elaborar Gráficos do Círculo e das Curvas

Trigonométricas

Achar a Área entre Curvas

.................................

...........................

Equações Paramétricas: Problema da Roda Gigante Demonstração do Teorema Fundamental de Cálculo Calcular Áreas de Polígonos Regulares com N Faces Elaborar Gráfico de Pagamento de Hipoteca

Verificar Memória Disponível Eliminar Itens da Memória

........................

...........................

Limpar Entradas e Elementos de Listas Repor as Definições Originais da TI-83

Como Começar: Enviar Variáveis LINK da TI-83

.....................................

Seleccionar Itens a Enviar Receber Itens Transmitir Itens

.....................................

...................................

Transmitir Listas para uma TI-82

.....................

...........................

......................

Transmitir de uma TI-82 para uma TI-83 Criar Cópia de Segurança da Memória

............

................

.................

................

.................

......

.....

17-2

17-5

17-7

17-9

17-11 17-12 17-13

17-14 17-15 17-16 17-19 17-21 17-24

18-2

18-3

18-4

18-5

19-2

19-4

19-5

19-7

19-9 19-12 19-13 19-15

Introdução vii

Índice

(cont.)

Apêndice A: Tabelas e Informações de Referência

Apêndice B: Informações Gerais

Índice Remissivo

Tabela de Funções e Instruções Mapa de Menus da TI-83 Variáveis Fórmulas Estatísticas Fórmulas Financeiras

.........................................

...............................

Informações Sobre Pilhas Em Caso de Dificuldades Condições de Erro

.................................

Informações Sobre Precisão

......................

............................

...........................

............................

.........................

Informações sobre a Assistência aos Produtos e

a Garantia TI

...................................

A-2 A-49 A-59 A-61 A-65

B-2

B-4

B-5 B-11

B-13

viii Introdução

Como Começar: O que fazer primeiro!

Índice

Teclado da TI.83 Menus da TI.83 Primeiros Passos Introduzir um Cálculo: A Fórmula Quadrática Definir uma Função: Caixa com Tampa

....................................

.....................................

...................................

..........

................

Definir uma Tabela de Valores: Caixa com Tampa Ampliar a Tabela: Caixa com Tampa

...................

Definir a Janela de Visualização: Caixa com Tampa Ver e Traçar o Gráfico: Caixa com Tampa Ampliar o Gráfico: Caixa com Tampa Achar o Máximo Calculado: Caixa com Tampa Outras Funções da TI.83

.............................

..............

..................

..........

.......

......

2 4 6

7 10 11 12 13 14 16 17 19

Como Começar 1

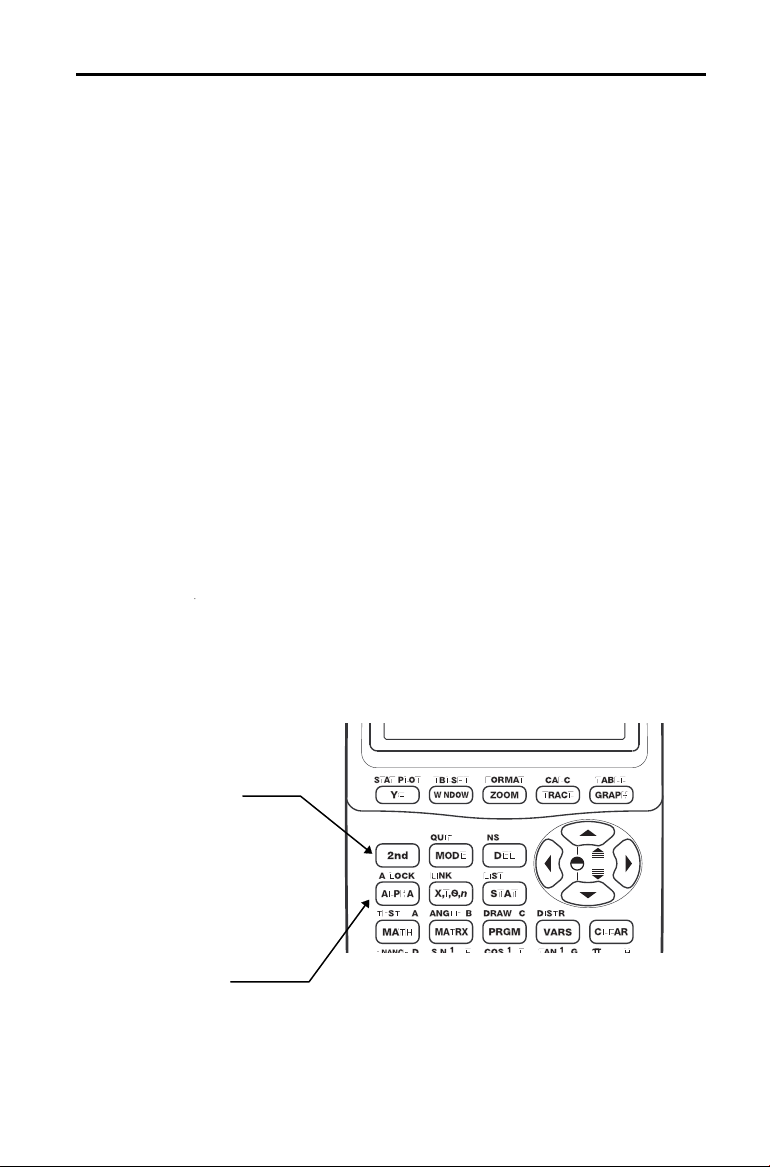
Teclado da TI.83

Utilizar o Teclado Codificado por Cores

Utilizar as Teclas 2nd e Alpha

A Tecla y acede à segunda função impressa a amarelo por cima de cada tecla.

As teclas da TI-83 estão codificadas por cores de forma a localizá-las mais facilmente quando precisar delas.

As teclas cinzentas são teclas numéricas. As teclas azuis localizadas do lado direito do teclado correspondem às funções matemáticas normais. As teclas azuis localizadas na parte superior do teclado permitem-lhe configurar e ver gráficos.

A função principal de cada tecla está impressa a branco na própria tecla. Por exemplo, quando prime , é apresentado o menu

MATH

A função secundária de cada tecla está impressa a amarelo acima da tecla. Quando prime a tecla y amarela, o carácter, a abreviatura ou a palavra impressa a amarelo acima das outras teclas fica activa para a tecla seguinte que premir.

Se, por exemplo, premir y e, depois, , visualizará o menu teclas como y [

. Este manual descreve esta combinação de

TEST

A função alfabética de cada tecla está impressa a verde acima da tecla. Quando prime a tecla ƒ verde, o carácter alfabético impresso a verde acima das outras teclas fica activo para a tecla seguinte que premir.

Se, por exemplo, premir ƒ e, depois, , será introduzida a letra de teclas como ƒ [

. Este manual descreve esta combinação

A Tecla ƒ acede à função alfabética impressa a verde por cima de cada tecla.

2 Como Começar

De um modo geral, o teclado está dividido nas seguintes áreas: teclas de

elaboração de gráficos, teclas de edição, teclas de funções avançadas e teclas de cálculo científico.

Teclas de Elaboração de Gráficos

Estas teclas são frequentemente utilizadas para aceder às funções interactivas de elaboração de gráficos da TI-83.

Teclas de Edi

ão

Teclas de Funções Avan

adas

Teclas de Cálculo Científico

Teclas de Elaboração de

Teclas de Edição

Teclas de Funções Avançadas

Estas teclas são frequentemente utilizadas para editar expressões e valores.

Estas teclas são frequentemente utilizadas para aceder às funções avançadas da TI-83.

Estas teclas são frequentemente utilizadas para aceder às funções de uma calculadora científica normal.

Teclas de Cálculo Científico

Como Começar 3

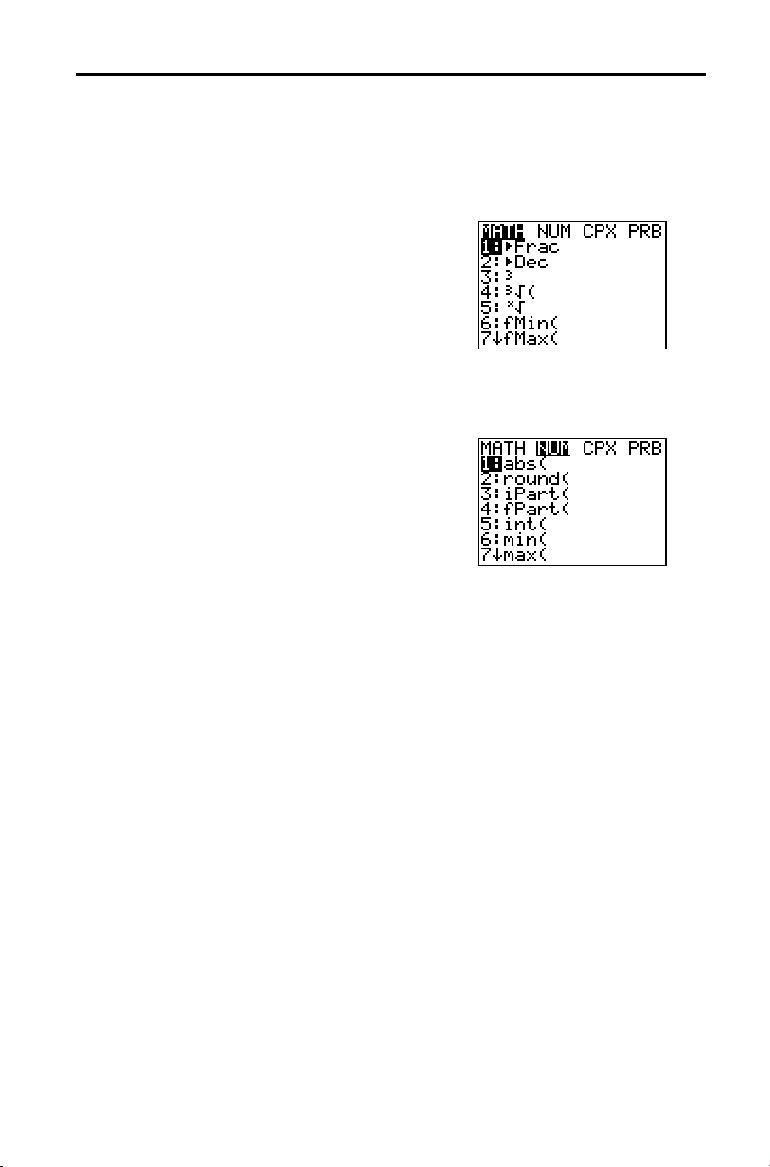
Menus da TI.83

A TI-83 dispõe de menus, apresentados em ecrã completo, que permitem o acesso a muitas operações. Os menus específicos são descritos noutros capítulos.

Ver um Menu

Quando prime uma tecla que apresenta um menu, este substitui temporariamente o ecrã no qual está a trabalhar. Por exemplo, quando prime , o menu ecrã completo.

Depois de seleccionar um item de um menu, o ecrã onde está a trabalhar é geralmente apresentado de novo.

Deslocar-se de um Menu para Outro

lgumas teclas permitem o acesso a mais do que um menu. Quando prime uma dessas teclas, os nomes de todos os menus disponíveis são apresentados na primeira linha. Quando realça o nome de um deles, são apresentados todos os itens desse menu. Prima ~ e | para realçar o nome de cada menu.

é apresentado em

MATH

4 Como Começar

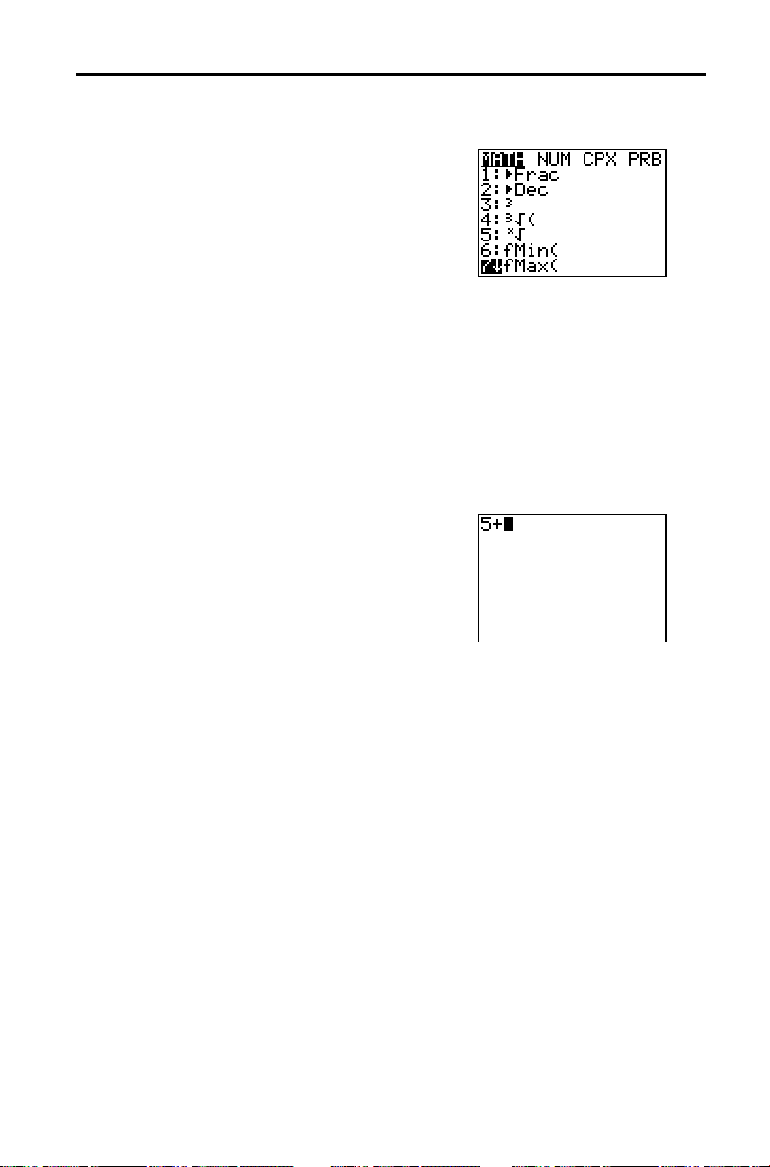
Seleccionar um Item de um Menu

O número ou a letra junto do item do menu actual fica realçada. Se o menu exceder os limites do ecrã, aparecerá uma seta para baixo ( $ ) em vez dos dois pontos (

) no último

item visualizado. Se percorrer o último item

isualizado, aparecerá uma seta para cima ( # )

em vez dos dois pontos no primeiro item

isualizado.

Pode seleccionar um item de duas formas. ¦ Prima † ou } para mover o cursor para o

número ou a letra do item e, depois, prima Í.

¦ Prima a tecla ou combinação de teclas

correspondentes ao número ou à letra junto do item.

Sair de um Menu sem Seleccionar

Pode sair de um menu sem seleccionar nada de três formas diferentes.

¦ Prima ‘ para regressar ao ecrã

anterior.

¦ Prima y [

] para regressar ao ecrã

QUIT

Home.

¦ Prima a tecla correspondente a outro menu

ou ecrã.

Como Começar 5

Primeiros Passos

Antes da abordagem dos exemplos práticos deste capítulo, siga os passos descritos nesta página para repor as definições do fabricante da TI-83 e limpar toda a memória, de forma a assegurar que os batimentos de teclas indicados neste capítulo têm os resultados ilustrados.

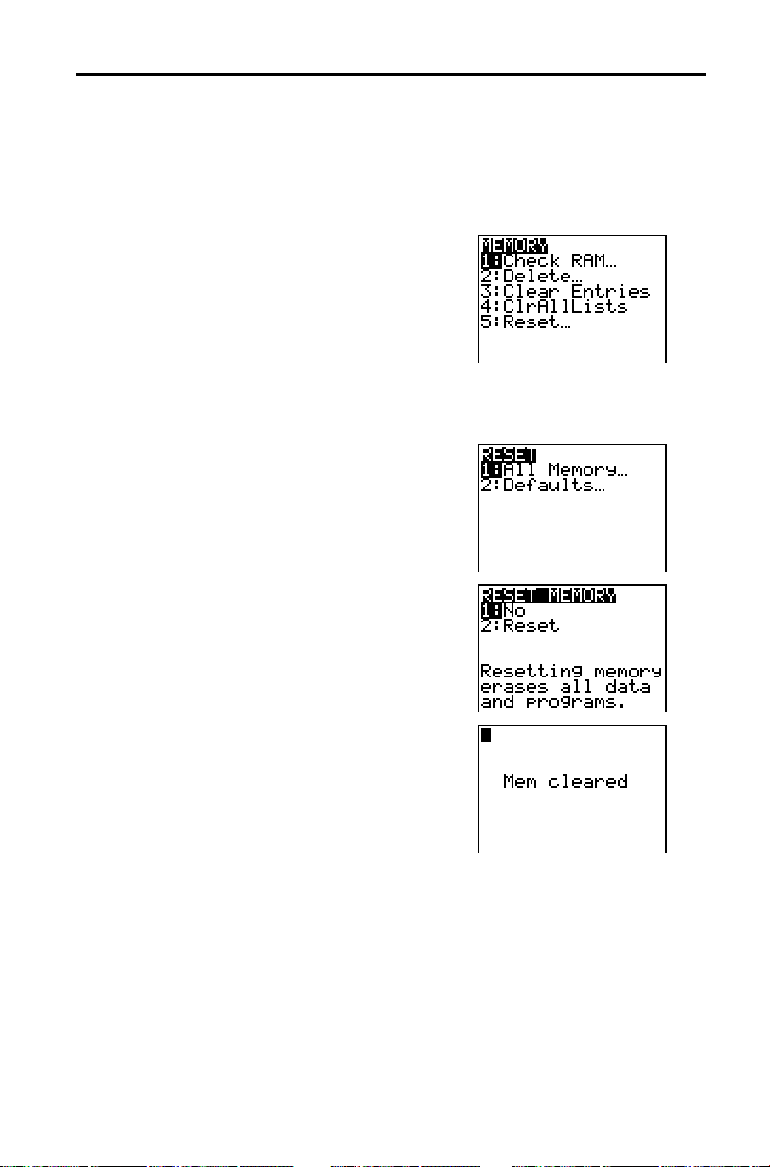
Para repor as definições originais da TI-83, siga estes passos:

1. Prima É para ligar a calculadora.

2. Prima e solte a tecla y e, depois, prima

[

] (acima de Ã).

MEM

Quando prime a tecla y, tem acesso à operação indicada a amarelo acima da tecla que premir em seguida. y da tecla Ã.

É apresentado o menu

3. Prima 5 para seleccionar

É apresentado o menu

é a operação

MEM

MEMORY

5:Reset

RESET

4. Prima 1 para seleccionar

É apresentado o menu

5. Prima 2 para seleccionar

1:All Memory

RESET MEMORY

2:Reset

Toda a memória será limpa e serão repostas as predefinições do fabricante da calculadora.

Quando repõe as definições originais da TI-83, repõe igualmente o contraste do visor.

¦ Se o visor estiver muito escuro, prima e solte

a tecla y e, depois, mantenha premida a tecla † para clarear o visor.

¦ Se o visor estiver muito claro ou branco,

prima e solte a tecla y e, depois, mantenha premida a tecla } para escurecer o visor.

6 Como Começar

Introduzir um Cálculo: A Fórmula Quadrática

Utilize a fórmula quadrática (fórmula resolvente das equações do segundo grau) para resolver as equações 3X

1. Prima

¿ ƒ [A] (acima de )

para armazenar o coeficiente do termo X

+ 5X + 2 = 0 e 2X2 N X + 3 = 0.

2. Prima ƒ [ : ]. Os dois pontos permitem-

lhe introduzir mais de uma instrução na mesma linha.

3. Prima

¿ ƒ [B] (acima de )

para armazenar o coeficiente do termo X. Prima ƒ [ instrução na mesma linha. Prima ƒ [

] para introduzir uma nova

] (acima de ) para armazenar

a constante.

4. Prima Í para armazenar o valor das

variáveis A, B e C.

5. Prima £ Ì ƒ [B] Ã y [‡] ƒ [B]

¡ ¹

ƒ [A] ƒ [C] ¤ ¤ ¥ £

ƒ [

] ¤ para introduzir a expressão de

uma das soluções para a fórmula quadrática.

−+ −bb ac

6. Prima Í para achar uma solução para a

equação 3X

+ 5X + 2 = 0.

A resposta é mostrada do lado direito do ecrã. O cursor passa para a linha seguinte, pronto para introduzir a expressão seguinte.

Como Começar 7

Introduzir um Cálculo: A Fórmula Quadrática (cont.)

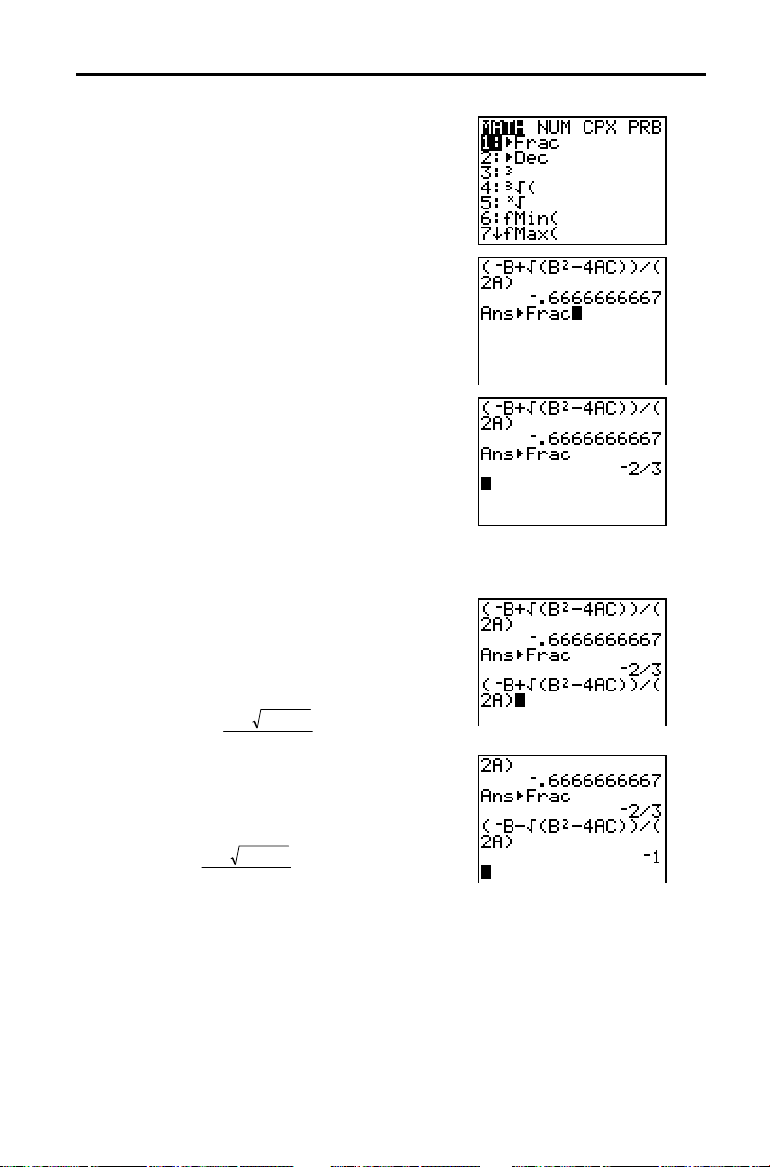
Pode mostrar a solução sob a forma de fracção.

7. Prima  para visualizar o menu

MATH

8. Prima 1 para seleccionar

menu Quando prime

no ecrã Home.

MATH

, é apresentado

é uma variável que

Ans

1:4Frac

Ans4Frac

contém a última resposta calculada.

9. Prima Í para converter o resultado

numa fracção.

Para armazenar batimentos de teclas, pode recuperar a última expressão introduzida e, depois, editá-la para um novo cálculo.

10. Prima y [

] (acima de Í) para

ENTRY

recuperar a entrada de conversão de fracção e, depois, prima novamente y [

] para recuperar a expressão da

ENTRY

fórmula quadrática.

bb ac

−+ −

11. Prima } para mover o cursor para o sinal

na fórmula. Prima ¹ para editar a expressão da fórmula quadrática da seguinte forma:

bb ac

−− −

12. Prima Í para achar a outra solução

para a equação quadrática

+ 5X + 2 = 0.

Nota: Outro modo de solucionar equações é utilizar o Equation Solver incorporado (menu MATH) e introduzir directamente a expressão Ax descrição detalhada desta Calculadora, consulte o capítulo 2.

+ Bx + C. Para obter uma

8 Como Começar

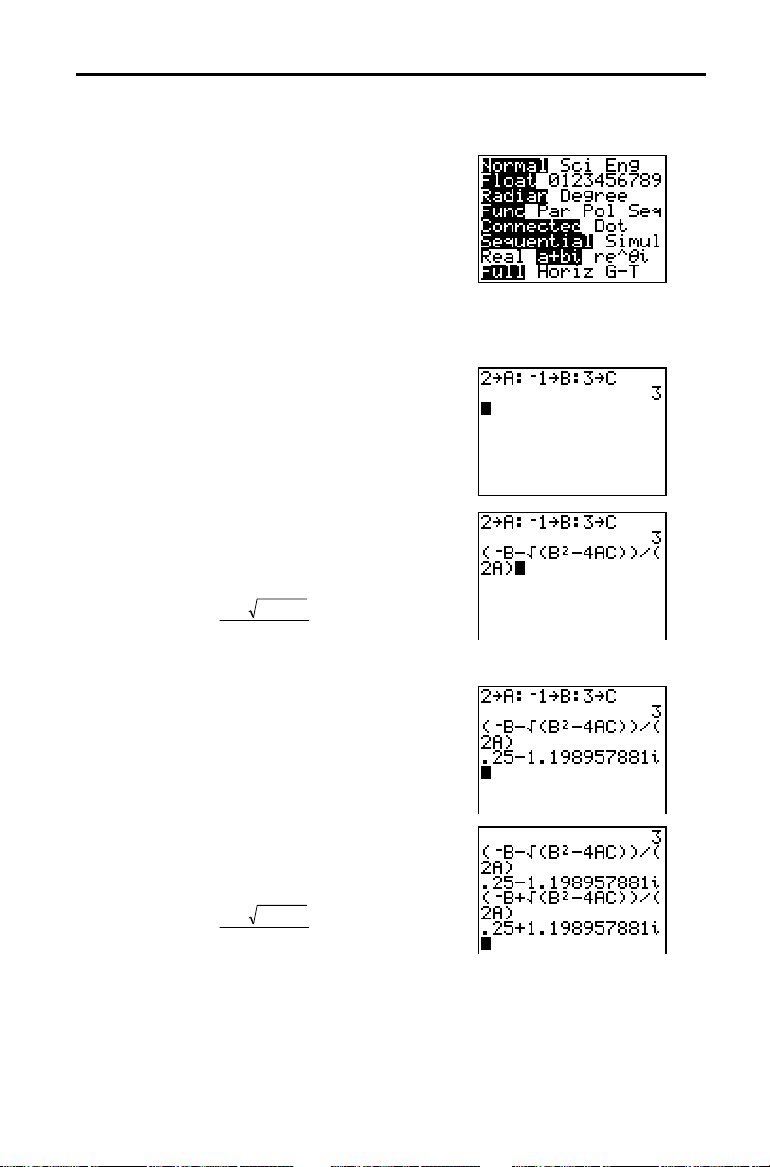
Resolva agora a equação 2X2 N X + 3 = 0. Quando define o modo de número complexo

i, a TI-83 apresenta resultados complexos.

a+b

13. Prima z † † † † † † (6 vezes) e,

depois, prima ~ para posicionar o cursor sobre modo de número complexo

i. Prima Í para seleccionar o

a+b

14. Prima y [

] (acima de z) para

QUIT

regressar ao ecrã Home e, depois, prima ‘ para o limpar.

15. Prima

¿ ƒ [A] ƒ [ : ] Ì

¿ ƒ [

] Í.

[

] ƒ [ : ] 3 ¿ ƒ

O coeficiente do termo X2, o coeficiente do termo X e a constante da nova equação são armazenados em A, B e C, respectivamente.

16. Prima y [

] para recuperar a

ENTRY

instrução para armazenar e, depois, prima novamente y [

] para recuperar a

ENTRY

expressão da fórmula quadrática.

bb ac

−− −

17. Prima Í para achar uma solução para a

equação 2X

18. Prima y [

-X+3=0.

] repetidamente até

ENTRY

visualizar esta expressão de fórmula quadrática.

bb ac

−+ −

19. Prima Í para achar a outra solução

para a equação quadrática

-X+3=0.

Como Começar 9

v A

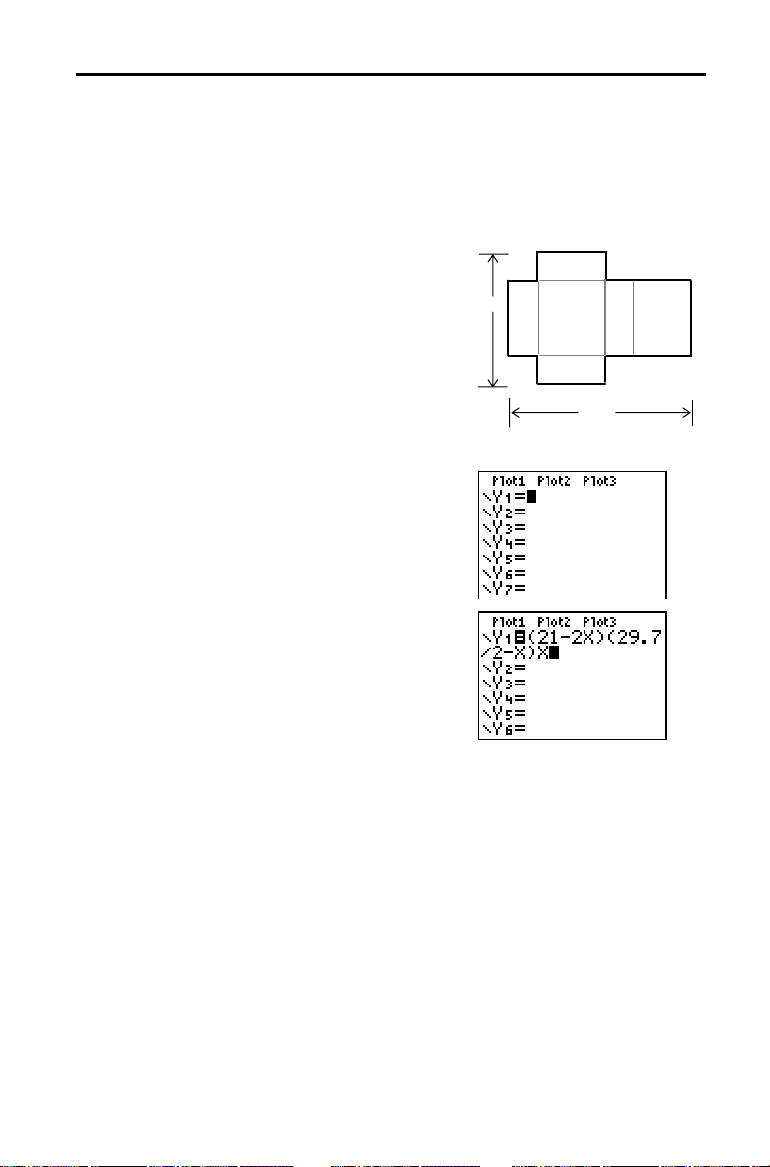
Definir uma Função: Caixa com Tampa

Pegue numa folha de papel com 21,0 cm × 29,7 cm e recorte quadrados de X × X de dois dos cantos. Recorte rectângulos de X × 14 cm dos outros dois cantos, conforme é mostrado no diagrama que se segue. Dobre o papel de modo a ter uma caixa com tampa. Qual deveria ser o valor de X para obter uma caixa com o maior volume V possível? Para determinar a solução, utilize os gráficos e a tabela.

Comece por definir uma função que descreva o

olume da caixa.

partir do diagrama: 2X + A = 21

2X + 2B = 29,7

V = ABX

Substituindo: V = (21 N 2X) (29,7à 2 N X)X

1. Prima ‘ para limpar o ecrã Home.

2. Prima o para visualizar o editor

, onde pode definir funções para a elaboração de tabelas e de gráficos.

29.7

3. Prima £

„ ¤ £

¹ „ ¤ „ Í para definir a função de volume como

em relação a X.

„ permite-lhe introduzir rapidamente o valor de sinal

, sem ter de premir ƒ. O

realçado indica que

está

seleccionado.

10 Como Começar

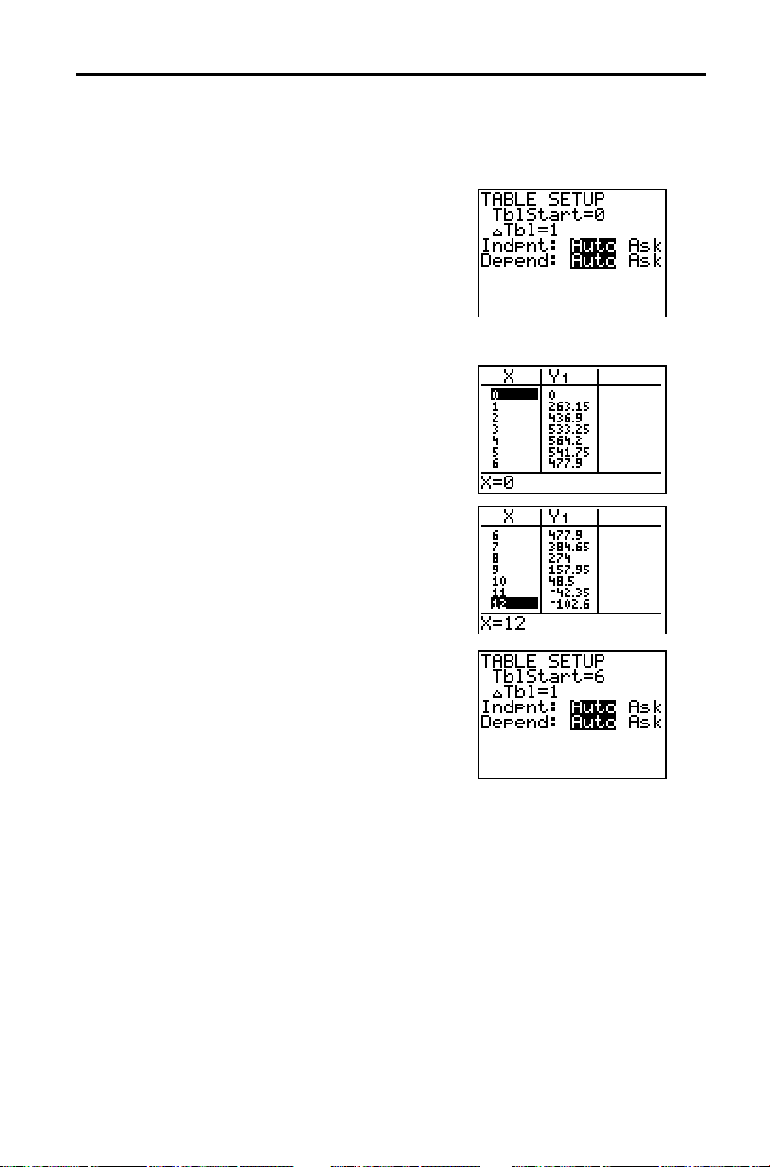
Definir uma Tabela de Valores: Caixa com Tampa

A função da TI-83 para elaboração de tabelas apresenta a informação numérica sobre uma função. Para calcular uma resposta para o problema, pode utilizar uma tabela de valores da função definida na página 9.

1. Prima y [

TBLSET

para visualizar o menu

2. Prima Í para aceitar

3. Prima 1 Í para definir os intervalos da tabela

Tbl=1

Depend: Auto

automaticamente.

4. Prima y [

TABLE

visualizar a tabela.

Tenha em atenção que máximo quando entre

e 5.

5. Mantenha premida a tecla † para percorrer a tabela até visualizar um resultado negativo para

Tenha em atenção que, neste problema, atinge o seu comprimento máximo quando

(volume) é negativo.

6. Prima y [

TBLSET

Tenha em atenção que o valor de foi alterado para 6, para reflectir a primeira linha da tabela tal como foi visualizada pela última vez. No ponto 5, o primeiro valor de

visualizado na tabela é 6.

] (acima de p)

TABLE SETUP

. Não altere

TblStart=0

Indpnt: Auto

para que a tabela seja gerada

] (acima de s) para

atinge o seu valor

é aproximadamente 4,

TblStart

Como Começar 11

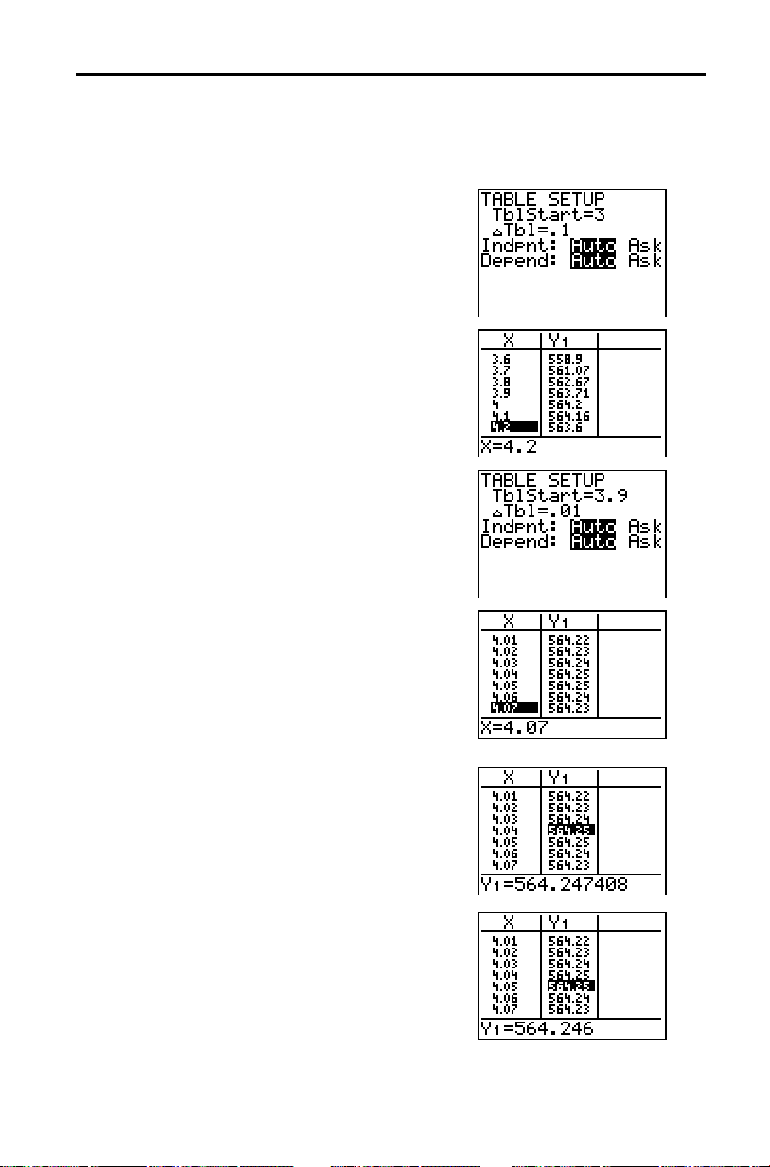
Ampliar a Tabela: Caixa com Tampa

Pode ajustar o modo de visualização de uma tabela de forma a obter mais informações sobre uma função definida. Com valores de ampliar uma tabela.

1. Ajuste a configuração da tabela de modo a obter uma estimativa mais exacta do valor de

para um volume máximo

Í para definir Í para definir

TblStart

Tbl

. Prima

. Prima Ë

inferiores, pode

Tbl

2. Prima y [

TABLE

3. Prima † e } para percorrer a tabela.

Tenha em atenção que o valor máximo para

máximo verifica-se com

4. Prima y [ para definir para definir

5. Prima y [

, o que se verifica com X=4. O

564.2

3.9<X<4.1

TBLSET

TABLE

]. Prima

Tbl

. Prima

TblStart

] e, depois, prima † e }

para percorrer a tabela.

São mostrados dois valores máximos equivalentes,

X=4.05

564.25

com X=

4.04

e com

6. Prima † e } para mover o cursor para o valor para a coluna

O valor de

. Prima ~ para mover o cursor

4.04

com X=

é apresentado na

4.04

última linha, sendo o seu valor rigoroso

564.247408

7. Prima † para visualizar o outro máximo.

O valor rigoroso de

. Isto seria o volume máximo da

564.246

com X=

4.05

caixa se medir a caixa com intervalos de 0,25 cm.

12 Como Começar

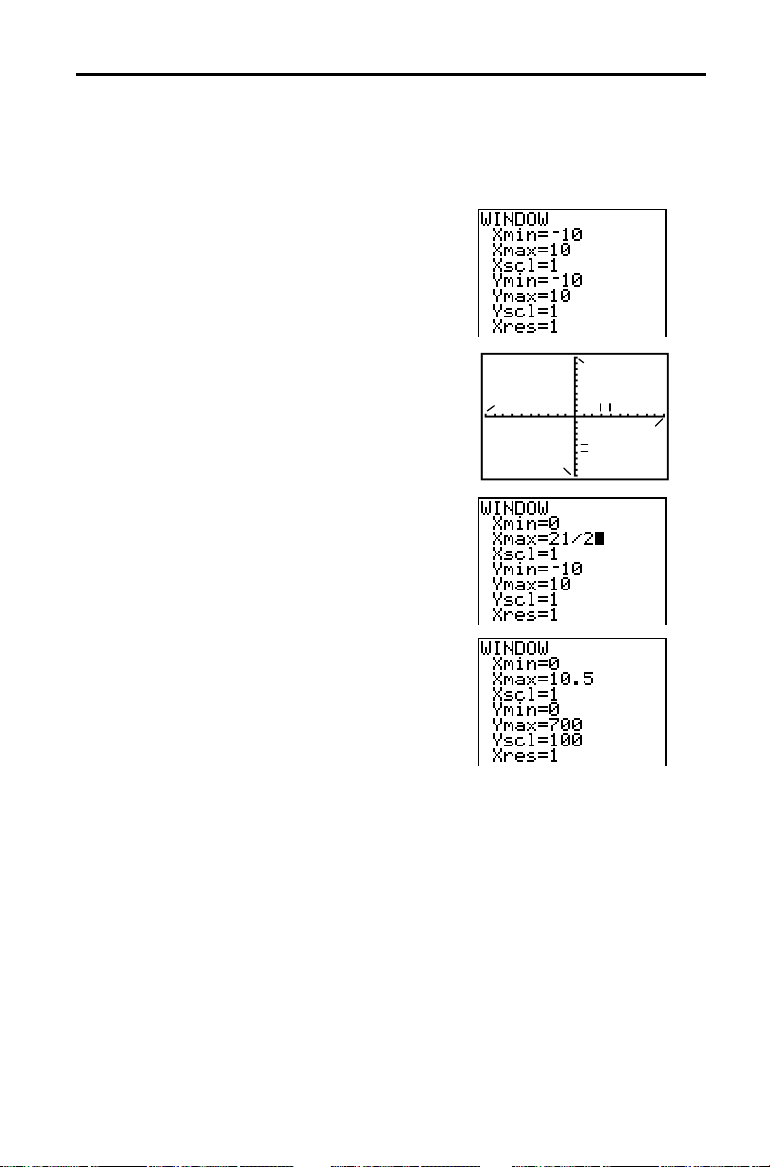
Definir a Janela de Visualização: Caixa com Tampa

As funções de elaboração de gráficos da TI-83 permitem-lhe achar o valor máximo de uma função previamente definida. Quando o gráfico está activado, a janela de visualização define a parte visualizada do plano de coordenadas. Os valores das variáveis da janela determinam o tamanho da janela de visualização.

1. Prima p para visualizar o editor de janela, onde poderá ver e editar os valores das variáveis de janela.

As variáveis standard da janela definem a janela de visualização conforme é mostrado.

Xmin, Xmax, Ymin

definem os limites do visor.

Xscl

Ymax

Yscl

definem a distância entre as marcas nos eixos

2. Prima 0

3. Prima

e Y.

controla a resolução.

Xres

para definir

Xmin

Xmax

utilizando

uma expressão.

4. Prima Í. A expressão é calculada e

é armazenado em

10.5

para aceitar

Xscl

5. Prima 0 Í

como 1.

700

. Prima Í

Xmax

100

para definir as restantes variáveis da janela.

Xmin

Ymax

Xscl

Xmax

Yscl

Ymin

Como Começar 13

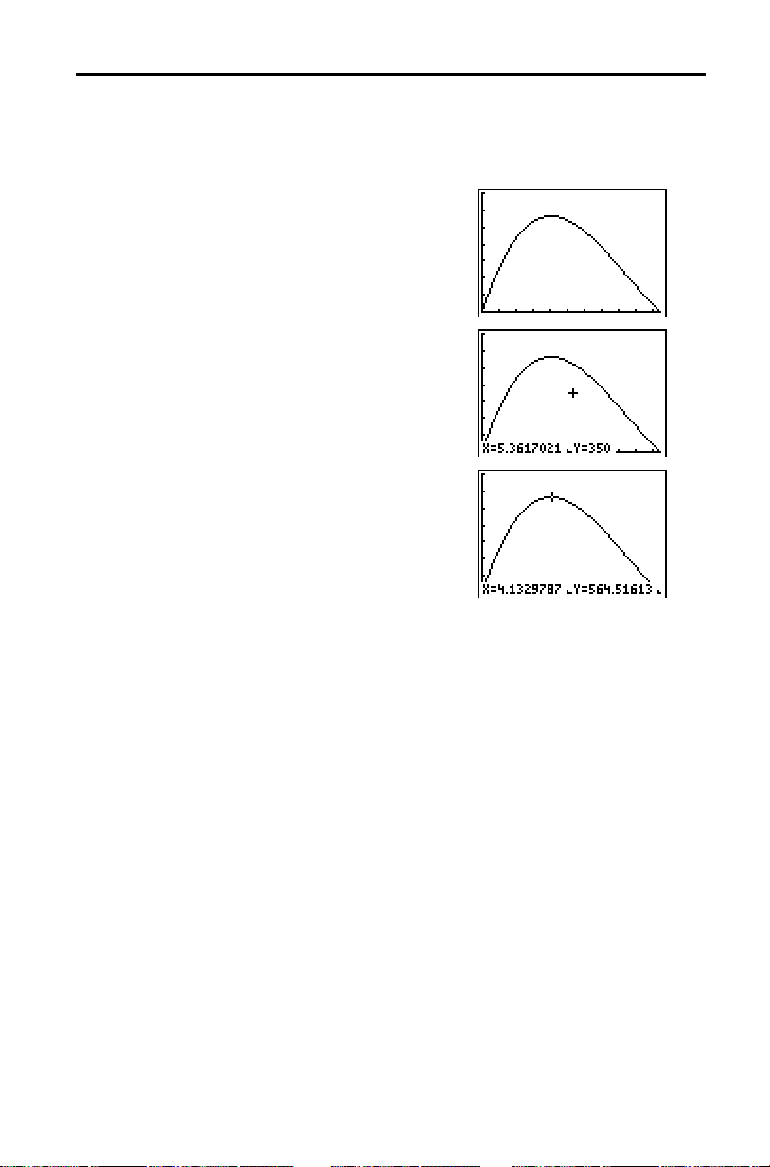
Ver e Traçar o Gráfico: Caixa com Tampa

Uma vez definida a função a partir da qual será elaborado um gráfico e definida a janela onde será elaborado, pode ver e explorar o gráfico. A função permite-lhe traçar o percurso de uma função.

1. Prima s para elaborar o gráfico da função seleccionada na janela de visualização. É apresentado o gráfico de

Y1=(21N2X)(29.7 à 2NX)X

2. Prima ~ para activar o cursor de movimento livre.

Os valores das coordenadas à posição do cursor do gráfico são apresentados na última linha.

3. Prima |, ~, } e † para mover o cursor de movimento livre para o máximo aparente da função. Os valores das coordenadas

são continuamente actualizados à medida

que move o cursor.

e Y relativos

TRACE

14 Como Começar

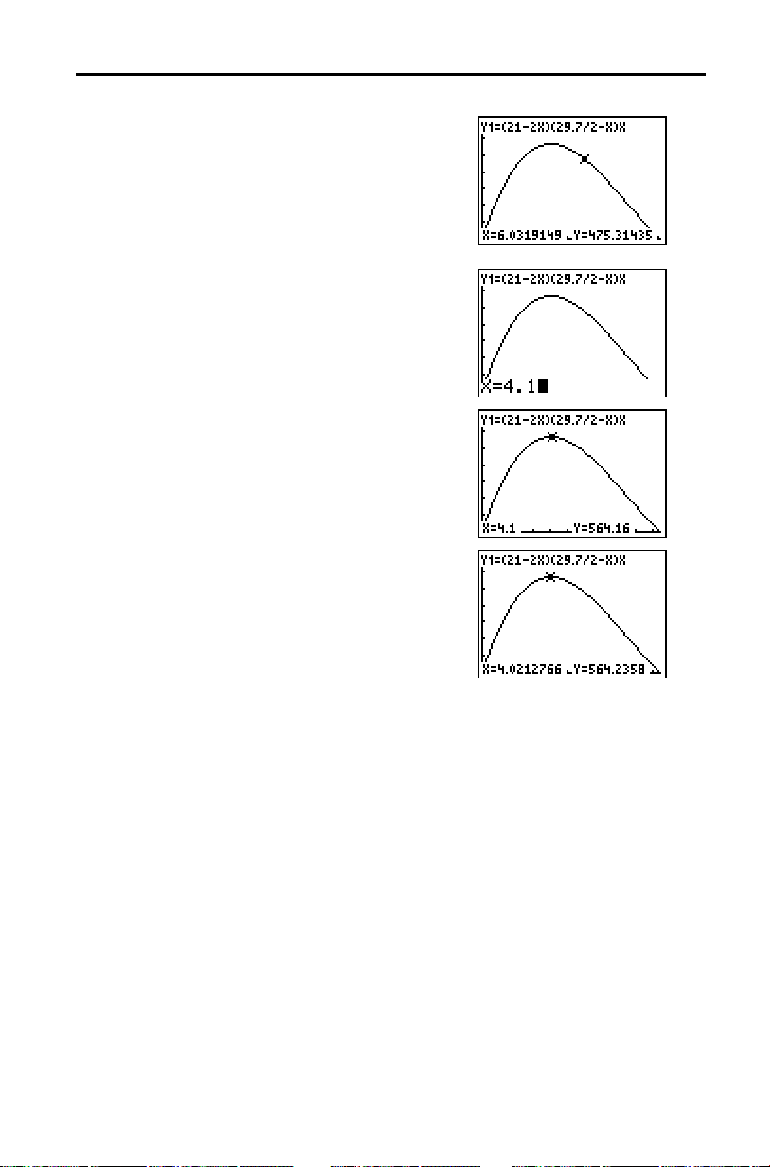
4. Prima r. O cursor de traçado é apresentado na função

. A função que

está a traçar é apresentada no canto superior esquerdo. Prima | e ~ para traçar o percurso de valor

de cada vez, calculando

ponto

, um ponto com o

a cada

Pode igualmente introduzir a sua estimativa para o valor máximo de

. Prima 4 Ë 1.

Quando prime uma tecla numérica em

TRACE,

a indicação X= é apresentada no

canto inferior esquerdo.

5. Prima Í. O cursor de traçado salta para o ponto da função de

introduzido.

calculado para o valor

6. Prima | e ~ até estar no valor máximo de

Este é o máximo pixel

. O máximo real e rigoroso pode

para os valores de

Y1(X)

encontrar-se entre valores de pixel.

Como Começar 15

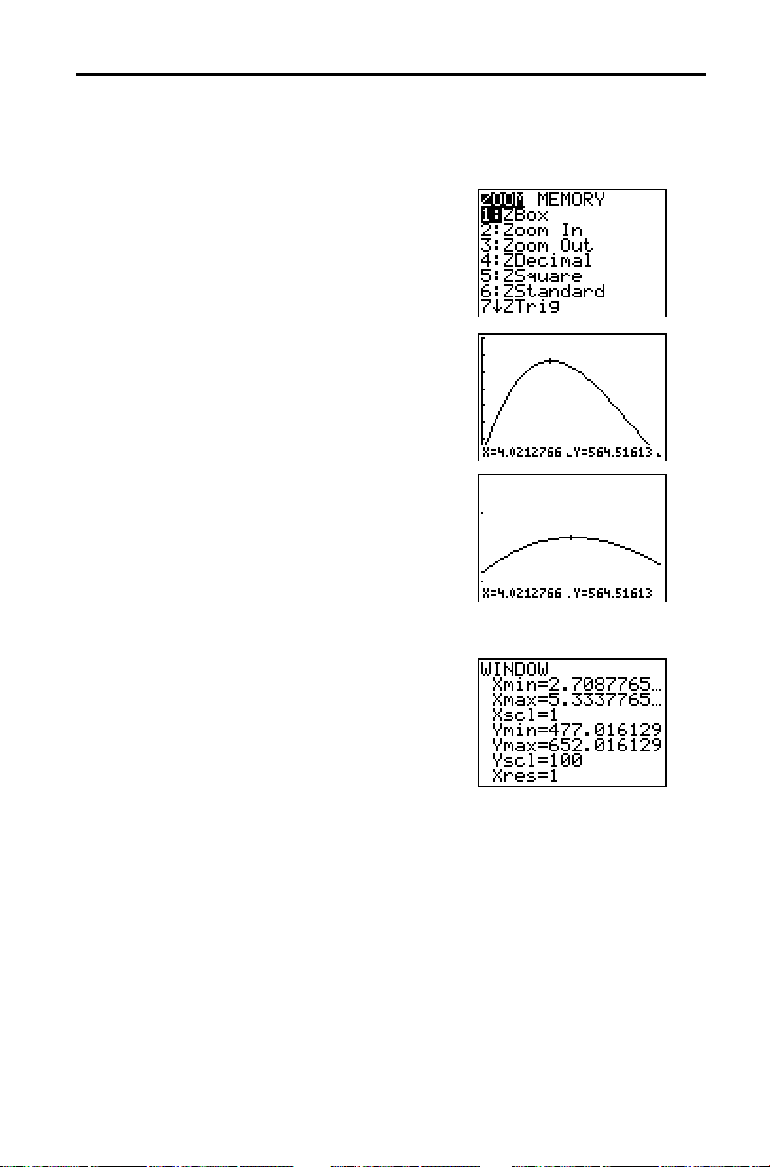
Ampliar o Gráfico: Caixa com Tampa

Utilizando as instruções

, pode ampliar a janela de visualização num

ZOOM

determinado ponto, o que o ajudará a identificar os máximos, mínimos, as raízes e intersecções de uma função.

1. Prima q para visualizar o menu

ZOOM

Este é um menu característico da TI-83. Para seleccionar um item, pode premir o número ou a letra junto do item ou premir † até que o número ou a letra do item seja realçada e, depois, premir Í.

2. Prima 2 para seleccionar

2:Zoom In

O gráfico é novamente apresentado. O cursor foi alterado de forma a indicar que está a utilizar a instrução

ZOOM

3. Com o cursor junto do valor máximo da função (conforme o passo 6 da página 12), prima Í.

É apresentada a nova janela de visualização. Tanto

YmaxNYmin

foram ajustados por factores

XmaxNXmin

como

de 4, os valores predefinidos dos factores

ZOOM

4. Prima p para visualizar as novas definições da janela.

16 Como Começar

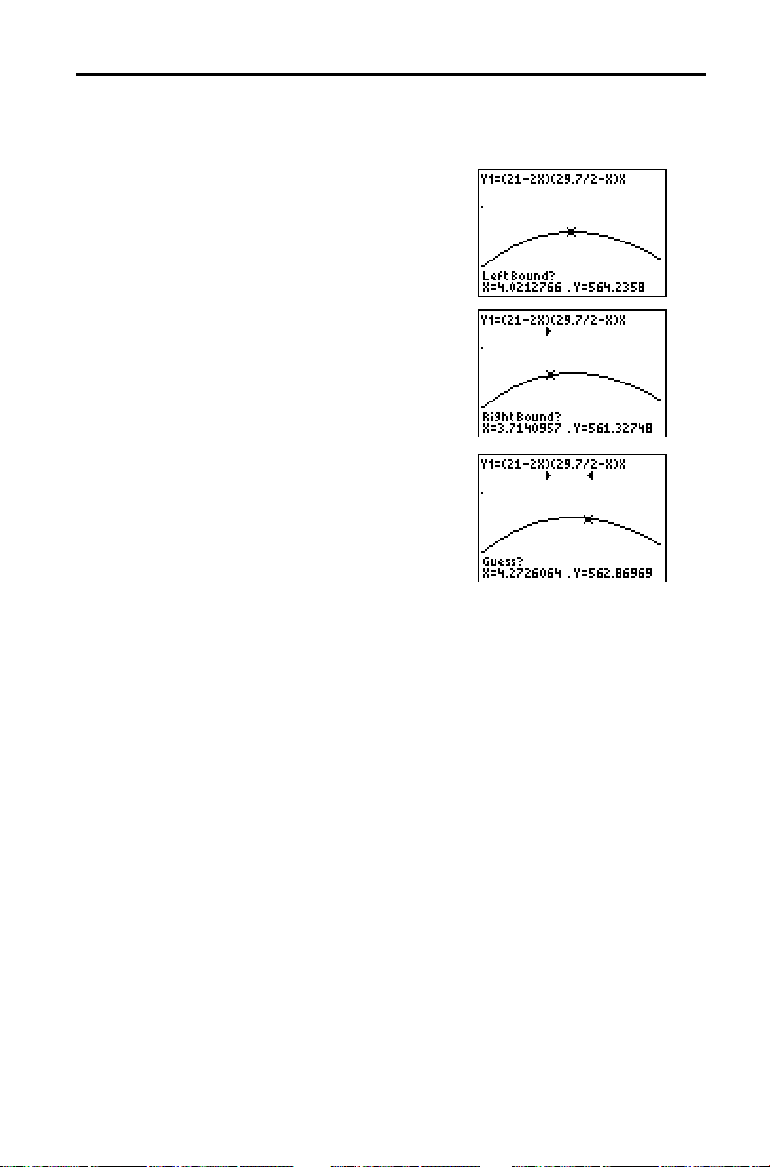
Achar o Máximo Calculado: Caixa com Tampa

Pode utilizar uma operação do menu

CALCULATE

num determinado ponto de uma função.

1. Prima y [

CALCULATE

4:maximum

] para visualizar o menu

CALC

. Prima 4 para seleccionar

O gráfico é novamente apresentado com a indicação

Left Bound?

2. Prima | para traçar o percurso da curva até um ponto à esquerda do máximo e, depois, prima Í.

O sinal 4 no início do ecrã indica o limite seleccionado. É apresentada a indicação

Right Bound?

3. Prima ~ para traçar o percurso de uma curva até um ponto à direita do máximo e, depois, prima Í.

O sinal 3 no início do ecrã indica o limite seleccionado. É apresentada a indicação

Guess?

para calcular um máximo

Como Começar 17

Achar o Máximo Calculado: Caixa com Tampa

4. Prima | para traçar até um ponto próximo do máximo e, depois, prima Í.

Poderá ainda indicar um valor de máximo. Prima

Ë 1 e, depois, prima Í.

Quando prime uma tecla numérica em

é apresentada a indicação X= no

TRACE,

canto inferior esquerdo.

Compare os valores obtidos através do máximo calculado com os máximos obtidos através do cursor de movimento livre, do cursor de traçado e da tabela.

Nota: Nos pontos 2 e 3 acima indicados, pode introduzir directamente valores para os limites esquerdo e direito, conforme é descrito no ponto 4

(cont.)

18 Como Começar

Outras Funções da TI.83

Este capítulo, Como Começar, descreveu as operações básicas da TI-83. Este manual descreve detalhadamente as funções utilizadas em Como Começar, abrangendo igualmente outras funções e capacidades desta calculadora.

Elaboração de Gráficos

Sucessões

Tabelas

Dividir o Ecrã

Matrizes

Listas

Pode armazenar, elaborar gráficos e analisar até 10 funções (Capítulo 3), até seis funções paramétricas (Capítulo 4), até seis funções polares (Capítulo 5) e até três sucessões (Capítulo 6). Pode ainda utilizar operações

DRAW

para

anotar gráficos (Capítulo 8).

Pode gerar sucessões e elaborar gráficos temporais de sucessões. Pode ainda representá-las sob a forma de traçados de Teia ou de Fase (Capítulo 6).

Pode criar tabelas de cálculo de funções para analisar simultaneamente várias funções (Capítulo 7).

Pode dividir o ecrã na horizontal para visualizar ao mesmo tempo um gráfico e um editor relacionado (tal como o editor

), a tabela, o editor de listas estatísticas ou o ecrã Home.

Pode igualmente dividir o ecrã na vertical para visualizar um gráfico e a respectiva tabela em simultâneo (Capítulo 9).

Pode introduzir e guardar até 10 matrizes e nelas executar operações standard de matrizes (Capítulo 10).

Pode introduzir e guardar tantas listas quantas a memória permitir para utilização em análises estatísticas. Para cálculo automático, pode ainda anexar fórmulas às listas. Pode utilizar as listas para calcular simultaneamente equações com valores múltiplos e para elaborar o gráfico de uma família de curvas (Capítulo 11).

Como Começar 19

Outras Funções da TI.83

(cont.)

Estatísticas

Estatística Inferencial

Funções Financeiras

CATALOG

Programação

Pode executar análises estatísticas baseadas em listas de uma ou duas variáveis, incluindo análises logísticas e de seno regressivo. Pode traçar os dados como um histograma, uma recta xy, um gráfico de dispersão, um gráfico “box-andwhisker” modificado ou regular, ou um gráfico de probabilidades normal. Pode ainda definir e armazenar até três definições de traçados estatísticos (Capítulo 12).

Pode realizar 16 testes de hipóteses e intervalos de confiança e 15 funções de distribuição. Os resultados dos testes de hipóteses podem ser representados gráfica ou numericamente. (Capítulo 13).

Pode utilizar funções de valor do dinheiro ao longo do tempo (TVM) para analisar instrumentos financeiros, tais como anuidades, empréstimos, hipotecas, alugueres e poupanças. (Capítulo 14).

CATALOG

é uma lista alfabética prática de todas as funções e instruções da TI-83. Pode colar qualquer função ou instrução do

CATALOG

na localização actual do cursor

(Capítulo 15).

Pode introduzir e armazenar programas que incluam instruções globais de controlo e de entrada/saída (Capítulo 16).

20 Como Começar

Capítulo 1: Utilização da TI-83

Índice

Ligar e Desligar a TI-83 Definir o Contraste do Visor O Visor

............................................

Introduzir Expressões e Instruções Teclas de Edição da TI-83 Definir Modos

......................................

Utilizar Nomes de Variáveis da TI-83 Armazenar Valores de Variáveis Recuperar Valores de Variáveis

..............................

..........................

....................

............................

..................

.......................

Área de Armazenamento ENTRY (Última Entrada) Área de Armazenamento Ans (Última Resposta) Menus da TI-83 Menus VARS e Y-VARS Equation Operating System (EOSé) Condições de Erro

.....................................

..............................

...................

..................................

.......

.....

2 3 5

7 10 11 15 17 18 19 21 22 24 26 28

Utilização da TI-83 1–1

Ligar e Desligar a TI-83

Ligar a Calculadora

Desligar a Calculadora

Pilhas

Para ligar a TI-83, prima É. ¦ Caso tenha desligado anteriormente a calculadora

premindo y [

], a TI-83 apresenta o ecrã Home, tal

OFF

como se encontrava da última vez que a utilizou, e limpa todos os erros.

¦ Caso a calculadora tenha sido desligada pela função

Desactivação Automática (APD

), a TI-83 ficará exactamente como a deixou, incluindo o ecrã apresentado, o cursor e quaisquer erros.

Para prolongar a duração das pilhas, a função APD desliga automaticamente a TI-83 depois de cerca de cinco minutos sem actividade.

Para desligar manualmente a TI-83, prima y [ ¦ Todas as definições e o conteúdo da memória são

conservados pela função Constant Memory

OFF

¦ São limpas todas as condições de erro.

A TI-83 funciona com quatro pilhas alcalinas AA e tem uma pilha de lítio (CR1616 ou CR1620) de reserva, substituível pelo utilizador. Para substituir as pilhas sem perda das informações armazenadas na memória, siga os passos descritos no Apêndice B.

1–2 Utilização da TI-83

Definir o Contraste do Visor

Ajustar o Contraste do Visor

Pode ajustar o contraste do visor de acordo com o seu ângulo de visão e as condições de iluminação. Quando altera a definição de contraste, aparece um número de claro) a

(o mais escuro) no canto superior direito

(o mais

indicando o nível actual. Talvez não consiga ver o número, caso o contraste seja demasiado claro ou demasiado escuro.

Nota: A TI-83 tem 40 definições de contraste; por isso, cada um dos números de 0 até 9 representa quatro definições.

A TI-83 conserva na memória a definição de contraste quando está desligada.

Para ajustar o contraste, siga estes passos.

1. Prima e solte a tecla y.

2. Mantenha premido † ou }, que se encontram abaixo e acima do símbolo de contraste (círculo amarelo, semisombreado).

¦ † clareia o ecrã. ¦ } escurece o ecrã.

Nota: Caso ajuste a definição de contraste para 0, o visor pode ficar totalmente branco. Para restaurar o ecrã, prima e solte y e, depois, mantenha premido } até que o ecrã reapareça.

Utilização da TI-83 1–3

Definir o Contraste do Visor

(cont.)

Quando substituir as pilhas

Quando as pilhas estão fracas, é apresentada uma mensagem de pilhas fracas quando liga a calculadora.

Para substituir as pilhas sem perda das informações na memória, siga os passos indicados no Apêndice B.

Em geral, a calculadora continuará a funcionar durante uma ou duas semanas depois de a mensagem de pilhas fracas ter aparecido pela primeira vez. Decorrido esse período, a TI-83 desligar-se-á automaticamente e a unidade não funcionará. As pilhas têm de ser substituídas. Conserva-se toda a memória.

Nota:

O período de funcionamento que se segue à primeira mensagem de pilhas fracas poderá ser superior a duas semanas caso não utilize frequentemente a calculadora.

1–4 Utilização da TI-83

O Visor

Tipos de Visualização

Ecrã Home

Ver Entradas e Respostas

A TI-83 apresenta texto e gráficos. O Capítulo 3 descreve os gráficos. O Capítulo 9 descreve a forma como a TI-83 pode apresentar um ecrã dividido na horizontal ou na vertical para mostrar simultaneamente gráficos e texto.

O ecrã Home é o ecrã principal da TI-83. Neste ecrã, pode introduzir instruções a executar e expressões a calcular. As respostas são visualizadas no mesmo ecrã.

Quando o texto é apresentado, o ecrã da TI-83 pode apresentar um máximo de oito linhas com um máximo de 16 caracteres por linha. Caso todas as linhas do ecrã estejam cheias, o texto é deslocado para além do início do ecrã. Caso alguma expressão no ecrã Home, no editor

(Capítulo 3)

ou no editor de programas (Capítulo 16) ocupe mais do que uma linha, é translineada para o início da linha seguinte. Nos editores numéricos, tais como o ecrã de janela (Capítulo 3), uma expressão longa é deslocada para a esquerda e para a direita.

Quando uma entrada é executada no ecrã Home, a resposta é apresentada do lado direito da linha seguinte.

Entrada Resposta

As definições de modo controlam a forma como a TI-83 interpreta expressões e apresenta respostas (página 1-11).

Caso uma resposta, como por exemplo uma lista ou matriz, seja demasiado longa para ser apresentada toda na mesma linha, são apresentadas reticências (

) à esquerda ou à

...

direita. Prima ~ e | para deslocar a resposta.

Entrada Resposta

Voltar ao Ecrã Home

Indicador de Ocupado

Para voltar ao ecrã Home a partir de qualquer outro ecrã, prima y [

QUIT

Quando a TI-83 está a calcular ou a elaborar gráficos, é apresentada uma linha móvel vertical como indicador de ocupado no canto superior direito do ecrã. Quando faz uma pausa num gráfico ou num programa, o indicador de ocupado transforma-se numa linha ponteada móvel vertical.

Utilização da TI-83 1–5

O Visor

(cont.)

Cursores de Visualização

Na maior parte dos casos, o aspecto do cursor indica o que acontece quando prime a tecla seguinte ou selecciona o item de menu seguinte para ser colado como

Cursor Aspecto Efeito do Batimento de

Tecla Seguinte

Entrada Rectângulo

preenchido

Inserção Sublinhado

É introduzido um no cursor; qualquer

carácter

substituído É inserido um

frente da localização do

carácter

existente é

carácter

cursor

Secundário Seta invertidaÞÉ introduzido um

carácter

secundário (a amarelo no teclado) ou é executada uma operação secundária

lfabético A invertido

Preenchido Rectângulo de

xadrez

É introduzido um

carácter

alfabético (a verde no teclado) ou é executado

SOLVE

Nenhuma entrada; foi introduzido o máximo de caracteres num pedido de informação ou a memória está cheia

Caso prima ƒ durante uma inserção, o cursor transforma-se num

sublinhado (A) Caso prima y durante

uma inserção, o cursor de sublinhado transforma-se numa #

sublinhada (

Por vezes, os gráficos e editores apresentam cursores adicionais, que são descritos noutros capítulos.

1–6 Utilização da TI-83

Introduzir Expressões e Instruções

O que é uma Expressão?

Introduzir uma Expressão

Uma expressão é um grupo de números, variáveis, funções e respectivos argumentos ou uma combinação destes elementos. Uma expressão é calculada resultando numa resposta. Na TI-83, pode introduzir uma expressão na mesma ordem em que a escreveria num papel. Por exemplo, p uma expressão.

Pode utilizar uma expressão no ecrã Home para calcular uma resposta. Na maior parte dos sítios em que é exigido um valor, pode utilizar uma expressão para introduzir um valor.

Para criar uma expressão, pode introduzir números, variáveis e funções a partir do teclado e dos menus. Uma expressão é completada quando prime Í, independentemente da localização do cursor. A expressão completa é calculada em conformidade com as normas do Equation Operating System (EOSè) (página 1-26) e é apresentada a resposta.

A maioria das funções e operações da TI-83 são símbolos compostos por vários caracteres. Tem de introduzir o símbolo a partir do teclado ou de um menu; não o escreva por extenso. Por exemplo, para calcular o logaritmo de 45, tem de premir « escreva multiplicação implícita das variáveis

, a TI-83 interpreta a entrada como

LOG

. Não introduza as letras L, O e G. Caso

e G.

L, O



Múltiplas Entradas numa Linha

Calcule 3,76 ÷ (L7,9 + ‡5) + 2 log 45.

3.76

¥ £ Ì

¤ ¤ Ã 2 « 45

Para introduzir duas ou mais expressões ou instruções numa linha, separe-as por dois pontos (ƒ [ : ]). Todas as instruções são armazenadas em conjunto na última entrada (

ENTRY

7.9

; página 1-19).

Ã y

ã‡ä

Utilização da TI-83 1–7

Introduzir Expressões e Instruções

(cont.)

Introduzir um Número em Notação Científica

Funções

Instruções

Para introduzir um número em notação científica, siga estes passos.

1. Introduza a parte do número que precede o expoente.

Este valor pode ser uma expressão.

2. Prima y [

]. åå é colado na localização do cursor.

3. Caso o expoente seja negativo, prima Ì e, depois,

introduza o expoente, que pode ser de um ou dois dígitos.

Quando introduz um número em notação científica, a TI-83 não apresenta automaticamente as respostas em notação científica ou de engenharia. As definições de modo (página 1-11) e o tamanho do número determinam o formato de visualização.

Uma função devolve um valor. Por exemplo,

, L, +, ‡(, e

log(

são as funções do exemplo na página 1-7. Em geral, a primeira letra de cada função apresenta-se em minúsculas na TI-83. A maior parte das funções apresenta pelo menos um argumento, o que é indicado por um parêntesis inicial ( seguir ao nome. Por exemplo,

valor

sin(

)

Uma instrução inicia uma acção. Por exemplo,

exige um argumento,

sin(

ClrDraw

) a

(

uma instrução que limpa quaisquer elementos desenhados de um gráfico. Não é possível utilizar instruções em expressões. Em geral, a primeira letra de cada nome de instrução apresenta-se em maiúsculas. Algumas instruções apresentam mais do que um argumento, o que é indicado por um parêntesis inicial, ( exige três argumentos,

) no fim do nome. Por exemplo,

(

raio

Circle(X,Y,

)

Circle(

1–8 Utilização da TI-83

Interromper um Cálculo

Enquanto a TI-83 está a calcular ou a elaborar gráficos, o indicador de ocupado está activo. Para interromper um cálculo ou um gráfico em curso, prima É. É apresentado o ecrã

ERR:BREAK.

¦ Para regressar ao ecrã Home, seleccione ¦ Para ir para o local da interrupção, seleccione

Nota: Para interromper um gráfico enquanto a TI-83 o estiver a elaborar, prima É. Para regressar ao ecrã Home, prima outra tecla.

1:Quit

2:Goto

‘

Utilização da TI-83 1–9

Teclas de Edição da TI-83

Batimentos de Teclas

Resultado

~ ou | Move o cursor numa expressão; estas teclas repetem } ou † Move o cursor de uma linha para outra, numa expressão que

ocupe mais do que uma linha; estas teclas repetem ¦ Na primeira linha de uma expressão, no ecrã Home,

} move o cursor para o início da expressão

¦ Na última linha de uma expressão, no ecrã Home, † move

o cursor para o fim da expressão

y | Move o cursor para o início de uma expressão y ~ Move o cursor para o fim de uma expressão Í Calcula uma expressão ou executa uma instrução ‘ ¦ Numa linha com texto, no ecrã Home, limpa a linha actual

¦ Numa linha em branco, no ecrã Home, limpa tudo o que

estiver no ecrã Home

¦ Num editor, limpa a expressão ou o valor na localização do

cursor; não armazena um zero

{ Elimina um carácter que se encontra na posição do cursor;

esta tecla repete

y [

] Altera o cursor para __ ; insere caracteres à frente do cursor

INS

de sublinhado; para terminar a inserção, prima y [

INS

] ou

prima |, }, ~ ou †

y Altera o cursor para Þ; o batimento de tecla seguinte executa

uma operação secundária (uma operação a amarelo acima e à esquerda de uma tecla); para cancelar uma operação secundária, prima novamente y

ƒ Altera o cursor para Ø; o batimento de tecla seguinte cola um

carácter alfabético (um carácter a verde acima e à direita de uma tecla) ou executa

SOLVE

(Capítulos 10 e 11); para

cancelar ƒ, prima ƒ ou prima |, }, ~ ou †

[

A-LOCK

] Altera o cursor para Ø; define o bloqueio alfabético; os

batimentos de teclas seguintes (num teclado alfabético) colam caracteres alfabéticos; para cancelar o bloqueio alfabético, prima ƒ; o pedido de informação de nomes define automaticamente o bloqueio alfabético

„ Com um batimento de tecla, cola um

no modo

Par

, um q no modo

Pol

ou um n no modo

no modo

Func

Seq

, um

1–10 Utilização da TI-83

Definir Modos

Verificar Definições de Modo

Alterar Definições de Modo

Definir um Modo a partir de um Programa

As definições de modo controlam a forma como a TI-83 apresenta e interpreta números e gráficos. As definições de modo são conservadas pela função Constant Memory quando a TI-83 está desligada. Todos os números, incluindo elementos de matrizes e listas, são apresentados em conformidade com as definições de modo activas.

Para visualizar as definições de modo, prima z. As definições activas são realçadas. As predefinições estão realçadas a seguir. As páginas seguintes descrevem em pormenor as definições de modo.

Normal Sci Eng Notação numérica Float 0123456789 Número de casas decimais Radian Degree Unidade de medida de ângulos Func Par Pol Seq Tipo de gráfico Connected Dot Ligar ou não pontos em gráficos Sequential Simul Traçar ou não simultaneamente Real a+bi re^qi

Real, complexo rectangular ou complexo polar

Full Horiz G-T

Ecrã completo, dois modos de dividir o ecrã

Para alterar as definições de modo, siga estes passos.

1. Prima † ou } para mover o cursor para a linha de

definições que quer alterar.

2. Prima ~ ou | para mover o cursor para a definição

pretendida.

3. Prima Í.

Pode definir um modo a partir de um programa introduzindo o nome do modo como uma instrução; por exemplo,

. Num pedido de informação em branco, seleccione a

Float

Func

definição de modo a partir do ecrã de modo; a instrução é colada na localização do cursor.

Utilização da TI-83 1–11

Definir Modos

(cont.)

Normal Sci Eng

Float Fix

Os modos de notação só afectam a forma como uma resposta é visualizada no ecrã Home. As respostas numéricas podem ser apresentadas com um máximo de 10 dígitos e com um expoente de dois dígitos. Pode introduzir um número em qualquer formato.

O modo de notação

é a forma normal em que

Normal

expressamos números, com dígitos à esquerda e à direita do decimal, como em

O modo de notação

12345.67

(científica) expressa números em

Sci

duas partes. Os números significativos são apresentados com um dígito à esquerda do carácter decimal. A potência de 10 adequada é apresentada à direita de

1.234567E4

O modo de notação

(de engenharia) é semelhante à

Eng

, como em

notação científica. No entanto, o número pode ter um, dois ou três dígitos antes do carácter decimal; e o expoente potência de 10 é um múltiplo de três, como em

Nota: Caso seleccione a notação Normal mas não seja possível apresentar a resposta em 10 dígitos (ou se o valor absoluto for inferior a 0,001), a TI-83 exprime a resposta em notação científica.

O modo decimal

(flutuante) apresenta até 10 dígitos,

Float

12.34567E3

mais o sinal e o carácter decimal.

O modo decimal fixo especifica o número de dígitos seleccionado (

to 9) à direita do carácter decimal. Coloque

o cursor no número de dígitos decimais pretendido e, depois, prima Í.

As definições decimais aplicam-se aos três modos de notação.

A definição decimal aplica-se a estes números.

¦ Uma resposta apresentada no ecrã Home. ¦ Coordenadas num gráfico (Capítulos 3, 4, 5 e 6) ¦ A instrução

valores

dy/dx

¦ Resultados de operações

tangente da equação da recta, x e dos

DRAW

(Capítulo 8)

CALCULATE

(Capítulos 3, 4, 5 e 6)

¦ Elementos de uma equação de regressão armazenada

depois da execução de um modelo de regressão (Capítulo 12)

1–12 Utilização da TI-83

Radian Degree

Func Par Pol Seq

Dot Connected

Os modos de ângulos controlam a forma como a TI-83 interpreta valores de ângulos em funções trigonométricas e em conversões polar/rectangular.

O modo

interpreta valores de ângulos como

Radian

radianos. As respostas são apresentadas em radianos.

O modo Degree interpreta valores de ângulos como graus. As respostas são apresentadas em graus.

Os modos de elaboração de gráficos definem os parâmetros dos gráficos. Os Capítulos 3, 4, 5 e 6 descrevem pormenorizadamente estes modos.

O modo de elaboração de gráficos funções, em que

é uma função de X (Capítulo 3).

O modo de elaboração de gráficos relações, em que

e Y são funções de T (Capítulo 4).

O modo de elaboração de gráficos em que

é uma função de q (Capítulo 5).

O modo de elaboração de gráficos

(função) traça

Func

(paramétrico) traça

Par

(polar) traça funções,

Pol

(sucessão) traça

Seq

sucessões (Capítulo 6).

O modo de traçado

Connected

desenha uma recta a ligar cada um dos pontos calculados para as funções seleccionadas.

O modo de traçado

traça apenas os pontos calculados

Dot

das funções seleccionadas.

Utilização da TI-83 1–13

Definir Modos

(cont.)

Sequential Simul

Real

a+b

re^q

Full Horiz G-T

O modo ordem do gráfico

Sequential

calcula e traça uma função por completo antes que a função seguinte seja calculada e traçada.

O modo ordem do gráfico todas as funções seleccionadas para um único valor de depois, calcula-as e traça-as com o valor seguinte de

Nota: Independentemente do modo de elaboração de gráficos seleccionado, a TI-83 traçará sequencialmente todos os gráficos estatísticos antes de traçar gráficos de quaisquer funções.

O modo

não apresenta resultados complexos, a menos

Real

(simultânea) calcula e traça

Simul

que sejam introduzidos números complexos como entrada.

Dois modos complexos apresentam resultados complexos. ¦ O modo complexo rectangular

i apresenta números

a+b

complexos no formato a+bi.

¦ O modo complexo polar

i apresenta números

re^q

complexos no formato re^qi.

O modo de ecrã

utiliza todo o ecrã para apresentar um

Full

gráfico ou ecrã de edição.

Cada modo de dividir o ecrã apresenta simultaneamente dois ecrãs.

¦ O modo

(horizontal) apresenta o gráfico actual na

Horiz

metade superior do ecrã; apresenta o ecrã Home ou um editor na metade inferior (Capítulo 9).

¦ O modo

(gráfico-tabela) apresenta o gráfico actual na

G-T

metade esquerda do ecrã; apresenta o ecrã da tabela na metade direita (Capítulo 9).

1–14 Utilização da TI-83

Utilizar Nomes de Variáveis da TI-83

Variáveis e Itens Definidos

Na TI-83, pode introduzir e utilizar vários tipos de dados, incluindo números reais e complexos, matrizes, listas, funções, gráficos estatísticos, bases de dados de gráficos, imagens gráficas e cadeias.

A TI-83 utiliza nomes atribuídos para variáveis e outros itens guardados na memória. Para as listas, pode igualmente criar os seus próprios nomes de cinco caracteres.

Tipo de Variável Nomes

Números reais Números complexos Matrizes Listas

, . . ., Z, q

A, B

, . . ., Z, q

A, B

ãAä, ãBä, ãCä

, . . . ,

ãJä

e nomes

definidos pelo utilizador Funções Equações paramétricas Funções polares Funções sequenciais Gráficos estatísticos Bases de dados de

, . . . ,

u, v, w

Plot1, Plot2, Plot3

GDB1, GDB2

, . . . ,

GDB9, GDB0

gráficos Imagens gráficas Cadeias

ariáveis do Sistema

Pic1, Pic2

Str1, Str2

Xmin, Xmax

, . . . ,

e outras

Pic9, Pic0

Str9, Str0

Utilização da TI-83 1–15

Utilizar Nomes de Variáveis da TI-83

(cont.)

Notas Sobre Variáveis

¦ Pode criar tantos nomes de lista quantos a memória

permita (Capítulo 11).

¦ Os programas têm nomes definidos pelo utilizador e

partilham a memória com as variáveis (Capítulo 16).

¦ No ecrã Home ou num programa, pode armazenar em

matrizes (Capítulo 10), listas (Capítulo 11), cadeias (Capítulo 15), variáveis do sistema tais como (Capítulo 1), (Capítulos 3, 4, 5 e 6).

¦ Num editor, pode armazenar em matrizes, listas e funções

(Capítulo 3).

¦ No ecrã Home, num programa ou num editor, pode

armazenar um valor num elemento de matriz ou num elemento de lista.

¦ Pode utilizar itens do menu

recuperar bases de dados de gráficos e imagens gráficas (Capítulo 8).

TblStart

(Capítulo 7) e todas as funções

DRAW STO

Xmax

para armazenar e

1–16 Utilização da TI-83

Armazenar Valores de Variáveis

Armazenar Valores numa Variável

Ver o Valor de uma Variável

Os valores das variáveis são armazenados e recuperados da memória utilizando nomes de variáveis. Quando uma expressão que contém o nome de uma variável é calculada, é utilizado o valor da variável nesse momento.

Para armazenar um valor numa variável a partir do ecrã Home ou de um programa utilizando a tecla ¿, comece numa linha em branco e siga estes passos.

1. Introduza o valor que quer armazenar. O valor pode ser

uma expressão.

2. Prima ¿. ! é copiado para a localização do cursor.

3. Prima ƒ, seguido da letra da variável em que quer

armazenar o valor.

4. Prima Í. Caso tenha introduzido uma expressão, é

calculada. O valor é armazenado na variável.

Para ver o valor de uma variável, introduza esse nome numa linha em branco do ecrã Home e prima Í.

Utilização da TI-83 1–17

Recuperar Valores de Variáveis

Utilizar a Recuperação (RCL)

Para recuperar e copiar o conteúdo de variáveis para a localização actual do cursor, siga estes passos. Para sair de

, prima ‘.

RCL

1. Prima y ã

RCL

ä.

e o cursor de edição são

Rcl

apresentados na última linha do ecrã.

2. Introduza o nome da variável de uma de cinco formas:

¦ Prima ƒ e, depois, a letra da variável. ¦ Prima y ã

(ou y e uma tecla numérica para

ä e, depois, seleccione o nome da lista

LIST

¦ Prima  e, depois, seleccione o nome da matriz. ¦ Prima  para visualizar o menu

para visualizar o menu

; depois, seleccione o

Y-VARS

VARS

ou  ~

tipo e, em seguida, o nome da variável ou função.

¦ Prima  | e, depois, seleccione o nome do

programa (apenas no editor de programas).

O nome da variável que seleccionou é apresentado na última linha e o cursor desaparece.

3. Prima Í. O conteúdo da variável é inserido no sítio

em que o cursor se encontrava antes de iniciar estes passos. Pode editar os caracteres colados na expressão sem afectar o valor em memória.

1–18 Utilização da TI-83

Área de Armazenamento ENTRY (Última Entrada)

Utilizar ENTRY (Última Entrada)



Aceder a uma Entrada Anterior



Quando prime Í no ecrã Home para calcular uma expressão ou executar uma instrução, a expressão ou instrução é colocada numa área de armazenamento chamada

(última entrada). Quando desliga a TI-83,

ENTRY

conservada na memória.

Para recuperar é colada na localização actual do cursor, onde pode editá-la e executá-la. No ecrã Home ou num editor, a linha actual é limpa e a última entrada é colada na linha.

Dado que a TI-83 só actualiza pode recuperar a entrada anterior mesmo que tenha começado a introduzir a expressão seguinte. Quando recupera

y [

A TI-83 conserva e actualiza muitas entradas anteriores possíveis em Para deslocar estas entradas, prima repetidamente y [ 128 bytes, é conservada para colocá-la na área de armazenamento

Í y

ENTRY

¿ ƒ

ENTRY

]

ENTRY

]. Caso uma única entrada tenha mais do que

A B

, prima y [

ENTRY

, substitui o que tinha introduzido.

, até atingir a capacidade de 128 bytes.

ENTRY

]. A última entrada

ENTRY

quando prime Í,

, mas não é possível

ENTRY



Quando prime y [ linha actual. Se premir y [ entrada armazenada mais antiga, a entrada mais recente armazenada é novamente apresentada, depois a anterior e assim sucessivamente.

ENTRY

], a entrada recuperada substitui a

ENTRY

] depois de visualizar a

ENTRY

Utilização da TI-83 1–19

Área de Armazenamento ENTRY (Últ. Entrada)

(cont.)

Reexecutar ENTRY Anterior



Valores Múltiplos de ENTRY numa Linha



Depois de ter colado e editado (se escolheu a edição) a última entrada no ecrã Home, pode executar a entrada. Para executar a última entrada, prima Í.

Para executar novamente a entrada apresentada, prima de novo Í. Cada reexecução apresenta uma resposta do lado direito da linha seguinte; a entrada em si não é apresentada de novo.

Í ƒ

N Ã 1 ¿

ã:ä

Í Í

Para armazenar em instruções, separe cada expressão ou instrução por dois pontos e, depois, prima Í. Todas as expressões e instruções separadas por dois pontos são armazenadas em

ENTRY

Quando prime y [ instruções separadas por dois pontos são coladas na localização actual do cursor. Pode editar qualquer uma das entradas e, depois, executá-las todas premindo Í.

Para a equação A=pr achar o raio de um círculo com 200 centímetros quadrados. Utilize 8 como primeira tentativa.

N ¡

duas ou mais expressões ou

ENTRY

], todas as expressões e

ENTRY

, utilize o método de tentativas para

ãpä

ENTRY

y | Í

Continue até que a resposta seja tão precisa quanto deseja.

Limpar ENTRY

1–20 Utilização da TI-83

Clear Entries

mantém na área de armazenamento

ƒ ƒ

7 y ãINS

ã:

ENTRY

R R ¡

]

(Capítulo 18) limpa todos os dados que a TI-83

Área de Armazenamento Ans (Última Resposta)

Utilizar Ans numa Expressão



Continuar uma Expressão



Quando uma expressão é calculada com êxito no ecrã Home ou num programa, a TI-83 armazena a resposta numa área de armazenamento chamada ser um número real ou complexo, uma lista, matriz ou cadeia. Quando desliga a TI-83, o valor de memória.

Pode utilizar a variável resposta na maioria dos locais. Prima y [ o nome da variável a expressão é calculada, a TI-83 utiliza o valor de cálculo.

Calcule a área de um canteiro de 1,7 metros por 4,2 metros. Em seguida, calcule a produção do canteiro por metro quadrado no caso de produzir um total de 147 tomates.

1.7

4.2

y [

147

Pode utilizar a variável expressão seguinte, sem introduzir novamente o valor nem premir y [ introduza a função. A TI-83 cola o nome da variável ecrã e, em seguida, a função.

Í ¯

9.9

Ans

]

ANS

]. Numa linha em branco do ecrã Home,

ANS

(última resposta).

Ans

para representar a última

Ans

para a localização do cursor. Quando

como primeira entrada na

Ans

ANS

pode

Ans

é retido na

] para copiar

Ans

Armazenar Respostas



Para armazenar uma resposta, armazene antes de calcular outra expressão.

Calcule a área de um círculo com um raio de 5 metros. Em seguida, calcule o volume de um cilindro com um raio de 5 metros e 3,3 metros de altura e armazene o resultado na variável V.

y Í ¯ Í ¿ ƒ Í

3.3

ãpä

Utilização da TI-83 1–21

numa variável

Ans

Menus da TI-83

Utilizar um Menu da TI-83

Deslocar um Menu

Pode aceder à maior parte das operações da TI-83 utilizando menus. Quando prime uma tecla ou uma combinação de teclas para visualizar um menu, aparece um ou mais nomes de menus na primeira linha do ecrã.

¦ O nome de menu que se encontra do lado esquerdo da

primeira linha é realçado. São apresentados até sete itens nesse menu, a começar pelo item

, que também está

realçado.

¦ Um número ou uma letra identifica o lugar de cada item

no menu. A ordem vai de

e assim sucessivamente. Os menus

B, C

PRGM EXEC

até 9 e 0.

PRGM EDIT

até 9, depois 0, em seguida A,

LIST NAMES

identificam apenas os itens de

¦ Quando o menu continua para além dos itens

apresentados, aparece uma seta para baixo ( $ ) em vez dos dois pontos junto ao último item apresentado.

¦ Caso um item de menu dê acesso a um menu secundário

ou a um editor, esse item termina com reticências.

Para visualizar qualquer outro menu listado na primeira linha, prima ~ ou | até que esse nome de menu fique realçado. A localização do cursor no menu inicial é irrelevante. O menu é apresentado com o cursor no primeiro item do menu.

Nota: O Mapa de Menus no Apêndice A mostra cada um dos menus, cada uma das operações de cada menu e a tecla ou combinação de teclas que prime para visualizar cada um dos menus.

Para deslocar os itens de menu para baixo, prima †. Para deslocar os itens de menu para cima, prima }.

Para avançar seis itens de menu de cada vez, prima ƒ †. Para recuar seis itens de menu de cada vez, prima ƒ }. As setas a verde entre † e } são os símbolos para avançar e recuar.

Para passar directamente para o último item de menu a partir do primeiro item de menu, prima }. Para passar directamente para o primeiro item de menu a partir do último item de menu, prima †. Alguns menus não permitem essa passagem.

1–22 Utilização da TI-83

Seleccionar um Item de um Menu

Sair de um Menu sem Seleccionar



Pode seleccionar um item a partir de um menu de uma de duas formas:

¦ Prima o número ou a letra do item que quer seleccionar.

O cursor poderá estar em qualquer sítio do menu e não é necessário que o item que seleccione esteja visível.

¦ Prima † ou } para mover o cursor para o item que

deseja e, em seguida, prima Í.

Depois de ter seleccionado um item de um menu, normalmente a TI-83 apresenta o ecrã anterior.

Nota:

Nos menus LIST NAMES, PRGM EXEC e PRGM EDIT, só pode seleccionar um dos primeiros dez itens, premindo um número de 1 até 9 ou 0. Prima um carácter alfabético ou q para mover o cursor para o primeiro item cuja inicial seja esse carácter alfabético. Caso nenhum item tenha esse carácter como inicial, o cursor passa para o item imediatamente a seguir.

Pode sair de um menu sem seleccionar nada de quatro maneiras.

¦ ¦ ¦

Calcule

 † † † Í

y [

Prima

‘ para voltar ao ecrã anterior.

Prima

uma tecla ou uma combinação de teclas para um

Prima

menu diferente, tais como  ou y [

uma tecla ou uma combinação de teclas para um

Prima

ecrã diferente, tais como o ou y [

‡27.

¤ Í

] para voltar ao ecrã Home.

QUIT

LIST

TABLE

Utilização da TI-83 1–23

Menus VARS e Y-VARS

Utilizar o Menu VARS

Utilizar o Menu Y-VARS

Pode introduzir os nomes de funções e variáveis do sistema numa expressão ou armazená-los directamente.

Para visualizar o menu menu

apresentam menus secundários, que mostram os

VARS

, prima . Todos os itens do

VARS

nomes das variáveis do sistema. Cada um dos seguintes menus dá acesso a mais do que um menu secundário:

...

5:Statistics

Variáveis Variáveis Variáveis Variáveis Variáveis

...

Variáveis Variáveis

Y-VARS

apresentam menus secundários das

3:Polar

Funções Funções

...

Funções Permite-lhe seleccionar/anular a selecção de funções

1:Window, 2:Zoom

VARS Y-VARS 1: Window 2: Zoom 3: GDB 4: Picture 5: Statistics 6: Table 7: String

...

Para visualizar o menu

2:Parametric

variáveis da função

VARS Y-VARS 1: Function 2: Parametric 3: Polar 4: On/Off

Nota: As variáveis de sucessões (u, v, w) estão localizadas no teclado como funções secundárias de ¬, − e ®.

...

X/Y, T/ ZX/ZY, ZT/Z BASE DE DADOS DE GRÁFICOS IMAGEM XY TABELA CADEIA

Yn Xn rn

U/V/W

, G, EQ,

TEST

, prima  ~.

PTS

1:Function

1–24 Utilização da TI-83

Seleccionar um Nome dos Menus VARS ou Y-VARS

Para seleccionar um nome de variável ou de função nos menus

1. Seleccione o menu

¦ Prima  para visualizar o menu ¦ Prima  ~ para visualizar o menu

2. Seleccione o tipo de nome de variável, tal como

do menu

VARS

, siga estes passos.

Y-VARS

VARS

3:Polar

Y-VARS

do menu

VARS

Y-VARS

. É

2:Zoom

apresentado um menu secundário.

3. Caso tenha seleccionado

5:Statistics

no menu

VARS

1:Window, 2:Zoom

, pode premir ~ ou | para

visualizar outros menus secundários.

4. Seleccione um nome de variável do menu. É copiado para

a localização do cursor.

Utilização da TI-83 1–25

Equation Operating System (EOSé)

Ordem de Cálculo

O Equation Operating System (EOS) define a ordem em que as funções e expressões são introduzidas e calculadas na TI-83. O EOS permite-lhe introduzir números e funções numa sequência simples e directa.

O EOS calcula as funções numa expressão por esta ordem:

1 Funções de um único argumento que precedem o

argumento, tais como

2 Funções introduzidas depois do argumento, tais

como

, !, ¡, r e conversões 3 Potências e raízes, tais como 4 Permutações (

‡(

sin(

) e combinações (

nPr

2^5

log(

nCr

‡32

) 5 Multiplicação, multiplicação implícita e divisão 6 Adição e subtracção 7 Funções relacionais, tais como > ou  8 Operador lógico 9 Operadores lógicos or e

and

xor

Dentro de um nível de prioridades, o EOS calcula funções da esquerda para a direita.

Os cálculos entre parênteses são efectuados em primeiro lugar. As funções com múltiplos argumentos, tais como

nDeriv(A2,A,6)

, são calculadas à medida que forem

encontradas.

Multiplicação Implícita

A TI-83 reconhece a multiplicação implícita. Por isso, não é necessário premir ¯ para exprimir multiplicação em todos os casos. Por exemplo, a TI-83 interpreta

(2ää5)7

Nota: As regras da multiplicação implícita da TI-83 diferem das da TI-82. Por exemplo, a TI-83 calcula 1/2X como (1/2)äX, enquanto que a TI-82 calcula 1/2X como 1/(2äX) (Capítulo 2).

1–26 Utilização da TI-83

2p, 4 sin(46), 5(1+2)

como multiplicação implícita.

Parênteses

Negação

Todos os cálculos entre parênteses são completados em primeiro lugar. Por exemplo, na expressão calcula em primeiro lugar a parte entre parênteses, depois multiplica a resposta,

, por 4.

4(1+2)

, o EOS

1+2

, e só

Pode omitir o parêntesis final ( ) ) no fim de uma expressão. Todos os elementos com parêntesis inicial são fechados automaticamente no fim de uma expressão. Isto é igualmente válido para elementos com parêntesis inicial que precedem as instruções para armazenamento ou para conversão de visualização

Nota: Um parêntesis inicial a seguir a um nome de lista, nome de matriz ou nome de função Y= não indica multiplicação implícita. Especifica elementos na lista (Capítulo 11) ou na matriz (Capítulo 10) e especifica um valor para o qual deve resolver a função Y=.

Para introduzir um número negativo, utilize a tecla de negação. Prima Ì e, em seguida, escreva o número. Na TI-83, a negação encontra-se no terceiro nível da hierarquia do EOS. As funções de primeiro nível, tais como calcular o quadrado, são calculadas antes da negação.

Por exemplo, M

, calcula para um número negativo (ou 0).

Utilize parênteses para calcular o quadrado de um número negativo.

Nota: Utilize a tecla ¹ para a subtracção e a tecla Ì para a negação. Caso prima ¹ para introduzir um número negativo, como em 9 ¯ ¹ 7, ou se premir Ì para indicar a subtracção, como em 9 Ì 7, ocorre um erro. Se premir interpretado como multiplicação implícita (A

A Ì

B).

B, será

Utilização da TI-83 1–27

Condições de Erro

Diagnosticar um Erro

Corrigir um Erro

A TI-83 detecta erros durante a execução das seguintes tarefas:

¦ Cálculo de uma expressão. ¦ Execução de uma instrução. ¦ Traçado de um gráfico. ¦ Armazenamento de um valor.

Quando a TI-83 detecta um erro, devolve uma mensagem de erro como título de menu, tal como

ERR:DOMAIN

. O Apêndice B descreve cada um dos tipos de

ERR:SYNTAX

erros e as razões possíveis para esses erros.

¦ Caso seleccione

(ou prima y [

1:Quit

QUIT

] ou ‘),

aparece o ecrã Home.

¦ Caso seleccione

, o ecrã anterior aparece com o

2:Goto

cursor perto ou na localização do erro.

Nota: Caso ocorra um erro de sintaxe no conteúdo de uma função Y= durante a execução do programa, a opção Goto regressa ao editor Y= e não ao programa.

Para corrigir um erro, siga estes passos.

1. Anote o tipo de erro (

2. Seleccione

, se estiver disponível. É apresentado o

2:Goto

tipo de erro).

ERR:

ecrã anterior com o cursor perto ou na localização do erro.

3. Determine o erro. Caso não consiga reconhecer o erro,

consulte o Apêndice B.

4. Corrija a expressão.

1–28 Utilização da TI-83

Capítulo 2: Operações Math, Angle e Test

Índice

Como Começr: Moeda ao Ar Operações Matemáticas no Teclado Operações MATH

...................................

Utilizar o Equation Solver Operações MATH NUM (Numéricas)

..........................

...................

............................

.................

Introduzir e Utilizar Números Complexos Operações MATH CPX (Complexas)

..................

Operações MATH PRB (Probabilidades) Operações ANGLE Operações TEST (Relacionais) Operações TEST LOGIC (Booleanas)

..................................

......................

.................

..............

2 3 6

9 14 17 19 21 24 27 28

Operações Math, Angle e Test 2–1

Como Começar: Moeda ao Ar

Como Começar é uma introdução. Leia o capítulo para obter detalhes.

Suponha que simula o lançamento de uma moeda ao ar 10 vezes. Quer determinar quantos desses 10 lançamentos resultam em caras e executar 40 vezes essa simulação. A probabilidade de um lançamento da moeda ao ar resultar em caras é de 0,5 e em coroas é de 0,5.

1. Comece no ecrã Home. Prima  | para visualizar o menu seleccionar

randBin(

é colado no ecrã Home. Prima

MATH PRB.

7:randBin(

para introduzir o número de lançamentos da moeda ao ar. Prima ¢. Prima Ë introduzir a probabilidade de sair caras. Prima ¢. Prima

para introduzir o número

de simulações. Prima ¤.

2. Prima Í para calcular a expressão. É apresentada uma lista de 40 elementos. A lista contém o total de caras resultantes de cada conjunto de 10 lançamentos da moeda ao ar. A lista tem 40 elementos porque esta simulação foi efectuada 40 vezes. Neste exemplo, a moeda apareceu cinco vezes como caras no primeiro conjunto de 10 lançamentos, cinco vezes no segundo conjunto de 10 lançamentos e assim sucessivamente.

3. Prima ¿ y ã

ä Í para armazenar

os dados com o nome de lista seguida, pode utilizar os dados noutra actividade, tal como o traçado de um histograma (Capítulo 12).

Prima 7 para

(binómio aleatório).

para

. Em

4. Prima ~ ou | para visualizar os totais adicionais na lista. As reticências ( indicam que a lista continua para além do ecrã.

Nota: Dado que randBin( gera números aleatórios, os elementos da sua lista podem diferir dos deste exemplo.

2–2 Operações Math, Angle e Test

)

...

Operações Matemáticas no Teclado

Utilizar Listas com Operações Matemáticas

+ (Adição) N (Subtracção)

ää

(Multiplicação)

à (Divisão)

Funções Trigonométricas

As operações matemáticas válidas para listas devolvem uma lista calculada elemento a elemento. Caso utilize duas listas na mesma expressão, ambas têm de ter a mesma extensão.

Pode utilizar + (adição, Ã), N (subtracção, ¹),

ää

(multiplicação, ¯) e à (divisão, ¥) com números reais e complexos, expressões, listas e matrizes. Não pode utilizar com matrizes.

valorA

valorB valorA-valorB

valorA

valorB valorA/valorB

Pode utilizar as funções trigonométricas (trig) (seno, ˜; coseno, ™; e tangente, š) com números reais, expressões e listas. Por exemplo,

.9880316241

valor

sin(

Pode utilizar as funções trigonométricas inversas (arco-seno, y [

SIN

y [

TAN

; no modo Degree devolve .5.

) cos(

]; arco-co-seno, y [

]) com números reais, expressões e listas. A

sin(30)

no modo

valor

) tan(

COS

devolve

Radian

valor

]; e arco-tangente,

)

definição do modo ângulo actual afecta a interpretação.

valor

sin

(

) cos

Nota: As funções trigonométricas não funcionam com números

complexos.

valor

(

) tan

valor

(

)

Operações Math, Angle e Test 2–3

Operações Matemáticas no Teclado

(cont.)

^ (Potência)

(Quadrado) ‡( (Raiz Quadrada)

(Inverso)

log(

ln(

e^( (Exponencial)

e (Constante)

Pode utilizar ^ (potência, ›), 2 (quadrado, ¡) e ‡( (raiz quadrada, y [ expressões, listas e matrizes. Não pode utilizar

‡

]) com números reais e complexos,

‡(

com

matrizes.

valor^potência valor

Pode utilizar

(inverso, —) com números reais e

‡(

valor

)

complexos, expressões, listas e matrizes. O inverso multiplicativo é equivalente ao recíproco, 1àx.

valor

Pode utilizar

y [

]) e

(logaritmo, «),

log(

(logaritmo natural, µ) com números reais

ln(

(potência de 10,

ou complexos, expressões e listas.

valor

log( e^(

)

(exponencial, y ã

uma potência. Pode utilizar

potência

]) devolve a constante e elevada a

) ln(

com números reais ou

e^(

valor

)

complexos, expressões e listas.

potência

e^(

(constante, y [e]) é armazenada como uma constante na

TI-83. Prima y [

)

] para copiar e para o local onde se

encontra o cursor. Nos cálculos, a TI-83 utiliza 2,718281828459 para

2–4 Operações Math, Angle e Test

L (Negação)

p (Pi)

(negação, Ì) devolve o simétrico do valor, que pode ser

um número real ou complexo, uma expressão, lista e matriz.

valor

As normas do EOS (Capítulo 1) determinam quando uma negação é calculada. Por exemplo,

devolve um número negativo porque o quadrado é calculado antes da negação. Utilize parênteses para elevar ao quadrado o simétrico de um número, como em

Nota: Na TI-83, o símbolo de negação (M) é mais curto e mais alto que o sinal de subtracção (N), sendo apresentado quando prime ¹.

(Pi) é armazenado como uma constante na TI-83. Prima

y [p] para copiar o símbolo

(LA)

para o local onde se encontra o cursor. Nos cálculos, a TI-83 utiliza 3,1415926535898 para

Operações Math, Angle e Test 2–5

Operações MATH

Menu MATH

Frac

Dec

Para visualizar o menu

MATH NUM CPX PRB 1:

4Frac

4Dec

‡( Calcula a raiz cúbica

‡

5: 6: fMin( Acha o mínimo de uma função 7: fMax( Acha o máximo de uma função 8: nDeriv( Calcula a derivada numérica 9: fnInt( Calcula o integral da função 0: Solver

Frac

(visualização como fracção) apresenta uma resposta

Apresenta a resposta em fracção Apresenta a resposta em decimal Calcula o cubo

Calcula a raiz

Apresenta o Equation Solver

...

MATH

, prima .

índice x

na forma do seu equivalente racional. valor pode ser um número real ou complexo, uma expressão, lista e matriz. Caso a resposta não possa ser simplificada ou o denominador resultante tenha mais de três dígitos, é devolvido o equivalente decimal. Só pode utilizar 4

Frac

seguir a valor.

Frac

valor4

Dec

(visualização como decimal) apresenta uma resposta

na forma de decimal. O valor pode ser um número real ou complexo, uma expressão, lista e matriz. Só pode utilizar

Dec

a seguir a valor.

Dec

valor

2–6 Operações Math, Angle e Test

(Cubo)

‡( (Raiz

Cúbica)

(cubo) devolve o cubo de um número real ou complexo,

uma expressão, lista e matriz quadrada.

valor

‡(

(raiz cúbica) devolve a raiz cúbica de um número real ou

complexo, uma expressão e lista.

valor

‡(

)

‡ (Root)

fMin( fMax(

‡

(raiz índice x) devolve a raiz índice x de um número

real ou complexo, uma expressão e lista.

raiz índice x

(mínimo da função) e

fMin(

‡

valor

(máximo da função)

fMax(

devolvem o valor em que ocorre o valor mínimo ou máximo da expressão relativamente à variável, entre os valores inferior e superior da variável.

fMin(

fMax(

não são válidos na expressão. A precisão é controlada pela tolerância (caso não seja especificado, a predefinição é 1â

N5).

expressão,variável,inferior,superior[,tolerância]

fMin(

expressão,variável,inferior,superior[,tolerância]

fMax(

Nota: Neste manual, os argumentos opcionais e as vírgulas que os

acompanham estão entre parênteses rectos ([ ]).

)

Operações Math, Angle e Test 2–7

Operações MATH

nDeriv(

aproximada da expressão relativamente à variável, dado o valor em que calcular a derivada e H (caso não seja

especificado, a predefinição é 1â

nDeriv( nDeriv(

aproxima o valor da derivada numérica como a inclinação da recta secante através destes pontos.

f¢(

À medida que H fica mais pequeno, normalmente a aproximação torna-se mais precisa.

(cont.)

(derivada numérica) devolve uma derivada

3).

expressão,variável,valor[,H]

utiliza o método cociente da diferença simétrica, que

+H)Nf(

) =

)

Pode utilizar

nDeriv(

utilizado para calcular valor derivado falso num ponto indiferenciável.

(integral da função) devolve o integral numérico

fnInt(

(método Gauss-Kronrod) da expressão relativamente a variável, dado o limite inferior, o limite superior e uma tolerância (caso não seja especificada, a predefinição é

1â

5).

expressão,variável,inferior,superior[,tolerância]

fnInt(

Sugestão: Para aumentar a velocidade do desenho de gráficos de

integração (quando utilizar fnInt( numa equação Y=), aumente o valor da variável de janela Xres antes de premir

2–8 Operações Math, Angle e Test

uma vez em expressão. Dado o método

, a TI-83 pode devolver um

nDeriv(

)

Utilizar o Equation Solver

apresenta o Equation Solver, em que pode solucionar

Solver

Introduzir uma Expressão no Equation Solver

Solver

qualquer variável de uma equação. Considera-se que a equação é igual a zero.

Quando selecciona ¦ O editor de equações (consulte a imagem do passo 1)

quando a variável da equação

¦ O editor do calculador interactivo (consulte a imagem do

passo 3, na página 2-10) quando uma equação é armazenada em

Para introduzir uma expressão no Equation Solver, partindo do princípio que a variável passos.

1. Seleccione

editor de equações.

2. Introduza a expressão de uma das três formas seguintes.

¦ Introduza a expressão directamente no Equation

Solver.

¦ Cole um nome de variável

Equation Solver.

¦ Prima y [

Y-VARS

Equation Solver.

A expressão é armazenada na variável a introduz.

, visualiza um de dois ecrãs.

Solver

se encontra vazia.

eqn

se encontra vazia, siga estes

eqn

0:Solver

no menu

], cole um nome de variável Y= do

RCL

para visualizar o

MATH

do menu

Y-VARS

e prima Í. A expressão é colada no

à medida que

eqn

Operações Math, Angle e Test 2–9

Utilizar o Equation Solver

(cont.)

Introduzir uma Expressão no Equation Solver (cont.)

Introduzir e Editar Valores de Variáveis

3. Prima Í ou †. É apresentado o editor do calculador

interactivo.

¦ A equação armazenada em

é apresentada na

eqn

primeira linha e definida como igual a zero.

¦ As variáveis da equação são listadas na ordem em que

aparecem na equação. São igualmente apresentados quaisquer valores armazenados nas variáveis listadas.

¦ Os limites inferior e superior predefinidos aparecem

na última linha do editor (

bound={L1å99.1å99}

¦ É apresentado $ na primeira coluna da última linha,

caso o editor ultrapasse os limites do ecrã.

Sugestão: Para utilizar o Solver para resolver uma equação como K=.5MV2, introduza eqn:0=KN.5MV

no editor de equações.

Quando introduz ou edita um valor de uma variável no editor do calculador interactivo, o novo valor é armazenado na memória para essa variável.

Pode introduzir uma expressão para um valor de variável. É calculado quando passa à variável seguinte. As expressões têm de ser resolvidas para números reais em cada passo, durante a iteração.

Pode armazenar equações em quaisquer variáveis de função

, tais como

Y-VARS

variáveis

da equação. O editor do calculador interactivo

apresenta todas as variáveis de todas as funções

e, em seguida, referenciar as

referenciadas na equação.

2–10 Operações Math, Angle e Test

Resolver uma Variável no Equation Solver

Para resolver uma variável utilizando o Equation Solver depois de uma equação ter sido armazenada em

eqn

, siga

estes passos.

1. Seleccione

0:Solver

no menu

para visualizar o

MATH

editor do calculador interactivo, caso ainda não esteja apresentado.

2. Introduza ou edite o valor de cada uma das variáveis

conhecidas. Todas as variáveis, à excepção da variável desconhecida, têm de conter um valor. Para mover o cursor para a variável seguinte, prima Í ou †.

3. Introduza uma estimativa inicial para a variável que está a

resolver. Isto é opcional, mas pode ajudá-lo a encontrar mais rapidamente a solução. Da mesma forma, no que respeita a equações com múltiplas raízes, a TI-83 tentará apresentar a solução mais próxima da sua estimativa.

A estimativa predefinida é calculada como

(superior-inferior)/2.

Operações Math, Angle e Test 2–11

Utilizar o Equation Solver

(cont.)

Resolver uma Variável no Equation Solver (cont.)

Editar uma Equação Armazenada em eqn

Equações com Múltiplas Raízes

4. Edite

bound={

inferior,superior

. inferior e superior são

}

os limites entre os quais a TI-83 procura uma solução. Isto é opcional, mas também pode ajudar a encontrar a solução mais rapidamente. A predefinição é

bound={L1å99.1å99}

5. Mova o cursor para a variável que está a tentar resolver e

prima

[

SOLVE

¦ A solução é apresentada junto à variável que resolveu.

Um quadrado preenchido na primeira coluna marca a variável que resolveu e indica que a equação está equilibrada. As reticências mostram que o valor continua para além do ecrã.

¦ Os valores das variáveis são actualizados na memória. ¦

dif é apresentado na última linha do editor. dif

leftNrt=

é a diferença entre os lados esquerdo e direito da equação. Um quadrado preenchido na primeira coluna, junto a

leftNrt=

indica que a equação foi

calculada com o novo valor da variável que resolveu.

Para editar ou substituir uma equação armazenada em

eqn

quando o Equation Solver interactivo é apresentado, prima

até que o editor de equações seja apresentado. Em

}

seguida, edite a equação.

Algumas equações têm mais do que uma solução. Pode introduzir uma nova estimativa inicial (página 2-9) ou novos limites (página 2-10) para procurar soluções adicionais.

2–12 Operações Math, Angle e Test

Outras Soluções

Controlar a Solução em Solver ou Solve(

Utilizar Solve( no Ecrã Home ou num Programa

Depois de ter *resolvido uma variável, pode continuar a explorar soluções a partir do editor do calculador interactivo. Edite os valores de uma ou mais variáveis. Quando edita qualquer valor de variável, os quadrados preenchidos junto à solução anterior e

leftNrt=

dif

desaparecem. Mova o cursor para a variável que quer resolver e prima ƒ [

SOLVE

A TI-83 resolve equações por um processo iterativo.

Para controlar esse processo, introduza limites que fiquem relativamente próximos da solução e introduza uma estimativa inicial dentro desses limites. Isto ajudará a encontrar uma solução mais rapidamente. Também definirá a solução que pretende para equações com múltiplas soluções.

só se encontra disponível no

solve(

CATALOG

ou num

programa. Devolve uma solução (raiz) de expressão para

variável, dada uma estimativa inicial e os limites inferior e superior dentro dos quais a solução é procurada. O limite inferior predefinido é L1â99. O limite superior predefinido é

1â99.

expressão,variável,estimativa[,{inferior,superior

solve(

})

expressão é assumido como sendo igual a zero. O valor de variável não será actualizado na memória. estimativa pode

ser um valor ou uma lista de dois valores. Os valores têm de ser armazenados para todas as variáveis em expressão, à excepção de variável, antes que expressão seja calculada. inferior e superior têm de ser introduzidos em formato de lista.

Operações Math, Angle e Test 2–13

Operações MATH NUM (Numéricas)

Menu MATH NUM

abs(

round(

Para visualizar o menu

MATH NUM CPX PRB 1: abs( Valor absoluto 2: round( 3: iPart( Parte inteira 4: fPart( Parte fraccionária 5: int( Inteiro maior 6: min( Valor mínimo 7: max( Valor máximo 8: lcm( Mínimo múltiplo comum 9: gcd( Máximo divisor comum

(valor absoluto) devolve o valor absoluto de um número

abs(

MATH NUM

Arredondado

, prima  ~.

real ou complexo (módulo), expressão, lista e matriz.

valor

abs(

Nota: abs( também se encontra disponível no menu MATH CPX.

round(

)

devolve um número, expressão, lista ou matriz arredondada para #decimais (9). Se #decimais for omitido, valor é arredondado para os dígitos apresentados, até um máximo de 10 dígitos.

valor[,#decimais]

round(

)

2–14 Operações Math, Angle e Test

iPart( fPart(

int(

min( max(

(parte inteira) devolve a(s) parte(s) inteira(s) de um

iPart(

número real ou complexo, expressão, lista e matriz.

valor

iPart( fPart(

)

(parte fraccionária) devolve a(s) parte(s) fraccionária(s) de um número real ou complexo, expressão, lista e matriz.

valor

fPart(

int(

)

(inteiro maior) devolve o maior inteiro  de um número

real ou complexo, expressão, lista e matriz.

valor

int(

Nota: O

inteiros negativos, excepto para um inteiro inferior a iPart( para números negativos não inteiros.

min(

)

valor

é o mesmo que iPart( para números não negativos e

(valor mínimo) devolve o valor mínimo de valorA e valorB ou o elemento mais pequeno de lista. Ao comparar listaA e listaB,

cada par de elementos. Ao comparar lista e valor,

devolve uma lista do mais pequeno de

min(

compara cada um dos elementos de lista com valor.

(valor máximo) devolve o maior de valorA e valorB ou

max(

o maior elemento de lista. Ao comparar listaA e listaB,

max(

devolve uma lista dos maiores de cada par de elementos. Ao comparar lista e valor,

compara cada um dos

max(

elementos de lista com valor.

valorA,valorB

min( min( min( min(

Nota: min( e max( encontram-se disponíveis no menu LIST MATH.

) max(

lista

listaA,listaB

lista,valor

) max(

valorA,valorB

)

lista listaA,listaB

lista,valor

)

Operações Math, Angle e Test 2–15

Operações MATH NUM (Numéricas)

devolve o mínimo múltiplo comum de valorA e valorB,

lcm( gcd(

lcm(

sendo ambos inteiros não negativos. Ao especificar listaA e listaB, lcm

devolve uma lista do mínimo múltiplo comum de

(

cada par de elementos. Ao comparar lista e valor, compara cada um dos elementos em lista com valor.

devolve o máximo divisor comum de valorA e valorB,

gcd(

sendo ambos inteiros não negativos. Ao especificar listaA e listaB, gcd

devolve uma lista do máximo divisor comum de

(

cada par de elementos. Ao comparar lista e valor, compara cada um dos elementos de lista com valor.

valorA,valorB

lcm(

listaA,listaB

lcm(

lista,valor

lcm(

) gcd(

(cont.)

valorA,valorB

listaA,listaB

lista,valor

lcm(

gcd(

)

2–16 Operações Math, Angle e Test

Introduzir e Utilizar Números Complexos

Modos de Números Complexos

A TI-83 exibe os números complexos nas formas retangular e polar. Para selecionar um modo de números complexos, pressione z e, em seguida, selecione um dos dois modos.

i (modo complexo-retangular)

a+b

i (modo complexo-polar)

re^q

Na TI-83, os números complexos podem ser armazenados em variáveis. Da mesma forma, os números complexos são elementos válidos da lista.

No modo retornam um erro, a menos que você tenha introduzido um número complexo como entrada. Por exemplo, no modo

Real, ln(L1)

uma resposta.

Modo Real Modo a+b

, os resultados dos números complexos

Real

retorna um erro; no modo

a+b

ln(L1)

retorna

Introduzindo Números Complexos

Nota sobre Modo Radiano x Grau

Os números complexos são armazenados na forma retangular, mas você pode introduzir um número complexo no formato retangular ou polar, independente da definição do modo. Os componentes dos números complexos podem ser números reais ou expressões dão números reais como resultado; as expressões são calculadas quando o comando é executado.

O modo radiano é recomendado para os cálculos com números complexos. Internamente, a TI-83 converte para radianos todos os valores trigonométricos introduzidos, porém não converte os valores das funções exponenciais, logarítmicas e hiperbólicas.

No modo grau, as identidades complexas como e^(iq) = cos(q) + i sin(q) geralmente não são verdadeiras porque os valores do seno e do coseno são convertidos para radianos, enquanto que os valores de e^() não são. Por exemplo, e^(i45) = cos(45) + i sin(45) é internamente tratado como e^(i45) = cos(p/4) + i sin(p/4). As identidades complexas são sempre tratadas no modo radiano.

Operações Math, Angle e Test 2–17

Introduzir e Utilizar Números Complexos

(cont.)

Interpretar Resultados Complexos

Modo RectangularComplexo

Modo PolarComplexo

Os números complexos dos resultados, incluindo elementos de lista, são apresentados com forma rectangular ou polar, conforme for especificado pela definição de modo ou por uma instrução de conversão de visualização (página 2-20).

No exemplo a seguir, estão activos os modos

re^q

i e

Degree

O modo rectangular reconhece e apresenta um número complexo na forma a+bi, em que a componente imaginária e i é uma constante igual a

é a componente real, b é

-1

Para introduzir um número complexo de forma rectangular, introduza o valor de

(componente real), prima Ã ou ¹,

introduza o valor de b (componente imaginária) e prima y [i] (constante).

componente real(

ou N) componente imagináriai

O modo polar reconhece e apresenta um número complexo na forma re^ natural,

i, em que r é a magnitude, e é a base do logaritmo

é o ângulo e i é uma constante igual a

-1

Para introduzir um número complexo na forma polar, introduza o valor de r (magnitude), prima y [ exponencial), introduza o valor de (constante).

magnitude

e^(

ânguloi

2–18 Operações Math, Angle e Test

] (função

(ângulo) e prima y [i]

)

Operações MATH CPX (Complexas)

Menu MATH CPX

conj(

real(

imag(

Para visualizar o menu

MATH CPX

, prima  ~ ~.

MATH NUM CPX PRB 1:conj(

Devolve o complexo conjugado

2:real( Devolve a parte real 3:imag( Devolve a parte imaginária 4;angle( 5:abs(

Devolve o ângulo polar Devolve a magnitude (módulo)

6:4Rect Apresenta o resultado na forma rectangular 7:4Polar Apresenta o resultado na forma polar

(conjugado ) devolve o complexo conjugado de um

conj(

número complexo ou uma lista de números complexos.

bi no modo

conj(a+bi) conj(re^(

real(

devolve um valor para a

devolve um valor para re^(

))

(parte real) devolve a parte real de um número

i) no modo

a+b

re^

complexo ou uma lista de números complexos.

real(a+bi) real(re^(

imag(

devolve um valor para a.

devolve um valor para r

))

cos(q).

(parte imaginária) devolve a parte imaginária (não real) de um número complexo ou uma lista de números complexos.

imag (a+bi) imag(re^(

devolve um valor para b.

devolve um valor para r

))

sin(q).

Operações Math, Angle e Test 2–19

Operações MATH CPX (Complexas)

devolve o ângulo polar de um número complexo ou

angle(

abs(

4Rect

angle(

uma lista de números complexos, calculados como

tan

(b/a), em que b é a parte imaginária e a é a parte real. O cálculo é ajustado por +p no segundo quadrante ou por no terceiro quadrante.

angle(a+bi) angle(re^(

abs(

(real

devolve um valor para tan

devolve um valor para q, em que Lp<q<p.

))

(valor absoluto) devolve a magnitude (módulo),

)

imag

, de um número complexo ou uma lista de

números complexos.

bi) devolve um valor para

abs(a+

abs(re^(

4Rect

devolve um valor para r (magnitude).

))

(visualização como rectangular) apresenta um resultado complexo na forma rectangular. Só é válido no final de uma expressão. Não é válido se o resultado for real.

resultado complexo

8Rect

devolve um valor para a+bi

(cont.)

(

(b/a).

)

8Polar

(visualização como polar) apresenta um resultado complexo na forma polar. Só é válido no fim de uma expressão. Não é válido se o resultado for real.

resultado complexo

2–20 Operações Math, Angle e Test

8Polar

devolve um valor para r

e^(

)

Operações MATH PRB (Probabilidades)

Menu MATH PRB

Utilizar rand para Gerar um Número Aleatório

Utilizar rand para Gerar uma Lista de Números Aleatórios

Para visualizar o menu

MATH NUM CPX PRB 1: rand Gerador de números aleatórios 2: nPr Número de permutações 3: nCr Número de combinações 4: ! Factorial 5: randInt( Gerador de inteiros aleatórios 6: randNorm( # aleatório da distribuição Normal 7: randBin( # aleatório da distribuição Binomial

(número aleatório) gera e devolve um ou mais números

rand

MATH PRB

, prima  |.

aleatórios > 0 e < 1. Para gerar uma sequência de números aleatórios, prima Í repetidas vezes.

númerotentativas

rand[(

Sugestão: Para gerar números aleatórios para além do intervalo de

0 a 1, pode incluir rand numa expressão. Por exemplo, rand 5 gera um número aleatório superior a 0 e inferior a 5.

Com cada execução de

]

)

, a TI-83 gera a mesma sequência

rand

de números aleatórios para um dado valor gerador. O valor gerador da TI-83 definido pela fábrica para

rand

é 0. Para gerar uma sequência de números aleatórios diferente, armazene qualquer valor gerador diferente de zero em

rand

Para restaurar o valor gerador definido pela fábrica, armazene

ou reponha as predefinições

rand

(Capítulo 18).

Nota: O valor gerador também afecta as instruções randInt(, randNorm(, e RandBin( (páginas 2-22, 2-23).

Para gerar uma sequência de números aleatórios apresentada em forma de lista, especifique um inteiro > 1 para númerotentativas (número de tentativas). A predefinição para númerotentativas é 1.

Operações Math, Angle e Test 2–21

Operações MATH PRB (Probabilidades)

(número de permutações) devolve o número de

nPr nCr

! (Factorial)

nPr

permutações de itens, um número de cada vez. itens e número têm de ser inteiros não negativos. Tanto itens como número podem ser listas.

itens

nCr

número

nPr

(número de combinações) devolve o número de

combinações de itens, um número de cada vez. itens e

número têm de ser inteiros não negativos. Tanto itens como número podem ser listas.

itens

(factorial) devolve o factorial de um inteiro ou um múltiplo

nCr

número

de 0,5. Tratando-se de uma lista, devolve factoriais para cada inteiro ou múltiplo de 0,5. valor tem de ser ‚ L0,5 e  69.

valor

(cont.)

Nota : O factorial é calculado de maneira repetitiva utilizando a

relação (n+1)! = nän!, até que n fique reduzido a 0 ou a L1/2. Nesse ponto, é utilizada a definição 0!=1 ou (L1/2)!=‡p para terminar o cálculo. Portanto : n!=nä(nN1)ä(n-2)ä ... ä2ä1, se n for um inteiro ‚ 0 n!= nä(nN1)ä(n-2)ä ... ä1/2 n! é falso se nem n nem n+1/2 for inteiro ‚ 0. (A variável n é representada por

(inteiro aleatório) gera e apresenta um inteiro

randInt(

aleatório num intervalo especificado por limites inteiros inferior e superior. Para gerar uma sequência aleatória inteira, prima

números aleatórios, especifique um inteiro > 1 para númerotentativas (número de tentativas; caso não seja especificado, a predefinição é 1).

inferior, superior[,númerotentativas]

randInt(

2–22 Operações Math, Angle e Test

‡p

, se n+1/2 for um inteiro ‚ 0

valor

)

repetidas vezes. Para gerar uma lista de

)

randNorm(

(aleatório Normal) gera e apresenta um número aleatório real a partir de uma distribuição Normal especificada. Cada valor gerado pode ser qualquer valor real, mas a maior parte situar-se-á no intervalo [mN3(s)

m+3(s)].

Para gerar uma lista de números aleatórios, especifique um inteiro > 1 para númerotentativas (número de tentativas. caso não seja especificado, a predefinição é 1).

númerotentativas]

randNorm(m,

[

)

randBin(

(aleatório Binomial) gera e apresenta um número aleatório real a partir de uma distribuição Binomial especificada. númerotentativas (número de tentativas) tem de ser ‚ 1. prob (probabilidade de êxito) tem de ser ‚ 0 e  1. Para gerar uma lista de números aleatórios, especifique um inteiro > 1 para númerosimulações (número de simulações; caso não seja especificado, a predefinição é 1).

randBin(

Nota: O valor gerador também afecta as instruções randInt(, randNorm( e RandBin( (página 2-21).

númerotentativas,prob[,númerosimulações]

)

Operações Math, Angle e Test 2–23

Operações ANGLE

Menu ANGLE

Notação de Entrada DMS

Para visualizar o menu

apresenta indicadores e instruções de ângulo. A

ANGLE

definição do modo

Radian/Degree

a TI-83 faz das entradas do menu

ANGLE 1:

2: ' Notação de minuto DMS

3: 4:

8DMS

5: R8Pr( Devolve r, dados X e 6: R8Pq( Devolve q, dados X e 7: P8Rx( Devolve x, dados R e 8: P8Ry( Devolve y, dados R e

Notação de graus

Notação de radianos Apresentado como graus/minutos/segundos

ANGLE

, prima y[

ANGLE

]. O menu

afecta a interpretação que

ANGLE

Y Y

q q

A notação de entrada DMS (graus/minutos/segundos) compreende o símbolo de graus ( minutos (

) e o símbolo de segundos (

), o símbolo de

. graus tem de ser

)

um número real; minutos e segundos têm de ser números reais ‚ 0.

graus

minutos'segundos

Por exemplo, introduza

30¡1'23''

para 30 graus, 1 minuto,

23 segundos. Caso o modo ângulo não esteja definido como

, tem de utilizar ¡ de a forma que a TI-83 possa

Degree

interpretar o argumento como graus, minutos e segundos.

Modo Degree Modo Radian

2–24 Operações Math, Angle e Test

¡ (Graus) ' (Minutos) " (Segundos)

(Radiano)

8DMS

(graus) designa um ângulo ou uma lista de ângulos como graus, independentemente da definição actual do modo ângulo. No modo

, pode utilizar ¡ para converter

Radian

graus em radianos.

valor¡

valor1,valor2,valor3,valor4

{

também designa graus (D) no formato DMS.

(minutos) designa minutos (M) no formato DMS.

...

valor n

}¡

" (segundos) designa segundos (S) no formato DMS.

Nota: " não existe no menu ANGLE. Para introduzir " , primaã].

(radiano) designa um ângulo ou uma lista de ângulos em radianos, independentemente da definição actual do modo ângulo. No modo

, pode utilizar r para converter

Degree

radianos em graus.

valor

Modo Radian Modo Degree

8DMS

(graus/minutos/segundos) apresente resposta no

formato DMS (página 2-24). A definição de modo tem de ser

para que resposta seja interpretado como graus,

Degree

minutos e segundos. 8

resposta

DMS

só é válido no fim de uma linha.

DMS

Operações Math, Angle e Test 2–25

Operações ANGLE

R8Pr( R8Pq ( P8Rx( P8Ry(

R8Pr(

polares e devolve um valor para coordenadas rectangulares em coordenadas polares e devolve um valor para

R8Pr(x,y) R8Pq (

P8Rx(

rectangulares e devolve um valor para coordenadas polares em coordenadas rectangulares e devolve um valor para

P8Rx(r,q) P8Ry(

(cont.)

converte coordenadas rectangulares em coordenadas

r. R8Pq(

. x e y podem ser listas.

x,y

)

Nota: O modo Radian está

activo.

converte coordenadas polares em coordenadas

. r e q podem ser listas.

,q)

Nota: O modo Radian está

activo.

converte

x. P8Ry(

converte

2–26 Operações Math, Angle e Test

Operações TEST (Relacionais)

Menu TEST

‚



Para visualizar o menu

Este operador... Devolve 1 (verdadeiro) se...

TEST LOGIC 1: = 2: ƒ 3: > 4: ‚ 5: < 6: 

, prima y [

TEST

Igual a Diferente de Maior que Maior ou igual a Menor que Menor ou igual a

TEST

Os operadores relacionais comparam valorA e valorB e devolvem

se o teste for verdadeiro ou 0 se o teste for falso.

valorA e valorB podem ser números reais ou complexos, expressões ou listas. Só

e ƒ funcionam com matrizes. Se

valorA e valorB forem matrizes, têm de ter as mesmas dimensões.

Os operadores relacionais são frequentemente utilizados em programas, para controlar o fluxo dos programas, e na elaboração de gráficos, para controlar o gráfico de uma função acima de valores específicos.

valorA

valorB valorAƒvalorB

valorA

valorB valorA‚valorB

valorA

valorB valorAvalorB

Utilizar Testes

Os operadores relacionais são calculados segundo funções matemáticas e em conformidade com as normas do EOS (Capítulo 1).

¦ A expressão

2+2=2+3

devolve 0. A TI-83 executa a adição em primeiro lugar, devido às normas do EOS, e compara 4 com 5.

¦ A expressão

2+(2=2)+3

devolve 6. A TI-83 executa o teste relacional em primeiro lugar, porque se encontra entre parênteses, e adiciona 2, 1 e 3.

Operações Math, Angle e Test 2–27

Operações TEST LOGIC (Booleanas)

Menu TEST LOGIC

Operadores Booleanos

and or xor

Para visualizar o menu

Este operador... Devolve um 1 (verdadeiro) se...

TEST LOGIC 1: and Ambos os valores são diferentes de

2: or Pelo menos um valor é diferente de zero

3: xor Só um valor é zero (falso) 4: not( O valor é zero (falso)

TEST LOGIC

zero (verdadeiro)

(verdadeiro)

prima y ã

TESTä

Os operadores Booleanos são frequentemente utilizados em programas, para controlar o fluxo dos programas, e na elaboração de gráficos, para controlar o gráfico de uma função acima de valores específicos. Os valores são interpretados como zero (falso) ou diferente de zero (verdadeiro).

and, or

expressão for verdadeira, ou

(ou exclusivo) devolvem um valor 1, se uma

xor

, se uma expressão for falsa,

em conformidade com a tabela a seguir. valorA e valorB podem ser números complexos ou reais, expressões ou listas.

valorA valorA valorA

valorA valorB

ƒ0 ƒ0 devolve ƒ0 0 devolve

valorB

and

valorB

xor

0 devolve

0 0 devolve

and or xor

110 011 011

devolve 1 se valor (que pode ser uma expressão) for 0.

not(

Utilizar Operações Booleanas

not(

valor

not(

)

A lógica Booleana é frequentemente utilizada em testes relacionais. No programa seguinte, as instruções armazenam

em C.

2–28 Operações Math, Angle e Test

Capítulo 3: Elaboração de Gráficos de Funções

Índice

Como Começar: Elaborar um Gráfico de Círculo Definir Gráficos Definir os Modos de Gráficos Definir Funções

....................................

.........................

....................................

Seleccionar e Anular Selecção de Funções Definir Estilos de Gráficos para Funções Definir as Variáveis da Janela de Visualização Definir o Formato do Gráfico Ver Gráficos

........................................

.........................

........

.............

...............

..........

Explorar Gráficos com o Cursor de Movimento Livre Explorar Gráficos com TRACE Explorar Gráficos com as Instruções ZOOM Utilizar ZOOM MEMORY Utilizar as Operações CALC (Cálculo)

.......................

............

.............................

................

....

2 3 4 5 7

9 12 14 16 18 19 21 24 26

Elaboração de Gráficos de Funções 3–1

Como Começar: Elaborar um Gráfico de Círculo

Como Começar é uma introdução. Leia o capítulo para obter detalhes.

Elaborar um gráfico de círculo de raio 10, com origem no centro da janela de visualização standard. Para traçar este círculo, terá de introduzir fórmulas separadas para as zonas superior e inferior do círculo. Em seguida, utilize

ZSquare

aparecerem como um círculo.

1. No modo

2. Prima q 6 para seleccionar

3. Para ajustar o visor de forma a que cada

(zoom do quadrado) para ajustar o visor de forma a fazer as funções

, prima o para visualizar o

Func

editor

. Prima y ã‡ä

¹ „ ¡

100

¤ Í para introduzir a expressão que define a metade superior do círculo Y=‡(100NX

A metade inferior do círculo é definida pela expressão Y=L‡(100NX2). No entanto, na TI-83, poderá definir uma função em relação a outra; assim, para definir

Y2=LY

, prima Ì para introduzir o sinal de negação. Prima  ~ para visualizar o menu

Y-VARS

seleccionar

FUNCTION

seleccionar

. Depois, prima Í para

1:Function

. O menu secundário

é apresentado. Prima 1 para

1:Y

VARS

6:Zstandard

. Este é um processo rápido de repor os valores standard das variáveis da janela. Também elabora os gráficos das funções; não é necessário premir s.

Note que as funções aparecem sob a forma de reticências na janela de visualização standard.

pixel represente uma largura e uma altura iguais, prima q

5:ZSquare

. As funções são traçadas

para seleccionar

novamente e aparecem agora, no visor, como um círculo.

4. Para ver as variáveis da janela

ZSquare

prima p e observe os novos valores para

Xmin, Xmax, Ymin

Ymax

3–2 Elaboração de Gráficos de Funções

Definir Gráficos

Similaridades no Modo de Elaboração de Gráfico da TI-83

Definir um Gráfico

Ver e Explorar um Gráfico

Guardar um Gráfico para Utilização Posterior

O Capítulo 3 descreve especificamente a elaboração de gráficos de funções. Os passos aqui apresentados são similares para cada modo de elaboração de gráficos na TI-83. Os Capítulos 4, 5 e 6 descrevem aspectos que são únicos na elaboração de gráficos paramétricos, polares e de sucessões.

Para definir um gráfico em qualquer modo de elaboração de gráficos, execute os seguintes passos. Alguns passos nem sempre são necessários.

1. Prima z e defina o modo de elaboração de gráficos adequado (página 3-4).

2. Prima o e escreva, edite ou seleccione uma ou mais funções no editor

(página 3-5).

3. Se necessário, anule a selecção de gráficos estatísticos (página 3-7).

4. Defina o estilo de gráfico para cada função (página 3-9).

5. Prima p e defina as variáveis de janela de visualização (página 3-12).

6. Prima y [

FORMAT

] e seleccione as definições do

formato de gráfico (página 3-14).

Uma vez definido um gráfico, poderá visualizá-lo premindo s. Explore o comportamento de uma ou mais funções utilizando as ferramentas da TI-83 descritas neste capítulo.

Os elementos que definem o gráfico actual podem ser armazenados numa das 10 variáveis de bases de dados de gráficos (

GDB1

GDB9

; Capítulo 8). Para recriar o

GDB0

gráfico actual posteriormente, basta recuperar a base de dados de gráficos onde armazenou o gráfico original.

Numa

, estão armazenados os tipos de informações que

GDB

se seguem. ¦ funções

¦ Definições de estilos de gráficos ¦ Definições de janela

Definições de formato

Pode igualmente armazenar uma imagem da visualização do gráfico actual numa das variáveis de 10 imagens gráficas (

Pic1

Pic9

; Capítulo 8). Posteriormente, poderá

Pic0

sobrepor uma ou mais imagens armazenadas ao gráfico actual.

Elaboração de Gráficos de Funções 3–3

Definir os Modos de Gráficos

Verificar e Alterar o Modo de Elaboração de Gráficos

Definir Modos a partir de um Programa

Para visualizar o ecrã de modo, prima z. As predefinições aparecerão realçadas a seguir. Para elaborar gráficos de funções, tem de seleccionar o modo

Func

antes de introduzir valores para as variáveis de janela e antes de introduzir as funções.

A TI-83 dispõe de quatro modos de elaboração de gráficos.

¦ ¦ ¦ ¦

(gráficos de funções)

Func

(gráficos paramétricos; Capítulo 4)

Par

(gráficos polares; Capítulo 5)

Pol

(gráficos de sucessões, Capítulo 6)

Seq

Outras definições de modo afectam os resultados da elaboração de gráficos. O Capítulo 1 descreve cada definição de modo.

¦ O modo decimal

Float

0123-9

(fixo) afecta as

coordenadas do gráfico visualizado.

¦ O modo de traçado

ou Degree afecta a

Radian

interpretação de algumas funções.

¦ O modo de de ângulo Connected ou Dot afecta a

interpretação de algumas funções.

¦ O modo de ordem de gráfico

Sequential

Simul

afecta o traçado de funções quando é seleccionada mais de uma função.

Para definir o modo de gráficos e outros modos a partir de um programa , comece numa linha em branco no editor do programa e siga estes passos.

1. Prima z para visualizar as definições de modo.

2. Prima †, ~, | e } para colocar o cursor no modo que pretende seleccionar.

3. Prima Í para colar o nome do modo na localização do cursor.

O modo é alterado quando o programa é executado.

3–4 Elaboração de Gráficos de Funções

Definir Funções

Ver Funções no Editor Y=

Definir ou Editar uma Função

Para visualizar o editor Y=, prima o. Pode armazenar até 10 funções nas variáveis de função

. Pode

elaborar um gráfico de uma ou mais funções definidas de uma só vez. No exemplo que se segue, as funções

são

definidas e seleccionadas.

Para definir ou editar uma função, siga estes passos:

1. Prima o para visualizar o editor Y=.

2. Prima † para mover o cursor para a função que pretende definir ou editar. Prima ‘ para apagar uma função.

3. Introduza ou edite a expressão para definir a função. ¦ Pode utilizar funções e variáveis (incluindo matrizes e

listas) na expressão. Se a expressão for calculada para um valor que não seja um número real, esse valor não será traçado; não são devolvidos erros.

¦ A variável independente na função é

. O modo

Func

define „ como X. Para introduzir X, prima „ ou prima ƒ [

¦ Quando introduz o primeiro carácter, o sinal

fica

realçado, indicando que a função foi seleccionada.

À medida que é introduzida, a expressão é armazenada na variável editor

como uma função definida pelo utilizador no

4. Prima Í ou † para mover o cursor para a função seguinte.

Elaboração de Gráficos de Funções 3–5

Definir Funções

(cont.)

Definir uma Função a partir do Ecrã Home ou de um Programa

Calcular Funções Y= em Expressões

Para definir uma função a partir do ecrã Home ou de um programa, comece numa linha em branco e siga estes passos.

1. Prima ƒ [

], introduza a expressão e, depois, prima

novamente ƒ [ã].

2. Prima ¿.

3. Prima  ~

VARS Y-VARS

e seleccione

1:Function

no menu

4. Seleccione o nome da função, que será colado na localização do cursor no ecrã Home ou no editor do programa.

5. Prima Í para terminar a instrução.

expressão

"!!Y

Depois de executada a instrução, a TI-83 armazena a expressão na variável

n designada, selecciona a função e

mostra a mensagem Done.

Pode calcular o valor Yn de uma função

. Uma lista de valores devolve uma lista.

especificado de

valor

Yn(

n({valor1,valor2,valor3, . . .,valor n

)

})

num valor

3–6 Elaboração de Gráficos de Funções

Seleccionar e Anular Selecção de Funções

Seleccionar e Anular Selecção de uma Função

Ligar ou Desligar um Gráfico Estatístico no Editor Y=

Pode seleccionar e anular a selecção (activar e dasactivar) de uma função no editor quando o sinal

está realçado. A TI-83 elabora gráficos

. Uma função é seleccionada

apenas das funções seleccionadas. Pode seleccionar uma ou todas as funções de

Para seleccionar ou anular a selecção de uma função no editor

siga estes passos

Y=,

1. Mova o para visualizar o editor Y=.

2. Mova o cursor para a função que pretende seleccionar ou desmarcar.

3. Prima | para colocar o cursor sobre o sinal

da função.

4. Para alterar o estado da selecção, prima Í.

Quando se introduz ou edita uma função, é automaticamente seleccionada. Quando limpa uma função, é desmarcada.

Para visualizar e alterar o estado de activado/desactivado de um gráfico estatístico no editor primeira linha do editor

, utilize

Plot1 Plot2 Plot3

). Quando um gráfico é activado,

o nome é realçado nesta linha.

Para alterar o estado activado/desactivado de um gráfico estatístico no editor em

Plot1, Plot2

, prima } e ~ para colocar o cursor

e, depois, prima Í.

Plot3

Plot1 está activado. Plot2 e Plot3 estão

desactivados.

Elaboração de Gráficos de Funções 3–7

Seleccionar e Anular Selecção de Funções

(cont.)

Seleccionar e Anular Selecção de Funções a partir do Ecrã Home ou de um Programa

Para seleccionar ou anular selecção de uma função a partir do ecrã Home ou de um programa, comece numa linha em branco e siga estes passos.

1. Prima  ~ para visualizar o menu

2. Seleccione

ON/OFF

3. Seleccione

para desactivar uma ou mais funções. A instrução

2:FnOff

4:On/Off

1:FnOn

para visualizar o menu secundário

para activar uma ou mais funções ou

VARS Y-VARS

seleccionada será copiada para a localização do cursor.

4. Introduza o número (

a 9 ou 0; não a variável

n) de

cada função que pretende activar ou desactivar. ¦ Se introduzir dois ou mais números, separe-os por

vírgulas.

¦ Para activar ou desactivar todas as funções, não

introduza nenhum número depois de

FnOn FnOff

[função#

função#

. . .

função n]

FnOn

FnOff

5. Prima Í. Quando a instrução é executada, o estado de cada função no modo actual é definido e é apresentada a mensagem Done.

Por exemplo, no modo desactivatodas as funções do editor Y= e, depois, activa

Func, FnOff :FnOn 1,3

3–8 Elaboração de Gráficos de Funções

Definir Estilos de Gráficos para Funções

Ícones de Estilos de Gráficos no editor Y=

Esta tabela descreve os estilos de gráficos disponíveis para gráficos de funções. Utilize os estilos para distinguir visualmente as funções que deverão ser representadas em gráfico em conjunto. Por exemplo, pode definir uma linha contínua,

com uma linha ponteada e

como

uma linha espessa.

Ícone Estilo Descrição

Linha

Uma linha contínua liga os pontos traçados; esta é a predefinição no modo

Espessa

Uma linha espessa contínua liga os pontos

Connected

traçados

Acima

Abaixo

Caminho

A área acima do gráfico é sombreada A área abaixo do gráfico é sombreada Um cursor circular traça a margem

esquerda do gráfico e desenha um caminho

Animação

Um cursor circular traça a margem esquerda do gráfico sem desenhar um caminho

Ponto

Um pequeno ponto representa cada um dos pontos traçados; esta é predefinição no modo Dot

Nota: Nem todos os estilos de gráficos estão disponíveis em todos os modos de elaboração de gráficos. Os capítulos 4, 5 e 6 listam os estilos dos modos Par, Pol e Seq.

Elaboração de Gráficos de Funções 3–9

Definir Estilos de Gráficos para Funções

(cont.)

Definir o Estilo do Gráfico

Sombrear Acima e Abaixo

Para definir o estilo do gráfico para uma função, siga estes passos:

1. Prima o para visualizar o editor

2. Prima † e } para mover o cursor para a função.

3. Prima | | para mover o cursor para a esquerda, a seguir ao sinal coluna. É apresentado o cursor de inserção. (A ordem dos passos 2 e 3 é aleatória.)

4. Prima Í repetidamente para fazer a rotação através dos estilos de gráficos. A rotação dos sete estilos de gráficos é feita na mesma ordem em que estão listados na tabela anterior.

5. Prima ~, } ou † quando tiver seleccionado um estilo.

Quando selecciona é ou ê para duas ou mais funções, a TI-83 faz a rotação através de quatro padrões de sombreado.

¦ Sombreado com linhas verticais para a primeira função

com um estilo de gráfico é ou ê.

¦ Sombreado com linhas horizontais para a segunda

função.

¦ Sombreado com linhas de inclinação negativa para a

terceira função.

¦ Sombreado com linhas de inclinação positiva para a

quarta função.

¦ A rotação regressa às linhas verticais para a quinta

função é ou ê, repetindo a ordem acima descrita.

, para o ícone do estilo de gráfico na primeira

3–10 Elaboração de Gráficos de Funções

Sombrear Acima e Abaixo (cont.)

Definir um Estilo de Gráfico a partir de um Programa

Quando as áreas a sombreadas se interceptam, os padrões sobrepõem-se.

Nota:

Quando selecciona é ou ê para uma função Y= que elabora uma família de curvas, tais como quatro padrões de sombreado para cada membro da família de curvas.

Y1={1,2,3}X

, é feita rotação dos

Para definir um estilo de gráfico a partir de um programa, seleccione visualizar este menu, prima do programa. #funçãoé o número da função gráficos actual. # estilo_gráficoé um inteiro de

H:GraphStyle(

o menu

PRGM CTL

enquanto estiver no editor



. Para

no modo de

a 7 que corresponde ao estilo de gráfico, tal como é apresentado a seguir.

= ç (linha)

= è (espessa)

= é (acima)

= ê (abaixo)

GraphStyle(

#função, #estilo_gráfico

= ë (caminho)

= ì (animação)

= í (ponto)

)

Por exemplo, quando este programa é executado no modo

Func, GraphStyle(1,3)

define

como é.( acima)

Elaboração de Gráficos de Funções 3–11

Definir as Variáveis da Janela de Visualização

A Janela de Visualização da TI-83

Ver as Variáveis da Janela

Alterar o Valor de uma Variável de Janela

A janela de visualização é a parte do plano de coordenadas definidas por

Xmin, Xmax, Ymin

marcas é definida por

Xscl

. A distância entre as

Ymax

(escala de X) no eixo X.

Yscl

(escala de Y) define a distância entre as marcas no eixo y. Para desactivar as marcas, defina

Ymax

Xmin

Xscl

Xmax

Yscl

Ymin

Xscl=0

Yscl=0

Para visualizar os valores actuais das variáveis de janela, prima p. O editor de janela acima e à direita mostra os valores predefinidos no modo de gráficos

e no modo de

Func

ângulo Radian. As variáveis da janela diferem de um modo de gráficos para outro.

define a resolução de pixels (1 a 8) apenas para

Xres

gráficos de funções. A predefinição é ¦ Em

, as funções são calculadas e traçadas em cada

Xres=1

pixel no eixo x..

¦ Em

, as funções são calculadas e traçadas de oito

Xres=8

em oito pixels ao longo do eixo x.

Sugestão: Os valores Xres mais baixos aumentam a resolução do gráfico, mas podem fazer com que a TI-83 desenhe os gráficos mais lentamente.

Para alterar o valor de uma variável de janela a partir do editor de janela, execute os seguintes passos:

1. Prima † ou } para mover o cursor para a variável de

janela que pretende alterar.

2. Edite o valor, que pode ser uma expressão.

¦ Introduza um novo valor, que limpará o valor original. ¦ Mova o cursor para um dígito específico e, em

seguida, edite-o.

3. Prima Í, † ou }. Se tiver introduzido uma

expressão, será caculada pela TI-83. O novo valor é armazenado.

Nota: As condições Xmin<Xmax e Ymin<Ymax têm de ser verdadeiras para poder elaborar o gráfico.

3–12 Elaboração de Gráficos de Funções

Armazenar numa Variável de Janela a partir do Ecrã Home ou de um Programa

X e @Y

Para armazenar um valor, que poderá ser uma expressão, numa variável de janela, comece numa linha em branco e siga estes passos.

1. Introduza o valor que pretende armazenar.

2. Prima ¿.

3. Prima  para visualizar o menu

4. Seleccione

janela

Func

1:Window

(menu secundário

para visualizar as variáveis de

X/Y

¦ Prima ~ para visualizar as variáveis de janela

(menu secundário

Pol

¦ Prima ~ ~ para visualizar as variáveis de janela

(menu secundário

U/V/W

VARS

Par

Seq

5. Seleccione a variável de janela na qual pretende

armazenar um valor. O nome da variável é colado na localização actual do cursor.

6. Prima Í para terminar a instrução.

Quando a instrução é executada, a TI-83 armazena o valor na variável de janela e apresenta-o.

As variáveis

VARS X/Y

(

1:Window

(itens 8 e 9 no menu secundário

)) definem a distância do centro de um pixel ao centro de qualquer pixel adjacente num gráfico (precisão do gráfico). valores de

Xmin, Xmax, Ymin

são calculados a partir dos

no momento da

Ymax

visualização do gráfico.

(Xmax - Xmin)

Pode armazenar valores em serão calculados a partir de

X, Xmin

(Ymax - Ymin)

. Se o fizer,

Ymin

Xmax

Ymax

Elaboração de Gráficos de Funções 3–13

Definir o Formato do Gráfico

Ver as Definições de Formato

Alterar uma Definição de Formato

RectGC PolarGC

Para visualizar as definições de formato, prima y [

FORMAT

]. As predefinições aparecem realçadas a seguir.

RectGC PolarGC Define as coordenadas do cursor CoordOn CoordOff Activa ou desactiva a visualização das

coordenadas

GridOff GridOn Activa ou desactiva a grelha AxesOn AxesOff Activa ou desactiva os eixos LabelOffLabelOn Activa ou desactiva as etiquetas dos

eixos

ExprOn ExprOff Activa ou desactiva a visualização de

expressões

As definições de formato determinam o aspecto de um gráfico no ecrã. As definições de formato aplicam-se a todos os modos de gráficos. O modo de gráficos

Seq

tem uma

definição de modo adicional (Capítulo 6).

Para alterar uma definição de formato, siga estes passos:

1. Prima †, ~, }

| como for necessário para mover o

cursor para a definição que pretende seleccionar.

2. Prima Í para seleccionar a definição realçada.

(coordenadas de gráficos rectangulares) apresenta a

RectGC

localização do cursor como coordenadas rectangulares

e Y.

PolarGC

localização do cursor como coordenadas polares

A definição

(coordenadas de gráficos polares) apresenta a

e q.

RectGC/PolarGC

determina quais as variáveis actualizadas no momento em que elabora o gráfico, move o cursor de movimento livre ou traça.

actualiza X e Y; se o formato CoordOn for

RectGC

seleccionado, serão apresentados

PolarGC

actualiza X, Y,

q; se o formato CoordOn, for

seleccionado, serão apresentados

e Y.

e q.

3–14 Elaboração de Gráficos de Funções

Texas instruments TI-83 User Manual [pt]

Specifications and Main Features

Frequently Asked Questions

User Manual

Índice

Como Começar: O que fazer primeiro!

Primeiros Passos

Introduzir um Cálculo: A Fórmula Quadrática

Definir uma Função: Caixa com Tampa

Definir uma Tabela de Valores: Caixa com Tampa

Ampliar a Tabela: Caixa com Tampa

Definir a Janela de Visualização: Caixa com Tampa

Ver e Traçar o Gráfico: Caixa com Tampa

Ampliar o Gráfico: Caixa com Tampa

Achar o Máximo Calculado: Caixa com Tampa

Capítulo 1: Utilização da TI-83

Ligar e Desligar a TI-83

Definir o Contraste do Visor

O Visor

Introduzir Expressões e Instruções

Teclas de Edição da TI-83

Definir Modos

Utilizar Nomes de Variáveis da TI-83

Armazenar Valores de Variáveis

Recuperar Valores de Variáveis

Área de Armazenamento ENTRY (Última Entrada)

Área de Armazenamento Ans (Última Resposta)

Menus da TI-83

Menus VARS e Y-VARS

Equation Operating System (EOSé)

Condições de Erro

Capítulo 2: Operações Math, Angle e Test

Como Começar: Moeda ao Ar

Operações Matemáticas no Teclado

Operações MATH

Utilizar o Equation Solver

Operações MATH NUM (Numéricas)

Introduzir e Utilizar Números Complexos

Operações MATH CPX (Complexas)

Operações MATH PRB (Probabilidades)

Operações ANGLE

Operações TEST (Relacionais)

Operações TEST LOGIC (Booleanas)

Capítulo 3: Elaboração de Gráficos de Funções

Como Começar: Elaborar um Gráfico de Círculo

Definir Gráficos

Definir os Modos de Gráficos

Definir Funções

Seleccionar e Anular Selecção de Funções

Definir Estilos de Gráficos para Funções

Definir as Variáveis da Janela de Visualização

Definir o Formato do Gráfico