Texas instruments TI-36X PRO User Manual

Calculadora TI-36X Pro

Informações importantes ....................................................... 2

Exemplos............................................................................... 3

Ligar e desligar a calculadora................................................ 3

Contraste do visor.................................................................. 3

Ecrã inicial ............................................................................. 4

2ª funções.............................................................................. 5

Modos.................................................................................... 6

Teclas multifunções ............................................................... 8

Menus.................................................................................... 8

Percorrer as expressões e o histórico ................................... 9

Comutação de respostas..................................................... 10

Última resposta.................................................................... 11

Ordem das operações ......................................................... 11

Apagar e corrigir .................................................................. 13

Fracções.............................................................................. 14

Percentagens....................................................................... 16

Tecla EE .............................................................................. 17

Potências, raízes e inversos................................................ 17

Pi.......................................................................................... 18

Matemática .......................................................................... 19

Funções numéricas ............................................................. 20

Ângulos................................................................................ 21

Rectangular para polar........................................................24

Trigonometria.......................................................................25

Funções hiperbólicas........................................................... 27

Funções exponenciais e logarítmicas..................................27

Derivada numérica............................................................... 28

Integral numérico ................................................................. 29

Operações guardadas.........................................................30

Variáveis guardadas e de memória..................................... 32

Editor de dados e fórmulas das listas.................................. 35

1

Estatística, regressões e distribuições ................................ 37

Probabilidade.......................................................................49

Tabela de funções ............................................................... 51

Matrizes ............................................................................... 54

Vectores............................................................................... 56

Solucionadores....................................................................58

Bases numéricas ................................................................. 63

Avaliação de expressões..................................................... 65

Constantes........................................................................... 66

Conversões.......................................................................... 68

Números complexos ............................................................ 71

Erros .................................................................................... 73

Informações das pilhas........................................................ 78

Em caso de dificuldade........................................................ 79

Apoio técnico, manutenção e garantia dos produtos Texas In-

struments............................................................................. 79

Informações importantes

A Texas Instruments não dá qualquer garantia, expressa ou
implícita, incluindo, mas não se limitando a quaisquer
garantias implícitas de comercialização e de adequação a um
propósito específico, com respeito a quaisquer programas ou
materiais de livros, e somente disponibiliza esses materiais
no estado em que se encontram.

Em hipótese alguma a Texas Instruments poderá ser
responsabilizada perante qualquer pessoa por danos
especiais, colaterais, incidentais ou conseqüenciais, que
tenham qualquer ligação ou que resultem da compra ou
utilização desses materiais, e a única e exclusiva
responsabilidade da Texas Instruments, independentemente
da forma de atuação, não deve exceder qualquer preço de
compra aplicável deste artigo ou material. Além disso, a
Texas Instruments não poderá estar sujeita a qualquer
reivindicação, seja de que espécie for, com respeito ao uso
desses materiais por qualquer outra parte.

2

MathPrint, APD, Automatic Power Down e EOS são marcas
comerciais da Texas Instruments Incorporated.

Copyright © 2010 Texas Instruments Incorporated

Exemplos

A seguir a cada secção aparecem instruções com exemplos
de sequências de teclas que demonstram as funções da
TI-36X Pro.

Os exemplos assumem todas as predefinições , conforme
apresentadas na secção Modos.

Alguns elementos do ecrã podem diferir dos elementos
apresentados neste documento.

Ligar e desligar a calculadora

& liga a calculadora. % ' desliga a calculadora. O
visor é apagado, mas o histórico, as definições e a memória
são retidos.

A função APD™ (Automatic Power Down™) desliga a
calculadora automaticamente se não premir nenhuma tecla
durante cerca de 5 minutos. Prima & após APD. O visor, as
operações pendentes, as definições e a memória são retidos.

Contraste do visor

O brilho e o contraste do visor podem depender da
iluminação do local em que a calculadora é utilizada, da
capacidade das pilhas e do ângulo de visualização.

Para ajustar o contraste:

1. Prima e liberte a tecla %.

2. Prima T (para escurecer o ecrã) ou U (para clarear o
ecrã).

3

Ecrã inicial

No ecrã inicial, pode introduzir funções e expressões
matemáticas juntamente com outras instruções. As respostas
aparecem no ecrã inicial. O ecrã da TI-36X Pro pode
apresentar um máximo de 4 linhas com um máximo de 16
caracteres por linha. Para entradas e expressões com mais
de 16 caracteres, pode deslocar-se para a esquerda e para a
direita (! e ") para ver a expressão ou a entrada completa.

No modo MathPrint™, pode introduzir até quatro níveis de
expressões e funções aninhadas, que incluem fracções,

raízes quadradas, expoentes com ^, Ü, e

Quando calcular uma entrada no ecrã inicial, dependendo do
espaço, a resposta aparece directamente à direita ou no lado
direito da linha seguinte.

Os indicadores especiais e os cursores podem aparecer no
ecrã para fornecerem informações adicionais relacionadas
com funções ou resultados.

Indicador Definição

2º 2ª função.
FIX Definição decimal fixa. (Consulte a

secção Modos.)

SCI, ENG Notação científica ou de engenharia

. (Consulte a secção Modos.)

DEG, RAD,
GRAD

Modo de ângulo (graus, radianos ou
grados). (Consulte a secção

Modos.)
L1, L2, L3 Mostra as listas no editor de dados.
H, B, O Indica o modo de base numérica

HEX, BIN ou OCT. Nenhum

indicador apresentado para o modo

DEC predefinido.

A calculadora está a efectuar uma

operação.

x

e 10x.

4

Indicador Definição

5 6 Uma entrada é guardada na

³´ Uma entrada ou menu mostra mais

memória antes e/ou depois do ecrã

activo. Prima # e $ para

percorrer.

de 16 dígitos. Prima ! ou " para

percorrer.

Cursor normal. Mostra onde o

próximo item escrito aparecerá.

Cursor de limite de entrada. Não

pode introduzir caracteres

adicionais.

Caixa do identificador para elemento

MathPrint™ vazio. Utilize as teclas

de setas para mover para a caixa.

Cursor MathPrint™. Continue a

introduzir o elemento MathPrint

actual ou prima uma tecla de seta

para sair do elemento.

2ª funções

%

A maioria das teclas pode efectuar mais de uma função. A
função principal é indicada na tecla e a função secundária
aparece por cima da tecla. Prima % para activar a função
secundária de uma determinada tecla. Não se esqueça de
que 2ª aparece como um indicador no ecrã. Para a cancelar
antes de introduzir dados, prima % novamente. Por
exemplo, %b 25 < calcula a raiz quadrada de 25 e
devolve o resultado 5.

5

Modos

q

Utilize q para seleccionar os modos. Prima $ # ! "
para seleccionar um modo e < para o seleccionar. Prima

- ou %s para voltar ao ecrã inicial e efectue o
trabalho com as definições do modo seleccionado.

As predefinições aparecem realçadas nestes ecrãs de
exemplo.

DEG RAD GRAD Define o modo de ângulo para graus,
radianos ou grados.

NORM SCI ENG Define o modo de notação numérica.
Os modos de notação numérica afectam apenas a
visualização dos resultados e não a precisão dos valores
guardados na unidade, que permanecem máximos.

NORM mostra os resultados com dígitos à esquerda e à
direita do decimal, como em 123456.78.

SCI expressa números com um dígito à esquerda do
número decimal e a potência de 10 adequada, como em

1.2345678
ENG mostra resultados como um número de 1 a 999

vezes 10 para a potência de um número inteiro. A potência
do número inteiro é sempre um múltiplo de 3.

Nota: E é uma tecla de atalho para introduzir um
número no formato de notação científica. O resultado
aparece no formato de notação numérica seleccionado no
menu do modo.

FLOAT 0 1 2 3 4 5 6 7 8 9 Define o modo de notação
decimal.

FLOAT (ponto decimal flutuante) mostra até 10 dígitos,
mais o sinal e o decimal.

0 1 2 3 4 5 6 7 8 9 (ponto decimal fixo) especifica o número
de dígitos (de 0 a 9) a mostrar do lado direito do decimal.

E5 (que é igual a 1.2345678×10

5

).

6

REAL a+bi r±q Define o formato dos resultados de
números complexos.

REAL resultados reais
a+bi resultados rectangulares
r±q resultados polares

DEC HEX BIN OCT Define a base numérica utilizada

para os cálculos.

DEC decimal
HEX hexadecimal (Para introduzir dígitos hexadecimais de

A a F, utilize %§, %¨, etc.)

BIN binário
OCT octal

CLASSIC MATHPRINT

O modo CLASSIC mostra as entradas e as saídas numa

linha.
O modo MathPrint™ mostra a maioria das entradas e

saídas em formato de livro de texto.

Exemplos de modos Classic e MathPrint™

Modo Classic Modo MathPrint™
Sci Sci

Modo Float e tecla de
comutação de resposta.

Modo Float e tecla de
comutação de resposta.

Fix 2 Fix 2 e tecla de comutação de

resposta.

7

Modo Classic Modo MathPrint™
U n/d U n/d

Exemplo de expoente Exemplo de expoente

Exemplo de raiz quadrada Exemplo de raiz quadrada

Exemplo de raiz cúbica Exemplo de raiz cúbica

Teclas multifunções

Uma tecla multifunções é a tecla que percorre várias funções
quando a prime.

Por exemplo, a tecla X contém funções trigonométricas sin

/, assim como as funções hiperbólicas sinh e sinh/.

e sin
Prima a tecla várias vezes para ver a função que pretende
introduzir.

As teclas multifunções incluem z, X, Y, Z, C,
D, H e g. As secções aplicáveis deste manual
descrevem como utilizar as teclas.

Menus

Os menus permitem aceder a várias funções da calculadora.
Algumas teclas dos menus, como, por exemplo, %h,
mostram um menu. Outras, como, por exemplo, d,
mostram vários menus.

8

Prima " e $ para percorrer e seleccionar um item de menu
ou prima o número correspondente junto ao item. Para voltar
ao ecrã anterior sem seleccionar o item, prima -. Para
sair de um menu e voltar ao ecrã inicial, prima %s.

%h (tecla com um menu):
RECALL VAR (com valores definidos para a predefinição de

0)
1: x = 0
2: y = 0
3: z = 0
4: t = 0
5: a = 0
6: b = 0
7: c = 0
8: d = 0

d (tecla com vários menus):

MATH NUM DMS R ³´ P

1:4

n

/d³´Un/

1: abs( 1:¡ 1: P ´Rx(

d

2: lcm( 2: round( 2: ¢ 2: P ´Ry(
3: gcd( 3: iPart( 3: £ 3: R ´Pr(
4: 4Pfactor 4: fPart( 4: r 4: R ´Pq(
5: sum( 5: int( 5: g
6: prod( 6: min( 6: ´DMS

7: max(
8: mod(

Percorrer as expressões e o histórico

! " # $
Prima ! ou " para mover o cursor numa expressão que

está a introduzir ou a editar. Prima %! ou % " para
mover o cursor directamente para o início ou o fim da
expressão.

9

Depois de avaliar uma expressão, a expressão e o resultado
são adicionados automaticamente ao histórico. Utilize # e
$ para percorrer o histórico. Pode reutilizar uma entrada
anterior , premindo < para a colar na linha inferior, onde
pode editá-la e avaliar uma nova expressão.

Exemplo

Percorrer 7 F U 4

(3 )(1 ) <

%b ## <
<

r

Comutação de respostas

r

Prima a tecla r para comutar o resultado apresentado
(quando possível) entre fracções e decimal, raízes quadradas
exactas e decimal, pi exacto e decimal.

Se premir r, aparece o último resultados em precisão total
do valor guardado, que pode não corresponder ao valor
arredondado.

Exemplo

Comutação
de
respostas

%b 8 <

r

10

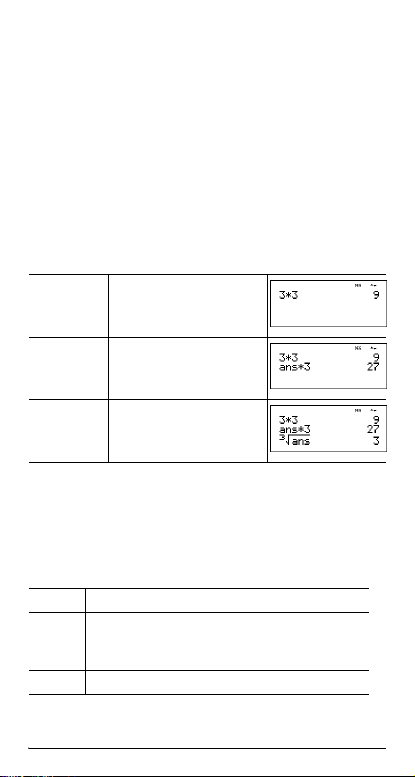
Última resposta

%i

A última entrada efectuada no ecrã inicial é guardada na
variável ans. Esta variável é retida na memória, mesmo
depois de desligar a calculadora . Para rechamar o valor de
ans:

•Prima %i (ans aparece no ecrã ) ou

• Prima qualquer tecla de operações (T, U, etc ) como a

primeira parte de uma entrada. ans e o operador
aparecem ambos .

Exemplos

ans 3 V 3 <

V 3 <

3 %c %i
<

Ordem das operações

A calculadora TI-36X Pro utiliza o Equation Operating System
(EOS™) para avaliar as expressões. Dentro de um nível de
prioridade, o EOS avalia as funções da esquerda para a
direita e pela seguinte ordem.

1ª Expressões entre parêntesis.
2º Funções que necessitam de um ) e precedem o

argumento, como, por exemplo, sin, log e
todos os itens do menu R³´P .

3ª Fracções.

11

4ª Funções que são introduzidas após o

argumento, como, por exemplo , x

2

e

modificadores de unidades de ângulos .

5ª

Exponenciação (^) e raízes (

x

‡).

Nota: No modo Classic, a exponenciação com
a tecla G é avaliada da esquerda para a
direita. A expressão 2^3^2 é avaliada como
(2^3)^2, com um resultado de 64.

No modo MathPrint™, a exponenciação com a
tecla G é avaliada da direita para a esquerda.
A expressão 2^3^2 é avaliada como 2^(3^2),
com um resultado de 512.

A calculadora avalia as expressões
introduzidas com F e a da esquerda para a
direita nos modos Classic e MathPrint. Se

premir 3 F F é calculado como (3

6ª

Negação (

M).

2)2

= 81.

7ª Arranjos sem repetição (nPr) e combinações

(nCr).

8ª Multiplicação, multiplicação implícita, divisão.
9ª Adição e subtracção.
10ª Conversões (n/d³´Un/d, F³´D, 4DMS).
11ª < completa todas as operações e fecha

todos os parêntesis abertos.

Exemplos

+ Q P M 6 0 T 5 V M1 2 <

12

(M) 1 T M 8 T 1 2 <

%b 9 T 16 <

( ) 4 V ( 2 T 3 ) <

4 ( 2 T 3 ) <

^ e ‡ %b 3 G 2 " T 4

G 2 <

Apagar e corrigir

%s Volta ao ecrã inicial.

- Apaga uma mensagem de erro.

Apaga os caracteres na linha de
entrada.
Move o cursor para a última entrada no
histórico assim que o visor estiver
limpo.

J Elimina o carácter no cursor.
%f Introduz um carácter no cursor.
%{ Apaga as variáveis x, y, z, t, a, b

para o valor predefinido de 0.

% 2 Reinicia a calculadora. Restaura a

unidade para as predefinições; apaga
as variáveis da memória, as operações
pendentes, todas as entradas do
histórico e os dados estatísticos; apaga
qualquer operação guardada e ans.

13

, c e d

Fracções

P%@d 1 %˜

No modo MathPrint™, as fracções com P podem incluir
números reais e complexos, teclas de operações (T, V,
etc.) e a maioria das teclas de funções (F, % _, etc.).

No modo Classic, as fracções com P não permitem teclas
de operações, funções ou fracções complexas no numerador
ou no denominador.

Nota: No modo Classic, apenas as entradas numéricas são
suportadas quando utilizar P. As fracções no modo Classic
são apresentadas com uma barra de fracção grossa dupla
(por exemplo, ). O numerador tem de ser um número
inteiro e o denominador tem de ser um número inteiro
positivo. Para calcular expressões mais complexas (funções,
variáveis, números complexos, etc.), utilize W juntamente
com ( e ).

A calculadora predefine a saída para fracções impróprias. Os
resultados são simplificados automaticamente.

• P introduz uma fracção simples. Premir P antes ou
depois de um número pode resultar num comportamento
diferente. Introduzir um número antes de premir P torna
esse número no numerador.

Para introduzir fracções com operadores ou radicais,
prima P antes de introduzir um número (apenas no modo
MathPrint™).

• No modo MathPrint™, prima $ entre a entrada do
numerador e do denominador.

• No modo Classic, prima P entre a entrada do numerador
e do denominador. A barra da fracção aparece mais
grossa do que a barra da divisão.

• Premir % # em qualquer nível do MathPrint, incluindo
o denominador ou um limite inferior, coloca o cursor no
histórico. Premir enter cola a expressão nesse nível do
MathPrint.

– Para colar uma entrada anterior no denominador,

coloque o cursor no denominador, prima %# para ir

14

para a entrada pretendida e, em seguida, prima <
para colar a entrada no denominador.

– Para colar uma entrada anterior no numerador ou na

unidade, coloque o cursor no numerador ou na unidade,
prima # ou %# para ir para a entrada pretendida
e, em seguida, prima < para colar a entrada no
numerador ou na unidade.

• % @ introduz um número misto. Prima as teclas de
setas para percorrer a unidade, o numerador e o
denominador.

• d 1 converte entre fracções simples e formato de
números mistos (4

n

/d³´Un/d).

• %˜ converte resultados entre fracções e decimais.

Exemplos Modo Classic

n

/d, Un/

3 P 4 T 1 % @ 7

d

P 12 <

n

/d³´Un/

9 P 2 d 1 <

d

F³´D 4 % @ 1 P 2

%˜ <

Exemplos ModoMathPrint™

n/d, U n/d P3 $ 4 " T 1

% @ 7 $12 <

n

/d³´Un/

9 P 2 " d 1 <

d

F³´D 4 % @ 1 $ 2 "

%˜ <

15

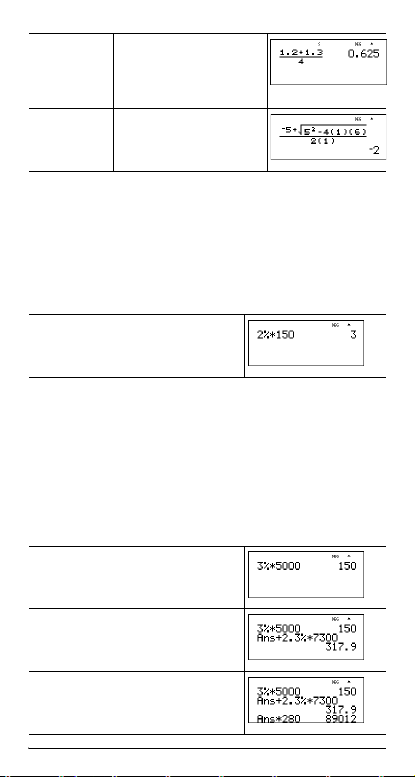
Exemplos
(apenas no
modo
MathPrint™)

(apenas no
modo
MathPrint™)

P1.2 T 1.3 $ 4 <

P M 5 T %b 5
F U 4 ( 1 ) ( 6
) $ 2 ( 1 ) <

Percentagens

%_

Para efectuar um cálculo que envolva uma percentagem,
prima %_ depois de introduzir o valor da percentagem.

Exemplo

2 %_ V 150 <

³ Problema

Uma empresa de extracção de minério extrai 5000 toneladas
de minério com uma concentração de metal de 3% e 7300
toneladas com uma concentração de 2,3%. Com base nestes
dois números de extracção, qual é a quantidade total de
metal obtida?

Se uma tonelada de metal valer 280 dólares, qual é o valor
total do metal extraído?

3 %_ V 5000 <

T 2.3 %_ V 7300 <

280 <

V

16

As duas extracções representam um total de 317,9 toneladas
de metal para um valor total de 89.012 dólares.

Tecla EE

E
E é uma tecla de atalho para introduzir um número no

formato de notação científica.

Exemplo

2 E 5 <

q $ " <

- <

Potências, raízes e inversos

F Calcula o quadrado de um valor. A calculadora

G Eleva um valor à potência indicada. Utilize "

%b Calcula a raiz quadrada de um valor não

%c Calcula a raiz índice n de qualquer valor não

TI-36X Pro avalia as expressões introduzidas
com F e a da esquerda para a direita nos
modos Classic e MathPrint.

para mover o cursor para fora da potência.

negativo.

negativo e de números negativos se o índice
for ímpar.

17

a Dá a inversa de um valor: 1/x. A calculadora

Exemplos

q$<­5 F T 4 G 2 T 1 "
<

10 G M 2 <

%b 49 <

%b 3 F T 2 G 4 <

6 %c 64 <

2 %a <

avalia as expressões introduzidas com F e
a da esquerda para a direita nos modos

Classic e MathPrint.

Pi

g (tecla multifunções)

p = 3.141592653590 para cálculos.
p = 3.141592654 para visualização.

Exemplo

p 2 V g <

18

r

³ Problema

Qual é a área de um círculo se o raio for 12 cm?
Lembrete: A = p×r

2

g V 12 F <
r

A área do círculo é 144 p cm2. A área do círculo é cerca de
452,4 cm2 quando arredondada para uma casa decimal.

Matemática

d MATH
d mostra o menu MATH:

n

/d³´Un/

1:4

2: lcm( Mínimo múltiplo comum
3: gcd( Máximo divisor comum
4: 4Pfactor Factores primos
5: sum( Soma
6: prod( Produto

Exemplos

n

/d³´Un/

Converte entre fracções simples e formato de

d

números mistos.

9 P 2 " d 1 <

d

lcm( d 2

6 %` 9 ) <

19

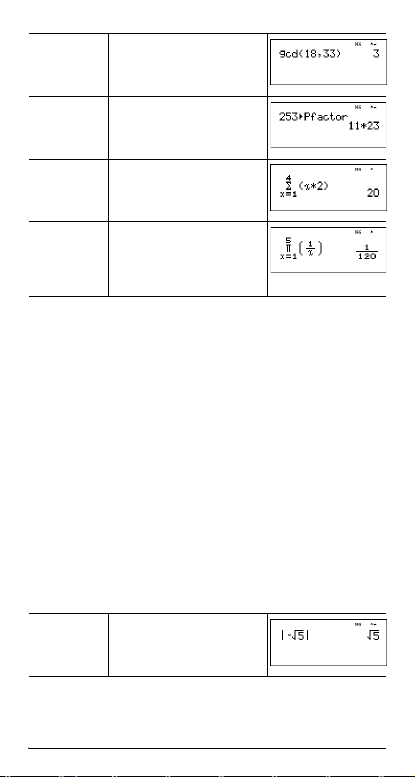
gcd( d 3

4Pfactor 253 d 4 <

18 %` 33 ) <

sum( d 5

prod(Sd 6

1 " 4 " z V 2
<

1 " 5 " 1 P z
" " <

Funções numéricas

d NUM
d " mostra o menu NUM:

1: abs( Valor absoluto
2: round( Valor arredondado
3: iPart( Parte inteira de um número
4: fPart( Parte decimal de um número
5: int( O maior número inteiro que é o número 
6: min( Mínimo de dois números
7: max( Máximo de dois números
8: mod( Módulo (resto da divisão do primeiro número

Exemplos

abs( d " 1

P pelo segundo número)

M % b 5

<

20

round( d " 2

iPart(
fPart(

int( d "5

1.245 %` 1 ) <

## <
!!!!! 5 <

4.9 L z <
d "3 z ) <
d "4 z )
V 3 <

M 5.6 ) <

min(
max(

mod( d "8

d "6
4 %`M5 ) <

"7

d

.6 %` .7 ) <

17 %` 12 ) <
## < !! 6 <

Ângulos

d DMS
d " " mostra o menu DMS:

1: ¡ Especifica o modificador da unidade de ângulos

2: ¢ Especifica o modificador da unidade de ângulos

3: £ Especifica o modificador da unidade de ângulos

4: r Especifica um ângulo radiano.
5: g Especifica um ângulo grado.
6: ´DMS Converte o ângulo de graus decimais para

Pode também converter entre o formato de coordenada
rectangular (R) e o formato de coordenada polar (P). (Para
mais informações, consulte Rectangular para polar.)

como graus (º).

como minutos (').

como segundos ('').

graus, minutos e segundos.

21

Seleccione um modo de ângulo no ecrã do modo. Pode
seleccionar entre DEG (predefinição), RAD ou GRAD. As
entradas são interpretadas e os resultados visualizados de
acordo com a definição do modo de ângulo sem necessitar
de introduzir um modificador da unidade de ângulo.

Exemplos

RAD q"<

­X 30 d""

1 ) <

DEG q<

-

2 g d " " 4
<

4DMSS 1.5 d"" 6 <

³ Problema

Os dois ângulos adjacentes medem 12¡ 31¢ 45£ e 26¡ 54¢
38£ , respectivamente. Adicione as medidas dos dois ângulos
e apresente o resultado em formato DMS. Arredonde os
resultados para duas casas decimais.

-q$$"""<

22

-12 d""

1
31 d""2
45 d"" 3
T 26 d""1
54 d"" 2
38 d"" 3 <

d"" 6 <

O resultado é 39 graus, 26 minutos e 23 segundos.

³ Problema

Sabe-se que 30¡ = p / 6 radianos. No modo predefinido,
graus, calcule o seno de 30¡. Defina a calculadora para o
modo de radianos e calcule o seno de p / 6 radianos.

Nota: Prima - para limpar o ecrã entre problemas.

- X 30 ) <

q " < ­X g P 6 " ) <

Retenha o modo de radianos na calculadora e calcule o seno
de 30¡. Altere a calculadora para o modo de graus e calcule o
seno de p / 6 radianos.

X 30 d"" <

) <

q < ­X g P 6 " d"" 4
) <

23

Rectangular para polar

d R³´P
d! mostra o menu R³´P , que tem funções para

converter coordenadas entre o formato rectangular (x,y) e
polar (r,q). Defina o modo Ângulo , conforme necessário,
antes de iniciar os cálculos.

1: P ´Rx( Converte polar para rectangular e mostra x.
2: P ´Ry( Converte polar para rectangular e mostra y.
3: R ´Pr( Converte rectangular para polar e mostra r.
4: R ´Pq( Converte rectangular para polar e mostra q.

Exemplo

Converta coordenadas polares (r, q)=(5, 30) para
coordenadas rectangulares. Converta coordenadas
rectangulares
(x, y) = (3, 4) para coordenadas polares. Arredonde os
resultados para uma casa decimal.

R³´P - q $ $ " "

Converter (r, q) = (5, 30) dá (x, y) = (4.3, 2.5) e
(x, y) = (3, 4) dá (r, q) = (5.0, 53.1).

<

- t ! 1
5 %` 30 ) <
d ! 2
5 %` 30

d !3
3 %` 4 ) <
d ! 4

3 %` 4 ) <

) <

24

Trigonometria

XYZ(teclas multifunções)
Introduza as funções trigonométricas (sin, cos, tan, sin

-1

, tan-1), como as escreveria . Defina o modo Ângulo

cos
pretendido antes de iniciar os cálculos trigonométricos.

Exemplo Modo Grau

-1

,

tan q $ $ < -

Z 45 ) <

()

tangente

­ZZ 1 ) <

cos -

5 V Y 60 ) <

Exemplo Modo Radiano

tan q " < -

Z g P 4 " )
<

tan

-1

­Z Z1 ) <

r

cos -

5 V Y g P 4 " )
<

r

25

³ Problema

A

Calcule a medida da amplitude do ângulo relativo ao vértice A
do triângulo rectângulo abaixo. De seguida calcule a medida
da amplitude do ângulo relatico ao vérticeB e a medida do
comprimento da hipotenusa c. Os comprimentos são em
metros. Arredonde os resultados para uma casa decimal.

Lembrete:

7

---

tan A = por isso, m±A = tan

3

7

-1

⎛

---

⎠⎞⎝

3

m±A + m±B + 90¡ = 180¡
por isso, m±B = 90¡ - m±A

272

c =

+

3

3

C

c

7

q < $ $ " " <

- ZZ 7 P 3 " ) <

90 U %i <

%b 3 F T 7 F <

B

r

Para uma casa decimal, a medida da amplitude do ângulo A
é 66,8¡, a medida da amplitude do ângulo B é 23,2¡ e a
medida do comprimento da hipotenusa é 7,6 metros.

26

Funções hiperbólicas

XYZ(teclas multifunções)
Premir uma destas teclas multifunções várias vezes permite

aceder a função hiperbólica correspondente ou hiperbólica
inversa. Os modos Ângulo não afectam os cálculos
hiperbólicos.

Exemplo

Definir
decimal
flutuante

HYP -

q $ $ <

XXX 5 ) T 2
<

# # < %!
XXXX <

Funções exponenciais e logarítmicas

DC(teclas multifunções)
D produz o logaritmo de um número para a base e

(e ≈ 2.718281828459).

DD produz o logaritmo comum de um número.
C eleva e à potência especificada.
CC eleva 10 à potência especificada.

Exemplos

LOG DD1 ) <

LN D 5 ) V 2 <

27

›

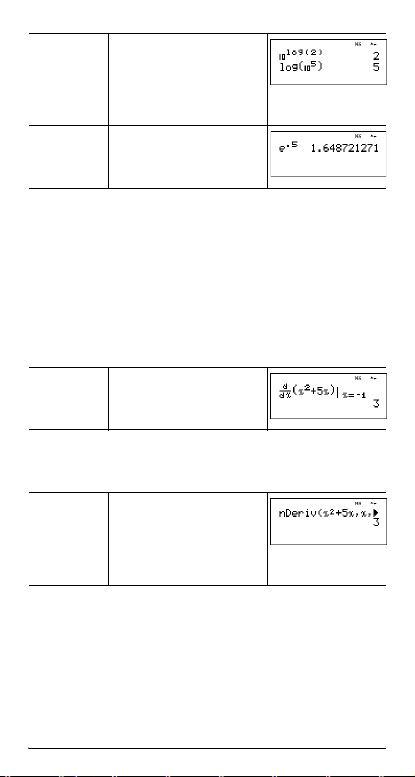
10

­CCDD
2 ) <
DDCC
5 " ) <

›

e

­C .5 <

Derivada numérica

%A
%A calcula uma derivada aproximada da expressão

em relação à variável, dado o valor para calcular a derivada
e H (se não especificada, a predefinição é 1
só é válida para números reais.

Exemplo no modo MathPrint

EM3). Esta função

%A %A

z F T 5 z ""
M 1 <

Exemplo no modo Classic

nDeriv(expressão,variável,valor[,H])

Classic:

%A %A

z F T 5 z
%`z
%`M1 )
<

nDeriv( utiliza o método do quociente da diferença simétrica,
que aproxima o valor da derivada numérica como o declive
da linha secante através destes pontos.

fx ε+()fx ε–()–

-----------------------------------------

f′ x()

=

2ε

28

À medida que H fica mais pequeno, a aproximação torna-se
geralmente mais precisa. No modo MathPrint™, o H
predefinido é 1
alterar H para investigações.

Pode utilizar nDeriv( uma vez na expressão. Devido ao
método utilizado para calcular nDeriv(, a calculadora pode
devolver um valor de derivada falso num ponto não
diferenciável.

³ Problema

Calcule o declive da recta tangente à curva f(x) = x

2

-------

x=

O que vê? (Fixe 3 casas decimais.)

q $$ """" <
%A
z G 3 " U 4 z ""
2 P % b 3
<

O declive da recta tangente em x = é zero. Um máximo

ou um mínimo da função tem de estar neste ponto!

EM3. Pode comutar para o modo Classic para

3

2

------­3

3

–4x em

Integral numérico

%Q
%Q calcula o integral da função numérica de uma

expressão em relação a uma variável x, dando um limite
inferior e um limite superior.

Exemplo no modo de ângulo RAD

%Q q " <-

%Q
0 " g" "
z X z" <

29

³ Problema

2

Calcule a área debaixo da curva f(x) = Mx

+4 de M2 a 0 e, em
seguida, de 0 a 2. O que vê? O que pode dizer sobre o
gráfico?

%Q M 2 " 0 "
Mz F T 4 " r

<

## <
%! "0 J
" 2

<

Não se esqueça de que ambas as áreas são iguais. Como é
uma parábola com o vértice em (4,0) e zeros em (M2, 0) e (2,

0), vê que as áreas simétricas são iguais.

Operações guardadas

%m %n
%n permite guardar uma sequência de operações.

%m reproduz a operação.

Para definir uma operação e rechamá-la :

1. Prima % n.

2. Introduza qualquer combinação de números, operadores

e/ou valores, até 44 caracteres.

3. Prima < para guardar a operação.

4. Prima %m para rechamar a operação guardada e

aplicá-la à última resposta ou à entrada actual .
Se aplicar %m directamente num resultado %m,

o n=1 contador de repetições é incrementado.

30

Exemplos

Apagar op

%n

Se existir uma op
guardada, clique em

- para a limpar.

Definir op V 2 T 3 <

Rechamar op%s

4 %m

%m

6 %m

Redefinir op %n -

F <

Rechamar op5 %m

20 %m

³ Problema

Dada a função afim y =5x – 2, calcule y para os seguintes
valores de x: -5; -1.

%n ­V 5 U 2 <

M 5 %m
M 1 %m

31

Variáveis guardadas e de memória

z L %h %{

A calculadora TI-36X Pro tem 8 variáveis de memória x, y, z,
t, a, b, c e d. Pode guardar um número complexo ou real, ou

o resultado de uma expressão numa variável de memória .
As funções da calculadora que utilizam variáveis (como, por

exemplo, os solucionadores) utilizam os valores guardados.
L permite guardar valores em variáveis . Prima L

para guardar uma variável e prima z para seleccionar a
variável para guardar. Prima < para guardar o valor na
variável seleccionada. Se esta variável já tiver um valor, esse
valor é substituído por um novo.

z é uma tecla multifunções que percorre os nomes das
variáveis x, y, z, t, a, b, c e d. Pode também utilizar z
para rechamar os valores guardados para estes variáveis. O
nome da variável é introduzido na entrada actual, mas o valor
atribuído é utilizado para avaliar a expressão. Para introduzir
duas ou mais variáveis sucessivamente, prima " após cada
uma delas.

%h rechama os valores das variáveis. Prima
%h para ver um menu de variáveis e os valores

guardados. Seleccione a variável que pretende voltar a
chamar e prima <. O valor atribuído à variável é
introduzido na entrada actual e utilizado para avaliar a
expressão.

%{ apaga os valores das variáveis. Prima
%{ e seleccione 1: Yes para apagar os valores de

todas as variáveis.

Exemplos

Começar
com o ecrã
limpo

Apagar Var %{

%s -

32

Guardar 1 (Selecciona Yes)

15 L z

<

Rechamar %h

< F <

Lzz

<

zz

< W 4 <

³ Problema

Numa pedreira, foram abertas duas escavações novas. A
primeira mede 350 metros por 560 metros, a segunda mede
340 metros por 610 metros. Que volume de gravilha tem a
empresa de extrair de cada escavação para atingir uma
profundidade de 150 metros? Para atingir 210 metros?
Mostra os resultados em notação de engenharia.

33

q $ " " < -

350 V 560 L z <

340 V 610 Lzz <

150 V %h

< <

210 V %h < <

150 V zz <

210 V zz <

Para a primeira escavação: A empresa necessita de extrair
29,4 milhões de metros cúbicos para atingir uma
profundidade de 150 metros e 41,16 milhões de metros
cúbicos para atingir uma profundidade de 210 metros.

Para a segunda escavação: A empresa necessita de extrair
31,11 milhões de metros cúbicos para atingir uma
profundidade de 150 metros e 43,554 milhões de metros
cúbicos para atingir uma profundidade de 210 metros.

34

Editor de dados e fórmulas das listas

v
v permite introduzir dados até 3 listas. Cada lista pode

conter até 42 itens. Prima % # para ir para o topo de uma
lista e % $ para ir para o fundo de uma lista.

As fórmulas das listas aceitam todas as funções da
calculadora e números reais.

Os modos de notação numérica, notação decimal e de
ângulo afectam a visualização de um elemento (excepto
fraccionários).

Exemplo

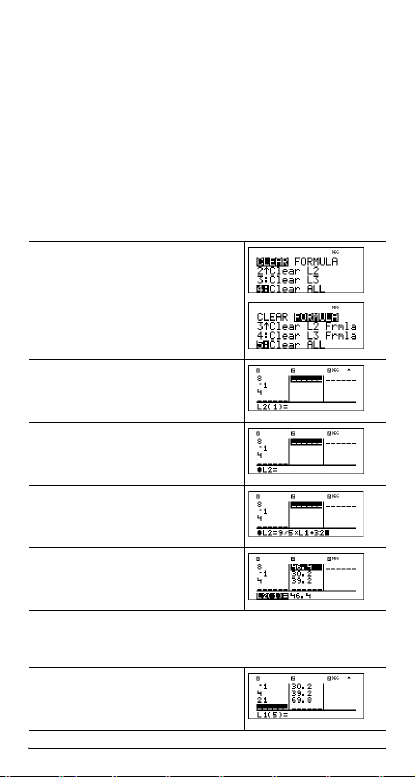
L1 v 1 P 4 $

Fórmula " v "

Não se esqueça de que L2 é calculada pela fórmula
introduzida e L2(1)= na linha de edição realçada para indicar
a lista é o resultado de uma fórmula.

2 P 4 $
3 P 4 $
4 P 4 <

<

v < %˜

<

35

³ Problema

Em Novembro, um boletim meteorológico na Internet listou as
seguintes temperaturas.

Paris, França 8¡C
Moscovo, Rússia M1¡C
Montreal, Canadá 4¡C

Converta estas temperatura de graus Celsius para graus
Fahrenheit. (Consulte também a secção em Conversões.)

9

Lembrete: F = C + 32

--­5

v v 4
v " 5

8 $ M 1 $ 4 $ "

v " 1

9 W 5 V v 1 T 32

<

Se estiverem 21¡C em Sidney, Austrália, calcule a
temperatura em graus Fahrenheit.

! $ $ $ 21 <

36

Estatística, regressões e distribuições

v%u
v permite introduzir e editar as listas de dados.
%u mostra o menu STAT-REG, que tem as

seguintes opções.
Nota: As regressões guardam as informações da regressão,

juntamente com a estatística de 2-Var para os dados em
StatVars (item do menu 1).

1: StatVars Mostra um menu secundário das variáveis

2: 1-Var Stats Analisa dados estatísticos de 1 conjunto

3: 2-Var Stats Analisa pares de dados de 2 conjunto de

4: LinReg ax+b Adapta a equação do modelo y=ax+b aos

de resultados estatísticos. Utilize $ e #
para localizar a variável pretendida e
prima < para a seleccionar. Se
seleccionar esta opção antes de calcular
estatísticas de 1-Var e 2-Var, ou qualquer
uma das regressões, aparece um
lembrete.

de dados com 1 variável medida, x. Os
dados de frequência podem ser incluídos.

dados com 2 variáveis quantitativas—x, a
variável independente , e y, a variável
dependente. Os dados de frequência
podem ser incluídos.
Nota: A estatística de 2-Var também
calcula uma regressão linear e preenche
os resultados da regressão linear.

dados com um ajuste dos mínimos
quadrados. Mostra os valores para a
(declive) e b (intersecção y); também

mostra os valores para r

2

e r.

37

5: QuadraticReg Adapta o polinómio de segundo grau

2

+bx+c aos dados. Mostra os valores

y=ax
para a , b e com; também mostra um valor

2

. Para três pontos de dados, a

para R
equação é um ajuste polinomial; para
quatro ou mais, é uma regressão
polinomial. São necessários pelo menos
três pontos de dados.

6: CubicReg Adapta o polinómio de terceiro grau

3

+bx2+cx+d aos dados. Mostra os

y=ax
valores para a , b , c e d; também mostra

um valor para R

2

. Para quatro pontos, a
equação é um ajuste polinomial; para
cinco ou mais, é uma regressão
polinomial. São necessários pelo menos
quatro pontos.

7: LnReg a+blnx Adapta a equação do modelo y=a+b ln(x)

aos dados com um ajuste dos mínimos
quadrados e os valores transformados
ln(x) e y. Mostra os valores para a e para

b; também mostra os valores para r

2

e

para r.

8: PwrReg ax^b

Adapta a equação do modelo y=ax

b

aos
dados com um ajuste dos mínimos
quadrados e valores transformados ln(x) e
ln(y). Mostra os valores para a e para b;

também mostra os valores para r

2

e

para r.

9: ExpReg ab^x

Adapta a equação do modelo y=ab

x

aos
dados com um ajuste dos mínimos
quadrados e valores transformados x e
ln(y). Mostra os valores para a e para b;

também mostra os valores para r

2

e

para r.

38

%u " mostra o menu DISTR, que tem as
seguintes funções de distribuição:

1: Normalpdf Calcula a função de densidade da

probabilidade (pdf) para a distribuição
normal num valor x especificado. As
predefinições são mu médio=0 e sigma do
desvio padrão=1. A função de densidade da
probabilidade (pdf) é:

2: Normalcdf Calcula a probabilidade de distribuição

3: invNorm Calcula a função de distribuição normal

4: Binompdf Calcula uma probabilidade em x para a

normal entre LOWERbnd e UPPERbnd
para o mu médio especificado e o sigma do
desvio padrão. As predefinições são mu=0;
sigma=1; com LOWERbnd = M1

UPPERbnd = 1
representa Minfinito para infinito.

cumulativa inversa para uma dada área na
curva de distribuição normal especificada
pelo mu médio e o sigma do desvio padrão.
Calcula o valor x associado a uma área à
esquerda do valor x. 0 { área { 1 tem de
ser verdadeiro. As predefinições são
área=1, mu=0 e sigma=1.

distribuição binomial discreta com o
numtrials especificado e a probabilidade de
sucesso (p) em cada tentativa. x é um
número inteiro não negativo e pode ser
introduzido com opções SINGLE, LIST ou
ALL (lista de probabilidades de 0 a
numtrials é devolvida). 0 { p { 1 tem de ser
verdadeiro. A função de densidade de
probabilidade (pdf) é:

E99. Nota: M1E99 to 1E99

39

E99 e

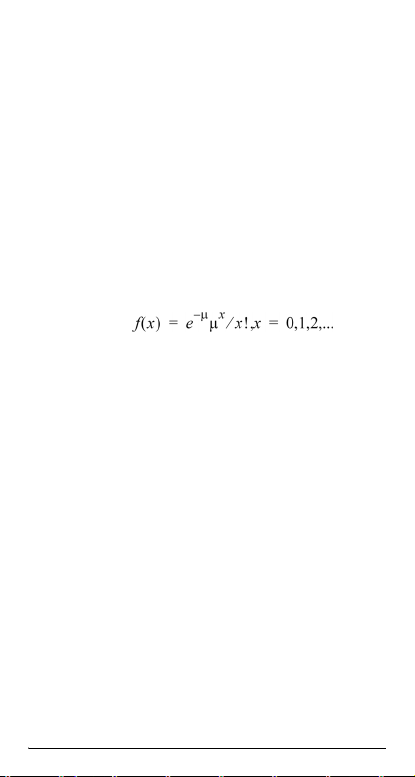
5: Binomcdf Calcula uma probabilidade cumulativa em x

para a distribuição binomial discreta com o
numtrials especificado e a probabilidade
de sucesso (p) em cada tentativa. x pode
ser um número inteiro não negativo e pode
ser introduzido com as opções SINGLE,
LIST ou ALL (uma lista de probabilidades
cumulativas é devolvida.) 0 { p { 1 tem de
ser verdadeiro.

6: Poissonpdf Calcula uma probabilidade em x para a

distribuição Poisson discreta com o mu
médio especificado (m), que tem de ser um
número real > 0. x pode ser um número
inteiro não negativo (SINGLE) ou uma lista
de números inteiros (LIST). A função de
densidade de probabilidade (pdf) é:

7: Poissoncdf Calcula uma probabilidade cumulativa em x

para a distribuição Poisson discreta com o
mu médio especificado, que tem de ser um
número real > 0. x pode ser um número
inteiro não negativo (SINGLE) ou uma lista
de números inteiros (LIST).

Nota: O valor predefinido para mu (m) é 0. Para Poissonpdf
e Poissoncdf, tem de o alterar para um valor > 0.

Resultados das estatísticas de 1-Var e 2-Var

Nota importante sobre os resultados: Muitas das
equações de regressão partilham as mesmas variáveis a, b,
c e d. Se efectuar qualquer cálculo de regressão, o cálculo de
regressão e a estatística de 2-Var para esses dados são
guardados no menu StatVars até ao cálculo estatístico ou de
regressão seguinte. Os resultados têm de ser interpretados
com base no tipo de cálculo estatístico ou de regressão
efectuado na última vez. Para o ajudar a interpretar
correctamente, a barra do título mostra o cálculo efectuado
pela última vez.

40

Variáveis Definição
n Número de pontos de dados x ou (x,y) .

v ou w Média de todos os valores x ou y .

Sx ou Sy Desvio padrão da amostra de x ou y.

sx ou sy Desvio padrão da população de x ou y.
Gx ou Gy Soma de todos os valores x ou y .

2

ou Gy2 Soma de todos os valores x2 ou y2 .

Gx
G xy Soma de (x…y) para todos os pares xy .

a (2-Var) Declive da regressão linear .
b (2-Var) Intersessão yda regressão linear.
r (2-Var) Coeficiente de correlação .
x¢ (2-Var) Utiliza a e b para calcular valor x previsível

quando introduzir um valor y .

y¢ (2-Var) Utiliza a e b para calcular o valor y

previsível quando introduzir um valor x .

MinX Mínimo dos valores x.
Q1 (1-Var) Mediana dos elementos entre MinX e Med

(1º quartil).

Med Mediana de todos os pontos de dados

(Apenas estatística de 1-Var).

Q3 (1-Var) Mediana dos elementos entre Med e MaxX

(3º quartil).

MaxX Máximos dos valores x.

Para definir pontos de dados estatísticos:

1. Introduza dados em L1, L2 ou L3. (Consultar Editor de
dados.)
Nota: São válidos os elementos de frequência não
inteiros. É útil quando introduzir frequências expressas
como percentagens ou partes que adicionam até 1. No
entanto, o desvio padrão da amostra, Sx, é indefinido para
frequências não inteiras, e Sx = Erro aparece para esse
valor. Aparecem todas as outras estatísticas.

41

2. Prima %u. Seleccione 1-Var ou 2-Var e
prima <.

3. Seleccione L1, L2 ou L3 e a frequência.

4. Prima < para ver o menu de variáveis.

5. Para apagar dados, prima v v
lista para apagar e prima

<.

, seleccione uma

Exemplo de 1-Var

Calcular a média de {45, 55, 55, 55}

Apagar

v v $ $ $
todos os
dados

Dados <

45 $ 55 $ 55 $ 55

<
Estatística %s

% u

2

(Selecciona 1-Var Stats)

$ $

<

Variável
estatística

2 <

V 2 <

42

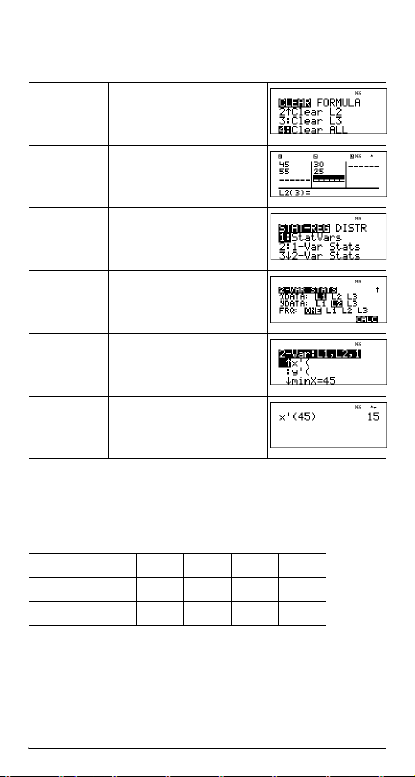
Exemplo de 2-Var

Dados: (45,30); (55,25). Calcular: x¢(45)

Apagar

v v $ $ $
todos os
dados

Dados < 45 $ 55 $ " 30

$ 25 $

Estatística %u

3

(Selecciona 2-Var Stats)

$ $ $

< %s

%u 1

# # # # # #

< 45 ) <

³ Problema

Nos últimos quatro testes, o António obteve os seguintes
resultados. Os testes 2 e 4 tiveram uma ponderação de 0,5 e
os testes 1 e 3 tiveram uma ponderação de 1.

Teste nº 1234
Resultado 12 13 10 11
Coeficiente 1 0.5 1 0.5

1. Calcule o nível médio do António (média ponderada).

2. O que representa o valor de n fornecido pela calculadora?
O que representa o valor de Gx fornecido pela
calculadora?

43

Lembrete: A média ponderada é

Σx

12()1() 13()0.5()10()1() 11()0.5()+++

------

--------------------------------------------------------------- -----------------------------------------

=

n

10.510.5+++

3. O professor deu ao Anthony mais 4 pontos no teste 4
devido a erro de classificação. Calcule o novo nível médio
do António.

v v $ $ $

<
v " $ $ $ $

<
12 $ 13 $ 10 $ 11 $
" 1 $ .5 $ 1 $ .5 <

%u

2 (Selecciona 1-Var Stats)

$ " " <

<

O António tem uma média (v) de 11,33 (para a centésima
mais próxima).

Na calculadora, n representa a soma total das ponderações.
n = 1 + 0.5 + 1 + 0.5.

Gx representa a soma ponderada dos resultados.
(12)(1) + (13)(0.5) + (10)(1) + (11)(0.5) = 34.

44

Mude o último resultado do António de 11 para 15.

v $ $ $ 15 <

%u 2
$ " " < <

Se o professor adicionar 4 pontos ao Teste 4, a média do
António é 12.

³ Problema

A tabela abaixo fornece os resultados de um teste de
travagem.

Teste nº 1 2 3 4
Velocidade

33 49 65 79

(km/h)
Distância

5.30 14.45 20.21 38.45
de
travagem
(m)

Utilize a relação entre a velocidade e a distância de travagem
para estimar a distância de travagem necessária para um
veículo que viaje a 55 km/h.

Um gráfico de dispersão destes pontos de dados sugere uma
relação linear. A calculadora utiliza o método do mínimo
quadrado para determinar a recta que melhor se ajuste,
y'=ax'+b, aos dados introduzidos nas listas.

v v $ $ $

<
33 $ 49 $ 65 $ 79 $ " 5.3
$ 14.45 $ 20.21 $ 38.45 <

45

%s
%u

3 (Selecciona 2-Var Stats)

$ $ $

<

Prima $ conforme necessário para
ver a e b.

Esta recta que melhor se ajuste,
y'=0.67732519x'N18.66637321 modela a tendência linear
dos dados.

Prima $ até realçar y'.

< 55 ) <

Este modelo linear dá uma distância de travagem prevista de
18,59 metros para um veículo que viaja a 55 km/h.

Exemplo de regressão 1

Calcule uma regressão linear ax+b para os seguintes dados:
{1,2,3,4,5}; {5,8,11,14,17}.

Apagar

v v $ $ $
todos os
dados

46

Dados <

1 $ 2 $ 3 $ 4 $

5 $ "

5 $ 8 $ 11 $ 14 $

17 <

Regressão %s

% u

$$$

<

$$$$ <

Prima $ para examinar

todas as variáveis dos

resultados.

Exemplo de regressão 2

Calcule uma regressão exponencial para os seguintes dados:
L1= {0, 1, 2, 3, 4}; L2={10, 14, 23, 35, 48}

Calcule o valor médio dos dados em L2.
Compare os valores da regressão exponencial para L2.

Apagar

v v 4
todos os
dados

Dados 0 $1 $ 2 $ 3 $ 4 $

"10 $ 14 $

23 $ 35

$ 48 <
Regressão % u

#

Guarde a
equação da
regressão
para f(x) no
menu I.

<$$$ " <

47

Equação de
regressão

<

Calcule o
valor médio
(y) dos
dados em L2
com
StatVars.

% u

1 (Selecciona StatVars)

$$$

$$$

$$$

Não se esqueça de
que a barra do
título mostra o
último cálculo
estatístico ou da
regressão.

Examine a

I 2

tabela de
valores da
equação da
regressão.

<

0 <

1 <

<<

Aviso: Se calcular a estatística de 2-Var nos dados, as
variáveis a e b (juntamente com r e r

2

) serão calculadas
como uma regressão linear. Não volte a calcular a estatística
de 2-Var após qualquer outro cálculo de regressão se quiser
manter os coeficientes de regressão (a, b, c, d) e os valores r
para o problema específico no menu StatVars.

Exemplo de distribuição

Calcule a distribuição pdf binomial nos valores x {3,6,9} com
20 tentativas e uma probabilidade de sucesso de 0.6.
Introduza os valores x na lista L1 e guarde os resultados
em L2.

48

Apagar

v v $ $ $
todos os
dados

Dados <

3 $ 6 $ 9 <

DISTR % u "

$ $ $

< "

<

20 $ 0.6

<$ $

<

Probabilidade

H%†
H é uma tecla multifunções que percorre as seguintes

opções:

! Um factorial é o produto dos números inteiros

positivos de 1 a n. n tem de ser um número inteiro
positivo { 69.

nCr Calcula o número de combinações possíveis de r

elementos retirados deumconjunto de n elementos,
dados n e r. A ordem dos objectos não é
importante, como numa mão de cartas.

49

nPr Calcula o número de arranjos possíveis de r

elementos retiradosde um conjunto de n
elementos, dados n e r. A ordem dos objectos é
importante, como numa corrida.

%† mostra um menu com as seguintes opções:
rand Gera um número real aleatório entre 0 e 1. Para

controlar uma sequência de números aleatórios,
guarde um número inteiro (valor semente) | 0
para rand. O valor semente muda aleatoriamente
sempre que um número aleatório é gerado.

randint( Gera um número inteiro aleatório entre 2

números inteiros, A e B, em que A { randint { B.
Separe os 2 números inteiros com uma vírgula.

Exemplos

! 4 H <

nCr 52 HH 5

<

nPr 8 HHH 3 <

STO 4 rand 5 L %†

1 (Selecciona rand)

<

Rand %† 1 <

50

Randint( %† 2

³ Problema

Uma loja de gelados anuncia que faz 25 sabores de gelado
caseiro. Deseja pedir três sabores diferentes num prato.
Quantas combinações de gelado pode experimentar num
Verão quente?

­25 HH 3 <

Pode escolher 2300 pratos com diferentes combinações de
sabores! Se o Verão quente tiver cerca de 90 dias, necessita
de comer cerca de 25 pratos de gelado por dia!

3 %` 5 ) <

Tabela de funções

I mostra um menu com as seguintes opções:
1: f( Cola f(x) existente numa área de entrada,

2: Edit function Permite definir a função f(x) e gera uma

A tabela de funções permite apresentar uma função definida
por uma lista de objectos e respectivas imagens. Para
configurar uma tabela de funções:

1. Prima I e seleccione Edit function.

2. Introduza uma função e prima <.

3. Seleccione o início da tabela, passo da tabela, auto ou
opções de pergunta x e prima <.

A tabela aparece com os valores especificados.

Início Especifica o valor inicial para a variável

como, por exemplo, o ecrã inicial para
calcular a imagen de um objecto pela
função (por exemplo, f(2)).

tabela de valores.

independente, x.

51

Passo Especifica o valor incremental para a variável

independente, x. O passo pode ser positivo ou
negativo.

Automático A calculadora gera automaticamente uma série

de valores com base no passo e início da
tabela.

Pergunta x Permite construir uma tabela manualmente,

introduzindo valores específicos para a
variável independente x.

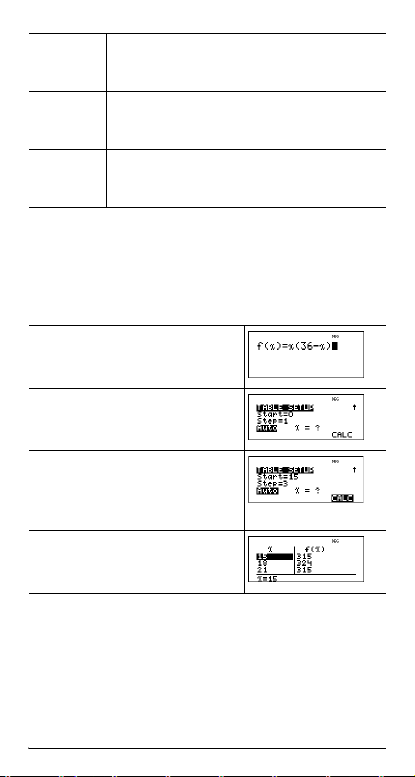
³ Problema

Calcule o vértice da parábola, y = x(36 - x) com uma tabela de
valores.

Lembrete: O vértice da parábola é o ponto na parábola que
está no seu eixo de simetria.

I 2 ­z ( 36 U z )

<

15 $ 3 $$

<

Depois de procurar junto a x = 18, o ponto (18, 324) parece
ser o vértice da parábola visto que parece ser o ponto de
viragem do conjunto de volores desta função. Para procurar
mais perto de x = 18, altere o valor do passo para valores
mais pequenos para ver pontos mais perto de (18, 324).

52

³ Problema

Uma organização de caridade angariou 3.600 dólares para
ajudar a suportar uma cozinha local. Serão dados 450 euros
à cozinha todos os meses até o fundo acabar. Quantos
meses a organização de caridade suportará a cozinha?

Lembrete: Se x = meses e y = dinheiro restante,

N 450x.

y = 3600

I 2

­3600 U 450 z

< 0 $ 1 $" < $ <

Introduza cada tentativa e prima
<.

Calcule o valor de f(8) no ecrã
inicial.
%s I

1 Selecciona f(
8 ) <

O apoio de 450 euros por mês durará 8 meses até y(8) =
3600 - 450(8) = 0 conforme se pode observar na tabela de
valores.

53

Matrizes

Além destas no menu MATH, são permitidas as seguintes
operações de matrizes. As matrizes têm de estar correctas:

• matriz + matriz

• matriz – matriz

• matriz × matriz

• Multiplicação escalar (por exemplo, 2 × matriz)

• matriz × vector (vector serão interpretados como um
vector da coluna)

% t NAMES
% t mostra o menu NAMES, que mostra as

dimensões das matrizes e permite utilizá-las nos cálculos.
1: [A] Matriz definível A

2: [B] Matriz definível B
3: [C] Matriz definível C
4: [Ans] Último resultado da matriz (apresentado como

5: [I2] Matriz de identidade 2×2 (não editável)
6: [I3] Matriz de identidade 3×3 (não editável)

% t MATH
% t " mostra o menu MATH, que permite efectuar

as seguintes operações:
1: Determinant Sintaxe: det(matriz)

2:
3: Inverse Sintaxe: matriz quadrada

4: ref reduced Forma tgriangular, sintaxe: ref(matriz)
5: rref reduced Forma triangular reduzida,

% t EDIT
% t ! mostra o menu EDIT, que permite definir ou

editar a matriz [A], [B] ou [C].

[Ans]=m×n) ou último resultado do vector
(apresentado como [Ans] dim=n). Não editável.

T Transpose Sintaxe: matrizT

–1

sintaxe: rref(matriz)

54

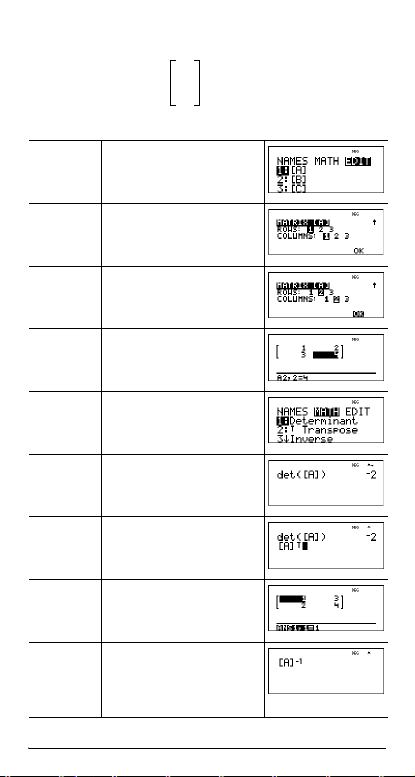
Exemplo de matriz

Definir matriz [A] como

12

34

Calcule o determinante, a transposta, a inversa e rref de [A].

Definir [A] % t !

<

Definir
dimensões

" < " <
<

Introduzir
valores< 1 $ 2 $ 3 $ 4 $

det([A]) -

% t "

<
% t < )
<

Transposta % t <

% t "$ <

<

Inversa -

% t <
% t "$$
<

55

<

rref -

% t " #

< % t
<)

<

Não se esqueça de que [A]
tem uma inversa e que [A]
é equivalente à matriz de
identidade.

Vectores

Além destas no menu MATH, são permitidas as seguintes
operações de vectores. As matrizes têm de estar correctas:

• vector + vector

• vector – vector

• Multiplicação escalar (por exemplo, 2 × vector)

• matriz × vector (vector serão interpretados como um
vector da coluna)

% … NAMES
% … mostra o menu NAMES, que mostra as

dimensões dos vectores e permite utilizá-los em cálculos.
1: [u] Vector definível u

2: [v] Vector definível v
3: [w] Vector definível w
4: [Ans] Último resultado da matriz (apresentado como

[Ans]=m×n) ou último resultado do vector
(apresentado como [Ans] dim=n). Não editável.

56

% … MATH
% … " mostra o menu MATH, que permite efectuar

os seguintes cálculos de vectores:
1: Produto Escalar Sintaxe: DotP(vector1, vector2)

Ambos os vectores têm de ter a
mesma dimensão.

2: Produto Vectorial Sintaxe: CrossP(vector1, vector2)

Ambos os vectores têm a mesma
dimensão.

3: Norma Sintaxe: norm(vector)

% … EDIT
% … ! mostra o menu EDIT, que permite definir ou

editar o vector [u], [v] ou [w].

Exemplo de vector

Definir vector [u] = [ 0.5 8 ]. Definir vector [v] = [ 2 3 ].
Calcule [u] + [v], DotP([u],[v]) e norm([v]).

Definir [u] % … !

<

" < <

.5 < 8 <

Definir [v] % … ! $ <

" < <

2 < 3 <

57

Adicionar
vectores-% … <

T
% … $ <

<

DotP -

norm -

% … " <

% … <
% `
% … $ <

) <

.5 V 2 T 8 V 3 <

Nota: DotP é calculado

aqui de duas formas.

%…" $$ <
%…$ < )
r<

%b 2 F T 3 F"
r <

Nota: norm é calculado
aqui de duas formas.

Solucionadores

Solucionador de equações numéricas

% ‰
% ‰ pede a equação e os valores das variáveis.

Seleccione a variável que pretende resolver. A equação está
limitada a um máximo de 40 caracteres.

58

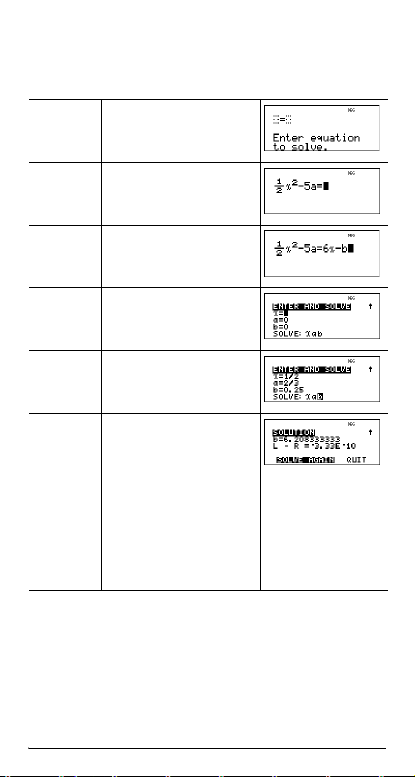
Exemplo

Lembrete: Se já tiver variáveis definidas, o solucionador
assume esses valores.

Num-solv % ‰

Primeiro
membro

1 P2 " zF
U5 z z z
z z ""

Segundo
membro

6 z U z z
zz z z

<

Val ore s
das
variáveis

Resolver
em ordem
a b

1 P 2 $
2 P 3 $

0.25 $ ""

<

Nota: Esquerda-Direita é
a diferença entre o
primeiro membro e
segundo membro da
equação avaliada na
solução. Esta diferença
mostra como perto a
solução está da resposta
exacta.

Solucionador de polinómios

%Š
% Š pede para seleccionar o solucionador de

equações cúbicas ou quadráticas. Introduza os coeficientes
das variáveis e resolva.

59

Exemplo de equação quadrática

Lembrete: Se já tiver variáveis definidas, o solucionador
assume esses valores.

Poly-solv % Š

Introduzir
coeficientes

<
1

$
M 2

$
2
<

Soluções <

$

$

Nota: Se seleccionar
guardar o polinómio em
f(x), pode utilizar I
para estudar a tabela de
valores.

$$" <

Forma do vértice
(apenas para
solucionador quadrático)

Nos ecrãs de soluções do solucionador de polinómios, pode
premir r para alternar o formato do número das soluções
x1, x2 e x3.

60

Sistema do solucionador de equações lineares

% ‹
% ‹ resolve os sistemas de equações lineares.

Seleccione os sistemas 2×2 ou 3×3.
Notas:

• Os resultados x, y e z são guardados automaticamente
nas variáveis x, y e z.

•Utilize r para alternar os resultados (x, y e z) conforme
necessário.

• O solucionador de equações 2x2 resolve uma solução
única ou mostra uma mensagem que indica um número
infinito de soluções ou nenhuma solução.

• O solucionador de equações 3x3 resolve uma solução
única ou soluções infinitas em formato fechado ou não
indica nenhuma solução.

Exemplo do sistema 2×2
Resolver: 1x + 1y = 1

1x – 2y = 3

Resolução

% ‹

de sistema

Sistema

<

2×2

Introduzir

1 < T1 < 1 <

equações

1 < U2 < 3 <

Resolver <

61

Alternar

r

tipo de
resultado

Exemplo do sistema 3×3

Resolver: 5x – 2y + 3z = -9

4x + 3y + 5z = 4
2x + 4y – 2z = 14

Resolução

% ‹ $

do sistema

Sistema

<

3×3

Primeira
equação

5 <
M2 <
3 <
M 9 <

Segunda
equação

4 <
3 <
5 <
4 <

Terceira
equação

2 <
4 <
M2 <
14 <

Soluções <

$
$

62

Exemplo do sistema 3×3 com soluções infinitas

Entrar no
sistema

% ‹ 2
1 <2 <3 <4

<
2 <4 <6 <8
<
3 <6 <9 <12
<

<

<

<

Bases numéricas

%—

Conversão da base

%— mostra o menu CONVR , que converte um
número real ao equivalente numa base especificada.

1: ´Hex Converte para hexadecimal (base 16).
2: ´Bin Converte para binário (base 2).
3: ´Dec Converte para decimal (base 10).
4: ´Oct Converte para octal (base 8).

Tipo de base

%— " mostra o menu TYPE, que permite indicar a
base de um número, independentemente do modo de base
numérica actual da calculadora.

1: h Indica um número inteiro hexadecimal.
2: b Especifica um número inteiro binário.

63

3: d Especifica um número decimal.
4: o Especifica um número inteiro octal.

Exemplos no modo DEC

Nota: Pode definir o modo DEC, BIN, OCT ou HEX. Consulte
a secção Modo.

d ´Hex -

127 %— 1 <

h ´Bin -

%¬ %¬
%— " 1
%— 2 <

b ´Oct -

10000000 %— "
2
%— 4 <

o ´Dec # <

Lógica booleana

%— ! mostra o menu LOGIC, que permite efectuar
a lógica booleana.

1: and Lógica binária AND de dois números inteiros
2: or Lógica binária OR de dois números inteiros
3: xor Lógica binária XOR de dois números inteiros
4: xnor Lógica binária XNOR de dois números inteiros
5: not( Lógica NOT de um número
6: 2’s( 2’s complemento de um número
7: nand Bitwise NAND de dois números inteiros

64

Exemplos

Modo BIN:
and, or

Modo BIN:
xor, xnor

Modo HEX:
not, 2’s

Modo DEC:

nand

q $$$$
"" <

1111 %— ! 1
1010 <
1111 %— ! 2
1010 <

11111 %— ! 3
10101 <
11111 %— ! 4
10101 <

q $$$$
" <
%— ! 6
%¬ %¬ )
<
%— ! 5
%i <

q $$$$ <

192 %— ! 7
48 <

Avaliação de expressões

%‡

Prima %‡ para introduzir e calcular uma expressão
com números, funções e variáveis/parâmetros. Se premir
%‡ a partir de um ecrã inicial, a expressão cola o
conteúdo em Expr=. Se o utilizador estiver numa linha do
histórico de entradas ou saídas quando premir %‡
, a expressão do ecrã inicial cola-se em Expr=.

Exemplo

%‡

65

2 z T z z z

< 2

< 5

<

%‡

< 4 < 6 <

Constantes

As constantes permitem aceder a constantes científicas para
colar em várias áreas da calculadora TI-36X Pro MultiView™.
Prima % Πpara aceder e ! ouo" para
seleccionar os menus NAMES ou UNITS das mesmas 20
constantes lógicas. Utilize # e $ para percorrer a lista de
constantes nos dois menus. O menu NAMES mostra um
nome abreviado junto ao carácter da constante. O menu
UNITS tem as mesmas constantes do menu NAMES, mas as
unidades da constante aparecem no menu.

66

Nota: Os valores das constantes apresentados são
arredondados. Os valores utilizados para cálculos são
fornecidos na tabela seguinte.

Constante Valor utilizado para cálculos

velocidade da luz 299792458 metros por segundo

c

g aceleração

gravitacional

H constante de Planck
NA número de

Avogadro
constante de gás

R

ideal

me massa de electrões
mp massa de protões
mn massa de neutrões
mμ massa muon
G gravitação universal

9.80665 metros por segundo

M

6.62606896×10

6.02214179×10

34

Joule segundos

23

moléculas por

mole

8.314472 Joules por mole por
Kelvin

9.109381215×10

1.672621637×10

1.674927211×10

1.88353130×10

6.67428×10

M31

M27

M27

M28

M11

metros3 por

quilograma por segundos

2

quilogramas
quilogramas

quilogramas

quilogramas

2

F constante Faraday 96485.3399 Coulombs por mole
a 0 raio Bohr

re raio do electrão

clássico

k constante de

Boltzmann

e carga de electrões
I unidade de massa

atómica

5.2917720859×10

2.8179402894×10

1.3806504×10
Kelvin

1.602176487×10

1.660538782×10

M11

M15

M23

Joules por

M19

Coulombs

M27

quilogramas

metros
metros

atm atmosfera padrão 101325 Pascals
H0 permeabilidade de

vácuo

m0 permeabilidade de

vácuo

Cc constante de

Coulomb

8.854187817620×10
por metro

1.256637061436×10
por ampere

8.987551787368×10
Farad

M12

Farads

M6

2

Newtons

9

metros por

67

Conversões

O menu CONVERSIONS permite efectuar 20 conversões (ou
40 se converter em ambos os sentidos).

Para aceder ao menu CONVERSIONS, prima % –.
Prima um dos números (1-5) para seleccionar ou prima # e
$ para percorrer e seleccione um dos submenus
CONVERSIONS. Os submenus incluem as categorias
Inglês-Métrica, Temperatura, Velocidade e Comprimento,
Pressão, Potência e Energia.

Inglês³´Conversão métrica

Conversão
pol 4 cm polegadas para centímetros
cm 4 pol centímetros para polegadas
pés 4 m pés para metros
m 4 pés metros para pés
jardas 4 m jardas para metros
m 4 jardas metros para jardas
milha 4 km milhas para quilómetros
km 4 milha quilómetros para milhas

2

acre 4 m

2

4 acre

m
gal EUA 4 L galões EUA para litros
L 4 gal EUA litros para galões EUA
gal GB 4 ltr galões GB para litros
ltr 4 gal GB litros para galões GB
oz 4 gm onças para gramas
gm 4 oz gramas para onças

acres para metros quadrados
metros quadrados para acres

68

lb 4 kg libras para quilogramas
kg 4 lb quilogramas para libras

Conversão de temperatura

Conversão

¡F 4 ¡C Farhrenheit para Celsius
¡C 4 ¡F Celsius para Fahrenheit
¡C 4 ¡K Celsius para Kelvin
¡K 4 ¡C Kelvin para Celsius

Conversão de velocidade e comprimento

Conversão
km/hr 4 m/s quilómetros/hora para metros/

segundo

m/s 4 km/hr metros/segundo para quilómetros/

hora

LtYr 4 m anos-luz por metro
m 4 LtYr metros para anos-luz
pc 4 m parsecs para metros
m 4 pc metros para parsecs
Ang 4 m Angstrom para metros
m 4 Ang metros para Angstrom

Conversão de potência e energia

Conversão
J 4 kkWh joules para quilowatt hora
kWh 4 kJ quilowatt hora para joules
J 4 kcal calorias para joules
cal 4 kJ joules para calorias
hp 4 kkWh cavalo potência para quilowatt hora

kkWh 4 hp quilowatt hora para cavalo potência

69

Conversão de pressão

Conversão
atm 4 kPa atmosferas para pascals
kPa 4 atm pascals para atmosferas
mmHg 4 kPa milímetros de mercúrio para pascals
Pa 4 mmHg pascals para milímetros de mercúrio

Exemplos

Temperatura

Velocidade,
Comprimento

Potência,
Energia

(M22)
%–2
<<

(Coloque números
negativos/expressões
negativas entre
parêntesis)

-

(60) %

–$$<

<<

-

(200) %

–$$$$
<"

<<

70

Números complexos

%ˆ

A calculadora efectua os seguintes cálculos de números
complexos:

• Adição, subtracção, multiplicação e divisão

• Cálculos de valores absolutos e argumentos

• Cálculos de recíprocos, quadrados e cubos

• Cálculos de números conjugados complexos

Definir formato completo:

Defina a calculadora para o modo DEC quando calcular com
números complexos.

q $ $ $ Seleccione o menu REAL. Utilize ! eo"
para percorrer o menu REAL para realçar o formato de
resultados complexos pretendido a+bi ou r±q e prima <.

REAL a+bi ou r±q defina o formato dos resultados de
números complexos.

a+bi resultados complexos rectangulares
r±q resultados complexos polares

Notas:

• Os resultados complexos não aparecem, a menos que se
introduzam números complexos.

• Para aceder a i no teclado, utilize a tecla multifunções
g.

• As variáveis x, y, z, t, a, b, c e d são reais ou complexas.

• Pode guardar os números complexos.

• Os números complexos não são permitidos em dados,
matriz, vector e em algumas outras áreas de entrada.

• Para conj(, real( e imag(, o argumento pode estar no
formato rectangular ou polar. A entrada de conj( é
determinada pela definição do modo.

• A saída de real( and imag( são números complexos.

• Defina o modo para DEG ou RAD dependendo da medida
do ângulo necessária.

71

Menu complexo Descrição

1:±± (carácter do ângulo polar)

Permite colar a representação polar de
um número complexo (como 5±p).

2 :ângulo polar angle(

Devolve o ângulo polar de um número
complexo.

3: magnitude abs( (ou |þ| no modo Mathprint™)

Devolve o módulo de um número
complexo.

4: 4 r±p Mostra um resultado complexo em

formato complexo. Válido apenas no fim
de uma expressão. Não válido se o
resultado for real.

5: 4 a+bi Mostra um resultado complexo em

formato rectangular. Válido apenas no fim
de uma expressão. Não válido se o
resultado for real.

6: conjugate conj(

Devolve o conjugado de um número
complexo.

7: real real(

Devolve a parte real de um número
complexo.

8: imaginário imag(

Devolve a parte imaginária (não real) de
um número complexo.

Exemplos (definir modo para RAD)

Carácter do
ângulo

-5%ˆ
<gP2<

polar:

±

Ângulo
polar:
angle(

-%ˆ$
<3 T4
ggg)<

72

Magnitude:
abs(

4 r±q -

4 a+bi -

Conjugado:
conj(

Real:
real(

-%ˆ3
(3 T4 ggg)
<

3 T 4 ggg
%ˆ 4
<

5 %ˆ<
3 g P 2 "

%ˆ5
<

­%ˆ6
5 U 6 ggg )
<

­%ˆ7
5 U 6 ggg)
<

Erros

Quando a calculadora detectar um erro, devolve uma
mensagem de erro com o tipo de erro. A lista seguinte
contém alguns dos erros que pode encontrar.

Para corrigir o erro, anote o tipo de erro e determine a causa
do erro. Se não conseguir reconhecer o erro, consulte a lista
seguinte.

Prima - para apagar a mensagem de erro. O ecrã
anterior aparece com o cursor junto ou no local do erro.
Corrija a expressão.

A lista seguinte encontra alguns dos erros que pode
encontrar.

0<area<1 — Este erro é devolvido quando introduzir um valor
inválido para a área invNormal.

ARGUMENT — Este erro é devolvido se:

73

• uma função não tem o número correcto de argumentos .

• o limite inferior é maior que o limite superior.

• o valor do índice é complexo.

BREAK — Premiu a tecla & para parar a avaliação de uma
expressão.

CHANGE MODE to DEC — Modo n base: Este erro aparece
se o modo não for DEC e premir ‰, Š,
‹, ‡, I, t, … ou –.

COMPLEX — Se utilizar um número complexo
incorrectamente numa operação ou na memória, obtém o
erro COMPLEX.

DATA TYPE — Introduziu um valor ou uma variável do tipo
de dados incorrecto.

• Para uma função (incluindo uma multiplicação implícita) ou
uma instrução, introduziu um argumento do tipo de dados
inválido, como, por exemplo, um número complexo em
que um número real é necessário.

• Tentou guardar um tipo de dados incorrecto, como, por
exemplo, uma matriz, numa lista.

• A introdução nas conversões complexas é real.

• Tentou para executar um número complexo numa área
não permitida.

DIM MISMATCH — Obtém este erro se

• tentar guardar um tipo de dados com uma dimensão não
permitida no tipo de dados de armazenamento.

• tentar uma matriz ou um vector de dimensão incorrecta
para a operação.

DIVIDE BY 0 — Este erro é devolvido quando:

• tentar dividir por 0.

• em estatística, n = 1.

DOMAIN — Especificou um argumento numa função fora do
intervalo válido. Por exemplo:

•Para x‡y: x = 0 ou y < 0 e x não é um número inteiro
ímpar.

74

•Para yx: y e x = 0; y < 0 e x não é um número inteiro.

•Para ‡x: x < 0.

•Para LOG ou LN: [ X ].

•Para TAN : x = 90¡, -90¡, 270¡, -270¡, 450¡, etc., e
equivalente para o modo radiano.

-1

•Para SIN

ou COS-1: [X]. >

•Para nCr ou nPr: n ou r não são números inteiros | 0.

•Para x!: x não é um número inteiro entre 0 e 69.

EQUATION LENGTH ERROR — Uma entrada excede os
limites de dígitos (80 para entradas estatísticas ou 47 para
entradas constantes); por exemplo, combinar uma entrada
com uma constante que excede o limite.

Exponent must be Integer — Este erro é devolvido se o
expoente não for um número inteiro.

FORMULA — A fórmula não contém um nome de lista (L1,
L2 ou L3) ou a fórmula para uma lista contém um nome de
lista próprio. Por exemplo, uma fórmula para L1 contém L1.

FRQ DOMAIN — Valor FRQ (nas estatísticas 1-Var e 2-Var)
< 0.

Highest Degree coefficient cannot be zero — Este erro
aparece se a num cálculo do solucionador de polinómios for
pré-preenchido com zero, ou se definir a para zero e mover o
cursor para a linha de entrada seguinte.

Infinite Solutions —A equação introduzida no sistema do
solucionador de equações lineares tem um número infinito de
soluções.

Input must be Real —Este erro aparece se uma variável for
pré-preenchida com um número não real em que é
necessário um número real e mover o cursor para além
dessa linha. O cursor é devolvido para a linha incorrecta e
tem de alterar a entrada.

Input must be non-negative integer — Este erro aparece
quando um valor inválido for introduzido para x e n nos
menus DISTR.

75

INVALID EQUATION — Este erro é devolvido quando:

• O cálculo contém demasiadas operações pendentes (mais
de 23). Se utilizar a funcionalidade da operação guardada
(op), tentou introduzir mais de quatro níveis de funções
aninhadas com fracções, raízes quadradas, exponentes

x

x

com ^, , e

e 10x.

y

•Prima < numa equação em branco ou numa equação
apenas com números.

Invalid Data Type — Num editor, introduziu um tipo não
permitido, como, por exemplo, um número complexo, uma
matriz ou um vector, como um elemento no editor de listas
estatísticas, editor de matrizes e editor de vectores.

Invalid domain — O solucionador de equações numéricas
não detectou uma mudança de sinal.

INVALID FUNCTION — Introduziu uma função inválida na
definição da função na tabela de funções.

Max Iterations Change guess — O solucionador de
equações numéricas excedeu o número máximo de iterações
permitidas. Mude a tentativa inicial ou verifique a equação.

Mean mu>0 — Um valor inválido é introduzido para a média
(mu = médio) em poissonpdf ou poissoncdf.

No sign change Change guess — O solucionador de
equações numéricas mão detectou uma mudança de sinal.

No Solution Found — A equação introduzida no sistema do
solucionador de equações lineares não tem solução.

Number of trials 0<n<41 — O número de tentativas está
limitado a 0<n<41 para binomialpdf e binomialcdf.

OP NOT DEFINED — A operação m não está definida.
OVERFLOW — Tentou introduzir ou calculou um número

para além do intervalo da calculadora.
Probability 0<p<1 — Introduziu um valor inválido para uma

probabilidade em DISTR.
sigma>0 sigma Real — Este erro é devolvido quando

introduzir um valor inválido para sigma nos menus DISTR.
SINGULAR MAT — Este erro aparece quando:

76

• Uma matriz singular (determinante = 0) não é válida como
o argumento para -1.

• A instrução SinReg ou a regressão polinomial gerou uma
matriz singular (determinante = 0) porque não conseguiu
encontrar uma solução ou não existe uma solução.

STAT — Tentou calcular estatísticas de 1-var ou 2-var sem
nenhum ponto de dados definido, ou tentou calcular
estatísticas de 2-var quando as listas de dados não tiverem
um comprimento igual.

SYNTAX — O comando contém um erro de sintaxe:
introduzir mais de 23 operações pendentes ou 8 valores
pendentes; ou ter funções, argumentos, parêntesis ou
vírgulas mal colocados. Se utilizar P, tente utilizar W e os
parêntesis adequados.

TOL NOT MET — Pediu uma tolerância para a qual o
algortimo não pode devolver um resultado preciso.

TOO COMPLEX — Se utilizar muito níveis de complexidade
MATHPRINT num cálculo, aparece o erro TOO COMPLEX
(este erro não se refere aos números complexos).

LOW BATTERY — Substitua as pilhas.
Nota: Esta mensagem aparece durante alguns segundos e,

em seguida, desaparece. Premir - não apaga esta
mensagem.

77

Informações das pilhas

Precauções com as pilhas

• Não deixe as pilhas ao alcance das crianças.

• Não misture pilhas novas com pilhas usadas. Não misture
marcas (ou tipos) de pilhas.

• Não misture pilhas recarregáveis com pilhas não
recarregáveis.

• Instale as pilhas de acordo com os diagramas de
polaridade (+ e -).

• Não coloque pilhas não recarregáveis num carregador de
pilhas.

• Elimine as pilhas usadas imediatamente.

• Não incinere nem desmonte as pilhas.

• Procure um médico imediatamente se engolir uma célula
ou pilha. (Nos EUA, contacte o National Capital Poison
Center através do número de telefone 1-800-222-1222.)

Eliminação das pilhas

Não mutile, fure ou coloque as pilhas num fogo. As pilhas
podem rebentar ou explodir, libertando produtos químicos
perigosos. Elimine imediatamente as pilhas usadas de
acordo com os regulamentos locais.

Como retirar ou substituir as pilhas

A calculadora TI-36X Pro utiliza uma pilha de lítio CR2032 de
3 volts.

Retire a tampa de protecção e rode a calculadora para baixo.

• Retire os parafusos do fundo da caixa com uma pequena
chave de parafusos.

• No fundo, separe cuidadosamente a parte frontal da parte
traseira. Tenha cuidado para não danificar qualquer peça
interna.

• Retire a pilha com uma pequena chave de parafusos (se
necessário).

78

• Para substituir a pilha, verifique a polaridade (+ e -) e faça
deslizar uma pilha nova. Prima a pilha nova para a
encaixar.
Importante: Quando substituir a pilha, evite qualquer
contacto com os outros componentes da calculadora.

Elimine a pilha gasta imediatamente de acordo com os
regulamentos locais.

Em caso de dificuldade

Reveja as instruções para se certificar de que os cálculos
foram efectuados correctamente.

Verifique a pilha para garantir que é nova e está instalada
correctamente.

Mude a pilha quando:

• & não ligar a unidade ou

• O ecrã aparecer em branco , ou

• Obter resultados imprevistos.

Apoio técnico, manutenção e garantia dos
produtos Texas Instruments

Apoio técnico e
manutenção

Garantia do produto Para conhecer melhor os termos e a

Para obter apoio técnico
relativamente a produtos Texas

Instruments, inclu
de uso e/ou manutenção/assistência
técnica, por favor contacte-nos,

[e-mail]

E-mail:
ou visite:

cobertura da garantia desta produto,
por favor consulte o Termo de
Garantia que o acompanha ou
contacte o distribuidor/revendedor
Texas Instruments mais próximo.

índo informações

education.ti.com

79