Texas instruments TI-30XS MULTIVIEW User Manual

TI-30XS MultiView™

En håndbok for lærere

Utviklet av

Texas Instruments Incorporated

Aktiviteter utviklet av

Gary Hanson, Aletha Paskett og Margo Lynn Mankus

Illustrert av

Jay Garrison og David Garrison

Om forfatterne

Gary Hanson

Sandy, Utah. De har utviklet flere av aktivitetene og bidratt til evalueringen av hvor godt eksemplene i delen “Slik bruker du

Margo Lynn Mankus

statlige universitetet i New York i New Paltz. Hun har gått gjennom og oppdatert materialet for TI-30XS MultiView

og

Aletha Paskett

arbeider for tiden ved det matematiske og teknologiske fakultetet i det

og utviklet flere aktiviteter for denne håndboken.

er matematikklærere i Jordan Independent School District i

TI-30XS MultiView™

” i denne håndboken passer.

Viktig

Texas Instruments gir ingen garantier, verken direkte eller indirekte, for salgbarhet eller egnethet til et bestemt formål, når det gjelder programmer eller trykte publikasjoner. Slikt materiale er tilgjengelig bare i den form det foreligger (“as-it-is”). Ingen underforståtte eller andre garantier gjelder for materialet.

Texas Instruments skal under ingen omstendigheter kunne holdes økonomisk ansvarlig for tap som måtte oppstå direkte, indirekte, tilfeldige eller som konsekvens av skader i forbindelse med eller som et resultat av kjøp eller bruk av dette materialet. Eventuelt økonomiske ansvar for Texas Instruments er, uansett årsak, begrenset til anvendbar innkjøpspris for dette produktet eller materialet. Dessuten kan Texas Instruments ikke holdes økonomisk ansvarlig for krav av noe slag i forbindelse med bruk av dette materialet fra noen annen part.

Texas Instruments Incorporated 7800 Banner Drive, M/S 3918 Dallas, TX 75251

Attention: Manager, Business Services

Trykt i USA.

MultiView, MathPrint, Automatic Power Down, APD og EOS er varemerker for Texas Instruments Incorporated.

Innholdsfortegnelse

KAPITTEL SIDE KAPITTEL SIDE

Om håndboken for lærere v

Om TI-30XS MultiView™-

kalkulatoren vi

Aktiviteter

En stjernereise

vitenskapelig notasjon 3

Pulsslag

statistikk med 1 variabel 7

På kino

dataformler på billettkontoret 13

Gi regelen et navn

algebraiske uttrykk 21

Slik bruker du TI-30XS MultiViewkalkulatoren

1 TI-30XS MultiView – enkle

operasjoner 29

2 Slette og korrigere 41

3 Enkel matematikk 45

4 Rekkefølge for operasjoner og

parenteser 49

5 Numerisk notasjon 55

6Brøker 59

7 Desimaltall og desimaler 65

8 Konstant 67

9 Minne og lagrede variabler 71

10 Dataredigeringsprogrammet og

listeformler 79

Slik bruker du TI-30XS MultiViewkalkulatoren

11 Statistikk 83

12 Sannsynlighet 89

13 Funksjonstabell 97

14 Potens, kvadratrot og inverse

verdier 101

15 Logaritmer og

eksponentfunksjoner 109

16 Pi 113

17 Innstillinger og omregninger

for vinkler 117

18 Polare og rektangulære

omregninger 121

19 Trigonometri 123

20 Hyperbolske funksjoner 131

Tillegg A

Hurtigreferanse for taster A-1

Tillegg B

Indikatorer på skjermen B-1

Tillegg C

Feilmeldinger C-1

Tillegg D

Informasjon om service og garanti på TI-produkter D-1

Tillegg E

Informasjon om batteriet E-1

(fortsettelse)

Om håndboken for lærere



Slik er lærerhåndboken organisert

Denne håndboken er for de vitenskapelige kalkulatorene TI-30XS MultiView™ og TI-30XB MultiView. Alle etterfølgende referanser i denne håndboken refererer til TI-30XS MultiView, men de gjelder også for TI-30XB MultiView.

Håndboken består av to deler: Aktiviteter og Slik

bruker du TI-30XS MultiView-kalkulatoren. Delen Aktiviteter er en samling med aktiviteter som

går ut på å integrere TI-30XS MultiView i matematikkundervisningen. Delen Slik bruker du TI-30XS MultiView-kalkulatoren er utformet for å hjelpe deg med å lære elevene hvordan kalkulatoren brukes.

I hver del brukes standardinnstillingene, inkludert modusen MathPrint™, hvis ikke noe annet er angitt.

Aktiviteter

Hver aktivitet er selvstendig og inkluderer følgende:

• En oversikt over det matematiske formålet med aktiviteten.

• De matematiske konseptene som utvikles.

• Materiellet som trengs for å utføre aktiviteten.

• En detaljert fremgangsmåte, inkludert trinnvise tastetrykk på TI-30XS MultiView.

• Et aktivitetsark for elever.

Slik bruker du TI-30XS MultiView

Denne delen inneholder eksempler på transparentmaler. Kapitlene er nummererte og inkluderer følgende:

• En introduksjonsside som beskriver kalkulatortastene som presenteres i eksemplet, plasseringen av disse tastene på TI-30XS MultiView og alle relevante notater om funksjonene.

• Transparentmaler som følger introduksjonssiden, og som inneholder eksempler på praktisk bruk av tasten(e) som blir diskutert. Tasten(e) som blir diskutert, vises i svart på tastaturet på TI-30XS MultiView. Modusinnstillingene for eksemplet vises også.

Nullstille TI-30XS MultiView

• Du kan sørge for at alle starter på samme punkt, ved å få elevene til å nullstille kalkulatoren: Trykk på & og - samtidig,

eller trykk på %  , og velg deretter 2 (Yes).

Konvensjoner som brukes i lærerhåndboken

• Hakeparentes [ ] rundt symbolet/navnet for en tast indikerer at tasten er en sekundær, eller alternativ, funksjon.

Eksempel: %Z

Om TI-30XS MultiView™-kalkulatoren

Startskjermen

På startskjermen kan du skrive inn matematiske uttrykk og funksjoner, sammen med andre instruksjoner. Svarene vises på startskjermen. Skjermen på TI-30XS MultiView kan vise opptil fire linjer med opptil 16 tegn per linje. For oppføringer og uttrykk på flere enn 16 tegn kan du rulle til venstre og til høyre (! og ") for å vise hele oppføringen eller uttrykket.

Når du trykker på %Q, nullstilles TI-30XS MultiView-kalkulatoren til en tom startskjerm. Trykk på # og $ hvis du vil vise tidligere oppføringer og bruke dem på nytt. (Se Tidligere oppføringer, side vii.)

I MathPrint™-modus kan du skrive inn opptil fire nivåer med etterfølgende nestede funksjoner og uttrykk, blant annet brøk, kvadratrot,

eksponenter med ^, , ex og 10x.

x

y

Modus

Bruk p til å velge modus. Trykk på $ # ! " for å velge en modus og på < for å bekrefte valget. Trykk på - eller %Q for å gå tilbake til startskjermen og utføre arbeidet med de valgte modusinnstillingene. Standardinnstillingene vises.

Classic-modus viser inntastinger og resultat på én enkelt linje.

MathPrint-modus viser de fleste inntastinger og resultat i tekstbokformat. Når du bruker MathPrint-modus, får du bedre visuell kontroll på at matematiske uttrykk er skrevet inn på riktig måte, og den fremhever også den korrekte matematiske oppstillingen på en bedre måte.

Når du beregner en oppføring på startskjermen, vises svaret enten direkte til høyre for oppføringen eller til høyre på neste linje, alt etter hva det er plass til.

Indikatorer på skjermen

Se i Tillegg B for en liste over indikatorene på skjermen.

Operasjonsrekkefølge

TI-30XS MultiView bruker EOS™ (Equation Operating System – ligningsoperasjonssystem) til å evaluere uttrykk. Operasjonsprioritetene er oppført på transparentmalen i kapittel 4, Rekkefølge for operasjoner og parenteser.

Siden operasjoner inne i parenteser utføres først, kan du bruke D E til å endre operasjonsrekkefølgen, og derfor til å endre resultatet.

Obs: Når du bytter modus mellom Classic og MathPrint, slettes kalkulatorloggen og konstantverdien.

Sekundære funksjoner

Hvis du trykker på %, vises indikatoren 2nd, og deretter kan du bruke funksjonen som vises over den neste tasten du trykker på. Eksempel: %b 25 < beregner kvadratroten av 25 og returnerer resultatet, 5.

Om TI-30XS MultiView™ (fortsatt)

Menyer

Enkelte taster viser menyer: H, %I, v, %t, %, %h og %{.

Trykk på " eller $ for å bla og velge et menyelement, eller trykk på det tilsvarende tallet ved siden av menyelementet. Hvis du vil gå tilbake til det forrige skjermbildet uten å velge elementet, trykker du på -. Hvis du vil avslutte en meny eller et program og gå tilbake til startskjermen, trykker du på %Q.

Tidligere oppføringer # $

Etter at et uttrykk er evaluert, kan du bruke # og $ til å bla gjennom tidligere oppføringer, som er lagret i loggen på TI-30XS MultiView. Du kan bruke en tidligere oppføring på nytt ved å trykke på < for å lime den inn på den nederste linjen, og deretter kan du redigere og evaluere et nytt uttrykk.

Bytte svar n

Nullstille TI-30XS MultiView

Hvis du trykker på & og - samtidig eller på %  og deretter velger 2 (Yes), nullstilles

kalkulatoren.

Nullstille kalkulatoren:

• Returnerer innstillingene til standarverdiene – standard notasjon (flytende desimal) og grademodus (DEG).

• Sletter variabler i minnet, ventende operasjoner, oppføringer i loggen, statistiske data, konstanter og Ans (siste svar).

Obs: Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

Automatic Power Down™ (APD™)

Hvis TI-30XS MultiView er inaktiv i omtrent 5 minutter, slås den av automatisk via APDfunksjonen. Trykk på & for å slå den på igjen. Skjermen, ventende operasjoner, innstillinger og minnet beholdes.

Byttetasten viser det sist beregnede resultatet i ulike visningsformater, der det er mulig. Trykk på n hvis du vil bytte mellom brøk- og desimalsvar, nøyaktig kvadratrot og desimal, og nøyaktig pi og desimal.

Siste svar (Ans)

Det sist beregnede resultatet er lagret i variabelen Ans. Ans beholdes i minnet, selv etter at TI-30XS MultiView er slått av. Slik henter du verdien for Ans:

•Trykk på % i (Ans vises på skjermen), eller

• Trykk på en hvilken som helst operasjonstast (T, U og så videre) som den første delen av en oppføring. Både Ans og operatoren vises.

Feilmeldinger

Se i Tillegg C for en liste over feilmeldinger.

Aktiviteter

En stjernereise

vitenskapelig notasjon 3

Pulsslag

statistikk med 1 variabel 7

På kino

dataformler på billettkontoret 13

Gi regelen et navn

algebraiske uttrykk 21

En stjernereise – vitenskapelig notasjon

Oversikt

Elevene studerer vitenskapelig notasjon ved å endre tall til vitenskapelig notasjon og deretter bruke dem i beregninger.

Innledning

Sett opp aktiviteten ved å fortelle elevene:

Standardformen for vitenskapelig notasjon er

nnnn

¿

10

aaaa enn 10, og nnnn er et heltall.

1. Få elevene til å øve på å skrive ned følgende tall i

, der aaaa er større enn eller lik 1 og mindre

1010

vitenskapelig notasjon ved å bruke blyant og papir.

a. 93 000 000 b. 384 000 000 000 c. 0,00000000000234 d. 0,0000000157

9,3 3,84 2,34 1,57

7

¿

10

11

¿

10

-12

¿

10

-8

¿

10

Matematiske konsepter

• vitenskapelig notasjon

•addisjon

•divisjon

Materiell

• TI-30XS MultiView™

•blyant

• elevaktivitet

2. Få elevene til å endre følgende tall til vitenskapelig notasjon (SCI) ved å bruke den vitenskapelige kalkulatoren TI-30XS MultiView.

¿

10

¿

10

-9

7

8

-6

a. 12 000 000 b. 974 000 000 c. 0,0000034 d. 0,000000004

Obs:

Obs: Svarene tar utgangspunkt i at standardinnstillingen for

Obs:Obs:

flytende desimaler brukes.

1,2 9,74 3,4 4

¿

3. Få elevene til å endre følgende tall til standard notasjon (NORM).

7

¿ 10

a. 5,8 b. 7,32 ¿ 10 c. 6,2 ¿ 10 d. 3 ¿ 10

Obs:

Obs: Når du skal skrive inn et negativt tall, trykker du på

Obs:Obs:

5

-6

-8

58 000 000 732 000 0,0000062 0,00000003

M og skriver inn tallet.

³ Følg disse trinnene:

1. Skriv inn det første tallet,

12000000.

2. Trykk på

3. Trykk på <for å vise tallet i vitenskapelig notasjon.

1.2Ã

³ Følg disse trinnene:

1. Skriv inn 5.8. Trykk på

2. Skriv inn 7. Trykk på

3. Trykk på

p. $ " < -

7

Ã10

ÃÃ

$ < - <.

58000000

C.

p.

En stjernereise – vitenskapelig notasjon (fortsettelse)

Aktivitet

Legg frem følgende problem for elevene:

Du er kaptein på et romskip i en fjern fremtid. Du har fått ordre om å dra til Alpha Centauri, og du har 5 år på deg til å komme dit. Avstanden fra

13

solen vår til Alpha Centauri er 2,5 x 10

engelske mil (heretter brukes bare benevnelsen mil). Avstanden fra jorden til solen er omtrent 9,3 x 10 mil.

Selv om vi ennå ikke har funnet ut hvordan vi kan reise med lysets hastighet, lever du i en tidsalder der romskipet kan reise med lysets hastighet.

Lyset tilbakelegger en omtrentlig avstand på 6x10

12

mil på 1 lysår. Du skal reise fra jorden via solen og deretter til Alpha Centauri. Klarer du å komme frem til Alpha Centauri i tide?

Fremgangsmåte

1. Bruk TI-30XS MultiView™-kalkulatoren til å

finne den totale avstanden du må tilbakelegge.

2,5 ¿ 10

13

+ 9,3 ¿ 10

7

= 2,5000093 ¿ 10

13

mil

2. Finn deretter ut hvor lang tid det vil ta deg å

tilbakelegge avstanden. (Tilbakelagt avstand lysår)

2.5000093 10

----------------------------------------610

×

13

×

12

4.1666821672=

år

3. Kan du gjennomføre reisen innen den tildelte tiden på 5 år?

Ja, hvis romskipet virkelig kan reise med lysets hastighet.

Tillegg

Lysets hastighet er 186 000 mil per sekund. Et lysår er avstanden lyset tilbakelegger på ett år. Få elevene til å regne om et lysår til tilbakelagte mil per lysår.

186 000mil,

----------------------------1s

60 s

------------ 1min

60min

--------------- -

××

1time

----------------

×

1d

24t

∅

gn

365d

----------------------

×

1°ar

∅

gn

≈

5.87 1012mil×

----------------------------------- 1°ar

7

¾ 1

Tips: Pass på at TI-30XS MultiViewkalkulatoren er i MathPrint™-modus for å løse dette problemet.

Jorden er omtrent 9.3 x 10

Tips:

solen.

³ Følg disse trinnene:

1. Trykk på 2.5

C13 " T 9,3

7

mil fra

C 7 <.

2,5000093Ã

2. Trykk på %i q 6 C 12

<.

4,166682167

³ Alt etter problemet må du minne

elevene på å ta med parenteser der det er nødvendig, for å sørge for at operasjonene utføres i den riktige rekkefølgen. Eksempel: (2,5000093 x 10 ha med parentesene for å få riktig resultat.

Ã10

ÃÃ

13

) ¾ (6 x 1012) må

Vi beregner denne verdien omtrentlig ved å bruke 6 x 10

Svar på elevtillegg: Det vil ta romskipet omtrent 15 år å komme til Delta Centauri.

12

mil for 1 lysår i denne aktiviteten.

³ Elevene kan lære mer om dette

emnet ved å besøke NASAs webområder på Internett.

En stjernereise –

Navn ___________________________

vitenskapelig notasjon

Dato ___________________________

Problemer

1. Skriv ned følgende tall i vitenskapelig notasjon.

Standard notasjon Vitenskapelig notasjon

a. 93 000 000 __________________________

b. 384 000 000 000 __________________________

c. 0,00000000000234 __________________________

d. 0,0000000157 __________________________

2. Bruk TI-30XS MultiView™-kalkulatoren til å endre følgende tall til vitenskapelig notasjon ved å bruke SCI-modus.

Standard notasjon Vitenskapelig notasjon

a. 12 000 000 __________________________

b. 974 000 000 __________________________

c. 0,0000034 __________________________

d. 0,000000004 __________________________

3. Bruk TI-30XS MultiView™-kalkulatoren til å endre følgende tall til standard desimalnotasjon ved å bruke NORM-modus.

Vitenskapelig notasjon Standard notasjon

a. 5,8 ¿ 10

b. 7,32 ¿ 10

c. 6,2 ¿ 10

d. 3 ¿ 10

7

5

-6

-8

_________________________

En stjernereise –

Navn ___________________________

vitenskapelig notasjon

Dato ___________________________

Problem

Du er kaptein på et romskip i en fjern fremtid. Du har fått ordre om å dra til Alpha Centauri, og du har 5 år på deg til å komme dit. Avstanden fra solen vår til Alpha Centauri er 2,5 x 1013 engelske mil (heretter brukes bare benevnelsen mil). Avstanden fra jorden til solen er omtrent 9,3 x 107 mil.

Selv om vi ennå ikke har funnet ut hvordan vi kan reise med lysets hastighet, lever du i en tidsalder der romskipet kan reise med lysets hastighet.

Lyset tilbakelegger omtrent 6 x 1012 mil på 1 lysår. Du skal reise fra jorden via solen og deretter til Alpha Centauri. Klarer du å komme frem til Alpha Centauri i tide?

Fremgangsmåte

1. Bruk TI-30XS MultiView™-kalkulatoren til å finne den totale avstanden du må tilbakelegge. For dette grove anslaget går du ut fra at du måler avstanden som en rett linje fra jorden til solen og deretter videre til Alpha Centauri.

____________________________________________________________________________

Tips: Pass på at kalkulatoren er i vitenskapelig notasjon før du begynner beregningen.

Finn deretter ut hvor lang tid det vil ta deg å tilbakelegge avstanden. (Tilbakelagt avstand ¾ 1 lysår)

Tips: Pass på at du bruker parenteser ved behov for å få riktig resultat for dette divisjonsproblemet. _________________________________________________________________

_________________________________________________________________

2. Kan du gjennomføre reisen innen den tildelte tiden på 5 år? _________________________________________________________________

Tillegg

Nå som det første oppdraget er utført på en vellykket måte, er du blitt spurt om å gjennomføre en ny reise. Avstanden fra solen til Delta Centauri er 9 x 1013 mil. Hvor lang tid vil det ta å komme dit fra jorden?

Tips: Jorden er omtrent 9,3 ¿ 107 mil fra solen.

Reisen med dette romskipet er en fiksjon. Hvis du er interessert i å finne ut mer om den nærmeste stjernen og kosmiske avstander, kan du besøke NASAs webområder på Internett.

Pulsslag – statistikk med 1 variabel

Oversikt

Elevene bruker dataredigeringsprogrammet og statistikkfunksjonen på TI-30XS MultiView™kalkulatoren til å studere effekten trening har på pulsen.

Innledning

Elevene kan plasseres i mindre grupper for denne aktiviteten, slik at datamengden som må skrives inn, blir så liten som mulig. Spør elevene:

• Hva tror dere den gjennomsnittlige pulsen er for noen på deres alder?

• Hvordan blir den etter trening?

Aktivitet

Få elevene til å utføre følgende undersøkelse for å kontrollere estimatene.

1. Få elevene til å kontrollere hvilepulsen ved å ta pulsen i 1 minutt. (Du kan få dem til å ta tiden i 10 sekunder og deretter multiplisere med 6, men dette kan være det roligste minuttet i løpet av arbeidsdagen din!)

Matematiske konsepter

• gjennomsnitt, minimum, maksimum og område

Materiell

• TI-30XS MultiView

• stoppeklokke eller en klokke med sekundviser

• elevaktivitet

2. Samle inn data i diagrammet. Skriv inn pulsen til hver elev, og legg til et merke i frekvenskolonnen. Når andre elever har samme puls, legger du til et nytt hakemerke i frekvenskolonnen.

3. Skriv inn pulsdataene på den vitenskapelige kalkulatoren TI-30XS MultiView.

a. Skriv inn den første pulsen i diagrammet i L1

og antallet merker for pulsen i L2. Du skal bruke L2 som frekvens.

b. Du må trykke på

Skriv for eksempel inn den første pulsen, og trykk deretter på

c. Anta for eksempel at du har en klasse på 22

elever:

$ mellom oppføringer.

$.

Puls Elever Puls Elever

603633 615641 626654

³ Følg disse trinnene:

1. Trykk på pulsene og frekvensene. Skriv inn pulsene i L1 og frekvensene i L2. Trykk på

og på

2. Fortsett med å skrive inn til du har skrevet inn alle pulsene og frekvensene.

3. Trykk på

4. Trykk på 1 for å velge statistikk med 1 variabel.

5. Velg L1 for dataene og L2 for frekvensen.

6. Trykk på dataene.

v for å skrive inn

$ mellom oppføringer

" for å gå fra L1 til L2.

% t.

$< for å vise

Pulsslag – statistikk med 1 variabe (fortsettelse)

4. Kontroller statistikkberegningene. Når elevene viser

Òx (Sigma x), forklarer du at Òx er summen

av alle pulsslagene. Spør elevene:

• Hvor mange pulsslag ble skrevet inn fra alle

elevene på ett minutt? Dette er

Òx

.

• Hvor mange elever ble skrevet inn? Dette er

nnnn.

• Hvordan kan vi beregne gjennomsnittlig puls?

Σx

Dette er

------

Ï

.

62.27272727=

n

• Er den gjennomsnittlige pulsen høyere eller

lavere enn du forventet?

5. Nå skal vi se hvilken effekt litt trening har på pulsen. For å ta hensyn til elevenes ulike behov setter du dem sammen med andre elever som vil kunne utføre oppgaven. Du kan også vurdere å lage en oppgave som én enkelt elev trygt kan gjennomføre for å øke pulsen. Si til elevene:

Hvis dere opplever smerte, tretthet eller mangel på pust i løpet av denne delen av aktiviteten, må dere stanse umiddelbart.

³ Følg disse trinnene:

1. Vis de statistiske dataene.

n skal være lik det totale antallet elever i aktiviteten. I dette eksemplet: n = 22.

2. Trykk på gjennomsnittlige pulsen. Ï = 62.27272727

3. Trykk på

Òx = 1370

Obs: Tallene viser resultatene for

eksemplet som er beskrevet i denne aktiviteten. Resultatene til elevene dine vil variere alt etter størrelsen på gruppen og pulsavlesningene.

$ til Ï for å se den

$ til du ser Òx.

6. Få elevene til å løpe på stedet i 2 minutter, og gi dem deretter følgende instruksjoner:

a.

Ta tiden på pulsen i 1 minutt.

b.

Registrer pulsslagene som tidligere. c. Skriv inn dataene på kalkulatoren. d. Sammenligne den gjennomsnittlige pulsen

etter løpingen med hvilepulsen.

7. Få deretter elevene til å hoppe i 2 minutter. Be dem ta pulsen i 1 minutt nok en gang, og registrer den som tidligere. Få dem til å skrive inn dataene på kalkulator på nytt og beregne den gjennomsnittlige pulsen etter hoppingen. Sammenligne med de andre 2 gjennomsnittene.

8. Be elevene om å lage et stolpediagram av de 3 settene med dataene de har samlet inn. Spør elevene:

• På hvilken måte er stolpediagrammene like?

• På hvilken måte er de forskjellige?

• Er dataene gruppert på samme måte, eller er

de mer spredt i ett diagram sammenlignet med et annet?

Pulsslag –

Navn ___________________________

statistikk

Dato ___________________________

Problem

Hva tror du den gjennomsnittlige pulsen er for noen på din alder? Hvordan blir den etter trening?

Fremgangsmåte

1. Bruk denne tabellen til å registrere data for klassen eller gruppen (hvilepuls).

Pulsslag per minutt

(hvilepuls)

Frekvens

2. Hva er gjennomsnittet for klassen (gruppen)? _____________________________

3. Bruk dataene til å svare på følgende spørsmål:

a. Hva er det totale antallet pulsslag for minuttet? Skriv ned symbolet og tallet

fra kalkulatoren.______________________________________________________

b. Hva er det totale oppgitte antallet pulsslag for elevene? Skriv ned symbolet og

tallet fra kalkulatoren. _______________________________________________

c. Hvordan vil du regne ut gjennomsnittlig puls? __________________________

Er svaret ditt det samme som i spørsmål 2? _____________________________

Pulsslag –

Navn ___________________________

statistikk

4. Bruk denne tabellen til å registrere data for klassen eller gruppen (etter løping).

Pulsslag per minutt

(etter løping)

Dato ___________________________

Frekvens

5. Hva er gjennomsnittet for klassen (gruppen)? _____________________________

6. Bruk dataene til å svare på følgende spørsmål:

a. Hva er det totale antallet pulsslag for minuttet? Skriv ned symbolet og tallet

fra kalkulatoren.____________________________________

b. Hva er det totale oppgitte antallet pulsslag for elevene? Skriv ned

symbolet og tallet fra kalkulatoren.

___________________________________________________

c. Hvordan vil du regne ut gjennomsnittlig puls?

___________________________________________________

Er svaret ditt det samme som i spørsmål 5? ___________

Pulsslag –

Navn ___________________________

statistikk

7. Bruk denne tabellen til å registrere data for klassen eller gruppen (etter hopping).

Pulsslag per minutt

(etter hopping)

Dato ___________________________

Frekvens

8. Hva er gjennomsnittet for klassen (gruppen)? _____________________________

9. Hva er det totale antallet pulsslag for minuttet? ___________________________

10.Bruk dataene til å svare på følgende spørsmål:

a. Hva er det totale antallet pulsslag for minuttet? Skriv ned symbolet og tallet

fra kalkulatoren.____________________________________________________

b. Hva er det totale oppgitte antallet pulsslag for elevene? Skriv ned symbolet og

tallet fra kalkulatoren. ______________________________________________

c. Hvordan vil du regne ut gjennomsnittlig puls? _________________________

Er svaret ditt det samme som i spørsmål 8? ____________________________

Pulsslag –

Navn ___________________________

statistikk

11. Lag et stolpediagram for hvert av de 3 settene med data du har samlet inn.

Hvilepuls Etter løping Etter hopping

Dato ___________________________

12.På hvilken måte er stolpediagrammene like? På hvilken måte er de forskjellige? _______________________________________________________________________

_______________________________________________________________________

13.Er dataene gruppert på samme måte, eller er de mer spredt i ett diagram

sammenlignet med et annet?_____________________________________________

_______________________________________________________________________ _______________________________________________________________________

På kino – dataformler på billettkontoret

Oversikt

Elevene undersøker en tabell med verdier og observerer mønstre i tabellen. Elevene bruker v på TI-30XS MultiView™-kalkulatoren til å skrive inn data i en liste og teste generaliseringer.

Innledning

Oppvarmingsspørsmålet er gitt for å hjelpe deg med å sette igang aktiviteten på elevarket. Du kan hoppe over oppvarmingsaktiviteten, men du må rettlede elevene mer under utforskningen av problemet på elevarket.

Oppvarming

Gi elevene rettledning i bruk av tabellene og v for å se et mønster og skrive ned en generalisering. Legg frem følgende problemhistorie.

Hver onsdag kommer Kari hjem fra arbeid til å gå på tur med hunden Max. Hun har spurt naboen Kim om å gå på tur med hunden etter at han kommer hjem fra skolen. Kim hjelper gladelig til! Kari betaler Kim €4 per uke for å gå på tur med Max. Kim liker å spare pengene. Lag en tabell over hvor mange penger Kim har hver uke i 5 uker.

Matematiske konsepter

•mønstre

•algebraiske uttrykk

•lineære funksjoner

•variabler

Materiell

• TI-30XS MultiView

•blyant

• millimeterpapir

• elevaktivitet

Gi elevene veiledning i å lage følgende tabell på papir. Du kan tenke på tabellen som en dataliste over to tall som er avhengige av hverandre. Det er viktig å få elevene til å skrive inn beregningen og resultatet i Penger-kolonnen (utdata) for at de skal kunne se noen mønstre. Dette hjelper dem med å skrive algebraiske setninger fra ordene og til å lage generaliseringer ved hjelp av induktiv resonnering.

Bruk disse kolonnene for andre

opplæringsstiler ved behov.

Uke Penger Gjentatt addisjon Påslag

11x4=4 4=4 4=4 2 2x4=8 4+4=8 4+4=8 3 3x4=12 4+4+4=12 8+4=12 4 4x4=16 4+4+4+4=16 12+4=16 5 5x4=20 4+4+4+4+4=20 16+4=20

På kino (fortsettelse)

Fremhev at Penger-kolonnen ser ut som multiplikasjonstabellen for tallet 4. Dette kobler elevene mot noe kjent å se tilbake på. Minn elevene på at de nå vet at Kim tjener €4 per uke. Dette er satsen for Kims sparing, og den kan skrives i brøkform som

sats =

Be elevene fylle ut mer av tabellen som beskriver hvor mye Kim vil spare. Be dem fylle ut tabellen for uke 6 og 7, og spør deretter om de kan finne ut hvor mye penger han har etter 10 uker, 25 uker og 100 uker. Spør dem til slutt om de kan fylle ut pengebeløpet etter et tilfeldig antall uker. Kall det ukjente antallet uker for en variabel, og bruk bokstaven U til å stå for uker. Bruk variabelen P til å stå for penger.

Uke (U) Penger (P)

11x4=4 22x4=8 33x4=12 44x4=16 55x4=20 66x4=24 77x4=28

€4

1 uke

10 10x4=40

25 25x4=100

UUx4*

uten

Alle disse undersøkelsene bør gjøres for disse enkle multiplikasjonsfaktaene. Hvis elevene trenger hjelp til multiplikasjonen, er det bedre å oppmuntre dem til å slå opp fakta i et diagram enn å bruke kalkulatoren, for å fremme hoderegning og riktig kalkulatorbruk.

Be elevene om å skrive utrykket for bergningen, ved å bruke U,

(Svar: U x 4)

x

og 4.*

kalkulator

På kino (fortsettelse)

Spør elevene om følgende: "Hvis du regner ut U uker ganger €4, får du et tall.

Hva betyr dette tallet for Kim?" Du ber elevene om å si penger (P), og deretter får du dem til å skrive formelen eller setningen med to variabler: P = U x 4. Vanligvis skriver du tallet og deretter bokstaven med den implisitte multiplikasjonen. Minn elevene på at faktorenes orden ved multiplikasjon er likegyldig, slik at P = U x 4 = 4 x U = 4U.

Støtt opp under undersøkelsen ved å bruke dataredigeringsprogrammet ( v) på TI-30XS MultiView™-kalkulatoren, ved å få elevene til å se på mange verdier i det algebraiske uttrykket for å se om de svarer til tabellen de har laget.

1. Få elevene til å skrive inn tabellen i datalisten. Legg merke til at det er tre tilgjengelige lister: L1, L2 og L3.

Få dem til å skrive inn ukeverdiene (U) i L1.

2. Få elevene til å skrive inn de tre første verdiene for U fra tabellen {1, 2, 3}.

3. Skriv inn en formel for å validere arbeidet: L2 = 4 x L1. Legg merke til at U = L1 og P = L2.

4. Legg til inndata i L1 for å se at L2 oppdateres automatisk med utdataverdien for formelen. Bla til en åpen oppføringsplass i L1. Be dem om å kontrollere tabellen for 4 uker og deretter 100 uker.

Få elevene til å slette dataene i listene før du starter gruppeundersøkelsen på elevarket.

(Fortsettelse)

³ Minn elevene på at de bruker

funksjonene i vog ikke i o for denne aktiviteten.

³ Hvis elevene ikke er kjent med

TI-30XS MultiView-kalkulatoren, må du få dem til å slå på kalkulatoren og trykke på p.

³ Kontroller at alle elevene har satt

modusen på kalkulatoren til følgende:

Trykk på - for å gå tilbake til startskjermen.

1. Skriv inn de tre første verdiene for U: v 1 $ 2 $ 3 $.

2. Skriv inn formelen:

" v " 1 4 V v 1 <.

3. Legg til inndata for L1:

! $ $ $

100 <.

4. Trykk på " v " 1 for å vise

formelen i L2 på nytt.

5. Rediger formelen om nødvendig, og trykk på < for å angi formelen igjen.

6. Trykk på

³ Tips: Husk at du kommer tilbake til

startskjermen ved å trykke på %Q .

4 <

v 4 for å slette dataene.

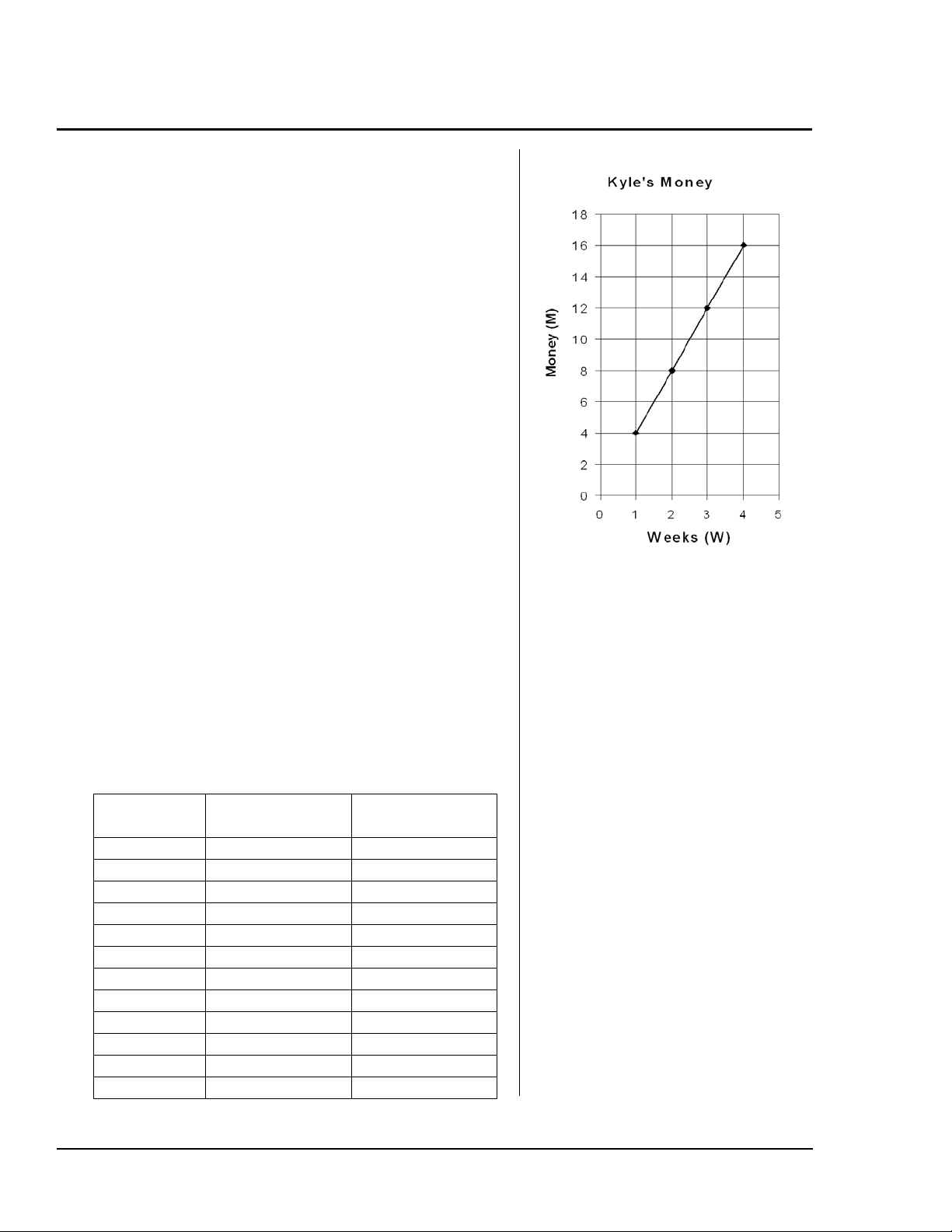
På kino (fortsettelse)

Nå har elevene hentet data fra ord til en tabell med verdier, til et mønster de kan vise, for å skrive et algebraisk uttrykk. Det neste trinnet er å vise dem en oversikt over hvordan nummermønsteret kan plottes på en graf. Hva er formen til P = 4U? Få elevene til å plotte de 4 første punktene i tabellen. Legg merke til at punktene danner en rett linje. Du kan nevne at de kan beskrive økningen av penger (P) som "for hver uke (U) Kim arbeider, øker pengesummen hans (P) med €4." Dette er en opplagt erklæring, men den utgjør grunnlaget for å snakke om satser og hvordan de virker inn på stigningsgraden til en linje (hellingen).

Både antallet uker og pengebeløpet er positive verdier, så det er fornuftig å plassere grafen i den første kvadranten. Få elevene til å bruke millimeterpapir til å lage grafer over dataene.

Aktivitet

Elevene gjentar en lignende undersøkelse i grupper ved å se på mønstre for å skrive algebraiske uttrykk og setninger. De lager også en graf over verdiene i tabellen. Få elevene til å lese gjennom problemet på elevarket før de deles inn i grupper, slik at de forstår oppgaven.

Elevene fyller ut tabellen ved å bruke hoderegning. De skriver ned alle beregninger som hjelper dem med å komme frem til formelen. De blir oppmuntret til å

før

bruke hoderegning så mye som mulig kalkulatoren til å finne resultatene for pengebeløpet.

Antall

Beregning Pengebeløp (P)

de bruker

personer (A)

1 1 x 11,50 €11,50 2 2 x 11,50 €23,00 3 3 x 11,50 €34,50 4 4 x 11,50 €46,00

...

10 10 x 11,50 €115,00

...

100 100 x 11,50 €1150,00

...

1000 1000 x 11,50 €11500,00

...

P A x 11,50 P = A x 11,50

På kino (fortsettelse)

Fremgangsmåte

Elevene skal skrive ned det algebraiske uttrykket basert på mønsteret som vises i tabellen: P = A x 11,50 eller ved å bruke implisitt multiplikasjon, P = 11,50 A.

Elevene kontrollerer formelen ved hjelp av dataredigeringsprogrammet ( TI-30XS MultiView™-kalkulatoren, som i

oppvarmingseksemplet.

1. Få elevene til å kontrollere hvordan kalkulatoren er satt opp.

2. Skriv inn de tre første verdiene i L1 {1, 2, 3}.

3. Oversett formelen til kalkulatorformelen, og skriv inn formelen i L2.

Formelen din: P = ____________________________ Formelen på kalkulatoren: L2 =

___________________

v) på

³ Kontroller at modusen på kalkulatoren

er satt til følgende:

1. Trykk på p.

2. Trykk på v 1 $ 2 $ 3 $.

3. Skriv inn formelen i L2. " v " 1

11 8 50 V v 1 <.

4. Trykk på ! $ $ $ 4 <

5 < 6 < 10 < 100 < 1000 <.

5. Trykk på 7500 <.

4. Skriv inn flere verdier i L1 for å kontrollere verditabellen og formelen. Denne aktiviteten validerer formelen for flere verdier.

5. Skriv inn 7500 i L1 for å finne pengebeløpet i L2. Skriv inn matematikken som P = 11,50 x 7500 = €86 250.

6. Lag en rapport ved å fylle ut en tabell med verdier og en graf. Skriv et avsnitt som beskriver arbeidet for presentasjonen.

Svarene i avsnittet vil variere. Pass på at elevene forklarer tabellen, grafen og det algebraiske uttrykket (formelen) i avsnittet.

AP

500 €5750 1000 €11500 1500 €17250 2000 €23000 2500 €28750

Navn ___________________________

På kino

Dato ___________________________

Problem

En storfilm har premiere denne helgen. På nyhetene hører du at billettene vil koste €11,50 per person. Reporteren sier at en familie på to vil bruke €23, og en familie på tre vil bruke €34,50. De viser et bilde med disse opplysningene i et tabellformat.

Antall personer Pengebeløp

1€11,50 2 €23,00 3 €34,50

Reporteren nevner også at den lokale kinoen, MultiPlex, har 25 filmsaler og har plass til 7500 personer. Storfilmen vil ha premiere i alle salene i kinoen. Eierne regner med at alle plassene vil bli solgt ut den første dagen!

Eierne av MultiPlex ønsker å vite hvor mye de kan forvente å tjene inn på billettkontoret. De er ute etter en generell formel, slik at de raskt kan finne pengebeløpet uansett hvor mange som kjøper billetter.

Jobben din: Du har fått jobb som regnskapsfører for MultiPlex! Gratulerer!Sjefen din vil ha en formel som forteller henne hvor mye som vil bli tatt inn på billettkontoret, alt etter hvor mange personer som kjøper billetter.

Fremgangsmåte

1. Bruk tabellen til å finne pengebeløpet som blir tatt inn på billettkontoret, avhengig av antallet personer som ser filmen. Fyll ut følgende tabell. Skriv ned alle beregningene i hvert trinn. Bruk hoderegning så mye som mulig resultatene for pengebeløpet.

Antall

Beregning Pengebeløp (P)

personer (A)

1 1 x 11,50 €11,50 2 2 x 11,50 €23,00 3 3 x 11,50 €34,50 4 5 6

...

10

...

100

...

1000

...

før

du bruker kalkulatoren til å finne

Navn ___________________________

På kino

Dato ___________________________

2. Hvilket mønster ser du i tabellen? Bruk opplysningene i tabellen til å skrive en formel (et algebraisk uttrykk) som beskriver pengebeløpet (P), avhengig av antallet personer (A) som kjøper en billett til forestillingen.

P = ___________________________

3. Kontroller formelen ved hjelp av dataredigeringsprogrammet ( TI-30XS MultiView™-kalkulatoren.

a. Skriv inn de tre første oppføringene fra listen over antall personer (A) fra tabellen

ovenfor, i kolonne L1. (Skriv inn {1, 2, 3}.)

b. Skriv inn formelen fra del 2 i L2. Vær forsiktig: Når du bruker kalkulatoren, må du

oversette variablene (bokstavene). Bokstaven A er nå L1 og P er L2. Skriv formelen på nytt ved å bruke L1 og L2, slik at du kan skrive inn formelen på

kalkulatoren. Formelen din: P = _________________________ Formelen på kalkulatoren: L2 = ________________________

c. Sammenligne tallene i L2 med tallene i tabellen ovenfor. Er det samsvar mellom

dem?

d. Skriv inn flere verdier fra listen over antallet personer fra tabellen i L1. Kontroller

verdiene i L2 sammenlignet med tabellen ovenfor. Er det samsvar mellom dem? Virker formelen?

v) på

4. Bruk dataredigeringsprogrammet på kalkulatoren til å finne pengebeløpet (P) som eierne vil ta inn på billettkontoret hvis hele kinoen fylles opp under én forestilling med 7500 personer (A). Skriv ned for hånd hvordan du kunne ha funnet dette svaret, ved å bruke formelen din.

Navn ___________________________

På kino

Dato ___________________________

5. Sjefen din vil at du skal lage en presentasjon til personene som investerer penger i MultiPlex. Investorene ønsker å se tall og grafer i presentasjonen! Fyll ut tabellen nedenfor ved å bruke dataredigeringsprogrammet på kalkulatoren. Plott punktene fra tabellen i en graf. Dette er en annen måte som en regnskapsfører kan bruke til å vise hvordan pengebeløpet (P) avhenger av antallet personer (A). Dette gir et bilde av dataene!

AP

500 1000 1500 2000 2500

Pengebeløp (P)

Antall personer (A)

6. Skriv et avsnitt nedenfor om hva du vil si til sjefen din og investorene om arbeidet ditt. Ta med hvordan du kom frem til formelen for pengebeløpet, og hva tabellen og grafen forteller dem om pengebeløpet som vil bli tatt inn på billettkontoret.

Gi regelen et navn!

Oversikt

Elevene skal gjette seg frem til det algebraiske uttrykket (en funksjon) basert på en tabell over verdier i et spillformat. Elevene bruker o på TI-30XS MultiView™-kalkulatoren til å angi et uttrykk som en funksjon (y=) for å kunne spille spillet.

Innledning

Elevene varmer opp for denne aktiviteten ved å evaluere uttrykk og fylle ut en tabell med verdier. Deretter spiller de et spill – "Gi regelen et navn!" Spillet bruker TI-30XS MultiView-kalkulatoren til å lage en tabell med verdier.

Få elevene til å fylle ut følgende tabeller som vises på elevarket.

Obs

Obs: Du kan bruke en annen bokstav for variabelen i

ObsObs oppvarmingen. Variabelen på kalkulatoren vil imidlertid alltid være x.

xx

-2 1 -2 2 2

+ 3

x

2x + 6 2(x + 3)*

Matematiske konsepter

• algebraiske uttrykk

• funksjoner

Materiell

• TI-30XS MultiView

•blyant

• elevaktivitet

•papirstrimler og papirkasse

-1 2 -1 4 4 03 06 6 14 18 8 25 210 10

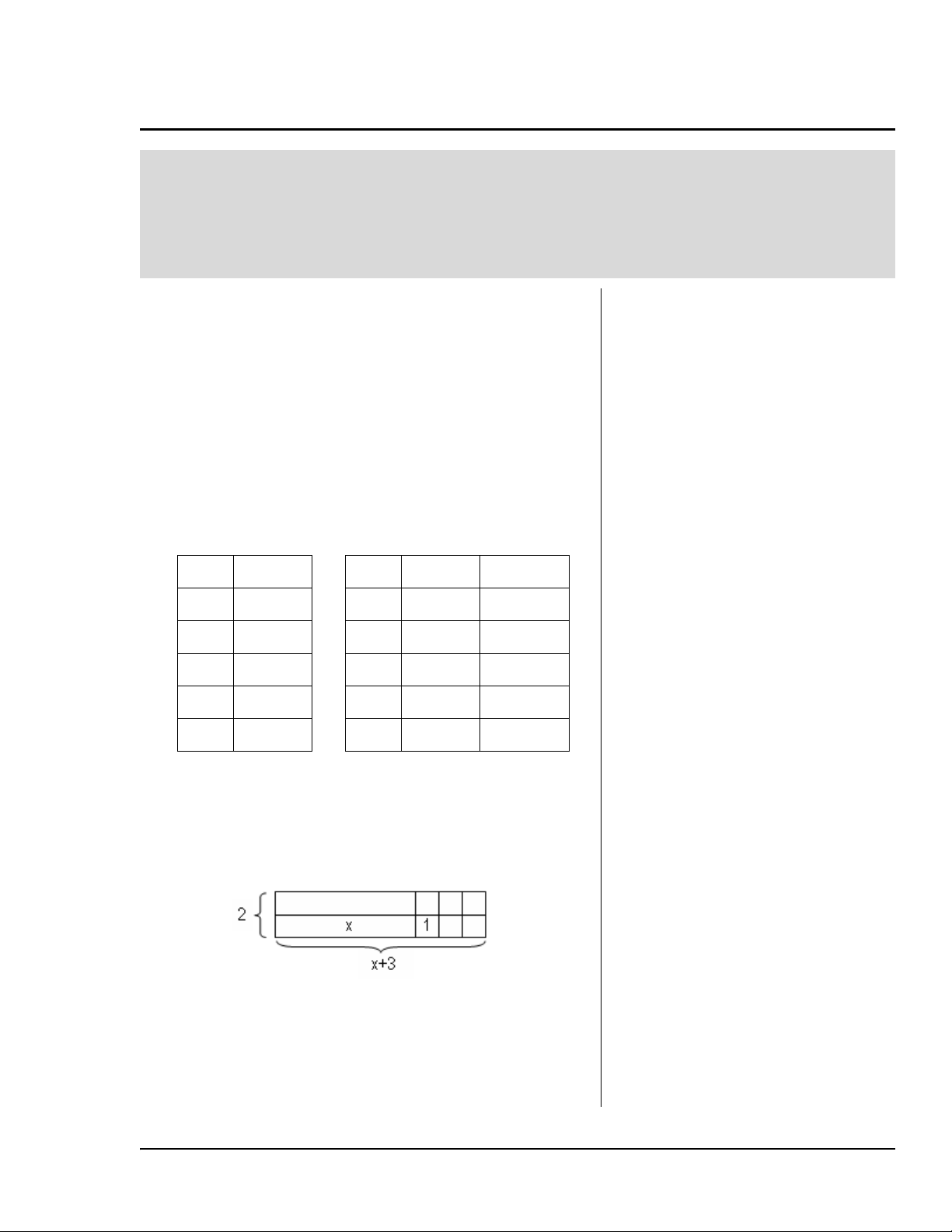
*Elevene bør legge merke til at tabellene for 2x + 6 og 2(x + 3) er like. Diskuter hvorfor disse uttrykkene er likeverdige, og kontroller dette ved å bruke fordelingsegenskapen ved multiplikasjon fremfor addisjon. Du kan også få elevene til å bruke brikker til å vise områdemodellen – 2(x + 3) = 2x + 6.

Vis elevene hvordan de angir uttrykket i o på TI-30XS MultiView. De angir uttrykket som en funksjon. Dette kan være et nytt konsept for elevene.

Gi regelen et navn! (fortsettelse)

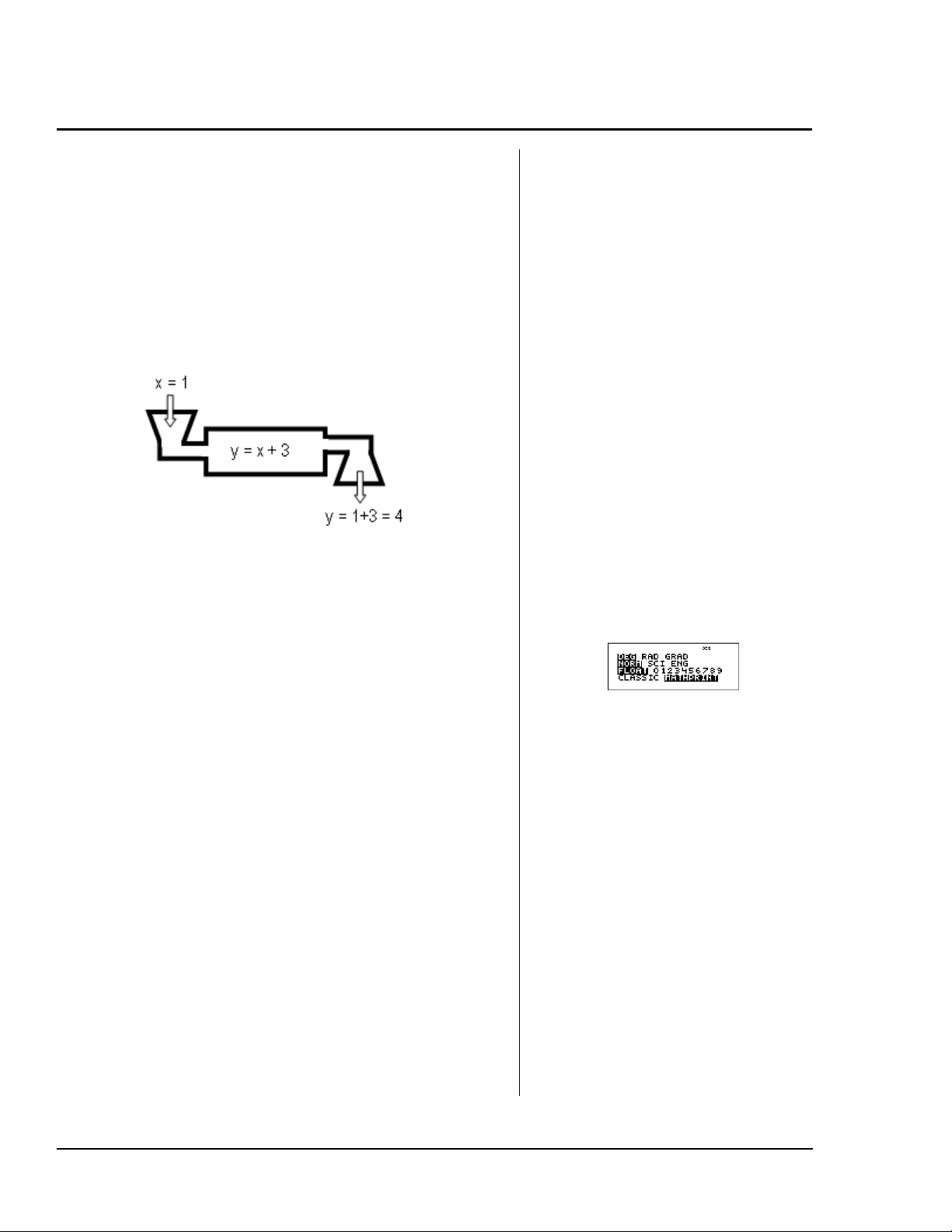
Bruk en funksjonsmaskin om nødvendig for å gi dem en alternativ tenkemåte om evaluering av et uttrykk for ulike verdier av

y

utdataene kan brukes som en regel til å finne må elevene tenke baklengs for å gjette seg frem til "regelen". Diskuter om nødvendig hvordan elevene følger reglene i sine favorittbrettspill. De må følge reglene for å spille. Når de evaluerer et uttrykk, følger de en regel for å bytte ett tall mot et annet.

= 1 + 3 = 4. Diskuter om uttrykket x+3

x

. Her gir inndataene x = 1

y

. Senere i spillet

Sett opp tabellen på kalkulatoren ved hjelp av Autofunksjonen i o. Auto setter automatisk opp en tabell med verdier som starter med en gitt verdi, og som øker med en gitt verdi. For å få kalkulatoren til å lage den samme tabellen som ovenfor setter du start på -2 og øker elevene til å sammenligne tabellen de har gjort for hånd, med kalkulatortabellen.

x

-verdiene med 1 per trinn. Få

Aktivitet

Spill ett eller to spill med “Gi regelen et navn!” med hele klassen, ved å bruke reglene på neste side. For å gi hele klassen en innføring i spillet spiller læreren rollen som styrer. Spillet bruker o Ask-

x

på TI-30XS MultiView™-kalkulatoren.

og funksjonen

³ Følg disse trinnene:

1. Trykk på p, og angi modusen som vist.

2. Skriv inn uttrykket y=x+3: o z T 3 <.

3. Angi oppsettsverdier for tabellen: M 2 $ $ $ <.

4. Bruk # og $ til å bla gjennom verdiene for x og y = x + 3.

³ Tips: Kopier spillarkene fra

elevaktivitetsdelen for så mange spill som du trenger.

Gi regelen et navn! (fortsettelse)

Regler for gruppespill

• Dann grupper på tre til fire elever.

• La én elev være styrer i spillet.

• Styreren har kontroll over kalkulatoren for spillet.

• Styreren velger et algebraisk uttrykk fra en papirkasse (eller en annen beholder) og holder det skjult for de andre elevene. Styreren kan også skrive et algebraisk uttrykk på et papirark for spillet og få godkjenning fra læreren til å bruke uttrykket.

• Styreren skriver inn det algebraiske uttrykket i o og velger funksjonen AskObs

Obs: Styreren må kanskje slette hver linje i tabellen

ObsObs Ask-

x

før en ny regel kan brukes til å spille med. (Se

instruksjoner om tastetrykk.)

• Alle spillerne (bortsett fra styreren) sier en verdi for

x

etter tur. Styreren skriver deretter inn verdien og

oppgir den resulterende

• Hver spiller beholder en verditabell som en spilleoversikt.

• En spiller kan bare gjette på uttrykket eller regelen når det er hans/hennes tur.

• Når en spiller har gjettet på en regel, må alle spillerne kontrollere om regelen stemmer for alle verdiene som allerede er spilt, eller sette regelen på prøve ved å finne en verdi som ikke passer.

• Hvis en spiller eller styreren finner ut at regelen er feil, må spilleren som gjettet på regelen, stå over neste gang det er hans/hennes tur.

• Hvis en spiller har gjettet på et algebraisk uttrykk som ikke er det samme uttrykket som styreren har skrevet inn, for eksempel 2( spillerne er enige om at uttrykket til spilleren er riktig, viser styreren uttrykket på kalkulatoren. Deretter må spilleren som gjettet på regelen, forklare hvorfor de to uttrykkene er likeverdige.

• Den første spilleren som gjetter riktig regel og forsvarer regelen, vinner.

• Styrerrollen går deretter videre til en annen spiller for neste spillerunde.

x

.

y

-verdien til spillerne.

x

+1) og 2x +2, og alle

³ Følg disse trinnene:

1. Trykk på p, og angi modusen som vist.

2. Skriv inn funksjonen y = 2x + 5:

- o 2 z T 5 <. Obs: Hvis en funksjon allerede er skrevet inn på skjermbildet y=, trykker du på - før du skriver inn en ny funksjon.

3. Angi oppsettsverdier for tabellen: $ $ " < $ <.

4. Angi x-verdier: 5 < 6 < 10 <.

³ Tips: Hvis du vil angi flere verdier,

uthever du en av de tre linjene i x- kolonnen, skriver inn tallet og trykker på <.

5. Trykk på o for å se gjennom skjermbildet y=. Du må bla gjennom oppsettsskjermbildet på nytt for å se verditabellen.

³ Slik spiller du på nytt:

1. Fjern det gamle uttrykket, velg et nytt og angi det: o -z T q1 $ 2.

2. Angi ønskede oppsettsverdier for tabellen, fremhev OK, og trykk på <.

Legg merke til at bare 3 forslag vises på skjermen. Elevene kan overskrive et tall for å se en ny utverdi.

Gi regelen et navn! (fortsettelse)

Liste over algebraiske uttrykk

Kopier disse eller andre uttrykk på papir, slik at styreren for hver spillergruppe kan velge uttrykket som skal brukes i spillet. Du kan også få styreren til å skrive et uttrykk som du kan godkjenne, før spillet starter. Å få elevene til å skrive et uttrykk selv gir dem et eierforhold, og det gir deg en mulighet til å vurdere kunnskapene.

Velg en liste eller bland listene, alt etter nivået til elevene. Utvid listene, alt etter nivået til elevene. Elevene må legge frem alt arbeid på elevarket.

Eksempler på: ett-trinns uttrykk

x

+ 3 2x + 3

x

– 9 -4x + 5

1

-- -+

x

2

x

– 2,5

x

+ 15 1,5 x + 2,5

1

x

–

-- -

5

Eksempler på: to-trinns uttrykk

2

x

+ 6 eller 2 (x + 3)

1

-- -x 4– 2

Modifiseringer av spillet

• Ta med uttrykk som må forenkles av spillerne, for

x

eksempel 2 5x - 2, må spilleren klargjøre at uttrykket er likeverdig med 2 vurderingsaspekt.

• Ta med uttrykk i ord, som "fire mindre enn to ganger et tall". Få styrerne til å velge uttrykket fra beholderen, og endre ordene til et uttrykk som du godkjenner, før de går tilbake til gruppen for å spille spillet.

+ 4 + 3x - 6. Hvis en spiller gjetter på

x

+ 4 + 3x - 6, som gir spillet nok et

Eksempel: Fire mindre enn to ganger et tall er valgt.Styreren oversetter dette til 2 om det er rett, og deretter går de tilbake til gruppen for å spille.

x

- 4, du sier fra

Gi regelen et navn!

Navn ___________________________

Dato ___________________________

Problem

Vi følger regler hver dag. Kan du følge reglene i favorittbrettspillet ditt? Må du følge reglene nøye for å spille? Vi følger også regler når vi arbeider med tall og uttrykk.

x

Eksempel: Hvis

= 1, må x + 3 = 1 + 3 = 4

Uttrykket tall. Du kan tenke på Verdiene for

-2 -2 -2

-1 -1 -1

1. Hva legger du merke til ved tabellen for 2

2. Kontroller tabellene ovenfor ved hjelp av o på TI-30XS MultiView™-kalkulatoren.

x

+ 3 har én variabel – x. Avhengig av verdien for x vil x + 3 være lik forskjellige

x

+ 3 som en regel. Fyll ut følgende tabell som en oppvarming.

x

har blitt valgt for deg.

xx

000 111 222

+ 3

x

2

x

+ 6

x

+ 6 og 2(x +3)?

x

2(x + 3)

3. Spill spillet "Gi regelen et navn!", ved å bruke spillearket på neste side. I dette spillet vet du ikke uttrykket (regelen). Du må gjette deg frem til regelen ved å tenke baklengs! Læreren gir deg spilleinstruksjoner.

?

Gi regelen et navn!

?

Tenk baklengs!

?

Navn på spillere: Styrer:

Læreren gir deg instruksjoner om hvordan du spiller. Bruk tabellen til å holde oversikt over

x

verdiene for kontrollere regelen. Hvis regelen til en spiller er feil, fortsetter spillet.

xy

og y for hver spillers tur under spillet. Bruk Forslag-kolonnene til å

-verdi på

kalkulator

Gjett på regelen basert på en tabell med verdier!

Forslag 1

y

= _______________________

x

Kontroller alle Er dette forslaget riktig? _______

-verdiene!

y

= _______________________ Kontroller alle Er dette forslaget riktig? _______

Forslag 2

?

x

-verdiene!

Forslag 4

x

-verdiene!

xy

-verdi på

kalkulator

Forslag 3

y

= _______________________

x

Kontroller alle Er dette forslaget riktig? _______

-verdiene!

y

= _______________________ Kontroller alle Er dette forslaget riktig? _______

Slik bruker du

TI-30XS MultiView™

kalkulatoren

TI-30XS MultiView - enkle operasjoner 29

Slette og korrigere 41

Enkel matematikk 45

Rekkefølge for operasjoner og parenteser 49

Numerisk notasjon 55

Brøker 59

Desimaltall og desimaler 65

Konstant 67

Minne og lagrede variabler 71

Dataredigeringsprogrammet og listeformler 79

Statistikk 83

Sannsynlighet 89

Funksjonstabell 97

Potens, kvadratrot og inverse verdier 101

Logaritmer og eksponentfunksjoner 109

Pi 113

Innstillinger og omregninger for vinkler 117

Polare og rektangulære omregninger 121

Trigonometri 123

Hyperbolske funksjoner 131

TI-30XS MultiView™ – enkle operasjoner

1

Taster

1. & slår på kalkulatoren.

2. % aktiverer 2nd-indikatoren og gjør at du kan bruke funksjonen som vises over den neste tasten du trykker på.

3. % ' slår av kalkulatoren og tømmer skjermen.

4. < fullfører operasjonen eller utfører kommandoen.

5. % i henter frem det sist beregnede resultatet og viser det som Ans.

6. n veksler svaret mellom formatene brøk og desimal, nøyaktig kvadratrot og desimaltall, og nøyaktig pi og desimaltall.

7. ! og " flytter markøren til venstre og høyre for å bla gjennom oppføringer på startskjermen, og for å navigere i menyer. %! eller % " blar til starten eller slutten av en gjeldende oppføring. # og $ flytter markøren opp og ned gjennom menyelementer, tidligere oppføringer på startskjermen og oppføringer i dataredigeringsprogrammet og funksjonstabellen. % # flytter markøren til den øverste oppføringen i den aktive kolonnen i dataredigeringsprogrammet, eller til den forrige oppføringen på startskjermen. Trykk på % # på nytt for å flytte markøren til den eldste oppføringen på startskjermen. I brøker kan du trykke på % # for å lime inn en tidligere oppføring i nevneren. (Se kapittel 6, Brøker, for mer informasjon.) % $ flytter markøren til den første tomme raden i den aktive kolonnen i dataredigeringsprogrammet, eller under den siste oppføringen på startskjermen.

8. p brukes til å angi modus for vinkel, numerisk, desimaltall og visning. Trykk på $# ! " for å velge en modus og på <

2

8

9

3

1

7

6

5 4

for å bekrefte valget. Trykk på - eller %Q for å avslutte modusmenyen.

9. %

Obs: Hvis du trykker på & og - samtidig, nullstilles kalkulatoren umiddelbart. Ingen menyer eller meldinger vises.

 viser menyen Reset.

• Trykk på 1 (No) for å gå tilbake til forrige

skjermbilde uten å nullstille kalkulatoren.

• Trykk på 2 (Yes) for å nullstille

kalkulatoren. Meldingen

CLEARED

vises.

MEMORY

TI-30XS MultiView™ – enkle operasjoner

(fortsettelse)

• Nullstille kalkulatoren: – Tilbakestiller innstillingene til

standardverdiene: grader (DEG) som vinkelmodus, vanlig numerisk notasjon (NORM), flytende desimalnotasjon (FLOAT) og MathPrint™ som visningsmodus.

– Sletter variabler i minnet, ventende

operasjoner, oppføringer i loggen, statistiske data, konstanter og Ans (siste svar).

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene (se side vi).

• n kan brukes i en oppføring før du trykker på <. Hvis du trykker på n flere ganger i en

gjeldende oppføring, kan det føre til en syntaksfeil. For å oppnå det ønskede resultatet kan du:

– Skrive inn uttrykket, trykke på n <

og deretter på n på nytt etter at resultatet vises.

– Skrive inn uttrykket og trykke på < og

deretter på n så mange ganger du vil, for å bytte visning og vise svaret i alternativt format.

• Når ³ eller ´ vises på skjermen, er det flere tegn til venstre eller høyre på oppføringslinjen.

• Trykk på & etter at funksjonen Automatic Power Down™ (APD™) er aktivert, for å slå strømmen på igjen. Skjermen, ventende operasjoner, innstillinger og minnet beholdes.

Sekundær, på-av, piler, enter

• Skriv inn 46 – 23.

• Endre 46 til 41. Endre 23 til 26 og fullfør operasjonen.

• Skriv inn + og fullfør

operasjonen.

• Slå TI-30XS MultiView™kalkulatoren av og på. Startskjermen er tom. Rull oppover for å vise loggen.

Trykk på Skjerm

2

--5

3

----10

46 U

%' ! "

# $ <

23 <

# # < !!!! 1 "" 6 < 2 q 5 " T 3 q 10 <

%' & # # #

Nullstille

Nullstill kalkulatoren.

Trykk på Skjerm

%

2

-

%

Hvis du trykker på & og samtidig, nullstilles også kalkulatoren umiddelbart. Ingen menyer eller meldinger vises.

Hvis du bruker % eller & og

-, returneres alle innstillingene til standardverdiene, og minnet tømmes.

Modus

p Bruk p til å velge modus. Trykk på

$ # ! " for å velge en modus og på < for å bekrefte valget. Trykk på

- eller %Q for å gå tilbake til

startskjermen og utføre arbeidet med de valgte modusinnstillingene.

Standard modusinnstillinger vises uthevet.

DEG RAD GRAD Setter

p

vinkelmodusen til grader, radianer eller gradienter.

NORM SCI ENG Angir modusen for numerisk notasjon. Moduser for numerisk notasjon virker bare inn på hvordan resultater vises, og ikke nøyaktigheten for verdiene som er lagret på kalkulatoren, som holder seg på det maksimale.

Modus (fortsettelse)

NORM viser resultatene med sifre

til venstre og høyre for desimaltegnet, som 123456,78.

SCI uttrykker tall med ett siffer til venstre for desimaltegnet og den aktuelle potensen av 10, som

5

1,2345678x10

(som er det

samme som 123456,78). ENG viser resultater som et tall

fra 1 til 1000 ganger 10 opphøyd i en heltallseksponent. Heltallseksponenten er alltid et

p

multiplum av 3.

Obs: C er en hurtigtast for å angi et tall i vitenskapelig notasjonsformat. Resultatet vises i det numeriske notasjonsformatet som er angitt i modusen.

FLOAT 0 1 2 3 4 5 6 7 8 9 Angir modusen for desimalnotasjon.

FLOAT (flytende desimalpunkt) viser opptil 10 sifre, pluss fortegn og desimaltall.

Modus (fortsettelse)

0 1 2 3 4 5 6 7 8 9 (fast

desimalpunkt) spesifiserer antallet sifre (0 til 9) som skal vises til høyre for desimaltegnet.

CLASSIC MATHPRINT angir hvordan inndata og utdata skal vises.

CLASSIC viser inntastinger og resultat på én enkelt linje.

MATHPRINT viser de fleste inntastinger og resultat i tekstbokformat. Når du bruker

p

MathPrint-modus, får du bedre visuell kontroll på at matematiske uttrykk er skrevet inn på riktig måte, og den fremhever også den korrekte matematiske oppstillingen på en bedre måte.

Obs: Når du bytter modus mellom Classic og MathPrint, slettes kalkulatorloggen og konstantverdien.

Menyer

Enkelte taster viser menyer: H, %I, v, %t, %, %h og %{. Enkelte

taster kan vise flere menyer.

Trykk på " og $ for å bla og velge et

menyelement, eller trykk på det tilsvarende tallet ved siden av menyelementet. Hvis du vil gå tilbake til det forrige skjermbildet uten å

velge elementet, trykker du på -.

Hvis du vil avslutte en meny eller et program og gå tilbake til

startskjermen, trykker du på

%Q. Startskjermen er tom. Rull oppover for å vise loggen.

Enkelte eksempelmenyer:

H % I

PRB RAND DMS R ¶¶¶¶P

1: nPr 1: rand 1: Ä 1: R ´Pr( 2: nCr 2: randint( 2: Å 2: R ´PÁ( 3: ! 3: Æ 3: P ´ Rx(

4: r 4: P ´Ry( 5: g 6: ´DMS

Menyer (fortsettelse)

v (Trykk én gang på v for å vise

dataredigeringsprogrammet. Trykk en gang til for å vise menyen.)

CLEAR FORMULA

1: Clear L1 1: Add/Edit Frmla 2: Clear L2 2: Clear L1 Frmla 3: Clear L3 3: Clear L2 Frmla 4: Clear ALL 4: Clear L3 Frmla

5: Clear ALL

Trykk på v når alternativet Add/ Edit Frmla på menyen FORMULA er aktivert, for å vise denne menyen:

%t

STATS

1: 1-Var Stats 2: 2-Var Stats

3: StatVars

Ls

1: L1 2: L2 3: L3

Dette menyalternativet vises etter at du har beregnet statistikk med 1 variabel eller 2 variabler.

StatVars-menyen: 1: n 2:

Ï

3: Sx Osv. Se kapittel 11, Statistikk, for en

fullstendig liste.

Siste svar (Ans)

Bruk siste svar (Ans) til å regne ut

2

5

+

Trykk på Skjerm

12

2

.

5 FT12

F<

%b% i<

%i

Bytte svar

Trykk på n hvis du vil bytte svaret som vises, mellom brøk- og desimalsvar, nøyaktig kvadratrot og desimaltall, og nøyaktig pi og desimaltall.

Trykk på Skjerm

% b

8 <

n

Slette og korrigere

2

Taster

1. - sletter tegn og feilmeldinger. Trykk én gang på - for å slette en ufullstendig oppføring. Trykk på nytt for å tømme skjermen. Du kan rulle oppover og bruke - til å slette oppføringer i loggen. - går tilbake ett skjermbilde i programmer.

2. % f gjør at du kan sette inn et tegn ved markøren.

3. J sletter tegnet ved markøren. Hver gang du deretter trykker på J, slettes 1 tegn til venstre for markøren.

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• Minnet, statistiske registre, vinkelenheter eller den numeriske notasjonen påvirkes ikke når du trykker på -.

2 3

1

Slette og sette inn

Skriv inn 4569 + 285, og endre det deretter til 459 + 2865. Fullfør oppgaven.

Trykk på Skjerm

4569 T 285

! ! ! ! ! ! J

" " " "

J

%f

%f 6

<

Fjerne

Skriv inn 21595. Fjern 95. Fjern oppføringen.

Trykk på Skjerm

21595

! ! -

(Fjerner til høyre)

-

(Fjerner oppføringen)

Enkel matematikk

3

Taster

1. T adderer.

U subtraherer.

2.

3. V multipliserer.

4.

W dividerer.

5. < fullfører operasjonen eller utfører

kommandoen.

M brukes til å skrive inn et negativt tall.

6.

7. % _ føyer til tegnet % for et tall.

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• TI-30XS MultiView™ støtter implisert multiplikasjon. Eksempel: 3 (4+3) = 21

• Du må ikke forveksle M med U. U tillater subtraksjon.

• Bruk om nødvendig parenteser til å gruppere fortegnet med tallet. Eksempel: M22 = M4, og (M2)2 = 4.

• Resultater av prosentberegninger vises i henhold til modusinnstillingen for desimaltallnotasjon.

4

7

3 2 1

5

6

Addere, subtrahere, multiplisere, dividere, er lik

Finn svaret:

2 + 54 16 x 21 =

1

x 10 =

--2

12 x (5 + 6) =

Trykk på Skjerm

½ 6 =

2 T 54 U 6 <

T U V W

<

16 V 21 <

1 q 2 " V 10 <

12 V D 5 T 6 E <

Negative tall

Temperaturen i Utah var 06:00. Klokken 10:00 hadde temperaturen steget med 12 ÄC. Hva var temperaturen klokken 10:00?

Trykk på Skjerm

M3 ÄC klokken

M 3 T

12 <

Temperaturen klokken 10:00 var 9 ÄC.

M

Prosent

Mikkel tjener €80 per uke. Han sparer

15 % av det han tjener. Hvor mye sparer Mikkel per uke?

Trykk på Skjerm

15

% _ V

80 <

Mikkel sparer

€12 per uke.

% _

Rekkefølge for operasjoner og parenteser

4

Taster

1. D åpner et parentesuttrykk.

2. E lukker et parentesuttrykk.

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• På transparentmalen der EOS™ (Equation Operating System – ligningsoperasjonssystem) vises, demonstreres rekkefølgen som TI-30XS MultiView™-kalkulatoren bruker til å utføre beregninger.

• Operasjoner inne i parenteser utføres først. Du kan bruke D E til å endre operasjonsrekkefølgen, og derfor til å endre resultatet. Eksempel: 1 + 2 x 3 = 7 (1 + 2) x 3 = 9

1

2

EOS™ (Equation Operating System)

1 (først) Uttrykk inne i D E 2 Funksjoner som trenger en E og som kommer

foran uttrykket, for eksempel >, A og enkelte

menyelementer 3Brøker 4 Funksjoner som er skrevet inn etter uttrykket,

for eksempel F og vinkelenhetsmodifikatorer (

¢, £, r, g)

5 Eksponent (G) og kvadratrot (%c)

Obs: I Classic-modus evalueres eksponenter ved

bruk av G-tasten fra venstre mot høyre.

Uttrykket 2^3^2 evalueres som (2^3)^2, med

resultatet 64.

I MathPrint™-modus evalueres eksponenter ved

bruk av G-tasten fra høyre mot venstre. Hvis du

3

trykker på 2 G 3 G 2, vises det som , med

2

resultatet 512.

Den vitenskapelige kalkulatoren TI-30XS

¡,

2

MultiView™ evaluerer uttrykk som er skrevet inn

med F og a, fra venstre mot høyre både i

Classic- og MathPrint-modus. Hvis du trykker på

22

3 F F, vises det som . Dette regnes ut

2)2

som (3

= 81.

3

EOS™ (Equation Operating System) (fortsettelse)

6 Fortegn (M) 7 Permutasjoner (nPr) og kombinasjoner (nCr) 8 Multiplikasjon, implisitt multiplikasjon og divisjon 9 Addisjon og subtraksjon 10 Omregninger (%O, %j, %R og

´DMS)

11 (siste) < utfører alle operasjoner og lukker alle åpne

parenteser.

Operasjonsrekkefølge

1 + 2 x 3 =

Trykk på Skjerm

1 T 2 V 3 <

1 + (2 x 3) =

Trykk på Skjerm

1 T D 2 V 3 E <

(1 + 2) x 3 =

T V D E

Trykk på Skjerm

D 1 T 2 E V 3 <

Operasjonsrekkefølge (fortsettelse)

2

5

Trykk på Skjerm

41()3()–

p$$$ <% b 5 F U 4 D 1 E D 3 E <

= (Classic-modus)

2

=

5

Trykk på Skjerm

41()3()–

(MathPrint™-modus)

p$$$ "<% b 5 F U 4 D 1 E D 3 E <

n

Numerisk notasjon

5

Taster

1. p lar deg velge fra følgende meny for

numerisk notasjon. NORM Gjenoppretter standardmodus

(flytende desimal).

SCI Aktiverer vitenskapelig modus og

viser resultater som et tall fra 1 til 10 (1 { n < 10) ganger 10 med en heltallspotens.

ENG Aktiverer teknisk modus og viser

resultater som et tall fra 1 til 1000 (1 { n < 1000) ganger 10 opphøyd i en heltallseksponent. Heltallseksponenten er alltid et multiplum av 3.

2. C er en hurtigtast for å angi et tall i

vitenskapelig notasjonsformat.

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• Du kan angi en verdi i vitenskapelig notasjon uavhengig av modusinnstillingen for numerisk notasjon. For en negativ eksponent trykker du på M før du angir den.

• Resultater som trenger flere enn 10 sifre, vises automatisk i vitenskapelig notasjon.

• For desimalnotasjonsmodus, se kapittel 7, Desimaltall og desimaler.

• Disse modusene (NORM, SCI og ENG) virker bare inn på visningen av resultater.

1

2

Teknisk, vitenskapelig, flytende desimal

Skriv inn 12543, som vil være i flytende desimalnotasjon og vanlig numerisk notasjon (begge er standardinnstillinger i resultatet på skjermen mellom vanlig, vitenskapelig og teknisk notasjon ved å endre innstillinger i modusskjermbildet.

Trykk på Skjerm

p). Bytt

12543 <

p

p$" <

-<

p$" "<

-<

Teknisk, vitenskapelig, flytende desimal (fortsettelse)

p$<

-<

p

Vitenskapelig notasjon

La TI-30XS MultiView™-kalkulatoren være i Norm-modus og MathPrint™modus (begge er standardinnstillinger), og angi følgende problem i vitenskapelig notasjon ved å bruke C-tasten.

Jorden er omtrent 1,5 x 10 fra Solen. Jupiter er omtrent 7,8 x 10 banene til planetene er sirkulære, og at planentene er på samme side av solen. Hvor nært vil Jupiter være

8

kilometer fra Solen. Anta at

8

kilometer

C

Jorden?

Trykk på Skjerm

7 8 8

C 8 " U 1 8 5 C

8 <

Jupiter og Jorden kan være omtrent 630 000 000 = 6,3 x 10 fra hverandre.

8

kilometer

Brøker

6

Taster

1. %N lar deg skrive inn blandede tall og brøker. Enheten må være et heltall. Telleren og nevneren kan ha desimaler.

Når du skal skrive inn et blandet tall, skriver du inn et heltall for enheten og trykker deretter på %N for å skrive inn en teller.

Hvis du trykker på %N i MathPrint™modus før du skriver inn et heltall, vises en brøkmal som bare tillater at du skriver inn ett siffer for enheten.

2. q lar deg skrive inn en enkel brøk. Å trykke på

q før eller etter et tall kan føre til ulike virkemåter. Hvis du skriver inn et tall i MathPrint™-modus før du trykker på q, blir vanligvis dette tallet telleren.

q i MathPrint-modus kan også brukes til mer kompliserte brøk- eller formelutregninger med operatorer og andre funksjoner på q før du skriver inn telleren.

I MathPrint™-modus trykker du på $ mellom oppføringen av telleren og nevneren. I Classicmodus trykker du på q mellom oppføringen av telleren og nevneren.

3. % O regner om en enkel brøk til et blandet tall, eller et blandet tall til en enkel brøk.

4. % j regner om en brøk til det tilsvarende desimaltallet, eller et desimaltall til den tilsvarende brøken, hvis det er mulig.

ved å trykke

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• I MathPrint-modus kan brøker med q inkludere operasjonstaster (T, V osv.) og de fleste funksjonstaster (F, %_ osv.). I

3

1 2

4

Classic-modus tillater ikke brøker q operasjonstaster, funksjoner eller sammensatte brøker i telleren eller nevneren.

• I MathPrint-modus kan du skrive inn variabler (x, y, z, t, a, b, og c) i telleren og nevneren i en brøk. I Classic-modus tillater ikke brøker med q variabler.

• I Classic-modus bruker dataredigeringsprogrammet og tabeller W sammen med D og E etter behov for å utføre sammensatte divisjonsproblemer.

Brøker (fortsettelse)

• Hvis du vil lime inn en tidligere oppføring i nevneren, plasserer du markøren i nevneren, trykker på % # for å bla til den ønskede oppføringen og trykker deretter på < for å lime inn oppføringen i nevneren.

• Hvis du vil lime inn en tidligere oppføring i telleren eller enheten, plasserer du markøren i telleren eller enheten, trykker på # eller % # for å bla til den ønskede oppføringen og trykker deretter på < for å lime inn oppføringen i telleren eller enheten.

• Brøkresultater og -oppføringer blir automatisk forenklest til lavest mulig benevnelse.

• Beregninger som bruker brøk, kan vise brøkeller desimalresultat, alt etter inndataene.

Brøker

5

På festen spiste du av

pepperonipizzaen og av

pølsepizzaen. Pizzaene er av samme størrelse. Hvor mye av en hel pizza spiste du hvis du legger stykkene sammen?

--6

1

----10

q

Trykk på Skjerm

5 q 6 " T1 q 10 <

14

Du spiste av en hel pizza. Det er

nesten en hel pizza!

---15

Blandede tall

Vekten til et spedbarn var 4 pund

ved fødselen. I løpet av de neste 6 månedene la hun på seg

3

2 pund. Hvor mye veier hun?

--4

3

--8

%N

%O

Trykk på Skjerm

4 %N 3

$ 8 " T 2 %N 3 $ 4 <

%O <

Etter 6 måneder veier barnet

1

7 pund.

--8

Regne om brøker og desimaltall

Jon svømmer 20 lengder på 5,72 minutter. Marie svømmer 20 lengder

på 5 minutter. Endre Maries tid til et desimaltall for å finne ut hvem som

svømmer raskest.

Trykk på Skjerm

3

--4

5 %N 3

$ 4 "

%j

<

%j

Jon svømmer raskere enn Marie siden han svømmer 20 lengder på 5,72 minutter.

Endre 2,25 til den tilsvarende brøken.

Trykk på Skjerm

2 8 25 %

j

<

eller 2 8 25 <

n

Desimaltall og desimaler

7

Taster

1. 8 angir et desimalpunkt.

2. p lar deg angi antallet desimaler. Trykk på $ $ og deretter på " til du har valgt ønsket antall desimaler. Trykk på < for å velge.

FLOAT Angir flytende desimalnotasjon

(standard).

0-9 Angir hvor mange desimaler som

vises. FIX vises når en desimalmodus er angitt fra 0-9.

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• Trykk på p $ $ < for å gå tilbake til standardnotasjon (flytende desimal).

• Innstillingen for desimalmodus virker inn på de fleste desimalresultater og desimalene i resultater i vitenskapelig og teknisk notasjon.

• TI-30XS MultiView™-kalkulatoren runder av resultatet automatisk til antallet desimaler som er valgt. Når for eksempel antallet desimaler er satt til 2, blir 0,147 til 0,15 når du trykker på <. TI-30XS MultiViewkalkulatoren runder også av eller fyller ut resulterende verdier med ekstra nulltall, alt etter hvilken innstilling som er valgt. Når for eksempel antallet desimaler er satt til 5, blir 0,147 til 0,14700 når du trykker på <.

• Hvis du nullstiller kalkulatoren, slettes desimalinnstillingen, og den stilles tilbake til standardinnstillingen – FLOAT.

• Desimalinnstillingen virker ikke inn på resultatenes interne nøyaktighet. Den virker

2

1

bare inn på hvordan resultatene vises.

Desimaler

Rund av 12,345 til hundredelsplassen, til tidelsplassen og deretter til flytende notasjon.

Trykk på Skjerm

12 8 345 <

p

$ $ "

""<

-<

p

$$"

"<

-<

p

$$

<

-<

Konstant

8

Taster

1. % l slår konstantfunksjonen på og av og lar deg definere et konstant tall, uttrykk eller en konstant operasjon for en snarvei når du gjentar et sett med tastetrykk. K vises når konstantmodus er aktivert.

2. < plasserer innholdet til K ved slutten av uttrykket på skjermen.

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• Alle operasjoner, funksjoner og verdier virker i konstantmodus.

• Slik angir du en konstant:

1. Trykk på % l. Hvis det allerede er

lagret en konstant, trykker du på for å slette den.

2. Angi konstanten (ethvert sett med

operasjoner, funksjoner og verdier).

3. Trykk på < for å aktivere

konstantfunksjonen. K vises på skjermen for å indikere at konstantfunksjonen er aktivert.

4. Trykk på - for å tømme skjermen.

5. Skriv inn en innledende verdi. Hvis du ikke

skriver inn en verdi, brukes 0, og Ans vises på skjermen.

6. Trykk på < for å plassere innholdet i K

ved slutten av uttrykket og evaluere det.

7. Fortsett med å trykke på < for å

gjenta konstanten.

8. Trykk på % l på nytt for å slå av

konstantfunksjonen.

1

2

Konstant

Tre personer sitter barnevakt for €5,25 hver per time. Den første personen arbeider 16 timer. Den andre personen arbeider 12 timer. Den tredje personen arbeider 17 timer. Hvor mye tjener den enkelte personen?

Trykk på Skjerm

%l

V 5,25 <

%l

-

16 <

12 <

17 <

Konstant (fortsettelse)

%l

(Konstantmodus er av.)

%l

Minne og lagrede variabler

9

Taster

1. L lar deg lagre verdier i variabler. Trykk på L for å lagre en variabel, og trykk på z

for å velge hvilken variabel du vil lagre. Trykk på < for å lagre verdien i den valgte variabelen. Hvis denne variabelen allerede har en verdi, erstattes denne verdien av den nye.

2. z gir tilgang til variabler. Trykk flere ganger på denne tasten for å velge x, y, z, t, a, b eller c. Du kan også bruke z til å hente frem de lagrede verdiene for disse variablene.

3. % { sletter alle variabler.

4. % h viser en meny over variabler x, y, z, t, a, b og c og lar deg vise de lagrede verdiene før du limer de inn på skjermen.

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• Du kan lagre et tall eller uttrykk som resulterer i et tall, i en variabel i minnet.

• Når du velger en variabel ved å bruke z, vises navnet på variabelen (x, y, z, t, a, b eller c). Navnet på variabelen settes inn i den gjeldende oppføringen, men verdien som er tildelt til variabelen, brukes til å evaluere uttrykket.

• Når du velger en variabel ved å bruke % h, vises en meny med verdiene for de lagrede variablene. Velg en variabel ved å trykke på det tilsvarende nummeret på menyen. Verdien som er tildelt til variabelen, settes inn i den gjeldende oppføringen og brukes til å evaluere uttrykket.

• Hvis du nullstiller kalkulatoren, slettes alle variablene i minnet.

3

2

4

1

Lagre, variabler

Nedenfor vises poengsummene dine for prøver og hjemmearbeid i matematikken.

Poengsummer på prøver: 96, 76, 85. Poengsummer på hjemmearbeid: 92, 83, 97, 86.

1. Finn karakteren din på prøvene som gjennomsnittet av poengsummene på prøvene.

2. Finn karakteren din på hjemmearbeidet som gjennomsnittet av

Lz

%h

poengsummene på hjemmearbeidet.

3.Læreren vil regne ut den endelige karakteren som gjennomsnittet av karakteren på prøvene og på hjemmearbeidet. Hva er den endelige karakteren? Læreren runder av til nærmeste hele tall om nødvendig.

Trykk på Skjerm 96 T 76 T 85 <

Lagre, variabler (fortsetter)

W 3 <

Lz <

92 T 83 T 97 T 86

< W 4 <

T z <

Lz

%h

W 2 <

Den endelige karakteren er 88, avrundet til nærmeste hele tall.

Lagre, hente

Du skal sende en gave til to venner. De skal få én gave hver. Du finner gavene til samme pris på to webområder. Områdene tar forskjellig pris for forsendelsen. Pakkene veier 4,5 pund og 3,2 pund. Lager A sender pakken for €2 pluss €1,40 per pund. Lager B sender pakken for €3 pluss €1,10 per pund. Hvilket lager tar lavest pris for å sende den enkelte gaven?

Trykk på Skjerm

4 8 5 L

L

%h

z <

2 T 8 40 E

3 T 8 10 E

Lager A tar €8,30, og lager B tar €7,95. Lager B tar minst for å sende

gaven som veier 4,5 pund.

z D1

<

z D1

<

Lagre, hente (fortsetter)

L

3 8 2 L z <

##### #<<

Lager A tar €6,48, og lager B tar €6,52. Lager A tar minst for å sende

gaven som veier 3,2 pund.

%h

Lagre, hente (fortsetter)

Butikk Kjøp Ant Pris Askjorter2€13,98 stk. B slips 3 €7,98 stk. C belte 1 €6,98

seler 1 €9,98

Hvor mye brukte du i hver butikk, og hvor mye brukte du til sammen?

Trykk på Skjerm

2 V 13 8 98 <

L

%h

Lz<

3 V 7 8 98 <

L z z <

Lagre, hente (fortsetter)

L

6 8 98 T 9 8 98 <

L z zz<

% h

1 T% h 2 T %

h 3 <

%h

Du brukte:

€27,96 i butikk A, €23,94 i butikk B, €16,96 i butikk C.

Du brukte €68,86 totalt i alle tre butikkene.

Dataredigeringsprogrammet og listeformler

10

Taster

1. v viser et dataredigeringsprogram med tre lister. Hver liste kan inneholde opptil 42 elementer. Gå til en liste og skriv inn et tall for å angi data. Trykk på piltastene for å navigere gjennom listeelementer.

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• Du kan bruke alle kalkulatorfunksjonene i listeformler.

•Bruk D og E rundt variabler eller navn på lister i formler, for å sørge for at operasjonene utføres i riktig rekkefølge.

• Hvis en formel angis i en liste, oppdateres formellisten automatisk hvis et henvist listeelement oppdateres.

Obs: Hvis du trykker på < i en formelliste, slettes formelen automatisk. Ingen meldinger vises.

• Når en formel er slettet, kan dataene fortsatt brukes. Dataene oppdateres imidlertid ikke lenger.

• Hvis du trykker på v på nytt i dataredigeringsprogrammet, åpnes menyer med alternativer for å tømme lister eller for å skrive inn og behandle formler.

• Hvis du trykker på v på nytt når alternativet for å legge til / redigere en formel valgt, åpnes en meny med navn på lister du kan bruke, når du legger til eller redigerer formler.

1

• Hvis du trykker på -, blir skjermbilder i dataredigeringsprogrammet sikkerhetskopiert.

• Hvis du trykker på % Q, avsluttes dataredigeringsprogrammet, og du kommer tilbake til startskjermen.

• I dataredigeringsprogrammet vises vitenskapelig notasjon som plass, men det vises fortsatt hvor stort et tall er.

Eksempel: 2 x 103 vises som 2E3.

E for å spare

Angi data og formler

På en dag i november viste en værrapport på Internett følgende temperaturer.

Paris, Frankrike 8 ÄC Moskva, Russland

½1 ÄC

Montreal, Canada 4 ÄC Regne om disse temperaturen fra

Celsius til Fahrenheit.

9

Omregningen: F= C+32.

--5

Trykk på Skjerm

v

v 8 $ M

$ 4 $ "

1

v "

1

9

W 5 V v

1 T 32

Angi data og formler (fortsettelse)

<

Legg merke til at L2 er fremhevet, siden dette er resultatet av en formel.

Grader Fahrenheit er: Paris, Frankrike 46,4 ÄF

Mokva, Russland 30,2 ÄF

v

Montreal, Canada 39,2 ÄF

Hvis Sydney, Australia er 21 ÄC, finn temperaturen i Fahrenheit.

! $ $ $

<

21

Temperaturen i Sydney, Australia er 69,8 ÄF.

Statistikk

11

Taster

1. v lar deg angi datapunkt (x for 1-Var- statistikk, x og y for 2-Var-statistikk). (Se kapittel 10, Dataredigeringsprogrammet og listeformler, for mer informasjon om v.)

2. %t viser en meny der du kan velge 1-Var,

2-Var eller StatVars. 1-Var Analyserer data fra 1 sett med

data med 1 målt variabel – x.

2-Var Analyserer sammenfattede data

fra 2 sett med data med 2 målte variabler – x, den uavhengige variabelen og y, den avhengige variabelen.

StatVars Dette alternativet vises bare

etter at du har beregnet statistikk med 1 variabel eller 2 variabler. Viser menyen med variabler med de gjeldende verdiene.

2

1

StatVars-menyen:

n

v eller w Gjennomsnittet for alle x- eller

Sx

eller

Antallet datapunkt for x (eller x,y).

y-verdiene.

Sy

Eksempelstandardavvik for x eller y.

sx eller sy Populasjonsstandardavvik for x

eller y.

Gx eller Gy Summen av alle x-verdiene eller

y-verdiene.

2

Gx

eller Gy2Summen av alle x2-verdiene eller

2

-verdiene.

y

Gxy Summen av produktet av x og y

for alle x-y-par i de 2 listene.

a Helling, lineær tilbakegang. b y-skjæringspunkt, lineær

tilbakegang.

r Korrelasjonskoeffisient. x ÅÅÅÅ (2-var) Bruker a og b til å regne ut

anslått x-verdi når du taster inn en y-verdi.

y ÅÅÅÅ (2-var) Bruker a og b til å regne ut

anslått y-verdi når du taster inn en x-verdi.

minX Minimum for x-verdiene. Q1 (1-var) Median for elementene mellom

minX og Med (første kvartil).

Med Median for alle datapunktene. Q3 (1-var) Median for elementene mellom

Med og maxX (tredje kvartil).

maxX Maksimum for x-verdiene.

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• Du kan endre datapunkt ved å gå til dataredigeringsprogrammet, navigere til dataelementet og endre verdien som er angitt. Obs: Du må deretter regne ut statistikken med 1-variabel eller 2-variabler for å vise StatVars-alternativet.

Angi stistikkdata med 1 variabel

Fem elever har hatt en matematikkprøve. Bruk poengsummene til å angi datapunktene – 85, 85, 97, 53, 77.

Trykk på Skjerm

v

85 $ 97 $ 53 $ 77 $

" 2 $1 $1 $1 $

%t v

Fortsettelse

Vise statistikken

Finn antallet datapunkt (n), gjennomsnittet (

v),

eksempelstandardavviket (Sx),

Gx),

2

), og

sx),

populasjonsstandardavviket ( summen av poengsummene (

summen av kvadratene (

Gx

sammendraget av dataene med fem tall, minX, Q1, Q2 og maxX.

Trykk på Skjerm

%t

1 $ " "

%t v

< $

<

$ $ $ $ $

$ $ $

$ $

Fjerne datapunkt

Stryk den laveste poengsummen ved å redigere dataene i L1 i dataredigeringsprogrammet. Pass på at du oppdaterer frekvenslisten, L2, om nødvendig. Finn det nye gjennomsnittet ( dataene fra alle listene.

Trykk på Skjerm

v). Slett til slutt

v

$ $

v

J " J

%t

1

$$<

vv 4

%Q

Angi stistikkdata med 2 variabler

Tabellen nedenfor viser antallet par med joggesko som ble solgt av en liten skobutikk. Tabellen viser det totale antallet skopar som ble solgt på to måneder, og det totale antallet par av merke A som ble solgt i løpet av de samme månedene. Skriv inn disse dataene i dataredigeringsprogrammet.

Måned April 58 35 Mai 47 28

Totalt ant. (x) Merke A (y)

%t v

Trykk på Skjerm

v58 $ 47 $

"35 $28 $

Vise statistikken

Anta at skosalget holder seg konstant. Du kan bruke to datapunkt til å forutsi salget i juni av merke A hvis du kjenner til det totale salget for juni. Bruk en linje med beste tilpassing til å finne salget i juni av merke A hvis butikken selger totalt 32 par i juni.

Tips: Finn y

Trykk på Skjerm

'(32).

%t

2 $ $ <

$ (rull ned til

y') <

32 E <

18 par av merke A vil bli solgt i juni hvis det totale salget er 32 par.

Sannsynlighet

12

Taster

1. H viser følgende meny med funksjoner.

nPr Regner ut antallet mulige

permutasjoner.

nCr Regner ut antallet mulige

kombinasjoner.

! Regner ut fakultetsverdien for

et tall.

Rand Genererer et tilfeldig tall

mellom 0 og 1.

Randint( Genererer et tilfeldig heltall

mellom 2 heltall, A og B, der

A

 Randint  B.

Merknader

• Alle eksemplene på transparentmalene tar utgangspunkt i standardinnstillingene.

• En kombinasjon er et arrangement med objekter der rekkefølgen ikke er viktig, som i en kortstokk.

• En permutasjon er et arrangement med objekter der rekkefølgen er viktig, som i et løp.

• En fakultetsverdi er produktet av alle de positive heltallene fra 1 til n, der n er et

positivt heltall  69.

• Du kan lagre (L) et heltall i Rand, på samme måte som du kan lagre verdier i variabler i minnet. Hvis du vil kontrollere de tilfeldige tallene som genereres av alle kalkulatorene i klassen, må du få elevene til å lagre det samme tallet i Rand. Rekkefølgen av tilfeldige tall er da den samme på alle kalkulatorene.

•For Randint bruker du et komma til å skille de 2 tallene du angir.

1

Kombinasjon (nCr)

Du har plass til 2 bøker i bokhyllen. Du har 4 bøker du vil sette i bokhyllen. Bruk denne formelen til å finne ut hvor mange måter du kan bruke til å plassere de 4 bøkene på 2 plasser.

4 nCr 2

ABCD

AB og BA teller bare som

AB AC AD BA

BC BD

H

1 kombinasjon

Trykk på Skjerm

CA DA

CB CD DB DC

4 H $

< 2 <

Det finnes 6 unike kombinasjoner av 2 bøker av et utvalg på 4 ulike bøker.

Permutasjon (nPr)

Fire personer deltar i et løp. Bruk denne formelen til å finne ut hvor mange måter de kan komme på 1. og

2. plass på.

4 nPr 2

ABC D

AB og BA teller som 2

AB AC AD BA BC BD

H

permutasjoner

Trykk på Skjerm

CA CB CD DA DB DC

4 H

<2 <

Det finnes 12 ulike permutasjoner for

1. og 2. plass i løpet.

Fakultetsverdi (!)

Nummerskilt inneholder ulike tall og bokstaver for å lage et unikt identifikasjonsnummer for hver bil. Lag dine egne skilt, der hvert skilt skal ha et 4-sifret tall. Bruk sifrene 1, 3, 7 og 9 uten å gjenta dem. Hvor mange 4-sifrede tall kan du lage?

Du kan bruke et trediagram til å lage følgende liste over nummerskilt. Er du sikker på at du har funnet alle? Tips: Finn 4!

1379 3179 7139

1397 3197 7193

1739 3719 7319

1793 3791 7391

1937 3917 7913

1973 3971 7931

H

9137

9173

9317

9371

9713

9731

Trykk på Skjerm

4 H $ $

< <

Du kan lage 24 unike nummerskilt ved å bruke 1, 3, 7 og 9 uten gjentakelse.

Texas instruments TI-30XS MULTIVIEW User Manual [no]

Specifications and Main Features

Frequently Asked Questions

User Manual