Texas instruments TI-30XS MULTIVIEW User Manual

TI-30XS MultiView™

Lärarhandledning

Utvecklad av

Texas Instruments Incorporated

Övningarna utvecklade av

Gary Hanson, Aletha Paskett och Margo Lynn Mankus

Illustrerad av

Jay Garrison och David Garrison

Om författarna

Gary Hanson

Sandy, Utah. De har utvecklat flera av övningarna och assisterat vid utvärderingen av exemplens användbarhet i delen Hur man använder

Margo Lynn Mankus

University of New York i New Paltz. Hon har gått igenom och uppdaterat materialet till TI-30XS MultiView

och

Aletha Paskett

arbetar för närvarande med matematik och teknikutbildningar vid State

och utvecklat flera övningar i den här handboken.

är matematiklärare på Jordan Independent School District i

TI-30XS MultiView™

i den här handboken.

Viktigt

Texas Instruments lämnar inga uttryckliga eller underförstådda garantier för något program eller bok. Detta innefattar, men är inte begränsat till, underförstådda garantier om säljbarhet eller lämplighet för ett visst ändamål. Materialet tillhandahålles enbart på “som det är”-basis. Inte i något fall skall Texas Instruments kunna hållas ansvarigt för speciella eller sekundära skador, skador på grund av olyckor eller följdskador i anslutning till eller härrörande från inköp eller användning av detta material. Det enda betalningsansvaret som Texas Instruments påtar sig, oaktat handling, skall inte överstiga något av de inköpspris som tillämpas för denna artikel eller detta material. Dessutom skall inte Texas Instruments ha något betalningsansvar för några krav avseende användning av detta material från annan part.

Texas Instruments Incorporated 7800 Banner Drive, M/S 3918 Dallas, TX 75251

Attention: Manager, Business Services

Tryckt i USA.

MathPrint, APD, Automatic Power Down, EOS, och MultiView är varumärken tillhörande Texas Instruments Incorporated.

Innehåll

KAPITEL SIDA KAPITEL SIDA

Om lärarhandledningen v Om TI-30XS MultiView™-räknaren vi

Övningar

En rymdfärd

Grundpotensform 3

Hjärtpuls

Statistik med en variabel 7

På bio

Dataformler vid biljettkassan 13

Gissa regeln!

Algebraiska uttryck 21

Hur man använder TI-30XS MultiView-räknaren

1 TI-30XS MultiView grundfunktioner 29

Hur du använder TI-30XS MultiView-räknaren

(Fortsättning)

11 Statistik 83 12 Sannolikhet 89 13 Funktionstabell 97 14 Potenser, rötter och inverterade

värden 101

15 Logaritmer och

exponentialfunktioner 109 16 Pi 113 17 Vinkelinställningar och

konverteringar 117 18 Polära och rektangulära

konverteringar 121 19 Trigonometri 123

2 Rensa och korrigera 41 3 Grundläggande matematik 45 4 Utförandeordning och parenteser 49 5 Numerisk notation 55 6Bråk 59 7 Decimaler och antal decimaler 65 8 Konstant 67 9 Minnet och lagrade variabler 71 10 Dataeditor och formellista 79

20 Hyperboliska funktioner 131

Appendix A

Snabbreferens till knapparna A-1 Appendix B

Indikationer på skärmen B-1 Appendix C

Felmeddelanden C-1 Appendix D

Support- och serviceinformation D-1 Appendix E

Batteriinformation E-1

Om lärarhandledningen



Hur lärarhandledningen är strukturerad

Den här handboken hör till TI-30XS MultiView-™ och TI-30XB MultiView-räknarna. Alla nedanstående referenser i handboken hänvisar till TI-30XS MultiView, men är också överförbara till TI-30XB MultiView.

Handboken består av två delar: Övningar och Hur man ska använda TI-30XS MultiView räknaren. Delen övningar innehåller en samling aktiviteter som intregrerar TI-30XS MultiView i matematikundervisningen. Delen Hur man ska använda TI-30XS MultiView-räknaren är utformad för att hjälpa er att lära eleverna hur de ska använda räknaren.

Varje del utgår från förinställningarna, inklusive MathPrint™-läget, om inget annat anges.

Övningar

Varje övning innehåller följande:

• En överblick över syftet med övningen.

• Beskrivning av det matematiska konceptet.

Hur man ska använda TI-30XS MultiView

Den här delen innehåller exempel på overheadmallar. Kapitlen är numrerade och innehåller följande.

• En introduktionssida som beskriver de av räknarens knappar som används i exemplen, knapparnas placering på TI-30XS MultiView, och all relevant information om deras funktioner.

• Overheadmallar som följer på introduktionssidan ger exempel på praktiska applikationer för de knappar som omtalas. Knapparna som omtalas visas med svart på TI-30XS MultiView. Lägesinställningarna i exemplen visas också.

Återställ TI-30XS MultiView

• Du kan förvissa dig om att alla har samma utgångspunkt genom att låta eleverna återställa sina räknare: Tryck & och -

samtidigt som du trycker %  och välj sedan 2 (Yes).

• Material som behövs för att utföra övningen.

• Tillvägagångsbeskrivning, inklusive steg-försteginstruktioner till knapptryckningarna på TI-30XS MultiView.

• Ett arbetsblad.

De konventioner som lärarhandledningen använder.

• I texten indikerar parenteser [ ] runt en knappsymbol/knappnamn att knappen är en sekundär, eller alternativ, funktion.

Exempel: %Z

Om TI-30XS MultiView™ -räknaren

Grundfönster

I grundfönstret kan du mata in matematiska uttryck och funktioner, tillsammans med andra instruktioner. Svaren visas i grundfönstret. Skärmen på TI-30XS MultiView-räknaren kan maximalt visa fyra rader med maximalt 16 tecken per rad. För inmatningar och uttryck med fler än 16 tecken kan man bläddra åt både vänster och höger (! och ") för att se hela inmatningen eller uttrycket.

När du trycker %Q, låter TI-30XS MultiViewräknaren dig återvända till ett tomt grundfönster. Tryck # och $ för att se och återanvända föregående inmatningar. (Se Föregående inmatningar, sida vii.)

I MathPrint™-läge, kan du mata in upp till fyra nivåer med konsekutivt nästlade funktioner och uttryck, som innehåller bråk, kvadratrötter, och

exponenter med ^, , ex, och 10x.

När du gör en inmatning i grundfönstret visas svaret, beroende på utrymme, antingen direkt till höger om inmatningen, eller till höger på nästa rad.

x

y

Visningsindikatorer

Se Appendix B för en lista med Visningsindikatorer.

Läge

Använd pför att välja läge. Tryck $ # ! " för att välja ett läge, och < för att aktivera det. Tryck - eller %Q för att återgå till grundfönstret och utföra dina beräkningar med vald lägesinställning. Förinställningarna visas.

Classic-läget visar inmatning och resultat på en enda rad.

MathPrint-läge visar de flesta inmatningar och resultat i ett textboksformat. Använd MathPrint-läge för att bekräfta att uttrycken matats in korrekt och för att stärka känslan korrekt matematisk notation.

Obs! Att växla mellan Classic och MathPrint rensar räknarens historia och konstanternas värde.

2:a funktion

Att trycka % visar indikatorn 2nd, och aktiverar funktionen skriven över nästa knapp som trycks. Till exempel, %b 25 < beräknar kvadratroten ur 25 och ger resultatet 5.

Utförandeordning

TI-30XS MultiView använder ekvationsoperativsystemet (EOS™) för att beräkna uttryck. Utförandeprioriteringen finns listad i overheadmallen i kapitel 4, utförandeordning och parenteser.

Eftersom tal inom parenteser utförs först, kan du använda D E för att ändra utförandeordningen och på så vis ändra resultatet.

Om TI-30XS MultiView™ (Fortsättning)

Menyer

Vissa knappar visar menyer: H, %I, v, %t, %, %h, och %{.

Tryck " eller $ bläddra och välj något från menyn, eller tryck numret intill menyvalet. För att återvända till föregående skärm utan att välja något, tryck -. För att lämna en meny eller applikation och återgå till grundfönstret tryck %Q.

Föregående inmatningar # $

Efter det att ett uttryck är behandlat, använd # och $ för att bläddra till föregående inmatningar, som har lagrats i TI-30XS MultiView historik. Du kan återanvända en gammal inmatning genom att trycka < och klistra in det på den nedre linjen, och sedan redigera och behandla ett nytt uttryck.

Svarsväxlare n

Knappen till svarsväxlaren visar senast beräknade resultat i olika format, när så är möjligt. Tryck n för att växla mellan svar i bråkeller decimalform, exakt kvadratrot eller i decimalform, och exakt pi eller i decimalform.

Återställa TI-30XS MultiView

Tryck & och - samtidigt eller tryck %  och välj sedan 2 (Yes)och räknaren

återställs.

Återställa räknaren:

• Återställer enheten till förvalda inställningar — standard notation (flytande decimaltecken) och grad (DEG)-läge.

• Rensar minnets variabler, pågående operationer, inmatningar i historik, statistiska data, konstanter, och Ans (Sista svaret).

Obs! Alla exemplen i overheadmallarna förutsätter förinställningar.

Automatisk avstägning™ (APD™)

Om TI-30XS MultiView förblir inaktiv omkring 5 minuter, slår APD-verktyget automatiskt av den. Tryck & för att slå på den igen. Skärmen, pågående operationer, inställningar och minnet återskapas.

Felmeddelanden

Se Appendix C för en lista med felmeddelanden.

Sista svaret (Ans)

Det allra senast beräknade svaret lagras i variabeln Ans. Ans blir kvar i minnet, även efter det att TI-30XS MultiView stängts av. För att återkalla värdet av Ans:

•Tryck % i (Ans visas på din skärm), eller

• Tryck på någon operationsknapp (T, U, och så vidare) som första ledet i en inmatning. Både Ans och operatorn visas.

Övningar

En rymdfärd —

Grundpotensform 3

Hjärtpuls —

statistik med en variabel 7

På bio —

Dataformler vid biljettkassan 13

Gissa regeln —

Algebraiska uttryck 21

En rymdfärd — grundpotensform

Översikt

Eleverna undersöker grundpotensform genom att omvandla tal till grundpotensform, och sedan använda dem i beräkningar.

Introduktion

Starta övningen genom att säga följande till eleverna:

Standardformen på grundpotensform är aaaa¿10 där aaaa är större än eller lika med 1 och mindre än 10, och nnnn är ett heltal.

1. Låt eleverna öva att skriva följande tal i

grundpotensform, med papper och penna.

a. 93 000 000 b. 384 000 000 000 c. 0.00000000000234 d. 0.0000000157

9.3

3.84

2.34

1.57

7

¿

10

11

¿

10

-12

¿

10

-8

¿

10

1010

Matematiska koncept

• Grundpotensform

•addition

• division

nnnn

,

Material

• TI-30XS MultiView™

• penna

• elevens övning

2. Låt eleverna ändra följande tal till

grundpotensform (SCI) genom att använda TI-30XS MultiView-räknaren.

¿

10

¿

10

-9

10

7

8

-6

a. 12 000 000 b. 974 000 000 c. 0.0000034 d. 0.000000004

Obs!

Obs! Svaren förutsätter förinställningen Flytande

Obs!Obs!

decimaltecken.

1.2

9.74

3.4 4

¿

3. Låt eleverna ändra följande tal till standard

(NORM) notation.

7

¿ 10

a. 5.8 b. 7.32 ¿ 10 c. 6.2 ¿ 10 d. 3 ¿ 10

Obs!

Obs! För att mata in ett negativt tal, tryck M och därefter

Obs!Obs!

talet.

5

-6

-8

58 000 000 732 000

0.0000062

0.00000003

³ Följ de här stegen:

1. Mata in första talet: 12000000.

2. Tryck

3. Tryck

³ Följ de här stegen:

1. Mata in 5.8; tryck

2. Mata in 7; tryck

3. Tryck

p. $ " < - <för

att visa talet i grundpotensform.

1.2Ã

Ã10

ÃÃ

7

C.

p.

$ < - <.

58000000

En rymdfärd — grundpotensform (Fortsättning)

Övning

Presentera följande problem för eleverna:

Du är kapten på ett rymdskepp i en fjärran framtid. Du har fått i uppdrag att ta dig till Alpha Centauri och du har 5 år på dig att komma dit. Avståndet mellan vår sol och Alpha Centauri är

13

2.5 x 10 och solen är uppskattningsvis 9.3 x 10

engelska mil. Avståndet mellan jorden

7

engelska

mil. Även om vi ännu inte lärt oss att färdas med

ljusets hastighet, lever du i en tid när ditt rymdskepp kan det.

Ljuset färdas en ungefärlig sträcka på 6 x 10 engelska mil på ett ljusår. Du tar vägen från jorden, över vår sol, och vidare mot Alpha Centauri. Kommer du att hinna till Alpha Centauri i tid?

Förfarande

1. Använd TI-30XS MultiView™-räknaren, och ta reda på den totala sträcka du måste färdas.

2.5 ¿ 10

13

+ 9.3 ¿ 10

7

= 2.5000093 ¿ 10

13

engelska mil

2. Därefter tar du reda på hur lång tid det tar att färdas den sträckan. (Sträcka som tillryggalagts

¾ 1 ljusår)

2.5000093 10

---------------------------------------------

610

×

3. Klarar du av att göra resan på den anvisade tiden 5år?

Ja, om ditt skepp verkligen kan färdas med ljusets hastighet.

13

×

12

4.1666821672

=

år

Extrauppgift

Ljuset färdas 186 000 engelska mil i sekunden. Ett ljusår är den sträcka ljuset färdas på ett år. Låt eleverna konvertera ett ljusår till engelska mil tillryggalagda under ett ljusår.

186 000 engmil,

--------------------------------------- 1 sek

60sek

------------ 1min

Vi uppskattar värdet till 6x10 ljusår i den här övningen.

Svar till elevernas extrauppgift: Det kommer att ta rymdskeppet uppskattningsvis 15 år att ta sig till Delta Centauri.

60min

----------------- -

××

1timme

24timmar

-----------------------

×

1dag

365 dgr

---------------- -

×

1a

12

engelska mil under 1

5.87 10

--------------------------------------------

≈

°

r

Tips: Se till att TI-30XS MultiViewräknaren är inställd på MathPrint™-läge när det här problemets behandlas.

Jorden är uppskattningsvis 9.3 x 10

12

engmil×

a°r

1

Tips:

engelska mil från solen.

³ Följ de här stegen:

1. Tryck 2.5 7

<.

2.5000093Ã

2. Tryck %i q 6 C 12

4.166682167

³ Beroende på vilket problem som

behandlas, påminn eleverna om att sätta in parenteser där det behövs, så att utförandeordningen bibehålls. Exempel: (2.5000093 x 10 måste innehålla parenteser för att resultatet ska bli korrekt.

³ Elverna kan lära sig mer om det här

genom att besöka NASAs hemsida på Internet.

C13 " T 9.3 C

13

Ã10

ÃÃ

<.

13

) ¾ (6 x 1012)

7

En rymdfärd —

Namn ___________________________

grundpotensform

Datum___________________________

Problem

1. Skriv följande tal i grundpotensform.

Standardnotation Grundpotensform

a. 93 000 000 __________________________

b. 384 000 000 000 __________________________

c. 0.00000000000234 __________________________

d. 0.0000000157 __________________________

2. Använd TI-30XS MultiView™-räknaren och gör om följande tal till grundpotensform genom att använda SCI-läget.

Standardnotation Grundpotensform

a. 12 000 000 __________________________

b. 974 000 000 __________________________

c. 0.0000034 __________________________

d. 0.000000004 __________________________

3. Använd TI-30XS MultiView-räknaren och gör om följande tal till standard decimal notation genom att använda NORM-läget.

Grundpotensform Standardnotation

a. 5.8 ¿ 10

b. 7.32 ¿ 10

c. 6.2 ¿ 10

d. 3 ¿ 10

7

5

-6

-8

_________________________

En rymdfärd —

Namn ___________________________

grundpotensform

Datum___________________________

Problem

Du är kapten på ett rymdskepp i en fjärran framtid. Du har fått i uppdrag att ta dig till Alpha Centauri och du har 5 år på dig att komma dit. Avståndet mellan solen och Alpha Centauri är 2.5 x 1013 engelska mil. Avståndet mellan jorden och solen är uppskattningsvis 9.3 x 107 engelska mil.

Även om vi ännu inte lärt oss att färdas med ljusets hastighet, lever du i en tid när ditt rymdskepp kan det.

Ljuset färdas uppskattningsvis en sträcka på 6 x 1012 engelska mil på 1 ljusår. Du tar vägen från jorden, över vår sol, och vidare mot Alpha Centauri. Kommer du att hinna till Alpha Centauri i tid?

Förfarande

1. Använd TI-30XS MultiView™-räknaren, för att beräkna den totala sträcka du behöver färdas. I den här grova uppskattningen, kan du anta att avståndet är en rät linje från jorden till solen och vidare till Alpha Centauri.

____________________________________________________________________________

Tips: Se till att din räknare är inställd på grundpotensform innan du gör beräkningen.

Därefter tar du reda på hur lång tid det tar att färdas den sträckan. (Tillryggalagd sträcka ¾ 1 ljusår)

Tips: I det här division-problemet ska du tänka på att använda parenteser, om det behövs, för att resultatet ska bli korrekt. _________________________________________________________________

_________________________________________________________________

2. Kan du göra resan på den anvisade tiden 5 år? _________________________________________________________________

Extrauppgift

Nu när du varit framgångsrik har du blivit ombedd att göra en ny resa. Avståndet mellan solen och Delta Centauri är 9 x 10 att färdas dit från jorden?

Tips: Jorden ligger uppskattningsvis 9.3 ¿ 107 engelska mil från solen.

Din resa med det här rymdskeppet är bara påhittad. Om du är intresserad av att veta mer om vår närmaste stjärna och kosmiska avstånd ska du besöka NASAs hemsida på Internet.

13

engelska mil. Hur långt tid skulle det ta

Hjärtpuls — statistik med en variabel

Översikt

Eleverna använder dataeditorn och statistikfunktionen på TI-30XS MultiView™-räknaren för att undersöka hur pulsen påverkas av ansträngningar.

Introduktion

Under övningen kan eleverna delas in i mindre grupper, så att mängden data som samlas in inte blir för stor. Fråga eleverna:

• Vad tror ni medelpulsen för någon i er ålder är?

• Och efter ansträngning?

Övning

Låt eleverna utföra följande undersökning för att kontrollera sina antaganden.

1. Låt eleverna ta reda på sin vilopuls, genom att ta pulsen i en minut. (Du kan låta eleverna ta pulsen i tio sekunder och sedan multiplicera det med 6, men den här minuten kan å andra sidan bli den här dagens tystaste minut!)

Matematiska koncept

• medelvärde, minimum, maximum, och intervall

Material

• TI-30XS MultiView

• Stoppur eller en klocka med sekundvisare

• elevens övning

2. Samla datan i diagrammet. Skriv varje elevs puls och markera i frekvenskolumnen. Om flera elever har samma puls, gör ytterligare ett streck i frekvenskolumnen.

3. Mata in pulsdatan i TI-30XS MultiViewräknaren.

a. Mata in den första pulsen från diagrammet i

L1, och det antal elever som haft den pulsen i L2. L2 kommer att användas för frekvens.

b. Du måste trycka

Till exempel, mata in den första pulsen och tryck sedan

c. Så här kan det se ut för en klass som har 22

elever:

$ mellan inmatningarna.

$.

Puls Elever Puls Elever

603633 615641 626654

³ Följ de här stegen:

1. Tryck

2. Fortsätt mata in tills du matat in alla

3. Tryck

4. Tryck 1 för att välja 1-var stats.

5. Välj L1 för data, och L2 för

6. Tryck

v för att mata in pulsen

och frekvensen. Mata in pulsen i L1 och frekvensen i L2. Tryck mellan varje inmatning, och " för att växla mellan L1 och L2.

pulser och frekvenser.

% t.

frekvens.

$ < för att se datan.

$

Hjärtpuls — statistik med en variabel (forts.)

4. Kontrollera de statistiska beräkningarna. Efter det att eleverna visar

Òx (Sigma x), förklara att

Òx är summan av alla pulser. Fråga eleverna:

• Hur många pulser tagna från eleverna under

Òx

en minut blev inmatade? Det är

.

• Hur många elever matades in? Det är nnnn.

• Hur kan vi beräkna medelpulsen? Det är

Σx

------

62.27272727=

n

Ï

.

• Är medelpulsen högre eller lägre än du trodde?

5. Nu ska vi se vilken effekt lite ansträngning har på pulsen. Ta hänsyn till elevernas olika möjligheter, genom att para ihop dem så att de tillsammans klarar av att slutföra uppgiften. Utforma övningarna så att varje elev tryggt kan åta sig att höja pulsen. Säg till eleverna:

Om du under övningarna känner smärta, svaghet eller får svårt att andas, ska du omedelbart avbryta.

6. Låt eleverna springa på stället i två minuter och ge dem sedan följande instruktioner:

a.

Mät din puls i en minut. Skriv ned pulsen på samma sätt som tidigare.

b.

c. Mata in data i räknaren. d. Jämför medelpulsen efter löpningen med

vilopulsen.

³ Följ de här stegen:

1. Visa statistiska data.

2. Tryck

3. Tryck

n ska motsvara det totala antalet av elever som deltagit. Till exempel, n = 22.

$ till Ï för att se

medelpulsen.

Ï = 62.27272727

$ tills du ser Òx.

Òx = 1370

Obs! Talen visar resultatet av exemplet som beskrivits i den här övningen. Dina elevers resultat kommer att variera, beroende på gruppens storlek och de uppmätta pulserna.

7. Låt nu eleverna hoppa jämfota i 2 minuter. Instruera dem att mäta pulsen i 1 minut och skriva ner den som tidigare. Låt dem åter mata in datan i räknaren och beräkna medelpulsen efter jämfotahoppen. Jämför med de andra två medelpulserna.

8. Låt eleverna göra stapeldiagram av de tre grupperna med data som de samlat in. Fråga eleverna:

• På vilket sätt liknar stapeldiagrammen

varandra?

• På vilket sätt är de olika?

• Är datan grupperad på samma sätt, eller är den

mer spridd i något diagram?

Hjärtpuls —

Namn ___________________________

Statistik med en variabel

Datum___________________________

Problem

Vad tror ni medelpulsen för någon i er ålder är? Och efter ansträgning?

Förfarande

1. Använd den här tabellen för att föra in din klass eller grupps data (i vila).

Hjärtslag per minut

(i vila)

Frekvens

2. Vilket är klassens (gruppens) medel? _____________________________________

3. Besvara följande fråga med hjälp av datan:

a. Vilken är den totala summan av alla hjärtslag per minut? Skriv av symbolen

och talet från räknaren. _______________________________________________

b. Vilket är det totala antalet hjärtslag som matats in? Skriv av symbolen och

talet från räknaren. __________________________________________________

c. Hur skulle du beräkna den genomsnitttliga pulsfrekvensen? _____________

Blir ditt svar det samma som för fråga 2? _______________________________

Hjärtpuls —

Namn ___________________________

Statistik med en variabel

4. Använd den här tabellen för att föra in din klass eller grupps data (vid löpning).

Hjärtslag per minut

(vid löpning)

Datum___________________________

Frekvens

5. Vilket är klassens (gruppens) medel? _____________________________________

6. Besvara följande fråga med hjälp av datan:

a. Vilken är den totala summan av alla hjärtslag per minut? Skriv av symbolen

och talet från räknaren. _____________________________

b. Vilket är det totala antalet hjärtslag som matats in? Skriv av

symbolen och talet från räknaren.

___________________________________________________

c. Hur skulle du beräkna den genomsnitttliga pulsfrekvensen?

___________________________________________________

Blir svaret det samma som för fråga 5? _______________

Hjärtpuls —

Namn ___________________________

Statistik med en variabel

7. Använd den här tabellen för att föra in din klass eller grupps data (vid hopp).

Hjärtslag per minut

(vid hopp)

Datum___________________________

Frekvens

8. Vilket är klassens (gruppens) medel? _____________________________________

9. Vilken är den totala summan av alla hjärtslag per minut? __________________

10.Besvara följande fråga med hjälp av datan:

a. Vilken är den totala summan av alla hjärtslag per minut? Skriv av symbolen

och talet från räknaren. _____________________________________________

b. Vilket är det totala antalet elevers hjärtslag som matats in? Skriv av

symbolen och talet från räknaren. ____________________________________

c. Hur skulle du beräkna den genomsnitttliga pulsfrekvensen? ____________

Blir svaret detsamma som för fråga 8? _________________________________

Hjärtpuls —

Namn ___________________________

Statistik med en variabel

11. Gör ett stapeldiagram för var och ett av de tre grupperna med data du samlat in.

Vid vila Vid löpning Vid hopp

Datum___________________________

12.På vilket sätt liknar stapeldiagrammen varandra? På vilket sätt är de olika?

_______________________________________________________________________ _______________________________________________________________________

13.Grupperar sig data på samma sätt eller är data mer spridd i något av diagrammen? ___________________________________________________________

_______________________________________________________________________ _______________________________________________________________________

På bio — dataformler vid biljettkassan

Översikt

Eleverna undersöker en tabells värden och observerar mönster i tabellen. Eleverna använder v på TI-30XS MultiView™-räknaren för att mata in data i en lista och undersöka sina generaliseringar.

Introduktion

Uppvärmningsfrågorna är till för att hjälpa dig att komma igång med elevernas arbetsblad. Du kan hoppa över uppvärmningen men då får du ge mer hjälp till eleverna under deras arbete med arbetsbladet.

Uppvärmning

Vägled eleverna i hur man använder tabeller och v att se mönster och göra en generalisering. Ge följande problem.

Varje onsdag kommer Keisha hem för sent från jobbet för att hinna gå ut med sin hund, Max. Hon ber sin granne Kyle att gå ut med hunden när han kommer hem från skolan. Kyle vill gärna hjälpa till! Keisha betalar Kyle €4 euro varje vecka för att gå ut med Max. Kyle tänker spara sina pengar. Skapa en tabell över hur mycket pengar Kyle får varje vecka i 5 veckor.

Matematiska begrepp

• mönster

•algebraiska uttryck

•linjära funktioner

•variabler

Material

• TI-30XS MultiView

• penna

• rutat papper

• elevens övning

Hjälp eleverna att skapa följande tabell på sina papper. Du kan tänka på den här tabellen som en datalista som består av två tal vilka är beroende av varandra. Det är viktigt att få eleverna att skriva sina beräkningar och svar i kolumnen Pengar om de ska kunna se några mönster. Det här hjälper dem att skriva algebraiska meningar utifrån en text och att dra slutsatser genom att använda induktiva resonemang.

Använd de här kolumnerna för

inlärningsstilar om det behövs.

Vecka Sparade

Upprepad addition Lägg till

pengar

11x4=4 4=4 4=4 2 2x4=8 4+4=8 4+4=8 3 3x4=12 4+4+4=12 8+4=12 4 4x4=16 4+4+4+4=16 12+4=16 5 5x4=20 4+4+4+4+4=20 16+4=20

På bio — dataformler vid biljettkassan (Fortsättning)

Påpeka att pengakolumnen ser ut som fyrans tabell. Det får dem att återknyta till något de redan känner till. Påminn dem om att Kyle tjänar €4 i veckan. Det här är takten i Kyle sparande och det kan skrivas som ett bråk

takt =

€4

1 vecka

Be eleverna att fylla i mer i tabellen som beskriver hur mycket Kyle kommer att spara. Låt dem fylla i tabellen för vecka 6 och 7, och fråga dem sedan om de kan förutsäga hur stor summa pengar det kommer att vara efter 10 veckor, 25 veckor, och 100 veckor. Slutligen frågar du dem om de kan fylla i summan pengar efter ett visst antal veckor. Kalla det okända antalet veckor för en variabel och använd bokstaven W som representation för veckor. Använd variabeln M som representation för pengar.

Veckor (W) Pengar (M)

11x4=4 22x4=8 33x4=12 44x4=16 55x4=20 66x4=24 77x4=28

10 10x4=40

25 25x4=100

WWx4*

utan

Hela undersökningen ska göras beträffar de här grundläggande multiplikationerna. Om eleverna behöver hjälp med multiplikationen, försök få dem att kolla upp svaret i en tabell, snarare än att använda räknaren. Detta för att uppmuntra huvudräkning och ett måttligt räknaranvändande.

Be eleverna skriva uttrycket för beräkningarna genom att använda W,

(Svar: W x 4)

x

, och 4.*

räknaren vad

På bio — dataformler vid biljettkassan (Fortsättning)

Be eleverna om följande: "Om du beräknar W veckor gånger €4, får du ett tal.

Vad betyder det talet för Kyle?" Du uppmanar eleverna att säga Pengar (M) och leder dem till att skriva formeln eller meningen med två variabler, M = W x 4. Du skriver siffran först, och sedan bokstäverna med multiplikationstecknet. Påminn eleverna att multiplikation är kommutativt, fungerar åt alla håll, så M = W x 4 = 4 x W = 4W.

Förstärk undersökningen genom att använda dataeditorn ( v) på TI-30XS MultiView™räknaren och låta eleverna se på flera värden hos deras utryck, och se om de stämmer överens med tabellen de skapat.

1. Låt eleverna mata in sin tabell i datalistan. Notera att det finns tre tillgängliga listor: L1, L2, och L3.

Samtala om att de ska mata in värden för veckor (W) i L1.

2. Låt eleverna mata in de tre första värdena för W från deras tabell, {1, 2, 3}.

3. Mata in en formel för att validera arbetet: L2 = 4 x L1. Lägg märke till att W = L1 och M = L2.

4. Gör tillägg i L1 och se att L2 uppdateras automatiskt med resultatet av formelns värde. Bläddra fram en tom plats i L1. Be dem kolla värdet för 4 veckor i tabellen, och därefter för 100 veckor.

Innan gruppundersökningen börjar på arbetsbladet måste eleverna rensa alla data i sina listor.

³ Påminn eleverna om att de i den

här övningen använder verktygen i voch inte o.

³ Om eleverna inte är bekanta med

TI-30XS MultiView-räknaren, låt dem slå på räknaren och trycka p.

³ Se till så att alla elevers räknare har

samma lägesinställning som visas här nedan:

För att återgå till grundfönstret, tryck

-.

1. Mata in de tre första värderna för W: v 1 $ 2 $ 3 $.

2. Mata in formeln:

" v " 1 4 V v 1 <.

3. Gör tillägg i L1:

! $ $ $

100 <.

4. För att se form eln i L2 igen , tryck

" v " 1.

5. Red igera formeln, om det behö vs, och tryck < för att se formeln igen.

6. För att rensa data, tryck

³ Tips: Kom ihåg att %Q tar dig

tillbaka till grundfönstret.

4 <

v 4.

(Fortsättning)

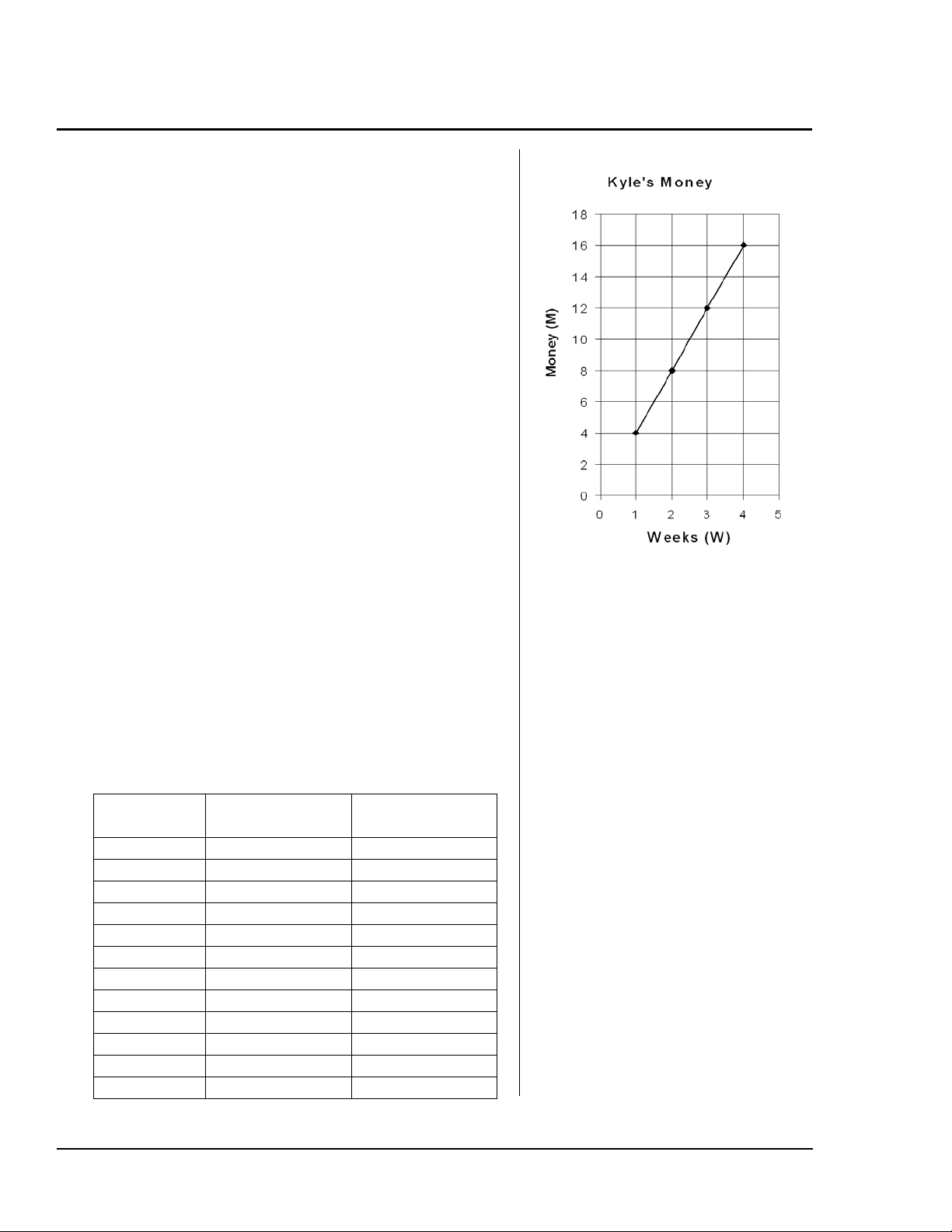
På bio — dataformler vid biljettkassan (Fortsättning)

Eleverna har nu fört över data från en text till en värdetabell, gjort ett mönster de kan se, och skrivit ett algebraiskt uttryck. Nästa steg är att visa dem hur siffermönstret bildar en graf. Hur ser formen för M = 4W ut? Låt eleverna rita de första 4 punkterna i tabellen. Lägg märke till att punkterna faller längs en rät linje. Du kan nämna att de kan beskriva ökningen av Pengar (M) som "för varje 1 vecka (W) Kyle jobbar, ökar hans summa (M) med €4." Uttalandet är en självklarhet, men det lägger grunden för hur man ska prata om antal och hur de påverkar en linjes lutning.

Antalet veckor och summan av pengarna är bägge positiva eftersom grafen bara är relevant i den första kvadranten. Låt dina elever använda ett graf-papper när de gör en graf över sina data.

Övning

Eleverna gör en liknande undersökning i grupp och söker efter mönster att skriva som algebraiska uttryck och meningar. De bildar också en graf av tabellens värden. Låt eleverna läsa problemet på arbetsbladet innan de delas in i smågrupper, och se till att alla förstår sin uppgift.

Eleverna ska fylla i tabellen med hjälp av huvudräkning. De skriver ner alla beräkningar, vilket hjälper dem att se formeln. De uppmuntras att använda huvudräkning så mycket som möjligt de använder räknaren för att hitta svaren på summan pengar.

Antal

Beräkning Summa Pengar

Personer (P)

1 A €11.50 2 A €23.00 3 A €34.50 4 A €46.00

...

10 A €115.00

...

100 A €1150.00

...

1000 A €11500.00

...

P P x 11.50 M = P x 11.50

innan

(M)

På bio — dataformler vid biljettkassan (Fortsättning)

Förfarande

Eleverna ska skriva det algebraiska uttrycket från mönstret som visas i deras tabell: M = P x 11.50 eller använd underförstådd multiplikation, M = 11.50 P.

Eleverna kontrollerar sina data genom att använda dataeditorn (

räknaren, som i uppvärmningsövningen.

1. Låt eleverna kontrollera hur räknaren ställs in.

2. Mata in de tre första värdena i L1 {1, 2, 3}.

v) på TI-30XS MultiView™-

³ Se till att räknarens lägesinställning är

som här nedan:

1. Tryck p.

3. Översätt din formel till räknarformel och mata in formeln i L2.

Din formel: M = ____________________________

Räknarens formel: L2 = ___________________

4. Mata in fler värden i L1 för att kontrollera värdetabellen och formeln. Den här övningen bekräftar formeln för flera värden.

5. Mata in 7500 i L1 och finn summan av pengarna i L2. Skriv på matematisk form som M = 11.50 x 7500 = €86,250.

6. Skapa en rapport genom att fylla i en värdetabell och göra en graf. Skriv ett stycke som beskriver arbetet med presentationen.

Svaren i stycket kommer att variera. Se till att eleverna förklarar tabellen, grafen och den algebraiska uttrycket (formeln) i stycket.

PM

2. Tryck v 1 $ 2 $ 3 $.

3. Mata in formeln i L2. " v " 1

11 8 50 V v 1 <.

4. Tryck ! $ $ $ 4 <

5 < 6 < 10 < 100 < 1000 <.

5. Tryck 7500 <.

500 €5750

1000 €11500

1500 €17250

2000 €23000

2500 €28750

Namn ___________________________

På bio

Datum___________________________

Problem

En film som är en kassasuccé har premiär den här helgen. På nyheterna hör du att biljetterna kostar €11.50 per person. Reportern säger att det kostar en familj på två €23 och en familj på tre €34.50. De visar den här informationen i tabellform.

Antal Personer Summa Pengar

1€11.50 2 €23.00 3 €34.50

Reportern nämner också att biografen, MultiPlex, har 25 salonger med sammanlagt 7,500 stolar. Den här kassasuccén visas i biografens samtliga salonger. Ägaren förutspår att alla biljetter kommer att säljas den första dagen!

Ägaren av MultiPlex vill veta hur mycket pengar de kan förvänta sig att få i biljettintäkter. De önskar sig en generell formel, så att de snabbt kan se summan pengar för vilket antal personer som köper biljetter som helst.

Ditt jobb: Du har fått anställning som ekonom på MultiPlex! Gratulerar! Din chef vill ha en formel som kan säga hur mycket pengar han får in på biljettförsäljningen, och hur det hänger ihop med hur många som köper biljetter.

Förfarande

1. Använd tabellen för att undersöka hur summan pengar i biljettkontoret beror på antal personer som ser filmen. Fyll i följande tabell. Skriv upp alla dina beräkningar vid varje steg. Använd huvudräkning så mycket du kan summan pengar.

Antal

Personer

Beräkning Summa

Pengar (M)

(P)

1 A €11.50 2 A €23.00 3 A €34.50 4 5 6

...

10

...

100

...

1000

...

innan

du använder räknaren för att se

Namn ___________________________

På bio

Datum___________________________

2. Vad kan du se för mönster i din tabell? Med hjälp av informationen du får i din tabell, ska du skriva en formel (ett algebraiskt uttryck) som beskriver summan pengar (M) i förhållande till antal personer (P) som köper biljett till filmen.

M = ___________________________

3. Kontrollera din formel med hjälp av datalisteditorn ( räknaren.

a. I kolumn L1, matar du bara in de tre första inmatningarna av antal personer (P) från

listan i tabellen här ovan. (Mata in {1, 2, 3}.)

b. Mata in din formel från del 2 i L2. Var noggrann: för att kunna använda räknaren

måste du översätta dina variabler (bokstäver). Bokstaven P är nu L1 och M är L2. Skriv om din formel och använd L1 and L2 så att du kan mata in formeln i din

räknare.

Din formel: M = _________________________

Räknarens formel: L2 = ________________________

c. Jämför siffrorna i L2 med siffrorna i din tabell här ovan. Stämmer de överens?

d. Mata in fler värden från listan med antal personer i L1. Jämför värdena i L2 med din

tabell här ovan. Matchar de varandra? Fungerar din formel?

v) i TI-30XS MultiView™-

4. Använd räknarens dataeditor för att hitta den summa pengar (M) som ägaren får in på biljettförsäljningen om hela biografen skulle fyllas med 7500 besökare (P). För hand ska du skriva ner hur du går till väga för att hitta svaret genom att använda din formel.

Namn ___________________________

På bio

Datum___________________________

5. Din chef vill göra en presentation för de som investerar pengar i MultiPlex. Investerarna vill se siffror och en graf i din presentation! Fyll i tabellen här nedan genom att använda din räknares dataeditor. Rita punkterna från den här tabellen. Det är är ett annat sätt som en ekonom kan visa hur summan pengar (M) beror på antal personer (P). Det här ger en bild av dina data!

PM

500

1000

1500

2000

2500

Summa Pengar (M)

Antal Personer (P)

6. Skriv ett stycke här nedan om vad du skulle säga till din chef och investerarna om ditt arbete. Se till att få med hur du bestämde formeln för summan pengar och vad tabellen och grafen kan säga dem om summan pengar som kommer in via biljettkassan.

Gissa regeln! — Algebraiska uttryck

Översikt

Eleverna gissar det algebraiska uttrycket (funktionen) från en värdetabell i ett spelformat. Eleverna använder o på TI-30XS MultiView™-räknaren för att mata in ett uttryck som en funktion (y=) för kunna spela.

Introduktion

Eleverna värmer upp för den här övningen genom att utvärdera uttryck och fylla i värdetabeller. Sedan spelar de ett spel, "Gissa regeln!" Spelet använder TI-30XS MultiView-räknaren för att skapa värdetabeller.

Låt eleverna fylla i följande tabell, som finns på arbetsbladet.

Obs

Obs! Överväg att variera bokstäver för variabeln

ObsObs under uppvärmningen. I räknaren kommer variabeln, hur som helst, att vara x hela tiden.

xx

-2 1 -2 2 2

+ 3

x

2x + 6 2(x + 3)*

Matematiska koncept

• algebraiska uttryck

•funktioner

Material

• TI-30XS MultiView

• penna

• elevens övning

• pappersremsor och papperspåse

-1 2 -1 4 4 03 06 6 14 18 8 25 210 10

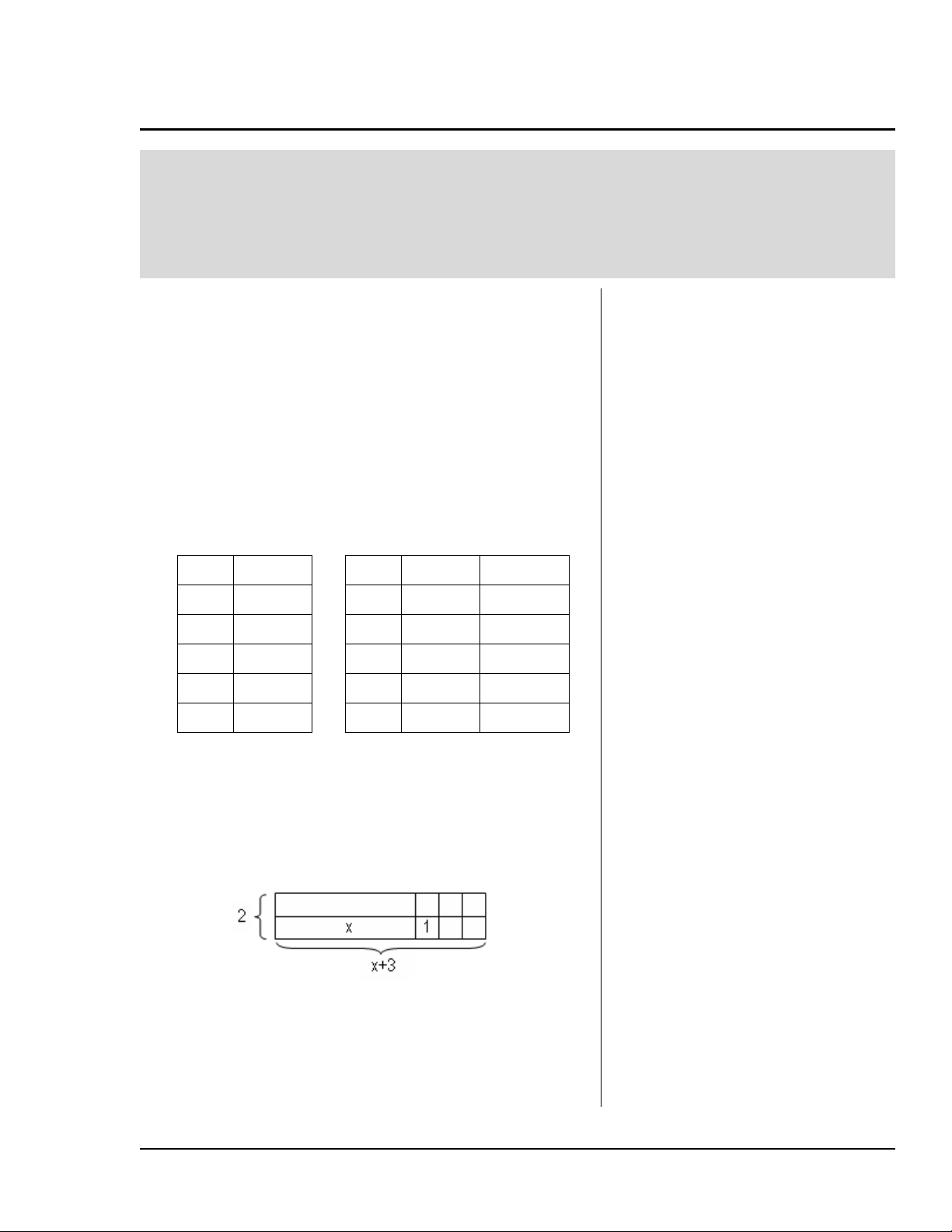
*Eleverna bör lägga märke till att tabellen för 2x + 6 och 2(x + 3) är densamma. Diskutera varför de är likvärdiga uttryck och belägg det genom att använda multiplikationens distributiva egenskap med summor. Du kan också låta eleverna använda kakelplattor för att visa areamodellen, 2(x + 3) =2x+6.

Visa eleverna hur de ska mata in uttryck i o på TI-30XS MultiView. Försök att mata in uttrycket som en funktion. Det här kan vara ett nytt begrepp för dina elever. Använd en funktionsmaskin om det skulle behövas.

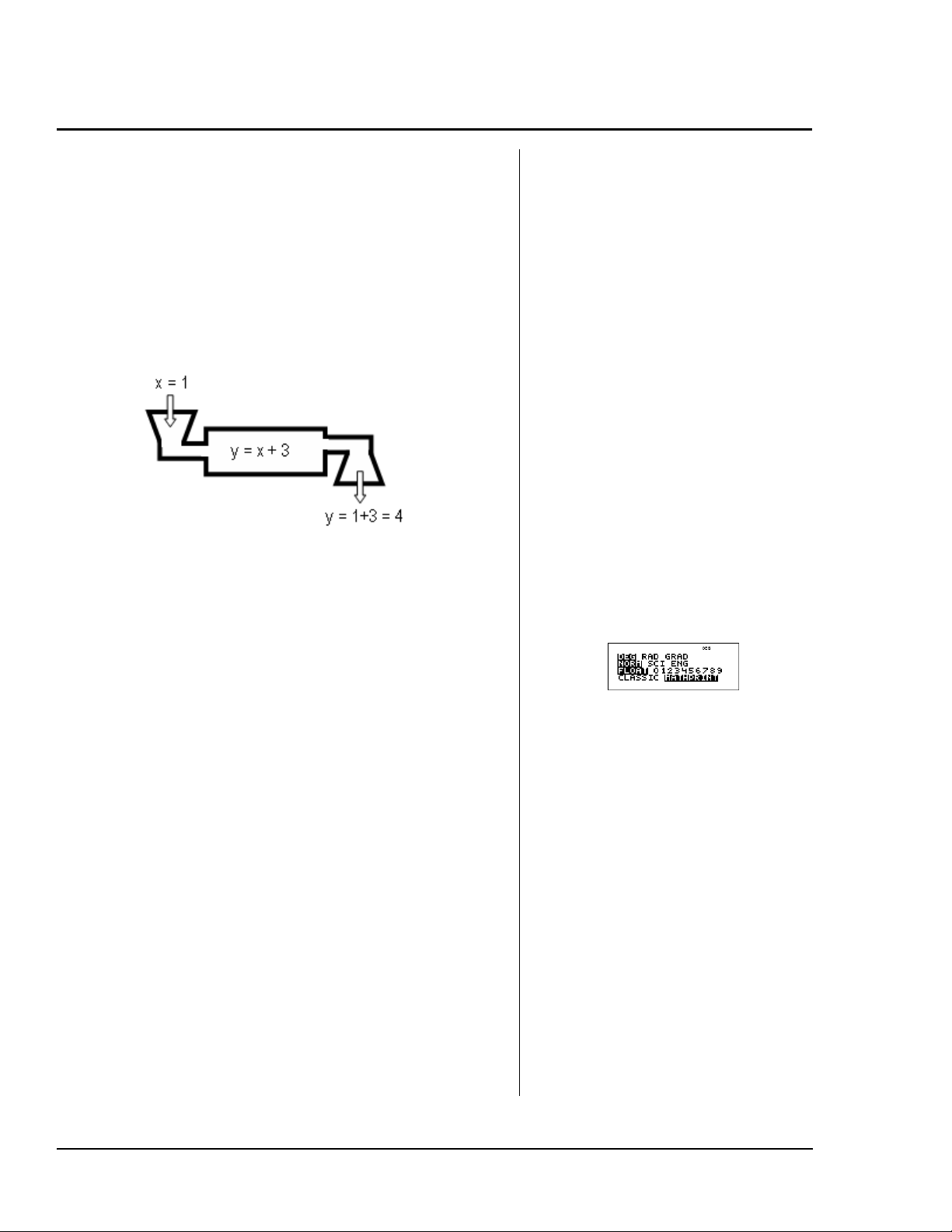
Gissa regeln! — Algebraiska uttryck (Fortsättning)

för att visa ett alternativt tänkesätt för att utvärdera

x

ett uttryck för olika värden för

x

= 1 leder till utdata på y=1+3=4. Diskutera att

x

uttrycket Senare i spelet kommer eleverna att tänka baklänges för att gissa "regeln". Om det behövs samtala om hur eleverna följer reglerna till sina favoritspel. För att kunna spela måste de följa reglerna. När de utvärderar ett uttryck, följer de regeln om hur man ändrar ett tal till ett annat.

+ 3, kan tänkas som regeln till att hitta y.

. Här, indata på

Skapa tabellen i räknaren genom att använda Autoverktyget i o. Auto skapar automatiskt en värdetabell som börjar vid ett givet värde och ökar med ett värde. För att få räknaren att skapa samma värdetabell som ovan, ställ in start på -2 och öka

x

-värdet med stegstorleken 1. Låt eleverna jämföra sina handgjorda tabeller med den som räknaren skapat.

Övning

Spela en eller två omgångar av “Gissa regeln!” med hela klassen, och använd reglerna som finns på nästa sida. I helklassgenomgången tar läraren rollen som Härskaren. Spelet använder o Fråga-

x

på TI-30XS MultiView™-räknaren.

och verktyget

³ Följ de här stegen:

1. Tryck p och ställ in läget som det visas.

2. Mata in uttrycket y=x+3: o z T 3 <.

3. Mata in tabelluppställningsvärden: M 2 $ $ $ <.

4. Använd # och $ och bläddra genom värden för x och y = x + 3.

³ Tips: Kopiera spelplanen från

övningsdelen i så många kopior som behövs.

Gissa regeln! — Algebraiska uttryck (Fortsättning)

Regler för spel i grupp

• Bilda grupper om tre eller fyra elever.

• Låt en elev vara spelets Härskare.

• Härskaren har i spelet kontroll över räknaren.

• Härskaren väljer ett algebraiskt uttryck från en papperspåse (eller annan behållare) och gömmer den för de övriga spelarna, alternativt skriver Härskaren en algebraisk funktion på en papperslapp och läraren godkänner att han kan använda det uttrycket.

• Härskaren matar in det algebraiska uttrycket i o och väljer verktyget FrågaObs

Obs! Härskaren kan behöva radera varje rad i

ObsObs

x

tabellen för Fråga-

innan man tar nästa regel. (Se

x

.

knapptryckningsinstruktionerna.)

• Alla spelare, förutom Härskaren, turas om att säga ett värde för säger vad

x

. Härskaren matar in det värdet och

y

-värdet blev.

• Varje spelare gör en värdetabell som håller koll på spelet.

• En spelare kan bara gissa uttrycket eller regeln när det är den spelarens tur.

• När en spelare gissar på en regel måste alla spelare kontrollera om regeln gäller för alla värden som redan spelats, eller utmana regeln och hitta ett värde som inte stämmer.

• Om en spelare eller härskaren lyckas påvisa att regeln man gissat är felaktig, förlorar den spelare som gissat sin nästa omgång.

• Om det algebraiska uttryck som en spelare gissat på inte är det samma som uttrycket som Härskaren matat in, till exempel, 2(

x

+1) och 2x +2, och alla spelare är överens om att det gissade uttrycket är korrekt, så visar Härskaren uttrycket i räknaren, och spelaren som gissat måste då förklara varför de två uttrycken är de samma.

• Den spelare som först gissar rätt och försvarar dess regel vinner.

• Rollen som Härskare övergår då till en ny spelare i nästa omgång .

³ Följ de här stegen:

1. Tryckp och ställ modeläget som det visas.

2. Mata in funktionen y = 2x + 5:

- o 2 z T 5 <. Obs! Om en funktion redan är inmatad i y=-skärmen, tryck innan den nya funktionen matas in.

3. Mata in tabelluppställningsvärden: $ $ " < $ <.

4. Mata in x-värd en: 5 < 6 < 10 <.

³ Tips: För att mata in fler värden,

markera någon av de tre raderna i x- kolumnen, mata in siffran, och tryck <.

5. För att återkalla fönstret y=, tryck o. Du måste scrolla genom inställningsfönstret igen för att se värdetabellen.

³ För att spela igen:

1. Rensa gam la uttryck, välj nästa uttryck, och mata in det: o -z T q1 $ 2.

2. Mata in det önskade tabelluppställningsvärdet , markera OK, och tryck <.

Lägg märke till att bara 3 gissningar visas i fönstret. Eleverna kan skriva över en siffra och se nya utdata.

Gissa regeln! — Algebraiska uttryck (Fortsättning)

Lista med algebraiska uttryck

Kopiera de här eller andra uttryck på pappersbitar så att Härskaren kan välja uttryck till spelet. Du kan också låta Härskaren skriva uttryck som du kan godkänna innan spelet börjar. Att låta eleverna skriva ett uttryck ger dem en känsla av att äga och ett mått på deras kunnande.

Välj en lista eller blanda listorna beroende på dina elevers nivå. Du kan också utvidga listorna beroende på dina elevers nivå. Eleverna ska dokumentera allt arbete på sina arbetsblad.

Exempel på ett-stegs-uttryck

x

+ 3 2x + 3

x

– 9 -4x + 5

1

---+

x

2

x

– 2.5

x

+ 15 1.5 x + 2.5

1

x

–

--5

Exempel på två-stegs-uttryck

2

x

+ 6 eller 2 (x + 3)

1

---

x

4–

2

Modifiera spelet

• Inkludera uttryck som måste förenklas av spelarna,

x

som 2 måste de påvisa att uttrycket är jämförbart med 2 utvärderingsmöjlighet av spelet.

• Använd uttryck i text som till exempel "fyra mindre än två gånger ett tal". Låt Härskarna välja uttrycket från behållaren och sedan ändra det till ett uttryck som du måste godkänna innan de får återvända till sin grupp och fortsätta spelet.

+ 4 + 3x - 6. Om en spelare gissar 5x - 2,

x

+ 4 + 3x - 6, vilket ger en ytterligare

Exempel: Fyra mindre än två gånger ett tal är draget. Härskaren översätter det till 2 att det är korrekt , och de återvänder till sin grupp för att spela.

x

-4, du säger

Gissa regeln!

Namn ___________________________

Datum___________________________

Problem

Vi följer regler varje dag. Kan du följa ditt favoritspels regler? Måste du följa reglerna noggrant när du spelar? Även när vi arbetar med tal och uttryck följer vi regler.

x

Exempel: Om

= 1, så x + 3 = 1 + 3 = 4

Uttrycket olika tal. Du kan tänka på

x

för

1. Vad lägger du märke till i tabellen för 2

2. Kontrollera tabellerna ovan genom att använda o på TI-30XS MultiView™-räknaren.

x

+ 3 har en variabel, x. Beroende på värdet för x, kommer x + 3 att vara lika med

x

+ 3 som en regel. Fyll i följande tabell som uppvärmning. Värdet

har valts åt dig.

xx

-2 -2 -2

-1 -1 -1

000

111

222

+ 3

x

2

x

+ 6

x

+ 6 och 2(x +3)?

x

2(x + 3)

3. Spela spelet "Gissa regeln!", genom att använda spelplanen på nästa sida. I det här spelet känner du inte till uttrycket (regel). Du måste gissa regeln genom att tänka baklänges! Din lärare kommer att ge dig instruktioner för spelet.

?

Gissa regeln!

?

Tänk baklänges!

?

Spelarnas namn: Härskare:

Din lärare kommer att instruera hur du ska spela. Använd tabellen för att hålla reda på

y

-värdena för varje spelares omgång under spelet. Använd kolumnen Gissning för att

och kontrollera regeln. Om en spelares regel inte är korrekt, fortsätt spela.

x

Räknarens

y

-värde

y

Kontrollera alla Är gissningen korrekt? _______

Gissa regeln från en värdetabell!

Gissning 1

= _______________________

x

-värden!

?

Gissning 2

y

= _______________________

x

Kontrollera alla Är gissningen korrekt? _______

-värden!

x-

x

Räknarens

y

-värde

Gissning 3

y

= _______________________

x

Kontrollera alla Är gissningen korrekt? _______

-värden!

y

= _______________________ Kontrollera alla Är gissningen korrekt? _______

Gissning 4

x

-värden!

Hur du använder

TI-30XS MultiView™

räknaren

TI-30XS MultiView grundfunktioner 29 Rensa och korrigera 41 Grundläggande matematik 45 Utförandeordning och parenteser 49 Numerisk notation 55 Bråk 59 Decimaler och decimalkommats placering 65 Konstant 67 Minnet och lagrade variabler 71 Dataeditor och formellista 79 Statistik 83 Sannolikhet 89 Funktionstabell 97 Potenser, rötter, och inverterade värden 101 Logaritmer och exponentialfunktioner 109 Pi 113 Vinkelinställningar och konverteringar 117 Polära och rektangulära konverteringar 121 Trigonometri 123 Hyperboliska funktioner 131

TI-30XS MultiView™ grundfunktioner

1

Knappar

1. & startar räknaren.

2. % aktiverar 2nd-indikatorn och ger tillgång

till funktionerna som visas över den knapp du trycker.

3. % ' stänger av räknaren och rensar skärmen.

4. < fullföljer operationen eller utför kommandot.

5. % i återkallar den senast utförda beräkningens resultat och visar det som Ans.

6. n växlar svaret mellan bråk- och decimalform, exakt kvadratrot och decimalform, samt exakt pi och decimalform.

7. ! och " flyttar markören åt vänster eller höger så du kan bläddra bland inmatningarna i grundfönstret samt röra dig i menyerna. %! eller % " låter dig bläddra till början eller slutet av en aktuell inmatning. # och $ flyttar markören upp eller ner i menyn, tidigare inmatningar, och grundfönstret när du befinner dig i Dataeditorn och Funktionstabellen. % # flyttar markören till inmatningen högst upp i en aktiv kolumn i Dataeditorn, eller till föregående inmatning i grundfönstret. Tryck % # en gång till för att flytta markören till den äldsta inmatningen i grundfönstret. I bråk, tryck % # för att klistra in ett värde som nämnare. (Se Kapitel 6, Bråk, för ytterligare information.) % $ flyttar markören till första tomma raden i den aktiva kolumnen i Data editorn, eller nedanför den senaste inmatningen i grundfönstret.

8. p låter dig ange lägena vinkel, numerisk, decimal och visa. Tryck $# ! " för att välja läge, och < för att aktivera det. Tryck

- eller %Q för att avsluta

2

8

9

3

1

7

6

5 4

lägesmenyn.

9. %  visar Återställnings -menyn.

•Tryck 1 (Nej)för att återgå till föregående

fönster utan att återställa räknaren.

•Tryck 2 (Ja) för att återställa räknaren.

Meddelandet MEMORY CLEARED visar i fönstret.

Obs! Tryck & och - samtidigt återställer omedelbart räknaren. Varken någon meny eller något meddelande visas.

TI-30XS MultiView™ grundfunktioner (Fortsättning)

• Återställa räknaren: – Återställer alla inställningar till

förinställningen: grader (DEG) vinkelläge, normal numerisk notation (NORM), flytande decimalkomma (FLOAT) och MathPrint™-visningsläge.

– Rensar variabler ur minnet, pågående

operationer, inmatningar i historik, statistiska data, konstanter, och Ans (Senaste svar).

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar (Se sida vi).

• n kan användas i en inmatning innan man trycker <. Att trycka

samma inmatning kan orsaka syntaxfel. För att få önskat resultat kan du:

– Mata in uttrycket, trycka

tryck därefter efter det att resultatet har visats.

– Mata in uttrycket och tryck <, tryck

sedan önskar för att växla fönster och se de alternativa svarsformaten.

•När ³ eller ´ visas i fönstret, innehåller inmatningsraden fler tecken, antingen till vänster, eller till höger.

• för att slå på räknaren igen tryck du & efter det att Automatic Power Down™ (APD™)-funktionen aktiverats. Fönstret, pågående operationer, inställningar och minnet återkallas.

n så många gånger som du

n ytterligare en gång,

n fler än en gång i

n <, och

Andra, av, pilar, mata in

• Mata in 46 – 23.

• Ändra 46 till 41. Ändra 23 till 26 och slutför operationen.

• Mata in + och slutför

operationen.

• Stäng av TI-30XS MultiView™räknaren och starta den igen. Grundfönstret är tomt; Bläddra uppåt för att se historik.

Tryck Visa

2

--5

3

----10

46 U

%' ! "

# $ <

23 <

# # < !!!! 1 "" 6 < 2 q 5 " T 3 q 10 <

%' & # # #

Återställ

Återställ räknaren.

Tryck Visa

%

2

-

%

Att trycka & och - på samma gång återställer också räknaren. Varken någon meny eller något meddelande visas.

Att använda % eller & och

- återkallar alla inställningar till förinställningen och rensar minnet.

Läge

p

Använd pför att välja läge. Tryck på $ # ! " # $ för att välja ett läge, och < för att aktivera det. Tryck på - eller %Q för att återgå till grundfönstret och utföra dina beräkningar med vald lägesinställning.

Lägets förinställningar visas i svart markering nedan.

p

DEG RAD GRAD Ställer in vinkelläget till grader, radianer, eller nygrader.

NORM SCI ENG anger läget för numerisk notation. Läget numerisk notation påverkar bara visningen av resultaten, och inte exaktheten hos de värden som lagrats i enheten. Den förblir maximal.

Läge (fortsättning)

NORM visar resultat med siffror

till vänster och höger om decimaltecknet, som i 123456.78.

SCI visar nummer med en siffra till vänster om decimaltecknet och gällande tiopotens, som i

5

1.2345678

(vilket är detsamma

som 123456.78). ENG visar resultat som ett tal

från 10 till 1000 gånger 10 upphöjt till ett heltal. Heltalspotensen är alltid en multipel av 3.

p

Obs! C är ett kortkommando för att mata in ett tal i grundpotensform Resultatet visas i det numeriska notations-läge som är inställt i läge.

FLOAT 0 1 2 3 4 5 6 7 8 9 Väljer läget för decimal notation.

FLOAT (flytande decimalkomma) visar upp till 10 siffror, plus tecknet och decimalkommat.

.

Läge (fortsättning)

0 1 2 3 4 5 6 7 8 9 (Fast

decimalkomma) anger antalet siffror som ska visas (0 till 9) till höger om decimaltecknet.

CLASSIC MATHPRINT anger inmatningar och resultat.

CLASSIC anger inmatning och resultat på en rad.

MathPrint-läge visar de flesta inmatningar och resultat i ett textboksformat. Använd MathPrint-läge för att kunna

p

bekräfta att uttrycken matats in korrekt och för att stärka känslan för matematisk notation.

Obs! Att växla mellan Classic och MathPrint rensar räknarens historik och konstanternas värde.

Menyer

Speciella knappar visar menyer: H, %I, v, %t, %, %h, och %{. Vissa

knappar kan visa mer än en meny.

Tryck " och $ för att bläddra och

välja ett meny -objekt, eller tryck motsvarande nummer intill menyobjektet. För att återvända till föregående skärm utan att göra

något val, tryck -. För att lämna

en meny eller applikation och återgå

till grundfönstret tryck %Q.

Grundfönstret är tomt; Bläddra uppåt för att se historik.

Några exempel menyer:

H % I

PRB RAND DMS R ¶P

1: nPr 1: rand 1: Ä 1: R ´Pr( 2: nCr 2: randint( 2: Å 2: R ´PÁ( 3: ! 3: Æ 3: P ´ Rx(

T4: P ´Ry( 5: g 6: ´DMS

Menyer (Fortsättning)

v (Tryck v en gång för att visa

skärmen för Dataeditorn. Tryck igen för att visa menyn.)

Rensa FORMULA (FORMEL)

1: Rensa L1 1: Lägg till/Redigera Frml 2: Rensa L2 2: Rensa L1 Frml 3: Rensa L3 3: Rensa L2 Frml 4: Rensa ALL 4: Rensa L3 Frml

5: Rensa ALL

Tryck v medan du är i läget Lägga till/Redigera Frml i FORMULA för att visa den här menyn:

%t

STATS

1: 1-Var Stats 2: 2-Var Stats

3: StatVars

Ls

1: L1 2: L2 3: L3

Den här menyn visas när du beräknat 1-var eller 2-var stats.

StatVars-menyn: 1: n 2:

Ï

3: Sx Etc. Se kapitel 11, Statistik, för en

komplett lista.

Senaste svar (Ans)

Använd Senaste svar (Ans) för att

2

5

beräkna .

Tryck Visa

+

2

12

5 FT12

F<

%b% i<

%i

Svars-växlaren

Tryck n för att växla mellan svar i bråk- eller decimalform, exakt kvadratrot och decimalform, samt exakt pi och decimalform.

Tryck Visa

% b

8 <

n

Rensa och korrigera

2

Knappar

1. - rensar siffror och felmeddelanden. Tryck

- en gång för att rensa en ofullständig

inmatning; Upprepa tryckningen för att rensa fönstret. Du kan bläddra upp och använda - för att rensa inmatningar i historik. - backar tillbaka en skärm i applikationer.

2. % f låter dig föra in en siffra vid markören.

3. J raderar siffran vid markören. Sedan, varje gång du trycker J, raderar den 1 siffra till vänster om markören.

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

• Att trycka -påverkar inte minnet, statistikregistret, vinkelenheter, eller numerisk notation.

2 3

1

Radera och infoga

Mata in 4569 + 285, och ändra det sedan till 459 + 2865. Fullfölj uppgiften.

Tryck Visa

4569 T 285

! ! ! ! ! ! J

" " " "

J

%f

%f 6

<

Rensa

Mata in 21595. Rensa bort 95. Rensa inmatningen.

Tryck Visa

21595

! ! -

(Rensa till höger)

-

(Rensa inmatningen)

Grundläggande matematik

3

Knappar

1. T adderar.

U subtraherar.

2.

3. V multiplicerar.

4.

W delar.

5. < fullföljer operationen eller utför

kommandot.

M låter dig mata in ett negativt tal.

6.

7. % _lägger till %-tecknet till ett tal.

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

• TI-30XS MultiView™ tillåter underförstådd multiplikation. Exempel: 3 (4+3) = 21

• Blanda inte ihop subtraktion.

• Använd parenteser för att hålla ihop minustecknet med talet, om det behövs.

Exempel: M22 = M4, and (M2)2 = 4.

• Resultatet i procentberäkningar visas enligt decimallägesinställningen.

M med U. U tillåter

4

7

3 2 1

5

6

Addera, subtrahera, multiplicera, dividera, lika med

Beräkna:

2 + 54 16 x 21 =

1

x 10 =

--2

12 x (5 + 6) =

Tryck Visa

½ 6 =

2 T 54 U 6 <

T U V W

<

16 V 21 <

1 q 2 " V 10 <

12 V D 5 T 6 E <

Negativa tal

Temperaturen i Umeå var klockan 6:00 på morgonen. Klockan 10:00 hade temperaturen stigit till 12Ä C. Vad var temperaturen klockan 10:00?

Tryck Visa

M3Ä C

M 3 T

12 <

Klockan 10:00 var temperaturen 9Ä C.

M

Procent

Mike tjänar €80 i veckan. Han sparar

15% av sin inkomst. Hur mycket sparar Mike i veckan?

Tryck Visa

15

% _ V

80 <

Mike sparar

€12 i veckan.

% _

Utförandeordning och parenteser

4

Knappar

1. D öppnar ett uttryck med parenteser.

2. E stänger ett uttryck med parenteser.

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

• Overheadmallen visar ekvationsoperativsystemet (EOS™) som demonstrerar i vilken utförandeordning TI-30XS MultiView™-räknaren utför operationerna.

• Operationer inom parenteser utförs först. Använd D E för att ändra utförandeordningen, och på så sätt förändra resultatet. Exempel: 1 + 2 x 3 = 7 (1 + 2) x 3 = 9

1

2

Ekvationsoperativsystemet (EOS™)

1 (först) Uttryck inuti D E 2 Funktioner som behöver E och föregår

uttrycket, som till exempel >, A, och vissa

menyval 3Bråk 4 Funktioner som är inmatade efter uttrycket,

som till exempel F och vinkelenhetsmodifierare

(

¡, ¢, £, r, g)

5 Exponentiering (G) och rötter (%c)

Obs! I Classic-läget, utvärderas exponenter som

använder G -knappen från vänster till höger.

Uttrycket 2^3^2 behandlas som (2^3)^2, med

resultatet 64.

I MathPrint™-läge, utvärderas exponentiering

som använder G -knappen från höger till

vänster. Att trycka

2

3

2 G 3 G 2 visas som , med resultatet 512.

2

TI-30XS MultiView™-räknaren utvärderar

uttryck inmatade med F och a från vänster

till höger i både Classic- och MathPrint-läget.

22

Att trycka 3 F F visas som . och beräknas

3

som (3

2)2

= 81.

Ekvationsoperativsystemet (EOS™) (Fortsättning)

6 Negation (M) 7 Permutationer (nPr) och kombinationer (nCr) 8 Multiplikation, underförstådd multiplikation, och

division 9 Addition och subtraktion 10 Konverteringar (%O, %j, %R,

och ´DMS) 11 (sist) < fullbordar alla operationer och stänger alla

öppna parenteser.

Utförandeordning

1 + 2 x 3 =

Tryck Visa

1 T 2 V 3 <

1 + (2 x 3) =

Tryck Visa

1 T D 2 V 3 E <

(1 + 2) x 3 =

T V D E

Tryck Visa

D 1 T 2 E V 3 <

Utförandeordning (fortsättning)

2

5

Tryck Visa

41()3()–

p$$$ <% b 5 F U 4 D 1 E D 3 E <

= (Classic-läge)

2

=

5

Tryck Visa

41()3()–

(MathPrint-läge)

p$$$ "<% b 5 F U 4 D 1 E D 3 E <

n

Numerisk notation

5

Knappar

1. p låter dig välja från följande meny för

numerisk notation. NORM Återställer standardläge (flytande

decimalkomma).

SCI Startar grundpotens-läget och visar

resultat som ett tal från 1 till 10 (1 { n < 10) gånger 10 upphöjt till en heltalspotens.

ENG Startar engineerings-notationsläget

och visar resultaten som ett tal från 1 till 1000 (1 { n < 1000) gånger 10 upphöjt till en heltalspotens. Heltalspotensen är alltid en multipel av 3.

2. C är ett kortkommando för att mata in

ett tal i grundpotensform.

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

• Du man mata in ett värde i grundpotensform oavsett inställningen i numeriska notationsläget. För en negativ exponent, tryck M innan du matar in talet.

• Resultat som kräver fler än 10 siffror visas automatiskt i grundpotensform.

• För mer information om decimalnoteringsläget, se kapitel 7, Decimaler och decimalkomman.

• Lägena (NORM, SCI, och ENG) påverkare bara visningen av resultatet.

1

2

Engineering-notation, grundpotensform, flytande decimalkomma

Mata in 12543, som kommer att visas med flytande decimalkomma och normal numerisk notation (båda är förinställning i resultatvisning mellan normal notation, grundpotensform, och engineering-notation genom att ändra inställningarna i lägesmenyn.

Tryck Visa

p). Växla

12543 <

p

p$" <

-<

p$" "<

-<

Engineering-notation, grundpotensform, flytande decimalkomma

p$<

-<

(Fortsättning)

p

Grundpotensform

Låt TI-30XS MultiView™-räknaren vara inställd på Norm- och MathPrint™-lägena (båda är förinställningar). Lös sedan följande problem genom beräkningar i grundpotensform, genom att trycka C.

Jorden befinner sig ungefär 1.5 x 10 kilometer från solen. Jupiter befinner sig ungefär 7.8 x 10 solen. Anta att deras omloppsbanor är cirkulära och att de befinner sig på

8

kilometer från

8

C

samma sida om solen, hur nära jorden kommer Jupiter att komma?

Tryck Visa

7 8 8

C 8 " U 1 8 5 C

8 <

Jupiter och Jorden skulle vara

8

ungefär 630 000 000 = 6.3 x 10 kilometer ifrån varandra.

Bråk

6

Knappar

1. %N låter dig mata inblandade tal (heltal + bråk). Enheten måste vara ett heltal. Täljaren och nämnaren kan innehålla decimaler.

För att mata in ett blandat tal, mata först in ett heltal och tryck %N för att mata in täljaren.

Att i MathPrint™-läget trycka %N innan du matar in ett heltal visar en bråkmall, och tillåter bara att du matar in en siffra.

2. q låter dig mata in ett enkelt bråk. Att

trycka q före eller efter en siffra kan resultera i olika beteenden. Att i MathPrint™-läget mata in ett tal innan man trycker q brukar göra det talet till täljare.

q i MathPrint-läget kan också användas för komplexa bråk, som formelberäkningar som innehåller operatorer och andra funktioner. trycker du q innan du matar in täljaren.

I MathPrint™-läget, tryck $ mellan inmatningen av täljare och nämnare. I Classic-läget, tryck q mellan inmatningen av täljare och nämnare.

3. % O konverterar ett enkelt bråk till blandat tal, eller ett blandat tal till ett enkelt bråk.

4. % j konverterar ett bråk till dess motsvarande decimalform, eller ett decimaltal till dess motsvarande bråk, om det är möjligt.

Då

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

• I MathPrint-läge, kan bråk med q innehålla operativa knappar (T, V, etc.) och de flesta

3 1 2

4

funktionsknapparna (F, %_, etc.). I Classic-läget, tillåter inte bråk med q användandet av operativa knappar, funktioner, eller komplexa bråk i täljaren och nämnaren.

• I MathPrint-läget kan du mata in variabler som (x, y, z, t, a, b, och c) i täljaren och nämnaren i ett bråk. I Classic-läget, tillåter inte bråk med q variabler.

• I Classic-läget. dataeditorn, och tabeller, använd W tillsammans med D och E när du behöver utföra komplexa divisioner.

Bråk (Fortsättning)

• För att klistra in en tidigare inmatning i nämnaren, placera markören i nämnaren, och tryck % # för att bläddra till den önskade inmatningen, tryck sedan < för att klistra in inmatningen i nämnaren.

• För att klistra in en tidigare inmatning i täljaren eller i heltalet, placera markören i täljaren eller heltalet, och tryck # eller % # för att bläddra till önskad inmatning. Tryck sedan < för att klistra in den i täljaren eller enheten.

• Resultaten av ett bråk och inmatningarna blir förenklade så långt som möjligt.

• Beräkningar som innehåller bråk kan visa svaret i bråk- eller decimalform beroende på inmatningarna.

Bråk

5

På partyt åt du av pepperonipizzan

1

och av korvpizzan. Pizzorna har

samma storlek. Om du lägger ihop de två delarna, hur stor del av en hel pizza åt du då?

----10

--6

q

Tryck Visa

5 q 6 " T1 q 10 <

14

Du åt av en hel pizza. Du åt alltså

nästan en hel pizza!

---15

Blandade tal

En baby väger 4 kilo vid födseln. De

första 6 månaderna ökar hon

3

2 kilo. Hur mycket väger hon då?

--4

3

--8

%N

%O

Tryck Visa

4 %N 3

$ 8 " T 2 %N 3 $ 4 <

%U <

Efter 6 månader vägde hon

1

7 kilo.

--8

Konvertera bråk och decimalform

Juan simmar 20 längder på 5.72 minuter. Mary simmar 20 längder på

3

5 minuter. Gör om Marys tid till

---

4 decimalform för att avgöra vem som simmade snabbast.

Tryck Visa

5 %N 3

$ 4 "

%j

<

%j

Juan simmade snabbare än Mary eftersom han simmade 20 längder på

5.72 minuter. Förvandla 2.25 till sin motsvarighet i

bråkform.

Tryck Visa

2 8 25 %

j

<

eller 2 8 25 <

n

Decimaler och decimalkommats placering

7

Knappar

1. 8 matar in ett decimalkomma.

2. p låter dig ange antal decimalplatser.

Tryck $ $ och sedan " till du kommer till önskat antal decimaler. Tryck < för att välja det.

FLOAT Aktiverar flytande decmalläge

(standard).

0-9 Anger antal decimalplatser som

visas. FIX visas när ett decimalläge mellan 0-9 är valt.

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

•Tryck p $ $ < för att återgå till standardnotation (flytande decimalkomma).

• Inställningen för decimalläge påverkar de flesta resultaten i decimalform, samt mantissan i resultat med grundpotensform och engineerings-notatation.

• TI-30XS MultiView™-räknaren avrundar automatiskt resultaten till det antal decimaler som valts. Till exempel, när antalet är inställt till 2 blir 0.147 förvandlat till 0.15 när du trycker <. TI-30XS MultiViewräknaren rundar också av, och fyller ut resulterande värden med extra nollor så att de passar vald inställning. Till exempel, när decimalerna är inställda på 5 platser blir

0.147 förvandlat till 0.14700 när du trycker <.

• Att återställa räknaren rensar decimalinställningarna och återställer förinställningen FLOAT.

• Decimalinställningen påverkar inte den

2

1

interna precisionen i resultatet. Det påverkar enbart sättet som resultatet visas på.

Decimal

Avrunda 12.345 till hundradelar, till tiondelar, och sedan till flytande notation.

Tryck Visa

12 8 345 <

p

$ $ "

""<

-<

p

$$"

"<

-<

p

$$

<

-<

Konstant

8

Knappar

1. % l stänger av och på konstantverktyget, och låter dig definiera konstantens värde, operation eller uttrycket för ett snabbkommando av upprepade kombinationer av knapptryckningar. K visar att konstantläget är på.

2. < placerar innehållet i K i slutet av uttrycket i fönstret.

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

• Alla operationer, funktioner och värden fungerar i konstant-läge.

• Mata in en konstant:

1. Tryck % l. Om en konstant redan är

lagrad, tryck - för att rensa den.

2. Mata in konstanten (vilken uppsättning

operationer, funktioner och värden som helst).

3. Tryck < för att aktivera

konstantverktyget. K visas i fönstret för att indikera att konstantverktyget är på.

4. Tryck - för att rensa fönstret.

5. Mata in ett initialvärde. Matar du inte in

något tal, antas värdet vara 0, och Ans blir synligt i fönstret.

6. Tryck < för att placera innehållet i K

vid slutet av uttrycket och utvärdera det.

7. Fortsätt att trycka < för att upprepa

konstanten.

8. Tryck % ll igen för att stänga av

konstantverktyget.

1

2

Konstant

Tre personer sitter barnvakt för

€5.25 var Person nummer ett

arbetar 16 timmar. Person nummer två arbetar 12 timmar. Person nummer tre arbetar 17 timmar. Hur mycket tjänar de, var och en?

Tryck Visa

%l

V 5.25 <

%l

-

16 <

12 <

17 <

Konstant (Fortsättning)

%l

(Konstant-läget är av.)

%l

Minnet och lagrade variabler

9

Knappar

1. L låter dig lagra värden till variabler. Tryck Lför att lagra en variabel, och tryck z

för att välja vilken variabel som ska lagras. Tryck < för att lagra den valda variabeln. Om variabeln redan har ett värde, ersätts det värdet med det nya.

2. z komma åt variabler. Upprepa knapptryckningen för att välja x, y, z, t, a, b, eller c. Du kan också använda z för att återkalla variablernas lagrade värde.

3. % { rensar alla variabler.

4. % h visar en meny med variablerna x, y, z, t, a, b, och c, och låter dig se deras lagrade värden innan du klistrar in dem i fönstret.

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

• Du kan lagra ett tal eller ett uttryck som resulterar i ett tal i en minnesvariabel.

• När du väljer en variabel, genom att använda z, visas variabelns namn (x, y, z, t, a, b, eller c). Variabelns namn infogas i den aktuella inmatningen, men variabelns tillskrivna värde används till att utvärdera uttrycket.

• När du väljer en variabel genom att använda % h, visas en meny med värdet av de lagrade variablerna. Välj variabel genom att trycka det motsvarande menynumret. Det tillskrivna värdet för variabeln infogas i aktuell inmatning och används för att utvärdera uttrycket.

• Att återställa räknaren rensar alla variabler i minnet.

3

2

4

1

Lagra, variabler

Här nedan följer resultat från dina matteläxor och provräkningar.

Provresultat: 96, 76, 85. Läxresultat: 92, 83, 97, 86.

1. Sök det betyg som är medelvärdet för dina provresultat.

2. Beräkna det betyg för läxorna som är medelvärdet av läxresultaten.

Lz

%h

3.Din lärare kommer att räkna ut ditt slutbetyg genom att beräkna medelvärdet på dina läx- och provresultat. Vad blir ditt slutbetyg? Din lärare avrundar till närmaste heltal om det skulle behövas.

Tryck Visa 96 T 76 T

85 <

Lagra, variabler (Fortsättning)

W 3 <

Lz <

92 T 83 T 97 T 86

< W 4 <

T z <

Lz

%h

W 2 <

Ditt slutbetyg är 88, avrundat till närmaste heltal.

Lagra, återkalla

Du ska skicka en present var till två av dina vänner. Du ser presenten på två olika webbplatser, men till samma pris. Men fraktkostnaden är olika på de två webbplatserna. Paketen väger

4.5 kg och 3.2 kg. Affär A kan skicka paketet för en kostnad på

€1.40 per kg. Affär B skickar paketet

för

€3, plus €1.10 per kg. Vilken affär

tar ut minst för att skicka vart och ett av paketen?

Tryck Visa

€2, plus

L

%h

4 8 5 L z <

2 T 8 40 E

3 T 8 10 E

Affär A tar ut ut skicka presenten som väger 4.5 kg.

z D1

<

z D1

<

€8.30 och affär B tar

€7.95. Affär B tar minst för att

Lagra, återkalla (Fortsättning)

L

3 8 2 L z <

##### #<<

Affär A tar

€6.52. Affär A tar ut minst för att

skicka presenten som väger 3.2 kg.

€6.48 och affär B tar

%h

Lagra, återkalla (Fortsättning)

Affär Köp Kvantitet Kostnad

Askjortor2 €13.98 /st. B slipsar 3 €7.98 /st. Cbälte1 €6.98

hängslen 1 €9.98

Hur mycket handlade du för i varje affär, och hur mycket betalade du sammanlagt?

Tryck Visa

2 V 13 8 98 <

L

%h

Lz<

3 V 7 8 98 <

L z z <

Lagra, återkalla (Fortsättning)

L

6 8 98 T 9 8 98 <

L z zz<

% D

1 T% h 2 T %

h 3 <

%h

Du gjorde av med:

€27.96 i affär A, €23.94 i affär B, €16.96 i affär C.

Du gjorde av med sammanlagt i de tre affärerna.

€68.86

Dataeditor och formellista

10

Knappar

1. v visar dataeditorn med tre listor. Varje lista kan innehålla upp till 42 element. För att mata in data, gå till en lista och mata in ett tal. Tryck pilknappen för att navigera mellan listelement.

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

• Listformlerna accepterar räknarens alla funktioner.

• I formler, använd D och E kring variabler så att rätt utförandeordning används.

• Om en formel matas in i en lista, blir formeln automatiskt uppdaterad om en referenslista uppdateras.

Obs! Att trycka < i en formellista raderar automatiskt formeln. Inget meddelande visas.

• När en formel raderas, kvarstår data och kan användas vidare. Data är då inte längre uppdaterad.

• Att trycka på v en gång till i ett fönster för en dataeditor öppnar en meny med möjlighet att rensa listor och hantera formler.

• Att trycka på v en gång till i “Lägga till/ redigera formler öppnar en meny som består av listnamn som du kan använda när du lägger till eller redigerar formler.

• Att trycka - backar tillbaka genom fönstren i dataeditorn.

1

• Att trycka % Q avslutar dataeditorn och du återvänder till grundfönstret.

• I dataeditorn, visas tal i grundpotensform med E för att spara utrymme.

3

Exempel: 2 x 10

visas som 2E3.

Mata in data och formler

En novemberdag listar en väderleksrapport på Internet följande temperaturer.

Paris 8Ä C Moskva

½1Ä C

Montreal, Kanada 4Ä C Omvandla temperaturerna från

Celsius till Fahrenheit.

9

Kom ihåg: F= C+32.

--5

Tryck Visa

v

v 8 $ M

$ 4 $ "

1

v "

1

9

W 5 V v

1 T 32

Mata in data och formler (Fortsättning)

<

Lägg märke till att L2 blir markerat, eftersom det är resultatet av en formel.

I Fahrenheit är graderna: Paris 46.4Ä F

Moskva 30.2Ä F

v

Montreal, Kanada 39.2Ä F

Om temperaturen i Sydney är 21Ä C, vad är den då i grader Fahrenheit?

! $ $ $

<

21

Temperaturen i Sydney, är 69.8Ä F.

Statistik

11

Knappar

1. v låter dig mata in datapunkter (x för 1-

Var statistik; x och y för 2-Var statistik). (Se

kapitel 10, Dataeditor och listformler, för ytterligare information om v.)

2. %t visar en meny från vilken du kan välja

1-Var, 2-Var eller StatVars. 1-Var Analyserar data från en

uppsättning data med en uppmätt variabel—-x.

2-Var Analyserar parade data från 2

uppsättningar data med 2 uppmätta variabler—x, den oberoende variabeln, och y, den beroende variabeln.

StatVars Det här alternativet kommer bara

ifråga när du gjort 1-var eller 2-var statistik. Visar menyn med variabler med deras aktuella värden..

2

1

StatVars-menyn:

n Antal x (eller x,y) datapunkter.

v eller w Medelvärde för alla x eller y

värden.

Sx eller Sy Standardavvikelse för stickprov

hos x eller y.

sx eller sy Standardavvikelse för

populationen hos x eller y.

Gx eller Gy Summan av alla x-värden eller

y-värden.

Gx

2

eller

2

Gy

Summan av alla x2 -värden eller y2-värden.

Gxy Summan av produkten av x och

y för alla x-y-par i de 2 listorna.

a Lutning hos regressionslinjen. b Lutning hos regresionslinjen,

skärning med y-axel.

r Korrelationskoefficient. x ÅÅÅÅ (2-var) Använder a och b för att

beräkna förutsagt x-värde när du matar in ett y-värde.

y ÅÅÅÅ (2-var) Använder a och b för att

beräkna förutsagt y-värde när du matar in ett x-värde.

minX Minsta x-värde. Q1 (1-var) Medianen av elementen mellan

minX och Med (1:a kvartil).

Med Medianen för alla datapunkter. Q3 (1-var) Medianen för alla element

mellan Med och maxX (3:e kvartil).

maxX Största x-värde.

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

• Du kan byta datapunkterna genom att gå till Dataeditorn, gå till dataelementet, och ändra det angivna värdet. Obs! Därefter måste du beräkna om 1-var eller 2-var statistik för att StatVars alternativet ska visas.

Mata in 1-Var statistik data

Fem elever gjorde ett matteprov. Mata först in —85, 85, 97, 53, 77.

Tryck Visa

v

85 $ 97 $ 53 $ 77 $

" 2 $1 $1 $1 $

%t v

Fortsättning

Visa statistiken

Sök antalet datapunkter (n), medelvärdet (

v), stickprovets

standardavvikelse (Sx), populationens standardavvikelse (

sx), summan av resultaten (Gx),

2

Gx

summan av kvadraterna (

),

medianen, minX, Q1, Q2, och maxX. Tryck Visa

%t

1 $ " " < $

%t v

<

$ $ $ $ $

$ $ $

$ $

Ta bort datapunkter

Ta bort det lägsta testresultatet genom att redigera datan i L1 i dataeditorn. Se till att du uppdaterar frekvenslistan, L2, om så behövs. Sök det nya medelvärdet ( Slutligen, rensa alla listor på data.

Tryck Visa

v).

v

$ $

v

J " J

%t

1

$$<

vv 4

%Q

Mata in 2-Var statistik data

Tabellen här nedan visar det antal sportskor som en liten skoaffär sålt. Tabellen visar det totala antal skor som sålts under två månader och antalet sålda av märke A under samma månader. Mata in data i dataeditorn.

Månad April 58 35 Maj 47 28

Tryck Visa

Totalt antal. (x) Märke A (y)

v58 $

%t v

47 $

"35 $28 $

Visa statistiken

Anta att antalet skor som säljs är konstant. Då kan du använda två data punkter för att förutspå försäljningen av Märke A i juni, om vi vet den totala försäljningen i juni. Använd en linje som bäst passar för att hitta junis försäljning av Märke A om affären totalt säljer 32 par skor i juni.

Tips: Sök y

Tryck Visa

'(32).

%t

2 $ $ <

$ (bläddra

ner till y') <

32 E <

I juni kommer 18 par skor att säljas av Märke A, om den totala försäljningen för månaden är 32 par.

Sannolikhet

12

Knappar

1. H visar följande meny med funktioner.

nPr Beräknar antalet möjliga

permutationer.

nCr Beräknar antalet möjliga

kombinationer.

! Beräknar ett tals fakultet.

Rand Skapar ett slumpmässigt tal

mellan 0 och 1.

Randint( Skapar ett slumpmässigt

heltal mellan två heltal, A och

B

, där A  Randint  B.

Anteckningar

• Alla exemplen i overheadmallarna förutsätter förinställningar.

• En kombination är ett arrangemang där objektens turordning saknar betydelse, ungefär som en korthand.

• En permutation är ett arrangemang där ordningen på objekten har betydelse, ungefär som vid en tävling.

• n-fakultet är produkten av alla positiva heltal från 1 till n, där n måste vara ett positivt

heltal  69.

• Du kan lagra (L) ett heltal i Rand precis som du lagrar värden i variabelminnet. Om du vill kontrollera det slumpmässiga tal som skapas av alla räknarna i klassrummet, låt eleverna lagra samma tal i Rand; sekvensen för de slumpmässiga talen blir då densamma på alla räknarna.

•I Randint ska de två tal du väljer separeras med ett komma.

1

Kombination (nCr)

Du har plats för två böcker i din bokhylla. Du har fyra böcker att ställa i hyllan. Använd den här formeln för att ta reda på hur många sätt du kan kombinera de fyra böckerna på de två platserna.

4 nCr 2

ABCD

AB och BA

AB AC AD

H

räknas bara som en kombination

Tryck Visa

BA CA DA

BC BD CB CD DB DC

4 H $

< 2 <

Det finns sex unika kombinationer av valda böcker från de fyra böckerna.

Permutation (nPr)

Fyra olika personer deltar i en springtävling. Använd den här formeln för att få reda på hur många sätt de kan komma etta och tvåa.

4 nPr 2

ABC D

AB och BA räknas som två

AB AC AD BA BC BD

H

permutationer

Tryck Visa

CA CB CD DA DB DC

4 H

<2 <

Det finns 12 olika permutationer för första och andra plats i springtävlingen.

n-Fakultet (!)

Registreringsskyltarna innehåller olika siffror och bokstäver för att kunna ge varje bil en unik kombination. Gör en egen registreringsskylt som innehåller ett fyrsiffrigt tal. Använd siffrorna 1, 3, 7, och 9 utan upprepning. Hur många fyrsiffriga tal kan du göra?

Du kan använda ett träddiagram för att skapa följande lista av registreringsskyltar. Är du säker på att du hittat alla? Ledtråd: Beräkna 4!

H

1379 3179 7139 9137

1397 3197 7193 9173

1739 3719 7319 9317

1793 3791 7391 9371

1937 3917 7913 9713

1973 3971 7931 9731

Tryck Visa

4 H $ $

< <

Du kan göra 24 unika registreringsskyltar om du använder 1, 3, 7 och 9 utan upprepning.

Texas instruments TI-30XS MULTIVIEW User Manual [sv]

Specifications and Main Features

Frequently Asked Questions

User Manual