Texas Instruments TI-30XS MultiView Guide [es]

Download

TI-30XS MultiView™

Manual del profesor

Desarrollado por

Texas Instruments Incorporated

Actividades desarrolladas por

Gary Hanson, Aletha Paskett y Margo Lynn Mankus

Ilustrado por

Jay Garrison y David Garrison

Antes de usar (ó ensamblar) el producto lea cuidadosamente este instructivo.

Acerca de los autores

Gary Hanson

Aletha Paskett

son profesores de matemáticas en el Independent School District, de Sandy, Utah. Han desarrollado algunas de las actividades que se ofrecen en esta guía y han contribuido a evaluar la idoneidad de los ejemplos incluidos en la sección Cómo utilizar la calculadora En la actualidad,

TI-30XS MultiView™

Margo Lynn Mankus

de este manual.

imparte clases de matemáticas y tecnología en la State University de Nueva York, en New Paltz. Ha revisado y actualizado los materiales utilizados para la calculadora

TI-30XS MultiView

y desarrollado algunas de las actividades de este manual.

Importante

Texas Instruments no ofrece garantía alguna, ya sea explícita o implícita, incluidas, sin limitarse a ellas, garantías implícitas de comerciabilidad o idoneidad para un uso concreto, en lo que respecta a los programas o manuales y ofrece dichos materiales únicamente “tal y como son”.

En ningún caso Texas Instruments será responsable ante ninguna persona por daños especiales, colaterales, accidentales o consecuentes relacionados o causados por la adquisición o el uso de los materiales mencionados, y la responsabilidad única y exclusiva de Texas Instruments, independientemente de la forma de acción, no sobrepasará el precio de compra del artículo o material que sea aplicable. Asimismo, Texas Instruments no puede hacerse responsable de las reclamaciones de cualquier clase contra el uso de dichos materiales por cualquier otra parte.

Texas Instruments Incorporated 7800 Banner Drive, M/S 3918 Dallas, TX 75251

Attention: Manager, Business Services

Impreso en EE. UU.

MathPrint, APD, Automatic Power Down, EOS y MultiView son marcas comerciales de Texas Instruments Incorporated.

Índice de contenidos

CAPÍTULO PÁGINA CAPÍTULO PÁGINA

Acerca del Manual del profesor v Acerca de la calculadora

TI-30XS MultiView™ vi

Actividades

Viaje estelar

Notación científica 3

Ritmos cardíacos

Estadística con una variable 7

En la taquilla del cine

Fórmulas de datos 13

Marcando reglas

Expresiones algebraicas 23

Cómo utilizar la calculadora TI-30XS MultiView

11 Estadística 85 12 Probabilidad 91 13 Tabla de funciones 99 14 Potencias, raíces y operaciones

inversas 103

15 Funciones logarítmicas y

exponenciales 111 16 Pi 115 17 Ángulos y conversiones 119 18 Conversiones polares

y rectangulares 123 19 Trigonometría 125 20 Funciones hiperbólicas 133

(Continuación)

1 TI-30XS MultiView: Operaciones

básicas 31 2 Borrado y corrección 43 3 Matemáticas básicas 47 4 Orden de operaciones y

paréntesis 51 5 Notación numérica 57 6 Fracciones 61 7 Decimales y número de decimales 67 8 Constante 69 9 Memoria y variables almacenadas 73 10 Fórmulas del editor de datos

y listas 81

Apéndice A

Referencia rápida para las teclas A-1

Apéndice B

Indicadores de pantalla B-1

Apéndice C

Mensajes de error C-1

Apéndice D

Información sobre soporte y servicio de atención al cliente D-1

Apéndice E

Información sobre las pilas E-1

Acerca del Manual del profesor



Cómo está organizado el Manual del profesor

Este manual es para las calculadoras científicas TI-30XS MultiView™ y TI-30XB MultiView. Aunque las instrucciones de este manual se indican para una calculadora TI-30XS MultiView, son igualmente válidas para una TI-30XB MultiView.

El manual consta de dos secciones: Actividades y Cómo utilizar la calculadora TI-30XS MultiView. La sección Actividades es un conjunto de actividades dirigidas a integrar la TI-30XS MultiView en la enseñanza de las matemáticas. La sección Cómo utilizar la calculadora TI-30XS MultiView se ha diseñado para facilitar el uso y aprendizaje de la calculadora.

A menos que se indique expresamente lo contrario, en cada sección se utilizan los valores de configuración predeterminados, incluidos los del modo MathPrint™.

Actividades

Cada actividad está considerada como un elemento independiente y contiene:

Cómo utilizar la calculadora TI-30XS MultiView

Esta sección contiene ejemplos en transparencias maestras. Los capítulos están numerados e incluyen:

• Una página de introducción en la que se describen las teclas de la calculadora TI-30XS MultiView que se utilizan en cada ejemplo, su ubicación en el teclado y notas sobre las funciones de cada una.

• Transparencias maestras con ejemplos prácticos de las teclas descritas en la página de introducción correspondiente. Las teclas de interés se indican en color negro en el teclado de la TI-30XS MultiView. La pantalla muestra también la configuración de modo correspondiente.

Restablecimiento de la TI-30XS MultiView

• Restablecer la calculadora es el mejor medio de asegurar que todos los alumnos comiencen a partir del mismo punto inicial; para ello: Pulse & y - al mismo tiempo o

pulse %  y, a continuación, seleccione 2 (Yes).

• Una visión global del objetivo matemático de que trata.

• El concepto matemático que se desarrolla.

• Los materiales necesarios para realizar cada actividad.

• El procedimiento detallado, incluidas cada una de las pulsaciones de tecla de la TI-30XS MultiView.

• Una hoja de actividades del alumno.

Convenciones utilizadas en el manual del profesor

• Los símbolos o nombres que aparece en el texto encerrados entre corchetes, [ ], indican una función secundaria o alternativa de la tecla en cuestión.

Por ejemplo: %Z

Acerca de la calculadora TI-30XS MultiView™

Pantalla de inicio

Puede utilizar la pantalla de inicio para introducir expresiones matemáticas, funciones y otras muchas instrucciones, cuyos resultados aparecerán también en la pantalla de inicio. La pantalla de la TI-30XS MultiView puede mostrar hasta cuatro líneas de texto con un máximo de 16 caracteres por línea. Si la entrada o la expresión contienen más de 16 caracteres, puede desplazar la pantalla a izquierda y derecha (teclas (! y " ) para ver todo el contenido.

Al pulsar la tecla %Q, la calculadora TI-30XS MultiView muestra una pantalla de inicio vacía. Pulse # y $ para ver las entradas y poder trabajar con ellas. (Consulte Entradas anteriores, en la página vii.)

En modo MathPrint™, puede introducir hasta cuatro niveles de funciones y expresiones anidadas consecutivamente; por ejemplo, fracciones, raíces cuadradas o potencias como

^, , e x y 10 x.

maestra del Capítulo 4, Orden de las operaciones y uso de paréntesis.

Dado que las operaciones entre paréntesis se efectúan en primer lugar, puede utilizar D E para cambiar el orden de las operaciones y, por consiguiente, el resultado.

Modo

Utilice la tecla p para seleccionar el modo que desee. Pulse $ # ! " # $ para resaltar un modo, y la tecla < para seleccionarlo. Pulse

- o %Q para regresar a la pantalla de inicio y trabajar con los valores de configuración del modo seleccionado. La pantalla muestra los valores de configuración de modo predeterminados.

Classic, este modo muestra las entradas y salidas en una única línea.

Cuando se calcula una entrada en la pantalla de inicio, y dependiendo del espacio disponible, la respuesta puede aparecer directamente a la derecha de la entrada o en el lateral derecho de la siguiente línea.

Indicadores de pantalla

En el Apéndice B se incluye una lista de los indicadores de pantalla.

Orden de las operaciones

Para calcular las expresiones, la TI-30XS MultiView utiliza el sistema operativo de ecuaciones (Equation Operating System (EOS™). La prioridad que se sigue para realizar las operaciones se describe en la transparencia

MathPrint, muestra las entradas y salidas en formato de texto de varias líneas. Utilice el modo MathPrint para confirmar visualmente que las expresiones matemáticas se han introducido correctamente y comprobar que el modo de notación matemática es correcto.

Nota: Cuando se cambia de modo Classic a MathPrint, se limpian tanto el historial de la calculadora como el valor de la constante.

Funciones secundarias

Cuando se pulsa %, la calculadora muestra el indicador 2nd y, a continuación, accede a la función impresa por encima de la tecla pulsada. Por ejemplo, % b 25 < calcula la raíz cuadrada de 25 y muestra el resultado, 5.

Acerca de la calculadora TI-30XS MultiView™ (Continuación)

Menús

Algunas teclas abren menús: H, %I, v, %t, %, %h y %{.

Pulse " o $ para desplazarse y seleccionar un elemento de menú, o pulse el número correspondiente situado junto al elemento de menú en cuestión. Para retroceder a la pantalla anterior sin seleccionar un elemento de menú, pulse -. Para salir de un menú o una aplicación y regresar a la pantalla de inicio, pulse %Q.

Entradas anteriores # $

Después de calcular una expresión, utilice las teclas # y $ para desplazarse por las entradas anteriores, que están almacenadas en el historial de la TI-30XS MultiView. Puede volver a utilizar una entrada anterior si pulsa la tecla < para pegarla en la línea inferior y, a continuación, edita y calcula la nueva expresión.

de una entrada. La pantalla muestra tanto

el indicador Ans como el operador.

Restablecimiento de la calculadora TI-30XS MultiView

Pulse & y - al mismo tiempo o pulse %  y, a continuación, seleccione 2 (Yes) para

restablecer la calculadora.

Cuando se restablece la calculadora:

• Se recuperan las configuraciones de modo predeterminadas en fábrica: notación estándar (decimal flotante) y grados (DEG).

• Se borran las variables de memoria, las operaciones pendientes, las entradas del historial, los datos estadísticos, las constantes y el indicador Ans (Última respuesta).

Nota: En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

Conmutar respuesta n

Siempre que sea posible, utilice esta tecla para cambiar el formato de las últimas respuestas calculadas. Pulse la tecla n para conmutar el formato de las respuestas mostradas, ya sea de fracción a decimal, de raíz cuadrada exacta a decimal, de pi exacto a decimal, o viceversa.

Última respuesta (Ans)

El resultado calculado en último lugar se almacena en la variable Ans. Ans se retiene en la memoria, incluso después de apagar la calculadora TI-30XS MultiView. Para recuperar el valor de Ans:

• Pulse % i (Ans se muestra en la

pantalla), o bien

• Pulse cualquier tecla de operaciones ( T, U, y así sucesivamente) como la primera parte

Automatic Power Down™ (APD™)

Si la TI-30XS MultiView se deja inactiva durante cinco minutos, la función APD apaga la calculadora automáticamente. Pulse & para encenderla de nuevo. No se perderán los valores en pantalla, las operaciones pendientes, los valores de configuración ni la memoria.

Mensajes de error

Consulte el Apéndice C para ver una lista de los mensajes de error.

Actividades

Viaje estelar —

Notación científica 3

Ritmos cardíacos —

Estadística con una variable 7

En la taquilla del cine —

Fórmulas de datos 13

Marcando reglas —

Expresiones algebraicas 23

Viaje estelar — Notación científica

Conceptos generales

Los alumnos investigan la notación científica cambiando números a notación científica y usándolos luego en los cálculos.

Introducción

Prepare la actividad indicando a los alumnos:

El formato de notación científica estándar es

nnnn

aaaa que 10, siendo nnnn un número entero.

1. Los alumnos deben practicar escribiendo los

, donde aaaa es mayor o igual que 1 y menor

1010

siguientes números en notación científica usando papel y lápiz.

a. 93 000 000 b. 384 000 000 000 c. 0,00000000000234 d. 0,0000000157

9,3 3,84 2,34 1,57

-12

-8

Conceptos matemáticos

• notación científica

•suma

• división

Materiales

• TI-30XS MultiView™

•lápiz

• actividad del alumno

2. Pida a los alumnos que cambien los siguientes números a notación científica (SCI) con la calculadora TI-30XS MultiView.

-9

-6

a. 12 000 000 b. 974 000 000 c. 0,0000034 d. 0,000000004

Nota:

Nota: En las respuestas se considera que el valor de

Nota:Nota:

configuración predeterminado es decimal flotante.

1,2 9,74 3,4 4

3. Pida a los alumnos que cambien los siguientes números a notación estándar (NORM).

¿ 10

a. 5,8 b. 7,32 ¿ 10 c. 6,2 ¿ 10 d. 3 ¿ 10

Nota:

Nota: Para introducir un número negat ivo , pulse M y, a

Nota:Nota:

-6

-8

continuación, escriba el número.

58 000 000 732 000 0,0000062 0,00000003

³ Siga los pasos que se indican a

continuación:

1. Introduzca el primer número,

12000000.

2. Pulse

3. Pulse

³ Siga los pasos que se indican a

1. Introduzca 5.8; pulse

2. Introduzca 7; pulse

3. Pulse

p. $ " < - <para

mostrar el número en notación científica.

1.2Ã

continuación:

Ã10

ÃÃ

$ < - <.

58000000

Viaje estelar — Notación científica (Continuación)

Actividad

Exponga el siguiente problema a los alumnos:

Eres el capitán de una nave espacial. Se te ha encargado la misión de ir a Alfa Centauro y debes llegar allí en cinco años. La distancia entre el Sol y

Alfa Centauro es de 2,5 x 10

de millas. La distancia de la Tierra al Sol es, aproximadamente, de 9,3 x 10

millas.

Aunque todavía no se ha descubierto la forma desplazarse a la velocidad de la luz, vives en un tiempo en el que se puede viajar a la velocidad de la luz.

La luz recorre una distancia aproximada de 6x10

millas en un año luz. Vas a partir de la Tierra en dirección al Sol, y luego, a Alfa Centauro. ¿Podrás llegar a Alfa Centauro en el tiempo proyectado?

Procedimiento

1. Utilizando la calculadora TI-30XS MultiView™,

halle la distancia total por recorrer.

2,5 ¿ 10

+ 9,3 ¿ 10

= 2,5000093 ¿ 10

millas

2. A continuación, halle el tiempo necesario para

recorrer la distancia. (distancia recorrida

¾ 1 año

luz).

2 5000093 10

----------------------------------------- -

610

×,

4 1666821672,=

años

3. ¿Puede hacerse el viaje en el tiempo de 5 años

señalado?

Sí, si fuera posible viajar a la velocidad de la luz.

Extensión

La luz viaja a 186.000 millas por segundo. Un año luz es la distancia que la luz puede recorrer en un año. Pida a los alumnos que convierta un año luz en millas recorridas en un año luz.

186.000millas

--------------------------------------1segundo

60segundo

-------------------------1minuto

60 minuto

-------------------------

××

1horas

24horas

-------------------- -

1día

365días

--------------------

1an˜o

587, 10

-------------------------------------------------

≈

1an

Sugerencia: Asegúrese de que la calculadora TI-30XS MultiView está en modo MathPrint™ antes de trabajar con este problema.

Sugerencia:

aproximadamente a 9.3 x 10

³ Siga los pasos que se indican a

³ Dependiendo del problema,

millas×

La Tierra está

millas del Sol.

continuación:

1. Pulse 2.5 7

2.5000093Ã

2. Pulse %i q 6 C 12

4.166682167

recuerde a los alumnos que deben incluir paréntesis cuando sea necesario para que las operaciones se realicen en el orden adecuado. Ejemplo: (2.5000093 x 10 necesario insertar los paréntesis para obtener el resultado correcto.

C13 " T 9.3 C

Ã10

ÃÃ

) ¾ (6 x 1012) es

Para aproximar este valor en la actividad vamos a utilizar 6 x 10

Respuesta a la extensión del alumno: El viaje estelar a Delta Centuro tardará unos 15 años.

millas en un año luz.í

³ Los alumnos pueden profundizar en

este tema visitando las páginas W eb de la NASA en Internet.

Viaje estelar —

Nombre ___________________________

Notación científica

Fecha ___________________________

Problemas

1. Escriba los siguientes números en notación científica.

Notación estándar Notación científica

a. 93 000 000 __________________________

b. 384 000 000 000 __________________________

c. 0,00000000000234 __________________________

d. 0,0000000157 __________________________

2. Utilizando la calculadora TI-30XS MultiView™, cambie los siguientes números a notación científica con el modo SCI.

Notación estándar Notación científica

a. 12 000 000 __________________________

b. 974 000 000 __________________________

c. 0,0000034 __________________________

d. 0,000000004 __________________________

3. Utilizando la calculadora TI-30XS MultiView, cambie los siguientes números a notación decimal estándar con el modo NORM.

Notación científica Notación estándar

a. 5,8 ¿ 10

b. 7,32 ¿ 10

c. 6,2 ¿ 10

d. 3 ¿ 10

-6

-8

_________________________

Viaje estelar —

Nombre ___________________________

Notación científica

Fecha ___________________________

Problema

Eres el capitán de una nave espacial. Se te ha encargado la misión de ir a Alfa Centauro y debes llegar allí en cinco años. La distancia entre el Sol y Alfa Centuro es de 2,5 x 1013 millas. La distancia entre la Tierra y el Sol es, aproximadamente, de

9,3 x 10 Aunque todavía no se ha descubierto la forma desplazarse a la velocidad de la luz,

vives en un tiempo en el que se puede viajar a la velocidad de la luz. La luz recorre una distancia aproximada de 6 x 10

de la Tierra en dirección al Sol, y luego, a Alfa Centauro. ¿Podrás llegar a Alfa Centauro en el tiempo proyectado?

millas.

millas en un año luz. Vas a partir

Procedimiento

1. Utilizando la calculadora TI-30XS MultiView™, halla la distancia total por recorrer. Para esta estimación aproximada, vamos a suponer que la distancia se mide trazando una recta entre la Tierra y el Sol, y luego otra hasta Alfa Centauro.

____________________________________________________________________________

Sugerencia: Antes de empezar el cálculo, debe comprobarse que la calculadora esté en modo de notación científica.

A continuación, halla el tiempo necesario para recorrer la distancia. (distancia recorrida ¾ 1 año luz).

Sugerencia: Asegúrate de utilizar los paréntesis que necesites para poder obtener el resultado correcto para este problema de división. __________________________________ ______________________________________

____________________________________________________________________________

¿Puede hacerse el viaje en el tiempo de cinco años señalado? _____________________________________________________________________________

Extensión

En vista del éxito de la misión anterior, se te ha encomendado una nueva. La distancia entre el Sol y Delta Centauro es de 9 x 1013 millas. ¿Cuánto tiempo tardarás en llegar viajando desde la Tierra?

Sugerencia: La distancia de la Tierra al Sol es, aproximadamente,

¿ 10

millas.

de 9,3

Naturalmente, se trata de un viaje estelar ficticio. Si deseas profundizar tus conocimientos sobre la estrella más cercana y las distancias cósmicas, visita las páginas Web de la NASA en Internet.

Ritmos cardíacos: Estadística con una variable

Conceptos generales

Los alumnos utilizan el editor de datos y la función de estadística de la calculadora TI-30XS MultiView™ para investigar el efecto del ejercicio sobre el ritmo cardíaco.

Introducción

Para reducir la cantidad de datos que deben introducirse para esta actividad distribuya los alumnos en pequeños grupos. Pregunte a los alumnos:

• ¿Cuál es el ritmo cardíaco medio para alguien de tu edad?

• ¿Crees que el ejercicio afecta al ritmo cardíaco?

Actividad

Los alumnos deben completar la siguiente investigación para comprobar sus estimaciones.

1. Pida a los alumnos que midan su ritmo cardíaco en reposo tomándose el pulso durante 1 minuto. (También podrían tomarse el pulso durante 10 segundos y multiplicar el resultado por 6, ¡pero se perdería el minuto más tranquilo de todo el día!)

Conceptos matemáticos

• media, mínimo, máximo y rango

Materiales

• TI-30XS MultiView

• cronómetro o reloj con segundero

• actividad del alumno

2. Recopile los datos en una tabla. Introduzca el ritmo cardíaco de cada alumno y haga una marca en la columna de frecuencia. Si hay otros alumnos con el mismo ritmo cardíaco, añada otra marca a la columna de frecuencia.

3. Introduzca los datos de ritmo cardíaco en la calculadora científica TI-30XS MultiView.

a. Introduzca el primer ritmo cardíaco en la

tabla, en L1, y el número de marcas por cada ritmo en L2. Los datos de L2 se van a utilizar como frecuencia.

b. Pulse

introduzca el primer ritmo cardíaco, y pulse luego

c. Por ejemplo, suponga una clase de 22

alumnos:

$ entre cada entrada. Por ejemplo,

Ritmo Alumnos Ritmo Alumnos

603633 615641 626654

³ Siga los pasos que se indican a

continuación:

1. Pulse

v para introducir los

ritmos cardíacos y las frecuencias. Introduzca los ritmos cardíacos en L1 y las frecuencias en L2. Pulse

$ entre cada entrada, y pulse "

para pasar de L1 a L2.

2. Repita el proceso hasta introducir todos los ritmos cardíacos y las frecuencias.

3. Pulse

4. Pulse 1 para seleccionar estadística

5. Seleccione L1 para los datos y L2

6. Pulse

% t.

con una variable.

para la frecuencia.

$< para ver los datos.

Ritmos cardíacos: Estadística con una variable (Cont.)

4. Revise los cálculos estadísticos. Cuando los estudiantes hayan mostrado hágales ver que cardíacos. Pregunte a los alumnos:

•

¿Cuál es el número de latidos de todos los

Òx es la suma de todos los ritmos

alumnos durante un minuto? Es el valor de

•

¿Cuántos alumnos hay en la clase? Es el valor de

Òx (Sigma x),

• ¿Cómo se puede calcular el ritmo cardíaco

Σx

medio? Es el valor de

------

62.27272727=

• El ritmo cardíaco medio, ¿es mayor o menor

que el esperado?

5. Ahora veremos el efecto del ejercicio en el ritmo cardíaco. Para facilitar el trabajo de los alumnos, divídalos en parejas de forma que entre los dos puedan completar la tarea. También puede añadir alguna tarea especial que un alumno concreto pueda realizar para aumentar su ritmo cardíaco sin peligro. Pida a los alumnos:

Que paren de inmediato si en algún momento de la actividad experimentan dolor, debilidad o dificultad para respirar.

6. Pida a los alumnos que corran sin moverse del sitio durante 2 minutos; a continuación indíqueles:

Que se tomen el pulso durante 1 minuto.

a. b.

Que registren el ritmo cardíaco como han

hecho anteriormente. c. Que introduzcan los datos en la calculadora. d. Que comparen el ritmo cardíaco medio después

del ejercicio con el medido en reposo.

7. Pida ahora a los alumnos que salten durante 2 minutos. Pídales que se vuelvan a tomar el pulso durante un minuto y lo registren como antes. Pídales que vuelvan a introducir los datos en la calculadora y calculen el ritmo cardíaco medio después de los saltos. Compare estos promedios con los dos anteriores.

8. Pida a los alumnos que creen un histograma con los tres conjuntos de datos recopilados. Pregunte a los alumnos:

• ¿En qué se parecen los histogramas?

• ¿En qué se diferencian?

• ¿Se agrupan los datos de la misma forma o se

dispersan más en un gráfico que en otro?

³ Siga los pasos que se indican a

continuación:

1. Compruebe los datos estadísticos.

n debería ser igual que el número total de alumnos de la muestra. Para

nnnn

este ejemplo, n = 22.

2. Pulse

3. Pulse

$ para Ï ver el ritmo

cardíaco medio.

Ï = 62.27272727

$ hasta que aparezca Òx.

Òx = 1370

Nota: Los números muestran los resultados del ejemplo descrito en esta actividad. Los resultados de los alumnos pueden variar dependiendo del tamaño del grupo y de las lecturas de los ritmos cardíacos.

Ritmos cardíacos:

Nombre ___________________________

Estadística con una variable

Fecha ___________________________

Problema

¿Cuál es el ritmo cardíaco medio para alguien de tu edad? ¿Crees que el ejercicio afecta al ritmo cardíaco?

Procedimiento

1. Utiliza esta tabla para registrar los datos de la clase o grupo (en reposo).

Latidos por minuto

(en reposo)

Frecuencia

2. ¿Cuál es el promedio de la clase (grupo)? __________________________________

3. Responde a las siguientes preguntas a partir de los datos:

a. ¿Cuál es el número total de latidos por minuto? Escribe el símbolo y el número

a partir de los datos de la calculadora. __________________________________

b. ¿Cuál es el número total de latidos cardíacos introducidos por los alumnos?

Escribe el símbolo y el número a partir de los datos de la calculadora. ________

c. ¿Cómo se calcularía el ritmo cardíaco medio? ____________________________

¿Es la respuesta igual a la de la pregunta 2?_____________________________

Ritmos cardíacos:

Nombre ___________________________

Estadística con una variable

4. Utiliza esta tabla para registrar los datos de la clase o grupo (corriendo).

Latidos por minuto

(corriendo)

Fecha ___________________________

Frecuencia

5. ¿Cuál es el promedio de la clase (grupo)? __________________________________

6. Responde a las siguientes preguntas a partir de los datos:

a. ¿Cuál es el número total de latidos por minuto? Escribe el símbolo y el número

a partir de los datos de la calculadora. ________________

b. ¿Cuál es el número total de latidos cardíacos introducidos por los

alumnos? Escribe el símbolo y el número a partir de los datos de la calculadora.

___________________________________________________

c. ¿Cómo se calcularía el ritmo cardíaco medio?

___________________________________________________

¿Es la respuesta igual a la de la pregunta 5?___________

Ritmos cardíacos:

Nombre ___________________________

Estadística con una variable

7. Utiliza esta tabla para registrar los datos de la clase o grupo (saltando).

Latidos por minuto

(saltando)

Fecha ___________________________

Frecuencia

8. ¿Cuál es el promedio de la clase (grupo)? __________________________________

9. ¿Cuál es el número total de latidos por minuto? ___________________________

10.Responde a las siguientes preguntas a partir de los datos:

a. ¿Cuál es el número total de latidos por minuto? Escribe el símbolo y el número

a partir de los datos de la calculadora. ________________________________

b. ¿Cuál es el número total de latidos cardíacos introducidos por los alumnos?

Escribe el símbolo y el número a partir de los datos de la calculadora. ________

c. ¿Cómo se calcularía el ritmo cardíaco medio? ___________________________

¿Es la respuesta igual a la de la pregunta 8?____________________________

Ritmos cardíacos:

Nombre ___________________________

Estadística con una variable

11. Crea un histograma para cada uno de los 3 grupos de datos recopilados.

En reposo Corriendo Saltando

Fecha ___________________________

12.¿En qué se parecen los histogramas? ¿En qué se diferencian? _______________

_______________________________________________________________________

13.¿Se agrupan los datos de la misma forma o se dispersan más en un gráfico que en otro? ___________________________________________________________________

_______________________________________________________________________

En la taquilla del cine: Fórmulas de datos

Conceptos generales

Los alumnos investigan una tabla de valores y observan los patrones que sigue. A continuación, los alumnos utilizan la tecla v de la calculadora TI-30XS MultiView™ para introducir datos en una lista y probar sus apreciaciones.

Introducción

La pregunta de entrenamiento se incluye como ayuda preparatoria a la actividad del alumno. Puede omitir la pregunta de entrenamiento si lo desea, pero deberá proporcionar más asistencia a los alumnos durante la investigación del problema.

Entrenamiento

Explique a los alumnos el uso de las tablas y la tecla v para ver un patrón y escribir una apreciación general. Exponga el siguiente problema a los alumnos:

Cada miércoles, Cristina sale de trabajar demasiado tarde para pasear con su perro, Max. Le ha pedido a su vecino Pablo que pasee al perro cuando salga de la escuela. Pablo está encantado de poder ayudarla. Cristina paga a Pablo 4 € semanales por pasear a Max. Pablo piensa ahorrar ese dinero. Cree una tabla que refleje la cantidad de dinero que Pablo tendrá semanalmente durante 5 semanas.

Conceptos matemáticos

•patrones

•expresiones algebraicas

• funciones lineales

•variables

Materiales

• TI-30XS MultiView

•lápiz

• papel pautado

• actividad del alumno

(Continuación)

En la taquilla del cine (Continuación)

Ayude a los alumnos a crear la siguiente tabla en el papel pautado. Considere esta tabla como una lista de datos de dos números dependientes entre sí. Es importante que los alumnos escriban sus cálculos y resultados en la columna Dinero (resultados) para poder ver los patrones. El objetivo de la práctica es ayudarles a escribir expresiones algebraicas a partir de palabras y crear apreciaciones generales utilizando razonamientos inductivos.

Utilice estas columnas para los

distintos estilos de enseñanza que sean necesarios.

Semana Dinero Suma repetida Suma

progresiva

1 1 x 4 = 4 4 = 4 4 = 4 2 2 x 4 = 8 4 + 4 = 8 4 + 4 = 8 3 3 x 4 = 12 4 + 4 + 4 = 12 8 + 4 = 12 4 4 x 4 = 16 4 + 4 + 4 + 4 = 16 12 + 4 = 16 5 5 x 4 = 20 4 + 4 + 4 + 4 + 4 = 20 1 6 + 4 = 20

Hágales ver que la columna Dinero se asemeja a la tabla de multiplicar del número 4. Es la conexión con un concepto que les resulta bastante familiar. Recuerde a los alumnos que ellos saben que Pablo gana €4 a la semana. Corresponde a la tasa de ahorros de Pablo y podría escribirse en forma de fracción como

tasa =

€4

1 semana

(Continuación)

En la taquilla del cine (Continuación)

Pida a los alumnos que añadan más datos a la tabla describiendo la cantidad que Pablo va a ahorrar. Pídales que incluyan en la tabla los datos de las semanas 6 y 7, y pregunte luego si pueden determinar la cantidad de dinero que correspondería a 10 semanas, 25 semanas y 100 semanas. Por último, pídales que indiquen la cantidad de dinero después de un cierto número de semanas. Asigne el nombre de variable al número de semanas desconocido y utilice la letra S para representar las semanas. Utilice la variable D para representar el dinero.

Semana

Dinero (D)

(S)

11 x 4 = 4 22 x 4 = 8 3 3 x 4 = 12 4 4 x 4 = 16 5 5 x 4 = 20 6 6 x 4 = 24 7 7 x 4 = 28

10 10 x 4 = 40

25 25 x 4 = 100

SS x 4*

Todas estas investigaciones deben hacerse calculadora, ya que los datos corresponden a multiplicaciones básicas. Si los alumnos necesitan apoyo para hacer sus multiplicaciones, anímeles a mostrar los datos de forma gráfica, en lugar de utilizar la calculadora, para favorecer el cálculo mental y el uso correcto de la calculadora.

sin

Pida a los alumnos que escriban la expresión para el cálculo utilizando S,

(Respuesta: S x 4)

y 4.*

En la taquilla del cine (Continuación)

Pregunte a los alumnos:

"Si sumamos las semanas S tantas veces como grupos de 4 €, obtenemos un número. ¿Qué significa ese número para Pablo?" Está pidendo a los alumnos que digan Dinero (D) y que lo escriban como una fórmula o expresión con dos variables, D = S x 4. Por lo general, se escribe primero el número y luego la letra de la mulplicación implícita. Recuerde a los alumnos que la multiplicación es conmutativa, por lo que D = S x 4 = 4 x S = 4S.

Apoye la investigación con el editor de datos (tecla

v) de la calculadora TI-30XS MultiView™ haciendo que los alumnos repasen los valores de sus expresiones algebraicas para ver si coinciden con los de la tabla creada.

1. Pida a los alumnos que introduzcan sus tablas en

la lista de datos Hágales ver que hay tres listas disponibles: L1, L2 y L3.

Explique que deben introducir los valores de Semana (S) en L1.

2. Pida a los alumntos que introduzcan los tres

primeros valores de S de sus tablas, {1, 2, 3}.

3. Escriba una fórmula para validar el trabajo: L2 =

4 x L1. Observe que S = L1 y D = L2.

4. Añada entradas a L1 para ver cómo L2 se

actualiza automáticamente con el resultado de la fórmula. Desplácese por L1 hasta un entrada vacía. Pídales que comprueben en sus tablas el valor de 4 semanas y luego el de 100 semanas.

³ Recuerde a los alumnos que para

esta actividad se utilizan las funciones de la tecla v y no las de la tecla o.

³ Si los alumnos no están familiarizados

con la calculadora TI-30XS MultiView , pídales que la apaguen y pulsen luego p.

³ Asegúrese de que todos los alumnos

tienen definidas sus calculadoras del modo siguiente:

Para regresar a la pantalla de inicio, pulse -.

1. Introduzca los tres primeros valores de S: v 1 $ 2 $ 3 $.

2. Introduzca la fórmula:

" v " 1 4 V v 1 <.

3. Añada las entradas a L1:

! $ $ $

100 <.

4. Para ver de nuevo la fórmula en L2, pulse

5. Edite la fórmula si fuera necesario, y pulse < para definirla de nuevo.

6. Para borrar los datos, pulse

4 <

" v " 1.

v 4.

Antes de iniciar la investigación de grupo en la hoja de los alumnos, pídales que borren los datos de las listas.

³ Sugerencia: Recuerde que si pulsa

%Q regresará a la pantalla de inicio.

Ahora los alumnos han convertido las palabras en datos y los han introducido en una tabla de valores, según un patrón que pueden ver, para escribir una expresión algebraica. El siguiente paso consiste en mostrarles cómo se representan gráficamente los patrones de números. ¿Cuál es la forma de D = 4S? Pida a los alumnos que representen los 4 primeros puntos de la tabla. Observe que los puntos forman

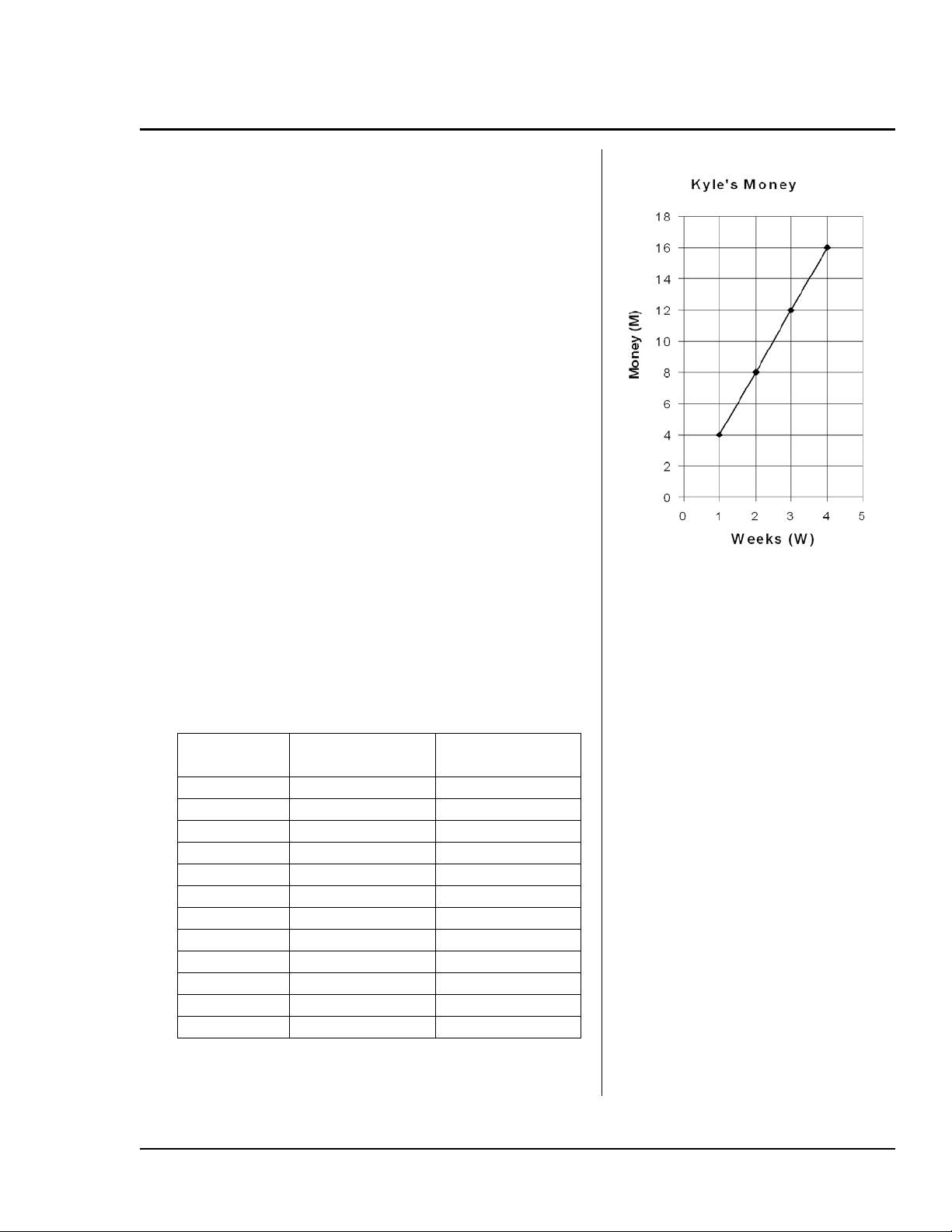
En la taquilla del cine (Continuación)

una línea recta. Puede mencionar que es posible describir el incremento de Dinero (D) como "por cada 1 de las semanas (S) que Pablo trabaja su cantidad de dinero (D) se incrementa en 4 €". Se trata de una expresión evidente, pero que sienta las bases para hablar de tasas y la forma en que afectan a la inclinación de una recta (pendiente).

El número de semanas y la cantidad de dinero son valores positivos y, por lo tanto, el gráfico tiene sentido en el primer cuadrante. Pida a los alumnos que utilicen papel pautado para crear los gráficos de sus datos.

Actividad

Los alumnos repiten una investigación similar, divididos en grupos y atendiendo a unos patrones dados, para escribir expresiones y ecuaciones algebraicas, y también para crear un gráfico con los valores de la tabla. Antes de dividir a los alumos en grupos, pídales que lean el problema para que comprendan la tarea que deben realizar.

Los alumnos deben rellenar la tabla utilizando el cálculo mental. Deben escribir todos los cálculos para que les resulte más fácil ver la fórmula. También deben esforzarse en utilizar el cálculo mental, tanto como les sea posible, para hallar el resultado de la cantidad de dinero.

Número de

personas (P)

1 1 x 11,50 €11,50 2 2 x 11,50 €23,00 3 3 x 11,50 €34,50 4 4 x 11,50 €46,00

...

10 10 x 11,50 €115,00

...

100 100 x 11,50 €1150,00

...

1000 1000 x 11,50 €11500,00

...

P P x 11,50 D = P x 11,50

antes

de utilizar la calculadora

Cálculo Cantidad de

dinero (D)

En la taquilla del cine (Continuación)

Procedimiento

Los alumnos deberán escribir la ecuación algebraica a partir del patrón mostrado en la tabla: D = P x 11,50 o utilizar la multiplicación implícita, D=11,50P.

A continuación, deberán comprobar sus fórmulas con el editor de datos ( TI-30XS MultiView™, igual que con el ejemplo de

entrenamiento.

1. Pida a los alumnos que comprueben si la calculadora está configurada.

2. Escriba los tres primeros valores en L1 {1, 2, 3}.

3. Traduzca la fórmula a la fórmula de la calculadora y escriba el resultado en L2.

Su fórmula: D = _____________________________

Fórmula de la calculadora: L2 = ________________

4. Introduzca más valores en L1 para comprobar la tabla de valores y la fórmula. Esta actividad valida la fórmula para varios valores.

v) de la calculadora

³ Asegúrese de que el modo definido en

la calculadora es el siguiente:

1. Pulse p.

2. Pulse v 1 $ 2 $ 3 $.

3. Introduzca la fórmula en L2. " v " 1

11 8 50 V v 1 <.

4. Pulse ! $ $ $ 4 <

5 < 6 < 10 < 100 < 1000 <.

5. Pulse 7500 <.

5. Introduzca 7500 en L1 para hallar la cantidad de dinero en L2. Escriba el valor como D = 11,50 x 7500 = €86.250.

6. Cree un informe rellenando una tabla de valores y un gráfico. Escriba un párrafo que describa el trabajo de la presentación.

Las respuestas del párrafo pueden variar. Asegúrese de que los alumnos explican la tabla, el gráfico y la expresión algebraica (fórmula) en el párrafo.

500 €5750 1000 €11500 1500 €17250 2000 €23000 2500 €28750

Nombre ___________________________

En la taquilla del cine

Fecha ___________________________

Problema

El cine de tu localidad estrena esta semana la película que todos están esperando. En las noticias, han dicho que cada entrada costará 11,50 €. El informador ha dicho que una pareja pagará 23 € y que una familia de tres personas gastará 34,50 €. Ha mostrado una tabla que refleja esta información de forma gráfica.

Número de personas Cantidad de dinero

1€11,50 2 €23,00 3 €34,50

El informador también ha comentado que el teatro local, MultiPlex, tiene 25 pantallas y una capacidad para 7.500 personas. La película se representará en todas las pantallas del teatro. Los propietarios han predicho que las entradas se venderán en cuestión de horas.

Los propietarios de MultiPlex quieren saber la cantidad de dinero que van a obtener en taquilla. Quieren utilizar una fórmula general de forma que puedan saber rápidamente la cantidad de dinero que obtendrán según la cantidad de personas que compre entradas.

Tu trabajo: Trabajas en la contabilidad del teatro MultiPlex. ¡Felicidades! Tu jefe te ha pedido una fórmula que le diga cuánto dinero ingresará en taquilla dependiendo de la cantidad de personas que compre entradas.

Procedimiento

1. Utiliza la tabla para investigar la cantidad de dinero que ingresará en taquilla según el número de personas que vaya al cine. Rellena la siguiente tabla. Escribe todos los cálculos de cada paso. Hasta donde sea posible, utiliza el cálculo mental la calculadora para hallar el resultado.

Número de

personas

Cálculo Cantidad de

dinero (D)

(P)

1 1 x 11,50 €11,50 2 2 x 11,50 €23,00 3 3 x 11,50 €34,50 4 5 6

...

100

...

1000

...

antes

de utilizar

Nombre ___________________________

En la taquilla del cine

Fecha ___________________________

2. ¿Qué patrón se observa en la tabla? Utilizando la información de su tabla, escribe una fórmula (una expresión algebraica) que describa la cantidad de dinero (D) en función del número de personas (P) que compre una entrada para el cine.

D = ___________________________

3. Comprueba la fórmula con el editor de listas ( TI-30XS MultiView™.

a. En la columna L1, escribe sólo las tres primeras entradas de la lista número de

personas (P) de la tabla anterior. (Introduce {1, 2, 3}.)

b. Escribe la fórmula de la parte 2 en L2. Presta atención a lo siguiente: para utilizar la

calculadora deberás traducir las variables (letras). La letra P es ahora L1 y D es L2. Vuelve a escribir la fórmula en términos de L1 y L2 para poder introducirla en la

calculadora.

Tu fórmula: D = _________________________

Fórmula de la calculadora: L2 = ________________________

c. Compara los números de L2 con los números de la tabla anterior. ¿Coinciden?

d. Introduce más valores de la lista de número de personas de la tabla en L1. Compara

los valores de L2 con los de la tabla anterior. ¿Coinciden? ¿Es válida la fórmula?

v) de la calculadora

4. Utiliza el editor de datos de la calculadora para hallar la cantidad de dinero (D) que los propietarios del teatro van a obtener de las ventas en taquilla suponiendo que asistan

7.500 personas (P) a un pase. Explica cómo calcularías la respuesta a mano con tu fórmula.

Nombre ___________________________

En la taquilla del cine

Fecha ___________________________

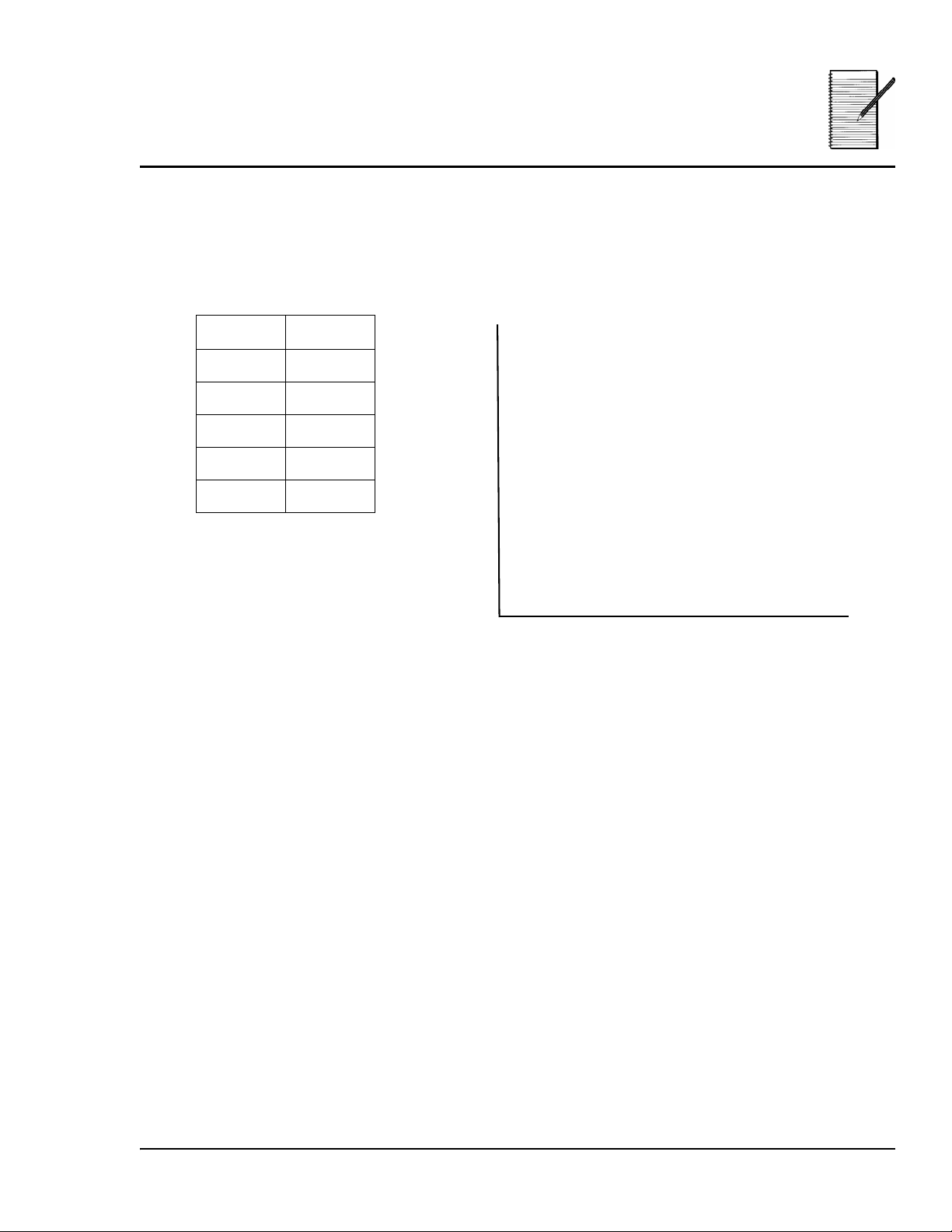
5. Tu jefe te ha pedido que hagas una presentación para los socios inversores de MultiPlex. Los inversores desean ver una presentación que refleje los números y los gráficos. Rellena la tabla siguiente utilizando el editor de datos de la calculadora. Representa gráficamente los puntos de esta tabla. Esta es otra forma que puede utilizar un contable para mostrar cómo la cantidad de dinero (D) depende del número de personas (P). ¡Y esta es la imagen de los datos!

500

1000

1500

2000

2500

Cantidad de dinero (D)

Número de personas (P)

6. Escribe un párrafo que muestre lo que dirías a tu jefe y a los inversores sobre el trabajo realizado. Incluye el procedimiento utilizado para determinar la fórmula para el aumento de dinero y lo que, tanto la tabla como el gráfico, indican sobre la cantidad de dinero que se va a recaudar en taquilla.

Marcando reglas

Conceptos generales

A partir de una tabla de valores, los alumnos calculan la expresión algebraica (función) siguiendo el formato de un juego. Para poder jugar, los alumnos deberán utilizar la tecla o de la calculadora TI-30XS MultiView™ para introducir una expresión como una función (y=).

Introducción

Para el proceso de entrenamiento de esta actividad, los alumnos deben evaluar expresiones y rellenar una tabla de valores. Participarán en un juego llamado "Marcando reglas", en el que se utiliza la calculadora TI-30XS MultiView para crear una tabla de valores.

Pida a los alumnos que rellenen las siguientes tablas que aparecen en la hoja de actividades.

Nota

Nota: Puede ser necesario cambiar la letra de

NotaNota variable del entrenamiento. No obstante, la variable que muestre la calculadora será siempre x.

+ 3

2x + 6 2(x + 3)*

Conceptos matemáticos

•expresiones algebraicas

• funciones

Materiales

• TI-30XS MultiView

•lápiz

• actividad del alumno

• trozos de papel y una bolsa

-2 1 -2 2 2

-1 2 -1 4 4

03 06 6

14 18 8

25 210 10

*Los alumnos deben observar que las tablas para 2x + 6 y 2(x + 3) son las mismas. Explique por qué esas expresiones son equivalentes y compruébelo utilizando la propiedad distributiva de la multiplicación con respecto a la suma. También puede pedir a los alumnos que utilicen mosaicos para mostrar el modelo de área, 2(x + 3) = 2x + 6.

Indique a los alummos cómo introducir la expresión en la tecla o de la calculadora TI-30XS MultiView. Introducen la expresión como una función, y puede ser un nuevo concepto para los alumnos.

Marcando reglas (Continuación)

Si fuera necesario, utilice una máquina de funciones para ofrecer un modo alternativo a la hora de evaluar expresiones para diferentes valores de

entrada de Hágales ver que la expresión, considerada como la regla con la que se ha de descubrir meditarán sobre cómo descubrir la "regla". Si fuera necesario, trate sobre el modo en que los alumnos siguen las reglas de sus juegos de mesa favoritos. Necesitan seguir las reglas para poder jugar. Cuando calculan una expresión, siguen una regla para cambiar un número por otro.

= 1 ofrece un resultado de y=1+3=4.

+ 3, puede ser

. Más tarde, durante el juego, los alumnos

. Aquí, una

Configure la tabla en la calculadora utilizando la función Auto de la tecla o. Esta función configura automáticamente una tabla de valores de inicio a partir de un valor dado que irán incrementando con un valor. Para que la calculadora cree la misma tabla de valores anterior, defina el valor de inicio en -2 e incremente los valores de alumnos que comparen las tablas que han hecho a mano con la de la calculadora.

en pasos de 1. Pida a los

Actividad

Juegue una o dos veces a “Marcando reglas” con toda la clase utilizando las reglas de la página siguiente. Para presentar el juego a toda la clase, el profesor desempeña el papel de Banca. Este juego utiliza la tecla o TI-30XS MultiView™.

y la función Ask-

de la calculadora

³ Siga los pasos que se indican a

continuación:

1. Pulse p para definir el modo como en la figura siguiente.

2. Introduzca la expresión y=x+3: o z T 3 <.

3. Introduzca los valores de configuración de la tabla: M 2 $ $ $ <.

4. Utilice las teclas # y $ para desplazarse por los valores de x y y = x + 3.

³ Sugerencia: Copie las hojas del juego

de la sección de actividades del alumno para tantos juegos como necesite.

Marcando reglas (Continuación)

Reglas para jugar en grupo

• Forme grupos de dos o tres alumnos.

• Designe a un alumno como Banca del juego.

• La Banca se encarga de manejar la calculadora durante el juego.

• La Banca toma una expresión algebraica de la bolsa (o cualquier otro contenedor previsto) y la mantiene oculta a los demás jugadores, o bien la Banca escribe una expresión algebraica en un trozo de papel y la enseña al profesor para que le indique si se puede utilizar en el ejemplo.

• La Banca introduce la expresión algebraica en la

o y selecciona la función AskNota

Nota: La Banca deberá borrar cada línea de la tabla

NotaNota Ask-

antes de cada nueva regla. (Consulte las

instrucciones sobre pulsaciones de tecla).

• Cada jugador, no la Banca, va diciendo por turno un valor para jugadores el resultado de

. La Banca introduce el valor y dice a los

• Cada jugador debe llevar un registro del juego en una tabla de valores.

• Cada jugador puede adivinar la expresión o la regla sólo durante su turno de juego.

• Cuando un jugador haya descubierto una regla, los demás deberán comprobar si es válida para todos los valores ya jugados, o probar la regla tratando de encontrar un valor que no sea válido.

• Si otro jugador o la Banca demuestran que la regla propuesta no es correcta, el jugador que la haya sugerido perderá el siguiente turno que le corresponda.

• Si la expresión propuesta por un jugador no está en la misma forma que la expresión introducida por la Banca, por ejemplo, 2(

+1) y 2x +2, y todos los jugadores acuerdan que la expresión es correcta, la Banca revelará la expresión de la calculadora y el jugador que haya propuesto la regla deberá explicar por qué las dos expresiones son iguales.

• Gana la partida el primer jugador que descubra la regla y la defienda correctamente.

• El papel de Banca pasará entonces a otro jugador para la siguiente partida.

³ Siga los pasos que se indican a

continuación:

1. Pulse p para definir el modo como en la figura siguiente.

2. Introduzca la función y = 2x + 5:

- o 2 z T 5 <. Nota: Si ya hay una función introducida en la pantalla y=, pulse

- antes de introducir otra nueva.

3. Introduzca los valores de configuración de la tabla: $ $ " < $ <.

4. Introduzca los valores de x: 5 < 6 < 10 <.

³ Sugerencia: Para introducir más

valores, resalte una de las tres líneas de la columna x, escriba el número y pulse <.

5. Para revisar la pantalla y=, pulse o. Deberá regresar a la pantalla de configuración para ver de nuevo la tabla de valores.

³ Para jugar de nuevo:

1. Borre la expresión antigua, seleccione la siguiente y, a continuación, introdúzcala: o - z T q1 $ 2.

2. Introduzca los valores de la tabla de configuración que desee, resalte OK y pulse <.

Observe que la pantalla muestra sólo 3 sugerencias. Los alumnos pueden sobrescribir un número para ver un nuevo resultado.

Marcando reglas (Continuación)

Lista de expresiones algebraicas

Copie estas u otras expresiones en trozos de papel para que la Banca de cada equipo de jugadores pueda tomar la expresión y comenzar el juego. O si lo desea, también puede pedir a la Banca que escriba una expresión y se la muestre para aprobarla o no antes de comenzar la partida. Pedir al alumno que escriba una expresión refuerza su grado de participación y permite valorar sus conocimientos.

La selección de la expresión en una lista depende del nivel de los alumnos. Amplíe las listas en función del nivel de la clase. Los alumnos deberán documentar el trabajo realizado en la hoja correspondiente.

Ejemplos de expresiones de un paso:

+ 3 2x + 3

– 9 -4x + 5

---+ 2

– 2,5

+ 15 1,5 x + 2,5

–

--5

Ejemplos de expresiones de dos pasos:

+ 6 o 2 (x + 3)

4–

--2

Modificaciones del juego

• Incluya expresiones que los alumnos deban

simplificar, como 2 propone 5x - 2, tendrá que justificar que la expresión es equivalente a 2 nivel de conocimientos al juego.

• Incluya las expresiones en términos como "cuatro menos que un número dos veces". Haga que las Bancas tomen una expresión de un contenedor y cambien las palabras por una expresión que debe ser aprobada antes de que vuelvan al grupo para jugar la partida.

+ 4 + 3x - 6. Si un alumno

+ 4 + 3x - 6, lo que añade otro

Ejemplo: Un alumno toma la expresión cuatro menos que un número dos veces. Las Bancas la escriben como 2 correcta, las bancas vuelven a sus grupos y comienzan el juego.

- 4 y se la enseñan; si la expresión es

Marcando reglas

Nombre ___________________________

Fecha ___________________________

Problema

Seguimos reglas a diario. ¿Puedes seguir las reglas de tu juego de mesa favorito? ¿Sigues cuidadosamente las reglas del juego? También seguimos reglas cuando trabajamos con números y expresiones.

Ejemplo: Si

La expresión diferentes números. Podemos considerar que como entrenamiento. La tabla contiene ya los valores de

-2 -2 -2

-1 -1 -1

000

111

= 1, entonces x + 3 = 1 + 3 = 4

+ 3 tiene una variable, x. Dependiendo del valor de x, x + 3 será igual a

+ 3 es una regla. Rellena la siguiente tabla

+ 3

+ 6

2(x + 3)

222

1. ¿Qué has observado en la tabla para 2

2. Comprueba las tablas anteriores utilizando la tecla o de la calculadora TI-30XS MultiView™.

3. Juega a "Marcando reglas", utilizando la página de juegos de la página siguiente. Para esta partida se desconoce la expresión (regla). Por lo que va a ser necesario descubrir la regla pensando desde el final hasta el principio. El profesor indicará las instrucciones del juego.

+ 6 y 2(x +3)?

Marcando reglas

¡Pensando hacia atrás!

Nombre de los jugadores: Banca:

El profesor indicará las instrucciones para jugar. Utiliza la tabla para hacer el seguimiento de los valores de Propuestas para comprobar la regla. Si la regla de un jugador no es correcta, el juego continúa.

Valo r de y

de la

calculadora

Cómo descubrir una regla a partir de una tabla de

valores

e y para el turno de cada jugador durante la partida. Utiliza la columna

Propuesta 1

= _______________________

Comprueba cada valor de ¿Es correcta la propuesta? ______

= _______________________ Comprueba cada valor de ¿Es correcta la propuesta? ______

Propuesta 2

Propuesta 4

Valo r de y

de la

calculadora

Propuesta 3

= _______________________

Comprueba cada valor de ¿Es correcta la propuesta? ______

= _______________________ Comprueba cada valor de ¿Es correcta la propuesta? ______

Cómo utilizar la

calculadora TI-30XS

MultiView™:

TI-30XS MultiView: Operaciones básicas 31 Borrado y corrección 43 Matemáticas básicas 47 Orden de operaciones y paréntesis 51 Notación numérica 57 Fracciones 61 Decimales y número de decimales 67 Constante 69 Memoria y variables almacenadas 73 Fórmulas del editor de datos y listas 81 Estadística 85 Probabilidad 91 Tabla de funciones 99 Potencias, raíces y operaciones inversas 103 Funciones logarítmicas y exponenciales 111 Pi 115 Ángulos y conversiones 119 Conversiones polares y rectangulares 123 Trigonometría 125 Funciones hiperbólicas 133

TI-30XS MultiView™: Operaciones básicas

Teclas

1. & enciende la calculadora.

2. % activa el indicador 2nd y permite

acceder a la función escrita por encima de la siguiente tecla que se pulse.

3. % ' apaga la calculadora y limpia la pantalla.

4. < completa la operación o ejecuta la orden.

5. % i vuelve a capturar el resultado calculado en último lugar y lo muestra como Ans.

6. n conmuta el formato de las respuesta, ya sea de fracción a decimal, de raíz cuadrada exacta a decimal, de pi exacto a decimal, y viceversa.

7. ! y " mueven el cursor a derecha e izquierda para desplazarse a las entradas de la pantalla de inicio y por los elementos de los menús. %! o % " permiten desplazarse al principio o al final de la entrada actual. # y $ mueven el cursor hacia arriba y abajo de los elementos de menú, las entradas anteriores de la pantalla de inicio y las entradas en el editor de datos y la tabla de funciones. % # mueve el cursor al principio de la columna activa, en el editor de datos, o a la entrada anterior, en la pantalla de inicio. Pulse % # de nuevo para mover el cursor a la entrada más antigua de la pantalla de inicio. En las fracciones, pulse % # para pegar una entrada anterior en el denominador. (Consulte el Capítulo 6, Fracciones, para obtener más información.) % $ mueve el cursor a la primera fila vacía de la columna activa, o debajo de la última entrada, en la pantalla de inicio.

8. p permite definir los modos ángulo, numérico, decimal y de pantalla. Pulse $#

! " para resaltar un modo, y la tecla <para seleccionarlo. Pulse - o

9 3 1

%Q para salir del menú de modo.

9. %

 muestra el menú Reset

(Restablecer) .

• Pulse 1 (No) para regresar a la pantalla

anterior sin restablecer la calculadora.

• Pulse 2 (Yes ) para restablecer la

calculadora. La pantalla muestra el mensaje MEMORY CLEARED.

TI-30XS MultiView™: Operaciones básicas

(Continuación)

Nota: Pulse & y - al mismo tiempo si

desea restablecer la calculadora inmediatamente. La pantalla no mostrará menú ni mensaje alguno.

• Cuando se restablece la calculadora: – Se recuperan los valores de configuración

predeterminados: grados ( DEG ) para modo de ángulo, ( NORM ) para notación numérica normal, ( FLOAT ) para notación decimal flotante y MathPrint™ para modo de pantalla.

– Se borran las variables de memoria, las

operaciones pendientes, las entradas del historial, los datos estadísticos, las constantes y el indicador Ans (Última respuesta).

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados (Consulte la página vi).

• Cuando la pantalla muestre que la línea de entrada tiene más caracteres a derecha e izquierda de los que puede mostrar.

• Pulse & después de la función Automatic Power Down™ (APD™) para volver a encender la calculadora. No se perderán los valores en pantalla, las operaciones pendientes, los valores de configuración ni la memoria.

³ o ´, significa

•Puede utilizar la tecla n en una entrada antes de pulsar <. Si n se pulsa más de una

vez en la entrada actual puede generar un error de sintaxis. Para mostrar el resultado apropiado puede:

– Introducir la expresión, pulsar n < y,

a continuación, pulsar n In de nuevo cuando aparezca el resultado.

– Introduzca la expresión y pulse <, y n

tantas veces como sean necesarias para conmutar el modo de pantalla y ver el formato o la respuesta alternativos.

Función secundaria, apagar, teclas de flecha, intro

• Introduzca 46 – 23.

• Cambie 46 por 41. Cambie 23 por 26 y complete la operación.

• Introduzca + y complete la

operación.

• Apague la calculadora

TI-30XS MultiView™ y vuelva a encenderla. La pantalla de inicio aparece vacía; desplácese hacia arriba para el ver historial

--5

----10

Pulse Pantalla

46 U

%' ! "

# $ <

23 < # # <

!!!! 1 "" 6 < 2 q 5 " T 3 q 10 <

%' & # # #

Restablecer

Restablece la calculadora.

Pulse Pantalla

%

Pulse & y - al mismo tiempo para restablecer la calculadora inmediatamente. La pantalla no mostrará menú ni mensaje alguno.

El uso de % o & y - recupera los valores de configuración predeterminados de la calculadora y limpia la memoria.

Modo

Utilice la tecla p para seleccionar el modo que desee. Pulse $ # ! " para resaltar un modo, y la tecla

< para seleccionarlo. Pulse - o %Q para regresar a la pantalla

de inicio y trabajar con los valores de configuración del modo seleccionado.

Los valores de configuración de modo predeterminados aparecen resaltados.

DEG RAD GRAD define el modo de ángulo en grados, radianes o grados centesimales.

NORM SCI ENG define el modo de notación numérica. Los modos de notación numérica afectan sólo a la presentación en pantalla de los resultados, no a la precisión de los valores almacenados en la unidad, que permanecen sin cambios.

Modo (Continuación)

NORM muestra los resultados con

dígitos a izquierda y derecha del separador decimal, como en 123456,78.

SCI expresa los números con un dígito a la izquierda del separador decimal y la potencia de 10 correspondiente, como en

1,2345678x10

(que es igual que

123456,78). ENG muestra los resultados como

el producto de un número

comprendido entre 1 y mil por una potencia de base 10 y exponente un número entero múltiplo de 3.

Nota: C es un modo de acceso directo del teclado para escribir un número en forma de notación científica. El resultado muestra el número en el formato de notación numérica definido en el modo.

FLOAT 0 1 2 3 4 5 6 7 8 9 define el modo de notación en decimal.

Modo (Continuación)

FLOAT

hasta 10 dígitos, más el signo y el decimal.

(decimal flotante) muestra

0 1 2 3 4 5 6 7 8 9 (decimal fijo)

especifica el número de dígitos (de 0 a 9) que aparece a la derecha del decimal.

CLASSIC MATHPRINT define el

modo de entrada y salida de la pantalla.

CLASSIC muestra las entradas y

salidas en una única línea.

MATHPRINT muestra las entradas

y salidas en formato de texto de varias líneas. Utilice el modo MathPrint para confirmar visualmente que las expresiones matemáticas se han introducido correctamente y comprobar que el modo de notación matemática es correcto.

Nota: Cuando se cambia de modo Classic a MathPrint, se limpian tanto el historial de la calculadora como el valor de la constante.

Menús

Algunas teclas muestran menús:

H, %I , v , %t , % , %h y %{.

Hay teclas que pueden abrir más de un menú.

Pulse " y $ para desplazarse y

seleccionar un elemento de menú, o pulse el número correspondiente situado junto al elemento en cuestión. Para regresar a la pantalla anterior sin seleccionar el elemento,

pulse -. Para salir de un menú o

una aplicación y regresar a la pantalla de inicio, pulse %Q. La pantalla de inicio aparece vacía; desplácese hacia arriba para el ver historial.

Algunos ejemplos de menú:

H % I

PRB RAND DMS R ¶P

1: nPr 1: rand 1: Ä 1: R ´ Pr( 2: nCr 2: randint( 2: Å 2: R ´ P Á( 3: ! 3: Æ 3: P ´ Rx(

4: r 4: P ´ Ry( 5: g 6: ´ DMS

Menús (Continuación)

v (Pulse v una vez para mostrar la

pantalla del editor de datos. Pulse de nuevo para mostrar el menú).

CLEAR FORMULA

1: Clear L1 1: Add/Edit Frmla 2: Clear L2 2: Clear L1 Frmla 3: Clear L3 3: Clear L2 Frmla 4: Clear ALL 4: Clear L3 Frmla

5: Clear ALL

Pulse

desde la opción Add/Edit Frmla (Añadir/Editar fórmula) del menú FORMULA para abrir este menú

1: L1 2: L2 3: L3

STATS

1: 1-Var Stats 2: 2-Var Stats

Esta opción de menú aparece

3: StatVars

después de calcular una estadística con 1- ó 2 variables.

Menú StatVars: 1: n 2:

3: Sx Etc. Consulte el Capítulo 11,

Estadística, para ver una lista completa.

Última respuesta (Ans)

Utilice la función Última respuesta (Ans) para calcular

Pulse Pantalla

5 FT 12

%b% i<

Conmutar respuesta

Pulse la tecla n para conmutar el formato de las respuestas mostradas, ya sea de fracción a decimal, de raíz cuadrada exacta a decimal, de pi exacto a decimal o viceversa.

Pulse Pantalla

% b

8 <

Borrado y corrección

Teclas

1. - borra caracteres y mensajes de error.

Pulse la tecla - una vez para borrar una entrada parcial; púlsela de nuevo para limpiar la pantalla. También puede desplazarse hacia arriba y utilizar - para borrar las entradas del historial. - hace una copia de seguridad de la pantalla en las aplicaciones.

2. % f permite insertar un carácter en el

lugar que ocupe el cursor.

3. J borra el carácter del lugar donde está

el cursor. A continuación y cada vez que se pulse la tecla J, se borra el carácter situado a la izquierda del cursor.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

• El uso de la tecla - no afecta a la memoria, los registros estadísticos, unidades de ángulo ni la notación numérica.

Borrado e inserción

Introduzca 4569 + 285, y cámbielos luego por 459 + 2865. Complete el problema.

Pulse Pantalla

4569 T 285

! ! ! ! ! ! J

" " " "

%f 6

Borrado

Introduzca 21595. Borre el 95. Borre la entrada.

Pulse Pantalla

21595

! ! -

(Borra hacia la derecha)

(Borra la entrada)

Matemáticas básicas

Teclas

1. T suma.

U resta.

3. V multiplica.

W divide.

5. < completa la operación o ejecuta la orden.

M permite introducir un número negativo.

7. % _ añade el símbolo % a un número.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

• La calculadora TI-30XS MultiView™ admite el uso de multiplicación implícita. Ejemplo: 3 (4 + 3) = 21

• No debe confundirse la tecla M con U.

U es la tecla de resta.

• Utilice paréntesis si necesita agrupar los números negativos. Ejemplo: M 2

• Muestra los resultados de los cálculos porcentuales según el modo de notación decimal elegido.

= M 4, y ( M 2) 2 = 4.

3 2 1

Suma, resta, multiplicación, división, igual a

Halle:

2 + 54 16 x 21 =

x 10 =

--2

12 x (5 + 6) =

Pulse Pantalla

½ 6 =

2 T 54 U 6 <

T U V W

16 V 21 <

1 q 2 " V 10 <

12 V D 5 T 6 E <

Números negativos

La temperatura de esta mañana era de

M 3 Ä C a las 6:00 a.m. A las 10:00

a.m., la temperatura ha subido 12 Ä C. ¿Qué temperatura había a las 10:00 a.m.?

Pulse Pantalla

M 3 T 12 <

La temperatura a las 10:00 a.m. era de 9 Ä C.

Por c ent a je

Miguel gana 80 € a la semana, y ahorra el 15% de sus ingresos. ¿Cuánto dinero ahorra Miguel cada semana?

Pulse Pantalla

% _ V 80 <

% _

Miguel ahorra 12

€ por semana.

Orden de las operaciones y paréntesis

Teclas

1. D abre un paréntesis para una expresión.

2. E cierra un paréntesis para una expresión.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

• La transparencia maestra utilizada por el programa Sistema operativo de ecuaciones (EOS™) indica el orden que sigue la calculadora TI-30XS MultiView™ para efectuar los cálculos.

• Las operaciones entre paréntesis se efectúan en primer lugar. Utilice D E para cambiar el orden de las operaciones y, en consecuencia, los resultados. Ejemplo: 1 + 2 x 3 = 7 (1 + 2) x 3 = 9

Sistema operativo de ecuaciones (EOS™)

(primero)

2 Funciones que necesitan un paréntesis de cierre, E,

3 Fracciones 4 Funciones que se han introducido después de la

Expresiones entre paréntesis, D E

que va delante del argumento; por ejemplo, >, A, y algunos elementos de menú

expresión; por ejemplo, F y modificadores de unidades de ángulo (

¡, ¢, £, r, g)

5 Exponenciaciones (G) y raíces (%c)

Nota: En modo Classic, las exponenciaciones que se calculan con la tecla G se calculan de izquierda a derecha. La expresión 2^3^2 se calcula como (2^3)^2, con un resultado de 64.

En modo MathPrint™, las exponenciaciones que se calculan con la tecla G se calculan de derecha a izquierda. Por ejemplo, al pulsar la tecla

2 G 3 G 2, la pantalla muestra , con un resultado

de 512. La calculadora científica TI-30XS MultiView™ calcula

las expresiones introducidas con las teclas F y a de izquierda a derecha en ambos modos, Classic y MathPrint. Cuando se pulsa 3 F F , la pantalla

muestra . La expresión se calcula como (3

2)2

= 81.

6Negación (M)

Sistema operativo de ecuaciones (EOS™)

(Continuación)

7 Variaciones (nPr) y combinaciones (nCr) 8 Multiplicación, multiplicación implícita, división 9 Suma y resta 10 Conversiones (%O, %j, %R y

´DMS)

11 (último) < finaliza todas las operaciones y cierra todos los

paréntesis abiertos.

Orden de las operaciones

1 + 2 x 3 =

Pulse Pantalla

1 T 2 V 3 <

1 + (2 x 3) =

Pulse Pantalla

1 T D 2 V 3 E <

(1 + 2) x 3 =

T V D E

Pulse Pantalla

D 1 T 2 E V 3 <

Orden de las operaciones (Continuación)

Pulse Pantalla

41()3()–

p$$$ <% b 5 F U 4 D 1 E D 3 E <

= (modo Classic))

Pulse Pantalla

41()3()–

(modo MathPrint™)

p$$$ "<% b 5 F U 4 D 1 E D 3 E <

Notación numérica

Teclas

1. p permite seleccionar entre las siguientes opciones del menú de notación numérica.

NORM recupera el modo estándar (decimal

flotante).

SCI activa el modo científico de la

calculadora y muestra el resultado como un número entero elevado a potencia 10 de 1 a 10 veces (1 { n < 10).

ENG activa el modo notación de ingeniería

y muestra los resultados como el producto de un número n por una potencia de base 10 y exponente un número entero (1 { n < 1000). Este exponente es siempre un número múltiplo de 3.

2. C es un modo de acceso directo del teclado para escribir un número en formato de notación científica.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

• Es posible introducir un número en notación científica independientemente del modo de notación numérica definido. Para indicar un exponente negativo, pulse la tecla M antes de introducirlo.

• Los resultados con más de 10 dígitos aparecen automáticamente en notación científica.

• Para obtener más información sobre el modo de notación decimal, consulte el Capítulo 7, Decimales y número de decimales.

• Los modos (NORM, SCI y ENG) afectan sólo a la forma en que aparecen los resultados.

Ingeniería, científica, decimal flotante

Introduzca 12543, que aparecerá tanto en notación decimal normal como en notación numérica normal (ambos valores de configuración se encuentran en la tecla alternativamente el resultado de notación normal a científica e ingeniería, y viceversa, modificando los valores de configuración de la pantalla de modo.

Pulse Pantalla

p). Cambie

12543 <

p$" <

p$" "<

Ingeniería, científica, decimal flotante (Continuación)

p$<

Notación científica

Con la calculadora TI-30XS MultiView™ en los modos Norm y MathPrint™ (ambos son los valores predeterminados), introduzca el siguiente problema en notación científica utilizando la tecla

La Tierra está aproximadamente a 1,5 x 10 está aproximadamente a 7,8 x 10 kilómetros del Sol. Suponiendo que las órbitas de los planetas son circulares y que los dos se

kilómetros del Sol. Júpiter

encuentran al mismo lado del Sol, ¿cuál sería la distancia entre Júpiter y la Tierra?

Pulse Pantalla

7 8 8

C 8 " U 1 8 5 C

8 <

La distancia entre Júpiter y la Tierra sería de 630.000.000 = 6,3 x 10 kilómetros, aproximadamente.

Fracciones

Teclas

1. %N permite introducir números mixtos y fracciones. La unidad debe ser un número entero. El numerador y el denominador pueden contener decimales.

Para introducir un número mixto, escriba un número entero para la unidad, y pulse luego %N para introducir el numerador.

Si en modo MathPrint™, pulsa la tecla %N antes de introducir un entero, la pantalla muestra una plantilla para fracciones en la que sólo podrá introducir un dígito para la unidad.

2. q permite introducir una fracción simple. La pulsación de q antes o después de un número puede generar distintos comportamientos. En modo MathPrint™, si se introduce un número antes de pulsar q, el número pasará a ser el numerador.

q se puede utilizar también en modo MathPrint para calcular, tanto fracciones más complejas como fórmulas que incluyan operadores y otras funciones; para ello, deberá pulsar q antes de introducir el numerador.

En modo MathPrint™, pulse $ entre la introducción del numerador y el denominador. En modo Classic, pulse q entre la introducción del numerador y el denominador.

3. % O convierte el formato de los números de fracción simple a número mixto o de número mixto a fracción simple.

4. % j convierte una fracción en su equivalente decimal o cambia un decimal por su equivalente fraccional siempre que sea posible.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los

1 2

predeterminados.

• En modo MathPrint, las fracciones con q pueden incluir teclas de operación ( T, etc.) y la mayoría de las teclas de función

( F, %_, etc.). En modo Classic, las fracciones con q no admiten el uso de teclas de operación, función ni fracciones complejas en el numerador ni el denominador.

• En modo MathPrint, es posible introducir variables ( x, y, z, t, a, b, y c ) tanto en el numerador como en el denominador de una fracción. En modo Classic, las fracciones con

q no admiten el uso de variables.

Fracciones (Continuación)

• En modo Classic, el editor de datos y las tablas utilizan la tecla W junto con la tecla D y E siempre que sea necesario realizar divisiones complejas.

• Para pegar una entrada anterior en el denominador, coloque el cursor en el denominador, pulse % # para desplazarse hasta la entrada apropiada y, a continuación, pulse < para pegar la entrada.

• Para pegar una entrada anterior en el numerador o la unidad, coloque el cursor en el lugar adecuado, pulse # o % # para desplazarse hasta la entrada apropiada y, por último, pulse < para pegar la entrada en el numerador o la unidad.

• Los resultados y las fracciones introducidas se simplifican al máximo automáticamente.

• Los cálculos que utilizan fracciones pueden mostrar los resultados en forma de fracción o decimal, dependiendo del método de introducción utilizado.

Fracciones

En una fiesta, has comido de la

pizza de pepperoni y de la pizza de

salchichas. Las pizzas eran del mismo tamaño. Si juntamos todos los trozos ¿cuántas partes de una pizza completa has comido?

----10

--6

Pulse Pantalla

5 q 6 " T 1 q 10 <

Has comido de una pizza

completa. ¡Casi una pizza!

---15

Números mixtos

Un bebé ha pesado al nacer 4 libras.

En los primeros 6 meses, ha ganado

2 libras. ¿Cuánto pesa?

--4

--8

Pulse Pantalla

4 %N 3

$ 8 " T 2 %N 3 $ 4 <

%O <

Después de 6 meses, el peso del bebé es de 7 libras.

--8

Conversión de fracciones y decimales

Juan nada 20 vueltas en 5,72 minutos. Mary nada 20 vueltas en

5 minutos. Cambie el tiempo de

--4

Mary a decimales para averiguar cuál de los dos nada más rápido.

Pulse Pantalla

5 % N 3

$ 4 " %j

Juan nada más rápido que Mary, ya que él nada 20 vueltas en 5,72 minutos.

Cambie 2,25 a su fracción equivalente.

Pulse Pantalla

2 8 25 %

o bien 2 8 25 <

Decimales y número de decimales

Teclas

1. 8 introduce un separador decimal.

p permite definir el número de decimales.

2. Pulse $ $ y luego " hasta llegar al número de decimales que desee. Pulse < para seleccionarlo.

FLOAT define el modo de notación decimal

en flotante (estándar).

0-9 define el número de decimales que

debe aparecer. FIX aparece cuando el modo decimal definido es de 0 a 9.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

•Pulse

• La configuración de modo decimal afecta a la

• La calculadora TI-30XS MultiView™ redondea

p $ $ < para regresar al

modo de notación estándar (decimal flotante).

mayoría de los resultados en formato decimal y a la mantisa de los resultados en notaciones científica y de ingeniería.

automáticamente el resultado al número de decimales seleccionado. Por ejemplo, si el número de decimales definido es 2, 0,147 se convierte en 0,15 cuando se pulsa la tecla <. Asimismo, la calculadora TI-30XS MultiView añade ceros para redondear los valores resultantes según el número de decimales seleccionado. Por ejemplo, si el número de decimales definido es 5, 0,147 se convierte en 0,14700 cuando se pulsa la tecla <.

• Cuando se restablece la calculadora se borra el número de decimales establecido y se vuelve a aplicar el valor predeterminado, FLOAT.

• El número de decimales no afecta a la precisión interna de los resultados, sólo a la forma en que la pantalla los muestra.

Decimal

Redondee el número 12,345 a centenas, a décimas y, por último, a notación flotante.

Pulse Pantalla

12 8 345 <

$ $ "

""<

$$"

Constante

Teclas

1. % l activa o desactiva la función de constante y permite definir el número de la constante numérica, operación o expresión que deba utilizarse al pulsar una determinada combinación de teclas. K aparece cuando el modo de constante está activado.

2. < inserta el contenido de K al final de la expresión que aparece en la pantalla.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

• Todas las operaciones, funciones y valores se realizan en modo de constante.

• Para introducir una constante:

1. Pulse % l. Si ya hay una constante

almacenada, pulse - para borrarla.

2. Introduzca la constante (cualquier

conjunto de operaciones, funciones y valores).

3. Pulse < para activar la función de

constante. K aparece en la pantalla para indicar que la función de constante está activada.

4. Pulse - para borrar la pantalla.

5. Introduzca un valor inicial. Si no introduce

un valor, la calculadora asume que se utiliza el valor 0 y muestra Ans en la pantalla.

6. Pulse < para colocar el contenido de K

al final de la expresión y calcularla.

7. Continúe pulsando < para repetir la

constante.

8. Vuelva a pulsar % l para desactivar la

función de constante.

Constante

Por cuidar niños, tres personas

ganan €5,25 cada una por hora. La

primera persona trabaja 16 horas. La segunda persona trabaja 12 horas. La tercera persona trabaja 17 horas. ¿Cuánto ha ganado cada persona?

Pulse Pantalla

V 5.25 <

16 <

12 <

17 <

Constante (Continuación)

(El modo de constante está desactivado).

Memoria y variables almacenadas

Teclas

1. L permite almacenar valores en variables. Pulse L para almacenar una variable; a continuación, pulse z para seleccionar la variable en la que se desea almacenar. Pulse < para almacenar el valor en la variable seleccionada. Si la variable tuviera ya un valor, el nuevo se sobrescribirá al anterior.

2. z permite acceder a las variables. Pulse esta tecla varias veces para seleccionar x, y, z, t, a, b o c. También puede utilizar z para recuperar los valores almacenados de estas variables.

3. % { borra todas las variables.

4. % h abre un menú de las variables x, y, z, t, a, b y c, y permite ver sus valores almacenados antes de pegarlos en la pantalla.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

• Cada variable de memoria permite almacenar un número o una expresión cuyo resultado sea un número real.

• Cuando se selecciona una variable con la tecla z , la pantalla muestra el nombre de la variable (x, y, z, t, a, b, c). El nombre de la variable se inserta en la entrada actual, pero el valor asignado a la variable se utiliza para calcular la expresión.

• Cuando se selecciona una variable con las teclas % h , aparece un menú que muestra el valor de las variables almacenadas. Para seleccionar una variable, pulse el número de menú correspondiente. El valor asignado a la variable se inserta en la entrada actual y se utiliza para calcular la expresión.

• Cuando se restablece la calculadora se borran todas las variables de la memoria.

3 2

Almacenar, variables

A continuación se indica las puntuaciones que los alumnos de matemáticas han obtenido en los exámenes y en las tareas para casa.

Puntuación por examen: 96, 76, 85. Puntuación por tareas: 92, 83, 97,

86.

1. Halle la media de las puntuaciones de los exámenes.

2.Halle la media de las puntuaciones por tareas de

casa.

3.El profesor calculará la nota final de cada alumno a partir de la media de puntuaciones por examen y por tareas. ¿Cuál es la nota final? En caso necesario, el profesor redondeará el valor al número entero más próximo.

Continúa

Almacenar, variables (Continuación)

Pulse Pantalla 96 T 76 T

85 <

W 3 <

L z <

92 T 83 T 97 T 86

W 4 <

T z <

W 2 <

La nota final redondeada al número entero más próximo es 88.

Almacenar, recuperar

Desea enviar un regalo a dos amigos. Ha visto los regalos en dos sitios Web por el mismo precio, pero los costes de envío son diferentes en cada uno. Los paquetes pesan 4,5 libras y 3,2 libras, respectivamente. El almacén A

envía el paquete por €2, más €1,40

por cada libra de peso. El almacén B

envía el paquete por €3, más €1,10

por cada libra. ¿Qué almacén cobra menos por enviar cada paquete?

Pulse Pantalla

4 8 5 L z <

2 T 8 40 E

3 T 8 10 E

Por enviar el paquete que pesa 4,5

libras, el almacén A cobra €8,30 y el almacén B cobra €7,95.

z D 1

Almacenar, recuperar (Continuación)

3 8 2 L z <

##### #<<

Por enviar el paquete que pesa 3,2

libras, el almacén A cobra €6,48 frente a los €6,52 que cobra el

almacén B.

Almacenar, recuperar (Continuación)

Tienda Artículo Cantidad Coste

A camisas 2 €13,98 unidad. B corbatas 3 €7,98 unidad. C cinturón 1 €6,98

tirantes 1 €9,98

¿Cuánto ha gastado en cada tienda, y cuánto en total?

Pulse Pantalla

2 V 13 8 98 <

Lz<

3 V 7 8 98 <

L z z <

Almacenar, recuperar (Continuación)

6 8 98 T 9 8 98 <

L z zz<

% h

1 T% h 2 T %

h 3 <

Ha gastado:

€27,96 en la tienda A, €23,94 en la tienda B y €16,96 en la tienda C.

En total, ha gastado €68,86 en las

tres tiendas.

Fórmulas del editor de datos y listas

Teclas

1. v muestra el editor de datos con tres listas. Cada lista puede contener hasta 42 elementos. Para introducir datos, desplácese hasta una lista y escriba un número. Pulse las teclas de flecha para desplazarse por los elementos de la lista.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

• Las fórmulas de listas aceptan todas las funciones de la calculadora.

• En las fórmulas, utilice las teclas D y E para encerrar entre paréntesis los nombres de variables o listas a fin de garantizar que las operaciones se efectúen en el orden apropiado.

• Cuando se introduce una fórmula en una lista, la lista de fórmulas se actualizará automáticamente cuando se actualice el elemento de la lista que esté relacionado con la fórmula.

Nota: Si se pulsa < en una lista de fórmulas, la fórmula se borra automáticamente. La pantalla no mostrará mensaje alguno.

• Cuando se borra una fórmula, los datos permanecen y siguen estando disponibles, aunque no se actualizarán.

• Si vuelve a pulsar v desde la pantalla del editor de datos, se abre un menú con opciones que puede utilizar para borrar listas

o introducir y trabajar con fórmulas.

• Si vuelve a pulsar v desde la opción “Add/ edit formula”, se abre un menú con nombres de lista que podrá utilizar para añadir o editar fórmulas.

• Al pulsar - vuelve a aparecer la pantalla del editor de datos.

• La tecla % Q permite salir del editor de datos y regresar a la pantalla de inicio.

• En el editor de datos, la notación científica aparece como E para ahorrar espacio, aunque sigue mostrando la magnitud de un número.

Ejemplo: 2 x 10

aparece como 2E3.

Introducción de datos y fórmulas

En un día de noviembre, el informe del tiempo publicado en Internet recogía las temperaturas siguientes.

París, Francia 8Ä C Moscú, Rusia

½1Ä C

Montreal, Canadá 4Ä C Convierta estas temperaturas de

grados Celsius a grados Fahrenheit.

Recordatorio: F= C+32.

--5

Pulse Pantalla

v 8 $ M

$ 4 $ "

v "

W 5 V v

1 T 32

Introducción de datos y fórmulas (Continuación)

Observe que L2 aparece resaltado, ya que es el resultado de una fórmula.

Los grados Fahrenheit son: París, Francia 46,4Ä F

Moscú, Rusia 30,2Ä F Montreal, Canadá 39,2Ä F

Si la temperatura de Sydney, Australia, es 21Ä C, halle la temperatura en grados Fahrenheit.

! $ $ $

La temperatura de Sydney, Australia es 69,8Ä F.

Estadística

Teclas

1. v permite introducir puntos de datos (x para

estadística con una variable, 1-Var; estadística con dos variables, 2-Var). (Consulte el Capítulo 10, Editor de datos y fórmulas de listas, para obtener más información sobre v).

2. %t muestra un menú con opciones donde

podrá elegir trabajar con 1-Var, 2-Var o StatVars. 1-Var analiza datos de un conjunto de

datos con respecto a una variable medida, x.

2-Var analiza pares de datos de conjuntos

de dos conjuntos de datos con respecto a dos variables medidas, x, la variable independiente, e y, la variable dependiente.

StatVars esta opción sólo aparece después de

haber calculado estadísticas con una o dos variables. Abre un menú de las variables con sus valores actuale

e y para

s..

Menú StatVars:

n Número de puntos de datos de x (o

x, y).

v o w

Media de todos los valores de x o de y.

Sx o Sy Desviación estándar de la muestra

de x o de y.

sx o sy Desviación estándar de la población

de x o de y.

Gx o Gy Suma de todos los valores de x o de

o Gy

Suma de todos los valores de x2 o de

Gxy Suma del producto de x e y para

todos los pares de x-y en las dos listas.

a Pendiente de regresión lineal. b Punto de corte con el eje Y de la

regresión lineal.

r Coeficiente de correlación. x ÅÅÅÅ (2-var) Utiliza a y b para calcular el valor

previsto de x cuando se introduce un valor para y.

y ÅÅÅÅ (2-var) Utiliza a y b para calcular el valor

previsto de y cuando se introduce un valor para x.

minX Mínimo de valores de x. Q1 (1-var) Mediana de los elementos entre

MínX y Med (primer cuartil).

Med Mediana de todos los puntos de

datos.

Q3 (1-var) Mediana de los elementos entre Med

y MáxX (tercer cuartil).

maxX Máximo de valores de x.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

• Si desea cambiar los puntos de datos, vaya al editor de datos, desplácese hasta el elemento de datos apropiado y cambie el valor por otro. Nota: A continuación deberá recalcular una estadística con 1-Var o 2-Var para que aparezca la opción StatVars.

Introducción de datos para estadística con una variable

Cinco alumnos han hecho un examen de matemáticas. Utilizando las puntuaciones obtenidas, introduzca los puntos de datos: 85, 85, 97, 53,

77. Pulse Pantalla

85 $ 97 $ 53 $ 77 $

" 2 $1 $1

%t v

$1 $

Visualización de estadísticas

Halle el número de puntos de datos (n), la media (

v), la desviación

estándar de la muestra (Sx), la desviación estándar de la población (

sx), la suma de las puntuaciones Gx), la suma de los cuadrados (Gx

(

) y el resumen de los cinco números de datos, minX, Q1, Q2 y maxX.

Pulse Pantalla

1 $ " "

%t v

< $

$ $ $ $ $

$ $ $

$ $

Eliminación de puntos de datos

Reduzca al mínimo la puntuación del examen editando los datos de la lista L1 del editor de datos. Asegúrese de actualizar la lista de frecuencia, L2, si fuese necesario. Halle la nueva media ( de todas las listas.

Pulse Pantalla

v). Por último, borre los datos

$ $

J " J

$$<

vv 4

Introducción de datos para estadística con dos variables

La tabla siguiente muestra el número de zapatillas de deporte vendidas en un pequeño comercio. La tabla muestra el número total de pares de zapatillas vendidos en dos meses y el número total de pares de la marca A vendidos en el mismo tiempo. Introduzca estos datos en el editor de datos.

Meses Abril 58 35 Mayo 47 28

Nº total (x) Marca A (y)

%t v

Pulse Pantalla

v58 $ 47 $

"35 $28 $

Visualización de estadísticas

Suponiendo que el porcentaje de zapatillas vendidas es una constante, utilice dos puntos de datos para predecir las ventas de la marca A durante el mes de junio, si ya conocemos las ventas totales de junio. Utilice la recta de mejor ajuste para hallar las ventas de junio de la marca A si la tienda vende un total de 32 pares en el mes de junio.

Sugerencia: Halle y'(32).

Pulse Pantalla

2 $ $ <

(desplácese hacia

abajo hasta y')

32 E <

En junio se venderán 18 pares de la marca A si el total de ventas es de 32 pares.

Probabilidad

Teclas

1. H muestra el siguiente menú de funciones.

nPr calcula el número de

variaciones.

nCr calcula el número de

combinaciones.

! calcula el factorial de un

número.

Rand genera un número real

aleatorio entre 0 y 1.

Randint( genera un número entero

aleatorio comprendido entre 2 enteros dados, A y B, donde A  Randint  B.

Notas

• En los ejemplos de las transparencias maestras se considera que los valores de configuración en uso son los predeterminados.

• Una combinación es una disposición de objetos en la que el orden no es importante, como en una mano de cartas.

• Una variación es una disposición de objetos en la que el orden es importante, como en una carrera.

• Un factorial es el producto de todos los enteros positivos de 1 a n, donde n es un

número entero positivo  69.

•Puede almacenar (L) un número entero en Rand exactamente igual que si guardara valores en las variables de memoria. Si desea controlar los números aleatorios generados por todas las calculadoras de la clase, pida a los alumnos que almacenen el mismo número en Rand; la secuencia de números aleatorios será la misma en todas las calculadoras.

•Para Randint, utilice una coma para separar los 2 números que especifique.

Combinaciones (nCr)

En su estantería tiene espacio para 2 libros, pero tiene 4 libros para colocar en la estantería. Utilice esta fórmula para hallar cuántas formas hay de colocar los 4 libros en el espacio para

4 nCr 2

ABCD

AB y BA cuentan como

AB AC AD BA

BC BD

una única combinación

Pulse Pantalla

CA DA

CB CD DB DC

4 H $

< 2 <

Sólo hay 6 combinaciones de 2 libros elegidos entre 4 libros distintos.

Texas Instruments TI-30XS MultiView Guide [es]

Specifications and Main Features

Frequently Asked Questions

User Manual