Texas instruments TI-30XS MULTIVIEW User Manual

TI-30XS MultiView™

Um manual para os

professores

Desenvolvido pela

Texas Instruments Incorporated

Actividades desenvolvidas por

Gary Hanson, Aletha Paskett e Margo Lynn Mankus

Ilustrado por

Jay Garrison e David Garrison

Acerca dos autores

Gary Hanson

e

Aletha Paskett

são professores de Matemática na Jordan Independent School District em Sandy, Utah. Desenvolveram várias actividades e avaliaram a adequação dos exemplos na secção Como utilizar a

Margo Lynn Mankus

trabalha actualmente em Educação Tecnológica e Matemática na State

TI-30XS MultiView™

University de Nova Iorque em New Paltz. Reviu e actualizou os materiais da

deste manual.

TI-30XS MultiView

e desenvolveu várias actividades para este manual.

Informações importantes

A Texas Instruments não dá qualquer garantia, expressa ou implícita, incluindo, mas não se limitando a quaisquer garantias implícitas de comercialização e de adequação a um propósito específico, com respeito a quaisquer programas ou materiais de livros, e somente disponibiliza esses materiais no estado em que se encontram.

Em hipótese alguma a Texas Instruments poderá ser responsabilizada perante qualquer pessoa por danos especiais, colaterais, incidentais ou conseqüenciais, que tenham qualquer ligação ou que resultem da compra ou utilização desses materiais, e a única e exclusiva responsabilidade da Texas Instruments, independentemente da forma de atuação, não deve exceder qualquer preço de compra aplicável deste artigo ou material. Além disso, a Texas Instruments não poderá estar sujeita a qualquer reivindicação, seja de que espécie for, com respeito ao uso desses materiais por qualquer outra parte.

Texas Instruments Incorporated 7800 Banner Drive, M/S 3918 Dallas, TX 75251

Attention: Manager, Business Services

Impresso nos EUA.

MultiView, MathPrint, Automatic Power Down, APD e EOS são marcas comerciais da Texas Instruments Incorporated.

Índice

CAPÍTULO PÁGINA CAPÍTULO PÁGINA

Acerca do manual do professor v Acerca da calculadora

TI-30XS MultiView™ vi

Actividades

Viagem às estrelas

Notação científica 3

Frequências cardíacas

Estatística de 1 variável 7

Nos cinemas

Fórmulas de dados na bilheteira 15

Nomear a regra (Name that rule)

Expressões algébricas 23

Como utilizar a calculadora TI-30XS MultiView

11 Estatística 85 12 Probabilidade 91 13 Tabela de funções 99 14 Potências, raízes e recíprocos 103 15 Funções exponenciais e

logarítmicas 111 16 Pi 115 17 Conversões e definições

de ângulos 119 18 Conversões polares e

rectangulares 123 19 Trigonometria 125 20 Hipérbole 133

(Continuação)

1 Operações básicas da

TI-30XS MultiView 31 2 Apagar e corrigir 43 3 Matemática básica 47 4 Ordem das operações e

parêntesis 51 5 Notação numérica 57 6 Fracções 61 7 Decimais e casas decimais 67 8 Constante 69 9 Variáveis guardadas e de memória 73 10 Editor de dados e fórmulas

das listas 81

Anexo A

Referência rápida das teclas A-1

Anexo B

Indicadores do ecrã B-1

Anexo C

Mensagens de erro C-1

Anexo D

Informações de assistência e suporte D-1

Anexo E

Informações das pilhas E-1

Acerca do manual do professor



Organização do manual do professor

Este manual destina-se às calculadoras científicas TI-30XS MultiView™ e TI-30XB MultiView. Todas as referências subsequentes neste manual referem-se à TI-30XS MultiView, mas também são aplicáveis à TI-30XB MultiView.

Este manual é composto por duas secções:

Actividades e Como utilizar a calculadora TI-30XS MultiView. A secção Actividades é um

conjunto de actividades para integrar a TI-30XS MultiView no ensino da matemática. A

secção Como utilizar a calculadora TI-30XS MultiView foi concebida para o ajudar a

ensinar os estudantes a utilizar a calculadora.

Cada secção utiliza as predefinições, incluindo o modo MathPrint™, excepto se indicado em contrário.

Actividades

Cada actividade é autónoma e inclui o seguinte:

Como utilizar a TI-30XS MultiView

Esta secção contém exemplos em acetatos. Os capítulos são numerados e incluem o seguinte.

• Uma página introdutória que descreve as teclas da calculadora apresentadas no exemplo, a localização das teclas na TI-30XS MultiView e qualquer nota pertinente sobre as funções.

• Os acetatos a seguir à página introdutória fornecem exemplos de aplicações práticas das teclas em discussão. As teclas em discussão aparecem a preto no teclado da TI-30XS MultiView. As definições do modo para o exemplo aparecem também.

Reiniciar a TI-30XS MultiView

• Pode garantir que todos os estudantes começam no mesmo ponto através da reinicialização das calculadoras dos estudantes: Prima & e -

simultaneamente ou prima %  e seleccione 2 (Yes).

• Uma apresentação do objectivo matemático da actividade.

• Conceitos matemáticos a desenvolver.

• Materiais necessários para efectuar a actividade.

• Procedimento detalhado, incluindo os batimentos das teclas da TI-30XS MultiView passo a passo.

• Folha de actividade do estudante.

Convenções utilizadas no manual do professor

• No texto, os parêntesis [ ] à volta do nome/ símbolo da tecla indicam que a tecla é uma função secundária ou alternativa.

Por exemplo: %Z

Acerca da calculadora TI-30XS MultiView™

Ecrã inicial

Pode introduzir funções e expressões matemáticas juntamente com outras instruções no ecrã inicial. As respostas aparecem no ecrã inicial. O ecrã da TI-30XS MultiView pode apresentar um máximo de 4 linhas com um máximo de 16 caracteres por linha. Para entradas e expressões com mais de 16 caracteres, pode deslocar-se para a esquerda e para a direita (! e ") para ver a expressão ou a entrada completa.

Quando premir %Q, a calculadora TI-30XS MultiView devolve um ecrã inicial em branco. Prima # e $ para ver e reutilizar as entradas prévias. (Ver entradas prévias, página vii.)

No modo MathPrint™, pode introduzir até quatro níveis de expressões e funções consecutivas, que incluem fracções, raízes quadradas, expoentes

x

com ^, , ex e 10x.

Quando calcular uma entrada no ecrã inicial, dependendo do espaço, a resposta aparece directamente à direita da entrada ou no lado direito da linha seguinte.

y

alterar a ordem das operações e, por conseguinte, alterar o resultado.

Modo

Utilize ppara seleccionar modos. Prima $ # ! " para escolher um modo e < para o

seleccionar. Prima - ou %Q para voltar ao ecrã inicial e efectuar o trabalho com as definições do modo escolhido. Aparecem as predefinições.

O modo CLASSIC mostra as entradas e as saídas numa linha.

O modo MATHPRINT mostra a maioria das entradas e saídas em formato de livro de texto. Utilize o modo MathPrint para melhor confirmação visual que as expressões matemáticas foram introduzidas correctamente e reforço da notação matemática correcta.

Nota: Se comutar o modo entre Classic e MathPrint, apaga o histórico da calculadora e o valor da constante.

Indicadores do ecrã

Consulte o Anexo B para obter uma lista de indicadores do ecrã.

Ordem das operações

A TI-30XS MultiView utiliza o Equation Operating System (EOS™) para avaliar as expressões. As prioridades das operações estão listadas no acetato no Capítulo 4, Ordem de operações e parêntesis.

Como as operações entre parêntesis são efectuadas primeiro, pode utilizar o D E para

2ª funções

Se premir %, aparece o indicador 2ª e, em seguida, acede à função impressa por cima da próxima tecla premida. Por exemplo, %b 25 < calcula a raiz quadrada de 25 e devolve o resultado 5.

Acerca da TI-30XS MultiView™ (Continuação)

Menus

Determinadas teclas mostram menus: H, %I, v, %t, %, %h e %{.

Prima " ou $ para percorrer e seleccionar um item do menu ou prima o número correspondente junto ao item do menu. Para voltar ao ecrã anterior sem seleccionar o item, prima -. Para sair de um menu ou uma aplicação e voltar ao ecrã inicial, prima %Q.

Entradas anteriores # $

Depois de avaliar uma expressão, utilize # e $ para percorrer as entradas anteriores guardadas no histórico da TI-30XS MultiView. Pode reutilizar uma entrada anterior, premindo < para a colar na linha inferior, editando e avaliando uma nova expressão.

Comutação de respostas n

A comutação de respostas apresenta o último resultado calculado em diferentes formatos de saída, onde for possível. Prima n para comutar o resultado apresentado entre fracções e decimal, raízes quadradas exactas e decimal, pi exacto e decimal.

Reiniciar a TI-30XS MultiView

Se premir & e - simultaneamente ou premir %  e seleccionar 2 (Yes), reinicia a

calculadora.

Reiniciar calculadora:

• Devolve as definições para as predefinições — notação standard (decimal flutuante) e modo de graus (DEG).

• Apaga as variáveis da memória, operações pendentes, entradas no histórico, dados estatísticos, constantes e Ans (Última resposta).

Nota: Os exemplos dos acetatos assumem todas as predefinições.

Automatic Power Down™ (APD™)

Se a TI-30XS MultiView permanecer inactiva durante cerca de 5 minutos, a funcionalidade APD desliga-a automaticamente. Prima & para ligar a calculadora novamente. O ecrã, as operações pendentes, as definições e a memória são retidos.

Mensagens de erro

Consulte o Anexo C para obter uma lista de

Última resposta (Ans)

O resultado calculado mais recentemente é guardado na variável Ans. Ans é retida na memória mesmo depois de desligar a TI-30XS MultiView. Para rechamar o valor de Ans:

•Prima % i (Ans aparece no ecrã) ou

• Prima qualquer tecla de operação (T, U, etc) como a primeira parte de uma entrada. Ans e o operador aparecem no ecrã.

mensagens de erro.

Actividades

Viagem às estrelas —

Notação científica 3

Frequências cardíacas —

Estatística de 1 variável 7

Nos cinemas —

Fórmulas de dados na bilheteira 15

Nomear a regra (Name that rule) —

Expressões algébricas 23

Viagem às estrelas — Notação científica

Apresentação

Os estudantes investigam a notação científica, alterando os números para notação científica e, em seguida, utilizando-os em cálculos.

Introdução

Configure a actividade, dizendo aos estudantes:

O formato standard da notação científica é aaaa¿10 em que aaaa é maior ou igual a 1 e menor que 10, e nnnn é um número inteiro.

1. Deixe os estudantes escreverem os seguintes

números em notação científica com lápis e papel.

a. 93 000 000 b. 384 000 000 000 c. 0.00000000000234 d. 0.0000000157

9.3

3.84

2.34

1.57

7

¿

10

11

¿

10

-12

¿

10

-8

¿

10

1010

Conceitos matemáticos

• Notação científica

•Adição

•Divisão

nnnn

,

Materiais

• TI-30XS MultiView™

•Lápis

• Actividade do estudante

2. Deixe os estudantes alterarem os seguintes números para notação científica (SCI) com a calculadora científica TI-30XS MultiView.

¿

10

¿

10

-9

7

8

-6

a. 12 000 000 b. 974 000 000 c. 0.0000034 d. 0.000000004

Nota:

Nota: As respostas assumem a predefinição de decimal

Nota:Nota:

flutuante.

1.2

9.74

3.4 4

¿

3. Deixe os estudantes alterarem os seguintes números para notação standard (NORM).

7

¿ 10

a. 5.8 b. 7.32 ¿ 10 c. 6.2 ¿ 10 d. 3 ¿ 10

Nota:

Nota: Para introduzir um número negativo, prima M e, em

Nota:Nota:

5

-6

-8

seguida, introduza um número.

58 000 000 732 000

0.0000062

0.00000003

³ Siga estes passos:

1. Introduza o primeiro número,

12000000.

2. Prima

3. Prima

³ Siga estes passos:

1. Introduza 5.8; prima

2. Introduza 7; prima

3. Prima

p. $ " < - <para

ver o número em notação científica.

1.2Ã

Ã10

ÃÃ

7

p.

$ < - <.

58000000

C.

Viagem às estrelas — Notação científica (Continuação)

Actividade

Apresente o seguinte problema aos estudantes:

É capitão de uma nave espacial no futuro distante. Recebeu como missão ir a Alpha Centauri e tem 5 anos para chegar lá. A distância do Sol a Alpha

13

Centauri é 2.5 x 10 ao Sol é cerca de 9.3 x 10

milhas. A distância da Terra

7

milhas.

Apesar de não saberem como é viajar à velocidade da luz, vive num tempo em que a nave pode viajar à velocidade da luz.

A luz viaja a uma distância aproximada de 6 x 10

12

milhas por ano luz. Trace um caminho da Terra ao Sol e, em seguida, para Alpha Centauri. Conseguirá chegar a tempo a Alpha Centauri?

Procedimento

1. Utilize a calculadora TI-30XS MultiView™ para

calcular a distância total da viagem.

2.5 ¿ 10

13

+ 9.3 ¿ 10

2. Em seguida, calcule o tempo que demorará a

percorrer a distância. (Distância percorrida ano luz)

2.5000093 10

---------------------------------------------

610

×

12

×

3. Consegue fazer a viagem no tempo atribuído de

5 anos?

Sim, se a nave conseguir viajar à velocidade da luz.

7

= 2.5000093 ¿ 10

13

4.1666821672

=

13

anos

milhas

¾ 1

Sugestão: Certifique-se de que a calculadora TI-30XS MultiView está no modo MathPrint™ para resolver este problema.

Sugestão:

milhas do Sol.

³ Siga estes passos:

A Terra está a cerca de 9.3 x 10

1. Prima 2.5 7

<.

2.5000093Ã

2. Prima %i q 6 C 12

4.166682167

C13 " T 9.3 C

13

Ã10

ÃÃ

<.

7

Extensão

A luz viaja a 186.000 milhas por segundo. Um ano luz é a distância que a luz pode viajar num ano. Deixe os estudantes converterem um ano luz para milhas viajadas por ano luz.

186 000milhas,

--------------------------------------1seg

60

------------ -

Aproximam-se deste valor com 6x10

seg

1min

××

60

min

-------------- 1hora

×

hrs

24

------------1dia

365

------------------ -

×

1ano

dias

5.87 10

------------------------------------------- -

≈

12

milhas num

12

1ano

milhas×

³ Dependendo do problema, não se

esqueça de dizer aos estudantes para incluírem parêntesis onde for necessário para garantirem a ordem das operações. Exemplo: (2.5000093 x 10 de incluir os parêntesis para obter o resultado correcto.

13

) ¾ (6 x 1012) tem

ano luz nesta actividade. Responder à extensão dos estudantes: A nave

demorará cerca de 15 anos a chegar a Delta Centauri.

³ Os estudantes podem aprender mais

sobre este tópico, visitando sítios Web da NASA na Internet.

Viagem às estrelas

Nome ___________________________

— Notação científica

Data ___________________________

Problemas

1. Escreva os seguintes números em notação científica.

Notação científica Notação científica

a. 93 000 000 __________________________

b. 384 000 000 000 __________________________

c. 0.00000000000234 __________________________

d. 0.0000000157 __________________________

2. Utilize a calculadora TI-30XS MultiView™ para alterar os seguintes números para notação científica com o modo SCI.

Notação científica Notação científica

a. 12 000 000 __________________________

b. 974 000 000 __________________________

c. 0.0000034 __________________________

d. 0.000000004 __________________________

3. Utilize a calculadora TI-30XS MultiView para alterar os seguintes números para notação decimal standard com o modo NORM.

Notação científica Notação standard

a. 5.8 ¿ 10

b. 7.32 ¿ 10

c. 6.2 ¿ 10

d. 3 ¿ 10

7

5

-6

-8

_________________________

Viagem às estrelas

Nome ___________________________

— Notação científica

Data ___________________________

Problema

É capitão de uma nave espacial no futuro distante. Recebeu como missão ir a Alpha Centauri e tem 5 anos para chegar lá. A distância do Sol a Alpha Centauri é 2.5 x 1013 milhas. A distância da Terra ao Sol é cerca de 9.3 x 107 milhas.

Apesar de não saberem como é viajar à velocidade da luz, vive num tempo em que a nave pode viajar à velocidade da luz.

A luz viaja a uma distância aproximada de 6 x 1012 milhas por ano luz. Trace um caminho da Terra ao Sol e, em seguida, para Alpha Centauri. Conseguirá chegar a tempo a Alpha Centauri?

Procedimento

1. Utilize a calculadora TI-30XS MultiView™ para calcular a distância total da viagem. Para esta precisão aproximada, assuma que está a medir a distância como uma linha recta da Terra ao Sol e, em seguida, para Alpha Centauri.

____________________________________________________________________________

Sugestão: Certifique-se de que a calculadora está no modo de notação científica antes de começar o cálculo.

Em seguida, calcule o tempo que demorará a percorrer a distância. (Distância percorrida ¾ 1 ano luz)

Sugestão: Certifique-se de que utiliza parêntesis para obter o resultado correcto para este problema de divisão. _________________________________________________________________

_________________________________________________________________

2. Consegue fazer a viagem no tempo atribuído de 5 anos? _________________________________________________________________

Extensão

Agora que foi bem-sucedido, foi-lhe pedido para fazer outra viagem. A distância do Sol a Delta Centauri é 9 x 1013 milhas. Quanto tempo demorará a viagem a partir da Terr a?

Sugestão: A Terra está a cerca de 9.3 ¿ 107 milhas do Sol.

A viagem neste nave é fictícia. Se estiver interessado em saber mais sobre as distâncias cósmicas e estrelas mais próximas, visite os sítios Web da NASA na Internet.

Frequências cardíacas — Estatísticas de 1 variável

Apresentação

Os estudantes utilizam o editor de dados e a função estatística da calculadora TI-30XS MultiView™ para investigarem o efeito do exercício na frequência cardíaca.

Introdução

Os estudantes podem formar pequenos grupos para esta actividade para minimizar a quantidade de dados a introduzir. Perguntar aos estudantes:

• Qual é a frequência cardíaca média para alguém da vossa idade?

• E depois de fazerem algum exercício?

Actividade

Peça aos estudantes para preencherem a seguinte investigação para verificar as previsões.

1. Peça aos estudantes para verificarem a frequência cardíaca, medindo o pulso durante 1 minuto. (Pode dizer-lhes para medirem durante 10 segundos e, em seguida, multiplicarem por 6, mas este pode ser o minuto mais sossegado do dia!)

Conceitos matemáticos

• Média, mínima, máxima e intervalo

Materiais

• TI-30XS MultiView

• Cronómetro ou um relógio com dois ponteiros

• Actividade do estudante

2. Recolha os dados no gráfico. Introduza a frequência cardíaca de cada estudante e uma marca na coluna de frequência. Como outros estudantes têm a mesma frequência cardíaca, adicione outra marca na coluna de frequência.

3. Introduza os dados da frequência cardíaca na calculadora científica TI-30XS MultiView.

a. Introduza a primeira frequência cardíaca em

L1 e o número de marcas para essa frequência cardíaca em L2. Utilizará L2 como a frequência.

b. Tem de premir

exemplo, introduza a primeira frequência cardíaca e prima

c. Por exemplo, assuma uma classe de 22

estudantes:

$ entre as entradas. Por

$.

Frequência Estudantes Frequência Estudantes

603633 615641 626654

³ Siga estes passos:

1. Prima

v para introduzir as

frequências e as frequências cardíacas. Introduza as frequências cardíacas em L1 e as frequências

em L2. Prima

$ entre as entrada e

" para ir de L1 para L2.

2. Continue a introduzir até seleccionar todas as frequências e frequências cardíacas.

3. Prima

4. Prima 1 para seleccionar a

5. Seleccione L1 para os dados e L2

6. Prima

% t.

estatística de 1 variável.

para a frequência.

$< para ver os dados.

Frequências cardíacas — Estatística de 1 variável

(Continuação)

4. Verifique os cálculos estatísticos. Depois de apresentar aos estudantes que a cardíacas. Perguntar aos estudantes:

Òx é a soma de todas as frequências

Òx (Sigma x), explique

• Quantos batimentos cardíacos foram

introduzidos de todos os estudantes num minuto? Isto é

Òx

.

• Quantos estudantes foram introduzidos? Isto é

nnnn.

• Como é que podemos calcular a frequência

Σx

cardíaca média? Isto é

------

Ï

.

62.27272727=

n

• A frequência cardíaca média é mais elevada ou

mais baixa do que o previsto?

5. Agora veremos o efeito de algum exercício na frequência cardíaca. Para acomodar as necessidades de vários estudantes, junte os estudantes com outros estudantes que sejam capazes de completar a tarefa. Considere também a concepção de alguma tarefa que um estudante possa fazer em segurança para aumentar a frequência cardíaca. Dizer aos estudantes:

Se em qualquer ponto da actividade sentirem dor, fraqueza ou insuficiência respiratória, parem imediatamente.

³ Siga estes passos:

1. Veja os dados estatísticos.

n deve ser igual ao número total de estudantes da amostra. Para este exemplo, n = 22.

2. Prima de frequência cardíaca média. Ï = 62.27272727

3. Prima

Òx = 1370

Nota: Os números mostram os

resultados para o exemplo descrito nesta actividade. Os resultados dos estudantes dependem do tamanho do grupo e das leituras das frequências cardíacas.

$ a Ï para ver a

$ até ver Òx.

6. Peça aos estudantes para correrem durante 2 minutos e dê-lhes estas instruções:

Medir o pulso durante 1 minuto.

a.

Registar a frequência cardíaca como

b.

anteriormente. c. Introduzir os dados na calculadora. d. Compare a frequência cardíaca média depois

de correr com a frequência cardíaca em

descanso.

(Continuação)

Frequências cardíacas — Estatística de 1 variável

7. Peça aos estudantes para saltarem durante 2 minutos. Instrua-os para medirem o pulso durante 1 minuto novamente e registarem como anteriormente. Peça-lhes para introduzirem os dados na calculadora novamente e calcularem a frequência cardíaca média depois dos saltos. Compare com as outras 2 médias.

8. Instrua os estudantes para fazerem um gráfico de barras dos 3 conjuntos de dados recolhidos. Perguntar aos estudantes:

• Quais são as semelhanças dos gráficos de

barras?

• Quais são as diferenças?

• Os dados agrupados são iguais ou mais

espalhados num gráfico em comparação com outro?

(Continuação)

Frequências cardíacas —

Nome ___________________________

Estatística de 1 variável

Data ___________________________

Problema

Qual é a frequência cardíaca média para alguém da vossa idade? E depois de fazerem algum exercício?

Procedimento

1. Utilize esta tabela para registar os dados do grupo ou da turma (em descanso).

Batimentos cardíacos

por minuto

(em descanso)

Frequência

2. Qual é a média da turma (grupo)? ________________________________________

3. Responda às seguintes questões a partir dos dados:

a. Qual é o número total de batimentos cardíacos por minuto? Escreva o símbolo

e o número na calculadora._____________________________________________

b. Qual é o número total de batimentos cardíacos dos estudantes introduzido?

Escreva o símbolo e o número na calculadora. __________________________

c. Como calcularia a frequência cardíaca média? ___________________________

A resposta é igual à resposta da questão 2? ______________________________

Frequências cardíacas —

Nome ___________________________

Estatística de 1 variável

4. Utilize esta tabela para registar os dados do grupo ou da turma (depois da corrida).

Batimentos cardíacos

por minuto

(depois da corrida)

Data ___________________________

Frequência

5. Qual é a média da turma (grupo)? ________________________________________

6. Responda às seguintes questões a partir dos dados:

a. Qual é o número total de batimentos cardíacos por minuto?

Escreva o símbolo e o número na calculadora.__________

b. Qual é o número total de batimentos cardíacos dos

estudantes introduzido? Escreva o símbolo e o número na calculadora.

___________________________________________________

c. Como calcularia a frequência cardíaca média?

___________________________________________________

A resposta é igual à resposta da questão 5? ____________

Frequências cardíacas —

Nome ___________________________

Estatística de 1 variável

7. Utilize esta tabela para registar os dados do grupo ou da turma (depois dos saltos).

Batimentos cardíacos

por minuto

(depois dos saltos)

Data ___________________________

Frequência

8. Qual é a média da turma (grupo)? ________________________________________

9. Qual é o número total de batimentos cardíacos por minuto? ________________

10.Responda às seguintes questões a partir dos dados:

a. Qual é o número total de batimentos cardíacos por minuto? Escreva o símbolo

e o número na calculadora.___________________________________________

b. Qual é o número total de batimentos cardíacos dos estudantes introduzido?

Escreva o símbolo e o número na calculadora. _________________________

c. Como calcularia a frequência cardíaca média? __________________________

A resposta é igual à resposta da questão 8? _____________________________

Frequências cardíacas —

Nome ___________________________

Estatística de 1 variável

11. Faça um gráfico de barras para cada um dos 3 conjuntos de dados recolhidos.

Descanso Corrida Saltos

Data ___________________________

12.Quais são as semelhanças dos gráficos de barras? Quais são as diferenças? __ _______________________________________________________________________

_______________________________________________________________________

13.Os dados agrupados são iguais ou mais espalhados num gráfico em comparação

com outro? _____________________________________________________________

_______________________________________________________________________ _______________________________________________________________________

Nos cinemas — Fórmulas de dados na bilheteira

Apresentação

Os estudantes investigam uma tabela de valores e observam os padrões na tabela. Os estudantes utilizam v na calculadora TI-30XS MultiView™ para introduzir dados numa lista e testar as generalizações.

Introdução

A questão de preparação é fornecida para o ajudar a lançar a actividade da folha do estudante. Pode ignorar a actividade de preparação, mas terá de orientar mais durante a investigação do problema na folha do estudante.

Preparação

Oriente os estudantes na utilização de tabelas e v para ver um padrão e escrever uma generalização. Apresente a seguinte história.

Todas as Quartas-feiras, a Joana chega demasiado tarde do trabalho para passear o seu cão Max. Pediu ao vizinho Pedro para passear o cão depois de vir da escola. O Pedro está muito contente por poder ajudar! A Joana paga €4 euros ao Pedro todas as semanas para passear Max. O Pedro gosta de poupar dinheiro. Criem uma tabela para determinar que dinheiro tem o Pedro cada semana durante 5 semanas.

Conceitos matemáticos

•Padrões

•Expressões algébricas

• Funções lineares

• Variáveis

Materiais

• TI-30XS MultiView

•Lápis

• Papel milimétrico

• Actividade do estudante

Oriente os estudantes para criarem a seguinte tabela no papel. Pode pensar nesta tabela como uma lista de dados de dois números que dependem um do outro. É importante que os estudantes escrevam o cálculo e o resultado na coluna Dinheiro (saída) para verem os padrões. Isto ajuda-os a escreverem frases algébricas a partir de palavras e a fazerem generalizações com o raciocínio indutivo.

Utilize estas colunas para diferentes estilos de aprendizagem, se for necessário.

Semana Dinheiro Adição repetida Adicionar em

1 1x4=4 4=4 4=4 2 2x4=8 4+4=8 4+4=8 3 3x4=12 4+4+4=12 8+4=12 4 4x4=16 4+4+4+4=16 12+4=16 5 5x4=20 4+4+4+4+4=20 16+4=20

Nos cinemas (Continuação)

Realce que a coluna Dinheiro parece a tabela de multiplicação para o número 4. Isto liga-os a algo familiar. Lembre aos estudantes que sabem que o Pedro ganha €4 euros por semana. Esta é a taxa de poupança do Pedro e pode ser escrita em formato de fracção como

taxa =

Peça aos estudantes para continuarem a preencher a tabela que descreve quanto poupará o Pedro. Mandeos preencher a tabela para as semanas 6 e 7 e pergunte-lhes se podem determinar o dinheiro para 10 semanas, 25 semanas e 100 semanas. Por fim, pergunte-lhes se conseguem preencher o dinheiro após algumas semanas. Chame variável ao número de semanas desconhecido e utilize a letra S para representar as semanas. Utilize a variável D para representar o dinheiro.

€4

1 semana

Semana (S) Dinheiro (D)

11x4=4 22x4=8 33x4=12 44x4=16 55x4=20 66x4=24 77x4=28

10 10x4=40

25 25x4=100

SSx4*

Todas estas investigações devem ser efectuadas a calculadora para estes factos de multiplicação básicos. Se os estudantes precisarem de ajuda para a multiplicação, encoraje-os a olharem para os factos numa tabela em vez de utilizarem a calculadora, para promover a matemática mental e a utilização adequada da calculadora.

sem

Peça aos estudantes para escreverem a expressão

x

para o cálculo com S, (Resposta: S x 4)

e 4.*

Nos cinemas (Continuação)

Perguntar aos estudantes: "Se calcular S semanas vezes €4, obtém um número.

O que significa esse número para o Pedro?" Está a pedir aos estudantes para dizerem Dinheiro(D) e conduzi-los para escreverem a fórmula ou a frase em duas variáveis, D = S x 4. Geralmente, escreve o número e a letra com a multiplicação implícita. Lembre aos estudantes que a multiplicação é comutativa, por isso, D = S x 4 = 4 x S = 4S.

Apoie a investigação com o editor de dados ( v) da calculadora TI-30XS MultiView™, pedindo aos estudantes para olharem para os vários valores da expressão algébrica para verem se corresponde à tabela criada.

1. Peça aos estudantes para introduzirem as tabelas na lista de dados. Não se esqueça que existem três listas disponíveis: L1, L2 e L3.

Explique-lhes que introduzirão os valores de Semana (S) em L1.

2. Peça aos estudantes para introduzirem os primeiros três valores de S das suas tabelas {1, 2, 3}.

3. Introduza uma fórmula para validar o trabalho: L2 = 4 x L1. Não se esqueça de que S = L1 e D = L2.

4. Adicione a entrada para L1 para ver L2 actualizar-se automaticamente com o valor de saída da fórmula. Vá para um espaço de entrada aberto em L1. Peça-lhes para verificarem as tabelas para 4 semanas e, em seguida, para 100 semanas.

Antes de começar a investigação de grupo na folha do estudante, peça aos estudantes para apagarem os dados das listas.

³ Lembre aos estudantes que para

esta actividade estão a utilizar as funcionalidades em ve não em o.

³ Se os estudantes não estiverem

familiarizados com a calculadora TI-30XS MultiView, peça-lhes para ligarem a calculadora e premirem p.

³ Certifique-se de que todos os

estudantes têm o modo de calculadora definido como apresentado:

Para voltar ao ecrã inicial, prima -.

1. Introduza os primeiros três valores de S: v 1 $ 2 $ 3 $.

2. Introduza a fórmula:

" v " 1 4 V v 1 <.

3. Adicione a entrada a L1:

! $ $ $

100 <.

4. Para ver a fórmula em L2 novamente, prima

5. Edite a fórmula, se for necessário, e prima < para definir a fórmula novamente.

6. Para apagar os dados, prima

³ Sugestão: Não se esqueça de que se

premir %Q , volta ao ecrã inicial.

4 <

" v " 1.

v 4.

(Continuação)

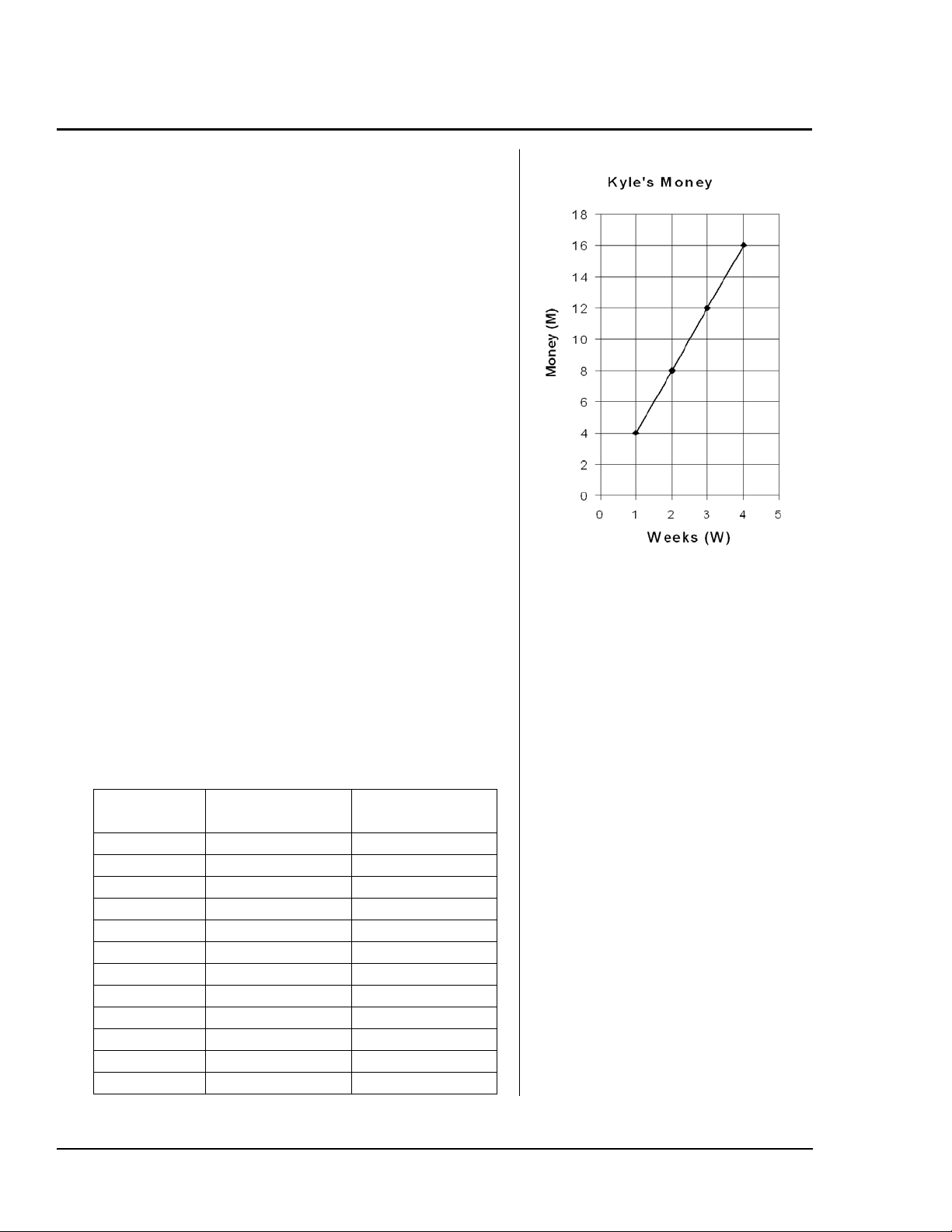
Nos cinemas (Continuação)

Os estudantes tiraram dados de palavras para uma tabela de valores, para um padrão que podem ver, para escreverem uma expressão algébrica. O próximo passo é mostrar-lhes uma vista de como o padrão de números aparece num gráfico. Qual é a forma de D = 4S? Peça aos estudantes para desenharem os primeiros 4 pontos na tabela. Não se esqueça de que os pontos ficam numa linha recta. Pode mencionar que podem descrever o aumento do Dinheiro (D) como "para todas as semanas (S) que o Pedro trabalha, o dinheiro (D) aumenta por 4€. " Isto é uma declaração óbvia, mas estabelece a base para falar sobre taxas e como afectam a inclinação de uma linha (declive).

O número de semanas e o dinheiro são ambos positivos, por isso, o gráfico faz sentido no primeiro quadrante. Peça aos estudantes para utilizarem o papel milimétrico para fazerem os gráficos dos dados.

Actividade

Os estudantes repetem uma investigação similar em grupos, procurando padrões para escreverem frases e expressões algébricas. Criam também um gráfico dos valores da tabela. Peça aos estudantes para lerem o problema na folha do estudantes antes de formarem grupos para que compreendam a tarefa.

Os estudantes preenchem a tabela com a matemática mental. Escrevem todos os cálculos para os ajudarem a ver a fórmula. São encorajados a utilizarem a matemática mental o mais que for possível utilizarem a calculadora para calcular os resultados do dinheiro.

Número de

Cálculo Dinheiro (D)

antes de

pessoas (P)

1 1 x 11.50 11.50€ 2 2 x 11.50 23.00€ 3 3 x 11.50 34.50€ 4 4 x 11.50 46.00€

...

10 10 x 11.50 115.00€

...

100 100 x 11.50 1150.00€

...

1000 1000 x 11.50 11500.00€

...

P P x 11.50 M = P x 11.50

Nos cinemas (Continuação)

Procedimento

Os estudantes devem escrever a equação algébrica a partir do padrão apresentado na tabela: D = P x 11.50 ou com a multiplicação implícita, D=11.50P.

Os estudantes verificam a fórmula com o editor de dados ( como no exemplo de preparação.

1. Peça aos estudantes para verificarem a

2. Introduza os primeiros três valores em L1 {1, 2,

3. Traduza a fórmula para a fórmula da calculadora

4. Introduza mais valores em L1 para verificar a

v) na calculadora TI-30XS MultiView™,

configuração da calculadora.

3}.

e introduza a fórmula em L2.

Fórmula: D = ____________________________ Fórmula da calculadora: L2 =

___________________

tabela de valores e a fórmula. Esta actividade valida a fórmula para vários valores.

³ Certifique-se de que o modo da

calculadora está definido como apresentado.

1. Prima p.

2. Prima v 1 $ 2 $ 3 $.

3. Introduza a fórmula em L2. " v " 1

11 8 50 V v 1 <.

4. Prima ! $ $ $ 4 <

5 < 6 < 10 < 100 < 1000 <.

5. Prima 7500 <.

5. Introduza 7500 em L1 para calcular o dinheiro em L2. Escreva a expressão matemática como D = 11.50 x 7500 =86,250 €.

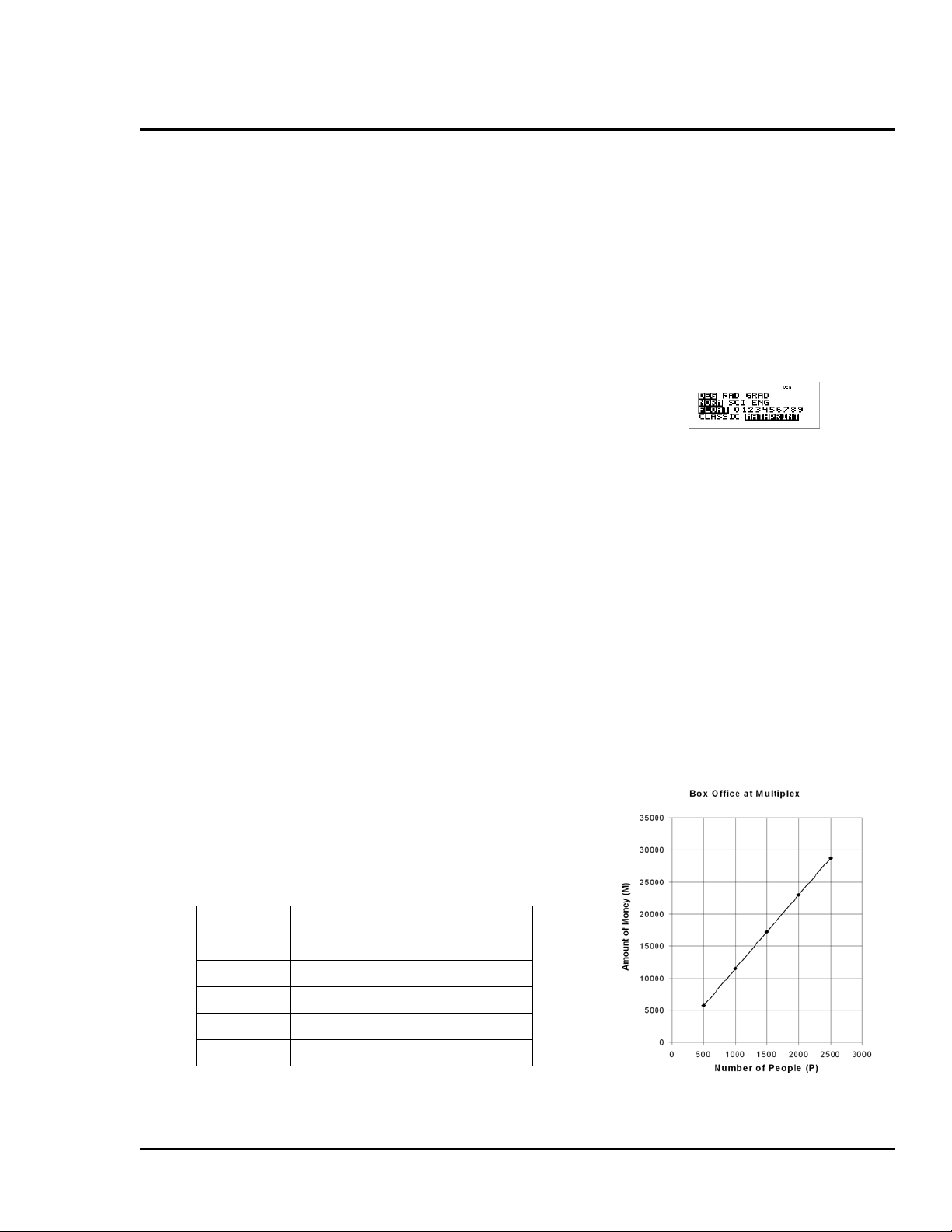
6. Preencha uma tabela de valores e um gráfico para criar um relatório. Escreva um parágrafo que descreva o trabalho para apresentação.

As respostas do parágrafo variam. Certifique-se de que os estudantes explicam a tabela, o gráfico e a expressão algébrica (fórmula) no parágrafo.

PD

500 5750€ 1000 11500€ 1500 17250€ 2000 23000€ 2500 28750€

Nome ___________________________

Nos cinemas

Data ___________________________

Problema

Vai abrir um blockbuster esta semana. O noticiário anuncia que os bilhetes custarão €11.50 por pessoa. O repórter diz que uma família de dois gastará €23 e uma família de três gastará €34.50. Mostram um gráfico com esta informação num formato de tabela.

Número de pessoas Dinheiro

111.50€ 2 23.00€ 3 34.50€

O repórter menciona também que o cinema local, MultiPlex, tem vinte e cinco ecrãs e pode acomodar 7.500 pessoas. Este blockbuster abrirá todos os ecrãs do cinema. Os proprietários prevêem que todos os lugares serão vendidos no primeiro dia!

Os proprietários do MultiPlex querem saber que quantia podem ganhar na bilheteira. Querem uma fórmula geral para que possam calcular a quantia para qualquer número de pessoas que comprem bilhetes.

Trabalho: Foi contratado como contabilista do MultiPlex! Parabéns! O patrão quer uma fórmula que lhe diga quanto dinheiro ganhará na bilheteira, dependendo do número de pessoas que comprem bilhetes.

Procedimento

1. Utilize a tabela para investigar o dinheiro ganho na bilheteira, dependendo do número de pessoas que vão ao cinema. Preencha a seguinte tabela. Escreva todos os cálculos em cada passo. Utilize a matemática mental até onde for possível calculadora para calcular os resultados do dinheiro.

Número de

Cálculo Dinheiro (D)

pessoas

(P)

1 1 x 11.50 11.50€ 2 2 x 11.50 23.00€ 3 3 x 11.50 34.50€ 4 5 6

...

10

...

100

...

1000

...

antes de

utilizar a

Nome ___________________________

Nos cinemas

Data ___________________________

2. Que padrão vê na tabela? Com as informações da tabela, escreva uma fórmula (uma expressão algébrica) que descreva o dinheiro (D), dependendo do número de pessoas (P) que comprem um bilhete para o espectáculo.

D = ___________________________

3. Verifique a fórmula com o editor da lista de dados ( TI-30XS MultiView™.

a. Na coluna L1, introduza apenas as três primeiras entradas na lista do número de

pessoas (P) da tabela acima. (Introduza {1, 2, 3}.)

b. Introduza a fórmula da parte 2 em L2. Tenha cuidado: para utilizar a calculadora,

tem de traduzir as variáveis (letras). A letra P é L1 e a letra D é L2. Rescreva a fórmula aqui em termos de L1 e L2 para que possa introduzir a fórmula

na calculadora. Fórmula: D = _________________________ Fórmula da calculadora: L2 = ________________________

c. Verifique os números em L2 com os números da tabela acima. Coincidem?

d. Introduza mais valores da lista do número de pessoas da tabela para L1. Verifique os

valores em L2 em relação à tabela acima. Coincidem? A fórmula funciona?

v) na calculadora

4. Utilize o editor de dados da calculadora para calcular o dinheiro (D) que os proprietários ganharão na bilheteira, se o cinema encher durante um espectáculo com 7500 pessoas (P). Escreva como calcularia esta resposta manualmente com a fórmula.

Nome ___________________________

Nos cinemas

Data ___________________________

5. O patrão quer fazer uma apresentação aos investidores do MultiPlex. Os investidores querem ver números e gráficos na apresentação! Preencha a tabela abaixo com o editor de dados da calculadora. Faça um gráfico dos pontos a partir desta tabela. Esta é outra forma que um contabilista tem para apresentar o dinheiro (D), dependendo do número de pessoas (P). Dá uma imagem dos dados!

PD

500 1000 1500 2000 2500

Dinheiro (D)

Número de pessoas (P)

6. Escreva um parágrafo sobre o que diria sobre o seu trabalho ao patrão e aos investidores. Inclua como calculou a fórmula do dinheiro e que a tabela e o gráfico indicam o dinheiro ganho na bilheteira.

Nomear a regra (Name that rule)!

Apresentação

Os estudantes descobrem a expressão algébrica (função) a partir de uma tabela de valores em formato de jogo. Os estudantes utilizam o na calculadora TI-30XS MultiView™ para introduzir uma expressão como uma função (y=) para jogarem.

Introdução

Os estudantes preparam esta actividade através da avaliação de expressões e do preenchimento de uma tabela de valores. Jogam o jogo "Nomear a regra (Name that rule)!" O jogo utiliza a calculadora TI-30XS MultiView para criar uma tabela de valores.

Peça aos estudantes para preencherem as tabelas seguintes que aparecem na folha do estudante.

Nota

Nota: Varie a letra da variável na preparação. No

NotaNota entanto, a variável da calculadora será sempre x.

xx

-2 1 -2 2 2

+ 3

x

2x + 6 2(x + 3)*

Conceitos matemáticos

•Expressões algébricas

• Funções

Materiais

• TI-30XS MultiView

•Lápis

• Actividade do estudante

• Faixas de papel e saco de papel

-1 2 -1 4 4 03 06 6 14 18 8 25 210 10

*Os estudantes devem detectar que as tabelas para 2x + 6 e 2(x + 3) são iguais. Diga por que razão estas são expressões equivalentes e verifique isto com a propriedade distributiva da multiplicação sobre a adição. Pode também pedir aos estudantes para utilizarem mosaicos para apresentarem o modelo da área, 2(x + 3) = 2x + 6.

Mostre aos estudantes como introduzir a expressão em o na TI-30XS MultiView. Os estudantes introduzem a expressão como uma função. Isto pode ser um conceito novo para os estudantes.

Nomear a regra (Name that rule)! (Continuação)

Se for necessário, utilize uma máquina de funçõespara fornecer uma forma de pensamento alternativa sobre a avaliação de uma expressão para diferentes valores de dá uma saída de

x

+ 3, pode ser pensada como a regra para calcular y. Posteriormente, os estudantes pensarão ao contrário para descobrirem a "regra". Se for necessário, fale sobre como os estudantes cumprem as regras nos seus jogos favoritos. Os estudantes têm de cumprir as regras para jogar. Quando avaliam uma expressão, cumprem uma regra para alterar um número para outro.

x

. Aqui, uma entrada de x = 1

y

=1+3=4. Diga que a expressão,

Configure a tabela na calculadora com a funcionalidade Auto em o. Auto configura automaticamente uma tabela de valores para começar num determinado valor e aumentar por um valor. Para a calculadora criar a mesma tabela de valores como acima, defina um início a -2 e aumente os valores para compararem a tabela efectuada manualmente em relação à tabela da calculadora.

x

com incremento 1. Peça aos estudantes

Actividade

Jogue um ou dois jogos de “Nomear a regra (Name that rule)!” com a turma inteira, utilizando as regras descritas na página seguinte. Para um jogo com a turma inteira, o professor desempenha o papel de Administrador. Este jogo utiliza o

x

da calculadora TI-30XS MultiView™.

e a função Ask-

³ Siga estes passos:

1. Prima p e defina o modo como apresentado.

2. Introduza a expressão y=x+3: o z T 3 <.

3. Introduza os valores de configuração da tabela: M 2 $ $ $ <.

4. Utilize # e $ para percorrer os valores de x e y = x + 3.

³ Sugestão: Copie as folhas de jogo da

actividade do estudante para os jogos que forem necessários.

Nomear a regra (Name that rule)! (Continuação)

Regras para o jogo de grupo

• Forme grupos de três a quatro estudantes.

• Atribua o papel de Administrador do jogo a um estudante.

• O Administrador é responsável pela calculadora para o jogo.

• O Administrador tira uma expressão algébrica de um saco de papel (ou outro contentor) e esconde-a dos outros jogadores ou o Administrador escreve uma expressão algébrica num pedaço de papel para o jogo e pede autorização para utilizar a expressão ao professor.

• O Administrador introduz a expressão algébrica para o e selecciona a função AskNota

Nota: O Administrador pode ter de eliminar cada

NotaNota

x

linha da tabela Ask-

antes de reproduzir uma regra

x

.

nova. (Consulte as instruções dos batimentos das teclas.)

• Cada jogador para além do Administrador pede um valor para valor e diz a saída do valor

x

à vez. O Administrador introduz esse

y

aos jogadores.

• Cada jogador mantém uma tabela de valores como um registo do jogo.

• Um jogador pode descobrir a expressão ou a regra apenas durante a jogada do jogador.

• Assim que uma regra for descoberta por um jogador, todos os jogadores têm de verificar se a regra é verdadeira para todos os valores já jogados, ou desafiar a regra para calcular um valor que não funcione.

• Se uma regra descoberta for considerada incorrecta por um jogador ou o Administrador, o jogador que descobriu a regra perde a vez ou a vez seguinte.

• Se a expressão algébrica descoberta por um jogador não estiver no mesmo formato da expressão introduzida pelo Administrador, por exemplo, 2(

x

+2, e todos os jogadores concordarem que a

e 2

x

+1)

expressão descoberta está correcta, o Administrador revela a expressão na calculadora e o jogador que descobriu a regra tem de explicar por que razão as duas expressões são iguais.

• O primeiro jogador a descobrir a regra correctamente e a definir a regra ganha.

• O papel de Administrador roda para outro jogador na próxima jogada.

³ Siga estes passos:

1. Prima p e defina o modo como apresentado.

2. Introduza a função y = 2x + 5:

- o 2 z T 5 <. Nota: Se já introduziu uma função no ecrã y=, prima - antes de introduzir uma função nova.

3. Introduza os valores de configuração da tabela: $ $ " < $ <.

4. Introduza os valores x-: 5 < 6 < 10 <.

³ Sugestão: Para introduzir mais valores,

realce qualquer uma das três linhas na coluna x, introduza o número e prima <.

5. Para rever o ecrã y=, prima o. Tem de percorrer o ecrã de configuração novamente para ver a tabela de valores.

³ Para jogar nov ament e :

1. Limpe a expressão antiga, escolha a expressão seguinte e introduza-a: o -z T q1 $ 2.

2. Introduza os valores de configuração da tabela pretendidos, realce OK e prima <.

Não se esqueça de que aparecem apenas 3 hipóteses no ecrã. Os estudantes podem substituir um número para ver uma saída nova.

Nomear a regra (Name that rule)! (Continuação)

Lista de expressões algébricas

Copie estas ou outras expressões em pedaços de papel para que o Administrador de cada equipa de jogadores possa escolher a expressão para jogar. Pode também pedir ao Administrador para escrever uma expressão que pode aprovar antes do início de um jogo. Deixar o estudante escrever uma expressão dálhe o domínio e permite fazer uma avaliação dos seus conhecimentos.

Escolha uma lista ou misture as listas, dependendo do nível dos estudantes. Expanda as listas, dependendo do nível dos estudantes. Os estudantes devem documentar todo o trabalho na folha do estudante.

Exemplos de expressões de um passote

x

+ 3 2x + 3

x

– 9 -4x + 5

1

x

---+ 2

x

– 2.5

x

+ 15 1.5 x + 2.5

1

x

–

--5

Exemplos de expressões de dois passos

2

x

+ 6 ou 2 (x + 3)

1

x

4–

--2

Modificações do jogo

• Inclua expressões que necessitem de ser simplificadas pelos jogadores, como 2 um jogador descobrir 5x - 2, terá de justificar que a

x

expressão é equivalente a 2 outra camada de avaliação ao jogo.

• Inclua expressões em palavras como "o dobro de um número menos quatro unidades". Deixe os Administradores escolherem a expressão do contentor e altere as palavras para uma expressão para aprovação antes de voltarem ao grupo para jogar.

Exemplo: É escolhido o dobro de um número menos quatro unidades. O Administrador traduz isto para 2

x

- 4, indique se estão correctas e, em seguida,

voltam ao grupo para jogar.

+ 4 + 3x - 6 que adiciona

x

+ 4 + 3x - 6. Se

Nomear a regra

Nome ___________________________

(Name that rule)!

Data ___________________________

Problema

Cumprimos as regras todos os dias. És capaz de cumprir as regras do teu jogo favorito? Tens que cumprir todas as regras do jogo, cuidadosamente? Também precisamos de cumprir regras quando trabalhamos números e expressões.

Exemplo: Se

A expressão diferentes números. Pode pensar em treino. Os valores de

x

= 1, x + 3 = 1 + 3 = 4

x

+ 3 tem uma variável, x. Dependendo do valor de x, x + 3 será igual a

x

+ 3 como uma regra. Preencha a tabela seguinte como

x

foram escolhidos para si.

xx

-2 -2 -2

-1 -1 -1 000 111 222

1. O que lhe chama à atenção na tabela para 2

2. Verifique as tabelas acima com o da calculadora TI-30XS MultiView™.

+ 3

x

2

x

+ 6

x

+ 6 e 2(x +3)?

x

2(x + 3)

3. Jogue o jogo "Nomear a regra (Name that rule)!", utilizando a folha de jogo na página seguinte. Neste jogo, não saberá a expressão (regra). Terá de descobrir a regra, pensando ao contrário! O professor dar-lhe-á instruções para jogar.

?

Nomear a regra

?

(Name that rule)!

?

Descubra a regra a partir de uma tabela de

Nomes dos jogadores: Administrador:

O professor dar-lhe-á instruções do jogo. Utilize a tabela para controlar os valores todas as vezes do jogador durante o jogo. Utilize as colunas Hipótese para verificar a regra. Se a regra do jogador não estiver correcta, continue a jogador.

x

Valo r y da

calculadora

y

= _______________________ Verifique todos os valores Esta hipótese está correcta? _____

Pense ao contrário!

valores!

Hipótese 1

x

?

x

e y para

Hipótese 2

y

= _______________________

!

Verifique todos os valores Esta hipótese está correcta? _____

x

!

Hipótese 4

x

!

x

Valo r y da

calculadora

Hipótese 3

y

= _______________________

x

Verifique todos os valores Esta hipótese está correcta? _____

!

y

= _______________________ Verifique todos os valores Esta hipótese está correcta? _____

Como utilizar a

calculadora

TI-30XS MultiView™

TI-30XS MultiView Operações básicas da 31 Apagar e corrigir 42 Matemática básica 47 Ordem das operações e dos parêntesis 51 Notação numérica 57 Fracções 61 Decimais e casas decimais 67 Constante 69 Variáveis guardadas e de memória 73 Editor de dados e fórmulas das listas 81 Estatística 85 Probabilidade 91 Tabela de funções 99 Potências, raízes e recíprocos 103 Funções exponenciais e logarítmicas 111 Pi 115 Conversões e definições de ângulos 119 Conversões polares e rectangulares 123 Trigonometria 125 Hipérbole 133

Operações básicas da TI-30XS MultiView™

1

Teclas

1. & liga a calculadora.

2. % liga o indicador 2nd e acede à função

apresentada por cima da próxima tecla premida.

3. % ' desliga a calculadora e apaga o ecrã.

4. < completa a operação ou executa o comando.

5. % i rechama o resultado calculado mais recentemente e apresenta-o como Ans.

6. n comuta a resposta entre os formatos de fracção e decimal, raiz quadrada exacta e decimal, pi exacto e decimal.

7. ! e " movem o cursor para a esquerda e para a direita para ir para as entradas no ecrã inicial e navegar nos menus. %! ou % " move para o início ou o fim da entrada actual. # e $ movem o cursor para cima e para baixo nos itens dos menus, entradas anteriores no ecrã inicial e entradas no editor de dados e tabela de funções. % # move o cursor para a entrada superior da coluna activa no editor de dados para a entrada anterior no ecrã inicial. Prima % # novamente para mover o cursor para a entrada mais antiga no ecrã inicial. Nas fracções, prima % # para colar uma entrada anterior no denominador. (Para mais informações, consulte o Capítulo 6, Fracções.) % $ move o cursor para a primeira linha em branco da coluna activa do editor de dados ou por baixo da última entrada no ecrã inicial.

8. p permite definir os modos de visualização, decimal, numérico e ângulo. Prima $# ! " para escolher um modo e < para o seleccionar. Prima - ou

2

8

9 3 1

7

6

5

4

%Q para sair do menu do modo.

9. %  mostra o menu Reset .

•Prima 1 (No) para voltar ao ecrã anterior

sem reiniciar a calculadora.

•Prima 2 (Yes) para reiniciar a calculadora.

Aparece a mensagem

Nota: Se premir & e - simultaneamente, reinicia a calculadora imediatamente. Não aparece nenhum menu ou mensagem.

MEMORY CLEARED

.

Operações básicas da TI-30XS MultiView™

(Continuação)

• Reiniciar calculadora: – Devolve as definições para as

predefinições: modo de ângulo de graus (DEG), notação numérica normal (NORM), notação decimal flutuante (FLOAT) e modo de visualização MathPrint™.

– Apaga as variáveis da memória,

operações pendentes, entradas no histórico, dados estatísticos, constantes e Ans (Última resposta).

Notas

• Os exemplos assumem todas as predefinições (Ver página vi).

• n pode ser utilizada numa entrada antes de premir <. Se premir n mais de uma vez na entrada actual, pode provocar um erro de

sintaxe. Para alcançar o resultado pretendido, pode:

– Introduzir a expressão, premir n < e,

em seguida, premir n novamente depois de aparecer o resultado.

– Introduzir a expressão, premir < e, em

seguida, premir n as vezes que desejar para alternar o ecrã e ver o formato alternativo da resposta.

•Quando ³ ou ´ aparecer no ecrã, a linha de entrada contém mais caracteres à esquerda ou à direita.

•Prima & depois de activar a função Automatic Power Down™ (APD™) para ligar a calculadora. O ecrã, as operações pendentes, as definições e a memória são retidos.

2ª, desligado, setas, enter

• Introduza 46 – 23.

• Mude de 46 para 41. Mude de 23 para 26 e complete a operação.

• Introduza + e complete a

operação.

• Desligue e ligue a calculadora TI-30XS MultiView™. O ecrã inicial está em branco; percorra para ver o histórico.

Premir Ecrã

2

--5

3

----10

46 U

%' ! "

# $ <

23 < # # <

!!!! 1 "" 6 < 2 q 5 " T 3 q 10 <

%' & # # #

Reiniciar

Reinicie a calculadora.

Premir Ecrã

%

2

-

%

Se premir & e simultaneamente, reinicia também a calculadora imediatamente. Não aparece nenhum menu ou mensagem.

Se utilizar % ou & e -, devolve todas as definições para as predefinições e apaga a memória.

Modo

p

Utilize ppara seleccionar modos. Prima $ # ! " para escolher um modo e < para o seleccionar. Prima - ou %Q para voltar ao ecrã inicial e efectue o trabalho com as definições do modo escolhido.

As predefinições do modo aparecem realçadas.

DEG RAD GRAD Define o

p

modo de ângulo para graus, radianos ou gradianos.

NORM SCI ENG Define o modo de notação numérica. Os modos de notação numérica afectam apenas a visualização de resultados e não a precisão dos valores guardados na calculadora, que permanecem máximos.

Modo (continuação)

NORM mostra os resultados com

dígitos à esquerda e à direita do decimal, como em 123456.78.

SCI expressa números com um dígito à esquerda do número decimal e a potência de 10 adequada, como em

5

1.2345678x10

(que é igual a

123456.78). ENG mostra resultados como um

número de 1 a 1000 vezes 10 para a potência de um número inteiro. A

p

potência do número inteiro é sempre um múltiplo de 3.

Nota: C é uma tecla de atalho para introduzir um número em formato de notação científica. O resultado aparece no formato de notação numérica definido no modo.

FLOAT 0 1 2 3 4 5 6 7 8 9 Define o modo de notação decimal.

FLOAT (ponto decimal flutuante) mostra até 10 dígitos, mais o sinal e o decimal.

Modo (continuação)

0 1 2 3 4 5 6 7 8 9 (ponto decimal

fixo) especifica o número de dígitos (de 0 a 9) a mostrar do lado direito do decimal.

CLASSIC MATHPRINT define a entrada e a saída do ecrã.

CLASSIC mostra as entradas e as saídas numa linha.

MATHPRINT mostra a maioria das entradas e saídas em formato de livro de texto. Utilize o modo MathPrint para melhor

p

confirmação visual que as expressões matemáticas foram introduzidas correctamente e reforço da notação matemática correcta.

Nota: Se comutar o modo entre Classic e MathPrint, apaga o histórico da calculadora e o valor da constante.

Menus

Determinadas teclas mostram menus: H, %I, v,

%t, %, %h e %{. Algumas teclas podem

mostrar mais de um menu.

Prima " e $ para percorrer e

seleccionar um item do menu ou prima o número correspondente junto ao item do menu. Para voltar ao ecrã anterior sem seleccionar o item,

prima -. Para sair de um menu ou

uma aplicação e voltar ao ecrã inicial,

prima %Q. O ecrã inicial está em

branco; mova para ver o histórico. Alguns menus de exemplo:

H % I

PRB RAND DMS R ¶P

1: nPr 1: rand 1: Ä 1: R ´Pr( 2: nCr 2: randint( 2: Å 2: R ´PÁ( 3: ! 3: Æ 3: P ´ Rx(

4: r 4: P ´Ry( 5: g 6: ´DMS

Menus (Continuação)

v (Prima v para ver o ecrã do editor

de dados. Prima novamente para ver o menu.)

CLEAR FORMULA

1: Clear L1 1: Add/Edit Frmla 2: Clear L2 2: Clear L1 Frmla 3: Clear L3 3: Clear L2 Frmla 4: Clear ALL 4: Clear L3 Frmla

5: Clear ALL

Prima v enquanto está na opção Add/Edit Frmla do menu FORMULA para ver este menu:

%t

STATS

1: 1-Var Stats 2: 2-Var Stats

3: StatVars

Ls

1: L1 2: L2 3: L3

Esta opção de menu aparece depois de calcular estatísticas de 1-variável ou 2 variáveis.

Menu StatVars: 1: n 2:

Ï

3: Sx Etc. Consulte o Capítulo 11,

Estatística, para obter uma lista completa.

Última resposta (Ans)

Utilize a Última resposta (Ans) para calcular

2

5

+

Premir Ecrã

12

2

.

5 FT12

F<

%b% i<

%A

Comutação de respostas

Prima n para comutar o resultado apresentado entre fracção e decimal, raiz quadrada exacta e decimal, pi exacto e decimal

Premir Ecrã

% b

8 <

n

Apagar e corrigir

2

Teclas

1. - apaga os caracteres e as mensagens de erro. Prima - para apagar uma entrada incompleta; prima-a novamente para apagar o ecrã. Pode percorrer e utilizar - para apagar as entradas do histórico. - efectua a cópia de segurança de um ecrã nas aplicações.

2. % f permite introduzir um carácter no cursor.

3. J elimina o carácter no cursor. Sempre que premir J, elimina 1 carácter à esquerda do cursor.

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

•Premir - não afecta a memória, registadores estatísticos, unidades dos ângulos ou notação numérica.

2

3

1

Eliminar e introduzir

Introduza 4569 + 285 e altere-o para 459 + 2865. Complete o problema.

Premir Ecrã

4569 T 285

! ! ! ! ! ! J

" " " "

J

%f

%f 6

<

Apagar

Introduza 21595. Apague o 95. Apague a entrada.

Premir Ecrã

21595

! ! -

(Apagar à direita)

-

(Apagar entrada)

Matemática básica

3

Teclas

1. T adiciona.

U subtrai.

2.

3. V multiplica.

4.

W divide.

5. < completa a operação ou executa o comando.

M permite introduzir um número negativo.

6.

7. % _ adiciona o sinal % a um número.

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

• A TI-30XS MultiView™ permite a multiplicação implícita. Exemplo: 3 (4+3) = 21

• Não confunda subtracção.

• Utilize os parêntesis para agrupar o sinal de negação com o número, se for necessário. Exemplo: M2

• Os resultados dos cálculos percentuais aparecem de acordo com a definição do modo de notação decimal.

M com U. U permite a

2

= M4 e (M2)2 = 4.

4

7

3 2 1

5

6

Adicionar, subtrair, multiplicar, dividir, igualar

Calcular:

2 + 54 16 x 21 =

1

x 10 =

--2

12 x (5 + 6) =

Premir Ecrã

½ 6 =

2 T 54 U 6 <

T U V W

<

16 V 21 <

1 q 2 " V 10 <

12 V D 5 T 6 E <

Números negativos

A temperatura em Lisboa foi 6:00. Às 10:00 a temperatura aumentou 12Ä C. Qual era a temperatura às 10:00?

Premir Ecrã

-3Ä C às

M 3 T

12 <

A temperatura às 10:00 era 9Ä C.

M

Per ce nt a g e m

O Miguel recebe €80 por semana. Poupa 15% dos rendimentos. Quanto poupa o Miguel por semana?

Premir Ecrã

15

% _ V

80 <

O Miguel poupa

€12 por semana.

% _

Ordem das operações e parêntesis

4

Teclas

1. D abre uma expressão envolvendo parêntesis.

2. E fecha uma expressão envolvendo parêntesis.

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

• O acetato que apresenta o Equation Operating System (EOS™) demonstra a ordem em que a calculadora TI-30XS MultiView™ conclui os cálculos.

• As operações entre parêntesis são efectuadas em primeiro lugar. Utilize D E para alterar a ordem das operações e, por conseguinte, alterar o resultado. Exemplo: 1 + 2 x 3 = 7 (1 + 2) x 3 = 9

1

2

Equation Operating System (EOS™)

1

(primeiro)

2

Expressões entre D E

Funções que necessitem de um expressão, como

>, A

e alguns itens de menus

E

e precedam a

3 Fracções 4 Funções introduzidas depois da expressão, como

F e modificadores das unidades de ângulos (

¢, £, r, g)

¡,

5 Exponenciação (G) e raízes (%c)

Nota: No modo Classic, a exponenciação com a tecla G é avaliada da esquerda para a direita. A expressão 2^3^2 é avaliada como (2^3)^2, com um resultado de 64.

No modo MathPrint™, a exponenciação com a tecla G é avaliada da direita para a esquerda.

2

3

Se premir 2, G 3 G 2 aparece como , com o

2

resultado de 512. A calculadora científica TI-30XS MultiView™

avalia as expressões introduzidas com F e a da esquerda para a direita nos modos Classic e MathPrint. Se premir 3, F F aparece como

3

22

. Este é calculado como (3

2)2

= 81.

Equation Operating System (EOS™) (Continuação)

6Negação (M) 7 Permutações (nPr) e combinações (nCr) 8 Multiplicação, multiplicação implícita e divisão 9 Adição e subtracção 10 Conversões (%O, %j, %R e

´DMS)

11

(último)

< conclui todas as operações e fecha todos os parêntesis abertos.

Ordem das operações

1 + 2 x 3 =

Premir Ecrã

1 T 2 V 3 <

1 + (2 x 3) =

Premir Ecrã

1 T D 2 V 3 E <

(1 + 2) x 3 =

T V D E

Premir Ecrã

D 1 T 2 E V 3 <

Ordem das operações (Continuação)

2

5

Premir Ecrã

41()3()–

p$$$ <% b 5 F U 4 D 1 E D 3 E <

= (Modo Classic)

2

=

5

Premir Ecrã

41()3()–

(Modo MathPrint™)

p$$$ "<% b 5 F U 4 D 1 E D 3 E <

n

Notação numérica

5

Teclas

1. p permite seleccionar a partir do menu de notação numérica.

NORM Restaura o modo standard (decimal

flutuante).

SCI Liga o modo científico e mostra os

resultados como um número de 1 de 10 (1 { n < 10) vezes uma potência de base 10 e expoente inteiro.

ENG Liga o modo de engenharia e mostra

os resultados como um número de 1 a 1000 (1 { n < 1000) vezes uma potência de base 10 e expoente inteiro. A potência do número inteiro é sempre um múltiplo de 3.

2. C é uma tecla de atalho para introduzir um número em formato de notação científica.

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

• Pode introduzir um valor em notação científica, independentemente da definição do modo de notação numérica. Para um expoente negativo, prima M antes de o introduzir.

• Os resultados que requeiram mais de 10 dígitos aparecem automaticamente em notação científica.

• Para o modo de notação decimal, consulte o Capítulo 7, Decimais e casas decimais.

• Estes modos (NORM, SCI e ENG) só afectam a visualização dos resultados.

1

2

Engenharia, científica e decimal flutuante

Introduza 12543, que será a notação de decimal flutuante e a notação numérica normal (ambas as predefinições em visualização dos resultados entre notações normais, científicas e de engenharia através da alteração das definições no ecrã de modos.

Premir Ecrã

p). Alterne a

12543 <

p

p$" <

-<

p$" "<

-<

Engenharia, científica, decimal flutuante (Continuação)

p$<

-<

p

Notação científica

Com a calculadora TI-30XS MultiView™ nos modos Norm e MathPrint™ (ambas as predefinições), introduza o problema seguinte em notação científica com a tecla C.

A Terra está a cerca de 1.5 x 10 quilómetros do Sol. Júpiter está a cerca de 7.8 x 10 Sol. Partindo do princípio que as órbitas dos planetas são circulares e os planetas estão do mesmo lado do

8

quilómetros do

8

C

Sol, qual é a proximidade entre Júpiter e a Terra?

Premir Ecrã

7 8 8

C 8 " U 1 8 5 C

8 <

Júpiter está a cerca de 630,000,000 = 6.3 x 10 quilómetros da Terra.

8

Fracções

6

Teclas

1. %N permite introduzir fracções e números mistos. A unidade tem de ser um número inteiro. O numerador e o denominador podem conter decimais.

Para introduzir um número misto, introduza um número inteiro para a unidade e prima %N para introduzir um numerador.

No modo MathPrint™, se premir %N antes de introduzir um número inteiro, aparece um modelo de fracção, e permite introduzir apenas um dígito para a unidade.

2. q permite introduzir uma fracção simples. Premir q antes ou depois de um número, pode resultar num comportamento diferente. No modo MathPrint™, se introduzir um número antes de premir q, torna esse número no numerador.

q no modo MathPrint pode também ser utilizado para mais cálculos de fórmulas e fraccionais mais complexos que incluam operadores e outras funções antes de introduzir o numerador.

No modo MathPrint™, prima $ entre a entrada do numerador e do denominador. No modo Classic, prima q entre a entrada do numerador e do denominador.

3. % O converte uma fracção simples para um número misto ou um número misto para uma fracção simples.

4. % j converte uma fracção para o decimal equivalente ou muda um decimal para a fracção equivalente, se possível.

, premindo q

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

• No modo MathPrint, as fracções com q podem incluir teclas de operações (T, V,

3 1 2

4

etc.) e a maioria das teclas de funções (F, %_, etc.). No modo Classic, as fracções com q não permitem teclas de operações, funções ou fracções complexas no numerador ou no denominador.

• No modo MathPrint, pode introduzir variáveis (x, y, z, t, a, b e c) no numerador e no denominador de uma fracção. No modo Classic, as fracções com q não permitem variáveis.

• No modo Classic, editor de dados e tabela, utilize W juntamente com D e E onde for necessário para efectuar problemas de divisão complexos.

Fracções (Continuação)

• Para colar uma entrada prévia no denominador, coloque o cursor no denominador, prima % # para ir para a entrada pretendida e, em seguida, prima < para colar a entrada no denominador.

• Para colar uma entrada prévia no numerador ou na unidade, coloque o cursor no numerador ou na unidade, prima # ou % # para ir para a entrada pretendida e, em seguida, prima < para colar a entrada no numerador ou na unidade.

• As entradas e os resultados fraccionais são simplificados automaticamente para os termos mais baixos.

• Os cálculos com fracções podem apresentar resultados em fracções ou decimais, dependendo da entrada.

Fracções

5

Na festa, comeu pizza de pepperoni

1

-----

e pizza de salsicha. As pizzas são

10 do mesmo tamanho. Se juntar as fatias, quanto comeu de uma pizza completa?

--6

q

Premir Ecrã

5 q 6 " T1 q 10 <

14

Comeu do tamanho de uma pizza

completa. Isso é quase uma pizza inteira!

---15

Números mistos

Um bebé pesava 4 quilos quando

nasceu. Nos 6 meses seguintes, ganhou

3

2 quilos. Quanto pesa?

--4

3

--8

%N

%O

Premir Ecrã

4 %N 3

$ 8 " T 2 %N 3 $ 4 <

%O <

Passados 6 meses, o bebé pesava

1

7 quilos.

--8

Converter fracções e decimais

O João nada 20 voltas em 5.72 minutos. A Maria nada 20 voltas em

3

5 minutos. Mude o tempo da Maria

---

4 para um número decimal para determinar quem nada mais depressa

Premir Ecrã

5 %N 3

$ 4 " %j <

%j

.

O João nada mais depressa do que a Maria visto que nada 20 voltas em

5.72 minutos.

Mude 2.25 para a fracção equivalente

Premir Ecrã

2 8 25 %

j <

ou 2 8 25 <

n

.

Decimais e casas decimais

7

Teclas

1. 8 introduz um ponto decimal.

2. p permite definir o número de casas

decimais. Prima $ $ e, em seguida, " para escolher o decimal pretendido. Prima < para o seleccionar.

FLOAT Define a notação decimal flutuante

(standard).

0-9 Define o número de casas decimais

apresentadas. FIX mostra quando um modo decimal está definido de 0 a 9.

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

•Prima p $ $ < para voltar à notação standard (decimal flutuante).

• A definição do modo decimal afecta a maioria dos resultados decimais e a mantissa de resultados de notação científica e de engenharia.

• A calculadora TI-30XS MultiView™ arredondada automaticamente o resultado para o número de casas decimais seleccionadas. Por exemplo, quando o decimal é definido para 2 casas, 0.147 passa para

0.15 quando premir <. A calculadora TI-30XS MultiView arredonda ou enche também os resultados resultantes com zeros à esquerda para ajustar a definição seleccionada. Por exemplo, quando o decimal estiver definido para 5 casas, 0.147 passa para 0.14700 quando premir <.

2

1

• A reinicialização da calculadora apaga a definição decimal e devolve a predefinição, FLOAT.

• A definição decimal não afecta a precisão interna dos resultados. Afecta apenas a forma de visualização dos resultados.

Decimal

Arredonde 12.345 para a casa das centésimas, para a casa das décimas e, em seguida, para a a notação flutuante.

Premir Ecrã

12 8 345 <

p

$ $ "

""<

-<

p

$$"

"<

-<

p

$$

<

-<

Constante

8

Teclas

1. % l liga e desliga a função constante e permite definir um número constante, operação ou expressão para um atalho quando repetir um conjunto de batimentos de teclas. K aparece quando o modo constante estiver ligado.

2. < coloca o conteúdo de K no fim da expressão no ecrã.

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

• Todos os valores, operações e funções funcionam no modo constante.

• Para introduzir uma constante:

1. Premir % l. Se já tiver guardado uma

constante, prima - para a apagar.

2. Introduza a constante (qualquer

conjunto de operações, funções e valores).

3. Prima < para ligar a função constante.

K aparece no ecrã para indicar que a função constante está ligada.

4. Prima - para apagar o ecrã.

5. Introduza um valor inicial. Se não

introduzir um valor, 0 é assumido e Ans aparecerá no ecrã.

6. Prima < para colocar o conteúdo de K

no fim da expressão e avaliá-la.

7. Continue a premir < para repetir a

constante.

8. Prima % l novamente para desligar a

função constante.

1

2

Constante

Três pessoas tomam conta de crianças a 5.25€ cada A primeira pessoa trabalha 16 horas. A segunda pessoas trabalha 12 horas. A terceira pessoa trabalha 17 horas. Quanto ganhou cada pessoa?

Premir Ecrã

%l

V 5.25 <

%l

-

16 <

12 <

17 <

Constante (Continuação)

%l

(O modo constante está desligado.)

%l

Variáveis guardadas e de memória

9

Teclas

1. L permite guardar valores em variáveis. Prima Lpara guardar uma variável e prima z para seleccionar a variável a guardar. Prima < para guardar o valor na variável seleccionada. Se esta variável já tiver um valor, esse valor é substituído por um novo.

2. z acede às variáveis. Prima esta tecla várias vezes para seleccionar x, y, z, t, a, b ou c. Pode também utilizar z para rechamar os valores guardados para estas variáveis.

3. % { apaga todas as variáveis.

4. % h mostra um menu das variáveis x, y, z, t, a, b, e c, e permite ver os valores guardados antes de colar no ecrã.

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

• Pode guardar um número ou uma expressão que resulta de um número para uma variável de memória.

• Quando seleccionar uma variável com z, aparece o nome da variável (x, y, z, t, a, b ou c). O nome da variável é inserido na entrada actual, mas o valor atribuído é utilizado para avaliar a expressão.

• Quando seleccionar uma variável com % h, aparece um menu com o valor das variáveis guardadas. Seleccione a variável, premindo o número do menu correspondente. O valor atribuído à variável é introduzido na entrada actual e utilizado para avaliar a expressão.

• A reinicialização da calculadora apagar todas as variáveis da memória.

3 2

4

1

Variáveis guardadas

Em seguida, aparecem os resultados dos testes e do trabalho de casa da aula de matemática.

Resultados dos testes: 96, 76, 85. Resultados dos trabalhos de casa: 92, 83, 97, 86.

1. Calcula a nota do teste como a média dos resultados do teste.

2.Calcula a nota do trabalho de casa como a média dos resultados do trabalho de casa.

Lz

%h

3.O professor calcula a nota final como a média da nota do teste e da nota do trabalho de casa. Qual é a nota final? O professor arredondará para o número inteiro mais próximo, se for necessário.

Premir Ecrã 96 T 76 T

85 <

Variáveis guardadas (Continuação)

W 3 <

L <

92 T 83 T 97 T 86

< W 4 <

z

Lz

%h

z <

T

W 2 <

A nota final é 88 arredondado para o número inteiro mais próximo.

Variáveis de memória

Vai enviar um presente para dois amigos. Vê os presentes em dois sítios Web com o mesmo preço. As despesas de envio são diferentes em cada sítio. Os pacotes pesam 4.5 quilos e 3.2 quilos. A loja A envia um

pacote por 2€ mais 1.40€ por quilo. A loja B envia o pacote por 3€ mais

1.10€ por quilo. Que loja cobra menos

pelo envio de cada presente?

Premir Ecrã

4 8 5 L

L

%h

z <

2 T 8 40 E

3 T 8 10 E

A loja A cobra 8.30€ e a loja B cobra

7.95€. A loja B cobra menos pelo

envio do presente que pesa 4,5 quilos.

z D1

<

z D1

<

Variáveis de memória (Continuação)

L

3 8 2 L z <

##### #<<

A loja A cobra 6.48€ e a loja B cobra

6.52€. A loja A cobra menos pelo

envio do presente que pesa 3.2 quilos.

%h

Variáveis de memória (Continuação)

Loja Compras Qtd Custo

AT-shirts 213.98€ cada uma. Bgravatas 37.98€ cada uma. Ccinto 16.98€

suspensórios 1 9.98€

Quanto gastou em cada loja e quanto gastou no total?

Premir Ecrã

2 V 13 8 98 <

Lz<

L

%h

3 V 7 8 98 <

L z z <

Variáveis de memória (Continuação)

L

6 8 98 T 9 8 98 <

L z zz<

% h

1 T% h 2 T %

h 3 <

%h

Gastou:

27.96€ na loja A,

23.94€ na loja B,

16.96€ na loja C. Gastou 68.86€ nas três lojas.

Editor de dados e fórmulas das listas

10

Teclas

1. v mostra um editor de dados com três listas. Cada lista pode conter até 42 itens. Para introduzir dados, navegue para uma lista e introduza um número. Prima as teclas de seta para navegar nos elementos da lista.

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

• As fórmulas das listas aceitam todas as funções da calculadora.

• Nas fórmulas, utilize D e E à volta das variáveis ou dos nomes da lista para garantir a ordem das operações pretendida.

• Se introduzir uma fórmula numa lista, a lista de fórmulas actualiza-se automaticamente, se um elemento da lista referenciada for actualizado.

Nota: Premir < numa lista de fórmulas elimina automaticamente a fórmula. Não aparece nenhuma mensagem.

• Quando eliminar uma fórmula, os dados podem ser utilizados. Os dados já não são actualizados.

• Se premir v novamente no ecrã do editor de dados, abre os menus com as opções para apagar as listas ou introduzir e gerir fórmulas.

• Se premir v novamente quando estiver na opção “Add/edit formula”, abre um menu com os nomes da lista que pode utilizar quando adicionar ou editar fórmulas.

1

• Se premir -, faz cópias de segurança dos ecrãs no editor de dados.

• Se premir % Q, sai do editor de dados e devolve o ecrã inicial.

• No editor de dados, a notação científica aparece como mas ainda mostra a magnitude de um número.

Exemplo: 2 x 10

E para conservar o espaço,

3

aparece como 2E3.

Introduzir dados e fórmulas

Em Novembro, um boletim meteorológico na Internet listou as seguintes temperaturas.

Paris, França 8ÄC Moscovo, Rússia

½1ÄC

Montreal, Canadá 4ÄC Converta estas temperatura de

graus Celsius para graus Fahrenheit.

9

Lembrete: F= C+32.

--5

Premir Ecrã

v

v 8 $ M

$ 4 $ "

1

v "

1

9

W 5 V v

1 T 32

Introduzir dados e fórmulas (Continuação)

<

Não se esqueça de que L2 está realçado, visto que é o resultado de uma fórmula.

Os graus Fahrenheit são: Paris, França 46.4ÄF

Moscovo, Rússia 30.2ÄF

v

Montreal, Canadá 39.2ÄF

Se Sidney, Austrália registar 21ÄC, calcule a temperatura em graus Fahrenheit.

! $ $ $

<

21

A temperatura em Sydney, Austrália é 69.8ÄF.

Estatística

11

Teclas

1. v permite introduzir os pontos de dados estatísticos (x para estatística de 1 variável;

x

e y para estatística de 2 variáveis). (Consulte Capítulo 10, Editor de dados e fórmulas das listas, para obter mais informações sobre v.)

2. %t apresenta um menu onde pode

seleccionar 1-Var, 2-Var ou StatVars.

1-Var

Analisa dos dados de 1 conjunto

de dados com 1 variável medida—x.

2-Var

Analisa os dados aos pares dos 2

conjuntos de dados com 2 variáveis medidas—x, a variável independente, e y, variável dependente.

StatVars Esta opção aparece apenas

depois de calcular a estatística de 1 variável ou 2 variáveis. Mostra o menu de variáveis com os valores actuais.

2

1

Menu StatVars:

n Número de pontos de dados x (ou

x,y).

v ou w Média de todos os valores x ou y.

Sx ou Sy Desvio padrão da amostra de x

ou y.

sx ou sy Desvio padrão da população de x

ou y.

Gx ou Gy Soma de todos os valores x ou y. G

x2 ou Gy2Soma de todos os valores x

Gxy Soma do produto de x e y para

todos os pares x-y das 2 listas.

a Declive da regressão linear. b Intercepção y da regressão linear. r Coeficiente de correlação. x ÅÅÅÅ (2-var) Utiliza a e b para calcular o valor

x previsível quando introduzir um valor y.

y ÅÅÅÅ (2-var) Utiliza a e b para calcular o valor

y previsível quando introduzir um valor x.

minX Mínimo dos valores x. Q1 (1-Var) Mediana dos elementos entre

minX e Med (1º quartil).

Med Mediana de todos os pontos de

dados.

Q3 (1-Var) Mediana dos elementos entre

Med e maxX (3º quartil).

maxX Máximo dos valores x.

2

ou y

2

.

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

• Pode alterar os pontos de dados, indo para o editor de dados, navegando para o elementos de dados e alterando o valor introduzido. Nota: Tem de recalcular estatísticas de 1-ou 2-variáveis para ver a opção StatVars.

Introduzir dados da estatística de 1 variável

Cinco estudantes fizeram um teste de matemática. Utilize os resultados para introduzir os pontos de dados—85, 85, 97, 53, 77.

Premir Ecrã

v

85 $ 97 $ 53 $ 77 $

" 2 $1 $1 $1 $

%t

v

Continuação

Ver as estatísticas

Calcule o número de pontos de dados (n), a média (

v), o desvio padrão da

amostra (Sx), o desvio padrão da população ( resultados (

quadrados (

sx), a soma dos

Gx), a soma dos

2

Gx

) e o resumo de cinco números dos dados, minX, Q1, Q2 e maxX.

Premir Ecrã

%t

1 $ " "

%t

v

< $

<

$ $ $ $ $

$ $ $

$ $

Remover os pontos de dados

Retire o resultado do teste mais baixo, editando os dados em L1 no editor de dados. Certifique-se de que actualiza a lista de frequência, L2, se for necessário. Calcule a média nova (

v). Apague os dados de todas as

listas. Premir Ecrã

v

$ $

v

J " J

%t

1

$$< vv 4

%Q

Introduzir dados da estatística de 2 variáveis

A tabela seguinte mostra o número de pares de ténis vendidos por uma pequena sapataria. A tabela mostra o número total de pares de sapatos vendidos durante dois meses e o número total de pares de sapatos da marca A vendidos durante os mesmos meses. Introduza estes dados no editor de dados.

Mês Abril 58 35 Maio 47 28

Nº total (x) Marca A (y)

%t v

Premir Ecrã

v58 $ 47 $

"35 $28 $

Ver as estatísticas

Partindo do princípio que a taxa de venda de sapatos é constante, pode utilizar os dois pontos de dados para prever as vendas de Junho da marca A se souber as vendas totais de Junho. Utilize umarecta de regressão para calcular as vendas de Junho da marca A, se a loja vender um total de 32 pares em Junho.

Sugestão: Calcule y

Premir Ecrã

'(32).

%C

%t

2 $ $ <

$ (ir para y') <

32 E <

Serão vendidos 18 pares da marca A em Junho, se as vendas totais forem 32 pares.

Probabilidade

12

Teclas

1. H mostra o seguinte menu de funções.

nPr Calcula o número de

permutações possíveis.

nCr Calcula o número de

combinações possíveis.

! Calcula o factorial de um

número.

Rand Gera um número aleatório

entre 0 e 1.

Randint( Gera um número inteiro

aleatório entre 2 números inteiros, A e B, em que A  Randint  B.

Notas

• Os exemplos dos acetatos assumem todas as predefinições.

• Uma combinação é uma disposição de objectos em que a ordem não é importante, como numa mão de cartas.

• Uma permutação é uma disposição de objectos em que a ordem é importante, como numa corrida.

• Um factorial é o produto de todos os números inteiros positivos de 1 a n, em que n

é um número inteiro positivo n‹o superior a

69.

• Pode guardar (L) um número inteiro para Rand tal como guardaria valores nas variáveis de memória. Se quiser controlar os números aleatórios gerados por todas as calculadoras da turma, deixe todos os estudantes guardarem o mesmo número para Rand; a sequência de números aleatórios é igual em todas as calculadoras.

•Para Randint, utilize uma vírgula para separar os 2 números especificados.

1

ç

Combinação (nCr)

Tem espaço para 2 livros na prateleira. Tem 4 livros para pôr na prateleira. Utilize esta fórmula para calcular o número de formas para escolher dois livros para ocuparem os espaços.

4 nCr 2

ABCD

AB e BA contam apenas

AB AC AD BA

BC BD

H

como 1 combina

Premir Ecrã

ão

CA DA

CB CD DB DC

4 H $

< 2 <

Existem 6 combinações únicas de 2 livros escolhidos a partir de 4 livros diferentes.

Texas instruments TI-30XS MULTIVIEW User Manual [pt]

Specifications and Main Features

Frequently Asked Questions

User Manual