Texas instruments TI-30XS MULTIVIEW User Manual

Download

Calculatrice

TI-30XS MultiView™

Guide de l’enseignant

Élaboré par

Texas Instruments Incorporated

Activités élaborées par

Gary Hanson, Aletha Paskett, Laurent Perret, et Margo Lynn Mankus

Illustré par

Jay Garrison et David Garrison

À propos des auteurs

Gary Hanson

School District à Sandy, dans l’Utah. Ils ont conçu plusieurs des activités proposées et participé à l’évaluation pédagogique des exemples contenus dans la section « Comment utiliser la calculatrice

Margo Lynn Mankus

mathématiques et des technologies à l’Université d’État de NewYork, à NewPaltz. Elle a vérifié et mis à jour le contenu de la documentation relative à la calculatrice conçu plusieurs activités proposées dans ce guide.

Laurent Perret

l’Environnement et du Cadre de Vie de la Chambre de commerce et d’industrie de Paris situé à Jouy-en-Josas. Il est également formateur T3 et a travaillé sur l’adaptation française de cette documentation.

Aletha Paskett

TI-30XS MultiView™

travaille actuellement dans le département d’enseignement des

est professeur de Mathématiques & Sciences Physiques à TECOMAH, l’Ecole de

sont enseignants de mathématiques au Jordan Independent

» de ce guide.

TI-30XS MultiView

Important

Texas Instruments n’offre aucune garantie, expresse ou tacite, concernant notamment, mais pas exclusivement, la qualité de ses produits ou leur capacité à remplir quelque application que ce soit, qu’il s’agisse de programmes ou de documentation imprimée. Ces produits sont en conséquence vendus “tels quels”. En aucun cas Texas Instruments ne pourra être tenu pour responsable des préjudices directs ou indirects, de quelque nature que ce soit, qui pourraient être liés ou dûs à l'achat ou à l'utilisation de ces produits. La responsabilité unique et exclusive de Texas Instruments, quelle que soit la nature de l'action, ne devra pas excéder le prix d'achat de cet article ou matériel.

Texas Instruments Incorporated 7800 Banner Drive, M/S 3918 Dallas, TX 75251

Attentnion: Manager, Business Services

Imprimé aux États-Unis d’Amérique.

MultiView, MathPrint, Automatic Power Down, APD et EOS sont des marques commerciales de Texas Instruments Incorporated.

Réglementation (France seulement)

TI-30XS MultiView les conditions d’usage des calculatrices aux examens et concours organisés par le Ministère de l’Éducation Nationale et dans les concours de recrutement des personnels enseignants en France, à compter de la session 2000.

est conforme à la circulaire française No 99-018 du 1-2-1999 qui définit

Table des matières

CHAPITRE PAGE CHAPITRE PAGE

À propos du guide de l’enseignant v À propos de la calculatrice

TI-30XS MultiView™

Activités

Voyage spatial

Notation scientifique 3

Rythme cardiaque

Statistiques 1-var 7

Au cinéma

Expressions algébriques appliquées aux films du « box office » 15

Trouvez la règle

Expressions algébriques 25

Comment utiliser la calculatrice

Comment utiliser la calculatrice TI-30XS MultiView

11 Statistiques 87 12 Probabilités 93 13 Table de fonction 101 14 Puissances, racines et inverses 105 15 Logarithmes et fonctions

exponentielles 113 16 Pi 117 17 Configuration et conversion

des angles 121 18 Conversions polaires et

rectangulaires 125 19 Trigonométrie 127 20 Hyperboles 135

(suite)

TI-30XS MultiView

1 Opérations de base de la

calculatrice TI-30XS MultiView 35 2 Effacer et modifier des entrées 47 3 Opérations de base 51 4 Ordre de priorité des opérations

et parenthèses 55 5 Notation numérique 61 6Fractions 65 7Décimales 69 8 Constante 71 9 Mémoire et variables mémorisées 75 10 Éditeur de données et listes 83

Annexe A

Référence aux touches A-1

Annexe B

Indicateurs d’affichage B-1

Annexe C

Messages d’erreur C-1

Annexe D

Informations sur les services et la garantie TI D-1

Annexe E

Informations sur la pile E-1

À propos du guide de l’enseignant



Organisation du guide de l’enseignant

Ce guide concerne les calculatrices scientifiques TI-30XS MultiView™ et TI-30XB MultiView. Toute référence ultérieure contenue dans ce guide se rapporte à la calculatrice TI-30XS MultiView, mais peut également s’appliquer à la calculatrice TI-30XB MultiView.

Ce guide est composé de deux sections : la section Activités et la section Comment utiliser

la calculatrice TI-30XS MultiView. La section Activités contient un certain nombre d’activités

permettant d’intégrer la calculatrice TI-30XS MultiView au programme d’enseignement des mathématiques. La section Comment utiliser la calculatrice TI-30XS MultiView a pour objectif d’aider les enseignants à apprendre à leurs élèves à utiliser leur calculatrice.

Sauf mention contraire, les activités et les exemples donnés utilisent les paramètres par défaut de la calculatrice, ainsi que le mode MathPrint™.

Activités

Chaque activité est autonome et présente les éléments suivants :

Comment utiliser la calculatrice TI-30XS MultiView

Cette section contient des fiches à utiliser comme des transparents. Chaque chapitre est numéroté et contient les éléments suivants :

• Une page d’introduction décrivant les touches de la calculatrice utilisées dans l’exemple, l’emplacement de ces touches sur la calculatrice TI-30XS MultiView, ainsi que toute note pertinente sur leurs fonctions.

• Les fiches disponibles après la page d’introduction contiennent des exemples d’application pratiques des touches abordées. Les touches abordées sont illustrées en noir sur le clavier de la calculatrice TI-30XS MultiView. Les paramètres du mode utilisé dans l’exemple sont également indiqués.

Réinitialisation de la calculatrice TI-30XS MultiView

• Pour vous assurer que le point de départ est le même pour tous les élèves, faites-leur réinitialiser leur calculatrice : Appuyez sur

& et - en même temps ou appuyez sur % , puis sur 2 (Yes).

• Une présentation de l’objectif de l’activité du point de vue mathématique.

• Le concept mathématique abordé.

• Le matériel nécessaire à la réalisation de l’activité.

• Toute la procédure en détail, ainsi que la combinaison successive des touches de la calculatrice TI-30XS MultiView à utiliser.

• Une fiche élève de l’activité.

Conventions utilisées dans le guide de l’enseignant

• Dans le texte, lorsque le symbole ou le nom d’une touche apparaît entre crochets [ ], cela signifie que cette touche représente une fonction secondaire ou une fonction alternative.

Par exemple : %Z

À propos de la calculatrice TI-30XS MultiView™

Écran d’accueil

L’écran d’accueil peut être utilisé pour entrer des expressions et des fonctions mathématiques, ainsi que d’autres instructions. Les réponses s’affichent dans l’écran d’accueil. L’écran de la calculatrice TI-30XS MultiView peut afficher jusqu’à quatre lignes de 16 caractères chacune. Pour consulter des entrées ou des expressions de plus de 16 caractères, vous pouvez faire défiler l’affichage à gauche et à droite (! et ") pour consulter l’entrée ou l’expression dans son intégralité.

Lorsque vous appuyez sur %Q, la calculatrice TI-30XS MultiView affiche l’écran d’accueil vide. Pour afficher et réutiliser des entrées précédentes, appuyez sur # et $ . (Voir Entrées précédentes, page vii.)

En mode MathPrint™, vous pouvez entrer jusqu’à quatre niveaux de fonctions et expressions imbriquées consécutives, y compris des fractions, des racines carrées et des exposants utilisant

les notations suivantes : ^, , ex et 10x.

Lorsque vous saisissez une entrée à calculer dans l’écran d’accueil, la réponse s’affiche soit à droite de l’entrée, soit sur la ligne suivante, en fonction de la place disponible.

chapitre 4, Ordre de priorité des opérations et parenthèses.

Étant donné que les opérations entre parenthèses sont effectuées en premier, si vous souhaitez modifier l’ordre de priorité des opérations et, par conséquent, modifier le résultat, utilisez les touches D E.

Mode

Pour changer de mode, utilisez la touche p. Appuyez sur $ # ! " pour choisir un mode et sur < pour le sélectionner. Appuyez sur ou sur %Q pour revenir à l’écran d’accueil et continuer à travailler en utilisant le mode sélectionné. Les paramètres par défaut sont indiqués.

Le mode Classic permet d’afficher les entrées et les réponses sur une seule ligne.

Le mode MathPrint permet d’afficher la plupart des entrées et des réponses selon deux colonnes (comme dans un cahier). Le mode MathPrint permet de mieux vérifier visuellement que les expressions ont été correctement entrées, mais également de renforcer l’utilisation appropriée des notations mathématiques.

Indicateurs d’affichage

Remarque : Le passage du mode Classic au mode

Pour obtenir la liste des indicateurs d’affichage, reportez-vous à l’annexe B.

MathPrint, et vice-versa, efface l’historique de la calculatrice, ainsi que la valeur de la fonction Constante.

Ordre de priorité des opérations

Fonctions secondaires (2nd)

La calculatrice TI-30XS MultiView utilise le système EOS™ (Equation Operating System Système d’exploitation d’équations) pour analyser les équations. L’ordre de priorité des opérations est présenté sur la fiche du

Pour accéder aux fonctions affichées au dessus de certaines touches, appuyez sur %, l’indicateur 2nd s’affiche, puis appuyez sur la touche appropriée. Par exemple, %b 25 < permet de calculer la racine carrée de 25 et renvoie la valeur 5.

À propos de la calculatrice

Menus

Certaines touches permettent d’afficher des menus : H, %I, v, %t, %, %h et %{. Appuyez sur " ou sur $ pour faire défiler l’écran et sélectionner un élément de menu, ou appuyez sur le numéro correspondant, situé en regard de l’élément de menu. Pour revenir à l’écran précédent sans sélectionner d’élément, appuyez sur -. Pour quitter un menu, ou une application, et revenir à l’écran d’accueil, appuyez sur %Q.

Entrées précédentes # $

Une fois qu’une expression a été analysée, vous pouvez utiliser les touches # et $ pour faire défiler les entrées précédentes, qui sont stockées dans l’historique de la calculatrice TI-30XS MultiView. Vous pouvez réutiliser une entrée précédente en appuyant sur < pour l’insérer dans la ligne du bas, la modifier, puis l’analyser en tant que nouvelle expression.

• Appuyez d’abord sur une touche d’opérateur (T, U, etc.). La valeur de Ans et l’opérateur s’affichent tous les deux.

Réinitialisation de la calculatrice TI-30XS MultiView

Pour réinitialiser la calculatrice, appuyez sur & et - en même temps ou appuyez sur % , puis sélectionnez 2 (Yes).

La réinitialisation de la calculatrice :

• Rétablit les paramètres par défaut : notation standard (virgule flottante) et mode degrés (DEG).

• Efface les variables en mémoire, les opérations en attente, les entrées de l’historique, les données statistiques, les constantes et la valeur de Ans (Dernière réponse).

Remarque : Les exemples des fiches supposent tous les réglages par défaut.

Affichages différents des réponses n

La touche de basculement permet d’afficher le résultat du dernier calcul sous plusieurs formes, si possible. Utilisez la touche n pour afficher la réponse sous la forme d’une fraction ou d’un nombre décimal, d’une racine carrée ou d’un nombre décimal, ou encore en utilisant pi ou un nombre décimal.

Dernière réponse (Ans)

Le dernier résultat de calcul est stocké dans la variable Ans. La valeur de Ans est gardée en mémoire, même après que la calculatrice TI-30XS MultiView ait été éteinte. Pour rappeler la valeur de Ans :

• Appuyez sur % i (l’indication Ans

s’affiche) ou

Fonction APD™ (Automatic Power Down™)

Lorsque la calculatrice TI-30XS MultiView reste inactive pendant plus de 5 minutes environ, la fonction APD (Automatic Power Down - Arrêt automatique) l’éteint automatiquement. Appuyez sur & pour la rallumer. L’affichage, les opérations en attente, les paramètres, ainsi que les valeurs mémorisées sont conservés.

Messages d’erreur

Pour obtenir la liste des messages d’erreur, reportez-vous à l’annexe C.

Activités

Voyage spatial —

Notation scientifique 3

Rythme cardiaque —

Statistiques 1-var 7

Au cinéma —

Expressions algébriques appliquées aux films du « box office » 15

Trouvez la règle —

Expressions algébriques 25

Voyage spatial — Notation scientifique

Présentation

Les élèves utilisent la notation scientifique pour écrire des nombres qu’ils utiliseront ensuite dans des calculs.

Introduction

Abordez l’activité en faisant part aux élèves du fait suivant :

La forme standard de la notation scientifique est aaaa à10 et où nnnn est un nombre entier.

1. Invitez les élèves à s’entraîner à écrire les

nnnn

, où aaaa est supérieur ou égal à 1 et inférieur

1010

nombres suivants en notation scientifique, à l’aide d’un crayon et de papier.

a. 93 000 000 b. 384 000 000 000 c. 0,00000000000234 d. 0,0000000157

9,3¿10 3,84¿10 2,34¿10 1,57¿10

-12

-8

Concepts mathématiques

•Notation scientifique

• Addition

• Division

Matériel requis

• La calculatrice TI-30XS MultiView™

•Un crayon

• La fiche élève de l’activité

2. Demandez aux élèves d’utiliser la notation scientifique (SCI) pour écrire les nombres suivants sur la calculatrice scientifique TI-30XS MultiView.

a. 12 000 000 b. 974 000 000 c. 0,0000034 d. 0,000000004

Remarque :

Remarque : Les réponses prennent en compte le paramètre

Remarque :Remarque :

de virgule flottante par défaut.

1,2¿10 9,74¿10 3,4¿10 4¿10

-6

-9

3. Demandez aux élèves d’écrire les nombres suivants en notation standard (NORM).

a. 5,8 b. 7,32 ¿ 10 c. 6,2 ¿ 10 d. 3 ¿ 10

Remarque :

Remarque : Pour entrer un nombre négatif, appuyez sur

Remarque :Remarque :

¿ 10

-6

-8

58 000 000 732 000 0,0000062 0,00000003

M, puis entrez le nombre.

³ Procédez comme suit :

1. Entrez le premier nombre,

12000000.

2. Appuyez sur p.

3. Appuyez sur $ " < - <pour afficher le nombre en notation scientifique.

1.2Ã

³ Procédez comme suit :

1. Entrez 5.8, appuyez sur C.

2. Entrez 7, appuyez sur p.

3. Appuyez sur $ < -

58000000

Ã10

ÃÃ

Voyage spatial — Notation scientifique (suite)

Activité

Soumettez le problème suivant aux élèves :

Vous êtes le commandant d’un vaisseau spatial dans un futur lointain. Votre mission consiste à vous rendre sur Alpha du Centaure et vous avez 5 ans pour y parvenir. La distance entre le soleil et Alpha du Centaure est de 2,5 x 10

miles (1 mile = 1,60934 km). La distance entre la Terre et le soleil est d’environ 9,3 x 10

miles.

Bien qu’à ce jour nous n’ayons pas encore découvert comment nous déplacer à la vitesse de la lumière, dans l’époque future dans laquelle vous vivez, votre vaisseau peut atteindre cette vitesse.

La lumière parcourt une distance d’environ 6x10

miles en une année-lumière. Votre trajectoire ira de la Terre au soleil, puis du soleil vers Alpha du Centaure. Pourrez-vous arriver sur Alpha du Centaure dans le délai imparti ?

Procédure

1. À l’aide de la calculatrice TI-30XS MultiView™,

calculez la distance totale à parcourir.

2,5¿1013 + 9,3¿107 = 2,5000093¿10

miles

2. Calculez ensuite le temps nécessaire pour

parcourir cette distance (distance parcourue

2 5000093 10

--------------------------------------------610

×,

¾ 1 année-lumière)

4 1666821672,=

années

3. Est-il possible d’effectuer le voyage dans le délai imparti de 5 ans ?

Oui, si le vaisseau peut réellement voyager à la vitesse de la lumière.

Complément

La lumière parcourt une distance de 186 000 miles par seconde. Une année-lumière correspond à la distance que peut parcourir la lumière en une année. Demandez aux élèves de calculer le nombre de miles parcourus en une année-lumière.

186.000 miles

--------------------------------- 1

Dans le cadre de cette activité, nous arrondirons cette valeur à 6 x 10

Réponse au complément de l’activité élève : il faudra environ 15 ans au vaisseau pour atteindre Delta du Centaure.

60s

------------ 1min

60min

--------------- -

××

24h

--------------

1jour

miles pour une année-lumière.

365jours

---------------------- -

1année

587, 1012miles×

-------------------------------------------

≈

1année

Astuce : Assurez-vous que la calculatrice TI-30XS MultiView est en mode MathPrint™ pour travailler sur ce problème.

Astuce :

soleil est d’environ 9,3 x 10

La distance entre la Terre et le

miles.

³ Procédez comme suit :

1. Appuyez sur 2.5 C13 C 7 <.

2.5000093Ã

2. Appuyez sur %i q 6 C 12 <.

4.166682167

³ Selon les calculs à effectuer,

rappelez aux élèves d’utiliser des parenthèses, si nécessaire, afin d’effectuer les opérations selon l’ordre de priorité souhaité. Exemple : (2,5000093 x 10 doit comprendre des parenthèses pour que le résultat souhaité soit généré.

³ Les élèves peuvent en savoir plus à

ce sujet en visitant le site Web de l’Agence spatiale européenne sur Internet.

Ã10

ÃÃ

" T 9.3

) ¾ (6 x 1012)

Voyage spatial —

Nom ___________________________

Notation scientifique

Date ___________________________

Problèmes

1. Écrivez les nombres suivants en notation scientifique.

Notation standard Notation scientifique

a. 93 000 000 __________________________

b. 384 000 000 000 __________________________

c. 0,00000000000234 __________________________

d. 0,0000000157 __________________________

2. Sur la calculatrice TI-30XS MultiView™, écrivez les nombres suivants en notation scientifique, à l’aide du mode SCI.

Notation standard Notation scientifique

a. 12 000 000 __________________________

b. 974 000 000 __________________________

c. 0,0000034 __________________________

d. 0,000000004 __________________________

3. Sur la calculatrice TI-30XS MultiView, écrivez les nombres suivants en notation décimale standard, à l’aide du mode NORM.

Notation scientifique Notation standard

a. 5,8 ¿ 10

b. 7,32 ¿ 10

c. 6,2 ¿ 10

d. 3 ¿ 10

-6

-8

_________________________

Voyage spatial —

Nom ___________________________

Notation scientifique

Date ___________________________

Problème

Vous êtes le commandant d’un vaisseau spatial dans un futur lointain. Votre mission consiste à vous rendre sur Alpha du Centaure et vous avez 5 ans pour y parvenir. La

distance entre le soleil et Alpha du Centaure est de 2,5 x 1013miles. La distance entre la Terre et le soleil est d’environ 9,3 x 107miles.

La lumière parcourt une distance d’environ 6 x 1012miles en une année-lumière. Votre trajectoire ira de la Terre au soleil, puis du soleil vers Alpha du Centaure. Pourrez-vous arriver sur Alpha du Centaure dans le délai imparti ?

Procédure

1. Sur la calculatrice TI-30XS MultiView™, calculez la distance totale à parcourir. Pour estimer cette distance, supposez que la distance à parcourir représente une ligne droite entre la Terre et le soleil, puis entre le soleil et Alpha du Centaure.

_____________________________________________________________________________

Astuce :

Calculez ensuite le temps nécessaire pour parcourir cette distance (distance parcourue ¾ 1 année-lumière).

Astuce : Veillez à utiliser des parenthèses afin d’effectuer les opérations selon l’ordre de priorité souhaité. ______________________________________________________________________________

____________________________________________________________________

2. Est-il possible d’effectuer le voyage dans le délai imparti de 5 ans ? ____________________________________________________________________

Assurez-vous que la calculatrice se trouve en mode de notation scientifique avant de commencer le calcul.

Complément

Maintenant que vous avez réussi, il vous est demandé d’entreprendre une nouvelle mission. La distance entre le soleil et Delta du Centaure est de 9 x 1013miles.

Combien de temps vous faudra-t-il pour vous y rendre à partir de la Terre ?

Astuce : La distance entre la Terre et le soleil est d’environ

¿ 10

9,3

Votre voyage dans ce vaisseau spatial est fictif. Si vous souhaitez en savoir plus sur l’étoile la plus proche et les distances cosmiques, visitez le site Web de l’Agence spatiale européenne sur Internet.

miles.

Rythme cardiaque — Statistiques 1-var

Présentation

Les élèves utilisent l’éditeur de données et la fonction de statistiques de la calculatrice TI-30XS MultiView™ pour étudier les effets de la pratique d’exercices physiques sur le rythme cardiaque.

Introduction

Les élèves peuvent être répartis en petits groupes pour cette activité afin de réduire la quantité de données à entrer. Posez aux élèves les questions suivantes :

• Quelle est, selon vous, le rythme cardiaque moyen d’une personne de votre âge ?

• Qu’en est-il de la pratique d’exercices physiques ?

Activité

Soumettez aux élèves l’expérience suivante afin qu’ils vérifient leurs estimations.

1. Invitez les élèves à mesurer leur rythme cardiaque au repos en comptant les pulsations pendant une minute. (Vous pourriez vous contenter de 10 secondes, puis multiplier le résultat obtenu par 6, mais vous passeriez alors à côté de ce qui pourrait être la minute la plus calme de votre journée !)

2. Rassemblez les données sur le graphique. Notez le rythme cardiaque de chaque élève, accompagné d’une marque dans la colonne des fréquences. Si d’autres élèves présentent le même rythme cardiaque, ajoutez une marque de pointage supplémentaire dans la colonne des fréquences.

3. Entrez les données sur le rythme cardiaque dans la calculatrice scientifique TI-30XS MultiView.

a. Entrez le premier rythme cardiaque du

graphique dans la liste L1 et le nombre de marques de pointage associées à ce rythme cardiaque dans la liste L2. Les valeurs de la liste L2 seront utilisées en tant que fréquence.

Concepts mathématiques

• moyenne, minimum, maximum et intervalle

³ Procédez comme suit :

1. Appuyez sur rythmes cardiaques et fréquences. Entrez les rythmes cardiaques dans la liste L1 et les fréquences dans la liste L2. Appuyez sur

chaque saisie et sur de L1 à L2.

2. Poursuivez la saisie jusqu’à ce que vous ayez entré tous les rythmes cardiaques et fréquences.

3. Appuyez sur

4. Appuyez sur 1 pour choisir les statistiques 1-var.

5. Choisissez la liste L1 pour les données et L2 pour la fréquence.

Matériel requis

• La calculatrice TI-30XS MultiView

• Un chronomètre ou une montre avec trotteuse

• La fiche élève de l’activité

v pour entrer les

$ entre

" pour passer

% t.

6. Appuyez sur les données.

$< pour afficher

Rythme cardiaque — Statistiques 1-var (suite)

a. Vous devez appuyer sur $ entre chaque

saisie. Par exemple, entrez le premier rythme cardiaque, puis appuyez sur

b. Supposons, par exemple, que vous ayez une

classe de 22 élèves :

Rythme Élèves Rythme Élèves

603633 615641 626654

4. Vérifiez les calculs statistiques. Une fois que les élèves ont obtenu est la somme de tous les rythmes cardiaques. Posez aux élèves les questions suivantes :

Òx (Sigma x), expliquez que Òx

• Combien de pulsations cardiaques ont été

enregistrées par tous les élèves en une

Òx

minute ? La réponse est

• Combien d’élèves ont été comptabilisés ? La

réponse est nnnn.

• Comment calculer le rythme cardiaque

Σx

moyen ? La réponse est

------

62.27272727=

• Le rythme cardiaque moyen est-il supérieur

ou inférieur à votre estimation ?

5. Nous allons maintenant étudier l’influence de la pratique d’exercices physiques sur le rythme cardiaque. Pour vous adapter aux différents besoins des élèves, demandez-leur de travailler par deux de façon à ce qu’ils s’entraident mutuellement. Songez également à définir une tâche que chacun des élèves peut réaliser en toute sécurité afin d’augmenter son rythme cardiaque. Dites aux élèves :

Si, à quelque stade que ce soit pendant cette phase de l’activité, vous ressentez une douleur, des vertiges ou le souffle court, arrêtez immédiatement.

³ Procédez comme suit :

1. Affichez les statistiques.

n doit correspondre au nombre total d’élèves comptabilisés. Dans cet exemple, n = 22.

2. Appuyez sur le rythme cardiaque moyen. Ï = 62.27272727

3. Appuyez sur vous voyiez

Òx = 1370

Remarque : Les nombres indiquent

les résultats de l’exemple décrit dans cette activité. Les résultats de vos élèves dépendront de la taille du groupe et des rythmes cardiaques collectés.

$ jusqu’à Ï pour voir

$ jusqu’à ce que

Òx.

Rythme cardiaque — Statistiques 1-var (suite)

6. Invitez les élèves à courir sur place pendant 2 minutes, puis donnez-leur les instructions suivantes :

Comptez vos pulsations pendant 1 minute.

Enregistrez votre rythme cardiaque comme

vous l’avez fait précédemment. c. Entrez les données dans la calculatrice. d. Comparez le rythme cardiaque moyen après

avoir couru avec le rythme cardiaque au

repos.

7. Demandez ensuite aux élèves de sautiller sur place pendant 2 minutes. Invitez-les à compter leurs pulsations pendant une minute et à réaliser les mêmes enregistrements qu’auparavant. Faites-leur entrer à nouveau les données dans la calculatrice, puis calculer le rythme cardiaque moyen après les sautillements. Comparez cette moyenne avec les deux autres.

8. Demandez aux élèves de construire un histogramme des 3 ensembles de données qu’ils ont collectés. Posez aux élèves les questions suivantes :

• Dans quelle mesure les histogrammes sont-ils

identiques ?

• Dans quelle mesure sont-ils différents ?

• Les données sont-elles regroupées ou

davantage dispersées sur un graphique que sur un autre ?

Rythme cardiaque —

Nom ___________________________

Statistiques 1-var

Date ___________________________

Problème

Quelle est, selon vous, le rythme cardiaque moyen d’une personne de votre âge ? Qu’en est-il de la pratique d’exercices physiques ?

Procédure

1. Utilisez ce tableau pour enregistrer les données de votre classe ou de votre groupe (au repos).

Pulsations cardiaques

par minute

(au repos)

Fréquence

2. Quel est le rythme cardiaque moyen de la classe ou du groupe ? _____________

3. Répondez aux questions suivantes à partir des données :

a. Quel est le nombre total de pulsations cardiaques comptées pendant cette

minute ? Inscrivez le symbole et le nombre affichés par la calculatrice._____

b. Quel est le nombre total de pulsations cardiaques entrées pour les élèves ?

Inscrivez le symbole et le nombre affichés par la calculatrice. ____________

c. Comment calculeriez-vous le rythme cardiaque moyen ? _________________

Votre réponse est-elle la même qu’à la question 2 ? _______________________

Rythme cardiaque —

Nom ___________________________

Statistiques 1-var

4. Utilisez le tableau ci-dessous pour enregistrer les données de votre classe ou votre groupe (après avoir couru).

Pulsations cardiaques

par minute

(après avoir couru)

Date ___________________________

Fréquence

5. Quel est le rythme cardiaque moyen de la classe ou du groupe ? ____________

6. Répondez aux questions suivantes à partir des données :

a. Quel est le nombre total de pulsations cardiaques comptées

pendant cette minute ? Inscrivez le symbole et le nombre affichés par la calculatrice.___________________________

b. Quel est le nombre total de pulsations cardiaques entrées

pour les élèves ? Inscrivez le symbole et le nombre affichés par la calculatrice.

___________________________________________________

c. Comment calculeriez-vous le rythme cardiaque moyen ?

___________________________________________________

Votre réponse est-elle la même qu’à la question 5 ?

___________________________________________________

Rythme cardiaque —

Nom ___________________________

Statistiques 1-var

7. Utilisez le tableau ci-dessous pour enregistrer les données de votre classe ou groupe (après avoir sautillé).

Pulsations cardiaques

par minute

(après avoir sautillé)

Date ___________________________

Fréquence

8. Quel est le rythme cardiaque moyen de la classe ou du groupe ? ____________

9. Quel est le nombre total de pulsations cardiaques calculées pendant cette minute ?

10.Répondez aux questions suivantes à partir des données :

a. Quel est le nombre total de pulsations cardiaques calculées pendant une

minute ? Inscrivez le symbole et le nombre affichés par la calculatrice.___

b. Quel est le nombre total de pulsations cardiaques entrées par les élèves ?

Inscrivez le symbole et le nombre affichés par la calculatrice. ___________

c. Comment calculeriez-vous le rythme cardiaque moyen ? ________________

Votre réponse est-elle la même qu’à la question 8 ?

Rythme cardiaque —

Nom ___________________________

Statistiques 1-var

11. Construisez un histogramme pour chacun des 3 ensembles de données que vous avez collectés.

Au repos Après avoir couru Après avoir sautillé

Date ___________________________

12.Dans quelle mesure les histogrammes sont-ils identiques ? Dans quelle mesure sont-ils différents ?

_______________________________________________________________________ _______________________________________________________________________

13.Les données sont-elles regroupées ou davantage dispersées sur un graphique que sur un autre ? __________________________________________________________

_______________________________________________________________________ _______________________________________________________________________

Au cinéma — Expressions algébriques appliquées aux films du « box office »

Présentation

Les élèves analysent un tableau de valeurs et observent les schémas mathématiques contenus dans le tableau. Les élèves utilisent la fonction v de la calculatrice TI-30XS MultiView™ pour entrer des données dans une liste et tester leurs hypothèses de généralisation.

Introduction

L’exercice d’entraînement ci-dessous vous permettra d’aborder l’activité avec les élèves. Si vous choisissez de l’ignorer, vous devrez fournir plus d’aide aux élèves lors de la phase d’analyse du problème sur papier.

Entraînement

Apprenez aux élèves à analyser les tableaux et à utiliser v afin de dégager un schéma mathématique et de trouver une règle de généralisation. Soumettez-leur le problème ci-dessous.

Chaque mercredi, Marie revient chez elle trop tard du travail pour pouvoir sortir son chien, Max. Elle a demandé à son voisin, Benjamin, de sortir Max après l’école. Benjamin en est ravi ! Marie paie Benjamin 4 € chaque semaine pour sortir Max. Benjamin aime économiser son argent. Créez un tableau représentant le montant gagné par Benjamin chaque semaine, pendant 5 semaines.

Concepts mathématiques

•Schémas mathématiques

• Expressions algébriques

• Fonctions linéaires

•Variables

Matériel requis

• La calculatrice TI-30XS MultiView

• Un crayon

• Du papier millimétré

• La fiche élève de l’activité

Apprenez aux élèves à créer le tableau suivant sur papier. Vous pouvez vous représenter ce tableau comme une liste de données à deux nombres dépendants l’un de l’autre. Il est important que les élèves écrivent leur calcul et que le résultat obtenu apparaisse dans la colonne Montant (résultat) afin qu’ils puissent dégager des schémas mathématiques.

Au cinéma (suite)

Cette approche leur permet de déduire des formules algébriques de leurs calculs écrits et d’émettre des hypothèses de généralisation par le biais d’un raisonnement inductif.

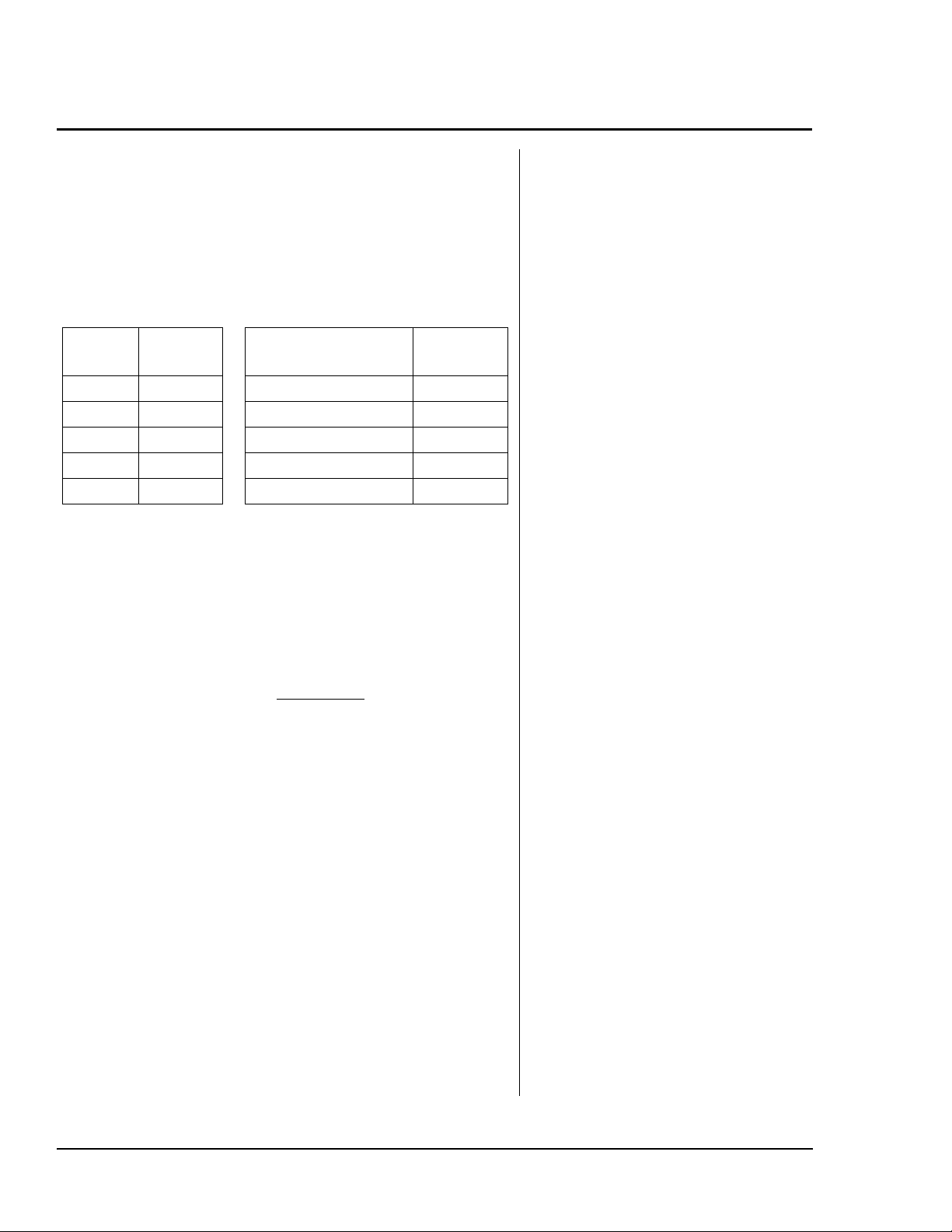
Si nécessaire, vous pouvez

utiliser ce tableau pour expliquer le problème selon une approche différente.

Semaine Montant Addition répétée Somme

cumulée

1 1x4=4 4=4 4=4 2 2x4=8 4+4=8 4+4=8 3 3x4=12 4+4+4=12 8+4=12 4 4x4=16 4+4+4+4=16 12+4=16 5 5x4=20 4+4+4+4+4=20 16+4=20

Faites remarquer aux élèves que le contenu de la colonne Montant ressemble à la table de multiplication du chiffre 4. Cette remarque permettra de faire référence à une notion qui leur est familière. Rappelez aux élèves qu’ils savent que Benjamin gagne 4 € par semaine. Il s’agit du taux d’épargne (économies) de Benjamin représenté par la fraction ci-dessous :

Taux =

4 €

1semaine

Demandez aux élèves de continuer à remplir le tableau décrivant l’épargne de Benjamin au fil des semaines. Invitez-les à remplir le tableau pour la sixième et la septième semaine, puis demandez-leur s’ils peuvent déterminer le montant épargné par Benjamin au bout de 10 semaines, 25 semaines et 100 semaines. Enfin, demandez-leur s’ils sont capables de calculer le montant épargné par Benjamin au bout d’un nombre donné de semaines.

Au cinéma (suite)

Expliquez aux élèves que ce nombre de semaines non défini est une variable que vous noterez S comme semaine. Utilisez la variable notée M pour représenter le montant épargné par Benjamin.

Semaine (S) Montant (M)

11x4=4 22x4=8 33x4=12 44x4=16 55x4=20 66x4=24 77x4=28

10 10 x 4 = 40

25 25 x 4 = 100

SSx4*

sans

Toute cette analyse doit être réalisée calculatrice car il s’agit de simples multiplications. Si les élèves ont besoin d’aide pour effectuer ces multiplications, encouragez-les à chercher dans les tables de multiplication plutôt que d’utiliser la calculatrice, ce qui favorisera le calcul mental et une utilisation à bon escient de la calculatrice.

Demandez aux élèves d’écrire l’expression algébrique du calcul en utilisant la variable S, le signe de multiplication

(Réponse : S x 4) Posez la question suivante aux élèves : « Lorsque vous effectuez le calcul de S semaines

multipliées par 4 €, vous obtenez un chiffre. À quoi correspond ce chiffre pour Benjamin ? » Les élèves doivent bien sûr vous répondre que ce résultat correspond au montant (M) gagné par Benjamin. Vous devez ensuite les inciter à écrire l’expression algébrique à deux inconnues (ou variables), M = S x 4. Par convention, on écrit d’abord le chiffre, puis la lettre sous forme de multiplication.

et le chiffre 4.*

³ Rappelez aux élèves que pour

cette activité, ils doivent utiliser la fonction vet non la fonction o.

³ Si certains élèves ne savent pas utiliser

la calculatrice TI-30XS MultiView, demandez-leur de l’allumer et d’appuyer sur p.

Au cinéma (suite)

Rappelez donc aux élèves que la multiplication est commutative, ce qui signifie que M=Sx4=4xS=4S.

Poursuivez l’analyse à l’aide de l’éditeur de données ( v) de la calculatrice TI-30XS MultiView™ en demandant aux élèves de vérifier que les valeurs résultant de l’expression algébrique trouvée correspondent à celles du tableau qu’ils ont créé.

1. Indiquez aux élèves d’entrer les valeurs de leur tableau dans la liste de données. Notez que trois listes sont disponibles : L1, L2 et L3.

Convenez avec les élèves d’entrer les valeurs de la variable Semaine (S) dans la liste L1.

2. Demandez aux élèves d’entrer les trois premières valeurs de la variable S apparaissant dans leur tableau, {1, 2, 3}.

3. Entrez la formule ci-dessous : L2 = 4 x L1. Notez que S = L1 et M = L2.

4. Ajoutez une entrée dans la liste L1 afin d’observer la mise à jour automatique de la liste L2 qui affiche le résultat de l’expression algébrique pour la valeur entrée. Déplacez le curseur sur une entrée vide de la liste L1. Demandez aux élèves de vérifier les résultats donnés par la calculatrice pour 4 et 100 semaines.

Avant de lancer la phase de recherche par groupe de l’activité, demandez aux élèves d’effacer les données entrées dans les listes.

³ Assurez-vous que la calculatrice des

élèves affiche le mode, tel qu’illustré ci-dessous :

Pour revenir à l’écran d’accueil, appuyez sur -.

1. Entrez les trois premières valeurs de la variable S : v 1 $ 2 $ 3 $.

2. Entrez la formule :

" v " 1

V v 1 <.

3. Ajoutez une entrée à la liste L1 :

! $ $ $

100 <.

4. Pour afficher à nouveau la formule dans la liste L2, appuyez sur

" 1.

5. Si nécessaire, modifiez l’expression, puis appuyez sur < pour définir l’expression à nouveau.

6. Pour effacer des données, appuyez sur

v 4.

4 <

" v

Les élèves ont su tirer d’un raisonnement transcrit sur papier des données qu’ils ont insérées dans un

³ Astuce : la touche %Q permet de

revenir à l’écran d’accueil.

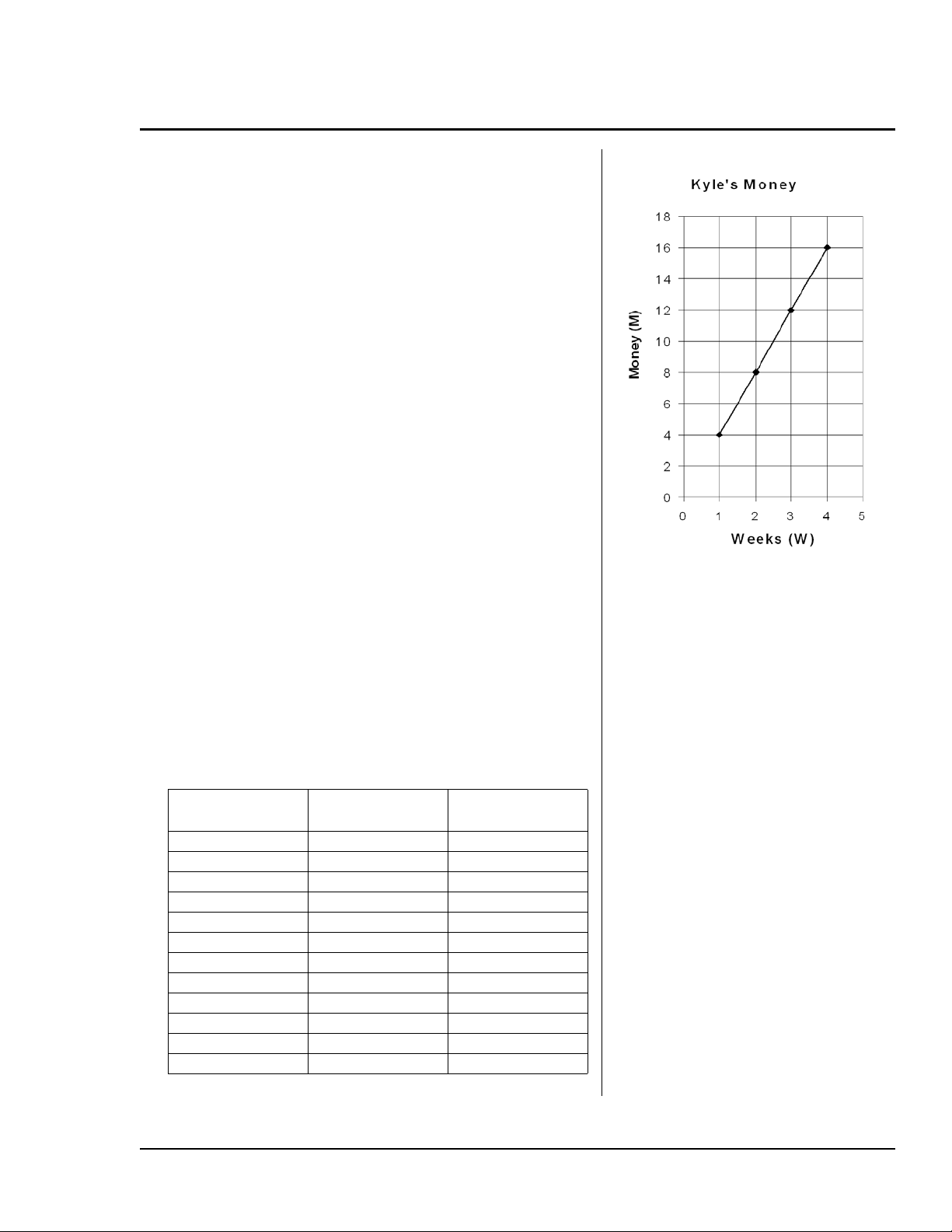
tableau de valeurs. Ce tableau leur a permis d’observer un schéma mathématique à partir duquel ils ont pu déduire une expression algébrique correspondante. La prochaine étape de l’exercice consiste à faire observer aux élèves la représentation graphique des points obtenus à l’aide de l’expression algébrique. Quelle est l’apparence de la courbe de l’expression M = 4W ? Demandez aux élèves de représenter graphiquement les quatre premiers points du tableau. Notez que tous les points appartiennent à la même droite. Vous pouvez indiquer aux élèves que l’augmentation du

Au cinéma (suite)

montant M peut être décrite de la manière suivante : « chaque semaine (S) de travail, le montant (M) gagné par Benjamin augmente de 4 € ». Il s’agit d’une affirmation évidente mais qui vous permettra d’aborder la notion de rapports, ainsi que leur influence sur le coefficient directeur (pente) d’une droite.

Le nombre de semaines et le montant gagné sont des valeurs positives, ce qui signifie que l’étude du graphique est pertinente dans le premier quadrant. Assurez-vous que les élèves utilisent du papier millimétré pour représenter leurs données graphiquement.

Activité

Les élèves travaillent en plusieurs groupes et réalisent à nouveau une analyse similaire consistant à observer des schémas mathématiques et à en déduire les expressions algébriques correspondantes. Ils représentent également les valeurs du tableau créé sous forme de graphique. Pour une meilleure compréhension du problème, assurez-vous que les élèves lisent individuellement l’énoncé avant de les laisser former les groupes de travail.

Les élèves doivent calculer les valeurs du tableau mentalement. Ils doivent mettre par écrit tous leurs calculs de façon à trouver l’expression algébrique le plus facilement possible. Encouragez-les à utiliser le calcul mental au maximum calculatrice pour calculer les montants.

Nombre de

avant

d’avoir recours à la

Calcul Montant (M)

personnes (P)

11x11,5011,50€ 2 2 x 11,50 23,00 € 3 3 x 11,50 34,50 € 4 4 x 11,50 46,00 €

...

10 10 x 11,50 115,00 €

...

100 100 x 11,50 1150,00 €

...

1 000 1 000 x 11,50 11500,00 €

...

P P x 11,50 M = P x 11,50

Au cinéma (suite)

Procédure

Les élèves doivent écrire l’expression algébrique qu’ils ont pu déduire du schéma mathématique mis en évidence par leur tableau : M = P x 11,50 ou M = 11,50 P (multiplication implicite).

Les élèves vérifient ensuite la pertinence de leur expression à l’aide de l’éditeur de données ( la calculatrice TI-30XS MultiView™. (Voir exercice

d’entraînement).

1. Demandez aux élèves de vérifier la configuration de leur calculatrice.

v) de

³ Assurez-vous que la calculatrice

affiche le mode approprié, tel qu’indiqué.

1. Appuyez sur p.

2. Entrez les trois premières valeurs dans la liste L1 {1, 2, 3}.

3. Adaptez votre expression de façon à ce qu’elle puisse être entrée dans la liste L2 de la calculatrice.

Votre expression est de la forme : M = ____________________________

L’expression à entrer dans la calculatrice est de la forme : L2 = ___________________

4. Entrez plusieurs valeurs dans la liste L1 afin de comparer les résultats du tableau de valeurs et celles de l’expression algébrique. Cette activité valide l’expression algébrique pour plusieurs valeurs.

5. Entrez la valeur 7 500 dans la liste L1 afin d’afficher le montant correspondant dans la liste L2. Écrivez l’expression sous la forme M = 11,50 x 7 500 = 86,250 €.

2. Appuyez sur v 1 $ 2 $ 3 $.

3. Entrez l’expression dans la liste L2. " v " 1

11 8 50 V v 1 <.

4. Appuyez sur ! $ $ $ 4 <

5 < 6 < 10 < 100 < 1000 <.

5. Appuyez sur 7500 <.

Au cinéma (suite)

6. Rédigez un rapport en remplissant un tableau de valeurs et en traçant un graphique. Expliquez votre démarche (1 paragraphe).

Ce paragraphe peut varier d’un élève à l’autre. Assurez-vous que les élèves y expliquent le calcul des valeurs du tableau, la représentation graphique et la définition de l’expression algébrique.

500 5 750 € 1 000 11 500 € 1 500 17 250 € 2 000 23 000 € 2 500 28 750 €

Nom ___________________________

Au cinéma

Date ___________________________

Problème

Un film évènement sort ce week-end dans les salles de cinéma. Aux informations, vous apprenez que la place coûtera 11,50 € par personne. Le journaliste déclare que deux personnes dépenseront 23 € et qu’une famille de trois personnes dépensera 34,50 €. Ces informations sont représentées sous la forme d’un tableau.

Nombre de personnes Montant

1 11,50 € 2 23,00 € 3 34,50 €

Le journaliste mentionne également que le complexe cinématographique local, le MultiPlex, propose 25 salles représentant au total 7 500 places assises. Ce film sera projeté dans toutes les salles du complexe. Les propriétaires de l’établissement estiment que toutes les places seront vendues le jour de la sortie du film !

Ces derniers souhaiteraient connaître le montant de la recette engendrée par ce film. Ils souhaiteraient disposer d’une expression algébrique générale leur permettant de calculer rapidement le montant de la recette du film en fonction du nombre de places vendues.

Votre mission est la suivante : vous avez été embauché comme comptable par le gérant du MultiPlex. Félicitations ! Votre patron souhaite disposer d’une expression mathématique qui lui indiquera la recette engendrée par ce film au box office, en fonction du nombre de places vendues.

Procédure

1. Utilisez un tableau afin d’étudier le montant de la recette en fonction du nombre de places vendues. Remplissez le tableau ci-dessous. Écrivez tous vos calculs, étape par étape. Utilisez le calcul mental au maximum calculer le montant de la recette.

Nombre de

Calcul Montant (M)

personnes (P)

11x11,5011,50€ 2 2 x 11,50 23,00 € 3 3 x 11,50 34,50 € 4 5 6

...

100

...

1 000

...

avant

d’avoir recours à la calculatrice pour

Nom ___________________________

Au cinéma

Date ___________________________

2. Quel schéma mathématique pouvez-vous tirer du tableau ? En vous inspirant des données du tableau, définissez une expression algébrique décrivant la variation du montant (M) de la recette en fonction du nombre de personnes (P) ayant acheté une place.

M = ___________________________

3. Vérifiez la pertinence de l’expression à l’aide de l’éditeur de données ( calculatrice TI-30XS MultiView™.

a. Dans la liste L1, entrez uniquement les trois premières valeurs correspondant au

nombre de personnes (P) du tableau. (Entrez {1, 2, 3}.)

b. Entrez l’expression algébrique définie à l’étape 2 dans la liste L2. Attention : pour

utiliser la calculatrice, vous devez adapter vos variables (lettres). La lettre P devient L1 et la lettre M devient L2.

Réécrivez l’expression algébrique en utilisant maintenant les notations L1 et L2 afin de pouvoir entrer l’expression dans la calculatrice.

Votre expression est de la forme : M = _________________________ L’expression à entrer dans la calculatrice est de la forme :

L2 = ________________________

c. Comparez les valeurs de la liste L2 et celles du tableau ci-dessus. Sont-elles

identiques ?

d. Entrez d’autres valeurs de la colonne du nombre de personnes de votre tableau dans

la liste L1. Comparez les valeurs de la liste L2 et celles du tableau ci-dessus. Sont-elles identiques ? Votre expression algébrique est-elle pertinente ?

v) de la

4. Utilisez l’éditeur de données de la calculatrice pour calculer le montant (M) de la recette qu’engendrera le film si toutes les séances sont complètes, soit 7 500 personnes (P). Retrouvez ce résultat manuellement à l’aide de l’expression algébrique. Justifiez votre raisonnement.

Nom ___________________________

Au cinéma

Date ___________________________

5. Votre patron souhaite élaborer une présentation destinée aux investisseurs du MultiPlex. Les investisseurs sont intéressés par les chiffres et les graphiques ! Remplissez le tableau ci-dessous en utilisant l’éditeur de données de la calculatrice. Représentez les points de ce tableau sous forme graphique. Le gérant dispose ainsi d’une alternative permettant d’observer la variation du montant (M) de la recette en fonction du nombre de personnes (P). Cela permet d’avoir une représentation visuelle des données !

500 1 000 1 500 2 000 2 500

Montant (M)

Nombre de personnes (P)

6. Expliquez à votre patron et aux investisseurs le travail que vous avez réalisé (un paragraphe). Détaillez la façon dont vous avez déterminé l’expression algébrique permettant de calculer le montant de la recette et expliquez ce que le tableau et le graphique peuvent apprendre sur la recette qu’engendrera le film.

Trouvez la règle !

Présentation

Les élèves doivent déduire une expression algébrique (fonction) à partir d’un tableau de valeurs, le tout sous forme de jeu. Pour cela, ils utilisent la touche o de la calculatrice TI-30XS MultiView™ afin d’entrer une expression sous forme de fonction (y=) pour pouvoir participer au jeu.

Introduction

Les élèves s’entraîneront pour cette activité en étudiant des expressions et en remplissant un tableau de valeurs. Ils participeront ensuite à un jeu appelé « Trouvez la règle ! », lequel fait appel à la calculatrice TI-30XS MultiView pour créer un tableau de valeurs.

Demandez aux élèves de remplir les tableaux suivants qui figurent sur leur fiche.

Remarque

Remarque : Pensez à éventuellement utiliser

RemarqueRemarque différentes notations pour les variables (lettres) pendant l’exercice d’entraînement. Sur la calculatrice en revanche, il s’agira toujours de la lettre x.

-2 1 -2 2 2

-1 2 -1 4 4 03 06 6 14 18 8 25 210 10

2x+6 2(x+3)*

Concepts mathématiques

•Expressions algébriques

• Fonctions

Matériel requis

• La calculatrice TI-30XS MultiView

•Un crayon

• La fiche élève de l’activité

• Des bandes de papier et un sac en papier

*Les élèves doivent remarquer que les colonnes du tableau correspondant aux expressions 2x + 6 et 2(x + 3) sont identiques. Débattez avec eux de la raison de cette équivalence entre les expressions et justifiez-la en utilisant la règle de distributivité de la multiplication par rapport à l’addition. Les élèves peuvent également utiliser des carreaux algébriques pour afficher la représentation de l’aire, 2(x + 3) = 2x + 6.

Indiquez aux élèves comment entrer l’expression à l’aide de la touche o de la calculatrice TI-30XS MultiView. L’expression doit être entrée comme une fonction. Il peut s’agir d’un concept nouveau pour vos élèves. Si nécessaire, utilisez un programme d’interprétation de fonctions

Trouvez la règle ! (suite)

afin de proposer une autre alternative au calcul d’une

expression pour différentes valeurs de présent, pour Expliquez aux élèves que l’expression envisagée comme la règle permettant de trouver Plus tard dans le jeu, les élèves devront faire le raisonnement inverse pour déduire la « règle ». Vous pouvez débattre de la méthode utilisée par les élèves pour suivre les règles de leurs jeux de société préférés. Ils doivent suivre des règles pour jouer. Lorsqu’ils évaluent une expression, ils suivent une règle pour passer d’un nombre à un autre.

= 1, on obtient y=1+3=4.

. Dans le cas

+3 peut être

Configurez le tableau à l’aide de la fonction automatique accessible via la touche o de la calculatrice. Cette fonction définit automatiquement un tableau de valeurs de sorte qu’il commence à une valeur donnée et qu’il soit incrémenté d’une certaine valeur. Pour que la calculatrice crée le même tableau de valeurs que ci-dessus, définissez la valeur de départ -2 et incrémentez les valeurs de de 1. Demandez aux élèves de comparer leur tableau avec celui de la calculatrice.

par pas

Activité

Jouez une ou deux parties de « Trouvez la règle ! » avec l’ensemble de la classe, en utilisant les règles énoncées à la page suivante. Pour la présentation du jeu à l’ensemble de la classe, le professeur joue le rôle d’arbitre. Ce jeu fait appel à la touche o

fonction AskTI-30XS MultiView™.

de la calculatrice

et à la

³ Procédez comme suit :

1. Appuyez sur p , puis définissez le mode tel qu’indiqué ci-dessous.

2. Entrez l’expression y = x +3 : o z T 3 <.

3. Entrez les valeurs de configuration du tableau : M 2 $ $ $ <.

4. Utilisez les touches # et $ pour faire défiler les valeurs de x et y = x +3.

³ Astuce : Copiez les fiches de jeu à

partir de la fiche élève en autant d’exemplaires que nécessaire.

Trouvez la règle ! (suite)

Règles pour une partie de groupe

• Formez des groupes de trois à quatre élèves.

• Attribuez à un élève le rôle d’arbitre du jeu.

• L’arbitre est responsable de la calculatrice pour la partie.

• Il tire une expression algébrique au sort dans un sac en papier (ou tout autre contenant) et la tient à l’abri du regard des autres joueurs. L’arbitre peut également écrire une expression algébrique sur un bout de papier et demander l’accord du professeur pour l’utiliser pour la partie.

• Il entre ensuite l’expression algébrique dans la calculatrice en utilisant la touche o, puis

sélectionne la fonction AskRemarque

Remarque : Il est possible que l’arbitre doive

RemarqueRemarque supprimer chaque ligne du tableau Askjouer une nouvelle partie (consultez les instructions sur l’utilisation des touches).

• Chaque joueur autre que l’arbitre donne une valeur à tour de rôle pour

. L’arbitre entre ces valeurs et

indique aux joueurs le résultat obtenu pour

• Chaque joueur conserve un tableau de valeurs en tant qu’enregistrement de jeu.

• Un joueur peut proposer une solution pour l’expression ou la règle à trouver uniquement lorsque son tour est venu.

• Une fois qu’une règle a été proposée par un joueur, chaque joueur doit vérifier si la règle est vraie pour toutes les valeurs déjà jouées ou mettre la règle à l’épreuve en tentant de trouver une valeur qui ne fonctionne pas.

• Si un joueur ou l’arbitre démontre que la règle proposée est incorrecte, le joueur ayant énoncé cette règle doit passer son tour suivant.

• Si l’expression algébrique proposée par un joueur n’est pas de la même forme que l’expression entrée par l’arbitre, par exemple 2 ( tous les joueurs s’accordent à dire que la règle est correcte, l’arbitre dévoile l’expression sur la calculatrice et le joueur ayant proposé la règle doit expliquer pourquoi les deux expressions sont équivalentes.

avant de

+1) et 2x+ 2, et si

³ Procédez comme suit :

1. Appuyez sur p , puis définissez le mode tel qu’indiqué ci-dessous.

2. Entrez la fonction y =2x +5:

- o 2 z T 5 <. Remarque : Si une fonction a déjà été entrée sur l’écran y=, appuyez sur - avant d’entrer une nouvelle fonction.

3. Entrez les valeurs de configuration du tableau : $ $ " < $ <.

4. Entrez les valeurs x : 5 < 6 < 10 <.

³ Astuce : Pour entrer des valeurs

supplémentaires, mettez en surbrillance l’une des trois lignes de la colonne x, entrez le nombre, puis appuyez sur <.

5. Pour revenir à l’écran y=, appuyez sur o. Vous devrez faire défiler à nouveau tout l’écran de configuration pour afficher le tableau de valeurs.

³ Pour rejouer, procédez comme suit :

1. Effacez l’ancienne expression, tirez au sort la nouvelle expression, puis entrez-la dans la calculatrice : o -z T q1 $ 2.

2. Entrez les valeurs de configuration de tableau souhaitées, mettez en surbrillance OK, puis appuyez sur <.

Notez que seules 3 solutions potentielles s’affichent à l’écran. Les élèves peuvent écraser un nombre pour afficher un nouveau résultat.

Trouvez la règle ! (suite)

• Le gagnant est le premier joueur qui propose la règle correcte et la défend.

• Le rôle d’arbitre est alors confié à un autre joueur pour la partie suivante.

Liste des expressions algébriques

Copiez ces expressions (ou d’autres) sur des bouts de papier afin que l’arbitre de chaque équipe puisse tirer au sort l’expression pour la partie. Celui-ci peut également écrire une expression que vous pouvez valider avant le début du jeu. Le fait que les élèves écrivent eux-mêmes une expression leur donne une certaine responsabilité et permet d’évaluer leurs connaissances.

Proposez une liste d'expressions algébriques ou créez-en une correspondant au niveau de vos élèves. Développez ces listes en fonction du niveau de vos élèves. Les élèves doivent documenter tout leur travail sur leur fiche.

Exemples d’expressions nécessitant une étape de résolution

+3 2x+3

–9 -4x+5

-- -+

–2,5

+15 1,5 x+2,5

–

-- -

Exemples d’expressions nécessitant deux étapes de résolution

+6 ou 2(x+3)

-- -x 4– 2

Adaptations du jeu

• Incluez des expressions que les joueurs devront

simplifier, par exemple 2 propose 5x - 2, il devra expliquer pourquoi l’expression est équivalente à 2 ajoute encore au côté pédagogique du jeu.

+4+3x- 6. Si un joueur

+4+3x- 6, ce qui

Trouvez la règle ! (suite)

• Intégrez des expressions sous forme de mots, telles que « quatre de moins que le double d’un nombre ». Demandez à l’arbitre de tirer au sort une expression algébrique dans le sac et de transformer les mots en une expression soumise à votre approbation avant qu’il ne retourne vers son équipe pour démarrer le jeu.

Exemple : L’expression « Quatre de moins que le double d’un nombre » est tirée au sort. L’arbitre traduit cela par l’expression algébrique 2 lui indiquez si sa transcription est correcte, puis il retourne avec son groupe pour commencer la partie.

-4, vous

Trouvez la règle !

Name ___________________________

Date ___________________________

Problème

Notre quotidien est fait de règles. Pouvez-vous suivre les règles de votre jeu de société préféré ? Devez-vous suivre scrupuleusement les règles pour jouer ? Nous suivons également des règles lorsque nous utilisons des nombres et des expressions.

Exemple : Si

L’expression des résultats. Vous pouvez considérer pour vous entraîner. Les valeurs de

-2 -2 -2

-1 -1 -1 000 111 222

=1, alors x+3=1+3=4

+ 3 se compose d’une variable, x. Selon la valeur de x, l’expression x+3 aura

+ 3 comme une règle. Remplissez le tableau suivant

ont été choisies pour vous.

2(x+3)

1. Que remarquez-vous sur le tableau pour 2

2. Vérifiez les tableaux ci-dessus en utilisant des tableaux créés dans la calculatrice TI-30XS MultiView™ à l’aide de la touche o.

3. Jouez à « Trouvez la règle ! » à l’aide de la fiche de jeu figurant sur la page suivante. Dans ce jeu, vous ignorerez l’expression (règle). Vous devrez déduire la règle en suivant le raisonnement inverse ! Votre professeur vous expliquera les règles du jeu.

+6 et 2(x+3)?

Trouvez la règle !

Raisonnez à l’inverse.

Noms des joueurs : Arbitre :

Votre professeur vous expliquera les règles du jeu. Utilisez le tableau pour garder une trace des valeurs de Proposition pour vérifier la règle. Si la règle d’un joueur n’est pas correcte, poursuivez la partie.

Valeur de y

donnée par

calculatrice

Déduisez la règle à partir d’un tableau de valeurs !

et de y proposées par chaque joueur pendant la partie. Utilisez les colonnes

Proposition 2

Proposition 1

= _______________________ Vérifiez chaque valeur de Cette proposition est-elle correcte ? _______

= _______________________

Vérifiez chaque valeur de Cette proposition est-elle correcte ? _______

Proposition 3

Valeur de y

donnée par

calculatrice

= _______________________ Vérifiez chaque valeur de Cette proposition est-elle correcte ? _______

= _______________________

Vérifiez chaque valeur de Cette proposition est-elle correcte ? _______

Proposition 4

Comment utiliser la

calculatrice

TI-30XS MultiView™

Opérations de base de la calculatrice TI-30XS MultiView 35

Effacer et modifier des entrées 47 Opérations de base 51 Ordre de priorité des opérations et

parenthèses 55 Notation numérique 61 Fractions 65 Décimales 69 Constante 71 Mémoire et variables mémorisées 75 Éditeur de données et listes 83 Statistiques 87 Probabilité 93 Table de fonction 101 Puissances, racines et inverses 105 Fonctions logarithmes et exponentielles 113 Pi 117 Configuration et conversion des angles 121 Conversions polaires et rectangulaires 125 Trigonométrie 127 Hyperboles 135

Opérations de base de la calculatrice TI-30XS MultiView™

Touche s

1. & permet d’allumer la calculatrice.

2. % active l’indicateur 2nd et donne accès

aux fonctions présentées au-dessus de certaines touches.

3. % ' permet d’éteindre la calculatrice et d’effacer l’affichage.

4. < lance l’opération ou exécute la commande.

5. % i rappelle le dernier résultat de calcul et l’affiche comme suit : Ans.

6. n permet d’afficher le résultat du calcul sous la forme d’une fraction ou d’un nombre décimal, d’une racine carrée ou d’un nombre décimal, ou encore en utilisant pi ou un nombre décimal.

7. ! et " déplacent le curseur à gauche et à droite afin de faire défiler les entrées sur l’écran d’accueil et de naviguer dans les menus. %! ou % " permettent d’atteindre le début ou la fin d’une entrée en cours. # et $ permettent de déplacer le curseur vers le haut et le bas pour parcourir les éléments du menu, visualiser les entrées précédentes sur l’écran d’accueil et visualiser les entrées dans l’éditeur de données et la table de fonction. % # permet de déplacer le curseur sur l’entrée supérieure de la colonne active de l’éditeur de données ou sur l’entrée précédente de l’écran d’accueil. Appuyez à nouveau sur % # pour déplacer le curseur sur l’entrée la plus ancienne de l’écran d’accueil. Dans les fractions, appuyez sur % # pour coller une entrée précédente dans le dénominateur. (Pour plus d’informations, reportez-vous au chapitre 6, Fractions). % $ déplace le curseur sur la première ligne vierge de la colonne active de l’éditeur de données ou au-dessous de la dernière entrée de l’écran d’accueil.

8. p permet de définir les modes angle,

3 1

5 4

numérique, décimal et affichage. Appuyez sur $# ! " pour choisir un mode et < pour le sélectionner. Appuyez sur - ou sur %Q pour quitter le menu des modes.

9. % affiche le menu Reset.

• Appuyez sur 1

précédent sans réinitialiser la calculatrice.

• Appuyez sur 2 (Yes) pour réinitialiser la

calculatrice. Le message

CLEARED

(No) pour revenir à l’écran

MEMORY

(mémoire effacée) s’affiche.

Opérations de base de la calculatrice TI-30XS MultiView™ (suite)

Remarque : Pour réinitialiser immédiatement la

calculatrice, appuyez en même temps sur & et

-. Aucun menu, ni message ne s’affiche.

• La réinitialisation de la calculatrice : – Rétablit les paramètres par défaut :

mode degrés (DEG), notation numérique normale (NORM), notation décimale (FLOAT) et MathPrint™.

– Efface les variables en mémoire, les

opérations en attente, les entrées de l’historique, les données statistiques, les constantes et la valeur de Ans (Dernière réponse).

Remarques

• Les exemples des fiches supposent tous les réglages par défaut (voir page vi).

• Vous pouvez utiliser la touche n dans une entrée avant d’appuyer sur <. Lorsque

vous appuyez plusieurs fois sur n dans une entrée en cours, une erreur de syntaxe peut survenir. Pour parvenir au résultat souhaité :

• Lorsque qu’il existe des caractères supplémentaires sur la gauche ou sur la droite.

• Appuyez sur & une fois la fonction APD™ (Automatic Power Down™ - Arrêt automatique) activée, pour rallumer la calculatrice. L’affichage, les opérations en attente, les paramètres, ainsi que les valeurs mémorisées sont conservés.

³ ou ´ s’affiche à l’écran, cela signifie

– Entrez l’expression, appuyez sur n <,

puis à nouveau sur n une fois que le résultat est affiché.

– Entrez l’expression, appuyez sur <,

puis sur n pour basculer entre les différents formats d’affichage de la réponse ;

autant de fois que nécessaire

2nd, off, flèches et enter

•Entrez 46–23. Remplacez 46 par 41 et

• 23 par 26 et exécutez l’opération.

• Entrez + et exécutez

l’opération. Éteignez, puis rallumez la

• calculatrice TI-30XS MultiView™. L’écran d’accueil est vide ; faites le défiler afin de consulter l’historique.

Touches Affichage

--5

----10

46 U

%' ! "

# $ <

23 < # # <

!!!! 1 "" 6 < 2 q 5 " T 3 q 10 <

%' & # # #

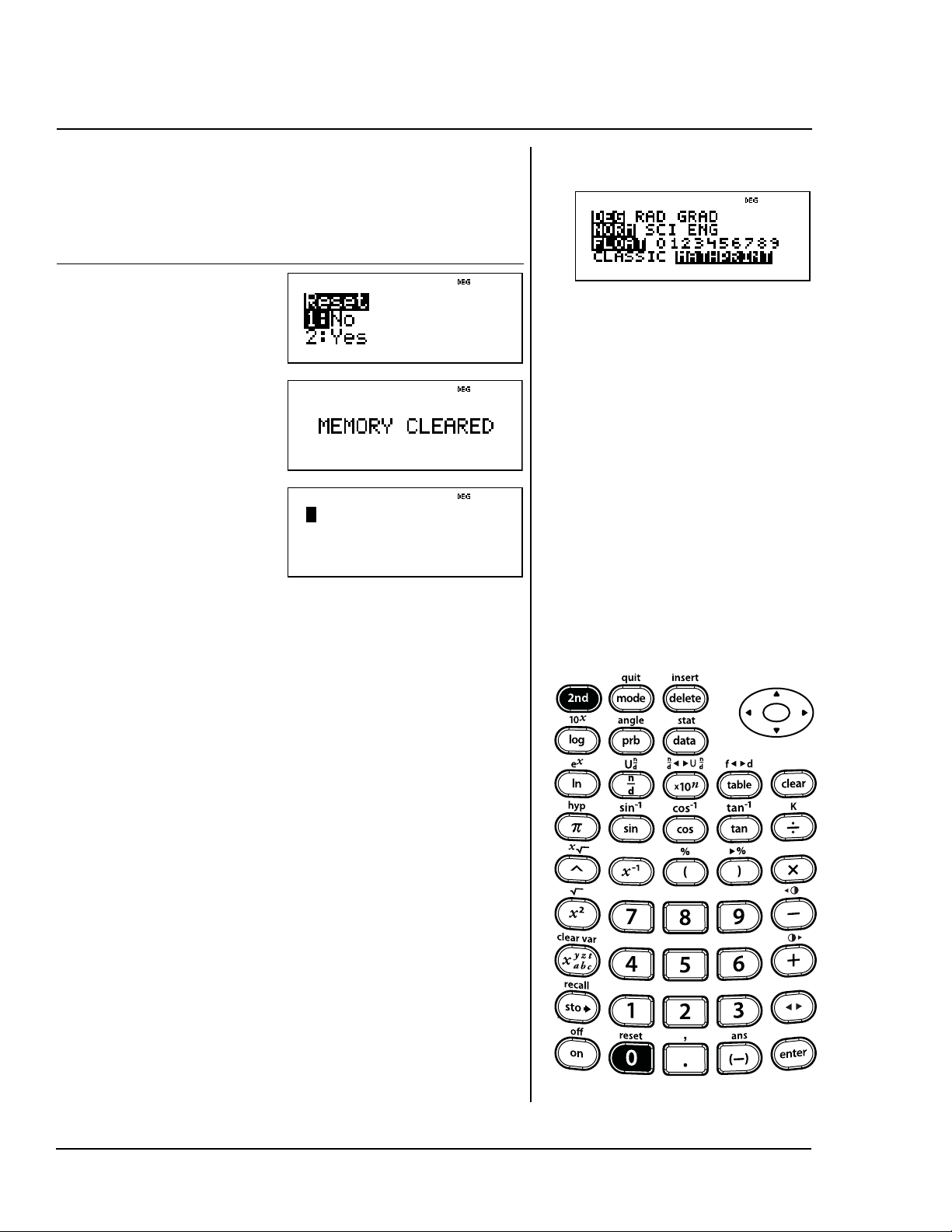
Réinitialise

Réinitialise la calculatrice.

Touches Affichage

%

Pour réinitialiser immédiatement la calculatrice, vous pouvez également appuyer en même temps sur & et

-. Aucun menu, ni message ne s’affiche.

Lorsque vous appuyez sur % ou, à la fois sur & et -, tous les paramètres par défaut sont rétablis et la mémoire est effacée.

Mode

Pour changer de mode, appuyez sur p. Appuyez sur $ # ! " pour choisir un mode et sur < pour le sélectionner. Appuyez sur - ou sur %Q pour revenir à l’écran d’accueil et continuer à travailler en utilisant le mode sélectionné.

Les paramètres de mode par défaut sont mis en surbrillance.

DEG RAD GRAD Permet de définir le mode d’angle sur degrés, radians ou grades.

NORM SCI ENG Permet de définir le mode de notation numérique. Le mode de notation numérique affecte uniquement l’affichage des résultats et non la précision des données stockées dans la calculatrice, précision qui reste maximale.

Mode (suite)

NORM affiche les résultats avec

des chiffres à gauche et à droite du séparateur décimal, ici un point, par exemple 123456.78.

SCI exprime les nombres avec un chiffre significatif à gauche du séparateur décimal et la puissance de 10 appropriée, par

exemple 1.2345678x10

(ce qui est

identique à 123456.78). ENG affiche les résultats sous la

forme d’un nombre de 1

à 999 multiplié par 10 élevé à une puissance correspondant à un nombre entier. L’exposant entier est toujours un multiple de 3.

Remarque : C est une touche de raccourci qui permet d’entrer une valeur en notation scientifique. Le résultat s’affiche en notation numérique selon les paramètres définis.

FLOAT 0 1 2 3 4 5 6 7 8 9 Définit le mode de notation décimale.

Mode (suite)

FLOAT (virgule flottante) affiche

jusqu’à 10 chiffres, plus le signe et la virgule.

0 1 2 3 4 5 6 7 8 9 (virgule fixe) indique le nombre de chiffres à afficher à droite de la décimale.

CLASSIC MATHPRINT permettent de définir l’affichage des entrées et des réponses.

CLASSIC permet d’afficher les entrées et les réponses sur une seule ligne.

MATHPRINT permet d’afficher la

plupart des entrées et des réponses selon deux colonnes (comme dans un cahier). Le mode MathPrint permet de mieux vérifier visuellement que les expressions ont été correctement entrées, mais également de renforcer l’utilisation appropriée des notations mathématiques.

Remarque : Le passage du mode Classic au mode MathPrint, et vice-versa, efface l’historique de la calculatrice, ainsi que la valeur de la fonction Constante.

Menus

Certaines touches permettent d’afficher des menus : H,

%I, v, %t, %, %h et %{. Certaines

touches peuvent afficher plusieurs menus.

Appuyez sur " et $ pour faire défiler

l’écran et sélectionner un élément de menu, ou appuyez sur le numéro correspondant, situé en regard de l’élément de menu. Pour revenir à l’écran précédent sans sélectionner d’élément, appuyez sur -. Pour quitter un menu ou une application et

revenir à l’écran d’accueil, appuyez sur

%Q. L’écran d’accueil est vide ; faites le défiler afin de consulter l’historique.

Voici quelques exemples de menus :

H % I

PRB RAND DMS R ¶¶¶¶P

1: nPr 1: rand 1: Ä 1: R ´Pr( 2: nCr 2: randint( 2: Å 2: R ´PÁ( 3: ! 3: Æ 3: P ´ Rx(

4: r 4: P ´Ry( 5: g 6: ´DMS

Menus (suite)

v Appuyez sur v une fois pour

afficher l’écran de l’éditeur de données. Appuyez à nouveau sur cette touche pour afficher le menu.

CLEAR FORMULA

1: Clear L1 1: Add/Edit Frmla 2: Clear L2 2: Clear L1 Frmla 3: Clear L3 3: Clear L2 Frmla 4: Clear ALL 4: Clear L3 Frmla

5: Clear ALL

Appuyez sur v pendant que vous êtes dans l’option Add/Edit Frmla du menu FORMULA pour afficher le menu suivant :

1: L1 2: L2 3: L3

STATS

1: 1-Var Stats 2: 2-Var Stats

Cette option de menu est affichée

3: StatVars

après le calcul de statistiques à 1 ou 2 variables.

StatVars menu: 1: n 2:

3: Sx Etc. Pour obtenir la liste complète,

reportez-vous au Chapitre 11, Statistiques.

Dernière réponse (Ans)

Utilisez l’option de dernière réponse

(Ans) pour calculer .

Touches Affichage

5 FT12

%b% i<

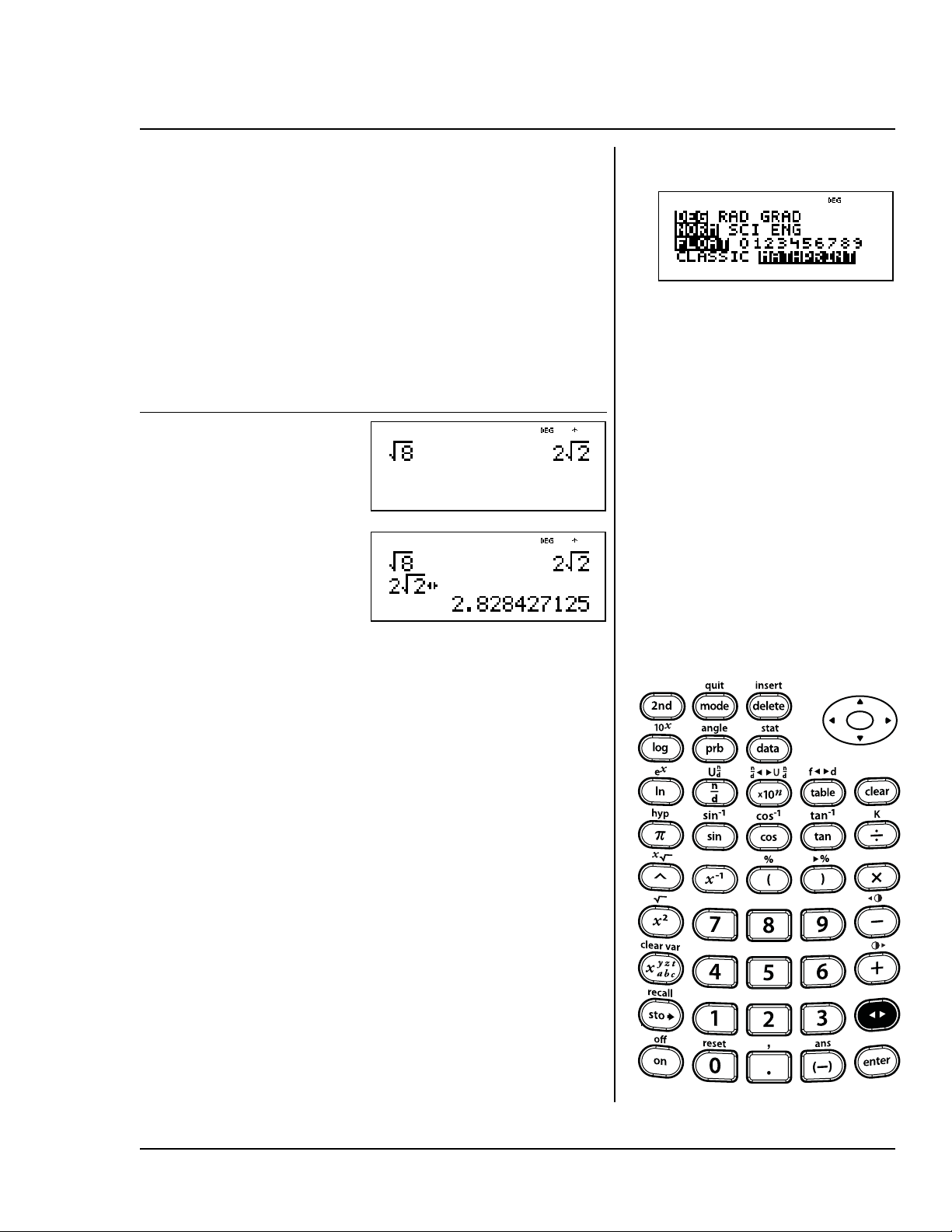
Affichages différents des réponses

Utilisez la touche n pour afficher le résultat du calcul sous la forme d’une fraction ou d’un nombre décimal, d’une racine carrée ou d’un nombre décimal, ou encore en utilisant pi ou un nombre décimal.

Touches Affichage

% b

8 <

Effacer et modifier des entrées

Touche s

1. La touche - permet d’effacer les caractères et les messages d’erreur. Appuyez une fois sur - pour effacer une saisie en cours ; appuyez à nouveau sur cette touche pour effacer tout ce qui apparaît à l’écran. Vous pouvez faire défiler l’écran et utiliser la touche - pour effacer les entrées de l’historique. Dans les applications, la touche

- permet de revenir à l’écran précédent.

2. La touche % f permet d’insérer un caractère au niveau du curseur.

3. La touche J permet de supprimer le caractère situé au niveau du curseur. Puis, à chaque fois que vous appuyez sur J, vous supprimez le premier caractère situé à gauche du curseur.

Remarques

• Les exemples des fiches supposent tous les réglages par défaut.

• La touche - n’a pas d’incidence sur les valeurs mémorisées, les registres statistiques, les unités d’angle et de la notation numérique définies.

2 3

Supprimer et insérer des entrées

Entrez 4569 + 285, puis modifiez la saisie en 459 + 2865. Exécutez l’opération.

Saisie Affichage

4569 T 285

! ! ! ! ! ! J

" " " "

%f 6

Effacer des entrées

Entrez 21595. Effacez les deux derniers chiffres : 95. Effacez l’entrée.

Saisie Affichage

21595

! ! -

(Effacer les éléments à

droite)

(Effacer l’entrée)

Opérations de base

Touche s

1. T additionne.

U soustrait.

3. V multiplie.

W divise.

5. < effectue l’opération ou exécute la commande.

M vous permet d’entrer un nombre négatif.

7. % _ ajoute le signe % à un nombre.

Remarques

• Les exemples des fiches supposent tous les réglages par défaut.

• La TI-30XS MultiView™ permet d’effectuer des multiplications implicites. Exemple : 3 (4+3) = 21

• Ne confondez pas la touche La touche

soustractions.

• Si nécessaire, utilisez les parenthèses pour regrouper le signe moins et le nombre. Exemple : M22 = M4 et (M2)2 = 4.

• Les résultats des calculs de pourcentage s’affichent selon le réglage du mode de notation décimale.

U permet d’effectuer des

M avec U.

3 2 1

Addition, soustraction, multiplication, division, égal

Trouvez :

2 + 54 16 x 21 =

x 10 =

--2

12 x (5 + 6) =

Touches Affichage

½ 6 =

2 T 54 U 6 <

T U V W

16 V 21 <

1 q 2 " V 10 <

12 V D 5 T 6 E <

Nombres négatifs

La température dans le Nord de la France était de 6 h 00 et 10 h 00, la température avait augmenté de 12Ä C. Quelle était la température à 10 h 00 ?

Touches Affichage

M3Ä C à 6 h 00. Entre

M 3 T

12 <

La température à 10 h 00 était de 9Ä C.

Pour c en t ag es

Mickaël gagne 80 € par semaine. Il économise 15 % de ses revenus. Combien Mickaël économise-t-il par semaine ?

Touches Affichage

% _ V 80 <

% _

Mickaël économise 12

€ par semaine.

Priorité des opérations et parenthèses

Touche s

1. D ouvre une expression entre parenthèses.

2. E ferme une expression entre parenthèses.

Remarques

• Les exemples des fiches supposent tous les réglages par défaut.

• La fiche présentant l’Equation Operating System (EOS™) montre la priorité des calculs effectués avec la calculatrice TI-30XS MultiView™.

• Les opérations entre parenthèses sont effectuées en premier. Utilisez les touches D E pour modifier la priorité des opérations et, par conséquent, modifier le résultat. Exemple : 1 + 2 x 3 = 7 (1 + 2) x 3 = 9

Equation Operating System (EOS™)

(en premier)

2 Fonctions qui nécessitent une E et précèdent

3 Fractions 4 Fonctions entrées après l’expression, notamment

Expressions entre D E

l’expression, notamment >, A et certaines options de menu.

F et les symboles d’unité d’angle (

¡, ¢, £, r, g)

5 Exposants (G) et racines (%c)

Remarque : En mode Classic, les expressions avec des exposants utilisant la touche G sont traitées de gauche à droite. L’expression 2^3^2 est traitée sous la forme (2^3)^2, avec un résultat de 64.

En mode MathPrint™, les expressions avec des exposants utilisant la touche G sont traitées de droite à gauche. Lorsque vous appuyez sur les touches 2 G 3 G 2, l’expression s’affiche sous la

forme , avec un résultat de 512.

La calculatrice scientifique TI-30XS MultiView™ traite les expressions entrées avec F et a de gauche à droite dans les modes Classic et MathPrint. Lorsque vous appuyez sur les touches

3 F F , l’expression s’affiche sous la forme

2)2

Le calcul est effectué comme suit : (3

=81.

Equation Operating System (EOS™) (suite)

6 Signe d’un nombre relatif (M) 7 Permutations (nPr) et combinaisons (nCr) 8 Multiplication, multiplication implicite et division 9 Addition et soustraction 10 Conversions (%O, %j, %R et

´DMS)

11 (en dernier)

< termine toutes les opérations et ferme toutes les parenthèses ouvertes.

Priorité des opérations

1 + 2 x 3 =

Touches Affichage

1 T 2 V 3 <

1 + (2 x 3) =

Touches Affichage

1 T D 2 V 3 E <

(1 + 2) x 3 =

T V D E

Touches Affichage

D 1 T 2 E V 3 <

Priorité des opérations (suite)

Touches Affichage

41()3()–

p$$$ <% b 5 F U 4 D 1 E D 3 E <

= (mode Classic)

Touches Affichage

41()3()–

(mode MathPrint™)

p$$$ "<% b 5 F U 4 D 1 E D 3 E <

Notation numérique

Touche s

1. p vous permet d’effectuer une sélection dans le menu de notation numérique suivant.

NORM Restaure le mode standard (virgule

flottante).

SCI Passe en mode scientifique et affiche

les résultats sous forme d’un nombre de 1 à 9 (1 { n < 9) multiplié par 10 avec un exposant entier.

ENG Passe en mode ingénieur et affiche les

résultats sous forme d’un nombre de 1 à 1000 (1 { n < 1000) multiplié par 10 avec un exposant entier. L’exposant entier est toujours un multiple de 3.

2. C est une touche de raccourci qui permet d’entrer une valeur en notation scientifique.

Remarques

• Les exemples des fiches supposent tous les réglages par défaut.

• Vous pouvez entrer une valeur en notation scientifique quel que soit le réglage du mode de notation numérique. Pour un exposant négatif, appuyez sur M avant de l’entrer.

• Les résultats nécessitant plus de 10 chiffres sont automatiquement affichés en notation scientifique.

• Pour le mode de notation décimale, reportezvous au Chapitre 7, Décimales.

•Ces modes (NORM, SCI et ENG) affectent uniquement l’affichage des résultats.

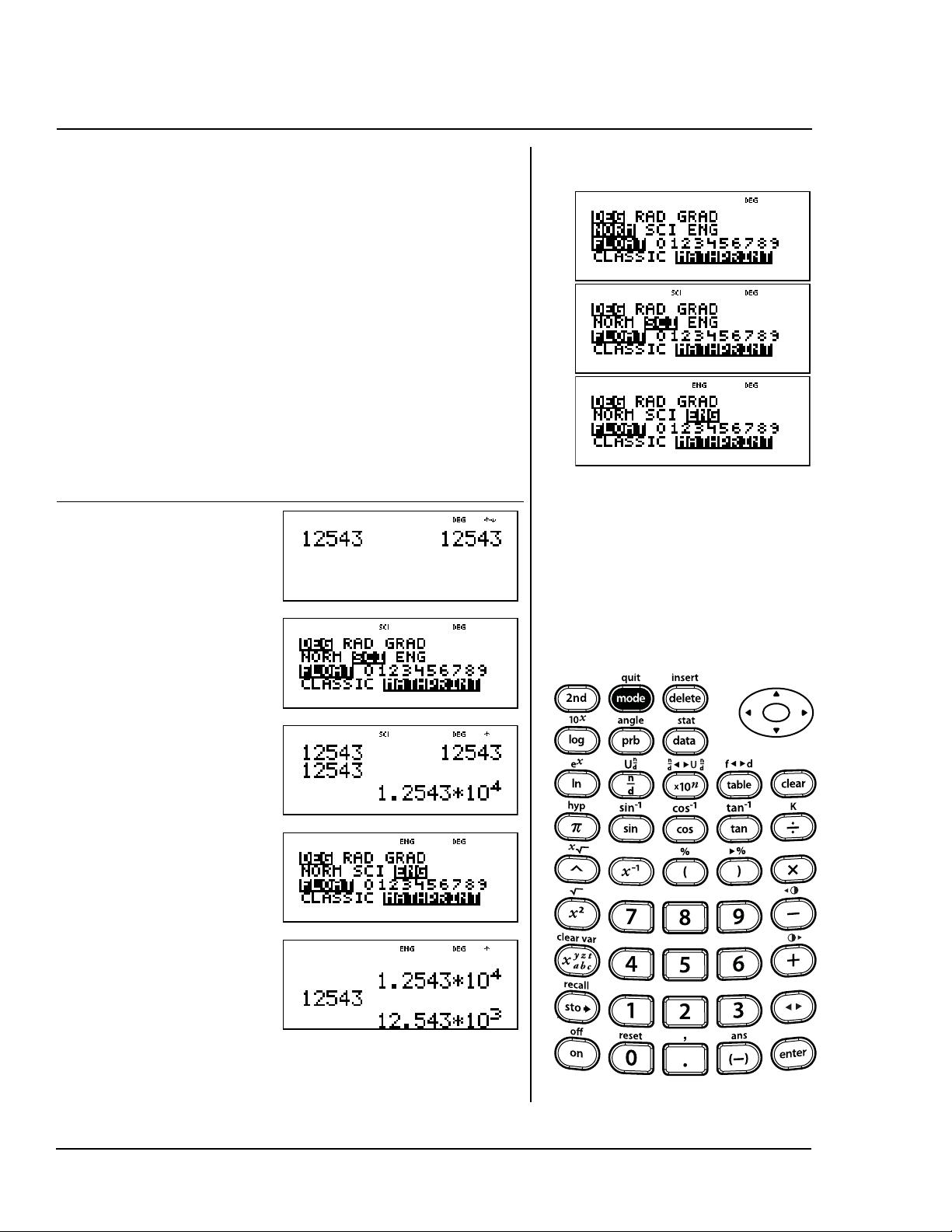
Notations ingénieur, scientifique et virgule flottante

Entrez 12543, qui sera en notation virgule flottante et en notation numérique normale (réglages par défaut dans p). Alternez le résultat à l’écran entre les notations normale, scientifique et ingénieur en changeant les réglages sur l’écran des modes.

Touches Affichage

12543 <

p$" <

p$" "<

Notations ingénieur, scientifique et virgule

p$<

Notation scientifique

Avec la calculatrice TI-30XS MultiView™ définie sur les modes Norm et MathPrint™ (modes par défaut), entrez le problème suivant en notation scientifique en utilisant la touche C

La Terre se trouve à environ 1.5 x 10 kilomètres du Soleil. Jupiter se trouve à environ 7.8 x 10 Soleil. En supposant que les orbites des planètes soient circulaires et que les planètes soient du même côté du

kilomètres du

Soleil, quelle distance sépare Jupiter de la Terre ?

Touches Affichage

7 8 8

C 8 " U 1 8 5 C

8 <

Jupiter et la Terre sont séparées

d’environ 630 000 000 = 6,3 x 10 kilomètres.

Fractions

Touche s

1. %N vous permet d’entrer des fractions en notation anglo-saxonne. L’unité doit être un entier. Le numérateur et le dénominateur peuvent contenir des décimales.

Pour entrer une fraction en notation anglosaxonne, entrez un entier pour l’unité, puis appuyez sur %N pour entrer un numérateur.

En mode MathPrint™, lorsque vous appuyez sur %N avant d’entrer un entier, un modèle de fraction s’affiche et vous ne pouvez entrer qu’un seul chiffre pour l’unité.

2. q vous permet d’entrer une fraction. Appuyer sur q avant ou après un nombre peut produire un comportement différent. En mode MathPrint™, lorsque vous entrez un nombre avant d’appuyer sur q , ce nombre devient généralement le numérateur.

En mode MathPrint, q peut également être utilisé pour des calculs plus complexes de fractions ou de formules qui incluent des opérateurs et d'autres fonctions. sur q avant d’entrer le numérateur.

En mode MathPrint™, appuyez sur $ entre l’entrée du numérateur et du dénominateur. En mode Classic, appuyez sur q entre l’entrée du numérateur et du dénominateur.

3. % O fait la conversion entre la notation sous forme de fraction et la notation anglo-saxonne et inversement.

4. % j convertit une fraction en son équivalent décimal et inversement.

Appuyez

Remarques

• Les exemples des fiches supposent tous les réglages par défaut.

• En mode MathPrint, vous pouvez entrer des fractions (q) avec toutes les touches

d’opération (T, V, etc.) et la plupart des touches de fonction (F, %_, etc.). En

1 2

mode Classic, vous ne pouvez pas entrer de fraction (q) avec les touches d’opération ou de fonction, ni entrer de fraction complexe comme numérateur ou dénominateur.

• En mode MathPrint, vous pouvez entrer des variables (x, y, z, t, a, b et c) dans le numérateur et le dénominateur d’une fraction. En mode Classic, les fractions avec q n’admettent pas de variables.

• En mode Classic, dans l’éditeur de données et la table de fonctions, utilisez W avec D et E où nécessaire pour résoudre des problèmes de division complexe.

Fractions (suite)

• Pour coller une entrée précédente dans le dénominateur, placez le curseur dans le dénominateur, appuyez sur % # pour rechercher l’entrée souhaitée, puis appuyez sur < pour coller l’entrée dans le dénominateur.

• Pour coller une entrée précédente dans le numérateur ou l’unité, placez le curseur dans le numérateur ou l’unité, appuyez sur # ou % # pour rechercher l’entrée désirée, puis appuyez sur < pour coller l’entrée dans le numérateur ou l’unité.

• Les résultats et les entrées sous forme de fractions sont automatiquement simplifiés.

• Selon l’entrée, les calculs utilisant des fractions peuvent afficher des résultats sous forme de fraction ou sous forme décimale.

Fractions

Pendant la fête, vous avez mangé

de la pizza au pepperoni et de la pizza à la saucisse. Les pizzas ont la

même taille. Si vous rassemblez les parts, quelle quantité d’une pizza entière avez-vous mangé ?

----10

--6

Touches Affichage

5 q 6 " T1 q 10 <

Vous avez mangé d’une pizza

entière. C’est pratiquement une pizza entière !

---15

Conversion de fractions et de nombres décimaux

A la piscine Julian fait 20 longueurs en 5.72 minutes. Marie fait 20

longueurs en minutes. Convertissez le temps de Marie en

nombre décimal pour déterminer qui nage le plus vite.

Touches Affichage

-----4

23 q 4 "

Julian nage plus rapidement que Marie car il parcourt 20 longueurs en 5,72 minutes.

Changez 2,25 en son équivalent fractionnaire.

Touches Affichage

2 8 25 %

ou 2 8 25 <

Décimales

Touche s

1. 8 entre une virgule décimale.

p vous permet de définir le nombre de

2. décimales. Appuyez sur $ $ puis sur " pour choisir la décimale souhaitée. Appuyez sur < pour la sélectionner.

FLOAT Définit la notation virgule flottante

(standard).

0-9 Définit le nombre de décimales

affichées. FIX s’affiche lorsqu’un mode décimal est défini entre 0-9.

Remarques

• Les exemples des fiches supposent tous les réglages par défaut.

•Appuyez sur p $ $ < pour revenir à la notation standard (virgule flottante).

• Le réglage du mode décimal influe sur la plupart des résultats décimaux et sur la mantisse des résultats des notations scientifique et ingénieur.

• La calculatrice TI-30XS MultiView™ arrondit automatiquement le résultat au nombre de décimales sélectionné. Par exemple, si le nombre de décimales est défini sur deux,

0.147 devient 0.15 lorsque vous appuyez sur <. De plus, la calculatrice TI-30XS MultiView arrondit ou complète les résultats avec des zéros à droite en fonction du réglage sélectionné. Par exemple, si le nombre de décimales est défini sur cinq,

0.147 devient 0.14700 lorsque vous appuyez sur <.

• La réinitialisation de la calculatrice efface le réglage des décimales et rétablit le réglage par défaut, FLOAT.

• Le réglage des décimales n’affecte pas la précision des résultats, mais uniquement leur affichage.

Décimale

Arrondissez 12,345 aux centaines, aux dizaines et ensuite à la notation virgule flottante.

Touches Affichage

12 8 345 <

$ $ "

""<

$$"

Constante

Touche s

1. % l active et désactive la fonction Constante, et vous permet de définir un nombre, une opération ou une expression de constante pour un raccourci lors de la répétition d’un ensemble de frappes. K s’affiche lorsque le mode Constante est activé.

2. < place le contenu de K à la fin de l’expression dans l’affichage.

Remarques

• Les exemples des fiches supposent tous les réglages par défaut.

• Toutes les opérations, fonctions et valeurs fonctionnent en mode Constante.

• Pour entrer une constante :

1. Appuyez sur % l. Si une constante

est déjà en mémoire, appuyez sur pour l’effacer.

2. Entrez la constante (un ensemble

quelconque d'opérations, de fonctions et de valeurs).

3. Appuyez sur < pour activer la fonction

Constante. K apparaît sur l’écran pour indiquer que la fonction Constante est activée.

4. Appuyez sur - pour effacer l’écran.

5. Entrez une valeur initiale. Si vous n’entrez

aucune valeur, la valeur 0 est supposée et Ans s’affiche à l’écran.

6. Appuyez sur < pour placer le contenu

de K à la fin de l’expression et pour l’évaluer.

7. Continuez à appuyer sur < pour

répéter la constante.

8. Appuyez à nouveau sur % l pour

désactiver la fonction Constante.

Constante

Trois personnes gardent des enfants

pour 5,25 € par heure. La première

personne travaille 16 heures. La deuxième personne travaille 12 heures. La troisième personne travaille 17 heures. Combien chaque personne gagne-t-elle ?

Touches Affichage

V 5.25 <

16 <

12 <

17 <

Constante (suite)

Touches Affichage

(Mode Constante désactivé.)

Mémoire et variables en mémoire

Touche s

1. L vous permet de stocker des valeurs dans les variables. Appuyez sur L pour sauvegarder une valeur et sur z pour sélectionner le nom de la variable. Appuyez sur < pour mémoriser la valeur dans la variable sélectionnée. Si cette variable contient déjà une valeur, elle est remplacée par la nouvelle.

2. z donne accès aux variables. Appuyez plusieurs fois sur cette touche pour choisir x, y, z, t, a, b ou c. Vous pouvez aussi utiliser z pour rappeler les valeurs mémorisées dans ces variables.

3. % { efface toutes les variables.

4. % h affiche un menu des variables x, y, z, t, a, b et c , et vous permet de visualiser leurs valeurs en mémoire avant de les coller à l’écran.

Remarques

• Les exemples des fiches supposent tous les réglages par défaut.

• Vous pouvez mémoriser un nombre ou une expression qui produit un nombre dans une variable en mémoire.

• Lorsque vous sélectionnez une variable avec la touche z, le nom de la variable (x, y, z, t, a, b ou c) s’affiche. Le nom de la variable est inséré dans l’entrée en cours, mais la valeur affectée à la variable sert à évaluer l’expression.

• Lorsque vous sélectionnez une variable avec la touche % h, un menu présentant la valeur des variables en mémoire s’affiche. Sélectionnez la variable en appuyant sur le numéro de menu correspondant. La valeur affectée à la variable est insérée dans l’entrée en cours et est utilisée pour évaluer l’expression.

• La réinitialisation de la calculatrice efface toutes les variables en mémoire.

3 2

Mémorisation de variables

Voici les pourcentages de vos contrôles et de vos devoirs de mathématiques.

Notes des contrôles : 96, 76, 85. Notes des devoirs : 92, 83, 97, 86.

1. Calculez la moyenne de vos notes d’examens.

2.Calculez la moyenne de vos notes de devoirs.

3.Votre professeur calculera votre

note finale en faisant la moyenne de votre note d’examens et de votre note de devoirs. Quelle est votre note finale ? Si nécessaire, votre professeur arrondira la note à l’entier le plus proche.

Touches Affichage 96 T 76 T

85 <

Mémorisation de variables (suite)

W 3 <

Lz <

92 T 83 T 97 T 86

< W 4 <

T z <

W 2 <

Votre note finale est arrondie à 88, l’entier le plus proche.

Rappel de variables

Vous allez expédier un cadeau à chacun de vos deux amis. Vous trouvez les cadeaux sur deux sites Web au même prix. Les frais d’expédition sont différents sur chaque site. Les colis pèsent 4,5 livres et 3,2 livres. Le magasin A

livrera le colis pour 2 € plus 1,40 € par

livre. Le magasin B livrera le colis pour

3 € plus 1,10 € par livre. Quel magasin

proposera le tarif le moins élevé pour l’expédition de chaque cadeau ?

Touches Affichage

4 8 5 L

z <

2 T 8 40 E

3 T 8 10 E

Le magasin A facture 8,30 € et le magasin B facture 7,95 €. Le

magasin B propose le tarif le moins

z D1

Rappel de variables (suite)

élevé pour l’expédition du cadeau pesant 4,5 livres.

3 8 2 L

z <

##### #<<

Le magasin A facture 6,48 € et le

magasin B facture 6,52 €. Le

magasin A propose le tarif le moins élevé pour l’expédition du cadeau pesant 3,2 livres.

Rappel de variables (suite)

Magasin Achats Qté Prix

A Chemises 2 13,98 € l’unité B Cravates 3 7,98 € l’unité C Ceinture 1 6,98 €

Bretelles 1 9,98 €

Combien avez-vous dépensé dans chaque magasin et au total ?

Touches Affichage

2 V 13 8 98 <

Lz<

3 V 7 8 98 <

L z z <

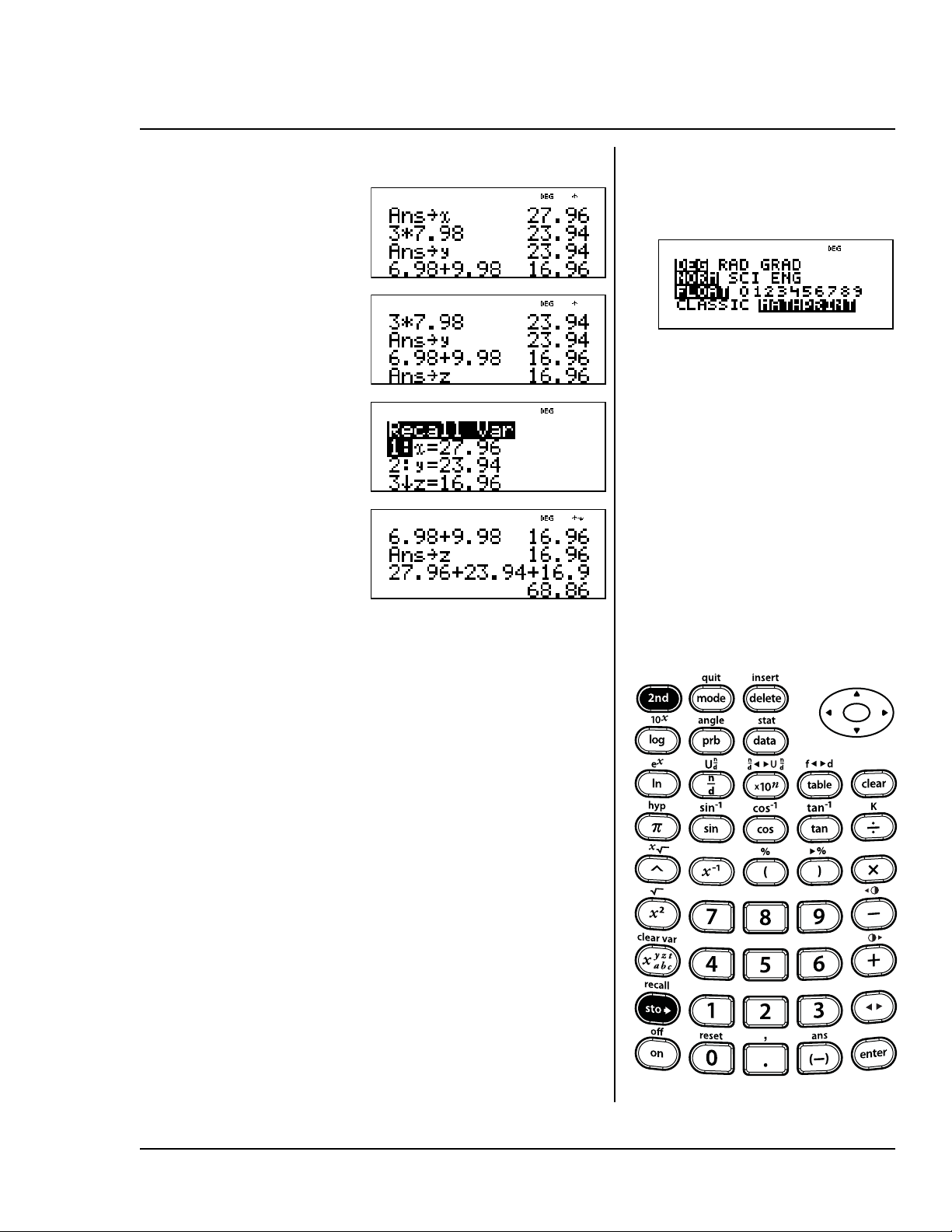
Rappel de variables (suite)

6 8 98 T 9 8 98 <

L z zz<

% h

1 T% h 2 T %

h 3 <

Vous avez dépensé :

27,96 € dans le magasin A, 23,94 € dans le magasin B, 16,96 € dans le magasin C.

Vous avez dépensé 68,86 € dans les

trois magasins.

Éditeur de données et listes

Touche s

1. v affiche un éditeur de données avec trois listes. Chaque liste peut contenir jusqu’à 42 éléments. Pour entrer des données, accédez à une liste et entrez un nombre. Appuyez sur les touches fléchées pour parcourir les éléments de la liste.

Remarques

• Les exemples des fiches supposent tous les réglages par défaut.

• Les listes acceptent toutes les fonctions de la calculatrice.

• Dans les formules, utilisez D et E autour des variables ou des noms de liste pour garantir la priorité des opérations souhaitée.

• Lorsqu’une formule est entrée dans une liste, la liste est automatiquement mise à jour si un élément de la liste référencé est mis à jour.

Remarque : Si vous appuyez sur < dans une liste, la formule est automatiquement effacée. Aucun message ne s’affiche.

• Lorsqu’une formule est supprimée, les données sont conservées mais ne sont plus mises à jour.

• Lorsque vous appuyez à nouveau sur v depuis l’écran de l’éditeur de données, vous accédez à des menus qui contiennent des options permettant d’effacer des listes ou d’entrer et de gérer des formules.

• Lorsque vous appuyez à nouveau sur v dans l’option « Add/edit a formula », vous accédez à un menu contenant des noms de liste que vous pouvez utiliser pour ajouter ou

éditer des formules.

• La touche - permet de sauvegarder des écrans dans l'éditeur de données.

• La séquence de touches % Q permet de quitter l’éditeur de données et de revenir à l’écran d’accueil.

• Dans l’éditeur de données, la notation scientifique s’affiche sous la forme gagner de l’espace mais elle représente toujours la grandeur d’un nombre.

Exemple : 2 x 103 apparaît sous la forme 2E3.

E pour

Saisie de données et de formules

Un jour de novembre, un bulletin météo sur Internet indiquait les températures suivantes.

Paris, France 8Ä C Moscou, Russie Montréal, Canada 4Ä C

Convertissez ces températures : de degrés Celsius en degrés Fahrenheit.

Rappel : F= C+32.

Touches Affichage

--5

½1Ä C

v 8 $ M 1 $ 4 $ "

v "

9 W 5 V v 1 T 32

Saisie de données et de formules (suite)

Notez que L2 s’affiche en surbrillance car il s’agit du résultat de la formule.

Les températures en degrés Fahrenheit sont les suivantes :

Paris, France 46,4Ä F Moscou, Russie 30,2Ä F

Montréal, Canada 39,2Ä F

Si la température à Sydney, en Australie, est de 21Ä C, quel est son équivalence en degrés Fahrenheit ?

! $ $ $

La température à Sydney, en Australie, est de 69,8Ä F.

Statistiques

Touche s

1. v vous permet d’entrer des valeurs (x pour

les statistiques 1-Var ; x et y pour les statistiques 2-Var). (Pour plus d’informations sur v, reportez-vous au Chapitre 10, Éditeur de données et listes.)

2. %t affiche un menu dans lequel vous

pouvez sélectionner 1-Var, 2-Var ou StatVars.

1-Var

2-Var analyse les données couplées de 2

StatVars Cette option est affichée

analyse les données d’un ensemble de données avec 1 variable mesurée (x).

ensembles de données avec 2 variables mesurées (x, la variable indépendante et y, la variable dépendante).

uniquement après le calcul des statistiques 1-var ou 2-var. Elle affiche le menu des variables avec leurs valeurs en cours.

Menu StatVars :

n Effectif total x (ou x, y).

v ou w Moyenne de toutes les valeurs x

ou y.

Sx ou Sy Écart type d’échantillon

standard de x ou y.

sx ou sy Écart type de population

standard de x ou y.

Gx ou Gy Somme de toutes les valeurs

de x ou de y.

ou Gy2Somme de toutes les valeurs

de x

ou de y2.

Gxy Somme du produit de x et y

pour tous les couples de données x-y dans les 2 listes.

a Coefficient directeur de la

droite de régression.

b Coordonnée à l’origine de la

droite de régression.

r Coefficient de corrélation. x ÅÅÅÅ (2-var) Utilise a et b pour calculer la

valeur x prévue lorsque vous entrez une valeur y.

y ÅÅÅÅ (2-var) Utilise a et b pour calculer la

valeur y prévue lorsque vous entrez une valeur x.

minX Minimum des valeurs x. Q1 (1-var) Médiane des points situés

entre minX et Med (1er quartile).

Med Médiane de toutes les valeurs. Q3 (1-var) Médiane des points situés

entre Med et maxX (3ème quartile).

maxX Maximum des valeurs x.

Remarques

• Les exemples des fiches supposent tous les réglages par défaut.

• Pour modifier des valeurs dans l’éditeur de données, accédez à l’élément de données et modifiez la valeur entrée. Remarque : Vous devez ensuite recalculer les statistiques 1-var ou 2-var pour afficher l’option StatVars.

Saisie de données statistiques 1-Var

Cinq élèves ont passé un contrôle de mathématiques. En utilisant leurs notes, entrez les valeurs 85, 85, 97, 53, 77.

Touches Affichage

85 $ 97 $ 53 $ 77 $

" 2 $1 $1 $1 $

%t v

Suite

Visualisation des statistiques

Trouvez l’effectif total (n), la moyenne (

v), l’écart type d'échantillon

standard (Sx), l’écart type de population standard ( des notes (

au carré (

Gx), la somme des notes

) et les cinq nombres

sx), la somme

récapitulatifs des données, minX, Q1, Q2, et maxX.

Touches Affichage

1 $ " "

%t v

< $

$ $ $ $ $

$ $ $

$ $

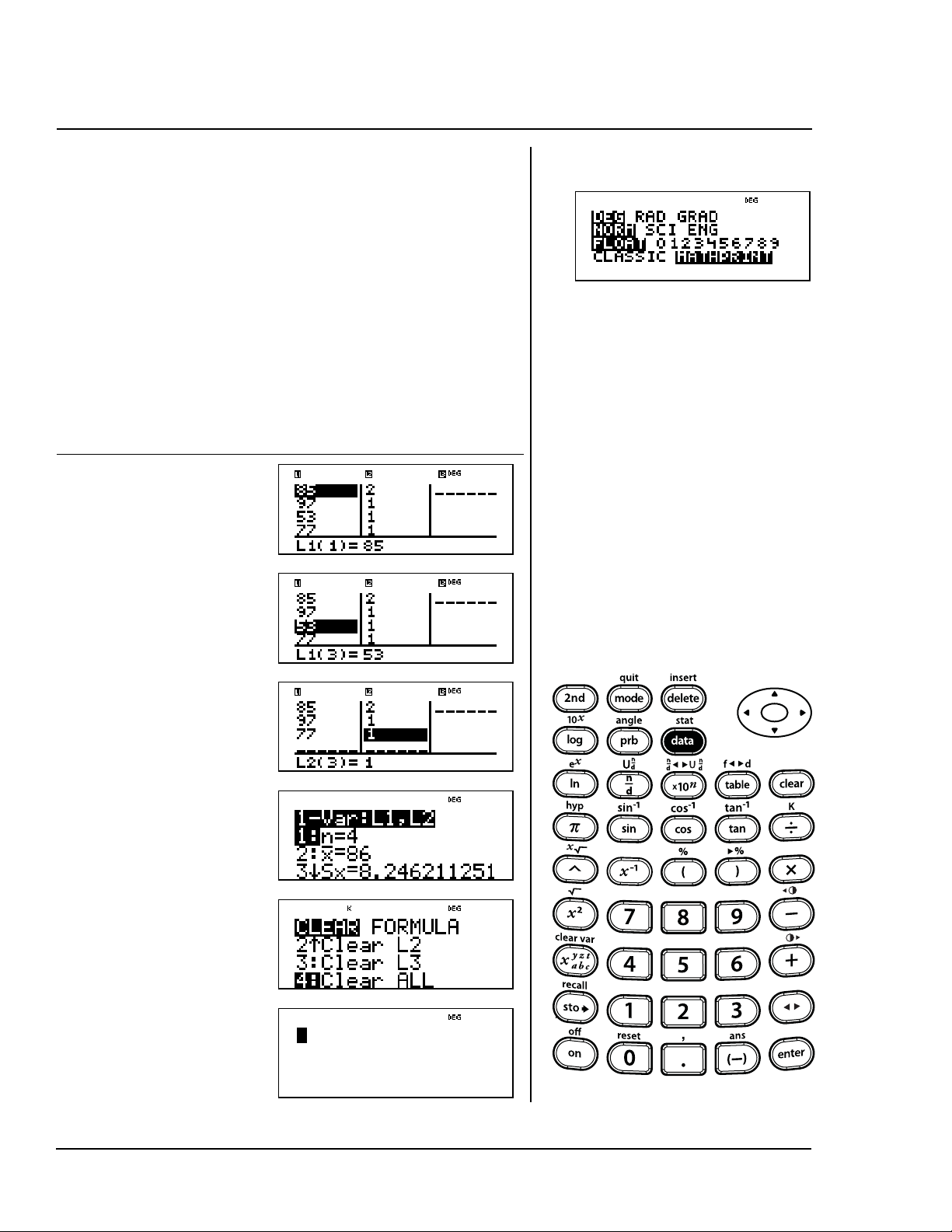
Retrait de valeurs

Éliminez la note la plus basse en modifiant les données dans L1 dans l’éditeur de données. Veillez à mettre à jour la liste de fréquence L2 si nécessaire. Calculez la nouvelle moyenne ( données de toutes les listes.

Touches Affichage

v). Enfin, effacez les

$ $

J " J

$$<

vv 4

Texas instruments TI-30XS MULTIVIEW User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual