Texas instruments TI-10 Teachers Manual

TI.10

Guide de l'enseignant

Conception :

Texas Instruments Incorporated

Conception des activités :

Jane Schielack

À propos de l'auteur

Jane Schielack est Maître de conférences de Mathématiques auprès du Département des Mathématiques de la Texas A&M University. Elle a conçu la section contenus dans le chapitre de ce guide

Utilisation de la TI-10

Activités

et a participé à l'évaluation de l'adéquation des exemples

Remarque importante concernant la documentation

Texas Instruments Texas Instruments n'émet aucune garantie expresse ou implicite, y compris sans s'y limiter, toute garantie implicite de valeur marchande et d'adéquation à un usage particulier, concernant les programmes ou la documentation, ceux-ci étant fournis “tels quels” être tenue responsable vis-àvis de quiconque pour quelque dommage de nature spéciale, collatérale, fortuite ou indirecte occasionné à un tiers, en rapport avec ou découlant de l'achat ou de l'utilisation desdits matériels, la seule et exclusive responsabilité de Texas Instruments, pour quelque forme d'action que ce soit, ne pouvant excéder le prix d'achat de cette publication. Par ailleurs, la responsabilité de Texas Instruments ne saurait être engagée pour quelque réclamation que ce soit en rapport avec l'utilisation desdits matériels par toute autre tierce partie.

sans autre

recours. En aucun cas, Texas Instruments ne peut

Remarque

dans la documentation fournie.

: l'utilisation d'autres calculatrices que la TIN10 peut générer des résultats différents de ceux indiqués

Autorisation en matière de reproduction et de photocopie

Les enseignants sont autorisés à reproduire ou à photocopier pour la classe, l'atelier ou le séminaire, les pages ou fiches de ce manuel portant l'avis de copyright de Texas Instruments. Ces pages sont conçues pour être reproduites par les enseignants qui les utiliseront dans leurs classes, ateliers ou séminaires, à condition que chaque copie réalisée porte l'avis de copyright. Ces copies ne peuvent être vendues et toute distribution ultérieure est expressément interdite. Sauf exception indiquée ci-dessus, l'autorisation écrite préalable de Texas Instruments Incorporated est nécessaire pour reproduire ou diffuser tout ou partie de ce manuel, sous toute autre forme et par tout autre moyen électronique ou mécanique, y compris tout système stockage d'information ou système de recherche, sauf autorisation expresse reconnue par les lois fédérales en matière de copyright.

Si la photocopie intégrale ou partielle de ce manuel est confiée à d'autres personnes, cette page devra leur être fournie (avec la notice d'autorisation ci-dessus).

Toute demande d'information doit être envoyée à l'adresse suivante :

Texas Instruments Incorporated 7800 Banner Drive, M/S 3918 Dallas, TX 75251 A l'attention du directeur des services commerciaux

education.ti.com

ti-cares@ti.com

Imprimé aux États-Unis.

Automatic Power Down, APD, et EOS sont des marques commerciales de Texas Instruments Incorporated.

Table des matières



CHAPITRE PAGE

À propos du Guide de l'enseignant À propos de la TI-10

.................................... v

........ iv

Activités.................................................1

Importance de la valeur de position........2

Valeur de position

Description du problème............................7

Expressions numériques, Résolution du problème

Comparaison de coûts.............................. 11

Résultat de division sous forme quotient/reste ou décimale

Utilisation de la TI-10........................15

1 Affichage, défilement, ordre des

opérations et parenthèses................16

2 Effacement et corrections ................19

3 Menus....................................................23

CHAPITRE PAG

Annexe A....................................................A-1

Référence rapide aux touches

Annexe B ....................................................B-1

Indicateurs d'affichage

Annexe C..................................................... C-1

Menus

Annexe D ....................................................D-1

Messages d'erreur

Annexe E ....................................................E-1

Assistance, SAP et garantie

4 Opérations fondamentales ..............26

5 Opérations avec une constante ......33

6 Nombres entiers et décimaux......... 38

7 Mémoire .................................................42

8 Résolution de problèmes :

mode Auto............................................ 47

9 Résolution de problèmes :

mode Manuel........................................54

10 Valeur de position...............................62

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

iii

À propos du Guide de l'enseignant

pprop

prop



Contenu du Guide de l'enseignant

Ce guide est composé de deux sections :

Activités Activités

à intégrer la TI-10 dans l'enseignement des mathématiques. La section

la TI-10

à apprendre aux élèves à utiliser la TI-10.

•

• •

Utilisation de la TI-10

offre une série d'activités destinées

Utilisation de

a été conçue pour aider les enseignants

Section

Les activités doivent être effectuées sous la direction de l'enseignant. Elles sont conçues conce la TI-10 comme outil d'enseignement. Cha activité constitue une unité indé et inclut les éléments suivants :

−

Activités

our aider à développer des

ts mathématiques tout en utilisant

erçu des éléments mathématiques

un a contenus dans l'activité ;

les conce devront être développés ;

le matériel servant à l'activité ;

une fiche d'activité destinée à l'élève.

ts mathématiques qui

Section Utilisation de la TI.10

. La section

endante

Points importants

Bien

•

ue plusieurs exemples proposés sur les trans utilisés mathémati conçus dans ce but exclusif.

Dans un souci de sou les exem

endants les uns des autres.

indé Il convient donc de sélectionner le trans les élèves doivent a

mathémati ensuite sélectionner une activité a mathématique que vous enseignez.

Si un exem au utilisez-le ou des touches et exem personnellement développés.

Pour s'assurer au même d'a effacer le contenu de la TI-10, la touche ” pour effacer l'affichage.

arent associé à la touche que

our développer les concepts

riée se rapportant au concept

rogramme d'études ou à votre classe,

les pertinents que vous aurez

uyer sur la touche b pour

arents puissent être

our développer des concepts

ues, ils n'ont pas été

lesse optimale,

les ou activités sont

rendre à utiliser

ues étudiés. Vous pouvez

le ne vous semble pas adapté

our enseigner la fonction de la

osez ensuite des

ue les élèves partent

oint, demandez-leur

uis sur

Cette section propose des exemples sur des su sont numérotés et incluent :

−

orts transparents. Les chapitres

age d'introduction décrivant les

Une touches de la TI-10 utilisées dans les exem touches sur le clavier de la TI-10 et des remar fonctions de ces touches.

Des su

exem touches étudiées. Les touches étudiées sont colorées en noir sur l'illustration re

les, l'emplacement de ces

ues utiles relatives aux

orts transparents suivant la

age d'introduction fournissent des

les d'applications pratiques des

résentant le clavier de la TI-10.

EXAS INSTRUMENTS INCORPORATED

Commande supplémentaire de Guides de l'enseignant

Pour commander des produits Texas Instruments (TI) ou obtenir des informations supplémentaires les concernant, contactez-nous.

Tel :

E-mail : Page d'accueil :

Vous pouvez télécharger et imprimer votre propre exemplaire de ce Guide de l'enseignant à partir de la page Web suivante :

education.ti.com/guides

TI-10 : Guide de l'enseignant

1-800-TI-CARES (1-800-842-2737)

ti-cares@ti.com

education.ti.com

À propos de la TI.10

Affichage sur deux lignes

La première ligne peut contenir une entrée

ortant jusqu'à 11 caractères. Les entrées

com sont affichées dans l'angle su Si les données saisies dé ligne, elles continuent sur la deuxième. Si l'es résultat sont affichés sur la première ligne.

La deuxième ligne caractères. Si les données saisies sont tro longues pour la première ligne, elles continuent sur la deuxième. Si les données saisies et le résultat dé résultat est affiché sur la deuxième, droite. Les résultats com chiffres sont affichés en notation scientifique.

Si les données saisies dé lignes, elles continuent sur les lignes suivantes de sorte soient tou de l'entrée, il vous suffit de faire défiler les lignes vers le haut. Dans ce cas, le résultat s'affiche uni la touche

ace le permet, les données saisies et le

eut contenir jusqu'à 11

assent la première ligne, le

ue les deux dernières lignes saisies

ours visibles. Pour afficher le début

uement lorsque vous appuyez sur

érieur gauche.

assent la première

ustifié à

ortant plus de 10

assent les deux

Les opérations à l'intérieur de parenthèses étant calculées les utiliser les touches X et Y l'ordre des o modifier le résultat.

érations et, par conséquent,

remières, vous pouvez

our modifier

Menus

La touche

• Pour se dé

• Pour dé

• Pour revenir à l'écran

• Pour sélectionner une o

• Pour revenir à l'écran

Pour de plus amples informations sur les menus, consultez l'Annexe C : Menus.

‡

permet d'afficher les menus.

lacer dans les menus, vers le haut ou vers le bas, a touches

une o touches ! ou ".

sélectionner d'o touches

uyez sur la touche

a l'option en question est soulignée.

appuyez sur les touches

ou $.

lacer le curseur et souligner

tion de menu, appuyez sur les

tion, appuyez sur les

”

‡

uyez sur les

récédent sans

tion de menu,

lorsque

récédent,

‡

”

Indicateurs d'affichage

Reportez-vous à l'Annexe B de ce manuel pour obtenir la liste des indicateurs d'affichage.

Messages d'erreur

Reportez-vous à l'Annexe D de ce manuel pour obtenir une liste des messages d'erreur.

Priorité des opérations

La TI-10 utilise l'Equation Operating System (EOSé) Les

érations sont indiquées sur le transparent

Affichage, défilement, priorité des opérations et TI-10.

our évaluer les expressions.

riorités affectées aux différentes

arenthèses

EXAS INSTRUMENTS INCORPORATED

, de la section

Utilisation de la

Entrées précédentes (Historique)

Une fois qu'une expression a été calculée, utilisez les touches

arcourir les entrées et les résultats récédents, stockés dans l'historique de la

TI-10.

et $ pour

Résolution de problèmes (‹)

L'outil Résolution de problèmes offre trois

ossibilités que les élèves peuvent utiliser

our se confronter avec les opérations mathémati valeur de position.

TI-10 : Guide de l'enseignant

ues de base et les problèmes d

À propos de la TI.10

prop

(Suite)

• Le mode Automati

roblèmes fournit une série d'exercices

de destinée à vérifier les connaissances des élèves sur les o soustraction, multiplication et division).

Dans ce mode, les élèves ont la

de sélectionner le niveau de difficulté (1, 2, ou 3) et le type d'opération (+, –, x,

• Le mode Manuel de l'outil Résolution des

roblèmes permet aux élèves de créer leurs

res problèmes, qui peuvent contenir des éléments man inégalités.

• La résolution de

Valeur de options qui permettent de :

− trouver la valeur de

chiffre donné ;

− trouver le nombre d'unités, dizaines,

centaines, milliers, dizièmes ou centièmes contenus dans un nombre donné ;

− trouver le chiffre occu

des unités, dizaines, centaines ou centièmes d'un nombre donné.

osition des chiffres offre trois

ue de l'outil Résolution

érations de base (addition,

ossibilité

ou ?).

uants ou comporter des

roblèmes concernant la

osition d'un

ant la position

Lorsque vous réinitialisez la TI-10, le message

MEM CLEARED

pour effacer le contenu de l'écran.

La réinitialisation de la TI-10 :

• rétablit les réglages

calculatrice :

− notation standard (en virgule

flottante)

− résolution de problèmes, mode

− résultats sous forme de

reste pour la division

− niveau de difficulté 1 (addition) défini

pour l'outil Résolution de problèmes

− type d'opération — addition

• efface :

− les opérations en cours

− les entrées de l'historique

− la constante (opération stockée)

− toute condition d'erreur

s'affiche. Appuyez sur

ar défaut de la

”

AUTO

uotient et

Automatic Power DownTM (APDTM)

Réinitialisation de la TI.10

Vous pouvez réinitialiser la TI-10 en utilisant l'une des méthodes suivantes :

• Appuyez sur

• Appuyez simultanément sur

• A

uyez sur

RESET

appuyez sur

EXAS INSTRUMENTS INCORPORATED

−

et sur

‡

, sélectionnez le menu

, sélectionnez Y (yes/oui) et

”

Si la TI-10 reste inactive pendant cinq minutes environ, la fonction Automatic Power Down (APD) l'éteint automatiquement. Pour rallumer la TI-10 après un APD, appuyez sur −. Les données

affichées, les opérations en cours, les

réglages et la mémoire sont conservés.

TI-10 : Guide de l'enseignant

Activités

Importance de la valeur de position 2

Quel est le problème ? 7

Comparaison de coûts 11

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Importance de la valeur de position

Aperçu

Les élèves développeront leurs capacités à manipuler des nombres en découvrant les relations qui existent entre les symboles numériques et leur représentation avec du matériel en base dix.

Introduction

1. Lisez le manuel

Clement. Évoquez d'autres types de questions qu'une personne peut poser concernant le nombre d'objets contenus dans ou sur d'autres objets.

2. Répartissez les élèves en plusieurs groupes.

Distribuez à chaque groupe une grande quantité d'unités (plus de 300) du matériel en base dix. Indiquez-leur qu'il s'agit du nombre de haricots contenus dans un pot que vous avez rempli. Demandez-leur de compter les “haricots”. Observez les techniques qu'ils emploient pour compter les haricots (un par un, par groupes de 10, etc.).

3. Dites aux élèves que vous n'avez plus

d'unités et demandez-leur :

Combien de bâtons (groupes de 10) devrais-je utiliser pour obtenir une quantité de “haricots” identique à la vôtre ?

4. Les élèves peuvent trouver la réponse à ce

problème en utilisant les unités dont ils disposent ou en appliquant leurs connaissances concernant la valeur de position. Montrez-leur ensuite comment trouver la réponse à l'aide de la TI-10.

5. Demandez aux élèves de comparer ensuite la

solution obtenue avec le matériel en base dix et le résultat affiché sur la TI-10. (Ils obtiennent 31 bâtons de dizaines pour 314 unités, avec un reste de 4 unités.)

Counting On Frank

de Rod

Concepts mathématiques

Niveaux 2 - 4

valeur de position des

•

nombres entiers (jusqu'aux milliers)

•

argent

Niveaux 4 - 6

valeur de position des

•

décimales (jusqu'aux centièmes)

unités métriques

•

(mètres, décimètres, centimètres)

Utilisation de l'outil Valeur de position

dans le cadre de cette activité :

1. Appuyez sur

2. Appuyez sur sélectionner le mode (manuel), si nécessaire.

3. Appuyer sur régler l'outil Valeur de position

11 –.

sur combien d'unités, de dizaines, de centaines, etc., sont contenues dans un nombre.

Remarque :

la fonction de position pour trouver le chiffre occupant la position des unités, dizaines, centaines, etc.

4. Appuyez sur l'écran de saisie.

Pour découvrir les réponses à ce

problèmes sur la TI-10 :

1. Si nécessaire, appuyez sur pour accéder à l'outil Résolution de problèmes.

2. Entrez 314, à savoir le nombre d'unités.

3. Appuyez sur nombre de dizaines qu'il y a dans 314. L'écran affiche c'est-à-dire qu'il y a 31 dizaines dans 314.

‹ "

Ceci permet de trouver

vous pouvez utiliser

– 1 –.

‡ pour revenir à

Matériel

TI-10

•

crayon

•

Counting on

•

Frank

Rod Clement

matériel en

•

base dix

activité de

•

l'élève (pages 5 et 6)

‡.

pour

MAN

pour

de l'outil Valeur

’ pour voir le

par

‹

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Importance de la valeur de position

(Suite)

Cueillette et organisation des données

Les élèves doivent utiliser leur matériel en base dix et la TI-10 pour continuer à découvrir, avec d'autres nombres, combien il y a d'unités, de dizaines, de centaines, et de milliers dans un nombre donné. Les élèves plus âgés pourront chercher combien il y a de dixièmes et de centièmes dans un nombre donné. Encouragez cette découverte en posant des questions telles que :

Combien y a-t-il de centaines dans le nombre

•

120 ? 2478 ? 3056 ?

Combien y a-t-il de dizaines dans le nombre

•

120 ? 2478 ? 3056 ?

Combien y a-t-il d'unités dans le nombre 120 ?

•

2478 ? 3056 ?

Quels nombres contiennent 12 unités ?

•

12 dizaines ? 12 centaines ?

Quels nombres contiennent 60 unités ?

•

60 dizaines ? 60 centaines ?

Analyse des données et conclusion

Les élèves doivent utiliser les tableaux

pages correspondantes de l'activité.

la valeur de position, où ils peuvent noter leurs résultats et identifier les patterns observés. Pour les aider à se concentrer sur les patterns, posez des questions du type :

fournis aux

Importance de

Lorsque la calculatrice se

trouve en mode manuel

MAN

(‹ de problèmes, les élèves peuvent utiliser l'option de l'outil Valeur de position pour vérifier leurs hypothèses. Par exemple, s'ils pensent que 1602 contient 160 centaines, ils doivent entrer sur Ils peuvent utiliser le matériel en base dix pour constater que le nombre 1602 ne contient que 16 centaines.

Remarque :

peuvent utiliser le

mode – 1 –.

chiffre correspondant aux centaines. À l'aide de ce mode, ils peuvent entrer

1602

lire que trouve à la position des centaines.

) de l'outil résolution

1602

Œ ‘

ê6êê

et lire

, appuyer sur

. Ce résultat signifie

est le chiffre qui se

les élèves pour trouver le

Œ ‘

, appuyer

êê

11 –.

•

Que peut-on faire pour comparer le nombre de dizaines contenues dans 1314 et le nombre 1314 ? Même chose pour 567 ? 2457 ? 4089, etc. ?

Si vous cachez le chiffre correspondant aux unités, vous pouvez voir le nombre de dizaines contenues dans un nombre.

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Importance de la valeur de position

Que peut-on faire pour comparer le nombre de

•

centaines contenues dans 1314 et le nombre 1314 ? Même chose pour 567 ? 2457 ? 4089, etc. ?

Si vous cachez les chiffres à la droite de la position des centaines, vous pouvez voir le nombre de centaines contenues dans un nombre.

Comment peut-on comparer l'affichage à l'écran de la

•

TI-10 et ce que vous pouvez faire avec le matériel en base dix ?

(Suite)

Si la TI-10 affiche mesure de faire 31 bâtons de dizaines à partir des 316 unités.

31_

, pour 316, vous devez être en

Suite des recherches

Appliquez les patterns observés sur la valeur de position à l'argent. Par exemple, demandez aux élèves :

Si chacun des “haricots” coûte un cent, combien de

•

cents dépense-t-on pour acheter 1314 haricots ?

1314 cents

Combien de pièces de 10 cents (dizaines)

•

dépense-t-on ?

131 pièces de 10 cents et encore 4 cents

Combien de dollars (centaines) ?

•

13 dollars, plus 14 cents, ou 1 pièce de 10 cents et 4 cents

Les élèves plus âgés peuvent noter la quantité d'argent et l'entrer sur la TI-10 sous forme décimale, c'est-à-dire 13.14. Ils peuvent ensuite utiliser la TI-10 pour mettre en rapport les pièces de 10 cents avec 1/10 (0.1) de dollar ($13.14 contient 131 pièces de 10 cents ou dixièmes). Ils peuvent également mettre en rapport les cents avec 1/100 (0.01) de dollar ($13.14 contient 1314 cents ou centièmes).

Les élèves plus âgés peuvent encore mettre en rapport les patterns observés sur la valeur de position avec les conversions des unités métriques. Par exemple, une mesure de 324 centimètres correspond également à 32.4 décimètres (ou à 32 dm, si on arrondit), puisque 1 dm = 10 cm, ou encore à 3.25 mètres (ou à 3 m, si on arrondit), puisque 1 m = 100 cm.

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Importance de la valeur

Nom ______________________

Date ______________________

de position, Partie A

Cueillette et organisation des données

1. Utilisez votre matériel en base dix et votre TI-10 pour découvrir combien il y a de dizaines, centaines et milliers dans un nombre. Notez vos remarques dans le tableau.

Nombre

Nombre de

milliers

2. Quels patterns observez-vous ?

Nombre de

centaines

Nombre de

dizaines

Analyse des données et conclusions : exemples

1. Écrivez 5 nombres contenant 15 dizaines.

__________________________________________________________________________________

2. Écrivez 5 nombres contenant 32 centaines.

__________________________________________________________________________________

3. Écrivez 5 nombres contenant 120 dizaines.

__________________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Importance de la valeur

Nom ______________________

Date ______________________

de position, Partie B

Cueillette et organisation des données

1. Utilisez votre matériel en base dix et votre TI-10 pour découvrir combien il y a de dixièmes et de centièmes dans un nombre. Notez vos remarques dans le tableau. Quels patterns observez-vous ?

Nombre Nombre de

dixièmes

2. Quels patterns observez-vous ?

Nombre de

centièmes

Analyse des données et conclusions : exemples

1. Écrivez 5 nombres contenant 15 dixièmes.

__________________________________________________________________________________

2. Écrivez 5 nombres contenant 32 centièmes.

__________________________________________________________________________________

3. Écrivez 5 nombres contenant 120 dixièmes.

__________________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Quel est le problème

Aperçu

Les élèves doivent mettre en relation les

ressions numériques avec les problèmes

osés et utiliser l'addition, la soustraction, la

multiplication et la division pour les résoudre.

Introduction

1. Affichez sur une bande ou à l'aide d'un rétroprojecteur une expression numérique, comme 8 + 2 = ?. Demandez aux élèves de trouver des situations et des questions qui se traduisent par cette expression numérique. Soumettez-leur ensuite le problème suivant :

Si j'achète huit cartes postales durant les vacances, et si j'avais déjà deux cartes postales à la maison, combien de cartes ai-je maintenant ?

2. Si nécessaire, les élèves peuvent faire un récit mimé du problème en utilisant des compteurs afin de déterminer que la valeur de ? est égale à 10.

Concepts mathématiques

Niveaux 1 - 5

addition,

•

soustraction

ressions

•

ues

numéri

quations)

(

Niveaux 3 - 5

lication,

multi

•

division inégalités

•

Pour afficher

1. Appuyez sur pour mettre la TI-10 en mode manuel ( Résolution de problèmes.

2. Appuyez sur le menu.

3. Appuyez sur La TI-10 affiche solution avec un nombre entier).

4. Entrez 10 et appuyez sur pour vérifier l'exactitude de la solution. La TI-10 affiche l'équation et

8 + 2 = ?

‹

‡ "

MAN

) de l'outil

‡ pour quitter

8 T 2 Z

1 SOL

YES

Matériel

TI-10

•

compteurs

•

crayon

•

activité de

•

l'élève (page 10)

 ®

(une

3. Montrez-leur comment afficher cette équation sur la TI-10 et indiquer à la TI-10 la valeur de ?.

4. Présentez-leur ensuite une équation du type ? - 10 = 4. Demandez aux élèves de trouver des situations et des questions qui se traduisent par cette expression numérique.

J'avais de l'argent dans ma poche et j'ai

Si une valeur incorrecte est entrée pour ?, la TI-10 affiche et propose une aide. Par exemple, si un élève entre 15 pour l'équation affiche revient à l'équation initiale.

Remarque :

réponses incorrectes, la TI-10 affiche la solution.

? - 10 = 4

, montre

après trois

, la TI-10

15 - 10 > 4

dépensé 10 cents. Il me reste 4 cents. Quelle était la somme que je possédais avant d'en dépenser une partie ?

Les élèves doivent s'entraîner à utiliser les touches nécessaires pour afficher cette équation et trouver la valeur correspondant à ?.

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Quel est le problème ?

5. Présentez aux élèves les autres types d'expressions numériques à étudier. Par exemple, ? x ? = 24 (avec 8 solutions de paires de facteurs, formées par des nombres entiers) et ? x 4 = 2 (dont la solution n'est pas un nombre entier).

Cueillette et organisation des données

En prolongement de l'activité, les élèves peuvent travailler par deux et utiliser la page

problème

résolution de problèmes. L'un des élèves s'occupe des calculs sur la TI-10 et l'autre écrit les expressions numériques.

1. L'élève chargé d'écrire doit créer une expression

2. L'élève qui utilise la TI-10 doit saisir l'expression

de l'activité pour créer des fiches de

numérique formant une addition, une soustraction, une multiplication ou une division à l'aide du symbole ?, puis noter cette expression dans le cadre situé en haut de la page 10.

numérique sur la calculatrice.

Quel est le

(Suite)

3. L'élève chargé d'écrire doit concevoir un problème et une question correspondant à l'expression numérique, puis noter ces informations dans le cadre du bas.

Les deux élèves peuvent travailler ensemble pour coller (avec colle ou ruban adhésif) les deux cadres sur les faces opposées d'une fiche index.

Les élèves doivent travailler ensemble sur la TI-10 pour trouver le nombre de solutions entières associées à l'équation et vérifier l'exactitude de ces solutions. Donnez-leur des idées en posant des questions telles que :

Quelles sont les actions qui peuvent se produire

•

dans votre histoire et qui correspondent à l'addition (soustraction, multiplication, ou division) ?

Comment pouvez-vous utiliser les compteurs

•

pour faire un récit mimé de cette expression numérique ?

Que peut représenter, dans votre histoire,

•

ce nombre de l'expression numérique ?

Que peut représenter, dans votre histoire, le point

•

d'interrogation contenu dans l'expression numérique ?

Pouvez-vous créer une histoire pour une

•

expression numérique commençant par un point d'interrogation ?

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Quel est le problème ?

Analyse des données et conclusions

Pour aider les élèves à approfondir les relations existant entre leurs histoires et les nombres et les opérations contenues dans leurs expressions numériques, posez-leur des questions telles que :

De quelle façon l'utilisation d'un nombre

•

différent à cet endroit peut-elle affecter votre histoire ?

De quelle façon l'utilisation du symbole

•

supérieur à ou inférieur à à la place du symbole égal dans l'expression numérique affecte-t-elle votre histoire ?

De quelle façon l'utilisation d'une autre

•

opération dans votre expression numérique affecte-t-elle votre histoire ?

Suite des recherches

(Suite)

•

Demandez aux groupes de deux élèves de créer et d'échanger des histoires. Chaque élève peut ensuite écrire une expression numérique traduisant l'histoire de l'autre élève.

•

Demandez aux élèves de classer leurs expressions numériques par catégorie. Par exemple, celles dont les solutions ne comportent pas de nombres entiers, celles avec 1 solution formée par un nombre entier, celles avec 2 solutions formées par un nombre entier et celles avec une infinité de solutions formées par un nombre entier.

•

Les élèves doivent tenter de trouver une équation ou une inégalité sans aucune solution formée par un nombre entier, avec 1 seule solution formée par un nombre entier, avec 2 solutions formées par un nombre entier, avec plus de 5 solutions formées par un nombre entier, etc.

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Nom _____________________________

Quel est le problème

Date _____________________________

1. Écrivez une expression numérique contenant une opération et le symbole ?.

2. Écrivez une histoire décrivant une situation et posez une question qui puisse être représentée par l'expression numérique.

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Comparaison de coûts

Aperçu

Les élèves doivent résoudre un problème à l'aide d'une division dont le résultat est un quotient formé par un nombre entier et un reste, résoudre le même problème à l'aide d'une division dont le résultat est un quotient sous forme décimale, puis comparer les résultats.

Introduction

1. Présentez le problème.

Le service de maintenance a calculé que l'entretien du terrain de football du quartier revient, chaque année, à 0.40 dollar par mètre carré. Le terrain de football mesure 80 mètres de largeur sur 110 mètres de longueur. Les six écoles qui jouent sur ce terrain ont décidé de partager les coûts de façon égale. Quel montant doit verser chaque école au fond destiné à l'entretien du terrain de football, cette année ?

2. Les élèves doivent utiliser la TI-10 pour résoudre ce problème en utilisant deux méthodes différentes :

Trouver le quotient entier et le reste.

•

Trouver le quotient sous forme décimale.

•

Concepts mathématiques

division

•

multiplication

•

fractions

•

décimales

•



Le réglage par défaut de la division sur la TI-10 ( affiche un quotient sous forme de nombre entier, avec un reste.

Matériel

•

TI-10

crayon

activité de l'élève (page

14)

)

Cueillette et organisation des données

Les élèves doivent noter leurs démarches et les résultats sur la page l'activité. Pour les aider à approfondir leur raisonnement, posez des questions telles que

Quelles données faut-il entrer sur la TI-10 pour

•

résoudre ce problème ?

110

−

de football.

0.40

−

Z pour trouver le coût total de

l'entretien.

−

Z pour trouver le coût pour chaque

école, sous forme décimale.

EXAS INSTRUMENTS INCORPORATED

Comparaison de coûts

Z pour déterminer l'aire du terrain

TI-10 : Guide de l'enseignant



Pour afficher un quotient sous forme décimale :

1. Appuyez sur réinitialiser la TI-10.

2. Appuyez sur souligner décimale).

3. Appuyez sur sélectionner le réglage décimal.

4. Appuyez sur quitter le menu et revenir à l'écran précédent.

(forme

”

pour

‡ "

pour

‡

pour

P (division)

pour

Comparaison de coûts

Existe-t-il une autre méthode permettant de

•

résoudre ce problème plus rapidement ? Si oui, laquelle ?

80 x 110 peut être calculé mentalement et ainsi réduire la séquence de touches à utiliser à

8800

En quoi les méthodes utilisées pour obtenir

•

chaque type de résultat se ressemblent-elles ?

Les méthodes utilisées requièrent le calcul du nombre de mètres carrés que mesure le terrain de football ; toutes utilisent les opérations de multiplication et de division.

En quoi diffèrent-elles ?

•

Vous utilisez des touches différentes pour demander à la TI-10 d'afficher la réponse sous la forme désirée.

(Suite)

Analyse des données et conclusions

Pour guider les élèves lors de l'analyse de leurs données, posez des questions telles que :

En quoi les deux formes de résultats obtenus se

•

ressemblent-elles ?

Tous les résultats ont un élément commun formé par un nombre entier, à savoir 586.

En quoi les deux résultats diffèrent-ils ?

•

La forme avec le reste indique simplement le nombre de dollars. La forme décimale indique le montant que chaque école doit payer en plus des 586 dollars.

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Comparaison de coûts

Que ce passe-t-il si vous multipliez chaque résultat

•

par 6 pour le vérifier ?

Si vous multipliez le résultat sous la forme quotient/reste, soit 586 par 6, vous obtenez 3516, à quoi il faut ajouter le reste de 4 pour obtenir le coût total de 3520 dollars.

Si vous multipliez le résultat décimal 586.6666667 par 6

586.6666667

( résultat n'est pas logique puisque 6 x 7 ne se termine pas par 0 !

Étant donné qu'il s'agit de calculs sur des montants d'argent, on peut limiter le résultat décimal,

586.6666667, à 2 décimales ( Si on multiplie le nombre arrondi 586.67 par 6

586.67

( pas logique, puisque 6 x 7 = 42.

Si vous réinitialisez et effacez le contenu de l'écran de la TI-10, et qu'ensuite vous multipliez 586.67 par 6 (

b ”

est logique.

Si vous étiez l'administrateur d'une école, pour quelle

•

forme de quotient opteriez-vous ?

Les réponses peuvent varier. Certains élèves peuvent préférer la forme décimale, puisqu'elle est la plus proche de la représentation de l'argent. D'autres peuvent opter pour la forme quotient entier/reste et suggérer que le reste de 4.00 dollars soit payé par le Bureau Central.

V 6 Z), vous obtenez 3520. Toutefois, ce

586.6666667

Š ™

V 6 Z), on obtient 3520.00. Ce résultat n'est

586.67

V 6 Z), vous obtenez 3520.02. Ce calcul

(Suite)



Pour la division d'un nombre entier (avec quotient et reste), la TI-10 utilise uniquement le quotient du résultat pour les calculs suivants. Le reste est toujours ignoré.



La TI-10 arrondit uniquement le résultat affiché. La valeur stockée à l'intérieur

n'est pas

vous limitez

586.6666667 à 2 décimales (586.67) et que vous multipliez ce nombre par 6, la TI-10

mémorise

d'origine (586.6666667) et l'utilise comme facteur. Mais si vous saisissez le nombre arrondi, 586.67, la TI-10 utilise ce nombre comme facteur et vous obtenez un produit de

3520.02.

arrondie. Si

le nombre

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Nom ______________________

Comparaison de coûts

Date ______________________

Cueillette et organisation des données

Le Service de maintenance a calculé que l'entretien du terrain de football du quartier revient, chaque année, à 4 dollars par mètre carré. Le terrain de football mesure 80 mètres de largeur et 110 mètres de longueur. Les 6 écoles qui jouent sur ce terrain ont décidé de partager les coûts de façon égale. Quel montant doit verser chaque école au fond destiné à l'entretien du terrain de football, cette année ?

1. Utilisez la division avec un quotient entier et un reste pour trouver la réponse.

2. Utilisez la division avec un quotient sous forme décimale pour trouver la réponse.

Analyse des données et conclusions

Écrivez un court paragraphe pour comparer en un court paragraphe les deux solutions obtenues.

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Utilisation

de la TI.10

1 Affichage, défilement, ordre des

opérations et parenthèses 16 2 Effacement et corrections 19 3 Menus 23 4 Opérations fondamentales 26 5 Opérations avec une constante 33 6 Nombres entiers et décimaux 38 7 Mémoire 42 8 Résolution de problèmes :

mode Auto 47 9 Résolution de problèmes :

mode Manuel 54 10 Valeur de position 62

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Affichage, défilement, priorité des

opérations et parenthèses

Touches

ouvre une ex

arenthèses. Vous pouvez ouvrir

jusqu'à huit parenthèses à la fois.

ferme une ex

parenthèses.

et "

curseur vers la gauche ou vers la droite.

et $ permettent de faire défiler

les entrées et résultats ainsi curseur vers le haut et vers le bas.

ermettent de déplacer le

ue les menus, en déplaçant le

ression entre

récédents,

Remarques

Les exemples fournis sur les

•

trans les réglages de la calculatrice le sont

ar défaut. Appuyez sur b ” pour rétablir les réglages TI-10 et effacer le contenu de l'écran.

Le transparent EOSTM montre l'ordre

•

dans lequel laTI-10 effectue les calculs. Au cours de calculs comportant des

•

arenthèses, si vous appuyez sur avant d'a affiche Syn Error . A pour revenir à l'écran précédent.

Les opérations entre parenthèses sont

•

calculées en

our changer l'ordre des opérations et donc modifier le résultat.

arents supposent que tous

ar défaut de la

uyer sur Y, l'écran

uyez sur

remier. Utilisez X et

”

Exemple : 1 + 2 x 3 = 7

(1 + 2) x 3 = 9

La première et la deuxième ligne de

•

l'écran caractères. Les entrées commencent à gauche de l'écran et défilent vers la droite. Une entrée

ligne suivante à l'endroit d'un opérateur. Lors de leur affichage, les résultats

•

sont d'un ligne, le résultat est affiché sur la deuxième.

•

Si le contenu d'une entrée dé les deux lignes, il se lignes suivantes. Pour afficher le début d'une entrée, a afin d'en faire défiler le contenu.

euvent contenir jusqu'à 11

asse toujours à la

ustifiés à droite. Si la longueur roblème dépasse la première

asse

oursuit sur les

uyez sur

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Equation Operating System, EOS™

Priorité Fonctions

1 (première) Expressions entre

parenthèses ( ).

Fonctions exigeant une

arenthèse de fermeture ) et récédant l'argument.

3 Négation (N).

4 Multiplication, multiplication

implicite, division (

5 Addition et soustraction (

6 (dernière)

termine toutes les

Q P

opérations.

Étant donné que les opérations entre

arenthèses sont calculées en premier lieu, vous pouvez utiliser les parenthèses pour changer l'ordre des opérations et, par conséquent, modifier le résultat.

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

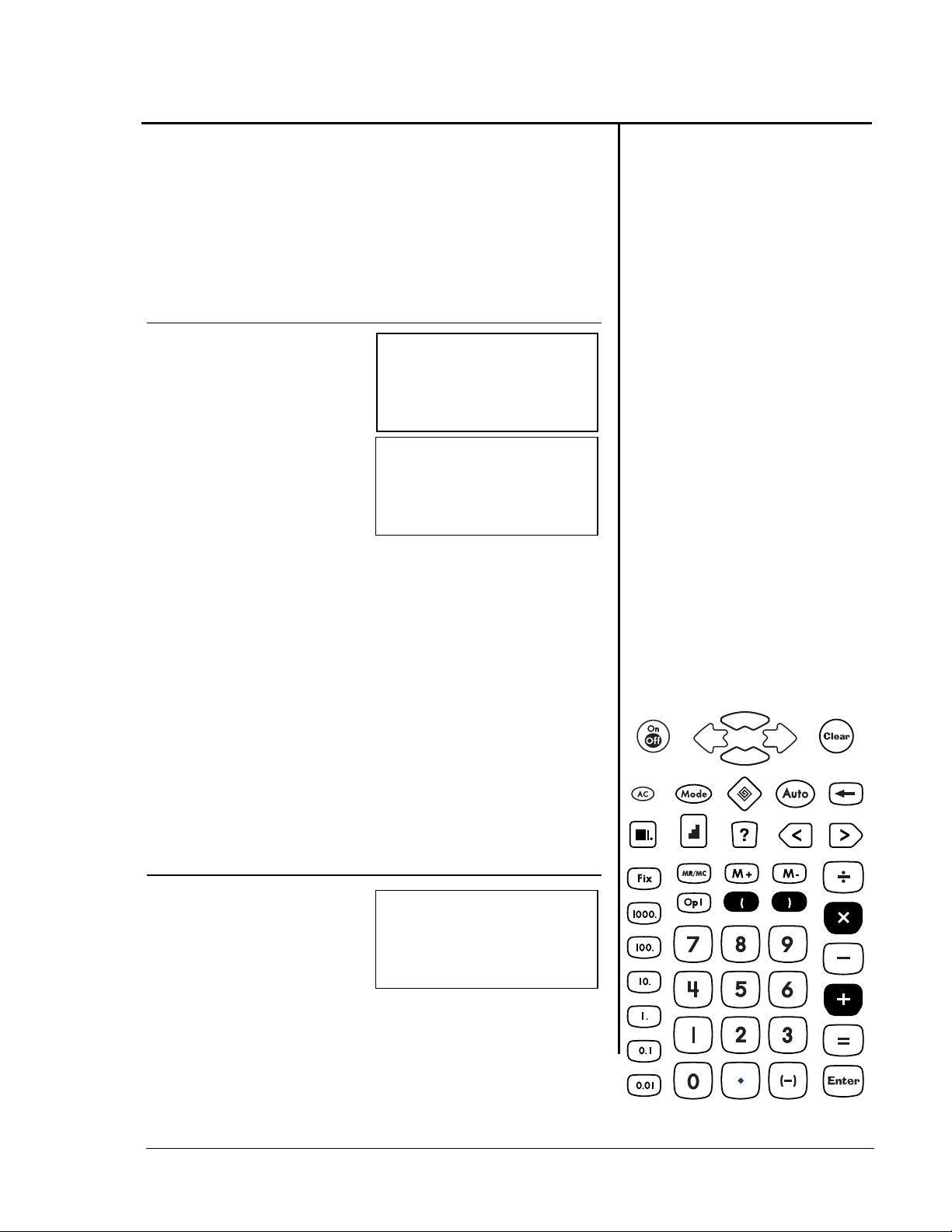
Ordre des opérations

(

1 + 2 x 3 =

Appuyez sur Affichage

b”

1Û2Ý3

Addition

Multiplication

Parenthèses

X Y

1 + 2) x 3 =

Appuyez sur Affichage

X V

1 3

Å1Û2ÆÝ3Ú

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

Effacement et corrections

Touches

allume et éteint la TI-10.

−

efface le dernier chiffre entré et

ermet ainsi de corriger une entrée

sans avoir à la reta

complètement.

3. Dans l'outil Calculatrice,

dernière entrée, toutes les o

érations en cours et toute condition d'erreur. Vous ensuite saisir un nouveau et continuer vos calculs.

réinitialise la TI-10.

efface la

”

ouvez

roblème

Remarques

Les exemples fournis sur les

•

trans

arents supposent que tous

les réglages de la calculatrice le sont

ar défaut. Appuyez sur b ” pour réinitialiser la TI-10 et effacer le contenu de l'écran.

Vous pouvez réinitialiser laTI-10 en

•

utilisant l'une des méthodes suivantes :

−

Appuyez sur b.

−

uyez simultanément sur

et ”.

−

uyez sur

, sélectionnez

‡

le menu RESET, sélectionnez Y (Yes) et appuyez sur

Lorsque vous réinitialisez la TI-10,

•

le message MEM CLEARED s'affiche. A

uyez sur ” pour

effacer l'écran.

−

EXAS INSTRUMENTS INCORPORATED

La réinitialisation de la TI-10

•

rétablit les réglages

ar défaut de

la calculatrice :

−

notation standard (en virgule flottante)

−

résolution de

roblèmes, mode

Auto

−

division avec quotient et reste

−

niveau de difficulté 1 (addition)

our l'outil Résolution de

problèmes

−

le ty

e d'opération par défaut

est l'addition

TI-10 : Guide de l'enseignant

Effacement et corrections

Remarques (suite)

efface :

•

−

les opérations en cours

−

les entrées de l'historique

−

la constante (opération stockée)

−

toute condition d'erreur

Une simple pression sur la touche

•

n'affecte pas les réglages de mode, la mémoire, l'histori constante.

Lorsque la calculatrice se trouve en

•

mode automati l'outil Résolution de l'utilisation de la touche d'effacer votre ré avant d'appuyer sur

Lorsque la calculatrice se trouve en

•

mode manuel (‹ Résolution de de la touche votre sur avant d'appuyer sur

roblème avant d'appuyer

”

ou d'effacer votre ré

ue ou la

ue (‹

onse de l'écran

MAN

roblèmes, l'utilisation

permet d'effacer

AUTO

roblèmes,

permet

”

) de l'outil

”

) de

onse

EXAS INSTRUMENTS INCORPORATED

TI-10 : Guide de l'enseignant

+ 59 hidden pages

Texas instruments TI-10 Teachers Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Table des matières

À propos du Guide de l'enseignant

Activités

Importance de la valeur de position

Quel est le problème

Comparaison de coûts

Equation Operating System, EOS™

Ordre des opérations

Effacement et corrections