Texas Instruments TI-84 Plus Guidebook [de]

Erste Schritte



7,3OXV$QZHQGXQJHQ
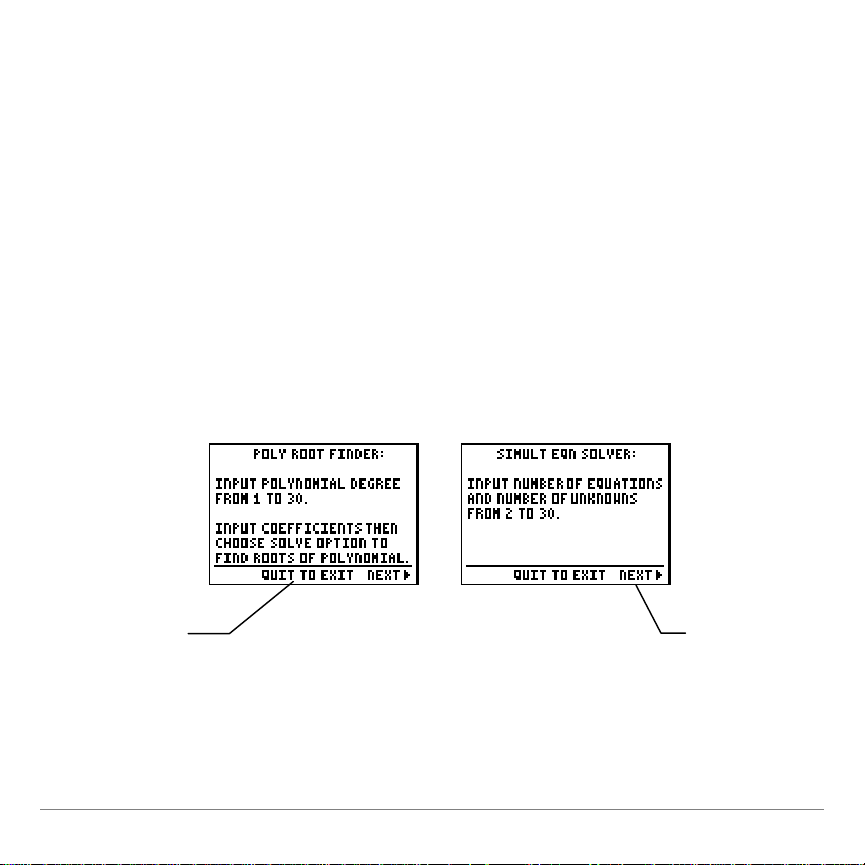
3RO\QRPLDO5RRW)LQGHU
6LPXOWDQHRXV(TXDWLRQ
6ROYHU

Polynomial Root Finder – Beispiel für den Analysis-Vorkurs
Polynomial Root Finder – Beispiel für die Analysis
Simultaneous Equation Solver

So wird’s gemacht…

Werte aus einer List e laden Werte aus einer Matrix laden
Werte in List en s peicher n Werte in Matrizen speichern

Beispiele

Die Wurzeln eines Polynoms finden
Lösen eines Gleichungssystems
Anzeigen einer Matrix in der reduzierten Diagonal-Form

Weitere Informationen

Kundendienst Fehlerbeseitigung

10/24/01 © 2001 Texas Instruments

:LFKWLJ

Texas Instruments übernimmt keine Gewährleistung, weder
ausdrücklich noch stillschweigend, einschließlich, aber nicht
beschränkt auf implizierte Gewährleistungen bezüglich der
handelsüblichen Brauchbarkeit und Geeignetheit für einen
speziellen Zweck, was sich auch auf die Programme und
Handbücher bezieht, die ohne eine weitere Form der
Gewährleistung zur Verfügung gestellt werden.

In keinem Fall haftet Texas Instruments für spezielle,
begleitende oder zufällige Beschädigungen in Verbindung mit
dem Kauf oder der Verwendung dieser Materialien. Die einzige
und ausschließliche Haftung von Texas Instruments übersteigt
unabhängig von ihrer Art nicht den geltenden Kaufpreis des
Gegenstandes bzw. des Materials. Darüber hinaus übernimmt
Texas Instruments keine Haftung gegenüber Ansprüchen Dritter.

Anwendungen für Grafikprodukte (Apps) sind lizenziert. Die
Einzelheiten entnehmen Sie bitte der Lizenzvereinbarung
dieses Produkt.

für

TI-GRAPH LINK und TI-Cares sind Warenzeichen von Texas Instruments. Alle anderen
Warenzeichen sind im Besitz der jeweiligen Eigentümer.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 2

:DVLVWGLH$QZHQGXQJ3RO\QRPLDO5RRW
)LQGHU6LPXOWHQRXV(TXDW LRQ6ROY HU"

(Polynomgleichungs- und Gleichungssystem Löser)

Mit der Anwendung Polynomial Root Finder berechnen Sie die
Wurzeln (Nullstellen) von Polynomen 1. bis 30. Grades, mit einer
bequemen und einfach einzusetzenden Oberfläche. Sie können
Lösungen in Listen abspeichern, Listen zur Bearbeitung in die
Anwendung laden und das Polynom grafisch darstellen. Die
Lösungen werden nur numerisch berechnet, weil die Anwendung
die Eigenwert-Routinen des Betriebssystems verwendet.

Mit der Anwendung Simultaneous Equation Solver finden Sie
Lösungen linearer Gleichungssysteme. Sie können Matrizen mit
Koeffizienten linearer Gleichungssysteme laden und feststellen,
ob ein vorgegebenes System genau eine, eine unendliche
Anzahl oder keine Lösung hat.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 3

:DV6LHIU,QVWDOODWL RQXQG(L QVDW]GHU
$QZHQGXQJEHQ|WLJHQ 

Um die Anwendung zu installieren und verwenden zu können,
benötigen Sie:

Einen Taschenrechner TI-83 Plus mit Betriebssystemsoftware

•

ab Version 1.13, um die Leistung Ihres Taschenrechners und
der Anwendung zu optimieren

-

Die Version des Betriebssystems prüfen Sie, indem Sie

, drücken und dann

y

Versionsnummer wird unter dem Produktnamen
angezeigt.

-

TI-GRAPH LINK™ Software, die kompatibel ist mit dem
TI-83 Plus. Eine kostenlose Kopie TI-GRAPH LINK der
Software können Sie von der Website

http://education.ti.com/softwareupdates

Folgen Sie den Links für Connectivity Software und dann
für TI-GRAPH LINK.

.

About

(info)

auswählen. Die

herunterladen.

Einen Computer auf dem Windowsë95/98/2000,

•

Windows NTëoder Apple® Mac® OS 7.0 oder neuer
installiert ist.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 4

A TI-GRAPH LINK™ in Computer-Rechner-

•

Verbindungskabel. Wenn Sie diese Kabel nicht besitzen,
rufen Sie Ihren oder bestellen Sie das Kabel online von TIs
Online-Shop unter online store

TI-GRAPH LINK Software, die kompatibel ist mit

•

demTI-83 Plus. Eine kostenlose Kopie TI-GRAPH LINK der
Software können Sie von education.ti.com/softwareupdates
herunterladen. Folgen Sie den Links für Connectivity
Software und dann für TI-GRAPH LINK.

.

:R6LH,QVWDOODW LRQVDQOHLWXQJHQ ILQGHQ

Ausführliche Installationsanleitungen finden Sie unter

http://education.ti.com/guides

Flash-Installationsanleitungen.

. Folgen Sie dem Link zu den

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 5

6RHUKDOWHQ6LH+LO IH 

Drücken Sie

y

5

, um die
Hilfebildschirme zu
verlassen und zum
Hauptmenü (Main
Menu)
zurückzukehren.

Drücken Sie ~,
um folgende
Bildschirme zu
sehen.

Diese Anwendung enthält eingebaute Hilfebildschirme, die Ihnen
Informationen zum Einsatz der Anwendungen Polynomial Root
Finder und Simultaneous Equation Solver geben. So erhalten Sie
Zugriff und verwenden Sie die Hilfebildschirme:

1. Wählen Sie im
oder

Simult Help

2. Drücken Sie

3. Drücken Sie
und zum

~

y 5

MAIN MENU (HAUPTMENÜ)

MAIN MENU (HAUPTMENÜ)

.

, um folgende Bildschirme zu sehen.

, um die Hilfebildschirme zu verlassen

zurückzukehren.

, entweder

Poly Help

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 6

3RO\QRPLDO5RRW)LQGHU$QZHQGXQJ

Hügel

Flugbahn des
Golfballs

(UVWH6FKULWWHPLWGHU3RO\QRPLDO5RRW)LQGHU$QZHQGXQJ 

Beispiel den Analysis-Vorkurs

Gehen Sie das folgende Beispiel durch, um sich mit den
wichtigsten Eigenschaften der Anwendung Polynomial Root
Finder vertraut zu machen.

Ein Golfspieler schlägt einen Ball am Fuß eines Hügels ab.

8

Der Hügel läßt sich wie folgt beschreiben y(x) = .8x. Der Ball
hat diese Flugbahn: y(x) =
Hügelboden, wenn ihn der Golfspieler am Fuß des Berges in
(0, 0) stehend abschlägt?

x2+ 12x. Wo erreicht der Ball den

M

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 7

1. Um dieses Problem zu lösen, müssen Sie herausfinden, wo
die Flugbahn des Golfballs y(x) =

x2+ 12x, den Hügel

M

erreicht, y(x) = .8x. Lösen Sie das Problem zuerst von Hand
und gehen Sie dann gemäß den folgenden Anweisungen
vor, um Ihre Berechnung zu überprüfen.

2. Als Erstes stellen Sie die beiden Gleichungen auf.

x2+ 12x =,8x

M

x2+ 11,2x = 0

M

3. Die Wurzeln des daraus resultierenden Polynoms ergeben
die Schnittpunkte der Flugbahn des Balls und des Hügels.

4. Drücken Sie

, um eine Liste von Anwendungen auf

Œ

Ihrem Taschenrechner angezeigt zu bekommen.

5. Wählen Sie

PolySmlt

. Der Informationsbildschirm wird

angezeigt.

6. Drücken Sie zum Fortzusetzen eine beliebige Taste. Das

MAIN MENU (HAUPTMENÜ)

7. Wählen Sie

Poly Root Finder

8. Geben Sie den Grad des Polynoms ein (
dann

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 8

Í

.

wird angezeigt.

.

) und drücken Sie

2

9. Geben Sie die Koeffizienten des Polynoms ein {M1, 11.2, 0}.
Drücken Sie nach jedem Koeffizienten

Í

, um den Cursor

zur nächsten Ziele zu verschieben.

10. Wählen Sie

SOLVE (LÖSE)

(drücken Sie

s

), um die

Wurzeln berechnen und anzeigen zu lassen.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 9

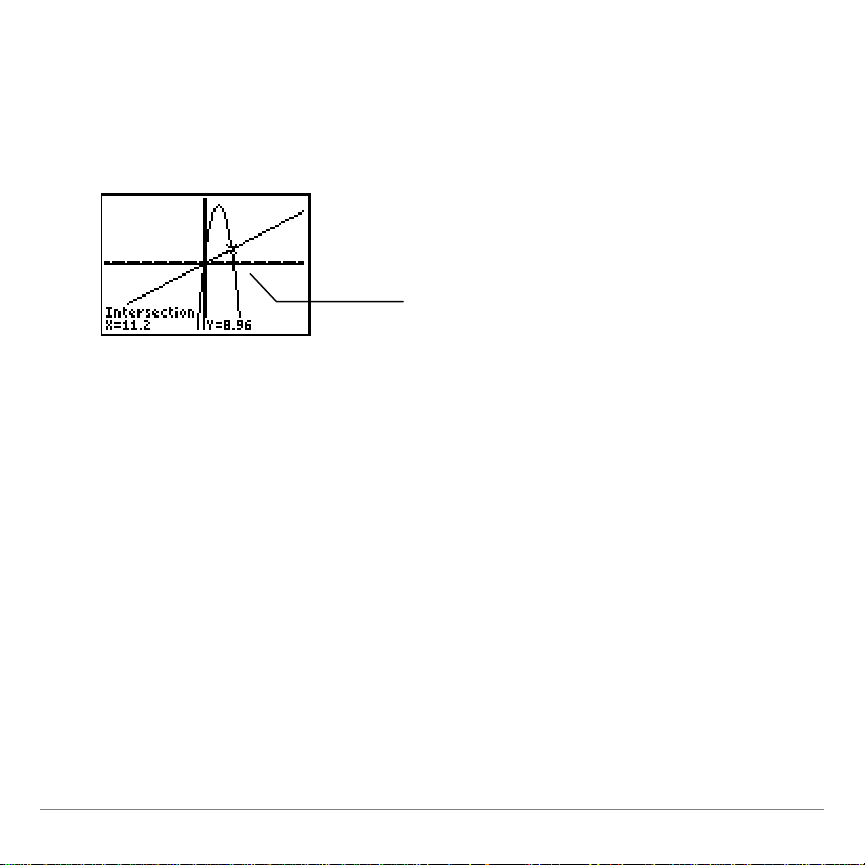
Zwei Antworten werden angezeigt x1= 11.2 and x2= 0. Wenn

So woird die Grafik angezeigt:

1. Drücken Sie

q

2. Wählen Sie Verkleinern (Zoom Out)

3. Bewegen Sie den Cursor in die Nähe
von (0,0)).

4. Drücken Sie

Í

.

Sie die Anwendung verlassen, die beiden Funktionen zeichnen
und ihre Schnittpunkte finden (drücken Sie
Sie

Intersect

), sehen Sie dass der Ball bei (0, 0) started und den

y

/

und wählen

Hügel bei (11.2, 8.96) trifft.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 10

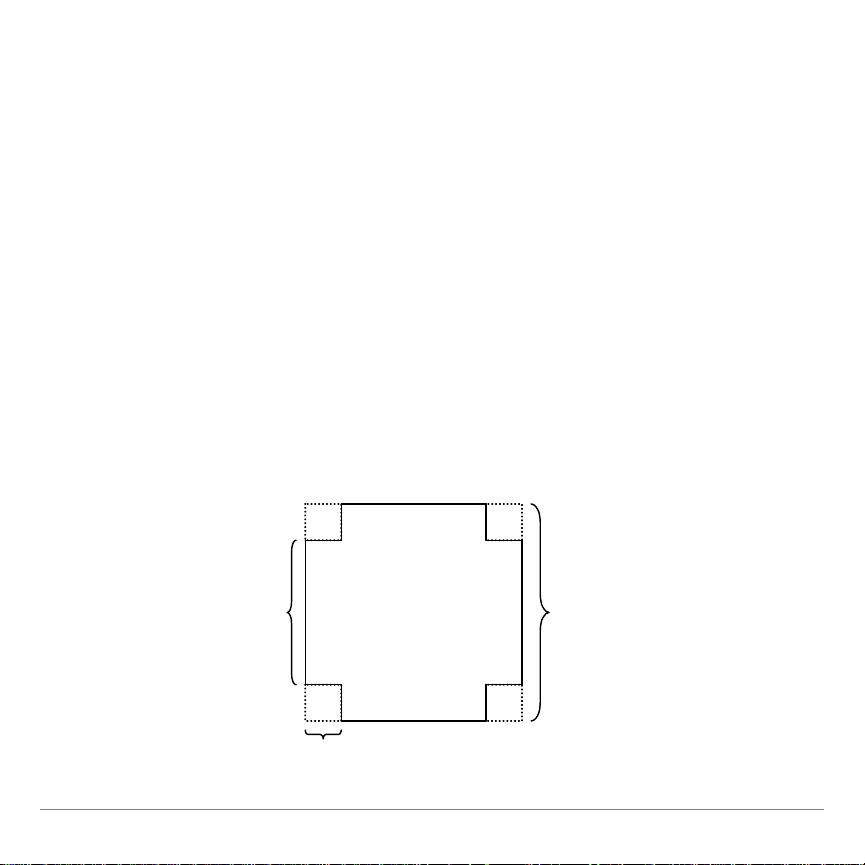
Beispiel für die Analysis

36 cm

x

36 – 2x cm

Gehen Sie das folgende Beispiel durch, um sich mit den
wichtigsten Eigenschaften der Anwendung Polynomial Root
Finder vertraut zu machen.

Aus einem quadratischen Stück Material mit 36 cm

8

Kantenlänge ist eine offene Schachtel herzustellen, indem
gleich große Quadrate aus den Ecken herausgeschnitten und
die entstandenen Seiten nach oben geklappt werden. Welches
maximale Volumen kann mit dieser Konstruktion der Schachtel
erreicht werden?

L = (36 – 2x)

W = (36 – 2x)
H = x
Das Volumen der Schachtel ist V(x) = x(36-2x)

2

.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 11

1. Um die Extrema des Volumens zu finden, setzen Sie die
erste Ableitung von V gleich Null.
V(x) = x(36-2x)
V(x) = 4x

3

V'(x) = 12x

2

x

– 24x + 108 = 0

2

– 144x2+ 1296x

2

– 288x + 1296 = 0

2. Wenn Sie jetzt die Wurzeln von x

2

– 24x + 108 = 0 finden,

finden Sie damit auch die kritischen Punkte der Funktion.

3. Drücken Sie

, um eine Liste von Anwendungen auf

Œ

Ihrem Taschenrechner angezeigt zu bekommen.

4. Wählen Sie

PolySmlt

. Der Informationsbildschirm wird

angezeigt.

5. Drücken Sie zum Fortzusetzen eine beliebige Taste. Das

MAIN MENU (HAUPTMENÜ)

6. Wählen Sie

Poly Root Finder

wird angezeigt.

.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 12

7. Geben Sie den Grad des Polynoms (2) ein, und drücken Sie
dann

Í

.

8. Geben Sie die Koeffizienten für das Polynom {1, L24, 108}
ein. Drücken Sie nach jedem Koeffizienten

Í

, um den

Cursor zur nächsten Ziele zu verschieben.

9. Wählen Sie

SOLVE (LÖSE)

(drücken Sie

s

), um die

Wurzeln zu berechnen und anzuzeigen.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 13

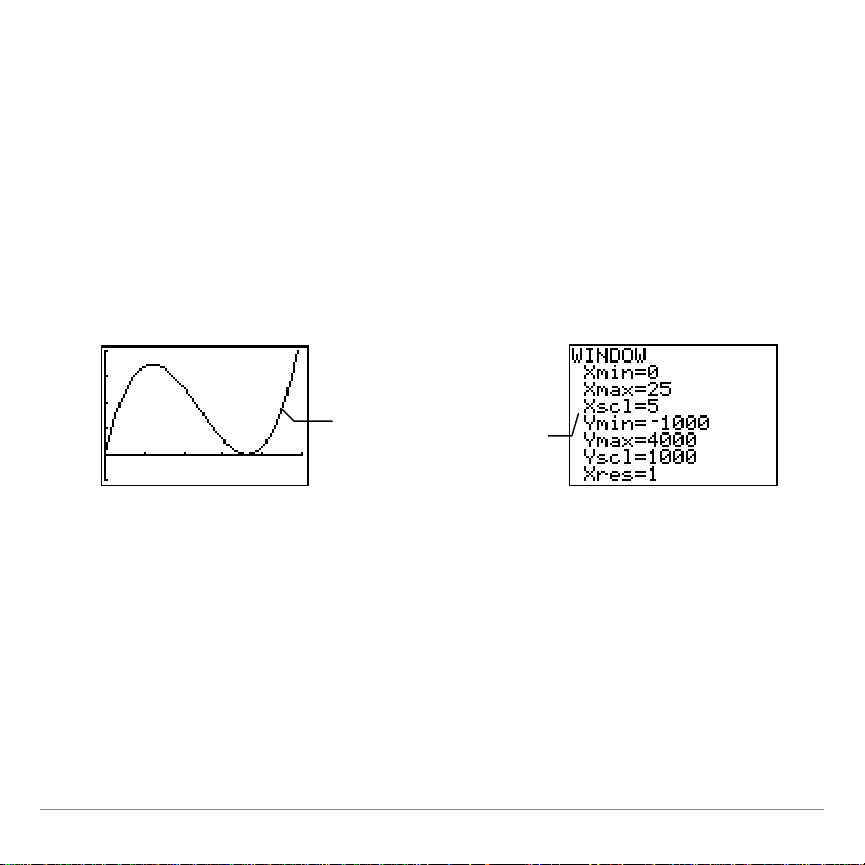
Es werden zwei Antworten angezeigt: x1= 18 and x2= 6.

0

(6)V

<′′

Der sinnvolle
physikalische Bereich von
x liegt zwischen 0 und 18
(faltet das Material in zwei
Hälften). In diesem
Fenster sehen Sie eine
gute Abbildung für die
Funktion im Wertebereich
von x=0 bis 25.

Welche können Sie wählen?

10. Vergessen Sie nicht zur Prüfung, ob x = 6 das Maximum ist,
das Vorzeichen der zweiten Ableitung bei x = 6 zu prüfen
(d.h. stellen Sie sicher, dass

).

Wenn Sie V(x) grafisch darstellen, können Sie sehen, dass 6
das Maximum von x ist, das Sie für die Herstellung einer
Schachtel verwenden können.

11. Da das Volumen der Schachtel V(x) = x(36-2x)2ist, können
Sie das maximale Volumen finden, indem Sie für x den Wert
6 einsetzen. (Ergebnis: 3456)

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 14

Nachdem Sie nun das Beispiel ‘Erste Schritte’ durchgearbeitet
haben, können Sie weitere Anleitungen dazu lesen, wie Sie die
Anwendung Polynomial Root Finder einsetzen können.
Interessante Themen sind z.B.:

Eine Liste von Koeffizienten in die Anwendung laden

•

Speichern von Koeffizienten in einer Liste

•

Speichern von Lösungen (Wurzeln) in einer Liste

•

Speichern der Gleichungen im Y= Editor

•

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 15

6WDUWHQXQG%HHQGHQGHU3RO\QRPLDO5RRW)LQGHU

Abkürzung

Sie können auch

y 5

drücken, um die Anwendung zu
verlassen. Wenn sich der Cursor an der Namenseingabe
befindet, müssen Sie

y 5

zwei mal drücken.

$QZHQGXQJ

Starten der Anwendung

Œ

1. Drücken Sie

, um eine Liste von Anwendungen auf

Ihrem Taschenrechner angezeigt zu bekommen.

2. Wählen Sie

PolySmlt

. Der Informationsbildschirm wird

angezeigt.

3. Drücken Sie eine beliebige Taste, um in das

(Hauptmenü)

4. Wählen Sie

ROOT FINDER

zu gelangen.

Poly Root Finder

wird angezeigt.

. Der Hauptbildschirm der

Main Menu

Beenden der Anwendung

5. Sie können auf jedem Bildschirm
zum

Main Menu (Hauptmenü)

6. Wählen Sie

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 16

Quit (Beenden) PolySmlt

zurückzukehren.

MAIN (HAUPT)

.

wählen, um

POLY

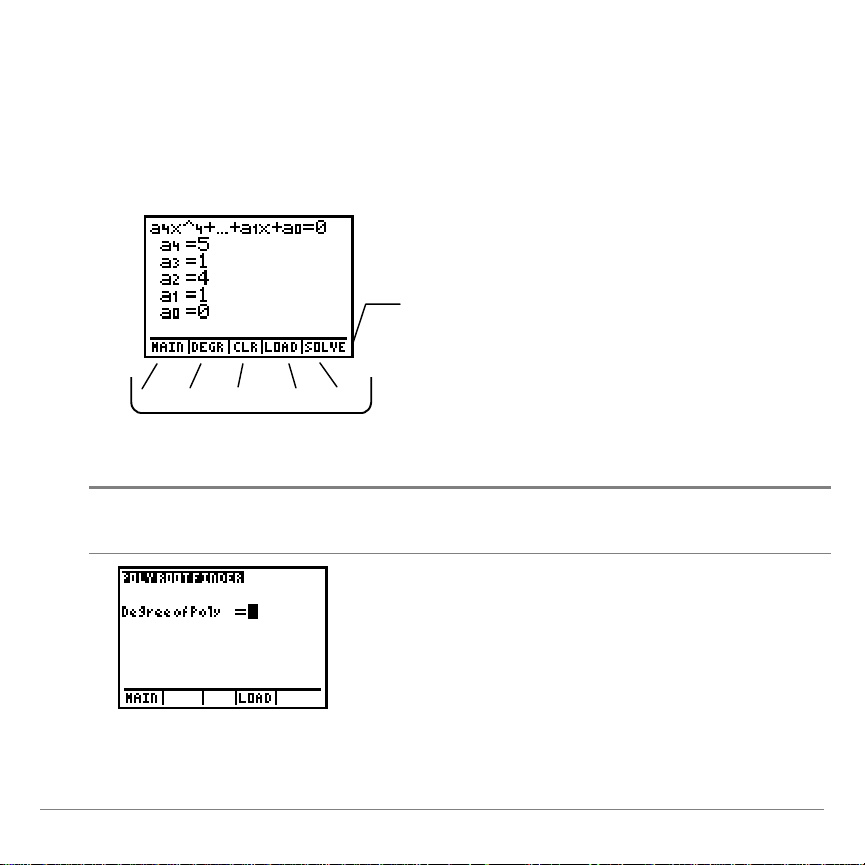
$XVZlKOHQYRQ2SWLRQHQIU3RO\QRPLDO5RRW)LQGHU

Verwenden von Optionen
auf diesem Bildschirm …

Gehen Sie wie folgt vor:

Eingabebildschirm für den Grad

MAIN (HAUPT) zeigt das Hauptmenü an.
LOAD (LADEN) zeigt eine Eingabeaufforderung an, so

dass Sie einen Listennamen eingeben können, der die
zu verwendenden Koeffizientenwerte enthält. Sie
müssen die Liste im Listeneditor einrichten, bevor Sie
die Liste in der Anwendung Polynomial Root Finder
verwenden können. Sie haben keinen Zugriff auf den
Listeneditor, während die Anwendung ausgeführt wird.

o p q r s

Drücken Sie eine
Grafiktaste, um eine
dieser Optionen
auszuwählen.

Auf jedem Bildschirm werden unten Optionen angezeigt, mit
denen Sie verschiedene Aufgaben lösen können. Um eine
Option auszuwählen, drücken Sie jeweils die direkt darunter
liegende Grafiktaste.

=XU9HUIJXQJVWHKHQGH2SWLRQHQ 

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 17

Verwenden von Optionen
auf diesem Bildschirm …

Gehen Sie wie folgt vor:

Eingabebildschirm für den

Koeffizienten

MAIN (HAUPT) zeigt das Hauptmenü an.
DEGR (GRAD) zeigt den Eingabebildschirm für

den Grad des Polynoms an, in dem Sie diesen
Wert anzeigen und ändern können.

CLR (LÖSCH) löscht alle von ihnen eingegebenen
Koeffizientenwerte.

LOAD (LADEN) zeigt eine Eingabeaufforderung an,
so dass Sie einen Listennamen eingeben können,
der die zu verwendenden Koeffizientenwerte
enthält. Sie müssen die Liste im Listeneditor
einrichten, bevor Sie die Liste in der Anwendung
Polynomial Root Finder verwenden können. Sie
haben keinen Zugriff auf den Listeneditor, während
die Anwendung ausgeführt wird.

SOLVE (LÖSE) berechnet die Wurzeln des
Polynoms und zeigt sie an.
Möglicherweise ist die Lösung für die komplette
Anzeige auf dem Bildschirm zu lang. Wenn auf der
linken Seite des Bildschirms Pfeile nach oben und
unten angezeigt werden, drücken Sie †und },
um die gesamte Lösung nach Bedarf anzuzeigen.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 18

Verwenden von Optionen
auf diesem Bildschirm …

Gehen Sie wie folgt vor:

Lösungsbildschirm

MAIN (HAUPT) zeigt das Hauptmenü an.
COEFS (KOEFS) zeigt den Eingabebildschirm für

die Koeffizienten an, in dem Sie diese Werte
anzeigen und ändern können.

STOa (SPEa) zeigt eine Listen­Eingabeaufforderung an der Sie die Liste angeben
können, unter dem die Koeffizienten gespeichert
werden sollen.

STOx (SPEx) zeigt eine Listen­Eingabeaufforderung an der Sie die Liste angeben
können, auf dem die Ergebnisse gespeichert
werden sollen.

STOy (SPEy) speichert die Polynomgleichung in
die nächste verfügbare y-Variable im Y= Editor.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 19

bQGHUXQJGHU0RGXVHLQVWHOOXQJHQ

Hinweis

•

Wenn das RAM zurückgesetzt wird, gehen die Einstellungen

von Polynomial Root Finder und Simultaneous Equation
Solver verloren.

•

Die Moduseinstellungen werden in einer Anwendungsvariablen

(engl. application variable, kurz AppVar) gespeichert. Wenn
Sie die Anwendung und Ihre Modus-Einstellungen mit einem
anderen TI-83 Plus -Benutzer gemeinsam nutzen wollen,
müssen Sie sowohl die Anwendung als auch die AppVar mit
der Bezeichnung APPVARO übertragen.

•

Wenn eine Listennamen-Eingabeaufforderung angezeigt wird

(zum Beispiel, STOx LIST = ), müssen Sie diese erst
verlassen, bevor Sie die Moduseinstellungen ändern können.

Diese Anwendung verfügt über einen eigenständigen
Einstellungsbildschirm auf Basis der Moduseinstellungen des
Taschenrechners. Diese Modus-Einstellungen werden nur wirksam,
während die Anwendung Polynomwurzelsuche/Gleichungssystem
Löser ausgeführt wird. Die Einstellungen wurden gespeichert und
werden bei jedem Ausführen der Anwendung wirksam. Wenn Sie
die Anwendung verlassen, werden die vorhergehenden
Moduseinstellungen des Rechners wiederhergestellt.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 20

So ändern Sie die Moduseinstellungen:

1. Starten Sie Polynomial Root Finder

Anwendung.

2. Drücken Sie auf einem beliebigen Bildschirm
Bildschirm

PolySmlt MODE Settings (PolySmlt Modus Einstellung)

angezeigt zu bekommen.

z

, um den

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 21

3. Verschieben Sie den Cursor auf eine Einstellung und

Einstellung

Erläuterung

Normal Sci Eng

Der Notationsmodus Normal

ist die übliche
Darstellungsweise für Zahlen, mit Ziffern links und
rechts vom Komma, wie bei 12345,67.

Im Notationsmodus Sci (Exp)

(wissenschaftl i ch,
engl. scientific) werden Zahlen in zwei Teilen
ausgedrückt. Die signifikanten Stellen werden mit
einer Stelle links vom Komma angezeigt. Die
entsprechende Zehnerpotenz wird rechts neben
dem Eangezeigt, wie in 1,234567E4.

Eng (Tech)

Der technischen Anzeigemodus
(engl. engineering) ist der wissenschaftlichen
Notation ähnlich. Allerdings kann die Zahl bis
zu drei Stellen vor dem Komma enhalten. Der
Zehnerexponent ist ein Vielfaches von 3, wie in
12,34567E3.

Float 0 1 2 3 4 5 6 7 8 9

Float (Flk)

Im Fließkommamodus werden bis zu
zehn Stellen plus Vorzeichen und Komma
angezeigt.

0123456789

(Festkomma)
Kommasetzungsmodus- gibt an, wieviele Stellen
(0 bis 9) rechts neben dem Komma angezeigt
werden.

drücken Sie

Í

, um die Einstellung auszuwählen.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 22

Einstellung

Erläuterung

Radian Degree

Im Modus Radian (Bogenmaß)

werden
Winkelwerte im Bogenmaß verwendet.
Antworten werden in Radian angezeigt.

Degree (Grad)

Modus interpretiert
Winkelangaben in Grad. Antworten werden in
Grad angezeigt.

Real a+bi re^qi

Im Modus Real (Reell)

werden keine komplexen
Ergebnisse angezeigt. Wenn Sie diese Modus­Einstellung wählen und die Antort komplex ist,
wird als Ergebnis

NONREAL (NICHT REELL)

angezeigt.

a+b

i

(kartesische Darstellung der komplexen
Ebene)- In diesem Modus werden komplexe
Zahlen in der Form a+bidargestellt. Sie müssen
möglicherweise ~drücken, um die ganze
komplexe Zahl angezeigt zu bekommen.

re^

q

i

(Polare Darstellung der komplexen Ebene)­In diesem Modus werden komplexe Zahlen in der
Form re

q

i

dargestellt. Sie müssen möglicherweise

~

drücken, um die ganze komplexe Zahl

angezeigt zu bekommen.

4. Wählen Sie

, um die Einstellungen zu speichern und

ESC

zum vorherigen Bildschirm zurückzukehren.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 23

(LQJHEHQXQG/|VHQHLQHU$XIJDEH 

Um die Wurzeln des Polynoms zu finden geben Sie den Grad
des Polynoms ein und dann den Wert jedes Koeffizienten. Der
Grad des Polynoms ist eine ganze Zahl zwischen 1 und 30. Die
Werte der Koeffizienten müssen reelle Zahlen sein.

Im folgenden Beispiel wird die Polynomial Root Finder zur
Berechnung der Wurzeln der Funktion verwendet:

f(x) = 7x

7

– 5x6+ 8x5+ 6x4– 9x3– 3x2+ 2x +1

1. Geben Sie den Grad des Polynoms ein, und drücken Sie
dann

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 24

Í

.

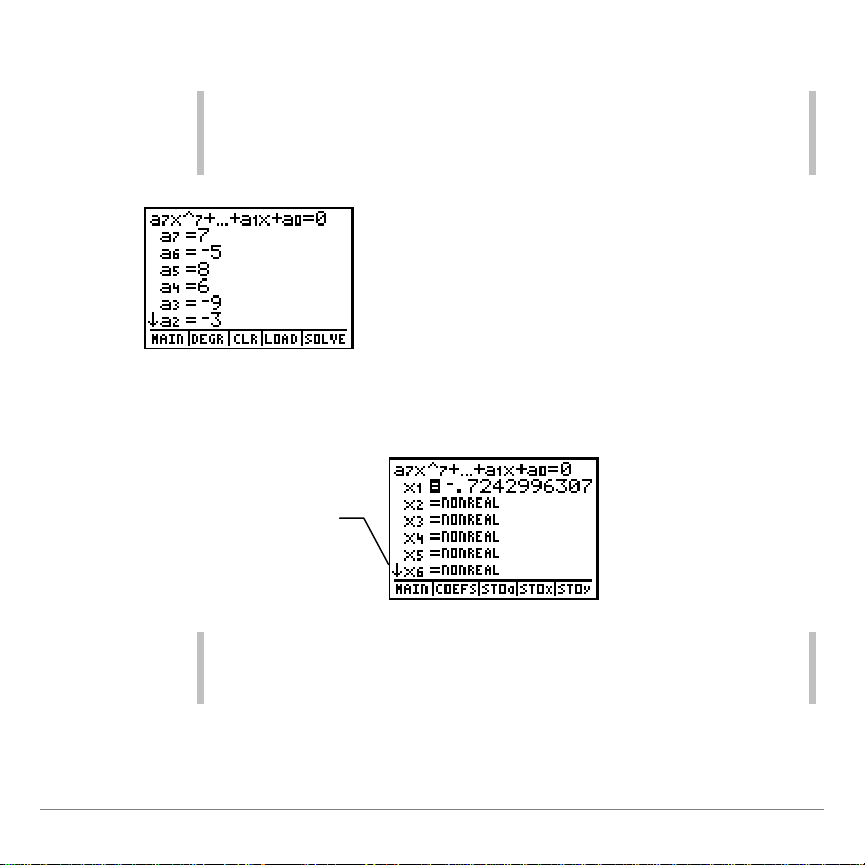
2. Geben Sie einen Wert für jeden Koeffizienten ein.

Tipp

•

Der Koeffizient des größten Terms kann nicht 0 sein.

•

Mit }und †können Sie durch die Liste der Koeffizienten

blättern und bei Bedarf Werte korrigieren.

Hinweis

Wenn NONREAL (NICHT REELL) angezeigt wird, ist der Modus
Poly/Simult auf REAL (REELL) gesetzt. Zur Anzeige komplexer
Ergebnisse ist der Modus a+bi oder re^qi einzustellen.

Der Pfeil zeigt, dass
Sie zur Anzeige der
verbleibenden
Wurzeln †drücken
müssen

3. Wählen Sie

SOLVE (LÖSE)

, um die Lösung angezeigt zu

bekommen. Dies kann einige Sekunden dauern.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 25

:HUWHODGHQ

Hinweis

Sie müssen die Liste im Listeneditor einrichten, bevor Sie die
Liste in der Anwendung Polynomial Root Finder verwenden
können. Sie haben keinen Zugriff auf den Listeneditor, während
die Anwendung ausgeführt wird.

Sie können vom Bildschirm

POLY ROOT FINDER

Koeffizienten-Bildschirm eine Liste von Koeffizienten laden.

Die Liste muss zwischen 2 und 31 Werte enthalten. Die Länge
der Liste muss dem Grad des Polynoms entsprechen. Wenn Sie
z.B. mit einem Polynom 5. Grades arbeiten wollen, muss die
Liste 6 Elemente enthalten.

So laden Sie eine Liste:

1. Wählen Sie auf dem Bildschirm

Degree of Poly (Grad des Poly)

oder dem Eingabebildschirm für die Koeffizienten

(LADE)

. Die Eingabeaufforderung

LOAD List (LADE Liste) =

wird angezeigt.

oder dem

LOAD

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 26

2. Geben Sie den Listennamen ein.

Tipp

•

Sie können mit einer der folgenden Methoden einen

Listennamen wählen:
Geben Sie den Listennamen an der Eingabeaufforderung ein.
Drücken Sie

y 9

, um die Liste von Matrizen auf Ihrem
Taschenrechner angezeigt zu bekommen und wählen Sie dann
einen Listennamen.
Wenn der Name ihrer Liste L1 – L6 ist, drücken Sie yund den
Namen der Liste (zum Beispiel,

y d

).

•

Drücken Sie zur Eingabe des Buchstaben

ƒ

und den

Buchstaben.

•

Wenn Sie die Alpha-Sperre aktivieren, können Sie ausschließlich

aus Buchstaben bestehende Listennamen ganz einfach
eingeben. Drücken Sie dazu

y 7

.

•

Drücken Sie zum Entfernen des Listennamens von der

Eingabezeile

‘

.

•

Drücken Sie zum Verlassen der Namens-Eingabeaufforderung

‘

.

3. Drücken Sie

Í

, um die Werte in die Koeffizientenliste zu

laden.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 27

'DWHQVSHLFKHUQ

Nach der Anzeige der Lösung können Sie die Koeffizienten und
Wurzeln des Polynoms in Listen speichern. Sie können das
Polynom auch in der nächsten verfügbaren y-Variablen im Y=
Editor speichern.

Speichern von Koeffizienten und Wurzeln

1. Wählen Sie auf dem Lösungsbildschirm
Koeffizienten oder
Die Eingabeaufforderung

STOx (SPEx)

STOa List =

, um Wurzeln zu speichern.

STOa (SPEa)

(bzw.

STOx List =

, um

) wird

angezeigt.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 28

2. Geben Sie den bis zu 5 Zeichen langen Namen der Liste ein

Tipp

•

Ein Listenname kann nicht mit einer Ziffer beginnen, aber

Ziffern enthalten. Drücken Sie zur Eingabe des Buchstaben

ƒ

und den Buchstaben

•

Wenn Sie die Alpha-Sperre aktivieren, können Sie

ausschließlich aus Buchstaben bestehende Listennamen ganz
einfach eingeben. Drücken Sie dazu

y 7

.

•

Drücken Sie zum Entfernen des Listennamens von der

Eingabezeile

‘

.

•

Drücken Sie zum Verlassen der Namens-Eingabeaufforderung

und anschließenden Rückkehr zum Bildschirm mit den
Lösungen

‘

.

•

Drücken Sie zur Eingabe eines Listennames L1 – L6 yund

den Listennamen (z.B.

y e

).

•

Wenn ein Listenname bereits vorhanden ist, wird die

Fehlermeldung "Liste bereits vorhanden" ("List already exists")
angezeigt, die Liste wird aber nicht überschrieben.

und drücken Sie anschließend

Í

gespeichert.

Speichern der Gleichungen im Y= Editor

. Die Liste ist jetzt

Wählen Sie zur Speicherung des Polynoms im Y= Editor

(SPEy)

. Das Polynom wird in der nächsten verfügbaren Funktion

STOy

im Y= Editor gespeichert. Zur Bestätigung der Speicherung des
Polynoms wird eine Meldung angezeigt.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 29

6LPXOWDQHRXV(TXDWLRQ 6ROYHU$QZHQGXQJ

(UVWH6FKULWWHPLWGHU6LPXOWDQHRXV(TXDWLRQ6ROYHU
$QZHQGXQJ

Gehen Sie das folgende Beispiel durch, um sich mit den
wichtigsten Eigenschaften der Anwendung Simultaneous
Equation Solver vertraut zu machen.

Eine kleine Firma nimmt zur Erweiterung Ihrer Produktlinie einen

8

Kredit von $500.000 auf. Ein Teil des Kredits wurde mit 9%, ein
Teil mit 10% und ein weiterer mit 12% Zinsen aufgenommen.
Wieviel wurde zu den jeweiligen Bedingungen geborgt, wenn die
Jahreszinsen $52.000 betrugen und die Menge des zu 10%
geborgten Geldes 2,5 mal so viel war, wie die Menge zu 9%?

Es sei x = Menge des zu 9% geborgten Geldes

y = Menge des zu 10% geborgten Geldes
z = Menge des zu 12% geborgten Geldes

1. Schreiben Sie eine Gleichung für jede Aussage.
x + y + z = 500.000
,09x +,1y +,12z = 52.000
y = 2,5x

2,5x – y = 0

"

2. Drücken Sie

, um eine Liste der Anwendungen auf

Œ

Ihrem Taschenrechner angezeigt zu bekommen.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 30

3. Wählen Sie

Tipp

Sie können }oder †betätigen, um den Cursor zu einem
Eintrag zu verschieben und diesen zu verändern.

PolySmlt

. Der Informationsbildschirm wird

angezeigt.

4. Drücken Sie zum Fortzusetzen eine beliebige Taste. Das

MAIN MENU (HAUPTMENÜ)

wird angezeigt.

5. Wählen Sie

Simult Eqn Solver

.

6. Geben Sie die Anzahl der Gleichungen (
der Unbekannten (

Í

.

) ein. Drücken Sie nach jeder Eingabe

3

) und die Anzahl

3

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 31

7. Geben Sie die Koeffizienten für die Variablen und die





0

52000

500000

01-

2.5

.12

.1

.0911

1



Diese Matrix zeigt
die Werte im
Modus Float an.

Konstanten in die Matrix ein:

8. Wählen Sie

SOLVE (LÖSE)

(drücken Sie

s

), um das
Gleichungssystem zu lösen. Sie sehen jetzt, dass die Firma
$100.000 zu 9%, $250.000 zu 10% und $150.000 zu 12%
borgte.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 32

Nachdem Sie nun das Beispiel ‘Erste Schritte’ durchgearbeitet
haben, können Sie weitere Anleitungen dazu lesen, wie Sie die
Anwendung Simultaneous Equation Solver einsetzen können.
Interessante Themen sind z.B.

Eine Matrix wird in die Anwendung geladen

•

Speichern von Daten in einer Matrix

•

Anzeigen einer Matrix in der reduzierten Diagonal-Form

•

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 33

6WDUWHQXQG%HHQGHQGHU$QZHQGXQJ6LPXOWDQHRXV
(TXDWLRQ6ROYHU

Starten der Anwendung

1. Drücken Sie

, um eine Liste von Anwendungen auf

Œ

Ihrem Taschenrechner angezeigt zu bekommen.

2. Wählen Sie

PolySmlt

. Der Informationsbildschirm wird

angezeigt.

3. Drücken Sie eine beliebige Taste, um in das Hauptmenü zu
gelangen.

4. Wählen Sie

SIMULT EQN SOLVER

Simult Eqn Solver

wird angezeigt.

. Der Hauptbildschirm von

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 34

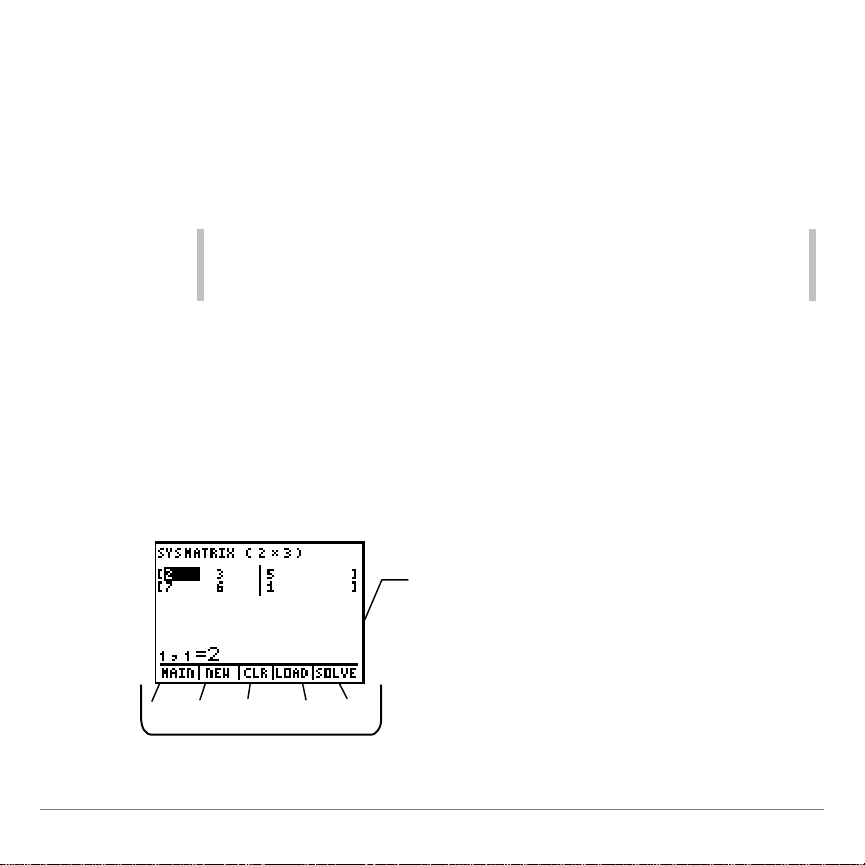
Beenden der Anwendung

Abkürzung

Sie können auch

y 5

drücken, um die Anwendung zu
verlassen. Wenn sich der Cursor an der Namenseingabe
befindet, müssen Sie

y 5

zwei mal drücken.

o p q r s

Drücken Sie eine
Grafiktaste, um eine
dieser Optionen
auszuwählen.

5. Sie können auf jedem Bildschirm
zum

.

6. Wählen Sie

Quit (Beenden) PolySmlt

$XVZDKOHQGHU2SWLRQHQGHU$QZHQGXQJ6LPXOWDQHRXV
(TXDWLRQ6ROYHU

Am unteren Rand des Bildschirms werden Optionen zur
Durchführung verschiedener Tätigkeiten angezeigt. Um eine
Option auszuwählen, drücken Sie jeweils die direkt darunter
liegende Grafiktaste.

MAIN (HAUPT)

.

wählen, um

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 35

=XU9HUIJXQJVWHKHQGH2SWLRQHQ 

Verwenden der Optionen auf
diesem Bildschirm…

Gehen Sie wie folgt vor:

Eingabebildschirm

Gleichungen/Unbekannte

(Equations/unknowns)

MAIN (HAUPT) zeigt das Hauptmenü an.
LOAD (LADEN) zeigt eine Eingabeaufforderung an, so

dass Sie einen Matrixnamen eingeben können, der die
zu verwendenden Matrixwerte enthält. Sie müssen die
Matrix im Matrixeditor einrichten, bevor Sie die Matrix in
der Anwendung Simultaneous Equation Solver
verwenden können. Sie haben keinen Zugriff auf den
Matrixeditor, während die Anwendung ausgeführt wird.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 36

Verwenden der Optionen auf
diesem Bildschirm…

Gehen Sie wie folgt vor:

SYSMATRIX-Bildschirm

MAIN (HAUPT) zeigt das Hauptmenü an.
NEW (NEU) zeigt den Eingabebildschirm für

Gleichungen/Unbekannte an, in dem Sie die Anzahl
der Gleichungen und Unbekannten anzeigen
lassen und ändern können.

CLR (LÖSCH) löscht alle von ihnen eingegebenen
Matrixwerte. (Bei Betätigung von

‘

werden die

Matrixwerte nicht gelöscht.)
LOAD (LADEN) zeigt eine Eingabeaufforderung an,

so dass Sie einen Matrixnamen eingeben können,
der die zu verwendenden Matrixwerte enthält. Sie
müssen die Matrix im Matrixeditor einrichten, bevor
Sie die Matrix in der Anwendung Simultaneous
Equation Solver können. Sie haben keinen Zugriff
auf den Matrixeditor, während die Anwendung
ausgeführt wird.

SOLVE (LÖSE) löst das Gleichungssystem. Es ist
möglich, dass die vollständige Lösung nicht auf einen
Bildschirm passt. Wenn auf der linken Seite des
Bildschirms ein Pfeil angezeigt wird, drücken Sie bei
Bedarf †und }, um die gesamte Lösung anzusehen.
Es ist möglich, das nicht jede Zeile der Matrix auf den
Bildschirm passt. Drücken Sie ~und gehen Sie in der
Anzeige nach rechts, um den ausserhalb der Anzeige
liegenden Bildschirmbereich angezeigt zu bekommen.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 37

Verwenden der Optionen auf
diesem Bildschirm…

Gehen Sie wie folgt vor:

Lösungsbildschirm

MAIN (HAUPT) zeigt das Hauptmenü an.
BACK (ZURÜCK) zeigt den Bildschirm

SYSMATRIX an, so dass Sie die Werte
anzeigen und ändern können.

STOsys (SPEsys) speichert die Koeffizienten in
der von Ihnen ausgewählten Matrix.

STOx (SPEx) speichert die Lösungen in der von
Ihnen ausgewählten Matrix.

Bildschirm Keine Lösung

gefunden

MAIN (HAUPT) zeigt das Hauptmenü an.
BACK (ZURÜCK) zeigt den Eingabebildschirm

der Matrix an, so dass Sie die Werte anzeigen
und ändern können.

STOsys (SPEsys) speichert die Koeffizienten in
der von Ihnen ausgewählten Matrix.

RREF zeigt die reduzierte Diagonal-Form einer
Matrix an, die entweder keine oder eine
unendliche Anzahl von Lösungen hat.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 38

Verwenden der Optionen auf
diesem Bildschirm…

Gehen Sie wie folgt vor:

RREF-Bildschirm

MAIN (HAUPT) zeigt das Hauptmenü an.
BACK (ZURÜCK) zeigt den Eingabebildschirm

der Matrix an, so dass Sie die Werte anzeigen
und ändern können.

STORE RREF (SPEICH RREF) speichert die
reduzierte Diagonal-Form einer Matrix in einer
Matrix-Variabglen, die Sie auswählen können.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 39

bQGHUXQJGHU0RGXVHLQVWHOOXQJHQ

Hinweis

•

Wenn das RAM zurückgesetzt wird, gehen die gespeicherten

Einstellungen von Polynomial Root Finder und Simultaneous
Equation Solver verloren.

•

Die Moduseinstellungen werden in einer Anwendungsvariablen

(engl. application variable, kurz AppVar) gespeichert. Wenn
Sie die Anwendung und Ihre Modus-Einstellungen mit einem
anderen TI-83 Plus -Benutzer gemeinsam nutzen wollen,
müssen Sie sowohl die Anwendung als auch die AppVar mit
der Bezeichnung APPVARO übertragen.

•

Die Moduseinstellungen können vom RREF-Matrix-Bildschirm

aus nicht verändert werden.

•

Wenn eine Matrix-Variablen-Eingabeaufforderung angezeigt

wird (z.B. STOsys MAT = ), müssen Sie zuerst die
Eingabeaufforderung verlassen, bevor Sie die
Moduseinstellungen ändern können.

Diese Anwendung verfügt über einen eigenständigen
Einstellungsbildschirm auf Basis der Moduseinstellungen des
Taschenrechners. Diese Modus-Einstellungen werden nur wirksam,
während die Anwendung Polynomial Root Finder / Simultaneous
Equation Solver ausgeführt wird. Die Einstellungen werden
gespeichert und bei jedem Ausführen der Anwendung wirksam.
Wenn Sie die Anwendung verlassen, werden die vorhergehenden
Moduseinstellungen des Rechners wiederhergestellt.

So ändern Sie die Moduseinstellungen:

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 40

1. Starten Sie Simultaneous Equation Solver Anwendung.

2. Drücken Sie

Einstellungsbildschirm)

z

, um den

PolySmlt MODE Settings (MODUS-

angezeigt zu bekommen.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 41

3. Verschieben Sie den Cursor auf eine Einstellung und

Einstellung

Beschreibung

Normal Sci Eng

Normal

Dieser Notationsmodus ist die übliche
Darstellungsart von Zahlen mit Stellen links und
rechts vom Komma, z.B. 12345,67.

Im Notationsmodus Sci (Exp)

(wissenschaftl ich,
engl. scientific) werden Zahlen in zwei Teilen
ausgedrückt. Die signifikanten Stellen werden mit
einer Stelle links vom Komma angezeigt. Die
entsprechende Zehnerpotenz wird rechts neben
dem Eangezeigt, wie in 1,234567E4.

Ing (Eng)

Der Anzeigemodus (engl. engineering)
ist der wissenschaftlichen Notation ähnlich.
Allerdings kann die Zahl bis zu drei Stellen vor
dem Komma enhalten. Der Zehnerexponent ist
ein Vielfaches von 3, wie in 12,34567E3.

Float 0 1 2 3 4 5 6 7 8 9

Float (Fließkomma)

Im Modus Fließkomma
(engl. floating) werden bis zu 10 Stellen, plus
Vorzeichen und Komma dargestellt.

0123456789

(Festkomma)
Kommasetzungsmodus- gibt an, wieviele
Stellen (0 bis 9) rechts neben dem Komma
angezeigt werden.

drücken Sie

Í

, um die Einstellung auszuwählen.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 42

Einstellung

Beschreibung

Radian Degree

Im Modus Radian (Bogenmaß)

werden
Winkelwerte im Bogenmaß verwendet.
Antworten werden im Bogenmaß angezeigt.

Degree (Grad)

Modus interpretiert
Winkelangaben in Grad. Antworten werden in
Grad angezeigt.

Real a+bi re^qi

Im Modus Real (Reell)

werden keine
komplexen Ergebnisse angezeigt. Wenn Sie
diese Modus-Einstellung wählen und die
Antwort komplex ist, wird als Ergebnis

NONREAL (NICHT REELL)

angezeigt.

a+b

i

(kartesische Darstellung der komplexen
Ebene)- In diesem Modus werden komplexe
Zahlen in der Form a+bidargestellt.

re^

q

i

(Polarkoordinaten-Darstellung der
komplexen Ebene)- in diesem Modus werden
komplexe Zahlen in der Form re

q

i

dargestellt.

4. Wählen Sie

ESC

, um die Einstellungen zu speichern und

zum vorherigen Bildschirm zurückzukehren.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 43

(LQJHEHQXQG/|VHQHLQHV3UREOHPV 

Hinweis

Der Simultaneous Equation Solver findet keine Lösungen zu
komplexen Systemen. Die erweiterte Matrix kann nur reelle
Zahlen enthalten.

Um ein Gleichungssystem zu lösen, geben Sie die Anzahl der
Gleichungen, die Anzahl der Unbekannten und dann die
erweiterte Matrix (enthält sowohl die Koeffizienten als auch die
Konstanten) des Systems ein.

Im folgenden Beispiel wird dieses Gleichungssystem gelöst:
x + y + z = 5

2x-,5y + z = 10
x- 2y + 3z = 15

1. Geben Sie die Anzahl der Gleichungen (
der Unbekannten ein (
Eingabe

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 44

Í

.

3

) und drücken Sie nach jeder

3

) und die Anzahl

2. Geben Sie einen Wert für jeden Koeffizienten und einen

Tipp

Sie können mittels }, †, ~und |durch die Liste der
Koeffizienten und Konstanten blättern, um bei Bedarf Werte zu
bearbeiten.

Wert für jede Konstante ein. Drücken Sie nach jeder Eingabe

Í

, um den Cursor zum nächsten Wert zu verschieben.

3. Wählen Sie

SOLVE (LÖSE)

, um die Lösung angezeigt zu

bekommen. Dies kann einige Sekunden dauern.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 45

/DGHHLQH0DWUL[

Sie können eine erweiterte Matrix aus dem Eingabebildschirm
für Gleichungen/Unbekannte oder dem Bildschirm

SYSMATRIX

laden. Sie müssen die Matrix im Matrixeditor einrichten, bevor
Sie die Matrix in der Anwendung Simultaneous Equation Solver
verwenden können. Sie haben keinen Zugriff auf den
Matrixeditor, während die Anwendung ausgeführt wird.

Die Größe der Matrix kann nicht kleiner als 2x3 oder größer als
30x30 sein. Die Größe der Matrix muss der Anzahl der
Gleichungen und der Anzahl der Unbekannten entsprechen.
Wenn Sie beispielsweise 5 als Anzahl der Gleichungen und 3 als
Anzahl der Unbekannten eingeben, muss die Größe der Matrix
5x4 sein.

So laden Sie eine Matrix:

1. Wählen Sie

LOAD Mat = (LADE Mat)

2. Drücken Sie

LOAD (LADEN)

y >

. Die Eingabeaufforderung

wird angezeigt.

, um eine Liste von Matrizen auf

Ihrem Taschenrechner angezeigt zu bekommen.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 46

3. Verwenden Sie }und †, um die Matrix zu wählen und

Tipp

•

Drücken Sie

‘

, um den Listennamen von der

Eingabeaufforderung

LOAD Mat =

zu entfernen.

•

Drücken Sie

‘

, um die Ladeoption abzubrechen, wenn

kein Listenname an der Eingabeaufforderung

LOAD Mat =

steht.

Hinweis

•

Wenn die geladene Matrix nicht die gleichen Diemensionen

hat, die auf dem Eingabebildschirm Gleichungen/Unbekannte
angegeben wurden, wird die Dimension der Matrix so
geändert, dass sie der geladenen Matrix entspricht.

•

Es wird davon ausgegangen, dass die Matrix eine erweiterte

Matrix ist. Falls nötig, wird die Anzahl der Unbekannten
automatisch geändert.

drücken Sie dann

LOAD Mat =

-Eingabeaufforderung zu kopieren.

Í

, um den Namen der Matrix zur

4. Drücken Sie

Í

, um die Werte in die Matrix zu laden.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 47

6SHLFKHUQGHU'DWHQ

Hinweis

Sie müssen einen ungenutzten Matrixnamen auswählen. Wenn
alle Matrixnamen in Benutzung sind, müssen Sie die Anwendung
verlassen und eine Matrix löschen, bevor Sie die neue Matrix
speichern können.

Sie können eine erweiterte Matrix (die Koeffizienten und
Konstanten enthält) und die Lösung des Gleichungssystems in
Matrizen speichern. Die Lösungen werden als Spaltenmatrizen
gespeichert. Wenn das Gleichungssystem keine Lösung oder
eine unendliche Anzahl von Lösungen hat, können Sie die
reduzierte Diagonal-Form der Matrix anzeigen lassen.

So speichern Sie Daten:

1. Wählen Sie
speichern,

STOx (SPEx)

speichern oder

STOsys (SPEsys)

, um die Lösung als Spaltenmatrix zu

STORE RREF (SPEICH RREF)

, um die erweiterte Matrix zu

, um die
reduzierte Diagonal-Matrix zu speichern. Die
Eingabeaufforderung
(oder

2. Drücken Sie

STOx Mat =

y >

Matrixnamen aus dem Menü

3. Drücken Sie

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 48

Í

STOsys Mat =

oder

STORE RREF

, und wählen Sie dann einen

NAMEN

, um die Matrix zu speichern.

) wird angezeigt.

.

$Q]HLJHQHLQHU0DWUL[LQGHUUHGX]LHUWHQ'LDJRQDO )RUP

Wenn das Gleichungssystem keine Lösung oder eine unendliche
Anzahl von Lösungen hat, können Sie die reduzierte Diagonal­Form der Matrix anzeigen lassen.

Im folgenden Beispiel wird dieses Gleichungssystem gelöst:
x Ny + 2z = 4

x + z = 6
2x N3y + 5z = 4
3x + 2y Nz = 1

1. Starten Sie Simultaneous Equation Solver

Anwendung.

2. Geben Sie die Anzahl der Gleichungen (4) und die Anzahl
der Unbekannten (3) ein und drücken Sie nach jeder
Eingabe

Í

.

3. Geben Sie einen Wert für jeden Koeffizienten und einen
Wert für jede Konstante ein. Drücken Sie nach jeder Eingabe

Í

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 49

, um den Cursor zur nächsten Wert zu verschieben.

4. Wählen Sie
bekommen.
wird angezeigt.

SOLVE (LÖSE)

No Solutions Found (Keine Lösungen gefunden)

, um die Lösung angezeigt zu

5. Wählen Sie
Form darzustellen.

, um die Matrix in der reduzierten Diagonal-

RREF

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 50

/|VFKHQGHU$QZHQGXQJXQG$SS9DUV

Tipp

Sie können mit Hilfe der Software TI-GRAPH LINK™ eine Kopie
der Anwendung auf Ihrem Computer speichern.

Durch das Löschen der Anwendung wird diese komplett von
Ihrem Taschenrechner entfernt.

Stellen Sie zum Löschen der Anwendung von Ihrem Rechner
sicher, dass der Hauptbildschirm (home) angezeigt wird und
folgen Sie dann den weiteren Anleitungen.

1. Drücken Sie

2.

Wählen Sie

y L

Mem Mgmt/Del (Spei Mgmt / Lö)

3. Verwenden Sie

4. Verwenden Sie

, um das Menü

oder }, um

†

oder }, um den Cursor auf

†

Apps (App)

MEMORY

anzuzeigen.

.

auszuwählen.

PolySmlt

zu

verschieben.

5. Drücken Sie

6. Wählen Sie

7. Drücken Sie

.

{

Yes (Ja)

‘

.

, um zum Hauptbildschirm (Home)

zurückzukehren.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 51

Wenn Sie auf Ihrem Rechner weiteres RAM freigeben wollen,

Hinweis

Wenn Sie die AppVars löschen, gehen die Moduseinstellungen
und zuletzt eingegebenen Daten verloren. In Listen und Matrizen
exportierte Daten gehen nicht verloren.

können Sie auch die AppVars löschen, welche die Anwendung
erstellt. Um die AppVars zu löschen, ist sicherzustellen, dass der
Hauptbildschirm (home) angezeigt wird. Folgen Sie dann den
weiteren Anleitungen zum Löschen von

APPVARO

.

APPVARL, APPVARM

und

1. Drücken Sie

2.

Wählen Sie

y L

Mem Mgmt/Del (Spei Mgmt /Lö)

3. Verwenden Sie

†

, um das Menü

oder }, um

MEMORY

anzuzeigen.

.

AppVars (AppVar)

auszuwählen.

4. Verwenden Sie

oder }, um den Cursor auf

†

APPVARL

zu

verschieben.

5. Drücken Sie

6. Verschieben Sie den Cursor auf
dann

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 52

{

.

{

.

APPVARM

, und drücken Sie

7. Verschieben Sie den Cursor auf
dann

{

.

APPVARO

, und drücken Sie

8. Drücken Sie
zurückzukehren.

‘

, um zum Hauptbildschirm (Home)

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 53

,QVWDOODWLRQV IHKOHUPHO GXQJHQ

Low Battery (Batterie leer)

Versuchen Sie nicht eine Flash-Anwendung herunterzuladen,
wenn die Meldung "Batterie leer" auf dem Hauptbildschirm des
TI-83 Plus erscheint. Die Batterieschwäche wird auf dem
Ausgangsbildschirm angezeigt. Wenn diese Meldung während
einer Installation ausgegeben wird, müssen Sie die Batterien
wechseln, bevor Sie es erneut versuchen.

Archive Full (Archiv voll)

Dieser Fehler tritt auf, wenn der TI-83 Plus nicht mehr über
ausreichend Speicher für eine Anwendung verfügt. Um Speicher
für eine neue Anwendung freizugeben, müssen Sie eine
Anwendung und/oder archivierte Variablen vom TI-83 Plus
löschen. Bevor Sie eine Anwendung von dem TI-83 Plus
löschen, können Sie diese auf Ihrem Computer speichern.
Verwenden Sie dazu die TI-GRAPH LINK™-software für den TI­83 Plus. Sie können die Anwendung auf Ihrem TI-83 Plus später
mit der Software TI-GRAPH LINK wiederherstellen.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 54

Link Transmission Error (Verbindungs-Übertragungsfehler)

Dieser Fehler zeigt, dass die Software TI-GRAPH LINK™ nicht
in der Lage ist, mit dem TI

83 Plus zu kommunizieren. Das

-

Problem ist gewöhnlich mit dem TI-GRAPH LINK-Kabel
verbunden und mit dessen Anschluss am TI

83 Plus und/oder

-

am Computer.

Vergewissern Sie sich, dass das Kabel fest mit dem E/A-

•

Anschluss des Rechners und mit dem Computer
verbunden ist.

Stellen Sie sicher, dass in den Einstellungen von

•

TI-GRAPH LINK™ der richtige Kabeltyp ausgewählt wurde.
Stellen Sie sicher, dass in den TI-GRAPH LINK-Link-

•

Einstellungen der richtige Anschluss (COM-Schnittstelle)
gewählt wurde.

Wenn diese Schritte das Problem nicht lösen, versuchen Sie es
mit einem anderen TI-GRAPH LINK-Kabel und starten Sie Ihren
Computer neu. Wenn der Fehler weiterhin auftritt, wenden Sie
sich bitte an den TI-Cares

Kundendienst zur Unterstützung.

é

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 55

Error in Xmit (Fehler bei Übertragung)

Diese Problem hängt meist mit dem Rechner-Rechner­Verbindungskabel und dessen Verbindung mit den TI-83 Plus
Rechnern zusammen. Vergewissern Sie sich, dass das Kabel
fest mit den E/A-Anschlüssen der beiden Rechner verbunden ist.

Wenn der Fehler weiterhin auftritt, wenden Sie sich bitte an den

TI-Cares

™ Customer Support.

Invalid Signatur e or Ce rtificate (Signatur oder Zerti fikat ungültig)

Entweder hat der Rechner kein Zertifikat zur Ausführung dieser
Anwendung, oder elektrische Störsignale verursachten einen
Verbindungsfehler. Versuchen Sie erneut, die Anwendung zu
installieren. Wenn der Fehler weiterhin auftritt, wenden Sie sich
bitte an den TI-Cares

Kundendienst.

Andere Fehler

Siehe Seiten B-6 bis B-10 im TI-83 Plus

-Handbuch. Dort finden

Sie weitere Informationen zu dem speziellen Fehler oder Kontakt
zum TI-Cares

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 56

Kundendienst.

3UIHQGHU9HUVLRQVQXPPHUQ XQGGHVIUHL HQ
6SHLFKHUSODW]HV 

9HULIL]LHUHQGHU9HUVLRQGHV%HWULHEVV\VWHPVXQGGHU,' 
1XPPHU

Die Anwendung Polynomial Root Finder/Simultaneous Equation
Solver ist kompatibel mit dem Betriebssystem TI-83 Plus ab
Version 1.13.

So überprüfen Sie die Version Ihres Betriebssystems:

1. Drücken Sie, während der Ausgangsbildschirm angezeigt

y L

wird

.

2. Wählen Sie
Die Versionsnummer des Betriebssystems wird unter dem

Namen des Produkts im Format x.yy angezeigt. Die ID-Nummer
erscheint in der Zeile unter der Produktnummer.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 57

ABOUT (INFO)

.

9HULIL]LHUHQGHU9HUVLRQGHU)ODVK$QZHQGXQJ 

1. Drücken Sie

2. Wählen Sie

PolySmlt

Œ

.

. Der Informationsbildschirm wird

angezeigt.

Die Versionsnummer wird auf dem Informationsbildschirm unter
dem Namen der Anwendung angezeigt.

Sie können auch auf den Informationsbildschirm gelangen,
indem Sie

About (Info)

im

MAIN MENU (HAUPTMENÜ)

der

Anwendung wählen.

3UIHQGHVIUHLHQ6SHLFKHUVIU)ODVK$QZHQGXQJHQ 

1. Drücken Sie, während der Hauptbildschirm angezeigt wird

y L

2. Wählen Sie

.

Mem Mgmt/Del (Spei Mgmt / Lö)

.

Die Anwendung Polynomwurzelsuche/Gleichungssystem Löser
benötigt mindestens 33.070 Byte des ARC FREE (Flash) zum
Laden der Anwendung.

Weiteren Informationen zum Speicher und zur
Speicherverwaltung finden Sie im TI-83 Plus

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 58

-Handbuch.

7H[DV,QVWUXPHQWV7,.XQGHQGLHQVWXQG
$XVNXQIW

$OOJHPHLQH$XVNQIWH

Email:
Telefon:

[e-mail]

1.800.TI.CARES (1.800.842.2737)
Nur für die USA, Kanada, Mexiko, Puerto Rico
und die Jungferninseln

Internet:

education.ti.com

7HFKQLVFKH$XVNQIWH

Telefon:

1.972.917.8324

3URGXNWNXQGHQGLHQVW*HUlWH

Kunden in den USA, Kanada, Mexiko, Puerto Rico und
auf den Jungferninseln:

Wenden Sie sich vor der
Rückgabe eines Produkts immer erst an den Kundendienst
von TI.

Alle anderen Kunden:

Beachten Sie das Informationsblatt,
das Ihrem Produkt beilag, oder wenden Sie sich an Ihren Ti­Händler bzw. einen Großhändler in Ihrer Nähe.

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 59

7(;$6,167580(176/,=(1=9(575$* 

DURCH DIE INSTALLATION DIESER SOFTWARE ERKLÄREN SIE SICH MIT FOLGENDEN
VERTRAGSBEDINGUNGEN EINVERSTANDEN:

LIZENZ

1.

2.

3.

4.

. HAFTUNGSBESCHRÄNKUNG

5

IN BESTIMMTEN STAATEN UND LÄNDER KANN HAFTUNG NICHT AUSGESCHLO SSEN

: Texas Instrument s Incorporated (”TI”) gewährt Ihnen eine Lizenz zum Einsatz und zum
Kopieren der Software (”Gegenstand der Lizenz ”), die sich auf dieser Dis kette/CD/Web site
befindet. Sie und jeder weitere Benutzer dürfen den Gegenstand der Lizenz nur auf Rechnern
von Texas Instrument s einsetzen.

BESCHRÄNKUNGEN

decompilieren. Sie dürfen Kopi en, die Sie anfertigen, nicht verkaufen, vermiet en oder zum
Mietkauf überlassen.

COPYRIGHT

Dokumentationsmaterial sind urheberrechtlich geschützt. Löschen Sie beim Herstellen von
Kopien den Urhebervermerk, das Warenzeic hen oder Schutzvermerke nicht aus den Kopien.

GEWÄHRLEISTUNG

Dokumentationsmaterial fehlerfrei oder für den von Ihnen vorgesehenen Z weck einsetzbar sind.
Der Gegenstand der Lizenz wird Ihnen und allen weit eren Nutzern "wie vorliegend" überlassen.

Gewährleistung beliebiger Art für den Gegenstand der Lizenz, einschließlich für dessen
Eignung als Wirtschaftsgut, die Anwendbarkeit und di e E ignung zu einem bestimmten Z weck.

TI ODER SEINE ZULIEFERER HAFTEN WEDER FÜR INDIREKTE, ZUFÄLLIGE ODER
FOLGESCHÄDEN NOCH FÜR GEW INNAUSFALL, BETRIEBSUNTERBRECHUNGEN,
ODER DATENVERLUST, UNGEACHTET DESSEN, OB SCHÄDEN ALS ERLITTENES
UNRECHT, VERTRAGSBRUCH ODE R AL S SCHADENSERSATZ GELTEND GEMACHT
WERDEN.

UND EINE HAFTUNGSBEGRENZUNG FÜR ZUFÄLLIGE O DER FOLGESCHÄDEN NICHT
FESTGESCHRIE BEN WERDEN. DIE GENANNT E HAFTUNGSBESCHRÄNKUNGEN
TREFFEN ALSO MÖGLICHERWEISE F ÜR SIE NICHT ZU.

: Der Gegenstand der Lizenz und das gesam te mitgelieferte

: Sie dürfen den Gegenstand der Lizenz ni cht disassemblieren oder

: TI gewährleistet nicht, daß der Gegenstand der Lizenz oder das

: TI übernimmt weder direkt noc h i ndi rekt eine Haftung oder

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 60

Seitenaufteilung

Dieses PDF-Dokument enthält elektronische Lesezeichen, die der
einfachen bildschirmgestützten Navigation dienen. Wenn Sie dieses
Dokument drucken möchten, sollten Sie bei der Suche nach bestimmten
Themen die folgenden Seitennummern beac ht en.

Wichtig..................................................................................................................2

Was ist die Anwendung Polynomial Root Finder & Simultenous Equation Solver?3

Was Sie für Installation und Einsatz der Anwendung benötigen.......................... 4

Wo Sie Installationsanleitungen finden................................................................. 5

So erhalten Sie Hilfe.............................................................................................6

Polynomial Root Finder Anwendung.....................................................................7

Erste Schritte mit der Polynomial Root Finder Anwendung........................... 7

Starten und Beenden der Polynomial Root Finder Anwendung...................16

Auswählen von Optionen für Polynomial Root Finder..................................17

Zur Verfügung stehende Optionen...............................................................17

Änderung der Moduseinstellungen ..............................................................20

Eingeben und Lösen einer Aufgabe............................................................. 24

Werte laden .................................................................................................26

Daten speichern........................................................................................... 28

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 61

Simultaneous Equation Solver Anwendung........................................................ 30

Erste Schritte mit der Simultaneous Equation Solver Anwendung .............. 30

Starten und Beenden der Anwendung Simultaneous Equation Solver........ 34

Auswahlen der Optionen der Anwendung Simultaneous Equation Solver .. 35

Zur Verfügung stehende Optionen...............................................................36

Änderung der Moduseinstellungen ..............................................................40

Eingeben und Lösen eines Problems ..........................................................44

Lade eine Matrix .......................................................................................... 46

Speichern der Daten.................................................................................... 48

Anzeigen einer Matrix in der reduzierten Diagonal-Form ............................ 49

Löschen der Anwendung und AppVars.............................................................. 51

Installationsfehlermeldungen..............................................................................54

Prüfen der Versionsnummern und des freien Speicherplatzes ..........................57

Prüfen des freien Speichers für FlashAnwendungen .........................................58

Texas Instruments (TI) Kundendienst und Auskunft ..........................................59

TEXAS INSTRUMENTS LIZENZVERTRAG......................................................60

TI-83 Plus Polynomial Root Finder / Simultaneous Equation Solver Application Seite 62