How it Works
Texas Instruments
Loading...
TI-30X Plus
Calculator
80 pgs671.62 Kb0
User Manual [de]
72 pgs1.57 Mb0
User Manual [de]
85 pgs1.83 Mb0
User Manual [de]
88 pgs724.53 Kb0
Table of contents
Loading...

Texas Instruments TI-30X Plus User Manual [de]

Wissenschaftlicher Schulrechner
TI-30X Plus MathPrint™
Handbuch
Dieses Handbuch ist gültig für die Software-Version 1.0. Gehen Sie auf
education.ti.com/eguide, um die aktuellste Version der Dokumentation
herunterzuladen.

Wichtige Informationen

MathPrint, APD, Automatic Power Down und EOS sind Marken von Texas Instruments Incorporated.
Copyright © 2018 Texas Instruments Incorporated
ii
Inhalt
Wichtige Informationen
Einstieg 1
Ein- und Ausschalten des Rechners Anzeigekontrast Hauptbildschirm Zweitbelegung Modi Tasten mit Mehrfachbelegung Menüs Beispiele Benutzung der Pfeiltasten zum Zurückblättern Umwandeln von Ergebnissen Letztes Ergebnis Rangfolge der Operatoren Löschen und Korrigieren Speicher und gespeicherte Variablen
11 11
Mathematische Funktionen 15
Brüche Prozentrechnung Wissenschaftliche Notation [EE] Potenzen, Wurzeln und Kehrwerte Pi (Symbol Pi) Math Numerische Funktionen Winkelmaße Kartesisch in polar Trigonometrie Hyperbelfunktionen Logarithmus- und Exponentialfunktionen Statistik, Regressionen und Verteilungen Wahrscheinlichkeit
15 17 18 19 20 20 21 23 26 26 28 29 30 42
ii
1 1 1 2 4 6 6 7 7 8 8 9
Mathematische Werkzeuge 44
Gespeicherte Operationen Dateneditor und Listenformeln Funktionstabelle Zahlensysteme Auswerten von Ausdrücken Konstanten
44 45 49 52 54 55
iii
Umrechnungen Komplexe Zahlen
56 59
Referenz 62
Fehler und Meldungen Batterie Problembehebung
62 65 67
Allgemeine Informationen 68
Texas Instruments – Kundendienst und Service Produktinformation Service und Garantie
68 68 68
iv

Einstieg

Dieser Abschnitt enthält Informationen über die grundlegenden Funktionen des Rechners.

Ein- und Ausschalten des Rechners

& schaltet den Rechner ein. % ' schaltet ihn aus. Die Anzeige wird gelöscht, Protokoll, Einstellungen und Speicher bleiben jedoch erhalten.
Die APD™ (Automatic Power Down™) Funktion schaltet den Rechner automatisch ab, wenn etwa 3 Minuten lang keine Taste gedrückt wird. Drücken Sie & nach einer solchen APD™-Abschaltung. Die Anzeige, nicht abgeschlossene Operationen, Einstellungen und der Speicher bleiben erhalten.

Anzeigekontrast

Helligkeit und Kontrast der Anzeige können je nach Beleuchtung des Raums, Batteriezustand und Blickwinkel unterschiedlich erscheinen.
So stellen Sie den Kontrast ein:
1. Drücken Sie % und lassen Sie die Taste wieder los.
2. Drücken Sie ] für eine dunklere oder [ für eine hellere Anzeige.
Hinweis: Dadurch wird der Kontrast um jeweils eine Stufe angepasst. Wiederholen
Sie Schritte 1 und 2 nach Bedarf.

Hauptbildschirm

Auf dem Hauptbildschirm können Sie mathematische Ausdrücke, Funktionen und andere Anweisungen eingeben. Die Ergebnisse werden ebenfalls auf dem Hauptbildschirm angezeigt.
Die TI-30X Plus MathPrint™ Anzeige kann bis zu vier Zeilen à 16 Zeichen anzeigen. Wenn eine Eingabe oder ein Ausdruck länger als der sichtbare Anzeigebereich ist, können Sie nach links oder rechts blättern (! und "), um die Eingabe bzw. den Ausdruck vollständig zu sehen.
Im MathPrint™ Modus können Sie Funktionen und Ausdrücke bis zu vier Ebenen tief verschachteln. Der Modus unterstützt Brüche, Quadratwurzeln, Exponenten mit ^, Ü, exund 10x.
Wenn Sie eine Eingabe auf dem Hauptbildschirm berechnen, wird das Ergebnis je nach verfügbarem Platz entweder direkt rechts neben der Eingabe oder rechts in der nächsten Zeile angezeigt.
Wenn zusätzliche Informationen zu einer Funktion oder einem Ergebnis vorhanden sind, wird dies ggf. durch spezielle Hinweis- oder Eingabemarken gekennzeichnet.
Einstieg 1
Anzeige Definition
2ND Zweitbelegung FIX Festkomma-Einstellung (siehe Abschnitt
SCI, ENG Wissenschaftliche oder technische Notation
DEG, RAD, GRAD
L1, L2, L3 Wird über den Listen im Dateneditor angezeigt H, B, O Gibt das Zahlensystem an (hexadezimal, binär,
5 6 Vor und/oder nach dem sichtbaren
´
„Modi“)
(siehe Abschnitt „Modi“) Winkelmodus (Grad, Bogenmaß oder Neugrad)
(siehe Abschnitt „Modi“)
oktal). Im Standardmodus (dezimal) erfolgt keine gesonderte Anzeige.
Der Rechner arbeitet einen Vorgang ab. Verwenden Sie &, um die Berechnung abzubrechen.
Anzeigebereich ist ein Eintrag im Speicher abgelegt. Drücken Sie # und $ zum Blättern.
Gibt an, dass die Taste mit Mehrfachbelegung aktiv ist.
Normale Anzeige des Cursors. Zeigt an, wo Ihre nächste Eingabe erscheint. Ersetzt das aktuelle Zeichen.
Cursor bei Erreichen der Eingabegrenze. Es können keine weiteren Zeichen eingegeben werden.
Einfüge-Cursor. Ein Zeichen wird vor der Cursorposition eingefügt.
Platzhalter für leeres MathPrint™ Element. Verwenden Sie die Pfeiltasten, um in das Kästchen zu springen.
MathPrint™ Cursor. Fahren Sie mit der Eingabe im aktuellen MathPrint™ Element fort oder drücken Sie ", um das Element zu verlassen.

Zweitbelegung

%
Die meisten Tasten sind mit mehr als einer Funktion belegt. Die primäre Funktion ist dann unten auf die Taste gedruckt, die zweite Funktion darüber. Drücken Sie %, um die zweite Funktion einer Taste zu aktivieren. In der Anzeige erscheint der Hinweis
2ND. Um die Eingabe rückgängig zu machen, drücken Sie noch einmal %. % b 25
2 Einstieg
< berechnet beispielsweise die Quadratwurzel von 25 und gibt das Ergebnis 5 zurück.
Einstieg 3

Modi

q
Drücken Sie q, um die Modi auszuwählen. Drücken Sie $ # ! ", um einen Modus auszuwählen, und <, um ihn zu aktivieren. Drücken Sie - oder % s, um zum Hauptbildschirm zurückzukehren und mit den gewählten Moduseinstellungen weiterzuarbeiten.
In den folgenden Beispielbildschirmen sind jeweils die Standardeinstellungen hervorgehoben.
DEGREE RADIAN GRADIAN – Legt den Winkelmodus fest: Grad, Bogenmaß,
Neugrad.
NORMAL SCI ENG – Legt die Notation von Zahlen fest. Die Notation ist nur für die
Anzeige von Ergebnissen relevant. Intern werden Werte stets mit maximaler Präzision gespeichert.
NORMAL – Ergebnisse werden mit Vor-und Nachkommastellen angezeigt. Beispiel:
123456.78.
SCI – Zahlen werden mit einer einzigen linksseitigen Dezimalstelle und der
entsprechenden Zehnerpotenz angezeigt. Beispiel: 1.2345678E5, was dem Wert (1.2345678×105) mit den Klammern für die richtige Rangfolge der Operatoren entspricht.
ENG – Zahlen werden als 1 bis 999 × 10 hoch einer ganzen Zahl angezeigt. Der
Exponent ist immer ein Vielfaches von 3.
Hinweis: Um eine Zahl in wissenschaftlicher Notation einzugeben, verwenden Sie
die Taste E. Das Ergebnis wird in der Notation angezeigt, die im Modusmenü ausgewählt ist.
FLOAT 0 1 2 3 4 5 6 7 8 9 – Legt die Anzahl der Nachkommastellen bei
Dezimalnotation fest.
FLOAT (Gleitkommamodus) – Es werden bis zu 10 Stellen plus Vorzeichen und
Komma angezeigt.
0 1 2 3 4 5 6 7 8 9 (Festkommamodus) – Nach dem Komma wird eine feste Anzahl
von Stellen (0 bis 9) angezeigt.
REAL a+bi r±q – Legt das Format von komplexen Ergebniswerten fest.
REAL Reelle Ergebnisse
a+bi Kartesische Ergebnisse
r±q Polare Ergebnisse
4 Einstieg
DEC HEX BIN OCT – Legt das Zahlensystem für Berechnungen fest.
DEC Dezimal
HEX Hexadezimal (Ziffern A bis F mit % §, % ¨ usw. eingeben)
BIN Binär
OCT Oktal
MATHPRINT CLASSIC
MATHPRINT – Die meisten Ein- und Ausgaben werden im Lehrbuchformat
angezeigt.
CLASSIC (klassisch) – Zeigt Ein- und Ausgaben in einer einzigen Zeile an.
Beispiele für die Modi MathPrint™ und Klassisch
MathPrint™ Modus Klassischer Modus
Sci Sci
Gleitkommamodus und Umwandlungstaste
Gleitkommamodus und Umwandlungstaste
Fix 2 und Umwandlungstaste Fix 2
Un/d Un/d Eingabe
Beispiel mit Exponent Beispiel mit Exponent
Beispiel mit Quadratwurzel Beispiel mit Quadratwurzel
Einstieg 5
MathPrint™ Modus Klassischer Modus
Beispiel mit Kubikwurzel Beispiel mit Kubikwurzel

Tasten mit Mehrfachbelegung

Bei Tasten mit Mehrfachbelegung können Sie durch wiederholtes Drücken unterschiedliche Funktionen aufrufen. Drücken Sie ", um die Mehrfachbelegung zu beenden.
Beispielsweise ist die Taste X sowohl mit den trigonometrischen Funktionen sin und
sin/ als auch den hyperbolischen Funktionen sinh und sinh/ belegt. Drücken Sie die
Taste so oft, bis die gewünschte Funktion angezeigt wird.
Zu den Tasten mit Mehrfachbelegung gehören z, X, Y, Z, C, D, H und g. Ihre Verwendung wird ausführlicher in den dazugehörigen Abschnitten dieser Anleitung beschrieben.

Menüs

Über Menüs haben Sie Zugriff auf eine große Vielzahl von Rechnerfunktionen. Bei manchen Menütasten wie z. B. % h wird ein einzelnes Menü angezeigt. Über andere Tasten wie etwa d werden hingegen mehrere Menüs angezeigt.
Verwenden Sie die Tasten " und $, um einen Menüeintrag auszuwählen und zu aktivieren, oder drücken Sie direkt die Nummer neben dem Eintrag. Um zum vorherigen Bildschirm zurückzukehren, ohne den Eintrag auszuwählen, drücken Sie
-. Um ein Menü zu verlassen und zum Hauptbildschirm zurückzukehren, drücken Sie % s.
% h (Taste mit einem einzelnen Menü):
RECALL VAR
1:x = 0 2:y = 0 3:z = 0 4:t = 0 5:a = 0 6:b = 0 7:c = 0 8:d = 0
6 Einstieg
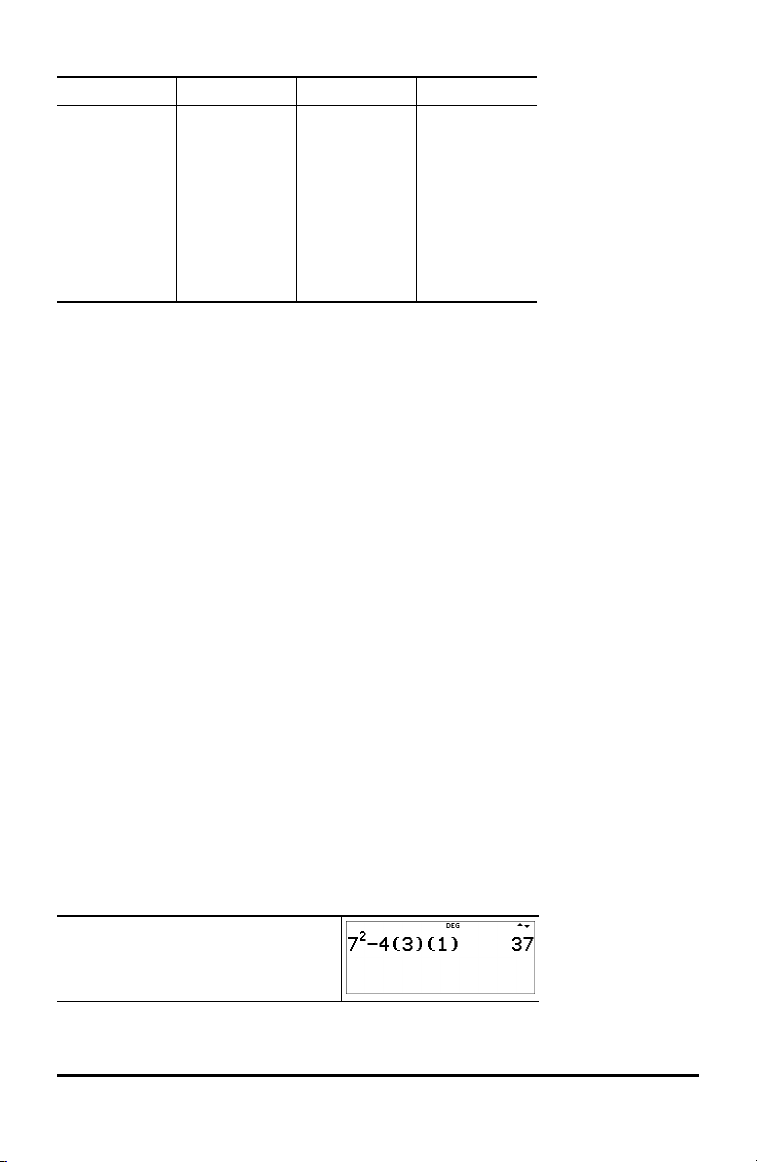
d (Taste mit mehreren Menüs):
MATH NUM DMS R³´P
1:4n/d³´Un/d 2:lcm( 3:gcd( 4:4Pfactor 5:sum( 6:prod(
1:abs( 2:round( 3:iPart( 4:fPart( 5:int( 6:min( 7:max( 8:mod(
1:¡ 2:¢ 3:£ 4:r 5:g 6:4DMS
1:P 4 Rx( 2:P 4 Ry( 3:R 4 Pr( 4:R 4 Pq(

Beispiele

Auf manche Abschnitte folgen Beispiele für Tasteneingaben, die die TI-30X Plus MathPrint™ Funktionen veranschaulichen.
Hinweise:
• Bei Beispielen wird vorausgesetzt, dass alle Standardeinstellungen (siehe
Abschnitt „Modi“) aktiv sind, sofern im Beispiel nichts anderes angegeben ist.
• Drücken Sie -, um den Hauptbildschirm nach Bedarf zu löschen.
• Die tatsächliche Bildschirmanzeige kann eventuell leicht von den Abbildungen in
diesem Dokument abweichen.
• Da Assistenten Eingaben speichern, können manche Tasteneingaben abweichen.

Benutzung der Pfeiltasten zum Zurückblättern

! " # $
Drücken Sie ! oder ", um den Cursor an die gewünschte Stelle in dem Ausdruck zu bewegen, den Sie gerade eingeben oder bearbeiten. Drücken Sie % ! oder % ", um den Cursor direkt an den Anfang bzw. das Ende des Ausdrucks zu setzen.
Mit # wird der Cursor von einem Ausdruck oder der Bearbeitungszeile zum Protokoll bewegt. Wenn Sie in einer Ein- oder Ausgabe im Protokoll < drücken, wird der Ausdruck wieder an der Cursorposition in der Bearbeitungszeile eingefügt.
Drücken Sie % # im Nenner eines Bruchs in der Bearbeitungszeile eines Ausdrucks, um den Cursor zum Protokoll zu bewegen. Wenn Sie in einer Ein- oder Ausgabe im Protokoll < drücken, wird der Ausdruck in den Nenner eingefügt.
Beispiel
7 F U 4
( 3 ) ( 1 ) <
Einstieg 7
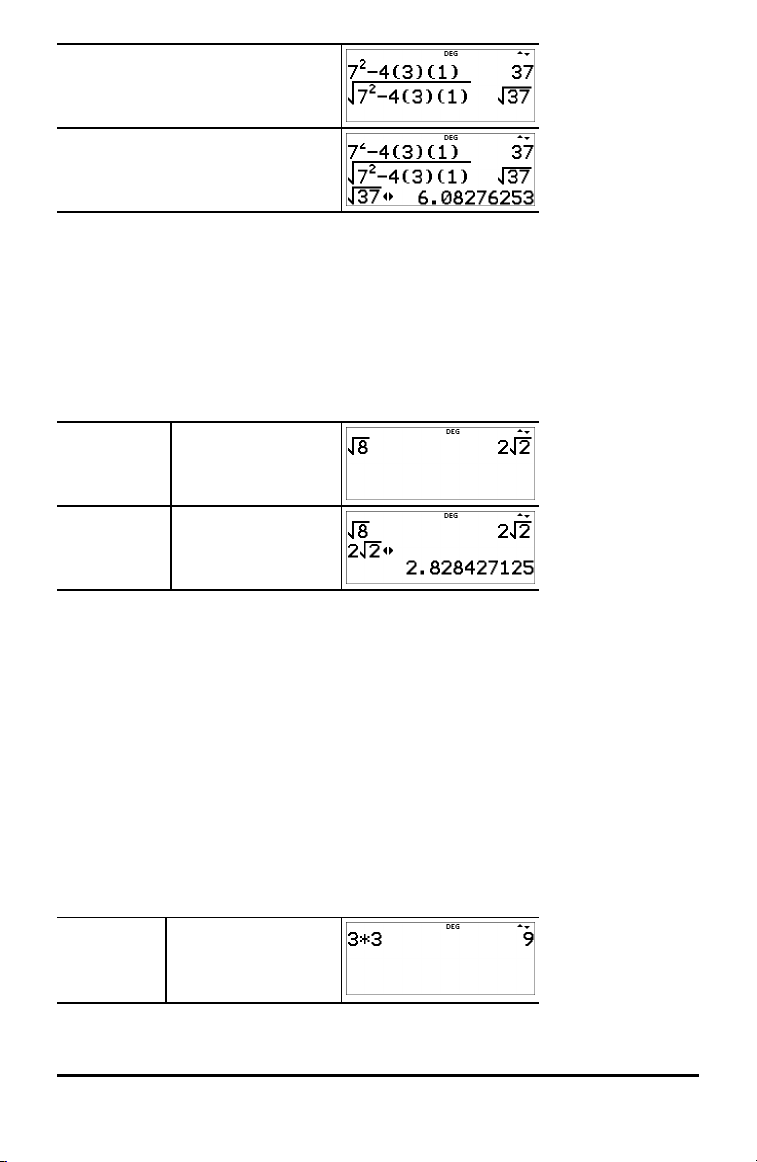
% b # # < <
r

Umwandeln von Ergebnissen

r
Drücken Sie r, um zwischen unterschiedlichen Darstellungsweisen eines Ergebnisses hin und her zu schalten (sofern möglich): Bruch oder Dezimaldarstellung, exakter Wurzelterm oder Näherungswert in Dezimaldarstellung, exakter Wert von Pi oder Näherungswert in Dezimaldarstellung.
Beispiel
Umwandeln von Ergebnissen
Hinweis: Mit r können auch Zahlenformate für Werte in Zellen in der
Funktionstabelle und im Dateneditor umgewandelt werden.
% b 8 <
r

Letztes Ergebnis

% i
Das Ergebnis der letzten Berechnung auf dem Hauptbildschirm wird in der Variablen
ans gespeichert. Diese Variable bleibt auch nach dem Ausschalten des Rechners im
Speicher erhalten. So rufen Sie den Wert von ans ab:
• Drücken Sie % i (ans wird auf dem Bildschirm angezeigt) oder
• Drücken Sie zu Anfang einer Eingabe die Taste einer beliebigen Operation (T, U
usw.). ans und der Operator werden angezeigt.
Beispiele
ans 3 V 3 <
8 Einstieg
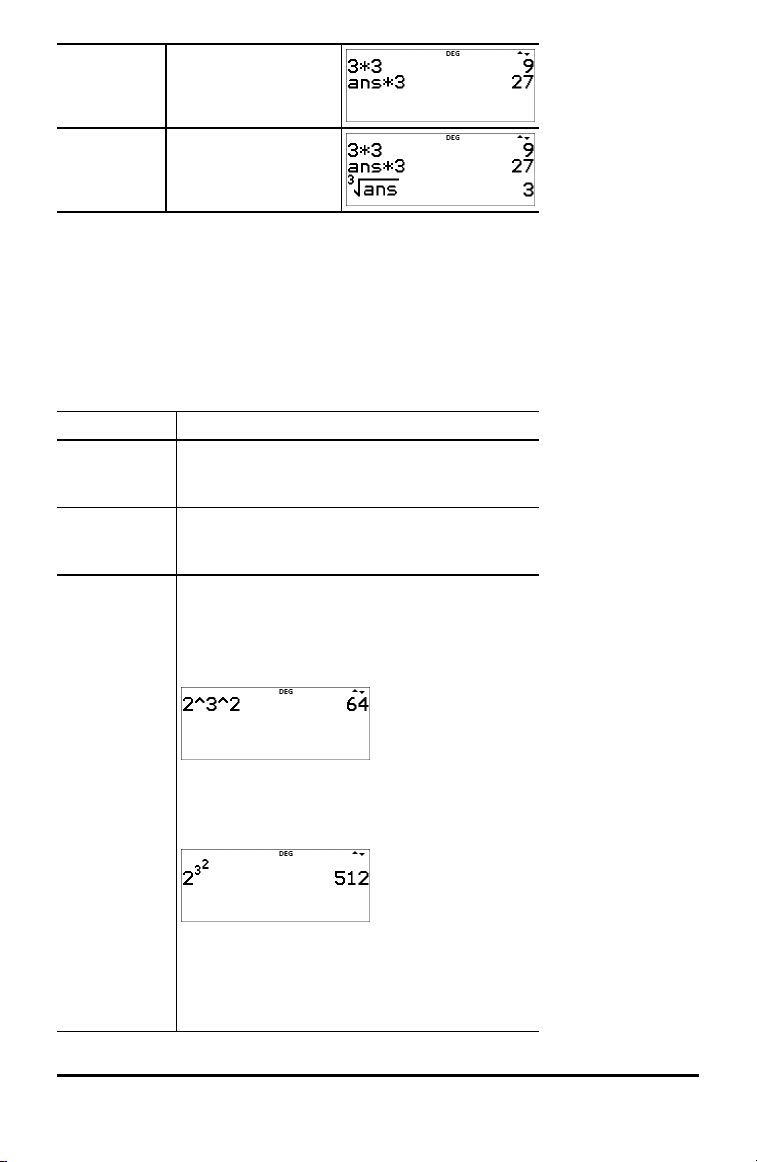
V 3 <
3 % c %
i <
Hinweis: Die Variable ans wird mit maximaler Präzision, d. h. mit 13 Stellen
gespeichert und eingefügt.

Rangfolge der Operatoren

Der TI-30X Plus MathPrint™ Rechner verwendet zum Auswerten von Ausdrücken das Equation Operating System (EOS™). EOS™ wertet Funktionen in der folgenden Reihenfolge aus. Funktionen derselben Prioritätsebene werden von links nach rechts abgearbeitet.
1. Ausdrücke in Klammern
2. Funktionen, die eine ) brauchen und vor dem
3. Funktionen, die nach dem Argument
4. Potenzen (^) und Wurzeln (x‡)
Argument stehen (z. B. sin, log), sowie alle Befehle im Menü R³´P.
eingegeben werden, z. B. x2und die Winkelmaßeinheiten.
Hinweis: Im klassischen Modus werden mit der
Taste G eingegebene Potenzen von links nach rechts abgearbeitet. Der Ausdruck 2^3^2 würde also als (2^3)^2 = 64 ausgerechnet.
Im MathPrint™ Modus werden mit der Taste G eingegebene Potenzen von rechts nach links abgearbeitet. Der Ausdruck 2^3^2 würde also als 2^(3^2) = 512 ausgerechnet.
Mit den Tasten F und a eingegebene Ausdrücke werden sowohl im klassischen als auch im MathPrint™ Modus von links nach rechts abgearbeitet. 3 F F wird also ausgerechnet als (32)2= 81.
Einstieg 9
5. Negation (M)
6. Brüche
7. Permutationen (nPr) und Kombinationen (nCr)
8. Multiplikation, implizite Multiplikation, Division
und Winkelindikator ±
9. Addition und Subtraktion
10. Logische Operatoren and, nand
11. Logische Operatoren or, xor, xnor
12. Umwandlungen wie 4n/d³´Un/d, F³´D, 4DMS
13.
L
14. < wertet den eingegebenen Ausdruck aus
Hinweis: Operatoren, die das Ende eines Ausdrucks angeben, und Umwandlungen mit
der Basis n wie 4Bin, Winkelumwandlung 4DMS, 4Pfactor und Umwandlungen von komplexen Zahlen 4Polar und 4Rectangle sind nur im Hauptbildschirm gültig. Sie werden in Assistenten, in der Anzeige von Funktionstabellen und Dateneditor­Funktionen ignoriert, wo das Ergebnis des Ausdrucks, sofern es gültig ist, ohne Umwandlung angezeigt wird.
Hinweis: Verwenden Sie Klammern, um eindeutig die Operatorrangfolge anzugeben,
die Sie für den eingegebenen Ausdruck erwarten. Bei Bedarf kann mit den Klammern die von den Algorithmen des Rechners befolgte Rangfolge der Operatoren übergangen werden. Sollte das Ergebnis nicht wie erwartet ausfallen, ist zu überprüfen, wie der Ausdruck eingegeben wurde. Fügen Sie dann nach Bedarf Klammern hinzu.
Beispiele
+ Q P M 60 T 5 V M 12 <
(M) 1 T M 8 T 12 <
‡ und + % b 9 T 16 <
( ) 4 V ( 2 T 3 ) <
10 Einstieg
( ) und + 4 ( 2 T 3 ) <
^ und ‡ % b 3 G 2 " T 4
( ) und M ( M 3 ) F <
G 2 <
M 3 F <

Löschen und Korrigieren

% s Rückkehr des Cursors zum Hauptbildschirm.
Verlässt schnell die folgenden Anwendungen: Auswerten von Ausdrücken, Mengenoperation, Funktionstabelle, Dateneditor, Statistik und Verteilungen.
-
J
% f Fügt an der Cursorposition ein Zeichen ein. % { 1 Setzt die Variablen x, y, z, t, a, b, c und d auf
%  2 Setzt den Rechner zurück.
Löscht eine Fehlermeldung. Löscht Zeichen in der Eingabezeile.
Löscht das Zeichen an der Cursorposition. Wenn sich der Cursor am Ende eines Ausdrucks
befindet, geht er eine Stelle zurück und löscht das Zeichen.
den Standardwert 0 zurück.
Stellt die Werkseinstellungen wieder her; löscht die Variablen im Speicher, die ausstehenden Operationen, alle Protokolleinträge und Statistikdaten; löscht gespeicherte Operationen und das unter ans gespeicherte Ergebnis.

Speicher und gespeicherte Variablen

z L % h % {
Der TI-30X Plus MathPrint™ Rechner hat 8 Speichervariablen: x, y, z, t, a, b, c und d. Folgendes können Sie in einer Speichervariablen speichern:
• reelle oder komplexe Zahlen
• das Ergebnis eines Ausdrucks
• Berechnungen aus verschiedenen Anwendungen wie Verteilungen
Einstieg 11
• Zellwerte des Dateneditors (die aus der Bearbeitungszeile gespeichert wurden)
Rechnerfunktionen, die Variablen verwenden, verwenden diese gespeicherten Werte.
L speichert Werte unter Variablen ab. Drücken Sie L, um eine Variable zu speichern, und wählen Sie anschließend mit z die gewünschte Variable aus. Drücken Sie <, um den Wert unter der ausgewählten Variablen zu speichern. Wenn die Variable bereits einen Wert hat, wird dieser durch den neuen Wert ersetzt.
z ist eine Taste mit Mehrfachbelegung, die bei wiederholtem Drücken nacheinander die verschiedenen Variablennamen aufruft: x, y, z, t, a, b, c und d. Außerdem können Sie mit z die gespeicherten Werte dieser Variablen abrufen. In den aktuellen Eintrag wird der Name der Variablen eingefügt, zur Auswertung des Ausdrucks wird jedoch der aktuelle Wert der Variablen verwendet. Um mehrere Variablen nacheinander einzugeben, drücken Sie nach jeder Variablen ".
% h ruft den Wert von Variablen ab. Drücken Sie % h, um ein Menü der Variablen und ihrer gespeicherten Werte anzuzeigen. Wählen Sie die Variable aus, deren Wert Sie abrufen möchten, und drücken Sie <. Der Variablenwert wird in den aktuellen Eintrag eingefügt und zu dessen Auswertung verwendet.
% { löscht den Wert einer Variablen. Drücken Sie % { und wählen Sie
1:Yes, um die Werte aller Variablen zu löschen.
Beispiele
Beginnen Sie
% s -
mit dem Löschen der Anzeige
Variable löschen
% {
1 (wählt Yes)
Speichern 15 L z
<
Abrufen % h
< F <
12 Einstieg
L z z
<
z z
< W 4 <
³ Aufgabe
In einem großen Kiestagebau sollen zwei neue Gruben entstehen. Die erste Grube misst 350 Meter x 560 Meter, die zweite 340 Meter x 610 Meter. Wie viel Kubikmeter Kies muss der Betreiber aus jeder der beiden Gruben fördern, wenn diese jeweils 150 Meter tief werden? Und wie viel für eine Tiefe von 210 Meter? Zeigen Sie das Ergebnis in technischer Notation an.
q $ " " < -
350 V 560 L z <
340 V 610 L z z <
-
150 V % h
< <
-
210 V % h < <
Erste Grube: Für eine Tiefe von 150 m muss der Betreiber 29,4 Mio. Kubikmeter fördern, für eine Tiefe von 210 m 41,16 Mio. Kubikmeter.
Einstieg 13
-
150 V z z <
210 V z z <
Zweite Grube: Für eine Tiefe von 150 m muss der Betreiber 31,11 Mio. Kubikmeter fördern, für eine Tiefe von 210 m 43,554 Mio. Kubikmeter.
14 Einstieg

Mathematische Funktionen

Dieser Abschnitt enthält Informationen zur Verwendung der mathematischen Funktionen des Rechners, wie Trigonometrie, Statistik und Wahrscheinlichkeit.

Brüche

P % @ d 1 % j
Die mit P eingegebenen Brüche können reelle und komplexe Zahlen, Operationstasten (T, V usw.) sowie die meisten Funktionstasten (F, % _ usw.) enthalten.
Im klassischen Modus oder bei klassischen Eingaben im MathPrint™ Modus wird der Bruchstrich P in derselben Zeile als dicker Strich angezeigt (Beispiel: ). Verwenden Sie Klammern, um eindeutig die Operatorrangfolge anzugeben, die Sie erwarten. Während die Regeln der Operatorrangfolge gelten, haben Sie die Kontrolle darüber, wie ein Ausdruck ausgewertet wird, wenn Sie bei Ihren Eingaben die Klammern richtig setzen.
Bruchergebnisse
• Bruchergebnisse werden automatisch vereinfacht und als unechte Brüche
ausgegeben.
• Wenn eine gemischte Zahl ausgegeben werden soll, verwenden Sie die
Umrechnung in eine gemischte Zahl 4n/d³´Un/d am Ende des eingegebenen Ausdrucks. Diese Funktion befindet sich in d 1: 4n/d³´Un/d.
• Es werden Bruchergebnisse ausgegeben, wenn der berechnete Wert in den
Grenzen des vom Rechner unterstützten Bruchformats angezeigt werden kann und im eingegebenen Ausdruck kein Dezimalwert eingegeben wurde.
• Wenn im Zähler oder Nenner eines Bruchs Dezimalzahlen verwendet oder
berechnet werden, wird das Ergebnis als Dezimalzahl angezeigt. Die Eingabe einer Dezimalzahl bewirkt, dass das Ergebnis im Dezimalformat angezeigt wird.
• Verwenden Sie % j (oben r), um Ergebnisse innerhalb der für die
Bruchanzeige geltenden Grenzen des Rechners von Bruch- in Dezimaldarstellung umzuwandeln.
Gemischte Zahlen und Umrechnungen
• % @ dient zur Eingabe einer gemischten Zahl. Drücken Sie die Pfeiltasten, um
zwischen ganzzahligem Teil, Zähler und Nenner zu wechseln.
• d 1 schaltet zwischen der Anzeige als einfachem Bruch und gemischter Zahl
um (4n/d³´Un/d).
• % j wandelt Ergebnisse von Bruch- in Dezimaldarstellung um und
umgekehrt.
Eingabe im MathPrint™ Modus
• Um im MathPrint™ Modus Zahlen oder Ausdrücke in Zähler und Nenner
einzugeben, drücken Sie P.
• Drücken Sie $ oder #, um den Cursor zwischen Zähler und Nenner zu bewegen.
Mathematische Funktionen 15
• Wird P vor oder nach Zahlen oder Funktionen gedrückt, kann der Zähler mit Teilen
des gewünschten Ausdrucks gefüllt werden. Achten Sie auf die Anzeige, wenn Sie Tasten drücken, um sicherzustellen, dass Sie den Ausdruck genau nach Bedarf eingeben.
Auf dem Hauptbildschirm
• Um einen vorherigen Eintrag aus dem Speicher in den Zähler oder in den
ganzzahligen Teil einzufügen, setzen Sie den Cursor an die gewünschte Stelle, drücken #, um zum gewünschten Eintrag zu blättern, und dann noch einmal <, um diesen in den Zähler bzw. den ganzzahligen Teil einzufügen.
• Um einen vorherigen Eintrag aus dem Speicher in den Nenner einzufügen, setzen
Sie den Cursor in den Nenner und drücken % #, um zum Speicher zu springen. Drücken Sie #, um zum gewünschten Eintrag zu blättern, und dann noch einmal <, um diesen in den Nenner einzufügen.
Auswertung des Ausdrucks
• Wenn Sie zur Auswertung des eingegebenen Ausdrucks < drücken, werden
möglicherweise Klammern angezeigt, die eindeutig angeben, wie der Ausdruck vom Rechner interpretiert und ausgerechnet wurde. Wenn das nicht dem entspricht, was Sie erwartet haben, kopieren Sie den eingegebenen Ausdruck und bearbeiten Sie ihn nach Bedarf.
Klassischer Modus oder klassischer Eintrag
• Wenn sich der Cursor in einem klassischen Eintrag befindet, geben Sie den
Zählerausdruck in Klammern ein, drücken dann P, um den dicken Bruchstrich anzeigen, und geben anschließend ebenfalls in Klammern den Nennerausdruck ein, damit das Ergebnis wie für Ihre Aufgabe erwartet berechnet wird.
Beispiele im MathPrint™ Modus
n/d, Un/d P 3 $ 4 " T 1 %
@ 7 $ 12 <
Hinweis: Klammern
werden automatisch hinzugefügt.
4n/d³´Un/d 9 P 2 " d 1 <
f³´d 4 % @ 1 $ 2 "
% j <
Beispiel P 1.2 T 1.3 $ 4
<
Hinweis: Das Ergebnis
ist dezimal, weil im Bruch Dezimalzahlen
16 Mathem atische Funktionen
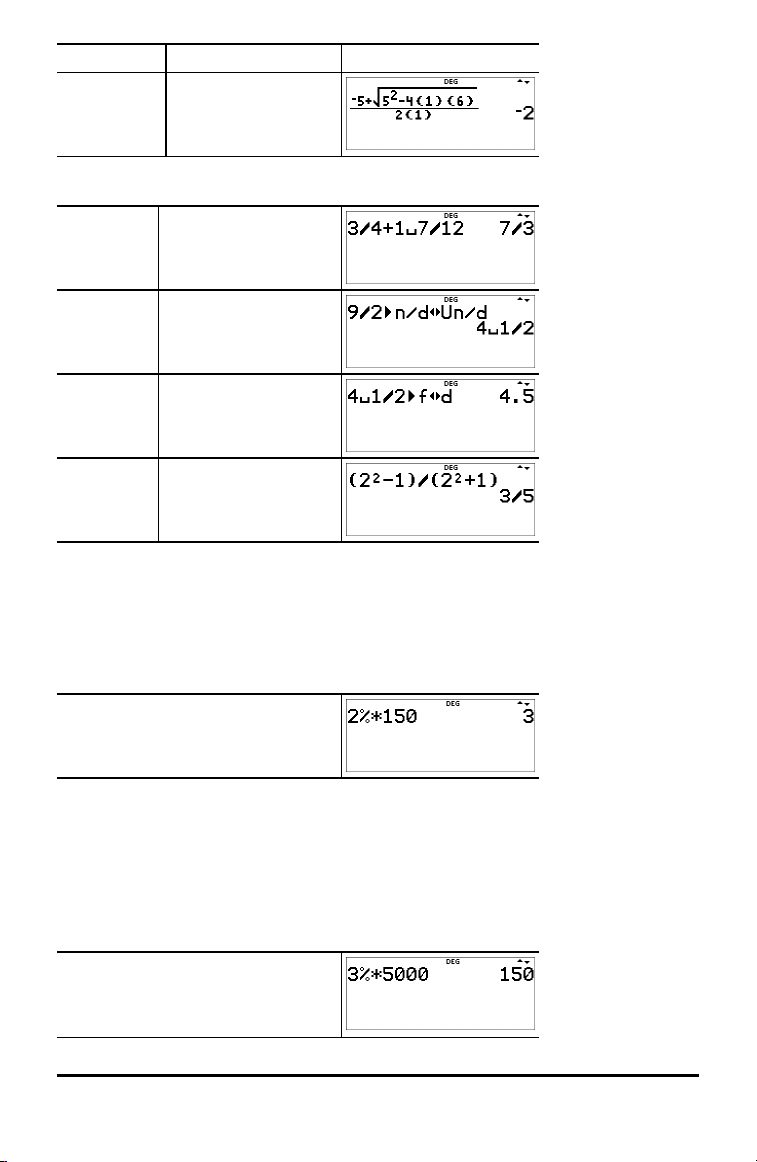
verwendet wurden.
Beispiel P M 5 T % b 5
F U 4 ( 1 ) ( 6
) $ 2 ( 1 ) <
Beispiele im klassischen Modus
n/d, Un/d 3 P 4 T 1 % @ 7
P 12 <
4n/d³´Un/d 9 P 2 d 1 <
f³´d 4 % @ 1 P 2 %
j <
Klammern ( 2 F U 1 ) P (
2 F T 1 ) <

Prozentrechnung

% _
Um mit Prozentwerten zu rechnen, drücken Sie nach dem Prozentwert % _.
Beispiel
2 % _ V 150 <
³ Aufgabe
Ein Bergbauunternehmen fördert 5000 Tonnen Erz mit einem Metallgehalt von 3 % und 7300 Tonnen mit einem Metallgehalt von 2,3 %. Wie viel Metall kann das Unternehmen auf der Grundlage dieser Zahlen insgesamt gewinnen?
Wie viel ist das gewonnene Metall insgesamt wert, wenn eine Tonne 280 Währungseinheiten wert ist?
3 % _ V 5000 <
Mathematische Funktionen 17
T 2.3 % _ V 7300 <
V 280 <
Insgesamt werden 317,9 Tonnen Metall mit einem Wert von
89.012 Währungseinheiten gewonnen.

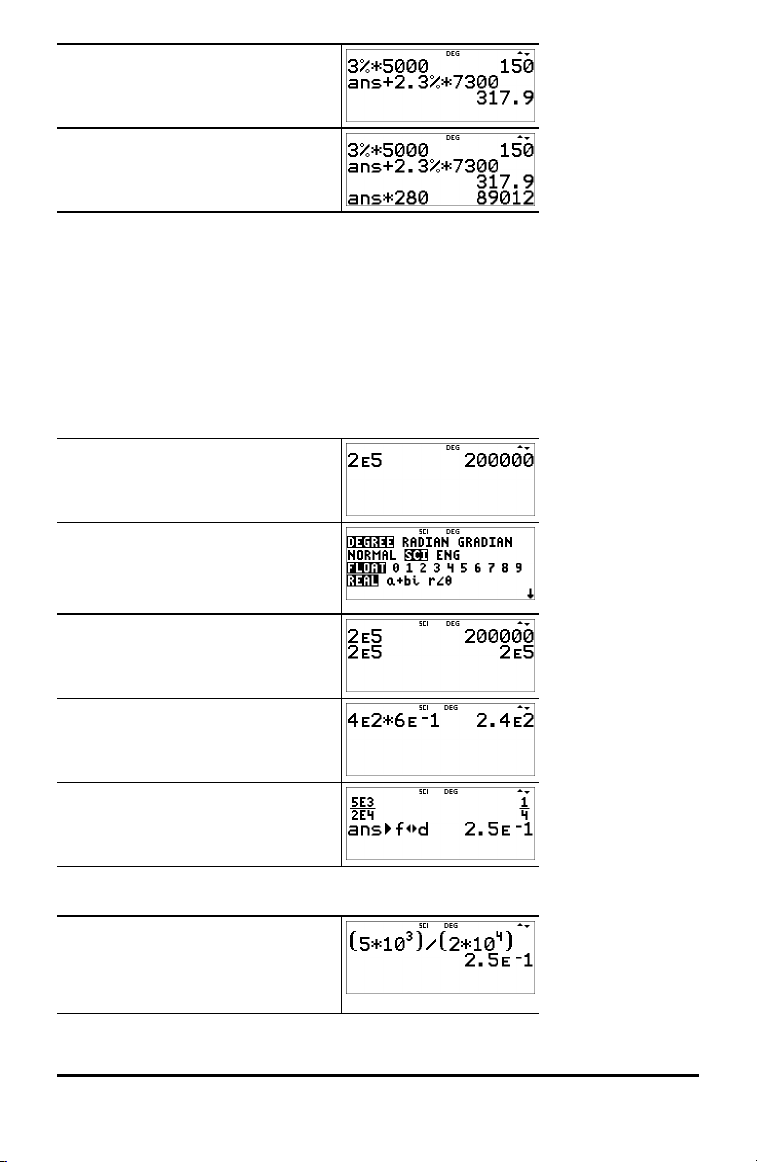
Wissenschaftliche Notation [EE]

E
Um eine Zahl in wissenschaftlicher Notation einzugeben, verwenden Sie die Taste E. Eine Zahl wie (1,2 x 10-4) wird als 1.2E-4 in den Rechner eingegeben.
Beispiel
2 E 5 < Hinweis: Gibt (2 x 10
5
) in der
Notation E des Rechners ein.
q $ " <
Hinweis: Die Moduseinstellung SCI
zeigt Ergebnisse in wissenschaftlicher Notation an.
- <
-
4 E 2 V 6 E M 1 <
P 5 E 3 $ 2 E 4 < % i % j
Beispiel
Textbuch-Aufgabe
­( 5 V 10 G 3 " ) W ( 2 V 10
G 4 " ) <
18 Mathem atische Funktionen
Loading...
+ 50 hidden pages
Buy Points How it Works FAQ Contact Us Questions and Suggestions Privacy Policy Cookie Policy Terms of Use