CITIZEN SRP-400G User Manual

Download

CALCULATRICES

Calculatrice Scientifique Graphique

SRP-400G

Mode d’emploi

Chapitre 1 Bien débuter

1 - 1 Alimentation

1 - 1 - 1 Pour éteindre ou allumer .................................................... 04

1 - 1 - 2 Remplacement des piles .................................................... 04

1 - 1 - 3 Fonction d’arrêt automatique ............................................. 04

1 - 2 Fonction de nettoyage des données ............................................... 04

1 - 3 Utiliser le menu des modes de fonctionnement .............................. 04

1 - 4 Afficher le menu ............................................................................... 05

1 - 5 Affichage .......................................................................................... 05

1 - 5 - 1 Affichage des caractères .................................................... 05

1 - 5 - 2 Réglage du contraste ......................................................... 06

1 - 6 Les touches ...................................................................................... 06

1 - 6 - 1 Le marquage des touches .................................................. 06

1 - 6 - 2 Pour utiliser les touches “2nd” et “ALPHA” ......................... 06

1 - 6 - 3 Le curseur ........................................................................... 06

1 - 7 L’ordre des opérations ....................................................................... 07

1 - 8 Précision et capacité ........................................................................ 07

1 - 9 Conditions d’erreur ........................................................................... 08

1 - 10 Statut et effaçage de la mémoire ...................................................... 08

1 - 10 - 1Pour vérifier le statut de la mémoire ................................... 08

1 - 10 - 2Pour effacer les contenus de la mémoire ........................... 09

Chapitre 2 Calculs simples

2 - 1 Calculs mixtes ................................................................................... 09

2 - 2 Formats d’affichage .......................................................................... 09

2 - 2 - 1 Nombre de décimales ........................................................ 09

2 - 2 - 2 Formats d’affichage des nombres ...................................... 10

2 - 3 Calculs entre parenthèses ................................................................ 10

2 - 4 Calculs des pourcentages ................................................................. 10

2 - 5 Fonctions de calculs utiles ................................................................ 10

2 - 5 - 1 Fonction de calcul continu .................................................. 10

2 - 5 - 2 Marquage des corrections pendant les entrées ................. 11

2 - 5 - 3 Fonction de révision ........................................................... 11

2 - 5 - 4 Fonction d’affichage d’erreur de position ........................... 11

2 - 5 - 5 Fonctions réponse ............................................................. 11

2 - 5 - 6 Multiplication implicite ........................................................ 11

2 - 6 Calculs à mémoire ............................................................................ 12

2 - 6 - 1 Mémoire indépendante ...................................................... 12

2 - 6 - 2 Variables standard ............................................................. 12

2 - 6 - 3 Sauvegarde d’équation ...................................................... 12

2 - 7 Logarithmes et Exponentielles ........................................................ 13

2 - 8 Calcul des fractions .......................................................................... 13

2 - 9 Conversions des unités d’angles ...................................................... 13

2 - 9 - 1 Réglage de l’unité d’angle par défaut ................................. 13

2 - 9 - 2 Notation DMS ..................................................................... 14

2 - 10 Fonction trigonométrique / Trig. - inversée ....................................... 14

2 - 11 Fonction hyperbolique / Hyp. - inversée ........................................... 15

2 - 12 Fonction mathématiques .................................................................. 15

2 - 12 - 1 Calculs numériques .................................................... 15

2 - 12 - 2 Quotient et reste d’une division .................................. 16

2 - 12 - 3 Permutation et combinaison ....................................... 16

2 - 12 - 4 Factorielles, arrondis, entiers, fractions, valeurs absolues,

2 - 12 - 5 Transformation de coordonnées ................................ 17

2 - 12 - 6 Simplification de fraction ............................................ 17

2 - 12 - 7 Notation ingénieur ..................................................... 17

2 - 13 Autres fonctions (x , Ö, Ö, x², Ù) .................................................... 18

2 - 14 Conversion d’unité ........................................................................... 18

2 - 15 Constantes physiques ...................................................................... 18

2 - 16 Fonction multidéclarations ................................................................ 19

2 - 17 Intégration et différentiation .............................................................. 19

2 - 17 - 1 Intégration .................................................................. 19

2 - 17 - 2 Différentiation ............................................................. 20

2 - 17 - 3 Application de l’intégration et de la différentiation ...... 20

2 - 18 Nombres complexes ........................................................................ 21

2 - 19 Menu des données variables (VARS) .............................................. 22

Chapitre 3 Calculs EVL & EQ

3 - 1 Système de deux équations à deux inconnues ............................... 23

3 - 2 Equations quadratiques ................................................................... 23

Chapitre 4 Graphiques

4 - 1 Avant d’essayer de dessiner un graphique ...................................... 24

4 - 2 Paramétrage de fenêtre V-Window .................................................. 24

4 - 2 - 1 Pour initialiser et standardiser la fenêtre V-Window ... 24

4 - 2 - 2 Mémoire V-Widow ...................................................... 25

4 - 3 Opérations Graphiques .................................................................... 25

4 - 3 - 1 Pour spécifier le type de graphique ............................ 25

4 - 3 - 2 Pour éditer des fonctions en mémoire ........................ 26

4 - 3 - 3 Pour dessiner un graphique ........................................ 26

4 - 4 Dessiner des graphiques manuellement ........................................... 27

4 - 5 Autres fonctions de graphisme ......................................................... 28

4 - 5 - 1 Type de création de graphique (D-TYPE) ................... 28

4 - 5 - 2 Affichage de fonction graphique (G-FUNC) ................ 29

4 - 5 - 3 Mode de graphique simultané (SIMUL-G) .................. 29

4 - 5 - 4 Trace .......................................................................... 29

4 - 5 - 5 Défilement .................................................................. 29

4 - 5 - 6 Zoom .......................................................................... 29

4 - 5 - 7 Fonction Sketch ......................................................... 31

nombres aléatoires .................................................... 16

-1 x

Chapitre 5 Fonctions de tableaux

5 - 1 Avant d’utiliser le mode TABLE ....................................................... 33

5 - 2 Enregistrer une fonction .................................................................. 33

5 - 3 Supprimer une fonction ................................................................... 33

5 - 4 Assigner des valeurs à une variable ............................................... 33

5 - 5 Générer un tableau numérique ....................................................... 34

5 - 6 Editer un tableau ............................................................................. 35

5 - 7 Afficher le graphique d’une fonction ................................................ 35

5 - 8 Assigner les contenus d’un tableau numérique à une liste ............. 35

Chapitre 6 Fonctions de liste

6 - 1 Avant d’utiliser le mode liste ............................................................ 36

6 - 2 Assigner des valeurs à une liste ...................................................... 36

6 - 2 - 1 Pour entrer des valeurs unes à unes ........................ 36

6 - 2 - 2 Pour entrer à la file une série de valeurs ................... 36

6 - 3 Editer et réaménager les listes ........................................................ 36

6 - 3 - 1 Pour éditer les valeurs d’une liste .............................. 37

6 - 3 - 2 Pour trier les valeurs d’une liste ................................. 38

6 - 4 Manipuler des données de liste ....................................................... 39

6 - 5 Calculs arithmétiques utilisant des listes ......................................... 42

6 - 5 - 1 Pour insérer une liste dans un calcul ........................ 42

6 - 5 - 2 Pour invoquer les contenus d’une liste ...................... 43

6 - 5 - 3 Pour appliquer une fonction en graphique

6 - 5 - 4 Pour entrer des calculs scientifiques dans une liste .. 44

6 - 5 - 5 Pour effectuer des calculs de fonctions scientifiques

Chapitre 7 calculs en mode base-n

7 - 1 Avant de commencer un calcul binaire, octal, décimal ou hexadécimal

........................................................................................................... 45

7 - 2 Convertir une valeur affichée d’un système numérique vers un autre

........................................................................................................... 46

7 - 3 Fonction de bloc ................................................................................ 46

7 - 4 Opérations arithmétiques .................................................................. 46

7 - 5 Valeurs négatives et opérations logiques .......................................... 46

Chapitre 8 Calculs statistiques et graphiques

8 - 1 Avant d’exécuter des calculs statistiques ......................................... 48

8 - 2 Spécifier des données statistiques et des paramètres ..................... 48

8 - 3 Exécuter des calculs statistiques ...................................................... 49

8 - 3 - 1 Calcul statistique à variable unique ............................. 49

8 - 3 - 2 Calcul statistique à variable double ............................. 50

8 - 3 - 3 Calculs de régression .................................................. 51

en utilisant une liste ................................................... 44

en utilisant une liste .................................................... 44

8 - 4 Graphiques statistiques .................................................................... 54

8 - 4 - 1 Paramètres généraux des graphiques statistiques ..... 54

8 - 4 - 2 Exemples de graphiques statistiques ......................... 55

8 - 5 Graphiques statistiques à variable double ........................................ 56

8 - 5 - 1 Histogramme (Hist) ..................................................... 56

8 - 5 - 2 Graphique en quartiles (Box) ...................................... 56

8 - 5 - 3 Courbe de distribution normale (N-Distr) .................... 57

8 - 5 - 4 Le graphique de contrôle du traitement statistiques (Spc)

8 - 5 - 5 Pour afficher les résultats d’un calcul statistique à

8 - 6 Graphiques statistiques à variable double / régression .................... 58

8 - 6 - 1 Graphique de régression linéaire (X) .......................... 58

8 - 6 - 2 Graphique de régression Med-Med (Med) .................. 58

8 - 6 - 3 Graphique de régression quadratique (X²) .................. 59

8 - 6 - 4 Graphique de régression logarithmique (Log) ............. 59

8 - 6 - 5 Graphique de régression exponentielle (Exp) ............. 60

8 - 6 - 6 Graphique de régression de puissance (Pwr) ............. 61

8 - 6 - 7 Graphique de dispersion (Scat) ................................... 61

8 - 6 - 8 Graphique par ligne xy (xyLin) ..................................... 62

8 - 6 - 9 Graphique de série temporelle (T-Ser) ........................ 62

8 - 6 - 10 Pour afficher les résultat d’un calcul statistique à double

8 - 6 - 11 Pour copier une formule de graphique de régression

8 - 7 Graphiques multiples ........................................................................ 63

8 - 8 Application manuelle de graphique ................................................... 64

8 - 8 - 1 Pour régler la largeur d’un histogramme ..................... 64

Chapitre 9 Jeux

9 - 1 Avant de commencer un jeux ............................................................ 64

9 - 2 MEMORY ........................................................................................... 64

9 - 3 ARTH ................................................................................................. 65

9 - 4 GHOST .............................................................................................. 65

9 - 5 GUESS .............................................................................................. 66

Chapitre 10 Programmer

10 - 1 Avant de programmer ........................................................................ 67

10 - 2 Créer un nouveau programme .......................................................... 67

10 - 2 - 1 Pour spécifier un type de programme et enregistrer un

10 - 2 - 2 Pour entrer les contenus du programme ..................... 68

10 - 2 - 3 Pour démarrer un programme ..................................... 68

..................................................................................... 57

variable unique ............................................................ 58

variable / régression .................................................... 62

vers le mode graphique ............................................... 63

nom de fichier .............................................................. 67

10 - 3 Débugger un programme .......................................................... 69

10 - 4 Chercher un fichier .................................................................... 69

10 - 5 Renommer un programme ........................................................ 70

10 - 6 Editer les contenus du programme ........................................... 70

10 - 7 Effacer un programme ............................................................... 70

10 - 8 Commandes de programme ...................................................... 71

10 - 9 Utiliser des fonctions de graphiques dans un programme

10 - 10 Utiliser les fonctions de tableau et de graphique dans un

10 - 11 Utiliser des fonctions de tri liste dans un programme ............... 77

10 - 12 Utiliser un calcul de graphique statistique dans un programme

10 - 13 Exemples de programmes ........................................................ 81

10 - 8 - 1 Commandes de programme de base .................. 71

10 - 8 - 2 Commandes d’éffaçage ....................................... 74

10 - 8 - 3 Opérateurs relationnels et logiques ..................... 74

.................................................................................................... 75

programme ................................................................................. 76

................................................................................................... 78

10 - 12 - 1 Pour spécifier les données de calcul statistique

10 - 12 - 2 Calculs statistiques ............................................. 78

10 - 12 - 3 Graphique statistiques ........................................ 79

............................................................................ 78

Chapitre 1 Bien débuter

1 - 1 Alimentation 1 - 1 - 1 Pour éteindre ou allumer

Pour allumer la calculatrice, pressez [ON/CL]; Pour éteindre la calculatrice, pressez [2nd] [OFF]

1 - 1 - 2 Remplacement des piles

Cet appareil est alimenté par trois piles. Deux piles de taille AAA (les piles principales, Lr03 (Am4) ou R03 (UM-4) prennent en charge les opérations normales, alors que la troisième pile, en lithium (pile de sauvegarde, Cr2032) alimente le stockage des données en mémoire. Quand la puissance des piles principales faiblit, le message “LOW BATTERY” s’affiche. Si vous continuez à utiliser la calculatrice, l’alimentation peut s’éteindre automatiquement et le fonctionnement va devenir impossible même si vous pressez la touche [ON/CL]. Veuillez remplacer les piles dès que possible.

Ne retirez jamais en même temps de l’unité les piles principales et la pile de

(A) Pour remplacer les piles principales

1. Pressez [2nd] [OFF] pour éteindre la calculatrice

2. Retirez dans la direction indiquée le couvercle du boîtier des piles à l’arrière de la calculatrice.

3. Retirez les deux anciennes piles et placez les deux neuves dans les directions de polarité indiquées.

4. Replacez le couvercle du boîtier et pressez [ON/CL] pour démarrer l’appareil. La pile de sauvegarde fournira son alimentation pendant que les batteries principales seront enlevées, ainsi nulle perte de mémoire ne sera occasionnée.

(B) Pour remplacer la mémoire de sauvegarde

1. Pressez [2nd] [OFF] pour éteindre la calculatrice

2. Retirez dans la direction indiquée le couvercle du boîtier à l’arrière de la calculatrice.

3. Retirez l’ancienne pile et placez la neuve dans la direction de polarité indiquée.

4. Replacez le couvercle du boîtier et pressez [ON/CL] pour démarrer l’appareil. Les piles principales fourniront leur alimentation à la mémoire lors de l’enlèvement de la pile de sauvegarde, ainsi nulle perte de mémoire ne sera occasionnée.

1 - 1 - 3 Fonction d’arrêt automatique.

La calculatrice s’éteint automatiquement lorsqu’elle n’est pas utilisée pendant environ 9 à 15 minutes. Elle peut être réactivée en pressant la touche [ON/CL]; l’affichage, la mémoire et les réglages reviendront en leur état d’avant l’arrêt.

!! IMPORTANT !!

sauvegarde

1 - 2 Fonction de nettoyage des données

Si la calculatrice allumée donne des résultats surprenants, pressez [MODE] 7 (RESET). Un message s’affiche pour confirmer si vous voulez réinitialiser ou non toutes les mémoires dans la calculatrice.

* * * RESET **** ALL MEMORIES RESET : N Y

Déplacez le curseur vers “Y” par la touche [u], puis pressez [EXE] pour réinitialiser toutes les mémoires de la calculatrice. Pour abandonner cette opération sans nettoyer la calculatrice choisissez “N”. Si la calculatrice cesse de fonctionner pour une raison quelconque, utilisez un objet pointu et fin pour presser le bouton RESET à l’arrière de l’instrument. Cela devreit provoquer l’apparition de l’écran de confirmation RESET. Effectuer la procédure précédente pour terminer l’opération de RESET.

Note : Une fois cette opération effectuée, le système sera revenu à ses paramètres par défaut

1 - 3 Utiliser le menu des Modes de fonctionnement

Le menu des Modes de fonctionnement vous permet de choisir le mode de calcul adapté à vos besoins. Vous pouvez faire apparaître ce menu des Modes de fonctionnement à tout moment en pressant [MODE].

Option MAIN GRAPH

STAT

TABLE

0MAIN 1GRAPH 2STAT 3TABLE 4LIST 5Base-n 6 PROG 7RESET

Signification

Utiliser ce mode pour les calculs arithmétiques et les calculs de fonction Utilisez ce mode pour enregistrer des fonctions de graphiques et les

utiliser pour dessiner des graphiques

Utilisez ce mode pour exécuter des calculs statistiques à variable unique (écart type) et à variable double (régression), et pour dessiner des graphiques statistiques

Utilisez ce mode pour stocker des fonctions, pour générer un tableau numérique de différentes solutions selon les valeurs assignées aux variables, et pour dessiner des graphiques

0VLE 1QE 2GAME 3CONT

LIST Base-n

PROG

RESET

VLE

QE GAME CONT

Exemple : Entrer en mode STAT (Méthode 1)

(Etape 1) : Pressez [MODE] pour afficher le menu des modes de fonctionnements. Déplacez-vous dans le menu par les touches du curseur jusqu’à ce que “2STAT” soit souligné. [MODE] [q]

Utilisez ce mode pour sauvegarder et éditer des données numériques Utilisez ce mode pour effectuer des calculs binaires, octaux, décimaux et

hexadécimaux

Utilsez ce mode pour stocker des programmes dans la zone de programmes et pour les effectuer

Utilisez ce mode pour vérifier la quantité de mémoire utilisée pour effacer des données de la mémoire et pour réinitialiser la calculatrice

Utilisez ce mode pour résoudre des systèmes de deux équations à deux inconnues

Utilisez ce mode pour résoudre des équations du second degré Utilisez ce mode pour jouer aux jeux Utilisez ce mode pour régler le contraste de l’affichage

0MAIN 1GRAPH 2STAT 3TABLE 4LIST 5Base-n 6 PROG 7RESET

(Etape 2) : Pressez [EXE] pour entrer en mode STAT

(Méthode 2)

(Etape 1) : Pressez [MODE] pour afficher le menu des modes de fonctionnement (Etape 2) : Entrez 2 pour choisir directement le mode “2STAT”

1 - 4 Afficher le menu

Chaque mode de fonctionnement de la calculatrice assigne divers paramètres et fonctions aux menus [FUNC], [SYSTEM], [MATH] ..., Etc. Ces paramètres et fonctions peuvent être affichés sous forme de menu. Vous devrez souvent accéder aux options à partir de ces menus.

(A) Pour sélectionner une option à partir d’un menu

Par exemple, pressez [MATH] pour afficher le menu ci-dessous dans le mode de fonctionnement principal “MAIN”.

0Min 1Max 2Med 3Sum 4Avg 5Sgn 6Int ¸ 7Rmdr

Indique que des pages supplémentaires se trouvent en bas de l’écran en cours

Si vous souhaitez sélectionner “Max”, * Soulignez l’option “Max” grâce aux touches du curseur, puis pressez [EXE]. * Vous pouvez aussi entrer directement le nombre correspondant à l’option voulue.

(B) Pour vous déplacer d’une page vers la suivante

Certains menus de fonctions possèdent plusieurs pages. Lorsque cela arrive, une barre indicatrice apparaît sur le côté droit de l’écran, indiquant que des pages supplémentaires se trouvent au dessous (ou au dessus) de l’écran actuel. Vous pouvez utiliser les touches de curseur ou presser encore une fois la touche menu pour avancer vers la page suivante.

Quelques options marquées en lettres capitales signifient qu’elles possèdent des sous menus. Après avoir entré l’option, il se trouve des options supplémentaires à sélectionner. Par exemple, pressez [2nd] [SYSTEM]

F-TYPE : Y =

[EXE]

D-TYPE : Conct ANGLE : Rad DISP : Flo

(D) Quitter un menu

Vous pouvez quitter un menu par chacune des trois méthodes suivantes :

- Pressez [EXIT] pour retourner à l’affichage précédent

- Pressez [2nd] [QUIT] pour retourner à l’écran de départ

- Pressez n’importe quelle touche pour un autre menu ou écran.

1 - 5 Affichage 1 - 5 - 1 Affichage des caractères

Cette calculatrice utilise deux type d’affichage : affichage texte et affichage graphique

0Y = 1Parm 2Y > 3Y< 4Y £ 5Y£

Affichage texte Affichage graphique

GRAPH R

G-Func : Y = Y1 6X² - X - 5

Y : Y3 :

L’affichage texte peut exposer 12 colonnes et 4 lignes de carctères. Les indicateurs suivants apparaissent pour vous indiquer le statut en cours de la calculatrice.

GRAPH R

Indicateur Signification M Mémoire indépendante

Les touches alphabétiques sont activées 2nd 2ème ensemble de fonctions activé GRAPH Le mode graphique est activé STAT Le mode statistique est activé TBLE Le mode tableaux est activé D R G Unités d’angles : Degrés, Radians ou Grades PROG Le mode programme est activé VLE Le mode de résolution de système de 2 équations à 2 inconnues est

activé

QE Le mode de résolution d’équation quadratique est activé ENGSCI Format d’affichage SCI (scientifique) ou ENG (ingénieur) FIX Le nombre de décimales est fixé HYP Une fonction trigonométrique hyperbolique est en cours de calcul d h b o Base décimale, hexadécimale, binaire et octale

y La valeur affichée est le résultat intermédiaire

Opération de touche inactive p q Il se trouve des pages ou des entrées supplémentaires masquées au

1 - 5 - 2 Réglage du contraste

Pressez les touches [MODE] [MODE] 3 (CONT) pour afficher le menu de contraste.

dessus ou en dessous de l’écran actuel. Ces deux indicateurs clignoteront quand une opération ou un programme seront en cours d’exécution.

* * CONTRAST **

[i] [h]

Pressez les touches [q] ou [p] pour accentuer ou diminuer le contraste.

1 - 6 Les touches 1 - 6 - 1 Le marquage des touches

Beaucoup des touches que présente cette calculatrice servent à exécuter plus d’une seule fonction. Les fonctions indiquées sur le clavier sont imprimées différemment pour vous aider à trouver rapidement et facilement celle que vous recherchez.

Marquage clavier Signification

Noir Entrée directe Jaune Pressez [2nd] puis la touche Blanc sur fond bleu Pressez [ALPHA] puis la touche

Note : Quelques modèles de clavier peuvent avoir reçu une impression en couleurs

différentes de celles décrites ci-dessus.

1 - 6 - 2 Pour utiliser les touches “2nd” et “ALPHA”

Pour utiliser les fonctions marquées en jaune (ou la couleur de la touche [2nd]), pressez [2nd] puis la touche souhaitée. Lorsque vous pressez [2nd], l’indicateur “2nd” vous indique que vous sélectionnez la seconde fonction de la prochaine touche que vous presserez. Si vous avez appuyé sur [2nd] par erreur, il vous suffit de presser [2nd] à nouveau pour annuler l’indicateur “2nd”. Pour exécuter les fonctions marquées en blanc sur fond bleu, pressez [ALPHA] puis la touche correspondante. Lorsque vous pressez [ALPHA], l’indicateur “ “ à l’écran vous annonce que vous sélectionnerez la fonction alphabétique de la prochaine touche que vous presserez. Si vous appuyez sur la touche [ALPHA] par erreur, il vous suffit de pressez [ALPHA] de nouveau pour annuler l’indicateur “ “. Presser [2nd] [ALPHA] verrouille la calculatrice dans ce mode et permet ensuite l’entrée de touches de fonctions alphabétiques, jusqu’à ce que [ALPHA] soit pressé.

1 - 6 - 3 Le curseur

Presser les touches [t] ou [u] déplace le curseur vers la gauche ou vers la droite. Maintenez ces touches pressées pour que le curseur se déplace à grande vitesse. Presser les touches [p] ou [q] déplace l’affichage vers le haut ou vers le bas quand il y a des entrées masquées. Vous pouvez réutiliser ou éditer une entrée précédente lorsqu’elle se trouve sur la ligne d’entrée. Presser [2nd] [t] ou [2nd] [u] déplace le curseur vers le commencement ou la fin de la ligne en cours. Presser [2nd] [p] ou [2nd] [q] déplace le curseur vers le haut ou le bas de la série des entrées.

1 - 7 L’ordre des opérations

Chaque calcul est effectué dans l’ordre suivant :

01) L’expression entre parenthèses

02) La transformation des coordonnées et des fonctions de Type B pour

lesquelles il faut presser la touche de fonction avant l’argument, par exemple, sin, cos, tan, sin , cos , tan , sinh, cosh, tanh, sinh , cosh ,

-1 x x

tanh , log, 10 , e , Ö, d/dx, ¦dx, Neg, Not, X’(), Y’(), Max, Min, Sum, Sgn, Avg, Abs, Int, Frac, List, Fill, Dim, Seq, Med, Intg : d, h, b, o.

03) Les fonctions de Type A pour lesquelles il faut entrer l’argument avant de

presser la touche de fonction, par exemple; X², X , X!, ° ‘ “, r, g, %

04) L’élévation à une puissance (Ù), Ö

05) Les fractions

06) Multiplication abrégée devant les variables, p, Rand, Randl

07) (-)

08) La multiplication abrégée devant les fonctions de Type B 2Ö3, Alog2, etc.

09) nPr, nCr

10) x, ¸, Int¸, Rmdr

11) +, -

12) Les opérateurs relationnels ==, <, >, ¹, £, ³

13) And, Nand -- Les calculs en Base-n

14) Or, Xor, Xnor -- Les calculs en Base-n

15) Uniquement conversions (A / |} /, F|}D, }DMS)

·La fonction de simplification (Simp) ne peut s’exécuter avec d’autres fonctions Elle ne peut pas non plus servir d’argument dans aucune autre fonction.

· Lorsque des fonctions à priorité sont utilisées à la suite, leur exécution est effectuée de droite à gauche.

e ln120 g e {ln (120) } Dans les autres cas, leur exécution s’effectue de gauche à droite

· Les fonctions composées sont exécutées de droite à gauche

-1 -1 -1 -1 -1

-1

· Tout ce qui est contenu entre parenthèses reçoit la plus haute priorité.

1 - 8 Précision et capacité

Caractères de calcul : jusqu’à 24 caractères La calculatrice peut afficher un résultat jusqu’à 10 chiffres suivi d’un exposant à deux chiffres jusqu’à 10±99. Les nombres utilisés en entrée doivent se situer dans les limites de la fonction donnée comme suit :

Fonctions

sin x, cos x, tan x

Gamme d’entrée

Deg : IXI < 4.5 x 10 deg Rad : IXI < 2.5 x 10 p rad Grad : IXI < 5 x 10 grad

10 8

-1 -1

sin x, cos x tan-1 x sinh x, cosh x tanh x

-1

sinh x

-1

cosh x

-1

tanh x log x, In x

e Öx x²

-1

x x! P (x,y) R (r,q)

DMS

Öy

NPr, nCr

Cependant, pour tan x Deg : IXI ¹ 90 (2n + 1) Rad : IXI ¹ (2n + 1) Grad : IXI ¹ 100 (2n + 1) (n est un entier)

IXI £ 1 IXI < 1 x 10

100

IXI £ 230.2585092 IXI < 1 x 10 IXI < 5 x 10 1 £ x < 5 x 10

100

IXI < 1

-99 100

1 x 10 £ x < 1 x 10

100

-1 x 10 < x < 100

100

-1 x 10 < x £ 230.2585092 0 £ x < 1 x 10 IXI <1 x 10 IXI < 1 x 10 , X ¹ 0

100

0 £ x £ 69 , x est un entier

x² + y² < 1 x 10 0 £ r < 1 x 10 Deg : IqI < 4.5 x 10 deg Rad : IqI < 2.5 x 10 p rad Grad : IqI < 5 x 10 grad Cependant, pour tan x

Deg : IqI ¹ 90 (2n + 1) Rad : IqI ¹ (2n + 1) Grad : IqI ¹ 100 (2n + 1) (n est un entier)

IDI, M, S < 1 x 10 , 0 £ M, S, IXI < 10 Y > 0 : x ¹ 0, -1 x 10 < log y < 100

y = 0 : x > 0 y < 0 : x = 2n + 1 ou I/n ; n est un entier (n ¹ 0) mais -1 x 10100 < log IyI < 100

0 £ r £ n, n < 10 , n et r sont des entiers

100

10 8

100 100

100 1

1 x

100

STAT

IXI < 1 x 10 , IyI < 1 x 10 1 - VAR : n £ 255, 2 - VAR : n £ 255 FREQ = n, InI < 1 x 10 sx, sy, x, y, a, b, c, r : n ¹ 0

100 100

100

Sx, Sy : n ¹ 0,1

BaseN

DEC : - 2147483648 £ x £ 2147483647 BIN : 10000000000000000000000000000000 £ x £ 11111111 111111111111111111111111 ( po ur le s n ég at iv es ) 0 £ x £ 01111111111111111111111111111111 (p our 0 , positif) OCT : 20000000000 £ x £ 3777777777 (pour les négatives) 0 £ x £ 17777777777 (pour zéro ou positif) HEX : 80000000 £ x £ FFFFFFFF (pour les négatives) 0 £ x £ 7FFFFFFF (pour zéro ou positif)

1 - 9 Conditions d’erreur

Un message d’erreur s’affiche, tout calcul devient impossible si l’une des conditions d’erreur suivantes est rencontrée.

Indicateur Signification

DOMAIN Er

DIVIDE BY O OVERFLOW Er

SYNTAX Er

(1) L’argument d’une fonction dépasse la gamme d’entrée de la fonction (2) Les dimensions ne correspondent pas entre deux listes ou plus (3) La valeur USL < la valeur LSL (4) Tentative d’exécution d’une liste ne contenant pas de données (5) Tentative d’invocation d’une zone de mémoire ne contenant pas de données (6) Vous avez entré une valeur C négative ou une valeur C

où C = , C =

USL + x

PU PL

x - LSL

Vous avez essayé de diviser par 0 Lorsque le résultat des calculs de fonctions dépasse l’étendue

spécifiée. (1) Des erreurs d’entrée ont été faites

(2) Des arguments inappropriés sont utilisés dans des commandes ou des fonctions qui nécessitent des arguments. (3) Il manque une commande End pour marquer la fin d’un programme (4) Utilisation d’une syntaxe inappropriée pour l’opération (5) Il ne se trouve pas de Data correspondantes dans la commande de données où la commande Read est utilisée.

(6) Le nombre dans la commande Locate que vous avez entré se trouve hors de l’étendue autorisée.

LENGTH Er

STAT E r

NEST Er

GOTO Er

GOSUB Er

MEMORY Er

NO SOLUTION MULTI SOLUTION

NO REAL SOL

LABLE Er

Une entrée dépasse les 88 caractères après multiplication implicite

(1) Vous devez entrer des données statistiques avant de réaliser un graphique statistique ou d’effectuer un calcul statistique. (2) Tentative de visualiser des points de résumé (x1, y1, x2, y2, x3, y3) alors que la régression Med-Med n’a pas été dessinée ou effectuée.

(1) Une insertion de sous-programme dépasse 4 niveaux (2) Une insertion If-Then-Else dépasse les 6 niveaux (3)Une insertion de boucles dépasse les 6 niveaux

(1) Il n’y a de Label n correspondant lorsque Goto est utilisé (2) Dans le mode MAIN, tentative de démarrer un programme dont le nom de fichier est invalide

Il n’y a pas de nom de fichier correspondant lorsque Gosub Prog < nom de fichier > est utilisé

Il n’y a pas assez de mémoire disponible pour ce que vous essayé d’accomplir.

Il n’y a pas de solution au système en mode VLE Il y a une infinité de solutions au système en mode VLE

Il n’y a pas de solution réelle à l’équation quadratique en mode QE

Tentative d’utiliser le même nom de label plus d’une fois

Pour annuler les erreurs ci-dessus, pressez la touche [ON/CL]

1 - 10 Statut et effaçage de la mémoire 1 - 10 - 1 Pour vérifier le statut de la mémoire

Vous pouvez vérifier combien de mémoire est utilisée pour le stockage de tout type de données. Vous pouvez aussi voir combien d’octets de mémoire restent disponibles. Dans le menu des modes de fonctionnement, pressez [MODE] 7 (RESET) 0 (MEM USAGE) pour afficher l’écran du statut de la mémoire.

MEMORY USAGE Program : 120 Yn = : 1175 Free 19485

Déplacez le curseur pour voir la quantité de mémoire (en octets) utilisée pour le stockage de chaque type de données.

Page

Le tableau suivant montre tous les types de données affichés dans l’écran de statut de mémoire.

Option Signification program Données de programme Yn = Fonctions de graphiques List Données de liste table Données de graphiques et de tableaux

1 - 10 - 2 Pour effacer les contenus de la mémoire

Pour effacer toutes les données d’un type spécifique, pressez [MODE] 7 (RESET) 1 (CLEAR) pour afficher le menu des types de données.

0Prog 1Yn 2List 3Table 4Var 5Aqn 6Stat 7V-win

Program ... Données de programme Yn ... Fonctions de graphique List ... Données de liste Table ... Données de graphiques et

Var ... Donnée de mémoire variable Eqn ... Stockage d’équation Qtat ... Variables de statistiques V-win ... Données de mémoire en

Sélectionnez le type de données que vous souhaitez effacer. [q]

[EXE]

Déplacer le curseur vers “Y” pour effacer le type de données ou vers “N” pour annuler l’opération sans rien supprimer.

de tableaux

fenêtre V-Window

0Prog 1Yn 2List 3Table 4Var 5Eqn 6Stat 7V-win

CLEAR : N Y

Chapitre 2 Calculs simples

2 - 1 Calculs mixtes

(A) Opérations arithmétiques

Pour les opérations arithmétiques mixtes, la multiplication et la division ont priorité sur l’addition et la soustraction

Exemple : 7 + 10 x 8 ¸ 2 = 47

7 [+] 10 [x] 8 [¸] 2 [EXE]

(B) Valeurs négatives

Pour les valeurs négatives, pressez[(-)] avant d’entrer la valeur

Exemple : - 3.5 + 8 ¸ 4 = - 1.5

[(-)] 3.5 [+] 8 [¸] 4 [EXE]

Vous pouvez entrer un nombre sous forme exponentielle avec la touche [EXP]

Exemple : (3.15 x 10 ) x (2.7 x 10 ) =8.505 x 10

3.15 [EXP] [(-)] 15 [x] 2.7 [EXP] 32 [EXE]

Les résultats plus grands que 10 ou plus petits que 10 sont affichés sous forme exponentielles

Exemple : 12369 x 7532 x 74103 = 6903680613000

12369 [x] 7532 [x] 74103 [EXE]

-15 32 17

10 -9

7 + 10 x 8 ¸ 2

-3.5 + 8 ¸ 4

3.15 E - 15 x 2.7

E 32

12369 x 7532 x 74103

2 - 2 Formats d’affichage

2 - 2 - 1 Nombre de décimales

Le nombre de décimales affiché (F0123456789) se règle en pressant [2nd] [SYSTEM] deux fois et en sélectionnant “FIX” pour afficher le menu. (Le réglage par défaut pour le nombre de décimales affiché est la notation de la virgule flottante .F)

-1.5

8.505

6.90368061

+17

+12

FIX : F

[EXE]

. F 0 0 1 1 2 2

3 3 4 4 5 5 6 6 7 7 8 8 9 9

Exemple : 6 ¸ 7 = 0.857142857

6 [¸] 7 [EXE]

[2nd] [SYSTEM] [2nd] [SYSTEM] (FIX) [EXE] 2 (2)

[EXIT] [EXE]

2 - 2 - 2 Formats d’affichage des nombres

Le format d’affichage des nombres (Flo, Sci, Eng) se règle en pressant [2nd] [SYSTEM] et en sélectionnant “DISP” pour afficher le menu. (Le réglage par défaut pour l’affichage des nombres est “Flo”)

F-TYPE : Y = D-TYPE : Conct ANGLE : Rad DISP : Flo

Les options du menu sont Flo (pour virgule flottante), Sci (pour scientifique) et Eng (pour ingénieur).

Exemple : 1 ¸ 6000 = 0.0001666...

[EXE]

1 [¸] 6000 [EXE]

[2nd] [SYSTEM] [q] [q] [q] (DISP) [EXE] 1 (Sci)

[EXIT] [EXE]

[2nd] [SYSTEM] [q] [q] [q] (DISP) [EXE] 2 (Eng)

[EXIT] [EXE]

6 ¸ 7

0.857142857

R FIX

FIX : 2

R FIX

6 ¸ 7

0.857142857

0.86

0Flo 1Sci 2Eng

1 ¸ 6000

0.000166667

R SCI

F-TYPE : Y = D-TYPE : Conct ANGLE : Rad DISP : Sci

R SCI

1 ¸ 6000

0.000166667

1.66666667

R ENG

F-TYPE : Y = D-TYPE : Conct ANGLE : Rad DISP : Eng

R SCI

1 ¸ 6000

0.000166667

1.66666667

166.666667

-04

-06

2 - 3 Calculs entre parenthèses

Les opérations entre parenthèses sont toujours exécutées en premier. La calculatrice peut traiter jusqu’à 12 niveaux de parenthèses consécutives dans un seul calcul.

Exemple : (5 - 2 x 1.5) x 3 = 6

[()] 5 [-] 2 [x] 1.5 [u] [x] 3 [EXE]

Les parenthèses fermées survenant immédiatement avant l’opération de la touche [EXE] peuvent être omises, quelque soit le nombre de parenthèses requis.

Exemple : 2 x { 7 + 6 x ( 5 + 4 ) } = 122

2 [x] [()] 7 [+] 6 [x] [()] 5 [+] 4 [EXE]

2 - 4 Calculs des pourcentages

[2nd] [%] divise le nombre affiché par 100. Vous pouvez utiliser cette séquence de touches pour calculer des pourcentages, ajouts, remises et rapports de pourcentages.

Exemple : 120 x 30% = 36

120 [x] 30 [2nd] [%] [EXE]

Exemple : 88 ¸ 55% = 160

( 5 - 2 x 1 . 5 ) x 3 6

2 x ( 7 + 6 x ( 5 + 4 ) ) 122

1 2 0 x 3 0 % 36

88 [¸] 55 [2nd] [%] [EXE]

8 8 ¸ 5 5 % 160

2 - 5 Fonctions de calculs utiles

2 - 5 - 1 Fonction de calcul continu

La calculatrice vous permet de répéter la dernière opération exécutée en pressant la touche [EXE] pour un calcul supplémentaire.

Exemple : 3 x 3 x 3 x 3 = 81

3 [x] 3 [EXE]

[x] 3 [EXE]

[EXE] [EXE]

3 x 3 9

3 x 3 9 Ans x 3 27

Ans x 3 27 81 243

2 - 5 - 2 Marquage des corrections pendant les entrées

Le curseur clignotant “t” signifie que la calculatrice se trouve en mode insertion. Pour supprimer un caractère, soulignez ce caractère grâce aux touches du curseur, puis pressez [DEL]. Pour insérer un caractère, déplacez le curseur sur le caractère déjà affiché suivant l’endroit où vous voulez opérer l’insertion, et le nouveau caractère que vous presserez sera inséré automatiquement devant le caractère marqué. Pour effacer tous les caractères, pressez [ON/CL].

Exemple : Pour changer 123 x 45 en 123 x 47

123 [x] 45 [t] 7 [DEL] [EXE]

1 2 3 x 4 7 5 7 8 1

Pour récupérer un caractère qui vient d’être supprimé par [DEL], pressez [2nd] [L]

2 - 5 - 3 Fonction de révision

Lorsque le résultat d’un calcul est affiché, vous pouvez utiliser [t] ou [u] pour déplacer le curseur à travers l’entrée qui a produit le résultat. Cela signifie que vous pouvez revenir à une étape et corriger des erreurs sans avoir à entrer à nouveau la totalité du calcul.

Exemple : Pour calculer 4.5 x 6.3 puis changer le calcul en 4.5 x 6.53

4.5 [x] 6.3 [EXE]

[t] [t] 5 [EXE]

4 . 5 x 6 . 3 2 8 . 3 5

4 . 5 x 6 . 5 3 2 9 . 3 8 5

2 - 5 - 4 Fonction d’affichage d’erreur de position

Lorsqu’un calcul mathématiquement erroné est exécuté ou qu’un programme que vous avez entré cause une erreur, un message d’erreur (voir “1-9 Conditions d’erreur”) apparaît 5 secondes, puis la fonction d’affichage de position d’erreur vous annonce grâce au curseur où se trouve l’erreur. Dans ce cas, veuillez effectuer les corrections nécessaires avant d’exécuter de nouveau les calculs.

Exemple : 14 ¸ 0 x 2.3 entré par erreur au lieu de 14 ¸ 10 x 2.3

14 [¸] 0 [x] 2.3 [EXE]

D I V I D E B Y 0

(5 secondes)

[t] 1 [EXE]

2 - 5 - 5 Fonction réponse

La fonction réponse enregistre les résultats du calcul le plus récent. L’enregistrement perdure même lorsque l’on éteint l’appareil. Quand une valeur numérique ou expression numérique est entrée et que [EXE] a été pressée, le résultat est sauvegardé par cette fonction.

Exemple : 123 + 456 = 579 g 789 - 579 = 210

123 [+] 456 [EXE]

1 4 ¸ 0 t 2 . 3

1 4 ¸ 1 0 x 2 . 3 3 . 2 2

1 2 3 + 4 5 6 5 7 9

Pour rappeler des opérations précédentes ou suivantes, utilisez [p] ou [q]

Exemple : Pour rappeler l’opération 1+2=3 après avoir exécuté 1+2, 3+4, 5+ 6

1 [+] 2 [EXE] 3 [+] 4 [EXE] 5 [+] 6 [EXE]

[p] [p] [p] [p] [p] [p] [EXE]

3 + 4 7 5 + 6 11

1 + 2 t

789 [-] [2nd] [ANS] [EXE]

Note : Même si l’exécution d’un calcul a pour résultat une erreur, la mémoire de réponse conserve le résultat du précédent calcul abouti.

2 - 5 - 6 Multiplication implicite

Vous pouvez omettre le signe de multiplication dans chacun des cas suivants.

· Devant les fonctions scientifiques suivantes : Sin, cos, tan, sin , cos , tan , log, In, 10 , e , Ö, Pol (x,y), Rec (r,q), d/dx, Seq, Min, Max, Avg, Med, List, Dim, Sum. Exemple : 2 sin30, 10log1.2, 2Ö3, etc

-1 -1 -1 x x

1 2 3 + 4 5 6 5 7 9 7 8 9 - Ans 2 1 0

· Devant les constantes, les noms de variables, le contenu de la mémoire de réponse.

Exemple : 2p, 2AB, 3Ans, 6X, etc

· Devant les parenthèses ouvertes.

Exemple : 3 (5 + 6), (A + 1) (B - 1)

2 - 6 Calculs avec mémoire

2 - 6 - 1 Mémoire indépendante

Pressez [M+] pour ajouter un chiffre à la mémoire vive. Pressez [2nd] [M-] pour soustraire la valeur à la mémoire vive. Pour rappeler la valeur de la mémoire vive, pressez [MRC] [EXE]. Pour vider la mémoire vive, pressez [MRC] deux fois.

Exemple : [ ( 3 x 5 ) + ( 5 6 ¸ 7 ) - ( 7 4 - 8 x 7 ) ] = 5

3 [x] 5 [M+] 56 [¸] 7 [M+] [MRC] [EXE]

74 [-] 8 [x] 7 [2nd] [M-] [MRC] [EXE]

[MRC] [MRC] [EXE]

2 - 6 - 2 Variables standard

La calculatrice possède 28 variables standards pour usage répété : A ~ Z, X1 et X2. Vous pouvez sauvegarder un nombre réel ou un nombre complexe dans chacune de ces variables.

· [SAVE] enregistre des valeurs dans une variable spécifique

M R

5 6 ¸ 7 8 M 2 3

M R

57 4 - 8 x 7 1 8 M 5

1 8 M 0

· [2nd] [RECALL] rappelle la valeur de la variable

· [ALPHA] + < nom de la variable (A~Z) > invoque le contenu d’une variable

spécifique. Pour effacer le contenu de toutes les variables, voyez <<1-10 Statut et effaçage de la mémoire>>

Exemple : (1) Pour enregistrer la valeur 30 dans la variable A

(2) Pour multiplier 5 par la variable A, puis sauvegarder le

résultat

(3) Pour ajouter 3 à la variable B

(1) 30 [SAVE] [u]

[EXE]

(2) 5 [x] [2nd] [RECALL] (A) [EXE] [EXE]

[SAVE] [u] [u] [EXE]

(3) [ALPHA] [B] [+] 3 [EXE]

Note : Pour assigner des données multiples de la même valeur à plus d’une variable,

la valeur peut être entrée en utilisant [ALPHA] [~]. Par exemple, pour assigner la valeur 98 aux variables de mémoire A, B, C, D, pressez 98 [SAVE] (g) [EXE] [ALPHA] [A] [ALPHA] [~] [ALPHA] [D] [EXE]

2 - 6 - 3 Sauvegarde d’équation

Vous pouvez sauvegarder une équation dans les mémoires E-PROG1 ou E-PROG2 pour les rappeler rapidement lorsque vous en avez besoin. Vous pouvez alors invoquer l’équation à tout moment, entrer des valeurs, et exécuter des calculs rapidement et facilement.

Exemple : Pour régler E-PROG1 = 3A + 5B, et calculer pour

3 [ALPHA] [A] [+] 5 [ALPHA] [B] [SAVE] [SAVE] [q] [q] (E-PROG1)

A = 20, B = 18 E-PROG1 = 150

[EXE]

g g A B C D E F G H I J K L M N O P Q

3 0 g A 3 0

3 0 g A 3 0 5 x 3 0 1 5 0

5 x 3 0 1 5 0 A n s g B 1 5 0

A n s g B 1 5 0 B + 3 1 5 3

g R S T U V W X Y Z X X E-PROG1 E-PROG2

3 A + 5 B g E - P R O G 1 0

[2nd] [RECALL] [2nd] [RECALL] [q] [q] (E-PROG1) [EXE] [EXE] 20 [EXE] 18 [EXE]

[EXE]

2 - 7 Logarithmes et exponentielles

La calculatrice peut calculer des logarithmes décimaux et népériens et leurs réciproques à l’aide de [LOG], [LN], [2nd] [10 ] et [2nd] [e ]

Exemple : In7 + log100 + 10² + e = 103.9526481

[LN] 7 [u] [+] [LOG] 100 [u] [+] [2nd] [10 ] 2 [u] [+] [2nd] [e ] [(-)] 5 [EXE]

2 - 8 Calcul des fractions

Pour entrer une fraction en écriture anglo-saxonne, entrez la partie entière, pressez [A / ], entrez le numérateur, pressez [A / ] et entrez le dénominateur. Pour entrer une fraction en écriture française, entrez le numérateur, pressez [A / ] et entrez le dénominateur. L’affichage de la valeur de fraction se fait comme suit :

-5

3 A + 5 B A = 2 0 B = 1 8

3 A + 5 B 1 5 0

I n ( 7 ) + l o g ( 1 0 0 ) +

Ù Ù

1 0 ( 2 ) + e ( - 5 )

1 0 3 . 9 5 2 6 4 8 1

Ecriture française Ecriture anglo-saxonne

821470

7 2 3 + 1 4 5 7

2 2 8 2 1

2 2 8 2 1 A n s u A/ |} / 4 7 0 2 1

5 12 affichage de 56 5 12 affichage de 56 +

2 3

5 7

En pressant [2nd] [A / |} / ], la valeur affichée sera convertie de l’écriture anglaise à l’écriture française et vice et versa.

Exemple : 7 + 14 = 22 =

bb bb

7 [A / ] 2 [A / ] 3 [+] 14 [A / ] 5 [A / ] 7 [EXE]

cc cc

[2nd] [A / |} / ] [EXE]

Pour convertir un résultat décimal en écriture fractionnaire ou vice et versa, pressez [2nd] [F|}D] et [EXE]

Exemple : = 3.4

187 [Ab/c] 55 [2nd] [F|}D] [EXE]

Les calculs contenant à la fois des fractions et des décimales sont affichés en format décimal.

Exemple : 8 + 3.75 = 12.55

8 [A / ] 4 [A / ] 5 [+] 3.75 [EXE]

[2nd] [F|}D] [EXE]

187

1 8 7 5 5 u F | } D 3 . 4

8 4 5 + 3 . 7 5 1 2 . 5 5

8 4 5 + 3 . 7 5 1 2 . 5 5 A n s u F | } D 1 2 1 1 2 0

2 - 9 Conversion des unités d’angle

2 - 9 - 1 Réglage de l’unité d’angle par défaut

L’unité d’angle (Deg, Rad, Grad) se règle en pressant [2nd] [SYSTEM] et en sélectionnant “ANGLE” pour afficher le menu. (Le réglage par défaut est “Rad”)

F-TYPE : Y =

[EXE]

D-TYPE : Conct ANGLE : Rad DISP : Flo

La relation entre les trois unités d’angles est :

180 Deg. = p Rad. = 200 Grad.

0 R a d 1 D e g 2 G r a d

Exemple : 2 p rad. = 360 deg. Étape 1 : Changez le réglage par défaut vers l’unité d’angle dans laquelle vous voulez

convertir. [2nd] [SYSTEM] [q] [q] (ANGLE) [EXE] 1 (Deg)

F-TYPE : Y = D-TYPE : Conct ANGLE : Deg DISP : Flo

Étape 2 : Entrez la valeur de l’unité à convertir, puis pressez [2nd] [DMS] pour afficher le menu. Les unités que vous pouvez sélectionner sont ° (degrés), ‘ (minutes), “ (secondes), r (radians), g (grades),ou DMS (Degrés-Minutes-Secondes).

[EXIT] 2 [2nd] [p] [2nd] [DMS] [u] [u] [u]

° ‘ “ r g u D M S

Pour convertir une valeur décimale en notation DMS, pressez [2nd] [DMS] et sélectionnez “uDMS”, ce qui convertit une entrée en notation DMS.

Exemple : 1.555 = 1°33’18” (DMS)

1.555 [2nd] [DMS] [u] [u] [u] [u] [u]

° ‘ “ r g u D M S

Étape 3 : Après avoir sélectionné les unités que vous souhaitez pour la conversion, pressez [EXE] deux fois.

[EXE] [EXE]

2 p 3 6 0

2 - 9 - 2 Notation DMS

Pour convertir une notation DMS en une valeur décimale, pressez [2nd] [DMS] et sélectionnez ° (degrés), ‘ (minutes), “ (secondes) pour l’entrée, c’est à dire que

2°45’10.5” représente 2 degrés (heures), 45 minutes, 10.5 secondes.

Note : Lorsque vous utilisez ces fonctions, assurez-vous que la calculatrice est

réglée sur l’unité d’angle que vous souhaitez.

Exemple : 2°45’10.5” = 2.752916667

2 [2nd] [DMS]

[EXE] 45 [2nd] [DMS] [u]

[EXE] 10.5 [2nd] [DMS] [u] [u]

[EXE] [EXE]

° ‘ “ r g u D M S

2 ° 4 5 ‘ 1 0 . 5 “ 2 . 7 5 2 9 1 6 6 6 7

[EXE] [EXE]

1 . 5 5 5 u D M S

1 ° 3 3 ‘ 1 8 “

2 - 10 Fonction trigonométrique / Trig. - inversée

La calculatrice fournit les fonctions trigonométriques et les fonctions trigonométriques inverses standards : sin, cos, tan, sin , cos et tan

Note : Quand vous utilisez ces touches, assurez-vous que la calculatrice est réglée

sur l’unité d’angle que vous souhaitez.

Exemple : sin30 Deg. = 0.5

[2nd] [SYSTEM] [q] [q] (ANGLE) [EXE] 1 (Deg)

[EXIT] [SIN] 30 [EXE]

Exemple : sin 0.5 = 33.33333333 Grad

[2nd] [SYSTEM] [q] [q] (ANGLE) [EXE] 2 (Grad)

[EXIT] [2nd] [SIN ] 0.5 [EXE]

-1

-1 -1 -1

F-TYPE : Y = D-TYPE : Conct ANGLE : Deg DISP : Flo

s i n ( 3 0 ) 0 . 5

F-TYPE : Y = D-TYPE : Conct ANGLE : Grad DISP : Flo

s i n ( 0 . 5 ) 3 3 . 3 3 3 3 3 3 3 3

-1

2 - 11 Fonction Hyperbolique / Hyp. - Inversée

La calculatrice propose [2nd] [HYP] pour calculer les fonctions hyperboliques et les fonctions hyperboliques inverses : sinh, cosh, tanh, sinh , cosh et tanh

Note : Quand vous utilisez ces touches, assurez-vous que la calculatrice est réglée

sur l’unité d’angle que vous souhaitez.

Exemple : cosh1.5 - sinh 7 = -0.291711146

[2nd] [HYP] [COS] 1.5 [u] [-] [2nd] [HYP] [2nd]

-1

[SIN ] 7 [EXE]

-1

-1 -1 -1

c o s h ( 1 . 5 ) - s i n h ( 7 )

- 0 . 2 9 1 7 1 1 1 4 6

-1

Exemple : Min (sin 30 Deg., Sin 90 Deg.) = Min (0.5, 1) = 0.5

[MATH] 0 (Min) [SIN] 30 [u] [ ] [SIN] 90 [EXE]

M i n ( s i n ( 3 0 ) , s i n ( 9 0 ) ) 0 . 5

Exemple : Max (sin 30 Deg., Sin 90 Deg.) = Max (0.5, 1) = 1

[MATH] 1 (Max) [SIN] 30 [u] [ ] [SIN] 90 [EXE]

M a x ( s i n ( 3 0 ) , s i n ( 9 0 ) ) 1

2 - 12 Fonction mathématique

La touche [MATH] donne accès à divers menus mathématiques avec les fonctions suivantes :

0 M i n 1 M a x 2 M e d 3 S u m 4 A v g 5 S g n 6 I n t ¸ 7 R m d r

0 n P r 1 n C r 2 X ! 3 R n d 4 I n t 5 F r a c 6 I n t g 7 A b s

1 pression ... 2 pressions ...

0 R u P r 1 R u P q 2 P u R x 3 P u r y 4 R a n d 5 R a n d l 6 S i m p

0 m 1 m 2 n 3p 4 f 5 K 6 M 7 G 8 T 9 P

3 pressions ... 4 pressions de la touche [MATH]

2 - 12 - 1 Calculs numériques

Min ... Donne le minimum des valeurs entrées Max ... Donne le maximum des valeurs entrées Med ... Donne la médiane des valeurs entrées Sum ... Donne la somme des valeurs entrées Avg ... Donne la moyenne des valeurs entrées Sgn ... Donne le signe du nombre entré : -1 si négatif

0 si c’est 0 1 si positif

Exemple : Med (12, 15, 17, 21, 33) = 17

[MATH] 2 (Med) 12 [ ] 15 [ ] 17 [ ] 21 [ ] 33 [EXE]

, , , ,

Exemple : Sum (13, 15, 23) = 51

[MATH] 3 (Sum) 13 [ ] 15 [ ] 23 [EXE]

, ,

Exemple : Avg (13, 15, 23) = 17

[MATH] 4 (Avg) 13 [ ] 15 [ ] 23 [EXE]

Exemple : Sgn (log 0.01) = Sgn (-2) = -1

[MATH] 5 (Sgn) [LOG] 0.01 [EXE]

M e d ( 1 2 , 1 5 , 1 7 , 2 1 , 3 3 ) 1 7

S u m ( 1 3 , 1 5 , 2 3 ) 5 1

A v g ( 1 3 , 1 5 , 2 3 ) 1 7

S g n ( l o g ( 0 . 0 1 ) )

-1

2 - 12 - 2 Quotient et reste d’une division

Int ¸ ... Donne le quotient d’une division euclidienne entre 2 entiers Rmdr ... Donne le reste d’une division euclidienne entre deux entiers

Note : Veuillez vous rappeler que vous ne pouvez utiliser que des entiers avec ces

deux fonctions (donc ni Ö2, ni sin 30)

Exemple : Pour afficher le quotient produit par 58 ¸ 9

58 [MATH] 6 (Int¸) 9 [EXE]

Exemple : Pour afficher le reste produit par 58 ¸ 9

[MATH] 7 (Rmdr) 9 [EXE]

5 8 I n t ¸ 9 6

5 8 R m d r 9 4

Note : Dans les exemples précédents, on a finalement 58 = 9 x 6 + 4

2 - 12 - 3 Permutation et Combinaison

nPr ... Permutation nCr ... Combinaison

Exemple : 7 ! ¸ [ ( 7-4) ! ] = P = 840

7 [MATH] [MATH] 0 (nPr) 4 [EXE]

Exemple : 7 ! ¸ [ (7-4) ! X 4 ! ] = C = 35

7 [MATH] [MATH] 1 (nCr) 4 [EXE]

2 - 12 - 4 Factorielles, arrondis, entiers, fractions, valeurs absolues, nombres

aléatoires

4 7

7 n P r 4 8 4 0

4 7

7 n C r 4 3 5

X ! ... Calcule la factorielle d’un entier positif donné n, où n £ 69 Rnd ... Arrondit le résultat pour l’adapter au nombre de décimales (FIX) Int ... Extrait la partie non décimale de la valeur entrée Frac ... Extrait la partie fractionnaire de la valeur entrée Intg ... Donne la partie entière de la valeur entrée

Abs ... Donne la valeur absolue du nombre entré Rand ... Génère un nombre aléatoire entre 0 et 1 Randl ... Genère un entier aléatoire entre deux entiers donnés A et B,

A £ valeur aléatoire £ B

Exemple : 5 ! = 120

5 [MATH] [MATH] 2 (X!) [EXE]

5 ! 1 2 0

Exemple : Rnd (82.3 ¸ 5) = Rnd (16.46) = 16.5 (si FIX = 1)

[MATH] [MATH] 3 (Rnd) 82.3 [¸] 5 [EXE]

R n d ( 8 2 . 3 + 5 ) 1 6 . 5

Exemple : Int (10 ¸ 8) = Int (1.25) = 1

[MATH] [MATH] 4 (Int) 10 [¸] 8 [EXE]

I n t ( 1 0 ¸ 8 ) 1

Exemple : Frac (10 ¸ 8) = Frac (1.25) = 0.25

[MATH] [MATH] 5 (Frac) 10 [¸] 8 [EXE]

F r a c ( 1 0 ¸ 8 ) 0 . 2 5

Exemple : Intg (25 ¸ 4) = Intg (6.25) = 6

[MATH] [MATH] 6 (Intg) 25 [¸] 4 [EXE]

I n t g ( 2 5 ¸ 4 ) 6

Exemple : Abs (log 0.01) = Abs (-2) = 2

[MATH] [MATH] 7 (Abs) [LOG] 0.01 [EXE]

A b s ( l o g ( 0 . 0 1 ) ) 2

Exemple : Génère un nombre aléatoire entre 0 et 1

[MATH] [MATH] [MATH] 4 (Rand) [EXE]

R a n d 0 . 4 6 4 3 7 0 7 2 8

Exemple : Génère un entier aléatoire entre 7 et 9

[MATH] [MATH] [MATH] 5 (Randl) 7 [ ] 9 [EXE]

R a n d l ( 7 , 9 ) 7

2 - 12 - 5 Transformation de coordonnées

R u Pr , R u P q ... Coordonnées rectangulaire ® coordonnée polaire P u Rx , P u Ry ... Coordonnée polaire ® coordonnée rectangulaire

Coordonnée rectangulaire « Coordonnée polaire

Y Y

0 0

Note : Lorsque vous utilisez ces fonctions, assurez-vous que la calculatrice est

réglée sur l’unité d’angle que vous souhaitez.

X + y i = r ( cos q + i sin q )

P ( x, y ) P ( r, q )

X X

Exemple : Si x = 5, y = 30, que sont r, q ? Rép : r = 30.41381265,

q = 80.53767779° (unité d’angle : Deg)

[MATH] [MATH] [MATH]

[EXE] 5 [ ] 30 [EXE]

[MATH] [MATH] [MATH] [u]

[EXE] 5 [ ] 30 [EXE]

0 R u P r 1 R u P q 2 P u R x 3 P u r y 4 R a n d 5 R a n d l 6 S i m p

R u P r (5 , 3 0 ) 3 0 . 4 1 3 8 1 2 6 5

0 R u P r 1 R u P q 2 P u R x 3 P u r y 4 R a n d 5 R a n d l 6 S i m p

R u P q (5 , 3 0 ) 8 0 . 5 3 7 6 7 7 7 9

2 - 12 - 6 Simplification de fraction

Simp ... Simplifier une fraction enutilisant votre facteur ou celui de la calculatrice.

(A) Pour simplifier en utilisant le diviseur de la calculatrice

Selon la syntaxe ci-dessous pour utiliser le facteur de simplification de la calculatrice

[ MATH ] [MATH ] [ MATH ] 6 (Simp) < fraction > [EXE ]

La calculatrice sélectionne automatiquement le plus petit diviseur premier possible (Factor, F = ) pour le simplification. Si nécessaire, vous pouvez répéter l’opération pour la simplifier encore jusqu’à ce qu’il soit affiché qu’aucune simplification supplémentaire n’est possible.

Exemple : Pour simplifier la fraction en utilisant le facteur de la calculatrice

[MATH] [MATH] [MATH] 6 (Simp) 42 [A / ] 24 [EXE]

[EXE]

(B) Pour simplifier en utilisant votre facteur

Selon la syntaxe ci-dessous pour spécifier votre facteur de simplification

[ MATH ] [ MATH ] [ MATH ] 6 (Simp) < fraction > [ ] < facteur >[EXE ]

Vous ne pouvez spécifier qu’un entier positif en tant que facteur.

Note : Si la valeur que vous spécifiez est invalide en tant que facteur pour la

simplification, la calculatrice emploie automatiquement le plus petit diviseur premier possible.

Exemple : Pour simplifier la fraction en utilisant votre facteur 6

[MATH] [MATH] [MATH] 6 (Simp) 42 [A / ]24

[ ] 6 [EXE]

42 24

S i m p ( 4 2 2 4 ) F = 2 2 1 1 2

F = 2

21 12

F = 3

7 4

42 24

S i m p ( 4 2 2 4 , 6) F = 6 7 4

2 - 12 - 7 Notation ingénieur

Cette calculatrice fournit aussi une liste de symboles pour l’entrée de valeurs par notation ingénieur. Il y a dix symboles dans le menu.

milli micro nano pico femto

-3 -6 -9 -12 -15

m = 10 m = 10 n = 10 p = 10 f = 10 kilo mega giga tera peta

3 6 9 12 15

K = 10 M = 10 G = 10 T = 10 P = 10

Exemple : 20 G byte + 0.1 K byte = 2.000000015 x 10 byte

20 [MATH] [MATH] [MATH] MATH] 7 (G) [+] 0.1 [MATH] [MATH] [MATH] [MATH] 5 (K) [EXE]

2 - 13 Autres fonctions(x , Ö, Ö, x², )

-1 x

La calculatrice fournit aussi des fonctions inverse ([x ]), de racine carrée ([Ö]), de carré ([x²]), de racine universelle ([ Ö]) et exponentiel ([Ù]).

1.25

-1

Exemple : + 2² + (4 + 21) + 81 + 5 = 137.8

1.25 [2nd] [X ] [+] 2 [X²] [+] [Ö] 4 [+] 21 [u] [+] 4 [2nd] [ Ö ] 81 [u] [+] 5 [ ] 3 [EXE]

2 0 G + 0 . 1 K 2 . 0 0 0 0 0 0 0 1

-1

1 . 2 5 + 2 ² + Ö ( 4 + 2 1 ) + 4 Ö ( 8 1 ) + 5 3 1 3 7 . 8

-1

x Ù

+10

2 - 14 Conversion d’unités

La calculatrice est munie d’un menu de conversion d’unités, qui vous permet de convertir des nombres en mesures anglaises et françaises . Il y a 7 menus : distance, surface, température, capacité, poids, énergie et pression, ce qui fait en tout 38 unités.

Exemple : 1yd² = 9ft² = 0.000000836 km²

Étape 1 : Entrez le nombre que vous voulez convertir, et déroulez la liste des

unités jusqu’à ce que le menu d’unités approprié soit désigné, puis

pressez [EXE]

1 [CONV] [CONV] [u] [EXE]

f t ² y d ² k m ² m ² h e c t a r e s m i l e s ² a c r e s 1

Étape 2 : Pressez [t] ou [u] pour convertir le nombre dans une autre unité.

[t]

[u] [u]

f t ² y d ² k m ² m ² h e c t a r e s m i l e s ² a c r e s 9

f t ² y d ² k m ² m ² h e c t a r e s m i l e s ² a c r e s 0 . 0 0 0 0 0 0 8 3 6

2 - 15 Constantes physiques

Vous pouvez utiliser un certain nombre de constantes physiques dans vos calculs. Avec les 40 constantes suivantes :

Symbole c g G Vm N

e m

h k IR IF mn mm

m e

a ge lc gp gcp lcn R¥ mp me mn mu

AU t atm pc

Vitesse de la lumière Accélération de la gravité Constante gravitationnelle Volume molaire du gaz idéal Nombre d’Avogadro Charge élémentaire Masse électronique Masse protonique Constante de Planck Constante de Boltzmann Constante du Gaz Constante de Faraday Masse neutronique Masse muonique Constante de la masse atomique Permittivité Diélectrique Permittivité magnétique Quantum de flux Rayon de Bohr Magnéton de Bohr Moment magnétique neutronique h = h/2p Constante de structure fine Rayon classique électronique Longueur d’onde électronique Compton Rapport gyromagnétique protonique Longueur d’onde protonique Compton Longueur d’onde neutronique Compton Constante de Rydberg Moment protonique blindé Moment électronique magnétique Moment magnétique neutronique Moment magnétique muonique Première constante de radiation Deuxième constante de radiation Constante de Stéfan-Boltzmann Unité astronomique Température Celsius Atmosphère standard Parsec

Signification

299792458 m/s

9.80665 m.s

6.6725985 x 10 N.m kg

6.022136736 x 10 mol

1.6021773349 x 10 C

9.109389754 x 10 kg

1.67262311 x 10 kg

6.62607554 x 10 JS

1.38065812 x 10 J.K

1.67492861 x 10 kg

1.66054021 x 10 kg

8.85418782 x 10 F / m

2.0678346161 x 10 Vs

5.2917724924 x 10 m

9.274015431 x 10 A . M²

5.05078662 x 10 J / T

1.05457266 x 10 J.s

-11 2 -2

0.0224141 m mol

8.3145107 J / mol . k

96485.30929 C / mol

3-1

23 -1

-23 -1

1.8835327 x 10 kg

-12

0.000001257 H / m

-24

-27

7.29735308 x 10

2.81794092 x 10 m

2.42631058 x 10 m 267522128 T s

1.32141002 x 10 m

1.3195911 x 10 m

10973731.53 m

1.411060761 x 10 J T

9.2847701 x 10 J T

9.6623707 x 10 J T

4.4904514 x 10 J T

3.7417749 x 10 W m²

5.67051 x 10 W m K

-26 -1

-24 -1

-27 -1

-26 -1

-16

0.01438769 m K

-8 -2 -4

1.4959787 x 10 m

273.15 K

101325 Pa

3.0856776 x 10 m

-2

-19

-31

-27

-34

-27

-28

-27

-15

-11

-34

-3

-15

-12

-1 -1

-15

-1

Pour insérer la valeur d’une constante à la position du curseur, pressez [2nd] [CONST] pour afficher le menu des constantes physiques. Déroulez le menu jusqu’à ce que la constante que vous souhaitez soit soulignée puis pressez [EXE].

Exemple : 3 x G = 2.00177955 x 10

3 [x] [2nd] [CONST] [q]

[EXE] [EXE]

-10

c g Vm NA me G e mp mn mu h k j a e 6 . 6 7 2 5 9 8 5

3 x 6 . 6 7 2 5 9 8 5 E

-11 2 . 0 0 1 7 7 9 5 5

000

-10

-11

2 - 16 Fonction multidéclarations

Les multidéclarations se forment en connectant plusieurs déclarations individuelles pour une exécution en séquence. Pour exécuter une fonction multidéclaration, séparez chaque déclaration individuelle par une commande de résultat affiché (y). Lorsque l’exécution atteint la fin d’une déclaration suivie par y, l’exécution s’arrête et le résultat à ce point s’affiche. Vous pouvez reprendre l’exécution en pressant [EXE].

Exemple : Utilisez la fonction multidéclarations pour les deux déclarations :

E x 13 = 195 180 ¸ E = 12

15 [SAVE] [u] [u] [u] [u] [u] (E) [EXE]

[ALPHA] [E] [x] 13 [ALPHA] [y] 180 [¸] [ALPHA] [E] [EXE]

[EXE]

où E=15

1 5 g E 1 5

1 5 g E 1 5 E x 1 3 y 1 8 0 ¸ E 1 9 5

E x 1 3 y 1 8 0 ¸ E 1 9 5 E x 1 3 y 1 8 0 ¸ E 1 2

1 9 5 E x 1 3 y 1 8 0 ¸ E 1 2 1 9 5

2 - 17 Intégration et Différentiation

Cette calculatrice peut effectuer des calculs d’’intégration et de différentiation numérique en pressant [ ò dx ] et [2nd] [d/dx]

2 - 17 - 1 Intégration

La calculatrice utilise la règle de Simpson pour effectuer des calculs d’intégration comme le montre l’exemple ci-dessous :

ò f(x)dx,N=2

où [a, b] est l’intervalle d’intégration et N est le nombre de divisions, (n est un entier de 1 à 9)

La règle de Simpson

y = f (x)

f (a)

Surface = { f (a) + 4 { f (a + h) + f (a + 3h) + ... + f (a + (N-1) h } + 2 { f (a + 2h) +

h 3

f (a + 4h) + ... + f (a + (N - 2) h) } + f (b) }, où h =

En général, plus n est grand, plus le temps de calcul requis est long et plus le résultat est précis. Dans quelques cas, les résultats de votre intégration peuvent être erronés même si le plus grand n est utilisé. En particulier, lorsque les chiffres concernés sont plus petits que 1, un message d’erreur apparaîtra quelquefois.

Note : Les calculatrices exécutent toujours l’intégration trigonométrique en utilisant

les radians en tant qu’unité de mesure des angles.

Note : Une intégration impliquant certains types de fonctions ou d’étendue peut

générer des erreurs relativement importantes dans les valeurs produites.

f (b)

b - a

Exemple : ò ( x + 1 ) d x = 320

Étape 1 : Entrez la fonction f(x). Vous pouvez utiliser la touche [X,T] pour entrer la

variable x dans la fonction

[ ò dx] [( )] [X,T] [+] 1 [u] [Ù] 3 [EXE]

Étape 2 : Entrez les limites inférieure et supérieure de l’intégration (a et b). Donnez le

nombre de division à spécifier 2 = N, où la valeur de n est un entier de 1 à 9

et la valeur par défaut est 5.

1 [EXE] 5 [EXE]

Étape 3 : Pressez [EXE]

[EXE]

ò ( ( X + 1 ) 3 ) dx a 1 = 0 b 1 = 0 2 I n1 = 5 ( 1 ~ 9 )

ò ( ( X + 1 ) 3 ) dx a 1 = 1 b 1 = 5 2 I n1 = 5 ( 1 ~ 9 )

ò ( ( X + 1 ) 3 ) dx 3 2 0

Plus x est petit, plus grand est le temps de calcul requis et plus le résultat est précis. En général, la précision est de ± 1 pour le chiffre le moins important du résultat. Vous n’avez toutefois pas besoin d’entrer une valeur x et il suffit de presser [EXE] pour passer cette étape. La calculatrice assigne automatiquement la valeur par défaut de

-8

10 .

Exemple : f (x) = x + 4x + x - 6 Þ f’ (3) = (3x + 8x + 1) = 52

Étape 1 : Entrez la fonction f(x). Vous pouvez utiliser [X,T] pour entrer la variable x

[2nd] [d/dx] [X,T] [Ù] 3 [+] 4 [X,T] [X²] [+] [X,T] [-] 6 [EXE]

Étape 2 : Entrez le point x1 = a pour déterminer le nombre dérivé en ce point. Puis

3 [EXE]

32 2

dans la fonction.

entrez l’augmentation / diminution de x ( x)

x=3

d / dx ( X 3 + 4 X ² x 1 = 0 x 1 = 1 - 0 8

d / dx ( X 3 + 4 X ² x 1 = 3 x 1 = 1 - 0 8

2 - 17 - 2 Différentiation

La calculatrice utilise la différence centrale pour exécuter des calculs différentiels, comme il est montré dans l’exemple ci-dessous :

f’ (a) = lim .

Où a est le point dont vous voulez déterminer le nombre dérivé et x l’augmentation / diminution de x.

Différence centrale

12Y

f’ (a) = ( + )

f(a + x) - f(a)

= ( + )

f(a + x) - f(a - x)

2 x

ÑY

ÑX

f(a) - f(a - x) x.

F (a + x) - f (a)

g 0

. x

f(a + x) - f(a - x) 2 x

a- x

y = f (x)

Ñy Ñx

y x

a+ x

Étape 3 : Pressez [EXE]

[EXE]

Note : Si le temps de calcul de l’intégration ou la différentiation est trop long et que

vous souhaitez l’interrompre, pressez [EXIT]

d / dx ( X 3 + 4 X ² + X - 6 )

5 2

2 - 17 - 3 Application de l’intégration et de la différentiation

Les intégrales et différentielles peuvent être additionnées, soustraites, multipliées et divisées les unes avec les autres. Par exemple : ò f(x) dx + ò g(x) dx, ò f(x) dx xò g(x) dx, f (a) ¸ ò g(x) dx ...

Exemple :

Þ f (10) - f (30) = [3cos (3x + 30)] - { - [3cos(x)² x sin(x)] }

= - 2.927765162 (Rad.)

b a

f (x) = sin(3x + 30)

f (x) = cos (x)

d c

b a

x=10 x=30

d c

b a

[2nd] [d/dx] [SIN] 3 [X,T] [+] 30 [u] [u] [-] [2nd] [d/dx] [( )] [COS] [X,T] [u] [Ù] 3 [EXE]

10 [EXE] [q] 30 [EXE] [EXE]

Les résultats intégrés ou différentiels peuvent être utilisés dans des additions, soustractions, multiplications et divisions, et dans des fonctions. Par exemple, 5 x ò f(x) dx, cos (ò f(x) dx)

Exemple : cos [ ò (x + 1) dx] = cos(320) = 0.766044443

b a

1 5

b a

[COS] [òdx] [( )] [X,T] [+] 1 [u] [Ù] 3 [EXE]

1 [EXE] 5 [EXE] [EXE]

Après avoir effectué une intégration, vous pouvez réintégrer le même f(x), avec différentes limites d’intégration, a et b, ou un nombre différent de divisions, n. De même vous pouvez calculer un autre nombre dérivé de f(x).

Exemple :

ò (x + 1) dx = 320

1 8

ò (x + 1) dx = 1576.25

[òdx] [( )] [X,T] [+] 1 [u] [Ù] 3 [EXE]

1 [EXE] 5 [EXE]

[EXE]

d / dx ( s i n ( 3 X + x 1 = 0 x 1 = 1 - 0 8 x 2 = 0

d / dx ( s i n ( 3 X + 3 0 ) ) d / dx ( (c o s ( X ) 3 ) )

- 2 . 9 2 7 7 6 5 1 6 2 1

c o s ( ò ( ( X + 1 ) a 1 = 0 b 1 = 0

2 I n1 = 5 ( 1 ~ 9 )

c o s ( ò ( ( X + 1 ) 3 ) dx )

0 . 9 0 3 7 0 5 1 1 2

ò ( ( X + 1 ) 3 ) dx a 1 = 0 b 1 = 0

2 I n1 = 5 ( 1 ~ 9 )

ò ( ( X + 1 ) 3 ) dx a 1 = 1 b 1 = 5

2 I n1 = 5 ( 1 ~ 9 )

ò ( ( X + 1 ) 3 ) dx )

3 2 0

[EXE] 3 [EXE] 8 [EXE]

[EXE]

Lorsque l’intervalle d’intégration [a,b] n’est pas disponible ou interrompu pour la fonction intégré, un message d’erreur est affiché. Cela signifie que vous devez modifier les limites inférieures et supérieures d’intégration (a,b) pour l’intégration.

Exemple : ò dx = 0.58789835

0.5

-0.5

(x² - 3x + 2)

[òdx] 1 [+] [( )] [X,T] [X²] [-] 3 [X,T] [+] 2 [EXE]

[( - )] 0.5 [EXE] 1.5 [EXE] 5 [EXE]

Après 5 secondes

[EXE] [( - )] 0.5 [EXE] 0.5 [EXE] 5 [EXE]

ò ( ( X + 1 ) 3 ) dx a 1 = 3 b 1 = 8 2 I n1 = 5 ( 1 ~ 9 )

ò ( ( X + 1 ) 3 ) dx )

1 5 7 6 . 2 5

ò ( 1 + ( X ² - 3 X + 2 a 1 = 0 b 1 = 0 2 I n1 = 5 ( 1 ~ 9 )

D I V I D E B Y 0

ò ( 1 + ( X ² - 3 X + 2 ) t

ò ( 1 + ( X ² - 3 X + 2 ) )

0 . 5 8 7 8 9 8 3 5

2 - 18 Nombres complexes

Vous pouvez additionner, soustraire, multiplier et diviser des nombres complexes. Les résultats d’une opération complexes sont affichés comme suit :

Re ... Valeur réelle Im ... Valeur imaginaire ab ... Valeur absolue ar ... Valeur d’argument

Note : Lorsque vous utilisez cette fonction, assurez-vous que la calculatrice est

réglée sur l’unité d’angle que vous souhaitez.

Exemple : ( 7 - 9 i) + ( 15 + 12 i ) = 22 + 3 i

ab = 22.20360331, ar = 7.765166018° (unité d’angle : Deg)

[( )] 7 [-] 9 [2nd] [i] [u] [+] [( )] 15 [+] 12 [2nd] [i] [EXE]

[u]

R e I m a b a r

2 2

R e I m a b a r

2 2 . 2 0 3 6 0 3 3 1

R e I m a b a r

7 . 7 6 5 1 6 6 0 1 8

2 - 19 Menu des données varables (VARS)

Vous pouvez utiliser le menu des données variables pour rappeler les données cidessous :

· Délimitation de la fenêtre graphique

· Etendue du tableau et contenus du tableau

· Facteur d’augmentation / de réduction de zoom

· Données graphiques

· Données statistiques à une ou deux variables

Pour rappeler des données variables, pressez [VARS] pour afficher le menu des données variables.

V-Window V_Xmin ... Minimum de l’axe des x V-Xmax ... Maximum de l’axe des x V-Xscl ... Echelle de l’axe des x V-Ymin ... Minimum de l’axe des y V-Ymax ... Maximum de l’axe des y V-Yscl ... Echelle de l’axe des y V-Tmin ... Minimum de T V-Tmax ... Maximum de T V-Tpth ... Pente de T

Etendue du tableau et contenus du tableau T Strt ... Valeur de départ du tableau T End ... Valeur de fin du tableau T pth ... Pas d’incrémentation des valeurs du tableau

Facteur d’augmentation / de réduction X fact ... Facteur d’augmentation / de réduction de l’axe des x Y fact ... Facteur d’augmentation / de réduction de l’axe des y

Fonctions graphiques Y ... Coordonnée rectangulaire ou fonction d’inégalité X t ... Fonction de graphique paramétrique X t Y t ... Fonction de graphique paramétrique Y t

Données statistiques STAT ... Données statistiques à une ou deux variables

(Voir “Chapitre 8 / Calculs statistiques et graphiques”)

V - Xmin V - Xmax V - X s c l V - Ymin V - Y max V - Y s c l

- 3 . 5

V - Tmin V - Tmax V - Tpth T S t r t T E n d T p t h 0

X f a c t Y f a c t Y X t Y t S T A T

Chapitre 3 Calculs EVL & EQ

3 - 1 Système de deux équations à deux inconnues

Dans le menu des modes de fonctionnement, sélectionnez VLE pour entrer en mode systèmes d’équations. S’affiche alors l’écran d’entrée des données dans le système de variables linéaires X et Y.

a x + b y = c , d x + e y = f a = 0 b = 0 c = 0

Dans ce mode on peut résoudre un système de 2 équations à deux inconnues, comme suit :

ax + by = c

où x et y sont des inconnues

dx + ey = f’

Il suffit d’entrer chaque coefficient ( a, b, c, d, e, f ) dans l’ordre correct et la calculatrice résout automatiquement x et y.

a x + b y = c , d x + e y = f a = - 1 5 7 . 2 3 3 5 7 7 b = 2 . 7 c = 0

Si le symbole “ = “ devient “-=”, “-=-” cela signifie qu’il y a des entrées masquées à droite ou à gauche de l’écran ou les deux. Pressez [t] ou [u] pour déplacer le curseur et lire ces entrées.

Exemple : Þ x = 5, y = - 2

3 x + 5 y = 5 x - 4 y = 13

[MODE] [MODE] 0

3 [EXE] 5 [EXE] 5 [EXE] 1 [EXE] [( - )] 4 [EXE] 13

[EXE]

[u]

R VLE

a x + b y = c , d x + e y = f a = 0 b = 0 c = 0

a x + b y = c , d x + e y = f d = 1 e = - 4 f = 1 3

X Y

- 2

R VLE

3 - 2 Equations Quadratiques

Dans le menu des modes de fonctionnement, sélectionnez la fonction QE pour entrer en mode de résolution d’équations quadratiques. S’affiche alors l’écran d’entrée des données dans les équations quadratiques.

a x ² + b x + c = 0 a = 0 b = 0 c = 0

R QE

Ce mode peut résoudre les équations comme suit : a x ² + b x + c = 0, où x est une inconnue. Il suffit d’entrer chaque coefficient (a, b, c) dans l’ordre correct et la calculatrice résout

automatiquement toutes les valeurs de x.

a x ² + b x + c = 0 a = 1 2 . 5 7 b = - 1 3 . 2 6 9 9 4 3 4 c = 6 4 5 . 4 8

Exemple : x ² - 5 x + 6 = 0 Þ X = 2 ou 3

[MODE] [MODE] 1

1 [EXE] [( - )] 5 [EXE] 6

[EXE]

[u]

R QE

a x ² + b x + c = 0 a = 0 b = 0 c = 0

a x ² + b x + c = 0 a = 1 b = - 5 c = 6

X1 X2

R QE

R VLE

Chapitre 4 Graphiques

4 - 1 Avant d’essayer de dessiner un graphique

Dans le menu des modes de fonctionnement, sélectionnez l’option GRAPH pour entrer en mode graphique. Apparaît alors le menu graphique (G-Func).

GRAPH R

G F u n c : Y = Y 1 : Y 2 : Y 3 :

4 - 2 Paramétrage de fenêtre V-Window

Il faut toujours régler les paramètres V-Window que l’on souhaite avant de dessiner un graphique. Pressez [V-WIN] en mode GRAPH ou en mode MAIN pour afficher le menu des paramètres V-Window.

GRAPH R

V - W i n d o w Xm i n = - 3 . 5 m a x = 3 . 5 s c l = 1

GRAPH R

V - W i n d o w Tm i n = 0 m a x = - 6 . 2 8 3 1 8 p t c h = - 0 . 0 6 2 8 3

Axe X Axe Y min ... Valeur minimum de l’axe x min ... Valeur minimum de l’axe y max ... Valeur maximum de l’axe x max ... Valeur maximum de l’axe y scl ... Echelle de l’axe x scl ... Echelle de l’axe y

Valeur T min ... Valeur minimum T max ... Valeur maximum T ptch ... Pente T

Init ... Paramètres initiaux V-Window Trig ... Paramètres initiaux V-Window avec l’unité d’angle spécifié Sto ... Mémoriser les paramètres V-Window Rcl ... Invoquer les paramètres V-Window de la mémoire

GRAPH R

V - W i n d o w Ym i n = - 1 . 5 m a x = 1 . 5 s c l = 1

GRAPH R

V - W i n d o w 0 I n i t 1 T r i g 2 S t o 3 R c l

L’illustration suivante montre la signification de chacun de ces paramètres :

X min

Y min

Y scl

Y max

X scl

X max

T ptch

T min

T max

4 - 2 1 Pour initialiser et standardiser la fenêtre V-Window

(A) Pour initialiser la fenêtre V-Window

Pressez [V-WIN] [p] 0 (Init) pour initialiser la fenêtre V-Window selon les paramètres suivants (Lorsque l’unité d’angle choisie est le radian) :

Xmin = -3.5, Xmax = 3.5, Xscl = 1 Ymin = -1.5, Ymax = 1.5, Yscl = 1 Tmin = 0, Tmax = 6.28318, Tptch = 0.0628318

(B) Pour standardiser la fenêtre V-Window

Pressez [V-WIN] [p] 1 (Trig) pour standardiser la fenêtre V-Window selon les paramètres suivants :

Mode Deg : Xmin = -360, Xmax = 360, Sxcl = 90

Mode Rad : Xmin = - 6.28318530718, Xmax = 6.28318530718

Mode Grad : Xmin = -400, Xmax = 400, Xscl = 100

Note : Les réglages de Tmin, Tmax et Tptch restent inchangés lorsque vous pressez

Ymin = - 1.1, Ymax = 1.1, Yscl = 0.5

Xscl = 1.570796326795, Ymin = -1.1, Ymax = 0.5, Yscl = 0.5

Ymin = -1.1, Ymax = 1.1, Yscl = 0.5

[V-WIN] [p] 1 (Trig).

4 - 2 - 2 Mémoire V-Window

Vous pouvez stocker un jeu de paramètres V-Window dans la mémoire V-Window, afin de les rappeler lorsque vous en avez besoin.

(A) Pour mémoriser les paramètres V-Window.

Pressez [V-WIN] [p] 2 (Sto) pour enregistrer les paramètres en cours.

Note : Quand vous enregistrez des paramètres V-Window, tous les paramètres

préalablement stockés sont remplacés

(B) Pour rappeler des paramètres V-Window

Pressez [V-WIN] [p] 3 (Rcl) pour rappeler les paramètres de fenêtre V-Window stockés en mémoire.

Note : Quand vous rappelez des paramètres V-Window, tous les paramètres de la

fenêtre en cours sont remplacés par ceux-ci.

4 - 3 Opérations Graphiques

Vous pouvez enregistrer jusqu’à 20 fonctions dans les zones de mémoire Y1 à Y20. Les fonctions en mémoire peuvent être éditées, rappelées et tracées.

GRAPH R

G - F u n c : Y = Y 1 6 X ² - X - 5

Zone de mémoire

Si le symbole “ = “ devient “-=”, “-=-” cela signifie qu’il y a des entrées masquées à droite ou à gauche de l’écran ou les deux. Pressez [t] ou [u] pour déplacer le curseur parmi ces entrées.

Y 2 = - 8 X ² - 1 8 + 9 Y 3 :

Type de fonction de graphique

4 - 3 - 1 Pour spécifier le type de graphique

Lorsque le menu Graphique (G-Func) est affiché, vous pouvez presser [FUNC] pour afficher le menu.

GRAPH R

0 S e l 1 D r a w 2 Y = 3 Y < 4 Y > 5 P a r m 6 Y £ 7 Y ³ 8 L i s t

Y = ... Graphique à coordonnée rectangulaire Y > ... Y > f(x) inégalité stricte Y < ... Y < f(x) inégalité stricte Parm ... Graphique paramétrique Y £ ... Y £ f(x) inégalité large Y ³ ... Y ³ f(x) inégalité large

(A) Pour enregistrer une fonction à coordonnée rectangulaire (Y=)

Exemple : Pour stocker l’expression suivante dans la zone de mémoire

Étape 1 : Lorsque le zone de mémoire que vous souhaitez est soulignée, pressez

[FUNC] 2 (Y=)

Étape 2 : Entrez l’expression et pressez [EXE] pour l’enregistrer. La variable indépendante X peut être définie en pressant (X,T].

6 [X,T] [X²] [ - ] [X,T] [ - ] 5 [EXE]

Note : On ne peut stocker une expression dans une zone qui contient déjà une

Y1: Y = 6X ² - X - 5

[FUNC] 2 (Y=) pour spécifier son type de graphique.

GRAPH R

G - F u n c : Y = Y 1 : Y 2 : Y 3 :

GRAPH R

G - F u n c : Y =

Y 1 6 X ² - X - 5 Y 2 : Y 3 :

fonction paramétrique. Il faut sélectionner une autre zone ou supprimer au préalable la fonction paramétrique qui s’y trouve. Cela s’applique aussi lorsque l’on enregistre des inégalités.

(B) Pour enregistrer une inégalité (Y <, Y £, Y ³, Y >)

Utilisez les mêmes procédures que celles utilisées pour l’expression. La seule différence consiste à spécifier le type d’inégalité (Y <, Y £, Y ³, Y >)

Exemple : Pour stocker les fonctions suivantes dans les zones de mémoire Xt3

et Yt3 : X = 5 sin T, Y = 4 cos T (L’unité d’angle choisie est le radian)

Étape 1 : Lorsque la zone de mémoire que vous souhaitez est soulignée, pressez

[FUNC] 5 (Parm) pour spécifier le type de graphique.

[FUNC] 5 (Parm)

GRAPH R

G - F u n c : P a r m X t 3 : Y t 3 : X t 4 :

Étape 2 : Entrez l’expression et pressez [EXE] pour l’enregistrer. La variable

indépendante T dans la fonction peut être définie en pressant [X,T]

5 [SIN] [X,T] [EXE]

4 [COS] [X,T] [EXE]

GRAPH R

G - F u n c : P a r m

X t 3 5 s i n ( T ) Y t 3 : X t 3 :

GRAPH R

G - F u n c : P a r m

X t 3 5 s i n ( T )

Y t 3 4 c o s ( T ) X t 4 :

4 - 3 - 2 Pour éditer des fonctions en mémoire

(A) Pour éditer une fonction en mémoire

Exemple : Pour changer l’expression dans la zone de mémoire :

Y1 de Y = 6X² - X - 5 à Y = 6X² - 4X - 5

Étape 1 : Lorsque la zone de mémoire que vous souhaitez est soulignée, pressez [u]

pour afficher le curseur.

[u]

Étape 2 : Modifiez les contenus souhaités.

[u] [u] [u] [u] 4

GRAPH R

G - F u n c : Y = Y 1 = t X ² - X - 5 Y 2 : Y 3 :

GRAPH R

G - F u n c : Y = Y 1 = 6 X ² - 4 X - 5 Y 2 : Y 3 :

Étape 3 : Pressez [EXE] pour enregistrer les changements

GRAPH R

[EXE]

(B) Pour supprimer une fonction

Lorsque la zone de mémoire que vous souhaitez est soulignée, pressez [DEL]. Un message apparaît pour confirmer si vous voulez supprimer cette fonction ou pas.

G - F u n c : Y =

Y 1 6 X ² - 4 X - 5 Y 2 : Y 3 :

GRAPH R

Y 1

DEL : N Y

Déplacez le curseur vers “Y” pour supprimer la fonction ou “N” pour abandonner la procédure sans rien supprimer.

4 - 3 - 3 Pour dessiner un graphique

Avant de dessiner effectivement un graphique, il faut spécifier le statut / non dessiné

(A) Pour spécifier le statut dessiné / non dessiné d’un graphique

En pressant [FUNC] 0 (Sel), vous pouvez préciser quelles fonctions parmi celles stockées en mémoire doivent être utilisées pour une opération de dessin.

Exemple Pour sélectionner les fonctions suivantes pour le dessin :

Étape 1 : Sélectionnez une zone de mémoire qui contient une fonction que vous

[q]

Y1 = 6 X² - X - 5 X : X = 5 sin (T), Y : Y = 4 cos (T)

t3 t3

Utilisez les paramètres de fenêtre V-Window suivants : Xmin = -5, Xmax = 5, Xscl = 1 Ymin = -5, Ymax = 5, Yscl = 1 Tmin = 0, Tmax = 6.2832, Tptch = 0.0629

voulez écarter du dessin.

GRAPH R

G - F u n c : P a r m Y 1 6 X ² - X - 5 Y 2 X 3 - 7 X + 6 X t 3 5 s i n ( T )

Étape 2 : Spécifiez “non-draw”. Le symbole “=” devient alors inaccentué sur l’écran.

[FUNC] 0 (Sel)

GRAPH R

G - F u n c : P a r m Y 1 6 X ² - X - 5

Y 2 £ X Ù 3 - 7 X + 6 X t 3 5 s i n ( T )

Étape 3 : Pressez [EXE] ou [FUNC] 1 (Draw) pour dessiner des graphiques.

[EXE]

GRAPH R

Étape 4 : En pressant [GnT] on retourne à l’affichage texte G-Func.

Note : Un graphique paramétrique paraîtra grossier si les paramètres que vous

avez choisis pour la fenêtre V-Window augmentent trop la valeur de la pente, relativement à la différence entre les paramètres min et max. Par contre, si les paramètres que vous avez choisis font que la valeur de la pente est trop petite relativement à la différence entre les paramètres min et max, le graphique sera très long à dessiner.

4 - 4 Dessiner des graphiques manuellement

En mode MAIN, vous pouvez dessiner des graphiques manuellement. Commencez par presser [GRAPH] pour appeler le menu des commandes de graphique, puis entrez la fonction Graphique.

0 C l s 1 P l o t 2 V e r t 3 L i n e 4 H z t l 5 P a r m 6 Y = 7 Y <

Cls ... Efface l’écran graphique Y = ... Graphique à coordonnées rectangulaire Y < ... Y < f(x) inégalité stricte Y > ... Y > f(x) inégalité stricte Y £ ... Y £ f(x) Inégalité large

0 Y > 1 Y £ 2 Y ³

Y ³ ... Y ³ f(x) inégalité large Parm ... Courbe paramétrée

(A) Pour un graphique utilisant des coordonnées rectangulaires (Y = )

Exemple : Pour appliquer en graphique Y = X + 3X - 6X - 8

Étape 1 : Dans l’écran de réglage, spécifiez le type de graphique approprié pour

Utilisez les paramètres de fenêtre V-Window suivants : Xmin = -8, Xmax = 8, Xscl = 2 Ymin = -15, Ymax = 15, Yscl = 5

F-TYPE

[2nd] [SYSTEM] (F-TYPE) [EXE] 0 (Y=)

Étape 2 : Entrez l’expression. La variable indépendante X dans la fonction se définit

en pressant [X,T]

[EXIT] [GRAPH] 0 (Cls) [EXE] [GRAPH] 6 (Y=) [X,T] [Ù] 3 [+] 3 [X,T] [X²] [-] 6 [X,T] [-] 8

F-TYPE : Y = D-TYPE : Conct ANGLE : Rad DISP : Flo

C l s

G r a p h Y = X 3 + 3 X² - 6 X - 8 t

Étape 3 : Pressez [EXE] pour dessiner le graphique

[EXE]

(B) Graphiques embarqués

Cette unité contient en tout 19 graphiques embarqués, qui permettent de produire des graphiques de fonctions de base : sin, cos, tan, sin , cos , tan , sinh, cosh, tanh, sinh , cosh , tanh , Ö, x², log, In, 10 , e , x

Note : Les paramètres de fenêtre V-Window sont automatiquement réglés à leur

Exemple : Pour le graphique de cosinus

[2nd] [SYSTEM] (F-TYPE) [EXE] 0 (Y=)

[EXIT] [GRAPH] 0 (Cls) [EXE] [GRAPH] 6 (Y=) [COS] [EXE]

Exemple : Pour dessiner les fonctions paramétriques suivantes :

Étape 1 : Dans l’écran de réglage, spécifiez le type de graphique approprié pour

[2nd] [SYSTEM] (F-TYPE) [EXE] 1 (Parm)

-1 -1 -1 x x -1

-1 -1 -1

optimum et tout graphique antérieurement affiché est effacé.

F - T Y P E : Y = D - T Y P E : C o n c t A N G L E : R a d D I S P : F l o

Vous pouvez dessiner des fonctions paramétriques exprimées dans le format suivant : Graph (X,Y) = f (T), g (T)

f (T) = sin (2T), g (T) = cos (3T) Utilisez les paramètres de fenêtre V-Window suivants : Xmin = -1, Xmax = 1, Xscl = 0.5 Ymin = -1.5, Ymax = 1.5, Yscl = 1 Tmin = 0, Tmax = 6.2832, Tptch = 0.01

F-TYPE. Réglez l’angle par défaut sur les radians (Rad)

F - T Y P E : Parm D - T Y P E : C o n c t A N G L E : R a d D I S P : F l o

Étape 2 : Entrez l’expression. La variable indépendante T dans la fonction se définit

en pressant la touche [X,T]

[EXIT] [GRAPH] 0 (Cls) [EXE] [GRAPH] 5 (Parm) [SIN] 2[X,T] [u] [ ] [COS] 3 [X,T]

0 G r a p h ( X , Y ) = s i n ( 2 T ) , c o s ( 3 T t

Étape 3 : Pressez [EXE] pour dessiner le graphique.

[EXE]

(D) Pour tracer des inégalités Vous pouvez dessiner les inégalités qui peuvent être exprimées dans les quatre formats suivants.

· y > f(x) · y < f(x) · y ³ f(x) · y £ f(x)

Exemple : Pour appliquer en graphique l’inégalité Y > X² - X - 6

Étape 1: Dans l’écran de réglage, spécifiez le type de graphique approprié pour

Utilisez les paramètres de fenêtre V-Window suivants : Xmin = -6, Xmax = 6, Xscl = 2 Ymin = -8, Ymax = 8, Yscl = 2

F-TYPE

[2nd] [SYSTEM] (F-TYPE] [EXE] 2 (Y>)

Étape 2 : Entrez l’expression. La variable indépendante X dans la fonction se définit

en pressant [X,T]

[EXIT] [GRAPH] 0 (Cls) [EXE] [GRAPH] [GRAPH] 0 (Y>) [X,T] [X²] [ - ] [X,T] [ - ] 6

F - T Y P E : Y > D - T Y P E : C o n c t A N G L E : R a d D I S P : F l o

C l s 0 G r a p h Y > X ² - X

- 6 t

Étape 3 : Pressez [EXE] pour dessiner le graphique

[EXE]

(E) Chevauchement des graphiques

Deux graphiques de fonction ou plus peuvent se superposer, ce qui facilite la détermination de points d’intersection et de solutions qui satisfont toutes les expressions. Lorsque la deuxième fonction est une fonction embarquée, il est nécessaire d’entrer la variable X sinon seule cette fonction sera tracée.

Exemple : Pour superposer Y = cos (x) sur le graphique Y = sin (X)

[2nd] [SYSTEM] (F-TYPE) [EXE] 0 (Y=)

[EXIT] [GRAPH] 0 (Cls) [EXE] [GRAPH] 6 (Y=) [SIN] [EXE]

F - T Y P E : Y = D - T Y P E : C o n c t A N G L E : R a d D I S P : F l o

[EXIT] [GRAPH] 6 (Y=) [COS] [X,T] [EXE]

4 - 5 Autres fonctions de graphisme

4 - 5 - 1 Type de création de graphique (D-TYPE)

En mode MAIN ou GRAPH, le type de graphique pour la connexion et le positionnement (Concr, Plot) se règle en pressant [2nd] [SYSTEM] et en sélectionnant “D-TYPE” pour afficher le menu. (Le réglage par défaut est “Conct”)

GRAPH R

D - T Y P E : C o n c t G - F U N C : O n S I M U L -G : O f f A N G L E : R a d

Conct ... Les points sont positionnés et connectés par des lignes pour créer une

courbe.

Plot ... Les points sont positionnés sans être connectés.

[EXE]

GRAPH R

0 C o n c t 1 P l o t

4 - 5 - 2 Affichage de fonction graphique (G-FUNC)

En mode GRAPH, l’affichage de fonction graphique (On, Off) se règle en pressant [2nd] [SYSTEM] et en sélectionnant “G-FUNC” pour afficher le menu. (Le réglage par défaut est “On”.

On ... Déclenche l’affichage de la fonction graphique durant le dessin et le traçage

Off ... Eteint l’affichage de la fonction graphique durant le dessin et le traçage

GRAPH R

D - T Y P E : C o n c t G - F U N C : O n S I M U L -G : O f f A N G L E : R a d

du graphique.

graphique.

[EXE]

GRAPH R

0 O n 1 O f f

4 - 5 - 3 Mode de graphique simultané (SIMUL-G)

En mode GRAPH, le mode de graphiques simultanés (On, Off) se règle en pressant [2nd] [SYSTEM] et en sélectionnant “SIMUL-G” pour afficher le menu. (Le réglage par défaut est “Off”)

GRAPH R

D - T Y P E : C o n c t G - F U N C : O n S I M U L -G : O f f A N G L E : R a d

On ... Déclenche les graphiques simultanés de toutes les fonctions en mémoire Off ... Le graphisme simultané est éteint; les graphiques sont dessinés un par un.

[EXE]

GRAPH R

0 O n 1 O f f

Étape 1 : Après avoir tracé les graphiques, pressez [TRACE] pour faire apparaître le

pointeur à l’écran. Utilisez [u] ou [t] pour déplacer le pointeur vers la première intersection.

[TRACE] [u] ~ [u]

GRAPH R

Y1 = - X 3 + 3X² - 6

X = 2 . 0 5 7 1 Y = 1 . 0 5 8 1

Étape 2 : Utilisez [q] et [p] pour déplacer le pointeur entre deux graphiques

[q]

GRAPH R

Y2 = - X + 2

X = 2 . 0 5 7 1 Y = - 0 . 0 5 7

Étape 3 : Pour quitter l’opération de traçage, pressez [TRACE] de nouveau

Note : Comme vous povez le voir, la fonction Trace peut être utilisée pour déplacer

le pointeur à intervalle fixe et le localiser à un point approximatif. En raison des limitations dues à l’affichage, la position actuelle du pointeur ne peut être qu’approximative.

4 - 5 - 5 Défilement

Vous pouvez faire défiler un graphique le long de ses axes x ou y. Chaque fois que vous pressez [t], [u], [p] ou [q], le graphique défile dans la direction correspondante.

4 - 5 - 4 Trace

Avec la fonction de traçage, vous pouvez déplacer un pointeur dans un graphique par les touches de curseur et obtenir le relevé des coordonnées à chaque point. La fonction Trace ne peut être utilisée qu’immédiatement après qu’un graphique ait été dessiné. Elle ne peut pas être utilisée après avoir modifié les paramètres d’un graphique.

Exemple : Utilisez la fonction Trace pour déterminer les points d’intersection

pour les graphiques produits par les fonctions suivantes :

Y1 : Y = X + 3X - 6X - 8 Y2 : Y = - X + 2 Utilisez les paramètres de fenêtre V-Window suivants : Xmin = -8, Xmax = 8, Xscl = 2, Ymin = -15, Ymax = 15, Yscl = 5

4 - 5 - 6 Zoom

La fonction de zoom vous permet d’agrandir ou de réduire l’affichage d’un graphique.

(A) Avant d’utiliser le zoom

Immédiatement après avoir dessiné un graphique, pressez [ZOOM] pour afficher le menu de Zoom.

GRAPH R

0 I n 1 O u t 2 B o x 3 O r i g 4 F A C T

In ... Agrandit le graphique en utilisant les facteurs de zoom Out ... Réduit le graphique en utilisant les facteurs de zoom Box ... Agrandit le graphique en utilisant la zone de zoom Orig ... Taille originale FACT ... Affiche l’écran de spécification des facteurs zoom

(B) Pour utiliser la zone de zoom

Avec la zone de zoom, vous tracez un espace pour spécifier une portion de graphique, puis en élargir les contenus dans les limites de zone.

Exemple : Pour utiliser la zone de zoom pour agrandir une portion du

Étape 1 : Après avoir tracé le graphique de cette fonction, pressez [ZOOM] 2 (Box),

graphique suivant : Y = (X + 5) (X + 7) (X + 9) (X + 10) Utilisez les paramètres de fenêtre V-Window suivants : Xmin = -20, Xmax = 20, Xscl = 5 Ymin = -15, Ymax = 15, Yscl = 5

puis utilisez les clés de curseur pour déplacer le pointeur ( ) vers l’un des coins de la zone que vous voulez dessiner sur l’écran. Pressez [EXE] pour adopter le coin choisi.

GRAPH R

[ZOOM] 2 [p] ~ [t] [EXE]

X = - 1 3 . 7 1 Y = 10

Étape 2 : Utilisez les curseurs pour déplacer le pointeur ( ) vers le coin

diagonalement opposé du premier coin.

[u] ~ [q]

Étape 3 : Pressez [EXE] pour entrer le lieu du second coin. La partie du

graphique à l’intérieur de la zone est alors immédiatement élargie pour remplir la totalité de l’écran.

[EXE]

GRAPH R

X = - 2 . 2 8 6 Y = - 6

GRAPH R

Avec le facteur zoom, vous pouvez agrandir ou réduire l’affichage, avec le pointeur en cours au centre du nouvel affichage.

Exemple : Pour appliquer en graphique les deux fonctions ci dessous, et les

Étape 1 : Après avoir dessiné les fonctions, pressez [ZOOM] 4 (FACT) pour afficher

[ZOOM] 4 (FACT) 4 [EXE] 4 [EXE]

Étape 2 : Presse [EXIT] 0 (In) pour les agrandir. Cet écran agrandit montre

agrandir afin de déterminer si elles sont tangentes ou pas :

Y1 : Y = X + 3X² - 6 X - 8 Y2 : Y = 1.5 X + 17 Utilisez les paramètres de fenêtre V-Window suivants : Xmin = -10, Xmax = 8, Xscl = 4 Ymin = -30, Ymax = 50, Yscl = 10

l’écran de détermination des facteurs, et entrez les facteurs pour les axes x et y. (Le réglage par défaut est : Xfat : 2, Yfat : 2)

GRAPH R

Z o o m F a c t o r X f a t = 4 Y f a t = 4 I n i t

évidemment que les graphiques des deux expressions ne sont pas tangentes.

GRAPH R

[EXIT] 0 (In)

X = - 1 Y = 10

Note : La procédure ci-dessus peut être utilisé pour réduire la taille d’un graphique.

Ensuite, pressez 1 (Out)

(D) Pour initialiser le facteur de zoom

Pressez [ZOOM] 4 (FACT) et sélectionner “Init” pour initialiser le facteur de zoom aux réglages par défaut : Xfat : 2, Yfat : 2

Etape 4 : Pour retourner au graphique original, pressez [ZOOM] 3 (Orig).

4 - 5 - 7 Fonction Sketch

La fonction Sketch vous permet de dessiner des lignes et de positionner des points sur un graphique déjà à l’écran.

Note : Le fonctionnement de la fonction Sketch en mode STAT, GRAPH ou TABLE

diffère du fonctionnement de la fonction Sketch en mode MAIN.

(A) Avant d’utiliser la fonction Sketch

· En mode MAIN, revenez à l’écran texte avec [G«T] puis pressez [GRAPH]

· En mode STAT, GRAPH ou TABLE, pressez [GRAPH]

Le menu Sketch suivant s’affiche alors :

0 C l s 1 P l o t 2 V e r t 3 L i n e 4 H z t l 5 P a r m 6 Y = 7 Y <

Cls ... Efface la ligne et le point Plot ... Affiche le menu de positionnement de points Vert ... Ligne verticale Line ... Affiche le menu des lignes Hztl ... Ligne horizontale

0 C l s 1 P l o t 2 V e r t 3 L i n e 4 H z t l 5 P a r m

(B) Pour positionner des points et tirer une ligne entre deux points repérés

·En mode STAT, GRAPH ou TABLE

Exemple : Pour positionner deux points sur le graphique de

Étape 1 : Après avoir appliqué la fonction en graphique, effectuez l’opération suivante

pour faire apparaître le pointeur sur l’écran de graphique.

Y1 = X + 3 X - 6 X - 8 et dessiner une ligne entre ces deux points. Utilisez les paramètres de fenêtre V-Window suivants : Xmin = -6, Xmax = 8, Xscl = 2 Ymin = -15, Ymax = 25, Yscl = 5

.GRAPH R

[GRAPH] 1 (Plot)

X = 1 Y = 5

Étape 2 : Utilisez les touches de curseur pour déplacer le pointeur ( ) vers les

endroits que vous souhaitez repérer et pressez [EXE] pour positionner.

.GRAPH R

[u] ~ [p] [EXE]

X = 2 . 6 Y = 1 7

Étape 3 : Utilisez les touches de curseur pour déplacer le ( ) vers l’autre point.

.GRAPH R

[t] ~ [q]

X = - 2 . 8 Y = 1 0 . 3 3 3

Étape 4 : Pressez [GRAPH] pour afficher le menu et effectuer l’opération suivante pour dessiner une ligne entre les deux points.

.GRAPH R

[GRAPH] 3 (Ligne)

X = - 2 . 8 Y = 1 0 . 3 3 3

· En mode MAIN

Voici la syntaxe pour le positionnement de points dans ce mode.

[ GRAPH ] 1 ( Plot ) < coordonnée X > [ ] < coordonnée Y > [ EXE ]

Exemple : Pour positionner un point (4, 15), utilisez les paramètres de

Étape 1 : Effectuez l’opération suivante pour faire apparaître le pointeur sur l’écran de

fenêtre V-Window suivants : Xmin = -6, Xmax = 8, Xscl = 2 Ymin = -15, Ymax = 25, Yscl = 5

graphique.

[GRAPH] 0 (Cls) [EXE] [GRAPH] 1 (Plot) 4 [ ] 15

. R

C l s

P l o t ( 4 , 1 5 )

Étape 2 : Pressez [EXE] pour positionner le point

[EXE]

. R

X = 4 Y = 1 5

Étape 3 : Pressez [G«T] pour retourner au menu de la fonction Graphique

[G«T]

Note : Si les coordonnées que vous avez spécifiées se trouvent au-delà de

l’étendue des paramètres de fenêtre V-Window, le pointeur n’est pas affiché.

. R

C l s

P l o t ( 4 , 1 5 )

D o n e

· En mode STAT, GRAPH ou TABLE

Exemple : Pour dessiner des lignes verticales et horizontales sur le

Étape 1 : Après avoir appliqué la fonction en graphique, effectuez l’opération suivante

graphique de Y1 = X + 3 X - 6X - 8, utilisez les paramètres de fenêtre V-Window : Xmin = -6, Xmax = 8, Xscl = 2 Ymin = -15, Ymax = 25, Yscl = 5

pour faire apparaître le pointeur sur l’écran de graphique .

[GRAPH] 2 (Vert)

Étape 2 : Utilisez les touches de curseur [t] et [u] pour déplacer la ligne à gauche ou

à droite et pressez [EXE] pour dessiner la ligne à l’endroit indiqué.

[u] ~ [u] [EXE]

Note : Pour dessiner une ligne horizontale, il suffit de presser 4 (Hztl) au lieu de 2

(Vert), et utilisez les touches de curseur [p] et [q] pour déplacer la ligne horizontale sur l’écran.

.GRAPH R

X = 2 Y = 5

· En mode MAIN

Voici la syntaxe pour le positionnement de points dans ce monde.

Ligne verticale : [ GRAPH ] 2 (Vert) < coordonnée X > [ EXE ]

Ligne horizontale : [GRAPH ] 4 (Hztl) < coordonnée Y > [ EXE ]

(D) Pour effacer les lignes et les points tracés

L’opération suivante efface tous les points et lignes tracés de l’écran.

· En mode STAT, GRAPH ou TABLE

Les lignes et points tracés en utilisant les fonctions du menu Sketch sont temporaires. Affichez le menu Sketch et pressez [GRAPH] 0 (Cls) pour effacer les lignes et points tracés, en laissant seulement le graphique de départ.

· En mode MAIN

Voici la syntaxe pour effacer les lignes et points tracés, ainsi que le graphique luimême.

[ GRAPH ] 0 (Cls) [ EXE ]

Chapitre 5 Fonctions de tableaux

5 - 1 Avant d’utiliser le mode TABLE

Dans le menu des modes de fonctionnement, sélectionnez la fonction TABLE pour entrer en mode Tableaux. Apparaît alors l’écran principal du mode tableaux.

TBLE R

T - F u n c : Y = Y 1 : Y 2 : Y 3 :

5 - 2 Enregistrer une fonction

Vous pouvez stocker jusqu’à 20 fonctions de tableau dans les zones de mémoire Y1 à Y20. Les fonctions en mémoire peuvent être éditées, rappelées et tracées.

Zone de mémoire

Si le symbole “=” devient “-=”, “-=-” ou “=-”, cela signifie que des entrées supplémentaires sont masquées à la droite ou la gauche du tableau, ou les deux. Pressez [t] ou [u] déplace le curseur à l’intérieur d’une entrée.

Exemple : Pour stocker la fonction Y = 6 X² - X - 5 dans la zone de mémoire Y1

Étape 1 : Utilisez [q] et [p] pour souligner la zone de mémoire que vous souhaitez.

[p] ~ [p]

Étape 2 : Entrez ensuite la fonction et pressez [EXE] pour la stocker.

6 [X,T] [X²] [ - ] [X,T] [ - ] 5 [EXE]

5 - 3 Supprimer une fonction

Utilisez [q] et [p] pour souligner la zone de mémoire que vous souhaitez supprimer , puis pressez [DEL]. Un message s’affiche pour confirmer si vous voulez supprimer la fonction ou pas.

TBLE R

T - F u n c : Y =

Y 1 6 X ² - X - 5 Y 2 = - 8 X ² - 1 8 X + 9 Y 3 :

Type de fonction de tableau

TBLE R

T - F u n c : Y = Y 1 : Y 2 : Y 3 :

TBLE R

T - F u n c : Y = Y 1 6 X ² - X - 5

Y 2 : Y 3 :

TBLE R

Y 1

D E L : N Y

Déplacez le curseur vers “Y” pour supprimer la fonction, ou “N” pour abandonner la procédure sans rien supprimer.

5 - 4 Assigner des valeurs à une variable

Avant de créer un tableau, vous devez assigner des valeurs à une variable. Vous pouvez utiliser l’une des méthodes suivantes.

· Assignation automatique dans une étendue spécifiée

· Assignation de valeurs depuis une liste.

La méthode par défaut est l’assignation automatique dans une étendue spécifiée.

(A) Pour assigner des valeurs automatiquement dans une étendue spécifiée

Avant de créer un tableau, pressez [FUNC] 2 (RANGE) pour afficher le menu des étendues de tableau.

Srt ... Valeur de départ de la variable X e n d ... Valeur de fin de la variable X p t c h ... Incrémentation de la variable X

Exemple : Pour assigner des valeurs de -5 à 5, en incréments de 1 (onze

valeurs en tout).

[FUNC] 2 (RANGE) [( - )] 5 [EXE] 5 [EXE] 1 [EXE]

(B) Pour assigner des valeurs depuis une liste

La méthode pour assigner des valeurs depuis une liste (L1 ~ L8) se règle en pressant [2nd] [SYSTEM] et en sélectionnant “VAR” pour afficher le menu. (Le réglage par défaut est l’étendue “Range”).

TBLE R

V A R : R a n g e G - F U N C : O n S I M U L 6 G : O f f A N G L E : R a d

TBLE R

T a b l e R a n g e X S r t : 1 e n d : 5 p t c h : 1

[EXE]

TBLE R

T a b l e R a n g e X S r t : - 5 e n d : 5 p t c h : 1

TBLE R

0 R a n g e 1 L 1 2 L 2 3 L 3 4 L 4 5 L 5 6 L 6 7 L 7 8 L 8

Exemple : Pour assigner des valeurs depuis L5

[2nd] [SYSTEM] (VAR) [EXE] 5 (L5)

Note : Après avoir sélectionné une liste pour l’assignation, pressez [FUNC] 2

(RANGE) la rend inactive.

TBLE R

V A R : L 5 G - F U N C : O n S I M U L 6 G : O f f A N G L E : R a d

5 - 5 Générer un tableau numérique

L’exemple ci-dessous est l’écran de génération d’un tableau numérique.

TBLE R

Y 1 = 6 X ² - X - 5 XY 1

- 5 u 1 5 0

Cellule

- 4 8 4

1 5 0

· Chaque cellule peut contenir jusqu’à six caractères (le signe négatif, le point décimal ou le symbole exponentiel prennent chacun un caractère).

· La valeur contenue dans la cellule sélectionnée apparaît en bas de l’écran

· Vous pouvez utiliser [t] [u] pour vous déplacer entre les colonnes et [p] [q]

pour vous déplacer entre les cellules d’un même tableau. L’écran défile automatiquement vers le bas lorsque le curseur atteint le bord de l’écran.

Avant de créer effectivement le nouveau tableau, il faut sélectionner les fonctions que vous voulez utiliser. Utilisez les touches de curseur [p] et [q] pour déplacer le curseur vers la fonction que vous voulez utiliser. Pressez [FUNC] 0 (Sel) pour sélectionner les fonctions dont vous voulez obtenir le tableau des valeurs. Le signe égal des fonctions sélectionnées est en surbrillance. Vous pouvez sélectionner plusieurs fonctions en même temps.

Exemple : Utilisez les fonctions suivantes pour créer un tableau

Étape 1 : Après avoir stocké les fonctions, spécifiez leur statut graphique / non-

numérique. Y1 = 6 X² - X - 5 Y2 = 32 X Utilisez les paramètres suivants : Srt = -5, end = 5, ptch = 1

graphique. Cet affichage montre Y1 et Y2 sélectionnés.

TBLE R

T - F u n c : Y = Y 1 6 X ² - X - 5

Y 2 3 2 X

Y 3 = X - 1 1

Étape 2 : Pressez [FUNC] 1 (Table) ou [EXE] pour générer un tableau numérique.

Cet affichage montre le tableau numérique généré.

[FUNC] 1 (Table)

Étape 3 : Vous pouvez utiliser le curseur dans le tableau en utilisant les touches de

curseur ([p] [q] [t] [u]). Déplacer le curseur hors de l’écran fait défiler le tableau là où se trouve des cellules en haut, en bas, à gauche ou à droite.

[u]

[u][q] [q]

TBLE R

XY 1

u- 5 1 5 0

- 4 9 5

TBLE R

Y 1 = 6 X ² - X - 5 XY 1

- 5 u 1 5 0

- 4 9 5

TBLE R

Y 2 = 3 2 X XY 2

- 4 - 1 2 8

- 3 u - 9 6

- 5

1 5 0

- 9 6

Étape 4 : Pour retourner à la liste T-Func, pressez [FUNC] 0 (Form)

TBLE R

[FUNC] 0 (Form)

T - F u n c : Y = Y 1 6 X ² - X - 5

Y 2 3 2 X

Y 3 = X - 1 1

5 - 6 Editer un tableau

Après avoir généré un tableau numérique, vous pouvez ajouter, insérer ou supprimer des lignes d’un tableau existant en pressant [FUNC].

TBLE R

0 F o r m 1 I n s 2 A d d 3 G - C o n 4 L i s t 5 G - P l t 6 D i m 7 L M E M

Ins ... Insère une nouvelle ligne là où se situe le curseur Add ... Insère une nouvelle ligne sous la ligne où le curseur se situe

Pour supprimer une ligne là où le curseur se situe, pressez [DEL]

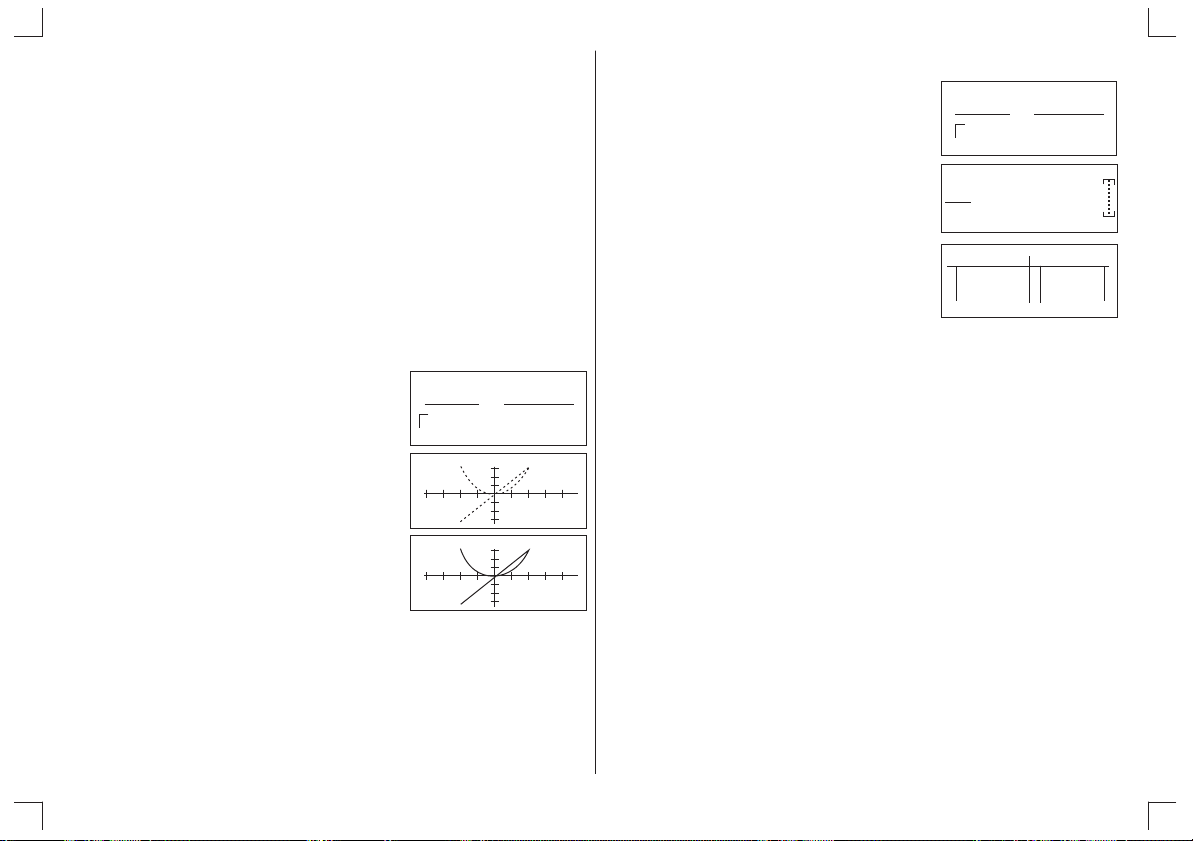
5 - 7 Afficher le graphique d’une fonction

Vous pouvez utiliser les deux touches de fonction suivantes pour produire un graphique à partir du tableau numérique affiché.

G-Con ... Graphique avec relevé de points connectés G-Plt ... Graphique avec relevé de points non connectés

Si l’on produit un graphique de tableau dont les valeurs ont été générées par plus d’une fonction, le graphique de toutes les fonctions sera affiché en même temps. Vous pouvez sélectionner les axes x- et y- grâce à la fenêtre V-WIN Pressez [GnT] pour retourner à l’écran du tableau numérique. Vous pouvez utiliser [GnT] pour permuter entre le graphique et son tableau, pourvu que vous n’effaciez pas le graphique. Pour revenir au menu des tableaux, pressez [2nd] [QUIT]

Exemple : Pour rendre en graphique les fonctions Y1 = 6 X² - X - 5 et Y = 32 X,

dont les tableaux de valeurs numériques se trouvent à l’écran, utilisez l’étendue suivante et les paramètres de fenêtre V-Window Srt = -5, end = 5, ptch = 1 Xmin = -10, Xmax = 10, Xscl = 2.5 Ymin = -150, Ymax = 150, Yscl = 50

TBLE R

XY 1

u- 5 1 5 0

- 4 9 5

TBLE R

- 5

[FUNC] 5 (G-Plt)

TBLE R

[FUNC] 3 (G-Con)

Exemple : Pour copier toutes les valeurs dans la colonne Y1 vers L4

TBLE R

Y 1 = 6 X ² - X - 5 XY 1

- 5 u 1 5 0

- 4 9 5

TBLE R

0 L 1 1 L 2 2 L 3

[FUNC] 7 (LMEM) [q]

3 L 4 4 L 5 5 L 6 6 L 7 7 L 8 8 N o n e

L 3 L 4

[EXE] [MODE] 4 [u] [u] [u]

L 4 ( 1 ) = 1 5 0

Note : Lorsque vous assignez les contenus d’un tableau numérique à une liste qui

possède déjà des nombres stockés, le contenu précédent de la liste sera remplacé.

1 5 0

1 1 u 1 5 0 1 5 9 5 1 3 5 2

5 - 8 Assigner les contenus d’un tableau numérique à une liste

Vous pouvez assigner une colonne de valeurs d’un tableau dans une liste spécifiée. Il vous suffit d’utiliser [t] et [u] pour déplacer le curseur vers la colonne dont vous voulez copier les valeurs. Le curseur peut se trouver dans n’importe quelle rangée de la colonne. On réalise l’opération de copie en pressant [FUNC] 7 (LMEM).

Chapitre 6 Fonctions de liste

6 - 1 Avant d’utiliser le mode liste

Dans le menu des modes de fonctionnement, sélectionnez l’otion LIST pour entrer en mode liste. S’affiche alors l’écran d’entrée des données dans une liste.

L 1 L 2

L 1 ( 1 ) =

6 - 2 Assigner des valeurs à une liste

Une liste est une sorte de réceptacle que vous pouvez utiliser pour stocker plusieurs données. Cette calculatrice vous permet d’entrer jusqu’à huit listes (L1 ~ L8) en mémoire, chaque liste pouvant utiliser jusqu’à 256 cellules. Leurs contenus peuvent être utilisés dans des calculs arithmétiques ou statistiques, ou pour des graphiques.

L 1 L 2

2 1 . 1 5

Cellule

L 2 = ( 5 ) = 4 5 2 3 5 8 7t

· Chaque cellule peut contenir jusqu’à six caractères (le signe négatif, la virgule décimale ou le symbole exponentiel prennent chacun un caractère).

· La valeur contenue dans la cellule sélectionnée apparaît en bas de l’écran.

· Vous pouvez utiliser [t] [u] pour vous déplacer entre les listes, et [p] [q]

pour vous déplacer entre les cellules d’un même tableau. L’écran défile automatiquement lorsque le curseur se trouve sur le côté.

Si le symbole “=” devient “-=”, “-=-é ou “=-”, cela signifie qu’il se trouve des entrées supplémentaires masquées à la droite ou la gauche de l’écran, ou les deux. Pressez [t] ou [u] pour déplacer le curseur dans une entrée.

2 2 7 . 5

Étape 2 : Pressez [EXE] pour l’enregistrer dans la liste. Le curseur se déplace

automatiquement vers la cellule en dessous pour la prochaine entrée. Continuez à entrer les valeurs 2 et 3.

[EXE] 2 [EXE] 3 [EXE]

L 1 L 2

L 1 ( 4 ) =

6 - 2 - 2 Pour entrer à la file une série de valeurs

Exemple : Pour entrer la série de valeurs suivante dans les cellules de

Étape 1 : Utilisez les touches de curseur pour déplacer le pointeur vers le nom de la

[u]

Étape 2 : Pressez [2nd] [ { } ], puis entrez les valeurs que vous souhaitez. Rappelez-

[2nd] [ { } ] 5 [ ] 6 [ ] 7 [ ] 8

L2 {5, 6, 7, 8}

liste.

vous de presser [ ] entre chacune des valeurs.

, , ,

L 1 u L 2

1 2 3

L 1 u L 2

1 2

{ 5 , 6 , 7 , 8 t

Étape 3 : Pressez [EXE] pour enregister toutes les valeurs dans votre liste.

[EXE]

L 1 L 2

L 2 ( 1 ) = 5

1 u 5 26 37

6 - 2 - 1 Pour entrer des valeurs unes à unes

Exemple : Pour assigner les valeurs {1, 2, 3} aux cellules de la liste L1

Étape 1 : Entrez une valeur

L 1 L 2

L 1 ( 1 ) = 1 t

6 - 3 Editer et réaménager les listes

Après l’entrée des données, presser [FUNC] affiche le menu d’édition et d’aménagements des listes.

0 S r t - A 1 S r t - D 2 D e l - A 3 I n s 4 L i s t 5 D i m 6 F i l l 7 S e q

Srt-A ... Trier les listes en ordre ascendant Srt-D ... Trier les listes en ordre descendant Del-A ... Supprimer toutes les cellules dans une liste Ins ... Insérer une nouvelle cellule

6 - 3 - 1 Pour éditer les valeurs d’une liste

(A) Pour changer la valeur d’une cellule

Utilisez [t] ou [u] pour déplacer le curseur vers la cellule dont vous voulez changer la valeur. Entrez la nouvelle valeur et pressez [EXE] pour remplacer les anciennes données par les nouvelles.

Exemple : Modifier la liste 3 (1;3;5;7;9;12) par (1;3;5;6;9;12)

Étape 1 : Entrez le contenu de la liste 3 (1;3;5;7;9;12)

1 [EXE] 3 [·] 5 [EXE] 7 [EXE] 9 [EXE] 12 [EXE]

Étape 2 : A l’aide des touches de curseur déplacez le pointeur vers la cellule que vous

voulez modifier

[p] [p] [p]

Étape 3 : Entrez la nouvelle valeur et pressez [EXE] pour remplacer l’ancienne valeur

par la nouvelle

6 [EXE] [p]

(B) Pour supprimer une cellule Exemple : Pour supprimer L2 (1) = 5

Étape 1 : Utilisez les touches de curseur pour déplacer le pointeur vers la cellule que

vous voulez supprimer.

[u]

L 2 L 3

29 1 2

L 3 ( 6 ) =

L 2 L 3

4 u 7 29

L 3 ( 3 ) = 7

L 2 L 3

4 u 6 29

L 3 ( 3 ) = 6

L 1 L 2

1 u 5 26

L 2 ( 1 ) = 5

3 7

1 2

Étape 2 : Pressez [DEL] pour supprimer la cellule sélectionnée et tout ce qui se

trouve plus bas s’élève d’un cran.

[DEL]

Note : L’opération de suppression de cellules ci-dessus n’affecte pas les cellules

des autres listes. Si les données dont vous voulez supprimer les cellules sont d’une manière quelconques liées aux données des cellules voisines, supprimer une cellule peut causer un faux alignement de valeurs liées.

L 1 L 2

1 u 6 27

L2 (1) = 6

3 8

Exemple : Pour supprimer toutes les cellules dans L2

Étape 1 : Utilisez les touches de curseur pour déplacer le pointeur vers le nom de la

liste dont vous voulez supprimer les cellules

[p] ~ [p]

Étape 2 : Pressez [FUNC] 2 (Del-A). Le menu des fonctions change pour confirmer si

vous voulez supprimer toutes les cellules dans la liste. Sélectionnez “Y” pour supprimer ou “N” pour abandonner l’opération sans rien supprimer.

[FUNC] 2 (Del-A) [u]

L 1 u L 2

1 6 27 3 8

D E L - A L L : N Y

Étape 3 : Pressez [EXE] pour supprimer toutes les cellules dans la L2

[EXE]

L 1 L 2

1 u 2

L 2 ( 1 ) =

(D) Pour insérer une nouvelle cellule

Exemple : Pour insérer une nouvelle valeur 6.5 à L2 (2)

Étape 1 : Utilisez les touches de curseur pour déplacer le pointeur vers l’endroit où

vous voulez insérer la nouvelle valeur.

[q]

Étape 2 : Pressez [FUNC] 3 (Ins), entrez la valeur et pressez [EXE]. Tout ce qui se

trouve en dessous est décalé vers le bas d’un cran.

[FUNC] 3 (Ins) 6.5 [EXE]

Note : L’opération d’insertion des cellules ci-dessus n’affecte pas les cellules des

autres listes. Si les cellules où vous voulez insérer une donnée sont liées d’une manière quelconque, insérer une cellule peut causer un faux alignement de valeurs liées.

L 1 L 2

1 6 2 u 7

L 2 ( 1 ) =

L 2 ( 3 ) = 7

3 8

L 1 L 2

1 6 2 6 . 5 3 u 7

6 - 3 - 2 Pour trier les valeurs d’une liste

Vous pouvez trier les listes soit en ordre croissant soit en ordre décroissant. La position en cours du curseur n’a pas d’influence sur les procédures qui suivent.

(A) Pour trier une liste unique

· Ordre croissant

Exemple : Pour trier les cellules dans la liste L3 ( 11, 15, 13) en ordre

Étape 1 : Quand les listes sont à l’écran, pressez [FUNC] 0 (Srt-A). La question

[FUNC] 0 (Srt-A)

Étape 2 : Entrez 1 pour indiquer que vous ne voulez trier qu’une liste. En réponse la

croissant

“HowMany L ?” Apparaît pour vous demander combien de listes vous voulez trier.

question “Sel L ?” Vous demande de sélectionner la liste que vous voulez trier.

u L 3 L 4

H o w M a n y L ? =

1 1 2 1 1 5 3 0 1 3 1 8

1 [EXE]

Étape 3 : Entrez ici 3 pour spécifier que vous voulez trier la liste 3. Les valeurs dans la

liste 3 sont triées en ordre croissant.

3 [EXE]

u L 3 L 4

S e l L ? =

u L 3 L 4

1 1 2 1 1 5 3 0 1 3 1 8

1 1 2 1 1 3 3 0 1 5 1 8

· Odre décroissant

Utilisez la même procédure que celle du tri par ordre croissant. La seule différence est que vous devez presser 1 (Srt-D) au lieu de 0 (Srt-A)

(B) Pour trier des listes multiples

Vous pouvez lier plusieurs listes pour un tri, de sorte que toutes leurs cellules soient réarrangées selon le tri d’une liste de base. La liste de base est triée soit en ordre croissant soit en ordre décroissant, tandis que les cellules des listes liées sont arrangées pour que la relation respective de toutes les cellules soit maintenue.

· Ordre croissant

Exemple : Pour trier les cellules de L3 (11, 15, 13) en ordre croissant et

Étape 1 : Quand les listes sont à l’écran, pressez [FUNC] 0 (Srt-A).

[FUNC] 0 (Srt-A)

Étape 2 : Vous voulez trier une liste de base à une autre liste soit 2 listes donc vous

2 [EXE]

Étape 3 : Entrez 3 pour spécifier la liste de base L3. En réponse la question “2nd L ? =”

réarranger les cellules de L4 (21, 30, 18)

La question “HowMany L ?” Apparaît pour vous demander combien de listes vous voulez trier.

entrez 2. En réponse la question “Base L ?” Vous demande de sélectionner la liste de base que vous voulez trier.

vous demande de sélectionner la liste que vous souhaitez lier à la liste de base.

u L 3 L 4

H o w M a n y L ? =

u L 3 L 4

B a s e L ? =

1 1 2 1 1 5 3 0 1 3 1 8

3 [EXE]

Étape 4 : Vous spécifiez par exemple la liste 4. Les valeurs de la liste 3 sont triées en

ordre croissant et celles de la liste 4 sont aussi réarrangées pour garder la même relation avec des cellules de la liste 3.

4 [EXE]

u L 3 L 4

2 n d L ? =

u L 3 L 4

1 1 2 1 1 5 3 0 1 3 1 8

1 1 2 1 1 3 1 8 1 5 3 0

· Ordre décroissant

Utilisez la même procédure que celle du tri par ordre croissant. La seule différence est que vous devez presser 1 (Srt-D) au lieu de 0 (Srt-A).

6 - 4 Manipuler des données de liste

Les données des listes peuvent être utilisées dans des calculs arithmétiques et de fonction. Il existe aussi toute une série de fonctions de manipulation de listes, qui vous permette de réaliser tout ce qui suit :

· Compter le nombre de valeurs d’une liste (Dim)

· Remplacer toutes les valeurs de cellule par la même valeur (Fill)

· Générer une séquence de nombres (Seq)

· Trouver la valeur minimum d’une liste (Min)

· Trouver la valeur maximum d’une liste (MAx)

· Trouver laquelle de deux listes contient la valeur minimum (Min)

· Trouver laquelle de deux listes contient la valeur maximum (Max)

· Calculer la moyenne des valeurs d’une liste (Avg)

· Calculer la moyenne des valeurs pondéres d’une liste (Avg)

· Calculer la médiane d’une liste (Med)

· Calculer la médiane des valeurs pondérées d’une liste (Med)

· Calculer la somme des valeurs d’une liste (Sum)

Vous pouvez utiliser les fonctions de manipulations des données de liste en mode MAIN, STAT, LIST, TABLE ou PROG. Pour accéder à ces fonctions pressez [FUNC] dans tous les cas. Toutes les syntaxes suivantes sont données en mode MAIN.

(A) Compter le nombre de valeurs (Dim)

[ FUNC ] 1 ( Dim ) [ FUNC ] 0 ( List ) < nom de liste 1~8 > [ EXE ]

· Le nombre de cellules contenant les données d’une liste est appelé sa “

Dimension (Dim)”

Exemple : Compter le nombre de valeurs dans la liste 1 (1, 2, 3)

[ON/CL] [FUNC] 1 (Dim) [FUNC] 0 (List) 1 [EXE]

Exemple : En mode LIST, utilisez la fonction Dim pour compter le nombre de

valeurs de la liste 1 (1, 2, 3)

[FUNC] 5 (Dim) [FUNC] 4 (List] 1

D i m ( L i s t 1 )

L 2 ( 1 ) = D i m ( L i s t 1 )

[EXE]

L 2 ( 1 ) = 3

L 1 L 2

1 u 2 3

L 1 L 2

1 u 3 2 3

(B) Remplacer toutes les valeurs de cellules par la même valeur (Fill)

[ FUNC ] 2 ( Fill ) < valeur > [ ] [ FUNC ] 0 ( List ) < nom de liste 1 ~8 > [ EXE ]

Note : Le résultat de cette opération est aussi enregistré dans la mémoire Ans.

Exemple : Pour remplacer toutes les valeurs dans la liste 1 (1, 2, 3) par 3

[ON/CL] [FUNC] 2 (Fill) 3 [ ] [FUNC] 0 (List) 1

[EXE]

F i l l ( 3 , L i s t 1 t

A n s

u 3

L ( 1 ) = 3

3 3

[ FUNC ] 3 (Seq) < expression > [ ] < nom de la variable > [ ] < valeur de départ > [ ] < valeur de fin > [ ] < valeur de pente > [EXE]

, ,

Note : Le résultat de cette opération est aussi enregistré dans la mémoire Ans.

Exemple : Pour entrer la séquence de nombres 12 ², 15 ², 18 ² dans une liste,

utilisez les paramètres suivants : Variable : x Valeur de départ : 12 Valeur de fin : 18 Incrémentation : 3

[ON/CL] [FUNC] 3 (Seq) [X,T] [X²] [ ] [X,T] [ ] 12

, ,

[ ] 18 [ ] 3

, ,

[EXE]

Exemple : En mode LIST, utilisez Seq pour générer la séquence de nombres

Étape 1 : Utilisez les touches de curseur pour déplacer le pointeur vers le nom de la

( 5² + 1 ; 5,1² + 1 ; 5,2² + 1 ; 5,3² + 1 ; 5,4² + 1 ; 5,5² + 1) dans la liste 3.

liste que vous souhaitez sélectionner.

S e q ( X², X , 1 2, 1 8, 3 ) t

A n s

u 1 4 4

L ( 1 ) = 1 4 4

[u] ~ [u] [p] ~ [p]

Étape 2 : Dans le menu FUNC sélectionnez l’option Seq puis entrez les paramètres de la séquence : Seq ( X² + 1, X, 5, 5.5, 0.1)

[FUNC] 7 (Seq) [X,T] [x²] [+] 1 [ ] [X,T] [ ] 5 [ ]

5 [·] 5 [ ] 0 [ ·] 1

, , ,

S e q ( X² + 1 , X , 5 , 5 . 5 , 0 . 1 )

[EXE]

L 3 ( 1 ) = 2 6

2 2 5 3 2 4

L 2 u L 3

L 2 L 3

3 u 2 6 2 7 . 0 1 2 8 . 0 4

(D) Pour trouver la valeur minimum d’une liste (Min)

[MATH] 0 (Min) [FUNC] 0 (List) < nom de liste 1~8 > [EXE]

Exemple : Pour trouver la valeur minimum dans la liste 1 (1, 2, 3)

[ON/CL] [MATH] 0 (Min) [FUNC] 0 (List) 1 [EXE]

Exemple : En mode LIST, déterminez le minimum de la liste 4 où

List 4 (sin20, cos20, sin30, cos30, tan20, tan30) à l’aide de la fonction Min.

M i n ( L i s t 1)

Étape 1 : Placez le curseur dans la liste 4, entrez le contenu de cette liste

[SIN] 20 [EXE] [COS] 20 [EXE] [SIN] 30 [EXE] [COS] 30 [EXE] [TAN] 20 [EXE] [TAN] 30 [EXE]

L 3 L 4 3 0 . 1 6 2 . 2 3 7 2 3 1 . 2 5 - 6 . 4 0 5

L 4 ( 7 ) =

Étape 2 : Choisissez l’option Min dans le menu MATH et appliquez la à la liste 4

[MATH] 0 (Min) [FUNC] 4 (List) 4

[EXE]

(E) Pour trouver la valeur maximum d’une liste (Max)

Utilisez la même procédure que pour trouver la valeur minimum, sauf qu’il faut presser 1 (Max) au lieu de 0 (Min)

L 3 L 4 3 0 . 1 6 2 . 2 3 7 2 3 1 . 2 5 - 6 . 4 0 5

L 4 ( 7 ) = M i n ( L i s t 4 )

L 4 ( 8 ) =

L 3 L 4 3 1 . 2 5 - 6 . 4 0 5

- 6 . 4 0 5

(F) Pour trouver laquelle de deux listes contient la valeur minimum (Min)

[MATH] 0 (Min) [FUNC] 0 (List) < non de liste 1-8 > [ ] [FUNC] 0 (List) < nom de liste 1-8 > [EXE]

Les deux listes doivent contenir le même nombre de valeurs. Dans le cas contraire une erreur survient.

Note : Le résultat de cette opération est aussi enregistré dans la mémoire Ans.

Exemple : Pour trouver si la liste 1 (1, 2, 3) ou la liste 2 (5, 6, 7) contient la

[ON/CL] [MATH] 0 (Min) [FUNC] 0 (List) 1 [ ] [FUNC] 0 (List) 2

[EXE]

valeur minimum.

M i n ( L i s t 1 , L i s t 2 )

A n s

u 1

L ( 1 ) = 1

2 3

(G) Pour trouver laquelle de deux listes contient la valeur maximum (Max)

Utilisez la même procédure que pour la valeur minimum, sauf qu’il faut 1 (Max) au lieu de 0 (Min).

(H) Pour calculer la moyenne des valeurs d’une liste (Avg)

[ MATH ] 4 (Avg ) [ FUNC ] 0 ( List ) < nom de liste 1-8 > [ EXE ]

Exemple : Pour calculer la moyenne des valeurs dans la liste 1 (1, 2, 3)

[ON/CL] [MATH] 4 (Avg) [FUNC] 0 (List) 1 [EXE]

A v g ( L i s t 1 )

Exemple : En mode LIST, calculer la moyenne des valeurs de la liste 1 (1,2,3)

Étape 1 : Entrez le contenu de la liste 1

1 [EXE] 2 [EXE] 3 [EXE]

L 1 L 2

L 1 ( 4 ) =

Étape 2 : Utilisez l’option Avg pour calculer la moyenne des valeurs de la liste 1

[MATH] 4 (Avg) [FUNC] 4 (List) 1

[EXE] [p]

(I) Pour calculer la moyenne des valeurs d’une liste pondérées par les valeurs d’une seconde liste

[ MATH ] 0 ( Avg ) [ FUNC ] 0 ( List ) < nom de liste 1-8 (données) > [ ] [ FUNC ] 0 ( List ) < nom de liste 1-8 (fréquence) > [ EXE ]

Cette procédure utilise deux listes : une qui contient les valeurs et une qui contient la fréquence de chaque valeur. Les deux listes doivent contenir le même nombre de valeurs. Dans le cas contraire une erreur survient.

L 1 L 2

L 1 ( 4 ) = A v g ( L i s t 1 )

u 2

L 1 ( 4 ) = 2

L 1 L 2

Exemple : Pour calculer la moyenne des valeurs dans la liste 1 (1, 2, 3) dont

[ON/CL] [MATH] 4 (Avg) [FUNC] 0 (List) 1 [ ] [FUNC] 0 (List) 2 [EXE]

la fréquence est indiquée par la liste 2 (5, 6, 7)

A v g ( L i s t 1 , L i s t 2 ) 2 . 1 1 1 1 1 1 1 1 1

(J) Pour calculer la médiane des valeurs d’une liste (Med)

[ MATH ] 2 ( Med ) [ FUNC ] 0 ( List ) < nom de liste 1-8 > [ EXE ]

Exemple : Pour calculer la médiane des valeurs dans la liste 1 (1, 2, 3)

[ON/CL] [MATH] 2 (Med) [FUNC] 0 (List) 1 [EXE]

Exemple : En mode LIST, déterminez la valeur médiane de la liste 5 (2, 3.5, 3.5

4 , 4, 4 ,5, 6, 7, 7, 8, 9) = 4.5

Étape 1 : Entrez le contenu de la liste 5

M e d ( L i s t 1 )

2 [EXE] 3 [·] 5 [EXE] 3 [·] 5 [EXE] 4 [EXE] 4 [EXE] 4 [EXE] 5 [EXE] 6 [EXE] 7 [EXE] 7 [EXE] 8 [EXE] 9 [EXE]

Étape 2 : Utilisez la fonction Med pour déterminer la médiane de la liste 5

L 5 ( 1 3 ) =

[MATH] 2 (Med) [FUNC] 4 (List) 5 [EXE]

L 5 ( 1 4 ) =

(K) Pour calculer la médiane des valeurs d’une liste pondérée par les valeurs

d’une seconde liste

[ MATH ] 2 ( Med ) [ FUNC ] 0 ( List ) < nom de liste 1-8 (données) > [ ] [FUNC ] 0 (List ) < nom de liste 1-8 (fréquence) > [ EXE ]

Cette procédure utilise deux listes : une qui contient les valeurs et une qui contient la fréquence de chaque valeur. Les deux liste doivent contenir le même nombre de valeurs. Dans le cas contraire une erreur survient.

L 4 L 5

8 9 u

L 4 L 5

9 4 . 5 u

Exemple : Pour calculer la médiane des valeurs dans la liste 1 (1, 2, 3) dont la

[ON/CL] [MATH] 2 (Med) [FUNC] 0 (List) 1 [ ] [FUNC] 0 (List) 2 [EXE]

fréquence est indiquée par la liste 2 (5, 6, 7)

M e d ( L i s t 1 , L i s t 2 ) 2

(L) Pour calculer la somme des valeurs d’une liste (Sum)

[ MATH ] 3 ( Sum ) [ FUNC ] 0 ( List ) < nom de liste 1-8 > [ EXE ]

Exemple : Pour calculer la somme des valeurs de la liste 1 (1, 2, 3)

[ON/CL] [MATH] 3 (Sum) [FUNC] 0 (List) 1 [EXE]

S u m ( L i s t 1 ) 6

6 - 5 Calculs aritmétiques utilisant des listes

Vous pouvez exécuter des calculs arithmétiques en utilisant deux listes ou une liste et une valeur numérique.

Valeur numérique de la liste Valeur numérique de la liste = liste

Un calcul impliquant deux listes effectue la même opération entre les cellules correspondantes. C’est pourquoi une erreur survient si les deux listes n’ont pas le même nombre de valeurs.

Exemple : Pour multiplier la liste 3 ( 11, 13, 15 ) par la liste ( 3, 2, 5 )

[ON/CL] [FUNC] 0 (List) 3 [x] [2nd] [ { } ] 3

[ ] 2 [ ] 5 [EXE]

Exemple : En mode LIST, effectuer les calculs suivants :

Étape 1 : Entrez le contenu de la liste 5; déplacez le pointeur vers le nom de la liste où

Liste 6 = Liste 5 x 2 et Liste 7 = Liste 6 + Liste 5 où Liste 5 ( 1, 2, 3 )

vous souhaitez placer le résultat du calcul Liste 5 x 2, puis effacez-la.

1 [EXE] 2 [EXE] 3 [EXE]

[u] [p] ~ [p]

[FUNC] 2 (Del-A) [u]

[EXE] [p]

A n s

u 3 3

2 6

L ( 1 ) = 3 3

L 5 ( 4 ) =

D E L - A L L = N Y

7 5

L 5 L 6

L 5 u L 6

1 7 28 3 9

L 5 u L 6

1 2 3

6 - 5 - 1 Pour insérer une liste dans un calcul

Il y a deux méthodes que vous pouvez utiliser pour insérer une liste dans un calcul.

(A) Pour entrer une liste donnée par son nom

Pressez [FUNC] 0 (List) et entrez le numéro de la liste que vous souhaitez utiliser

Exemple : Pour entrer la liste 3

[FUNC] 0 (List) 3

(B) Pour entrer directement une liste de valeurs

Vous pouvez aussi entrer directement une liste de valeurs en utilisant [2nd] [ { } ] et

[ ] . La liste résultant est enregistrée dans la mémoire Ans.

L i s t 3 t

Étape 2 : Utilisez la touche [FUNC] pour effectuer l’opération voulue

[FUNC] 4 (List) 5 [x] 2

[EXE]

Étape 3 : Déplacez le pointeur vers L7, effacez le contenu de cette liste et effectuez

l’opération voulue

L 5 u L 6

1 2 3

L i s t 5 x 2

L 5 L 6

1 u 2 24 3 6

L 6 ( 1 ) = 2

[u] [p] [FUNC] 2 (Del-A) [u] [EXE] [p]

[FUNC] 4 (List) 5 [+] [FUNC] 4 (List) 6

[EXE]

Utilisez “g” pour assigner les contenus d’une liste à une autre liste.

L 6 u L 7

2 4 6

L 6 u L 7

2 4

L i s t 5 + L i s t 6

L 7 ( 1 ) = 3

L 6 L 7

2 u 3 4 6 6 9

Exemple : Pour assigner les contenus de la liste 3 (11, 13, 15 ) à la liste 1

[FUNC] 0 (List) 3 [SAVE]

[EXE] [FUNC] 0 (List) 1 [EXE]

[MODE] 4

Note : Au lieu de l’opération [FUNC] 0 (List) 3 dans la procédure ci-dessus, vous

pouvez entrer [2nd] [ { } ] 11 [ ] 13 [ ] 15 [ u]

, ,

g g A B C D E F G H I J K L M N O P Q

L i s t 3 g L i s t 1

u 1 1 5

L 1 ( 1 ) = 1 1

D o n e

L 1 L 2

1 3 6 1 5 7

Exemple : Pour assigner les valeurs de la liste en mémoire Ans à la liste 5

[FUNC] 0 (List) [2nd] [Ans] [SAVE]

g g A B C D E F G H I J K L M N O P Q

[EXE] [FUNC] 0 (List) 5 [EXE]

L i s t A n s g L i s t 5

[MODE] 4 [u] [u] [u] [u]

L 5 ( 1 ) = 1 1

(D) Pour entrer une seule valeur de cellule de liste dans un calcul

Vous pouvez extraire la valeur d’une cellule spécifique d’une liste et l’utiliser dans un calcul. Spécifiez le numéro de cellule entre des parenthèses carrées ( [ ] ).

D o n e

L 4 L 5

2 1 u 1 1

3 0 1 3

1 8 1 5

Exemple : Pour calculer la racine carrée de la valeur stockée dans L3(1) = 144

[Ö] [FUNC] 0 (List) 3 [2nd] [ [ ] ] 1 [EXE]

(E) Pour remplacer une cellule spécifique

Vous pouvez remplacer une cellule spécifique dans une liste. La valeur précédemment stockée dans la dite cellule est alors remplacée par la nouvelle valeur.

Ö ( l i s t 3 [ 1 ] )

Exemple : Pour remplacer la cellule 4 de la liste 3 en tant que valeur 17

[ON/CL] 17 [SAVE] (g) [EXE] [FUNC] 0 (List) 3 [2nd] [ [] ] 4 [EXE]

1 7 g L i s t 3 [ 4 ]

6 - 5 - 2 Pour rappeler les contenus d’une liste

(A) Pour rappeler une liste spécifique par son nom

Pressez [FUNC] 0 (List) et entrer le numéro de la liste que vous voulez rappeler. L’opération affiche le contenu de la liste voulue et les enregistre aussi dans la mémoire Ans. Vous pouvez alors utiliser les contenus de la mémoire Ans dans un calcul.

Exemple : Pour invoquer les contenus de la liste 3 (11, 13, 15)

[FUNC] 0 (List) 3 [EXE]

A n s

u 1 1

L ( 1 ) = 1 1

1 3

1 5

(B) Pour utiliser la liste en mémoire Ans dans un calcul

Exemple : Pour multiplier le contenu de la liste en mémoire Ans par 6

[FUNC] 0 (List) [2nd] [Ans] [x] 6 [EXE]

A n s

u 6 6

7 8

L ( 1 ) = 6 6

9 0

6 - 5 - 3 Pour appliquer une fonction en graphique en utilisant une liste

Lorsque vous utilisez les fonctions de graphique de la calculatrice, vous pouvez entrer une fonction telle que Y1 = List1 X. Si la liste 1 contient les valeurs 1, 2, 3 cette fonction va produire trois graphiques : Y = X, Y = 2X, Y = 3X

Exemple : Utilisez les paramètres de fenêtre V-Window suivants pour le

[GRAPH] 0 (Cls) [EXE] [GRAPH] 6 (Y = ) [FUNC] 0 (List) 1 [X,T] [EXE]

Exemple : Utilisez les paramètres de fenêtre V-Window suivants pour le

[GRAPH] 0 (Cls) [EXE] [GRAPH] 6 (Y=) [X,T] [Ù] [FUNC] 0 (List) 1 [EXE]

graphique Y1 = List1 X, où la liste 1 (1, 2, 3) Xmin = -10, Xmax = 10, Xscl = 2 Ymin = -10, Ymax = 10, Yscl = 2

graphique Y2 = X où List 1 ( 1, 2, 3 ) : Xmin = -10, Xmax = 10, Xscl = 2 Ymin = -10, Ymax = 10, Yscl = 2

Ù List1

TBLE R

6 - 5 - 4 Pour entrer des calculs scientifiques dans une liste

Vous pouvez entrer des nombres résultants de calculs de fonctions scientifiques dans une liste en passant par l’intermédiaire d’un tableau. Pour ce faire :

· Créer un tableau en mode TABLE, correspondant aux calculs souhaités

· Copier le dans la liste voulue grâce à LMEM

Exemple : En mode TABLE créer un tableau de valeurs de la fonction

Y3 = ÖX + 1 avec les paramètres suivants : Xsrt = 0, Xend = 10, Xpcth = 0.5 Copier ensuite ce tableau dans la liste 8 en utilisant LMEM

[MODE] 3 (TABLE) [q] [q] [q] [Ö] [X,T] [u] [+] [1] [EXE] [p]

[FUNC] 2 (Range) 0 [EXE] 10 [EXE] 0 [·] 5 [EXE]

[EXIT] [EXE] [u]

[FUNC] 7 (LMEM) 7 (L8) [MODE] 4 (List) [u] [u] [u] [u] [u] [u] [u]

6 - 5 - 5 Pour effectuer des calculs de fonctions scientifiques en utilisant une

liste.

Les listes peuvent être utilisées dans des calculs de fonctions scientifiques. La machine effectuera alors le calcul de cette fonction avec chacune des valeurs de la liste. Lorsque le calcul produit une liste en tant que résultat, celle-ci est enregistrée dans la mémoire Ans.

TBLE R

T - F u n c : Y = Y 2 : Y 3 Ö ( x ) + 1

Y 4 =

TBLE R

T a b l e R a n g e X S r t = 0 e n d = 1 0 p t c h = 0 . 5

TBLE R

Y 3 = Ö ( x ) + 1 XY 3

0u 1 0 . 5 1 . 7 0 7 1

L 5 L 6

L 8 ( 1 ) = 1

3 u 1

6 1 . 7 0 7 1

9 2

Exemple : Utiliser la liste 3 (10, 100, 1000) pour exécuter log (List 3)

[LOG] [FUNC] 0 (List) 3 [EXE]

Exemple : Utiliser la liste 1 (1, 2, 3) et la liste 2 (5, 6, 7) pour exécuter liste 1

(cela crée une liste avec les résultats 1 , 2 , 3 ).

[FUNC] 0 (List) 1 [Ù] [FUNC] 0 (List) 2 [EXE]

A n s

u 1

L ( 1 ) = 1

567

A n s

u 1

2 1 8 7

L ( 1 ) = 1

6 4

liste2

Chapitre 7 Calculs en mode base-n

7 - 1 Avant de commencer un calcul en base binaire, octal, décimal ou hexadécimal

Vous pouvez utiliser le mode base-n pour effectuer des calculs pour des valeurs binaires, octales, décimales et hexadécimales. Vous pouvez aussi convertir entre les systèmes numériques et exécuter des opérations logiques. Si vous essayez d’entrer une valeur invalide pour le système numérique (binaire, octal, décimal, hexadécimal) que vous êtes en train d’utiliser, la calculatrice affiche un message d’erreur (SYNTAX Er). Voici les nombres utilisés dans chaque système numérique. Base binaire : 0, 1 Base octale : 0, 1, 2, 3, 4, 5, 6, 7 Base décimale : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Base hexadécimale : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, /A, IB, IC, ID, IE, IF En mode base-n, vous pouvez entrer les caractères alphabétiques (/A, IB, IC, ID, IE, IF) utilisés dans les nombres hexadécimaux en pressant les touches [A]~[F]. Ces caractères alphabétiques (/A, IB, IC, ID, IE, IF) sont affichés de manière distincte des caractères de texte : Texte normal : A, B, C, D, E, F Valeurs hexadécimales : /A, IB, IC, ID, IE, IF Sélectionnez le mode base-n dans le menu des modes de fonctionnement pour entrer le mode en base-n. S’affiche alors l’écran ci dessous :

Système numérique en cours

0 d 1 h 2 b 3 o

d ... Choisir la base décimale pour l’entrée suivante h ... Choisir la base hexadécimale pour l’entrée suivante b ... Choisir la base binaire pour l’entrée suivante o ... Choisir la base octale pour l’entrée suivante

Utilisez-les pour spécifier la base de chaque valeur que vous entrez.

Exemple : Utilisez la touche [dhbo] pour entrer A alors que la base de

calcul choisie est la base binaire. Faites de même avec 7 et 5

810

[2nd] [SYSTEM] [EXE] 2 (Bin)

[EXIT] [dhbo] [u]

[EXE] [A] [EXE]

B A S E : B i n

0 d 1 h 2 b 3 o

h A

1 0 1 0

(A) Pour spécifier le système numérique en cours

Pressez [2nd] [SYSTEM] pour afficher le menu.

B A S E : D e c

Dec ... Choisir la base décimale comme système numérique Hex ... Choisir la base hexadécimale comme système numérique Bin ... Choisir la base binaire comme système numérique Oct ... Choisir la base octale comme système numérique

(B) Pour spécifier le système numérique dans lequel est exprimé chaque

entrée.

Pressez [dnbo] pour afficher le menu suivant :

[EXE]

0 D e c 1 H e x 2 B i n 3 O c t

o 7

[ON/CL] [dhbo] 3 (0) 7 [EXE]

d 5

[ON/CL] [dhbo] 0 (d) 5 [EXE]

Chaque système numérique peut afficher un nombre de chiffres précis.

1 1 1

1 0 1

Système numérique Nombre de chiffres affichés

Binaire Jusqu’à 32 chiffres ( 8 chiffres x 4 blocs )

Octal Jusqu’à 11 chiffres

Décimal Jusqu’à 10 chiffres

Hexadécimal Jusqu’à 8 chiffres

7 - 2 Convertir une valeur affichée d’un système numérique vers un autre

Exemple : Pour convertir “1 IF ” en sa valeur décimale et octale, quand le

système numérique par défaut est décimal.

[2nd] [SYSTEM] [EXE] 0 (Dec)

[EXIT] [dhbo] 1 (h) 1 [F] [EXE]

B A S E : D e c

h 1 IF

3 1

D H B O

1 b 1 1 1 1 0 0 1 1

[p] ¯

D H B O

4 b 1 0 0 1 1 0 0 1

Exemple : 4777 = 1001010101001

10 2

[2nd] [SYSTEM] [EXE] 2 (Bin)

[EXIT] [dhbo] 0 (d) 4777 [EXE]

D H B O

[p]

2 b 1 0 1 0 1 0 0 1

D H B O

[p]

3 b 0 0 1 1 0 0 1 0

1er bloc second bloc

B A S E : B i n

h 4 7 7 7

1 0 1 0 1 0 0 1

1 0 0 1 0

[dhbo] [u] [u] [u]

Donc 1IF = 31 = 37

16 10 8

D H B O

3 7

7 - 3 Fonction de bloc

Un résultat en base binaire qui dépasse 8 chiffres sera affiché sous forme de blocs. Le maximum de 32 chiffres s’affiche en 4 blocs de 8 chiffres.

Bloc 4 1 0 0 1 1 0 0 1 Bloc 3 0 0 1 1 0 0 1 0 Bloc 2 1 0 1 0 1 0 0 1 Bloc 1 1 1 1 1 0 0 1 1

En mode binaire, le bloc 1 (1b) est affiché immédiatement apès le calcul. Les autres blocs (2b ~ 4b) s’affichent en pressant [p].

7 - 4 Opérations arithmétiques

Exemple : Pour calculer “1234 + 1 IEIF ¸ 24 ” et afficher la valeur octale

du résultat.

10 16

[2nd] [SYSTEM] [EXE] 3 (Oct)

[EXIT] [dhbo] 0 (d) 1234 [+] [dhbo] 1 (h) 1 [E] [F] [¸] [dhbo] 3 (o) 24 [EXE]

B A S E : O c t

D 1 2 3 4 + h 1 IE IF ¸ o 2 4

2 3 5 2

7 - 5 Valeurs négatives et opérations logiques

Pressez [2nd] [TEST] pour afficher un menu d’opérateurs négatifs et logiques.

0 N e g 1 N o t 2 A n d 3 O r 4 N a n d 5 X o r 6 X n o r

Neg ... Négation Not ... NON logique And ... ET logique Or ... OU logique Nand ... NON ET logique Xor ... OU EXCLUSIF Xnor ... Négation de Xor logique logique

(A) Valeurs négatives

Exemple : Pour déterminer la négation de 3/A

[2nd] [SYSTEM] [EXE] 1 (Hex)

[EXIT] [2nd] [TEST] 0 (Neg) [dhbo] 1 (h) 3 [/A] [EXE]

B A S E : H e x

N e g h 3 /A

IF IF IF IF IF IF IC 6

(B) Opérations logiques

Exemple : Pour afficher le résultat de “1010 , And (A Or 7 )” en valeur

binaire.

[2nd] [SYSTEM] [EXE] 2 (Bin)

16 16

B A S E : B i n

[EXE]

[ON/CL] [dhbo] 2 (b) 10 [VARS] 3 (Or) [dhbo] 1 (h) [F] [EXE]

[ON/CL] [dhbo] 3 (o) 61 [VARS] 1 (Not) [dhbo] 0 (d) 127

[EXE]

b 1 0 O r h IF 1 1 1 1

0 6 1 N o t d 1 2 7

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 0 0 0 0 0 0 0

[EXIT] [dhbo] 2 (b) 1010 [2nd] [TEST] 2 (And) [ ( ) ] [dhbo] 1 (h) [A] [2nd] [TEST] 3 (Or) [dhbo] 1 (h) 7 [EXE]

Exemple : Choisissez la base de calcul binaire et effectuez les calculs

suivants : Neg d 7, b 10 Or h F, o 61 Not d 127

[2nd] [SYSTEM] [EXE] 2 (Bin)

[EXIT] [VARS] 0 (Neg) [dhbo] 0 (d) 7

b 1 0 1 0 A n d ( h /A O r h 7 ) 1 0 1 0

B A S E : B i n

N e g d 7

Chapitre 8 Calculs statistiques et graphiques

8 - 1 Avant d’exécuter des calculs statistiques

Dans le menu des modes de fonctionnement, sélectionnez STAT pour entrer en mode STAT. S’affiche alors une liste de données statistiques.

Vous pouvez utiliser la liste de données statistiques pour entrer des données et exécuter des calculs statistiques et des graphiques.

Exemple : Pour entrer les deux groupes de données suivants.

List 1 (0.7, 1.5, 2.5, 4.5, 6) List 2 ( -2.5, 0.5, 1.8, 2.6, 3.5)

0.7 [EXE] 1.5 [EXE] 2.5 [EXE] 4.5 [EXE] 6 [EXE] [u]

[ ( - ) ] 2.5 [EXE] 0.5 [EXE] 1.8 [EXE] 2.6 [EXE] 3.5 [EXE]

Le mode STAT utilise les mêmes listes de données que le mode LIST, il n’est donc pas nécessaire d’entrer les mêmes données dans différents modes.

Pressez [FUNC] pour afficher les menus ci-dessous.

STAT R

0 G R A P H: 1 C A L C 2 S r t - A 3 S r t - D 4 D e l - A 5 I n s 6 L i s t 7 D i m

GRAPH ... Menu graphiques CALC ... Menu calcul statistique Srt-A ... Tri croissant des listes Srt-D ... Tri décroissant des listes Del-A ... Supprimer toutes les cellules d’une liste Ins ... Insérer une nouvelle cellule dans une liste List ... Entrer une liste spécifique par son nom Dim ... Compter les dimensions d’une liste Seq ... Générer une séquence de nombres Fill ... Remplacer toutes les cellules avec la même valeur

STAT R

L 1 L 2

L 1 ( 1 ) =

STAT R

L 2 ( 1 ) =

STAT R

L 2 ( 6 ) =

STAT R

0 F i l l 1 S e q

L 1 L 2

0 . 7 u 1 . 5 2 . 5

L 1 L 2

4 . 5 2 . 6 6 3 . 5 u

Les procédures utiles pour l’édition et le réarrangement des données sont les mêmes que celles de la fonction Liste. Pour les détails voir “Chapitre 6 Fonction de liste”.

8 - 2 Spécifier des données statistiques et des paramètres

(A) Pour spécifier des données statistiques

Vous devez entrer les données statistiques pour le calcul ou le graphique que vous voulez exécuter et entrer les paramètres de ces données avant d’effectuer un calcul ou un graphique. Lorsque les données statistiques sont affichées, pressez [FUNC] 1 (CALC) 9 (SET) pour afficher les menus suivants :

STAT R

1 - V A R X : L 1 1 - V A R F : 1

1-VAR X ... Spécifier la liste de données pour les calculs à variable unique 1-VAR F ... Spécifier la liste des valeurs de fréquence des données précédentes

2-VAR X ... Spécifier la liste de données X pour les calculs à deux variables 2-VAR Y ... Spécifier la liste de données Y pour les calculs à deux variables 2-VAR F ... Spécifier la liste des valeurs de fréquence des couples de données

Les réglages initiaux par défaut pour la liste de données statistiques sont Liste 1 pour les données statistiques à variable unique, Liste 1 et Liste 2 pour les données statistiques à variable double, 1 pour la valeur de fréquence.

Vous pouvez spécifier la liste de données statistiques pour 1-VAR X / 2-VAR X / 2VAR Y, ou les valeurs 1-VAR F / 2-VAR F. Utilisez [p] et [q] pour souligner l’objet que vous souhaitez spécifier, et pressez [EXE]. Entrez alors le nom de la liste de données statistiques que vous voulez utiliser.

en mode 1-VAR

précédentes en mode 2 variables

STAT R

2 - V A R X : L 1 2 - V A R Y : L 2 2 - V A R F : 1

( 1-VAR X / 2-VAR X / 2-VAR Y) (1-VAR F / 2-VAR F)

STAT R

0 L 1 1 L 2 2 L 3 3 L 4 4 L 5 5 L 6 6 L 7 7 L 8 8 N o n e

STAT R

0 1 1 L 1 2 L 2 3 L 3 4 L 4 5 L 5 6 L 6 7 L 7 8 L 8

L1~L8 ... List 1 ~ List 8 None ... Aucune des listes 1 ... Pour affecter la fréquence 1 à toutes les données

(B) Pour régler les paramètres de distribution normale et de capacité de

traitement.

Après avoir entré les données statistiques vous pouvez régler les paramètres de distribution normale et de capacité de traitement ainsi : Pressez [FUNC] 1 (CALC) 8 (L/D SET) pour faire apparaître l’écran suivant :

D I S T R / L I M I T a x = 0 X L S L = 0 X U S L = 0

Entrez alors les données suivantes :

ax ... Valeur aléatoire dans la distribution normale X LSL ... Valeur limite de plus basse spécification pour les données X X USL ... Valeur limite de plus haute spécification pour les données X Y LSL ... Valeur limite de plus basse spécification pour les données Y Y USL ... Valeur limite de plus haute spécification pour les données Y

[q] ¯

D I S T R / L I M I T Y L S L = 0 Y U S L = 0

8 - 3 Exécuter des calculs statistiques

8 - 3 - 1 Calcul statistique à variable unique

Pressez [FUNC] 1 (CALC) 0 (1-VAR) affiche les menus de résultat du calcul statistique à variable unique.

n x X m i n X m a x S x s x S x S x ² C a x C p x C p k x

Où :

n ... Nombre de données entrées x ... Moyenne des données x Xmin ... Minimum des données x Xmax ... Maximum des données x Sx ... Ecart type sur un échantillon de n-1 données x

sx ... Ecart type sur les données x Sx ... Somme des données x Sx² ... Somme des carrés des données x

Cax ... Précision de capacité pour les données x,

Cpx ... Précision de capacité potentielle pour les données x, C =

t P ( t ) Q ( t ) R ( t ) Q 1 M e d Q 3 M o d C V R p p m

X + X

( - x )

USL LSL

X - X

USL LSL

X - X

USL LSL

6 s

Cpkx ... Minimum (C , C ) pour les données x, où C est la limite supérieure de

spécification de capacité de précision et C est la limite inférieure de spécification de capacité de précision. C = Min (C , C ) = C (1 - C )

t ... Valeur de test P (t) ... Représente la fraction cumulative de la distribution normale standard qui

R (t) ... Représente la fraction cumulative de la distribution normale résidant entre

Q (t) ... Représente la fraction cumulative de la distribution normale standard

Q1 ... Premier quartile Med ... Médiane Q3 ... Troisième quartile Mod ... Mode ppm ... Parties par million, défection par million d’opportunités

pkx PU PL px ax

est inférieure à la valeur t.

les valeurs t et 0 R (t) = 1 - P (t)

supérieure à la valeur t Q (t) = I 0.5 - R (t) I

Exemple : Pour trouver n, Cax, Q (t), Mod

PU PL PU

Utilisez les paramètres SET et L/D SET suivants : 1-VAR X = L1, où List 1 (3, 2, 10, 7) 1-VAR F = L2, où List 2 (5, 9, 4, 12) ax = 6, X LSL = 1, X USL = 13

Étape 1 : Entrez les groupes de données de la liste 1 et de la liste 2

3 [EXE] 2 [EXE] 10 [EXE] 7 [EXE] [u] 5 [EXE] 9 [EXE] 4 [EXE] 12 [EXE]

Étape 2 : Spécifier la liste de données statistiques pour 1-VAR X et 1-VAR F

[FUNC] 1 (CALC) 9 (SET) [q]

[EXE] 2 (L2)

L 1 L 2

1 0 4

7 1 2

L 2 ( 5 ) =

STAT R

1 - V A R X : L 1 1 - V A R F : 1

STAT R

1 - V A R X : L 1 1 - V A R F : L 2

Étape 3 : Spécifier les valeurs pour ax, X LSL, X USL

[EXIT] 8 (L/D SET) 6 [EXE] 1 [EXE] 13 [EXE]

D I S T R / L I M I T a x = 6 X L S L = 1 X U S L = 1 3

Étape 4 : Pressez [FUNC] 1 (CALC) 0 (1-VAR) pour afficher les menus de résultat .

Vous pouvez utiliser les touches de curseur pour visualiser les caractéristiques de variables.

[EXIT] 0 (1-VAR)

[q] [q]

[q] [u] [u]

[u] [u] [u] [u] [u]

n x X m i n X m a x S x s x S x S x ² C a x C p x C p k x

t P ( t ) Q ( t ) R ( t ) Q 1 M e d Q 3 M o d C V R p p m

STAT R

3 0

STAT R

0 . 2 9 4 4 4 4 4 4 4

STAT R

0 . 1 0 5 3

STAT R

8 - 3 - 2 Calcul statistique à variable double

Pressez [FUNC] 1 (CALC) 1 (2-VAR) affiche les menus de résultat du calcul statistique à variable double.

n x X m i n X m a x S x s x S x S x ² C a x C p x C p k x

Où :

n ... Nombre d’options de données x ... Moyenne des données x Xmin ... Minimum des données x Xmax ... Maximum des données x Sx ... Ecart type sur un échantillon de n-1 données x

sx ... Ecart type sur les données x

STAT R

y Y m i n Y m a x S y s y S y S y ² S x y C a y C p y C p k y

STAT R

Sx ... Somme des données x Sx² ... Somme des carrés des données x

Cax ... Précision de capacité pour les données x,

Cpx ... Précision de capacité potentielle pour les données x, C =

( - x )

X + X

USL LSL

X - X

USL LSL

X - X

USL LSL

6 s

Cpkx ... Minimum (C , C ) pour les données x, où C est la limite supérieure de

spécification de capacité de précision et C est la limite inférieure de spécification de capacité de précision. C = Min (C , C ) = C (1 - C )

y ... Moyenne des données y Ymin ... Minimum des données y Ymax ... Maximum des données y Sy ... Ecart type sur un échantillon de n-1 données y

sy ... Ecart type sur les données y

pkx PU PL px ax

PU PL PU

Sy ... Somme des données y Sy² ... Somme des carrés des données y

Cay ... Précision de capacité pour les données y,

Cpy ... Précision de capacité potentielle pour les données y, C = Cpky ... Minimum (C , C ) pour les données y, où C est la limite supérieure de

spécification de capacité de précision et C est la limite inférieure de spécification de capacité de précision. C = Min (C , C ) = C (1 - C )

pky PU PL py ay

Exemple : Pour trouver n, Ymin, Cpy, Mod

PU PL PU

Utilisez les paramètres SET et L/D SET suivants 2-VAR X = L3, où List 3 (63, 57, 81, 90) 2-VAR Y = L4, où List 4 (18, 22, 31, 43) 2-VAR F = 1 X LSL = 55, X USL = 95, Y LSL = 15, Y USL = 44

( - y )

Y + Y

USL LSL

Y - Y

USL LSL

Y - Y

USL LSL

6 s

Étape 1 : Entrez les groupes de données de la liste 3 et de la liste 4

63 [EXE] 57 [EXE] 81 [EXE] 90 [EXE] [u] 18 [EXE] 22 [EXE] 31 [EXE] 43 [EXE]

Étape 2 : Spécifier les listes de données de calcul statistique pour 2-VAR X ,

2-VAR Y et 2-VAR F

[FUNC] 1 (CALC) 9 (SET) [q] [q]

[EXE] 2 (L3) [q] [EXE] 3 (L4)

L 3 L 4

8 1 3 1

9 0 4 3

L 4 ( 5 ) =

STAT R

2 - V A R X : L 1 2 - V A R Y : L 2 2 - V A R F : 1

STAT R

2 - V A R X : L 3 2 - V A R Y : L 4 2 - V A R F : 1

Étape 3 : Spécifiez les valeurs pour X LSL, X USL, Y LSL, Y USL

[EXIT] 8 (L/DSET) [q] 55 [EXE] 95 [EXE] [q] 15 [EXE] 44

Étape 4 : Pressez [FUNC] 1 (CALC) 1 (2-VAR) pour afficher les menus de résultat et

utilisez les touches de curseur pour visualiser la valeur de chaque calcul.

[EXE] [EXIT] 1 (2-VAR)

[q] [q] [q] [u]

[q] [q] [u]

D I S T R / L I M I T Y L S L = 1 5 Y U S L = 4 4 t

n x X m i n X m a x S x s x S x S x ² C a x C p x C p k x

y Y m i n Y m a x S y s y S y S y ² S x y C a y C p y C p k y

STAT R

1 8

STAT R

0 . 5 0 3 2 2 6 5 6 6 6

8 - 3 - 3 Calculs de régression

(A) Pour afficher les résultats de la régression

Dans le menu CALC (pressez [FUNC] 1 (CALC)), se trouvent les six types de régression suivants :

Type de régression Formule

Régression linéaire (X) y = ax + b Régression Med-Med (MED) y = ax + b Régression Logarithmique (LOG) y = a + b In x Régression Quadratique (X²) y = ax² + b x + c Régression Exponentielle (EXP) y = a · e

Puissance de régression (PWR) y = a · x

Les calculs de régression sont disponibles seulement dans des calculs statistiques à deux variables.

Linéaire a ... Coefficient de régression (pente)

y = a x + b

a b r

Med-Med a ... Pente de graphique Med-Med

y = a x + b

a b

Quadratique a ... Deuxième coefficient de régression

y = a x ² + b x + c

a b c

Logarithmique a ... Terme de constante de régression

y = a + b · I n ( x )

a b r

Exponentielle a ... Coefficient de régression

y = a · e b ( x )

a b r

Puissance a ... Coefficient de régression

y = a · x b

a b r

Exemple : Avec les données suivantes effectuez deux calculs de

STAT R

b ... Terme de constante de régression

(interception avec l’axe des ordonnées)

r ... Coefficient de corrélation

b ... Ordonnée à l’origine du graphique

Med-Med

b ... Premier coefficient de régression c ... Terme de constante de régression

(interception avec l’axe des ordonnées)

b ... Coefficient de régression (pente) r ... Coefficient de corrélation.

b ... Terme de constante de régression r ... Coefficient de corrélation

b ... Puissance de régression r ... Coefficient de corrélation

régression : l’un linéaire, l’autre quadratique.

x i 1,2 2,4 3 3,8 4,6 y i 1,5 5,5 9,2 14,6 21

Étape 1 : Entrez les valeurs x i et y i dans L1 et L2

1 [·] 2 [EXE] 2 [·] 4 [EXE] 3 [EXE] 3 [·] 8 [EXE] 4 [·] 6 [EXE] [u] [p] ~ [p]

1 [·] 5 [EXE] 5 [·] 5 [EXE] 9 [·] 2 [EXE] 14 [·] 6 [EXE] 21 [EXE]

STAT R

L1 L 2 1 . 2 u 1

2 . 4 4

L 2 ( 1 ) = 1

STAT R

L 2 ( 6 ) = 1

3 9

L1 L 2 3 . 8 1 4 . 6

4 . 6 2 1

Étape 2 : Spécifiez 2-VAR X = L 1

[FUNC] 1 (CALC) 9 (SET) [q] [q] [EXE] 0(L1) [q] [EXE] 1 (L2) [q] [EXE] 0 (1)

Étape 3 : Sélectionnez X pour effectuer un calcul de régression linéaire.

[EXIT]

2 (X)

[u]

2-VAR Y = L 2 2-VAR F = 1

2 - V A R X : L 1 2 - V A R Y : L 2 2 - V A R F : 1

0 1 - V A R 1 2 - V A R 2 X 3 M E D 4 L O G 5 X ² 6 E X P 7 P W R 8 L / D S E T 9 S E T

y = a x + b

a b r

y = a x + b

a b r

y = a x + b

a b r

STAT R

5 . 7 7 6 4 7 0 5 8 8

STAT R

- 6 . 9 6 9 4 1 1 7 6 5

STAT R

0 . 9 8 3 3 4 2 6 8 8

L’équation de régression linéaire est donc y = 5.776470588 x - 6.969411765

Étape 4 : Sélectionnez X² pour effectuer un calcul de régression quadratique

[EXIT] 5 (X²)

[u]

y = a x ² + b x + c

a b c

y = a x ² + b x + c

a b c

y = a x ² + b x + c

a b c

STAT R

0 . 9 7 2 2 1 2 4 6 4

STAT R

0 . 1 4 9 0 7 6 0 9 1

STAT R

0 . 1 5 9 3 4 9 3 9 9

Donc l’équation de régression est y » 0.97 x² + 0.15x + 0.16

(B) Pour calculer les valeurs estimées

En mode STAT et MAIN, vous pouvez presser [VARS] pour trouver les objets cidessous pour calculer les valeurs estimées des paramètres x et y du graphique de régression.

x’ ... Valeurs de x estimées étant donné la valeur de y y’ ... Valeurs de y estimées étant donné la valeur de x

Si vous ne voulez pas sortir du mode STAT pour calculer les valeurs estimées, le résultat de ces valeurs estimées sera automatiquement inséré dans la cellule où se trouve le curseur.

Note : Vous ne pouvez pas calculer les valeurs estimées pour les graphiques Med-

Med et les graphiques de régression quadratique.

Exemple : Pour effectuer une régression linéaire en utilisant les données

Étape 1 : Entrez les valeurs x et y dans L5 et L6

15 [EXE] 17 [EXE] 21 [EXE] 28 [EXE] [u] 451 [EXE] 475 [EXE] 525 [EXE] 678 [EXE]

Étape 2 : Spécifier les listes de données de calcul statistique pour 2-VAR X,2-VAR Y

[FUNC] 1 (CALC) 9 (SET) [q] [q]

[EXE] 4 (L5) [q] [EXE] 5 (L6)

Étape 3 : Pressez 2 (X) pour afficher le menu de régression linéaire. Vous pouvez

[EXIT] 2 (X) [u]

suivantes et en estimer les valeurs quand x = 19 et y = 573

x 15 17 21 28

y 451 475 525 678

2-VAR F

alors presser les touches de curseur pour afficher les résultats du calcul de régression.

L 5 L 6

2 1 5 2 5

2 8 6 7 8

L 6 ( 5 ) =

STAT R

2 - V A R X : L 1 2 - V A R Y : L 2 2 - V A R F : 1

STAT R

2 - V A R X : L 5 2 - V A R Y : L 6 2 - V A R F : 1

y = a x + b

a b r

STAT R

1 7 6 . 1 0 6 3 2 9 1

Étape 4 : En mode STAT pour trouver “x’” et “y’” et calculer la valeur estimée.

[VARS] [VARS] [VARS] [q] [u] [u] [u]

[EXE] [u] (2-VAR) [EXE] [t] [t]

X f a c t Y f a c t Y X t Y t S T A T

x 1y 1 x 2 y 2 x 3 y 3a b c r x ‘ y ‘

STAT R

Attention ! : Ne pas tenir compte du message d’erreur qui s’affiche.

[EXE] 573

[EXE]

[VARS] [VARS] [VARS] [q] [u] [u] [u] [EXE] (2-VAR) [EXE] [t]

L 5 L 6

2 1 5 2 5 2 8 6 7 8

L 6 ( 5 ) = X’( 5 7 3 t

L 6 ( 6 ) = X

x 1y 1 x 2 y 2 x 3 y 3a b c r x ‘ y ‘

L 5 L 6

2 8 6 7 8

2 2 . 5 6 7

STAT R

Étape 1 : Entrez les valeurs x et y dans L7 et L8

57 [EXE] 61 [EXE] 67 [EXE] [u] 101 [EXE] 117 [EXE] 155 [EXE]

Étape 2 : Spécifiez les listes de données de calcul statistique : 2-VARX, 2-VARY et 2VARF

[FUNC] 1 (CALC) 9 (SET) [q] [q]

[EXE] 6 (L7) [q] [EXE] 7 (L8)

Étape 3 : Pressez 7 (PWR) pour afficher le menu de régression quadratique. Vous

pouvez presser les touches de curseur ([t] [u] [p] [q])pour visualiser les caractéristiques de variables.

[EXIT] 7 (PWR)

L 7 L 8

6 1 1 1 7

6 7 1 5 5

L 8 ( 4 ) =

2 - V A R X : L 1 2 - V A R Y : L 2 2 - V A R F : 1

2 - V A R X : L 7 2 - V A R Y : L 8 2 - V A R F : 1

y = a · x b

a b r

STAT R

0 . 0 0 2 0 3 5 1 2

[EXE] 19

[EXE]

Donc si y = 573 la valeur estimée de x est de 22.567; et si x = 19 la valeur estimée de y est 510.27

Exemple : Pour effectuer la régression de puissance en utilisant les

données suivantes et estimer les valeurs de x quand y = 143

x 57 61 67

Y 101 117 155

L 5 L 6

2 8 6 7 8

L 6 ( 6 ) = y‘ ( 1 9 t

L 6 ( 6 ) =

L 5 L 6

2 2 . 5 6 7

5 1 0 . 2 7

Étape 4 : Entrez en mode MAIN pour trouver “x’” et “y’” et estimer le calcul de valeur.

[MODE] 0 [VARS] [VARS] [VARS] [q] [u] [u] [u]

[EXE] [u] (2-VAR) [EXE] [t] [t]

X f a c t Y f a c t Y X t Y t S T A T

x 1 y 1 x 2 y 2 x 3 y3 a b c r x ‘ y ‘

STAT R

Attention ! : Ne pas tenir compte du message d’erreur qui s’affiche

[EXE] 143 [EXE]

x ‘ ( 1 4 3 )

STAT R

6 5 . 2 2 9 8 2 6 9

8 - 4 Graphiques statistiques

8 - 4 - 1 Paramètres généraux des graphiques statistiques

Cette section décrit l’utilisation des menus de paramétrage de graphique (Gph1, Gph2, Gph3)

(A) Menus de paramétrage de graphiques

Lorsque les données statistiques sont affichées, pressez [FUNC] 0 (GRAPH) 3 (SET) pour afficher les menus de paramétrage de graphiques.

S - G R A P H : G p h 1 G - T Y P E : S c a t X L I S T : L 1 Y L I S T : L 2

GRAPH R

F R E Q : 1 M A R K : o

GRAPH R

· Les paramètres montrés ici ont seulement valeur d’exemple. Les paramètres sur votre écran de paramétrage de graphiques peuvent être différents. Voici la liste des paramètres possibles à régler selon le type de graphique choisi.

G-TYPE S-GRAPH X LIST Y LIST T LIST Y1~Y5 LIST FREQ MARK

Scat þ þþ¨ ¨ þþ

xyLin þ þþ¨ ¨ þþ

Hist þ þ¨¨¨þ¨

Box þ þ¨¨¨þ¨

N-Dist þ þ¨¨¨þ¨

X þ þþ¨ ¨ þ¨

Med þ þþ¨ ¨ þ¨

Log þ þþ¨ ¨ þ¨

X² þ þþ¨ ¨ þ¨

Exp þ þþ¨ ¨ þ¨

Pwr þ þþ¨ ¨ þ¨

T-Ser þ þþþ þ þþ

Spc þ þ¨¨¨þ¨

(B) Zone de graphique statistique (S-GRAPH)

Lorsque le menu de paramétrage de graphique est affiché, sélectionnez l’option “SGRAPH” et pressez [EXE].

0 G r h 1 4 G r p h 2 2 G p h 3

Vous pouvez alors choisir entre :

Gph1 ... Graph 1 Gph2 ... Graph 2 Gph3 ... Graph 3

Le paramètre initial de type de graphique par défaut est le graphique par dispersion. Vous pouvez le changer pour l’un des nombreux autres types de graphique statistique, et ce pour chaque graphique : Graph1, Graph2 et Graph3. Pour cela, ouvrez l’écran de réglage des paramètres graphique en tapant : [FUNC] 0 (GRAPH) 3 (SET), sélectionnez l’option “G-TYPE” et pressez [EXE]. L’écran suivant apparaît alors :

0 S c a t 1 x y L i n 2 H i s t 3 B o x 4 N - D i s t 5 X 6 M e d 7 L o g

GRAPH R

0 X ² 1 E x p 2 P w r 3 T - S e r

[q] i

4 S p c

GRAPH R

Vous pouvez alors choisir le type de graphique voulu parmi les 13 suivants :

Scat ... Diagramme par dispersion xyLin ... Graphique en ligne xy Hist ... Histogramme Box ... Graphique en quartiles N-Dist ... Courbe de distribution normale X ... Graphique de régression linéaire Med ... Graphique Med-Med Log ... Graphique de régression logarithmique X² ... Graphique de régression Quadratique Exp ... Graphique de régression exponentielle Pwr ... Graphique de régression de puissance T-Ser ... Graphique de série temporelle Spc ... Graphique de contrôle de processus staistique

(D) Liste de données (X LIST, Y LIST, T LIST, Y1 LIST ~Y5 LIST)

Vous pouvez spécifier quelle liste de données statistiques vous voulez utiliser. Lorsque le menu de paramétrage de graphique est affiché, sélectionnez l’option “X LIST” (ou “Y LIST”, “T LIST”, “Y1 LIST” ~ “Y5 LIST”) et pressez [EXE]

0 L 1 1 L 2 2 L 3 3 L 4 4 L 5 5 L 6 6 L 7 7 L 8 8 None

Choisissez alors parmi les listes celle voulue.

L1 ~ L8 ... List 1 ~ List 8 None ... Aucune liste

(E) Liste de données de fréquence (FREQ)

Normalement, chaque donnée ou paire de données d’une liste de données statistiques est représentée sur un graphique par un point. Toutefois, quand vous travaillez avec un grand nombre d’options de données, cela peut causer des problèmes à cause du nombre de points de positionnement sur le graphique. Lorsque cela arrive, vous pouvez spécifier une liste de fréquence qui contient des valeurs indiquant le nombre d’instances (la fréquence) des données y. Quand vous faites comme cela, un seul point est positionné pour les multiples données séparées, ce qui rend le graphique plus facile à lire. Lorsque le menu de paramétrage de graphique est affiché, sélectionnez l’option “FREQ”, et pressez [EXE].

0 1 1 L 1 2 L 2 3 L 3 4 L 4 5 L 5 6 L 6 7 L 7 8 L 8

1 ... Positionnez toutes les données à 1 L1~L8 ... Les données des listes 1~8 sont des données de fréquence

(F) Type de marque de positionnement (MARK)

Ce paramètre vous permet de spécifier la forme des points de positionnement sur le graphique. Lorsque le menu de paramétrage de graphique est affiché, sélectionnez l’option “MARK” et pressez [EXE].

0 S q u a r e ( ¨ ) 1 D o t ( · ) 2 C r o s s ( x )

Choisissez alors la forme des points voulue :

Square (¨) ... Positionnement avec ¨ Dot (·) ... Positionnement avec ·

STAT R

Cross (x) ... Positionnement avec X

8 - 4 - 2 Exemples de graphiques statistiques

Le paramètre initial de type de graphique par défaut est le graphique par dispersion (Gph1 à Gph3), mais vous pouvez changer pour l’un des nombreux autres types de

graphique.

Exemple : Selon les paramètres suivants, pour dessiner un graphique en

Étape 1 : Après avoir entré les groupes de données de la liste 3 et de la liste 4,

[FUNC] 0 (GRAPH) 3 (SET)

Étape 2 : Sélectionnez la zone de graphique que vous voulez utiliser.

[EXE] 1 (Gph2)

ligne xy dans Gph 2. X LIST : L3, Y LIST : L4, FREQ : 1, MARK : Cross Où la liste 3 (0.7, 1.5, 2.5, 4.5, 6) et la liste 4 (-2.5, 0.5, 1.8, 2.6, 3.5)

pressez [FUNC] 0 (GRAPH) 3 (SET) pour afficher le réglage du graphique.

S - G R A P H : G p h 1 G - T Y P E : S c a t X L I S T : L 1 Y L I S T : L 2

S - G R A P H : G p h 2 G - T Y P E : S c a t X L I S T : L 1 Y L I S T : L 2

GRAPH R

Étape 3 : Sélectionnez le type de graphique que vous voulez utiliser

[q] [EXE] 1 (xyLin)

Étape 4 : Spécifiez les listes de données et les listes de données de fréquence que

vous voulez utiliser.

[q][EXE] 2 (L3) [q] [EXE] 3 (L4) [q] [EXE] 0 (1)

S - G R A P H : G p h 2 G - T Y P E : x y - L i X L I S T : L 1 Y L I S T : L 2

F R E Q : 1 M A R K : o

GRAPH R

Étape 5 : Sélectionnez le type de point de positionnement que vous voulez utiliser.

[q] [EXE] 2 (Cross)

Étape 6 : Pressez [EXIT] 1 (Gph2) pour dessiner le graphique. Les paramètres de la

fenêtre V-Window sont ajustés automatiquement et le graphique en ligne xy est affiché.

F R E Q : 1 M A R K : x

[EXIT] 1 (Gph2)

GRAPH R

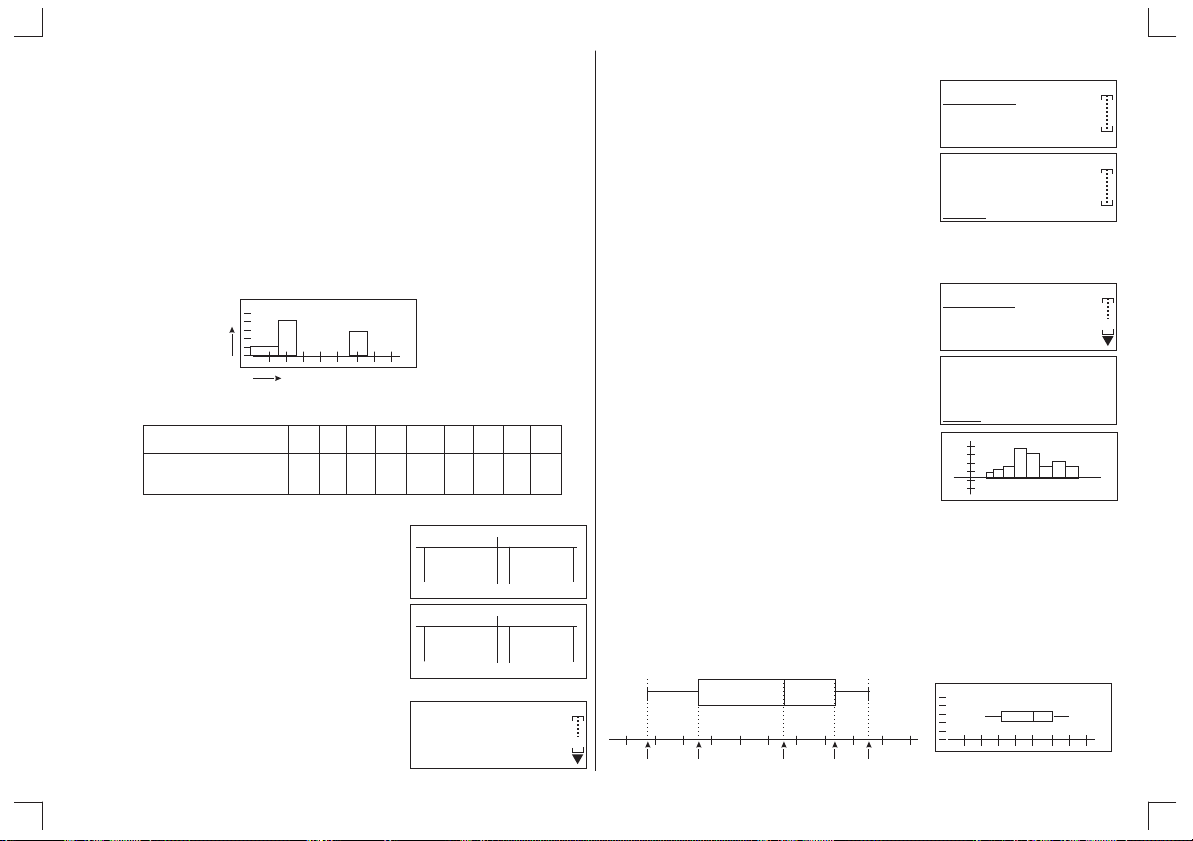
Note : Les paramètres de fenêtre V-Wondow sont normalement réglés

automatiquement pour les graphiques statistiques. Si vous voulez régler les paramètres de fenêtre V-Window manuellement, vous devez changer l’option “S-WIND” en “Manual”. Voir “8 - 8 Graphiques manuels).

8 - 5 Graphiques statistiques à variable unique

8 - 5 - 1 Histogramme (Hist)

Un histogramme donne une vue graphique de la distribution des données x et permet souvent une perception plus riche des données que ne vous le permettent des représentations numériques comme la moyenne, la médiane ou le mode. L’axe horizontal est constitué par les données x. L’axe vertical est le nombre d’occurrence des données x.

Fréquence des données x

Esemple : Voici les résultats d’une classe de seconde au devoir de math.

Tracez l’histogramme de ces données :

GRAPH R

Données x

Note 0 3 5 7 10 12 13 15 17

Nbre d’éleve 1123 9 7 2 3 2 Ayant eu cette note

Étape 1 : Entrez les données précédentes dans L7 et L8

0 [EXE] 3 [EXE] 5 [EXE] 7 [EXE] 10 [EXE] 12 [EXE] 13 [EXE] 15 [EXE] 17 [EXE]

[u]1 [EXE] 1 [EXE] 2 [EXE] 3 [EXE] 9 [EXE] 7 [EXE] 2 [EXE] 3 [EXE] 2 [EXE]

Étape 2 : Spécifier 1-VAR X = L7 et 1-VAR F = L8

[FUNC] 1 (CALC) 9 (SET) [EXE] 6 (L7) [q] [EXE] 8 (L8)

STAT R

L 7 L 8

1 5

L 7 ( 1 0 ) =

STAT R

L 8 ( 1 0 ) =

STAT R

1 - V A R X : L 7 1 - V A R F : L 8

1 7

L 7 L 8

1 5 3 1 7 2

Étape 3 : Entrez les paramètres du graphique à l’aide de la fonction SET.

[EXIT] [EXIT] 0 (GRAPH] 3 (SET)

[q] [EXE] 2 (Hist) [ q] [EXE] 6 (L7) [q] [EXE] 8 (L8)

Étape 4 : Réglez le paramétrage fenêtre sur manuel (Man) puis sélectionnez Gph1

pour tracer l’histogramme avec les paramètres de fenêtre suivants : X Srt = 0 et X ptch = 2

[2nd] [SYSTEM] [EXE] 1 (Man)

[EXIT] [FUNC] 0 (GRAPH) 0 (Gph1) 0 [EXE] 2 [EXE]

STAT R

S - G R A P H : G p h 1 G - T Y P E : S c a t X L I S T : L 1 F R E Q : 1

STAT R

S - G R A P H : G p h 1 G - T Y P E : H i s t X L I S T : L 7 F R E Q : L 8

STAT R

S - W I N D : M a n G - F U N C : O n A N G L E : R a d D I S P : F l o

STAT R

S e t I n t e r v a l X S r t = 0 p t c h = 2 D r a w

STAT R

[EXE]

8 - 5 - 2 Graphique en quartiles (Box)

Le graphique en quartiles vous permet de voir qu’un grand nombre d’options de données sont groupées dans des étendues. Un ensemble rectangulaire comprend toutes les données x dans une zone allant du 25ème centile (premier quartile, Q1) jusqu’au 75ème centile (troisième quartile, Q3), avec une ligne tirée au 50ème centile (Médiane, Med). Les lignes s’étendent des deux extrémités de l’ensemble jusqu’à un minimum (Xmin) et un maximum (Xmax) des données.

STAT R

Xmin Q1 Med Q3 Xmax

Exemple : Tracez un diagramme en quartiles avec les données suivantes :

[2nd] [SYSTEM] [EXE] 0 (Auto)

[EXIT] [FUNC] 0 (GRAPH) 3 (SET) [EXE] 1 (Gph2) [q] [EXE] 3 (Box) [q] [EXE] 6 (L7) [q] [EXE] 0 (1)

[EXIT] 4 (SEL) [EXE] 1 (Off) [q] [EXE] 0 (On) [q] [EXE] 1 (Off)

S-WIND : Auto X-LIST : L7 (0, 3, 5, 7, 10, 12, 13, 15, 17) Gph1 : Off FREQ : 1 Gph2 : On Gph3 : Off

STAT R

S - W I N D : A u t o G - F U N C : O n A N G L E : R a d D I S P : F l o

STAT R

S - G R A P H : G p h 2 G - T Y P E : B o x X L I S T : L 7 F R E Q : 1

STAT R

S - G p h 1 : O f f S - G p h 2 : O n S - G p h 3 : O f f 0 D r a w

STAT R

[EXIT] 4 (SEL) [EXE] 1 (Off) [q] [EXE] 1 (Off) [q] [EXE] 0 (On)

[EXIT] 2 (Gph3)

STAT R

S - G p h 1 : O f f S - G p h 2 : O f f S - G p h 3 : O n 0 D r a w

STAT R

8 - 5 - 4 Le graphique de contrôle du traitement Statistique (Spc)

Le contrôle du traitement statistique est un outil essentiel à la fois pour la direction et les travailleurs pour résoudre des problèmes et contrôler les performances d’un procédé pour s’assurer qu’il fonctionne d’une manière acceptable.

STAT R

[EXIT] 1 (Gph2)

8 - 5 - 3 Courbe de distribution normale (N-Dist)

La courbe de distribution normale positionne la relation entre les déviations moyenne et standard des données x. La courbe de distribution normale représente la fonction de distribution normale ci dessous :

(x-x)² 2xs ²

Y = e

(2p) xs

Exemple : Tracez la courbe de distribution normale correspondant aux

[2nd] [SYSTEM] [EXE] 0 (Auto) [EXIT] [FUNC] 0 (GRAPH) 3 (SET) [EXE] 2 (Gph3) [q] [EXE] 4 (N-Dist) [q] [EXE] 6 (L7) [q] [EXE] 0 (1)

données suivantes : S-WIND : Auto X-LIST : L7 (0, 3, 5, 7, 10, 12, 13, 15, 17) Gph1 : Off FREQ : 1 Gph2 : Off Gph3 : On

STAT R

S - G R A P H : G p h 3 G - T Y P E : N - D i s X L I S T : L 7 F R E Q : 1

Exemple : Tracez le graphique de contrôle du traitement statistique

[2nd] [SYSTEM] [EXE] 0 (Auto)

[EXIT] [FUNC] 0 (GRAPH) 3 (SET) [EXE] 0 (Gph1) [q] [EXE] [ q] ~ [q] 4 (Spc) [q] [EXE] 6 (L7) [q] [EXE] 0 (1)

[EXIT] 4 (SEL) [EXE] 0 (On) [q] [EXE] 1 (Off) [q] [EXE] 1 (Off)

correspondant aux données suivantes : S-WIND : Auto X-LIST : L7 (0, 3, 5, 7, 10, 12, 13, 15, 17) Gph1 : On FREQ : 1 Gph2 : Off Gph3 : Off

STAT R

S - W I N D : A u t o G - F U N C : O n A N G L E : R a d D I S P : F l o

STAT R

S - G R A P H : G p h 1 G - T Y P E : S p c X L I S T : L 7 F R E Q : 1

STAT R

S - G p h 1 : O n S - G p h 2 : O f f S - G p h 3 : O f f 0 D r a w

STAT R

[EXIT] 0 (Gph1)

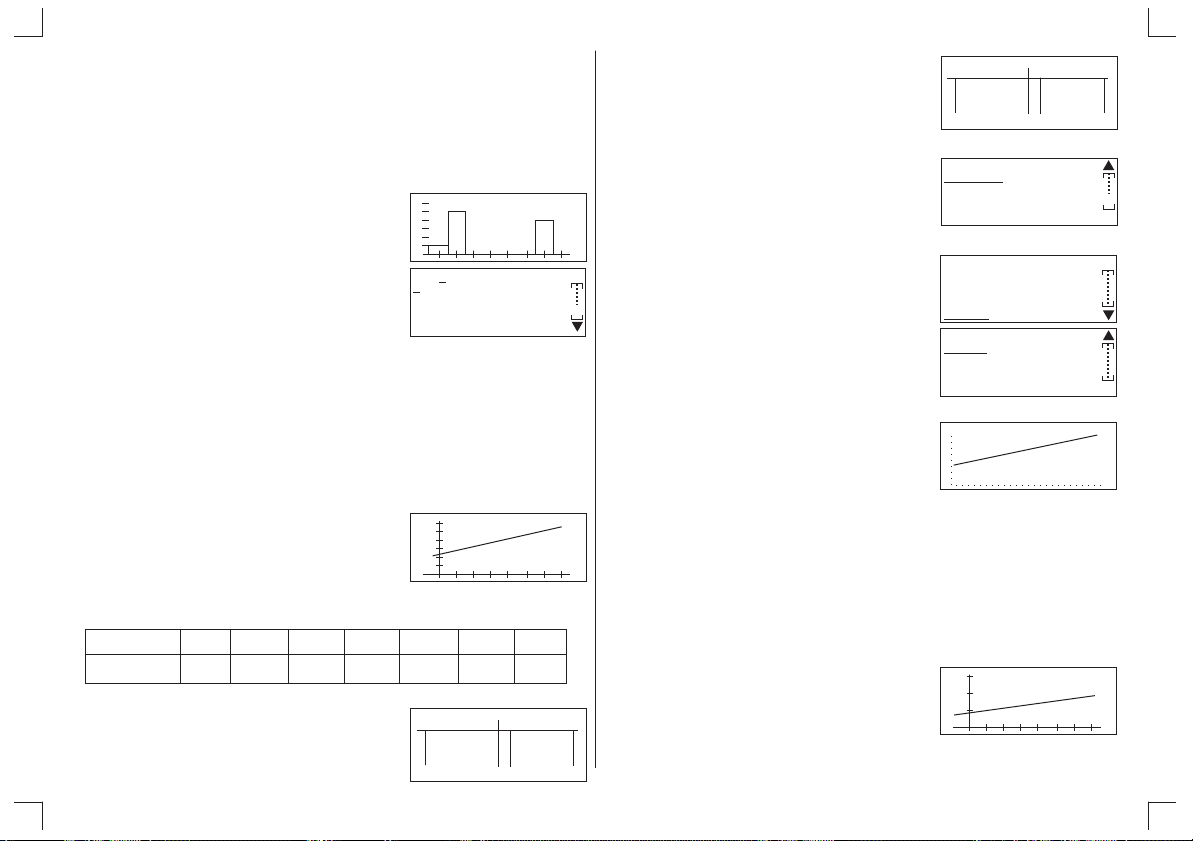
8 - 5 - 5 Pour afficher les résultats d’un calcul statistique à variable unique

Lorsqu’un graphique statistique à variable unique est affiché, les résultats du calcul peuvent être rappelés immédiatement en tapant [FUNC] 0 (1-VAR) pour visualiser les menus de résultat.

Exemple : Pour voir les résultats d’un calcul statistique à variable unique

[FUNC] 0 (1-VAR)

Vous pouvez utiliser les touches de curseur pour visualiser les caractéristiques de variables.

lorsqu’un histogramme graphique est affiché.

STAT R

n x X m i n X m a x S x s x S x S x ² C a x C p x C p k x

STAT R

80 [·] 9 [EXE] 81 [·] 1 [EXE] 81 [·] 4 [EXE] 81 [·] 8 [EXE] 82 [·] 0 [EXE] 82 [·] 4 [EXE] 82 [·] 7 [EXE]

STAT R

L 1 L 2

1 9 9 8 8 2 . 4 2 0 0 0 8 2 . 7

L 2 ( 8 ) =

Étape 2 : Specifier 2-VAR X = L1, 2-VAR Y = L2 et 2-VAR F = 1

[FUNC] 1 (CALC) 9 (SET) [q] [q] [EXE] 0 (L1) [q] [EXE] 1 (L2) [q] [EXE] 0 (1)

2 - V A R X : L 1 2 - V A R Y : L 2 2 - V A R F : 1

STAT R

Étape 3 : Entrez les paramètres du graphique à l’aide de la fonction SET

[EXIT] [EXIT] 0 (GRAPH) 3 (SET) [EXE] 0 (Gph1) [q] [EXE] 5 (X) [q] [EXE] 0 (L1) [q] [EXE] 1 (L2)

[q] [EXE] 0 (1)

STAT R

S - G R A P H : G p h 1 G - T Y P E : L i n e r X L I S T : L 1 Y L I S T : L 2

STAT R

F R E Q : 1

8 - 6 Graphiques statistiques à variable double / régression

8 - 6 - 1 Graphique de régression linéaire (X)

La régression linéaire positionne une ligne droite qui passe près d’autant de points de données que possible et retourne le valeurs de la pente et de l’ordonnée à l’orignine.

Exemple : Voici les résultats d’une étude de l’INSEE sur l’évolution de

Année x 1990 1991 1992 1994 1996 1998 2000

Espérance y 80,9 81,1 81,4 81,8 82,0 82,4 82,7

l’espérance de vie des femmes à la naissance

Étape 1 : Entrez les données précédentes dans L1 et L2

1990 [EXE] 1991 [EXE] 1992 [EXE] 1 994 [EXE] 1996 [EXE] 1998 [EXE] 2000 [EXE] [u]

STAT R

L 1 L 2

1 9 9 0 u 1 9 9 1 1 9 9 2

L 2 ( 1 ) =

Étape 4 : Tracez le graphique en sélectionnant Gph1

[EXIT] 0 (Gph1)

STAT R

8 - 6 - 2 Graphique de régression Med-Med (Med)

Lorsque l’on suspecte l’existence d’un grand nombre de valeurs extrêmes, un graphique Med-Med peut être utilisé au lieu de la méthode des carrés inférieurs. Il s’agit aussi d’une sorte de régression linéaire, mais qui minimise les effets des valeurs extrêmes. Il est tout spécialement utile dans la production de régressions linéaires de haute fiabilité à partir de données comprenant des fluctuations irrégulières, comme des études périodiques.

STAT R

Exemple : Modifiez l’exemple précédent pour effectuer un graphique de

[FUNC] 0 (GRAPH) 3 (SET) [q] [EXE] 6 (Med)

[EXIT] 0 (Gph1)

régression Med-Med

STAT R

S - G R A P H : G p h 1 G - T Y P E : M e dt X L I S T : L 1 Y L I S T : L 2

STAT R

8 - 6 - 3 Graphique de régression quadratique (X²)

Un graphique de régression quadratique représente la connexion des points de données d’un diagramme par dispersion. Il s’agit en fait de la dispersion de points qui sont assez proches pour être connectés. La formule qui représente cela est une régression quadratique.

STAT R

Étape 2 : Spécifier 2-VAR X = L3, 2-VAR Y = L4 et 2-VAR F = 1

[FUNC] 1 (CALC) 9 (SET) [q] [q] [EXE] 2 (L3) [q] [EXE] 3 (L4) [q] [EXE] 0 (1)

2 - V A R X : L 3 2 - V A R Y : L 4 2 - V A R F : 1

STAT R

Étape 3 : Entrez les paramètres du graphique à l’aide de la fonction SET

STAT R

[EXIT] [EXIT] 0 [GRAPH] 3 (SET) [EXE] 0 (Gph1) [q] [EXE] [q]~ [q] 0 (X²) [q] [EXE] 2 (L3) [q] [EXE] 3 (L4)

[q] [EXE] 0 (1)

Étape 4 : Tracez le graphique en sélectionnant Gph1

S - G R A P H : G p h 1 G - T Y P E : Q u a d X L I S T : L 3 Y L I S T : L 4

F R E Q : 1

STAT R

[EXIT] 0 (Gph1)

Exemple : Une étude a composé l’évolution de l’indice des salaires sur sept

Rang x 0 1 2 3 4 5 6 7

Indice y 100 97,6 96,8 98,4 98,3 99,8 103,3 106,7

ans; en voici les résultats. Dans le tableau suivant le rang 0 correspond à l’année 1992.

Tracez le graphique de régressions quadratique correspondant à ces données.

Étape 1 : Entrez les données précédentes dans les listes L3 et L4

STAT R

0 [EXE] 1 [EXE] 2 [EXE] 3 [EXE] 4 [EXE] 5 [EXE] 6 [EXE] 7 [EXE] [u]

100 [EXE] 97 [·] 6 [EXE] 96 [ ·] 8 [EXE] 98 [·] 4 [EXE] 98 [·] 3 [EXE] 99 [·] 8 [EXE] 103 [·] 3 [EXE] 106 [·] 7 [EXE]

L 3 L 4

0 u 1

L 4 ( 1 ) =

STAT R

L 4 ( 9 ) =

L 3 L 4

6 1 0 3 . 3 7 1 0 6 . 7 UU

8 - 6 4 Graphique de régression logarithmique (Log)

Le graphique de régression logarithmique exprime y en tant que fonction logarithmique de x. La formule de régression logarithmique standard est y = a + b In x, donc si on dit que X = In x, la formule correspond à la formule de régression linéaire y = a + bX

Exemple : Voici l’évolution de la production en pétrole de l’OPEP durant

Rang xi 1 2 3 4 5 6 7 8 9 10

Production en milliers de 944 1065 1137 1232 1231 1297 1322 1333 1368 1408 Tonnes

neuf ans

STAT R

Utilisez ces données pour tracer un graphique de régression logarithmique.

Étape 1 : Entrez les données précédentes dans les listes L5 et L6

STAT R

1 [EXE] 2 [EXE] 3 [EXE] 4 [EXE] 5 [EXE] 6 [EXE] 7 [EXE] 8 [EXE] 9 [EXE] [ u]

944 [EXE] 1065 [EXE] 1137 [EXE] 1232 [EXE] 1231 [EXE] 1297 [EXE] 1322 [EXE] 1333 [EXE] 1368 [EXE] 1408 [EXE]

L 5 L 6

L 6 ( 1 ) =

STAT R

L 5 L 6

1 0 1 4 0 8

L 6 ( 1 1 ) =

Étape 2 : Spécifiez 2-VAR X = L5, 2-VAR Y = L6 et 2-VAR F = 1

[FUNC] 1 (CALC) 9 (SET) [q] [q] [EXE] 4 (L5) [q] [EXE] 5 (L6) [q] [EXE] 0 (1)

2 - V A R X : L 5 2 - V A R Y : L 6 2 - V A R F : 1

Étape 3 : Entrez les paramètres graphiques à l’aide de la fonction SET

[EXIT] [EXIT] 0 (GRAPH) 3 (SET) [EXE] 0 (Gph1) [q] [EXE] 7 (Log) [q] [EXE] 4 (L5) [q] [EXE] 5 (L6)

[q] [EXE] 0 (1)

STAT R

S - G R A P H : G p h 1 G - T Y P E : L o g X L I S T : L 5 Y L I S T : L 6

STAT R

F R E Q : 1

Étape 4 : Tracez le graphique en sélectionnant Gph1

[EXIT] 0 (Gph1)

STAT R

1 u 2 3

9 1 3 6 8

STAT R

GRAPH R

Exemple : Paul vient d’acheter une voiture d’une valeur de 50 000 euros. Il

consulte ensuite sa cotation à l’argus au fils des ans; l’année 0 étant l’année d’achat de la voiture.

Année x 0 1 2 3 4 5 6 7

Prix y 50000 42500 36150 30700 26100 22200 18850 16000

Grâce à la calculatrice, effectuez un graphique de régression exponentielle correspondant à ces données.

Étape 1 : Entrez les données précédentes dans les listes L7 et L8

0 [EXE] 1 [EXE] 2 [EXE] 3 [EXE] 4 [EXE] 5 [EXE] 6 [EXE] 7 [EXE] [u] 50000 [EXE] 42500 [EXE] 36150 [EXE] 30700 [EXE] 26100 [EXE] 22200 [EXE] 18850 [EXE] 16000 [EXE]

STAT R

L 7 L 8

6 1 8 8 5 0 7 1 6 0 0 0

L 8 ( 9 ) =

Étape 2 :Spécifiez 2-VAR X = L7, 2-VAR Y = L8 et 2-VAR F = 1

[FUNC] 1 (CALC) 9 (SET) [q] [q] [EXE] 6 (L7) [q] [EXE] 7 (L8) [q] [EXE] 0 (1)

2 - V A R X : L 7 2 - V A R Y : L 8 2 - V A R F : 1

STAT R

Étape 3 : Entrez les paramètres graphiques puis tracez-le

[EXIT] [EXIT] 0 (GRAPH) 3 (SET) [EXE] 0 (Gph1) [q] [EXE] [q] ~ [q]1 (Exp) [q] [EXE] 6 (L7) [q] [EXE] 7 (L8)

[q] [EXE] 0 (1)

STAT R

S - G R A P H : G p h 1 G - T Y P E : E x p X L I S T : L 7 Y L I S T : L 8

STAT R

F R E Q : 1

8 - 6 - 5 Graphique de régression exponentielle (Exp)

La régression exponentielle exprime y en tant que proportion de la fonction exponentielle de x. La formule de régression exponentielle standard est y = a · e, donc si on prend les logarithmes des deux côtés, on obtient log y = log a + b x. Ensuite, si on dit Y = log y et A = log a, la formule correspond à la formule de régression linéaire Y = A + b x.

[EXIT] 0 (Gph1)

STAT R

8 - 6 - 6 Graphique de régression de puissance (Pwr)

La régression exponentielle exprime y en tant que proportion de la puissance de x. La formule de régression exponentielle standard est y = a · x , donc si on prend les logarithmes des deux côtés, on obtient log y = log a +b logx. Ensuite, si on dit X = log x et A = log a, la formule correspond à la formule de régression linéaire Y = A + b X.

Exemple : A partir des données qui suivent tracez un graphique de

régression de puissance.

x 1 1,5 2,4 3,1 4 5,2 5,7 6,2 7,3

y 1,1 2,15 5,5 9,4 15,7 26,8 32,5 38,2 53

STAT R

Étape 1 : Entrez les données précédentes dans les listes L1 et L2

1 [EXE] 1 [·] 5 [EXE] 2 [·] 4 [EXE] 3 [·] 1[EXE] 4 [EXE] 5 [·] 2 [EXE] 5 [·] 7 [EXE] 6 [·] 2[EXE] 7 [·3 [EXE] [u] 1[·] 1 [EXE] 2 [·] 15 [EXE] 5 [ ·] 5 [EXE] 9[·] 4 [EXE]15 [·]7 [EXE]26[·]8[EXE]32[·] 5 [EXE] 38 [·] 2 [EXE] 53 [EXE]

Étape 2 :Spécifiez 2-VAR X = L1, 2-VAR Y = L2 et 2-VAR F = 1

[FUNC] 1 (CALC) 9 (SET) [q] [q] [EXE] 0 (L1) [q] [EXE] 1 (L2) [q] [EXE] 0 (1)

STAT R

L 1 L 2

6 . 2 3 8 . 2 7 . 3 5 3

L 2 ( 1 0 ) =

2 - V A R X : L 1 2 - V A R Y : L 2 2 - V A R F : 1

STAT R

Étape 3 : Entrez les paramètres graphiques puis tracez-le

STAT R

[EXIT] [EXIT] 0 (GRAPH) 3 (SET) [EXE] 0 (Gph1) [q] [EXE] [q] ~ [q]2 (Pwr) [q] [EXE] 0 (L1) [q] [EXE] 1 (L2)

[q] [EXE] 0 (1)

S - G R A P H : G p h 1 G - T Y P E : P o w e r X L I S T : L 1 Y L I S T : L 2

STAT R

F R E Q : 1

8 - 6 - 7 Graphique de dispersion (Scat)

La dispersion positionne les points de données de la liste X et de la liste Y en tant que paires coordonnées, montrant chaque point par un Square (¨), une Cross (X) ou un Dot (·).

GRAPH R

Exemple : Effectuez le graphique de dispersion des données suivantes

x32054

y67461

Étape 1 : Entrez les données précédentes dans les listes L3 et L4

STAT R

3 [EXE] 2 [EXE] 0 [EXE] 5 [EXE] 4 [EXE] [u] 6 [EXE] 7 [EXE] 4 [EXE] 6 [EXE] 1 [EXE]

Étape 2 :Spécifiez 2-VAR X = L3, 2-VAR Y = L4 et 2-VAR F = 1

[FUNC] 1 (CALC) 9 (SET) [q] [q] [EXE] 2 (L3) [q] [EXE] 3 (L4) [q] [EXE] 0 (1)

L 3 L 4

5 6 4 1

L 4 ( 6 ) =

2 - V A R X : L 3 2 - V A R Y : L 4 2 - V A R F : 1

STAT R

Étape 3 : Entrez les paramètres du graphique puis tracez-le

STAT R

[EXIT] [EXIT] 0 (GRAPH) 3 (SET) [EXE] 0 (Gph1) [q] [EXE] 0 (Scat) [q] [EXE] 2 (L3) [q] [EXE] 3 (L4)

[q] [EXE] 0 (1) [q] [EXE] 0 (Square (¨))

[EXIT] 0 (Gph1)

S - G R A P H : G p h 1 G - T Y P E : S c a t X L I S T : L 3 Y L I S T : L 4

STAT R

F R E Q : 1 M A R K : ¨

STAT R

[EXIT] 0 (Gph1)

STAT R

8 - 6 - 8 Graphique par ligne xy (xyLin)

La ligne xy est un positionnement par dispersion dans laquelle les points de données sont positionnés et connectés selon leur ordre d’apparition dans la liste X et la liste Y.

Exemple : Avec les données précédentes, modifiez l’exemple précédent

[FUNC] 0 (GRAPH) 3 (SET) [q][EXE] 1 (xyLin)

pour tracer un graphique par ligne xy.

STAT R

S - G R A P H : G p h 1 G - T Y P E : x y L i n X L I S T : L 3 Y L I S T : L 4

[EXIT] 0 (Gph1)

STAT R

8 - 6 - 9 Graphique de série temporelle (T-Ser)

Une série temporelle est une séquence d’observations ordonnées dans le temps. Si les observations sont effectuées sur un phénomène dans le temps, le graphique est très judicieux pour afficher les données dans leur ordre d’apparition.

(A) En espace bidimensionnel

Le bidimensionnel pour un graphique de série temporelle positionne les points de données de la liste T et de la liste Y. Les données temporelles de la liste T se placent sur l’axe des abscisses; celles de la liste Y sur l’axe des ordonnées.

STAT R

8 - 6 - 10 Pour afficher les résultats d’un calcul statistique à double variable /

régression.

Lorsqu’un graphique statistique à double variable est affiché, les résultats du calcul statistique à deux variables ou n’importe lequel des six calculs de régression peuvent être rappelés immédiatement en pressant [FUNC] pour afficher le menu ci-dessous.

0 2 - V A R 1 X 2 M E D 3 L O G 4 X ² 5 E X P 6 P W R

STAT R

Choisissez :

2-VAR ...Statistique à variable double : pour afficher l’écran des résultats du calcul

statistique à deux variables

X ... Graphique de régression linéaire : pour afficher l’écran des résultats du

calcul de régression linéaire

MED ... Graphique Med-Med : pour afficher l’écran des résultats du

calcul de régression Med-Med

LOG ... Graphique de régression logarithmique : pour afficher l’écran des résultats

du calcul de régression logarithmique

X² ... Graphique de régression quadratique : pour afficher l’écran des résultats

du calcul de régression quadratique.

EXP ... Graphique de régression exponentielle : pour afficher l’écran des résultats

du calcul de régression exponentielle

PWR ... Graphique de régression de puissance : : pour afficher l’écran des résultats

du calcul de régression de puissance

Exemple : Pour afficher les résultats d’un calcul de régression lorsqu’un

graphique de régression linéaire est affiché.

STAT R

(B) En l’espace tridimensionnel

Le tridimensionnel pour un graphique de série temporelle positionne les points de données de la liste X et de la liste Y (ou liste Y1~Liste Y5). Les données de la liste X se placent sur l’axe des abscisses, celles de la liste Y sur l’axe des ordonnées. Les points de données sont positionnés et connectés selon la liste temporelle (Liste T).

STAT R

[FUNC] 1 (X)

Vous pouvez utiliser les touches de curseur pour visualiser les résultats du calcul. Lorsque vous effectuez un calcul de régression Med-Med, vous avez accès aux points de résumé (x1, y1, x2, y2, x3, y3). Pour ce faire, sélectionnez “STAT” dans le menu [VARS] et défilez vers le bas de l’écran.

STAT R

y = a x + b 0 C o p y 1 D r a w a b r 3 . 5

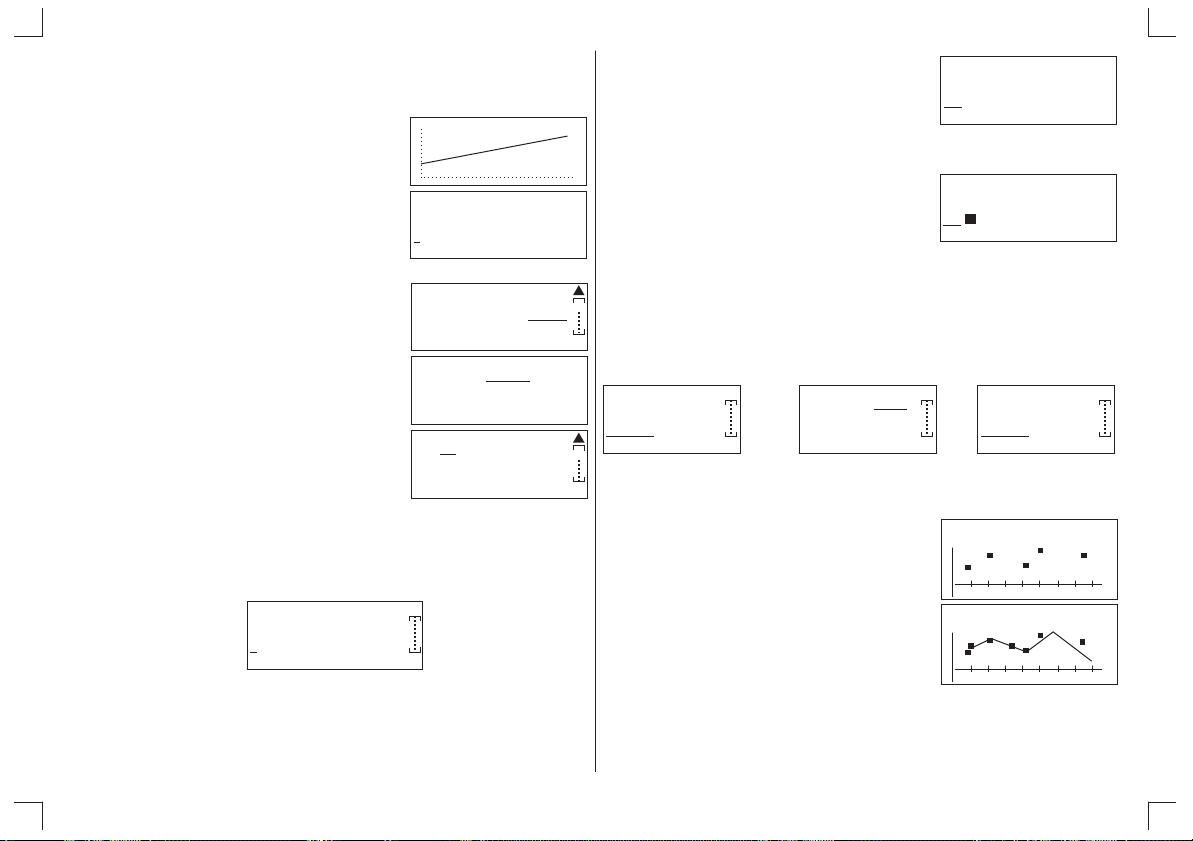
Exemple : Reprenons l’exemple du graphique de régression Med-Med.

[FUNC] 2 (MED)

Lorsque le graphique est affiché, il est possible d’afficher les résultats du calcul de régression Med-Med à l’aide de la touche [FUNC].

y = a x + b 0 C o p y 1 D r a w a b 0 . 1 8 2 3 5 2 9 4 1

STAT R

Accédons maintenant aux points de résumé :

[EXIT] [EXIT] [EXIT] [VARS] [VARS] [VARS] [q] [u] [u] [u]

[EXE] [u]

8 - 6 - 11 Pour copier une formule de graphique de régression vers le mode

graphique.

Après avoir effectué un calcul de régression, vous pouvez copier sa formule vers le mode GRAPH.

y = a x + b 0 C o p y 1 D r a w a b 3 . 5

Copy ... Enregistre la formule de régression affichée dans le mode GRAPH Draw ... Applique en graphique la formule de régression affichée

Pressez 0 (Copy) pour copier la formule de régression qui a produit les résultats affichés vers le mode GRAPH. Utilisez [q] ou [p] pour sélectionner la zone de mémoire que vous souhaitez.

STAT R

X f a c t Y f a c t Y X t Y t S T A T

1 - V A R 2 - VA R

x 1 y 1 x 2 y 2 x 3 y 3 a b c r x’ y’

8 1

STAT R

GRAPH R

0 (COPY) [q]

Pressez [EXE] pour enregistrer la formule de graphique copiée et retourner à l’affichage antérieur du résultat du calcul de régression. Voici les contenus en mode GRAPH.

G - F u n c : Y = Y 1 : Y 2 : Y 3 :

GRAPH R

G - F u n c : Y = Y 1 : Y 2 3 . 5 + 1 . 8

Y 3 :

8 - 7 Graphiques multiples

Vous pouvez dessiner plusieurs graphiques dans le même affichage en réglant le statut de dessin des graphiques statistiques sur On ou Off pour un, deux ou trois graphiques. Pressez [FUNC] 0 (GRAPH) 4 (SEL) pour spécifier la zone du graphique statistique (S-Gph1 ~ S-Gph3) qui est dessiné ou non.

STAT R

S - G p h 1 : O n S - G p h 2 : O n S - G p 3 : O n 0 D r a w

Pressez 0 (Draw) pour afficher les graphiques multiples. Le texte en haut de l’écran indique le graphique actuellement sélectionné (S-Graph1 = S-Gph 1, S-Graph2 = SGph 2, S-Graph3 = S-Gph 3).

[EXE][u] [EXE]

0 (Draw)

STAT R

0 O n 1 O f f

S - G p h 1 : O n S - G p h 2 : O n S - G p 3 : O f f 0 D r a w

STAT R

S - G r a p h 1

STAT R

S - G r a p h 2

STAT R

8 - 8 Application manuelle de graphique

Dans tous les exemples d’applications graphiques jusqu’ici, les valeurs étaient calculées selon les paramètres de fenêtre V-Window et les graphiques étaient réalisés automatiquement. Cette application automatique se déclenche lorsque l’option “S-WIND” de la fenêtre V-Window est réglée sur “Auto” (auto graphiques). Vous pouvez aussi produire des graphiques manuellement, quand les capacités de graphiques automatiques de cette calculatrice ne donnent pas des résultats qui vous conviennent. Sélectionnez pour cela l’option “S-WIND” Man.

8 - 8 - 1 Pour régler la largeur d’un histogramme

En mode STAT, pressez [2nd] [SYSTEM]. Lorsque l’option “S-WIND” de la fenêtre de visualisation est réglée sur “Man” (graphiques manuels), un écran apparaît où vous pouvez spacifier le point de départ et l’espacement des barres d’histogramme.

STAT R

S - W I N D : A u t o G - F U N C : O n A N G L E : R a d D I S P : F l o

Voici les significations des options qui apparaissent sur cet écran lorsque vous choisissez de tracer un histogramme manuellement.

XStrt ... Point de départ de l’histogramme (coordonnées x) ptch ... Espacement de barre (spécifier en tant qu’unité d’échelle)

Ici nous allons illustrer cette opération en réglant les paramètres d’histogramme pour le Graph 1, où X Strt = 2 et ptch = 4 Lorsque la liste de données statistiques est affichée, exécutez la procédure suivante.

STAT R

S e t I n t e r v a l X s r t = - 3 . 5 p t c h = 1 D r a w

[2nd] [SYSTEM] (S-WIND) [EXE] 1 (Man)

[EXIT] [FUNC] 0 (GRAPH) 0 (Gph 1)

2 [EXE] 4 [EXE] [EXE]

[EXE]

STAT R

0 A u t o 1 M a n

STAT R

S - W I N D : M a n G - F U N C : O n A N G L E : R a d D I S P : F l o

STAT R

S e t I n t e r v a l X s r t = - 3 . 5 p t c h = 1 D r a w

GRAPH R

Chapitre 9 Jeux

9 - 1 Avant de commencer un jeu

Dans le menu des modes de fonctionnement, sélectionnez la fonction GAME pour entrer en mode Jeux. Le menu des jeux est alors affiché.

0 M E M O R Y 1 A R I T H 2 G H O S T 3 G U E S S

Il y a quatre jeux : MEMORY, ARITH, GHOST, GUESS.

· Lorsqu’on dépasse la période d’entrée du choix, l’écran de sommeil apparaît.

Pressez n’importe quelle touche pour revenir à l’écran précédent.

· Si vous avez gagné une session, vous êtes automatiquement amené au niveau supérieur. Si vous avez perdu une session, vous êtes automatiquement amené au niveau inférieur. L’indicateur “LV:” sur l’écran vous montre quel est votre niveau actuel.

9 - 2 MEMORY

Dans le menu principal des jeux, pressez 0 (MEMORY) pour accéder à ce jeu. Sélectionnez 1 (SET) pour régler le niveau de difficulté du jeu de 1 à 9 et le statut affiché / non affiché (On, Off) des lettres L et R.

0 P L A Y 1 S E T

Pressez 0 (PLAY) pour démarrer le jeu.

Règle :

· Lorsque le jeu commence, des séries de chiffres et de lettres parcourent l’écran en séquence. Si votre mémoire est vraiment bonne, augmentez la difficulté par la vitesse d’apparition en pressant [q] ou [ + ].

· Entrez ensuite les chiffres de la première série et pressez [EXE]

L e v e l : 1 2 3 4 5 6 7 8 9

[EXE]

T y p e : O n O f f

P E A S E

R E P E A T 1 s t

L = - R = +

L 4 t

Lorsque vous jouez avec les lettres, entrez le caractère R en pressant [ + ]; pour enter le caractère L, pressez [ - ].

· Si vous entrez une réponse incorrecte, un message d’erreur s’affiche. Vous pouvez alors sélectionner “CONTINUE” pour ouvrir une nouvelle session, ou “REPLAY” pour rejouer la dernière question.

W R O N G L V : 1

0 R E P L A Y 1 C O N T I N U E

· Si vous sélectionnez “REPLAY”, un message apparaît pour confirmer si vous voulez rejouer la dernière question ou pas.

R E P L A Y : N Y

· Lorsque “N” est sélectionné, la réponse correcte s’affiche.

A N S W E R

R 4

1 C O N T I N U E

9 - 3 ARITH

Dans le menu principal des jeux, pressez 1 (ARITH) pour jouer à Arith. Sélectionnez 1 (SET) pour régler le niveau de difficulté du jeu de 1 à 9 et le type arithmétique (+, -, x,

¸, +-, x ).

0 P L A Y 1 S E T

[EXE]

L e v e l : 1 2 3 4 5 6 7 8 9 T y p e : + - x ¸ x

Pressez 0 (PLAY) pour démarrer le jeu.

Règle :

· Lorsque le jeu commence, des calculs apparaissent en séquence. Si votre calcul

arithmétique est vraiment bon, augmentez la difficulté en changeant de vitesse par [q] ou [ + ]

· Après l’affichage, entrez la réponse et prssez [EXE].

A N S W E R

L = - R = +

3 7 5 t

· Si vous entrez une réponse incorrecte, un message d’erreur s’affiche. Vous pouvez sélectionner “CONTINUE” pour ouvrir une nouvelle session ou “REPLAY” pour réessayer.

W R O N G L V : 1

0 R E P L A Y 1 C O N T I N U E

· Si vous sélectionnez “REPLAY”, un message apparaît pour confirmer si vous

voulez rejouer la dernière question ou pas.

R E P L A Y : N Y

· Lorsque “N” est sélectionné, la réponse correcte s’affiche.

A N S W E R :

3 7 7

1 C O N T I N U E

9 - 4 GHOST

Dans le menu principal des jeux, pressez 2 (GHOST) pour jouer à Ghost. Sélectionnez 1 (SET) pour régler le niveau de difficulté du jeu de 1 à 9.

0 P L A Y 1 S E T

G|} T = G R A P H = X

L e v e l : 1 2 3 4 5 6 7 8 9

[EXE]

Pressez 0 (PLAY) pour démarrer le jeu.

Règle :

· Des fantômes ( ) apparaissent au hasard dans la zone de jeu. Utilisez les

touches de curseur ([t] [u] [p] [q]) pour déplacer le curseur ( ) là où se trouve un fantôme. Pressez [G«T] ou [GRAPH] pour l’éliminer et gagner des points.

H : 2 5 P : 10

· Chaque fois que dix fantômes sont éléminés, vous êtes récompensé par une manche supplémentaire ( ). Ne l’éliminez pas sinon vos points seraient supprimés.

· Essayez d’éliminer autant de fantômes que possible. Les meilleurs points (H)

seront placés sur le côté gauche de l’écran.

· Pour interrompre un jeu en cours, pressez [EXIT].

· Si le nombre de fantômes à l’écran dépasse dix-huit, le jeu est fini et vous avez

perdu. Vous pouvez sélectionner “CONTINUE” pour ouvrir une nouvelle session.

H : 2 5 P : 1 7 G A M E O V E R

1 C O N T I N U E

9 - 5 GUESS

Dans le menu principal des jeux, pressez 3 (GUESS) pour jouer à Guess. Sélectionnez 2 (SET) pour régler le niveau de difficulté du jeu de 1 à 4 et la limite de réponses incorrectes en session (10, 20, 30)

0 S I N G L E 1 D O U B L E 2 S E T

L e v e l : 1 2 3 4 T y p e : 1 0 2 0 30

[EXE]

Par exemple, “2A2B” “2A” signifie que deux nombres sont corrects et à la bonne place “2B” signifie que vous avez trouvé deux nombres mais qu’il ne sont pas à la bonne place.

9 8 7 6 0 A 1 B

4 3 1 8 2 A 1 B 2 4 1 8 2 A 2 B u 4 2 1 8

· Le jeu continue alors, et vous gagnez si vous trouvez le code caché. Vous pouvez sélectionner “CONTINUE” pour ouvrir une nouvelle session.

y o u a r e g o o d

1 C O N T I N U E

Ù Ù

· Selon vos paramètres, il y a une limite de réponses incorrectes pour la même session. Lorsque cette limite est atteinte, le jeu est fini et le code caché apparaît. Vous pouvez sélectionner “CONTINUE” pour ouvrir une nouvelle session.

y o u a r e l o s t 2 9 5 1

1 C O N T I N U E

(B) Statut double

· Après le démarrage d’un nouveau jeu, réglez votre code caché.

S E T N U M B ER

P L E A S E ?

u 4 2 1 8

Pressez 0 (SINGLE) pour jouer tout seul; pressez 1 (DOUBLE) pour jouer avec la calculatrice.

Règle : (A) Statut seul

· Après avoir commencé un nouveau jeu, un code caché est placé dans la mémoire de la calculatrice. Utilisez les nombres possible de 0 à 9 pour entrer votre combinaison (les chiffres ne peuvent pas être répétés), et pressez [EXE]. La calculatrice répond par un certain nombre de “A” et de “B” juste après votre combinaison.

· Les procédures et règles sont similaires à celles du statut unique, sauf que c’est vous et la calculatrice qui devinez et répondez à votre tour.

c 5 6 7 8 1 A 0 B u : 4 1 2 8 A B

uu 4 7 3 8 A B

c 5 6 7 8 u : 4 1 2 8 u 0 A B

u 4 7 3 8 0 A 1 B

· Rappelez-vous de ne pas faire de réponse incorrecte à la calculatrice, ce qui provoquerait l’affichage d’un message d’erreur.

· Le jeu continue alors, jusqu’à ce que vous ou la calculatrice trouvez le code caché. Si vous avez perdu, vous pouvez sélectionner “CONTINUE” pour ouvrir une nouvelle session.

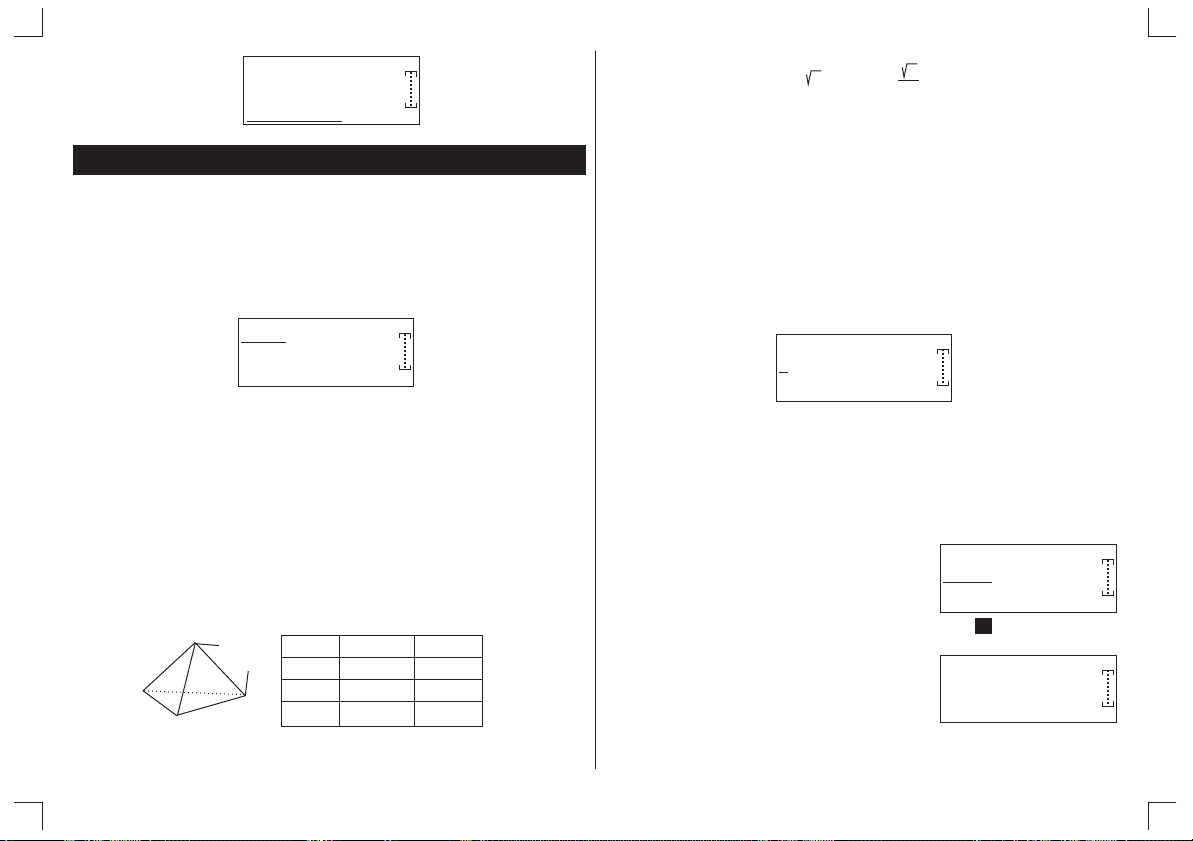
:C O D E : 4 2 1 8 Y O U L O S T !

1 C O N T I N U E

Chapitre 10 Programmer

10 - 1 Avant de programmer

La fonction de programmation aide à réaliser rapidement des calculs complexes et répétés. Les commandes et calculs sont exécutés en séquence, exactement comme les multidéclarations manuelles. Les programmes multiples peuvent être enregistrés sous des noms de fichiers pour une utilisation et une édition rapides. Dans le menu des modes de fonctionnement, sélectionnez l’option PROG pour entrer en mode PROG. L’écran suivant s’affiche alors :

0 N E W 1 E DI T 2 R U N 3 D E L 4 T R A C E 5 R E N A M

Vous pouvez choisir entre :

NEW ... Sélectionnez NEW pour commencer un nouveau programme EDIT ... Sélectionnez EDIT pour éditer un programme RUN ... Sélectionnez RUN pour exécuter un programme DEL ... Sélectionnez DEL pour effacer un programme TRACE ... Sélectionnez TRACE pour entrer en mode de debuggage d’un

RENAM ... Sélectionnez RENAM pour changer le nom d’un programme

programme

10 - 2 Créer un nouveau programme

Exemple : Pour enregistrer un programme qui calcule la zone de surface (S) et

3.5 ? Cm² ? Cm

Voici les formules utilisées pour calculer la zone de surface (S) et le volume (V) d’un tétraèdre régulier dont la longueur sur un côté (A) est connue.

le volume (V) d’un tétraèdre régulier dont la longueur sur un côté (A) est connue. Enregistrez la formule de calcul sous le nom de fichier TETRA.

PROG

ASV

5 ? Cm² ? Cm 12 ? Cm² ? Cm

S = 3 A ² V = A

10 - 2 - 1 Pour spécifier un type de programme et enregistrer un nom de

PROG TYPE : Chaque programme doit se voir spécifié un mode de fonctionnement

que la calculatrice choisit en exécutant le programme que vous avez entré. Pour tous les programmes classiques choisissez le mode MAIN (MA); pour les calculs logiques de base, sélectionnez le mode Base-N (BA).

Filename : Lorsque vous entrez un nouveau programme, vous devez enregistrer le nom de fichier puis entrer le programme en question. Le nom de fichier peut être long d’au plus sept caractères et les caractères que vous pouvez utiliser vont de A à Z, ou de 0 à 9. Si vous essayez d’utiliser un nom de fichier semblable à ceux existants, un message apparaît pour confirmer si vous voulez écraser le programme précédent ou pas.

Déplacez le curseur vers “Y” pour écraser le programme ou “N” pour abandonner la procédure sans rien écraser.

Exemple : Pour enregistrer le nom de fichier TETRA, dont le type de

Étape 1 : Lorsque l’écran initial du mode de programme est affiché, pressez

fichier

O V E R W R I T E : N Y

PROG

programme est MAIN.

0 (NEW) et spécifiez le type de programme que vous souhaitez créer.

0 (NEW)

Étape 2 : Entrez le nom du fichier. Le verrouillage Alpha “ “ est enclenché. Le

curseur change de forme pour indiquer l’entrée de caractère alpha.

[EXE] [T] [E] [T] [R] [A]

P R O G T Y P E 0 M A I N 2 B a s e - n

F i l n a m e : M A [ T E T R A t ]

PROG

Étape 3 : Pressez [EXE] pour enregistrer le nom de fichier et afficher l’écran d’entrée du programme.

[EXE]

Note :

· Vous pouvez supprimer un caractère lors de l’entrée d’un nom de fichier en

déplaçant le curseur vers le caractère que vous voulez supprimer, pressez ensuite [DEL]

· Pour sortir de l’écran d’entrée du nom de fichier et retourner à l’écran principal

sans enregistrer un nom de fichier, pressez [EXIT]

10 - 2 - 2 Pour entrer les contenus du programme

Les contenus du programme s’entre en utilisant les mêmes procédures de base que vous utilisez pour les calculs manuels. Chaque ligne de commande se termine automatiquement par un point-virgule ( ; ) lorsque vous pressez [EXE]. Pour entrer plus d’une seule instruction ou expression dans une seule ligne de commande, veuillez les séparer toutes par un point-virgule ( ; ). Voici comment vous pouvez entrer les formules requises en tant que calcul manuel ou en tant que programme.

· Calcul manuel Zone de surface (S) ... [ Ö ] 3 [u] [x] < valeur de A > [X²] Volume (V) ... [ Ö ] 2 [u] [¸] 12 [x] < valeur de A > [Ù] 3

· Programme Zone de surface (S) ... [ Ö ] 3 [u] [x] [ALPHA] [A] [X²] Volume (V) ... [ Ö ] 2 [u] [¸] 12 [x] [ALPHA] [A] [Ù] 3

Exemple : Pour entrer les contenus du programme pour le nom de fichier

Suivez les étapes suivantes pour entrer les contenus du programme.

TETRA

Contenus : < Input A ; Étapes : < [2nd] [INST] 2 (Input) [ALPHA] [A] [EXE]

Contenus : = S = Ö (3) x A² ; Étapes : = [ALPHA] [S] [ALPHA] [=] [Ö] 3 [u] [x] [ALPHA] [A] [X²] [EXE]

= T E T R A =

E n d

PROG

Contenus : > V = Ö (2) ¸ 12 x A Ù 3 ; Étapes : > [ALPHA] [V] [ALPHA] [=] [Ö] 2 [u] [¸] 12 [x] [ALPHA] [A] [Ù] 3

Contenus : ? Print “S=”, S ; Étapes : ? [2nd] [INST] [2nd] [INST] [2nd] [INST] 0 (Print) [ALPHA] [”]

Contenus : @ Print “V=”, V ; Étapes : @ [2nd] [INST] [2nd] [INST] [2nd] [INST] 0 (Print) [ALPHA] [”]

Contenus : A End

Pour plus d’exemples de programmes, voyez “10-13 Programme exemples)

10 - 2 - 3 Pour exécuter un programme

Exemple : Pour exécuter le programme TETRA

Étape 1 : Lorsque l’écran principal est affiché, pressez 2 (RUN) et choisissez un nom

de fichier. Lorsque la liste de noms de fichiers est affichée, utilisez [p] ou [q] pour déplacer le curseur vers le nom du programme que vous voulez démarrer.

2 (RUN) [q] ~ [q]

Étape 2 : Pressez [EXE] pour démarrer le programme et entrer une valeur pour A

[EXE] 3.5

Étape 3 : Pressez [EXE] pour exécuter le programme. Le résultat final est affiché.

[EXE] [p]

Étape 4 : Pour redémarrer le programme depuis le début, veuillez presser [EXE] pour

entrer encore la valeur A

[EXE]

[ALPHA] [S] [ALPHA] [=] [ALPHA] [”] [ ] [ALPHA] [S] [EXE]

[ALPHA] [V] [ALPHA] [=] [ALPHA] [”] [ ] [ALPHA] [V] [EXE]

Essayons d’exécuter le programme que nous avons entré.

, ,

B A : B I N M A : L I N E

PROG

* R U N *

u M A : T E T R A

A = 3 . 5 t

S = 2 1 . 2 1 7 6 2 2 3

9 2 7 2

V = 5 . 0 5 2 8 6 7 2 0 7 2 2 9

A S V

3.5 21.21762239272 cm² 5.052867207229 cm 5 43.30127018922 cm² 14.73139127472 cm 12 249.4153162899 cm² 203.6467529817 cm

Note : Vous pouvez aussi démarrer le programme en mode MAIN en entrant :

PROG < nom de fichier >.

10 - 3 Débugger un programme

Un problème dans un programme qui empêche le programme de fonctionner correctement s’appelle un “bug”, et l’opération consistant à éliminer de tels problèmes s’appelle le “débuggage”. N’importe lequel des symptômes suivants indique que votre programme contient des bugs et q’un débugage est nécessaire.

(A) Pour éliminer les bugs qui causent des messages d’erreurs

Un message d’erreur, comme celui montré ci-dessous, apparaît pendant 5 secondes lorsque quelque chose d’erroné ou un calcul interdit est survenu pendant l’exécution du programme.

Après un message d’erreur, le curseur clignotant montre l’emplacement de l’erreur. Consultez “1-9 Conditions d’erreur” et corrigez-la. Vous pouvez aussi sélectionner “TRACE” dans le menu principal de programme pour entrer en mode TRACE de débugage. Le système vérifie le programme étape par étape et vous dire où se trouve l’erreur, s’il y a lieu.

(B) Pour éliminer les bugs qui causent de mauvais résultats

Si votre programme produit des résultats qui ne sont pas ceux que l’on attendrait normalement, vérifiez les contenus du programme et effectuez les changements nécessaires. Voir “10-6 Editer les contenus du programme” pour les détails sur la façon de changer les contenus du programme.

PROG

S Y N T A X E E r

10 - 4 Chercher un fichier

Vous pouvez chercher un nom de fichier spécifique en utilisant n’importe laquelle des trois méthodes suivantes.

(A) Recherche par défilement

Lorsque la liste des noms de fichiers est affichée, utilisez [p] ou [q] pour déplacer

le pointeur sur le nom du programme que vous voulez, puis pressez [EXE] pour l’éditer.

* R U N *

u M A : T E T R A

(B) Recherche par nom de fichier

Lorsque la liste de noms de fichiers est affichée, pressez [FUNC] 0 (Search) pour afficher l’écran de recherche et entrer le nom du fichier. Après avoir pressé [EXE], les contenus du programme sont invoqués.

S e a r c h F o r

[ T E T R A t ]

Note : S’il se trouve pas de programme dont le nom de fichier correspond à celui

que vous avez entré, le message “Not Found” s’affiche alors. Si cela arrive, pressez [EXIT] pour effacer le message d’erreur et entrer un nom correct.

Lorsque les différents noms de fichiers sont affichés, pressez [FUNC] 0 (Search) pour afficher l’écran de recherche et entrer les caractères initiaux du fichier que vous voulez trouver. Tous les fichiers dont les noms de fichiers commencent par les caractères que vous avez invoqués seront affichés.

S e a r c h F o r

[ T t ]

Utilisez [p] ou [q] pour déplacer le pointeur vers le nom du programme que vous voulez, puis pressez [EXE]. Les contenus du programme sont invoqués.

Note : S’il ne se trouve pas de programme dont le nom de fichier commence par les

caractères que vous avez entrés, le message “Not Found” s’affiche alors. Si cela arrive, pressez [EXIT] pour effacer le message d’erreur et entrer des caractères corrects.

PROG

P r o g r a m

B A : B I N M A : L I N E

[EXE]

PROG

P r o g r a m

* R U N * u B A : T A N

M A : T E T R A M A : T H I N

PROG

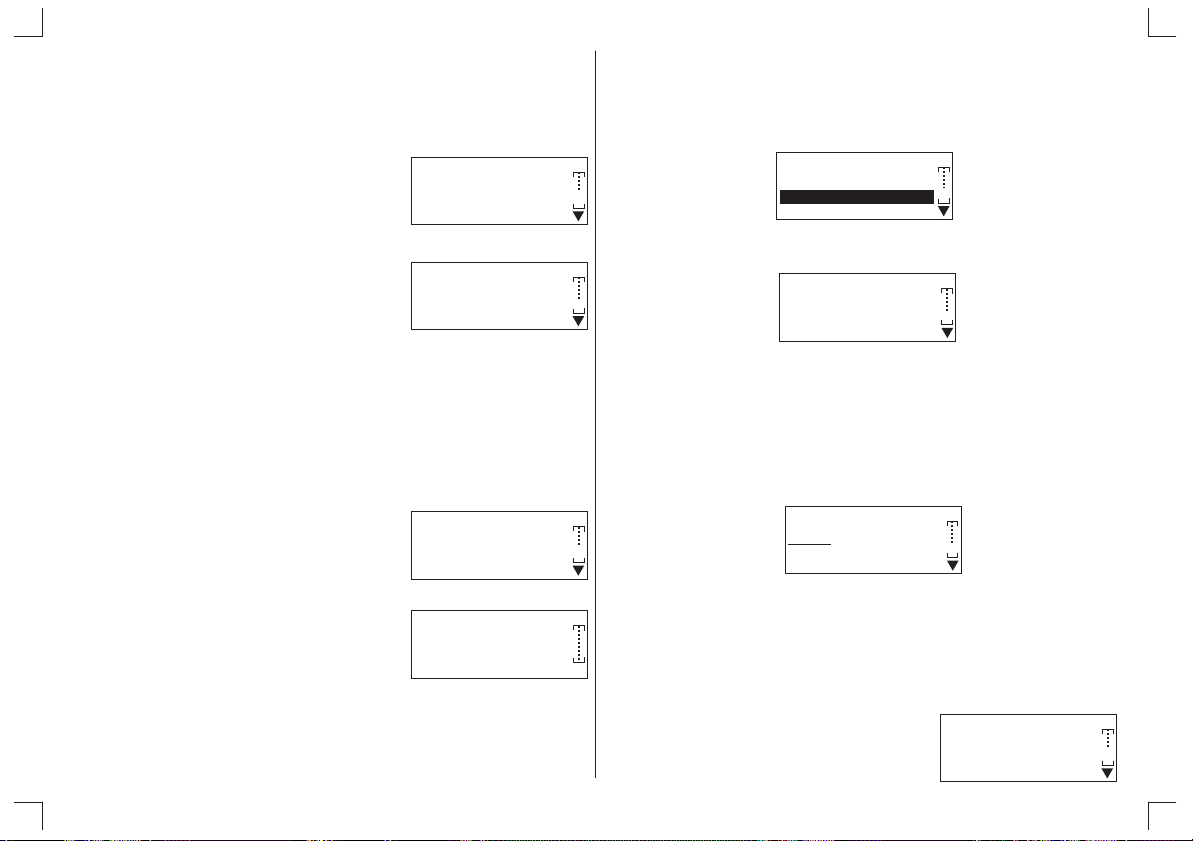
10 - 5 Renommer un programme

Exemple : Pour renommer un nom de fichier TETRA

Étape 1 : Lorsque le menu principal de programme est affiché, pressez 5 (RENAM).

Trouvez le nom de fichier du programme que vous voulez renommer dans la liste de noms de fichier.

5 (RENAM) [q]

* R E N A M E *

u M A : T E T R A

Étape 2 : Effectuez la correction du nom de fichier pour le renommer

[EXE] [u] ~ [u] [H]

* R E N A M E *

u M A : T E T R A H t ]

PROG

B A : T A N

M A : T H I N

PROG

B A : T A N

M A : T H I N

Étape 3 : Pressez [EXE] pour l’enregistrer

10 - 6 Editer les contenus du programme

Exemple : Pour éditer les contenus du programme nommé TETRA

Étape 1 : Lorsque le menu principal du mode programme est affiché, pressez

1 (EDIT). Trouvez le nom de fichier du programme que vous voulez éditer dans la liste des noms de fichiers.

1 (EDIT) [q]

* R E N A M E *

u M A : T E T R A H t ]

PROG

B A : T A N

M A : T H I N

Étape 2 : Pressez [EXE] pour éditer le programme

PROG

[EXE]

Note : Les procédures que vous utilisez pour corriger les contenus du programme

édité sont identiques à celles utilisées pour éditer les calculs manuels, sauf que [ON/CL] devient inactif. Pour les détails, voir “2-5-2 Effectuer des corrections pendant l’entrée”.

= T E T R A =

I n p u t A ; u S = Ö ( 3 ) x A ² ; V = Ö ( 2 ) ¸ 1 2 x A Ù

Les fonctions “COPY” et “Paste” sont aussi utiles lorsqu’on édite les contenus du programme. Dans les contenus du programme, déplacez le curseur vers l’endroit où vous voulez commencer la copie, puis pressez [FUNC] 6 (COPY) 0 (Begin). Continuez en déplaçant le curseur vers l’endroit où vous voulez terminer la copie, puis pressez [FUNC] 6 (COPY) 1 (End). La ligne de commande sélectionnée est marquée comme suit.

V = Ö ( 2 ) ¸ 1 2 x A Ù

Pour coller la ligne de commande que vous venez de copier, déplacez le curseur vers l’endroit désiré et pressez [FUNC] 7 (Paste) pour la coller.

3 I n p u t B ; S = Ö ( 3 ) x A ²

Note : Vous ne pouvez pas copier une ligne de commande depuis un programme

existant pour la coller dans un autre programme existant.

PROG

= T E T R A =

I n p u t A ;

S = Ö ( 3 ) x A ² ;

PROG

= T E T R A =

10 - 7 Effacer un programme

Lorsque le menu principal est affiché, pressez 3 (DEL) pour effacer un ou plusieurs programmes. Il existe deux manières différentes de supprimer un nom de fichier et son programme.

D E L E T E : 0 O N E 1 A L L

ONE ... Suppression d’un programme spécifique ALL ... Suppression de tous les programmes

PROG

(A) Pour supprimer un programme spécifique

Étape 1 : Pressez 0 (ONE) pour afficher la liste des programmes existants. Utilisez

[p] ou [q] pour déplacer le pointeur vers le nom du programme que vous voulez supprimer.

0 (ONE) [q] ~ [q]

* D E L *

u M A : T E T R A

B A : B I N M A : L I N E

PROG

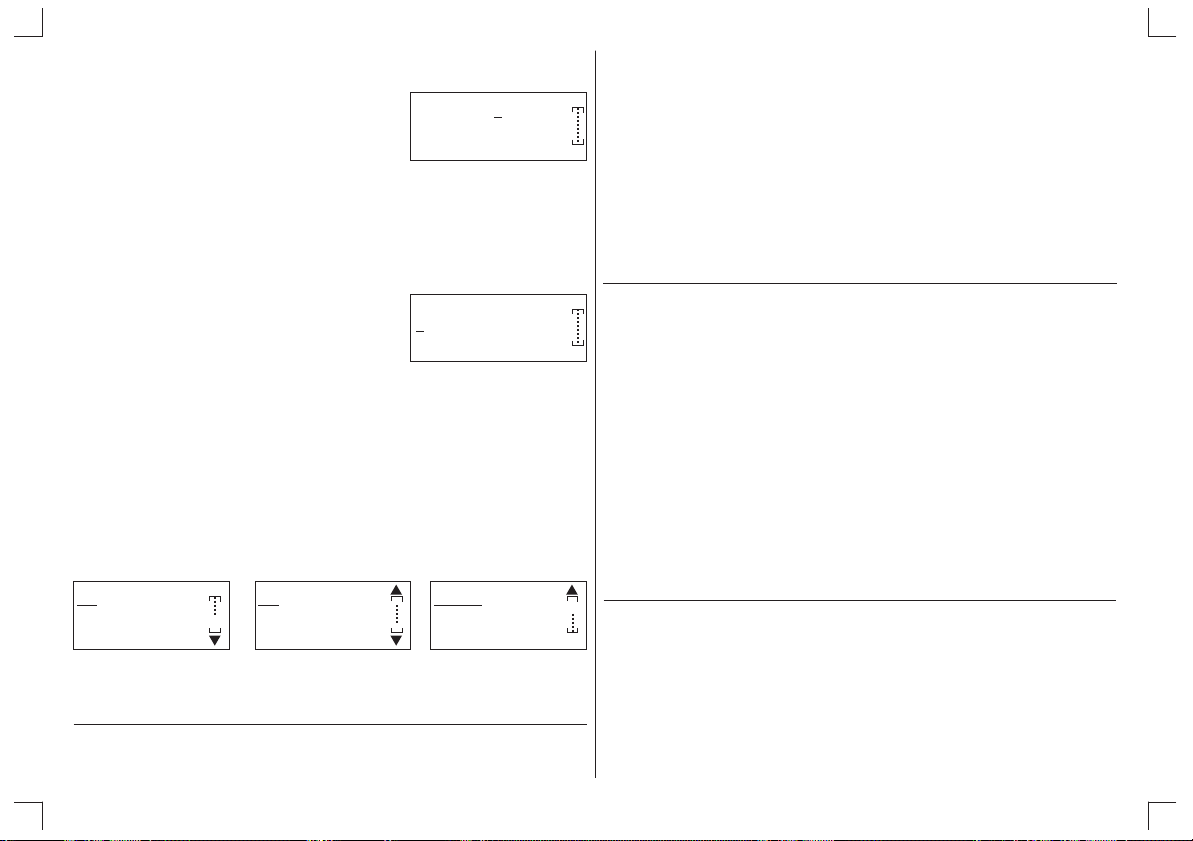
Étape 2 : Après avoir pressé [EXE], un message apparaît pour confirmer si vous

voulez supprimer le contenu du programme ou pas.

[EXE]

Étape 3 : Déplacez le curseur vers “Y” pour supprimer le programme ou “N” pour

abandonner la procédure sans rien supprimer.

D E L E T E : N Y

PROG

(B) Pour supprimer tous les programmes

Étape 1 : Après avoir pressé 1 (ALL), un message apparaît pour confirmer si vous

voulez supprimer tous les programmes ou pas.

1 (ALL)

Étape 2 : Déplacez le curseur vers “Y” pour supprimer tous les programmes ou “N”

pour abandonner la procédure sans rien supprimer.

Note : Vous pouvez aussi supprimer tous les programmes en utilisant le mode

RESET. Voir “1-10 Statut et effaçage de la mémoire”

D E L E T E A L L : N Y

PROG

10 - 8 Commandes de programme

En plus des commandes de calcul, cette calculatrice inclut aussi diverses commandes relationnelles et de saut qui peuvent être utilisées pour créer rapidement et facilement des programmes. Pressez [2nd] [INST] pour afficher les menus de commandes de programme.

0 I f 1 T h e n 2 I n p u t 3 E l s e 4 G o t o 5 F o r 6 G o s u b 7 L a b e l

PROG

0 - - 1 + + 2 D a t a 3 L o c a t 4 R e a d 5 S l e e p 6 R e m 7 R S t o r e

PROG

0 P r i n t 1 S w a p 2 E n d

PROG

10 - 8 - 1 Commandes de programme de base

Commande : Input Fonction : Demande l’entrée de valeurs pour assignation à des variables

pendant exécution du programme.

Syntaxe : (1) Input < nom de variable > ;

Exemple : (1) Input A ;

Description :

1. Cette commande interrompt momentanément l’exécution du programme et

(2) Input < nom de variable >, < nom de variable >, ..., < nom de

variable > ;

(2) Input A, B, S ;

demande l’entrée d’une valeur pour un nom de variable ou une expression. Lorsque la commande Input est exécutée, “< nom de variable > =” s’affiche et la calculatrice attend l’entrée de la valeur.

2. Pour entrer plus d’un nom de variable, veuillez les séparer par une virgule (,).

Commande : If ~ Then ~ Else

Fonction : Une branche conditionnelle est exécutée seulement si certaines

expressions relationnelles sont vérifiées.

Syntaxe : (1) I¦ (< condition > ) Then { < déclaration > } ;

(2) I¦ ( < condition > ) Then { < déclaration > } ; Else { < déclaration > } ;

Exemple : (1) I¦ (A = = 0 ) Then { B = 3 C } ;

(2) I¦ (A = = 0 ) Then { B = 3 C } ; Else { S = 5 C } ;

Description :

1. Pour la commande If-Then, la déclaration Then est exécutée seulement quand les expressions conditionnelles introduites par If sont vraies. Sinon, la déclaration Then n’est pas exécutée

2. Pour la commande If-Then, la déclaration Then est exécutée seulement quand les expressions relationnelles introduites par If sont vraies. Sinon, la déclaration Else est exécutée.

Commande : Print Fonction : Imprimer le texte à l’intérieur des apostrophes et la valeur du nom de

Syntaxe : (1) Print “ < texte > “ ;

Exemple : (1) Print “POWER = “ ;

variable pendant l’exécution du programme.

(2) Print < nom de variable > (3) Print “ < texte > “, < nom de variable > ;

(2) Print A ; (3) Print “POWER = “, A ;

Description :

1. Les options multiples dans une commande Print sont séparées par des virgules (,)

Commande : For

Fonction : Cette commande permet d’exécuter des boucles, c’est à dire la même

Syntaxe : For ( condition de départ ; condition de continuation ; ré-évaluation )

Exemple : For ( A = 1 ; A £ 4 ; A + + )

Description :

L’ordre de traitement de chaque partie pour une boucle For :

1. La première partie de la boucle For, “ For (A = 1;”, initialise la valeur de A pour 1.

2. Ensuite, A = 2 sur l’itération. A £ 4 est toujours vrai, donc le bloc de déclaration

3. A est incrémenté à nouveau, la condition re-évaluée etc ..., Jusqu’à ce que A

Commande : + + , - -

Fonction : Cette commande permet d’augmenter ou de diminuer de 1

Syntaxe : Post-fixée : < nom de variable > + + ; ou < nom de variable > - - ;

Exemple : A + + ; , A - - ; , ++ A ; , --A ;

Commande : Goto ~ Label

Fonction : La commande Goto effectue un saut vers un emplacement Label

Syntaxe : Goto < valeur > ;

opération pour plusieurs valeurs entrant dans une gamme délimitée.

{ déclaration ] ;

A = 1 sur l’itération. A £ 4 est vrai, donc le bloc de déclaration est exécuté et à la fin de l’itération, A est incrémenté de 1.

est exécuté. A la fin de l’itération, A est augmenté de 1. Et ainsi de suite.

atteigne une valeur de 5. Lorsque cela survient, A £ 4 est faux, donc le bloc de déclaration n’est pas exécuté et cela termine le programme.

Préfixée : + + < nom de variable > ; ou - - < nom de variable > ;

spécifié.

Label < valeur > ;

Exemple : Goto 1;

Description :

1. Lorsque le programme en cours d’exécution atteint la déclaration “Goto n”, il

2. S’il n’y a pas de déclaration Label dont les valeurs correspondent à celles

Commande : GoSub

Fonction : Cette commande demande l’exécution d’un autre programme en tant

Syntaxe : GoSub PROG < nom de fichier > ;

Exemple : GoSub PROG ABC ;

Description :

1. Cette commande permet d’invoquer un second programme lors de l’exécution

2. Vous écrivez la commande GoSub en tant que partie du programme principal

3. Si un sous-programme avec le nom de fichier spécifié par la commande

Commande : Data ~ Read

Fonction : La commande Read lit les contenus dans la commande Data.

Syntaxe : Data ( < données >, < données >, ... < données > ) ;

Exemple : Data ( 52, 31, 23 ) ;

Label 1 ;

saute vers “Label n” (n est le même pour Goto n et Label n et n est compris entre 0 et 9). Cela est utile pour faire revenir l’exécution au départ pour des calculs répétitifs, ou pour répéter des calculs depuis un point fixe du programme.

spécifiées par la déclaration Goto, une erreur (GOTO Er) survient.

que sous-programme.

d’un programme principal.

(programme invoqueur). Le principal (programme invoqueur) transfère le contrôle au sous-programme, le sous-programme termine son opération et le contrôle est ramené au programme principal.

Gosub PROG n’existe pas, une erreur (GOSUB Er) survient.

Read ( < nom de variable >, < nom de variable >, ... , < nom de variable > )

Read ( I, A, Q ) ;

Description :

1. Lorsque vous utilisez plusieurs variables dont vous souhaitez entrer les valeurs, vous pouvez utiliser les commandes Data / Read dans le programme pour affecter toutes ces valeurs plus rapidement qu’avec une commande d’entrée classique.

2. La commande Read provoque la lecture des données fournies par une ou plusieurs commandes Data.

3. Lorsqu’une commande Read est exécutée le programme entier est inspecté, commençant à la première ligne, pour chercher une commande Data. Lorsqu’ une telle commande est repérée autant de données que nécessaire sont extraites et stockées dans les noms de variables spécifiés par la commande Read. S’il ne se trouve pas assez de données dans la commande Data, une autre est recherchée.

4. Si une autre déclaration Read est rencontrée, elle continue à chercher des données là où la dernière lecture s’étaient interrompue. Les données ne sont pas réutilisées. Si la commande Read ne trouve pas assez de données pour occuper toutes ses variables, elle produit un message d’erreur et le programme arrête l’exécution.

Commande : Restore

Fonction : La commande réinitialise les données

Syntaxe : Restore ;

Description :

1. Une fois qu’une donnée est LUE, elle ne peut pas être LUE à nouveau, à moins que vous n’utilisiez une commande Restore. La commande Restore réinitialise toutes les données, et la prochaine donnée qui sera LUE sera donc la première donnée de la première commande Data dans le programme, sans considération du nombre de données qui ont été lues précédemment.

Commande : Rem

Fonction : Vous pouvez inclure des commentaires dans votre programme grâce

à la commande Rem. Le programme ignore complètement les lignes Rem, mais leur but est d’aider une personne qui essaie de comprendre comment votre programme fonctionne

Syntaxe : Rem < déclaration > ;

Exemple : Rem PRESSURE CONVERSION ;

Commande : Locate

Fonction : Cette commande affiche les contenus de la commande Input à un

Syntaxe : (1) Locate ( < numéro de colonne >, < numéro de ligne > ) ;

Exemple : (1) Locate ( 2, 2 ) ;

Description :

1. Cette commande affiche les valeurs (y compris les contenus de variables) ou le

2. Le numéro de ligne est désigné par un entier de 1 à 4, et le numéro de colonne est

3. Dans quelques cas, la commande ClrText doit être exécutée avant de démarrer

endroit spécifique sur l’écran de la calculatrice. Celui-ci est considéré comme un tableau à 4 lignes et 12 colonnes.

Input < nom de la variable > ;

(2) Locate ( < numéro de colonne >, < numéro de ligne > ) ;

Print “ < texte > “ ;

Input A ; Affiche :

(2) Locate ( 1, 3 ) ;

Print “ ANSWER “ ;

A =

A N S W E R

texte à un endroit spécifique de l’écran.

désigné par un entier de 1 à 12.

( 1 , 1 )

( 1 , 4 )

PROG

( 12 , 1 )

( 12 , 4 )

le programme ci-dessus.

Commande : Swap

Fonction : Cette commande peut intervertir les contenus de deux variables de

mémoire.

Syntaxe : Swap ( < nom de variable >, < nom de variable > ) ;

Exemple : Swap ( A, B )

Commande : Sleep

Fonction : Cette commande peut suspendre l’exécution du programme pendant

un temps donné en secondes. Le nombre maximum de secondes est d’environ 105. Cela est utile pour afficher des résultats intermédiaires et d’autres informations.

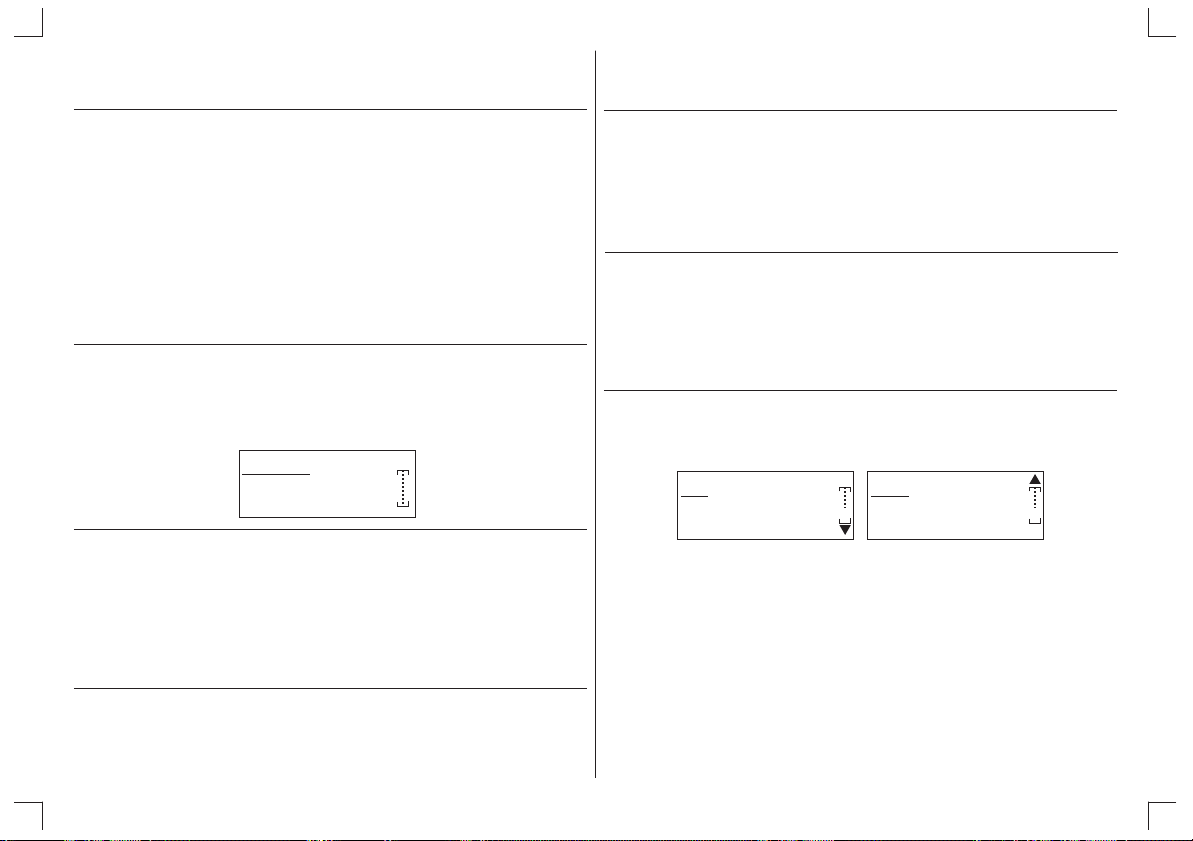
Syntaxe : Sleep ( < temps > ) ;

Exemple : Sleep ( 5 ) ;

Commande : End

Fonction : La déclaration End signifie la fin du programme et doit être la dernière

déclaration exécutée quand un programme est lancé (RUN).

Syntaxe : End ;

Exemple : End ;

Description :

1. La commande End doit être la dernière déclaration dans tout programme.

2. Normalement, lorsque l’on crée un nouveau programme, la commande End va être ajoutée et affichée automatiquement sur l’écran.

10 - 8 - 2 Commandes d’effaçage

Une commande d’effaçage s’entre en pressant [FUNC] 0 (CLR) pour afficher le menu ci-dessous.

0 C l r T e x t 1 C l r G r a p h 2 C l r L i s t 3 C l r D i s p l a y

PROG

Commande : ClrGraph

Fonction : Cette commande efface l’écran graphique

Syntaxe : ClrGraph ;

Description :

Cette commande efface les contenus graphiques et l’écran pendant l’exécution du programme.

Commande : ClrList

Fonction : Cette commande efface les données de liste.

Syntaxe : ClrList ;

Description :

Cette commande efface les contenus de la liste actuellement sélectionnée (Liste 1 à Liste 8) pendant l’exécution du programme.

Commande : ClrText

Fonction : Cette commande efface les contenus textes de l’écran.

Syntaxe : ClrText ;

Description :

Cette commande efface le texte de l’écran pendant l’exécution du programme

Commande : ClrDisplay

Fonction : Cette commande efface l’écran

Syntaxe : ClrDisplay ;

Description :

Cette commande effacetout l’écran pendant l’exécution du programme.

10 - 8 - 3 Opérateurs relationnels et logiques

Pressez [2nd] [TEST] pour afficher le menu ci-dessous.

PROG d

0 = = 1 ¹ 2 < 3 > 4 £ 5 ³

Les opérateurs relationnels peuvent être utilisés avec une boucle For et une commande If dans votre programme

PROG d

0 N e g 1 N o t 2 A n d 3 O r 4 N a n d 5 X o r 6 X n o r

= = ... Egal à ¹ ... Différent de < ... Inférieur à > ... Supérieur à £ ... Inférieur ou égal à ³ ... Supérieur ou égal à

Les opérateurs logiques peuvent être utilisés pour effectuer des calculs en Base-n dans votre programme.

Neg ... Négation Not ... NOT logique And ... AND logique Or ... OR logique Nand ... NAND logique Xor ... XOR logique Xnor ... XNOR logique

10 - 9 Utiliser des fonctions de graphiques dans des programmes

Vous pouvez incorporer des fonctions de graphiques dans un programme pour dessiner des graphiques et pour superposer des graphiques les uns sur les autres. Voici ci-dessous divers types de syntaxe dont vous aurez besoin dans la programmation avec graphiques de fonction.

(A) Visualiser la fenêtre

Pressez [V-WIN] pour afficher le menu ci-dessous.

0 V - w i n d o w 1 S t o V - w i n 2 R c l V - w i n

PROG

· La commande de fenêtre V-Window peut régler les paramètres de la fenêtre graphique utilisant la syntaxe suivante :

ViewWindow ( < Xmin valeur >, < Xmax valeur >, < Xscl valeur >, < Ymin valeur >, < Ymax valeur >, Yscl valeur >, Tmin valeur >, < Tmax valeur >, < Tptch valeur > )

· La commande RclV-Win peut rappeler les réglages de la fenêtre V-Window stockés en mémoire en utilisant la syntaxe suivante :

RclV-Win ;

· La commande StoV-Win peut stocker les réglages actuels de la fenêtre VWindow en utilisant la syntaxe suivante :

StoV-Win ;

(B) Fonction graphique

Une commande pour un type de fonction graphique (Y = Type, Parm Type, Y > Type, Y < Type, Y ³ Type, Y £ Type) s’entre en pressant [FUNC] 4 (GRAPH) pour afficher le menu ci-dessous.

PROG d

0 G - S e l O n 1 G - S e l O f f 2 Y = T y p e 3 P a r m T y p e

PROG d

0 Y > T y p e 1 Y < T y p e 2 Y ³ T y p e 3 Y £ T y p e

< expression > ® Y ( < paramètre > ) ;

Où le paramètre pour la zone de mémoire est un entier de 1 à 20. Cela permet d’enregistrer une expression dans une zone de mémoire de fonction Y1 ... Y 20.

(D) Statut dessiné / non dessiné

La commande pour le statut Dessin ou Non dessin (G-SelOn, G-SelOff) s’entre en pressant [FUNC] 4 (GRAPH) pour afficher le menu.

Statut Dessin : G-SelOn ( < paramètre > ) ; Statut Non dessin : G-SelOff Y ( < paramètre > ) ;

Où le paramètre pour la zone de mémoire est un entier de 1 à 20.

(E) Opération de type de graphique

Pressez [2nd] [SYSTEM] et trouvez les commandes ‘G-Con” et “G-Plot”. Ces commandes produisent des graphiques selon les conditions définies dans le programme. “G-Con” produit un graphique de type connexion, alors que “G-Plot” produit un graphique de type positionnement.

Type de connexion : G-Connect ; Type de positionnement : G-Plot ;

(F) L’operation d’agrandissement du facteur

La commande d’agrandissement du facteur (Factor) s’entre en pressant [ZOOM] 0 (Factor).

Factor ( < X factor >, < Y factor > ) ;

(G) L’opération d’application de graphique

Pressez [FUNC] 1 (DISP) et trouvez la commande “DrawGraph”. Cette commande dessine un graphique selon les conditions définies dans le programme.

DrawGraph ;

Exemple : Pour créer un programme dont le graphique Y1 = X + 3X ² - 6X - 8

Utilise les paramètres de fenêtre V-Window suivants : Xmin = -8, Xmax = 8, Xscl = 2 Ymin = -15, Ymax = 15, Yscl = 5

Suivez les étapes suivantes pour entrer les contenus du programme.

Contenus : < ClrGraph ; Étapes : < [FUNC] 0 (CLR) 1 (ClrGraph) [EXE]

Contenus : = ViewWindow ( -8, 8, 2, -15, 15, 5) Étapes : = [V-WIN] 0 (V-Window) [(-)] 8 [ ] 8 [ ] 2 [ ] [(-)] 15 [ ] 15 [ ] 5 [u]

[EXE]

, , , , ,

Contenus : > Y = Type ; Étapes : > [FUNC] 4 (GRAPH) 2 (Y = Type) [EXE]

Contenus : ? X 3 + 3X² - 6X - 8 ® Y ( 1) ; Étapes : ? [ALPHA] [X] [ ] 3 [+] 3 [ALPHA] [X] [X²] [ - ] 6 [ALPHA] [X] [ - ] 8

Contenus : @ G-SelOn Y (1) ; Étapes : @ [FUNC] 4 (GRAPH) 0 (G-SelOn) 1 [u] [EXE]

Contenus : A DrawGraph ; Étapes : A [FUNC] 1 (DISP) 1 (DrawGraph) [EXE]

Contenus : B End L’exécution de ce programme produit le résultat ci-dessous.

10 - 10 Utiliser les fonctions de tableau et de graphique dans un programme

Les fonctions de tableau et de graphique dans un programme peuvent générer des tableaux numériques et effectuer des opérations de graphiques. Voici ci-dessous divers types de syntaxe dont vous aurez besoin pour programmer avec les fonctions de tableau et de graphique.

(A) Etendue du tableau

La commande pour l’étendue d’un tableau se règle en pressant [2nd] [SYSTEM] deux fois pour afficher le menu ci-dessous.

0 V a r - R 1 V a r - L 1 2 V a r - L 2 3 V a r - L 3 4 V a r - L 4 5 V a r - L 5 6 V a r - L 6 7 V a r - L 7

Étendue spécifiée : Depuis le menu TABLE Var-R,

(B) Géneration d’un tableau numérique

Pressez [FUNC] 1 (DISP) et trouvez la commande “DispTable”. Cela génère des tableaux numériques pendant l’exécution du programme selon les conditions définies dans le programme.

[SAVE] [VARS] [VARS] [VARS] [q] (Y) [EXE] 1 [u] [EXE]

PROG

Etendue spécifiée depuis une liste L1 ~ L8

0 V a r - L 8 1 S - w i n A u t o 2 S - w i n M a n 3 G - C o n 4 G - P l o t

PROG

DispTable ;

La commande pour le statut Générer / Non-Générer (T-SelOn, T-SelOff) s’entre en pressant [FUNC] 5 (TBLE) pour afficher le menu voulu.

Statut Générer : T-SelOn Y ( < paramètre > ) ; Statut Non-générer : T-SelOff Y ( < paramètre > ) ;

Où le paramètre pour la zone de mémoire est un entier de 1 à 20.

(D) Opération de type de graphique de tableau

Pressez [FUNC] 1 (DISP) et trouvez les commandes “DrawTG-Con” et “DrawTG-Plt”. Ces commandes dessinent les fonctions graphiques selon les conditions définies dans le programme. “DrawTG-Con” produit un graphique de type connexion, alors que “DrawTG-Plt” produit un graphique de type positionnement.

Type connexion : DrawTG-Con ; Type positionnement : DrawTG-Plt ;

Exemple : Utilisez la fonction Y2 = 6 X² - X - 5 pour créer un programme qui

Après avoir enregistré les valeurs dans les paramètres d’étendue, suivez les étapes ci dessous pour entrer les contenus du programme.

Contenus : < ClrGraph ; Étapes : < [FUNC] 0 (CLR) 1 (ClrGraph) [EXE]

Contenus : = ClrText ; Étapes : = [FUNC] 0 (CLR) 0 (ClrText) [EXE]

Contenus : > ViewWindow (-10, 10, 2.5, -150, 150, 50) ; Étapes : > [V-WIN] 0 (V-window) [ ( - ) ] 10 [ ] 10 [ ] 2.5 [ ] [ ( - ) ] 150 [ ] 150

Contenus : ? Y = Type ; Étapes : ? [FUNC] 4 (GRAPH) 2 (Y = Type) [EXE]

génère un tableau numérique. Utilisez les paramètres d’étendue suivants : Xsrt = - 5, Xend = 5, Xptch = 1 Utilisez les paramètres de fenêtre V-Window suivants : Xmin = -10, Xmax = 10, Xscl = 2.5 Ymin = -150, Ymax = 150, Yscl = 50

, , , ,

[ ] 50 [u] [EXE]

Contenus : @ 6X² - X - 5 ®Y(2) ; Étapes : @ 6 [ALPHA] [X] [X²] [ - ] [ALPHA] [X] [ - ] 5 [SAVE] [VARS] [VARS]

[VARS] [q] (Y) [EXE] 2 [u] [EXE]

Contenus : A T-SelOn Y (2) ; Étapes : A [FUNC] 5 (TABL) 0 (T-SelOn) 2 [u] [EXE]

Contenus : B Sleep (5) Étapes : B [2nd] [INST] [2nd] [INST] 5 (Sleep) 5 [u] [EXE]

Contenus : C VarRange ; Étapes : C [2nd] [SYSTEM] [2nd] [SYSTEM] 0 (VAR-R) [EXE]

Contenus : D DispTable ; Étapes : D [FUNC] 1 (DISP) [p] (DispTable) [EXE] [EXE]

Contenus : <;DrawTG-Con ; Étapes : <;[FUNC] 1 (DISP) 2 (DrawTG-Con) [EXE]

Contenus : <<End L’exécution de ce programme produit le résultat ci-dessous :

Table numérique

PROG

XY 1

- 5 1 5 0

- 4 9 5

- 5

PROG

Graphique

NB : Vous pouvez alors retourner en mode TABLE pour revenir sur ce tableau.

10 - 11 Utiliser des fonctions de tri de liste dans un programme

Pressez [FUNC] 3 (LIST) pour afficher les fonctions de tri de liste.

0 L i s t 1 F i l l 2 D i m 3 S r t - A 4 S e q 5 S r t - D

PROG

(A) Pour entrer une liste spécifique par son nom

Cette fonction vous permet de spécifier la liste que vous voulez en entrant le nombre (1 ~ 8).

List < nombre >

(B) Pour remplacer toutes les valeurs en cellules par la même valeur

Cette fonction vous permet de remplacer toutes les cellules dans une liste spécifiée par la même valeur selon la syntaxe suivante :

Fill ( < valeur > , < nom de liste > ) ;

Exemple : Fill ( 3 , List1 ) remplit toutes les cellules de la liste 1 par la valeur 3

Cette fonction vous permet de compter le nombre des valeurs dans une liste spécifiée.

Dim ( < nom de liste > ) ;

Exemple : Dim (List2) donne la dimension, c’est à dire le nombre de valeurs

(D) Ordre croissant

Cette fonction vous permet de trier les données dans des listes jusqu’à huit listes en ordre croissant.

de la liste 2.

Srt-A (< nom de liste > , < nom de liste > , ... , < nom de liste > ) ;

Exemple : Srt-A (Liste 3, Liste 4) trie les listes 3 et 4 en ordre croissant

(E) Ordre décroissant

Cette fonction vous permet de trier les données dans des listes jusqu’à huit listes en ordre décroissant.

Srt-D ( < nom de liste >, < nom de liste >, ..., < nom de liste > ) ;

Exemple : Srt-D (Liste 1, Liste 2) trie les listes 1 et 2 en ordre décroissant

(F) Pour générer une séquence de nombres

Cette fonction vous permet de générer une séquence de nombres selon la syntaxe suivante :

Seq ( < expression >, < variable >, < valeur de départ >, < valeur de fin >, < valeur de pente > ) ;

Exemple : Seq ( X² + 1, X, 0, 5, 1 ) va donner la suite de nombres suivants :

10 - 12 Utiliser un calcul de graphique statistique dans un programme

Pressez [FUNC] 2 (STAT) pour afficher le menu ci-dessous. Les calculs statistiques et les opérations de graphiques dans un programme vous permettent de calculer et d’appliquer en graphique des données statistiques.

10 - 12 - 1 Pour spécifier les données de calcul statistique

(A) Entrée de données statistiques

{ < données >, < données >, < données >, ..., < données > } ® < nom de liste > ; Où le paramètre pour le nom de liste est L1 ~ L8

(B) Entrée de données L /D SET

La commande L/D Set permet de régler les paramètres de limite spécifiée pour la capacité de traitement et la valeur a pour la distribution normale en utilisant la syntaxe suivante :

L/D set ( < a valeur>, < X LSL valeur >, < X USL valeur >, < Y LSL valeur >, < Y USL valeur > ) ;

10 - 12 - 2 Calculs statistiques

Les commandes de calcul statistique sont disponibles en pressant [FUNC] 2 (STAT) 4 (CALC). Le menu ci-dessous s’affiche alors :

(A) Calcul statistique à variable unique

Pressez 0 (1-Var) pour effectuer un calcul statistique à variable unique selon la syntaxe suivante :

1, 2, 5, 10, 17, 26

0 D R A W 1 G R A P H 2 L I S T 3 M A R K 4 C A L C 5 L / D S e t

0 1 - V a r 1 2 - V a r 2 X 3 M e d 4 X ² 5 L o g 6 E x p 7 P w r

PROG

1-Variable ( < nom de la liste X >, < fréquence > ) ;

Où les paramètres pour la liste de données X sont L1 ~ L8 Où les paramètres pour la fréquence sont 1, ou L1 ~ L8

(B) Calcul statistique à variable double

Pressez 1 (2-VAR) pour effectuer un calcul statistique à 2 variables selon la syntaxe suivante :

2-variable ( < nom de la liste X >, < nom de la liste Y >, < fréquence > ) ;

Où les paramètres pour la liste de données X ou Y sont L1 ~ L8 Où les paramètres pour la fréquence sont 1, ou L1 ~ L8

La syntaxe est la suivante :

LinearReg ( < nom de la liste X >, < nom de la liste Y >, < fréquence > ) ;

Où les paramètres pour la liste de données X sont L1 ~ L8 Où les paramètres pour la fréquence sont 1, ou L1 ~ L8

Note : Chacun des types suivants peut être choisi en tant que type de régression :

Régression Linéaire (X) ................... LinearReg

Régression Med-Med (Med) ... ....... Med-MedLine

Régression Quadratique (X²) ........... QuadReg

Régression Logarithmique (Log) ..... LogReg

Régression Exponentielle (Exp) ...... ExpReg

Régression de Puissance (Pwr) ...... PowerReg

Exemple : Pour créer un programme qui effectue un calcul à deux variables.

Contenus : < { 63, 57, 81, 90 } ® List 1 ; Étapes : < [2nd] [ { } ] 63 [ ] 57 [ ] 81 [ ] 90 [u] [SAVE] [FUNC] 3 (LIST)

Contenus : = { 18, 22, 31, 43 } ® List 2 ; Étapes : = [2nd] [ { } ] 18 [ ] 22 [ ] 31 [ ] 43 [u] [SAVE] [FUNC] 3 (LIST)

Utilisez les paramètres suivants : Liste données X : L1, Liste données Y : L2, fréquence : 1 Où la liste 1 ( 63, 57, 81, 90 ) et la liste 2 (18, 22, 31, 43 ) ax = 6, X LSL = 1, X USL = 13, Y LSL = 15, Y USL = 44

, , ,

0 (List ) 1 [EXE]

,,,

0 (List ) 2 [EXE]

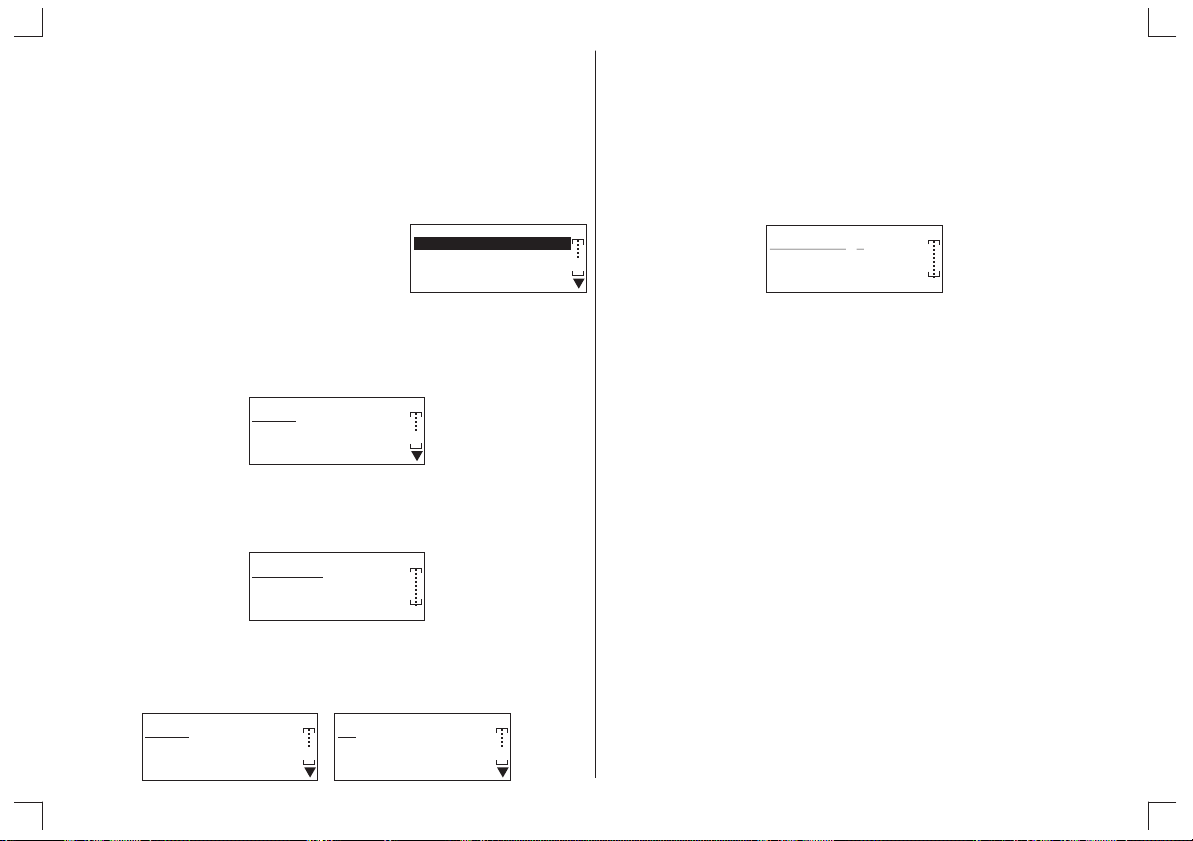
Contenus : > L/D set ( 6, 1, 13, 15, 44 ) Étapes : > [FUNC] 2 (STAT) 5 (L/D set) 6 [ ] 1 [ ] 13 [ ] 15 [ ] 44 [u] [EXE]

Contenus : ? 2-Variable ( L1, L2, 1 ) ; Étapes : ? [FUNC] 2 (STAT) 4 (CALC) 1 (2-Var) [FUNC] 2 (STAT) 2 (LIST)

Contenus : @ End L’exécurion de ce programme produit le résultat ci-dessous. Vous pouvez presser les touches de curseur pour visualiser les différents résultats.

[p] ~ [p]

0 (L1) [ ] [FUNC] 2 (STAT) 2 (LIST) 1 (L2) [ ] 1 [u] [EXE]

, , , ,

n = 4

x.=.......... 7 2 . 7 5

Xmin = 5 7 Xmax = 9 0

PROG

(D) Listes de données X et Y, liste de données de fréquence

(Sauf le graphique de données temporelles)

Liste de données X ou Y : L1 ~ L8, None Fréquence : L1 ~ L8 pour les praphiques statistiques à une variable, L1 ~ L8

(E) Type de marquage

La commande pour le type de marquage (Square, Cross, Dot) s’obtient en pressant [FUNC] 2 (STAT) 3 (MARK) pour afficher le menu ci-dessous.

ou 1 pour ceux à deux variables.

0 S q u a r e ( ¨ ) 1 D o t ( · ) 2 C r o s s ( x )

PROG

10 - 12 - 3 Graphique statistique

(A) Zone de graphique statistique

La commande pour la zone de graphique statistique (S-Gph1, S-Gph2, S-Gph3) s’obtient en pressant [FUNC] 2 (STAT) 1 (GRAPH) pour afficher le menu ci dessous.

0 S c a t 1 S - G p h 1 2 x y L i n 3 S - G p h 2 4 H i s t 5 S - G p h 3 6 B o x 7 N - D i s t

Sélectionnez le graphique voulu et pressez [EXE].

(B) Statut Dessin / Non dessin

La commande pour le statut Dessin / Non dessin (DrawOn, DrawOff) s’entre en pressant [FUNC] 2 (STAT) 0 (DRAW) pour afficher le menu ci-dessous.

0 D r a w O n 1 D r a w O f f

Les commandes pour le type de graphique statistique (Scat, xyLin, Hist, Box, N-Dist, W, Med, X², Log, Exp, Pwr, T-Ser, Spc) s’obtiennent en pressant [FUNC] 2 (STAT) 1 (GRAPH) pour afficher le menu ci-dessous.

0 S c a t 1 S - G p h 1 2 x y L i n 3 S - G p h 2 4 H i s t 5 S - G p h 3 6 B o x 7 N - D i s t

PROG

0 X 1 M e d 2 X ² 3 L o g 4 E x p 5 P w r 6 T - s e r 7 S p c

PROG

(F) Opération de dessin d’un graphique

Pressez [FUNC] 1 (DISP) et trouvez la commande “DrawStat”. Cette commande dessine un graphique statistique selon les conditions définies dans le programme.

Exemple : Créer un programme pour tracer un histogramme

Contenus : < ClrGraph ; Étapes : < [FUNC] 0 (CLR) 1 (ClrGraph) [EXE]

Contenus : = S-WinAuto ; Étapes : = [2nd] [SYSTEM] [2nd] [SYSTEM] [2nd] [SYSTEM] 1 (S-winAto)

Contenus : > S-Gph1 DrawOn ; Étapes : > [FUNC] 2 (STAT) 1 (GRAPH) 1 (S-Gph 1) [FUNC] 2 (STAT)

Contenus : ? Hist (L1, L2) ; Étapes : ? [FUNC] 2 (STAT) 1 (GRAPH) 4 (Hist) [FUNC] 2 (STAT) 2 (LIST)

Contenus : @ DrawStat ; Étapes : @ [FUNC] 1 (DISP) 0 (DrawStat) [EXE]

Contenus : A End

L’exécution de ce programme produit l’histogramme suivant :

[EXE]

0 (Draw) 0 (DrawOn) [EXE]

0 (L1) [ ] [FUNC] 2 (STAT] 2 (LIST) 1 (L2) [u] [EXE]

GRAPH R

Note : Le même programme peut être utilisé pour les types de graphiques

suivants, en remplaçant simplement “Hist” dans les spécifications ci-dessus par le type de graphique qui convient. Graphique par quadrille ... MedBox Graphique de distribution normale ... N-Dist Graphique de contrôle de traitement statistique (Spc) ... Spc

· Voici un exemple de programme traçant un graphique statistique à 2 variables :

Contenus : < ClrGraph ; Étapes : < [FUNC] 0 (CLR) 1 (ClrGraph) [EXE]

Contenus : = S-WinAuto ; Étapes : = [2nd] [SYSTEM] [2nd] [SYSTEM] [2nd] [SYSTEM] 1 (S-winAuto)

Contenus : > S-Gph1 DrawOn ; Étapes : > [FUNC] 2 (STAT) 1 (GRAPH) 1 (S-Gph1) [FUNC] 2 (STAT)

Contenus : ? Linear ( L1, L2, 1 ) ; Étapes : ? [FUNC] 2 (STAT) 1 (GRAPH) [q] [q] [q] [q] 0 (X) [FUNC]

Contenus : @ DrawStat ; Étapes : @ [FUNC] 1 (DISP) 0 (DrawStat) [EXE]

Contenus : A End L’execution de ce programme produit la régression linéaire ci-dessous :

Note : Chacun des types suivant peut être spécifié en tant que type de graphique.

[EXE]

0 (DRAW) 0 (DrawOn) [EXE]

2 (STAT) 2 (LIST) 0 (L1) [ ] [FUNC] 2 (STAT) 2 (LIST) 1 (L2) [ ] 1 [u] [EXE]

STAT R

Régression Linéaire (X) ... Linear Régression Med-Med (Med) ... Med-Med Régression Quadratique (X²) ... Quad

, ,

Régression logaritmique (Log) ... Log

Régression Exponentielle (Exp) ... Exp Régression de Puissance (Pwr) ... Power

· Ci-dessous se trouve un exemple de programme pour tracer un diagramme par dispersion :

Contenus : < ClrGraph ; Étapes : < [FUNC] 0 (CLR) 1 (ClrGraph) [EXE]

Contenus : = S-WinAuto ; Étapes : = [2nd] [SYSTEM] [2nd] [SYSTEM] [2nd] [SYSTEM] 1 (S-winAuto)

Contenus : > S-Gph1 DrawOn ; Étapes : > [FUNC] 2 (STAT) 1 (GRAPH) 1 (S-Gph1) [FUNC] 2 (STAT)

Contenus : ? Scatter( L1, L2, 1, Dot ) ; Étapes : ? [FUNC] 2 (STAT) 1 (GRAPH) 0 (Scat) [FUNC] 2 (STAT) 2 (LIST)

Contenus : @ DrawStat ; Étapes : @ [FUNC] 1 (DISP) 0 (DrawStat) [EXE]

Contenus : A End L’execution de ce programme produit le diagramme par dispersion ci-dessous :

Note : Dans le cas d’un graphique de ligne xy, remplacez “Scatter” dans la

· La syntaxe pour un graphique de série temporelle se présente comme suit :

T-Ser ( < nom de la liste X >, < nom de la liste Y >, < Fréquence >, < nom de la liste Y1 >, < nom de la liste Y2 >, < nom de la liste Y3 >, < nom de la liste Y4 >, < nom de la liste Y5 >, < nom de la liste T >, < type de marquage > )

(A) Voici un exemple de syntaxe de graphique bidimensionnel :

T-Ser (None, < nom de la liste Y >, < fréquence >, None, None, None, None, None, < nom de la liste T >, < Type de marquage > )

[EXE]

0 (DRAW) 0 (DrawOn) [EXE]

0 (L1) [ ] [FUNC] 2 (STAT) 2 (LIST) 1 (L2) [ ] 1[FUNC] 2 (STAT) 3 (MARK) 1 (Dot) [u] [EXE]

PROG

spécification ci-dessus par “xyLine”.

Où les paramètres pour la liste des données X et T sont L1 ~ L8 Où les paramètres pour la fréquence sont 1, ou L1 ~ L8 Où le type de marque est un square, une Cross ou un Dot.

(B) Voici un exemple de syntaxe de graphique tridimensionnelle :

T-Ser (< nom de la liste X >, < nom de la liste Y >, < Fréquence >, < nom de la liste Y1 >, < nom de la liste Y2 >, < nom de la liste Y3 >, < nom de la liste Y4 >, < nom de la liste Y5 >, < nom de la liste T >, < Type de marquage > )

Où les paramètres pour la liste des données X et T sont L1 ~ L8 Où les paramètres pour la fréquence sont 1, ou L1 ~ L8 Où les paramètres pour la liste des données Y, Y1~ Y5 sont L1~ L8 ou None (spécifier l’une des listes Y, Y1 ~ Y5 est indispensable, les quatre autres listes sont facultatives) Où le type de marque est un square, une Cross ou un Dot.

10 - 13 Exemples de programmes

Exemple : Créer un programme pour calculer le n itéré d’une suite

arithmétique de raison D et de premier terme A. Calculer aussi la somme des n premiers termes de cette suite :

S (N) = A + (A + D) + (A + 2D) + (A + 3D) + ... =

ème

N itéré : A (N) = A + ND

ème

(N + 1) (2A + ND)

PROG TYPE : MAIN Filename : DIFFER

Content

P r i n t “ 1 : A ( N ) 2 : S ( N ) “ ; S l e e p ( 5 ) ; L o c a t e ( 1 , 3 ) ; I n p u t P , A , D , N ; I f ( P == 1 ) T h e n { G o t o 1 } ; S = ( N + 1 ) ( 2 A + N D ) ¸ 2 ; R e m S U M ; P r i n t “ S ( “ , N , “ ) = “ , S ; G o t o 2 ; L a b e l 1 : T = A + N D ; R e m N I T E M ; P r i n t “ A ( “ , N , “ ) = “ , T ; L a b e l 2 : E n d

Quand le message “ 1 : A ( N ) 2 : S ( N ) “ s’affiche, vous pouvez entrer une valeur “P” pour chacune des valeurs suivantes pour spécifier le type d’opération à exécuter.

Si P = 1 ... A ( N ) Si P = 2 ... S ( N )

P = 1 < A = 3, D = 2, N = 4 Þ A (N) = A (4) = 11

(5 secondes ) 1

[EXE] 3 [EXE] 2 [EXE] 4

[EXE]

1 : A ( N ) 2 : S ( N )

P = 1 t

P = 1 A = 3 D = 2 N = 4 t

A ( 4 ) = 11

PROG

P = 2 = A = 5, D = 11, N = 15 Þ S ( N) = S (15) = 1581

[EXE] (5 secondes ) 2

[EXE] 5 [EXE] 11 [EXE] 15

[EXE]

Exemple : Créer trois sous-programmes pour stocker les formules ci-

dessous et utiliser la commande GoSub-PROG pour écrire un programme principal (programme invoqueur) pour l’exécution. Sous-programme 1 : CHARGE = N x 3 Sous-programme 2 : POWER = I ¸ A

1 : A ( N ) 2 : S ( N )

P = 2 t

P = 2 A = 5 D = 11 N = 15 t

S ( 15 ) = 1 5 8 1

PROG

Sous-programme 3 : VOLTAGE = I ¸ (B x Q x A)

PROG TYPE : MAIN Filename : CHARGE Note : Subroutine

Content

xn3t;

“ C H A R G E = “ , Q ;

PROG TYPE : MAIN Filename : POWER Note : Subroutine

Content

J = I ¸ A ; P r i n t “ P O W E R = “ , J ; E n d

PROG TYPE : MAIN Filename : VOLTAGE Note : Subroutine

Content

V = I ¸ ( B x Q x A ) ; P r i n t “ V O L T A G E = “ , V ; E n d

PROG TYPE : MAIN Filename : CALL Note : Calling program

Content

I n p u t N ; G o s u b P R O G C H A R G E ; I n p u t I , A ; G o s u b P R O G P O W E R ; B = 2 7 ; G o s u b P R O G V O L T A G E ; E n d

RUN

N = 1.5, I = 486, A = 2 Þ CHARGE = 4.5, POWER = 243, VOLTAGE = 2

[EXE]

N = t

PROG

1.5 [EXE] 486 [EXE] 2

[EXE] [p]

Exemple : Utiliser la commande For pour créer un programme qui calcule

9 x 1 = 9 8 x 1 = 8 ........... 2 x 1 = 2 1 x 1 = 1

9 x 2 = 18 8 x 2 = 16 ........... 2 x 2 = 4 1 x 2 = 2

: : : :

9 x 8 = 72 8 x 8 = 64 ........... 2 x 8 = 16 1 x 8 = 8

9 x 9 = 81 8 x 9 = 72 ........... 2 x 9 = 18 1 x 9 = 9

N = 1 . 5 C H A R G E = 4 . 5 I = 4 8 6 A = 2 t

P O W E R = 2 4 3 V O L T A G E = 2

PROG TYPE : MAIN Filename : LOOP

Content

F o r ( A = 9 ; A ³ 1 ; A - - ) ; { F o r ( B = 1 ; B £ 9 ; B ++ ) { C = A x B ; P r i n t A , “ x “ , B , “ = , C } } E n d

RUN

[EXE]

Exemple : Régler le type de programme de la zone de programme en “Base-

n” et créer un programme qui calcule l’expression suivante :

ANS = 1010 And (Y Or 7 )

216

9 x 1 = 9 9 x 2 = 1 8 9 x 3 = 2 7 9 x 4 = 3 6

1 x 9 = 9

PROG

PROG TYPE : Base-n (Décimal) Filename : LOGICAL

Content

I n p u t Y ; C = b 1 0 1 0 A n d ( Y O r h 7 ) ; P r i n t “ A N S = “ , C ; E n d

RUN

< Y = /A Þ A ns = 10

16 10

[EXE]

Y = t

PROG

< Y = 11011 Þ A ns = 1010

[EXE]

[dhbo] 3 ( o ) 11011

[EXE]

RUN

Y = t

Y = o 1 1 0 1 1 t

AN S = 1 0 1 0

PROG

PROG d

PROG b

[dhbo] [u]

[EXE] [A]

[EXE]

[EXE] [q]

[2nd] [SYSTEM] [q]

[EXE] [ALPHA] [ ; ]

EDIT

PROG d

0 d 1 h 2 b 3 o

PROG d

Y = h /A t

PROG d

AN S = 1 0

PROG d

= L O G I C A L = I n p u t Y ; t = b 1 0 1 0 A n d ( Y O r h 7 ) ;

PROG d

0 D e c 1 H e x 2 B i n 3 O c t

PROG d

= L O G I C A L = I n p u t Y ; B i n ; C = b 1 0 1 0 A n d ( Y O r h 7

Exemple : Utiliser les commandes Data-Read pour créer un programme qui

3.5 ? Cm² ? Cm

calcule les formules suivantes utilisées pour calculer la zone de surface (S) et le volume (V) d’un tétraèdre régulier dont la longueur d’un côté (A) est 3.5, 5, 12

S = Ö3 A² V = A

Ö2

A S V

5 ? Cm² ? Cm 12 ? Cm² ? Cm

PROG TYPE : MAIN Filename : DIFFER

Content

L a b e l 1 : R e a d ( A ) ; D a t a ( 3 . 5 , 5 , 1 2 ) ; S = Ö ( 3 ) x A ² ; V = Ö ( 2 ) ¸ 1 2 x A Ù 3 ; P r i n t “ A = “ , A ; P r i n t “ S = “ , S ; P r i n t “ V = “ , V ; I f ( A ¹ 1 2 ) T h e n { G o t o 1 } ; G o t o 2 ; L a b e l 2 : E n d

RUN

L’exécution de ce programme produit les résultats ci-dessous.

AS V

3.5 21.21762239272 cm² 5.052867207229 cm 5 43.30127018922 cm² 14.73139127472 cm 12 249.4153162899 cm² 203.6467529817 cm

RUN

[EXE]

[p] [p]

[p] [p] [p]

V = 2 0 3 . 6 4 6 7 5 2

9 8 1 7

A = 1 2

S = 2 4 9 . 4 1 5 3 1 6 2 8 9 9 V = 2 0 3 . 6 4 6 7 5 2

A = 5

S = 4 3 . 3 0 1 2 7 0 1 8 9 2 2 V = 1 4 . 7 3 1 3 9 1 2

A = 3 . 5

S = 2 1 . 2 1 7 6 2 2 3 9 2 7 2 V = 5 . 0 5 2 8 6 7 2 0

PROG

Exemple : Créer un programme qui simule un jeu de loterie pour tirer des

numéros gagnants, où les numéros gagnants sont une combinaison de 4 nombres possibles 1 à 42 et aucun nombre ne peut être répété.

PROG TYPE : MAIN Filename : LOTTERY

Content

A = R a n d l ( 1 , 4 2 ) ; L a b e l 1 : B = R a n d l ( 1 , 4 2 ) I f ( B == A ) T h e n { G o t o 1 } ; L a b e l 2 : C = R a n d l ( 1 , 4 2 ) I f ( C == A ) T h e n { G o t o 2 } ; I f ( C == B ) T h e n { G o t o 2 } ; L a b e l 3 : D = R a n d l ( 1 , 4 2 ) I f ( D == A ) T h e n { G o t o 3 } ; I f ( D == B ) T h e n { G o t o 3 } ; I f ( D == C ) T h e n { G o t o 3 } ; P r i n t “ * L O T T E R Y * “ ; P r i n t “ A , “ “ , B , “ “ , C , “ “ , D ; E n d

RUN

PROG

* L O T T E R Y *

[EXE] [p]

1 3 5 2 7 3 1

NEMA CITIZEN

76 ter, rue du Réveil Matn

78800 HOUILLES Tél. : 01 39 57 45 64 Fax : 01 39 57 09 81

E-mail : nema.citizen@wanadoo.fr

Site : citizen-france.com

CITIZEN SRP-400G User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual