Page 1

TI.10
Manual del profesor
Desarrollado por
Texas Instruments Incorporated
Actividades desarrolladas por la
Dra. Jane Schielack
Page 2

Acerca de la autora
La Dra. Jane Schielack es profesora asociada al Departamento de Matemáticas de la Universidad A&M de Texas
(EE UU). Se ha encargado del desarrollo de la sección
ejemplos incluidos en la sección
Cómo utilizar la TI-10
Actividades
de este manual.
y ha contribuido a evaluar la idoneidad de los
Aviso importante relacionado con los materiales
Texas Instruments no ofrece ninguna garantía, ya sea expresa o implícita, incluida pero no limitada cualquier otra
garantía de comerciabilidad y adecuación a un propósito concreto, en relación con cualquier programa o material
impreso, y pone a su disposición los mencionados materiales “tal cual” y
circunstancia, Texas Instruments será responsable ante nadie por ningún daño especial, colateral, incidental o a
consecuencia de, o en conexión con, o derivado de la compra o el uso de estos materiales; la única y exclusiva
responsabilidad de Texas Instruments, sea cual sea la forma de la acción, no podrá superar el precio de compra de
este libro. Por otra parte, Texas Instruments no será responsable de ninguna reclamación de cualquier tipo que
pueda plantearse por el uso de estos materiales por cualquier otra parte.
Nota
: El uso de otras calculadoras que no sean TIN10 puede producir resultados diferentes a los descritos en este
material.
sólo
a efectos de referencia. Bajo ninguna
Permiso de reimpresión o fotocopia
Este documento autoriza a los profesores a reimprimir o fotocopiar para su uso en clase, taller de trabajo o
seminario, las páginas u hojas de este libro que ostenten el aviso de propiedad intelectual (copyright) de
Texas Instruments. Estas páginas están diseñadas para su reproducción y uso en clases, talleres de trabajo o
seminarios, siempre que cada copia lleve el aviso de propiedad intelectual (copyright) correspondiente. Queda
expresamente prohibida la venta y distribución posterior de dichas copias. Excepto en la forma autorizada
anteriormente, es necesario obtener autorización por escrito de Texas Instruments Incorporated previa a la
reproducción o transmisión de este trabajo o parte del mismo en cualquier otra forma o por cualquier otro medio
electrónico o mecánico, incluido cualquier sistema de almacenaje y recuperación de información, con excepción de
aquellos que la ley federal de propiedad intelectual permite expresamente.
Si ha de hacer fotocopias de todo o parte de este libro con destino a terceros, deberá proporcionar esta página
(con las indicaciones de permiso anteriores) al servicio de reproducción de fotocopias.
Las consultas deben dirigirse a:
Texas Instruments Incorporated
7800 Banner Drive, M/S 3918
Dallas, TX 75251
A la atención de: Manager, Business Services
education.ti.com
ti-cares@ti.com
Copyright © 2001 Texas Instruments Incorporated
Reservados todos los derechos, excepto los que se garantizan específicamente en este documento.
Impreso en los Estados Unidos de América.
Automatic Power Down, APD, y EOS son marcas comerciales de Texas Instruments Incorporated.
Page 3

Índice de contenidos
CAPÍTULO PÁGINA
Acerca del Manual del profesor
Acerca de la TI-10
........................................ v
.............. iv
Actividades............................................1
Valor del valor de posición.........................2
Valor de posición
¿Cuál es el problema?..................................7
Sentencia de números, Resolución de
problemas
Comparación de costes ............................11
División con cociente y resto o
resultado decimal
Cómo utilizar la TI-10.........................15
1 Pantalla, desplazamiento, orden de las
operaciones y uso de paréntesis .....16
2 Borrado y corrección...........................19
3 Menús....................................................23
CAPÍTULO PÁGINA
Apéndice A ................................................A-1
Referencia rápida a teclas
Apéndice B.................................................B-1
Indicadores de pantalla
Apéndice C................................................. C-1
Mapa de menús
Apéndice D.................................................D-1
Mensajes de error
Apéndice E.................................................E-1
Soporte, servicio y garantía
4 Operaciones básicas..........................26
5 Operaciones con una constante .....33
6 Números enteros y decimales ........ 38
7 Memoria.................................................42
8 Resolución de problemas:
Modo Auto ........................................... 47
9 Resolución de problemas:
Modo Manual.......................................54
10 Valor de posición.................................62
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
iii
Page 4

Acerca del Manual del profesor
p
p
p
j
p
p
p
p
q
jemp
p
p
p
p
q
q
p
p
p
j
jemp
p
p
p
p
p
p
prop
jemp
p
q
p
p
Cómo está organizado el Manual del
profesor
El manual está formado por dos secciones:
Actividades
La sección
actividades dirigidas a integrar la TI-10 en la
enseñanza de las matemáticas. La sección
Cómo utilizar la TI-10
facilitar el uso y aprendizaje de la TI-10.
•
Sección
Todas las actividades deben estar
dirigidas
de ayudar a desarrollar los conce
matemáticos e incor
una herramienta de enseñanza. Cada
actividad está considerada como un
elemento independiente y contiene:
−
y
Cómo utilizar la TI-10
Actividades
es un conjunto de
se ha diseñado para
Actividades
or el profesor. Su objetivo es el
orar la TI-10 como
Una visión global del ob
matemático de que trata.
.
tos
etivo
Observaciones a tener en cuenta
Aun
•
•
•
ue la mayoría de los ejemplos de las
trans
desarrollar conce
se han diseñado es
cumplir tal propósito.
Al ob
flexibilidad, cada e
elementos com
del resto. Seleccione la trans
maestra corres
los estudiantes van a necesitar
desarrollar el conce
se dis
seleccione la actividad a
concepto matemático de que se trate.
Si algún e
nivel o grado de enseñanza de la clase,
utilícelo
teclas y desarrolle sus propios ejemplos.
arencias pueden utilizarse para
tos matemáticos, no
ecíficamente para
eto de proporcionar la máxima
lo y actividad son
letos e independientes
arencia
ondiente a la tecla que
ara
to matemático que
one a explicar. A continuación,
iada al
lo no parece adecuado al
ara ilustrar la función de las
El conce
−
desarrolla.
Los materiales necesarios
−
cada actividad.
Una hoja de actividades del alumno.
−
•
Sección
Esta sección contiene ejemplos en
trans
están numerados e incluyen:
−
−
arencias maestras. Los capítulos
Una
describen las teclas de la TI-10
utilizan en cada e
en el teclado de la TI-10, y notas sobre
las funciones de cada una.
Trans
rácticos de las teclas descritas en la
ágina de introducción correspondiente.
Cada ca
teclado de la TI-10 en el
descritas aparecen resaltadas en negro.
to matemático que se
Cómo utilizar la TI.10
ágina de introducción en la que se
arencias maestras con ejemplos
ítulo incluye una ilustración del
ara realizar
ue se
lo, su ubicación
ue las teclas
Para tener la certeza de
•
alumnos
ulsar b para borrar la TI-10, y luego
pulsar ” para borrar la pantalla.
arten del mismo punto, deben
ue todos los
Cómo solicitar más ejemplares del
Manual del profesor
Para pedir más manuales u obtener
información adicional sobre los productos
de Texas Instruments (TI), puede dirigirse a:
Teléfono:
Correo-e:
Página principal:
Puede descargar e imprimir una copia de
este Manual del profesor tras acceder a la
página Web.
education.ti.com/guides
1-800-TI-CARES
(1-800-842-2737)
ti-cares@ti.com
education.ti.com
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
iv
Page 5
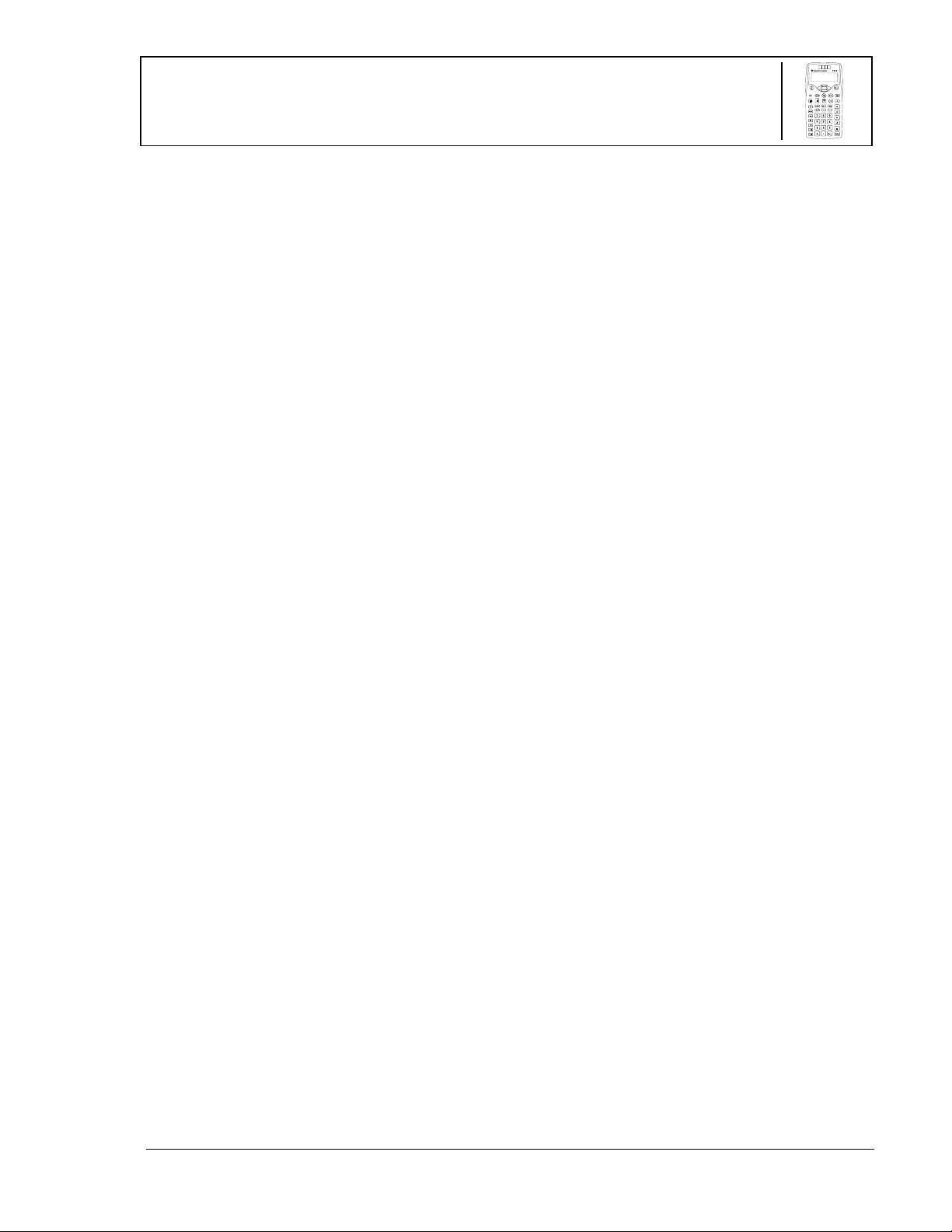
Acerca de la TI.10
p
p
p
p
p
p
j
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
q
p
p
j
p
Pantalla de dos líneas
La primera línea muestra una entrada con un
máximo de 11 caracteres. Las entradas
comienzan en la
Si la entrada no cabe en la
laza a la segunda. Cuando el espacio lo
des
ermite, tanto la entrada como el resultado
aparecen en la primera línea.
La segunda línea admite un máximo de 11
caracteres. Si la entrada es demasiado extensa
ara caber en la primera línea, se desplaza a la
segunda. Si la entrada y el resultado no caben
en la
segunda línea
resultados con más de 10 dígitos a
notación científica.
Cuando una entrada no cabe en dos líneas
continúa el des
siem
de la entrada. Para ver el
entrada,
contenido de la
pulse
rimera línea, el resultado aparece en la
re sean visibles las dos últimas líneas
uede desplazar hacia arriba el
®
sólo aparecerá el resultado.
arte superior izquierda.
rimera línea se
ustificado a la derecha. Los
arecen en
lazamiento, de forma que
rincipio de la
antalla. En tal caso, cuando
Indicadores de pantalla
En el Apéndice B se incluye una lista de los
indicadores de pantalla.
Mensajes de error
Consulte el Apéndice D para ver la lista de
mensajes de error.
Dado que las operaciones entre paréntesis
se efectúan en primer lugar, puede utilizar
y Y para cambiar el orden de las
operaciones y, por consiguiente, el resultado.
X
Menús
La tecla
• Para des
• Para des
• Para retroceder a la
• Para seleccionar un elemento de menú,
• Para retroceder a la
Para obtener más información sobre los
menús, consulte el Apéndice C: Mapa de
menús.
‡
permite mostrar los menús.
lazarse por los menús en
sentido ascendente o descendente,
pulse
elemento de menú, pulse ! o ".
sin seleccionar un elemento de menú,
pulse
ulse
cuestión aparezca subrayado.
pulse
o $.
#
lazar el cursor y resaltar un
antalla anterior
‡
®
‡
”
.
o
mientras el elemento en
antalla anterior,
”
.
o
Entradas anteriores (Historial)
Después de calcular una expresión, utilice
y $ para examinar las entradas y
#
resultados anteriores almacenados en el
historial de la TI-10.
Resolución de problemas (‹)
Orden de las operaciones
Para calcular las expresiones, la TI-10 utiliza
el sistema o
erating System, EOSé). La prioridad que
O
se sigue
describe en la trans
Pantalla, desplazamiento, orden de las
eraciones
o
Cómo utilizar la TI-10
© 2001 T
erativo de ecuaciones (Equation
ara realizar las operaciones se
arencia maestra
uso de paréntesis
y
.
EXAS INSTRUMENTS INCORPORATED
de la sección
La herramienta Resolución de problemas
ofrece tres modos de funcionamiento con
ue los alumnos podrán ejercitarse en el
los
uso de las o
básicas y el valor de posición.
• El modo Automático de Resolución de
roblemas cuenta con un conjunto de
ercicios destinados a mejorar las
e
habilidades de los alumnos en o
de suma, resta, multiplicación y división.
TI-10: Manual del profesor
eraciones matemáticas
eraciones
v
Page 6

Acerca de la TI.10
p
p
p
p
p
p
q
p
(continuación)
Asimismo, el modo Automático
seleccionar el nivel de dificultad (1, 2 ó 3) y el
tipo de operación (+, –, x,
• Con el modo Manual de Resolución de
roblemas los alumnos podrán crear y
lantear problemas en los que pueden
incluir incógnitas o inecuaciones.
• La o
ción Valor de posición de Resolución de
roblemas tiene tres opciones con las que
podrá:
− Hallar el valor de
dado.
− Hallar la cantidad de unidades,
decenas, centenas, millares, décimas o
centésimas contenidas en un número
dado.
− Hallar el dígito
las unidades, decenas, centenas,
millares, décimas o centésimas de un
número dado.
P
osición de un dígito
ue ocupe la posición de
ermite
o ?).
Al restablecer la TI-10:
• Se recu
configuración predeterminados:
− Notación estándar (decimal flotante)
− Modo
− División con cociente y resto
− Nivel de dificultad 1 (suma) en la
− Tipo de operación, suma
• Se borran:
− Operaciones pendientes
− Entradas del historial
− Constante (operación almacenada)
− Cualquier condición de error
eran los valores de
AUTO
de Resolución de
problemas
herramienta Resolución de problemas
Automatic Power DownTM Apagado
automático (APDTM)
Restablecimiento de la TI.10
Para restablecer la TI-10, puede utilizar uno
de los métodos siguientes:
• Pulsar
• Pulsar
• Pulsar
elegir Y (Sí), y pulsar
Cuando se restablece la TI-10, la pantalla
muestra
borrar la pantalla.
b
.
”
−
y
simultáneamente.
‡
, seleccionar el menú
MEM CLEARED
®
.
. Pulse
”
RESET
para
Si la TI-10 se deja inactiva durante cinco
minutos se activa la función Automatic
Power Down (APD) y la calculadora se apaga
automáticamente. Para activar la TI-10 de
nuevo tras un apagado automático, APD,
pulse −. No se perderán los valores en
pantalla, las operaciones pendientes,
,
los valores de configuración ni la memoria.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
vi
Page 7

Actividades
Valor del valor de posición 2
¿Cuál es el problema? 7
Comparación de costes 11
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
1
Page 8

Valor del valor de posición
Visión general
Los alumnos deben ejercitar su flexibilidad en el
uso de los números; para ello, analizarán la
relación existente entre los símbolos numéricos y
su representación por medio de materiales de
base diez.
Introducción
1. Lea el manual
Clement. Analice las distintas formas de
preguntar cuántos objetos caben o admiten otros.
2. Forme varios grupos de alumnos. Entregue a
cada grupo una cantidad considerable de
unidades (más de 300) de un material de base
diez. Indíqueles que se trata de hallar cuántas
pastillas de goma caben en un recipiente que
ha llenado con anterioridad. Pídales que
cuenten las “pastillas de goma”. Observe las
técnicas que utilizan para contar (de una en
una, formando grupos de 10, etc.).
3. Dígales que ha agotado todas sus unidades y
pregunte:
¿Cuántas filas (grupos de 10) necesitaré
para formar una pila de “pastillas de goma”
del mismo tamaño que las vuestras?
4. Pida a los alumnos que analicen la respuesta del
problema con sus unidades, o bien que apliquen
los conocimientos que tengan sobre el valor de
posición. A continuación, muéstreles cómo
deben analizar la respuesta con la TI-10.
5. Pídales que comparen los resultados
obtenidos con los materiales de base diez con
la respuesta que muestra la pantalla de la
TI-10. (Con las 314 unidades, pueden formar
31 filas de diez unidades y les sobran 4.)
Counting On Frank
de Rod
Conceptos
matemáticos
Grados 2 - 4
valor de posición de
•
números enteros
(mediante centenas)
•
dinero
Grados 4 - 6
valor de posición de
•
decimales (mediante
centésimas)
unidades métricas
•
(metros, decímetros,
centímetros)
³
Para utilizar la función Valor de
posición con esta actividad:
1. Pulse
2. Pulse
seleccionar el modo
(manual), si fuese necesario.
3. Pulse $
establecer la función Valor de
posición en 11. De este modo,
podrá hallar la cantidad de
unidades, decenas, centenas,
etc. de un número.
Nota:
función
posición para hallar el dígito
que ocupe el lugar de las
unidades, decenas,
centenas, etc.
4. Pulse
la pantalla de entrada.
³
Para analizar las respuestas al
problema en la TI-10:
1. Si es necesario, pulse
para activar la herramienta
Resolución de problemas.
2. Introduzca 314, el número
de unidades.
3. Pulse
cantidad de decenas que hay
en 314. La pantalla muestra
31
hay 31 decenas.
‹
‡.
®
"
®
Puede utilizar la otra
– 1 –.
‡ para regresar a
Œ
’ para ver la
, para indicar que en 314
ê
Materiales
TI-10
•
lápiz
•
•
Counting
on Frank
de Rod
Clement
materiales
•
de base
diez
actividad
•
del alumno
(páginas 5
y 6)
para
MAN
para
de Valor de
‹
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
2
Page 9

Valor del valor de posición
Recopilación y organización de datos
Los alumnos utilizar·n los materiales de base diez y
la TI-10 para avanzar en el análisis de otros números
e identificar la cantidad de unidades, decenas,
centenas y millares que contenga un número. Los
alumnos mayores pueden hallar la cantidad de
décimas y centésimas. Para estimular su capacidad
de investigación, puede utilizar preguntas como:
¿Cuántas centenas hay en 120? ¿En 2.478?
•
¿En 3.056?
¿Cuántas decenas hay en 120? ¿En 2.478?
•
¿En 3.056?
¿Cuántas unidades (unos) hay en 120?
•
¿En 2.478? ¿En 3.056?
¿Qué número puedes encontrar que tenga
•
12 unidades?, ¿12 decenas?, ¿12 centenas?
¿Qué número puedes encontrar que tenga
•
60 unidades?, ¿60 decenas?, ¿60 centenas?
(continuación)
³
En ‹ (Resolución de
11 –.
– 1 –.
1602
ê6êê
MAN
de Valor
para ver
para hallar
, pulsar
. Este
6
es el
problemas) con modo
(manual), los alumnos pueden
utilizar la función
de posición para probar sus
conjeturas. Por ejemplo, si
consideran que 1.602 tiene 160
centenas, deben introducir
1602
, pulsar
16
. Pueden utilizar los
êê
materiales de base diez para ver
por qué en 1.602 hay sólo 16
centenas.
Nota:
Los alumnos pueden
utilizar el modo
el dígito que ocupe la posición
de las centenas. Con este modo
deben introducir
Œ ‘
resultado indica que
dígito que ocupa la posición de
las centenas.
Œ ‘
para ver
Análisis de datos y trazado de conclusiones
Pida a los alumnos que utilicen las tablas de las
páginas de Actividades del alumno de
valor de posición
para registrar sus resultados e
identificar los patrones que pueden observar.
Para ayudarles en el enfoque de los patrones,
haga preguntas como:
¿Cómo comparar el número de decenas de
•
1.314 con el número 1.314? ¿Y con el número
567? ¿Con 2.457? 4.089, etc.?
Si tapa el dígito que ocupa la posición de las
unidades, podrá ver la cantidad de decenas
que tiene un número.
¿Cómo comparar el número de centenas de
•
1.314 con el número 1.314? ¿Y con el número
567? ¿Con 2.457? ¿Con 4.089, etc.?
Si tapa los dígitos situados a la derecha de las
centenas, podrá ver la cantidad de centenas
que hay en un número.
¿Cómo comparar la pantalla de la TI-10 con lo que
•
puede hacerse con los materiales de base diez?
Valor del
© 2001 T
Si la pantalla de la TI-10 muestra
31_
, para 316,
significa que con 316 unidades pueden
formarse 31 filas de decenas.
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
3
Page 10

Valor del valor de posición
Continuando con la investigación
Establezca la relación entre los patrones del valor
de posición y el dinero. Por ejemplo, pregunte:
Si cada “pastilla de goma” cuesta un centavo,
•
¿cuántos centavos debes gastar para comprar
1.314 pastillas de goma?
1.314 centavos
¿Cuántas monedas de diez centavos
•
(decenas) gastarías?
131 monedas de diez centavos y 4 centavos
más
¿Cuántos dólares (centenas)?
•
13 dólares, más 14 centavos, o 1 moneda de
diez centavos y 4 centavos
Los alumnos mayores pueden registrar el dinero y
escribirlo en la TI-10 en formato decimal, 13,14.
A continuación, pueden utilizar la TI-10 para
relacionar monedas de diez centavos con 1/10
(0,1) de dólar (13,14 dólares estadounidenses
tienen 131 decenas). También pueden relacionar
los centavos con 1/100 (0,01) de dólar (13,14
dólares estadounidenses tienen 1.314 centavos o
centésimas).
(continuación)
Los alumnos más mayores pueden también
relacionar los patrones del valor de posición con la
conversión entre unidades métricas. Por ejemplo,
una medida de 324 centímetros podría registrarse
como 32,4 decímetros (o redondearse a 32 dm), ya
que 1 dm = 10 cm, o bien podría registrarse como
3,25 metros (o redondearse a 3 m), ya que 1 m =
100 cm.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
4
Page 11

Valor del valor de
Nombre _____________________________
Fecha _____________________________
posición, Parte A
Recopilación y organización de datos
1. Utilice los materiales de base diez y la TI-10 para hallar la cantidad de
decenas, centenas y millares que contenga un número. Registre los
resultados en la tabla.
Número
Número de
millares
2. ¿Qué patrones se observan?
Número de
centenas
Número de
decenas
Análisis de datos y trazado de conclusiones: Patrones
1. Escriba 5 números que contengan 15 decenas.
__________________________________________________________________________________
2. Escriba 5 números que contengan 32 centenas.
__________________________________________________________________________________
3. Escriba 5 números que contengan 120 decenas.
__________________________________________________________________________________
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
5
Page 12

Valor del valor de
Nombre _____________________________
Fecha _____________________________
posición, Parte B
Recopilación y organización de datos
1. Utilice los materiales de base diez y la TI-10 para hallar la cantidad de
décimas y centésimas que hay en un número. Registre los resultados
en la tabla. ¿Qué patrones se observan?
Número Número de
décimas
2. ¿Qué patrones se observan?
Número de
centésimas
Análisis de datos y trazado de conclusiones: Patrones
1. Escriba 5 números que contengan 15 décimas.
__________________________________________________________________________________
2. Escriba 5 números que contengan 32 centésimas.
__________________________________________________________________________________
3. Escriba 5 números que contengan 120 décimas.
__________________________________________________________________________________
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
6
Page 13

¿Cuál es el problema?
p
p
p
Visión general
Los alumnos relacionarán sentencias de números
con enunciados de
soluciones
or medio de operaciones de suma, resta,
roblemas y hallarán las
multiplicación y división.
Introducción
1. Utilice la pizarra o el retroproyector para mostrar
una sentencia de números, como 8 + 2 = ?. Pida
a los alumnos que imaginen situaciones en las
que puedan utilizar estos números, y pregunte:
Si durante mis vacaciones he comprado ocho
postales y ya tenía dos ¿cuántas postales tengo
ahora?
2. Si es necesario, permita que los alumnos utilicen
contadores para determinar que el valor de ? es 10.
3. Indique a los alumnos lo que deben hacer para
mostrar esta ecuación en la TI-10 y para
preguntar a la TI-10 cuál es el valor de ?.
4. Muestre ahora una ecuación, por ejemplo,
? - 10 = 4. Plantee situaciones relacionadas con
estos números y sus posibles significados.
Tenía algún dinero en el bolsillo y gasté 10
centavos. Si sólo me quedan ahora 4 centavos.
¿Cuánto dinero había en mi bolsillo?
Permita que los alumnos practiquen con las
pulsaciones de tecla necesarias para mostrar esta
ecuación y probar el valor que le han dado a ?.
5. Continúe con esta actividad durante un cierto
periodo de tiempo para que los alumnos se
acostumbren a manejar y analizar distintos tipos
de sentencias de números. Por ejemplo, ? x ? = 24
(que tiene 8 soluciones de pares de números
enteros) y ? x 4 = 2 (que no tiene solución con
números enteros).
Conceptos
matemáticos
Grados 1 - 5
suma, resta
•
sentencias de
•
números
(ecuaciones)
Grados 3 - 5
licación,
multi
•
división
inecuaciones
•
³
Para mostrar
1. Pulse
2. Pulse
3. Pulse
4. Introduzca 10 y
³
Si el valor que se comprueba
para ? es incorrecto, la TI-10
muestra
sugerencia. Por ejemplo, si un
alumno prueba 15 para la
ecuación
indica
y regresa a la ecuación
original.
Nota:
respuestas erróneas, la
TI-10 muestra la correcta.
‹
que la TI-10 active el modo
MAN
(manual) de
Resolución de problemas.
‡ para salir del
menú.
8 T 2 Z
La TI-10 muestra
(una única solución con
números enteros).
®
pulse
solución. La TI-10
muestra la ecuación y la
respuesta
no
? - 10 = 4
no
, muestra
Después de tres
Materiales
•
•
•
•
8 + 2 = ?
‡ "
®
para probar la
YES
.
junto con una
, la TI-10
15 - 10 > 4
TI-10
contadores
lápiz
actividad
del alumno
(página 10)
:
®
para
.
1 SOL
,
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
7
Page 14

¿Cuál es el problema?
Recopilación y organización de datos
Como actividad progresiva, pida a los alumnos que
trabajen en parejas y utilicen la página Actividad del
alumno de
de resolución de problemas. Un miembro de la pareja
es el responsable de realizar las operaciones en la
TI-10, y el otro de escribir las sentencias de números.
1. Pida al responsable de escribir que cree sentencias
de suma, resta, multiplicación o división en las que
se utilice el signo ? y, a continuación, registre la
sentencia de números en el cuadro superior de la
página 10.
2. Pida al responsable de la TI-10 que introduzca la
sentencia de números en la calculadora.
3. Pida al responsable de escribir que cree una
situación y formule una pregunta con la
sentencia de números y luego registre esta
información en el cuadro inferior.
¿Cuál es el problema?
para crear tarjetas
(continuación)
Ambos responsables pueden trabajar juntos para
pegar o fijar con cinta adhesiva los dos cuadros en
lados opuestos de una tarjeta de índice.
Pida a los alumnos que trabajen juntos y utilicen la
TI-10 para hallar la cantidad de soluciones con
números enteros de la ecuación y probar las
soluciones. Ofrézcales ideas que faciliten el análisis
con preguntas como:
¿Qué habría sucedido de haber utilizado una
•
suma (resta, multiplicación o división)?
¿Cómo habrías utilizado los contadores para
•
hallar la sentencia de números?
¿Qué representa este número en la secuencia de
•
números que has imaginado?
¿Qué representa el signo de interrogación en la
•
historia que has inventado?
¿Podrías crear un problema que comenzase con
•
un signo de interrogación?
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
8
Page 15

¿Cuál es el problema?
(continuación)
Análisis de datos y trazado de conclusiones
Para ayudar a los alumnos a centrar su atención en
hallar la relación entre los problemas que han
inventado y los números y operaciones de las
sentencias de números, formule preguntas como:
¿Cómo cambiaría el problema que has
•
inventado si utilizaras otro número?
¿Cómo se vería afectado tu problema si en la
•
sentencia de números utilizases un signo mayor
que o menor que en lugar de un signo igual?
¿Cómo cambiaría tu problema si realizases una
•
operación distinta en la sentencia de números?
Continuando con la investigación
•
Pida a los alumnos que creen problemas y los
intercambien. Cada miembro de la pareja debe
escribir una sentencia de números que continúe
la historia del otro.
•
Pida a los alumnos que ordenen las sentencias de
números respectivas en categorías. Por ejemplo, las
que no tienen solución con números enteros, las
que tienen 1 solución con números enteros, las que
tienen 2 soluciones con números enteros y las que
tienen infinitas soluciones con números enteros.
•
Pida a los alumnos que intenten hallar una
ecuación o una inecuación que no tenga solución
con números enteros, una con 1 solución con
números enteros, con 2, con más de 5, etc.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
9
Page 16

Nombre _____________________________
¿Cuál es el problema?
Fecha _____________________________
1. Escriba una sentencia de números utilizando una operación y el signo ?.
2. Escriba una historia que describa un problema y formule una
pregunta que se pueda representar con una sentencia de números.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
10
Page 17

Comparación de costes
Visión general
Los alumnos deben resolver un problema utilizando
una división con cociente entero y resto, a
continuación, resolverán el mismo problema con un
cociente decimal y, por último, compararán los
resultados.
Introducción
1. Plantee el siguiente problema:
El departamento de mantenimiento ha calculado
que el coste anual del mantenimiento del campo
de fútbol es de 0,40 dólares estadounidenses por
yarda cuadrada. El campo de fútbol tiene
80 yardas de ancho por 110 de largo. Los seis
colegios que utilizan el campo han acordado
sufragar los gastos a partes iguales. ¿Cuál será
la contribución anual de cada colegio?
2. Pida a los alumnos que utilicen la TI-10 para
resolver este problema de dos formas:
Hallando el cociente entero y el resto.
•
Hallando el cociente con decimales.
•
Conceptos
matemáticos
división
•
multiplicación
•
fracciones
•
decimales
•
El valor de configuración
predeterminado para división
de la TI-10 (
cociente entero y un resto.
Materiales
•
•
•
QR
) muestra un
TI-10
lápiz
actividad
del alumno
(página 14)
Recopilación y organización de datos
Los alumnos deben registrar los procedimientos y
resultados en la página
Actividad del alumno. Para ayudarles a enfocar el
problema, formule preguntas como
¿Qué cantidad se ha introducido en la TI-10
•
para resolver el problema?
80
110
−
V
Z para determinar el área del
campo de fútbol.
0,40
V
−
Z para hallar el coste total del
mantenimiento.
6
W
−
Z para hallar el coste por colegio en
formato decimal.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
Comparación de costes
:
Para mostrar el cociente en
formato decimal:
de la
TI-10: Manual del profesor
1. Pulse
restablecer la TI-10.
2. Pulse ‡ " para
subrayar
decimal).
3. Pulse
seleccionar la
configuración decimal.
4. Pulse ‡ para salir del
menú
regresar a la pantalla
anterior.
”
para
b
(formato
Ù
®
para
P (división) y
11
Page 18

Comparación de costes
¿Se podría solucionar el problema de forma
•
más eficaz? ¿Cómo?
80 x 110 se puede calcular mentalmente y
simplificar las pulsaciones de tecla a
6
W
Z.
¿Qué procedimientos parecidos utilizarías para
•
cada tipo de solución?
Para todos los procedimientos es necesario
hallar las dimensiones del campo en yardas, lo
que supone el uso de operaciones de
multiplicación y división.
¿En qué se diferencian?
•
Se han utilizado teclas diferentes para indicar a la
TI-10 el modo en que se desea mostrar el resultado.
8800
V
(continuación)
0,4
Análisis de datos y trazado de conclusiones
Para ayudar a los alumnos a realizar el an·lisis de los
datos, formule preguntas como:
¿Qué aspecto tiene cada una de las dos formas
•
del resultado?
Todas las soluciones tienen 586 como
componente de número entero.
¿En qué se diferencian los dos resultados?
•
La forma con resto indica sólo la cantidad de
dólares sobrante. La forma decimal indica cuánto
más de 586 dólares tiene que pagar cada colegio.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
12
Page 19

Comparación de costes
¿Qué ocurre si se multiplica cada resultado por
•
6 como prueba?
Para la forma con cociente y resto, al multiplicar
586 por 6 se obtiene 3.516, a lo que deberá sumar
el resto, 4, para obtener el coste total, 3.520
dólares estadounidenses.
Si se multiplica el resultado decimal 586,6666667
586,67
586,6666667
586,6666667
V 6 Z), el resultado es 3.520.
Š ™
®
).
V 6 Z), el resultado es 3.520,00. Este
b ”
586,67
V 6 Z), el resultado es
por 6 (
No obstante, este resultado no tiene sentido,
ya que al multiplicar 6 x 7 ¡no se obtiene 0 como
dígito final!
Al referirnos a operaciones con dinero, puede
fijarse un resultado decimal, 586,6666667, con 2
posiciones (
Al multiplicar el número redondeado, 586,67, por 6
(
resultado carece de sentido ya que 6 x 7 = 42.
Si se restablece la TI-10, y se multiplica 586,67
por 6 (
3.520,02. Esta operación no es correcta.
Imagina que formas parte de uno de los colegios,
•
¿qué forma de cociente querrías utilizar?
Las respuestas pueden variar. Algunos alumnos
pueden preferir la forma decimal, ya que es la
que más se acerca a la representación del dinero.
Algunos otros podrían decantarse por la forma
de cociente entero y resto y proponer que la
Oficinacentralse haga cargo de los 4,00 dólares
restantes.
(continuación)
Para una división con enteros
(con cociente y resto), la TI-10
utiliza sólo el cociente del
resultado en las operaciones
que debe realizar a
continuación. El resto se
desestima siempre.
La TI-10 redondea sólo el
resultado que muestra en
pantalla. El valor almacenado
internamente
Cuando se fija 586,6666667
en 2 posiciones decimales
(586,67) y se multiplica por 6,
la TI-10
original (586,6666667) y lo
utiliza como factor. Sin
embargo, cuando se introduce
el número redondeado,
586,67, la TI-10 utiliza como
factor el número introducido y
calcula un producto de
3.520,02.
recuerda
no
se redondea.
el número
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
13
Page 20

Nombre _____________________________
Comparación de
Fecha _____________________________
costes
Recopilación y organización de datos
El departamento de mantenimiento ha calculado que el coste anual del
mantenimiento del campo de fútbol es de 4 dólares estadounidenses por
yarda cuadrada. El campo de fútbol tiene 80 yardas de ancho por 110 de
largo. Los seis colegios que utilizan el campo han acordado sufragar los
gastos a partes iguales. ¿Cuál será la contribución anual de cada colegio?
1. Halle el resultado utilizando una división con cociente entero y resto.
2. Halle el resultado utilizando una división con cociente decimal.
Análisis de datos y trazado de conclusiones
Escriba unas líneas comparando los dos resultados.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
14
Page 21

Cómo utilizar
la TI.10
1 Pantalla, desplazamiento, orden de las
operaciones y uso de paréntesis 16
2 Borrado y corrección 19
3 Menús 23
4 Operaciones básicas 26
5 Operaciones con una constante 33
6 Números enteros y decimales 38
7 Memoria 42
8 Resolución de problemas: Modo Auto 47
9 Resolución de problemas: Modo Manual 54
10 Valor de posición 62
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
15
Page 22

Pantalla, desplazamiento, orden de
p
p
p
q
j
q
p
p
p
p
p
p
p
q
p
j
p
p
p
p
las operaciones y uso de paréntesis
1
Teclas
1.
2.
3.
abre un
X
ex
resión. Puede haber hasta ocho
paréntesis a la vez.
cierra un
Y
expresión.
! y"
y derecha, respectivamente.
y $ mueven el cursor hacia
#
arriba y aba
resultados anteriores, y en los
menús.
aréntesis para una
aréntesis para una
mueven el cursor a iz
o de las entradas y
uierda
3
Notas
En los ejemplos de las transparencias
•
”
ue los
para
maestras se considera
valores de configuración en uso son
redeterminados. Pulse b
los
ara restablecer la TI-10 a los valores
predeterminados y borrar la pantalla.
La transparencia maestra del
•
TM
EOS
TI-10 para realizar las operaciones.
Al trabajar con paréntesis, si se
•
a
sincronización. Pulse
retroceder a la pantalla anterior.
Las operaciones entre paréntesis
•
se efectúan en
X
las o
el resultado.
Ejemplo: 1 + 2 x 3 = 7
muestra el orden que sigue la
ulsa Z antes de pulsar Y,
arece Syn Error, error de
rimer lugar. Utilice
y Y
ara cambiar el orden de
eraciones y, por lo tanto,
(1 + 2) x 3 = 9
”
© 2001 T
EXAS INSTRUMENTS INCORPORATED
Las dos primeras líneas muestran
•
las entradas hasta un máximo de
11 caracteres. Las entradas van de
uierda a derecha, y siempre se
iz
1
2
•
•
TI-10: Manual del profesor
lazan a la línea siguiente en el
des
lugar que ocupa el operador.
Los resultados aparecen
ustificados a la derecha. Si el
roblema completo no cabe en la
rimera línea, el resultado se
desplaza a la segunda.
Cuando una entrada no cabe en dos
líneas, continúa des
Para ver el
utilice
contenido de la pantalla.
#
rincipio de una entrada,
para desplazar el
lazándose.
16
Page 23
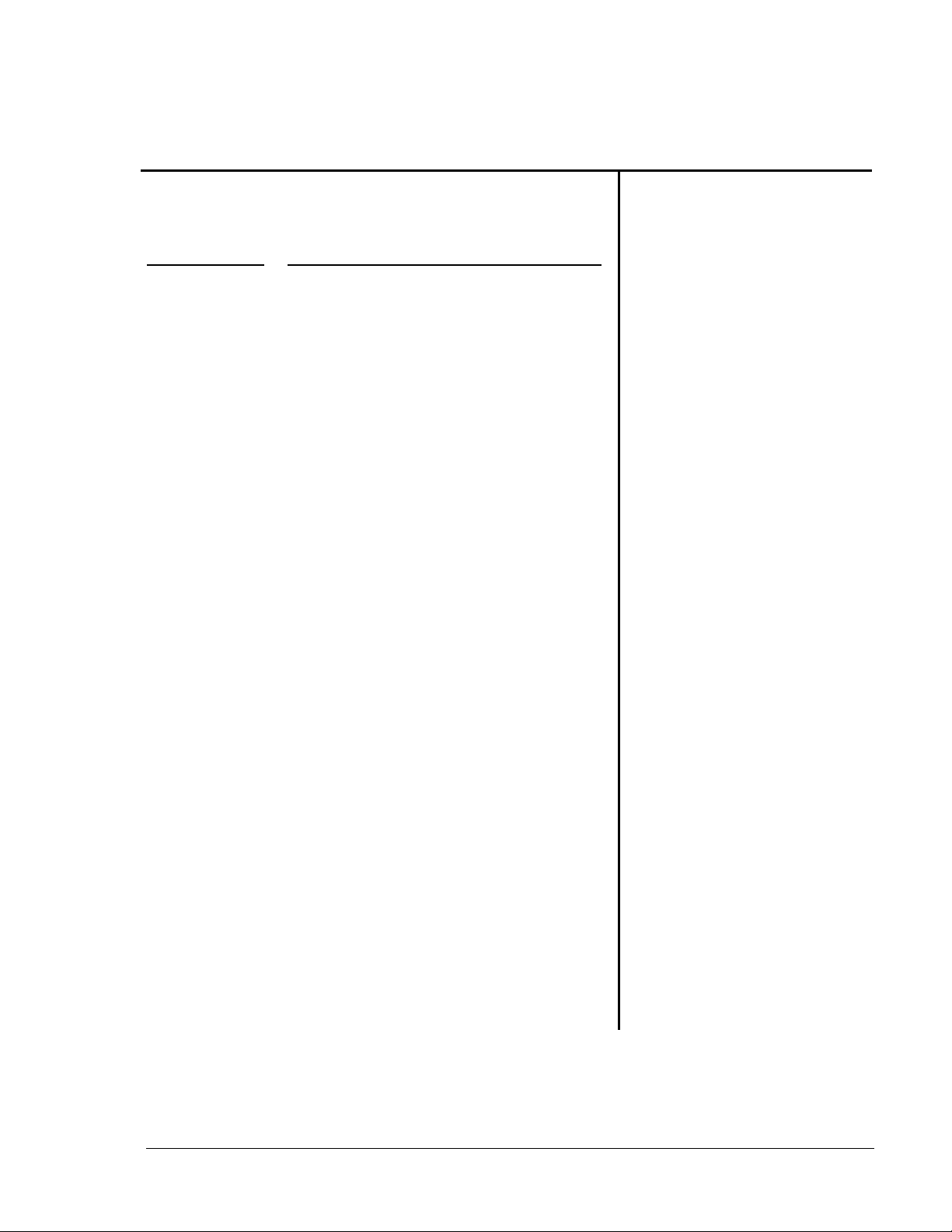
Equation Operating System, EOS™
q
p
p
p
(Sistema operativo de ecuaciones)
Prioridad Funciones
1 (primero) Expresiones entre paréntesis ( ).
Funciones
ue requieren un
2
aréntesis de cierre ) y
receden al argumento.
3 Negación (N).
4 Multiplicación, multiplicación
implícita, división (
5 Suma y resta (
6 (último)
completa todas las
Z
+
N
Q P
).
).
operaciones.
Dado que las operaciones entre paréntesis
se efectúan en primer lugar, puede utilizar
aréntesis para cambiar el orden de las
operaciones y, por lo tanto, el resultado.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
17
Page 24
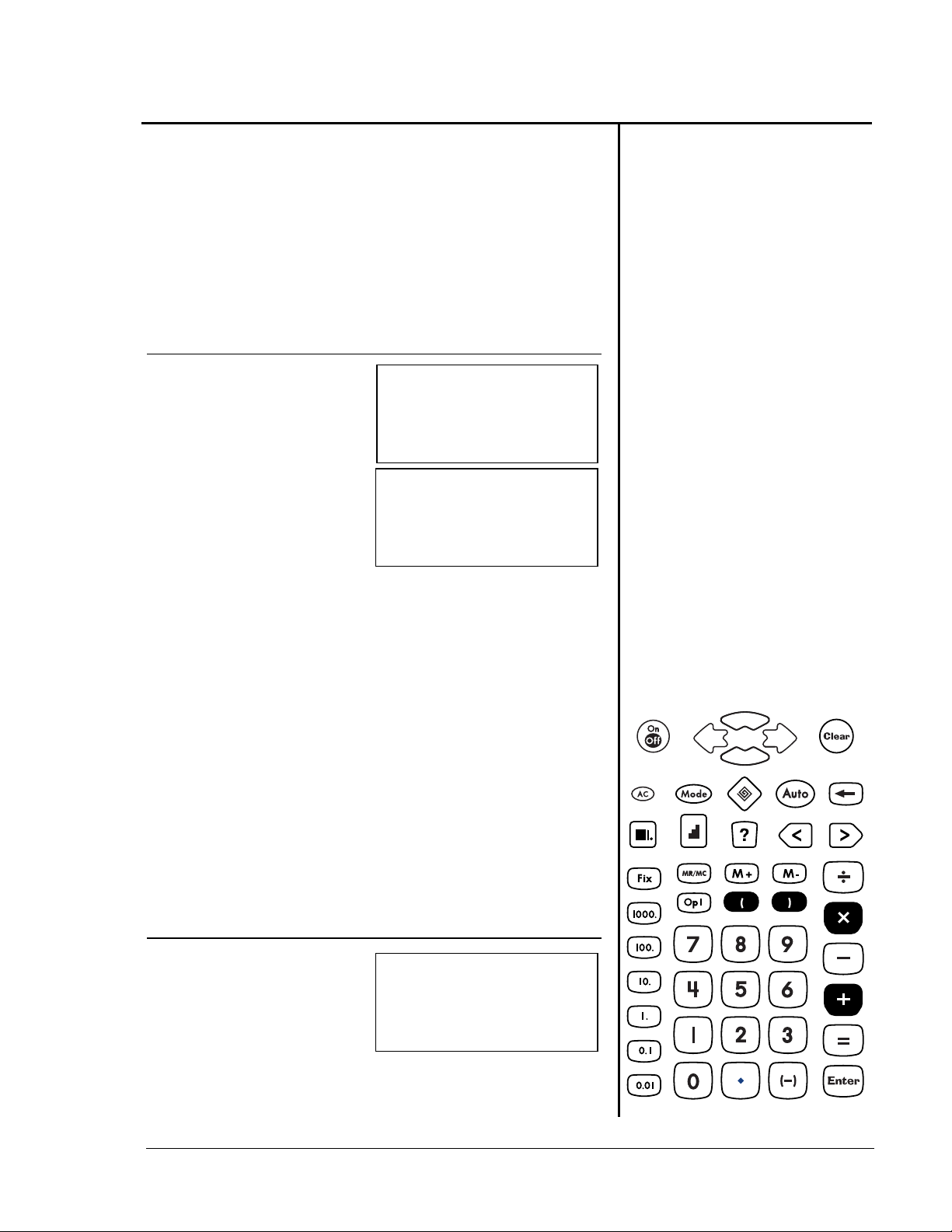
Orden de las operaciones
(
1 + 2 x 3 =
La pantalla
Pulse muestra
b”
á
1
T
2
V
3
1Û2Ý3
Z
Sumar
T
Multiplicar
V
Paréntesis
X Y
Ú
7
1 + 2) x 3 =
La pantalla
Pulse muestra
1
X
3
V
© 2001 T
EXAS INSTRUMENTS INCORPORATED
T
Z
2
Y
Å1Û2ÆÝ3Ú
9
TI-10: Manual del profesor
18
Page 25

Borrado y corrección
p
q
p
p
q
p
p
p
p
(
(
(op
2
Teclas
1.
2.
enciende y apaga la TI-10.
−
borra el dígito introducido en
w
último lugar y
entrada sin tener
ermite corregir una
ue introducir el
número completo.
3. En la herramienta Calculadora,
borra la última entrada, todas las
o
eraciones pendientes y cualquier
condición de error. Puede introducir
un nuevo
roblema y continuar con la
operación.
4.
restablece la TI-10.
b
”
Notas
En los ejemplos de las transparencias
•
maestras se considera
ue los
valores de configuración en uso son
redeterminados. Pulse b
los
ara restablecer la TI-10 y borrar la
pantalla.
Para restablecer la TI-10, puede
•
utilizar uno de los métodos
siguientes:
−
Pulsar b.
−
Pulsar − y ” simultáneamente.
−
Pulsar
, seleccionar el menú
‡
RESET, eligir Y (Sí), y pulsar
Cuando se restablece la TI-10 la
•
antalla muestra el mensaje
MEM CLEARED. Pulse ”
ara
borrar la pantalla.
”
®
.
Al restablecer la TI-10 se recuperan
•
los valores de configuración
predeterminados:
−
Notación estándar
decimal
flotante)
1
3
−
Modo Automático de
Resolución de problemas
4
2
−
División con cociente y resto
−
Nivel de dificultad 1
suma) en
Resolución de problemas
−
Suma como Tipo de operación
Se borran:
•
−
Operaciones pendientes
−
Entradas del historial
−
La constante
eración
almacenada)
−
Cualquier condición de error
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
19
Page 26

Borrado y corrección
p
p
p
p
p
Notas (continuación)
Cuando se pulsa ” sin ninguna otra
•
tecla no se cambian la configuración
de modo, la memoria, el historial ni la
constante.
En ‹ (Resolución de problemas) con
•
modo
pantalla antes de pulsar
En ‹ (Resolución de problemas) con
•
modo
obtenido antes de pulsar
AUTO
uede cambiar el resultado de la
MAN
uede borrar el problema antes de
ulsar
(automático), si
®
(manual), si
®
, o bien borrar el resultado
ulsa
®
ulsa
.
”
.
”
2
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
20
Page 27

Borrado de entradas
p
p
1. Introduzca 35 + 10.
2. Borre la entrada y la o
endiente.
3. Introduzca 35 N 9.
4. Complete la operación.
La pantalla
Pulse muestra
b”
á
35
T
10
35Û10á
Borrar
eración
”
”
35
Z
U
9
á
35Ü9
35Ü9
Ú
26
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
21
Page 28
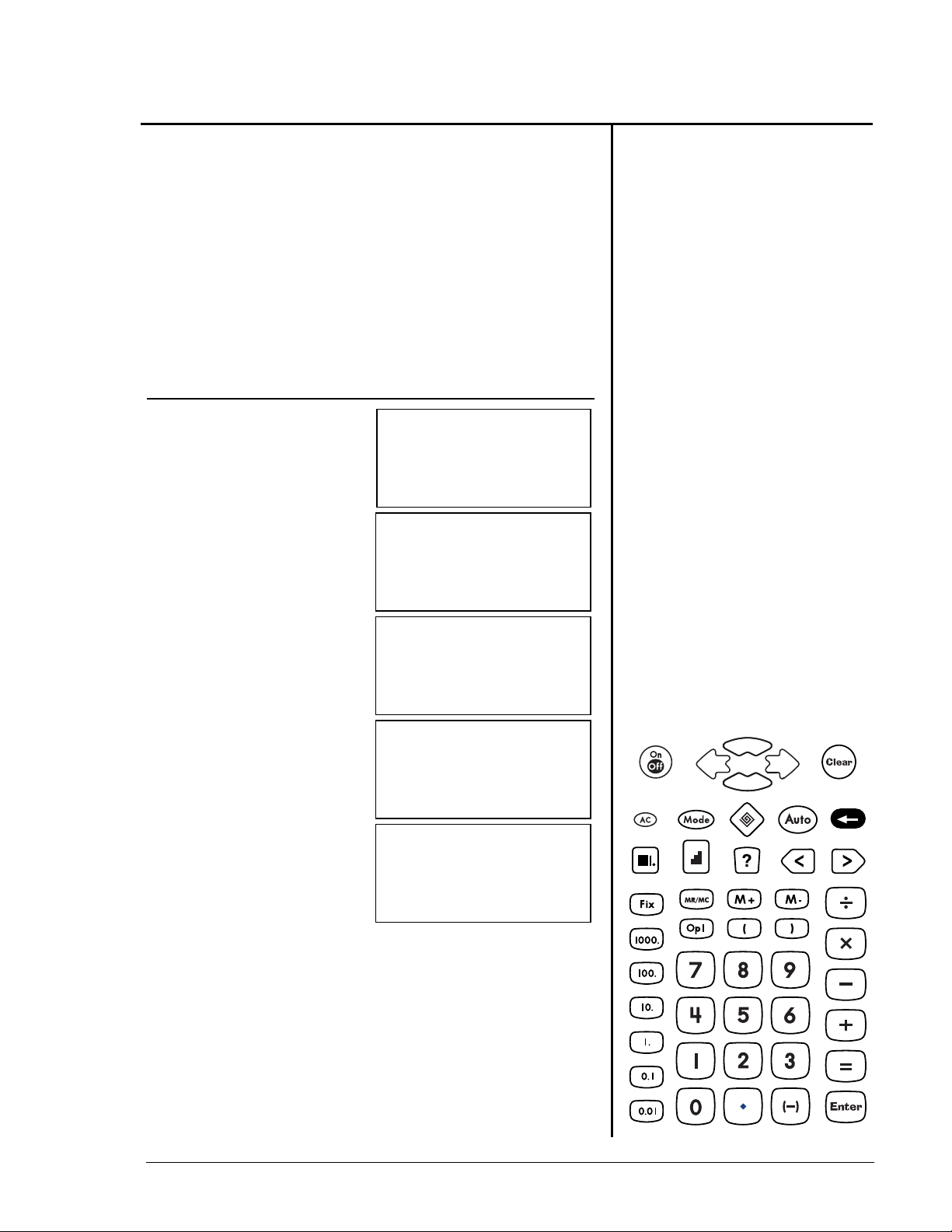
Corrección de errores de entrada con
p
w
1. Introduzca 69 + 3.
2. Cambie el 9
or un 8.
3. Sume 3.
4. Complete la operación.
La pantalla
Pulse muestra
b”
á
69
T
3
69Û3á
Retroceso
w
w w w
T
3
Z
8
68á
68Û3á
68Û3
Ú
71
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
22
Page 29

Menús
p
p
pág
p
p
q
(
3
Teclas
1.
muestra los menús de la
‡
herramienta Calculadora (consulte
la página 24).
2.
‹ ‡
muestra los menús de la
herramienta Resolución de
problemas (consulte la página 25).
Notas
En los ejemplos de las transparencias
•
maestras se considera que los valores
de configuración en uso son los
redeterminados. Pulse b ” para
restablecer la TI-10 y borrar la pantalla.
La herramienta Calculadora se activa
•
al encender la TI-10. Con la
herramienta Calculadora activa,
ulse
para acceder a los menús
‡
de Calculadora. Consulte, en la
ina 24, las opciones del menú
Calculadora.
Pulse ‹ para acceder a la
•
herramienta Resolución de problemas.
Cuando la herramienta Resolución de
roblemas está activa, el indicador
aparece en la línea superior de la
‹
antalla de la TI-10. Con la
herramienta Resolución de problemas
activa, pulse
para acceder a los
‡
menús de Resolución de problemas.
Consulte, en la página 25, las
opciones del menú Resolución de
problemas.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
Consulte el Apéndice C para ver el
•
21
mapa de menús completo.
Para seleccionar una opción de
•
cualquier menú, resalte el elemento
ue desee y pulse
menú, pulse
Pulse
•
]
‡
para pasar
. Para salir del
®
de nuevo.
alternativamente del modo AUTO
automático) al MAN (manual) de la
herramienta Resolución de problemas.
Pulse c para cambiar el nivel de
•
dificultad siempre que el modo
seleccionado sea AUTO. Una vez
alcanzado el Nivel 3, la TI-10
retrocede al Nivel 1.
TI-10: Manual del profesor
23
Page 30

Menús
(continuación)
Herramienta Calculadora
Pulse Menú Opción Explicación Ejemplo
3
b
‡
b
‡
b
‡
”
”
$
”
$$
P
(División)
OP
(Operación
con
constante)
CLEAR OP1 Y
n
QR
Ù
+ 1
?
(Sí)
(No)
Muestra los resultados de
la división en forma de
cociente y resto.
Muestra los resultados de
la división con decimales.
Muestra en la pantalla la
operación con una
constante.
Oculta la operación con la
constante.
Borra la operación y el
valor almacenados en OP1.
Retiene el valor y la
operación almacenados en
OP1.
2 r 1
2.25
1 x 5
15
15
Y
CLEAR OP1
Y
CLEAR OP1
n
n
b
”
‡
© 2001 T
RESET
$$$
EXAS INSTRUMENTS INCORPORATED
(No)
n
Y
(Sí)
No restablece la
calculadora.
Restablece la calculadora.
TI-10: Manual del profesor
n
n
Y
RESET
Y
RESET
24
Page 31

Menús
(continuación)
Herramienta Resolución de problemas
Pulse Menú Opción Explicación Ejemplo
3
b
”
‹ ‡
(Modo)
AUTO
(automático)
MAN
(manual)
Predeterminado. Muestra
los problemas con una
incógnita.
Permite plantear
problemas y elegir las
incógnitas.
Modo AUTO (automático) de Resolución de problemas
Pulse Menú Opción Explicación Ejemplo
b
”
‹ ‡
$
OR
ê ë ì
(Nivel de
dificultad)
1 2 3
Una vez alcanzado el
Nivel 3, la TI-10 retrocede
al Nivel 1.
c
b
”
‹ ‡
$$
Û Ü Ý Þ Ã
(Tipo de
operación)
Sumar, restar, multiplicar,
dividir, hallar el operador.
‹
5 + 2 = ?
‹
5 + ?= 7
‹
4 + ? = 10
‹
10 - ? = 4
Auto
Auto
Auto
Modo MAN (manual) de Resolución de problemas
Muestra opciones sólo para el Valor de posición de Resolución de problemas.
Pulse Menú Opción Explicación Ejemplo
b
”
‹ ] ‡
$
© 2001 T
EXAS INSTRUMENTS INCORPORATED
å
(Valor de
posición)
11 -.
- 1 -.
Permite hallar la cantidad
de unidades, centenas,
millares, décimas o
centésimas de un número.
Permite hallar el dígito que
ocupa un lugar
determinado en un
número.
TI-10: Manual del profesor
Pulse 1234
Œ‘
‹ ƒ
1234
12_ _
Pulse 1234
Œ‘
‹ ƒ
1234
_2_ _
25
Page 32

Operaciones básicas
p
q
p
p
p
p
p
p
p
p
p
j
p
Teclas
1.
2.
3.
4.
5.
6.
7. M
Notas
•
suma.
T
resta.
U
multiplica.
V
divide.
W
completa la operación.
Z
completa la entrada.
®
ermite introducir un número
negativo.
En los ejemplos de las transparencias
maestras se considera
ue los valores
de configuración en uso son los
redeterminados. Pulse b ” para
restablecer la TI-10 y borrar la pantalla.
Hay dos opciones para mostrar los
•
resultados de una división.
−
Cuando está seleccionada la
o
ción QR, el resultado de la
división a
arece en forma de
cociente y resto (__ r __). QR
es el valor de configuración
predeterminado.
−
Cuando está seleccionada la
ción decimal (Ù), el resultado
o
de la división a
arece en forma
decimal.
Si el resultado de la división se
•
utiliza en una o
sólo se em
eración posterior,
lea el cociente. El resto
se desestima.
4
El número máximo de dígitos para
•
cociente y resto es 5. El número
total de caracteres del cociente,
resto y el carácter r no
uede ser
superior a 11.
Cuando se ha seleccionado la
•
o
ción QR para una división, todos
los números deben ser enteros
positivos.
Si intenta dividir por 0, la pantalla
•
4
3
2
1
5
6
7
mostrará un mensaje
T, U, V, W, ®
•
con las constantes integradas.
El símbolo de negación (L)
•
a
arecerá en la pantalla más
pequeño que el signo menos (N).
0 ERROR.
P
y Z traba
an
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
26
Page 33

7
Operaciones básicas
2 + 5 N 6 =
La pantalla
Pulse muestra
b”
2
6
T
Z
5
U
á
2Û5Ü6
Sumar, Restar
T U
Multiplicar, Dividir
V W
Igual
Ú
1
Z
3 x 4 P 2 =
La pantalla
Pulse muestra
b”
3
V
4
W
2
á
3Ý4Û 2
Ú
Z
6½0
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
2
Page 34

Búsqueda de patrones en problemas anteriores
p
Introduzca los problemas.
1 + 1 =
1 + 2 =
1 + 3 =
Revise el historial (
roblemas
anteriores) para determinar el patrón.
La pantalla
Pulse muestra
b”
á
1
T
1
Z
1Û1
Ú
2
Sumar
T
Historial
#
$
1
1
T
T
2
3
##
$
Z
Z
1Û2
1Û3
1Û1
1Û2
1Û2
1Û3
Ú
Ú
Ú
Ú
Ú
Ú
3
4
2
3
3
4
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
28
Page 35

Introducción de números negativos
p
La temperatura de esta mañana era
A.M
de L3° C a las 6:00
A.M
., la temperatura ha subido hasta
12° C. ¿Qué tem
10:00
Pulse muestra
A.M
.?
eratura había a las
La pantalla
. A las 10:00
b”
á
Negativo
M
M
3
T
12
Z
3Û12
ä
Ú
9
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
29
Page 36

División y resto
p
Cristina tiene 27 caramelos.
Desea re
artirlos equitativamente
con otros 5 amigos. ¿Cuántos
caramelos tendrá cada uno?
¿Cuántos caramelos le quedarán?
La pantalla
Pulse muestra
b”
á
27
W
6
Z
27
Ú
6
Þ
4½3
Dividir
W
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
30
Page 37
División con resultado decimal
Defina la opción de pantalla para
división en formato decimal y divida
27 entre 6.
La pantalla
Pulse muestra
b ”
á
Ù Þ
‡ " ®
·
Ù
ê
Þ
‡
á
Ù Þ
Dividir
W
27
W
6
Z
27
Ù Þ
Ú
6
Þ
4Ù5
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
31
Page 38

Cálculo de unidades de tiempo equivalentes
p
Sara ha corrido 2 kilómetros en
450 segundos. Convierta su tiem
en minutos y segundos.
450 segundos = ? minutos
? segundos
La pantalla
Pulse muestra
b”
á
Dividir
o
W
450
Z
W
60
450Þ60
(7 minutos, 30 segundos)
Ú
7½30
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
32
Page 39

Operaciones con una constante
p
(
)
p
q
s
p
a
j
p
p
p
p
p
q
p
p
p
p
p
p
p
Teclas
La operación con una constante se
1.
›
como constante en o
repetidas.
Notas
En los ejemplos de las transparencias
•
maestras se considera
de configuración en uso son los
restablecer la TI-10 y borrar la pantall
La operación con constante se
•
define
realizan o
utilizan las teclas T, U, V o W.
ermite almacenar un operador
+ N Q
redeterminados. Pulse b ” para
y un número para utilizar
P
eraciones
ue los valore
unto con › cuando se
eraciones en las que se
•
uede realizar tanto con números
enteros como con decimales.
Cuando se utiliza este tipo de
•
o
eración (›) el contador
a
arece en la parte izquierda de la
antalla y el resultado a la
derecha. El contador indica las
veces
constante. No obstante, no
a
número situado a la derecha tiene
más de 6 dígitos. Cuando llega a
99, el contador se pone a cero (0).
Si al realizar la operación con una
•
constante utiliza una división,
elegir un formato con cociente y
resto - (QR) o decimal (
o
continuación, el formato QR utiliza
sólo el cociente y desestima el resto.
ue se ha repetido la
arecerá en la pantalla si el
eraciones que deban realizarse a
). En las
.
5
uede
Para borrar una operación con
•
constante almacenada:
−
Pulse b
TI-10. (Pulse
a la pantalla anterior.)
1
© 2001 T
EXAS INSTRUMENTS INCORPORATED
−
Pulse
al menú CLEAR OP1, seleccione
Y
, y
ulse
ulse
pantalla anterior.
Nota:
de
”
TI-10: Manual del profesor
ara restablecer la
para retroceder
”
‡
‡
$ $
®
para retroceder a la
La sim
no borra la constante.
para acceder
. A continuación,
le pulsación
33
Page 40

La suma como “recuento continuo”
q
q
En un estanque hay 4 ranas. Si 3
ranas más saltan al estan
ue de
una en una, ¿cuántas ranas habrá
en el estan
Pulse muestra
ue?
La pantalla
b”
á
Operación con
una constante
›
Sumar
T
› T
(almacenar la operación)
1
›
4
(inicializar con 4)
›
(sumar 1, de uno en uno)
›
›
Op1
Û
1
Op1
4á
Op1
4Û1
15
Op1
5Û1
26
Op1
6Û1
© 2001 T
37
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
34
Page 41
La multiplicación como “suma repetida”
p
p
q
p
p
(
)
María ha cambiado el suelo de su
cocina. Ha
uesto 4 filas de
baldosas con 5 baldosas en cada
una. Utilice la suma re
hallar la cantidad de baldosas
ha necesitado. Antes de em
seleccione en TI-10 la o
etida para
ue
ezar,
ción para
ocultar la operación con constante.
La pantalla
Pulse muestra
Operación con
una constante
›
Sumar
T
b”
‡ $ "
(ocultar operación con
constante)
®
‡
(borrar el menú)
› T
(almacenar la operación
con constante)
Continúa
5
›
á
Û1
á
Û
5
Op1
¼Á
Ã
ííí
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
35
Page 42

La multiplicación como “suma repetida”
(continuación)
La pantalla
Pulse muestra
0
(inicializar con 0)
›
›
›
›
Op1
0á
Op1
1 5
Op1
210
Op1
315
Op1
© 2001 T
420
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
36
Page 43

Borrado de la operación con una constante
p
Antes de comenzar una nueva
eración en OP1, deberá borrar los
o
valores actuales.
La pantalla
Pulse muestra
b”
á
‡
·
êê
Op1
ê
Þ
Menú Modo
‡
Ù
$ $
®
(borrar OP1)
‡
(salir del menú modo)
Op1
À»
ê
ç
Op1
À»
ê
ç
á
î
¼ÁÏ
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
37
Page 44

Números enteros y decimales
q
p
p
q
p
p
q
Teclas
6
1.
2.
introduce un separador decimal.
r
define el número de decimales en
Š
combinación con las teclas del Valor
de posición.
3.
Š
redondea el resultado al
millar más próximo.
4. Š
redondea el resultado a la
‘
centena más próxima.
5. Š ’ redondea el resultado a la
decena más próxima.
6. Š “ redondea el resultado a la
unidad más próxima.
7.
Š ˜
redondea el resultado a la
décima más próxima.
8. Š
redondea el resultado a la
™
centésima más próxima.
Notas
En los ejemplos de las transparencias
•
maestras se considera
ue los
valores de configuración en uso son
los
redeterminados. Pulse b
ara restablecer la TI-10 y borrar la
pantalla.
De forma automática, la TI-10
•
redondea el resultado al número de
decimales seleccionado. Sólo se
redondea al valor
ue aparece en la
antalla. El redondeo no afecta a
los valores almacenados. Si es
necesario, el valor calculado se
rellena con ceros.
”
2
3
4
5
6
7
8
© 2001 T
EXAS INSTRUMENTS INCORPORATED
Para eliminar el ajuste decimal fijo,
•
pulse Š r.
Debe pulsar Š antes de pulsar
•
una tecla de Valor de
vez
ue desee cambiar el número
osición cada
de posiciones para redondear.
1
TI-10: Manual del profesor
38
Page 45

Números enteros y decimales
j
q
q
q
6
Notas
•
•
•
(continuación)
Todos los resultados se muestran
con el número de decimales fi
hasta
tecla Š r o restablecer la TI-10.
El uso de r permite introducir
cual
cual sea el decimal fijo.
Puede aplicar el ajuste Fix a un
número
resultado.
ue decida borrarlo con la
uier número de decimales, sea
ue haya introducido o a un
o
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
39
Page 46

Definición del número de decimales
Redondee 12,345 a centésimas,
a décimas, y a decenas.
A continuación, cancele el ajuste Fix.
La pantalla
Pulse muestra
b”
á
12
r
345
12Ù345
Ú
®
12Ù345
Š ™
Fix
12Ù345Ú12Ù35
Fijar decimal
Š
Centésimas
™
Décimas
˜
Decenas
’
Š
˜
Š ’
Š r
(cancelar Fix)
Fix
12Ù345
Fix
12Ù345
12Ù345
Ú
12Ù3
Ú
Ú
12Ù345
10
Ù
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
40
Page 47

Suma con dinero
José se ha gastado 3,50 dólares
en helados, 2,75 en galletas y 0,99
en un refresco. ¿Cuánto dinero ha
gastado en total?
La pantalla
Pulse muestra
b”
á
Š ™
Fix
Fijar decimal
Š
Centésimas
™
3
2
r
r
50
r
75
99
Z
T
T
Fix
3Ù50Û2Ù75
ÛÙ
99
Ú
7Ù24
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
41
Page 48

Memoria
p
p
q
p
p
q
p
7
Teclas
1.
suma el resultado mostrado al
`
valor en memoria.
2.
resta el resultado mostrado del
a
valor en memoria.
3.
|
recu
era en la pantalla el
contenido de la memoria. Cuando
se
ulsa dos veces, borra la
memoria.
Notas
En los ejemplos de las transparencias
•
maestras se considera
ue los
valores de configuración en uso son
los
redeterminados. Pulse b
ara restablecer la TI-10 y borrar la
pantalla.
Puede almacenar números enteros
•
y decimales.
La pantalla muestra M siempre
•
ue el valor en memoria sea
distinto de 0.
Para borrar la memoria,
•
pulse
Para completar una operación,
•
debe
|
ulsar Z a fin de introducir el
dos veces.
resultado en la memoria.
”
1
3
© 2001 T
EXAS INSTRUMENTS INCORPORATED
2
TI-10: Manual del profesor
42
Page 49

Uso de la memoria para sumar productos
p
(
)
Hamburguesas 2 1,19 dólares =
Batidos 3 1,25 dólares =
Descuento
or
batido 3 0,20 dólares =
Total =
La pantalla
Pulse muestra
b ”
á
Fix
Š ™
á
Sumar a
memoria
`
Restar de
memoria
a
Recuperar
memoria
|
2
V
1
r
19
Z
`
(sumar hamburguesas a valor
en memoria)
3
V
1
r
25
Z
`
(sumar batidos a valor en
memoria)
3
V r
(calcular descuento)
20
Z
Fix
2Ý1Ù19
Fix M
2Ý1Ù19
Fix M
3Ý1Ù25
Fix M
3Ý1Ù25
Fix M
3
ÝÙ
20
Ú
Ú
Ú
Ú
Ú
2Ù38
2Ù38
3Ù75
3Ù75
0Ù60
Continúa
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
43
Page 50

Uso de la memoria para sumar productos
(continuación)
La pantalla
Pulse muestra
a
(deducir descuento del valor
en memoria)
|
(recuperar total)
|
(borrar memoria)
Fix M
ÝÙ
3
20
Fix M
5Ù53
Fix
5Ù53
Ú
0Ù60
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
44
Page 51

Uso de la memoria para hallar medias
p
p
p
p
En varias pruebas, Diana ha
obtenido 96 y 85
untos. Los
untos semanales han sido 87 y
98. Halle la media de cada gru
ruebas y halle la media de las dos
medias en formato decimal.
La pantalla
Pulse muestra
b”
á
‡"®
·
Þ
Sumar a memoria
`
o de
Sumar
T
Recuperar
memoria
|
Ù Þ
Ù
Ü
Z
2
96
Z
‡
85
W
`
87
(Continúa)
T
98
T
Z
96Û85
181Þ2
M
181Þ2
M
87Û98
Ù Þ
Ú
Ú
Ú
Ú
181
Ù Þ
90Ù5
Ù Þ
90Ù5
Ù Þ
185
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
45
Page 52
Uso de la memoria para hallar medias
(continuación)
La pantalla
Pulse muestra
W
T
W
2
Z
_ Z
2
Z
M
185Þ2
92Ù5Û90Ù5
183Þ2
Ú
M
M
Ú
Ù Þ
92Ù5
Ù Þ
Ú
183
Ù Þ
91Ù5
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
46
Page 53

Resolución de problemas: Modo Auto
p
p
j
p
p
p
(
)
(
)
p
p
p
p
Teclas
8
1.
activa la herramienta Resolución de
‹
roblemas. En modo
AUTO
herramienta Resolución de
muestra e
eraciones de suma, resta,
o
ercicios en los que se utilizan
, la
roblemas
multiplicación y división.
2.
‡
modo
Automático
MAN
ermite acceder al menú de
ara cambiar entre los modos
AUTO
. En modo
y Manual
AUTO
, puede
acceder a los menús Nivel de
dificultad y Tipo de operación.
Nota:
Los valores de configuración
redeterminados son Auto, Nivel 1 y Suma.
3.c cambia al siguiente nivel de
dificultad. Una vez alcanzado el Nivel
3, vuelve a comenzar desde el Nivel 1.
4.
conmuta los modos MAN y
]
AUTO
de la herramienta Resolución
de problemas.
Notas
En los ejemplos de las transparencias
•
maestras se considera que los
valores de configuración en uso son
los predeterminados. Pulse b
ara restablecer la TI-10 y borrar la
pantalla.
En modo AUTO (predeterminado),
•
la TI-10 muestra problemas con
una incógnita (por ejemplo, 5+2=?,
5+?=7, 5?2=7).
Si el alumno introduce una
•
respuesta incorrecta, la
TI-10 indica no y ofrece una
sugerencia en la forma < o >.
Después de tres respuestas
•
erróneas, la TI-10 muestra la
respuesta correcta.
”
1
2
3
© 2001 T
EXAS INSTRUMENTS INCORPORATED
Cada cinco problemas, la TI-10
•
muestra un marcador que refleja
4
las respuestas correctas e
incorrectas.
El uso de la tecla
•
, que abre el
‡
marcador durante unos instantes,
ermite comprobar los progresos en
cualquier momento. Pulse
#
para
revisar los problemas anteriores.
Resolución de problemas permite
•
repasar y examinar problemas,
pero no corregirlos.
Para salir de Resolución de
•
roblemas, pulse ‹ de nuevo.
Cuando se cierra la herramienta se
borran tanto el marcador como las
entradas anteriores.
TI-10: Manual del profesor
47
Page 54

Selección del nivel de dificultad
Elija un nivel de dificultad.
La pantalla
Pulse muestra
b ”
á
‹ ‡
‹
жи
ккккк
Resolución de
problemas
‹
Modo
‡
Auto
Auto
êëì
Auto
ê
êëì
Auto
808
$
®
"
‡
(para salir)
(Los problemas pueden ser distintos del
ejemplo que muestra la ilustración.)
‹
1 2 3
ê
‹
1 2 3
‹
ÛÃÚ
8
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
48
Page 55

Selección del nivel de dificultad con
c
Elija un nivel de dificultad.
La pantalla
Pulse muestra
b ”
á
‹
(predeterminado en Nivel 1)
‹
3Û20Ú
á
Resolución de
problemas
‹
Modo
‡
Auto
Ã
c
(cambiar a Nivel 2)
‡
(ver el ajuste del nivel de
dificultad)
$
‡
(regresar al problema)
‹
Ã
êëì
ÚÃ
2Û70Ú
á
‹
1 2 3
‹
2Û70
á
Auto
Auto
ê
Auto
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
49
Page 56
Selección del tipo de operación
p
Elija un tipo de operación:
– suma (+)
– resta (N)
– multi
licación (Q)
– división (P)
– hallar el operador (?)
La pantalla
Pulse muestra
b ”
á
‹ ‡
‹
жи
ккккк
Resolución de
problemas
‹
Modo
‡
Auto
$
$
" ®
‡
(para salir)
‹
1 2 3
ê
‹
Û Ü Ý Þ Ã
ê
‹
Û
Ü Ý Þ
Ü
‹
4Ü1Ú
Auto
êëì
Auto
Auto
Auto
Ã
Ã
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
50
Page 57

Comprobación de progresos
p
p
p
p
Escriba las soluciones a los
roblemas que presenta la TI-10.
La pantalla
Pulse muestra
b ”
á
‹ ‡
‡
(la pantalla muestra el
roblema)
‹
жи
ккккк
‹
8Û3Ú
á
Auto
Auto
Ã
Resolución de
problemas
‹
Modo
‡
11
®
(siguiente problema; el
orden de los
aleatorio)
4
®
(la pantalla vuelve a
mostrar el
5
®
roblemas es
roblema)
‹
Auto
8Û3Ú11
À¹¾
‹
ÛÃÚ
2
Auto
7
á
‹
Auto
2Û4Ç7
»¼
‹
ÛÃÚ
2
Auto
7
á
‹
Auto
2Û5Ú7
À¹¾
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
51
Page 58

Comprobación del marcador
q
p
p
p
p
p
Cada cinco problemas, la TI-10
muestra un marcador
las res
uestas correctas e
ue refleja
incorrectas.
El marcador
durante unos instantes
de la tecla
Pulse muestra
‹
(la pantalla muestra el
roblema)
uede mostrarse
‡
.
La pantalla
‹
ХЫГЪЧ
or medio
Auto
Resolución de
problemas
‹
Modo
‡
‡
(El marcador aparece de
forma momentánea)
‡
(salir del menú; regresar al
roblema)
‹
À¹¾ »¼
‹
æè
êêêê
‹
ХЫГЪЧ
Auto
50
Auto
Auto
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
52
Page 59

Búsqueda del operador
p
p
Cambie el tipo de operación para
“hallar el o
erador” (?) y resolver el
problema que presente la TI-10.
La pantalla
Pulse muestra
b ”
á
Auto
‹ ‡
‹
À¹¾ »¼
00
Resolución de
problemas
‹
Modo
‡
$ $
" " " "
®
‡
V ®
(Los problemas pueden ser
distintos del ejem
muestra la ilustración.)
lo que
Auto
‹
Û Ü Ý Þ Ã
ê
Auto
‹
Û Ü Ý Þ Ã
Auto
‹
8Ã6Ú48
Auto
‹
8Ý6Ú48
À¹¾
ê
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
53
Page 60

Resolución de problemas: Modo Manual
p
p
(
)
(
)
j
p
p
p
p
q
p
p
p
p
p
p
p
Teclas
9
1.
activa la herramienta Resolución
‹
de problemas.
2.
‡
modo
Automático
MAN
ermite acceder al menú de
ara cambiar entre los modos
AUTO
. En modo
y Manual
puede
MAN
acceder al menú Valor de posición.
Nota: 11-.
redeterminado.
3.
es el a
permite al alumno crear
uste de Valor de posición
roblemas con una incógnita cuando
se trabaja en modo
4.
[, \
y Z
ermite al alumno
MAN
.
robar las ecuaciones y las
inecuaciones de un problema
5.
conmuta los modos MAN y
]
AUTO de la herramienta Resolución
de problemas.
Notas
En los ejemplos de las transparencias
•
maestras se considera
ue los
valores de configuración en uso son
los
redeterminados. Pulse b
”
ara restablecer la TI-10 y borrar la
pantalla.
En modo MAN cada alumno puede
•
lantear los problemas que haya
imaginado.
.
En modo MAN , la TI-10 acepta
•
sólo números enteros
las o
eraciones, con excepción de
ara todas
las inecuaciones.
El número máximo de caracteres
•
que admite la pantalla es 11.
1
2
5
tengan una solución, varias
soluciones o sin solución. Por ejemplo:
3
4
−
1 solución: 2+5=?, 2+?=7, 2?5=7
−
Varias soluciones: ?+?=1, ?+?=6
−
0 soluciones: 3P2=?
Pueden plantearse problemas que
•
(No hay solución de número
entero positivo.)
Cuando un problema no tiene
•
solución, la TI-10 muestra la
alabra no y reanuda el
lanteamiento del problema hasta
que se pulsa
”
.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
54
Page 61

Resolución de problemas: Modo Manual
p
p
p
p
p
p
p
p
p
p
Notas (continuación)
El modo Manual de Resolución de
•
roblemas se ha diseñado para
tratar con números enteros
ositivos. El algunos casos,
la función de igualdad/inecuación
permite introducir decimales.
Los problemas con dos incógnitas
•
ueden tener varias soluciones.
(Así, ?x?=24 tiene ocho soluciones.)
Estos
la forma ?operador?=número.
Si desea comprobar los progresos,
•
ulse
marcador. Pulse
problemas anteriores.
roblemas deben indicarse en
para mostrar el
‡
para revisar los
#
9
La primera vez que se pulsa
•
la
antalla muestra el marcador
durante los instantes
apertura del menú.
En las pruebas de inecuaciones,
•
cuando la res
, a
no
de forma inmediata.
Resolución de problemas permite
•
re
no corregirlos.
Para salir de Resolución de
•
problemas, pulse ‹.
arece la respuesta correcta
asar y examinar problemas, pero
uesta de la TI-10 es
revios a la
‡
,
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
55
Page 62

Problemas con una solución
p
j
Los problemas con una solución son
ecuaciones con una incógnita (
e
emplo, 7+2=? o 7+?=9). Introduzca
or
un problema y halle la solución.
La pantalla
Pulse muestra
b ”
á
‹
‹ ‡"
®
‡
æè
‹
á
êêêê
Resolución de
problemas
‹
Modo
‡
Incógnita
5
U
3
®
2
®
5
T Z
9
®
(Continúa)
Z
‹
5Ü3
‹
5Ü3Ú2
‹
5
ÚÃ
1
ÛÃÚ
1
¾¼º
À¹¾
9
¾¼º
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
56
Page 63

7
Problemas con una solución
La pantalla
Pulse muestra
(continuación)
3
4
®
®
‹
5Û3Ç9
»¼
‹
5Û4Ú9
À¹¾
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
5
Page 64
Problemas con más de una solución
p
p
p
p
Los problemas con dos incógnitas
ueden tener más de una solución.
Introduzca un
roblema, halle el
número de soluciones y luego,
halle la solución del problema.
La pantalla
Pulse muestra
b ”
á
‹ ‡ "
®
‹
æè
êêêê
Resolución de
problemas
‹
Modo
‡
Incógnita
‡
T Z
3
®
2
®
1
®
(Pruebe con otra solución,
o bien
introducir un nuevo
roblema.)
ulse ” para
‹
á
‹
ÃÛÃÚ
4
‹
ÛÃÚ
2
‹
ÛÏÚ
2
3
¾¼º
3
3
À¹¾
S
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
58
Page 65

Problemas sin solución
p
p
p
La TI-10 no ha sido diseñada para
resolver determinados ti
os de
roblemas. Tales problemas tendrán
como res
uesta
0 SOL
(sin solución)
por parte de la TI-10.
La pantalla
Pulse muestra
b ”
á
‹ ‡ "
®
‹
æè
êêêê
Resolución de
problemas
‹
Modo
‡
Incógnita
‡
1
U
2
Z
®
”
‹
á
‹
1Ü2ÚÃ
0
‹
á
¾¼º
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
59
Page 66
Menor que, mayor que, igual que
p
La herramienta Resolución de
roblemas permite probar las
igualdades y las inecuaciones de los
números.
La pantalla
Pulse muestra
b ”
á
‹‡ "
®
‡
‹
æè
‹
á
êêêê
Resolución de
problemas
‹
Modo
‡
Igual
Z
Mayor que
\
Menor que
2
T
2
T
5
T
®
5
r
50
r
1
Z
®
4
\
®
1
[
10
‹
2Û1Ú1Û2
À¹¾
‹
5Û4Ç10
À¹¾
‹
Ù5ÈÙ
‹
Ù5ÚÙ
50
»¼
50
À¹¾
[
S
S
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
60
Page 67

Comprobación del marcador
q
p
p
p
p
p
Cada cinco problemas, la TI-10
muestra un marcador
las res
uestas correctas e
ue refleja
incorrectas.
El marcador
durante unos instantes
de la tecla
Pulse muestra
‹
(la pantalla muestra el
roblema)
uede mostrarse
‡
.
La pantalla
‹
ХЫГЪЧ
or medio
Auto
Resolución de
problemas
‹
Modo
‡
‡
(El marcador aparece de
forma momentánea)
‡
(salir del menú; regresar al
roblema)
‹
À¹¾ »¼
‹
æè
êêêê
‹
ХЫГЪЧ
Auto
50
Auto
Auto
v
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
61
Page 68

Valor de posición
p
p
p
j
p
p
p
q
p
p
p
p
p
p
Teclas
10
1.
activa la herramienta Resolución
‹
de problemas.
2.
‡
modo
ermite acceder al menú de
ara cambiar entre los modos
Automático (
(
MAN
). En modo
AUTO
MAN
) y Manual
uede
acceder al menú Valor de posición.
Nota: 11-.
redeterminado.
es el a
uste de Valor de posición
3.
activa la función Valor de
Œ
osición cuando la TI-10 se
encuentra en modo MAN de
Resolución de
roblemas. Actúa
también en combinación con las
teclas siguientes:
La tecla Muestra
‘
’
“
˜
™
Número de millares
Número de centenas
Número de decenas
Número de unidades
Número de décimas
Número de centésimas
Notas
En los ejemplos de las transparencias
•
maestras se considera
ue los
valores de configuración en uso son
los
redeterminados. Pulse b
ara restablecer la TI-10 y borrar la
pantalla.
”
La función Valor de posición sólo
•
2
1
uede activarse cuando el modo
definido en Resolución de
problemas es MAN (manual).
Cuando la función Valor de posición
•
3
está activada, la TI-10 muestra el
indicador ƒ en la línea su
erior de
la pantalla.
Para salir de Valor de posición,
•
ulse ”. La TI-10 regresa al modo
MAN de Resolución de problemas.
Para salir y cerrar Resolución de
•
roblemas, pulse ‹.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
62
Page 69

Valor de posición
¿Cuál es el valor de posición de un dígito dado?
(continuación)
10
El modo ‹ de Resolución de problemas debe ser
Siga estos pasos (consulte el ejemplo de la página 65).
1. Pulse b ” para restablecer la TI-10 y borrar la pantalla.
2. Pulse
de problemas.
3. Pulse
4. Pulse Œ.
5. Pulse el dígito cuyo valor de posición desee conocer.
Si introduce 6, la TI-10 mostrará ____._6 durante unos instantes para
indicar la posición del 6 y, a continuación, mostrará su valor, 6 –> 0,01,
lo que significa que 6 ocupa la posición de las centésimas.
Una vez activado Valor de posición, no es necesario pulsar Œ antes de cada
dígito que desee comprobar. No obstante, para probar con un nuevo número,
deberá pulsar ”, introducir el número, y pulsar Œ de nuevo.
¿Cuántas unidades, decenas, centenas, millares, décimas o centésimas hay en
un número dado?
‡ " ®
para salir del menú; introduzca 1234,56.
‡
para seleccionar el modo
MAN
MAN
(manual).
del menú Resolución
El modo ‹ de Resolución de problemas debe ser
presentación debe estar definida en
Siga estos pasos (consulte el ejemplo de la página 67).
1. Pulse b ” para restablecer la TI-10 y borrar la pantalla.
2. Pulse
de problemas.
3. Pulse
4. Subraye
5. Pulse
6. Pulse Œ.
7. Pulse “, ’,
Si pulsa
tiene 12 centenas. Cuando se pulsa
indicar que el número tiene 123.456 centésimas.
‡ " ®
.
$
y pulse
11 –.
para salir del menú, y escriba 1234,56.
‡
‘, , ˜
, la TI-10 mostrará 1 2 _ _ . _ _ , lo que significa que el número
‘
para seleccionar el modo
.
®
o
™
11 –.
.
™
, la TI-10 muestra 1 2 3 4 5 6 para
(manual) y la opción de
MAN
del menú Resolución
MAN
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
63
Page 70

Valor de posición
Si un número tiene un dígito repetido, la TI-10 analiza primero el dígito que ocupa
la posición situada más a la derecha. Para hallar el valor de posición de otras
coincidencias del mismo dígito, pulse el dígito dos veces para indicar que se
trata de la segunda coincidencia, tres veces para el de la tercera, etc. Cada una
de las veces sucesivas que pulse el dígito, la pantalla mostrará el dígito situado
a la izquierda del anterior. (Consulte la página 66 para ver un ejemplo.)
(continuación)
10
Para salir de Valor de posición, pulse
(manual) de Resolución de problemas.
MAN
¿Qué dígito de un número ocupa una posición dada?
El modo ‹ de Resolución de problemas debe ser
presentación debe estar definida en
Siga estos pasos (consulte el ejemplo de la página 68).
1. Pulse b ” para restablecer la TI-10 y borrar la pantalla.
2. Pulse
de problemas.
3. Pulse
4. Subraye
5. Pulse
6. Pulse Œ.
7. Pulse “, ’,
‡ " ®
.
$
y pulse
– 1 –.
‡
para salir del menú, y escriba 1234,56.
‘, , ˜
para seleccionar el modo
®
.
™
o
y la TI-10 regresará al modo
”
MAN
– 1 –.
MAN
.
(manual) y la opción de
del menú Resolución
Si pulsa
que el 2 ocupa la posición de las centenas. Acto seguido, la respuesta se borra
para que pueda introducir otro dígito u otra tecla de valor de posición.
Pulse
Resolución de problemas.
© 2001 T
‘
, la TI-10 mostrará _ 2 _ _ . _ _ durante unos instantes para indicar
para salir de Valor de posición. La TI10 regresa al modo
”
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
MAN
de
64
Page 71
Determinación del valor de posición
êêêê
Escriba 1234,56. Determine el valor
de posición de 6 y 4.
La pantalla
Pulse muestra
b ”
á
‹‡ "
‹
æè
®
‡
‹
á
Resolución de
problemas
‹
Valor de posición
Œ
1234
Œ
6
4
r
56
‹
ƒ
1234Ù56
á
‹ ƒ
1234Ù56
ннннЩн
‹ ƒ
1234Ù56
ÜÈ0Ù
6
‹ ƒ
1234Ù56
ííí4Ùíí
‹ ƒ
1234Ù56
6
01
© 2001 T
4
EXAS INSTRUMENTS INCORPORATED
ÜÈ
1
TI-10: Manual del profesor
65
Page 72

Dígitos repetidos
êêêê
Escriba 123,43. Determine el valor
de posición de cada 3.
La pantalla
Pulse muestra
b ”
á
‹ ‡ "
‹
æè
®
‡
‹
á
Resolución de
problemas
‹
Valor de posición
Œ
123
Œ
3
33
r
43
‹ ƒ
123Ù43
á
‹ ƒ
123Ù43
нннЩн
‹ ƒ
123Ù43
ÜÈ0Ù
3
‹ ƒ
123Ù43
íí3Ùíí
ƒ
‹
123Ù43
3
01
© 2001 T
3
EXAS INSTRUMENTS INCORPORATED
ÜÈ
1
TI-10: Manual del profesor
66
Page 73

¿Cuántas?
êêêê
¿Cuántas centenas hay en
1234,56? ¿Cuántas centésimas?
La pantalla
Pulse muestra
b ”
á
‹ ‡"
‹
æè
®
Resolución de
problemas
‹
Valor de posición
Œ
Centenas
‘
Centésimas
™
‡
1234
Œ
‘
™
r
56
‹
á
‹ ƒ
1234Ù56
‹ ƒ
1234Ù56
ннЩнн
12
‹ ƒ
1234Ù56
123456
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
67
Page 74

¿Qué dígito?
¿Qué dígito ocupa la posición de las
centenas en el número 1234,56?
La pantalla
Pulse muestra
b ”
á
‹ ‡"
®
" ®
$
‹
æè
‹
ÜÙ ÜÏÜÙ
11
êêêê
кккккк
Resolución de
problemas
‹
Valor de posición
Œ
‡
1234
Œ
‘
r
56
‹
á
‹
ƒ
1234Ù56
‹
ƒ
1234Ù56
н2ннЩнн
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
68
Page 75

Referencia rápida a teclas
Tecla Función
A
−
”
b
− ”
" !
# $
w
‡
Enciende la calculadora. Si ya está encendida, la apaga.
Borra la pantalla y cualquier condición de error.
Restablece la TI-10. La pantalla muestra el mensaje
Restablece la TI-10. Mantenga pulsadas las teclas − y ” durante unos
segundos y suéltelas simultáneamente. La pantalla muestra
El restablecimiento de la TI-10 no sólo borra totalmente la
Nota:
calculadora sino que supone la eliminación de todos los ajustes de menú,
entradas del historial, valores que haya almacenados en la memoria y la
pantalla. Se recuperan todos los valores de configuración predeterminados.
Mueven el cursor a derecha e izquierda, respectivamente, lo que permite
ver entera la línea de entrada o seleccionar un elemento de menú.
Mueven el cursor arriba y abajo, respectivamente, lo que permite ver las
entradas y resultados anteriores o acceder a las listas de menús.
Borra el carácter situado a la izquierda del cursor antes de pulsar
En la herramienta Calculadora, muestra menús que permiten:
Seleccionar el formato del resultado de
una división. Puede elegir entre cociente
con resto (QR) o decimal (.).
/·
êê
.
MEM CLEARED
MEM CLEARED
Þ
.
®
Ù
.
.
‡
$
‡
$ $
‡
$ $ $
© 2001 T
Mostrar (+1) u ocultar (?) en
operador de una constante y el
operando.
Borrar la operación con una constante
(
).
OP1
Restablecer la TI-10.
EXAS INSTRUMENTS INCORPORATED
el
OP1
/Û1 Ã
êê
,
Àß
ê
¼Á
/ç//î
//ß À//
//ê ·¹Ó¹Ê
TI-10: Manual del profesor
A-1
Page 76
Referencia rápida a teclas
Tecla Función
A
‹
‹ ‡
‹ ‡
‹ ‡
‹ ‡
$
$$
(
MAN
)
$
Pasa de la herramienta Calculadora a Resolución de problemas y viceversa.
La herramienta Resolución de problemas, muestra menús que permiten:
Seleccionar el modo
(automático) o
Seleccionar el Nivel de dificultad.
MAN
AUTO
(manual).
‹
æè
‹
Auto
Auto
++1++2++3
êëì
Auto
ê
Auto
Seleccionar el Tipo de operación.
Seleccionar opciones de presentación
para la función Valor de posición.
(Esta opción sólo está disponible
cuando el modo seleccionado es
MAN
..ê
‹
+ЫЬЭЮГ
‹
ППЬЩО-- ÜÏÜÙ
êêêê
.)
]
c
[
\
Conmuta los modos
Pasa al siguiente Nivel de dificultad. Una vez alcanzado el Nivel 3, la TI-10
vuelve a comenzar desde el Nivel 1.
Nivel 1: operaciones básicas
Nivel 2: un número digital o dos números digitales con ceros en el
lugar de las unidades
Nivel 3: hasta tres números digitales
En ‹ (Resolución de problemas) con modo
permite indicar la incógnita de una ecuación.
En ‹ (Resolución de problemas) con modo
permite probar las inecuaciones.
En ‹ (Resolución de problemas) con modo
permite probar las inecuaciones.
AUTO
y
de Resolución de problemas.
MAN
(manual),
MAN
(manual),
MAN
(manual),
MAN
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
A-2
Page 77

Referencia rápida a teclas
Tecla Función
A
Œ
d
Œ
Œ
Œ ‘
Œ ’
Œ “
Œ ˜
Œ ™
En ‹ (Resolución de problemas) con modo
determinar el valor de posición de un dígito concreto de un número dado
o, en combinación con las teclas de valor de posición, permite determinar
la cantidad de millares, centenas, etc. contenidas en un número, o el
dígito que ocupa una posición dada.
Determina el valor de posición del dígito d (0 - 9) de un número dado.
Indica la cantidad de millares que contiene un número dado o el dígito
que ocupa la posición de los millares.
Indica la cantidad de centenas que contiene un número dado o el dígito
que ocupa la posición de las centenas.
Indica la cantidad de decenas que contiene un número dado o el dígito
que ocupa la posición de las decenas.
Indica la cantidad de unidades que contiene un número dado o el dígito
que ocupa la posición de las unidades.
Indica la cantidad de décimas que contiene un número dado o el dígito
que ocupa la posición de las décimas.
Indica la cantidad de centésimas que contiene un número dado o el
dígito que ocupa la posición de las centésimas.
(manual), permite
MAN
Š
Š
Š ‘
Š ’
Š “
Š ˜
Š ™
Š r
q h i j k l
m n o p
T
Define el número de decimales en combinación con las teclas de Valor de
posición. Sólo se redondea el resultado que aparece en la pantalla;
el redondeo no afecta al valor almacenado internamente. Si es
necesario, el valor calculado se rellena con ceros.
Redondea el resultado al millar más próximo.
Redondea el resultado a la centena más próxima.
Redondea el resultado a la decena más próxima.
Redondea el resultado a la unidad más próxima.
Redondea el resultado a la décima más próxima.
Redondea el resultado a la centésima más próxima.
Elimina el ajuste de decimal fijo y activa el decimal flotante.
Introducen los números de 0 a 9, respectivamente.
Suma. En modo Resolución de problemas, introduce el símbolo de suma.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
A-3
Page 78

Referencia rápida a teclas
p
Tecla Función
A
U
V
W
Z
®
r
M
X
Y
Resta. En modo Resolución de problemas, introduce el símbolo de resta.
Multiplica. En modo Resolución de problemas, introduce el símbolo de
multiplicación.
Divide. En modo Resolución de problemas, introduce el símbolo de división
con el resultado en forma de cociente y resto o decimal, de acuerdo con
lo seleccionado en la opción de menú.
Finaliza las operaciones. En ‹ (Resolución de problemas) con modo
(manual), permite introducir el signo igual (=) para probar las
MAN
igualdades.
Prueba una solución en la herramienta Resolución de problemas.
Selecciona un menú en cualquiera de las herramientas Calculadora o
Resolución de problemas. Finaliza una operación.
Inserta un separador decimal.
Introduce un signo negativo. No actúa como operador.
Abre un paréntesis para una expresión.
Cierra un paréntesis para una expresión.
`
a
|
›
‡
$ $
®
Suma el resultado de la pantalla al valor en memoria.
Resta el resultado de la pantalla del valor en memoria.
Cuando se pulsa una vez, recupera el valor en la memoria para utilizarlo
en una operación. Cuando se pulsa dos veces, borra la memoria.
Almacena una operación con un valor de constante, que se puede repetir
al pulsar la tecla › tantas veces como sean necesarias. Para almacenar
una operación en
1. Pulse ›, inserte el o
operación.
2. Pulse › para recuperar la operación almacenada.
Para borrar el contenido de
y pulse
operaciones para utilizarlas varias veces.
. A partir de este momento puede almacenar otras
®
y recuperarla:
OP1
erador y el valor, y pulse › para guardar la
OP1
, pulse
‡
$ $
, subraye Y,
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
A-4
Page 79

Indicadores de pantalla
p
B
Indicador
‹
ƒ
Fix
M
Op1
Auto
Ù
P
y
z
w
x
Significado
La TI-10 tiene activada la herramienta Resolución de problemas.
La TI-10 tiene activada la función Valor de posición.
La TI-10 está redondeando a una posición determinada.
Indica que la memoria contiene un valor distinto de cero.
Hay un operador y un valor almacenados en
Indica que la herramienta Resolución de problemas ‹ está en modo
Indica que el resultado de la función de división aparecerá en formato
decimal.
Las entradas anteriores están almacenadas en el historial, o hay más
menús dis
para acceder a las listas de menús adicionales.
Pulse
Es necesario pulsar
onibles. Pulse # para acceder al historial. Pulse $ y
!
y " para desplazar el contenido de los menús y subrayar uno.
para completar la selección.
®
OP1
.
AUTO
#
.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
B-1
Page 80
Mapa de menús
b
La TI-10 incluye dos herramientas: Calculadora y Resolución de problemas.
C
Herramienta Calculadora Herramienta Resolución de
pro
lemas
P
Menú Formato de división
OP
Menú
Operación con una constante
CLEAR OP1
Menú
Borrar operación con una
constante
RESET
Menú Restablecer
AUTO MAN
Menú Modo
êëì
Menú Nivel de
dificultad
+ - x P ?
Menú
Tipo de operación
ƒ
Menú
Valor de posición
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
C-1
Page 81

Mapa de menús
p
p
(continuación)
Herramienta Calculadora
La herramienta Calculadora se activa al encender la TI-10. Con la herramienta Calculadora
activa, pulse
muestran las pantallas del menú Calculadora.
para acceder a los menús de Calculadora. Las ilustraciones siguientes
‡
C
P
Menú
Formato de división
OP
Menú Operación con una
constante
CLEAR OP1
Menú
Borrar operación con una
constante
RESET
Menú
Restablecer
Muestra el resultado de la división en
formato de cociente y resto
·
êêê
Ù
Þ
Û1
êêê
Ã
¼Á
À»
ê
ç
ß À
ê
·¹¾¹Ê
¼ÁÏ
(predeterminado).
Muestra el resultado de la división
en formato decimal.
Muestra la línea que contenga la
operación con una constante
(predeterminado).
Oculta la línea que contenga la
eración con una constante.
o
Sí. Borra la operación con una
constante (predeterminado).
No. No borra la operación con una
constante.
No. No restablece la TI-10
(predeterminado).
Sí. Restablece la TI-10 a los
valores
redeterminados.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
C-2
Page 82

Mapa de menús
(continuación)
Herramienta Resolución de problemas
C
Esta herramienta tiene dos modos de funcionamiento:
El modo
permite acceder al menú Valor de posición.
MAN
Menú Modo —
Dos modos para seleccionar:
AUTO
•
•
(predeterminado) muestra problemas para
resolver.
MAN
permite crear problemas propios.
‹
1 2 3
ê
‹
Û Ü Ý Þ Ã
ê
permite acceder a los menús Nivel de dificultad y Tipo de operación. El modo
AUTO
Auto
1 - más fácil
(predeterminado)
2
Modo
Auto
êëì
Auto
AUTO
‹
жи
ккккк
Menú Nivel de dificultad
— Tres niveles para
seleccionar:
•
•
•
3 - más difícil
Menú Tipo de operación —
Cinco opciones para
seleccionar:
•
Suma (predeterminado)
•
Resta
•
Multiplicación
•
División
•
Hallar el operador
(Automático) y
AUTO
(Manual).
MAN
MAN
Modo
‹
11
ÜÙ ÜÏÜÙ
ккккк
å
Menú Valor de posición —
Dos opciones para
seleccionar:
•
¿Cuántas unidades,
decenas, etc. hay en un
número?
(predeterminado)
•
¿Qué dígito ocupa la
posición de las
unidades, decenas, etc.?
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
C-3
Page 83

Mensajes de error
Mensaje Significado
D
Arith Error
Syn Error
P
0 Error
Mem Error
Op Error
Overflow Error
Underflow Error
Error aritmético. Se ha introducido una entrada o un parámetro que no
son válidos.
Error de sintaxis. Se ha introducido una ecuación que no es válida o no
es correcta; por ejemplo,
Error de división por cero (0). Se ha intentado efectuar una división por 0.
Se ha producido un error al intentar almacenar una entrada en la memoria.
Se ha producido un error al seguir los pasos para utilizar
Desbordamiento. El resultado es demasiado extenso para caber en los
límites de la pantalla.
Subflujo. El resultado es demasiado pequeño para los límites de la pantalla.
5++2
o
(5+2
.
.
OP1
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
D-1
Page 84

Soporte, servicio y garantía
E
Asistencia al
producto
Clientes de Estados Unidos, Canadá, Puerto Rico y las Islas
Vírgenes
Para preguntas generales, póngase en contacto con la Asistencia
Técnica de Texas Instruments:
teléfono:
e-mail:
Para consultas técnicas, llame al Grupo de Asistencia de Programación
de Asistencia al Cliente:
teléfono:
1-800-TI-CARES (1-800-842-2737)
ti-cares@ti.com
1-972-917-8324
Clientes fuera de Estados Unidos, Canadá, Puerto Rico y las
Islas Vírgenes
Póngase en contacto con TI por correo electrónico o visite la página de
las calculadoras TI en la World Wide Web.
e-mail:
internet:
ti-cares@ti.com
education.ti.com
Servicio al
producto
Otros
productos y
servicios TI
Clientes en Estados Unidos y Canadá solamente
Siempre póngase en contacto con Asistencia Técnica de Texas
Instruments antes de devolver un producto para servicio.
Clientes fuera de Estados Unidos y Canadá
Consulte la hoja incluida con este producto o póngase en contacto con
el distribuidor local de Texas Instruments.
Visite la página de las calculadoras TI en la World Wide Web.
education.ti.com
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
E-1
Page 85

Soporte, servicio y garantía
(Continuación)
E
Información sobre la
garantía
Clientes en Estados Unidos y Canadá solamente
Garantía limitada de un año para producto electrónico
La garantía de este producto electrónico Texas Instruments ("TI") se
extiende sólo al comprador y usuario original del producto.
Duración de la garantía.
comprador original por el periodo de un (1) año a contar de la fecha de
compra original.
Cobertura de la garantía.
por defectos de materiales y fabricación. ESTA GARANTÍA QUEDA
NULA SI EL PRODUCTO HA SIDO DAÑADO POR ACCIDENTE O USO
INDEBIDO, NEGLIGENCIA, REPARACIÓN INADECUADA U OTRAS
CAUSAS NO ASOCIADAS CON DEFECTOS DE MATERIALES O
FABRICACIÓN
Negación de garantía.
LA VENTA, INCLUIDAS SIN RESTRICCIÓN LAS GARANTÍAS IMPLÍCITAS
DE VIABILIDAD COMERCIAL Y APTITUD PARA UN PROPÓSITO
PARTICULAR, SE LIMITAN EN DURACIÓN AL PERIODO DE UN AÑO
ANTES MENCIONADO. TEXAS INSTRUMENTS NO ASUMIRÁ
RESPONSABILIDAD POR PÉRDIDA DE USO DEL PRODUCTO U OTROS
COSTOS, GASTOS O DAÑOS INCIDENTALES O DERIVADOS EN LOS
QUE INCURRIERE EL CONSUMIDOR U OTRO USUARIO.
Algunos estados/provincias no permiten la exclusión o limitación de las
garantías implícitas o daños incidentales, por lo que las limitaciones o
exclusiones anteriores pueden no aplicarse en su caso.
Este producto electrónico TI se garantiza al
Este producto electrónico TI es garantizado
CUALQUIER GARANTÍA IMPLÍCITA DERIVADA DE
Recursos legales.
sin perjuicio de otros derechos que pueden variar de una estado a otro y
de una provincia a otra.
Cumplimiento de la garantía
garantía de un (1) año, el producto defectuoso puede ser reparado o
reemplazado por un modelo reacondicionado de calidad similar (a opción
de TI) si el producto es devuelto, con envío postal prepagado, a las
Instalaciones de Servicio de Texas Instruments. La garantía de la
reparación o el reemplazo de la unidad continuará por el resto de la
garantía de la unidad original o seis (6) meses, el tiempo más largo.
Salvo el pago del envío postal, no se cobrará por las reparaciones o el
reemplazo. TI recomienda asegurar el valor del producto antes de
enviarlo.
Software.
que conceden sus licencias no garantizan que el software no tiene errores o
cumple requerimientos específicos.
Copyright.
producto están protegidos por ley de propiedad intelectual.
El software se concede en licencia, no se vende. TI y las entidades
El software y la documentación suministrada con este
Esta garantía otorga derechos legales específicos,
. Durante el mencionado periodo de
El software se entrega "TAL CUAL".
Todos los clientes fuera de Estados Unidos y Canadá
Para informaciones sobre el plazo y las condicíones de la garantia,
diríjase al paquete y/o a la declaracíon de garantía adjunto con este
producto, o comuniquese con su vendedor o distribuidor local de Texas
Instruments.
© 2001 T
EXAS INSTRUMENTS INCORPORATED
TI-10: Manual del profesor
E-2
 Loading...
Loading...