Apple Newton Works Graphing Calculator User Manual

1 Tap New.

Introduction

The Newton Works graphing calculator program lets you perform calculations and display the results in a graph or table. You can copy and paste the calculations or graph into other programs using Newton Works commands. To learn about Newton

e e

300

’

anua

Works, see the chapters on Newton Works in the

Creating a new document for calculations

To create a new document in which to do calculations, do the following from inside Newton Works:

2 In the list that appears, tap Calculations.

A blank document and a title slip appear.

3 If desired, type in a title for the calculation document.

Note:

This title doesn’t appear when you print a calculation document.

tit

ere

’

ini

urn

ere

4 Press Return or tap X.

Here’s an example of a typical calculation document.

t t

ere

efere

2 Chapter 1

d, d

elete

t t

Setting preferences

You can set preferences for the graphing calculator. You can choose the default measurement to use for angles and the default number format.

You can enter numbers in the way they’re typically expressed, with digits to the left and right of the decimal. For example,

123.4567

–4.32

You can also enter scientific or engineering notation. For example,

1.234567E2

To set the default number format for new calculation documents, follow these steps:

1 Tap the Information button ;, then tap Calculations Prefs.

The Calculations Prefs slip appears.

ere

t t

eme

ere

t t

2 Tap “u Measure Angles in” and in the list that appears, tap your choice.

Introduction 3

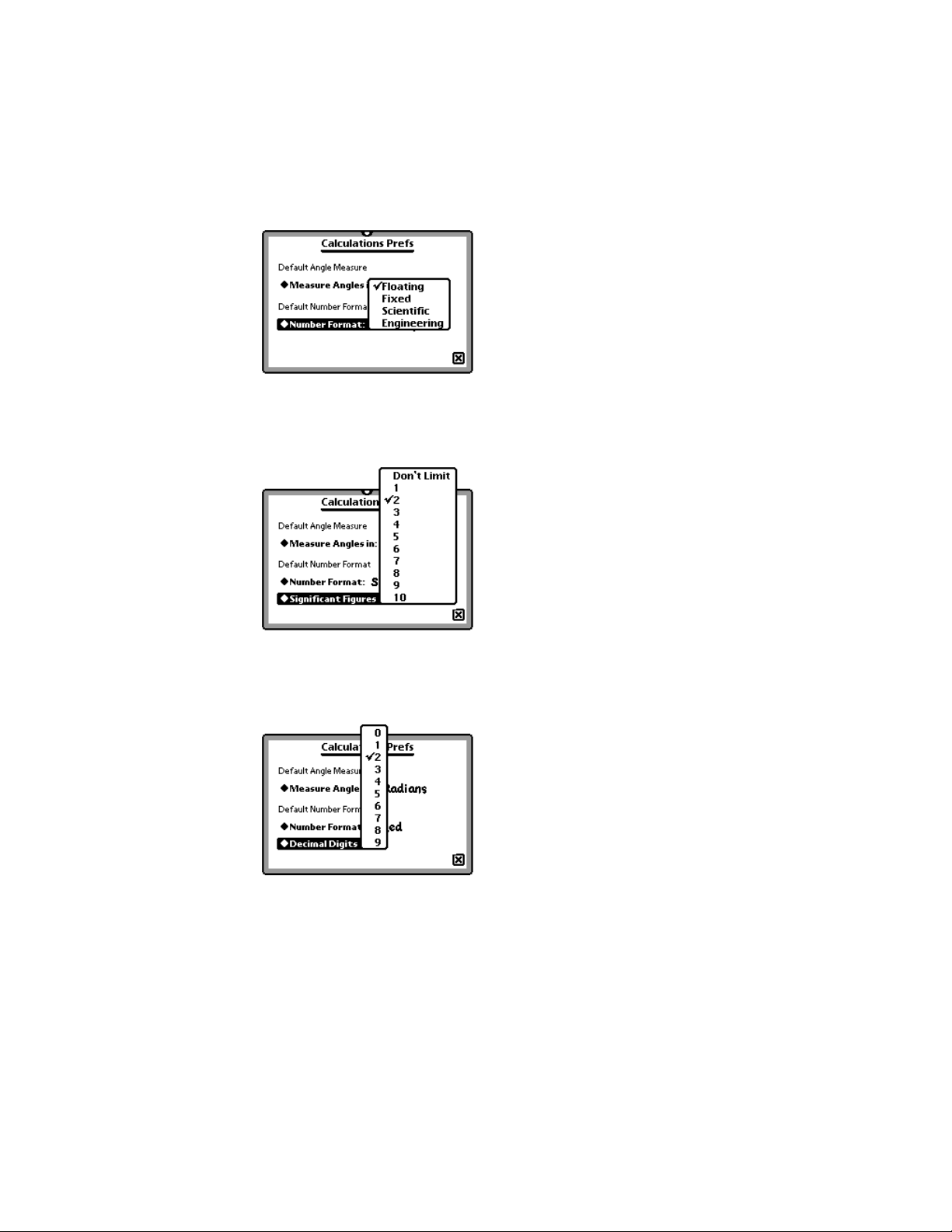
3 Tap u Number Format and in the list that appears, tap your choice.

4 If you choose Scientific or Engineering, tap u Significant Figures and in the list that

appears, tap your choice.

4 Chapter 1

5 If you choose Fixed, tap u Decimal Digits and in the list that appears, tap your

choice for the number of digits you want after the decimal point.

To change the number format for the open calculation document follow these steps:

1 Tap Tools, then tap u Number Format.

2 Tap u Number Format and in the list that appears, tap your choice.

3 If you choose Scientific or Engineering, tap u Significant Figures, then tap the

number of significant digits to be displayed.

4 If you choose Fixed, tap u Decimal Digits and in the list that appears, tap your

choice for the number of digits you want after the decimal point.

Using operators

You can use the following operators in your calculations:

For Type this Example

Addition + 3 + 4

Subtraction – 10 – 3

Multiplication * (or a space) 43 * 2

Division / 8/2

Absolute value || |x|

Factorial ! 36!

Power ^ 2^3

Tip:

You don’t need to type the multiplication symbol (*) before an expression. A number before a symbol or a space between symbols is interpreted as multiplication. For example:

3sin(x) is interpreted as 3 multiplied by the sine of x.

Introduction 5

x y z is interpreted as x multiplied by y, then that product multiplied by z.

Use parentheses to avoid ambiguity about the order of calculations. The expressions in parentheses are solved first.

For example, if you type:

3*(4+6)

then the calculation 4 + 6 will be performed first.

For more information, see “Order of Evaluation,” next.

Order of evaluation

The graphing calculator evaluates calculations in the following order:

m Calculations inside parentheses. For example, in the expression 3 * (4 + 6), 4 + 6

is evaluated first and the result (10) is multiplied by 3.

m Functions, such as sin or log m Factorials (evaluated left to right) m Exponent operator (evaluated right to left) m Unary minus (for example, –a)

6 Chapter 1

m Multiplication and division (evaluated left to right). For example, in the expression

2 + 3 * 6, 3 * 6 is evaluated first.

m Addition and subtraction (evaluated left to right)

Viewing the results

To see the results of your calculation, do one of the following:

m Tap Tools and then tap Evaluate. m Press Enter. m Press x-Return.

The results of your calculation appear. A checkmark appears at the right of the calculation area if you are defining a variable or function. If any errors are found, an error message appears.

rror

Correcting mistakes

If you make a mistake, you can correct it by doing one of the following. (To learn how to perform these actions, see the documentation that came with your Newton device.)

m Position the caret to the right of the information you want to delete and press the

Delete key.

m Scrub out the information you want to delete. m Select the information you want to delete and press the Delete key.

Note:

Error messages and results are automatically deleted when you edit the line

they are located on.

Clearing the display

To clear all calculations from a graphing calculator document, do the following:

1 Select all the calculations by pressing x-A. (Or tap Edit then tap Select All.)

2 Tap Edit, then tap Clear (or press Delete).

Introduction 7

Saving a calculation document

Like other Newton Works documents, your calculation document is automatically saved as you enter information. There is no save command or button.

For more information on Newton Works, see the chapters on Newton Works in the

e e

300

’

anua

Filing a calculation document

If you are using the full Newton System, you can file calculation documents into folders using the Folder button. When you create a new calculation document, it is automatically stored in the current folder you are viewing. You can file calculation documents into other folders at any time.

Note:

If you are using your eMate in Classroom Mode, you can’t file items

into folders.

1 Go to the calculation document you want to file.

2 Tap the Folder button F.

The folder slip appears.

3 Tap the name of the folder you want the item to be stored in, then tap File.

t t

8 Chapter 1

If you move a document to a folder you’re not currently viewing, the document will disappear from your screen.

ere

’

For more information on filing a document (or multiple documents), see the chapter on organizing information in the

e e

300

’

anua

Viewing your calculation documents

You may want to see a list of all the calculation documents you created, especially if you’re trying to find a particular document.

m To see a list of items press Overview.

An overview appears.

s s

ese

m Press Scroll Up or Scroll Down or the Up and Down Arrow keys on your keyboard

to move up and down in the list.

m If desired, tap an item in the list to go to it.

Printing, beaming, and faxing

You can print, fax, and beam calculation documents. For more detailed information, see the chapter on printing, faxing, and beaming in the

’

anua

e e

300

Reinstalling the Newton Works graphing calculator software

If you inadvertently delete the Newton Works graphing calculator, you can reinstall the software using the

ivi

CD that came with your eMate. For more information, see the documentation that came with the CD, and the documentation that came with the Newton Connection Utilities software.

Introduction 9

Using Functions and Variables

This chapter describes how to use the built-in functions of the graphing calculator and how to create your own functions and variables.

Using the built-in functions

The graphing calculator has several built-in functions that you can use with your calculations. These functions are grouped as follows:

m Integer m Math m Tr igonometry m Series m Hyperbolic m Financial

You can enter functions by typing function names on the keyboard or by selecting the functions from a list.

To use any of the built-in functions, do one of the following: m Type the function name on the keyboard, or

1 Tap Tools, and then tap Functions.

The function slip appears. (Your slip may not look exactly like the illustration.)

y y

2 Tap the diamond u at the top of the slip.

3 In the list that appears, tap the type of function you want (Integer, Math, Trig, Series,

Hyperbolic, Advanced, or Financial).

12 Chapter 2

Functions of that type are shown.

4 Tap the function that you want to use in your calculation, then tap Insert.

The function appears and the caret is placed between the parentheses.

5 If desired, tap X to close the function slip.

6 Enter the arguments for the function.

Using the integer functions

The Integer list contains the following functions:

Function Abbreviation Description

Ceiling Ceiling(x) Returns the smallest integer greater than x

Floor Floor(x) Returns the largest integer less than x

Round Round(x) Returns the nearest integer to x (rounds to even

integers on x.5 values)

Truncate Trunc(x) Returns the numbers to the left of the

decimal point of x

Examples

y(x) = Ceiling(2.3x+3.6)

y(x) = Round(3*x/4)

mymodulus(x,y) = x–y*Trunc(x/y)

Using Functions and Variables 13

Using the math functions

The Math list contains the following functions:

Function Abbreviation Description

Square Root Sqrt(x) Returns the square root of x

Natural logarithm Ln(x) Returns the natural logarithm of x

Exponential Exp(x) Returns the exponential (inverse of the

natural logarithm) of x

Gamma Gamma(x) Returns the gamma of x (Factorial(x – 1) for

positive integers)

Logarithm Log(x) Returns the logarithm of x, base 10

Modulus Mod(x,y) Returns the modulus of x with respect to y

(that is, the remainder of x/y)

Remainder Remainder(x,y) Returns x – y * round(x/y)

Factorial Factorial(x) Returns the factorial of x

Using the Remainder function

14 Chapter 2

The Remainder function is not simply the remainder of x/y (the modulus function is). The Remainder function returns x – y * round(x/y). A different definition is x – remainder(x,y), which gives the closest value to x that is evenly divisible by y.

Examples

y(x) = 0.5*ln((1+x)/(1–x))

y(x) = 1/sqrt(4*x^2+1)

y(x) = exp(x)/(1–exp(2*x))

Using the trig functions

The Trig list contains the following functions:

Function Abbreviation Description

Cosine Cos(x) Returns the cosine of x

Sine Sin(x) Returns the sine of x

Tangent Tan(x) Returns the tangent of x

Arc cosine ArcCos(x) Returns the inverse cosine (arc cosine) of x

Arc sine ArcSin(x) Returns the inverse sine (arc sine) of x

Arc tangent ArcTan(x) Returns the inverse tangent (arc tangent) of x

Examples

5cos(.5)

y(x) = sin(x–/2)

Changing the measured angle

By default, trigonometric arguments are interpreted as radians. To use degrees or gradients, follow these steps:

1 Tap measured angle.

2 Tap the desired measurement from the list.

Graphs and tables are updated automatically when you change the angle. Results in the math window are not automatically updated.

Using Functions and Variables 15

Using the series functions

The Series functions perform operations on lists. The Series list contains the following functions:

Function Abbreviation Description

Summation Sum(list) Returns the sum of the entries in the list

Minimum Min(list) Returns the smallest value in the list

Maximum Max(list) Returns the largest value in the list

Mean Mean(list) Returns the arithmetic mean

Median Median(list) Returns the median

Mode Mode(list) Returns the value that occurs most

frequently in the list, or multiple values if they occur with equal frequency

Variance Variance(list) Returns the mean of the squared deviations

Standard deviation StDev(list) Returns the positive square root of the

variance

Sort Sort(list) Sorts the entries in the list from smallest

to largest

16 Chapter 2

Size Size(list) Returns the number of elements in the list

Element Element(list,index) Returns the

Note: index starts with 0 for the first entry

entry in the list

For more information on lists, see Chapter 4, “Creating and Using Lists.”

Examples

y(x) = Sum([3,sin(x),trunc(x/2)])

element([1,2,3,4,5,6],2) -> 3

mean([0,1,2,3,4,5,6])

mode([0,0,1,2,3,4,5,5,6]) ->[0,5]

Using the hyperbolic functions

The Hyperbolic list contains the following functions:

Function Abbreviation Description

Hyperbolic cosine CosH(x) Returns the hyperbolic cosine of x

Hyperbolic sine SinH(x) Returns the hyperbolic sine of x

Hyperbolic tangent TanH(x) Returns the hyperbolic tangent of x

Hyperbolic arc cosine ArcCosH(x) Returns the inverse hyperbolic cosine of x

Hyperbolic arc sine ArcSinH(x) Returns the inverse hyperbolic sine of x

Hyperbolic arc tangent ArcTanH(x) Returns the inverse hyperbolic tangent of x

Examples

y(x) = sinh(4x)*cosh(2x)

y(x) = tanh(sin(x))

y(x) = x*arcsinh(2x)

Using Functions and Variables 17

Using the financial functions

The Financial list contains the following functions:

Function Abbreviation Description

Annuity Annuity(rate,periods) Returns the present value of an annuity

(1 – (1 + r)^n)/r

Compound Compound(rate,periods) Returns (1 + r)^n

Examples

Calculate your savings after two years if you deposited $3000 at 5.25% interest, compounded annually.

3000*compound(.0525,2) -> 3323.27

Calculate the current principal if you’ve made 12 payments of $320 at a rate of 8.5%.

320*annuity(.085,12)

Creating your own functions

You can create functions and use functions that you define. Functions must have a function name followed by the argument names in parentheses on the left side of the equals sign and an expression on the right.

18 Chapter 2

Note:

You must enter a function name for each expression.

The following are examples of valid functions:

y(x)=sin(x–0.5*pi)

z(x)=sqrt(16–x^2)

r(t)=8cos(t)

p(t)=[4cos(t),3sin(t)]

qrts(a,b,c)=[(–b+sqrt(b^2–4a*c))/(2a),(–b–sqrt(b^2–

4a*c))/(2a)]

andtin the above examples are the function parameters. You specify the values for these parameters when you use the function in a calculation. For example, to evaluate the function

z(x)=sqrt(16–x^2) with x = 2, type z(2) and

press Enter.

To create a function: m Enter the function and press Enter.

If no errors are found, a checkmark appears to the right of your function and your function is added to the Your Functions list. Functions are saved automatically. There is no save command or button.

Using Functions and Variables 19

Creating parametric functions

An example of a parametric function is shown below:

x=t2, y=t–3

To enter parametric equations into the Newton Works graphing calculator, you can use the following format:

x(t)=f(t)

y(t)=g(t)

p(t)=[x(t),y(t)]

p(t)=[f(t),g(t)]

For example, using the above parametric equation, you can enter:

x(t)=t^2

y(t)=t–3

p(t)=[x(t),y(t)]

20 Chapter 2

p(t)=[t^2,t–3]

You can graph parametric functions or view the results in tabular format, just like any other function.

Using your function

To use your function, do one of the following: m Type the function name on the keyboard, or

1 Tap Tools, and then tap Functions.

2 Tap the diamond u at the top of the slip, then tap User Functions.

3 Tap the function that you want to use in your calculation, then tap Insert.

The caret is placed between the parentheses.

4 Enter the arguments, if any, for the function.

Using constants

The graphing calculator has four constants defined:

m e m pi () m infinity m negative infinity

Tip:

Pressing Option-P is a shortcut for entering the pi symbol ().

Using Functions and Variables 21

To use these constants, do one of the following: m Type the function name from the keyboard, or

1 Tap Tools, and then tap Functions.

2 Tap the diamond u, then tap Constants.

3 In the list that appears, tap the constant that you want to use in your calculation.

t t

’

ini

ere

t t

22 Chapter 2

4 Tap Insert.

Using variables

A variable can represent a number, an expression, or a list. Variable names are not case-sensitive, can be up to 255 characters in length, and must begin with a letter.

Variables can consist of other variables. For example,

Dist = High–Low

To define your own variable, follow these steps:

1 Enter the variable name and its value.

Use the format

myvar = 3+y

e=e

For example, myvar = 3 or

2 Tap Tools, then tap Evaluate (or press Enter).

Your variable is added to the User Variables list.

Displaying the value of a variable

To display the value of a variable, follow these steps:

1 Enter the variable name.

2 Tap Tools, then tap Evaluate (or press Enter).

Changing the value of a variable

To change the value of a variable, follow these steps:

1 Enter the variable name and its new value.

2 Tap Tools, then tap Evaluate (or press Enter or Return).

Graph and table variables

The graphing calculator has some predefined system variables that define the graph and table views.

Using Functions and Variables 23

The graph variables and their default values are:

Variable name Definition Default value

xMin Minimum x value to display –12

xMax Maximum x value to display 12

xScl Increment between tick marks on the x axis 1

yMin Minimum y value to display –12

yMax Maximum y value to display 12

yScl Increment between tick marks on the y axis 1

tMin Minimum value for t in parametric functions 0

tMax Maximum value for t in parametric functions 99

tStep Increment between t values 1

thetaMin Minimum value for

thetaMax Maximum value for  in polar functions 2

thetaStep Increment between  values /128

 in polar functions 0

For more information on using these graph variables, see “Changing the Scale of an Axis” in Chapter 3.

The table variables and their default values are as follows:

Variable name Definition Default value

tblStart Starting value of the table 0

tblDelta Increment between values 0.1

tblStop Stopping value of the table 10

These names are not case-sensitive. You can use these system variables in calculations. You can also change their values and store them.

24 Chapter 2

Additional examples

Find the range, mean, and standard deviation of these observations:

16,4,8,14,3,10,2,24,11,7,9

An object is released from rest and falls freely. Calculate its position and velocity after 1, 5, and 10 seconds. Take the origin 0 as the elevation of the starting point, the y-axis vertical, and the upward direction as positive.

The initial coordinate and initial velocity are both negative. The acceleration is downward, or –32 ft/s

position = v0t + .5at2= –16t

velocity = v0+ at = –32t

Using Functions and Variables 25

A 32-lb. weight is attached to the lower end of a coil spring suspended from the ceiling. The weight comes to rest in its equilibrium position, stretching the spring 2 ft. The weight is then pulled down 5 in. below its equilibrium position and released at t = 0. No external forces are present; but the resistance of the medium in pounds is equal to 4(dx/dt), where dx/dt is the instantaneous velocity in feet per second. Plot the damped oscillatory motion.

Using the above information with the basic differential equation for free, damped motion:

m * d2x/dt2+ a * dx/dt + k * x = 0

Solving for the root and differentiating with respect to t, the solution is:

x = sqrt(3)/3 * e^(–2t) * cos(2sqrt(3) * t – /6)

26 Chapter 2

Creating Graphs and Tables

This chapter describes how to plot a function and view results in tabular format.

Creating graphs

You can create graphs in cartesian (x,y) coordinates:

Creating Graphs and Tables 2727

Or polar coordinates:

To plot a function, follow these steps:

1 Create your function.

See “Creating Your Own Functions” in Chapter 2.

2 Position the cursor on the line of the function you want to graph.

28 Chapter 3

3 Tap Tools, then tap Graph or Graph Polar.

A graph of your function appears.

If you change a graphed function in the math window, the graph is updated automatically after you evaluate the function. If a function is dependent on a variable, the graph is updated automatically when you change the value of that variable.

Plotting multiple functions on a graph

You can plot multiple curves on a single graph. The graph icon next to the function shows the line style used to draw the curve associated with that function.

Note:

To plot multiple functions, make sure the functions have different names.

To plot multiple curves, follow these steps:

1 In the math window, move the caret to the function you want to add to the graph.

2 Tap Tools, and then tap Graph or Graph Polar, depending on the graph you already

have displayed.

s s

Creating Graphs and Tables 29

Changing the zoom factor

To change the level of detail in your graph, tap View and then tap Zoom In or Zoom Out.

To zoom in to a particular section of a curve, draw a rectangle around that section.

1 Hold the pen where you want one corner of the rectangle, until you hear a beep.

Note:

Make sure the volume on your eMate is turned up so that you can hear the

beep noise.

2 Drag the pen until the section of the graph you want to view is enclosed in

the rectangle.

t t

30 Chapter 3

The other View options are as follows:

m Tap Zoom Full to view the entire graph. m Tap Zoom Default to set the x and y min and max values to –12 and +12,

respectively.

m Tap Constrain Aspect Ratio to make sure the graph is always square. m You can also change the zoom factor with the Scale slip. See “Changing the Scale

of an Axis” next.

Changing the scale of an axis

The Graph Variables define the scale of the axes for graphs.

You can change these scales by entering new graph variables in the math window or the Scale slip.

1 Tap View, and then tap Scale.

The Scale slip appears.

Note:

xMin must be less than xMax and yMin must be less than yMax.

You can enter expressions with e or  in the Scale slip. For example, you can set

Max = 2.

Creating Graphs and Tables 31

If xScl or yScl are set to values that would generate too few or too many tick marks on the graph window, their default values are used.

For more information on these variables, see “Graph and Table Variables” in the section “Using Variables” in Chapter 2.

Viewing a point on the graph

Tapping a curve marks that point with a box and displays the (x,y) values of that point. Use the left and right arrow keys on your keyboard to move the box to the left and right, respectively. The box will follow the curve of the graph.

To view the (x,y) values of a point that’s not on a curve, tap the point. An X appears and the (x,y) values of that point are displayed.

Hint:

If you have problems tapping on a curve, tap above (or below) the curve, then press the arrow keys on your keyboard to move the point in small increments to the curve. When it reaches the curve, the X changes to a box.

If you have multiple graphs plotted, you can use the Tab key on your keyboard to move the point between lines.

32 Chapter 3

Moving around a graph

After tapping a point on a curve (or any point on the graph), you can use the arrow keys on your keyboard to move around the graph. Pressing the arrow keys while holding down the Shift or x key moves the box or X in larger increments.

Closing graphs

To close the graph window: m Tap Graph, then tap Close Graph.

To remove a curve from the graph, follow these steps:

1 In the math window, tap the function you want to remove from the graph (or tap the

line in the graph window).

2 Tap Graph, then tap Ungraph.

Creating a table

You can display your function in a tabular format.

1 Create your function.

2 Tap Tools, and then tap Table.

A table appears showing the input and output values of your function. An example is shown below.

Creating Graphs and Tables 33

You can display multiple functions in a table. m In the math window, move the caret to the function you want to add to the table.

Tap Tools, and then tap Table.

Moving through the table

To scroll through a table, tap any entry in the table and press the Up or Down Arrow keys on your keyboard. Pressing the arrow keys while holding down the x key moves in larger increments. Press the Left or Right Arrow keys to move from one function to the next.

34 Chapter 3

Changing the table scale

The tblStart, tblStop, and tblDelta system variables define the initial table view. You can change these variables in the math window. For example:

tblStart=10

tblStop=15

tblDelta=.25

Note:

tblStop is used only in printing or copy-and-drag operations. You can scroll

beyond the tblStart and tblStop values in the table window.

Closing a table

To close the table window: m Tap Tools, then tap Close Table.

To remove a function from the table, follow these steps:

1 In the math window, tap the function you want to remove from the table.

2 Tap Tools, then tap Untable.

Creating Graphs and Tables 35

Creating and UsingLists

You can use lists to provide values for function arguments and to store and manipulate data. This chapter describes how to create and use lists in your calculations and functions.

Creating lists

To create a list, type a series of numbers separated by commas and enclosed in square brackets. You can enclose lists within lists and place functions in lists. The following are examples of lists:

[1,2,3,4,5]

[1,2,[3,4]]

[1,2,x^2,sin(x)]

Performing operations on lists

You can perform any operation on a list of numbers. If multiple lists are used in an operation, they must be the same length. The following are some examples of simple operations done with lists:

Operation Example Result

Addition [1,2] + 3 [4,5]

[1,2] + [3,4] [4,6]

3 + [1,2,[3,4]] [4,5,[6,7]]

Subtraction [1,7,1] – [2,3,1] [–1,4,0]

[6,7] – 3 [3,4]

Multiplication 3 * [4,5] [20,25]

[1,2,[3,4]] * [4,5,6] [4,10,[18,24]]

Division [3,4,5]/2 [1.5,2,2.5]

[4,5,6]/[2,3,4] [2,1.6667,1.5]

38 Chapter 4

Simple functions [2,3]^2 [4,9]

log([1,10]) [0,1]

The above functions perform operations on each element in the list. Other functions perform operations on the entire list—for example sum([list]). For more information on lists and functions, see Chapter 2, “Using Functions and Variables.”

Using variables with lists

You can assign a list to a variable and perform operations on that variable. For example:

a=[1,2,[3,4]]

3+a -> [4,5,[6,7]]

For more information on variables, see “Using Variables” in Chapter 2.

Graphing lists

You can use lists to graph a family of curves. Use one of the following formats for the list:

m [[x1,y1,x2,y2,x3,y3...] m [[x1,y1],[x2,y2],[x3,y3],...] m [[x1,x2,x3,...],[y1,y2,y3,...]]

An example is shown below:

An advantage of the format [[x1,x2,x3,...],[y1,y2,y3,...]] is that you can perform operations on the x and y coordinates independently.

The following example shifts the graph to the right (shifts the x coordinates) by 10 units:

list1=[[0,1,2,3,4],[5,6,7,8,9]]

list2=list1+[10,0] -> [[10,11,12,13,14],[5,6,7,8,9]]

Creating and Using Lists 39



Newton Works

Graphing Calculator

User’s Manual

K Apple Computer, Inc.

Every effort has been made to ensure that the information in this manual is accurate. Apple is not responsible for printing or clerical errors.

Apple, the Apple logo, the Light bulb logo, Macintosh, and Newton are trademarks of Apple Computer, Inc., registered in the U.S. and other countries

eMate is a trademark of Apple Computer, Inc.

Adobe, Adobe Illustrator, Adobe Photoshop, and PostScript are trademarks of Adobe Systems Incorporated, which may be registered in certain jurisdictions.

Helvetica is a registered trademark of Linotype-Hell AG and/or its subsidiaries.

Simultaneously published in the United States and Canada.

Mention of third-party products is for informational purposes only and constitutes neither an endorsement nor a recommendation. Apple assumes no responsibility with regard to the performance or use of these products.

Contents

1Introduction 1

Creating a new document for calculations 1 Setting preferences 3 Using operators 5 Order of evaluation 6 Viewing the results 7 Correcting mistakes 7 Clearing the display 7 Saving a calculation document 8 Filing a calculation document 8 Viewing your calculation documents 9 Printing, beaming, and faxing 9 Reinstalling the Newton Works graphing calculator software 9

2 Using Functions and Variables 11

Using the built-in functions 11 Creating your own functions 18 Using constants 21 Using variables 22 Additional examples 25

iii

3Creating Graphs and Tables 27

Creating graphs 27 Creating a table 33

4Creating and Using Lists 37

Creating lists 37 Performing operations on lists 38 Using variables with lists 38 Graphing lists 39

iv Contents

Apple Newton Works Graphing Calculator User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual