
TI-86 Inferential Statistics and
Distribution Functions
Loading and Installing Inferential Statistics and
Distribution Features on Your TI-86...............................................................2
Loading the Inferential Statistics and Distribution Features into TI-86 Memory................................. 2
Installing the Inferential Statistics and Distribution Features for Use.................................................2
Displaying the STAT (Inferential Statistics and Distribution) Menu..................................................... 3
The STAT Menu................................................................................................................................... 3
Uninstalling the Inferential Statistics and Distribution Features.........................................................3
Deleting the Inferential Statistics and Distribution Program from TI-86 Memory...............................4
Example: Mean Height of a Population ......................................................... 4
Interpreting the Results......................................................................................................................5
Inferential Statistics Editors ........................................................................... 7
Displaying the Inferential Statistics Editors.........................................................................................7
Using an Inferential Statistics Editor...................................................................................................7
Bypassing the Inferential Statistics Editors.........................................................................................8
Inferential Statistics Editors for the STAT TESTS Instructions ....................9
STAT TESTS (Inferential Statistics Tests) Menu...................................................................................9
Inferential Statistics and Distribution Input Descriptions.........................24
Test and Interval Output Variables.............................................................. 26
Distribution (DISTR) Functions......................................................................28
STAT DISTR (Inferential Statistics Distribution) Menu.......................................................................28
DRAW (Distribution Shading) Functions ...................................................... 33
STAT DRAW (Inferential Statistics Draw) Menu................................................................................33
FUNC (Function) Parameters ......................................................................... 35
STAT FUNC (Inferential Statistics Functions) Menu.......................................................................... 35
Menu Map for Inferential Statistics and Distribution Functions .............. 39
MATH menu (where STAT is automatically placed)..........................................................................39
(MATH) STAT (Inferential Statistics and Distribution) Menu.............................................................39
STAT TESTS (Inferential Statistics Tests) Menu.................................................................................39
STAT DISTR (Inferential Statistics Distribution) Menu.......................................................................39
STAT DRAW (Inferential Statistics Draw) Menu................................................................................39
STAT FUNC (Inferential Statistics Functions) Menu.......................................................................... 39

Assembly Language Programming: Inferential Statistics and Distribution Functions
t
Loading and Installing Inferential Statistics and
Distribution Features on Your TI-86
To load the inferential statistics and distribution features onto your TI-86, you
need a computer and the TI-86 Graph Link software and cable. You also need to
download the statistics program file from the Internet and save it on your
computer.
Loading the Inferential Statistics and Distribution Features into TI-86 Memory
When sending a program
from your computer to the
TI-86, the calculator must no
be in Receive mode. The
Receive mode is used when
sending programs or data
from one calculator to
another.
1
Start the TI-86 Graph Link on
your computer.
2
Turn on your TI-86 and display
the home screen.
3
Click on the Send button on the
TI-86 Graph Link toolbar to
display the Send dialog box.
WLink86.exe
^
- l
2
Other files associated with
the assembly language
program (
statedit
PRGM NAMES
need not do anything with
them.
For assembly language
programs that must be
installed, up to three can be
installed at a time (although
the TI-86 can store as many
as permitted by memory). To
install a fourth, you must first
uninstall (page 3) one of the
others.
exstats, exstats2
) appear on the
menu, but you
,
4
Specify the statistics program
file as the file you want to send.
5
Send the program to the TI-86.
The program and its associated
executable file become items on
PRGM NAMES
the
6
Exit Graph Link.
menu.
infstat1.86g
Installing the Inferential Statistics and Distribution Features for Use
Use the assembly language program
Infstats
to install the inferential statistics and
distribution features directly into the TI-86’s built-in functions and menus. After
installation, the inferential statistics and distribution features are available each
time you turn on the calculator. You do not need to reinstall them each time.
When you run assembly language programs that do not install themselves into the
- Π/ menu, their features are lost when you turn off the calculator.
All examples assume that
on your TI-86. The position of
Infstats
STAT
is the only assembly language program installed
on the
MATH
menu may vary, depending on
how many other assembly language programs are installed.
1
2
Asm(
Select
to paste it to a blank line on the
home screen.
Select
NAMES
to the home screen as an
argument.
from the
Infstat
from the
menu to paste
CATALOG
PRGM
Infstats
- w &
#
(move 4 to
Asm(
b
)
8 &
Infstat
(select
E

Assembly Language Programming: Inferential Statistics and Distribution Functions
3
The variables that will be
overwritten are listed on
page 26.
If other assembly language
programs are installed,
may be in a menu cell other
- Π/ '
than
STAT
.
3
Run the installation program.
Caution:
If you have values
b
stored to variables used by the
statistical features, they will be
overwritten. To save your
values, press * to exit, store
them to different variables, and
then repeat this installation.
4
Continue the installation. Your
&
version number may differ from
the one shown in the example.
5
Display the home screen.
:
Displaying the STAT (Inferential Statistics and Distribution) Menu - Π/
When you install the inferential statistics and distribution program on your TI-86
and activate it,
NUM PROB ANGLE HYP MISC 4 INTER STAT
STAT
becomes the last item on the
Inferential Statistics and Distribution Menu
MATH
menu.
When you uninstall the
inferential statistics and
distribution features, the
statistics assembly language
programs (
exstats2,
remain in memory, but the
STAT
the
Infstats, exstats,
statedit
and
option is removed from
MATH
menu.
)
The STAT Menu - Π/ '
TESTS DISTR DRAW FUNC Uninst 4 RsltOn RsltOf
Inferential Distribution Uninstall Results Off
Statistics Shading Instruction (Default)
Test Editors
Functions Statistics (Intermediate calculation
Distribution Inferential Results On
Test Functions results display)
Uninstalling the Inferential Statistics and Distribution Features
1
Display the
then select
2
If you are sure you want to
uninstall, select
confirmation menu. The
menu is removed and the home
screen is displayed. Your version
number may differ from the one
shown in the example.
STAT
Uninst
menu, and
.
Yes
from the
- Π/ '
*
)
STAT

Assembly Language Programming: Inferential Statistics and Distribution Functions
Deleting the Inferential Statistics and Distribution Program from TI-86 Memory
Deleting the program does
not delete the variables
associated with the program.
1
2
Select
menu.
Select
DELET
DELET
PRGM
menu.
from the
from the
MEM
MEM
- ™ '
/ *
4
3
Move the selection cursor to
Infstats
4
Move the selection cursor to
exstats
down and delete
statedit
5
Display the home screen.
, and then delete it.
and then delete it. Scroll
exstats2
.
and
#
(as needed)
b
#
(as needed)
b
:
Example: Mean Height of a Population
Estimate the mean height of a population of women, given the random sample
below. Because heights among a biological population tend to be normally
distributed, a t distribution confidence interval can be used when estimating the
mean. The 10 height values below are the first 10 of 90 values, randomly generated
from a normally distributed population with an assumed mean of 65 inches and a
standard deviation of 2.5 inches.
This example uses an inferential statistics editor. An editor prompts you for test
information. See page 7 for another example of using an inferential statistics
editor. You can also enter test parameters without using an editor. See page 8 for
an example of bypassing the inferential statistics editors.
Height (in Inches) of Each of 10 Women
66.7 66.3 62.8 66.9 62.9 71.4 67.4 63.8 65.8 62.8
1
Create a new list column. The
cursor indicates that alpha-lock
is on. The existing list name
columns shift to the right.
Note:
Your statistics editor may
not look like the one pictured
here, depending on the lists you
have already stored.
2
Enter the list name at the
prompt. The list to which you
will store the women’s height
data is created.
3
Move the cursor onto the first
row of the list.
displayed on the bottom line.
HGHT(1)=
Name=
is
- š ' }
Ø
y p
[H] [G] [H] [T]
Í
†

Assembly Language Programming: Inferential Statistics and Distribution Functions
66
4
Enter the first height value. As
you enter it, it is displayed on
the bottom line.
The value is displayed in the first
row, and the rectangular cursor
moves to the next row. Enter the
other nine height values the
same way.
Ë
7
5
Í
5
Display the inferential statistics
TInterval
editor for
the
6
Select
7
Enter the test requirements:
¦
¦
¦
8
Calculate
are displayed on the home
screen.
Note:
b
the screen.
TIntl
(
STAT TESTS
Data
Set alpha-lock and enter the
List
name.
Enter 1 at the
Enter a 99 percent
confidence level at the
C-Level=
Press .,
to clear the results from
menu.
Inpt
in the
Freq=
prompt.
the test. The results
:
. - Œ
) from
field. If
prompt.
, or
/ ' & /
(
press |
† 1 1
[H] [G] [H] [T]
†
† Ë
&
Stats
1
99
is selected,
Í
Interpreting the Results
The first line
(62.887,68.473)
shows that the 99 percent confidence interval for the
population mean is between about 62.9 inches (5 feet 2.9 inches) and 68.5 inches
(5 feet 8.5 inches). This is about a 5.6-inch spread.
The .99 confidence level indicates that in a very large number of samples, we
expect 99 percent of the intervals calculated to contain the population mean. The
actual mean of the population sampled is 65 inches, which is in the calculated
interval.
The second line gives the mean height of the sample þ used to compute this
interval. The third line gives the sample standard deviation
gives the sample size
.
n
. The bottom line
Sx
To obtain a more precise bound on the population mean m of women’s heights,
increase the sample size to 90. Use a sample mean þ of 64.5 and sample standard
deviation
Stats
(summary statistics) input option.
of 2.8 calculated from the larger random sample. This time, use the
Sx

Assembly Language Programming: Inferential Statistics and Distribution Functions
6
The parameters are
invnm(
area[, m, s
]).
9
Display the inferential statistics
and distribution editor for
and select
J
Enter the test requirements:
¦
Store 64.5 to
¦
Store 2.8 to
¦
Store 90 to
K
Calculate the test. The
Stats
in the
þ
Sx
n
Inpt
results
TIntl
field.
: - Œ
/ ' & /
( ~ Í
64
Ë 5
Í
Í
†
2
Ë 8
90
Í
&
are displayed on the home
screen.
If the height distribution among a population of women is normally distributed
with a mean
of 65 inches and a standard deviation σ of 2.5 inches, what height is
m
exceeded by only 5 percent of the women (the 95th percentile)?
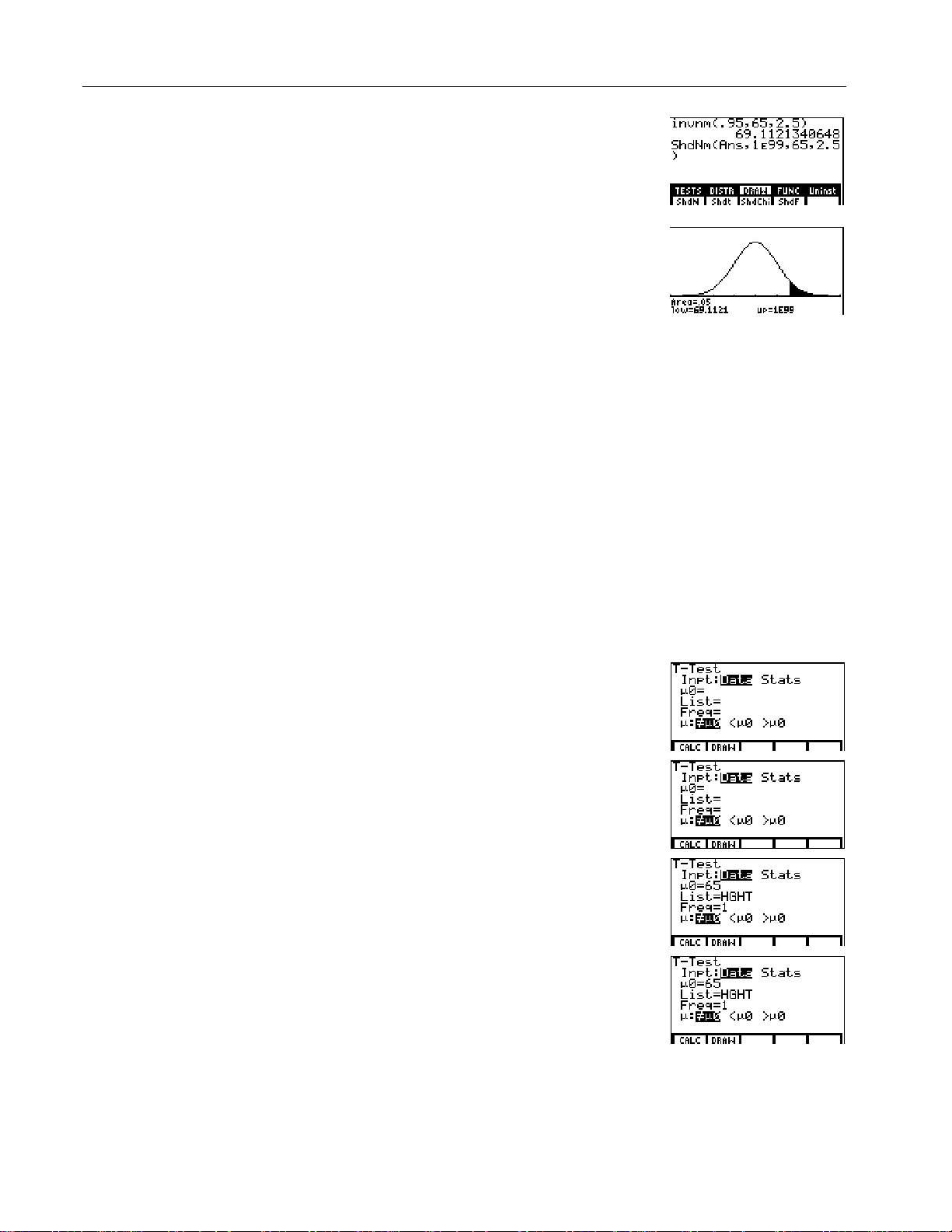
invnm(
invnm
STAT DISTR
to the home
stands for
‘ y Œ
/ ' '
(
95
¢
Í
65
¢
Ë
5
¤
2
Ë
L
Display the
(Distributions) menu.
M
Paste
screen. (
Inverse Normal.)
N
Enter .95 as the area, 65 as µ,
and 2.5 as σ.
The result is displayed on the home screen; it shows that five percent of the
women are taller than 69.1 inches (5 feet 9.1 inches).
Now graph and shade the top five percent of the population.
O
Set the window variables to these
values:
xMin=55 yMin=L.05 xRes=1
xMax=75 yMax=.2
xScl=2.5 yScl=0
P
Display the
Q
Paste
screen. (
STAT DRAW
ShdNm(
ShdNm
to the home
stands for Shade
Normal.)
menu.
6 '
. y Œ
/ ' (
&
Assembly Language Programming: Inferential Statistics and Distribution Functions
7
The parameters are
ShdNm(
upperbound
lowerbound,
, m, s
[
R
The answer (
)
.
]
from step 14 is the lower bound.
1å99 is the upper bound. The
Ans
69.1121340648)
y ¡ ¢
99
¢ 65 ¢ 2 Ë
¤
1
C
5
normal curve is defined by a
mean µ of 65 and a standard
deviation σ of 2.5.
S
Plot and shade the normal curve.
Area=
is the area above the 95th
percentile.
bound.
low=
is the lower
up=
is the upper bound.
Í
You can remove the menu from
the bottom of the screen.
:
Inferential Statistics Editors
Displaying the Inferential Statistics Editors
When you select a hypothesis test or confidence interval instruction from the
home screen, the appropriate inferential statistics editor is displayed. The editors
vary according to each test or interval’s input requirements.
When you select the
ANOVA(
instruction, it is pasted to the home screen.
does not have an editor screen.
ANOVA(
Data
Select
lists as input. Select
enter summary statistics,
such as v, Sx, and n as
inputs.
Most of the inferential
statistics editors for the
hypothesis tests prompt you
to select one of three
alternative hypotheses.
to enter the data
Stats
to
Using an Inferential Statistics Editor
This example uses the inferential statistics editor for
1
Select a hypothesis test or
confidence interval from the
STAT TESTS
menu. The
appropriate editor displays.
2
Select
Data
or
Stats
input, if the
selection is available.
3
Enter real numbers, list names,
or expressions for each
argument in the editor. See the
input descriptions table on
page 24.
4
Select the alternative hypothesis
against which to test, if the
selection is available.
- Π/ '
& '
(displays
TTest
the
"
#
[H] [G] [H] [T]
1
#
or !
65
#
editor)
b
#
b
TTest
.
Assembly Language Programming: Inferential Statistics and Distribution Functions
8
Select No or
Pooled option, if the selection
is available. The Pooled
option is available for
TInt2
and
! b
¦ Select
want the variances pooled.
Population variances can
be unequal.
¦ Select
variances pooled.
Population variances are
assumed to be equal.
Yes
for the
only. Press " or
to select an option.
No
if you do not
Yes
if you want the
Tsam2
5
Select
Calc
or
Draw
(when Draw
&
or
'
is available) to execute the
instruction.
¦
When you select
results are displayed on the
Calc
, the
&
home screen.
¦
When you select
Draw
, the
'
results are displayed in a
graph (not available for a
confidence interval).
Bypassing the Inferential Statistics Editors
You can paste a hypothesis test or confidence interval instruction to the home
screen without displaying the corresponding inferential statistics editor. You can
also paste a hypothesis test or confidence interval instruction to a command line
in a program.
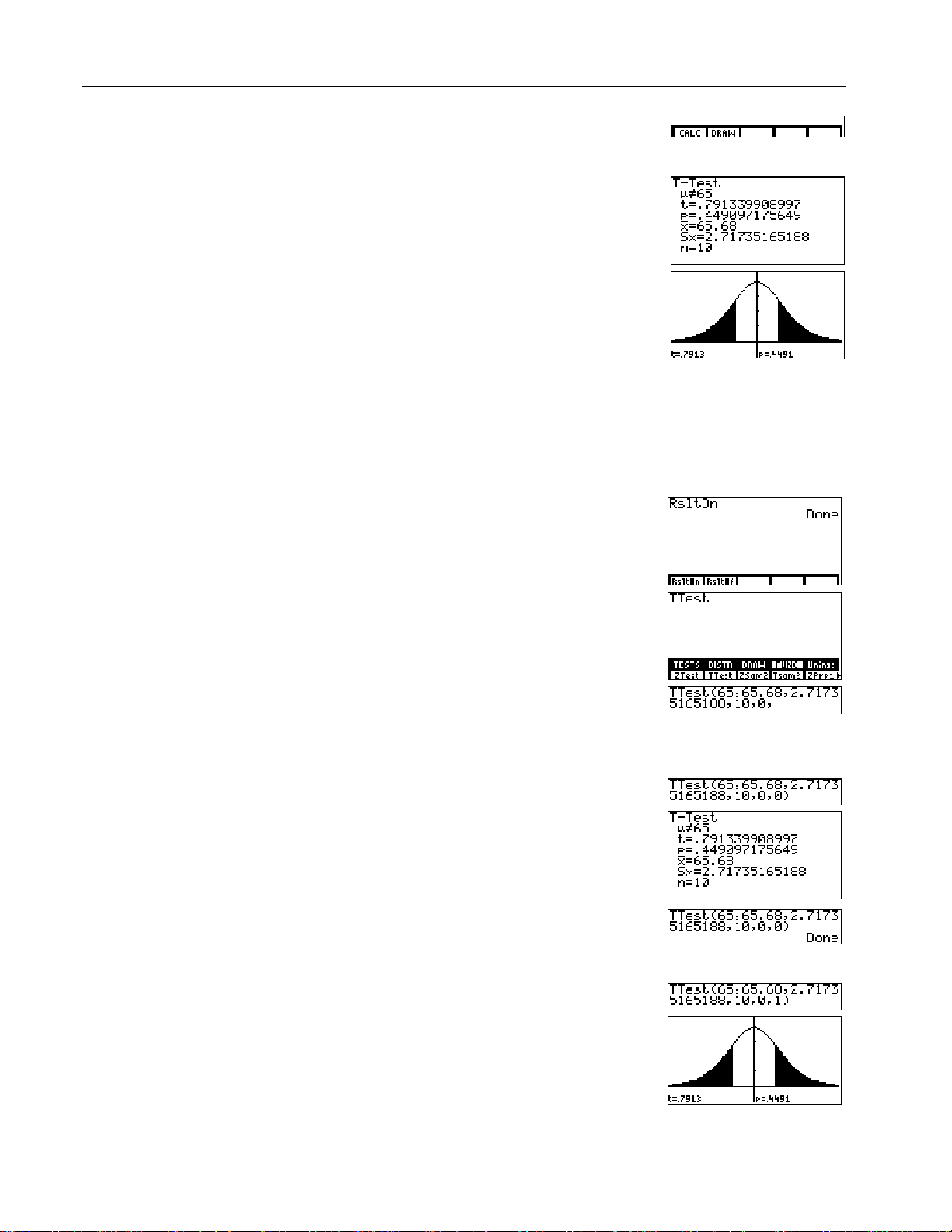
1
RsltOn
Turn
Note:
The default is
(Results Off).
(Results On).
RsltOf
- Π/ '
/ & b
This example uses summary
statistics. See pages 35-38
for a list of
menu parameters.
FUNC
(Function)
2
Select the instruction from the
STAT FUNC
3
Input the syntax for each
menu.
hypothesis test and confidence
interval instruction. Complete
the syntax by using one of the
options below:
¦
Enter 0 (zero) as the last
parameter to display the
results on the home screen.
Note:
The home screen does
not display the results if you
RsltOf
use
.
– or –
¦
Enter 1 as the last parameter
to display the results in a
graph. The graph is drawn
whether you use
RsltOf
.
RsltOn
or
: / ) '
(for the
TTest
instruction)
65 P 65.68
D
2.71735165188
0
10
P
0
E b
1
b
E
P
P
P
You can remove the menu
from the bottom of the screen.
:

Assembly Language Programming: Inferential Statistics and Distribution Functions
Inferential Statistics Editors for the STAT TESTS
Instructions
STAT TESTS (Inferential Statistics Tests) Menu - Π/ ' &
9
TESTS DISTR DRAW FUNC Uninst
ZTest TTest Zsam2 Tsam2 ZPrp1
4
RsltOn RsltOf
4
ZPrp2 ZIntl TIntl ZInt2 TInt2
4
ZPin1 ZPin2 Chitst FSam2 TLinR
4
ANOVA
Test Name Description Function
ZTest
TTest
Zsam2
Tsam2
ZPrp1
ZPrp2
ZIntl
TIntl
ZInt2
TInt2
ZPin1
ZPin2
Chitst
FSam2
TLinR
ANOVA
One-sample Z-test Test for one m , known
One-sample t-test Test for one m, unknown
Two-sample Z-test Test comparing two m’s, known s’s
Two-sample t-test Test comparing two m’s, unknown s’s
One-proportion Z-test Test for one proportion
Two- proportion Z-test Test comparing two proportions
One-sample Z confidence interval Confidence interval for one m,
s
known
One-sample t confidence interval Confidence interval for one m,
unknown
Two-sample Z confidence
interval
Two-sample t confidence interval Confidence interval for difference of
One-proportion Z confidence
interval
Two-proportion Z confidence
interval
Chi-square test Chi-square test for two-way tables
Two-sample Û-test Test comparing two s’s
Linear regression t-test t-test for regression slope and
One-way analysis of variance One-way analysis of variance
Confidence interval for difference of
two m’s, known s’s
two m’s, unknown s’s
Confidence interval for one
proportion
Confidence interval for difference of
two proportions
s
s
s
r
This section provides a description of each
STAT TESTS
instruction and shows the
unique inferential statistics editor for that instruction with example arguments.
Descriptions of instructions that offer the
¦
Data/Stats
input choice show both
types of input screens.
Descriptions of instructions that do not offer the
¦
Data/Stats
input choice show
only one input screen.
The description then shows the unique output screen for that instruction with the
example results.
Descriptions of instructions that offer the
¦
Calculate/Draw
output choice show
both types of screens: calculated and drawn results.
Descriptions of instructions that offer only the
¦
Calculate
output choice show the
calculated results on the home screen.
Assembly Language Programming: Inferential Statistics and Distribution Functions
d
All examples on pages 10 through 23 assume a fixed-decimal mode setting of four.
If you set the decimal mode to
Float
or a different fixed-decimal setting, your
output may differ from the output in the examples.
Be sure to turn off the y= functions before drawing results.
To remove the menu from a drawing, press :.
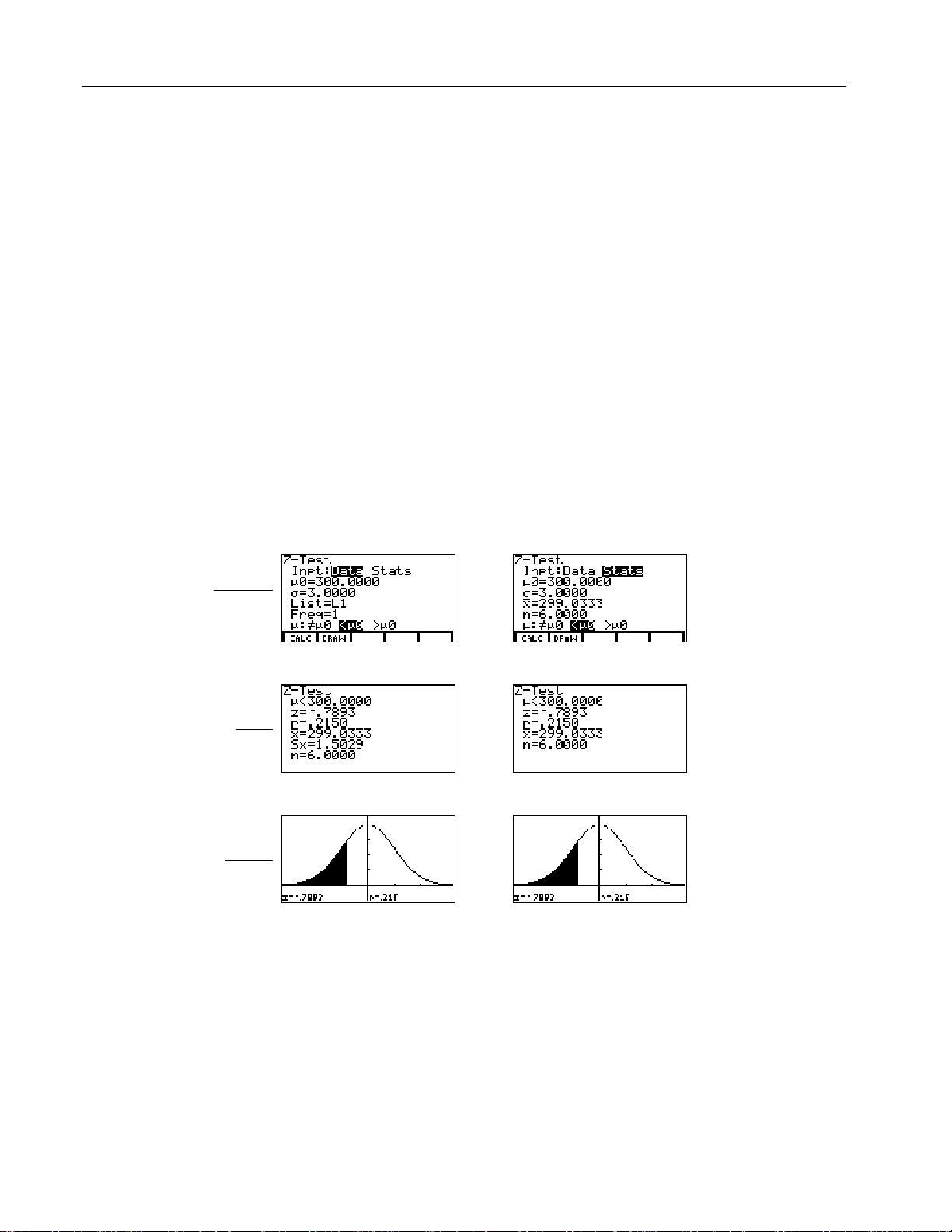
Ztest
Z-Test
This one-sample Z-test, shown as
in the editor, performs a hypothesis test
for a single unknown population mean m when the population standard
deviation
is known. It tests the null hypothesis H0: m=
s
alternatives below.
against one of the
m
0
10
Input
Calculate
Results
:
H
mƒm
¦
a
: m<
H
¦
a
: m>
H
¦
a
ƒm
(m:
)
0
0
m
(m:<
(m:>
)
0
m
)
0
m
0
m
0
In the example:
L1=
{299.4 297.7 301 298.9 300.2 297}
Data Stats
$$
$$
Drawn
Results
Assembly Language Programming: Inferential Statistics and Distribution Functions
d
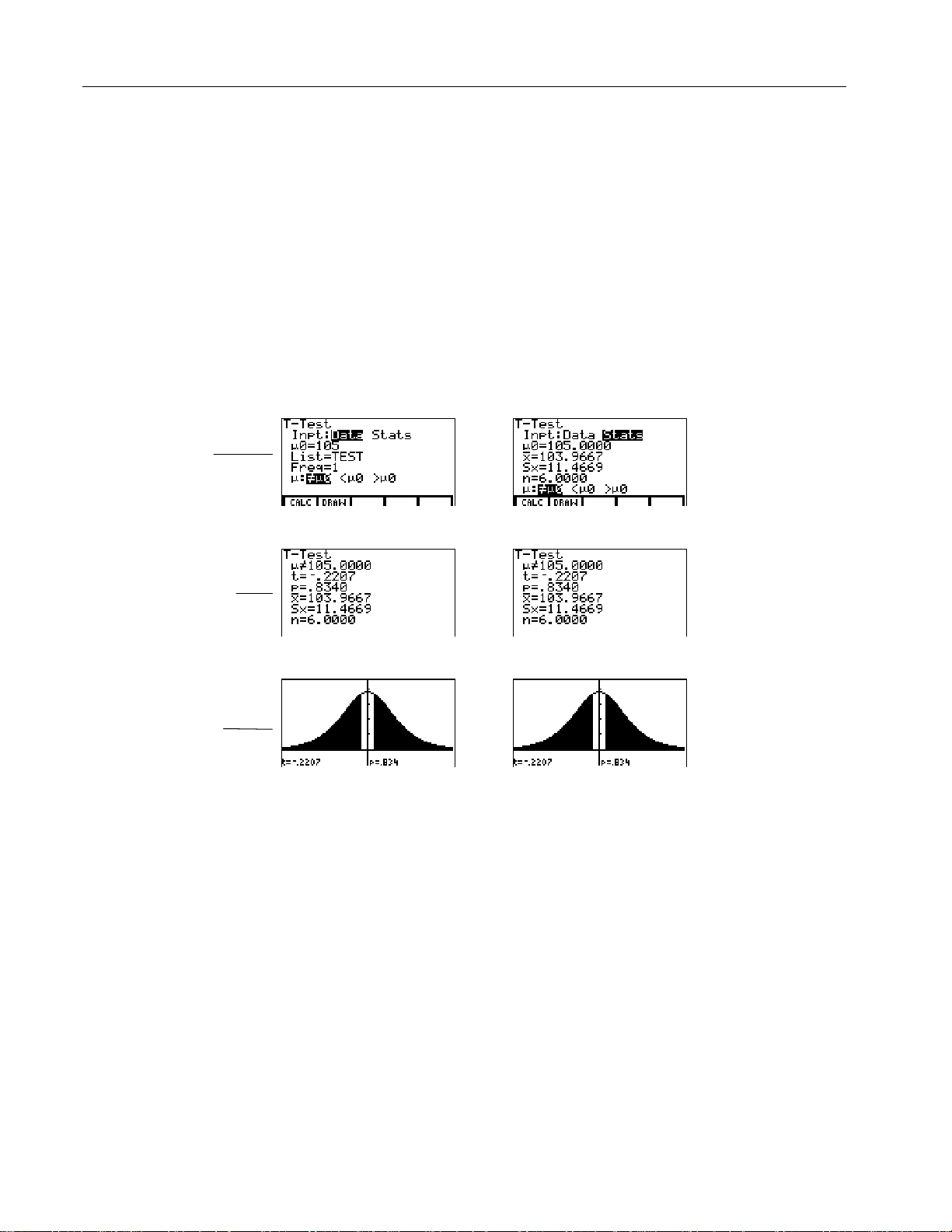
TTest
T-Test
This one-sample t-test, shown as
in the editor, performs a hypothesis test
for a single unknown population mean m when the population standard deviation
is unknown. It tests the null hypothesis H
s
below.
: m=
against one of the alternatives
m
0
0
11
Input
Calculate
Results
:
H
mƒm
¦
a
: m<
H
¦
a
: m>
H
¦
a
ƒm
(m:
)
0
0
m
(m:<
(m:>
)
0
m
)
0
m
0
m
0
In the example:
TEST=
{91.9 97.8 111.4 122.3 105.4 95}
Data Stats
$$
$$
Drawn
Results
Assembly Language Programming: Inferential Statistics and Distribution Functions
d
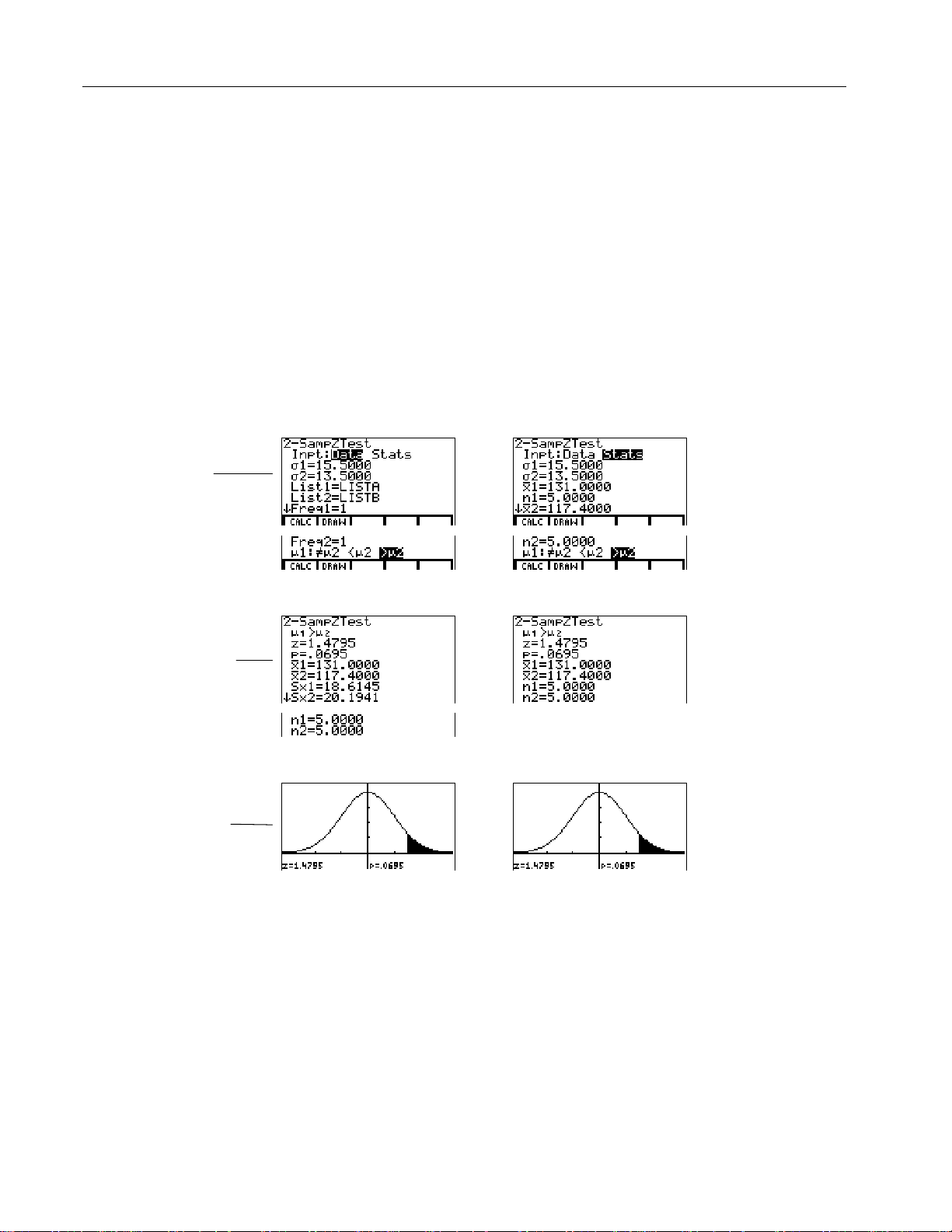
Zsam2
This two-sample Z-test, shown as
the means of two populations (
both population standard deviations (
H
:
=
is tested against one of the alternatives below.
m
m
0
1
2
:
H
¦
a
:
H
¦
a
:
H
¦
a
m
m
m
1ƒm2
<
m
1
>
m
1
(m1:ƒm2)
(m1:<m2)
2
(m1:>m2)
2
2-SampZTest
and
m
1
s
) based on independent samples when
m
2
and
1
In the example:
in the editor, tests the equality of
) are known. The null hypothesis
s
2
12
Input
Calculate
Results
LISTA=
LISTB=
{154 109 137 115 140}
{108 115 126 92 146}
Data Stats
$$
$$
Drawn
Results

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
Tsam2
m
1
and
2-SampTTest
) based on independent samples when
m
2
or
s
1
This two-sample t-test, shown as
means of two populations (
neither population standard deviation (
H
:
=
is tested against one of the alternatives below.
m
m
0
1
2
:
H
¦
a
:
H
¦
a
:
H
¦
a
m
m
m
1ƒm2
<
m
1
>
m
1
(m1:ƒm2)
(m1:<m2)
2
(m1:>m2)
2
In the example:
in the editor, tests the equality of the
) is known. The null hypothesis
s
2
13
Input
Calculate
Results
SAMP1=
SAMP2=
{12.207 16.869 25.05 22.429 8.456 10.589}
{11.074 9.686 12.064 9.351 8.182 6.642}
The pooled option is available for
variances can be unequal.
Yes
means that population variances are assumed to be
equal.
Data Stats
$$
Tsam2
and
TInt2
only. No means that population
$$
Drawn
Results

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
ZPrp1
This one-proportion Z-test, shown as
1-PropZTest
an unknown proportion of successes (prop). It takes as input the count of
successes in the sample x and the count of observations in the sample n.
tests the null hypothesis H0: prop=p0 against one of the alternatives below.
: propƒp0
Input
H
¦
H
¦
H
¦
a
: prop<p0
a
: prop>p0
a
(prop:ƒp0)
(prop:<p0)
(prop:>p0)
$
14
in the editor, computes a test for
ZPrp1
Calculate
Results
Drawn
Results
phat represents
Ç
$

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
ZPrp2
This two-proportion Z-test, shown as
2-PropZTest
compare the proportion of successes (p1 and p2) from two populations. It takes
as input the count of successes in each sample (x1 and x2) and the count of
observations in each sample (n1 and n2).
ZPrp2
H0: p1=p2 (using the pooled sample proportion
below.
in the editor, computes a test to
tests the null hypothesis
Ç
) against one of the alternatives
15
Input
Calculate
Results
Drawn
Results
Phat represents
: p
ƒ
a
1
: p1<p2
a
: p1>p2
a
p
(p1:ƒp2)
2
(p1:<p2)
(p1:>p2)
H
¦
H
¦
H
¦
$
$
Ç
in the editor. Phat1 represents
phat1 represents
phat2 represents
phat represents
Ç
, and phat2 represents
1
Ç
1
Ç
2
Ç
Ç
.
2

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
d
ZIntl
This one-sample Z confidence interval, shown as
confidence interval for an unknown population mean m when the population
standard deviation
is known. The computed confidence interval depends on the
s
user-specified confidence level.
In the example:
L1=
{299.4 297.7 301 298.9 300.2 297}
Data Stats
Input
$$
Calculate
Results
ZInterval
16
in the editor, computes a
Input
Calculate
Results
TIntl
This one-sample t confidence interval, shown as
TInterval
in the editor, computes a
confidence interval for an unknown population mean m when the population
standard deviation s is unknown. The computed confidence interval depends on
the user-specified confidence level.
In the example:
L6=
{1.6 1.7 1.8 1.9}
Data Stats
$$

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
ZInt2
This two-sample Z confidence interval, shown as
computes a confidence interval for the difference between two population means
(
) when both population standard deviations (
m
1Nm2
computed confidence interval depends on the user-specified confidence level.
In the example:
2-SampZInt
and
s
1
in the editor,
) are known. The
s
2
17
Input
Calculate
Results
LISTC=
LISTD=
{154 109 137 115 140}
{108 115 126 92 146}
Data Stats
$$

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
TInt2
This two-sample t confidence interval, shown as
computes a confidence interval for the difference between two population means
(
) when both population standard deviations (
m
1Nm2
computed confidence interval depends on the user-specified confidence level.
In the example:
2-SampTInt
and
s
1
in the editor,
) are unknown. The
s
2
18
Input
Calculate
Results
SAMP1=
SAMP2=
{12.207 16.869 25.05 22.429 8.456 10.589}
{11.074 9.686 12.064 9.351 8.182 6.642}
The pooled option is available for
variances can be unequal.
means that population variances are assumed to be
Yes
equal.
Data Stats
$$
TInt2
and
only. No means that population
Tsam2

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
d
ZPin1
This one-proportion Z confidence interval, shown as
computes a confidence interval for an unknown proportion of successes. It takes
as input the count of successes in the sample x and the count of observations in
the sample n. The computed confidence interval depends on the user-specified
confidence level.
Input
$
Calculate
Results
ZPin2
This two-proportion Z confidence interval, shown as
computes a confidence interval for the difference between the proportion of
successes in two populations (p
each sample (x
and x2) and the count of observations in each sample (n1 and n2) .
1
The computed confidence interval depends on the user-specified confidence level.
). It takes as input the count of successes in
p
N
1
2
1-PropZInt
2-PropZInt
19
in the editor,
in the editor,
Input
Calculate
Results
$

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
Chitst
2
Chi
Test
-
This test, shown as
in the editor, computes a chi-square test for
association on the two-way table of counts in the matrix you specify at the
Observed
prompt. The null hypothesis H0 for a two-way table is: no association
exists between row variables and column variables. The alternative hypothesis is:
the variables are related.
20
Matrix
Editor
Input
Calculate
Results
Before computing a
matrix variable name at the
Chitst
, enter the observed counts in a matrix. Enter that
Observed
prompt in the editor. At the
Expected
prompt, enter the matrix variable name to which you want the computed expected
counts to be stored.
Note:
Press -
b
to select Matrix A from
the MATRX EDIT menu.
‰ '
[A]
$
Note:
$
Press -
b
to display Matrix B.
‰ '
[B]
Drawn
Results

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
ÜSam2
This two-sample Û-test, shown as
2-SampÜTest
compare two normal population standard deviations (
means and standard deviations are all unknown.
sample variances Sx1
2
/Sx22, tests the null hypothesis H0:
alternatives below.
:
:
:
s
1ƒs2
s
1
s
1
<
s
>
s
(s1:ƒs2)
(s1:<s2)
2
(s1:>s2)
2
H
¦
a
H
¦
a
H
¦
a
In the example:
21
in the editor, computes an Û-test to
and
s
1
Sam2
, which uses the ratio of
ÜÜ
). The population
s
2
=
against one of the
s
s
1
2
Input
Calculate
Results
Drawn
Results
SAMP4=
SAMP5=
{7 L4 18 17 L3 L5 1 10 11 L2}
{L1 12 L1 L3 3 L5 5 2 L11 L1 L3}
Data Stats
$$
$$

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
TLinR
This linear regression t-test, shown as
LinRegTTest
regression on the given data and a t-test on the value of slope b and the correlation
coefficient r for the equation y=a+bx. It tests the null hypothesis H
For the regression equation,
you can use the fix-decimal
mode setting to control the
number of digits stored after
the decimal point. However,
limiting the number of digits
to a small number could
affect the accuracy of the fit.
(equivalently,
: bƒ0 and rƒ0
H
¦
a
: b<0 and r<0
H
¦
a
: b>0 and r>0
H
¦
a
The regression equation is automatically stored to
/ '
). If you enter a y= variable name at the
regression equation is automatically stored to the specified
example below, the regression equation is stored to
(turned on).
=0) against one of the alternatives below.
r
(b & r:ƒ0)
b
(
& r:<0)
b
(
& r:>0)
In the example:
L3=
{38 56 59 64 74}
L4=
{41 63 70 72 84}
Input
in the editor, computes a linear
: b=0
0
RegEQ
RegEQ
y1
- š * /
(
prompt, the calculated
y=
equation. In the
, which is then selected
22
Calculate
Results
$

Assembly Language Programming: Inferential Statistics and Distribution Functions
d
ANOVA
This test computes a one-way analysis of variance for comparing the means of 2 to
20 populations. The ANOVA procedure for comparing these means involves
analysis of the variation in the sample data. The null hypothesis H
tested against the alternative H
ANOVA(
list1,list2
...,list20]
,
[
)
:. Not all
a
m
In the example:
L1=
7 4 6 6 5}
{
L2=
6 5 5 8 7}
{
L3=
{4 7 6 7 6}
Input
$
Intermediate calculation
results display only when
Calculate
Results
RsltOn is selected from the
STAT menu.
...
m
1
are equal.
k
23
:
=
=...=
m
m
0
1
2
is
m
k
SS is sum of squares and MS
is mean square.

Assembly Language Programming: Inferential Statistics and Distribution Functions
Inferential Statistics and Distribution Input
Descriptions
This table describes the inferential statistics and distribution inputs. You enter
values for these inputs in the inferential statistics editors. The table presents the
inputs in the same order as they appear in the editor examples on pages 10-23.
Input Description
m
0
s
List
Freq
Calculate/Draw
v
, Sx, n
s
1
s
2
List1, List2
Freq1, Freq2
v
1, Sx1, n1, v2,
Sx2, n2
Pooled
p
0
x
n
x1
x2
n1
n2
C-Level
Hypothesized value of the population mean that you are testing.
The known population standard deviation; must be a real number
> 0.
The name of the list containing the data you are testing.
The name of the list containing the frequency values for the data in
List
. Default=1. All elements must be integers | 0.
Determines the type of output to generate for tests and intervals.
Calculate
displays the output on the home screen. In tests,
draws a graph of the results.
Summary statistics (mean, standard deviation, and sample size) for
the one-sample tests and intervals.
The known population standard deviation from the first population
for the two-sample tests and intervals. Must be a real number > 0.
The known population standard deviation from the second
population for the two-sample tests and intervals. Must be a real
number > 0.
The names of the lists containing the data you are testing for the
two-sample tests and intervals.
The names of the lists containing the frequencies for the data in
List1
and
List2
for the two-sample tests and intervals. Defaults=1.
All elements must be integers | 0.
Summary statistics (mean, standard deviation, and sample size) for
sample one and sample two in the two-sample tests and intervals.
Specifies whether variances are to be pooled for
No
does not pool the variances.
The expected sample proportion for
such that 0 < p
< 1.
0
The count of successes in the sample for the
be an integer ‚ 0.
The count of observations in the sample for the
Must be an integer > 0.
The count of successes from sample one for the
Must be an integer ‚ 0.
The count of successes from sample two for the
Must be an integer ‚ 0.
The count of observations in sample one for the
Must be an integer > 0.
The count of observations in sample two for the
Must be an integer > 0.
The confidence level for the interval instructions. Must be ‚ 0 and
<100. If it is ‚ 1, it is assumed to be given as a percent and is divided
by 100. Default=0.95.
Yes
pools the variances.
ZPrp1
. Must be a real number
ZPrp1
Tsam2
and
ZPrp1
ZPrp2
ZPrp2
ZPrp2
ZPrp2
and
ZPin1
and
and
and
and
and
Draw
TInt2
. Must
ZPin1
ZPin2
ZPin2
ZPin2
ZPin2
24
.
.
.
.
.

Assembly Language Programming: Inferential Statistics and Distribution Functions
Input Description
Observed
(Matrix)
Expected
(Matrix)
Xlist, Ylist
RegEQ
y
The matrix name that represents the columns and rows for the
observed values of a two-way table of counts for the
Observed
must contain all integers ‚ 0. Matrix dimensions must be
at least 2×2.
The matrix name that specifies where the expected values should
be stored.
Chitst
.
Expected
is created upon successful completion of the
The names of the lists containing the data for
dimensions of
Xlist
and
Ylist
The prompt for the name of the y= variable where the calculated
regression equation is to be stored. If a
equation is automatically selected (turned on). The default is to
store the regression equation to the
Always use lowercase characters for stored regression equations.
must be the same.
y=
variable is specified, that
RegEQ
variable only.
TLinR
Chitst
. The
25
.

Assembly Language Programming: Inferential Statistics and Distribution Functions
Test and Interval Output Variables
The inferential statistics and distribution variables are calculated as indicated
below. To access these variables for use in expressions, press - w and
then select the menu listed in the
below.
All inferential statistics variables begin with the letters
other variables.
If you upload TI-86 variables that contain the sigma (s) or mu (m) symbols to your
computer, the Graph Link program will prompt you to rename them. This is
because computer file names cannot contain these symbols. When you download
the renamed variables to your TI-86, Graph Link restores the symbols and the files
are loaded in the calculator under their original names.
Variables and Catalog/Variables Menu
column
st
to separate them from
26
Important:
If you do not rename the sigma variables (sts.86n, sts1.86n, and
sts2.86n), they are stored on the computer under the names st_.86n, st_1.86n, and
st_2.86n. You cannot delete or rename these files on your computer, and you will
not be able to download them to your calculator.
TI-86 Variables
Variables and
Catalog / Variables Menu
p-value
REAL
test statistics
REAL
degrees of freedom
REAL
sample mean of x values for
sample 1 and sample 2
REAL
sample standard deviation of x
for sample 1 and sample 2
REAL
number of data points for
sample 1 and sample 2
REAL
pooled standard deviation
REAL
estimated sample proportion
REAL
estimated sample proportion
for population 1
REAL
estimated sample proportion
for population 2
REAL
confidence interval pair
REAL
mean of x values
REAL
sample standard deviation of x
REAL
Tests Intervals
stp stp p
stz, stt,
stchi, stF
stdf stdf stdf df
stmean1,
stmean2
stSx1,
stSx2
stn1, stn
stSxp stSxp stSxp Sx
stphat stphat
stphat1 stphat1
stphat2 stphat2
stxbar stxbar
stSx stSx Sx
2
stmean1,
stmean2
stSx1,
stSx2
stn1, stn
stLOWER,
stUPPER
2
TLinR,
ANOVA
stt, stF
Math
Symbols
2
c
Ü
,
z, t,
v
v
,
1
2
Sx1,
Sx
2
n1, n
2
P
ÇÇ
1
ÇÇ
2
ÇÇ
lower,
upper
v

Assembly Language Programming: Inferential Statistics and Distribution Functions
27
TI-86 Variables
Variables and
Catalog / Variables Menu
number of data points
REAL
standard error about the line
REAL
regression/fit coefficients
STAT
correlation coefficient
REAL
coefficient of determination
REAL
regression equation
STAT
factor DF, degrees of freedom
REAL
factor SS, sum of square
REAL
factor MS, mean square
REAL
error DF, degrees of freedom
REAL
error SS, sum of square
REAL
error MS, mean square
REAL
TLinR,
Tests Intervals
stn stn n
ANOVA
sts s
a, b a, b
str r
stlrsqr r
RegEQ RegEQ
stfDF DF
stfSS SS
stfMS MS
steDF DF
steSS SS
steMS MS
Math
Symbols
2

Assembly Language Programming: Inferential Statistics and Distribution Functions
Distribution (DISTR) Functions
STAT DISTR (Inferential Statistics Distribution) Menu - Π/ ' '
TESTS DISTR DRAW FUNC Uninst 4RsltOn RsltOf
nmpdf nmcdf invnm tpdf tcdf 4 chipdf chicdf Fpdf Fcdf bipdf
4
bicdf pspdf pscdf gepdf gecdf
Instruction Function
nmpdf
nmcdf
invnm
tpdf
tcdf
chipdf
chicdf
Ü
pdf
Ü
cdf
bipdf
bicdf
pspdf
pscdf
gepdf
gecdf
Normal probability density
Normal distribution probability
Inverse cumulative normal distribution
Student-t probability density
Student-t distribution probability
Chi-square probability density
Chi-square distribution probability
Û
probability density
Û
distribution probability
Binomial probability
Binomial cumulative density
Poisson probability
Poisson cumulative density
Geometric probability
Geometric cumulative density
28
For plotting the normal
distribution, you can set
window variables
so that the mean m falls
xMax
between them, and then
6 ( / &
press
fit the graph in the window.
xMin
and
to
L1å99 and 1å99 approximate infinity. If you want to view the area left of
Note:
upperbound, for example, specify lowerbound=
1å99.
L
nmpdf
) for the normal distribution at a
Computes the probability density function (
specified x value. The defaults are mean
the normal distribution, paste
2
()
x
−
µ
−
()
nmpdf(x[,m,
πσ
2
]
s
1
=>
fx e
2
2
σ
,
)
σ
0
Note:
xMin = 28
xMax = 42
xScl = 1
yMin = 0
yMax = .25
yScl = 1
xRes = 1
to the
nmpdf
For this example,
pdf
=0 and standard deviation s=1. To plot
m
y
= editor. The
pdf
is:

Assembly Language Programming: Inferential Statistics and Distribution Functions
nmcdf
Computes the normal distribution probability between lowerbound and
upperbound for the specified mean
=0 and s=1.
m
lowerbound,upperbound[
nmcdf(
and standard deviation s. The defaults are
m
,m,
)
]
s
invnm
Computes the inverse cumulative normal distribution function for a given area
under the normal distribution curve specified by mean
It calculates the x value associated with an area to the left of the x value. 0 area
1 must be true. The defaults are
area[
invnm(
,m,
)
]
s
=0 and s=1.
m
tpdf
Computes the probability density function (pdf) for the Student-t distribution at a
specified x value. df (degrees of freedom) must be > 0. To plot the Student-t
tpdf
distribution, paste
++
Γ
df
1221
[( ) ]
=
()
fx
Γ
df
()
/
to the y= editor. The
2
/
xdf
/
()
()
df
−+
π
df
12
/
pdf
29
and standard deviation s.
m
is:
tpdf(x,df)
Note:
For this example,
xMin = L4.5
xMax = 4.5
xScl = 1
yMin = 0
yMax = .4
yScl = 1
xRes = 1
tcdf
Computes the Student-t distribution probability between lowerbound and
upperbound for the specified df (degrees of freedom), which must be > 0.
lowerbound,upperbound,df
tcdf(
)

Assembly Language Programming: Inferential Statistics and Distribution Functions
chipdf
Computes the probability density function (pdf) for the
distribution at a specified x value. df (degrees of freedom) must be an integer > 0.
To plot the
2
distribution, paste
c
chipdf
to the y= editor. The pdf is:
2
(chi-square)
c
30
1
=≥
()
fx
Γ
2
()
/
df
df df x
// /
(1/2)
221 2
xex
−−
,
0
chipdf(x,df)
Note:
For this example,
xMin = 0
xMax = 30
xScl = 1
yMin = L.02
yMax = .132
yScl = 1
xRes = 1
chicdf
2
c
Computes the
(chi-square) distribution probability between lowerbound and
upperbound for the specified df (degrees of freedom), which must be an
integer > 0.
lowerbound,upperbound,df
chicdf(
pdf
Ü
)
Computes the probability density function (pdf) for the Û distribution at a
specified x value. numerator df (degrees of freedom) and denominator df must
be integers > 0. To plot the Û distribution, paste Ü
n
/
fx
()
=
/
nd
[( ) ]
Γ
nd
()()
ΓΓ
2
+
//
22
2
n
nnd
//
21 2
−−+
xnxd x
10
()
d
+≥
()
/,
pdf
to the y= editor. The
pdf
is:
where n = numerator degrees of freedom
d = denominator degrees of freedom
Ü
numerator df,denominator df
pdf(x,
)
Note:
For this example,
xMin = 0
xMax = 5
xScl = 1
yMin = 0
yMax = 1
y Scl = 1
xRes = 1

Assembly Language Programming: Inferential Statistics and Distribution Functions
cdf
ÜÜ
Computes the Û distribution probability between lowerbound and upperbound for
the specified numerator df (degrees of freedom) and denominator df. numerator
df and denominator df must be integers > 0.
Ü
lowerbound,upperbound,numerator df,denominator df
cdf(
bipdf
Computes a probability at x for the discrete binomial distribution with the
specified numtrials and probability of success (p) on each trial. x can be an
integer or a list of integers. 0 p 1 must be true. numtrials must be an integer
> 0. If you do not specify x, a list of probabilities from 0 to numtrials is returned.
The
pdf
is:
n
fx
pp x n
x
xnx
=
() ( )
−
−=
101,,,,
K
where n = numtrials
numtrials,p[,x]
bipdf(
)
31
)
bicdf
Computes a cumulative probability at x for the discrete binomial distribution with
the specified numtrials and probability of success (p) on each trial. x can be a
real number or a list of real numbers. 0 p 1 must be true. numtrials must be an
integer > 0. If you do not specify x, a list of cumulative probabilities is returned.
numtrials,p[,x]
bicdf(
)
pspdf
Computes a probability at x for the discrete Poisson distribution with the
specified mean m, which must be a real number > 0. x can be an integer or a list of
integers. The
==
fx e x x
() !
pspdf(m,x)
pdf
x
−µ
µ
/, ,,,
is:
012
K

Assembly Language Programming: Inferential Statistics and Distribution Functions
pscdf
Computes a cumulative probability at x for the discrete Poisson distribution with
the specified mean m, which must be a real number > 0. x can be a real number or
a list of real numbers.
pscdf(m,x)
gepdf
Computes a probability at x, the number of the trial on which the first success
occurs, for the discrete geometric distribution with the specified probability of
success p. 0 p 1 must be true. x can be an integer or a list of integers. The
1
x
() ( )
=− =
fx p p x
gepdf(p,x)
−
112
,,,
K
pdf
32
is:
gecdf
Computes a cumulative probability at x, the number of the trial on which the first
success occurs, for the discrete geometric distribution with the specified
probability of success p. 0 p 1 must be true. x can be a real number or a list of
real numbers.
gecdf(p,x)

Assembly Language Programming: Inferential Statistics and Distribution Functions
DRAW (Distribution Shading) Functions
STAT DRAW (Inferential Statistics Draw) Menu - Π/ ' (
33
TESTS DISTR DRAW FUNC Uninst
ShdN Shdt ShdChi ShdF
4
RsltOn RsltOf
4
Instruction Function
ShdN
Shdt
ShdChi
ShdF
DRAW
instructions draw various types of density functions, shade the area
Shades normal distribution
Shades Student-t distribution
Shades
Shades Û distribution
2
c
distribution
specified by lowerbound and upperbound, and display the computed area value.
DRAW
Before you execute a
Set the window variables so the desired distribution fits the screen.
¦
Turn off the y= functions.
¦
To clear the drawings, select
instruction:
CLDRW
from the
GRAPH DRAW
menu.
To remove the menu from a drawing, press :.
ShdN
Draws the normal density function specified by mean
and standard deviation
m
and shades the area between lowerbound and upperbound. The defaults are m=0
and
=1.
s
lowerbound,upperbound[
ShdN(
,m,
]
s
)
s
Note:
For this example,
xMin = 55
xMax = 72
xScl = 1
yMin = L.05
yMax = .2
yScl = 1
xRes = 1
Shdt
Draws the density function for the Student-t distribution specified by df (degrees
of freedom) and shades the area between lowerbound and upperbound.
lowerbound,upperbound,df
Shdt(
)
Note:
For this example,
xMin = L3
xMax = 3
xScl = 1
yMin = L.15
yMax = .5
yScl = 1
xRes = 1

Assembly Language Programming: Inferential Statistics and Distribution Functions
ShdChi
2
Draws the density function for the
(chi-square) distribution specified by df (degrees
c
of freedom) and shades the area between lowerbound and upperbound.
ShdChi(
lowerbound,upperbound,df
Note:
xMin = 0
xMax = 35
xScl = 1
yMin = L.025
yMax = .1
yScl = 1
xRes = 1
)
For this example,
ShdÜ
Draws the density function for the
distribution specified by numerator df
Û
(degrees of freedom) and denominator df and shades the area between
lowerbound and upperbound.
lowerbound,upperbound,numerator df,denominator df
ShdÜ(
Note:
For this example,
xMin = 0
xMax = 5
xScl = 1
yMin = L.25
yMax = .9
yScl = 1
xRes = 1
34
)

Assembly Language Programming: Inferential Statistics and Distribution Functions
FUNC (Function) Parameters
STAT FUNC (Inferential Statistics Functions) Menu - Π/ ' )
35
TESTS DISTR DRAW FUNC Uninst
Ztest TTest ZSam2 Tsam2 ZPrp1
Test Name Function
ZTest
TTest
ZSam2
Tsam2
ZPrp1
ZPrp2
ZIntl
TIntl
ZInt2
TInt2
ZPIn1
ZPIn2
Chitst
FSam2
TLinR
ANOVA
Test for 1 m , known
Test for 1 m, unknown
Test comparing 2 m’s, known s’s
Test comparing 2 m’s, unknown s’s
Test for 1 proportion
Test comparing 2 proportions
Confidence interval for 1 m, known
Confidence interval for 1 m, unknown
Confidence interval for difference of 2 m’s, known s’s
Confidence interval for difference of 2 m’s, unknown s’s
Confidence interval for 1 proportion
Confidence interval for difference of 2 proportions
Chi-square test for 2-way tables
Test comparing 2 s’s
t-test for regression slope and
One-way analysis of variance
s
4
RsltOn RsltOf
4
ZPrp2 ZIntl TIntl ZInt2 TInt2
4
ZPIn1 ZPIn2 Chitst FSam2 TLinR
4
ANOVA
s
s
s
r
You can bypass the inferential statistics editors and paste a hypothesis test or
confidence interval instruction to the home screen. This section provides the
parameters of each
Instructions that offer the
¦
STAT FUNC
instruction.
Data/Stats
input choice show both sets of input
parameters.
Instructions that do not offer the
¦
Data/Stats
input choice show one set of input
parameters.
The following table lists the function arguments alphabetically.

Assembly Language Programming: Inferential Statistics and Distribution Functions
Function Argument and Result
ANOVA(
list1,list2
list3,...,list20]
,
[
)
Performs a one-way analysis of variance for comparing the means of
2 to 20 populations.
observedmatrix,expectedmatrix[,drawflag]
Chitst(
Performs a chi-square test. drawflag=1 draws results; drawflag=
calculates results.
36
)
0
listname1,listname2
FSam2
where listname1
Performs a two-sample Û-test. alternative=
alternative=
,
[freqlist1
listname2 refers to lists you have created in the list editor.
,
1
is >. drawflag=1 draws results; drawflag=0 calculates
freqlist2,alternative,drawflag]
,
L
1
is < ; alternative=0 is ƒ ;
results.
FSam2
Sx1
where Sx1
Sx2,n2[,alternative,drawflag]
,n1,
Sx2,n2 refers to summary statistics that you must enter.
,n1,
L
Performs a two-sample Û-test. alternative=
alternative=
1
is >. drawflag=1 draws results; drawflag=0 calculates
1
is < ; alternative=0 is ƒ ;
results.
TInt2
listname1
where listname1
listname2[,freqlist1,freqlist2,confidence level,pooled]
,
listname2 refers to lists you have created in the list editor.
,
Computes a two-sample t confidence interval. pooled=1 pools
0
does not pool variances.
TInt2
where
variances; pooled=
1,Sx1,n1
v
1,Sx1,n1
v
2,Sx2,n2[,confidencelevel,pooled]
,
v
2,Sx2,n2 refers to summary statistics that you must enter.
,
v
Computes a two-sample t confidence interval. pooled=1 pools
0
does not pool variances.
confidence level]
,
TIntl
variances; pooled=
listname
,
[freqlist
where listname refers to a list you have created in the list editor.
Computes a t confidence interval.
TIntl
v
where
confidence level]
,Sx,n[,
n refers to summary statistics that you must enter.
,Sx,
v
Computes a t confidence interval.
Xlistname,Ylistname
TLinR
where Xlistname
Performs a linear regression and a t-test. alternative=
alternative=
listname1,listname2
Tsam2
where listname1
Computes a two-sample t-test. alternative=
alternative=
variances. drawflag=
,
[freqlist
Ylistname refers to lists you have created in the list editor.
,
0
is ƒ ; alternative=1 is >.
,
[freqlist1
listname2 refers to lists you have created in the list editor.
,
1
is >. pooled=1 pools variances; pooled=0 does not pool
1
alternative,regequ]
,
L
1
is < ;
freqlist2,alternative,pooled,drawflag]
,
L
1
is < ; alternative=0 is ƒ ;
draws results; drawflag=0 calculates results.

Assembly Language Programming: Inferential Statistics and Distribution Functions
Function Argument and Result
Tsam2
where
1,Sx1,n1
v
1,Sx1,n1
v
2,Sx2,n2[,alternative,pooled,drawflag]
,
v
2,Sx2,n2 refers to summary statistics that you must enter.
,
v
Computes a two-sample t-test. alternative=
alternative=
variances. drawflag=
1
is >. pooled=1 pools variances; pooled=0 does not pool
1
draws results; drawflag=0 calculates results.
L
1
is < ; alternative=0 is ƒ ;
37
TTest
where
0,listname[,freqlist,alternative,drawflag]
m
0,listname refers to the hypothesized value and to a list you have
m
created in the list editor.
L
1
L
1
is < ;
is < ;
)
TTest
where
ZInt2(
where
Performs a t-test with frequency freqlist. alternative=
alternative=
drawflag=
0,
,Sx,n[,
m
v
0
,
,Sx,
v
m
0
is ƒ ; alternative=1 is >. drawflag=1 draws results;
0
calculates results.
alternative,drawflag]
n refers to summary statistics that you must enter.
Performs a t-test with frequency freqlist. alternative=
alternative=
drawflag=
listname1,listname2[,freqlist1,freqlist2,confidence level]
,
,
s
s
1
2
listname1,listname2 refers to the known population standard
,
,
s
s
1
2
0
is ƒ ; alternative=1 is >. drawflag=1 draws results;
0
calculates results.
deviations (from the first and second populations) and lists you have created in
the list editor.
Computes a two-sample Z confidence interval.
1,n1
ZInt2(
where
,
,
s
s
v
1
2
,
s
s
1
2
2,n2[,confidence level]
,
v
1,n1
,
v
2,n2 refers to summary statistics that you must enter.
,
v
)
Computes a two-sample Z confidence interval.
listname[,freqlist,confidence level]
ZIntl
,
s
listname refers to the known population deviation and a list you have
where
,
s
created in the list editor.
Computes a Z confidence interval.
ZIntl
where
confidence level]
,n[,
s,v
n refers to summary statistics that you must enter.
,
s,v
Computes a Z confidence interval.
ZPIn1(x,n[,
confidence level]
Computes a one-proportion Z confidence interval.
ZPIn2(x1,n1,x2,
Computes a two-proportion Z confidence interval.
ZPrp1(p0,x,n[,
Computes a one-proportion Z-test. alternative=
; alternative=
ƒ
results.
ZPrp2(x1,n1,x2,
Computes a two-proportion Z-test. alternative=
; alternative=
ƒ
results.
)
n2[,confidence level]
alternative,drawflag]
1
is >. drawflag=1 draws results; drawflag=0 calculates
)
n2[,alternative,drawflag]
1
is >. drawflag=1 draws results; drawflag=0 calculates
)
L
1
is < ; alternative=0 is
)
L
1
is < ; alternative=0 is

Assembly Language Programming: Inferential Statistics and Distribution Functions
Function Argument and Result
ZSam2(
where
listname1,listname2[,freqlist1,freqlist2,alternative,drawflag]
,
,
s
s
2
1
listname1,listname2 refers to the known population standard
,
,
s
s
2
1
deviations (from the first and second populations) and lists you have created in
the list editor.
Computes a two-sample Z-test. alternative=
alternative=
1
is >. drawflag=1 draws results; drawflag=0 calculates
results.
ZSam2(
where
1,n1
,
,
s
s
v
2
1
1,n1
,
,
s
s
v
2
1
2,n2[,alternative,drawflag]
,
v
2,n2 refers to summary statistics that you must enter.
,
v
Computes a two-sample Z-test. alternative=
alternative=
1
is >. drawflag=1 draws results; drawflag=0 calculates
results.
0
ZTest(
where
listname[,freqlist,alternative,drawflag]
,s,
m
0
listname refers to the hypothesized value, the known population
,s,
m
deviation, and a list you have created in the list editor.
Performs a Z-test with frequency freqlist. alternative=
alternative=
drawflag=
0
is ƒ ; alternative=1 is >. drawflag=1 draws results;
0
calculates results.
L
1
is < ; alternative=0 is ƒ ;
)
L
1
is < ; alternative=0 is ƒ ;
)
L
1
is < ;
38
)
ZTest(
where
0
m
m
alternative,drawflag]
,s,v,n[,
0
n refers to summary statistics that you must enter.
,s,v,
Performs a Z-test. alternative=
alternative=
1
is >. drawflag=1 draws results; drawflag=0 calculates
results.
)
L
1
is < ; alternative=0 is ƒ ;

Assembly Language Programming: Inferential Statistics and Distribution Functions
Menu Map for Inferential Statistics and Distribution
Functions
MATH menu (where STAT is automatically placed) - Œ
39
NUM PROB ANGLE HYP MISC
4
INTER STAT
(MATH) STAT (Inferential Statistics and Distribution) Menu - Π/ '
TESTS DISTR DRAW FUNC Uninst
4
RsltOn RsltOf
STAT TESTS (Inferential Statistics Tests) Menu - Π/ ' &
TESTS DISTR DRAW FUNC Uninst
ZTest Ttest Zsam2 Tsam2 ZPrp1
4
RsltOn RsltOf
4
ZPrp2 ZIntl TIntl ZInt2 TInt2
4
ZPin1 ZPin2 Chitst FSam2 TLinR
4
ANOVA
STAT DISTR (Inferential Statistics Distribution) Menu - Π/ ' '
TESTS DISTR DRAW FUNC Uninst
nmpdf nmcdf invnm tpdf tcdf
4
RsltOn RsltOf
4
chipdf chicdf Fpdf Fcdf bipdf
4
bicdf pspdf pscdf gepdf gecdf
STAT DRAW (Inferential Statistics Draw) Menu - Π/ ' (
TESTS DISTR DRAW FUNC Uninst
ShdN Shdt ShdChi ShdF
4
RsltOn RsltOf
4
STAT FUNC (Inferential Statistics Functions) Menu - Π/ ' )
TESTS DISTR DRAW FUNC Uninst
ZTest Ttest ZSam2 Tsam2 ZPrp1
4
RsltOn RsltOf
4
ZPrp2 ZIntl TIntl ZInt2 TInt2
4
ZPIn1 ZPIn2 Chitst FSam2 TLinR
4
ANOVA
 Loading...
Loading...