Texas instruments TI-15 User Manual [pt]

Download

TI.15

Manual do Instrutor

Desenvolvido pela

Texas Instruments Incorporated

Atividades desenvolvidas por

Jane Schielack

Sobre a autora

Jane Schielack é Professora Adjunta de matemática no Departamento de Matemática da Texas A&M University. Ela desenvolveu a seção

neste manual.

a TI-15

Atividades

e ajudou na avaliação da aplicabilidade dos exemplos contidos em

Como Usar

Nota importante relativa a materiais bibliográficos

A Texas Instruments renuncia a todas as garantias, expressas ou implícitas, incluindo mas não se limitando às garantias implícitas de comercialização e adequabilidade a um fim específico, relativas a qualquer programa ou livro e disponibiliza esses materiais exclusivamente da forma como estão. Em nenhuma hipótese a Texas Instruments se responsabilizará por quaisquer prejuízos específicos, relativos, incidentais ou conseqüentes ligados a ou oriundos da aquisição ou uso desses materiais e a única e exclusiva responsabilidade da Texas Instruments, independentemente da reivindicação, não será superior ao preço deste manual. A Texas Instruments não será responsabilizada por nenhuma reivindicação de nenhuma espécie, contrária ao uso destes materiais por terceiros. Nota: O uso de calculadoras diferentes da TIN15 pode produzir resultados diferentes dos descritos nestes materiais.

Permissão para reimpressão ou fotocópia

É concedida permissão aos instrutores, neste ato, para reimprimir ou fotocopiar as páginas ou folhas deste trabalho que portem o aviso de copyright da Texas Instruments, em quantidades apropriadas para uso em salas de aula, workshops ou seminários. Estas páginas foram projetadas para serem reproduzidas pelos instrutores para uso em salas de aula, workshops ou seminários, desde que cada cópia feita exiba o aviso de copyright. Essas cópias não podem ser vendidas e sua ulterior distribuição fica expressamente proibida. Exceto conforme autorizado acima, deve ser obtida permissão escrita prévia da Texas Instruments com fins de reprodução ou transmissão deste trabalho ou de partes dele de qualquer outra forma ou por qualquer outro meio eletrônico ou mecânico, incluindo qualquer armazenamento de informações ou sistema de recuperação, a menos que isso seja expressamente permitido por uma lei federal de copyright. Envie suas consultas para este endereço:

Texas Instruments Incorporated 7800 Banner Drive, M/S 3918 Dallas, TX 75251 - USA Attention: Manager, Business Services

Caso solicite fotocópias do todo ou de parte deste manual a terceiros, é necessário incluir esta página (com a autorização acima) ao prestador de serviços de fotocópia.

www.ti.com/calc

ti-cares@ti.com

Excetuando os direitos específicos aqui concedidos, todos os direitos estão reservados.

Impresso nos Estados Unidos da América.

Automatic Power Down, APD e EOS são marcas registradas da Texas Instruments Incorporated.

EXAS INSTRUMENTS INCORPORATED

Índice



CAPÍTULO PÁGINA

Sobre o Manual do Instrutor Sobre a TI-15

Atividades

Padrões em Porcentagem.........................2

Formas de Frações.....................................6

Comparando Custos..................................11

Taquigrafia Numérica................................15

Procedimentos Correlatos..................... 20

No Intervalo................................................24

A Importância do Valor Posicional........29

Qual o Problema? ......................................34

Como Usar a

1 Visor, Rolagem, Ordem de

Operações, Parênteses..................... 39

................................................vi

...........................................1

TI.15.........................38

....................v

CAPÍTULO PÁGINA

Anexo A ..................................................... A-1

Referência Rápida às Teclas

Anexo B.......................................................B-1

Indicadores do Visor

Anexo C ......................................................C-1

Mensagens de Erro

Anexo D ....................................................D-1

Suporte, Serviços e Garantia

2 Apagando e Corrigindo.......................42

3 Menus de Modo...................................45

4 Operações Básicas............................48

5 Operações com Constantes.............55

6 Números Inteiros e Decimais ..........63

7 Memória ................................................68

8 Frações................................................... 71

9 Porcentagem .......................................80

10 Pi............................................................ 84

11 Potências e Raízes Quadradas.......88

12 Solução de Problemas: Modo

Auto ...................................................... 94

13 Solução de Problemas: Modo

Manual.................................................100

14 Valor Posicional .................................106

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

iii

Sobre o Manual do Instrutor



Organização do Manual do Instrutor

Este guia consiste em duas seções:

Atividades Atividades

para integrar a TI-15 no ensino da matemática. A seção criada para ajudar você a ensinar seus alunos a usar a calculadora.

Como Usar a TI-15

é uma coletânea de atividades

Como Usar a TI-15

. A seção

foi

Seção de Atividades

As atividades foram criadas para ser dirigidas pelo instrutor. Seu objetivo é ajudar a desenvolver conceitos matemáticos incorporando a TI-15 como uma ferramenta de ensino. As atividades são independentes e incluem o seguinte.

• Uma visão geral do propósito

matemático da atividade.

• Os conceitos matemáticos que estão

sendo desenvolvidos.

• Os materiais necessários para o

desempenho da atividade.

• Uma folha de atividades do estudante.

Seção Como Usar a TI-15

Lembretes

• Embora muitos dos exemplos nos

modelos de transparências possam ser usados no desenvolvimento de conceitos matemáticos, eles não foram criados especificamente para esse propósito.

• Para maior flexibilidade, cada exemplo e

atividade é independente dos outros. Selecione o exemplo de modelo de transparência apropriado para a tecla que você está tentando ensinar ou selecione a atividade que tenha funções apropriadas para o conceito matemático que você está ensinando.

• Se um exemplo de um modelo de transpa-

rência não parecer apropriado ao seu nível ou grau curricular, use-o para ensinar a função de uma tecla (ou teclas) e, em seguida, forneça seus exemplos apropriados.

• Para garantir que todos comecem no mesmo

ponto, antes de começar peça aos estudantes que reinicializem a calculadora pressionando − e ” simultaneamente, ou pressionando ‡, selecionando selecionando Y (yes), e, em seguida ®.

RESET

Esta seção contém exemplos de modelos de transparências. Os capítulos são numerados e incluem o seguinte.

• Uma página introdutória descrevendo as

teclas da calculadora, apresentadas no exemplo, a posição dessas teclas na TI-15 e outras notas pertinentes sobre suas funções.

• Um ou mais exemplos de transparências

após a página introdutória, com um ou mais exemplos de aplicações práticas da(s) tecla(s) que está(ão) sendo discutida(s). A(s) tecla(s) que está(ão) sendo discutida(s) é (são) mostrada(s) com um círculo no teclado da TI-15.

Como Solicitar Manuais Adicionais

Para fazer um pedido ou solicitar informações adicionais sobre as calculadoras da Texas Instruments (TI), ligue para o nosso número gratuito:

1-800-TI-CARES (1-800-842-2737)

Ou use o nosso endereço de correio eletrônico:

ti-cares@ti.com

Ou ainda visite a home page das calculadoras TI:

http://www.ti.com/calc

EXAS INSTRUMENTS INCORPORATED

Sobre a TI.15

Visor de Duas Linhas

A primeira linha exibe uma entrada com até 11 caracteres. As entradas começam no topo à esquerda. Se a entrada não couber na primeira linha, ela avançará para a segunda linha. Quando o espaço permitir, tanto a entrada quanto o resultado aparecerão na primeira linha.

A segunda linha exibe até 11 caracteres. Se a entrada for longa demais para caber na primeira linha, ela avançará para a segunda linha. Se a entrada e o resultado não couberem na primeira linha, o resultado será exibido justificado à direita na segunda linha. Os resultados com mais de 10 dígitos serão exibidos em notação científica.

Se uma entrada não couber em duas linhas, ela continuar a avançar; você pode visualizar o início da entrada rolando-a para cima. Neste caso, apenas o resultado aparecerá quando você pressionar ®.

Indicadores do Display

Consulte uma lista dos indicadores do display no Apêndice B.

Mensagens de Erro

Consulte a lista de mensagens de erro no Apêndice C.

Ordem das Operações

A TI-15 usa o Equation Operating System (EOSTM) para calcular expressões. As prioridades das operações estão listadas no modelo de transparência no Capítulo 1,

Rolagem, Ordem das Operações e Parênteses

Como as operações de dentro dos parênteses são executadas primeiro, você pode usar X Y para alterar a ordem das operações e, por conseguinte, alterar os resultado.

Visor,

Menus

Duas teclas da TI-15 exibem menus: ‡ e ¢.

Pressione $ ou # para navegar para cima ou para baixo na lista do menu. Pressione ! ou " para mover o cursor e realçar um item do menu. Para voltar à tela anterior sem selecionar o item, pressione ” ou ‡. Para selecionar um item de menu, pressione < enquanto o item estiver sublinhado.

Entradas Anteriores

Após o cálculo de uma expressão, use # e $ para ver as entradas anteriores, que

estão armazenadas no histórico da TI-15.

Solucionador de Problemas (‹)

A ferramenta Solucionador de Problemas tem três recursos que os estudantes podem usar para desafiar-se a si mesmos com operações matemáticas básicas ou valor da posição.

O Solucionador de Problemas (Modo Automático) fornece um conjunto de exercícios eletrônicos para desafiar a habilidade do estudante em adição, subtração, multiplicação e divisão. Os estudantes podem selecionar o modo, o nível de dificuldade e o tipo de operação.

O Solucionador de Problemas (Modo Manual) permite que os estudantes componham seus próprios problemas, que podem incluir incógnitas ou desigualdades.

O Solucionador de Problemas (Valor da

Posição) permite que os estudantes exibam o valor da posição de um dígito específico, ou exiba o número de unidades, dezenas, centenas, milhares, décimos, centésimos ou milésimos de um dado número.

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Sobre a TI.15

(

Continuação

Reinicialização da TI.15

Pressionar − e ” simultaneamente ou pressionando ‡, selecionando RESET, selecionando Y (sim) e, em seguida, pressionando < reinicia a calculadora.

Reinicialização da calculadora:

• Retorna a configuração para as definições

padrão: notação padrão Standard (Ponto Flutuante), números mistos, simplificação manual, modo Automático do Solucionador de Problemas e Nível de Dificuldade 1 (adição) no Solucionador de Problemas.

• Apaga as operações pendentes, as

entradas no histórico e as constantes (operações armazenadas).

)

Desligar Automático (Automatic Power

Se a TI-15 permanecer inativa durante cerca de 5 minutos, Desligar Automático (APDTM) desliga-a automaticamente. Pressione − depois de APD. O visor, as operações pendentes, as definições e a memória são retidos.

Down

, APDTM)

EXAS INSTRUMENTS INCORPORATED

Atividades

Padrões em Porcentagem 2

Formas de Frações 6

Comparando Custos 11

Taquigrafia Numérica 15

Procedimentos Correlatos 20

No Intervalo 24

A Importância do Valor Posicional 29

Qual o Problema? 34

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Padrões em Porcentagem

Séries: 4ª à 6ª

Visão geral

Os estudantes usarão a tecla ª para coletar dados sobre porcentagens de um determinado número. Em seguida eles organizam os dados e buscam padrões de porcentagens. (Por exemplo, 10% de 20 é duas vezes 5% de 20.)

Introdução

1. Depois que os estudantes usarem manipulações para desenvolver o significado da porcentagem (1% = 1 parte de 100 partes), peça que eles estudem o que acontece quando eles pressionarem ª na calculadora.

2. Apresente aos estudantes a seguinte situação:

Metropolis East (M.E.) e Metropolis West (M.W.) são cidades vizinhas. O imposto sobre as vendas em M.E. é de 10%, mas em M.W. esse imposto é de apenas 5%. Colete os dados e exiba os resultados de cada porcentagem em uma tabela para comparar os valores em dinheiro que você pagaria pelos diversos itens em cada cidade.

3. Peça que os estudantes levantem hipóteses sobre as porcentagens baseadas nos padrões observados. Os estudantes podem usar elementos de manipulação para verificar suas hipóteses.

Exemplos:

• Os estudantes podem observar que, para cada

item, 10% de seu preço é duas vezes 5% desse preço.

• Os estudantes podem observar que é fácil

estimar 10% de um número inteiro usando a função valor posicional e olhando os dígitos à direita da casa das unidades.

Conceitos Matemáticos

• multiplicação

• frações equivalentes, decimais e porcentagens

³ Quando um estudante

digita 6, a TI-15 exibe

6. Então, quando o estudante pressionar

ª ®

para 0.06 para mostrar que 6% é uma maneira diferente de escrever

0.06 ou 6/100.

³ Será necessário

mostrar aos estudantes como usar a multiplicação na TI-15 para expressar a porcentagem de uma determinada quantidade. Por exemplo, para mostrar 10% de $20:

1. Digite 10.

2. Pressione ª V.

3. Digite 20; pressione

Os estudantes podem verificar o visor da calculadora exibindo usando manipulações para mostrar que 10% de $20 = $2.

, o visor muda

Materiais

• TI-15

• lápis

• atividade do estudante (página 4)

Coletando e Organizando Dados

Para orientar os estudantes na organização de seus dados para deduzir sobre os padrões, faça perguntas do tipo:

Como você organizaria os seus dados para

•

comparar a alíquota de 5% com a alíquota de 10%? Por que seria útil manter 5% na coluna da

•

esquerda da tabela das unidades até embaixo e mudar apenas a quantidade total?

EXAS INSTRUMENTS INCORPORATED

Padrões em Porcentagem

Como pode ser feita uma tabela semelhante

•

para 10%, para comparar os seus dados? O que você acha que ocorreria se você ordenasse

•

os valores das quantidades totais do menor para o maior?

De que outra forma você poderia organizar seus

•

dados para comparar as duas alíquotas e encontrar os padrões nas porcentagens?

Analisando Dados e Extraindo Conclusões

Para focalizar a atenção do estudante na procura de padrões em seus dados, faça perguntas do tipo:

Qual a semelhança entre as porcentagens

•

(valores do imposto) na sua tabela de 5% e os valores na tabela de 10%?

Qual a comparação entre 5% de um item de $20

•

e 5% de um item de 10%? Qual a comparação entre 10% de um item de

•

$20 e 10% de um item de $10?

(continuação)

Qual a comparação entre 10% do custo de um

•

item e o custo total desse item? Que conjecturas você pode fazer sobre como

•

calcular 10% de um número? Que conjecturas você pode fazer sobre como

•

calcular 5% de um número? Como você pode usar manipulações para testar

•

as suas hipóteses?

Continuando com a Pesquisa

Os estudantes podem criar outras situações para pesquisar padrões em porcentagens. Por exemplo, pergunte aos estudantes:

O que acontece se você aumentar o ICMS em um

•

ponto percentual por dia? Como mudaria o imposto sobre um item de $20

•

que muda todos os dias? Como muda o imposto sobre um item de $40 a

•

cada dia? Que comparação você faz dos impostos nos 2

•

itens?

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Nome __________________________

Padrões em Porcentagem

Data __________________________

Coletando e Organizando Dados

Use a sua calculadora para coletar dados sobre a porcentagem, organizá-lo na tabela abaixo e, em seguida, procurar os padrões.

Preço do item Imposto em

Metropolis East

Alíquota: ___%

Imposto em

Metropolis West

Alíquota: ___%

EXAS INSTRUMENTS INCORPORATED

Nome ___________________________

Padrões em Porcentagem

Data ___________________________

Analisando Dados e Extraindo Conclusões

1. Que padrões você observa nas suas tabelas?

__________________________________________________________________________

2. Que conjecturas você pode fazer a partir destes padrões?

__________________________________________________________________________

3. Repita a atividade com uma porcentagem diferente na coluna da esquerda e compara os seus resultados.

__________________________________________________________________________

4. Repita a atividade mudando as porcentagens na coluna da esquerda, enquanto mantém constante a quantidade total. Que padrões você vê agora? Que conjecturas você pode fazer?

__________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Formas de Frações

Séries: 4ª à 6ª

Visão geral

Os estudantes irão comparar os resultados de usar a divisão para criar frações em diferentes configurações de modo, para exibir frações, e fazer comentários sobre os padrões observados por eles.

Introdução

1. Apresente o seguinte tipo de problema aos estudantes:

Na despensa de uma pequena lanchonete sobraram 6 xícaras de açúcar para serem colocadas em 4 açucareiros. Como você deseja que todos eles contenham a mesma quantidade de açúcar, que quantidade de açúcar deve ser colocada em cada açucareiro?

2. Peça aos estudantes que apresentem suas soluções para o problema. Estimule-os a encontrar o maior número possível de diferentes formas de representar a solução.

Conceitos Matemáticos

• divisão

• multiplicação

• fatores comuns

• frações equivalentes

 Consulte outras

informações mais detalhadas, na página 45, sobre as configurações de modo na TI-15.

Materiais

• TI-15

• lápis

• atividade do estudante (página 9)

Exemplos:

• Se eles pensaram em usar uma concha de ¼ de

xícara para encher os açucareiros, cada açucareiro receberia 6 conchas, ou 6/4 xícaras de açúcar.

• Se eles pensaram em separar cada xícara em

meias xícaras, haveria 12 meias xícaras, e cada açucareiro receberia 3 meias xícaras, ou 3/2 xícaras de açúcar.

• Se uma xícara de medida de 1 xícara houvesse

sido usada inicialmente, cada açucareiro receberia 1 xícara de açúcar, em seguida as últimas duas xícaras seriam divididas em oito quartos para dar 1 2/4 xícaras por açucareiro.

• As últimas duas xícaras poderiam ser divididas

em 4 metades para dar 11/2 xícaras por açucareiro.

3. Peça aos estudantes que identifiquem a operação e anotem a equação que poderiam usar com a calculadora para representar a ação a adotar nessa situação (6 xícaras ÷ 4 açucareiros = número de xícaras por açucareiro).

 A divisão pode ser

representada por 6 P 4 ou 6/4 (digitado na calculadora como 6  4 ¥). Nesta atividade, usa-se a representação fracionária.

EXAS INSTRUMENTS INCORPORATED

Formas de Fração

(continuação)

4. Peça que os estudantes digitem a divisão para mostrar os quocientes na forma de fração, e anote os resultados exibidos.

5. Peça aos estudantes que testem o quociente com as diferentes combinações de configurações e discutam os diferentes conteúdos do visor. Se necessário, peça-lhes que manipulem os dados para associar os significados das quatro diferentes formas de frações.

6. Peça aos estudantes que, trabalhando em grupos de quatro, escolham um denominador e anotem as diferentes formas de frações na folha de atividade fornecida.

7. Peça aos estudantes que compartilhem os resultados entre si, verifiquem os padrões e façam comentários.

Coletando e Organizando Dados

Para orientar os estudantes sobre como criar dados que exibirão padrões nos quocientes fracionários, faça perguntas do tipo:

 Por exemplo, para 6 ÷ 4

na forma de fração, digite 6  4 ¥. Os visores nos diferentes modos terão o seguinte aspecto:

man

d n

auto

man 1

d n

auto 1

6 4

3 2

2 4

1 2

Que denominador você preferiu testar? Por quê?

•

Que denominadores você obteve com as

•

configurações

man

Que denominadores você obteve com as

•

configurações

auto

Que denominador você escolherá para o

•

n d

? Com as configurações

man

? Com as configurações

auto

próximo teste?

Exemplo:

Após testar com os denominadores de 2 e 3, você pode sugerir um teste com um denominador de 6 e comparar os resultados.

Como você pode organizar os resultados para

•

procurar padrões?

Exemplo:

n d

Continuando a aumentar os numeradores de 1 a cada vez.

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Formas de Fração

(continuação)

Analisando Dados e Tirando Conclusões

Para concentrar a atenção dos estudantes nos padrões de suas frações e nas relações entre esses padrões e os denominadores, faça perguntas do tipo:

Que padrões você vê em seus resultados?

•

Exemplo:

Quando um denominador 4 é usado na coluna cada quarto número usado será um número inteiro.

Como é possível comparar os resultados de

•

quando se usa um denominador 2 comparado com os resultados ao se usar um denominador 4?

Como é possível comparar um denominador 5

•

com um denominador d de valor 10? Que outros denominadores parecem estar

•

relacionados?

Exemplo:

n d

auto,

O padrão ao se usar um divisor de 6 está relacionado com os padrões de 2 e 3.

Que padrão você observa nos denominadores

•

relacionados?

Exemplo:

Eles estão relacionados como fatores e múltiplos.

Continuando a Pesquisa

Peça aos estudantes que simulem situações em que prefeririam usar as combinações das configurações das formas de frações uns dos outros.

Exemplo:

• Ao trabalhar com as probabilidades que

poderiam ser adicionadas, o uso da configuração denominadores das probabilidades iguais e simplificaria a adição mental.

• Numa situação na qual os resultados estimados

são bastante próximos, o uso da configuração

auto

componente inteiro do número resultante e se a parte fracionária adicional é maior ou menor que

½.

n d

facilita, e vê-se mais rápidamente o

manteria os

man

EXAS INSTRUMENTS INCORPORATED

Nome ___________________________

Formas de Fração

Data ___________________________

Coletando e Organizando Dados

1. Peça a cada pessoa do grupo que configure sua calculadora para uma das seguintes combinações de modos de exibição de fração. (Cada uma deve escolher uma configuração diferente.)

• imprópria/manual simp

• imprópria/auto simp

• número misto/manual simp

• número misto/auto simp

2. Selecione um denominador: _____________

3. Use esse denominador com vários numeradores e anote os resultados de cada pessoa na tabela abaixo.

Numerador Denominador

Man

Auto U

Man U

Auto

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Formas de Fração

(continuação)

Analisando Dados e Tirando Conclusões

1. Que padrões você observa?

___________________________________________________________________________

2. Que deduções você pode tirar?

___________________________________________________________________________

3. Tente esta atividade novamente usando um denominador diferente e compare os seus resultados com os dois denominadores.

___________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

Comparando Custos

Séries: 3ª à 5ª

Visão geral

Os estudantes resolverão um problema usando a divisão com um quociente inteiro e um resto, a divisão com o quociente na forma fracionária e a divisão com o quociente na forma decimal, e farão uma comparação dos resultados.

Introdução

1. Apresente o seguinte problema:

O departamento de manutenção determinou que custará $0.40 por metro quadrado por ano para fazer a manutenção do campo de futebol do bairro. O campo de futebol mede 80 metros de largura por 110 metros de comprimento. As seis escolas que jogam no campo decidiram dividir o custo por igual. Com quanto cada escola deve contribuir para o fundo de manutenção do campo de futebol este ano?

2. Peça aos estudantes que usem a calculadora para resolver este problema de três maneiras:

• Encontrando um quociente inteiro e um

resto.

• Encontrando o quociente na forma de fração.

• Encontrando o quociente na forma decimal.

Coletando e Organizando Dados

Os estudantes devem anotar seus resultados e procedimentos na página Atividade do Estudante. Para ajudá-los a se concentrar em seu pensamento, faça perguntas do tipo:

O que você digitou na calculadora para resolver

•

o problema?

Conceitos Matemáticos

• divisão

• multiplicação

• frações

• decimais

 Para exibir um

quociente inteiro com um resto, use a tecla

 Para exibir um

quociente na forma de fração, pressione

‡ " ®

selecionar n/d e, em seguida, use a tecla W.

 Para exibir um

quociente na forma decimal, pressione

‡ ! ®

selecionar seguida, use a tecla W.

para

e, em

Materiais

• TI-15

• lápis

• atividade do estudante (página 14)

Exemplo:

Um estudante pode ter digitado

110

® para calcular a área do campo de futebol e depois V de manutenção e, depois, W

0.40

® para encontrar o custo total

® para calcular o custo para cada escola na forma de fração ou decimal.

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Comparando Custos

Você teria resolvido o problema de forma mais

•

eficiente? Como?

Exemplo:

Um estudante pode observar que 80 x 110 poderia ser calculado mentalmente e as teclas a pressionar poderiam ser simplificadas para 8800 V .4 W 6 ®.

Qual a semelhança entre os seus procedimentos

•

para cada tipo de solução?

Exemplos:

Todos eles envolvem o cálculo da quantidade de metros quadrados do campo de futebol; todos eles envolvem multiplicação e divisão.

Qual a diferença?

•

Você usa teclas diferentes para informar à calculadora de que maneira você deseja que a resposta seja exibida.

(continuação)

Analisando Dados e Tirando Conclusões

Para orientar os estudantes a analisar seus dados, faça perguntas do tipo:

Qual a semelhança entre as suas três soluções?

•

Todas elas têm um componente número inteiro de 586.

Qual a diferença entre as três soluções?

•

A forma do resto indica apenas quantos reais estão sobrando. As formas fracionária e decimal indicam quanto além dos $586 cada escola tem que pagar.

EXAS INSTRUMENTS INCORPORATED

Comparando Custos

O que acontece se você multiplicar cada solução

•

por 6 para verificar?

(continuação)

Para a forma do resto, você tem que multiplicar 586 x 6 e depois adicionar 4 para obter o custo total de $3520. Você pode multiplicar 586 na forma de fração para obter $3520. Se você digitar 586.666667 x 6 e pressionar ®, obterá 3520, mas isso não faz sentido, porque 6 x 7 não termina em 0!

Se você digitar 586.66667, então fixe o quociente decimal para centésimos, visto que se trata de dinheiro, e depois calcule 586.67 x 6, você ainda obterá 3520.00, que ainda não faz sentido porque 6 x 7 = 42. Se você apagar a calculadora e digitar

586.67 x 6 e pressionar ® , então o visor exibirá 3520.02, que não faz sentido.

Na condição de escola, que forma de quociente

•

você desejaria usar?

As respostas podem variar. Alguns estudantes podem desejar usar a forma decimal, já que ela é a que mais se aproxima da representação de dinheiro. Alguns estudantes podem desejar usar a forma de quociente inteiro e resto e sugerir que a Administração Municipal pague os $4.00 restantes.

/3 x 6

 Quando você fixa

586.666667 para 2 casas decimais e depois multiplica por 6, a calculadora se “lembra” do número original e o utiliza como o fator. O produto arredondado para o centésimo mais próximo, usando o fator original, é 3520.00. Quando você digita

586.67, a calculadora usa este número como fator, mostrando o produto real de

3520.02.

Embora a forma fracionária do quociente descreva a quantia exata que cada escola deve pagar, a maioria dos estudantes observará, por comparação com a forma decimal, que a forma fracionária não é facilmente convertida em dinheiro.

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Nome __________________________

Comparando Custos

Data __________________________

Coletando e Organizando Dados

O departamento de Manutenção determinou que custará $4.00 por metro quadrado por ano para fazer a manutenção do campo de futebol do bairro. O campo de futebol mede 80 metros de largura por 110 metros de comprimento. As 6 escolas que jogam no campo decidiram dividir o custo por igual. Com quanto cada escola deve contribuir para o fundo de manutenção do campo de futebol este ano?

1. Use divisão com um quociente inteiro e resto:

2. Use divisão com um quociente na forma de fração:

3. Use divisão com um quociente na forma decimal:

Analisando Dados e Tirando Conclusões

Escreva um breve parágrafo comparando as três soluções.

EXAS INSTRUMENTS INCORPORATED

Taquigrafia Numérica: Notação Científica

Séries: 5ª à 6ª

Visão geral

Os estudantes usarão padrões criados na calculadora com a operação de constante (› ou œ) para desenvolver uma compreensão da notação científica.

Introdução

1. Peça aos estudantes que analisem o padrão criado ao utilizarem 10 como fator.

Exemplo:

1 x 10 = 10 2 x 10 = 20 3 x 10 = 30 10 x 10 = 100

2. Pergunte aos estudantes:

Com base neste padrão, o que você acha que ocorre quando multiplicamos por 10 repetidas vezes?

Conceitos Matemáticos

• multiplicação

• potências de 10

• expoentes

Materiais

• TI-15

• lápis

• atividade do estudante (página 18)

3. Após os estudantes compartilharem suas suposições, peça que utilizem › para testar suas hipóteses. Enquanto os estudantes pressionam ›, peça que registrem os valores exibidos na página Atividade do Estudante.

4. Quando os estudantes chegarem ao ponto em que o contador do lado esquerdo não for mais exibido, pergunte o que acham que aconteceu com a calculadora. (O produto ficou tão grande que não existe espaço para exibi-lo e ao contador, sendo assim o contador foi ignorado.)

Peça aos estudantes que continuem a registrar os dados do contador, mesmo que ele não apareça mais na calculadora.

5. Quando o contador do lado esquerdo reaparecer, peça aos estudantes que descrevam o que aconteceu com o produto mostrado. (Ele foi substituído por uma exibição, à direita, da notação científica: por exemplo,

1x10^11

 Para multiplicar

repetidamente por 10, digite:

› V

1. Isto “programa” a

operação com a constante.

2. Digite 1 como o fator de partida.

3. Pressione ›.

Quando você pressiona

›

pela primeira vez, a calculadora realiza a operação 1 x 10 e o visor exibe:

1x10 110

O 1 representa a utilização de vez.

›

x 10

uma

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Taquigrafia Numérica: Notação Científica

(continuação)

6. Peça aos estudantes que continuem a pressionar › e anotar os resultados.

7. Peça aos estudantes que analisem seus dados e tirem conclusões sobre o visor da notação científica.

Por exemplo, 1 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10.

Explique aos estudantes que a notação exponencial ou científica é uma simplificação de fatores repetidos:

1 x 10

8. Peça aos estudantes que continuem a experimentar o uso da notação científica para representar a multiplicação repetida por 10 com outros fatores de partida. (Por exemplo, quando se usa 2 como o fator de partida, o visor representa a multiplicação de 2 por 10 onze vezes, ou 2 x 10

1x10^11

representa o produto:

Coletando e Organizando Dados

Para concentrar a atenção dos estudantes nas importantes mudanças no visor da calculadora, faça perguntas do tipo:

O que significa o conteúdo

•

3 1000

do visor?

2x10^11

Quando desapareceu o contador à esquerda? O

•

que você acha que aconteceu? Quando reapareceu o contador à esquerda? O

•

que mais mudou?

O produto parece diferente. Ele mudou de 1000000000 para 1x10^10.

Como fica o conteúdo do visor após ocorrer a

•

mudança?

O 1x10 permanece o mesmo, mas o número do lado direito (o expoente) aumenta de um cada vez que › é pressionado e fica igual ao valor do contador à esquerda.

EXAS INSTRUMENTS INCORPORATED

Taquigrafia Numérica: Notação Científica

(continuação)

Analisando Dados e Tirando Conclusões

Para concentrar a atenção dos estudantes na relação entre os fatores de 10 repetidos e o conteúdo do visor em notação científica, faça perguntas do tipo:

Que padrões você observa nos produtos antes

•

que o contador desapareça?

Todos eles têm um 1 seguido pelo mesmo número de zeros que os fatores de 10 usados no produto.

Se você continuasse com esse padrão, qual seria

•

o produto no ponto em que o conteúdo do produto no visor mudasse? Que relação tem o produto com o novo conteúdo do visor?

Por exemplo, produto deveria ser 100.000.000.000. O visor

1x10^11

O que acontece se você usar 2 como o fator de

•

partida e multiplicar por 10 repetidamente?

O conteúdo do visor é o mesmo, exceto que o primeiro número em todos os produtos é 2. O conteúdo do visor

2 x 10

1x10^11

representa o produto 1 x 1011.

está no lugar onde o

2x10^11

representa o produto

Continuando com a Pesquisa

Os estudantes podem usar outras potências de 10 como o fator de repetição, anotar os resultados na tabela e buscar a ocorrência de padrões. Por exemplo, usar 100 como fator de repetição faz com que a parte exponencial exibida da notação científica aumente de 2 cada vez que › é pressionada.

Os estudantes podem usar um fator de partida de 10 ou mais, anotar os resultados na tabela e buscar padrões. Por exemplo, usar 12 como fator de partida logo resulta em um visor de conteúdo onde a parte exponencial do conteúdo do visor é um a mais do que o número de vezes em que 10 foi usado como fator.

12 1.2 x10^13

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Taquigrafia Numérica:

Nome __________________________

Notação Científica

Data __________________________

Coletando e Organizando Dados

Programe o recurso de operação com constante na sua calculadora para multiplicar por 10. Anote os resultados na tabela abaixo para cada vez que você pressionar ›.

Número de

Vezes

___

Usada como

Fator

0 (fator de partida)

Visor

EXAS INSTRUMENTS INCORPORATED

Taquigrafia Numérica:

Nome ___________________________

Notação Científica

Data ___________________________

Analisando Dados e Tirando Conclusões

1. Que padrões você observa?

__________________________________________________________________________

2. O que significa quando o conteúdo do lado direito do visor muda? (Por exemplo,

__________________________________________________________________________

1x10^15

__________________________________________________________________________

3. Tente a atividade novamente com outro múltiplo de 10 e compare os resultados.

__________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Procedimentos Relacionados

Séries: 2ª à 6ª

Visão geral

Os estudantes usarão as duas operações com constantes (› e œ) para comparar os resultados dos diferentes procedimentos matemáticos e determinar a relação entre eles.

Introdução

1. Peça aos estudantes que programem › com +2 e œ com -2.

2. Peça aos estudantes que digitem 8 em suas calculadoras, pressionem › e leiam a saída (1 10, o que significa que adicionar 2 uma vez a 8 resulta em 10).

3. Peça aos estudantes que pressionem œ para aplicar a segunda operação com constantes à saída da primeira operação com constantes e depois ler a saída (1 8, o que significa que subtrair 2 uma vez de 10 resulta em 8).

4. Peça aos estudantes que continuem este processo com vários números como a primeira entrada. Discuta os resultados. (Pressionar › e depois œ sempre leva de volta ao primeiro número de entrada, o que significa que › e œ são procedimentos inversos.)

5. Desafie os estudantes a encontrar mais pares de procedimentos para › e œ que seguirão o mesmo padrão, e a anotar suas experiências usando Procedimentos Relacionados na página de atividade do estudante.

Conceitos Matemáticos

• números inteiros

• adição, subtração, multiplicação, divisão

• frações (Séries: 5ª à 6ª)

• decimais (Séries: 5ª à 6ª)

³ Para usar › e œ:

1. Pressione › (ou

2. Digite a operação e o número (por exemplo,

2).

3. Pressione › (ou œ).

4. Digite o número ao qual deseja aplicar a operação com constantes.

5. Pressione › (ou

). O visor terá um esquerda e o resultado à direita. Se você pressionar (ou œ) novamente, a calculadora aplicará a operação com constantes à saída anterior e exibirá um à esquerda, indicando que a operação com constantes foi aplicada duas vezes à entrada original.

Materiais

• TI-15

• lápis

• atividade do estudante (página 23)

›

EXAS INSTRUMENTS INCORPORATED

Procedimentos Relacionados

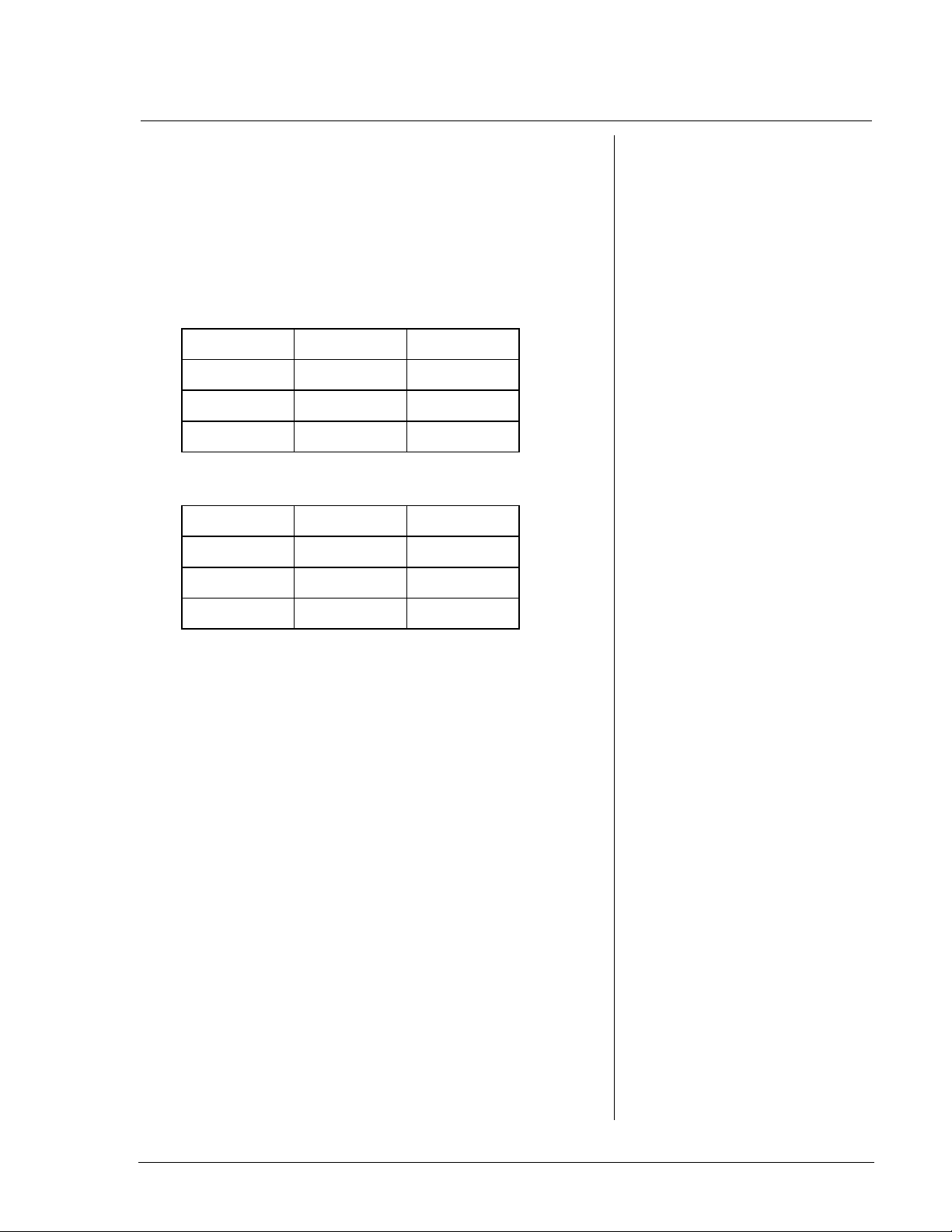
Coletando e Organizando Dados

À medida que os estudantes usam › e œ, peça que anotem seus resultados nas tabelas apropriadas na página Atividade do Estudante. Se um estudante estiver estudando a relação entre exemplo, a tabela poderia ter o seguinte aspecto:

x 2

÷ 2

, por

(continuação)

Tabela para

Entrada Procedimento Saída

Tabela para

Entrada Procedimento Saída

›

1x22 2x24 3x26

2 4 6

Analisando Dados e Tirando Conclusões

Pergunte aos estudantes:

Que padrão você observa nos seus dados?

•

Os procedimentos são inversos uns dos outros?

•

Como você sabe?

Se o número da saída de › for usado como o número de entrada para œ e der um número de saída igual ao número de entrada original para ›, então os procedimentos podem ser inversos

x 2

÷ 2

entre si, como em

O padrão funciona com números especiais

•

como 1 e 0? Com frações e decimais? Com inteiros positivos e negativos?

³ Para reconhecer os

procedimentos equivalentes, os estudantes podem precisar usar a tecla

para mudar as saídas da forma decimal para fração ou vice-versa.

• O que acontece se você usar œ primeiro e

depois ›?

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Procedimentos Relacionados

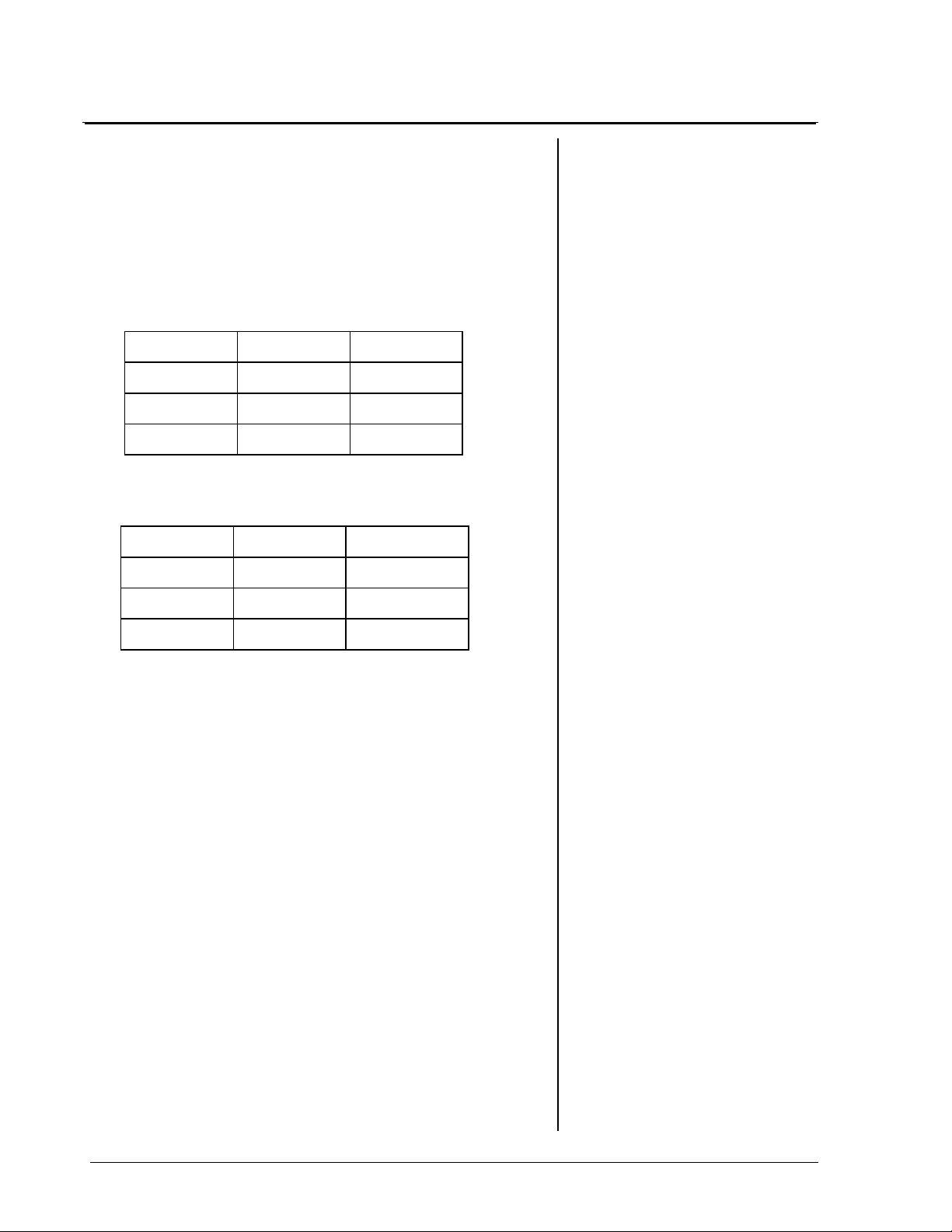
Continuando a Pesquisa

Os estudantes mais adiantados podem experimentar procedimentos equivalentes, como dividir por um número e multiplicar por seu recíproco. Se um estudante estiver testando a relação entre exemplo, a tabela pode ter a seguinte aparência:

x ½

÷ 2

, por

(continuação)

Tabela para

Entrada Procedimento Saída

Tabela para

Entrada Procedimento Saída

›

1x 2x 3x

½½ ½ ½

1 2 3

P2 0,5 = P 2 P 2 1,5 = 1

10 =

1½

1,5 = 1

EXAS INSTRUMENTS INCORPORATED

Procedimentos

Nome ___________________________

Relacionados

Data ___________________________

Coletando e Organizando Dados

1. Escolha um procedimento para › (por exemplo,

2. Escolha um procedimento para œ (por exemplo,

3. Selecione um número de entrada ao qual o procedimento será aplicado e anote os números de entrada e saída na tabela apropriada.

4. Use a tabela abaixo para registrar e comparar seus resultados usando › e œ.

Tabela para › Tabela para œ

Entrada Procedimento Saída Entrada Procedimento Saída

x ½

÷ 2

Analisando Dados e Tirando Conclusões

5. Que comparação você faz entre os dois procedimentos?

__________________________________________________________________________

6. Que padrões você observa?

__________________________________________________________________________

7. Os dois procedimentos estão relacionados? Explique.

__________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

No Intervalo

Séries: 3ª à 6ª

Visão geral

Os estudantes interpretarão o arredondamento envolvido na medição, para identificar o possível intervalo de valores de uma dada medição.

Introdução

1. Peça aos estudantes que meçam o comprimento de uma mesa ou escrivaninha na sala e anotem o valor da medição com aproximação de milímetros, por exemplo, 1357 mm.

Comente como as medidas em milímetros podem ser anotadas como 1357 mm ou como milésimos de metros, 1,357 m. Observe que a medida foi arredondada para 1357 mm porque ficava entre ½ milímetro menos que 1357 mm (1356,5 mm) e ½ milímetro mais que 1357 mm (1357,5 mm).

Conceitos Matemáticos

• arredondando números inteiros

• arredondando decimais

• medição usando unidades métricas (comprimento, massa, capacidade)

Materiais

• TI-15

• lápis

• varetas de medição ou fitas métricas

• atividade do estudante (página 27)

1356,5 1357 1357,5

2. Então peça aos estudantes que usem o arredondamento para anotar a mesma medida com aproximação de centímetros (136 cm ou 1,36 m).

3. Digite a medida original na calculadora como 1,357 e fixe o visor em duas casas decimais.

4. Peça aos estudantes que fixem o visor para uma casa decimal. Pergunte: O que representa este número? (A medida arredondada até o décimo mais próximo de um metro ou a medida arredondada para 14 decímetros.)

³ Para fixar o visor em 2

casas decimais, pressione Š ™ ®.

³ Peça aos estudantes

que comentem como

1.36 (1,36)

o arredondamento da medida de 136 cm.

EXAS INSTRUMENTS INCORPORATED

coincide com

No Intervalo

(continuação)

5. Peça aos estudantes que fixem o visor para nenhuma casa decimal. Pressione Š e depois “ para exibir O que representa este número? (A medida arredondada até o metro mais próximo.)

6. Introduza o jogo In the Range (No Intervalo) digitando secretamente na calculadora um número de três casas decimais para representar uma medida em milímetros; por exemplo, 2.531. Em seguida, exiba o número arredondado até o número inteiro mais próximo (3). Mostre o visor aos estudantes.

7. Informe aos estudantes que esse número representa a medição do comprimento de uma tábua até o metro mais próximo. Pergunte aos estudantes:

Qual seria a sua medição se ela houvesse sido feita até o decímetro mais próximo?

(2,5 m a 3,5 m)

8. Arredonde o número original até o décimo mais próximo (2,5). Pergunte aos estudantes:

O valor está no intervalo que nós identificamos?

. Pergunte:

³ Para arredondar até o

número inteiro mais próximo, pressione

Š “ ®

³ Para arredondar até o

décimo mais próximo, pressione Š ˜ ®.

9. Repita a medição até o centímetro (centésimo) e até o milímetro (milésimo) mais próximos. (O intervalo para os centímetros deve ser de 2,45 a 2,55, estando 2,53 contido nesse intervalo; e o intervalo para os milímetros deve ser de 2,525 a 2,535, estando 2,531 contido nesse intervalo.)

10. Peça aos estudantes que trabalhem em pares para participar do jogo e anotar suas observações nas páginas de atividade do estudante.

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

No Intervalo

(continuação)

Coletando e Organizando Dados

Enquanto os estudantes estão jogando, concentre a atenção deles nos padrões que estão desenvolvendo, fazendo perguntas do tipo:

Quando você anota uma medida, por que o

•

arredondamento está sempre envolvido? Quando você faz uma medição, que intervalo

•

essa medição deve sempre indicar? (½ unidade a menos ou ½ unidade a mais)

Que aspecto teria este intervalo em uma trena

•

(ou vareta de medição)? Como é que ½ é representado no sistema

•

métrico? Qual a sua decisão sobre como representar o

•

intervalo de possíveis medidas? Que padrões você está usando?

Analisando Dados e Tirando Conclusões

Para ajudar os estudantes a analisar seus dados, faça perguntas do tipo :

Que intervalo é indicado por cada medida?

•

Que padrões você usou para identificar o

•

intervalo de possíveis medidas? Como você usaria esses padrões para

•

arredondar 256,0295 até o décimo mais próximo?

Continuando com a Pesquisa

Peça aos estudantes que substituam as unidades de comprimento por unidades de massa (gramas, centigramas) ou capacidade (litros, mililitros) para observar os mesmos padrões.

Peça aos estudantes que discutam o motivo pelo qual a abordagem do valor posicional com a calculadora não funciona para as medidas em jardas, pés e polegadas. Peça-lhes que identifiquem em que intervalo estaria uma medição, se ela fosse medida para a jarda mais próxima, até o pé mais próximo e para a polegada mais próxima. (Por exemplo, 2 jardas estariam entre 1 jarda e 18 polegadas, e 2 jardas e 18 polegadas.)

EXAS INSTRUMENTS INCORPORATED

Nome ___________________________

No Intervalo

Data ___________________________

Coletando e Organizando Dados

Peça ao seu colega que secretamente digite uma medida com três casas decimais na calculadora e em seguida fixe o número a ser arredondado até o número inteiro mais próximo. Agora observe o visor e responda às seguintes perguntas:

1. Qual a medida até o metro mais próximo? _____________________

a. Qual poderia ser o intervalo da medida se houvesse sido feita até o

décimo mais próximo de um metro (decímetros)?

_______________________________________________________________________

b. Configure Š até o décimo mais próximo (˜).

Qual é a medida até o décimo mais próximo? ________________

Esse valor está no intervalo que você identificou? ____________

2. Qual é a medida até o décimo mais próximo de um metro? _______

a. Qual poderia ser o intervalo da medida se houvesse sido feita até o

centésimo mais próximo de um metro (centímetros)?

_______________________________________________________________________

b. Configure Š até o centésimo mais próximo (™).

Qual é a medida até o centésimo mais próximo? ______________

Esse valor está no intervalo que você identificou? ____________

3. Qual é a medida até o centésimo mais próximo de um metro? _____

a. Qual poderia ser o intervalo da medida se houvesse sido feita até o

milésimo mais próximo de um metro (milímetros)?

_______________________________________________________________________

b. Configure Š até o milésimo mais próximo (š).

Qual é a medida até o milésimo mais próximo? _______________

Esse valor está no intervalo que você identificou? ____________

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Nome __________________________

No Intervalo

Data __________________________

Analisando Dados e Tirando Conclusões

Identifique três medidas até o milímetro mais próximo que seriam:

a. 10 m quando arredondados até o metro mais próximo. ________

b. 9,0 m quando arredondados até o décimo mais próximo de um

metro (decímetro).

_______________________________________________________________________

c. 9,05 m quando arredondados até o centésimo mais próximo de um

metro (centímetro).

_______________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

A Importância do Valor Posicional

Séries: 2ª à 6ª

Visão geral

Os estudantes desenvolverão sua habilidade em utilizar números, explorando as relações entre os símbolos numéricos e sua representação através de materiais de base dez.

Introdução

1. Leia Counting On Frank (Contando com Frank) de Rod Clement. Comente sobre outros tipos de perguntas que uma pessoa faria sobre quantos objetos cabem dentro de outros objetos ou sobre eles.

2. Dê a cada grupo de estudantes uma grande quantidade de unidades (mais de 300) dos materiais de base dez, e diga-lhes que esta é a quantidade máxima de jujubas que cabe no pote que você encheu. Peça-lhes que contem as “jujubas” e observe as técnicas usadas (contando uma por vez, fazendo grupos de 10, etc.)

3. Diga aos estudantes que não existem mais jujubas, então pergunte:

Conceitos Matemáticos

Séries: 2ª à 4ª

• valor posicional de números inteiros (até os milhares)

• dinheiro

Séries: 4ª à 6ª

• valor posicional decimal (até os milésimos)

• unidades métricas (metros, decímetros, centímetros)

³ Para usar o recurso Valor

Posicional para esta atividade:

1. Pressione ‹ ‡.

2. Pressione " ® para selecionar MAN (Manual).

3. Pressione $ ® para configurar o modo

Value

para saber quantas unidades, dezenas, centenas, etc., existem em um número. (O modo – localizar o dígito na casa das unidades, das dezenas, das centenas, etc.)

Materiais

• TI-15

• lápis

Counting on

•

Frank (Contando com Frank)

de Rod Clement

• materiais de base 10

• atividade do estudante (páginas 32 e 33)

–. Isto permite

– . é usado para

Place

Quantos “bastões” (grupos de 10) eu precisaria usar para fazer uma pilha de jujubas do mesmo tamanho da sua?

4. Peça aos estudantes que reflitam sobre a resposta para este problema usando seus materiais ou apliquem o conhecimento do valor posicional. Depois mostre-lhes como explorar a resposta usando a calculadora.

5. Peça aos estudantes que comparem suas soluções usando seus materiais de base dez com o resultado da calculadora. (Eles podem fazer 31 dezenas de bastões com as 314 unidades, sobrando 4 unidades.)

EXAS INSTRUMENTS INCORPORATED

³ Para explorar as respostas

para este problema na calculadora:

1. Pressione ‹.

2. Digite o número de unidades (por exemplo,

314).

3. Pressione Œ ’ para observar o visor. (Usando 314, o visor mostra significando que existem 31 dezenas em 314.)

TI-15: Manual do instrutor

A Importância do Valor Posicional

(continuação)

Coletando e Organizando Dados

Peça aos estudantes que usem seus materiais de base dez e a calculadora para continuar a experimentação com outros números, identificando quantas centenas e milhares (e 0.1s e 0.01s para os estudantes mais adiantados). Estimule a exploração com perguntas do tipo:

Quantas centenas existem em 120? 2478?

•

3056? Quantas dezenas existem em 120? 2478? 3056?

•

Quantos elementos (unidades) existem em 120?

•

2478? 3056? Que números têm 12 unidades? 12 dezenas? 12

•

centenas? Que números têm 60 unidades? 60 dezenas? 60

•

centenas?

Analisando Dados e Tirando Conclusões

Peça aos estudantes que usem a tabela em A Importância do Valor Posicional - página Atividade

do Estudante para anotar seus achados e identificar os padrões observados. Para ajudá-los a concentrar sua atenção nos padrões, faça perguntas do tipo:

³ Os estudantes podem

usar o modo

Place Value para

– .

testar suas suposições. Por exemplo, se acharem que 1602 tem 160 centenas, digitam

1602

, pressionam Œ

íí

– 1

– .

16.

para

íí

‘ e vêem Podem então usar os materiais de base dez para ver por que existem apenas 16 centenas em 1602. (Se os estudantes usarem o modo localizar o dígito que ocupa a casa das centenas, verão í no visor, mostrando que 6 é o dígito que ocupa a casa das centenas.

Qual a comparação entre o número de dezenas em

•

1314 e o próprio número 1314? E em 567? 2457? 4089, etc.?

Se cobrir o dígito da casa das unidades, você verá quantas dezenas existem em um número.

Qual a comparação entre o número de centenas em

•

1314 e o próprio número 1314? E em 567? em 2457? em 4089, etc.?

Se cobrir os dígitos à direita da casa das centenas, você verá quantas centenas existem em um número.

Qual a comparação entre o conteúdo do visor da

•

calculadora e aquilo que você pode fazer com os materiais de base dez?

Se a calculadora mostra 31_, para 316, então eu devo ser capaz de fazer 31 dezenas de bastões com as 316 unidades que eu tenho.

EXAS INSTRUMENTS INCORPORATED

A Importância do Valor Posicional

Continuando a Pesquisa

Relacione os padrões do valor posicional com o valor do dinheiro. Por exemplo, pergunte aos estudantes:

Se cada uma das suas “jujubas” custar um

•

centavo, quantos centavos você gastaria com 1314 jujubas?

1314 centavos.

Quantas moedas de de 10 centavos (dezenas)

•

você gastaria?

131 moedas de de 10 centavos e mais 4 centavos.

Quantos dólares (centenas)?

•

13 reais, mais 14 centavos, ou 1 moedasde de 10 centavos e 4 centavos.

Os estudantes mais adiantados podem anotar o valor do dinheiro (e digitar na calculadora) na forma decimal, 13.14. Então eles podem usar a calculadora para relacionar as moedas de de 10 centavos com um décimo (0,1) de um dólar ($13.14 tem 131 moedas de de 10 centavos ou décimos) e os centavos com um centésimo (0,01) de um real ($13.14 tem 1314 centavos ou centésimos).

(continuação)

Para os estudantes mais adiantados, relacione os padrões do valor posicional com as conversões entre unidades métricas. Por exemplo, uma medida de 324 centímetros também pode ser anotada como 32,4 decímetros (ou arredondada para 32 dm) porque 1 dm = 10 cm, ou pode ser anotada como 3,25 metros (ou arredondada para 3 m), porque 1 m = 100 cm.

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Nome _____________________________

A Importância do Valor

Data _____________________________

Posicional, Parte A

Coletando e Organizando Dados

1. Use seus materiais de base dez e a sua calculadora para verificar quantas dezenas, centenas e milhares existem em um número. Anote as suas observações na tabela. Que padrões você vê?

Número

Número de

milhares

Número de

centenas

Número de

dezenas

Analisando Dados e Tirando Conclusões

2. Escreva 5 números que tenham 15 dezenas.

___________________________________________________________________________

3. Escreva 5 números que tenham 32 centenas.

___________________________________________________________________________

4. Escreva 5 números que tenham 120 dezenas.

___________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

Nome _____________________________

A Importância do Valor

Data _____________________________

Posicional, Parte B

Coletando e Organizando Dados

1. Use seus materiais de base dez e a sua calculadora para explorar quantos décimos, centésimos e milésimos existem em um número. Anote as suas observações na tabela. Que padrões você vê?

Número Número de

décimos

Número de

centésimos

Número de

milésimos

Analisando Dados e Tirando Conclusões

2. Escreva 5 números que tenham 15 décimos.

__________________________________________________________________________

3. Escreva 5 números que tenham 32 centésimos.

__________________________________________________________________________

4. Escreva 5 números que tenham 120 décimos.

__________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Qual o Problema?

Séries: 2ª à 5ª

Visão geral

Os estudantes associarão sentenças numéricas a situações de problemas e usarão adição, subtração, multiplicação e divisão para resolver os problemas.

Introdução

1. Utilizando uma faixa com a sentença ou usando uma transparência, exiba uma sentença numérica como “8 + 2 = ?” Faça com que os estudantes pensem em situações e questões associadas que poderiam ser representadas por essa sentença. Por exemplo, “Se eu comprei oito cartões postais nas férias e já tinha dois cartões em casa, quantos cartões postais tenho agora?”

2. Se necessário, peça aos estudantes que simulem a situação com contadores e determinem que o valor de “?” é 10.

3. Demonstre como exbir esta equação na calculadora e como informar à calculadora qual é o valor de ?.

4. Agora exiba uma equação do tipo ? - 10 = 5. Peça aos estudantes que reflitam sobre as situações e questões relacionadas que poderiam ser representadas por esta sentença numérica. Por exemplo, “Eu tinha algum dinheiro no bolso e gastei 10 centavos. Agora só me restam 5 centavos. Quanto eu tinha em dinheiro no começo?” Peça aos estudantes que pratiquem a seqüência de teclas necessária para exibir esta equação e testar o valor de “?” determinado por eles.

5. Durante um certo tempo, continue a apresentar diferentes tipos de sentenças numéricas para os estudantes testarem. Por exemplo, ? - 8 < 5 (que tem 13 soluções de números inteiros) e ? x ? = 24 (que tem 8 soluções de pares de fatores de números inteiros) e ? x 4 = 2 (que não tem solução de número inteiro).

Conceitos Matemáticos

• adição, subtração

• multiplicação, divisão (Séries: 3ª à 5ª)

• sentenças numéricas (equações)

• desigualdades (Séries: 3ª à 5ª)

³ Para exibir esta

equação na calculadora, coloque a calculadora no modo Solução de Problemas pressionando a tecla ‹. Em seguida, digite a equação 8 + 2 = ? e pressione ®. O visor da calculadora (1 SOL) informa quantas soluções de número inteiro existem para a equação.

Para testar a sua solução para a equação, digite o valor de 10 e pressione ®. A calculadora exibirá YES.

³ Se um valor incorreto

for testado para ?, a calculadora exibirá NO e fornecerá uma dica. Por exemplo, se um estudante testar 5 para a equação ? - 10= 5, a calculadora exibe NO, depois mostra 5 - 10 < 5 e, em seguida, volta à equação original.

Materiais

• TI-15

• contadores

• lápis

• atividade do estudante (página

37)

EXAS INSTRUMENTS INCORPORATED

Qual o Problema?

(continuação)

Coletando e Organizando Dados

Como uma atividade contínua, peça aos estudantes que trabalhem em pares e use a folha Qual o Problema? Atividade do Estudante para criar os cartões de solução de problemas. Peça que o colega crie uma sentença numérica com uma adição, subtração, multiplicação ou divisão usando a “?” e anote na caixa superior e registre na calculadora. Se possível, o outro colega cria uma situação e uma pergunta que serão anexadas à sentença numérica e a registra na caixa inferior. As duas caixas podem ser fixadas com cola ou fita gomada aos lados opostos de um cartão de fichário.

Peça aos estudantes que trabalhem junto com a calculadora para testar quantas soluções de números inteiros a equação tem e que testem quais são as soluções. Forneça idéias para esse estudo, fazendo perguntas do tipo:

Que ações poderiam estar acontecendo na sua

•

história para necessitar da adição (subtração, multiplicação ou divisão)?

Como estes contadores poderiam ser usados

•

para representar esta sentença numérica? O que representaria este número na sentença

•

numérica da sua história? O que representaria o ponto de interrogação da

•

sentença numérica na sua história? Você conseguiria fazer uma história para uma

•

sentença numérica que comece com um ponto de interrogação?

Analisando Dados e Tirando Conclusões

Para concentrar o pensamento dos estudantes nas relações entre suas histórias, números e as operações de suas sentenças numéricas, faça perguntas do tipo:

De que maneira a utilização de um número

•

diferente aqui modificaria a sua história? De que maneira usar um símbolo de maior que

•

ou menor que, ao invés de um sinal de igualdade na sentença numérica, modificaria a sua história?

•

De que maneira usar uma operação diferente na sua sentença numérica modificaria a sua história?

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Qual o Problema?

(continuação)

Continuando a Pesquisa

• Peça aos colegas que criem histórias e as

troquem. Cada colega pode então escrever uma sentença numérica para ser usada com a história do outro colega.

• Peça aos estudantes que classifiquem as

sentenças numéricas que fizeram em categorias: exemplo, as com 0 soluções de números inteiros, as com uma solução de números inteiros, as com duas soluções de números inteiros, as com um número infinito de soluções de números inteiros.

• Peça aos estudantes que encontrem uma equação

ou inequação com exatamente 0 soluções de números inteiros, exatamente 1 solução de números inteiros, exatamente 2 soluções de números inteiros, mais de 5 soluções de números inteiros, etc.

EXAS INSTRUMENTS INCORPORATED

Nome ___________________________

Qual o Problema?

Data ___________________________

Escreva uma sentença numérica usando uma operação e o “?”

Escreva uma história que descreva uma situação e faça perguntas que possam ser representadas pela sentença numérica.

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Como Usar

a TI.15

Visor, Rolagem, Ordem de

Operações, Parênteses 39 Apagando e Corrigindo 42 Menus de Modo 45 Operações Básicas 49 Operações com Constantes 55 Números Inteiros e Decimais 63 Memória 68 Frações 7 1 Porcentagem 80 Pi 84 Potências e Raízes Quadradas 88 Solução de Problemas: Modo Auto 94 Solução de Problemas: Modo Manual 100 Valor Posicional 106

EXAS INSTRUMENTS INCORPORATED

Visor, Rolagem, Ordem das Operações e Parênteses

Teclas

abre uma expressão entre

parênteses. É possível ter até 8 parênteses por vez.

fecha uma expressão entre

parênteses.

e " movem o cursor para a

esquerda e para a direita, rolando a linha de entrada.

e $ movem o cursor para cima e

para baixo mostrando as entradas anteriores e resultados.

Notas

Os exemplos dos modelos de

•

transparência assumem todas as definições padrão.

O modelo de transparência EOS

•

demonstra a seqüência na qual são realizados os cálculos na TI-15.

Ao usar os parênteses, se pressione

•

antes de pressionar Y,

Syn Error

pressionar

ou Y,

As operações dentro dos parênteses

•

são realizadas primeiro. Use X ou para mudar a ordem das operações e, portanto, alterar o resultado.

Exemplo:

será exibido. Se você

antes de pressionar

Error ?

1 + 2 x 3 = 7 (1 + 2) x 3 = 9

será exibido.

A primeira e a segunda linhas exibem

•

entradas com até 11 caracteres mais

um ponto decimal, um sinal negativo e um expoente negativo ou positivo com 2 dígitos. As entradas começam à esquerda e rolam para a direita. Uma entrada sempre apresentará uma quebra de linha no operador.

Os resultados são exibidos alinhados

•

à direita. Se todo o problema não couber na primeira linha, o resultado será exibido na segunda linha.

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Equation Operating System (Sistema de Operação de Equação)

Prioridade Funções

EOS

1 (primeiro)

X Y

¨ ¬

V W

T U

¦ Ÿ

8 (último)

Como as operações de dentro dos

parênteses são

executadas primeiro, você pode usar X Y para mudar a ordem das operações e, portanto, alterar o resultado.

EXAS INSTRUMENTS INCORPORATED

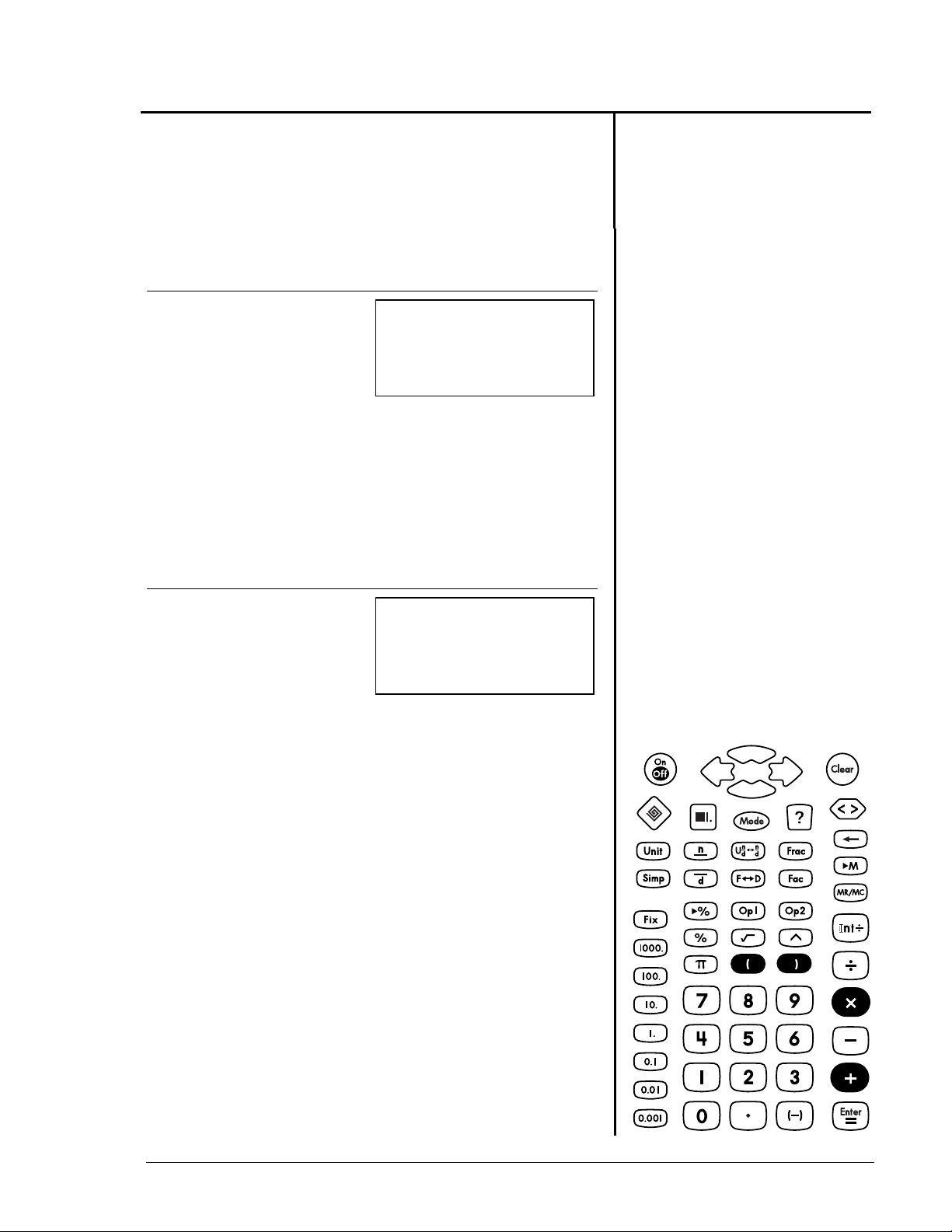
Ordem das operações

1 + 2 x 3 =

Pressionar Visor

1Û2Ý3Ú 7

(1 + 2) x 3 =

Pressionar Visor

Adicionar

Multiplicar

Parênteses

X Y

X V

1 3

Å1Û2ÆÝ3Ú 9

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Apagando e Corrigindo

Teclas

3. ” apaga a última entrada e qualquer

liga e desliga a calculadora.

−

apaga o último dígito introduzido,

permitindo a correção de uma entrada sem digitar todo o número novamente.

condição de erro. Você pode digitar um novo número e continuar com o cálculo. Quando pressionada duas vezes, apaga todas as operações pendentes. Assim que o visor se apaga, move o cursor para entrada mais recente.

Notas

Os exemplos dos modelos de

•

transparência assumem todas as definições padrão.

Pressionar − e ” simultaneamente

•

reinicializa a calculadora. Reinicialização da calculadora:

Retorna as definições aos valores

−

padrão. Apaga a memória e as

−

constantes.

Pressionar ” não afeta as memórias

•

nem as constantes.

EXAS INSTRUMENTS INCORPORATED

Apagando entradas

1. Digite 335 + 10.

2. Apague a entrada e as operações pendentes.

3. Digite 335 N 9.

4. Complete o cálculo.

Pressionar Visor

335

335Û103

”

(apague a entrada)

335

335Ü9

Apagar

”

335Ü9Ú 326

Nota: ” apaga a tela, mas não o histórico.

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Corrigindo erros de entrada usando w

1. Digite 1569 + 3.

2. Troque o 9 por um 8.

3. Adicione 3.

4. Complete o cálculo.

Pressionar Visor

1569

w w w

1569Û3á

1568á

1568Û3á

Backspace

1568Û3Ú 1571

EXAS INSTRUMENTS INCORPORATED

Menus de Modo

Teclas

Veja nas próximas duas páginas as tabelas contendo os detalhes de cada opção de configuração do modo.

exibe o menu Modo Calculadora a

‡

seguir, do qual você pode selecionar:

Configuração Opções

Divisão (P)

Constantes (Op)

Apagar Ops

RESET

(decimal)

. n/d

+1 ?

Op 1 Op 2

N Y

(fração) (exibir)

(ocultar)

(apagar Op 1) (apagar Op 2)

(Não) (Sim)

‹ ‡

de Problemas apresentado a seguir, do qual você pode selecionar:

Configuração Opções

Modo

Nível de dificuldade Operação

Opção do visor

As opções do visor só aparecem se você houver selecionado o modo Manual. Nível de dificuldade e operação só aparecem se você houver selecionado o modo Automático.

apresentado a seguir, do qual você pode selecionar:

exibe o menu Modo Solução

Auto

(Manual)

Man 1 2 3

+ – x P ?

(adicionar, subtrair, multiplicar, dividir, localizar a operação)

11-. 1-.

exibe o menu Frações,

Configuração Opções

Exibir Simplificar

Notas

Os exemplos dos modelos de

•

transparência assumem todas as definições padrão.

É necessário estar em Solução de

•

Problemas (‹) para ver seu menu ao pressionar verá o menu Modo Calculadora.

Pressione

•

Modo Calculadora, menu Modo de Solução de Problemas, ou

Fração. Pressione seleção e, em seguida, pressione ou

‡

para exibir o menu

‡

para exibir o menu Modo de

novamente para sair do menu.

U n/d n/d Man

. Caso contrário, você

‹‡

para exibir o

após efetuar a

Auto

‡

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Menus de Modo

(continuação)

Menu do Modo Calculadora

Configuração Opção Explicação Exemplo

Division (Þ)

Constant Operations (OP)

Clear OP1 Quando selecionada, apaga Op1

Reset N Não; não reinicializa a calculadora.

n/d Exibe os resultados da divisão como

+1 Mostra a operação com constante no

? Oculta a operação com constante

OP2 Quando selecionada, apaga Op2

Y Sim; reinicializa a calculadora.

Exibe os resultados da divisão como decimal

fração

visor

Menu do Modo Solucionador de Problemas

.75

3 4

1x5 15

Configuração SubMenu Opção Exemplo

Auto

Manual Opção do visor

Nível de dificuldade

Operação

(somente para o Valor da Posição no Solucionador de Problemas)

1 2 3

+ – x P ?

multiplica, divide e localiza a operação)

(Exibe o número de unidades,

11-.

dezenas, centenas ou milhares)

(Exibe o dígito que está casa das

1-.

unidades, dezenas, centenas ou milhares)

(adiciona, subtrai,

1234 For ‘: 12_ _

1234 For ‘: _ 2 _ _

EXAS INSTRUMENTS INCORPORATED

Menus de Modo

(continuação)

Menu de Frações

Configuração Opção Explicação Exemplo

Display

Simplify Man Permite simplificação manual

U n/d

n/d Exibe os resultados como frações

Auto Simplifica automaticamente para a

Exibe os resultados como números mistos

impróprias

forma mais reduzida da fração

3 4

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Operações Básicas

Teclas

adiciona.

subtrai.

multiplica.

divide. O resultado pode ser exibido

como um d ecimal ou como uma fração, dependendo da configuração de modo selecionada.

divide um número inteiro por outro

inteiro e exibe o resultado como um quociente e um resto.

completa a operação.

permite a introdução de um número

negativo.

Notas

Os exemplos dos modelos de

•

transparência assumem todas as definições padrão.

O resultado de Divisão de Inteiro

•

aparece sempre como quociente e resto (__

O número máximo de dígitos para o

•

quociente ou para o resto ( quociente, o resto e o caractere r não podem totalizar mais de 10 caracteres.

Se o resultado da divisão de inteiros

•

for usado em outro cálculo, apenas o quociente será usado. O resto é ignorado.

Todos os números usados com

•

devem ser números inteiros positivos.

__).

) é 5. O

Se você tentar dividir por 0, uma

•

mensagem de erro será exibida.

T, U, V, W, ®

•

com as constantes incorporadas.

funcionam

EXAS INSTRUMENTS INCORPORATED

Operações Básicas

Adicionar, Subtrair

2 + 54 N 6 =

Pressionar Visor

2 6

3 x 4 P 2 =

Pressionar Visor

2Û54Ü6Ú 50

T U

Multiplicar, Dividir

V W

Igual

3Ý4P2Ú 6

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Digitando números negativos

A temperatura em Utah era de N3° C às 6 horas. Às 10 horas, a temperatura havia subido 12° C. Qual era a temperatura às 10 horas?

Pressionar Visor

3Û12Ú 9

Negativa

EXAS INSTRUMENTS INCORPORATED

Divisão com restos

Cris tem 27 tabletes de chicletes. Ele deseja dividir os tabletes igualmente entre ele mesmo e 5 amigos. Quantos tabletes receberá cada pessoa? Quantos tabletes sobrarão?

Pressionar Visor

27Þ

6Ú 4½3

Divisão de Inteiro

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Divisão com resultado decimal

Configure a opção de exibição da divisão para decimal e divida 27 por 6.

Pressionar Visor

‡ ®

»Ä¸

‡

27Þ

6 Ú 4Ù5

Dividir

EXAS INSTRUMENTS INCORPORATED

Divisão com resultado fracionário

Configure a opção de exibição da divisão para fracionária e divida 27 por 6.

Pressionar Visor

‡" ®

»Ä¸ êêêê

‡

27Þ

6Ú 4

Dividir

êêêê

¤®

5 1

êêêê

êêê

10 2

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Calculando unidades de tempo equivalentes

Sara correu 2 quilômetros em 450 segundos. Converta o tempo dela para minutos e segundos.

450 segundos = ? minutos

? segundos

Pressionar Visor

450

450Þ60Ú 7½30

Divisão de Inteiro

EXAS INSTRUMENTS INCORPORATED

Operações com Constantes

Teclas

Notas

•

permite que você defina ou execute

›

a operação 1.

permite que você defina ou execute

a operação com constante 2.

Os exemplos dos modelos de transparência assumem todas as definições padrão.

A memória constante é definida em

•

conjunto com faz um cálculo que usa

A função constante funciona com

•

números inteiros, decimais e frações. Ao usar

•

contador à esquerda e o total aparece à direita do visor. O contador mostra quantas vezes a constante foi repetida. Se o número à direita do visor exceder a 6 dígitos, o contador não será mostrado. O contador volta a 0 após chegar a 99.

e ¨.

›

, aparece um

quando você

T, U, V, W

Ao usar

•

constante, os cálculos subseqüentes são realizados com a parte do quociente do resultado. O resto é ignorado.

Você pode apagar uma constante

•

armazenada reinicializando a calculadora (pressionando − e simultaneamente) ou pressionando

‡

, pressionando $ para navegar até o menu CLEAR, selecionando OP1 (ou OP2) e pressionando Pressionar apenas − não apaga a função constante.

com a função

”

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Adição do tipo “contagem sucessiva”

Existem 4 rãs em um tanque. Se outras 3 rãs pularem no tanque, uma de cada vez, quantas rãs haverá no tanque?

Pressionar Visor

› T

(armazena a

›

Û1

Op1

Operações com

Constantes

›

Adicionar

operação)

(inicializa usando 4)

›

(adiciona 1 por vez)

4Û1 15

›

5Û1 26

›

6Û1 37

Op1

EXAS INSTRUMENTS INCORPORATED

Multiplicação do tipo “adição repetida”

Maria colocou novos azulejos na cozinha. Ela fez 4 fileiras de 5 azulejos em cada fileira. Use a adição repetida para determinar quantos azulejos ela usou. Antes de começar, configure a calculadora para ocultar a operação com a constante.

Operações com

Constantes

›

Pressionar Visor

‡$"

+1 Ã

‡

á+

› T

(armazena a operação)

›

Û5

(inicializa usando 0)

0á

êê

¼Á

Op1

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Multiplicação do tipo “adição repetida”

Press Display

›

1 5

›

210

›

315

›

420

Op1

EXAS INSTRUMENTS INCORPORATED

Potências como “multiplicação repetida”

Use esta fórmula e a multiplicação repetida para calcular o volume de um cubo com uma base de 5 metros.

V = l x w x h = 5 x 5 x 5 = 5

Pressionar Visor

› V

(armazena a

›

Ý5

Op1

Operações com

Constantes

›

Multiplicar

operação)

1á

(inicializa usando 1)

›

1Ý5 15

›

5Ý5 225

›

25Ý5 3 125

Op1

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Usando ¨ como uma constante

Use esta fórmula para calcular o volume de cada cubo.

V = base

Pressionar Visor

› ¨

›

Op1

É3

Operações com

Constantes

›

Potências

›

Op1

2É3 18

Op1

›

3É3 127

Op1

›

4É3 164

EXAS INSTRUMENTS INCORPORATED

Usando OP 1 e OP 2 juntos

Ming recebeu 5 decalques para cada tarefa doméstica que ela realizou. Ela deu 2 decalques ao irmão dela para ajudá-la em cada tarefa. Se eles concluiram 3 tarefas, com quantas decalques ela ficou?

Pressionar Visor

› T

œ U

›

Û5

Ü2

Op1

Op1 Op2

Operações com

Constantes

›

0á

›

0Û5 15

5Ü2 13

›œ

8Ü2 16

›œ

11Ü2

Op1 Op2

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Apagando operações com constantes

Antes de digitar uma nova operação em OP1 ou OP2, é necessário apagar os valores atuais.

Press Display

‡

Ù ßÄ¸

$ $

¼ÁÏ ¼Á2 êêêê

(apaga OP1)

¼ÁÏ ¼Á2 êêêê

Menu Mode

‡

" ®

(apaga OP2)

‡

(sai do menu Modo)

Nota:

com constantes.

Pressionar ” não apaga as operações

¼ÁÏ ¼Á2

êêêê

EXAS INSTRUMENTS INCORPORATED

Números Inteiros e Decimais

Teclas

introduz um ponto decimal.

define o número de casas decimais

em conjunto com as teclas de Valor Posicional (de 3 a 9 na ilustração abaixo). Apenas o valor exibido é arredondado; o valor armazenado internamente não é arredondado. O valor calculado será completado com zeros à esquerda, se necessário.

Š 

milhar.

arredonda os resultados no

Š ‘

centena.

Š ’

dezena.

Š “

unidade.

Š ˜

décimo mais próximo.

Š ™

o centésimo mais próximo.

Š š

o milésimo mais próximo.

arredonda os resultados na

arredonda os resultados até o

arredonda os resultados até

Š r

decimal fixo. É necessário pressionar Š antes de

uma tecla de Valor Posicional cada vez que você desejar alterar o número de casas para arredondamento.

Notas

Os exemplos dos modelos de

•

transparência assumem todas as definições padrão.

A calculadora automaticamente

•

arredonda o resultado, de acordo com o número selecionado de casas

2 3

4 5

decimais. (Apenas o valor exibido é arredondado. O valor armazenado internamente não é arredondado.)

remove a configuração de

8 9

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Números Inteiros e Decimais

Notas

•

(continuação)

Todas as entradas são exibidas com a configuração fixa, até que você apague a configuração pressionando Š r ou reinicialize a calculadora.

Você pode definir de 0 a 3 casas decimais.

Se os estudantes ficarem confusos quando tentarem arredondar .555 (,555 ) até o número inteiro mais próximo, por exemplo, e o resultado for 1, talvez seja necessário recapitular com eles as regras do arredondamento.

Você pode usar Š para definir o número de casas decimais durante um cálculo. No entanto, você ainda pode usar r para digitar números com um decimal flutuante, independentemente da configuração decimal fixa.

É necessário pressionar

•

FIX seja ativado.

para que

EXAS INSTRUMENTS INCORPORATED

Definindo o número de casas decimais

Arredonde 12,345 para a casa centesimal, depois para a casa decimal, para a casa milesimal e, em seguida, cancele a configuração FIX.

Pressionar Visor

345

12Ù345Ú

12Ù345

Fix

Š ™

12Ù345Ú 12Ù35

Fix

Š ˜

12Ù345Ú 12Ù3

Decimal fixo

Š š

Para cancelar Fix:

Š r

Fix

12Ù345Ú

12Ù345

12Ù345Ú

12Ù345

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Adição com dinheiro

José comprou sorvete por $3.50, biscoitos por $2.75 e um refrigerante grande por $.99. Quanto ele gastou?

Pressionar Visor

Fix

Š ™ ®

3 2

3Ù50Û2Ù75

ÛÙ99Ú 7Ù24

Fix

Decimal fixo

EXAS INSTRUMENTS INCORPORATED

Convertendo decimais para frações

Converta o decimal 0,5 para uma fração e, em seguida, veja o decimal novamente após a conversão.

Pressionar Visor

ÙÓÚ ØÙÓ

ÙÓÚ Ó

(Voltar a decimal)

ØÙÓ

êêêê

ÏØ

Decimal fixo

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Memória

Teclas

funções conforme mostradas abaixo:

z ®

z T

z U

z V

z W

z £

Armazena o valor visualizado sobre o valor memorizado. Adiciona o valor visualizado à memória. Subtrai o valor visualizado do valor memorizado. Multiplica o valor visualizado pelo valor memorizado. Divide o valor visualizado pelo valor memorizado. Efetua divisão de inteiros com o valor visualizado e o valor memorizado.

de memória para o visor. Quando pressionada duas vezes, apaga a memória.

Notas

Os exemplos dos modelos de

•

transparência assumem todas as definições padrão.

Os resultados são armazenados em

•

memória e não são exibidos. O visor permanece o mesmo.

É possível armazenar frações,

•

decimais e números negativos em memória.

chama novamente o conteúdo

•

1 2

é exibido sempre que a memória

contiver um valor diferente de 0. Para apagar a memória, pressione

duas vezes.

EXAS INSTRUMENTS INCORPORATED

Usando a memória para adicionar itens

Hambúrgueses 2 $1,19 = Milk shakes 3 $1,25 = Desconto para cada

um milk shake 3 $0,20 =

Custo total =

Pressionar Visor

2Ý1Ù19Ú 2Ù38

z ®

2Ý1Ù19Ú 2Ù38

3Ý1Ù25Ú 3Ù75

Armazenar na

memória

Chamar novamente

z T

Adicionar milk

(

shakes à memória.)

V r

z U

Deduzir desconto

(

da memória.)

Chamar novamente

(

o custo total.)

3Ý1Ù25Ú 3Ù75

3ÝÙ20Ú 0Ù6

5Ù53

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Usando a memória para calcular médias

As notas das provas de Franco foram 96 e 85. Suas notas da semana foram 87 e 98. Calcule a média de cada grupo de notas e a média das médias.

Pressionar Visor

96Û85Ú 181

181Þ2Ú 90Ù5

Armazenar na

memória

Adicionar

Chamar novamente

z ®

T | ®

181Þ2Ú 90Ù5

87Û98Ú 185

185Þ2Ú 92Ù5

92Ù5Û90Ù5Ú

183

183Þ2Ú 91Ù5

EXAS INSTRUMENTS INCORPORATED

Frações

Teclas

exibe um menu de 4 configurações

de modo do qual você pode selecionar a maneira como os resultados das frações serão exibidos. Você seleciona 2 elementos.

(padrão) exibe resultados

U n/d

como números mistos.

exibe resultados fracionários.

n/d

(padrão) exibe resultados

Man

fracionários não simplificados para que você possa simplificá-los manualmente.

Auto

exibe resultados fracionários

simplificados em seus mínimos termos.

3. permite digitar o numerador de

4. ¥ permite digitar o denominador de

permite digitar a parte inteira de



um número misto.

uma fração.

transforma um número misto

em fração e vice-versa.

simplifica uma fração usando o

mínimo fator primo comum. Se você desejar escolher o fator (em vez de deixar a calculadora fazê-lo), pressione inteiro) e, em seguida, pressione

, digite o fator (um

É necessário estar no modo Manual para usar esta função.

transforma uma fração em seu

equivalente decimal e vice-versa.

exibe o divisor (fator) usado para

simplificar o resultado da última fração. É necessário estar no modo Manual para usar esta função.

Notas

Os exemplos dos modelos de

•

transparência assumem todas as definições padrão.

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Frações

Notas (continuação)

Dividir uma fração por outra fração dá

•

resultados fracionários independente da configuração da divisão (decimal ou fração).

As configurações do modo

•

proporcionam 4 eventuais opções de exibição para resultados de cálculos exibidos na forma de fração. Por exemplo, para 6 ÷ 4, os visores teriam o seguinte aspecto:

manual simp/imprópria (n/d):

auto simp/imprópria (n/d):

manual simp/número misto (U n/d):

auto simp/número misto (U n/d): Você pode digitar o denominador ou o

•

numerador primeiro. Você pode digitar de 1 a 1000 para o denominador.

Ao multiplicar ou dividir frações e

•

decimais, o resultado é exibido como decimal. Um decimal não pode ser convertido em uma fração se o resultado exceder o número de dígitos no visor.

O apagamento com a tecla de

•

retrocesso w ocorre da direita na base para a esquerda no topo. Se você acidentalmente pressionar

4 3 2 2

após digitar o numerador, sem primeiro digitar um numeral para o denominador, w não corrigirá esse erro. Será necessário apagar e digitar a entrada novamente.

Se o número de casas decimais

•

estiver configurado com 0, o decimal equivalente de uma fração não será exibido.

EXAS INSTRUMENTS INCORPORATED

Adicionando números mistos

Ao nascer, uma garotinha pesava 4 de quilogramas. Nos 6 meses

seguintes, ganhou 2

de quilograma.

Quanto ela pesa?

Pressionar Visor

Tecla do numerador



Tecla do

denominador

Tecla da unidade



Conversão de mista

para imprópria







¥ ®

êêê

3 3 1

êêê

84 8

êêêêêê

ккккк

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Simplificando frações

Método 1: A calculadora escolhe um fator comum

Simplificar

Pressionar Visor

(Digite a fração.)



ккккк

(Prepare-se para simplificar.)

(Simplifique a fração.)

18 S

ккккк

à¾á

18 9

à¾

24 12

Tecla do

numerador



Tecla do

denominador

Simplificar

Fatorial

êêêêккккк

(Opcional: Verifique o fator. É necessário estar no modo Manual.)

(Volte para a fração.)

¤ ®

(Continue simplificando.)

êêêê

9 3

à¾

êêêê

êêê

12 4

EXAS INSTRUMENTS INCORPORATED

Simplificando frações

Método 2: Você escolhe um fator comum

Simplificar

Pressionar Visor

(Digite a fração.)



êêêê

Prepare-se para

(

simplificar.)

à¾á

Tecla do

numerador



Tecla do

denominador

Simplificar

(Digite um fator comum.)

(Simplifique a fração.)

êêêê

à¾Ôá

18 3

à¾Ôá

24 4

êêêêêêê

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Convertendo frações para decimais

Converta a fração

para decimal e,

em seguida, visualize a fração original após a conversão.

Pressionar Visor



íííí

10 10

Tecla do

numerador



Tecla do

denominador

Fração em decimal

(Volte para a fração.)

para decimal.)

(Volte

N D

n d

0Ù5

íííí

0Ù5

EXAS INSTRUMENTS INCORPORATED

Convertendo decimais para frações

Converta o decimal 0,5 para uma fração e, em seguida, veja o decimal novamente após a conversão.

Pressionar Visor

Ù5Ú 0Ù5

Ù5Ú 5

Tecla do

numerador



Tecla do

denominador

Fração em

decimal

íííí

para decimal.)

(Volte

0Ù5

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Convertendo frações em números mistos

Converta a fração imprópria número misto.

Pressionar Visor

¿ »Ä¸ »Д¸ кккккк

èæ êêêê

em um

Tecla do

numerador



Tecla do

denominador

Modos de Fração

¢ ®



2 1

à¾

4 2

êêêêêê

êêê

EXAS INSTRUMENTS INCORPORATED

Comparando frações e decimais

Linda nada 20 voltas em 5,72 minutos. Juan nada 20 voltas em 5 ¾ minutos. Quem nada mais rápido?

Para comparar os tempos como decimais:

Pressionar Visor





ííí

5Ù75

нннннн

100

Tecla do numerador



Tecla do

denominador

Para comparar os tempos como frações:

EXAS INSTRUMENTS INCORPORATED

5Ù72Ú 5Ù72

кккккк

100

TI-15: Manual do instrutor

Porcentagem

Teclas

converte um decimal ou fração em

porcentagem.

converte uma porcentagem em um

decimal.

Notas

Os exemplos dos modelos de

•

transparência assumem todas as definições padrão.

EXAS INSTRUMENTS INCORPORATED

Convertendo em porcentagem

Converta 25% em um decimal.

Pressionar Visor

ª ®

25ãÚ 0Ù25

Converta

em uma porcentagem.

100

Pressionar Visor



100

кккккк

àã25

y ®

100

Porcentagem

Converter em porcentagem

Converta 3 em uma porcentagem.

Pressionar Visor

y ®

3àã 300ã

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Convertendo frações em porcentagem

Converta 25% em uma fração, simplifique em seus termos mínimos e, em seguida, converta a fração em decimal.

Pressionar Visor

ª ®

25ãÚ 0Ù25

кккккк

100

N/D"n/d

25 5

кккккк

à¾

êêêê

100 20

Porcentagem

Fração em Decimal

¤ ®

N/D"n/d

êêêê

à ¾

êêê

20 4

0Ù25

0Ù25àã 25ã

EXAS INSTRUMENTS INCORPORATED

Dicas de cálculo

A família Chen foi jantar em um restaurante. A conta foi de $31.67. De quanto foi a gorjeta, se eles deixaram 15% da conta para o garçom? Qual o total da conta, incluindo a gorjeta?

Pressionar Visor

31.67

31Ù67Ú 31Ù67

Fix

Š ™

31Ù67Ú 31Ù67

ª ®

31Ù67Ý15Ú

Fix

Porcentagem

Converter em porcentagem

31.67

4.75

4Ù75

31Ù67Û4Ù75Ú

36Ù42

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Teclas

introduz o valor de pi arredondado

com sete casas decimais (3.1415927).

Notas

Os exemplos dos modelos de

•

transparência assumem todas as definições padrão.

Internamente, pi é armazenado com

•

12 casas decimais (3.141592653590). Apenas 9 casas decimais são exibidas.

Para converter do pi simbólico em um

•

valor decimal, pressione

EXAS INSTRUMENTS INCORPORATED

Usando pi para calcular a circunferência

Use esta fórmula para calcular a quantidade de borda necessária, caso você deseje colocar uma borda circular de 3 metros em torno da árvore do seu jardim.

C = 2pr = 2 x p x 3

Pressionar Visor

V ©

2Ýß

2ÝßÝ3Ú Ôß

18Ù8495592

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Usando pi para calcular a área

Use esta fórmula para calcular a quantidade de gramado a ser molhada pelo borrifador com 4 metros de raio.

A = pr

2 =

x 12

Pressionar Visor

ßÝ

ßÝ12ÉÐ

ßÝ12ÉÐÚS 144ß

452Ù3893421

EXAS INSTRUMENTS INCORPORATED

Usando pi para calcular volume

Use esta fórmula para calcular o espaço ocupado por uma bola.

4pr

V =

5 cm

Pressionar Visor

V © V

ÒÝßÝ

ТЭЯЭУЙС

ТЭЯЭУЙСЮС

ТЭЯЭУЙСЮСЪ

523 Ù5987756

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Potências e Raízes Quadradas

Teclas

permite especificar uma potência

para o valor digitado. Ao pressionar

, o valor será exibido se estiver

dentro do intervalo da calculadora.

calcula a raiz quadrada de valores

positivos, incluindo frações.

Notas

Os exemplos dos modelos de

•

transparência assumem todas as definições padrão.

EXAS INSTRUMENTS INCORPORATED

Calculando a área de um quadrado

Use esta fórmula para calcular o tamanho da lona necessária para cobrir toda a área interna do campo de beisebol.

A = x

= 90

Potências

Pressionar Visor

EXAS INSTRUMENTS INCORPORATED

ЧШЙРЪ 8100

TI-15: Manual do instrutor

Calculando a raiz quadrada

Use esta fórmula para calcular o comprimento do lado da sede do clube, de formato quadrado, se um carpete de 36 metros quadrados tiver que ser usado para cobrir o piso.

L =

x = 36

36 m

of carpet

Raiz Quadrada

Pressionar Visor

âÅ36ÆÚ 6

EXAS INSTRUMENTS INCORPORATED

Calculando potências

Dobre um pedaço de papel pela metade, depois novamente na metade e assim por diante, até não poder fisicamente dobrá-lo novamente. Quantas partes ficaram após dobrar 10 vezes?

Pressionar Visor

Potências

2ÉÏØÚ 1024

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Calculando potências negativas

Calcule os números padrão para as seguintes potências:

-3

-2

-3

(1/2)

Pressionar Visor

¨ M

2ÉÜÑÚ ШЩПРУ

Potências

Negativo



¨ M

Ь2ЙЬСЪ ЬШЩПРУ

Ù2ÉÜÑÚ ÏÐÓ

1. 2

êêê

ÉÜÑÚ Ö

EXAS INSTRUMENTS INCORPORATED

Calculando potências de 10

1.3 x 103 = ?

Pressionar Visor

Potências

1 10

¨ M

1.3 x 10

1Щ3ЭПШЙСЪ

1300

= ?

1Щ3ЭПШЙЬСЪ

0Ù0013

EXAS INSTRUMENTS INCORPORATED

TI-15: Manual do instrutor

Solução de Problemas: Modo Auto

Teclas

ativa a Solução de Problemas. Esta

‹

função proporciona um conjunto de exercícios eletrônicos com o intuito de desafiar a habilidade do estudante em adição, subtração, multiplicação e divisão.

‹ ‡

modo, o nível de dificuldade e o tipo de operação.

Modo: Nível: Tipo:

Auto é a configuração do modo padrão.

exibe o menu para selecionar o

Auto Man 123 +- x

(Manual)

Notas

•

Os exemplos assumem todas as definições padrão.

No modo Auto (padrão), a TI-15 apresenta problemas com um elemento ausente (por exemplo 5+2=? ou 5+?=7 ou 5?2=7).

Se a resposta não estiver correta, a calculadora exibe “no” e dá uma dica da forma “<” ou “>”.

Após digitar três respostas incorretas, a calculadora fornece a resposta certa.

Após cada cinco problemas, a TI-15 exibe um quadro de pontuação discriminando as respostas corretas e incorretas do estudante.

Os instrutores podem verificar o progresso de um estudante a qualquer momento, pressionando

para exibir o quadro de

‡

pontuação.

Para sair da Solução de Problemas,

•

pressione ‹ novamente. Ao sair, o quadro de pontuação é apagado.

EXAS INSTRUMENTS INCORPORATED

Texas instruments TI-15 User Manual [pt]

Specifications and Main Features

Frequently Asked Questions

User Manual