Texas instruments TI-15 GUIDE FOR TEACHERS

TI-15

Guide de l’enseignant

TI.15

:

Guide de l’enseignant

Rédigé par

Texas Instruments Incorporated

Activités élaborées par

Jane Schielack

À propos de l'auteure

Jane Schielack est Professeure associée de mathématiques au Département des Mathématiques de l'université Texas A&M. Elle a élaboré la section section

Comment utiliser la TI-15

Activités

de ce guide.

et a participé à l'évaluation de la pertinence des exemples dans la

Avis important concernant le matériel de ce livre

Texas Instruments n'accorde aucune garantie, expresse ou implicite, incluant sans toutefois se limiter à, toute garantie implicite de commerciabilité et d'aptitude à un usage particulier, concernant le matériel (programmes ou documents) et rend ce matériel disponible "en l'état" tenue responsable de dommages spéciaux, collatéraux, fortuits ou indirects en relation avec, ou imputables à l'achat ou à l'utilisation de ce matériel. La seule responsabilité exclusive de Texas Instruments, indépendamment de la forme d'action, ne saurait dépasser le prix d'achat de ce livre. De plus, Texas Instruments dénie toute responsabilité quant aux plaintes de quelque nature que ce soit, portées par un tiers contre l'utilisation de ce matériel.

Remarque

décrits dans ce matériel.

: L'utilisation de toute autre calculatrice que TIN15 peut entraîner des résultats différents de ceux

seulement

. En aucun cas, Texas Instruments ne saurait être

Permission de reproduction ou de photocopie

Par la présente, une permission est accordée aux enseignants qui veulent reproduire ou photocopier dans la classe, l'atelier ou le séminaire des pages ou des feuilles de ce livre qui portent un avis de Texas Instruments sur les droits d'auteur. Ces pages sont conçues pour être reproduites par des enseignants à des fins d'utilisation dans les classes, les ateliers ou les séminaires si chaque copie affiche l'avis sur les droits d'auteur. Ces copies ne peuvent pas être vendues et toute autre distribution est expressément interdite. À l'exception de l'autorisation décrite cidessus, une permission écrite préalable doit être obtenue de Texas Instruments Incorporated pour reproduire ou transmettre ce travail ou une partie de ce travail sous toute autre forme ou par un moyen électronique ou mécanique quelconque, y compris un système de stockage ou de récupération d'informations, à moins d'une permission expressément donnée conformément à la loi fédérale sur les droits d'auteur.

Faites parvenir vos demandes à l'adresse suivante :

Texas Instruments Incorporated 7800 Banner Drive, M/S 3918 Dallas, TX 75251 Attention : Manager, Business Services

Si vous faites la demande de photocopies de la totalité ou de portions de ce livre à un tiers, vous devez inclure cette page (avec la déclaration de permission ci-dessus) pour le fournisseur des services de photocopie.

www.ti.com/calc

ti-cares@ti.com

À l'exception des droits spécifiques accordés par la présente, tous les droits sont réservés.

Imprimé aux États-Unis d'Amérique.

Automatic Power Down, APD et EOS sont des marques de Texas Instruments Incorporated.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

ii

Table des matières

E



C

HAPITRE

Au sujet de Guide........................................ v

À propos de TI.15 .......................................vi

P

AGE

Activitiés................................................1

Régularités dans les pourcentages ........2

Formes de répresentation des

fractions.......................................................6

Comparaison de coûts..............................11

Écriture des nombres...............................15

Procédures inverses.................................20

Dans l’intervalle.........................................24

L'importance de la valeur de position..29

Quel est le problème ? .............................34

Comment utiliser la TI.15................38

1 Affichage, défilement, priorité des

opérations, parenthèses...................39

C

HAPITRE

Comment utiliser la TI.15

12 Résolution de problèmes :

Mode Auto........................................... 94

13 Résolution de problèmes :

Mode Manuel......................................100

14 Valeur de position .............................106

Annexe A: ..................................................A-1

Référence rapide aux touches

Annexe B: ..................................................B-1

Indicateurs d'affichage

Annexe C:.................................................... C-1

Messages d'erreur

Annexe D: ..................................................D-1

Service technique, réparations et

garantie

(suite)

P

AG

2 Effacement et correction..................42

3 Menus de la touche mode.................45

4 Opérations élémentaires...................48

5 Opérations avec des constantes....55

6 Nombres entiers et nombres

décimaux...............................................63

7 Mémoire ................................................68

8 Fractions............................................... 71

9 Pourcentage........................................ 80

10 Pi.............................................................84

11 Puissances et racines carrées........ 88

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

iii

A propos du guide de l’enseignant



Comment est organisé le Guide de l’enseignant

Ce guide est composé de deux parties:

Activités et Mode d’emploi de la TI-15

section permettant d’intégrer la TI-15 à l’enseignement des mathématiques.

d’emploi de la TI-15

à enseigner à vos élèves comment utiliser la calculatrice.

Activités

est un ensemble d’activités

est conçu pour vous aider

. La

Le mode

Activités

Les activités sont conçues pour être dirigées par l’enseignant. Elles ont pour but d’aider à développer des concepts mathématiques tout en incorporant la TI-15 comme outil d’enseignement. Chaque activité est indépendante et inclut :

Un aperçu du but mathématique de l’activité.

•

Les concepts mathématiques étant

•

développés.

Le matériel nécessaire pour exécuter

•

l’activité.

Une fiche d’activité pour l’élève.

•

Mode d’emploi de la TI.15

Cette partie contient des exemples sur des transparents originaux. Les chapitres sont numérotés et incluent :

Une page d’introduction décrivant les

•

touches de la calculatrice présentées dans les exemples, l’endroit où elles se trouvent sur la TI-15, ainsi que toute remarque relative à leurs fonctions.

Des transparents originaux suivent la page

•

d’introduction et offrent des exemples d’applications pratiques des ou de la touche(s)dont il est question. Les touches (ou la touche) en question apparaissent en noir sur un dessin représentant le clavier de la TI-15.

A garder à l’esprit

Bien que de nombreux exemples sur les

•

transparents originaux peuvent être utilisés pour développer des concepts mathématiques, ils n’ont cependant pas été conçus dans ce but spécifique.

Pour une flexibilité maximale, les exemples et

•

activités sont indépendants les uns des autres. Sélectionnez le transparent original qui concerne la touche que vos élèves doivent utiliser pour développer les concepts mathématiques que vous enseignez. Sélectionnez une activité appropriée au concept mathématique que vous enseignez.

Si un exemple ne semble pas approprié à

•

votre programme ou au niveau scolaire, utilisez-le pour enseigner la fonction d’une touche (ou de plusieurs touches), puis donnez vos propres exemples appropriés.

Pour vous assurez que tout le monde

•

commence au même point, demandez aux élèves de remettre à zéro la calculatrice en appuyant simultanément sur les touches

et

−

sélectionnant RESET, sélectionnant Y (oui), puis en appuyant sur

ou en appuyant sur

”

<

‡

.

,

Commander des Guides de l’enseignant

supplémentaires

Pour passer une commande ou pour demander des informations supplémentaires sur les calculatrices (TI) Texas Instruments, appelez notre numéro de téléphone gratuit

1-800-TI-CARES (1-800-842-2737)

Ou utilisez notre adresse de courrier électronique

Ou visitez la page web des calculatrices TI

:

ti-cares@ti.com

http://www.ti.com/calc

:

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

iv

À propos de TI.15

p

j

p

q

p

pp

p

pp

p

q

p

j

p

prop

p

Affichage sur deux lignes

La première ligne affiche une entrée composée d'un maximum de 11 caractères. Les entrées commencent dans le coin su l'entrée ne tient continue sur la seconde ligne. Si l'es

ermet, l'entrée et le résultat apparaissent

sur la première ligne.

La seconde ligne affiche un maximum de 11 caractères. Si l'entrée est tro sur la ligne. Si l'entrée et le résultat ne tenir sur la sur la seconde ligne et résultats de notation scientifique.

Si une entrée ne tient continue à être renvoyée ; vous le début de l'entrée en faisant défiler vers le haut. Dans ce cas, seul le résultat est affiché lorsque vous appuyez sur

remière ligne, elle continue sur la seconde

as sur la première ligne, elle

remière ligne, le résultat est affiché

ustifié à droite. Les

lus de 10 chiffres sont affichés en

érieur gauche. Si

ace le

longue pour tenir

euvent pas

as sur deux lignes, elle

ouvez afficher

®

.

Indicateurs d'affichage

Reportez-vous à l'annexe B pour consulter la liste des indicateurs d'affichage.

Messages d'erreur

Reportez-vous à l'annexe C pour consulter la liste des messages d'erreur.

Ordre des opérations

La calculatrice TI-15 utilise le système

uation Operating System (EOSé) pour

E évaluer des ex

érations sont indiquées dans le

o trans

arent principal au chapitre 1,

défilement, ordre des o parenthèses.

Les opérations entre parenthèses étant exécutées en

X

ou Y

et, par conséquent, le résultat.

ressions. Les priorités des

Affichage,

érations et

remier, vous pouvez utiliser

our changer l'ordre des opérations

Menus

Deux touches du TI-15 permettent d'afficher des menus :

uyez sur $ ou # pour monter ou

A descendre dans la liste des menus. A sur ! ou " souligner un élément de menu. Pour retourner à l'écran l'élément, a élément de menu, a que l'élément est souligné.

‡

our déplacer le curseur et

récédent sans sélectionner

uyez sur ”. Pour sélectionner un

Entrées précédentes #

Après l'évaluation d'une expression, utilisez

#

et $ résultats l'historique TI-15.

our défiler parmi les entrées et

récédents qui sont stockés dans

¢

et

uyez sur

.

uyez

®

pendant

$

Résolution de problème (‹)

L'outil Résolution de problème comprend trois fonctions de se lancer des défis avec des o mathémati position.

L'outil Résolution de offre un re étudiants en matière d'addition, de soustraction, de multi division. Les étudiants le mode, le niveau de difficulté et le ty d'opération.

L'outil Résolution de

ermet aux étudiants de composer leurs

éléments manquants ou des inégalités.

L'outil Résolution de

osition) permet aux étudiants d'afficher la valeur de d'afficher le nombre d'unités, de dizaines, de centaines, de milliers, de dizièmes, de centièmes ou de millièmes dans un nombre donné.

eu d'exercices électroniques qui

résente un défi pour les capacités des

res problèmes, pouvant inclure des

ermettant aux étudiants

érations

ues de base ou une valeur de

roblème (mode Auto)

lication et de

euvent sélectionner

e

roblème (mode Manuel)

roblème (Valeur de

osition d'un chiffre précis ou

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

v

À propos de TI.15

p

q

p

Remise à zéro de TI.15

L'appui simultané de − et ” ou l'appui de

, la sélection de RESET, la sélection de Y

‡

(oui), à zéro.

Remise à zéro de la calculatrice :

uis l'appui de

remet la calculatrice

®

(suite)

Ramène les réglages à leurs valeurs

•

défaut : Notation standard (virgule flottante), nombres mixtes, simplification manuelle, Résolution de problème en mode Auto et le Niveau de difficulté 1 (addition) dans la Résolution de problème.

Efface les opérations en cours, les entrées

•

dans l'historique et les constantes (opérations stockées).

ar

Automatic Power DownTM (APDTM)

Si la calculatrice TI-15 reste inactive pendant environ 5 minutes, Automatic Power Down (APD) l'éteint automati

rès APD. L'affichage, les opérations en

a

−

cours, les réglages et la mémoire sont conservés.

uement. Appuyez sur

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

vi

Activitiés

Régularités dans les pourcentages 2

Formes de répresentation des fractions 6

Comparaison de coûts 11

Écriture des nombres 15

Procédures inverses 20

Dans l’intervalle 24

L'importance de la valeur de position 29

Quel est le problème ? 34

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

1

Régularités dans les pourcentages

prop

p

q

p

4e à 6e année

Description

Les élèves utiliseront la touche ª pour rassembler des données à

os des pourcentages d'un nombre donné. Ils organiseront ensuite les données et rechercheront des Régularités dans les

ourcentages. (Par exemple, 10% de

20 est deux fois plus que 5% de 20.)

Introduction

1. Après que les élèves aient utilisé des méthodes

manipulatoires pour développer leur compréhension de pourcentage (1% = 1 partie de 100 parties), demandez-leur d'explorer ce qui se produit lorsqu'ils appuient sur ª sur la calculatrice.

2. Présentez le scénario suivant aux élèves :

Metropolis East (M.E.) et Metropolis West (M.W.) sont des villes voisines. La taxe de vente à M.E. est de 10%, mais la taxe de vente à M.W. est de 5% seulement. Collectez des données et affichez vos résultats de chaque pourcentage dans un tableau pour comparer les montants d'argent payés en taxes de divers articles dans chaque ville.

3. Demandez aux élèves d'élaborer des conjectures

à propos des pourcentages en fonction des régularités observés. Les élèves peuvent alors utiliser des méthodes manipulatoires pour vérifier leurs conjectures.

Exemples :

•

Les élèves peuvent remarquer que pour chaque article, 10% de son prix est deux fois plus que 5% de son prix.

•

Les élèves peuvent noter qu'il est facile d'estimer 10% d'un nombre entier en utilisant la valeur de position et en examinant les chiffres à droite de la position des unités.

Concepts mathématiques

• multiplication

• fractions é

uivalentes, nombres décimaux et

ourcentages

³

Lorsqu'un élève entre un 6, la TI-15 affiche 6. Ensuite, lorsque l'élève appuie sur ª ®, l'affichage change à

0,06

pour montrer que 6% est une autre façon d'écrire 0,06 ou 6/100.

³

Vous devrez montrer aux élèves comment utiliser la multiplication avec la TI-15 pour exprimer le pourcentage d'une quantité donnée. Par exemple, pour afficher 10% de 20 $ :

1. Entrez 10.

2. Appuyez sur ª V.

3. Entrez 20 ; appuyez sur ®.

Les élèves peuvent vérifier l'affichage de 2 sur la calculatrice en utilisant des méthodes manipulatoires pour expliquer que 10% de 20 $ = 2 $.

Matériel

• TI-15

• crayon

• activité de l’élève (page 4)

Collecte et organisation des données

Pour guider les élèves dans l'organisation de leurs données pour faire ressortir les régularités, demandez des questions telles que :

Comment pouvez-vous organiser vos données

•

afin de pouvoir comparer le taux de taxe de 5% au taux de taxe de 10% ?

Pourquoi serait-il pratique de garder 5% dans

•

la colonne de gauche d'un tableau jusqu'en bas et de changer seulement la quantité totale ?

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

2

Régularités dans les pourcentages

Comment pouvez-vous créer un tableau

•

similaire dans le cas de 10% pour comparer vos données ?

Que se passerait-il si vous ordonnez les

•

montants de la quantité totale du plus petit au plus grand ?

De quelle autre façon pourriez-vous organiser

•

vos données pour comparer les deux taxes de vente et trouver des régularités dans les pourcentages ?

Analyse des données et déductions

Pour attirer l'attention des élèves sur la recherche de régularités dans leurs données, posez des questions telles que :

Comment les pourcentages (montants de la taxe)

•

dans votre tableau de 5% sont-ils comparables aux montants dans le tableau de 10% ?

(suite)

Comment pouvez-vous comparer 5% d'un article

•

de 20 $ à 5% d'un article de 10 $ ?

Comment pouvez-vous comparer 10% d'un

•

article de 20 $ à 10% d'un article de 10 $ ?

Comment 10% du coût d'un article se compare-

•

t-il au coût total de l'article ?

Quelles conjectures pouvez-vous élaborer à

•

propos de la recherche de 10% d'un nombre ?

Quelles conjectures pouvez-vous élaborer à

•

propos de la recherche de 5% d'un nombre ?

Comment pouvez-vous utiliser des méthodes

•

manipulatoires pour vérifier vos conjectures ?

Poursuite de l'explanation

Les élèves peuvent créer d'autres scénarios de pourcentage pour explorer des régularités dans les pourcentages. Par exemple, demandez aux élèves :

Que se passe-t-il si vous augmentez la taxe de

•

vente d'un point de pourcentage chaque jour ?

Comment la taxe sur un article de 20 $

•

changera-t-elle chaque jour ?

•

Comment la taxe sur un article de 40 $ changera-t-elle chaque jour ?

Comment les taxes sur les 2 articles se comparent-elles ?

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

3

Nom ___________________________

Régularités dans les

Date ___________________________

pourcentages

Collecte et organisation des données

Utilisez votre calculatrice pour collecter des données sur le pourcentage, organisez-les dans le tableau ci-dessous, puis recherchez des régularités.

Coût de l'article Montant de la taxe à

Metropolis West

Pourcentage (taux de

la taxe) : ______%

Montant de la taxe à

Metropolis East

Pourcentage (taux de

la taxe) : ______%

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

4

Nom ___________________________

Regularités dans le

Date ___________________________

pourcentage

Analyse des données et déductions

1. Quelles régularités voyez-vous dans vos tableaux ?

__________________________________________________________________________

2. Quelles conjectures pouvez-vous faire à partir de ces régularités ?

__________________________________________________________________________

3. Répétez l'activité avec un pourcentage différent dans la colonne de gauche et comparez vos résultats.

__________________________________________________________________________

4. Répétez l'activité, en changeant les pourcentages dans la colonne de gauche tout en maintenant la quantité totale constante. Quelles régularités voyez-vous maintenant ? Quelles conjectures pouvez-vous énoncer ?

__________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

5

Formes de representation des fractions

p

4e à 6e année

Description

Les élèves vont comparer les résultats de l'utilisation de la division

our créer des fractions selon les différents réglages du mode de l'affichage des fractions et faire des généralisations à des régularités observées.

Introduction

1. Présentez aux élèves un problème tel que :

Dans un petit bistro, il reste 6 tasses de sucre dans la cuisine à partager entre 4 bols de sucre. Si vous voulez qu'ils contiennent tous la même quantité de sucre, combien de sucre doît-on verser dans chaque bol ?

2. Demandez aux élèves de présenter leurs

solutions au problème. Encouragez-les à trouver autant de façons possibles de représenter la solution.

artir

Concepts mathématiques

• division

• multiplication

• facteurs communs

• fractions équivalentes



Reportez-vous à la page 45 pour des informations détaillées sur les réglages du mode d’affichage de la calculatrice TI-15.

Matérial

• TI-15

• crayon

• activité de l’élève (page 9)

Exemples:

•

En prévoyant utiliser une pelle à sucre de ¼ de tasse pour remplir les bols, chaque bol recevrait 6 pelles, ou

•

En prévoyant de partager chaque tasse en demi-

6

/4 de tasse de sucre.

tasses, il y aurait 12 demi-tasses et chaque bol recevrait 3 demi-tasses ou

•

Si une tasse à mesurer de 1 tasse était utilisée en

3

/2 tasse de sucre.

premier, chaque bol recevrait 1 tasse de sucre, puis les deux dernières tasses seraient divisées

2

en huit quarts pour donner 1

•

Les deux dernières tasses seraient divisées en 4 demies pour donner 1

1

/2 tasse par bol.

/4 tasse par bol.

3. Demandez aux élèves d'identifier l'opération et d'enregistrer l'équation qu'ils peuvent utiliser avec leur calculatrice pour représenter la situation (6 tasses ÷ 4 bols = nombre de tasses par bol).



La division peut être représentée par 6 P 4 ou 6/4 (entré sur la calculatrice comme étant 6  4 ¥). Dans cette activité, l’affichage de fractions est utilisé.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

6

Formes de represéntations des fractions

(suite)

4. Demandez aux élèves d'entrer la division pour afficher les quotients sous forme de fraction, et enregistrez les affichages qui en résultent.

5. Demandez aux élèves d'explorer le quotient avec les différentes combinaisons de réglages et discutez des différents affichages qui se produisent. Si nécessaire, demandez-leur d'utiliser des méthodes manipulatoires pour établir des liens entre les significations des quatre différentes formes de représentation de fractions.

6. Demandez aux élèves, travaillant par groupes de quatre, de choisir un dénominateur et d'enregistrer les différentes formes de représentation de fractions sur la feuille d'activité fournie.

7. Demandez aux élèves de partager leurs résultats, de rechercher des régularités et de faire des généralisations.

Collecte et organisation des données

Pour guider les élèves dans la création de données qui afficheront des régularités dans les quotients sous forme de fraction, posez des questions telles que :



Par exemple, pour 6 ÷ 4 en tant que fraction, entrez 6  4 ¥. Les affichages sous les différents réglages se présenteront sous la forme suivante :

n

man

d n

auto

d

n

U

man 1

d n

U

auto 1

d

6 4

3 2

2 4

1 2

Quel dénominateur avez-vous choisi

•

d'explorer ? Pourquoi ?

Quels dénominateurs obtenez-vous avec les

•

réglages

Quels dénominateurs obtenez-vous avec les

•

réglages

Quel dénominateur choisirez-vous d'explorer

•

n

man

d

n

auto

d

? Avec les réglages

U

n d

U

man

n

auto

d

ensuite ?

Exemple :

Après avoir exploré les dénominateurs 2 et 3, vous pouvez suggérer d'explorer le dénominateur 6 et de comparer les résultats.

Comment pouvez-vous organiser vos résultats

•

de façon à rechercher des régularités ?

Exemple :

En continuant d'augmenter les numérateurs de 1 à chaque fois.

?

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

7

Formes de répresentation des fractions

(suite)

Analyse des données et déductions

Pour attirer l'attention des élèves sur les régularités observées sur leurs fractions et la lien de ces régularités avec les dénominateurs, posez des questions telles que :

Quels régularités voyez-vous dans vos résultats ?

•

Exemple :

Lorsque la dénominateur 4 est utilisé dans la

n

colonne

nombre entier.

Comment les résultats de l'utilisation du

•

dénominateur 2 se comparent-ils avec les résultats de l'utilisation du dénominateur 4 ?

Comment le dénominateur 5 se compare-t-il au

•

dénominateur 10 ?

Quels autres dénominateurs semblent être associés ?

•

auto

d

, chaque quatrième nombre est un

Exemple :

La régularité utilisant le diviseur 6 est associé aux régularités des diviseurs 2 et 3.)

Quel modèle voyez-vous dans les dénominateurs

•

associés ?

Exemple :

Ils sont associés en tant que facteurs et multiples.

Porsuite de l'exploration

Demandez aux élèves de penser à des situations dans lesquelles ils préféreraient utiliser chacune des combinaisons de réglages des formes de représentaion des fractions.

Exemple :

•

En travaillant avec des probabilités qui pourraint être additionnées, utilisant le

n

réglage

dénominateurs des probabilités et faciliterait le calcul mental de l’addition.

•

Dans une situation où les résultats estimés sont suffisamment rapprochés, l'utilisation du réglage

n

U

d

nombre entier composant le résultat et si la partie fraction est supérieure ou inférieure à

man

conserverait les

d

auto

faciliterait la visualisation rapide du

½.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

8

p

Nom ___________________________

Formes de

Date ___________________________

re

résentation des

fractions

Collecte et organisation des données

1. Demandez à chaque personne de votre groupe de régler sa calculatrice sur l'une des combinaisons de réglages suivantes pour l'affichage des fractions. (Chaque personne doit choisir un réglage différent.)

impropre/simp manuelle

•

impropre/simp auto

•

nombre fractionnaire/simp manuelle

•

nombre fractionnaire/simp auto

•

2. Sélectionnez un dénominateur :__________

3. Utilisez ce dénominateur avec plusieurs numérateurs et enregistrez les résultats de chaque personne dans le tableau ci-dessous.

Numérateur Dénomina-

teur

0

1

2

3

4

n

Man

d

n

Auto U

d

n

Man U

d

n d

Auto

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

9

Formes de représentation des fractions

(suite)

Analyse des données et déductions

1. Quelles régularités voyez-vous ?

__________________________________________________________________________

2. Quelles généralisations pouvez-vous faire ?

__________________________________________________________________________

3. Essayez cette activité de nouveau avec un dénominateur différent et comparez vos résultats avec les deux dénominateurs.

__________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

10

Comparaison des coûts

q

3e à 5e années

Description

Les élèves vont résoudre un problème en utilisant la division avec un avec le le

uotient sous forme de fraction et la division avec

uotient sous forme décimale et ils vont comparer les

uotient entier et un reste, la division

résultats.

Introduction

1. Présentez le problème suivant :

Le service d'entretien a déterminé qu'il en coûterait 0,40 $ la verge (yard) carrée pour entretenir le terrain de soccer du district chaque année. Le terrain de soccer est d'une largeur de 80 verges et d'une longueur de 100 verges. Les six écoles qui jouent sur le terrain ont décidé de partager le coût de façon égale. Combien chaque école devra-t-elle contribuer au fond d'entretien du terrain de soccer cette année ?

2. Demandez aux élèves d'utiliser la calculatrice pour résoudre ce problème de trois façons :

•

Recherche d'un quotient entier et d'un reste.

•

Recherche du quotient sous forme de fraction.

•

Recherche du quotient sous forme décimale.

Collecte et organisation des données

Les élèves devraient noter leurs procédures et les résultats sur la feuille Activité de l’élève . Pour les aider dans leur cheminemet, posez des questions telles que

Qu'avez-vous entré dans la calculatrice pour

•

résoudre le problème ?

:

Concepts mathématiques

• division

• multiplication

• fractions

• nombres décimaux



Pour afficher un quotient entier et un reste, utilisez la touche

£

.



Pour afficher un quotient sous forme de fraction, appuyez sur

‡ " ®

sélectionner utilisez la touche W.



Pour afficher un quotient sous forme décimale, appuyez sur

‡ ! ®

sélectionner utilisez la touche W.

Matérial

• TI-15

• crayon

• activité

pour

n/d

pour

.

, puis

de l'élève (page 14)

, puis

Exemple :

80

Il se peut qu'un élève ait entré calculer l’aire du terrain de football V pour calculer le coût d'entretien total, puis W

®

pour calculer le coût de contribution de

V

110

® pour

0.40

®

6

chaque école sous forme de fraction ou sous forme décimale.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’ enseignant

11

Comparaison des coûts

Auriez-vous pu résoudre le problème de façon

•

plus efficace ? Comment ?

Exemple :

Un élève peut réaliser que 80 x 110 peut être calculé mentalement, et les pressions des touches peuvent être simplifiées à

Comment vos procédures sont-elles similaires

•

pour chaque type de solution ?

Exemples :

Elles impliquent toutes le calcul du nombre de verges carrées dans le terrain de soccer ; elles impliquent toutes la multiplication et la division.

Comment diffèrent-elles ?

•

Vous utilisez des touches différentes pour indiquer à la calculatrice sous quelle forme vous voulez afficher la réponse.

8800

V .

4

W

6

®

.

(suite)

Analyse des données et déductions

Pour guider les élèves dans l'analyse de leurs données, posez des questions telles que :

Comment vos solutions sous les trois formes

•

sont-elles semblables ?

Elles ont toutes une partie entière égale à 586.

En quoi vos trois solutions diffèrent-elles ?

•

La forme avec reste vous indique seulement le reste en dollars. Les formes “fractions” et décimale informent sur le montant excédant 586 que chaque école doit payer.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’ enseignant

12

Comparaison des coûts

Que se passe-t-il si vous multipliez chaque

•

solution par 6 pour la vérifier ?

Pour la forme quotient avec reste, vous devez multiplier 586 x 6 puis ajouter 4 pour obtenir le coût total de 3520 $. Pour la fome “fractions” vous pouvez multiplier 586 Pour la fome décimale si vous entrez

x 6

et que vous appuyez sur ®, vous obtenez

3520

, mais cela n'est pas logique car 6 x 7 ne se

termine pas avec un 0 !

Si vous entrez

586,66667

quotient décimal aux centièmes puisqu'il s'agit d'argent, et que vous obtenez 586,67 x 6, vous

obtenez

encore 3520,00, qui n'est toujours pas logique car 6 x 7 = 42. Si vous remettez la calculatrice à zéro et entrez vous appuyez sur ® , l'affichage indique alors

3520,02

En tant qu'école, quelle forme de quotient

•

, ce qui est logique.

voudriez-vous utiliser ?

2

/3 x pour obtenir 3520 $.

586,666667

, puis corrigez le

586,67 x 6

, et que

(suite)



Lorsque vous tanslformez 586,666667 pour obtenir 2 décimales, puis multipliez par 6, la calculatrice se souvient du nombre initial et l'utilise comme facteur. Le produit arrondi au centième le plus rapproché, en utilisant le facteur initial, est 3520,00. Lorsque vous entrez 586,67, la calculatrice utilise ce nombre comme facteur, affichant le produit réel de 3520,02.

Les réponses peuvent varier. Certains élèves peuvent vouloir utiliser la forme décimale, puisqu'elle est la plus rapprochée de la représentation en argent. Certains élèves peuvent vouloir utiliser la forme avec quotient entier et reste et suggérer que le Bureau central paie le 4,00 $ qui reste.

Bien que le quotient sous forme de fraction décrive le montant exact devant être payé par chaque école, la plupart des élèves vont reconnaître, après comparaison avec la forme décimale, que la forme “fraction” ne se traduit pas aussi facilement en argent.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’ enseignant

13

Nom ___________________________

Comparaison des

Date ___________________________

coûts

Collecte et organisation des données

Le service d'entretien a déterminé qu'il en coûterait 4,00 $ la verge (yard) carrée pour entretenir le terrain de soccer du district chaque année. Le terrain de soccer est d'une largeur de 80 verges et d'une longueur de 110 verges. Les 6 écoles qui jouent sur ce terrain ont décidé de partager le coût de façon égale. Combien chaque école devra-t-elle contribuer au fond d'entretien du terrain de soccer cette année ?

1. Utilisez la division avec un quotient entier et un reste :

2. Utilisez la division avec un quotient sous forme de fraction :

3. Utilisez la division avec un quotient sous forme décimale :

Analyse des données et déductions

Rédigez un court paragraphe comparant les trois solutions.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’ enseignant

14

Écriture des nombres : Notation scientifique

p

5e et 6e années

Description

Les élèves vont se servir des régularités créés sur la calculatrice en utilisant une l'o (› ou œ)

our les aider à comprendre la notation

ération constante

scientifique.

Introduction

1. Demandez aux élèves de revoir le régularité obtenue en utilisant 10 comme facteur.

Exemple :

1 x 10 = 10 2 x 10 = 20 3 x 10 = 30 10 x 10 = 100

2. Demandez aux élèves :

En vous basant sur cette régularité, que se passe-t-il si vous multipliez par 10 sans arrêt ?

Concepts mathématiques

• multiplication

• puissances de 10

• exposants

Matériel

• TI-15

• crayon

• activité de l'élève (page 18)

3. Après que les élèves aient partagé leurs conjectures, demandez-leur d'utiliser › pour les vérifier. À mesure que les élèves appuient sur

›

, demandez-leur de noter les affichages de la

calculatrice sur la feuille Activité de l'élève.

4. Lorsque les élèves atteignent le point où le compteur de gauche ne s'affiche plus, demandezleur d'interpréter que fait la calculatrice. (Le produit est devenu tellement important que l'espace est insuffisant pour afficher à la fois le produit et le compteur, alors le compteur a été supprimé de l'affichage.)

Demandez aux élèves de continuer à noter les données du compteur, même si ce dernier n'est plus affiché sur la calculatrice.

5. Lorsque le compteur de gauche réapparaît, demandez aux élèves de décrire l'affichage du produit. (Il a été remplacé par un en notation scientifique : par exemple,

1x10^11.

)



Pour multiplier par 10 de façon répétée, entrez :

› V

1. Cela “programme” une

opération de constante.

2. Entrez 1 comme facteur de départ.

3. Appuyez sur›.

Lorsque vous appuyez sur › pour la première fois, la calculatrice effectue l'opération 1 x 10 et l'affichage indique :

1x10 110

Le 1 représente l'utilisation de fois.

10

›

x 10

une

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

15

Écriture des nombres : Notation scientifique

(suite)

6. Demandez aux élèves de continuer à appuyer sur

›

et d'enregistrer les résultats.

7. Demandez aux élèves d'analyser leurs données et de présenter certaines conclusions à propos de l'affichage de la notation scientifique .

Par exemple, 1 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10.

Expliquez aux élèves que la notation exponentielle ou scientifique est une écriture pour les facteurs répétés : 1 x 10

8. Demandez aux élèves de continuer à explorer l'utilisation de la notation scientifique pour représenter une multiplication répétée par 10 avec d'autres facteurs de départ. (Par exemple, l'utilisation de 2 comme facteur de départ, l'affichage de 2 par 10 onze fois ou 2 x 10

1x10^11

2x10^11

représente le produit :

11

.

représente la multiplication

11

.

Collecte et organisation des données

Pour attirer l'attention des élèves sur les changements pertinents dans l'affichage de la calculatrice, posez des questions telles que :

Que signifie l'affichage de

•

Quand le compteur de gauche a-t-il disparu ?

•

Que s'est-il passé selon vous ?

3 1000

?

•

Quand le compteur de gauche a-t-il réapparu ? Quoi d'autre a changé ?

Le produit semble différent. Il a changé de 1000000000 à 1x10^10.

À quoi ressemblent les affichages après ce changement ?

Le 1x10 reste pareil mais le nombre de droite (l'exposant) augmente de un chaque fois que la touche › est appuyée, et cela concorde avec le compteur de gauche.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

16

Écriture des nombres : Notation scientifique

(suite)

Analyse des données et déductions

Pour attirer l'attention des élèves sur le lien entre les facteurs répétés 10 et l'affichage de la notation scientifique, posez des questions telles que :

Quelles régularités voyez-vous dans les produits

•

avant que le compteur disparaisse ?

Ils ont tous un 1 suivi du même nombre de zéros que les facteurs 10 qui ont été utilisés dans le produit.

Si vous continuez cette régularité, quel serait le

•

produit au moment où l'affichage du produit a changé ? Comment le produit est-il lié au nouvel affichage ?

Par exemple, produit serait de 100 000 000 000. L'affichage

1x10^11

Que se passe-t-il si vous utilisez 2 comme

•

facteur de départ et que vous le multipliez par 10 de façon répétée ?

Les affichages sont les mêmes, à l'exception du premier nombre dans tous les produits qui est 2. L'affichage

1x10^11

représente le produit 1 x 1011.

2x10^11

apparaît à l’endroit où le

représente le produit 2 x 1011.

Poursuite de l'exploration

Les élèves peuvent utiliser d'autres puissances de 10 comme facteur répété, noter les résultats dans le tableau et rechercher des régularités. Par exemple, l'utilisation de 100 comme facteur répété entraîne la partie exposant de l'affichage de la notation scientifique à augmenter par 2 chaque fois que vous appuyez sur › .

Les élèves peuvent utiliser le facteur de départ de 10 ou plus, noter les résultats dans le tableau et rechercher des régularités. Par exemple, l'utilisation de 12 comme facteur de départ entraîne rapidement un affichage tel que exposant de l'affichage est un de plus que le nombre de fois où 10 a été utilisé comme facteur.

12 1.2 x10^13

, où la partie

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

17

É

criture des

q

Nom ___________________________

nombres: Notation scientifi

ue

Date ___________________________

Collecte et organisation des données

Programmez la fonction d'opération constante sur votre calculatrice en une multiplication par 10. Notez les résultats dans le tableau ci-dessous à chaque fois que vous appuyez sur

Nombre de

fois

___

Utilisé comme

facteur

0 (facteur de départ)

1

›

.

Affichage

2

3

4

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

18

É

criture des

q

Nom ___________________________

nombres : Notation scientifi

ue

Date ___________________________

Analyse des données et déductions

1. Quelles régularités voyez-vous ?

__________________________________________________________________________

2. Que signifie le changement de l'affichage de droite ? (Par exemple,

__________________________________________________________________________

1x10^15

.)

__________________________________________________________________________

3. Répétez cette activité avec un autre multiple de 10 et comparez vos résultats.

__________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

19

Procédures inverses

p

2e à 6e année

Description

Les élèves vont utiliser les deux opérations constantes (› et œ)

our comparer les résultats de différentes

rocédures mathématiques et déterminer si elles sont

inverses.

Introduction

1. Demandez aux élèves de programmer › avec +2 et œ avec -2.

2. Demandez aux élèves d'entrer 8 sur leur calculatrice, d'appuyer sur › et de lire le résultat ( une fois avec 8 donne 10).

3. Demandez aux élèves d'appuyer sur œ pour appliquer la seconde opération constante au résultat de la première opération constante, puis de lire le résultat. ( soustraction de 2 une fois de 10 donne 8).

4. Demandez aux élèves de continuer ce processus avec divers nombres comme première entrée. Discutez de leurs résultats. (L'appui de › et puis de œ vous ramène toujours au premier nombre entré, ce qui signifie que › et œ sont des procédures inverses.)

5. Défiez les élèves de trouver d'autres paires de procédures pour › et œ qui respecteront le même régularité et de noter leurs explorations sur la feuille d'activité de l'élève

inverses

1 10

.

, qui signifie que l'addition de 2

1 8

, qui signifie que la

Procédures

Concepts mathématiques

• nombres entiers

• addition, soustraction, multi

lication,

division

• fractions (5e et 6e années)

• nombres décimaux (5e et 6e année)

³

Pour utiliser › et œ:

1. Appuyez sur › (ou

œ

).

2. Entrez l'opération et le nombre (par exemple,

T

2).

3. Appuyez sur › (ou

œ

).

4. Entrez le nombre auquel vous voulez appliquer l'opération de constante.

5. Appuyez sur › (ou

œ

).

L'affichage montre un

sur la gauche et le

1

résultat sur la droite. Si vous appuyez sur (ou œ) à nouveau, la calculatrice appliquera l'opération constante au résultat précédent et affichera un gauche, indiquant que l'opération constante a été appliquée deux fois à l'entrée initiale.

Matériel

• TI-15

• crayon

• activité de l'élève (page 23)

›

à

2

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

20

Procédures inverses

(suite)

Collecte et organisation des données

Lorsque les élèves utilisent › et œ, demandezleur de noter leurs résultats dans les tableaux appropriés de la feuille Activité de l'élève. Par exemple, si un élève explore le lien entre les tableaux peuvent ressembler à ceci :

x 2

et

÷ 2

,

Tableau pour

Entrée Procédure Sortie

1x22 2x24 3x26

Tableau pour

Entrée Procédure Sortie

2 4 6

›

œ

P

21

P

22

P

23

Analyse des données et déductions

Demandez aux élèves :

Quelles régularités voyez-vous dans vos données ?

•

Les procédures sont-elles inverses l'une de

•

l'autre ? Comment pouvez-vous le savoir ?

Si le nombre à la sortie pour › est utilisé comme nombre d'entrée pour œ et donne un nombre ‡ la sortie égal au nombre à l’initial pour

›

, les procédures peuvent être l'inverse l'une de

x 2

l'autre, comme dans

et

÷ 2

.

³

Pour reconnaître des procédures équivalentes, les élèves devront peutêtre utiliser la touche

Ÿ

pour changeur nombre à la sortie de forme décimale en fraction ou vice versa.

•

Le régularité fonctionne-t-elle avec des nombres spéciaux tels que 1 et 0 ? Avec des fractions et des nombres décimaux ? Avec des entiers positifs et négatifs ?

Que se passe-t-il si vous utilisez

œ

en

premier, et puis › ?

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

21

Procédures inverses

(suite)

Poursuite de l’exploration

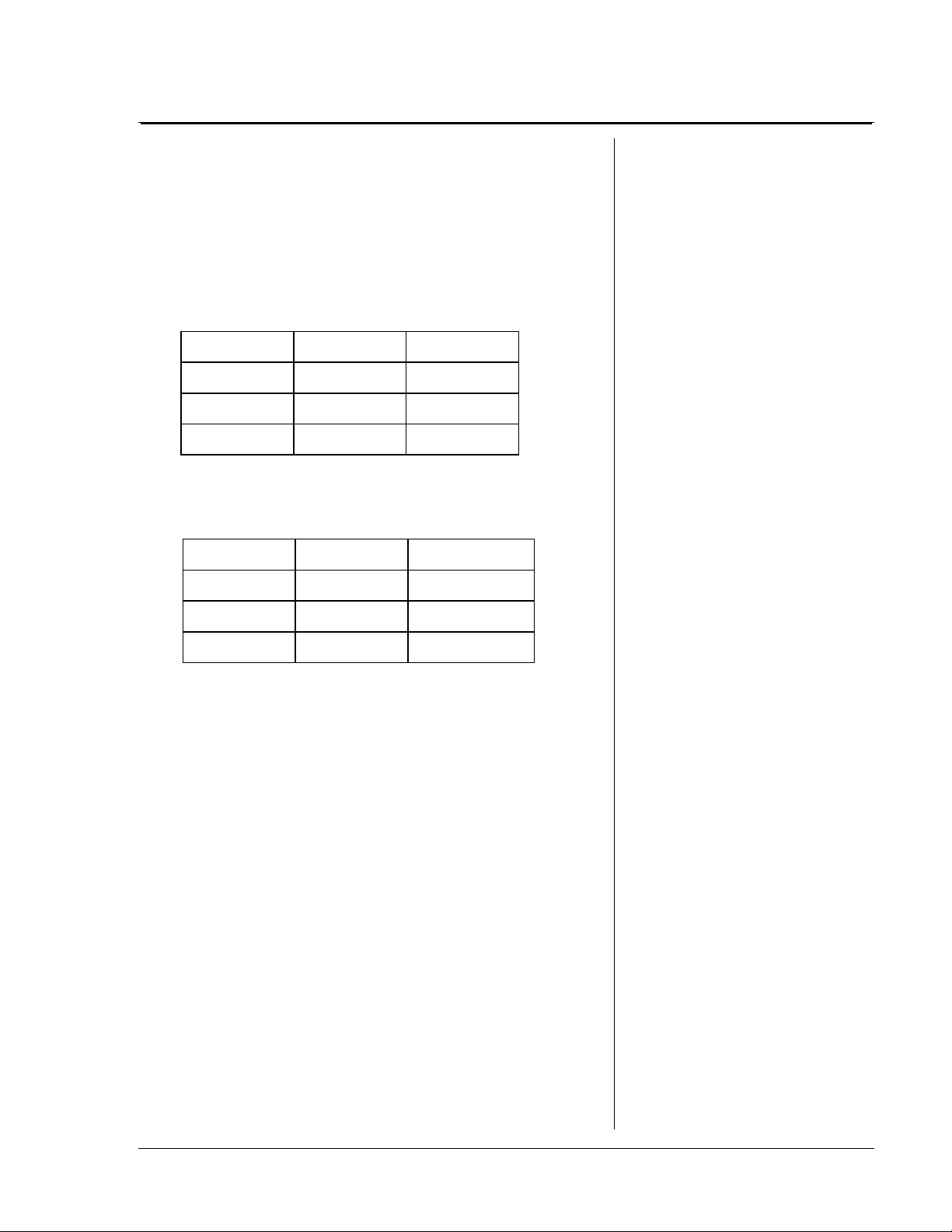
Les élèves plus âgés peuvent explorer des procédures équivalentes, telles que la division par un nombre et la multiplication par le nombre inverse. Par exemple, si un élève explore le lien entre

2

, les tableaux peuvent ressembler à ceci :

x ½

et

÷

Tableau pour

Entrée Procédure Sortie

Tableau pour

Entrée Procédure Sortie

›

1x 2x½1 3x½1.5 = 1

œ

1 2 3

½½

2 0.5 =

P

2

P

2 1.5 = 1

P

5

/

1

5

10 =

/

½

10 =

½

1½

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

22

Nom ___________________________

Procédures inverses

Date ___________________________

Collecte et organisation des données

1. Choisissez une procédure pour

2. Choisissez une procédure pour

3. Sélectionnez un nombre à l’entrée pour appliquer la procédure et notez les nombres à l’entrée et à la sortie dans le tableau approprié.

4. Utilisez les tableaux ci-dessous pour noter et comparer vos résultats en utilisant › et

Tableau pour

œ

›

.

Entrée Procédure Sortie Entrée Procédure Sortie

(par exemple,

›

(par exemple,

œ

).

x ½

).

÷ 2

Tableau pour

œ

Analyse des données et déduction de conclusions

5. Comment se comparent les deux procédures ?

__________________________________________________________________________

6. Quelles régularités voyez-vous ?

__________________________________________________________________________

7. Les deux procédures sont-elles inverses ? Expliquez.

__________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

23

Dans l’intervalle

p

q

p

3e à 6e année

Description

Les élèves vont interpréter l'arrondissement impliqué dans la valeur d’une mesure

our identifier l’intervalle

possible d'une mesure donnée.

Introduction

1. Demandez aux élèves de mesurer la longueur d'une table ou d'un bureau dans la pièce et de noter la mesure au millimètre le plus proche, par exemple, 1 357 mm.

Discutez de la façon dont les mesures en millimètres peuvent être notées comme 1 357 mm ou en millièmes de mètres, soit 1,357 m. Remarquez que la mesure a été arrondie à 1 357 mm car elle se situe entre ½ millimètre de moins que 1 357 mm (1 356,5 mm) et ½ millimètre de plus que 1 357 mm (1 357,5 mm).

Concepts mathématiques

• arrondissement de nombres entiers

• arrondissement de nombres décimaux

• mesure avec des unités métri (longueur, masse, capacité)

ues

Matériel

• TI-15

• crayon

• mètres liants ou

galons métriques

• activité de

l'élève (p.27)

1356.5 1357 1357.5

2. Demandez aux élèves d'arrondir pour noter la même mesure au centimètre le plus proche (136 cm ou 1,36 m).

3. Entrez la mesure initiale sur la calculatrice comme étant 1,357 et réglez l'affichage à deux décimales.

4. Demandez aux élèves de règler l'affichage à une décimale. Demandez :

Que représente ce nombre ?

(La mesure arrondie au dixième de mètre le plus proche ou la mesure arrondie à 14 décimètres.)

EXAS INSTRUMENTS INCORPORATED

³

Pour regler l'affichage à 2 décimales, appuyez sur Š ™ ®.

³

Demandez aux élèves de discuter de la façon dont l'affichage de correspond à leur arrondissement de la mesure à 136 cm.

TI-15 : Guide de l’enseignant

1,36

24

Dans l’intervalle

(suite)

5. Demandez aux élèves de régler l'affichage à aucune décimale. Appuyez sur Š et puis “ pour afficher

Que représente ce nombre ?

au mètre le plus proche.)

6. Introduisez la partie secrètement un nombre sur la calculatrice avec trois décimales pour représenter une mesure en millimètres; par exemple, 2,531. Affichez ensuite le nombre arrondi au nombre entier le plus proche (3). Montrez cet affichage aux élèves.

7. Informez les élèves que ce nombre représente la mesure d'une longueur de carton au mètre le plus proche. Demandez aux élèves :

Que pourrait être sa mesure si elle avait été prise au décimètre le plus proch e?

(2,5 m à 3,5 m)

8. Arrondissez le nombre initial au dixième le plus proche (2,5). Demandez aux élèves :

Cela se situe-t-il dans l’intervalle que nous avons identifié ?

1

. Demandez :

(La mesure arrondie

Dans l’intervalle

en entrant

³

Pour arrondir au nombre entier le plus proche, appuyez sur

“ ®

³

Pour arrondir au dixième le plus proche, appuyez sur Š

®

.

Š

˜

9. Répétez en mesurant au centimètre le plus proche (centièmes) et au millimètre le plus proche (millièmes). (L’intervalle des centimètres serait de 2,45 à 2,55, avec 2,53 se situant dans l’intervalle ; et l’intervalle des millimètres serait de 2,525 à 2,535, avec 2,531 se situant dans l’intervalle.)

10. Demandez aux élèves de travailler en groupes de 2 pour jouer à la partie et noter leurs observations sur la feuille d'activité de l'élève.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

25

Dans l’intervalle

(suite)

Collecte et organisation des données

Pendant que les élèves jouent la partie, attirez leur attention sur les régularités qui se développent en posant des questions telles que:

Lorsque vous notez une mesure, pourquoi faut-

•

il toujours l’arrondir ? Lorsque vous lisez une mesure, quel intervalle

•

cette mesure doit-elle toujours indiquer ?

unité de moins ou ½ unité de plus

À quoi ressemble cet intervalle surla droite

•

numérique (ou mètre pliant) ? Comment est représenté ½ dans le système

•

métrique ? Comment décider de la façon de représenter

•

l’intervalle des mesures possibles ? Quelels régularités utilisez-vous ?

)

Analyse des données et déductions

Pour guider les élèves dans l'analyse de leurs données, posez des questions telles que:

(½

Quel intervalle est indiquée par chaque mesure ?

•

Quelels régularités avez-vous utilisées pour

•

identifier l’intervalle des mesures possibles ? Comment utiliseriez-vous ces régularités pour

•

arrondir 256,0295 au dixième le plus proche ?

Poursuite de l’exploration

Demandez aux élèves de remplacer les unités de longueur par des unités de masse (grammes, centigrammes) ou capacité (litres, millilitres) pour remarquer les mêmes régularités.

Demandez aux élèves de discuter pourquoi cette approche de valeur de position décimale avec la calculatrice ne fonctionne pas avec les mesures en verges (yards), pieds et pouces. Demandez-leur d'identifier l’intervalle de la mesure si elle est calculée à la verge la plus proche, au pied le plus proche, and au pouce le plus proche. (Par exemple, 2 verges se situent entre 1 verge et 18 pouces et 2 verges et 18 pouces.)

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

26

Nom ___________________________

Dans l’intervalle

Date ___________________________

Collecte et organisation des données

Demandez à votre partenaire d'entrer secrètement une mesure à trois décimales sur la calculatrice, puis réglez l’affichage du nombre à arrondir au nombre entier le plus proche. Regardez maintenant l'affichage et répondez aux questions suivantes:

1. Quelle est la mesure au mètre le plus proche ? __________________

a. Que pourrait être l’intervalle de la mesure si celle-ci était exprimée

au dixième de mètre le plus proche (décimètres) ?

_______________________________________________________________________

b. Réglez Š sur le dixième le plus proche (˜).

Quelle est la mesure au dixième le plus proche ? _____________

Cela se situe-t-il dans l’intervalle que vous avez identifiée ? ____

2. Quelle est la mesure au dixième le plus proche d'un mètre ? ______

a. Que pourrait être l’intervalle de la mesure si elle avait été mesurée

au centième de mètre le plus proche (centimètres) ?

_______________________________________________________________________

b. Réglez Š sur le centième le plus proche (

™

).

Quelle est la mesure au centième le plus proche ? ____________

Cela se situe-t-il dans l’intervalle que vous avez identifié ? _____

3. Quelle est la mesure au centième le plus proche d'un mètre ? _____

a. Que pourrait être l’intervalle de la mesure si elle si elle avait été

exprimée au millième de mètre le plus proche (millimètres) ?

_______________________________________________________________________

b. Réglez Š sur le millième le plus proche (

š

).

Quelle est la mesure au millième le plus proche ? _____________

Cela se situe-t-il dans l’intervalle que vous avez identifié ? _____

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

27

Nom ___________________________

Dans l’intervalle

Date ___________________________

Analyse des données et déductions

Identifiez trois mesures au millimètre le plus proche qui seraient :

a. 10 m lorsqu'arrondie au mètre le plus proche. ________________

b. 9,0 m lorsqu'arrondie au dixième de mètre le plus proche

(décimètre).

_______________________________________________________________________

c. 9,05 m lorsqu'arrondie au centième de mètre le plus proche

(centimètre).

_______________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

28

L'importance de la valeur de position

p

2e à 6e année

Description

Les élèves vont travailler leur souplesse d'utilisation des nombres en ex nombres et leur re

lorant les liens entre les symboles des

résentation en base dix.

Introduction

1. Lisez

2. Donnez à chaque groupe d'élèves une grande

3. Dites aux élèves que vous êtes à court de blocs-unités

Counting On Frank.

(En comptant sur Frank) de Rod Clement. Discutez d'autres types de questions qu'une personne peut poser à propos du nombre d'objets pouvant tenir dans ou sur d'autres objets.

quantité de blocs-unités du matériel de base dix (plus de 300), et dites-leur qu'il s'agit du nombre de jujubes pouvant tenir dans un bocal que vous avez rempli. Demandez-leur de compter les “jujubes” et observez les techniques utilisées (en comptant un à la fois, en formant des groupes de 10, etc.)

puis demandez :

Combien de groupes de dix devrais-je utiliser pour obtenir le même nombre de jujubes de vous ?

Concepts mathématiques

2e à 4e années

• valeur de position d’ un nombre entier (jusque dans les milliers)

• argent

4e à 6e années

• valeur de position d’ un nombre décimal (jusque dans les millièmes)

• unités métriques (mètres, décimètres, centimètres)

³

Pour utiliser la fonction Valeur de position dans cette activité :

1. Appuyez sur ‹

2. Appuyez sur " ® pour sélectionner (Manuel).

3. Appuyez sur $ ® pour régler le mode

position

permet de trouver combien d'unités, de dizaines, de centaines, etc., sont contenues dans un nombre. (Le mode – pour trouver quel chiffre occupe la place des unités, des dizaines, des centaines, etc.)

sur

Matériel

• TI-15

• crayon

•

• matériel de

• activité de

‡

MAN

Valeur de

11

–.

Cela vous

1

– .

est utilisé

Counting on Frank

comptant sur Frank) de Rod Clement

base dix

l’'élève (pages 32 et 33)

(En

.

4. Demandez aux élèves d'explorer la réponse à ce problème avec leur blocs-unités ou d'appliquer leur connaissance de la valeur de position. Montrez-leur ensuite comment explorer la réponse en utilisant la calculatrice.

5. Demandez aux élèves de comparer leurs solutions obtenues avec le matériel de base dix et l'affichage de la calculatrice. (Ils peuvent créer 31 groupes de dix à partir des 314 unités, avec 4 unités en reste.)

EXAS INSTRUMENTS INCORPORATED

³

Pour explorer des réponses à ce problème sur la calculatrice :

1. Appuyez sur ‹.

2. Entrez le nombre d'unités (par exemple, 314).

3. Appuyez sur Œ ’ pour voir l'affichage. (En utilisant 314, l'affichage est 31 dizaines dans 314.)

TI-15 : Guide de l’enseignant

31

í

, signifiant

29

L'importance de la valeur de position

(suite)

Collecte et organisation des données

Demandez aux élèves d'utiliser leur matériel de base dix et la calculatrice pour continuer l'exploration avec d'autres nombres, en identifiant combien de centaines et de milliers (et 0,1 et 0,01 avec les élèves plus âgés). Encouragez l'exploration avec des questions telles que :

Combien de centaines a-t-on dans 120 ? 2 478 ?

•

3 056 ? Combien de dizaines a-t-on dans 120 ? 2 478 ?

•

3 056 ? Combien d'unités a-t-on dans 120 ? 2 478 ?

•

3 056 ? Quels nombres pouvez-vous trouver qui ont 12

•

unités ? 12 dizaines ? 12 centaines ? Quels nombres pouvez-vous trouver qui ont 60

•

unités ? 60 dizaines ? 60 centaines ?

Analyse des données et déductions

Demandez aux élèves d'utiliser le tableau

L'importance de la valeur de position

Activité de l'élève pour noter leurs découvertes et identifier les régularités perçues. Pour les aider observer les régularités, posez des questions telles que :

dans la feuille

³

Les élèves peuvent utiliser le mode Valeur de position vérifier leurs conjectures. Par exemple, si ils pensent que 1 602 contient 160 centaines, ils entrent

1602

, appuient sur

‘

et voient peuvent alors utiliser le matérielde base dix pour expliquer qu’il y a seulement 16 centaines dans 1 602. (Si les élèves utilisent le mode

1

–

– .

chiffre occupe la position des centaines, ils verront pour indiquer que 6 est le chiffre qui occupe la position des centaines.

11

16

pour trouver quel

í

íí

6

pour

Œ

íí

. Ils

affiché

Comment le nombre de dizaines dans 1 314 se

•

compare-t-il au nombre 1 314 ? Qu'en est-il de 567 ? 2 457 ? 4 089, etc. ?

Si vous couvrez le chiffre qui occupe la position des unités, vous voyez combien de dizaines il y a dans un nombre.

Comment le nombre de centaines dans 1 314 se

•

compare-t-il au nombre 1 314 ? Qu'en est-il de 567 ? dans 2 457 ? dans 4 089, etc. ?

Si vous couvrez les chiffres qui se trouvent à droite de la position des centaines, vous voyez combien de centaines il y a dans un nombre.

Comment l'affichage sur la calculatrice se compare-

•

t-il à ce que vous pouvez faire avec le matériel de base dix ?

Si la calculatrice affiche 31_, pour 316, je devrais être en mesure de créer 31 groupes de dix à partir des 316 unités que j'ai.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

30

L'importance de la valeur de position

Poursuite de l’exploration

Associez les régularités observèes surles valeurs de position à de l'argent. Par exemple, demandez aux élèves :

Si chaque “jujube” coûte un cent, combien de cents

•

dépenseriez-vous pour 1 314 jujubes ?

1 314 cents.

Combien de pièces de dix cents (dizaines)

•

dépenseriez-vous ?

131 pièces de dix cents et 4 cents supplémentaires.

Combien de dollars (centaines) ?

•

13 dollars, plus 14 cents supplémentaires ou 1 pièce de dix cents et 4 cents.

Les élèves plus âgés peuvent noter l'argent (et l'entrer dans la calculatrice) sous forme décimale, 13,14. Ils peuvent ensuite utiliser la calculatrice pour associer les pièces de dix cents à un dixième (0,1) d'un dollar (13,14 $ comprend 131 pièces de dix cents ou dizaines) et les cents à un centième (0,01) d'un dollar (13,14 $ comprend 1 314 cents ou centièmes).

(suite)

Avec les élèves plus âgés, associez les régularités observèes sur les valeurs de position aux conversions entre les unités de mesure métrique. Par exemple, une mesure de 324 centimètres peut aussi être notée comme 32,4 décimètres (ou arrondie à 32 dm) car 1 dm = 10 cm, ou elle peut être notée comme 3,25 mètres (ou arrondie à 3 m), car 1 m = 100 cm.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

31

L'importance de la

p

Nom _____________________________

Date _____________________________

valeur de

osition,

Partie A

Collecte et organisation des données

1. Utilisez votre matérial de base dix et votre calculatrice pour explorer combien de dizaines, de centaines et de milliers sont contenus dans un nombre. Notez vos observations dans le tableau. Quelles régularités voyez-vous ?

Nombre Nombre de

milliers

Nombre de

centaines

Nombre de

dizaines

Analyse des données et déductions : Régularités

2. Écrivez 5 nombres qui ont 15 dizaines.

__________________________________________________________________________

3. Écrivez 5 nombres qui ont 32 centaines.

__________________________________________________________________________

4. Écrivez 5 nombres qui ont 120 dizaines.

__________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

32

L'importance de la

p

Nom _____________________________

Date _____________________________

valeur de

osition,

Partie B

Collecte et organisation des données

1. Utilisez votre matériel de base dix et votre calculatrice pour explorer combien de dizièmes, de centièmes et de millièmes sont contenus dans un nombre. Notez vos observations dans le tableau. Quelles régularités voyez-vous ?

Nombre Nombre de

dixièmes

Nombre de

centièmes

Nombre de

millièmes

Analyse des données et déductions : Régularités

2. Écrivez 5 nombres qui ont 15 dixièmes.

__________________________________________________________________________

3. Écrivez 5 nombres qui ont 32 centièmes.

__________________________________________________________________________

4. Écrivez 5 nombres qui ont 120 dixièmes.

__________________________________________________________________________

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

33

Quel est le problème ?

p

q

2e à 5e années

Description

Les élèves vont associer des phrases mathématiques à des situations de soustraction, la multi

roblème et utiliser l'addition, la

lication et la division pour

résoudre les problèmes.

Introduction

1. Au tableau ou sur un rétro-projecteur, affichez une phrase mathématique telle que “8 + 2 = ?” Demandez aux élèves de penser à des situations et à des questions que cette phrase pourrait représenter. Par exemple, “Si j'ai acheté huit cartes postales pendant mes vacances et que j'avais déjà deux cartes postales à la maison, combien de cartes postales ai-je maintenant ?”

2. Au besoin, demandez aux élèves de mettre la situation en action à l'aide de compteurs et de déterminer que la valeur de “?” est 10.

3. Montrez comment afficher cette équation sur la calculatrice et comment indiquer à la calculatrice quelle est la valeur de ?.

4. Affichez maintenant une équation telle que “? - 10 = 5”. Demandez aux élèves de penser à des situations et des questions que cette phrase mathématique pourrait représenter. Par exemple, “J'avais de l'argent dans ma poche et j'ai dépensé 10 cents du total. Il me reste seulement 5 cents. Combien d'argent avais-je dans ma poche au départ ?” Demandez aux élèves d’appuyer sur les touches nécessaires pour afficher cette équation et de vérifier la valeur qu'ils ont déterminée pour “?”.

5. Pendant un certain temps, continuez à initier lles élèves aux différents types de phrases de phrases mathématiques à explorer. Par exemple, “? - 8 < 5” (qui a 13 solutions entières) et “? x ? = 24” (qui a 8 solutions de paires de facteurs entierd) et “? x 4 = 2” (qui n'a aucune solution entiËre).

Concepts mathématiques

• addition, soustraction

• multi

•

• inégalités (3e à

lication, division (3e à 5e années)

hrases mathémati (équations)

5e années)

³

Pour afficher cette équation sur la calculatrice, mettez la calculatrice en mode Résolution de problème en appuyant sur la touche ‹. Entrez ensuite l'équation

= ?

L'affichage de la calculatrice ( indique le nombre de solutions entierères qui sont possibles dans l'équation.

Pour vérifier votre solution à l'équation, entrez la valeur de et appuyez sur ®. La calculatrice affichera

YES

³

Si une valeur incorrecte est vérifiée pour ?, la calculatrice affichera

NO

Par exemple, si un élève vérifie 5 pour l'équation calculatrice affiche NO, puis affiche et revient ensuite à l'équation initiale.

ues

et appuyez sur ®.

.

et offrira un indice.

Matériel

• TI-15

• compteurs

• crayon

• activité de l'élève (page 37)

1 SOL

? - 10= 5

5 - 10 < 5

8 + 2

)

10

, la

,

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

34

Quel est le problème ?

Collecte et organisation des données

Pour réaliser cette activité, demandez aux élèves de travailler en petits groupes de 2 et d'utiliser la feuille d’ activité de l’élève des cartes de résolution de problème. Demandez à un partenaire de créer une phrase mathématique contenant une addition, unr soustraction, une multiplication ou une division en utilisant le symbole “?” et de le noter dans la zone supérieure de la feuille d’ activité de l’élève et sur la calculatrice. Si possible, l'autre partenaire crée une situation et une question associées à la phrase mathématique et les note dans la zone inférieure de la feuille d’ activité de l’élève. Les deux zones peuvent être collées ensemble sur les deux côtés d'une carte.

Demandez aux élèves de travailler ensemble avec la calculatrice pour explorée le nombre de solutions entières qui sont offertes par l'équation et vérifiez les solutions. Donnez des idées d'exploration en posant des questions telles que :

Quel est le problème

pour créer

(suite)

Quelles actions pourraient se produire dans une

•

situation se traduisant par une addition (une soustraction,une multiplication ou une division) ?

Comment pourriez-vous utiliser les compteurs pour

•

mettre en situation cette phrase mathématique ?

Que pourrait représenter ce nombre dans la

•

phrase mathématique de votre situation ?

Que pourrait représenter le point

•

d'interrogation dans la phrase mathématique de votre situatione ?

Pouvez-vousinventer une situation se

•

traduisant par une phrase mathématique qui commence par un point d'interrogation ?

Analyse des données et déductions

Pour centrer la pensée des élèves sur les liens entre leurs situations et les nombres et les opérations de leurs phrases mathématiques, posez des questions telles que :

Comment l'utilisation d'un nombre différent

•

changera-t-elle votre situation ?

Comment l'utilisation d'un symbole supérieur à

•

ou inférieur à plutôt qu'un signe égal changerat-elle votre situation ?

•

Comment l'utilisation d'une opération différente dans votre phrase mathématique change-t-elle votre situation ?

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

35

Quel est le problème ?

Poursuite de l’exploration

•

Demandez aux élèves de créer des situations et de les échanger. Chaque partenaire peut ensuite rédiger une phrase mathématique pour traduire la situation de l'autre partenaire.

•

Demandez aux élèves de trier les phrases mathématiques créées par catégories : par exemple, celles qui n'ont aucune solution entière, celles qui ont une solution se traduisant par un nombre entier et celles qui ont deux solutions se traduisant par un nombre entier, celles qui ont un nombre infini de solutions se traduisant par un nombre entier.

•

Demandez aux élèves d'essayer de trouver une équation ou une inégalité avec exactement 0 solution se traduisant en nombre entier, exactement 1 solution se traduisant par un nombre entier, exactement 2 solutions se traduisant par un nombre entier, plus de 5 solutions se traduisant par un nombre entier, etc.

(suite)

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

36

Nom ___________________________

Quel est le problème ?

Date ___________________________

Rédigez une phrase mathématique en utilisant une opération et le symbole “?”

Rédigez une situation et posez une question qui peut être représentée par la phrase mathématique.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

37

Comment

utiliser

la TI.15

Affichage, défilement, priorité des

opérations, parenthèses 39 Effacement et correction 42 Menus de la touche mode 45 Opérations élémentaires 48 Opérations avec des constantes 55 Nombres entiers et nombres décimaux 63 Mémoire 68

Fractions71 Pourcentage 80 Pi 84 Puissances et racines carrées 88 Résolution de problèmes : Mode Auto 94 Résolution de problèmes : Mode Manuel 100 Valeur de position 106

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

38

Affichage, défilement, priorité des

p

pp

p

pp

p

jusq

p

j

p

opérations, parenthèses

1

Touches

1.

2.

3.

ouvre une ex

X

arenthèses. Vous pouvez avoir jusqu'à

8 parenthèses à la fois.

ferme une ex

Y

parenthèses.

et " dé

!

gauche et la droite d'entrée.

et $ dé

#

haut et le bas précédentes et résultats.

ression entre

lacent le curseur vers la

our défiler la ligne

lacent le curseur vers le

armi les entrées

Remarques

Les exemples affichés sur les

•

originaux des trans su

osent tous les réglages par

défaut. L’original du transparent EOSTM

•

résente la priorité dans laquel le TI-

15 effectue les calculs. Lorsque vous utilisez les parenthèses

•

a

uyez sur ® avant d'appuyer sur

Y, Syn Error s'affiche. Les opérations qui se trouvent entre

•

arenthèses sont exécutées en remier. Utilisez X ou Y pour

modifier la par conséquent, le résultat.

Exemple : 1 + 2 x 3 = 7

riorité des opérations et,

(1 + 2) x 3 = 9

arents

Les première et seconde lignes

•

affichent des entrées com

3

•

1

2

u'à 11 caractères incluant la

artie décimale, un signe négatif et un

ex

osant positif ou négatif à deux chiffres. Les entrées commencent à gauche et défilent vers la droite. Une entrée est tou l'opération.

L'affichage des résultats est justifié à droite. Si un tient résultat s'affiche sur la seconde ligne.

as sur la première ligne, le

ours renvoyée à

roblème entier ne

renant

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

39

Système d'exploitation d'équations

p

Priorité Fonctions

(EOS)

1 (première)

2

3

4

5

6

7

X Y

¢

¨ ¬

M

V W

T U

¦ Ÿ

8 (dernière)

®

Les opérations entre parenthèses étant exécutées en

remier, vous ouvez utiliser X Y pour modifier la riorité des opérations et, par

conséquent, le résultat.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

40

Priorité des opérations

1 + 2 x 3 =

Appuyez sur Affichage

1

T

2

V

3

1Û2Ý3Ú 7

®

(1 + 2) x 3 =

Appuyez sur Affichage

Aditionner

T

Multiplier

V

Parenthèses

X Y

X V

1 3

T

2

®

Y

Å1Û2ÆÝ3Ú 9

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

41

Effacement et correction

p

q

p

2

Touches

1.

2.

3.

met en marche et éteint la

−

calculatrice.

efface le dernier chiffre entré

w

vous sans avoir à ressaisir le nombre en entier.

”

condition d'erreur. Vous entrer un nouveau nombre et votre calcul. Lors elle efface toutes les o cours. Une fois l'affichage effacé, elle dé récente.

ermettre de corriger une entrée

efface la dernière entrée et toute

ouvez alors

oursuivre

u'appuyée deux fois,

érations en

lace le curseur vers l'entrée la plus

our

Remarques

Les exemples sur les originaux des

•

trans réglages par défaut.

Appuyez sur − et ” simultanément

•

our remettre à zéro la calculatrice.

Remise à zéro de la calculatrice :

−

L'appui de ” n'affecte pas la mémoire

•

ou les constantes.

arents supposent tous les

Ramène les réglages à leurs valeurs par défaut.

Efface la mémoire et les constantes.

1

EXAS INSTRUMENTS INCORPORATED

3

2

TI-15 : Guide de l’enseignant

42

Effacement des entrées

p

1. Entrez 335 + 10.

2. Effacez l'entrée et l'o cours.

3. Entrez 335 N 9.

4. Terminez le calcul.

Appuyez sur Affichage

335

T

10

335Û10á

ération en

”

(effacez l'entrée)

á

Effacer

”

335

U

9

335Ü9

®

335Ü9Ú 326

Remarque : ” efface l'écran mais non l'historique.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

43

Correction d'erreurs de saisie à l'aide de

p

w

1. Entrez 1569 + 3.

2. Changez le 9

3. Aditionnez 3.

4. Terminez le calcul.

Appuyez sur Affichage

1569

w w w

T

3

T

3

8

ar un 8.

1569Û3á

1568á

1568Û3á

Retour arrière

w

®

1568Û3Ú 1571

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

44

Menus de la touche mode

Touches

Consultez les tableaux des deux pages suivantes pour obtenir les détails sur chaque option de paramètre de mode.

1.

affiche le menu du mode

‡

Calculatrice à partir duquel vous pouvez sélectionner les options suivantes :

Réglage Options

Division (P)

Constants (Op)

Clear Ops

RESET

(décimal)

.

(fraction)

n/d

+1 ?

Op 1 Op 2

N Y

(afficher)

(masquer)

(effacer Op 1)

(effacer Op 2)

(Non)

(Oui)

2.

3.

3

‹ ‡

Résolution de problèmes à partir duquel vous pouvez sélectionner les options suivantes :

Réglage Options

Mode

Niveau de difficulté

Opération

Option d'affichage

¢

partir duquel vous pouvez sélectionner les options suivantes :

Réglage Options

Affichage

affiche le menu du mode

Auto Man

1 2 3

+ – x P ?

11-. 1-.

affiche le menu Fractions à

(nombre

U n/d

fractionnaire)

n/d

(impropre)

Simplification

Remarques

1

2

3

Les exemples sur les originaux des

•

transparents supposent tous les réglages par défaut.

Vous devez être en mode Résolution

•

de problèmes (‹) pour voir son menu lorsque vous appuyez sur vous voyez le menu du mode Calculatrice.

Appuyez sur

•

menu du mode Calculatrice, sur

‹‡

Résolution de problèmes ou sur pour afficher le menu du mode Fractions. Appuyez sur avoir fait votre sélection, puis appuyez sur nouveau pour quitter le menu.

pour afficher le menu du mode

‡

Man Auto

pour afficher le

‡

ou sur

(Manuelle)

. Sinon,

‡

¢

après

®

de

¢

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

45

Menus de la touche mode

(suite)

Menu du mode Calculatrice

Réglage Option Signification Exemple

3

Division (Þ)

Constant Operations (OP)

Clear OP1 Lorsque sélectionné, efface Op1

Reset N Non ; ne remet pas la calculatrice à

.

n/d Affiche les résultats de la division sous

+1 Affiche l'opération de constante sur

? Masque l'opération de constante

OP2 Lorsque sélectionné, efface Op2

Y Oui ; remet la calculatrice à zéro.

Affiche les résultats de la division sous forme décimale

forme de fraction

l'affichage

zéro.

0,75

3 4

1x5 15

15

Menu du mode Résolution de problèmes

Réglage Sous-menu Option Exemple

Auto

Manual Option

Niveau de difficulté

Opération

d'affichage (pour Résolution de problèmes Valeur de position seulement)

1 2 3

+ – x P ?

multiplie, divise, trouve l'opération)

(Affiche le nombre d'unités, de

11-.

dizaines, de centaines ou de milliers)

(Affiche le chiffre à la place des

1-.

unités, des dizaines, des centaines ou des milliers)

(additionne, soustrait,

1234 pour ‘: 12_ _

1234 pour ‘: _ 2 _ _

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

46

Menus de la touche mode

Menu Fractions

Réglage Option Signification Exemple

(suite)

3

Display

Simplify Man Permet la simplification manuelle

U n/d

n/d Affiche les résultats en tant que

Auto Simplifie automatiquement à la forme

Affiche les résultats en tant que nombres mixtes

fractions incorrectes

de fraction la plus réduite

3

1

4

7

4

3

6

=

4

8

3 4

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

47

Opérations élémentaires

p

pp

q

p

q

4

Touches

1.

2.

3.

4.

aditionne.

T

soustrait.

U

multiplie.

V

divise. Le résultat

W

eut être affiché sous forme décimale ou sous forme de fraction selon le réglage du mode sélectionné.

5.

divise un nombre entier

£

nombre entier et affiche le résultat comme un quotient et un reste.

6.

7.

termine l'opération.

®

M

vous

ermet d'entrer un nombre

négatif.

ar un

Remarques

Les exemples sur les originaux des

•

trans

arents supposent tous les

réglages par défaut. Le résultat de la division de nombres

•

entiers £ a un quotient et un reste (__

Le nombre maximum de chiffres pour

•

le

uotient ou le reste (r) est 5. Le

araît toujours comme

r

uotient, le reste et le caractère r ne euvent pas totaliser plus de 10

caractères. Si vous utilisez le résultat de la

•

division de nombres entiers dans un autre calcul, seul le

uotient est

utilisé. Le reste n'est pas utilisé. Tous les nombres utilisés avec £

•

doivent être des nombres entiers positifs.

__).

Si vous tentez de diviser par 0, un

•

message d'erreur s'affiche. T, U, V, W, ®, et £

•

fonctionnent avec les constantes intégrées.

5

4

3

2

1

6

7

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

48

Opérations élémentaires

2 + 54 N 6 =

Additionner,

Soustraire

T U

Multiplier, Diviser

Appuyez sur Affichage

2 6

T

54

®

U

2Û54Ü6Ú 50

3 x 4 P 2 =

Appuyez sur Affichage

3

V

4

W

2

3Ý4Þ2Ú 6

®

V W

Est égal à

®

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

49

Saisie de nombres négatifs

p

La température dans l'état de Utah était de N3° C à 6 heures. À 10 heures, la tem Quelle était la tem

érature était montée de 12° C.

érature à 10

heures ?

Appuyez sur Affichage

M

3

T

12

3Û12Ú 9

Ü

®

Négatif

M

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

50

Division de nombres entiers avec reste

p

q

Christian a 27 morceaux de gomme à mâcher. Il veut

artager les morceaux de façon égale entre 5 amis et luimême. Combien de morceaux seront donnés à cha

ue personne ? Combien de

morceaux restera-t-il ?

Appuyez sur Affichage

27

£

6

27Þ

6Ú 4½3

®

Division de

nombres entiers

£

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

51

Résultat de division sous forme décimale

Réglez l'option d'affichage de division sur forme décimale et divisez 27 par 6.

Appuyez sur Affichage

‡ ®

Ù

ê

»Ä¸

/

‡

á

27

W

6

®

27Þ

6 Ú 4Ù5

Diviser

W

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

52

Résultat de division sous frome de fraction

1

Réglez l'option d'affichage de division sur fraction et divisez 27 par 6.

Appuyez sur Affichage

‡" ®

Ù

»Ä¸ êêêê

/

‡

á

n

27

W

6

®

27Þ

6Ú 4

P

Diviser

W

5

êêêê

0

¤

n

P

5 1

êêêê

4

êêê

4

10 2

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

53

Calcul d'unités équivalentes de temps

p

Sarah a couru 2 kilomètres en 450 secondes. Convertissez le tem

s en

minutes et secondes.

450 secondes = ? minutes

? secondes

Appuyez sur Affichage

450

£

60

450Þ60Ú 7½30

®

Division de

nombres entiers

£

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

54

Opérations avec des constantes

Touches

1.

2.

Remarques

•

vous permet de définir ou d'exécuter

›

l'opération 1.

vous permet de définir ou

œ

d'exécuter l'opération de constante 2.

Les exemples sur les originaux des transparents supposent tous les réglages par défaut.

La mémoire des constantes est réglée en combinaison avec lorsque vous exécutez un calcul qui utilise T, U, V, W,

›

£

et

œ

, et ¨.

La fonction Constante fonctionne

•

avec des nombres entiers, des nombres décimaux et des fractions.

Lorsque vous utilisez

•

compteur apparaît à gauche et le résultat apparaît à droite dans l'affichage. Le compteur affiche le nombre de fois que la constante est répétée. Si le nombre situé à droite dans l'affichage dépasse 6 chiffres, le compteur n'apparaît pas. Le compteur revient à 0 après avoir atteint 99.

Lorsque vous utilisez

•

fonction Constante, les calculs suivants sont exécutés avec la partie quotient du résultat. Le reste n'est pas utilisé.

›

£

ou

œ

avec la

5

, un

Vous pouvez effacer une constante

•

stockée en mémoire en remettant à zéro la calculatrice (en appuyant sur

et ” simultanément) ou en

−

appuyant sur sur $ pour faire défiler le menu

1

2

CLEAR, puis en sélectionnant OP1 (ou OP2) et en appuyant sur de − seule n'efface pas la fonction Constante.

, et en appuyant

‡

®

. L'appui

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

55

Addition en tant que “comptage”

Il y a 4 grenouilles dans un étang. Si 3 autres grenouilles sautent dans l'étang 1 à la fois, combien de grenouilles seront dans l'étang ?

Appuyez sur Affichage

› T

(stocke

1

›

Û1

Op1

Opérations avec

des constantes

›

Additionner

T

l'opération)

4

(initialise en utilisant 4)

›

(additionne 1, un à la fois)

›

Op1

4

Op1

4Û1 15

Op1

5Û1 26

Op1

6Û1 37

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

56

Multiplication en tant que “addition répétée”

p

Marie installe de nouveaux carreaux dans sa cuisine. Elle a fait 4 rangées de 5 carreaux chacune. Utilisez une addition ré

étée pour trouver le nombre de carreaux utilisés. Avant de commencer, réglez la calculatrice de façon à masquer l'opération de constante.

Appuyez sur Affichage

Opérations avec

des constantes

›

‡$"

‡

› T

(stocke l'opération)

5

0

(initialise en utilisant 0)

(suite)

›

Û1 Ã

¼Á

á

Op1

Û5

Op1

0á

êê

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

57

Multiplication en tant que “addition répétée”

(suite)

Appuyez sur Affichage

›

Op1

1 5

Op1

210

Op1

315

Op1

420

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

58

Puissances en tant que “multiplication répétée”

p

Utilisez cette formule et la multi

lication répétée pour trouver le volume d'un cube ayant une arête de 5 mètres.

V = L x l x h = 5 x 5 x 5 = 5

Appuyez sur Affichage

3

Opérations avec

des constantes

›

Multiplier

V

› V

(stocke l'opération)

5

1

(initialise en utilisant 1)

›

Op1

Ý5

Op1

1á

Op1

1Ý5 15

Op1

5Ý5 225

Op1

25Ý5

3 125

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

59

Utilisation de

¨

en tant que constante

Utilisez cette formule pour trouver le volume de chaque cube.

V = base

Appuyez sur Affichage

› ¨

3

›

3

Op1

É3

Opérations avec

des constantes

›

Puissances

¨

2

3

4

›

Op1

2É3 18

Op1

›

3É3 127

Op1

›

4É3 164

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

60

Utilisation de OP 1 et OP 2 ensemble

q

p

q

p

Ming a reçu 5 collants pour chaque tâche domesti donné 2 collants à son frère aidée avec cha ont accom

ue accomplie. Elle a

our l'avoir

ue tâche. Si les deux

li 3 tâches, combien de

collants a-t-elle ?

Appuyez sur Affichage

› T

œ U

5

2

›

Û5

œ

Ü2

Op1

Op1 Op2

Opérations avec

des constantes

›

œ

0

›

œ

›œ

Op1 Op2

0á

Op1 Op2

0Û5 15

Op1 Op2

5Ü2 13

Op1 Op2

8Ü2 16

Op1 Op2

11Ü2

EXAS INSTRUMENTS INCORPORATED

19

TI-15 : Guide de l’enseignant

61

Effacement d'une opération constante

Avant d'entrer une nouvelle opération dans OP1 ou OP2, vous devez effacer les valeurs actuelles.

Appuyez sur Affichage

‡

Ù ßÄ¸

ê

Þ

$$

¼ÁÏ ¼Á2

êêêê

ç

Menu Mode

‡

®

(efface OP1)

¼ÁÏ ¼Á2

êêêê

ç

" ®

(efface OP2)

¼ÁÏ ¼Á2

êêêê

ç

‡

(quitte le menu Mode)

Remarque : L'appui de ” n'efface pas l’opération avec constante.

á

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

62

Nombres entiers et nombres décimaux

p

pp

p

q

p

q

p

j

q

pp

7

Touches

1.

2.

3.

entre une décimale.

r

règle le nombre de décimales en

Š

combinaison avec les touches de Valeur de

osition (3 à 9 dans l'illustration cidessous). Seul le résultat affiché est arrondi ; la valeur stockée à l’interne n'est est com significatifs au besoin.

Š 

milliers.

as arrondie. La valeur calculée

létée avec des zéros non

arrondit les résultats en

4.

Š ‘ arrondit les résultats en centaines.

5.

Š ’ arrondit les résultats en dizaines.

6.

Š “ arrondit les résultats en unités.

7.

Š ˜ arrondit les résultats au dizième le plus proche.

8.

Š ™ arrondit les résultats au centième le plus proche.

9.

Š š arrondit les résultats au millième le plus proche.

6

Š r su virgule fixe.

Vous devez a touche de Valeur de fois

ue vous voulez modifier le nombre de décimales à l'arrondissement.

Remarques

Les exemples sur les originaux des

•

trans réglages par défaut.

La calculatrice arrondit

•

automati nombre de décimales sélectionné.

2

3

4

5

6

1

8

9

(Seule la valeur affichée est arrondie. La valeur stockée à l’interne n'est arrondie.)

Toutes les entrées sont affichées

•

selon le réglage de

ue vous effaciez le réglage en

a

uyant sur Š r ou en remettant

la calculatrice à zéro.

rime le réglage de la

uyer sur Š avant une

osition chaque

arents supposent tous les

uement le résultat au

as

à fixé jusqu'à ce

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

63

Nombres entiers et nombres décimaux

p

pp

p

6

Remarques

Vous pouvez définir de 0 à 3 décimales.

•

Si les élèves sont incertains en

•

arrondissant 0,555 au nombre entier le

lus proche, par exemple, et que le résultat est 1, vous devrez leur ra l'arrondissement.

Vous pouvez utiliser Š pour définir le

•

nombre de décimales Ce saisir des nombres avec une virgule flottante, nombre de décimales.

Vous devez appuyer sur

•

FIX entre en vigueur.

(suite)

eut-être

eler les règles concernant

endant un calcul.

endant, vous pouvez utiliser r pour

eu importe le réglage du

avant que

®

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

64

Réglage du nombre de décimales

p

Arrondissez 12,345 au centième, au dixième, au millième,

uis annulez le

réglage Fix.

Appuyez sur Affichage

r

12

345

12Ù345Ú

®

12Ù345

Fix

Š ™

12Ù345Ú 12Ù35

Fix

Š ˜

12Ù345Ú 12Ù3

Virgule fixe

Š

Š š

Pour annuler Fix :

Š r

Fix

12Ù345Ú

12Ù345

12Ù345Ú

12Ù345

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

65

Addition de valeurs en argent

José a acheté pour 3,50 $ de crème glacée, 2,75 $ de biscuits et un grand verre de boisson gazeuse à 0,99 $. Combien a-t-elle dépensé ?

Appuyez sur Affichage

Fix

Š ™ ®

r

3

r

75

99

50

T r

®

T

2

3Ù50Û2Ù75 ÛÙ99Ú 7Ù24

Fix

Virgule fixe

Š

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

66

Conversion de nombres décimaux en fractions

p

Convertissez le nombre décimal 0,5 en fraction,

uis affichez de nouveau le

nombre décimal après la conversion.

Appuyez sur Affichage

r

5

®

ÙÓÚ ØÙÓ

n

N

Ÿ

ÙÓÚ Ó

&

êêêê

ÏØ

Ÿ

(Revenir au nombre décimal)

ØÙÓ

Virgule fixe

Š

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

67

Mémoire

p

j

p

pp

p

q

Touches

1.

fonctionne de la façon suivante :

z

z ®

z T

z U

z V

z W

Stocke la valeur affichée en rem de Additionne la valeur affichée à la valeur en mémoire. Soustrait la valeur affichée de la valeur en mémoire.

Multi

Divise la valeur en mémoire

laçant la valeur en

à en mémoire.

lie la valeur affichée

ar la valeur en mémoire.

ar la valeur affichée.

z £ Effectue la division de

nombres entiers de la valeur en mémoire affichée.

2. | ra

mémoire sur l'affichage. Une seconde pression vide la mémoire.

Remarques

Les exemples sur les originaux des

•

trans réglages par défaut.

Les résultats sont stockés en

•

mémoire et ne sont L'affichage reste le même.

arents supposent tous les

ar la valeur

elle le contenu de la

as affichés.

7

Vous pouvez stocker des fractions,

•

des nombres décimaux et des nombres négatifs en mémoire.

•

1

2

s'affiche cha

M

autre que 0 est en mémoire.

Pour effacer la mémoire, appuyez deux fois sur |.

ue fois qu'une valeur

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

68

Utilisation de la mémoire pour additionner

pp

p

pp

z T

pp

)

des coûts

Hamburgers 2 1,19 $ = Laits fra Bon

our chaque

lait fra

és 3 1,25 $ =

é 3 0,20 $ =

Coût total =

Appuyez sur Affichage

2

V

1

r

19

2Ý1Ù19Ú 2Ù38

®

z ®

M

2Ý1Ù19Ú 2Ù38

3

V

1

r

25

3Ý1Ù25Ú 3Ù75

M

®

Stocker en mémoire

z

Rappel de la

mémoire

|

Additionner le coût

(

des laits fra valeur en mémoire.

V r

3

és à la

20

®

z U

Déduire la valeur des

(

bons de la mémoire.)

|

Rappeler le coût

(

total.)

EXAS INSTRUMENTS INCORPORATED

M

3Ý1Ù25Ú 3Ù75

M

3ÝÙ20Ú 0Ù6

M

3ÝÙ20Ú 0Ù6

M

5Ù53

TI-15 : Guide de l’enseignant

69

Utilisation de la mémoire pour calculer des

q

moyennes

Daniel a des notes d'examen de 96 et

85. Il a des notes de travaux hebdomadaires de 87 et 98. Calculez la moyenne de cha

ue groupe de notes et

la moyenne de l'ensemble des notes.

Appuyez sur Affichage

96

T

85

96Û85Ú 181

®

W

2

®

181Þ2Ú 90Ù5

Stocker en mémoire

z

Additionner

T

Rappel de mémoire

|

z ®

87

T

98

®

W

2

®

T | ®

W

2

®

M

181Þ2Ú 90Ù5

M

87Û98Ú 185

M

185Þ2Ú 92Ù5

M

92Ù5Û90Ù5Ú

183

M

183Þ2Ú 91Ù5

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

70

Fractions

p

pp

p

pp

p

Touches

1.

affiche un menu de 4 réglages à

¢

artir desquels vous pouvez sélectionner la façon dont les résultats ex

rimés en fractions seront affichés.

Vous sélectionnez 2 éléments.

ar défaut) affiche des

(

U n/d

résultats de nombres fractionnaires.

affiche des résultats sous forme de

n/d

fraction.

(

Man

ar défaut) affiche des résultats

sous forme de fraction non sim

our que vouspuissiez les simplifier manuellement.

Auto

affiche des résultats sous forme

d’une fraction irréductible équivalente.

lifiée

8

2.  vous permet d'entrer la partie

entière d'un nombre fractionnaire.

3.  vous

numérateur d'une fraction.

4. ¥ vous

dénominateur d'une fraction.

5. ¦ change un nombre fractionnaire

en une fraction impropre et vice versa.

6. ¤ sim

le

lus petit facteur premier commun. Si vous voulez choisir le facteur (

lutôt que de laisser la calculatrice le choisir), a facteur (un nombre entier), a Vous devez être en mode Manuel utiliser cette fonction.

ermet d'entrer le

lifie une fraction en utilisant

uyez sur ¤, entrez le

uis

uyez sur ®.

our

7. Ÿ change une fraction

ar son

équivalent décimal et vice versa.

8. § affiche le diviseur (facteur) utilisé

our simplifier le dernier résultat sous forme de fraction. Vous devez être en mode Manuel

3

2

6

4

5

1

8

7

fonction.

Remarques

Les exemples sur les originaux des

•

trans

arents supposent tous les

our utiliser cette

réglages par défaut.

La division d'une fraction par une

•

fraction donne des résultats sous forme de fraction

eu importe le réglage de la division (décimal ou fraction).

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

71

Fractions

Remarques (suite)

Les réglages du mode

•

options d'affichage possibles pour les résultats de calcul affichés sous forme de fraction. Par exemple, pour 6 ÷ 4, les affichages ressemblent à ceci :

simp manuelle /impropre (n/d) :

simp auto /impropre (n/d) :

simp manuelle /nombre

•

fractionnaire (U n/d) :

simp auto / nombre

fractionnaire (U n/d) :

Vous pouvez entrer le dénominateur ou le numérateur en premier.

Vous pouvez entrer un nombre de 1 à

•

1000 comme dénominateur.

¢

offrent 4

8

Lorsque vous multipliez ou divisez des

•

fractions et des nombres décimaux, le résultat est affiché sous la forme décimale. Un nombre décimal ne peut pas être converti en fraction si le

6

4 3 2 2

1

4

1

2

résultat ne peut pas tenir dans l'affichage.

Tout effacement à l'aide de la touche

•

retour arrière w dans les fractions se fait du coin inférieur droit au coin supérieur gauche. Si vous appuyez par inadvertance sur la touche du dénominateur ¥ après avoir entré le numérateur, sans avoir d'abord entré un nombre comme dénominateur, la touche de retour arrière w ne corrigera pas cette erreur. Vous devrez effacer et recommencer l'entrée.

Si le nombre de décimales est réglé

•

sur 0, l'équivalent décimal pour une fraction ne sera pas affiché.

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

72

Addition de nombres fractionnaires

p

Un bébé fille pesait 4

3

livres à la

8

/ naissance. Dans les 6 mois suivants, elle a

ris 2

3

livres. Combien pèse-t-

4

/

elle ?

Touche du

numérateur



Touche du

dénominateur

¥

Touche d'unité



Conversion de

nombre

Appuyez sur Affichage



4



3



2

¥ ®

4

T

8

3

¥



3

4

3 3 1

Û

ííí

8

Û

2

84 8

¦

fractionnaire à

fraction impropre

¦

íííííí

Ú

ííí

74

57

ннннн

8

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

73

Simplification de fractions

Méthode 1 : La calculatrice choisit un facteur commun

18

Simplifier

.

24

Appuyez sur Affichage

18

(Entrez la fraction.)



24

¥

18

ннннн

24

¤

18 S

(Préparez à simplifier.)

ннннн

24

à¾á

N

n

&

®

18 9

(Simplifiez la fraction.)

ннннн

à¾

íííí

24 12

Touche du

numérateur



Touche du

dénominateur

¥

Simplifier

¤

Facteur

§

(Optionnel : Vérifiez le facteur. Vous devez être en mode Manuel.)

§

(Revenez à la fraction.)

¤ ®

(Continuez la simplification.)

EXAS INSTRUMENTS INCORPORATED

N

n

&

íííí

12

9 3

íííí

à¾

ííí

12 4

TI-15 : Guide de l’enseignant

2

9

74

Simplification de fractions

¤

(

p

Méthode 2 : Vous choisissez un facteur commun

18

Simplifier

Appuyez sur Affichage

18

(Entrez la fraction.)

sim



24

Préparez à

lifier.)

24

.

¥

18

íííí

24

18

íííí

24

á

à¾á

Touche du

numérateur



Touche du

dénominateur

¥

Simplifier

¤

6

(Entrez un facteur commun.)

®

(Simplifiez la fraction.)

18

íííí

à¾Ôá

24

18 3

íííí

à¾Ôá

24 4

ííí

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

75

Conversion de fractions en nombres décimaux

p

5

Convertissez la fraction

en un

Touche du

nombre décimal,

uis affichez la fraction

initiale après la conversion.

Appuyez sur Affichage



5

®

10

¥

55

íííí íííí

Ú

10 10

Ÿ

(Revenez à la

N

n

&

n

&

0Ù5

5

íííí

numérateur



Touche du

dénominateur

¥

Fraction à nombre

décimal

Ÿ

fraction.)

Ÿ

(Revenez au nombre décimal.)

EXAS INSTRUMENTS INCORPORATED

10

0Ù5

TI-15 : Guide de l’enseignant

76

Conversion de nombres décimaux en fractions

p

Convertissez le nombre décimal 0,5 en une fraction,

uis affichez de nouveau le

nombre décimal après la conversion.

Appuyez sur Affichage

r

5

®

Ù5Ú 0Ù5

N

n

&

Ÿ

Ù5Ú 5

íííí

10

Touche du

numérateur



Touche du

dénominateur

¥

Fraction à nombre

décimal

Ÿ

(Revenez au nombre décimal.)

0Ù5

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

77

Conversion de fractions en nombres fractionnaires

6

Convertissez la fraction impropre

en

Touche du

un nombre fractionnaire.

Appuyez sur Affichage

¢

¿ »Ä¸ »Д¸ кккккк

$

èæ êêêê

numérateur



Touche du

dénominateur

¥

Mode de fraction

¢

6



®

¤ ®

¦

EXAS INSTRUMENTS INCORPORATED

4

n

N

&

62

Ú

44

2 1

ííí

1 1

4 2

ííííííí

1

íííí

3

íííí

2

TI-15 : Guide de l’enseignant

78

Comparaison de fractions et de nombres

p

décimaux

Linda nage 20 longueurs de piscine en 5,72 minutes. Juan nage 20 longueurs de en 5 ¾ minutes. Qui nage le Pour com

arer les résultats sous forme

lus vite ?

iscine

décimale :

Appuyez sur Affichage



5

¥ ®

3



4

33

ííí

=

5

ííí

5

44

Ÿ

5Ù75

N

n

&

Ÿ

72

5

нннннн

100

Touche du

numérateur



Touche du

dénominateur

¥

Pour comparer les résultats sous forme de fractions :

5

r

72

®

5Ù72Ú 5Ù72

Ÿ

72

EXAS INSTRUMENTS INCORPORATED

N

n

&

нннннн

5

100

TI-15 : Guide de l’enseignant

79

Pourcentage

p

9

Touches

1.

2.

convertit un nombre décimal ou une

y

fraction en pourcentage.

convertit un

ª

nombre décimal.

ourcentage en un

Remarques

Les exemples sur les originaux des

•

trans réglages par défaut.

arents supposent tous les

1

2

EXAS INSTRUMENTS INCORPORATED

TI-15: Guide de l’enseignant

80

Conversion en pourcentage

Convertissez 25% en un nombre décimal.

Appuyez sur Affichage

25

Convertissez

Appuyez sur Affichage

ª ®

25ãÚ 0Ù25

25

en un pourcentage.

100

Pourcentage

ª

Convertir en

pourcentage

y

25



100

¥

25

íííí

àã 25

y ®

100

Convertissez 3 en un pourcentage.

Appuyez sur Affichage

y ®

3

3àã 300ã

%

EXAS INSTRUMENTS INCORPORATED

TI-15: Guide de l’enseignant

81

Conversion de fractions en pourcentage

p

q

Convertissez 25% en une fraction, sim é

lifiez en une fraction irréducible

uivalente, puis convertissez cette

fraction en un nombre décimal.

Appuyez sur Affichage

25

ª ®

25ãÚ 0Ù25

N/D"n/d

Ÿ

25

Pourcentage

ª

Fraction à nombre

décimal

Ÿ

нннннн

100

¤ ®

Ÿ

y

N/D"n/d

25 5

нннннн

à¾

100 20

5

íííí

à

¾

20 4

0Ù25àã 25ã

N/D"n/d

0Ù25

íííí

ííí

1

EXAS INSTRUMENTS INCORPORATED

TI-15: Guide de l’enseignant

82

Indices de calcul

p

La famille Chen est allée manger au restaurant. Leur facture était de 31,67 $. Quel était le

ourboire s'ils ont laissé 15% de leur facture ? Quel était le total avec le pourboire ?

Appuyez sur Affichage

31.67

®

31Ù67Ú 31Ù67

Fix

Š ™

31Ù67Ú 31Ù67

V

15

ª ®

31Ù67Ý15%Ú

Fix

Pourcentage

ª

Convertir en

pourcentage

y

31.67

4.75

®

4Ù75

T

31Ù67Û4Ù75Ú

36Ù42

EXAS INSTRUMENTS INCORPORATED

TI-15: Guide de l’enseignant

83

Pi

p

10

Touches

1.

affiche la valeur de

©

sept décimales (3,1415927).

i arrondie à

Remarques

Les exemples sur les originaux des

•

trans réglages par défaut.

La valeur de pi est stockée avec dix

•

décimales dans la calculatrice (3,1415926535). Seulement se décimales sont affichées.

Pour exprimer la valeur de pi sous

•

forme décimale, appuyez sur Ÿ.

arents supposent tous les

t

1

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

84

Utilisation de pi pour calculer la circonférence

p

q

p

Utilisez cette formule

our trouver la longueur

de la clôture

ue vous devez acheter si vous voulez

lacer une clôture circulaire autour d'un arbre de votre jardin, la clôture étant située à 3 m de l’arbre.

C = 2pr = 2 x p x 3

Pi

©

Appuyez sur Affichage

V ©

2

2Ýß

V

3

®

2ÝßÝ3Ú Ôß

Ÿ

18Ù84955592

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

85

Utilisation de pi pour calculer l’aire

q

Utilisez cette formule pour calculer l’aire de gazon

ui sera couverte par un

aspersoir ayant un rayon de 12 mètres.

A = pr

2 =

p

x 12

2

Pi

©

Appuyez sur Affichage

© V

ßÝ

¨

12

2

ЯЭПРЙР

®

ЯЭПРЙРЪS 144Я

Ÿ

452Ù3893421

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

86

Utilisation de pi pour calculer le volume

Utilisez cette formule pour calculer l'espace occupé par un ballon.

3

p

4

r

V =

Appuyez sur Affichage

3

5 cm

Pi

©

V © V

4

¨

5

W

3

®

ÒÝßÝ

ТЭЯЭУЙС

ТЭЯЭУЙСЮС

ТЭЯЭУЙСЮСЪ

523 Ù5987756

EXAS INSTRUMENTS INCORPORATED

TI-15 : Guide de l’enseignant

87

Puissances et racines carrées

p

q

p

11

Touches

1.

2.

vous

¨

uissance pour la valeur entrée. Lors valeur est affichée si elle se situe dans le limite de l’affichage de la calculatrice.

calcule la racine carrée de valeurs

¬

positives, y compris des fractions.

ermet de préciser une

ue vous appuyez sur

®

, la

Remarques

Les exemples sur les originaux des

•

trans réglages par défaut

arents supposent tous les

12

EXAS INSTRUMENTS INCORPORATED

TI-15: Guide de l’enseignant

88

Mesurer l’aire d'un carré

p

Utilisez cette formule pour mesurer la taille de la toile nécessaire recouvrir tout le cham

intérieur d’un

our

terrain de baseball.

A = x

2

= 90

2

Puissances

¨

Appuyez sur Affichage

90

¨

EXAS INSTRUMENTS INCORPORATED

2

®

ЧШЙРЪ 8100

TI-15: Guide de l’enseignant

89

Calcul de la racine carrée

p

q

Utilisez cette formule pour calculer la longueur du côté d'un 36 mètres carrés de mo

avillon carré si

uette peuvent

recouvrir le plancher.

L =

x = 36

36 m

de moquette

2

Racine carrée

¬

Appuyez sur Affichage

¬

36

®

â36Ú 6

EXAS INSTRUMENTS INCORPORATED

TI-15: Guide de l’enseignant

90

Calcul de puissances

q

p

Pliez un morceau de papier en deux, puis en deux à nouveau, et ainsi de suite jus le de sections avez-vous a

u'à ce qu'il ne soit plus possible de

lier physiquement en deux. Combien

rès dix

pliages ?

Appuyez sur Affichage

Puissances

¨

2

¨

10

®

2ÉÏØÚ 1024

EXAS INSTRUMENTS INCORPORATED

TI-15: Guide de l’enseignant

91

Calcul de puissances négatives

Exprimez la valeur des puissances suivantes sous fome de nombres (décimaux):

-3

2

=

-3

-2

=

-3

.2

=

(1/2)

Appuyez sur Affichage

¨ M

2

3

-3

=

2ÉÜÑÚ ШЩПРУ

®

Puissances

¨

Négatif

M

2

M

3

r

2

®



1

®

3

¨

®

¨ M

2

3

Ь2ЙЬСЪ ЬШЩПРУ

Ù2ÉÜÑÚ ÏÐÓ

1.

ííí

ÉÜÑÚ Ö

2

EXAS INSTRUMENTS INCORPORATED

TI-15: Guide de l’enseignant

92

Utilisation de puissances de 10

1.3 x 103 = ?

Appuyez sur Affichage

Puissances

¨

r

1 10

r

1 10

®

V

3

¨

3

V

3

¨ M

®

1.3 x 10

3

1Щ3ЭПШЙСЪ

1300

3

L

= ?

1Щ3ЭПШЙЬСЪ

0Ù0013

EXAS INSTRUMENTS INCORPORATED

TI-15: Guide de l’enseignant

93

Texas instruments TI-15 GUIDE FOR TEACHERS

Specifications and Main Features

Frequently Asked Questions

User Manual

Guide de l’enseignant

Table des matières

A propos du guide de l’enseignant

Activitiés

Régularités dans les pourcentages

Formes de representation des fractions

Comparaison des coûts

Écriture des nombres : Notation scientifique

Procédures inverses

Dans l’intervalle

L'importance de la valeur de position

Quel est le problème ?

Système d'exploitation d'équations

Priorité des opérations

Effacement et correction

Effacement des entrées

Menus de la touche mode

Opérations élémentaires

Saisie de nombres négatifs

Division de nombres entiers avec reste

Résultat de division sous forme décimale

Résultat de division sous frome de fraction

Calcul d'unités équivalentes de temps

Opérations avec des constantes

Addition en tant que “comptage”

Multiplication en tant que “addition répétée”

Puissances en tant que “multiplication répétée”

Utilisation de OP 1 et OP 2 ensemble

Effacement d'une opération constante

Nombres entiers et nombres décimaux

Réglage du nombre de décimales

Addition de valeurs en argent

Conversion de nombres décimaux en fractions

Mémoire

Fractions

Addition de nombres fractionnaires

Simplification de fractions

Conversion de fractions en nombres décimaux

Conversion de nombres décimaux en fractions

Conversion de fractions en nombres fractionnaires

Pourcentage

Conversion en pourcentage

Conversion de fractions en pourcentage

Indices de calcul

Pi

Utilisation de pi pour calculer la circonférence

Utilisation de pi pour calculer l’aire

Utilisation de pi pour calculer le volume

Puissances et racines carrées

Mesurer l’aire d'un carré

Calcul de la racine carrée

Calcul de puissances

Calcul de puissances négatives

Utilisation de puissances de 10