Analog Devices AD650KP, AD650JP Datasheet
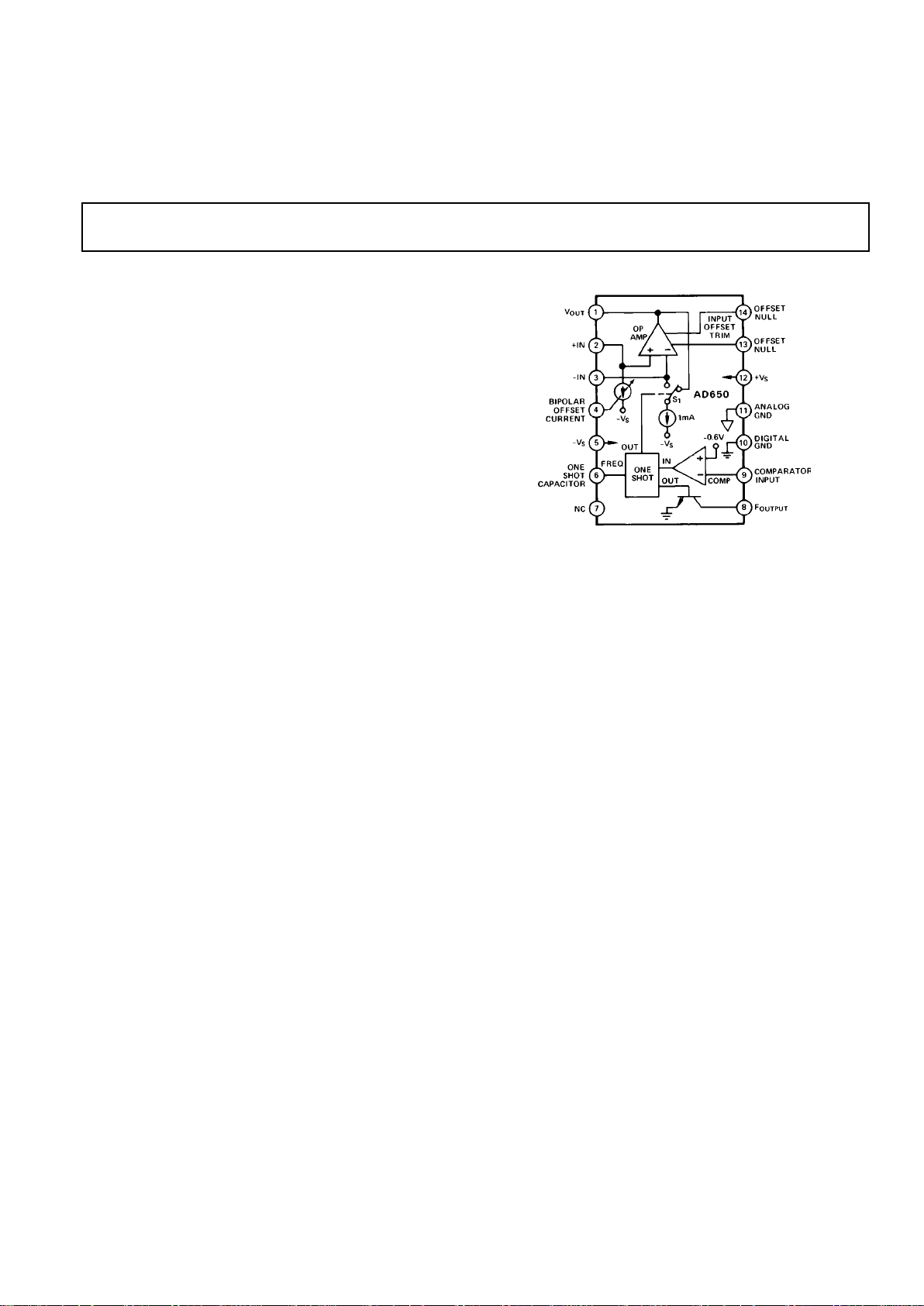
PIN CONFIGURATION
REV. A
Information furnished by Analog Devices is believed to be accurate and
reliable. However, no responsibility is assumed by Analog Devices for its
use, nor for any infringements of patents or other rights of third parties
which may result from its use. No license is granted by implication or
otherwise under any patent or patent rights of Analog Devices.
a
Voltage-to-Frequency and
Frequency-to-Voltage Converter
AD650
FEATURES
V/F Conversion to 1 MHz
Reliable Monolithic Construction
Very Low Nonlinearity
0.002% typ at 10 kHz
0.005% typ at 100 kHz
0.07% typ at 1 MHz
Input Offset Trimmable to Zero
CMOS or TTL Compatible
Unipolar, Bipolar, or Differential V/F
V/F or F/V Conversion
Available in Surface Mount
MIL-STD-883 Compliant Versions Available
PRODUCT DESCRIPTION
The AD650 V/F/V (voltage-to-frequency or frequency-to-voltage
converter) provides a combination of high frequency operation
and low nonlinearity previously unavailable in monolithic form.
The inherent monotonicity of the V/F transfer function makes
the AD650 useful as a high-resolution analog-to-digital converter.
A flexible input configuration allows a wide variety of input voltage and current formats to be used, and an open-collector output with separate digital ground allows simple interfacing to
either standard logic families or opto-couplers.
The linearity error of the AD650 is typically 20 ppm (0.002%
of full scale) and 50 ppm (0.005%) maximum at 10 kHz full
scale. This corresponds to approximately 14-bit linearity in an
analog-to-digital converter circuit. Higher full-scale frequencies
or longer count intervals can be used for higher resolution conversions. The AD650 has a useful dynamic range of six decades
allowing extremely high resolution measurements. Even at 1 MHz
full scale, linearity is guaranteed less than 1000 ppm (0.1%) on
the AD650KN, KP, BD and SD grades.
In addition to analog-to-digital conversion, the AD650 can be
used in isolated analog signal transmission applications, phased
locked-loop circuits, and precision stepper motor speed controllers. In the F/V mode, the AD650 can be used in precision
tachometer and FM demodulator circuits.
The input signal range and full-scale output frequency are userprogrammable with two external capacitors and one resistor.
Input offset voltage can be trimmed to zero with an external
potentiometer.
The AD650JN and AD650KN are offered in a plastic 14-pin
DIP package. The AD650JP and AD650KP are available in a
One Technology Way, P.O. Box 9106, Norwood, MA 02062-9106, U.S.A.
Tel: 617/329-4700 Fax: 617/326-8703
20-pin plastic leaded chip carrier (PLCC). Both plastic packaged
versions of the AD650 are specified for the commercial (0°C to
+70°C) temperature range. For industrial temperature range
(–25°C to +85°C) applications, the AD650AD and AD650BD
are offered in a ceramic package. The AD650SD is specified for
the full –55°C to +125°C extended temperature range.
PRODUCT HIGHLIGHTS
1. In addition to very high linearity, the AD650 can operate at
full-scale output frequency up to 1 MHz. The combination of
these two features makes the AD650 an inexpensive solution
for applications requiring high resolution monotonic A/D
conversion.
2. The AD650 has a very versatile architecture that can be configured to accommodate bipolar, unipolar, or differential input voltages, or unipolar input currents.
3. TTL or CMOS compatibility is achieved using an open collector frequency output. The pull-up resistor can be connected to voltages up to +30 V, or +15 V or +5 V for
conventional CMOS or TTL logic levels.
4. The same components used for V/F conversion can also be
used for F/V conversion by adding a simple logic biasing network and reconfiguring the AD650.
5. The AD650 provides separate analog and digital grounds.
This feature allows prevention of ground loops in real-world
applications.
6. The AD650 is available in versions compliant with MILSTD-883. Refer to the Analog Devices Military Products
Databook or current AD650/883B data sheet for detailed
specifications.
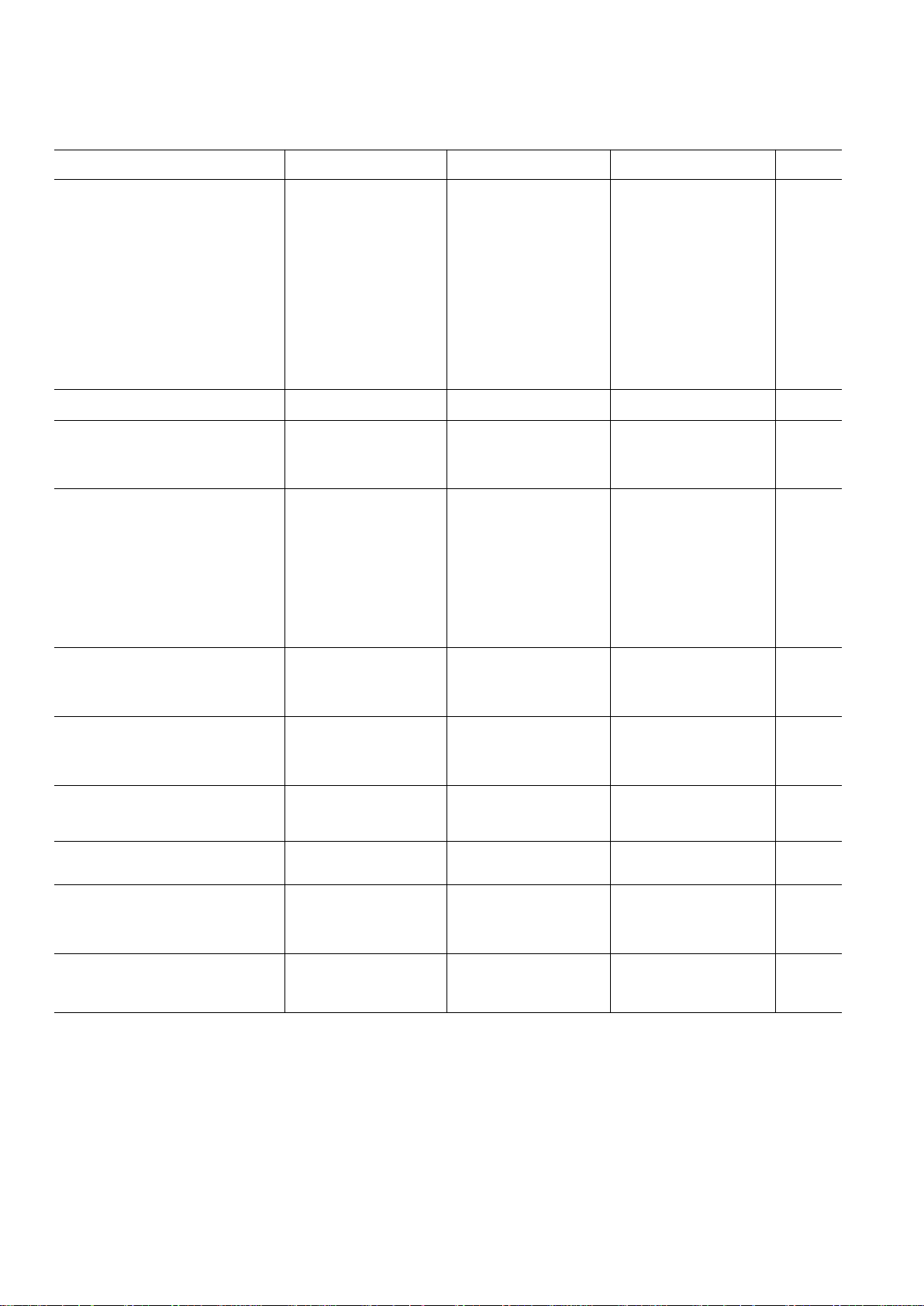
AD650J/AD650A AD650K/AD650B AD650S
Model Min Typ Max Min Typ Max Min Typ Max Units
DYNAMIC PERFORMANCE
Full-Scale Frequency Range 1 1 1 MHz
Nonlinearity
1
f
MAX
= 10 kHz 0.002 0.005 0.002 0.005 0.002 0.005 %
Nonlinearity
1
f
MAX
= 100 kHz 0.005 0.02 0.005 0.02 0.005 0.02 %
Nonlinearity
1
f
MAX
= 500 kHz 0.02 0.05 0.02 0.05 0.02 0.05 %
Nonlinearity
1
f
MAX
= 1 MHz 0.1 0.05 0.1 0.05 0.1 %
Full-Scale Calibration Error
2
, 100 kHz ±5 ±5 ±5%
Full-Scale Calibration Error2, 1 MHz ±10 ±10 ±10 %
vs. Supply
3
–0.015 +0.015 –0.015 +0.015 –0.015 +0.015 % of FSR/V
vs. Temperaturc
A, B, and S Grades
at 10 kHz ± 75 ±75 ± 75 ppm/°C
at 100 kHz ± 150 ± 150 ± 150 ppm/°C
J and K Grades
at 10 kHz ± 75 ±75 ppm/°C
at 100 kHz ± 150 ± 150 ppm/°C
BIPOLAR OFFSET CURRENT
Activated by 1.24 kΩ Between Pins 4 and 5 0.45 0.5 0.55 0.45 0.5 0.55 0.45 0.5 0.55 mA
DYNAMIC RESPONSE
Maximum Settling Time for Full Scale
Step Input 1 Pulse of New Frequency Plus 1 µs 1 Pulse of New Frequency Plus 1 µs 1 Pulse of New Frequency Plus 1 µs
Overload Recovery Time
Step Input 1 Pulse of New Frequency Plus 1 µs 1 Pulse of New Frequency Plus 1 µs 1 Pulse of New Frequency Plus 1 µs
ANALOLG INPUT AMPLIFIER (V/F Conversion)
Current Input Range (Figure 1) 0 +0.6 0 +0.6 0 +0.6 mA
Voltage Input Range (Figure 5) –10 0 –10 0 –10 0 V
Differential Impedance 2 MΩi10 pF 2 MΩi10 pF 2 MΩi10 pF
Common-Mode Impedance 1000 MΩi10 pF 1000 MΩi10 pF 1000 MΩi10 pF
Input Bias Current
Noninverting Input 40 100 40 100 40 100 nA
Inverting Input ±8 620 ±8 620 ±8 620 nA
Input Offset Voltage
(Trimmable to Zero) 64 64 64 mV
vs. Temperature (T
MIN
to T
MAX
) ±30 ±30 ±30 µ V/°C
Safe Input Voltage ±V
S
±V
S
±V
S
C
COMPARATOR (F/V Conversion)
Logic “0” Level –V
S
–1 –V
S
–1 –V
S
+1 V
Logic “1” Level 0 +V
S
0+V
S
0+V
S
V
Pulse Width Range
4
0.1 (0.3 × tOS) 0.1 (0.3 × tOS) 0.1 (0.3 × tOS) µs
Input Impedance 250 250 250 kΩ
OPEN COLLECTOR OUTPUT (V/F Conversion)
Output Voltage in Logic “0”
I
SINK
≤ 8 mA, T
MIN
to T
MAX
0.4 0.4 0.4 V
Output Leakage Current in Logic “1” 100 100 100 nA
Voltage Range
5
0 +36 0 +36 0 +36 V
AMPLIFIER OUTPUT (F/V Conversion)
Voltage Range (1500 Ω min Load Resistance) 0 +10 0 +10 0 +10 V
Source Current (750 Ω max Load Resistance) 10 10 10 mA
Capacitive Load (Without Oscillation) 100 100 100 pF
POWER SUPPLY
Voltage, Rated Performance ±9 618 ±9 618 ±9 618 V
Quiescent Current 88 8mA
TEMPERATURE RANGE
Rated Performance – N Package 0 +70 0 +70 °C
Rated Performance – D Package –25 +85 –25 +85 –55 +125 °C
Storageated Perfor – N Package –25 +85 –25 +85 °C
Rated Performance – D Package –65 +150 –65 +150 –65 +150 °C
PACKAGE OPTIONS
6
PLCC (P-20A) AD650JP AD650KP
Plastic DIP (N-14) AD650JN AD650KN
Ceramic DIP (D-14) AD650AD AD650BD AD650SD
NOTES
1
Nonlinearity is defined as deviation from a straight line from zero to full scale, expressed as a fraction of full scale.
2
Full-scale calibration error adjustable to zero.
3
Measured at full-scale output frequency of 100 kHz.
4
Refer to F/V conversion section of the text.
5
Referred to digital ground.
6
D = Ceramic DIP; N = Plastic DIP; P = Plastic Leaded Chip Carrier.
Specifications subject to change without notice.
Specifications shown in boldface are tested on all production units at final electrical test. Results from those test are used to calculate outgoing quality levels. All min and max
specifications are guaranteed, although only those shown in boldface are tested on all production units.
AD650–SPECIFICATIONS
(@ + 258C, with VS = 615 V, unless otherwise noted)
REV. A
–2–
AD650
REV. A
–3–
ABSOLUTE MAXIMUM RATINGS
Total Supply Voltage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 V
Storage Temperature Ceramic . . . . . . . . . . . . –55°C to +165°C
Storage Temperature Plastic . . . . . . . . . . . . . –25°C to +125°C
Differential Input Voltage (Pins 2 and 3) . . . . . . . . . . . . ±10 V
Maximum Input Voltage . . . . . . . . . . . . . . . . . . . . . . . . . . ±V
S
Open Collector Output Voltage Above Digital GND . . . . . 36 V
Open Collector Output Current . . . . . . . . . . . . . . . . . . 50 mA
Amplifier Short Circuit to Ground . . . . . . . . . . . . . . . Indefinite
Comparator Input Voltage (Pin 9) . . . . . . . . . . . . . . . . . . . ±V
S
ORDERING GUIDE
Gain
Tempco Specified
ppm/ 8C 1 MHz Temperature
Model
1
100 kHz Linearity Range 8C Package
AD650JN 150 typ 0.1% typ 0 to +70 Plastic DIP
AD650KN 150 typ 0.1% max 0 to +70 Plastic DIP
AD650JP 150 typ 0.1% typ 0 to +70 PLCC
AD650KP 150 typ 0.1% max 0 to +70 PLCC
AD650AD 150 max 0.1% typ –25 to +85 Ceramic
AD650BD 150 max 0.1% max –25 to +85 Ceramic
AD650SD 150 max 0.1% max –55 to +125 Ceramic
NOTE
1
For details on grade and package offerings screened in accordance with
MIL-STD-883B, refer to the Analog Devices Military Products Databook or
current AD650/883B data sheet.
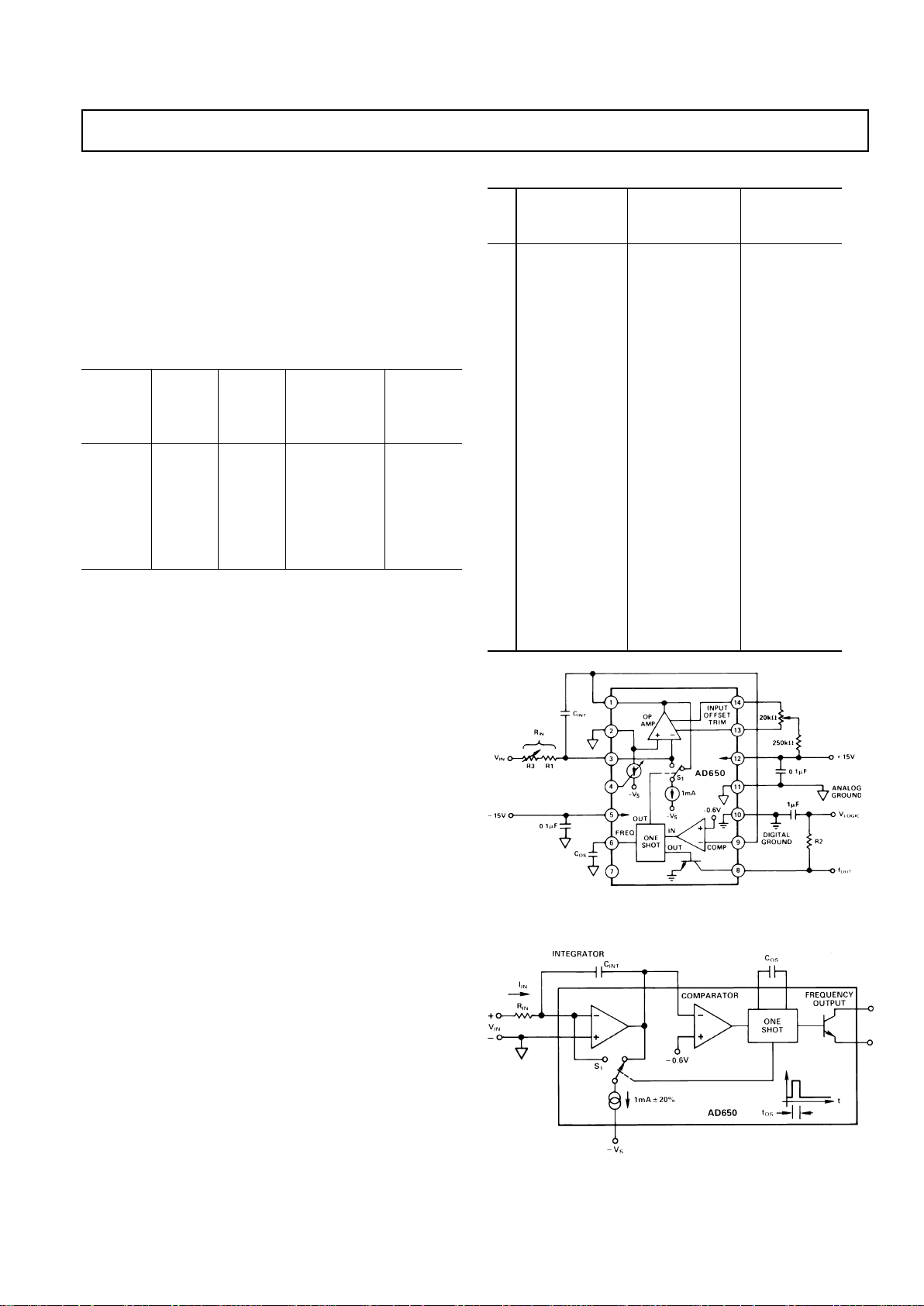
CIRCUIT OPERATION
UNIPOLAR CONFIGURATION
The AD650 is a charge balance voltage-to-frequency converter.
In the connection diagram shown in Figure 1, or the block diagram of Figure 2a, the input signal is converted into an equivalent current by the input resistance R
IN
. This current is exactly
balanced by an internal feedback current delivered in short,
timed bursts from the switched 1 mA internal current source.
These bursts of current may be thought of as precisely defined
packets of charge. The required number of charge packets, each
producing one pulse of the output transistor, depends upon the
amplitude of the input signal. Since the number of charge packets delivered per unit time is dependent on the input signal amplitude, a linear voltage-to-frequency transformation will be
accomplished. The frequency output is furnished via an open
collector transistor.
A more rigorous analysis demonstrates how the charge balance
voltage-to-frequency conversion takes place.
A block diagram of the device arranged as a V-to-F converter is
shown in Figure 2a. The unit is comprised of an input integrator, a current source and steering switch, a comparator and a
one-shot. When the output of the one-shot is low, the current
steering switch S
1
diverts all the current to the output of the op
amp; this is called the Integration Period. When the one-shot
has been triggered and its output is high, the switch S
1
diverts
all the current to the summing junction of the op amp; this is
called the Reset Period. The two different states are shown in
Figure 2 along with the various branch currents. It should be
noted that the output current from the op amp is the same for
either state, thus minimizing transients.
PIN CONFIGURATION
PACKAGE
PIN “D” “N” “P”
NO. CERAMIC DIP PLASTIC DIP PLCC
1V
OUT
V
OUT
NC
2 +IN +IN V
OUT
3 –IN –IN +IN
4 BIPOLAR OFFSET BIPOLAR OFFSET –IN
CURRENT CURRENT
5–V
S
–V
S
NC
6 ONE SHOT ONE SHOT BIPOLAR OFFSET
CAPACITOR CAPACITOR CURRENT
7NC NC NC
8F
OUTPUT
F
OUTPUT
–V
S
9 COMPARATOR COMPARATOR ONE SHOT
INPUT INPUT CAPACITOR
10 DIGITAL GND DIGITAL GND NC
11 ANALOG GND ANALOG GND NC
12 +V
S
+V
S
F
OUTPUT
13 OFFSET NULL OFFSET NULL COMPARATOR
INPUT
14 OFFSET NULL OFFSET NULL DIGITAL GND
15 NC
16 ANALOG GND
17 NC
18 +V
S
19 OFFSET NULL
20 OFFSET NULL
Figure 1. Connection Diagram for V/F Conversion,
Positive Input Voltage
Figure 2a. Block Diagram
AD650
REV. A
–4–
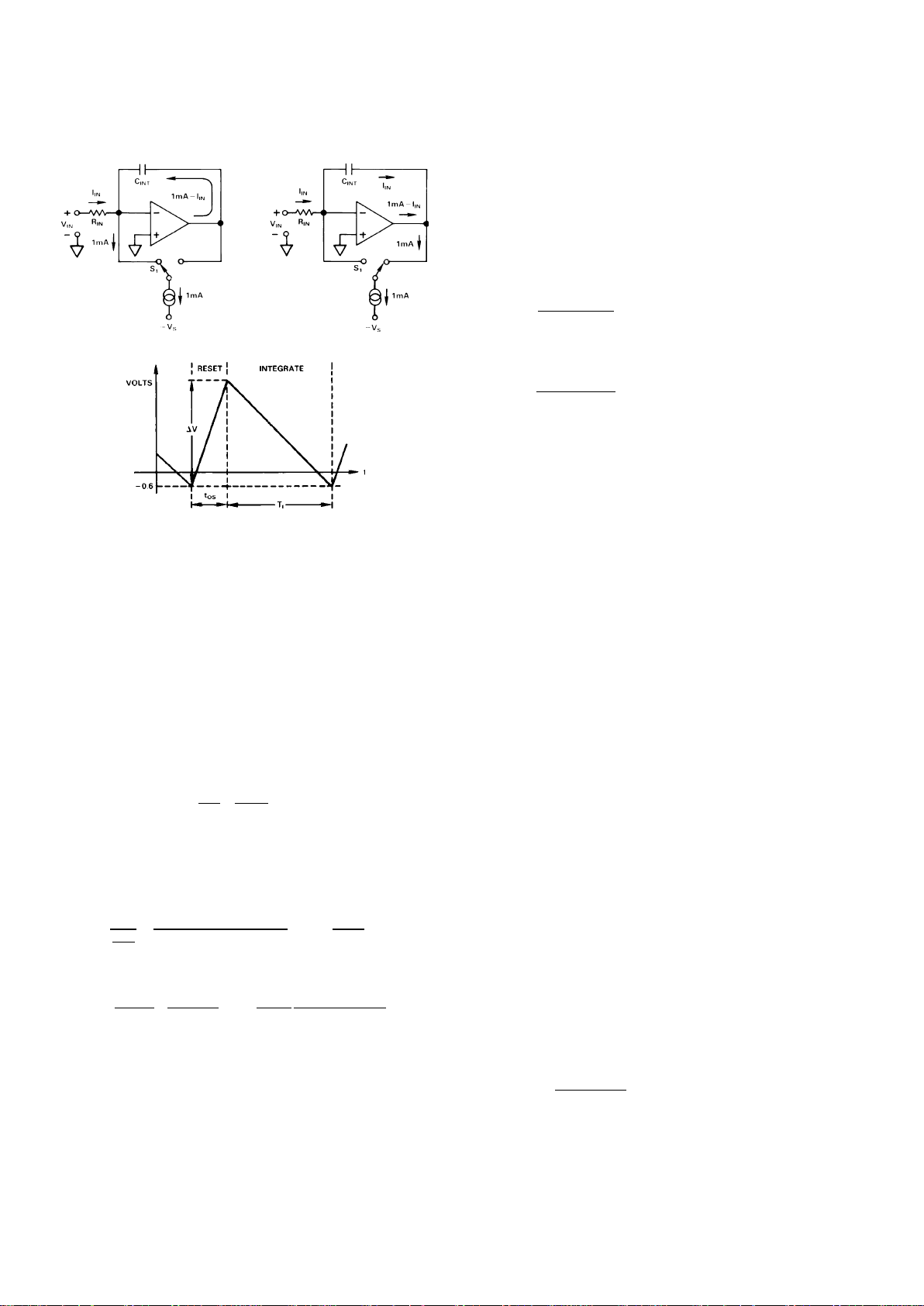
Figure 2b. Reset Mode Figure 2c. Integrate Mode
Figure 2d. Voltage Across C
INT
The positive input voltage develops a current (IIN = VIN/RIN)
which charges the integrator capacitor C
INT
. As charge builds up
on C
INT
, the output voltage of the integrator ramps downward
towards ground. When the integrator output voltage (Pin 1)
crosses the comparator threshold (–0.6 volt) the comparator
triggers the one shot, whose time period, t
OS
is determined by
the one shot capacitor C
OS
.
Specifically, the one shot time period is:
tOS= COS×6.8 ×103sec/F + 3.0 ×10
–7 sec
(1)
The Reset Period is initiated as soon as the integrator output
voltage crosses the comparator threshold, and the integrator
ramps upward by an amount:
∆V = tOS•
dV
dt
=
t
OS
C
INT
1mA – I
N
()
(2)
After the Reset Period has ended, the device starts another Integration Period, as shown in Figure 2, and starts ramping downward again. The amount of time required to reach the
comparator threshold is given as:
T
I
=
∆
V
dV
dt
=
t
OS/CINT
(1 mA – IIN)
I
N/CINT
= t
OS
1mA
I
IN
–1
(3)
The output frequency is now given as:
f
OUT
=
1
t
OS+TI
=
I
IN
tOS×1 mA
= 0.15
F•Hz
A
VIN/R
IN
COS+ 4.4 ×10
–11
F
(4)
Note that C
INT
, the integration capacitor has no effect on the
transfer relation, but merely determines the amplitude of the
sawtooth signal out of the integrator.
One Shot Timing
A key part of the preceding analysis is the one shot time period
that was given in equation (1). This time period can be broken
down into approximately 300 ns of propagation delay, and a
second time segment dependent linearly on timing capacitor
C
OS
. When the one shot is triggered, a voltage switch that holds
Pin 6 at analog ground is opened allowing that voltage to
change. An internal 0.5 mA current source connected to Pin 6
then draws its current out of C
OS
, causing the voltage at Pin 6 to
decrease linearly. At approximately –3.4 V, the one shot resets
itself, thereby ending the timed period and starting the V/F conversion cycle over again. The total one shot time period can be
written mathematically as:
tOS=
∆VC
OS
I
DISCHARGE
+T
GATE DELAY
(5)
substituting actual values quoted above,
tOS=
–3.4 V × C
OS
–0.5 ×10–3A
+300 ×10
–9
sec
(6)
This simplifies into the timed period equation given above.
COMPONENT SELECTION
Only four component values must be selected by the user. These
are input resistance R
IN
, timing capacitor COS, logic resistor R2,
and integration capacitor C
INT
. The first two determine the
input voltage and full-scale frequency, while the last two are
determined by other circuit considerations.
Of the four components to be selected, R2 is the easiest to define. As a pull-up resistor, it should be chosen to limit the current through the output transistor to 8 mA if a TTL maximum
V
OL
of 0.4 V is desired. For example, if a 5 V logic supply is
used, R2 should be no smaller than 5 V/8 mA or 625 Ω. A larger
value can be used if desired.
R
IN
and COS are the only two parameters available to set the fullscale frequency to accommodate the given signal range. The
“swing” variable that is affected by the choice of R
IN
and COS is
nonlinearity. The selection guide of Figure 3 shows this quite
graphically. In general, larger values of C
OS
and lower full-scale
input currents (higher values of R
IN
) provide better linearity. In
Figure 3, the implications of four different choices of R
IN
are
shown. Although the selection guide is set up for a unipolar configuration with a zero to 10 V input signal range, the results can
be extended to other configurations and input signal ranges. For
a full scale frequency of 100 kHz (corresponding to 10 V input),
you can see that among the available choices, R
IN
= 20 k and
C
OS
= 620 pF gives the lowest nonlinearity, 0.0038%. Also, if
you wish to use the highest frequency that will give the 20 ppm
minimum nonlinearity, it is approximately 33 kHz (40.2 kΩ and
1000 pF).
For input signal spans other than 10 V, the input resistance
must be scaled proportionately. For example, if 100 kΩ is called
out for a 0 V–10 V span, 10k would be used with a 0 V–1 V
span, or 200 kΩ with a ± 10 V bipolar connection.
The last component to be selected is the integration capacitor
C
INT
. In almost all cases, the best value for C
INT
can be calcu-
lated using the equation:
C
INT
=
10
–4
F / sec
f
MAX
(1000 pF minimum)
(7)
When the proper value for C
INT
is used, the charge balance
architecture of the AD650 provides continuous integration of
the input signal, hence large amounts of noise and interference
 Loading...
Loading...