SHARP EL-506W User Manual [fr]

Download

EL-506W EL-546W

CALCULATRICE SCIENTIFIQUE

MODE D’EMPLOI

MODÈLE

MEM RESET

0 1

DRG FSE TA B

0 1

x x x

2 3

P (x,y )

P (r,θ )

FRANÇAIS

PRINTED IN CHINA / IMPRIMÉ EN CHINE

06HGK (TINSF1270EHZZ)

INTRODUCTION

Nous vous remercions de votre achat d’une calculatrice scientifique SHARP modèle EL-506W/546W. En ce qui concerne les exemples de calcul (y compris certaines formules et

tableaux), reportez-vous au verso du mode d’emploi en anglais. Pour l’utilisation, reportez-vous au numéro à la droite de chaque titre.

Après avoir lu ce document, veuillez le conserver afin de pouvoir vous y reporter le moment venu. Remarque: Quelques-uns des modèles décrits dans ce mode d’emploi sont

susceptibles de ne pas être disponibles dans certains pays.

Remarques sur l’utilisation

•

Ne transportez pas la calculatrice dans la poche arrière de votre pantalon, sous peine de la casser en vous asseyant. L’afficheur étant en verre, il est particulièrement fragile.

•

Éloignez la calculatrice des sources de chaleur extrême comme sur le tableau de bord d’une voiture ou près d’un chauffage et évitez de la placer dans des environnements excessivement humides ou poussiéreux.

•

Cet appareil n’étant pas étanche, il ne faut pas l’utiliser ou l’entreposer dans des endroits où il risquerait d’être mouillé, par exemple par de l’eau. La pluie, l’eau brumisée, l’humidité, le café, la vapeur, la transpiration, etc. sont à l’origine de dysfonctionnement.

•

Nettoyez avec un chiffon doux et sec. N’utilisez pas de solvants, ni de chiffon mouillé.

•

Évitez les chocs; manipulez la calculatrice avec soin.

•

Ne jetez jamais les piles dans le feu.

•

Gardez les piles hors de portée des enfants.

•

Ce produit, y compris les accessoires, peut varier suite à une amélioration sans préavis.

AVIS

•

SHARP recommande fortement de garder de façon permanente et séparée une trace écrite de toutes les données importantes, car celles-ci peuvent être perdues ou altérées dans pratiquement tous les produits à mémoire électronique dans certaines circonstances. SHARP n’assumera donc aucune responsabilité pour les données perdues ou bien rendues inutilisables que ce soit à la suite d’une mauvaise utilisation, de réparations, vices, remplacement des piles, utilisation après expiration de la durée de vie spécifiée de la pile ou toute autre cause.

•

SHARP ne sera pas tenu responsable de tout dommage matériel ou économique imprévu ou consécutif à la mauvaise utilisation et/ou au mauvais fonctionnement de cet appareil et de ses périphériques, à moins qu’une telle responsabilité ne soit reconnue par la loi.

♦

Appuyez sur le bouton RESET (au dos), avec la pointe d’un stylo à bille ou un objet identique, uniquement dans les cas suivants. N’utilisez pas un objet avec une pointe cassable ou affilée. Prenez note qu’une pression sur le bouton RESET effacera toutes les données stockées dans la mémoire.

•

Lors de la première utilisation

•

Après remplacement des piles

•

Pour effacer la mémoire entièrement

•

Lorsqu’une anomalie survient et qu’aucune autre solution ne fonctionne. Si un entretien est nécessaire à cette calculatrice, demandez seulement les services d’un fournisseur spécialisé SHARP, un service d’entretien agréé par SHARP ou un centre de réparation SHARP où cela est disponible.

Boîtier

AFFICHEUR

Affichage

des équations

•

Pendant le fonctionnement tous les symboles ne sont pas affichés en même temps.

•

Certains symboles inactifs peuvent apparaître visibles si on regarde la calculatrice d’un angle éloigné.

•

Seuls les symboles nécessaires à l’utilisation expliquée sont présentés dans l’affichage et les exemples de calcul de ce mode d’emploi.

: Apparaît sur l’afficheur lorsque l’équation ou la réponse ne peut pas être

xy/rθ: Indique le mode d’expression des résultats en mode calcul avec nombres

: Indique que des données sont visibles en haut/bas de l’afficheur.

2ndF

: S’affiche si @ a été pressée.

HYP

: Lorsque la touche h a été pressée, cette indication s’affiche pour

→

donnée en un seul affichage. Appuyez sur les touches </> pour lire la partie restante (cachée).

complexes.

Appuyez sur [/] pour faire défiler en haut/bas la vue.

vous signaler que les fonctions hyperboliques sont accessibles. Si vous employez la combinaison @H, les indications “2ndF HYP” s’affichent pour vous signaler que les fonctions hyperboliques inverses sont accessibles.

←Symbole

ExposantMantisse

ALPHA

: S’affiche si K (STAT VAR), O ou R a été pressée.

FIX/SCI/ENG DEG/RAD/GRAD

: Indique la notation employée pour afficher une valeur.

: Indique les unités angulaires. : Apparaît lorsque le mode matrice est sélectionné. : Apparaît lorsque le mode liste est sélectionné. : Apparaît lorsque le mode statistique est sélectionné.

: Indique qu’une valeur a été sauvegardée dans la mémoire indépendante.

: Indique que la calculatrice attend l’entrée d’une valeur numérique, comme

en mode de simulation.

: Apparaît lorsque la calculatrice affiche un résultat sous forme d’angle, en

mode calcul avec nombres complexes.

: Indique qu’une partie imaginaire est affichée, en mode calcul avec nombres

complexes.

AVANT D’UTILISER CETTE CALCULATRICE

Représentation des touches dans ce mode d’emploi

Dans ce mode d’emploi, la représentation des touches est décrite de la manière suivante:

Pour spécifier ex: @e Pour spécifier ln : I Pour spécifier F : Kü

Pour utiliser les fonctions gravées en orange sur les touches, vous devez d’abord presser la touche @, avant la touche de fonction. Lorsque vous sélectionnez la mémoire, appuyez d’abord sur K. Les nombres pour l’entrée de valeur ne sont pas représentés comme les touches mais comme des nombres ordinaires.

Mise sous tension et hors tension

Appuyez sur la touche ª pour mettre la calculatrice sous tension et employez la combinaison @F pour la mettre hors tension.

Effacement de l’entrée et des mémoires

Opération Entrée M A-F, X,Y STAT*1matA-D*

ª ×× × × @c ×

Choix du mode de fonctionnement

@∏00* @∏10*

Bouton RESET

: Efface × : Garde en mémoire

*1Données statistiques (données entrées).

x¯, sx, σx, n, Σx, Σx2, ¯y, sy, σy, Σy, Σy2, Σxy, r, a, b, c.

Mémoires de matrice (matA, matB, matC et matD)

Mémoires de liste (L1, L2, L3 et L4)

Toutes les variables sont effacées.

Cette combinaison de touches fonctionne de la même manière que le bouton RESET.

[Touche effacement de la mémoire]

Appuyez sur @∏ pour afficher le menu.

•

Pour effacer toutes les variables (M, A-F, X, Y, ANS, F1F4, STAT VAR, matA-D, L1-4), appuyez sur 00 ou 0®.

•

Pour réinitialiser (RESET) la calculatrice, appuyez sur 10 ou 1®. L’opération de réinitialisation (RESET) effacera toutes les données stockées en mémoire et ramènera la calculatrice aux réglages par défaut.

(Affichage) F1-F4 ANS STAT VAR*2L1-4*

Entrée et correction d’une équation

[Touches curseur]

•

Appuyez sur < ou > pour déplacer le curseur. Vous pouvez également revenir à l’équation après avoir obtenu une réponse en appuyant sur > (<). Voir le paragraphe suivant pour l’utilisation des touches [ et ].

•

Reportez-vous au ‘Menu SET UP’ pour l’utilisation du curseur dans le menu SET UP.

[Mode d’insertion et mode de réécriture dans l’affichage équation]

•

Une pression sur @‘ commute entre les deux modes d’édition: le mode d’insertion (par défaut) et le mode de réécriture. Un curseur triangulaire indique qu’une entrée sera insérée à l’endroit du curseur, tandis qu’un curseur rectangulaire indique la réécriture des données existantes à chaque nouvelle entrée.

•

Pour insérer un nombre en mode d’insertion, déplacez le curseur immédiatement après l’endroit où vous souhaitez insérer, puis entrez le nombre. En mode de réécriture, les données sous le curseur seront réécrites par le nombre saisi.

•

Le mode établi sera maintenu jusqu’à la prochaine réinitialisation (RESET).

[Touche d’effacement]

Pour effacer un nombre/fonction, déplacez le curseur sur le nombre/fonction que

• vous souhaitez effacer, puis appuyez sur d. Si le curseur est situé à l'extrémité droite d'une équation, la touche d fonctionnera comme une touche de retour arrière.

Fonction de rappel multi-ligne

Les équations précédentes peuvent être rappelées en mode normal. Les équations incluent aussi les instructions de fin de calculs telles que “=” et un maximum de 142 caractères peut être mis en mémoire. Lorsque la mémoire est pleine, les équations sauvegardées sont supprimées dans l’ordre chronologique inverse à partir de la plus ancienne. Si vous pressez [, l’équation précédente apparaîtra à l’écran. Si vous appuyez plusieurs fois sur la touche [, les équations d’avant seront affichées (après être revenu à l’équation précédente, appuyez sur la touche ] pour visualiser les équations, dans l’ordre). De plus, vous pouvez utiliser la combinaison @[ pour passer directement à l’équation la plus ancienne.

•

La mémoire multi-ligne est effacée en suivant la procédure suivante: @c, changement de mode, RESET, conversions en base N. et effacement de la mémoire (@∏).

Niveaux de priorité dans le calcul

Les opérations sont effectuées en tenant compte de la priorité suivante:

Fractions (1l4, etc.) W ∠, préfixes d'ingénierie ELes fonctions pour lesquelles l’argument précède (x mémoire (2Y, etc.)

Multiplication d’une fonction (2sin30, etc.)

}

OR, XOR, XNOR q=, M+, M–, ⇒M, |DEG, |RAD, |GRAD, DATA, CD, →rθ,

→xy et autres instructions de fin de calcul.

•

Les calculs entre parenthèses ont la priorité sur tout les autres calculs.

-1

, x2, n!, etc.) RYx,

Les fonctions pour lesquelles l’argument suit (sin, cos, etc.)

Multiplication d’une valeur en

InCr, nPr O×, ÷ P+, – {AND

OPÉRATIONS PRÉLIMINAIRES

Choix du mode de fonctionnement

m0: Mode normal (NORMAL) m1: Mode statistique (STAT) m2: Mode équation (EQN) m3: Mode nombre complexe (CPLX) m4: Mode matrice (MAT) m5: Mode liste (LIST)

Menu SET UP

Appuyez sur ” pour afficher le menu SET UP.

•

Un élément du menu peut être sélectionné en:

•

déplaçant le curseur clignotant avec ><, puis appuyez sur ® (touche =), ou

•

appuyant sur la touche numérique correspondant au nombre de l’élément du menu.

•

Si ou est affiché sur l’écran, appuyez sur [ ou ] pour consulter l’écran de menu précédent/suivant.

•

Appuyez sur ª pour quitter le menu SET UP.

[Choix de l’unité angulaire]

Les trois unités angulaires suivantes (degrés, radians et grades) peuvent être spécifiées.

•

DEG (°) : Appuyez sur ”00.

•

RAD (rad) : Appuyez sur ”01.

•

GRAD (g) : Appuyez sur ”02.

[Choix de la notation et du nombre de décimales]

Quatre systèmes de notation sont utilisés pour l’affichage du résultat d’un calcul: virgule flottante, virgule décimale fixe, notation scientifique et notation d’ingénierie.

•

Lorsque les symboles FIX, SCI ou ENG sont affichés, le nombre de décimales (TAB) peut avoir une valeur quelconque entre 0 et 9. Les valeurs affichées seront arrondies de la manière appropriée selon le nombre de décimales.

[Réglage du système des nombres à virgule flottante en notation scientifique]

Deux réglages sont utilisés pour l’affichage d’un nombre à virgule décimale flottante: NORM1 (réglage par défaut) et NORM2. Un nombre est automatiquement affiché en notation scientifique en dehors de la plage préétablie:

•

NORM1: 0.000000001 ≤ x ≤ 9999999999

•

NORM2: 0.01 ≤ x ≤ 9999999999

CALCULS SCIENTIFIQUES

•

Appuyez sur les touches m0 pour sélectionner le mode normal.

•

Dans chaque exemple, appuyez sur ª pour effacer l’affichage. Si le voyant FIX, SCI ou ENG est affiché, effacez-le en sélectionnant ‘NORM1’ dans le menu SET UP.

Calculs arithmétiques

•

La parenthèse de fermeture ) juste avant = ou ; peut être omise.

Calculs avec constantes

•

Lors des calculs à constante, le cumulateur devient une constante. Les soustractions et divisions sont effectuées de la même façon. Dans les multiplications, le multiplicande devient une constante.

•

Lors des calculs de constantes, celles-ci seront représentées par un K.

Fonctions scientifiques

•

Reportez-vous aux exemples de calcul de chaque fonction.

•

Avant d’effectuer un calcul de fonctions, précisez l’unité angulaire.

Fonctions Différentielles/Intégrales

Les calculs différentiels et intégraux sont disponibles seulement en mode normal. Pour des conditions initiales de calcul telles que la valeur de x en calcul différentiel ou le point initial en calcul intégral, seules les valeurs numériques peuvent être entrées et des équations telles que 2 réutilisée autant de fois que désirée et résolue en changeant seulement les conditions sans avoir à l’entrer une nouvelle fois dans la calculatrice.

•

Effectuer un calcul effacera la valeur dans la mémoire X.

•

Pour effectuer un calcul différentiel, entrez d’abord la formule, puis entrez la valeur en calcul différentiel et l’intervalle en minute (dx). Si une valeur numérique n’est pas spécifiée pour l’intervalle en minute, x≠0 sera valeur de la dérivée numérique.

•

Pour effectuer un calcul intégral, entrez d’abord la formule, puis entrez une plage d’intégrale (a, b) et les intervalles partiels (n). Si une valeur numérique n’est pas spécifiée pour les intervalles partiels, le calcul sera effectué en utilisant n=100.

Comme les calculs différentiels et intégraux se basent sur les équations suivantes, des résultats incorrects peuvent survenir dans certains cas, assez rares, lors de calculs spéciaux contenant des points de discontinuité.

Calcul intégral (règle de Simpson):

S=—h{ƒ(a)+4{ƒ(a+h)+ƒ(a+3h)+······+ƒ(a+(N–1)h)}

3 +2{ƒ(a+2h)+ƒ(a+4h)+······+ƒ(a+(N–2)h)}+f(b)}

Calcul différentiel:

[Lorsque vous réalisez des calculs intégraux]

Les calculs intégraux prennent plus de temps. Ce temps dépend de l’intégrande et des sous-intervalles d’intégration. Pendant le calcul, “Calculating!” sera affiché. Pour arrêter le calcul, pressez Notez qu’il y aura d’autant plus d’erreurs d’intégration que les fluctuations des valeurs de l’intégrale sont grandes avec une modification légère de la plage d’intégration et pour une fonction périodique, etc., lorsque des valeurs positive et négative de l’intégrale existent selon l’intervalle d’intégration.

ne peuvent être spécifiées. Une même équation peut être

x

×10–5 et x=0 sera 10–5 à partir de la

b – a ——

N=2n

a ≤ x≤ b

   

dx2dx

f(x+––)–f(x –––)

f’(x)=————————

   

En ce qui concerne le premier exemple, divisez les intervalles d’intégration en intervalles

P (x,y )

P (r,θ )

aussi petits que possibles. Pour l’exemple suivant, séparez valeurs positives et négatives. Si vous suivez ces conseils, vous obtiendrez des résultats de précision meilleure et cela réduira aussi votre temps de calcul.

Fonction aléatoire

La fonction Aléatoire comprend quatre réglages pour l’utilisation en mode normal, statistique, matrice et liste. (Cette fonction ne peut pas être sélectionnée en même temps que la fonction Base N.) Pour générer davantage de nombres aléatoires à la suite, appuyez sur ®. Appuyez sur ª pour quitter.

•

La série de nombres pseudo-aléatoires générée est stockée dans la mémoire Y. Chaque nombre aléatoire est basé sur une série de nombres.

[Nombres aléatoires]

Un nombre pseudo-aléatoire à trois chiffres significatifs compris entre 0 et 0.999, peut être créé en employant la combinaison @`0®.

[Dé aléatoire]

Pour simuler un lancer de dé, un nombre entier aléatoire compris entre 1 et 6 peut être généré en appuyant sur @`1®.

[Pile ou face aléatoire]

Pour simuler un lancer de pièce, 0 (face) ou 1 (pile) peut être généré de façon aléatoire en appuyant sur @`2®.

[Nombre entier aléatoire]

Un nombre entier entre 0 et 99 peut être généré de façon aléatoire en appuyant sur @`3®.

Conversion des unités angulaires

L’unité angulaire change successivement chaque fois que @g sont pressées.

Calculs avec mémoires

Mode ANS M, F1-F4 A-F, X,Y NORMAL

STAT ×× EQN ××× CPLX × MAT × LIST ×

: Disponible × : Non disponible

[Mémoires temporaires (A-F, X et Y)]

Appuyez sur O et une touche de variable pour mettre une valeur en mémoire. Appuyez sur R et une touche de variable pour rappeler une valeur de la mémoire. Pour placer une variable dans une équation, appuyez sur K, suivi d’une touche de variable souhaitée.

[Mémoire indépendante (M)]

En plus de toutes les caractéristiques des mémoires indépendantes, vous pouvez ajouter ou soustraire une valeur sauvegardée auparavant dans la mémoire. Appuyez sur ªOM pour effacer la mémoire indépendante (M).

[Mémoire de la dernière réponse (ANS)]

Le résultat du calcul obtenu après avoir appuyé sur = ou toute autre valeur de fin de calcul est automatiquement sauvegardé en mémoire de la dernière réponse. Un résultat sous le format Matrice/Liste n'est pas sauvegardé.

[Mémoires de formules (F1-F4)]

Des formules ayant jusqu’à 256 caractères en tout peuvent être enregistrées dans F1 F4. (Les fonctions tels que sin, etc. seront comptées comme une lettre). Enregistrer une nouvelle équation dans chaque mémoire remplacera automatiquement l’équation existante.

Remarque:

•

Les résultats des calculs obtenus à partir des fonctions indiquées ci-dessous sont automatiquement sauvegardés dans les mémoires X et Y en remplacement des valeurs existantes.

•

Fonction aléatoire ................. mémoire Y

•

→rθ, →xy ............................ mémoire X (r ou x), mémoire Y (θ ou y)

•

Utiliser R ou K rappellera la valeur mise en mémoire jusqu’à 14 chiffres.

Calculs horaires, décimaux et sexagésimaux

La conversion entre nombres décimaux et sexagésimaux peut être effectuée, ainsi que, tout en utilisant des nombres sexagésimaux, la conversion vers la notation en minutes et secondes. Elle peut également effectuer les quatre opérations arithmétiques et des calculs avec mémoires dans le système sexagésimal. La notation hexadécimale est la suivante:

Changements de coordonnées

•

Calculs faisant appel à des constantes physiques

Consultez la carte référence rapide et le verso du mode d’emploi en anglais. Une constante est rappelée en appuyant sur ß suivi du numéro de la constante physique désigné par un nombre à deux chiffres. La constante s’affiche en tenant compte du mode d’affichage choisi et du nombre de décimales précisé. Les constantes physiques peuvent être rappelées dans le mode normal (sous réserve que vous n’ayez pas choisi les systèmes de numération binaire, pentale, octale ou hexadécimale), dans le mode statistique, le mode équation, le mode matrice et le mode liste.

Remarque: Les constantes physiques et les conversions métriques, reposent sur

Calculs à la chaîne

•

Le résultat précédemment obtenu peut être utilisé pour le calcul qui suit. Toutefois il ne peut pas être rappelé après entrée d’instructions multiples ou lorsque le résultat du calcul est sous le format Matrice/Liste.

•

Dans le cas de l’utilisation des fonctions postfixes (¿ , sin, etc.), un calcul à la chaîne est possible même si le résultat du calcul précédent est effacé par l’utilisation de la touche ª.

Calculs avec fractions

Les opérations arithmétiques et les calculs à mémoire peuvent être effectués à l’aide de fractions, ainsi que la conversion entre un nombre décimal et une fraction.

•

Si le nombre de chiffres à afficher est supérieur à 10, le nombre est converti en nombre décimal et affiché comme tel.

Conversion des unités

Consultez la carte référence rapide et le verso du mode d’emploi en anglais. Les conversions d’unités peuvent être effectuées en mode normal (sous réserve que vous n’ayez pas choisi les systèmes de numération binaire, pentale, octale ou hexadécimale), dans le mode statistique, le mode équation, le mode matrice et le mode liste.

Calculs avec des nombres binaires, pentaux, octaux, décimaux et hexadécimaux (Base N)

Les conversions peuvent être effectuées entre des nombres en base N. Les quatre opérations arithmétiques de base, des calculs avec parenthèses et des calculs avec mémoire peuvent aussi être effectués, ainsi que les opérations logiques AND, OR, NOT, NEG, XOR et XNOR sur des nombres binaires, pentaux, octaux et hexadécimaux. Les conversions sont obtenues au moyen des combinaisons suivantes:

@ê (“ s’affiche.), @ì (“

” s’affiche.), @û (“ ” s’affiche.), @î (“ ”

” s’affiche.), @í (“ ”, “ ”, “ ” et “ ”

disparaissent.) Remarque: Les signes A-F utilisés pour un nombre hexadécimal sont introduits en

employant les touches ß, ™, L, ÷, l, et I, et affichés comme suit:

A → ï, B → ∫, C → ó, D → ò, E → ô, F → ö

Dans les systèmes binaire, pental, octal et hexadécimal, il n’est pas possible d’utiliser un nombre ayant une partie décimale. Lors de la conversion d’un nombre du système décimal présentant une partie décimale en un nombre binaire, pental, octal ou hexadécimal, la partie décimale est ignorée. Pareillement, si le résultat d’un calcul en binaire, pental, octal ou hexadécimal comporte une partie décimale, cette partie décimale est ignorée. Dans les systèmes binaire, pental, octal et hexadécimal, un nombre négatif est affiché sous la forme de son complément.

Calculs utilisant des préfixes d’ingénierie

Les calculs peuvent être effectués en mode normal (à l’exception de la base N) en utilisant les 9 types de préfixes suivants.

degré seconde

minute

Avant tout calcul choisissez l’unité angulaire.

↔

Coordonnées cartésiennes

Les résultats des calculs sont automatiquement placés en mémoires X et Y.

•

Valeur de r ou x: Mémoire X

les valeurs recommandées par la Commission des Données Scientifiques et Techniques (CODATA 2002) ou l’édition 1995 du “Guide for the Use of the International System of Units (SI)” publiée par NIST (National Institute of Standards and Technology) soit celles des prescriptions ISO.

No. Constante

01 Vitesse de la lumière dans le vide 02 Constante de gravitation

newtonienne 03 Accélération standard de la gravité 04 Masse de l’électron 05 Masse du proton 06 Masse du neutron 07 Masse du Muon 08 Relation unité-kilogramme de

masse atomique 09 Charge élémentaire 10 Constante de Planck 11 Constante de Boltzmann 12 Constante magnétique 13 Constante électrique 14 Rayon classique de l’électron 15 Constante de structure fine 16 Rayon de Bohr 17 Constante de Rydberg 18 Quantum de flux magnétique 19 Magnéton de Bohr 20 Moment magnétique de l’électron 21 Magnéton nucléaire 22 Moment magnétique du proton 23 Moment magnétique du neutron 24 Moment magnétique du muon 25 Longueur d’onde de Compton 26 Longueur d’onde de Compton du

proton 27 Constante de Stefan Boltzmann

No. Remarques

1in: pouce 2cm: centimètre 3ft: pied 4m : mètre 5yd: yard 6m : mètre 7 mile : mille 8km: kilomètre

9n mile : mille nautique 10 m : mètre 11 acre : acre 12 m2: mètre carré 13 oz : once 14 g : gramme 15 lb : livre 16 kg : kilogramme 17 °F : degré Fahrenheit 18 °C : degré Celsius 19 gal (US) : gallon américain 20 l : litre 21 gal (UK) : gallon impérial 22 l : litre

Coordonnées polaires

•

Valeur de θ ou y: Mémoire Y

No. Constante

28 Constante d’Avogadro 29 Volume molaire du gaz idéal

(273,15 K, 101,325 kPa)

Constante du gaz de masse molaire 31 Constante de Faraday 32 Constante de Von Klitzing 33 Charge de l’électron vers quotient

de la masse 34 Quantum de circulation 35 Rapport gyromagnétique du

proton 36 Constante de Josephson 37 Électronvolt 38 Température Celsius 39 Unité astronomique 40 Parsec 41 Masse molaire du carbone 12 42 Constante de Planck sur 2 pi 43 Énergie de Hartree 44 Quantum de conductance 45 Inverse constante de structure fine 46 Rapport de masse proton-électron 47 Constante de masse molaire 48 Longueur d’onde de Compton du

neutron 49 Première constante de radiation 50 Seconde constante de radiation 51 Impédance caractéristique du vide 52 Atmosphère standard

No. Remarques

23 fl oz(US): once liquide américain 24 ml : millilitre 25 fl oz(UK): once liquide impériale 26 ml : millilitre 27 J : Joule 28 cal : calorie 29 J : Joule 30 cal15 : Calorie (15n°C) 31 J : Joule 32 calIT : Calorie I. T. 33 hp : cheval vapeur 34 W : Watt 35 ps : cheval vapeur français 36 W : Watt 37 38 Pa : Pascal 39 atm : atmosphère 40 Pa : Pascal 41 (1 mmHg = 1 Torr) 42 Pa : Pascal 43 44 J : Joule

EL-506W EL-546W

CALCULATRICE SCIENTIFIQUE

MODE D’EMPLOI

MODÈLE

SHARP CORPORATION

MEM RESET

0 1

DRG FSE TA B

0 1

x x x

2 3

Préfixe Opération Unité

P (x,y )

P (r,θ )

FRANÇAIS

k(kilo) ∑10 10 M(Méga) ∑11 10 G (Giga) ∑12 10 T (Téra) ∑13 10 m (milli) ∑14 10 µ(micro) ∑15 10 n (nano) ∑16 10 p (pico) ∑17 10 f (femto) ∑18 10

–3

–6

–9

–12

–15

Fonction de modification

Les résultats de calcul sont obtenus en interne en notation scientifique avec une mantisse pouvant aller jusqu’à 14 caractères. Cependant, comme les résultats du calcul sont affichés selon la forme indiquée sur l’écran, le résultat du calcul interne peut être différent de celui affiché. En utilisant la fonction de modification, la valeur interne est modifiée pour représenter la valeur affichée, de façon à ce que celle-ci puisse être utilisée sans changement dans les opérations qui suivent.

Fonction de résolvant

La valeur x peut être trouvée qui réduit une équation saisie à “0”.

•

Cette fonction utilise la méthode de Newton pour obtenir une approximation. Selon la fonction (ex, périodique) ou la valeur de ‘Start’ (départ), une erreur peut avoir lieu (Error 2) suite à l’absence de convergence vers la solution pour l’équation.

•

La valeur obtenue par cette fonction peut comprendre une marge d’erreur. Si elle est plus grande qu’il n’est acceptable, recalculez la solution après avoir changé les valeurs de ‘Start’ (départ) et dx.

•

Changez la valeur de ‘Start’ (départ) (ex, à une valeur négative) ou la valeur dx (ex, à une valeur inférieure) si:

•

aucune solution ne peut être trouvée (Error 2).

•

plus de deux solutions semblent possibles (ex, une équation cubique).

•

pour améliorer la précision arithmétique.

•

Le résultat du calcul est automatiquement sauvegardé dans la mémoire X.

[Effectuer la fonction de résolvant]

Appuyez sur m0.

Q W

Saisissez une formule avec une variable x.

Appuyez sur ∑0.

Saisissez la valeur de ‘Start’ (départ) et appuyez sur ®. La valeur par défaut est “0”.

Saisissez la valeur dx (intervalle par minute).

Appuyez sur ®.

CALCUL DE SIMULATION (ALGB)

Vous devez trouver consécutivement une valeur, en utilisant la même formule, par exemple, lorsque vous devez représenter la courbe de l’équation 2x trouver une variable qui résolve l’équation 2x + 2y = 14. Une fois l’équation entrée en mémoire, tout ce que vous avez à faire, c’est de spécifier la valeur de la variable dans la formule. Variables utilisables: A-F, M, X et Y Fonctions non-utilisables: Fonction aléatoire

•

Les calculs de simulation ne peuvent être effectués qu’en mode normal.

•

Les instructions de fin de calcul différentes de = ne peuvent pas être employées.

+ 1, ou bien

Mode opératoire

Employez la combinaison m0.

Entrez une formule ayant au moins une variable.

Appuyez sur la touche @≤.

L’écran d’entrée des variables apparaîtra. Entrez la valeur de la variable clignotante, puis appuyez sur ® pour confirmer. Le résultat du calcul s’affichera après avoir entré toutes les variables utilisées.

•

Seules les valeurs numériques peuvent servir de variables. L’entrée de formules n’est pas permise.

•

Après avoir achevé le calcul, appuyez sur la touche @≤ pour réaliser d’autres calculs en utilisant la même formule.

•

Les variables et les valeurs numériques seront affichées sur l’écran d’entrée des variables. Pour changer une valeur numérique, entrez la nouvelle valeur puis appuyez sur ®.

•

Procéder au calcul de simulation provoquera la réécriture des emplacements de mémoire par de nouvelles valeurs.

CALCULS STATISTIQUES

Appuyez sur m1 pour sélectionner le mode statistique. Les sept calculs statistiques indiqués ci-dessous peuvent être effectués. Une fois sélectionné le mode statistique, sélectionnez le sous-mode désiré en appuyant sur la touche numérique correspondant à votre choix. Pour changer le sous-mode statistique, resélectionnez le mode statistique (appuyez sur m1), puis sélectionnez le sous-mode requis.

0 (SD) : Statistique à variable simple 1 (LINE) : Calcul de régression linéaire 2 (QUAD) : Calcul de régression quadratique 3 (EXP) : Calcul de régression exponentielle 4 (LOG) : Calcul de régression logarithmique 5 (PWR) : Calcul de régression de puissance 6 (INV) : Calcul de régression inverse

Les statistiques suivantes peuvent être obtenues pour chaque calcul statistique (reportez-vous au tableau ci-dessous):

Calcul statistique à variable simple

Valeurs statistiques du tableau Q et valeurs de la densité de probabilité de la loi normale

Calcul de régression linéaire

Statistique de Q et W ainsi qu’estimation d’y pour x donné (estimation d’y´) et estimation de x pour y donné (estimation de x´).

Calcul de régression exponentielle, régression logarithmique, régression de puissance et régression inverse

Statistique de Q et W ainsi qu’estimation d’y pour x donné et estimation de x pour y donné. (Comme la calculatrice convertit chaque formule en une formule de régression linéaire avant que le calcul proprement dit ait lieu, elle obtient toutes les statistiques, sauf les coefficients a et b, des données converties plutôt que des données entrées.)

Calcul de régression quadratique

Statistique de Q et W et coefficients a, b, c dans la formule de régression quadratique (y = a + bx + cx corrélation (r) ne peut être obtenu.) Lorsqu’il existe deux valeurs d’x´, appuyez sur @≠.

Lors de calculs avec a, b et c, une seule valeur numérique peut être maintenue.

•

Utilisez K et R pour effectuer un calcul de variable STAT.

). (Pour les calculs de régression quadratique, aucun coefficient de

x Moyenne des échantillons (données x)

sx Écart type de l’échantillon (données x)

x Écart type de la population (données x)

n Nombre d’échantillons

x Somme des échantillons (données x)

x2Somme des carrés des échantillons (données x)

y Moyenne des échantillons (données y)

sy Écart type de l’échantillon (données y)

y Écart type de la population (données y)

y Somme des échantillons (données y)

y2Somme des carrés des échantillons (données y)

xy Somme des produits des échantillons (x, y) r Coefficient de corrélation a Coefficient de l’équation de régression b Coefficient de l’équation de régression c Coefficient de l’équation de régression quadratique

Entrée des données et correction

Les données entrées sont gardées en mémoire jusqu’à @c ou la sélection du mode. Avant d’entrer de nouvelles données, veillez à effacer le contenu des mémoires.

[Entrée des données]

Données de variable simple

Donnée

Donnée & fréquence

Données de variable double

Données

x &

Données

x &

mêmes données x et y.)

•

Un maximum de 100 éléments de données peut être entré. Dans le cas de données de variable simple, un élément de données sans attribution de fréquence est compté comme un élément de données, alors qu’un élément attribué avec fréquence est stocké comme un groupe de deux éléments de données. Dans le cas de données de variable double, un groupe d’éléments de données sans attribution de fréquence est compté comme deux éléments de données, alors qu’un groupe d’éléments attribué avec fréquence est stocké comme un groupe de trois éléments de données.

[Correction des données]

Correction avant la frappe de la touche k juste après une entrée de données:

Effacez les données erronées au moyen de la touche ª, puis entrez les données correctes.

Correction après la frappe de la touche k

Utilisez [] pour afficher les données précédemment saisies. Appuyez sur ] pour afficher les éléments de données en ordre ascendant (le plus ancien en premier). Pour inverser l’ordre d’affichage à l’ordre descendant (le plus récent en premier), appuyez sur la touche [. Chaque élément est affiché avec ‘Xn=’, ‘Yn=’, ou ‘Nn=’ (n est le nombre séquentiel du groupe de données). Affichez un élément de données à modifier, entrez la valeur correcte, puis appuyez sur k. En utilisant &, vous pouvez corriger les valeurs du groupe de données toutes en même temps.

•

Pour effacer un groupe de données, affichez un élément du groupe de données à effacer, puis appuyez sur @J. Le groupe de données sera effacé.

•

Pour ajouter un nouveau groupe de données, appuyez sur ª et entrez les valeurs, puis appuyez sur k.

k (Pour entrer des multiples de la même donnée.)

Données

y k

Données

y &

fréquence

k (Pour entrer des multiples des

Formules statistiques

Type Formule de régression Linéaire y = a + bx Exponentiel y = a • e Logarithmique y = a + b • ln x Puissance y = a • x

Inverse

Quadratique y = a + bx + cx

Lors de l’emploi des formules de calculs statistiques, il y a survenance d’une erreur si:

•

la valeur absolue d’un résultat intermédiaire ou du résultat définitif est égale ou supérieur à 1 × 10

•

le dénominateur est nul.

•

la valeur dont il faut extraire la racine carrée est négative.

•

aucune solution n’existe dans le calcul de régression quadratique.

Calculs de probabilité selon la loi normale

•

P(t), Q(t) et R(t) prendront toujours des valeurs positives, même lorsque t<0, parce que ces fonctions suivent le même principe que celui utilisé lors de résolution pour une surface. Les valeurs de P(t), Q(t) et R(t) sont données avec 6 décimales.

RÉSOLUTION D’UN SYSTÈME D’ÉQUATIONS LINÉAIRES

Une équation linéaire simultanée à 2 inconnues (2-VLE) ou à 3 inconnues (3-VLE) peut être résolue par cette fonction.

2-VLE: m20

3-VLE: m21

•

Une erreur survient si le déterminant D est nul.

•

Une erreur survient si un résultat intermédiaire ou le résultat définitif est égal ou supérieur à 1 × 10

•

Un coefficient (a1, etc.) peut être le résultat d’une opération arithmétique ordinaire.

•

Pour effacer les coefficients tapés, utilisez la combinaison @c.

y = a + b —

100

•

Si vous appuyez sur la touche ® alors que le déterminant D est affiché, vous provoquez le rappel des coefficients. A chaque pression sur la touche ®, un coefficient s’affiche (l’ordre est le même que celui de la frappe), ce qui vous permet une vérification. (En appuyant sur @®, les coefficients sont affichés dans le sens inverse.) Pour modifier le coefficient affiché, tapez une autre valeur puis appuyez sur la touche ®.

RÉSOLVANT D’ÉQUATION QUADRATIQUE ET CUBIQUE

L’équation quadratique (ax2 + bx + c = 0) ou cubique (ax3 + bx2 + cx + d = 0) peut être résolue par cette fonction.

Résolvant d’équation quadratique: m22

Résolvant d’équation cubique: m23

•

Appuyez sur ® après avoir saisi chaque coefficient.

•

Le résultat sera affiché en appuyant sur ® après avoir saisi tous les coefficients. Lorsqu’il y a plus de 2 résultats, la solution suivante s’affichera.

•

Lorsque le résultat est un nombre imaginaire, le symbole “xy” s’affichera. L’affichage peut être commuté entre partie imaginaire et réelle en appuyant sur @≠.

•

Les résultats obtenus par cette fonction peuvent comprendre une marge d’erreur.

CALCULS AVEC NOMBRES COMPLEXES

Pour effectuer des additions, soustractions, multiplications et divisions avec des nombres complexes, appuyez sur m3 pour sélectionner le mode nombres complexes. Les résultats d’un calcul avec des nombres complexes sont exprimés de deux manières:

@}: Coordonnées cartésiennes (rectangulaires). (xy s’affiche.)

@{: Coordonnées polaires. (

s’affiche.)

Frappe d’un nombre complexe

Coordonnées cartésiennes

coordonnée x

Coordonnées polaires

r: valeur absolue θ: argument

•

Lors de la sélection d’un autre mode, la partie imaginaire d’un nombre complexe enregistré dans la mémoire indépendante (M) s’efface.

•

Un nombre complexe exprimé en coordonnées cartésiennes pour lequel la valeur de y est nulle, ou un nombre complexe exprimé en coordonnées polaires pour lequel la valeur de l’argument est nulle, est traité comme un nombre réel.

•

Appuyez sur ∑0 pour ramener le conjugué complexe du nombre complexe spécifié.

coordonnée x

coordonnée y

+Ü

coordonnée y

CALCULS DE MATRICE

Cette fonction permet la sauvegarde d’un maximum de 4 matrices (4 lignes × 4 colonnes) pour les calculs. Appuyez sur m4 pour passer au mode matrice.

•

Les données de la matrice doivent être saisies avant d’effectuer le calcul. Une pression sur [/] affichera le tampon d'édition de la matrice en même temps que (COLONNE), puis chaque élément, ex. ‘MAT1,1’) et appuyez sur k après chaque entrée. Une fois saisis tous les éléments, appuyez sur ª, puis appuyez sur °2 et spécifiez matA-D pour sauvegarder les données.

•

Pour éditer les données sauvegardées dans matA-D, appuyez sur °1 et spécifiez matA-D pour rappeler les données vers le tampon d'édition de la matrice. Une fois édité, appuyez sur ª, puis appuyez sur °2 et spécifiez matAD pour sauvegarder les données.

•

Avant de procéder aux calculs, appuyez sur ª pour fermer le tampon d'édition de la matrice.

•

Lorsque les résultats du calcul sont sous le format matrice, le tampon d’édition de la matrice avec ces résultats sera affiché. (À cet instant, vous ne pouvez revenir à l'équation.) Pour sauvegarder les résultats dans matA-D, appuyez sur ª, puis appuyez sur °2 et spécifiez matA-D.

•

Étant donné qu’il n’y a qu’un tampon d’édition de la matrice, les données précédente seront écrasées par le nouveau calcul.

•

En plus des quatre fonctions arithmétiques (à l'exception des divisions entre matrices),

, x2, et x–1, les commandes suivantes sont disponibles:

dim(

nom de la matrice,

ligne,colonne

fill(

valeur,ligne,colonne

cumul

nom de la matrice

aug(

nom de la matrice,

nom de la matrice

identity

rnd_mat(

det

nom de la matrice

trans

mat→list (∑5)

matA→list (∑6)

. Entrez la valeur de chaque élément (‘ROW’ (LIGNE), ‘COLUMN’

Ramène une matrice avec les dimensions modifiées

)

valeur

ligne,colonne

comme spécifié.

) Remplit chaque élément avec une valeur spécifique.

Ramène la matrice cumulative. Joint la seconde matrice à la première comme nouvelles

colonnes. La première et seconde matrices doivent avoir

)

le même nombre de lignes. Ramène la matrice identifiée avec une valeur spécifique de

lignes et colonnes.

) Ramène une matrice aléatoire avec des valeurs

spécifiques de lignes et colonnes. Ramène le déterminant d’une matrice carrée. Ramène la matrice avec les colonnes transposées vers les

lignes et les lignes transposées vers les colonnes. Crée des listes avec des éléments de la colonne gauche

dans chaque matrice. (matA→L1, matB→L2, matC→L3, matD→L4) Le mode passe du mode matrice au mode liste.

Crée des listes avec des éléments de chaque colonne dans la matrice. (matA→L1, L2, L3, L4) Le mode passe du mode matrice au mode liste.

CALCULS DE LISTES

Cette fonction permet la sauvegarde d’un maximum de 4 listes de 16 éléments pour les calculs. Appuyez sur m5 pour passer au mode liste.

•

Les données de la liste doivent être saisies avant d’effectuer le calcul. Une pression sur [/] affichera le tampon d'édition de la liste en même temps que

. Entrez la valeur de chaque élément (‘SIZE’ (TAILLE), puis chaque élément, ex. ‘LIST1’) et appuyez sur k après chaque entrée. Une fois saisis tous les éléments, appuyez sur ª, puis appuyez sur °2 et spécifiez L1-4 pour sauvegarder les données.

•

SHARP CORPORATION

P (x,y )

P (r,θ )

Pour éditer les données sauvegardées dans L1-4, appuyez sur °1 et spécifiez L1-4 pour rappeler les données vers le tampon d'édition de la matrice. Une fois édité, appuyez sur ª, puis appuyez sur °2 et spécifiez L1-4 pour sauvegarder les données.

•

Avant de procéder aux calculs, appuyez sur ª pour fermer le tampon d'édition de la liste.

•

Lorsque les résultats du calcul sont sous le format liste, le tampon d’édition de la liste avec ces résultats sera affiché. (À cet instant, vous ne pouvez revenir à l'équation.) Pour sauvegarder les résultats dans L1-4, appuyez sur ª, puis appuyez sur °2 et spécifiez L1-4.

•

Étant donné qu’il n’y a qu’un tampon d’édition de la liste, les données précédente seront écrasées par le nouveau calcul.

•

En plus des quatre fonctions arithmétiques, x3, x2, et x–1, les commandes suivantes sont disponibles:

sortA

nom de la liste

sortD

nom de la liste

dim(

nom de la liste,taille

fill(

valeur,taille

cumul

nom de la liste

df_list

nom de la liste

aug(

nom de la liste,

nom de la liste

min

nom de la liste

max

nom de la liste

mean

nom de la liste

med

nom de la liste

sum

nom de la liste

prod

nom de la liste

stdDv

nom de la liste

vari

nom de la liste

o_prod(

nom de la liste,

nom de la liste

i_prod(

nom de la liste,

nom de la liste

abs

nom de la liste

list→mat (∑5)

list→matA (∑6)

) Saisit la valeur pour tous les éléments dans la liste

)

Trie la liste en ordre ascendant. Trie la liste en ordre descendant.

) Ramène une liste avec la taille modifiée comme spécifié.

spécifiée. Accumule séquentiellement chaque élément dans la liste. Ramène une nouvelle liste en utilisant la différence entre

les éléments adjacents dans la liste. Ramène une liste jointe aux listes.

Ramène la valeur minimale dans la liste. Ramène la valeur maximale dans la liste. Ramène la valeur significative des éléments dans la liste. Ramène la valeur médiane des éléments dans la liste. Ramène la somme des éléments dans la liste. Ramène la multiplication des éléments dans la liste. Ramène la déviation standard de la liste. Ramène la variance de la liste. Ramène le produit externe de 2 listes (vecteurs).

Ramène le produit interne de 2 listes (vecteurs).

Ramène la valeur absolue de la liste (vecteur). Crée des matrices avec des données de la colonne

gauche dans chaque liste. (L1→matA, L2→matB, L3→matC, L4→matD) Le mode passe du mode liste au mode matrice.

Crée une matrice avec des données de la colonne dans chaque liste. (L1, L2, L3, L4→mat) Le mode passe du mode liste au mode matrice.

ERREURS ET PLAGES DE CALCUL

Erreurs

Il y a erreur lorsqu’une opération excède la capacité de calcul, ou bien lorsque vous tentez d’effectuer une opération mathématiquement interdite. Lorsqu’il y a une erreur, le curseur est automatiquement placé sur l’endroit où se trouve l’erreur dans l’équation en appuyant sur < (ou >). Éditez l’équation ou appuyez sur la touche ª pour effacer l’équation.

Code d’erreur et nature de l’erreur

Erreur de syntaxe (Error 1):

•

Tentative d’exécution d’une opération illégale.

Ex. 2 @{

Erreur de calcul (Error 2):

•

La valeur absolue d’un résultat intermédiaire ou du résultat final est supérieure ou égale à

100

•

Tentative de division par 0 (ou un calcul intermédiaire dont le résultat est zéro).

•

Un calcul a entraîné un dépassement de la plage de calcul possible.

Erreur de profondeur (Error 3):

•

Le nombre de tampons disponibles a été dépassé. (Il y a 10 tampons* de valeurs numériques et 24 tampons d'instructions de calculs en mode normal.) *5 tampons dans les autres modes et 1 tampon pour les données Matrice/Liste.

•

Les éléments de données dépassaient 100 en mode statistique.

Équation trop longue (Error 4):

•

L’équation a dépassé son tampon d’entrée maximal (142 caractères). Une équation doit être inférieure à 142 caractères.

Erreur de rappel d’équation (Error 5):

•

L’équation mise en mémoire contient une fonction non-disponible dans le mode utilisé pour la rappeler. Par exemple, si une valeur numérique avec des chiffres différents de 0 et 1 est enregistrée comme un décimal, etc, elle ne peut être rappelée si la calculatrice est réglée en mode binaire.

Erreur excès mémoire (Error 6):

•

L’équation a dépassé le tampon de mémoire de la formule (256 caractères en tout dans F1 - F4).

Erreur invalide (Error 7):

•

Erreur de définition de la matrice/liste ou saisie d’une valeur invalide.

Erreur de dimension (Error 8):

•

Dimensions de matrice/liste inconsistantes avec le calcul.

Erreur DIM invalide (Error 9):

•

Taille de matrice/liste dépasse la plage de calcul.

Pas d’erreur définie (Error 10):

•

Matrice/liste indéfinie utilisée dans calcul.

Plages de calcul

•

Dans les limites définies ci-après, cette calculatrice fournit un résultat avec une erreur ne dépassant pas ±1 sur le chiffre le moins significatif de la mantisse. Néanmoins une erreur de calcul augmente dans les calculs en chaîne suite à l’accumulation de chaque erreur de calcul. (C’est la même chose pour y

n!, e

, ln, calculs de Matrice/Liste, etc., où des calculs en chaîne sont effectués intérieurement.) En outre, une erreur de calcul s’accumulera et deviendra plus grande à proximité des points d’inflexion et points singuliers de fonction.

x, x

•

Plages de calcul

–99

~ ±9.999999999×1099 et 0.

±10 Si la valeur absolue d’un nombre introduit au clavier, ou si la valeur absolue d’un résultat final ou intermédiaire est inférieure à 10 comme nulle aussi bien pour les calculs que pour l’affichage.

–99

, cette valeur est considérée

REMPLACEMENT DES PILES

Remarques sur le remplacement des piles

Une utilisation incorrecte des piles peut occasionner une fuite d’électrolyte ou une explosion. Assurez-vous d’observer les règles de manipulation:

•

Remplacez les deux piles en même temps.

•

Ne mélangez pas les piles usagées et neuves.

•

Vérifiez l’exactitude du type de piles utilisées

•

Veillez à installer les piles dans le bon sens, comme indiqué sur la calculatrice.

•

Les piles sont installées dans l’usine avant transport et peuvent s’être déchargées avant d’atteindre la durée de service indiquée dans la fiche technique.

Remarques sur l’effacement du contenu de la mémoire

Au remplacement de la pile, tout le contenu de la mémoire est effacé. Le contenu peut également être effacé si la calculatrice est défectueuse ou quand elle est réparée. Notez toutes les données importantes contenues dans la mémoire en prévision d’un effacement accidentel.

Quand faut-il remplacer les piles

Si l’affichage manque de contraste ou que rien n’apparaît à l’écran même si vous appuyez sur la touche ª en éclairage réduit, les piles doivent être changées.

Attention

•

Le fluide provenant d’une pile qui fuit peut causer de sérieuses blessures s’il pénétrait accidentellement dans un œil. Si cela se produisait, rincez à l’eau vive et consultez un médecin immédiatement.

•

Si le fluide provenant d’une pile qui fuit entrait en contact avec votre peau ou vos vêtements, nettoyez immédiatement à l’eau vive.

•

Si vous n’avez pas l’intention d’utiliser l’appareil pendant une période prolongée, retirez les piles et conservez-les dans un endroit sûr, afin d’éviter toute fuite.

•

Ne laissez pas des piles usées à l’intérieur de l’appareil.

•

Ne mélangez pas des piles partiellement usées, ni des piles de type différent.

•

Tenez les piles hors de portée des enfants.

•

Une pile usagée peut fuire et endommager la calculatrice.

•

Des risques d’explosion peuvent exister à cause d’une mauvaise manipulation.

•

Ne jetez pas la pile dans une flamme vive, elle peut exploser.

Méthode de remplacement

1. Mettez la calculatrice hors tension en utilisant la combinaison @F.

2. Devissez les deux vis. (Fig. 1)

3. Faites glisser légèrement le couvercle des piles; il suffit ensuite de le soulever pour

le retirer.

4. Ôtez les piles usagées, en vous servant d’un stylo à bille ou d’un instrument à

pointe similaire. (Fig. 2)

5. Installez deux piles neuves. Assurez-vous que le signe “+” est vers le haut.

6. Remettez le couvercle et les vis.

7. Appuyez sur la touche RESET (dos de la calculatrice).

•

Assurez-vous que l’affichage a l’aspect de la figure ci-dessous. Dans le cas contraire, retirez les piles puis mettez-les en place à nouveau et vérifiez l’affichage.

(Fig. 1) (Fig. 2)

Mise hors tension automatique

Cette calculatrice se met d’elle-même hors tension si vous n’appuyez sur aucune touche pendant environ 10 minutes.

FICHE TECHNIQUE

Calculs: Calculs scientifiques, calculs de nombres com-

Calculs internes: Mantisses jusqu’à 14 chiffres Calculs maximaux: 24 calculs, 10 valeurs numériques en mode

Alimentation: Cellules solaires intégrées

Température de fonctionnement: 0°C – 40°C Dimensions extérieures: 79,6 mm (W) × 154,5 mm (D) × 13,2 mm (H) Poids: Environ 97 g (en incluant les piles) Accessoires: Piles × 2 (installées) et mode d’emploi, carte de

POUR PLUS D’INFORMATIONS SUR LA CALCULATRICE SCIENTIFIQUE

Visitez notre site web. http://sharp-world.com/calculator/

plexes, résolvants d’équation, calculs statistiques, etc.

normal (5 valeurs numériques dans les autres modes et 1 valeur numérique pour données de Matrice/Liste)

3V ¶ (DC): Piles de secours (piles alcalines (LR44 ou équivalent) × 2)

référence rapide et boîtier

EL-506W

•

x =

Σx

y =

Σy

sy =

Σy

– ny

n – 1

sx =

Σx

– nx

n – 1

σy =

Σy

– ny

σx =

Σx

– nx

EL-546W

CALCULATION EXAMPLES ANWENDUNGSBEISPIELE EXEMPLES DE CALCUL EJEMPLOS DE CÁLCULO EXEMPLOS DE CÁLCULO ESEMPI DI CALCOLO REKENVOORBEELDEN PÉLDASZÁMÍTÁSOK

PŘÍKLADY VÝPOČTŮ

RÄKNEEXEMPEL LASKENTAESIMERKKEJÄ

икаеЦкх ЗхуалгЦзав

UDREGNINGSEKSEMPLER

CONTOH-CONTOH PENGHITUNGAN CONTOH-CONTOH PERHITUNGAN

[]

13(5+2)= ª 3 ( 5 + 2 )= 23×5+2= 3 * 5 + 2 = 33×5+3×2= 3 * 5 + 3 * 2 =

→1 @[ →2 ] →3 ] →2 [

”

100000÷3= [NORM1] ª 100000 / 3 = →[FIX] ”10 [TAB 2] ”2 2

→[SCI] ”11 →[ENG] ”12 →[NORM1] ”13

3÷1000= [NORM1] ª 3 / 1000 =

→[NORM2] ”14 3.× →[NORM1] ”13

+-*/()±E

45+285÷3= ª 45 + 285 / 3 =

18+6

15–8 ( 15 - 8 =

42×(–5)+120= 42 *± 5 + 120 =

(5×103)÷(4×10–3)= 5 E 3 / 4 E

34+57= 34 + 57 = 45+57= 45 + 57 =

68×25= 68 * 25 = 68×40= 68 * 40 =

sutSUTVhH Ile¡•L÷⁄™ $#!qQ%

sin60[°]= ªs 60 =

cos — [rad]=

tan–11=[g] ”02@T 1 =

(cosh 1.5 + ª(hu 1.5 +h sinh 1.5)2 = s 1.5 )L=

tanh–1— =

5 7

••••

( 18 + 6 )/

*1 (5 ±) *

± 3 =

”01u( @V/ 4 )=

”00

@Ht( 5 / 7 )=

33’333.33333 33’333.33333

33’333.33

33’333.33333

21.

17.

21.

17.

21.

17.

3.33×10

33.33×10

0.003 10

0.003

140.

3.428571429

–90.

1’250’000.

91.

102.

1’700. 2’720.

0.866025403

0.707106781

50.

20.08553692

0.895879734

••••

ln 20 = I 20 =

log 50 = l 50 =

e3 = @e 3 =

1.7

= @¡ 1.7 =

1 — + — = 6

8–2 – 34 × 52 =8 ™± 2 - 3 ™

1 4

(123)—=

49 –4¿

81 = @⁄ 49 - 4 @$

27 @# 27 =

4! = 4 @!=

= 10 @q 3 =

10P3

=5 @Q 2 =

5C2

500×25%= 500 * 25 @%

120÷400=?% 120 / 400 @%

500+(500×25%)= 500 + 25 @%

400–(400×30%)= 400 - 30 @%

04–

03–

6 @•+ 7 @

•=

4 * 5 L=

12 ™ 3 ™ 4

@•=

8 ÷=

81 =

θ = sin–1 x, θ = tan–1 x θ = cos–1 x

DEG –90 ≤ θ ≤ 90 0 ≤ θ ≤ 180

–03

RAD – — ≤ θ ≤ — 0 ≤ θ ≤ π

GRAD –100 ≤ θ ≤ 100 0 ≤ θ ≤ 200

Åè

d/dx (x4 – 0.5x3 + 6x2) ªKˆ™ 4 - 0.5 K



x=2 ˆ÷+ 6 KˆL



dx=0.00002 @Å 2 ®®

 

x=3 ® 3 ® 0.001 ®



dx=0.001



(x2 – 5)dx ªKˆL- 5

∫

n=100 è 2 ® 8 ®® n=10 ®®® 10 ®

90°→ [rad] ª 90 @g → [g] @g → [°] @g

sin–10.8 = [°] @S 0.8 =

→ [rad] @g → [g] @g → [°] @g

KRO;:?≥∆˚¬

24÷(8×2)= 24 /KM= (8×2)×5= KM* 5 =

$150×3:M1 150 * 3 ; +)$250:M2 =M1+250 250 ; –)M2×5% RM* 5 @% M @:RM

••••

ª 8 * 2 OM

ªOM

2.995732274

1.698970004

20.08553692

50.11872336

0.309523809

–2’024.984375

6.447419591

512.

24.

720.

10.

125.

30.

625.

280.

50.

130.5000029

138.

1.570796327

100.

90.

53.13010235

0.927295218

59.03344706

53.13010235

16.

1.5

80.

450.

250.

35.

665.

••••

$1=¥110 110 OY ¥26,510=$? 26510 /RY=

$2,750=¥? 2750 *RY=

r=3cm (r→Y) 3 OY πr2=? @VKYL=

—— = 2.4...(A) 24 /( 4 + 6 )=

4+6

3×(A)+60÷(A)=

πr2⇒F1 @VKYL

V = ? R≥* 4 / 3 =

3 *K?+ 60 /

K?=

O≥ 3 OY

6+4=ANS ª 6 + 4 = ANS+5 + 5 =

8×2=ANS 8 * 2 =

ANS

44+37=ANS 44 + 37 =

√

ANS= @⁄=

124

3— + — = [a—] ª 3 \ 1 \ 2 +

→[a.xxx] \ →[d/c] @|

—

(—)

5 1

(—)

—— = @⁄ 64 \ 225 =

225

2 — =

1.2 —– =

2.3 1°2’3”

——– =

1×10 ——– =

2×10 A = 7 ª 7 OA

— =4 \KA=

1.25 + — = [a.xxx] 1.25 + 2 \ 5 = →[a—] \

4 l5 l6

b c

2 3

= @¡ 2 \ 3 =

=7 \ 5 ™ 5 =

—

2 5

b c

= 4—

4 \ 3 =

1 \ 8 ™ 1 \ 3

( 2 ™ 3 ) \ ( 3 ™ 4 ) =

1.2 \ 2.3 =

1 o 2 o 3 \ 2 =

1 E 3 \ 2 E 3 =

5 6

кыомнгв†д аб

DEC(25)→BIN ª@í 25 @ê

HEX(1AC) @ì 1AC

→BIN @ê →PEN @û →OCT @î →DEC @í

BIN(1010–100) @ê( 1010 - 100 ) ×11 = * 11 =

BIN(111)→NEG ã 111 =

HEX(1FF)+ @ì 1FF @î+ OCT(512)= 512 = HEX(?) @ì

2FEC– ªOM@ì 2FEC 2C9E=(A) 2C9E ;

+)2000– 2000 -

1901=(B) 1901 ;

1011 AND ª@ê 1011 † 101 = (BIN) 101 =

5A OR C3 = (HEX) @ì 5A ä C3 =

NOT 10110 = @êâ 10110 = (BIN)

24 XOR 4 = (OCT) @î 24 à 4 =

B3 XNOR @ì B3 á 2D = (HEX) 2D = →DEC @í

110.

241.

302’500.

28.27433388

32.2

37.69911184

256.

4 l5 l6

4.833333333 29 l6

4.641588834

16807 l3125

1 l2

8 l15

8 l81

12 l23

0°31’1.5”

1 l2

4 l7

1.65

1 l13 l20

11001.

110101100.

3203.

654.

428.

10010.

1111111001.

1511.

349.

34E.

6FF. A4d.

db.

1111101001.

20.

FFFFFFFF61.

–159.

2.4

10.

15.

16.

81.

o_° (→sec, →min)

x =

Σx

y =

Σy

sy =

Σy

– ny

n – 1

sx =

Σx

– nx

n – 1

σy =

Σy

– ny

σx =

Σx

– nx

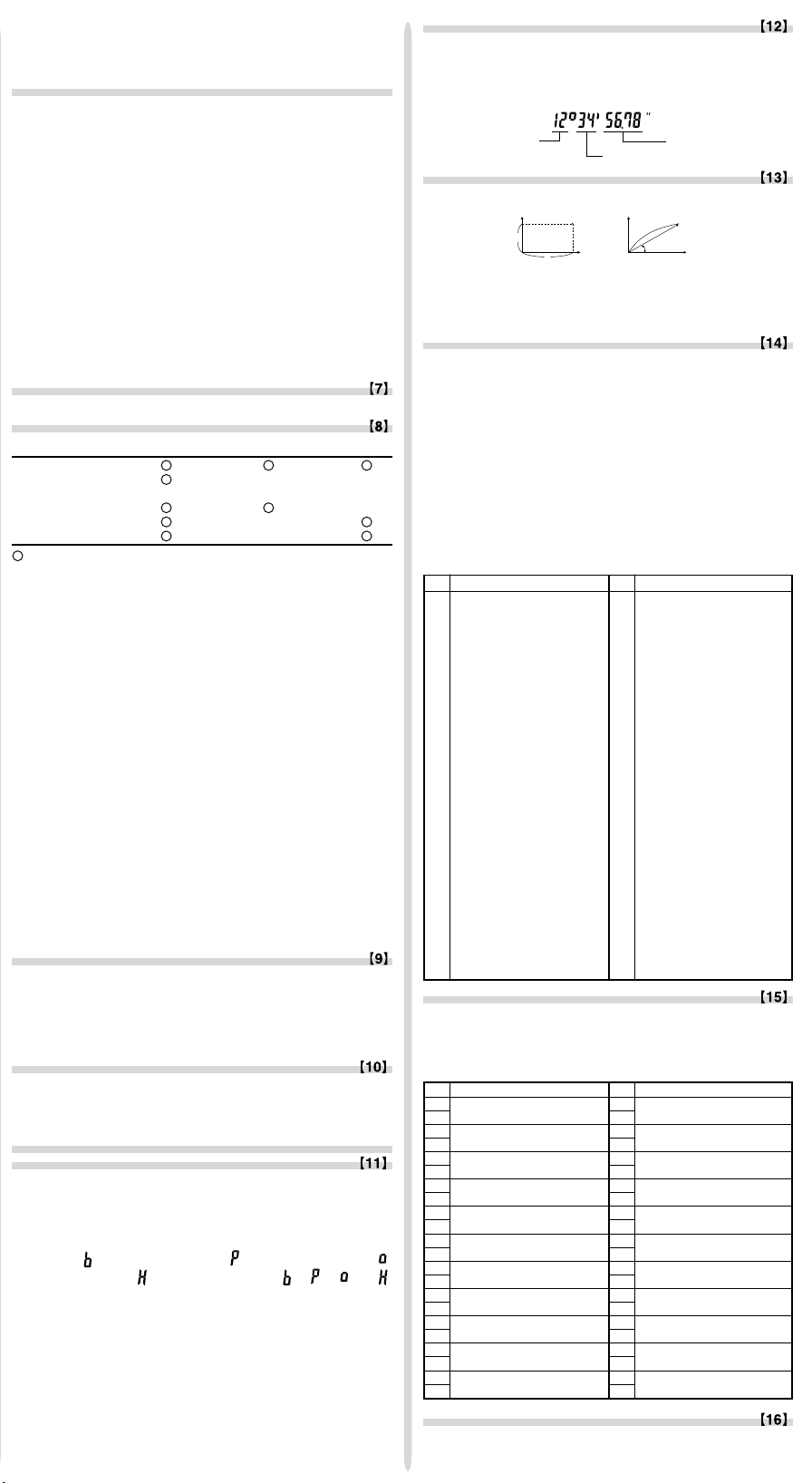
12°39’18.05” ª 12 o 39 o 18.05 →[10] @_

123.678→[60] 123.678 @_

3h30m45s + 3 o 30 o 45 + 6 o 6h45m36s = [60] 45 o 36 =

1234°56’12” + 1234 o 56 o 12 + 0°0’34.567” = [60] 0 o 0 o 34.567 =

3h45m – 3 o 45 - 1.69 =

1.69h = [60] @_

sin62°12’24” = [10] s 62 o 12 o 24=

24°→[ ” ] 24 o°2

1500”→[ ’ ]0 o 0 o 1500 °3

12.65501389

123°40’40.8”

10°16’21.”

1234°56’47.”

2°3’36.”

0.884635235 86’400.

{},≠

  

ª 6 @, 4

@≠[r]

14 @, 36

@≠[x]

]

7.211102551

33.69006753

7.211102551

11.32623792

8.228993532

11.32623792



x = 6 →r = @{[



y = 4 θ = [°] @≠[θ]





r = 14 →x = @}[x]



θ = 36[°] y = @≠[y]



V0 = 15.3m/s ª 15.3 * 10 + 2 @•* t = 10s ß 03 * 10 L=

V0t+ — gt2 = ?m

643.3325

125yd = ?m ª 125 @¥ 5 =

∑ (k, M, G, T, m,

100m×10k= 100 ∑14*

ÌÌ

Ì, n, p, f)

ÌÌ

10 ∑10=

j”

5÷9=ANS ª”10”2 1 ANS×9= 5 / 9 = [FIX,TAB=1] * 9 =*

5 / 9 =@j * 9 =*

5.5555555555555×10–1×9

0.6×9

”13

∑ (SOLV)

sin x–0.5 ªsKˆ- 0.5 Start= 0 ∑0 0 ®® Start= 180 ® 180 ®®

≤

f(x) = x

–3x2+2 Kˆ™ 3 - 3 K

x = –11 ±® x = –0.5 @≤ 0.5 ±®

A2+B

A = 2, B = 3 2 ® 3 ® A = 2, B = 5 @≤® 5 ®

ˆL+ 2 @≤

@⁄(KAL+ KBL)@≤

3.605551275

5.385164807

25.

114.3

1’000.

0.6

5.0

0.6

5.4

30.

150.

–2.

1.125

k&~£pnzw^ ¢PZWvrab© xy≠° (→t, P(, Q(, R()

DATA

95 m10 80 95 k 80 80 k 75 k 75 75 & 3 k 75 50 k 50

–

x= R~

σx= Rp

n= Rn

Σx= Rz

Σx2= Rw

sx= R£

sx2= L=

(95––x)

×10+50=

x = 60 → P(t) ? °1 60 °0)=

t = –0.5 → R(t) ? °3 0.5 ±)=

xy m11

2 5 2 & 5 k 2 5 k 12 24 12 & 24 k 21 40 21 & 40 & 3 k 21 40 15 & 25 k 21 40 Ra 15 25 Rb

x=3 → y′=? 3 @y y=46 → x′=? 46 @x

xy m12

12 41 12 & 41 k 8 13 8 & 13 k 5 2 5 & 2 k 23 200 23 & 200 k 15 71 15 & 71 k

x=10 → y′=? 10 @y y=22 → x′=? 22 @x

( 95 -K~) /K£* 10 + 50 =

Rr R£ R¢

Ra Rb R©

@≠ @≠

–3.120289663

–3.432772026

k[]

DATA

30 m10 40 30 k 40 40 & 2 k 50 50 k

↓

DATA

30 ]]]

45 45 & 3 k X2= 45 ] N2= 45 60 ] 60 k X3=

Σx = x1 + x2 + ··· + x

Σx2 = x

+ x

+ ··· + x

75.71428571

12.37179148

530.

41’200.

13.3630621

178.5714286

64.43210706

0.102012

0.691463

1.050261097

1.826044386

0.995176343

8.541216597

15.67223812

6.528394256

24.61590706

5.357506761

0.503334057

24.4880159

9.63201409

45.

60.

Σxy = x1y1 + x2y2 + ··· + xny Σy = y1 + y2 + ··· + y

Σy2 = y

+ y

+ ··· + y

•

t = ––––

x – x

σx

Standardization conversion formula Standard Umrechnungsformel Formule de conversion de standardisation Fórmula de conversión de estandarización Fórmula de conversão padronizada Formula di conversione della standardizzazione Standaardisering omzettingsformule

Standard átváltási képlet Vzorec pro přepočet rozdělení

Omvandlingsformel för standardisering Normituksen konversiokaava

îÓÏÛÎ‡ ÒÚ‡Ì‰‡ÚËÁÓ‚‡ÌÌÓ„Ó ÔÂÓ·‡ÁÓ‚‡ÌËﬂ

Omregningsformel for standardisering

Rumus penukaran pemiawaian Rumus konversi standarisasi

θ1

θ2

x =

Σx

y =

Σy

sy =

Σy

– ny

n – 1

sx =

Σx

– nx

n – 1

σy =

Σy

– ny

σx =

Σx

– nx

m (2-VLE)

a1x + b1y = c a2x + b2y = c



2x + 3y = 4 2 ® 3 ® 4 ®



5x + 6y = 7 5 ® 6 ® 7



x = ? ® [x]

m20

y = ? ® [y] det(D) = ? ® [det(D)]

D =

a1 b a2 b

m (3-VLE)

a1x + b1y + c1z = d

a2x + b2y + c2z = d a3x + b3y + c3z = d

m21

x + y – z = 9 1 ® 1 ® 1 ±® 9 ®



6x + 6y – z = 17 6 ® 6 ® 1 ±® 17 ®



14x – 7y + 2z = 42 14 ® 7 ±® 2 ® 42



x = ? ® [x] y = ? ® [y] z = ? ® [z]

det(D) = ? ® [det(D)]

D =

a1 b1 c

a2 b2 c a3 b3 c

3.238095238

–1.638095238

m (QUAD, CUBIC)

m22

@®

m23

@≠

@≠ [y] @≠ [x]

@≠ [y]

–6.333333333

–1.233600307

0.216800153

1.043018296

0.216800153

–

1.043018296

13.85640646

+ 4x – 95 = 0 3 ® 4 ®± 95

x1 = ? ® x2 = ? ®

+4x2+3x +7=0 5 ® 4 ® 3 ® 7

x1 = ? ® x2 = ? ®

x3 = ? ®

m (CPLX)

(12–6i) + (7+15i) – 12 - 6 Ü+ 7 + 15 Ü- (11+4i) = ( 11 + 4 Ü)= [x]

6×(7–9i) × 6 *( 7 - 9 Ü)* (–5+8i) = ( 5 ±+ 8 Ü)= [x]

16×(sin30°+ 16 *(s 30 +

icos30°)÷(sin60°+ Üu 30 )/(s 60 + icos60°)= Üu 60 )= [x]

••••

–7.4

105.

222.

606.

••••

@{ 8 Ö 70 + 12 Ö 25 = [r] @≠ [θ]

r1 = 8, θ1 = 70° r2 = 12, θ2 = 25°

↓ r = ?, θ = ?°

(1 + i) @} 1 +Ü= ↓ @{ [r] r = ?, θ = ?° @≠ [θ]

= = [x]

(2 – 3i)

@}( 2 - 3 Ü)L

@≠ [y]

1 ( 1 +Ü)@•= [x]

—— = 1 + i @≠ [y]

CONJ(5+2i)

∑0( 5 + 2 Ü)= [x] @≠ [y]

m (MAT)

1 2

→ matA

3 4 3 k 4 k 3 1

→ matB

2 6

matA × matB =

matA

7 13 17 27

–2

–1

1.5 –0.5

dim(matA,3,3) = 1 2 0

dim(matA,3,3) = 3 4 0

dim(matA,3,3) = 0 0 0

fill(5,3,3) = 5 5 5

–1.

–3.

cumul matA =

1 2 4 6

aug(matA,matB) =

identity 3 = 1 0 0

identity 3 = 0 1 0 ª∑34 3 =

identity 3 = 0 0 1

rnd_mat(2,3)

det matA = –2

trans matB =

mat → list

3 2 1 6

L1: {1 3} L2: {3 2}

m4 ] 2 k 2 k 1 k 2 k

ª∑20 ] 2 k 2 k 3 k 1 k 2 k 6 k ª∑21

ª∑00*∑01=

ª∑00@•=

ª∑30∑00 @, 3 @, 3 )=

ª∑31 5 @, 3 @, 3 )=

ª∑32∑00=

1 2 3 1 ª∑33∑00 3 4 2 6 @,∑01)=

ª∑35 2 @, 3 )=

ª∑40∑00=

ª∑41∑01=

ª∑5

m (LIST)

2, 7, 4 → L1 ] 3 k 2 k 7 k 4 k

–3, –1, –4 → L2

L1+L2 = {–1 6 0}

sortA L1 = {2 4 7}

sortD L1 = {7 4 2}

dim(L1,5) = {2 7 4 0 0}

fill(5,5) = {5 5 5 5 5}

cumul L1 = {2 9 13}

df_list L1 = {5 –3}

aug(L1,L2) = {2 7 4 –3 –1 –4} ª∑36∑00

min L1 = 2

max L1 = 7

mean L1 = 4.333333333

med L1 = 4

sum L1 = 13

prod L1 = 56

••••

ª∑20 ] 3 k ± 3 k± 1 k± 4 k ª∑21

ª∑00+∑01=

ª∑30∑00=

ª∑31∑00=

ª∑32∑00 @, 5 )=

ª∑33 5 @, 5 )=

ª∑34∑00=

ª∑35∑00=

@,∑01)=

ª∑40∑00=

ª∑41∑00=

ª∑42∑00=

ª∑43∑00=

ª∑44∑00=

ª∑45∑00=

18.5408873

∠

42.76427608

1.414213562

•••• ••••

stdDv L1 = 2.516611478

vari L1 = 6.333333333

o_prod(L1,L2) = {–24 –4 19}

ª∑46∑00=

ª∑47∑00=

∑48∑00

@,∑01)=

i_prod(L1,L2) = –29

∑49∑00

@,∑01)=

abs L2 = 5.099019514

list → matA matA: 2 –3

∠

–

list → matA matA: 7 –1 ª∑6

45.

list → matA matA: 4 –4

–5.

12.

0.5

–

Function Dynamic range Funktion zulässiger Bereich Fonction Plage dynamique

Función Rango dinámico Função Gama dinâmica

ª∑4A∑01=

Funzioni Campi dinamici

Functie Rekencapaciteit

Függvény Megengedett számítási tartomány

Funkce Dynamický rozsah

Funktion Definitionsområde

Funktio Dynaaminen ala

îÛÌÍˆËﬂ СЛМ‡ПЛ˜ВТНЛИ ‰Л‡Ф‡БУМ

Funktion Dynamikområde

Fungsi Julat dinamik Fungsi Kisaran dinamis

DEG: | x | < 10

sin x, cos x,

RAD: | x | < —– × 10

tan x (tan x : | x | ≠ — (2n–1))*

GRAD: | x | < —– × 10

sin–1x, cos–1x | x | ≤ 1

tan–1x,

x | x | < 10

In x, log x 10

–99

≤ x < 10

• y > 0: –10

• y = 0: 0 < x < 10

• y < 0: x = n

• y > 0: –10

¿y • y < 0: x = 2n–1

10 sinh x, cosh x,

tanh x

• y = 0: 0 < x < 10

100

–10

< x ≤ 230.2585092

100

–10

< x < 100

| x | ≤ 230.2585092

sinh–1 x | x | < 10 cosh–1 x 1 ≤ x < 10 tanh–1 x | x | < 1

x 0 ≤ x < 10

–1

| x | < 10 | x | < 2.15443469 × 10

| x | < 10

(tan x : | x | ≠ 90 (2n–1))*

180

(tan x : | x | ≠ 100 (2n–1))*

100

< x log y < 100

(0 < l x l < 1: — = 2n–1, x ≠ 0)*,

100

–10

< x log | y | < 100

100

< — log y < 100 (x ≠ 0)

(0 < | x | < 1 : — = n, x ≠ 0)*,

100

–10

< — log | y | < 100

100

(x ≠ 0)

100

n! 0 ≤ n ≤ 69*

nPr

0 ≤ r ≤ n ≤ 9999999999*

100

—— < 10

(n-r)!

0 ≤ r ≤ n ≤ 9999999999*

nCr

↔

DEG, D°M’S

x, y → r, θ x2 + y2 < 10

r, θ → x, y RAD: | θ | < —– × 10

DRG |

(A+Bi)+(C+Di) | A + C | < 10 (A+Bi)–(C+Di)| A – C | < 10

(A+Bi)×(C+Di)

0 ≤ r ≤ 69

100

—— < 10

(n-r)!

0°0’0.00001” ≤ | x | < 10000°

100

0 ≤ r < 10 DEG: | θ | < 10

GRAD : | θ | < — × 10

DEG→RAD, GRAD→DEG: | x | < 10 RAD→GRAD: | x | < — × 10

(AC – BD) < 10 (AD + BC) < 10

180 10

100

, | B + D | < 10

100

, | B – D | < 10

100

••••

x =

Σx

y =

Σy

sy =

Σy

– ny

n – 1

sx =

Σx

– nx

n – 1

σy =

Σy

– ny

σx =

Σx

– nx

AC + BD

(A+Bi)÷(C+Di)

→DEC DEC : | x | ≤ 9999999999 →BIN BIN : 1000000000 ≤ x ≤ 1111111111 →PEN 0 ≤ x ≤ 111111111 →OCT PEN : 2222222223 ≤ x ≤ 4444444444 →HEX 0 ≤ x ≤ 2222222222

AND OCT : 4000000000 ≤ x ≤ 7777777777 OR 0 ≤ x ≤ 3777777777 XOR HEX : FDABF41C01 ≤ x ≤ FFFFFFFFFF XNOR 0 ≤ x ≤ 2540BE3FF

NOT

NEG

C2 + D

BC – AD

C2 + D

C2 + D2 ≠ 0

BIN : 1000000000 ≤ x ≤ 1111111111

PEN : 2222222223 ≤ x ≤ 4444444444

OCT : 4000000000 ≤ x ≤ 7777777777

HEX : FDABF41C01 ≤ x ≤ FFFFFFFFFF

BIN : 1000000001 ≤ x ≤ 1111111111

PEN : 2222222223 ≤ x ≤ 4444444444

OCT : 4000000001 ≤ x ≤ 7777777777

HEX : FDABF41C01 ≤ x ≤ FFFFFFFFFF

100

< 10

100

< 10

0 ≤ x ≤ 111111111

0 ≤ x ≤ 2222222221

0 ≤ x ≤ 3777777777

0 ≤ x ≤ 2540BE3FE

0 ≤ x ≤ 111111111

0 ≤ x ≤ 2222222222

0 ≤ x ≤ 3777777777

0 ≤ x ≤ 2540BE3FF

* n, r: integer / ganze Zahlen / entier / entero / inteiro / intero /

geheel getal / egész számok / celé číslo / heltal / kokonaisluku / ˆÂÎ˚Â / heltal /

/ /

integer / bilangan bulat

In Europe:

This equipment complies with the requirements of Directive 89/336/ EEC as amended by 93/68/EEC.

Dieses Gerät entspricht den Anforderungen der EG-Richtlinie 89/336/ EWG mit Änderung 93/68/EWG.

Ce matériel répond aux exigences contenues dans la directive 89/336/ CEE modifiée par la directive 93/68/CEE.

Dit apparaat voldoet aan de eisen van de richtlijn 89/336/EEG, gewijzigd door 93/68/EEG.

Dette udstyr overholder kravene i direktiv nr. 89/336/EEC med tillæg nr. 93/68/EEC.

Quest’ apparecchio è conforme ai requisiti della direttiva 89/336/EEC come emendata dalla direttiva 93/68/EEC.

           89/336/, !  "! ! "#$ !   93/68/.

Este equipamento obedece às exigências da directiva 89/336/CEE na sua versão corrigida pela directiva 93/68/CEE.

Este aparato satisface las exigencias de la Directiva 89/336/CEE modificada por medio de la 93/68/CEE.

Denna utrustning uppfyller kraven enligt riktlinjen 89/336/EEC så som kompletteras av 93/68/EEC.

Dette produktet oppfyller betingelsene i direktivet 89/336/EEC i endringen 93/68/EEC.

Tämä laite täyttää direktiivin 89/336/EEC vaatimukset, jota on muutettu direktiivillä 93/68/EEC.

Ñ‡ÌÌÓÂ ÛÒÚÓÈÒÚ‚Ó ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ ÚÂ·Ó‚‡ÌËﬂÏ ‰ËÂÍÚË‚˚ 89/336/ EEC Ò Û˜ÂÚÓÏ ÔÓÔ‡‚ÓÍ 93/68/EEC.

Ez a készülék megfelel a 89/336/EGK sz. EK-irányelvben és annak 93/ 68/EGK sz. módosításában foglalt követelményeknek.

Tento pﬁístroj vyhovuje poÏadavkÛm smûrnice 89/336/EEC v platném znûní 93/68/EEC.

Endast svensk version/For Sweden only:

Miljöskydd

Denna produkt drivs av batteri. Vid batteribyte skall följande iakttagas:

• Det förbrukade batteriet skall inlämnas till er lokala handlare eller till kommunal miljöstation för återinssamling.

• Kasta ej batteriet i vattnet eller i hushållssoporna. Batteriet får ej heller utsättas för öppen eld.

OPMERKING: ALLEEN VOOR NEDERLAND/ NOTE: FOR NETHERLANDS ONLY

• Physical Constants and Metric Conversions are shown in the tables.

• Physikalischen Konstanten und metriche Umrechnungen sind in der Tabelle aufgelistet.

• Les constants physiques et les conversion des unités sont indiquées sur les tableaux.

• Las constants fisicas y conversiones métricas son mostradas en las tables.

• Constantes Fisicas e Conversões Métricas estão mostradas nas tablelas.

• La constanti fisiche e le conversioni delle unità di misura vengono mostrate nella tabella.

• De natuurconstanten en metrische omrekeningen staan in de tabellen hiernaast.

• A fizikai konstansok és a metrikus átváltások a táblázatokban találhatók.

• Fyzikální konstanty a převody do metrické soustavy jsou

uvedeny v tabulce.

• Fysikaliska konstanter och metriska omvandlingar visas i tabellerna.

• Fysikaaliset vakiot ja metrimuunnokset näkyvät taulukoista.

• З Ъ‡·ОЛˆ‡ı ФУН‡Б‡М˚ ЩЛБЛ˜ВТНЛВ НУМТЪ‡МЪ˚ Л

ПВЪЛ˜ВТНЛВ ФВУ·‡БУ‚‡МЛﬂ.

• Fysiske konstanter og metriske omskrivninger vises i tabellen.

•

• Pemalar Fizik dan Pertukaran Metrik ditunjukkan di dalam

jadual.

• Konstanta Fisika dan Konversi Metrik diperlihatkan di dalam tabel.

PHYSICAL CONSTANTS ß 01 — 52

No. SYMBOL UNIT No. SYMBOL UNIT No. SYMBOL UNIT 01 - c, c0m s 02 - G m3 kg–1 s–220 03 - gnm s 04 - mekg 22 05 - mpkg 23 06 - mnkg 24 07 - mµkg 25 08 - lu kg 26 09 - e C 27 - 10 - h J s 28 - N 11 - k J K 12 -

13 -

14 - rem 32 - RKOhm 50 - c2m K 15 -

16 - a0m 34 - h/2mem2 s 17 - R∞m 18 - Φ0Wb 36 - KJHz V

–1

19 -

–2

21 -

–1

29 - Vmm3 mol–147 - Mukg mol

–2

N A

F m

30 - R J mol–1 K–148 -

–1

31 - F C mol–149 - c1W m

33 - -e/meC kg

–1

35 -

–1

J T

–1

J T

–1

J T

–1

J T

–1

J T

–1

J T

m43 - EhJ

m44 - G0s

c, p

W m–2 K–445 -

–1

L mol

–1

s–1 T

–1

37 - eV J 38 - t K 39 - AU m 40 - pc m 41 - M(12C) kg mol 42 - h-J s

–1

46 - mp/m

c, n

51 - Z0Ω 52 - Pa

–1

Nur für Deutschland/For Germany only:

Umweltschutz

Das Gerät wird durch eine Batterie mit Strom versorgt. Um die Batterie sicher und umweltschonend zu entsorgen, beachten Sie bitte folgende Punkte:

• Bringen Sie die leere Batterie zu Ihrer örtlichen Mülldeponie, zum Händler oder zum Kundenservice-Zentrum zur Wiederverwertung.

• Werfen Sie die leere Batterie niemals ins Feuer, ins Wasser oder in den Hausmüll.

Seulement pour la France/For France only:

Protection de l’environnement

L’appareil est alimenté par pile. Afin de protéger l’environnement, nous vous recommandons:

• d’apporter la pile usagée ou à votre revendeur ou au service après-vente, pour recyclage.

• de ne pas jeter la pile usagée dans une source de chaleur, dans l’eau ou dans un vide-ordures.

METRIC CONVERSIONS

No. UNIT No. UNIT No. UNIT 1in→cm 16 kg→lb 31 J→calIT 2cm→in 17 °F→°C32calIT→J 3ft→m18°C→°F33hp→W 4m→ft 19 gal (US)→l 34 W→hp 5yd→m20l→gal (US) 35 ps→W 6m→yd 21 gal (UK)→l 36 W→ps 7 mile→km 22 l→gal (UK) 37 kgf/cm2→Pa 8km→mile 23 fl oz (US)→ml 38 Pa→kgf/cm 9 n mile→m24ml→fl oz (US) 39 atm→Pa 10 m→n mile 25 fl oz (UK)→ml 40 Pa→atm 11 acre→m 12 m2→acre 27 J→cal 42 Pa→mmHg 13 oz→g 28 cal→J 43 kgf·m→J 14 g→oz 29 J→cal15 44 J→kgf·m 15 lb→kg 30 cal15→J

26 ml→fl oz (UK) 41 mmHg→Pa

x @¥ 1 — 44

SHARP EL-506W User Manual [fr]

Specifications and Main Features

Frequently Asked Questions

User Manual