
®
EL-5230
EL-5250
PROGRAMMIERBARER
WISSENSCHAFTLICHER
RECHNER
BEDIENUNGSANLEITUNG

This equipment complies with the requirements of Directive 89/336/EEC as amended by 93/
68/EEC.
Dieses Gerät entspricht den Anforderungen der EG-Richtlinie 89/336/EWG mit Änderung 93/
68/EWG.
Ce matériel répond aux exigences contenues dans la directive 89/336/CEE modifiée par la
directive 93/68/CEE.
Dit apparaat voldoet aan de eisen van de richtlijn 89/336/EEG, gewijzigd door 93/68/EEG.
Dette udstyr overholder kravene i direktiv nr. 89/336/EEC med tillæg nr. 93/68/EEC.
Quest’ apparecchio è conforme ai requisiti della direttiva 89/336/EEC come emendata dalla
direttiva 93/68/EEC.
89/336/, 93/68/
.
Este equipamento obedece às exigências da directiva 89/336/CEE na sua versão corrigida pela
directiva 93/68/CEE.
Este aparato satisface las exigencias de la Directiva 89/336/CEE modificada por medio de la
93/68/CEE.
Denna utrustning uppfyller kraven enligt riktlinjen 89/336/EEC så som kompletteras av 93/68/
EEC.
Dette produktet oppfyller betingelsene i direktivet 89/336/EEC i endringen 93/68/EEC.
Tämä laite täyttää direktiivin 89/336/EEC vaatimukset, jota on muutettu direktiivillä 93/68/
EEC.
чÌÌÓ ÛÒÚÓÈÒÚ‚Ó ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ Ú·ӂ‡ÌËflÏ ‰ËÂÍÚË‚˚ 89/336/EEC Ò Û˜ÂÚÓÏ
ÔÓÔ‡‚ÓÍ 93/68/EEC.
Ez a készülék megfelel a 89/336/EGK sz. EK-irányelvben és annak 93/68/EGK sz.
módosításában foglalt követelményeknek.
Tento pfiístroj vyhovuje poÏadavkÛm smûrnice 89/336/EEC v platném znûní 93/68/EEC.
Nur für Deutschland/For Germany only:
Umweltschutz
Das Gerät wird durch eine Batterie mit Strom versorgt.
Um die Batterie sicher und umweltschonend zu entsorgen, beachten Sie bitte folgende
Punkte:
• Bringen Sie die leere Batterie zu Ihrer örtlichen Mülldeponie, zum Händler oder zum
Kundenservice-Zentrum zur Wiederverwertung.
• Werfen Sie die leere Batterie niemals ins Feuer, ins Wasser oder in den Hausmüll.

1
SHARP EL-5230/5250
Programmierbarer wissenschaftlicher Rechner
Einleitung
Anhang
Kapitel 1:
Vor der ersten Verwendung
Kapitel 2:
Allgemeine Informationen
Kapitel 3:
Wissenschaftliche Berechnungen
Kapitel 4:
Statistische Berechnungen
Kapitel 5:
Gleichungslöser
Kapitel 6:
Berechnungen mit komplexen Zahlen
Kapitel 7:
Programmierung
Kapitel 8:
Anwendungsbeispiele

2
Inhalt
Einleitung ...............................................................7
Betriebshinweise ...................................................................................... 8
Tastenbezeichnungen in dieser Anleitung............................................... 9
Kapitel 1: Vor der ersten Verwendung ...............11
Vorbereitungen vor dem ersten Gebrauch des Rechners .................... 11
Zurücksetzen des Rechners .......................................................... 11
Schutzabdeckung .................................................................................. 12
Rechner-Aufbau und Displaysymbole ................................................... 13
Betriebsarten (Modi) .............................................................................. 15
Wählen eines Modus...................................................................... 15
Möglichkeiten der Modi .................................................................. 15
Kurzanleitung ......................................................................................... 16
Ein- und Ausschalten des Rechners.............................................. 16
Eingeben und Berechnen eines Ausdrucks................................... 16
Bearbeiten eines Ausdrucks .......................................................... 17
Verwenden von Variablen ............................................................... 18
Verwenden der Simulationsberechnung (ALGB) ........................... 19
Verwenden der Solver-Funktion ..................................................... 21
Weitere Funktionen ........................................................................ 22
Kapitel 2: Allgemeine Informationen .................23
Löschen von Eingaben und Speichern ................................................. 23
Speicher-Löschtaste ...................................................................... 23
Bearbeiten und Korrigieren einer Gleichung ......................................... 24
Cursor-Tasten ................................................................................. 24
Modus für Einfügen und Überschreiben ........................................ 24
Löschtaste ...................................................................................... 25
Mehrzeilen-Playback-Funktion....................................................... 25
Das SET UP-Menü ................................................................................ 26
Änderung der Winkeleinheit ........................................................... 26
Wahl des Anzeigeformats und Festlegen der Anzahl der
Dezimalstellen ................................................................................ 26

3
Inhalt
Einstellen des Gleitkommasystems bei wissenschaftlicher
Notation .......................................................................................... 26
Arbeiten mit Speichern .......................................................................... 27
Arbeiten mit Buchstaben ................................................................ 27
Arbeiten mit globalen Variablen ..................................................... 27
Arbeiten mit lokalen Variablen ....................................................... 28
Verwendung von Variablen in einer Gleichung oder
einem Programm ............................................................................ 29
Verwendung des letzten Ergebnisses ........................................... 30
Globale Variable M ......................................................................... 30
Arbeiten mit Speichern in verschiedenen Modi ............................. 31
Zurücksetzen des Rechners .......................................................... 32
Kapitel 3: Wissenschaftliche Berechnungen ....33
NORMAL-Modus .................................................................................... 33
Einfache Berechnungen ................................................................. 33
Berechnungen mit Konstanten....................................................... 34
Funktionen ............................................................................................. 34
Funktionen des Mathematik-Menüs (MATH) ......................................... 36
Differential-/Integralfunktion................................................................... 38
Differentialfunktion ......................................................................... 38
Integralfunktion ............................................................................... 39
Ausführen von Integralberechnungen............................................ 40
Zufallszahlen-Funktion........................................................................... 41
Zufallszahlen .................................................................................. 41
Zufalls-Würfel ................................................................................. 41
Zufalls-Münze ................................................................................. 41
Ganzzahlige Zufallszahlen ............................................................. 41
Umwandeln der Winkeleinheiten ........................................................... 42
Kettenberechnungen.............................................................................. 42
Bruchrechnung ....................................................................................... 43
Rechnungen mit Binär-, Pental-, Oktal-, Dezimal- und
Hexadezimalzahlen (N-Basis) ............................................................... 44
Zeitberechnungen sowie dezimale und sexagesimale
Berechnungen ........................................................................................ 46
Koordinaten-Umwandlungen ................................................................. 47
Berechnungen mit physikalischen Konstanten ..................................... 48
Berechnungen mit Vorsilben physikalischer Maßeinheiten .................. 50

4
Inhalt
Modifizierungsfunktion ........................................................................... 51
Die Solver-Funktion ............................................................................... 52
Eingeben und Lösen einer Gleichung ........................................... 52
Ändern des Wertes von Variablen und Bearbeiten einer
Gleichung ....................................................................................... 52
Lösen einer Gleichung ................................................................... 53
Wichtige Hinweise .......................................................................... 54
Simulationsberechnung (ALGB) ............................................................ 55
Eingabe eines Ausdrucks für Simulationsberechnung .................. 55
Ändern des Wertes von Variablen und Bearbeiten eines
Ausdrucks ....................................................................................... 55
Simulieren einer Gleichung für verschiedene Werte ..................... 56
Speichern von Gleichung in eine Datei ................................................. 58
Speichern einer Gleichung ............................................................ 58
Laden und Löschen einer Gleichung ............................................. 59
Kapitel 4: Statistische Berechnungen ...............61
Statistische Berechnungen mit Einzel-Variablen ........................... 62
Berechnen linearer Regressionen ................................................. 62
Berechnen exponentieller, logarithmischer, Potenz-
und inverser Regressionen ............................................................ 62
Berechnen quadratischer Regressionen ....................................... 63
Dateneingabe und Korrektur ................................................................. 63
Dateneingabe ................................................................................. 63
Korrektur der Daten........................................................................ 63
Formeln für Regressionen statistischer Berechnungen ........................ 65
Berechnen der Normalverteilung .......................................................... 66
Beispiele statistischer Berechnungen ................................................... 67
Kapitel 5: Gleichungslöser .................................69
Lineare Gleichungssysteme .................................................................. 69
Solver für Gleichungen 2. und 3. Grades .............................................. 71
Kapitel 6:
Berechnungen mit komplexen Zahlen ...
73
Eingabe komplexer Zahlen .................................................................... 73

5
Inhalt
Kapitel 7: Programmierung ................................75
PROG-Modus......................................................................................... 75
Einschalten des PROG-Modus ...................................................... 75
Wahl des NORMAL-Programm-Modus oder des
NBASE-Programm-Modus ............................................................. 75
Konzept der Programmierung ........................................................ 75
Tasten und Display ......................................................................... 76
Erzeugen eines neuen Programms (NEW) ........................................... 76
Erzeugen eines neuen Programms (NEW) ................................... 76
Verwenden von Variablen ............................................................... 77
Programmierbefehle .............................................................................. 79
Eingabe- und Display-Befehle ....................................................... 79
Ablaufsteuerung ............................................................................. 81
Gleichwertigkeiten und Ungleichwertigkeiten................................ 82
Statistische Befehle ............................................................................... 83
Bearbeiten eines Programms ................................................................ 84
Fehlermeldungen ................................................................................... 85
Löschen von Programmen..................................................................... 86
Kapitel 8: Anwendungsbeispiele .......................87
Programmbeispiele ................................................................................ 87
Celsius-Fahrenheit-Umrechnung ................................................... 87
Die Heronische Formel .................................................................. 89
Umrechnen in andere Zahlensysteme........................................... 91
T Test .............................................................................................. 93
Bestimmen eines Kreises, der 3 gegebene Punkte schneidet ..... 95
Radioaktiver Zerfall ........................................................................ 97
Delta-Y Impedanz-Kreis-Transformation ....................................... 99
Bestimmen der Zugspannung von Fäden ................................... 102
Kauf mit n-monatlicher Ratenzahlung ......................................... 104
Digitaler Würfel ............................................................................. 106
Wie viele Stellen können Sie sich merken? ................................ 107
Berechnungsbeispiele ......................................................................... 110
Geosynchrone Umlaufbahnen ..................................................... 110
Scheinbare Helligkeit der Sterne ................................................. 111
Speicherberechnungen ................................................................ 113
Die Staatslotterie .......................................................................... 114

6
Inhalt
Anhang ...............................................................115
Auswechseln der Batterien .................................................................. 115
Verwendete Batterien ................................................................... 115
Hinweis zum Auswechseln der Batterien .................................... 115
Zeitpunkt des Batteriewechsels ................................................... 115
Warnungen ................................................................................... 116
Vorgehen beim Batteriewechsel .................................................. 116
Automatische Abschaltfunktion.................................................... 117
Das Optionsmenü (OPTION) ............................................................... 118
Die Optionsanzeige (OPTION) .................................................... 118
Kontrast ........................................................................................ 118
Speicherprüfung ........................................................................... 118
Löschen von Gleichungsdateien und Programmen .................... 119
Wenn eine Betriebsstörung auftritt ...................................................... 119
Fehlermeldungen ................................................................................. 120
Effektive Verwendung der Solver-Funktion ......................................... 121
Newton-Verfahren ........................................................................ 121
Lösungstoleranz des Näherungsverfahrens ................................ 121
Bereich der Erwartungswerte ...................................................... 121
Berechnungsgenauigkeit ............................................................. 122
Ändern des Bereichs der Erwartungswerte ................................. 122
Schwer lösbare Gleichungen ....................................................... 123
Technische Informationen .................................................................... 124
Rechenbereiche ........................................................................... 124
Speicherverwendung ................................................................... 126
Priorisierung der Berechnungen .................................................. 127
Technische Daten ................................................................................ 128
Weitere Informationen zu diesem wissenschaftlichen Rechner ......... 129

7
Einleitung
Besten Dank für den Kauf dieses programmierbaren wissenschaftlichen
Rechners von SHARP, Modell EL-5230/5250.
Diese Anleitung sollte als Referenz gut aufbewahrt werden.
•Wenn das Modell nicht explizit genannt wird , beziehen sich Text und alle
Hinweise in dieser Anleitung auf beide Modelle (EL-5230 und EL-5250).
• Manche in dieser Anleitung beschriebenen Modelle sind möglicherweise
nicht in allen Ländern erhältlich.
• Die in dieser Anleitung abgebildeten Anzeigenbeispiele entsprechen
möglicherweise nicht der Anzeige des Rechners. So geben die Anzeigenbeispiele nur etwa die zur Erklärung einer bestimmten Berechnung
erforderlichen Symbole wieder.
• Alle anderen Firmen- und/oder Produktnamen können Marken oder
eingetragene Marken ihrer Eigentümer sein.

8
Einleitung
Betriebshinweise
• Den Rechner nicht in der hinteren Hosentasche herumtragen, da er beim
Hinsetzen beschädigt werden kann. Das Display ist aus Glas und daher
besonders empfindlich.
• Den Rechner von extremer Hitzeeinwirkung, wie z.B. auf dem Armaturenbrett eines Fahrzeugs oder neben einem Heizgerät, fernhalten. Vermeiden
Sie weiterhin besonders feuchte oder staubige Umgebungen.
• Da dieses Produkt nicht wasserdicht ist, sollten Sie es nicht an Orten
benutzen oder lagern, die extremer Feuchtigkeit ausgesetzt sind. Schützen
Sie das Gerät vor Wasser, Regentropfen, Sprühwasser, Saft, Kaffee,
Dampf, Schweiß usw., da der Eintritt von irgendwelchen Flüssigkeiten zu
Funktionsstörungen führen kann.
• Mit einem weichen, trockenen Tuch reinigen. Keine Lösungsmittel oder
feuchte Tücher verwenden.
• Den Rechner nicht fallen lassen und keine Gewalt anwenden.
• Die Batterien niemals in offenes Feuer werfen.
• Die Batterien außerhalb der Reichweite von Kindern aufbewahren.
• Produktverbesserungen dieses Gerätes, einschließlich des Zubehörs,
bleiben ohne Vorankündigung vorbehalten.
HINWEIS
• SHARP empfiehlt Ihnen, separat schriftliche Aufzeichnungen aller
wichtigen im Taschenrechner gespeicherten Daten zu erstellen.
Unter bestimmten Umständen können Daten in praktisch jedem
elektronischen Speicher verlorengehen oder geändert werden.
Daher übernimmt SHARP keine Haftung für Daten, die aufgrund von
falscher Verwendung, Reparaturen, Defekten, Batteriewechsel,
Verwendung nach Ablauf der angegebenen Batterielebensdauer
oder aus irgendwelchen anderen Gründen verlorengehen oder
anderweitig unbrauchbar werden.
• SHARP übernimmt keine Verantwortung oder Haftung für irgendwelche zufälligen oder aus der Verwendung folgenden wirtschaftlichen oder sachlichen Schäden, die aufgrund der falschen Verwendung bzw. durch Fehlfunktionen dieses Gerätes und dessen
Zubehör auftreten, ausgenommen diese Haftung ist gesetzlich
festgelegt.

9
Einleitung
Tastenbezeichnungen in dieser Anleitung
In dieser Anleitung werden folgende Tastenbezeichnungen verwendet:
Bestimmung von ex: @ " .............. 햲
Bestimmung von In : i
Bestimmung von F : ; F .................... 햳
Bestimmung von d/c : @ F .............. 햲
Bestimmung von a
b
/
c
: k
Bestimmung von H : ; H.................... 햳
Bestimmung von i : Q ....................... 햴
햲 Für die Verwendung der zweiten Funktion einer Taste (in Orangerot
oberhalb der Taste aufgedruckt) zuerst @ drücken und anschließend
die Funktionstaste drücken.
햳 Um einen Speicherplatz (A-Z) festzulegen (in Blau oberhalb der Taste
aufgedruckt ) erst ; drücken.
Die Eingabe von Buchstaben wird nicht als Tasten sondern als regulärer
Buchstabe dargestellt.
햴 Funktionen, die in Grau neben den Tasten aufgedruckt sind, sind nur in
bestimmten Modi verfügbar.
Hinweis:
• Um den Cursor in den Abbildungen dieser Anleitung deutlich
sichtbarer zu machen, ist er als “_” unterhalb des entsprechenden
Zeichens dargestellt, obwohl er im Display als Rechteck erscheint.
Beispiel
Drücken Sie j @ s ; R
A k S 10
• @ s und ; R bedeutet, dass
Sie @ gefolgt von der Taste ` und
; gefolgt von der Taste 5 drücken
müssen.
NORMAL MODE
0.
πRŒ˚–10_

10
11
Kapitel 1
Vor der ersten Verwendung
Vorbereitungen vor dem ersten Gebrauch des
Rechners
Vor dem ersten Gebrauch des Rechners müssen Sie ihn zurücksetzen und
den Kontrast einstellen.
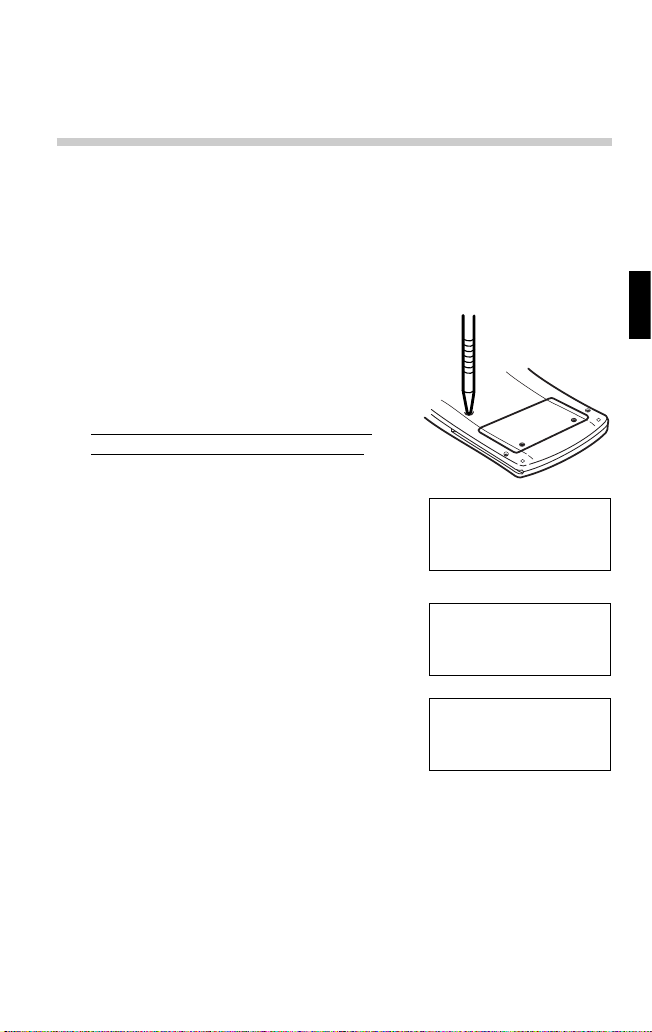
Zurücksetzen des Rechners
1. Den RESET-Schalter auf der Rückseite
des Rechners mit der Spitze eines
Kugelschreibers oder eines ähnlich
spitzen Gegenstandes eindrücken.
Verwenden Sie keine Gegenstände mit
zerbrechlichen oder scharfen Spitzen.
•Wenn Sie die Meldung rechts nicht sehen,
kann es sein, dass die Batterie falsch
eingelegt ist. Schlagen Sie unter “Auswechseln der Batterien” (s. Seite 115)
nach und setzen Sie die Batterien neu ein.
2. y drücken.
• Die Anfangsanzeige des NORMAL-Modus
erscheint.
3. @ o 0 und + oder -
drücken, um den Displaykontrast einzustellen, und dann j drücken.
• @ o bedeutet, dass Sie die Taste
@ und anschließend S drücken
müssen.
• Siehe “Das Optionsmenü (OPTION)” für weitere Informationen zu
optionalen Funktionen. (s. Seite 118)
zALL DATA CL?z
z YES¬[DEL] z
z NO¬[ENTER]z
NORMAL MODE
0.
LCD CONTRAST
[+] [-]
DARK® ¬LIGHT
12
Kapitel 1: Vor der ersten Verwendung
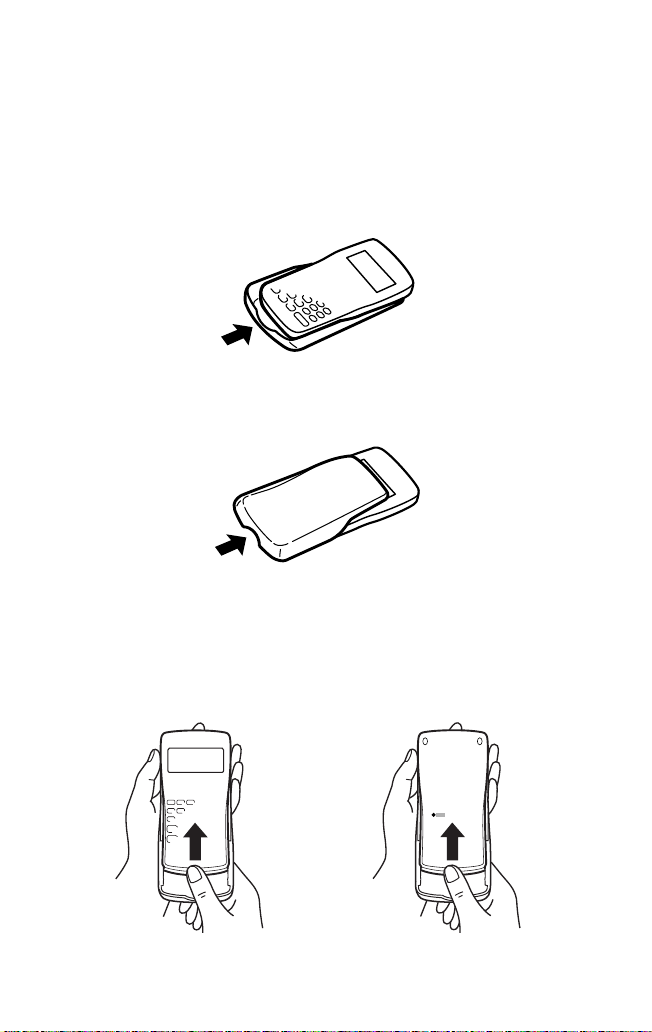
Schutzabdeckung
Ihr Rechner wird mit einer Schutzabdeckung geliefert, um Tastatur und
Display bei Nichtgebrauch zu schützen.
Vor der Verwendung des Rechners nehmen Sie die Schutzabdeckung ab
und schieben Sie sie auf die Rückseite, um sie nicht zu verlieren.
(s. Abbildung)
Bei Nichtverwendung des Rechners schieben Sie die Schutzabdeckung über
Tastatur und Display. (s. Abbildung)
• Schieben Sie die Schutzabdeckung ganz bis zur Kante.
• Die Schnell-Referenz-Karte befindet sich innen in der Schutzabdeckung.
• Nehmen Sie die Schutzabdeckung ab, während Sie sie mit den Fingern an
den unten gezeigten Stellen greifen.
13
Kapitel 1: Vor der ersten Verwendung
Rechner-Aufbau und Displaysymbole
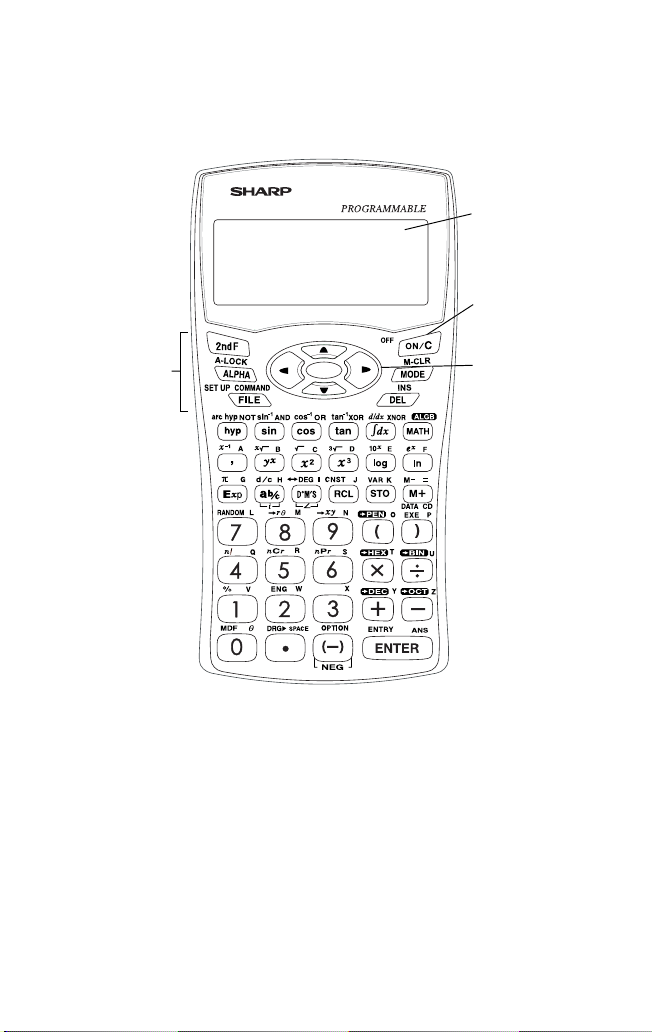
Rechner-Aufbau
1 Display-Anzeigebild: Das Rechnerdisplay besteht aus einer 14 × 3
Zeilen Punktmatrix (5 × 7 Punkte pro Zeichen) und einer 2-stelligen
Exponentialanzeige pro Zeile.
2 ON/OFF- und Lösch-Taste: Schaltet den Rechner ein. Zum Ausschalten
des Rechners drücken Sie @ und anschließend o. Diese Taste
kann auch zum Löschen des Bildschirms verwendet werden.
3 Tastenbedienungstasten:
@: Aktiviert die zweite Funktion (in Orangerot aufgedruckt), die der
nächsten gedrückten Taste zugewiesen wird.
;: Aktiviert die Variable (in Blau aufgedruckt), die der nächsten
gedrückten Taste zugewiesen wird.
4 Cursor-Tasten: Ermöglichen die Cursorbewegung in vier Richtungen.
1 Display-
Anzeigebild
2 ON/OFF- und
Lösch-Taste
3 Tasten-
bedienungstasten
4 Cursor-Tasten

14
Kapitel 1: Vor der ersten Verwendung
Display-Anzeige
Symbol
Exponent
Mantisse
PunktmatrixAnzeige
•Während der Verwendung werden nicht alle Symbole gleichzeitig angezeigt.
• In der Anleitung werden nur diejenigen Symbole angezeigt, die für die
jeweilige Beschreibung bzw. für das jeweilige Anwendungsbeispiel
notwendig sind.
: Zeigt an, dass bestimmte Inhalte in den anzeigten Richtungen
versteckt sind.
Drücken Sie die Cursor-Tasten, um den verbleibenden (versteckten)
Teil anzuzeigen.
BUSY
: Erscheint bei der Ausführung einer Berechnung.
2ndF : Erscheint, wenn @ gedrückt wird.
xy/r
θ
: Zeigt an, in welcher Form die Ergebnisse bei Berechnungen mit
komplexen Zahlen dargestellt werden.
HYP : Zeigt an, dass H gedrückt wurde; die hyperbolischen Funktio-
nen sind aktiviert. Wenn @ > gedrückt werden, erscheint die
Anzeige “2ndF HYP”; die inversen hyperbolischen Funktionen sind
jetzt aktiviert.
ALPHA: Erscheint, wenn ;, @ a, x oder t gedrückt wird.
FIX/SCI/ENG: Anzeige des Darstellungsformats einer Zahl.
DEG/RAD/GRAD: Zeigt die Winkeleinheit an.
: Erscheint, wenn der Statistik-Modus gewählt wurde.
M:Zeigt an, dass ein Wert im Speicher M gespeichert wurde.

15
Kapitel 1: Vor der ersten Verwendung
NORMAL MODE
0.
<MODE-2>
›CPLX
<MODE-1>
ƒNORMAL ⁄STAT
¤PROG ‹EQN
Betriebsarten (Modi)
Dieser Rechner hat fünf Modi, um verschiedene Verfahren auszuführen.
Diese Modi wählen Sie mit der MODE-Taste aus.
Wählen eines Modus
1. b drücken.
Die Menüanzeige erscheint. Um zur
Anzeige der nächsten Menüseite zu
gelangen, d drücken.
2. Drücken Sie 0, um den NORMAL-
Modus einzustellen.
• In der Menü-Anzeige drücken Sie die
zugewiesene Zahl, um eine Auswahl
vorzunehmen.
Möglichkeiten der Modi
NORMAL-Modus:
Ermöglicht übliche wissenschaftliche Berechnungen, Differential-/
Integralfunktionen, N-Basis-Berechnungen, Solver-Funktion,
Simulationsberechnungen auszuführen.
STAT-Modus (Statistik):
Beinhaltet statistische Berechnungen.
PROG-Modus:
Ermöglicht, Programme zu erzeugen und zu verwenden, um einfache
oder komplexe Berechnungen zu automatisieren.
EQN-Modus (Gleichung):
Bietet die Möglichkeit, Gleichungen zu lösen (z.B. quadratische
Gleichungen).
CPLX-Modus (Komplex):
Beinhaltet arithmetische Verfahren mit komplexen Zahlen.

16
Kapitel 1: Vor der ersten Verwendung
NORMAL MODE
0.
Kurzanleitung
In diesem Abschnitt werden kurz die einfachen arithmetischen Funktionen
des Rechners und auch die Hauptfunktionen wie z.B. die Solver-Funktion
erklärt.
Ein- und Ausschalten des Rechners
1. Zum Einschalten des Rechners die Taste
j oben rechts auf der Tastatur drücken.
• Um die Batterielebensdauer zu verlängern,
schaltet der Rechner sich automatisch aus,
wenn er einige Minuten lang nicht
verwendet wird.
2. Zum Ausschalten des Rechners drücken Sie @ o.
• Um eine Funktion oder einen Befehl verwenden zu können, der in
Orangerot oberhalb einer Taste aufgedruckt ist, wird @ und
anschließend die entsprechende Taste gedrückt.
Eingeben und Berechnen eines Ausdrucks
Arithmetische Ausdrücke sollten in derjenigen Reihenfolge eingegeben
werden, in der sie auch auf Papier geschrieben werden. Für die Berechnung
eines Ausdrucks e unten rechts auf der Tastatur drücken; diese Taste hat
die gleiche Funktion wie die Taste mit dem Gleichheitszeichen bei einigen
Rechnern.
Beispiel
Den folgenden Ausdruck berechnen:
82 ÷ 았앙3 – 7 × -10.5
1. 8 A z @ * 3 -
7 k S 10.5
• Dieser Rechner hat eine Minustaste
- für die Subtraktion und eine
Vorzeichenänderungstaste S für die
Eingabe negativer Zahlen.
• Für die Korrektur eines Eingabefehlers die Cursor-Tasten l r
u d verwenden, um zu der fehlerhaften Position im Display zu
gelangen und den vorhandenen Ausdruck zu überschreiben.
NORMAL MODE
0.
8Œ©‰3-7˚–10.5_
17
Kapitel 1: Vor der ersten Verwendung
2. e drücken, um das Ergebnis zu
bestimmen.
• Während der Rechner ein Ergebnis
berechnet, erscheint “BUSY” oben links
im Display.
• Der Cursor muss nicht am Ende eines Ausdrucks stehen, um ein
Ergebnis berechnen zu können.
Bearbeiten eines Ausdrucks
Nach der Bestimmung des Ergebnisses kann der Ausdruck wieder aufgerufen
und modifiziert werden. Dazu werden die Cursor-Tasten gedrückt, bevor
erneut e gedrückt wird.
Beispiel
Den letzten Ausdruck aufrufen und folgendermaßen ändern:
82 ÷
았앙앙앙앙앙앙
3 – 7 × -10.5
1. Um zum letzten Ausdruck zurückzugelangen, d oder r drücken.
• Der Cursor befindet sich jetzt am Anfang
des Ausdrucks (in diesem Fall der “8”).
• Durch Drücken von u oder l
nach der Bestimmung des Ergebnisses kehrt der Cursor zum Ende
des letzten Ausdrucks zurück.
• Um den Cursor in den Abbildungen dieser Anleitung deutlich
sichtbarer zu machen, ist er als “_” unter dem Zeichen dargestellt,
obwohl er im Display als Rechteck erscheint.
2. r viermal drücken, um den Cursor
an die Stelle zu bringen, an der die
Änderung vorgenommen werden soll.
• Der Cursor hat sich vier Stellen nach
rechts bewegt und blinkt jetzt über der “3”.
3. Drücken Sie @ O.
• Dadurch wird der Zeicheneingabemodus von “Überschreiben” auf
“Einfügen” geändert.
•Wenn @ gedrückt wird, sollte das Symbol 2ndF oben im Display
erscheinen. Wenn das nicht geschieht, haben Sie die Taste nicht fest
genug gedrückt.
• Die Form des blinkenden Cursors zeigt an, welcher Zeicheneingabemodus eingestellt ist. Ein dreieckiger Cursor zeigt den Modus
“Einfügen”, während ein rechteckiger Cursor den Modus
“Überschreiben” anzeigt.
0.
8Œ©‰3-7˚–10.5=
110.4504172
8Œ©‰3-7˚–10.5=
110.4504172
8Œ©‰3-7˚–10.5
8Œ©‰3-7˚–10.5=
110.4504172
8Œ©‰3-7˚–10.5
18
Kapitel 1: Vor der ersten Verwendung
2
S = πr
r
NORMAL MODE
0.
2„Ò_
0.
2„ÒR
8.
4. ( drücken und anschließend den
Cursor an das Ende des Ausdrucks
bewegen (@ r).
• Beachten Sie, dass der Cursor sich jetzt
in der zweiten Zeile befindet, da der
Ausdruck jetzt mehr als 14 Zeichen lang ist.
5. ) und e drücken, um das
Ergebnis für den neuen Ausdruck zu
bestimmen.
Verwenden von Variablen
Sie können bis zu 27 Variablen (A-Z und θ) in dem NORMAL-Modus
verwenden. Eine als Variable gespeicherte Zahl kann entweder durch
Eingabe des Namens der Variablen oder durch Verwendung von t
aufgerufen werden.
Beispiel 1
Speichern von 23 als Variable R.
1. Drücken Sie j 2 1 und
anschließend x.
• j löscht den Bildschirm.
• “ALPHA” erscheint automatisch, wenn
Sie x drücken. Sie können jetzt
Buchstaben oder θ (in Blau oberhalb der Tasten aufgedruckt)
eingeben.
2. Drücken Sie R, um das Ergebnis von 2
3
in R zu speichern.
• Die gespeicherte Zahl wird in der
nächsten Zeile angezeigt.
• “ALPHA” ist im Display nicht mehr
sichtbar.
Sie können auch eine Zahl direkt eingeben, statt das Resultat eines
Ausdrucks zu speichern.
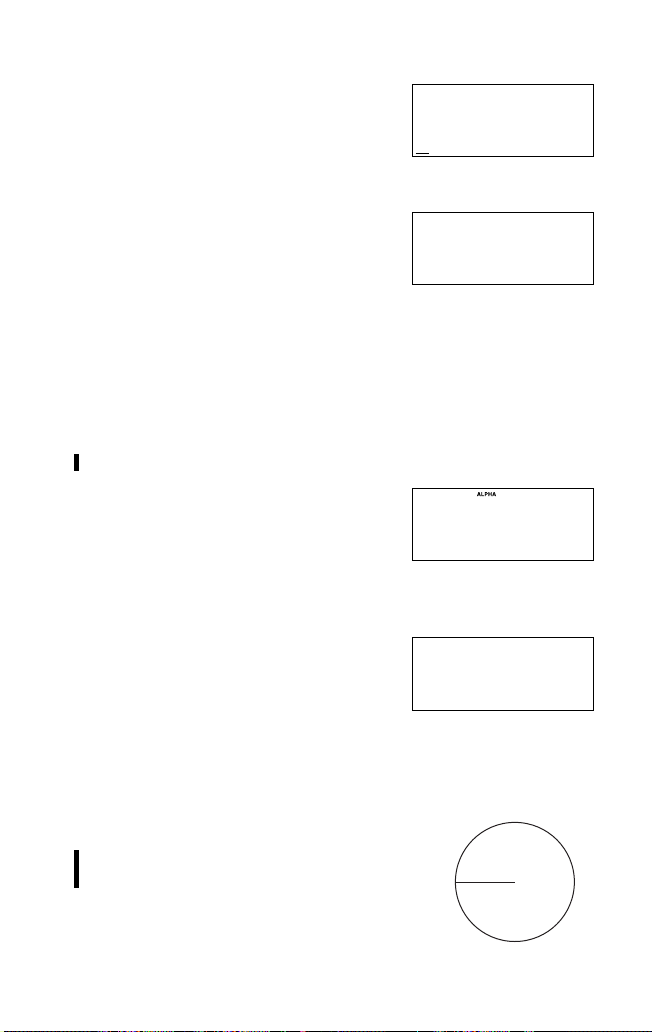
Beispiel 2
Berechnung der Fläche eines Kreises mit dem
Radius R.
8Œ©‰(3-7˚–10.5
)=
7.317272966
110.4504172
8Œ©‰(3-7˚–10.5
19
Kapitel 1: Vor der ersten Verwendung
Geben Sie einen Ausdruck mit der
Var iablen R (hier gleich 8) aus dem letzten
Beispiel ein.
1. Drücken Sie j @ s und
anschließend ;.
•Wenn Sie eine in Blau auf der Tastatur
abgebildete Funktion verwenden wollen,
drücken Sie vorher ;. “ALPHA”
erscheint dann oben im Display.
2. Drücken Sie R und anschließend
A.
• “ALPHA” verschwindet nach dem
Drücken der Funktionstaste im Display.
3. e drücken, um das Resultat zu
ermitteln.
Verfahren Sie auf gleiche Weise wie
oben, aber drücken Sie t anstelle von ; in Schritt 1.
Sie erhalten das gleiche Resultat.
Verwenden der Simulationsberechnung (ALGB)
Wenn Sie mehr als eine Lösung mit der gleichen Formel oder allgemeinen
mathematischen Gleichung finden wollen, können Sie dies schnell und leicht
mit Hilfe der Simulationsberechnung tun.
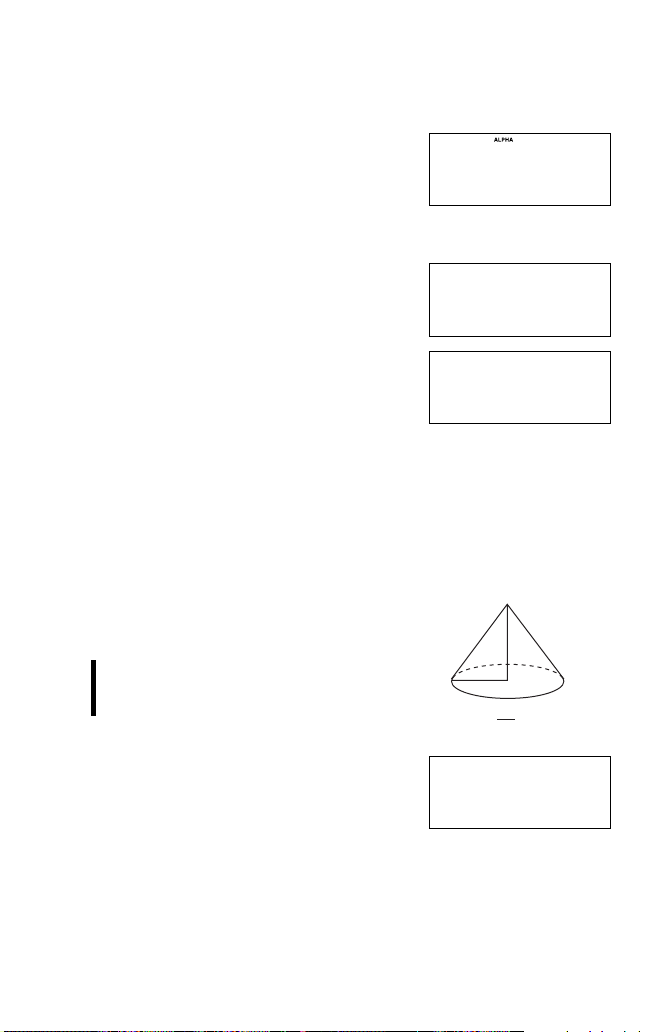
Beispiel
Das Volumen zweier Kegel berechnen:
1 mit der Höhe 10 und dem Radius 8 und
2 mit der Höhe 8 und dem Radius 9.
1. j 1 k 3 @ s ; R
A ; H für die Eingabe der
Formel drücken.
• Beachten Sie, dass “1l3” den Bruch 1/3
(d.h. 1 geteilt durch 3) darstellt.
•Variablen können nur durch Großbuchstaben dargestellt werden.
2
V
=
πr h
3
1
r
h
0.
πRŒ=
201.0619298
NORMAL MODE
0.
π_
NORMAL MODE
0.
πRŒ_
NORMAL MODE
0.
1ı3πRŒH_

20
Kapitel 1: Vor der ersten Verwendung
2. Zum Beenden der Eingabe dieser
Gleichung @ G (I Taste)
drücken.
• Der Rechner findet die in dieser
Gleichung verwendeten Variablen
automatisch in alphabetischer Reihenfolge und fordert zur Eingabe
von Werten für die Variablen auf.
•“
” unten im Display erinnert daran, dass eine weitere Variable im
Ver lauf dieser Gleichung verwendet wird.
3. 10 e drücken, um die Höhe
einzugeben. Dann zur nächsten
Var iable übergehen.
• Der Rechner fordert nun zur Eingabe
eines Wertes für die nächste Variable auf.
• Beachten Sie, dass die Variable R bereits mit einem Wert im Speicher
abgelegt ist und der Rechner diese Zahl aufruft.
•“
” erinnert daran, dass eine weitere Variable vorher in dieser
Gleichung verwendet wurde.
4. Geben Sie 8 für den Radius ein.
Die Eingabe aller Variablen ist jetzt abgeschlossen.
5. e drücken, um die Lösung zu
bestimmen.
• Das Ergebnis (Volumen des Kegels 1)
wird in der dritten Zeile angezeigt.
6. e und 8 drücken, um die Höhe des
Kegels 2 einzugeben.
• Die Anzeige schaltet auf eine Eingabemaske für die Werte um, bei der “8” für
“10” in der Variablen H ersetzt wird.
7. e drücken, um die Änderung zu
bestätigen.
8. Für die Eingabe des neuen Radius 9
drücken, und anschließend e
drücken, um die Gleichung zu lösen.
• Das Volumen des Kegels 2 wird jetzt
angezeigt.
• Nach den Schritten 2-8 drücken Sie @ h, um die Lösung mit
den für die Variablen eingegebenen Werten zu bestimmen.
1ı3πRŒH
H=z 0.
1ı3πRŒH
R=z 8.
1ı3πRŒH=
678.5840132
1ı3πRŒH=
670.2064328
1ı3πRŒH
H=8_
1ı3πRŒH
R=z 8.
21
Kapitel 1: Vor der ersten Verwendung
2
V
=
πr h
3
1
r
h
Verwenden der Solver-Funktion
Sie können eine Gleichung nach jeder Variablen auflösen, indem Sie
bekannte Werte den restlichen Variablen zuweisen. Zum Vergleich zwischen
der Solver-Funktion (Lösungsmodus) und der Simulationsberechnung soll
der gleiche Ausdruck wie im letzten Beispiel verwendet werden.
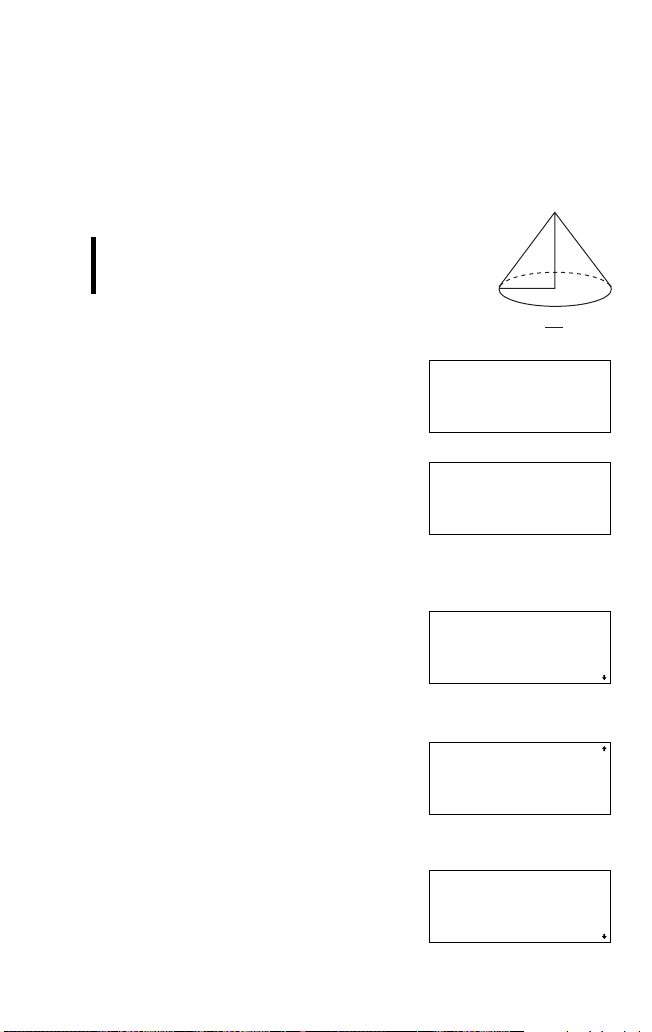
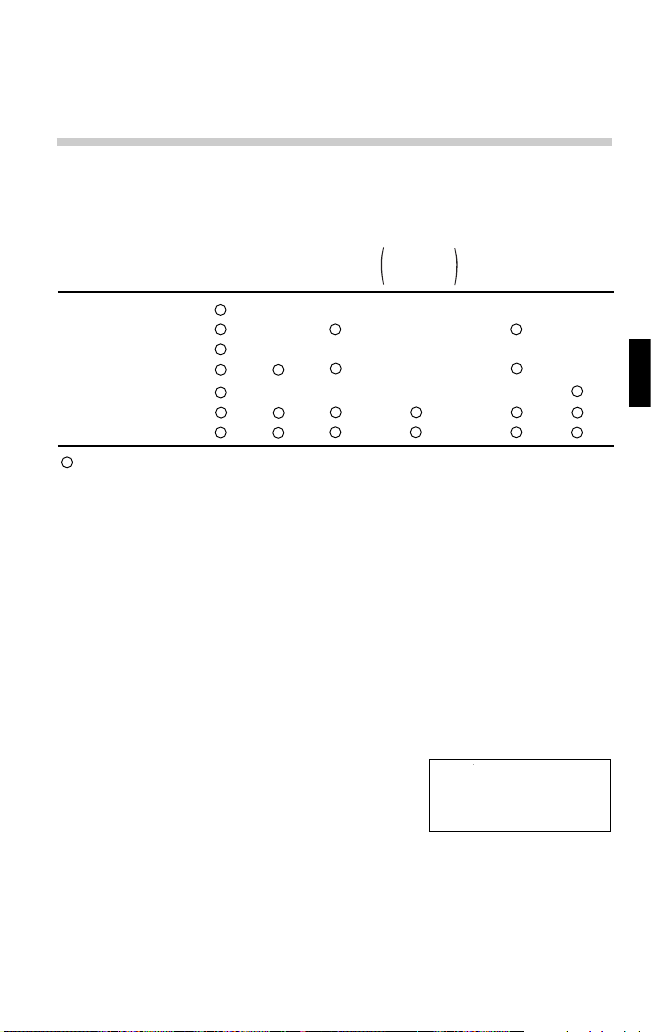
Beispiel
Wie hoch ist der Kegel 3, wenn der Radius 8
beträgt und das Volumen dem vom Kegel 2 (r = 9,
h = 8) im letzten Beispiel entspricht?
9. Das Ergebnis von Schritt 8 auf der
vorherigen Seite in Variable V
speichern.
Zweimal j drücken und anschließend ; < x V drücken.
10. Die Gleichung (einschließlich “=”) im
NORMAL-Modus eingeben.
; V ; = drücken und
anschließend den Rest des Ausdrucks
eingeben.
Um das Zeichen “=” einzugeben, drücken Sie statt e die Tasten
; = (m Taste).
11. I 5 drücken, um zur Variablen-
Eingabemaske zu gelangen.
• Beachten Sie, dass die Werte, die den
Var iablen im letzten Beispiel der
Simulationsberechnung zugewiesen
wurden, hier übernommen und angezeigt werden.
12. Für die Eingabe der Höhe d
drücken, und anschließend für die
Eingabe des Radius (R) 8 e
drücken.
• Der Cursor befindet sich jetzt bei V. Der in
Schritt 9 gespeicherte Wert wird angezeigt. (Volumen des Kegels 2)
13. u u drücken, um zur Variablen
H zurückzugehen.
• Diesmal wird der Wert von H aus dem
Speicher ebenfalls angezeigt.
V=1ı3πRŒH
H=z 8.
V=1ı3πRŒH
V=z678.5840132
AnsÒV
678.5840132
V=1ı3πRŒH_
0.
AnsÒV
678.5840132
V=1ı3πRŒH
H=z 8.

22
Kapitel 1: Vor der ersten Verwendung
14. @ h drücken, um die Höhe
des Kegels 3 zu finden.
• Beachten Sie, dass der Rechner die
Werte der Variablen findet, auf der
sich der Cursor befindet, wenn Sie
@ h drücken.
• Jetzt haben Sie die Höhe des Kegels
3 mit dem gleichen Volumen wie der
Kegel 2.
•R→ und L→ sind die Werte, die nach dem Newton-Verfahren
berechnet wurden, um die Genauigkeit der Lösung zu bestimmen.
Weitere Funktionen
Dieser Rechner hat eine Reihe weiterer Funktionen, die in verschiedenen
Situationen genutzt werden können, aber in der Kurzanleitung nicht
aufgeführt werden konnten. Einige der wichtigsten Funktionen werden kurz
im folgenden beschrieben.
Statistische Berechnungen:
Für bewertende Statistik mit einer oder zwei Variablen, Berechnungen
von Regressionen und Berechnungen der Normalverteilung. Statistische Ergebnisse enthalten Mittelwerte, Standardabweichungen,
Standardabweichungen der Grundgesamtheit, Summe der Daten und
Summe der Quadratwurzeln der Daten. (s. Kapitel 4)
Gleichungslöser:
Für das Lösen linearer Gleichungssysteme mit zwei bzw. drei Unbekannten oder Gleichungen 2. und 3. Grades. (s. Kapitel 5)
Berechnungen mit komplexen Zahlen:
Zur Ausführung von Addition, Subtraktion, Multiplikation und Division.
(s. Kapitel 6)
Programmierung:
Sie können Ihren Rechner so programmieren, dass bestimmte Berechnungen automatisiert werden. Jedes Programm kann sowohl im
Programmbetrieb NORMAL als auch NBASE verwendet werden.
(s. Kapitel 7)
H= 10.125
R¬ 678.5840132
L¬ 678.5840132
Volumen von Kegel 3
Rechte und linke Seite des
Ausdrucks nach der Substitution der bekannten Variablen
23
Kapitel 2
Allgemeine Informationen
Löschen von Eingaben und Speichern
Verfahren
ANS
*
3
: Wird gelöscht : Wird nicht gelöscht
×
STAT
*
4
STAT VAR
*
5
A-Z,
θ
*
1
Eingabe
(Anzeige)
Gespeicherte Gleichungen
*
2
einschließlich
gespeicherte
lokale Variablen
Mehrzeilen-
Playback,
j
Wahl des Modus
@ P 0
RESET-Schalter
@ P 1 y
@ P 3 y
×
×
×
@ P 2 y
×
×
×
×
×
××
*
6
×
×
×
×
×
×
×
×
×
Lokale
Variablen
*1Globale variable Speicher.
*2Mit der Speicher-Funktion für Gleichungen und lokale Variablen
*3Speicher des letzten Ergebnisses
*4Statistische Daten (eingegebene Daten)
*5n, x
-
, sx, σx, Σx, Σx2, y-, sy, σy, Σy, Σy2, Σxy, a, b, c, r.
*6Wird beim Wechsel zwischen den Untermenüs innerhalb des STAT-Modus
gelöscht.
Hinweis:
• Um einen Variablen-Speicher für globale Variablen und lokale
Var iablen zu löschen, drücken Sie j x und wählen anschließend den Speicher.
Speicher-Löschtaste
Für die Anzeige des Menüs @ P
drücken.
• Drücken Sie 0, um die Anzeige zu
initialisieren. Die Parameter sind wie folgt
eingestellt:
• Winkeleinheit: DEG (s. Seite 26)
• Anzeigeart: NORM1 (s. Seite 26)
• N-Basis: DEC (s. Seite 44)
• Zum Löschen aller Variablen (ausschließlich lokaler Variablen gespeicherter
Gleichungen, Statistischer Daten und STAT Variablen) 1 y drücken.
<M-CLR>
ƒDISP ⁄MEMORY
¤STAT ‹RESET

24
Kapitel 2: Allgemeine Informationen
• Zum Löschen statistischer Daten und STAT Variablen 2 y drücken.
• Um den Rechner zurück zu setzen, drücken Sie 3 y. Bei diesem
Vorgang werden alle gespeicherten Daten gelöscht und die Grundeinstellungen des Rechners wieder eingestellt.
Bearbeiten und Korrigieren einer Gleichung
Cursor-Tasten
Tippfehler können mit den Cursor-Tasten (l r u d) korrigiert
werden.
Beispiel
Geben Sie 123456 ein und ändern Sie die Eingabe in 123459.
1. j 123456 drücken.
2. y 9 e drücken.
•Wenn sich der Cursor am rechten Ende
einer Gleichung befindet, funktioniert die
Taste y als Rückschritt-Taste.
• Um nach der Anzeige des Ergebnisses
in die Gleichung zurückzugelangen, drücken Sie die Cursor-Tasten.
Nach dem Zurückgehen in die Berechnungszeile sind die folgenden
Verfahren nützlich;
@ l oder @ r: für die sofortige Bewegung des Cursors
an den Anfang oder das Ende der Gleichung.
Modus für Einfügen und Überschreiben
• Durch Drücken von @ O wird zwischen den folgenden zwei
Bearbeitungsmodi umgeschaltet: Modus zum Überschreiben (Grundeinstellung) und Modus zum Einfügen. Ein rechteckiger Cursor bedeutet,
dass vorher eingegebene Daten durch Eingabe überschrieben werden,
während ein dreieckiger Cursor anzeigt, dass die Eingabe an der Cursorposition eingefügt wird.
• Beim Überschreiben wird eine Eingabe unter dem Cursor durch den neu
eingegebenen Wert überschrieben. Für die Eingabe einer Zahl im
Einfügemodus bewegen Sie den Cursor direkt links neben die Stelle, hinter
der die Zahl eingefügt werden soll. Nehmen Sie anschließend die Eingabe
vor.
0.
123459=
123459.
NORMAL MODE
0.
123456_

25
Kapitel 2: Allgemeine Informationen
• Der ausgewählte Modus bleibt eingeschaltet, bis @ O gedrückt wird
oder ein RESET, d.h. ein Rückstellvorgang, ausgeführt wird.
Löschtaste
• Zum Löschen einer Zahl/Funktion den Cursor auf die zu löschende Zahl/
Funktion bringen und dann y drücken. Wenn sich der Cursor am
rechten Ende einer Gleichung befindet, funktioniert die Taste y als
Rückschritt-Taste.
Mehrzeilen-Playback-Funktion
Bereits eingegebene Gleichungen können im NORMAL-, STAT- oder CPLXModus erneut aufgerufen werden. Bis zu 160 Zeichen von Gleichungen
können gespeichert werden.
Wenn der Speicher voll ist, werden die gespeicherten Gleichungen in der
Reihenfolge ihrer Eingabe (älteste Gleichung zuerst) gelöscht.
• Durch Drücken von @ g wird die vorhergehende Gleichung
angezeigt. Bei weiterem Drücken von @ g werden weitere Gleichung angezeigt, die zuvor eingegeben worden waren.
• Sie können die wieder aufgerufenen Gleichung bearbeiten.
• Der Inhalt des Mehrfachzeilen-Speichers wird durch die folgenden
Operationen gelöscht: Änderung des Modus, Speicherlöschung (@
P 1 y), RESET, Umwandlungen zwischen Zahlensystemen.
Beispiel
Drei Ausdrücke eingeben und anschließend erneut aufrufen.
1 3(5+2)=
2 3×5+2=
3 3×5+3×2=
1. Drücken Sie j 3 ( 5 +
2 ) e
3 k 5 + 2 e
3 k 5 + 3 k 2 e
2. @ g drücken, um Ausdruck 3
aufzurufen.
3. @ g drücken, um Ausdruck 2
aufzurufen.
17.
3˚5+3˚2=
21.
3˚5+3˚2=
21.
3˚5+3˚2
3˚5+3˚2=
21.
3˚5+2

26
Kapitel 2: Allgemeine Informationen
4. @ g drücken, um Ausdruck 1
aufzurufen.
Das SET UP-Menü
Das SET UP-Menü ermöglicht das Ändern von Winkeleinheiten und
Anzeigeformaten.
• Für die Anzeige des SET UP-Menüs @
J drücken.
• Für das Beenden des SET UP-Menus j
drücken.
Änderung der Winkeleinheit
Die folgenden drei Winkeleinheiten (Kreisgrad, Radiant und Gradient)
können ausgewählt werden.
• DEG(°) : @ J 0 0 drücken
• RAD (rad) : @ J 0 1 drücken.
• GRAD (g) : @ J 0 2 drücken
Wahl des Anzeigeformats und Festlegen der Anzahl der Dezimalstellen
Für die Anzeige von Berechnungsergebnissen stehen fünf Anzeigeformate
zur Verfügung: Zwei Einstellungen für Gleitkomma (NORM1 und NORM2),
Festkomma (FIX), wissenschaftliche Notation (SCI) und technische Notation
(ENG).
•Wenn @ J 1 0 (FIX) oder @ J 1 2 (ENG)
gedrückt wird, erscheint “TAB (0-9)?” und die Anzahl der Dezimalstellen
(TAB) kann auf einen Wert zwischen 0 und 9 eingestellt werden.
•Wenn @ J 1 1 (SCI) gedrückt wird, erscheint “SIG (0-9)?”
und die Anzahl der effektiven Stellen (TAB) kann auf einen Wert zwischen
0 und 9 eingestellt werden. Durch Eingabe von 0 wird eine 10-stellige
Anzeige eingestellt.
•Wenn eine Gleitkommazahl nicht in den festgelegten Bereich passt, zeigt
der Rechner das Resultat in wissenschaftlicher Notation (exponentieller
Notation) an. Einzelheiten siehe nächster Abschnitt.
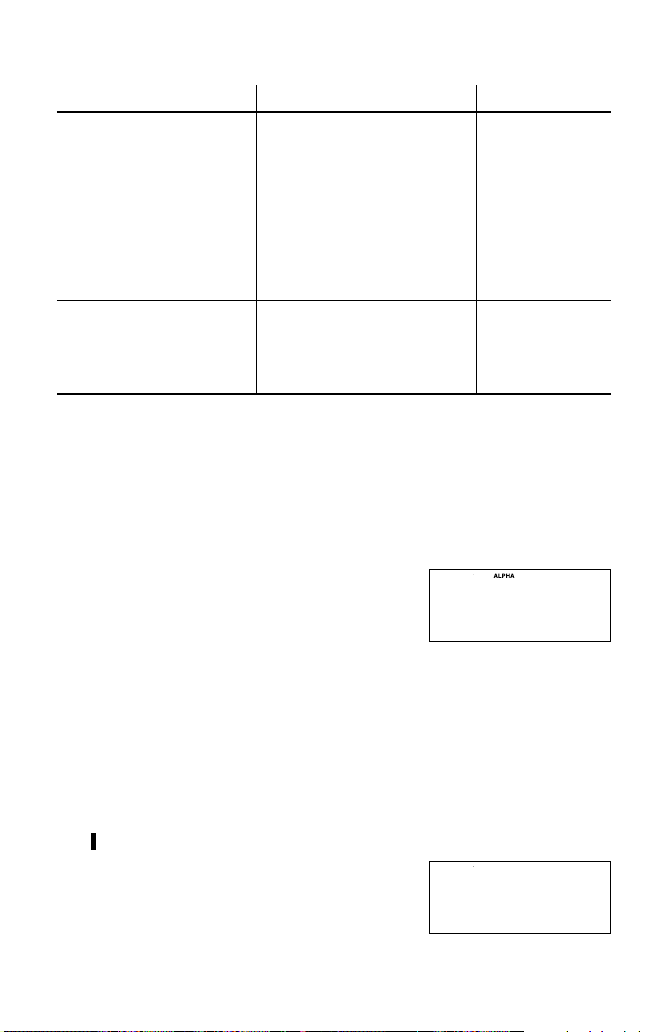
Einstellen des Gleitkommasystems bei wissenschaftlicher Notation
Der Rechner verfügt über zwei Einstellungen für die Anzeige einer
Gleitkommazahl: NORM1 (Grundeinstellung) und NORM2. Sollte eine Zahl
außerhalb des eingestellten Bereichs liegen, wird diese bei jeder Einstellung
automatisch in wissenschaftlicher Notation angezeigt:
• NORM1: 0.000000001 ≤ |x| ≤ 9999999999
• NORM2: 0.01 ≤ |x| ≤ 9999999999
3˚5+3˚2=
21.
3(5+2)
<SET UP>
ƒDRG ⁄FSE
¤---
27
Kapitel 2: Allgemeine Informationen
100000÷3=
[Gleitkommasystem (NORM1)]
→[Festkomma-System
und TAB auf 2]
→[wissenschaftl. Notation, SCI
und SIG auf 3 ]
→[Techn. Notation, ENG
und TAB auf 2]
→[Gleitkommasystem (NORM1)]
3÷1000=
[Gleitkommasystem (NORM1)]
→[Gleitkommasystem (NORM2)]
→[Gleitkommasystem (NORM1)]
Beispiel
Tastenfolge
Ergebnis
33333.33333
33333.33333
0.003
0.003
33333.33
3.33˚10
04
33.33˚10
03
3.˚10
-03
j @ J 1 3
100000 z 3 e
@ J 1 2 2
@ J 1 3
j 3
z 1000 e
@ J 1 1 3
@ J 1 0 2
@ J 1 4
@ J 1 3
Arbeiten mit Speichern
Der Rechner verwendet globale variable Speicher (A–Z und θ), lokale
variable Speicher (maximal neun Variablen pro Gleichung) sowie einen
Speicher für das letzte Ergebnis beim Lösen von Gleichungen.
Arbeiten mit Buchstaben
Sie können einen Buchstaben (in Blau oberhalb
der Tasten abgebildet) eingeben, wenn “ALPHA”
oben im Display erscheint. Zum Einschalten
dieses Modus drücken Sie ;.
Zur Eingabe von mehr als einem alphabetischen Zeichen @ a drücken, um den Alphabet-Eingabemodus
einzuschalten. ; drücken, um diesen Modus zu verlassen.
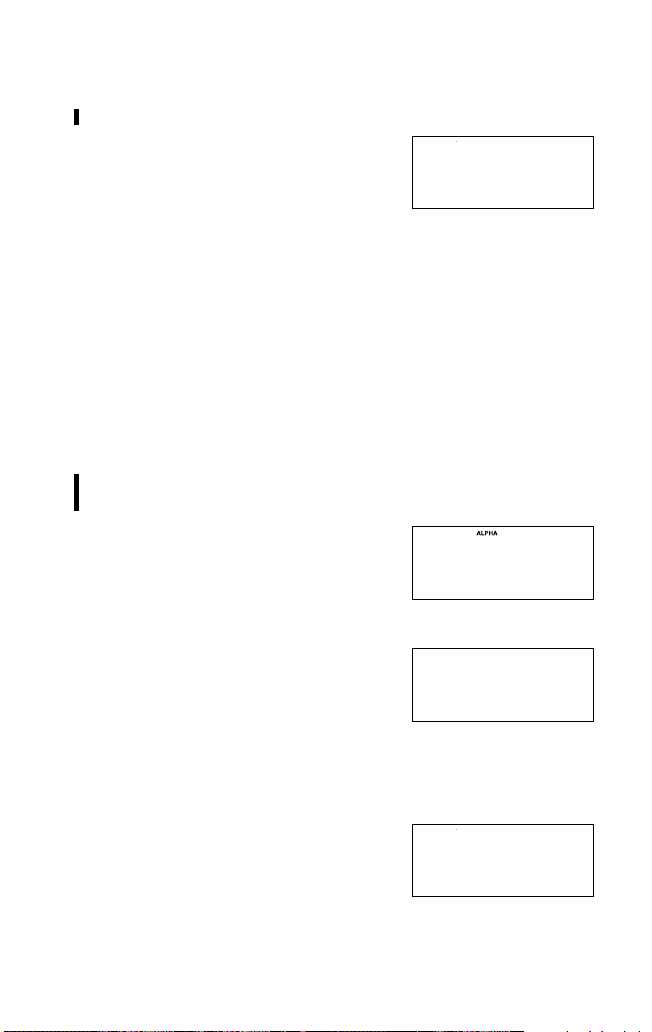
Arbeiten mit globalen Variablen
Sie können globalen Variablen Werte (Zahlen) zuweisen, indem Sie x
und anschließend A–Z und θ drücken.
Beispiel 1
Speichern von 6 in globaler Variable A.
1. j 6 x A drücken.
• Es ist nicht erforderlich, ; zu
drücken, weil ALPHA automatisch mit
ausgewählt wird, wenn Sie x
drücken.
NORMAL MODE
0.
0.
6ÒA
6.
28
Kapitel 2: Allgemeine Informationen
Beispiel 2
Aufrufen der globalen Variablen A.
1. t A drücken.
• Es ist nicht erforderlich, ; zu
drücken, weil ALPHA automatisch mit
ausgewählt wird, wenn Sie t drücken.
Arbeiten mit lokalen Variablen
Neben den globalen Variablen können in jeder Gleichung und in jedem
Programm bis zu neun lokale Variablen verwendet werden. Im Unterschied
zu den globalen Variablen werden die Werte lokaler Variablen zeitgleich mit
der Gleichung unter der Verwendung der Speicher-Funktion für Gleichungen
gespeichert. (s. Seite 58)
Für die Verwendung lokaler Variablen müssen Sie zuerst den Namen der
lokalen Variablen mit zwei Zeichen zuweisen: Das erste Zeichen muss ein
Buchstabe von A bis Z oder θ sein und das zweite muss eine Zahl von 0 bis 9
sein.
Beispiel
Speichern Sie 1.25 × 10-5 als lokale Variable A1 (in NORMAL-Modus)
und rufen Sie die gespeicherte Zahl auf.
1. @ v drücken.
• Das VAR-Menü erscheint.
•Wenn noch keine lokalen Variablen
gespeichert sind, erscheint ALPHA
automatisch und der Rechner ist zur
Eingabe eines Namens bereit.
2. A1 e drücken.
•“¬” zeigt an, dass bereits die Zuweisung
des Namens A1 vorgenommen wurde.
• Um weitere Namen zuzuweisen, drücken
Sie d. Der Cursor wandert zu VAR 1.
Wiederholen Sie das obige Verfahren.
3. j drücken.
• Dies bringt Sie zur vorherigen Anzeige zurück.
4. 1.25 ` S 5 x @ v
0 drücken.
• Sie brauchen keinen Buchstaben
einzugeben. Bestimmen Sie einfach die
entsprechende lokale Variable mit einer
Zahl von 0 bis 8, oder bewegen Sie den Pfeil zur geeigneten
Var iablen und drücken dann e.
6.
A=
6.
¬ƒA¡ ‹ fl
⁄ › ‡
¤ fi °
ƒz ‹ fl
⁄ › ‡
¤ fi °
0.
1.25
E
–5ÒA1
0.0000125

29
Kapitel 2: Allgemeine Informationen
5. @ v 0 e drücken.
• Der Wert von VAR 0 wird aufgerufen.
• Alternativ können Sie eine Variable durch
Bewegen des Pfeils an die entsprechende
Stelle und zweimaliges Drücken von
e aufrufen.
Hinweis:
• Sie können den Namen einer lokalen Variablen ändern, indem Sie ihn
im VAR-Menü überschreiben. Der Cursor erscheint, wenn r im
VAR-Menü gedrückt wird.
• Lokale Variablen, die nicht mit der Speicher-Funktion für Gleichungen
gespeichert sind, werden gelöscht, sobald der Modus gewechselt
oder ein Speicher gelöscht (@ P 1 y) wird.
• Lokale Variablen werden durch Erstellen eines neuen Programms
sowie durch Bearbeiten und Ausführen eines Programms gelöscht.
Verwendung von Variablen in einer Gleichung oder einem Programm
Sowohl globale als auch lokale Variablen können direkt in einer Gleichung
oder einem Programm verwendet werden. Lokale Variablen sind nützlich,
wenn Sie Variablen wie X1 und X2 gleichzeitig in einer anderen Gleichung
verwenden müssen. Die Namen lokaler Variablen und ihre Werte können in
jeder Gleichung gespeichert werden. (s. Seite 58)
Beispiel
Lösen Sie folgende Gleichung mit A (6) und A1 (0.0000125) aus den
letzten beiden Beispielen.
1
—
A1
– 1000A
1. j 1 k drücken.
• Beginnen Sie mit der Eingabe des
Ausdrucks.
2. @ v drücken.
3. 0 - 1000 ; A e
drücken.
• Die Anzeige schaltet automatisch zum
vorangegangenen Bildschirm um,
nachdem Sie die lokale Variable gewählt
haben. Sie können die Eingabe des
Ausdrucks fortsetzen.
0.0000125
A1=
0.0000125
NORMAL MODE
0.
1ı_
¬ƒA¡ ‹ fl
⁄ › ‡
¤ fi °
0.
1ıA¡-1000A=
74000.

30
Kapitel 2: Allgemeine Informationen
• Sie brauchen nicht k einzugeben, wenn Sie eine Variable
verwenden wollen. Die Variable muss allerdings ein Faktor sein.
Verwendung des letzten Ergebnisses
Der Rechner behält immer das letzte Ergebnis im ANS-Speicher und ersetzt
es jedesmal durch das neue Ergebnis, wenn Sie eine abschließende
Anweisung (e, x usw.) drücken. Sie können das letzte Ergebnis
aufrufen und in der nächsten Berechnung verwenden.
Beispiel
Berechnen Sie die Grundfläche (S = 32π)
und das Volumen eines Zylinders (V = 5S)
mit dem Speicher des letzten Ergebnisses.
1. j 3 A @ s e
drücken.
• Die Grundfläche wird jetzt berechnet.
• Die Zahl 28.27433388 wird im ANSSpeicher gespeichert.
2. j 5 ; < e drücken.
• Sie haben jetzt das Volumen des
Zylinders.
Das letzte Ergebnis wird gelöscht (d.h. auf 0
gestellt), wenn Sie den RESET-Schalter
drücken, den Modus ändern oder den Speicher löschen (@ P 1
y), aber nicht wenn Sie den Rechner ausschalten.
Globale Variable M
Bei Verwendung des Speichers M zusätzlich zu den Merkmalen der globalen
Var iablen kann ein Wert auch zum Inhalt des unabhängigen Speichers
addiert oder von diesem subtrahiert werden.
Beispiel
Tastenfolge
Ergebnis
j x M
0.
450.
250.
35.
@ M t M
665.
$150×3:M
a
+)$250:Mb=Ma+250
–)M
b
×5%
M
150 k 3 m
250 m
t M k 5 @ %
• m und @ M können nicht im STAT-Modus verwendet werden.
h = 5
r = 3
0.
3ι=
28.27433388
0.
5Ans=
141.3716694

31
Kapitel 2: Allgemeine Informationen
Arbeiten mit Speichern in verschiedenen Modi
: verfügbar : nicht verfügbar
Modus ANS M A-L, N-Z,
Lokale Variablen
NORMAL
STAT
PROG
EQN
CPLX
*
1
*
1
*1 nur zum Abrufen der im Speicher abgelegten Daten verfügbar.
Hinweise:
• Berechnungsergebnisse der unten angegebenen Funktionen werden
automatisch in dem unten angegebenen Speicher gespeichert und
bestehende Werte dabei überschrieben.
• →rθ, →xy ........................ Speicher R (r)
Speicher θ (θ)
Speicher X (x)
Speicher Y (y)
• Durch Drücken von t oder ; werden gespeicherte Werte mit
bis zu 14 Stellen Genauigkeit aufgerufen.

32
Kapitel 2: Allgemeine Informationen
Zurücksetzen des Rechners
Wenn Sie alle Speicher, Variablen, Dateien und Daten löschen wollen, oder
wenn keine der Tasten (einschließlich j) Wirkung zeigt, drücken Sie den
RESET-Schalter auf der Rückseite des Rechners.
In seltenen Fällen können alle Tasten wirkungslos werden. Es sei denn, der
Rechner wird beim Gebrauch sehr starken elektrischen Störungen oder
starken Stößen ausgesetzt. Folgen Sie den Anweisungen unten, um den
Rechner zurückzusetzen.
Vorsicht:
• Beim Rückstellvorgang werden alle gespeicherten Daten gelöscht
und die Grundeinstellungen des Rechners eingestellt.
1. Den RESET-Schalter auf der Rückseite des
Rechners mit der Spitze eines Kugelschreibers oder eines ähnlichen Gegenstandes
eindrücken.
Verwenden Sie keine Gegenstände mit zerbrechlichen oder scharfen
Spitzen.
• Eine Abfrage erscheint im Display, die zur
Bestätigung auffordert, ob der Rechner
wirklich zurückgesetzt werden soll.
2. y drücken.
• Alle Speicher, Variablen, Dateien und
Daten werden gelöscht.
• Im Display erscheint die Anfangsanzeige
im NORMAL-Modus.
• Der Rechner kehrt zu den allerersten
Einstellungen zurück, die bei der ersten
Inbetriebnahme vorgenommen wurden.
Oder drücken Sie e, um das Verfahren abzubrechen.
Hinweis:
• Bei Datenfehlern kann es vorkommen, dass der Rücksetzvorgang
automatisch ausgeführt wird, wenn Sie den RESET-Schalter drücken.
• Durch Drücken von @ P und 3 y können Sie ebenfalls
alle Speicher, Variablen, Dateien und Daten wie oben beschrieben
löschen.
zALL DATA CL?z
z YES¬[DEL] z
z NO¬[ENTER]z
z ALL DATA z
z CLEARED! z
z z
NORMAL MODE
0.

33
Kapitel 3
Wissenschaftliche
Berechnungen
NORMAL-Modus
Der NORMAL-Modus dient den üblichen wissenschaftlichen Berechnungen
und umfasst die größte Anzahl an Funktionen. Viele der in diesem Kapitel
beschriebenen Funktionen stehen auch in anderen Modi zur Verfügung.
Drücken Sie b 0, um den NORMAL-Modus einzuschalten.
• Die Differential-/Integralfunktionen, N-Basis-Funktionen, Solver-Funktionen
und Simulationsberechnungen (ALGB) in diesem Kapitel werden alle im
NORMAL-Modus ausgeführt.
•Drücken Sie bei jedem Beispiel in diesem Kapitel zuerst j, um die
Anzeige zu löschen. Wenn das Symbol FIX, SCI oder ENG angezeigt wird,
löschen Sie dieses Symbol durch die Wahl von ‘NORM1’ im SET UP-Menü.
Wenn nicht anders angegeben stellen Sie die Winkeleinheiten auf “DEG”
ein. (@ P 0)
Einfache Berechnungen
Beispiel Tastenfolge Ergebnis
3.428571429
–90.
140.
1250000.
45+285÷3= j 45 + 285 z 3 e
18+6
=
(
18 + 6 ) z
15–8 (
15 - 8 ) e
42×(–5)+120=
42 k S 5 + 120 e
(5×10
3
)÷(4×10–3)= 5 ` 3 z 4 ` S
3 e

34
Kapitel 3: Wissenschaftliche Berechnungen
Berechnungen mit Konstanten
Beispiel Tastenfolge Ergebnis
34+57= 34 + 57 e
45+57= 45 e
68×25= 68 k 25 e
68×40= 40 e
91.
102.
1700.
2720.
• Beim Rechnen mit Konstanten wird der zweite Summand zu einer
Konstanten. Subtraktion und Division werden in gleicher Weise behandelt.
Bei Multiplikationen wird der Multiplikand zu einer Konstanten.
• Bei den Konstantenberechnungen werden Konstanten mit ∆ angezeigt.
Funktionen
0.866025403
ErgebnisBeispiel Tastenfolge
sin60 [°]= j v 60 e
cos — [rad]=
@ J 0 1 $
@ s k 4 e
tan–11 [g]= @ J 0 2 @ y 1
e
@ P 0
π
4
0.707106781
50.
• Der Bereich der Ergebnisse inverser trigonometrischer Funktionen
θ = sin–1 x, θ = tan–1 x θ = cos–1 x
DEG –90 ≤θ≤ 90 0 ≤θ≤ 180
RAD 0 ≤θ≤π
GRAD –100 ≤θ≤100 0 ≤θ≤ 200
–
—
≤θ≤
—
π
2
π
2

35
Kapitel 3: Wissenschaftliche Berechnungen
Beispiel Tastenfolge Ergebnis
(cosh 1.5 +
sinh 1.5)2 =
tanh
–1
— =
0.895879734
ln 20 =
2.995732274
log 50 =
1.698970004
e3 =
20.08553692
10
1.7
=
50.11872336
— + — =
0.309523809
8–2 – 34 × 52 =
-2024.984375
(123)—=
6.447419591
83 =
512.
4.
3.
4! =
24.
10P3
=
720.
5C2
=
10.
500×25%=
125.
120÷400=?%
30.
500+(500×25%)=
625.
400–(400×30%)=
j ( H $
1.5 +
H v
1.5 ) A e
@ > t (
5
z 7 ) e
i
20 e
l
50 e
@ "
3 e
@ Y
1.7 e
6 @ Z +
7 @
Z e
4 k 5 A e
4 @ B e
5 @ c 2 e
8 m S 2 - 3 m
8 1 e
12 m 3 m 4
@ Z e
@ *
49 - 4 @ D
81 e
@ q
27 e
10 @ e 3 e
500 k 25 @ %
120 z 400 @ %
500 + 25 @ %
400 - 30 @ %
280.
5
7
1
6
1
7
1
4
49 –481
=
3
27 =
20.08553692

36
Kapitel 3: Wissenschaftliche Berechnungen
Funktionen des Mathematik-Menüs (MATH)
Neben der ersten und zweiten Belegung der Taste stehen Ihnen bei diesem
Rechner noch weitere Funktionen zur Verfügung. Der Zugriff auf diese
anderen Funktionen erfolgt über das Mathematik-Funktionsmenü . Das
Mathematik-Menü bietet für jeden Modus verschiedene Inhalte.
Für die Anzeige des Mathematik-Menüs I drücken. Die folgenden
Funktionen können im NORMAL-Modus aufgerufen werden.
<MATH MENU-1>
ƒabs ⁄ipart
¤int ‹fpart
→
<MATH MENU-2>
›ÒRAND fiSOLVE
flΩsec ‡Ωmin
d
• Blättern Sie innerhalb dieser Anzeige mit d u weiter.
0: abs
Zeigt den absoluten Wert einer
Zahl an.
1: ipart
Zeigt den ganzzahligen Wert einer
Zahl an.
2: int
Zeigt die größte ganze Zahl an,
die kleiner oder gleich der
angegebenen Zahl ist.
3: fpart
Zeigt nur die Nachkommastellen
einer Dezimalzahl an.
Funktion Tastenfolge Ergebnis
I 0 S
7 e
I 1 S
7.94 e
I 2 S
7.94 e
I 3 S
7.94 e
abs–7=
7.
ipart–7.94=
–7.
int–7.94=
–8.
fpart–7.94=
–0.94

37
Kapitel 3: Wissenschaftliche Berechnungen
Funktion Tastenfolge Ergebnis
4: ⇒RAND
Vor der Verwendung der
Zufallszahlenfunktion bestimmen
Sie 0.001 der 0.999 verfügbaren
Zufallszahlensequenzen. Der
Rechner kann dann die gleichen
Zufallszahlen ein weiteres Mal
generieren.
Wenn Sie zu den normalen
Zufallszahlen zurückgehen wollen,
drücken Sie 0 I 4.
5: SOLVE
Einschalten des Solver-Modus.
(s. Seite 52)
6: Ωsec
Sexagesimale Zahlen werden in
Sekunden-Notation umgewandelt.
(s. Seite 46)
7: Ωmin
Sexagesimale Zahlen werden in
Minuten-Notation umgewandelt.
(s. Seite 46)
24∂Ωsec
86400.
0∂0∂1500Ωmin
25.
0.001 I 4
@ w 0
e
I 5
24 [ I
6
0 [ 0 [
1500 I 7
0.001ÒRAND
0.001
random=
0.232

38
Kapitel 3: Wissenschaftliche Berechnungen
Differential-/Integralfunktion
Differential- und Integralberechnungen können nur im NORMAL-Modus
ausgeführt werden. Es ist möglich, dieselbe Gleichung immer wieder zu
verwenden und dabei nur die Werte zu ändern, ohne die Gleichung neu
eingeben zu müssen.
• Bei der Ausführung einer Berechnung wird der Wert im X-Speicher gelöscht.
• Sie können sowohl globale als auch lokale Variablen in der Gleichung
verwenden.
• Das berechnete Ergebnis wird im Speicher für das letzte Ergebnis
gespeichert.
• Das berechnete Ergebnis kann durchaus einen Lösungsfehler enthalten,
so dass ein Fehler auftritt. In diesem Fall führen Sie die Berechnung
erneut durch, nachdem Sie das Intervall (dx) oder Teilintervall (n) präzisiert
haben.
• Da bei Differential- und Integralrechnungen auf die folgenden Formeln
zurückgegriffen wird, kann es in einzelnen seltenen Fällen wie etwa bei der
Ausführung von Funktionen mit Unstetigkeitsstellen zu unkorrekten
Ergebnissen kommen.
Integralrechnung (Simpsonsche Regel):
S=—h{f (a)+4{f (a+h)+f (a+3h)+······+f (a+(N–1)h)}
+2{f (a+2h)+f (a+4h)+······+f (a+(N–2)h)}+f(b)}
N=2n
h=
b – a
N
a≤x ≤ b
1
3
——
Differentialrechnung:
f(x+ ––)–f(x – ––)
dx
2
dx
2
f
’(x)= ————————
dx
Differentialfunktion
Die Differentialfunktion wird wie folgt verwendet.
1. Drücken Sie b 0, um den NORMAL-Modus einzuschalten.
2. Eine Formel mit einer x Variable eingeben.
3. @ 3 drücken.
4. Den Wert x eingeben und e drücken.
5. Das genaue Intervall (dx) eingeben.
6. Zum Berechnen e drücken.

39
Kapitel 3: Wissenschaftliche Berechnungen
• Zum Beenden der Differentialfunktion drücken Sie j.
• Nach der Ermittlung des Ergebnisses drücken Sie e, um zur Anzeige
für die Eingabe des Wertes x und dem genauen Intervall zurückzugelangen. Drücken Sie @ h, um die Berechnung in einem anderen
Punkt erneut auszuführen.
d/dx
(x4–0.5x3+6x2) j ; X* m 4 - 0.5
; X 1 + 6 ;
X A @ 3
x
= 2
dx
= 0.00002
d/dx
= ?
2 e e
x
= 3
dx
= 0.001
d/dx
= ?
e 3 e 0.001 e
X^4-0.5X„+6XŒ
X=
z
0.
dx: 0.00001
X^4-0.5X„+6XŒ
d/dx=
50.
X^4-0.5X„+6XŒ
d/dx=
130.5000029
Beispiel Tastenfolge Ergebnis
* Speicher X wird durch Drücken von ; und anschließendes Drücken der
Taste 3 bestimmt.
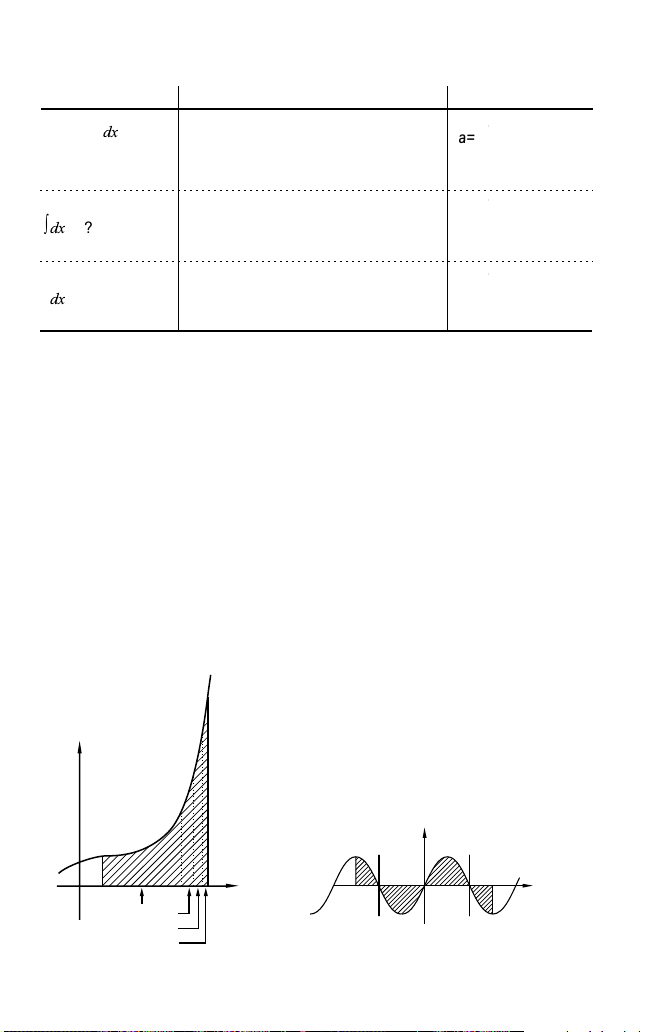
Integralfunktion
Die Integralfunktion wird wie folgt verwendet:
1. Drücken Sie b 0, um den NORMAL-Modus einzuschalten.
2. Eine Formel mit einer x Variable eingeben.
3. { drücken.
4. Geben Sie den Anfangswert (a) eines Bereiches des Integrals ein und
drücken Sie e.
5. Geben Sie den Endwert (b) eines Bereiches des Integrals ein und
drücken Sie e.
6. Geben Sie das Teilintervall (n) ein.
7. Für die Berechnung e drücken.
• Um die Integralfunktion zu beenden, drücken Sie j.
• Nach der Ermittlung des Ergebnisses drücken Sie e, um zur Anzeige
für die Eingabe eines Bereiches für Integral und Teilintervall zurückzugelangen. Drücken Sie @ h, um die Berechnung in einem anderen
Punkt erneut auszuführen.
40
Kapitel 3: Wissenschaftliche Berechnungen
j ; X A - 5
{
n = 100 2 e 8 e e
∫
8
2
( x2–5)
@N
∫
@N
= ?
n = 10 e e e 10 e
∫
@N
= ?
a=z 0.
b= 0.
n= 100.
XŒ-5
∫dx=
138.
XŒ-5
∫dx=
138.
Beispiel Tastenfolge Ergebnis
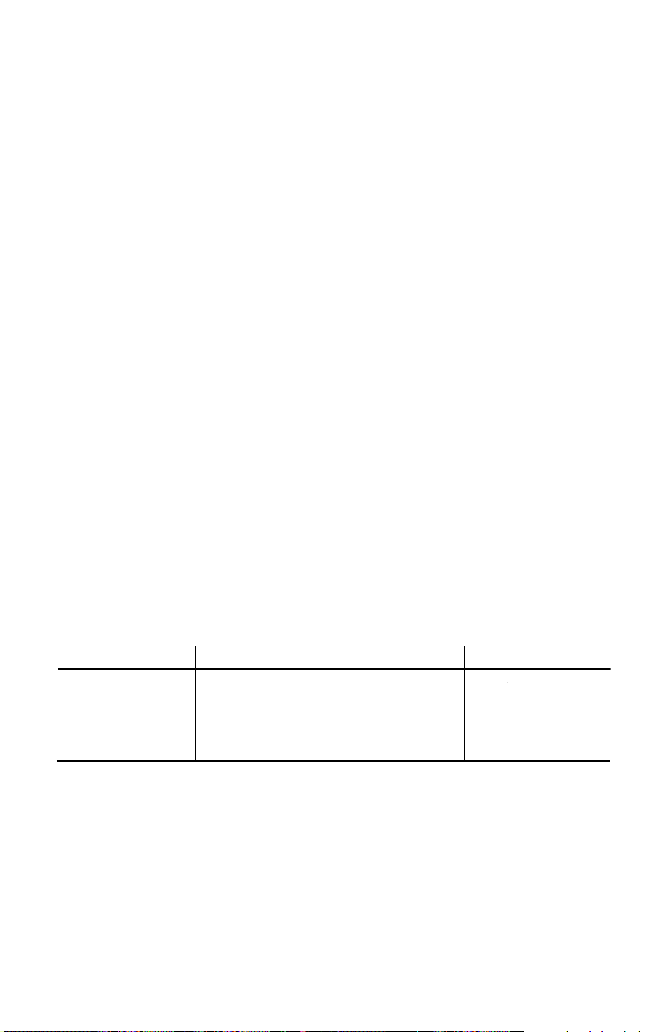
Ausführen von Integralberechnungen
Bei Integralberechnungen wird je nach eingegebenen Integranden und
Teilintervallen längere Zeit für die Berechnung beansprucht. Während der
Berechnung erscheint auf der Anzeige das Wort “calculating!” (= “wird
berechnet”). Um die Berechnung zu unterbrechen, drücken Sie j. Bitte
beachten Sie, dass es zu größeren Integralfehlern kommen kann, wenn z.B.
in den Integralwerten größere Schwankungen bei gleichzeitig geringen
Ver änderungen des Integralbereiches auftreten, oder auch bei periodischen
Funktionen, die sowohl positive als auch negative Integralwerte innerhalb
eines Intervalles aufweisen können.
Im ersten Fall wählen Sie das zu integrierende Intervall so klein wie möglich.
Im zweiten Fall trennen Sie die positiven und negativen Werte.
Auf diese Weise werden die Berechnungsergebnisse genauer und die
Berechnungszeit kürzer.
y
x
b
xx
xx
a
0
13
2
y
a
b
x
x
x
x
x
1
0
2
3
41
Kapitel 3: Wissenschaftliche Berechnungen
Zufallszahlen-Funktion
Die Zufallszahlen-Funktion hat vier Einstellungen für die Modi NORMAL,
STAT und PROG. (Nicht verfügbar ist diese Funktion, wenn die N-BasisFunktion verwendet wird.)
Zufallszahlen
Eine Pseudo-Zufallszahl mit drei effektiven Stellen von 0 bis 0.999 kann
durch Drücken von @ w 0 e generiert werden. Zum Generieren
weiterer Zufallszahlen mehrmals e drücken. Zum Beenden j drücken.
• Der Rechner kann die gleiche Zufallszahl erneut generieren. (s. Seite 36)
Zufalls-Würfel
Zum Simulieren eines Würfels kann durch Drücken von @ w 1
e eine Zufallszahl zwischen 1 und 6 generiert werden. Zum Generieren
weiterer Zufallszahlen mehrmals e drücken. Zum Beenden j drücken.
Zufalls-Münze
Zum Simulieren eines Münzwurfes kann 0 (Kopf) oder 1 (Zahl) durch
Drücken von @ w 2 e zufällig generiert werden. Zum Generie-
ren weiterer Zufallszahlen mehrmals e drücken. Zum Beenden j
drücken.
Ganzzahlige Zufallszahlen
Zum Generieren einer ganzzahligen Zufallszahl zwischen 0 und 99 @
w 3 e drücken. Zum Generieren weiterer Zufallszahlen mehrmals
e drücken. Zum Beenden j drücken.
j @ w 0
k 10 e
Wählen Sie eine
zufällige Zahl
zwischen 0 und
9.99.
Beispiel Tastenfolge Ergebnis
0.
random˚10=
6.31
• Das Ergebnis ist möglicherweise nicht bei jeder Ausführung dieser
Operation gleich.

42
Kapitel 3: Wissenschaftliche Berechnungen
Umwandeln der Winkeleinheiten
Die Winkeleinheit wird bei jedem Drücken von @ ] (. Taste)
geändert.
90°→ [rad] j 90 @ ]
1.570796327
→ [g] @ ]
100.
→ [°] @ ]
90.
sin–10.8 = [°] @ w 0.8 e
53.13010235
→ [rad] @ ]
0.927295218
→ [g] @ ]
59.03344706
→ [°] @ ]
53.13010235
Beispiel Tastenfolge Ergebnis
Kettenberechnungen
Das Ergebnis einer vorhergehenden Berechnung kann für die nächste
Berechnung weiterverwendet werden. Es kann aber nicht mehr aufgerufen
werden, wenn weitere Rechnungsanweisungen eingegeben wurden.
• Bei Verwendung einer vorangestellten Funktionen (앀앙, sin usw.) können
Kettenberechnungen ausgeführt werden, selbst wenn das vorherige
Berechnungsergebnis mit j gelöscht wurde.
6+4=ANS j 6 + 4 e
10.
ANS+5 + 5 e
15.
8×2=ANS 8 k 2 e
16.
ANS
2
A e
256.
44+37=ANS 44 + 37 e
81.
ANS= @ * e
9.
Beispiel Tastenfolge Ergebnis

43
Kapitel 3: Wissenschaftliche Berechnungen
Bruchrechnung
Arithmetische Operationen und Speicherberechnungen können mit Brüchen
ausgeführt werden. Auch Umwandeln zwischen Dezimalzahlen und Brüchen
ist möglich.
•Wenn mehr als 10 Ziffern angezeigt werden sollen, muss die Zahl
umgewandelt und als Dezimalzahl angezeigt werden.
3— + — = [a—] j 3 k 1 k 2 +
4 k 3 e
4ı5ı6
*
→[a.xxx] k
4.833333333
→[d/c] @ F
29ı6
10
—
= @ Y 2 k 3 e
4.641588834
(—)
5
=
16807ı3125
(—)
—
=
1 k 8 m 1 k 3 e
7 k 5 m 5 e
1ı2
—— = @ * 64 k 225 e
8ı15
2
3
( 2 m 3 ) k
3
4
( 3 m 4 ) e
8ı81
1.2
1.2 k 2.3 e
12ı23
2.3
1°2’3”
1 [
2 [ 3 k 2 e
0∂31∂1.5∂
2
1×10
3
1 ` 3 k 2 ` 3 e
1ı2
2×10
3
A = 7 j 7 x A
7.
— = 4 k ; A e
4ı7
1.25 + — = [a.xxx] 1.25 + 2 k 5 e
1.65
→[a—] k
1ı13ı20
*
4ı5ı6
= 4—
124
3
b
c
2
3
7
5
1
8
1
3
64
225
— =
—– =
——– =
——– =
4
A
2
5
b
c
5
6
Beispiel Tastenfolge Ergebnis

44
Kapitel 3: Wissenschaftliche Berechnungen
Rechnungen mit Binär-, Pental-, Oktal-, Dezimalund Hexadezimalzahlen (N-Basis)
Dieser Rechner kann Umrechnungen zwischen Zahlen ausführen, die im
Binär-, Pental-, Oktal- und Hexadezimalsystem ausgedrückt sind. Die vier
Grundrechenarten, Berechnungen mit Klammern und Speicherberechnungen können ebenfalls mit Binär-, Pental-, Oktal- und Hexadezimalzahlen ausgeführt werden. Des weiteren kann der Rechner logische
Operationen mit AND, OR, NOT, NEG, XOR und XNOR mit Binär-, Pental-,
Oktal- und Hexadezimalzahlen ausführen.
Umwandlungen in die verschiedenen Zahlensysteme erfolgen mit Hilfe der
folgenden Tasten:
@ z:Wandelt in das Binärsystem um. “?” erscheint.
@ r:Wandelt in das Pentalsystem um. “q” erscheint.
@ g:Wandelt in das Oktalsystem um. “f” erscheint.
@ h:Wandelt in das Hexadezimalsystem um. “6” erscheint.
@ /:Wandelt in das Dezimalsystem um. “?”, “q”, “f” und “6”
verschwinden aus der Anzeige.
Die Umwandlung wird auf dem angezeigten Wert ausgeführt, wenn diese
Tasten gedrückt werden.
Hinweis: Die Hexadezimalzahlen A - F werden durch Drücken von ,,
m, A, 1, l und i in den Rechner eingegeben.
Im Binär-, Pental-, Oktal- und Hexadezimalsystem gibt es keine Kommastellen. Wird eine Dezimalzahl mit Nachkommastellen in eine Binär-, Pental-,
Oktal- oder Hexadezimalzahl umgewandelt, so wird der Teil nach dem
Komma vernachlässigt. Sollte das Ergebnis einer Berechnung mit Binär-,
Pental-, Oktal- oder Hexadezimalzahlen eine Nachkommastelle aufweisen,
wird diese in gleicher Weise vernachlässigt. Negative Zahlen werden im
Binär-, Pental-, Oktal- oder Hexadezimalsystem als Komplement angezeigt.

45
Kapitel 3: Wissenschaftliche Berechnungen
DEC(25)→BIN j @ / 25 @ z
11001
.
b
HEX(1AC) @ a 1AC
→BIN @ z
110101100
.
b
→PEN @ r
3203
.
P
→OCT @ g
654
.
0
→DEC @ /
428.
BIN(1010–100) @ z ( 1010 - 100
×11 = ) k 11 e
10010
.
b
BIN(111)→NEG d 111 e
1111111001
.
b
HEX(1FF)+ @ a 1FF @ g +
OCT(512)= 512 e
1511
.
0
HEX(?) @ a
349
.
H
2FEC– j x M @ a 2FEC
2C9E=(A) - 2C9E m
34E
.
H
+)2000– 2000 -
1901=(B) 1901 m
6FF
.
H
(C) t M
A4D
.
H
1011 AND j @ z 1011 4
101 = (BIN) 101 e
1
.
b
5A OR C3 = (HEX) @ a 5A p C3 e
DB
.
H
NOT 10110 = @ z n 10110 e
1111101001
.
b
(BIN)
24 XOR 4 = (OCT) @ g 24 x 4 e
20
.
0
B3 XNOR @ a B3 C
2D = (HEX) 2D e
FFFFFFFF61
.
H
→DEC @ /
–159.
Beispiel Tastenfolge Ergebnis
46
Kapitel 3: Wissenschaftliche Berechnungen
Zeitberechnungen sowie dezimale und
sexagesimale Berechnungen
Umwandlungen zwischen dezimalen und sexagesimalen Zahlen können
ausgeführt werden; bei der Verwendung von sexagesimalen Zahlen ist auch
die Umwandlung von Sekunden- und Minuten-Notationen möglich. Weiterhin
können die vier Grundrechenarten und Speicherberechnungen mit dem
sexagesimalen System ausgeführt werden. Die Notation von sexagesimalen
Zahlen ist wie folgt zu verstehen:
12∂34∂56.78∂
Winkelgrad Winkelsekunde
Winkelminute
12°39’18.05” j 12 [ 39 [ 18.05
→[10] @ :
12.65501389
123.678→[60] 123.678 @ :
123∂40∂40.8
∂
3h30m45s + 3 [ 30 [ 45 + 6 [
6h45m36s = [60] 45 [ 36 e
10∂16∂21.∂
1234°56’12” + 1234 [ 56 [ 12 +
0°0’34.567” = [60] 0 [ 0 [ 34.567 e
1234∂56∂47.∂
3h45m – 3 [ 45 - 1.69 e
1.69h = [60] @ :
2∂3∂36.∂
sin62°12’24” = [10] v 62 [ 12 [ 24 e
0.884635235
24°→[”] 24 [ I 6
86400.
1500”→[’] 0 [ 0 [ 1500 I 7
25.
Beispiel Tastenfolge Ergebnis

47
Kapitel 3: Wissenschaftliche Berechnungen
Koordinaten-Umwandlungen
Umwandlungen können zwischen Rechteck- und Polarkoordinaten ausgeführt werden.
P (x, y )
X
Y
0
y
x
P (r,θ)
X
Y
0
r
θ
Rechtwinkelige Koordinaten Polarkoordinaten
•Vor der Durchführung einer Berechnung ist eine Winkeleinheit zu wählen.
• Das Rechenergebnis wird automatisch in folgende Speicher gespeichert.
•Wert von r: Speicher R
•Wert von θ: Speicher θ
•Wert von x: Speicher X
•Wert von y: Speicher Y
•Werte r und x werden im Speicher für das letzte Ergebnis gespeichert.
j 6 , 4
x = 6 →r =
@ u
r
= 7.211102551
y = 4
θ
= [°]
= 33.69006753
14 , 36
r = 14 →x =
@ E
x
= 11.32623792
θ
= 36[°] y =
y
= 8.228993532
Beispiel Tastenfolge Ergebnis

48
Kapitel 3: Wissenschaftliche Berechnungen
Berechnungen mit physikalischen Konstanten
Rufen Sie eine Konstante durch Drücken von @ c gefolgt von der
Nummer der physikalischen Konstante auf, die mit einer zweistelligen Ziffer
zugewiesen wurde.
Die aufgerufene Konstante erscheint im gewählten Anzeige-Modus mit der
jeweils möglichen Zahl von Dezimalstellen.
Physikalische Konstanten können im NORMAL-Modus (allerdings nicht bei
Einstellung auf Binär-, Pental-, Oktal- oder Hexadezimalzahlen), STATModus, PROG-Modus und EQN-Modus aufgerufen werden.
Hinweis: Physikalische Konstanten basieren entweder auf den von 2002
CODATA empfohlenen Werten oder der Ausgabe 1995 des “Guide
for the Use of the International System of Units (SI)” (Anleitung für
die Verwendung des Internationalen Einheitensystems (SI)) des
NIST (National Institute of Standards and Technology) oder auf
ISO-Normen.
01 Lichtgeschwindigkeit im Vakuum
02 Gravitationskonstante
03 Gravitationsbeschleunigung
04 Elektronenmasse
05 Protonenmasse
06 Neutronenmasse
07 Muonen-Ruhemasse
08 Relative Atommasse
09 Elementarladung
10 Plancksches Wirkungsquantum
11 Boltzmann-Konstante
12 Magnetische Konstante
13 Elektrische Konstante
14 Klassischer Elektronenradius
15 Feinstrukturkonstante
16 Bohr’scher Radius
17 Rydberg-Konstante
18 Magnetisches Flussquant
19 Bohr’sches Magneton
20 Magnetisches Moment des Elektrons
21 Kernmagneton
22 Magnetisches Moment des Protons
Nr. Konstante Symbol Einheit
c, c
0
m s
–1
µ
B
J T
–1
G
m
3
kg–1 s
–2
µ
e
J T
–1
g
n
m s
–2
µ
N
J T
–1
m
e
kg
µ
p
J T
–1
m
p
kg
m
n
kg
m
µ
kg
lu
kg
e
C
h
J s
k
J K
–1
µ
0
N A
–2
ε
0
F m
–1
r
e
m
a
0
α
m
R
∞
m
–1
Φ
0
Wb

49
Kapitel 3: Wissenschaftliche Berechnungen
23 Magnetisches Moment des Neutrons
24 Magnetisches Moment des Muons
25 Compton-Wellenlänge
26 Compton-Wellenlänge des Protons
27 Stefan-Boltzmannsche Konstante
28 Lochschmidtsche Zahl
29 Molarvolumen idealer Gase (273,15K,
101,325kPa)
30 Molare Gaskonstante
31 Faraday-Konstante
32 Von-Klitzing-Konstante
33 Ladungs-Masse-Verhältnis des Elektrons
34 Quantum des Umlaufintegrals
35 Gyromagnetisches Verhältnis des Protons
36 Josephson-Konstante
37 Elektronenvolt
38 Temperatur in Celsius
39 Astronomische Einheit
40 Parsek
41 Molare Masse von Kohlenstoff-12
42 Planck-Konstante über 2 pi
43 Hartree-Energie
44 Quantum der Leitfähigkeit
45 Inverse Feinstrukturkonstante
46 Masse-Verhältnis Elektron-Proton
47 Molare Massekonstante
48 Compton-Wellenlänge des Neutrons
49 Erste Strahlenkonstante
50 Zweite Strahlenkonstante
51 Charakteristische Impedanz des Vakuums
52 Standard des atmosphärischen Drucks
eV J
t K
AU m
pc m
M(
12
C) kg mol
–1
µ
µ
J T
–1
h
-
J s
λ
c
m
E
h
J
λ
c, p
m
0
G s
σ
W m–2 K
–4
α
–1
N
Α
,
L mol
–1
mp/m
e
V
m
m3 mol
–1
M
u
kg mol
–1
R J mol–1 K
–1
λ
c, n
m
F C mol
–1
c
1
W m
2
R
K
Ohm
c
2
m K
-
e/m
e
C kg
–1
Z
0
Ω
h/2m
e
m2 s
–1
γ
p
–1
Ts
–1
K
J
Hz V
–1
Nr. Konstante Symbol Einheit
Beispiel Tastenfolge Ergebnis
µ
n
J T
–1
Pa
V
0
= 15.3 m/s
t = 10 s
V
0
t + gt2 = ? m
j 15.3 k 10 + 2 @
Z k @ c 03 k 10
A e
1
2
643.3325

50
Kapitel 3: Wissenschaftliche Berechnungen
Berechnungen mit Vorsilben physikalischer
Maßeinheiten
Berechnungen können im NORMAL-Modus (ausgenommen N-Basis), STATModus und PROG-Modus mit den folgenden 12 Vorzeichen ausgeführt
werden.
Vorzeichen Tastenfolge Wert
E
P
T
G
M
k
m
µ
n
p
f
a
(Exa)
(Peta)
(Tera)
(Giga)
(Mega)
(kilo)
(milli)
(micro)
(nano)
(pico)
(femto)
(atto)
@ j 0
@ j 1
@ j 2
@ j 3
@ j 4
@ j 5
@ j 6
@ j 7
@ j 8
@ j 9
@ j A
@ j B
10
18
10
15
10
12
10
9
10
6
10
3
10
–3
10
–6
10
–9
10
–12
10
–15
10
–18
100m × 10k =
100 @ j 6 k
10 @ j 5 e
1000.
Beispiel Tastenfolge Ergebnis

51
Kapitel 3: Wissenschaftliche Berechnungen
Modifizierungsfunktion
Berechnungsergebnisse werden intern in der wissenschaftlichen Notation
mit bis zu 14 Stellen für die Mantisse berechnet. Die Darstellung der
Ergebnisse erfolgt allerdings nach der zugewiesenen Anzeigeart und Anzahl
der Dezimalstellen; die internen Ergebnisse stimmen daher nicht unbedingt
mit den dargestellten Ergebnissen überein. Mit der Modifizierungsfunktion
werden die internen Werte so umgewandelt, dass sie den Ergebnissen auf
der Anzeige entsprechen; die angezeigten Werte können dann ohne weitere
Änderungen für Folgeberechnungen verwendet werden.
5÷9=ANS j @ J 1 0 1
ANS×9= 5 z 9 e
0.6
[FIX,TAB=1] k 9 e *
1
5.0
5 z 9 e @ n
0.6
k 9 e*
2
5.4
@ P 0
*
1
5.5555555555555×10–1×9
*
2
0.6×9
Beispiel Tastenfolge Ergebnis

52
Kapitel 3: Wissenschaftliche Berechnungen
Die Solver-Funktion
Diese Funktion ermöglicht das Bestimmen einer beliebigen Variable in einer
Gleichung.
Eingeben und Lösen einer Gleichung
Die Solver-Funktion wird wie folgt verwendet.
1. Drücken Sie b 0, um den NORMAL-Modus einzuschalten.
2. Geben Sie beide Seiten einer Gleichung mit “=” und Variablennamen ein.
3. I 5 drücken.
4. Geben Sie den Wert der bekannten Variablen ein.
5. Bewegen Sie den Cursor an die Stelle der unbekannten Variablen.
6. @ h drücken.
• Die Solver-Funktion kann eine beliebige
Var iable in einer Gleichung finden. Sie
kann sogar Variablen finden, die mehrmals
in einer Gleichung vorkommen.
• Sie können sowohl globale als auch lokale
Var iablen in der Gleichung verwenden. (s. Seite 58)
• Bei der Ausführung der Solver-Funktion werden die Variablen-Speicher
mit neuen Werten überschrieben.
• Zum Beenden der Solver-Funktion drücken Sie j.
Ändern des Wertes von Variablen und Bearbeiten einer
Gleichung
Das Display zeigt die Lösung an. Drücken Sie e, um zur Anzeige für die
Eingabe der Variablenwerte zurückzugelangen. Kehren Sie anschließend zur
Gleichungsanzeige in den NORMAL-Modus zurück, indem Sie j
drücken.
R= 1.127251652
R¬ 9.
L¬ 9.
→
TŒ=(4π©GM)R
G=z 1.5
→
NORMAL MODE
0.
TŒ=(4π©GM)R_
e j
NORMAL MODE
0.
TŒ=(4π©GM)R_
Eingeben Gleichung Display
Lösungsanzeige Verwenden Sie
d u, um den
Cursor von Variable
zu Variable zu
bewegen.
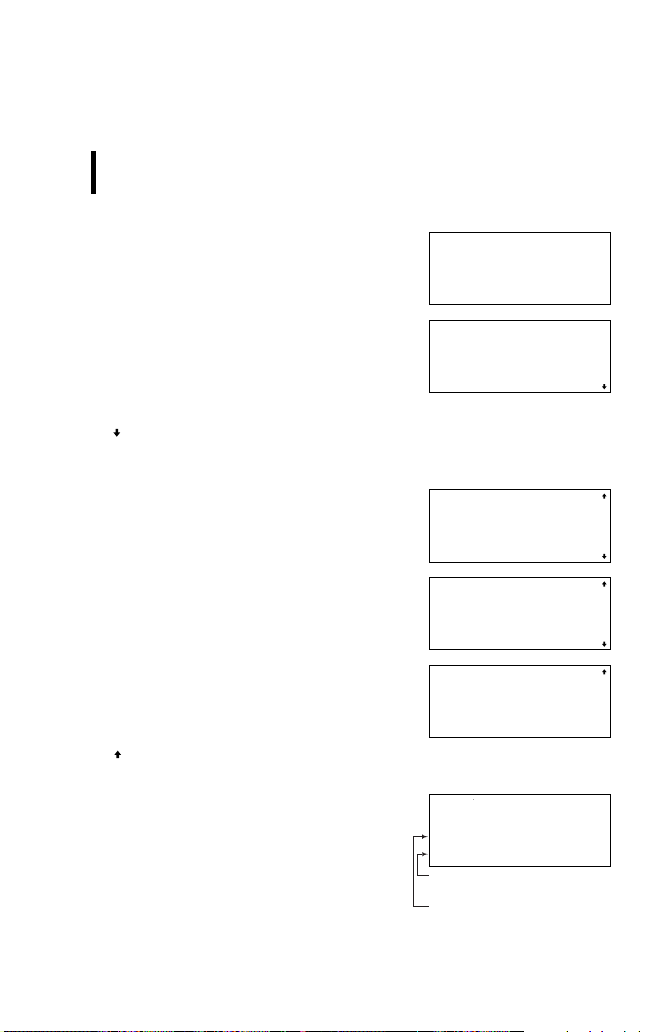
53
Kapitel 3: Wissenschaftliche Berechnungen
Werte der rechten Seite der
Gleichung.
Werte der linken Seite der
Gleichung.
D= 20.
R¬ 50.
L¬ 50.
NORMAL MODE
0.
A˚B=C˚D_
A˚B=C˚D
A=z 0.
A˚B=C˚D
D=z 0.
A˚B=C˚D
B=z 0.
A˚B=C˚D
C=z 0.
Lösen einer Gleichung
Beispiel
Bestimmen Sie die Variablen in der untenstehenden Gleichung.
A × B = C × D
1. Drücken Sie b 0 , um den NORMAL-Modus einzuschalten.
2. ; A k ; B ; = ;
C k ; D drücken.
• Geben Sie die gesamte Gleichung ein.
3. I 5 drücken.
• Der Rechner ruft automatisch die
Anzeige für die Eingabe der Variablen
auf und zeigt die Variablen in alphabetischer Reihenfolge an.
•“
” zeigt an, dass es mehrere Variablen gibt.
•Wenn eine Variable bereits einen Wert hat, zeigt der Rechner diesen
Wert automatisch an.
4. 10 e drücken.
• Gibt einen Wert für die bekannte Variable
A ein.
• Der Cursor geht zur nächsten Variablen.
5. 5 e drücken.
• Gibt einen Wert für die bekannte Variable
B ein.
6. 2.5 e drücken.
• Gibt einen Wert für die bekannte Variable
C ein.
• Der Cursor geht zur nächsten Variablen.
“
” zeigt an, dass dies die letzte Variable
ist.
7. @ h drücken.
• Nach der Anzeige von “calculating!”
(“wird berechnet”) im Display findet der
Rechner den Wert für die unbekannte
Var iable, die vom Cursor angezeigt
wurde.

54
Kapitel 3: Wissenschaftliche Berechnungen
• Die zu lösende Gleichung muss nicht auf 0 gesetzt sein, um sie lösen
zu können.
• Das Ergebnis erscheint in der obersten Zeile, die Werte der linken
und rechten Seiten der Gleichung erscheinen unten.
8. e drücken.
• Schaltet zur Anzeige für die Eingabe der
Var iablen zurück.
9. d 8 e drücken.
• Substituiert den Wert 8 für B.
• Der Cursor geht zur nächsten Variable C.
10. @ h drücken.
• Sie können alle Unbekannten in der
gleichen Gleichung finden.
Wichtige Hinweise
Für die Verwendung der Solver-Funktion sind mehrere wichtige Punkte zu
beachten:
• Um die Berechnung zu unterbrechen, drücken Sie j, wenn
“calculating!” (= “wird berechnet”) erscheint.
•Vor der Eingabe der Gleichung muss die geeignete Winkeleinheit gewählt
sein.
• Der Rechner verwendet das Newton-Verfahren zum Lösen von Gleichungen. Darum kann es Gleichungen geben, die hier nicht gelöst werden
können, obwohl sie lösbar sind. (s. Seite 123)
• Der Rechner stoppt den Rechenvorgang, wenn der für die linke und rechte
Seite der Gleichung erhaltene Wert sehr nah ist. Deshalb kann es in
bestimmten Fällen vorkommen, dass die erhaltene Lösung nicht das wahre
Ergebnis ist. (s. Seite 122)
• In bestimmten Fällen kann der Rechner eine Berechnung abbrechen und
die rechts gezeigte Meldung anzeigen.
(s. Seite 121)
A˚B=C˚D
A=z 10.
A˚B=C˚D
C=z 2.5
C= 4.
R¬ 80.
L¬ 80.
- ERROR 02 CALCULATION

55
Kapitel 3: Wissenschaftliche Berechnungen
Simulationsberechnung (ALGB)
Diese Funktion ermöglicht das schnelle Bestimmen anderer Lösungen einer
Reihe verschiedener Werte unter Verwendung des gleichen Berechnungsausdrucks.
Eingabe eines Ausdrucks für Simulationsberechnung
Die Simulationsberechnung wird wie folgt verwendet.
1. Drücken Sie b 0, um den NORMAL-Modus einzuschalten.
2. Geben Sie einen Ausdruck mit mindestens einer Variablen ein.
3. @ G drücken.
4. Geben Sie die Werte der Variablen ein. Das Berechnungsergebnis wird
nach Eingabe der Werte für alle verwendeten Variablen angezeigt.
• Sie können sowohl globale Variablen als auch lokale Variablen in Ihrer
Gleichung verwenden, aber nur die lokalen Variablen werden beim
Speichern der Gleichung gespeichert. (s. Seite 58)
• Sie müssen nur die Seite der Gleichung eingeben, die die Variablen
enthält.
• Bei der Ausführung von Simulationsberechnungen werden die Variablen-Speicher von den neuen Werten überschrieben.
• Das berechnete Ergebnis wird im Speicher für das letzte Ergebnis
gespeichert.
• Zum Beenden der Simulationsberechnung drücken Sie j.
Ändern des Wertes von Variablen und Bearbeiten eines
Ausdrucks
Das Display zeigt die Lösung an. Drücken Sie e, um zur Anzeige für die
Eingabe der Variablenwerte zurückzugelangen. Kehren Sie anschließend zur
Gleichungsanzeige in den NORMAL-Modus zurück, indem Sie j
drücken.
πRŒH=
785.3981634
→
πRŒH
H=z 5.
→
NORMAL MODE
0.
πRŒH_
e j
Lösungsanzeige Verwenden Sie
d u, um den
Cursor von Variable
zu Variable zu
bewegen.
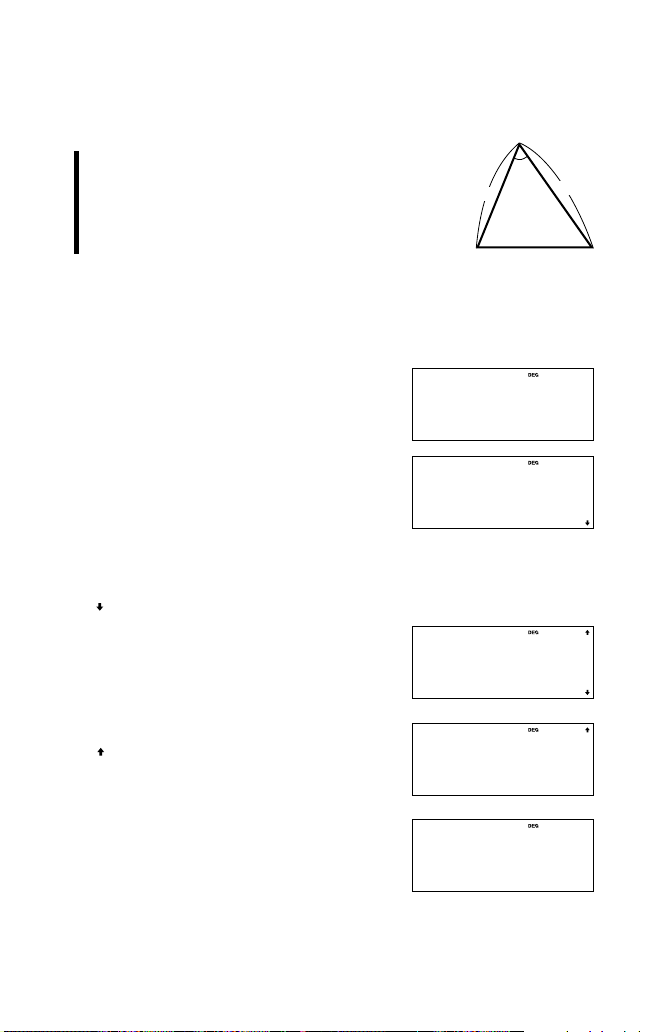
56
Kapitel 3: Wissenschaftliche Berechnungen
Simulieren einer Gleichung für verschiedene Werte
Beispiel
Berechnen Sie die Fläche S = bc sin A ÷ 2 wenn
folgendes gilt:
1 b = 3, c = 5 und A = 90° (DEG)
2 b = 3, c = 5 und A = 45° (DEG)
3 b = 4, c = 5 und A = 45° (DEG)
1. Drücken Sie b 0, um den NORMAL-
Modus einzuschalten.
2. @ J 0 0 j drücken.
• Die Winkeleinheiten werden auf DEG gesetzt.
3. ; B ; C v ; A z 2
drücken.
• Die Gleichung wird auf normale Weise
eingegeben.
4. @ G drücken.
• Der Rechner ruft automatisch die
Anzeige für die Eingabe der Variablen
auf und zeigt die Variablen in alphabetischer Reihenfolge.
•Wenn eine Variable bereits einen Wert hat, zeigt der Rechner diesen
Wert automatisch an.
•“
” zeigt an, dass mehrere Variablen vorhanden sind.
5. 90 e drücken.
• Der Rechner ruft die nächste Variable
auf.
6. 3 e 5 drücken.
•“
” zeigt an, dass dies die letzte Variable
ist.
7. e drücken.
NORMAL MODE
0.
BCsinA©2_
BCsinA©2
A=z 0.
BCsinA©2
B=z 0.
BCsinA©2
C=5_
b
c
A
S =
S
bc sin A ÷ 2
Die Fläche des Dreiecks
1 beträgt 7.5 Quadrateinheiten.
BCsinA©2=
7.5

57
Kapitel 3: Wissenschaftliche Berechnungen
8. e und anschließend 45 e
drücken.
• Nach der Ermittlung des Ergebnisses
drücken Sie e, um zur Anzeige für
die Eingabe der Variablen zurückzugelangen.
9. @ h drücken.
• Die Seiten b und c haben die gleiche
Länge im Dreieck 2 wie im Dreieck 1,
so dass Sie diese Werte nicht neu
eingeben müssen.
10. e und dann d 4 e @
h drücken.
2BCsinA©2
B=z 3.
BCsinA©2=
5.303300859
Die Fläche des Dreiecks
2 wird angezeigt.
BCsinA©2=
7.071067812
Die Fläche des Dreiecks
3 wird angezeigt.
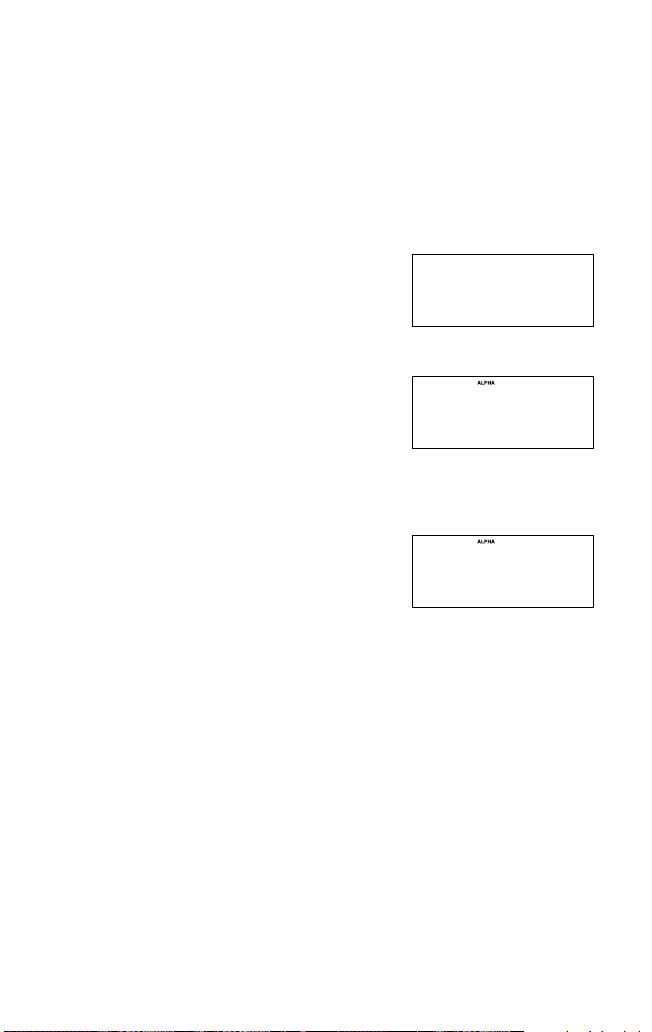
58
Kapitel 3: Wissenschaftliche Berechnungen
Speichern von Gleichung in eine Datei
Wenn der Rechner sich im NORMAL-Modus (ausgenommen N-Basis)
befindet, können Sie die Gleichungen in eine Gleichungsdatei speichern.
Gespeicherte Gleichungen können im NORMAL-Modus gelöscht werden.
Drücken Sie f im NORMAL-Modus, um das Gleichungsdatei-Menü
aufzurufen.
• Drücken Sie 0, 1 oder 2, um
auszuwählen, ob eine Gleichung geladen,
gespeichert oder gelöscht werden soll.
Speichern einer Gleichung
Sie können eine Gleichung wie folgt speichern.
1. Nach der Eingabe einer Gleichung im
NORMAL-Modus drücken Sie 1 im
Gleichungsdatei-Menü.
• Der Benutzer wird zur Eingabe eines Titels
der Gleichung aufgefordert.
• Der Rechner schaltet automatisch auf die Alphabeteingabe um. Zum
Aufheben der Alphabet-Einstellung drücken Sie ;.
2. Geben Sie den Titel der Datei ein (bis zu
sieben Zeichen).
•Wenn Sie sich anders entscheiden und die
Gleichung nicht mehr speichern wollen,
drücken Sie j.
3. Drücken Sie e zum Speichern der
Gleichung.
• Der Bildschirm zeigt die letzte Anzeige vor dem Drücken von f an.
Hinweis:
• Beim Speichern einer Gleichung werden lokale Variablen
(einschließlich ihrer Werte), die in der Gleichung verwendet
werden, zur gleichen Zeit gespeichert.
<EQTN FILE>
ƒLOAD ⁄SAVE
¤DEL
SAVE:TITLE?
SAVE:RING_
“RING” wird als
Dateiname eingegeben.

59
Kapitel 3: Wissenschaftliche Berechnungen
Laden und Löschen einer Gleichung
Die Verfahren zum Aufrufen (Laden) und Löschen einer gespeicherten
Gleichung sind gleich. Einziger Unterschied ist, dass Sie das Löschen einer
Funktion bestätigen müssen.
Das Aufrufen (Laden) oder Löschen einer Gleichung geschieht wie folgt:
1. Drücken Sie zum Aufrufen (Laden) oder
Löschen f und anschließend 0
bzw. 2.
2. Verwenden Sie d u, um den Titel
der gewünschten Datei anzuzeigen, und
drücken Sie e.
• Beim Löschen einer Gleichung erscheint im
Display die Aufforderung zur Bestätigung
des Löschvorgangs. Drücken Sie y, um
mit dem Löschvorgang fortzusetzen oder e, um den Vorgang
abzubrechen.
Hinweis:
• Wenn die aufgerufene Gleichung lokale Variablen enthält, werden
die Namen und die Werte der lokalen Variablen zusammen mit
der Gleichung aufgerufen.
• Jede andere Gleichung in der Anzeige und lokale Variablen vor
dem Aufruf der Gleichung werden gelöscht.
TITLE:RING
DELETE¬[DEL]
QUIT¬[ENTER]
DEL ¬º⁄RING
º¤AREA-3
º‹CIRCUIT
DEL wurde gewählt.

60

61
Kapitel 4
Statistische Berechnungen
Der STAT-Modus ermöglicht Ihnen das Ausführen statistischer Berechnungen.
Der Statistik-Modus wird durch Drücken von b 1 ausgewählt. Die
unten aufgeführten sieben statistischen Berechnungen können verwendet
werden. Nach dem Einschalten des Statistik-Modus wählen Sie den
gewünschten Unter-Modus durch Drücken der entsprechenden Zahlentaste
aus.
Zum Wechseln des Unter-Modus müssen Sie erst den Statistik-Modus
erneut anwählen (b 1 drücken) und dann den gewünschten UnterModus auswählen.
0 (SD) : Statistische Berechnungen mit Einzel-Variablen
1 (LINE) : Berechnungen linearer Regressionen
2 (QUAD) : Berechnungen quadratischer Regressionen
3 (EXP) : Berechnungen exponentieller Regressionen
4 (LOG) : Berechnungen logarithmischer Regressionen
5 (POWER) : Berechnungen von Potenz-Regressionen
6 (INV) : Berechnungen inverser Regressionen

62
Kapitel 4: Statistische Berechnungen
Die folgenden statistischen Werte (s. untenstehende Tabelle) können für die
jeweiligen statistischen Berechnungen ermittelt werden.
I 0 0
I 0 1
I
0
2
I
0
3
I
0
4
I 0 5
I
0
6
I 0 7
I
0
8
I
0
9
I
0
A
I
0
B
I 2 0
I 2 1
I
2
2
I
2
3
Q
n
Anzahl der Stichproben
Mittelwert einer Stichprobe (x-Daten)
Standardabweichung einer Stichprobe (x-Daten)
Standardabweichung der Gesamtheit (x-Daten)
Summe der Stichproben (x-Daten)
Quadratsumme der Stichproben (x-Daten)
Mittelwert einer Stichprobe (y-Daten)
Standardabweichung einer Stichprobe (y-Daten)
Standardabweichung der Gesamtheit (y-Daten)
Summe der Stichproben (y-Daten)
Quadratsumme der Stichproben (y-Daten)
Summe der Produkte der Stichproben (x, y)
Koeffizient der Regressionsgleichung
Koeffizient der Regressionsgleichung
Koeffizient der quadratischen Regressionsgleichung
Korrelationskoeffizient
¯
y
sy
W
r
a
b
c
σ
¯
x
sx
x
σ
x
Σ
x
2
Σ
y
y
2
xy
Σ
y
Σ
Σ
Variablen Bezeichnung Tastenfolge
• Für Ausführung von Berechnungen mit statistischen Variablen die Taste
I verwenden.
Statistische Berechnungen mit Einzel-Variablen
Die unter 1 angeführten statistischen Werte sowie der Wert für die
Normalverteilungsfunktion.
Berechnen linearer Regressionen
Die statistischen Werte von 1 und 2 (ausgenommen Koeffizienten c);
weiterhin Schätzung von y für ein bestimmtes x
(Schätzwert y´) und
Schätzung von x
für ein bestimmtes y (Schätzwert x´)
Berechnen exponentieller, logarithmischer, Potenz- und
inverser Regressionen
Statistische Werte von 1 und 2 (ausgenommen Koeffizienten c). Weiterhin
Schätzung von y
für ein bestimmtes x (Schätzwert y´) und Schätzung von x
für ein bestimmtes y (Schätzwert x´). (Da dieser Rechner jede Formel in eine
lineare Regressionsformel umwandelt, ehe er eine Berechnung ausführt,
werden alle statistischen Werte, ausgenommen die Koeffizienten a
und b,
aus umgewandelten Daten ermittelt, nicht etwa von den eingegebenen.)

63
Kapitel 4: Statistische Berechnungen
Berechnen quadratischer Regressionen
Die statistischen Werte von 1 und 2 und die Koeffizienten a, b, c der
allgemeinen quadratischen Regressionsformel (y = a + bx + cx2). (Für
Berechnungen quadratischer Regressionen kann kein Korrelationskoeffizient
(r) ermittelt werden.)
Dateneingabe und Korrektur
Alle Daten werden im Speicher abgelegt, bis eine Speicherlöschung (@
P 2
y) ausgeführt oder ein neuer Modus ausgewählt wird. Vor der
Eingabe neuer Daten sollte der Speicherinhalt gelöscht werden.
Dateneingabe
Daten mit 1 Variablen
Daten
_
Daten , Häufigkeit
_ (Angabe der Häufigkeit, um ein
wiederholtes Eingeben gleicher Daten zu vermeiden)
Daten mit 2 Variablen
Daten
x ,
Daten
y _
Daten
x ,
Daten
y ,
Häufigkeit
_ (Angabe der Häufigkeit,
um ein wiederholtes Eingeben gleicher Daten zu vermeiden x und y.)
• Es können bis zu 100 einzelne Daten eingegeben werden. Bei Daten mit 1
Var iablen werden die Daten ohne Häufigkeitsangabe als einfache Daten
gewertet, während Daten, die mehr als einmal in der Stichprobe vorkommen als ein Satz von mehreren gleichen Daten gespeichert werden. Bei
Daten mit 2 Variablen werden Daten ohne Häufigkeitsangabe als Satz von
zwei Daten gewertet, während Daten mit einer Häufigkeitsangabe als ein
Satz von drei Daten gespeichert werden.
Korrektur der Daten
Korrektur vor dem Drücken von _ direkt nach der Dateneingabe:
Falsche Daten mit j löschen, dann die korrekten Daten eingeben.

64
Kapitel 4: Statistische Berechnungen
Korrektur nach dem Drücken von _:
Drücken Sie u d, um den zuletzt eingegebenen Datensatz
angezeigt zu bekommen.
Drücken Sie
d
, um die Daten in aufsteigender Reihenfolge (älteste
zuerst) angezeigt zu bekommen. Zum Wechseln zur Anzeige in absteigender Reihenfolge (neueste zu erst) die Taste
u
drücken.
Jeder Datensatz wird angezeigt mit “X=”, “Y=” oder “N:” (N ist die
laufende Nummer des Datensatzes).
X=z 75.
› 3.
X=z 4.
Y= 3.
› 3.
x
-Daten
Häufigkeit
Häufigkeit
Datensatz-Zahl
x
-Daten
y
-Daten
Datensatz-Zahl
Bewegen Sie den Cursor mit u d, um den zu modifizierenden
Datensatz aufzurufen. Geben Sie den korrekten Wert ein und drücken
Sie anschließend
_
oder e.
• Zum Löschen eines Datensatzes bewegen Sie den Cursor mit u
d an eine Stelle des Datensatzes, und drücken Sie @ #
Der Datensatz wird gelöscht.
• Um einen neuen Datensatz hinzuzufügen, drücken Sie j. Die
Anzeige der vorher eingegebenen Daten verschwindet. Geben Sie die
neuen Werte ein und drücken Sie _.
Daten
30
b 1 0
40
30
_
40
40
, 2 _
50
50
_
Daten
30
d d d
45 45 _
X= 45.
45 3 _
¤ 3.
45
60 d 60 _
X= 60.
Stat 0 [SD]
0.
DATA SET= 1.
DATA SET= 2.
DATA SET= 3.
Beispiel
ErgebnisTastenfolge

65
Kapitel 4: Statistische Berechnungen
Formeln für Regressionen statistischer
Berechnungen
Art der Regression Regressionsformel
Linear y = a + bx
Exponentiell y = a • e
bx
Logarithmisch y = a + b • ln x
Potenz y = a • x
b
Invers y = a + b —
Quadratisch y = a + bx + cx
2
1
x
Bei den Regressionsformeln für statistische Berechnungen können in
folgenden Situationen Fehler auftreten:
•Wenn der absolute Wert eines Zwischenergebnisses oder eines Endergebnisses größer oder gleich 1 × 10
100
ist.
•Wenn der Nenner gleich Null ist.
•Wenn versucht wurde, die Quadratwurzel einer negativen Zahl zu
berechnen.
•Wenn Berechnungen für eine quadratische Regression keine Lösung
haben.
xy = x1y1 + x2y2 + ··· + xny
n
y = y1 + y2 + ··· + y
n
x = x1 + x2 + ··· + x
n
x2 = x
1
2
+ x
2
2
+ ··· + x
n
2
y2 = y
1
2
+ y
2
2
+ ··· + y
n
2
sx =
x
2
– nx
2
n – 1
sy =
y
2
– ny
2
n – 1
y =
y
n
x =
x
n
x =
x
2
– nx
2
n
y =
y
2
– ny
2
n
Σ
Σ
Σ
σ
Σ
Σ
Σ
Σ
Σ
σ
Σ
Σ
Σ

66
Kapitel 4: Statistische Berechnungen
Berechnen der Normalverteilung
•P(
t
), Q(t) und R(t) nehmen immer positive Werte an, auch wenn t<0 gilt,
weil diese Funktionen auch als Fläche unter einer Kurve gedeutet werden
können.
• Die Werte für P(
t
), Q(t) und R(t) werden auf sechs Dezimalstellen genau
angegeben.
–
x – x
x
σ
t =
Standard Umrechnungsformel

67
Kapitel 4: Statistische Berechnungen
Beispiele statistischer Berechnungen
Daten
95
b 1 0
80
95 _
80
80 _
75
_
75
75 , 3 _
75
50 _
50
–
x = I
0 1 e
@
P 2 y
= I
0 3 e
n = I
0 0 e
= I
0 4 e
= I
0 5 e
sx = I
0 2 e
sx
2
= A e
(95––x)
×10+50=
( 95 - I
0 1 )
sx
z I
0 2 k 10
+ 50 e
x = 60 → I
1 1 60 I 1 0
) e
t = –0.5 I
1 3 S 0.5 ) e
Σ
x
2
Σ
˛= 75.71428571
σ
≈
= 12.37179148
n= 7.
Í≈= 530.
Í≈Œ= 41200.
= 13.3630621
sx
178.5714286
64.43210706
0.102012
0.691463
Stat 0 [SD]
0.
x
σ
x
→R(t) ?
DATA SET= 1.
DATA SET= 2.
DATA SET= 3.
DATA SET= 4.
DATA SET= 5.
P(t) ?
Beispiel ErgebnisTastenfolge

68
Kapitel 4: Statistische Berechnungen
Beispiel ErgebnisTastenfolge
Daten
b 1 1
2 5
2 , 5 _
2 5
_
12 24
12 , 24 _
21 40
21 , 40 , 3 _
21 40
15 , 25 _
21 40
I
2 0 e
15 25
I
2 1 e
I
2 3 e
I
0 2 e
I
0 7 e
x=3 → y'=? 3 I
2 5
y=46 → x' =? 46 I
2 4
b 1 2
@ P 2 y
@ P 2 y
12 , 41 _
8 , 13 _
5 , 2 _
23 , 200 _
15 , 71 _
I
2 0 e
I 2 1 e
I
2 2 e
x=10 → y'=? 10 I
2 5
y=22 → x'=? 22 I
2 4
xy
12 41
8 13
5 2
23 200
15 71
xy
Daten
Stat 1 [LINE]
0.
Stat 2 [QUAD]
0.
DATA SET= 1.
DATA SET= 2.
DATA SET= 3.
DATA SET= 4.
DATA SET= 5.
DATA SET= 1.
DATA SET= 2.
DATA SET= 3.
DATA SET= 4.
DATA SET= 5.
= 5.357506761
=-3.120289663
= 0.503334057
≈¡: 9.63201409
≈™:-3.432772026
= 1.050261097
= 1.826044386
= 0.995176343
=8.541216597
=15.67223812
6.528394256
24.61590706
=
=
=
=
=
a
b
r
a
b
c
sx
sy
a
b
r
=
a
=
b
=
c
sx
sy
24.4880159

69
Kapitel 5
Gleichungslöser
Lineare Gleichungssysteme
Lineare Gleichungssysteme mit 2 Unbekannten (2-VLE) oder mit 3 Unbekannten (3-VLE) können mit dieser Funktion gelöst werden.
1 2-VLE: b 3 0
a1x + b1y = c
1
a2x + b2y = c
2
a1 b
1
a2 b
2
D =
2 3-VLE: b 3 1
a1x + b1y + c1z = d
1
a2x + b2y + c2z = d
2
a3x + b3y + c3z = d
3
a1 b1 c
1
a2 b2 c
2
a3 b3 c
3
D =
• Ist die Determinante D = 0, so erscheint eine Fehlermeldung im Display.
•Wenn der absolute Wert eines Zwischenergebnisses oder eines Endergebnisses größer oder gleich 1 × 10
100
ist, tritt ebenfalls ein Fehler auf.
• Die mit dieser Funktion erhaltenen Ergebnisse unterliegen daher einer
Fehlertoleranz.
Beispiel 1
2x+3y = 4 x = ?
5x+6y = 7Òy = ?
det(D) = ?
1. Drücken Sie b 3 0, um 2-
VLE innerhalb des EQN-Modus
einzustellen.
2. Geben Sie den Wert jedes Koeffizienten ein (a1, usw.)
2 e 3 e 4 e
5 e 6 e 7
• Bei der Eingabe von Koeffizienten können die allgemeinen Grundrechenarten verwendet werden.
• Zum Löschen der eingegebenen Koeffizienten drücken Sie j.
• Um den Cursor zeilenweise zu bewegen, drücken Sie d oder
u. Für den Sprung in die letzte oder oberste Zeile drücken Sie
@ d
oder
@ u
.
a⁄z 0.
b⁄ 0.
c⁄ 0.

70
Kapitel 5: Gleichungslöser
3. Nach der Eingabe des letzten
Koeffizienten drücken Sie e, um
die 2 Variablen zu bestimmen.
• Nach der Berechnung der Lösung
drücken Sie e oder j, um zur
Anzeige für die Eingabe des Koeffizienten zurückzugelangen. Sie
können unabhängig von der Cursorposition @ h drücken, um
die 2 Variablen zu bestimmen.
Beispiel 2
x+y-z = 9 x = ?
6x+6y-z = 17 Ò y = ?
14x-7y+2z = 42 z = ?
det(D) = ?
1. Drücken Sie b 3 1,
innerhalb des EQN-Modus
einzustellen.
2. Geben Sie den Wert jedes Koeffizienten ein (a1, usw.)
1 e 1 e S 1 e 9 e
6 e 6 e S 1 e 17 e
14 e S 7 e 2 e 42
• Bei der Eingabe von Koeffizienten können die allgemeinen Grundrechenarten verwendet werden.
• Zum Löschen der eingegebenen Koeffizienten drücken Sie j.
• Um den Cursor zeilenweise zu bewegen, drücken Sie d oder
u. Für den Sprung in die letzte oder oberste Zeile drücken Sie
@ d oder @ u.
3. Nach der Eingabe des letzten
Koeffizienten drücken Sie e, um
die 3 Variablen zu bestimmen.
• Für die Anzeige von det(D) drücken Sie
d.
• Nach der Berechnung der Lösung
drücken Sie e oder j, um zur
Anzeige für die Eingabe des Koeffizienten zurückzugelangen. Sie können
unabhängig von der Cursorposition @
h drücken, um die 3 Variablen zu bestimmen.
x= –1.
y= 2.
D= –3.
a⁄z 0.
b⁄ 0.
c⁄ 0.
x= 3.238095238
y=–1.638095238
Z
= –7.4
D= 105.

71
Kapitel 5: Gleichungslöser
Solver für Gleichungen 2. und 3. Grades
Quadratische Gleichungen (ax2 + bx + c = 0) oder auch kubische
Gleichungen (ax3 + bx2 + cx + d = 0) können mit Funktionen des SOLVERModus gelöst werden.
1 Solver für quadratische Gleichungen (QUAD): b 3 2
2 Solver für Gleichungen 3. Grades(CUBIC): b 3 3
•Falls es mehr als 2 Lösungen gibt, können diese wie unten im Beispiel
angezeigt werden.
• Die mit dieser Funktion ermittelten Lösungen unterliegen einer Fehlertoleranz.
Beispiel 1
3x2 + 4x – 95 = 0 → x = ?
1. Drücken Sie b 3 2, um
QUAD im EQN-Modus auszuwählen.
2. Geben Sie den Wert für jeden
Koeffizienten ein (a, usw.)
3 e 4 e S 95
• Bei der Eingabe von Koeffizienten können die allgemeinen Grundrechenarten verwendet werden.
• Zum Löschen der eingegebenen Koeffizienten drücken Sie j.
• Um den Cursor zeilenweise zu bewegen, drücken Sie d oder
u.
3. Zum Lösen der quadratischen
Gleichung drücken Sie nach der
Eingabe des letzten Koeffizienten
e.
• Nach der Berechnung der Lösung
drücken Sie e oder j, um zur Anzeige für die Eingabe des
Koeffizienten zurückzugelangen. Sie können unabhängig von der
Cursorposition @ h zum Lösen der quadratischen Gleichung
verwenden.
a=z 0.
b= 0.
c= 0.
X⁄ 5.
X¤–6.333333333

72
Kapitel 5: Gleichungslöser
Beispiel 2
5x3 + 4x2 +3x + 7 = 0 → x = ?
1. Drücken Sie b 3 3, um
CUBIC im EQN-Modus auszuwählen.
2. Geben Sie den Wert jedes Koeffizienten ein (a, usw.)
5 e 4 e 3 e 7
• Bei der Eingabe von Koeffizienten können die allgemeinen Grundrechenarten verwendet werden.
• Zum Löschen der eingegebenen Koeffizienten drücken Sie j.
• Um den Cursor zeilenweise zu bewegen, drücken Sie d oder
u. Für den Sprung in die letzte oder oberste Zeile drücken Sie
@ d oder @ u.
3. Nach der Eingabe des letzten
Koeffizienten drücken Sie e zum
Lösen der Gleichung 3. Grades.
• Nach der Berechnung der Lösung
drücken Sie e oder j, um zur
Anzeige für die Eingabe des Koeffizienten zurückzugelangen. Sie
können unabhängig von der Cursorposition @ h für das Lösen
der Gleichung 3. Grades verwenden.
a=z 0.
b= 0.
c= 0.
X⁄–1.233600307
X¤ 0.216800153
+1.043018296i
-

73
Kapitel 6
Berechnungen mit
komplexen Zahlen
Der CPLX-Modus für komplexe Zahlen ermöglicht die Addition, Subtraktion,
Multiplikation und Division komplexer Zahlen. Drücken Sie b 4, um
den Modus für komplexe Zahlen auszuwählen.
Ergebnisse von Berechnungen mit komplexen Zahlen werden auf zwei Arten
dargestellt:
1 @ E: Mit Hilfe von rechtwinkligen Koordinaten (xy
erscheint).
2 @ u: Mit Hilfe von Polarkoordinaten (r
θ
erscheint).
Eingabe komplexer Zahlen
1 Rechtwinklige Koordinaten werden wie folgt eingegeben:
x-Koordinate + y-Koordinate Q
oder x-Koordinate + Q y-Koordinate
2 Polarkoordinaten werden wie folgt eingegeben:
r R θ
r: absoluter Wert
θ: Argument
• Beim Wechsel in einen anderen Modus wird der im Speicher M
gespeicherte imaginäre Teil einer komplexen Zahl gelöscht.
• Eine in rechtwinkligen Koordinaten angegebene komplexe Zahl mit dem
y-Wert gleich Null oder eine in Polarkoordinaten angegebene komplexe
Zahl mit dem Winkel Null wird als reelle Zahl behandelt.
•Drücken Sie I 0, um auf den komplex konjugierten Wert der
angegebenen komplexen Zahl zurückzugelangen.

74
Kapitel 6: Berechnungen mit komplexen Zahlen
b 4
(12–6i) + (7+15i) –
(11+4i) =
( 11 + 4 Q ) e
8.
+5.i
6×(7–9i)× 6 k ( 7 - 9 Q )
(–5+8i) = k ( S 5 + 8 Q
222.
+606.i
16×(sin30°+ 16 k ( v 30 +
icos30°)÷(sin60°+
icos60°)=
13.85640646
+8.i
@ u 8 R 70 + 12
R 25 e
18.5408873
∠
∠
42.76427608
r1 = 8, θ1 = 70°
r2 = 12, θ2 = 25°
↓
r = ?, θ = ?°
(1 + i) @ E 1 + Q e
1.
+1.i
↓
@ u
1.414213562
r = ?, θ = ?°
45.
@ E ( 2 - 3 Q
(2 – 3i)
2
=
) A e
–5.
–12.i
1
( 1 + Q ) @
Z e
0.5
1 + i
=
–0.5i
conj(5+2i) =
I 0
( 5 + 2
Q
) e
5.
–2.i
( 12 - 6 Q ) +
( 7 + 15 Q ) -
Q $ 30 ) z (
Q $ 60 ) e
v 60 +
) e
0.
COMPLEX MODE
Beispiel Tastenfolge Ergebnis

75
Kapitel 7
Programmierung
PROG-Modus
Ein Programm ermöglicht Ihnen, eine Reihe von einfachen oder auch
komplexen Berechnungen zu automatisieren. Programme werden entweder
im NORMAL-Programm-Modus oder im NBASE-Programm-Modus geschrieben.
Einschalten des PROG-Modus
1. Drücken Sie b 2, um den PROG-
Modus einzuschalten.
2. Drücken Sie 0, um ein Programm
auszuführen (RUN), drücken Sie 1, um
ein neues Programm zu schreiben (NEW),
drücken Sie 2, um ein Programm zu bearbeiten (EDIT), und drücken
Sie 3, um ein Programm zu löschen (DELETE).
Wahl des NORMAL-Programm-Modus oder des NBASEProgramm-Modus
Vor dem Schreiben eines neuen Programms (b 2 1) wählen Sie
entweder den NORMAL-Programm-Modus oder den NBASE-ProgrammModus aus.
Im NORMAL-Programm-Modus können Sie einfache mathematische sowie
statistische Berechnungen ausführen. Im NBASE-Programm-Modus können
Sie logische Operationen mit Zahlen verschiedener Zahlensysteme ausführen.
Konzept der Programmierung
Es würde den Rahmen dieser Bedienungsanleitung sprengen, detaillierte
Beispielprogramme für den Rechner aufzuzeigen. Vorhandene Programmiererfahrung ist zum Verständnis dieses Abschnitts erforderlich. Die Programmiersprache für diesen Rechner ähnelt anderen heute verwendeten
Programmiersprachen.
Alle herkömmlichen Rechner und Rechnerprogramme verwenden fundamentale Elemente wie Eingabe, Ablaufsteuerung, Schleifen, Berechnung
und Ausgabe. Die Programmiersprache Ihres Rechners enthält Befehle, die
es Ihnen erlauben, alle diese fundamentalen Elemente in Ihren Programmen
einzusetzen. Eine Liste der Befehle ist im Abschnitt “Programmierbefehle”
aufgeführt. (s. Seite 79)
PROGRAM MODE
ƒRUN ⁄NEW
¤EDIT ‹DEL
76
Kapitel 7: Programmierung
MODE
ƒNORMAL ⁄NBASE
SLOPE_ :NORMAL
TITLE? :NORMAL
Hinweis:
•
Befehle müssen mit dem Befehlsmenü (COMMAND) (i) eingegeben
werden. Schreiben Sie Befehle NICHT manuell mit Hilfe der Taste ;.
Tasten und Display
Im PROG-Modus bewirken bestimmte Tasten und Anzeigen etwas anderes
als in den anderen Modi, um die Programmierung zu erleichtern. Die
Unterschiede werden kurz im folgenden beschrieben:
• Drücken Sie i (die Taste f) für den direkten Zugriff auf das
Befehlsmenü für die Programmierung. Die Funktion zum Speichern von
Gleichungen in eine Datei arbeitet im PROG-Modus nicht.
• Während der Eingabe eines Programmtitels sind die Tasten automatisch
auf Alphabet-Modus (A-LOCK) gesetzt.
• In einem Programm kann eine einzelne Zeile bis zu 160 Buchstaben
enthalten, wobei alle Befehle als jeweils einzelne Buchstaben gezählt
werden. Während Sie eine Zeile schreiben, läuft der Text nach links weiter.
Ein Zeilenumbruch geschieht im PROG-Modus nicht.
Erzeugen eines neuen Programms (NEW)
Nachdem Sie das Programm mit einem Titel versehen haben, speichert der
Rechner automatisch und zeitgleich das gesamte Programm unter diesem
Namen ab. Es ist nicht nötig, das Programm manuell (durch Bestätigung) zu
speichern.
Erzeugen eines neuen Programms (NEW)
1. Drücken Sie b 2, um den PROG-
Modus einzuschalten. Anschließend
drücken Sie 1, um ein neues
Programm zu erzeugen.
• Die Anzeige fordert zum Wählen des
NORMAL-Programm-Modus oder des NBASE-Programm-Modus auf.
2. Für dieses Beispiel drücken Sie 0, um
den NORMAL-Programm-Modus einzuschalten.
• Die Anzeige fordert zur Eingabe eines
Programmtitels auf.
3. Schreiben Sie den Namen des Programms
(z.B., SLOPE).
• Ein Programmname kann bis zu 7
Buchstaben haben.
• Der Rechner schaltet automatisch auf den Alphabet-Eingabemodus um.
Sie brauchen für die Buchstabeneingabe nicht mehr die Taste ; zu
drücken.

77
Kapitel 7: Programmierung
4. Nach der Eingabe drücken Sie e.
• Sie können jetzt das neue Programm
eingeben.
• Jede Programmzeile wird gespeichert,
sobald Sie u, d oder e drücken.
• Sie können sowohl die regulären Funktionen des Rechners als Befehle
als auch die zusätzlichen Programmierbefehle im Menü i verwenden.
Verwenden von Variablen
Globale und lokale Variablen werden im PROG-Modus unterschiedlich
behandelt.
• Die Buchstaben A – Z und θ stellen im Falle, dass sie alleine verwendet
werden, globale Variablen dar. Globale Variablen entsprechen den
Speichern des Rechners (z.B. bedeutet “C” in einem Programm Speicher
C im Rechner). Globale Variablen ermöglichen den Programmen den
direkten Zugriff auf gespeicherte Werte oder die Weitergabe von Variablen
von einem Programm zu einem anderen Programm. Ebenso ermöglichen
globale Variablen, Ergebnisse von Programmen zu speichern und in einem
anderen Modus zu verwenden.
• Sie können auch bis zu neun lokale Variablen benennen und verwenden
(@ v). Lokale Variablen speichern Werte nur in einem individuellen
Programm.
Wenn eine Zeile in Ihrem Programm eine
Gleichung wie z.B. Y = M1X + 5 enthält, wird die
globale Variable Y gleich (M1 × X) + 5 gesetzt.
Wenn diese Gleichung bei der Ausführung des
Programms auftritt und der Wert der lokalen
Variable M1 nicht vorher im Programm definiert
wurde, fordert der Rechner mit der Anzeige
“M1=?” zur Eingabe eines Werts für M1 auf. Die
globale Variable X ist bereits auf den zuletzt in
diesem Speicher gespeicherten Wert gestellt.
Mit nur ein wenig Übung sind sie schnell in der
Lage, Programme in Ihren Rechner einzugeben.
Beispiel
Schreiben Sie ein einfaches Programm, das zur Eingabe der Grundlinie
(B1) und Höhe (H1) eines Dreiecks auffordert und dann die Fläche (A)
berechnet. Nach dem Erstellen führen Sie das Programm mit RUN
aus, um die Fläche eines Dreiecks mit einer Basis von 4 Einheiten und
einer Höhe von 3 Einheiten zu bestimmen.
SLOPE :NORMAL
Y=M¡X+5
_
SLOPE :NORMAL
M¡=?
SLOPE :NORMAL
PROGRAM?

78
Kapitel 7: Programmierung
1. Vorbereitung zum Erstellen eines neuen Programms (NEW)
b 2
1
0
e
AREA
AREA :NORMAL
PROGRAM?
Einschalten des PROG-Modus.
NEW wählen.
Verfahren
Tastenfolge Anzeige
Den NORMAL-Modus einschalten.
Den Namen des Programms schreiben.
Den Namen des Programms eingeben.
2. Eingeben des Programms
Print“B≥=BASE
i 1 @ v B1 e e @
Print“H≥=HEIGHT
a = BASE ; e
i 1 @ v d H1 e e
@
a = HEIGHT ; e
;
A ; = 1 k 2 @ v
e @ v d e e
A=1ı2B≥H≥
Print“AREA
i 1 @ a AREA ; e
i
0 ; A e
Print A
Programmcode Tastenfolge
• Zur Eingabe von mehr als einem alphabetischen Zeichen @ a
drücken, um den Alphabet-Eingabemodus einzuschalten. ; drücken,
um diesen Modus zu verlassen.
3. Ausführen des Programms
Verfahren
Zum Zurückkehren zur
anfänglichen PROG-Anzeige.
Das Programm auswählen
und ausführen.
4 für B
1
eingeben
3 für H
1
eingeben
j
0
(Das Programm auswählen.)
e
4
e
3
e
Tastenfolge Anzeige
AREA
A=
6.
RUN ¬º⁄AREA
•Wenn der Wert einer lokalen Variablen, die Sie mit @ v definier t
haben, unbekannt ist, fordert das Programm automatisch zur Eingabe
eines Wertes auf.
79
Kapitel 7: Programmierung
• Zum Beenden des Programms drücken Sie j. Zum erneuten Ausführen des Programms drücken Sie e.
• Beim Ausführen des Programms wird der im Programm im Zusammenhang mit dem Print-Befehl verwendete Text bei Bedarf in der nächsten
Zeile fortgesetzt.
• Pro Zeile kann nur ein Befehl eingegeben werden, ausgenommen
Sonderfälle wie z.B. die Struktur “If...Goto”.
•Weitere Programmierbeispiele finden Sie in Kapitel 8: Anwendungsbeispiele.
Programmierbefehle
In diesem Abschnitt werden alle Befehle beschrieben, die im PROG-Modus
zur Verfügung stehen, mit Ausnahme von Tastaturbefehlen und I-
Menübefehlen.
Eingabe- und Display-Befehle
1. Beim Schreiben oder Bearbeiten eines
Programms drücken Sie i, um auf das
COMMAND-Menü zuzugreifen.
• Die erste Seite des COMMAND-Menüs
erscheint.
• Drücken Sie d oder u für das seitenweisen Weiterblättern.
• Sie können einen Befehl direkt eingeben, indem Sie die entsprechende
Buchstabentaste drücken, ohne zuerst die relevante Seite im
COMMAND-Menü zu benutzen.
Befehl Beschreibung
Tasten-
folge
Beispiele
i 0
i
1
i
2
Print A
Input A
Input B≥
Print B≥
Print” SHARP
Print
<Variable>
Zeigt den Wert der bestimmten
Variable an. Das Anzeigeformat
wird vom SET UP-Menü
bestimmt.
Zeigt den nach dem Anführungszeichen eingegebenen Text an.
Wenn der Text drei Zeilen
überschreitet, werden nur die
letzten drei Zeilen angezeigt.
Stoppt das Programm kurzzeitig
und fordert zur Eingabe eines
Werts für die Variable mit der
Anzeige “<Variable>=?” auf.
Print”
<Text>
Input
<Variable>
<COMMAND-1>
ƒPrint ⁄Print"
¤Input ‹Wait

80
Kapitel 7: Programmierung
i 4
i
5
Rem TIME TABLE
End
Zeigt an, dass die Zeile eine
Anmerkung und kein Befehl ist,
wodurch Sie Kommentare im
Programm einfügen können.
Jede Zeile, die mit “Rem”
anfängt, wird bei der Ausführung
eines Programms ignoriert.
Durch übertriebene Verwendung
dieses Befehls wird außerordentlich viel Speicherplatz gebraucht.
Beendet das Programm. Wenn
das Programm durch den letzten
Befehl beendet wird, ist der
Befehl End nicht erforderlich.
Wenn kein End-Befehl im
Programm enthalten ist, wird am
Ende des Programms das letzte
berechnete Ergebnis angezeigt.
Sie können mehr als einen EndBefehl im gleichen Programm
verwenden, um verschiedene
Zweige, Subroutinen usw. nach
ihrer Ausführung zu beenden.
Rem
<Text>
End
i 3
Wait 5
(HexadezimalModus)
(Binär-Modus)
Schaltet das Programm für die
angegebene Anzahl von
Sekunden auf Pause.
Die maximale Wartezeit beträgt
255 Sekunden. Wenn keine
Wartezeit bestimmt ist, schaltet
das Programm auf Pause, bis
Sie eine beliebige Taste
drücken. Die BUSY-Anzeige
leuchtet, solange wie das
Programm wartet.
Wait
<Zahl>
Wait FF
Wait 1010
Befehl Beschreibung
Tasten-
folge
Beispiele

81
Kapitel 7: Programmierung
Ablaufsteuerung
i 6
i
7
i
8
i 9
i
9
Label LOOP1
Clrt
Goto LOOP2
Label LOOP2
If B≥=1 Goto
LOOP1
Label
<Label-Name>
Zeigt einen Zielpunkt für die AblaufAnweisungen Goto und Gosub an.
Bis zu sieben Buchstaben können
für den Label-Namen verwendet
werden.
Jeder Label-Name muss
unverwechselbar (eindeutig) sein.
Sie können nicht den gleichen LabelNamen mehr als einmal in einem
Programm verwenden. Bis zu 20
verschiedene Label können in jedem
Programm verwendet werden.
Löscht den auf dem Bildschirm
angezeigten Text.
Bewirkt, dass das Programm
zum angegebenen Label springt
(bezeichnet durch einen LabelBefehl). Eine Goto-Anweisung
muss eine entsprechende LabelAnweisung in der Zeile haben,
die den Zielort angibt.
Der “If”-Abfrage muss eine
konditionale Anweisung und
anschließend ein Goto-Befehl
folgen. Goto ist der einzige
Befehl, der nach der If-Abfrage
verwendet werden darf. Sie
können ; s vor dem
Goto-Befehl eingeben, um die
Zeile besser lesbar zu machen.
Clrt
Goto
<Label-Name>
If
<Bedingung>
Goto
<Label-Name>
Befehl Beschreibung
Tasten-
folge
Beispiele
i A
Gosub PART1
Führt die Subroutine beginnend
mit dem angegebenen Label
(bezeichnet durch einen LabelBefehl) aus. Eine GosubAnweisung muss eine
entsprechende Subroutine haben,
die nach der Label-Anweisung
startet und mit einem ReturnBefehl endet. Subroutinen können
auf bis zu zehn Ebenen
verschachtelt werden.
Gosub
<Label-Name>

82
Kapitel 7: Programmierung
i B
Return
Definiert das Ende einer
Subroutine. Die Operation kehrt
zu dem der entsprechenden
Gosub-Anweisung folgendem
Befehl zurück.
Return
Befehl Beschreibung
Tasten-
folge
Beispiele
Gleichwertigkeiten und Ungleichwertigkeiten
Diese Ausdrücke dienen dazu, die bedingte Anweisung in der If-Abfrage zu
bilden. Sie sind die Grundlage für Schleifen und für die Ablaufsteuerung in
Programmen.
Das Gleichheitszeichen (“=”) dient als Funktion, um einen Substitutionsbefehl für Variablen bilden zu können.
Sie können auch “=” eingeben, indem Sie einfach ; = drücken.
i C
If B=0 Goto ZERO
=
Gleich. Diese Funktion
dient u.a. zur Bildung eines
Substitutionsbefehls, der
einer Variablen einen
neuen Wert zuweist,
einschließlich
inkrementieren oder
dekrementieren.
If B<0 Goto NGTV
i D Kleiner als
<
If B>=0 Goto RECALC
i F Größer gleich
>=
If B≥>0 Goto PSTV
i G Größer als
>
If A ≠ B Goto DIF
i H Ungleich
≠
If B≥<=0 Goto CALC
i E Kleiner gleich
<=
A=A+1
Symbole Beschreibung
Tasten-
folge
Beispiele

83
Kapitel 7: Programmierung
Statistische Befehle
Im PROG-Modus stehen statistische Befehle nur dann zur Verfügung, wenn
der NORMAL-Programm-Modus ausgewählt wurde. Wenn der NBASEProgramm-Modus ausgewählt wurde, kann das Menü für statistische Befehle
nicht aufgerufen werden.
• Sobald Sie die Befehle STATx oder STATxy verwenden, löscht der Rechner
alle zuvor in der STAT-Funktion gespeicherten Daten.
i I
STATx
Wählt den Modus für
statistische Berechnungen
mit 1 Variablen (SD).
STATx
i J
STATxy
Wählt den Modus für
Berechnungen linearer
Regressionen (LINE).
STATxy
i K
Data 5
Data 25,2
Data 72,175
Data 9,96,3
Eingabe neuer statistischer
Daten. Das Datenformat
muss mit dem gewählten
Statistik-Modus übereinstimmen (Einzelvariable
oder lineare Regression).
Ein im PROG-Modus
eingegebener statistischer
Datensatz kann später nicht
bei der Verwendung einer
Statistik-Funktionen
aufgerufen werden.
Data
<x>
Data
<x,
Frequenz
>
Data
<x, y>
Data
<
x, y,
Frequenz
>
Befehl Beschreibung
Tasten-
folge
Beispiele

84
Kapitel 7: Programmierung
Bearbeiten eines Programms
1. b 2 zum Einschalten des PROG-Modus drücken, und
anschließend 2 drücken, um den Bearbeiten-Modus auszuwählen.
2. Das zu bearbeitende Programm auswählen und dann e drücken.
•Wenn Sie Text im Programm hinzufügen wollen, drücken Sie vor der
Bearbeitung @ O.
•Wenn Sie Zeilen im Programm einfügen wollen, drücken Sie @ O
(Der Cursor nimmt die Form eines Dreiecks an.). Bewegen Sie den
Cursor dann an den Anfang einer Zeile und drücken Sie e, um an
dieser Stelle eine neue Zeile einzufügen.
• Beachten Sie, dass pro Zeile nur ein Befehl eingegeben werden kann,
ausgenommen bei Sonderfällen wie z.B. dem “If...Goto”-Befehl.
Versuchen Sie bitte nicht, zwei oder mehr Befehle in einer Zeile
einzugeben.
• Die zu modifizierende Zeile wird nach dem Drücken von u, d
oder e gespeichert. Wenn Sie die Zeile nicht ändern wollen, drücken
Sie j zweimal. (Die Zeile verschwindet an dieser Stelle, aber die
Inhalte der Zeile werden nicht gelöscht.)
• Zum Löschen einer gesamten Zeile des Programms j und
anschließend u, d oder e drücken. Zum Löschen einer
leeren Zeile bewegen Sie den Cursor zur leeren Zeile und drücken
y.
• Leere Zeilen werden beim Ausführen des Programms ignoriert.
• y löscht das gerade eingegebene Zeichen an derselben Cursorposition.
• Sie können den Titel eines Programms ändern, indem Sie den vorhandenen Titel überschreiben. Zum Bewegen des Cursors zur Titelzeile
u drücken, dann den neuen Namen schreiben und e drücken.
3. Zum Beenden der EDIT-Modus drücken Sie j.

85
Kapitel 7: Programmierung
Fehlermeldungen
Der Rechner zeigt eine Fehlermeldung an, wenn ein Programm auf ein
Problem stößt. Die Fehlermeldung zeigt die Fehlerart an, während der
Rechner in diejenige Zeile springt, wo das Problem aufgetreten ist.
Nach der Eingabe eines Programms ist es häufig erforderlich, das
Programm zunächst zu testen. Um das Auffinden von Fehlern zu erleichtern,
zeigt der Rechner eine Fehlermeldung an, sobald er bei der Ausführung des
Programms auf ein Problem stößt.
Wenn Sie z.B. mehr als ein Label mit dem
gleichen Namen in Ihrem Programm eingegeben haben, erscheint die rechts abgebildete
Fehlermeldung im Display.
Für die Anzeige der fehlerhaften Zeile im EDITModus drücken Sie r oder l. Um zum
Programm-Menü zurückzukehren, drücken Sie
j.
Sie können jederzeit j drücken, um die
Ausführung des Programms zu stoppen. Dies ist
z.B. nötig, wenn Ihr Programm in eine Endlosschleife gerät.
In diesem Falle erscheint die Meldung “BREAK!” kurzzeitig im Display. Die
anfängliche Anzeige des PROG-Modus wird erneut angezeigt. Im Anhang
finden Sie eine Liste aller Fehlermeldungen. (s. Seite 120)
- ERROR 04 LBL DUPLICATE
BREAK!

86
Kapitel 7: Programmierung
PROGRAM MODE
ƒRUN ⁄NEW
¤EDIT ‹DEL
DEL ¬º⁄AREA
º¤TEMP
º‹STAT
TITLE:AREA
DELETE¬[DEL]
QUIT¬[ENTER]
Löschen von Programmen
Sie können so viele Programme erstellen, wie es die Speicherkapazität des
Rechners es zulässt. Um Platz für neue Programme zu schaffen, müssen
alte gelöscht werden.
1. Drücken Sie b 2, um den PROG-
Modus einzuschalten.
2. 3 drücken.
• In der DEL-Anzeige werden alle gespeicherten Programme aufgelistet.
3. Den Cursor an die Position des zu
löschenden Programms bewegen und
anschließend e drücken.
• Der Rechner fordert zur Bestätigung auf,
ob das Programm gelöscht werden soll.
•Drücken Sie y, um das Programm zu löschen oder e, um diesen
Vorgang abzubrechen.

87
Kapitel 8
Anwendungsbeispiele
Programmbeispiele
Die folgenden Beispiele zeigen die grundlegende Verwendung der
Programmierbefehle einschließlich Drucken, Eingabe und Ablaufsteuerungen. Nehmen Sie die Beispiele als Referenz zur Programmierung.
Celsius-Fahrenheit-Umrechnung
Dieses Programm dient zur Umrechnung von Temperaturen von Celsius in
Fahrenheit und umgekehrt.
1. b 2 1 0 drücken, um ein
neues Programm zu erstellen.
2. Geben Sie TEMP als Programmtitel ein, und
drücken Sie anschließend e.
• Ein neues Programm mit dem Titel
“TEMP” wird erstellt.
3. Geben Sie das Programm wie folgt ein:
• Siehe “*” unten für weitere Erklärungen.
Programmcode Tastenfolge
Label START i 6 @ a START ;
e
Print”(1) C TO F i 1 ( 1 ) @ a
s C s TO s F ; e
Print”(2) F TO C i 1 ( 2 ) @ a
s F s TO s C ; e
Input T i 2 ; T e
TEMP :NORMAL
PROGRAM?
* Das Programm fordert zur
Wahl des gewünschten
Umwandlungstyps auf. Drücken
Sie 1 für “C TO F” und 2
für “F TO C”.

88
Kapitel 8: Anwendungsbeispiele
Programmcode Tastenfolge
If T=1 Goto CTOF i 8 ; T ; = 1 ;
s i 9 @ a CTOF
; e
If T=2 Goto FTOC i 8 ; T ; = 2 ;
s i 9 @ a FTOC
; e
Goto START i 9 @ a START ;
e
Label CTOF i 6 @ a CTOF ;
e
F=(9©5)C≠+32 ; F ; = ( 9 z 5
) @ v C0 e e +
32 e
Print F i 0 ; F e
End i 5 e
Label FTOC i 6 @ a FTOC ;
e
C=(5©9)˚(F≠-32) ; C ; = ( 5 z 9
) k ( @ v d F0
e e - 32 ) e
Print C i 0 ; C e
End i 5 e
Ausführen des Programms
4. Um zum PROG-Menü zurückzukehren,
drücken Sie j.
5. Drücken Sie 0, wählen Sie das
Programm “TEMP” aus und drücken Sie
e.
• Das Programm fordert zur Wahl des gewünschten Umwandlungstyps
und anschließend zur Eingabe des Temperaturwertes auf.
PROGRAM MODE
ƒRUN ⁄NEW
¤EDIT ‹DEL
* Das Programm fordert
automatisch zur Eingabe eines
Wertes für die lokale Variable
C0 auf.
* Das Programm fordert
automatisch zur Eingabe eines
Wertes für die lokale Variable
F
0 auf.

89
Kapitel 8: Anwendungsbeispiele
Die Heronische Formel
Bestimmen Sie den Flächeninhalt S des
Dreiecks mit den Seitenlängen A, B und C mit
der Heronischen Formel, die für jedes ebene
Dreieck gilt.
1. b 2 1 0 drücken, um ein
neues Programm zu erstellen.
2. Geben Sie HERON als Programmtitel ein,
und drücken Sie anschließend e.
• Ein neues Programm mit dem Titel “HERON” wird erstellt.
3. Geben Sie das Programm wie folgt ein:
Programmcode Tastenfolge
Label START i 6 @ a START ;
e
Print”SIDE LENGTHS i 1 @ a SIDE s
LENGTHS ; e
Input A i 2 ; A e
Input B i 2 ; B e
Input C i 2 ; C e
If (A+B)<=C Goto ERROR i 8 ( ; A + ; B
) i E ; C ; s
i 9 @ a ERROR ;
e
If (B+C)<=A Goto ERROR i 8 ( ; B + ; C
) i E ; A ; s
i 9 @ a ERROR ;
e
If (C+A)<=B Goto ERROR i 8 ( ; C + ; A
) i E ; B ; s
i 9 @ a ERROR ;
e
T=(A+B+C)©2 ; T ; = ( ; A +
; B + ; C ) z 2
e
S = √ T (T – A) (T – B) (T – C)
T = —————
A + B + C
2
A
B
C
S

90
Kapitel 8: Anwendungsbeispiele
Programmcode Tastenfolge
S=‰(T(T-A)(T-B)(T-C)) ; S ; = @ * (
; T ( ; T - ; A
) ( ; T - ; B )
( ; T - ; C ) )
e
Print S i 0 ; S e
End i 5 e
Label ERROR i 6 @ a ERROR ;
e
Print”NO TRIANGLE i 1 @ a NO s
TRIANGLE ; e
Wait 1 i 3 1 e
Print”REENTER i 1 @ a REENTER ;
e
Goto START i 9 @ a START ;
e
Beispiel
Bestimmen Sie den Flächeninhalt des Dreiecks mit den Seitenlängen
20 cm (A), 35 cm (B) und 40 cm (C).
4. Um zum PROG-Menü zurückzukehren, drücken Sie j.
5. Drücken Sie 0, wählen Sie das
Programm “HERON” aus, und drücken Sie
e.
•Wenn die eingegebenen Werte nicht den
notwendigen Eigenschaften eines Dreiecks
(A + B > C, wobei A, B und C die Seitenlängen sind) entsprechen,
fordert das Programm zur Neueingabe der Werte auf. Wenn Sie das
Programm stoppen wollen, drücken Sie j.
6. Geben Sie 20 für A, 35 für B und 40 für C ein.
Ergebnis
Die Fläche des Dreiecks beträgt etwa
350 cm2.
HERON :NORMAL
SIDE LENGTHS
A=?
40
S=
349.944192

91
Kapitel 8: Anwendungsbeispiele
Umrechnen in andere Zahlensysteme
Die Umwandlungsfunktionen und logischen Operationen können im NBASEProgramm-Modus verwendet werden. Das folgende einfache Programm
wandelt eine Dezimalzahl in binäre, pentale, oktale und hexadezimale
Zahlenformate um.
1. b 2 1 1 drücken, um ein
neues Programm im NBASE-Modus zu
erstellen.
2. Geben Sie NBASE als Titel ein und
drücken Sie e.
• Ein neues Programm mit dem Titel “NBASE” wird erstellt.
3. Geben Sie das Programm wie folgt ein:
Programmcode Tastenfolge
Print”ENTER A i 1 @ a ENTER s A
; e
Print”DECIMAL NUMBER i 1 @ a DECIMAL s
NUMBER ; e
Input Y i 2 ; Y e
Y¬BIN ; Y @ z e
Print”BINARY i 1 @ a BINARY ;
e
Print Y i 0 ; Y e
Wait i 3 e
Y¬PEN ; Y @ r e
Print”PENTAL i 1 @ a PENTAL ;
e
Print Y i 0 ; Y e
Wait i 3 e
NBASE :NBASE
PROGRAM?

92
Kapitel 8: Anwendungsbeispiele
Programmcode Tastenfolge
Y¬OCT ; Y @ g e
Print”OCTAL i 1 @ a OCTAL ;
e
Print Y i 0 ; Y e
Wait i 3 e
Y¬HEX ; Y @ h e
Print”HEXADECIMAL i 1 @ a HEXADECIMAL
; e
Print Y i 0 ; Y e
Ausführen des Programms
4. Um zum PROG-Menü zurückzukehren, drücken Sie j.
5. Drücken Sie 0, wählen Sie das Programm “NBASE” aus und
drücken Sie e.
• Das Programm fordert zur Eingabe einer Dezimalzahl auf und zeigt
diese dann im Binärformat an.
• Drücken Sie eine beliebige Taste, um die Zahl im Pentalformat zu
zeigen, drücken Sie dann wieder eine beliebige Taste, um sie im
Oktalformat zu sehen, und drücken Sie erneut eine beliebige Taste, um
sie im Hexadezimalformat zu sehen.
• Seien Sie vorsichtig beim Verwenden des Befehls “Wait” im ProgrammModus NBASE. Die hinter dem “Wait”-Befehl stehenden Zahlen werden
entsprechend der aktuellen Zahlenbasis verarbeitet, also binär, pental,
oktal, dezimal oder hexadezimal.
Zur Eingabe der Wartezeit im Dezimalformat definieren Sie vorher eine
Var iable (z.B. T = 5) für die Wartezeit und verwenden Sie im “Wait”Befehl (d.h. Wait T).

93
Kapitel 8: Anwendungsbeispiele
T Test
Der T-Test-Wert wird durch den Vergleich der Mittelwerte von Stichprobenwerten und dem erwarteten Durchschnitt der Stichprobenwerte ermittelt.
Unter Verwendung der t-Verteilungstabelle kann die Zuverlässigkeit eines
Mittelwertes bewertet werden.
t = ———
m = erwarteter Mittelwert, geschätzt anhand von Stichproben
n = Anzahl der Stichproben
x = tatsächlicher Mittelwert der Stichprobe
sx = Standardabweichung der Stichprobe
x – m
sx
2
n
——
–
–
Beispiel
Im Geschäft von A werden Kekse in Packungen verkauft, die laut Beschriftung 100 g enthalten sollen. Kaufen Sie als Stichprobe 6 Packungen und
prüfen Sie, ob die Angabe richtig ist.
• Durch die Festlegung eines erwarteten Mittelwertes von 100 (m = 100 g)
kann ein t-Testwert ermittelt werden. Wenn er größer ist als der aus der
t-Verteilungstabelle erwartete t-Wert (bei 5% Risikorate), ist die
Schätzung falsch. (In diesem Fall verkauft das Geschäft A nicht ehrlich.)
Stichprobe 1 2 3 4 5 6
Gramm 102 95 107 93 110 98
1. b 2 1 0 drücken, um ein neues Programm zu erstellen.
2. Geben Sie TTEST als Titel ein, und drücken Sie e.
• Ein neues Programm mit dem Titel “TTEST” wird erstellt.
3. Geben Sie das Programm wie folgt ein:

94
Kapitel 8: Anwendungsbeispiele
Programmcode Tastenfolge
STATx i I e
Data 102 i K 102 e
Data 95 i K 95 e
Data 107 i K 107 e
Data 93 i K 93 e
Data 110 i K 110 e
Data 98 i K 98 e
Print”MEAN i 1 @ a MEAN ; e
Input M i 2 ; M e
T=(˛-M)©‰(sxŒ©˜) ; T ; = ( I 5
1 - ; M ) z @
* ( I 5 2 A z
I 5 0 ) e
Print T i 0 ; T e
End i 5 e
Ausführen des Programms
4. Um zum PROG-Menü zurückzukehren, drücken Sie j.
5. Drücken Sie 0, wählen Sie das Programm “TTEST” aus und drücken
Sie e.
6. Den erwarteten Mittelwert “100” eingeben und e drücken.
Ergebnis
Der t-Testwert von 0.303 ist kleiner als der Wert 2.571, der erwartete
Mittelwert aus der t-Test-Verteilungstabelle (bei 5% Risikorate). Das zeigt,
dass das Geschäft ehrlich verkauft.
100
T=
0.303058133

95
Kapitel 8: Anwendungsbeispiele
Bestimmen eines Kreises, der 3 gegebene Punkte schneidet
Wenn drei verschiedene Punkte P (X1, Y1), Q (X2, Y2), S (X3, Y3) gegeben
sind, können Sie die Koordinaten O (X, Y) des Mittelpunktes und den Radius
R desjenigen Kreises, der durch diese Punkte verläuft, bestimmen.
Um die obigen Bedingungen zu erfüllen, müssen die Abstände zwischen P,
Q, S und O gleich sein, da sie auf dem
Radius des gleichen Kreises liegen.
Deshalb gilt:
PO = QO = SO = R
Mit dem Satz des Pythagoras erhält man:
PO
2
= (X1 – X
)
2
+ (Y1 – Y
)
2
= R
2
QO2 = (X2 – X
)
2
+ (Y2 – Y
)
2
= R
2
SO2 = (X3 – X
)
2
+ (Y3 – Y
)
2
= R
2
daraus ergibt sich:
(X
1
2
+Y
1
2
-X
2
2
-Y
2
2
)(Y2–Y3) – (X
2
2
+Y
2
2
-X
3
2
-Y
3
2
)(Y1–Y2)
2{(X
1–X2
)(Y2–Y3) – (X2–X3)(Y1–Y2)}
X = ------ 1
(X
1
2
+Y
1
2
-X
2
2
-Y
2
2
)(X2–X3) – (X
2
2
+Y
2
2
-X
3
2
-Y
3
2
)(X1–X2)
2{(Y
1–Y2
)(X2–X3) – (Y2–Y3)(X1–X2)}
Y = ------ 2
R =
(X – X1)2 + (Y – Y1)
2
------ 3
Zur Verbesserung der Lesbarkeit und der Schreibbarkeit des Programms
werden Zwischenvariablen G, H, I, J, K und M verwendet.
Die obigen Gleichungen werden dafür vereinfacht zu:
GM – HK
2 (IM – JK)
X =
GJ – HI
2 (KJ – MI)
Y =
1. b 2 1 0 drücken, um ein neues Programm zu erstellen.
2. Gebens Sie CIRCLE als Titel ein, und drücken Sie e.
• Ein neues Programm mit dem Titel “CIRCLE” wird erstellt.
3. Geben Sie das Programm wie folgt ein:
Programmcode Tastenfolge
Print”ENTER COORDS i 1 @ a ENTER s COORDS
; e
G=X≥Œ+Y≥Œ-X√Œ-Y√Œ ; G ; = @ v X1 e
e A + @ v d Y1 e
e A - @ v d d X2
e e A - @ v d
d d Y2 e e A e
P (X1, Y1)
S (X
3, Y3)
Q (X
2, Y2)
O (X, Y)
X1–X
Y
1–Y
R
R
R
* Berechnen der Zwischen-
ergebnisse.

96
Kapitel 8: Anwendungsbeispiele
Programmcode Tastenfolge
H=X√Œ+Y√Œ-X…Œ-Y…Œ
; H ; = @ v 2 A
+ @ v 3 A - @ v
d d d d X3 e e A
- @ v d d d d d
Y3 e e A e
I=X≥-X√ ; I ; = @ v 0 -
@ v 2 e
J=X√-X… ; J ; = @ v 2 -
@ v 4 e
K=Y≥-Y√ ; K ; = @ v 1 -
@ v 3 e
M=Y√-Y… ; M ; = @ v 3 -
@ v 5 e
X=(GM-HK)©2(IM-JK)
; X ; = ( ; G ; M ; H ; K ) z 2 ( ; I
; M - ; J ; K ) e
Print X i 0 ; X e
Wait i 3 e
Y=(GJ-HI)©2(KJ-MI)
; Y ; = ( ; G ; J ; H ; I ) z 2 ( ; K
; J - ; M ; I ) e
Print Y i 0 ; Y e
Wait i 3 e
R=‰((X-X≥)Œ+(Y-Y≥)Œ)
; R ; = @ * ( ( ; X
- @ v 0 ) A + ( ;
Y - @ v 1 ) A ) e
Print R i 0 ; R e
Beispiel
Bestimmen Sie dieKoordinaten (X, Y) des Mittelpunktes und des Radius R
desjenigen Kreises, der durch die Punkte P (1, 9), Q (7, 1) und S (0, 2)
verläuft.
4. Um zum PROG-Menü zurückzukehren, drücken Sie j.
5. Drücken Sie 0, wählen Sie das Programm “CIRCLE” aus, und
drücken Sie e.
6. Geben Sie die Koordinaten (X1 bis X3, Y1 bis Y3) für die drei Punkte ein.
* Gleichung 1 ausführen.
* Gleichung 2 ausführen.
* Gleichung 3 ausführen.

97
Kapitel 8: Anwendungsbeispiele
Ergebnis
Der Mittelpunkt liegt in (4, 5) und der Radius beträgt 5.
Radioaktiver Zerfall
Kohlenstoff-14 (14C) ist ein natürlich vorkommendes radioaktives Isotop von
Kohlenstoff, das bei der Kohlenstoffaltersbestimmung verwendet wird. Da
Kohlenstoff-14 mit einer gleichmäßigen Rate zerfällt, ist es möglich, das
Alter von Fossilien durch Messung der enthaltenen Restmengen an
14
C zu
bestimmen.
Die Masse von 14C wies in einer Stichprobe die der folgenden
Gleichung entsprechenden Veränderungen auf:
M = M
0
e
–kt
oder t = –––––––––
wobei M
1
= Masse von 14C zur Zeit t
M
0
= Ursprüngliche Masse von 14C
k = Radioaktive Zerfallskonstante (für
14
C, k = 1.2118 × 10–4 Jahr–1)
t = Vergangene Zeit in Jahren
M
1
M
0
k
–ln ( ––– )
Beispiel
Dieses Programm fordert zur Eingabe einer Original-Masse und der
aktuellen Masse von 14C auf und teilt dann das Alter des Exemplars mit. Es
berechnet anschließend die Halbwertszeit von 14C.
1. b 2 1 0 drücken, um ein neues Programm zu erstellen.
2. Geben Sie DECAY als Titel ein, und
drücken Sie e.
• Ein neues Programm mit dem Titel
“DECAY” wird erstellt.
3. Geben Sie das Programm wie folgt ein:
Programmcode Tastenfolge
Print”ORIGINAL MASS i 1 @ a ORIGINAL s
MASS ; e
Input M≠ i 2 @ v M0 e e
e
Print”CURRENT MASS i 1 @ a CURRENT s
MASS ; e
DECAY :NORMAL
PROGRAM?

98
Kapitel 8: Anwendungsbeispiele
Programmcode Tastenfolge
Input M≥ i 2 @ v d M1 e
e e
T=-(ln(M≥© M≠))© ; T ; = S ( i
1.2118œ-4 ( @ v 1 z @
v 0 ) ) z 1.2118
` S 4 e
Print T i 0 ; T e
Print”YEARS i 1 @ a YEARS ;
e
End i 5 e
• Die Halbwertszeit eines radioaktiven Isotops ist die Zeit, in der die
Hälfte seiner Masse zerfällt.
Ausführen des Programms
4. Um zum PROG-Menü zurückzukehren, drücken Sie j.
5. Drücken Sie 0, wählen Sie das
Programm “DECAY” aus, und drücken Sie
e.
6. Geben Sie 100 für M0 und 50 für M1 ein.
Ergebnis
Die Halbwertszeit von 14C beträgt
5719.980034 Jahre.
DECAY :NORMAL
ORIGINAL MASS
Mº=?
T=
5719.980034
YEARS
 Loading...
Loading...