
42 High Frequency Electronics
High Frequency Design
BROADBAND DESIGN
Broadband VHF/UHF
Amplifier Design Using
Coaxial Transformers
By C. G. Gentzler and S.K. Leong
Polyfet RF Devices
T
he desire of the
armed forces to
maintain instant
communications with all
forces requires the design
of miniature broadband
power amplifiers with
greater than decade
bandwidth (30 to 512
MHz). This bandwidth is
required for all-band transceivers that cover
tactical ground and air frequencies in addition
to civil telecommunication frequencies and the
frequencies of our allies. All-band radios are
commonplace in virtually every deployment of
new platforms, as well as in the retrofitting of
existing communications systems.
This paper will discuss the design of miniature coaxial structures and examine the
implementation of improved design techniques to enable the designer to obtain insight
into matching the load line of power MOSFET
transistors over decade bandwidths.
This article presents the development of
large signal parameters for a typical power
MOSFET device and the development of a
suitable load line using coaxial transmission
line transformers in conjunction with embedded lumped structures, enabling an efficient
load line match across a decade of bandwidth.
Simulation Methodology.
Linear simulation assumes that a circuit
with active devices is operated at such a low
power that the simulated measurements are
no longer power dependent. This simulation
can be achieved by two methods. First the circuit uses a nonlinear model and nonlinear
simulator. The quiescent current is set at a
nominal condition and the power level used in
the simulation is set to a low level so as not to
make the output data power dependent.
Another linear simulation method is to use
tabular data to describe an active device and
simulate with a linear simulator. Usually the
data file is in S-parameter format although
other formats have been used in the past at
lower frequencies (e.g. impedance magnitude
and angle). If the nonlinear model and the
data file agree, both simulations will yield the
same measurement data. In the case of using
a non-linear model with a nonlinear simulator, the simulation results are generally very
close to actual amplifier performance.
Nonlinear simulators provide gain compression, power output, efficiency and harmonic power data. With somewhat less accuracy, intermodulation distortion can be simulated, but not with the same accuracy as the
single tone measurements. To obtain accurate
results, the device model would have to track
an actual device transfer curve closer than 5
percent. Five percent accuracy is generally
acceptable for gain compression and efficiency
measurements, but not for the slight nonlinearity that causes low to intermediate levels
of intermodulation distortion. Modeling technology is slowing improving and it is expected
that intermodulation performance may be
accurately modeled in the future. Nonlinear
simulators generally are more costly, but are
really the only choice if large signal performance simulation is desired, as in the case of
this article.
Amplifier Design
First one must determine the optimum
load line impedance required by the device.
This article describes the
methods used to design
broadband coaxial trans-
former matching networks
for an LDMOS power ampli-
fier that delivers consistent
performance over more
than a decade bandwidth
From May 2003 High Frequency Electronics
Copyright © 2003 Summit Technical Media, LLC
44 High Frequency Electronics
High Frequency Design
BROADBAND DESIGN
Computer load pull or optimization is
required since any actual load pull
techniques are only generally available for much higher frequencies. The
physical structures for generating
load impedances at frequencies below
500 MHz are too large to be practical
to implement. Additionally, since the
band width is multi-octave, broadband matching structures must be
used to determine the load line
rather than multiple narrow band
measurements. A computer with suitable software and good device models
is the most practical approach. In
this article we will use popular software packages such as Applied Wave
Research’s (AWR) Microwave Office
and Agilent Technologies’ ADS, used
together with Polyfet RF Spice
Models to demonstrate broadband
matching techniques.
Impedance Behavior of
Transistors
At low frequencies, the device’s
output impedance is relatively high
compared with the calculated load
line required to produce the desired
power. As the operating frequency is
increased, the output capacitance
(C
oss
), reverse capacitance (C
rss
) and
an increased saturation voltage lowers the optimum load line to achieve
satisfactory performance.
Over a decade of bandwidth, the
optimum impedance can drop by a
factor of two. That is to say that if the
low frequency load line is 6 ohms, the
upper operating frequency could
require an impedance of 3 ohms with
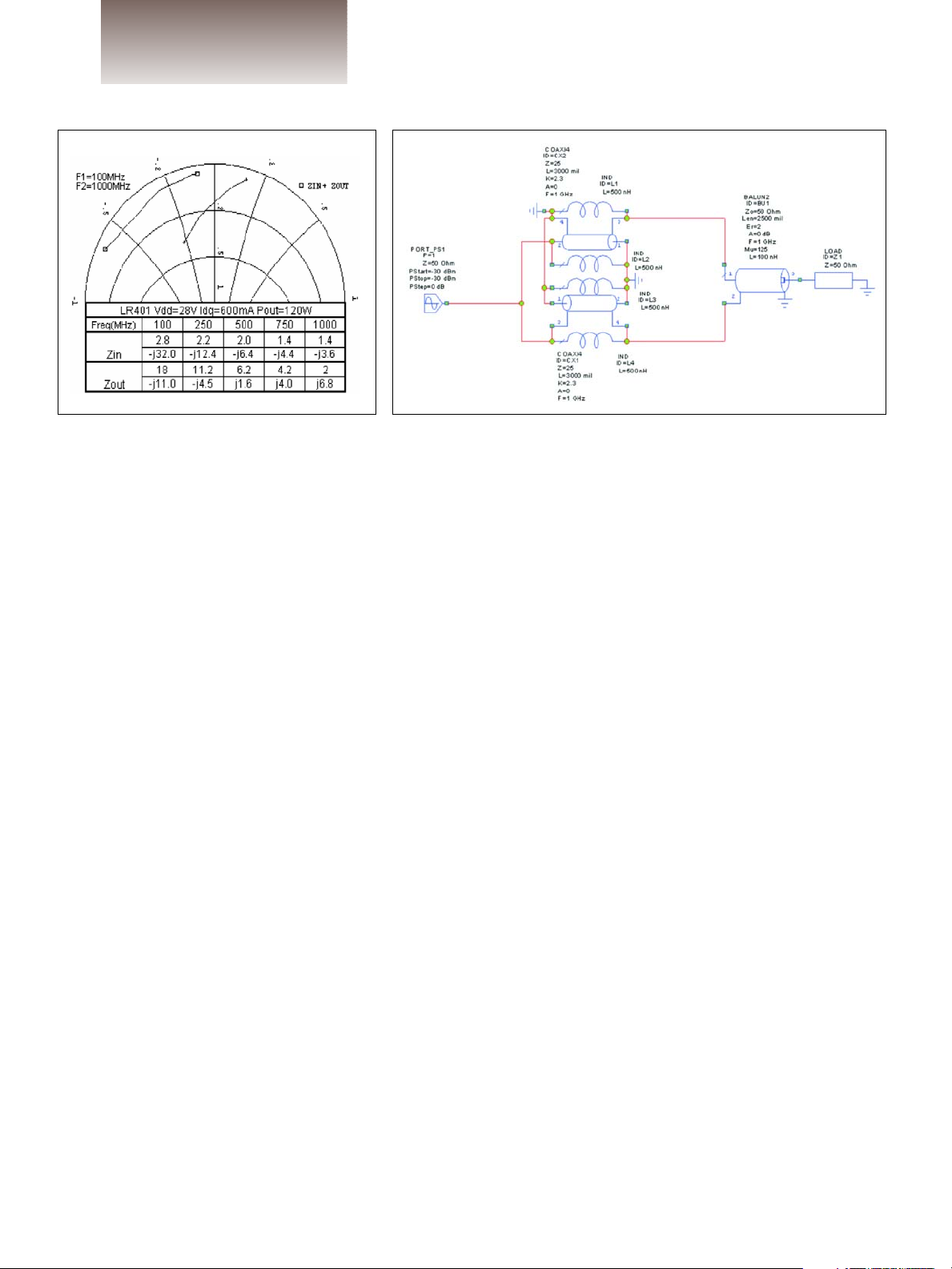
some amount of inductive or capacitive reactance. Figure 1 shows real
value of Z
out
dropping from 11 ohms
at low frequencies to 2 ohms at high
frequency for the transistor LR401.
There has been considerable
experimental and developmental
work published on the attributes of
coaxial transformers to achieve
extremely wide bandwidths. This
paper will explore how to combine
the coaxial transformer with lumped
components to achieve optimal power
matching in a MOSFET power amplifier over more than a decade of bandwidth.
Computer simulated load pulling
will be utilized to extract the first
order magnitude of load line matching. This impedance information is
only the starting point, since it will
be extracted by a narrow band technique. Broadband extraction is an
area that will be explored in the
future as the results will take into
account more realistic harmonic loading and allow more accurate broadband design implementation. In the
case of Polyfet transistors, Z
in/Zout
data can be found for each transistor
in its respective data sheet.
Once the approximate load line
has been determined, let us review
the coaxial transformer matching
techniques and explore the use of
physical length, cable impedance,
and lumped components in addition
to ferrite loading to achieve optimum
performance.
Of all the coaxial transformer
designs, one of the most practical for
wideband impedance matching is the
4:1 design with a balun transformer
to achieve optimum balance. The
standard accepted equation for transformation is that the Z
0
of the cable
should be the square root of the product of the input and output
impedances. For example, if the input
impedance is 12.5 ohms and the output impedance is 50 ohms, then the
square root of 12.5 × 50 = 25. A 25ohm impedance cable would give the
optimum results across a wide operating bandwidth.
Figure 3 shows a uniform
impedance transformation ratio of
four across the frequency band. It
should be noted for the purpose of
load line design, impedance is measured drain to drain. This allows single ended impedance measurements.
Simply divide the impedance data by
two to obtain individual device load
impedance. At 30 MHz the ratio falls
off due to reactive shunt losses,
which could be compensated with
Figure 1 · Zinand Z
out
vs. frequency. Figure 2 · Conventional 4:1 transformer with balun.

46 High Frequency Electronics
High Frequency Design
BROADBAND DESIGN
ferrite loading. The object is to
design a load line that lowers the
real resistance as the frequency
increases. This requires some
rethinking as to how one might
exploit the benefits of transmission
line matching in conjunction with
techniques mentioned above to
achieve a satisfactory load line over
a decade of bandwidth.
A Novel Approach
The following is a presentation of
how to embed a lumped matching
network into a transmission matching network to achieve a suitable
broad band power match. A conventional design allows the coaxial
transformer to transform the
impedance to obtain a match the low
end of the band, then add additional
lowpass matching sections to lower
the impedance at the upper band
edge. Although this technique performs satisfactorily, a microstrip
implementation would occupy considerable space.
A novel approach to this problem,
shown in Figure 4, is to use the effective inductance of the coaxial transmission lines as the inductive component in a pi matching network. Only
small chip capacitors will be needed
to complete the transformation at the
upper band edge. By a selection of the
transmission line impedance and
electrical length, a load line may be
created that will essentially provide
the basic transformation ratios at the
lower band edge. As the operating
frequency is increased the combination of the transmission line effective
inductance and the shunt capacitance will lower the load line to effectively match the device at the upper
band edge. Figure 5 shows the
impedance dropping with increasing
frequency. This can be accomplished
with the same physical constraints as
just a broadband transformer alone.
This technique enables one to construct decade bandwidth power
amplifiers with physical dimensions
no larger than the transformers and
the device. The savings in size can be
critical in some applications.
Designing the Load Line
To design our example 80 watt
broadband amplifier that covers 30
512 MHz band, one would first calculate the load line for the lower band
edge. Using a simple approximation
of Steve Cripps law [1],
let’s calculate the low frequency load
line. (28–5)
2
/(2×80) = 3.31 ohms or
6.62 ohms for two push-pull devices.
A 6.25-ohm load line that is achieved
with a 4:1 coaxial transformer and a
1:1 balun easily accomplishes this
task.
Next, using simulator generated
Frequency Coax transformer
(GHz) Z
in
[1] Zin[1]
(Real) (Imag.)
0.03 11.10 4.92
0.08 12.94 1.91
0.13 13.07 0.94
0.18 12.99 0.45
0.23 12.87 0.17
0.28 12.73 0.02
0.33 12.60 –0.05
0.38 12.49 –0.06
0.43 12.41 –0.04
0.48 12.37 0.00
0.53 12.36 0.05
0.58 12.37 0.08
0.6 12.38 0.09
Figure 3 · Uniform 4:1 transformation
across the frequency band.
Figure 4 · Variable 4:1 impedance transformer and matching network.
Frequency Coax transformer
(GHz) Z
in
[1] Zin[1]
(Real) (Imag.)
0.03 11.91 4.13
0.08 12.17 –1.02
0.13 10.06 –2.17
0.18 8.35 –1.77
0.23 7.29 –0.79
0.28 6.75 0.34
0.33 6.64 1.42
0.38 6.83 2.33
0.43 7.21 2.95
0.48 7.62 3.22
0.53 7.86 3.20
0.58 7.80 3.05
0.6 7.69 2.99
Figure 5 · Impedance decreases
with frequency.
VV
()
=
dd sat
2
R
load
2
−
P
out

48 High Frequency Electronics
High Frequency Design
BROADBAND DESIGN
large signal impedance data, review
the optimum match at the upper
band edge. The next step is to use a
linear simulator to embed the matching structure into the transformer
structure. In order to successfully
embed the upper edge matching network into the transformer the electrical length of the transformer should
be shorter that 1/8 wavelength at the
highest operating frequency. This will
keep the transmission line acting as
an inductance. Both the length and
impedance may be varied to optimize
the performance over the band.
For example, to design an embedded matching network for the Polyfet
LR401 push-pull MOSFET device,
one would start with the power level
desired and determine the low frequency load line. Since the low frequency load line is output power
related and not necessarily a function
of the output impedance of the
device, we will use a 4:1 coaxial
transformer followed by a 1:1 balun
transform to establish a solid 6.25
ohm load line from the lower band
edge up to several octaves higher or
around 120 MHz. Above 120 MHz,
the large signal impedance will
determine the impedance transformation required to maintain adequate performance. The technique in
broadband matching is normally to
match the highest frequency and use
the fact the power impedance contours where satisfactory operation
can be obtained become larger as the
operating frequency is reduced.
Large Signal Simulation
Once the load line has been
designed, it is time for large signal
simulation. The input matching section is designed in a similar manner
as the output section with the exception that since the return loss can be
measured during simulation, it is
much easier to either manually tune
or automatically optimize the input
circuit.
Assuming the tentative circuit
design has been completed, the next
step is nonlinear simulation. It is
strongly recommended to start the
simulation at a low input power level
and check for small signal gain, gain
flatness, and input return loss. The
input return loss may be tuned under
small signal conditions since it will
not change significantly as the power
level is increased. Do not attempt to
tune on the output matching section
under small signal operation, since
the load line tuning is extremely
power sensitive. Once satisfactory
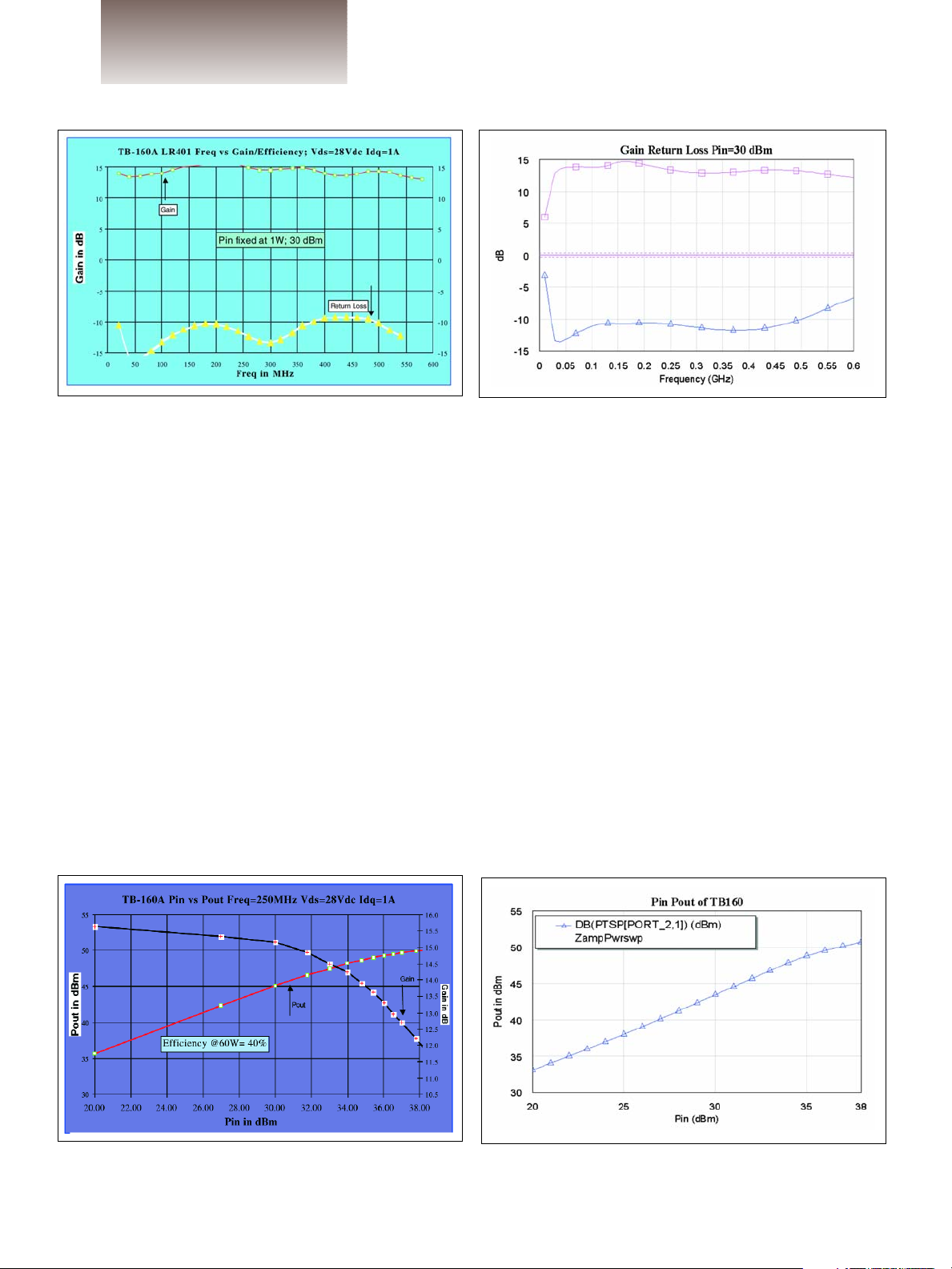
Figure 6 · Input schematic for nonlinear simulation.
Figure 7 · Input circuit layout diagram. Figure 8 · Actual amplifier; note the small size.
50 High Frequency Electronics
High Frequency Design
BROADBAND DESIGN
gain and return loss has been
obtained under small signal condition, slowly raise the input power
until the amplifier starts to compress. Typically, the compression will
first occur at mid to higher frequencies. The goal of high power optimization is to obtain a flat compression
point across the highest octave of
amplifier operation. Manual tuning
or an optimization feature may
accomplish this goal. Manual tuning
is usually the best avenue of
approach since most optimization
routines are somewhat linear simulation based, and variables (component
values) have to be constrained greatly in order to get meaningful results.
With today’s Pentium computers and
improved EDA software, nonlinear
simulation speeds approach that of
linear simulation just a few years
earlier.
Real time nonlinear tuning is a
capability of present simulators. As
the optimum load line is approached,
slight optimization of the input circuit will be required to obtain an optimum input return loss. Since the output load line tuning has minimal
effect on the input tuning only a
slight adjustment should be required.
The circuit used in simulation
shown in Figure 6 consists of similar
input and output matching networks,
as described earlier in this article.
The series R-C on the output of the
input balun acts as series gate resistance to lower the gain of the transistor. A series RLC network between
gate and source is added to stabilize
the transistor from low frequency
oscillations and series RLC drain to
gate feedback is added to further
enhance stability and achieve a flat
gain over the band. The schematic
shows additional inductances to represent the printed circuit board pads
for component mounting. The drains
of the transistors are fed to DC supplies through chokes that are represented by air coils. At the DC supply
feed, there is a choke with a parallel
resistor to further increase the stability of the amplifier. Figure 7 shows
the computer generated artwork
courtesy of AWR [2] and Figure 8 is a
photo of the actual amplifier built
from the simulation and artwork.
Simulation Results
Very good correlation between
simulated and actual measurements
Figure 12 · Simulated Pin vs. Pout.Figure 11 · Measured Pin vs. Pout.
Figure 9 · Measured gain and return loss. Figure 10 · Simulated values of gain and return loss.

May 2003 51
can be seen between Figures 9 and 10
and between Figures 11 and 12, verifying validity of models of both active
and passive components.
Figures 9 and 10 show the measured and simulated gain and return
loss performance across the full 30 to
512 MHz bandwidth. Very good
return loss was achieved. The gate
series resistance improves return
loss in addition to lowering device
gain. By its nature, the LDMOS transistor yielded very high gain of 14 dB
across the entire bandwidth at high
power out. Figures 11 and 12 show
the results for P
in
and P
out
, This measures the accuracy of simulation at
both low and high power.
The simulation results shown
here are from AWR Microwave Office.
Similar results were achieved with
Agilent’s ADS software. Simulation
files for both simulators can be downloaded from Polyfet’s website:
www.polyfet.com. At this website,
data sheet, S-parameter and spice
model for the LR401, as well as other
transistors are also available.
This topic was presented at the
MicroApps seminar at the 2002 MTT-S
International Microwave Symposium.
The slide presentation is also available
at the Polyfet website for download
(www.polyfet.com).
Conclusion
In conclusion, by implementing
lumped impedance matching embedded into coaxial transmission line
impedance transformation, an amplifier has been designed that possesses
wide bandwidth, gain flatness, reasonable input VSWR, linearity and
efficiency in a physically small footprint. It has also been demonstrated
the feasibility to accurately simulate
a high power broadband amplifier
using off the shelf commercial non
linear simulators.
References
1. Steve Cripps, RF Power
Amplifiers for Wireless Communications, Artech House, 1999.
Acknowledgment
2. Thanks to Ryan Welch of
Applied Wave Research, Inc.,
provider of Microwave Office, for creating the amplifier layout drawing.
Author Information
S.K.Leong is the Founder and
President of Polyfet RF Devices, 1110
Avenida Acaso, Camarillo, CA 93012.
He can be reached by e-mail at:
sk_leong@polyfet.com.
Charles Gentzler is CTO of
Paradigm Wireless Systems and a
member of the Board of Directors of
Polyfet RF Devices.
 Loading...
Loading...