3B Scientific Pohl's Torsion Pendulum User Manual

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

U15040 Drehpendel nach Prof. Pohl

Bedienungsanleitung

12/03 ALF

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

9

8

7

6

5

4

bl bm bn bo bp

bq br bs

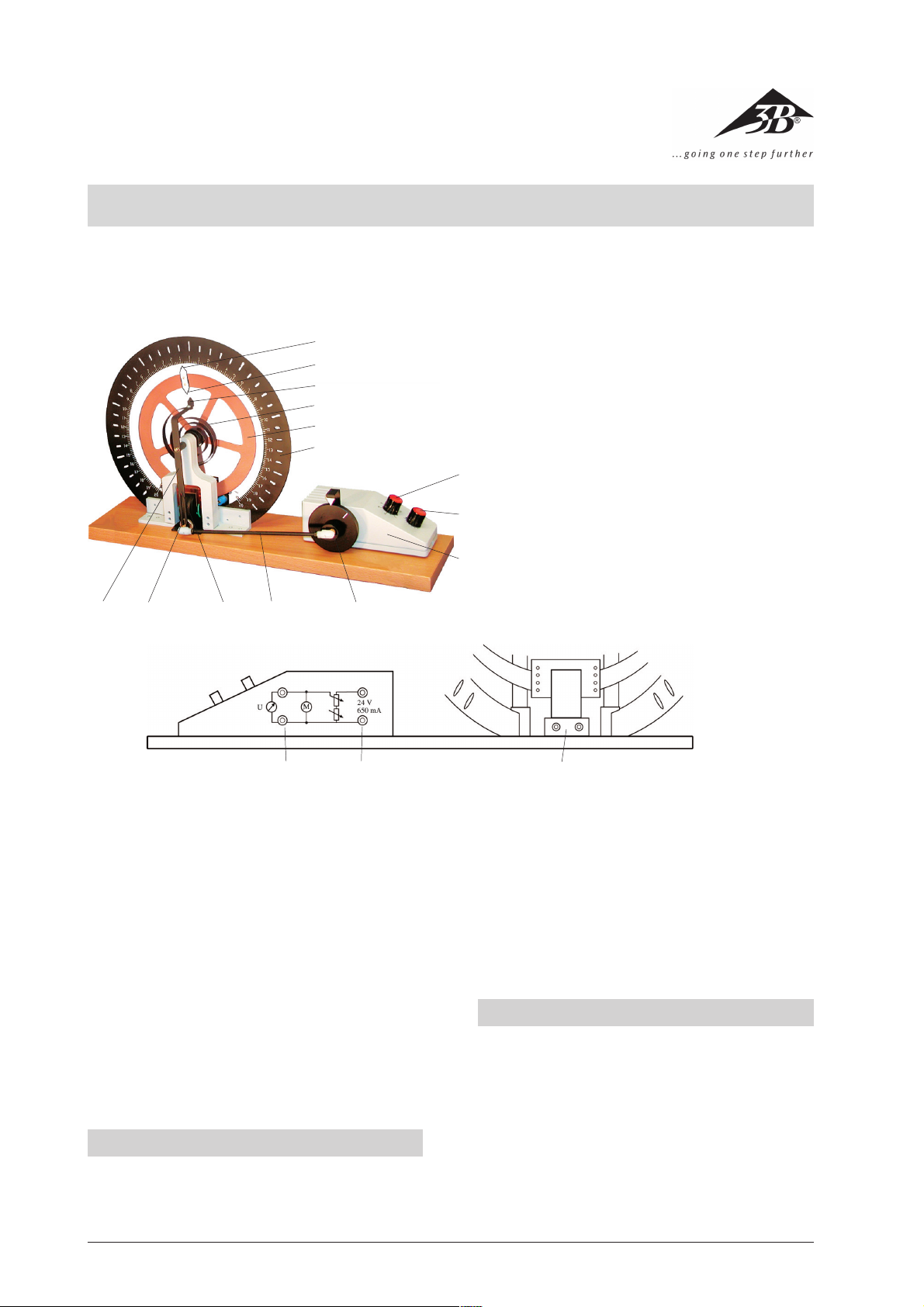
1 Erregermotor 2 Drehknopf zur Feineinstellung der Erregerspannung 3 Drehknopf zur Grobeinstellung der Erregerspannung 4 Skalenring 5 Pendelkörper 6 Schneckenfeder 7 Zeiger zur Phasenlage des Erregers 8 Zeiger zur Phasenlage des Pendelkörpers 9 Zeiger für Auslenkung des Pendelkörpers

3

bl Erreger bm Wirbelstrombremse bn Führungsschlitz und Schraube zur Einstellung der Erreger-

2

amplitude

bo Schubstange bp Antriebsrad mit Exzenter

1

bq 4-mm-Sicherheitsbuchsen zum Messen der Erregerspannung br 4-mm-Sicherheitsbuchsen zur Versorgung des Erregermotors bs 4-mm-Sicherheitsbuchsen zur Versorgung der Wirbelstrom-

bremse

Das Drehpendel dient zur Untersuchung von freien, erzwungenen und chaotischen Schwingungen bei verschiedenen Dämpfungen.

Versuchsthemen:

• Freie Drehschwingungen bei verschiedenen Dämp-

fungen (Schwingfall mit mäßiger Dämpfung, aperiodische Schwingung und aperiodischer Grenzfall)

• Erzwungene Schwingungen und deren Resonanz-

kurven bei verschiedenen Dämpfungen

• Phasenverschiebung zwischen Erreger und Resona-

tor im Resonanzfall

• Chaotische Drehschwingungen

• Statische Bestimmung der Richtgröße D

• Dynamische Bestimmung des Trägheitsmoments J

1. Sicherheitshinweise

• Das Drehpendel bei der Entnahme aus der Verpa-

ckung nicht am Skalierring anfassen! Beschädi-

gungsgefahr! Entnahme immer mit Entnahmehilfe (Innenverpackung) vornehmen!

• Zum Tragen des Drehpendels Gerät immer an der

Grundplatte halten.

• Maximal zulässige Versorgungsspannung des

Erregermotors (24 V DC) nicht überschreiten.

• Das Drehpendel keinen unnötigen mechanischen

Belastungen aussetzen.

2. Beschreibung, technische Daten

Das Drehpendel nach Prof. Pohl besteht aus einem auf einer hölzernen Grundplatte montiertem schwingenden System und einem Elektromotor. Das schwingende System ist ein kugelgelagertes Kupferrad (5), das über eine Spiralfeder (6), die das rücktreibende Moment liefert, mit dem Erregergestänge verbunden ist. Zur Anregung des Drehpendels dient ein Gleichstrommotor mit grob- und fein einstellbarer Drehzahl, der über einen Exzenter (14) mit Schubstange (13) die Spi-

1

ralfeder in periodischer Folge auseinanderzieht und

ω

0

2

=

D

J

zusammendrückt und so das Kupferrad in Schwingung versetzt. Für die Dämpfung wird eine elektromagnetische Wirbelstrombremse (11) verwendet. Ein Skalenring (4) mit Schlitzen und Skala in 2-mm-Teilung umgibt das schwingende System; Zeiger befinden sich an Erreger und Resonator. Das Gerät kann auch in der Demonstration zur Schattenprojektion verwendet werden. Für die Stromversorgung wird ein DC-Netzgerät für Drehpendel U11755 benötigt.

Eigenfrequenz: ca. 0,5 Hz. Erregerfrequenz: 0 bis 1,3 Hz (stufenlos einstellbar) Anschlüsse: Motor: max. 24 V DC, 0,7 A,

über 4-mm-Sicherheitsbuchsen

Wirbelstrombremse:0 bis 24 V DC, max. 2 A,

über 4-mm- Sicherheitsbuchsen Skalenring: 300 mm Ø Abmessungen: 400 mm x 140 mm x 270 mm Masse: 4 kg

2.1 Lieferumfang

1 Drehpendel 2 Zusatzmassen 10 g 2 Zusatzmassen 20 g

3. Theoretische Grundlagen

3.1 Verwendete Formelzeichen

D = Winkelrichtgröße J = Massenträgheitsmoment M = Rücktreibendes Drehmoment T = Periodendauer T0= Periodendauer des ungedämpften Systems Td= Periodendauer des gedämpften Systems



= Amplitude des Erreger-Drehmoments

M

E

b = Dämpfungsmoment n = Periodenzahl t = Zeit

Λ = Logarithmisches Dekrement δ = Dämpfungskonstante

ϕ

= Auslenkwinkel



ϕ

= Amplitude zur Zeit t = 0 s

0



ϕ

= Amplitude nach n Perioden

n



ϕ

= Erregeramplitude

E



ϕ

= Systemamplitude

S

ω0= Eigenfrequenz des schwingenden Systems ωd= Eigenfrequenz des gedämpften Systems ωE= Erregerkreisfrequenz ωE

= Erregerkreisfrequenz für max. Amplitude

res

Ψ0S= Systemnullphasenwinkel

3.2 Harmonische Drehschwingung

Eine harmonische Schwingung liegt vor, wenn die rücktreibende Kraft proportional zur Auslenkung ist. Bei harmonischen Drehschwingungen ist das rück-

treibende Drehmoment proportional zum Auslenkwinkel ϕ:

M = D ·

ϕ

Der Proportionalitätsfaktor D (Winkelrichtgröße) lässt sich durch Messung des Auslenkwinkels und des auslenkenden Moments errechnen. Die Eigenkreisfrequenz des Systems ω0 ergibt sich nach Messung der Periodendauer T aus

ω

= 2 π/T

0

und das Massenträgheitsmoment J aus

3.3 Freie gedämpfte Drehschwingung

Bei einem schwingenden System, bei dem durch Reibungsverluste Energie verloren geht, ohne dass diese durch von außen zugeführte Energie kompensiert wird, verringert sich die Amplitude ständig, d.h. die Schwingung ist gedämpft. Dabei ist das Dämpfungsmoment b proportional zur Winkelgeschwindigkeit

.

ϕ

. Aus dem Drehmoment-Gleichgewicht ergibt sich die Bewegungsgleichung

.

..

JbD⋅+⋅+⋅=

ϕϕϕ

0

Für die ungedämpfte Schwingung ist b = 0 Beginnt die Schwingung zur Zeit t = 0 s mit der maxi-



malen Amplitude

ϕ

ergibt sich die Lösung der Diffe-

0

renzialgleichung bei einer nicht zu starken Dämpfung (δ² < ω0²) (Schwingfall)



–δ ·t

ϕ

=

· e

· cos (

ω

0

d

· t)

δ = b/2 J ist die Dämpfungskonstante und

2

ωωδ

=−

d

2

0

die Eigenfrequenz des gedämpften Systems. Bei einer starken Dämpfung (δ² > ω0²) schwingt das System nicht, sondern kriecht in die Ruhelage (Kriechfall). Die Periodendauer Td des gedämpft schwingenden Systems ändert sich gegenüber T0 des ungedämpft schwingenden Systems bei nicht zu starker Dämpfung nur geringfügig. Durch Einsetzen von t = n · Td in die Gleichung



–δ ·t

ϕ

ϕ =

und für die Amplitude nach n Perioden ϕ = man mit der Beziehung



ϕ



ϕ

· e

0

n

0

δ

−⋅

n

=⋅

eT

· cos (

ω

= 2 π/T

d

ω

· t)

d



ϕ

erhält

n

d

und daraus das logarithmische Dekrement Λ:

Λ

=⋅ =⋅

δ

T

d





ϕ

1 n

n



In In





ϕ

0











ϕ



=

 

n











ϕ

n+1





2

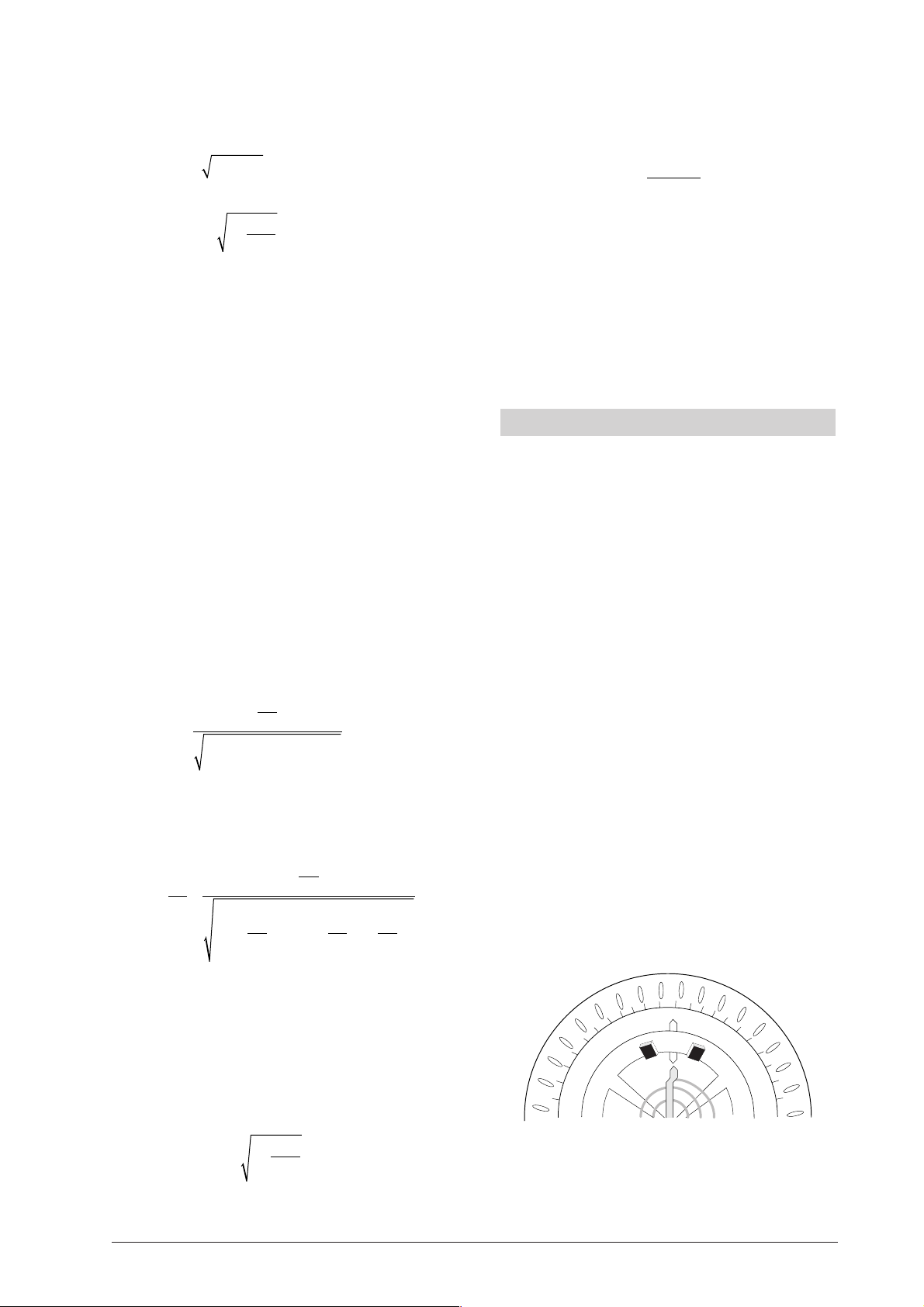
Durch Einsetzen von δ = Λ / Td ,

Ψ

ω

= 2π / Td in die Gleichung

d

2

ωωδ

=−

d

2

0

ω

= 2 π / T0 und

0

erhält man:

2

TT

=⋅+1

d0

Λ

2

4

π

womit sich die Periodendauer Td genau berechnen lässt, wenn T0 bekannt ist.

3.4 Erzwungene Drehschwingung

Bei erzwungenen Drehschwingungen wirkt von außen ein periodisch mit einer Sinusfunktion veränderliches Drehmoment auf das schwingende System. In der Bewegungsgleichung ist dieses Erregermoment zu ergänzen

.

..

JbD M t⋅+⋅+⋅= ⋅ ⋅

ϕϕϕ ω



sin

E

()

E

Nach einer Einschwingzeit schwingt das Drehpendel in einem stationären Zustand mit derselben Kreisfrequenz wie der Erreger, dabei kann ωE noch gegen ω phasenverschoben sein. Ψ0S ist der System-Nullphasenwinkel, die Phasenverschiebung zwischen dem schwingenden System und dem Erreger.



ϕ

=

· sin (

ω

· t –

Ψ

S

E

Für die Systemamplitude



ϕ

=

2

ωω δω

−

()

02E

M

J

2

)

0S



ϕ

gilt

S

E

2

+⋅

4

2

E

Für das Verhältnis von Systemamplitude zu Erregeramplitude gilt



M



ϕ

S

=



ϕ

E





ω

E



−

14



ω



0





E

J

2







+









2





δ





ω

0





2





ω

E

⋅





ω

0





Bei starker Dämpfung gibt es keine Amplitudenüberhöhung. Für den System-Nullphasenwinkel Ψ0S gilt



arctan

 

ωω



=

0S



δω

2



22



−

ω

0



Für ωE = ω0 (Resonanz) ist der System-Nullphasenwinkel Ψ0S = 90°. Dies gilt auch für δ = 0 mit entsprechendem Grenzübergang. Bei gedämpften Schwingungen (δ > 0) und ωE < ω ergibt sich 0° ≤ Ψ0S ≤ 90°, für ωE > ω0 gilt 90° ≤ Ψ

0

0S

≤ 180°. Bei ungedämpften Schwingungen (δ = 0) gilt Ψ0S = 0° bei ωE < ω0 und Ψ0S = 180° für ωE > ω0.

4.Bedienung

4.1 Freie gedämpfte Drehschwingung

• Wirbelstrombremse mit dem Ausgang für einstell-

bare Spannung des Drehpendel-Netzgeräts verbinden.

• Amperemeter in den Stromkreis schalten.

0

• Dämpfungskonstante in Abhängigkeit vom Strom

bestimmen.

4.2 Erzwungene Drehschwingung

• Anschlussbuchsen (16) des Erregermotors mit dem

Festspannungsausgang des Drehpendel-Netzgeräts verbinden.

• Voltmeter mit den Anschlussbuchsen (15) des

Erregermotors verbinden.

• Bestimmung der Schwingungsamplitude in Abhän-

gigkeit der Erregerfrequenz bzw. der Versorgungsspannung.

• Bei Bedarf Wirbelstrombremse mit dem Ausgang

für einstellbare Spannung des Drehpendel-Netzgeräts verbinden.

4.3 Chaotische Schwingungen

• Zur Erzeugung chaotischer Schwingungen stehen 4

Zusatzmassen zur Verfügung, die das lineare Rückstellmoment des Drehpendels verändern.

• Dazu Zusatzmasse am Pendelkörper (5) anschrau-

ben.

Bei ungedämpften Schwingungen steigt die Amplitude im Resonanzfall (ωE gleich ω0) theoretisch unendlich an und führt zur „Resonanzkatastrophe“. Bei gedämpften Schwingungen und nicht zu starker Dämpfung wird die Systemamplitude maximal, wobei die Erregerkreisfrequenz ω

kleiner ist als die Eigen-

E res

kreisfrequenz des Systems. Diese Frequenz ergibt sich aus

2

δ

ωω

=⋅−1

Eres 0

2

ω

0

3

5. Versuchsbeispiele

5.1 Freie gedämpfte Drehschwingung

• Zur Bestimmung des logarithmischen Dekrements Λ werden die Amplituden in mehrfachen Durch-

läufen gemessen und gemittelt. Dazu werden in zwei Messreihen die Ausschläge des Drehpendels auf der Skala jeweils links und rechts abgelesen.

• Der Startpunkt des Pendelkörpers lag bei 15 bzw. –15 auf der Skala. Fünf Ausschläge wurden abgelesen.

• Aus dem Verhältnis der Amplituden ergibt sich Λ nach der Formel







ϕ

n



Λ

=

In

n









ϕ

n+1







ϕ

–



ϕ

+

0 –15 –15 –15 –15 15 15 15 15 1 –14,8 –14,8 –14,8 –14,8 14,8 14,8 14,8 14,8 2 –14,4 –14,6 –14,4 –14,6 14,4 14,4 14,6 14,4 3 –14,2 –14,4 –14,0 –14,2 14,0 14,2 14,2 14,0 4 –13,8 –14,0 –13,6 –14,0 13,8 13,8 14,0 13,8 5 –13,6 –13,8 –13,4 –13,6 13,4 13,4 13,6 13,6

nØ



ϕ

– Ø



ϕ

+

Λ

–

Λ

+

0 –15 15 1 –14,8 14,8 0,013 0,013 2 –14,5 14,5 0,02 0,02 3 –14,2 14,1 0,021 0,028 4 –13,8 13,8 0,028 0,022 5 –13,6 13,5 0,015 0,022

• Der gemittelte Wert für Λ beträgt Λ = 0,0202.

• Für die Schwingungsdauer T des Pendels gilt

t = n · T. Dazu die Zeit für 10 Schwingungen mit einer Stoppuhr messen und T berechnen.

T = 1,9 s

• Aus diesen Werten lässt sich die Dämpfungskonstante δ mit δ = Λ / T bestimmen.

δ

= 0,0106 s

–1

• Für die Eigenfrequenz ω gilt

2

π





2

ω

=

 

ω

= 3,307 Hz

−

δ



T



5.2 Freie gedämpfte Drehschwingung

• Zur Bestimmung der Dämpfungskonstante δ in Abhängigkeit vom Strom Ι durch den Elektromagne- ten wurde der gleiche Versuch mit zugeschalteter Wirbelstrombremse bei Ι = 0,2 A, 0,4 A und 0,6 A durchgeführt.

ΙΙ

Ι = 0,2 A

ΙΙ



n



ϕ

– Ø

ϕ

– Λ –

0 –15 –15 –15 –15 –15 1 –13,6 –13,8 –13,8 –13,6 –13,7 0,0906 2 –12,6 –12,8 –12,6 –12,4 –12,6 0,13 3 –11,4 –11,8 –11,6 –11,4 –11,5 0,0913 4 –10,4 –10,6 –10,4 –10,4 –10,5 0,0909 5 9,2 –9,6 –9,6 –9,6 –9,5 0,1

• Bei T = 1,9 s und gemitteltem Λ = 0,1006 ergibt



ϕ

– Λ –

–1

sich die Dämpfungskonstante: δ = 0,053 s

ΙΙ

Ι = 0,4 A

ΙΙ



n

ϕ

– Ø

0 –15 –15 –15 –15 –15 1 –11,8 –11,8 –11,6 –11,6 –11,7 0,248 2 –9,2 –9,0 –9,0 –9,2 –9,1 0,25 3 –7,2 –7,2 –7,0 –7,0 –7,1 0,248 4 –5,8 –5,6 –5,4 –5,2 –5,5 0,25 5 –4,2 –4,2 –4,0 –4,0 –4,1 0,29

• Bei T = 1,9 s und gemitteltem Λ = 0,257 ergibt sich die Dämpfungskonstante: δ = 0,135 s

ΙΙ

Ι = 0,6 A

ΙΙ



n

ϕ

– Ø

–1



ϕ

– Λ –

0 –15 –15 –15 –15 –15 1 –9,2 –9,4 –9,2 –9,2 –9,3 0,478 2 –5,4 –5,2 –5,6 –5,8 –5,5 0,525 3 –3,2 –3,2 –3,2 –3,4 –3,3 0,51 4 –1,6 –1,8 –1,8 –1,8 –1,8 0,606 5 –0,8 –0,8 –0,8 –0,8 –0,8 0,81

• Bei T = 1,9 s und gemitteltem Λ = 0,5858 ergibt sich die Dämpfungskonstante: δ = 0,308 s

–1

5.3 Erzwungene Drehschwingung

• Zur Bestimmung der Schwingungsamplitude in Abhängigkeit der Erregerfrequenz bzw. der Versorgungsspannung wird der maximale Ausschlag des Pendelkörpers abgelesen.

T = 1,9 s



Motorspannung V

ϕ

3 0,8 4 1,1 5 1,2 6 1,6 7 3,3

7,6 20,0

8 16,8 9 1,6

10 1,1

4

• Die Eigenkreisfrequenz des Systems ω0 ergibt sich

nach Messung der Periodendauer T aus

ω

= 2 π/T = 3,3069 Hz

0

• Bei einer Motorspannung von 7,6 V findet die größ-

te Auslenkung statt, d.h. der Resonanzfall tritt ein.

• Dann wurde der gleiche Versuch mit zugeschalteter Wirbelstrombremse bei Ι = 0,2 A, 0,4 A und 0,6 A durchgeführt.

ΙΙ

Ι = 0,2 A

ΙΙ



Motorspannung V

ϕ

3 0,9 4 1,1 5 1,2 6 1,7 7 2,9

7,6 15,2

8 4,3 9 1,8

10 1,1

ΙΙ

Ι = 0,6 A

ΙΙ

Motorspannung V

7,6 3,6

5 1,3 6 1,8 7 3,6 7,6 7,4 8 3,6 9 1,6

10 1,0



ϕ

3 0,9 4 1,1 5 1,2 6 1,6 7 2,8

8 2,6 9 1,3

10 1,0

ΙΙ

Ι = 0,4 A

ΙΙ

Motorspannung V

3 0,9 4 1,1

A

[skt]

20

15

10

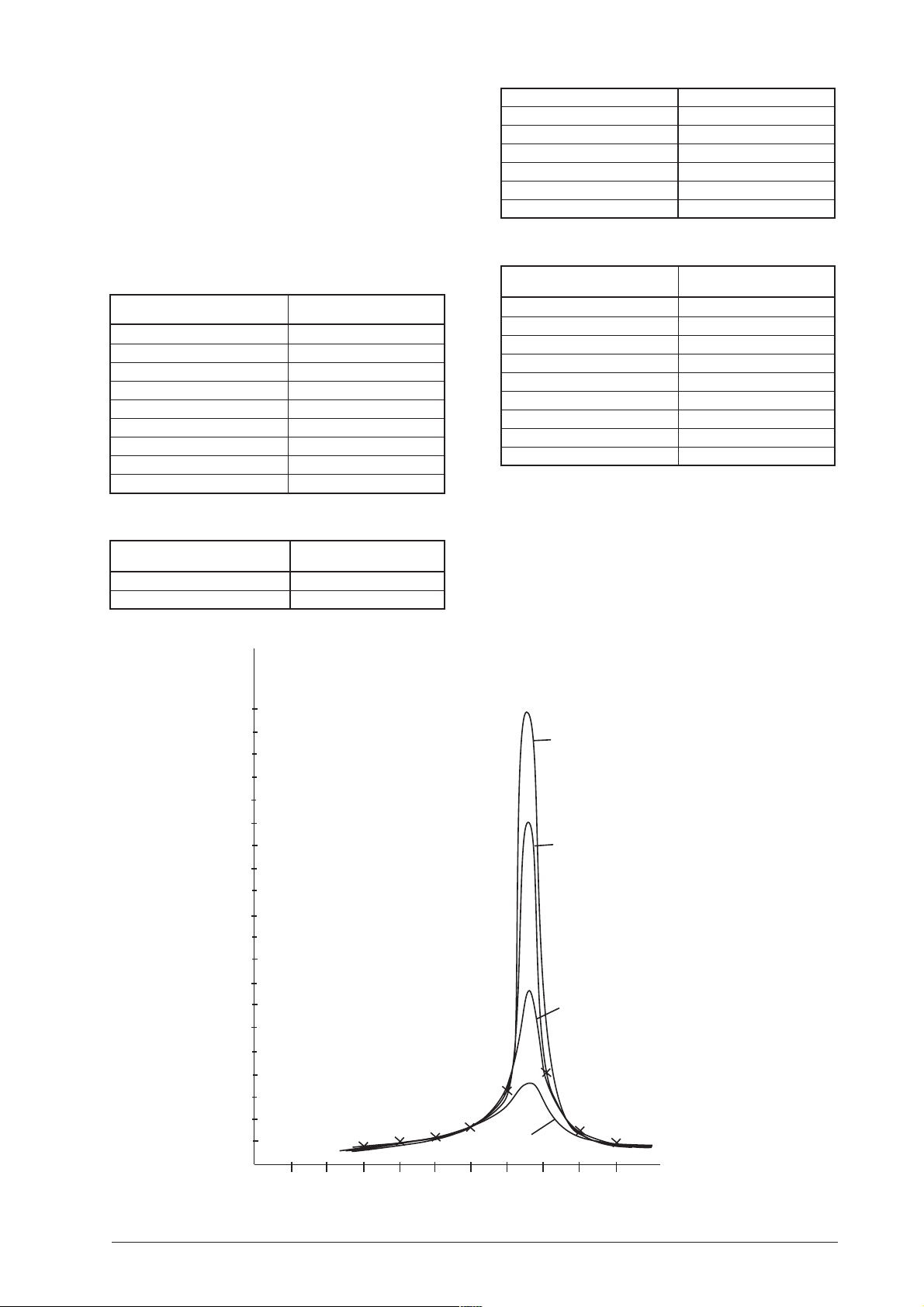
• Aus diesen Messungen lassen sich die Resonanz-

kurven grafisch darstellen, indem man die Ampli-



ϕ

tuden in Abhängigkeit zur Motorspannung aufträgt.

• Aus der Halbwertsbreite des Grafen kann die Reso-

nanzfrequenz grafisch ermittelt werden.

I=0,0A

I=0,2A

I=0,4A

5

1

Resonanzkurven

012

3

567 8910

4

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Deutschland • www.3bscientific.com • Technische Änderungen vorbehalten

I=0,6A

u[v]

5

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

U15040 Torsion pendulum according to Professor Pohl

Operating instructions

12/03 ALF

9

8

7

6

5

4

bl bm bn bo bp

bq br bs

1 Exciter motor 2 Control knob for fine adjustment of the exciter voltage 3 Control knob for coarse adjustment of the exciter voltage 4 Scale ring 5 Pendulum body 6 Coil spring 7 Pointer for the exciter phase angle 8 Pointer for the pendulum’s phase angle 9 Pointer for the pendulum’s deflection

3

bl Exciter bm Eddy current brake bn Guide slot and screw to set the exciter amplitude

2

bo Connecting rod bp Eccentric drive wheel bq 4-mm safety socket for exciter voltage measurement

1

br 4-mm safety sockets for the exciter motor power supply bs 4-mm safety sockets for the eddy current brake power

supply

The torsion pendulum may be used to investigate free, forced and chaotic oscillations with various degrees of damping.

Experiment topics:

• Free rotary oscillations at various degrees of damp-

ing (oscillations with light damping, aperiodic oscillation and aperiodic limit)

• Forced rotary oscillations and their resonance

curves at various degrees of damping

• Phase displacement between the exciter and reso-

nator during resonance

• Chaotic rotary oscillations

• Static determination of the direction variable D

• Dynamic determination of the moment of inertia J

1. Safety instructions

• When removing the torsional pendulum from the

packaging do not touch the scale ring. This could

lead to damage. Always remove using the handles provided in the internal packaging.

• When carrying the torsional pendulum always hold

it by the base plate.

• Never exceed the maximum permissible supply

voltage for the exciter motor (24 V DC).

• Do not subject the torsional pendulum to any un-

necessary mechanical stress.

2. Description, technical data

The Professor Pohl torsional pendulum consists of a wooden base plate with an oscillating system and an electric motor mounted on top. The oscillating system is a ball-bearing mounted copper wheel (5), which is connected to the exciter rod via a coil spring (6) that provides the restoring torque. A DC motor with coarse and fine speed adjustment is used to excite the torsional pendulum. Excitement is brought about via an eccentric wheel (14) with connecting rod (13) which

6

unwinds the coil spring then compresses it again in a periodic sequence and thereby initiates the oscillation of the copper wheel. The electromagnetic eddy current brake (11) is used for damping. A scale ring (4) with slots and a scale in 2-mm divisions extends over the outside of the oscillating system; indicators are located on the exciter and resonator. The device can also be used in shadow projection demonstrations. A DC power supply unit for the torsional pendulum U11755 is required to power the equipment.

Natural frequency: 0.5 Hz approx. Exciter frequency: 0 to 1.3 Hz (continuously adjustable) Terminals: Motor: max. 24 V DC, 0.7 A,

via 4-mm safety sockets

Eddy current brake: 0 to 24 V DC, max. 2 A,

via 4-mm safety sockets Scale ring: 300 mm Ø Dimensions: 400 mm x 140 mm x 270 mm Ground: 4 kg

2.1 Scope of supply

1 Torsional pendulum 2 Additional 10 g weights 2 Additional 20 g weights

3. Theoretical Fundamentals

3.1 Symbols used in the equations

D = Angular directional variable J = Mass moment of inertia M = Restoring torque T = Period T0= Period of an undamped system Td= Period of the damped system



= Amplitude of the exciter moment

M

E

b = Damping torque n = Frequency t = Time

Λ = Logarithmic decrement δ = Damping constant

ϕ

= Angle of deflection



ϕ

= Amplitude at time t = 0 s

0



ϕ

= Amplitude after n periods

n



ϕ

= Exciter amplitude

E



ϕ

= System amplitude

S

ω0= Natural frequency of the oscillating system ωd= Natural frequency of the damped system ωE= Exciter angular frequency ωE

= Exciter angular frequency for max. amplitude

res

Ψ0S= System zero phase angle

3.2 Harmonic rotary oscillation

A harmonic oscillation is produced when the restoring torque is proportional to the deflection. In the case of

harmonic rotary oscillations the restoring torque is proportional to the deflection angle ϕ:

M = D ·

ϕ

The coefficient of proportionality D (angular direction variable) can be computed by measuring the deflection angle and the deflection moment. If the period duration T is measured, the natural resonant frequency of the system ω0 is given by

ω

= 2 π/T

0

and the mass moment of inertia J is given by

D

2

ω

=

0

J

3.3 Free damped rotary oscillations

An oscillating system that suffers energy loss due to friction, without the loss of energy being compensated for by any additional external source, experiences a constant drop in amplitude, i.e. the oscillation is damped. At the same time the damping torque b is proportional to the deflectional angle

.

ϕ

. The following motion equation is obtained for the torque at equilibrium

.

..

JbD⋅+⋅+⋅=

ϕϕϕ

0

b = 0 for undamped oscillation.



If the oscillation begins with maximum amplitude

ϕ

at t = 0 s the resulting solution to the differential equation for light damping (δ² < ω0²) (oscillation) is as follows



–δ ·t

ϕ

=

· e

· cos (

ω

0

d

· t)

δ = b/2 J is the damping constant and

2

ωωδ

=−

d

2

0

the natural frequency of the damped system. Under heavy damping (δ² > ω0²) the system does not oscillate but moves directly into a state of rest or equilibrium (non-oscillating case). The period duration Td of the lightly damped oscillating system varies only slightly from T0 of the undamped oscillating system if the damping is not excessive. By inserting t = n · Td into the equation



–δ ·t

ϕ

ϕ =



and ϕ =

ϕ

tain the following with the relationship



ϕ



ϕ

· e

· cos (

ω

0

for the amplitude after n periods we ob-

n

0

δ

−⋅

n

=⋅

eT

d

· t)

ω

= 2 π/T

d

and thus from this the logarithmic decrement Λ:

Λ

=⋅ =⋅

δ

T

d





ϕ

1



In In



n



ϕ





n

 

0









ϕ

n



=









ϕ

n+1





0

7

By inserting δ = Λ / Td ,

Ψ

ω

= 2 π / T0 and

0

ω

= 2π / T

d

into the equation

2

ωωδ

=−

d

2

0

we obtain:

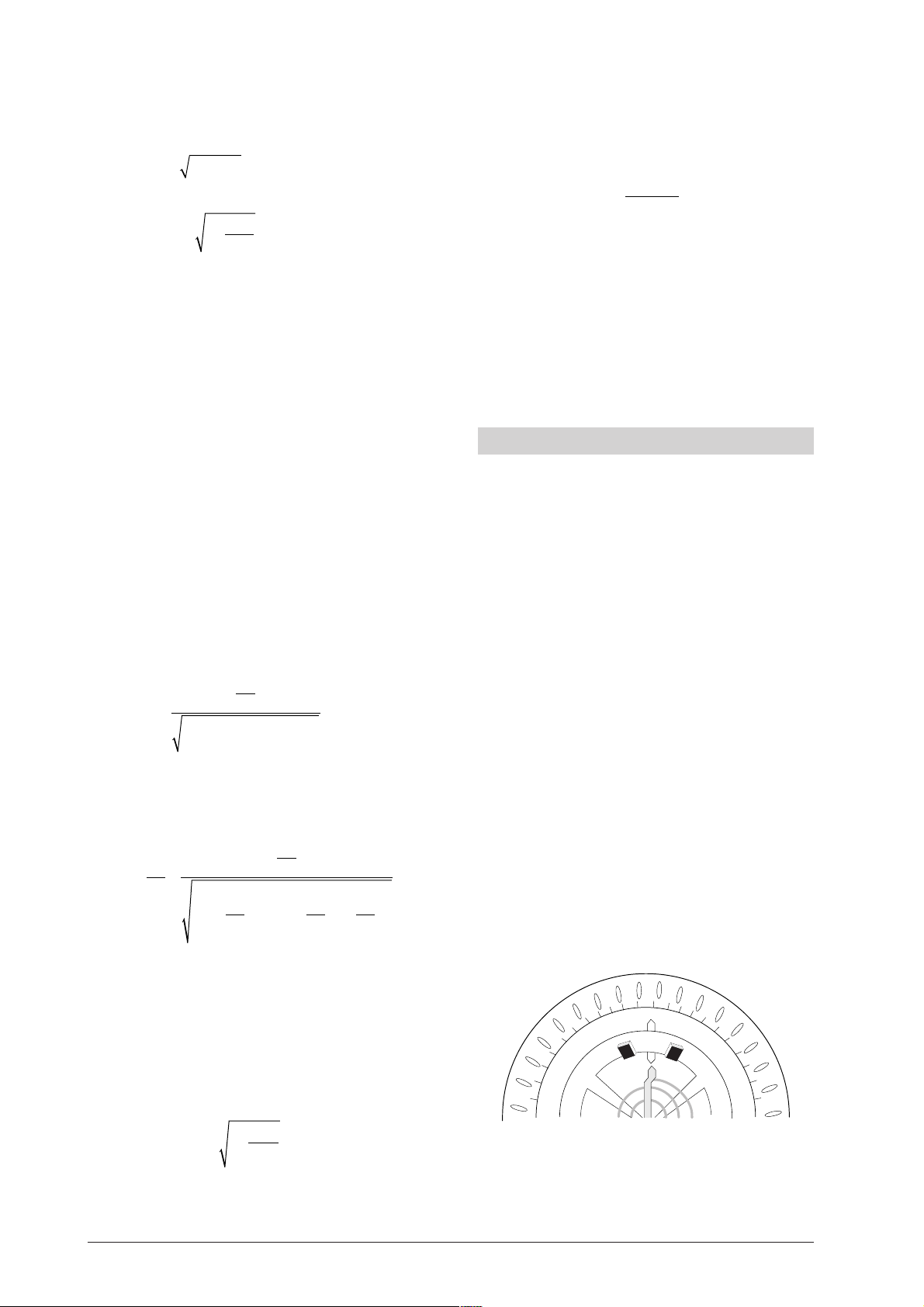
2

TT

=⋅+1

d0

Λ

2

4

π

whereby the period Td can be calculated precisely provided that T0 is known.

3.4 Forced oscillations

In the case of forced oscillations a rotating motion with sinusoidally varying torque is externally applied to the system. This exciter torque can be incorporated into the motion equation as follows:

.

..

JbD M t⋅+⋅+⋅= ⋅ ⋅

ϕϕϕ ω



sin

E

()

E

After a transient or settling period the torsion pendulum oscillates in a steady state with the same angular frequency as the exciter, at the same time ωE can still be phase displaced with respect to ω0. Ψ0S is the system’s zero-phase angle, the phase displacement between the oscillating system and the exciter.



ϕ

=

· sin (

ω

· t –

Ψ

S

E

The following holds true for the system amplitude



M

−

02E

J

2



ϕ

=

ωω δω

()

)

0S

E

2

+⋅

4



ϕ

2

E

The following holds true for the ratio of system amplitude to the exciter amplitude



M



ϕ

S

=



ϕ

E





ω

E



−

14



ω



0





E

J

2







+









2





δ





ω

0





2





ω

E

⋅





ω

0





d

Stronger damping does not result in excessive amplitude. For the system’s zero phase angle Ψ0S the following is true:



arctan

 

ωω



=

0S



δω

2



22



−

ω

0



For ωE = ω0 (resonance case) the system’s zero-phase angle is Ψ0S = 90°. This is also true for δ = 0 and the oscillation passes its limit at this value. In the case of damped oscillations (δ > 0) where ωE < ω0, we find that 0° ≤ Ψ0S ≤ 90° and when ωE > ω

0

it is found that 90° ≤ Ψ0S ≤ 180°. In the case of undamped oscillations (δ = 0), Ψ0S = 0° for ωE < ω0 and Ψ0S = 180° for ωE > ω0.

4. Operation

4.1 Free damped rotary oscillations

• Connect the eddy current brake to the variable volt-

age output of the DC power supply for torsion pendulum.

• Connect the ammeter into the circuit.

• Determine the damping constant as a function of

the current.

4.2 Forced oscillations

S

• Connect the fixed voltage output of the DC power

supply for the torsion pendulum to the sockets (16) of the exciter motor.

• Connect the voltmeter to the sockets (15) of the

exciter motor.

• Determine the oscillation amplitude as a function

of the exciter frequency and of the supply voltage.

• If needed connect the eddy current brake to the

variable voltage output of the DC power supply for the torsion pendulum.

4.3 Chaotic oscillations

• To generate chaotic oscillations there are 4 supple-

mentary weights at your disposal which alter the torsion pendulum’s linear restoring torque.

• To do this screw the supplementary weight to the

body of the pendulum (5).

In the case of undamped oscillations, theoretically speaking the amplitude for resonance (ωE equal to ω0) increases infinitely and can lead to “catastrophic resonance”. In the case of damped oscillations with light damping the system amplitude reaches a maximum where the exciter’s angular frequency ω

is lower than the sys-

E res

tem’s natural frequency. This frequency is given by

2

δ

ωω

=⋅−1

Eres 0

2

ω

0

8

5. Example experiments

5.1 Free damped rotary oscillations

• To determine the logarithmic decrement Λ, the

amplitudes are measured and averaged out over several runs. To do this the left and right deflections of the torsional pendulum are read off the scale in two sequences of measurements.

• The starting point of the pendulum body is located

at +15 or –15 on the scale. Take the readings for five deflections.

• From the ratio of the amplitudes we obtain Λ us-

ing the following equation







ϕ

n



Λ

=

n

In









ϕ

n+1







ϕ

–



ϕ

+

0 –15 –15 –15 –15 15 15 15 15 1 –14.8 –14.8 –14.8 –14.8 14.8 14.8 14.8 14.8 2 –14.4 –14.6 –14.4 –14.6 14.4 14.4 14.6 14.4 3 –14.2 –14.4 –14.0 –14.2 14.0 14.2 14.2 14.0 4 –13.8 –14.0 –13.6 –14.0 13.8 13.8 14.0 13.8 5 –13.6 –13.8 –13.4 –13.6 13.4 13.4 13.6 13.6

nØ



ϕ

– Ø



ϕ

+

Λ

–

Λ

+

0 –15 15 1 –14.8 14.8 0.013 0.013 2 –14.5 14.5 0.02 0.02 3 –14.2 14.1 0.021 0.028 4 –13.8 13.8 0.028 0.022 5 –13.6 13.5 0.015 0.022

• The average value for Λ comes to Λ = 0.0202.

• For the pendulum oscillation period T the follow-

ing is true: t = n · T. To measure this, record the time for 10 oscillations using a stop watch and calculate T.

T = 1.9 s

• From these values the damping constant δ can be determined from δ = Λ / T.

δ

= 0.0106 s

–1

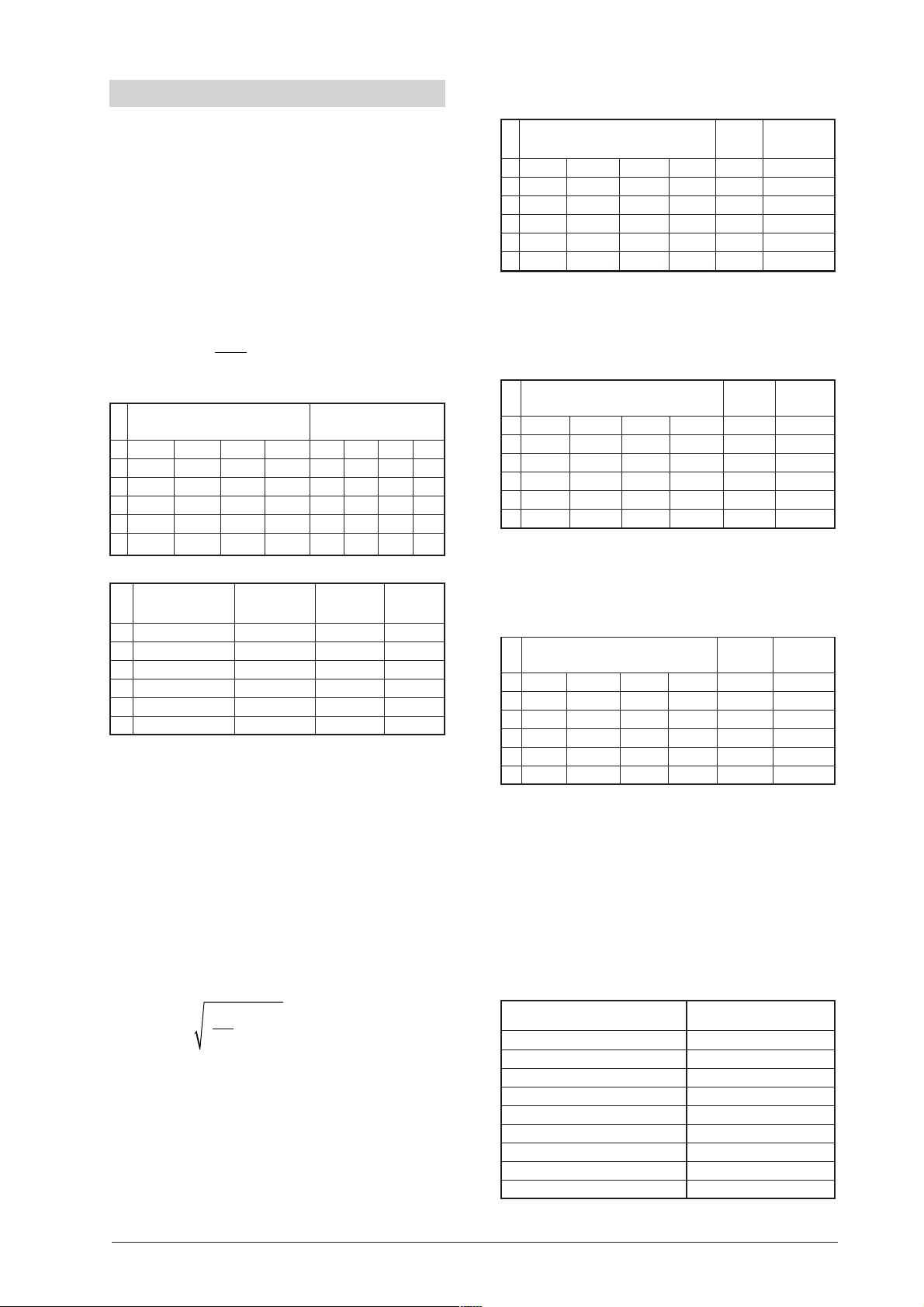
• For the natural frequency ω the following holds true

2

π

2





ω

=

 

ω

= 3.307 Hz

T

2

δ

−

 

5.2 Free damped rotary oscillations

• To determine the damping constant δ as a function of the current Ι flowing through the electromagnets the same experiment is conducted with an eddy current brake connected at currents of

Ι = 0.2 A, 0.4 A and 0.6 A.

ΙΙ

Ι = 0.2 A

ΙΙ



n



ϕ

– Ø

ϕ

– Λ –

0 –15 –15 –15 –15 –15 1 –13.6 –13.8 –13.8 –13.6 –13.7 0.0906 2 –12.6 –12.8 –12.6 –12.4 –12.6 0.13 3 –11.4 –11.8 –11.6 –11.4 –11.5 0.0913 4 –10.4 –10.6 –10.4 –10.4 –10.5 0.0909 5 9.2 –9.6 –9.6 –9.6 –9.5 0.1

• For T = 1.9 s and the average value of Λ = 0.1006 we obtain the damping constant: δ = 0.053 s

ΙΙ

Ι = 0.4 A

ΙΙ

n



ϕ

– Ø



ϕ

– Λ –

–1

0 –15 –15 –15 –15 –15 1 –11.8 –11.8 –11.6 –11.6 –11.7 0.248 2 –9.2 –9.0 –9.0 –9.2 –9.1 0.25 3 –7.2 –7.2 –7.0 –7.0 –7.1 0.248 4 –5.8 –5.6 –5.4 –5.2 –5.5 0.25 5 –4.2 –4.2 –4.0 –4.0 –4.1 0.29

• For T = 1.9 s and an average value of Λ = 0.257 we



ϕ

– Λ –

–1

obtain the damping constant: δ = 0.135 s

ΙΙ

Ι = 0.6 A

ΙΙ



n

ϕ

– Ø

0 –15 –15 –15 –15 –15 1 –9.2 –9.4 –9.2 –9.2 –9.3 0.478 2 –5.4 –5.2 –5.6 –5.8 –5.5 0.525 3 –3.2 –3.2 –3.2 –3.4 –3.3 0.51 4 –1.6 –1.8 –1.8 –1.8 –1.8 0.606 5 –0.8 –0.8 –0.8 –0.8 –0.8 0.81

• For T = 1.9 s and an average value of Λ = 0.5858 we obtain the damping constant: δ = 0.308 s

–1

5.3 Forced rotary oscillation

• Take a reading of the maximum deflection of the pendulum body to determine the oscillation amplitude as a function of the exciter frequency or the supply voltage.

T = 1.9 s



Motor voltage V

ϕ

3 0.8 4 1.1 5 1.2 6 1.6 7 3.3

7.6 20.0 8 16.8 9 1.6

10 1.1

9

• After measuring the period T the natural frequency of the system ω0 can be obtained from

ω

= 2 π/T = 3.3069 Hz

0

• The most extreme deflection arises at a motor voltage of 7.6 V, i.e. the resonance case occurs.

• Then the same experiment is performed with an eddy current brake connected at currents of

Ι = 0.2 A, 0.4 A and 0.6 A.

ΙΙ

Ι = 0.2 A

ΙΙ



Motor voltage V

ϕ

3.0 0.9

4.0 1.1

5.0 1.2

6.0 1.7

7.0 2.9

7.6 15.2

8.0 4.3

9.0 1.8

10.0 1.1

ΙΙ

Ι = 0.6 A

ΙΙ

Motor voltage V

5.0 1.3

6.0 1.8

7.0 3.6

7.6 7.4

8.0 3.6

9.0 1.6

10.0 1.0

3.0 0.9

4.0 1.1

5.0 1.2

6.0 1.6

7.0 2.8

7.6.0 3.6

8.0 2.6

9.0 1.3

10.0 1.0



ϕ

ΙΙ

Ι = 0.4 A

ΙΙ

Motor voltage V

3.0 0.9

4.0 1.1

A

[skt]

20

15

10

• From these measurements the resonance curves can

be plotted in a graph depicting the amplitudes



ϕ

against the motor voltage.

• The resonant frequency can be determined by find-

ing the half-width value from the graph.

I=0,0A

I=0,2A

I=0,4A

5

1

012

Resonance curves

3

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Germany • www.3bscientific.com • Technical amendments may occur

567 8910

4

10

I=0,6A

u[v]

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

U15040 Pendule tournant d’après Prof. Pohl

Instructions d‘utilisation

12/03 ALF

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

®

9

8

7

6

5

4

bl bm bn bo bp

1 Moteur excitateur 2 Bouton tournant pour le réglage fin de la tension d’excita-

tion

3 Bouton tournant pour le réglage grossier de la tension

d’excitation

4 Bague graduée 5 Corps du pendule 6 Ressort conique 7 Pointeur indiquant la phase de l’excitateur 8 Pointeur indiquant la phase du corps du pendule

3

9 Pointeur indiquant la déviation du corps du pendule bl Excitateur

2

bm Frein à courants de Foucault bn Fente de guidage et vis pour le réglage de l’amplitude

d’excitation

bo Barre de traction

1

bp Roue d’entraînement à excentrique bq Douilles de sécurité de 4 mm pour la mesure de la tension

d’excitation

br Douilles de sécurité de 4 mm pour l’alimentation du moteur

excitateur

bs Douilles de sécurité de 4 mm pour l’alimentation du frein à

courants de Foucault

bq br bs

Le pendule tournant sert à l’analyse d’oscillations libres, forcées et chaotiques en présence de différents amortissements.

Thèmes des expériences :

• Libres oscillations tournantes avec différents amor-

tissements (oscillations avec amortissement modéré, oscillation apériodique et cas limite apériodique)

• Oscillations forcées et ses courbes de résonance avec

différents amortissements

• Déphasage entre l’excitateur et le résonateur en cas

de résonance

• Oscillations tournantes chaotiques

• Détermination statique de la grandeur direction-

nelle D

• Détermination dynamique du moment d’inertie J

1. Consignes de sécurité

• Lorsque vous retirez le pendule de l’emballage, ne

le saisissez pas à hauteur de la bague graduée ! Risque d’endommagement ! Retirez-le toujours en saisissant l’emballage intérieur.

• Pour porter le pendule, tenez toujours l’appareil

par la plaque de base.

• Ne pas dépasser la tension d’alimentation maxi-

mum admissible du moteur excitateur de 24 V CC.

• Ne pas exposer le pendule à des charges mécani-

ques inutiles.

2. Description, caractéristiques techniques

Le pendule tournant d’après Prof. Pohl est constitué d’un système oscillant monté sur une plaque de base en bois et d’un moteur électrique. Le système oscillant est constitué d’une roue en cuivre (5) montée sur un roulement à billes qui est reliée à la barre de l’excitateur par un ressort spiral (6) fournissant le couple de rappel. Le pendule est excité par un moteur à courant continu à vitesse réglage (réglages grossier et fin) qui, par l’action d’un excentrique (14) à barre de

11

traction (13), étire et comprime régulièrement le res-

ω

0

2

=

D

J

sort spiral et fait ainsi osciller la roue en cuivre. Un frein électromagnétique à courants de Foucault (11) est utilisé pour l’amortissement. Une bague graduée (4) à fentes et graduation en pas de 2 mm entoure le système oscillant ; l’excitateur et le résonateur sont pourvus de pointeurs. L’appareil peut aussi être utilisé en démonstration pour la projection d’ombres. L’alimentation électrique nécessite une alimentation CC pour pendule tournant U11755.

Fréquence propre : env. 0,5 Hz. Fréquence d’excitateur : 0 à 1,3 Hz

(réglable en continu)

Connexions :

Moteur : max. 24 V CC, 0,7 A,

douilles de sécurité

de 4 mm Frein à courants de Foucault : 0 à 24 V CC, max. 2 A,

douilles de sécurité

de 4 mm Bague graduée : Ø 300 mm Dimensions : 400 mm x 140 mm x 270 mm Masse : 4 kg

2.1 Matériel fourni

1 pendule tournant 2 masses supplémentaires de 10 g 2 masses supplémentaires de 20 g

3. Notions théoriques

3.1 Symboles utilisés dans les formules

D = grandeur directionnelle angulaire J = moment d’inertie de masse M = couple de rappel T = durée d’une période T0= durée d’une période du système non amorti Td= durée d’une période du système amorti



= amplitude du couple de l’excitateur

M

E

b = couple d’amortissement n = nombre de périodes t = temps

Λ = décrément logarithmique δ = constante d’amortissement

ϕ

= angle de déviation



ϕ

= amplitude au temps t = 0 s

0



ϕ

= amplitude après n périodes

n



ϕ

= amplitude de l’excitateur

E



ϕ

= amplitude du système

S

ω0= propre fréquence du système oscillant ωd= propre fréquence du système amorti ωE= fréquence angulaire de l’excitateur ωE

= fréquence angulaire de l’excitateur

res

pour l’amplitude max.

Ψ0S= angle de phase nulle du système

3.2 Oscillation tournante harmonique

Une oscillation est harmonique lorsque la force de rappel est proportionnelle à la déviation. En présence d’oscillations tournantes harmoniques, le couple de rappel est proportionnel à l’angle de déviation ϕ:

M = D ·

ϕ

Le facteur de proportionnalité D (grandeur directionnelle angulaire) peut être déterminé en mesurant l’angle de déviation et le couple déviant. D’après la mesure de la durée d’une période T, la fréquence angulaire propre du système ω

résulte de

0

l’équation suivante :

ω

= 2 π/T

0

et le moment d’inertie de masse de l’équation suivante :

3.3 Oscillation tournante amortie libre

En présence d’un système oscillant où de l’énergie est perdue suite à des pertes dues aux frottements, sans qu’elle ne soit compensée par de l’énergie apportée de l’extérieur, l’amplitude diminue continuellement, c’est-à-dire que l’oscillation est amortie. Le couple d’amortissement b est proportionnel à la vitesse angulaire

.

ϕ

. L’équation suivante du mouvement résulte de l’équilibre du couple :

.

..

JbD⋅+⋅+⋅=

ϕϕϕ

0

Si l’oscillation n’est pas amortie, b = 0. Si l’oscillation commence au moment t = 0 s avec une



amplitude maximale

ϕ

on obtient l’équation diffé-

0

,,

,

,,

rentielle avec un amortissement pas trop élevé (δ² < ω0²) (cas d’oscillation)



–δ ·t

ϕ

=

· e

· cos (

ω

0

d

· t)

δ = b/2 J représente la constante d’amortissement et

2

ωωδ

=−

d

2

0

la propre fréquence du système amorti. Si l’amortissement est élevé (δ² > ω0²) le système n’oscille plus, mais rampe en position de repos (cas de rampement). Lorsque l’amortissement n’est pas trop important, la durée Td d’une période du système oscillant amorti ne se modifie que légèrement par rapport à T0 du système oscillant non amorti. En remplaçant t = n · Td dans l’équation



–δ ·t

ϕ

ϕ =

et pour l’amplitude après n périodes ϕ = tient avec l’équation



ϕ



ϕ

· e

0

ω

n

0

δ

−⋅

n

=⋅

eT

· cos (

= 2 π/T

d

ω

· t)

d



ϕ

, on ob-

n

d

12

et ainsi le décrément logarithmique Λ:

Ψ

Λ

=⋅ =⋅

δ

1

T

d

In In

n

En remplaçant δ = Λ / Td ,





ϕ

n







ϕ

0



ω

= 2 π / T0 et

0









ϕ



=

 

n











ϕ

n+1





ω

= 2π / T

d

dans l’équation

2

ωωδ

=−

d

2

0

on obtient :

2

TT

=⋅+1

d0

Λ

2

4

π

ce qui permet de calculer avec précision la durée d’une période Td, dans la mesure où l’on connaît T0.

3.4 Oscillation tournante forcée

En présence d’oscillations tournantes forcées, un couple modifiable périodiquement par une fonction sinusoïdale agit de l’extérieur sur le système oscillant. Ce couple d’excitation doit être complété dans l’équation de mouvement

.

..

JbD M t⋅+⋅+⋅= ⋅ ⋅

ϕϕϕ ω



sin

E

()

E

Après une certaine période transitoire, le pendule tournant oscille dans un état stationnaire à la même fréquence angulaire que l’excitateur, ωE pouvant encore être déphasé par rapport à ω0. Ψ0S représente l’angle de phase nulle du système, le déphasage entre le système oscillant et l’excitateur.



ϕ

=

· sin (

ω

· t –

Ψ

S

E

Pour l’amplitude du système

)

0S



ϕ

, on a l’équation sui-

S

vante :



M

E

−

02E

J

2

+⋅

4

2

E



ϕ

=

ωω δω

()

Pour le rapport entre l’amplitude du système et celle de l’excitateur, on a l’équation suivante :



M



ϕ

S

=



ϕ

E





ω

E



−

14



ω



0





E

J

2







+









2





δ





ω

0





2





ω

E

⋅





ω

0





Cette fréquence résulte de

2

δ

ωω

=⋅−1

Eres 0

2

ω

0

Si l’amortissement est trop important, l’amplitude

d

n’augmente pas. L’équation suviante s’applique à l’angle de phase nulle du système Ψ0S :

 

arctan

=

0S



ωω





2

δω



22



−

ω

0



Si ωE = ω0 (résonance), l’angle de phase nulle du système Ψ0S = 90°. Ceci s’applique également pour δ = 0 avec un passage correspondant à la limite. Avec des oscillations amorties (δ > 0) et ωE < ω0, on obtient 0° ≤ Ψ0S ≤ 90°, avec ωE > ω0 on obtient 90° ≤

Ψ0S ≤ 180°.

Avec des oscillations amorties (δ = 0), Ψ0S = 0° à ωE < ω

0

et Ψ0S = 180° à ωE > ω0.

4. Manipulation

4.1 Oscillation tournante amortie libre

• Relier le frein à courants de Foucault à la sortie de

tension réglable de l’alimentation du pendule tournant.

• Connecter l’ampèremètre au circuit électrique.

• Déterminer la constante d’amortissement en fonc-

tion du courant.

4.2 Oscillation tournante forcée

• Relier les douilles de connexion (16) du moteur

excitateur à la sortie de tension fixe de l’alimentation du pendule tournant.

• Relier le voltmètre aux douilles de connexion (15)

du moteur excitateur.

• Déterminer l’amplitude de l’oscillation en fonction

de la fréquence de l’excitateur et de la tension d’alimentation.

• Au besoin, relier le frein à courants de Foucault à

la sortie destinée à la tension réglable de l’alimentation du pendule tournant.

4.3 Oscillations chaotiques

• Pour générer des oscillations chaotiques, on peut

utiliser les 4 masses supplémentaires qui permettent de modifier le couple de rappel linéaire du pendule tournant.

• Visser pour cela la masse au corps du pendule (5).

En cas de résonance (ωE = ω0), si les oscillations ne sont pas amorties, l’amplitude augmente théoriquement jusqu’à l’infini et entraîne une « catastrophe de résonance ». Si les oscillations sont amorties et l’amortissement pas trop important, l’amplitude du système est maximale, la fréquence angulaire de l’excitateur ω

étant infé-

E res

rieure à la fréquence angulaire propre du système.

13

5. Exemples d’expériences

5.1 Oscillation tournante amortie libre

• Pour définir le décrément logarithmique Λ, mesu-

rer et déterminer les amplitudes en plusieurs passages. Pour cela, au cours de deux séries de mesures, lire les déviations du pendule tournant sur la graduation à gauche et à droite.

• Le point de départ du corps du pendule était 15 ou

–15 sur la graduation. Cinq déviations ont été lues.

• A partir du rapport des amplitudes, on obtient Λ à

l’aide de la formule suivante :







ϕ

n



Λ

=

In









ϕ

n+1





ΙΙ

Ι = 0,2 A

ΙΙ



n



ϕ

– Ø

ϕ

– Λ –

0 –15 –15 –15 –15 –15 1 –13,6 –13,8 –13,8 –13,6 –13,7 0,0906 2 –12,6 –12,8 –12,6 –12,4 –12,6 0,13 3 –11,4 –11,8 –11,6 –11,4 –11,5 0,0913 4 –10,4 –10,6 –10,4 –10,4 –10,5 0,0909 5 9,2 –9,6 –9,6 –9,6 –9,5 0,1

• Avec T = 1,9 s et la moyenne Λ = 0,1006, on ob-

tient la constante d’amortissement : δ = 0,053 s

ΙΙ

Ι = 0,4 A

ΙΙ

–1

n



ϕ

–



ϕ

+

0 –15 –15 –15 –15 15 15 15 15 1 –14,8 –14,8 –14,8 –14,8 14,8 14,8 14,8 14,8 2 –14,4 –14,6 –14,4 –14,6 14,4 14,4 14,6 14,4 3 –14,2 –14,4 –14,0 –14,2 14,0 14,2 14,2 14,0 4 –13,8 –14,0 –13,6 –14,0 13,8 13,8 14,0 13,8 5 –13,6 –13,8 –13,4 –13,6 13,4 13,4 13,6 13,6

nØ



ϕ

– Ø



ϕ

+

Λ

–

Λ

+

0 –15 15 1 –14,8 14,8 0,013 0,013 2 –14,5 14,5 0,02 0,02 3 –14,2 14,1 0,021 0,028 4 –13,8 13,8 0,028 0,022 5 –13,6 13,5 0,015 0,022

• La valeur déterminée pour Λ est Λ = 0,0202.

• Pour la durée d’oscillation T du pendule, t = n · T.

Pour cela, mesurer avec un chronomètre la durée de 10 oscillations et calculer T.

T = 1,9 s

• Ces valeurs permettent de déterminer la constante d’amortissement δ avec δ = Λ / T.

δ

= 0,0106 s

–1

• Pour la fréquence propre ω, on a l’équation

2

π

2





ω

=

 

ω

= 3,307 Hz

T

2

δ

−

 

5.2 Oscillation tournante amortie libre

• Pour déterminer la constante d’amortissement δ en fonction de l’intensité Ι par l’électro-aimant, la même expérience a été réalisée avec un frein à courants de Foucault à Ι = 0,2 A, 0,4 A et 0,6 A.

n



ϕ

– Ø



ϕ

– Λ –

0 –15 –15 –15 –15 –15 1 –11,8 –11,8 –11,6 –11,6 –11,7 0,248 2 –9,2 –9,0 –9,0 –9,2 –9,1 0,25 3 –7,2 –7,2 –7,0 –7,0 –7,1 0,248 4 –5,8 –5,6 –5,4 –5,2 –5,5 0,25 5 –4,2 –4,2 –4,0 –4,0 –4,1 0,29

• Avec T = 1,9 s et la moyenne Λ = 0,257, on obtient la constante d’amortissement : δ = 0,135 s

ΙΙ

Ι = 0,6 A

ΙΙ



n

ϕ

– Ø



ϕ

–1

– Λ –

0 –15 –15 –15 –15 –15 1 –9,2 –9,4 –9,2 –9,2 –9,3 0,478 2 –5,4 –5,2 –5,6 –5,8 –5,5 0,525 3 –3,2 –3,2 –3,2 –3,4 –3,3 0,51 4 –1,6 –1,8 –1,8 –1,8 –1,8 0,606 5 –0,8 –0,8 –0,8 –0,8 –0,8 0,81

• Avec T = 1,9 s et la moyenne Λ = 0,5858 on obtient la constante d’amortissement : δ = 0,308 s

–1

5.3 Oscillation tournante forcée

• Pour déterminer l’amplitude de l’oscillation en fonction de la fréquence de l’excitateur et de la tension d’alimentation, lire la déviation maximale du corps du pendule.

T = 1,9 s



Tension moteur V

ϕ

3 0,8 4 1,1 5 1,2 6 1,6 7 3,3 7,6 20,0 8 16,8 9 1,6

10 1,1

14

• D’après la mesure de la durée d’une période T, la fréquence angulaire propre du système ω0 résulte de l’équation suivante :

ω

= 2 π/T = 3,3069 Hz

0

• La déviation maximale a lieu avec une tension de moteur de 7,6 V, c’est-à-dire qu’il y a résonance.

• Puis, la même expérience a été réalisée avec un frein à courants de Foucault à Ι = 0,2 A, 0,4 A et 0,6 A.

ΙΙ

Ι = 0,2 A

ΙΙ



Tension moteur V

ϕ

3 0,9 4 1,1 5 1,2 6 1,7 7 2,9 7,6 15,2 8 4,3 9 1,8

10 1,1

ΙΙ

Ι = 0,4 A

ΙΙ



Tension moteur V

ϕ

3 0,9 4 1,1

5 1,3 6 1,8 7 3,6 7,6 7,4 8 3,6 9 1,6

10 1,0

ΙΙ

Ι = 0,6 A

ΙΙ



Tension moteur V

ϕ

3 0,9 4 1,1 5 1,2 6 1,6 7 2,8 7,6 3,6 8 2,6 9 1,3

10 1,0

• A partir de ces mesures, on peut représenter les

courbes de résonance sous forme graphique en reportant les amplitudes en fonction de la tension de moteur.

• La largeur de valeur moyenne du graphe permet

de représenter dans un graphique la fréquence de résonance.

A

[skt]

20

15

10

I=0,0A

I=0,2A

I=0,4A

5

1

012

Courbes de résonance

3

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Allemagne • www.3bscientific.com • Sous réserve de modifications techniques

567 8910

4

15

I=0,6A

u[v]

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

U15040 Pendolo di torsione del Prof. Pohl

Istruzioni per l’uso

12/03 ALF

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

9

8

7

6

5

4

bl bm bn bo bp

1 Motore ad eccitazione 2 Manopola di microregolazione della tensione di eccitazione 3 Manopola di macroregolazione della tensione di eccitazione 4 Anello graduato: 5 Corpo del pendolo 6 Molle a spirale 7 Indicatore della posizione di fase dell’eccitatore 8 Indicatore della posizione di fase del corpo del pendolo 9 Indicatore per la deviazione del corpo del pendolo bl Eccitatore

3

bm Freno a corrente di Foucault: bn Fessura di guida e vite per la regolazione dell’ampiezza

2

dell’eccitatore

bo Leva di trasmissione bp Ruota motrice con eccentrico bq Jack di sicurezza da 4 mm per la misurazione della tensione

1

di eccitazione

br Jack di sicurezza da 4 mm per l’alimentazione del motore

ad eccitazione

bs Jack di sicurezza da 4 mm per l’alimentazione del freno a

corrente di Foucault

bq br bs

Il pendolo di torsione serve per esaminare oscillazioni libere, forzate e caotiche con smorzamenti diversi.

Argomenti degli esperimenti:

• oscillazioni di torsione libere con smorzamenti di-

versi (oscillazione con smorzamento moderato, oscillazione aperiodica e caso limite aperiodico)

• oscillazioni forzate e relative curve di risonanza con

smorzamenti diversi

• spostamento di fase tra eccitatore e risonatore in

caso di risonanza

• oscillazioni di torsione caotiche

• determinazione statica della costante di collega-

mento D

• determinazione dinamica del momento d’inerzia J

1. Norme di sicurezza

• Durante l’estrazione dall’imballaggio, non afferra-

re il pendolo di torsione in corrispondenza dell’anello graduato! Rischio di danneggiamento! Du-

rante l’estrazione utilizzare sempre l’opportuno ausilio (imballaggio interno)!

• Per trasportare il pendolo di torsione, tenere sem-

pre l’apparecchio sulla piastra di base.

• Non superare la tensione di alimentazione max.

ammessa del motore ad eccitazione (24 V CC).

• Non sottoporre il pendolo di torsione a sollecita-

zioni meccaniche non necessarie.

2. Descrizione, caratteristiche tecniche

Il pendolo di torsione del Prof. Pohl è composto da un sistema oscillante montato su una piastra di base in legno e da un motore elettrico. Il sistema oscillante si compone di una ruota di rame con cuscinetti a sfera (5), collegata all’asta di eccitazione tramite una molla a spirale (6), che fornisce il momento di richiamo. Per eccitare il pendolo di torsione è necessario un motore a corrente continua con velocità a regolazione fine e grossolana, che mediante un eccentrico (14) con leva di trasmissione (13) separa e comprime le molle a spi-

16

rale in sequenza periodica, mettendo in tal modo in moto la ruota di rame. Per lo smorzamento si utilizza un freno elettromagnetico a corrente di Foucault (11). Un anello graduato (4) con fessure e scala con divisioni da 2 mm circonda il sistema oscillante; sull’eccitatore e sul risonatore si trovano indicatori. L’apparecchio può essere utilizzato anche nella dimostrazione della proiezione d’ombra. Per l’alimentazione di corrente è necessario un alimentatore CC per pendolo di torsione U11755.

Frequenza propria: ca. 0,5 Hz. Frequenza di eccitazione: da 0 a 1,3 Hz

(regolabile di continuo) Connessioni: Motore: max. 24 V CC, 0,7 A,

mediante jack di

sicurezza da 4 mm Freno a corrente di Foucault: da 0 a 24 V CC, max. 2 A,

mediante jack di

sicurezza da 4 mm Anello graduato: 300 mm Ø Dimensioni: 400 mm x 140 mm x 270 mm Peso: 4 kg

2.1 Fornitura

1 pendolo di torsione 2 masse supplementari da 10 g 2 masse supplementari da 20 g

3. Principi teorici

3.1 Simboli delle formule utilizzati

D = costante di collegamento angolare J = momento di inerzia delle masse M = momento torcente di richiamo T = periodo T0= periodo del sistema non smorzato Td= periodo del sistema smorzato



= ampiezza del momento torcente

M

E

dell'eccitatore b = momento di smorzamento n = frequenza t = tempo

Λ = decremento logaritmico δ = costante di smorzamento

ϕ

= angolo di deviazione



ϕ

= ampiezza relativa al tempo t = 0 s

0



ϕ

= ampiezza dopo n periodi

n



ϕ

= ampiezza di eccitazione

E



ϕ

= ampiezza del sistema

S

ω0= frequenza propria del sistema oscillante ωd= frequenza propria del sistema smorzato ωE= frequenza del circuito di eccitazione ωE

= frequenza del circuito di eccitazione per

res

ampiezza max.

Ψ0S= angolo di fase zero del sistema

3.2 Oscillazione di torsione armonica

Un'oscillazione armonica è presente se la forza di ri-

chiamo è proporzionale alla deviazione. In caso di oscillazioni di torsione armoniche il momento torcente di richiamo è proporzionale all'angolo di deviazione ϕ:

M = D ·

ϕ

Il fattore di proporzionalità D (costante di collegamento angolare) può essere calcolato mediante misurazione dell'angolo di deviazione e del momento deviante. La frequenza del circuito proprio del sistema ω0 si ottiene dalla misurazione del periodo T

ω

= 2 π/T

0

e il momento di inerzia delle masse J da

D

2

ω

=

0

J

3.3 Oscillazione di torsione smorzata libera

In un sistema oscillante, nel quale si verificano perdite di energia a causa di perdite per attriti, senza che l'energia venga compensata da energia apportata dall'esterno, l'ampiezza si riduce costantemente, ossia l'oscillazione è smorzata. In ciò il momento di smorzamento b è proporzionale alla velocità angolare

.

ϕ

. Dall'equilibrio del momento torcente si ottiene l'equazione del moto

.

..

JbD⋅+⋅+⋅=

ϕϕϕ

0

Per l'oscillazione non smorzata, b = 0 Se inizia l'oscillazione relativa al tempo t = 0 s con



l'ampiezza massima

ϕ

si ottiene la soluzione del-

0

l'equazione differenziale con uno smorzamento non troppo potente (δ² < ω0²) (oscillazione)



–δ ·t

ϕ

=

· e

· cos (

ω

0

d

· t)

δ = b/2 J è la costante di smorzamento e

2

ωωδ

=−

d

ω

= frequenza propria del sistema smorzato.

d

2

0

In caso di smorzamento potente (δ² > ω0²) il sistema non oscilla ma scorre in posizione di riposo (scorrimento). In caso di smorzamento non troppo potente, il periodo Td del sistema oscillante smorzato cambia solo leggermente rispetto a T0 del sistema oscillante non smorzato. Inserendo t = n · Td nell'equazione



–δ ·t

ϕ

ϕ =

e per l'ampiezza in base a n periodi ϕ = con la definizione



ϕ



ϕ

· e

0

ω

= 2 π/T

d

n

0

δ

−⋅

n

=⋅

eT

· cos (

d

ω

· t)

d



ϕ

si ottiene

n

d

e da ciò il decremento logaritmico Λ:

Λ

=⋅ =⋅

δ

T

d





ϕ

1



In In



n



ϕ





n

 

0









ϕ

n



=









ϕ

n+1





17

Inserendo δ = Λ / Td ,

Ψ

ω

= 2 π / T0 e

0

ω

= 2π / T

d

nell'equazione

2

ωωδ

=−

d

2

0

si ottiene:

2

TT

=⋅+1

d0

Λ

2

4

π

dove il periodo Td può essere calcolato con precisione, se è noto T0.

3.4 Oscillazione di torsione forzata

In caso di oscillazioni di torsione forzate agisce dall'esterno un momento torcente variabile periodicamente con una funzione sinusoidale sul sistema oscillante. Questo momento di eccitazione deve essere integrato nell'equazione del moto.

.

..

JbD M t⋅+⋅+⋅= ⋅ ⋅

ϕϕϕ ω



sin

E

()

E

Dopo un tempo di assestamento il pendolo di torsione oscilla in uno stato stazionario con la stessa frequenza del circuito dell'eccitatore, dove ωE può essere ulteriormente spostato di fase verso ω0. Ψ0S è l'angolo di fase zero del sistema, lo spostamento di fase tra il sistema oscillante e l'eccitatore.



ϕ

=

· sin (

ω

· t –

Ψ

S

E

Per l'ampiezza del sistema



M

−

02E

J

2



ϕ

=

ωω δω

()

)

0S



ϕ

vale

S

E

2

+⋅

4

2

E

Per il rapporto tra l'ampiezza del sistema e l'ampiezza dell'eccitatore vale



M



ϕ

S

=



ϕ

E





ω

E



14

−



ω



0





E

J

2







+









2





δ





ω

0





2





ω

E

⋅





ω

0





Con oscillazioni non smorzate aumenta l'ampiezza in caso di risonanza (ωE uguale a ω0) teoricamente all'infinito e viene determinata una "catastrofe di risonanza". Con oscillazioni smorzate e uno smorzamento non troppo potente, l'ampiezza del sistema diventa massima, dove la frequenza del circuito dell'eccitatore ω

E res

è inferiore rispetto alla frequenza del circuito proprio del sistema. Questa frequenza si ottiene da

2

δ

ωω

=⋅−1

Eres 0

2

ω

0

d

In caso di smorzamento potente non si verifica alcun incremento di ampiezza. Per l'angolo di fase zero del sistema Ψ0S vale



arctan

 

ωω



=

0S



δω

2



22



−

ω

0



Per ωE = ω0 (risonanza) l'angolo di fase zero del sistema Ψ0S = 90°. Ciò vale anche per δ = 0 con relativa transizione. Con oscillazioni smorzate (δ > 0) e ωE < ω0 si ottiene 0° ≤ Ψ0S ≤ 90°, per ωE > ω0 vale 90° ≤ Ψ0S ≤ 180°. Con oscillazioni non smorzate (δ = 0) vale Ψ0S = 0° con

ωE < ω0 e Ψ0S = 180° per ωE > ω0.

4. Comandi

4.1 Oscillazione di torsione smorzata libera

• Collegare il freno a corrente di Foucault con l'usci-

ta per la tensione regolabile dell'alimentatore del pendolo di torsione.

• Attivare l'amperometro nel circuito elettrico.

• Determinare la costante di smorzamento in fun-

zione della corrente.

4.2 Oscillazione di torsione forzata

• Collegare i jack di raccordo (16) del motore ad ecci-

tazione con l'uscita di tensione fissa dell'alimentatore del pendolo di torsione.

• Collegare il voltmetro con i jack di raccordo (15)

del motore ad eccitazione.

• Determinazione dell'ampiezza di oscillazione in

funzione della frequenza dell'eccitatore o della tensione di alimentazione.

• Se necessario, collegare il freno a corrente di

Foucault con l'uscita per la tensione regolabile dell'alimentatore del pendolo di torsione.

4.3 Oscillazioni caotiche

• Per la produzione di oscillazioni caotiche sono di-

sponibili 4 masse supplementari, che modificano il momento di rovesciamento lineare del pendolo di torsione.

• A tale scopo avvitare la massa supplementare sul

corpo del pendolo (5).

18

5. Esempi di esperimenti

5.1 Oscillazione di torsione smorzata libera

• Per la determinazione del decremento logaritmico Λ le ampiezze vengono misurate in più flussi e ven-

gono determinati i valori medi. A tale scopo le deviazioni del pendolo di torsione sulla scala di volta in volta a sinistra e a destra vengono lette in due serie di misure.

• Il punto di partenza del corpo del pendolo era compreso tra 15 e –15 sulla scala. Sono state lette cinque deviazioni.

• Dal rapporto delle ampiezze si ricava Λ in base alla formula







ϕ

n



Λ

=

In









ϕ

n+1





ΙΙ

Ι = 0,2 A

ΙΙ



n



ϕ

– Ø

ϕ

– Λ –

0 –15 –15 –15 –15 –15 1 –13,6 –13,8 –13,8 –13,6 –13,7 0,0906 2 –12,6 –12,8 –12,6 –12,4 –12,6 0,13 3 –11,4 –11,8 –11,6 –11,4 –11,5 0,0913 4 –10,4 –10,6 –10,4 –10,4 –10,5 0,0909 5 9,2 –9,6 –9,6 –9,6 –9,5 0,1

• Con T = 1,9 s e Λ = 0,1006 medio si ottiene la costante di smorzamento: δ = 0,053 s

ΙΙ

Ι = 0,4 A

ΙΙ



n

ϕ

– Ø

–1



ϕ

– Λ –

n



ϕ

–



ϕ

+

0 –15 –15 –15 –15 15 15 15 15 1 –14,8 –14,8 –14,8 –14,8 14,8 14,8 14,8 14,8 2 –14,4 –14,6 –14,4 –14,6 14,4 14,4 14,6 14,4 3 –14,2 –14,4 –14,0 –14,2 14,0 14,2 14,2 14,0 4 –13,8 –14,0 –13,6 –14,0 13,8 13,8 14,0 13,8 5 –13,6 –13,8 –13,4 –13,6 13,4 13,4 13,6 13,6

nØ



ϕ

– Ø



ϕ

+

Λ

–

Λ

+

0 –15 15 1 –14,8 14,8 0,013 0,013 2 –14,5 14,5 0,02 0,02 3 –14,2 14,1 0,021 0,028 4 –13,8 13,8 0,028 0,022 5 –13,6 13,5 0,015 0,022

• Il valore medio per Λ ammonta a Λ = 0,0202.

• Per la durata dell'oscillazione T del pendolo vale

t = n · T. A tale scopo misurare il tempo per 10 oscillazioni con un cronometro e calcolare T.

T = 1,9 s

• Da questi valori è possibile determinare la costante di smorzamento δ con δ = Λ / T.

δ

= 0,0106 s

–1

• Per la frequenza propria ω vale

2

π

2





ω

=

 

ω

= 3,307 Hz

T

2

δ

−

 

5.2 Oscillazione di torsione smorzata libera

• Per la determinazione della costante di smorzamento δ in funzione della corrente Ι mediante l'elettromagnete è stato eseguito lo stesso tentativo con il freno a corrente di Foucault inserito con Ι = 0,2 A, 0,4 A e 0,6 A.

0 –15 –15 –15 –15 –15 1 –11,8 –11,8 –11,6 –11,6 –11,7 0,248 2 –9,2 –9,0 –9,0 –9,2 –9,1 0,25 3 –7,2 –7,2 –7,0 –7,0 –7,1 0,248 4 –5,8 –5,6 –5,4 –5,2 –5,5 0,25 5 –4,2 –4,2 –4,0 –4,0 –4,1 0,29

• Con T = 1,9 s e Λ = 0,257 medio si ottiene la costante di smorzamento: δ = 0,135 s

ΙΙ

Ι = 0,6 A

ΙΙ



n

ϕ

– Ø

–1



ϕ

– Λ –

0 –15 –15 –15 –15 –15 1 –9,2 –9,4 –9,2 –9,2 –9,3 0,478 2 –5,4 –5,2 –5,6 –5,8 –5,5 0,525 3 –3,2 –3,2 –3,2 –3,4 –3,3 0,51 4 –1,6 –1,8 –1,8 –1,8 –1,8 0,606 5 –0,8 –0,8 –0,8 –0,8 –0,8 0,81

• Con T = 1,9 s e Λ = 0,5858 medio si ottiene la costante di smorzamento: δ = 0,308 s

–1

5.3 Oscillazione di torsione forzata

• Per la determinazione dell'ampiezza di oscillazione in funzione della frequenza di eccitazione o della tensione di alimentazione viene letta la deviazione massima del corpo del pendolo.

T = 1,9 s



Tensione motore V

ϕ

3 0,8 4 1,1 5 1,2 6 1,6 7 3,3 7,6 20,0 8 16,8 9 1,6

10 1,1

19

• La frequenza del circuito proprio del sistema ω0 si

ottiene dalla misurazione del periodo T

ω

= 2 π/T = 3,3069 Hz

0

• In caso di tensione del motore pari a 7,6 V ha luo-

go la deviazione massima, ossia si verifica la risonanza.

• Quindi è stato eseguito lo stesso tentativo con freno a corrente di Foucault inserito con Ι = 0,2 A, 0,4 A e 0,6 A.

ΙΙ

Ι = 0,2 A

ΙΙ



Tensione motore V

ϕ

3 0,9 4 1,1 5 1,2 6 1,7 7 2,9 7,6 15,2 8 4,3 9 1,8

10 1,1

ΙΙ

Ι = 0,4 A

ΙΙ



Tensione motore V

ϕ

3 0,9 4 1,1

5 1,3 6 1,8 7 3,6 7,6 7,4 8 3,6 9 1,6

10 1,0

ΙΙ

Ι = 0,6 A

ΙΙ



Tensione motore V

ϕ

3 0,9 4 1,1 5 1,2 6 1,6 7 2,8 7,6 3,6 8 2,6 9 1,3

10 1,0

• Da queste misurazioni è possibile rappresentare

graficamente le curve di risonanza, tracciando le ampiezze in funzione della tensione del motore.

• Dalla semilarghezza del grafo può essere determi-

nata graficamente la frequenza della risonanza.

A

[skt]

20

15

10

I=0,0A

I=0,2A

I=0,4A

5

1

012

Curve di risonanza

3

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Germania • www.3bscientific.com • Con riserva di modifiche tecniche

567 8910

4

20

I=0,6A

u[v]

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

U15040 Péndulo oscilatorio según Pohl

Instrucciones de uso

12/03 ALF

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

9

8

7

6

5

4

bl bm bn bo bp

bq br bs

1 Motor de excitación 2 Botón para ajuste fino de la tensión de excitación 3 Botón para ajuste grueso de la tensión de excitación 4 Anillo graduado 5 Cuerpo pendular 6 Muelle espiral 7 Indicador de la posición de fase del excitador 8 Indicador de la posición de fase del péndulo 9 Indicador de desviación del péndulo bl Excitador

3

bm Freno de corrientes parásitas bn Ranura guía y tornillo para el ajuste de la amplitud de

2

excitación

bo Biela bp Rueda con palanca excéntrica bq Clavijeros de seguridad de 4 mm para medición de la

1

tensión de excitación

br Clavijeros de seguridad de 4 mm para alimentación del

motor de excitación

bs Clavijeros de seguridad de 4 mm para alimentación del

freno de corrientes parásitas

El péndulo oscilatorio sirve para el estudio de oscilaciones libres, forzadas y caóticas frente a diferentes atenuaciones.

Temas experimentales:

• Oscilaciones torsionales libres con distintas atenua-

ciones (caso oscilante con atenuación media, oscilación no periódica y caso límite no periódico)

• Oscilaciones forzadas y sus características de reso-

nancia frente a diferentes atenuaciones

• Desfase entre excitador y resonador en caso de re-

sonancia

• Oscilaciones torsionales caóticas

• Determinación estática de la magnitud de referen-

cia D

• Determinación dinámica del momento de inercia J

1. Aviso de seguridad

• ¡Al retirar el péndulo oscilatorio de su embalaje no

se lo debe tomar por el anillo graduado! ¡Peligro

de daño! ¡El equipo siempre se debe retirar con ayuda de material auxiliar (envoltura interna)!

• Para transportar el péndulo oscilatorio se lo debe

sujetar siempre de la placa base.

• No se debe sobrepasar la máxima tensión de ali-

mentación permitida del motor de excitación (24 V c.c.).

• El péndulo oscilatorio no se debe someter a esfuer-

zos mecánicos innecesarios.

2. Descripción, datos técnicos

El péndulo según Pohl se compone de un sistema oscilatorio, montado sobre una placa base de madera, y de un motor eléctrico. El sistema oscilatorio consta de un rueda de cobre (5) asentada sobre un rodamiento de bolas y conectada a la varilla de excitación por medio de un muelle espiral (6), que suministra el momento de retroceso. Para la excitación del péndulo oscilatorio se utiliza un motor de corriente continua, con velocidad de giro de ajuste grueso y fino, el cual

21

presiona y estira el muelle espiral, en secuencias pe-

ω

0

2

=

D

J

riódicas, por medio de una palanca excéntrica (14), dotada de una biela (13), provocando de esta manera la oscilación de la rueda de cobre. Para la atenuación se emplea un freno electromagnético de corrientes parásitas (11). Un anillo graduado (4), con ranuras y escala con división de 2 mm, rodea el sistema oscilatorio; los indicadores se encuentran en el excitador y el resonador. El equipo también se puede utilizar para experimentos de demostración con proyección de sombras. Para la alimentación de corriente se requiere una fuente de alimentación de c.c. U11755 para péndulo oscilatorio.

Frecuencia propia: aprox. 0,5 Hz. Frecuencia de excitación: 0 a 1,3 Hz

(ajuste continuo) Conexiones: Motor: máx. 24 V c.c., 0,7 A,

a través de clavijeros

de seguridad de 4 mm Freno de corrientes parásitas: 0 a 24 V c.c., máx. 2 A,

a través de clavijeros

de seguridad de 4 mm Anillo graduado: 300 mm Ø Dimensiones: 400 mm x 140 mm x 270 mm Peso: 4 kg

2.1 Volumen de suministro

1 péndulo oscilatorio 2 pesas adicionales de 10 g 2 pesas adicionales de 20 g

3. Fundamentos teóricos

3.1 Símbolos empleados

D = magnitud de referencia angular J = momento de inercia de masa M = momento de giro de retroceso T = duración de periodo T0= duración de periodo del sistema

sin atenuación

Td= duración de periodo del sistema

con atenuación



= amplitud del momento de giro del excitador

M

E

b = momento de atenuación n = cantidad de periodos t = tiempo

Λ = decremento logarítmico δ = constante de atenuación

ϕ

= ángulo de desviación



ϕ

= amplitud para tiempo t = 0 s

0



ϕ

= amplitud tras n periodos

n



ϕ

= amplitud del excitador

E



ϕ

= amplitud del sistema

S

ω0= frecuencia propia del sistema oscilatorio ωd= frecuencia propia del sistema amortiguado ωE= frecuencia angular del excitador

ωE

= frecuencia angular del excitador para

res

la máx. amplitud

Ψ0S= ángulo de fase cero del sistema

3.2 Oscilación torsional armónica

Una oscilación armónica se presenta cuando la fuerza de reacción es proporcional a la desviación. En el caso de las oscilaciones torsionales armónicas, el par de giro de retroceso es proporcional al ángulo de desviación ϕ:

M = D ·

ϕ

El factor de proporcionalidad D (magnitud de referencia angular) se puede calcular a partir de la medición del ángulo de desviación y del momento de desviación. La frecuencia angular propia del sistema ω0 se obtiene de la medición de la duración de periodo T a partir de:

ω

= 2 π/T ,

0

mientras que el momento de inercia de masa J se obtiene de:

3.3 Oscilación torsional sin amortiguación

En un sistema oscilatorio cuya energía decrece debido a las pérdidas por fricción, sin que dicha energía se vea compensada por una alimentación externa, la amplitud disminuye constantemente, esto es, la oscilación sufre una amortiguación. En este caso, el momento de amortiguación b es proporcional a la velocidad angular

.

ϕ

. Partiendo del equilibrio del momento se obtiene la ecuación de movimiento:

.

..

JbD⋅+⋅+⋅ =

ϕϕϕ

0

En el caso de la oscilación sin amortiguación, b es igual a 0. Si con el tiempo t = 0 s, la oscilación se inicia con la



amplitud máxima

ϕ

, se obtiene la solución de la

0

ecuación diferencial con una amortiguación no muy elevada (δ² < ω0²) (caso oscilante)



–δ ·t

ϕ

=

· e

· cos (

ω

0

d

· t)

δ = b/2 J es la constante de amortiguación y

2

ωωδ

=−

d

2

0

la frecuencia propia del sistema amortiguado. Frente a una amortiguación fuerte (δ² > ω0²) el sistema no oscila, sino que se arrastra hacia el estado de reposo. Frente a una amortiguación no muy fuerte, la duración de periodo Td del sistema oscilante varía de manera mínima en relación al periodo T0 del sistema oscilante no amortiguado. Si se sustituye t = n · Td en la ecuación



–δ ·t

ϕ

ϕ =

0

· e

· cos (

ω

· t)

d

22



Ψ

y para la amplitud tras n periodos ϕ = lo siguiente, con la relación



ϕ

n



ϕ

0

δ

−⋅

n

=⋅

eT

ω

= 2 π/T

d

ϕ

, se obtiene

n

d

y, a partir de ello, el decremento logarítmico Λ:

Λ

=⋅ =⋅

δ

1

T

d

In In

n

Si se reemplaza δ = Λ / Td ,





ϕ

n







ϕ

0



ω

= 2 π / T0 y

0









ϕ



=

 

n











ϕ

n+1





ω

= 2π / T

d

en la ecuación

En el caso de las oscilaciones no amortiguadas, si se presenta el caso de resonancia (ωE es igual a ω0), teóricamente, la amplitud aumenta hasta el infinito, lo cual produciría la destrucción del sistema. Con oscilaciones atenuadas por una amortiguación no demasiado fuerte, se alcanza la máxima amplitud del sistema, siendo la frecuencia angular del excitador ω

E res

menor que la frecuencia angular propia del sistema. Esta frecuencia se obtiene a partir de:

2

δ

ωω

=⋅−1

d

Eres 0

2

ω

0

2

ωωδ

=−

d

2

0

se obtiene:

2

TT

=⋅+1

d0

Λ

2

4

π

con lo que se puede calcular exactamente la duración del periodo Td, si se conoce el valor de T0.

3.4 Oscilación torsional forzada

Las oscilaciones torsionales forzadas se generan cuando, sobre el sistema oscilante, actúa externamente un par de giro de variación periódica con una función sinusoidal. Se debe sustituir este momento de excitación en la ecuación de movimiento

.

..

JbD M t⋅+⋅+⋅= ⋅ ⋅

ϕϕϕ ω



sin

E

()

E

Una vez transcurrido el tiempo de establecimiento de la oscilación, el péndulo oscilatorio alcanza un estado estacionario con la misma frecuencia angular que la del excitador, siendo incluso factible que ωE se encuentre desfasada en relación a ω0. Ψ0S es el ángulo de fase cero del sistema, el desfase entre el sistema oscilante y el excitador.



ϕ

=

· sin (

ω

· t –

Ψ

S

E

)

0S

Si se tiene una amortiguación fuerte, no se producen excesos de amplitud. Para el ángulo de fase cero Ψ0S del sistema es válido:

 

arctan

=

0S



ωω





2

δω



22



−

ω

0



Para ωE = ω0 (resonancia), el ángulo de fase cero Ψ del sistema es igual a 90°. Esto también es válido para δ = 0, en donde la oscilación sobrepasa su valor límite. Con oscilaciones amortiguadas (δ > 0) y ωE < ω0 se obtiene 0° ≤ Ψ0S ≤ 90°, para ωE > ω0 es válido 90° ≤

Ψ0S ≤ 180°. Con oscilaciones no amortiguadas (δ = 0) es válido Ψ0S = 0° con ωE < ω0 y Ψ0S = 180° para ωE > ω0.

4. Servicio

4.1 Oscilación torsional de amortiguación libre

• Conectar el freno de corrientes parásitas a la salida

de tensión regulable de la fuente de alimentación del péndulo oscilatorio.

• Conectar el amperímetro al circuito de corriente.

• Determinar la constante de amortiguación en fun-

ción de la corriente.

0S



Para la amplitud



ϕ

es válido lo siguiente:

S



M

E

−

02E

J

2

+⋅

=

ωω δω

()

2

4

E

Para la relación entre la amplitud del sistema y la del excitador se aplica:



M



ϕ

S

=



ϕ

E





ω

E



−

14



ω



0





E

J

2







+









2





δ





ω

0





2





ω

E

⋅





ω

0





4.2 Oscilación torsional forzada

• Conectar el clavijero (16) del motor de excitación a

la salida de tensión fija de la fuente de alimentación del péndulo oscilatorio.

• Conectar el voltímetro a los clavijeros de conexión

(15) del motor de excitación.

• Determinar la amplitud de oscilación en función

de la frecuencia del excitador o de la tensión de alimentación.

• En caso de ser necesario, conectar el freno de co-

rrientes parásitas a la salida de tensión ajustable de la fuente de alimentación del péndulo oscilatorio.

4.3 Oscilaciones caóticas

• Para generar oscilaciones caóticas se dispone de 4

pesas adicionales que varían el momento lineal de retroceso del péndulo oscilatorio.

23

• Lo anterior se realiza atornillando las pesas al cuer-

po del péndulo (5).

• Para la frecuencia propia ω es válido

2

π

2





ω

=

 

ω

= 3,307 Hz

T

2

δ

−

 

5.2 Oscilación torsional de amortiguación libre

• Para determinar la constante de amortiguación δ

en función de la corriente Ι que fluye por los electroimanes, se realizó el mismo experimento conectándose adicionalmente el freno de corrientes parásitas con Ι = 0,2 A, 0,4 A y 0,6 A.

5. Ejemplos de experimentos

5.1 Oscilación torsional de amortiguación libre

• Para determinar el decremento logarítmico Λ se

miden y se promedian las amplitudes de varios ciclos, para lo cual se leen las oscilaciones del péndulo tanto a la derecha como a la izquierda de la escala.

• El punto de partida del cuerpo pendular se encon-

traba en 15, ó bien en –15, de la escala. Se leyeron cinco oscilaciones.

• A partir de la relación de amplitud se obtiene Λ de

acuerdo con la fórmula:







ϕ

n



Λ

=

In

n









ϕ

n+1







ϕ

–



ϕ

+

0 –15 –15 –15 –15 15 15 15 15 1 –14,8 –14,8 –14,8 –14,8 14,8 14,8 14,8 14,8 2 –14,4 –14,6 –14,4 –14,6 14,4 14,4 14,6 14,4 3 –14,2 –14,4 –14,0 –14,2 14,0 14,2 14,2 14,0 4 –13,8 –14,0 –13,6 –14,0 13,8 13,8 14,0 13,8 5 –13,6 –13,8 –13,4 –13,6 13,4 13,4 13,6 13,6

nØ



ϕ

– Ø



ϕ

+

Λ

–

Λ

+

0 –15 15 1 –14,8 14,8 0,013 0,013 2 –14,5 14,5 0,02 0,02 3 –14,2 14,1 0,021 0,028 4 –13,8 13,8 0,028 0,022 5 –13,6 13,5 0,015 0,022

• El valor promedio de Λ es igual a 0,0202.

• Para la duración de oscilación T del péndulo es

válido t = n · T. Medir para ello, con un cronómetro, el tiempo necesario para 10 oscilaciones y calcular el valor de T.

T = 1,9 s

• A partir de estos valores se puede determinar la constante de amortiguación δ por medio de

δ = Λ /T.

δ

= 0,0106 s

–1

ΙΙ

Ι = 0,2 A

ΙΙ



n



ϕ

– Ø

ϕ

– Λ –

0 –15 –15 –15 –15 –15 1 –13,6 –13,8 –13,8 –13,6 –13,7 0,0906 2 –12,6 –12,8 –12,6 –12,4 –12,6 0,13 3 –11,4 –11,8 –11,6 –11,4 –11,5 0,0913 4 –10,4 –10,6 –10,4 –10,4 –10,5 0,0909 5 9,2 –9,6 –9,6 –9,6 –9,5 0,1

• Con T = 1,9 s y el valor promedio Λ = 0,1006 se obtiene la constante de amortiguación: δ = 0,053 s

ΙΙ

Ι = 0,4 A

ΙΙ



n

ϕ

– Ø



ϕ

–1

– Λ –

0 –15 –15 –15 –15 –15 1 –11,8 –11,8 –11,6 –11,6 –11,7 0,248 2 –9,2 –9,0 –9,0 –9,2 –9,1 0,25 3 –7,2 –7,2 –7,0 –7,0 –7,1 0,248 4 –5,8 –5,6 –5,4 –5,2 –5,5 0,25 5 –4,2 –4,2 –4,0 –4,0 –4,1 0,29

• Con T = 1,9 s y el valor promedio Λ = 0,257 se obtiene la constante de amortiguación: δ = 0,135 s

ΙΙ

Ι = 0,6 A

ΙΙ

n



ϕ

– Ø



ϕ

– Λ –

–1

0 –15 –15 –15 –15 –15 1 –9,2 –9,4 –9,2 –9,2 –9,3 0,478 2 –5,4 –5,2 –5,6 –5,8 –5,5 0,525 3 –3,2 –3,2 –3,2 –3,4 –3,3 0,51 4 –1,6 –1,8 –1,8 –1,8 –1,8 0,606 5 –0,8 –0,8 –0,8 –0,8 –0,8 0,81

• Con T = 1,9 s y el valor promedio Λ = 0,5858 se obtiene la constante de amortiguación: δ = 0,308 s

–1

5.3 Oscilación torsional forzada

• Para determinar la amplitud de oscilación en función de la frecuencia del excitador, o bien de la tensión de alimentación, se lee la máxima oscilación del cuerpo pendular.

24

T = 1,9 s



Tensión del motor V

ϕ

3 0,8 4 1,1 5 1,2 6 1,6 7 3,3 7,6 20,0 8 16,8 9 1,6

10 1,1

• La frecuencia circular propia del sistema ω0 se ob-

tiene de la medición de la duración de periodo T a partir de:

ω

= 2 π/T = 3,3069 Hz

0

• Con una tensión del motor de 7,6 V se presenta la

mayor desviación, esto es, se presenta el caso de resonancia.

• A continuación se llevó a cabo el mismo experi-

mento con la presencia adicional del freno de corrientes parásitas con I = 0,2 A, 0,4 A y 0,6 A.

ΙΙ

Ι = 0,2 A

ΙΙ



Tensión del motor V

ϕ

3 0,9 4 1,1

A

[skt]

5 1,2 6 1,7 7 2,9 7,6 15,2 8 4,3 9 1,8

10 1,1

ΙΙ

Ι = 0,4 A

ΙΙ

Tensión del motor V

3 0,9 4 1,1 5 1,3 6 1,8 7 3,6 7,6 7,4 8 3,6 9 1,6

10 1,0

ΙΙ

Ι = 0,6 A

ΙΙ

Tensión del motor V

3 0,9 4 1,1 5 1,2 6 1,6 7 2,8 7,6 3,6 8 2,6 9 1,3

10 1,0



ϕ



ϕ

20

15

10

5

1

012

• A partir de estas mediciones se pueden represen-

tar gráficamente las características de resonancia,

I=0,0A

trazando la amplitud en función de la tensión del motor.

• A partir del valor promedio del ancho de los gráfi-

cos se puede obtener la frecuencia de resonancia.

I=0,2A

I=0,4A

I=0,6A

3

567 8910

4

u[v]

Curvas de resonancia

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Alemania • www.3bscientific.com • Se reservan las modificaciones técnicas

25

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

U15040 Pêndulo de torção segundo Prof. Pohl

Instruções para o uso

12/03 ALF

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

9

8

7

6

5

4

bl bm bn bo bp

1 Motor do excitador 2 Botão rotativo para o ajuste fino da tensão do excitador 3 Botão rotativo para o ajuste grosseiro da tensão do

excitador

4 Anel graduado 5 Corpo pendular 6 Mola caracol 7 Indicador da situação de fase do excitador 8 Indicador da situação de fase do corpo pendular 9 Indicador do ângulo de oscilação do corpo pendular

3

bl Excitador bm Freio de corrente parasita

2

bn Fresta de controle e parafuso para o ajuste da

amplitude do excitador

bo Vara para impulso bp Roda de acionamento com excêntrico

1

bq Tomadas de segurança de 4 mm para a medição

da tensão do excitador

br Tomadas de segurança de 4 mm para a alimentação do

motor do excitador

bs Tomadas de segurança de 4 mm para a alimentação do

freio de corrente parasita

bq br bs

O pêndulo de torção serve para a análise de oscilações livres, forçadas e caóticas em diferentes casos de amortecimento.

Temas para experiências:

• Vibrações de torção livres em diferentes amorteci-

mentos (queda na oscilação com amortecimento moderado, oscilação aperiódica e queda aperiódica da limitação)

• Oscilações forçadas e suas curvas de ressonância

em vários casos de amortecimentos

• Transição fásica entre excitador e ressonador com

queda de ressonância

• Oscilações de torção caóticas

• Determinação estática da grandeza de referência D

• Determinação dinâmica do momento de inércia J

1. Indicações de segurança

• Ao retirar o pêndulo de torção da sua embalagem,

nunca o pegue pelo anel graduado! Podem ocor-

rer danos! Sempre retire o aparelho com o dispositivo previsto para isto! (Interior da embalagem).

• Para transportar o pêndulo de torção, sempre pegar o aparelho pela base.

• Não ultrapassar a tensão de alimentação máxima admitida do motor do excitador (24 V DC).

• O pêndulo de torção não deve ser sujeito a qualquer esforço físico desnecessário.

2. Descrição, dados técnicos

O pêndulo de torção segundo Prof. Pohl consiste num sistema oscilatório montado sobre uma placa base de madeira e um motor elétrico. O sistema oscilatório consiste numa roda de cobre com rolamento (5), a qual está conectada com a vara do excitador por meio de uma mola espiral (6) que por sua vez fornece o momento de restituição. Para a excitação do pêndulo de torção, utiliza-se um motor de corrente contínua com número de rotações ajustável de modo aproximado ou preciso, o qual expande e comprime a mola espiral

26

numa seqüência periódica através de um excêntrico (14) com uma vara de impulso (13), levando assim a roda de cobre a oscilar. Para o amortecimento é utilizado um freio de corrente parasita eletromagnético (11). Um anel graduado (4) com frestas e uma escala com divisões de 2 mm envolve o sistema oscilatório; indicadores encontram-se no excitador e no ressoador. O aparelho também pode ser utilizado para a projeção de sombras em demonstrações. Para a alimentação elétrica é necessária a unidade de alimentação elétrica DC para o pêndulo de torção U11755.

Freqüência própria: aprox. 0,5 Hz. Freqüência do excitador: 0 até 1,3 Hz (ajustável sem

escalonamento) Conexões: motor: máx. 24 V DC, 0,7 A,

por tomadas de segurança

de 4 mm freio de corrente parasita: 0 até 24 V DC, máx. 2 A,

por tomadas de segurança

de 4 mm Anel graduado: 300 mm Ø Medidas: 400 mm x 140 mm x 270 mm Massa: 4 kg

2.1 Fornecimento

1 pêndulo de torção 2 massas adicionais de 10 g 2 massas adicionais de 20 g

3. Fundamentos teóricos

3.1 Símbolos utilizados nas fórmulas

D = Grandeza de referência angular J = Momento de inércia da massa M = Momento de torção de restituição T = Duração do período T0= Duração do período do sistema sem

amortecimento

Td= Duração do período do sistema com

amortecimento



M

= Amplitude do momento de torção do

E

excitador b = Momento do amortecimento n = Número de períodos t = Tempo

Λ = Decremento logarítmico δ = Constante de amortecimento

ϕ

= Deslocamento angular



ϕ

= Amplitude no tempo t = 0 s

0



ϕ

= Amplitude após n períodos

n



ϕ

= Amplitude do excitador

E



ϕ

= Amplitude do sistema

S

ω0= Freqüência própria do sistema oscilatório ωd= Freqüência própria do sistema amortecido ωE= Freqüência circular do excitador

ωE

= Freqüência circular para a amplitude máx.

res

Ψ0S= Ângulo de fase do sistema

3.2 Oscilações de torção harmônicas

Uma oscilação de torção harmônica se dá quando a força de restituição é proporcional ao deslocamento angular. Nas oscilações de torção harmônicas, o momento de torção de reação é proporcional ao deslocamento angular ϕ:

M = D ·

ϕ

O fator de proporcionalidade D (grandeza de referência angular) pode ser calculado através da medição do deslocamento angular e do momento deslocador. A freqüência própria circular do sistema ω0 resulta das medições da duração do período T a partir de

ω

= 2 π/T

0

e do momento de inércia da massa J a partir de

D

2

ω

=

0

J

3.3 Oscilações de torção livres amortecidas

Num sistema oscilatório no qual energia é perdida por causa de perdas por atrito sem que esta energia seja compensada por aporte externo de energia, a amplitude diminui constantemente, ou seja, a oscilação é amortecida. Enquanto isso, o momento de amortecimento b é proporcional à velocidade angular

.

ϕ

. A partir do equilíbrio de momentos de torção resulta a equação de movimento

.

..

JbD⋅+⋅+⋅ =

ϕϕϕ

0

Para a oscilação sem amortecimento vale b = 0 Se a oscilação no tempo t = 0 s começa com a amplitu-



de máxima

ϕ

a solução da equação diferencial com

0

um amortecimento não muito forte resulta em (δ² < ω0²) (caso oscilatório)



–δ ·t

ϕ

=

· e

· cos (

ω

0

d

· t)

δ = b/2 J é a constante de amortecimento e

2

ωωδ

=−

d

2

0

é a freqüência própria do sistema amortecido. No caso de um amortecimento forte (δ² > ω0²) o sistema não oscila, mais se arrasta para o ponto de descanso (caso de arraste). A duração de período Td do sistema oscilatório amortecido só varia muito pouco com relação ao valor T do sistema oscilatório sem amortecimento. Pela introdução de t = n · Td na equação



–δ ·t

ϕ

ϕ =

e a amplitude após n períodos ϕ = a relação

ω



ϕ



ϕ

· e

0

= 2 π/T

d

n

0

d

δ

−⋅

n

=⋅

eT

· cos (

d

ω

· t)

d



ϕ

obtém-se com

n

0

27

e a partir disso o decremento logarítmico Λ:

Ψ





ϕ

Λ

=⋅ =⋅

δ

T

d

1 n

n



In In





ϕ

0



Pela introdução de δ = Λ / Td ,

  







ϕ



=





ϕ



ω

= 2 π / T0 e

0

n+1



n

 



/ Td na equação

2

ωωδ

=−

d

2

0

freqüência resulta de

2

δ

ωω

=⋅−1

Eres 0

2

ω

0

Com amortecimento forte não há aumento excessivo

ω

= 2

π

d

de amplitude. Para o ângulo de fase do sistema Ψ0S é válido

 

arctan

=

0S



ωω





2

δω



22



−

ω

0



obtém-se:

2

TT

=⋅+1

d0

Λ

2

4

π

pelo qual a duração de período Td pode ser calculada exatamente se o valor T0 é conhecido.

3.4 Oscilações de torção forçadas

No caso de oscilações de torção forçadas, um momento de torção variável periodicamente com uma função seno age do exterior sobre o sistema oscilatório. Completa-se esse momento do excitador na equação de movimento

.

..

JbD M t⋅+⋅+⋅= ⋅ ⋅

ϕϕϕ ω



sin

E

()

E

Depois da iniciação da oscilação, o pêndulo de torção oscila num estado estacionário com a mesma freqüência circular que o excitador, sendo que não se encontra defasado nem com ωE ou contra ω0. Ψ0S é o ângulo de fase do sistema, a defasagem entre o sistema oscilatório e o excitador.



ϕ

=

· sin (

ω

· t –

Ψ

S

E

Para a amplitude do sistema



M

−

02E

J

2



ϕ

=

ωω δω

()

)

0S



ϕ

é válido

S

E

2

+⋅

4

2

E

Para ωE = ω0 (ressonância), o ângulo de fase do sistema Ψ0S = 90°. Isto é válido também para δ = 0 com a extrapolação correspondente. No caso das oscilações amortecidas (δ > 0) e ωE < ω resulta 0° ≤ Ψ0S ≤ 90°, para ωE > ω0 é válido 90° ≤ Ψ ≤ 180°. No caso de oscilações sem amortecimento (δ = 0) é válido Ψ0S = 0° com ωE < ω0 e Ψ0S = 180° para ωE > ω0.

4. Utilização

4.1 Oscilações de torção livres amortecidas

• Conectar o freio de corrente parasita com a saída

para tensão ajustável do transformador de alimentação do pêndulo de torção.

• Conectar o amperímetro com o circuito elétrico.

• Determinar a constante de amortecimento depen-

dendo da corrente.

4.2 Oscilações de torção forçadas

• Conectar as tomadas de conexão (16) do motor do

excitador com a saída de tensão fixa do transformador do pêndulo de torção.

• Conectar o voltímetro com as tomadas de conexão

(15) do motor do excitador.

• Determinar a amplitude de oscilação em relação

de dependência com a freqüência do excitador ou com a tensão de alimentação.

• Caso seja necessário, conectar o freio de corrente

parasita com a saída de tensão ajustável do transformador do pêndulo de torção.

0

0S

Para a relação entre a amplitude do sistema e a amplitude do excitador é válido



M



ϕ

S

=



ϕ

E





ω

E



−

14



ω



0





E

J

2







+









2





δ





ω

0





2





ω

E

⋅





ω

0





Nas oscilações sem amortecimento, a amplitude, em caso de ressonância (ωE igual a ω0) cresce teoricamente infinitamente e leva ao “colapso por ressonância”. Nas oscilações amortecidas e com amortecimento não muito forte a amplitude do sistema atinge seu máximo, sendo que a freqüência circular do excitador ω

E res

é menor do que a freqüência própria do sistema. Esta

4.3 Oscilações caóticas

• Para a produção de oscilações caóticas, encontram-

se 4 massas adicionais, estas modificam o momento de restauração linear do pêndulo de torção.

• Para tal, aparafusar as massas adicionais no corpo

pendular (5).

28

5. Exemplos de experiências

5.1 Oscilações de torção livres amortecidas

• Para determinar o decremento logarítmico Λ, me-

dem-se e estabelece-se a média das amplitudes em várias operações. Para tal, registra-se o balanço do pêndulo na escala em duas séries de medições, a cada vez com leitura à esquerda e à direita.

• O ponto inicial do pêndulo encontrava-se em 15

ou –15 na escala. Cinco deslocamentos foram registrados.

• Da relação entre as amplitudes, obtém-se Λ com a

fórmula







ϕ

n



Λ

=

n

In









ϕ

n+1







ϕ

–



ϕ

+

0 –15 –15 –15 –15 15 15 15 15 1 –14,8 –14,8 –14,8 –14,8 14,8 14,8 14,8 14,8 2 –14,4 –14,6 –14,4 –14,6 14,4 14,4 14,6 14,4 3 –14,2 –14,4 –14,0 –14,2 14,0 14,2 14,2 14,0 4 –13,8 –14,0 –13,6 –14,0 13,8 13,8 14,0 13,8 5 –13,6 –13,8 –13,4 –13,6 13,4 13,4 13,6 13,6

nØ



ϕ

– Ø



ϕ

+

Λ

–

Λ

+

0 –15 15 1 –14,8 14,8 0,013 0,013 2 –14,5 14,5 0,02 0,02 3 –14,2 14,1 0,021 0,028 4 –13,8 13,8 0,028 0,022 5 –13,6 13,5 0,015 0,022

• O valor obtido para Λ é Λ = 0,0202.

• Para duração de oscilação T do pêndulo é válido

t = n · T. Para tal, medir o tempo par 10 oscilações com um cronômetro e calcular T.

T = 1,9 s

• A partir destes valores pode-se determinar a constante de amortecimento δ com δ = Λ / T.

δ

= 0,0106 s

–1

• Para a freqüência própria ω é válido

2

π





2

ω

=

 

ω

= 3,307 Hz

−

δ



T



5.2 Oscilações de torção livres amortecidas

• Para determinar a constante de amortecimento δ em relação de dependência com a corrente Ι através do imã eletromagnético, foi realizado o mesmo ensaio com o freio de corrente parasita ligado com Ι = 0,2 A, 0,4 A e 0,6 A.

ΙΙ

Ι = 0,2 A

ΙΙ



n



ϕ

– Ø

ϕ

– Λ –

0 –15 –15 –15 –15 –15 1 –13,6 –13,8 –13,8 –13,6 –13,7 0,0906 2 –12,6 –12,8 –12,6 –12,4 –12,6 0,13 3 –11,4 –11,8 –11,6 –11,4 –11,5 0,0913 4 –10,4 –10,6 –10,4 –10,4 –10,5 0,0909 5 9,2 –9,6 –9,6 –9,6 –9,5 0,1

• Com T = 1,9 s e média de Λ = 0,1006 resulta a



ϕ

– Λ –

–1

constante de amortecimento: δ = 0,053 s

ΙΙ

Ι = 0,4 A

ΙΙ



n

ϕ

– Ø

0 –15 –15 –15 –15 –15 1 –11,8 –11,8 –11,6 –11,6 –11,7 0,248 2 –9,2 –9,0 –9,0 –9,2 –9,1 0,25 3 –7,2 –7,2 –7,0 –7,0 –7,1 0,248 4 –5,8 –5,6 –5,4 –5,2 –5,5 0,25 5 –4,2 –4,2 –4,0 –4,0 –4,1 0,29

• Com T = 1,9 s e média de Λ = 0,257 resulta a constante de amortecimento: δ = 0,135 s

ΙΙ

Ι = 0,6 A

ΙΙ



n

ϕ

– Ø

–1



ϕ

– Λ –

0 –15 –15 –15 –15 –15 1 –9,2 –9,4 –9,2 –9,2 –9,3 0,478 2 –5,4 –5,2 –5,6 –5,8 –5,5 0,525 3 –3,2 –3,2 –3,2 –3,4 –3,3 0,51 4 –1,6 –1,8 –1,8 –1,8 –1,8 0,606 5 –0,8 –0,8 –0,8 –0,8 –0,8 0,81

• Com T = 1,9 s e média de Λ = 0,5858 resulta a constante de amortecimento: δ = 0,308 s

–1

5.3 Oscilações de torção forçadas

• Para determinar amplitude de oscilação dependendo da freqüência do excitador ou da tensão de alimentação registra-se a oscilação máxima do corpo pendular.

T = 1,9 s



Tensão do motor V

ϕ

3 0,8 4 1,1 5 1,2 6 1,6 7 3,3 7,6 20,0 8 16,8 9 1,6

10 1,1

29

• A freqüência circular do sistema ω0 obtém-se pela

medição da duração de período T

ω

= 2 π/T = 3,3069 Hz

0

• Com uma tensão de motor de 7,6 V ocorre a maior

distância angular, ou seja, ocorre o caso de ressonância.

• Logo foi efetuado o mesmo ensaio com o freio de corrente parasita ligado com Ι = 0,2 A, 0,4 A e 0,6 A.

ΙΙ

Ι = 0,2 A

ΙΙ



Tensão do motor V

ϕ

3 0,9 4 1,1 5 1,2 6 1,7 7 2,9 7,6 15,2 8 4,3 9 1,8

10 1,1

10 1,0

ΙΙ

Ι = 0,6 A

ΙΙ

Tensão do motor V

10 1,0

5 1,3 6 1,8 7 3,6 7,6 7,4 8 3,6 9 1,6



ϕ

3 0,9 4 1,1 5 1,2 6 1,6 7 2,8 7,6 3,6 8 2,6 9 1,3

ΙΙ

Ι = 0,4 A

ΙΙ

Tensão do motor V



ϕ

3 0,9 4 1,1

A

[skt]

20

15

10

• A partir destas medições pode-se representar as

curvas de ressonância de forma gráfica integrando as amplitudes dependendo da tensão do motor.

• Pela amplitude dos valores médios do gráfico pode-

se determinar graficamente a freqüência de ressonância.

I=0,0A

I=0,2A

I=0,4A

5

1

012

Curvas de ressonância

3

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Alemanha • www.3bscientific.com • Sob reserva de modificações técnicas

567 8910

4

30

I=0,6A

u[v]

3B Scientific Pohl's Torsion Pendulum User Manual [en, de, es, fr, it]

Specifications and Main Features

Frequently Asked Questions

User Manual