Page 1

fx-9860G SD
fx-9860G
Manual de Instruções
Po
http://edu.casio.com
Page 2
CASIO Europe GmbH
Bornbarch 10, 22848 Norderstedt,
Germany
Importante!
Por favor guarde este manual e todas as informações
à mão para futuras referências.
Page 3

ANTES DE UTILIZAR ESTA CALCULADORA
2
PELA PRIMEIRA VEZ...
No acto de compra, esta calculadora não contém pilhas. Antes de utilizar a calculadora
pela primeira vez, realize os seguintes procedimentos para colocar as pilhas, realizar a
reinicialização da calculadora e ajustar o contraste.
1. Assegure-se de que não carrega acidentalmente na tecla o, deslize a tampa sobre
a calculadora e vire-a. Retire a tampa traseira da calculadora, fazendo-a deslizar com
o dedo no ponto
2. Carregue as quatro pilhas que acompanham a calculadora.
• Assegure-se de que o lado positivo (+) e negativo (–) das pilhas estão orientados
correctamente.
1.
1
3. Remova a película protectora do local indicado “BACK UP”, retirando-a na direcção
indicada pela seta.
4. Volte a colocar a tampa traseira, assegurando-se de que as suas linguetas entram nos
orifícios marcados com 2 e volte a calculadora para cima. A calculadora será ligada
automaticamente e o menu principal (MAIN MENU) aparecerá no visor.
20060601
Page 4

• Se o menu principal mostrado à direita não aparecer no
visor, abra a tampa traseira da calculadora e prima o
botão P localizado no interior do compartimento das
pilhas.
Botão P
5. Utilize as teclas de cursor (f, c, d, e) para seleccionar o ícone SYSTEM, prima
w e, em seguida, 1(
) para visualizar o ecrã de ajuste do contraste.
6. Ajuste o contraste.
•A tecla de cursor e torna o contraste mais escuro.
•A tecla de cursor d torna o contraste mais claro.
• 1(INIT) reajusta o contraste para os seus valores iniciais.
7. Para sair do ecrã de ajuste do contraste, prima m.
20060601
Page 5
Início Rápido
MANEIRA DE LIGAR E DESLIGAR A CALCULADORA
UTILIZAÇÃO DOS MODOS
CÁLCULOS BÁSICOS
FUNÇÃO DE REPETIÇÃO
CÁLCULOS COM FRACÇÕES
EXPOENTES
FUNÇÕES GRÁFICAS
GRÁFICO DUPLO
GRÁFICO DINÂMICO
FUNÇÃO DE TABELA
20050401
Page 6

1
Início Rápido
Início Rápido
Bem-vindo ao mundo das calculadoras gráficas.
O Início Rápido não é um manual completo, mas uma referência às funções mais
comuns, desde o ligar da calculadora até às complexas equações gráficas. No final, terá
aprendido as operações básicas desta calculadora e estará preparado para continuar a
utilizar o manual para aprender todas as funções disponíveis.
Cada passo dos exemplos no Início Rápido é representado graficamente de modo a
que possa avançar fácil e rapidamente pelas instruções. Quando necessitar introduzir
o número 57, por exemplo, indicamos da seguinte maneira:
Prima fh.
Sempre que necessário, incluímos exemplos do que deve aparecer no ecrã. Se
verificar que o seu ecrã não coincide com o exemplo, pode reiniciar as instruções,
premindo o botão de “Limpeza Total”
MANEIRA DE LIGAR E DESLIGAR A CALCULADORA
o
.
Para ligar a calculadora, prima o.
Para desligar a calculadora, prima
A calculadora desliga-se automaticamente se não for realizada nenhuma operação
dentro do limite de tempo especificado. Este limite pode ser especificado entre 6 e 60
minutos.
!
OFF
o
.
UTILIZAÇÃO DOS MODOS
Esta calculadora permite-lhe realizar uma grande variedade de cálculos, mediante a
simples selecção do modo apropriado. Antes de realizar os exemplos de operações e
de cálculos, vejamos como navegar entre os modos.
Selecção do modo RUN
1. Prima m para visualizar o menu principal.
•
MAT
20050401
Page 7
2
Início Rápido
2. Utilize defc para seleccionar
•
RUN
MAT e prima w.
Este é o ecrã inicial do modo RUN
pode executar cálculos manuais, cálculos de
matriz e executar programas.
•
MAT, onde
CÁLCULOS BÁSICOS
Nos cálculos básicos, as fórmulas são introduzidas da esquerda para a direita. Nas
fórmulas que incluêm operadores aritméticos e parênteses, a calculadora aplica
automaticamente a lógica algébrica verdadeira para calcular o resultado.
Exemplo:
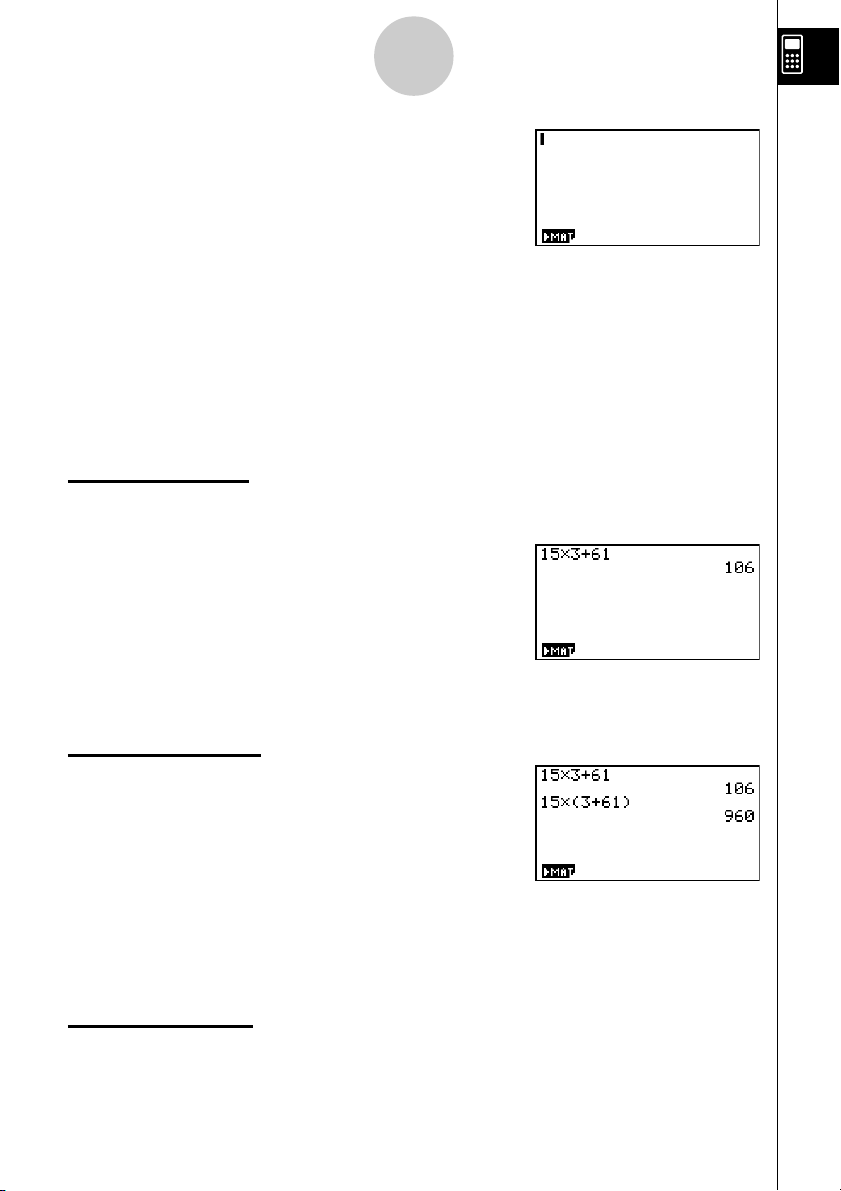
1. Prima
2. Primabf*d+gbw.
15 × 3 + 61
o para limpar a calculadora.
Cálculos com parênteses
Exemplo:
1. Prima
15 × (3 + 61)
bf*(d
+gb)w.
Funções incorporadas
Esta calculadora inclui um certo número de funções científicas incorporadas, entre
elas funções trigonométricas e algorítmicas.
Exemplo:
Importante!
Assegure-se de que especifica Deg (graus) como a unidade angular antes de
realizar este exemplo.
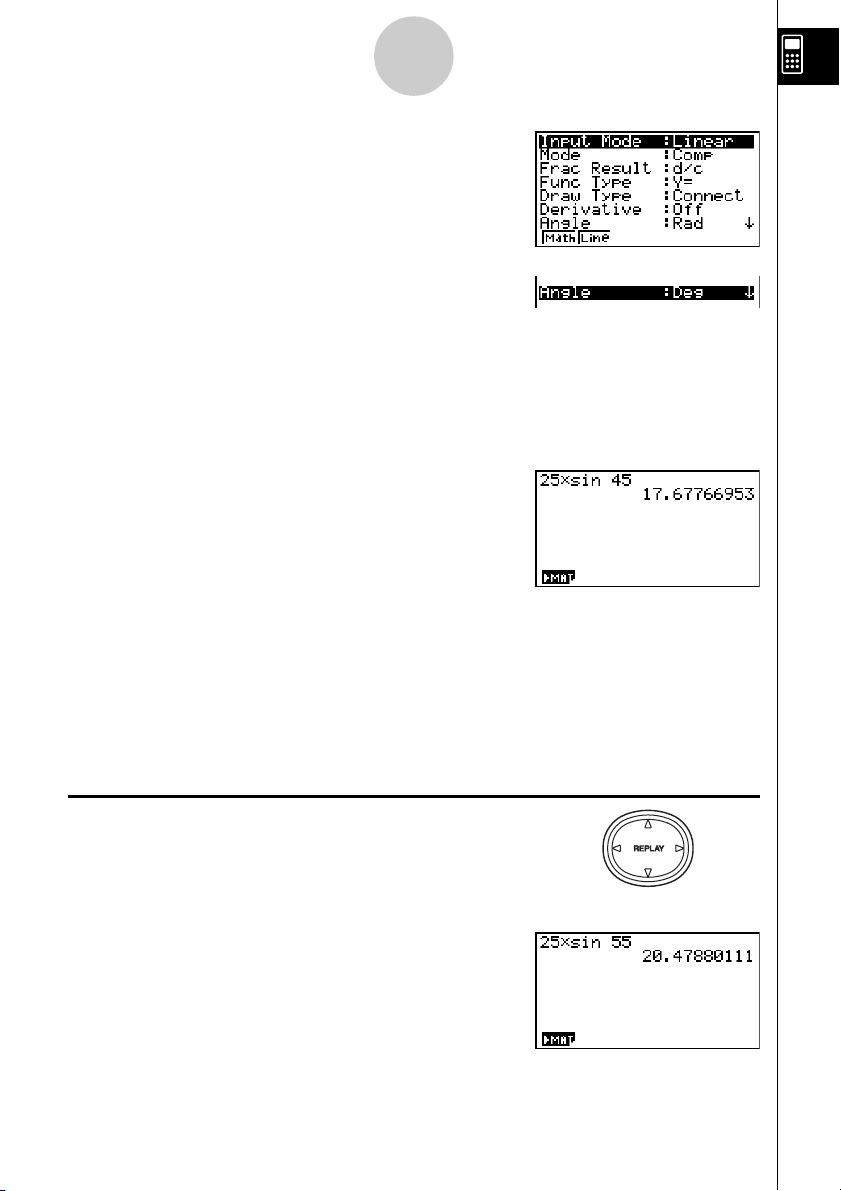
25 × sin 45˚
20050401
Page 8
3
Início Rápido
SET UP
1. Prima !m para visualizar o ecrã de
configuração.
2. Prima
3. Prima J para limpar o menu.
4. Prima o para limpar a unidade.
5. Prima cf*sefw.
cccccc1(Deg)
para especificar graus como a unidade angular.
FUNÇÃO DE REPETIÇÃO
Com a função de repetição, prima simplesmente d ou e para chamar o último
cálculo que foi executado de modo a poder ser alterado ou ser executado novamente
tal como está.
Exemplo:
1. Prima d para visualizar o último cálculo.
2. Prima
Para alterar o cálculo do último exemplo de (25 × sin 45˚) para
(25 × sin 55˚)
d para mover o cursor (
de 4.
I
) para o lado direito
3. Prima
4. Prima f.
5. Prima w para executar novamente o cálculo.
D para apagar o 4.
20050401
Page 9
4
Início Rápido
CÁLCULOS COM FRACÇÕES
Pode utilizar a tecla $ para introduzir fracções nos cálculos. O simbolo “ { ” é
utilizado para separar as diferentes partes da fracção.
Exemplo:
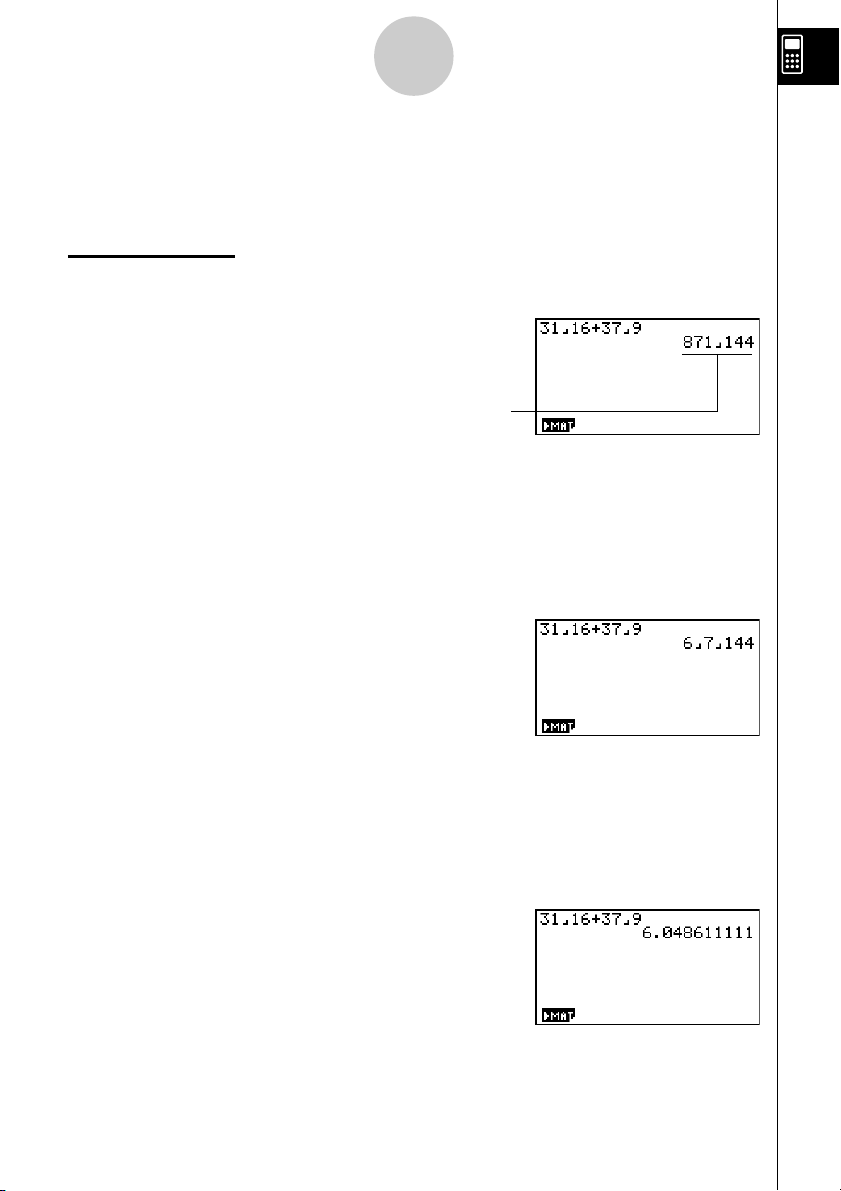
31
/16 + 37/
9
1. Prima o.
2. Prima db$bg+
dh$jw.
871
Indica
Conversão de uma fracção imprópria numa fracção
mista
Com a fracção imprópria no ecrã, prima !M para convertê-la numa fracção
mista.
<
Prima novamente !M para converter de novo em fracção imprópria.
<
/
144
Conversão de uma fracção para o seu equivalente
decimal
Com a fracção no ecrã, prima M para convertê-la no seu equivalente decimal.
Prima novamente M para converter de novo em fracção.
20050401
Page 10

EXPOENTES
5
Início Rápido
Exemplo:
1. Prima o.
2. Prima bcfa*c.ag.
3. Prima
4. Prima f. O ^5 que se visualiza no ecrã indica que 5 é o expoente.
5. Prima w.
1250 × 2,06
M e o indicador ^ surgirá no ecrã.
5
20050401
Page 11
6
Início Rápido
FUNÇÕES GRÁFICAS
As capacidades gráficas desta calculadora permitem desenhar gráficos complexos
utilizando, quer coordenadas rectangulares (eixo horizontal: x ; eixo vertical: y) quer
θ
coordenadas polares (ângulo:
Todos os exemplos gráficos seguintes são realizados a partir do ajuste da calculadora
com efeito imediato após a operação de reinicialização.
; distância desde a origem: r).
Exemplo
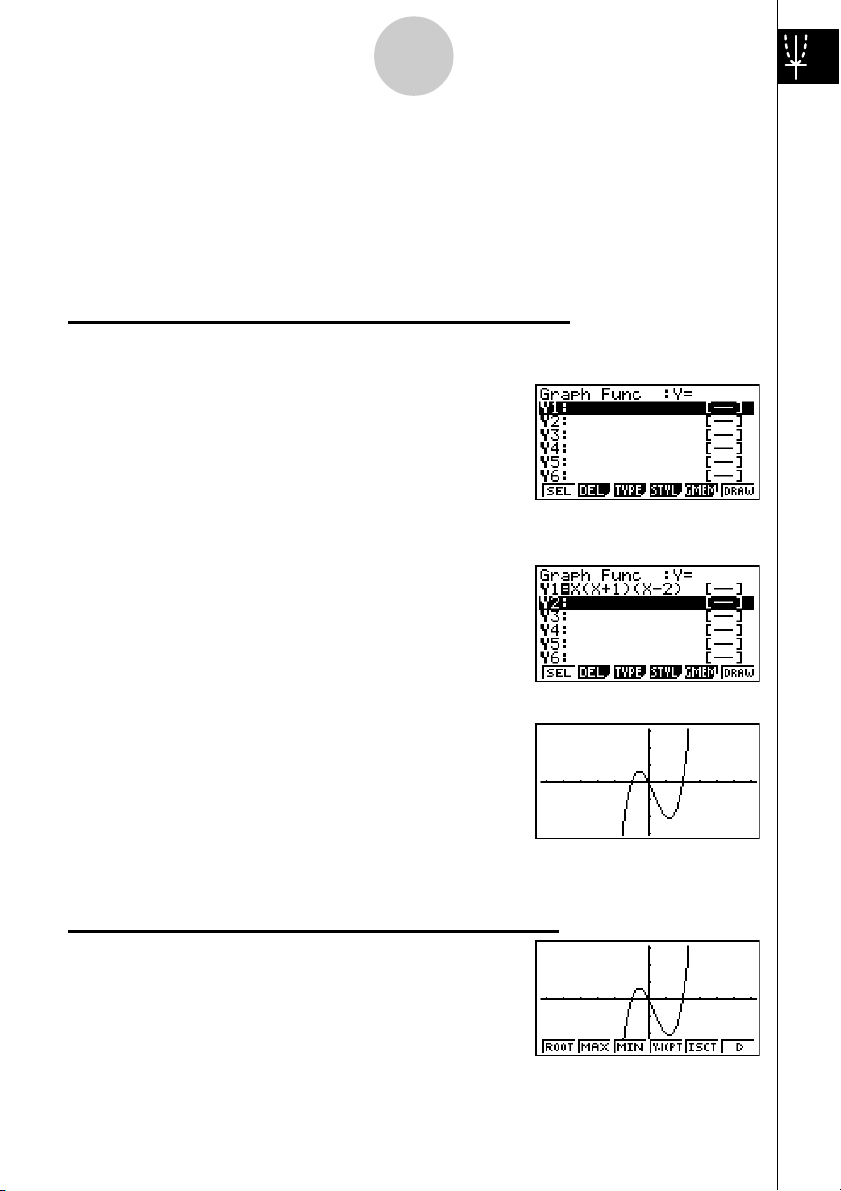
1. Prima
2. Utilize defc para realçar
3. Introduza a fórmula.
1: Para representar graficamente Y = X(X + 1)(X – 2)
m.
GRAPH, e prima w.
v(v+b)
(v-c)w
4. Prima 6(DRAW) ou w para desenhar
o gráfico.
Exemplo
1. Prima
2: Para determinar as raízes de Y = X(X + 1)(X – 2)
!5(G-SLV).
20050401
Page 12
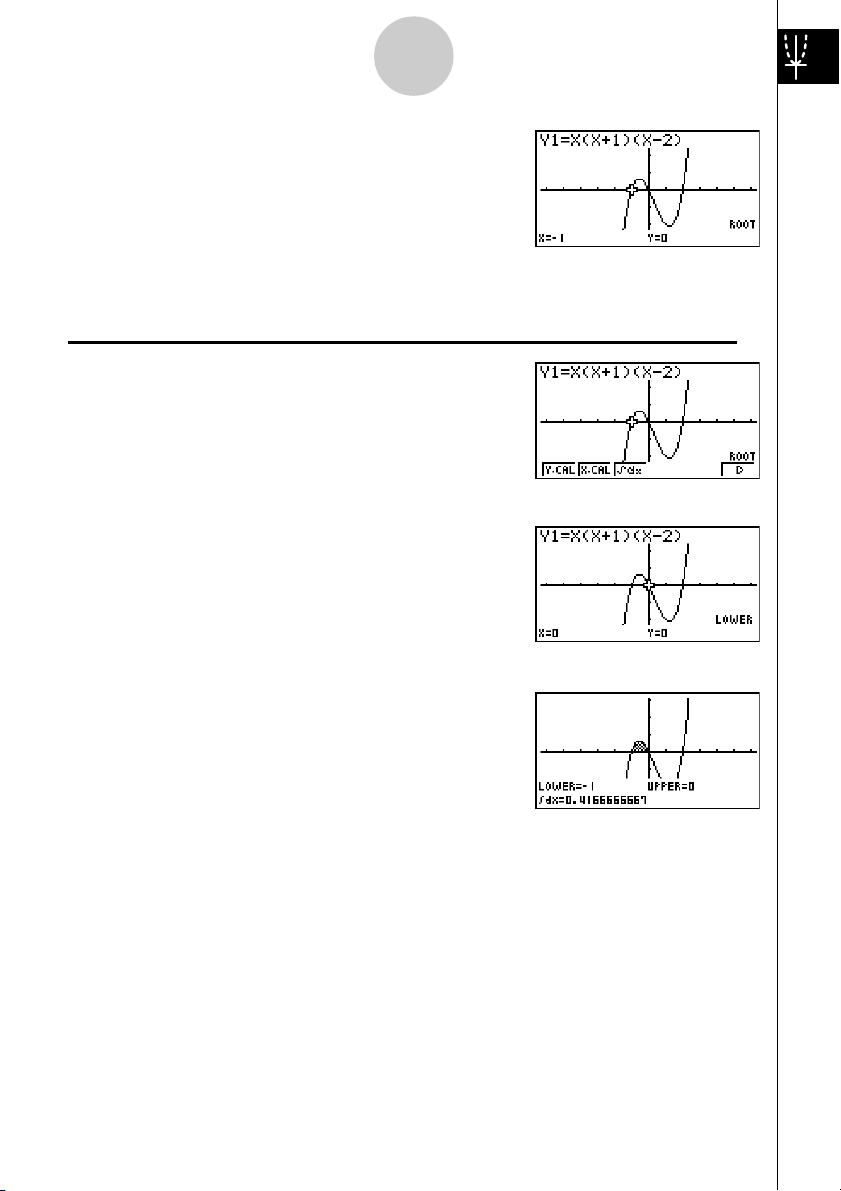
2. Prima 1(ROOT).
Prima e para outras raízes.
7
Início Rápido
Exemplo
1. Prima
2. Prima 3(∫dx).
3. Utilize d para mover o ponteiro para a localização
3: Para determinar a área limitada pela origem e a raiz X = –1 obtida
para Y = X(X + 1)(X – 2)
!5(G-SLV)6(g).
onde X = –1 e prima w. A seguir, utilize e
para mover o ponteiro para a localização onde
X = 0 e prima
que torna-se a sombreado no ecrã.
para o limite de integração,
w
20050401
Page 13

8
Início Rápido
GRÁFICO DUPLO
Com esta função pode dividir o ecrã em duas áreas e visualizar duas janelas de
gráficos.
Exemplo:
intersecção
1. Prima !mcc1(G+G)
para especificar “G+G” para o ajuste Dual Screen.
2. Prima
Para desenhar os dois gráficos seguintes e determinar os pontos de
Y1 = X(X + 1)(X – 2)
Y2 = X + 1,2
SET UP
J, e introduza as duas funções.
v(v+b)
(v-c)w
v+b.cw
3. Prima 6(DRAW) ou w para desenhar
os gráficos.
Zoom de caixa
Utilize a função de zoom de caixa para especificar as áreas de um gráfico para
ampliar.
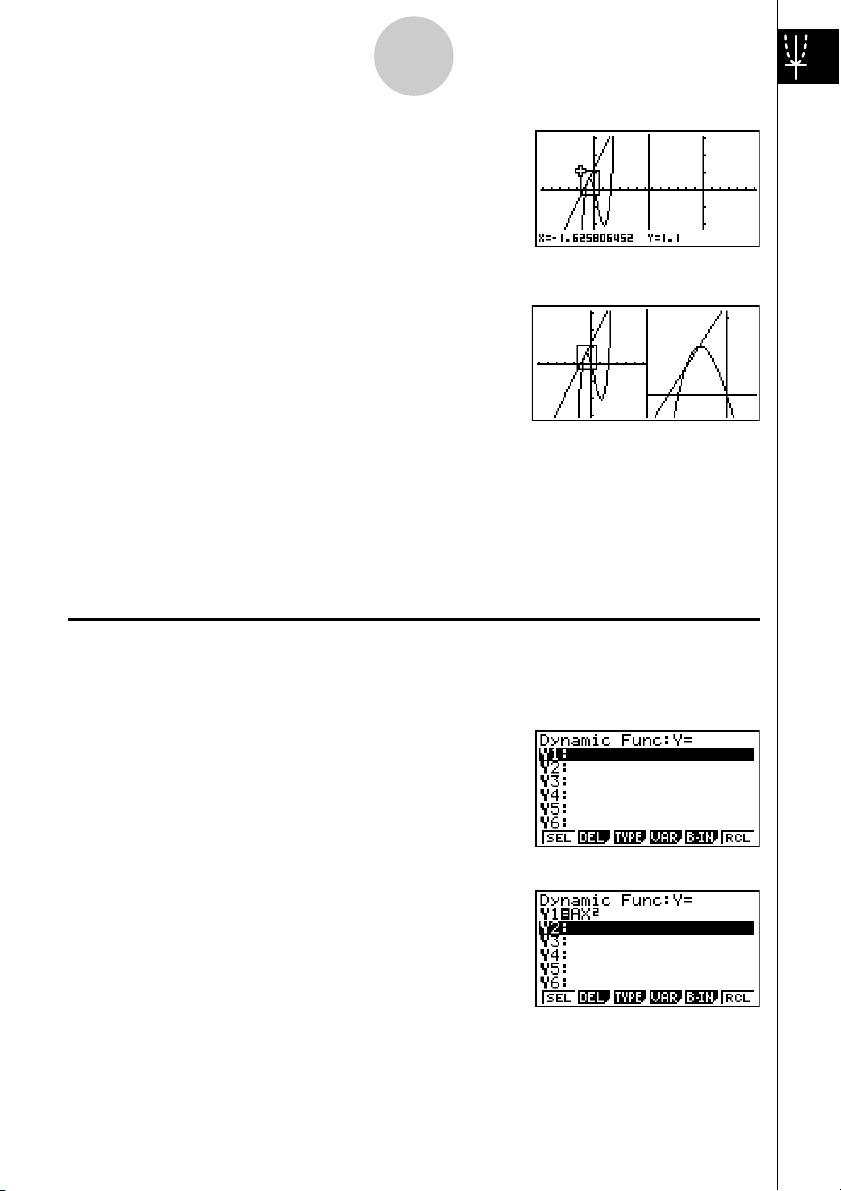
1. Prima
2. Utilize
!2(ZOOM) 1(BOX).
d e f c para mover o ponteiro
para um dos cantos da área que pretende especificar
e prima
w
.
20050401
Page 14
9
Início Rápido
3. Utilize d e f c para mover o ponteiro
novamente. Ao fazer isso, aparece uma caixa no
visor. Mova o ponteiro de modo que a caixa
envolva a área que deseja ampliar.
4. Prima w, e a área ampliada surge no ecrã
inactivo (lado direito).
GRÁFICO DINÂMICO
O gráfico dinâmico permite-lhe ver como a forma de um gráfico é afectada à medida
que o valor especificado de um dos coeficientes da sua função é alterado.
Exemplo:
1. Prima m.
2. Utilize d e f c para realçar
DYNA, e prima w.
3. Introduza a fórmula.
a
Para desenhar gráficos à medida que o valor do coeficiente A na seguinte
função muda de 1 para 3
Y = AX
v
2
A
vxw
20050401
12356
Page 15
10
Início Rápido
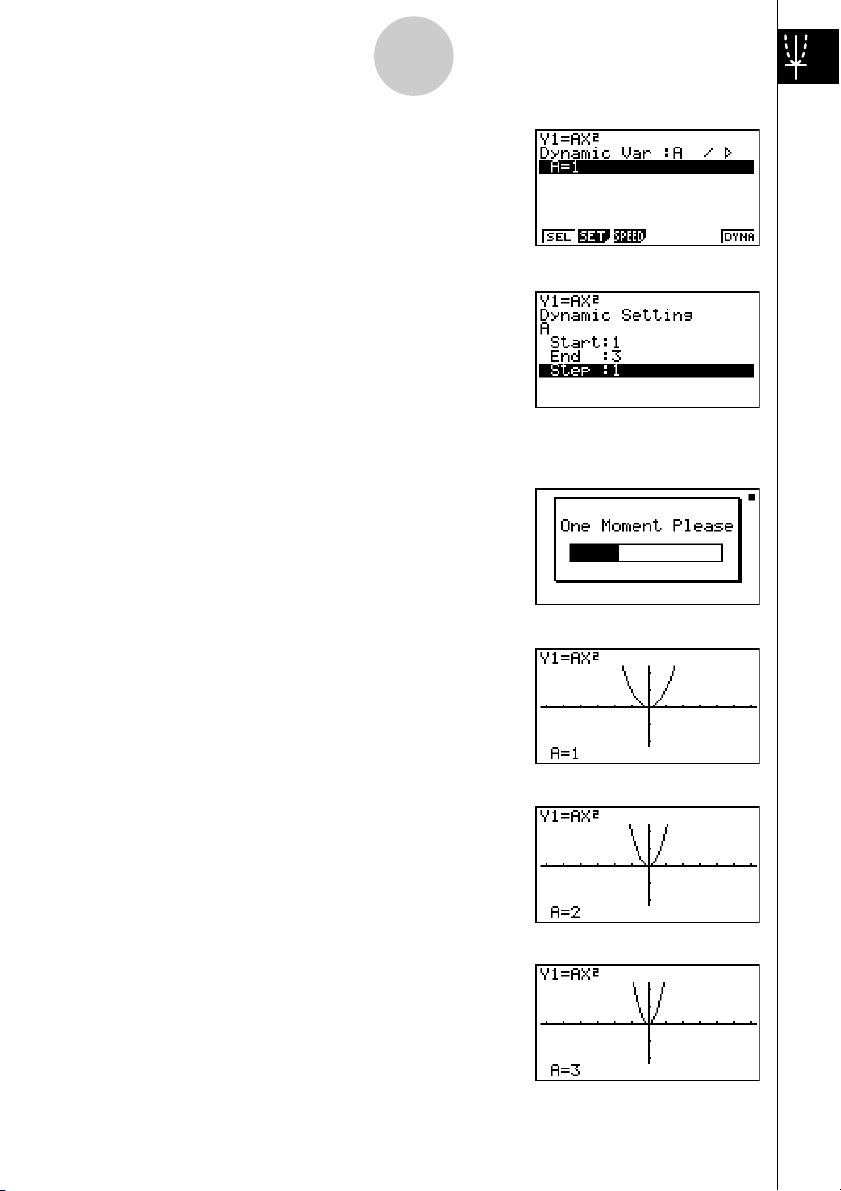
4. Prima 4(VAR) bw para especificar
um valor inicial de 1 para o coeficiente A.
5. Prima
2(SET) bwdwb
wpara especificar o limite e o incremento
de mudança no coeficiente A.
6. Prima
7. Prima 6(DYNA) para iniciar o gráfico dinâmico.
J.
Os gráficos são desenhados 10 vezes.
• Para interromper uma operação de desenho de
gráfico dinâmico em progresso, prima
o.
↓
↓↑
20050401
↓↑
Page 16
11
Início Rápido
FUNÇÃO DE TABELA
A função de tabela permite-lhe gerar uma tabela de soluções à medida que se
especifica diferentes valores nas variáveis de uma função.
Exemplo:
Para criar uma tabela numérica para a função seguinte
Y = X (X+1) (X–2)
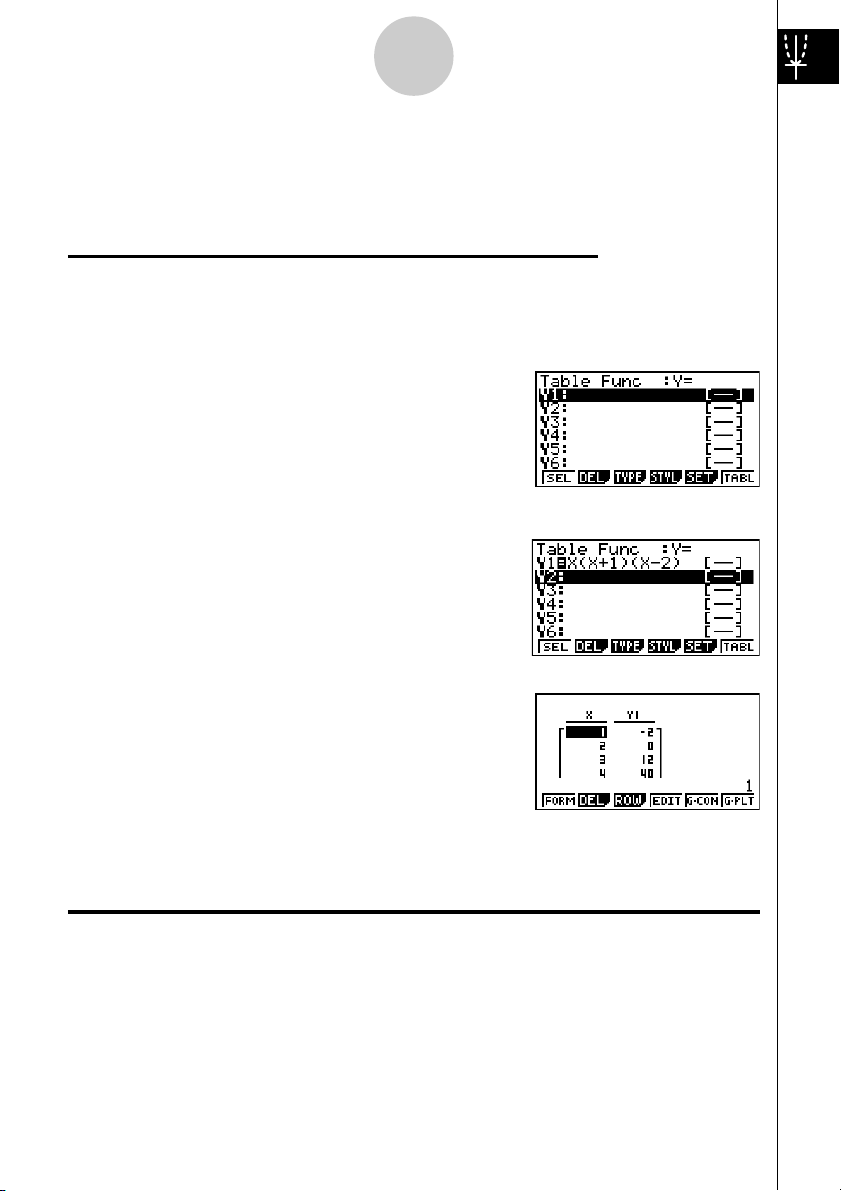
1. Prima m.
2. Utilize defc para realçar
TABLE, e prima w.
3. Introduza a fórmula.
v(v+b)
(v-c)w
4. Prima 6(TABL) para gerar a tabela
numérica.
Para aprender tudo sobre as poderosas funções desta calculadora, leia e explore!
20050401
Page 17
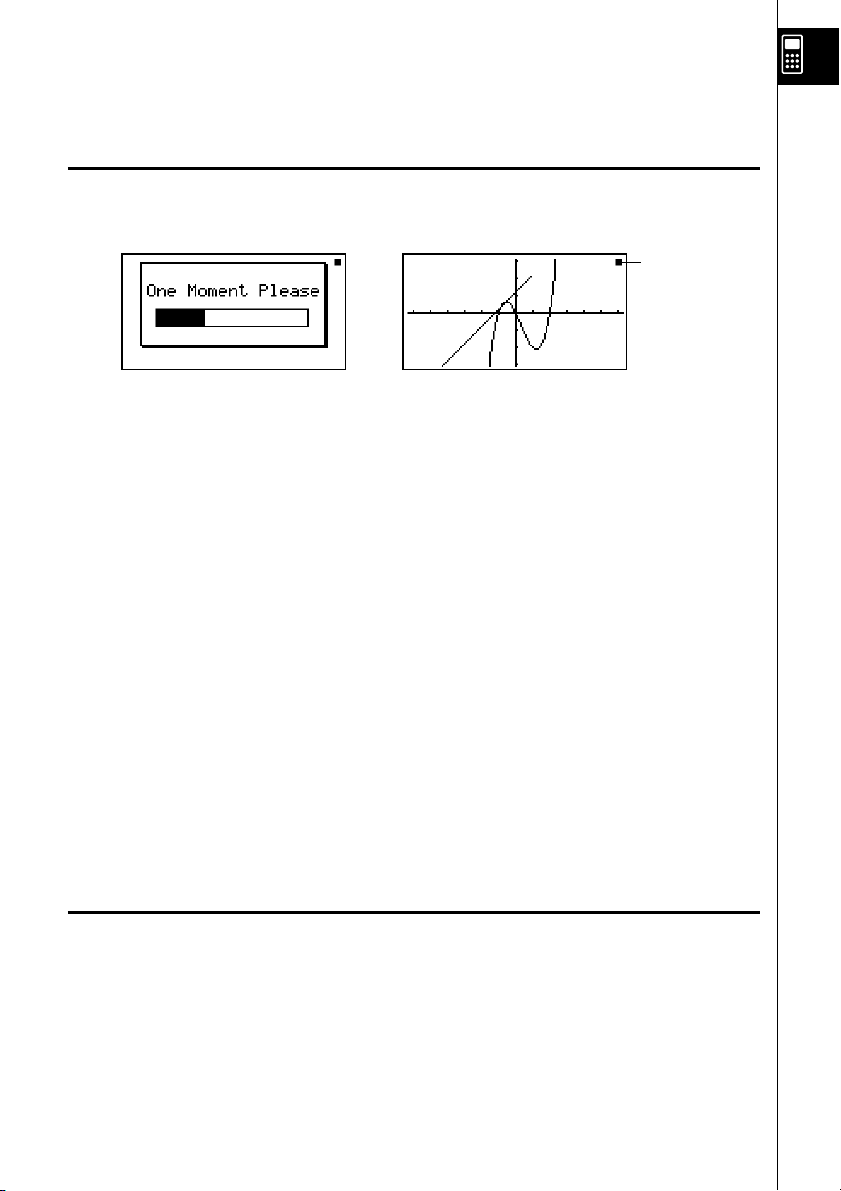
Precauções ao utilizar este produto
Uma barra de progresso e/ou um indicador de ocupado aparece no visor sempre que a
calculadora está a realizar um cálculo, a escrever na memória (incluindo a memória flash),
ou a ler da memória (incluindo a memória flash).
Indicador de
ocupado
Barra de progresso
Nunca prima o botão P nem retire as pilhas da calculadora quando a barra de progresso ou
o indicador de ocupado estiver no visor. Fazer isso pode causar a perda do conteúdo da
memória, bem como pode causar um mau funcionamento da calculadora.
Esta calculadora é dotada de uma memória flash para o armazenamento de dados.
Recomendamos que sempre faça uma cópia de segurança dos seus dados para a memória
flash. Para mais detalhes sobre o procedimento de cópia de segurança, consulte “12-7
Modo MEMORY” no manual de instruções.
Ta mbém pode transferir dados para um computador utilizando o software Program-Link (FA-
124) que vem incluído com a calculadora. O software Program-Link também pode ser
utilizado para fazer uma cópia de segurança para um computador.
u Apenas fx-9860G SD
Se a mensagem “No Card” aparecer quando houver um cartão SD colocado na abertura
para cartão SD, isso significa que a calculadora não está a reconhecer o cartão por alguma
razão. Tente retirar o cartão e, em seguida, coloque-o de novo. Se isso não funcionar, entre
em contacto com o fabricante do cartão SD. Repare que alguns cartões SD podem não ser
compatíveis com esta calculadora.
Precauções ao ligar a um computador
Um controlador USB especial deve estar instalado em seu computador para que possa ligar
a calculadora a ele. O controlador é instalado junto com o software Program-Link (FA-124)
que vem incluído com a calculadora. Certifique-se de instalar o software Program-Link (FA-
124) no computador antes de tentar ligar a calculadora a ele. Tentar ligar a calculadora a um
computador que não tenha o software Program-Link instalado pode causar um mau
funcionamento. Para mais informações sobre como instalar o software Program-Link,
consulte o manual de instruções no CD-ROM incluído.
20050401
Page 18

Precauções relativas à manipulação
•Esta calculadora é feita de componentes de precisão. Nunca a desmonte.
•Evite deixar cair a calculadora e sujeitá-la a grandes impactos.
•Não guarde nem deixe a calculadora em lugares expostos a grandes temperaturas, humidade
ou pó. Quando exposta a baixas temperaturas, a calculadora pode precisar de mais tempo para
realizar os cálculos, podendo mesmo deixar de funcionar. A calculadora regressa ao seu normal
funcionamento assim que voltar à temperatural normal.
•O ecrã fica em branco e as teclas deixam de funcionar durante o processamento dos cálculos.
Ao utilizar o teclado, verifique o ecrã de modo a assegurar que todas as operações estão a ser
realizadas correctamente.
•Substitua as pilhas principais de 1 em um ano, independentemente de quanto a calculadora for
utilizada durante esse período. Nunca deixe pilhas velhas dentro da calculadora, uma vez que
podem danificar a unidade.
•
Mantenha as pilhas fora do alcance das crianças. Se engolidas, consulte de imediato um médico.
•Evite utilizar líquidos voláteis para limpar a calculadora. Limpe-a com um pano macio e seco ou
com um pano humedecido numa solução de água e detergente neutro, devidamente
expremido.
• Limpe sempre suavemente o ecrã, de modo a não o riscar.
• Em nenhum caso, pode o fabricante e os seus distribuidores serem responsáveis por qualquer
dano, despesa, perda de lucro, perda de poupanças ou outros danos provocados pela perda de
informação e/ou fórmulas devido a falhas de funcionamento, reparação ou substituição das
pilhas. É sua responsabilidade ter registos físicos de dados importantes para evitar a sua perda
total.
•Não destrua as pilhas, o painel de cristal líquido ou outros componentes pelo fogo.
•Assegure-se de que a calculadora está desligada quando substituir as pilhas.
•Se a calculadora for exposta a uma grande carga electrostástica, o conteúdo da memória pode
ficar danificado e as teclas deixarem de funcionar. Em tal caso, realize a operação de
reinicializaçao para limpar a memória e restaurar o normal funcionamento das teclas.
•Se por algum motivo a calculadora deixar de funcionar, utilize um objecto fino e pontiagudo
para premir o botão P que se encontra na parte de trás da calculadora. Tenha em conta que tal
operação apaga todos os dados da memória da calculadora.
•Tenha em conta que uma forte vibração ou impacto durante a execução de programas pode
provocar a sua paragem ou pode danificar o conteúdo da memória.
•O uso da calculadora pode provocar interferências na televisão ou rádio, quando utilizada perto
destes aparelhos.
•Antes de supor o mau funcionamento da calculadora, leia novamente este manual e assegurese de que o problema não se deve à falta de pilhas, erros de programação ou erros
operacionais.
•A vida útil das pilhas pode ser reduzida dramaticamente por certas operações e pelo uso de
certos tipos de cartões SD.
20050401
Page 19

Assegure-se de que tem registos físicos de todos os dados importantes!
Pilhas fracas ou a sua incorrecta substituição pode provocar danos nos dados armazenados na
memória ou mesmo a sua perca total. Os dados armazenados podem também ser afectados por
grandes cargas electrostásticas ou grandes impactos. É sua responsabilidade manter cópias de
segurança dos dados de modo a precaver-se contra a sua perda.
Em caso algum será a CASIO Computer Co., Ltd. responsável perante terceiros pelos danos
especiais, colaterais, acidentais ou consequentes relacionados ou devido à compra ou uso
destes materiais. Mais ainda, a CASIO Computer Co., Ltd. não se responsabiliza perante
nenhuma reclamação provocada pelo uso destes materiais por terceiros.
•O conteúdo deste manual está sujeito a alterações sem aviso prévio.
•Nenhuma parte deste manual pode ser reproduzida sob nenhuma forma sem o expresso
consentimento do fabricante.
•As opções descritas no Capítulo 12 deste manual podem não estar disponíveis em
determinadas áreas geográficas. Para informações mais detalhadas sobre a disponibilidade
na sua área, consulte o distribuidor CASIO mais próximo.
20050401
Page 20

1
Índice
Índice
Conhecimento da calculadora — Leia isto primeiro!
Capítulo 1 Operações básicas
1-1 Teclas ............................................................................................... 1-1-1
1-2 Visor ................................................................................................. 1-2-1
1-3 Introdução e edição de cálculos ....................................................... 1-3-1
1-4 Menu de opções (OPTN) ................................................................. 1-4-1
1-5 Menu de dados de variáveis (VARS) ............................................... 1-5-1
1-6 Menu de programas (PRGM) ........................................................... 1-6-1
1-7 Utilização do ecrã de configuração .................................................. 1-7-1
1-8 Utilização da captura de ecrã ........................................................... 1-8-1
1-9 Ao encontrar problemas... ................................................................ 1-9-1
Capítulo 2 Cálculos manuais
2-1 Cálculos básicos .............................................................................. 2-1-1
2-2 Funções especiais ............................................................................ 2-2-1
2-3 Especificação da unidade angular e do formato de visualização..... 2-3-1
2-4 Cálculos com funções ...................................................................... 2-4-1
2-5 Cálculos numéricos .......................................................................... 2-5-1
2-6 Cálculos com números complexos................................................... 2-6-1
2-7 Cálculos binários, octais, decimais e hexadecimais com números
inteiros .............................................................................................. 2-7-1
2-8 Cálculos com matrizes ..................................................................... 2-8-1
Capítulo 3 Função de lista
3-1 Introdução e edição de uma lista ..................................................... 3-1-1
3-2 Manipulação dos dados de uma lista ............................................... 3-2-1
3-3 Cálculos aritméticos utilizando listas ................................................ 3-3-1
3-4 Mudança entre ficheiros de lista....................................................... 3-4-1
Capítulo 4 Cálculos de equações
4-1 Equações lineares simultâneas........................................................ 4-1-1
4-2 Equações quadráticas e cúbicas...................................................... 4-2-1
4-3 Cálculos de resolução ...................................................................... 4-3-1
4-4 O que fazer quando surge um erro .................................................. 4-4-1
20050401
Page 21

2
Índice
Capítulo 5 Representação gráfica
5-1 Gráficos de exemplo ........................................................................ 5-1-1
5-2 Controlo do que surge num ecrã de gráficos ................................... 5-2-1
5-3 Desenho de um gráfico .................................................................... 5-3-1
5-4 Armazenamento de um gráfico na memória de imagem ................. 5-4-1
5-5 Desenho de dois gráficos no mesmo ecrã ....................................... 5-5-1
5-6 Representação gráfica manual ........................................................ 5-6-1
5-7 Utilização de tabelas ........................................................................ 5-7-1
5-8 Gráficos dinâmicos ........................................................................... 5-8-1
5-9 Representação gráfica de uma fórmula de recursão ....................... 5-9-1
5-10 Mudança da aparência de um gráfico ............................................ 5-10-1
5-11 Análise de função ........................................................................... 5-11-1
Capítulo 6 Cálculos e gráficos estatísticos
6-1 Antes de realizar cálculos estatísticos ............................................. 6-1-1
6-2 Cálculos e gráficos estatísticos de variável simples ........................ 6-2-1
6-3 Cálculos e gráficos estatísticos de variáveis binárias ...................... 6-3-1
6-4 Realização de cálculos estatísticos.................................................. 6-4-1
6-5 Testes ............................................................................................... 6-5-1
6-6 Intervalo de confiança ...................................................................... 6-6-1
6-7 Distribuição....................................................................................... 6-7-1
Capítulo 7 Cálculos financeiros (TVM)
7-1 Antes de realizar cálculos financeiros .............................................. 7-1-1
7-2 Juros simples ................................................................................... 7-2-1
7-3 Juros compostos .............................................................................. 7-3-1
7-4 Fluxo de caixa (Avaliação de investimento) ..................................... 7-4-1
7-5 Amortização ..................................................................................... 7-5-1
7-6 Conversão de taxa de juros ............................................................. 7-6-1
7-7 Custo, preço de venda, margem de lucro ........................................ 7-7-1
7-8 Cálculos de dias/datas ..................................................................... 7-8-1
20050401
Page 22

Capítulo 8 Programação
8-1 Passos de programação básicos ..................................................... 8-1-1
8-2 Teclas de função do modo PRGM.................................................... 8-2-1
8-3 Edição do conteúdo dos programas................................................. 8-3-1
8-4 Gestão dos ficheiros......................................................................... 8-4-1
8-5 Referência de comandos ................................................................. 8-5-1
8-6 Utilização das funções da calculadora em programas ..................... 8-6-1
8-7 Lista de comandos do modo PRGM ................................................ 8-7-1
8-8 Biblioteca de programas................................................................... 8-8-1
Capítulo 9 Folha de cálculo
9-1 Perfil geral da folha de cálculo ......................................................... 9-1-1
9-2 Operações de ficheiro e re-cálculo................................................... 9-2-1
9-3 Operações básicas no ecrã da folha de cálculo............................... 9-3-1
9-4 Introdução e edição de dados nas células ....................................... 9-4-1
9-5 Comandos do modo S
9-6 Gráficos estatísticos ......................................................................... 9-6-1
9-7 Utilização da função CALC .............................................................. 9-7-1
9-8 Utilização da memória no modo S
Capítulo 10 eActivity
10-1 Perfil geral da eActivity................................................................. 10-1-1
10-2 Trabalho com ficheiros eActivity................................................... 10-2-1
10-3 Introdução e edição de dados de um ficheiro eActivity ................ 10-3-1
10-4 Utilização do editor de matriz e editor de listas............................ 10-4-1
10-5 Ecrã de utilização da memória de ficheiros eActivity ................... 10-5-1
3
Índice
• SHT............................................................ 9-5-1
• SHT ......................................... 9-8-1
Capítulo 11 Menu de ajuste do sistema
11-1 Utilização do menu de sistema .................................................... 11-1-1
11-2 Ajustes do sistema ....................................................................... 11-2-1
11-3 Lista de versões ........................................................................... 11-3-1
11-4 Reinicialização ............................................................................. 11-4-1
Capítulo 12 Comunicação de dados
12-1 Conexão de duas calculadoras .................................................... 12-1-1
12-2 Conexão da calculadora a um computador pessoal .................... 12-2-1
12-3 Operação de comunicação de dados .......................................... 12-3-1
12-4 Precauções com a comunicação de dados ................................. 12-4-1
12-5 Transferência de imagem ............................................................ 12-5-1
12-6 Adições ........................................................................................ 12-6-1
12-7 Modo MEMORY ........................................................................... 12-7-1
20050401
20060601
Page 23

4
Índice
Capítulo 13 Utilização de cartões SD (apenas fx-9860G SD)
13-1 Utilização de um cartão SD.......................................................... 13-1-1
13-2 Formatação de um cartão SD ...................................................... 13-2-1
13-3 Precauções com um cartão SD durante o uso ............................ 13-3-1
Apêndice
1Tabela de mensagens de erro ............................................................α-1-1
2Intervalos de introdução .....................................................................
3 Especificações .....................................................................................α-3-1
4Índice de teclas ....................................................................................
5 Botão P (Em caso de bloqueio da calculadora) ..................................
6 Fonte de alimentação .........................................................................α-6-1
α
α
α
-2-1
-4-1
-5-1
20050401
Page 24

Conhecimento da calculadora
— Leia isto primeiro!
Sobre este manual do utilizador
u! x( )
A referência anterior indica que deve premir ! seguido de x para introduzir o símbolo
, sendo esta a indicação para todas as operações que requerem a introdução de
múltiplas teclas. Indica-se a tecla de acesso, seguido do carácter a introduzir ou comando
em parênteses.
u m EQUA
Isto indica que deve premir m primeiro, utilizar as teclas de cursor (f, c, d, e)
para seleccionar o modo EQUA e, em seguida, premir w. As operações que precisa
realizar para entrar em um modo a partir do menu principal são indicadas assim.
0
uTeclas de função e menus
•Muitas das operações realizadas por esta calculadora podem ser executadas premindo-
se as teclas de função de 1 a 6. A operação associada a cada tecla de função
depende do modo em que a calculadora está a funcionar, sendo a actual operação
associada indicada pelos menus de funções que surgem no ecrã.
•O manual indica a operação associada à respectiva tecla de função em parênteses
seguido da tecla de acesso para essa tecla. 1(Comp), por exemplo, indica que ao
premir 1 selecciona {Comp}, que também é indicado no menu de funções.
•Quando (g) é indicado no menu de funcões para a tecla 6, significa que ao premir 6
visualiza-se a página seguinte ou a anterior das opções de menu.
uu
uTítulos dos menus
uu
•Os títulos dos menus neste manual incluêm a operação de tecla necessária para
visualizar o menu explicado. A operação de tecla para um menu que é visualizado
premindo-se K seguido de {MAT} é mostrado da seguinte forma: [OPTN]-[MAT].
•As teclas de funções 6(g) para mudar para outra página de menu não são mostradas
nas operações de tecla do título do menu.
20050401
Page 25
Conhecimento da calculadora
0-1-1
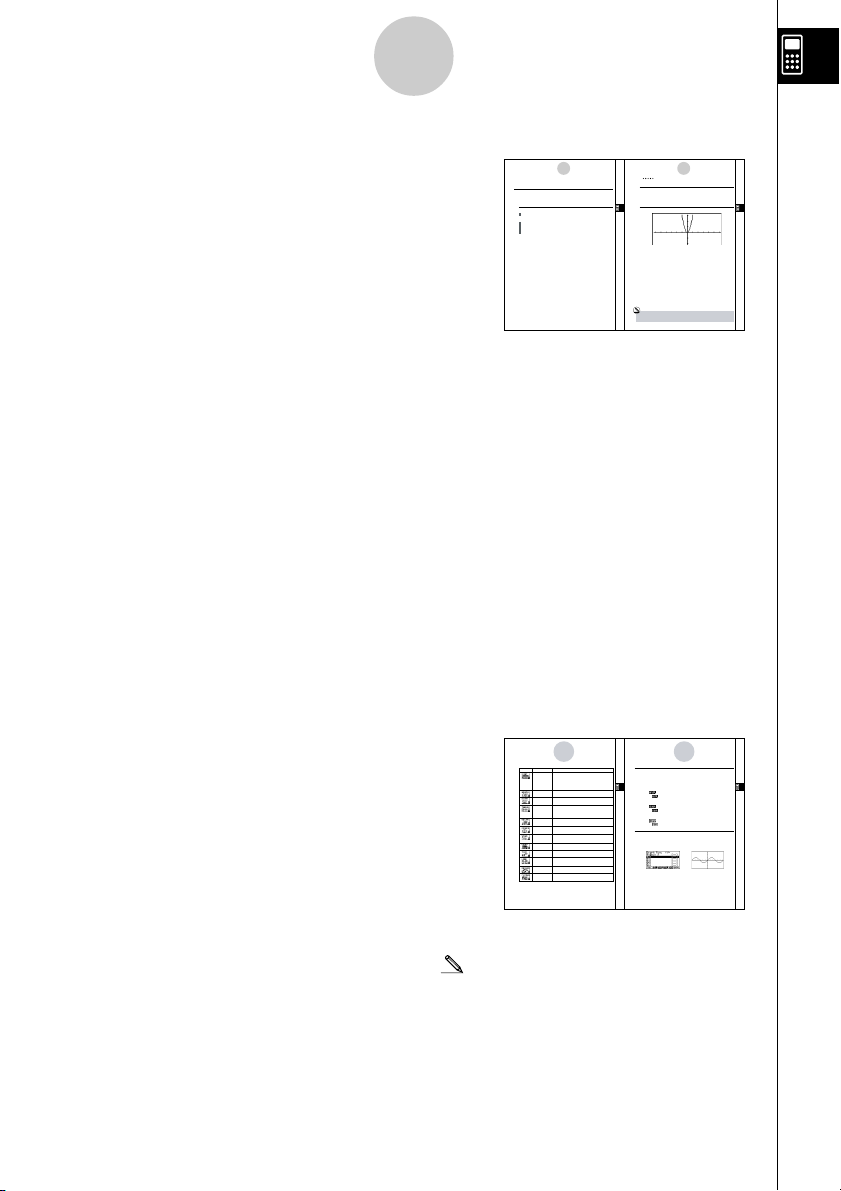
uGráficos
Como regra geral, as operações de gráficos são
mostradas em páginas abertas, encontrando-se os
exemplos dos gráficos nas páginas do lado direito.
Pode produzir o mesmo gráfico na sua calculadora,
realizando os passos dos procedimentos que se
5-1-1
Gráficos de exemplo
5-1 Gráficos de exemplo
kkkkkComo desenhar um gráfico simples (1)
Descrição
Para desenhar um gráfico, simplesmente introduza a função correspondente.
Configuração
1. A partir do menu principal, entre no modo GRAPH.
Execução
2.Introduza a função para a qual pretende desenhar o gráfico.
Deve utilizar o ecrã de visualização para especificar o intervalo e os outros parâmetros
do gráfico. Consulte a secção 5-2-1.
3.Desenhe o gráfico.
encontram antes do gráfico.
Procure o tipo de gráfico que pretende na página do
lado direito e de seguida a página indicada para esse
gráfico. Os passos do “Procedimento” utilizam sempre
20050401 20050401
as definições iniciais de RESET.
Os números dos passos nas secções “Configuração” e “Execução” que se encontam nas
páginas do lado esquerdo correspondem aos números dos passos do “Procedimento” que
se encontram nas páginas do lado direito.
Exemplo:
Página do lado esquerdo Página do lado direito
3. Desenhe o gráfico. 3 5(DRAW)(ou w)
uu
uLista de comandos
uu
A lista de comandos do modo PRGM (página 8-7) proporciona uma tabela dos vários
menus das teclas de função e demonstra como chegar ao menu de comandos que
necessita.
Exemplo: A operação seguinte visualiza Xfct: [VARS]-[FACT]-[Xfct]
Gráficos de exemplo
Exemplo Para reprensentar graficamente y= 3
Procedimento
1m GRAPH
2dvxw
36(DRAW) (ou w)
Ecrã de resultados
#PremirA enquanto um gráfico estiver no
visor voltará ao ecrã no passo 2.
5-1-2
2
x
uu
uConteúdos da página
uu
Números constituidos por três partes encontram-se
centrados no topo de cada página. O número de
página “1-2-3”, por exemplo indica capítulo 1, secção
2, página 3.
uu
uInformação suplementar
uu
1-2-2
Visor
Ícone Nome do modo Descrição
S•SHT Utilize este modo para executar cálculos em uma folha de
(folha de cálculo) cálculo. Cada ficheiro contém uma folha de cálculo de 26
colunas⋅ 999 linhas. Além dos comandos incorporados da
•
calculadora e dos comandos do modo S
SHT, também pode
executar cálculos estatísticos e dados estatísticos de gráfico
utilizando os mesmos procedimentos utilizados no modo
STAT.
GRAPH
Utilize este modo para armazenar funções de gráfico
(gráfico)
para desenhar gráficos utilizando as funções
DYNA
Utilize este modo para armazenar funções gráficas e
(gráfico dinâmico)
paradesenhar múltiplas versões de gráficos, alterando
osvalores associados às variáveis de uma função.
TABLE Utilize este modo para armazenar as funções, para gerar
(tabela)
uma tabela numérica de soluções diferentes à medida
que os valores designados para as variáveis em uma
função mudam, e para desenhar gráficos.
RECUR
Utilize este modo para armazenar fórmulas e para criar
(recursão)
tabelas numéricas diferentes consuante as variáveis de
uma função e para desenhar gráficos.
CONICS
Utilize este modo para desenhar gráfico de secções cónicas.
(secções cónicas)
EQUA
Utilize este modo para solucionar equações lineares com
(equação)
duas a seis incógnitas, equações quadráticas, e
equações cúbicas.
PRGM
Utilize este modo para armazenar programas na área de
(programa)
programas e para executar programas.
TVM Utilize este modo para executar cálculos financeiros e para
(financeiro) desenhar o fluxo de caixa e outros tipos de gráficos. make
LINK
Utilize este modo para transferir o conteúdo da memória
(ligação)
ou para fazer cópias de segurança para outra unidade ou
um computador.
MEMORY
Utilize este modo para gerir os dados na memória.
(memória)
SYSTEM
Utilize este modo para inicializar a memória, para ajustar
(sistema)
o contraste e para outros ajustes do sistema.
20050401
20050401 20050401
e
.
1-2-3
Visor
kk
kSobre o menu de funções
kk
Utilize as teclas de função (1 a 6
) para aceder aos menus e comandos da barra de
menus que se encontra na parte de baixo do ecrã. Pode saber se um item da barra de
menus é um menu ou um comando pela sua aparência.
• Próximo menu
Exemplo:
Seleccionar exibe um menu de funções hiperbólicas.
• Introdução de comando
Exemplo:
Seleccionar introduz o comando sinh.
• Execução de comando direta
Exemplo:
Seleccionar executa o comando DRAW.
kk
kSobre os ecrãs
kk
Esta calculadora tem dois tipos de ecrãs: um ecrã de texto e um ecrã de gráfico. O de texto
tem capacidade para 21 colunas e 8 linhas de caracteres, sendo a última linha utilizada para
o menu de teclas de função. O ecrã de gráfico utiliza uma área de 127 (L) ⋅ 63 (A) pontos.
Ecrã de texto Ecrã de gráfico
O contéudo de cada um dos ecrãs é armazenado em áreas de memória independentes.
Prima!6(G T) para alternar entre o ecrã de texto e o ecrã de gráfico.
20050401
No final de cada página encontra-se um bloco “ (Notas)” com informação suplementar.
indica uma nota sobre um termo que surge na mesma página que a nota.
*
# indica uma nota de informação geral sobre um tópico abrangido pela mesma secção que
a nota.
20050401
Page 26

Capítulo
Operações básicas
1-1 Teclas
1-2 Visor
1-3 Introdução e edição de cálculos
1-4 Menu de opções (OPTN)
1-5 Menu de dados de variáveis (VARS)
1-6 Menu de programas (PRGM)
1-7 Utilização do ecrã de configuração
1-8 Utilização da captura de ecrã
1-9 Ao encontrar problemas...
1
20050401
Page 27

1-1 Teclas
1-1-1
Teclas
20050401
Page 28
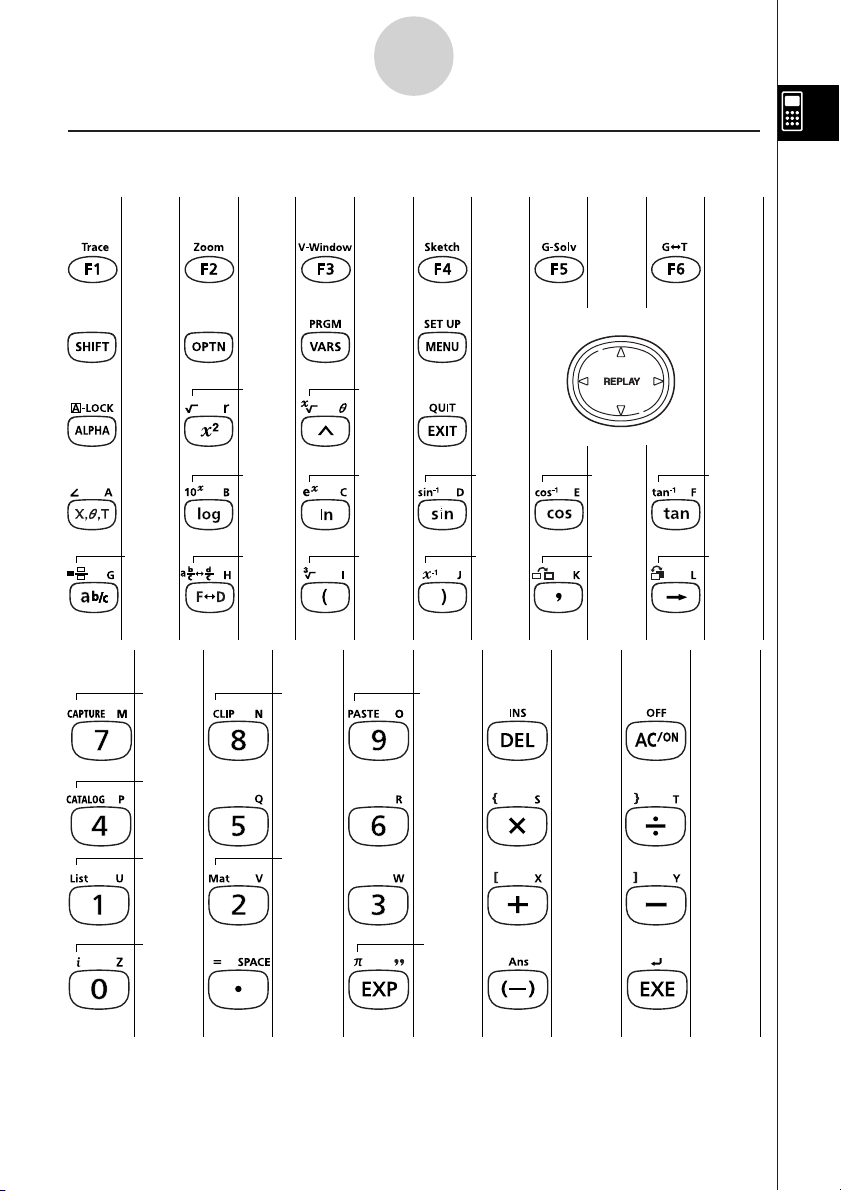
1-1-2
Teclas
kk
k Tabela das teclas
kk
Página Página Página Página Página Página
5-11-1
5-2-7 5-2-1
1-6-1
5-10-1 5-11-9
1-7-1
1-1-3 1-4-1 1-5-1 1-2-1
2-4-7 2-4-5
1-1-3 2-4-7 2-4-5
2-4-5 2-4-5
2-4-5 2-4-5
2-4-10
2-4-10
Página Página Página Página Página
1-8-1
2-4-12
2-4-11
1-3-5
2-4-7
2-1-1
2-4-4 2-4-4
2-4-4 2-4-4
2-4-7
2-1-1
1-3-7
10-3-13 10-3-12
1-3-2
1-3-1
1-3-7
2-1-1
2-1-1
1-2-3
2-4-4
2-4-4
2-2-1
3-1-2
2-8-11
2-6-2 2-4-4
20050401
2-1-1
2-2-5
2-1-12-1-1
2-1-1
Page 29

1-1-3
Teclas
kk
k Marcação das teclas
kk
Muitas das teclas da calculadora permitem realizar mais do que uma função. As diversas
funções inscritas no teclado estão codificadas por cores de modo a poder encontrá-las mais
facíl e rapidamente.
Função Operação de teclas
1 log l
2 10
x
!l
3 B al
A tabela seguinte descreve o código de cores utilizado nas inscrições das teclas.
Cor Operação de teclas
Laranja Prima ! e, em seguida, a tecla para realizar a função inscrita.
Vermelho Prima a e, em seguida, a tecla para realizar a função inscrita.
# Bloqueio alfanumérico
Normalmente, premir a e, em seguida, uma
tecla para introduzir um caracter alfanumérico,
o teclado reverte para as suas funções
principais.
Se premir ! e a, o teclado fica bloqueado
introdução alfanumérica até que se prima
novamente a.
20050401
Page 30

1-2-1
Visor
1-2 Visor
k Selecção dos ícones
Esta secção descreve como seleccionar um ícone no menu principal para entrar no modo
desejado.
uu
u Para seleccionar um ícone
uu
1. Prima m para visualizar o menu principal.
2. Utilize as teclas de cursor (d, e, f, c) para seleccionar o ícone desejado.
Ícone seleccionado
3. Prima w para visualizar o ecrã inicial do ícone seleccionado.
Aqui entraremos no modo STAT.
•Pode também escolher o modo, introduzindo o número ou letras que se encontram no
canto inferior direito do ícone.
A tabela seguinte explica o significado de cada ícone.
Ícone Nome do modo Descrição
•
RUN
MAT Utilize este modo para cálculos aritméticos e de funções,
(executar
•
matrizes)
para cálculos que envolvam valores binários, octais,
decimais, e hexadecimais e matrizes.
STAT Utilize este modo para executar cálculos estatísticos de
(estatísticas) variável simples (desvio padrão) e de variáveis binárias
(regressão) para realizar testes, para analisar dados e
para desenhar gráficos estatísticos.
•
e
ACT eActivity permite-lhe introduzir texto, expressões
(eActivity) matemáticas, e outros dados em uma interface similar a um
bloco de anotações. Utilize este modo quando quiser
armazenar textos ou fórmulas, ou dados de uma aplicação
incorporada em um ficheiro.
20050401
Page 31

1-2-2
Visor
Ícone Nome do modo Descrição
•
S
SHT Utilize este modo para executar cálculos em uma folha de
(folha de cálculo) cálculo. Cada ficheiro contém uma folha de cálculo de 26
colunas × 999 linhas. Além dos comandos incorporados da
calculadora e dos comandos do modo S
executar cálculos estatísticos e dados estatísticos de gráfico
utilizando os mesmos procedimentos utilizados no modo
STAT.
GRAPH Utilize este modo para armazenar funções de gráfico e
(gráfico) para desenhar gráficos utilizando as funções.
DYNA Utilize este modo para armazenar funções gráficas e
(gráfico dinâmico) para desenhar múltiplas versões de gráficos, alterando
os valores associados às variáveis de uma função.
TABLE Utilize este modo para armazenar as funções, para gerar
(tabela) uma tabela numérica de soluções diferentes à medida
que os valores designados para as variáveis em uma
função mudam, e para desenhar gráficos.
RECUR Utilize este modo para armazenar fórmulas e para criar
(recursão) tabelas numéricas diferentes consuante as variáveis de
uma função e para desenhar gráficos.
CONICS
Utilize este modo para desenhar gráfico de secções cónicas.
(secções cónicas)
EQUA Utilize este modo para solucionar equações lineares com
(equação) duas a seis incógnitas, equações quadráticas, e
equações cúbicas.
PRGM Utilize este modo para armazenar programas na área de
(programa) programas e para executar programas.
•
SHT, também pode
TVM Utilize este modo para executar cálculos financeiros e para
(financeiro) desenhar o fluxo de caixa e outros tipos de gráficos. make
LINK Utilize este modo para transferir o conteúdo da memória
(ligação) ou para fazer cópias de segurança para outra unidade ou
um computador.
MEMORY Utilize este modo para gerir os dados na memória.
(memória)
SYSTEM Utilize este modo para inicializar a memória, para ajustar
(sistema) o contraste e para outros ajustes do sistema.
20050401
Page 32

1-2-3
Visor
kk
k Sobre o menu de funções
kk
Utilize as teclas de função (1 a 6) para aceder aos menus e comandos da barra de
menus que se encontra na parte de baixo do ecrã. Pode saber se um item da barra de
menus é um menu ou um comando pela sua aparência.
• Próximo menu
Exemplo:
Seleccionar exibe um menu de funções hiperbólicas.
• Introdução de comando
Exemplo:
Seleccionar introduz o comando sinh.
• Execução de comando direta
Exemplo:
Seleccionar executa o comando DRAW.
kk
k Sobre os ecrãs
kk
Esta calculadora tem dois tipos de ecrãs: um ecrã de texto e um ecrã de gráfico. O de texto
tem capacidade para 21 colunas e 8 linhas de caracteres, sendo a última linha utilizada para
o menu de teclas de função. O ecrã de gráfico utiliza uma área de 127 (L) × 63 (A) pontos.
Ecrã de texto Ecrã de gráfico
O contéudo de cada um dos ecrãs é armazenado em áreas de memória independentes.
Prima !6(G↔T) para alternar entre o ecrã de texto e o ecrã de gráfico.
20050401
Page 33

1-2-4
Visor
kk
k Visualização normal
kk
Normalmente a calculadora visualiza valores com um máximo de 10 dígitos. Os valores que
execedem esse limite são automaticamente convertidos e mostrados no formato exponecial.
u Como interpretar o formato exponencial
1.2E+12 indica que o resultado é equivalente a 1,2 × 1012. Isto significa que deve mover o
ponto decimal 1,2 doze casas para a direita porque o expoente é positivo, resultando no
valor 1.200.000.000.000.
1.2E–03 indica que o resultado é equivalente a 1,2 × 10–3. Isto significa que deve mover o
ponto décimal 1,2 três casas para a esquerda porque o expoente é negativo, resultando no
valor 0,0012.
Pode especificar um de dois limites diferentes para mudança automática para o ecrã
normal.
Norm 1 .................. 10–2 (0,01) > |x|, |x| > 10
Norm 2 .................. 10–9 (0,000000001) > |x|, |x| > 10
10
10
Todos os exemplos neste manual mostram os resultados dos cálculos utilizando Norm 1.
Consulte a página 2-3-2 para detalhes sobre como alternar entre Norm 1 e Norm 2.
20050401
Page 34

1-2-5
Visor
kk
k Formatos de visualização especiais
kk
Esta calculadora utiliza formatos de visualização especiais para indicar fracções, valores
hexadecimais e valores de graus/minutos/segundos.
u Fracções
................. Indica: 456
u Valores hexadecimais
................. Indica: 0ABCDEF1(16), que é
igual a 180150001(10)
u Graus/Minutos/Segundos
................. Indica: 12° 34’ 56,78”
•Além do referido anteriormente, esta calculadora utiliza também indicadores e símbolos
que serão descritos à medida que surjam na secção relevante.
kk
k Indicador de execução de cálculos
kk
Cada vez que a calculadora estiver ocupada a desenhar um gráfico ou a executar um longo
e complexo cálculo ou programa, surge um quadrado preto “k” a piscar no canto superior
direito do visor. Este quadrado significa que a calculadora está a realizar uma operação
interna.
12
––––
23
20050401
Page 35

Introdução e edição de cálculos
1-3-1
1-3 Introdução e edição de cálculos
Nota
•Salvo indicação específica em contrário, todas as operações nesta secção são explicadas
utilizando o modo de entrada linear.
kk
k Introdução de cálculos
kk
Quando estiver preparado para introduzir um cálculo, primeiro prima A para limpar o ecrã.
A seguir, introduza as suas fórmulas de cálculo tal como são escritas, da esquerda para a
direita, e prima w para obter o resultado.
○○○○○
Exemplo 1 2 + 3 – 4 + 10 =
Ac+d-e+baw
○○○○○
Exemplo 2 2(5 + 4) ÷ (23 × 5) =
Ac(f+e)/
(cd*f)w
k Edição de cálculos
Utilize as teclas d e e para mover o cursor para a posição que pretende alterar e, em
seguida, realize uma das operações descritas abaixo. Depois de editar o cálculo, pode
executá-lo, premindo w. Ou pode utilizar e para ir para o fim do cálculo e introduzir mais.
u Para alterar um passo
○○○○○
Exemplo Para alterar cos60 para sin60
Acga
ddd
D
s
20050401
Page 36

Introdução e edição de cálculos
1-3-2
No modo de entrada linear, premir !D(INS) altera o cursor para ‘‘ ’’.
A próxima função ou valor que introduzir é substituído na localização de ‘‘ ’’.
Acga
ddd!D(INS)
s
Para cancelar, prima novamente !D(INS).
u Para apagar um passo
○○○○○
Exemplo Para alterar 369 × × 2 para 369 × 2
Adgj**c
dD
No modo de inserção, a tecla D funciona como uma tecla de retrocesso.
#O cursor é uma linha intermitente vertical (I)
quando o modo de inserção está
seleccionado. O cursor é uma linha
intermitente horizontal (
substituição está seleccionado.
) quando o modo de
#A predefinição inicial para o modo de entrada
linear é o modo de inserção. Pode mudar para o
modo de substituição premindo 1Y(INS).
20050401
Page 37

Introdução e edição de cálculos
1-3-3
u Para inserir um passo
○○○○○
Exemplo Para alterar 2,362 para sin2,36
Ac.dgx
ddddd
s
u Para alterar o último passo introduzido
○○○○○
Exemplo Para alterar 369 × 3 para 369 × 2
Adgj*d
D
c
2
20050401
Page 38

Introdução e edição de cálculos
1-3-4
kk
k Utilização da memória de releitura
kk
O último cálculo realizado é sempre amazenado na memória de releitura. Pode chamar o
seu conteúdo, premindo d ou e.
Se premir e, o cálculo surge com o cursor no início. Se premir d, o cálculo surge com o
cursor no fim. Pode realizar as alterações que quiser e executá-las novamente.
○○○○○
Exemplo 1 Para executar os dois cálculos seguintes
4,12 × 6,4 = 26,368
4,12 × 7,1 = 29,252
Ae.bc*g.ew
dddd
!D(INS)
h.b
w
Depois de premir A, pode premir f ou c para chamar cálculos anteriores,
sequencialmente, do mais recente para o mais antigo (Função de Releitura Múltipla). Uma
vez chamado o cálculo, pode utilizar e e d para mover o cursor pelo cálculo e alterá-lo
de modo a criar um novo.
○○○○○
Exemplo 2
Abcd+efgw
cde-fghw
A
f (Um cálculo atrás)
f (Dois cálculos atrás)
#O cálculo permanece armazenado na
memória de releitura até executar outro
cálculo.
#O conteúdo da memória de releitura não é
apagado ao premir a tecla A, assim
pode chamar o cálculo e executá-lo
mesmo depois de premir a tecla A.
#A memória de releitura é activada somente no
modo de entrada linear. No modo de entrada
matemática, a função de história é utilizada no
lugar da memória de releitura. Para mais
detalhes, consulte “Função de história” (página
2-2-6).
20050401
20050901
Page 39

Introdução e edição de cálculos
1-3-5
k Correcções no cálculo original
○○○○○
Exemplo 14 ÷ 0 × 2,3 introduzido por engano em vez de 14 ÷ 10 × 2,3
Abe/a*c.d
w
Prima J.
O cursor é colocado automaticamente no
local onde ocorreu o erro.
Realize as alterações necessárias.
db
Execute novamente.
w
kk
k Utilização da área de transferência para copiar e colar
kk
Pode copiar (ou cortar) uma função, comando, ou outros dados para a área de transferência
e, em seguida, colar o conteúdo da área de transferência numa outra posição.
u Para especificar o intervalo de cópia
Modo de entrada linear
1. Mova o cursor (I) para início ou fim do intervalo do texto que pretende copiar e prima
!i(CLIP). Isso faz que o cursor mude para “ ”.
2. Utilize as teclas de cursor para mover o cursor e realçar o intervalo do texto que
pretende copiar.
#O intervalo de cópia de texto que pode
especificar depende da definição “Input Mode”
actual.
Modo de entrada linear: 1 carácter
1 linha
Linhas múltiplas
Modo de entrada matemática: Apenas 1 linha
20050401
Page 40

Introdução e edição de cálculos
1-3-6
3. Prima 1(COPY) para copiar o texto realçado para a área de transferência e sair do
modo de especificação do intervalo de cópia.
Os caracteres seleccionados não são
alterados ao copiá-los.
Para cancelar a selecção de texto sem realizar a operação de cópia, prima J.
Modo de entrada matemática
1. Utilize as teclas de cursor para mover o cursor para a linha que pretende copiar.
2. Prima !i(CLIP) . O cursor mudará para “ ”.
3. Prima 1(CPY
•
L) para copiar o texto realçado para a área de transferência.
u Para cortar o texto
1. Mova o cursor (I) para o início ou fim do intervalo de texto que pretende cortar e prima
!i(CLIP). Isso muda o cursor para “ ”.
2. Utilize as teclas de cursor para mover o cursor e realçar o intervalo de texto que
pretende cortar.
3. Prima 2(CUT) para cortar o texto realçado para a área de transferência.
A operação de corte faz com que os
caracteres originais sejam apagados.
A operação CUT só é suportada para o modo de entrada linear. Ela não é suportada para o
modo de entrada matemática.
20050401
Page 41

Introdução e edição de cálculos
1-3-7
u Para colar texto
Mova o cursor para a localização onde pretende colar o texto e prima !j(PASTE).
O conteúdo da área de transferência é copiado para a posição do cursor.
A
!j(PASTE)
kk
k Função de catálogo
kk
O catálogo é uma lista alfabética de todos os comandos disponíveis na calculadora. Pode
introduzir um comando, chamando o catálogo e seleccionando o comando desejado.
u Para utilizar do catálogo para introduzir um comando
1. Prima !e(CATALOG) para visualizar a lista de catálogo alfabética dos comandos.
2. Introduza a primeira letra do comando que deseja introduzir. Isso visualizará o primeiro
comando que começa com tal letra.
3. Utilize as teclas de cursor (f, c) para realçar o comando que deseja introduzir e,
em seguida, prima w.
○○○○○
Exemplo Para utilizar o catálogo para introduzir o comando ClrGraph
A!e(CATALOG)I(C)c~cw
Premir J ou !J(QUIT) fecha o catálogo.
20050401
Page 42

Introdução e edição de cálculos
1-3-8
k Operações de entrada no modo de entrada matemática
Seleccionar “Math” para a definição “Input Mode” no ecrã de configuração (página 1-7-1)
activa o modo de entrada matemática, o que permite a entrada e visualização natural de
certas funções, exactamente como elas apareceriam em um livro de texto.
Nota
•A definição “Input Mode” inicial é “Linear” (modo de entrada linear). Antes de tentar realizar
qualquer uma das operações explicadas nesta secção, certifique-se de alterar a definição
“Input Mode” para “Math”.
•No modo de entrada matemática, qualquer entrada é introduzida no modo de inserção (e
não no modo de substituição). Repare que a operação !D(INS) (página 1-3-2)
utilizada no modo de entrada linear para alternar para a entrada no modo de inserção
realiza uma função completamente diferente no modo de entrada matemática. Para mais
informação, consulte “Inserção de uma função em uma expressão existente” (página 1-3-
13).
•Salvo indicação específica em contrário, todas as operações nesta secção são realizadas
no modo RUN
•
MAT.
20050401
Page 43

Introdução e edição de cálculos
1-3-9
u Funções e símbolos do modo de entrada matemática
As funções e símbolos relacionados abaixo podem ser utilizados para a entrada natural no
modo de entrada matemática. A coluna “Bytes” mostra o número de bytes de memória que
são utilizados por uma entrada no modo de entrada matemática.
Função/Símbolo Operação de teclas Bytes
Fracção (Imprópria) $ 9
Fracção mista*
Potência M 4
Quadrado x 4
Potência negativa (Recíproca) !)(x
Raiz cúbica !((3
Raiz de potência !M(x)9
x
e
x
10
log(a,b) (Entrada a partir do menu MATH*2)7
Abs (Valor absoluto) (Entrada a partir do menu MATH*2)6
Diferencial linear*
Diferencial quadrático*
Integral*
Cálculo de Σ*
Matriz (Entrada a partir do menu MATH*2) 14*
Parênteses ( e ) 1
Chaves (Utilizadas durante a
entrada de lista)
Colchetes (Utilizados durante a
entrada de matriz)
1
!$(&)14
–1
)5
!x( )6
)9
!I(ex)6
!l(10x)6
3
3
3
4
(Entrada a partir do menu MATH*2)7
(Entrada a partir do menu MATH*2)7
(Entrada a partir do menu MATH*2)8
(Entrada a partir do menu MATH*2)11
5
!*( { ) e !/( } ) 1
!+( [ ) e !-( ] ) 1
*1A fracção mista é suportada apenas no modo
de entrada matemática.
2
*
Para mais informações sobre a entrada de
funções a partir do menu de funções MATH,
consulte “Utilização do menu MATH” na
página 1-3-10.
3
*
A tolerância não pode ser especificada no modo
de entrada matemática. Se quiser especificar a
tolerância, utilize o modo de entrada linear.
4
*
Para o cálculo de Σ no modo de entrada
matemática, o passo é sempre 1. Se quiser
especificar um passo diferente, utilize o modo de
entrada linear.
5
*
Este é o número de bytes para uma matriz 2 × 2.
20050401
Page 44

Introdução e edição de cálculos
1-3-10
u Utilização do menu MATH
No modo RUN
Pode utilizar este menu para a entrada natural de matrizes, diferenciais, integrais, etc.
•{MAT} ... {visualiza o submenu MAT, para a entrada natural de matrizes}
•{logab} ... {inicia uma entrada natural de um logaritmo log ab}
•{Abs} ... {inicia uma entrada natural de um valor absoluto |X|}
•{d/dx} ... {inicia uma entrada natural de um diferencial linear
•{d2/dx2} ... {inicia uma entrada natural de um diferencial quadrático
•{∫dx} … {inicia uma entrada natural de uma integral
•{Σ(} … {inicia uma entrada natural de um cálculo de
•
MAT, premir 4(MATH) visualiza o menu MATH.
•{2×2} ... {introduz uma matriz 2 × 2}
•{3×3} ... {introduz uma matriz 3 × 3}
•{m×n} ... {introduz uma matriz com m linhas e n colunas (até 6 × 6)}
d
f(x)
x = a
dx
d
b
a
β
Σ
α
x=α
f(x)dx
f(x)
dx
}
}
}
2
f(x)
}
x = a
2
u Exemplos de entrada no modo de entrada matemática
Esta secção oferece um certo número de exemplos que mostram como o menu de
funções MATH e outras teclas podem ser utilizados durante a entrada natural no modo de
entrada matemática. Certifique-se de prestar atenção à posição do cursor de entrada ao
introduzir valores e dados.
○○○○○
Exemplo 1 Para introduzir 23 + 1
AcM
d
e
+b
w
20050401
Page 45

Introdução e edição de cálculos
1-3-11
○○○○○
Exemplo 2 Para introduzir
A(b+
$
cc
f
e
)x
w
J
○○○○○
Exemplo 3 Para introduzir
Ab+4(MATH)6(g)1(∫dx)
2
2
1+
(
)
5
1
1+ x + 1dx
0
a+(X)+b
ea
fb
e
w
J
20050401
Page 46

Introdução e edição de cálculos
1-3-12
○○○○○
Exemplo 4 Para introduzir
2 ×
1
2
2
1
2
2
Ac*4(MATH)1(MAT)1(2×2)
$bcc
ee
!x( )ce
e!x( )cee$bcc
w
u Quando o cálculo não entra dentro da janela de visualização
Aparece uma seta na borda esquerda, direita, superior ou inferior do visor para lhe avisar
quando há mais do cálculo fora do ecrã na direcção correspondente.
Ao ver uma seta, pode utilizar as teclas de cursor para rolar o conteúdo do ecrã e ver a
parte desejada.
20050401
Page 47

Introdução e edição de cálculos
1-3-13
u Inserção de uma função em uma expressão existente
No modo de entrada matemática, pode inserir uma função de entrada natural em uma
expressão existente. Realizar isso fará que o valor ou expressão com parênteses para a
direita do cursor se torne o argumento da função inserida. Utilize !D(INS) para inserir
uma função em uma expressão existente.
u Para inserir uma função em uma expressão existente
○○○○○
Exemplo Para inserir a função em uma expressão 1 + (2 + 3) + 4 para a
1. Mova o cursor de modo que fique localizado directamente à esquerda da parte da
2. Prima !D(INS).
3. Prima !x( ) para inserir a função .
expressão com parênteses que se tornará o argumento da função
expressão que deseja que se torne o argumento da função que inserirá.
• Isso muda o cursor para um cursor de inserção (').
• Isso insere a função e torna a expressão com parênteses o seu argumento.
u Regras de inserção de funções
As regras básicas que governam como um valor ou expressão se torna o argumento de
uma função inserida são as seguintes.
•Se um cursor de inserção está localizado imediatamente à esquerda de um parêntese
de abertura, tudo a partir do parêntese de abertura até o seguinte parêntese de
fechamento será o argumento da função inserida.
•Se o cursor de entrada estiver localizado imediatamente à esquerda de um valor ou
fracção, tal valor ou fracção será o argumento da função inserida.
# No modo de entrada linear, premir
!D(INS) mudará para o modo de
inserção. Consulte a página 1-3-2 para mais
informações.
20050401
Page 48

Introdução e edição de cálculos
1-3-14
u Funções que suportam a inserção
As funções que podem ser inseridas utilizando o procedimento descrito em “Para inserir
uma função em uma expressão existente” (página 1-3-13) são as seguintes. Também são
dadas informações sobre como a inserção afecta o cálculo existente.
Função Operação de teclas
Fracção imprópria $
Potência M
!x( )
3
Raiz cúbica !((
Raiz de potência !M(
x
e
10
x
!I(
!l(10x)
)
x
)
e
x
)
log(a,b) 4(MATH)2(logab)
Valor absoluto 4(MATH)3(Abs)
Diferencial linear 4(MATH)4(
Diferencial quadrático 4(MATH)5(
Integral
Cálculo de Σ
4(MATH)6(g)
1(
∫dx
4(MATH)6(g)
Σ
( )
2(
d/dx
2
d
/
dx
)
)
2
)
Expressão
original
Expressão após a
inserção
u Edição de cálculos no modo de entrada matemática
Os procedimentos para editar cálculos no modo de entrada matemática são basicamente
os mesmos que aqueles para o modo de entrada linear. Para mais informações, consulte
“Edição de cálculos” (página 1-3-1).
Repare, entretanto, que os seguintes pontos são diferentes entre o modo de entrada
matemática e o modo de entrada linear.
• Uma entrada do modo de substituição que está disponível no modo de entrada linear
não é suportada no modo de entrada matemática. No modo de entrada matemática, uma
entrada é
•No modo de entrada matemática, premir a tecla D realiza sempre uma operação de
retrocesso.
inserida
sempre na localização actual do cursor.
20050401
Page 49

Introdução e edição de cálculos
1-3-15
•Observe as seguintes operações do cursor que pode utilizar enquanto introduz um
cálculo com o formato de visualização natural.
Para fazer isto: Prima esta tecla:
Mover o cursor do fim até ao começo do cálculo e
Mover o cursor do começo até ao fim do cálculo d
u Visualização do resultado de um cálculo no modo de entrada matemática
As fracções, matrizes e listas produzidas pelos cálculos no modo de entrada matemática
são visualizadas no formato natural, exactamente como apareceriam em um livro de texto.
Visualizações dos resultados dos cálculos de amostra
#As fracções são visualizadas como fracções
impróprias ou fracções mistas, dependendo
da definição “Frac Result” no ecrã de
configuração. Para mais detalhes, consulte
“1-7 Utilização do ecrã de configuração”.
#As matrizes são visualizadas no formato
natural, até 6 × 6. Uma matriz que tenha
mais de seis linhas ou colunas será
visualizada em um ecrã MatAns, que é o
mesmo ecrã utilizado no modo de entrada
linear.
#As listas são visualizadas no formato natural
para até 20 elementos. Uma lista que tenha
mais de 20 elementos será visualizada em
um ecrã ListAns, que é o mesmo ecrã
utilizado no modo de entrada linear.
# Aparece uma seta na borda esquerda,
direita, superior ou inferior do visor para lhe
avisar quando há mais dados fora do ecrã na
direcção correspondente.
Pode utilizar as teclas de cursor para deslocar o
ecrã e ver os dados desejados.
# Premir 2(DEL)1(DEL
• L) enquanto um
resultado de cálculo estiver seleccionado
apagará tanto o resultado como o cálculo que o
produziu.
# O sinal de multiplicação não pode ser omitido
logo antes de uma fracção imprópria ou fracção
mista. Certifique-se sempre de introduzir um
sinal de multiplicação neste caso.
Exemplo: 2 × —
2
5
c*$ccf
# Uma operação de teclas M, x ou !)(
não pode ser seguida imediatamente por outra
operação de teclas M, x ou !)(
Neste caso, utilize parênteses para manter as
operações de teclas separadas.
Exemplo: (3
2)–1
(dx)!)(x–1)
20050401
20060601
–1
x
)
–1
x
).
Page 50

Introdução e edição de cálculos
1-3-16
u Restrições de entrada no modo de entrada matemática
Observe as seguintes restrições que são aplicadas durante a entrada no modo de entrada
matemática.
•Certos tipos de expressões podem fazer que a largura vertical de uma fórmula de
cálculo fique maior do que uma linha de visualização. A largura vertical máxima
permissível de uma fórmula de cálculo é de aproximadamente dois ecrãs de visualização
(120 pontos). Não é possível introduzir nenhuma expressão que exceda desse limite.
20050401
20060601
Page 51

Menu de opções (OPTN)
1-4-1
1-4 Menu de opções (OPTN)
O menu de opções permite-lhe aceder a funções científicas e a recursos que não estão
assinalados no teclado da calculadora. O conteúdo do menu de opções varia de acordo com
o modo em que se encontra ao premir a tecla K.
Para mais detalhes sobre o menu de opções (OPTN), consulte “8-7 Lista de comandos do
modo PRGM”.
u Menu de opções no modo RUN
•
MAT ou PRGM
•{LIST} ... {menu de funções de lista}
•{MAT} ... {menu de operações de matrizes}
•{CPLX} ... {menu de cálculos com números complexos}
•{CALC} ... {menu de análise de funções}
•{STAT} ... {menu de valores estimados de estatísticas com variáveis binárias}
•{HYP} ... {menu de cálculos com funções hiperbólicas}
•{PROB} ... {menu de cálculos de probabilidade/distribuição}
•{NUM} ... {menu de cálculos numéricos}
•{ANGL} ... {menu para conversão de ângulos/coordenadas, introdução/conversão DMS}
•{ESYM} ... {menu de símbolos de engenharia}
•{PICT} ... {menu de memória de imagem}*
•{FMEM} ... {menu de memória de funções}*
1
1
•{LOGIC} ... {menu de operadores lógicos}
•{CAPT} ... {menu de captura de ecrã}
#O menu de opções (OPTN) não aparece
durante cálculos binários, decimais e
hexadecimais.
1
*
Os itens PICT, FMEM e CAPT não são
visualizados quando “Math” é seleccionado
como o modo de entrada.
20050401
Page 52

Menu de opções (OPTN)
1-4-2
u Menu de opções durante a introdução de dados numéricos nos modos
STAT, TABLE, RECUR, EQUA e S
• {LIST}/{CPLX}/{CALC}/{HYP}/{PROB}/{NUM}/{ANGL}/{ESYM}/{FMEM}/{LOGIC}
uu
u Menu de opções durante a introdução de fórmulas nos modos GRAPH,
uu
•
SHT
DYNA, TABLE, RECUR e EQUA
• {List}/{CALC}/{HYP}/{PROB}/{NUM}/{FMEM}/{LOGIC}
Mostram-se a seguir os menus de funções que surgem noutras situações.
u Menu de opções quando um valor de tabela numérica é visualizado no
modo TABLE ou RECUR
•{LMEM} … {menu da memória de lista}
•{
}/{ENG}/{ENG}
° ’ ”
O significado dos item do menu de opções é descrito nas secções dos respectivos modos.
20050401
Page 53

Menu de dados de variáveis (VARS)
1-5-1
1-5 Menu de dados de variáveis (VARS)
Para aceder aos dados de variáveis, prima
J
para visualizar o menu de dados de variáveis
{V-W IN}/{FACT}/{STAT}/{GRPH}/{DYNA}/
{TABL}/{RECR}/{EQUA*1}/{TVM*1}
Para mais detalhes sobre o menu de dados variáveis (VARS), consulte a secção “8-7 Lista
de comandos do modo PRGM”.
u V-WIN — Chamada de valores do ecrã de visualização
• {X}/{Y}/{T,
• {R-X}/{R-Y}/{R-T,
• {min}/{max}/{scal}/{dot}/{ptch}
θ
}
... {menu do eixo-x}/{menu do eixo-y}/{menu de T, θ}
θ
}
...{menu do eixo-x}/{menu do eixo-y}/{menu de T,
θ
} para o lado direito de um
gráfico dual
... {valor mínimo}/{valor máximo}/{escala}/{valor de ponto*2}/{passo}
u FACT — Chamada dos factores de zoom
•{Xfact}/{Yfact}
... {factor do eixo-x}/{factor do eixo-y}
.
*1Os itens EQUA e TVM surgem apenas
quando acede ao menu de dados de variáveis
a partir do modo RUN
ACT.
# Se o número de sistema por defeito for
binário, octal, decimal, ou hexadecimal, o
menu de dados de variáveis não surgirá ao
premir J.
•
MAT, PRGM ou e
2
*
O valor de ponto indica o intervalo de
•
visualização (valor Xmax – valor Xmin) dividido
pelo passo do ponto (126) de ecrã.
O valor de ponto é normalmente calculado
automaticamente a partir dos valores mínimos e
máximos. Ao alterar o valor de ponto, o máximo
é calculado automaticamente.
20050401
Page 54

Menu de dados de variáveis (VARS)
1-5-2
u STAT — Chamada de dados estatísticos
• {X} … {dados x de variável simples/variáveis binárias}
•{n}/{
oo
o}/{Σx }/{Σx
oo
2
}/{x
σ
n}/{xσn–1}/{minX}/{maxX}
…{número de dados}/{média}/{soma}/{soma dos quadrados}/{desvio padrão
populacional}/{desvio padrão da amostra}/{valor mínimo}/{valor máximo}
• {Y} ... {dados y de variáveis binárias}
•{
pp
p
}/{Σ
pp
2
y}/{Σ y
}/{Σ
xy}/{ y
σ
n}/{
y
σ
n–1}/{minY}/{maxY}
…{média}/{soma}/{soma dos quadrados}/{soma dos produtos de dados x e y}/
{desvio padrão populacional}/{desvio padrão da amostra}/{valor mínimo}/{valor
mínimo}
•{GRPH} ... {menu de dados de gráficos}
•{a}/{b}/{c}/{d}/{e}
... {coeficiente de regressão e coeficientes polinomiais}
•{r}/{r2} ... {coeficiente de correlação}/{coeficiente de determinação}
•{MSe} ... {erro médio quadrático}
•{Q1}/{Q3}
... {primeiro quartil}/{terceiro quartil}
•{Med}/{Mod}
... {mediana}/{modo} de dados introduzidos
•{Strt}/{Pitch}
... {divisão de início}/{intervalo} do histograma
•{PTS} ... {menu de dados do ponto de sumário}
•{x1}/{y1}/{x2}/{y2}/{x3}/{y3} ... {coordenadas dos pontos de sumário}
20050401
20050401
Page 55

Menu de dados de variáveis (VARS)
1-5-3
u GRPH — Chamada de funções gráficas
•{Y}/{r} ... {função de coordenada rectangular ou desigualdade}/{função de coordenada
polar}
•{Xt}/{Yt}
... função de gráfico paramétrico {Xt}/{Yt}
•{X} ... {função de gráfico de X = constante}
(Prima uma dessas teclas antes de introduzir um valor para especificar a memória de
armazenamento.)
u DYNA — Chamada de dados de ajuste do gráfico dinâmico
•{Strt}/{End}/{Pitch}
... {valor inicial do intervalo de coeficiente}/{valor final do intervalo de coeficiente}/
{valor de incremento do coeficiente}
u TABL — Chamada de dados de conteúdo e ajustes de tabela
•{Strt}/{End}/{Pitch}
... {valor inicial do intervalo de tabela}/{valor final do intervalo de tabela}/{incre-
mento do valor de tabela}
•{Reslt*1}
... {matriz de conteúdos de tabela}
1
*
O item “Reslt” surge apenas quando o menu
TABL é visualizado no modo RUN
PRGM ou e
•
ACT.
•
MAT,
20050401
Page 56

Menu de dados de variáveis (VARS)
1-5-4
u RECR — Chamada de uma fórmula de regressão*
1
, intervalo de tabela, dados
de conteúdo de tabela
• {FORM}
... {menu de dados da fórmula de regressão}
• {an}/{an+1}/{an+2}/{bn}/{bn+1}/{bn+2}/{cn}/{cn+1}/{cn+2}
... expressões {an}/{an+1}/{an+2}/{bn}/{bn+1}/{bn+2}/{cn}/{cn+1}/{cn+2}
• {RANG} ... {menu de dados do intervalo de tabela}
• {Strt}/{End}
... {valor inicial}/{valor final} do intervalo de tabela
• {a0}/{a1}/{a2}/{b0}/{b1}/{b2}/{c0}/{c1}/{c2}
... valor {a0}/{a1}/{a2}/{b0}/{b1}/{b2}/{c0}/{c1}/{c2}
• {anSt}/{bnSt}/{cnSt}
... origem do gráfico de convergência/divergência da fórmula de recursão {an }/{bn}/
{cn} (gráfico WEB)
• {Reslt*2} ... {matriz do conteúdo de tabela*
3
}
u EQUA — Chamada dos coeficientes de equações e soluções*
• {S-Rlt}/{S-Cof}
... matriz das {soluções}/{coeficientes} para equações lineares com duas a seis
incógnitas*
6
• {P-Rlt}/{P-Cof}
... matriz da {solução}/{coeficientes} para uma equação quadrática ou cúbica
u TVM — Chamada dos dados de cálculos financeiros
•{n}/{I%}/{PV}/{PMT}/{FV}
... {períodos (prestações) de pagamento}/{juros (%)}/{principal}/{quantia do
pagamento}/{saldo da conta ou principal mais juros após a última prestação}
•{P/Y}/{C/Y}
... {número de prestações por ano}/{número de períodos de capitalização por ano}
4
5
*
1
*
Produz-se erro quando não existe nenhuma
função ou tabela numérica de fórmula de
recursão em memória.
2
*
“Reslt” apenas está disponível nos modos
RUN
•
MAT, PRGM e e
3
*
O conteúdo da tabela é armazenado
automaticamente na memória de respostas de
matrizes (MatAns).
4
*
Coeficientes e soluções também são
armazenados automaticamente na memória
de respostas de matrizes (MatAns).
•
ACT.
20050401
5
*
As seguintes condições produzem erros.
- Quando não existem coeficientes
introduzidos na equação.
- Quando não existem soluções obtidas para
a equação.
6
*
Os dados de memória de solução e de
coeficiente de uma equação linear não podem
ser chamados ao mesmo tempo.
Page 57

Menu de programas (PRGM)
1-6-1
1-6 Menu de programas (PRGM)
Para visualizar o menu de programas (PRGM), primeiro entre no modo RUN
•
MAT ou no
modo PRGM a partir do menu principal e prima !J(PRGM). As selecções disponivéis
no menu de programas (PRGM) são as seguintes:
• {COM} ...... {menu de comandos de programa}
• {CTL} ........ {menu de comandos de controlo de programa}
• {JUMP} .... {menu de comando de salto}
• {?} ............ {indicador de introdução}
• {^} ........... {comando de saída}
• {CLR} ....... {menu de comando de limpeza}
• {DISP} ...... {menu de comando de visualização}
• {REL} ....... {menu de operadores relacionais de salto condicional}
• {I/O} .......... {menu de comando de transferência/controlo I/O}
• {:} ............. {conector de instruções múltiplas}
O menu de teclas de função seguinte surge se premir !J(PRGM) no modo RUN
•
MAT
ou no modo PRGM quando o sistema binário, octal, decimal ou hexadecimal estiver definido
por omissão.
• {Prog} ...... {chamada do programa}
• {JUMP}/{?}/{^}/{REL}/{:}
As funções especificadas para as teclas de função são as mesmas do modo Comp.
Consulte a secção “8. Programação”, para mais detalhes sobre os comandos disponíveis
nos diversos menus do menu de programas.
20050401
Page 58

Utilização do ecrã de configuração
1-7-1
1-7 Utilização do ecrã de configuração
O ecrã de configuração do modo mostra as especificações actuais do modo e permite
alterar essas especificações. O procedimento seguinte exemplifica como realizar essas
alterações.
u Para alterar o ajuste de modo
1. Seleccione o ícone desejado e prima w para introduzir o modo e visualizar o seu
ecrã inicial. No nosso exemplo escolhemos o modo RUN
2. Prima !m(SET UP) para visualizar o ecrã
de configuração do modo.
•Este ecrã de configuração é um dos muitos
exemplos possíveis. O conteúdo do ecrã de
configuração varia de acordo com o modo
especificado e as suas especificações.
•
MAT.
...
3. Utilize as teclas de cursor f e c para mover o realce para o item cujos ajustes
pretende alterar.
4. Prima a tecla de função (1 a 6) associada ao ajuste que pretende realizar.
5. Após fazer todas as alterações, prima J para sair do ecrã de configuração.
k Menu de teclas de funções do ecrã de configuração
Esta secção descreve as especificações que pode realizar utilizando as teclas de função no
ecrã de configuração.
indica a especificação por defeito.
u Input Mode (modo de entrada)
•{Math}/{Line}... modo de entrada {matemática}/{linear}
20050401
20050401
Page 59

Utilização do ecrã de configuração
1-7-2
u Mode (modo de cálculo/binário, octal, decimal, hexadecimal)
•{Comp} ... {modo de cálculo aritmético}
•{Dec}/{Hex}/{Bin}/{Oct}
... {decimal}/{hexadecimal}/{binário}/{octal}
u Frac Result (formato de visualização de resultado fraccionário)
•{d/c}/{ab/c}... fracção {imprópria}/{mista}
u Func Type (tipo de função de gráfico)
Premir uma das seguintes teclas de função muda também a função da tecla v.
•{Y=}/{r=}/{Parm}/{X=c}
... {coordenada rectangular}/{coordenada polar}/{coordenada paramétrica}/
gráfico {X = constante}
•{Y>}/{Y<}/{Yt}/{Ys}
... {y>f(x)}/{y<f(x)}/{y≥f(x)}/{y≤f(x)} gráfico de desigualdades
u Draw Type (método de desenho de gráfico)
•{Con}/{Plot}
... {pontos ligados}/{pontos não ligados}
u Derivative (ecrã de valor de derivadas)
•{On}/{Off}
... {ecrã activado}/{ecrã desactivado} quando se utiliza gráfico para tabela, tabela
e gráfico e traçado
u Angle (unidade de ângulo por omissão)
•{Deg}/{Rad}/{Gra}
... {graus}/{radiais}/{graus centesimais}
u Complex Mode (modo complexo)
•{Real} ... {cálculo apenas no intervalo do número real}
•{a + bi}/{r ∠θ}
... {formato rectangular}/{formato polar} visualização de cálculo complexo
u Coord (ecrã de coordenada de indicador de gráficos)
•{On}/{Off}
... {visualização activada}/{visualização desactivada}
u Grid (ecrã de grade de gráficos)
•{On}/{Off}
... {visualização activada}/{visualização desactivada}
20050401
Page 60

Utilização do ecrã de configuração
1-7-3
u Axes (visualização do eixo de gráficos)
•{On}/{Off}
... {visualização activada}/{visualização desactivada}
u Label (visualização de rótulos do eixo de gráficos)
•{On}/{Off}
... {visualização activada}/{visualização desactivada}
u Display (formato de visualização)
•{Fix}/{Sci}/{Norm}/{Eng}
... {especificação do número fixo das casas decimais}/{especificação do número
de dígitos significantes}/{especificação de visualização normal}/{modo de
engenharia}
u Stat Wind (método de especificação do ecrã de visualização de gráficos
estatísticos)
•{Auto}/{Man}
... {automático}/{manual}
u Resid List (cálculo residual)
•{None}/{LIST}
... {sem cálculo}/{especificação da lista para os dados de cálculo residual}
u List File (especificações de ecrã do ficheiro de lista)
•{FILE} ... {especificações do ficheiro de lista no ecrã}
u Sub Name (atribuição do nome de uma lista)
•{On}/{Off}
... {visualização activada}/{visualização desactivada}
u Graph Func (especificações na criação de tabelas e de desenhos gráficos)
•{On}/{Off}
... {visualização activada}/{visualização desactivada}
u Dual Screen (especificações do modo de ecrã duplo)
•{G+G}/{GtoT}/{Off}
... {gráficos em ambos os lados do ecrã duplo}/{gráfico num dos lados do ecrã
duplo e tabela numérica no outro}/{ecrã duplo desactivado}
u Simul Graph (modo de gráficos simultâneos)
•{On}/{Off}
... {gráficos simultâneos activados (todos os gráficos desenhados
simultaneamente)}/{gráficos simultâneos desactivados (gráficos desenhados
em sequência numérica de área)}
20050401
Page 61

Utilização do ecrã de configuração
1-7-4
u Background (fundo da visualização de gráficos)
•{None}/{PICT}
... {sem fundo}/{especificação da imagem de fundo do gráfico}
u Sketch Line (tipo de linha sobreposta)
•{ }/{ }{ }/{ }
... {normal}/{grossa}/{interrompida}/{pontilhada}
u Dynamic Type (tipo de gráfico dinâmico)
•{Cnt}/{Stop}
... {sem parar (contínuo)}/{paragem automática após 10 desenhos}
u Locus (modo de lugar geométrico de gráfico dinâmico)
•{On}/{Off}
... {lugar geométrico é desenhado}/{lugar geométrico não é desenhado}
u Y=Draw Speed (velocidade de desenho de gráfico dinâmico)
•{Norm}/{High}
... {normal}/{alta velocidade}
u Variable (ajustes de criação de tabelas e de desenhos gráficos)
•{RANG}/{LIST}
... {utilizar intervalo de tabelas}/{utilizar dados de lista}
u Σ Display (visualização do valor Σ na tabela de recursão)
•{On}/{Off}
... {visualização activada}/{visualização desactivada}
u Slope (visualização da derivada no local do cursor no gráfico de secções
cónicas)
•{On}/{Off}
... {visualização activada}/{visualização desactivada}
u Payment (definição do período de pagamento)
•{BGN}/{END}
... definição do {começo}/{fim} do período de pagamento
20050401
20050401
Page 62

Utilização do ecrã de configuração
1-7-5
u Date Mode (definição do número de dias por ano)
•{365}/{360}
... cálculos de juros utilizando {365}*1/{360} dias por ano
u Auto Calc (cálculo automático de folha de cálculo)
•{On}/{Off}
... {executar}/{não executar} as fórmulas automaticamente
u Show Cell (modo de visualização de célula de folha de cálculo)
•{Form}/{Val} ... {fórmula}*2/{valor}
u Move (direcção do cursor de célula de folha de cálculo)*
•{Low}/{Right} ... {mover para baixo}/{mover para a direita}
3
*1O ano de 365 dias deve ser utilizado para
cálculos de datas no modo TVM. Caso
contrário, ocorrerá um erro.
2
*
Seleccionar “Form” (fórmula) faz que uma
fórmula na célula seja visualizada como uma
fórmula. A opção “Form” não afecta dados que
não sejam uma fórmula na célula.
3
*
Especifica a direcção em que o cursor de célula se
move quando se preme a tecla w para registar a
entrada da célula, quando o comando Sequence
gera uma tabela numérica, e quando se chama
dados da memória de listas.
20050401
Page 63

Utilização da captura de ecrã
1-8-1
1-8 Utilização da captura de ecrã
Qualquer vez enquanto estiver a operar a calculadora, pode capturar uma imagem do ecrã
actual e guardá-la na memória de captura.
u Para capturar uma imagem de ecrã
1. Opere a calculadora e visualize o ecrã que deseja capturar.
2. Prima !h(CAPTURE).
• Isso visualiza a caixa de diálogo de selecção da
área de memória.
3. Introduza um valor de 1 a 20 e, em seguida, prima w.
• Isso captura a imagem do ecrã e guarda-a na área de memória de captura com o
nome “Capt n” (n = valor introduzido).
•Não é possível capturar a imagem do ecrã de uma mensagem que indica uma operação
ou comunicação de dados em progresso.
•Ocorrerá um erro de memória se não houver espaço suficiente na memória principal para
armazenar a captura do ecrã.
u Para chamar uma imagem de ecrã da memória de captura
1. No modo RUN
1(RCL).
2. Introduza um número da memória de captura no intervalo de 1 a 20 e, em seguida,
prima w.
•Também pode utilizar o comando RclCapt em um programa para chamar uma imagem de
ecrã da memória de captura.
•
MAT (modo de entrada linear), prima K6(g)6(g)5(CAPT)
20050401
Page 64

Ao encontrar problemas...
1-9-1
1-9 Ao encontrar problemas...
Quando tiver problemas na realização de operações, realize os procedimentos seguintes
antes de assumir que existe algo de errado com a calculadora.
kk
k Restauração das definições originais da calculadora
kk
1. A partir do menu principal, entre no modo SYSTEM.
2. Prima 5(RSET).
3. Prima 1(STUP) e, em seguida, 1(Yes).
4. Prima Jm para voltar ao menu principal.
Agora entre no modo correcto e execute novamente o cálculo, acompanhando os resultados
no ecrã.
kk
k Em caso de bloqueio
kk
•Caso a unidade bloquear-se e deixar de responder, prima o botão P que se encontra na
parte de trás da calculadora para restaurar as definições iniciais da calculadora (consulte a
página α-5-1). Tenha em conta que este procedimento apaga todos os dados da memória
da calculadora.
20050401
Page 65

Ao encontrar problemas...
1-9-2
kk
k Mensagem de pilhas fracas
kk
Se algumas das mensagens seguintes surgir no ecrã, desligue de imediato a calculadora e
troque as pilhas principais seguindo as instruções.
Se continuar a utilizar a calculadora sem trocar as pilhas principais, a alimentação será
desligada automaticamente para proteger o conteúdo da memória. Quando isso ocorrer, não
será possivel ligar novamente a calculadora, havendo o perigo de danificar o conteúdo da
memória ou mesmo perdê-la completamente.
# Não é possível realizar comunicações de
dados depois de surgir a mensagem de
pilhas fracas.
20050401
Page 66

Capítulo
Cálculos manuais
2-1 Cálculos básicos
2-2 Funções especiais
2-3 Especificação da unidade angular e do formato de
visualização
2-4 Cálculos com funções
2-5 Cálculos numéricos
2-6 Cálculos com números complexos
2-7 Cálculos binários, octais, decimais e hexadecimais com
números inteiros
2-8 Cálculos com matrizes
2
Modo de entrada linear/matemática (página 1-3-8)
•A menos que seja indicado especificamente ao contrário, todas as operações
neste capítulo são explicadas utilizando o modo de entrada linear.
•Quando necessário, o modo de entrada é indicado pelos seguintes símbolos.
<Math>.... Modo de entrada matemática
<Line> ..... Modo de entrada linear
20050401
Page 67

2-1-1
Cálculos básicos
2-1 Cálculos básicos
kk
k Cálculos aritméticos
kk
• Introduza os cálculos aritméticos tal como são escritos, da esquerda para a direita.
•Utilize a tecla - para introduzir o sinal menos antes do valor negativo.
•Os cálculos são realizados internamente com uma mantissa de 15 dígitos. O resultado é
arredondado para uma mantissa de 10 dígitos antes de ser mostrado no ecrã.
•Para cálculos aritméticos mistos, a multiplicação e a divisão têm prioridade sobre a
adição e a subtracção.
Exemplo Operação
23 + 4,5 – 53 = –25,5 23+4.5-53w
56 × (–12) ÷ (–2,5) = 268,8 56*-12/-2.5w
(2 + 3) × 102 = 500 (2+3)*1E2w*
1
1 + 2 – 3 × 4 ÷ 5 + 6 = 6,6 1+2-3*4/5+6w
100 – (2 + 3) × 4 = 80 100-(2+3)*4w
2 + 3 × (4 + 5) = 29 2+3*(4+5w*
(7 – 2) × (8 + 5) = 65 (7-2)(8+5)w*
6
= 0,3
4 × 510
3
<Line>
6 /(4*5)w*
<Math>
2
3
4
$6c4*5w
(1 + 2i) + (2 + 3i) = 3 + 5i (b+c!a(i))+(c+
d!a(i))w
(2 + i) × (2 – i) = 5 (c+!a(i))*(c-!a(i)
)w
3
*1A operação (2+3)E2 não produz o
resultado correcto. Assegure-se de introduzir
o cálculo tal como é exemplificado.
2
*
O símbolo de fechar parênteses (antes da
operação da tecla w) pode ser omitido,
independentemente de quantos são
necessários.
*
O sinal de multiplicação antes de um parêntese
de abertura pode ser omitido.
4
*
Isto é identico a 6 / 4 / 5 w.
20050401
Page 68

2-1-2
Cálculos básicos
kk
k Número de casas decimais, número de dígitos significativos, intervalo
kk
de visualização normal
[SET UP]- [Display] -[Fix] / [Sci] / [Norm]
•Mesmos depois de ser especificado o número de casas decimais dos dígitos
significativos, os cálculos internos continuam a ser realizados com base numa mantissa
de 15 dígitos e os valores visualizados são armazenados com base numa mantissa de
10 dígitos. Utilize Rnd do menu de cálculos numéricos (NUM) (página 2-4-1) para
arredondar o valor visualizado para o número de casas decimais e de dígitos
significativos especificados.
•As especificações do número de casas decimais (Fix) e de dígitos significativos (Sci)
permanecem em efeito até que sejam alteradas ou até que altere as especificações do
intervalo de visualização normal (Norm).
○○○○○
Exemplo 100 ÷ 6 = 16,66666666...
Condição Operação Visualização
100/6w 16.66666667
4 casas decimais !m(SET UP) f (ou c 12 vezes)
1(Fix)ewJw 16.6667
5 dígitos significativos !m(SET UP) f (ou c 12 vezes)
2(Sci)fwJw 1.6667E+01
Cancela a especificação !m(SET UP) f (ou c 12 vezes)
3(Norm)Jw 16.66666667
*1Os valores apresentados são arredondados
por defeito para a casa especificada.
1
*
1
*
20050401
Page 69

2-1-3
Cálculos básicos
Exemplo 200 ÷ 7 × 14 = 400
Condição Operação Visualização
200/7*14w
3 casas decimais
!m(SET UP) f (ou c 12 vezes)
1(Fix)dwJw
O cálculo continua
utilizando a capacidade de
visualização de 10 dígitos
200/7w
*
14w
Ans ×
• Caso o mesmo cálculo seja realizado utilizando o número de dígitos especificado:
200/7w
O valor armazenado
internamente é arredondado
para o número de casas
K6(g)4(NUM)4(Rnd)w
*
14w
Ans ×
decimais especificado no
ecrã de configuração.
200/7w 28.571
Também pode especificar o
número de casas decimais
para o arredondamento dos
valores internos para um
cálculo específico.*
1
6(RndFi)!-(Ans),2)
w
*
14w
RndFix(Ans,2)
Ans ×
(Exemplo: Para especificar o
arredondamento para duas
casas decimais)
400
400.000
28.571
I
400.000
28.571
28.571
I
399.994
28.570
I
399.980
k Sequência de prioridade dos cálculos
Esta calculadora utiliza a lógica algébrica verdadeira para realizar parte dos cálculos de
uma fórmula na seguinte ordem:
1 Funções de tipo A
Transformação de coordenadas Pol (
Derivadas, segundas derivadas, integrações, cálculos de
d/dx, d2/dx2, ∫dx, Σ, Mat, Solve, FMin, FMax, List→Mat, Seq, Min, Max, Median, Mean,
Augment, Mat
Funções compostas*
*1 Para desactivar o arredondamento,
especifique 10 para o número de dígitos
significativos.
*2 Pode combinar os conteúdos das localizações
da memória de funções múltiplas (fn) e
localizações da memória de gráfico (Yn, rn,
Xtn, Ytn, Xn) para as funções compostas.
Especificar fn1(fn2), por exemplo, resulta na
→List, P(, Q(, R(, t(, List, RndFix, log ab
2
fn, Yn, rn, Xtn, Ytn, Xn
x, y), Rec (r,
θ
)
Σ
função composta fn1°fn2 (vide página 5-3-3).
Uma função composta pode consistir em até cinco
funções.
# Não pode utilizar uma expressão de cálculo
diferencial, diferencial quadrático, integração, Σ,
valor máximo/mínimo, resolução, RndFix ou log ab
dentro de um termo de um cálculo RndFix.
20061001
20070101
Page 70

2-1-4
1
2
3
4
5
6
1
2
3
4
5
6
Cálculos básicos
2 Funções de tipo B
Nestas funções, primeiro introduza o valor e só depois prima a tecla de função.
x2, x–1, x!, ° ’ ”, simbolos ENG, unidade angular °, r,
g
3 Potência/raiz ^(xy), x'
b
4 Fracções a
/
c
5 Formato de multiplicação abreviado em frente π, nome de memória ou nome da variável.
2π, 5A, etc.
6 Funções de tipo C
Nestas funções, primeiro prima a tecla de função e só depois introduza o valor.
', 3', log, In, ex, 10x, sin, cos, tan, sin–1, cos–1, tan–1, sinh, cosh, tanh, sinh–1, cosh–1,
tanh–1, (–), d, h, b, o, Neg, Not, Det, Trn, Dim, Identity, Sum, Prod, Cuml, Percent, AList,
Abs, Int, Frac, Intg, Arg, Conjg, ReP, ImP
7 Formato de multiplicação abreviado antes de funções de tipo A, funções de tipo C e
parênteses.
2'3, A log2, etc.
8 Permutação, combinação nPr, nCr, ∠
9 ×, ÷
0 +, –
! Operadores relacionais =, ≠, >, <, ≥, ≤
@ And (operador lógico), and (operador bitwise)
# Or (operador lógico), or, xor, xnor (operador bitwise)
Exemplo 2 + 3
# Quando são utilizadas funções com a
mesma prioridade em série, a execução
realiza-se da direita para a esquerda.
exIn 120 → ex{In( 120)}
Caso contrário, a execução é da esquerda
para a direita.
× (log sin2π2 + 6,8) = 22,07101691 (unidade angular = Rad)
# As funções combinadas são executadas da
direita para a esquerda.
# Tudo o que se encontra entre parênteses
recebe prioridade máxima.
20061001
20070101
Page 71

2-1-5
Cálculos básicos
k Operações de multiplicação sem o sinal de multiplicação
É possivel omitir o sinal de multiplicação (×) nas seguintes operações:
• Antes das funções de tipo A (
1 na página 2-1-3) e funções de tipo C (6 na página 2-1-
4), excepto para os sinais negativos.
Exemplo 2sin30, 10log1,2, 2
'3, 2Pol(5, 12), etc.
• Antes de constantes, nomes de variáveis e nomes de memória.
Exemplo 2π, 2AB, 3Ans, 3Y1, etc.
• Antes de um parentêse de abertura
Exemplo 3(5 + 6), (A + 1)(B – 1), etc.
k Excesso da capacidade e erros
Quando se excede um limite de cálculo ou de entrada, ou se realiza uma operação
ilegal, surge uma mensagem de erro, sendo impossível realizar outra operação enquanto
tal mensagem permanecer no ecrã. Os exemplos seguintes fazem surgir no ecrã uma
mensagem de erro.
• Quando qualquer erro, quer intermédio, quer final, ou qualquer valor na memória excede
±9,999999999 × 1099 (Ma ERROR).
• Quando se tenta realizar um cálculo de função que exceda o limite de introdução (Ma
ERROR).
• Quando se tenta realizar uma operação ilegal durante cálculos estatísticos (Ma ERROR).
Por exemplo, tentar obter 1VAR sem introduzir dados.
• Quando é especificado um tipo de dados impróprios para o argumento de um cálculo de
função (Ma ERROR).
• Quando se excede a capacidade da pilha de valores numéricos ou de comandos (Stack
ERROR). Por exemplo, introduzir 25 successivos ( seguido de 2 + 3 * 4 w.
• Quando se tenta realizar um cálculo utilizando uma fórmula ilegal (Syntax ERROR). Por
exemplo, 5 ** 3 w.
# Muitas das teclas da calculadora estão
inacessíves enquanto estiver no ecrã a
mensagem de erro.
J para limpar o erro e ver onde
Prima
se encontra o erro (consulte página
1-3-5).
# Consulte a “Tabela de mensagens de erro” na
página α-1-1 para mais informação sobre outros
erros.
20061001
20070101
Page 72

2-1-6
Cálculos básicos
•Quando se tenta realizar um cálculo que exceda da capacidade da memória (Memory
ERROR).
•Quando se utiliza um comando que requer um argumento, mas não se especifica um
argumento válido (Argument ERROR).
•Quando se tenta utilizar uma dimensão ilegal durante os cálculos de matrizes (Dimension
ERROR).
• Quando se tenta realizar um cálculo que tem um argumento de número real e produz uma
solução de número complexo, com “Real” seleccionado na definição Complex Mode no
ecrã de configuração (Non-Real ERROR).
k Capacidade da memória
No modo de entrada, cada vez que preme uma tecla, utiliza-se um ou dois bytes. Algumas
das funções que utilizam um byte são: b, c, d, sin, cos, tan, log, In, e π. Algumas
das funções que utilizam dois bytes são d/dx(, Mat, Xmin, If, For, Return, DrawGraph, SortA(,
PxIOn, Sum e an+1.
Para mais detalhes sobre o número de bytes requerido para cada função no modo de entrada
matemática, consulte a página 1-3-9.
#À medida que introduz valores ou comandos,
eles surgem alinhados à esquerda do ecrã.
Os resultados dos cálculos, pelo contrário,
surgem alinhados à direita do ecrã.
#O intervalo permitido para a introdução de
valores é de 15 dígitos para a mantissa e dois
dígitos para o expoente. Os cálculos internos
são realizados utilizando uma mantissa de 15
dígitos e um expoente de dois dígitos.
20050401
Page 73

2-2-1
Funções especiais
2-2 Funções especiais
kk
k Cálculos com variáveis
kk
Exemplo Operação Visualização
193.2aav(A)w 193.2
193,2 ÷ 23 = 8,4 av(A)/23w 8.4
193,2 ÷ 28 = 6,9 av(A)/28w 6.9
kk
k Memória
kk
uVariáveis (Memória de alfabeto)
A calculadora vem com 28 variáveis. Pode utilizar as variáveis para armazenar valores que
pretenda utilizar nos cálculos. As variáveis são identificadas por nomes de uma letra,
compostos pelas 26 letras do alfabeto, mais r e θ. O tamanho máximo de valores que pode
atribuir às variáveis é de 15 dígitos para a mantissa e 2 dígitos para o expoente.
u Para atribuir um valor a uma variável
[valor] a [nome da variável] w
○○○○○
Exemplo Para atribuir 123 à variável A
Abcdaav(A)w
○○○○○
Exemplo Para adicionar 456 à variável A e armazenar o resultado na variável B
Aav(A)+efgaa
l(B)w
# Os conteúdos das variáveis permanecem
armazenados mesmo que a calculadora seja
desligada.
20050401
Page 74

2-2-2
Funções especiais
u Para visualizar o conteúdo de uma variável
○○○○○
Exemplo Para visuzalizar o conteúdo da variável A
Aav(A)w
u Para limpar uma variável
○○○○○
Exemplo Para limpar a variável A
Aaaav(A)w
u Para especificar o mesmo valor a mais do que uma variável
[valor]a [nome da primeira variável*1]a3(~) [nome da última variável*1]w
○○○○○
Exemplo Para especificar o valor 10 da variável A até à F
Abaaav(A)
a3(~)at(F)w
uMemória de função [OPTN]-[FMEM]
A memória de função (f1~f20) é conveniente para armazenar temporariamente as expressões
mais usadas. Para um armazenamento a longo prazo, recomenda-se que utilize o modo
GRAPH para expressões e o modo PRGM para programas.
•{STO}/{RCL}/{fn}/{SEE} ... {armazenar função}/{chamar função}/{especificação da área
de função como nome de variável dentro de uma expressão}/{lista de funções}
*1 Não pode utilizar “r” ou “θ” como o nome de
uma variável.
20050401
Page 75

2-2-3
Funções especiais
u Para armazenar uma função
○○○○○
Exemplo Para armazenar a função (A+B) (A–B) como função de memória
número 1
(av(A)+al(B))
(av(A)-al(B))
K6(g)6(g)3(FMEM)
1(STO)bw
JJJ
u Para chamar uma função
○○○○○
Exemplo Para chamar o conteúdo da memória de função número 1
K6(g)6(g)3(FMEM)
2(RCL)bw
u Para chamar uma função como uma variável
daav(A)w
baal(B)w
K6(g)6(g)3(FMEM)3(fn)
b+cw
u Para visualizar a lista de funções disponíveis
K6(g)6(g)3(FMEM)
4(SEE)
# Se o número da memória de função já tiver
uma função, esta será subtituida pela nova.
#A função chamada surge no ecrã onde estiver o
cursor.
20050401
Page 76

2-2-4
Funções especiais
u Para apagar uma função
○○○○○
Exemplo Para apagar o conteúdo da memória de número 1
AK6(g)6(g)3(FMEM)
1(STO)bw
•Se o ecrã estiver vazio e executar a operação de armazenamento, a função que estiver
armazenada na memória de função será apagada.
u Para utilizar memórias armazenadas
○○○○○
Exemplo Para armazenar x3 + 1, x2 + x na memória de função e desenhar o
!m(SET UP)ccc1(Y=)J
AvMd+bK6(g)6(g)3(FMEM)
1(STO)bw(armazena (x3 + 1))
JAvx+v1(STO)cw(armazena (x2 + x))
gráfico: y = x3 + x2 + x + 1
Utilize as seguintes definições para o ecrã de visualização.
Xmin = – 4, Xmax = 4, Xscale = 1
Ymin = –10, Ymax = 10, Yscale = 1
JA!4(SKTCH)1(Cls)w
5(GRPH)1(Y=)
K6(g)6(g)3(FMEM)3(fn)b+
3(fn)cw
•Para detalhes completos sobre gráficos, consulte “5. Representação gráfica”.
#Também pode utilizar a para armazenar
uma função na memória de funções num
programa. Neste caso, deve encerrar a
função com aspas.
20050401
Page 77

2-2-5
Funções especiais
k Função de resposta
A função de resposta armazena automaticamente o último resultado calculado, bastando
para isso premir w (a menos que a operação da tecla w resulte num erro). O resultado é
armazenado na memória de resposta.
u Para utilizar o conteúdo da memória de resposta num cálculo
Exemplo 123 + 456 = 579
789 – 579 = 210
Abcd+efgw
hij-!-(Ans)w
No modo de entrada matemática, a memória de resposta é actualizada com cada
cálculo. Repare, entretanto, que a operação de chamada do conteúdo da memória de
resposta difere da operação utilizada no modo de entrada linear. Para mais detalhes,
consulte “Função de história” (página 2-2-6).
k Execução de cálculos contínuos
A memória de resposta permite também utilizar o resultado de um cálculo como argumento
no próximo cálculo.
Exemplo 1
÷ 3 =
1 ÷ 3 × 3 =
Ab/dw
(continuando)*dw
Os cálculos contínuos também podem ser utilizados com funções de tipo B (x2, x–1, x!,
página 2-1-4), +, –, ^(xy), x', ° ’ ”, etc.
# O valor máximo da memória de resposta é
de 15 dígitos para a mantissa e 2 dígitos
para o expoente.
# Apenas valores numéricos e resultados de
cálculos podem ser armazenados na
memória de resposta.
# O conteúdo da memória de resposta não se
apaga quando se preme a tecla A ou quando
se desliga a calculadora.
# Quando “Linear” é seleccionado como o modo
de entrada, o conteúdo da memória de resposta
não é alterado pela operação que atribui valores
à memória de alfabeto (tal como: fa�
av(A)w).
20061001
20070101
Page 78

2-2-6
Funções especiais
kk
k Função de história
kk
A função de história mantém uma história das expressões de cálculo e dos resultados no
modo de entrada matemática. Até 30 conjuntos de expressões de cálculo e resultados são
mantidos.
b+cw
*cw
Ta mbém pode editar as expressões de cálculo que são mantidas pela função de história
e calcular de novo. Isso recalculará todas as expressões a partir da expressão editada.
○○○○○
Exemplo Para mudar “1+2” para “1+3” e recalcular
Realize a seguinte operação seguindo a amostra mostrada acima.
ffffdDdw
#O valor armazenado na memória de resposta
depende sempre do resultado produzido pelo
último cálculo executado. Se os conteúdos
da história incluírem operações que utilizam
a memória de resposta, editar um cálculo
pode afectar o valor da memória de resposta
utilizado em cálculos subsequentes.
- Se tiver uma série de cálculos que utilizam a
memória de resposta para incluir o resultado do
cálculo anterior no cálculo seguinte, editar um
cálculo afectará os resultados de todos os
outros cálculos que vierem depois do mesmo.
- Quando o primeiro cálculo da história incluir
conteúdos da memória de resposta, o valor da
memória de resposta será “0”, porque não há
cálculo antes do primeiro na história.
20050401
20050901
20050901
Page 79

2-2-7
Funções especiais
k Pilhas
A calculadora utiliza blocos de memória, denominados
comandos de baixa prioridade. Existe uma
pilha de comando
ocorre se realizar um cálculo tão complexo que exceda a capacidade da pilha de valores
numéricos disponíveis, o espaço da pilha de comando ou se a execução de uma sub-rotina
de um programa exceder a capacidade da pilha da sub-rotina.
○○○○○
Exemplo
de 26 níveis e uma
pilha de valores numéricos
pilha de sub-rotina de programa
pilhas
, para armazenar valores e
de 10 níveis, uma
de 10 níveis. Um erro
Pilha de valores
numéricos
1
2
2
3
3
4
4
5
5
4
...
#Os cálculos são realizados de acordo com a
sequência de prioridades. Uma vez realizado
um cálculo, o mesmo é limpado da pilha.
Pilha de
comandos
b
×
c
(
d
(
e
+
f
×
g
(
h
+
...
#Armazenar números complexos ocupa dois níveis
da pilha de valor numérico.
#Armazenar funções de dois bytes ocupa dois
níveis da pilha de valores numéricos.
20050401
20050901
Page 80

2-2-8
Funções especiais
k Utilização de instruções múltiplas
As instruções múltiplas são formadas pela ligação de instruções individuais para a execução
sequencial. Pode utilizar instruções múltiplas em cálculos manuais e em cálculos
programados. Existem duas formas diferentes de ligar instruções para formar instruções
múltiplas.
•Dois pontos (:)
As instruções que utilizam dois pontos são executadas da esquerda para a direita, sem
parar.
•Comando de visualização de resultado (
^^
^)
^^
Quando a execução chega ao fim de uma instrução seguida do comando de visualização
de resultado, a execução pára e o resultado parcial surge no ecrã. Pode continuar a
execução do cálculo premindo a tecla w.
○○○○○
Exemplo 6,9 × 123 = 848,7
123 ÷ 3,2 = 38,4375
Abcdaav(A)
!J(PRGM)6(g)5(:)g.j
*av(A)!J(PRGM)5(^)
av(A)/d.cw
w
# Não é possivel contruir uma intrução múltipla,
em que uma das instruções utiliza o resultado
de instrução anterior.
Exemplo: 123 × 456: × 5
Inválido
20050401
20050901
Page 81

Especificação da unidade angular e do formato de visualização
2-3-1
2-3 Especificação da unidade angular e do
formato de visualização
Antes de realizar o primeiro cálculo, deve utilizar o ecrã de configuração para especificar a
unidade angular e o formato de visualização.
kk
k Definição da unidade angular [SET UP]- [Angle]
kk
1. No ecrã de configuração, seleccione “Angle”.
2. Prima a tecla de função da unidade angular desejada e prima J.
•{Deg}/{Rad}/{Gra} ... {graus}/{radianos}/{grados}
•A relação entre graus, grado e radianos é a seguinte:
360° = 2π radianos = 400 grados
90° = π/2 radianos = 100 grados
kk
k Definição do formato de visualização [SET UP]- [Display]
kk
1. No ecrã de configuração, seleccione “Display”.
2. Prima a tecla de função do item que deseja especificar e prima J.
•{Fix}/{Sci}/{Norm}/{Eng} ... {especificação do número fixo de casas decimais}/
{especificação do número de dígitos significativos}/{visualização normal}/{modo
de engenharia}
u Para especificar o número de casas decimais (Fix)
○○○○○
Exemplo Para especificar duas casas decimais
1(Fix) cw
Prima a tecla numérica correspondente ao
número de casas decimais desejado
n
= 0 a 9).
(
#Os valores visualizados são arredondados
para o número de casa decimais
especificado.
20050401
Page 82

Especificação da unidade angular e do formato de visualização
2-3-2
u Para especificar o número de dígitos significativos (Sci)
○○○○○
Exemplo Para especificar três dígitos significativos
2(Sci) dw
Prima a tecla numérica que corresponde
ao número de dígitos significativos que
deseja especificar (
Se especificar 0, o número de dígitos
significativos será 10.
n
= 0 a 9).
u Para especificar a visualização normal (Norm 1/Norm 2)
Prima 3(Norm) para alterar entre Norm 1 e Norm 2.
Norm 1: 10
Norm 2: 10
–2
(0,01)>|x|, |x| >10
–9
(0,000000001)>|x|, |x| >10
Ab/caaw (Norm 1)
10
10
(Norm 2)
u Para especificar a visualização da notação de engenharia (modo Eng)
Prima 4(Eng) para alterar entre a notação de engenharia e a notação normal. O
indicador “/E” permanece no ecrã enquanto a notação de engenharia estiver activa.
Pode utilizar os símbolos seguintes para converter valores para a notação de
engenharia, tal como 2.000 (= 2 × 103) → 2k.
E (Exa) × 10
P (Peta) × 10
T (Tera) × 10
G (Giga) × 10
M (Mega) × 10
k (kilo) × 10
18
15
12
9
6
3
#Os valores visualizados são arredondados para
o número de dígitos significativos especificados.
m (milli) × 10
µ (micro) × 10
n (nano) × 10
p (pico) × 10
f (femto) × 10
#O símbolo de engenharia que faz da mantissa
um valor entre 1 e 1000 é automaticamente
seleccionado pela calculadora quando a
notação de engenharia está em efeito.
20050401
–3
–6
–9
–12
–15
Page 83

2-4-1
Cálculos com funções
2-4 Cálculos com funções
k Menus de funções
Esta calculadora inclui cinco menus de funções que lhe dão acesso a funções científicas
que não estão descritas no teclado.
•O conteúdo do menu de funções difere de acordo com o modo escolhido no menu
principal antes que a tecla K. Os exemplos seguintes demonstram os menus
disponíveis no modo RUN
uu
u Cálculos com funções hiperbólicas (HYP) [OPTN]-[HYP]
uu
•{sinh}/{cosh}/{tanh} ... {seno}/{co-seno}/{tangente} hiperbólicos
•{sinh–1}/{cosh–1}/{tanh–1} ... {seno}/{co-seno}/{tangente} hiperbólicos inversos
uu
u Cálculos de probalidades/distribuição (PROB) [OPTN]-[PROB]
uu
•{x!} ... {prima depois de ter introduzido um valor para obter o seu factorial}
•{nPr}/{nCr} ... {permutação}/{combinação}
•{Ran#}... {gera um número pseudo aleatório (0 a 1)}
•{P(}/{Q(}/{R(} ... probabilidade de distribuição normal {P(t)}/{Q(t)}/{R(t)}
•{t(} ... {valor da variável normalizada t(x)}
•
MAT.
uu
u Cálculos numéricos (NUM) [OPTN]-[NUM]
uu
•{Abs} ... {seleccione este item e introduza um valor para obter o seu valor absoluto}
•{Int}/{Frac} ... Seleccione este item e introduza um valor para extrair a parte {inteira}/
•{Rnd} ... {arredonda o valor utilizado para cálculos internos para 10 dígitos significativos
(para coincidir com o valor na memória de resposta), ou para o número de casas
decimais (Fix) e número de dígitos significativos (Sci) especificado}
•{Intg} ... {seleccione este item e introduza um valor para obter o maior número inteiro
que não seja maior que o valor}
•{RndFi} ... {arredonda o valor usado para os cálculos internos para os dígitos
especificados (0~9) (consulte a página 2-1-3)}
{fraccionária}.
20050401
Page 84

2-4-2
Cálculos com funções
uu
u Operações com unidades angulares, conversão de coordenadas,
uu
sexagesimais (ANGL)
[OPTN]-[ANGL]
•{°}/{r}/{g} ... {graus}/{radianos}/{grados} para um valor específico
•{° ’ ”} ... {especifica graus (horas), minutos, segundos quando se introduz um valor de
graus/minutos/segundos}
•{
} ... {converte valores decimais para valores em graus/minutos/segundos}*
° ’ ”
1
•{Pol(}/{Rec(} ... converte coordenadas {rectangular a polar}/{polar a rectangular}
•{'DMS} ... {converte um valor decimal para um valor sexagesimal}
uu
u Símbolo de engenharia (ESYM) [OPTN]-[ESYM]
uu
•{m}/{µ}/{n}/{p}/{f} ... {milli (10–3)}/{micro (10–6)}/{nano (10–9)}/{pico (10
–12
)}/{femto (10
–15
)}
•{k}/{M}/{G}/{T}/{P}/{E} ... {kilo (103)}/{mega (106)}/{giga (109)}/{tera (1012)}/{peta (1015)}/
{exa (1018)}
•{ENG}/{ENG} ... altera a casa decimal do valor visualizado três dígitos para a
{esquerda}/{direita} e {diminui}/{aumenta} o expoente em três.*
2
Quando utiliza a notação de engenharia, o símbolo de engenharia é devidamente
alterado.
*1A operação do menu {
apenas quando existe um resultado de um
cálculo no ecrã.
2
*
As operações dos menus {ENG} e {ENG}
estão dísponiveis apenas quando existe um
resultado de um cálculo no ecrã.
} está dísponivel
° ’ ”
#A comutação ENG/ENG é desactivada para os
seguintes tipos de resultados de cálculo.
- Resultado de cálculo matricial introduzido no
modo de entrada matemática
- Resultado de cálculo de lista introduzido no
modo de entrada matemática
20050401
Page 85

2-4-3
Cálculos com funções
kk
k Unidades angulares
kk
Para alterar a unidade angular de um valor introduzido, prima K6(g)5(ANGL). No
menu que surge, seleccione “°”, “r” ou “g”.
•Assegure-se de especificar o modo Comp no ecrã de configuração.
Exemplo Operação
Para converter 4,25 radianos
para graus:
243,5070629 4.25K6(g)5(ANGL)2(r)w
!m(SET UP)cccccc1(Deg)J
47,3° + 82,5rad = 4774,20181°
2°20⬘30⬙ + 39⬘30⬙ = 3°00⬘00⬙
2,255° = 2°15⬘18⬙
47.3+82.5K6(g)5(ANGL)2(r)w
2K6(g)5(ANGL)4(° ’ ”) 204(° ’ ”) 30
4(° ’ ”)+04(° ’ ”)394(° ’ ”)304(° ’ ”)w
5(
)
° ’ ”
2.255K6(g)5(ANGL)6(g)3('DMS)w
# Uma vez especificada a unidade angular, ela
permanece em efeito até ser especificada
outra unidade. A especificação permanece
mesmo que se desligue a calculadora.
20050401
Page 86

2-4-4
Cálculos com funções
kk
k Funções trigonométricas e trigonométricas inversas
kk
•Assegure-se de que especifica a unidade angular antes de realizar cálculos com funções
trigonométricas e trigonométricas inversas.
π
(90° = ––– radianos = 100 grados)
2
•Assegure-se de que especifica o modo Comp no ecrã de configuração.
Exemplo Operação
sin 63° = 0,8910065242 !m(SET UP)cccccc
1(Deg)J
s63w
π
cos (–– rad) = 0,5 !m(SET UP)cccccc
3
2(Rad)J
<Line>
c(!E(π)/3)w
<Math>
c$!E(π)c3w
tan (– 35gra) = – 0,6128007881 !m(SET UP)cccccc
3(Gra)J
t-35w
2 • sin 45° × cos 65° = 0,5976724775 !m(SET UP)cccccc
cosec 30° =
1(Deg)J
2*s45*c65w*
1
= 2
sin30° 1(Deg)J
!m(SET UP)cccccc
1
<Line>
1/s30w
<Math>
$1cs30w
sin-10,5 = 30° !m(SET UP)cccccc
(x quando sinx = 0,5) 1(Deg)J
!s(sin–1)0.5*2w
*1* pode ser omitido. *2A introdução de zeros à esquerda não é
necessária.
20050401
Page 87

2-4-5
Cálculos com funções
k Funções logarítmicas e exponenciais
•Assegure-se de que especifica o modo Comp no ecrã de configuração.
Exemplo Operação
log 1,23 (log101,23) = 0,08990511144 l1.23w
log2 8 = 3 <Line>
K4(CALC)6(g)4(logab)2,8)w
<Math>
4(MATH)2(logab) 2e8w
In 90 (loge90) = 4,49980967 I90w
1,23
10
= 16,98243652 !l(10x)1.23w
(Obter o antilogoritmo do logaritmo
natural 1,23)
4,5
e
= 90,0171313 !I(ex)4.5w
(Obter o antilogoritmo do logaritmo
natural 4,5)
(–3)4 = (–3) × (–3) × (–3) × (–3) = 81 (-3)M4w
–34 = –(3 × 3 × 3 × 3) = –81 -3M4w
7
123
1
(= 1237) = 1,988647795
<Line>
7!M(x )123w
<Math>
!M(x )7e123w
<Line>
2 + 3 × 3 – 4 = 10 2+3*3!M(x )64-4w*
64
<Math>
2+3*!M(x )3e64e-4w
1
*1^ (xy) e x têm precedência sobre a
multiplicação e a divisão.
# Não pode utilizar uma expressão de cálculo
diferencial, diferencial quadrático, integração,
Σ, valor máximo/mínimo, resolução, RndFix ou
log ab dentro de um termo de um cálculo log
ab.
#O modo de entrada linear e o modo de entrada
matemática produzem resultados diferentes
quando duas ou mais potências são introduzidas
em série, como: 2M3M2.
Modo de entrada linear: 2^3^2 = 64
Modo de entrada matemática:
Isso ocorre porque, internamente, o modo de
entrada matemática trata a entrada acima
como: 2^(3^(2)).
20050401
= 512
Page 88

2-4-6
Cálculos com funções
k Funções hiperbólicas e hiperbólicas inversas
•Assegure-se de que especifica o modo Comp no ecrã de configuração.
Exemplo Operação
sinh 3,6 = 18,28545536 K6(g)2(HYP)1(sinh)3.6w
cosh 1,5 – sinh 1,5 K6(g)2(HYP)2(cosh)1.5-
= 0,2231301601 1(sinh)1.5w
–1,5
= e
(Visualização: –1,5) I!-(Ans)w
(Prova de cosh x ± sinh x = e±x)
20
cosh–1
= 0,7953654612
15
Determine o valor de x
quando tanh 4 x = 0,88
–1
tanh
0,88 <Line>
=
x
4
= 0,3439419141
<Line>
K6(g)2(HYP)5(cosh–1)(20/15)w
<Math>
K6(g)2(HYP)5(cosh–1)$20c15w
K6(g)2(HYP)6(tanh–1)0.88/4w
<Math>
$K6(g)2(HYP)6(tanh–1)0.88c4w
20050401
Page 89

2-4-7
Cálculos com funções
k Outras funções
•Assegure-se de que especifica o modo Comp no ecrã de configuração
Exemplo Operação
+ =
25
(3 + i)
(–3)2 = (–3) × (–3) = 9 (-3)xw
–32 = –(3 × 3) = –9 -3xw
3,65028154 !x( )2+!x( )5w
= 1,755317302 <Line>
+0,2848487846i !x( )(d+!a(i))w
<Math>
!x( )d+!a(i)w
1
–––––– = 12
11
–– – ––
34
<Line>
(3!)(x
<Math>
–1
)-4!)(x–1))!)(x–1)w
$1c$1c3e-$1c4w
8! (= 1 × 2 × 3 × .... × 8) 8K6(g)3(PROB)1(x!)w
= 40320
3
Qual é o valor absoluto
do logaritmo comum de
3
log | = 0,1249387366
|
4
= 42 <Line>36 × 42 × 49
3
?
4
!((
<Math>
!((
3
)(36*42*49)w
3
)36*42*49w
<Line>
K6(g)4(NUM)1(Abs)l(3/4)w
<Math>
4(MATH)3(Abs)l$3c4w
Qual é a parte inteira de K6(g)4(NUM)2(Int)-3.5w
– 3,5? – 3
Qual é a parte decimal de K6(g)4(NUM)3(Frac)-3.5w
– 3,5? – 0,5
Qual é o inteiro mais perto K6(g)4(NUM)5(Intg)-3.5w
sem exceder – 3,5? – 4
20050401
Page 90

2-4-8
Cálculos com funções
k Geração de número aleatório (Ran#)
Esta função gera um número aleatório sequencial ou um número aleatório verdadeiro de 10
dígitos maior que zero e menor que 1.
•É gerado um número aleatório verdadeiro se não especificar nenhum argumento.
Exemplo Operação
Ran# (Gera um número aleatório.) K6(g)3(PROB)4(Ran#)w
(Cada vez que preme w gera um novo w
número aleatório.) w
•Especificar um argumento de 1 a 9 gera números aleatórios com base nessa sequência.
•Especificar um argumento de 0 inicia a sequência.*
Exemplo Operação
Ran# 1
(Gera o primeiro número aleatório em sequência de 1.)
(Gera o segundo núemro aleatório em sequeência de 1.) w
Ran# 0 (Inicializa a sequência.) 4(Ran#)aw
Ran# 1
(Gera o primeiro número aleatório em sequência de 1.)
1
K6(g)3(PROB)
4(Ran#)bw
4(Ran#)bw
*1Alterar para uma sequência diferente ou
gerar um número totalmente aleatório (sem
um argumento) inicializa a sequência.
20050401
Page 91

2-4-9
Cálculos com funções
k Conversão de coordenadas
uu
u Coordenadas rectagulares
uu
•Com as coordenadas polares, θ pode ser calculado e visualizado dentro do intervalo
–180°< θ < 180° (radianos e grados têm o mesmo intervalo).
•Assegure-se de especificar o modo Comp no ecrã de configuração.
Exemplo Operação
Calcular r e θ° quando x = 14 e y = 20,7 !m(SET UP)cccccc
1 24.989 → 24,98979792 (r)
2 55.928 → 55,92839019 (θ)
Calcular x e y quando r = 25 e θ = 56° 2(Rec()25,56)w
1 13.979 → 13,97982259 (x)
2 20.725 → 20,72593931 (y)
uu
u Coordenadas polares
uu
1(Deg)J
K6(g)5(ANGL)6(g)1(Pol()
14,20.7)wJ
20050401
Page 92

2-4-10
Cálculos com funções
k Permutação e combinação
uu
u Permutação
uu
n! n!
nPr = ––––– nCr = –––––––
(n – r)! r! (n – r)!
•Assegure-se de especificar o modo Comp no ecrã de configuração.
○○○○○
Exemplo Para calcular o número de combinações diferentes utilizando 4 itens
seleccionados de entre 10 itens
Fórmula Operação
10P4 = 5040 10K6(g)3(PROB)2(nPr)4w
○○○○○
Exemplo Para calcular o número possível de combinações de 4 itens que
podem ser seleccionados de entre 10 itens
Fórmula Operação
10C4 = 210 10K6(g)3(PROB)3(nCr)4w
uu
u Combinação
uu
kk
k Fracções
kk
A maneira que deve introduzir fracções depende do modo de entrada que está seleccionado
actualmente.
Fracção imprópria Fracção mista
Modo de entrada
matemática
7
3
($7c3)(1$(()2e1c3)
1
2
3
7 { 32 { 1 { 3
Modo de entrada
linear
Numerador Denominador
(7$3)(2$1$3)
Parte inteira
Numerador
•Para mais detalhes sobre o modo de entrada matemática, consulte “Operações de entrada
no modo de entrada matemática” (página 1-3-8).
•Os resultados dos cálculos fraccionários são sempre reduzidos antes de serem
visualizados.
20050401
Denominador
Page 93

2-4-11
Cálculos com funções
•Assegure-se que especifica o modo Comp no ecrã de configuração.
Exemplo Operação
2173
–– + 3 –– = –––
5420
<Math>
$2c5e+!$(&)3e1c4 w
<Line>
2$5+3$1$4w
11
––––– + –––––
2578 4572
1
–– × 0,5 = 0,25*
2
1,5 + 2,3i = –– + –– i
112
–––––– =
11 7
–– + ––
34
= 6,066202547 × 10–4*
2
323
210
––
Visualização:
3{2
+23{10i
<Math>
1
$1c2578e+$1c4572w
<Line>
1$2578+1$4572w
<Math>
$1c2e*.5w
<Line>
1$2*.5w
1.5+2.3!a(i)w
3
MM*
<Math>
$1c$1c3e+$1c4w
<Line>
1$(1$3+1$4)w
*1Quando o número total de caracteres
incluindo o inteiro, numerador, denominador
e delimitador excedem 10, a fracção é
automaticamente visualizada no formato
decimal.
2
*
Cálculos que contêm fracções e decimais
são realizados no formato decimal.
*3Premir uma vez M quando se converte a parte
decimal de um número complexo numa fracção,
faz com que primeiro se visualize a parte real e
a parte imaginária em linhas separadas.
20050401
Page 94

2-4-12
Cálculos com funções
Mudança entre o formato de fracção imprópria e fracção mista
Premir !M(
fracção imprópria.
) alterna a fracção visualizada entre o formato de fracção mista e
<
Mudança entre o formato de fracção e decimal
⇒
M
⇐
•Se o resultado do cálculo incluir uma fracção, o formato de visualização (fracção imprópria
ou fracção mista) corresponderá à definição “Frac Result” do ecrã de configuração. Para
mais detalhes, consulte “1-7 Utilização do ecrã de configuração”.
•Não é possível mudar do formato decimal para o formato de fracção mista se o número
total de dígitos usado na fracção mista (incluindo a parte inteira, numerador, denominador
e símbolos de separador) for maior que 10.
k Cálculos de notação de engenharia
Introduza os símbolos de engenharia utilizando o menu de notação de engenharia.
•Assegure-se de especificar o modo Comp no ecrã de configuração.
Exemplo Operação
!m(SET UP) f (ou c 12 vezes)
999k (kilo) + 25k (kilo) 999K6(g)6(g)1(EYSM)6(g)1(k)+
= 1,024M (mega) 251(k)w
4(Eng)J
9 ÷ 10 = 0,9 = 900m (milli) 9/10w
= 0,9 K6(g)6(g)1(EYSM)6(g)6(g)3(ENG)*
= 0,0009k (kilo) 3(ENG)*
= 0,9 2(ENG)*
= 900m 2(ENG)*
*1Converte o valor visualizado na unidade de
engenharia mais alta, colocando a vírgula
decimal três casas à direita.
1
2
2
*2Converte o valor visualizado na unidade de
engenharia mais baixa, colocando a vírgula
decimal três casas à esquerda.
20050401
1
Page 95

2-5-1
Cálculos numéricos
2-5 Cálculos numéricos
A seguir descreve-se os itens disponíveis nos menus utilizados nos cálculos de diferenciais/
diferenciais quadráticos, integração, Σ, valor máximo/valor mínimo e resoluções.
Com o menu de opões no ecrã, prima 4(CALC) para visualizar o menu de análise de
funções. Os itens deste menu são utilizados quando se realiza determinados tipos de
cálculos.
• {
Solve}/{d/dx}/{d2/dx2}/{∫dx}/{FMin}/{FMax}/{Σ(} ... cálculos de {resolução}/{diferencial}/
{diferencial quadrático}/{integração}/{valor mínimo}/{valor máximo}/{Σ (sigma)}
k Cálculos de resolução
A seguir apresenta-se a sintaxe da função de resolução utilizada num programa.
Solve( f(x), n, a, b) (a: límite inferior, b: límite superior, n: valor inicial estimado)
Existem dois métodos de introdução que podem ser utilizados em cálculos de resolução:
especificação directa e introdução da tabela de variáveis.
No método de especificação directa (descrito aqui), especifica-se directamente valores às
variáveis. Este método é idêntico ao utilizado com o comando de resolução no modo PRGM.
A introdução da tabela de variáveis é utilizada com a função de resolução no modo EQUA.
Este método é recomendado para a maioria das introduções da função de resolução normal.
Quando não existe convergência da solução, ocorre um erro (Time Out).
Consulte a página 4-3-1 para informação sobre cálculos de resoluções.
# Não pode utilizar uma expressão de cálculo
diferencial, diferencial quadrático, integração,
Σ, valor máximo/mínimo, resolução, RndFix
ou log ab dentro de um termo de um cálculo
de resolução.
A durante o cálculo de resolução
# Premir
(quando o cursor não está no ecrã) interrompe
o cálculo.
20061001
20070101
Page 96

2-5-2
Cálculos numéricos
k Cálculos diferenciais [OPTN]-[CALC]-[d
Para realizar cálculos diferenciais, primeiro visualize o menu de análise de funções e, em
seguida, introduza os valores utilizando a seguinte sintaxe.
K4(CALC)2(
d/dx ( f (x), a) ⇒ ––– f (a)
A diferenciação para este tipo de cálculo é a seguinte:
f '(a) = lim –––––––––––––
Nesta definição,
f (a + Ax) – f (a)
Ax→0
infinitesimal
valor na proximidade de f ' (a) calculado como:
f (a + Ax) – f (a)
f '(a) –––––––––––––
De forma a obter a melhor precisão, esta calculadora emprega a diferença central para
executar os cálculos diferenciais.
Utilização de cálculos diferenciais numa função gráfica
• Omitir o valor de tolerância (tol ) quando se utiliza o comando diferencial numa função
gráfica simplifica o cálculo no desenho do gráfico. Em tal caso, é sacrificada a precisão
a favor de um desenho mais rápido. O valor de tolerância é especificado, o gráfico é
desenhado com a mesma precisão quando se realiza um cálculo diferencial.
• Pode também omitir a introdução do ponto derivado, utilizando o seguinte formato para
o gráfico diferencial: Y2=d/dx(Y1). Neste caso, o valor da variável X é utilizado como o
ponto derivado.
d/dx) f(x),a,tol)
d
dx
Ax
é substituido por uma Ax,
Ax
(a: ponto para o qual pode derterminar a
derivada, tol: tolerância)
pequena suficientemente
, com o
/dx]
20050401
Page 97

2-5-3
Cálculos numéricos
Exemplo Para determinar a derivada no ponto x = 3 para a função
3
y = x
+ 4x2 + x – 6, com uma tolerância de “tol” = 1E – 5
Introduza a função f(x).
AK4(CALC)2(d/dx)vMd+evx+v-g,
Introduza o ponto x = a para o qual deseja determinar a derivada.
d,
Introduza o valor da tolerância.
bE-f)
w
<Math>
A4(MATH)4(d/dx)vMde
+evx+v-ged
w
# Na função f(x), apenas X pode ser utilizado
como variável em expressões. Outras
variáveis (A a Z excluindo X, r, θ) são tratadas
como constantes e o valor especificado a
essa variável é aplicada durante o cálculo.
# A introdução do valor da tolerância (tol) e o
parêntese de fecho pode ser omitido. Se omitir
o valor da tolerância, a calculadora utiliza
automaticamente como valor para tol, 1E-10.
# Especifique um valor de tolerância (tol) de
1E-14 ou maior. Ocorre um error (Time Out)
quando nenhuma solução satisfaz o valor de
tolerância obtido.
# No modo de entrada matemática, o valor de
tolerância é fixado em 1E-10 e não pode ser
alterado.
# Resultados imprecisos e erros podem ocorrer
devido às seguintes condições:
- pontos descontínuos nos valores
- mudanças extremas nos valores x
- inclusão do ponto máximo local e ponto mínimo
local nos valores x
- inclusão do ponto de inflexão nos valores x
- inclusão de pontos não diferenciáveis nos
valores x
- resultados de cálculos diferenciais que se
aproximam a zero
20061001
20070101
x
Page 98

2-5-4
Cálculos numéricos
u Aplicações de cálculos diferenciais
•Os diferenciais podem ser adicionados, subtraídos, multiplicados ou divididos entre si.
dd
––– f (a) = f '(a), ––– g (a) = g'(a)
dx dx
Assim:
f '(a) + g'(a), f '(a) × g'(a), etc.
•Os resultados dos diferenciais pode ser utilizados na soma, subtracção, multiplicação e
divisão e em funções.
2 × f '(a), log ( f '(a)), etc.
•As funções podem ser utilizadas em qualquer um dos termos ( f (x), a, tol) de um
diferencial.
d
––– (sinx + cosx, sin0,5, 1E - 8), etc.
dx
# Não pode utilizar uma expressão de cálculo
diferencial, diferencial quadrático, integração,
Σ, valor máximo/mínimo, resolução, RndFix ou
log ab dentro de um termo de um cálculo
diferencial.
#Premir A durante o cálculo de um diferencial
(quando o cursor não está no ecrã) interrompe
o cálculo.
#Utilize sempre radianos (modo Rad) como a
unidade angular quando realizar diferenciais
trigonométricos.
20050401
Page 99

d
2
d
2
––– (
f(x), a
)
⇒
–––
f(a
)
dx
2
dx
2
d
2
d
2
––– (
f(x), a
)
⇒
–––
f(a
)
dx
2
dx
2
f
''(a) =
180h
2
2 f(a + 3h) – 27 f(a + 2h) + 270 f(a + h) – 490 f(a) + 270 f(a – h) – 27 f(a –2h) + 2 f(a – 3h)
f
''(a) =
180h
2
2 f(a + 3h) – 27 f(a + 2h) + 270 f(a + h) – 490 f(a) + 270 f(a – h) – 27 f(a –2h) + 2 f(a – 3h)
2-5-5
Cálculos numéricos
k Cálculos diferenciais quadráticos [OPTN]-[CALC]-[d2/dx
Após visualizar o menu de análise de funções, pode introduzir diferenciais quadráticos
utilizando a seguinte sintaxe.
K4(CALC)3(d2/dx2) f(x),a,tol)
(a: ponto do coeficiente do diferencial, tol: tolerância)
Os cálculos de diferenciais quadráticos produzem um valor diferecnial aproximado utilizando
a seguinte fórmula de segunda ordem, que se baseia na interpretação do polinómio de
Newton.
Nesta expressão, os valores para os “incrementos suficientemente pequenos de h” são
utilizados para obter um valor que se aproxima de f ”(a).
Exemplo Para determinar o coeficiente do diferencial quadrático no ponto onde
x = 3 para a função y = x
Utiliza-se aqui uma tolerância tol = 1E – 5
Introduza a função f(x).
AK4(CALC)3(d2/dx2) vMd+
evx+v-g,
3
+ 4x2 + x – 6
2
]
Introduza 3 como ponto a, que é o ponto do coeficiente do diferencial.
d,
Introduza o valor de tolerância.
bE-f)
w
# Na função f(x), apenas X pode ser utilizado
como variável em expressões. Outras
variáveis (A a Z excluindo X, r, θ) são tratadas
como constantes e o valor especificado para
essa variável é aplicada durante o cálculo.
# A introdução do valor de tolerância (
parêntese de fecho podem ser omitidos.
# Especifique um valor de tolerância (tol) de 1E-14
ou maior. Ocorre um error (Time Out) quando
nenhuma solução satisfaz o valor de tolerância
obtido.
20061001
20070101
tol) e o
Page 100

d
2
d
2
–––
f
(
a
) =
f ''(a
),
–––
g
(
a
) =
g''(a
)
dx
2
dx
2
d
2
d
2
–––
f
(
a
) =
f ''(a
),
–––
g
(
a
) =
g''(a
)
dx
2
dx
2
d
2
–––
(sin
x
+
cos
x
,
sin
0,5, 1
E
- 8), etc.
dx
2
d
2
–––
(sin
x
+
cos
x
,
sin
0,5, 1
E
- 8), etc.
dx
2
2-5-6
Cálculos numéricos
<Math>
A4(MATH)5(d2/dx2)vMde
+evx+v-gedw
u Aplicações de diferenciais quadráticos
• As operações aritméticas podem ser realizadas utilizando dois diferenciais quadráticos.
Assim:
f ''(a) +
g
(a), f ''(a) ×
''
g
(a), etc.
''
• O resultado de um cálculo diferencial quadrático pode ser utilizado num cálculo
aritmético ou de função subseguinte.
2 ×
''(a), log ( f ''(a) ), etc.
f
• As funções podem ser utilizadas nos termos (
f(x), a, tol ) de uma expressão de
diferencial quadrático.
# No modo de entrada matemática, o valor de
tolerância é fixado em 1
alterado.
# As regras que são aplicadas para o diferencial
linear também são aplicadas quando se
utiliza um cálculo diferencial quadrático para a
fórmula gráfica (consulte a página 2-5-2).
# Resultados imprecisos e erros podem ocorrer
devido às seguintes condições:
- pontos descontínuos nos valores
- mudanças extremas nos valores x
- inclusão do ponto máximo local e ponto
mínimo local nos valores
- inclusão do ponto de inflexão nos valores x
- inclusão de pontos não diferenciáveis nos
x
valores
- resultados de cálculos diferenciais que se
aproximam a zero
E-10 e não pode ser
x
x
# Pode interromper um cálculo diferencial
quadrático premindo a tecla
# Utilize radianos (modo Rad) como a unidade
angular sempre que realizar diferenciais
quadráticos trigonométricos.
# Não pode utilizar uma expressão de cálculo
diferencial, diferencial quadrático, integração,
valor máximo/mínimo, resolução, RndFix ou log
ab dentro de um termo de um cálculo diferencial
quadrático.
# Com cálculos diferenciais quadráticos, a
precisão do cálculo será de até cinco dígitos
para a mantissa.
A.
Σ,
20070101
20061001
 Loading...
Loading...