3B Scientific Resistance Bridge User Manual
3B SCIENTIFIC
Resistance Bridge 1009885
Instruction sheet
01/13 ALF
1 Plastic base
2 Connection sockets
3 Rail with scale
1. Safety instructions
®
PHYSICS
4 Resistance wire
5 Slide contact with pointer
3. Technical data
• Do not exceed a maximum permissible volt-
age of 8 V.
• Do not exceed a maximum permissible cur-
rent of 1.5 A.
2. Description
The resistance bridge is used in determining the
resistance in bridge circuits as well as in investigating the voltage drop along a wire.
The device consists of a rail with scale mounted
on two bases with a resistance wire. A slide
contact, is attached on top of the resistance
wire. This defines the resistances R
(see Fig. 1).
and R
1
2
Di me nsions: approx. 1300x100x90 mm³
Rail: approx. 30x30 mm²
Scale: 0 – 1000 mm
Scale divisions: mm
Resistance wire: 1 m, 0.5 mm diam.
Material: NiCr
Resistance: 5.3 Ω
Connection: 4 mm safety jacks
Maximum voltage: 8 V
Maximum current: 1.5 A
In order to determine a resistance a Wheatstone
bridge circuit is set up (see Fig. 1).
To do this a resistance wire of length l = l
and with specific resistivity ρ (Ωm) is connected
into a circuit consisting of the resistor R
measured and a known resistor R
4. Operating principle
. A DC volt-
0
+ l
1
to be
X
2
1
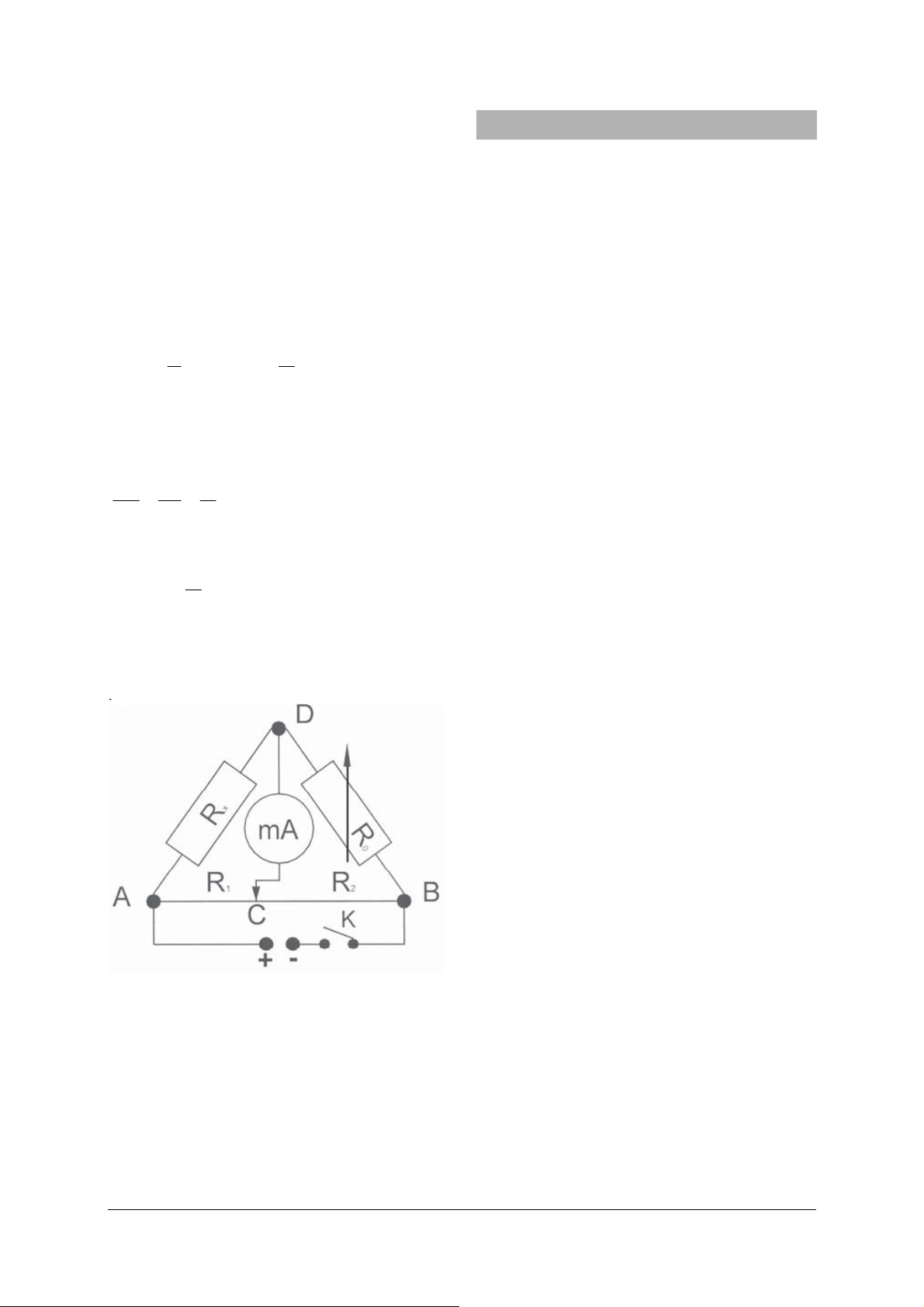
age U is applied to this circuit. The ammeter is
F
F
used to measure the current flowing between
the point D and the moveable tapping point C
located on the resistance wire.
The partial resistances of the wire R
and R
1
can
2
be varied using the slide contact on the resistance wire.
Now it is important to calibrate the measurement
bridge, i.e. to adjust the slide contact so that
there is no voltage between points C and D and
thus a current no longer flows. The partial resistances are:
l
R
1
1
⋅ρ= and
R
l
2
⋅ρ=
2
whereby F is the cross-sectional area of the
wire.
For the resistance ratios the following then holds
true:
X
R
0
1
1
==
l
R
2
2
l
R
R
From this we can deductively compute the unknown resistance:
X
The resistor R
calibration of the bridge l
l
2
should be selected so that upon
0
and l
1
are approxi-
2
l
1
⋅=
RR
0
mately equal, in order to keep the error to a
minimum.
Fig. 1
5. Sample experiments
5.1 Determining resistance in a Wheatstone
bridge circuit
Additionally required:
1 AC/DC Power Supply 12 V, 3 A (230 V, 50/60 Hz)
1002776
or
1 AC/DC Power Supply 12 V, 3 A (115 V, 50/60 Hz)
1002775
1 Zero Galvanometer CA 403 1002726
1 Resistance Decade 1 Ω 1002730
or
1 Resistance Decade 10 Ω 1002731
or
1 Resistance Decade 100 Ω 1002732
1 Incandescent lamp with socket
8 Experiment cables (500 mm)
1 Switch (optional)
• Connect up the experiment setup as illus-
trated (see Fig. 1).
• An incandescent lamp is used as the un-
known resistance.
• A voltage of 4 to 6 V is applied.
• Close switch K and slowly move the slide
contact from A to B to A again.
• At the same time observe the deflection of
the ammeter. When the pointer deflection in
the proximity of point A is zero, this means
that the value of R
is very high and that it
0
must be reduced. If the zero value is in the
proximity of point B, then the value of R
0
is
too low and must be increased.
• Select the R
value so that when the power
0
is switched on again the pointer of the ammeter does not deflect when the slide contact is in the middle of the wire, i.e. the
measurement bridge is calibrated.
• If there is no appropriate resistance avail-
able, use a resistor R
, for which the
0
pointer's deflection is smallest and then
carry out the calibration.
• Obtain readings of partial lengths of the
resistance wire.
• Repeat the experiment with varied voltage
levels, enter your findings in a table and
compute the resistance R
.
X
5.2 Determine the specific resistivity ρ of a
wire
• Experiment set-up according to Fig. 1, but
this time use a resistance wire with a length
from 1 to 3 m instead of the incandescent
lamp.
2
Loading...