3B Scientific Resistance Apparatus User Manual

3B SCIENTIFIC

Resistance Apparatus 1009949

Instruction sheet

09/12 ADP BJK

1 4-mm connectors
2 Base plate
3 Resistance wires

®

PHYSICS

1. Safety instructions

If the current is too high, it can lead to the resis­tance wires becoming destroyed.

• Do not exceed the stated values for current.
The resistance wires are thin and can stretch or

snap.

• Always carry the device by the base plate,

never try to lift the wires.

2. Description

The resistance measurement bridge is a useful
tool for exploring the factors that contribute to a
wire’s overall resistance. It is used to investigate
the dependency of electrical resistance on con­ductor length, conductor cross-section and ma­terial.

The resistance measurement bridge is made up
of six wires laid out side by side on a base plate
with both ends connected to 4-mm sockets.

3. Technical data

Material Diameter Current

Constantan 1 mm 2 A max.

Constantan
2x

Constantan 0.5 mm 1.5 A max.

Constantan 0.35 mm 1 A max.

Brass 0.5 mm 2.5 A max.

Dimensions: 1085 x 70 x 55 mm
Length of wires: 1000 mm
Weight: approx. 1.5 kg

It is recommended to use the analogue multime­ter AM51 (1003074) to determine the resistance
of the wires.

To avoid measuring errors, it is necessary to
take account of the resistance of cables.

• The multimeter leads should be shorted

together so that only their resistance is
measured and the meter should then be
calibrated to register that resistance as zero.

0.7 mm 2 A max.

3

4. Sample experiments

1

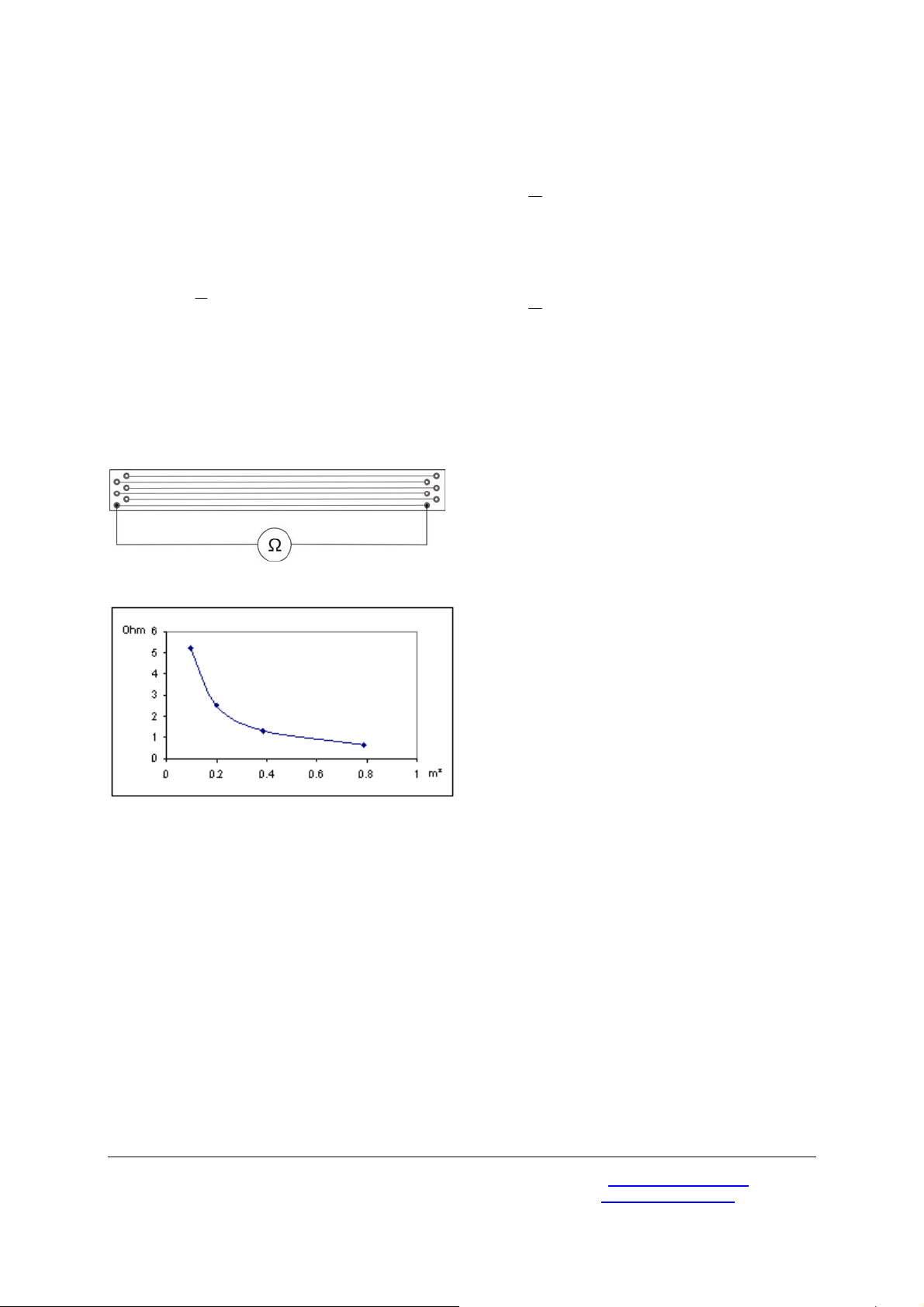
4.1 Resistance as a function of cross­sectional area

• Connect the LCR meter to the sockets of the

Constantan wire with the smallest diameter
(refer to fig. 1).

• Measure its resistance R and fill it in a table.

• Calculate the cross sectional area A of the

wire by using the equation

A

⎟

⎜

2

⎠

⎝

d

⎞

⎛

⋅π=

• Be sure to convert the diameter d into me-

ters before substituting.

• Repeat the procedure with the other Con-

stantan wires.

• Plot the graph of the resitance vs. cross

sectional area (refer to fig. 2).

Fig. 1 Experimental set-up

4.2 Calculating the resistivity ρ of a wire

The equation for resistance R of a wire is given

by

L

R ⋅ρ=

A

with L = length of the wire, A = cross sectional
area of the wire and ρ = resistivity of the material

Solving our equation of resistance for ρ, we get:

A

R⋅=ρ

L

• Set up the experiment according to fig. 1.

• Connect the LCR to any of the constantan

wires and determine its resistance.

• Calculate the resistivity of Constantan.

• Repeat the experiment with the brass wire

and compare the resistivity of Constantan
and Brass.

Fig. 2 Resistance as a function of the cross sectional
area

Elwe Didactic GmbH ▪ Steinfelsstr. 5 ▪ 08248 Klingenthal ▪ Germany ▪ www.elwedidactic.com

3B Scientific GmbH ▪ Rudorffweg 8 ▪ 21031 Hamburg ▪ Germany ▪ www.3bscientific.com

Subject to technical amendments

© Copyright 2012 3B Scientific GmbH