3B Scientific Laser Optics Supplemental Set User Manual [en, de, es, fr, it]

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

®

Demonstrations-Laseroptik-Satz U17300 und Ergänzungssatz U17301

Bedienungsanleitung

1/05 ALF

Inhaltsverzeichnung

Seite Exp - Nr. Experiment Gerätesatz

1 Einleitung
2 Leiferumfang
3 E1 Reflexion an Planspiegel U17300/U17301
3 E2 Reflexion an zwei Planspiegeln U17301
3 E3a Reflexion an Konkavspiegel – Lichtstrahlen parallel zur optischen Achse U17300
4 E3b Reflexion an Konkavspiegel – Lichtstrahlen nicht parallel

zur optischen Achse U17300
4 E4a Reflexion an Konvexspiegel – Lichtstrahlen parallel zur optischen Achse U17300
4 E4b Reflexion an Konvexspiegel – Lichtstrahlen nicht parallel zur

optischen Achse U17300
5 E5a Brechung eines Lichtstrahls beim Übergang von Luft in Acryl U17300
5 E5b Scheinbare Tiefe eines Objekts U17301
5 E6a Brechung eines Lichtstrahls beim Übergang von Acryl in Luft U17300
6 E6b Brechung an einem Acrylprisma U17300/U17301
6 E6c Kritischer Winkel, Totalreflexion U17300
6 E6d Totalreflexion – Ausbreitung von Licht in Lichtleitern U17300
7 E7 Verschiebung eines Lichtstrahls, planparallele Acrylplatte U17300/U17301
7 E8 Verschiebung eines Lichtstrahls, Luft zwischen zwei

planparallelen Acrylplatten U17301
7 E9a Ablenkung eines Lichtstrahls durch ein Acrylprisma U17300/U17301
8 E9b Minimale Ablenkung durch ein Acrylprisma U17300/U17301
8 E10a Ablenkung eines Lichtstrahls durch ein Luftprisma U17301
8 E10b Minimale Ablenkung durch ein Luftprisma U17301
9 E11a Reflexion an einer Kante eines Acrylprismas U17301
9 E11b Reflexion an zwei Kanten eines Acrylprismas U17301
9 E11c Reflexion an zwei Acrylprismen U17301
10 E11d Reflexion an zwei Acrylprismen U17301
10 E11e Reflexion an zwei Acrylprismen U17301
10 E12 Reflexion an einem Luftprisma U17301
11 E13a Durchgang eines Lichtstrahls durch eine konvexe Grenzfläche Luft-Acryl U17301
11 E13b Durchgang von Lichtstrahlen durch eine konvexe Grenzfläche Luft-Acryl U17301
11 E14a Durchgang eines Lichtstrahls durch eine konkave Grenzfläche Luft-Acryl U17301
12 E14b Durchgang von Lichtstrahlen durch eine konkave Grenzfläche Luft-Acryl U17301
12 E15a Durchgang eines Lichtstrahls durch eine konvexe Grenzfläche Acryl-Luft U17301
12 E15b Durchgang von Lichtstrahlen durch eine Grenzfläche Acryl-Luft U17301
13 E16a Durchgang eines Lichtstrahls durch eine konkave Grenzfläche Acryl-Luft U17301
13 E16b Durchgang von Lichtstrahlen durch eine konkave Acryl-Luft U17301
13 E17a Durchgang von Lichtstrahlen durch eine konvexe Acryllinse –

Lichtstrahlen parallel zur optischen Achse U17300/U17301
14 E17b Durchgang von Lichtstrahlen durch eine konvexe Acryllinse –

Lichtstrahlen nicht parallel zur optischen Achse U17300/U17301
14 E17c Durchgang von Lichtstrahlen durch eine dicke konvexe Acryllinse U17301
14 E18a Durchgang von Lichtstrahlen durch eine konkave Acryllinse –

Lichtstrahlen parallel zur optischen Achse U17300/U17301

1

15 E18b Durchgang von Lichtstrahlen durch eine konkave Acryllinse –

Lichtstrahlen nicht parallel zur optischen Achse U17300/U17301

15 E19a Durchgang von Lichtstrahlen durch eine konvexe Luftlinse –

Lichtstrahlen parallel zur optischen Achse U17301

15 E19b Durchgang von Lichtstrahlen durch eine konvexe Luftlinse –

Lichtstrahlen nicht parallel zur optischen Achse U17301

16 E20a Durchgang von Lichtstrahlen durch eine konkave Luftlinse –

Lichtstrahlen parallel zur optischen Achse U17301

16 E20b Durchgang von Lichtstrahlen durch eine konkave Luftlinse –

Lichtstrahlen nicht parallel zur optischen Achse U17301
16 E21a Parameter von dicken Linsen – Bestimmung des Krümmungsradius U17300/U17301
17 E21b Parameter von dicken Linsen – Brennweite U17300/U17301
17 E22a Augenmodell U17300
17 E22b Augenmodell, Kurzsichtigkeit U17300
18 E22c Augenmodell, Weitsichtigkeit U17300
18 E23a Korrektur der sphärischen Aberration durch Verringerung des

Durchmessers des Strahlenbündels U17300/U17301
18 E23b Korrektur der sphärischen Aberration durch eine Kombination von Linsen U17300
19 E24a Teleskop nach Kepler U17300
19 E24b Teleskop nach Galilei U17300
19 E25 Kamera U17300

Demonstrations-Laseroptik-Satz U17300
Ergänzungssatz U17301

Die Spalte "Gerätesatz" listet den für das jeweilige Experiment benötigten Gerätesatz auf, U17300, U17301 oder beide.

Einleitung

Der Demonstrations-Laseroptik-Satz ermöglicht einfa­che und klare Versuchsaufbauten zur Darstellung der
Grundlagen der geometrischen Optik sowie der
Funktionsweise verschiedener optischer Geräte. Als
Lichtquelle dient der Diodenlaser, 5 Strahlen U17302.
In dieser Bedienungsanleitung sind zahlreiche grund­legende Versuche mit den optischen Elementen der
beiden Gerätesätze U17300 und U17301 beschrieben.
Jede Versuchsbeschreibung besteht aus drei Teilen:

1. Eine einfache Beschreibung des Versuchs

2. Eine grafische Darstellung des Versuchs

3. Eine Abbildung des Versuchsaufbaus
Unter dem jeweiligen Titel steht in Klammern mit wel­chem Gerätesatz der Versuch durchgeführt werden
kann, U17300, U17301 oder U17300/U17301. Die glei­che Angabe befindet sich auch in der letzten Spalte
der Inhaltsübersicht.
Ein sehr wichtiger Bestandteil der Versuchsaufbauten
ist der Diodenlaser U17302. Fünf Laserdioden erzeu­gen fünf parallele Lichtstrahlen. Die Anzahl der aus­tretenden Lichtstrahlen lässt sich auswählen. Dazu wird
eine im Lieferumfang des Lasers enthaltene Metall­platte mit Bohrungen vor den Diodenlaser gesetzt.
Beim Einsatz des Laser ist ein direkter Augenkontakt
mit dem Laserstrahl zu vermeiden.

Lieferumfang

Demonstrations-Laseroptik-Satz U17300

1 Bikonkav Linse
2 Bikonvex Linse

3 Bikonvex Linse
4 Bikonvex Linse
5 Bikonvex Linse
6 Kleine plankonkave Linse
7 Kleine plankonvexe Linse
8 Große plankonvexe Linse
9 Spiegel, konkav
10 Spiegel, konvex
11 Planspiegel
12 Planparallele Platte
13 Prisma
14 Lichtleiter

Folien

A Augenmodell
B Kamera
C Teleskop nach Galilei
D Teleskop nach Kepler
E Sphärische Aberration
F Winkelskala 360°

Ergänzungssatz U17301

21 Bikonkav Luftlinse
22 Bikonkav Linse
23 Bikonvex Luftlinse
24 Bikonvex Linse
25 Luftprisma
26 Gleichseitiges Prisma
27 2 Rechtwinklige Prismen
28 Planparallele Platte, quadratisch
29 2 Planparallele Platten, rechteckig
11 2 Planspiegel

2

E1 Reflexion an Planspiegel

(U17300/U17301)

Darstellung des Reflexionsgesetzes. Ein Lichtstrahl, der
unter dem Einfallswinkel α auf eine plane Spiegelfläche
trifft, wird unter dem Winkel ß reflektiert

α = ß

Beide Winkel werden zum Einfallslot hin gemessen.

E3a Reflexion an Konkavspiegel – Lichtstrahlen

parallel zur optischen Achse

(U17300)
Die Brennweite f eines Hohlspiegels wird durch die
Länge der Strecke VF bestimmt. Der Krümmungsradius
lässt sich mit der Formel

fr=

2

berechnen. Die Strecke VS ist doppelt so lang wie VF.

E2 Reflexion an zwei Planspiegeln

(U17301)

Demonstration der Beziehung:

δ = 2 γ
wobei der Winkel δ vom einfallenden und dem reflek­tierten Lichtstrahl gebildet wird und γ der Winkel zwi­schen den Spiegelflächen ist.

E3b Reflexion an Konkavspiegel – Lichtstrahlen

nicht parallel zur optischen Achse

(U17300)

Die Achse ϕ steht senkrecht auf der optischen Achse
und verläuft durch den Brennpunkt. Sie wird als Brenn­ebene bezeichnet. Die einfallenden parallelen Strah­len werden reflektiert und treffen sich in einem Punkt
auf der Brennebene ϕ. Sind die Strahlen parallel zur
optischen Achse, so liegt der Punkt darauf und heißt
Brennpunkt F.

3

E4a Reflexion an Konvexspiegel – Lichtstrahlen

parallel zur optischen Achse

(U17300)
Die reflektierten Strahlen scheinen von einem Punkt
hinter dem Spiegel auszugehen. Er heißt virtueller
Brennpunkt. Die Strecke VF bestimmt die Brennweite
des Spiegels. Der Krümmungsradius lässt sich mit der
Formel

fr=

2

berechnen. Die Strecke VS ist doppelt so lang wie VF.

E5a Brechung eines Lichtstrahls beim Übergang

von Luft in Acryl

(U17300, Folie F)

Beim Übergang eines Lichtstrahls von einem Medium
mit dem Brechungsindex n1 in ein anderes Medium
mit dem Brechungsindex n2 wird seine Richtungs­änderung durch das Snelliussche Brechungsgesetz be­stimmt:
n

sin α = n

1

sin ß

2

α ist der Einfallswinkel in Medium n1 und ß ist der
Brechungswinkel im Medium n2.

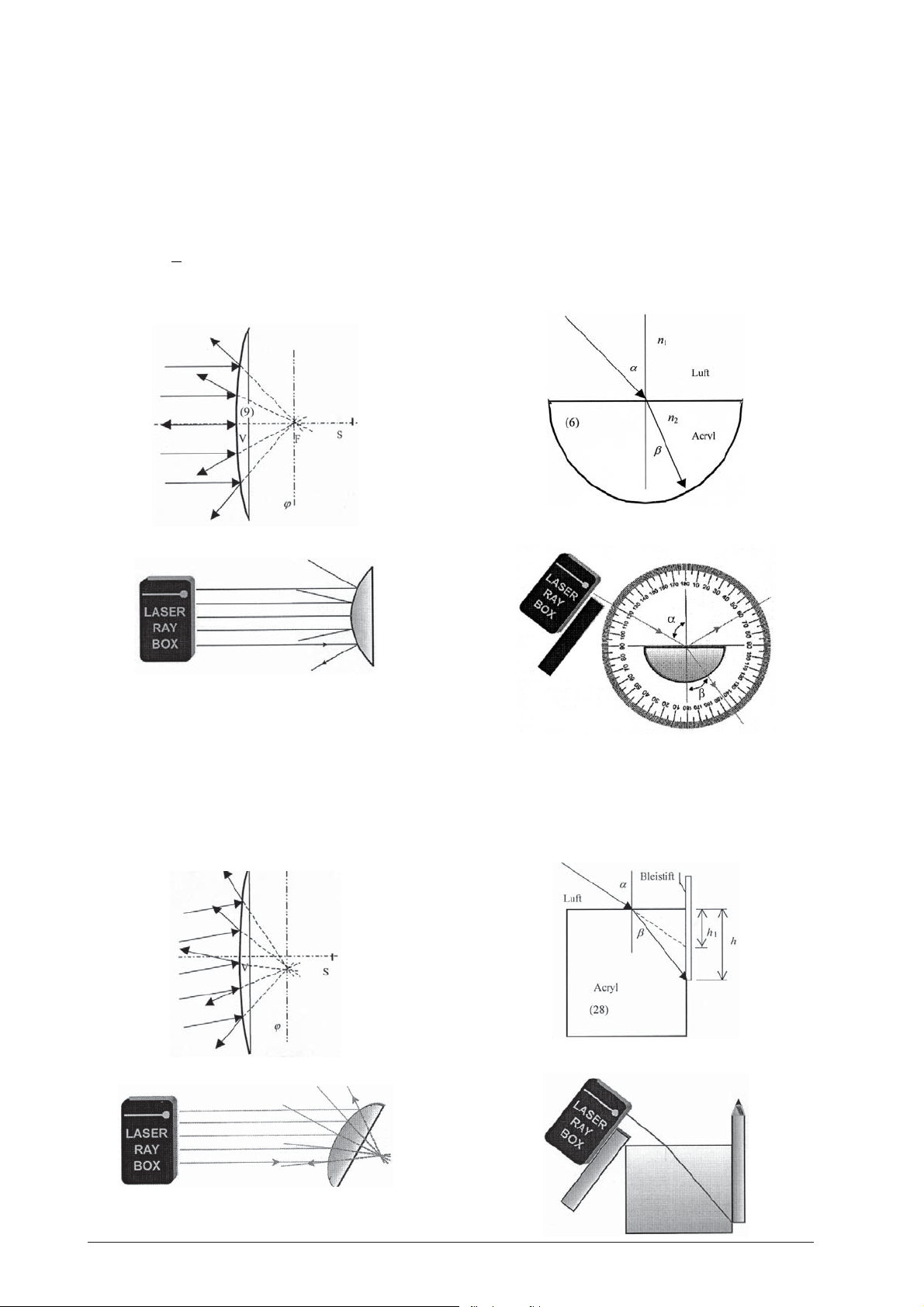
E4b Reflexion an Konvexspiegel – Lichtstrahlen

nicht parallel zur optischen Achse

(U17300)
Die Achse ϕ steht senkrecht auf der optischen Achse
und verläuft durch den Brennpunkt. Sie wird als Brenn­ebene bezeichnet. Fallen parallele Strahlen auf den
Spiegel, so werden sie so gestreut, dass sie von einem
Punkt auf der Brennebene ϕ hinter dem Spiegel aus­zugehen scheinen.

E5b Scheinbare Tiefe eines Objekts

(U17301)
Versuchsaufbau zur Beobachtung der scheinbaren Tie­fe eines Objekts in Wasser oder hinter Acryl von Luft
aus gesehen.

4

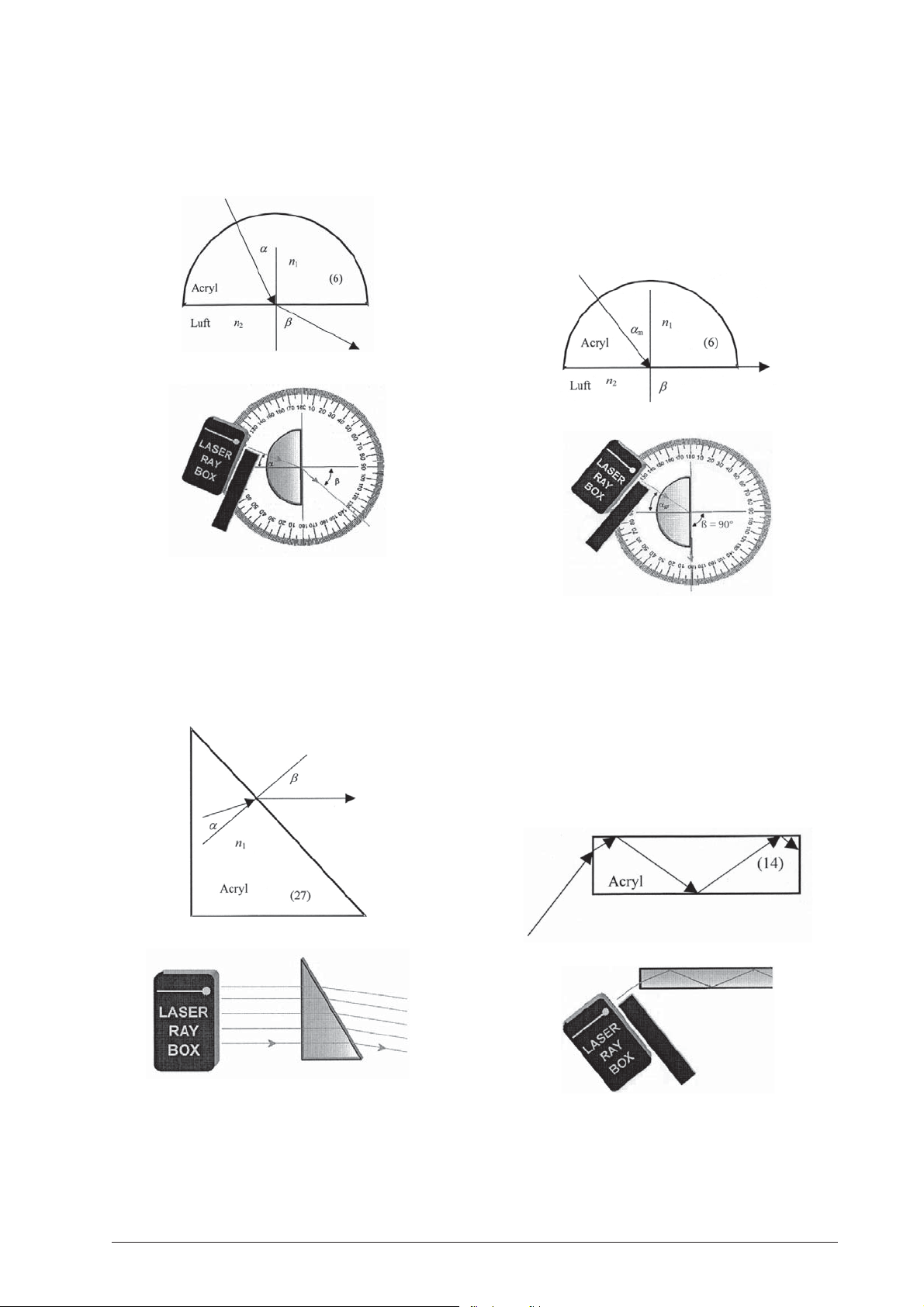
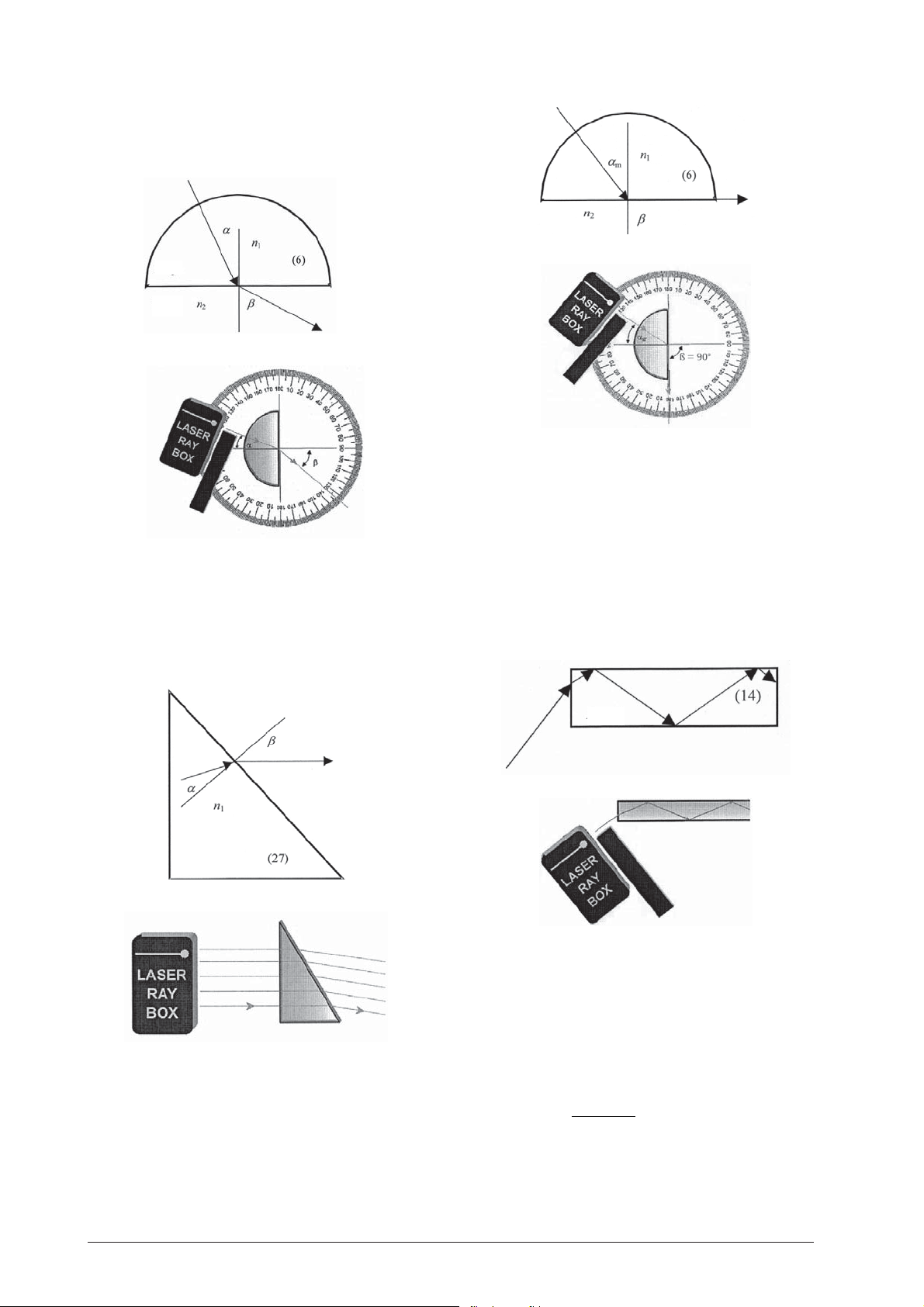
E6a Brechung eines Lichtstrahls beim Übergang

von Acryl in Luft

(U17300, Folie F)

Der Brechungswinkel ß ist größer als der Einfallswin-

kel α. Der Strahl wird vom Einfallslot weg gebrochen.

E6c Kritischer Winkel, Totalreflexion

(U17300, Folie F)
Je größer der Einfallswinkel desto größer der
Brechungswinkel. Wenn n1 < n2, existiert ein kritischer
Winkel α. Der gebrochene Strahl liegt dann an der
Grenzfläche zwischen zwei Medien. Ist der Einfallswin­kel größer als der kritische Winkel, dann gibt es keine
Brechung mehr und das ganze Licht wird reflektiert.
In diesem Fall spricht man von Totalreflexion.

E6b Brechung an einem Acrylprisma

(U17300/U17301)
Beim Übergang eines Lichtstrahls von Acryl in Luft kann
das Snelliussche Gesetz in folgender Form geschrieben
werden:

n

sin α = sin ß

1

Brechungsindex von Luft n2 = 1.

E6d Totalreflexion – Ausbreitung von Licht in

Lichtleitern

(U17300)
Licht breitet sich mit Hilfe der Totalreflexion in einem
Lichtleiter aus. Der Parameter, numerische Apertur,
bestimmt, welcher Winkel dabei nicht überschritten
werden darf. Er entspricht dem Sin des maximalen Ein­trittswinkel des Lichts. Auch wird der kleinste Radius,
wenn der Lichtleiter gebogen wird, durch diesen Para­meter bestimmt. Er darf nicht unterschritten werden,
wenn der Lichtleiter installiert wird.

5

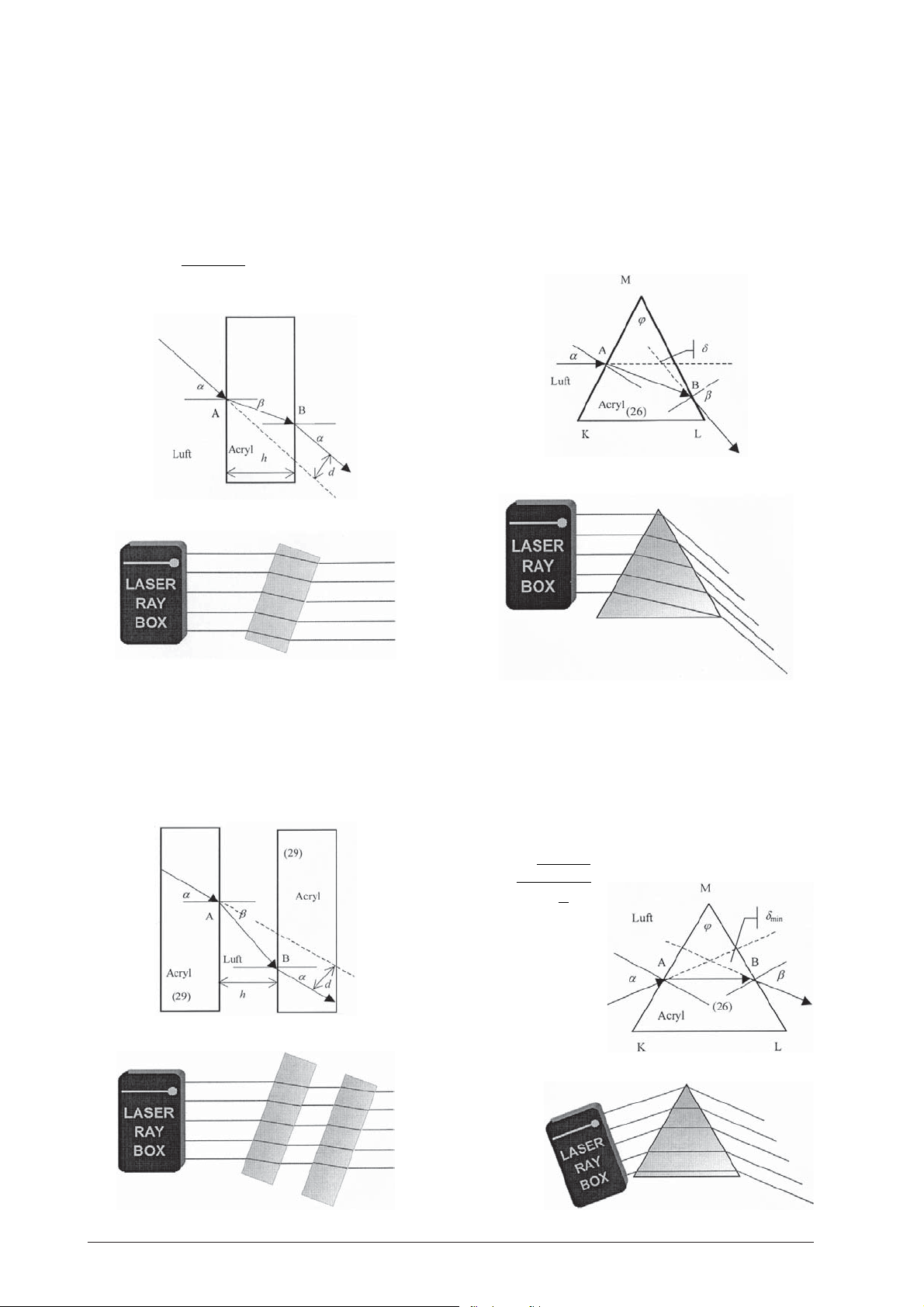
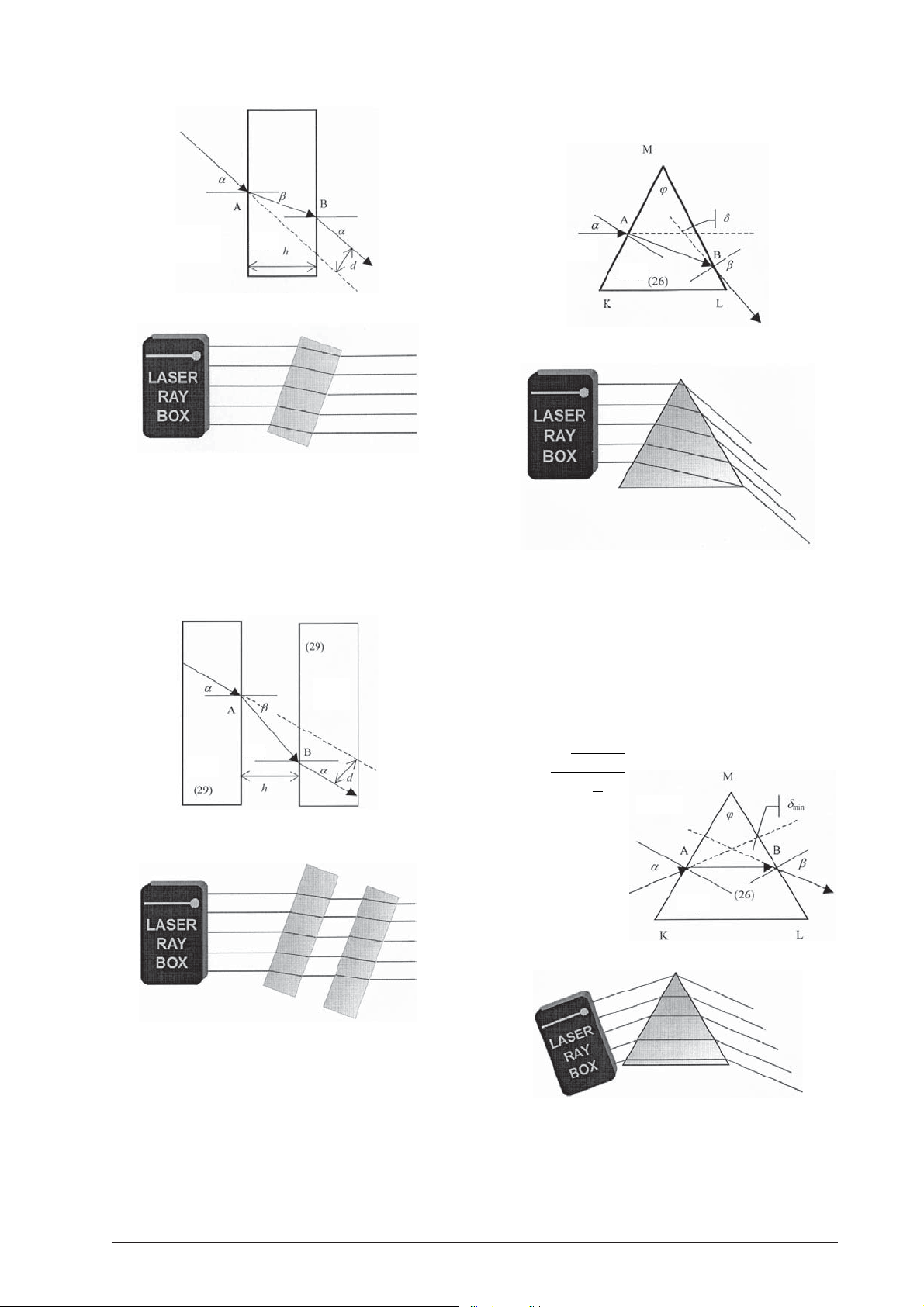
E7 Verschiebung eines Lichtstrahls, planparallele

Acrylplatte

(U17300/U17301)
Wenn ein Lichtstrahl durch eine planparallele Platte
geht, wird seine Richtung nicht verändert. Der austre­tende Strahl ist um den Betrag d verschoben. Bei einer
Plattendicke h ergibt sich für d:

sin

αβ

−

dh=

()

cos

β

E9a Ablenkung eines Lichtstrahls durch ein

Acrylprisma

(U17300/U17301)
In einem Acrylprisma wird ein einfallender Lichtstrahl
im Punkt A hin zum Einfallslot gebrochen. Am Aus­trittspunkt B findet die Brechung weg vom Einfallslot
statt. Die Summe aller Brechungswinkel ist der Ab­lenkungswinkel δ. Es ist der Winkel zwischen dem ein­fallenden und austretenden Lichtstrahl.

E8 Verschiebung eines Lichtstrahls, Luft zwischen

zwei planparallelen Acrylplatten

(U17301)
In diesem Fall findet eine Verschiebung zwischen dem
einfallenden und dem austretenden Strahl statt. Die
Verschiebung geht jedoch in die umgekehrte Richtung
als bei der Acrylplatte.

E9b Minimale Ablenkung durch ein Acrylprisma

(U17300/U17301)

Es kann gezeigt werden, dass der Einfallswinkel α bei
minimalstem Ablenkungswinkel δ

gleich dem Aus-

min

trittswinkel ß ist. Der gebrochene Strahl verläuft dann
im Prisma parallel zu der Seite, die nicht durchgangen
wird. Für den Brechungsindex des Prismas gilt:

+

δϕ

min

sin

sin

2

ϕ

2

n =

6

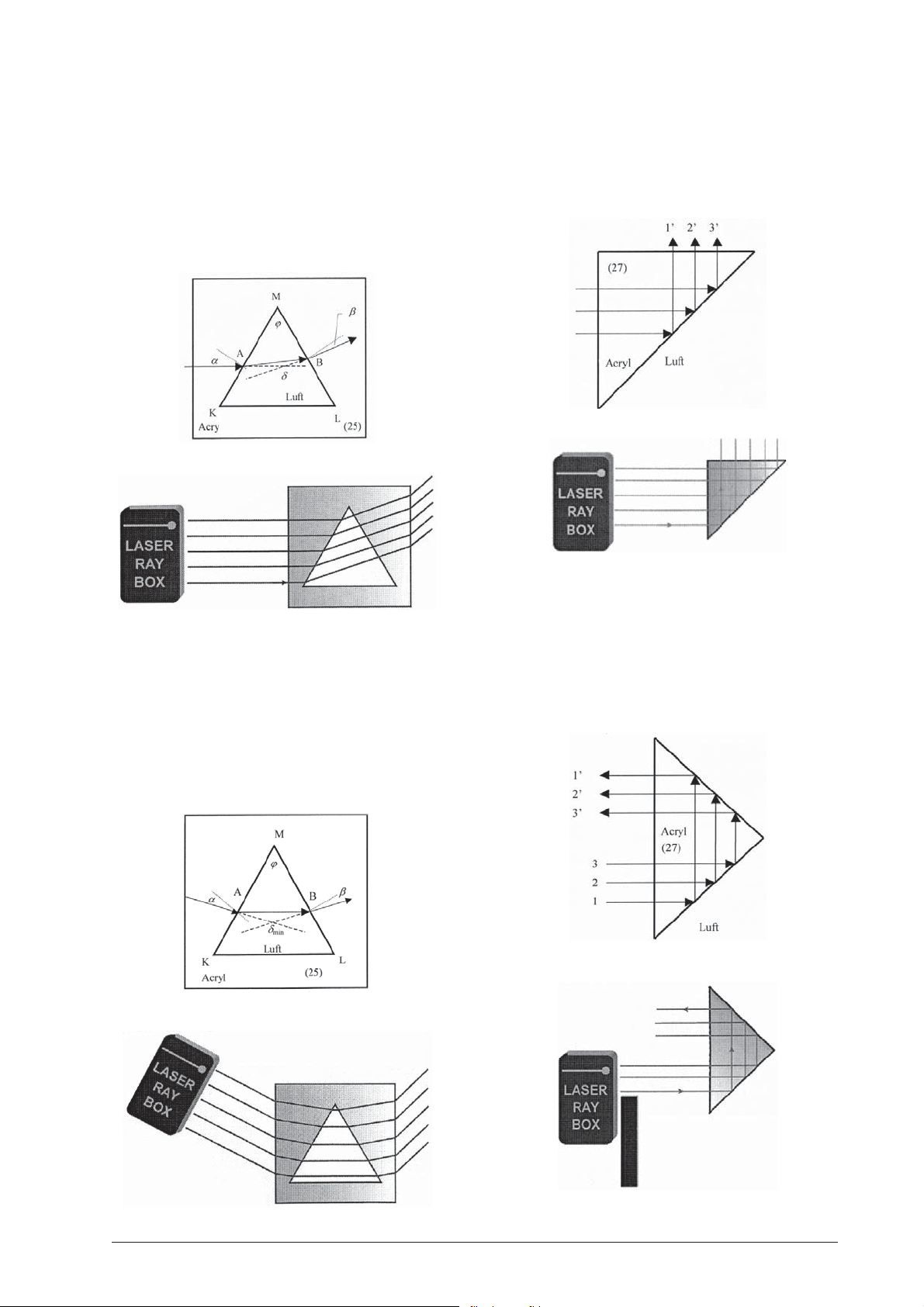
E10a Ablenkung eines Lichtstrahls durch ein

Luftprisma
(U17301)

Licht tritt an Punkt A durch die Grenzfläche Acryl-Luft.
Der Lichtstrahl wird vom Einfallslot weg gebrochen. Am
Austrittspunkt B wird er hin zum Einfallslot gebrochen.
Die Summe aller Brechungswinkel ist der Ablenkungs­winkel δ. Es ist der Winkel zwischen dem einfallenden
und austretenden Lichtstrahl.

E11a Reflexion an einer Kante eines Acrylprismas

(U17301)

Wenn die Lichtstrahlen auf die Kante treffen, werden
sie total reflektiert. Bei leichtem Drehen des Prismas
kann sowohl Brechung als auch Reflexion beobachtet
werden.

E10b Minimale Ablenkung durch ein Luftprisma

(U17301)

Im Fall der minimalsten Ablenkung δ

ist der Ein-

min

fallswinkel α gleich dem Austrittswinkel ß. Der gebro­chene Strahl verläuft dann im Prisma parallel zu der
Seite, die nicht durchgangen wird. Für den Brechungs­index des Prismas gilt: (siehe E9b). Die Richtung der
Ablenkung ist umgekehrt der in einem Acrylprisma.

E11b Reflexion an zwei Kanten eines Acrylprismas

(U17301)

In diesem Fall sind die Bedingungen für Totalreflexi­on an beiden Kanten des Prismas erfüllt. Wird der
oberste einfallende Strahl ausgeblendet, so verschwin­det der unterste austretende Strahl. Das Bild ist um
180° gedreht.

7

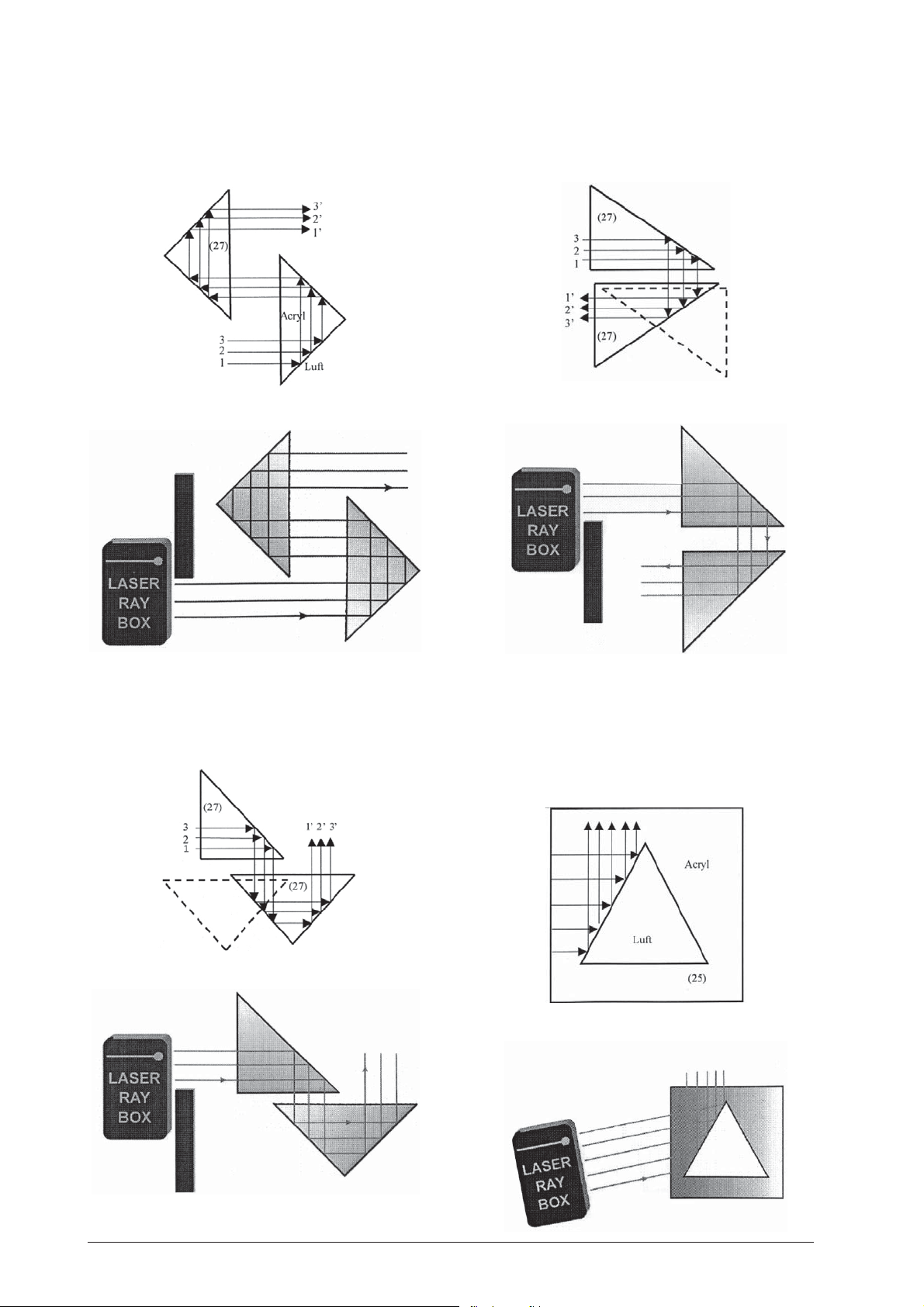
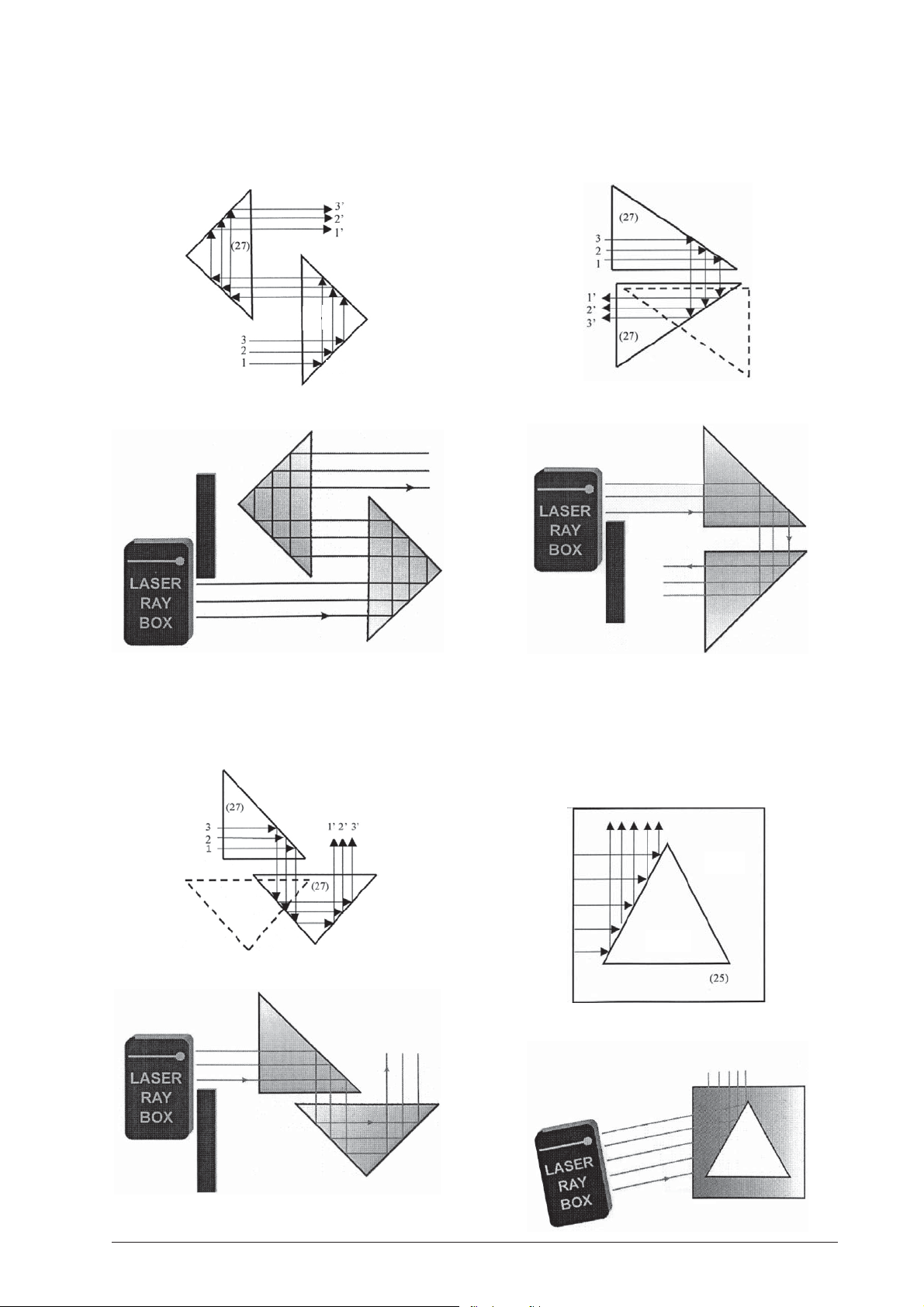
E11c Reflexion an zwei Acrylprismen

(U17301)

Die Bedingungen für Totalreflexion sind an allen Kan­ten der Prismen erfüllt.

E11e Reflexion an zwei Acrylprismen

(U17301)

Die Bedingungen für Totalreflexion sind an allen Kan­ten der Prismen erfüllt.

E11d Reflexion an zwei Acrylprismen

(U17301)

Die Bedingungen für Totalreflexion sind an allen Kan­ten der Prismen erfüllt.

E12 Reflexion an einem Luftprisma

(U17301)
Wenn der Einfallwinkel der Lichtstrahlen kleiner ist als
der kritische Winkel (42°), werden die Lichtstrahlen ins
Acryl hin reflektiert. Ist der Winkel größer, geht ein Teil
des Lichts durch das Luftprisma.

8

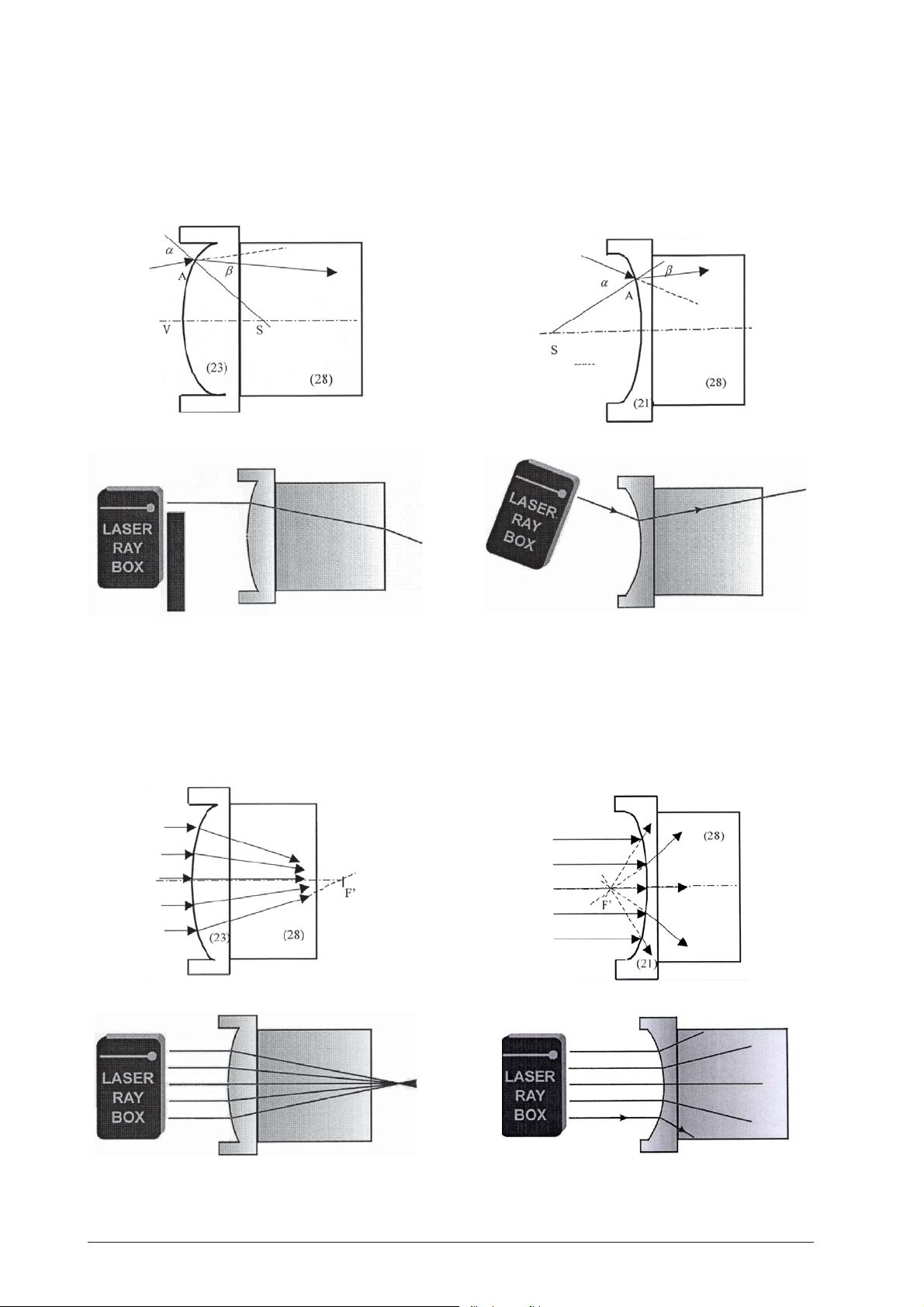
E13a Durchgang eines Lichtstrahls durch eine

konvexe Grenzfläche Luft-Acryl
(U17301)

Wenn ein Lichtstrahl an Punkt A durch die Grenzfläche
Luft-Acryl tritt, wird er hin zum Einfallslot gebrochen.
Das Einfallslot ist die Gerade von Punkt A zum
Krümmungsmittelpunkt S.

E14a Durchgang eines Lichtstrahls durch eine

konkave Grenzfläche Luft-Acryl
(U17301)

Wenn der Lichtstrahl durch Punkt A auf der Grenzflä­che tritt, ist eine Brechung hin zum Einfallslot zu beo­bachten. Das Einfallslot ist die Gerade von Punkt A zum
Krümmungsmittelpunkt S.

E13b Durchgang von Lichtstrahlen durch eine

konvexe Grenzfläche Luft-Acryl
(U17301)

Die einfallenden Lichtstrahlen werden zweimal gebro­chen und treffen sich im Punkt F auf der optischen
Achse, dem Brennpunkt.

E14b Durchgang von Lichtstrahlen durch eine

konkave Grenzfläche Luft-Acryl
(U17301)

Nach Durchgang durch die Grenzfläche Acryl-Luft wird
das Strahlenbündel divergent gebrochen. Werden die
gebrochenen Strahlen nach hinten verlängert, so tref­fen sie sich in einem Punkt auf der optischen Achse.
Dieser Punkt heißt virtueller Brennpunkt F'.

9

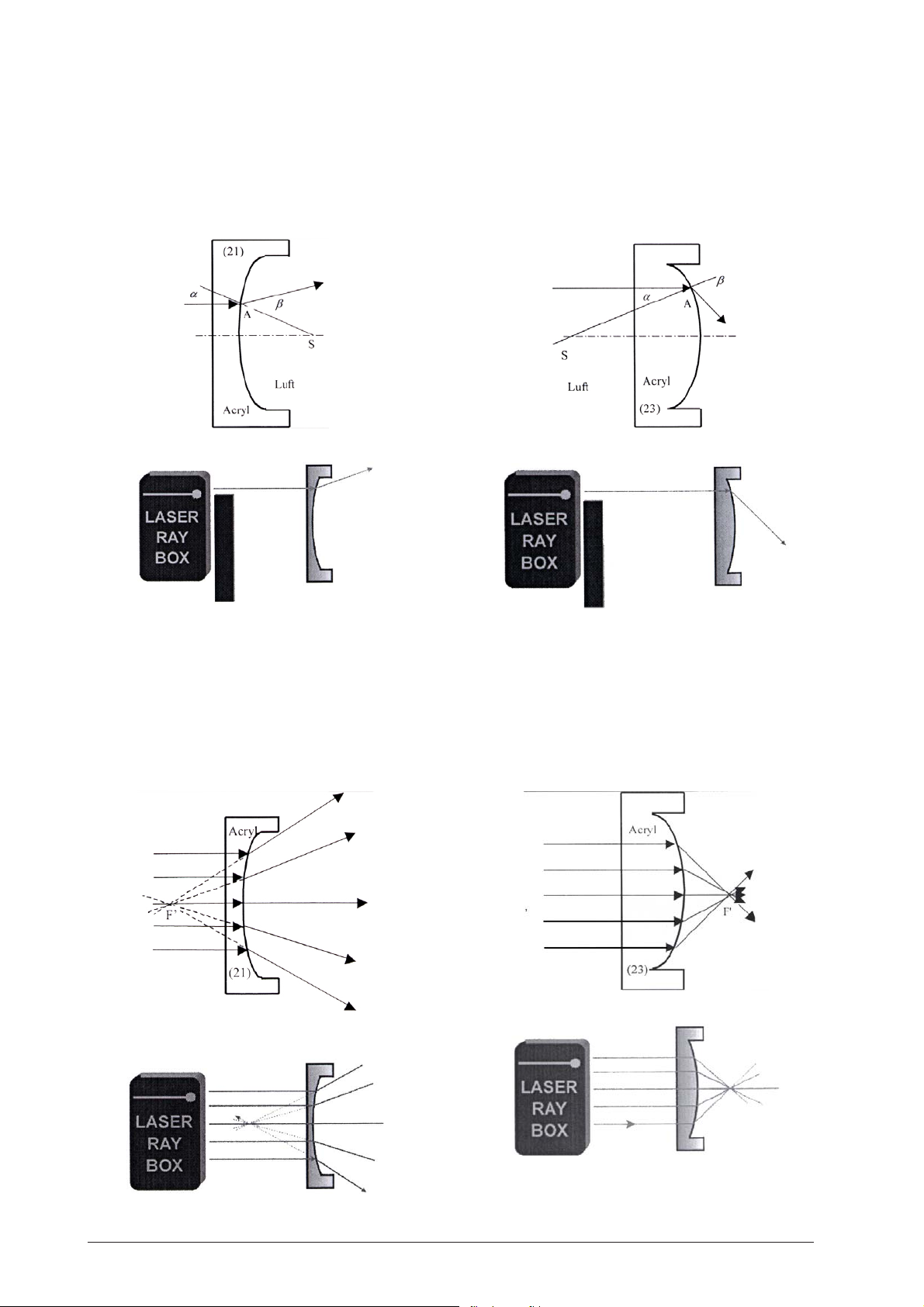
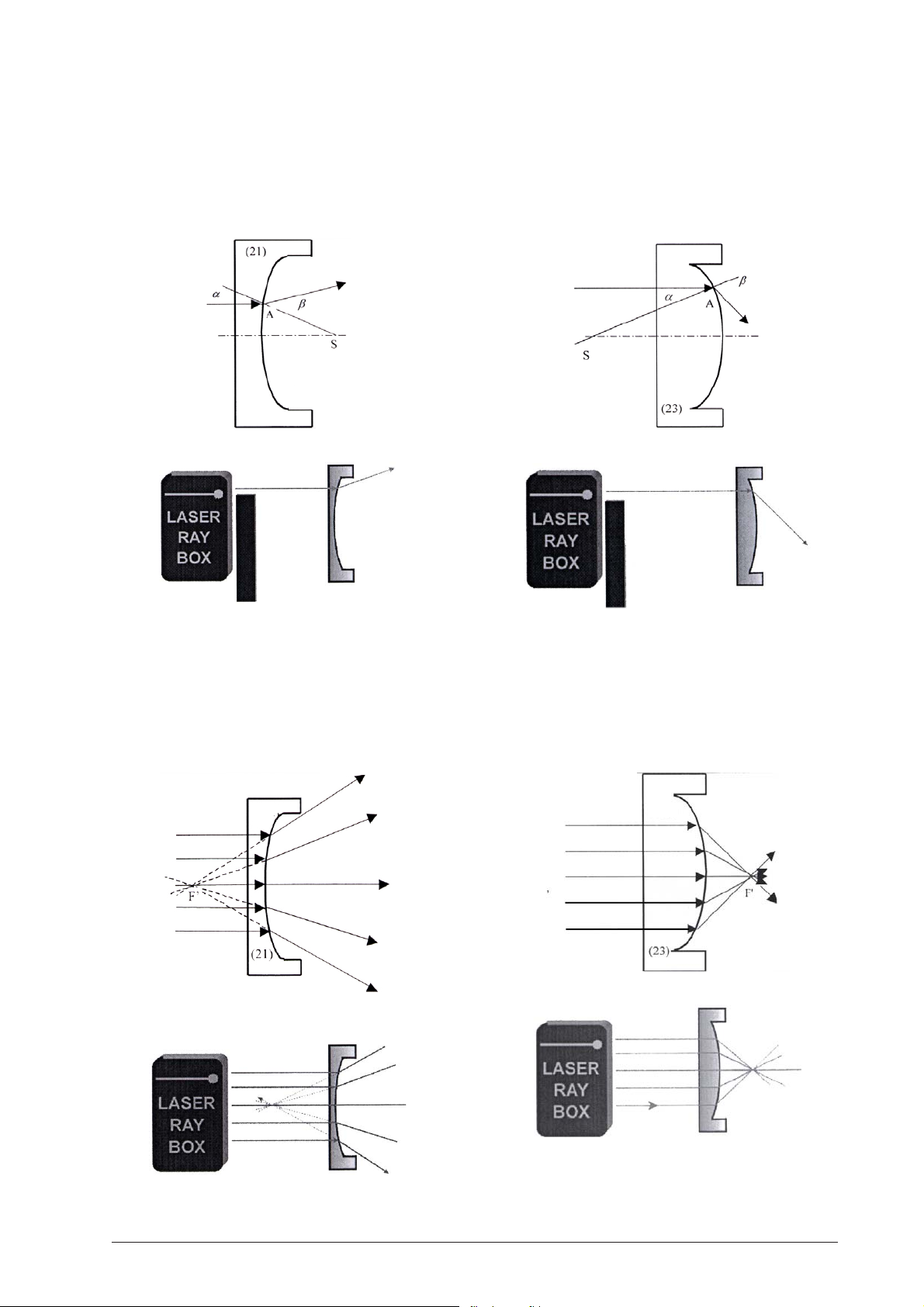
E15a Durchgang eines Lichtstrahls durch eine

konvexe Grenzfläche Acryl-Luft
(U17301)

Nach Durchgang des Lichtstrahls durch Punkt A wird
er vom Einfallslot weg gebrochen. Das Einfallslot ist
die Gerade von Punkt A zum Krümmungsmittelpunkt
S.

E16a Durchgang eines Lichtstrahls durch eine

konkave Grenzfläche Acryl-Luft

(U17301)

Nach Durchgang des Lichtstrahls durch Punkt A wird
er vom Einfallslot weg gebrochen. Das Einfallslot ist
die Gerade von Punkt A zum Krümmungsmittelpunkt
S.

E15b Durchgang von Lichtstrahlen durch eine

konvexe Grenzfläche Acryl-Luft
(U17301)

Nach Durchgang durch die Grenzfläche Acryl-Luft wird
das Strahlenbündel divergent gebrochen. Verlängert
man die gebrochenen Strahlen nach hinten, so treffen
sie sich in einem Punkt auf der optischen Achse. Die­ser Punkt heißt virtueller Brennpunkt F'.

E16b Durchgang von Lichtstrahlen durch eine

konkave Grenzfläche Acryl-Luft

(U17301)

Nach Durchgang durch die Grenzfläche ist das Strah­lenbündel konvergent. Parallele Strahlen treffen sich
in einem Punkt auf der optischen Achse, dem Brenn­punkt F.

10

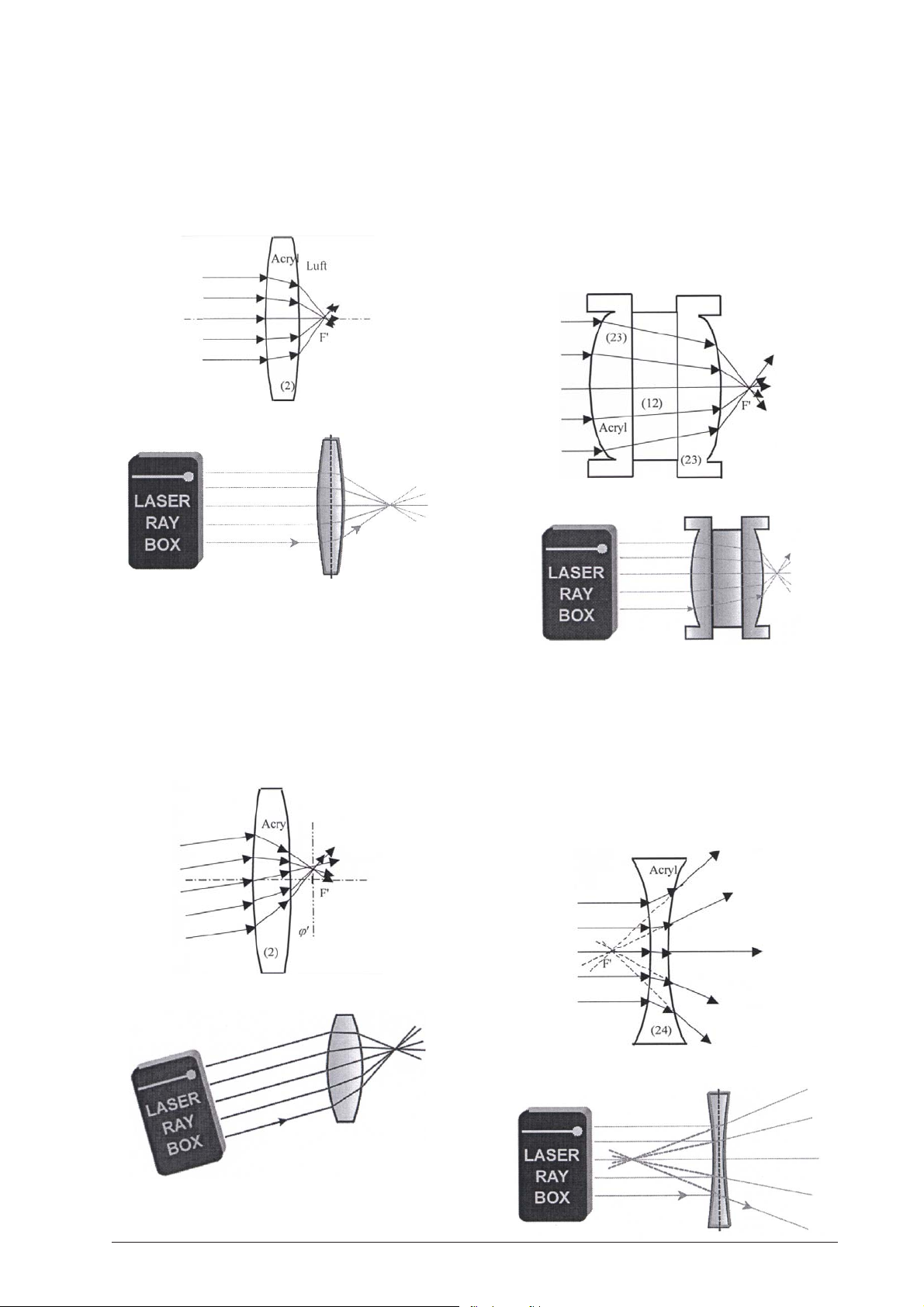
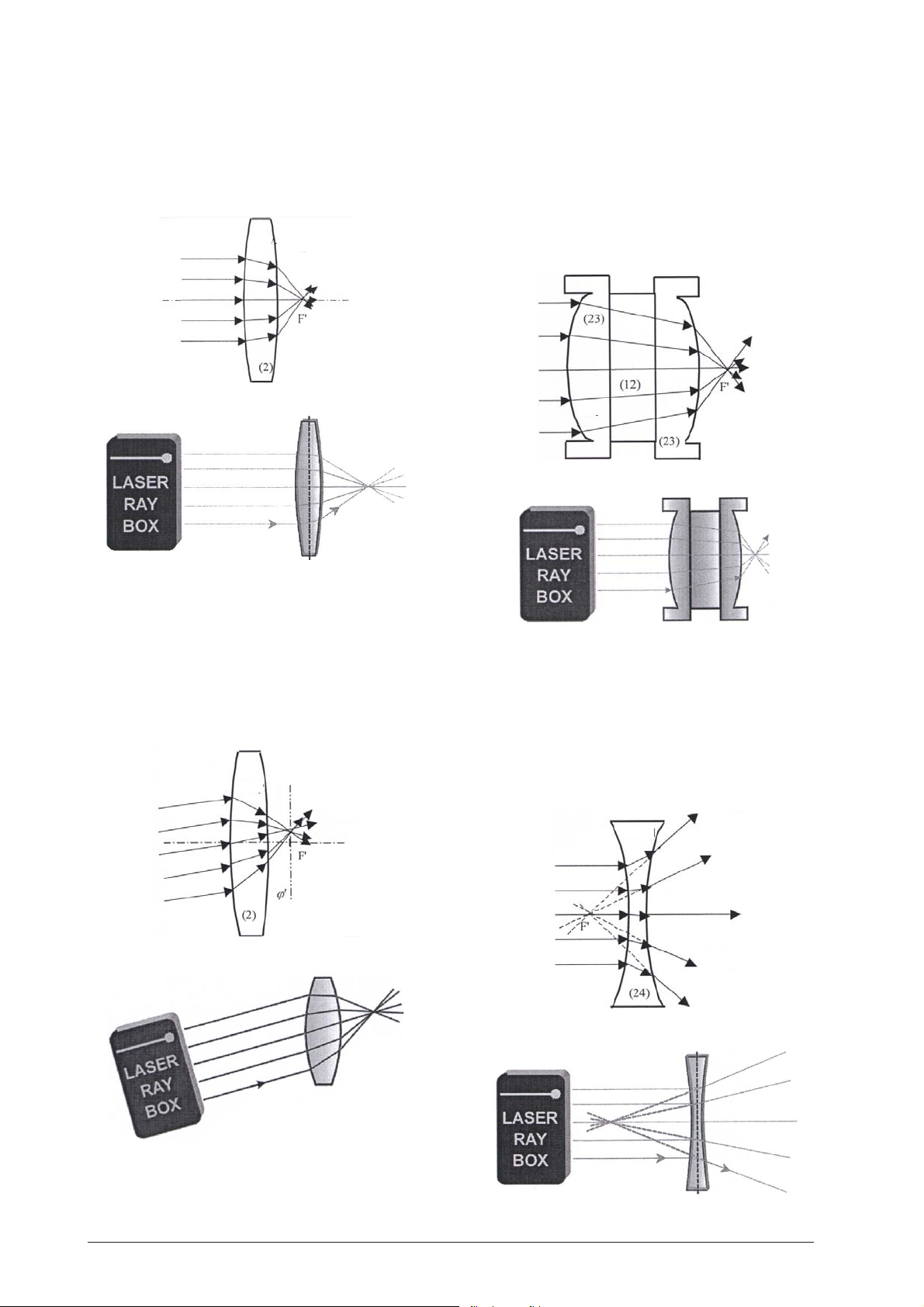
E17a Durchgang von Lichtstrahlen durch eine

konvexe Acryllinse – Lichtstrahlen parallel
zur optischen Achse
(U17300/U17301)

Eine konvexe Acryllinse ist eine Sammellinse und die
Lichtstrahlen treffen sich nach Durchgang durch die
Linse im Brennpunkt F'.

E17c Durchgang von Lichtstrahlen durch eine

dicke konvexe Acryllinse
(U17301)

Durch Platzieren einer planparallelen Platte zwischen
zwei Linsen (23) kann das Modell einer dicken Linse
verwirklicht werden. Mit Veränderung der Dicke d der
Linse verändert sich auch die Brennweite, je dicker die
Linse desto kleiner die Brennweite. Ab einer kritischen
Dicke wird aus der Sammellinse eine Zerstreuungslin­se.

E17b Durchgang von Lichtstrahlen durch eine

konvexe Acryllinse - Lichtstrahlen nicht
parallel zur optischen Achse
(U17300/U17301)

Die Achse ϕ' steht senkrecht auf der optischen Achse
und verläuft durch den Brennpunkt F'. Sie wird als
Brennpunktebene bezeichnet. Die einfallenden Strah­len werden gebrochen und treffen sich in einem Punkt
auf der Achse ϕ'.

E18a Durchgang von Lichtstrahlen durch eine

konkave Acryllinse – Lichtstrahlen parallel
zur optischen Achse
(U17300/U17301)

Die Lichtstrahlen sind divergent nach Durchgang durch
die Linse. Sie bildet kein Objekt ab. Nach hinten ver­längert, treffen sich die Strahlen im virtuellen Brenn­punkt F'.

11

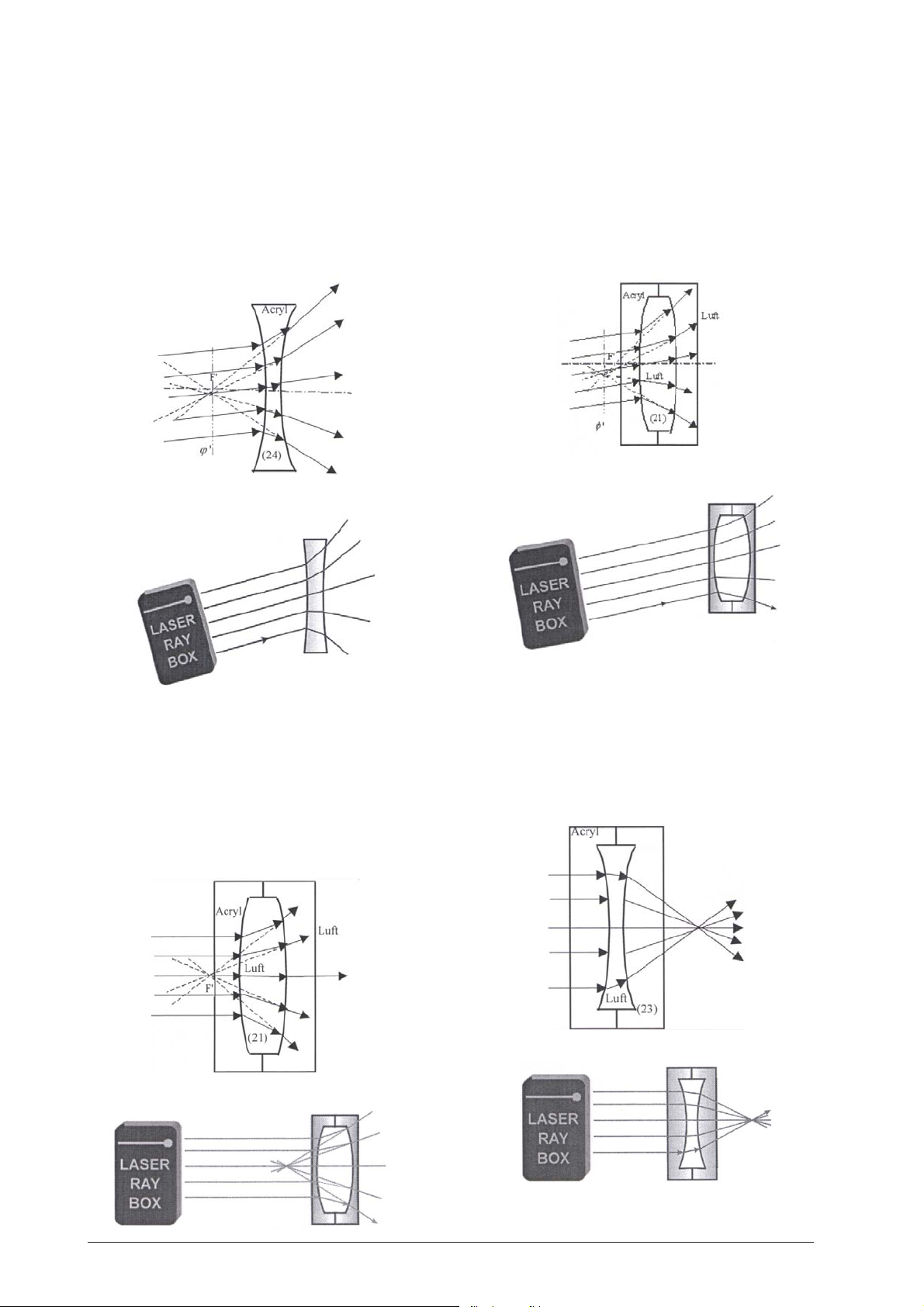
E18b Durchgang von Lichtstrahlen durch eine

konkave Acryllinse – Lichtstrahlen nicht
parallel zur optischen Achse
(U17300/U17301)

Die Achse ϕ' steht senkrecht auf der optischen Achse
und verläuft durch den virtuellen Brennpunkt F'. Sie
wird als Brennpunktebene bezeichnet. Die Verlänge­rung der gebrochenen Strahlen treffen sich in einem
Punkt auf der Achse ϕ'.

E19b Durchgang von Lichtstrahlen durch eine

konvexe Luftlinse – Lichtstrahlen nicht

parallel zur optischen Achse

(U17301)

Die Achse ϕ' steht senkrecht auf der optischen Achse
und verläuft durch den virtuellen Brennpunkt F'. Sie
wird als Brennpunktebene bezeichnet. Die Verlänge­rung der gebrochenen Strahlen treffen sich in einem
Punkt auf der Achse ϕ'.

E19a Durchgang von Lichtstrahlen durch eine

konvexe Luftlinse – Lichtstrahlen parallel zur
optischen Achse
(U17301)

Die Lichtstrahlen sind divergent nach Durchgang durch
die Linse. Sie bildet kein Objekt ab. Nach hinten ver­längert, treffen sich die Strahlen im virtuellen Brenn­punkt F'.

E20a Durchgang von Lichtstrahlen durch eine

konkave Luftlinse – Lichtstrahlen parallel zur

optischen Achse

(U17301)

Ein konkave Luftlinse verhält sich wie eine Sammellin­se und die gebrochenen Strahlen treffen sich im Brenn­punkt F' nach Durchgang durch die Linse.

12

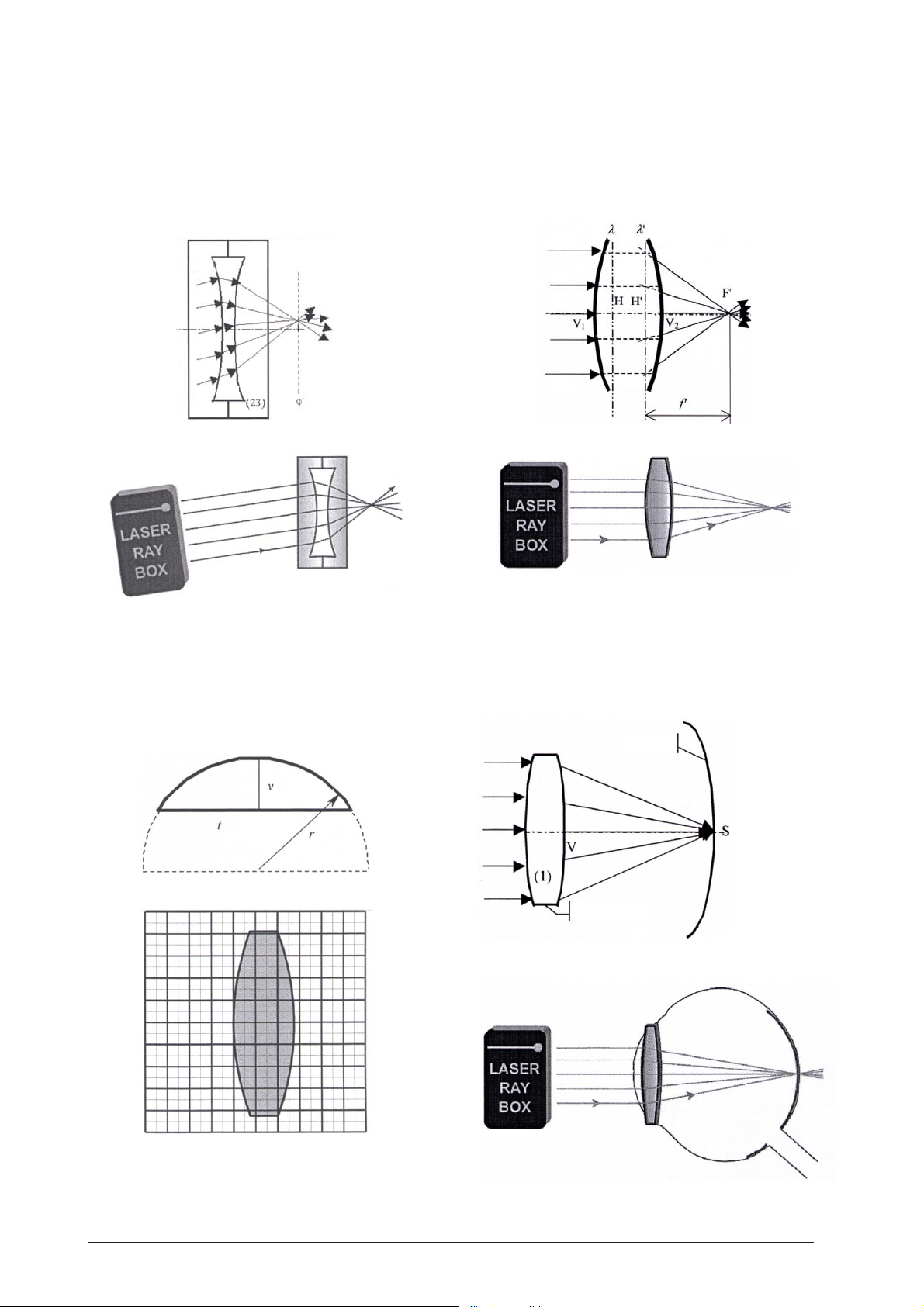
E20b Durchgang von Lichtstrahlen durch eine

konkave Luftlinse – Lichtstrahlen parallel
zur optischen Achse
(U17301)

Die Achse ϕ' steht senkrecht auf der optischen Achse
und verläuft durch den Brennpunkt F'. Sie wird als
Brennpunktebene bezeichnet. Die gebrochenen Strah­len treffen sich in einem Punkt auf der Achse ϕ'.

E21b Parameter von dicken Linsen – Brennweite

(U17300/U17301)

Dicke Linsen sind Linsen, bei denen die Dicke nicht
vernachlässigbar ist. Bei der Definition der Brennwei­te muss der Abstand zwischen den beiden Haupt­ebenen H and H' berücksichtigt werden.

E21a Parameter von dicken Linsen – Bestimmung

des Krümmungsradius
(U17300/U17301)

Die Linsen im Laseroptik-Satz besitzen eine zylindri­sche Brechungsfläche auf kreisförmiger Grundfläche
mit gleichen Krümmungsradien. Mit Hilfe von Milli­meterpapier lassen sich diese Radien bestimmen.

E22a Augenmodell

(U17300, Folie A)

Lichtstrahlen parallel zur optischen Achse werden
durch die Augenlinse gebrochen und treffen sich in
einem Punkt auf der Netzhaut.
Augenlinse (1) direkt hinter der Linie O2 platzieren.

13

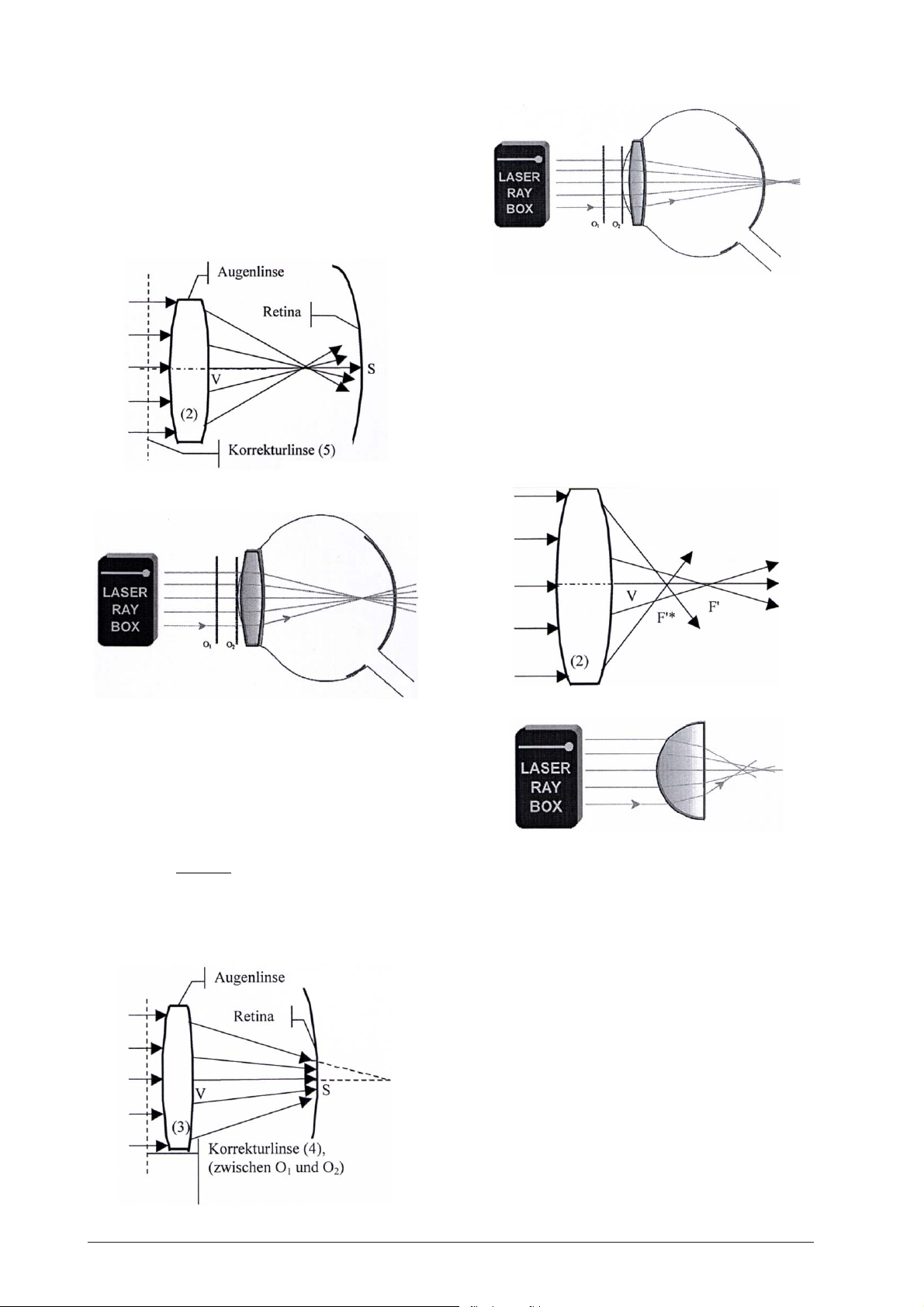
E22b Augenmodell, Kurzsichtigkeit

(U17300, Folie A)

Lichtstrahlen parallel zur optischen Achse werden
durch die Augenlinse gebrochen und treffen sich in
einem Punkt vor der Netzhaut.
Augenlinse (2) direkt hinter der Linie O2 und die
Korrekturlinse (5) zwischen die Linien O1 und O2 plat­zieren.

E23a Korrektur der sphärischen Aberration durch

Verringerung des Durchmessers des

Strahlenbündels(

U17300/U17301)
Sphärische Aberration einer Linse kann durch Verrin­gerung des Durchmessers des Strahlenbündels, das
durch die Linse geht, reduziert werden. Dazu die äu­ßersten Strahlen ausblenden.

E22c Augenmodell, Weitsichtigkeit

(U17300, Folie A)

Lichtstrahlen parallel zur optischen Achse werden
durch die Augenlinse gebrochen und treffen sich in
einem Punkt hinter der Netzhaut. Die Korrekturlinse
ist eine Sammellinse. Für die Brennweite f' des Linsen­systems gilt:

ff

’’

12

f

’

=

ff

’’

+

12

wobei f1' die Brennweite der Augenlinse und f2' die der
Korrekturlinse ist.

E23b Korrektur der sphärischen Aberration durch

eine Linsenkombination

(U17300, Folie E)

Sphärische Aberration von Sammel- und Zerstreuungs­linsen haben einen umgekehrten Effekt. Durch eine
Kombination von Linsen lässt sich der Fehler korrigie­ren. Die Aberration ∆f = f

– f2 ist definiert als die Dif-

1

ferenz zwischen der Brennweite f1 der äußeren und f
der inneren Strahlen. Bei Sammellinsen hat die Aber­ration ein positives bei Zerstreuungslinsen ein negati­ves Vorzeichen.

2

14

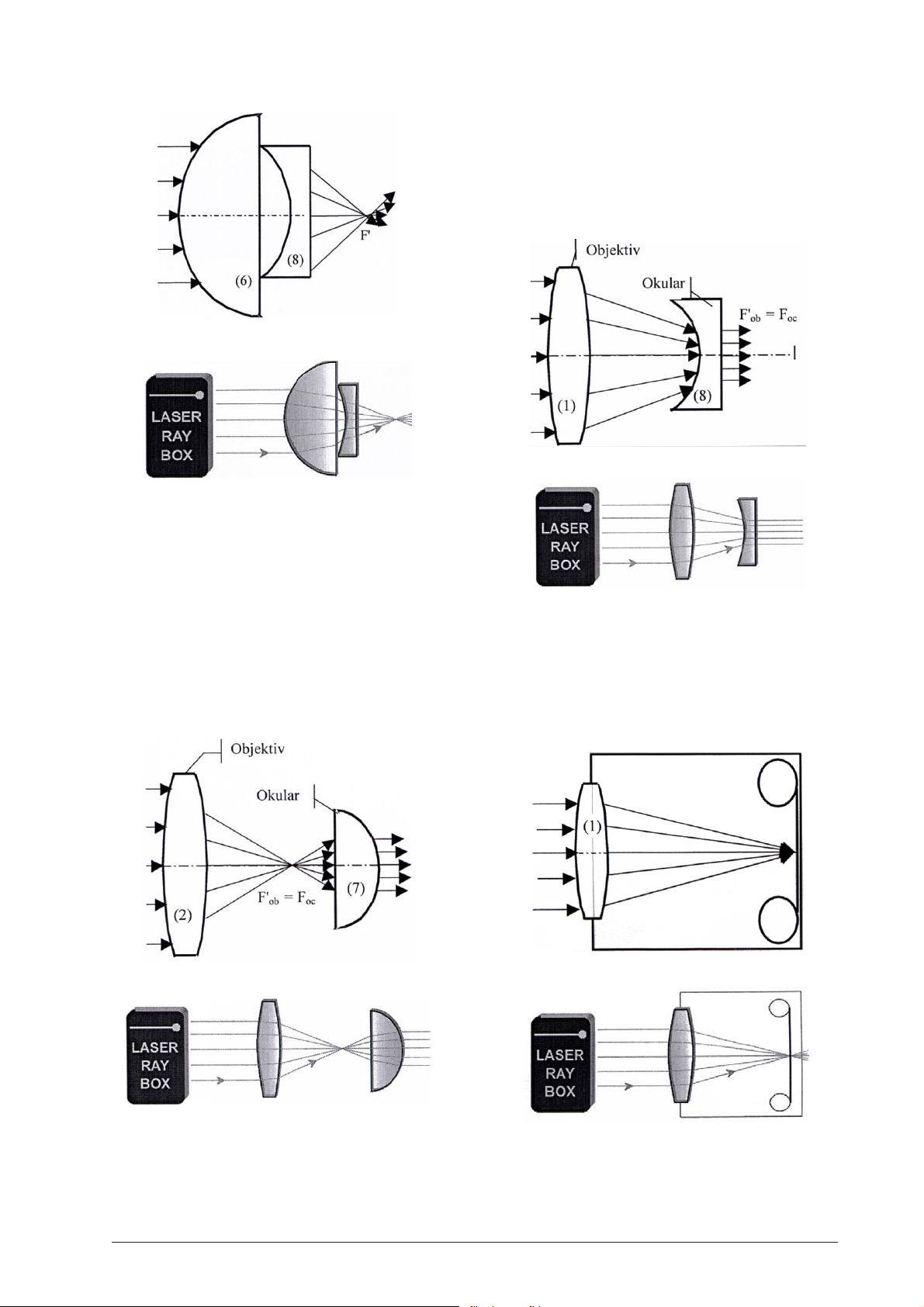
E24a Teleskop nach Kepler

(U17300, Folie D)

Das Objektiv in Keplers Teleskop erzeugt ein verklei­nertes reelles Bild des betrachteten Objekts, das vom
Okular wie durch eine Lupe vergrößert wird. Es ent­steht eine umgekehrte (oben und unten sowie rechts
und links sind vertauscht), stark vergrößerte Abbildung.
Zur Demonstration dieses Sachverhalts einen der äu­ßeren Lichtstrahlen ausblenden. Wird der oberste ein­fallende Strahl ausgeblendet, so verschwindet der un­terste ausgehende Strahl.

E24b Teleskop nach Galilei

(U17300, Folie C)

Beim Galilei-Fernrohr treffen die vom Objektiv kom­menden Strahlen auf eine Zerstreuungslinse bevor sie
den Brennpunkt erreichen. Die Strahlen gelangen als
parallele Strahlen ins Auge. Die Abbildung des Objekts
ist vergrößert, aufrecht und seitenrichtig.

E25 Kamera

(U17300, Folie B)
Die Linse der Kamera ist eine Sammellinse. Sie bildet
ein Objekt in einem reellen Bild auf dem Kopf stehend
auf dem an der Rückseite der Kamera befindlichen Film
ab.

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Deutschland • www.3bscientific.com • Technische Änderungen vorbehalten

15

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

®

U17300 Laser Optics Demonstration Set and

U17300 Laser Optics Supplement Set

Instruction sheet

1/05 ALF

Table of contents

Page No. of Exp. Experiment Gerätesatz

1 Introduction
2 Tables of the settlements
3 E1 Reflection on planar mirror U17300/U17301
3 E2 Reflection on two planar mirrors U17301
3 E3a Reflection of light rays on concave mirror – rays are parallel to optical axis U17300
4 E3b Reflection of light rays on concave mirror – rays are non-parallel

to optical axis U17300
4 E4a Reflection of light rays on convex mirror – rays are parallel to optical axis U17300
4 E4b Reflection of light rays on convex mirror – rays are non-parallel

to optical axis U17300
5 E5a Refraction of light passing air-glass boundary U17300
5 E5b Apparent depth of objects U17301
5 E6a Refraction of light passing glass-air boundary U17300
6 E6b Refraction on glass prism edge U17300/U17301
6 E6c Critical angle, total reflection U17300
6 E6d Total reflection – propagating of light in optical fibres U17300
7 E7 Light ray shift by glass planparallel plate U17300/U17301
7 E8 Light ray shift by air planparallel plate U17301
7 E9a Glass prism deviation of light ray U17300/U17301
8 E9b Glass prism minimal deviation U17300/U17301
8 E10a Air prism deviation of light U17301
8 E10b Air prism minimal deviation U17301
9 E11a Reflection of light on one edge of glass prism U17301
9 E11b Reflection of light on two edges of glass prism U17301
9 E11c Reflection of light on two glass prisms U17301
10 E11d Reflection of light on two glass prisms U17301
10 E11e Reflection of light on two glass prisms U17301
10 E12 Reflection of light on air prisms U17301
11 E13a Light ray passing a convex air-glass boundary U17301
11 E13b Light beam passing through convex air-glass boundary U17301
11 E14a Light ray passing through concave air-glass boundary U17301
12 E14b Light beam passing through concave air-glass boundary U17301
12 E15a Light ray passing through convex glass-air boundary U17301
12 E15b Light beam passing through the glass-air boundary U17301
13 E16a Light ray tracing passing concave glass-air boundary U17301
13 E16b Light beam passing through concave glass-air boundary U17301
13 E17a Light beam passing through glass convex lens - beam is parallel

to the optical axis U17300/U17301
14 E17b Light beam passing through glass convex lens – the rays are non-parallel

to the optical axis U17300/U17301
14 E17c Light beam passing through thick glass convex lens U17301
14 E18a Light beam passing through glass concave lens – the rays are parallel

to the optical axis U17300/U17301

16

15 E18b Light beam passing through glass concave lens – the rays are non-parallel

to the optical axis U17300/U17301

15 E19a Light beam passing through air convex lens – the rays are parallel

to the optical axis U17301

15 E19b Light beam passing through air convex lens – the rays are non-parallel

to the optical axis U17301

16 E20a Light beam passing through air concave lens – the rays are parallel

to the optical axis U17301

16 E20b Light beam passing through air concave lens – the rays are non-parallel

to the optical axis U17301
16 E21a Parameters of thick lenses – determination of radius of curvature U17300/U17301
17 E21b Parameters of thick lenses – focal length U17300/U17301
17 E22a Model of a normal eye U17300
17 E22b Model of short-sighted eye U17300
18 E22c Model of long-sighted eye U17300
18 E23a Correction of spherical aberration by reducing the beam diameter U17300/U17301
18 E23b Correction of spherical aberration by combination of lenses U17300
19 E24a Keplerian telescope U17300
19 E24b Galileian telescope U17300
19 E25 Camera U17300

Laser Optics Demonstration Set U17300
Laser Optics Supplement Set U17301

The column "SET TO USE" informs you which set is appropriate for which experiment (either U17300, or U17301, or
both).

Introduction

The demonstration set U17300 was designed for easy
and clear demonstration of basic optical effects and
devices. Using diode laser as a light source for experi­ments enables both teacher and student to understand
the principle of simple and more complicated optical
systems. In this guide book you can find many basic
experiments and demonstrations using U17300 and
U17301, which is an additional set of optical elements
containing air lenses, air prisms etc. Every experiment
in this book has three parts:

1. A simple description of the experiment

2. A geometric diagram of the experiment

3. A diagram showing what the experiment

looks like when it is set up.
Shown in brackets under the title of the experiment is
whether it can be demonstrated with the U17300 or
U17301 set, or both. The same note can be find also in
the table of contents in the last row. It is clear now,
that some experiments cannot be done with U17300
and some of them with U17301.
A very important constituent of the experiments is the
LASER RAY BOX which consists of five laser diodes. Be
careful to avoid direct eye contact with the laser beam!
If you have basic set U17300 and you are interested in
realizing experiments for additional set U17301, please,
contact your distributor of didactic aids.

Table of set elements

U17300 Basic Set

1 Biconcave lens

2 Biconvex lens
3 Biconvex lens
4 Biconvex lens
5 Biconvex lens
6 Small planeconcave lens
7 Large planeconvex lens
8 Small planeconvex lens
9 Concave mirror
10 Convex mirror
11 Planar mirror
12 Planparallel plate
13 Prism
14 Optical fibre

Working sheets

A Human Eye Model
B Camera
C Galileian Telescope
D Keplerian Telescope
E Correction of Spherical Aberration
F Hartle's circle

U17301, Additional Set

21 Biconcave air lens
22 Biconcave glass lens
23 Biconvex air lens
24 Biconvex glass lens
25 Optical air prism
26 Equilateral optical glass prism
27 Rectangular optical glass prism (2 pc)
28 Square glass planparallel plate
29 Rectangular glass planparallel plate (2 pc)
11 Planar mirror (2 pc)

17

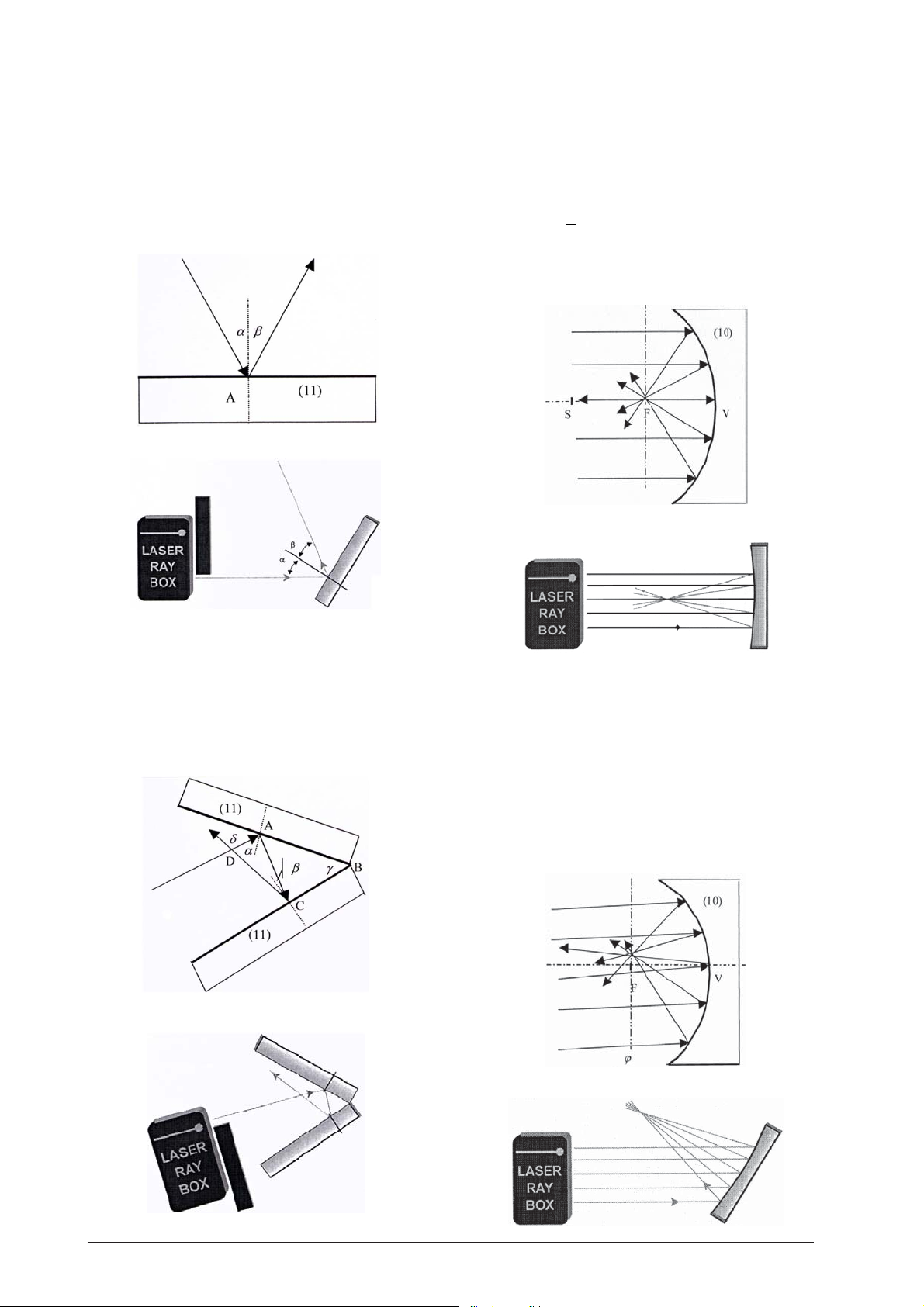
E1 Reflraction on planar mirror

(U17300/U17301)

The law of reflection is demonstrated. When a light
ray impinges a plane mirror under an angle α it is re­flected under the same angle ß

α = ß

Both angles are measured from the perpendicular line
to the mirror plane.

E3a Reflection of light rays on concave mirror –

rays are parallel to optical axis

(U17300)
The focal length f of the concave mirror is determined
by the length of the line VF. The curvature radius can
be obtained using the known formula:

fr=

2

The distance of the centre of curvature S is twice as

long as the distance of the focus F.

E2 Reflection on two planar mirrors

(U17301)

An interesting relation can be shown:

δ = 2 γ
where δ is the angle between the incident and the
reflected ray and γ is the angle between the mirrors'
planes.

E3b Reflection of light rays on concave mirror –

rays are non-parallel to optical axis

(U17300)

The axis ϕ which is perpendicular to the optical axis
and passes through the focus is referred as the focal
plane of the concave mirror. If the parallel rays im­pinge the mirror, they meet at one point of the axis ϕ
after the reflection. In the case of the rays parallel to
the optical axis, the point belongs to the axis and is
called the focus (F).

18

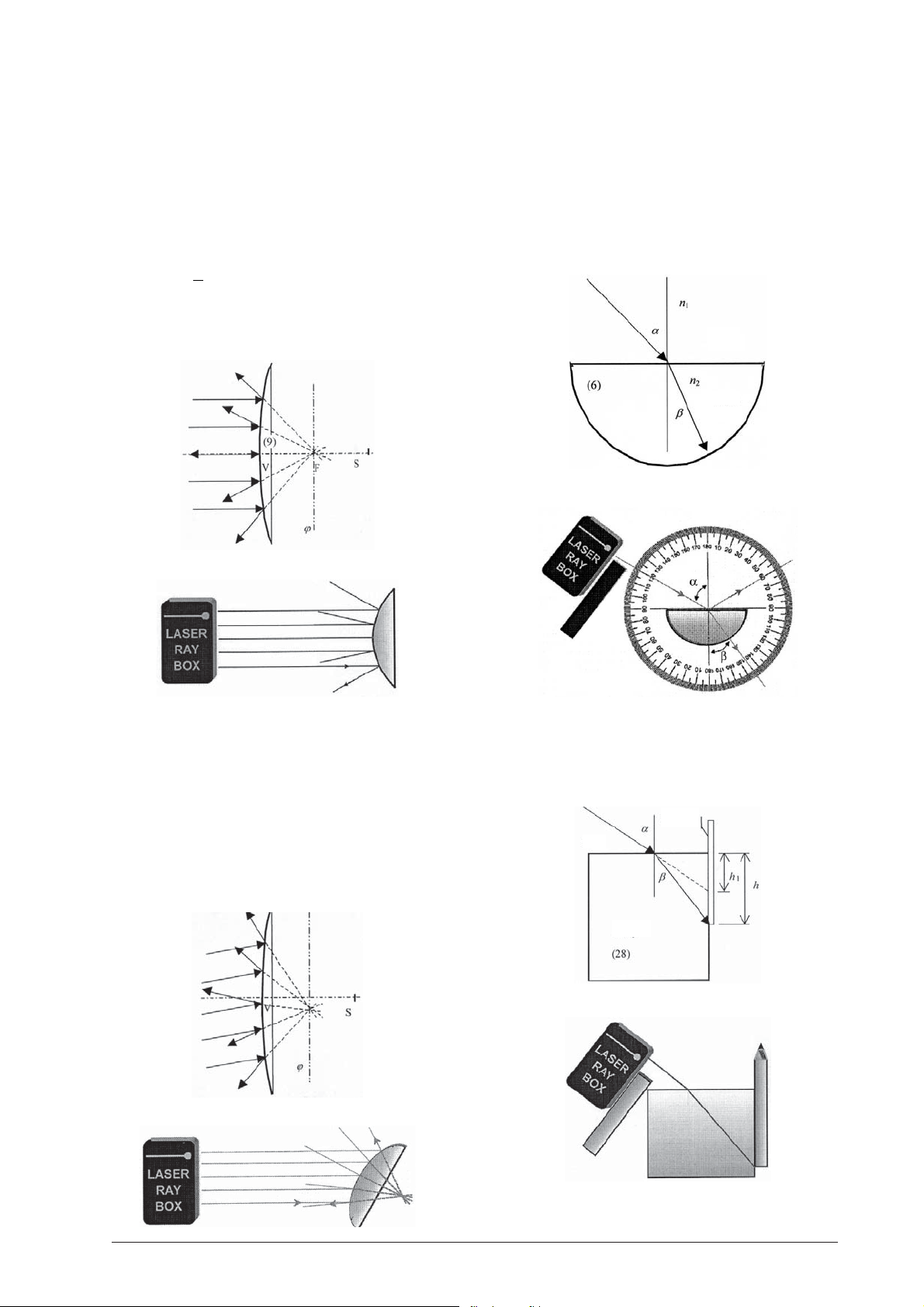
E4a Reflection of light rays on convex mirror –

rays are parallel to optical axis

(U17300)
The reflected rays, parallel to the optical axis, appear
to start from one point on the right side behind the
mirror. This point is referred to as the figure focus. The
length of line VF determines the focal length f of the
mirror. The radius of curvature can be obtained from
the next formula.

fr=

2

The distance of the centre of curvature S is two times
longer than the distance of the focus F.

E5a Refraction of light passing air-glass boundary

(U17300, transparency F)

If light passes through one optical medium character­ized by refraction index n1 into the other with refrac­tion index n2 its direction is changed by Snell’s law:
n

sin α = n

1

where α is an incidence angle in the medium n

sin ß

2

and

1

ß is an angle of refraction in the medium n2. The angles
are measured from the normal to the planar boundary.

Air

Acrylic

E4b Reflection of light rays on convex mirror –

rays are non-parallel to optical axis

(U17300)
The axis ϕ which is perpendicular to the optical axis
and passes through the focus is referred to as the focal
plane of the convex mirror. If parallel rays impinge
the mirror, they are scattered in such a way that they
appear to start from one point of the plane ϕ. In the
case of incidence rays parallel to the optical axis this
point belongs to the axis.

E5b Apparent depth of objects

(U17301)
You can build up the model of observing the depth of
objects in water or glass from air.

Pencil

Air

Acrylic

19

E6a Refraction of light passing glass-air boundary

(U17300, transparency F)

The ray is refracted with the refraction angle ß, which
is larger than α. The ray is bent away from the normal.

Acrylic

Air

E6b Refraction on glass prism edge

(U17300/U17301)
When light passes through glass to air, Snell’s law can
be written in the next form:

n

sin α = sin ß

1

Refractive index of air n2 = 1.

Acrylic

Air

E6d Total reflection – propagating of light in

optical fibres

(U17300)
If light enters the optical fibre under some angles it
propagates in it using the total reflection on the bor­ders of the fibre. An important parameter determines
what angle should not be overcome. This parameter is
called the numerical aperture. It is SIN of the maxi­mum entrance angle of the light. Also the minimal
radius of the fibre bent is set by this parameter. It
cannot be smaller, when the fibre is installed.

Acrylic

E6c Critical angle, total reflection

(U17300, transparency F)
The larger the incidence angle the larger the refrac­tion angle. If n1 < n

a critical angle α exists. In other

2

words, the refracted ray lies on the border of two me­diums. When the incidence angle is larger than the
critical angle, there is no more refracted light and all
light energy is reflected, this is called total reflection.

Acrylic

E7 Light ray shift by glass planparallel plate

(U17300/U17301)
If a light ray passes through a planparallel plate its
direction is not changed. The outgoing ray is shifted in
accordance with the incoming one. The shift d can be
estimated with respect to the thickness h of the plate
using the formula:

sin

αβ

−

dh=

()

cos

β

20

Air

Acrylic

E8 Light ray shift by air planparallel plate

(U17301)
In this case, a shift between the incoming and the out­going ray can be observed. This shift has an opposite
direction than in the case of the glass plate.

Acrylic

angle δ. It is the angle between the incidence and the
outgoing ray.

Air

Acrylic

E9b Glass prism minimal deviation

(U17300/U17301)

It can be seen that in the case of minimal deviation

δ

the incidence angle α is equal to the angle of the

min

outgoing ray ß. The direction of the refraction of light
in the prism is parallel to the edge the ray does not
pass through. The refractive index of the prism obeys
the formula:

Acrylic

Air

E9a Glass prism deviation of light ray

(U17300/U17301)
If the prism is glass, after the light impinges the point
A, it is bent toward the normal and refracts to point B.
At this point it is bent into the air away from the nor­mal. The sum of all refraction angles is the deviation

sin

n =

+

δϕ

min

2

ϕ

sin

2

Air

Acrylic

21

E10a Air prism deviation of light

(U17301)

Light passes through the glass-air border at point A.
Then it is directed away from the normal axis and af­ter light passes through point B, it is then directed to­ward the normal. The sum of the refraction angles is
referred as the deviation angle δ. It is the angle be­tween the incidence and the outgoing ray.

E11a Reflection of light on one edge of glass prism

(U17301)

When the rays impinge the edge, they are totally re­flected. If the prism is slightly adjusted reflection and
refraction can be observed.

Air

Acrylic

E10b Air prism minimal deviation

(U17301)

In the case of minimal deviation δ

the incidence

min,

angle α is equal to the angle of the outgoing ray ß. The
direction of the refracted light in the prism is parallel
to the edge the ray does not pass through. The refrac­tive index of the prism obey formula (see E9b). The
deviation has an opposite direction as in the case of a
glass prism.

Acrylic

Air

E11b Reflection of light on two edges of glass

prism

(U17301)
The conditions for total reflections are fulfilled on both
edges of the prism. If the top ray of the incidence
light is eliminated, the bottom ray of the outgoing light
disappears. The picture is 180° rotated.

Acrylic

Acrylic

Air

Air

22

E11c Reflection of light on two glass prisms

(U17301)

Conditions for total reflection are fulfilled on every
edge.

Acrylic

Air

E11e Reflection of light on two glass prisms

(U17301)

Conditions necessary for total reflection are fulfilled
on every edge.

E11d Reflection of light on two glass prisms

(U17301)

Conditions necessary for total reflection are fulfilled
on every edge.

E12 Reflection of light on air prism

(U17301)
If the incidence angle of light to the edge of the prism
(25) is smaller than critical angle (42°), the rays are
reflected into the glass. If the angle is greater, a part of
the light passes through the air prism.

Acrylic

Air

23

E13a Light ray passing a convex air-glass boundary

(U17301)

When a ray impinges the air-glass boundary at point
A, it is directed toward the normal. The normal is de­fined as the line from point A to the centre of bound­ary curvature S.

E14a Light ray passing through concave air-glass

boundary

(U17301)
When a ray impinges the boundary at point A, refrac­tion towards the normal is observed. The normal is
defined as the line from point A to the centre of bound­ary curvature S.

Acrylic

Air

E13b Light beam passing through convex air-glass

boundary

(U17301)
Using a boundary of convenient curvature radius and
an auxiliary glass element, where the rays are refracted,
one can observe that the rays are met at the point F' in
the optical axis – figure focus.

Air

Acrylic

E14b Light beam passing through concave air-glass

boundary

(U17301)
The beam after passing the boundary is divergent.
Elongating the refracted light to the other side one can
find a point on the optical axis where the line meets. It
is figure focus F'.

Acrylic

Acrylic

24

E15a Light ray passing through convex glass-air

boundary

(U17301)
When a ray impinges the boundary at point A, refrac­tion away from the normal is observed. The normal
can be defined as the line from point A to the centre of
boundary curvature S.

E16a Light ray passing through concave glass-air

boundary

(U17301)
When a ray impinges the boundary at point A, refrac­tion away from the normal is observed. The normal is
defined as the line from point A to the centre of bound­ary curvature S.

Acrylic

Air

E15b Light beam passing through convex glass-air

boundary

(U17301)
The beam after passing the boundary is divergent. Elon­gating the refracted light to the other side one can find
a point on the optical axis where the line meets. It is
figure focus F'.

Acrylic

Air

E16b Light beam passing through concave glass-air

boundary
(U17301)

The beam is convergent after passing the boundary.
Parallel rays meet in one point of the optical axis –
figure focus F'.

Acrylic

Acrylic

25

E17a Light beam passing through glass convex lens

– beam is parallel to the optical axis

(U17300/U17301)
A convex glass lens behaves as a convergent optical
system and the rays meet at figure focus F' after pass­ing through the lens.

Acrylic

Air

E17c Light beam passing through thick glass

convex lens

(U17301)
By inserting planparallel plates into the space between
two elements (23), a model of a thick lens can be con­structed. The thickness d of the lens can be changed.
If the thickness increases the focal length of the lens
decreases. For a critical thickness the lens changes from
convergent to divergent.

Acrylic

E17b Light beam passing through glass convex lens

– the rays are non-parallel to the optical axis

(U17300/U17301)

The plane ϕ' which is perpendicular to the optical axis,
combined with the figure focus F' is called a figure fo­cus plane. If a beam of perpendicular rays impinges
the convex glass lens, the rays cross the plane ϕ' at
one point.

Acrylic

E18a Light beam passing through glass concave

lens – the rays are parallel to the optical axis

(U17300/U17301)

The rays are divergent after passing a concave glass
lens, they do not create a real figure. By elongating the
rays it is seen that the lines have a common intersec­tion – figure focus F'.

Acrylic

26

E18b Light beam passing through glass concave

lens – the rays are non-parallel to the optical
axis
(U17300/U17301)

The plane ϕ' which is perpendicular to the optical axis,
combined with the figure focus F' is called a figure focus
plane. If a beam of perpendicular rays impinges the
concave glass lens, the elongated lines of the rays cross
the plane ϕ' at one point.

Acrylic

E19b Light beam passing through air convex lens –

the rays are non-parallel to the optical axis
(U17301)

The plane ϕ' which is perpendicular to the optical axis,
combined with the figure focus F' is called a figure focus
plane. If a beam of perpendicular rays impinges the
convex air lens, the elongated lines of the rays cross
the plane ϕ' at one point.

Acrylic

Air

Air

E19a Light beam passing through air convex lens –

the rays are parallel to the optical axis

(U17301)
The rays are divergent after passing a convex air lens,
they do not create a real figure. By elongating the rays
one can see the lines has a common intersection –
figure focus F'.

Acrylic

Air

Air

E20a Light beam passing through air concave lens

– the rays are parallel to the optical axis

(U17301)
A concave air lens behaves as a convergent optical sys­tem and the rays meet at figure focus F' after passing
through the lens.

Acrylic

Air

27

E20b Light beam passing through air concave lens

– the rays are non-parallel to the optical axis

(U17301)

The plane ϕ' which is perpendicular to the optical axis,
combined with figure focus F' is called a figure focus
plane. If a beam of perpendicular rays impinges the
concave air lens, the rays cross the plane ϕ' at one point.

Acrylic

E21b Parameters of thick lenses – focal length

(U17300/U17301)

In the case of a thick lens (a lens with not negligible
thickness) the definition of the focal length as a dis­tance of the focus from the main planes (points – H
and H'), must be taken into account.

Air

E21a Parameters of thick lenses – determination

of radius of curvature

(U17300/U17301)
The lenses in the set have cylindrical refraction sur­faces with circular bottoms with equal radia of curva­ture. You can measure these radii by using a milimetre
grid.

Air

Acrylic

E22a Model of a normal eye

(U17300, transparency A)

Display rays parallel to the optical axis intersect after
passing through uncorrected eye lens at one point of
the retina.
Place the eye lens (1) directly behind the line O2.

Retina

28

Eye lens

E22b Model of short-sighted eye

(U17300, transparency A)

Display rays parallel to the optical axis intersect after
passing through uncorrected eye lens at one point of
the optical axis before the retina.
Place the eye lens (2) directly behind the line O2 and
the correction lens (5) between the lines O1 and O2.

Eye lens

Retina

Correction lens (5)

E23a Correction of spherical aberration by

reducing the beam diameter

(U17300/U17301)
Spherical aberration of a lens can be reduced by re­ducing the diameter of the beam which impinges the
lens. The rays which are far away from the optical axis
must be obscured.

E22c Model of long-sighted eye

(U17300, transparency A)

Display rays parallel to the optical axis intersect after
passing through uncorrected eye lens at one point of
the optical axis after the retina. A correction lens must
be convergent. The focal length f' of the system of eye
lens and the correction lens is:

ff

’’

12

f

’

=

ff

’’

+

12

where f1' is the focal length of the eye lens and f2' is
the focal length of the correction lens.

Eye lens

Retina

Correction lens (4),

(between O1 and O2)

E23b Correction of spherical aberration by

combination of lenses

(U17300, transparency E)

The spherical aberrations of divergent and convergent
lenses have an inverse effect. By a convenient
combination of these two types of lenses the aberra­tion can be corrected. The aberration ∆f = f

– f2 is

1

defined as the difference between the focal length f
of marginal beam rays and the focal length f2 of
paraxial rays. In the case of a convergent lens the
aberration is of a plus sign and for a divergent lens it is
a minus sign.

1

29

E24a Keplerian telescope

(U17300, transparency D)

The figure from Kepler's telescope is reversed. This can
be verified by obscuring a marginal ray. One can see
that if the top ray is obscured, in the output ray the
bottom ray disappears. The figure is unreal and
magnified.

Objective

The figure is created by parallel rays, so it is unreal
and magnified. If the top ray of the incident beam is
obscured, the top ray of the output beam disappears.

Objective

Ocular

E25 Camera

(U17300, transparency B)
The lens of the camera is a convergent optical system.
The figure which appears on the rear part of the cam­era is real and reversed. It is directed onto the optical
material.

Ocular

E24b Galileian telescope

(U17300, transparency C)

In this experiment the incident angle can be changed.
The larger change of the output angle is observed (the
viewing angle is magnified – the figure is magnified).

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Germany • www.3bscientific.com • Technical amendments are possible

30

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

Jeu d’optique laser de démonstration U17300 et jeu complémentaire U17301

Manuel d’utilisation

1/05 ALF

Sommaire

®

Page Exp. n

1 Introduction
2 Eléments fournis
3 E1 Réflexion sur un miroir plan U17300/U17301
3 E2 Réflexion sur deux miroirs plans U17301
3 E3a Réflexion sur un miroir concave – Rayons lumineux parallèles

4 E3b Réflexion sur un miroir concave – Rayons lumineux non parallèles

4 E4a Réflexion sur un miroir convexe – Rayons lumineux parallèles

4 E4b Réflexion sur un miroir convexe – Rayons lumineux non parallèles

5 E5a Réfraction d'un rayon lumineux lors du passage de l'air vers l'acrylique U17300
5 E5b Profondeur virtuelle d'un objet U17301
5 E6a Réfraction d'un rayon lumineux lors du passage de l'acrylique vers l'air U17300
6 E6b Réfraction sur un prisme acrylique U17300/U17301
6 E6c Angle critique, réflexion totale U17300
6 E6d Réflexion totale – Propagation de la lumière dans des fibres optiques U17300
7 E7 Décalage d'un rayon lumineux, lame acrylique à faces parallèles U17300/U17301
7 E8 Décalage d'un rayon lumineux, air entre deux lames acryliques

7 E9a Déflexion d'un rayon lumineux à travers un prisme acrylique U17300/U17301
8 E9b Déflexion minimum à travers un prisme acrylique U17300/U17301
8 E10a Déflexion d'un rayon lumineux à travers un prisme d'air U17301
8 E10b Déflexion minimum à travers un prisme d'air U17301
9 E11a Réflexion sur une arête d'un prisme acrylique U17301
9 E11b Réflexion sur deux arêtes d'un prisme acrylique U17301
9 E11c Réflexion sur deux prismes acryliques U17301
10 E11d Réflexion sur deux prismes acryliques U17301
10 E11e Réflexion sur deux prismes acryliques U17301
10 E12 Réflexion sur un prisme d'air U17301
11 E13a Passage d'un rayon lumineux à travers une surface limite

11 E13b Passage de rayons lumineux à travers une surface limite

11 E14a Passage d'un rayon lumineux à travers une surface limite

12 E14b Passage de rayons lumineux à travers une surface limite

12 E15a Passage d'un rayon lumineux à travers une surface limite

12 E15b Passage de rayons lumineux à travers une surface limite acrylique-air U17301

o

Expérience Jeu d’appareils

à l'axe optique U17300

à l'axe optique U17300

à l'axe optique U17300

à l'axe optique U17300

à faces parallèles U17301

convexe air-acrylique U17301

convexe air-acrylique U17301

concave air-acrylique U17301

concave air-acrylique U17301

convexe acrylique-air U17301

31

13 E16a Passage d'un rayon lumineux à travers une surface limite

concave acrylique-air U17301

13 E16b Passage de rayons lumineux à travers une surface limite

acrylique-air concave U17301

13 E17a Passage de rayons lumineux à travers une lentille convexe -

Rayons lumineux parallèles à l'axe optique U17300/U17301

14 E17b Passage de rayons lumineux à travers une lentille convexe –

Rayons lumineux non parallèles à l'axe optique U17300/U17301

14 E17c Passage de rayons lumineux à travers une lentille acrylique

convexe épaisse U17301

14 E18a Passage de rayons lumineux à travers une lentille concave –

Rayons lumineux parallèles à l'axe optique U17300/U17301

15 E18b Passage de rayons lumineux à travers une lentille concave –

Rayons lumineux non parallèles à l'axe optique U17300/U17301

15 E19a Passage de rayons lumineux à travers une lentille d'air convexe –

Rayons lumineux parallèles à l'axe optique U17301

15 E19b Passage de rayons lumineux à travers une lentille d'air convexe –

Rayons lumineux non parallèles à l'axe optique U17301

16 E20a Passage de rayons lumineux à travers une lentille d'air concave –

Rayons lumineux parallèles à l'axe optique U17301

16 E20b Passage de rayons lumineux à travers une lentille d'air concave –

Rayons lumineux non parallèles à l'axe optique U17301
16 E21a Paramètres de lentilles épaisses – Détermination du rayon de courbure U17300/U17301
17 E21b Paramètres de lentilles épaisses – Distance focale U17300/U17301
17 E22a Modèle d'un œil U17300
17 E22b Modèle d'un œil, myopie U17300
18 E22c Modèle d'un œil, hypermétropie U17300
18 E23a Correction d'une aberration sphérique par la réduction du diamètre

de faisceau U17300/U17301
18 E23b Correction de l'aberration sphérique par une combinaison de lentilles U17300
19 E24a Télescope d'après Kepler U17300
19 E24b Télescope d'après Galilée U17300
19 E25 Appareil photo U17300

Jeu d'optique laser de démonstration U17300
Jeu complémentaire laser de démonstration U17301

La colonne " Jeu d'appareils " propose le jeu d'appareils requis pour l'expérience en question, soit U17300, soit
U17301, soit les deux.

Einleitung

Le jeu d'optique laser de démonstration permet le
montage simple et clair d'expériences destinées à il­lustrer les principes de l'optique géométrique ainsi que
le mode de fonctionnement de divers appareils opti­ques. Le laser à diodes, 5 rayons, U17302, servira de
source lumineuse.
Ce manuel d'utilisation décrit de nombreuses expérien­ces fondamentales utilisant les éléments optiques des
deux jeux d'appareils U17300 et U17301. Chaque des­cription d'expérience est composée de trois parties :

1. une description sommaire de l'expérience

2. une représentation graphique de l'expérience

3. une illustration du montage
Sous chaque titre, vous trouverez entre parenthèses le
jeu d'appareils qui permet de réaliser l'expérience,
U17300, U17301 ou U17300/U17301. La même indi­cation est précisée dans la dernière colonne du som­maire.

Le laser à diodes U17302 constitue un élément central
des expériences. Cinq diodes laser génèrent cinq rayons
lumineux parallèles. Vous pouvez sélectionner le nom­bre de rayons lumineux émergents. Une plaque mé­tallique fournie, présentant des alésages, est placée
devant le laser à diodes. Evitez tout contact direct des
yeux avec le rayon laser.

Eléments fournis

Jeu d'optique laser de démonstration U17300

1 Lentille biconcave
2 Lentille biconvexe
3 Lentille biconvexe
4 Lentille biconvexe
5 Lentille biconvexe
6 Petite lentille plan-concave
7 Petite lentille plan-convexe
8 Grande lentille plan-convexe

32

9 Miroir concave
10 Miroir convexe
11 Miroir plan
12 Lame à faces parallèles
13 Prisme
14 Fibre optique

Feuilles

A Modèle d'un œil
B Appareil photo
C Télescope d'après Galilée
D Télescope d'après Kepler
E Aberration sphérique
F Graduation angulaire 360°

Jeu complémentaire U17301

21 Lentille d'air biconcave
22 Lentille biconcave
23 Lentille d'air biconvexe
24 Lentille biconvexe
25 Prisme d'air
26 Prisme équilatéral
27 2 prismes en angle droit
28 Lame à faces parallèles carrée
29 2 lame à faces parallèles rectangulaires
11 2 miroirs plans

E2 Réflexion sur deux miroirs plans

(U17301)

Démonstration de l'équation :

δ = 2 γ
l'angle δ étant formé par le rayon incident et le rayon
réfléchi et γ représentant l'angle entre les surfaces du
miroir.

E1 Réflexion sur un miroir plan

(U17300/U17301)
Illustration de la loi de la réflexion. Un rayon lumi­neux qui rencontre la surface plane d'un miroir dans
un angle d'incidence α est réfléchi dans un angle ß.

α = ß

Les deux angles sont mesurés par rapport à la norma­le.

E3a Réflexion sur un miroir concave – Rayons

lumineux parallèles à l'axe optique

(U17300)
La focale f d'un réflecteur de concentration est déter­minée par la distance VF. Le rayon de courbure peut
être calculé à l'aide de la formule

fr=

2

La distance VS est deux fois plus longue que VF.

33

E3b Réflexion sur un miroir concave – Rayons

lumineux non parallèles à l'axe optique

(U17300)

L'axe ϕ est perpendiculaire à l'axe optique et traverse
le foyer. On l'appelle le plan focal. Les rayons incidents
parallèles sont réfléchis et se rencontrent sur le plan
focal ϕ. Si les rayons sont parallèles à l'axe optique, le
foyer F se situe par-dessus.

E4b Réflexion sur un miroir convexe – Rayons

lumineux non parallèles à l'axe optique

(U17300)

L'axe ϕ est perpendiculaire à l'axe optique et traverse
le foyer. On l'appelle le plan focal. Si les rayons tombant
sur le miroir sont parallèles, ils sont divergés de telle
sorte qu'on a l'impression qu'ils partent d'un point
situé sur le plan focal ϕ derrière le miroir.

E4a Réflexion sur un miroir convexe – Rayons

lumineux parallèles à l'axe optique

(U17300)
Les rayons réfléchis semblent partir d'un point situé
derrière le miroir. Il s'agit du foyer virtuel. La distance
VF détermine la focale du miroir. Le rayon de courbure
peut être calculé à l'aide de la formule

fr=

2

La distance VS est deux fois plus longue que VF.

E5a Réfraction d'un rayon lumineux lors du

passage de l'air vers l'acrylique

(U17300, feuille F)

Lors du passage d'un rayon d'un milieu d'indice de
réfraction n1 vers un milieu d'indice de réfraction n2,
son changement de direction est déterminé par la loi
de la réfraction de Snellius :
n

sin α = n

1

α est l'angle d'incidence dans le milieu n

sin ß

2

et ß l'angle

1

de réfraction dans le milieu n2.

Air

Acrylique

34

E5b Profondeur virtuelle d'un objet

(U17301)
Expérience permettant d'observer la profondeur vir­tuelle d'un objet dans de l'eau ou derrière de
l'acrylique, vu depuis l'air.

Crayon

Air

Acrylique

E6b Réfraction sur un prisme acrylique

(U17300/U17301)
Lors du passage d'un rayon lumineux de l'acrylique
vers l'air, on peut écrire la loi de Snellius sous la forme
suivante :

n

sin α = sin ß

1

Indice de réfraction n2 = 1.

Acrylique

E6a Réfraction d'un rayon lumineux lors du

passage de l'acrylique vers l'air

(U17300, feuille F)

L'angle de réfraction ß est supérieur à l'angle
d'incidence α. Le rayon est réfracté en s'écartant de la
normale.

Acrylique

Air

E6c Angle critique, réflexion totale

(U17300, feuille F)
Plus l'angle d'incidence est élevé, plus l'angle de
réfraction est important. Si n1 < n2, on obtient un ang­le critique α. Le rayon réfracté se situe alors à la surface
limite entre les deux milieux. Si l'angle d'incidence est
supérieur à l'angle critique, il n'y a plus de réfraction
et toute la lumière est réfléchie. Dans ce cas, on parle
de réflexion totale.

Acrylique

Air

35

E6d Réflexion totale – Propagation de la lumière

dans des fibres optiques

(U17300)
De la lumière se propage dans une fibre optique par la
réflexion totale. Le paramètre, l'ouverture numérique,
détermine l'angle qui ne doit pas être dépassé. Il
correspond au sinus de l'angle d'entrée maximum de
la lumière. Lorsque la fibre optique est pliée, ce
paramètre détermine également le plus petit rayon. Il
ne peut pas passer au-dessous de la valeur minimum
lorsque la fibre optique est installée.

Acrylique

E8 Décalage d'un rayon lumineux, air entre deux

lames acryliques à faces parallèles

(U17301)
Dans ce cas, on observe un décalage entre le rayon
incident et le rayon émergent. En revanche, ce décalage
va dans le sens contraire à celui observé dans le cas de
la plaque acrylique.

Acrylique

Acrylique

Air

E7 Décalage d'un rayon lumineux, lame

acrylique à faces parallèles

(U17300/U17301)
Lorsqu'un rayon lumineux traverse une lame à faces
parallèles, sa direction n'est pas modifiée. Le rayon
émergent est décalé de la distance d. Avec une
épaisseur de lame h, on obtient pour d :

sin

αβ

−

dh=

()

cos

β

Acrylique

Air

E9a Déflexion d'un rayon lumineux à travers un

prisme acrylique

(U17300/U17301)
Dans un prisme acrylique, un rayon incident est
réfracté au point A vers la normale. Au point
d'émergence B, la réfraction s'écarte de la normale.
La somme de tous les angles de réfraction est l'angle
de déflexion δ. Il s'agit de l'angle entre le rayon incident
et le rayon émergent.

Air

Acrylique

36

E9b Déflexion minimum à travers un prisme

acrylique

(U17300/U17301)

On peut montrer que l'angle d'incidence α, avec un
angle de déflexion minimum δ

, est égal à l'angle

min

d'émergence ß. Dans le prisme, le rayon réfracté est
alors parallèle au côté qui n'est pas traversé. On peut
appliquer l'équation suivante pour calculer l'indice de
réfraction du prisme :

+

δϕ

min

sin

sin

2

ϕ

2

Air

n =

E10b Déflexion minimum à travers un prisme d'air

(U17301)

En présence d'un angle de déflexion minimum δ

min

l'angle d'incidence α est égal à l'angle d'émergence ß.
Dans le prisme, le rayon réfracté est alors parallèle au
côté qui n'est pas traversé. On peut appliquer
l'équation suivante pour calculer l'indice de réfraction
du prisme : (voir E9b). Le sens de la déflexion est
l'inverse de celui d'un prisme acrylique.

Air

,

Acrylique

E10a Déflexion d'un rayon lumineux à travers un

prisme d'air
(U17301)

De la lumière traverse la surface limite acrylique-air
au point A. Le rayon est réfracté en s'écartant de la
normale. Au point B, il est réfracté dans la direction
de la normale. La somme de tous les angles de
réfraction est l'angle de déflexion δ. Il s'agit de l'angle
entre le rayon incident et le rayon émergent.

Acrylique

E11a Réflexion sur une arête d'un prisme

acrylique
(U17301)

Lorsqu'ils touchent l'arête, les rayons sont entièrement
réfléchis. Si l'on tourne légèrement le prisme, on peut
observer tant une réfraction qu'une réflexion.

Acrylique

Air

Acrylique

Air

37

E11b Réflexion sur deux arêtes d'un prisme

acrylique
(U17301)

Dans ce cas, les conditions sont remplies pour obtenir
une réflexion totale sur les deux arêtes. Si le rayon
incident supérieur est masqué, le rayon émergent
inférieur disparaît. L'image est inversée à 180°.

Acrylique

Air

E11d Réflexion sur deux prismes acryliques

(U17301)

Les conditions sont remplies pour obtenir une réflexion
totale sur toutes les arêtes des prismes.

E11c Réflexion sur deux prismes acryliques

(U17301)

Les conditions sont remplies pour obtenir une réflexion
totale sur toutes les arêtes des prismes.

Acrylique

Air

E11e Réflexion sur deux prismes acryliques

(U17301)

Les conditions sont remplies pour obtenir une réflexion
totale sur toutes les arêtes des prismes.

38

E12 Réflexion sur un prisme d'air

(U17301)
Si l'angle d'incidence des rayons lumineux est inférieur
à l'angle critique (42°), les rayons sont réfléchis vers
l'acrylique. Si l'angle est supérieur, une partie de la
lumière traversera le prisme d'air.

Acrylique

E13b Passage de rayons lumineux à travers une

surface limite convexe air-acrylique
(U17301)

Les rayons incidents sont réfractés à deux reprises et
se rencontrent sur l'axe optique au point F', au foyer.

Air

E13a Passage d'un rayon lumineux à travers une

surface limite convexe air-acrylique

(U17301)

Si un rayon lumineux traverse la surface limite air­acrylique au point A, il est réfracté vers la normale. La
normale est la droite reliant le point A au point central
de courbure S.

Acrylique

E14a Passage d'un rayon lumineux à travers une

surface limite concave air-acrylique
(U17301)

Si le rayon lumineux rencontre la surface limite au
point A, on observe une réfraction vers la normale. La
normale est la droite reliant le point A au point central
de courbure S.

Acrylique

Air

39

Air

Acrylique

E14b Passage de rayons lumineux à travers une

surface limite concave air-acrylique
(U17301)

Lorsque le faisceau a traversé la surface limite
acrylique-air, il subit une réfraction divergente. Si les
rayons réfractés sont prolongés vers l'arrière, ils se
rencontrent en un point de l'axe optique. Ce point est
le foyer virtuel F'.

Acrylique

E15b Passage de rayons lumineux à travers une

surface limite convexe acrylique-air
(U17301)

Lorsque le faisceau a traversé la surface limite
acrylique-air, il subit une réfraction divergente. Si les
rayons réfractés sont prolongés vers l'arrière, ils se
rencontrent en un point de l'axe optique. Ce point est
le foyer virtuel F'.

Acrylique

E15a Passage d'un rayon lumineux à travers une

surface limite convexe acrylique-air
(U17301)

Lorsque le faisceau a traversé le point A, il est réfracté
en s'écartant de la normale. La normale est la droite
reliant le point A au point central de courbure S.

Air

Acrylique

E16a Passage d'un rayon lumineux à travers une

surface limite concave acrylique-air
(U17301)

Lorsque le faisceau a traversé le point A, il est réfracté
en s'écartant de la normale. La normale est la droite
reliant le point A au point central de courbure S.

Air

Acrylique

40

E16b Passage de rayons lumineux à travers une

surface limite concave acrylique-air

(U17301)

Lorsque le faisceau a traversé la surface limite, il
devient convergent. Des rayons parallèles se
rencontrent en un point de l'axe optique, le foyer F'.

Acrylique

incidents sont réfractés et se rencontrent en un point
sur l'axe ϕ'.

Acrylique

E17a Passage de rayons lumineux à travers une

lentille convexe – Rayons lumineux

parallèles à l'axe optique

(U17300/U17301)

Une lentille acrylique convexe est une lentille de
convergence et, après avoir traversé la lentille, les
rayons lumineux se rencontrent au foyer F'.

Acrylique

Air

E17c Passage de rayons lumineux à travers une

lentille acrylique convexe épaisse
(U17301)

En plaçant une lame à faces parallèles entre deux
lentilles (23), on peut illustrer le modèle d'une lentille
épaisse. En modifiant l'épaisseur d de la lentille, on
modifie en même temps la focale. Plus la lentille est
épaisse, plus la focale est petite. A partir d'une
épaisseur critique, la lentille de convergence devient
une lentille divergente.

Acrylique

E17b Passage de rayons lumineux à travers une

lentille convexe – Rayons lumineux non

parallèles à l'axe optique

(U17300/U17301)

L'axe ϕ' est perpendiculaire à l'axe optique et traverse
le foyer F'. On l'appelle le plan focal. Les rayons

41

E18a Passage de rayons lumineux à travers une

lentille concave – Rayons lumineux
parallèles à l'axe optique
(U17300/U17301)

Après avoir traversé la lentille, les rayons lumineux sont
divergents. La lentille ne projette aucune d'image.
Prolongés vers l'arrière, les rayons se rencontrent au
foyer virtuel F'.

E19a Passage de rayons lumineux à travers une

lentille d'air convexe – Rayons lumineux
parallèles à l'axe optique
(U17301)

Après avoir traversé la lentille, les rayons lumineux sont
divergents. La lentille ne projette aucune d'image.
Prolongés vers l'arrière, les rayons se rencontrent au
foyer virtuel F'.

Acrylique

E18b Passage de rayons lumineux à travers une

lentille concave – Rayons lumineux non
parallèles à l'axe optique
(U17300/U17301)

L'axe ϕ' est perpendiculaire à l'axe optique et traverse
le foyer virtuel F'. On l'appelle le plan focal. Si les rayons
réfractés sont prolongés, ils se rencontrent en un point
sur l'axe ϕ'.

Acrylique

Acrylique

Air

Air

E19b Passage de rayons lumineux à travers une

lentille d'air convexe – Rayons lumineux
non parallèles à l'axe optique
(U17301)

L'axe ϕ' est perpendiculaire à l'axe optique et traverse
le foyer virtuel F'. On l'appelle le plan focal. Si les rayons
réfractés sont prolongés, ils se rencontrent en un point
sur l'axe ϕ'.

Acrylique

Air

42

Air

E20a Passage de rayons lumineux à travers une

lentille d'air concave – Rayons lumineux

parallèles à l'axe optique

(U17301)

Une lentille d'air concave se comporte comme une
lentille de convergence et, après avoir traversé la
lentille, les rayons lumineux se rencontrent au foyer
F'.

Acrylique

Air

E21a Paramètres de lentilles épaisses –

Détermination du rayon de courbure
(U17300/U17301)

Les lentilles du jeu d'optique laser présentent une
surface de réfraction cylindrique sur base circulaire
avec les mêmes rayons de courbure. Du papier
millimétrique permet de déterminer ces rayons.

E20b Passage de rayons lumineux à travers une

lentille d'air concave – Rayons lumineux

parallèles à l'axe optique

(U17301)

L'axe ϕ' est perpendiculaire à l'axe optique et traverse
le foyer F'. On l'appelle le plan focal. Si les rayons
réfractés sont prolongés, ils se rencontrent en un point
sur l'axe ϕ'.

Acrylique

Air

E21b Paramètres de lentilles épaisses – Distance

focale
(U17300/U17301)

Ce sont des lentilles dont l'épaisseur n'est pas
négligeable. Lors de la définition de la focale, il faut
tenir compte de l'écart entre les deux plans principaux
H et H'.

Air

Acrylique

43

E22a Modèle d'un œil

f

ff

ff

’

’’

’’

=

+

12

12

(U17300, feuille A)

Les rayons parallèles à l'axe optique sont réfractés par
la lentille oculaire et se rencontrent en un point sur la
rétine.
Placer la lentille oculaire (1) directement derrière la
ligne O2.

Rétine

Lentille oculaire

E22c Modèle d'un œil, hypermétropie

(U17300, feuille A)

Les rayons parallèles à l'axe optique sont réfractés par
la lentille oculaire et se rencontrent en un point
derrière la rétine. Une lentille de correction est une
lentille de convergence. L'équation suivante permet
de calculer la focale f' du système de lentilles :

f1' étant la focale de la lentille oculaire et f2' la lentille

de correction.

E22b Modèle d'un œil, myopie

(U17300, feuille A)

Les rayons parallèles à l'axe optique sont réfractés par
la lentille oculaire et se rencontrent en un point devant
la rétine.
Placez la lentille oculaire (2) directement derrière la
ligne O2 et la lentille de correction (5) entre les lignes
O1 et O2.

Lentille oculaire

Rétine

Lentille oculaire

Rétine

Lentille de correction (4),

(entre O1 et O2)

Lentille de correction (5)

44

E23a Correction d'une aberration sphérique par la

réduction du diamètre de faisceau

(U17300/U17301)
Pour réduire l'aberration sphérique d'une lentille, on
peut diminuer le diamètre du faisceau qui traverse la
lentille. Il suffit de masquer les rayons se trouvant sur
les bords extérieurs.

E24a Télescope d'après Kepler

(U17300, feuille D)

L'objectif dans le télescope de Kepler génère une image
réelle réduite de l'objet observé, agrandie par l'oculaire
qui fait fonction de loupe. L'image est inversée (le haut
et le bas, ainsi que la gauche et la droite sont inversés)
et fortement agrandie. Pour illustrer ce phénomène,
masquez l'un des rayons se trouvant sur les bords
extérieurs. Si le rayon incident supérieur est masqué,
le rayon émergent inférieur disparaît.

E23b Correction de l'aberration sphérique par une

combinaison de lentilles

(U17300, feuille E)

L'aberration sphérique de lentilles de convergence et
de divergence ont un effet inverse. Une combinaison
de lentilles permet de corriger cette erreur. L'aberration
∆f = f

– f2 est définie comme la différence entre la

1

focale f1 des rayons extérieurs et la focale f2 des rayons
intérieurs. Avec les lentilles convergentes, l'aberration
a un signe positif et avec les lentilles divergentes, elle
présente un signe négatif.

Objectif

Oculaire

45

E24b Télescope d'après Galilée

(U17300, feuille C)

Dans la lunette de Galilée, les rayons provenant de
l'objectif rencontrent une lentille divergente avant
d'atteindre le foyer. Les rayons atteignent l'œil
parallèlement. L'image de l'objet est agrandie, droite
et à l'endroit.

Objectif

Oculaire

E25 Appareil photo

(U17300, feuille B)
La lentille de l'appareil photo est une lentille de
convergence. Sur le film se trouvant à l'arrière de
l'appareil, elle génère une image réelle, mais à l'envers,
d'un objet.

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Allemagne • www.3bscientific.com • Sous réserve de modifications techniques

46

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

®

Set dimostrativo di ottiche per laser U17300

e set supplementare U17301

Istruzioni per l’uso

1/05 ALF

Sommario

Pagina N. esp. Esperimento Kit da utilizzare

1 Introduzione
2 Fornitura
3 E1 Riflessione su specchio piano U17300/U17301
3 E2 Riflessione su due specchi piani U17301
3 E3a Riflessione su specchio concavo – Fasci luminosi paralleli

all'asse ottico U17300

4 E3b Riflessione su specchio concavo – Fasci luminosi non paralleli

all'asse ottico U17300

4 E4a Riflessione su specchio convesso – Fasci luminosi paralleli

all'asse ottico U17300

4 E4b Riflessione su specchio convesso – Fasci luminosi non paralleli

all'asse ottico U17300

5 E5a Rifrazione di un fascio luminoso durante il passaggio dall'aria

all'acrilico U17300
5 E5b Profondità apparente degli oggetti U17301
5 E6a Rifrazione di un fascio luminoso durante il passaggio dall'acrilico

all'aria U17300
6 E6b Rifrazione su un prisma di acrilico U17300/U17301
6 E6c Angolo critico, riflessione totale U17300
6 E6d Riflessione totale – Diffusione di luce in fotoconduttori U17300
7 E7 Spostamento di un fascio luminoso mediante lastra

di acrilico pianparallela U17300/U17301
7 E8 Spostamento di un fascio luminoso mediante aria tra due lastre

di acrilico pianparallele U17301
7 E9a Deviazione di un fascio luminoso attraverso un prisma di acrilico U17300/U17301
8 E9b Deviazione minima attraverso un prisma di acrilico U17300/U17301
8 E10a Deviazione di un fascio luminoso attraverso un prisma di aria U17301
8 E10b Deviazione minima attraverso un prisma di aria U17301
9 E11a Riflessione su un bordo di un prisma di acrilico U17301
9 E11b Riflessione su due bordi di un prisma di acrilico U17301
9 E11c Riflessione su due prismi di acrilico U17301
10 E11d Riflessione su due prismi di acrilico U17301
10 E11e Riflessione su due prismi di acrilico U17301
10 E12 Riflessione su un prisma di aria U17301
11 E13a Passaggio di un fascio luminoso attraverso una superficie limite

convessa di aria-acrilico U17301
11 E13b Passaggio di fasci luminosi attraverso una superficie limite

convessa di aria-acrilico U17301
11 E14a Passaggio di un fascio luminoso attraverso una superficie limite

concava di aria-acrilico U17301
12 E14b Passaggio di fasci luminosi attraverso una superficie limite

concava di aria-acrilico U17301

47

12 E15a Passaggio di un fascio luminoso attraverso una superficie limite

convessa di acrilico-aria U17301

12 E15b Passaggio di fasci luminosi attraverso una superficie limite

convessa di acrilico-aria U17301

13 E16a Passaggio di un fascio luminoso attraverso una superficie limite

concava di acrilico-aria U17301

13 E16b Passaggio di fasci luminosi attraverso una superficie limite

concava di acrilico-aria U17301

13 E17a Passaggio di fasci luminosi attraverso una lente convessa di acrilico –

lasci luminosi paralleli all'asse ottico U17300/U17301

14 E17b Passaggio di fasci luminosi attraverso una lente convessa di acrilico –

fasci luminosi non paralleli all'asse ottico U17300/U17301

14 E17c Passaggio di fasci luminosi attraverso una lente convessa

di acrilico spessa U17301

14 E18a Passaggio di fasci luminosi attraverso una lente concava di acrilico –

fasci luminosi paralleli all'asse ottico U17300/U17301

15 E18b Passaggio di fasci luminosi attraverso una lente concava di acrilico –

fasci luminosi non paralleli all'asse ottico U17300/U17301

15 E19a Passaggio di fasci luminosi attraverso una lente convessa di aria –

fasci luminosi paralleli all'asse ottico U17301

15 E19b Passaggio di fasci luminosi attraverso una lente convessa di aria –

fasci luminosi non paralleli all'asse ottico U17301

16 E20a Passaggio di fasci luminosi attraverso una lente concava di aria –

fasci luminosi paralleli all'asse ottico U17301

16 E20b Passaggio di fasci luminosi attraverso una lente concava di aria –

fasci luminosi non paralleli all'asse ottico U17301
16 E21a Parametri di lenti spesse – determinazione del raggio di curvatura U17300/U17301
17 E21b Parametri di lenti spesse – distanza focale U17300/U17301
17 E22a Modello di occhio U17300
17 E22b Modello di occhio miope U17300
18 E22c Modello di occhio ipermetrope U17300
18 E23a Correzione dell'aberrazione sferica mediante riduzione del diametro

del fascio di raggi U17300/U17301
18 E23b Correzione dell'aberrazione sferica mediante una combinazione di lenti U17300
19 E24a Telescopio kepleriano U17300
19 E24b Telescopio galileiano U17300
19 E25 Fotocamera U17300

Set dimostrativo di ottiche per laser U17300
Kit aggiuntivo U17301

La colonna "Kit da utilizzare" elenca i kit necessari per i rispettivi esperimenti, U17300, U17301 o entrambi.

Introduzione

Il set dimostrativo di ottiche per laser consente di ot­tenere strutture per esperimenti semplici e chiare per
la rappresentazione dei principi dell'ottica geometri­ca e del funzionamento di apparecchi ottici diversi.
Come sorgente luminosa si utilizza il laser a diodi a 5
raggi U17302.
Le presenti istruzioni per l'uso contengono le descri­zioni di vari esperimenti fondamentali con gli elementi
ottici dei due kit U17300 e U17301. Ciascuna descri­zione degli esperimenti è suddivisa in tre parti:

1. Una descrizione semplice dell'esperimento

2. Una rappresentazione grafica
dell'esperimento

3. Una raffigurazione della struttura
dell'esperimento

Sotto il titolo dell'esperimento, tra parentesi è indica­to il kit da utilizzare per l'esecuzione dell'esperimen­to, U17300, U17301 o U17300/U17301. La stessa nota
è riportata anche nell'ultima colonna del sommario.
Una parte molto importante delle strutture degli espe­rimenti è il laser a diodi U17302. Cinque diodi laser
generano cinque fasci luminosi paralleli. È possibile
scegliere il numero dei fasci luminosi emessi. A tale
scopo, la dotazione del laser comprende una piastra
di metallo con fori da collocare davanti al laser a diodi.
Durante l'uso del laser, evitare di rivolgere lo sguardo
direttamente verso il raggio laser.

48

Fornitura

Set dimostrativo di ottiche per laser U17300

1 Lente biconcava
2 Lente biconvessa
3 Lente biconvessa
4 Lente biconvessa
5 Lente biconvessa
6 Lente pianoconcava piccola
7 Lente pianoconvessa piccola
8 Lente pianoconvessa grande
9 Specchio, concavo
10 Specchio, convesso
11 Specchio piano
12 Lastra pianparallela
13 Prisma
14 Fotoconduttore

Pellicole

A Modello di occhio
B Fotocamera
C Telescopio galileiano
D Telescopio kepleriano
E Aberrazione sferica
F Scala angolare 360°

E2 Riflessione su due specchi piani

(U17301)

Dimostrazione del rapporto:

δ = 2 γ
dove δ è l'angolo tra il fascio luminoso incidente e
quello riflesso e γ è l'angolo tra le superfici degli spec­chi.

Set supplementare U17301

21 Lente di aria biconcava
22 Lente biconcava
23 Lente di aria biconvessa
24 Lente biconvessa
25 Prisma di aria
26 Prisma equilatero
27 2 prismi rettangolari
28 Lastra pianparallela, quadrata
29 2 lastre pianparallele, rettangolari
11 2 Specchio piano

E1 Riflessione su specchio piano

(U17300/U17301)

Rappresentazione della legge di riflessione. Un fascio
luminoso incidente sotto l'angolo di incidenza α su
una superficie a specchio piana, viene riflesso sotto
l'angolo ß

α = ß

Entrambi gli angoli vengono misurati verso la perpen­dicolare incidente.

49

E3a Riflessione su specchio concavo – Fasci

luminosi paralleli all'asse ottico

(U17300)
La distanza focale f di uno specchio concavo è deter­minata dalla lunghezza della distanza VF. Il raggio di
curvatura può essere calcolato con la formula

fr=

2

La distanza VS è il doppio della distanza VF.

E4a Riflessione su specchio convesso – Fasci

luminosi paralleli all'asse ottico

(U17300)
I raggi riflessi sembrano partire da un punto dietro lo
specchio. Questo punto si chiama fuoco virtuale. La
lunghezza della linea VF determina la distanza focale
dello specchio. Il raggio di curvatura può essere calco­lato con la formula

fr=

2

La distanza VS è il doppio della distanza VF.

E3b Riflessione su specchio concavo – Fasci

luminosi non paralleli all'asse ottico

(U17300)

L'asse ϕ è perpendicolare all'asse ottico e attraversa il
fuoco. Viene definito piano focale. I raggi paralleli in­cidenti vengono riflessi e si incontrano in un punto sul
piano focale ϕ. Se i raggi sono paralleli all'asse ottico,
il punto si trova sull'asse e viene chiamato fuoco F.

E4b Riflessione su specchio convesso – Fasci

luminosi non paralleli all'asse ottico

(U17300)
L'asse ϕ è perpendicolare all'asse ottico e attraversa il
fuoco. Viene definito piano focale. Se lo specchio vie­ne colpito da raggi paralleli, questi vengono diffusi in
modo che sembrino partire da un punto sul piano
focale ϕ dietro lo specchio.

50

E5a Rifrazione di un fascio luminoso durante il

passaggio dall'aria all'acrilico

(U17300, pellicola F)

Se un fascio luminoso passa da un mezzo con indice di
rifrazione n1 in un altro mezzo con indice di rifrazione

n2, è possibile determinarne la deviazione di direzio-

ne con la legge di rifrazione di Snellius:
n

sin α = n

1

sin ß

2

α è l'angolo di incidenza nel mezzo n1 e ß è l'angolo
di rifrazione nel mezzo n2.

Aria

Acrilico

E6a Rifrazione di un fascio luminoso durante il

passaggio dall'acrilico all'aria

(U17300, pellicola F)

L'angolo di rifrazione ß è maggiore dell'angolo di inci­denza α. Il raggio viene interrotto dalla perpendicola-
re incidente.

Acrilico

Aria

E5b Profondità apparente degli oggetti

(U17301)
Struttura dell'esperimento per l'osservazione delle pro­fondità apparenti di un oggetto in acqua o dietro
acrilico visto dall'aria.

Matita

Aria

Acrilico

E6b Rifrazione su un prisma di acrilico

(U17300/U17301)
Se un fascio luminoso passa dall'acrilico all'aria, la leg­ge di Snellius può essere scritta nella forma seguente:

n

sin α = sin ß

1

Indice di rifrazione dell'aria n2 = 1.

Acrilico

E6c Angolo critico, riflessione totale

(U17300, pellicola F)
Tanto più grande è l'angolo di incidenza, quanto più
grande è l'angolo di rifrazione. Se n1 < n2, esiste un
angolo critico α. Il raggio interrotto si trova pertanto
sulla superficie limite tra i due mezzi. Se l'angolo di

51

incidenza è maggiore dell'angolo critico, non si verifi­ca più alcuna rifrazione e tutta la luce viene riflessa.
In tal caso si parla di riflessione totale.

Acrilico

Aria

E7 Spostamento di fasci luminosi mediante

lastra di acrilico pianparallela

(U17300/U17301)
Se un fascio luminoso attraversa una lastra pianparal­lela la sua direzione non cambia. Il raggio uscente vie­ne spostato del valore d. Con spessore della piastra h,
d è uguale a:

sin

αβ

−

dh=

()

cos

β

E6d Riflessione totale – Diffusione di luce in

fotoconduttori

(U17300)
La luce si diffonde mediante la riflessione totale in un
fotoconduttore. Il parametro apertura numerica de­termina l'angolo da non superare. Corrisponde al seno
dell'angolo di ingresso massimo della luce. Anche il
raggio minimo viene determinato da questo parame­tro quando il fotoconduttore è piegato e non può es­sere inferiore quando il fotoconduttore è installato.

Acrilico

Aria

Acrilico

E8 Spostamento di un fascio luminoso mediante

aria tra due lastre di acrilico pianparallele

(U17301)
In questo caso si verifica uno spostamento tra il fascio
luminoso incidente e quello uscente. Lo spostamento
va in direzione opposta rispetto a quella nella lastra di
acrilico.

Acrilico

52

Aria

Acrilico

E9a Deviazione di un fascio luminoso attraverso

un prisma di acrilico

(U17300/U17301)
In un prisma di acrilico un fascio luminoso incidente
viene interrotto nel punto A verso la perpendicolare
incidente. Sul punto di uscita B la rifrazione si verifica
lontano dalla perpendicolare incidente. La somma di
tutti gli angoli di rifrazione è l'angolo di deflessione δ.
Si tratta dell'angolo che si forma tra il fascio luminoso
incidente e quello uscente.

Aria

Acrilico

E10a Deviazione di un fascio luminoso attraverso

un prisma di aria
(U17301)

La luce penetra nel punto A attraverso la superficie
limite di acrilico-aria. Il fascio luminoso viene inter­rotto dalla perpendicolare incidente. Il fascio lumino­so viene interrotto nel punto di uscita B verso la per­pendicolare incidente. La somma di tutti gli angoli di
rifrazione è l'angolo di deflessione δ. Si tratta dell'an­golo che si forma tra il fascio luminoso incidente e
quello uscente.

E9b Deviazione minima attraverso un prisma di

acrilico

(U17300/U17301)
È possibile dimostrare che l'angolo di incidenza α, in
caso di angolo di deflessione minima δ

, è uguale

min

all'angolo di uscita ß. Il raggio interrotto scorre quindi
nel prisma parallelo al lato che non viene attraversa­to. Per l'indice di rifrazione del prisma vale la formula
seguente:

+

δϕ

min

sin

sin

2

ϕ

2

Aria

Acrilico

n =

Aria

Acrilico

E10b Deviazione minima attraverso un prisma di

aria
(U17301)

Nel caso della deflessione minima δ

, l'angolo di in-

min

cidenza α è uguale all'angolo di uscita ß. Il raggio in­terrotto scorre quindi nel prisma parallelo al lato che

53

non viene attraversato. Per l'indice di rifrazione del
prisma vale la formula seguente: (ved. E9b). La dire­zione della deviazione risulta opposta a quella nel pri­sma di acrilico.

Aria

E11b Riflessione su due bordi di un prisma di

acrilico (U17301)

In questo caso, le condizioni per la riflessione totale
sono soddisfatte su entrambi i bordi del prisma. Se il
raggio incidente superiore viene oscurato, il raggio
uscente inferiore scompare. L'immagine risulta ruotata
di 180°.

Acrilico

Acrilico

E11a Riflessione su un bordo di un prisma di

acrilico
(U17301)

Se i fasci luminosi si incontrano sul bordo, vengono
riflessi completamente. Ruotando leggermente il pri­sma, è possibile osservare sia la rifrazione che la rifles­sione.

Aria

E11c Riflessione su due prismi di acrilico

(U17301)

Le condizioni per la riflessione totale sono soddisfatte
su tutti i bordi del prisma.

Acrilico

Aria

Acrilico

Aria

54

E11d Riflessione su due prismi di acrilico

(U17301)

Le condizioni per la riflessione totale sono soddisfatte
su tutti i bordi del prisma.

E12 Riflessione su un prisma di aria

(U17301)
Se l'angolo di incidenza dei fasci luminosi è inferiore
all'angolo critico (42°), i fasci luminosi vengono rifles­si nell'acrilico. Se l'angolo è maggiore, una parte della
luce attraversa il prisma di aria.

Acrilico

Aria

E11e Riflessione su due prismi di acrilico

(U17301)

Le condizioni per la riflessione totale sono soddisfatte
su tutti i bordi del prisma.

E13a Passaggio di un fascio luminoso attraverso

una superficie limite convessa di aria-acrilico

(U17301)

Se un fascio luminoso penetra nel punto A attraverso
la superficie limite di aria-acrilico, viene interrotto ver­so la perpendicolare incidente. La perpendicolare in­cidente è definita come la linea retta dal punto A al
punto centrale della curva S.

55

Acrilico

Aria

Aria

Acrilico

E13b Passaggio di fasci luminosi attraverso una

superficie limite convessa di aria-acrilico
(U17301)

I fasci luminosi incidenti vengono interrotti due volte
e si incontrano nel punto F' sull'asse ottico, ovvero il
fuoco.

Acrilico

E14b Passaggio di fasci luminosi attraverso una

superficie limite concava di aria-acrilico
(U17301)

Dopo aver attraversato la superficie limite di acrilico­aria, il fascio di raggi viene interrotto in modo diver­gente. Se i raggi interrotti vengono allungati all'indie­tro, si incontrano in un punto sull'asse ottico. Questo
punto viene definito fuoco virtuale F'.

Acrilico

E14a Passaggio di un fascio luminoso attraverso

una superficie limite concava di aria-acrilico
(U17301)

Se un fascio luminoso penetra sulla superficie limite
attraverso il punto A, è possibile osservare una rifra­zione verso la perpendicolare incidente. La perpendi­colare incidente è definita come la linea retta dal pun­to A al punto centrale della curva S.

E15a Passaggio di un fascio luminoso attraverso

una superficie limite convessa di acrilico-aria
(U17301)

Dopo aver attraversato il punto A, il fascio luminoso
viene interrotto dalla perpendicolare incidente. La
perpendicolare incidente è definita come la linea ret­ta dal punto A al punto centrale della curva S.

56

Acrilico

E16a Passaggio di un fascio luminoso attraverso

una superficie limite concava di acrilico-aria

(U17301)

Dopo aver attraversato il punto A, il fascio luminoso
viene interrotto dalla perpendicolare incidente. La
perpendicolare incidente è definita come la linea ret­ta dal punto A al punto centrale della curva S.

Aria

E15b Passaggio di fasci luminosi attraverso una

superficie limite convessa di aria-acrilico
(U17301)

Dopo aver attraversato la superficie limite di acrilico­aria, il fascio di raggi viene interrotto in modo diver­gente. Se i raggi interrotti vengono allungati all'indie­tro, si incontrano in un punto sull'asse ottico. Questo
punto viene definito fuoco virtuale F'.

Acrilico

Aria

Acrilico

E16b Passaggio di fasci luminosi attraverso una

superficie limite concava di acrilico-aria

(U17301)

Dopo aver attraversato la superficie limite, il fascio di
raggi risulta convergente. I raggi paralleli si incontra­no in un punto sull'asse ottico, ovvero il fuoco F'.

Acrilico

57

E17a Passaggio di fasci luminosi attraverso una

lente convessa di acrilico – fasci luminosi
paralleli all'asse ottico
(U17300/U17301)

Una lente di acrilico convessa funge da lente collettrice
e i fasci luminosi si incontrano, dopo aver attraversato
la lente, nel fuoco F'.

Acrilico

Aria

E17c Passaggio di fasci luminosi attraverso una

lente convessa di acrilico spessa
(U17301)

Collocando una lastra pianparallela tra due lenti (23),
è possibile realizzare un modello di lente spessa. Mo­dificando lo spessore d della lente, cambia anche la
distanza focale. Maggiore è lo spessore della lente,
minore è la distanza focale. A partire da uno spessore
critico, la lente passa da collettrice a divergente.

Acrilico

E17b Passaggio di fasci luminosi attraverso una

lente convessa di acrilico – fasci luminosi
non paralleli all'asse ottico
(U17300/U17301)

L'asse ϕ' è perpendicolare all'asse ottico e attraversa il
fuoco F'. Viene definito piano focale. I raggi incidenti
vengono interrotti e si incontrano in un punto sull'as­se ϕ'.

Acrilico

E18a Passaggio di fasci luminosi attraverso una

lente concava di acrilico – fasci luminosi
paralleli all'asse ottico
(U17300/U17301)

I fasci luminosi sono divergenti dopo avere attraversa­to la lente. Non danno forma ad alcun oggetto. Allun­gati all'indietro, i raggi si incontrano nel fuoco virtua­le F'.

Acrilico

58

E18b Passaggio di fasci luminosi attraverso una

lente concava di acrilico – fasci luminosi
non paralleli all'asse ottico

(U17300/U17301)

L'asse ϕ' è perpendicolare all'asse ottico e attraversa il
fuoco virtuale F'. Viene definito piano focale. I prolun­gamenti dei raggi interrotti si incontrano in un punto
sull'asse ϕ'.

Acrilico

E19b Passaggio di fasci luminosi attraverso una

lente convessa di aria – fasci luminosi non

paralleli all'asse ottico

(U17301)

L'asse ϕ' è perpendicolare all'asse ottico e attraversa il
fuoco virtuale F'. Viene definito piano focale. I prolun­gamenti dei raggi interrotti si incontrano in un punto
sull'asse ϕ'.

Acrilico

Aria

Aria

E19a Passaggio di fasci luminosi attraverso una

lente convessa di aria – fasci luminosi
paralleli all'asse ottico
(U17301)

I fasci luminosi sono divergenti dopo avere attraversa­to la lente. Non danno forma ad alcun oggetto. Allun­gati all'indietro, i raggi si incontrano nel fuoco virtua­le F'.

Acrilico

Aria

Aria

E20a Passaggio di fasci luminosi attraverso una

lente concava di aria – fasci luminosi
paralleli all'asse ottico

(U17301)
Una lente concava di aria funge da lente collettrice e i
raggi interrotti si incontrano nel fuoco F' dopo aver
attraversato la lente.

Acrilico

Aria

59

E20b Passaggio di fasci luminosi attraverso una

lente concava di aria – fasci luminosi
paralleli all'asse ottico
(U17301)

L'asse ϕ' è perpendicolare all'asse ottico e attraversa il
fuoco F'. Viene definito piano focale. I raggi interrotti
si incontrano un punto sull'asse ϕ'.

Acrilico

E21b Parametri di lenti spesse – distanza focale

(U17300/U17301)

Le lenti spesse sono lenti il cui spessore non può esse­re ignorato. Nella definizione della distanza focale, è
necessario tenere in considerazione la distanza tra i
due piani principali H e H'.

Aria

E21a Parametri di lenti spesse – determinazione

del raggio di curvatura
(U17300/U17301)

Le lenti del set di ottiche per laser sono caratterizzate
da una superficie di rifrazione cilindrica su una super­ficie di base circolare con raggi di curvatura identici.
Questi raggi possono essere determinati con l'ausilio
della carta millimetrata.

Aria

Acrilico

E22a Modello di occhio

(U17300, pellicola A)

I fasci luminosi paralleli all'asse ottico vengono inter­rotti dalla lente dell'occhio e si incontrano in un pun­to sulla retina.
Collocare la lente dell'occhio (1) direttamente dietro
la linea O2.

Retina

60

Lente dell'occhio

E22b Modello di occhio miope

(U17300, pellicola A)

I fasci luminosi paralleli all'asse ottico vengono inter­rotti dalla lente dell'occhio e si incontrano in un pun­to davanti alla retina.
Collocare la lente dell'occhio (2) direttamente dietro
la linea O2 e la lente di correzione (5) tra le linee O1 e
O2.

Lente dell'occhio

Retina

Lente di correzione (5)

E22c Modello di occhio ipermetrope

(U17300, pellicola A)

I fasci luminosi paralleli all'asse ottico vengono inter­rotti dalla lente dell'occhio e si incontrano in un pun­to dietro la retina. La lente di correzione è una lente
collettrice. Per la distanza focale f' del sistema di lenti,
vale la formula seguente:

ff

’’

12

f

’

=

ff

’’

+

12

dove f1' è la distanza focale della lente dell'occhio e f2'
è la distanza focale della lente di correzione.

Lente dell'occhio

Retina

E23a Correzione dell'aberrazione sferica mediante

riduzione del diametro del fascio di raggi

(U17300/U17301)
L'aberrazione sferica di una lente può essere ridotta
riducendo il diametro del fascio di raggi che attraver­sa la lente. A tale scopo, oscurare i raggi più esterni.

E23b Correzione dell'aberrazione sferica mediante

una combinazione di lenti

(U17300, pellicola E)

Le aberrazioni sferiche di lenti collettrici e divergenti
hanno effetti inversi. L'errore può essere corretto me­diante una combinazione di lenti. L'aberrazione ∆f =

f1 – f2 è definita come la differenza tra la distanza focale
f1 dei raggi esterni e la distanza focale f2 dei raggi in-

terni. Nelle lenti collettrici, l'aberrazione ha un segno
positivo, mentre nelle lenti divergenti ha un segno
negativo.

Lente di correzione (4)

(fra O1 e O2)

61

E24a Telescopio kepleriano

(U17300, pellicola D)

L'obiettivo del telescopio kepleriano genera un'imma­gine reale ridotta dell'oggetto osservato, che viene in­grandito dall'oculare come attraverso una lente. Si for­ma quindi un'immagine invertita (da sopra a sotto e
da destra a sinistra) e fortemente ingrandita. Per di­mostrare questo comportamento, oscurare uno dei
fasci luminosi esterni. Se viene oscurato il raggio inci­dente più in alto, scompare il raggio uscente più in
basso.

Obiettivo

Oculare

Obiettivo

Oculare

E24b Telescopio galileiano

(U17300, pellicola C)

Nel cannocchiale galileiano, i raggi provenienti dal­l'obiettivo si incontrano su una lente divergente pri­ma di raggiungere il fuoco. I raggi raggiungono l'oc­chio come raggi paralleli. L'immagine dell'oggetto ri­sulta ingrandita, verticale e non speculare.

E25 Fotocamera

(U17300, pellicola B)
La lente della fotocamera è una lente collettrice. L'im­magine che appare sulla pellicola posta nella parte
posteriore della fotocamera è reale e capovolta.

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Germania • www.3bscientific.com • Con riserva di modifiche tecniche

62

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

®

Juego de demostración de óptica de laser U17300

y juego complementario U17301

Instrucciones de servicio

1/05 ALF

Índice

Página Exp. Nr. Experimento Equipo

1 Introducción
2 Volumen de suministro
3 E1 Reflexión en un espejo plano U17300/U17301
3 E2 Reflexión en dos espejos planos U17301
3 E3a Reflexión en espejo cóncavo – rayos de luz paralelos al eje óptico U17300
4 E3b Reflexión en espejo cóncavo – rayos de luz no paralelos al eje óptico U17300
4 E4a Reflexión en espejo convexo – rayos de luz paralelos al eje óptico U17300
4 E4b Reflexión en espejo convexo – rayos de luz no paralelos al eje óptico U17300
5 E5a Refracción de un haz de luz durante su paso del aire al acrílico U17300
5 E5b Profundidad aparente de un objeto U17301
5 E6a Refracción de un haz de luz durante su paso del acrílico al aire U17300
6 E6b Refracción en un prisma acrílico U17300/U17301
6 E6c Ángulo crítico, reflexión total U17300
6 E6d Reflexión total – propagación de la luz en conductores ópticos U17300
7 E7 Desplazamiento de un haz de luz, placa acrílica planoparalela U17300/U17301
7 E8 Desplazamiento de un haz de luz, aire entre dos placas acrílicas

planoparalelas U17301
7 E9a Desviación de un haz de luz por medio de un prisma acrílico U17300/U17301
8 E9b Desviación mínima por medio de un prisma acrílico U17300/U17301
8 E10a Desviación de un haz de luz por medio de un prisma de aire U17301
8 E10b Desviación mínima por medio de un prisma de aire U17301
9 E11a Reflexión en una cara de un prisma acrílico U17301
9 E11b Reflexión en dos caras de un prisma acrílico U17301
9 E11c Reflexión en dos prismas acrílicos U17301
10 E11d Reflexión en dos prismas acrílicos U17301
10 E11e Reflexión en dos prismas acrílicos U17301
10 E12 Reflexión en un prisma de aire U17301
11 E13a Paso de un haz de luz a través de una superficie de separación

de aire-acrílico U17301
11 E13b Paso de rayos de luz a través de una superficie de separación convexa

de aire-acrílico U17301
11 E14a Paso de un haz de luz a través de una superficie de separación cóncava

de aire-acrílico U17301
12 E14b Paso de rayos de luz a través de una superficie de separación cóncava

de aire-acrílico U17301
12 E15a Paso de un haz de luz a través de una superficie de separación convexa

de aire-acrílico U17301
12 E15b Paso de rayos de luz a través de una superficie de separación

de aire-acrílico U17301
13 E16a Paso de un haz de luz a través de una superficie de separación cóncava

de aire-acrílico U17301
13 E16b Paso de rayos de luz a través de una superficie de separación cóncava

de aire-acrílico U17301

63

13 E17a Paso de rayos de luz a través de una lente acrílica convexa –

rayos de luz paralelos al eje óptico U17300/U17301

14 E17b Paso de rayos de luz a través de una lente acrílica convexa –

rayos de luz no paralelos al eje óptico U17300/U17301
14 E17c Paso de rayos de luz a través de una lente acrílica convexa gruesa U17301
14 E18a Paso de rayos de luz a través de una lente acrílica cóncava –

rayos de luz paralelos al eje óptico U17300/U17301
15 E18b Paso de rayos de luz a través de una lente acrílica cóncava –

rayos de luz no paralelos al eje óptico U17300/U17301
15 E19a Paso de rayos de luz a través de una lente de aire convexa –

rayos de luz paralelos al eje óptico U17301
15 E19b Paso de rayos de luz a través de una lente de aire convexa –

rayos de luz no paralelos al eje óptico U17301
16 E20a Paso de rayos de luz a través de una lente de aire cóncava –

rayos de luz paralelos al eje óptico U17301
16 E20b Paso de rayos de luz a través de una lente de aire cóncava –

rayos de luz no paralelos al eje óptico U17301
16 E21a Parámetros de lentes gruesas – determinación del radio de curvatura U17300/U17301
17 E21b Parámetros de lentes gruesas – distancia focal U17300/U17301
17 E22a Modelo del ojo humano U17300
17 E22b Modelo del ojo humano, miopía U17300
18 E22c Modelo del ojo humano, presbicia U17300
18 E23a Corrección de la aberración esférica por disminución del diámetro

del haz de rayos U17300/U17301
18 E23b Corrección de la aberración esférica por medio una combinación

de lentes U17300
19 E24a Telescopio según Kepler U17300
19 E24b Telescopio según Galilei U17300
19 E25 Cámara U17300

Juego demostración de óptica de láser U17300
Equipo complementario U17301

En la columna "Equipo" se enumeran los componentes de equipo necesarios para cada experimento, provenientes de
U17300 y U17301, o de ambos juegos.

Introducción

El equipo de demostración de óptica de láser permite
un montaje de experimentos sencillo y claro para la
representación de los fundamentos de la geometría
óptica, al igual que para el funcionamiento de dife­rentes equipos de óptica. Como fuente de luz, se em­plea el láser de diodos de 5 rayos U17302.
En estas instrucciones de uso se describen numerosos
experimentos básicos con los elementos ópticos de los
juegos de equipos U17300 y U17301. Cada descripción
experimental se compone de tres partes:

1. Sencilla descripción del experimento

2. Representación gráfica del experimento

3. Imagen del montaje experimental
Debajo del título respectivo, se anota entre paréntesis
con qué equipo se puede llevar a cabo el experimen­to, esto es, U17300, U17301 ó U17300/U17301. La mis­ma indicación se encuentra en la última columna de
la sinopsis del índice.
El láser de diodos U17302 es un componente muy im­portante de los arreglos experimentales. Cinco diodos
láser generan cinco rayos de luz paralelos. La cantidad
de rayos emitidos es seleccionable. Para ello, delante

del láser de diodos, se coloca la placa metálica con
perforaciones, incluida en el suministro. Durante el uso
de este equipo, se debe evitar un contacto ocular di­recto con el rayo láser.

Volumen de suministro

Juego demostración de óptica de láser U17300

1 Lente bicóncava
2 Lente biconvexa
3 Lente biconvexa
4 Lente biconvexa
5 Lente biconvexa
6 Pequeña lente plano cóncava
7 Pequeña lente plano convexa
8 Lente grande plano convexa
9 Espejo, cóncavo
10 Espejo, convexo
11 Espejo plano
12 Placa planoparalela
13 Prisma
14 Conductor óptico

64

Láminas

A Modelo del ojo humano
B Cámara
C Telescopio según Galilei
D Telescopio según Kepler
E Aberración esférica
F Escala angular de 360°

Juego complementario U17301

21 Lente bicóncava de aire
22 Lente bicóncava
23 Lente biconvexa de aire
24 Lente biconvexa
25 Prisma de aire
26 Prisma equilateral
27 2 prismas rectangulares
28 Placa planoparalela, cuadrada
29 2 placas planoparalelas, cuadrangulares
11 2 espejos planos

E1 Reflexión en un espejo plano

(U17300/U17301)
Representación de la ley de reflexión. Un rayo de luz
que incide sobre una superficie especular plana, con
un ángulo de incidencia α, se refleja con el ángulo ß

α = ß

Ambos ángulos se miden con la normal.

E3a Reflexión en un espejo cóncavo – rayos de luz

paralelos al eje óptico

(U17300)
La distancia focal f de un espejo hueco se determina
por medio de la longitud de la distancia VF. El radio de
curvatura se puede determinar a partir de la fórmula:

E2 Reflexión en dos espejos planos

(U17301)

Demostración de la relación:

δ = 2 γ
en donde el ángulo δ está formado por el rayo de inci­dencia, y el reflectante γ es el ángulo entre las superfi­cies especulares.

fr=

2

La distancia VS es dos veces más larga que VF.

65

E3b Reflexión en un espejo cóncavo – rayos de luz

no paralelos al eje óptico

(U17300)

El eje ϕ presenta un posición vertical en relación al eje
óptico y pasa por el foco. Recibe el nombre de plano
focal. Los rayos de incidencia paralela se reflejan y se
encuentran en un punto del plano focal ϕ. Si los rayos
son paralelos al eje óptico, el punto se encontrará por
encima y recibe el nombre de punto focal F.

E4b Reflexión en espejo convexo – rayos de luz no

paralelos al eje óptico

(U17300)

El eje ϕ presenta un posición vertical en relación al eje
óptico y pasa por el foco. Recibe el nombre de plano
focal. Si sobre el espejo inciden rayos paralelos, éstos se
dispersan de manera que parecen provenir de un pun­to del plano focal ϕ que se encuentra detrás del espejo.

E4a Reflexión en espejo convexo – rayos de luz

paralelos al eje óptico

(U17300)
Los rayos reflectantes parecen provenir de un punto
que se encuentra por detrás del espejo. A éste se lo
denomina foco virtual. La longitud de la línea VF de­termina la distancia focal del espejo. El radio de cur­vatura se puede determinar a partir de la fórmula:

fr=

2

La distancia VS es dos veces más larga que VF.

E5a Refracción de un rayo de luz durante su paso

del aire al acrílico

(U17300, lámina F)
Cuando un rayo de luz pasa de un medio con un índi­ce de refracción n1 a otro medio con un índice de re­fracción n2 su cambio de dirección se determina por
medio de la ley de refracción de Snellius:
n

sin α = n

1

Aquí, α es el ángulo de incidencia en el medio n

sin ß

2

y ß es

1

el ángulo de refracción en el medio n2.

Aire

Acrílico

66

E5b Profundidad aparente de un objeto

(U17301)
Montaje experimental para la observación de la pro­fundidad aparente de un objeto que se encuentra su­mergido en el agua, o detrás de material acrílico, ob­servado desde fuera.

Lápiz

Aire

Acrílico

E6b Refracción en un prisma acrílico

(U17300/U17301)
Durante el paso de un rayo de luz de acrílico hacia el
aire, la ley de Snellius se puede describir de la siguien­te manera:

n

sin α = sin ß

1

El índice de refracción del aire es n2 = 1.

Acrílico

E6a Refracción de un rayo de luz durante su paso

del acrílico al aire

(U17300, lámina F)

El ángulo de refracción ß es mayor que el ángulo de
incidencia α. El rayo se rompe en la normal.

Acrílico

Aire

E6c Ángulo crítico, reflexión total

(U17300, lámina F)
Mientras mayor sea el ángulo de incidencia, mayor será
el ángulo de refracción. Si n1 < n2, existe un ángulo
crítico α. El rayo cortado se encuentra entonces en la
superficie limitante de ambos medios. Si el ángulo de
incidencia es mayor que el ángulo crítico, entonces ya
no se encuentra presente ninguna refracción y se re­fleja toda la luz. En este caso se habla de reflexión to­tal.

Acrílico

Aire

67

E6d Reflexión total – propagación de la luz en

conductores ópticos

(U17300)
En un conductor óptico, la luz se propaga gracias a la
reflexión total. El parámetro denominado apertura nu­mérica determina, en este caso, el ángulo que no se
debe sobrepasar. Corresponde al seno del ángulo máxi­mo de incidencia de la luz. Por medio de este parámetro
también se determina el radio menor, en el caso de que
el conductor se pliegue. Cuando se instala el conductor
óptico, este radio no se debe sobrepasar.

E8 Desplazamiento de un rayo de luz, presencia

de aire entre dos placas acrílicas planoparale­las (U17301)

En este caso se presenta un desplazamiento entre el
rayo incidente y el reflejado. No obstante, el desplaza­miento va en dirección contraria al de la placa acrílica.

Acrílico

Acrílico

E7 Desplazamiento de un haz de luz, placa

acrílica planoparalela

(U17300/U17301)
Si un rayo de luz atraviesa una placa planoparalela, su
dirección no se modifica. El rayo de reflexión se ha
desplazado en una distancia d. Si se tiene un espesor
de placa h, para d se obtiene:

sin

αβ

−

dh=

()

cos

β

Aire

Acrílico

E9a Desviación de un rayo de luz por medio de un

prisma acrílico (U17300/U17301)

En un prisma acrílico, un rayo de luz incidente sobre
el punto A se corta hacia el eje de incidencia. En el
punto de salida B, la refracción se realiza en un lugar
distante de la normal. La suma de todos los ángulos
de refracción conforma el ángulo de desviación δ. Se
trata del ángulo entre la luz incidente y el rayo de luz
reflejado.

Aire

Acrílico

Aire

Acrílico

68

E9b Desviación mínima por medio de un prisma

acrílico

(U17300/U17301)

Se puede demostrar que el ángulo de incidencia α,
con el ángulo mínimo de desviación δ

, es igual al

min

ángulo de salida ß. El rayo interrumpido pasa por el
prisma paralelamente al lado por el que no pasa la
luz. Para el índice de refracción del prisma es válido:

+

δϕ

min

sin

sin

2

ϕ

2

Aire

Acrílico

n =

E10b Desviación mínima por medio de un prisma

de aire

(U17301)

En el caso de que se tenga la desviación mínima δ

min

el ángulo de incidencia α es igual al ángulo de reflexión
ß. El rayo partido pasa a través del prisma paralelo al
lado que no atraviesa. Para el índice de refracción del
prisma es válido: (véase E9b). La dirección de la des­viación es inversa a la de un prisma acrílico.

Aire

Acrílico

,

E10a Desviación de un rayo de luz por medio de

un prisma de aire
(U17301)

La luz incide en el punto A a través de la superficie de
separación acrílico-aire. La normal corta y desplaza el
rayo de luz. En el punto de salida B, se corta hacia la
normal. La suma de todos los ángulos de refracción
conforma el ángulo de desviación δ. Se trata del ángu­lo entre la luz incidente y el rayo de luz reflejado.

Aire

Acrílico

E11a Reflexión en una cara de un prisma acrílico

(U17301)

Cuando los rayos de luz llegan a la base del prisma, se
reflejan totalmente. Si se gira levemente el prisma, se
puede observar refracción al igual que reflexión.

Acrílico

Aire

69

E11b Reflexión en dos caras de un prisma acrílico

(U17301)

En este caso se cumplen las condiciones para la re­flexión total en ambas caras. Si el rayo superior se su­prime, desaparece el rayo inferior de reflexión. La ima­gen tiene un giro de 180°.

Acrílico

Aire

E11d Reflexión en dos prismas acrílicos

(U17301)

Las condiciones para la reflexión total se cumplen en
todas las caras del prisma.

E11c Reflexión en dos prismas acrílicos (U17301)
Las condiciones para la reflexión total se cumplen en
todos las caras del prisma.

Acrílico

Aire

E11e Reflexión en dos prismas acrílicos

(U17301)

Las condiciones para la reflexión total se cumplen en
todas las caras del prisma.

70

E12 Reflexión en un prisma de aire

(U17301)
Si el ángulo de incidencia de los rayos de luz es menor
que el ángulo crítico (42°), los rayos de luz se reflejan
en el material acrílico. Si el ángulo es mayor, una par­te de la luz atraviesa el prisma de aire.

Acrílico

Aire

E13b Paso de rayos de luz a través de una

superficie de separación convexa de aire­ acrílico
(U17301)

Los rayos de luz incidentes se parten dos veces y se
encuentran en el punto F' del eje óptico, esto es, el
punto focal.

Acrílico

E13a Paso de un haz de luz a través de una

superficie convexa de separación de aire-

acrílico

(U17301)

Si un rayo de luz incide en el punto A, a través de la
superficie de separación aire-acrílico, se parte hacia la
normal. La normal es la recta que va del punto A al
punto central de curvatura S.

Acrílico

Aire

E14a Paso de un haz de luz a través de una

superficie de separación cóncava de aire­ acrílico
(U17301)

Si el rayo de luz incide sobre la superficie, a través del
punto A, se observa una refracción hacia la normal. La
normal es la recta que va del punto A al punto central
de curvatura S.

Aire

Acrílico

71

E14b Paso de rayos de luz a través de una

superficie de separación cóncava de aire­ acrílico
(U17301)

Después del paso a través de la superficie de aire­acrílico, el haz de rayos se parte de manera divergen­te. Si los rayos partidos se prolongan hacia atrás, se
encuentran en un punto del eje óptico. Este punto se
denomina punto focal virtual F'.

Acrílico

E15b Paso de rayos de luz a través de una

superficie de separación convexa de acrílico­ aire (U17301)

Después del paso a través de la superficie de aire­acrílico, el haz de rayos se parte de manera divergen­te. Si los rayos partidos se prolongan hacia atrás, se
encuentran en un punto del eje óptico. Este punto se
denomina punto focal virtual F'.

Acrílico

E15a Paso de un rayo de luz a través de una

superficie de separación convexa de aire­ acrílico
(U17301)

Después de que el rayo de luz ha atravesado el punto
A, se ve desplazado de la normal. La normal es la recta
que va del punto A al punto central de curvatura S.

Aire

Acrílico

E16a Paso de rayos de luz a través de una

superficie de separación cóncava de aire­ acrílico (U17301)

Después de que el rayo de luz ha atravesado el punto
A, se ve desplazado por la normal. La normal es la rec­ta que va del punto A al punto central de curvatura S.

Aire

Acrílico

72

E16b Paso de rayos de luz a través de una

superficie de separación cóncava de
acrílico-aire

(U17301)
Después de atravesar la superficie de separación, el
haz de rayos se vuelve convergente. Los rayos parale­los se encuentran en un punto del eje óptico, esto es,
el punto focal F'.

E17b Paso de rayos de luz a través de una lente

acrílica convexa – rayos de luz no paralelos
al eje óptico (U17300/U17301)

El eje ϕ' presenta un posición vertical en relación al
eje óptico y pasa por el punto focal F'. Recibe el nom­bre de plano focal. Los rayos incidentes se parten y se
encuentran en un punto del eje ϕ'.

Acrílico

E17a Paso de rayos de luz a través de una lente

acrílica convexa – rayos de luz paralelos al
eje óptico
(U17300/U17301)

Una lente acrílica convexa es una lente convergente y,
una vez que la han atravesado, los rayos de luz se en­cuentran en el punto focal F'.

Acrílico

Aire

Acrílico

E17c Paso de rayos de luz a través de una lente

acrílica convexa gruesa (U17301)

Se puede obtener el modelo de una lente gruesa em­plazando una placa planoparalela ente dos lentes (23):
Al modificarse el espesor d de la lente, varía también
la distancia focal; mientras más gruesa sea la lente, la
distancia focal será menor. A partir de un espesor crí­tico, la lente convergente se convierte en una lente
divergente.

73

Acrílico

E18a Paso de rayos de luz a través de una lente

acrílica cóncava – rayos de luz paralelos al
eje óptico (U17300/U17301)

Después de atravesar la lente, los rayos de luz se vuel­ven divergentes. No reflejan ningún objeto. Si se pro­longan hacia atrás, se encuentran en el punto focal
virtual F'.

Acrílico

E19a Paso de rayos de luz a través de una lente de

aire convexa – rayos de luz paralelos al eje
óptico

(U17301)
Después de atravesar la lente, los rayos de luz se vuel­ven divergentes. No reflejan ningún objeto. Si se pro­longan hacia atrás, se encuentran en el punto focal
virtual F'.

Acrílico

Aire

Aire

E18b Paso de rayos de luz a través de una lente

acrílica cóncava – rayos de luz no paralelos
al eje óptico (U17300/U17301)

El eje ϕ' presenta un posición vertical en relación al
eje óptico y pasa por el punto focal virtual F'. Recibe el
nombre de plano focal. La prolongación de los rayos
desviados se encuentra en un punto del eje ϕ'.

Acrílico

E19b Paso de rayos de luz a través de una lente de

aire convexa – rayos de luz no paralelos al

eje óptico

(U17301)

El eje ϕ' presenta un posición vertical en relación al
eje óptico y pasa por el punto focal virtual F'. Recibe el
nombre de plano focal. La prolongación de los rayos
desviados se encuentra en un punto del eje ϕ'.

Acrílico

Aire

Aire

74

E20a Paso de rayos de luz a través de una lente de

aire cóncava – rayos de luz paralelos al eje
óptico
(U17301)

Una lente de aire cóncava se comporta como una len­te convergente y los rayos desviados se encuentran en
el punto focal F' después de atravesar la lente.

Acrílico

Aire

E21a Parámetros de lentes gruesas –

determinación del radio de curvatura
(U17300/U17301)

En el juego de óptica de láser, las lentes poseen una
superficie de refracción cilíndrica, sobre una superfi­cie base circular, con iguales radios de curvatura. Es­tos radios se pueden determinar empleando papel
milimetrado.

E20b Paso de rayos de luz a través de una lente de

aire cóncava – rayos de luz paralelos al eje
óptico
(U17301)

El eje ϕ' presenta un posición vertical en relación al
eje óptico y pasa por el punto focal F'. Recibe el nom­bre de plano focal. La prolongación de los rayos des­viados se encuentra en un punto del eje ϕ'.

Acrílico

Aire

E21b Parámetros de lentes gruesas – distancia

focal
(U17300/U17301)

Se habla de lentes gruesas cuando el espesor de éstas
no es despreciable. Durante la definición de la distan­cia focal, se debe tomar en cuenta la distancia entre
ambos planos principales H y H'.

Aire

Acrílico

75

E22a Modelo del ojo humano

f

ff

ff

’

’’

’’

=

+

12

12

(U17300, lámina A)

Los rayos de luz paralelos al eje óptico se desvían por
la acción de la lente ocular y se encuentran en un punto
de la retina. Emplazar la lente ocular (1) directamente
detrás de la línea O2.

Retina

Lente ocular

E22c Modelo del ojo humano, presbicia

(U17300, lámina A)

Los rayos de luz paralelos al eje óptico se desvían por
la acción de la lente ocular y se encuentran en un punto
situado detrás de la retina. La lente de corrección es
una lente convergente. Para la distancia focal f' del
sistema de lentes es válido:

en donde f1' es la distancia focal de la lente ocular y f2'
la de la lente de corrección.

E22b Modelo de ojo humano, miopía

(U17300, lámina A)

Los rayos de luz paralelos al eje óptico se desvían por
la acción de la lente ocular y se encuentran en un punto
situado delante de la retina.
Emplazar la lente ocular (2) directamente detrás de la
línea O2 y la lente de corrección (5) entre las líneas O1 y
O2.

Lente ocular

Retina

Lente ocular

Retina

Lente de corrección (4),

(entre O1 y O2)

Lente de corrección (5)

76

E23a Corrección de la aberración esférica por

disminución del diámetro del haz de rayos

(U17300/U17301)
La aberración esférica de una lente se puede reducir
disminuyendo el diámetro del haz de rayos que atra­viesa la lente. Para ello se suprimen los rayos exter­nos.

E24a Telescopio según Kepler

(U17300, lámina D)

En el telescopio de Kepler, el objetivo genera una ima­gen real reducida del objeto observado, la cual se ve
ampliada por el ocular como si se tratara de una lupa.
Se obtiene una imagen invertida enormemente am­pliada (tanto las partes superior e inferior, así como la
derecha e izquierda se encuentran permutadas). Este
hecho se puede demostrar suprimiendo uno de los
rayos de luz externos. Si el rayo superior incidente se
suprime, desaparece el rayo inferior de salida.

E23b Corrección de la aberración esférica por

medio de una combinación de lentes

(U17300, lámina E)

La aberración esférica de las lentes convergentes y di­vergentes tienen un efecto inverso. El error se puede
corregir por medio de una combinación de lentes. La
aberración ∆f = f

– f2 se define como la diferencia

1

entre la distancia focal f1 de los rayos externos y f2 de
los rayos internos. En el caso de las lentes convergen­tes, la aberración tiene signo positivo, mientras que
en las divergentes el signo es negativo.

Objetivo

Ocular

77

E24b Telescopio según Galilei

(U17300, lámina C)

En el telescopio de Galilei, los rayos provenientes del
objetivo pasan por una lente divergente antes de arri­bar al punto focal. Los rayos llegan al ojo en forma de
rayos paralelos. La imagen del objeto está ampliada,
derecha y no invertida.

Objetivo

Ocular

E25 Cámara

(U17300, lámina B)
La lente de una cámara es una lente convergente. Re­fleja un objeto en una imagen real, volteada de cabe­za, en la película que se encuentra en la parte poste­rior de la cámara.

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Alemania • www.3bscientific.com • Se reservan las modificaciones técnicas

78

3B SCIENTIFIC3B SCIENTIFIC

3B SCIENTIFIC®

3B SCIENTIFIC3B SCIENTIFIC

PHYSICSPHYSICS

PHYSICS

PHYSICSPHYSICS

®

Kit de ótica laser de demonstração U17300

e kit complementar U17301

Manual de instruções

1/05 ALF

Índice de conteúdo

Página Exp - N° Experiência Kit de aparelhos
1 Introdução
2 Fornecimento
3 E1 Reflexão num espelho plano U17300/U17301
3 E2 Reflexão em dois espelhos planos U17301
3 E3a Reflexão num espelho côncavo – Raios luminosos paralelos ao eixo ótico U17300
4 E3b Reflexão num espelho côncavo – Raios luminosos não paralelos

ao eixo ótico U17300
4 E4a Reflexão num espelho convexo – Raios luminosos paralelos ao eixo ótico U17300
4 E4b Reflexão num espelho convexo – Raios luminosos não paralelos

ao eixo ótico U17300
5 E5a Refração de um raio luminoso ao passar do ar para o acrílico U17300
5 E5b Profundidade aparente de um objeto U17301
5 E6a Refração de um raio luminoso ao passar do acrílico para o ar U17300
6 E6b Refração num prisma de acrílico U17300/U17301
6 E6c Ângulo crítico, reflexão total U17300
6 E6d Reflexão total – Propagação da luz em condutores de luz U17300
7 E7 Deslocamento de um raio luminoso, placas de acrílico plano paralelas U17300/U17301
7 E8 Deslocamento de um raio luminoso, ar entre duas placas de acrílico

plano paralelas U17301
7 E9a Desvio de um raio luminoso por um prisma de acrílico U17300/U17301
8 E9b Desvio mínimo através de um prisma de acrílico U17300/U17301
8 E10a Desvio de um raio luminoso por um prisma de ar U17301
8 E10b Desvio mínimo através de um prisma de ar U17301
9 E11a Reflexão numa aresta de um prisma de acrílico U17301
9 E11b Reflexão em duas arestas de um prisma de acrílico U17301
9 E11c Reflexão em dois prismas de acrílico U17301
10 E11d Reflexão em dois prismas de acrílico U17301
10 E11e Reflexão em dois prismas de acrílico U17301
10 E12 Reflexão num prisma de ar U17301
11 E13a Percurso de um raio luminoso através de uma superfície de

separação ar-acrílico convexa U17301
11 E13b Percurso de um raio luminoso através de uma superfície de

separação ar-acrílico convexa U17301
11 E14a Percurso de um raio luminoso através de uma superfície de

separação ar-acrílico côncava U17301
12 E14b Percurso de um raio luminoso através de uma superfície de

separação ar-acrílico côncava U17301
12 E15a Percurso de um raio luminoso através de uma superfície de

separação acrílico-ar convexa U17301
12 E15b Percurso de um raio luminoso através de uma superfície de

separação acrílico-ar convexa U17301
13 E16a Percurso de um raio luminoso através de uma superfície de

separação acrílico-ar côncava U17301

79

13 E16b Percurso de um raio luminoso através de uma superfície de

separação acrílico-ar côncava U17301

13 E17a Percurso de raios luminosos através de uma lente de acrílico convexa –

Raios luminosos paralelos ao eixo ótico U17300/U17301

14 E17b Percurso de raios luminosos através de uma lente de acrílico convexa –

Raios luminosos não paralelos ao eixo ótico U17300/U17301

14 E17c Percurso de raios luminosos através de uma lente de acrílico convexa

grossa U17301

14 E18a Percurso de raios luminosos através de uma lente de acrílico côncava –

Raios luminosos paralelos ao eixo ótico U17300/U17301

15 E18b Percurso de raios luminosos através de uma lente de acrílico côncava –

Raios luminosos não paralelos ao eixo ótico U17300/U17301

15 E19a Percurso de raios luminosos através de uma lente de ar convexa –

Raios luminosos paralelos ao eixo ótico U17301

15 E19b Percurso de raios luminosos através de uma lente de ar convexa –

Raios luminosos não paralelos ao eixo ótico U17301

16 E20a Percurso de raios luminosos através de uma lente de ar côncava –

Raios luminosos paralelos ao eixo ótico U17301

16 E20b Percurso de raios luminosos através de uma lente de ar côncava –

Raios luminosos não paralelos ao eixo ótico U17301
16 E21a Parâmetros de lentes grossas – Determinação do raio de curvatura U17300/U17301
17 E21b Parâmetros de lentes grossas – Distância focal U17300/U17301
17 E22a Modelo de olho U17300
17 E22b Modelo de olho, miopia U17300
18 E22c Modelo de olho, hipermetropia U17300
18 E23a Correção da aberração esférica através da redução do diâmetro

do feixe de raios luminosos U17300/U17301
18 E23b Correção da aberração esférica através de uma combinação de lentes U17300
19 E24a Telescópio segundo Kepler U17300
19 E24b Telescópio segundo Galileu U17300
19 E25 Câmera U17300

Kit de ótica laser de demonstração U17300
Kit complementar U17301

A coluna "Kit de aparelhos" indica o kit de aparelhos necessário para cada experiência, U17300, U17301 ou ambos.

Introdução

O kit de ótica laser de demonstração permite uma
montagem simples e clara das experiências para a re­presentação dos fundamentos da ótica geométrica
assim como do modo de funcionamento de diversos
aparelhos óticos. Um laser diodo de 5 feixes U17302
serve de fonte luminosa.
Neste manual de instruções encontram-se descritas
numerosas experiências fundamentais com os elemen­tos óticos de ambos kits, U17300 e U17301. Cada des­crição de experiência está composta por três partes:

1. Uma descrição simples da experiência

2. Uma representação gráfica da experiência

3. Uma representação da montagem da
experiência

Debaixo de cada título encontra-se indicado entre
parênteses com qual kit de aparelhos a experiência
pode ser executada, U17300, U17301 ou U17300/
U17301. A mesma informação encontra-se também na
última coluna do índice de conteúdo.
Um elemento constituinte fundamental das monta-

gens de experiências é o laser diodo U17302. Cinco
diodos laser produzem cinco raios luminosos parale­los. O número de feixes produzidos pode ser escolhi­do. Para tal, coloca-se a placa de metal com perfura­ções incluída no fornecimento na frente do diodo laser.
Ao utilizar o laser deve-se evitar o contato direto do
olho com o feixe do laser.

Fornecimento

Kit de ótica laser de demonstração U17300

1 Lente bicôncava
2 Lente biconvexa
3 Lente biconvexa
4 Lente biconvexa
5 Lente biconvexa
6 Lente plano côncava pequena
7 Lente plano convexa pequena
8 Lente plano convexa grande
9 Espelho, côncavo
10 Espelho, convexo

80

11 Espelho plano
12 Placa plano paralela
13 Prisma
14 Condutor de luz

Transparências

A Modelo de olho
B Câmera
C Telescópio segundo Galileu
D Telescópio segundo Kepler
E Aberração esférica
F Escala angular de 360°

Kit complementar U17301

21 Lente de ar bicôncava
22 Lente bicôncava
23 Lente de ar biconvexa
24 Lente biconvexa
25 Prisma de ar
26 Prisma equilátero
27 2 prismas retangulares
28 Placa plano paralela, quadrada
29 2 placas plano paralelas, retangular
11 2 espelhos planos

E1 Reflexão no espelho

(U17300/U17301)
Representação da lei dos reflexos. Um raio luminoso
que incide na superfície espelhada plana com um ân­gulo de incidência α, será refletido com o ângulo ß

α = ß

Ambos ângulos são medidos em relação à normal da

superfície.

E3a Reflexão em espelhos côncavos – raios

paralelos ao eixo ótico

(U17300)
A distância focal f de um espelho côncavo é determi-
nada pelo comprimento do percurso VF. O raio de cur­vatura pode ser calculado com a fórmula

fr=

2

O percurso VS é duas vezes mais longo que VF.

E2 Reflexão em dois espelhos planos

(U17301)

Demonstração da relação:

δ = 2 γ
sendo que o ângulo δ é formado pelo raio incidente e
o raio refletido e γ é o ângulo formado pelas superfíci­es dos espelhos.

81

E3b Reflexão em espelhos côncavos – Raios

luminosos não paralelos ao eixo ótico

(U17300)

O eixo ϕ perpendicular ao eixo ótico e passa pelo pon­to focal. Ele é chamado de plano focal. Os raios inci­dentes paralelos são refletidos e convergem num pon­to no plano focal ϕ. Se os raios são paralelos ao eixo
ótico, então o ponto encontra-se lá e este chama-se
ponto focal F.

E4b Reflexão em espelhos convexos – Raios

luminosos não paralelos ao eixo ótico

(U17300)

O eixo ϕ perpendicular ao eixo ótico e passa pelo pon­to focal. Ele é chamado de plano focal. Se raios parale­los incide sobre o espelho eles são divergidos de modo
que parece que eles têm a sua origem num ponto do
plano focal ϕ atrás do espelho.

E4a Reflexão em espelhos convexos – Raios

luminosos paralelos ao eixo ótico

(U17300)
Os raios refletidos parecem ter origem num ponto atrás
do espelho. É o chamado ponto focal virtual. O percur­so VF determina a distância focal do espelho. O raio de
curvatura pode ser calculado com a fórmula

fr=

2

O percurso VS é duas vezes mais longo que VF.

E5a Refração de um raio luminoso ao passar do ar

para o acrílico

(U17300, transparência F)

Na passagem de um raio luminoso de um meio com o
índice de refração n1 para um meio com índice de re­fração n2, a sua mudança de direção é determinada
pela Lei da refração de Snellius:
n

sin α = n

1

α é o ângulo de incidência no meio n

sin ß

2

e ß é o ângulo

1

de refração no meio n2.

Ar

Acrílico

82

E5b Profundidade aparente de um objeto

(U17301)
Montagem da experiência para a observação da pro­fundidade aparente de um objeto na água ou por trás
de acrílico visto pelo ar.

Lápis

Ar

Acrílico

E6b Refração num prisma de acrílico

(U17300/U17301)
Na passagem de um raio luminoso do acrílico para o
ar, a Lei de Snellius pode ser escrita da seguinte for­ma:

n

sin α = sin ß

1

Índice de refração do ar n2 = 1.

Acrílico

E6a Refração de um raio luminoso ao passar do

acrílico para o ar

(U17300, transparência F)

O ângulo de refração ß é maior do que o ângulo de

incidência α. O raio é refratado para além da normal
à superfície.

Acrílico

Ar

E6c Ângulo crítico, reflexão total

(U17300, transparência F)
Quanto maior é o ângulo de incidência, maior será o
ângulo de refração. Se n1 < n2, então existe um ângulo
crítico α. O raio refratado encontra-se então na super­fície de separação entre dois meios. Caso o ângulo de
incidência for maior que o ângulo crítico não há mais
refração e a totalidade da luz é refletida. Neste caso
fala-se de reflexão total.

Acrílico

Ar

83

E6d Reflexão total – Propagação da luz em

condutores de luz

(U17300)
A luz se propaga num condutor de luz graças à refle­xão total. O parâmetro, a abertura numérica, determi­na qual é o ângulo que não deve ser ultrapassado. Ele
corresponde ao seno do ângulo de entrada máximo
da luz. Também determina-se o menor rádio, quando
o condutor é dobrado, por esse parâmetro. Ele não deve
ser ultrapassado quando o condutor de luz for instala­do.

Acrílico

E8 Deslocamento de um raio luminoso, ar entre

duas placas de acrílico plano paralelas

(U17301)
Neste caso ocorre um deslocamento entre o raio inci­dente e o raio emergente. Porém, o deslocamento ocor­re no sentido contrário do deslocamento com a placa
de acrílico.

Acrílico

Ar

Acrílico

E7 Deslocamento de um raio luminoso, placa de

acrílico plano paralela

(U17300/U17301)
Quando um raio luminoso atravessa uma placa plano
paralela, a sua direção não é alterada. O raio emer­gente é deslocado num valor d. Para uma placa de es­pessura h resulta para d:

sin

αβ

−

dh=

()

cos

β

Ar

Acrílico

E9a Desvio de um raio luminoso através de um

prisma de acrílico

(U17300/U17301)
Um raio luminoso incidente num prisma de acrílico
no ponto A é refratado em direção à normal da super­fície. No ponto de saída B a refração ocorre para fora
da normal da superfície. A soma de todos os ângulos
de refração resulta no ângulo de desvio δ. Este é o ân­gulo formado pelo raio luminoso incidente e o raio
luminoso emergente.

Ar

Acrílico

84

E9b Desvio mínimo através de um prisma de

acrílico

(U17300/U17301)

Pode ser demonstrado que o ângulo de incidência a,
no caso do ângulo mínimo de desvio δ

, é igual ao

min

ângulo de saída ß. O raio refratado atravessa então o
prisma paralelamente ao lado que não é atravessado.
Para o índice de refração do prisma é valido:

+

δϕ

min

sin

sin

2

ϕ

2

Ar

n =

E10b Desvio mínimo através de um prisma de ar

(U17301)

No caso do desvio mínimo δ

, o ângulo de incidência

min

α é igual ao ângulo de saída ß. O raio refratado atra­vessa o prisma então paralelamente ao lado que não é
atravessado. Para o índice de refração do prisma é va­lido: (veja E9b). A direção do desvio é oposta à do caso
do prisma de acrílico.

Ar

Acrílico

E10a Desvio de um raio luminoso através de um

prisma de ar
(U17301)

A luz atravessa a superfície de separação acrílico/ar no
ponto A. O raio luminoso é refratado para fora da nor­mal da superfície. No ponto de saída B ele é refratado
em direção à normal da superfície. A soma de todos os
ângulos de refração resulta no ângulo de desvio δ. Este
é o ângulo formado pelo raio luminoso incidente e o
raio luminoso emergente.

Acrílico

E11a Reflexão numa aresta de um prisma de

acrílico
(U17301)

Quando os raios luminosos atingem a aresta, eles são
totalmente refletidos. Girando levemente o prisma
pode-se observar tanto a refração quanto a reflexão.

Acrílico

Ar

Acrílico

Ar

85

E11b Reflexão em duas arestas de um prisma de

acrílico (U17301)

Neste caso encontram-se reunidas as condições para a
reflexão total em ambas arestas. Se o raio incidente
superior for interrompido, então desaparece o raio
emergente inferior. A imagem está invertida em 180°.

Acrílico

Ar

E11d Reflexão em dois prismas de acrílico

(U17301)

As condições para a reflexão total estão reunidas em
todas as arestas do prisma.

E11c Reflexão em dois prismas de acrílico (U17301)
As condições para a reflexão total estão reunidas em
todas as arestas do prisma.

Acrílico

Ar

E11e Reflexão em dois prismas de acrílico

(U17301)

As condições para a reflexão total estão reunidas em
todas as arestas do prisma.

86

E12 Reflexão num prisma de ar (U17301)
Quando o ângulo de incidência dos raios luminosos é
menor do que o ângulo crítico (42°), os raios lumino­sos são refletidos para dentro do acrílico. Se o ângulo
é maior, uma parte da luz passa pelo prisma de ar.

Acrílico

Ar

E13b Percurso de um raio luminoso através de

uma superfície de separação ar-acrílico
convexa
(U17301)

Os raios luminosos incidentes são refratados duas ve­zes e se encontram no ponto F' no eixo ótico, o ponto
focal.

Acrílico

E13a Percurso de um raio luminoso através de

uma superfície de separação ar-acrílico
convexa (U17301)

Quando um raio luminoso atravessa a superfície de
separação ar/acrílico no ponto A ele é refratado em
direção à normal da superfície. A normal da superfície
é a reta que vai do ponto A ao ponto S centro da curva­tura.

Acrílico

Ar

E14a Percurso de um raio luminoso através de

uma superfície de separação ar-acrílico
côncava
(U17301)

Se o raio luminoso atinge a superfície de separação no
ponto A, observa-se uma refração em direção à nor­mal da superfície. A normal da superfície é a reta que
vai do ponto A ao ponto S centro da curvatura.

Ar

Acrílico

87

E14b Percurso de um raio luminoso através de

uma superfície de separação ar-acrílico
côncava
(U17301)

Após a passagem pela superfície de separação acríli­co/ar o feixe luminoso é refratado de modo divergen­te. Se os raios refratados fossem prolongados para trás,
então eles se encontrariam num ponto no eixo ótico.
Esse ponto chama-se ponto focal virtual F'.

Acrílico

E15b Percurso de um raio luminoso através de

uma superfície de separação acrílico-ar

convexa (U17301)

Após a passagem pela superfície de separação acríli­co/ar o feixe luminoso é refratado de modo divergen­te. Se os raios refratados fossem prolongados para trás,
então eles se encontrariam num ponto no eixo ótico.
Esse ponto chama-se ponto focal virtual F'.

Acrílico

E15a Percurso de um raio luminoso através de

uma superfície de separação acrílico-ar
convexa
(U17301)

Após a passagem do raio luminoso pelo ponto A este é
refratado para fora da normal da superfície. A normal
da superfície é a reta que vai do ponto A ao ponto S
centro da curvatura.

Ar

Acrílico

E16a Percurso de um raio luminoso através de

uma superfície de separação acrílico-ar

côncava (U17301)

Após a passagem do raio luminoso pelo ponto A este é
refratado para fora da normal da superfície. A normal
da superfície é a reta que vai do ponto A ao ponto S
centro da curvatura.

Ar

Acrílico

88

E16b Percurso de um raio luminoso através de

uma superfície de separação acrílico-ar
côncava
(U17301)

Após a passagem através da superfície de separação o
feixe de raios luminosos é convergente. Raios parale­los encontram-se num ponto do eixo ótico, o ponto
focal F'.

Acrílico

E17b Percurso de raios luminosos através de uma

lente de acrílico convexa – Raios luminosos
não paralelos ao eixo ótico (U17300/U17301)

O eixo ϕ' perpendicular ao eixo ótico e passa pelo ponto
focal F'. Ele é chamado de plano focal. Os raios inci­dentes são refratados e convergem num ponto no eixo
ϕ'.

Acrílico

E17a Percurso de raios luminosos através de uma

lente de acrílico convexa – Raios luminosos
paralelos ao eixo ótico
(U17300/U17301)

Uma lente de acrílico convexa é uma lente convergen­te e os raios luminosos se encontram no ponto focal F'
após atravessar a lente.

Acrílico

Ar

E17c Percurso de raios luminosos através de uma

lente de acrílico convexa grossa (U17301)

Colocando uma placa plano paralela entre duas len­tes (23) pode-se realizar o modelo de uma lente gros­sa. Com a alteração da espessura d da lente também
altera-se a distância focal, quanto mais grossa a lente,
menor a distância focal. A partir de uma espessura crí­tica, a lente convergente torna-se uma lente divergen­te.

Acrílico

89

E18a Percurso de raios luminosos através de uma

lente de acrílico côncava – Raios luminosos
paralelos ao eixo ótico (U17300/U17301)

Os raios luminosos são divergentes após a passagem
pela lente. Não é projetado um objeto. Se prolonga­dos para trás, os raios se encontram no ponto focal
virtual F'.

Acrílico

E19a Percurso de raios luminosos através de uma

lente de ar convexa – Raios luminosos

paralelos ao eixo ótico

(U17301)

Os raios luminosos são divergentes após a passagem
pela lente. Eles não projetam um objeto. Se prolonga­dos para trás, os raios se encontram no ponto focal
virtual F'.

Acrílico

Ar

Ar

E18b Percurso de raios luminosos através de uma

lente de acrílico côncava – Raios luminosos
não paralelos ao eixo ótico (U17300/U17301)

O eixo ϕ' perpendicular ao eixo ótico e passa pelo ponto
focal virtual F'. Ele é chamado de plano focal. Os pro­longamentos dos raios refratados se encontram num
ponto no eixo ϕ'.

Acrílico

E19b Percurso de raios luminosos através de uma

lente de ar convexa – Raios luminosos não

paralelos ao eixo ótico

(U17301)

O eixo ϕ' perpendicular ao eixo ótico e passa pelo ponto
focal virtual F'. Ele é chamado de plano focal. Os pro­longamentos dos raios refratados se encontram num
ponto no eixo ϕ'.

Acrílico

Ar

Ar

90

E20a Percurso de raios luminosos através de uma

lente de ar côncava – Raios luminosos
paralelos ao eixo ótico
(U17301)

Uma lente de ar côncava se comporta como uma lente
convergente e os raios refratados se encontram no
ponto focal F' após a passagem pela lente.

Acrílico

Ar

E21a Parâmetros de lentes grossas – Determinação

do raio de curvatura

(U17300/U17301)
As lentes do kit de ótica laser possuem uma superfície
de refração cilíndrica sobre uma base circular com de
curvatura iguais. Com a ajuda de papel milimetrado
pode-se determinar esses rádios.

E20b Percurso de raios luminosos através de uma

lente de ar côncava – Raios luminosos
paralelos ao eixo ótico
(U17301)

O eixo ϕ' perpendicular ao eixo ótico e passa pelo ponto
focal virtual F'. Ele é chamado de plano focal. Os raios
refratados se encontram num ponto no eixo ϕ'.

Acrílico

Ar

E21b Parâmetros de lentes grossas – Distância

focal

(U17300/U17301)

Lentes grossas são aquelas nas quais a espessura não é
desprezível. Ao definir-se a distância focal deve-se le­var em consideração a distância entre os dois planos
principais H e H'.

AcrílicoAr

91

E22a Modelo de olho

f

ff

ff

’

’’

’’

=

+

12

12

(U17300, transparência A)

Raios luminosos paralelos ao eixo ótico são refratados
pelo cristalino e se encontram num ponto sobre a reti­na.
Colocar o cristalino (1) diretamente atrás da linha O2.

Retina

Lente ocular

E22c Modelo de olho, hipermetropia

(U17300, transparência A)

Raios luminosos paralelos ao eixo ótico são refratados
pelo cristalino e se encontram num ponto atrás da re­tina. A lente de correção é uma lente convergente. Para
a distância focal f' do sistema de lentes vale:

sendo que f1' é a distância focal do cristalino e f2' é a
da lente de correção.

Lente ocular

Retina

Lente de correção (4)

(entre O1 e O2)

E22b Modelo de olho, miopia

(U17300, transparência A)

Raios luminosos paralelos ao eixo ótico são refratados
pelo cristalino e se encontram num ponto antes da
retina.
Colocar o cristalino (2) diretamente atrás da linha O2 e
a lente de correção (5) entre a linha O1 e O2.

Lente ocular

Retina

Lente de correção (5)

E23a Correção da aberração esférica através da

redução do diâmetro do feixe de raios
luminosos (U17300/U17301)

A aberração esférica de uma lente pode ser reduzida
pela diminuição do diâmetro do feixe de raios lumi­nosos que atravessa a lente. Para tal, utilizar os raios
mais exteriores.

92

E23b Correção da aberração esférica através de

uma combinação de lentes
(U17300, transparência E)

As aberrações esféricas de lentes convergentes e diver­gentes têm efeitos opostos. Por uma combinação de
lentes pode-se corrigir esses erros. A aberração ∆f = f
– f2 é definida como a diferença entre a distância focal

f1 dos raios exteriores e a f2 dos raios interiores. No

caso das lentes convergentes a aberração tem um va­lor com sinal positivo, no das lentes divergentes com
sinal negativo.

E24b Telescópio segundo Galileu

(U17300, transparência C)

No telescópio de Galileu, os raios que vêm da objetiva
encontram uma lente divergente antes de atingir o
ponto focal. Os raios chegam aos olhos como raios

1

paralelos. A imagem do objeto é ampliada, de pé e
lateralmente correta.

Objetiva

Ocular

E24a Telescópio segundo Kepler

(U17300, transparência D)

A objetiva no telescópio de Kepler produz uma ima­gem real reduzida do objeto observado, a qual é am­pliada pelo ocular como por uma lupa. Resulta disto
uma imagem invertida (acima e abaixo como esquer­da e direita estão invertidos) e fortemente ampliada.
Para a demonstração desse comportamento apagar um
dos raios mais periféricos. Se o raio incidente superior
é interrompido, então o raio emergente inferior desa­parece.

Objetiva

Ocular

E25 Câmera

(U17300, transparência B)
A lente da câmera é uma lente convergente. Ela proje­ta um objeto numa imagem real, de cabeça para bai­xo, no filme que se encontra na parte traseira da
câmera.

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Alemanha • www.3bscientific.com • Sob reserva de modificações técnicas

93