HP 40g, 39g User Manual [de]

Download

Exakte Berechnungen

und

Mathematik

mit HP40G

Version 1.0

Renée de Graeve

Außerordentlicher Professor in Grenobel I

Exakte Berechnungen und Mathematik mit HP40G

Danksagung

Alle wußten, daß es unmöglich ist, allein ein leistungsfähiges Programm für exakte Berechnungen zu bilden … nur der aufgeklärte Bernard Parisse wußte dies nicht … und dachte gleich so ein Programm aus!

Sie haben vor sich sein Programm für exakte Berechnungen (das so genannte ERABLE), das schon das zweite Mal die Software eines H P Taschenrechners bildet.

Bernard Parisse hat das Pr ogramm soweit verändert, daß die Funktionen der exakten Berechnungen editiert und die Ergebnisse im Editor der Gleichungen angezeigt werden konnten.

Entdecken Sie die Fähigkeiten dieses Rechners während des Lesens dieses Handbuches.

Ich danke:

Bernard Parisse für seine wertvollen Ratschläge, Anmerkungen zu diesem

Text, für die Korrektur und dafür, daß er so fr eundlich war, die von uns geforderten Funktionen wirksam z u beschreiben.

Jean Tavenas für das Interesse, das er bei der Beendigung dieses

Handbuches gezeigt hat.

Jean Yves Avenard dafür, daß er unseren Bitten zugehört hat und daß er

sehr schlagfe rtig die Anweisung PROMPT beschrieben hat.

elektronischer Form oder in Buchform kopiert, übersetzt und distribuiert werden. Ohne schriftlicher Zustimmung des Rechtsinhabers zu Copyright ist es verboten, das Handbuch für kommerziellen Zwecke zu benutzen. Dieses Handbuch wird unter gege bener Sachlage ohne Gewähr geliefert. Der Rechtsinhab er zu Cop yri ght haftet nicht für Schäden, verursacht durc h die Verwendung dieses Handbuches. Für seinen Inhalt trä gt weder die Gesellschaft Hewlett-Packard noch deren Distributionspartner Verantwortung.

2 Danksagung

Exakte Berechnungen und Mathematik mit HP40G

Vorwort

Der Rechner HP 40G bedeutet eine neue Etappe in der Arbeit mit den exakten Berechnungen. Einerseits durch seinen Konkurrenzpreis, andererseits durch die

Möglichkeiten, wie man die Grundalgorithmen, die im Mathematikunterricht an französischen Obersc hulen und in den ersten Studienjahren der Hochschulen unterrichtet werden, berechnet.

Notwendig war jedoch, dazu noch eine Dokumentation zu bearbeiten, am besten aus der Feder eines Mannes, der Mathematik unterrichtet. Sie finden das Ergebnis in diesem Handbuch, erstellt durch Renée De Graeve, außerordentlicher Professor an der Université de Grenoble I und führende Persönlichkeit am IREM de Grenoble. Das Handbuch beinhaltet die gesamten Hinweise auf die Funktionen der exakten Berechnungen, es wird jedoch auch durch ausgewählte Beispiele aus den Abitur und Bakkalaureusprüfungen gezeigt, wie man intelligent die Berechnungsmöglichkeiten dieses Rechners ausnutzen kann. Zum Schluß widmet er sich in zwei Kapiteln der Programmierung: im dem ersten Kapitel erfahren Sie, wie man programmiert. Im zweite Kapitel werden die Algorithmen beschrieben, die in einem spezielle n arithmetischen Programm der letzten, Studienjahre an den französischen Oberschulen benutzt werden.

Inhalt 3

Exakte Berechnungen und Mathematik mit HP40G

Inhalt

1 Zu Beginn 13

1.1 Allgemeine Informationen 13

1.1.1 Start 13

1.1.2 Was sieht man? 13

1.2 Bezeichnung 15

1.2.1 Hilfe 15

2 Aplets 17

2.1 Taste APLET 17

2.2 Verschiedene Aplets 17

2.3 Beispiele mit Benutzung von Aplet Sequence 19

2.4 Tasten SYMB NUMB PLOT 22

3 Tastatur und CAS 23

3.1 Taste CAS auf der Leiste 23

3.2 Leiste des Editors der Gleichungen 24

3.3 Tasten und Editor der Gleichungen 25

3.3.1 Taste MATH 25

3.3.2 Taste SHIFT MATH (CMDS) 26

3.3.3 Taste VARS 26

3.3.4 Taste SHIFT 2 (SYNTAX) 27

3.3.5 Taste HOME 27

3.3.6 Taste SHIFT SYMB 28

3.3.7 Taste SHIFT 28

3.3.8 Taste PLOT 29

3.3.9 Taste NUM 29

3.3.10 Taste VIEWS 30

3.3.11 Tastenabkürzungen 30

3.4 CAS nach HOME 30

3.4.1 PUSH 31

3.4.2 POP 31

3.5 Tastatur Aus Dem Fenster Home 31

3.5.1 Taste MATH 31

3.5.2 Die Taste SHIFT F6 31

3.5.3 Taste SHIFT 2 (SYNTAX) 32

3.5.4 Taste SHIFT 1 (PROGRAMM) 33

Inhalt 5

Exakte Berechnungen und Mathematik mit HP40G

4 Ausdruckssatz der Leiste CAS 35

4.1 Editor der Gleichungen 35

4.1.1 Zutritt zum Editor der Gleichungen 35

4.1.2 Wie verläuft die Eingabe ? 35

4.1.3 Wie ändert man den Ausdruck 40

4.1.4 Betriebsart Cursor 41

4.1.5 Möglichkeit einer gesamten Darstellung 41

4.2 Benutzung der Funktionen CAS 42

4.2.1 Wie schreibt man XQG

4.2.2 Wie schreibt man infixe Funktionen 43

4.2.3 Wie schreibt man präfixe Funktionen 44

4.3 Variablen 47

4.3.1 STO

4.3.2 STORE 48

4.3.3 Vordefinierte Variablen der Leiste CAS 48

5 Funktion der exakten Berechnungen 51

5.1 Leiste CAS 51

5.1.1 CFG 51

5.1.2 TOOL 52

5.1.3 ALGB 52

5.1.4 DIFF 53

5.1.5 Taste MATH 53

5.1.6 REWRITE 54

5.1.7 SOLVER 54

5.1.8 TRIGO 55

5.2 Modus „Schritt für Schritt“ 55

5.3 Normale Schreibweise 56

5.3.1 DEF 56

5.4 Ganze Zahlen (und Gauß-Ganzzahlen) 57

5.4.1 DIVIS 58

5.4.2 EULER 58

5.4.3 FACTOR 58

5.4.4 GCD 59

5.4.5 IEGCD 59

5.4.6 IQUOT 60

5.4.7 IREMAINDER MOD 60

5.4.8 ISPRIME? 61

5.4.9 LCM 62

5.4.10 NEXTPRIME 62

6 Inhalt

Exakte Berechnungen und Mathematik mit HP40G

5.4.11 PREVPRIME 62

5.5 Modulare Berechnungen 62

5.5.1 ADDTMOD 63

5.5.2 DIVMOD 63

5.5.3 EXPANDMOD 63

5.5.4 FACTORMOD 64

5.5.5 GCDMOD 64

5.5.6 INVMOD 64

5.5.7 MODSTO 64

5.5.8 MULTMOD 65

5.5.9 POWMOD 65

5.5.10 SUBTMOD 65

5.6 Rationale Zahlen 65

5.6.1 PROPFRAC 66

5.7 Reelle Zahlen 67

5.7.1 FLOOR 67

5.7.2 MOD 67

5.8 Komplexe Zahlen 68

5.8.1 ARG 69

5.8.2 CONJ 69

5.8.3 DROITE 70

5.9 Algebraische Ausdrücke 70

5.9.1 COLLECT 70

5.9.2 EXPAND 71

5.9.3 FACTOR 71

5.9.4 72

5.9.5 SUBST 72

5.10 Polynome 72

5.10.1 DEGREE 73

5.10.2 EGCD 73

5.10.3 FACTOR 73

5.10.4 GCD 74

5.10.5 HERMITE 74

5.10.6 LCM 75

5.10.7 LEGENDRE 75

5.10.8 PARTFRAC 76

5.10.9 PROPFRAC 76

5.10.10 PTAYL 77

5.10.11 QUOT 77

5.10.12 REMAINDER 78

5.10.13 TCHEBYCHEFF 78

Inhalt 7

Exakte Berechnungen und Mathematik mit HP40G

5.11 FUNKTION 79

5.11.1 DEF 79

5.11.2 IFTE 80

5.11.3 DERVX 80

5.11.4 DERIV 81

5.11.5 TABVAR 82

5.11.6 FOURIER 82

5.11.7 IBP 83

5.11.8 INTVX 84

5.11.9 LIMIT 86

5.11.10 LIMIT und  87

5.11.11 PREVAL 88

5.11.12 RISCH 88

5.12 Limitierte Und Asymptonische Entwicklungen 88

5.12.1 DIVPC 89

5.12.2 LIMIT 89

5.12.3 SERIE 90

5.12.4 TAYLOR0 93

5.12.5 TRUNC 93

5.13 Funktion Konvertierung (Wertumformung) 94

5.13.1 DISTRIB 94

5.13.2 EPSX0 94

5.13.3 EXP2POW 95

5.13.4 EXPLN 95

5.13.5 FDISTRIB 95

5.13.6 LIN 96

5.13.7 LNCOLLECT 96

5.13.8 POWEXPAND 97

5.13.9 SIMPLIFY 97

5.13.10 XNUM 97

5.13.11 XQ 98

5.14 GLEICHUNGEN 98

5.14.1 ISOLATE 98

5.14.2 SOLVEVX 99

5.14.3 SOLVE 99

5.15 Lineare Systeme 100

5.15.1 LINSOLVE 100

5.16 Differentialgleichungen 102

5.16.1 DESOLVE und SUBST 102

5.16.2 LDEC 103

5.17 Trigonometrische Ausdrücke 103

8 Inhalt

Exakte Berechnungen und Mathematik mit HP40G

5.17.1 ACOS2S 103

5.17.2 ASIN2C 104

5.17.3 ASIN2T 104

5.17.4 ATAN2S 105

5.17.5 HALFTAN 105

5.17.6 SINCOS 106

5.17.7 TAN2CS2 106

5.17.8 TAN2SC 107

5.17.9 TAN2SC2 107

5.17.10 TCOLLECT 108

5.17.11 TEXPAND 108

5.17.12 TLIN 109

5.17.13 TRIG 109

5.17.14 TRIGCOS 110

5.17.15 TRIGSIN 110

5.17.16 TRIGTAN 110

6 Lösen von Aufgaben mit dem Rechner HP 40

6.1 Einleitung 111

6.2 Beispiele bei einer Bakkalaureusprüfung 112

6.2.1 Beispiel 1 112

6.2.2 Beispiel 2 113

6.2.3 Beispiel 3 114

6.2.4 Beispiel 4 115

6.2.5 Beispiel 116

6.3 Beispiele bei dem Abitur 118

6.3.1 Beispiel 1 118

6.3.2 Beispiel 2 (Sonderbeispiel) 124

6.3.3 Beispiel 3 (Sonderbeispiel) 129

6.4 Schlußbemerkung 134

111

7 Programmieren 135

7.1 Implementierung 135

7.1.1 Wie man Programme aufruft und speichert 135

7.1.2 Wie repariert man ein Programm 135

7.1.3 Wie wird mit den Programmen gearbeitet? 135

7.1.4 Wie ändert man ein Programm 136

7.2 Kommentare 136

7.3 Variablen 137

Inhalt 9

Exakte Berechnungen und Mathematik mit HP40G

7.3.1 Namen 137

7.3.2 Kenntnis der lokalen Variablen 137

7.3.3 Kenntnis der Parameter 137

7.4 Eingaben 137

7.4.1 Erläuterung im Algorithmus 137

7.4.2 Erläuterung HP40G 137

7.5 Ausgaben 138

7.5.1 Erläuterung der Algorithmen 138

7.5.2 Erläuterung HP40G 138

7.6 Folge der Instruktionen bzw. Aktion 138

7.6.1 Erläuterung in der Algorithmik 138

7.6.2 Erläuterung HP40G 138

7.7 Instruktion der Zuordnung 138

7.7.1 Erläuterung in der Algorithmik 138

7.7.2 Erläuterung HP40G 139

7.8 Bedingte Instruktionen IF … THEN … ELSE 139

7.8.1 Erläuterung in der Algorithmik 139

7.8.2 Erläuterung HP40G 139

7.9 Instruktion For (für) 139

7.9.1 Erläuterung in der Algorithmik 139

7.9.2 Erläuterung HP40G 139

7.10 Instruktion WHILE … REPEAT 140

7.10.1 Erläuterung in der Algorithmik 140

7.10.2 Erläuterung HP40G 140

7.11 Boolensche Ausdrücke 140

7.11.1 Erläuterung in der Algorithmik 140

7.11.2 Erläuterung HP40G 140

7.12 Logische Operatoren 140

7.12.1 Erläuterung in der Algorithmik 140

7.12.2 Erläuterung HP40G 140

7.13 Listen (Reihen) 141

7.13.1 Erläuterung in der Algorithmen 141

7.13.2 Erläuterung HP40G 141

7.14 Beispiel: Eratosthenesgitter (Tabelle) 142

7.14.1 Beschreibung 142

7.14.2 Schreiben der Algorithmen 142

7.14.3 Erläuterung HP40G 144

8 Arithmetische Programme 147

8.1 P GCD Euklids Algorithmus 147

10 Inhalt

Exakte Berechnungen und Mathematik mit HP40G

8.1.1 Algorithmische Erläuterung 147

8.1.2 Erläuterung HP40G 148

8.2 Bezogst Identität mit Hilfe des euklidischen Algorithmus. 151

8.2.1 Iteration – nochmalige Version mit Reihen 152

8.2.2 Erläuterung HP40G 153

8.2.3 Rekursive Versionen mit Hilfe von Registern 154

8.2.4 Rekursive Versionen ohne Register 155

8.2.5 Interpretation HP40G 155

8.3 Verteilung auf Primfaktoren 157

8.3.1 Algorithmen und deren Erläuterung 157

8.3.2 Erläuterung HP40G 160

8.4 Berechnung AP mod N 161

8.4.1 Algorithmische Erläuterung 161

8.4.2 Erläuterung HP4OG 163

8.5 Funktion Ist-eine-Primzahl 164

8.5.1 Algorithmische Erläuterung 164

8.5.2 Erläuterung HP40G 166

8.6 Wahrscheinlichkeitsmethode des Herrn Rabin 167

8.6.1 Algorithmische Übersetzung 168

8.6.2 Übersetzung (Erläuterung) HP40G 169

9 GNU Free Documentation License 171 Stichwortverzeichnis 179

Inhalt 11

Exakte Berechnungen und Mathematik mit HP40G

1 Zu Beginn

1.1 Allgemeine Informationen

1.1.1 Start

Durch das Dr ücken der T aste ON befinden Sie sich im Fenster Im Arbeitsmodus lösc ht die Taste ON die gerade durchgeführt e Operation: sie

hat die Funktion Das Ausschalten des Rechners wird durc h das Drücken der Taste

danach

ON (OFF)

CANCEL.

durchgeführt.

HOME

SHIFT

und

1.1.2 Was sieht man?

Von oben nach unten:

1. das Fenster HOME a. den Rechnerstatus b. eine Waagerechte c. eine Leiste mit Anweisungen

2. eine Tastatur

Fenster

1.a Der Rechnerst atus beschre i bt den zugänglichen Mod us im Fenster HOME: RAD oder DEG oder GRD je nach dem, ob in Radianten oder in Grad

gearbeitet wird.

{FUNCTION} kennzeichnet den Namen Aplet, dieser Name wird mit

Hilfe von:

Aplet Function

gewählt.

EH]HLFKQHWGDGHUQDFKREHQJHULFKWHWH3IHLO&XUVRUHLQH

chronologische Griffübersichtanzeige ermöglicht.

1.b Waagerechte:

Über der Waagerechten befindet sich, die im Fenster HOME durchgeführte Berechnungsübersicht.

Prinzip: im Fenster wird die gewünschte Berechnung links und das Ergebnis rechts gesc hrieben.

Zu Beginn 13

Exakte Berechnungen und Mathematik mit HP40G

Unter der Waagerechten befindet sich die Anweisungszeile.

Mit Hilfe des Pfeiles (Cursor), der nach oben gerichtet ist, ist es möglich in die Übersicht zu gelangen und durch die Anweisung

COPY

in der Leiste, den vorhergehenden Ausdruck oder das Ergebnis in die Anweisungszeile zu kopieren.

1.c Leiste: Die Anweisungen auf der Leiste werden durch 6 graue (Funktions-)Tasten

ohne Benennung betäti gt. Diese Tasten werden folgend benannt: F1 F2 F3 F4 F5 F6. Die Leiste kann Register mit Befehlsdateien beinhalten. Sie sind bestimmbar. Die Anweisung auf der Leiste wird durch das Drücken der zuständigen

Funktionstaste

aktiviert.

Im Fenster

STO

HOME

beinhaltet die Leiste zwei Anweisungen:

ermöglicht einen bestimmten Wert auf eine Variable zu übertragen

(speichern) und

CAS

ermöglicht den Editor der Gleichungen (Computer Algebra System) für

exakte Berechnungen zu öffnen. 2 Tastatur

Sie wissen schon: Die Taste ON startet oder beendet die laufende Berechnung und durch das

Drücken vo n

SHIFT ON

wird der Rechner ausgeschaltet.

Es ist notwendig sich folgendes anzueignen:

vier Pfeile (linker, rechter, nach oben, nach unten) ermöglichen de n Cursor

im CAS, im Menü usw. zu bewegen.

die Taste

die Taste ALP HA zum schrei ben von gro ßen Buchstab en und

ALPHA

SHIFT

ändert die Funktion jeder Taste auf eine andere Funktion.

zum Schreib en von klei nen Buchstab en. Damit man im

SHIFT

ausgewählten Alphabetmodus verbleibt, ist es notwe ndig die Taste

ALPHA

X T

Die Taste

ständig zu b etätigen.

ermöglicht laut Kontext direkt X, T, zu schreiben.

ENTER

bestätigt die Anweisung.

14 Zu Beginn

Exakte Berechnungen und Mathematik mit HP40G

1.2 Bezeichnung

Die vier Richtungspfeile des Cursors sind hier in folgender Form:

STO auf der Leiste ist im Programm folgend geschrieb e n:

STO

oder

Die Cursorposition im Editor der Gleichungen wird folgend bezeichnet:

1.2.1 Hilfe

Dieser Rechner hat eine sehr leistungsfähige Hilfe. Im Fenster

Rechners aufrufen. Tastenbedienung:

SHIFT

geschrieben. Man muß nur den Name der Anweisung schreiben, zum Beispiel

man erhält di e Struktur (Syntax) die s er Anweisung. Im Fenster

aufrufen. Sie kann vom Fen st er

HELP

Vom CAS kann man Hilfe für verschiedene Funktionen erhalten. Tastenbedienung:

SHIFT

Sollte die Funktion

CAS HELP ON

ist, eine bestimmte Funktion hervo rzuheben und OK zu schreiben, damit man zu dieser Funktion Hilfe bekommt.

Sollte im Editor, die Funktion Menü

HOME

kann man di e Hilfe über verschiedene Anweisungen des

SYNTAX

2 (

HOME

in die Anweisungszeile schreibt.

SYNTAX

2 (

CAS HELP ON

) (pv 2.3.4) und

kann man auch eine allgemeine Hilfe für die Funktion

) (pv 2.3.4)

CAS

im Editor nicht gewählt sein, so öffnet man das Menü

durch die Menüliste im Editor der Gleichungen. Ausreichend

zeigt direkt die Hilfe für

HELPWITH

HOME

CAS

gewählt sein, zum Beispiel

wird in der Anweisungszeile

INPUT

so ausgewählt werden, indem man

FACTOR

an.

und

CAS

(45),

Zu Beginn 15

2 Aplets

2.1 Taste APLET

Exakte Berechnungen und Mathematik mit HP40G

Die Taste

Dieser Rechner ermöglicht tatsächlich mit Was ist eigentlich

Aplet

Ansichten zu gewinnen (eine symbolische, numerische und eine graphische Ansicht). Das alles wurd e schon programmiert!

Verschiedene Beispiel Funktionen, Reihen, statistischen Folgen usw., zu arbeiten.

Einige

Aplet

macht die Liste der benutzbaren

Aplet

ist ein Programm im Rechner, das durch eine einfache Art ermöglicht 3

Aplets

ermöglichen mit mathematischen Effekten, wie zum

Aplets

sind Programme, die Teile des Unterrichtes illustrieren.

Aplets

zugreifbar.

zu arbeiten:

2.2 Verschiedene Aplets

Befindet man sich im HOME, so erfähr t man den Namen des gewählten

APLET

Hier sind einige Auswahlmöglichkeiten der Taste

Sequence

Dieser U1, U2 … U9, U0 Man definiert U1(N):

von der Zustandsze ile .

APLET

sei eine Funk tion N,

ermöglicht Reihen, die folgende Namen tragen, zu definieren:

APLET

aufgelistet:

sei eine Funk tion U1(N – 1).

Sei eine Funktion U1(N – 1) und U1(U – 2). Man definiert zum Beispiel: U1(N) = N*N+1 und die Wer te U1(1) und U1(2) werden berechnet und geschri eben. Durch das Anstreichen von U1, danach durch das Drücken der Taste

werden die Werte U1(N) angezeigt.

Aplets 17

NUM

Exakte Berechnungen und Mathematik mit HP40G

Weitere Verwendungsbeispiele von

Kapitel und zwar als Berechnung

Aplet Sequence

PGCD

zweier Zahlen (pv 1.3) und

finden Sie im nächsten

Berechnung der Quotienten der Bezouts Identität (pv 1.3)

Function

Aplet

Dieser

ermöglicht Funktionen zu definieren, die folgend kennzeichnet

sind: F1(X), F2(X) … F9(X), FO(X) Es wird die Funktion F1(X) definiert:

entweder dur ch den Ausdruck der Funktio n X:

Zum Beispiel die Formel:

(x) = x.ln (x)

oder, sollte die Funktion fortschreitend definiert sein, mit Benutzung

boolenscher Zahlen:

X>0 usw … Zum Beispiel die Formel in Form: F1(X) = X*(X<0)+2*X*(X<0) definiert die Funktion:

(x) = x wen n x < 0 und

(x) = 2·x wenn x > 0

Parametric Polar Solve Statistic Inference

18 Aplets

zur Setzung der Kurven in Parameterkoordinaten.

zur Setzung der Kurven der Polarkoordinaten.

zur Lösung numerischer Gleichungen.

für Statistik.

inferentiale Statistiken.

Exakte Berechnungen und Mathematik mit HP40G

2.3 Beispiele mit Benutzung von Aplet Sequence

Schreibweise der Basis b

Gegeben ist a und b, Sie möchten die Reihe qn (n ³ 1) und rn (n ³ 2) der Quotienten und der Reste, die Sie durch die Division durch die Basis b dieser q erhalten, ge wi nne n:

= a

= b·q2 + r2 (0 £ r

= b·q3 + r3 (0 £ r

……

= b·qn + rn (0 £ r

n – 1

Beachten Sie, daß wenn r

= b, dann ist die Anzahl rn r

n+1

… r3 r2 eine

n – 1

Schreibweise der Basis b von a. Zu B wird der Wert der Basis zugeordnet, zum Beispiel:

STO

und zu A die Zahl zur Schreibweise der Basis B (zum Beispiel 1789 Nun definieren Sie zwei Reihen:

U1(1)=A U1(2)= U1(N)=

FLOOR

(A/B)

(U1(N – 1)/B)

danach

U2(1)=0 U2(2)=U1(1) U2(N)=U1(N – 1)

So ist also q

=U1(N) und rn=U2(N)

MOD

STO

Aplets 19

Exakte Berechnungen und Mathematik mit HP40G

Berechnung PGCD

Weiter unten ist die Durchführung des Euklids Algorithmus mit dem Rechner angeführt:

Hier ist die Beschreibung dieses Algorithmus: Sie führen eine sukzessive Euklid Division durch:

A = B ´ Q

B = R

+ R1 0 £ R

´ Q2 + R2 0 £ R

A = R2 ´ Q3 + R3 0 £ R

Man hat also:

PGCD PGCD

(A,B) =

n – 1, Rn

PGCD (B, R

) =

PGCD (R

) = …

n – 1,

0) =

n – 1

Mit Hilfe der Reihen werden die Reihen der Reste geschrieben. Benutzen Sie

Sequence

und dann

Aplet Sequence

START

am Rechner (Taste

auf der Leiste).

Aplet

, danach wählen Sie

Wenn Sie PGCD(78,56) definieren möchten, wählen Sie die folgende Reihe:

U1(1) = 78 U1(2) = 56 U1(N) = U1(N – 2)

MOD

U1(N – 1).

Sie bedienen die Taste NUM, damit Sie eine numerische Reihe U1(N) erhalten, bzw. eine Reihe der Reste der sukzessiven Division …

Der letzte Rest ungleich Null ist 2, also

PGCD

(78056) = 2. BEMERKUNG Im Fenster

HOME

kann man di e Variable n A und B benutzen, damit man

beide Zahlen U1(1) = A U1(2) = B speichert und implementiert. Es ist auch zu erwähnen, daß A

MOD

0 = A.

Koeffizientberechnung der Bézouts Identität

Euklids Algorithmus ermöglicht das Paar U, V zu finden und zu prüfen, daß:

A ´ U ´ B ´ V = PGCD(A, B)

Mit Hilfe der Reihen:

20 Aplets

Exakte Berechnungen und Mathematik mit HP40G

Sie definieren „die Reihen der Reste“ Rn und zwei Reihen Un und Vn so, daß in jeder Phase folgendes gilt:

Denn es gilt, daß: R Beziehung (Q R

über R

n – 2

A + Vn ´ B.

n = Un ·

= ganze Quotient

n – 1

n = Rn – 2

– Q

n ´ Rn – 1

, Un und V prüft die gesamte ind uktive

Am Anfang hat man:

= A R2 =B

=1 U2 = 0 denn A = 1 ´ A + 0

=1 V2 = 0 denn B = 0 ´ A + 1

Dank der Funktion

Aplet Sequence

kann man mit dem Rechn e r di e Reste und

die Reihen U2 und U3 definieren, die für alle N folgendes haben werden: U/N)=A

U2(N)+B* U3(N).

Dazu braucht man eine Reihe von Koeffizienten, die man in U4 eingliedert. Die Reihen U1, U2, U3 beweisen eine gleiche Induktionsbeziehung:

= U

Qn =U4(N) =

– Qn ´ U

n – 2

n – 1

FLOOR

gemeinsam mit

(U1(N – 2)/U1(N – 1)) Man definiert also: U1(1)=A U1(2)=B U1(N)=U1(N – 2) – U4(N)·U1(N – 1) U2(1)=1 U2(2)=0 U2(N)=U2(N – 2) – U4(N)·U2(N – 1) U3(1)=0 U3(2)=1 U3(N)=U3(N –2) –U4(N)·U3(N –1) U4(1)=0 U4(2)=0 U4(N)=FLOOR(U1(N –2)/U1(N –1)

Aplets 21

Exakte Berechnungen und Mathematik mit HP40G

Es ist zu bemerken, daß U4(N) nur für N > 2 benutzt wird, es wurden also die ersten zwei Werte (die nicht gebraucht werden) als Null definiert.

NUM

zeigt also die Werte dieser verschiedenen Reihen und bei dem letzten

nullfreien Rest wird man die Koeffizienten der B ezouts Identität haben.

2.4 Tasten SYMB NUMB PLOT

Aplet kann man all ge mei n dur c h dre i Art en se he n:

NUM

PLOT

SETUP

SYMB

) gedrückt werden, werden

Symbolische Ansicht, entspricht die Taste

Numerische Ansicht, entspricht die Taste

Graphische Ansicht, entspricht die Taste

Wenn alle Tasten gemeinsam mit Shift ( verschiedene benutzte Parameter gewählt (Wahl der Winkeleinheiten, Parameter des graphischen Fe nsters us w … ).

22 Aplets

Exakte Berechnungen und Mathematik mit HP40G

3 Tastatur und CAS

3.1 Taste CAS auf der Leiste

CAS ermöglicht eine exakte oder eine symbolische Berechnung (CAS = Computer Algebra System).

Man muß zwischen dem folgenden einen Unterschied sehen: Zwischen der exakten oder der symbolischen Berechnung. Diese Berechnung

ist diejenige, die man mit den Funktionen CAS durchführt. Man arbeitet im mode exact mit einer unendlichen Genauigkeit und es is t möglich deren Berechnung Schritt für Schritt zu führen; und

Zwischen der numerischen Berechnung. Diese Berechnung ist diejenige, die man mit den Funktionen MATH im Fenster HOME oder Aplets durchführt.

Beispiel: Befindet man sich im Radians im Fenster HOME so: ARG (1 + i) hat einen Wert von 0,785398163397 Während in CAS, wo nur in Radians gearbeitet wird:

ARG (1 + i) hat einen Wert von

Wenn man eine exakte Berechnung durchführen möchte, ist es notwendig CAS auf der Leiste zu drücken und somit den CAS Modus zu öffnen. Für die Rückkehr in das Fenster HOME dann ON drücken.

In den folgenden Kapiteln werden wir dann lernen mit der Funktion CAS umzugehen.

BEMERKUNG Einige Funktionen der e xakten Berec hnungen ka nn man direkt im Fenster

HOME benutzen, die laufende Variable ist also systematisch eine Variable S1, zum Beispiel:

FACTOR

ACHTUNG, einige Berechnungen werden nur annähernd in Hinsicht auf die Unbestimmtheit zwischen den reellen und den ganzen Zahlen im Fenster

HOME

exaktes Argument auf ein annäherndes Argument (pv 2.3.4) umzusetzen.

Tastatur und CAS 23

(S1^2 – 4)

durchgeführt. Die Anwendung de r Anweisung XQ ermöglicht ein

Exakte Berechnungen und Mathematik mit HP40G

3.2 Leiste des Editors der Gleichungen

Der Editor der Gleichungen ermöglicht, ähnlich wie beim Sc hreiben mit d er Hand, die Schreibweise der Ausdrücke, die man vereinfachen möchte, zu differenzieren, zu integrieren etc.

Es ist ein Editor der Register beinhaltet:

Edit expr., Change font, View expr.

Cursor

Edit

diesen Ausdruck zu ändern.

Change

Buchstaben zu wählen(diese Wahl ist stets zugänglich).

View

2. Das Register

zu arbeiten: Fakultäten durchzuführen, Zerlegung und Vereinfachung …

3. Das Register

ermöglichen: Derivation, Integration, limitierte Zerlegung …

4. Das Register

Ausdruck anders oder neu einzugeben.

5. Das Register

trigonometrische Ausdrücke zu ändern.

6. Das Register

Gleichungen, lineare Systeme und differentiale Gleichungen zu lösen.

Im Kapitel 3 finden Sie eine Anleitung, wie man den Ausdruck in den Editor der Gleichungen schreibt, wie man einen Unterausdruck wählt und wie man die Funktionen aus

mode

ermöglicht zum Modus Cursor (pv 3.1.4) zu übergehen.

expr.

Editiert den hervorgehobenen Ausdrucks, er ermöglicht also

font

ermöglicht entweder kleine Buchstaben oder große

expr.

ermöglicht eine einfache Sicht auf großen Ausdrücke.

ALBG

beinhaltet Funktionen, die ermöglichen, mit Algebra

DIFF

beinhaltet Funktionen, die eine Differentialrechnung

REWRITE

TRIGO

SOLVER

CAS

aufruft.

beinhalt et Funktio nen, die er möglichen, einen

beinhaltet Funktionen, die ermöglichen

beinhaltet Funktionen, die ermöglichen,

Cursor mode,

Im Kapitel 4 finden Sie alle Funktionen der exakten Berechnungen, beinhaltet in diesen Registern jeweils mit Beispielen, wie man sie verwendet.

SHIFT 2 (SYNTAX

Funktionen, die zur Verfügung stehen, dienen dann zu deren Eingabe.

24 Tastatur und CAS

) (pv 2.3.4) dient zum Öffnen der Hilfe für die sonstigen

SHIFT MATH (CMDS

) (pv 2.3.2)

Exakte Berechnungen und Mathematik mit HP40G

3.3 Tasten und Editor der Gleichungen

Die Tasten, über denen in diesem Abschnitt gesprochen wird, haben im Editor der Gleichungen keine gleiche Funktion wie im Fenster

Wie diese Tasten außerhalb des Editoren der Gleichungen funktionieren, ist aus dem Haupthandbuch zu entnehmen.

3.3.1 Taste MATH

Diese Taste öffnet das Menü der Funktionen. Schon im Editor der Gleichungen fi ndet man Funktionen für eine exakte

Berechnung.

HOME

Zusätzlich ze igt die gedr ückte Taste folgendes an:

den Register

zusammengesetzten Zahlen zu arbeiten.

den Register

die gesamte Arithmetik durchzuführen.

den Register

zu arbeiten. Den Wert p beinhaltet die Variable

den Register

ermöglichen, mit Polynomen zu rechnen.

den Register

ASSUME

Parameter und so die Variable REALASSUME (pv 3.3.3) zu modifizieren

CMPLX

CONSTANTS INTEGER

HYPERBOLIC MODULAR

POLYNOMINAL

TEST

UNASSUME

… der Funktionen beinhaltet, die ermöglichen, mit

… der folgendes beinhaltet:

³ < £ = = ¹

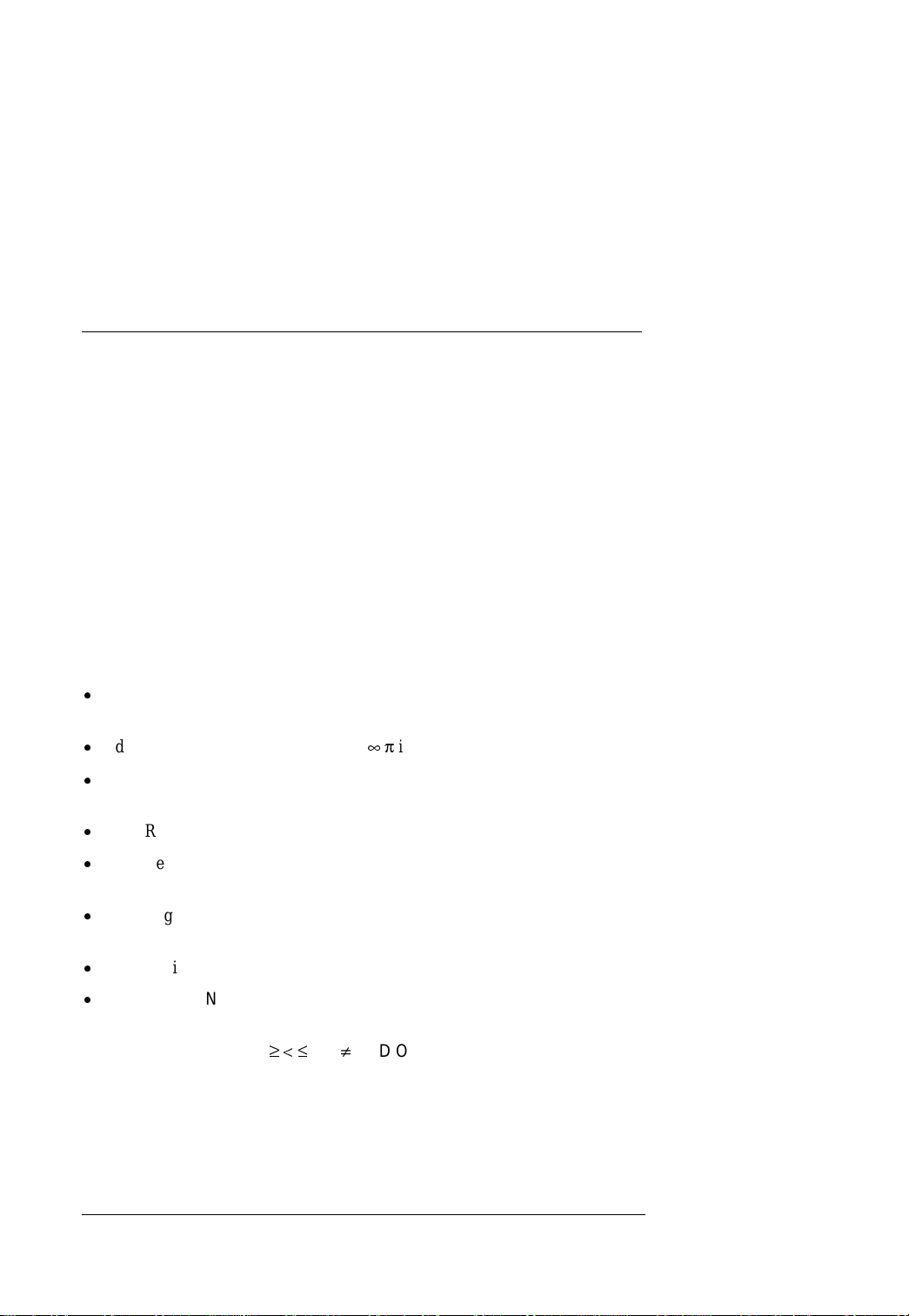
MATH

im Editor der Gleichungen

… (e i ¥ p i)

… der Funktionen beinhaltet, die ermöglichen,

… der hyperbolische Funktionen beinha ltet.

… der ermöglicht, in Z/pZ oder Z/pZ[X] mit p

MODULO

… der Funktionen beinhaltet, die

(zur Durchführung von Hypothesen über

AND OR NOT.

Tastatur und CAS 25

Exakte Berechnungen und Mathematik mit HP40G

3.3.2 Taste SHIFT MATH (CMDS)

Im HOME ermöglicht diese Taste den Zugriff zu den Anweisungen, die

folgendes zu steuern ermöglichen:

Aplets

Programme zu schreiben

Graphen zu zeichnen

Statistiken zu erstellen

Im Editor der Gleichungen findet man einen Katalog aller Funktionen der exakten Berechnungen.

Genau so die Funktionen, die anderswo nicht vorkommen, können aus diesem Menü aufgerufen werde n, womit man das Eintasten im Modus vermeiden

Alpha

3.3.3 Taste VARS

Durch Betätigen dieser Taste werden im Editor der Gleichungen die Namen der in CAS definierten Variablen angezeigt.

Wir unterscheiden namV X, das den Namen der laufenden Varia ble beinhaltet. Zur Darstellung des Inha l tes jeder Variable ge nügt es, den markierten Namen

durch Betätigen von F2 für VIEW in der Displayleiste anz usehen. Zur Änderung des Inhaltes der Variable genügt es, den markierten Namen

anzugeben und F3 für EDIT der Liste zu betätigen. In der Liste wird ebenfalls folgendes angezeigt: PURGE, löscht die entsprechnede Variable. RENAME, ändert die bestehenden Variable. NEW, ermöglicht eine neue Variabl e zu besti mmen: es genügt, auf den Inhalt

(Objekt), dann auf deren Namen (Name) zu klicken. siehe auch Teil 3.3.

26 Tastatur und CAS

Exakte Berechnungen und Mathematik mit HP40G

3.3.4 Taste SHIFT 2 (SYNTAX)

Wenn man sich im Editor der Gleichungen befindet, öffnet die Kombination der Tasten: SHIFT 2 (SYNTAX) das Menü CAS HELP ON. Sollte die Funktion des gewählten CAS im Editor nicht vorhanden sein, schlägt dieses Menü eine Liste der aus dem Editor der Gleichu ngen verwendbaren Fun kt ionen vor. Es genügt also, die Funktion zu markieren und O K zu drücke n, um für diese Funktion die Hilfe zu bekommen.

Wenn im Editor die Funktion CAS gewählt wird, z.B.: FACTOR (45), öffnet das Menü CAS HELP ON direkt die Hilfe auf der Seite von FACTOR. Die Hilfe besteht in einer kurzen Beschreibung der Anweisung, eines Beispiels und seiner Antwort. Jedes Beispiel kann im Editor der Gleichungen mit Hilfe von ECHO der Liste im bestehenden Zustand angegeben werden oder es kann geändert werden.

Es ist zu bemerken, daß in den Beispielen der Hilfe als laufende Variable VX=X gewählt wurde. Sollte es nicht der Fall sein, wird das B e ispiel automatisch mit Rücksicht auf Ihr VX im Laufe der Übertragung mit Hilfe von ECHO geändert.

Sie haben ebenfalls die Möglichkeit, die Hilfe einer Anweisung direkt in SEE zu öffnen: mit Hilfe von SEE1, SEE2 … der Liste.

3.3.5 Taste HOME

Das Drücken der Taste Übersicht

Die Übersicht der durchgeführten Berechnungen im der Berechnungen durchgeführt i n HOME ist unterschie dlich.

Genau so wie in der Übersicht des Fensters Berechnungen links und die Ergebnisse rechts geschrieben werden. Durch den Pfeil der nach oben zielt kann man in die Übersicht zurückkehren.

Dank schon eingegebene Anweisung kopieren.

Tastatur und CAS 27

CAS

einzuspr ingen.

ECHO

auf der Leiste kann man das vorhe rgehende Ergebnis od er die

HOME

im Editor der Gleichungen ermöglicht in die

CAS

und die Übersicht

HOME,

wo die eingegebenen

Exakte Berechnungen und Mathematik mit HP40G

3.3.6 Taste SHIFT SYMB

Befindet man sich im Editor der Gleichungen, so sind die Tasten

SYMB (SETUP

usw … auf der Leiste pv 4.1.1) Das ermöglicht folgendes zu präzisieren: den Namen der Variable beinhaltet in VX durch d as Eintasten d eren Namen

Inder var

vor

Modulo,

Modus durch Akti vie re n vo n reellen Modus arbeiten möchte/oder im Komplex des Modus durch Aktivieren

Complex

von Wenn man im Modus

wird auf der Leiste wenn Ihre Polynome nach den abnehmenden Po tenzen (oder der zuneh menden,

wenn man Pow und CHK auf der Leiste aktiviert) geschrieben sind, wenn man symbolische Primfaktor en (oder numerische, we nn man Num Fac tor

und CHK auf der Leiste anstreicht) erhalten möchte, wenn man im freien Modus (oder im exakten Modus, wenn man Rigourous und

CHK auf der Leiste aktiviert, damit man die absoluten Werte beachtet!) arbeiten möchte.

Man bestätigt durch OK oder durch ENTER.

) analogisch zu

,den Wert

wenn man im exakten Mous arbeiten möchte (oder im annähernden

und

MODULO

CHK

auf der Leiste),

Direct

Step/Step

CFG

(die erste Wahl aus dem Menü

durch das Eintasten ihre s Wertes vor

Aprox

arbeiten möchte(oder im Modus

und

CHK

und

CHK

auf der Leiste),wenn man im

auf der Leiste anktiviert),

SHIFT

ALBG

Step/Step

, dann

3.3.7 Taste SHIFT

Befindet man sich im Editor der Gleichungen, dann haben die Tasten: SHIFT, (MEMORY) eine Aufgabe „undo“. Das ist sehr nüt zlich, wenn man sich getäuscht hat, die vorhergehende Ein gabe

zu löschen.

28 Tastatur und CAS

Exakte Berechnungen und Mathematik mit HP40G

3.3.8 Taste PLOT

Drückt man PLOT im Editor der Gleichungen, so fragt Sie das Dia l ogfenster, ob Sie eine Parameterkurve oder ei ne Polarkurve festlegen möchten. Je nach dem, was gewählt wird, wird der hervorgehobene Ausdruck in das zuständige

Aplets

ACHTUNG: dies erfordert, daß die laufende Variable auch als Variable der zuständigen Funktion ist, denn während des Kopieren wird der Ausdruck aufgewertet und die laufende Variable (die, was im VX beinhaltet ist) wird zu

;7RGHU

Wenn es einen ausgewählt en Ausdruck mit reellen Werten gib t :

auf eine Stel le, die man näher besti mmt, kopiert.

ODXW$UWGHV*UDSKHVJHändert.

so kann man entweder zum Type:

Wenn es einen ausgewählt en Ausdruck mit komplexen Werte n gibt: so muß man Aplet Parametric wählen und der Graph wird den Type:

Parametric haben. Wenn man folgendes auswählt:

Aplet Function, der hervorgehobene Ausdruck wird in die ausgewählte

Funktion Fi kopiert und die laufende Variable wird sich während des Kopieren zu X ändern,

Aplet Parametric, reeller und imaginärer Teil

des hervorgehobenen Au sdruckes werden in die ausgewählten Fu nktionen

Xi, Yi kopieren und die laufende Variable ändert sich zu T während des Kopieren,

Aplet Polar, der hervorgehobene Wert wird in die ausgewählte Funktion

Ri kopiert und die laufende Variable ändert sich während des Kopieren auf



Aplet Function

Function

oder Aplet Polar wählen, der Graph wird dann

Polar

oder

3.3.9 Taste NUM

Drückt man Ausdruck durch einen nu merisch annähernden Wer t ersetzt.

NUM

im Editor der Gleichungen, so wird der hervorgehobene

Tastatur und CAS 29

Exakte Berechnungen und Mathematik mit HP40G

3.3.10 Taste VIEWS

Beim Betätigen von VIEWS aus dem Editor der Gleichungen kann der markierte Ausdruck durch die Cursorbewegung mittels der Pfeile > und < vollständig angezeigt werden. Zur Rückkehr in den Editor der Gleichungen OK drücken.

3.3.11 Tastenabkürzungen

Es ist zu bemerken, daß man im Editor der Gleichungen mit der Tastatur diese abgekürzten Anweisungen benutzen kann:

SHIFT

0 für

SHIFT

1 für i

SHIFT

3 für

SHIFT

5 für

SHIFT

6 für

SHIFT

8 für

SHIFT

9 für

3.4 CAS nach HOME

Es ist möglich bestimmte genaue Funkt i onen direkt im Fenster H OME, mit Hilfe eini gen Maßnahmen, zu benut zen:

die Anwendung der genauen Rechenfunktion, die sich im CAS auf der

Taste MATH (im Fenster HOME) befindet. Übliche Variable ist also die systematische Variable S1, z. B.:

-die Anwendung der Variable S1, S2, … S5 als symbolische Variablen,

wenn Sie mit den symbolischen Matrixen arbeiten wollen, ist nötig die Matrixen als L1, L2, … L9, L0 zu speichern, sonst werden diese Matrixen als die Liste der Listen interpretieren (die numerische Matrixen müssen als M1, M2, … M9, M0 gespeichert werden).z.B.:

Sie können auch mit der Hilfe des Befehls PUSH und POP die Ausdrücke aus dem Speicher ins Fenster HOME auf den Speicher CAS übertragen.

30 Tastatur und CAS

12)241(

SSSDERVX ⋅=⋅−

1)]2(,11[ LSTOXQS >+

Exakte Berechnungen und Mathematik mit HP40G

3.4.1 PUSH

Aus dem Fenster HOME können Sie die Ausdrücke aus dem Speicher CAS mit der Hilfe des Befehls PUSH schicken.

Im Fenster HOME drücken wir : PUSH(S1+1) und S1+1 schreiben wir in den Speicher CAS.

3.4.2 POP

Sie können Dank dem Befehl POP im Fenster HOME wieder den zuletzt geschriebenen Ausdruck im Speicher CAS erwerben.

Im Fenster schreiben wir: POP und z·B·S1 +1 schreiben wir im Speicher des Fensters HOME.

3.5 Tastatur Aus Dem Fenster Home

3.5.1 Taste MATH

Sie öffnet das Menü der mathematischen Funktionen. Durch Betätigen dieser T aste aus dem Fenster H OME wird ein Fenster mit

mathematischen (numerischen) Funktionen, die den Themen nach geordnet sind, geöffnet, weil die MTH-Wahl aus der Liste (Taste F1) falsch angestrichen ist.

Wenn man CAS d er Liste dieses Fensters (Taste F3) drückt, setzt man dieselben Register wie beim Betätigen der Taste MATH aus dem Editor der Gleichungen zurück: so gelangt man ebenfalls zu den Funktionen der ge nauen Berechnung, die den Themen nach geordnet sind und die aus dem Fenster HOME verwendbar sind (nicht vergessen, daß im Fenster HO ME nur S1, S2 … S5 symbolische Variablen sind).

3.5.2 Die Taste SHIFT F6

Die Kombination der Tasten SHIFT+F6 (SHIFT CAS auf der Leiste) öffnet das Fenster der Konfiguration CAS. Es er möglicht die Konfiguration CAS im Fenster HOME (vergleiche es mit 2.5.6).

Tastatur und CAS 31

Exakte Berechnungen und Mathematik mit HP40G

3.5.3 Taste SHIFT 2 (SYNTAX)

Die Kombination der Tasten SHIFT 2 (SYNTAX) plaziert HELPWITH in die

Anweisungszeile. Es genügt, diese Zeile mit dem Namen der Anweisung oder dem Namen der CAS-Funktion, für die Sie die Hilfe wollen, zu ergänzen. Zur Rückkehr in die CAS-Fu nktion MATH CAS verwenden, es muß jedoch dara uf geachtet werden, daß die Klammer entfernt wird.

Zum Beispiel: HELPWITH DERVX öffnet für Sie die CAS-Hilfe auf der Seite DERVX.

Wenn Sie eine allgemeine Hilfe für CAS aus dem Fenster HOME brauchen, muß HELP, dann ENTER gedrückt werden: somit steht Ihnen di e Hilfe zu den CAS-Funktionen, die aus dem Fenster HOME verwendbar sind, zur Verfügung.

Jedes Beispiel kann aus dem Menü des Fensters HOME über ECHO der Liste zugänglich gemacht werden und kann im bestehenden oder in einem veränderten Zustand verwendet werden (die Variable X wird selbstverstä ndlich durch S1 ersetzt).

Jedes Beis piel kann man in die chronologische Üb ersicht durc h Drücken von ECHO auf der Leiste eintragen und weiter in der bestehenden oder in der

umgeänderten Form (und zwar damit, daß die Variable X durch S1 ersetzt wird) verarbeiten.

Manchmal wird man selbst die Namen einiger Variablen (zum Beispiel Y durch S2 ersetzen) ändern müssen, weil in HOME die Variablen A, … X, Y, Z numerische Variablen sind, die STETS einen Wert haben.

Man wird manchmal im HOME die reellen Zahlen auf ganze Zahlen dank der Funktion XQ ändern müssen und zum Be i s piel MODST O (XQ(13) ) eingeben.

Ausführlicheres Beispie l: In HOME:

(PROPFRAC =

während

(XQ(PROPFRAC +=

32 Tastatur und CAS

..5833.3)

3)) 12

Exakte Berechnungen und Mathematik mit HP40G

3.5.4 Taste SHIFT 1 (PROGRAMM)

Das Drücken dieser Tasten in CAS ermöglicht eine imaginäre Zahl i zu schreiben.

Durch ein Drücken dieser Taste in

CATALOG.

Angezeigt wird:

die Liste der die durch uns geschriebener Programme,

die Leiste mit Anweisungen:

EDIT NEW RUN SEND RECV. EDIT ermöglicht das hervorgehobene Programm zu editieren, NEW ermöglicht ein neues Programm zu erstellen, RUN startet das hervorgehobene Programm, SEND und RECV sind Funktionen, die eine Verbindung zwischen Rechner

und Ihrem Computer er möglichen. Zum Beispiel:

benutzt:

SEND

auf der Leiste klickt, so fragt der Rechner folgendes:

HP 40G

Wenn man auf HP40G oder Disk drive Durch die Vorhebung von

anderen Rec hner und durch Vorhebung des Diskdrive zum Computer. Dann OK auf der Leiste. Unten angeführt erfahren sie zum Beispiel, wie man das Programm

Linuxu

HOME

öffnet sich das Fenster

sendet man d as Programm z u einem

PROGRAM

Kermit

von

Schließen Sie den Rechner an die Übertragungseinheit an. in den Compute r schreibt man: kermit set line/dev/ttyS0 (oder S1 … nach dem Seriellnummer, Achtung, S0

entsprechend COM1 im MS-DOS) Es ist möglich, daß dieser Befehl verursacht ein Fehler „access to device

denied“ In dem Fall müssen Sie als root folgender Befehl durchführen: chmod 666/dev/ttyS0 (oder/dev/ttyS1 nach dem Seriellnummer)

Tastatur und CAS 33

Exakte Berechnungen und Mathematik mit HP40G

Es ist auch möglich, daß dieser Befehl verursacht ein Fehler – write access to UUCP lockfile directory denied-, in dem Fall müssen Sie als root folgender Befehl durchführen:

chmod 1777/var/lock Nachdem schreiben Sie folgende Befehle: set speed 9600 set carrier-watch off serv Auf dem Rechner: heben Sie das Programm mit dem Namen

SEND

auf der Leiste und heben Sie Disk drive hervor. Dann OK auf der

Leiste, daß das Programm mit dem Namen

NOM

hervor, danach drücken Sie

NOM

, das sich in Ihr em Rechner

befindet, in Ihren Computer kopiert wird. oder Auf dem Rechner: Drücken Sie

RECV

auf der Leiste und heben Sie Disk drive hervor. Dann OK auf der Leiste: der Rechner zeigt die Liste der Programme, die sich in Ihrem Computer befindet, an (auf jeden Fall müssen Sie im Computer ein Register, wo die Programme vom Rechner aufbewahrt werden, haben).

Dann heben Sie

PGCD

hervor, damit das Programm mit dem Namen

PGCD

das sich in Ihrem Computer befindet, in Ihren Rechner kopiert wird. Wählen Sie PGCD so aus, damit das Programm, der PGCD heißt, und der sich

in Ihrem Computer befindet, im HP 40G kopiert wird. Beachten Sie, daß die Befehle kermit können auch automatisch durchgeführt werden, so, daß die in die Kartei. Kermc den Wurzelindex des Benutzers übertragen sind, bilden Sie z.B. folgende Kartei:

set line /dev/ttyS0 set speed 9600 set carrier-watch off set file names literal

und speichern Sie die unter dem Name ~/.kermrc Weiter Informationen, die die Benutzung Kermit mit den Taschenrec hnern HP

betreffen, finden Sie in URL: http://www.columbia.edu/kermit/hp48.html

34 Tastatur und CAS

Exakte Berechnungen und Mathematik mit HP40G

4 Ausdruckssatz der Leiste CAS

4.1 Editor der Gleichungen

4.1.1 Zutritt zum Editor der Gleichungen

Die Taste CAS ermöglicht einen Zutritt in den Editor der Gleichungen. Dieser Edit or ist für das Schreiben, Ve reinfach ung und Tra nsformation der

mathematischen Ausdrücke sehr leistungsfähig. Befindet man sich im Editor der Gleichungen, kann man Ausdrücke schreiben,

wobei der gerade ausgewählte Operator stets mit dem zuständigen Ausdruck oder mit dem durch Ihnen ausgewählten Ausdruck verknüpft ist.

Es ist nicht notwendig, sich mit dem Schreiben der Klammern zu beschäftigen, es wird nur eine Auswahl durchgeführt.

Die mathematischen Ausdrücke betrachtet man als einen Baum, ohne daß dieser binär wäre und daraus versteht man, daß die vier Pfeile ermöglichen, den gesamten Baum ungezwungen durchgehen zu können:

Der rechte und der linke Pfeil ermöglichen von einem Baum zum anderen zu gelangen

Mit dem oberen und mit dem unteren Pfeil kann man den Baum nach oben und nach unten durc h gehe n

Der rechte und der linke Pfeil gemeinsam mit der Taste SHIFT ermöglichen verschiedene Auswahlen (siehe Seite 5 Beispiel 3).

4.1.2 Wie verläuft die Eingabe?

In den Eingabemodus kann man durch zwei Möglichkeiten einspringen

Der Pfeil ¨HUP|JOLFKW,KQHQLQGLH$XVZDKOEHWULHEVDUWHLQ]XVSULQJHQXQG

sucht ein Element, das zum Cursor passt, aus. Beispiel:

1 + 2 + 3 + 4 ¨

durch die Ei ngabe von 4 u nd durch das Drücken von ¨ZLUGGHUJDQ]H Baum 1 + 2 + 3 + 4 gewählt.

Ausdruckssatz der Leiste CAS 35

Exakte Berechnungen und Mathematik mit HP40G

Der Pfeil > ermöglicht in die Auswahlbetriebsart einzuspringen und sucht

einen Teilbaum, der zum Cursor paßt, aus. Wenn Sie nochmals das Symbol > drücken, erweitern sie die

Auswahlmöglichkeit des passenden Teilbaumes, und zwar links von Ihrer Auswahl.

Beispiel:

1 + 2 + 3 + 4

durch die Ei ngabe von 3 + 4 und durch das Drücken von > wird 2 + 3 + 4 gewählt, danach wird dur ch das Drücken von > 1 + 2 + 3 + 4 gewählt

Achtung: wenn geradezu eine Funktion, die mehrere Argumente hat,

eingeben wird (wie zum B eispiel RGHU oder SUBST usw.), ermöglicht der Pfeil > das Schreiben durch eine

Änderung der Cursorpositionierung fortzusetzen. An und für sich sind es die Pfeile > und >, die ermöglichen, von einem Argument zum anderen zu

übergehen. In diesem Falle ist es notwendig, stets mit Hilfe des Pfeiles ¨

einzugeben (siehe 1.2.1). Beispiele über die Funktion dieses Editors: Durch das Dr ücken der Taste CAS öffnet man den Editor der Gleic hungen,

dann gibt man die Ausdrücke der Beispiele ein. Beispiel 1 unter Schreib en des Ausdruc kes:

2 + X * 3 – X

versteht man:

2 + X·3 – X

man drückt für die Eingabe des Ausdruckes >

dann die Ta st e ENTER und erhält das Ergebnis:

2 + 2·X

Wenn man einen Ausd r uck sc hre ib t:

2 + X > * 3 – X

36 Ausdruckssatz der Leiste CAS

Exakte Berechnungen und Mathematik mit HP40G

ist dieser Ausdruck mit dem folgenden Ausdruck äquivalent:

(2 + X)·3 – X

Zur Eingabe des Ausdruckes drückt man > >, dann die Ta st e ENTER und man erhält das Er gebnis:

6 + 2·X

Tastenbedienung:

2 + X > * ¨±;

ergibt:

(2 + X)·(3 – X)

zur Eingabe des Ausdruckes drückt man > >

dann die Ta st e ENTER und man erhält das Er gebnis:

–(X² – X – 6) Beispiel 2 Wenn man folgend e s schr ei be n mö cht e :

X² – 3·X + 1

Tastenbedienung:

2 > – 3X + 1

Wenn man folgend e s schr ei be n mö cht e :

–X² – 3·X + 1

Tastenbedienung:

–Xx

> > – 3·X > > + 1

Es ist notwendig bevor man weitere Angaben schr eibt noch zuvor –X² einzugeben.

Beispiel 3 Wenn man folgend e s schr ei be n mö cht e :

1 2

+++

Ausdruckssatz der Leiste CAS 37

Exakte Berechnungen und Mathematik mit HP40G

Hier, ist die Baumspitze „ + “ und es sind hier 4 Teilbäume. Jeder dieser Teilbäume hat als Spitze „ ¸ „ und besitzt zwei Blätter.

Durch das Drücken der Leistentaste CAS wird der Editor der Gleichungen geöffnet, d ann wird der e rste Teilbaum geschrieben:

1 ÷ 2

ferner wählt man diesen Baum mit Hilfe

aus Dann drückt man das Symbol

und den zweiten Teilbaum:

1 ÷ 3

dann wird dieser Baum mit Hilfe

eingegeben

danach schreibt man

und den dritten Teilbaum:

1 ÷ 4

ferner wird dieser Baum mit Hilfe

eingegeben

dann schreibt ma n

und den vier ten Teilba um:

1 ÷ 5

38 Ausdruckssatz der Leiste CAS

Exakte Berechnungen und Mathematik mit HP40G

und ferner wird dieser Baum mit Hilfe

eingegeben.

Nun, der Sollwert

1 2

ist im Editor der Gleich ungen geschrieben und

+++

ist eingegeben.

Es wird der Baum durchgegangen und die Eingab e durchgeführt

das Symbol:

für die Eingabe von 1/3 drücken – dann die Taste

SHIFT

ermöglicht die Eingabe von zwei passenden Teilbäumen, und zwar des eingegebenen und seines N achbars auf der rechten Seite, hier:

Bedeutung: Mit Hilfe d er Taste ENTER kann gefo rdert werden, daß eine Berechnung des eingegebenen Teiles durchgeführt wird ergibt:

eingegeben ist. Wenn man jetzt eine Teilrech nung durchführen möcht e

Ausdruckssatz der Leiste CAS 39

Exakte Berechnungen und Mathematik mit HP40G

muß man zuerst eine Permutation durchführen, damit einander be finden, und das durch Drücken von

SHIFT die das eingegebene Element mit seinem Nachbar links austauscht . Ergibt:

und

die folgendes eingibt, betätigen

es kann die Taste ENTER wieder gedrückt werden.

- Zusammengefaßt: SHIFT> ermöglicht eine Eingabe des ausgewählten Elements und seines Nachbars auf der rechten Seite.

SHIFT< ermöglicht das gewählte Element (die Reihenfolge) mit seinem Nachbar auf der linken Seit e auszutauschen (zu ändern).

ist eingegeben, dann die Taste

SHIFT

1 2

und

sich neben

Das eingegebene Element hat seine Stelle geändert, aber es bleibt stets eingegeben.

4.1.3 Wie ändert man den Ausdruck

Wenn Sie gerade einen Ausdruck schreiben, ermöglicht Ihnen die Taste DEL alles, was gerade geschrieb en wurde, zu löschen.

Wenn Sie gerade eine Eingabe durchführen, so können Sie: entweder durch das Drücken vo n DEL die Auswahl löschen, der Ausdr uck wird jedoch nicht gelöscht.

Der Cursor befindet sich am Ende des Ausdruckes, dessen Eingabe abgebrochen werden soll.

Entweder man ersetzt die Eingabe durch einen anderen Ausdruck: man schreibt den Ausdruck.

40 Ausdruckssatz der Leiste CAS

Exakte Berechnungen und Mathematik mit HP40G

Oder man tauscht den eingegebenen Ausdruck so, daß man eine Funktion de r Leiste CAS anwendet: man ruft also die Funktion vo n der Auswahlliste der Leiste CAS auf, oder man bricht den eingegebenen Ausdruck mit Hilfe von

SHIFT DEL (CLEAR) ab Oder man bricht die Spitze des eingegebenen Baumes so ab, daß man

Remove op aus dem Menü TOOL eingibt. Zum Beispiel, wenn man den Ausdruck SIN durch den Ausdruck COS ersetzen

möchte, löscht man SIN so, daß man SIN eingibt, betätigt die Taste Remove op, und drüc kt COS.

Den binäre n Operator kann man nicht a bbrechen: man drückt den Ausdruck so aus, indem man

Edit expr. vom Menü TOOL eingibt und die Korrektur durchführt. Entweder man schreibt das Element aus dem History Speicher durch Drücken

der Taste HIST ab. Die neue Abschrift wird an der Stelle des Cursors oder an der Stelle der Auswahl, wenn man die Taste ENTER direkt vom History Speicher drückt, durchgeführt.

4.1.4 Betriebsart Cursor

Die Betriebsart Cursor e rmöglicht einen großen Ausdruck schnell einzugeben. Für den Zutritt in die Betriebsart Cursor, gibt man Cursor mode im Menü TOOL ein,

dann benutzt man Pfeile zur Markierung der Auswahl, die wir in die Box geben möchten, weiter betätigt man die Taste ENTER zur Bestätigung der Auswahl des Boxinhaltes.

4.1.5 Möglichkeit einer gesamten Darstellung

Durch Eingabe „Change font“ aus dem Menü TOOL, vergrößert man oder verkleinert man die Schriftgröße: in manchen Fällen ermöglicht dieses den gesamten Ausdruck im allgemeinen zu sehen.

Sollte dies nicht ausreichend sein, ist es notwendig i n die Betriebsart Cursor umzustellen:

Ausdruckssatz der Leiste CAS 41

Exakte Berechnungen und Mathematik mit HP40G

Die Betriebsart Cursor aus dem Menü TOOL auswählen, dann den Pfeil > für das Rollen des Ausdruckes, denn man nicht ganz sehen kann, drücken.

man kann auch folgendes benutzen: „View expr.“ aus dem Menü TOOL, durch das Drücken des Pfeiles > für das

Rollen des Ausdruckes.

4.2 Benutzung der Funktionen CAS

Wenn man sich im Editor der Gleichungen befinde t, kann man alle Funktionen CAS benutzen und man kann e inen Satz nach verschiedenen Arten durchführen.

4.2.1 Wie schreibt man  und

befindet sich auf der Tastatur, man muß nur folgende Tasten:

SHIFT + (S) in der Betriebsart ALPHA, drücken. Das Symbol  befindet sich auch auf der Tastatur, es reicht wenn man folgende

Tasten betätigt:

SHIFT d/dX ( 

Die Symbole undS werden für im vora us fest ge legte Funktio ne n, die einige Argumente (unabhängige Va riablen) besitzen, gehalten.

 und

voraus festgelegt), falls es dieses gi bt, positioniert. Der Cursor ist auf einer durch uns ausgewählten Stelle positioniert und man

betätigt ihn mit Hilfe der Pfeile.

Die Ausdrücke, die man eingibt, richten sich nach dem Eingabegesetz, erklärt im vorhergehenden Kapitel, es ist jedoch notwendig, in die Betriebsart Eingabe mit Hilfe ¨HLQ]XWUHWHQ

Achtung – den Zeiger „ i“ nicht zur Summendefinition benutzen, denn „i“ bezeichnet die komplexe Anzahl der Lösungen x² + 1 = 0, bzw.

werden automatisch vor das eingegebene Element (Funktion im

> <

1−=i .

42 Ausdruckssatz der Leiste CAS

Exakte Berechnungen und Mathematik mit HP40G

Die numerische Betriebsart S führt Näherungsberechnungen durch.

Zum Beispiel:

∑

indem

1 =++++

Das Symbol „! „ erhält man so, daß man die Taste SHIFTx drückt. Es ist notwendig zu wissen, daß S symbolisch die Summen der rationalen

Brüche und hypergeometrische Serien, die eine diskrete primitive Funktion zulassen, ausrechnen kann.

Beispiel: Wenn ein Ausdruck eingegeben wird:

3342.70833333

65 24

∞

∑

)1(

=+⋅1

Nach dem Drücken der Taste ENTER er hält man:

4.2.2 Wie schreibt man infixe Funktionen

Diese Funktionen schrei bt man zwischen die Argumente (unabhängige Variablen),

AND | MOD Man kann: entweder in der Betriebsart Alpha schreiben, und dann die Argumente

(unabhängige Variabl en) schreiben, oder sie von der Auswahlliste der Leiste CAS oder mit Hilfe einer der Tasten

abrufen, unter Bedingung, daß man das erste Argument geschrieben und eingegeben ha t.

Mit Hilfe der Pfeile > < geht man von einem Argument zum anderen.

Ausdruckssatz der Leiste CAS 43

wie zum Beispiel:

Exakte Berechnungen und Mathematik mit HP40G

4.2.3 Wie schreibt man präfixe Funktionen

Diese Funkti onen schrei bt man vor deren Argumente, dies is t ein allgemein geltender Fall.

Im diesen Falle ist alles möglich! Man kann das erste Argument schreiben, man kann es eingeben und dann die

Funktion mit H ilfe des Menüs abrufen. Oder man kann die Funktion aus dem Menü abrufen oder man kann sie in die

Betriebsart Alpha schreiben, und dann ihr Argument oder Argumente schreiben.

Beim folgendem Beispiel werden verschiedene Möglichkeiten des Schreibens ausgeführt.

Beispiel: Sie möchten den Ausdruck

42−x faktorisieren und dann seinen Wert für

4=x erhalten.

Sie wissen, daß ein FACTOR zur Faktorisierung dient und daß sich diese Funktion im Menü ALGB befindet.

Sie wissen, daß SUBST die Variable im Ausdruck ersetzen soll, und zwar durch einen anderen We rt, und daß sich diese Funktion im Men ü ALGB befindet.

Erste Möglichkeit: Eingabe, die früher als die Argumente durchgeführt wird

Drücken Sie die Taste, die ALGB aktiviert, und heben Sie FACTOR hervor und dann drücken Sie die Taste ENTER.

FACTOR (3) wird in den Editor in Klammern mit Hilfe des Cursors geschrieben. Schreiben Sie Ihren Ausdr uck laut den Regeln für die Eingabe und zwar so, wie es in den vorherigen Kapiteln beschrieben wurde:

2 > – 4 >

wird folgendes eingegeben:

FACTOR (X² – 4)

weiter mit der Taste ENTER und man erhält das Ergebnis:

(X + 2)·(X – 2)

Das Ergebnis ist eingegeben und ersetzt die Anweisung.

44 Ausdruckssatz der Leiste CAS

Exakte Berechnungen und Mathematik mit HP40G

Man sieht es ni cht auf de m er sten Blick, jedoch nach jedem Drücken der Tast e ENTER wird dies in den History Speicher gespeichert, also FACTOR(X² – 4) und (X + 2)·(X – 2) werden in d en History Spe i cher geschri eben. Nun löschen Sie das vorherige Ergebnis mit Hilfe der Tasten SHIFT DEL (CLEAR), weil dieses Ergebnis jetzt eingegeben ist.

Drücken Sie die Taste, die ALGB aktiviert, heben Sie SUBS T hervor und dann drücken Sie di e Taste ENTE R .

SUBST(3,



wird durch den Cursor in Klammern in den Editor anstatt des ersten Arguments geschrieben.

Sie schreibe n Ihren Ausdruck laut den oben angeführ t en Regeln. Achtung! hier hat SUBST zwei Argumente, deshal b muß man in di e

Betriebsart Eingabe mit Hilfe

¨einspringen:

Xxy 2 ¨¨±! X = 4 >

wird folgendes eingeben:

SUBST(X² – 4,X = 4)

dann betätigt man die Taste ENTER und man erhält da s Ergebnis:

4² – 4

Dieses Ergebnis ist ein Ausdruck, in dem die Variablen durch einen Wert ersetzt werden und nach dem Drücken de r Taste ENTER ergibt sich ein verkürztes Ergebnis:

Natürlich sind (X² – 4, X = 4), 4² – 4 und 12 im History Speicher weiter vorhanden.

Bemerkung: Wenn man eine der Funktionen der Leist e CAS zuvor als deren Ar gumente

benutzt, kann man sie in der Betriebsart Alpha mi t Klammern schreiben.

Zweite Möglichkeit: Eingabe erst nach den Argumenten

Erst wird der Ausdruck, d en man nach den oben angeführten Regeln für die Eingabe eingibt, geschrieben.

Hier schreibt man:

2 > – 4

Ausdruckssatz der Leiste CAS 45

Exakte Berechnungen und Mathematik mit HP40G

Dann drückt man die Taste FACTOR: Man drückt die Taste, die ALGB aktiviert und wählt die Anweis ung FACTOR

durch das Drücken der Ta st e ENTER. Ergibt:

FACTOR(X² – 4)

dann drückt man die Taste ENTER und man erhält das Ergebnis:

(X + 2)·(X – 2) Dieses Ergebnis ersetzt die Anweisung und ist eingegeben. Natürlich sind die Anweisungen FACTOR(X² – 4) und (X + 2)·(X – 2) im

History Speicher weiter vorhanden. Sie bemerken nun, daß das Ergebnis eingegeben ist, Sie sind also bereit, eine

andere Anweisung zum Ergebnis anzuwenden. Sie können also SUBST abrufen: drücken Sie die Taste, die ALGB aktiviert,

und wählen Sie SUBST, dann drücken Sie die Taste ENTER.

SUBST((X + 2)·(X – 2), 3)

wird in den Editor mit Klammern, mit Ihrem Ausdruck als mit dem ersten Argument und mit dem Cursor an der Stelle des zweiten Arguments, geschrieben.

Nun genügt folgendes z u schreiben: X = 4 dann

> >

und die Taste ENTER betätigen.

Ergibt:

(4 + 2)·(4 – 2)

dann drückt man die Tast e ENTER und erhält:

Natürlich sind SUBST (X² – 4, X = 4), (4 + 2)·(4 – 2) und 12 im History Speicher weiter vorhanden.

Bemerkung: Während des A usdruckssatzes können Sie eine der Funkt i onen der Leist e CAS

abrufen. Diese Funktion wird als das erste Argument das, was eingegeben worden ist, haben. Sollte nichts eingegeben worden sein, so befindet sich der Cursor an der richtigen Stelle, um Argumente zu ergänzen.

46 Ausdruckssatz der Leiste CAS

Exakte Berechnungen und Mathematik mit HP40G

4.3 Variablen

Sie können die Objekte in Variablen lassen und sie wieder so benutzen, daß Sie den Namen der Variabl e benutzen.

Achtung!!!

1. Variablen, die in CAS benutzt werden, kann man nicht in der

Betriebsart HOME oder im Editor der Programme benutzen und man schreibt sie in die Reihen STO>

2. Man benutzt STO

Betriebsart HOME oder vom Editor der Programme und man schreibt sie in die Reihen STO > oder >.

3. In CAS benutzt man die Anweisung STORE (sie he 1.3.2) z ur Erhaltung

der Variablenwerte.

4. Die Taste VARS zeigt das Menü, daß alle Variablen beinhaltet, die zur

Verfügung stehen, an. Wenn man sich in der Betriebsart HOME befindet, dann werden d urch das Drücken der Ta ste VARS die Na men der bewilligten Variablen in HOME und in Aplets, jedoch unterschiedlich als in CAS, angezeigt. Wenn man sich im Editor der Gleichungen befindet, dann werden durch das Drücken dieser Taste, die Namen der Var i ablen, definiert in CAS, angezeigt.

zum Speichern des Objektes in derVariable von der

oder

4.3.1 STO>

STO> ermöglicht das Objekt in einer der Var i ablen des Menü s HOME zu erhalten.

Die Namen de r zahligen Variablen i m Menü HOME hab en 26 Buchsta ben des Alphabetes und die Namen der symbolischen Variablen in der Betriebsart HOME sind S1… S5

ACHTUNG! Die Variablen A … Z stehen Ihnen ständig zur Verfügung und beinhalten

stets einen Wert . Zum Beispiel, bei Verwendung STO> vom Bereich HOME oder vom Edito r

der Programme, schreibt man: 1 STO> A

dies wird auf dem Display folgend angezeigt:

Ausdruckssatz der Leiste CAS 47

Exakte Berechnungen und Mathematik mit HP40G

1 > A und hat zur Folge, daß der vorherige Wert A abgebrochen wird und

durch 1 ersetzt wird. A wurde ausgewertet und kennzeichnet den Inhalt A

4.3.2 STORE

In CAS ist es notwendig die Anweisung STORE zum Speichern des Objektes in der Variable zu benutzen.

Man kann jeden belieb i gen Namen der Variable auswählen, jedoch in STORE muß vor diesem Namen die Funktion QUOTE benutzt werden, diese ermöglicht, den Namen der Variable QUOTE(ABC) von ihrem Inhalt ABC zu unterscheiden.

STORE und QUOTE befinden sich im Menü ALGB auf der Leiste des Editors der Gleichungen.

Beispiel: Tastenbedienung:

STORE(X² – 4, QUOTE(ABC)

Oder Tastenbedienung:

X² – 4 das man eingibt, weiter mit der Taste STORE, und dann schreibt man QUOTE(ABC) Die Taste ENTER bestätigt die Definition der Variab le ABC. Wenn man die Variable abbrechen möchte, ist es notwendig die Anweisung

UNASSIGN aus dem Menü ALGB zu benutzen, man schreibt zum Beispiel: UNASSIGN(QUOTE(ABC))

4.3.3 Vordefinierte Variablen der Leiste CAS

VX enthalten den Namen der üblichen symbolis chen Vari able. Meistens ist es X, man kann also X als Na men der numerischen Var iable nicht

benutzen, oder den Inhalt X mit Hilfe der Anweisung UNASSIGN aus dem Menü ALGB löschen, bevor man die symbolische Berechnung nicht durchgeführt hat– man schreibt zum Beispiel: UNASSIGN(QUOTE(X)).

EPS enthält einen Wert des Ypsilons, benutzt in der Anweisung EPSX0 ( siehe

4.13.2).

48 Ausdruckssatz der Leiste CAS

Exakte Berechnungen und Mathematik mit HP40G

EQ beinhaltet eine Gleichung des letzten realisierten Graphen. MODULO beinhaltet den Wert p, um eine symbolische Berechnung in Z/p.Z

durchführen zu können. Man kann de n Wert p mit Hilfe der Anweisung MODSTO aus dem Menü

MODULAR so ändern, daß man zum Beispiel folgendes schreibt: MODSTO(13), damit der p Wert 13 ist, oder man benutzt CFG der Leiste CAS.

PERIOD muß eine Perio de der Funktion beinhalten, für die ma n die FourierKoeffiziente festlegen möchte. (siehe 2.10.3).

PRIMIT enthält eine primitive Funktion der letzten integrierten Funktion. REALASSUME enthält den Namen der symbolischen Variablen, die man für

reell hält, es sind: X, Y, t, S1, S2 und alle benutzte Integralvariable. Natürlich wenn Sie im Menü Konfiguration CFG die Wahl Real vars

auswählen, werden alle symbolische Variablen als reelle gehalten (vergleiche es mit 4.1.1).

Man kann auch Postulate, betreffend den Bereich Definition der Variablen, wie zum Beispiel X>1, machen.

In diesem Falle ist es notwendig, die Anweisung ASSUME(X>1) zu verwenden, damit REALASSUME X>1 beinhaltet.

Die Anweisung UNASSUME(X) beseitigt alle Voraussetzungen, die in X gemacht wurd en.

Zur Darstellung dieser V ariablen und ebenfalls der, welche in CAS definiert sind, muß VARS aus dem Fenster des Edito r s d e r Gleichunge n be tätigt werden (Artikel 2.5.3).

Ausdruckssatz der Leiste CAS 49

Exakte Berechnungen und Mathematik mit HP40G

5 Funktion der exakten

Berechnungen

5.1 Leiste CAS

Nur das Menü TOOL enthält Anweisungen, die ande ren Menüs beinhalten eine Aufbereitung und Zurechtlegen der Konfigura tion und algebraische Funktionen, die man in der Betriebsa rt Alpha schrei ben kann.

5.1.1 CFG

Im jedem Menü sehen Sie den St and Ihrer Konfiguration und Sie haben d i e Möglichkeit sie zu ändern.

Zum Beispiel: Sie sehen die Nummer 0:

CFG: R= ‘X’

das bedeutet, daß Sie sich in der exakten reellen Betriebsart befinden und daß X eine übliche Variable ist.

Man hebt die Nummer 0 hervor und drückt die Taste OK. Im Menükopf erscheint

CFG:R = STEP

was bedeutet, daß Sie sich in der exakten reellen Betriebsart befinden, daß die Betriebsart „Schritt für Schritt“ eingegeben ist und daß die Polynome je nach der steigenden Potenz ( des Exponenten) geschrieben werden

Ferner, daß X eine übliche Variable ist, daß die modalen Berechnungen in Z/3Z (p = 3) durchgeführt werden, und das Sie sich in der Betriebsart Rigourous (es werden Absolutwerte ei ngegeben) be finden.

Sie können diese Konfiguration durch Eingabe eines der folgenden Ausdrücke ändern:

1. Complex (oder Real)

2. Aprox (oder Exact)

3. Direct (oder Step/Step wenn man in der Betriebsart Schritt für Schritt

bleiben möchte)

4. x² + x +1 (oder 1 + x + x² … zum Schreiben der Polynome)

Funktion der exakten Berechnungen 51

‘X’ 3

Exakte Berechnungen und Mathematik mit HP40G

5. Change VX (zur Änderung der Variable VX)

6. Change MOD (zur Änderung der Variable MODULO)

7. Rigourous (oder Sloopy, damit man keine Absolutwerte eingeben muß)

8. Symb factor (oder Num.factor)

9. Default cfg (Konfiguratio n R = DRCT Durch das Drücken der Taste OK bestätigen Sie Ihre Eingabe.

Aus dem Menü CFG kann man wenn man CANCEL drückt, austreten. Bemerkung: im CAS sind die Winkel stets in Radianten dargestellt.

; 

5.1.2 TOOL

Wir kommen zum Abschnitt betreffend die Beschreibung der Funktionen, die sich im Register TOOL befinden, zurück.

Cursor mode Edit expr. Change font Remmove op. History Undo View expr.

5.1.3 ALGB

COLLECT DEF EXPAND FACTOR PARTFRAC QUOTE STORE

SUBST TEXPAND UNASSIGN

52 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

5.1.4 DIFF

DERIV DERVX DIVPC FOURIER IBP INTVX LIMIT PREVAL RISCH SERIES TAYLOR0 TRUNC

5.1.5 Taste MATH

CMPLX … (ABS ARG CONJ FLOOR IM MOD – RE SIGN) CONSTANTS … (e i +¥ –¥ pi) HYPERBOLIC … (ACOSH ASINH ATANH COSH SINH TANH) INTEGER … (DIVIS EULER FACTOR GCD IEGCD IQUOT

IREMAINDER ISPRIME? LCM NEXTPRIME PREVPRIME) MODULAR … (ADDTMOD DIVMOD ESPANDMOD FACTORMOD

GCDMOD INVMOD MODSTO MULTMOD POWMOD SUBTMOD) POLYNOMIAL … (FACTOR GCD HERMITE LCM LEGENDRE

PARTFRAC PROPFRAC PTAYL QUOT REMAINDER TCHEBYCHEFF) TEST … (ASSUME UNASSUME > ³ < £ = = ¹ AND OR NOT)

Funktion der exakten Berechnungen 53

Exakte Berechnungen und Mathematik mit HP40G

5.1.6 REWRITE

DISTRIB EPSX0 EXP2POW FDISTRIB LNCOLLECT LIN EXPLN POWEXPAND SINCOS SIMPLIFY XNUM XQ

5.1.7 SOLVER

DESOLVE ISOLATE LDEC LINSOSVE SOLVE SOLVX

54 Funktion der exakten Berechnungen

5.1.8 TRIGO

ACOS2S ASIN2C ASIN2T ATAN2S FOURIER HALFTAN SIMPLIFY SINCOS TAN2CS2 TAN2SC TAN2SC2 TCOLLECT TRIG TRIGCOS

Exakte Berechnungen und Mathematik mit HP40G

TRIGSIN TRIGTAN TEXPAND TLIN

5.2 Modus „Schritt für Schritt“

Den Modus „Schritt für Schritt“ ( wenn man eine Berechnung ausführlich anzeigen möchte.

Auf dem Display erscheint die ausführliche Berechnung und für den weiteren „Schritt“ ist es notwendig OK in der Displayleiste zu drücken.

Manchmal wird das Display zur Anzeige aller Informationen ausreichen: man zeigt sie mit Hilfe des Pfeiles an. Dieser Pfeil ist entweder unten ( (

 auf dem Display angebracht. Danach, damit man den restlichen Teil sieht,

benutzt man die Pfe ile sr zum Rollen des Displays.

Funktion der exakten Berechnungen 55

Step/Step

oder abge kürzt S) wählt man,

oder oben

Exakte Berechnungen und Mathematik mit HP40G

5.3 Normale Schreibweise

Der Rechner kann mit ganzen Zahlen mit einer u nendlichen Genauigkeit arbeiten, probieren Sie folgendes aus:

100

Das Symbol „ ! „ erhält man durch da s Drücken von: SHIFT x In Ansehung dessen, daß die Dezimalschreibweise von 100! sehr lang ist, kann

man das Ergebnis durch die Anweisung View expr., die sich im Menü TOOL befindet, sehen.

5.3.1 DEF

Oder ein weiteres Beispiel:

Rechnen Sie die ersten sechs Fermantzahlen sagen Sie, ob es Primzahlen sind.

Man schreibt die Formel

ergibt 17, dann wird die Anweisung ISPRIME?( ) gegeben. Diese Anweisung befindet sich im Menü INTEGER Taste MATH.

F für k = 1..6 aus und

122+=

Die Antwort ist 1., was bedeutet, daß es richtig ist. Dank des History Speichers (History au s dem Menü TOOL) kann man d en Ausdruck

2 2

+ 1 in den Editor der Gleichungen abschreiben und man ändert ihn auf

Oder, und das ist die beste Art, man definiert die Funktion F (K) mit Hil fe DEF aus dem Menü ALGB so, daß man folgendes schreibt:

)12)(F(DEF

+=KK

Die Antwort ist 12

und F schreibt man unter die Variablen (VARS

drücken, damit man es prüfen kann).

56 Funktion der exakten Berechnungen

Um K = 5 zu erhalten, schreibt man:

ergibt:

4294967297

Exakte Berechnungen und Mathematik mit HP40G

F(5)

Man kann F

mit FACTOR, den man im Menü ALGB findet, faktorisiere n:

Tastenbedienung:

FACTOR(F(5))

ergibt

641Â

für F(6) fi ndet man:

18446744073709551617

Man faktorisiert mit Hilfe des FACTOR, man bekommt:

274177.67280421310721

Achtung auf den Unterschied zwischen:

5.2 =

5 2

und

1052 =⋅

5.4 Ganze Zahlen (und Gauß-Ganzzahlen)

Alle Funktionen aus diesem Abschnitt befinden sic h im Menü INTEGER Taste MATH.

Für einige Funktionen kann man Gauß-Ganzzahlen, Zahlen in Form a + ib mit a und b als ganze Zahlen, anstatt der klassischen ganze n Zahlen, benutzen.

Funktion der exakten Berechnungen 57

Exakte Berechnungen und Mathematik mit HP40G

5.4.1 DIVIS

DIVIS gibt u ns eine Aufste llung der Teiler der ganzen Zahlen. Tastenbedienung

DIVIS(12)

ergibt:

12 OR 6 OR 3 OR 4 OR 2 OR 1

5.4.2 EULER

EULER kennzeichnet den Bezeichner EULER der ganzen Zahl. EULER ist der Hauptzahl (der Kardinalzahl) aus der Gruppe der Zahlen kleiner

als n und der ersten Zahl mit n gleich. Tastenbedienung: EULER(21) ergibt: 12

Tatsächlich beinhaltet die Menge: E=^2,4,5,7,8,10,11,13,15,16,17,19`Zahlen kleiner als 21, die unteilbar mit

21 sind, und E als Hauptzahl (Kardinalzahl) die 12 hat.

5.4.3 FACTOR

FACTOR zerlegt die ganzen Zahlen in Produkte der Primzahlen. Tastenbedienung:

FACTOR(90)

ergibt:

2Â² Â

58 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

5.4.4 GCD

GCD kennzei chnet den größten gemeinsamen Teiler von zwei ganzen Zahlen. Tastenbedienung:

GCD(18,15)

ergibt:

In der Betriebsart „Schritt für Schritt“ schreibt man:

GCD(78,24) ergibt: 78 mod 24 = 6 24 mod 6 = 0 Result 6 ENTER sendet die Zahl 6 in den Editor der Gleichungen.

5.4.5 IEGCD

IEGCD(A,B) kennzeichnet den erwe i terten größten gemeinsamen Tei l er (Bezouts-Identität) von zwei ganzen Zahlen.

IEGCD(A,B) sendet U AND V = D mit U, V, D und prüft die Gültigkeiten: AU+BV=D und D=NSD(A,B). Tastenbedienung:

IEGCD(48,30)

ergibt

2 AND –3 = 6

In Wirklichkeit:

2Â±Â  In der Betriebsart „Schritt für Schritt“ erhält man: z=u*48+v*30 [48,1,0] [30,0,1] * –1

Funktion der exakten Berechnungen 59

Exakte Berechnungen und Mathematik mit HP40G

[18,1, –1]* –1 [12,1, –2]* –1 [6,2, –3]* –2 Result: [6,2, –3] Dann betätigt man die Taste ENTER, 2 AND – 3 = 6 wird in den Editor der Gleichungen geschrieben.

5.4.6 IQUOT

IQUOT kennzeichnet den ganzen Quotient der Euklidesdivision von zwei ganzen Zahle n.

Tastenbedienung:

IQUOT(148,5)

ergibt:

5.4.7 IREMAINDER MOD

IREMAINDER kennzeichnet den ganzen Euklidesdivisonsrest der zwei ganzen Zahlen.

IREMAINDER befindet sich im Menü INTEGER und MOD befindet sich im Menü CMPLX der Taste MATH.

Tastenbedienung:

IREMAINDER(148,5)

Oder

148 MOD 5

ergibt:

IREMAINDER arbeitet mit ganzen Zahlen oder mit Gauß-Ganzzahlen und dadurch unterscheidet er sich von MOD.

Beispiel: IREMAINDER(2+3·i,1+i) setzt i zurück

60 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

MOD nimmt die tatsächlichen Zahlen an (7.5 mod 2 = 1.5), jedoch nicht die Gauß-Ganzzahlen.

Probieren Sie folgendes a us: IREMAINDER(148!,5!+2) (! Man erhält dieses mit Hilfe von SHIFT x). In der Betriebsart „Schritt für Schritt“, führt man die Division wie in der

Schule, mit Hilfe des Algorithmus, benannt als „Galgen“, durch.

5.4.8 ISPRIME?

ISPRIME?(N) setzt 1. zurück (richtig) wenn N eine Pseudoprimzahl ist und setzt 0 zurück.

(falsch) wenn N keine Primzahl ist. Definition: Für Zahlen niedriger als 10

zu sein bedeutet das gleiche! … jedoch über 10

ist die Pseudoprimzahl mit großer Wahrscheinlichkeit eine

Primzahl (siehe Rabins Algorithmus Abschnitt 4.6). Tastenbedienung:

als Pseudoprimzahlen und Primzahlen

ISPRIME?(13)

ergibt:

Tastenbedienung:

ISPRIME?(14)

ergibt:

Funktion der exakten Berechnungen 61

Exakte Berechnungen und Mathematik mit HP40G

5.4.9 LCM

LCM kennze ichnet das kl einste ge meinsame Viel fache von zwei ganzen Zahlen.

Tastenbedienung:

LCM(18,15)

ergibt:

5.4.10 NEXTPRIME

NEXTPRIME(N) kennzeichnet die kleinste Pseudoprimzahl, größer als N. Tastenbedienung:

NEXTPRIME(75)

ergibt:

5.4.11 PREVPRIME

PREVPRIME(N) kennzeichnet die größte Pseudoprimzahl, kleiner als N. Tastenbedienung:

PREVPRIME(75)

ergibt:

5.5 Modulare Berechnungen

Alle Funktionen dieses Abschnittes befi nden sich im Menü MODULAR der Taste MATH.

Man kann Berechnungen modulo p, d.h. in Z/pZ oder in Z/pZ[X] durchführen. Achtung, für einige Anweisungen ist es notwendig, die Zahl p als erste

auszuwählen (Primzahl ?). Die folgenden Beispiele werden mit Hilfe von p = 13 bearbeitet.

62 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

Setzen wir voraus, daß wir folgendes geschrieb e n hab en :

MODSTO(13)

oder daß MODULO im geöffneten Fenster mit den Tasten SHIFT SYMB (SETUP) geändert wurde.

Die gewählte Darstellung ist eine symmetrische Darstellung (–1 anstat t 6 modulo 7).

5.5.1 ADDTMOD

ADDTMOD führt die Summe in Z/pZ[X] durch. Tastenbedienung:

ADDTMOD(11X + 5,8X + 6)

ergibt:

6X – 2

5.5.2 DIVMOD

Als Argumente sind zwei Polynome A[X] und B[X]. Als Ergebnis ist ein

[]

rationaler Bruch

[]

vereinfacht im Z/pZX]. Tastenbedienung:

DIVMOD(2X² + 5,5X² + 2X – 3)

ergibt:

6635++X

5.5.3 EXPANDMOD

EXPANDMOD hat als Argument einen polynomialen Ausdruck. EXPANDMOD entwickelt diesen Ausdruck im Z/pZ[X]. Tastenbedienung:

EXPANDMOD(2X² + 12)·(5X – 4)

ergibt:

–(3X³ – 5X² + 5X – 4)

Funktion der exakten Berechnungen 63

Exakte Berechnungen und Mathematik mit HP40G

5.5.4 FACTORMOD

FACTORMOD hat als Argu ment einen Polynom. FACTORMOD faktorisiert diesen Polynom im Z/pZ[X] unter Bedingung, daß

man p97 und p als erstes hat. Tastenbedienung:

FACTORMOD(–(3X³ – 5X² +5X – 4)

ergibt:

–((3X – 5)(X² + 6))

5.5.5 GCDMOD

GCDMOD hat als Argumente zwei Polynome. GCDMOD rechnet NSD von zwei Polynomen im Z/pZ[X] aus. Tastenbedienung:

GCDMOD(2X² + 5,5X² + 2X – 3)

ergibt:

–(4X – 5)

5.5.6 INVMOD

INVMOD hat als Argument eine ganze Zahl. INVMOD rechnet das Gegenteil diese r ganzen Zahl im Z/pZ aus. Tastenbedienung:

INVMOD(5)

ergibt (weil 5x –5 = –25 = 1 (mod 13)):

–5

5.5.7 MODSTO

Es ist notwendig, in die Variable MODULO den Wert p mit Hilfe der Anweisung MODSTO einzugeben.

Hier, sind die Beispiele mit Hilfe von p=13 ausgerechnet. Setzen wir voraus, daß wir folgendes geschrieb e n hab en : MODSTO(13)

64 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

5.5.8 MULTMOD

MULTMOD führt die Multiplikation im Z/pZ[X] durch. Tastenbedienung:

MULTMOD(11X + 5,8X + 6)

ergibt:

–(3X² – 2X – 4)

5.5.9 POWMOD

POWMOD(X,N) rechnet X potenziert N im Z/pZ[X] aus. Tastenbedienung:

POWMOD(2X + 1,5)

ergibt:

6·X

+ 2·X4 + 2·X3 + X2 – 3·X + 1 weil: 10 = –3 (mod 13) 40 = 1 (mod 13) 80 = 2 (mod 13) 32 = 6 (mod 13)

5.5.10 SUBTMOD

SUBTMOD realisiert das Subtrahieren im Z/pZ[X]. Tastenbedienung:

SUBTMD(11X + 5,8X + 6)

ergibt:

3X – 1

5.6 Rationale Zahlen

Rechnen Sie:

123

Funktion der exakten Berechnungen 65

Exakte Berechnungen und Mathematik mit HP40G

Durch die Eingabe des vorherigen Ausdruckes und durch das Drücken der Taste ENTE R erhält man das E rgebnis:

365

Wenn man die Funktion XNUM aus dem Menü REWRITE anwendet, so ist das Ergebnis:

12.9642857143

Wenn man diese zwei Darstellungen gleichzeitig in einem Ausdruck benutzt, zum Beispiel:

5.0

wird der Rechner fordern, um in die Betriebsart approx einzuspringen, zwecks Durchführung der Berechnung. Hier ist es notwendig mit yes zu antworten, man erhält:

1 Dann geht man in die Betriebsart exact (CFG usw…) zurück.

5.6.1 PROPFRAC

PROPFRAC befindet sich im Menü POLYNOMIAL der Taste MATH.

PROPFRAC Form:

Q +

Tastenbedienung:

s 0 5< B

PROPFRAC

ergibt:

66 Funktion der exakten Berechnungen

)(

schreibt den Bruch

43 12

in Form von Doppelbrüchen, d.h. in

5.7 Reelle Zahlen

Rechnen Sie:

Exakte Berechnungen und Mathematik mit HP40G

Sie führen die Eingabe durch, dann drücken Sie die Taste ENTER und die Antwort ist:

Wenn man die Funktion SNUM aus dem Menü REWRITE anwendet, ist die Antwort:

1263794.7537

Finden Sie im Menü CMPLX der Taste MATH, folgende Funktionen, die als ein Parameter einen Ausdruck mit ei nem reelle n Wert haben:

)20*(EXP

)*5*2(EXP

5.7.1 FLOOR

Tastenbedienung:

FLOOR(3.53)

ergibt:

5.7.2 MOD

MOD ist eine nicht konst ante Funktion, deren unabhängige Variable ganze Zahlen sind.

MOD setzt den Rest der euklidischen Division der unabhängigen Variablen zurück.

Man betätigt:

3 MOD 2

Man bekommt das Ergebni s:

Funktion der exakten Berechnungen 67

Exakte Berechnungen und Mathematik mit HP40G

5.8 Komplexe Zahlen

Darstellung: die komplexen Zahlen in Form von reellen a und b können als (a, b) oder a + b geschrieben wer den. i.

Operationen +, –, *, /, ˆ werden durchgeführt. Tastenbedienung:

)21( i⋅+

Man führt ei ne Auswahl durch, danach

ENTER

Falls man sich nicht im Modus complex b efindet, so fordert der Rechner eine Änderung des Modus, dann ist

YES

einzugeben, damit man die folgende

Anwort erhält:

)43( i⋅−−

Es ist zu erwähnen, daß dieser Ausdruck nicht weiter vereinfacht wird (die Ergebnisse heben jedesmal die kompl exe Zahl des positiven reellen Tei les im Modus exact hervor).

Im Menü

CMPLX

der Taste MATH finden Sie folgend e Funktionen, deren

Parameter ein Ausdruck mit einem komplexen Wert ist: Als Parameter

DROITE

des Afix z

ARG

bestimmt die Variable des Parameters,

ABS

bestimmt das Parametermodul,

CONJ

bestimmt die zugeordnete Zahl des Parameters,

bestimmt den reellen Parameterteil,

bestimmt den imaginären Parameterteil,

bestimmt den Gegenparameter,

DROITE

sind zwei komplexe Zahlen z1, z

sendet dann die Gleichung von de m re chten Teil über zwei Punkte

, z2.

SIGN

bestimmt den Parameterquotienten seines Mod uls.

68 Funktion der exakten Berechnungen

5.8.1 ARG

Tastenbedienung:

Exakte Berechnungen und Mathematik mit HP40G

)43(ARG i⋅+

Anzeige (denn in CAS wird mit

Bemerkung: Den selben Ausdr uck ka nn ma n in

Ergebnis in Zahlen 0.64250 … (wenn man in

Radians

HOME

gearbeitet):

)

(ATAN

durchführen, man erhält jedoch ein

Radians

arbeitet)

5.8.2 CONJ

Wir schreiben:

CONJ(1 + 2·i)

Wir bekommen:

1 – 2·i

Achtung! Wenn sie im Menü Konfiguration CFG die Wahl Real vars auswählen, bekommen Sie CONJ(Z)=Z, und wenn Sie Camplx vars auswählen, CONJ(Z) wird sich von Z unter dem Bedingung unterscheiden, daß Z funktioniert nicht in der Liste, die Variable REALASUMME umfaßt ist.

Oft ist besser e i nen Quotena usdruck zu schreiben: QUOTE(Ausdruck), damit wir nicht mehr dieser Ausdruck schreiben müssen.

z.B. wenn wir uns Real vars ausgesucht haben, schrei ben wir:

SUBST(QUOTE(CONJ(Z)),Z = 1 + i)

Wir bekommen:

CONJ(1+i)

Während:

SUBST(CONJ(Z),Y = 1 + i)

Ergibt uns:

1 + i

Funktion der exakten Berechnungen 69

Exakte Berechnungen und Mathematik mit HP40G

Natürlich, wenn wir Cmplx vars ausgesucht haben und Z ist nicht in d er Liste, die Variable REALASUMME umfaßt:

SUBST(CONJ(Z),Z = 1 + i)

Ergibt uns:

CONJ(1 + i)

5.8.3 DROITE

Tastenbedienung:

))1,0(),2,1((DRIOTE

oder Tastenbedienung:

),21(DRIOTE ii⋅+

21+−= xy

danach ENTER und ergibt das Ergebnis:

1+= xy

5.9 Algebraische Ausdrücke

Alle Funktionen von diesem Abschnitt befinden sich im Menü ALGB der Leiste CAS.

5.9.1 COLLECT

COLLECT hat als Parameter irgendeinen Ausdruck. COLLECT fa kt orisiert den Ausdruck auf ganze Zahlen. Beispiel: Auf ganze zahlen fakto risieren: x² – 4 Tastenbedienung:

COLLECT(X² – 4)

70 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

In der reellen Betriebsart erhält man:

(X + 2)·(X – 2)

Faktorisierung auf ganz e Zahlen:

X² – 2

Tastenbedienung:

COLLECT(X² – 2)

ergibt:

X² – 2

5.9.2 EXPAND

EXPAND hat a l s Parameter irgendeinen Ausdruck. EXPAND erweitert und vereinfacht diesen Ausdruck. Beispiel – man erweitert das vorherige Ergebnis mit Hilfe von EXPAND:

))1X2X()1X2X((EXPAND

+⋅−⋅+⋅+

Und ergibt wiederholt:

+ 1

5.9.3 FACTOR

FACTOR hat als Parameter irgendeinen Ausdruck. FACTOR faktorisiert diesen Ausdruck. Beispiel: Faktorisieren Sie

+ 1

Tastenbedienung:

FACTOR(X FACTOR find et man im Menü ALGB. In der reellen Betriebsart findet man:

Funktion der exakten Berechnungen 71

+ 1)

)12()12(

+⋅−⋅+⋅+ XXXX

Exakte Berechnungen und Mathematik mit HP40G

In der kompl exen Betriebsart find et man (dazu benutzt man Menü CFG):

⋅+−⋅⋅++

)2)1(2()2)1(2( iXiX

)2)1(2()2)1(2( ⋅−−⋅⋅−+ iXiX

5.9.4

| ist ein infixer Operator geeignet zum Ersetzen der Variable im Ausdruck e (im gewissen Maße wie die Funktion SUBST).

Tastenbedienung:

X² – 1 |X = 2

ergibt:

2² – 1

5.9.5 SUBST

SUBST hat zwei Parameter: einen Ausdruck abhängig vom Paramete r und eine Gleichung (Parameter = Substitutionswert).

SUBST führt di e gewünschte Substitution im Ausdruck (in der Formel) durch. Tastenbedienung:

SUBST(A² + 1,A = 2)

ergibt:

2² + 1

5.10 Polynome

Alle Funktionen von diesem Abschnitt befinden sich im Menü POLYNOMIAL der Tas t e MATH.

72 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

5.10.1 DEGREE

DEGREE hat als unabhängige Variabl e ein Polynom der laufenden Variable. DEGREE setzt den Grad dieses Polynoms zurück. ACHTUNG: der Grad des Nullpolynoms ist gleich –1. Man betätigt:

DEGREE(X

+ X + 1)

Wir bekommen das Ergeb nis:

5.10.2 EGCD

Es handelt sich um Bézouts Identität (Extended Greatest Common Divisor). EGCD(A(X), B(X)) setzt U(X) AND V(X) = D(X) mit Hilfe von D,U,V durch eine Überp rüfung zurück:

D(X) = U(X)·A(X) + V(X)·B(X)

Man betätigt:

EGCD(X

+ 2·X + 1,X2 – 1)

Wir bekommen das Ergeb nis:

1 AND – 1 = 2·X + 2

Man betätigt:

EGCD(X

+ 2·X + 1,X3 – 1)

Wir bekommen das Ergeb nis:

–(X + 2) AND 1 = 3·X + 3

5.10.3 FACTOR

Als Argument der Anweisung FACTOR ist ein Polynom. FACTOR faktorisiert diesen Polynom. Tastenbedienung:

FACTOR(X² – 2)

Funktion der exakten Berechnungen 73

Exakte Berechnungen und Mathematik mit HP40G

ergibt:

Tastenbedienung:

FACTOR(X² + 2·X + 1)

ergibt:

(X + 1)²

Tastenbedienung:

FACTOR(X

– 2·X² + 1)

ergibt:

(X – 1)²·(X + 1)²

Tastenbedienung:

FACTOR(X³ – 2·X² + 1)

ergibt:

)2X()2X( −⋅+

))51(X2()51X2()1X( +−⋅+−+⋅−

5.10.4 GCD

GCD kennzei chnet den gr ößeren gemeinsamen Teiler beider Polynome. Tastenbedienung:

GCD(X² + 2·X + 1,X² – 1)

ergibt:

X + 1

5.10.5 HERMITE

HERMITE hat als unabhängige Variable eine ganze Zahl n. HERMITE setzt das Polynom von HERMITE des Grades n zurück. Es handelt sich um das Polynom:

Hn(x) = (–1)

Man hat also:

74 Funktion der exakten Berechnungen

·e x2/2 d n/dxn e –x2/2

Exakte Berechnungen und Mathematik mit HP40G

für n  0

(x) – xH n(x) + nHn(x) = 0

und für n  1

(x) – xHn(x) + nH

n+1

(x) = nH

n – 1

(x)

(x) = 0

Man betätigt:

HERMITE(6)

Man bekommt das Ergebni s:

64·X

– 480·X4 + 720·X2 – 120

5.10.6 LCM

LCM kennzeichnet das kleinste gemeinsame Vielfache zweier Polynome. Tastenbedienung:

LCM(X² + 2·X + 1,X² – 1)

ergibt:

(X² + 2·X + 1)·(X – 1)

5.10.7 LEGENDRE

LEGENDRE hat als unabhängige Variable eine ganze Zahl n. LEGENDRE setzt das Polynom Ln non zurück, keine Lösung der Differentialgleichung:

(x² – 1)·y Man hat also: für n  0 Rodriguèzs Formel

und für n  1

Man betätigt:

Funktion der exakten Berechnungen 75



– 2·x·y– n(n + 1)·y = 0

(x) = 1/n!2n d n/dxn (x2 – 1)

(n + 1)L

(x) = (2n + 1)xLn(x) – nL

n+1

LEGENDRE(4)

n – 1

(x)

Exakte Berechnungen und Mathematik mit HP40G

ergibt:

+⋅−⋅ XX

33035

5.10.8 PARTFRAC

Die Anweisung PARTFRAC verteilt den rationalen Br uch auf einfache

unteilbare Brüche:

+×−

234

Man benutzt die Anweisung PARTFRAC. Tastenbedienung:

1222

+×−×+×−

xxxx



PARTFRAC

In der reellen Betriebsart erhält man:

In der komplexen Betriebsart erhält man:

  

−

⋅−

+×−

234

−

XiX

−

⋅−

−

  

+×−×+×−

1222

XXXX



5.10.9 PROPFRAC

PROPFRAC ha t als Argument einen rationalen Bruch. PROPFRAC set zt diesen geschriebenen r ationalen Bruch nach solch einer Art

zurück, damit sein ganzer Teil sichtbar ist (rationaler Doppelbruch).

[]

PROPFRAC( A( X)) schreibt e inen ratio nalen Bruch

[]

XQ +

[]

XR XB

[]

in Form:

[]

76 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

Mit Hilfe R[X] = 0 oder 0 £ deg(R[X] < deg (B[X]) Tastenbedienung:

−⋅+⋅

)1()35(

 



ergibt:

PROPFRAC

 



125

+−⋅XX

5.10.10 PTAYL

Die Anweisung PTAYL setzt den Polynom, der zur Variable X um einen Wert

a versetzt ist, zurück. PTAYL hat z we i Parameter: einen Po lynom P und eine Zahl a. Tastenbedienung:

PTAYL(X² + 2·X + 1,2)

ergibt den Polynom Q[X] :

X² + 6·X + 9

Achtung, man ha t:

P(X) = Q(X – 2)

Also man hat:

Q(X) = P(X + 2)

5.10.11 QUOT

QUOT gibt uns einen Quotient von zwei Polynomen während der Teilung, j e nach den ab nehmenden P otenzen.

Tastenbedienung:

QUOT(X² + 2·X + 1·X)

ergibt:

X + 2

Funktion der exakten Berechnungen 77

Exakte Berechnungen und Mathematik mit HP40G

5.10.12 REMAINDER

REMAINDER gibt den Rest der Teilung von zwei Polynomen (Teilung laut den abnehmenden Pote nzen).

Tastenbedienung:

REMAINDER(X³ – 1,X² – 1)

ergibt:

X – 1

5.10.13 TCHEBYCHEFF

TCHEBYCHEFF hat als Argument eine ganze Zahl n. Wenn n > 0, TCHEBYCHEFF setzt den Polynom T

[x] = cos(n.arccos(x))

folgend zurück:

Man hat also: für n 0

(x) = [n/2] k=0 C 2k n(x2 – 1)k x

n – 2k

für n 0

)T00n(x) – xT0n (x) + n2Tn(x) = 0

(1 – x

für n 1

(x) = 2xTn(x) – T

n+1

n – 1

(x)

Wenn n < 0 ist, setzt TCHEBYCHEFF Tchebycheffs Polynom zweiten Grades

zurück:

Tn[x] =

os(x))sin(n.arcc

(x))sin(arccos

Tastenbedienung:

TCHEBYCHEFF(4)

ergibt:

8·X

– 8·X² + 1 in Wirklichkeit: cos(4·x) = Re((cos(x) + i.sin(x))

78 Funktion der exakten Berechnungen

)

Exakte Berechnungen und Mathematik mit HP40G

cos(4·x) = cos(x)4 – 6·cos(x)²·(– cos(x)²) + ((1 – cos(x)²)² cos(4·x) = T

(cos(x))

Tastenbedienung:

TCHEBYCHEFF(–4)

ergibt:

8·X³ – 4·X

in Wirklichkeit:

sin(4·x) = sin(x)·(8·cos(x) ³ – 4·cos(x))

5.11 FUNKTION

Alle Funktionen dieses Absatzes sind im Menü DIFF der Liste vorhanden, außer DEF, das sich im Menü ALGB befindet, und IFTE, das sich im Menü Tests der Taste MATH befindet.

5.11.1 DEF

DEF hat als unabhängige Variable eine Übereinstimmung zwischen dem Namen einer Funktion mit Klammern, in denen der Name der Variable enthalten ist, und einem Ausdruck, der die Funktion definiert.

DEF bestimmt diese Funktion und setzt die Übereinstimmung zurück. Man betätigt:

DEF(U(N) = 2

+ 1)

Man bekommt das Ergebni s:

U(N) = 2

+ 1

Danach betätigt man:

U(3)

Man bekommt das Ergebni s:

Funktion der exakten Berechnungen 79

Exakte Berechnungen und Mathematik mit HP40G









5.11.2 IFTE

IFTE hat drei unabhängige Variablen, eine boolensche Variable (achten Sie auf = = für den Test!) und zwei Ausdrücke expr1, expr2.

IFTE wertet den Te st aus, setzt expr1 zurück, wenn der Test richtig ist, und setzt expr2 zurück, wenn der Test falsch ist.

Man betätigt:

STORE(2,QUOTE(N))

IFTE(N = = 0,1, N + 1 / N)

Man bekommt das Ergebni s:

3 / 2

Man kann selbstverständlich eine F unktion mit Hilfe von IFTE definieren, zum Beispiel:

DEF(F(X) = IFTE(X = = 0,1, SIN(X) / X)) bestimmt die Funktion f mit Hilfe von: f(x) = 1 wenn x = 0

sin(x)/x wenn x 

5.11.3 DERVX

Die Anweisung DERVX leitet den Ausdruck (Funktion) laut der Variable X ab. Entweder

)(

−

Die Ableitung f ausrechnen. Tastenbedienung:

)(

−

oder, wenn man den Ausdruck f (x) in die Variable F gespeichert hat

DERVX(F)

80 Funktion der exakten Berechnungen









−









−

Exakte Berechnungen und Mathematik mit HP40G

Oder wenn man F(X) mit Hilfe von DEF definiert hat:







)(DEF

−











−



DERVX(F(X))

Man findet einen komplizierten A usdruck, den man durch die folgende Eingabe vere in fa c ht:

(ENTER). ergibt:

−

+⋅−

5.11.4 DERIV

DERIV hat zwei Argumente: einen Ausd ruck (oder eine Funktion) und eine Variable.

DERIV setzt die Ableitung des Ausdruckes (oder die Funktion) in Bezug auf

die gegebene V ariable als zweiten Par ameter der Fu nktion zurück (nützlich für die Berechnung (von Teilableitungen)!).

Beispiel: Entweder für die Berechnung:

yxzyx

⋅+⋅⋅∂ )(

∂

Tastenbedienung:

DERIV(X·Y²·Z³ + X·Y, Z)

ergibt:

3·X·Y²·Z²

Funktion der exakten Berechnungen 81

Exakte Berechnungen und Mathematik mit HP40G

5.11.5 TABVAR

Als Parameter des

TABVARs

ist ein Ausdruck mit einer rationellen

Derivation.

TABVAR

sendet die Variationstabelle in Abhängigkei t von der laufenden

Variablen. Tastenbedienung:

))(LN(TABVAR XX +

Im Modus „Schritt für Schritt“ wird folgendes angezeigt:

XXLNF

))((:

′

→

Variation table:

∞++−∞−

 



0?1?

?1.??

 

∞+↑∞−−



ACHTUNG: es ist nur mit den Werten X > 0 zu rechnen: Der Rechner rechnet nämlich damit, daß für x £ 0 die Funktion ln (x) definiert

ist und daß sie mit komplexen Werten ist.

5.11.6 FOURIER

FOURIER hat zwei Parameter: den Ausdruck f(x) und eine ganze Zahl n. FOURIER setzt den Fourier-Koefizient c

Funktion bei Interval [O,T] und Periode T (T ist dem Inhalt der Variable PERIOD gleich) zurück.

wenn f(x) e i ne diskrete Reihe ist:

)(

Beispiel: Die Fourier-Koefiziente der period ischen Funktion f der Periode 2· und definiert auf [0 2·p] mit Hilfe f(x) = x² bestimmen.

82 Funktion der exakten Berechnungen

von f(x), erwägt als eine definierte

inx

+∞

∑

ecxf

−∞=

Tastenbedienung:

STORE(2·p, QUOTE(PERIOD))

FOURIER(X²,N)

Nach der Vereinfachung erhält man:

Wenn also n ¹ 0 ist, erhält man:

Weiter wird folgendes geschriebe n: FOURIER(X²,0) ergibt:

Wenn: n = 0 ist, so hat man:

Exakte Berechnungen und Mathematik mit HP40G

22NNi +⋅⋅⋅

22NNi

+⋅⋅⋅

⋅

5.11.7 IBP

IBP hat zwei Parameter: einen Ausdruck der Form u(x)·v´(x) und v(x). IBP setzt AND Gruppen u(x)·v(x) und –v(x)·u´(x), d.h. Glieder, die man

ausrechnen muß, wenn man eine Inte gration in Teilen (per partes) d urchführt, zurück.

Es besteht noch das Integral des zweiten Gl i edes AND auszurechnen, dann mit dem ersten Glied AND zusammenzählen und man erhält eine primitive Funktion

u(x)·v´(x). Tastenbedienung:

IBP(LN(X),X)

Funktion der exakten Berechnungen 83

Exakte Berechnungen und Mathematik mit HP40G









ergibt:

X·LN(X) AND – 1 Die Eingliederung wird durch den Aufruf der Funktion INTVX beendet: INTVX(X·LN(X) AND – 1) Man bekommt a lso das Erge bnis:

X·LN(X) – X

Bemerkung: Wenn der erste Parameter IBP AND der beiden Ele mente ist, so wirkt IBP nur auf das letzte Element AND und gibt ein integriertes Glied zum ersten Element AND hinzu (so, daß man einige IBP sukzessiv durchführen kann).

5.11.8 INTVX

Berechnung einer primitiven Funktion Entweder

)(

−

Man berechnet die primitive Funktion f(x).









−

Tastenbedienung:

)(

−

Oder wenn man den Ausdruck f (x) in F gespeichert hat

INTVX(F)



Oder wenn man F(X) mit Hilfe DEF

definiert hat . Man findet:



⋅ XX

LN +⋅+−⋅+



−



84 Funktion der exakten Berechnungen

  

 











−

 

 

() ()

1LN

)(DEF

3 2

−

1LN

 





−





Übung 1

Ausrechnen:

Exakte Berechnungen und Mathematik mit HP40G

∫

Tastenbedienung:

INTVX

Man findet:

Bemerkung: Man kann auch folgendes schreiben:

Dadurch erhält man ein gl eiches Ergebnis inklusive Konst ante der I nt egration die folgend gleich ist:

Übung 2

 



)(ATAN3

∫

246

+⋅+

xxx

XXX

+⋅+

103 +⋅

 

246

XXX

+⋅+



−−⋅−

246

Ausrechnen:

∫

Tastenbedienung:



INTVX

Funktion der exakten Berechnungen 85



 

⋅+

xx )2sin()sin(

 



⋅+ )2(SIN)(SIN



Exakte Berechnungen und Mathematik mit HP40G

Man findet:

1 6

−

Bemerkung wenn der Parameter INTVX AND der beiden Elemente ist, so wirkt INTVX nur auf das zweite Element AND.

)1)(COS(LN

−+⋅⋅

++⋅+−⋅− )1)(COS(LN

)2(LN)1)(COS2(LN

5.11.9 LIMIT

Für n > 2 einen Grenzwert finden, wenn x nach 0 konvergiert, von:

)tan()tan(

xnxn

×−×

)sin()sin(

xnxn

×−×

Man benutzt die Anweisung LIMIT. Tastenbedienung:

 

LIMIT

 

ergibt:

Den Grenzwert finden, wenn x zu +¥ groß wird:

⋅−⋅



⋅−⋅

)(TAN)(TAN

XNXN



)(SIN)(SIN

XNXN



xxxx −++

Tastenbedienung:

),(LIMIT +∞−++ XXXX

Nach einer Weile erhält man:

1 2

86 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

Achtung!!!

kann man durch die Abkürzung der Taste: SHIFT 0 erhalten –¥ erhält man, wenn man fo l gend e s schr ei bt :

(–)

+¥ erhält man, wenn ma n fol ge nd e s schr ei b t:

(–) (–)

Das Symbol ¥ findet man auch im Menü CONSTANTS der Taste MATH.

5.11.10 LIMIT und 

Den Grenzwert bestimmen, wenn a zum Unendli chen neigt:





∫

−













−



Man schreibt in den Editor der Gleichungen: +

+∞





∫



Achtung, da s Symbol +¥ erhält man, wenn man folgendes schr ei bt :

ergibt:

−

(–) (–) ¥ (SHIFT 0)

−∞+

Und nach de r Vereinfachung:

Funktion der exakten Berechnungen 87















−



)3(7 LN⋅

Exakte Berechnungen und Mathematik mit HP40G

5.11.11 PREVAL

PREVAL hat d rei Parameter: einen Ausdruck (Funkti on) F(VX) abhängig von der Variable, beinhaltet in VX, und zwei Ausdrüc ke A und B.

PREVAL führ t F(B ) -F(A) durch. PREVAL ist für das Rechne n eines definie rten Integr als geeignet, wenn man

von der pri mitiven Funktion ausgeht: Man wertet diese primitive Funktion an dem von Ihnen eingegebenen Intervall

des Definitionsbereiches des Inte grals aus. Tastenbedienung: PREVAL (X² + X, 2,3) ergibt: 12 – 6

5.11.12 RISCH

RISCH hat zwei Parameter: einen Ausdruck und einen N amen der V ariable. RISCH setzt die primitive Funktion des ersten Parameters in Bezug auf die

spezifizierte Variable im zweiten Parameter zurück. Tastenbedienung:

RISCH((2·X² +1)·EXP(X²+1),X) ergibt: X·EXP(X² + 1) Bemerkung: Wenn der Parameter RISCH AND von zwei Elemen ten ist, so

wirkt RISCH nur auf das zweite Element AND.

5.12 Limitierte Und Asymptonische

Entwicklungen

Bemerkung: Alle Funktionen von diesem Abschnitt befinden sich im Menü DIFF der Leiste CAS.

88 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

5.12.1 DIVPC

DIVPC hat drei Argumente: zwei Polynome A(X), B(X) (mit B(O)¹0) und eine ganze Zahl n.

DIVPC setzt den Quotient Q(X) der Division A(X) laut den steigenden Potenzen mit deg(Q)£ n oder Q = 0 zurück.

[]

Q[X] ist also eine limitierte Entwicklu ng der Anweisung n v von Umgebung

X = 0. Tastenbedienung:

DIVPC(1 + X² + X³, 1 + X²,5)

ergibt:

1 + X³ – X

Achtung: Der Rechner fordert in die „steigenden Potenzen“ zu übe rgehen, und yes zu antworten.

in der

[]

5.12.2 LIMIT

LIMIT hat als Argument einen Ausdruck abhängig von der Variablen und von der Gleichung (Variable = Wert, für den man einen Grenzwert ausrechnen möchte).

Oft ist es geeigneter einen „quotierten“ Ausdruck (QUOTE(expression)) zu schreiben, damit man ein wiederholtes Schreiben dieses Ausdruckes in der normalen Form (damit man keine rationale Vereinfachung der Argumente hat) vor der Durchführung d er Anweis ung LIMIT vermeidet.

Man schreibt zum Beispiel:

   

ergibt:

Funktion der exakten Berechnungen 89

 

X ,

 



⋅− X

EXP)12(QUOTELIMIT

 





−



 

+∞=

 

Exakte Berechnungen und Mathematik mit HP40G

5.12.3 SERIE

Erweiterung in der Umgebung des Punktes x = a Beispiel: Eine limite Erweiterung des 4. Stellenwertes in der Umgeb ung

)2cos(6xodx ×=

Muster zur Benutzung der Anweisung SERIES. Tastenbedienung:

=⋅ 4,

 



ergibt:

 

,)2(COSSERIES





 



Erweiterung in der Umgebung x= +¥ oder x = –



432



−++−

hhhh





−= Xh

Beispiel 1: Erweiterungsanweisung arctan(x) in den 5. Stellenwert in der Umgebung x = +¥ und zwar, daß man als unendlich klein

h1=

nimmt

Tastenbedienung:

SERIES(ATAN(X),X = +¥, 5)

ergibt:





 





−+−

h1=



532



Beispiel 2:

Erweiterung

)12(−−xex in den 2. Stellenwert in der Umgebung x= +

und

zwar, daß man als unendlich klein folgendes nimmt

90 Funktion der exakten Berechnungen

h1=





Tastenbedienung:

Exakte Berechnungen und Mathematik mit HP40G

 

()

 

EXP12SERIES X

⋅− 3,,









−





ergibt:

hh +++

h1=

(

)

Beispiel 3:

Erweiterung

)12(−−xex in den 2. Stellenwert in der Umgebung x= –

zwar, daß man als unendlich klein folgendes nimmt

h1−=

Tastenbedienung:

 

()

⋅− 3,,







EXP12SERIES X





−





ergibt:

hh +−+−

Expans:

(

gerichtete Erweiterung

 

+∞=

 

und

 

−∞=



h1−=

)

Es ist notwendig, für die Reihe eine positive reelle Zahl (zum Beispiel 4) zu benutzen, für die Durchführung de r Erweiter ung in der Umgebung

x = a mit Hilfe von x > a und eine ne gative reel le Zahl (zum Beispiel – 4) für die Durchführung der Erweiterung in der Umgebung

x = a mit Hilfe von x< a.

Funktion der exakten Berechnungen 91

Exakte Berechnungen und Mathematik mit HP40G

Beispiel 1:

Erweiterung

)1(XXX+

in den 2. Stelle nwert in der Umgebung X = 0

Tastenbedienung:

(SERIES

ergibt:

ehe

⋅−⋅

22h

 

⋅





−

 

Beispiel 2:

)1(XXX+

Erweiterung von

in den 2. Stellenwert in der Umgebung X = 0–.

Tastenbedienung:

)1(

(SERIES

)1(

h = X

)2,,

−+X

ergibt:

ehe

⋅−⋅



−



22h









h = X

⋅

Beispiel 3:

Erweiterung von

92 Funktion der exakten Berechnungen

)1(XXX+

in den 2. Stellenwert in der Umgebung X = 0.

Exakte Berechnungen und Mathematik mit HP40G

Tastenbedienung:

)1(

(SERIES

)2,,

ergibt:

ehe

⋅−⋅



−



22h









h = X

⋅

5.12.4 TAYLOR0

TAYLOR0 hat nur ein Argument: die Funktion x zu erweitern, und setzt die limite Erweiterung in den relativen 4. Stellenwert in der Umgebung x=0 (falls x

eine übliche Variable ist) zurück. Tastenbedienung:

TAYLORO

 

 



⋅−⋅

)(SIN)(TAN

XPXP



⋅−⋅

)(SIN)(TAN

XQXQ



ergibt:

PQP

⋅−

4 Q

⋅

+⋅

Achtung: 4. St ellenwert bedeutet, daß die eingegebene Funkt i on zum rela tiven

4. Stellenwert des Zählers und des Nenners verglichen wird ((hier der absolute

5. Stellenwert für den Zähler und den Nenner, womit man eigentlich 2 (5-3) erhält, denn der Exponent des Nenners ist 3).

5.12.5 TRUNC

TRUNC ermöglicht einen Polynom aus der gegebenen Folge herauszulösen (geeignet, wenn man ei ne limite Erweiterung durchführ t).

TRUNC hat zwei Argumente: Polynom und X TRUNC setzt den herausgerissenen Polynom in die Fo l ge n–1 zurüc k (sind

keine Symbole ³ als X

Funktion der exakten Berechnungen 93

Exakte Berechnungen und Mathematik mit HP40G

Tastenbedienung:

ergibt:

1((

1 2

432

),)

XXXTRUNC ⋅++

+⋅+⋅+⋅ XXX

5.13 Funktion Konvertierung

(Wertumformung)

Alle Funktionen von diesem Abschnit t befinden sich im Menü REWRITE de r Leiste CAS.

5.13.1 DISTRIB

DISTRIB ermöglicht, die Distributivheit der Multiplikation in der Beziehung zur Addition nur durch eine Operation anzuwenden.

DISTRIB e rmöglicht, we nn man ihn mehrmals anwendet, die Di st ributivität Schritt für Schritt durchzuführen.

Tastenbedienung:

DISTRIB ((X + 1)·(X + 2)·(X + 3))

ergibt:

X·(X + 2)·(X + 3) + 1·(X + 2)·(X + 3)

5.13.2 EPSX0

EPSX0 hat als Parameter einen Ausdruck X und setzt den Ausdruck und in Stellen, wo die Werte kleiner als EPS waren, zurück, diese Werte wurden durch Null ersetzt.

Tastenbedienung:

EPSX0(0.001 + X)

ergibt: (mit Hilfe EPS=0.01):

0 + X

ergibt: (mit Hilfe EPS=0.0001):

.001 + X

94 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

5.13.3 EXP2POW

EXP2POW e rmöglicht den Ausdruck, der eine Form exp(n*ln(x)) hat, in die Potenz, x, zu transformieren.

Tastenbedienung: EXP2POW(EXP(N*LN(X))) ergibt: X Den Unterschied mit LNCOLLECT bemerken: Man hat: LNCOLLECT(EXP(N*LN(X))) = EXP(N*LN(X)) LNCOLLECT(EXP(LN(X)/3)) = EXP(LN(X)/3) EXP2POW(EXP(LN(X)/3)) = X

1/3

5.13.4 EXPLN

EXPLN hat als Argument einen trigonometrischen Ausdruck. EXPLN transformiert trigonometrische Funktionen auf exponentielle und

logarithmische Funktionen, ohne daß er sie linearisiert. EXPLN konvertiert in die komplexe Betriebsart. Tastenbedienung:

EXPLN(SIN(X))

ergibt:

)(EXP

−⋅ ⋅

)(EXP

⋅

5.13.5 FDISTRIB

FDISTRIB ermöglicht, eine Distributivität der Multiplikation in Beziehung zur Addition nur durch eine Operation zu realisieren.

Tastenbedienung:

FDISTRIB((X + 1)·(X + 2)·(X + 3))

ergibt:

X³ + 6 X ²+ 11·X + 6

Funktion der exakten Berechnungen 95

Exakte Berechnungen und Mathematik mit HP40G

5.13.6 LIN

LIN hat als Argument einen Ausdruck der exponentiale und trigonometrische

Funktionen enthält. LIN linearisiert diesen Ausdruck (er äußert ihn in Bezug auf exp(n.x)). LIN konvertiert in die komplexe Betriebsart, in Falle der trigonometrischen

Funktionen. Beispiel 1: Tastenbedienung: LIN((SIN(X)) ergibt:

( Xi

Beispiel 2: Tastenbedienung: LIN((COS(X)²) ergibt:

( XiXi ⋅⋅−⋅++⋅⋅⋅−

Beispiel 3: Tastenbedienung: LIN((EXP(X) + 1)³) ergibt:

3·EXP(X) + 1 + 3·EXP(2·X) + EXP3·X)

))(EXP

))2(EXP

))((EXP

⋅−⋅+⋅⋅−

))2((EXP

5.13.7 LNCOLLECT

LNCOLLECT hat als Argument einen Ausdruck, der Logarithmen enthä l t. LNCOLLECT konjugiert logarithmische Glied e r , es ist deshalb günstig, ihn bei

einem faktorisierten Ausdruck zu benutzen (man benutzt FACTOR). Wenn man folgend e s schr ei bt :

LNCOLLECT(LN(X + 1) + LN(X – 1))

Erhält man: LN((X + 1) (X – 1))

96 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

5.13.8 POWEXPAND

POWEXPAND schreibt die Potenz in Form eines Produktes. Tastenbedienung:

POWEXPAND((X + 1)³)

ergibt:

(X + 1)·(X + 1)·(X + 1)

5.13.9 SIMPLIFY

SIMPLIFY vereinfacht alle Ausdrücke so, daß er sie auf komplexe Exponentialfunktionen transformiert (konvertiert sie in die komplexe Betriebsart).

Tastenbedienung:

)7(SIN)3(SIN

⋅+⋅

(SIMPLIFY

Nach der Vereinfachung erhält man:

XXX⋅

1)(EXPXiXi

+⋅

)(EXP

⋅

)

)5(SIN

5.13.10 XNUM

XNUM hat als Parameter irgendeinen Ausdruck. XNUM konvertiert in die approximative Betriebsart und setzt den numerischen

Wert des Ausdruckes zurück. Tastenbedienung:

)2(XNUM

ergibt:

1.41421356237

Funktion der exakten Berechnungen 97

Exakte Berechnungen und Mathematik mit HP40G

5.13.11 XQ

XQ hat als Parameter einen reellen numerischen Ausdruck. XQ konvertiert in die exakte Betriebsart und gibt dem Ausdruck eine rationale

oder reelle Annäherung. Tastenbedienung:

XQ(1.41422)

ergibt:

66441 46981

Tastenbedienung:

XQ(1.414213562)

ergibt:

5.14 GLEICHUNGEN

Alle Funktionen von diesem Abschnitt sind im Menü SOLV der Leiste CAS enthalten.

5.14.1 ISOLATE

ISOLATE isoliert die Variable im Ausdruck oder in der Gleichung. Die Variable darf nur einmal erscheinen.

ISOLATE hat zwei Parameter, einen Ausdruck oder eine Gleichung und einen Namen der Variable, die er isolieren soll.

Achtung: ISOLATE setz t nur eine Lösung zurück. Tastenbedienung:

(X =

– 1 = 3,X)

2 )

ISOLATE(X

ergibt:

98 Funktion der exakten Berechnungen

Exakte Berechnungen und Mathematik mit HP40G

5.14.2 SOLVEVX

SOLVEVX hat als Parameter eine Gleichung zwischen zwei Ausdrücken der Variable, beinhaltet in VX, oder einen Ausdruck (=0 ist so mit vorausgesetzt).

SOLVEVX löst eine Gleichung. Beispiel 1: Tastenbedienung: SOLVEVX(X In der reellen Betriebsart erhält man:

– 1 = 3)

(X = –

2 ) OR (X = 2 )

In der komplexen Betriebsart erhält man:

(X = –

2 ) OR (X = 2 ) OR (X = –i· 2 ) OR (X = i 2 )

Beispiel 2: Tastenbedienung: SOLVEVX((X – 2)·SIN(X)) In der reellen Betriebsart:

)2(OR)2(OR)2(

=⋅⋅=⋅⋅−= XnXnX

5.14.3 SOLVE

SOLVE hat als Argument eine Gleichung zwischen zwei Ausdrücken oder einen Ausdruck (= 0 ist vorausgesetzt ), und eine n Namen der Variable.

SOLVE löst die Gleichungen: Tastenbedienung:

SOLVE(X In der reellen Betriebsart erhält man:

(X = –

– 1 = 3,X)

2 ) OR (X = 2 )

In der kompl exen Betriebsart erhält man:

(X = –

Funktion der exakten Berechnungen 99

2 ) OR (X = 2 ) OR (X = – i · 2 ) OR (X = i· 2 )

Exakte Berechnungen und Mathematik mit HP40G

5.15 Lineare Systeme

Alle Funktionen dieses Abschnittes befi nden sich im Menü SOLV der Leiste CAS.

5.15.1 LINSOLVE

LINSOLVE ermöglicht das System der linearen Gleichungen z u lösen. Man setzt voraus, daß verschiedene Gle ichungen in folgender Form

geschrieben sind: Ausdruck = 0. LINSOLVE hat zwei Argumente: Die ersten Glieder verschiedener Gleichungen getrennt durch AND und die

Namen verschiedener Va riablen get rennt durch AND. Beispiel 1: Tastenbedienung:

LINSOLVE(X + Y + 3 AND X – Y + 1, X AND Y)

ergibt:

(X = –2)AND(Y = –1) Falls man sich in der Betriebsart Schritt für Schritt b e fi ndet, erhält man CFG: L2 = L2 – L1

311

 



ENTER L1 = 2L1 – L2

 



ENTER Reduction Result

 



ENTER

100 Funktion der exakten Berechnungen

 

− 111



311

 

−− 220



402

 

−− 220



HP 40g, 39g User Manual [de]

Specifications and Main Features

Frequently Asked Questions

User Manual