Emerson Fisher 249, Fisher 249P, Fisher 249VS, Fisher 249W, Fisher 249BP Instruction Manual
...
Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
Simulation of Process Conditions for Calibration
of Fisherr Level Controllers and
Transmitters—Supplement to 249 Sensor
Instruction Manuals
Displacer / torque tube sensors are transducers that convert a buoyancy change into a shaft rotation. The change in
buoyancy is proportional to the volume of fluid displaced, and the density of the fluid. The change in rotation is
proportional to the change in buoyancy, the moment arm of the displacer about the torque tube, and the torque rate.
The torque rate itself is a function of the torque tube material, the temperature of the material, the wall thickness, and
the length. If the density of the process fluid, process temperature, and torque tube material of the sensor are known,
simulation of process conditions may be accomplished by one of the following means
1. Weight or Force Method:
The interface application is the most general case. The level application can be considered an interface with the upper
fluid SG = 0, and the density application can be considered as a variable SG application with the interface at the top of
the displacer. The buoyancy for a given interface level on the displacer is given by:
(1)
:
=
F
B
Where:
F
B
ρ
w
V
D
H
disp
SG
U
SG
L
* V
*
ρ
D
[
w
SGU)H
= buoyant force
= density of water at 4_C, 1
atmosphere = 1.0000 Kg/liter
(0.03613 lb/in
= displacer volume
= height of interface on displacer,
normalized to displacer length
= specific gravity of upper fluid
(0.0 for Level)
= specific gravity of lower fluid
disp
SG
(
*
3
)
L
- SG
(1)
)
U
]
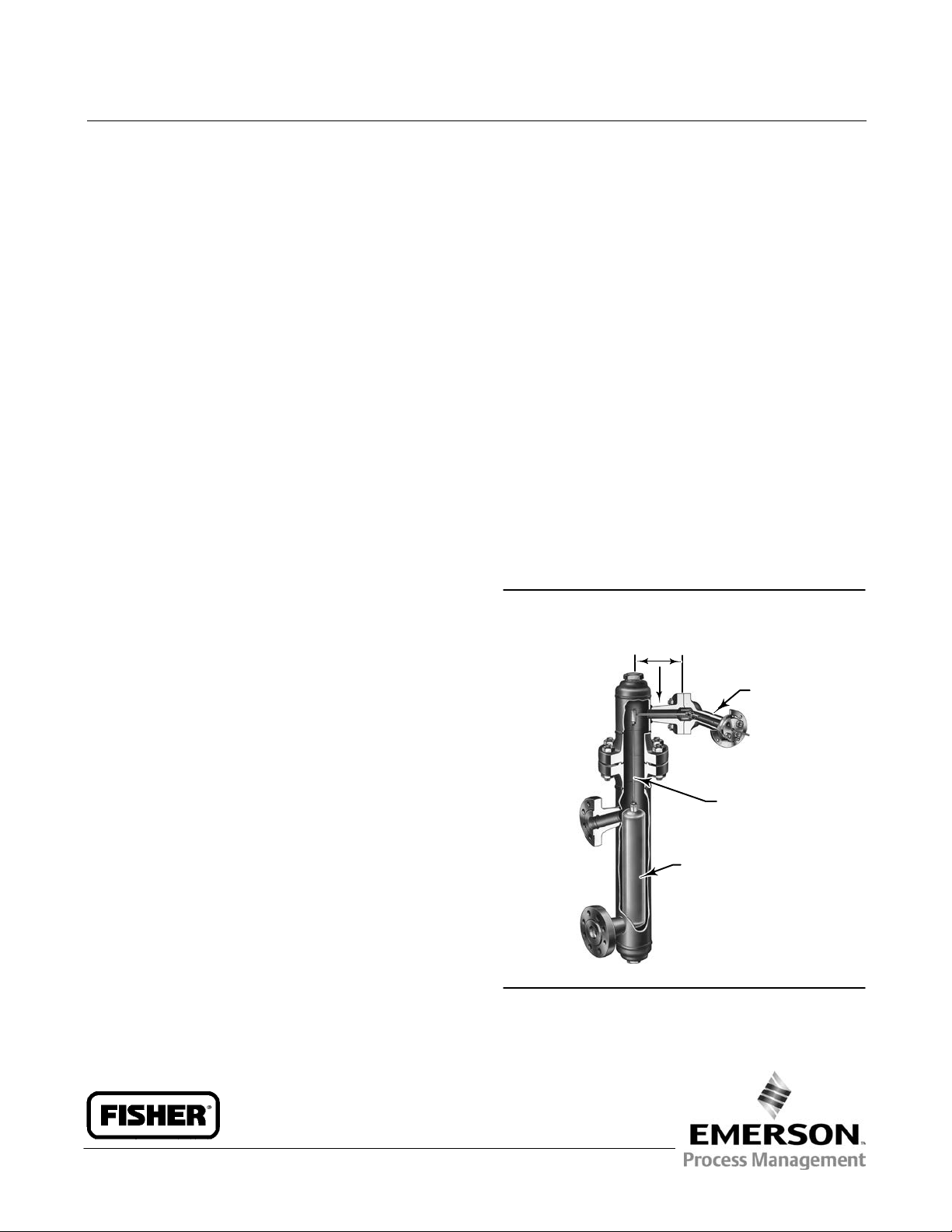
Figure 1. Cutaway View of Fisher 249 Displacer
Sensor
DRIVER ROD
TORQUE TUBE
SUSPENSION ROD
LIQUID DISPLACER
W2141-1
1. Note that this document does not consider the effects of the thermal expansion of
the moment arm, or the thermal expansion of displacer volume.
www.Fisher.com
249 Sensors
March 2014
Instruction Manual Supplement
D103066X012
Figure 2. Fisher 2500 or 2503 Level Controller
Transmitter on Caged 249 Sensor
2500 OR 2503
CONTROLLER/
TRANSMITTER
249 SENSOR
W8334
For the density application, H
= 1.0, SGu = lowest expected density, and SGL becomes the independent variable, the
disp
Figure 3. FIELDVUE™ DLC3010 Digital Level
Controller
actual process density.
The net load on the driver rod is then computed from the equation:
W7977
(2)
net
=
W
- F
D
B
W
Where:
W
W
net
D
= net load on driver rod
= weight of displacer
To simplify equations in the following discussion, let us define a few intermediate terms:
The minimum buoyancy, developed when the interface level is at the bottom of the displacer, is given by:
(3)
SG
V
*
FB
min
ρ
=
*
w
U
D
The change in buoyant force as the normalized interface level rises on the displacer is:
(4)
ΔF
=
ρ
*
V
B
w
D
- SGU) *
(SG
*
L
H
disp
The maximum change in buoyancy, developed when the interface level is at the top of the displacer is:
(5)
B)max
=
ρ
*
V
*
(SG
- SGU)
w
D
L
(ΔF
2
Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
Temperature Effect
As process temperature increases, the torque rate decreases due to the change in modulus of rigidity. This effect can
be represented by normalizing the modulus vs. temperature curve for a given material to the room temperature value,
and using it as a scale factor on the torque rate. See figure 4 and table 1 or 2.
Because we can simulate the rotation of a more compliant torque tube by increasing the load, the weight value may be
divided by the same scale factor to simulate the process condition:
(6)
W
- F
D
W
Where:
W
net_test
G
norm
net_test
=
= net load adjusted to simulate
process temperature effect
= normalized modulus of torque
tube material, a function of
temperature.
G
B
norm
Displacer Rise Effect
Note that equation 6 simulates the process level on the displacer. The actual level in the cage or vessel will be
different, due to the rise of the displacer as the torque tube load is decreased by the increasing buoyancy.
On a 14‐inch displacer, or on a 249VS with a long driver rod, the displacer rise can become a significant fraction of the
span. If the torque tube rate and driver rod length are known, change in rotation can be computed by dividing the
torque change by the rate.
(7)
*
ΔF
ΔAngle
=
R
Where:
ΔAngle = resulting change in torque tube
Driver = driver rod length
R
amb
= Torque rate (torque per
Driver
B
amb
*
G
norm
(
*
angle in radians
_rotation) at ambient
temperature
π
/
180_
)
3
249 Sensors
Instruction Manual Supplement
March 2014
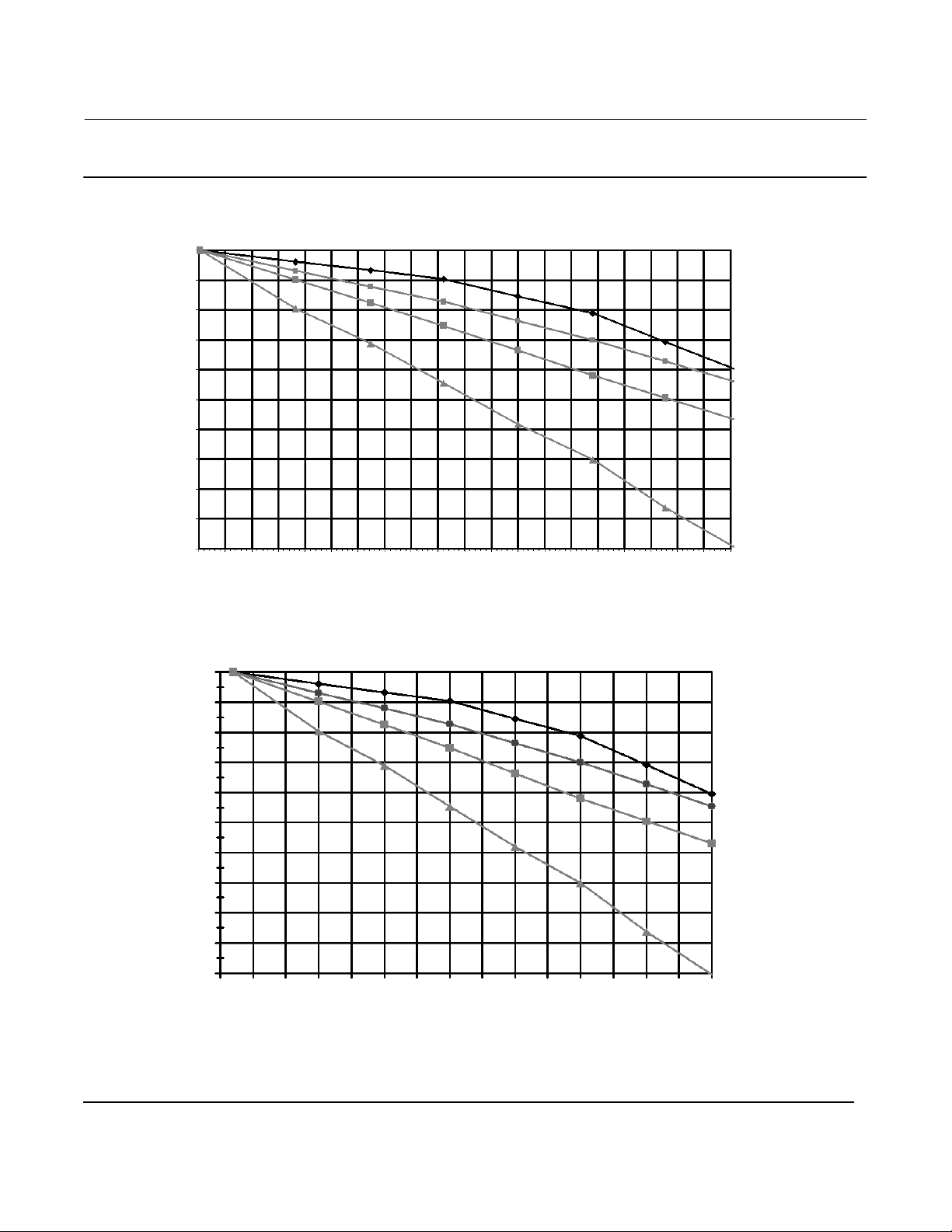
Figure 4. “Gnorm”: Theoretical Temperature Effect on Torque Rate for Most Commonly Used Materials
TORQUE RATE REDUCTION
1.00
0.98
0.96
0.94
(NORMALIZED MODULUS OF RIGIDITY)
D103066X012
0.92
0.90
norm
G
0.88
0.86
0.84
0.82
0.80
20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400 420
TEMPERATURE (_C)
TORQUE RATE REDUCTION
(NORMALIZED MODULUS OF RIGIDITY)
1.00
0.98
0.96
0.94
0.92
norm
0.90
G
0.88
N05500
N06600
N10276
S31600
N05500
N06600
N10276
0.86
0.84
0.82
0.80
50 100 150 200 250 300 350 400 450 500 550 600 650 700 750 800
S31600
TEMPERATURE (_F)
NOTE: THIS CHART DEPICTS THE REVERSIBLE CHANGE ONLY. THE IRREVERSIBLE DRIFT IS A FUNCTION OF THE NET LOAD, THE ALLOY, AND THE LEVEL OF STRESS EQUALIZATION
ACHIEVED IN MANUFACTURING. (THE IRREVERSIBLE EFFECT CAN ONLY BE COMPENSATED BY PERIODIC ZERO TRIM.) N05500 IS AN APPROPRIATE SPRING MATERIAL FOR
TEMPERATURES BELOW AMBIENT AND UP TO 232_C (450_F). ABOVE 260_C (500_F), THE INDUSTRY DOES NOT RECOMMEND USING IT AS A SPRING MATERIAL. N06600 IS
CONSIDERED ACCEPTABLE TO APPROXIMATELY 399_C (750_F) WITH PROPER STRESS EQUALIZATION.
4
Loading...