Casio FX-9860GII, FX-9860G SD, FX-9860G AU, FX-9750GII, FX-9860GII SD User Manual [de]

...

fx-9860GII SD fx-9860GII fx-9860G AU PLUS

fx-9860G Slim

(Aktualisiert auf OS 2.00)

fx-9860G SD (Aktualisiert auf OS 2.00) fx-9860G (Aktualisiert auf OS 2.00) fx-9860G AU (Aktualisiert auf OS 2.00) fx-9750GⅡ fx-7400GⅡ Software-Version 2.00

Bedienungsanleitung

CASIO Weltweite Schulungs-Website

http://edu.casio.com

CASIO SCHULUNGSFORUM

http://edu.casio.com/forum/

• Änderungen des Inhalts dieser Bedienungsanleitung ohne Vorankündigung vorbehalten.

• Reproduktion dieser Bedienungsanleitung, auch ausschnittsweise, ist ohne die schriftliche Genehmigung des Herstellers nicht gestattet.

• Die in Kapitel 13 dieser Bedienungsanleitung beschriebenen Zusatzgeräte sind in bestimm-ten Ländern nicht erhältlich. Wegen weiterer Einzelheiten über die Verfügbarkeit in Ihrem Land wenden Sie sich bitte an Ihren CASIO-Fachhändler oder an einen Kundendienst.

• Bitte bewahren Sie die gesamte Benutzerdokumentation für späteres Nachschlagen auf.

Inhalt

Einführung — Bitte dieses Kapitel zuerst durchlesen!

Kapitel 1 Grundlegende Operationen

1. Tastenanordnung .......................................................................................................... 1-1

2. Display .......................................................................................................................... 1-2

3. Eingabe/Editieren von Berechnungsformeln ................................................................. 1-6

4. Verwendung des Math-Ein-/Ausgabemodus ............................................................... 1-11

5. Optionsmenü (OPTN) ................................................................................................. 1-24

6. Variablendatenmenü (VARS) ...................................................................................... 1-25

7. Programmmenü (PRGM) ...........................................................................................1-28

8. Zugeordnetes SET-UP-Menü (Voreinstellungen) ....................................................... 1-28

9. Verwendung der Displayanzeigen-Einfangfunktion .................................................... 1-32

10. Falls Probleme auftreten… ........................................................................................ 1-33

Kapitel 2 Manuelle Berechnungen

1. Grundrechenarten ......................................................................................................... 2-1

2. Spezielle Taschenrechnerfunktionen ............................................................................ 2-6

3. Festlegung des Winkelmodus und des Anzeigeformats (SET UP) ............................. 2-10

4. Funktionsberechnungen .............................................................................................. 2-12

5. Numerische Berechnungen ......................................................................................... 2-21

6. Rechnen mit komplexen Zahlen .................................................................................. 2-31

7. Rechnen mit (ganzen) Binär-, Oktal-, Dezimal- und Hexadezimalzahlen ................... 2-34

8. Matrizenrechnung ....................................................................................................... 2-37

9. Umrechnen von Maßeinheiten .................................................................................... 2-50

Kapitel 3 Listenoperationen

1. Eingabe in eine Liste und Editieren einer Liste ............................................................. 3-1

2. Operationen mit Listendaten ......................................................................................... 3-5

3. Arithmetische Operationen mit Listen (Listenarithmetik) ............................................. 3-10

4. Umschaltung zwischen Listendateien ......................................................................... 3-14

Kapitel 4 Lösung von Gleichungen

1. Eindeutig lösbare lineare Gleichungssysteme ..............................................................4-1

2. Gleichungen höherer Ordnung (2. bis 6. Grades) ......................................................... 4-2

3. Allgemeine Nullstellengleichungen ...............................................................................4-4

Kapitel 5 Grafische Darstellungen

1. Grafikbeispiele .............................................................................................................. 5-1

2. Voreinstellungen verschiedenster Art für eine optimale Grafikanzeige ......................... 5-3

3. Zeichnen einer Grafik .................................................................................................... 5-6

4. Speicherung einer Grafik im Bildspeicher ................................................................... 5-11

5. Zeichnen von zwei Grafiken im gleichen Display ........................................................ 5-12

6. Manuelle grafische Darstellung ................................................................................... 5-13

7. Verwendung von Wertetabellen .................................................................................. 5-16

8. Dynamische Grafik (Grafikanimation einer Kurvenschar) ........................................... 5-21

9. Grafische Darstellung von Rekursionsformeln ............................................................ 5-24

10. Grafische Darstellung eines Kegelschnitts .................................................................. 5-29

11. Vervollständigung einer Grafik durch weitere Grafikelemente .................................... 5-30

12. Funktionsanalyse (Kurvendiskussion) ......................................................................... 5-31

Kapitel 6 Statistische Grafiken und Berechnungen

1. Vor dem Ausführen statistischer Berechnungen ........................................................... 6-1

2. Berechnungen und grafische Darstellungen mit einer eindimensionalen Stichprobe ... 6-4

3. Berechnungen und grafische Darstellungen mit einer zweidimensionalen

Stichprobe ..................................................................................................................... 6-9

4. Ausführung statistischer Berechnungen und Ermittlung von Wahrscheinlichkeiten ... 6-16

5. Statistische Testverfahren ........................................................................................... 6-25

6. Konfidenzintervall ........................................................................................................6-38

7. Wahrscheinlichkeitsverteilungen .................................................................................6-41

8. Ein- und Ausgabebedingungen für statistische Testverfahren, Konfidenzintervalle

und Wahrscheinlichkeitsverteilungen .......................................................................... 6-55

9. Statistikformeln ............................................................................................................ 6-57

Kapitel 7 Finanzmathematik (TVM)

1. Vor dem Ausführen finanzmathematischer Berechnungen ........................................... 7-1

2. Einfache Kapitalverzinsung ........................................................................................... 7-2

3. Kapitalverzinsung mit Zinseszins .................................................................................. 7-3

4. Cashflow-Berechnungen (Investitionsrechnung) ..........................................................7-5

5. Tilgungsberechnungen (Amortisation) .......................................................................... 7-7

6. Zinssatz-Umrechnung ................................................................................................. 7-10

7. Herstellungskosten, Verkaufspreis, Gewinnspanne .................................................... 7-11

8. Berechnung der Zinstage (Datumsberechnungen) ..................................................... 7-12

9. Abschreibung .............................................................................................................. 7-13

10. Anleihenberechnungen ............................................................................................... 7-15

11. Finanzmathematik unter Verwendung von Funktionen ............................................... 7-18

Kapitel 8 Programmierung

1. Grundlegende Programmierschritte .............................................................................. 8-1

2. PRGM-Menü-Funktionstasten ....................................................................................... 8-2

3. Editieren von Programminhalten ................................................................................... 8-4

4. Programmverwaltung .................................................................................................... 8-5

5. Befehlsreferenz ............................................................................................................. 8-7

6. Verwendung von Rechnerbefehlen in Programmen ...................................................8-22

7. PRGM-Menü-Befehlsliste ............................................................................................ 8-40

8. Programmbibliothek .................................................................................................... 8-45

Kapitel 9 Tabellenkalkulation

1. Grundlagen der Tabellenkalkulation und das Funktionsmenü ...................................... 9-1

2. Grundlegende Operationen in der Tabellenkalkulation ................................................. 9-2

3. Verwenden spezieller Befehle des S • SHT-Menüs .................................................... 9-14

4. Zeichnen von statistischen Grafiken sowie Durchführen von statistischen

Berechnungen und Regressionsanalysen ..................................................................9-16

5. Speicher des S • SHT-Menüs ..................................................................................... 9-21

Kapitel 10 eActivity

1. Beschreibung von eActivity ......................................................................................... 10-1

2. eActivity Funktionsmenüs ........................................................................................... 10-2

3. eActivity Bedienungsvorgänge .................................................................................... 10-3

4. Eingabe und Editieren von Daten ............................................................................... 10-4

5. eActivity Guide .......................................................................................................... 10-13

Kapitel 11 Speicherverwalter

1. Verwendung des Speicherverwalters .......................................................................... 11-1

iii

Kapitel 12 Systemverwalter

1. Verwendung des Systemverwalters ............................................................................ 12-1

2. Systemeinstellungen ................................................................................................... 12-1

Kapitel 13 Datenkommunikation

1. Verbindung von zwei CASIO-Rechnern ...................................................................... 13-1

2. Verbindung des CASIO-Rechners mit einem Personalcomputer ............................... 13-1

3. Ausführung der Datenübertragung .............................................................................. 13-2

4. Hinweise zur Datenübertragung .................................................................................. 13-5

5. Bildschirmkopie senden ............................................................................................ 13-12

Kapitel 14 Verwendung von SD-Karten (nur fx-9860GⅡ SD)

1. Verwenden einer SD-Karte .........................................................................................14-1

2. Formatieren einer SD-Karte ........................................................................................ 14-2

3. Vorsichtsmaßregelen für den Benutzung von SD-Karten ...........................................14-3

Anhang

1. Tabelle der Fehlermeldungen1. Tabelle der Fehlermeldungen ......................................................................................A-1

2. Für die Eingabe zugelassene Zahlenbereiche2. Für die Eingabe zugelassene Zahlenbereiche ............................................................. A-6

E-CON2 Application (English)

1 E-CON2 Overview 2 Using the Setup Wizard 3 Using Advanced Setup 4 Using a Custom Probe 5 Using the MULTIMETER Mode 6 Using Setup Memory 7 Using Program Converter 8 Starting a Sampling Operation 9 Using Sample Data Memory 10 Using the Graph Analysis Tools to Graph Data 11 Graph Analysis Tool Graph Screen Operations 12 Calling E-CON2 Functions from an eActivity

Einführung — Bitte dieses Kapitel zuerst

durchlesen!

I Informationen zu dieser Bedienungsanleitung

S Modellspezifische Funktion und Unterschiede in der Anzeige

Diese Bedienungsanleitung beinhaltet mehrere verschiedene Rechnermodelle. Beachten Sie, dass es einige der hier beschriebenen Funktionen nicht bei allen in dieser Bedienungsanleitung beschriebenen Modellen gibt. Alle Screenshots in dieser Bedienungsanleitung zeigen die Anzeige des fx-9860G der anderen Modelle kann leicht abweichen.

S Natürliche Eingabe und Anzeige von MATH

In den ursprünglichen Standardeinstellungen, ist der fx-9860GII SD, fx-9860GII oder fx-9860G AU PLUS so eingestellt, dass er den „Math-Ein-/Ausgabemodus“ verwendet, welches die natürliche Eingabe und Anzeige von mathematischen Gleichungen aktiviert. Das bedeutet, dass Sie Bruchzahlen, Quadratwurzeln, Differenzialen und andere Gleichungen genau so eingeben können, wie sie geschrieben werden. Im „Math-Ein-/Ausgabemodus“ erscheinen die meisten Ergebnisse der Berechnungen auch als natürliche Anzeige.

Wenn Sie wünschen, können Sie ebenfalls einen „Lineares Ein-/Ausgabemodus“ auswählen, um Berechnungen in einer einzigen Zeile einzugeben und anzeigen zu lassen. Die ursprüngliche Standardeinstellung des fx-9860G Ein-/Ausgabemodus ist der Math-Ein-/Ausgabemodus.

II SD und die Anzeigenerscheinung

SD, fx-9860GII, und fx-9860G AU PLUS

Die Beispiele in der Bedienungsanleitung werden hauptsächlich mithilfe des linearen Ein-/ Ausgabemodus dargestellt. Beachten Sie folgende Hinweise, wenn Sie einen fx-9860G fx-9860GII oder fx-9860G AU PLUS verwenden.

• Informationen bezüglich Wechseln zwischen dem Math-Ein-/Ausgabemodus und dem

linearen Ein-/Ausgabemodus erhalten Sie in der Beschreibung der „Input/Output“ (Eingabe/ Ausgabe) im Abschnitt „Zugeordnetes SET-UP-Menü (Voreinstellungen)“ (Seite 1-27).

• Informationen bezüglich der Eingabe und Anzeige mithilfe des Math-Ein-/Ausgabemodus

erhalten Sie im Abschnitt „Verwendung des Math-Ein-/Ausgabemodus“ (Seite 1-11).

S Für Besitzer eines Modells, das kein Math-Ein-/Ausgabemodus enthält

(fx-7400G

Der fx-7400GII und der fx-9750GII besitzen kein Math-Ein-/Ausgabemodus. Wenn Sie die Berechnungen dieses Handbuchs mit diesen Modellen durchführen möchten, verwenden Sie den linearen Eingabemodus. Besitzer des fx-7400GII und des fx-9750GII ignorieren alle Beschreibungen diesese Handbuchs bezüglich des Math-Ein-/Ausgabemodus.

Ⅱ, fx-9750GⅡ)...

S V()

Die obige Tastenfolge besagt, dass Sie die -Taste gefolgt von der V-Taste drücken sollen. Dadurch wird das -Symbol eingegeben. Auf diese Weise werden alle Tasten dargestellt, die hintereinander gedrückt werden müssen. Die Tastenbezeichnungen sind aufgeführt, gefolgt von dem tatsächlich eingegebenen Zeichen oder Befehl in Klammern.

II SD,

S K EQUA

Damit wird angezeigt, dass Sie zuerst K drücken, die Cursortasten (D, A, B, C) zur Wahl von EQUA verwenden und danach U drücken müssen. Die Bedienungsvorgänge, die Sie für das Aufrufen eines Menüs aus dem Hauptmenü verwenden müssen, sind auf diese Weise angegeben.

S Funktionstasten und Menüs

• Viele der in diesem Rechner vorhandenen Operationen können durch Drücken der

Funktionstasten  bis  ausgeführt werden. Die jeder Funktionstaste zugeordneten Operationen oder Befehle ändern sich in Abhängigkeit von dem Menü, in dem der Rechner momentan arbeitet. Dabei werden die aktuell zugeordneten Operationen durch die Funktionstastenmenüs angezeigt, die im unteren Teil des Displays erscheinen.

• In dieser Bedienungsanleitung ist die aktuell einer Funktionstaste zugeordnete Operation

nach der Tastenbezeichnung in Klammern aufgeführt. So wird zum Beispiel mit (Comp) angezeigt, dass durch das Drücken der -Taste die Operation {Comp} gewählt wird, die auch im Funktionstastenmenü angezeigt ist.

• Wenn ein symbolischer Pfeil (E) im Funktionstastenmenü für die Taste  angezeigt

wird, dann bedeutet dies, dass durch das Drücken der -Taste das nächste oder vorhergehende Fenster der Menüoptionen angezeigt wird.

S Menüsymbole

• Die Menüsymbole in dieser Bedienungsanleitung schließen die erforderlichen

Tastenbetätigungen ein, um das erläuterte Menü zu öffnen und damit anzuzeigen. Die Tastenbetätigung z.B. für ein Untermenü, das durch Drücken von * gefolgt von {LIST} geöffnet wird, würde dann wie folgt dargestellt werden: [OPTN]-[LIST].

• Auf die (E)-Tastenbetätigungen für das Umschalten auf ein anderes Menüfenster wird in

den Menüsymbol-Tastenbetätigungen nicht extra hingewiesen.

S Befehlsliste

Die PRGM-Menü-Befehlsliste (Seite 8-40) enthält ein grafisches Flussdiagramm der verschiedenen Funktionstastenmenüs und zeigt an, wie Sie in das Menü der erforderlichen Befehle gelangen können.

Beispiel: Die folgende Tastenbetätigung zeigt Xfct an: [VARS]-[FACT]-[Xfct]

S E-CON2

Dieses Handbuch beinhaltet nicht das E-CON2-Menü. Weitere Informationen über das E-CON2-Menü erhalten Sie im E-CON2-Handbuch (nur englische Version), das Sie hier

herunterladen können: http://edu.casio.com.

I Kontrasteinstellung

Stellen Sie den Kontrast ein, wenn die Anzeige auf dem Display dunkel erscheint oder schwierig zu sehen ist.

1. Verwenden Sie die Cursortasten (D, A, B, C), um das SYSTEM-Symbol auszuwählen und drücken Sie U und dann ( zu erhalten.

), um die Kontrasteinstellungsanzeige

2. Stellen Sie den Kontrast ein.

• Drücken Sie die C-Cursortaste, um den Kontrast des

Displays zu verdunkeln.

• Drücken Sie die B-Cursortaste, um den Kontrast des Displays heller einzustellen.

• Drücken Sie die (INIT)-Taste, um den Kontrast des Displays auf seine Vorgabe-

Einstellung zurückzustellen.

3. Um die Kontrasteinstellung zu verlassen, drücken Sie erneut die K-Taste.

Kapitel 1 Grundlegende Operationen

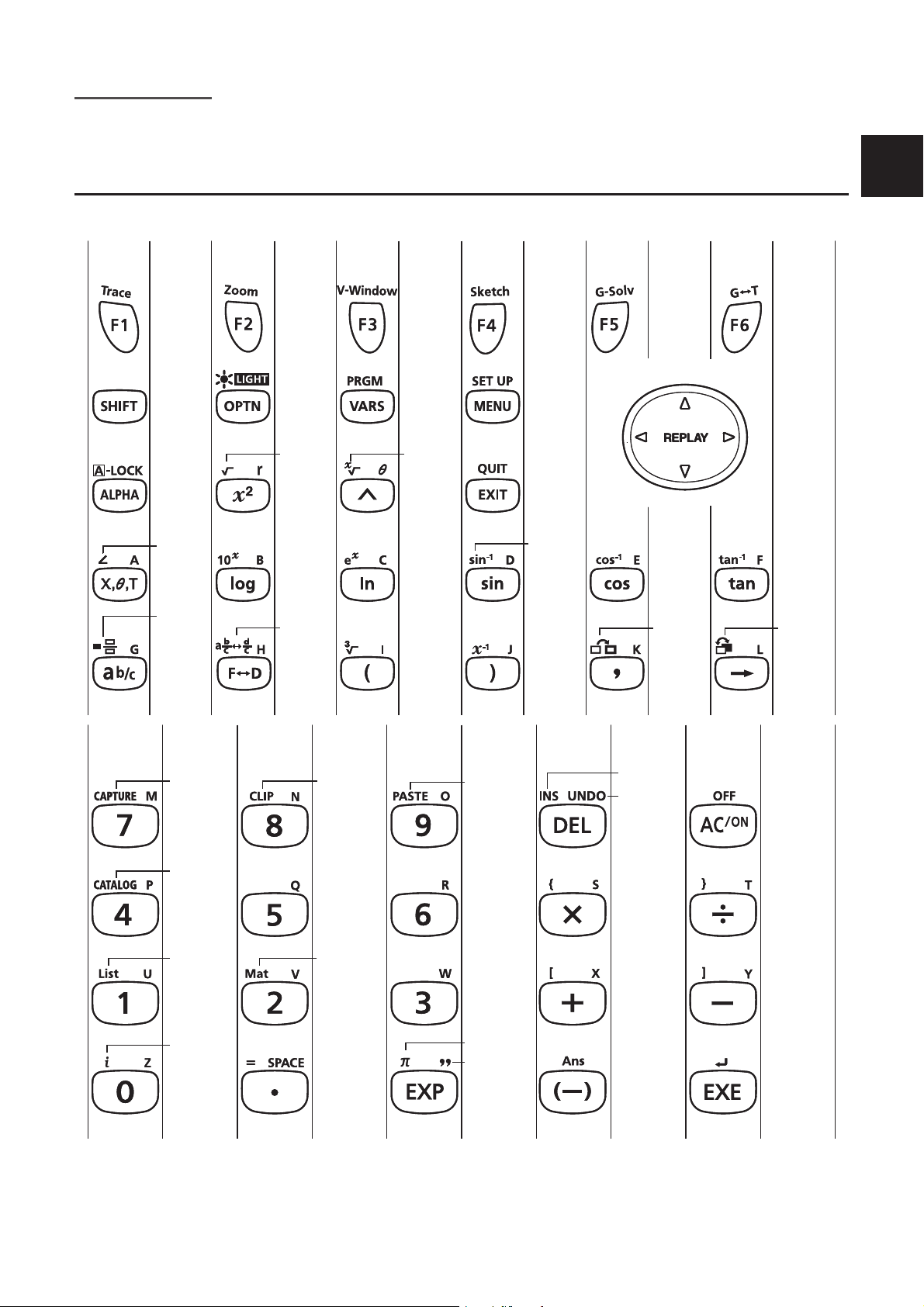
1. Tastenanordnung

I Tastentabelle

Seite Seite Seite Seite Seite Seite

5-31 5-5 5-3

1-28 1-29

1-2 1-24 1-25 1-2

1-20,

1-20, 2-14

2-14

2-1

2-7

2-7 1-2

1-2

2-31

1-12

1-14

1-14 1-20

1-20 2-19

2-19

2-15

2-15 2-14

2-14

2-19

1-20

1-20 2-19

2-19

5-30 5-33 5-1

2-14

2-14 2-14

2-1 2-6

5-26

10-11 10-10

SeiteSeiteSeiteSeiteSeite

1-6,1-16

1-10

1-32

1-10

3-2

2-31

Nicht alle der oben beschriebenen Funktionen sind bei allen in diesem Handbuch beschriebenen Modellen verfügbar. Je nach Rechnermodell kann es sein, dass sich einige der oben angegebenen Tasten nicht auf Ihrem Rechner befinden.

1-9

2-43

1-10

2-14

2-14 2-7

2-7

2-1

1-6,1-16 1-17

1-17 1-7

1-7

2-1

2-9

2-9 2-1

2-1

1-11

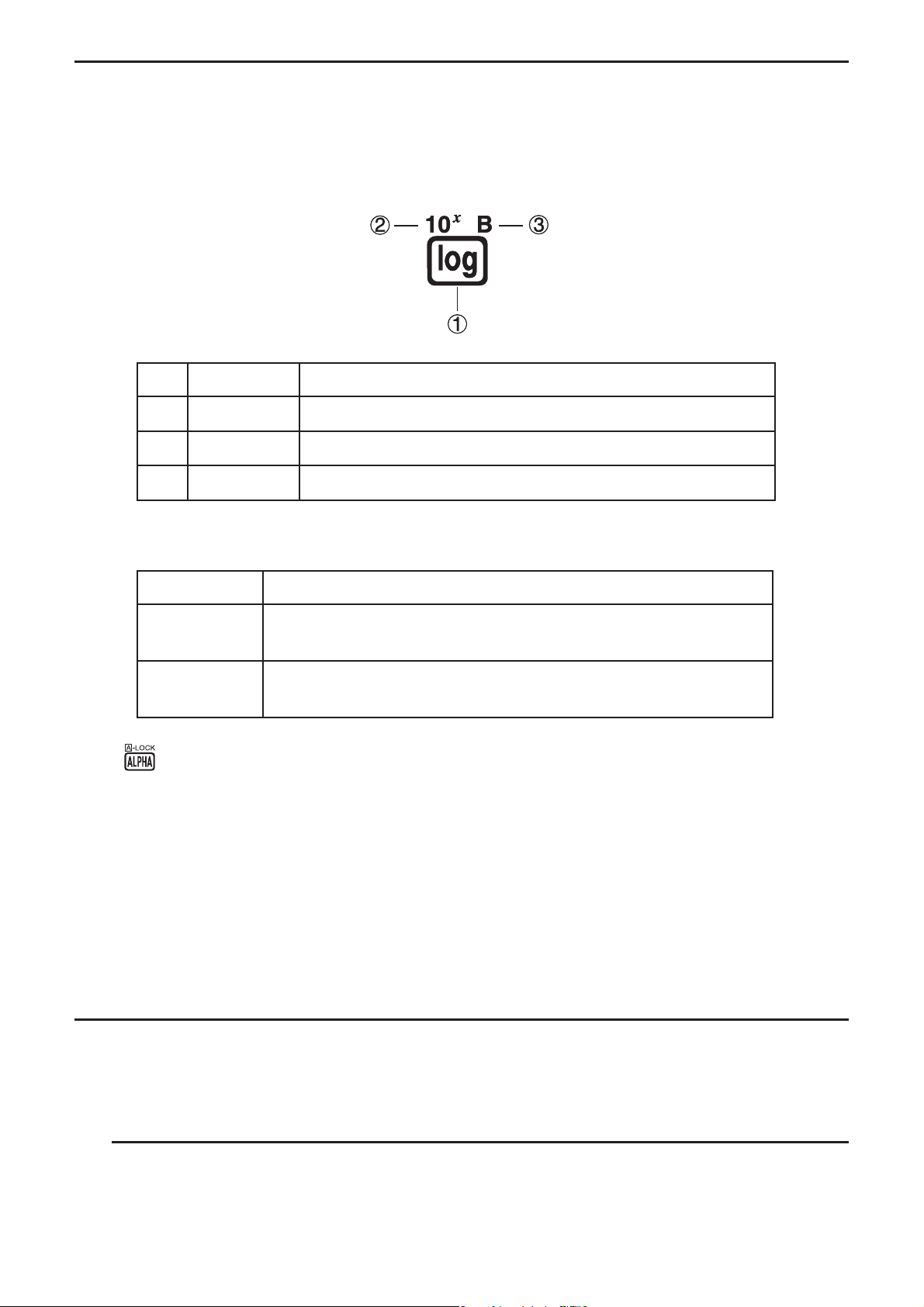
I Tastenmarkierungen (Mehrfachbelegung einer Taste)

Viele der Tasten des Rechners werden für die Ausführung von mehr als einer Funktion verwendet. Die auf der Tastatur markierten Funktionen weisen eine Farbcodierung auf, um Ihnen beim schnellen und einfachen Auffinden der benötigten Funktion zu helfen.

Funktion Tastenbetätigung

Rot

log

J

Drücken Sie die -Taste und danach die gewünschte Taste, um die markierte Funktion auszuführen.

Drücken Sie die ?-Taste und danach die gewünschte Taste, um die markierte Funktion auszuführen.







Nachfolgend ist die für die Tastenmarkierungen verwendete Farbcodierung beschrieben.

Farbe Tastenbetätigung

Gelb

Buchstaben-Feststeller

•

Wenn Sie normalerweise die ?-Taste und danach eine andere Taste drücken, um ein

alphabetisches Zeichen einzugeben, wird die Tastatur sofort wieder auf die primären Funktionen zurückgeschaltet. Falls Sie die -Taste gefolgt von der ?-Taste drücken, wird die Tastatur auf die Eingabe der alphabetischen Zeichen solange fest eingestellt, bis Sie die ?-Taste erneut drücken.

2. Display

I Wahl eines Icons

Dieser Abschnitt beschreibt, wie Sie ein Icon im Hauptmenü auswählen können, um das gewünschte Menü aufzurufen.

S Wählen eines Icons

1. Drücken Sie die K-Taste, um das Hauptmenü anzuzeigen.

1-22

2. Verwenden Sie die Cursortasten (B, C, D, A), um

Gegenwärtig gewähltes IconGegenwärtig gewähltes Icon

das gewünschte Icon zu markieren.

3. Drücken Sie die U-Taste, um den Eingangsbildschirm des ausgewählten Icons an-zuzeigen. Hier wollen wir das STAT-Menü öffnen.

• Sie können auch ein Menü öffnen, ohne ein Icon im Hauptmenü zu markieren, indem Sie

die Nummer oder den Buchstaben eingeben, die/der in der rechten unteren Ecke des Icons angegeben ist.

• Benutzen Sie nur das oben beschriebene Verfahren, um ein Menü aufzurufen. Falls Sie

ein anderes Verfahren anwenden, können Sie in ein anderes als das gewünschte Menü gelangen.

Nachfolgend sind die Bedeutungen der einzelnen Icons (Menüs) erläutert.

Icon Menübezeichnung Beschreibung

RUN (nur fx-7400Gnur fx-7400G

RUN • MAT*1 (Ausführen •Ausführen • Matrizenrechnung)

STAT (Statistik)Statistik)

e • ACT*2 (eActivity)eActivity)

S • SHT*2 (Tabellenkalkulation)Tabellenkalkulation)

II)

Verwenden Sie dieses Menü für arithmetische und Funktionsberechnungen sowie für Berechnungen mit Binär-, Oktal-, Dezimal- und Hexadezimal-Werten.

Verwenden Sie dieses Menü für arithmetische und Funktions-berechnungen, für Matrizenrechnung sowie für Berechnungen mit Binär-, Oktal-, Dezimal- und Hexadezimal-Werten.

Verwenden Sie dieses Menü, um statistische Berechnungen für eindimensionale Stichproben (z. B. Standardabweichung) oder zweidimensionale Stichproben (Regression) auszuführen, Daten zu analysieren, Tests vorzunehmen und statistische Grafiken zu zeichnen.

eActivity lässt Sie Text, mathematische Ausdrücke und andere Daten in einem Notebook-ähnlichem Interface eingeben. Verwenden Sie dieses Menü, wenn Sie Text oder Formelterme bzw. die integrierten Applikationsdaten in einer Datei speichern möchten.

Verwenden Sie dieses Menü für die Ausführung von Tabellen-kalkulationen. Jede Datei enthält eine 26-Spalten × 999-Zeilen Tabellenkalkulation. Zusätzlich zu den integrierten Befehlen und den Befehlen des S • SHT-Menüs, können Sie auch statistische Berechnungen ausführen und statistische Daten grafisch darstellen, indem Sie die gleichen Vorgänge wie in dem STAT-Menü einhalten.

GRAPH Verwenden Sie dieses Menü, um Grafikfunktionen zu

speichern und Grafiken mit den Funktionen zu zeichnen.

1-33

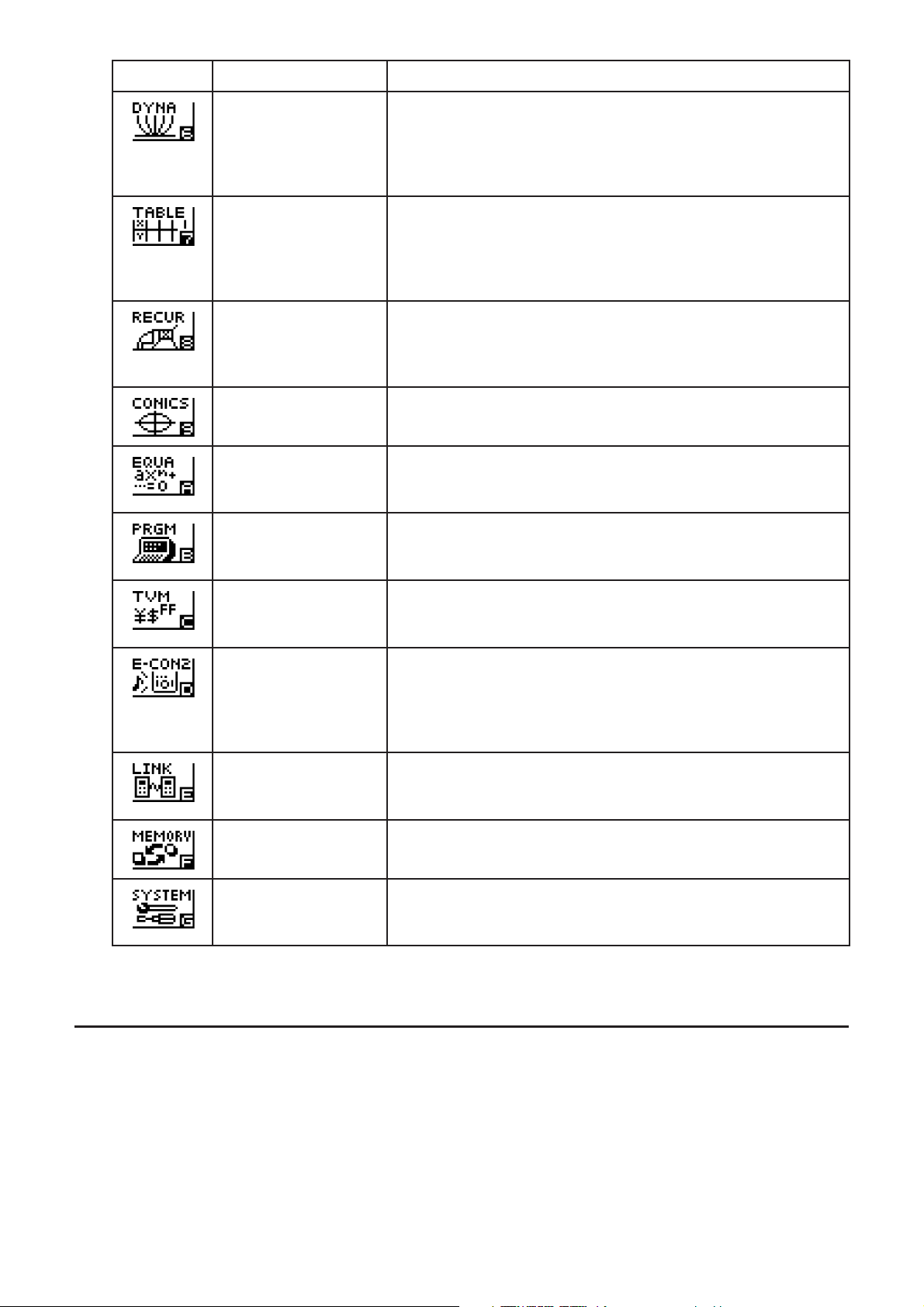
Icon Menübezeichnung Beschreibung

DYNA*1 (Dynamische Grafik)Dynamische Grafik)

TABLE Verwenden Sie dieses Menü, um Funktionen zu speichern,

RECUR*1 (Rekursion)Rekursion)

CONICS*

EQUA (Gleichungslöser)Gleichungslöser)

PRGM (Programme)Programme)

Verwenden Sie dieses Menü, um Grafikfunktionen mit einem Parameter abzuspeichern und mehrere Varianten des Graphen zu zeichnen, indem die dem Parameter in der Funktion zugeordneten Werte geändert werden (Kurvenschar, Animation).

eine Wertetabelle von unterschiedlichen Lösungen zu generieren, wenn die den Variablen in einer Funktion zugeordneten Werte sich ändern, und um eine Grafik zu zeichnen.

Verwenden Sie dieses Menü, um Rekursionsformeln zu speichern, numerische Tabellen unterschiedlicher Werte zu erstellen, wenn sich die den Variablen in einer Funktion zugeordneten Werte ändern, und Grafiken zu zeichnen.

Verwenden Sie dieses Menü für das Zeichen von Kegelschnitten.

Verwenden Sie dieses Menü, um lineare Gleichungen mit zwei bis sechs Unbekannten und Gleichungen höherer Ordnung vom 2ten bis 6ten Gradmaß zu lösen.

Verwenden Sie dieses Menü, um Programme im Programmbereich zu speichern und Programme auszuführen.

TVM*1 (Finanzmathematik)Finanzmathematik)

E-CON2*

LINK Verwenden Sie dieses Menü, um Speicherinhalte oder

MEMORY (Speicher)

SYSTEM Verwenden Sie dieses Menü, um alle Speicher neu zu

Verwenden Sie dieses Menü zur Ausführung von finanzmathematischen Berechnungen und für das Zeichnen von Cashflow- und anderen Typen von Grafiken.

Verwenden Sie dieses Menü zur Kontrolle des optional verfügbaren EA-200 Datenanalyseprogramms. Weitere Informationen über das E-CON2-Menü erhalten Sie im E-CON2-Handbuch (nur englische Version), das Sie hier herunterladen können: http://edu.casio.com.

Sicherungsdaten zu einem anderem Rechner oder PC zu übertragen.

Verwenden Sie dieses Menü für die Verwaltung der im Speicher abgelegten Daten.

initialisieren, den Kontrast einzustellen und um andere Systemeinstellungen auszuführen.

*1 Nicht verfügbar beim fx-7400GII.

Nicht verfügbar beim fx-7400GII/fx-9750GII.

I Das Funktionstastenmenü

Verwenden Sie die Funktionstasten ( bis ), um auf die Menüs und Befehle in der Menüleiste im unteren Teil der Displayanzeige zuzugreifen. Die Tastensymbole einer der Menüleiste zugeordneten Funktionstaste sehen bei einem Untermenü anders aus als bei einem Sofortbefehl.

1-44

I Die Displayanzeigen

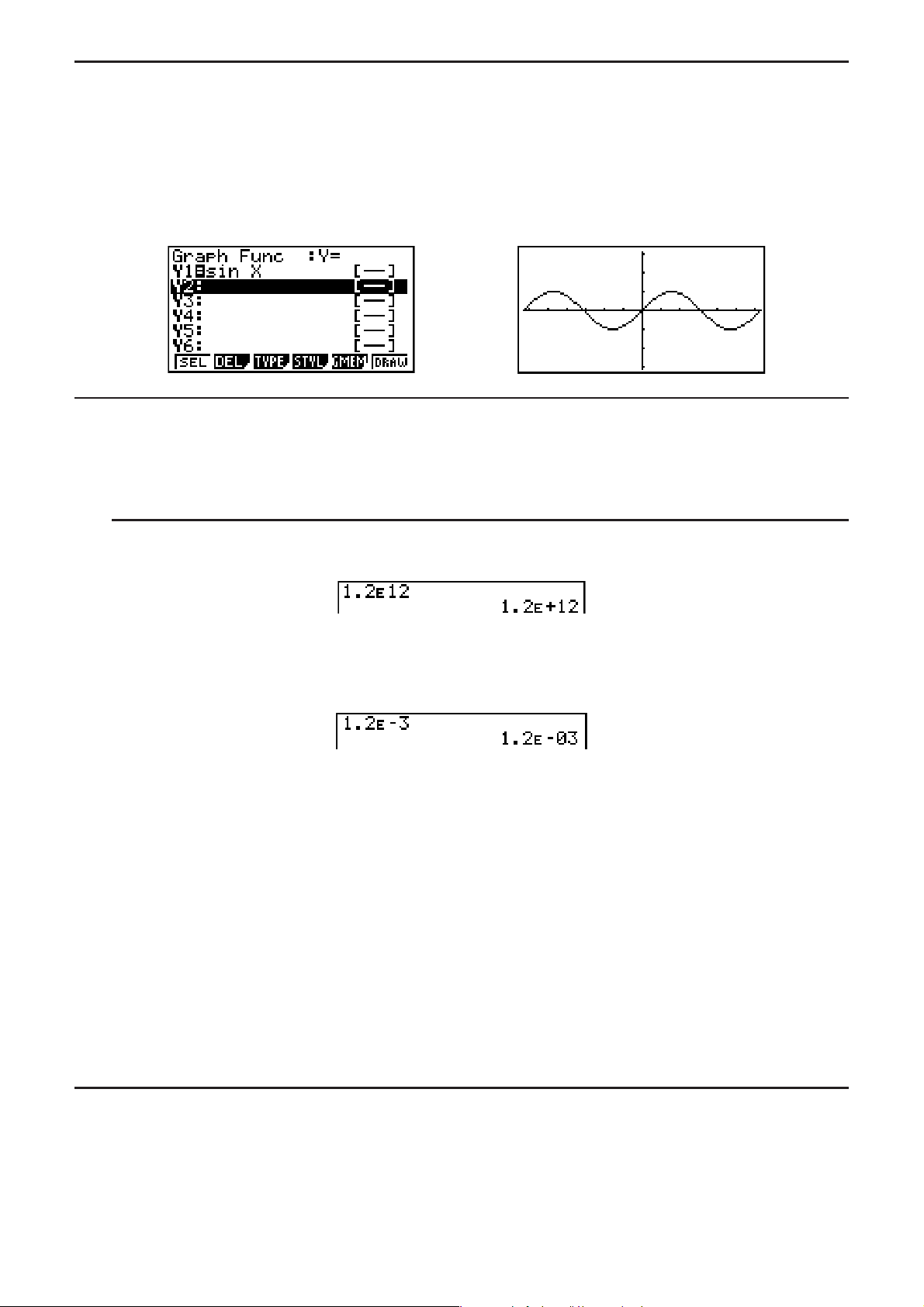
Dieser Rechner verwendet zwei Arten von Displayanzeigen: eine Textanzeige und eine Grafikanzeige. Die Textanzeige kann 21 Spalten und 8 Zeilen von Zeichen anzeigen, wobei die unterste Zeile für das Funktionstastenmenü verwendet wird. Die Grafikanzeige verwendet einen Bereich von 127 (B) × 63 (H) Punkten.

Textanzeige Grafikanzeige

I Normal-Anzeige

Der Rechner zeigt normalerweise Werte mit bis zu 10 Stellen an. Werte mit mehr als 10 Stellen werden automatisch umgewandelt und im Eponentialformat angezeigt.

S Interpretation des Exponentialformats

1.2E+12 bedeutet, dass das Ergebnis gleich 1,2 s 1012 ist. Dies bedeutet, dass Sie den

Dezimalpunkt in 1,2 um zwölf Stellen nach rechts verschieben müssen, weil der Exponent positiv ist. Dies ergibt den Wert 1.200.000.000.000.

-03 bedeutet, dass das Ergebnis gleich 1,2 s 10–3 ist. Dieses bedeutet, dass Sie den

1.2

Dezimalpunkt in 1,2 um drei Stellen nach links verschieben müssen, weil der Exponent negativ ist. Dies ergibt den Wert 0,0012.

Sie können innerhalb der Normal-Anzeige zwischen zwei unterschiedlichen Zahlenbereichen für die automatische Umwandlung in das Exponentialformat wählen.

Norm 1 ................... 10

Norm 2 ................... 10

−22

(0,01) > |x|, |x|  10

−99

(0,000000001) > |x|, |x|  10

Alle in dieser Anleitung aufgeführten Beispiele zeigen die Rechenergebnisse unter der Voreinstellung (im SET-UP-Menü) auf „Norm 1“ an.

Zu Einzelheiten über das Umschalten zwischen Norm 1 und Norm 2 siehe Seite 2-11.

I Spezielle Anzeigeformate

Dieser Rechner verwendet spezielle Anzeigeformate für die Anzeige von gemeinen Brüchen, Hexadezimalzahlen und Sexagesimalzahlen (Grad/Minuten/Sekunden).

1-55

S Brüche

S Hexadezimalzahlen

.................... Bedeutet: 456

12 23

.................... Bedeutet: 0ABCDEF1 Bedeutet: 0ABCDEF1Bedeutet: 0ABCDEF1

gleichwertig mit 180150001

, das ist

(16)

(10)

S Grad/Minuten/Sekunden

.................... Bedeutet: 12° 34’ 56.78“

• Zusätzlich zu den obigen speziellen Anzeigeformaten verwendet der Rechner auch

Indikatoren und Symbole, die dann in den entsprechenden Abschnitten dieser Anleitung beschrieben sind.

3. Eingabe/Editieren von Berechnungsformeln

I Eingabe von Berechnungsformeln

Wenn Sie eine Berechnungsformel eingeben möchten, drücken Sie zuerst die -Taste, um vorhandene Anzeigen im Display zu löschen. Danach geben Sie die Berechnungsformel genau so wie sie auf Papier geschrieben ist von links nach rechts ein und drücken danach die U-Taste, um das Ergebnis anzuzeigen.

Beispiel 2 + 3 – 4 + 10 =

ABC@?U

I Editieren von Berechnungsformeln

Verwenden Sie die B- und C-Tasten, um den Cursor an die Stelle zu bringen, die Sie ändern möchten, und führen Sie danach einen der nachfolgend beschriebenen Vorgänge aus. Nachdem Sie die Berechnungsformel editiert haben, können Sie die Berechnung durch Drücken der U-Taste ausführen. Sie können auch die C-Taste verwenden, um an das Ende der Rechnung zu gelangen und weitere Daten einzugeben.

• Sie können für die Eingabe*

Überschreiben, ersetzt der Text den Sie eingeben den Text, der sich am aktuellen Cursorstandort befindet. Sie können zwischen Einfügen und Überschreiben wählen und folgende Operationen ausführen: #(INS). Beim Einfügen erscheint der Cursor als „I“ und beim Überschreiben als „ “.

Bei allen Modellen bis auf beim fx-7400G Bei allen Modellen bis auf beim fx-7400GBei allen Modellen bis auf beim fx-7400GII/fx-9750GII, ist die Wahl zwischen Einfügen

und Überschreiben nur dann möglich, wenn der lineare Ein-/Ausgabemodus (Seite 1-32) ausgewählt ist.

entweder Einfügen oder Überschreiben auswählen. Mit

1-66

S Ändern einer Position in der Formel (Operand oder Operationszeichen)

Beispiel Ändern Sie cos60 auf sin60

AE?

BBB

S Löschen einer Position in der Berechnungsformel

Beispiel Korrigieren Sie 369 s s 2 zu 369 s 2

BEHA

In dem Einfügemodus funktioniert die Taste # als Rückschritttaste.

S Einfügen einer Position in der Berechnungsformel

Beispiel Ändern Sie 2,362 in sin2,36

ABEV

BBBBB

I Verwendung des Wiederholungsspeichers

Die zuletzt ausgeführte Berechnungsformel wird immer im Wiederholungsspeicher abgelegt. Sie können den Inhalt des Wiederholungsspeichers aufrufen, imdem Sie B oder C drücken.Wenn Sie C drücken, erscheint die Berechnungsformel mit dem Cursor am Anfang. Drücken Sie dagegen die B-Taste, dann wird die Berechnungsformel mit dem Cursor am Ende der Formel angezeigt. Sie können nun die gewünschten Änderungen in der Berechnungsformel vornehmen und diese danach nochmals ausführen.

• Der Wiederholungsspeicher ist nur im linearen Ein-/Ausgabemodus aktiviert. Im Math-Ein-/

Ausgabemodus wird die Historyfunktion anstelle des Wiederholungsspeichers verwendet. Näheres siehe unter „Historyfunktion“ (Seite 1-19).

Beispiel 1 Um folgende zwei Berechnungen durchzuführen

4,12 s 6,4 = 26,368 4,12 s 7,1 = 29,252

1-77

C@AECU

BBBB

#(INS)

F@

Nachdem Sie die -Taste gedrückt haben, können Sie die D- oder A-Taste betätigen, um frühere Berechnungsformeln in der Reihenfolge von der neuesten bis zur ältesten Formel aufzurufen (Multi-Wiederholungsfunktion). Sobald Sie eine ältere Formel aufgerufen haben, können Sie die C- und B-Tasten verwenden, um den Cursor in der Formel zu verschieben und die gewünschten Änderungen vorzunehmen, damit eine neue Berechnungsformel entsteht.

Beispiel 2

@ABCDEU

ABCDEFU

D (Eine Berechnung zurück)

D (Zwei Berechnungen zurück)

• Eine Berechnungsformel verbleibt solange im Wiederholungsspeicher, bis Sie eine andere

Berechnung ausführen.

• Die Inhalte des Wiederholungsspeichers werden nicht gelöscht, wenn Sie die -Taste

drücken. Sie können daher eine Berechnung zurück holen und ausführen, auch nachdem Sie die -Taste gedrückt haben.

I Berichtigung der ursprünglichen Berechnungsformel

Beispiel 14 w 0 s 2,3 wurde fälschlich anstatt 14 w 10 s 2,3 eingegeben.

@C?AB

Drücken Sie ).

Der Cursor wird automatisch an der Stelle positioniert, die den Fehler verursacht hat.

1-88

Nehmen Sie die erforderlichen Änderungen vor.

Führen Sie die Berechnung nochmals aus. U

I Verwendung der Zwischenablage für das Kopieren und Einfügen

Sie können eine Funktion, einen Befehl oder eine andere Eingabe in die Zwischenablage kopieren (oder ausschneiden) und danach den Inhalt der Zwischenablage an einer anderen Stelle einfügen.

• Die hier beschriebenen Vorgehensweisen verwenden alle den linearen Ein-/Ausgabemodus.

Weitere Details über die Funktion „Kopieren und Einfügen“ während der Math-Ein-/ Ausgabemodus ausgewählt ist, erhalten Sie im Abschnitt „Verwendung der Zwischenablage für das Kopieren und Einfügen im Math-Ein-/Ausgabemodus“ (Seite 1-20).

S Markieren des Kopierbereichs

1. Verschieben Sie den Cursor (I) an den Beginn oder das Ende des Bereichs des Textes, den Sie kopieren möchten, und drücken Sie danach die Tasten G(CLIP). Dadurch wechselt der Cursor auf „ “.

2. Verwenden Sie die Cursortasten, um den Cursor zu verschieben und den Bereich des zu kopierenden (z.B. numerischen) Textes zu markieren.

3. Drücken Sie die (COPY)-Taste, um den markierten Text in die Zwischenablage zu übernehmen. Verlassen Sie danach den Kopierbereich-Auswahlmodus (COPY-Modus).

Die markierten Zeichen werden nicht geändert, wenn Sie diese kopieren.

Um den markierten Text wieder freizugeben, ohne eine Kopieroperation auszuführen, drücken Sie die )-Taste.

S Ausschneiden von Text

1. Verschieben Sie den Cursor (I) an den Beginn oder das Ende des Bereichs des Textes, den Sie ausschneiden möchten, und drücken Sie danach die Tasten G(CLIP). Dadurch wechselt der Cursor auf „ “.

1-99

2. Verwenden Sie die Cursortasten, um den Cursor zu verschieben und den Bereich des auszuschneiden (z.B. numerischen) Textes zu markieren.

3. Drücken Sie die (CUT)-Taste, um den markierten Text in die Zwischenablage zu übernehmen.

Durch das Ausschneiden werden die ursprünglichen Zeichen gelöscht.

S Einfügen von (z.B. numerischem) Text

Verschieben Sie den Cursor an die Stelle, an der Sie den Text einfügen möchten, und drücken Sie danach die Tasten H(PASTE). Der Inhalt der Zwischenablage wird dadurch an der Cursorposition eingefügt.

H(PASTE)

I Katalogfunktion

Der Katalog ist eine alphabetische Liste alle auf diesem Rechner verfügbaren Befehle. Sie können einen Befehl eingeben, indem Sie den Katalog aufrufen und dann den gewünschten Befehl auswählen.

S Verwenden des Katalogs, um einen Befehl einzugeben

1. Drücken Sie C(CATALOG), um einen alphabetischenen Katalog von Befehlen anzuzeigen.

• Die Anzeige, die als ersten erscheint, ist die, die sie zuletzt zur Eingabe eines Befehls

verwendet haben.

• Beim fx-9860G Slim erscheinen zuerst zwei Zeilen Beschreibungstext zum aktuell Beim fx-9860G Slim erscheinen zuerst zwei Zeilen Beschreibungstext zum aktuellBeim fx-9860G Slim erscheinen zuerst zwei Zeilen Beschreibungstext zum aktuell

ausgewählten Befehl unten auf der Anzeige. Drücken Sie (HELP), um den Text, den Sie lesen möchten, im Vollbildschirmmodus anzuzeigen. Wenn der Text nicht in eine einzelne Anzeige passt, können Sie D und A zum Blättern verwenden.

(HELP)

m k

)

Um die Hilfetextanzeige zu schließen, drücken Sie ).

1-1010

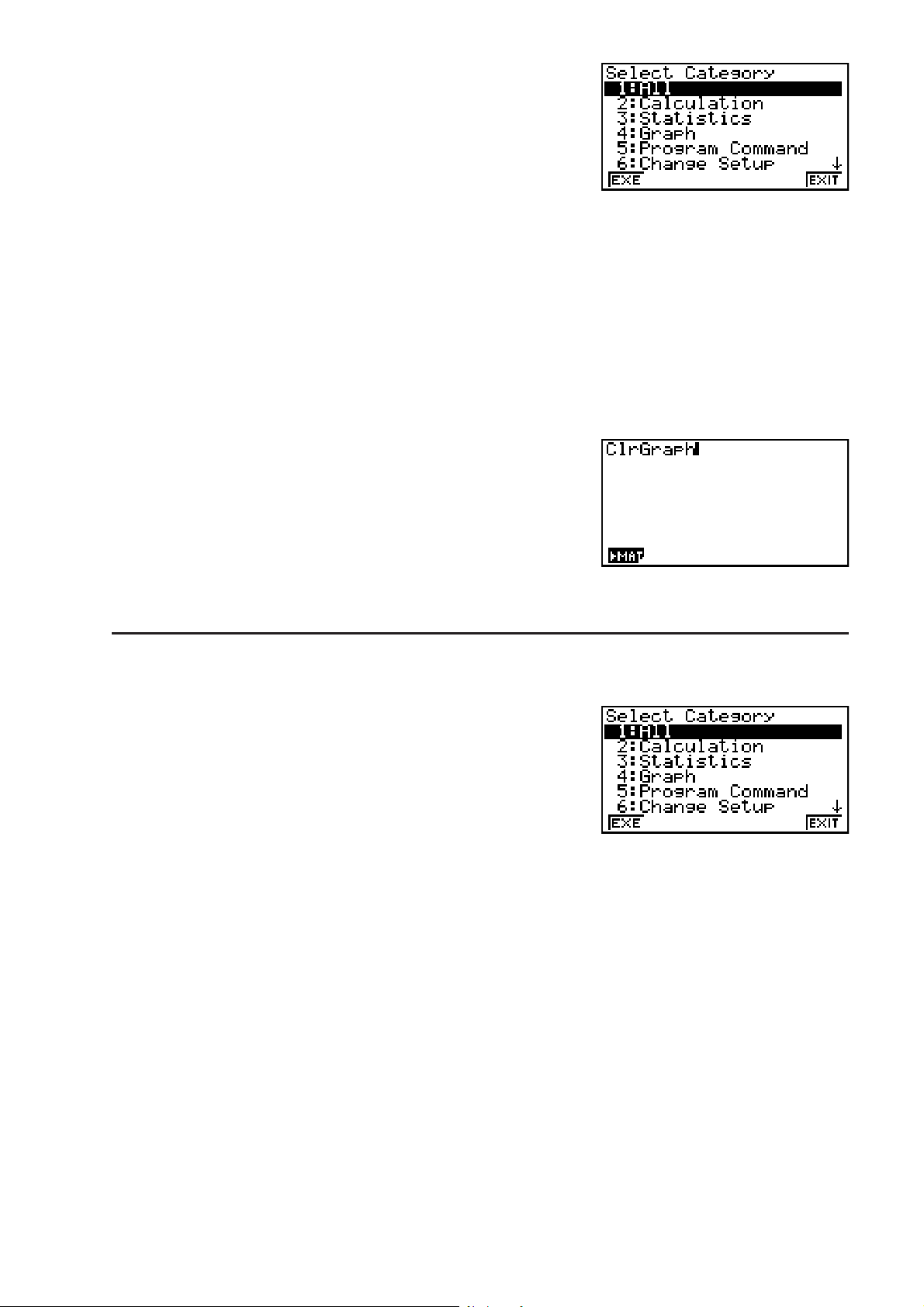
2. Drücken Sie (CTGY), um die Katalogliste anzuzeigen.

• Wenn Sie möchten, können Sie diesen Schritt Wenn Sie möchten, können Sie diesen SchrittWenn Sie möchten, können Sie diesen Schritt

überspringen und direkt mit Schritt 5 fortfahren.

3. Verwenden Sie die Cursortasten (D, A), um die gewünschte Befehlskategorie zu markieren und drücken Sie dann (EXE) oder U.

• Zeigt eine Liste der Befehle in der momentan ausgewählten Kategorie an.

4. Geben Sie den ersten Buchstaben des Befehls ein, den Sie eingeben möchten. Dies zeigt den ersten Befehl, der mit diesem Buchstaben anfängt, an.

5. Verwenden Sie die Cursortasten (D, A), um den Befehl, den Sie eingeben möchten, zu markieren und drücken Sie dann (INPUT) oder U.

Beispiel Verwenden des Katalogs, um den ClrGraph-Befehl einzugeben

C(CATALOG)((C)A~AU

Drücken Sie ) oder )(QUIT), um den Katalog zu schließen.

S Um einen Befehl mit ; einzugeben (nur fx-9860G Slim)

1. Drücken Sie ;.

• Dadurch wird der Kategorienauswahlbildschirm

angezeigt.

•  (EXE)... {zeigt eine Liste der Befehle in der momentan ausgewählten Kategorie an}

•  (EXIT)... {beendet den Kategorienauswahlbildschirm}

2. Fahren Sie mit Schritt 3 des Vorgehensweise unter „Verwenden des Katalogs, um einen Befehl einzugeben“ fort.

4. Verwendung des Math-Ein-/Ausgabemodus

Wichtig!

• Der fx-7400G

Durch die Wahl von „Math“ für die Einstellung „Input/Output“ auf der Einstellanzeige (Seite 1-

32) wird der Math-Ein-/Ausgabemodus eingeschaltet, der Ihnen die natürliche Eingabe und die

Anzeige bestimmter Funktionen gestattet, gleich wie sie in Ihrem Textbuch erscheinen.

II und der fx-9750GII besitzen keinen Math-Ein-/Ausgabemodus.

1-1111

• Die Operationen in diesem Abschnitt werden alle im Math-Ein-/Ausgabemodus durchgeführt.

- Die ursprüngliche Standardeinstellung des fx-9860G

II SD/fx-9860GII/fx-9860G AU PLUS

ist der Math-Ein-/Ausgabemodus. Wenn Sie in den linearen Ein-/Ausgabemodus gewechselt sind, wechseln Sie zum Math-Ein-/Ausgabemodus zurück bevor Sie die Operationen aus diesem Abschnitt durchführen. Weitere Informationen darüber, wie Sie die Menüs wechseln, erhalten Sie im Abschnitt „Zugeordnetes SET-UP-Menü (Voreinstellungen)“ (Seite 1-28).

- Die ursprüngliche Standardeinstellung des fx-9860G Slim/fx-9860G SD/fx-9860G/fx-9860G AU ist der lineare Ein-/Ausgabemodus. Wechseln Sie in den Math-Ein-/Ausgabemodus, bevor Sie die Operationen aus diesem Abschnitt durchführen. Weitere Informationen darüber, wie Sie die Menüs wechseln, erhalten Sie im Abschnitt „Zugeordnetes SET-UPMenü (Voreinstellungen)“ (Seite 1-28).

• In dem Math-Ein-/Ausgabemodus werden alle Eingaben in dem Einfügemodus (nicht dem Überschreibungsmodus) getätigt. Achten Sie darauf, dass die Eingabe #(INS) (Seite 1-6), die Sie in dem linearen Ein-/Ausgabemodus für das Umschalten der Eingabe auf den Einfügemodus verwenden, in dem Math-Ein-/Ausgabemodus eine vollständig unterschiedliche Funktion aufweist. Weitere Informationen erhalten Sie im Abschnitt „Werte und Terms als Argumente verwenden“ (Seite 1-16).

• Wenn nicht speziell anders aufgeführt, werden alle in diesem Abschnitt beschriebenen Bedienungsvorgänge im RUN•MAT • MAT•MAT MATMAT-Menü ausgeführt.

I Eingabevorgänge im Math-Ein-/Ausgabemodus

S Funktionen und Symbole des Math-Ein-/Ausgabemodus

Sie können die nachfolgend aufgelisteten Funktionen und Symbole für die natürliche Eingabe

im Math-Ein-/Ausgabemodus verwenden. In der Spalte „Byte“ ist die Anzahl der Byte aufgeführt, die durch die Eingabe der entsprechenden Funktion im Math-Ein-/Ausgabemodus in dem Speicher belegt wird.

Funktion/Symbol Tastenbetätigung Byte

Bruch (unechter) Gemischter Bruch*

Potenz Quadrat Negative Potenz (Kehrwert)



Kubikwurzel Potenzwurzel

6()

–1

(

)

V()

( ,(

)

((ex)

J(10x)

log(a,b) (Eingabe aus dem MATH-Menü* Abs (Absolutwert) (Eingabe aus dem MATH-Menü* Lineares Differenzial* Quadratisches Differential* Integral*

(Eingabe aus dem MATH-Menü*2)7 (Eingabe aus dem MATH-Menü*2)7 (Eingabe aus dem MATH-Menü*2)8

4 4 5 6 9 9

6 6

1-1212

Funktion/Symbol Tastenbetätigung Byte

3-Rechnung*

(Eingabe aus dem MATH-Menü*2)11

Matrix (Eingabe aus dem MATH-Menü*

) 14*

Runde Klammern Geschweifte Klammern (Werden für

die Listeneingabe verwendet.) Eckige Klammern (Werden für die

Matrixeingabe verwendet.)

Gemischte Brüche werden nur im Math-Ein-/Ausgabemodus unterstützt.

Weitere Informationen über die Funktionseingabe aus dem MATH-Funktionsmenü erhalten

 und 

( { ) und ( } )

( [ ) und ( ] )

Sie im unten beschriebenen Abschnitt „Verwendung des MATH-Menüs“.

Sie können die Toleranz im Math-Ein-/Ausgabemodus nicht spezifizieren. Falls Sie die

Toleranz spezifizieren möchten, verwenden Sie den linearen Ein-/Ausgabemodus.

Für eine 3-Rechnung im Math-Ein-/Ausgabemodus beträgt die Teilung immer 1. Falls Sie

eine unterschiedliche Teilung spezifizieren möchten, verwenden Sie den linearen Ein-/ Ausgabemodus.

Dies ist die Anzahl der Byte für eine 2 × 2 Matrix.

S Verwendung des MATH-Menüs

Drücken Sie (MATH) im RUN • MAT-Menü, um das MATH-Menü anzuzeigen. Sie können dieses Menü für die natürliche Eingabe von Matrizen, Differenzials, Integrals usw. verwenden.

• {MAT} ... {Zeigt das MAT-Untermenü für die natürliche Eingabe von Matrizen an}

• {2s2} ... {Gibt eine a 2 × 2 Matrix ein}

• {3s3} ... {Gibt eine a 3 × 3 Matrix ein}

msn} ... {Gibt eine Matrix mit m Zeilen und n Spalten ein (bis zu 6 × 6)}

• {

• {log

b} ... {Startet die natürliche Eingabe des Logarithmus logab}

• {Abs} ... {Startet die natürliche Eingabe des Absolutwertes |X|}

(x)

d/dx} ... {Startet die lineare Eingabe des linearen Differenzials

• {

/dx2} ... {Startet die lineare Eingabe des quadratischen Differenzials

• {

dx} … {Startet die natürliche Eingabe des Integrals

• {°

• {3(} … {Startet die natürliche Eingabe der 3-Rechnung

f(x)dx

x=A

f(x

)

}

f(x

)

}

S Eingabebeispiele für den Math-Ein-/Ausgabemodus

In diesem Abschnitt ist eine Anzahl von unterschiedlichen Beispielen aufgeführt, die zeigen,

wie Sie das MATH-Funktionsmenü und andere Tasten für die natürliche Eingabe in dem Math-Ein-/Ausgabemodus verwenden können. Beachten Sie unbedingt die Position des Eingabecursors, wenn Sie die Werte und Daten eingeben.

Beispiel 1 Einzugeben ist 2

+ 1

1-1313

@

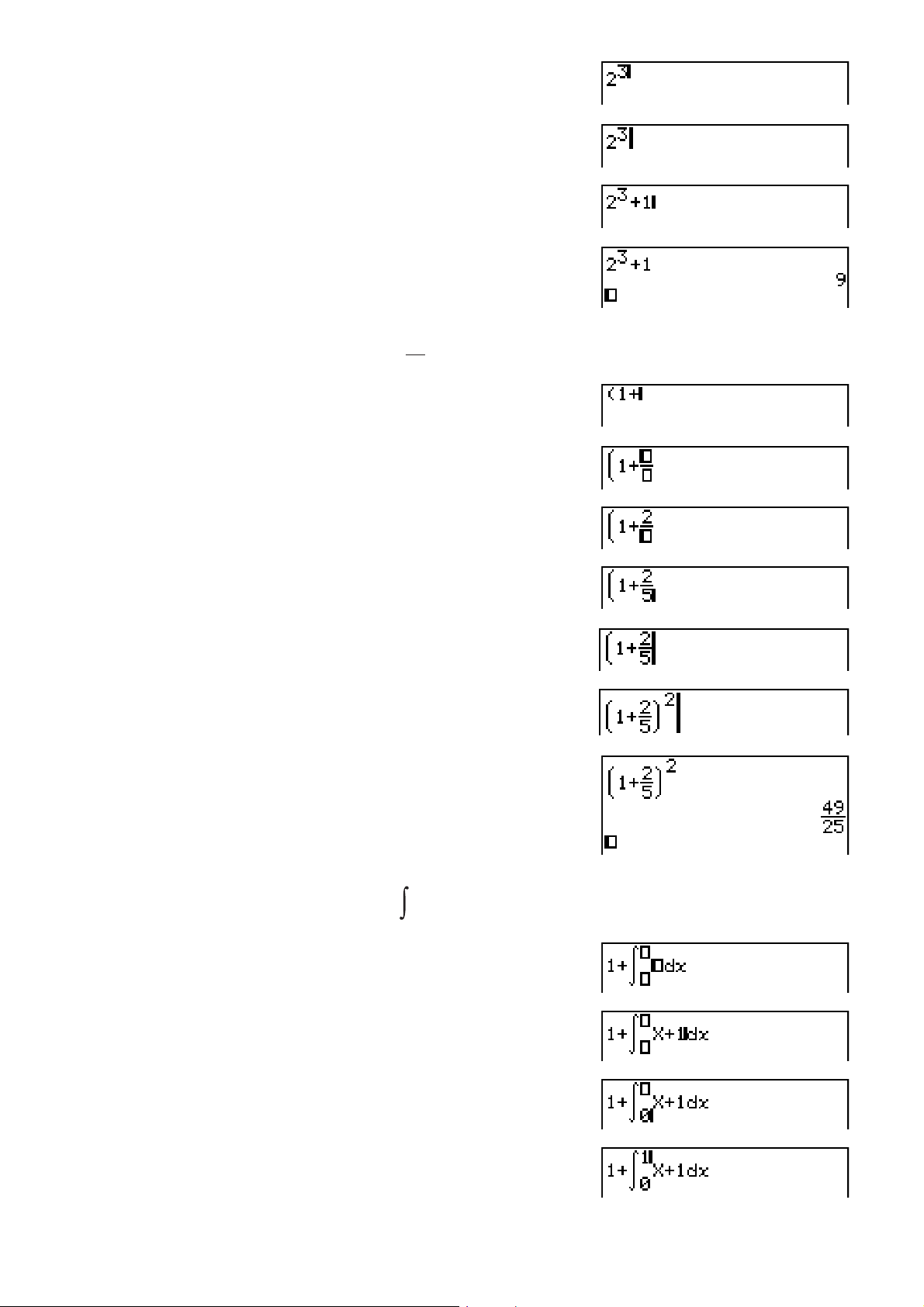
Beispiel 2 Einzugeben ist

@

(

)

V

Beispiel 3 Einzugeben ist

@(MATH)(E)(

T@

1+ x + 1dx

)

1-1414

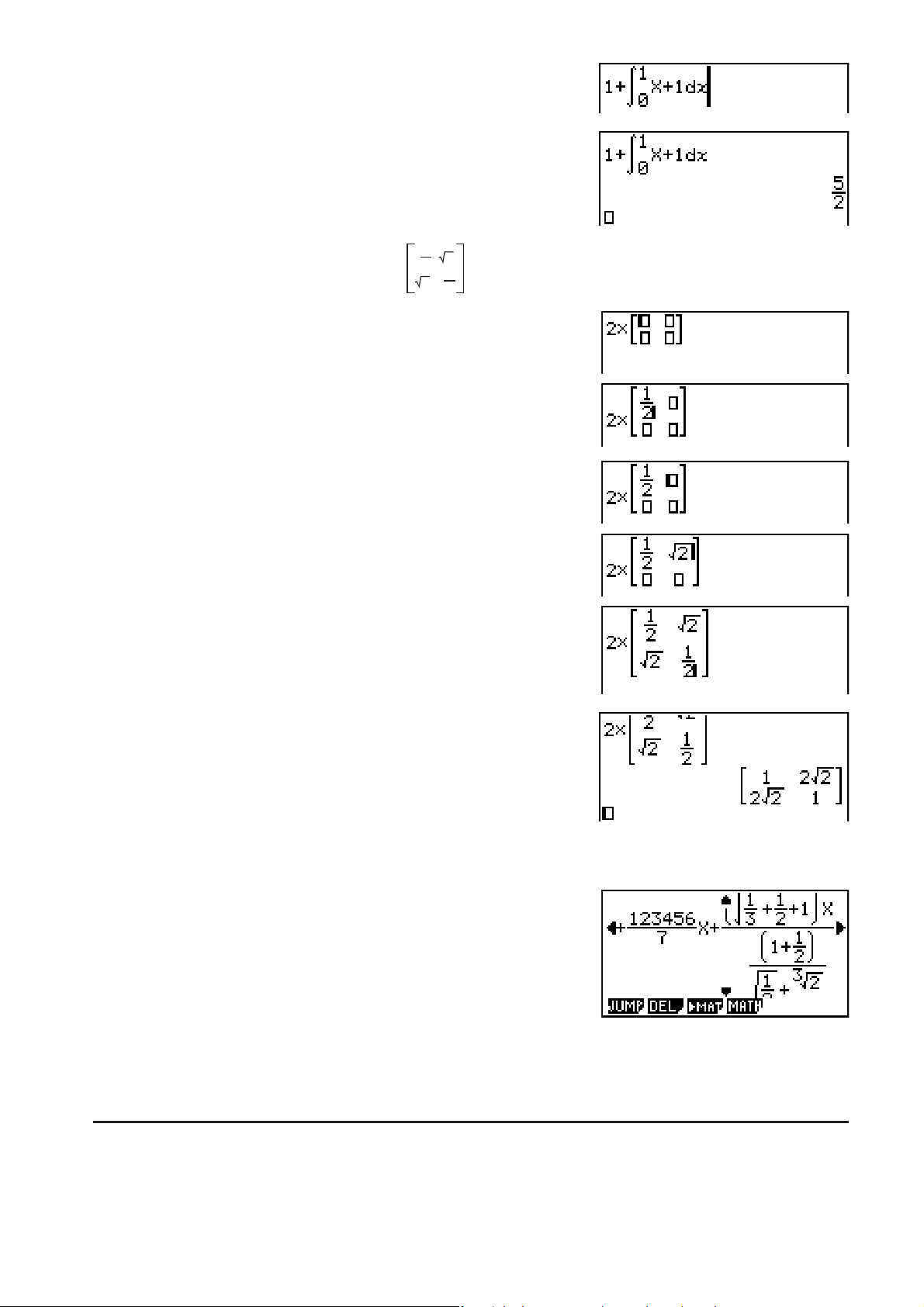
Beispiel 4 Einzugeben ist

2 ×

A(MATH)(MAT)(2×2)

6@AA

V()AC

CV()ACC6@AA

S Wenn die Rechnung nicht in das Anzeigefenster passt

Pfeile erscheinen an dem linken, rechten, oberen oder

unteren Rand des Displays, um Ihnen mitzuteilen, dass weitere Zeichen der Rechnung in der von dem Pfeil angezeigten Richtung vorhanden sind, die nicht auf dem Display angezeigt sind.

Falls Sie einen Pfeil sehen, können Sie die Cursortasten

verwenden, um den Inhalt der Displayanzeige zu verschieben und den gewünschten Teil zu betrachten.

S Eingaberestriktionen für den Math-Ein-/Ausgabemodus

Bestimmte Typen von Ausdrücken können dazu führen, dass die vertikale Breite einer Berechnungsformel größer als die auf dem Display angezeigte Zeile ist. Die maximal zulässige vertikale Breite einer Berechnungsformel beträgt etwa zwei Displayanzeigen (120 Punke). Sie können keinen Ausdruck eingeben, der diese Begrenzung übersteigt.

1-1515

S Werte und Terms als Argumente verwenden

Ein Wert oder ein Term, den Sie bereits eingegeben haben, kann als Argument für eine Funktion verwendet werden. Nach dem Sie zum Beispiel „(2+3)“ eingegeben haben, können Sie diese Formel zum Argument von  machen, was

Beispiel

1. Verschieben Sie den Cursor an die Position unmittelbar links von dem Teil des Ausdrucks,

den Sie zum Argument der einzufügenden Funktion machen möchten.

2. Drücken Sie #(INS).

• Dadurch wechselt der Cursor auf einen Einfügecursor ().

3. Drücken Sie V(), um die -Funktion einzufügen.

• Dadurch wird die -Funktion eingefügt, und der Klammerausdruck wird zu deren Argument.

(2+3)

ergibt.

Wie oben dargestellt wird der Wert oder Term rechts neben dem Cursor nach #(INS) gedruckt und wird zum Argument der Funktion, die als nächstes festgelegt wird. Der abgegrenzte Bereich als Argument umfasst alles bis zur ersten offenen Klammer an der rechten Seite, wenn es eine gibt, oder alles bis zur ersten Funktion an der rechten Seite (sin(30), log2(4) usw.).

Diese Funktion kann mit folgenden Funktionen verwendet werden.

Funktion Tastenbetätigung

Unechter Bruch

Potenz



Kubikwurzel

Potenzwurzel

V()

(

,(

)

((ex)

J(10x)

Ursprünglicher

Ausdruck

Ausdruck nach dem

Einfügen

log(a,b)

Absolutwert

Lineares Differenzial

Quadratisches Differenzial

(MATH)(log

(MATH)(Abs)

(MATH)(

(MATH)(

d/dx)

/dx2)

1-1616

Funktion Tastenbetätigung

Ursprünglicher

Ausdruck

Ausdruck nach dem

Einfügen

Integral

3-Rechnung

• Falls Sie #(INS) in dem linearen Ein-/Ausgabemodus drücken, dann wird auf den Einfügemodus umgeschaltet. Für weitere Informationen siehe Seite 1-6.

(MATH)(E)(°

(MATH)(E)(3( )

dx)

S Bearbeitung der Rechnungen in dem Math-Ein-/Ausgabemodus

Die Vorgänge für die Bearbeitung der Rechnungen in dem Math-Ein-/Ausgabemodus sind

grundlegend gleich mit den in dem linearen Ein-/Ausgabemodus verwendeten Vorgängen. Für weiter Informationen siehe „Editieren von Berechnungsformeln“ (Seite 1-6).

Achten Sie jedoch darauf, dass die folgenden Punkte unterschiedlich zwischen dem Math-Ein-/

Ausgabemodus und dem linearen Ein-/Ausgabemodus sind.

• Die in dem linearen Ein-/Ausgabemodus verfügbare Überschreibmoduseingabe wird von dem Math-Ein-/Ausgabemodus nicht unterstützt. In dem Math-Ein-/Ausgabemodus wird die Eingabe immer an der aktuellen Cursorposition eingefügt.

• In dem Math-Ein-/Ausgabemodus können Sie durch Drücken der #-Taste immer einen Rückschrittvorgang ausführen.

• Beim Eingeben von Berechnungen im Math-Ein-/Ausgabemodus ist folgende Cursorsteuerung möglich.

Um dies zu tun: Drücken Sie diese Taste:

Cursor vom Ende der Berechnung zum Anfang bewegen Cursor vom Anfang der Berechnung zum Ende bewegen

C B

I Verwenden der Operationen Rückgängig und Wiederholen

Sie können folgende Vorgehensweisen während der Eingabe von Rechnungsterms im Math-Ein-/Ausgabemodus verwenden (bis Sie die U-Taste drücken), um die letzte Tastenoperation rückgängig zu machen und die Tastenoperation, die Sie gerade rückgängig gemacht haben, zu wiederholen.

- Um die letzte Tastenoperation rückgängig zu machen, drücken Sie: ?#(UNDO).

- Um eine Tastenoperation, die Sie gerade rückgängig gemacht haben, zu wiederholen, drücken Sie: Wieder ?#(UNDO).

• Sie können ebenfalls UNDO dazu verwenden, um eine -Tastenoperation abzubrechen. Nachdem Sie die -Taste gedrückt haben, um einen Term, den Sie eingegeben haben, zu löschen, wird das Drücken von ?#(UNDO), das wiederherstellen, was auf dem Display angezeigt wurde, bevor Sie gedrückt haben.

• Sie können ebenfalls UNDO dazu verwenden, um eine Cursortastenoperation abzubrechen. Wenn Sie während der Eingabe die C-Taste drücken und dann ?#(UNDO) drücken, dann kehrt der Cursor wieder dahin zurück, wo er war, bevor Sie die C-Taste gedrückt haben.

• Die UNDO-Operation ist deaktiviert solange die Buchstaben der Tastatur festgestellt sind. Durch Drücken von ?#(UNDO), während die Buchstaben der Tastatur festgestellt sind, wird die gleiche Löschoperation durchgeführt, wie durch alleiniges Drücken der #-Taste.

1-1717

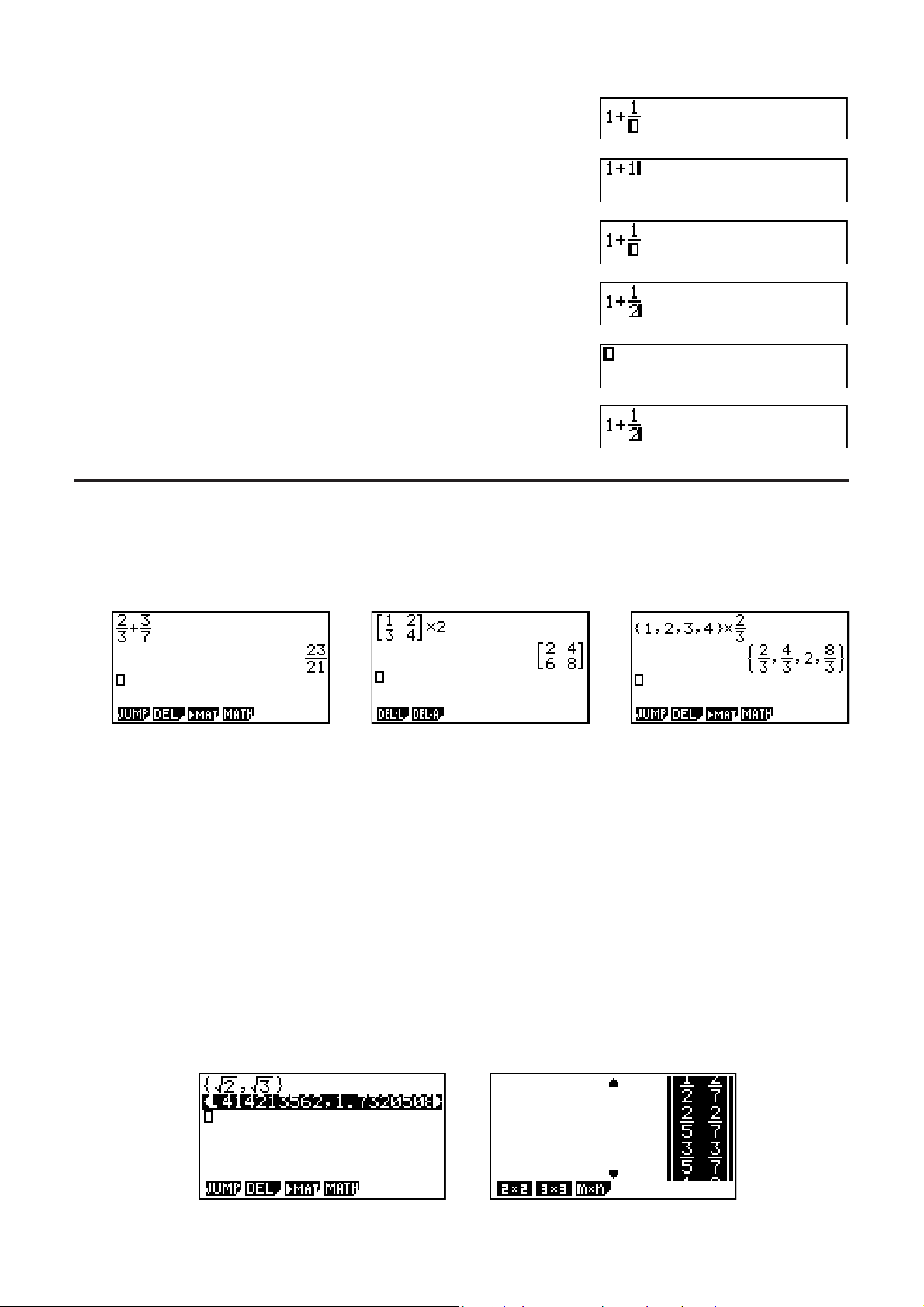
Beispiel

@6@C

?#(UNDO)

I Anzeige des Rechnungsergebnisses in dem Math-Ein-/Ausgabemodus

Brüche, Matrizen und Listen, die durch Rechnungen im Math-Ein-/Ausgabemodus erhalten

wurden, werden in dem natürlichen Format angezeigt, gleich wie sie in Ihrem Textbuch erscheinen.

Anzeigebeispiele für Rechenergebnisse

• Brüche werden entweder als unechte Brüche oder als gemischte Brüche angezeigt, abhängig von der Einstellung „Frac Result“ auf der Einstellungsanzeige. Für Einzelheiten siehe „Zugeordnetes SET-UP-Menü (Voreinstellungen)“ (Seite 1-28).

• Matrizen werden im natürlichen Format bis zu 6 × 6 angezeigt. Eine Matrix mit mehr als sechs Reihen oder Spalten wird auf einer MatAns-Anzeige angezeigt, die der in dem linearen Ein-/Ausgabemodus verwendeten Anzeige entspricht.

• Die Listen werden in dem natürlichen Format mit bis zu 20 Elementen angezeigt. Eine Liste mit mehr als 20 Elementen wird auf einer ListAns-Anzeige angezeigt, die der in dem linearen Ein-/Ausgabemodus verwendeten Anzeige entspricht.

• Pfeile erscheinen an dem linken, rechten, oberen oder unteren Rand des Displays, um Ihnen mitzuteilen, dass weitere Daten in der entsprechenden Richtung vorhanden sind, die nicht gleichzeitig angezeigt werden können.

1-1818

Sie können die Cursortasten verwenden, um die Anzeige zu verschieben, damit Sie die

gewünschten Daten ablesen können.

• Falls Sie (DEL)(DEL

•

L) bei gewähltem Rechnungsergebnis drücken, dann werden

sowohl das Ergebnis als auch die dafür verwendete Berechnungsformel gelöscht.

• Das Multiplikationszeichen darf unmittelbar vor einem unechten Bruch oder einem gemischten Bruch nicht weggelassen werden. Geben Sie daher in einem solchen Fall immer das Multiplikationszeichen ein.

2×

Beispiel:

• Einer ,, V oder (

AA6D

–1

)-Tastenoperation darf nicht sofort eine andere ,, V oder

(x–1)-Tastenoperation folgen. In einem solchen Fall sollten Sie Klammern verwenden,

um die Vorgänge getrennt zu halten.

2)–1

Beispiel: (3 (3(3

BV(x–1)

I Historyfunktion

Die Historyfunktion zeichnet die Ausdrücke und Ergebnisse der Berechnungen im Math-Ein-/ Ausgabemodus auf. Die Funktion hält max. 30 Datensätze mit Ausdrücken und Ergebnissen aufrecht.

@AU AU

Sie können die von der Historyfunktion aufrecht erhaltenen mathematischen Ausdrücke auch bearbeiten und neu berechnen lassen. Dadurch werden alle Ausdrücke neu berechnet, beginnend mit dem bearbeiteten Ausdruck.

Beispiel „1+2“ in „1+3“ ändern und neu berechnen

Führen Sie nach dem oben gezeigten Muster folgende Bedienung aus.

DDDDB#BU

• Der im Antwortspeicher gespeicherte Wert ist stets vom Ergebnis der letzten durchgeführten Berechnung abhängig. Wenn der History-Inhalt Operationen einschließt, die den Antwortspeicher verwenden, kann sich das Bearbeiten einer Berechnung auf den in nachfolgenden Berechnungen verwendeten Antwortspeicherwert auswirken.

- Wenn Sie eine Serie von Berechnungen vornehmen, die den Antwortspeicher verwenden,

um das Ergebnis der vorherigen Berechnung in die nächste Berechnung einzubeziehen, kann sich das Bearbeiten einer Berechnung auf die Ergebnisse aller danach folgenden anderen Berechnungen auswirken.

- Wenn die erste Berechnung in der History Antwortspeicherinhalte einbezieht, beträgt der

Antwortspeicherwert „0“, da vor der ersten Berechnung in der History noch keine andere vorhanden ist.

1-1919

I Verwendung der Zwischenablage für das Kopieren und Einfügen im

Math-Ein-/Ausgabemodus

Sie können eine Funktion, einen Befehl oder eine andere Eingabe in die Zwischenablage kopieren und danach den Inhalt der Zwischenablage an einer anderen Stelle einfügen.

• Sie können im Math-Ein-/Ausgabemodus nur eine Zeile als Kopierbereich festlegen.

• Der CUT-Bedienungsvorgang wird nur in dem linearen Ein-/Ausgabemodus unterstützt. In dem Math-Ein-/Ausgabemodus wird er nicht unterstützt.

S Kopieren von Text

1. Verwenden Sie die Cursortasten, um den Cursor auf den zu kopierenden Zeile zu

verschieben.

2. Drücken Sie G(CLIP). Der Cursor ändert auf „

3. Drücken Sie (CPY

(Clipboard) zu kopieren.

•

L), um den hervorgehobenen Text in den Zwischenspeicher

“.

S Einfügen von Text

I Rechenoperationen im Math-Ein-/Ausgabemodus

Dieser Abschnitt beinhaltet Rechenbeispiele im Math-Ein-/Ausgabemodus.

• Details zu Rechenoperationen finden Sie im „Kapitel 2 Manuelle Berechnungen“.

S Durchführen von Funktionsrechnungen im Math-Ein-/Ausgabemodus

Beispiel Tastenfolge

4×5610

6645U



cos

( )

log

8 = 3

123 = 1,988647795

2 + 3 ×

3 4

+ 3 =

1,5 + 2,3

( )

(Winkel: Rad)

64 − 4 = 10

= 0,1249387366log

+ 4

+ x − 6

x = 3

= 52

A$(P)63CU

(MATH)(logab) 2C8U ,( 23,(

(MATH)(Abs)J364U

265C36()1C4U

1.52.3?(

(MATH)(d/dx)T,3C4 TVT6C3U

) 7C123U

1-2020

) 3C64C4U

i)U,



+ 3x + 4

404

(MATH)(E)(°dx) 2TV3T4C1 C5U

− 3k + 5) = 55

(

∑

(MATH)(E)(3)?(K)V3?(K) 5C?(K)C2C6U

I Durchführen von Matrixrechnungen im Math-Ein-/Ausgabemodus

S Festlegen der Dimension (Größe) einer Matrix

1. Drücken Sie K(SET UP)(Math)) im RUN • MAT • MAT• MAT MATMAT-Menü.

2. Drücken Sie (MATH), um das MATH-Menü anzuzeigen.

3. Drücken Sie (MAT), um das nachfolgend dargestellte Menü anzuzeigen.

• {2s2} ... {Gibt eine 2 × 2 Matrix ein}

• {3s3} ... {Gibt eine 3 × 3 Matrix ein}

msn} … {Gibt eine Matrix mit m Reihen × n Spalten ein (bis zu 6 × 6)}

• {

Beispiel Zu erstellen ist eine Matrix mit 2 Reihen s 3 Spalten.

(

msn)

Geben Sie die Anzahl der Reihen ein. AU Geben Sie die Anzahl der Spalten ein. BU U

S Eingeben von Zellenwerten

Beispiel Auszuführen ist die nachfolgend dargestellte Rechnung.

Der nachfolgende Bedienungsvorgang ist eine Fortsetzung des Berechnungsbeispiels von der vorhergehenden Seite.

× 8

1-2121

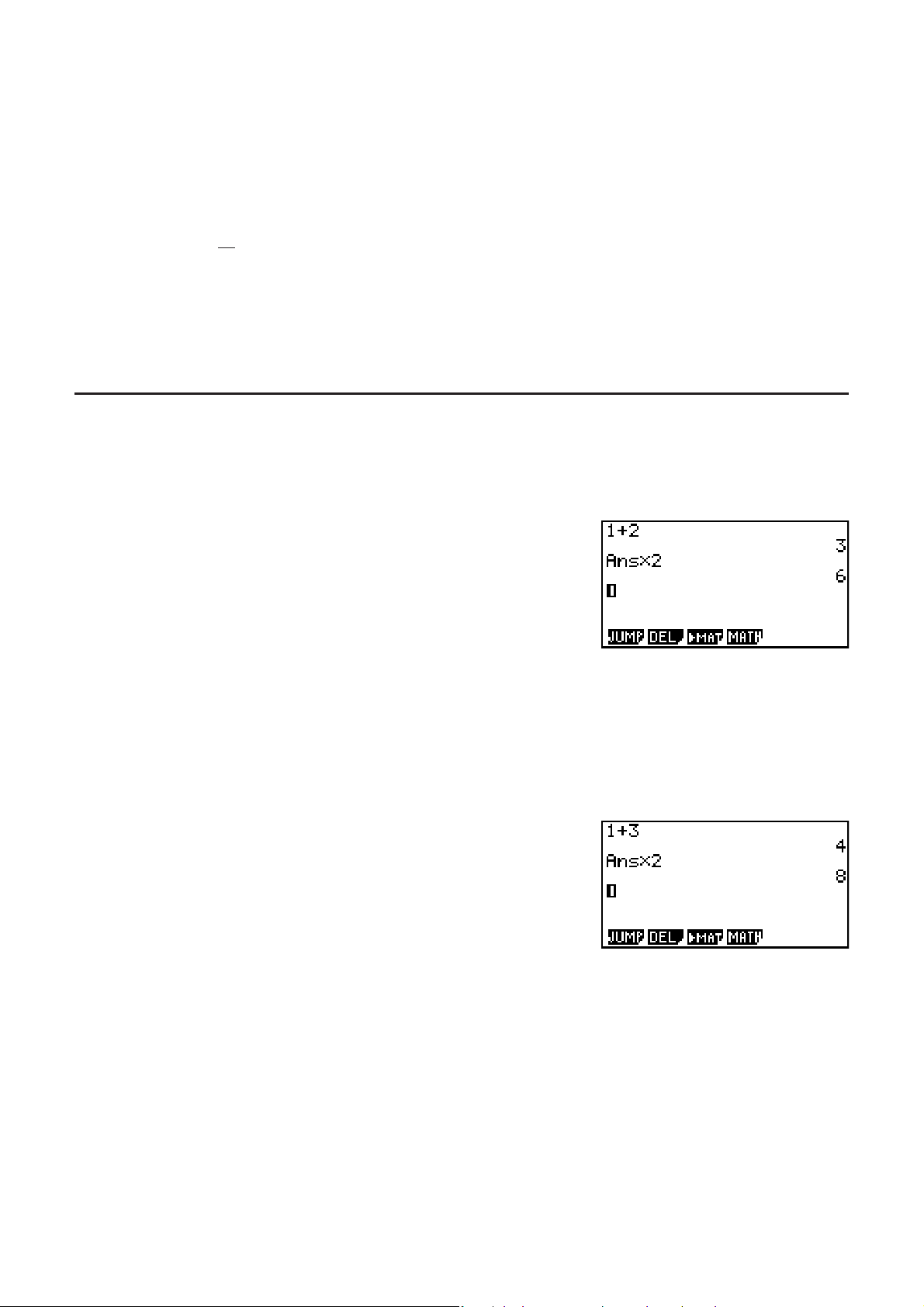
@C@6ACCBBC @B6CCCDCEC GU

S Zuordnen einer unter Verwendung des Math-Ein-/Ausgabemodus erstellten

Matrix zu einer Matrix des MAT-Modus

Beispiel Das Rechnungsergebnis ist Mat J zuzuordnen.

A(Mat)(Ans)?

A(Mat)?(J)U

• Falls Sie die #-Taste drücken, wenn sich der Cursor an der Oberseite (oben links) der Matrix befindet, wird die gesamte Matrix gelöscht.



I Verwenden von Grafikmodus und EQUA-Modus im Math-Ein-/Ausgabe-

modus

Durch Verwendung des Math-Ein-/Ausgabemodus mit einem beliebigen unten angegebenem Modus, können Sie numerische Terms genauso eingeben, wie Sie sie in Ihrem Heft schreiben und können die Ergebnisse der Rechnung im natürlichen Anzeigeformat betrachten.

Menüs, die die Eingabe von Terms, wie man sie im Heft schreibt, unterstützen: RUN•MAT, e • ACT, GRAPH, DYNA, TABLE, RECUR, EQUA • MAT, e • ACT, GRAPH, DYNA, TABLE, RECUR, EQUA•MAT, e• ACT, GRAPH, DYNA, TABLE, RECUR, EQUA MAT, e • ACT, GRAPH, DYNA, TABLE, RECUR, EQUAMAT, e•ACT, GRAPH, DYNA, TABLE, RECUR, EQUA • ACT, GRAPH, DYNA, TABLE, RECUR, EQUA•ACT, GRAPH, DYNA, TABLE, RECUR, EQUA ACT, GRAPH, DYNA, TABLE, RECUR, EQUAACT, GRAPH, DYNA, TABLE, RECUR, EQUA (SOLV)

Menüs, die ein natürliches Anzeigeformat unterstützen: RUN•MAT, e • ACT, EQUA • MAT, e • ACT, EQUA•MAT, e• ACT, EQUA MAT, e • ACT, EQUAMAT, e•ACT, EQUA • ACT, EQUA• ACT, EQUA ACT, EQUAACT, EQUA

Folgende Beschreibungen zeigen Operationen im Math-Ein-/Ausgabemodus in den GRAPH-, DYNA-, TABLE-, RECUR- und EQUA-Menüs und eine Ergebnisanzeige von natürlichen Rechnungen im EQUA-Menü.

• Weitere Details über die Operation erhalten Sie in den Abschnitten, die jede Rechnung beinhalten.

• Details über Eingabeoperationen im Math-Ein-/Ausgabemodus und Ergebnisanzeigen von Rechnungen im RUN•MAT • MAT•MAT MATMAT-Menü erhalten Sie im Abschnitt „Eingabevorgänge im Math-Ein-/ Ausgabemodus“ (Seite 1-12) und „Rechenoperationen im Math-Ein-/Ausgabemodus“ (Seite 1-20).

• Eingabeoperationen im e • ACT • ACT•ACT ACTACT-Menü und Ergebnisanzeigen sind die gleichen wie die im RUN•MAT • MAT•MAT MATMAT-Menü. Informationen über Operationen im e•ACT • ACT• ACT ACTACT-Menü, erhalten Sie in „Kapitel 10 eActivity“.

1-2222

Wichtig!

• Bei einem Modell, dessen Betriebssystem von einer älteren OS-Version auf OS 2.00 aktualisiert wurde, wird die Eingabe im Math-Ein-/Ausgabemodus und die Ergebniseinzeige in keinem Modus unterstützt außer im RUN•MAT • MAT•MAT MATMAT-Menü und e•ACT • ACT• ACT ACTACT-Menü.

S Eingabe des Math-Ein-/Ausgabemodus im GRAPH-Menü

Sie können den Math-Ein-/Ausgabemodus für die Eingabe des Grafikausdrucks in den

GRAPH-, DYNA-, TABLE- und RECUR-Menüs verwenden.

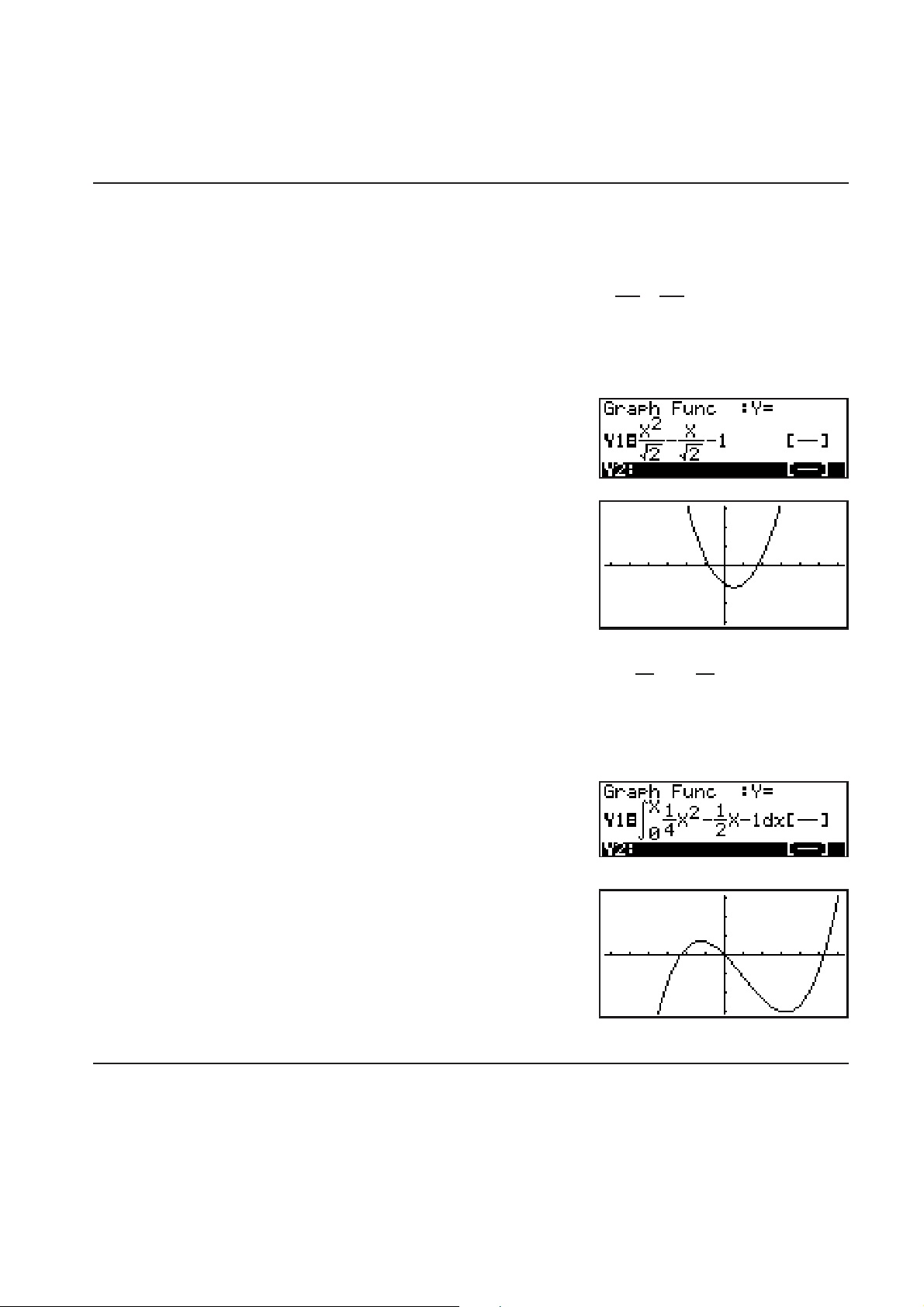
Beispiel 1 Geben Sie im GRAPH-Menü die Funktion

lassen Sie sich diese dann darstellen. Vergewissern Sie sich, dass im Betrachtungsfenster die ursprüngliche Standardeinstellungen konfiguriert sind.

KGRAPHTV6V()A\

CCT6V()ACC\ @U

(DRAW)

−−1 2

ein und

Beispiel 2 Geben Sie im GRAPH-Menü die Funktion

und lassen Sie sich diese dann darstellen. Vergewissern Sie sich, dass im Betrachtungsfenster die ursprüngliche Standardeinstellungen

konfiguriert sind.

KGRAPH*(CALC)(°dx)

@6CCTV@6AC T@C?CTU

(DRAW)



−

− 1

ein

• Eingabe des Math-Ein-/Ausgabemodus und Ergebnisanzeige im EQUAMenü

Sie können den Math-Ein-/Ausgabemodus im EQUA-Menü verwenden, um Berechnungen wie unten dargestellt einzugeben und anzuzeigen.

• Bei linearen Gleichungssystemen ((SIML)) und Gleichungen höherer Ordnung ((POLY)), werden die Lösungen wenn möglich im natürlichen Anzeigeformat ausgegeben (Brüche, , P werden im natürlichen Format angezeigt).

1-2323

• Bei Lösern ((SOLV)), können Sie die natürliche Eingabe des Math-Ein-/Ausgabemodus verwenden.

Beispiel Zu bestimmen ist die Lösung der quadratischen Gleichung

0 im EQUA-Menü

KEQUAK(SET UP) AAAA(Complex Mode)

+ 3x + 5 =

(a+b

(POLY)(2)@UBUDUU

i))

5. Optionsmenü (OPTN)

Das Optionsmenü ermöglicht Ihnen den Zugriff auf höhere mathematische Funktionen und Merkmale, die nicht unmittelbar auf der Tastatur des Rechners angegeben sind. Der Inhalt des Optionsmenüs unterscheidet sich in Abhängigkeit davon, in welchem Menü Sie sich gerade befinden, wenn Sie die *-Taste drücken.

• Das Optionsmenü erscheint nicht, wenn * gedrückt wird und das Binär-, Oktal-, Dezimaloder Hexadezimalsystem als das Vorgabe-Zahlensystem eingestellt ist.

• Details über die Befehle einschließlich des Optionsmenüs (OPTN) erhalten Sie im „* key“-Eintrag in der „PRGM-Menü-Befehlsliste“ (Seite 8-40).

• Die Bedeutungen der einzelnen Befehle des Optionsmenüs sind in den Abschnitten beschrieben, in denen das entsprechende Menü behandelt wird.

Folgende Liste beinhaltet das Optionsmenü, das angezeigt wird, wenn das RUN•MAT- • MAT-•MAT- MAT-MAT- (oder RUN-) oder PRGM-Menü ausgewählt wurde.

Eintragsnamen, die darunter mit einem Sternchen (*) markiert sind, sind beim fx-7400G verfügbar.

• {LIST} ... {Listenfunktionsmenü}

• {MAT}* ... {Matrixoperationsmenü}

• {CPLX} ... {Menü für Berechnungen mit komplexen Zahlen}

• {CALC} ... {Funktionsanalysemenü}

• {STAT} ... {Menü zum zweidimensional statistisch geschätzen Wert} (fx-7400G {Menü zum zweidimensional statistisch geschätzen Wert} (fx-7400G{Menü zum zweidimensional statistisch geschätzen Wert} (fx-7400G {Menü zum zweidimensional statistisch geschätzten Wert, Verteilung, Standardabweichung, Varianz und Testfunktionen} (alle Modelle außer fx-7400G

• {CONV} ... {Menü zur metrischen Umrechnung}

• {HYP} ... {Hyperbelfunktionsmenü}

• {PROB} ... {Menü zur Wahrscheinlichkeitsrechnung}

• {NUM} ... {Menü für numerisches Berechnungen}

• {ANGL} ... {Menü für Winkel-/Koordinatenumwandlung, Sexagesimal-Eingabe/Umwandlung}

• {ESYM} ... {Menü für technische Symbole}

• {PICT} ... {Menü zum Speichern/Aufrufen von Grafiken}

• {FMEM} ... {Funktionsspeichermenü}

Ⅱ)

Ⅱ nicht

Ⅱ)

• {LOGIC} ... {Logikoperatormenü}

• {CAPT} ... {Anzeigeneinfangmenü}

1-2424

• {TVM}* ... {Finanzmathematikmenü}

• PICT, FMEM und CAPT werden nicht angezeigt, wenn Sie „Math“ als Ein-/Ausgabemodus gewählt haben.

6. Variablendatenmenü (VARS)

Um abgespeicherte Werte spezieller Variablen aufzurufen, drücken Sie die )-Taste, um das Variablendatenmenü zu öffnen.

{V-WIN}/{FACT}/{STAT}/{GRPH}/{DYNA}/{TABL}/{RECR}/{EQUA}/{TVM}/{Str}

• Beachten Sie, dass die EQUA- und TVM-Einträge für Funktionstasten ( und ) nur dann erscheinen, wenn Sie auf das Variablendatenmenü aus dem RUN•MAT • MAT•MAT MATMAT- (oder RUN-) oder PRGM-Menü zugreifen.

• Das Variablendatenmenü erscheint nicht, wenn ) gedrückt wird und das Binär-, Oktal-, Dezimal- oder Hexadezimalsystem als das Vorgabe-Zahlensystem eingestellt ist.

• Je nach Rechnermodell, sind einige Menüeintrage eventuell nicht vorhanden.

• Details über die Befehle einschließlich des Variablendatenmenüs (VARS) erhalten Sie im „)-Taste“-Eintrag in der „PRGM-Menü-Befehlsliste“ (Seite 8-40).

• Eintragsnamen, die darunter mit einem Sternchen (*) markiert sind, sind beim fx-7400G nicht verfügbar.

S V-WIN — Aufrufen der Einzelwerte für das Betrachtungsfenster

• {X}/{Y}/{T,θ} ... {Menü der x-Achse}/{Menü der y-Achse}/{T,θ-Menü}

{R-X}/{R-Y}/{R-T,θ} ... {Menü der x-Achse}/{Menü der y-Achse}/{T,θ-Menü} für die

• rechte Seite der Doppelgrafik

• {min}/{max}/{scal}/{dot}/{ptch} ... {Minimalwert}/{Maximalwert}/{Skalierung}/

}/{Schrittweite}

{Punktwert*

Der Punktwert zeigt den Anzeigebereich (Xmax-Wert – Xmin-Wert) geteilt durch die Punktteilung (126) des Displays an. Der Punktwert wird normalerweise automatisch anhand der Minimal- und Maximalwerte be-rechnet. Durch eine Änderung des Punktwertes wird das Maximum automatisch berechnet.

S FACT — Aufrufen des Zoomfaktors

• {Xfct}/{Yfct} ... {Faktor der x-Achser}/{Faktor der y-Achse}

S STAT — Aufrufen von statistischen Kennzahlen und Parametern

• {X} … {x-Daten einer eindimensionalen oder zweidimensionalen Stichprobe}

• { {Mittelwert}/{Summe der Einzelwerte}/{Summe der Quadrate}/{Grundgesamtheits-

n}/{¯x}/{3x}/{3x

Standardabweichung}/{Stichproben-Standardabweichung}/{Minimalwert}/ {Maximalwert}

}/{σx}/{sx}/{minX}/{maxX} ... {Anzahl der Daten, Stichprobenumfang}/

Ⅱ

{Y} ... {y-Daten einer zweidimensionalen Stichprobe}

•

• { {Summe der Quadrate}/{Summe der Produkte der x-Daten und y-Daten}/

ӯ}/{3y}/{3y

{Grundgesamtheits-Standardabweichung}/{Stichproben-Standardabweichung}/ {Minimalwert}/{Maximalwert}

}/{3xy}/{σx}/{sy}/{minY}/{maxY} ... {Mittelwert}/{Summe der Einzelwerte}/

1-2525

•

{GRPH} ... {Grafikdatenmenü}

• {a}/{b}/{c}/{d}/{e} ... {Regressionskoeffizient und Polynomkoeffizienten}

• {r}/{r

} ... {Korrelationskoeffizient}/{Bestimmtheitsmaß (bei quasilinearer Dreifach-

Regression)}

• {MSe} ... {mittlerer quadratischer Fehler (Restvarianz aus der Streuungszerlegung)}

• {Q

}/{Q3} ... {erstes Quartil}/{drittes Quartil}

• {Med}/{Mod} ... {Median}/{Modalwert} der Eingabedaten

• {Strt}/{Pitch}... Histogramm {Start-Reduktionslage}/{Klassenbreite}

{PTS} ... {Datenmenü der Medianpunkte einer Med-Med-Regression}

•

• {

•

• {n}/{¯x}/{sx}/{n1}/{n2}/{¯x1}/{¯x2}/{s

}/{y1}/{x2}/{y2}/{x3}/{y3} ... {Koordinaten der Medianpunkte/Summierungspunkte}

{INPT}* ... {Eingabewerte der statistischen Berechnung}

}/{s

}/{sp} ... {Stichprobenumfang}/{Mittelwert der

Stichprobe}/{empirische Standardabweichung}/{Stichprobenumfang 1}/

{Stichprobenumfang 2}/{Mittelwert der Stichprobe 1}/{Mittelwert der Stichprobe 2}/ {empirische Standardabweichung 1}/{empirische Standardabweichung 2}/{empirische Standardabweichung p}

{RESLT}* ... {Ausgabewerte der statistischen Berechnung}

•

• {TEST} ... {Testberechnungsergebnisse}

• {

p}/{z}/{t}/{Chi}/{F}/{ ˆp}/{ ˆp

}/{ ˆp2}/{df}/{se}/{r}/{r 2}/{pa}/{Fa}/{Adf}/{SSa}/{MSa}/{pb}/{Fb}/

{Bdf}/{SSb}/{MSb}/{pab}/{Fab}/{ABdf}/{SSab}/{MSab}/{Edf}/{SSe}/{MSe}... {p-Wert}/

{z-Ergebnis}/{t-Ergebnis}/{C2-Wert}/{F-Wert}/{geschätzter Stichprobenanteil}/

{geschätzter Stichprobenanteil 1}/{geschätzter Stichprobenanteil 2}/{Freiheitsgrade}/ {Standardfehler}/{Korrelationskoeffizient}/{Bestimmtheitsmaß}/{Faktor A p-Wert}/ {Faktor A F-Wert}/{Faktor A Freiheitsgrade}/{Faktor A Summe der Quadrate}/ {Faktor A Mittelwert der Quadrate}/{Faktor B p-Wert}/{Faktor B F-Wert}/{Faktor B Freiheitsgrade}/{Faktor B Summe der Quadrate}/{Faktor B Mittelwert der Quadrate}/ {Faktor AB p-Wert}/{Faktor AB F-Wert}/{Faktor AB Freiheitsgrade}/{Faktor AB Summe der Quadrate}/{Faktor AB Mittelwert der Quadrate}/{Fehler Freiheitsgrade}/ {Fehler Summe der Quadrate}/{Fehler Mittelwert der Quadrate}

• {{INTR} ... {Berechnungsergebnisse des Konfidenzintervals}

• {Left}/{Right}/{ ˆp}/{ ˆp1}/{ ˆp2}/{df} ... {untere Grenze des Konfidenzintervals (linker Rand)}/{obere Grenze des Konfidenzintervalls (rechter Rand)}/{geschätzter

Stichprobenanteil}/{geschätzter Stichprobenanteil 1}/{geschätzter Stichprobenanteil 2}/{Freiheitsgrade}

• {DIST} ... {Verteilungsberechnungsergebnisse}

• { der Verteilungswahrscheinlichkeit oder Summenverteilung (

p}/{xInv}/{x1Inv}/{x2Inv}/{zLow}/{zUp}/{tLow}/{tUp} ... {Berechnungsergebnis

p-Wert)}/{Umkehrversion

Student-t, C2, F, binomial, Poisson, geometrische oder hypergeometrisch kumulative Verteilungsberechnungsergebnis}/{Umkehrversion normale kumulative obere Grenze der Verteilung (rechter Rand) oder untere Grenze (linker Rand)}/{Umkehrversion normale kumulative obere Grenze der Verteilung (rechter Rand)}/{normale kumulative untere Grenze der Verteilung (linker Rand)}/{normale kumulative obere Grenze der Verteilung (rechter Rand)}/{Student-t kumulative untere Grenze der Verteilung (linker Rand)}/{Student-

t kumulative obere Grenze der Verteilung (rechter

Rand)}

S GRPH — Aufrufen von Grafikfunktionen

• {Y}/{r} ... {Funktionsgleichungen oder -ungleichungen in kartesischen Koordinaten}/

{Funktionsgleichungen in Polarkoordinaten}

• {Xt}/{Yt} ... Funktionsgleichungen in Parameterdarstellung {Xt}/{Yt}

1-2626

• {X} ... {X=Konstant} vertikale Geraden

• Drücken Sie diese Tasten vor der Eingabe eines Wertes, um den Speicherbereich

auszuwählen.

S DYNA* — Aufrufen der Einstelldaten für eine dynamische Grafik

• {Strt}/{End}/{Pitch} ... {Dynamik-Variable/Scharparameter-Startwert}/{Dynamik-Variable/ Scharparameter-Endwert}/{Dynamik-Variable/Scharparameter-Schrittweite}

S TABL — Aufrufen der Tabellen-Einstellungswerte und der Wertetabellen

• {Strt}/{End}/{Pitch} ... {Tabellenbereich-Startwert des Arguments}/{Tabellenbereich- Endwert des Arguments}/{Tabellenbereich-Schrittweite des Arguments}

• {Reslt *

Der Ergebniseintrag erscheint nur dann, wenn das TABL-Menü im RUN • MAT- (oder

} ... {Wertetabelle als Matrix}

RUN-) und PRGM-Menü angezeigt wird.

S RECR* — Aufrufen der Rekursionsformeln*1, des Tabellenbereichs und der

Wertetabellen

• {FORM} ... {Datenmenü der Rekursionsformeln}

• {an}/{a {c

}/{a

} Terms

}/{bn}/{b

}/{c

}/{b

}/{cn}/{c

}/{c

} ... {an}/{a

}/{a

}/{bn}/{b

}/{b

}/{cn}/

• {RANG} ... {Tabellenbereich-Datenmenü}

• {Strt}/{End}... Tabellenbereich {Startwert}/{Endwert}

• {

}/{a1}/{a2}/{b0}/{b1}/{b2}/{c0}/{c1}/{c2} ... {a0}/{a1}/{a2}/{b0}/{b1}/{b2}/{c0}/{c1}/{c2} Wert

St}/{bnSt}/{cnSt} ... Startwerte {an}/{bn}/{cn} in der WEB-Grafik für eine Konvergenz-/

Divergenzuntersuchung einer Zahlenfolge/Rekursionsformel

• {Reslt*

Es kommt zu einer Fehlermeldung, wenn sich keine Zahlenfolge- oder Rekursionsformel-

}* ... {Wertetabelle (der Werte der Folgenglieder) als Matrix*3}

Wertetabelle im Speicher befindet.

„Result“ steht nur im RUN•MAT • MAT•MAT MATMAT-Menü und PRGM-Menü zur Verfügung.Menü zur Verfügung. zur Verfügung.

Die Tabelleninhalte werden automatisch im Matrixantwortspeicher (MatAns) gespeichert.

S EQUA* — Aufrufen der Gleichungskoeffizienten und Lösungen*1 *

• {S-Rlt}/{S-Cof} ... Matrix von {Lösungen}/{Koeffizienten} für lineare Gleichungen mit zwei bis sechs Unbekannten*

• {P-Rlt}/{P-Cof} ... Matrix von {Lösungen}/{Koeffizienten} für eine quadratische oder kubische Gleichung

Die Koeffizienten und Lösungen werden automatisch im Matrixantwortspeicher (MatAns)

gespeichert.

Die folgenden Bedingungen führen zu einer Fehlermeldung:

- wenn keine Koeffizienten für die Gleichung eingegeben wurden;

- wenn keine Lösungen für die Gleichung erhalten wurden (z. B. nicht eindeutig lösbares Gleichungssystem).

Die Koeffizienten- und Lösungsspeicherdaten für ein lineares Gleichungssystem können nicht gleichzeitig aufgerufen werden.chzeitig aufgerufen werden.

1-2727

S TVM* — Aufrufen der finanziellen Rechnungsdaten

• {n}/{I%}/{PV}/{PMT}/{FV} ... {Zahlungsperiode (Raten)}/{Jahreszinssatz}/{Anfangswert}/ {Zahlung}/{Endwert}

• {

P/Y}/{C/Y} ... {Ratenperioden pro Jahr}/{Verzinsungsperioden pro Jahr}

S Str — Str Befehl

• {Str} ... {Kettenspeicher}

7. Programmmenü (PRGM)

Um das Programmmenü (PRGM) anzuzeigen, wechseln Sie zuerst in das RUN•MAT • MAT•MAT MATMAT- (oder RUN-) oder PRGMGM-Menü aus dem Hauptmenü aus und drücken Sie dann aus dem Hauptmenü aus und drücken Sie dann )(PRGM).

Die folgenden Positionen stehen im Programmmenü (PRGM) zur Auswahl zur Verfügung.

• {COM} ...... {Programmbefehlsmenü}

• {CTL} ....... {Programm-Steuerbefehlsmenü}

• {JUMP} ..... {Sprungbefehlsmenü}

• {?} ............ {Eingabebefehl}

• {<} .......... {Ausgabebefehl}

• {CLR} ....... {Löschbefehlsmenü}

• {DISP} ...... {Anzeigebefehlsmenü}

• {REL} ....... {Menü der Verhältnisoperatoren für bedingten Sprung}

• {I/O} ......... {E/A-Steuerungs-/Übertragungsbefehlsmenü}

• {:} ............. {Mehrfachanweisungsbefehl}

• {STR} ....... {Stringbefehl}

Folgendes Funktionstastenmenü erscheint, wenn Sie im RUN•MAT • MAT•MAT MATMAT-Menü (oder (oder RUN-Menü)) oder im PRGM-Menü )(PRGM) drücken, während Binär-, Oktal-, Dezimal- oder Hexadezimal als Standardnummernsystem festgelegt ist.

• {Prog} ....... {Aufrufen eines (Unter-)Programms}

• {JUMP}/{?}/{<}/{REL}/{:}

Die den Funktionstasten zugeordneten Funktionen sind die gleichen wie im Comp-Modus, der in der Einstellanzeige voreingestellt werden kann.

Für Einzelheiten zu den Befehlen in den verschiedenen Menüs, die Sie aus dem Programmmenü aufrufen können, siehe „Kapitel 8 Programmierung“.

8. Zugeordnetes SET-UP-Menü (Voreinstellungen)

Jedem Menü, das aus dem Hauptmenü heraus geöffnet werden kann, ist ein spezielles SET-UP-Menü zugeordnet, in dem der aktuelle Status der Voreinstellungen eingesehen oder gewünschte Änderungen vorgenommen werden können. Dazu gehen Sie wie folgt vor.

1-2828

S Ändern einer Voreinstellung für ein gewähltes Menü

1. Wählen Sie das gewünschte Icon aus und drücken Sie die U-Taste, um ein Menü

aufzurufen und dessen Eingangsbildschirm anzuzeigen. Hier soll das RUN•MAT • MAT•MAT MATMAT-Menü (oder RUN-Menü) geöffnet werden, um dessen zugeordnetes SET-UP-Menü einsehen zu können.

2. Drücken Sie die Tasten K(SET UP), um das SET-UP

des Menüs anzuzeigen.

• Die Einstellanzeige (SET UP) ist nur ein mögliches Beispiel.

Der tatsächliche Inhalt der Einstellanzeige hängt von dem Menü, in dem Sie sich gerade befinden, und dessen aktuellen Voreinstellungen ab.

3. Verwenden Sie die D- und A-Cursortasten, um die Positionen zu markieren, dessen

Voreinstellung Sie ändern möchten.

4. Drücken Sie die Funktionstaste ( bis ), die derjenigen Auswahl-Einstellung

zugeordnet ist, die Sie in das SET UP übernehmen möchten.

5. Nachdem Sie die gewünschten Änderungen ausgeführt haben, drücken Sie die )-Taste,

um in den Eingangsbildschirm des geöffneten Menüs zurückzukehren.

I Funktionstastenmenü im zugeordneten SET-UP-Menü

Dieser Abschnitt beschreibt die Voreinstellungen, die Sie unter Verwendung der Funktionstasten im zugeordneten SET-UP-Menü ausführen können.

identifiziert Standardeinstellungen.

Eintragsnamen, die darunter mit einem Sternchen (*) markiert sind, sind beim fx-7400G verfügbar.

S Mode (Berechnungs/Binär-, Oktal-, Dezimal-, Hexadezimalmodus)

• {Comp} ... {Modus für arithmetische Berechnungen}

• {Dec}/{Hex}/{Bin}/{Oct} ... {dezimal}/{hexadezimal}/{binär}/{oktal}

S Frac Result (Bruchergebnis-Anzeigeformat)

• {d/c}/{ab/c} ... {Unechter}/{Gemischter} Bruch

Ⅱ nicht

S Func Type (Grafikfunktionstyp)

Drücken Sie eine der folgenden Funktionstasten, um auch die Funktionsweise der TTaste umzuschalten.

• {Y=}/{r=}/{Parm}/{X=} ... Grafiken mit {kartesischen Koordinaten (Y= {Polarkoordinaten}/{parametrisch}/{kartesischen Koordinate (X=

• {Y>}/{Y<}/{YP}/{YO} ... Ungleichungsgrafik {

• {X>}/{X<}/{XP}/{XO} ... Ungleichungsgrafik {

y>f(x)}/{y<f(x)}/{yrf(x)}/{ybf(x)} x>f(y)}/{x<f(y)}/{xrf(y)}/{xbf(y)}

1-2929

f (x) Typ)}/

f (y) Typ)}

S Draw Type (Grafikzeichnungsmethode)

• {Con}/{Plot} ... {verbundene Punkte, Liniengrafik}/{nicht verbundene Punkte, Punkteplot}

S Derivative (Anzeige der Ableitung)

• {On}/{Off} ... {Ableitungs-Anzeige eingeschaltet}/{Ableitungs-Anzeige ausgeschaltet} während Grafik-auf-Tabelle, Tabelle & Grafik oder Trace verwendet werden

S Angle (Winkelmodus)

• {Deg}/{Rad}/{Gra} ... {Altgrad}/{Bogenmaß}/{Neugrad}

S Complex Mode (Modus für komplexe Zahlen)

• {Real} ... {Berechnungen nur im reellen Zahlenbereich}

a+bi}/{rθ} ... {Kartesisches Format, arithmetische Darstellung}/{Polarformat,

• { exponentielle Darstellung} der Anzeige einer Berechnung mit komplexen Zahlen

S Coord (Koordinaten des Grafikcursors)

• {On}/{Off} ... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}

S Grid (Grafik-Gitterlinien)

• {On}/{Off} ... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}

S Axes (Grafikachsen)

• {On}/{Off} ... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}

S Label (Grafikachsen-Bezeichnungen)

• {On}/{Off} ... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}

S Display (Anzeigeformat der Zahlendarstellung)

• {Fix}/{Sci}/{Norm}/{Eng} ... {Festlegung der Anzahl der Dezimalstellen}/{Festlegung der Mantissenlänge}/{Normal-Anzeige, in Norm1 oder Norm2 umschaltbar}/

{Techniknotation}

S Stat Wind (Einstellung des Betrachtungsfensters der statistischen Grafiken)

• {Auto}/{Man} ... {automatische}/{manuelle} Grafik-Fenstereinstellung

S Resid List (Residuenberechnung)

• {None}/{LIST} ... {keine Berechnung}/{Listenvorgabe für die berechneten Residuen}

S List File (Listendatei-Einstellanzeige)

• {FILE} ... {Einstellung der im Display gewählten Listendatei}

S Sub Name (Listenbenennung)

• {On}/{Off} ... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}

S Graph Func (Anzeige der Funktionsformel in der Grafikdarstellung und bei

Benutzung der Trace-Funktion)

• {On}/{Off} ... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}

1-3030

S Dual Screen (Status für Doppelanzeige)

• {G+G}/{GtoT}/{Off} ... {Grafik auf beiden Seiten der Doppelanzeige}/{Grafik auf der einen Seite und numerische Wertetabelle auf der anderen Seite der Doppelanzeige}/

{Doppelanzeige ausgeschaltet, d.h. kein unterteilter Bildschirm}

S Simul Graph (Simultaner Grafikmodus)

• {On}/{Off} ... {simultane Grafikdarstellung eingeschaltet (alle Grafiken werden gleichzeitig gezeichnet)}/{simultane Grafikdarstellung ausgeschaltet (Grafiken werden in der

numerischen Reihenfolge der Speicherbelegung einzeln gezeichnet)}

S Background (Hintergrund der Grafikanzeige)

• {None}/{PICT} ... {keine Hintergrundgrafik}/{Auswahl eines Bildes als Hintergrundgrafik}

S Sketch Line (Linie skizzieren) (Überlagerter Linientyp)

• { }/{ }/{ }/{ } ... {normal}/{dick}/{strichliert}/{punktiert}

S Dynamic Type* (Dynamischer Grafik-Typ)

• {Cnt}/{Stop} ... {ohne Stopp (kontinuierlich)}/{automatischer Stopp nach 10 Durchläufen}

S Locus* (Locus-Modus für dynamische Grafik)

• {On}/{Off} ... {Locus gezeichnet}/{Locus nicht gezeichnet}

S Y=Draw Speed* (Zeichenngeschwindigkeit für dynamische Grafik)

• {Norm}/{High} ... {normal}/{hohe Geschwindigkeit}

S Variable (Einstellungen für Tabellengenerierung und Grafikdarstellung)

• {RANG}/{LIST} ... {Tabellenbereichsvorgaben verwenden}/{Listendaten verwenden}

S 3 Display* (3-Wert-Anzeige (Partialsummenfolge) in Zahlenfolge-Tabelle)

• {On}/{Off} ... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}

S Slope* (Anzeige der 1. Ableitung für die aktuelle Cursorposition bei

Kegelschnitt-Grafik - CONICS-Menü)

• {On}/{Off} ... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}

S Payment* (Zahlungsperiode)

• {BGN}/{END} ... {Beginn}/{Ende} der Zahlungsperiode

S Date Mode* (Anzahl der Tage pro Jahr)

• {365}/{360} ... Zinssatzberechnungen mithilfe {365}*1/{360} Tage pro Jahr

Das Jahr mit 365 Tagen muss für Datumsrechnungen im Das Jahr mit 365 Tagen muss für Datumsrechnungen imDas Jahr mit 365 Tagen muss für Datumsrechnungen im TVM-Menü verwendet werden.

Anderenfalls kommt es zu einer Fehlermeldung.

S Periods/YR. * (Festlegung des Zahlungsintervalls)

• {Annu}/{Semi} ... {jährlich}/{halbjährlich}

S Ineq Type (Festlegung von Ungleichungen)

• {AND}/{OR} ... Graphische Darstellung von mehrere Ungleichungen, {Füllbereiche, wo alle Bedingungen für Ungleichungen erfüllt sind}/{Füllbereiche, wo jede Bedingung

für Ungleichungen erfüllt ist}

1-3131

S Simplify (Berechnungsergebnis der automatischen/manuellen

Reduktionsfestlegung)

• {Auto}/{Man} ... {automatischen reduzieren und anzeigen}/{Anzeigen ohne Reduzierung}

S Q1Q3 Typ (Q1/Q3 Berechnungsformeln)

• {Std}/{OnData} ... {Dividieren Sie die Grundgesamtheit im Mittelpunkt zwischen oberen und unteren Gruppen mit dem Median der unteren Gruppe Q1 und dem

Median der oberen Gruppe Q3}/{Erstellen Sie den Wert des Elements, dessen Partialsummenverhältnis größer als 1/4 ist und 1/4 Q1 am nächsten liegt und den Wert des Elements, dessen Partialsummenverhältnis größer als 3/4 ist und 3/4 Q3 am nächsten liegt}

Folgende Einträge sind beim fx-7400G

Ⅱ/fx-9750GⅡ nicht verfügbar.

S Input/Output (Ein-/Ausgabemodus)

• {Math}/{Line}*1 ... {Math}/{Linear} Ein-/Ausgabemodus

S Auto Calc (automatische Berechnung der Tabellenkalkulation)

• {On}/{Off} ... {ausführen}/{nicht ausführen} automatisch für Formeln

S Show Cell (Tabellenkalkulations-Zellenanzeigemodus)

• {Form}/{Val} ... {Formel}*2/{Wert}

S Move (Tabellenkalkulationszellen-Cursorrichtung)*3

• {Low}/{Right} ... {nach unten}/{nach rechts}

Die ursprüngliche Standardeinstellung vom fx-9860G Slim (OS 2.00)/fx-9860G SD (OS Die ursprüngliche Standardeinstellung vom fx-9860G Slim (OS 2.00)/fx-9860G SD (OSDie ursprüngliche Standardeinstellung vom fx-9860G Slim (OS 2.00)/fx-9860G SD (OS/fx-9860G SD (OS

2.00)/fx-9860G (OS 2.00)/fx-9860G AU (OS 2.00) ist der „Line“ Ein-/Ausgabemodus. ist der „Line“ Ein-/Ausgabemodus.

Durch die Wahl von „Form“ (Formel) wird eine Formel in der Zelle als Formel angezeigt. Durch die Wahl von „Form“ (Formel) wird eine Formel in der Zelle als Formel angezeigt.Durch die Wahl von „Form“ (Formel) wird eine Formel in der Zelle als Formel angezeigt.

Die „Form“ beeinträchtigt andere Daten in der Zelle nicht, wenn es sich dabei nicht um Formeln handelt.

Spezifiziert die Bewegungsrichtung des Zellencursors, wenn Sie die Spezifiziert die Bewegungsrichtung des Zellencursors, wenn Sie dieSpezifiziert die Bewegungsrichtung des Zellencursors, wenn Sie die U-Taste zum

Registrieren der Zelleneingabe drücken, wenn der Sequenzbefehl eine Wertetabelle generiert und wenn Sie Daten aus dem Listenspeicher aufrufen.

9. Verwendung der DisplayanzeigenEinfangfunktion

Falls der Rechner in Betrieb ist, können Sie eine Abbildung der aktuellen Displayanzeige einfangen und diese in dem Einfangspeicher ablegen.

S Einfangen einer Anzeigenabbildung

1. Bedienen Sie den Rechner, und zeigen Sie die einzufangende Displayanzeige an.

2. Drücken Sie F(CAPTURE).

• Dadurch erscheint das Speicherbereich-Wahlfeld.

1-3232

3. Geben Sie einen Wert von 1 bis 20 ein, und drücken Sie danach U.

• Dadurch wird die Anzeigenabbildung eingefangen und in dem mit „Capt

Ihnen eingegebene Wert) bezeichneten Einfangspeicherbereich abgelegt.

• Sie können die Anzeigenabbildung einer Meldung, die den Ablauf eines Betriebs- oder

Kommunikationsvorganges anzeigt, nicht einfangen.

• Es kommt zu einem Speicherfehler, wenn im Speicher nicht ausreichend Platz für die

Speicherung der eingefangenen Anzeigenabbildung vorhanden ist.

n“ (n = der von

S Aufrufen einer Anzeigenabbildung aus dem Einfangspeicher

Diese Operation ist nur verfügbar, wenn der lineare Ein-/Ausgabemodus ausgewählt ist.

1. Im RUN • MAT • MAT• MAT MATMAT-Menü (oder RUN-Menü), drücken Sie

*(E)(E)(CAPT)((CAPT) beim fx-7400G (RCL).

2. Geben Sie eine Einfangsspeichernummer in dem Bereich von 1 bis 20 ein, und drücken Sie

danach U.

• Dies zeigt die gespeicherten Bilder in dem von Ihnen festgelegten Einfangsspeicher an.

Ⅱ)

3. Um die Bilderanzeige zu verlassen und zu der Anzeige zurückzukehren, mit der Sie in

Schritt 1 angefangen habe, drücken Sie ).

• Sie können auch den RclCapt-Befehl in einem Programm verwenden, um eine

Anzeigenabbildung aus dem Einfangspeicher aufzurufen.

10. Falls Probleme auftreten…

Falls Probleme bei der Arbeit mit dem Rechner auftreten, ergreifen Sie die folgenden Maßnahmen, bevor Sie einen Defekt in Ihrem Rechner vermuten.

I Zurückstellung des Rechners auf seine Standard-Voreinstellungen

1. Rufen Sie das SYSTEM-Menü aus dem Hauptmenü heraus auf.

2. Drücken Sie die (RSET)-Taste.

3. Drücken Sie die (STUP)-Taste und danach die (Yes)-Taste.

4. Drücken Sie die Tasten )K, um in das Hauptmenü zurückzukehren. Öffnen Sie nun das richtige Menü und führen Sie Ihre Berechnung erneut aus, wobei Sie die

Ergebnisse im Display überwachen.

I Neu starten und Rückstellung

S Neu starten

Wenn der Rechner anfängt, ungewöhnlich zu reagieren, können Sie ihn erneut starten indem Sie den RESTART-Knopf (P-Knopf) drücken. Beachten Sie jedoch, dass Sie den RESTART-

1-3333

Knopf nur im Notfall verwenden sollten.Normalerweise startet das Betriebssystem des Rechners neu, wenn Sie den RESTART-Knopf drücken, sodass Programme, graphische Funnktionen und andere Daten im Speicher des Rechners erhalten bleiben.

RESTART-

RESTARTKnopf

Knopf

fx-9860G SD

fx-9860G SD fx-9860G

fx-9860G fx-9860G AU PLUS

fx-9860G AU PLUS

fx-9750G

fx-9750G fx-7400G

fx-7400G

fx-9860G SD

fx-9860G SD fx-9860G

fx-9860G

P-Knopf

fx-9860G Slim

Wichtig!

Der Rechner erstellt Sicherheitskopien der Benutzerdaten (Hauptspeicher) wenn Sie ihn ausschalten und lädt diese Sicherheitskopien sobald Sie den Rechner wieder anschalten.

Wenn Sie den RESTART-Knopf drücken, startet der Rechner neu und lädt die Daten der Sicherheitskopie.Wenn Sie den RESTART-Knopf drücken nachdem Sie ein Programm, graphische Funktionen oder andere Daten bearbeitet haben, von denen keine Sicherheitskopie erstellt wurde, bedeutet dies, dass die Daten verloren gehen.

S Rückstellung

Verwenden Sie die Rückstellfunktion wenn Sie alle Daten löschen möchten, die sich aktuell im Speicher des Rechners befinden und alle Moduseinstellungen auf die Standardeinstellung zurücksetzen möchten.

Bevor Sie die Rückstelloperation verwenden, fertigen Sie zuerste eine schriftliche Kopie von allen wichtigen Daten an. Details erhalten Sie im Abschnitt „Rückstellung“ (Seite 12-4).

I Meldung für niedrige Batteriespannung

Falls die folgende Meldung auf dem Display erscheint, schalten Sie den Rechner unverzüglich aus und erneuern Sie die Batterien gemäß Instruktion.

Falls Sie jedoch den Rechner weiterhin verwenden, ohne die Batterien auszutauschen, wird die Stromversorgung schließlich automatisch ausgeschaltet, um die Speicherinhalte zu schützen. In diesem Fall können Sie die Stromversorgung nicht mehr einschalten, wobei die Gefahr besteht, dass Speicherinhalte verfälscht oder gar gelöscht werden.

• Sie können keine Datenübertragungen aus-führen, nachdem eine Meldung für niedrige

Batteriespannung erschienen ist.

1-3434

Kapitel 2 Manuelle Berechnungen

1. Grundrechenarten

I Arithmetische Berechnungen

• Geben Sie die arithmetischen Berechnungsformeln oder Rechenaufgaben wie geschrieben

von links nach rechts ein.

• Verwenden Sie anstatt des Operationszeichens „minus“ die -Taste, um ein

Minusvorzeichen vor einem negativen Wert einzugeben.

• Alle Berechnungen werden intern mit einer 15stelligen Mantisse durchgeführt. Das Ergebnis

wird dann auf eine 10stellige Mantisse gerundet, bevor es im Display zur Anzeige kommt.

• Bei gemischten arithmetischen Operationen werden der Multiplikation und Division Priorität

vor der Addition und Subtraktion eingeräumt (übliche Vorrangregeln).

Beispiel Tastenfolge

56 × (–12) ÷ (–2,5) = 268,8

(2 + 3) × 10

2 + 3 × (4 + 5) = 29

= 0,3

4 × 5

Die schließenden Klammern (unmittelbar vor der Betätigung der U-Taste) können

weggelassen werden, wie viele auch erforderlich wären.

= 500

56122.5U

231$2U

2345U*

645U

I Anzahl der Dezimalstellen, Mantissenlänge, Normal-Anzeige

• Auch nachdem Sie die Anzahl der Dezimalstellen oder die Mantissenlänge voreingestellt

haben, werden die internen Rechnungen mit einer 15-stelligen Mantisse ausgeführt, wobei jedoch die berechneten Werte mit einer 10-stelligen Mantisse angezeigt werden. Verwenden Sie „Rnd“ des numerischen Berechnungsmenüs (NUM) (Seite 2-12), um den angezeigten Wert auf die gewünschte Anzahl der Dezimalstellen und die gewünschte Mantissenlänge zu runden.

• Die Einstellungen der Anzahl der Dezimalstellen (Fix) und der Mantissenlänge (Sci) bleiben

normalerweise solange wirksam, bis Sie diese ändern oder bis Sie die Einstellungen der Normal-Anzeige (Norm mit Auswahl zwischen Norm1 oder Norm2) ändern.

[SET UP]- [Display]

[Fix]

[Sci] / [Norm]

Beispiel 1 100 w 6 = 16,66666666...

Bedingung Tastenfolge Anzeige

4 Dezimalstellen

Mantissenlänge 5

K(SET UP) DD

2-11

1006U

(Fix)CU)U

(Sci)DU)U

16.66666667

16.6667

*1*

1.6667

+01

*1*

Ersetzt die bisherige Vorgabe „Fix“ oder „Sci“

Die angezeigten Werte werden auf die von Ihnen vorgegebene Stellenanzahl gerundet.

K(SET UP) DD

(Norm))U

16.66666667

Beispiel 2 200 w 7 s 14 = 400

Bedingung Tastenfolge Anzeige

200714U

3 Dezimalstellen

Die Berechnung wird mit einer Anzeigekapazität von 10 Stellen fortgesetzt.

K(SET UP) DD

(Fix)BU)U

2007U



14U

Ans s

400.000

28.571

400.000

• Wenn die gleiche Berechnung mit der vorgegebenen Anzahl von Stellen ausgeführt wird:

28.571

399.994

Der intern abgespeicherte Wert wird auf die Anzahl an Dezimalstellen abgerundet,

2007U

*(E)(NUM)*(Rnd)U



14U

Ans s

die in der Einstellanzeige spezifiziert wurden.

Sie können auch die Anzahl der Dezimalstellen für das Runden der internen Werte einer speziellen Berechnung

2007U

(E)(RndFi)(Ans)2



14U

RndFix(Ans,2)

Ans s

28.571

28.570

399.980

spezifizieren. (Beispiel: Festlegung der Rundung auf zwei Dezimalstellen)

400

* fx-7400G

I Prioritäten der Rechenoperationen während der Berechnung

Dieser Rechner arbeitet mit der üblichen Algebralogik, um Teilschritte einer Formel mit folgenden Prioritäten zu berechnen:

 Funktionen vom Typ A:

• Koordinatenumrechnung Pol (

• Funktionen, die Klammern enthalten (wie z. B. Ableitungen, Integrale, 3 usw.)

d/dx, d

/dx2, °dx, 3, Solve, FMin, FMax, ListmMat, Fill, Seq, SortA, SortD, Min, Max,

Median, Mean, Augment, MatmList, P(, Q(, R(, t(, RndFix, log

• Zusammengesetzte (verkettete) Funktionen*  Funktionen vom Typ B Bei diesen Funktionen wird zuerst das Argument eingegeben, und danach wird die

Funktionstaste gedrückt.

, x–1, x!, ° ’ ”, ENG-Symbole, Winkelargumente °, r,

 Potenzen/Wurzeln ^(xy), x  Gemeine Brüche (gemischte Zahlen)

x, y), Rec (r,

2-22

)

, List, Mat, fn, Yn, rn, Xtn, Ytn, Xn

II: (NUM)

 Abgekürztes Multiplikationsformat (ohne Multplikationszeichen) vor P, vor einer Speicher-

oder Variablenbezeichnung, z. B. 2P, 5A, Xmin, F Start usw.  Funktionen vom Typ C Bei diesen Funktionen wird zuerst die Funktionstaste gedrückt und danach wird ein

Argument eingegeben.

,

, log, In, ex, 10x, sin, cos, tan, sin–1, cos–1, tan–1, sinh, cosh, tanh, sinh–1, cosh–1,

–1

tanh

, (–), d, h, b, o, Neg, Not, Det, Trn, Dim, Identity, Ref, Rref, Sum, Prod, Cuml, Percent,

List, Abs, Int, Frac, Intg, Arg, Conjg, ReP, ImP

 Abgekürztes Multiplikationsformat (ohne Multiplikationszeichen) vor Typ A Funktionen, Typ

C Funktionen und Klammern. 23, A log2 usw.

 Variation (Permutation), Kombination

nPr, nCr

 Befehle für die metrische Umwandlung  s, ÷, Int÷, Rnd

 +, –

 Relationszeichen =, x, >, <, r, b  And (Logikoperator), and (bitweiser Operator)  Or, Xor (Logikoperator), or, xor, xnor (bitweiser Operator)

Sie können den Inhalt mehrerer Funktionsspeicher (fn) oder Grafikspeicher (Yn, rn, Xtn,

Ytn, Xn) in zusammengesetzten (verketteten) Funktionen verknüpfen. Falls Sie zum Beispiel fn1(fn2) definieren, wird die zusammengesetzte Funktion fn1°fn2 erhalten (siehe Seite 5-8). Eine zusammengesetzte Funktion kann aus bis zu fünf verketteten Funktionen (äußeren und inneren Funktionen) bestehen.

Beispiel 2 + 3 s (log sin2P

+ 6,8) = 22,07101691 (Winkeleinheit = Rad)

• Achten Sie darauf, dass ein Ableitungsbefehl für die 1. oder 2. Ableitung, ein Integrations-,

3-, Maximalwert-/Minimalwert-, Nullstellenberechnungs- (Solve-), RndFix- oder logab-Befehl

nicht innerhalb eines RndFix-Berechnungsbefehls verwendet werden kann.

• Wenn Funktionen mit der gleichen Priorität hintereinander angewendet werden, erfolgt die

Ausführung von rechts nach links, also von der inneren zur äußeren Funktion.

In 120 m ex{In( 120)}

Andernfalls erfolgt die Ausführung von links nach rechts.

• Verkettete Funktionen werden ebenfalls von rechts nach links ausgeführt.

• Klammerterme haben höchste Priorität.

I Anzeige von irrationalen Zahlen als Ergebnisse

Sie können den Rechner so konfigurieren, dass er Ergebnisse im Format für irrationale Zahlen (einschließlich  oder P) anzeigt. Wählen Sie dazu in der Einstellanzeige für die Moduseinstellung „Input/Output“ den Eintrag „Math“.

(nur fx-9860GII SD/fx-9860GII/fx-9860G AU PLUS)

2-33

Beispiel 2 + 8 = 32 (Input/Output: Math)

V()ACV()GU

S Rechenergebnis-Anzeigebereich mit 

Die Anzeige eines Rechenergebnisses im -Format wird für Ergebnisse mit  in bis zu zwei Gliedern unterstützt. Rechenergebnisse im -Format können wie folgt aussehen:

110

a'b

+ d´

• Nachfolgend finden Sie die Bereiche für die einzelnen Koeffizienten (a, b, c, d, e, f), die im

-Rechenergebnisformat dargestellt werden können. 1  0 

• In den unten dargestellten Fällen kann ein Rechenergebnis im -Format angezeigt werden,

selbst wenn dessen Koeffizienten ( Rechenergebnisse im -Format verwenden einen gemeinsamen Nenner.

Da das Rechenergebnis einen gemeinsamen Nenner verwendet, kann es immer noch im -Format angezeigt werden, selbst wenn die Koeffizienten ( zutreffenden Koeffizientenbereichs (a, c, d) liegen.

Beispiel:

ab, p d p ab, p

a < 100, 1 < b < 1000, 1  c < 100 d < 100, 0  e < 1000, 1  f < 100

a'b

d'e

10'3 + 11'2

d'e

a, c, d) außerhalb der obigen Bereiche liegen.

* c´ ist das kleinste gemeinsame Vielfache von c

und

a´, c´, d´) außerhalb des

Rechenbeispiele

Rechenaufgabe Anzeigetyp

2 s (3 – 25) = 6 – 45 -Format

352 s 3 = 148,492424 (=

150'2

23 s (5 – 23) = 35,32566285 (=

2 + 3 + 8 = 3 + 32 -Format

Dezimalformat, da die Werte außerhalb des Bereichs liegen.

Dezimalformat, da das Rechenergebnis aus drei Gliedern besteht.

= 8,485281374*

2 + '3 + '6

= 5,595754113*

105

2)*

115

– 463)*

2-44

Dezimalformat

• Das Rechenergebnis wird im Dezimalformat angezeigt, selbst wenn ein Zwischenergebnis

größer als zwei Glieder ist. Beispiel: (1 + 2 + 3) (1 – 2 – 3) (= – 4 – 26) = –8,898979486

• Wenn die Berechnungsformel ein -Glied und ein Glied, das nicht als Bruch angezeigt

werden kann, enthält, wird das Rechenergebnis im Dezimalformat angezeigt. Beispiel: log3 + 2 = 1,891334817

S Rechenergebnis-Anzeigebereich mit P

Rechenergebnisse werden in den folgenden Fällen im P-Format angezeigt:

• Wenn das Rechenergebnis in der Form

n ist eine ganze Zahl bis maximal |10

• Wenn das Rechenergebnis in der Form Allerdings muss die {Anzahl von

oder kleiner sein, wenn obiges

Anzahl der zulässigen c Stellen drei.*

*1 Falls c < b ist, wird die Anzahl der a, b und c Stellen gezählt, wenn der Bruch von einem

unechten Bruch (

) in einen gemischten Bruch (

a Stellen + Anzahl von b Stellen + Anzahl von c Stellen} 9

Wenn „Manual“ für die Einstellung „Simplify“ der Einstellanzeige angegeben wird, kann

das Rechenergebnis im Dezimalformat angezeigt werden, selbst wenn diese Bedingungen erfüllt werden.

Rechenbeispiele

Rechenaufgabe Anzeigetyp

78Ps 2 = 156PP-Format

123456P s 9 = 3490636,164 (=

11111104

nP angezeigt werden kann

oder

P oder

gekürzt wird.*1*2 Außerdem beträgt die maximale

P)*

P angezeigt werden kann

Dezimalformat

) umgewandelt wird.

568 824

258

P = 105

P =

105

3238

Dezimalformat, da der ganzzahlige Teil des Rechenergebnisses |106| oder größer ist.

Dezimalformat, da die Anzahl der Nennerstellen für die

ist.

103

6,533503684

129

1619

P-Format

2

Dezimalformat

P-Form vier beträgt oder größer

I Multiplikationsoperationen ohne Multiplikationszeichen

Sie können das Multiplikationssymbol (s) in folgenden Operationen weglassen:

• Vor Funktionen des Typs A ( auf Seite 2-2) und des Typs C ( auf Seite 2-2),

ausgenommen bei negativen Vorzeichen

Beispiel 1 2sin30, 10log1,2, 2

, 2Pol(5, 12) usw.

2-55

• Vor Konstanten, Variablen- oder Speicherbezeichnungen

Beispiel 2 2P, 2AB, 3Ans, 3Y

• Vor einer öffnenden Klammer

Beispiel 3 3(5 + 6), (A + 1)(B – 1) usw.

1 usw.

I Überlauf und Fehler

Bei Überschreiten eines bestimmten Eingabe- oder Berechnungsbereiches bzw. bei einer unzulässigen Eingabe wird eine Fehlermeldung im Display angezeigt. Während der Fehleranzeige ist jede weitere Funktion des Rechners deaktiviert. Einzelheiten finden Sie in der „Tabelle der Fehlermeldungen“ auf Seite A-1.

• Wenn eine Fehlermeldung angezeigt wird, sind die meisten Tasten des Rechners gesperrt.

Drücken Sie ), um den Fehler zu löschen und zum normalen Betrieb zurückzukehren.

I Speicherkapazität

Mit jedem Drücken einer Taste werden ein Byte oder zwei Byte verwendet. Zu den Funktionen, die ein Byte benötigen, gehören: @, A, B, sin, cos, tan, log, In, und P. Zu den Funktionen, die zwei Byte benötigen, zählen d/dx(, Mat, Xmin, If, For, Return,

DrawGraph, SortA(, PxIOn, Sum und

• Die erforderliche Anzahl von Bytes zur Eingabe von Funktionen und Befehlen ist im linearen

Ein-/Ausgabemodus und im Math-Ein-/Ausgabemodus jeweils unterschiedlich. Einzelheiten

zur erforderlichen Anzahl von Bytes für die einzelnen Funktionen im Math-Ein-/

Ausgabemodus finden Sie auf Seite 1-11.

2. Spezielle Taschenrechnerfunktionen

I Berechnungen mit Variablen

Beispiel Tastenfolge Anzeige

193,2 ÷ 23 = 8,4

193,2 ÷ 28 = 6,9

I Speicher

193.2??T(A)U

?T(A)23U

?T(A)28U

193.2

8.4

6.9

S Variablen (Alphabetspeicher)

Der Rechner verfügt standardmäßig über 28 Variablen. Sie können die Variablen für das Abspeichern von Werten verwenden, die innerhalb von Berechnungen benötigt werden. Variablen werden jeweils mit einem Buchstaben bezeichnet, indem die 26 Buchstaben des Alphabets sowie r und Q verwendet werden. Der Maximalwert, der Variablen zugewiesen werden kann, weist in Gleitkommadarstellung 15 Stellen für die Mantisse und 2 Stellen für den Exponenten auf.

• Die abgespeicherten Werte der Variablen bleiben erhalten, auch wenn Sie den Rechner

ausschalten.

2-66

S Wertzuweisung für eine Variable

[Wert] ? [Variablenbezeichnung] U

Beispiel 1 Wertzuweisung von 123 zur Variablen A

@AB??T(A)U

Beispiel 2 Abspeicherung der Summe A+456 in der Variablen B

?T(A)CDE?

?J(B)U

S Wertzuweisung des gleichen Wertes zu mehr als einer Variablen

[Wert] ? [Bezeichnung der ersten Variablen] ?(~) [Bezeichnung der letzten Variablen] U

• Sie können hier jedoch „

Beispiel Der Wert 10 ist den Variablen A bis F zuzuweisen.

@???T(A) ?(~)?R(F)U

r“ oder „

Q

“ nicht als Variablenbezeichnung verwenden.

S Kettenspeicher

Sie können bis zu 20 Ketten (mit Str 1 bis Str 20 bezeichnet) im Kettenspeicher ablegen. Gespeicherte Ketten können auf dem Display angezeigt oder in Funktionen und Befehlen verwendet werden, die die Verwendung von Ketten als Argumente unterstützen.

Einzelheiten zu Kettenoperationen finden Sie unter „Ketten“ (Seite 8-19).

Beispiel Zuweisen von Kette „ABC“ zu Str 1 und anschließende Ausgabe von Str

1 auf dem Display

?( J(B)((C)$(”)?(Entsperrt den Buchstaben-Feststeller.)

-LOCK)$(”)T(A)

?)(E)(Str)*@U

(Str)*@U * fx-7400G

• Führen Sie die obige Operation im linearen Ein-/Ausgabemodus aus. Eine Durchführung im

Math-Ein-/Ausgabemodus ist nicht möglich.

II: (Str)

Die Kette wird linksbündig angezeigt.

2-77

S Funktionstermspeicher (Termspeicher) [OPTN]-[FMEM]

Der Funktionstermspeicher ist nützlich für das temporäre Abspeichern häufig verwendeter Formelterme. Für eine längere Speicherung wird empfohlen, dass Sie das GRAPH-Menü zum Abspeichern von Formeltermen und das PRGM-Menü zum Abspeichern von Programmen nutzen.

• {STO}/{RCL}/{fn}/{SEE} ... {Funktionsterm speichern}/{Funktionsterm aufrufen}/

{Funktionsspeicherposition als Variablenbezeichnung in einem Term}/{Termspeicherliste öffnen}

S Speichern einer Funktion

Beispiel Abspeichern des Funktionsterms (A+B)(A–B) unter der

Funktionsspeicherposition 1

?T(A)?J(B) ?T(A)?J(B)

*(E)(E)(FMEM)* (STO)@U * fx-7400G

)))

• Falls die Funktionsspeicherposition, der Sie einen Funktionsterm zuweisen, bereits einen

Funktionsterm enthält, dann wird der vorhandene Term durch den neuen Term ersetzt.

• Sie können auch die ?-Taste verwenden, um in einem

Programm einen Funktionsterm im Funktionstermspeicher

abzulegen. In diesem Fall müssen Sie die Funktion in

doppelte Anführungszeichen setzen.

II: (FMEM)

S Abruf eines Funktionsterms

Beispiel Abruf des Funktionsterms unter der Funktionsspeicherposition 1

*(E)(E)(FMEM)* (RCL)@U * fx-7400G

• Der aufgerufene Funktionsterm erscheint an der aktuellen Cursorposition im Display.

II: (FMEM)

S Aufrufen einer Funktion als Variable

B??T(A)U @??J(B)U *(E)(E)(FMEM)*(fn) @AU * fx-7400G

II: (FMEM)

2-88

S Anzeige der Belegung des Funktionstermspeichers

*(E)(E)(FMEM)* (SEE) * fx-7400G

II: (FMEM)

S Löschen einer Funktion

Beispiel Löschen des Funktionsterms unter der Funktionsspeicherposition 1

*(E)(E)(FMEM)* (STO)@U * fx-7400G

• Mit Ausführung der Speicheroperation bei leerem Display wird der Funktionsterm aus der

von Ihnen bezeichneten Funktionsspeicherposition gelöscht.

II: (FMEM)

I Antwortspeicherfunktionen der Taschenrechners

Die Antwortspeicherfunktion speichert automatisch das zuletzt berechnete Ergebnis durch Drücken der U-Taste (wenn nicht die U-Tastenfunktion zu einem Fehler führt). Das jeweils letzte Ergebnis wird im Antwortspeicher abgelegt und kann dort abgerufen werden.

• Der größte Zahlenwert, der im Antwortspeicher abgelegt werden kann, weist 15 Stellen für

die Mantisse und 2 Stellen für den Exponenten auf.

• Der Inhalt des Antwortspeichers wird nicht gelöscht, wenn Sie die -Taste drücken oder

die Stromversorgung ausschalten.

S Verwendung des Inhalts des Antwortspeichers in einer Rechnung

Beispiel 123 + 456 = 579

789 – 579 = 210

@ABCDEU FGH(Ans)U

Benutzer der Modelle fx-7400G

II, fx-9750GII...

• Die Inhalte des Antwortspeichers können durch einen Bedienungsvorgang, der die Werte

dem Alphabetspeicher zuordnet, nicht geändert werden (Beispiel: D??J(B)U).

2-99

Benutzer der Modelle fx-9860GII SD, fx-9860GII, fx-9860G AU PLUS, fx-9860G Slim...

• Im Math-Ein-/Ausgabemodus unterscheidet sich das Vorgehen zum Abrufen der Inhalte des

Antwortspeichers vom Vorgehen im linearen Ein-/Ausgabemodus. Näheres finden Sie unter

„Historyfunktion“ (Seite 1-19).

• Bei einer Operation, die dem Alphabetspeicher einen Wert zuordnet (wie z. B.

D??J(B)U), wird der Inhalt des Antwortspeichers zwar im Math-Ein-/

Ausgabemodus, nicht jedoch im linearen Ein-/Ausgabemodus aktualisiert.

I Ausführen von „Ketten-Rechnungen“

Das Ergebnis einer Berechnung kann unmittelbar als erster Operand in der nachfolgenden Berechnung verwendet werden, indem der Antwortspeicher durch Eingabe eines Operationszeichens automatisch abgerufen wird.

Beispiel 1 w 3 =

1 w 3 s 3 =

@BU (Fortsetzung)BU

Eine derartige „Ketten-Rechnung“ kann auch mit Typ B Funktionen ( +, –, ^(xy), x, ° ’ ” usw. ausgeführt werden.

, x–1, x!, auf Seite 2-2),

3. Festlegung des Winkelmodus und des Anzeigeformats (SET UP)

Vor der erstmaligen Ausführung einer Berechnung sollten Sie die Einstellanzeige (SET-UPMenü) verwenden, um den Winkelmodus und das Anzeigeformat festzulegen.

I Einstellen des Winkelmodus [SET UP]- [Angle]

1. Markieren Sie „Angle“ in der Einstellanzeige (SET-UP-Menü).

2. Drücken Sie die Funktionstaste für den festzulegenden Winkelmodus. Drücken Sie danach

die )-Taste.

• {Deg}/{Rad}/{Gra} ... {Altgrad}/{Bogenmaß}/{Neugrad}

• Der Zusammenhang zwischen Altgrad, Bogenmaß und Neugrad lautet wie folgt: 360° (Altgrad) = 2P rad = 400 gon (Neugrad) 90° (Altgrad) = P/2 rad = 100 gon (Neugrad)

I Einstellen des Anzeigeformats für Zahlen [SET UP]- [Display]

1. Markieren Sie „Display“ in der Einstellanzeige (SET-UP-Menü).

2. Drücken Sie die Funktionstaste für das einzustellende Anzeigeformat. Drücken Sie danach

die )-Taste.

• {Fix}/{Sci}/{Norm}/{Eng} ... {Festlegung eine festen Anzahl von Dezimalstellen}/

{Festlegung der Mantissenlänge}/{Normal-Anzeige mit Norm1 oder Norm2 einstellbar}/ {Technik-Notation}

2-1010

S Festlegung der Anzahl der Dezimalstellen (Fix)

Beispiel Festlegung auf zwei Dezimalstellen

(Fix)AU

Drücken Sie die Zahlentaste, die der Anzahl der Dezimalstellen entspricht, die Sie festlegen möchten (

n = 0 bis 9).

• Angezeigte Zahlenwerte werden auf die von Ihnen festgelegte Anzahl von Dezimalstellen

gerundet.

S Festlegung der Mantissenlänge (Sci)

Beispiel Einstellung auf die Mantissenlänge 3

(Sci)BU

Drücken Sie die Zahlentaste, die der Länge der Mantisse entspricht, die Sie voreinstellen möchten (

n = 0 bis 9). Durch die Vorgabe von 0 wird die Mantissenlänge auf 10 eingestellt.

• Die angezeigten Werte werden auf die von Ihnen vorgegebene Mantissenlänge gerundet.

S Einstellung auf Normal-Anzeige (Norm 1 oder Norm 2)

Drücken Sie die (Norm)-Taste, um zwischen Norm 1 und Norm 2 umzuschalten.

–2

Norm 1: 10

(0,01) > |x|, |x| 10

Norm 2: 10–9 (0,000000001) > |x|, |x| 10

S Einstellung der Anzeige auf die Technik-Notation (Eng)

Drücken Sie (Eng), um zwischen der technischen Schreibweise und der Standardschreibweise umzuschalten. Der Indikator „/E“ wird im SET-UP-Display angezeigt, wenn die technische Schreibweise wirksam ist.

Sie können folgende Symbole für die Umwandlung von Werten in die technische Schreibweise

verwenden, wie zum Beispiel 2000 (= 2 × 10

E (Exa)

P (Peta)

s 10

) m 2k.

m (Milli)

M (Mikro) s 10

s 10

–3

–6

T (Tera)

G (Giga)

M (Mega)

k (Kilo)

s 10

n (Nano)

p (Piko)

f (Femto)

s 10

–9

–12

–15

• Das SI-Symbol, das die Mantisse auf einen Wert von 1 bis 1000 eingrenzt, wird automatisch

vom Rechner gewählt, wenn die Technik-Notation voreingesellt ist.

2-1111

4. Funktionsberechnungen

I Funktionsuntermenüs

Dieser Rechner besitzt fünf Funktionsuntermenüs, die Ihnen Zugriff auf höhere mathematische Funktionen ermöglichen, die nicht auf der Tastatur markiert sind.

• Der Inhalt dieser Funktionsuntermenüs unterscheidet sich in Abhängigkeit vom gewählten

Menü, das Sie im Hauptmenü aufgerufen hatten, bevor Sie die *-Taste gedrückt haben. Die folgenden Beispiele zeigen Funktionsuntermenüs an, die im RUN • MAT- (oder RUN-) oder PRGM-Menü erscheinen.

SHyperbel- und Areafunktionen (HYP) [OPTN]-[HYP]

• {sinh}/{cosh}/{tanh} ... Hyperbel-{Sinus-}/{Cosinus-}/{Tangens-}Funktionen

–1

• {sinh

S Wahrscheinlichkeitsrechnung (PROB) [OPTN]-[PROB]

x!} ... {nach der Eingabe eines Wertes drücken, um die Fakultät dieses Wertes zu erhalten}

• {

}/{cosh–1}/{tanh–1} ... Hyperbel-{Sinus-}/{Cosinus-}/{Tangens-}Umkehrfunktionen

• {

nPr}/{nCr} ... {Variation (Permutation)}/{Kombination}

• {RAND} ... {Generieren einer Zufallszahl}

• {Ran#}/{Int}/{Norm}/{Bin}/{List} ... {Generieren einer Zufallszahl (zwischen 0 und 1)}/ {Generieren einer zufälligen Ganzzahl}/{Generieren einer Zufallszahl entsprechend der Normalverteilung auf der Grundlage eines Mittelwertes Standardabweichung Binomialverteilung auf der Grundlage einer Anzahl von Versuchen bzw. Stichproben und einer Wahrscheinlichkeit p}/{Generieren einer Zufallszahl (zwischen 0 und 1) und Speicherung des Ergebnisses in ListAns}

• {P(}/{Q(}/{R(} ... Wahrscheinlichkeit entsprechend Normal- oder Gaußverteilung {P( {R(t)}

t(} ... {Wert der standardisierten Zufallsvariablen t(x)}

• {

σ}/{Generieren einer Zufallszahl entsprechend der

μ und einer

t)}/{Q(t)}/

S Numerische Berechnungen (NUM) [OPTN]-[NUM]

• {Abs} ... {Um den Absolutwert/Betrag einer Zahl zu erhalten, wählen Sie die Abs-Funktion und geben die Zahl ein}

• {Int}/{Frac} ... Um den {ganzzahligen Teil}/{Bruchteil} einer Zahl zu erhalten, wählen Sie die Int- oder Frac-Funktion und geben die Zahl ein.

• {Rnd} ... {Rundet den Wert, der für interne Berechnungen verwendet wird, auf die Mantissenlänge 10 (um der Darstellung im Antwortspeicher zu entsprechen) oder auf die von Ihnen festgelegte Anzahl von Dezimalstellen (Fix) oder die von Ihnen festgelegte Mantissenlänge (Sci)}

• {Intg} ... {Um für eine vorgegebene Zahl die größte ganze Zahl zu erhalten, die nicht größer als die Zahl selbst ist, wählen Sie die Intg-Funktion und geben die Zahl ein}

• {RndFi} ... {rundet den für die interne Berechnung verwendeten Wert auf die festgelegte

Anzahl von Stellen (0 bis 9) ab (siehe Seite 2-2)}

• {GCD} ... {größter gemeinsamer Teiler zweier Zahlen}

• {LCM} ... {kleinstes gemeinsames Vielfaches zweier Zahlen}

2-1212

• {MOD} ... {Divisionsrest (Ausgabe des Rests, wenn n durch m) dividiert wird}

• {MOD

•

E} ... {Rest, wenn eine Division einer Potenzzahl erfolgt (Ausgabe des Rests, wenn n

mit p potenziert und dann durch m) dividiert wird}

S Winkelsymbole, Koordinatenumrechnung, Sexagesimal-Operationen

(ANGL)

• {°}/{r}/{g} ... Bezeichnet {Altgrad}/{Bogenmaß}/{Neugrad} für einen Eingabewert.

• {° ’ ”} ... {bezeichnet Grad (Stunden), Minuten und Sekunden, wenn ein Sexagesimalwert eingegeben wird}

• {

• Die Menü-Operation {

• {Pol(}/{Rec(} ... wandelt {kartesische in Polarkoordinaten}/{Polar- in kartesische Koordinaten}

• {DMS} ... {wandelt einen Dezimalwert in einen Sexagesimalwert um}

} ... {wandelt einen Dezimalwert in einen Sexagesimalwert Grad/Minuten/Sekunden um}

° ’ ”

} steht nur dann zur Verfügung, wenn ein Berechnungsergebnis

° ’ ”

im Display angezeigt wird.

[OPTN]-[ANGL]

S Technik-Notation, SI-Symbole (ESYM) [OPTN]-[ESYM]

• {m}/{

μ}/{n}/{p}/{f} ... {Milli (10

–3

)}/{Mikro (10–6)}/{Nano (10–9)}/{Piko (10

• {k}/{M}/{G}/{T}/{P}/{E} ... {Kilo (10 {Exa (1018)}

)}/{Mega (106)}/{Giga (109)}/{Tera (1012)}/{Peta (1015)}/

–12

)}/{Femto (10

–15

)}

• {ENG}/{ENG} ... Verschiebt das Komma im berechneten Wert um drei Stellen nach {rechts}/ {links} und {vermindert}/{erhöht} den Exponenten um drei.

Wenn Sie die technische Notation verwenden, wird das SI-Symbol ebenfalls

entsprechend geändert.

• Die Menü-Operationen {ENG} und {ENG} stehen nur dann zur Verfügung, wenn ein

Berechnungsergebnis im Display angezeigt wird.

I Winkelmodus

• Wählen Sie in der Einstellanzeige (SET UP) unbedingt „Comp“ für „Mode“.

Beispiel Tastenfolge

Umwandeln von 4,25 rad in Altgrad: 243,5070629 243,5070629

47,3° + 82,5 rad = 4774,20181°

2°20´30˝ + 39´30˝ = 3°00´00˝

K(SET UP)AAAAAA*(Deg))

4.25*(E)(ANGL)**(r)U

47.382.5*(E)(ANGL)**(r)U

2*(E)(ANGL)**(° ’ ”) 20(° ’ ”) 30

(° ’ ”)0(° ’ ”)39(° ’ ”) 30(° ’ ”)U (

° ’ ”

)

2,255° = 2°15´18˝

* fx-7400G

2.255*(E)(ANGL)**(E)(DMS)U

II, fx-9750GII: AAAAA ** fx-7400GII: (ANGL)

2-1313

I Trigonometrische und Arkusfunktionen

• Stellen Sie unbedingt den Winkelmodus korrekt ein, bevor Sie Berechnungen mit trigonometrischen oder Arkusfunktionen vornehmen.



90° (Altgrad) = rad (Bogenmaß) = 100 Gon (Neugrad)

• Wählen Sie in der Einstellanzeige (SET UP) unbedingt „Comp“ für „Mode“.

Beispiel Tastenfolge



cos (

rad) = 0,5

•

sin 45° s cos 65° = 0,5976724775

sin–10,5 = 30°

K(SET UP)AAAAAA*(Rad)) A$(P)3U

K(SET UP)AAAAAA*(Deg))

2Q45A65U*

–1

Q(sin

) 0.5*2U

(x wenn sinx = 0,5)

 kann weggelassen werden. * fx-7400GII, fx-9750GII: AAAAA

Die Eingabe von vorangestellten Nullen ist nicht erforderlich.

I Logarithmische und Exponentialfunktionen (Potenzen)

• Wählen Sie in der Einstellanzeige (SET UP) unbedingt „Comp“ für „Mode“.

Beispiel Tastenfolge

log 1,23 (log

8 = 3

log

= (–3) s (–3) s (–3) s (–3) = 81

(–3)

123 (= 123

1,23) = 0,08990511144

1 7

) = 1,988647795

J1.23U

*(CALC)*(E)(logab) 28U

3,4U

7,(

)123U

* fx-7400G

II: (CALC)

• Der lineare Ein-/Ausgabemodus und der Math-Ein-/Ausgabemodus erzeugen unterschiedliche Ergebnisse, wenn zwei oder mehrere Potenzen in Serie eingegeben werden, wie: 2 , 3 , 2.

Linearer Ein-/Ausgabemodus: 2^3^2 = 64 Math-Ein-/Ausgabemodus:

= 512

Dies ist darauf zurückzuführen, dass der Math-Ein-/Ausgabemodus die obige Eingabe intern

wie folgt behandelt: 2^(3^(2)).

I Hyperbel- und Areafunktionen

• Wählen Sie in der Einstellanzeige (SET UP) unbedingt „Comp“ für „Mode“.

Beispiel Tastenfolge

sinh 3,6 = 18,28545536

–1

cosh

= 0,7953654612

*(E)(HYP)*(sinh) 3.6U

*(E)(HYP)*(cosh–1)2015U

* fx-7400G

II: (HYP)

2-1414

I Andere Funktionen

• Wählen Sie in der Einstellanzeige (SET UP) unbedingt „Comp“ für „Mode“.

Beispiel Tastenfolge

2 + 5 = 3,65028154

(–3)

= (–3) s (–3) = 9

8! (= 1 s 2 s 3 s .... s 8) = 40320

Was ist der ganzzahlige Teil von –3,5? – 3

V() 2V()5U

3VU

8*(E)(PROB)*1(x!)U

*(E)(NUM)*2(Int)3.5U

*1 fx-7400GII: (PROB) *2 fx-7400GII: (NUM)

I Generieren einer Zufallszahl (RAND)

S Generieren einer Zufallszahl (0 bis 1) (Ran#, RanList#)

Ran# und RanList# generieren auf zufällige oder sequenzielle Weise 10 Dezimalstellen aufweisende Zufallszahlen zwischen 0 und 1. Ran# gibt eine einzige Zufallszahl zurück, während RanList# mehrere Zufallszahlen in Form einer Liste zurückgibt. Nachfolgend ist die Syntax von Ran# und RanList# dargestellt.

Ran# [a] 1  RanList# (n [,a]) 1 

a  9 n  999

n ist die Anzahl der Versuche bzw. Stichproben. RanList# generiert die Anzahl von

• Zufallszahlen, die

n einen Wert einzugeben.

für

• „

a“ ist die Zufallsfolge. Erfolgt keine Eingabe für „a“, werden Zufallszahlen zurückgegeben.

Bei Eingabe einer ganzen Zahl zwischen 1 und 9 für a wird die entsprechende sequenzielle Zufallszahl zurückgegeben.

• Mit Ausführung der Funktion Ran# 0 werden die Folgen von Ran# und RanList# initialisiert. Die Folge wird außerdem initialisiert, wenn eine sequenzielle Zufallszahl mit einer anderen Folge als vorher unter Verwendung von Ran# oder RanList# generiert wird oder wenn eine Zufallszahl generiert wird.

Beispiele für Ran#

Ran# (Generiert eine Zufallszahl.)

(Mit jedem Drücken der U-Taste wird eine neue Zufallszahl generiert.)

Ran# 1 (Generiert die erste Zufallszahl der Zufallszahlen-Folge 1.)

n entsprechen, und zeigt sie auf der ListAns-Anzeige an. Es ist notwendig,

Beispiel Tastenfolge

*(E)(PROB)*(RAND) (Ran#)U

U U

*(E)(PROB)*(RAND) (Ran#)1U

(Generiert die zweite Zufallszahl der Zufallszahlen-Folge 1.)

2-1515

Ran# 0 (Initialisiert die Zufallsfolge.) (Initialisiert die Zufallsfolge.)(Initialisiert die Zufallsfolge.)

(Ran#)0U

Ran# 1 (Generiert die erste Zufallszahl der Zufallszahlen-Folge 1.)

Beispiele für RanList#

Beispiel Tastenfolge

RanList# (4) (Generiert vier Zufallszahlen und zeigt die Ergebnisse auf der ListAns-Anzeige an.)

RanList# (3, 1) (Generiert die erste, zweite und dritte Zufallszahl aus der Zufallszahlen-Folge 1 und zeigt das Ergebnis auf der ListAnsAnzeige an.)

(Generiert dann die vierte, fünfte und sechste Zufallszahl aus der ZufallszahlenFolge 1 und zeigt das Ergebnis auf der ListAns-Anzeige an.)

(Ran#)1U

* fx-7400G

*(E)(PROB)*(RAND)(List)

4U

)*(E)(PROB)*(RAND) (List) 31U

II: (PROB)

Ran# 0 (Initialisiert die Zufallsfolge.) (Initialisiert die Zufallsfolge.)

RanList# (3, 1) (Generiert erneut die erste, zweite und dritte Zufallszahl aus der Zufallszahlen-Folge 1 und zeigt das Ergebnis auf der ListAnsAnzeige an.)

)(Ran#) 0U

(List) 31U

* fx-7400G

II: (PROB)

S Generieren einer zufälligen Ganzzahl (RanInt#)

RanInt# generiert zufällige Ganzzahlen, die zwischen zwei vorgegebenen Ganzzahlen liegen. RanInt# (A, B [,n]) A < B |A|,|B| < 1

• A ist der Startwert und B ist der Endwert. Wird für Rückgabe einer entsprechend dem Ist-Zustand generierten Zufallszahl. Durch Vorgabe eines Wertes für n erhalten Sie die gewünschte Anzahl von Zufallszahlen in Form einer Liste.

Beispiel Tastenfolge

RanInt# (1, 5) (Generiert eine zufällige Ganzzahl im Bereich von 1 bis 5.)

E10 B – A < 1E10 1  n  999

n kein Wert eingegeben, erfolgt die

*(E)(PROB)*(RAND)(Int)

15U

RanInt# (1, 10, 5) (Generiert fünf zufällige Ganzzahlen im Bereich von 1 bis 10 und zeigt das Ergebnis auf der ListAns-Anzeige an.)

2-1616

*(E)(PROB)*(RAND)(Int)

1105U

* fx-7400GII: (PROB)

S Generieren einer Zufallszahl entsprechend der Normalverteilung

(RanNorm#)

Diese Funktion generiert eine Zufallszahl mit 10 Dezimalstellen entsprechend der Normalverteilung auf der Grundlage eines spezifizierten Mittelwertes μ und einer Standardabweichung σ.

RanNorm# (

• Wird für generierten Zufallszahl. Durch Vorgabe eines Wertes für n erhalten Sie die gewünschte Anzahl von Zufallszahlen in Form einer Liste.

RanNorm# (8, 68) (Erzeugt auf zufällige Weise einen Körperlängen-Wert, der entsprechend der Normalverteilung einer Gruppe von Säuglingen von unter einem Jahr mit einer mittleren Körperlänge von 68 cm und einer Standardabweichung von 8 erhalten wird.)

RanNorm# (8, 68, 5) (Erzeugt auf zufällige Weise für fünf Säuglinge im obigen Beispiel KörperlängenWerte und zeigt sie in einer Liste an.)

σ, μ [,n]) σ > 0 1  n  999

n kein Wert eingegeben, erfolgt die Rückgabe einer entsprechend dem Ist-Zustand

Beispiel Tastenfolge

*(E)(PROB)*(RAND)(Norm)

868U

*(E)(PROB)*(RAND)(Norm)

8685U

* fx-7400GII: (PROB)

S Generieren einer Zufallszahl entsprechend der Binomialverteilung

(RanBin#)

Diese Funktion generiert zufällige Ganzzahlen entsprechend der Binomialverteilung, auf der Grundlage von Werten, die für die Anzahl der Stichproben bzw. Versuche n und die Wahrscheinlichkeit p vorgegeben wurden.

RanBin# (n, p [,m]) 1 

• Wird für generierten Zufallszahl. Durch Vorgabe eines Wertes für m erhalten Sie die gewünschte Anzahl von Zufallszahlen in Form einer Liste.

RanBin# (5, 0,5) (Erzeugt auf zufällige Weise die Anzahl, in der bei fünfmaligem Werfen einer Münze entsprechend der Binominalverteilung „Kopf“ erwartet werden kann, wobei die Wahrscheinlichkeit für „Kopf“ 0,5 beträgt.)

RanBin# (5, 0,5, 3) (Realisiert die gleiche Münzwurfserie wie oben beschrieben dreimal und zeigt die Ergebnisse in einer Liste an.)

m kein Wert eingegeben, erfolgt die Rückgabe einer entsprechend dem Ist-Zustand

Beispiel Tastenfolge

n  100000 1  m  999 0  p  1

*(E)(PROB)*(RAND)(Bin)

50.5U

*(E)(PROB)*(RAND)(Bin)

50.53U

2-1717

* fx-7400G

II: (PROB)

I Koordinatenumwandlung

S Karthesische Koordinaten S Polarkoordinaten

• In Polarkoordinaten wird der Winkel von –180°<

• Wählen Sie in der Einstellanzeige (SET UP) unbedingt „Comp“ für „Mode“.

Berechnen von 20,7

1 24,98924,98979792 (r)

1 24,98924,98979792 (r) 2 55,928  55,92839019 ( )

2 55,928  55,92839019 ( )

Berechnen von x und y für r = 25 und θ = 56°

1 13,97913,97982259 (x)

1 13,97913,97982259 (x) 2 20,725  20,72593931 (y)

2 20,725  20,72593931 (y)

θ  180° berechnet und angezeigt (im Bogenmaß oder Neugrad entsprechend).

Beispiel Tastenfolge

r und θ° für x = 14 und y =

* fx-7400G

θ innerhalb des Hauptwinkelbereichs

K(SET UP)AAAAAA* (Deg)) *(E)(ANGL)**(E)(Pol() 1420.7U)



(Rec() 2556U

II, fx-9750GII: AAAAA ** fx-7400GII: (ANGL)

I Variation (Permutation) und Kombination

S Variation (Permutation) S Kombination ohne ohne Wiederholung Wiederholung

n–r

nCr

nPr

(

r!(n–r

• Wählen Sie in der Einstellanzeige (SET UP) unbedingt „Comp“ für „Mode“.

Beispiel 1 Berechnen der Anzahl der möglichen Variationen, wenn 4

unterschiedliche Elemente aus 10 möglichen ausgewählt werden.

Formel Tastenfolge

10P4 = 5040

Beispiel 2 Berechnen der Anzahl der möglichen Kombinationen, wenn 4

unterschiedliche Elemente aus 10 möglichen ausgewählt werden.

Formel Tastenfolge

10C4 = 210

10*(E)(PROB)*(nPr) 4U

* fx-7400G

10*(E)(PROB)*(nCr) 4U

* fx-7400G

2-1818

II: (PROB)

I Größter gemeinsamer Teiler (GCD), kleinstes gemeinsames Vielfaches

–

(LCM)

Beispiel Tastenfolge

Bestimmen des größten gemeinsamen Teilers von 28 und 35:

*(E)(NUM)*(E)(GCD) 28 35U

(GCD (28, 35) = 7)

Bestimmung des kleinsten gemeinsamen Vielfachen von 9 und 15:

*(E)(NUM)*(E)(LCM) 915 U

(LCM (9, 15) = 45)

I Divisionsrest (MOD), Rest bei Division von Zahlen in

Potenzschreibweise (MOD Exp)

Beispiel Tastenfolge

Bestimmen des Rests, wenn 137 durch 7 dividiert wird: (MOD (137, 7) = 4)

Bestimmung des Rests, wenn 5

durch 3 dividiert wird: (MOD • E (5, 3, 3) = 2)

*(E)(NUM)*(E)(MOD) 1377 U

*(E)(NUM)*(E)(MOD • E)

533U

* fx-7400GII: (NUM)

* fx-7400G

II: (NUM)

I Brüche

• Im Math-Ein-/Ausgabemodus ist die Verfahrensweise zur Eingabe von Bruchzahlen von der nachfolgend beschriebenen verschieden. Zur Eingabe von Bruch-Termen im Math-Ein-/ Ausgabemodus siehe Seite 1-11.

• Wählen Sie in der Einstellanzeige (SET UP) unbedingt „Comp“ für „Mode“.

Beispiel Tastenfolge

2 1 73

–+3––=––

5 4 20

= 3,65 (Dezimalumrechnung)*

1 1

–––– + –––––

2578 4572

s 0,5 = 0,25*

–

Brüche können in Dezimalwerte umgerechnet werden und umgekehrt.

Wenn die Gesamtanzahl der Zeichen für die ganze Zahl, Zähler, Nenner und Begrenzungszeichen

= 6,066202547 s 10

–4 *2

10 übersteigt, dann wird der Bruch automatisch im Dezimalzahlenformat angezeigt.

Berechnungen, die sowohl gemeine Brüche als auch Dezimalzahlen enthalten, werden im

Dezimalzahlenformat ausgeführt.

25314U

1257814572U

12.5U

• Drücken Sie die Tasten ,(



), um die Bruchanzeige zwischen dem Format für

gemischte Brüche und dem Format für unechte Brüche umzuschalten.

2-1919

I Berechnungen in technischer Notation (SI-Symbole)

Unter Verwendung des Untermenüs für die technische Notation können Sie die SI-Symbole (Internationales Einheitensystem) eingeben.

• Wählen Sie in der Einstellanzeige (SET UP) unbedingt „Comp“ für „Mode“.

Beispiel Tastenfolge

999k (Kilo) + 25k (Kilo) = 1,024M (Mega)

9 w 10 = 0,9 = 900m (Milli) = 0,9

= 0,0009k (Kilo) = 0,9 = 900 m

K(SET UP)DD(Eng))999*(E)(E) (ESYM)*(E)(k)25(k)U

910U *(E)(E)(ESYM)*(E)(E)(ENG)*

(ENG)* (ENG)* (ENG)*

* fx-7400GII: (ESYM)

Wandelt den angezeigten Wert in die nächst höhere SI-Einheit um, indem der Dezimalpunkt

um drei Stellen nach links verschoben wird.

Wandelt den angezeigten Wert in die nächst niedrigere SI-Einheit um, indem der

Dezimalpunkt um drei Stellen nach rechts verschoben wird.

I Logikoperatoren (AND, OR, NOT, XOR) [OPTN]-[LOGIC]

Das Logikoperator-Menü enthält eine Auswahl an Logikoperatoren.

• {And}/{Or}/{Not}/{Xor} ... {logisches AND}/{logisches OR}/{logisches NOT}/{logisches XOR}

• Wählen Sie in der Einstellanzeige (SET UP) unbedingt „Comp“ für „Mode“.

Beispiel Was ist das logische AND von A und B, wenn A = 3 und B = 2 ist?

A AND B = 1

Tastenfolge Anzeige

3??T(A)U

2??J(B)U

?T(A)*(E)(E)

(LOGIC)*(And)?J(B)U

* fx-7400G

II: (LOGIC)

S Logikoperationen

• Eine Logikoperation erzeugt immer 0 oder 1 als Ergebnis.

• Die folgende Tabelle zeigt alle möglichen Ergebnisse, die von AND-, OR- und XOROperationen erzeugt werden können, auf.

Wert oder Ausdruck A Wert oder Ausdruck B A AND B A OR B A XOR B

A x 0B x 0

A x 0

B = 0 0 1 1

110

2-2020

A = 0

A = 0 B = 0 0 0 0

• Die nachstehende Tabelle zeigt die von NOT-Operationen erzeugten Ergebnisse.

Wert oder Ausdruck A NOT A

B x 0

011

A x 0

A = 0 1

5. Numerische Berechnungen

Nachfolgend werden die numerischen Berechnungen erläutert, die in dem Funktionsuntermenü enthalten sind, das angezeigt wird, wenn die Tastenfolge *(CALC) ((CALC am fx-7400GII) ) gedrückt wird. Es sind folgende Berechnungen möglich:

• {Int÷}/{Rmdr}/{Simp} ... {Quotient}/{Rest}/{Vereinfachung}

• {Solve}/{

• {FMin}/{FMax}/{3(}/{log

d/dx}/{d

{Integration}/{f(x) Funktionswert}

logab}

I Quotient einer Ganzzahl ÷ Ganzzahl [OPTN]-[CALC]-[Int÷]

/dx2}/{°dx}/{SolvN} ... {Lösen der Gleichung}/{1. Ableitung}/{2. Ableitung}/

b} ... {Minimalwert}/{Maximalwert}/{Summenbildung}/{Logarithmus

Die „Int÷“-Funktion kann verwendet werden, um den ganzzahligen Teil des Quotienten zu bestimmen, wenn eine Ganzzahl durch eine andere Ganzzahl dividiert wird.

Beispiel Berechnen des ganzzahligen Teils des Quotienten von 107 ÷ 7:

@?F*(CALC)*(E) (E)(Int÷)F U * fx-7400G

II: (CALC)

I Rest einer Ganzzahl ÷ Ganzzahl [OPTN]-[CALC]-[Rmdr]

Die „Rmdr“-Funktion kann verwendet werden, um den Rest zu bestimmen, wenn eine Ganzzahl durch eine andere Ganzzahl dividiert wird.

Beispiel Berechnen des Rests von 107 ÷ 7:

@?F*(CALC)*(E) (E)(Rmdr)F U * fx-7400G

II: (CALC)

2-2121

I Vereinfachung [OPTN]-[CALC]-[Simp]

Die „Simp“-Funktion kann verwendet werden, um Brüche manuell zu vereinfachen. Zur Vereinfachung eines nicht vereinfachten Berechnungsergebnisses, das im Display angezeigt wird, können folgende Operationen verwendet werden:

• {Simp} U ... Diese Funktion vereinfacht automatisch das angezeigte Berechnungsergebnis

unter Verwendung der kleinsten verfügbaren Primzahl. Die verwendete Primzahl und das vereinfachte Ergebnis werden im Display angezeigt.

• {Simp}

Dieser Rechner ist zu Anfang so voreingestellt, dass er Ergebnisse von Bruchrechnungen automatisch vereinfacht, bevor er sie anzeigt. Um die folgenden Beispiele nachvollziehen können, müssen Sie zunächst in der Einstellanzeige (SET UP) die Einstellung von „Simplify“ von „Auto“ auf „Manual“ ändern (Seite 1-32).

• Wenn für den „Complex Mode“ in der Einstellanzeige (SET UP) „a+b voreingestellt wurde, werden die Ergebnisse von Bruchrechnungen immer vereinfacht, bevor sie angezeigt werden, auch wenn für „Simplify“ „Manual“ (manuell) eingestellt ist.

• Falls Sie Brüche manuell vereinfachen möchten (Simplify: Manual), stellen Sie sicher, dass für „Complex Mode“ „Real“ ausgewählt ist.

Beispiel 1 Vereinfachen von:

@DE?U *(CALC)*(E)(E)(Simp)U

* fx-7400G

n U ... Diese Funktion nimmt eine Vereinfachung entsprechend dem vorgegebenen

Teiler n vor.

15 60

2014

i“ oder „r

“

II: (CALC)

(Simp)U

Der Wert bei „F=“ ist der Teiler.

Beispiel 2 Vereinfachen von

AFEBU*(CALC)* (E)(E)(Simp)HU

* fx-7400G

• Es kommt zu einer Fehlermeldung, wenn sich mit dem vorgegebenen Teiler keine Vereinfachung durchführen lässt.

• Bei Ausführung von Simp während der Anzeige eines Terms, der sich nicht vereinfachen lässt, wird der ursprünglichen Term ausgegeben, wobei „F=“ nicht angezeigt wird.

bei Vorgabe von 9 als Teiler

II: (CALC)

27 63

2-2222

I Nullstellenberechnung [OPTN]-[CALC]-[Solve]

Nachfolgend ist die Syntax für die Verwendung des Solve-Befehls zur Lösung einer Nullstellengleichung in einem Programm aufgeführt.

Solve(

Es gibt zwei unterschiedliche Methoden zur Eingabe der Nullstellengleichung: direkte Eingabe eines Formelterms oder Eingabe mittels Koeffiziententabelle.

Bei der direkten Eingabe eines Formelterms (die hier beschriebene Methode) nutzen Sie den Funktionsterm zur Berechnung der Funktionswerte. Diese Art der Eingabe ist identisch mit der Eingabe, die Sie mit dem Solve-Befehl im PRGM-Menü verwenden können.

Die Eingabe mittels Koeffiziententabelle wird im EQUA-Menü verwendet. Diese Eingabemethode wird in den meisten Fällen praktiziert und empfohlen.

Es kommt zu einer Fehlermeldung (Time Out), wenn das Iterationsverfahren zur Nullstellenbestimmung nicht konvergiert und keine Nullstelle gefunden wird.

Weitere Informationen über Nullstellengleichungen können Sie Seite 4-4 entnehmen.

• Innerhalb der obigen Funktionen dürfen Sie keine 2. Ableitung, keine 3-Berechnung, keine

• Durch Drücken der -Taste während der Berechnung einer Solve (wenn der Cursor nicht

f(x), n, a, b) (a: untere Grenze, b: obere Grenze, n: geschätzter Anfangswert)

Maximal-/Minimalwertberechnung und keinen Solve-Berechnungsausdruck verwenden.

im Display angezeigt wird) können Sie die Rechnung unterbrechen.

I Berechnen der Nullstellen einer Funktion f(x) [OPTN]-[CALC]-[SolvN]

Verwenden Sie SolvN, um die Nullstellen einer Funktion bestimmen. Nachfolgend ist die Syntax für die Eingabe aufgeführt.

SolveN (linke Seite [=rechte Seite] [,Variable] [, unterer Grenzwert, oberer Grenzwert])

• Die rechte Seite, die Variable, der untere und obere Grenzwert können jeweils weggelassen werden.

• „linke Seite[=rechte Seite]“ ist der Ausdruck, für den eine Lösung zu ermitteln ist. Unterstützte Variablen sind A bis Z, angenommen, dass die rechte Seite = 0 ist, und dafür eine Lösung ermittelt.

• Die Variable legt die Variable innerhalb des Ausdrucks fest, für die eine Lösung zu ermitteln ist (A bis Z,

• Die untere Grenze und die obere Grenze legen den Wertebereich der Lösung fest. Für den Bereich können Sie einen Wert oder einen Ausdruck eingeben.

• Die folgenden Funktionen können nicht innerhalb der Argumente verwendet werden:

Solve(,

Bis zu 10 Berechnungsergebnisse lassen sich gleichzeitig im ListAns-Format anzeigen.

• Die Meldung „No Solution“ wird angezeigt, falls keine Lösung existiert.

). Wenn Sie keine Variable vorgeben, wird X als Variable verwendet.

/dx2, FMin(, FMax(, 3(

r und

. Wenn Sie die rechte Seite weglassen, wird

f(x) durch numerische Analyse zu

• Die Meldung „More solutions may exist.“ (Es gibt noch mehr Lösungen.) wird angezeigt, wenn es neben den durch SolvN angezeigten Lösungen noch weitere gibt.

2-2323

Beispiel Lösung für x2 – 5x – 6 = 0

*(CALC)*(SolvN) TVDTEU

* fx-7400G

II: (CALC)

)

I Ableitungsberechnungen (1. Ableitung) [OPTN]-[CALC]-[d/dx]

Um eine 1. Ableitung numerisch zu berechnen, öffnen Sie zuerst das Funktionsanalysemenü und geben danach die Werte unter Verwendung der nachfolgenden Syntax ein.

*(CALC)* (

(

a: Stelle, an der Sie die Ableitung bestimmen möchten, tol: Genauigkeit (Toleranzwert))

d/dx

(f

(x)

d/dx) f(x)atol * fx-7400GII: (CALC)

(a)

)



,



,



(a)

Die Berechnung der Ableitung wird wie üblich über den Differenzenquotienten definiert:

f(a

f (a

) = lim



f(a

–––––––––––––



x)–f(a

)

Nach dieser Definition wird ein unendlich kleiner Wert durch einen ausreichend kleinen Wert

x ersetzt, wobei der Wert in der Umgebung von f

f(a

f (a

f(a

)

–––––––––––––



x)–f(a

)

(a) berechnet wird als:

Um eine optimale Genauigkeit zu erreichen, wird hier die Zentraldifferenz für die Berechnung von Ableitungen verwendet.

Beispiel Bestimmen der Ableitung an der Stelle

y = x

+ 4x2 + x – 6, mit einer Genauigkeit (Toleranzwert) „tol“ = 1E – 5

Geben Sie die Funktion

*(CALC)* (

f(x) ein:

d/dx)T,BCTVTE

* fx-7400G

Geben Sie die Stelle

x = a ein, an der Sie die 1. Ableitung bestimmen möchten.

x = 3 für die Funktion

II: (CALC)

B

Geben Sie die Genauigkeitsschranke, d. h. den Toleranzwert, ein.

@$DU

2-2424

Verwendung der Ableitungsberechnung in einer Grafikfunktion

–

• Wenn der Ableitungsbefehl in einer Grafikfunktion verwendet wird, kann durch Weglassen des Toleranzwertes (tol) die Berechnung für die Grafikdarstellung vereinfacht werden. In einem solchen Falle wird auf Genauigkeit verzichtet, um ein schnelleres Zeichnen zu ermöglichen. Wird der Toleranzwert vorgegeben, erfolgt das Zeichnen der Grafik mit der gleichen Genauigkeit, wie Sie es bei normalen Ableitungsberechnungen gewöhnt sind.

• Sie können die Eingabe der Ableitungsstellen auch weglassen, indem Sie die folgende Syntax für die Grafik der 1. Ableitung nutzen: Y2=

d/dx(Y1). In diesem Fall wird der Wert der

Variablen X als Ableitungsstelle verwendet.

Hinweise zur Berechnung der ersten Ableitung

• In der Funktion f(x) kann nur X als die Variable des Funktionsterms verwendet werden. Andere Variablen (A bis Z (aber ausschließlich X), und bei der Berechnung wird der diesen Variablen aktuell zugeordnete Wert verwendet.

r, θ) werden wie Konstanten behandelt

• Die Eingabe des Toleranzwertes (

tol) und der schließenden Klammern kann weggelassen

werden. Wenn Sie den Toleranzwert (tol) weglassen, verwendet der Rechner automatisch den Wert für tol 1E–10.

• Vorgegeben werden kann ein Toleranzwert (

tol) von 1E–14 oder größer. Es kommt zu einer

Fehlermeldung (Time Out), wenn keine Lösung gefunden werden kann, die die geforderte Genauigkeit (Toleranzwert) aufweist.

• Durch Drücken der -Taste während der Berechnung einer Ableitung (wenn der Cursor nicht im Display angezeigt wird) können Sie die Rechnung unterbrechen.

• Ungenaue Ergebnisse und Fehler können durch Folgendes verursacht werden:

- Unstetigkeitsstellen bei den

- Extreme Änderungen bei den

- Einschluss des lokalen Minimums und lokalen Maximums in die

- Einschluss des Wendepunktes in die

- Einschluss von nicht differenzierbaren Punkten in die

x-Werten

x-Werte

- Differenzialrechnungsergebnisse nähern sich Null

• Verwenden Sie immer das Bogenmaß (Rad-Modus) als Winkelmodus für die Ableitungsberechnung bei trigonometrischen Funktionen.

• Beachten Sie, dass ein Ableitungsbefehl für die 1. oder 2. Ableitung, ein Integrations-, 3-, Maximalwert-/Minimalwert-, Nullstellen-berechnungs- (Solve-), RndFix- oder log

b-Befehl

nicht innerhalb eines Ableitungsbefehls selbst verwendet werden kann.

• Im Math-Ein-/Ausgabemodus ist der Toleranzwert auf 1

E–10 festgelegt und kann nicht

geändert werden.

I Berechnung zweiter Ableitungen [OPTN]-[CALC]-[d2/dx

]

Nachdem das Funktionsanalysemenü geöffnet wurde, können Sie 2. Ableitungen unter Verwendung der folgenden Syntax berechnen.

*(CALC)*( (

a: Ableitungsstelle, tol: Genauigkeit (Toleranzwert))

f(x), a

–– (

/dx2) f(x)atol * fx-7400GII: (CALC)

f(a

–––

f(a

)



2-2525

Die Berechnung 2. Ableitungen erfolgt näherungsweise unter Verwendung der folgenden

Differenzenformel zweiter Ordnung, die auf der Newton'schen Polynom-Interpolation beruht.

2 f(a + 3h) – 27 f(a + 2h) + 270 f(a + h) – 490 f(a) + 270 f(a – h) – 27 f(a –2h) + 2 f(a – 3h)

''(a) =

2 f(a + 3h) – 27 f(a + 2h) + 270 f(a + h) – 490 f(a) + 270 f(a – h) – 27 f(a –2h) + 2 f(a – 3h)

180h

In dieser Formel werden „ausreichend kleine Zuwächse von Näherungswert zu erhalten, der sich an f"(a) annähert.

Beispiel Bestimmung der 2. Ableitung an der Stelle

y = x

+ 4x2 + x – 6

Hier soll eine Genauigkeit (Toleranzwert)

Geben Sie die Funktion f(x) ein:

*(CALC)* ( * fx-7400G

Geben Sie 3 als die Stelle B

Geben Sie die Genauigkeitsschranke, d. h. den Toleranzwert, ein. @$D U

a ein, an der die Ableitung berechnet werden soll.

/dx2) T,BCTVTE

h“ verwendet, um einen

x = 3 der Funktion

tol = 1E – 5 verwendet werden.

Hinweise zur Berechnung der zweiten Ableitung

II: (CALC)

• In der Funktion f(x) kann nur X als die Variable des Funktionsterms verwendet werden. Andere Variablen (A bis Z (aber ausschließlich X), r, θ) werden wie Konstanten behandelt und bei der Berechnung wird der diesen Variablen aktuell zugeordnete Wert verwendet.

• Die Eingabe des Toleranzwertes ( werden.

• Vorgegeben werden kann ein Toleranzwert ( Fehlermeldung (Time Out), wenn kein Integrationsergebnis gefunden werden kann, das die geforderte Genauigkeit (Toleranzwert) aufweist.

• Die für die 1. Ableitung geltenden Regeln gelten auch bei Verwendung der Berechnung einer

2. Ableitung in der Grafikformel (siehe Seite 2-24).

• Ungenaue Ergebnisse und Fehler können durch Folgendes verursacht werden:

- Unstetigkeitsstellen bei den

- Extreme Änderungen bei den

- Einschluss des lokalen Minimums und lokalen Maximums in die

- Einschluss des Wendepunktes in die

- Einschluss von nicht differenzierbaren Punkten in die

- Differenzialrechnungsergebnisse nähern sich Null

• Sie können die Berechnung einer 2. Ableitung durch Drücken der -Taste unterbrechen.

tol) und der schließenden Klammern kann weggelassen

tol) von 1E–14 oder größer. Es kommt zu einer

x-Werten

x-Werte

• Verwenden Sie immer das Bogenmaß (Rad-Modus) als Winkelmodus, wenn Sie 2. Ableitungen trigonometrischer Funktionen berechnen.

• Beachten Sie, dass ein Ableitungsbefehl für die 1. oder 2. Ableitung, ein Integrations-, 3-, Maximalwert-/Minimalwert-, Nullstellen-berechnungs- (Solve-), RndFix- oder log nicht innerhalb eines Ableitungsbefehls für die 2. Ableitung selbst verwendet werden kann.

2-2626

b-Befehl

• Bei Berechnung zweiter Ableitungen beträgt die Genauigkeit der Berechnung bis zu fünf





Stellen für die Mantisse.

• Im Math-Ein-/Ausgabemodus ist der Toleranzwert auf 1 geändert werden.

E–10 festgelegt und kann nicht

I Integralrechnung (bestimmte Integrale) [OPTN]-[CALC]-[°dx]

Um ein bestimmtes Integral zu berechnen, öffnen Sie zuerst das Funktionsanalysemenü und geben danach die Werte unter Verwendung der nachfolgenden Syntax ein.

*(CALC)* (°

(

: Anfangspunkt, b: Endpunkt,

f(x),a





f(x),a

dx) f(x)  a  b  tol  * fx-7400GII: (CALC)

: Genauigkeit (Toleranzwert))

tol

f(x)d

b, tol

)



f(x)d





Berechnet wird die Fläche von

f(x)dx



Wie in der obigen Abbildung zu erkennen ist, werden die bestimmten Integrale ermittelt, indem die vorzeichenbehafteten Flächenanteile zwischen dem Graphen y = f(x), wobei

a  x  b, und der x-Achse f(x)  0 von a bis b aufsummiert werden. Damit wird praktisch der

Flächeninhalt der schattierten Fläche in der Abbildung berechnet.

Beispiel Ausführung der Integrationsberechnung für die nachfolgend

dargestellte Funktion mit einer Genauigkeit (Toleranzwert) von „

tol“ = 1E – 4

(2x2 + 3x + 4) dx

Geben Sie die Funktion

*(CALC)* (° * fx-7400G

Geben Sie die Integrationsgrenzen, d. h. den Anfangspunkt und den Endpunkt, ein.

@D

Geben Sie die Genauigkeitsschranke, d. h.den Toleranzwert, ein.

@$CU

(x) ein:

dx)ATVBTC

II: (CALC)

Achten Sie bei einer Flächeninhaltsberechnung auf folgende Punkte, um richtige Integrationsergebnisse zu erhalten:

2-2727

(1) Wenn Funktionen mit wechselndem Vorzeichen integriert werden, führen Sie die Berech-



nung für einzelne Intervalle mit vorzeichenkonstanten Funktionswerten aus oder integrieren zunächst über alle positiven Flächenanteile und dann über alle negativen Flächenanteile. Anschließend werden die Teilergebnisse zusammengefaßt:

Positiver

)

Anteil (

+ (–

f(x)dx

)

+.....+

f(x)dx





f(x)dx



)

Negativer Anteil (

f(x)dx =



Positiver Anteil (S) Negativer Anteil (S)

(2) Wenn viele Oszillationen innerhalb des Integrationsbereiches zu großen Abweichungen

im Integrationsergebnis führen können, berechnen Sie die Flächenanteile stückweise (die Abschnitte mit großen Oszillationen in kleinere Abschnitte zerlegen). Anschließend werden die Teilergebnisse zusammengefasst.



f(x)dx



f(x)dx =





f(x)dx







• Durch Drücken der -Taste während der Berechnung eines Integrals (wenn der Cursor nicht im Display angezeigt wird) können Sie die Rechnung unterbrechen.

• Verwenden Sie immer das Bogenmaß (Rad-Modus) als Winkelmodus, wenn Sie trigonometrische Funktionen integrieren.

• Es kommt zu einer Fehlermeldung (Time Out), wenn kein Integrationsergebnis gefunden werden kann, das die geforderte Genauigkeit (Toleranzwert) aufweist.

Hinweise zur Integralrechnung (bestimmte Integrale)

• Die Eingabe von „ „tol“, weglassen, verwendet der Rechner automatisch den Vorgabewert von 1E–5.

• Integrationsberechnungen können lange dauern.

• Im Math-Ein-/Ausgabemodus ist der Toleranzwert auf 1 geändert werden.

tol“ und der schließenden Klammern kann weggelassen werden. Wenn Sie

b-Befehl

E–5 festgelegt und kann nicht

2-2828

I 3-Berechnungen (Partialsummen einer Zahlenfolge) [OPTN]-[CALC]-[3(]

Um 3-Berechnungen auszuführen, öffnen Sie zuerst das Funktionsanalysemenü und geben danach die Werte unter Verwendung der nachfolgenden Syntax ein.

*(CALC)* (E)(3( )



(



n: Schrittweite)

(

,

)



k =

ak  k 



 B  n  * fx-7400GII: (CALC)



+........+



Beispiel Berechnen Sie folgende Summe:

(

–3k+5)

(

–3k+5)



k = 2

Verwenden Sie

n = 1 als Schrittweite.

*(CALC)*(E)(3( )?(K) VB?(K)D ?(K)AE@U

* fx-7400GII: (CALC)

Hinweise zur3-Berechnung

• Der Wert der vorgegebenen Variablen ändert sich während einer 3-Berechnung. Bevor Sie die Rechnung durchführen, sollten Sie die Werte für die vorgegebenen Variablen unbedingt schriftlich notieren, um später darauf zurückgreifen zu können.

• Sie können nur eine Variable in der Funktion für die Eingabefolge

• Geben Sie nur ganze Zahlen für den Anfangsindex ( Folge

• Sie können die Eingabe von

ak ein.

n und der schließenden Klammer weglassen. Wenn Sie n

) der Folge ak und den Endindex (B) der

ak verwenden.

weglassen, wird automatisch n = 1 verwendet.

• Achten Sie darauf, dass der als Endindex

verwendete Wert größer als der als

Anfangsindex A verwendete Wert ist. Andernfalls kommt es zu einer Fehlermeldung.

• Um eine 3-Berechnung (wenn der Cursor nicht im Display angezeigt wird) zu unterbrechen, drücken Sie die -Taste.

• Beachten Sie, dass ein Ableitungsbefehl für die 1. oder 2. Ableitung, ein Integrations-, 3-, Maximalwert-/Minimalwert-, Nullstellen-berechnungs- (Solve-), RndFix- oder log

b-Befehl

nicht innerhalb eines 3-Berechnungsbefehls verwendet werden kann.

• Im Math-Ein-/Ausgabemodus ist die Schrittweite (

n) auf 1 festgelegt und kann nicht geändert

werden.

2-2929

I Maximalwert/Minimalwert-Berechnungen [OPTN]-[CALC]-[FMin]/[FMax]

Nach den Öffnen des Funktionsanalysenmenüs können Sie Maximalwert/MinimalwertBerechnungen unter Verwendung der nachfolgenden Formate eingeben und so die Punkte für das Maximum oder Minimum einer Funktion innerhalb des Intervalls

S Minimalwert

*(CALC)* (E)(FMin) f (x)  a  b  n  * fx-7400GII: (CALC)

a: Anfangspunkt des Intervalls, b: Endpunkt des Intervalls, n: Genauigkeit (n = 1 bis 9))

(

S Maximalwert

*(CALC)* (E)(FMax) f (x) a  b  n  * fx-7400GII: (CALC)

a: Anfangspunkt des Intervalls, b: Endpunkt des Intervalls, n: Genauigkeit (n = 1 bis 9))

(

Beispiel Bestimmen des Minimums in dem Intervall das durch den Anfangspunkt

a = 0 und den Entpunkt b = 3 definiert ist, mit einer Genauigkeit von n = 6 der Funktion y = x

Geben Sie f (x) ein:

*(CALC)* (E)(FMin)TVCTH

– 4x + 9

a  x  b berechnen.

* fx-7400G

Geben Sie die Grenzen des Intervalls ein:

?B

Geben Sie den Genauigkeitsparameter

EU

• In der Funktion Andere Variablen (A bis Z (aber ausschließlich X), r, θ) werden wie Konstanten behandelt und bei der Berechnung wird der diesen Variablen aktuell zugeordnete Wert verwendet.

• Sie können die Eingabe von

• Unstetigkeitsstellen und Intervalle mit starken Oszillationen können die Genauigkeit beeinträchtigen und sogar einen Berechnungsfehler verursachen.

• Durch Eingabe eines größeren Wertes für wobei jedoch die Ausführung der Berechnung länger dauert.

• Der für den Endpunkt des Intervalls ( Anfangspunkt (a) eingegebene Wert. Andernfalls kommt es zu einer Fehlermeldung.

(x) kann nur X als die Variable des Funktionsterms verwendet werden.

n und der schließenden Klammer weglassen.

a = 0, b = 3.

n = 6 ein.

n wird die Genauigkeit der Berechnung erhöht,

b) eingegebene Wert muss größer sein als der für den

II: (CALC)

• Sie können die Ausführung einer Maximalwert/Minimalwert-Berechnung durch Drücken der

-Taste unterbrechen.

• Sie können eine ganze Zahl im Bereich von 1 bis 9 als Wert für eines Wertes außerhalb dieses Bereichs führt zu einer Fehlermeldung.

• Beachten Sie, dass ein Ableitungsbefehl für die 1. oder 2. Ableitung, ein Integrations-, 3-, Maximalwert-/Minimalwert-, Nullstellen-berechnungs- (Solve-), RndFix- oder log nicht innerhalb eines Maximalwert/Minimalwert-Befehls verwendet werden kann.

2-3030

n eingeben. Die Eingabe

b-Befehl

6. Rechnen mit komplexen Zahlen

Mit komplexen Zahlen können Sie Additionen, Subtraktionen, Multiplikationen, Divisionen, Klammerrechnungen, Funktionsberechnungen und Speicherrechnungen ausführen, genau wie bei den auf den Seiten 2-1 bis 2-15 beschriebenen manuellen Berechnungen.

Sie können den Darstellungsmodus für komplexe Zahlen festlegen, indem Sie in der Einstellanzeige (SET UP) für die Position „Complex Mode“ eine der folgenden Einstellungen auswählen.

• {Real} ... Berechnungen nur im reellen Zahlenbereich*

• {a+bi} ... Berechnungen mit komplexen Zahlen und Anzeige der Ergebnisse in arithmetischer Darstellung (kartesische Koordinaten)

• {

rθ} ... Berechnungen mit komplexen Zahlen und Anzeige der Ergebnisse in exponentieller

Darstellung (Polarkoordinaten)*

*1 Falls eine Eingabegröße als Argument eine Zahl mit einem Imaginärteil hat, wird die

Berechnung in komplexen Zahlen ausgeführt, wobei das Ergebnis in kartesischen

Koordinaten angezeigt wird. Beispiele: Komplexer Hauptwert von ln 2 Komplexer Hauptwert von ln 2i + ln (– 2) = (Non-Real ERROR)

Der für θ angezeigte Winkelbereich hängt vom Winkelmodus ab, der in der Einstellanzeige

(SET UP) unter „Angle“ eingestellt wurde.

• Deg ... –180 <

• Rad ... – P <

• Gra ... –200 <

Drücken Sie die Tasten *(CPLX) (*(CPLX) am fx-7400G für das Rechnen mit komplexen Zahlen anzuzeigen, welches die folgenden Positionen enthält:

θ  180 (Neugrad)

θ  P (Bogenmaß)

θ  200 (Neugrad)

i = 0,6931471806 + 1,570796327i

II), um das Untermenü

i} ... {Eingabe der imaginären Einheit i}

• {

• {Abs}/{Arg} ... Berechnung des {Absolutwertes (Betrages)}/{Arguments (Winkels)}

• {Conj} ... Berechnung der {konjugiert komplexen Zahl}

• {ReP}/{ImP} ... Berechnung des {Realteils}/{Imaginärteils} einer komplexen Zahl

rθ}/{a+bi} ... Umwandlung des Ergebnisses in {Polarkoordinaten}/{kartesische

• { Koordinaten}

• Sie können auch ?( (i) verwenden.

• Die im Realmodus erhaltenen Lösungen mit (xy) unterschiedlich, wenn x < 0 und y = m/n rational ist, wobei n eine ungerade Zahl darstellt.

Beispiel: 3

= 1 + 1,732050808i (a+bi) = 260 (rθ)

• Zum Eingeben des „  “-Operators in den Term in Polarkoordinaten ( T().

 (– 8) = – 2 (Real)

i) anstelle von *(CPLX) (*(CPLX) beim fx-7400GII)

a+bi und rθ sind beim allgemeinen Potenzieren

rθ), drücken Sie

2-3131

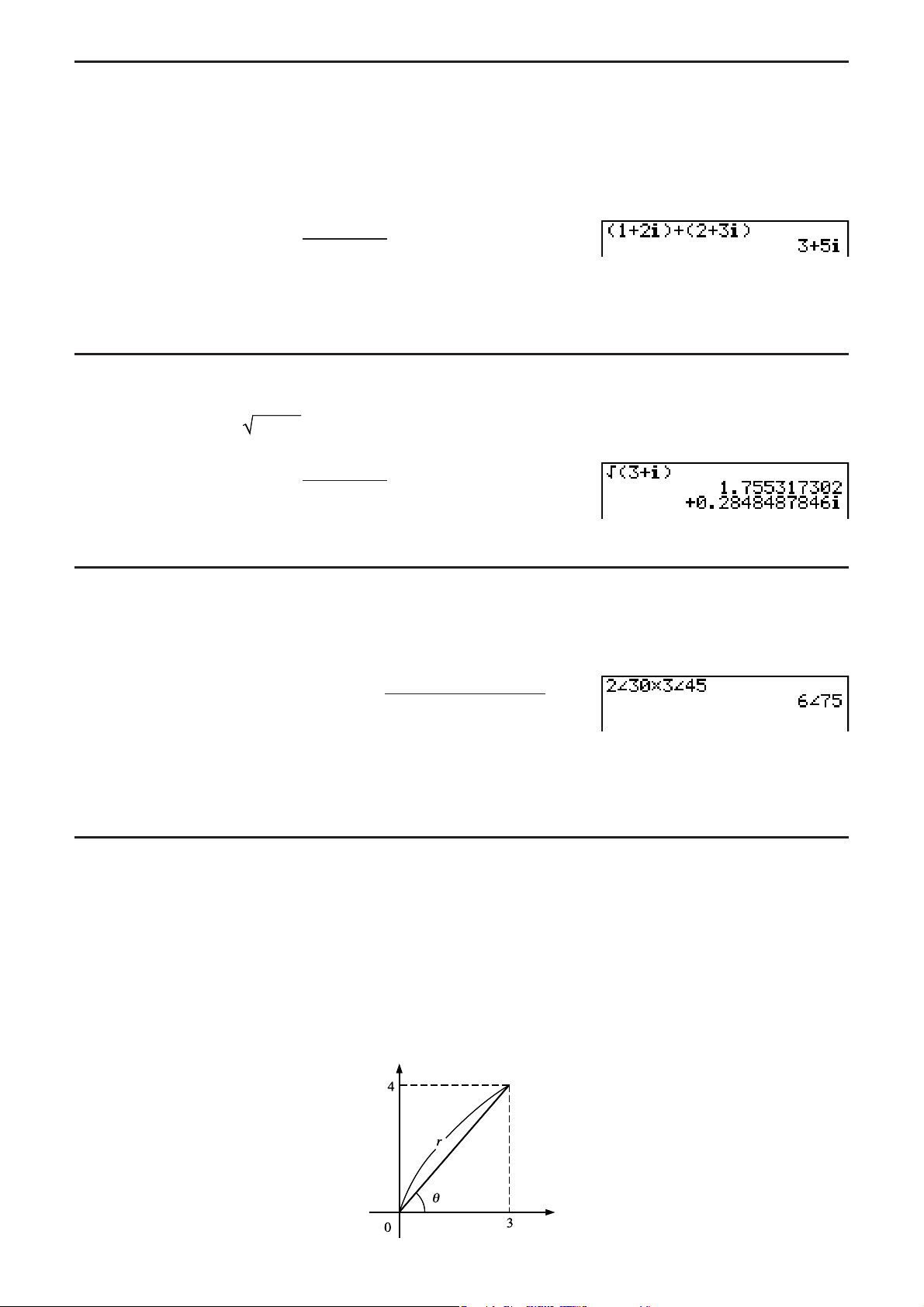
I Arithmetische Operationen [OPTN]-[CPLX]-[i]

Die arithmetischen Operationen sind die gleichen wie bei manuellen Rechnungen. Sie können auch Klammern und den Speicher verwenden.

Beispiel (1 + 2

*(CPLX)* @A( AB( * fx-7400G

i) + (2 + 3i)

i)

i)U

II: (CPLX)

I Kehrwerte, Quadratwurzeln und Quadrate

Beispiel (3 + i)

*(CPLX)* V()B( * fx-7400G

i)U

II: (CPLX)

I Format für komplexe Zahlen unter Verwendung der Polarkoordinaten

Beispiel 230 s 345 = 675

K(SET UP)AAAAAA* (Deg)A( AT()B?B T()CDU * fx-7400G

rθ))

II, fx-9750GII: AAAAA

I Absolutwert und Argument [OPTN]-[CPLX]-[Abs]/[Arg]

Der Rechner interpretiert jede komplexe Zahl in der Form Gauß'schen Zahlenebene und berechnet den Absolutwert ²Z ²und das Argument (arg).

Beispiel Berechnen des Absolutwertes (der euklidischen Vektorlänge) (

des Arguments (θ) für die komplexe Zahl 3 + 4i, wobei der Winkelmodus auf Altgrad eingestellt sein soll.

Imaginäre Achse

a + bi als Koordinate in der

r) und

Reelle Achse

2-3232

*(CPLX)*(Abs) BC( (Berechnung des Absolutwertes) * fx-7400G

*(CPLX)*(Arg) BC( (Berechnung des Arguments (Winkels)) * fx-7400G

• Das Ergebnis der Argumentberechnung ist je nach aktuell eingestelltem Winkelmodus (Altgrad, Bogenmaß, Neugrad) verschieden.

i)U

II: (CPLX)

i)U

II: (CPLX)

I Konjugiert komplexe Zahlen [OPTN]-[CPLX]-[Conj]

Eine komplexe Zahl der Form

Beispiel Berechnen der konjugiert komplexen Zahl zur komplexen Zahl 2 + 4

*(CPLX)*(Conj)

a + bi wird in die konjugiert komplexe Zahl a – bi umgeformt.

AC( * fx-7400G

i)U

II: (CPLX)

I Berechnen des Real- und des Imaginärteils [OPTN]-[CPLX]-[ReP]/[lmP]

Verfahren Sie wie folgt, um den Realteil Form a + bi zu berechnen.

Beispiel Berechnen von Real- und Imaginärteil der komplexen Zahl 2 + 5

*(CPLX)*(E)(ReP) AD(E)( (Berechnung des Realteils) * fx-7400G

*(CPLX)*(E)(ImP) AD(E)( (Berechnung des Imaginärteils)

a oder den Imaginärteil b einer komplexen Zahl der

i)U

II: (CPLX)

i)U

* fx-7400G

II: (CPLX)

I Umrechnen zwischen exponentieller und arithmetischer Darstellung

[OPTN]-[CPLX]-[rθ]/[a+bi]

Verfahren Sie wie folgt, um eine in der arithmetischen Darstellung angezeigte komplexe Zahl in die exponentielle Darstellung umzurechnen bzw. umgekehrt.

2-3333

Beispiel Die arithmetische Darstellung der komplexen Zahl 1 + 3 i ist in die

exponentielle Darstellung umzuformen.

K(SET UP)AAAAAA* (Deg)A( @V()B *(CPLX)**( * fx-7400G ** fx-7400G

AT()E? *(CPLX)*(E)( * fx-7400G

• Der Ein-/Ausgabe-Bereich für komplexe Zahlen umfasst für jede Koordinate 10 Stellen für die Mantisse und zwei Stellen für den Exponenten.

• Wenn eine komplexe Zahl mehr als 21 Stellen aufweist, werden der Realteil und der Imaginärteil in unterschiedlichen Zeilen des Displays angezeigt.

• Die folgenden Funktionen können auf komplexen Zahlen angewendet werden:

, ENG, ° ’ ”,

, x–1, ^(xy), 3, x, In, log, logab, 10x, ex, Int, Frac, Rnd, Intg, RndFix(, Fix, Sci, ENG,

/c, d/c

° ’ ”

a+bi))

i)(E)(r

II, fx-9750GII: AAAAA II: (CPLX)

a+bi)U

II: (CPLX)

7. Rechnen mit (ganzen) Binär-, Oktal-, Dezimalund Hexadezimalzahlen

Sie können das RUN • MAT-Menü (oder RUN-Menü) und eine Binär-, Oktal-, Dezimal- oder Hexadezimaleinstellung (SET UP) verwenden, um Berechnungen mit Binär-, Oktal-, Dezimaloder Hexadezimalzahlen auszuführen. Sie können auch Umrechnungen zwischen den Zahlensystemen und logische Operationen ausführen.

• Die höheren mathematischen Funktionen sind nicht für Berechnungen mit Binär-, Oktal-,

Dezimal- oder Hexadezimalzahlen verwendbar.

• Sie können nur ganze Zahlen in Berechnungen mit Binär-, Oktal-, Dezimal- oder

Hexadezimalzahlen verwenden, d. h. Dezimalbrüche oder gemeine Brüche sind nicht zulässig. Falls Sie einen Wert mit einem Dezimalstellenanteil eingeben, schneidet der Rechner den Dezimalstellenanteil automatisch ab.

• Falls Sie den Versuch unternehmen, einen für das verwendete Zahlensystem (binär,

oktal, dezimal oder hexadezimal) nicht zugelassenen Wert einzugeben, zeigt der Rechner eine Fehlermeldung an. Nachfolgend sind die Ziffern aufgeführt, die im zutreffenden Zahlensystem verwendet werden können.

Binär: 0, 1 Oktal: 0, 1, 2, 3, 4, 5, 6, 7 Dezimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Hexadezimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

2-3434

• Negative Binär-, Oktal- sowie Hexadezimalzahlen werden durch das Komplement des

ursprünglichen Wertes zu „Null“ erzeugt, so dass X + Neg X = „Null“ = (1)0...0 gilt. Die führende Ziffer (1) wird wegen Überschreitung der Anzeigekapazität nicht dargestellt.

• Nachfolgend sind die Anzeigekapazitäten für jedes Zahlensystem angegeben.

Zahlensystem Binär Oktal Dezimal Hexadezimal

Anzeigekapazität 16 Stellen 11 Stellen 10 Stellen 8 Stellen

• Die für Hexadezimalzahlen verwendeten alphabetischen Zeichen erscheinen in anderer

Darstellung, um sie von den normalen Textzeichen unterscheiden zu können.

Normaler Text ABCDEF

Hexadezimalzahlen

Tasten

• Nachfolgend sind die Zahlenbereiche der einzelnen Zahlensysteme aufgeführt, innerhalb

derer Berechnungen durchgeführt werden können. Binärzahlen (Dualzahlen, Anzeige mit 16 Stellen)) Positiv: 0 

Negativ: 1000000000000000  Oktalzahlen (Anzeige mit 11 Stellen)

Positiv: 0  Negativ: 20000000000  Dezimalzahlen

Positiv: 0  Negativ: –2147483648  Hexadezimalzahlen

Positiv: 0  Negativ: 80000000 

x  111111111111111

x  17777777777

x  2147483647

x  7FFFFFFF

x  FFFFFFFF

STUVW X

TJ ( Q A R

x  1111111111111111

x  37777777777

x  –1

S Ausführen einer Binär-, Oktal-, Dezimal- oder Hexadezimalzahlenrechnung

[SET UP]-[Mode]-[Dec]/[Hex]/[Bin]/[Oct]

1. Wählen Sie das RUN • MAT-Menü (oder RUN-Menü) im Hauptmenü aus.

2. Drücken Sie die Tasten K(SET UP). Verschieben Sie mit den Cursurtasten die

Markierung auf „Mode“ und wählen Sie danach Ihr Vorgabe-Zahlensystem für die Moduseinstellung durch Drücken der Taste (Dec), (Hex), (Bin) oder (Oct) aus.

3. Drücken Sie die )-Taste, um in das Display für die Berechnungseingabe zu wechseln.

Hierbei erscheint das Funktionsmenü mit den folgenden Positionen:

• {d~o}/{LOG}/{DISP} ... {Zahlensystem-Identifikationsmenü}/{Logikoperations-Menü}/

{Dezimal-/Hexadezimal-/Binär-/Oktal-Umrechnungsmenü}

I Auswahl eines Zahlensystems

Sie können das Dezimal-, Hexadezimal-, Binär- oder Oktalzahlensystem als VorgabeZahlensystem einstellen, indem Sie die Einstellanzeige (SET UP) verwenden.

2-3535

S Auswahl eines Zahlensystems für einen Eingabewert direkt im Display

Sie können für jeden Eingabewert jeweils ein individuelles Zahlensystem nutzen. Drücken Sie (d~o), um ein Untermenü der Zahlensystemsymbole anzuzeigen. Drücken Sie danach die Funktionstaste gemäß dem Symbol, das Sie wählen möchten, und geben Sie unmittelbar danach den Wert ein.

• {d}/{h}/{b}/{o} ... {dezimal}/{hexadezimal}/{binär}/{oktal}

S Eingeben von Zahlenwerten bei unterschiedlichen Zahlensystemen

Beispiel Eingeben von 12310, wenn das voreingestellte Zahlensystem das

Hexadezimalsystem ist:

K(SET UP) Bewegen Sie mit den Cursortasten die

Markierung auf „Mode“ und drücken Sie danach (Hex)).

(d~o)(d)@ABU

I Negative Werte und Logikoperationen

Drücken Sie (LOG), um ein Untermenü der Negation und Logikoperationen zu öffnen.

• {Neg} ... {Negation}*

• {Not}/{and}/{or}/{xor}/{xnor} ... {NOT}*2/{AND}/{OR}/{XOR}/{XNOR}*

*1 Zweierkomplement

Einerkomplement (bitweises Komplement)

Logikoperationen: bitweises AND, bitweises OR, bitweises XOR, bitweises XNOR

S Negative Werte

Beispiel Bestimmen des negativen Wertes von 1100102

K(SET UP) Bewegen Sie mit den Cursortasten die

(LOG)(Neg)

Markierung auf „Mode“ und drücken Sie danach (Bin)).

@@??@?U

• Negative Binär-, Oktal- und Hexadezimalzahlen werden erzeugt, indem das binäre

Zweierkomplement im ursprünglichen Zahlensystem dargestellt wird. Im Dezimalsystem

werden negative Werte mit einem Minuszeichen angezeigt.

2-3636

S Logikoperationen

Beispiel Eingabe und Darstellung von „12016 and AD16“

K(SET UP) Bewegen Sie mit den Cursortasten die

Markierung auf „Mode“ und drücken Sie

danach (Hex)). @A?(LOG) (and) #U

I Wechsel des Zahlensystems

Drücken Sie die (DISP)-Taste, um das Untermenü für die Befehle zum Wechseln des Zahlensystems anzuzeigen.

Dec}/{Hex}/{Bin}/{Oct} ... Umwandlung der angezeigten Zahlendarstellung in ihre

• {

gleichwertige {Dezimal-}/{Hexadezimal-}/{Binär-}/{Oktal-} Zahlendarstellung

S Umwandeln einer angezeigten Zahlendarstellung von einem Zahlensystem in

ein anderes

Beispiel Umwandeln von 2210 (Vorgabe-Zahlensystem) in den entsprechenden

Binär- oder Oktalwert

K(SET UP) Bewegen Sie mit den Cursortasten die

Markierung auf „Mode“ und drücken Sie

danach (Dec)). (d~o)(d)AAU

)(DISP)(Bin)U

(Oct)U

8. Matrizenrechnung

Wichtig!

• Mit dem fx-7400GII ist keine Matrizenrechnung möglich.

Rufen Sie das RUN • MAT-Menü vom Hauptmenü her auf und drücken Sie die (MAT)- Taste, um Matrizenrechnung betreiben zu können.

26 Matrixspeicher (Mat A bis Mat Z) plus ein Matrix-Antwortspeicher (MatAns) ermöglichen die Ausführung der folgenden Matrizenoperationen:

• Addition, Subtraktion, Multiplikation und Division von Matrizen

• Multiplikation einer Matrix mit einem skalaren Faktor

• Determinantenberechnung (für eine quadratische Matrix)

2-3737

• Transponieren einer (beliebigen) Matrix

• Invertieren einer (regulären) Matrix

• Quadrieren einer (quadratischen) Matrix

• Potenzieren einer (quadratischen) Matrix (Matrixpotenzen)

• Berechnen des Absolutwertes, Abspalten der Ganzzahl, des gebrochenen Teils,

Berechnung der maximalen Ganzzahl in jeweils allen Matrixelementen einer rellen Matrix

• Eingabe komplexer Zahlen in Matrixelemente und Verwendung von Funktionen mit

komplexen Zahlen

• Matrix-Umformungen unter Verwendung von Matrixbefehlen Für eine Matrix können maximal 999 Zeilen und 999 Spalten vorgegeben werden.

Zum Matrix-Antwortspeicher (MatAns):

• Der Rechner speichert Ergebnisse der Matrizenrechnung automatisch im Matrix-

Antwortspeicher. Beachten Sie die folgenden Punkte hinsichtlich des MatrixAntwortspeichers.

• Wenn Sie eine Matrizenrechnung ausführen, wird der aktuelle Inhalt des Matrix-

Antwortspeichers durch das neue Ergebnis ersetzt. Der frühere Inhalt wird überschrieben und kann nicht mehr zurückgerufen werden.

• Die Eingabe von Werten in eine Matrix hat keine Auswirkung auf den Inhalt des Matrix-

Antwortspeichers.

I Eingeben und Editieren von Matrizen

Drücken Sie die (MAT)-Taste, um eine Matrix-Editieranzeige (den Matrix-Editor) zu öffnen. Verwenden Sie den Matrix-Editor, um Matrizen einzugeben oder zu editieren.

None… Keine Matrix voreingestellt

•

• {DEL}/{DEL

• {DIM} ... {Vorgabe der Matrixdimensionen (Typ der Matrix)}

A}... Löscht {eine bestimmte Matrix}/{Alle Matrizen}

S Erstellen einer Matrix

Um eine Matrix zu erstellen, müssen Sie zuerst ihre Dimensionen (Typ) im Matrix-Editor definieren. Danach können Sie Werte (Matrixelemente) in die Matrix eingeben.

m s n … m (Zeile) s n (Spalte) -Matrix

S Festlegen der Dimensionen (Typ) einer Matrix

Beispiel Erstellen einer Matrix mit 2 Zeilen s 3 Spalten im mit Mat B bezeichneten

Speicherbereich:

Markieren Sie Mat B. A (DIM) (Dieser Schritt kann übersprungen werden.)

2-3838

Geben Sie die Anzahl der Zeilen ein. AU Geben Sie die Anzahl der Spalten ein. BU U

• Alle Elemente der neuen Matrix enthalten zunächst den Wert 0.

• Eine Änderung der Dimensionen einer Matrix löscht ihren aktuellen Inhalt.

• Falls neben dem Matrix-Bereichsnamen der Schriftzug „Memory ERROR“ verbleibt,

nachdem Sie die Dimensionen eingegeben haben, bedeutet dies, dass nicht genügend freier Speicherplatz für das Erstellen der gewünschten Matrix vorhanden ist.

S Eingeben von Matrixelementen

Beispiel Eingeben der folgenden Daten in die Matrix B:

1 2 3

1 2 3 4 5 6

4 5 6

Der nachfolgende Bedienungsvorgang ist eine Fortsetzung des Berechnungsbeispiels von der vorhergehenden Seite.

@UAUBU CUDUEU (Die Daten werden im Matrix-Editor jeweils

in die markierte Zelle eingegeben. Mit

jedem Drücken der U-Taste wird die

Markierung zur nächsten Zelle nach rechts

verschoben.)

• Die Matrixelemente (Zellenwerte) werden im Display bei positiven ganzen Zahlen mit bis zu

sechs Stellen und bei negativen ganzen Zahlen mit bis zu fünf Stellen (eine Stelle wird für das Minuszeichen verwendet) angezeigt. Exponentialwerte werden mit bis zu zwei Stellen für den Exponenten angezeigt. Gemeine Brüche werden nicht als Bruch angezeigt.

S Löschen von Matrizen

Sie können entweder eine bestimmte Matrix oder alle im Matrix-Speicher enthaltenen Matrizen löschen.

S Löschen einer bestimmten Matrix

1. Wenn der Matrix-Editor im Display angezeigt wird, verwenden Sie die D- und A-Tasten,

um die zu löschende Matrix zu markieren.

2. Drücken Sie (DEL).

3. Drücken Sie die (Yes)-Taste, um die Matrix zu löschen, oder die (No)-Taste, um die

Lösch-Operation abzubrechen, ohne etwas zu löschen.

2-3939

S Löschen aller Matrizen

1. Wenn der Matrix-Editor im Display angezeigt wird, drücken Sie die (DEL • A)-Taste.

2. Drücken Sie die (Yes)-Taste, um die Matrix zu löschen, oder die (No)-Taste, um die

Lösch-Operation abzubrechen, ohne etwas zu löschen.

I Operationen mit Matrixelementen (Matrixzellen)

Verfahren Sie wie folgt, um die Matrix für die Zellenoperationen vorzubereiten:

1. Wenn der Matrix-Editor im Display angezeigt wird, verwenden Sie die D- und A-Tasten,

um den Namen der zu verwendenden Matrix hervorzuheben. Durch die Eingabe des Buchstabens, der dem Matrixnamen entspricht, springen Sie zu einer bestimmten Matrix. Durch die Eingabe von beispielsweise ?G(N), springen Sie zu Mat N. Durch Drücken der Tasten (Ans) springen Sie zum aktuellen Matrix-Speicher.

2. Drücken Sie die U-Taste. In der unteren Zeile des Matrix-Editors, der nun geöffnet ist,

erscheint das Funktionsmenü mit den folgenden Positionen:

• {R-OP} ... {Zeilenoperationsmenü}

• {ROW}

• {DEL}/{INS}/{ADD} ... {Löschen}/{Einfügen}/{Hinzufügen} von Zeilen

• {COL}

• {DEL}/{INS}/{ADD} ... {Löschen}/{Einfügen}/{Hinzufügen} von Spalten

• {EDIT} ... {Editieranzeige für das markierte Element}

Alle nachfolgenden Beispiele verwenden Matrix A.

S Zeilenoperationen

Das folgende Menü erscheint, wenn Sie (R-OP) drücken, während eine aufgerufene Matrix im Display angezeigt wird.

• {Swap} ... {Vertauschen von Zeilen}

• {sRw} ... {Multiplikation eines Skalars mit der markierten Zeile}

• {sRw+} ... {Addition des skalaren Vielfachen der markierten Zeile zu einer anderen Zeile}

• {Rw+} ... {Addition der markierten Zeile zu einer anderen Zeile}

S Vertauschen zweier Zeilen

Beispiel Vertauschen der Zeilen 2 und 3 der folgenden Matrix:

Alle Bedienungsbeispiele verwenden die folgende Matrix:

1 2

Matrix A =

(R-OP)(Swap) Geben Sie die Zeilen-Nummern der zu vertauschenden

Zeilen ein. AUBUU

3 4 5 6

2-4040

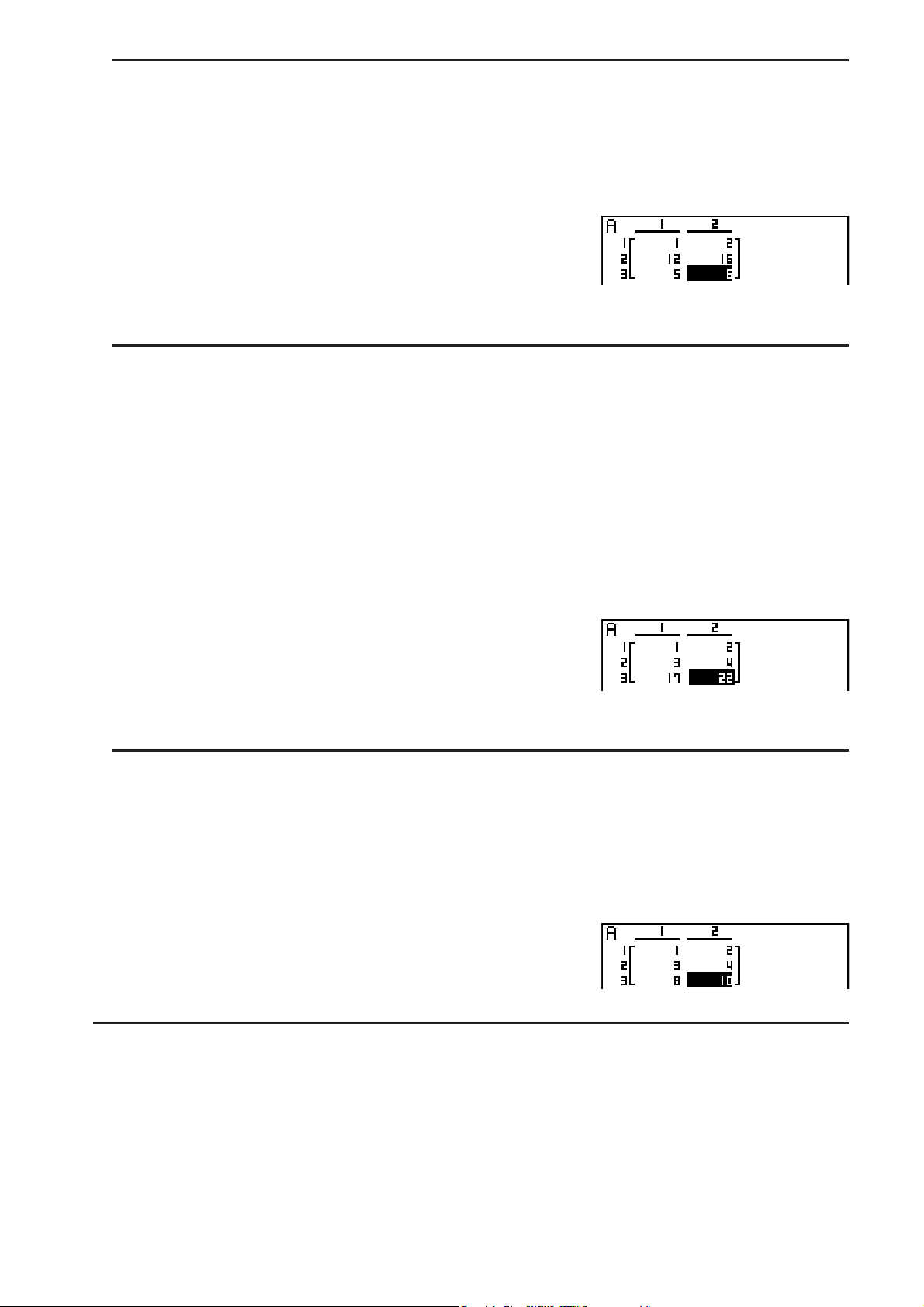
S Skalare Multiplikation einer Zeile

Beispiel Multiplizieren von Zeile 2 mit dem skalaren Faktor 4:

(R-OP)(sRw) Geben Sie den skalaren Faktor (Multiplikator)* ein. CU Geben Sie die Zeilen-Nummer ein. AUU * Es kann auch eine komplexe Zal als Multiplikator (k) eingegeben werden.

S Skalare Multiplikation einer Zeile und Addition des Ergebnisses zu einer

anderen Zeile

Beispiel Berechnen des Produkts von Zeile 2 und Faktor 4 und anschließendes

Addieren des Ergebnisses zu Zeile 3:

(R-OP)(sRw+) Geben Sie den skalaren Faktor (Multiplikator)* ein. CU Geben Sie die Nummer der Zeile, deren Vielfaches berechnet werden soll, ein. AU Geben Sie die Nummer der Zeile, zu der das Ergebnis

addiert werden soll, ein. BUU

* Es kann auch eine komplexe Zahl als Multiplikator (k) eingegeben werden.

S Addition zweier Zeilen

Beispiel Addieren der Zeile 2 zur Zeile 3:

(R-OP)(Rw+) Geben Sie die Nummer der Zeile, die addiert werden soll, ein.

AU Geben Sie die Nummer der Zeile, zu der addiert werden

soll, ein. BUU

S Zeilenoperationen

• {DEL} ... {Zeile löschen}

• {INS} ... {Zeile einfügen}

• {ADD} ... {Zeile am Ende hinzufügen}

2-4141

S Löschen einer Zeile

Beispiel Löschen der Zeile 2

(ROW)A

(DEL)

S Einfügen einer Zeile

Beispiel Einfügen einer neuen Zeile zwischen den Zeilen 1 und 2:

(ROW)A (INS)

S Anfügen einer Zeile

Beispiel Hinzufügen einer neuen Zeile unterhalb der Zeile 3:

(ROW)AA (ADD)

S Spaltenoperationen

• {DEL} ... {Spalte löschen}

• {INS} ... {Spalte einfügen}

• {ADD} ... {Spalte am Ende hinzufügen}

S Löschen einer Spalte

Beispiel Löschen der Zeile 2

(COL)C (DEL)

2-4242

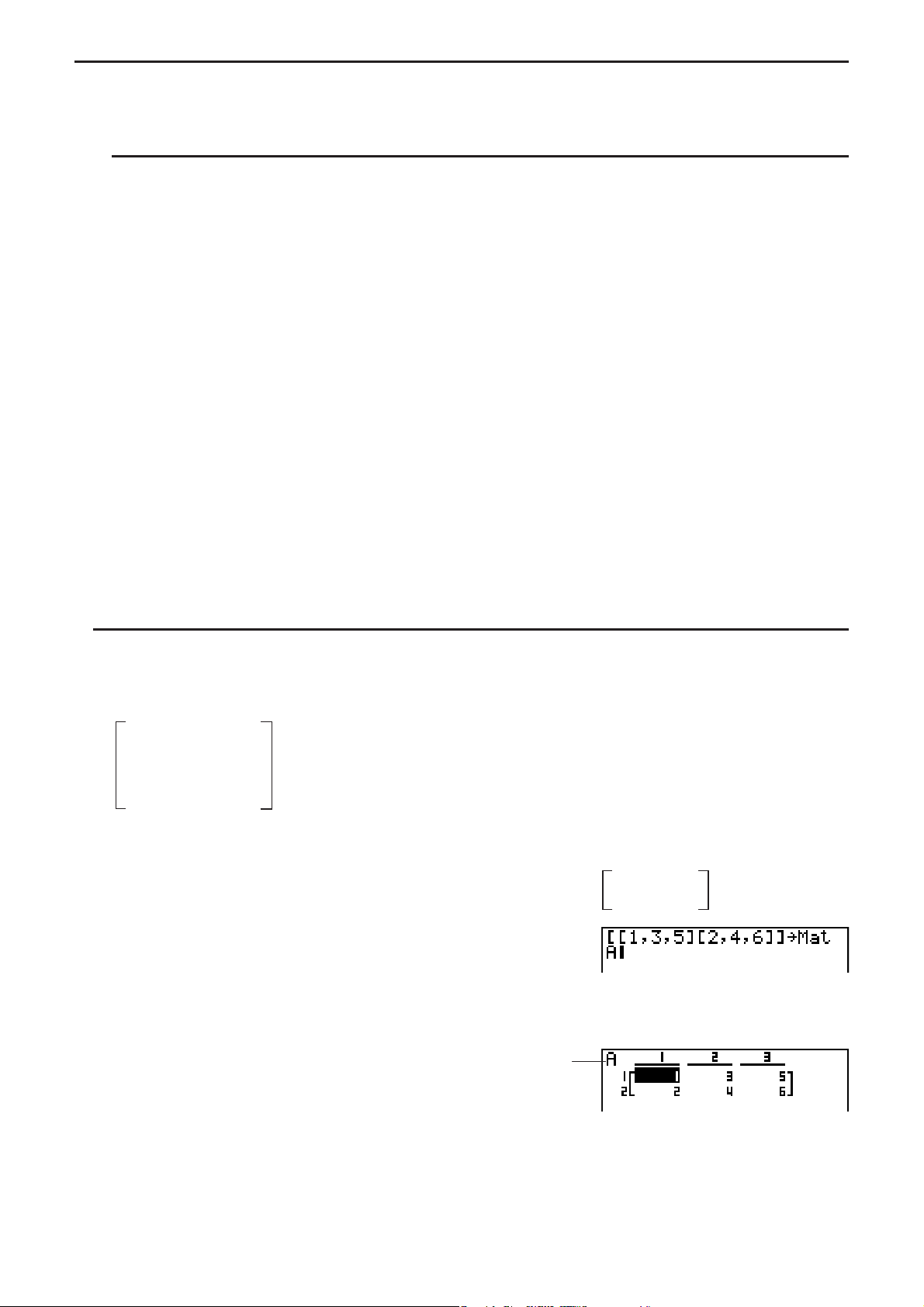
I Umformen von Matrizen unter Verwendung von Matrixbefehlen

S Anzeigen der Matrixbefehle

1. Rufen Sie das RUN • MAT-Menü aus dem Hauptmenü heraus auf.

2. Drücken Sie die *-Taste, um das Optionsmenü anzuzeigen.

3. Drücken Sie die (MAT)-Taste, um das Matrixbefehlsmenü zu öffnen.

Nachfolgend sind nur die Positionen des Matrixbefehlsmenüs beschrieben, die für das Erstellen von Matrizen und die Eingabe von Matrixdaten verwendet werden können.

• {Mat} ... {Mat-Befehl (Matrix-Auswahlbefehl)}

• {MmL} ... MatmList-Befehl (ordnet den Inhalt einer gewählten Spalte einer Listendatei zu)}

• {Aug} ... {Augment-Befehl (fügt zwei Matrizen zusammen)}

• {Iden} ... {Identity-Befehl (Eingabe einer Einheitsmatrix)}

• {Dim} ... {Dim-Befehl (Dimensionsbefehl)}

• {Fill} ... {Fill-Befehl (identische Matrixelemente eingeben)}

[OPTN]-[MAT]

• Sie können auch die Tasten A(Mat) anstelle der Tasten *(MAT)(Mat)

verwenden.

S Matrixdaten-Eingabeformat [OPTN]-[MAT]-[Mat]

Nachfolgend ist das Eingabeformat dargestellt, das Sie verwenden sollten, wenn Sie Daten zum Erstellen einer Matrix unter Verwendung des Mat-Befehls eingeben.

a11 a

a11 a a21 a

a21 a

am1 a

m Mat [Buchstabe A bis Z]

Beispiel Eingabe der folgenden Daten als Matrix A:

( [ )( [ )@BD ( ] )( [ )ACE ( ] )( ] )?*(MAT)

...

a1n

...

a1n

...

a2n

...

a2n

... a

...

= [ [a

, a12, ..., a

] [a21, a22, ..., a

] .... [a

, a

1 3 5

1 3 5 2 4 6

2 4 6

, ..., amn] ]

(Mat)?T(A)

• Der Maximalwert sowohl für

m als auch für n ist 999.

Matrixname

• Es kommt zu einer Fehlermeldung, wenn der Speicher während der Eingabe von Daten

überläuft.

• Sie können das obige Eingabeformat auch in einem Programm verwenden, das Matrixdaten

einliest.

2-4343

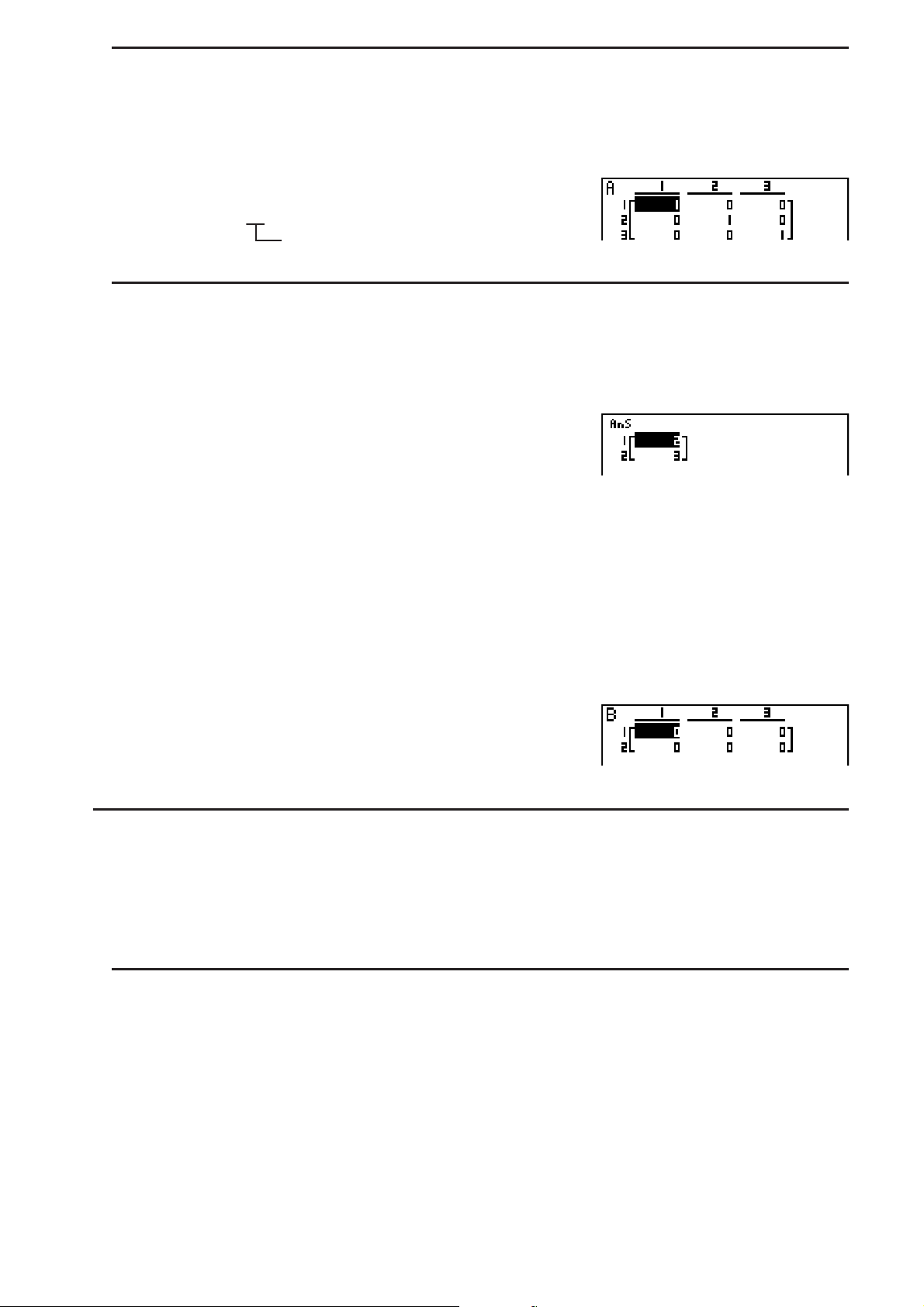
S Eingeben einer Einheitsmatrix [OPTN]-[MAT]-[Iden]

Verwenden Sie den Identity-Befehl, um eine Einheitsmatrix zu erstellen.

Beispiel Erstellen einer 3 s 3 Einheitsmatrix als Matrix A:

*(MAT)(E)(Iden) B?(E)(Mat)?T(A)U

Anzahl der Zeilen/Spalten

S Abfrage der Dimensionen einer Matrix [OPTN]-[MAT]-[Dim]

Verwenden Sie den Dim-Befehl, um die Dimensionen einer vorhandenen Matrix abzufragen.

Beispiel 1 Abfragen der Dimensionen der Matrix A

*(MAT)(E)(Dim) (E)(Mat)?T(A)U

Das Display zeigt im Listenformat an, dass die Matrix A aus zwei Zeilen und drei Spalten besteht. Da das Ergebnis des Dim-Befehls ein Listentyp-Datenwert ist, wird es im ListAns-Speicher abgelegt.

Sie können {Dim} auch verwenden, um die Dimensionen (Typ) der Matrix festzulegen.

Beispiel 2 Festlegen der Dimensionen (2, 3), d. h. 2 Zeilen und 3 Spalten, für die

Matrix B:

( H )AB( J )? *(MAT)(E)(Dim) (E)(Mat)?J(B)U

S Umformen von Matrizen unter Verwendung von Matrixbefehlen

Sie können Matrixbefehle auch verwenden, um Werte einer Matrix zuzuordnen oder Werte von einer bestehenden Matrix abzurufen, um alle Elemente einer bestehenden Matrix mit dem gleichen Wert zu belegen, um zwei Matrizen zu einer einzigen Matrix zu verbinden oder um den Inhalt einer Matrixspalte einer Listendatei zuzuordnen.

S Zuordnen von Werten zu und Aufrufen von Werten von einer bestehenden

Matrix

Verwenden Sie die folgende Syntax mit dem Mat-Befehl, um ein Element für das Zuordnen oder Abrufen eines Wertes zu beschreiben.

[OPTN]-[MAT]-[Mat]

Mat X [ X = Matrixname (A bis Z oder Ans)

m, n]

m = Zeilennummer n = Spaltennummer

2-4444

Beispiel 1 Zuordnen des Wertes 10 zu dem Element in Zeile 1, Spalte 2 der

folgenden Matrix A:

1 2

Matrix A =

@??*(MAT)(Mat) ?T(A)( F )@A ( G )U

Beispiel 2 Multiplizieren des Wertes des Elements in Zeile 2, Spalte 2 der obigen

Matrix mit 5

*(MAT)(Mat) ?T(A)( F )AA ( G )DU

3 4 5 6

S Belegen der Elemente einer Matrix mit identischen Werten und

Zusammenfügen zweier Matrizen zu einer einzigen Matrix

Verwenden Sie den Fill-Befehl, um alle Elemente einer vorhandenen Matrix mit einem identischen Wert zu belegen, oder den Augment-Befehl, um zwei vorhandene Matrizen zu einer einzigen Matrix zusammenzufügen.

[OPTN]-[MAT]-[Fill]/[Aug]

Beispiel 1 Überschreiben aller Elemente der Matrix A mit dem Wert 3.

*(MAT)(E)(Fill) B(E)(Mat)?T(A)U (Mat)?T(A)U

Beispiel 2 Zusammenfügen der zwei folgenden Matrizen zu einer neuen Matrix:

A =

*(MAT)(Aug) (Mat)?T(A) (Mat)?J(B)U

• Die beiden Matrizen, die Sie zusammenfügen möchten, müssen die gleiche Zeilenanzahl

aufweisen. Es kommt zu einer Fehlermeldung, falls Sie das Zusammenfügen zweier Matrizen versuchen, die unterschiedliche Zeilenanzahlen haben.

• Sie können den Matrix-Antwortspeicher verwenden, um das Ergebnis der obigen Matrix-

Eingabe- und Editieroperationen einer neuen Matrixvariablen zuzuweisen. Dazu verwenden Sie folgende Syntax:

1 2

B =

3 4

n, Mat

Fill ( Augment (Mat

Oben sind A, B und G bliebige Variablenbezeichnungen A bis Z und n ist ein beliebiger Wert.

Der Inhalt des Matrix-Antwortspeichers wird davon nicht beeinflusst.

)

, Mat B) m Mat

2-4545

S Zuordnen des Inhalts einer Matrixspalte zu einer Liste [OPTN]-[MAT]-[MmL]

Verwenden Sie die folgende Syntax mit dem Mat mList-Befehl, um eine Spalte einer ausgewählten Liste zuzuordnen.

Mat m List (Mat X, X = Matrixname (A bis Z)

Beispiel Zuordnen des Inhalts der Spalte 2 der Matrix A zur Liste 1:

Matrix A =

*(MAT)(MmL) (Mat)?T(A)A ?*(LIST)(List)@U (List)@U

m = Spaltennummer n = Listennummer

m) m List n

1 2 3 4 5 6

I Matrizenrechnung [OPTN]-[MAT]

Verwenden Sie das Matrixbefehlsmenü, um die folgenden Matrixoperationen auszuführen.

S Anzeigen der Matrixbefehle

1. Rufen Sie das RUN • MAT-Menü aus dem Hauptmenü heraus auf.

2. Drücken Sie die *-Taste, um das Optionsmenü anzuzeigen.

3. Drücken Sie die (MAT)-Taste, um das Matrixbefehlsmenü zu öffnen.

Nachfolgend sind nur die Matrixbefehle beschrieben, die für Matrizenarithmetik-Operationen verwendet werden.

• {Mat} ... {Mat-Befehl (Matrix-Auswahlbefehl)}

• {Det} ... {Det-Befehl (Determinantenberechnung)}

• {Trn} ... {Trn-Befehl (Befehl zum Transponieren einer Matrix)}

• {Iden} ... {Identity-Befehl (Eingabe einer Einheitsmatrix)}

• {Ref} ... {Ref-Befehl (Befehl zur Umformung in die zeilengestaffelte Stufenform)}

• {Rref} ... {Rref-Befehl (Befehl zur Umformung in die reduzierte Stufenform)}

Alle nachfolgenden Beispiele gehen davon aus, dass die Matrixdaten bereits im Speicher abgespeichert und von dort abrufbar sind.

S Matrizenarithmetik [OPTN]-[MAT]-[Mat]/[Iden]

Beispiel 1 Addition der beiden folgenden Matrizen (Matrix A und Matrix B):

A =

2 1

B =

2 3

2 3 2 1

2 1

2-4646

*(MAT)(Mat)?T(A) (Mat)?J(B)U

Beispiel 2 Multiplikation der beiden Matrizen vom Beispiel 1 (Matrix A s Matrix B)

in der angegebenen Reihenfolge:

*(MAT)(Mat)?T(A) (Mat)?J(B)U

• Die beiden Matrizen müssen die gleichen Dimensionen aufweisen, um addiert oder

subtrahiert werden zu können. Falls versucht wird, Matrizen mit unterschiedlichen Dimensionen zu addieren oder zu subtrahieren, kommt es zu einer Fehlermeldung.

• Für eine Matrizen-Multiplikation (Matrix 1 s Matrix 2) muss die Anzahl der Spalten in Matrix

1 mit der Anzahl der Zeilen in Matrix 2 übereinstimmen. Andernfalls kommt es zu einer Fehlermeldung.

S Determinante (Kennzahl einer quadratischen Matrix) [OPTN]-[MAT]-[Det]

Beispiel Berechnung der Determinante der folgenden Matrix:

1 2 3

Matrix A =

4 5 6

−1 −2 0

*(MAT)(Det)(Mat) ?T(A)U

• Determinanten können nur für quadratische Matrizen (gleiche Anzahl von Zeilen und

Spalten) berechnet werden. Falls versucht wird, die Determinante für eine nicht quadratische Matrix zu bestimmen, kommt es zu einer Fehlermeldung.

• Die Determinante einer 2 s 2-Matrix wird wie folgt berechnet:

a11a

| A | =

21a22

=a11a22–a12a

• Die Determinante einer 3 s 3-Matrix wird wie folgt berechnet:

|A| =

a11a12a a21a22a a31a32a

= a11a22a33 + a12a23a31 + a13a21a

– a

11a23a32

– a12a21a33 – a13a22a

S Transponieren einer Matrix [OPTN]-[MAT]-[Trn]

Eine Matrix wird transponiert, indem ihre Zeilen zu Spalten und ihre Spalten zu Zeilen werden.

Beispiel Transponieren der folgenden Matrix:

1 2

Matrix A =

*(MAT)(Trn)(Mat) ?T(A)U

3 4 5 6

2-4747

S Zeilengestaffelte Stufenform (Echelon-Form) [OPTN]-[MAT]-[Ref]

Dieser Befehl wendet das Gauß-Verfahren an, um die Matrix in eine Stufenform zu bringen.

Beispiel Ermitteln der Stufenform (Echelon-Form) der Matrix A:

1 2 3

Matrix A =

1 2 3 4 5 6

4 5 6

*(MAT)(E)(Ref) (E)(Mat)?T(A)U

S Reduzierte Stufenform [OPTN]-[MAT]-[Rref]

Mit diesem Befehl wird die reduzierte Stufenform einer Matrix ermittelt.

Beispiel Ermitteln der reduzierten Stufenform der Matrix A:

2 −1 3 19

Matrix A =

1 1 −5 −21

1 1 −5 −21 0 4 3 0

0 4 3 0

*(MAT)(E)(Rref) (E)(Mat)?T(A)U

• Möglicherweise liefern die Operationen zur Ermittlung der Stufenform und der reduzierten

Stufenform aufgrund von Rundungseffekten in den Kommastellen keine genauen Ergebnisse.

S Matrix-Inversion (einer regulären quadratischen Matrix) [x

Beispiel Invertieren der Matrix A:

1 2

Matrix A =

1 2 3 4

3 4

–1

]

*(MAT)(Mat) ?T(A)(

–1

• Nur reguläre quadratische Matrizen (mit einer von Null verschiedenen Determinante) können

invertiert werden. Falls das Invertieren einer nicht quadratischen oder nicht regulären Matrix versucht wird, kommt es zu einer Fehlermeldung.

• Eine Matrix mit einer Determinante von Null (singuläre Matrix) kann nicht invertiert werden.

Falls das Invertieren einer Matrix mit der Determinante 0 versucht wird, kommt es zu einer Fehlermeldung.

2-4848

• Die Rechengenauigkeit wird bei einer Matrix-Inversion mit einer Determinante nahe Null

möglicherweise beeinträchtigt.

• Für eine inverse Matrix vom Typ (2, 2) gilt die nachfolgend gezeigte Gleichheit:

A A–1 = A–1 A = E =

1 0 0 1

Nachfolgend ist die Formel aufgeführt, die verwendet wird, um für eine Matrix A vom Typ

d–b

–c a

–1

zu berechnen.

Man beachte, dass det A = ad – bc x 0 ist.

(2, 2) die inverse Matrix A

a b c d

ad – bc

A =

A–1=

S Quadrieren einer (quadratischen) Matrix [x

Beispiel Die folgende Matrix ist mit sich selbst zu multiplizieren, d. h. zu

quadrieren:

1 2

Matrix A =

*(MAT)(Mat)?T(A)VU

1 2 3 4

3 4

]

S Potenzieren einer Matrix (Matrizenpotenzen) [^]

Beispiel Die folgende quadratische Matrix ist in die dritte Potenz zu erheben:

1 2

Matrix A =

1 2 3 4

3 4

*(MAT)(Mat)?T(A) ,BU

• Beim Rechnen mit Matrizenpotenzen sind Berechnungen bis zur 32766-ten Potenz möglich.

S Bestimmung des Absolutwertes, des ganzzahligen Teils, des gebrochenen

Teils und der maximalen Ganzzahl einer Matrix

Beispiel Bestimmen des Absolutwertes bei allen Elementen der folgenden

Matrix:

1 –2

Matrix A =

1 –2 –3 4

–3 4

[OPTN]-[NUM]-[Abs]/[Frac]/[Int]/[Intg]

*(E)(NUM)(Abs) *(MAT)(Mat)?T(A)U

2-4949

S Rechnen mit komplexen Zahlen in einer Matrix

Beispiel Bestimmen des Absolutwertes bei den komplexzahligen Elementen der

folgenden Matrix:

–1 + i 1 +

Matrix D =

*(E)(NUM)(Abs) *(MAT)(Mat)?Q(D)U

• Es werden die folgenden komplexzahlige Argumente aufweisenden Funktionen in Matrizen

unterstützt:

i, Abs, Arg, Conjg, ReP, ImP, a+bi, r

Beachten Sie jedoch, dass „a+bi“ und „rQ“ im linearen Ein-/Ausgabemodus nicht

verwendet werden können.

–1 + i 1 +

1 + i –2 + 2



Hinweise zur Matrizenrechnung

• Determinanten und inverse Matrizen können aufgrund von Rundungseffekten in den

Kommastellen mit gewissen numerischen Fehlern behaftet sein.

• Matrixoperationen werden individuell für jedes Element ausgeführt, so dass die

Berechnungen sehr viel Zeit in Anspruch nehmen können.

• Die Rechengenauigkeit der angezeigten Ergebnisse für die Matrizenrechnung beträgt p1 für

die niedrigstwertige Stelle.

• Falls das Ergebnis der Matrizenrechnung zu groß ist, um in den Matrix-Antwortspeicher zu

passen, kommt es zu einer Fehlermeldung.

• Sie können folgenden Bedienablauf verwenden, um den Inhalt des Matrix-Antwortspeichers

in eine andere Matrix (oder wenn der Matrix-Antwortspeicher eine Determinante enthält, auf eine Variable) zu übertragen:

MatAns m Mat Bei der obigen Operation ist A ein beliebiger Variablenname A bis Z. Der Inhalt des Matrix-

Antwortspeichers wird durch die obige Speicher-Operation nicht beeinflusst.

9. Umrechnen von Maßeinheiten

Sie können Werte von einer Maßeinheit in eine andere umrechnen. Die Maßeinheiten sind wie nachfolgend angegeben in 11 Kategorien eingeteilt. Die Indikatoren in der Spalte „angezeigter Name“ repräsentieren den Text, der im Funktionsmenü des Rechners erscheint.

Angezeigter

Name

LENG Länge TMPR Temperatur PRES Druck

AREA Fläche VELO Geschwindigkeit ENGY

Kategorie

Angezeigter

Name

2-5050

Kategorie

Angezeigter

Name

Kategorie

Energie/ Arbeit

VLUM Volumen MASS Masse PWR Leistung

TIME Zeit FORC Kraft/Gewicht

Innerhalb einer Kategorie können Sie von einer Maßeinheit in eine andere umrechnen.

• Falls versucht wird, von einer Maßeinheit einer Kategorie (wie etwa „AREA“) in eine

Maßeinheit einer anderen Kategorie (wie etwa „TIME“) umzurechnen, kommt es zu einem Umrechnungsfehler (Conversion ERROR).

• Weitere Informationen über die Maßeinheiten, die jede Kategorie umfasst, können Sie der

„Liste der Befehle zur Umrechnung von Maßeinheiten“ (Seite 2-52) entnehmen.

I Umrechnen von Maßeinheiten [OPTN]-[CONV]

Um eine Maßeinheitenumrechnung vorzunehmen, geben Sie den Wert, der umgerechnet werden soll, und die Umrechnungsbefehle unter Verwendung der nachfolgenden Syntax ein.

{umzurechnender Wert}{Umrechnungsbefehl 1}  {Umrechnungsbefehl 2}

• Mit dem {Umrechnungsbefehl 1} legen Sie die Maßeinheit fest, aus der umgerechnet wird,

und mit dem {Umrechnungsbefehl 2} legen Sie die Maßeinheit fest, in die umgerechnet wird.

•  ist ein Befehl, der die zwei Umrechnungsbefehle verknüpft. Dieser Befehl ist unter ()

des Umrechnungsmenüs stets verfügbar.

• Der umzurechnende Wert kann eine reelle Zahl oder eine Liste, die reelle Zahlen enthält,

sein. Wenn umzurechnende Werte in eine Liste eingegeben werden (oder wenn ein Listenspeicher vorgegeben wird), erfolgt die Umrechnung für jedes Element der Liste und die Berechnungsergebnise werden im Listenformat (ListAns-Anzeige) zurückgegeben.

• Für eine komplexe Zahl kann keine Maßeinheitenumrechnung vorgenommen werden.

Auch wenn nur ein einziges Element einer Liste, für die eine Maßeinheitenumrechnung vorgesehen ist, eine komplexe Zahl enthält, kommt es zu einer Fehlermeldung.

Beispiel 1 Umrechnung von 50 cm in Zoll (Inch)

D?*(E)(CONV)*(LENG) D(cm)()(LENG)CA(in)U * fx-7400G

Beispiel 2 Umrechnung von {175, 162, 180} Zentimetern in Fuß

({)@FD@EA @G?(}) *(E)(CONV)*(AREA)A(m

II: (CONV)

) ()(AREA)B(ha)U * fx-7400G

II: (CONV)

2-5151

I Liste der Befehle zur Umrechnung von Maßeinheiten

Kat.

Angezeigter

Länge

Angezeigter

Name

Maßeinheit

Kubikzentimeter

Name

fm Fermi

Maßeinheit Kat.

Å Angstöm mL Milliliter

mm Millimeter m

cm Zentimeter in

m Meter ft

km Kilometer fl_oz(UK)

Mikrometer L Liter

Kubikmeter

Kubikzoll

Kubikfuß

Flüssigkeits-Unze (GB)

Astronomische Einheit

fl_oz(US)

Volumen

Flüssigkeit-Unze (USA)

l.y. Lichtjahr gal(US) Gallone (USA)

pc Parsec gal(UK) Gallone (GB)

Mil 1/1000 Zoll (Inch) pt Pint

Fläche

in Zoll (Inch) qt Quart

ft Fuß tsp Teelöffel

yd Yard tbsp Esslöffel

fath Faden cup Tasse

rd Rute (= 5,5 Yards)

mile Meile

ns Nanosekunden

Mikrosekunde

n mile Seemeile ms Millisekunde

ha Hektar h Stunde

Quadratzentimeter s Sekunde

Quadratmeter min Minute

Zeit

Quadratkilometer day Tag

Quadratzoll (-inch) week Woche

Quadratfuß yr Jahr

Quadratyard s-yr Siderisches Jahr

acre Morgen t-yr Tropisches Jahr

mile

Quadratmeile

2-5252

Kat.

Angezeigter

Name

Maßeinheit Kat.

Angezeigter

Name

Maßeinheit

Temperatur

Geschwindigkeit

°C Grad Celsius

Pa Pascal

K Kelvin kPa Kilopascal

°F Grad Fahrenheit mmH

°R Grad Rankine mmHg

Millimeter Wassersäule

Millimeter Quecksilbersäule

m/s Meter pro Sekunde atm Atmosphäre

km/h Kilometer pro Stunde inH

Druck

knot Knoten inHg

ft/s

Fuß pro Sekunde (Foot per Second)

lbf/in

Zoll Wassersäule (Inch of water)

Zoll Quecksilbersäule (Inch of Mercury)

Pfund pro Quadratzoll (Pound per Square Inch)

mile/h Meilen pro Stunde bar Bar

u Atommasseneinheit kgf/cm

Kilopond pro Quadratzentimeter

Masse

Kraft/Gewicht

mg Milligramm

eV Elektronenvolt

g Gramm J Joule

kg Kilogramm cal

mton Tonne cal

oz Avoirdupois-Unze cal

lb Avoirdupois-Pfund kcal

slug Slug kcal

ton(short)

ton(long)

Amerikanische Tonne (2000 lbm)

Britische Tonne (2240 lbm)

Energie/Arbeit

kcal

l-atm Literatmosphäre

Kalorie

Kalorie (15°C)

Kalorie

Kilokalorie

Kilokalorie (15°C)

Kilokalorie

N Newton kW•h Kilowattstunde

lbf

tonf

Pfund als Einheit der Kraft

Tonne als Einheit der Kraft

•

lbf Foot-pound

Btu British Thermal Unit

dyne Dyn erg Erg

kgf Kilopond kgf

2-5353

•

m Kilopondmeter

Kat.

Angezeigter

Name

Maßeinheit

W Watt

/s Kalorien pro Sekunde

cal

hp Pferdestärke(n)

Foot-pound pro

•

Leistung

lbf/s

Sekunde (Foot-pound per Second)

British Thermal Unit

Btu/min

pro Minute (British thermal unit per minute)

Quelle: NIST Special Publication 811 (1995)

2-5454

Kapitel 3 Listenoperationen

Eine Liste ist ein Speicherplatz für eine Vielzahl von Datenpositionen. Der Rechner gestattet die Speicherung von bis zu 26 Listen in einer einzigen Datei, und Sie können bis zu sechs derartiger Listen-Dateien im Speicher abspeichern. Listen können danach für arithmetische, statistische oder Matrix-Berechnungen sowie für grafische Darstellungen verwendet werden.

Elementnummer Anzeigebereich Element Spalte

List 1 List 2 List 3 List 4 List 5 List 26

SUB

1 2 37 2 75 6 0 0

2 37 2 75 6 0 0 3 21 4 122 2.1 0 0

3 21 4 122 2.1 0 0 4 69 8 87 4.4 2 0

4 69 8 87 4.4 2 0 5 40 16 298 3 0 0

5 40 16 298 3 0 0 648 32 48 6.8 3 0

648 32 48 6.8 3 0 7 93 64 338 2 9 0

7 93 64 338 2 9 0 8 30 128 49 8.7 0 0

8 30 128 49 8.7 0 0

•

• •••••

56 1 107 3.5 4 0

••••••

•

Listenname Untername

Zeile

1. Eingabe in eine Liste und Editieren einer Liste

Wenn Sie das STAT-Menü aufrufen, erscheint zuerst der Listen-Editor. Sie können den Listen-Editor für die Eingabe der Daten in eine Liste verwenden und verschiedene andere Listendatenvorgänge ausführen.

S Einzel-Eingabe der Listenelemente

Verwenden Sie die Cursortasten, um die Markierung auf den zu wählenden Listennamen oder die zu wählende Zelle zu verschieben. Achten Sie darauf, dass A die Markierung nicht auf eine Zelle verschiebt, die keinen Wert enthält.

Die Anzeige rollt automatisch, wenn die Markierung am Rand der Anzeige positioniert wird. Das folgende Beispiel beginnt damit, dass die Markierung auf dem 1. Element der Liste 1

steht.

1. Geben Sie einen Wert ein und drücken Sie die U-Taste,

um den Wert in der Liste abzuspeichern.

• Die Markierung wird für die Eingabe automatisch nach unten zum nächsten Element verschoben.

2. Geben Sie den Wert 4 als zweites Element und die Summe 2 + 3 als nächstes Element ein.

CUABU

3-11

• Sie können als Listen-Element auch den Wert eines Terms oder eine komplexe Zahl

eingeben.

• Sie können bis zu 999 Elemente in eine einzige Liste eingeben.

S Listenweise Eingabe einer Folge von Werten

1. Verwenden Sie die Cursortasten, um die Markierung auf eine andere Liste zu verschieben.

2. Drücken Sie die Tasten ( { ) und geben Sie danach die gewünschten Werte ein, wobei die -Taste zwischen den einzelnen Elementen zu drücken ist. Drücken Sie die Tasten ( } ), nachdem Sie den letzten Wert eingegeben haben.

( { )EFG( } )

3. Drücken Sie die U-Taste, um alle Werte in der Liste abzuspeichern.

• Denken Sie daran, dass das Komma die Elemente einer Folge trennt, jedoch nach dem

letzten Element ist kein Komma einzugeben. Richtig: {34, 53, 78} Falsch: {34, 53, 78,}

Sie können auch Listenarithmetik betreiben, d.h. Listennamen innerhalb eines mathematischen Terms verwenden, um die Element einer neuen Lste zu erzeugen. Das folgende Beispiel zeigt, wie die Werte in den einzelnen Zeilen der Liste 1 und Liste 2 addiert und die Summe der Listen als Liste 3 abgespeichert wird.

1. Verwenden Sie die Cursortasten, um die Markierung

auf den Namen der Liste zu verschieben, in die das Rechenergebnis eingegeben werden soll.

2. Drücken Sie die *-Taste und geben Sie den Ausdruck

ein.

*(LIST)(List)@ *(LIST)(List)AU

• Sie können auch die Tasten @(List) anstelle der Tasten *(LIST)(List) drücken.

I Editieren von Listenwerten

S Ändern eines Zellwertes

Verwenden Sie die Cursortasten, um die Markierung auf das Element zu verschieben, dessen

3-22

Wert Sie ändern möchten. Geben Sie den neuen Wert ein und drücken Sie die U-Taste, um den alten Wert mit dem neuen Wert zu überschreiben.

S Editieren eines Elements

1. Verwenden Sie die Cursortasten, um die Markierung auf das Element zu verschieben,

dessen Inhalt Sie editieren möchten.

2. Drücken Sie die Tasten (E)(EDIT).

3. Nehmen Sie die gewünschten Änderungen vor.

S Löschen eines Elements

1. Verwenden Sie die Cursortasten, um die Markierung auf das Element zu verschieben, das

Sie löschen möchten.

2. Drücken Sie (E)(DEL), um das markierte Element zu löschen und alle darunter

liegenden Werte nach oben zu verschieben.

• Die Löschoperation für Elemente beeinflusst nicht die Elemente in anderen Listen. Falls

die Daten in der Liste, deren Elemente Sie löschen, in Zusammenhang mit den Daten in

benachbarten Listen stehen, kann es durch das Löschen eines Elementes dazu kommen,

dass verbundene Listen nicht mehr richtig zugeordnet sind.

S Löschen aller Elemente in einer Liste

Verwenden Sie das folgende Verfahren, um alle Daten in einer Liste zu löschen.

1. Verwenden Sie die Cursortasten, um die Markierung auf ein beliebiges Element der Liste zu

verschieben, deren Inhalt Sie komplett löschen möchten.

2. Drücken Sie (E)(DEL

3. Drücken Sie (Yes), um alle Elemente in der gewählten Liste zu löschen, oder (No),

um die Löschoperation abzubrechen, ohne etwas zu löschen.

•

A), wodurch eine Bestätigungsmeldung im Display erscheint.

S Einfügen eines neuen Elements

1. Verwenden Sie die Cursortasten, um die Markierung in die Position zu verschieben, vor der

Sie ein neues Element einfügen möchten.

2. Drücken Sie (E)(INS), um ein neues Element einzufügen, das zunächst den Wert 0

enthält. Dabei werden die folgenden Elemente nach unten verschoben.

• Die Element-Einfügeoperation beeinflusst nicht die Elemente in anderen Listen. Falls

die Daten in der Liste, in die ein neues Element eingefügt wurde, in einem bestimmten

Zusammenhang mit den Daten in benachbarten Listen stehen, kann das Einfügen eines

neuen Elementes dazu führen, dass die verbundenen Listen nicht mehr richtig zugeordnet

sind.

I Benennung einer Liste

Sie können List 1 bis List 26 „Unternamen“ mit jeweils bis zu acht Byte zuordnen.

S Benennen einer Liste

1. Auf der Einstellanzeige heben Sie „Sub Name“ hervor, und drücken Sie danach

(On)).

3-33

2. Verwenden Sie die Cursortasten, um die Hervorhebung an die SUB-Zelle der neu zu

benennenden Liste zu verschieben.

3. Tippen Sie den Namen ein, und drücken Sie danach U.

• Um einen Namen unter Verwendung der alphabetischen Buchstaben einzutippen, drücken Sie ?, um auf den ALPHA-LOCK-Modus zu schalten.

Beispiel: YEAR

(Y)A(E)T(A)E(R)U

• Mit dem nachfolgenden Bedienungsvorgang können Sie einen Unternamen in dem

•

RUN

MAT (oder RUN)-Menü anzeigen.

@(List)

n = Listennummer von 1 bis 26)

(

n( [ )?( ] )U

• Obwohl Sie bis zu acht Byte für den Unternamen eingeben können, werden nur die innerhalb die Zelle des Listen-Editors passenden Zeichen angezeigt.

• Die SUB-Zelle des Listen-Editors wird nicht angezeigt, wenn Sie „Off“ (Aus) für „Sub Name“ (Untername) in der Einstellanzeige gewählt haben.

I Sortieren von Listenwerten

Sie können die Elemente innerhalb der Listen entweder nach aufsteigender oder abfallender Größenordnung sortieren. Die Markierung der zu sortierenden Liste kann dabei auf jedem beliebigen Element der Liste positioniert sein.

S Sortieren einer einzelnen Liste

Reihenfolge der Elemente der Vorrangliste in aufsteigender Größenordnung

•

1. Während die Dateilistenanzeige angezeigt wird, drücken Sie (E)(TOOL)(SRT

2. Es erscheint die Eingabemitteilung „How Many Lists?:“, um Sie zu fragen, wie viele Listen

Sie sortieren möchten. Geben Sie hier 1 ein, da ja nur eine Liste sortiert werden soll.

3. Als Antwort auf die Eingabemitteilung „Select List List No:“ geben Sie nun die Nummer der

Liste ein, die Sie sortieren möchten.

3-44

A).

Reihenfolge der Listenelemente in abfallender Größenordnung

Verwenden Sie das gleiche Verfahren wie für das Sortieren nach aufsteigender Größenordnung. Der einzige Unterschied besteht darin, dass Sie die (SRT

•

anstelle der (SRT

A)-Taste drücken müssen.

•

D)-Taste

S Sortieren von mehreren Listen

Sie können mehrere Listen für das Sortieren verknüpfen, so dass deren Elemente beim Umsortieren in Zuordnung mit der Sortierung einer Basisliste verbleiben. Die Elemente der Vorrangliste können entweder nach aufsteigender oder abfallender Größenordnung sortiert werden. Die Elemente der mit der Vorrangliste verbundenen Listen werden automatisch so angeordnet, dass die ursprüngliche zeilenweise Zuordnung der Elemente erhalten bleibt.

Reihenfolge der Elemente der Vorrangliste in aufsteigender Größenordnung

1. Während die Dateilistenanzeige angezeigt wird, drücken Sie (E)(TOOL)(SRT

2. Es erscheint die Eingabemitteilung „How Many Lists?:“, um Sie zu fragen, wie viele Listen

Sie sortieren möchten. Die X-Liste soll die Vorrangliste sein, die Y-Liste ist durch die Datenpaare der X-Liste zugeordnet.

•

A).

3. Als Antwort auf die Eingabemitteilung „Select Base List List No: “ geben Sie nun die

Listen-Nummer der Vorrangliste ein, die Sie nach aufsteigender Größenordnung sortieren möchten. Hier soll dies die Liste 1 sein.

4. Als Antwort auf die Eingabemitteilung „Select Second List List No:“ geben Sie die Listen-

Nummer der Liste ein, die mit der Vorrangliste verknüpft ist. Hier soll dies die Liste 2 sein.

Reihenfolge der Listenelemente in abfallender Größenordnung

Verwenden Sie das gleiche Verfahren wie für das Sortieren nach aufsteigender

•

Größenordnung. Der einzige Unterschied besteht darin, dass Sie die (SRT anstelle der (SRT

•

A)-Taste drücken müssen.

D)-Taste

• Sie können eine Zahl von 1 bis 6 als Anzahl der zu sortierenden Listen angeben.

• Falls Sie eine Liste mehr als einmal für eine einzige Sortieroperation auswählen, kommt es zu einer Fehlermeldung.

Es kommt auch zu einer Fehlermeldung, wenn die für das Sortieren ausgewählten Listen

nicht die gleiche Anzahl von Elementen besitzen, also keine zeilenweise Zuordnung bestehen kann.

2. Operationen mit Listendaten

Listendaten können in arithmetischen Berechnungen und Funktionsberechnungen verwendet werden. Zusätzlich machen verschiedene Listendaten-Befehle das Rechnen mit Listendaten schnell und einfach.

Sie können die Listendaten-Befehle im RUN •

PRGM-Menü verwenden.

MAT- (oder RUN-), STAT-, TABLE-, EQUA- und

3-55

Casio FX-9860GII, FX-9860G SD, FX-9860G AU, FX-9750GII, FX-9860GII SD User Manual [de]

Specifications and Main Features

Frequently Asked Questions

User Manual

Inhalt

Kapitel 1 Grundlegende Operationen

1. Tastenanordnung

2. Display

3. Eingabe/Editieren von Berechnungsformeln

4. Verwendung des Math-Ein-/Ausgabemodus

5. Optionsmenü (OPTN)

6. Variablendatenmenü (VARS)

7. Programmmenü (PRGM)

8. Zugeordnetes SET-UP-Menü (Voreinstellungen)

Kapitel 2 Manuelle Berechnungen

1. Grundrechenarten

2. Spezielle Taschenrechnerfunktionen

3. Festlegung des Winkelmodus und des Anzeigeformats (SET UP)

4. Funktionsberechnungen

5. Numerische Berechnungen

6. Rechnen mit komplexen Zahlen

8. Matrizenrechnung

9. Umrechnen von Maßeinheiten

Kapitel 3 Listenoperationen

1. Eingabe in eine Liste und Editieren einer Liste

2. Operationen mit Listendaten