Texas Instruments TI-Nspire Reference Guide
Reference Guide
This guidebook applies to TI-Nspire™ software version 3.0. To obtain the
latest version of the documentation, go to education.ti.com/guides.
Important Information
Except as otherwise expressly stated in the License that accompanies a
program, Texas Instruments makes no warranty, either express or
implied, including but not limited to any implied warranties of
merchantability and fitness for a particular purpose, regarding any
programs or book materials and makes such materials available solely on
an "as-is" basis. In no event shall Texas Instruments be liable to anyone
for special, collateral, incidental, or consequential damages in connection
with or arising out of the purchase or use of these materials, and the sole
and exclusive liability of Texas Instruments, regardless of the form of
action, shall not exceed the amount set forth in the license for the
program. Moreover, Texas Instruments shall not be liable for any claim of
any kind whatsoever against the use of these materials by any other
party.
License
Please see the complete license installed in C:\Program Files\TI
Education\TI-Nspire.
© 2006 - 2011 Texas Instruments Incorporated
ii
Contents
Expression templates
Fraction template ........................................ 1
Exponent template ...................................... 1
Square root template .................................. 1
Nth root template ........................................1
e exponent template ................................... 2
Log template ................................................ 2
Piecewise template (2-piece) .......................2
Piecewise template (N-piece) ......................2
System of 2 equations template ................. 3
System of N equations template .................3
Absolute value template .............................3
dd°mm’ss.ss’’ template ................................3
Matrix template (2 x 2) ................................3
Matrix template (1 x 2) ................................4
Matrix template (2 x 1) ................................4
Matrix template (m x n) .............................. 4
Sum template (G) ......................................... 4
Product template (Π) ................................... 4
First derivative template ............................. 5
Second derivative template ........................ 5
Definite integral template ..........................5
Alphabetical listing
A
abs() .............................................................. 6
amortTbl() .................................................... 6
and ................................................................ 6
angle() ..........................................................7
ANOVA .........................................................7
ANOVA2way ................................................ 8
Ans ................................................................9
approx() ......................................................10
4approxFraction() ....................................... 10
approxRational() ........................................ 10
arccos() ........................................................10
arccosh() ..................................................... 10
arccot() ........................................................10
arccoth() ..................................................... 11
arccsc() ........................................................ 11
arccsch() ......................................................11
arcsec() ........................................................ 11
arcsech() ......................................................11
arcsin() ........................................................11
arcsinh() ......................................................11
arctan() .......................................................11
arctanh() ..................................................... 11
augment() ...................................................11
avgRC() ....................................................... 12
B
bal() .............................................................12
4Base2 .........................................................12
4Base10 .......................................................13
4Base16 .......................................................14
binomCdf() ................................................. 14
binomPdf() ................................................. 14
C
ceiling() ...................................................... 14
centralDiff() ............................................... 15
char() .......................................................... 15
2
c
2way ........................................................ 15
2
Cdf() ........................................................ 16
c
2
GOF ......................................................... 16
c
2
Pdf() ........................................................ 16
c
ClearAZ ....................................................... 16
ClrErr .......................................................... 17
colAugment() ............................................. 17
colDim() ...................................................... 17
colNorm() ................................................... 17
completeSquare() ...................................... 18
conj() .......................................................... 18
constructMat() ........................................... 18
CopyVar ...................................................... 18
corrMat() .................................................... 19
cos() ............................................................ 19
cos/() .......................................................... 20
cosh() .......................................................... 21
cosh/() ........................................................ 21
cot() ............................................................ 21
cot/() .......................................................... 22
coth() .......................................................... 22
coth/() ........................................................ 22
count() ........................................................ 22
countif() ..................................................... 23
cPolyRoots() ............................................... 23
crossP() ....................................................... 23
csc() ............................................................. 24
csc/() ........................................................... 24
csch() ........................................................... 24
csch/() ......................................................... 24
CubicReg .................................................... 25
cumulativeSum() ........................................ 25
Cycle ........................................................... 26
4Cylind ........................................................ 26
D
dbd() ........................................................... 26
4DD ............................................................. 27
4Decimal ..................................................... 27
Define ......................................................... 27
Define LibPriv ............................................ 28
Define LibPub ............................................ 28
deltaList() ................................................... 29
DelVar ........................................................ 29
delVoid() .................................................... 29
det() ............................................................ 29
diag() .......................................................... 30
dim() ........................................................... 30
Disp ............................................................. 30
4DMS ........................................................... 31
dotP() .......................................................... 31
E
e^() ............................................................. 31
eff() ............................................................. 32
iii
eigVc() .........................................................32
eigVl() .........................................................32
Else ..............................................................32
ElseIf ............................................................33
EndFor .........................................................33
EndFunc ......................................................33
EndIf ............................................................33
EndLoop ...................................................... 33
EndPrgm ..................................................... 33
EndTry .........................................................33
EndWhile ....................................................33
euler() .........................................................34
Exit ..............................................................34
exp() ............................................................35
expr() ...........................................................35
ExpReg ........................................................35
F
factor() ........................................................36
FCdf() ..........................................................36
Fill ................................................................36
FiveNumSummary ...................................... 37
floor() ..........................................................37
For ...............................................................38
format() ......................................................38
fPart() ..........................................................38
FPdf() ..........................................................38
freqTable4list() ............................................39
frequency() .................................................39
FTest_2Samp .............................................. 39
Func .............................................................40
G
gcd() ............................................................40
geomCdf() ...................................................41
geomPdf() ...................................................41
getDenom() ................................................ 41
getLangInfo() ............................................. 41
getLockInfo() ..............................................42
getMode() ...................................................42
getNum() .................................................... 43
getType() ....................................................43
getVarInfo() ................................................43
Goto ............................................................44
4Grad ...........................................................44
I
identity() .....................................................45
If ..................................................................45
ifFn() ............................................................46
imag() ..........................................................46
Indirection .................................................. 47
inString() .....................................................47
int() .............................................................47
intDiv() ........................................................47
interpolate() ...............................................48
2
() ......................................................... 48
invc
invF() ...........................................................48
invNorm() ....................................................48
invt() ............................................................48
iPart() ..........................................................49
irr() ..............................................................49
isPrime() ......................................................49
isVoid() ....................................................... 49
L
Lbl ............................................................... 50
lcm() ............................................................ 50
left() ............................................................ 50
libShortcut() ............................................... 51
LinRegBx ..................................................... 51
LinRegMx ................................................... 52
LinRegtIntervals ......................................... 52
LinRegtTest ................................................ 54
linSolve() ..................................................... 55
@List() .......................................................... 55
list4mat() ..................................................... 55
ln() .............................................................. 55
LnReg .......................................................... 56
Local ........................................................... 57
Lock ............................................................ 57
log() ............................................................ 58
Logistic ....................................................... 58
LogisticD ..................................................... 59
Loop ............................................................ 60
LU ................................................................ 60
M
mat4list() ..................................................... 60
max() ........................................................... 61
mean() ........................................................ 61
median() ..................................................... 61
MedMed ..................................................... 62
mid() ........................................................... 62
min() ........................................................... 63
mirr() ........................................................... 63
mod() .......................................................... 64
mRow() ....................................................... 64
mRowAdd() ................................................ 64
MultReg ...................................................... 64
MultRegIntervals ....................................... 65
MultRegTests ............................................. 65
N
nCr() ............................................................ 66
nDerivative() .............................................. 67
newList() ..................................................... 67
newMat() .................................................... 67
nfMax() ....................................................... 67
nfMin() ....................................................... 68
nInt() ........................................................... 68
nom() .......................................................... 68
norm() ......................................................... 68
normCdf() ................................................... 69
normPdf() ................................................... 69
not .............................................................. 69
nPr() ............................................................ 69
npv() ........................................................... 70
nSolve() ....................................................... 70
O
OneVar ....................................................... 71
or ................................................................ 72
ord() ............................................................ 72
P
iv
P4Rx() ...........................................................72
P4Ry() ...........................................................73
PassErr .........................................................73
piecewise() ..................................................73
poissCdf() .................................................... 73
poissPdf() ....................................................73
4Polar .......................................................... 74
polyEval() .................................................... 74
polyRoots() ................................................. 74
PowerReg ...................................................75
Prgm ...........................................................76
prodSeq() .................................................... 76
Product (PI) ................................................. 76
product() ..................................................... 76
propFrac() ................................................... 77
Q
QR ............................................................... 77
QuadReg .....................................................78
QuartReg ....................................................78
R
R4Pq() ..........................................................79
R4Pr() ...........................................................79
4Rad .............................................................80
rand() ..........................................................80
randBin() ..................................................... 80
randInt() ..................................................... 80
randMat() ................................................... 80
randNorm() ................................................. 80
randPoly() ................................................... 81
randSamp() ................................................. 81
RandSeed .................................................... 81
real() ........................................................... 81
4Rect ............................................................81
ref() ............................................................. 82
remain() ......................................................83
Request ....................................................... 83
RequestStr .................................................. 84
Return .........................................................84
right() .......................................................... 84
rk23() .......................................................... 85
root() ...........................................................85
rotate() .......................................................85
round() ........................................................86
rowAdd() ....................................................86
rowDim() ....................................................87
rowNorm() ..................................................87
rowSwap() ..................................................87
rref() ............................................................87
S
sec() ............................................................. 88
sec/() ...........................................................88
sech() ...........................................................88
sech/() ......................................................... 88
seq() ............................................................89
seqGen() .....................................................89
seqn() ..........................................................90
setMode() ................................................... 90
shift() ..........................................................91
sign() ...........................................................92
simult() ........................................................ 92
sin() ............................................................. 93
sin/() ........................................................... 93
sinh() ........................................................... 94
sinh/() ......................................................... 94
SinReg ........................................................ 95
SortA .......................................................... 95
SortD .......................................................... 96
4Sphere ....................................................... 96
sqrt() ........................................................... 96
stat.results .................................................. 97
stat.values .................................................. 98
stDevPop() .................................................. 98
stDevSamp() ............................................... 98
Stop ............................................................ 99
Store ........................................................... 99
string() ........................................................ 99
subMat() ..................................................... 99
Sum (Sigma) ............................................... 99
sum() ........................................................... 99
sumIf() ...................................................... 100
sumSeq() ................................................... 100
system() .................................................... 100
T
T (transpose) ............................................ 100
tan() .......................................................... 101
tan/() ........................................................ 101
tanh() ........................................................ 102
tanh/() ...................................................... 102
tCdf() ........................................................ 103
Text ........................................................... 103
Then ......................................................... 103
tInterval .................................................... 103
tInterval_2Samp ....................................... 104
tPdf() ........................................................ 104
trace() ....................................................... 104
Try ............................................................. 105
tTest .......................................................... 105
tTest_2Samp ............................................. 106
tvmFV() ..................................................... 106
tvmI() ........................................................ 107
tvmN() ...................................................... 107
tvmPmt() .................................................. 107
tvmPV() ..................................................... 107
TwoVar ..................................................... 108
U
unitV() ...................................................... 109
unLock ...................................................... 109
V
varPop() .................................................... 109
varSamp() ................................................. 110
W
warnCodes() ............................................. 110
when() ...................................................... 110
While ........................................................ 111
“With” ...................................................... 111
X
xor ............................................................ 111
v
Z
zInterval ....................................................112
zInterval_1Prop ........................................112
zInterval_2Prop ........................................113
zInterval_2Samp .......................................113
zTest ..........................................................114
zTest_1Prop .............................................. 114
zTest_2Prop .............................................. 115
zTest_2Samp .............................................115
Symbols
+ (add) .......................................................116
N(subtract) ................................................116
·(multiply) ............................................... 117
à (divide) ...................................................117
^ (power) .................................................. 118
2
(square) ................................................118
x
.+ (dot add) ...............................................119
.. (dot subt.) ..............................................119
·(dot mult.) .............................................119
.
. / (dot divide) ...........................................119
.^ (dot power) ..........................................119
L(negate) ...................................................120
% (percent) ...............................................120
= (equal) ....................................................121
ƒ (not equal) .............................................121
< (less than) ..............................................121
{ (less or equal) ........................................122
> (greater than) ........................................122
| (greater or equal) ..................................122
! (factorial) ................................................122
& (append) ................................................122
d() (derivative) ..........................................123
‰() (integral) ..............................................123
‡() (square root) .......................................123
Π() (prodSeq) ............................................124
G() (sumSeq) ..............................................124
GInt() .........................................................125
GPrn() ........................................................ 125
# (indirection) .......................................... 126
E (scientific notation) ............................... 126
g (gradian) ............................................... 126
R(radian) .................................................... 126
¡ (degree) ................................................. 127
¡, ', '' (degree/minute/second) ................. 127
± (angle) .................................................. 127
_ (underscore as an empty element) ...... 127
10^() .......................................................... 128
^/(reciprocal) ........................................... 128
| (“with”) .................................................. 128
& (store) ................................................... 129
:= (assign) ................................................. 129
© (comment) ............................................ 129
0b, 0h ........................................................ 130
Empty (void) elements
Calculations involving void
elements ................................................... 131
List arguments containing void
elements ................................................... 131
Shortcuts for entering math
expressions
EOS™ (Equation Operating
System) hierarchy
Error codes and messages
Warning codes and messages
Texas Instruments Support and
Service
vi
TI-Nspire™
This guide lists the templates, functions, commands, and operators available for evaluating
math expressions.
Reference Guide
Expression templates
Expression templates give you an easy way to enter math expressions in standard mathematical
notation. When you insert a template, it appears on the entry line with small blocks at positions
where you can enter elements. A cursor shows which element you can enter.
Use the arrow keys or press
or expression for the element. Press
Fraction template
Note: See also / (divide), page 117.
Exponent template
Note: Type the first value, press l, and then type the exponent.
To return the cursor to the baseline, press right arrow (¢).
Note: See also ^ (power), page 118.
Square root template
Note: See also ‡() (square root), page 123.
Nth root template
e to move the cursor to each element’s position, and type a value
· or /· to evaluate the expression.
/p keys
Example:
l key
Example:
/q keys
Example:
/l keys
Example:
Note: See also root(), page 85.
TI-Nspire™ Reference Guide 1
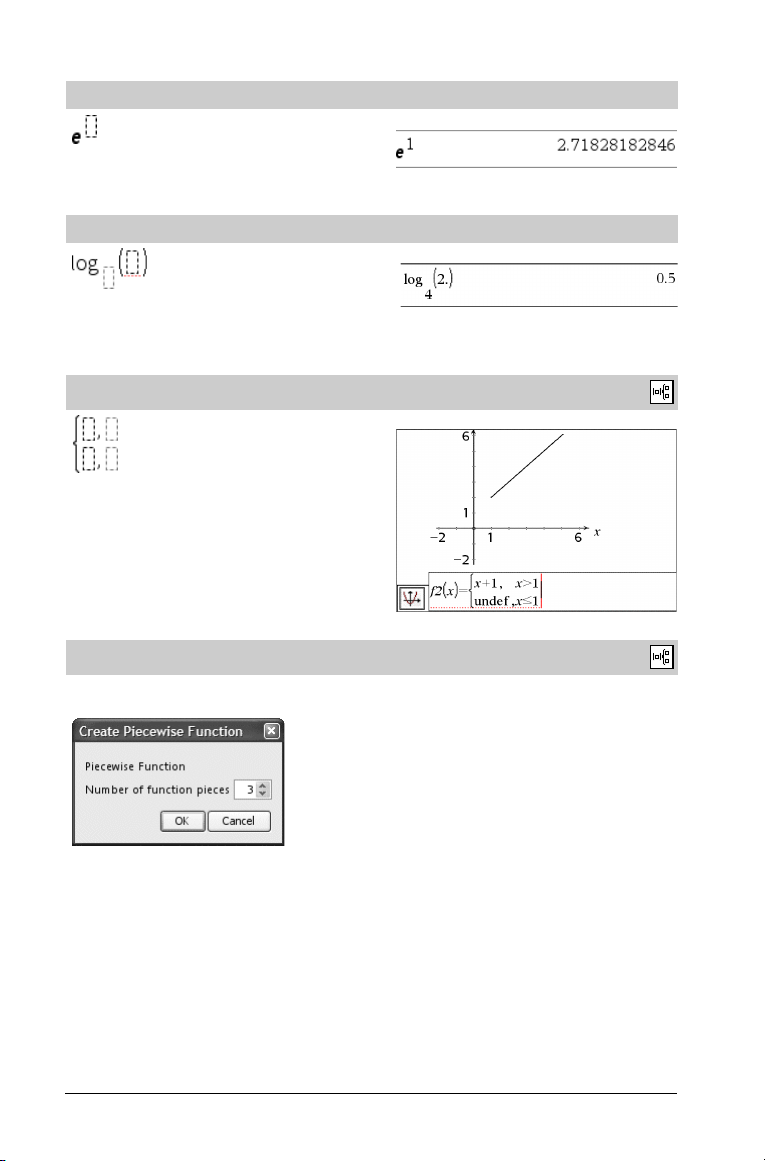
e exponent template
Natural exponential e raised to a power
Note: See also e^(), page 31.
u keys
Example:
Log template
Calculates log to a specified base. For a default of base 10, omit the
base.
Note: See also log(), page 58.
Piecewise template (2-piece)
Lets you create expressions and conditions for a two-piece piecewise
function. To add a piece, click in the template and repeat the
template.
Note: See also piecewise(), page 73.
Piecewise template (N-piece)
Lets you create expressions and conditions for an N-piece piecewise
function. Prompts for N.
Example:
Catalog >
Example:
Catalog >
Example:
See the example for Piecewise template (2-piece).
/s key
Note: See also piecewise(), page 73.
2 TI-Nspire™ Reference Guide
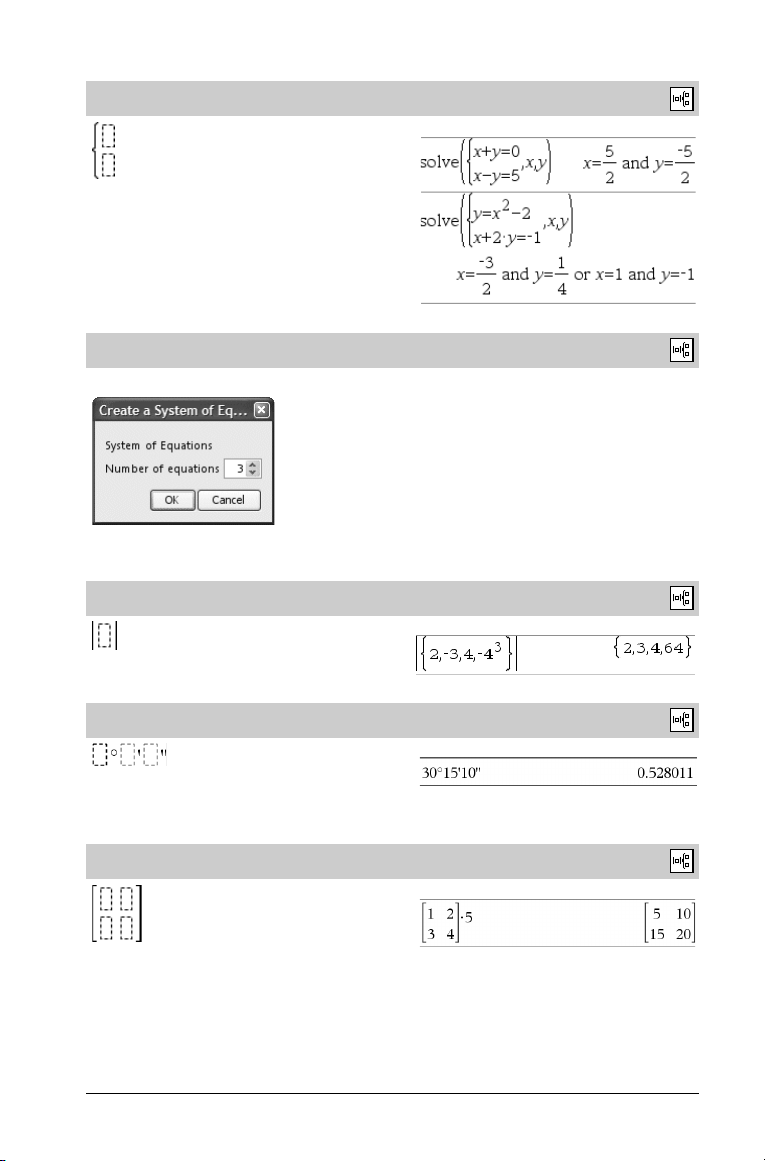
System of 2 equations template
Creates a system of two linear equations. To add a r ow to an existing
system, click in the template and repeat the template.
Note: See also system(), page 100.
Catalog >
Example:
System of N equations template
Lets you create a system of N linear equations. Prompts for N.
Note: See also system(), page 100.
Absolute value template
Note: See also abs(), page 6.
dd°mm’ss.ss’’ template
Lets you enter angles in dd°mm’ss.ss’’ format, where dd is the
number of decimal degrees, mm is the number of minutes, an d ss.ss
is the number of seconds.
Matrix template (2 x 2)
Catalog >
Example:
See the example for System of equations template (2-equation).
Catalog >
Example:
Catalog >
Example:
Catalog >
Example:
Creates a 2 x 2 matrix.
TI-Nspire™ Reference Guide 3
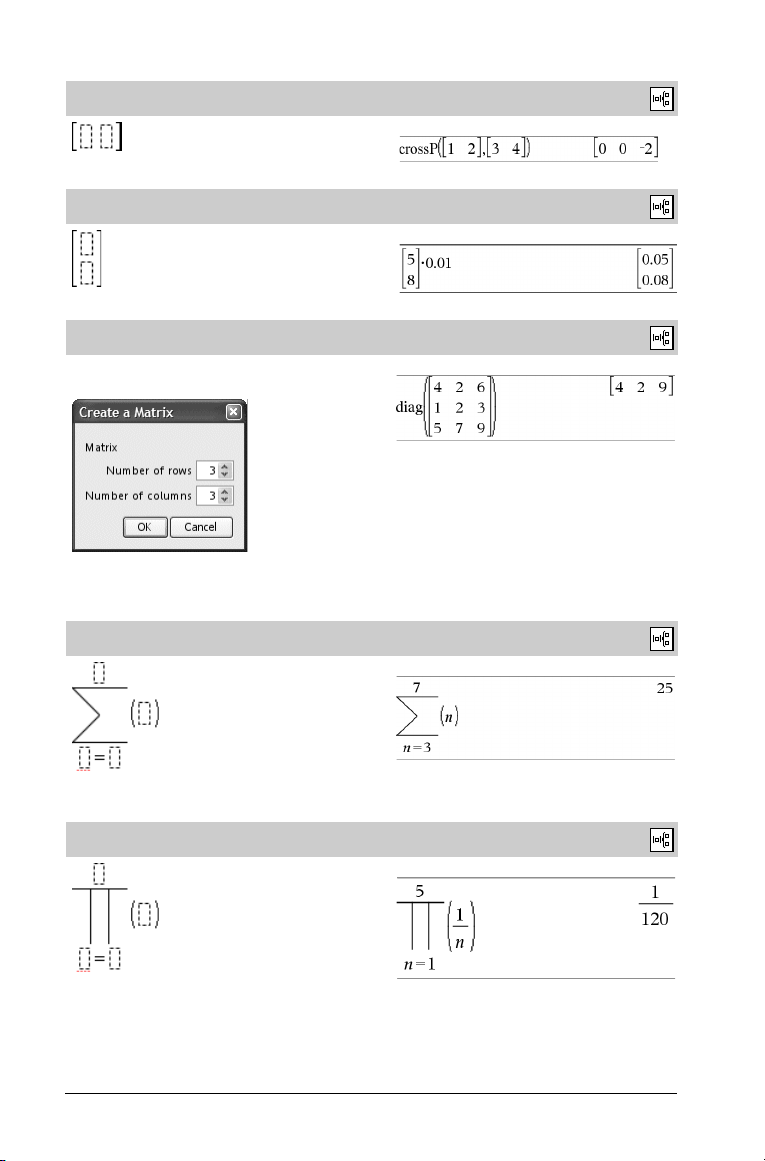
Matrix template (1 x 2)
.
Catalog >
Example:
Matrix template (2 x 1)
Matrix template (m x n)
The template appears after you are prompted to specify the number
of rows and columns.
Note: If you create a matrix with a large number of rows and
columns, it may take a few moments to appear.
Sum template (G)
Catalog >
Example:
Catalog >
Example:
Catalog >
Example:
Note: See also G() (sumSeq), page 124.
Product template (Π)
Note: See also Π() (prodSeq), page 124.
4 TI-Nspire™ Reference Guide
Catalog >
Example:
First derivative template
The first derivative template can be used to calculate first derivative
at a point numerically, using auto differentiation methods.
Note: See also d() (derivative), page 123.
Catalog >
Example:
Second derivative template
The second derivative template can be used to calculate second
derivative at a point numerically, using auto differentiation methods.
Note: See also d() (derivative), page 123.
Definite integral template
The definite integral template can be used to calculate the definite
integral numerically, using the same method as nInt().
183Note: See also nInt(), page 68.
Catalog >
Example:
Catalog >
Example:
TI-Nspire™ Reference Guide 5
Alphabetical listing
Items whose names are not alphabetic (such as +, !, and >) are listed at the end of this section,
starting on page
116. Unless otherwise specified, all examples in this section were performed in
the default reset mode, and all variables are assumed to be undefined.
A
abs()
abs(Val u e 1 ) ⇒ value
abs(
List1) ⇒ list
abs(Matrix1) ⇒ matrix
Returns the absolute value of the argument.
Note: See also Absolute value template, page 3.
If the argument is a complex number, returns the number’s modulus.
amortTbl()
amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],
roundValue]) ⇒ matrix
[
Amortization function that returns a matrix as an amortization table
for a set of TVM arguments.
NPmt is the number of payments to be included in the table. The
table starts with the first payment.
N, I, PV, Pmt, FV, PpY, CpY, and PmtAt are described in the table
of TVM arguments, page 107.
• If you omit Pmt, it defaults to
Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).
• If you omit FV, it defaults to FV=0.
• The defaults for PpY, CpY, and PmtAt are the same as for the
TVM functions.
roundValue specifies the number of decimal places for rounding.
Default=2.
The columns in the result matrix are in this order: Payment number,
amount paid to interest, amount paid to principal, and balance.
The balance displayed in row n is the balance after payment n.
You can use the output matrix as input for the other amortization
functions GInt() and GPrn(), page 125, and bal(), page 12.
Catalog
Catalog
>
>
and
BooleanExpr1 and BooleanExpr2 ⇒ Boolean expression
BooleanList1 and BooleanList2 ⇒ Boolean list
BooleanMatrix1 and BooleanMatrix2 ⇒ Boolean matrix
Returns true or false or a simplified form of the original entry.
6 TI-Nspire™ Reference Guide
Catalog
>
and
Integer1 and Integer2 ⇒ integer
Compares two real integers bit-by-bit using an and operation.
Internally, both integers are converted to signed, 64-bit binary
numbers. When corresponding bits are compared, the result is 1 if
both bits are 1; otherwise, the result is 0. The returned value
represents the bit results, and is displayed according to the Base
mode.
You can enter the integers in any number base. For a binary or
hexadecimal entry, you must use the 0b or 0h prefix, respectively.
Without a prefix, integers are treated as decimal (base 10).
Catalog
>
In Hex base mode:
Important: Zero, not the letter O.
In Bin base mode:
In Dec base mode:
Note: A binary entry can have up to 64 digits (not counting the
0b prefix). A hexadecimal entry can have up to 16 digits.
angle()
angle(Val u e 1 ) ⇒ value
Returns the angle of the argument, interpreting the argument as a
complex number.
In Degree angle mode:
In Gradian angle mode:
In Radian angle mode:
angle(List1) ⇒ list
angle(Matrix1) ⇒ matrix
Returns a list or matrix of angles of the elements in List1 or Matrix1,
interpreting each element as a complex number that represents a
two-dimensional rectangular coordinate point.
ANOVA
ANOVA List1,List2[,List3,...,List20][,Flag]
Performs a one-way analysis of variance for comparing the means of
two to 20 populations. A summary of results is stored in the
stat.results variable. (See page 97.)
Flag=0 for Data, Flag=1 for Stats
Output variable Description
stat.F Value of the F statistic
stat.PVal Smallest level of significance at which the null hypothesis can be rejected
stat.df Degrees of freedom of the groups
stat.SS Sum of squares of the groups
stat.MS Mean squares for the groups
stat.dfError Degrees of freedom of the errors
Catalog
Catalog
>
>
TI-Nspire™ Reference Guide 7
Output variable Description
stat.SSError Sum of squares of the errors
stat.MSError Mean square for the errors
stat.sp Pooled standard deviation
stat.xbarlist Mean of the input of the lists
stat.CLowerList 95% confidence intervals for the mean of each input list
stat.CUpperList 95% confidence intervals for the mean of each input list
ANOVA2way
ANOVA2way List1,List2[,List3,…,List10][,levRow]
Computes a two-way analysis of variance for comparing the means of
two to 10 populations. A summary of results is stored in the
stat.results variable. (See page 97.)
LevRow=0 for Block
LevRow=2,3,...,Len-1, for Two Factor, where
Len=length(List1)=length(List2) = … = length(List10) and
Len / LevRow ∈ {2,3,…}
Outputs: Block Design
Output variable Description
stat.FF statistic of the column factor
stat.PVal Smallest level of significance at which the null hypothesis can be rejected
stat.df Degrees of freedom of the column factor
stat.SS Sum of squares of the column factor
stat.MS Mean squares for column factor
stat.FBlock F statistic for factor
stat.PValBlock Least probability at which the null hypothesis can be rejected
stat.dfBlock Degrees of freedom for factor
stat.SSBlock Sum of squares for factor
stat.MSBlock Mean squares for factor
stat.dfError Degrees of freedom of the errors
stat.SSError Sum of squares of the errors
stat.MSError Mean squares for the errors
stat.s Standard deviation of the error
Catalog
>
COLUMN FACTOR Outputs
Output variable Description
stat.Fcol F statistic of the column factor
8 TI-Nspire™ Reference Guide
Output variable Description
stat.PValCol Probability value of the column factor
stat.dfCol Degrees of freedom of the column factor
stat.SSCol Sum of squares of the column factor
stat.MSCol Mean squares for column factor
ROW FACTOR Outputs
Output variable Description
stat.FRow F statistic of the row factor
stat.PValRow Probability value of the row factor
stat.dfRow Degrees of freedom of the row factor
stat.SSRow Sum of squares of the row factor
stat.MSRow Mean squares for row factor
INTERACTION Outputs
Output variable Description
stat.FInteract F statistic of the interaction
stat.PValInteract Probability value of the interaction
stat.dfInteract Degrees of freedom of the interaction
stat.SSInteract Sum of squares of the interaction
stat.MSInteract Mean squares for interaction
ERROR Outputs
Output variable Description
stat.dfError Degrees of freedom of the errors
stat.SSError Sum of squares of the errors
stat.MSError Mean squares for the errors
s Standard deviation of the error
Ans
Ans ⇒ value
Returns the result of the most recently evaluated expression.
/v
keys
TI-Nspire™ Reference Guide 9
approx()
approx(Val u e 1 ) ⇒ number
Returns the evaluation of the argument as an expression containing
decimal values, when possible, regardless of the current Auto or
Approximate
This is equivalent to entering the argument and pressing
·
approx(List1) ⇒ list
approx(Matrix1) ⇒ matrix
Returns a list or matrix where each element has been evaluated to a
decimal value, when possible.
mode.
/
.
Catalog
>
4approxFraction()
4
Val u e
approxFraction([Tol ]) ⇒ value
4
List
approxFraction([Tol ]) ⇒ list
4
Matrix
approxFraction([Tol ]) ⇒ matrix
Returns the input as a fraction, using a tolerance of To l. If To l is
omitted, a tolerance of 5.E-14 is used.
Note: You can insert this function from the computer keyboard by
typing @>approxFraction(...).
approxRational()
approxRational(Val u e [, Tol ]) ⇒ value
approxRational(List[, Tol ]) ⇒ list
approxRational(Matrix[, Tol ]) ⇒ matrix
Returns the argument as a fraction using a tolerance of To l . If Tol is
omitted, a tolerance of 5.E-14 is used.
arccos()
arccosh()
arccot()
Catalog
>
Catalog
>
See cos/(), page 20.
See cosh/(), page 21.
See cot/(), page 22.
10 TI-Nspire™ Reference Guide
arccoth()
See coth/(), page 22.
arccsc()
arccsch()
arcsec()
arcsech()
arcsin()
arcsinh()
arctan()
arctanh()
augment()
augment(List1, List2) ⇒ list
Returns a new list that is List2 appended to the end of List1.
augment(Matrix1, Matrix2) ⇒ matrix
Returns a new matrix that is Matrix2 appended to Matrix1. When
the “,” character is used, the matrices must have equal row
dimensions, and Matrix2 is appended to Matrix1 as new columns.
Does not alter Matrix1 or Matrix2.
See csc/(), page 24.
See csch/(), page 24.
See sec/(), page 88.
See sech/(), page 88.
See sin/(), page 93.
See sinh/(), page 94.
See tan/(), page
See tanh/(), page
Catalog
>
101
102
.
.
TI-Nspire™ Reference Guide 11
avgRC()
avgRC(Expr1, Va r [=Value] [, Step]) ⇒ ex pression
avgRC(Expr1, Va r [=Value] [, List1]) ⇒ list
avgRC(List1, Va r [=Value] [, Step]) ⇒ list
avgRC(Matrix1, Var [=Value] [, Step]) ⇒ matrix
Returns the forward-difference quotient (average rate of change).
Expr1 can be a user-defined function name (see Func).
When Val u e is specified, it overrides any prior variable assignment or
any current “with” substitution for the variable.
Step is the step value. If St ep is omitted, it defaults to 0.001.
Note that the similar function centralDiff() uses the centraldifference quotient.
B
Catalog
>
bal()
bal(NPmt,N,I,PV ,[Pmt], [FV], [PpY], [CpY], [PmtAt],
roundValue]) ⇒ value
[
bal(NPmt,amortTable) ⇒ value
Amortization function that calculates schedule balance after a
specified payment.
N, I, PV, Pmt, FV, PpY, CpY, and PmtAt are described in the table
of TVM arguments, page 107.
NPmt specifies the payment number after which you want the data
calculated.
N, I, PV, Pmt, FV, PpY, CpY, and PmtAt are described in the table
of TVM arguments, page 107.
• If you omit Pmt, it defaults to
Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).
• If you omit FV, it defaults to FV=0.
• The defaults for PpY, CpY, and PmtAt are the same as for the
TVM functions.
roundValue specifies the number of decimal places for rounding.
Default=2.
bal(NPmt,amortTable) calculates the balance after payment number
NPmt, based on amortization table amortTable. The amortTable
argument must be a matrix in the form described under amortTbl(),
page 6.
Note: See also GInt() and GPrn(), page 125.
4
Base2
Integer1 4Base2 ⇒ integer
Note: You can insert this operator from the computer keyboard by
typing @>Base2.
Converts Integer1 to a binary number. Binary or hexadecimal
numbers always have a 0b or 0h prefix, respectively.
Catalog
Catalog
>
>
12 TI-Nspire™ Reference Guide
4
Base2
Zero, not the letter O, followed by b or h.
0b binaryNumber
0h hexadecimalNumber
A binary number can have up to 64 digits. A
hexadecimal number can have up to 16.
Without a prefix, Integer1 is treated as decimal (base 10). The result
is displayed in binary, regardless of the Base mode.
Negative numbers are displayed in “two's complement” form. For
example,
N1 is displayed as
0hFFFFFFFFFFFFFFFF in Hex base mode
0b111...111 (64 1’s) in Binary base mode
63
N2
is displayed as
0h8000000000000000 in Hex base mode
0b100...000 (63 zeros) in Binary base mode
If you enter a decimal integer that is outside the range of a signed,
64-bit binary form, a symmetric modulo operation is used to bring the
value into the appropriate range. Consider the following examples of
values outside the range.
263 becomes N263 and is displayed as
0h8000000000000000 in Hex base mode
0b100...000 (63 zeros) in Binary base mode
264 becomes 0 and is displayed as
0h0 in Hex base mode
0b0 in Binary base mode
63
N2
N 1 becomes 2
0h7FFFFFFFFFFFFFFF in Hex base mode
0b111...111 (64 1’s) in Binary base mode
63
N 1 and is displayed as
Catalog
>
4Base10
Integer1 4Base10 ⇒ integer
Note: You can insert this operator from the computer keyboard by
typing @>Base10.
Converts Integer1 to a decimal (base 10) number. A binary or
hexadecimal entry must always have a 0b or 0h prefix, respectively.
0b binaryNumber
0h hexadecimalNumber
Zero, not the letter O, followed by b or h.
A binary number can have up to 64 digits. A hexadecimal number can
have up to 16.
Without a prefix, Integer1 is treated as decimal. The result is
displayed in decimal, regardless of the Base mode.
Catalog
>
TI-Nspire™ Reference Guide 13
4Base16
4Base16 ⇒ integer
Integer1
Note: You can insert this operator from the computer keyboard by
typing @>Base16.
Converts Integer1 to a hexadecimal number. Binary or hexadecimal
numbers always have a 0b or 0h prefix, respectively.
0b binaryNumber
0h hexadecimalNumber
Zero, not the letter O, followed by b or h.
A binary number can have up to 64 digits. A hexadecimal number can
have up to 16.
Without a prefix, Integer1 is treated as decimal (base 10). The result
is displayed in hexadecimal, regardless of the Base mode.
If you enter a decimal integer that is too large for a signed, 64-bit
binary form, a symmetric modulo operation is used to bring the value
into the appropriate range. For more information, see
page 12.
4Base2,
Catalog
>
binomCdf()
binomCdf(n,p) ⇒ number
binomCdf(n,p,lowBound,upBound) ⇒ number if lowBound
upBound are numbers, list if lowBound and upBound are
and
lists
binomCdf(
upBound is a number, list if upBound is a list
Computes a cumulative probability for the discrete binomial
distribution with n number of trials and probability p of success on
each trial.
For P(X { upBound), set lowBound=0
binomPdf()
binomPdf(n,p) ⇒ number
binomPdf(n,p,XVal) ⇒ number if XVal is a number, list if
XVal is a list
Computes a probability for the discrete binomial distribution with n
number of trials and probability p of success on each trial.
n,p,upBound) for P(0{X{upBound) ⇒ number if
C
ceiling()
ceiling(Val u e 1 ) ⇒ value
Returns the nearest integer that is | the argument.
The argument can be a real or a complex number.
Note: See also floor().
ceiling(List1) ⇒ list
ceiling(Matrix1) ⇒ matrix
Returns a list or matrix of the ceiling of each element.
Catalog
Catalog
Catalog
>
>
>
14 TI-Nspire™ Reference Guide
centralDiff()
centralDiff(Expr1,Va r [=Value][,Step]) ⇒ expression
centralDiff(Expr1,Va r [,Step ])|Var =Va l u e ⇒ expression
centralDiff(Expr1,Va r [=Value][,List]) ⇒ list
centralDiff(List1,Va r [=Value][,St ep]) ⇒ list
centralDiff(Matrix1,Va r [=Value][,Step]) ⇒ matrix
Returns the numerical derivative using the centra l difference quotient
formula.
When Val u e is specified, it overrides any prior variable assignment or
any current “with” substitution for the variable.
Step is the step value. If St ep is omitted, it defaults to 0.001.
When using List1 or Matrix1, the operation gets mapped across the
values in the list or across the matrix elements.
Note: See also avgRC().
Catalog
>
char()
char(Integer) ⇒ character
Returns a character string containing the character numbered Integer
from the handheld character set. The valid range for Integer is 0–
65535.
2
c
2way
2
c
2way obsMatrix
chi22way obsMatrix
Computes a c2 test for association on the two-way table of counts in
the observed matrix obsMatrix. A summary of results is stored in the
stat.results variable. (See page 97.)
For information on the effect of empty elements in a matrix, see
“Empty (void) elements” on page 131.
Output variable Description
stat.c2 Chi square stat: sum (observed - expected)2/expected
stat.PVal Smallest level of significance at which the null hypothesis can be rejected
stat.df Degrees of freedom for the chi square statistics
stat.ExpMat Matrix of expected elemental count table, assuming null hypothesis
stat.CompMat Matrix of elemental chi square statistic contributions
Catalog
Catalog
>
>
TI-Nspire™ Reference Guide 15
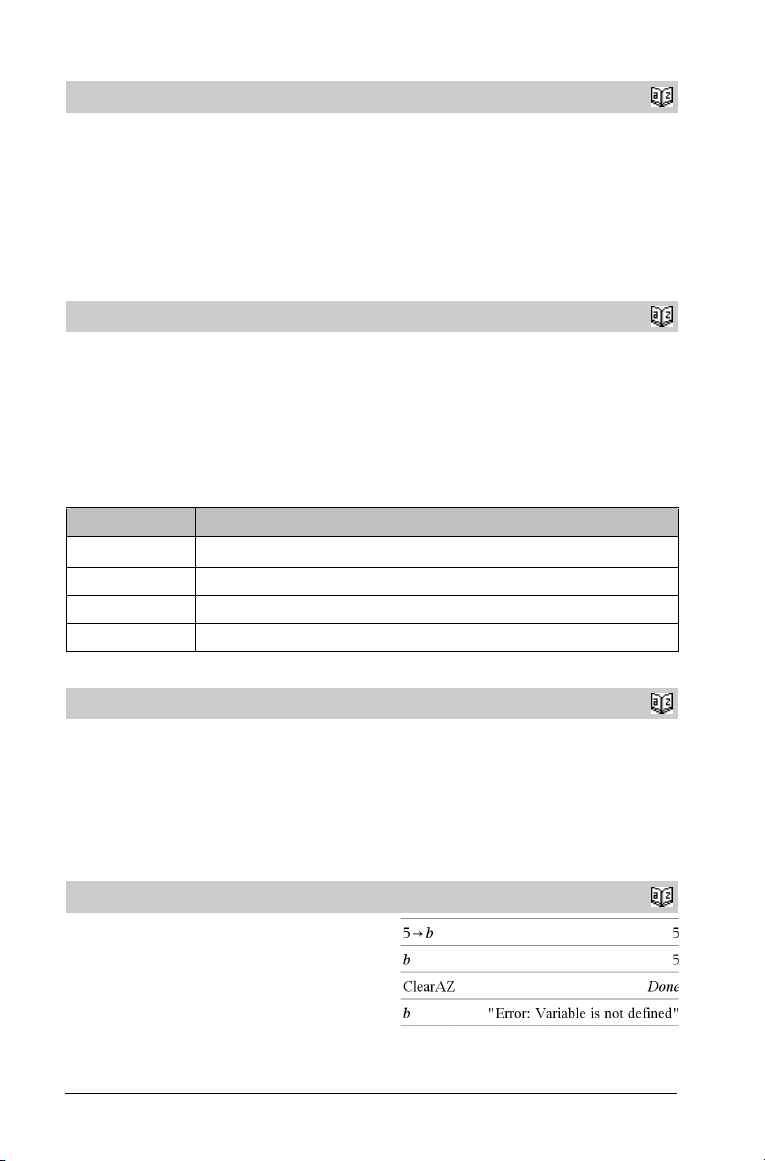
2
c
Cdf()
2
c
Cdf(lowBound,upBound,df) ⇒ number if lowBound and
upBound are numbers, list if lowBound and upBound are lists
chi2Cdf(lowBound,upBound,df) ⇒ number if lowBound and
upBound are numbers, list if lowBound and upBound are lists
Computes the c2 distribution probability between lowBound and
upBound for the specified degrees of freedom df.
{ upBound), set lowBound = 0.
For P(X
For information on the effect of empty elements in a list, see “Empty
(void) elements” on page 131.
2
c
GOF
2
c
GOF obsList,expList,df
chi2GOF obsList,expList,df
Performs a test to confirm that sample data is from a population that
conforms to a specified distribution. obsList is a list of counts and
must contain integers. A summary of results is stored in the
stat.results variable. (See page 97.)
For information on the effect of empty elements in a list, see “Empty
(void) elements” on page 131.
Output variable Description
stat.c2 Chi square stat: sum((observed - expected)2/expected
stat.PVal Smallest level of significance at which the null hypothesis can be rejected
stat.df Degrees of freedom for the chi square statistics
stat.CompList Elemental chi square statistic contributions
Catalog
Catalog
>
>
2
c
Pdf()
2
c
Pdf(XVal,df) ⇒ number if XVal is a number, list if XVal is a
list
chi2Pdf(
XVal,df) ⇒ number if XVal is a number, list if XVal is
a list
Computes the probability density function (pdf) for the c2 distribution
at a specified XVal value for the specified degrees of freedom df.
For information on the effect of empty elements in a list, see “Empty
(void) elements” on page 131.
ClearAZ
ClearAZ
Clears all single-character variables in the current problem space.
If one or more of the variables are locked, this command displays an
error message and deletes only the unlocked variables. See unLock,
page 109.
16 TI-Nspire™ Reference Guide
Catalog
Catalog
>
>
ClrErr
ClrErr
Clears the error status and sets system variable errCode to zero.
The Else clause of the Try...Else...EndTry block should use ClrErr
or PassErr. If the error is to be processed or ignored, use ClrErr. If
what to do with the error is not known, use PassErr to send it to the
next error handler. If there are no more pending Try...Else...EndTry
error handlers, the error dialog box will be displayed as normal.
Note: See also PassErr, page 73, and Try, page 105.
Note for entering the example: In the Calculator application
on the handheld, you can enter multi-line definiti ons by pressing @
instead of · at the end of each line. On the computer keyboard,
hold down Alt and press Enter.
Catalog
For an example of ClrErr, See Example 2 under the Try
command, page 105.
>
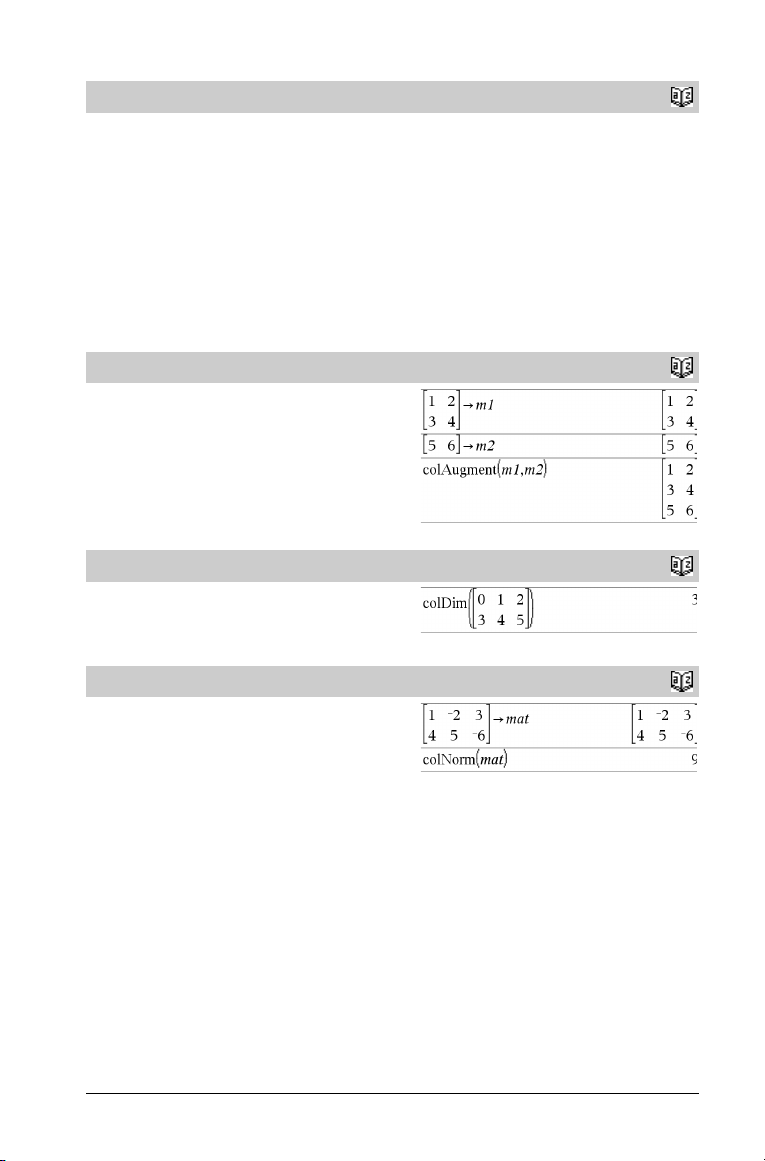
colAugment()
colAugment(Matrix1, Matrix2) ⇒ matrix
Returns a new matrix that is Matrix2 appended to Matrix1. The
matrices must have equal column dimensions, and Matrix2 is
appended to Matrix1 as new rows. Does not alter Matrix1 or
Matrix2.
colDim()
colDim(Matrix) ⇒ expression
Returns the number of columns contained in Matrix.
Note: See also rowDim().
colNorm()
colNorm(Matrix) ⇒ expression
Returns the maximum of the sums of the absolute values of the
elements in the columns in Matrix.
Note: Undefined matrix elements are not allowed. See also
rowNorm().
Catalog
Catalog
Catalog
>
>
>
TI-Nspire™ Reference Guide 17
completeSquare()
completeSquare(ExprOrEqn, Var ) ⇒ expression or equation
completeSquare(ExprOrEqn, Var ^ Po w e r)
equation
completeSquare(ExprOrEqn, Var1, Var2 [,...])
equation
completeSquare(ExprOrEqn, {Var1, Var2 [,...]})
or equation
⇒ expression or
⇒ expression or
⇒ expression
Converts a quadratic polynomial expression of the form a·x2+b·x+c
into the form a·(x-h)2+k
- or -
Converts a quadratic equation of the form a·x2+b·x+c=d into the
form a·(x-h)2=k
The first argument must be a quadratic expression or equation in
standard form with respect to the second argument.
The Second argument must be a single univariate term or a single
univariate term raised to a rational power, for example x, y2,orz
The third and fourth syntax attempt to complete the square with
respect to variables Var 1 , Va r2 [,… ]).
(1/3)
Catalog
>
.
conj()
conj(Val u e 1 ) ⇒ value
conj(List1) ⇒ list
conj(Matrix1) ⇒ matrix
Returns the complex conjugate of the argument.
constructMat()
constructMat(Expr,Var 1 ,Var 2 ,numRows,numCols)
⇒ matrix
Returns a matrix based on the arguments.
Expr is an expression in variables Va r 1 and Va r 2 . Elements in the
resulting matrix are formed by evaluating Expr for each incremented
value of Var 1 and Va r 2.
Var 1 is automatically incremented from 1 through numRows. Within
each row, Va r2 is incremented from 1 through numCols.
CopyVar
CopyVar Var 1 , Va r 2
CopyVar Var 1 ., Va r2 .
CopyVar Var 1 , Va r2 copies the value of variable Var 1 to variable
Var 2 , creating Va r 2 if necessary. Variable Va r1 must have a value.
If Var 1 is the name of an existing user-defined function, copies the
definition of that function to function Va r 2. Function Va r 1 must be
defined.
Var 1 must meet the variable-naming requirements or must be an
indirection expression that simplifies to a variable name meeting the
requirements.
Catalog
Catalog
Catalog
>
>
>
18 TI-Nspire™ Reference Guide
CopyVar
CopyVar Var 1 ., Va r 2. copies all members of the Va r 1 . variable
group to the Var 2
Var 1 . must be the name of an existing variable group, such as the
statistics stat.nn results, or variables created using the
LibShortcut() function. If Var 2
replaces all members that are common to both groups and adds the
members that do not already exist. If one or more members of Va r 2 .
are locked, all members of Va r 2
. group, creating Var 2. if necessary.
. already exists, this command
. are left unchanged.
Catalog
>
corrMat()
corrMat(List1,List2[,…[,List20]])
Computes the correlation matrix for the augmented matrix [List1,
List2, ..., List20].
cos()
cos(Val u e 1 ) ⇒ value
cos(List1) ⇒ list
cos(Va lu e 1 ) returns the cosine of the argument as a value.
cos(List1) returns a list of the cosines of all elements in List1.
Note: The argument is interpreted as a degree, gradian or radian
angle, according to the current angle mode setting. You can use ¡,G,
or R to override the angle mode temporarily.
In Degree angle mode:
In Gradian angle mode:
In Radian angle mode:
Catalog
>
μ key
TI-Nspire™ Reference Guide 19
cos()
cos(squareMatrix1) ⇒ squareMatrix
Returns the matrix cosine of squareMatrix1. This is not the same as
calculating the cosine of each element.
When a scalar function f(A) operates on squareMatrix1 (A), the
result is calculated by the algorithm:
Compute the eigenvalues (li) and eigenvectors (Vi) of A.
squareMatrix1 must be diagonalizable. Also, it cannot have symbolic
variables that have not been assigned a value.
Form the matrices:
μ key
In Radian angle mode:
Then A = X B X
X/ where:
cos(B) =
All computations are performed using floating-point arithmetic.
cos/()
cos/(Va lu e 1 ) ⇒ value
cos/(List1) ⇒ list
cos/(Va lu e 1 ) returns the angle whose cosine is Va l ue 1 .
cos/(List1) returns a list of the inverse cosines of each element of
List1.
Note: The result is returned as a degree, gradian or radian angle,
according to the current angle mode setting.
Note: You can insert this function from the keyboard by typing
arccos(...).
cos/(squareMatrix1) ⇒ squareMatrix
Returns the matrix inverse cosine of squareMatrix1. This is not the
same as calculating the inverse cosine of each element. For
information about the calculation method, refer to cos().
squareMatrix1 must be diagonalizable. The result always contains
floating-point numbers.
/and f(A) = X f(B) X/. For example, cos(A) = X cos(B)
μ key
In Degree angle mode:
In Gradian angle mode:
In Radian angle mode:
In Radian angle mode and Rectangular Complex Format:
To see the entire result, press £ and then use ¡ and ¢ to
move the cursor.
20 TI-Nspire™ Reference Guide
cosh()
cosh(Va lu e 1 ) ⇒ value
cosh(List1) ⇒ list
cosh(Va lu e 1 ) returns the hyperbolic cosine of the argument.
cosh(List1) returns a list of the hyperbolic co sines of each element of
List1.
cosh(squareMatrix1) ⇒ squareMatrix
Returns the matrix hyperbolic cosine of squareMatrix1. This is not
the same as calculating the hyperbolic cosine of each element. For
information about the calculation method, refer to cos().
squareMatrix1 must be diagonalizable. The result always contains
floating-point numbers.
In Radian angle mode:
Catalog
>
cosh/()
cosh/(Va lu e 1 ) ⇒ value
cosh/(List1) ⇒ list
cosh/(Va lu e 1 ) returns the inverse hyperbolic cosine of the
argument.
cosh/(List1) returns a list of the inverse hyperbolic cosines of each
element of List1.
Note: You can insert this function from the keyboard by typing
arccosh(...).
cosh/(squareMatrix1) ⇒ squareMatrix
Returns the matrix inverse hyperbolic cosine of squareMatrix1. This
is not the same as calculating the inverse hyperbolic cosine of each
element. For information about the calculation method, refer to
cos().
squareMatrix1 must be diagonalizable. The result always contains
floating-point numbers.
cot()
cot(Val u e 1 ) ⇒ value
cot(List1) ⇒ list
Returns the cotangent of Val u e1 or returns a list of the cotangents of
all elements in List1.
Note: The argument is interpreted as a degree, gradian or radian
angle, according to the current angle mode setting. You can use ¡,G,
or R to override the angle mode temporarily.
Catalog
>
In Radian angle mode and In Rectangular Complex Format:
To see the entire result, press £ and then use ¡ and ¢ to
move the cursor.
μ key
In Degree angle mode:
In Gradian angle mode:
In Radian angle mode:
TI-Nspire™ Reference Guide 21
cot/()
cot/(Va lu e 1 ) ⇒ value
cot/(List1) ⇒ list
Returns the angle whose cotangent is Va l ue 1 or returns a list
containing the inverse cotangents of each element of List1.
Note: The result is returned as a degree, gradian or radian angle,
according to the current angle mode setting.
Note: You can insert this function from the keyboard by typing
arccot(...).
μ key
In Degree angle mode:
In Gradian angle mode:
In Radian angle mode:
coth()
coth(Val u e 1 ) ⇒ value
coth(List1) ⇒ list
Returns the hyperbolic cotangent of Va l ue 1 or returns a list of the
hyperbolic cotangents of all elements of List1.
coth/()
coth/(Va lu e 1 ) ⇒ value
coth/(List1) ⇒ list
Returns the inverse hyperbolic cotangent of Va l u e1 or returns a list
containing the inverse hyperbolic cotangents of each element of
List1.
Note: You can insert this function from the keyboard by typing
arccoth(...).
count()
count(Val u e 1 or L i s t1 [,Value2orList2 [,...]]) ⇒ value
Returns the accumulated count of all elements in the arguments that
evaluate to numeric values.
Each argument can be an expression, value, list, or matrix. You can
mix data types and use arguments of various dimensions.
For a list, matrix, or range of cells, each element is evaluated to
determine if it should be included in the count.
Within the Lists & Spreadsheet application, you can use a range of
cells in place of any argument.
Empty (void) elements are ignored. For more information on empty
elements, see page 131.
Catalog
Catalog
Catalog
>
>
>
22 TI-Nspire™ Reference Guide
countif()
countif(List,Criteria) ⇒ value
Returns the accumulated count of all elements in List that meet the
specified Criteria.
Criteria can be:
• A value, expression, or string. For example, 3 counts only those
elements in List that simplify to the value 3.
• A Boolean expression containing the symbol ? as a placeholder
for each element. For example, ?<5 counts only those elements
in List that are less than 5.
Within the Lists & Spreadsheet application, you can use a range of
cells in place of List.
Empty (void) elements in the list are ignored. For more information on
empty elements, see page 131.
Note: See also sumIf(), page 100, and frequency(), page 39.
Counts the number of elements equal to 3.
Counts the number of elements equal to “def.”
Counts 1 and 3.
Counts 3, 5, and 7.
Counts 1, 3, 7, and 9.
Catalog
>
cPolyRoots()
cPolyRoots(Poly,Var ) ⇒ list
cPolyRoots(ListOfCoeffs) ⇒ list
The first syntax, cPolyRoots(Poly,Va r), returns a list of complex
roots of polynomial Poly with respect to variable Var .
Poly must be a polynomial in expanded form in one variable. Do not
use unexpanded forms such as y2·y+1 or x·x+2·x+1
The second syntax, cPolyRoots(ListOfCoeffs), returns a list of
complex roots for the coefficients in ListOfCoeffs.
Note: See also polyRoots(), page 74.
crossP()
crossP(List1, List2) ⇒ list
Returns the cross product of List1 and List2 as a list.
List1 and List2 must have equal dimension, and the dimension must
be either 2 or 3.
crossP(Vector1, Vector2) ⇒ vector
Returns a row or column vector (depending on the arguments) that is
the cross product of Vector1 and Vector2.
Both Vector1 and Vector2 must be row vectors, or both must be
column vectors. Both vectors must have equal dimension, and the
dimension must be either 2 or 3.
Catalog
Catalog
>
>
TI-Nspire™ Reference Guide 23
csc()
csc(Val u e 1 ) ⇒ value
csc(List1) ⇒ list
Returns the cosecant of Va lu e 1 or returns a list containing the
cosecants of all elements in List1.
μ key
In Degree angle mode:
In Gradian angle mode:
In Radian angle mode:
csc/()
csc/(Va l ue 1 ) ⇒ value
csc/(List1) ⇒ list
Returns the angle whose cosecant is Va l ue 1 or returns a list
containing the inverse cosecants of each element of List1.
Note: The result is returned as a degree, gradian or radian angle,
according to the current angle mode setting.
Note: You can insert this function from the keyboard by typing
arccsc(...).
csch()
csch(Val u e 1 ) ⇒ value
csch(List1) ⇒ list
Returns the hyperbolic cosecant of Va lu e 1 or returns a list of the
hyperbolic cosecants of all elements of List1.
csch/()
csch/(Val u e ) ⇒ value
csch/(List1) ⇒ list
Returns the inverse hyperbolic cosecant of Va l u e1 or returns a list
containing the inverse hyperbolic cosecants of each element of List1.
Note: You can insert this function from the keyboard by typing
arccsch(...).
In Degree angle mode:
In Gradian angle mode:
In Radian angle mode:
Catalog
Catalog
μ key
>
>
24 TI-Nspire™ Reference Guide
Loading...