Texas Instruments TI-Nspire Reference Guide [de]

Referenzhandbuch

Dieser Leitfaden îst gültig für die TI-Nspire Software-Version 1.4. Die aktuellste Version der Dokumentation finden Sie unter education.ti.com/guides.

Wichtige Informationen

Außer im Fall anderslautender Bestimmungen der Lizenz für das Programm gewährt Texas Instruments keine ausdrückliche oder implizite Garantie, inklusive aber nicht ausschließlich sämtlicher impliziter Garantien der Handelsfähigkeit und Eignung für einen bestimmten Zweck, bezüglich der Programme und der schriftlichen Dokumentationen, und stellt dieses Material nur im „Ist-Zustand“ zur Verfügung. Unter keinen Umständen kann Texas Instruments für besondere, direkte, indirekte oder zufällige Schäden bzw. Folgeschäden haftbar gemacht werden, die durch Erwerb oder Benutzung dieses Materials verursacht werden, und die einzige und exklusive Haftung von Texas Instruments, ungeachtet der Form der Beanstandung, kann den in der Programmlizenz festgesetzten Betrag nicht überschreiten. Zudem haftet Texas Instruments nicht für Forderungen anderer Parteien jeglicher Art gegen die Anwendung dieses Materials.

Lizenz

Bitte lesen Sie die vollständige Lizenz im Verzeichnis C:\Programme\TI

Education\TI-Nspire

Macintosh®, Windows®, Excel®, Vernier EasyLink®, EasyTemp®, Go!®Link, Go!®Motion, und Go!®Temp sind Warenzeichen und Eigentum der jeweiligen Besitzer.

Inhaltsverzeichnis

Wichtige Informationen Vorlagen für Ausdrücke

Vorlage Bruch ..............................................1

Vorlage Exponent ........................................ 1

Vorlage Quadratwurzel ...............................1

Vorlage n-te Wurzel ....................................1

Vorlage e Exponent .....................................2

Vorlage Logarithmus ................................... 2

Vorlage Stückweise (2 Teile) .......................2

Vorlage Stückweise (n Teile) .......................2

Vorlage Absolutwert ...................................2

Vorlage dd°mm’ss.ss’’ ..................................3

Vorlage Matrix (2 x 2) .................................. 3

Vorlage Matrix (1 x 2) .................................. 3

Vorlage Matrix (2 x 1) .................................. 3

Vorlage Matrix (m x n) ................................ 3

Vorlage Summe (G) ......................................3

Vorlage Produkt (Π) .....................................4

Alphabetische Auflistung A

abs() (Absolutwert) ...................................... 5

amortTbl() .................................................... 5

and (und) ......................................................5

angle() (Winkel) ...........................................6

ANOVA .........................................................6

ANOVA2way (ANOVA 2fach) ......................7

Ans (Antwort) .............................................. 9

approx() (Approximieren) ........................... 9

approxRational() .......................................... 9

augment() (Erweitern) ................................. 9

avgRC() (Durchschnittliche Änderungsrate) . 10

bal() .............................................................10

4Base2 .........................................................10

4Base10 .......................................................11

4Base16 .......................................................11

binomCdf() ................................................. 11

binomPdf() ................................................. 12

ceiling() (Obergrenze) ............................... 12

char() (Zeichenstring) .................................12

2way ........................................................12

Cdf() .........................................................13

GOF ......................................................... 13

Pdf() .........................................................13

ClearAZ (LöschAZ) ...................................... 13

ClrErr (LöFehler) ......................................... 14

colAugment() (Spaltenerweiterung) .........14

colDim() (Spaltendimension) ..................... 14

colNorm() (Spaltennorm) ........................... 14

conj() (Komplex Konjugierte) ....................14

constructMat() ............................................ 15

CopyVar ...................................................... 15

corrMat() (Korrelationsmatrix) ................. 15

cos() (Kosinus) ............................................ 16

cosê() (Arkuskosinus) ................................. 17

cosh() (Cosinus hyperbolicus) .................... 17

coshê() (Arkuskosinus hyperbolicus) ........ 17

cot() (Kotangens) ....................................... 18

cotê() (Arkuskotangens) ............................ 18

coth() (Kotangens hyperbolicus) ............... 18

cothê() (Arkuskotangens hyperbolicus) ...18

count() (zähle) ............................................ 19

countIf() ..................................................... 19

crossP() (Kreuzprodukt) ............................. 19

csc() (Kosekans) .......................................... 20

cscê() (Inverser Kosekans) .......................... 20

csch() (Kosekans hyperbolicus) .................. 20

cschê() (Inverser Kosekans hyperbolicus) . 20

CubicReg (Kubische Regression) ............... 21

cumSum() (Kumulierte Summe) ................ 21

Cycle (Zyklus) ............................................. 22

4Cylind (Zylindervektor) ............................ 22

dbd() ........................................................... 22

4DD (Dezimalwinkel) ................................. 23

4Decimal (Dezimal) .................................... 23

Definiere .................................................... 23

Definiere LibPriv (Define LibPriv) ............. 24

Definiere LibPub (Define LibPub) ............. 25

DelVar ........................................................ 25

det() (Matrixdeterminante) ....................... 25

diag() (Matrixdiagonale) ........................... 26

dim() (Dimension) ...................................... 26

Disp (Zeige) ................................................ 26

4DMS (GMS) ................................................ 27

dotP() (Skalarprodukt) ............................... 27

e^() ............................................................. 27

eff() ............................................................. 28

eigVc() (Eigenvektor) ................................. 28

eigVl() (Eigenwert) .................................... 28

Else ............................................................. 28

ElseIf ........................................................... 29

EndFor ........................................................ 29

EndFunc ...................................................... 29

EndIf ........................................................... 29

EndLoop ..................................................... 29

EndWhile .................................................... 29

EndPrgm ..................................................... 29

EndTry ........................................................ 29

Exit (Abbruch) ............................................ 30

exp() (e hoch x) .......................................... 30

expr() (String in Ausdruck) ........................ 30

ExpReg (Exponentielle Regression) .......... 31

factor() (Faktorisiere) ................................. 31

Fill (Füllen) ................................................. 32

FiveNumSummary ...................................... 32

FCdf() ......................................................... 32

iii

floor() (Untergrenze) .................................33

For ...............................................................33

format() (Format) .......................................33

fPart() (Funktionsteil) .................................34

FPdf() ..........................................................34

freqTable4list() ............................................34

frequency() (Häufigkeit) ............................34

FTest_2Samp (Zwei-Stichproben F-Test) ...35

Func .............................................................35

gcd() (Größter gemeinsamer Teiler) .........36

geomCdf() ...................................................36

geomPdf() ...................................................36

getDenom() (Nenner holen) ......................36

getLangInfo() .............................................37

getMode() ...................................................37

getNum() (Zähler holen) ............................38

getVarInfo() ................................................38

Goto (Gehe zu) ...........................................39

4Grad (Neugrad) .........................................39

identity() (Einheitsmatrix) ..........................39

If ..................................................................40

ifFn() ............................................................41

imag() (Imaginärteil) ..................................41

Umleitung ...................................................41

inString() (In String) ...................................41

int() (Ganze Zahl) .......................................42

intDiv() (Ganzzahl teilen) ..........................42

() .........................................................42

invc

invF() ...........................................................42

invNorm() ....................................................42

invt() ............................................................42

iPart() (Ganzzahliger Teil) ..........................43

irr() ..............................................................43

isPrime() (Primzahltest) ..............................43

Lbl (Marke) .................................................44

lcm() (Kleinstes gemeinsames Vielfaches) 44

left() (Links) ................................................44

libShortcut() ................................................45

LinRegBx .....................................................45

LinRegMx ....................................................46

LinRegtIntervals (Lineare Regressions-t-In-

tervalle) .......................................................46

LinRegtTest (t-Test bei linearer Regression) . 48

@list() (Listendifferenz) ..............................48

list4mat() (Liste in Matrix) ..........................49

ln() (Natürlicher Logarithmus) ...................49

LnReg ..........................................................49

Local (Lokale Variable) ..............................50

log() (Logarithmus) ....................................51

Logistic ........................................................51

LogisticD .....................................................52

Loop (Schleife) ............................................53

LU (Untere/obere Matrixzerlegung) .........53

mat4list() (Matrix in Liste) ..........................53

max() (Maximum) ...................................... 54

mean() (Mittelwert) ................................... 54

median() (Median) ..................................... 54

MedMed ..................................................... 55

mid() (Teil-String) ....................................... 55

min() (Minimum) ........................................ 56

mirr() ........................................................... 56

mod() (Modulo) ......................................... 56

mRow() (Matrixzeilenoperation) .............. 57

mRowAdd() (Matrixzeilenaddition) .......... 57

MultReg ...................................................... 57

MultRegIntervals ....................................... 57

MultRegTests ............................................. 58

nCr() (Kombinationen) .............................. 59

nDeriv() (Numerische Ableitung) .............. 59

newList() (Neue Liste) ................................ 60

newMat() (Neue Matrix) ........................... 60

nfMax() (Numerisches Funktionsmaximum) . 60 nfMin() (Numerisches Funktionsminimum) .. 60

nInt() (Numerisches Integral) .................... 60

nom() .......................................................... 61

norm() ......................................................... 61

normCdf() (Normalverteilungswahrscheinli-

chkeit) ......................................................... 61

normPdf() (Wahrscheinlichkeitsdichte) ....61

not .............................................................. 61

nPr() (Permutationen) ............................... 62

npv() ........................................................... 63

nSolve() (Numerische Lösung) ................... 63

OneVar (Eine Variable) .............................. 64

or ................................................................ 65

ord() (Numerischer Zeichencode) ..............65

P4Rx() (Kartesische x-Koordinate) .............65

P4Ry() (Kartesische y-Koordinate) .............66

PassErr (ÜbgebFeh) .................................... 66

piecewise() (Stückweise) ............................66

poissCdf() .................................................... 66

poissPdf() .................................................... 66

4Polar .......................................................... 67

polyEval() (Polynom auswerten) ............... 67

PowerReg ................................................... 67

Prgm ........................................................... 68

Product (PI) (Produkt) ................................ 68

product() (Produkt) .................................... 68

propFrac() (Echter Bruch) .......................... 69

QR ............................................................... 69

QuadReg .................................................... 70

QuartReg .................................................... 70

R4Pq() (Polarkoordinate) ............................ 71

R4Pr() (Polarkoordinate) ............................ 71

4Rad (Bogenmaß) ....................................... 72

rand() (Zufallszahl) .....................................72

randBin() (Zufallszahl aus Binomialvertei-

lung) ...........................................................72

randInt() (Ganzzahlige Zufallszahl) ..........72

randMat() (Zufallsmatrix) .......................... 72

randNorm() (Zufallsnorm) ......................... 73

randPoly() (Zufallspolynom) ...................... 73

randSamp() (Zufallsstichprobe) .................73

RandSeed (Zufallszahl) ..............................73

real() (Reell) ................................................73

4Rect (Kartesisch) ........................................73

ref() (Diagonalform) ..................................74

remain() (Rest) ............................................ 74

Return (Rückgabe) ..................................... 75

right() (Rechts) ...........................................75

root() (Wurzel) ...........................................75

rotate() (Rotieren) ......................................75

round() (Runden) ....................................... 76

rowAdd() (Zeilenaddition) ........................76

rowDim() (Zeilendimension) .....................77

rowNorm() (Zeilennorm) ...........................77

rowSwap() (Zeilentausch) ..........................77

rref() (Reduzierte Diagonalform) .............. 77

sec() (Sekans) .............................................. 78

sec/() (Arkussekans) ................................... 78

sech() (Sekans hyperbolicus) ......................78

sechê() (Arkussekans hyperbolicus) .......... 78

seq() (Folge) ................................................ 79

setMode ...................................................... 79

shift() (Verschieben) ...................................80

sign() (Zeichen) ...........................................81

simult() (Gleichungssystem) ....................... 81

sin() (Sinus) .................................................82

sinê() (Arkussinus) ......................................82

sinh() (Sinus hyperbolicus) .........................83

sinhê() (Arkussinus hyperbolicus) ..............83

SinReg .........................................................84

SortA (In aufsteigender Reihenfolge sortier-

en) ...............................................................84

SortD (In absteigender Reihenfolge sortier-

en) ...............................................................85

4Sphere (Kugelkoordinaten) .....................85

sqrt() (Quadratwurzel) ...............................85

stat.results .................................................. 86

stDevPop() (Populations-Standardabwei-

chung) ......................................................... 87

stDevSamp() (Stichproben-Standardabwei-

chung) ......................................................... 87

stat.values ...................................................87

Stop (Stopp) ............................................... 88

Store (Speichern) ........................................88

string() (String) ...........................................88

subMat() (Untermatrix) ............................. 88

Summe (Sigma) ..........................................88

sum() (Summe) ...........................................88

sumIf() .........................................................89

T (Transponierte) ....................................... 89

tan() (Tangens) ...........................................90

tanê() (Arkustangens) ................................90

tanh() (Tangens hyperbolicus) .................. 91

tanhê() (Arkustangens hyperbolicus) ....... 91

tCdf() .......................................................... 92

Then ........................................................... 92

tInterval ...................................................... 92

tInterval_2Samp (Zwei-Stichproben-t-Konfi-

denzintervall) ............................................. 92

tPdf() .......................................................... 93

trace() ......................................................... 93

Try (Versuche) ........................................... 94

tTest ............................................................ 94

tTest_2Samp (t-Test für zwei Stichproben) .. 95

tvmFV() ....................................................... 95

tvmI() .......................................................... 96

tvmN() ........................................................ 96

tvmPmt() .................................................... 96

tvmPV() ....................................................... 96

TwoVar (Zwei Variable) ............................ 97

unitV() (Einheitsvektor) ............................. 98

varPop() (Populationsvarianz) ................... 98

varSamp() (Stichproben-Varianz) .............. 98

when() (Wenn) ........................................... 99

While .......................................................... 99

“With” ........................................................ 99

xor (Boolesches exklusives oder) ............. 100

zInterval (z-Konfidenzintervall) .............. 100

zInterval_1Prop (z-Konfidenzintervall für

eine Proportion) ...................................... 101

zInterval_2Prop (z-Konfidenzintervall für

zwei Proportionen) .................................. 101

zInterval_2Samp (z-Konfidenzintervall für

zwei Stichproben) .................................... 101

zTest ......................................................... 102

zTest_1Prop (z-Test für eine Proportion) 102 zTest_2Prop (z-Test für zwei Proportionen) 103 zTest_2Samp (z-Test für zwei Stichproben) . 103

Sonderzeichen

+ (addieren) ............................................. 105

N(subtrahieren) ........................................ 105

·(multiplizieren) ..................................... 106

à (dividieren) ............................................ 106

^ (Potenz) ................................................. 107

(Quadrat) ............................................. 108

.+ (Punkt-Addition) .................................. 108

.. (Punkt-Subt.) ......................................... 108

·(Punkt-Mult.) ........................................ 108

. / (Punkt-Division) ................................... 108

.^ (Punkt-Potenz) ..................................... 109

ë(Negation) .............................................. 109

% (Prozent) ..............................................109

= (gleich) ...................................................110

ƒ (ungleich) ..............................................110

< (kleiner als) ............................................111

{ (kleiner oder gleich) ..............................111

> (größer als) ............................................111

| (größer oder gleich) ..............................111

! (Fakultät) ................................................112

& (anfügen) ..............................................112

‡() (Quadratwurzel) .................................112

Π() (Produkt) .............................................112

G() (Summe) ..............................................113

GInt() .........................................................113

GPrn() ........................................................114

# (Umleitung) ...........................................114

í (Wissenschaftliche Schreibweise) .........114

g (Neugrad) ..............................................115

ô(Bogenmaß) ............................................115

¡ (Grad) ..................................................... 115

¡, ', '' (Grad/Minute/Sekunde) ................. 115

 (Winkel) ................................................ 116

10^() .......................................................... 116

^ê (Kehrwert) ........................................... 116

| (“with”) .................................................. 117

& (speichern) ............................................ 117

:= (zuweisen) ............................................ 117

0b, 0h ........................................................ 118

Fehlercodes und -meldungen Hinweise zu TI Produktservice

und Garantieleistungen

TI-Nspire™

In diesem Handbuch sind die Vorlagen, Funktionen, Befehle und Operatoren aufgelistet, die zur Auswertung mathematischer Ausdrücke verfügbar sind.

Referenzhandbuch

Vorlagen für Ausdrücke

Vorlagen für Ausdrücke bieten Ihnen eine einfache Möglichkeit, mathematische Ausdrücke in der mathematischen Standardschreibweise einzugeben. Wenn Sie eine Vorlage eingeben, wird sie in der Eingabezeile mit kleinen Blöcken an den Positionen angezeigt, an denen Sie Elemente eingeben können. Der Cursor zeigt, welches Element eingegeben werden kann.

Verwenden Sie die Pfeiltasten oder drücken Sie der Elemente zu bewegen, und geben Sie für jedes Element einen Wert oder Ausdruck ein.

Drücken Sie

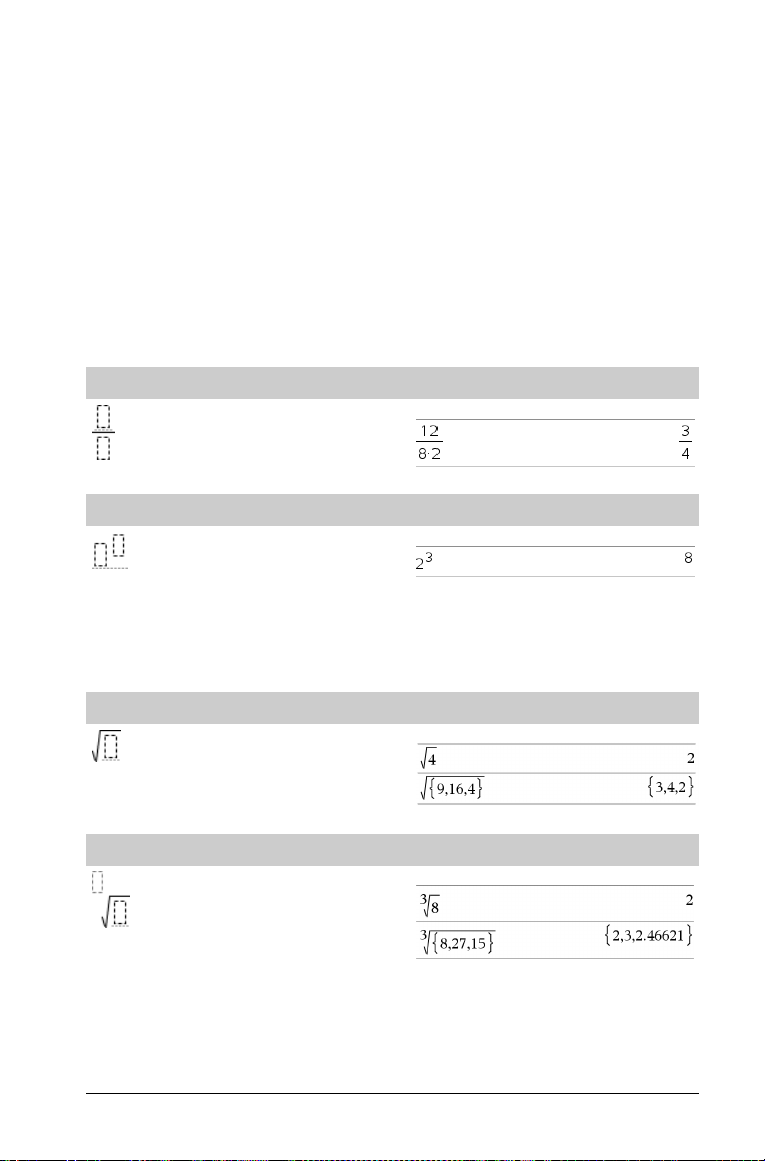
Vorlage Bruch

· oder /·, um den Ausdruck auszuwerten.

Hinweis: Siehe auch / (Dividieren), Seite 106.

e, um den Cursor zur jeweiligen Position

/p Tasten

Beispiel:

Vorlage Exponent

Hinweis: Geben Sie den ersten Wert ein, drücken Sie l und

geben Sie dann den Exponenten ein. Um den Cursor auf die Grundlinie zurückzusetzen, drücken Sie die rechte Pfeiltaste (¢).

Hinweis: Siehe auch ^ (Potenz), Seite 107.

Vorlage Quadratwurzel

Hinweis: Siehe auch

Vorlage n-te Wurzel

Hinweis: Siehe auch root(), Seite 75.

‡

() (Quadratwurzel), Seite 112.

l Taste

Beispiel:

/q Tasten

Beispiel:

/l Tasten

Beispiel:

TI-Nspire™ Referenzhandbuch 1

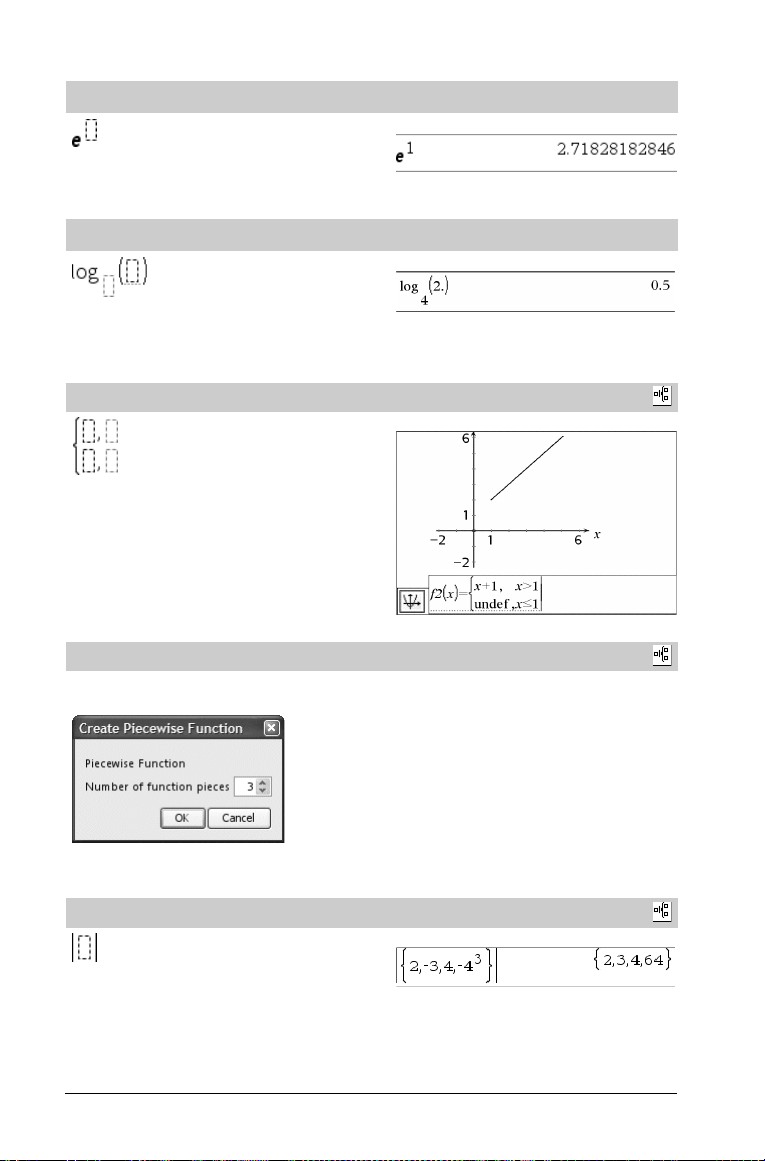
Vorlage e Exponent

Potenz zur natürlichen Basis e

Hinweis: Siehe auch e^(), Seite 27.

u Tasten

Example:

Vorlage Logarithmus

Berechnet den Logarithmus zu einer bestimmten Basis. Bei der Standardbasis 10 wird die Basis weggelassen.

Hinweis: Siehe auch log(), Seite 51.

Vorlage Stückweise (2 Teile)

Ermöglicht es, Ausdrücke und Bedingungen für eine stückweise definierte Funktion aus zwei-Stücken zu erstellen. Um ein Stück hinzuzufügen, klicken Sie in die Vorlage und wiederholen die Vorlage.

Hinweis: Siehe auch piecewise(), Seite 66.

Vorlage Stückweise (n Teile)

Ermöglicht es, Ausdrücke und Bedingungen für eine stückweise definierte Funktion aus n-Teilen zu erstellen. Fragt nach n.

/s Taste

Beispiel:

Katalog >

Beispiel:

Katalog >

Beispiel: Siehe Beispiel für die Vorlage Stückweise (2 Teile).

Hinweis: Siehe auch piecewise(), Seite 66.

Vorlage Absolutwert

Beispiel:

Hinweis: Siehe auch abs(), Seite 5.

Katalog >

2 TI-Nspire™ Referenzhandbuch

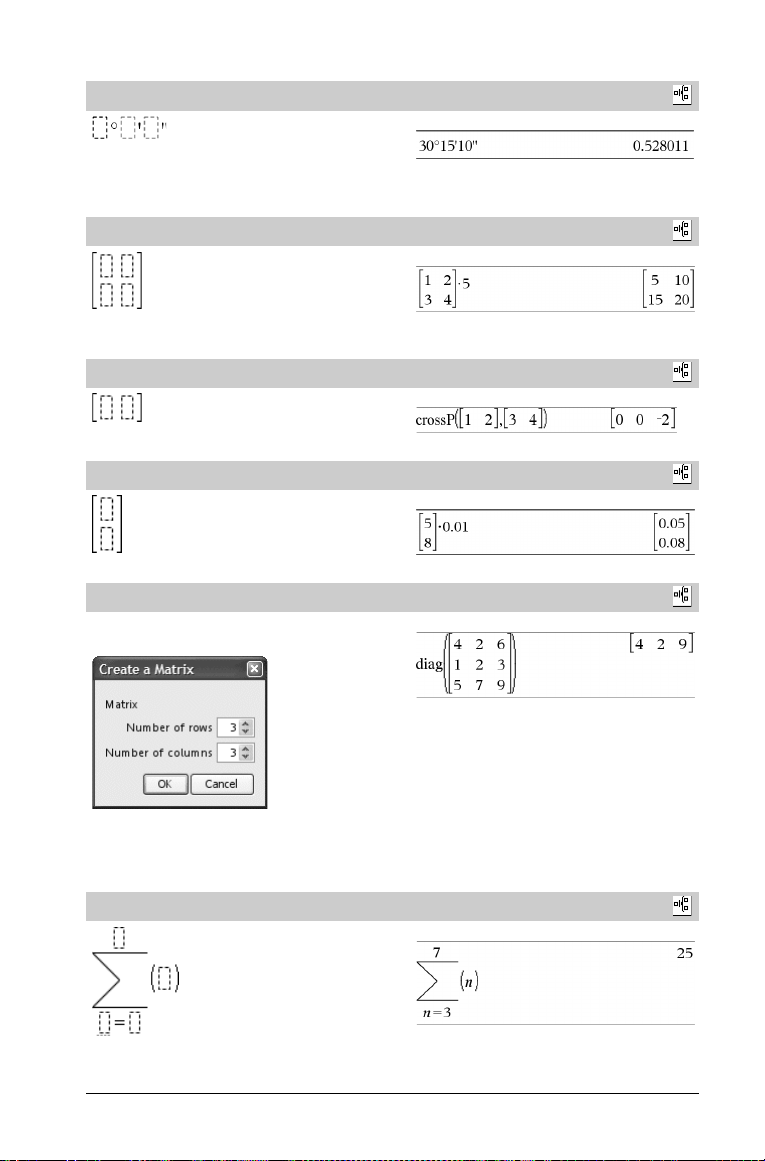
Vorlage dd°mm’ss.ss’’

Ermöglicht es, Winkel im Format dd°mm’ss.ss’’ einzugeben, wobei

dd für den Dezimalgrad, mm die Minuten und ss.ss die Sekunden

steht.

Katalog >

Beispiel:

Vorlage Matrix (2 x 2)

Erzeugt eine 2 x 2 Matrix.

Vorlage Matrix (1 x 2)

Vorlage Matrix (2 x 1)

Vorlage Matrix (m x n)

Die Vorlage wird angezeigt, nachdem Sie aufgefordert wurden, die Anzahl der Zeilen und Spalten anzugeben.

Katalog >

Beispiel:

Katalog >

Beispiel:

Katalog >

Beispiel:

Katalog >

Beispiel:

Hinweis: Wenn Sie eine Matrix mit einer großen Zeilen- oder Spaltenanzahl erstellen, dauert es möglicherweise einen Augenblick, bis sie angezeigt wird.

Vorlage Summe (G)

Beispiel:

Katalog >

TI-Nspire™ Referenzhandbuch 3

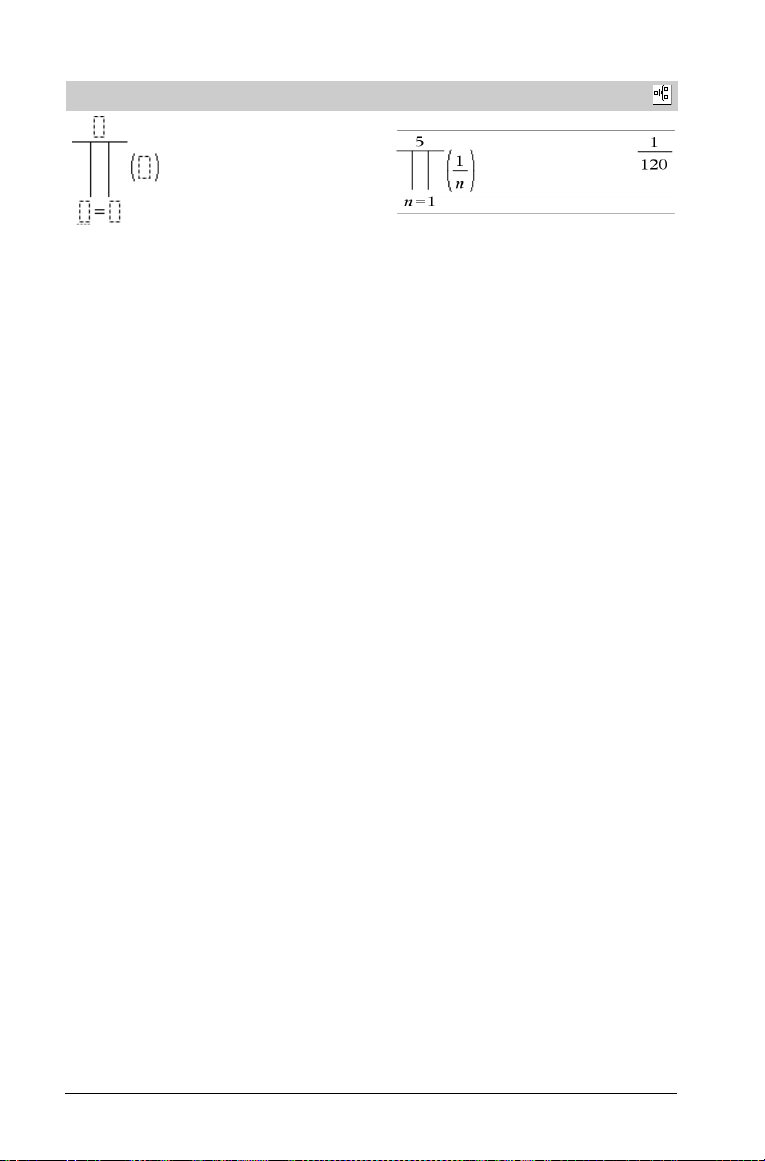
Vorlage Produkt (Π)

Hinweis: Siehe auch Π() (Produkt), Seite 112.

Katalog >

Beispiel:

4 TI-Nspire™ Referenzhandbuch

Alphabetische Auflistung

Elemente, deren Namen nicht alphabetisch sind (wie +, !, und >) finden Sie am Ende dieses Abschnitts ab Seite 105. Wenn nicht anders angegeben, wurden sämtliche Beispiele im standardmäßigen Reset-Modus ausgeführt, wobei alle Variablen als nicht definiert angenommen wurden.

abs() (Absolutwert)

abs(Wer t 1) ⇒ We r t abs(

Liste1) ⇒ Liste

abs(Matrix1) ⇒ Matrix

Gibt den Absolutwert des Arguments zurück.

Hinweis: Siehe auch Vorlage Absolutwert, Seite 2.

Ist das Argument eine komplexe Zahl, wird der Betrag der Zahl zurückgegeben.

Hinweis: Alle undefinierten Variablen werden als reelle Variablen

behandelt.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],

[

WertRunden]) ⇒ Matrix

Amortisationsfunktion, die eine Matrix als Amortisationstabelle für eine Reihe von TVM-Argumenten zurückgibt.

NPmt ist die Anzahl der Zahlungen, die in der Tabelle enthalten sein müssen. Die Tabelle beginnt mit der ersten Zahlung.

N, I, PV, Pmt, FV, PpY, CpY und PmtAt werden in der TVMArgumentetabelle auf Seite 96 beschrieben.

• Wenn Sie Pmt nicht angeben, wird standardmäßig Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt) eingesetzt.

• Wenn Sie FV nicht angeben, wird standardmäßig FV=0 eingesetzt.

• Die Standardwerte für PpY, CpY und PmtAt sind dieselben wie bei den TVM-Funktionen.

WertRunden (roundValue) legt die Anzahl der Dezimalstellen für das Runden fest. Standard=2.

Die Spalten werden in der Ergebnismatrix in der folgenden Reihenfolge ausgegeben: Zahlungsnummer, Zinsanteil, Tilgungsanteil, Saldo.

Der in Zeile n angezeigte Saldo ist der Saldo nach Zahlung n. Sie können die ausgegebene Matrix als Eingabe für die anderen

Amortisationsfunktionen GInt() und GPrn(), Seite 113, und bal(), Seite 10, verwenden.

Katalog

and (und)

Boolescher Ausdr1 and Boolescher Ausdr2

⇒ Boolescher Ausdruck

Boolesche Liste1 and Boolesche Liste2

⇒ Boolesche Liste

Boolesche Matrix1 and Boolesche Matrix2

⇒ Boolesche Matrix

Gibt „wahr“ oder „falsch“ oder eine vereinfachte Form des ursprünglichen Terms zurück.

Katalog

TI-Nspire™ Referenzhandbuch 5

and (und)

Ganzzahl1 and Ganzzahl2 ⇒ Ganzzahl

Vergleicht zwei reelle ganze Zahlen mit Hilfe einer für Bit. Intern werden beide ganzen Zahlen in binäre 32-Bit-Zahlen mit Vorzeichen konvertiert. Beim Vergleich der sich entsprechenden Bits ist das Ergebnis dann 1, wenn beide Bits 1 sind; anderenfalls ist das Ergebnis 0. Der zurückgegebene Wert stellt die Bit-Ergebnisse dar und wird im jeweiligen Basis-Modus angezeigt.

Sie können die ganzen Zahlen in jeder Basis eingeben. F ür eine binäre oder hexadezimale Eingabe ist das Präfix 0b bzw. 0h zu verwenden. Ohne Präfix werden ganze Zahlen als dezimal behandelt (Basis 10).

Geben Sie eine dezimale ganze Zahl ein, die für eine 32-Bit-Dualform mit Vorzeichen zu groß ist, dann wird eine symmetrische ModuloOperation ausgeführt, um den Wert in den erforderlichen Bereich zu bringen.

and-Operation Bit

Katalog

Im Hex-Modus:

Wichtig: Null, nicht Buchstabe O.

Im Bin-Modus:

Im Dec-Modus:

Hinweis: Eine binäre Eingabe kann bis zu 64 Stellen haben

(das Präfix 0b wird nicht mitgezählt). Eine hexadezimale Eingabe kann bis zu 16 Stellen aufweisen.

angle() (Winkel)

angle(Wer t 1) ⇒ We r t

Gibt den Winkel des Arguments zurück, wobei das Argument als komplexe Zahl interpretiert wird.

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

angle(Liste1) ⇒ Liste angle(Matrix1) ⇒ Matrix

Gibt als Liste oder Matrix die Winkel der Elemente aus Liste1 oder Matrix1 zurück, wobei jedes Element als komplexe Zahl interpretiert

wird, die einen zweidimensionalen kartesischen Koordinatenpunkt darstellt.

ANOVA

ANOVA Liste1,Liste2[,Liste3,...,Liste20][,Flag]

Führt eine einfache Varianzanalyse durch, um die Mittelwerte von zwei bis maximal 20 Grundgesamtheiten zu vergleichen. Eine Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (Siehe Seite 86.)

Flag=0 für Daten, Flag=1 für Statistik

Ausgabevariable Beschreibung

stat.F Wert der F Statistik

stat.PVal Kleinste Signifikanzebene, bei der die Nullhypothese verworfen werden kann

stat.df Gruppen-Freiheitsgrade

stat.SS Summe der Fehlerquadrate zwischen den Gruppen

stat.MS Mittlere Quadrate der Gruppen

Katalog

6 TI-Nspire™ Referenzhandbuch

Ausgabevariable Beschreibung

stat.dfError Fehler-Freiheitsgrade

stat.SSError Summe der Fehlerquadrate

stat.MSError Mittleres Quadrat für die Fehler

stat.sp Verteilte Standardabweichung

stat.xbarlist Mittelwerte der Eingabelisten

stat.CLowerList 95 % Konfidenzintervalle für den Mittelwert jeder Eingabeliste

stat.CUpperList 95 % Konfidenzintervalle für den Mittelwert jeder Eingabeliste

ANOVA2way (ANOVA 2fach)

ANOVA2way Liste1,Liste2[,Liste3,…,Liste10][,LevZei]

Berechnet eine zweifache Varianzanalyse, um die Mittelwerte von zwei bis maximal 10 Grundgesamtheiten zu vergleichen. Eine Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (Siehe Seite 86.)

LevZei=0 für Block

LevZei=2,3,...,Len-1, für Faktor zwei, wobei Len=length(Liste1)=length(Liste2) = … = length(Liste10) und Len / LevZei ∈ {2,3,…}

Ausgaben: Block-Design

Ausgabevariable Beschreibung

stat.FF Statistik des Spaltenfaktors

stat.PVal Kleinste Signifikanzebene, bei der die Nullhypothese verworfen werden kann

stat.df Freiheitsgrade des Spaltenfaktors

stat.SS Summe der Fehlerquadrate des Spaltenfaktors

stat.MS Mittlere Quadrate für Spaltenfaktor

stat.FBlock F Statistik für Faktor

stat.PValBlock Kleinste Wahrscheinlichkeit, bei der die Nullhypothese verworfen werden kann

stat.dfBlock Freiheitsgrade für Faktor

stat.SSBlock Summe der Fehlerquadrate für Faktor

stat.MSBlock Mittlere Quadrate für Faktor

stat.dfError Fehler-Freiheitsgrade

stat.SSError Summe der Fehlerquadrate

stat.MSError Mittlere Quadrate für die Fehler

stat.s Standardabweichung des Fehlers

Katalog

TI-Nspire™ Referenzhandbuch 7

Ausgaben des SPALTENFAKTORS

Ausgabevariable Beschreibung

stat.Fcol F Statistik des Spaltenfaktors

stat.PValCol Wahrscheinlichkeitswert des Spaltenfaktors

stat.dfCol Freiheitsgrade des Spaltenfaktors

stat.SSCol Summe der Fehlerquadrate des Spaltenfaktors

stat.MSCol Mittlere Quadrate für Spaltenfaktor

Ausgaben des ZEILENFAKTORS

Ausgabevariable Beschreibung

stat.Frow F Statistik des Zeilenfaktors

stat.PValRow Wahrscheinlichkeitswert des Zeilenfaktors

stat.dfRow Freiheitsgrade des Zeilenfaktors

stat.SSRow Summe der Fehlerquadrate des Zeilenfaktors

stat.MSRow Mittlere Quadrate für Zeilenfaktor

INTERAKTIONS-Ausgaben

Ausgabevariable Beschreibung

stat.FInteract F Statistik der Interaktion

stat.PValInteract Wahrscheinlichkeitswert der Interaktion

stat.dfInteract Freiheitsgrade der Interaktion

stat.SSInteract Summe der Fehlerquadrate der Interaktion

stat.MSInteract Mittlere Quadrate für Interaktion

FEHLER-Ausgaben

Ausgabevariable Beschreibung

stat.dfError Fehler-Freiheitsgrade

stat.SSError Summe der Fehlerquadrate

stat.MSError Mittlere Quadrate für die Fehler

s Standardabweichung des Fehlers

8 TI-Nspire™ Referenzhandbuch

Ans (Antwort)

Ans ⇒ We rt

Gibt das Ergebnis des zuletzt ausgewerteten Ausdrucks zurück.

Taste

approx() (Approximieren)

approx(Wer t 1) ⇒ Zahl

Gibt die Auswertung des Arguments ungeachtet der aktuellen Einstellung des Modus Auto oder Näherung als Dezimalwert zurück, sofern möglich.

Gleichwertig damit ist die Eingabe des Arguments und Drücken von

·.

approx(Liste1) ⇒ Liste approx(Matrix1) ⇒ Matrix

Gibt, sofern möglich, eine Liste oder Matrix zurück, in der jedes Element dezimal ausgewertet wurde.

approxRational()

approxRational(Expr[, tol]) ⇒ expression approxRational(List[, tol]) ⇒ list approxRational(Matrix[, tol]) ⇒ matrix

Gibt das Argument mit der Toleranz tol als Bruch zurück. Wird tol weggelassen, so wird die Toleranz 5.E-14 verwendet.

augment() (Erweitern)

augment(Liste1, Liste2) ⇒ Liste

Gibt eine neue Liste zurück, die durch Anfügen von Liste2 ans Ende von Liste1 erzeugt wurde.

augment(Matrix1, Matrix2) ⇒ Matrix

Gibt eine neue Matrix zurück, die durch Anfügen von Matrix2 an Matrix1 erzeugt wurde. Wenn das Zeichen “,” verwendet wird,

müssen die Matrizen gleiche Zeilendimensionen besitzen, und

Matrix2 wird spaltenweise an Matrix1 angefügt. Verändert weder Matrix1 noch Matrix2.

Katalog

TI-Nspire™ Referenzhandbuch 9

avgRC() (Durchschnittliche Änderungsrate)

avgRC(Ausdr1, Var [=Wert] [, H]) ⇒ Ausdruck avgRC(Ausdr1, Var [=Wert] [, Liste1]) ⇒ Liste avgRC(Liste1, Va r [=Wert] [, H]) ⇒ Liste avgRC(Matrix1, Var [=Wert] [, H]) ⇒ Matrix

Gibt den rechtsseitigen Differenzenquotienten zurück (durchschnittliche Änderungsrate).

Ausdr1 kann eine benutzerdefinierte Funktion sein (siehe Wenn Wer t angegeben wird, setzt er jede vorausgegangene

Variablenzuweisung oder jede aktuelle Ersetzung für die Variable außer Kraft.

H ist der Schrittwert. Wird H nicht angegeben, wird als Vorgabewert 0,001 benutzt.

Beachten Sie, dass die ähnliche Funktion Differenzenquotienten benutzt.

nDeriv() den zentralen

Func).

Katalog

bal()

bal(NPmt,N,I,PV,[Pmt], [FV], [PpY], [CpY], [PmtAt],

[

WertRunden]) ⇒ We rt

bal(NPmt,AmortTabelle) ⇒ We rt

Amortisationsfunktion, die den Saldo nach einer angegebenen Zahlung berechnet.

N, I, PV, Pmt, FV, PpY, CpY und PmtAt werden in der TVMArgumentetabelle auf Seite 96 beschrieben.

NPmt bezeichnet die Zahlungsnummer, nach der die Daten berechnet werden sollen.

N, I, PV, Pmt, FV, PpY, CpY und PmtAt werden in der TVMArgumentetabelle auf Seite 96 beschrieben.

• Wenn Sie Pmt nicht angeben, wird standardmäßig Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt) eingesetzt.

• Wenn Sie FV nicht angeben, wird standardmäßig FV=0 eingesetzt.

• Die Standardwerte für PpY, CpY und PmtAt sind dieselben wie bei den TVM-Funktionen.

WertRunden (roundValue) legt die Anzahl der Dezimalstellen für das Runden fest. Standard=2.

bal(NPmt,AmortTabelle) berechnet den Saldo nach jeder

Zahlungsnummer NPmt auf der Grundlage der Amortisationstabelle AmortTabelle. Das Argument AmortTabelle (amortTable) muss eine Matrix in der unter amortTbl(), Seite 5, beschriebenen Form sein.

Hinweis: Siehe auch GInt() und GPrn(), Seite 113.

Base2

Ganzzahl1 4Base2 ⇒ Ganzzahl

Konvertiert Ganzzahl1 in eine Dualzahl. Dual- oder Hexadezimalzahlen weisen stets das Präfix 0b bzw. 0h auf.

Katalog

10 TI-Nspire™ Referenzhandbuch

Base2

0b binäre_Zahl 0h hexadezimale_Zahl

Null (nicht Buchstabe O) und b oder h. Eine Dualzahl kann bis zu 64 Stellen haben, eine Hexadezimalzah l bis

zu 16. Ohne Präfix wird Ganzzahl1 als Dezimalzahl behandelt (Basis 10).

Das Ergebnis wird unabhängig vom Basis-Modus binär angezeigt. Geben Sie eine dezimale ganze Zahl ein, die für eine 64-Bit-Dualform

mit Vorzeichen zu groß ist, dann wird eine symmetrische ModuloOperation ausgeführt, um den Wert in den erforderlichen Bereich zu bringen.

Base10

Ganzzahl1 4Base10 ⇒ Ganzzahl

Konvertiert Ganzzahl1 in eine Dezimalzahl (Basis 10). Ein binärer oder hexadezimaler Eintrag muss stets das Präfix 0b bzw. 0h aufweisen.

0b binäre_Zahl 0h hexadezimale_Zahl

Null (nicht Buchstabe O) und b oder h. Eine Dualzahl kann bis zu 64 Stellen haben, eine Hexadezimalzah l bis

zu 16. Ohne Präfix wird Ganzzahl1 als Dezimalzahl behandelt. Das Ergebnis

wird unabhängig vom Basis-Modus dezimal angezeigt.

Base16

Ganzzahl1 4Base16 ⇒ Ganzzahl

Wandelt Ganzzahl1 in eine Hexadezimalzahl um. Dual- oder Hexadezimalzahlen weisen stets das Präfix 0b bzw. 0h auf.

0b binäre_Zahl 0h hexadezimale_Zahl

Null (nicht Buchstabe O) und b oder h. Eine Dualzahl kann bis zu 64 Stellen haben, eine Hexadezimalzah l bis

zu 16. Ohne Präfix wird Ganzzahl1 als Dezimalzahl behandelt (Basis 10).

Das Ergebnis wird unabhängig vom Basis-Modus hexadezimal angezeigt.

Geben Sie eine dezimale ganze Zahl ein, die für eine 64-Bit-Dualform mit Vorzeichen zu groß ist, dann wird eine symmetrische ModuloOperation ausgeführt, um den Wert in den erforderlichen Bereich zu bringen.

Katalog

binomCdf()

binomCdf(n,p,untereGrenze,obereGrenze) ⇒ Zahl, wenn

untereGrenze und obereGrenze Zahlen sind, Liste, wenn untereGrenze und obereGrenze Listen sind

binomCdf(

Zahl ist,

Berechnet die kumulative Wahrscheinlichkeit für die diskrete Binomialverteilung mit n Versuchen und der Wahrscheinlichkeit p für einen Erfolg in jedem Einzelversuch.

Für P(X  obereGrenze) setzen Sie untereGrenze=0

n,p,obereGrenze) ⇒ Zahl, wenn obereGrenze eine

Liste, wenn obereGrenze eine Liste ist

Katalog

TI-Nspire™ Referenzhandbuch 11

binomPdf()

binomPdf(n,p) ⇒ Zahl binomPdf(n,p,XWert) ⇒ Zahl, wenn XWert eine Zahl ist,

Liste, wenn XWert eine Liste ist

Berechnet die Wahrscheinlichkeit an einem XWert für die diskrete Binomialverteilung mit n Versuchen und der Wahrscheinlichkeit p für den Erfolg in jedem Einzelversuch.

Katalog

ceiling() (Obergrenze)

ceiling(Wer t 1) ⇒ We r t

Gibt die erste ganze Zahl zurück, die ‚ dem Argument ist.

Das Argument kann eine reelle oder eine komplexe Zahl sein.

Hinweis: Siehe auch floor().

ceiling(Liste1) ⇒ Liste ceiling(Matrix1) ⇒ Matrix

Für jedes Element einer Liste oder Matrix wird die kleinste ganze Zahl, die größer oder gleich dem Element ist, zurückgegeben.

char() (Zeichenstring)

char(Ganzzahl) ⇒ Zeichen

Gibt ein Zeichenstring zurück, das das Zeichen mit der Nummer Ganzzahl aus dem Zeichensatz des Handhelds enthält. Der gültige Wertebereich für Ganzzahl ist 0–65535.

2way

2way BeobMatrix

chi22way BeobMatrix

Berechnet eine c2 Testgröße auf Grundlage einer beobachteten Matrix BeobMatrix. Eine Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (Siehe Seite 86.)

Ausgabevariable Beschreibung

stat.c2 Chi-Quadrat-Testgröße: sum(beobachtet - erwartet)2/erwartet

stat.PVal Kleinste Signifikanzebene, bei der die Nullhypothese verworfen werden kann

stat.df Freiheitsgrade der Chi-Quadrat-Testgröße

stat.ExpMat Berechnete Kontingenztafel der erwarteten Häufigkeiten bei Annahme der Nullhypothese

stat.CompMat Berechnete Matrix der Chi-Quadrat-Summanden in der Testgröße

Katalog

12 TI-Nspire™ Referenzhandbuch

Cdf()

Cdf(untereGrenze,obereGrenze,Freigrad) ⇒ Zahl, wenn

untereGrenze und obereGrenze Zahlen sind, Liste, wenn untereGrenze und obereGrenze Listen sind

chi2Cdf(

untereGrenze,obereGrenze,Freiheitsgrad) ⇒ Zahl,

untereGrenze und obereGrenze Zahlen sind, Liste, wenn

wenn

untereGrenze und obereGrenze Listen sind

Berechnet die Verteilungswahrscheinlichkeit c2 zwischen

untereGrenze und obereGrenze für die angegebenen Freiheitsgrade FreiGrad.

Für P(X  obereGrenze) setzen Sie untereGrenze= 0.

GOF

GOF BeobListe,expListe,FreiGrad

chi2GOF BeobListe,expListe,FreiGrad

Berechnet eine Testgröße, um zu überprüfen, ob die Stichprobendaten aus einer Grundgesamtheit stammen, die einer bestimmten Verteilung genügt. obsList ist eine Liste von Zählern und muss Ganzzahlen enthalten. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Ausgabevariable Beschreibung

stat.c2 Chi-Quadrat-Testgröße: sum((beobachtet - erwartet)2/erwartet

stat.PVal Kleinste Signifikanzebene, bei der die Nullhypothese verworfen werden kann

stat.df Freiheitsgrade der Chi-Quadrat-Testgröße

stat.CompList Liste der Chi-Quadrat-Summanden in der Testgröße

Katalog

Pdf()

Pdf(XWert,FreiGrad) ⇒ Zahl, wenn Xwert eine Zahl ist,

Liste, wenn XWert eine Liste ist

chi2Pdf(

XWert,FreiGrad) ⇒ Zahl, wenn XWert eine Zahl ist,

Liste, wenn XWert eine Liste ist

Berechnet die Wahrscheinlichkeitsdichtefunktion (Pdf) einer c2Verteilung an einem bestimmten XWert für die vorgegebenen Freiheitsgrade FreiGrad.

ClearAZ (LöschAZ)

ClearAZ

Katalog

Löscht alle Variablen mit einem Zeichen im aktuellen Problembereich.

TI-Nspire™ Referenzhandbuch 13

ClrErr (LöFehler)

ClrErr

Löscht den Fehlerstatus und setzt die Systemvariable FehlerCode (errCode) auf Null.

Das Else im Block Try...Else...EndTry muss ClrErr oder PassErr

ÜbgebFehler) verwenden. Wenn der Fehler verarbeitet oder

( ignoriert werden soll, verwenden Sie ClrErr. Wenn nicht bekannt ist, was mit dem Fehler zu tun ist, verwenden Sie den nächsten Error Handler zu übergeben. Wenn keine weiteren

Try...Else...EndTry Error Handler unerledigt sind, wird das

Fehlerdialogfeld als normal angezeigt.

Hinweis: Siehe auch PassErr, Seite 66, und Try , Seite 94. Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen

PassErr, um ihn an

eingeben, indem Sie am Ende jeder Zeile @ statt · drücken. Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Ein Beispiel für

Versuche (Try), Seite 94.

zum Befehl

Katalog

ClrErr finden Sie als Beispiel 2 im Abschnitt

colAugment() (Spaltenerweiterung)

colAugment(Matrix1, Matrix2) ⇒ Matrix

Gibt eine neue Matrix zurück, die durch Anfügen von Matrix2 an Matrix1 erzeugt wurde. Die Matrizen müssen gleiche Spaltendimensionen haben, und Matrix2 wird zeilenweise an Matrix1 angefügt. Verändert weder Matrix1 noch Matrix2.

colDim() (Spaltendimension)

colDim(Matrix) ⇒ Ausdruck

Gibt die Anzahl der Spalten von Matrix zurück.

Hinweis: Siehe auch rowDim().

colNorm() (Spaltennorm)

colNorm(Matrix) ⇒ Ausdruck

Gibt das Maximum der Summen der absoluten Elementwerte der Spalten von Matrix zurück.

Hinweis: Undefinierte Matrixelemente sind nicht zulässig. Siehe

auch rowNorm().

conj() (Komplex Konjugierte)

conj(Wer t 1) ⇒ We r t conj(Liste1) ⇒ Liste conj(Matrix1) ⇒ Matrix

Gibt das komplex Konjugierte des Arguments zurück.

Hinweis: Alle undefinierten Variablen werden als reelle Variablen

behandelt.

Katalog

14 TI-Nspire™ Referenzhandbuch

constructMat()

constructMat(Ausdr,Var 1 ,Var 2 ,AnzZeilen,AnzSpalten)

⇒ Matrix

Gibt eine Matrix auf der Basis der Argumente zurück. Ausdr ist ein Ausdruck in Variablen Va r 1 und Va r 2 . Die Elemente in

der resultierenden Matrix ergeben sich durch Berechnung von Ausdr für jeden inkrementierten Wert von Va r 1 und Var 2 .

Var 1 wird automatisch von Zeile wird Va r2 inkrementiert von 1 bis AnzSpalten.

1 bis AnzZeilen inkrementiert. In jeder

Katalog

CopyVar

CopyVar Var 1 , Va r 2 CopyVar Var 1 ., Va r2 .

CopyVar Var 1 , Var 2 kopiert den Wert der Variablen Va r 1 auf die

Variable Var 2 und erstellt ggf. Va r 2. Variable Var 1 muss einen Wert haben.

Wenn Va r1 der Name einer vorhandenen benutzerdefinierten Funktion ist, wird die Definition dieser Funktion nach Funktion Va r 2 kopiert. Funktion Va r 1 muss definiert sein.

Var 1 muss die Benennungsregeln für Variablen erfüllen oder muss ein indirekter Ausdruck sein, der sich zu einem Variablennamen vereinfachen lässt, der den Regeln entspricht.

CopyVar Var 1 ., Va r2 . kopiert alle Mitglieder der Var 1 . -

Variablengruppe auf die Va r2 . -Gruppe und erstellt ggf. Va r 2 .. Var 1 . muss der Name einer bestehenden Variablengruppe sein, wie

die Statistikergebnisse stat.nn oder Variablen, die mit der Funktion

LibShortcut() erstellt wurden. Wenn Var 2 . schon vorhanden ist,

ersetzt dieser Befehl alle Mitglieder, die zu beiden Gruppen gehören, und fügt die Mitglieder hinzu, die noch nicht vorhanden sind. Wenn eine einfache (Nichtgruppen-) Variable namens Va r 2 existiert, tritt ein Fehler auf.

corrMat() (Korrelationsmatrix)

corrMat(Liste1,Liste2[,…[,Liste20]])

Berechnet die Korrelationsmatrix für die erweiterte Matrix [Liste1 Liste2 . . . Liste20].

Katalog

TI-Nspire™ Referenzhandbuch 15

cos() (Kosinus)

cos(Wer t1 ) ⇒ We rt cos(Liste1) ⇒ Liste

cos(Wer t1 ) gibt den Kosinus des Arguments als Wert zurück. cos(Liste1) gibt in Form einer Liste für jedes Element in Liste1 den

Kosinus zurück.

Hinweis: Der als Argument angegebene Winkel wird gemäß der

aktuellen Winkelmoduseinstellung als Grad, Neugrad oder Bogenmaß interpretiert. Sie können ó,G oderôbenutzen, um den Winkelmodus

vorübergend aufzuheben.

n Taste

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

cos(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den Matrix-Kosinus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Kosinus jedes einzelnen Elements.

Wenn eine skalare Funktion f(A) auf Quadratmatrix1 (A) angewendet wird, erfolgt die Berechnung des Ergebnisses durch den Algorithmus:

Berechnung der Eigenwerte (li) und Eigenvektoren (Vi) von A.

Quadratmatrix1 muss diagonalisierbar sein. Sie darf auch keine symbolischen Variablen ohne zugewiesene Werte enthalten.

Bildung der Matrizen:

Dann ist A = X B Xêund f(A) = X f(B) Xê. Beispiel: cos(A) = X cos(B) Xê, wobei:

cos (B) =

Alle Berechnungen werden unter Verwendung von FließkommaOperationen ausgeführt.

Im Bogenmaß-Modus:

16 TI-Nspire™ Referenzhandbuch

cosê() (Arkuskosinus)

cosê(Wer t 1) ⇒ Wer t cosê(Liste1) ⇒ Liste

/n Tasten

Im Grad-Modus:

cosê(Wer t 1) gibt den Winkel zurück, dessen Kosinus We r t1 ist.

cosê(Liste1) gibt in Form einer Liste für jedes Element aus Liste1

den inversen Kosinus zurück.

Hinweis: Das Ergebnis wird gemäß der aktuellen

Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben.

cosê(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den inversen Matrix-Kosinus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des inversen Kosinus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

cosh() (Cosinus hyperbolicus)

cosh(Wer t 1) ⇒ We r t cosh(Liste1) ⇒ Liste

cosh(Wer t 1) gibt den Cosinus hyperbolicus des Arguments zurück. cosh(Liste1) gibt in Form einer Liste für jedes Element aus Liste1

den Cosinus hyperbolicus zurück.

cosh(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den Matrix-Cosinus hyperbolicus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Cosinus hyperbolicus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:

Um das ganze Ergebnis zu sehen, drücken Sie £ und verwenden dann ¡ und ¢, um den Cursor zu bewegen.

Katalog

Im Bogenmaß-Modus:

coshê() (Arkuskosinus hyperbolicus)

coshê(Wer t 1) ⇒ Wer t coshê(Liste1) ⇒ Liste

cosh

(Wer t 1) gibt den inversen Cosinus hyperbolicus des

Arguments zurück.

cosh

(Liste1) gibt in Form einer Liste für jedes Element aus Liste1

den inversen Cosinus hyperbolicus zurück.

Katalog

TI-Nspire™ Referenzhandbuch 17

coshê() (Arkuskosinus hyperbolicus)

coshê(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den inversen Matrix-Cosinus hyperbolicus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des inversen Cosinus hyperbolicus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

Katalog

Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:

Um das ganze Ergebnis zu sehen, drücken Sie £ und verwenden dann ¡ und ¢, um den Cursor zu bewegen.

cot() (Kotangens)

cot(Wer t1 ) ⇒ We rt cot(Liste1) ⇒ Liste

Gibt den Kotangens von We rt 1 oder eine Liste der Kotangens aller Elemente in Liste1 zurück.

Hinweis: Der als Argument angegebene Winkel wird gemäß der

aktuellen Winkelmoduseinstellung als Grad, Neugrad oder Bogenmaß interpretiert. Sie können ó,G oderôbenutzen, um den Winkelmodus

vorübergend aufzuheben.

cotê() (Arkuskotangens)

cotê(Wer t 1) ⇒ Wer t cotê(Liste1) ⇒ Liste

Gibt entweder den Winkel, dessen Kotangens We r t1 ist, oder eine Liste der inversen Kotangens aller Elemente in Liste1 zurück.

Hinweis: Das Ergebnis wird gemäß der aktuellen

Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben.

coth() (Kotangens hyperbolicus)

coth(Wer t 1) ⇒ We r t coth(Liste1) ⇒ Liste

Gibt den hyperbolischen Kotangens von Ausdr1 oder eine Liste der hyperbolischen Kotangens aller Elemente in Liste1 zurück.

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Katalog

cothê() (Arkuskotangens hyperbolicus)

cothê(Wer t 1) ⇒ Wer t cothê(Liste1) ⇒ Liste

Gibt den inversen hyperbolischen Kotangens von We rt 1 oder eine Liste der inversen hyperbolischen Kotangens aller Elemente in Liste1 zurück.

Katalog

18 TI-Nspire™ Referenzhandbuch

count() (zähle)

count(Wert1oderListe1 [,Wert2oderListe2 [,...]]) ⇒ We rt

Gibt die kumulierte Anzahl aller Elemente in de n Argumenten zurück, deren Auswertungsergebnisse numerische Werte sind.

Jedes Argument kann ein Ausdruck, ein Wert, eine Liste oder eine Matrix sein. Sie können Datenarten mischen und Argumente unterschiedlicher Dimensionen verwenden.

Für eine Liste, eine Matrix oder einen Zellenbereich wird jedes Element daraufhin ausgewertet, ob es in die Zählung eingeschlossen werden soll.

Innerhalb der Lists & Spreadsheet Applikation können Sie anstelle eines beliebigen Arguments auch einen Zellenbereich verwenden.

Katalog

countIf()

countIf(Liste,Kriterien) ⇒ We rt

Gibt die kumulierte Anzahl aller Elemente in der Liste zurück, die die festgelegten Kriterien erfüllen.

Kriterien können sein:

• Ein Wert, ein Ausdruck oder eine Zeichenfolge. So zählt zum Beispiel 3 nur Elemente in der Liste, die vereinfacht den Wert 3 ergeben.

• Ein Boolescher Ausdruck, der das Sonderzeichen ? als Platzhalter für jedes Element verwendet. Beispielsweise zählt ?<5 nur die Elemente in der Liste, die kleiner als 5 sind.

Innerhalb der Lists & Spreadsheet Applikation können Sie anstelle der Liste auch einen Zellenbereich verwenden.

Hinweis: Siehe auch sumIf(), Seite 89, und frequency(), Seite

34.

crossP() (Kreuzprodukt)

crossP(Liste1, Liste2) ⇒ Liste

Gibt das Kreuzprodukt von Liste1 und Liste2 als Liste zurück. Liste1 und Liste2 müssen die gleiche Dimension besitzen, die

entweder 2 oder 3 sein muss.

crossP(Vektor1, Vektor2) ⇒ Vektor

Gibt einen Zeilen- oder Spaltenvektor zurück (je nach den Argumenten), der das Kreuzprodukt von Vektor1 und Vektor2 ist.

Entweder müssen Vektor1 und Vektor2 beide Zeilenvektoren oder beide Spaltenvektoren sein. Beide Vektoren müssen die gleiche Dimension besitzen, die entweder 2 oder 3 sein muss.

Katalog

Zählt die Anzahl der Elemente, die 3 entsprechen.

Zählt die Anzahl der Elemente, die “def.” entsprechen

Zählt 1 und 3.

Zählt 3, 5 und 7.

Zählt 1, 3, 7 und 9.

Katalog

TI-Nspire™ Referenzhandbuch 19

csc() (Kosekans)

csc(Wer t 1) ⇒ We r t csc(Liste1) ⇒ Liste

Gibt den Kosekans von We rt 1 oder eine Liste der Konsekans aller Elemente in Liste1 zurück.

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Katalog

cscê() (Inverser Kosekans)

cscê(We rt 1) ⇒ We rt cscê(Liste1) ⇒ Liste

Gibt entweder den Winkel, dessen Kosekans We r t1 entspricht, oder eine Liste der inversen Kosekans aller Elemente in Liste1 zurück.

Hinweis: Das Ergebnis wird gemäß der aktuellen

Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben.

csch() (Kosekans hyperbolicus)

csch(Wer t1 ) ⇒ We rt csch(Liste1) ⇒ Liste

Gibt den hyperbolischen Kosekans von We rt 1 oder eine Liste der hyperbolischen Kosekans aller Elemente in Liste1 zurück.

cschê() (Inverser Kosekans hyperbolicus)

cschê(Wer t 1) ⇒ We rt cschê(Liste1) ⇒ Liste

Gibt den inversen hyperbolischen Kosekans von We r t1 oder eine Liste der inversen hyperbolischen Kosekans aller Elemente in Liste1 zurück.

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Katalog

20 TI-Nspire™ Referenzhandbuch

CubicReg (Kubische Regression)

CubicReg X, Y[, [Häuf] [, Kategorie, Mit]]

Berechnet die kubische polynomiale Regression y = a·x3+b· x2+c·x+d auf Listen X und Y mit der Häufigkeit Häuf. Eine

Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Alle Listen außer Mit müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element

in Häuf gibt die Häufigkeit für jeden entsprechenden Datenpunkt X und Y an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen

| 0 sein.

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden Daten X und Y.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Ausgabevariable Beschreibung

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.R

stat.Resid Residuen von der Regression

stat.XReg Liste der Datenpunkte in der modifizierten X List, die schließlich in der Regression mit den

stat.YReg Liste der Datenpunkte in der modifizierten Y List, die schließlich in der Regression mit den

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

Regressionsgleichung: a·x3+b·x2+c·x+d

Regressionskoeffizienten

Bestimmungskoeffizient

Beschränkungen für Häufigkeit, Kategorieliste und Mit Kategorien verwendet wurde

Katalog

cumSum() (Kumulierte Summe)

cumSum(Liste1) ⇒ Liste

Gibt eine Liste der kumulierten Summen der Elemente aus Liste1 zurück, wobei bei Element 1 begonnen wird.

cumSum(Matrix1) ⇒ Matrix

Gibt eine Matrix der kumulierten Summen der Elemente aus Matrix1 zurück. Jedes Element ist die kumulierte Summe der Spalte von oben nach unten.

Katalog

TI-Nspire™ Referenzhandbuch 21

Cycle (Zyklus)

Übergibt die Programmsteuerung sofort an die nächste Wiederholung der aktuellen Schleife (

Cycle ist außerhalb dieser drei Schleifenstrukturen (For, While

Loop) nicht zulässig.

oder

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Cylind (Zylindervektor)

Vek t o r 4Cylind

Zeigt den Zeilen- oder Spaltenvektor in Zylinderkoordin aten [r,q, z] an.

Vek t o r muss genau drei Elemente besitzen. Er kann entweder ein Zeilen- oder Spaltenvektor sein.

For, While oder Loop).

@ statt · drücken.

Katalog

Funktionslisting, das die ganzen Zahlen von 1 bis 100 summiert und dabei 50 überspringt.

Katalog

dbd()

dbd(Datum1,Datum2) ⇒ We rt

Zählt die tatsächlichen Tage und gibt die Anzahl der Tage zwischen

Datum1 und Datum2 zurück. Datum1 und Datum2 können Zahlen oder Zahlenlisten innerhalb des

Datumsbereichs des Standardkalenders sein. Wenn sowohl Datum1 als auch Datum2 Listen sind, müssen sie dieselbe Länge haben.

Datum1 und Datum2 müssen innerhalb der Jahre 1950 und 2049 liegen.

Sie können Datumseingaben in zwei Formaten vornehmen. Die Datumsformate unterscheiden sich in der Anordnung der Dezimalstellen.

MM.TTJJ (üblicherweise in den USA verwendetes Format) TTMM.JJ (üblicherweise in Europa verwendetes Format)

Katalog

22 TI-Nspire™ Referenzhandbuch

DD (Dezimalwinkel)

4DD ⇒ We rt

Zahl Liste1 4DD ⇒ Liste Matrix1

4DD ⇒ Matrix

Gibt das Dezimaläquivalent des Arguments zurück. Das Argument ist eine Zahl, eine Liste oder eine Matrix, die gemäß der Moduseinstellung als Neugrad, Bogenmaß oder Grad interpretiert wird.

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Katalog

4Decimal (Dezimal)

4Decimal

Wer t 1

4Decimal

Liste1 Matrix1

Zeigt das Argument in Dezimalform an. Dieser Operator kann nur am Ende der Eingabezeile verwendet werden.

Definiere

Define Var = Expression Define Function(Param1, Param2, ...) = Expression

Definiert die Variable Va r oder die benutzerdefinierte Funktion Function.

Parameter wie z.B. Param1 enthalten Platzhalter zur Übergabe von Argumenten an die Funktion. Beim Aufrufen benutzerdefinierter Funktionen müssen Sie Argumente angeben (z.B. Werte oder Variablen), die zu den Parametern passen. Beim Aufruf wertet die Funktion Ausdruck (Expression) unter Verwendung der übergebenen Parameter aus.

Var und Funktion (Function) dürfen nicht der Name einer Systemvariablen oder einer integrierten Funktion / eines integrierten Befehls sein.

Hinweis: Diese Form von Definiere (Define) ist gleichwertig mit

der Ausführung folgenden Ausdrucks: expression & Function(Param1,Param2).

Decimal

⇒ Wer t ⇒ Wer t

⇒ Wer t

Katalog

TI-Nspire™ Referenzhandbuch 23

Definiere

Define Function(Param1, Param2, ...) = Func

Block

EndFunc

Program(Param1, Param2, ...) = Prgm

Define

Block

EndPrgm

In dieser Form kann die benutzerdefinierte Funktion bzw. das benutzerdefinierte Programm einen Block mit mehr eren Anweisungen ausführen.

Block kann eine einzelne Anweisung oder eine Serie von Anweisungen in separaten Zeilen sein. Block kann auch Ausdrücke und Anweisungen enthalten (wie If, Then, Else und For).

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste. Hinweis: Siehe auch Definiere LibPriv (Define LibPriv),

Seite 24, und Definiere LibPub (Define LibPub), Seite 25.

Katalog

Definiere LibPriv (Define LibPriv)

Define LibPriv Var = Expression Define LibPriv Function(Param1, Param2, ...) = Expression

Define LibPriv Function(Param1, Param2, ...) = Func

Block

EndFunc Define LibPriv

Block

EndPrgm

Funktioniert wie Define, definiert jedoch eine Variable, eine Funktion oder ein Programm für eine private Bibliothek. Private Funktionen und Programme werden im Katalog nicht angezeigt.

Hinweis: Siehe auch Definiere (Define), Seite 23, und Definiere LibPub (Define LibPub), Seite 25.

Program(Param1, Param2, ...) = Prgm

Katalog

24 TI-Nspire™ Referenzhandbuch

Definiere LibPub (Define LibPub)

Define LibPub Var = Expression Define LibPub Function(Param1, Param2, ...) = Expression

Define LibPub Function(Param1, Param2, ...) = Func

Block

EndFunc Define LibPub

Block

EndPrgm

Funktioniert wie Definiere (Define), definiert jedoch eine Variable, eine Funktion oder ein Programm für eine öffentliche Bibliothek. Öffentliche Funktionen und Programme werden im Katalog angezeigt, nachdem die Bibliothek gespeichert und aktualisiert wurde.

Hinweis: Siehe auch Definiere (Define), Seite 23, und Definiere LibPriv (Define LibPriv), Seite 24.

Program(Param1, Param2, ...) = Prgm

Katalog

DelVar

DelVar Var 1 [, Va r 2] [, Va r 3 ] ... DelVar

Var .

Löscht die angegebene Variable oder Variablengruppe im Speicher.

DelVar Var . löscht alle Mitglieder der Variablengruppe Va r. (wie

die Statistikergebnisse stat.nn oder Variablen, die mit der Funktion

LibShortcut() erstellt wurden). Der Punkt (.) in dieser Form des

Befehls DelVar begrenzt ihn auf das Löschen einer Variablengruppe; die einfache Variable Va r ist nicht davon betroffen.

det() (Matrixdeterminante)

det(Quadratmatrix[, Toleranz]) ⇒ Ausdruck

Gibt die Determinante von Quadratmatrix zurück. Jedes Matrixelement wird wahlweise als 0 behandelt, wenn sein

Absolutwert kleiner als Toleranz ist. Diese Toleranz wird nur dann verwendet, wenn die Matrix Fließkommaelemente aufweist und keinerlei symbolische Variablen ohne zugewiesene Werte enthält. Anderenfalls wird Toleranz ignoriert.

• Wenn Sie

oder Näherung

Berechnungen in Fließkomma-Arithmetik durchgeführt.

•Wird Toleranz weggelassen oder nicht verwendet, so wird die Standardtoleranz folgendermaßen berechnet:

5EM14 ·max(dim(Quadratmatrix))·

rowNorm(Quadratmatrix)

verwenden oder den Modus Autom.

auf 'Approximiert' einstellen, werden

Katalog

TI-Nspire™ Referenzhandbuch 25

diag() (Matrixdiagonale)

diag(Liste) ⇒ Matrix diag(Zeilenmatrix) ⇒ Matrix diag(Spaltenmatrix) ⇒ Matrix

Gibt eine Matrix mit den Werten der Argumentliste oder der Matrix in der Hauptdiagonalen zurück.

diag(Quadratmatrix) ⇒ Zeilenmatrix

Gibt eine Zeilenmatrix zurück, die die Elemente der Hauptdiagonalen von Quadratmatrix enthält.

Quadratmatrix muss eine quadratische Matrix sein.

Katalog

dim() (Dimension)

dim(Liste) ⇒ Ganzzahl

Gibt die Dimension von Liste zurück.

dim(Matrix) ⇒ Liste

Gibt die Dimensionen von Matrix als Liste mit zwei Elementen zurück {Zeilen, Spalten}.

dim(Strin g) ⇒ Ganzzahl

Gibt die Anzahl der in der Zeichenkette Str ing enthaltenen Zeichen zurück.

Disp (Zeige)

Disp [AusdruckOderString1] [, AusdruckOderString2] ...

Zeigt die Argumente im Calculator Protokoll an. Die Argumente werden hintereinander angezeigt, dabei werden Leerzeichen zur Trennung verwendet.

Dies ist vor allem bei Programmen und Funktionen nützlich, um die Anzeige von Zwischenberechnungen zu gewährleisten.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Katalog

26 TI-Nspire™ Referenzhandbuch

DMS (GMS)

4DMS

Zahl Liste 4DMS Matrix 4DMS

Interpretiert den Parameter als Winkel und zeigt die entsprechenden GMS-Werte (engl. DMS) an (GGGGGG¡MM'SS.ss''). Siehe ¡, ', ''

auf Seite 115 zur Erläuterung des DMS-Formats (Grad, Minuten, Sekunden).

Hinweis: 4DMS wandelt Bogenmaß in Grad um, wenn es im

Bogenmaß-Modus benutzt wird. Folgt auf die Eingabe das GradSymbol ¡, wird keine Umwandlung vorgenommen. Sie können 4DMS nur am Ende einer Eingabezeile benutzen.

Im Grad-Modus:

Katalog

dotP() (Skalarprodukt)

dotP(Liste1, Liste2) ⇒ Ausdruck

Gibt das Skalarprodukt zweier Listen zurück.

dotP(Vektor1, Vektor2) ⇒ Ausdruck

Gibt das Skalarprodukt zweier Vektoren zurück. Es müssen beide Zeilenvektoren oder beide Spaltenvektoren sein.

e^()

e^(Wer t 1) ⇒ We r t

Gibt e hoch Wer t1 zurück.

Hinweis: Siehe auch Vorlage e Exponent, Seite 2. Hinweis: Das Drücken von u zum Anzeigen von

das gleiche wie das Drücken von E auf der Tastatur.

Sie können eine komplexe Zahl in der polaren Form re Verwenden Sie diese aber nur im Winkelmodus Bogenmaß, da die Form im Grad- oder Neugrad-Modus einen Bereichsfehler verursacht.

e^(Liste1) ⇒ Liste

Gibt e hoch jedes Element der Liste1 zurück.

e^(Quadratmatrix1) ⇒ Quadratmatrix

Ergibt den Matrix-Exponenten von Quadratmatrix1. Dies ist nicht gleichbedeutend mit der Berechnung von e hoch jedes Element. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

^( ist nicht

eingeben.

Katalog

u Taste

TI-Nspire™ Referenzhandbuch 27

eff()

eff(Nominalzinssatz, CpY) ⇒ We rt

Finanzfunktion, die den Nominalzinssatz Nominalzinssatz in einen jährlichen Effektivsatz konvertiert, wobei CpY als die Anzahl der Verzinsungsperioden pro Jahr gegeben ist.

Nominalzinssatz muss eine reelle Zahl sein und CpY muss eine reelle Zahl > 0 sein.

Hinweis: Siehe auch nom(), Seite 61.

Katalog

eigVc() (Eigenvektor)

eigVc(Quadratmatrix) ⇒ Matrix

Ergibt eine Matrix, welche die Eigenvektoren für eine reelle oder komplexe Quadratmatrix enthält, wobei jede Spalte des Ergebnisses zu einem Eigenwert gehört. Beachten Sie, dass ein Eigenvektor nicht eindeutig ist; er kann durch einen konstanten Faktor skaliert werden. Die Eigenvektoren sind normiert, d. h. wenn V = [x1, x2, …, xn],

Im Komplex-Formatmodus “kartesisch”:

Katalog

dann:

+ … + x

= 1

Um das ganze Ergebnis zu sehen, drücken Sie £ und verwenden dann ¡ und ¢, um den Cursor zu bewegen.

Katalog

Im Komplex-Formatmodus “kartesisch”:

Quadratmatrix wird zunächst mit Ähnlichkeitstransformationen bearbeitet, bis die Zeilen- und Spaltennormen so nahe wie möglich bei demselben Wert liegen. Die Quadratmatrix wird dann auf die obere Hessenberg-Form reduziert, und die Eigenvektoren werden mit einer Schur-Faktorisierung berechnet.

eigVl() (Eigenwert)

eigVl(Quadratmatrix) ⇒ Liste

Ergibt eine Liste von Eigenwerten einer reellen oder komplexen

Quadratmatrix. Quadratmatrix wird zunächst mit Ähnlichkeitstransformationen

bearbeitet, bis die Zeilen- und Spaltennormen so nahe wie möglich bei demselben Wert liegen. Die Quadratmatrix wird dann auf die obere Hessenberg-Form reduziert, und die Eigenwerte werden aus der oberen Hessenberg-Matrix berechnet.

Um das ganze Ergebnis zu sehen, drücken Sie £ und verwenden dann ¡ und ¢, um den Cursor zu bewegen.

Else Siehe If, Seite 40.

28 TI-Nspire™ Referenzhandbuch

ElseIf

If Boolescher Ausdr1 Then

Block1

ElseIf Boolescher Ausdr2 Then

Block2

Boolescher AusdrN Then

ElseIf

BlockN

EndIf

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Katalog

EndFor

EndFunc Siehe Func, Seite 35.

EndIf Siehe If, Seite 40.

EndLoop Siehe Loop, Seite 53.

EndWhile Siehe While, Seite 99.

EndPrgm Siehe Prgm, Seite 68.

EndTry Siehe Try, Seite 94.

Siehe For, Seite 33.

TI-Nspire™ Referenzhandbuch 29

Exit (Abbruch)

Beendet den aktuellen For, While, oder Loop Block.

Exit ist außerhalb dieser drei Schleifenstrukturen (For, While oder Loop) nicht zulässig.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

@ statt · drücken.

Funktionslisting:

Katalog

exp() (e hoch x)

exp(Wer t 1) ⇒ Wer t

Gibt e hoch We rt 1 zurück.

Hinweis: Siehe auch Vorlage e Exponent, Seite 2.

Sie können eine komplexe Zahl in der polaren Form re Verwenden Sie diese aber nur im Winkelmodus Bogenmaß, da die Form im Grad- oder Neugrad-Modus einen Bereichsfehler verursacht.

exp(Liste1) ⇒ Liste

Gibt e hoch jedes Element der Liste1 zurück.

exp(Quadratmatrix1) ⇒ Quadratmatrix

Ergibt den Matrix-Exponenten von Quadratmatrix1. Dies ist nicht gleichbedeutend mit der Berechnung von e hoch jedes Element. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

expr() (String in Ausdruck)

expr(Stri ng) ⇒ Ausdruck

Gibt die in Strin g enthaltene Zeichenkette als Ausdruck zurück und führt diesen sofort aus.

q eingeben.

u Taste

Katalog

30 TI-Nspire™ Referenzhandbuch

ExpReg (Exponentielle Regression)

ExpReg X, Y [, [Häuf] [, Kategorie, Mit]]

Berechnet die exponentielle Regression y = a·(b)xauf Listen X und Y mit der Häufigkeit Häuf. Eine Zusammenfassung der Ergebnisse

wird in der Variablen stat.results gespeichert. (Siehe Seite 86.) Alle Listen außer Mit müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden Datenpunkt X und Y an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0

sein. Kategorie ist eine Liste numerischer Kategoriecodes für die

entsprechenden Daten X und Y. Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur

solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Ausgabevariable Beschreibung

stat.RegEqn

stat.a, stat.b Regressionskoeffizienten

stat.r

stat.r Korrelationskoeffizient für transformierte Daten (x, ln(y))

stat.Resid Mit dem exponentiellen Modell verknüpfte Residuen

stat.ResidTrans Residuum für die lineare Anpassung der transformierten Daten.

stat.XReg Liste der Datenpunkte in der modifizierten X List, die schließlich in der Regression mit den

stat.YReg Liste der Datenpunkte in der modifizierten Y List, die schließlich in der Regression mit den

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

Regressionsgleichung: a·(b)

Koeffizient der linearen Bestimmtheit für transformierte Daten

Beschränkungen für Häufigkeit, Kategorieliste und Mit Kategorien verwendet wurde

Katalog

factor() (Faktorisiere)

factor(RationaleZahl) ergibt die rationale Zahl in Primfaktoren

zerlegt. Bei zusammengesetzten Zahlen nimmt di e Berechnungsdauer exponentiell mit der Anzahl an Stellen im zweitgrößten Faktor zu. Das Faktorisieren einer 30-stelligen ganzen Zahl kann beispielsweise länger als einen Tag dauern und das Faktorisieren einer 100-stelligen Zahl mehr als ein Jahrhundert.

Hinweis: Um eine Berechnung anzuhalten (abzubrechen), drücken

Sie auf w.

Möchten Sie hingegen lediglich feststellen, ob es sich bei einer Zahl um eine Primzahl handelt, verwenden Sie isPrime(). Dieser Vorgang ist wesentlich schneller, insbesondere dann, wenn RationaleZahl keine Primzahl ist und der zweitgrößte Faktor mehr als fünf Stellen aufweist.

TI-Nspire™ Referenzhandbuch 31

Katalog

FCdf()

FCdf(UntGrenze,ObGrenze,FreiGradZähler,FreiGradNenner)

⇒ Zahl, wenn UntGrenze und ObGrenze Zahlen sind, Liste,

UntGrenze und ObGrenze Listen sind

wenn

FCdf(

UntGrenze,ObGrenze,FreiGradZähler,FreiGradNenner)

⇒ Zahl, wenn UntGrenze und ObGrenze Zahlen sind, Liste,

wenn

UntGrenze und ObGrenze Listen sind

Berechnet die F Verteilungswahrscheinlichkeit zwischen UntGrenze und ObGrenze für die angegebenen FreiGradZähler (Freiheitsgrade) und FreiGradNenner.

Für P(X  obereGrenze) setzen Sie untereGrenze = 0.

Katalog

Fill (Füllen)

Fill Zahl, MatrixVar ⇒ Matrix

Ersetzt jedes Element in der Variablen MatrixVar durch Zahl. MatrixVar muss bereits vorhanden sein.

Fill Zahl, ListeVar ⇒ Liste

Ersetzt jedes Element in der Variablen ListeVar durch Zahl. ListeVar muss bereits vorhanden sein.

FiveNumSummary

FiveNumSummary X[,[Häuf][,Kategorie,Mit]]

Bietet eine gekürzte Version der Statistik mit 1 Variablen auf Liste X. Eine Zusammenfassung der Ergebnisse wird in der Variablen

stat.results gespeichert. (Siehe Seite 86.) X stellt eine Liste mit den Daten dar. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden X-Wert an. Der

Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein.

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden X-Werte.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Ausgabevariable Beschreibung

stat.MinX Minimum der x-Werte

stat.Q1X 1. Quartil von x

stat.MedianX Median von x

stat.Q3X 3. Quartil von x

stat.MaxX Maximum der x-Werte

Katalog

32 TI-Nspire™ Referenzhandbuch

floor() (Untergrenze)

floor(Wer t1 ) ⇒ Ganzzahl

Gibt die größte ganze Zahl zurück, die { dem Argument ist. Diese Funktion ist identisch mit int().

Das Argument kann eine reelle oder eine komplexe Zahl sein.

floor(Liste1) ⇒ Liste floor(Matrix1) ⇒ Matrix

Für jedes Element einer Liste oder Matrix wird die größte ganze Zahl, die kleiner oder gleich dem Element ist, zurückgegeben.

Hinweis: Siehe auch ceiling() und int().

Katalog

For

For Var , Vo n , Bis [, Schritt]

Block

EndFor

Führt die in Block befindlichen Anweisungen für jeden Wert von Va r zwischen Vo n und Bis aus, wobei der Wert bei jedem Durchlauf um

Schritt inkrementiert wird. Var darf keine Systemvariable sein. Schritt kann positiv oder negativ sein. Der Standardwert ist 1. Block kann eine einzelne Anweisung oder eine Serie von

Anweisungen sein, die durch “:” getrennt sind.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

format() (Format)

format(Wer t[, FormatString]) ⇒ Strin g

Gibt We rt als Zeichenkette im Format der Formatvorlage zurück. FormatString ist eine Zeichenkette und muss diese Form besitzen:

“F[n]”, “S[n]”, “E[n]”, “G[n][c]”, wobei [ ] optionale Teile bedeutet. F[n]: Festes Format. n ist die Anzahl der angezeigten

Nachkommastellen (nach dem Dezimalpunkt). S[n]: Wissenschaftliches Format. n ist die Anzahl der angezeigten

Nachkommastellen (nach dem Dezimalpunkt). E[n]: Technisches Format. n ist die Anzahl der Stellen, die auf die erste

signifikante Ziffer folgen. Der Exponent wird auf ein Vielfaches von 3 gesetzt, und der Dezimalpunkt wird um null, eine oder zwei Stellen nach rechts verschoben.

G[n][c]: Wie Festes Format, unterteilt jedoch auch die Stellen links des Dezimaltrennzeichens in Dreiergruppen. c ist das Gruppentrennzeichen und ist auf "Komma" voreingestellt. Wenn c auf "Punkt" gesetzt wird, wird das Dezimaltrennzeichen zum Komma.

[Rc]: Jeder der vorstehenden Formateinstellungen kann als Suffix das Flag Rc nachgestellt werden, wobei c ein einzelnes Zeichen ist, das den Dezimalpunkt ersetzt.

Katalog

TI-Nspire™ Referenzhandbuch 33

fPart() (Funktionsteil)

fPart(Ausdr1) ⇒ Ausdruck fPart(Liste1) ⇒ Liste fPart(Matrix1) ⇒ Matrix

Gibt den Bruchanteil des Arguments zurück. Bei einer Liste bzw. Matrix werden die Bruchanteile aller Elemente

zurückgegeben. Das Argument kann eine reelle oder eine komplexe Zahl sein.

Katalog

FPdf()

FPdf(XWert,FreiGradZähler,FreiGradNenner) ⇒ Zahl, wenn

XWert eine Zahl ist, Liste, wenn XWert eine Liste ist

FPdf(

XWert,FreiGradZähler,FreiGradNenner) ⇒ Zahl, wenn

XWert eine Zahl ist, Liste, wenn XWert eine Liste ist

Berechnet die F Verteilungswahrscheinlichkeit bei XWert für die angegebenen FreiGradZähler (Freiheitsgrade) und FreiGradNenner.

freqTable4list()

freqTable4list(Liste1,HäufGanzzahlListe) ⇒ Liste

Gibt eine Liste zurück, die die Elemente von Liste1 erweitert gemäß den Häufigkeiten in HäufGanzzahlListe enthält. Diese Funktion kann zum Erstellen einer Häufigkeitstabelle für die Applikation 'Data & Statistics' verwendet werden.

Liste1 kann eine beliebige gültige Liste sein. HäufGanzzahlListe muss die gleiche Dimension wie Liste1 haben

und darf nur nicht-negative Ganzzahlelemente enthalten. Jedes Element gibt an, wie oft das entsprechende Liste1-Element in der Ergebnisliste wiederholt wird. Der Wert 0 schließt das entsprechende Liste1-Element aus.

frequency() (Häufigkeit)

frequency(Liste1,binsListe) ⇒ Liste

Gibt eine Liste zurück, die die Zähler der Elemente in Liste1 enthält. Die Zähler basieren auf Bereichen (bins), die Sie in binsListe definieren.

Wenn binsListe {b(1), b(2), …, b(n)} ist, sind die festgelegten Bereiche {?{b(1), b(1)<?{b(2),…,b(n-1)<?{b(n), b(n)>?}. Die Ergebnisliste enthält ein Element mehr als die binsListe.

Jedes Element des Ergebnisses entspricht der Anzahl der Elemente aus Liste1, die im Bereich dieser bins liegen. Ausgedrückt in Form der

countIf() Funktion ist das Ergebnis { countIf(Liste, ?{b(1)),

countIf(Liste, b(1)<?{b(2)), …, countIf(Liste, b(n-1)<?{b(n)), countIf(Liste, b(n)>?)}.

Elemente von Liste1, die nicht “in einem bin platziert” werden können, werden ignoriert.

Innerhalb der Lists & Spreadsheet Applikation können Sie für beide Argumente Zellenbereiche verwenden.

Hinweis: Siehe auch countIf(), Seite 19.

Katalog

Erklärung des Ergebnisses:

2 Elemente aus Datenliste (Datalist) sind {2.5 4 Elemente aus Datenliste sind >2.5 und {4.5 3 Elemente aus Datenliste sind >4.5

Das Element "Hallo" ist eine Zeichenfolge und kann nicht in einem der definierten bins platziert werden.

34 TI-Nspire™ Referenzhandbuch

FTest_2Samp (Zwei-Stichproben F-Test)

FTest_2Samp

Liste1,Liste2[,Häufigkeit1[,Häufigkeit2[,Hypoth]]]

FTest_2Samp

Liste1,Liste2[,Häufigkeit1[,Häufigkeit2[,Hypoth]]]

(Datenlisteneingabe)

FTest_2Samp sx1,n1,sx2,n2[,Hypoth]

FTest_2Samp

(Zusammenfassende statistische Eingabe)

Führt einen F -Test mit zwei Stichproben durch. Eine Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (Siehe Seite 86.)

Für Ha: s1 > s2 setzen Sie Hypoth>0 Für Ha: s1 ƒ s2 (Standard) setzen Sie Hypoth =0 Für Ha: s1 < s2 setzen Sie Hypoth<0

Ausgabevariable Beschreibung

Statistik.F

stat.PVal Kleinste Signifikanzebene, bei der die Nullhypothese verworfen werden kann

stat.dfNumer Freiheitsgrade des Zählers = n1-1

stat.dfDenom Freiheitsgrade des Nenners = n2-1

stat.sx1, stat.sx2 Stichproben-Standardabweichungen der Datenfolgen in Liste 1 und Liste 2

stat.x1_bar stat.x2_bar

stat.n1, stat.n2 Stichprobenumfang

sx1,n1,sx2,n2[,Hypoth]

Berechnete ó Statistik für die Datenfolge

Stichprobenmittelwerte der Datenfolgen in Liste 1 und Liste 2

Katalog

Func

Block

EndFunc

Vorlage zur Erstellung einer benutzerdefinierten Funktion. Block kann eine einzelne Anweisung, eine Reihe von durch das

Zeichen “:” voneinander getrennten Anweisungen oder eine Reihe von Anweisungen in separaten Zeilen sein. Die Funktion kann die Anweisung Zurückgeben (Return) verwenden, um ein bestimmtes Ergebnis zurückzugeben.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Definieren Sie eine stückweise definierte Funktion:

Ergebnis der graphischen Darstellung g(x)

Katalog

TI-Nspire™ Referenzhandbuch 35

gcd() (Größter gemeinsamer Teiler)

gcd(Zahl1, Zahl2) ⇒ Ausdruck

Gibt den größten gemeinsamen Teiler der beiden Argumente zurück.

gcd zweier Brüche ist der gcd ihrer Zähler dividiert durch das

Der kleinste gemeinsame Vielfache (

In den Modi Auto oder Approximiert ist der Fließkommabrüchen 1,0.

gcd(Liste1, Liste2) ⇒ Liste

Gibt die größten gemeinsamen Teiler der einander entsprechenden Elemente von Liste1 und Liste2 zurück.

gcd(Matrix1, Matrix2) ⇒ Matrix

Gibt die größten gemeinsamen Teiler der einander entsprechenden Elemente von Matrix1 und Matrix2 zurück.

geomCdf()

geomCdf(p,untereGrenze,obereGrenze) ⇒ Zahl, wenn

untereGrenze und obereGrenze Zahlen sind, Liste, wenn untereGrenze und obereGrenze Listen sind

geomCdf(

p,obereGrenze) ⇒ Zahl, wenn obereGrenze eine

Liste, wenn obereGrenze eine Liste ist

Zahl ist,

Berechnet die kumulative geometrische Wahrscheinlichkeit von UntereGrenze bis ObereGrenze mit der angegebenen Erfolgswahrscheinlichkeit p.

Für P(X  obereGrenze) setzen Sie untereGrenze = 1.

geomPdf()

geomPdf(p,XWert) ⇒ Zahl, wenn XWert eine Zahl ist, Liste,

XWert eine Liste ist

wenn

Berechnet die Wahrscheinlichkeit an einem XWert, die Anzahl der Einzelversuche, bis der erste Erfolg eingetreten ist, für die diskrete geometrische Verteilung mit der vorgegebenen Erfolgswahrscheinlichkeit p.

lcm) ihrer Nenner.

gcd von

Katalog

getDenom() (Nenner holen)

getDenom(Bruch1) ⇒ We rt

Transformiert das Argument in einen Ausdruck mit gekürztem gemeinsamem Nenner und gibt dann den Nenner zurück.

Katalog

36 TI-Nspire™ Referenzhandbuch

getLangInfo( )

getLangInfo() ⇒ Zeichenkette

Gibt eine Zeichenkette zurück, die der Abkürzung der gegenwärtig aktiven Sprache entspricht. Sie können den Befehl zum Beispiel in einem Programm oder einer Funktion zum Bestimmen der aktuellen Sprache verwenden.

Englisch = "en" Dänisch = "da" Deutsch = "de" Finnisch = "fi" Französisch = "fr" Italienisch = "it" Holländisch = "nl" Holländisch (Belgien) = "nl_BE" Norwegisch = "no" Portugiesisch = "pt" Spanisch = "es" Schwedisch = "sv"

Katalog

getMode()

getMode(ModusNameGanzzahl) ⇒ We rt getMode(0) ⇒ Liste

getMode(ModusNameGanzzahl) gibt einen Wert zurück, der die

aktuelle Einstellung des Modus ModusNameGanzzahl darstellt.

getMode(0) gibt eine Liste mit Zahlenpaaren zurück. Jedes Paar

enthält eine Modus-Ganzzahl und eine Einstellungs-Ganzzahl. Eine Auflistung der Modi und ihrer Einstellungen finden Sie in der

nachstehenden Tabelle.

Wenn Sie die Einstellungen mit getMode(0) & var speichern, können Sie setMode(var) in einer Funktion oder in einem Programm verwenden, um die Einstellungen nur innerhalb der Ausführung dieser Funktion bzw. dieses Programms vorübergehend wiederherzustellen. Siehe setMode(), Seite 79.

Modus Name

Angezeigte Ziffern

Winkel

Exponentialformat

Reell oder komplex

Auto oder Approx.

Vektorformat

Basis

Modus Ganzzahl Einstellen von Ganzzahlen

=Fließ, 2=Fließ 1, 3=Fließ 2, 4=Fließ 3, 5=Fließ 4, 6=Fließ 5, 7=Fließ 6, 8=Fließ 7,

9=Fließ 8, 10=Fließ 9, 11=Fließ 10, 12=Fließ 11, 13=Fließ 12, 14=Fix 0, 15=Fix 1, 16=Fix 2, 17=Fix 3, 18=Fix 4, 19=Fix 5, 20=Fix 6, 21=Fix 7, 22=Fix 8, 23=Fix 9, 24=Fix 10, 25=Fix 11, 26=Fix 12

=Bogenmaß, 2=Grad, 3=Neugrad

=Normal, 2=Wissenschaftlich, 3=Technisch

=Reell, 2=Kartesisch, 3=Polar

=Auto, 2=Approximiert

=Kartesisch, 2=Zylindrisch, 3=Sphärisch

=Dezimal, 2=Hex, 3=Binär

Katalog

TI-Nspire™ Referenzhandbuch 37

getNum() (Zähler holen)

getNum(Bruch1) ⇒ We rt

Transformiert das Argument in einen Ausdruck mit gekürztem gemeinsamem Nenner und gibt dann den Zähler zurück.

Katalog

getVarInfo()

getVarInfo() ⇒ Matrix oder Str ing getVarInfo(BiblioNameString) ⇒ Matrix oder Strin g

getVarInfo() gibt eine Informationsmatrix (Name, Typ und

Erreichbarkeit einer Variablen in der Bibliothek) für a lle Variablen und Bibliotheksobjekte zurück, die im aktuellen Problem definiert sind.

Wenn keine Variablen definiert sind, gibt getVarInfo() die Zeichenfolge "KEINE" (NONE) zurück.

getVarInfo(BiblioNameString) gibt eine Matrix zurück, die

Informationen zu allen Bibliotheksobjekten enthält, die in der Bibliothek BiblioNameString definiert sind. BiblioNameString muss eine Zeichenfolge (in Anführungszeichen eingeschlossener Text) oder eine Zeichenfolgenvariable sein.

Wenn die Bibliothek BiblioNameString nicht existiert, wird ein Fehler angezeigt.

Beachten Sie das Beispiel links, in dem das Ergebnis von

getVarInfo() der Variablen vs zugewiesen wird. Beim Versuch,

Zeile 2 oder Zeile 3 von vs anzuzeigen, wird der Fehler "Liste oder Matrix ungültig" zurückgegeben, weil mindestens eines der Elemente in diesen Zeilen (Variable b zum Beispiel) eine Matrix ergibt.

Dieser Fehler kann auch auftreten, wenn Ans zum Neuberechnen eines getVarInfo()-Ergebnisses verwendet wird.

Das System liefert den obigen Fehler, weil die aktuelle Version der Software keine verallgemeinerte Matrixstruktur unterstützt, bei der ein Element einer Matrix eine Matrix oder Liste sein kann.

Katalog

38 TI-Nspire™ Referenzhandbuch

Goto (Gehe zu)

Goto MarkeName

Setzt die Programmausführung bei der Marke MarkeName fort. MarkeName muss im selben Programm mit der Anweisung

definiert worden sein.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Grad (Neugrad)

Ausdr1 4 Grad ⇒ Ausdruck

Wandelt Ausdr1 ins Winkelmaß Neugrad um.

Lbl

Im Grad-Modus:

Im Bogenmaß-Modus:

Katalog

identity() (Einheitsmatrix)

identity(Ganzzahl) ⇒ Matrix

Gibt die Einheitsmatrix mit der Dimension Ganzzahl zurück. Ganzzahl muss eine positive ganze Zahl sein.

Katalog

TI-Nspire™ Referenzhandbuch 39

If Boolescher Ausdr Anweisung If Boolescher Ausdr Then

Block

EndIf

Wenn Boolescher Ausdr wahr ergibt, wird die Einzelanweisung Anweisung oder der Anweisungsblock Block ausgeführt und danach

mit EndIf fortgefahren. Wenn Boolescher Ausdr falsch ergibt, wird das Programm

fortgesetzt, ohne dass die Einzelanweisung bzw. der Anweisungsblock ausgeführt werden.

Block kann eine einzelne Anweisung oder eine Serie von Anweisungen sein, die durch “:” getrennt sind.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste. If Boolescher Ausdr Then

Block1

Else

Block2

EndIf

Wenn Boolescher Ausdr wahr ergibt, wird Block1 ausgeführt und dann Block2 übersprungen.

Wenn Boolescher Ausdr falsch ergibt, wird Block1 übersprungen, aber Block2 ausgeführt.

Block1 und Block2 können einzelne Anweisungen sein.

If Boolescher Ausdr1 Then

Block1

ElseIf

Boolescher Ausdr2 Then

Block2

Boolescher AusdrN Then

ElseIf

BlockN

EndIf

Gestattet Programmverzweigungen. Wenn Boolescher Ausdr1 wahr ergibt, wird Block1 ausgeführt. Wenn Boolescher Ausdr1 falsch ergibt, wird Boolescher Ausdr2 ausgewertet usw.

Katalog

40 TI-Nspire™ Referenzhandbuch

ifFn()

ifFn(BoolescherAusdruck,Wert_wenn_wahr [,Wert_wenn_falsch

Wert_wenn_unbekannt]]) ⇒ Ausdruck, Liste oder Matrix

Wertet den Booleschen Ausdruck BoolescherAusdruck (oder jedes einzelne Element von BoolescherAusdruck) aus und erstellt ein Ergebnis auf der Grundlage folgender Regeln:

• BoolescherAusdruck kann einen Einzelwert, eine Liste oder eine Matrix testen.

• Wenn ein Element von BoolescherAusdruck als wahr bewertet wird, wird das entsprechende Element aus Wert_wenn_wahr zurückgegeben.

• Wenn ein Element von BoolescherAusdruck als falsch bewertet wird, wird das entsprechende Element aus Wert_wenn_falsch zurückgegeben. Wenn Sie Wert_wenn_falsch weglassen, wird Undef zurückgegeben.

• Wenn ein Element von BoolescherAusdruck weder wahr noch falsch ist, wird das entsprechende Element aus

Wert_wenn_unbekannt zurückgegeben. Wenn Sie Wert_wenn_unbekannt weglassen, wird Undef zurückgegeben.

• Wenn das zweite, dritte oder vierte Argument der Funktion

ifFn() ein einzelnen Ausdruck ist, wird der Boolesche Test für

jede Position in BoolescherAusdruck durchgeführt.

Hinweis: Wenn die vereinfachte Anweisung BoolescherAusdruck

eine Liste oder Matrix einbezieht, müssen alle anderen Listen- oder Matrixanweisungen dieselbe(n) Dimension(en) haben, und auch das Ergebnis wird dieselben(n) Dimension(en) haben.

Katalog

Testwert von 1 ist kleiner als 2.5, somit wird das entsprechende Wert_wenn_wahr-Element von 5 in die Ergebnisliste kopiert.

Testwert von 2 ist kleiner als 2.5, somit wird das entsprechende Wert_wenn_wahr-Element von 6 in die Ergebnisliste kopiert.

Testwert von 3 ist nicht kleiner als 2.5, somit wird das entsprechende Wert_wenn_falsch-Element von 10 in die Ergebnisliste kopiert.

Wert_wenn_wahr ist ein einzelner Wert und entspricht einer beliebigen ausgewählten Position.

Wert_wenn_falsch ist nicht spezifiziert. Undef wird verwendet.

Ein aus Wert_wenn_wahr ausgewähltes Element. Ein aus Wert_wenn_unbekannt ausgewähltes Element.

imag() (Imaginärteil)

imag(We rt 1) ⇒ Wer t

Katalog

Gibt den Imaginärteil des Arguments zurück.

Hinweis: Alle undefinierten Variablen werden als reelle Variablen

behandelt. Siehe auch real(), Seite 73

imag(Liste1) ⇒ Liste

Gibt eine Liste der Imaginärteile der Elemente zurück.

imag(Matrix1) ⇒ Matrix

Gibt eine Matrix der Imaginärteile der Elemente zurück.

Umleitung Siehe

inString() (In String)

inString(Quellstring, Teilstring[, Start]) ⇒ Ganzzahl

Gibt die Position des Zeichens von Quellstring zurück, an der das erste Vorkommen von Teilstring beginnt.

Start legt fest (sofern angegeben), an welcher Zeichenposition innerhalb von Quellstring die Suche beginnt. Vorgabe = 1 (das erste Zeichen von Quellstring).

Enthält Quellstring die Zeichenkette Teilstring nicht oder ist Start > Länge von Quellstring, wird Null zurückgegeben.

, Seite 114.

#()

Katalog

TI-Nspire™ Referenzhandbuch 41

int() (Ganze Zahl)

int(Zahl) ⇒ Ganzzahl int(Liste1) ⇒ Liste int(Matrix1) ⇒ Matrix

Gibt die größte ganze Zahl zurück, die kleiner oder gleich dem Argument ist. Diese Funktion ist identisch mit

floor().

Das Argument kann eine reelle oder eine komplexe Zahl sein. Für eine Liste oder Matrix wird für jedes Element die größte ganze

Zahl zurückgegeben, die kleiner oder gleich dem Element ist.

Katalog

intDiv() (Ganzzahl teilen)

intDiv(Zahl1, Zahl2) ⇒ Ganzzahl intDiv(Liste1, Liste2) ⇒ Liste intDiv(Matrix1, Matrix2) ⇒ Matrix

Gibt den mit Vorzeichen versehenen ganzzahligen Teil von (Zahl1 ÷ Zahl2) zurück.

Für eine Liste oder Matrix wird für jedes Elementpaar der mit Vorzeichen versehene ganzzahlige Teil von (Argument 1 ÷ Argument 2) zurückgegeben.

invc2()

invc2(Fläche,FreiGrad)

Fläche,FreiGrad)

invChi2(

Berechnet die inverse kumulative c2 (Chi-Quadrat) Wahrscheinlichkeitsfunktion, die durch Freiheitsgrade FreiGrad für eine bestimmte Fläche unter der Kurve festgelegt ist.

invF()

invF(Fläche,FreiGradZähler,FreiGradNenner)

Fläche,FreiGradZähler,FreiGradNenner)

invF(

Berechnet die inverse kumulative F Verteilungsfunktion, die durch FreiGradZähler und FreiGradNenner für eine bestimmte Fläche unter der Kurve festgelegt ist.

invNorm()

invNorm(Fläche[,m,s])

Berechnet die inverse kumulative Normalverteilungsfunktion für eine bestimmte Fläche unter der Normalverteilungskurve, die durch m und s festgelegt ist.

Katalog

invt()

invt(Fläche,FreiGrad)

Berechnet die inverse kumulative Student-tWahrscheinlichkeitsfunktion, die durch Freiheitsgrade, FreiGrad, für eine bestimmte Fläche unter der Kurve festgelegt ist.

Katalog

42 TI-Nspire™ Referenzhandbuch

iPart() (Ganzzahliger Teil)

iPart(Zahl1) ⇒ Ganzzahl iPart(Liste1) ⇒ Liste iPart(Matrix1) ⇒ Matrix

Gibt den ganzzahligen Teil des Arguments zurück. Für eine Liste oder Matrix wird der ganzzahlige Teil jedes Elements

zurückgegeben. Das Argument kann eine reelle oder eine komplexe Zahl sein.

Katalog

irr()

irr(CF0,CFListe [,CFFreq]) ⇒ We rt

Finanzfunktion, die den internen Zinsfluss einer Investition berechnet. CF0 ist der Anfangs-Cash-Flow zum Zeitpunkt 0; dies muss eine

reelle Zahl sein. CFListe ist eine Liste von Cash-Flow-Beträgen nach dem Anfangs-

Cash-Flow CF0. CFFreq ist eine optionale Liste, in der jedes Element die Häufigkeit

des Auftretens für einen gruppierten (fortlaufenden) Cash-FlowBetrag angibt, der das entsprechende Element von CFListe ist. Der Standardwert ist 1; wenn Sie Werte eingeben, müssen diese positive Ganzzahlen < 10.000 sein.

Hinweis: Siehe auch mirr(), Seite 56.

isPrime() (Primzahltest)

isPrime(Zahl) ⇒ Boolescher konstanter Ausdruck

Gibt “wahr” oder “falsch” zurück, um anzuzeigen, ob es sich bei Zahl um eine ganze Zahl ‚ 2 handelt, die nur durch sich sel bst oder 1 ganzzahlig teilbar ist.

Übersteigt Zahl ca. 306 Stellen und hat sie keine Faktoren {1021, dann zeigt isPrime(Zahl) eine Fehlermeldung an.Hinweis zur

Eingabe des Beispiels:

Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie

In der Calculator-Applikation des

am Ende jeder Zeile @ statt · drücken. Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Katalog

Funktion zum Auffinden der nächsten Primzahl nach einer angegebenen Zahl:

TI-Nspire™ Referenzhandbuch 43

Lbl (Marke)

Lbl MarkeName

Definiert in einer Funktion eine Marke mit dem Namen MarkeName. Mit der Anweisung Goto MarkeName können Sie die Ausführung

an der Anweisung fortsetzen, die unmittelbar auf die Marke folgt. Für MarkeName gelten die gleichen Benennungsregeln wie für

einen Variablennamen.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

lcm() (Kleinstes gemeinsames Vielfaches)

lcm(Zahl1, Zahl2) ⇒ Ausdruck lcm(Liste1, Liste2) ⇒ Liste lcm(Matrix1, Matrix2) ⇒ Matrix

Gibt das kleinste gemeinsame Vielfache der beiden Argumente zurück. Das lcm zweier Brüche ist das lcm ihrer Zähler dividiert durch den größten gemeinsamen Teiler (gcd) ihrer Nenner. Das lcm von Dezimalbruchzahlen ist ihr Produkt.

Für zwei Listen oder Matrizen wird das kleinste gemeinsame Vielfache der entsprechenden Elemente zurückgegeben.

left() (Links)

left(Quellstring[, Anz]) ⇒ St ring

Gibt Anz Zeichen zurück, die links in der Zeichenkette Quellstring enthalten sind.

Wenn Sie Anz weglassen, wird der gesamte Quellstring zurückgegeben.

left(Liste1[, Anz]) ⇒ Liste

Gibt Anz Elemente zurück, die links in Liste1 enthalten sind. Wenn Sie Anz weglassen, wird die gesamte Liste1 zurückgegeben.

left(Vergleich) ⇒ Ausdruck

Gibt die linke Seite einer Gleichung oder Ungleichung zurück.

Katalog

44 TI-Nspire™ Referenzhandbuch

libShortcut()

libShortcut(BiblioNameString, VerknNameString [, BiblioPrivMerker]) ⇒ Liste von Variablen

Erstellt eine Variablengruppe im aktuellen Problem, die Verweise auf alle Objekte im angegebenen Bibliotheksdokument BiblioNameString enthält. Fügt außerdem die Gruppenmitglieder dem Variablenmenü hinzu. Sie können dann auf jedes Objekt mit VerknNameString verweisen.

Setzen Sie BiblioPrivMerker= auszuschließen (Standard) Setzen Sie BiblioPrivMerker=1, um private Bibliotheksobjekte einzubeziehen

Informationen zum Kopieren einer Variablengruppe finden Sie unter

CopyVar auf Seite 15.

Informationen zum Löschen einer Variablengruppe finden Sie unter

DelVar auf Seite 25.

0, um private Bibliotheksobjekte

LinRegBx

LinRegBx X,Y[,[Häuf][,Kategorie,Mit]]

Berechnet die lineare Regression y = a+b·x auf Listen X und Y mit der Häufigkeit Häuf. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Alle Listen außer Mit müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden Datenpunkt X und Y an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0

sein. Kategorie ist eine Liste numerischer Kategoriecodes für die

entsprechenden Daten X und Y. Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur

solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Katalog

Dieses Beispiel setzt ein richtig gespeichertes und aktualisiertes Bibliotheksdokument namens linalg2 voraus, das als clearmat, gauss1 und gauss2 definierte Objekte enthält.

Katalog

Ausgabevariable Beschreibung

stat.RegEqn

Regressionsgleichung: a+b·x

stat.a, stat.b Regressionskoeffizienten

stat.r

Bestimmungskoeffizient

stat.r Korrelationskoeffizient

stat.Resid Residuen von der Regression

stat.XReg Liste der Datenpunkte in der modifizierten X-Liste, die in der Regression mit den Beschränkungen für

stat.YReg Liste der Datenpunkte in der modifizierten Y- Li ste , die schließlich in der Regression mit den

Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Beschränkungen für Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

stat.FreqReg Liste der Häufigkeiten für stat.FreqReg und stat.YReg

TI-Nspire™ Referenzhandbuch 45

LinRegMx

LinRegMx X,Y[,[Häuf][,Kategorie,Mit]]

Berechnet die lineare Regression y = m·x+b auf Liste X und Y mit der Häufigkeit Häuf. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Katalog

Alle Listen außer Mit müssen die gleiche Dimension besitzen. X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden Datenpunkt X und Y an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0

sein. Kategorie ist eine Liste numerischer Kategoriecodes für die

entsprechenden Daten X und Y. Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur

solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Ausgabevariable Beschreibung

stat.RegEqn

Regressionsgleichung: m·x+b

stat.m, stat.b Regressionskoeffizienten

stat.r

Bestimmungskoeffizient

stat.r Korrelationskoeffizient

stat.Resid Residuen von der Regression

stat.XReg Liste der Datenpunkte in der modifizierten X-Liste, die in der Regression mit den Beschränkungen für

stat.YReg Liste der Datenpunkte in der modifizierten Y- Li ste , die schließlich in der Regression mit den

Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Beschränkungen für Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

LinRegtIntervals (Lineare Regressions-t-Intervalle)

LinRegtIntervals X,Y[,Häuf[,0[,KNiv]]]

Für Steigung. Berechnet ein Konfidenzintervall des Niveaus K für die Steigung.

LinRegtIntervals X,Y[,Häuf[,1,XWert[,KNiv]]]

Für Antwort. Berechnet einen vorhergesagten y-Wert, ein Niveau-KVorhersageintervall für eine einzelne Beobachtung und ein Niveau-KKonfidenzintervall für die mittlere Antwort.

Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Katalog

Alle Listen müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden X- und Y-

Datenpunkt an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein.

46 TI-Nspire™ Referenzhandbuch

Ausgabevariable Beschreibung

stat.RegEqn

stat.a, stat.b Regressionskoeffizienten

stat.df Freiheitsgrade

stat.r

stat.r Korrelationskoeffizient

stat.Resid Residuen von der Regression

Nur für Steigung

Ausgabevariable Beschreibung

[stat.CLower, stat.CUpper]

stat.ME Konfidenzintervall-Fehlertoleranz

stat.SESlope Standardfehler der Steigung

stat.s Standardfehler an der Linie

Nur für Antwort

Ausgabevariable Beschreibung

[stat.CLower, stat.CUpper]

stat.ME Konfidenzintervall-Fehlertoleranz

stat.SE Standardfehler der mittleren Antwort

[stat.LowerPred , stat.UpperPred]

stat.MEPred Vorhersageintervall-Fehlertoleranz

stat.SEPred Standardfehler für Vorhersage

stat.y

Regressionsgleichung: a+b·x

Bestimmungskoeffizient

Konfidenzintervall für die Steigung

Konfidenzintervall für die mittlere Antwort

Vorhersageintervall für eine einzelne Beobachtung

a + b·XWert

TI-Nspire™ Referenzhandbuch 47

LinRegtTest (t-Test bei linearer Regression)

LinRegtTest X,Y[,Häuf[,Hypoth]]

Berechnet eine lineare Regression auf den X- und Y-Listen und einen t-Test auf dem Wert der Steigung b und den Korrelationskoeffizienten

r für die Gleichung y=a+bx. Er berechnet die Null-Hypothese

:b=0 (gleichwertig, r=0) in Bezug auf eine von drei alternativen

Hypothesen. Alle Listen müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden X- und Y-

Datenpunkt an. Der Standardwert ist 1. Alle Elemente müssen

| 0 sein.

Ganzzahlen

Hypoth ist ein optionaler Wert, der eine von drei alternativen Hypothesen angibt, in Bezug auf die die Nullhypothese (H0:b=r=0) untersucht wird.

Für Ha: bƒ0 und rƒ0 (Standard) setzen Sie Hypoth=0 Für Ha: b<0 und r<0 setzen Sie Hypoth<0 Für Ha: b>0 und r>0 setzen Sie Hypoth>0

Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Ausgabevariable Beschreibung

stat.RegEqn

stat.t t-Statistik für Signifikanztest

stat.PVal Kleinste Signifikanzebene, bei der die Nullhypothese verworfen werden kann

stat.df Freiheitsgrade

stat.a, stat.b Regressionskoeffizienten

stat.s Standardfehler an der Linie

stat.SESlope Standardfehler der Steigung

stat.r

stat.r Korrelationskoeffizient

stat.Resid Residuen von der Regression

Regressionsgleichung: a + b·x

Bestimmungskoeffizient

Katalog

list() (Listendifferenz)

Katalog

@list(Liste1) ⇒ Liste

Ergibt eine Liste mit den Differenzen der aufeinander folgenden Elemente in Liste1. Jedes Element in Liste1 wird vom folgenden Element in Liste1 subtrahiert. Die Ergebnisliste enthält stets ein Element weniger als die ursprüngliche Liste1.

48 TI-Nspire™ Referenzhandbuch

list4mat() (Liste in Matrix)

list4mat(Liste [, ElementeProZeile]) ⇒ Matrix

Gibt eine Matrix zurück, die Zeile für Zeile mit den Elementen aus

Liste aufgefüllt wurde. ElementeProZeile gibt (sofern angegeben) die Anzahl der Elemente

pro Zeile an. Vorgabe ist die Anzahl der Elemente in Liste (eine Zeile). Wenn Liste die resultierende Matrix nicht vollständig auffüllt, werden

Nullen hinzugefügt.

Katalog

ln() (Natürlicher Logarithmus)

ln(We rt 1 ) ⇒ We rt ln(Liste1) ⇒ Liste

Gibt den natürlichen Logarithmus des Arguments zurück. Gibt für eine Liste die natürlichen Logarithmen der einzelnen

Elemente zurück.

ln(Quadratmatrix1) ⇒ Quadratmatrix

Ergibt den natürlichen Matrix-Logarithmus von Quadratmatrix1. Dies ist nicht gleichbedeutend mit der Berechnung des natürlichen Logarithmus jedes einzelnen Elements. Näheres zum Berechnungsverfahren finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

LnReg

LnReg X, Y[, [Häuf] [, Kategorie, Mit]]

Berechnet die logarithmische Regression y = a+b·ln(x) auf Listen X und Y mit der Häufigkeit Häuf. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Alle Listen außer Mit müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element

in Häuf gibt die Häufigkeit für jeden entsprechenden X- und Y- Datenpunkt an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein.

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden Daten X und Y.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Bei Komplex-Formatmodus reell:

Bei Komplex-Formatmodus kartesisch:

Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:

Um das ganze Ergebnis zu sehen, drücken Sie £ und verwenden dann ¡ und ¢, um den Cursor zu bewegen.

Katalog

Tasten

TI-Nspire™ Referenzhandbuch 49

Ausgabevariable Beschreibung

stat.RegEqn

Regressionsgleichung: a+b·ln(x)

stat.a, stat.b Regressionskoeffizienten

stat.r

Koeffizient der linearen Bestimmtheit für transformierte Daten

stat.r Korrelationskoeffizient für transformierte Daten (ln(x), y)

stat.Resid Mit dem logarithmischen Modell verknüpfte Residuen

stat.ResidTrans Residuen für die lineare Anpassung transformierter Daten

stat.XReg Liste der Datenpunkte in der modifizierten X-Liste, die in der Regression mit den Beschränkungen für

stat.YReg Liste der Datenpunkte in der modifizierten Y- Li ste , die schließlich in der Regression mit den

Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Beschränkungen für Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

Local (Lokale Variable)

Local Var 1 [, Va r 2] [, Va r 3 ] ...

Deklariert die angegebenen Variablen Variable als lokale Variablen. Diese Variablen existieren nur während der Auswertung einer Funktion und werden gelöscht, wenn die Funktion beendet wird.

Hinweis: Lokale Variablen sparen Speicherplatz, da sie nur

temporär existieren. Außerdem stören sie keine vorhandenen globalen Variablenwerte. Lokale Variablen müssen für For-Schleifen und für das temporäre Speichern von Werten in mehrzeiligen Funktionen verwendet werden, da Änderungen globaler Variablen in einer Funktion unzulässig sind.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Katalog

50 TI-Nspire™ Referenzhandbuch

log() (Logarithmus)

log(Wer t 1[,We rt 2 ]) ⇒ We rt log(Liste1[,We rt 2]) ⇒ Liste

Gibt für den Logarithmus des Arguments zur Basis Ausdr2 zurück.

Hinweis: Siehe auch Vorlage Logarithmus, Seite 2.

Gibt bei einer Liste den Logarithmus der Elemente zur Basis We r t2 zurück.

Wenn Wer t weggelassen wird, wird 10 als Basis verwendet.

Bei Komplex-Formatmodus reell:

Bei Komplex-Formatmodus kartesisch:

Tasten

log(Quadratmatrix1[,Zahl2]) ⇒ Quadratmatrix

Gibt den Matrix-Logarithmus von Zahl2 zur Basis Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Logarithmus jedes Elements zur Basis Zahl2. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

Wenn das Basisargument weggelassen wird, wird 10 als Basis verwendet.

Logistic

Logistic X, Y[, [Häuf] [, Kategorie, Mit]]

Berechnet die logistische Regression y = (c/(1+a·e und Y mit der Häufigkeit Häuf. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Alle Listen außer Mit müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden X- und Y-

Datenpunkt an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein.

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden Daten X und Y.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

-bx

)) auf Listen X

Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:

Um das ganze Ergebnis zu sehen, drücken Sie £ und verwenden dann ¡ und ¢, um den Cursor zu bewegen.

Katalog

TI-Nspire™ Referenzhandbuch 51

Ausgabevariable Beschreibung

stat.RegEqn

Regressionsgleichung: c/(1+a·e

-bx

)

stat.a, stat.b, stat.c Regressionskoeffizienten

stat.Resid Residuen von der Regression

stat.XReg Liste der Datenpunkte in der modifizierten X-Liste, die in der Regression mit den Beschränkungen für

stat.YReg Liste der Datenpunkte in der modifizierten Y- Li ste , die schließlich in der Regression mit den

Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Beschränkungen für Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

LogisticD

LogisticD X, Y [, [Iterationen], [Häuf] [, Kategorie, Mit] ]

Berechnet die logistische Regression y = (c/(1+a·e X und Y mit der Häufigkeit Häuf unter Verwendung einer bestimmten Anzahl von Iterationen. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

-bx

)+d) auf Listen

Katalog

Alle Listen außer Mit müssen die gleiche Dimension besitzen. X und Y sind Listen von unabhängigen und abhängigen Variablen. Iterationen ist ein optionaler Wert, der angibt, wie viele

Lösungsversuche maximal stattfinden. Bei Auslassung wird 64 verwendet. Größere Werte führen in der Regel zu höherer Genauigkeit, aber auch zu längeren Ausführungszeiten, und umgekehrt.

Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in Häuf gibt die Häufigkeit für jeden entsprechenden X- und Y-

Datenpunkt an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein.

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden Daten X und Y.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Ausgabevariable Beschreibung

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

Regressionsgleichung: c/(1+a·e

Regressionskoeffizienten

-bx

)+d)

stat.Resid Residuen von der Regression

stat.XReg Liste der Datenpunkte in der modifizierten X-Liste, die in der Regression mit den Beschränkungen für

stat.YReg Liste der Datenpunkte in der modifizierten Y- Li ste , die schließlich in der Regression mit den

Häuf, Kategorieliste und Mit -Kategorien verwendet wurde

Beschränkungen für Häuf, Kategorieliste und Mit -Kategorien verwendet wurde

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

52 TI-Nspire™ Referenzhandbuch

Loop (Schleife)

Loop

Block

EndLoop

Führt die in Block enthaltenen Anweisungen wiederholt aus. Beachten Sie, dass dies eine Endlosschleife ist. Beenden Sie sie, indem Sie die Anweisung

Block ist eine Folge von Anweisungen, die durch das Zeichen “:” voneinander getrennt sind.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Goto oder Exit in Block ausführen.

Katalog

LU (Untere/obere Matrixzerlegung)

LU Matrix, lMatName, uMatName, pMatName[, Tol ]

Berechnet die Doolittle LU-Zerlegung einer reellen oder komplexen Matrix. Die untere Dreiecksmatrix ist in lMatName gespeichert, die obere Dreiecksmatrix in uMatName und die Permutationsmatrix (in welcher der bei der Berechnung vorgenommene Zeilentausch dokumentiert ist) in pMatName.

lMatName · uMatName = pMatName · Matrix

Sie haben die Option, dass jedes Matrixelement als Null behandelt wird, wenn dessen absoluter Wert geringer als To l ist. Diese Toleranz wird nur dann verwendet, wenn die Matrix Fließkommaelemente aufweist und keinerlei symbolische Variablen ohne zugewiesene Werte enthält. Anderenfalls wird Tol ignoriert.

• Wenn Sie

•Wird Tol weggelassen oder nicht verwendet, so wird die

Der LU-Faktorisierungsalgorithmus verwendet partielle Pivotisierung mit Zeilentausch.

oder Näherung

Berechnungen in Fließkomma-Arithmetik durchgeführt.

Standardtoleranz folgendermaßen berechnet: 5EM14 ·max(dim(Matrix)) ·rowNorm(Matrix)

· verwenden oder den Modus Auto

auf Approximiert einstellen, werden

mat4list() (Matrix in Liste)

mat4list(Matrix) ⇒ Liste

Gibt eine Liste zurück, die mit den Elementen aus Matrix gefüllt wurde. Die Elemente werden Zeile für Zeile aus Matrix kopiert.

Katalog

TI-Nspire™ Referenzhandbuch 53

max() (Maximum)

max(We rt 1, We r t2 ) ⇒ Ausdruck max(Liste1, Liste2) ⇒ Liste max(Matrix1, Matrix2) ⇒ Matrix

Gibt das Maximum der beiden Argumente zurück. Wenn die Argumente zwei Listen oder Matrizen sind, wird eine Liste bzw. Matrix zurückgegeben, die den Maximalwert für jedes entsprechende Elementpaar enthält.

max(Liste) ⇒ Ausdruck

Gibt das größte Element von Liste zurück.

max(Matrix1) ⇒ Matrix

Gibt einen Zeilenvektor zurück, der das größte Element jeder Spalte von Matrix1 enthält.

Hinweis: Siehe auch min().

Katalog

mean() (Mittelwert)

mean(Liste[, Häufigkeitsliste]) ⇒ Ausdruck

Gibt den Mittelwert der Elemente in Liste zurück. Jedes Häufigkeitsliste-Element gewichtet die Elemente von Liste in

der gegebenen Reihenfolge entsprechend.

mean(Matrix1[, Häufigkeitsmatrix])

⇒ Matrix

Ergibt einen Zeilenvektor aus den Mittelwerten aller Spalten in

Matrix1. Jedes Häufigkeitsmatrix-Element gewichtet die Elemente von

Matrix1 in der gegebenen Reihenfolge entsprechend.

median() (Median)

median(Liste) ⇒ Ausdruck

Gibt den Medianwert der Elemente in Liste zurück.

median(Matrix1) ⇒ Matrix

Gibt einen Zeilenvektor zurück, der die Medianwerte der einzelnen Spalten von Matrix1 enthält.

Hinweis: Alle Elemente der Liste bzw. der Matr ix müssen zu Zahlen

vereinfachbar sein.

Im Vektorformat kartesisch:

Katalog

54 TI-Nspire™ Referenzhandbuch

MedMed

MedMed X,Y [, Häuf] [, Kategorie, Mit]]

Berechnet die Median-Median-Linie y = (m·x+b) auf Listen X und Y mit der Häufigkeit Häuf. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Alle Listen außer Mit müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden X- und Y-

Datenpunkt an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein.

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden Daten X und Y.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Ausgabevariable Beschreibung

stat.RegEqn

stat.m, stat.b Modellkoeffizienten

stat.Resid Residuen von der Median-Median-Linie

stat.XReg Liste der Datenpunkte in der modifizierten X-Liste, die in der Regression mit den Beschränkungen für

stat.YReg Liste der Datenpunkte in der modifizierten Y- Li ste , die schließlich in der Regression mit den

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

Median-Median-Linien-Gleichung: m·x+b

Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Beschränkungen für Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Katalog

mid() (Teil-String)

mid(Quellstring, Start[, Anzahl]) ⇒ Stri ng

Gibt Anzahl Zeichen aus der Zeichenkette Quellstring ab dem Zeichen mit der Nummer Start zurück.

Wird Anzahl weggelassen oder ist sie größer als die Länge von Quellstring, werden alle Zeichen vonQuellstring ab dem Zeichen mit der Nummer Start zurückgegeben.

Anzahl muss ‚ 0 sein. Bei Anzahl = 0 wird eine leere Zeichenkette zurückgegeben.

mid(Quellliste, Start [, Anzahl]) ⇒ Liste

Gibt Anzahl Elemente aus Quellliste ab dem Element mit der Nummer Start zurück.

Wird Anzahl weggelassen oder ist sie größer als die Dimension von Quellliste, werden alle Elemente von Quellliste ab dem Element mit der Nummer Start zurückgegeben.

Anzahl muss ‚ 0 sein. Bei Anzahl = 0 wird eine leere Liste zurückgegeben.

mid(QuellstringListe, Start[, Anzahl]) ⇒ Liste

Gibt Anzahl Strings aus der Stringliste QuellstringListe ab dem Element mit der Nummer Start zurück.

Katalog

TI-Nspire™ Referenzhandbuch 55

min() (Minimum)

min(Wer t1 , We rt 2) ⇒ Ausdruck min(Liste1, Liste2) ⇒ Liste min(Matrix1, Matrix2) ⇒ Matrix

Gibt das Minimum der beiden Argumente zurück. Wenn die Argumente zwei Listen oder Matrizen sind, wird eine Liste bzw. Matrix zurückgegeben, die den Minimalwert für jedes entsprechende Elementpaar enthält.

min(Liste) ⇒ Ausdruck

Gibt das kleinste Element von Liste zurück.

min(Matrix1) ⇒ Matrix

Gibt einen Zeilenvektor zurück, der das kleinste Element jeder Spalte von Matrix1 enthält.

Hinweis: Siehe auch max().

Katalog

mirr()

mirr(Finanzierungsrate,Reinvestitionsrate,CF0,CFListe[,CFFre

q])

Finanzfunktion, die den modifizierten internen Zinsfluss einer Investition zurückgibt.

Finanzierungsrate ist der Zinssatz, den Sie für die Cash-FlowBeträge zahlen.

Reinvestitionsrate ist der Zinssatz, zu dem die Cash-Flows reinvestiert werden.

CF0 ist der Anfangs-Cash-Flow zum Zeitpunkt 0; dies muss eine reelle Zahl sein.

CFListe ist eine Liste von Cash-Flow-Beträgen nach dem AnfangsCash-Flow CF0.

CFFreq ist eine optionale Liste, in der jedes Element die Häufigkeit des Auftretens für einen gruppierten (fortlaufenden) Cash-FlowBetrag angibt, der das entsprechende Element von CFListe ist. Der Standardwert ist 1; wenn Sie Werte eingeben, müssen diese positive Ganzzahlen < 10.000 sein.

Hinweis: Siehe auch irr(), Seite 43.

mod() (Modulo)

mod(Wer t 1, We rt 2 ) ⇒ Ausdruck mod(Liste1, Liste2) ⇒ Liste mod(Matrix1, Matrix2) ⇒ Matrix

Gibt das erste Argument modulo das zweite Argument gemäß der folgenden Identitäten zurück:

mod(x,0) = x mod(x,y) = x -ìy floor(x/y)

Ist das zweite Argument ungleich Null, ist das Ergebnis in diesem Argument periodisch. Das Ergebnis ist entweder Null oder besitzt das gleiche Vorzeichen wie das zweite Argument.

Sind die Argumente zwei Listen bzw. zwei Matrizen, wird eine Liste bzw. Matrix zurückgegeben, die den Modulus jedes Elementpaars enthält.

Hinweis: Siehe auch remain(), Seite 74

Katalog

56 TI-Nspire™ Referenzhandbuch

mRow() (Matrixzeilenoperation)

mRow(Zahl, Matrix1, Index) ⇒ Matrix

Gibt eine Kopie von Matrix1 zurück, in der jedes Element der Zeile Index von Matrix1 mit Zahl multipliziert ist.

Katalog

mRowAdd() (Matrixzeilenaddition)

mRowAdd(Zahl, Matrix1, Index1, Index2) ⇒ Matrix

Gibt eine Kopie von Matrix1 zurück, wobei jedes Element in Zeile Index2 von Matrix1 ersetzt wird durch:

Zahl × Zeile Index1 + Zeile Index2

MultReg

MultReg Y, X1[,X2[,X3,…[,X10]]]

Berechnet die lineare Mehrfachregression der Liste Y für die Listen X1, X2, …, X10. Eine Zusammenfassung der Ergebnisse wird in der

Variablen stat.results gespeichert. (Siehe Seite 86.) Alle Listen müssen die gleiche Dimension besitzen.

Ausgabevariable Beschreibung

stat.RegEqn

Regressionsgleichung: b0+b1·x1+b2·x2+ ...

stat.b0, stat.b1, ... Regressionskoeffizienten

stat.R

Multiples Bestimmtheitsmaß

stat.yList yList = b0+b1·x1+ ...

stat.Resid Residuen von der Regression

MultRegIntervals

MultRegIntervals Y,

X1[,X2[,X3,…[,X10]]],XWertListe[,KNiveau]

Berechnet einen vorhergesagten y-Wert, ein Niveau-KVorhersageintervall für eine einzelne Beobachtung und ein Niveau-KKonfidenzintervall für die mittlere Antwort.

Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Alle Listen müssen die gleiche Dimension besitzen.

Katalog

Ausgabevariable Beschreibung

stat.RegEqn

Regressionsgleichung: b0+b1·x1+b2·x2+ ...

stat.y Eine Punktschätzung: y = b0 + b1 · xl + ... für XWertListe

stat.dfError Fehler-Freiheitsgrade

stat.CLower, stat.CUpper Konfidenzintervall für eine mittlere Antwort

TI-Nspire™ Referenzhandbuch 57

Ausgabevariable Beschreibung

stat.ME Konfidenzintervall-Fehlertoleranz

stat.SE Standardfehler der mittleren Antwort

stat.LowerPred, stat.UpperrPred

Vorhersageintervall für eine einzelne Beobachtung

stat.MEPred Vorhersageintervall-Fehlertoleranz

stat.SEPred Standardfehler für Vorhersage

stat.bList Liste der Regressionskoeffizienten, {b0,b1,b2,...}

stat.Resid Residuen von der Regression

MultRegTests

MultRegTests Y, X1[,X2[,X3,…[,X10]]]

Der lineare Mehrfachregressionstest berechnet eine lineare Mehrfachregression für die gegebenen Daten sowie die globale F- Teststatistik und t-Teststatistik für die Koeffizienten.

Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Katalog

Ausgaben

Ausgabevariable Beschreibung

stat.RegEqn

Regressionsgleichung: b0+b1·x1+b2·x2+ ...

stat.F Globale F-Testgröße

stat.PVal Mit globaler F-Statistik verknüpfter P-Wert

stat.R

stat.AdjR

Multiples Bestimmtheitsmaß

Angepasster Koeffizient des multiplen Bestimmtheitsmaßes

stat.s Standardabweichung des Fehlers

stat.DW Durbin-Watson-Statistik; bestimmt, ob in dem Modell eine Autokorrelation erster Ordnung vorhanden ist

stat.dfReg Regressions-Freiheitsgrade

stat.SSReg Summe der Regressionsquadrate

stat.MSReg Mittlere Regressionsstreuung

stat.dfError Fehler-Freiheitsgrade

stat.SSError Summe der Fehlerquadrate

stat.MSError Mittleres Fehlerquadrat

stat.bList {b0,b1,...} Liste der Koeffizienten

stat.tList Liste der t-Testgrößen, eine für jeden Koeffizienten in b-Liste

stat.PList Liste der P-Werte für jede t-Testgröße

stat.SEList Liste der Standardfehler für Koeffizienten in b-Liste

stat.yList yList = b0+b1·x1+...

58 TI-Nspire™ Referenzhandbuch

Ausgabevariable Beschreibung

stat.Resid Residuen von der Regression

stat.sResid Standardisierte Residuen; wird durch Division eines Residuums durch die Standardabweichung ermittelt

stat.CookDist Cookscher Abstand; Maß für den Einfluss einer Beobachtung auf der Basis von Residuum und Hebelwert

stat.Leverage Maß für den Abstand der Werte der unabhängigen Variable von den Mittelwerten (Hebelwerte)

nCr() (Kombinationen)

nCr(We rt 1 , Wer t2 ) ⇒ Ausdruck

Für ganzzahlige We rt 1 und We rt 2 mit We rt 1 ‚ We rt 2 ‚ 0 ist nCr() die Anzahl der Möglichkeiten, We rt 1 Elemente aus We r t2 Elementen auszuwählen (auch als Binomialkoeffizient bekannt).

nCr(Wer t , 0) ⇒ 1

Wer t , negGanzzahl) ⇒ 0

nCr(

Wer t , posGanzzahl) ⇒ We r t·(We rt N1)...

nCr(

(Wer t NposGanzzahl+1)/ posGanzzahl!

Wer t , keineGanzzahl) ⇒ Ausdruck!/

nCr(

((Wer tNkeineGanzzahl)!·keineGanzzahl!)

nCr(

Liste1, Liste2) ⇒ Liste

Gibt eine Liste von Binomialkoeffizienten auf der Basis der entsprechenden Elementpaare der beiden Listen zurück. Die Argumente müssen Listen gleicher Größe sein.

nCr(Matrix1, Matrix2) ⇒ Matrix

Gibt eine Matrix von Binomialkoeffizienten auf der Basis der entsprechenden Elementpaare der beiden Matrizen zurück. Die Argumente müssen Matrizen gleicher Größe sein.

nDeriv() (Numerische Ableitung)

nDeriv(Ausdr1, Va r [=Wert] [, H]) ⇒ Ausdruck nDeriv(Ausdr1, Va r [, H] | Var=Wert) ⇒ Ausdruck

nDeriv(Ausdr1, Va r [=Wert], Liste) ⇒ Liste nDeriv(Liste1, Va r [=Wert] [, H]) ⇒ Liste nDeriv(Matrix1, Va r [=Wert] [, H]) ⇒ Matrix

Gibt die numerische Ableitung als Ausdruck zurück. Benutzt die Zentraldifferenzenquotientenformel.

Wenn Wer t angegeben wird, setzt er jede vorausgegangene Variablenzuweisung oder jede aktuelle Ersetzung für die Variable außer Kraft.

H ist der Schrittwert. Wird H nicht angegeben, wird als Vorgabewert 0,001 benutzt.

Wenn Sie Liste1 oder Matrix1 verwenden, wird die Operation über die Werte in der Liste oder die Matrixelemente abgebildet.

Hinweis: Siehe auch avgRC().

Katalog

TI-Nspire™ Referenzhandbuch 59

newList() (Neue Liste)

newList(AnzElemente) ⇒ Liste

Gibt eine Liste der Dimension AnzElemente zurück. Jedes Element ist Null.

Katalog

newMat() (Neue Matrix)

newMat(AnzZeil, AnzSpalt) ⇒ Matrix

Gibt eine Matrix der Dimension AnzZeil mal AnzSpalt zurück, wobei die Elemente Null sind.

nfMax() (Numerisches Funktionsmaximum)

nfMax(Ausdr, Var ) ⇒ Wer t nfMax(Ausdr, Var , UntereGrenze) ⇒ We rt nfMax(Ausdr, Var , UntereGrenze, ObereGrenze) ⇒ We rt nfMax(Ausdr, Var) | UntereGrenze<Var <ObereGrenze ⇒ Wer t

Gibt einen möglichen numerischen Wert der Variablen Va r zurück, wobei das lokale Maximum von Ausdr auftritt.

Wenn Sie UntereGrenze und ObereGrenze angeben, sucht die Funktion zwischen diesen Werten nach dem lokalen Maximum.

nfMin() (Numerisches Funktionsminimum)

nfMin(Ausdr, Var ) ⇒ Wer t nfMin(

Ausdr, Va r, UntereGrenze) ⇒ We rt

nfMin(

Ausdr, Va r, UntereGrenze, ObereGrenze) ⇒ Wer t

nfMin(

Ausdr, Var) | UntereGrenze<Var <ObereGrenze ⇒ We rt

Gibt einen möglichen numerischen Wert der Variablen Va r zurück, wobei das lokale Minimum von Ausdr auftritt.

Wenn Sie UntereGrenze und ObereGrenze angeben, sucht die Funktion zwischen diesen Werten nach dem lokalen Minimum.

nInt() (Numerisches Integral)

nInt(Ausdr1, Var, Untere, Obere) ⇒ Ausdruck

Wenn der Integrand Ausdr1 außer Va r keine anderen Variablen enthält und wenn Untere und Obere Konstanten oder positiv ˆ oder

negativ ˆ sind, gibt nInt() eine Näherung für ‰(Ausdr1, Va r , Untere, Obere) zurück. Diese Näherung ist der gewichtete

Durchschnitt von Stichprobenwerten des Integranden im Intervall Untere<Var <Obere.

Das Berechnungsziel sind sechs signifikante Stellen. Der angewende te Algorithmus beendet die Weiterberechnung, wenn das Ziel hinreichend erreicht ist oder wenn weitere Stichproben wahrscheinlich zu keiner sinnvollen Verbesserung führen.

Wenn es scheint, dass das Berechnungsziel nicht erreicht wurde, wird die Meldung “Zweifelhafte Genauigkeit” angezeigt.

Sie können nInt() verschachteln, um mehrere numerische Integrationen durchzuführen. Die Integrationsgrenzen können von außerhalb liegenden Integrationsvariablen abhängen.

Katalog

60 TI-Nspire™ Referenzhandbuch

nom()

nom(Effektivzins,CpY) ⇒ We rt

Finanzfunktion zur Umrechnung des jährlichen Effektivzinssatzes Effektivzins in einen Nominalzinssatz, wobei CpY als Anzahl der Verzinsungsperioden pro Jahr gegeben ist.

Effektivzins muss eine reelle Zahl sein und CpY muss eine re elle Zahl > 0 sein.

Hinweis: Siehe auch eff(), Seite 28.

Katalog

norm()

norm(Matrix) ⇒ Ausdruck norm(Ve k to r ) ⇒ Ausdruck

Gibt die Frobeniusnorm zurück.

normCdf() (Normalverteilungswahrscheinlichkeit)

normCdf(untereGrenze,obereGrenze[,m[,s]]) ⇒ Zahl, wenn

untereGrenze und obereGrenze Zahlen sind, Liste, wenn untereGrenze und obereGrenze Listen sind

Berechnet die Normalverteilungswahrscheinlichkeit zwischen untereGrenze und obereGrenze für die angegebenen m (Standard = 0) und s (Standard = 1).

Für P(X  obereGrenze) setzen Sie untereGrenze = .9E999.

normPdf() (Wahrscheinlichkeitsdichte)

normPdf(XWert[,m[,s]]) ⇒ Zahl, wenn XWert eine Zahl ist,

Liste, wenn XWert eine Liste ist

Berechnet die Wahrscheinlichkeitsdichtefunktion für die Normalverteilung an einem bestimmten XWert für die vorgegebenen

m und s.

not

not BoolescherAusdr1 ⇒ BoolescherAusdruck

Gibt „wahr“ oder „falsch“ oder eine vereinfachte Form des Arguments zurück.

Katalog

TI-Nspire™ Referenzhandbuch 61

not

not Ganzzahl1 ⇒ Ganzzahl

Gibt das Einerkomplement einer reellen ganzen Zahl zurück. Intern wird Ganzzahl1 in eine 32-Bit-Dualzahl mit Vorzeichen umgewandelt. Für das Einerkomplement werden die Werte aller Bits umgekehrt (so dass 0 zu 1 wird und umgekehrt). Die Ergebnisse werden im jeweiligen Basis-Modus angezeigt.

Sie können die ganzen Zahlen mit jeder Basis eingeben. Für eine binäre oder hexadezimale Eingabe ist das Präfix 0b bzw. 0h zu verwenden. Ohne Präfix wird die ganze Zahl als dezimal behandelt (Basis 10).

Katalog

Im Hex-Modus:

Wichtig: Null, nicht Buchstabe O.

Im Bin-Modus:

Um das ganze Ergebnis zu sehen, drücken Sie verwenden dann ¡ und ¢, um den Cursor zu bewegen.

Hinweis: Eine binäre Eingabe kann bis zu 64 Stellen haben

(das Präfix 0b wird nicht mitgezählt). Eine hexadezimale Eingabe kann bis zu 16 Stellen aufweisen.

£ und

nPr() (Permutationen)

nPr(We rt 1 , Wer t2 ) ⇒ Ausdruck

Für ganzzahlige We rt 1 und We rt 2 mit We rt 1 ‚ We rt 2 ‚ 0 ist nPr() die Anzahl der Möglichkeiten, We rt 1 Elemente unter Berücksichtigung der Reihenfolge aus We rt 2 Elementen auszuwählen.

nPr(Wer t, 0) ⇒ 1

Wer t , negGanzzahl)

nPr(

⇒ 1/((Wer t +1)·(Wer t+2)... (We r tNnegGanzzahl))

Wer t , posGanzzahl)

nPr(

⇒ Wer t ·(Wer tN1)... (We r tNposGanzzahl+1)

nPr(

Wer t , keineGanzzahl)

⇒ We rt ! / (Wer t NkeineGanzzahl)!

Liste1, Liste2) ⇒ Liste

nPr(

Gibt eine Liste der Permutationen auf der Basis der entsprechenden Elementpaare der beiden Listen zurück. D ie Argumente müssen Listen gleicher Größe sein.

nPr(Matrix1, Matrix2) ⇒ Matrix

Gibt eine Matrix der Permutationen auf der Basis der entsprechenden Elementpaare der beiden Matrizen zurück. Die Argumente müssen Matrizen gleicher Größe sein.

Katalog

62 TI-Nspire™ Referenzhandbuch

npv()

npv(Zinssatz,CFO,CFListe[,CFFreq])

Finanzfunktion zur Berechnung des Nettobarwerts; die Summe der Barwerte für die Bar-Zuflüsse und -Abflüsse. Ein positives Ergebnis für npv zeigt eine rentable Investition an.

Zinssatz ist der Satz, zu dem die Cash-Flows (der Geldpreis) für einen Zeitraum.

CF0 ist der Anfangs-Cash-Flow zum Zeitpunkt 0; dies muss eine reelle Zahl sein.

CFListe ist eine Liste der Cash-Flow-Beträge nach dem anfänglichen Cash-Flow CF0.

CFFreq ist eine Liste, in der jedes Element die Häufigkeit des Auftretens für einen gruppierten (fortlaufenden) Cash-Flow-Betrag angibt, der das entsprechende Element von CFListeist. Der Standardwert ist 1; wenn Sie Werte eingeben, müssen diese positive Ganzzahlen < 10.000 sein.

Katalog

nSolve() (Numerische Lösung)

nSolve(Gleichung,Var [=Schätzwert]) ⇒ Zahl oder

Fehler_String

nSolve(Gleichung,Var [=Schätzwert],UntereGrenze)

⇒ Zahl oder Fehler_String

nSolve(Gleichung,Var [=Schätzwert],UntereGrenze,ObereGrenz

e) ⇒ Zahl oder Fehler_String

nSolve(Gleichung,Var [=Schätzwert]) |

UntereGrenze<Var <ObereGrenze

⇒ Zahl oder Fehler_String

Ermittelt iterativ eine reelle numerische Näherungslösung von

Gleichung für deren eine Variable. Geben Sie die Variable an als:

Variable

– oder – Variable = reelle Zahl

Beispiel: x ist gültig und x=3 ebenfalls.

nSolve() versucht entweder einen Punkt zu ermitteln, wo der

Unterschied zwischen tatsächlichem und erwartetem Wert Null ist oder zwei relativ nahe Punkte, wo der Restfehler entgegengesetzte Vorzeichen besitzt und nicht zu groß ist. Wenn nSolve() dies nicht mit einer kleinen Anzahl von Versuchen erreichen kann, wird die Zeichenkette “Keine Lösung gefunden” zurückgegeben.

Katalog

Hinweis: Existieren mehrere Lösungen, können Sie mit Hilfe

einer Schätzung eine bestimmte Lösung suchen.

TI-Nspire™ Referenzhandbuch 63

OneVar (Eine Variable)

OneVar [1,]X[,[Häufigkeit][,Kategorie,Mit]] OneVar [

n,]X1,X2[X3[,…[,X20]]]

Berechnet die 1-Variablenstatistik für bis zu 20 Listen. Eine Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (Siehe Seite 86.)

Alle Listen außer Mit müssen die gleiche Dimension besitzen.

Die X-Argumente sind Datenlisten. Häufigkeit ist eine optionale Liste von Häufigkeitswerten.

Jedes Element in Häufigkeit gibt die Häufigkeit für jeden entsprechenden X-Wert an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein.

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden X-Werte.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Ausgabevariable Beschreibung

stat.v

stat.Gx

stat.sx Stichproben-Standardabweichung von x

stat.ssssx Populations-Standardabweichung von x

stat.n Anzahl der Datenpunkte

stat.MinX Minimum der x-Werte

stat.Q1X 1. Quartil von x

stat.MedianX Median von x

stat.Q3X 3. Quartil von x

stat.MaxX Maximum der x-Werte

stat.SSX Summe der Quadrate der Abweichungen der x-Werte vom Mittelwert

Mittelwert der x-Werte

Summe der x-Werte

Summe der x2-Werte

Katalog

64 TI-Nspire™ Referenzhandbuch

Boolescher Ausdr1 or Boolescher Ausdr2

⇒ Boolescher Ausdruck

Gibt „wahr“ oder „falsch“ oder eine vereinfachte Form des ursprünglichen Terms zurück.

Gibt “wahr” zurück, wenn ein Ausdruck oder beide Ausdrücke zu ”wahr” ausgewertet werden. Gibt nur dann “falsch” zurück, wenn beide Ausdrücke “falsch” ergeben.

Hinweis: Siehe xor. Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Ganzzahl1 or Ganzzahl2 ⇒ Ganzzahl

Vergleicht zwei reelle ganze Zahlen mit Hilfe einer or-Operation Bit für Bit. Intern werden beide ganzen Zahlen in binäre 32-Bit-Zahlen mit Vorzeichen konvertiert. Beim Vergleich der sich entsprechenden Bits ist das Ergebnis dann 1, wenn eines der Bits 1 ist; das Ergebnis ist nur dann 0, wenn beide Bits 0 sind. Der zurückgegebene Wert stellt die Bit-Ergebnisse dar und wird im jeweiligen Basis-Modus angezeigt.

Hinweis: Siehe xor.

Katalog

Im Hex-Modus:

Wichtig: Null, nicht Buchstabe O.

Im Bin-Modus:

Hinweis: Eine binäre Eingabe kann bis zu 64 Stellen haben

(das Präfix 0b wird nicht mitgezählt). Eine hexadezimale Eingabe kann bis zu 16 Stellen aufweisen.

ord() (Numerischer Zeichencode)

ord(Str ing) ⇒ Ganzzahl ord(Liste1) ⇒ Liste

Gibt den Zahlenwert (Code) des ersten Zeichens der Zeichenkette Strin g zurück. Handelt es sich um eine Liste, wird der Code des ersten Zeichens jedes Listenelements zurückgegeben.

Katalog

P4Rx() (Kartesische x-Koordinate)

P4Rx(rAusdr, qAusdr) ⇒ Ausdruck

P4Rx(rListe, qListe) ⇒ Liste P4Rx(rMatrix, qMatrix) ⇒ Matrix

Gibt die äquivalente x-Koordinate des Paars (r, q) zurück.

Hinweis: Das q-Argument wird gemäß deraktuellen

Winkelmoduseinstellung als Grad, Neugrad oder Bogenmaß interpretiert. Ist das Argument ein Ausdruck, können Sie ó,G oder

ôbenutzen, um die Winkelmoduseinstellung temporär zu ändern.

Im Bogenmaß-Modus:

TI-Nspire™ Referenzhandbuch 65

Katalog

P4Ry() (Kartesische y-Koordinate)

P4Ry(rWert, qWer t) ⇒ Wer t P4Ry(rListe, qListe) ⇒ Liste P4Ry(rMatrix, qMatrix) ⇒ Matrix

Gibt die äquivalente y-Koordinate des Paars (r, q) zurück.

Hinweis: Das q-Argument wird gemäß deraktuellen

Winkelmoduseinstellung als Grad, Neugrad oder Bogenmaß interpretiert.

Im Bogenmaß-Modus:

Katalog

PassErr (ÜbgebFeh)

PassErr

Übergibt einen Fehler an die nächste Stufe. Wenn die Systemvariable Fehlercode (errCode) Null ist, tut

PassErr nichts.

Das Else im Block Try...Else...EndTry muss ClrErr oder PassErr verwenden. Wenn der Fehler verarbeitet oder ignoriert werden soll, verwenden Sie ClrErr. Wenn nicht bekannt ist, was mit dem Fehler zu tun ist, verwenden Sie PassErr, um ihn an den nächsten Error Handler zu übergeben. Wenn keine weiteren Try...Else...EndTry Error Handler unerledigt sind, wird das Fehlerdialogfeld als normal angezeigt.

Hinweis: Siehe auch ClrfErr, Seite 14, und Try, Seite 94. Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

piecewise() (Stückweise)

piecewise(Ausdr1 [, Bedingung1 [, Ausdr2 [, Bedingung2 [, … ]]]])

Gibt Definitionen für eine stückweise definierte Funktion in Form einer Liste zurück. Sie können auch mit Hilfe einer Vorlage stückweise Definitionen erstellen.

Hinweis: Siehe auch Vorlage Stückweise, Seite 2.

poissCdf()

poissCdf(l,untereGrenze,obereGrenze) ⇒ Zahl, wenn

untereGrenze und obereGrenze Zahlen sind, Liste, wenn untereGrenze und obereGrenze Listen sind

poissCdf(

l,obereGrenze) (für P(0XobereGrenze) ⇒ Zahl,

wenn

obereGrenze eine Zahl ist, Liste, wenn obereGrenze eine

Liste ist

Berechnet die kumulative Wahrscheinlichkeit für die diskrete PoissonVerteilung mit dem vorgegebenen Mittelwert l.

Für P(X  obereGrenze) setzen Sie untereGrenze = 0

Katalog

Ein Beispiel zu PassErr finden Sie im Beispiel 2 unter Befehl

Versuche (Try), Seite 94.

Katalog

poissPdf()

poissPdf(l,XWert) ⇒ Zahl, wenn XWert eine Zahl ist, Liste,

XWert eine Liste ist

wenn

Berechnet die Wahrscheinlichkeit für die diskrete Poisson-Verteilung mit dem vorgegebenen Mittelwert l.

Katalog

66 TI-Nspire™ Referenzhandbuch

Polar

4Polar

Vek t o r

Zeigt Vektor in Polarform [r q] an. Der Vektor muss die Dimension 2 besitzen und kann eine Zeile oder eine Spalte sein.

Hinweis: 4Polar ist eine Anzeigeformatanweisung, keine

Konvertierungsfunktion. Sie können sie nur am Ende einer Eingabezeile benutzen, und sie nimmt keine Aktualisierung von ans vor.

Hinweis: Siehe auch 4Rect, Seite 73.

komplexerWert 4Polar

Zeigt komplexerVektor in Polarform an.

• Der Grad-Modus für Winkel gibt (rq) zurück.

• Der Bogenmaß-Modus für Winkel gibt re

komplexerWert kann jede komplexe Form haben. Eine re verursacht jedoch im Winkelmodus Grad einen Fehler.

Hinweis: Für eine Eingabe in Polarform müssen Klammern (rq)

verwendet werden.

q zurück.

q-Eingabe

Im Bogenmaß-Modus:

Im Neugrad-Modus:

Im Grad-Modus:

Katalog

polyEval() (Polynom auswerten)

polyEval(Liste1, Ausdr1) ⇒ Ausdruck polyEval(Liste1, Liste2) ⇒ Ausdruck

Interpretiert das erste Argument als Koeffizienten eines nach fallenden Potenzen geordneten Polynoms und gibt das Polynom bezüglich des zweiten Arguments zurück.

PowerReg

PowerReg X,Y [, Häuf] [, Kategorie, Mit]]

Berechnet die Potenzregression y = (a·(x)b) auf Listen X und Y mit der Häufigkeit Häuf. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Alle Listen außer Mit müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden X- und Y-

Datenpunkt an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein.

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden Daten X und Y.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Ausgabevariable Beschreibung

stat.RegEqn

Regressionsgleichung: a·(x)

Katalog

TI-Nspire™ Referenzhandbuch 67

Ausgabevariable Beschreibung

stat.a, stat.b Regressionskoeffizienten

stat.r

Koeffizient der linearen Bestimmtheit für transformierte Daten

stat.r Korrelationskoeffizient für transformierte Daten (ln(x), ln(y))

stat.Resid Mit dem Potenzmodell verknüpfte Residuen

stat.ResidTrans Residuen für die lineare Anpassung transformierter Daten

stat.XReg Liste der Datenpunkte in der modifizierten X-Liste, die in der Regression mit den Beschränkungen für

stat.YReg Liste der Datenpunkte in der modifizierten Y- Li ste , die schließlich in der Regression mit den

Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Beschränkungen für Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

Prgm

Block

EndPrgm

Vorlage zum Erstellen eines benutzerdefinierten Programms. Muss mit dem Befehl Definiere (Define), Definiere LibPub

(Define LibPub)

verwendet werden. Block kann eine einzelne Anweisung, eine Reihe von durch das

Zeichen “:” voneinander getrennten Anweisungen oder eine Reihe von Anweisungen in separaten Zeilen sein.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen

oder Definiere LibPriv (Define LibPriv)

eingeben, indem Sie am Ende jeder Zeile @ statt · drücken. Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Product (PI) (Produkt)

product() (Produkt)

product(Liste[, Start[, Ende]]) ⇒ Ausdruck

Gibt das Produkt der Elemente von Liste zurück. Start und Ende sind optional. Sie geben einen Elementebereich an.

Katalog

GCD berechnen und Zwischenergebnisse anzeigen.

Siehe Π(), Seite 112.

Katalog

68 TI-Nspire™ Referenzhandbuch

product() (Produkt)

product(Matrix1[, Start[, Ende]]) ⇒ Matrix

Gibt einen Zeilenvektor zurück, der die Produkte der Elemente aus den Spalten von Matrix1 enthält. Start und Ende sind optional. Sie geben einen Zeilenbereich an.

Katalog

propFrac() (Echter Bruch)

propFrac(We rt 1[, Va r ]) ⇒ Wer t

propFrac(rationale_Wert) gibt rationale_Wert als Summe einer

ganzen Zahl und eines Bruchs zurück, der das gleiche Vorzeichen besitzt und dessen Nenner größer ist als der Zähler.

propFrac(rationaler_Ausdruck,Var ) gibt die Summe der echten

Brüche und ein Polynom bezüglich Va r zurück. Der Grad von Va r im Nenner übersteigt in jedem echten Bruch den Grad von Va r im Zähler. Gleichartige Potenzen von Va r werden zusammengefasst. Die Terme und Faktoren werden mit Va r als der Hauptvariablen sortiert.

Wird Var weggelassen, wird eine Entwicklung des echten Bruchs bezüglich der wichtigsten Hauptvariablen vorgenommen. Die Koeffizienten des Polynomteils werden dann zuerst bezüglich der wichtigsten Hauptvariablen entwickelt usw.

QR Matrix, qMatrix, rMatrix[, Tol ]

Berechnet die Householdersche QR-Faktorisierung einer reellen oder komplexen Matrix. Die sich ergebenden Q- und R-Matrzen werden in den angegebenen Matrix gespeichert. Die Q-Matrix ist unitär. Bei der R-Matrix handelt es sich um eine obere Dreiecksmatrix.

• Wenn Sie

•Wird Tol weggelassen oder nicht verwendet, so wird die

Die QR-Faktorisierung wird anhand von Householderschen Transformationen numerisch berechnet. Die symbolische Lösung wird mit dem Gram-Schmidt-Verfahren berechnet. Die Spalten in

qMatName sind die orthonormalen Basisvektoren, die den durch Matrix definierten Raum aufspannen.

· verwenden oder den Modus Auto

oder Näherung

Berechnungen in Fließkomma-Arithmetik durchgeführt.

Standardtoleranz folgendermaßen berechnet: 5Eë14 ·max(dim(Matrix)) ·rowNorm(Matrix)

auf Approximiert einstellen, werden

Katalog

Die Fließkommazahl (9,) in m1 bewirkt, dass das Ergebnis in Fließkommaform berechnet wird.

TI-Nspire™ Referenzhandbuch 69

QuadReg

QuadReg X,Y [, Häuf] [, Kategorie, Mit]]

Berechnet die quadratische polynomiale Regression y =

·x

+b·x+c auf Listen X und Y mit der Häufigkeit Häuf. Eine

Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Alle Listen außer Mit müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden X- und Y-

Datenpunkt an. Der Standardwert ist 1. Alle Elemente müssen

| 0 sein.

Ganzzahlen

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden Daten X und Y.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Ausgabevariable Beschreibung

stat.RegEqn

stat.a, stat.b, stat.c Regressionskoeffizienten

stat.R

stat.Resid Residuen von der Regression

stat.XReg Liste der Datenpunkte in der modifizierten X-Liste, die in der Regression mit den Beschränkungen für

stat.YReg Liste der Datenpunkte in der modifizierten Y- Li ste , die schließlich in der Regression mit den

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

Regressionsgleichung: a·x2+b·x+c

Bestimmungskoeffizient

Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Beschränkungen für Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Katalog

QuartReg

QuartReg X,Y [, Häuf] [, Kategorie, Mit]]

Berechnet die polynomiale Regression vierter Ordnung y = a·x4+b·x3+c· x2+d·x+e auf Listen X und Y mit der

Häufigkeit Häuf. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Alle Listen außer Mit müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in

Häuf gibt die Häufigkeit für jeden entsprechenden X- und Y-

Datenpunkt an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein.

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden Daten X und Y.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Katalog

70 TI-Nspire™ Referenzhandbuch

Ausgabevariable Beschreibung

stat.RegEqn

stat.a, stat.b, stat.c, stat.d, stat.e

stat.R

stat.Resid Residuen von der Regression

stat.XReg Liste der Datenpunkte in der modifizierten X-Liste, die in der Regression mit den Beschränkungen für

stat.YReg Liste der Datenpunkte in der modifizierten Y- Li ste , die schließlich in der Regression mit den

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

Regressionsgleichung: a·x4+b·x3+c· x2+d·x+e

Regressionskoeffizienten

Bestimmungskoeffizient

Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Beschränkungen für Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

R4Pq() (Polarkoordinate)

R4Pq (xWert, yWert) ⇒ We rt R4Pq (xListe, yListe) ⇒ Liste R4Pq (xMatrix, yMatrix) ⇒ Matrix

Gibt die äquivalente q-Koordinate des Paars (x,y) zurück.

Hinweis: Das Ergebnis wird gemäß der aktuellen

Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben.

R4Pr() (Polarkoordinate)

R4Pr (xWert, yWert) ⇒ We rt R4Pr (xListe, yListe) ⇒ Liste R4Pr (xMatrix, yMatrix) ⇒ Matrix

Gibt die äquivalente r-Koordinate des Paars (x,y) zurück.

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Katalog

TI-Nspire™ Referenzhandbuch 71

4Rad (Bogenmaß)

4Rad ⇒ We rt

Wer t 1

Wandelt das Argument ins Winkelmaß Bogenmaß um.

Im Grad-Modus:

Im Neugrad-Modus:

Katalog

rand() (Zufallszahl)

rand() ⇒ Ausdruck rand(#Trials) ⇒ Liste

rand() gibt einen Zufallswert zwischen 0 und 1 zurück. rand(#Trials) gibt eine Liste zurück, die #Trials Zufallswerte

zwischen 0 und 1 enthält.

randBin() (Zufallszahl aus Binomialverteilung)

randBin(n, p) ⇒ Ausdruck randBin(n, p, #Trials) ⇒ Liste

randBin(n, p) gibt eine reelle Zufallszahl aus einer angegebenen

Binomialverteilung zurück.

randBin(n, p, #Trials) gibt eine Liste mit #Trials reellen

Zufallszahlen aus einer angegebenen Binomialverteilung zurück.

randInt() (Ganzzahlige Zufallszahl)

randInt(lowBound,upBound) ⇒ Ausdruck randInt(lowBound,upBound,#Trials) ⇒ Liste

randInt(lowBound,upBound) gibt eine ganzzahlige Zufallszahl

innerhalb der durch UntereGrenze (lowBound) und ObereGrenze (upBound) festgelegten Grenzen zurück.

randInt(lowBound,upBound,#Trials) gibt eine Liste mit #Trials

ganzzahligen Zufallszahlen innerhalb des festgelegten Bereichs zurück.

randMat() (Zufallsmatrix)

randMat(AnzZeil, AnzSpalt) ⇒ Matrix

Gibt eine Matrix der angegebenen Dimension mit ganzzahligen Werten zwischen -9 und 9 zurück.

Beide Argumente müssen zu ganzen Zahlen vereinfachbar sein.

Katalog

Setzt Ausgangsbasis für Zufallszahlengenerierung.

Katalog

Hinweis: Die Werte in dieser Matrix ändern sich mit jedem

Drücken von ·.

72 TI-Nspire™ Referenzhandbuch

randNorm() (Zufal lsnorm)

randNorm(m, s [,AnzVersuche]) ⇒ Ausdruck

Gibt eine Dezimalzahl aus der Gaußschen Normalverteilung zurück. Dies könnte eine beliebige reelle Zahl sein, die Werte konzentrieren

sich jedoch stark in dem Intervall [mN3·s, m+3·s].

Katalog

randPoly() (Zufallspolynom)

randPoly(Va r , Ordnung) ⇒ Ausdruck

Gibt ein Polynom in Va r der angegebenen Ordnung zurück. Die Koeffizienten sind zufällige ganze Zahlen im Bereich ë9 bis 9. Der führende Koeffizient ist nie Null.

Ordnung muss zwischen 0 und 99 betragen.

randSamp() (Zufallsstichprobe)

randSamp(List,#Trials[,noRepl]) ⇒ Liste

Gibt eine Liste mit einer Zufallsstichprobe von #Trials Versuchen aus Liste (List) zurück mit der Möglichkeiten, Stichproben zu ersetzen

(noRepl=0) oder nicht zu ersetzen (noRepl=1). Die Vorgabe ist mit Stichprobenersatz.

RandSeed (Zufallszahl)

RandSeed Zahl

Zahl = 0 setzt die Ausgangsbasis (“seed”) für den Zufallszahlengenerator auf die Werkseinstellung zurück. Bei Zahl ƒ 0 werden zwei Basen erzeugt, die in den Systemvariablen seed1 und seed2 gespeichert werden.

real() (Reell)

real(We rt 1) ⇒ Wer t

Gibt den Realteil des Arguments zurück.

Hinweis: Alle undefinierten Variablen werden als reelle Variablen

behandelt. Siehe auch imag(), Seite 41.

real(Liste1) ⇒ Liste

Gibt für jedes Element den Realteil zurück.

real(Matrix1) ⇒ Matrix

Gibt für jedes Element den Realteil zurück.

Katalog

Rect (Kartesisch)

Katalog

Vek t o r 4Rect

Zeigt Vek t o r in der kartesischen Form [x, y, z] an. Der Vektor muss die Dimension 2 oder 3 besitzen und kann eine Zeile oder eine Spalte sein.

Hinweis: 4Rect ist eine Anzeigeformatanweisung, keine

Konvertierungsfunktion. Sie können sie nur am Ende einer Eingabezeile benutzen, und sie nimmt keine Aktualisierung von ans vor.

Hinweis: Siehe auch 4Polar, Seite 67.

TI-Nspire™ Referenzhandbuch 73

Rect (Kartesisch)

komplexerWert 4Rect

Zeigt komplexerWert in der kartesischen Form a+bi an. KomplexerWert kann jede komplexe Form haben. Eine re

verursacht jedoch im Winkelmodus Grad einen Fehler.

Hinweis: Für eine Eingabe in Polarform müssen Klammern (rq)

verwendet werden.

q-Eingabe

Katalog

Im Bogenmaß-Modus:

Im Neugrad-Modus:

Im Grad-Modus:

Hinweis: Wählen Sie zur Eingabe von  das Symbol aus der

Sonderzeichenpalette des Katalogs aus.

ref() (Diagonalform)

ref(Matrix1[, To l]) ⇒ Matrix

Gibt die Diagonalform von Matrix1 zurück. Sie haben die Option, dass jedes Matrixelement als Null behandelt

wird, wenn dessen absoluter Wert geringer als To l ist. Diese Toleranz wird nur dann verwendet, wenn die Matrix Fließkommaelemente aufweist und keinerlei symbolische Variablen ohne zugewiesene Werte enthält. Anderenfalls wird Tol ignoriert.

• Wenn Sie

•Wird Tol weggelassen oder nicht verwendet, so wird die

Hinweis: Siehe auch rref(), Seite 77.

remain() (Rest)

remain(Wer t1 , Wer t 2) ⇒ We r t remain(Liste1, Liste2) ⇒ Liste remain(Matrix1, Matrix2) ⇒ Matrix

Gibt den Rest des ersten Arguments bezüglich des zweiten Arguments gemäß folgender Definitionen zurück:

remain(x,0)  x remain(x,y)  xNy·iPart(x/y)

Als Folge daraus ist zu beachten, dass remain(Nx,y) 

Nremain(x,y). Das Ergebnis ist entweder Null oder besitzt das

gleiche Vorzeichen wie das erste Argument.

Hinweis: Siehe auch mod(), Seite 56.

oder Näherung

Berechnungen in Fließkomma-Arithmetik durchgeführt.

Standardtoleranz folgendermaßen berechnet: 5Eë14 ·max(dim(Matrix1)) ·rowNorm(Matrix1)

· verwenden oder den Modus Auto

auf Approximiert einstellen, werden

Katalog

74 TI-Nspire™ Referenzhandbuch

Return (Rückgabe)

Return [Ausdr]

Gibt Ausdr als Ergebnis der Funktion zurück. Verwendbar in einem Block

Func...EndFunc.

Hinweis: Verwenden Sie Zurück (Return) ohne Argument

innerhalb eines beenden.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Prgm...EndPrgm Blocks, um ein Programm zu

@ statt · drücken.

Katalog

right() (Rechts)

right(Liste1[, Anz]) ⇒ Liste

Gibt Anz Elemente zurück, die rechts in Liste1 enthalten sind. Wenn Sie Anz weglassen, wird die gesamte Liste1 zurückgegeben.

right(Quellstring[, Anz]) ⇒ Str ing

Gibt Anz Zeichen zurück, die rechts in der Zeichenkette Quellstring enthalten sind.

Wenn Sie Anz weglassen, wird der gesamte Quellstring zurückgegeben.

right(Ver g le i c h ) ⇒ Ausdruck

Gibt die rechte Seite einer Gleichung oder Ungleichung zurück.

root() (Wurzel)

root(Wer t ) ⇒ root root(Wer t 1, We rt 2) ⇒ Wurzel

root(Wer t ) gibt die Quadratwurzel von Wer t zurück. root(Wer t 1, We rt 2) gibt die We rt 2. Wurzel von We rt 1 zurück.

Wer t 1 kann eine reelle oder komplexe Gleitkommakonstante, eine ganze Zahl oder eine komplexe rationale Konstante sein.

Hinweis: Siehe auch Vorlage n-te Wurzel, Seite 1.

rotate() (Rotieren)

rotate(Ganzzahl1[,#Rotationen]) ⇒ Ganzzahl

Rotiert die Bits in einer binären ganzen Zahl. Ganzzahl1 kann mit jeder Basis eingegeben werden und wird automatisch in eine 32-BitDualform konvertiert. Ist der Absolutwert von Ganzzahl1 für diese Form zu groß, wird eine symmetrische Modulo-Operation ausgeführt, um sie in den erforderlichen Bereich zu bringen.

Katalog

Im Bin-Modus:

Um das ganze Ergebnis zu sehen, drücken Sie £ und verwenden dann ¡ und ¢, um den Cursor zu bewegen.

TI-Nspire™ Referenzhandbuch 75

rotate() (Rotieren)

Ist #Rotationen positiv, erfolgt eine Rotation nach links. ist #Rotationen negativ, erfolgt eine Rotation nach rechts. Vorgabe ist

ë1 (ein Bit nach rechts rotieren).

Beispielsweise in einer Rechtsrotation:

Im Hex-Modus:

Katalog

Jedes Bit rotiert nach rechts. 0b00000000000001111010110000110101 Bit ganz rechts rotiert nach ganz links. Es ergibt sich: 0b10000000000000111101011000011010 Das Ergebnis wird gemäß dem jeweiligen Basis-Modus angezeigt.

rotate(Liste1[,#Rotationen]) ⇒ Liste

Gibt eine um #Rotationen Elemente nach rechts oder links rotierte Kopie von Liste1 zurück. Verändert Liste1 nicht.

Ist #Rotationen positiv, erfolgt eine Rotation nach links. ist #Rotationen negativ, erfolgt eine Rotation nach rechts. Vorgabe ist

ë1 (ein Element nach rechts rotieren).

rotate(String1[,#Rotationen]) ⇒ Strin g

Gibt eine um #Rotationen Zeichen nach rechts oder links rotierte Kopie von String1 zurück. Verändert String1 nicht.

Ist #Rotationen positiv, erfolgt eine Rotation nach links. ist #Rotationen negativ, erfolgt eine Rotation nach rechts. Vorgabe ist

ë1 (ein Zeichen nach rechts rotieren).

round() (Runden)

round(We rt 1[, Stell en]) ⇒ Wer t

Gibt das Argument gerundet auf die angegebene Anzahl von Stellen nach dem Dezimaltrennzeichen zurück.

Stell en muss eine ganze Zahl im Bereich 0–12 sein. Wird Stellen weggelassen, wird das Argument auf 12 signifikante Stellen gerundet.

Hinweis: Die Anzeige des Ergebnisses kann von der Einstellung

"Angezeigte Ziffern" beeinflusst werden.

round(Liste1[, Stellen]) ⇒ Liste

Gibt eine Liste von Elementen zurück, die auf die angegebene Stellenzahl gerundet wurden.

round(Matrix1[, Stel len]) ⇒ Matrix

Gibt eine Matrix von Elementen zurück, die auf die angegebene Stellenzahl gerundet wurden.

Wichtig: Geben Sie eine Dual- oder Hexadezimalzahl stets mit dem Präfix 0b bzw. 0h ein (Null, nicht der Buchstabe O).

Im Dec-Modus:

Katalog

rowAdd() (Zeilenaddition)

rowAdd(Matrix1, rIndex1, rIndex2) ⇒ Matrix

Gibt eine Kopie von Matrix1 zurück, in der die Zeile rIndex2 durch die Summe der Zeilen rIndex1 und rIndex2 ersetzt ist.

Katalog

76 TI-Nspire™ Referenzhandbuch

rowDim() (Zeilendimension)

rowDim(Matrix) ⇒ Ausdruck

Gibt die Anzahl der Zeilen von Matrix zurück.

Hinweis: Siehe auch colDim(), Seite 14.

Katalog

rowNorm() (Zeilennorm)

rowNorm(Matrix) ⇒ Ausdruck

Gibt das Maximum der Summen der Absolutwerte der Elemente der Zeilen von Matrix zurück.

Hinweis: Alle Matrixelemente müssen zu Zahlen vereinfachbar sein.

Siehe auch colNorm(), Seite 14.

rowSwap() (Zeilentausch)

rowSwap(Matrix1, rIndex1, rIndex2) ⇒ Matrix

Gibt Matrix1 zurück, in der die Zeilen rIndex1 und rIndex2 vertauscht sind.

rref() (Reduzierte Diagonalform)

rref(Matrix1[, To l]) ⇒ Matrix

Gibt die reduzierte Diagonalform von Matrix1 zurück.

• Wenn Sie

•Wird Tol weggelassen oder nicht verwendet, so wird die

Hinweis: Siehe auch ref(), Seite 74.

· verwenden oder den Modus Auto

oder Näherung

Berechnungen in Fließkomma-Arithmetik durchgeführt.

Standardtoleranz folgendermaßen berechnet: 5Eë14 ·max(dim(Matrix1)) ·rowNorm(Matrix1)

auf Approximiert einstellen, werden

Katalog

TI-Nspire™ Referenzhandbuch 77

sec() (Sekans)

sec(Wer t 1) ⇒ We rt sec(Liste1) ⇒ Liste

Gibt den Sekans von We rt 1 oder eine Liste der Sekans aller Elemente in Liste1 zurück.

Hinweis: Der als Argument angegebene Winkel wird gemäß der

aktuellen Winkelmoduseinstellung als Grad, Neugrad oder Bogenmaß interpretiert. Sie können

vorübergend aufzuheben.

sec/() (Arkussekans)

sec/(Wer t 1) ⇒ We rt sec/(Liste1) ⇒ Liste

Gibt entweder den Winkel, dessen Sekans We rt 1 entspricht, oder eine Liste der inversen Sekans aller Elemente in Liste1 zurück.

Hinweis: Das Ergebnis wird gemäß der aktuellen

Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben.

sech() (Sekans hyperbolicus)

sech(Wer t 1) ⇒ We rt sech(Liste1) ⇒ Liste

Gibt den hyperbolischen Sekans von We rt 1 oder eine Liste der hyperbolischen Sekans der Elemente in Liste1 zurück.

sechê() (Arkussekans hyperbolicus)

sechê(We rt 1 ) ⇒ Wer t sechê (Liste1) ⇒ Liste

Gibt den inversen hyperbolischen Sekans von We rt 1 oder eine Liste der inversen hyperbolischen Sekans aller Elemente in Liste1 zurück.

ó,

oderôbenutzen, um den Winkelmodus

Katalog

Im Grad-Modus:

Katalog

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Katalog

Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:

78 TI-Nspire™ Referenzhandbuch

seq() (Folge)

seq(Ausdr, Var , Vo n , Bis[, Schritt]) ⇒ Liste

Erhöht die Variable Va r in Stufen von Schritt ab dem Ausgangswert Von bis zum Wert Bis, wertet den Ausdr aus und gibt die Ergebnisse

als Liste zurück. Der ursprüngliche Inhalt von Va r ist nach Beendigung von

seq() weiterhin vorhanden.

Var darf keine Systemvariable sein.

Der Vorgabewert für Schritt

ist 1.

Katalog

Drücken Sie zum Berechnen Ctrl+Enter /·:

setMode

setMode(ModusNameGanzzahl, GanzzahlFestlegen)

⇒ Ganzzahl

setMode(Liste) ⇒ Liste mit ganzen Zahlen

Nur gültig innerhalb einer Funktion oder eines Programms.

setMode(ModusNameGanzzahl, GanzzahlFestlegen)

schaltet den Modus ModusNameGanzzahl vorübergehend in GanzzahlFestlegen und gibt eine ganze Zahl entsprechend der

ursprünglichen Einstellung dieses Modus zurück. Die Änderung ist auf die Dauer der Ausführung des Programms / der Funktion begrenzt.

ModusNameGanzzahl gibt an, welchen Modus Sie einstellen möchten. Hierbei muss es sich um eine der Modus-Ganzzahlen aus der nachstehenden Tabelle handeln.

GanzzahlFestlegen gibt die neue Einstellung für den Modus an. Für den Modus, den Sie festlegen, müssen Sie eine der in der nachstehenden Tabelle aufgeführten Einstellungs-Ganzzahlen verwenden.

setMode(Liste) dient zum Ändern mehrerer Einstellungen.

Liste enthält Paare von Modus- und Einstellungs-Ganzzahlen.

setMode(Liste) gibt eine ähnliche Liste zurück, deren

Ganzzahlen-Paare die ursprünglichen Modi und Einstellungen angeben.

Wenn Sie alle Moduseinstellungen mit getMode(0) & var gespeichert haben, können Sie setMode(var) verwenden, um diese Einstellungen wiederherzustellen, bis die Funktion oder das Programm beendet wird. Siehe getMode(), Seite 37.

Hinweis: Die aktuellen Moduseinstellungen werden an

aufgerufene Subroutinen weitergegeben. Wenn eine der Subroutinen eine Moduseinstellung ändert, geht diese Modusänderung verloren, wenn die Steuerung zur aufrufenden Routine zurückkehrt.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt ·

drücken. Auf der Computertastatur halten Sie Alt gedrückt und drücken die Eingabetaste.

Katalog

Zeigen Sie den Näherungswert von pan, indem Sie die Standardeinstellung für Zahlen anzeigen (Di splay Digits) verwenden, und zeigen Sie dann p mit einer Einstellung von Fix 2 an. Kontrollieren Sie, dass der Standardwert nach Beendigung des Programms wiederhergestellt wird.

TI-Nspire™ Referenzhandbuch 79

Modus Name

Angezeigte Ziffern

Winkel

Exponentialformat

Reell oder komplex

Auto oder Approx.

Vektorformat

Basis

Modus Ganzzahl Einstellen von Ganzzahlen

=Fließ, 2=Fließ 1, 3=Fließ 2, 4=Fließ 3, 5=Fließ 4, 6=Fließ 5, 7=Fließ 6, 8=Fließ 7,

9=Fließ 8, 10=Fließ 9, 11=Fließ 10, 12=Fließ 11, 13=Fließ 12, 14=Fix 0, 15=Fix 1, 16=Fix 2, 17=Fix 3, 18=Fix 4, 19=Fix 5, 20=Fix 6, 21=Fix 7, 22=Fix 8, 23=Fix 9, 24=Fix 10, 25=Fix 11, 26=Fix 12

=Bogenmaß, 2=Grad, 3=Neugrad

=Normal, 2=Wissenschaftlich, 3=Technisch

=Reell, 2=Kartesisch, 3=Polar

=Auto, 2=Approximiert

=Kartesisch, 2=Zylindrisch, 3=Sphärisch

=Dezimal, 2=Hex, 3=Binär

shift() (Verschieben)

shift(Ganzzahl1[,#Verschiebungen]) ⇒ Ganzzahl

Verschiebt die Bits in einer binären ganzen Zahl. Ganzzahl1 kann mit jeder Basis eingegeben werden und wird automatisch in eine 32-BitDualform konvertiert. Ist der Absolutwert von Ganzzahl1 für diese Form zu groß, wird eine symmetrische Modulo-Operation ausgeführt, um sie in den erforderlichen Bereich zu bringen.

Ist #Verschiebungen positiv, erfolgt die Verschiebung nach links. ist #Verschiebungen negativ, erfolgt die Verschiebung nach rechts. Vorgabe ist ë1 (ein Bit nach rechts verschieben).

In einer Rechtsverschiebung wird das ganz rechts stehende Bit abgeschnitten und als ganz links stehendes Bit eine 0 oder 1 eingesetzt. Bei einer Linksverschiebung wird das Bit ganz links abgeschnitten und 0 als letztes Bit rechts eingesetzt.

Beispielsweise in einer Rechtsverschiebung: Alle Bits werden nach rechts verschoben. 0b0000000000000111101011000011010 Setzt 0 ein, wenn Bit ganz links 0 ist,

und 1, wenn Bit ganz links 1 ist. Es ergibt sich: 0b00000000000000111101011000011010 Das Ergebnis wird gemäß dem jeweiligen Basis-Modus angezeigt.

Führende Nullen werden nicht angezeigt.

shift(Liste1 [,#Verschiebungen]) ⇒ Liste

Gibt eine um #Verschiebungen Elemente nach rechts oder links verschobene Kopie von Liste1 zurück. Verändert Liste1 nicht.

Ist #Verschiebungen positiv, erfolgt die Verschiebung nach links. ist #Verschiebungen negativ, erfolgt die Verschiebung nach rechts. Vorgabe ist ë1 (ein Element nach rechts verschieben).

Dadurch eingeführte neue Elemente am Anfang bzw. am Ende von Liste werden auf “undef” gesetzt.

Katalog

Im Bin-Modus:

Im Hex-Modus:

Wichtig: Geben Sie eine Dual- oder Hexadezimalzahl stets mit

dem Präfix 0b bzw. 0h ein (Null, nicht der Buchstabe O).

Im Dec-Modus:

80 TI-Nspire™ Referenzhandbuch

shift() (Verschieben)

shift(String1 [,#Verschiebungen]) ⇒ Strin g

Gibt eine um #Verschiebungen Zeichen nach rechts oder links verschobene Kopie von Liste1 zurück. Verändert String1 nicht.

Ist #Verschiebungen positiv, erfolgt die Verschiebung nach links. ist #Verschiebungen negativ, erfolgt die Verschiebung nach rechts. Vorgabe ist ë1 (ein Zeichen nach rechts verschieben).

Dadurch eingeführte neue Zeichen am Anfang bzw. am Ende von Strin g werden auf ein Leerzeichen gesetzt.

Katalog

sign() (Zeichen)

sign(We rt 1 ) ⇒ We rt sign(Liste1) ⇒ Liste sign(Matrix1) ⇒ Matrix

Gibt für reelle und komplexe We rt 1 We rt 1 / abs(Wer t 1) zurück, wenn Wer t 1 ƒ 0.

Gibt 1 zurück, wenn We rt 1 positiv ist. Gibt ë1 zurück, wenn We rt 1 negativ ist.

sign(0) gibt „1 zurück, wenn als Komplex-Formatmodus Reell

eingestellt ist; anderenfalls gibt es sich selbst zurück.

sign(0) stellt im komplexen Bereich den Einheitskreis dar.

Gibt für jedes Element einer Liste bzw. Matrix das Vorzeichen zurück.

simult() (Gleichungssystem)

simult(KoeffMatrix, KonstVektor[, Tol ]) ⇒ Matrix

Ergibt einen Spaltenvektor, der die Lösungen für ein lineares Gleichungssystem enthält.

KoeffMatrix muss eine quadratische Matrix sein, die die Koeffizienten der Gleichung enthält.

KonstVektor muss die gleiche Zeilenanzahl (gleiche Dimension) besitzen wie KoeffMatrix und die Konstanten enthalten.

• Wenn Sie den Modus Auto oder Näherung auf Approximiert einstellen, werden Berechnungen in Fließkomma-Arithmetik durchgeführt.

•Wird Tol weggelassen oder nicht verwendet, so wird die Standardtoleranz folgendermaßen berechnet:

5Eë14 ·max(dim(KoeffMatrix)) ·rowNorm(KoeffMatrix)

simult(KoeffMatrix, KonstMatrix[, Tol ]) ⇒ Matrix

Löst mehrere lineare Gleichungssysteme, die alle dieselben Gleichungskoeffizienten, aber unterschiedliche Konstanten haben.

Jede Spalte in KonstMatrix muss die Konstanten für ein Gleichungssystem enthalten. Jede Spalte in der sich ergebenden Matrix enthält die Lösung für das entsprechende System.

Bei Komplex-Formatmodus Reell:

Auflösen nach x und y: x + 2y = 1 3x + 4y = ë1

Die Lösung ist x=ë3 und y=2.

Auflösen: ax + by = 1 cx + dy = 2

Auflösen:

x + 2y = 1

3x + 4y = ë1

x + 2y = 2

3x + 4y = ë3

Katalog

Für das erste System ist x=ë3 und y=2. Für das zweite System ist x=ë7 und y=9/2.

TI-Nspire™ Referenzhandbuch 81

sin() (Sinus)

sin(We rt 1) ⇒ Wer t sin(Liste1) ⇒ Liste

sin(Wer t 1) gibt den Sinus des Arguments zurück. sin(Liste1) gibt eine Liste zurück, die für jedes Element von Liste1

den Sinus enthält.

Hinweis: Das Argument wird entsprechend dem aktuellen

Winkelmodus als Winkel in Grad, Neugrad oder Bogenmaß interpretiert. Sie können ó,G oder ô benutzen, um die

Winkelmoduseinstellung temporär zu ändern.

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Taste

sin(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den Matrix-Sinus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Sinus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt

cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

sinê() (Arkussinus)

sinê(Wer t 1) ⇒ Wer t sinê(Liste1) ⇒ Liste

sinê(Wer t 1) gibt den Winkel, dessen Sinus We r t1 ist, zurück.

sinê(Liste1) gibt in Form einer Liste für jedes Element aus Liste1

den inversen Sinus zurück.

Hinweis: Das Ergebnis wird gemäß der aktuellen

Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben.

sinê(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den inversen Matrix-Sinus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des inversen Sinus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

Im Bogenmaß-Modus:

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:

Um das ganze Ergebnis zu sehen, drücken Sie £ und verwenden dann ¡ und ¢, um den Cursor zu bewegen.

Tasten

82 TI-Nspire™ Referenzhandbuch

sinh() (Sinus hyperbolicus)

sinh(We rt 1) ⇒ Wer t sinh(Liste1) ⇒ Liste

sinh (Wer t 1) gibt den Sinus hyperbolicus des Arguments zurück. sinh (Liste1) gibt in Form einer Liste für jedes Element aus Liste1

den Sinus hyperbolicus zurück.

sinh(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den Matrix-Sinus hyperbolicus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Sinus hyperbolicus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

Im Bogenmaß-Modus:

Katalog

sinhê() (Arkussinus hyperbolicus)

sinhê(Wer t 1) ⇒ Wer t sinhê(Liste1) ⇒ Liste

sinhê(Wer t 1) gibt den inversen Sinus hyperbolicus des Arguments

zurück.

sinhê(Liste1) gibt in Form einer Liste für jedes Element ausListe1

den inversen Sinus hyperbolicus zurück.

sinhê(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den inversen Matrix-Sinus hyperbolicus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des inversen Sinus hyperbolicus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

Im Bogenmaß-Modus:

Katalog

TI-Nspire™ Referenzhandbuch 83

SinReg

SinReg X, Y [, [Iterationen],[ Periode] [, Kategorie, Mit] ]

Berechnet die sinusförmige Regression auf Listen X und Y. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Alle Listen außer Mit müssen die gleiche Dimension besitzen.

X und Y sind Listen von unabhängigen und abhängigen Variablen. Iterationen ist ein Wert, der angibt, wie viele Lösungsversuche

(1 bis 16) maximal unternommen werden. Bei Auslassung wird 8 verwendet. Größere Werte führen in der Regel zu höherer Genauigkeit, aber auch zu längeren Ausführungszeiten, und umgekehrt.

Periode gibt eine geschätzte Periode an. Bei Auslassung sollten die Werte in X sequentiell angeordnet und die Differenzen zwischen ihnen gleich sein. Wenn Sie Periode jedoch angeben, können die Differenzen zwischen den einzelnen x-Werten ungleich sein.

Kategorie ist eine Liste numerischer Kategoriecodes für die entsprechenden Daten X und Y.

Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten.

Die Ausgabe von Winkelmoduseinstellung immer im Bogenmaß (rad).

Ausgabevariable Beschreibung

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.Resid Residuen von der Regression

stat.XReg Liste der Datenpunkte in der modifizierten X-Liste, die in der Regression mit den Beschränkungen für

stat.YReg Liste der Datenpunkte in der modifizierten Y- Li ste , die schließlich in der Regression mit den

stat.FreqReg Liste der Häufigkeiten für stat.XReg und stat.YReg

SinReg erfolgt unabhängig von der

Regressionsgleichung: a·sin(bx+c)+d

Regressionskoeffizienten

Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Beschränkungen für Häuf, Kategorieliste und Mit-Kategorien verwendet wurde

Katalog

SortA (In aufsteigender Reihenfolge sortieren)

SortA Liste1[, Liste2] [, Liste3] ... SortA

Vektor1[, Vektor2] [, Vektor3] ...

Sortiert die Elemente des ersten Arguments in aufsteigender Reihenfolge.

Bei Angabe von mehr als einem Argument werden die Elemente der zusätzlichen Argumente so sortiert, dass ihre neue Position mit der neuen Position der Elemente des ersten Arguments übereinstimmt.

Alle Argumente müssen Listen- oder Vektornamen sein. Alle Argumente müssen die gleiche Dimension besitzen.

Katalog

84 TI-Nspire™ Referenzhandbuch

SortD (In absteigender Reihenfolge sortieren)

SortD Liste1[, Liste2] [, Liste3] ...

Vektor1[,Vektor2] [,Vektor3] ...

SortD

Identisch mit SortA mit dem Unterschied, dass SortD die Elemente in absteigender Reihenfolge sortiert.

Sphere (Kugelkoordinaten)

Vek t o r 4Sphere

Zeigt den Zeilen- oder Spaltenvektor in Kugelkoordinaten [r q

f] an.

Vek t o r muss die Dimension 3 besitzen und kann ein Zeilen- oder ein Spaltenvektor sein.

Hinweis: 4Sphere ist eine Anzeigeformatanweisung, keine

Konvertierungsfunktion. Sie können sie nur am Ende einer Eingabezeile benutzen.

Katalog

(ρ,θ,φ)

sqrt() (Quadratwurzel)

sqrt(Wer t 1) ⇒ We r t sqrt(Liste1) ⇒ Liste

Gibt die Quadratwurzel des Arguments zurück. Bei einer Liste wird die Quadratwurzel für jedes Element von Liste1

zurückgegeben.

Hinweis: Siehe auch Vorlage Quadratwurzel, Seite 1.

Katalog

TI-Nspire™ Referenzhandbuch 85

stat.results

Zeigt Ergebnisse einer statistischen Berechnung an. Die Ergebnisse werden als Satz von Namen-Wert-Paaren angezeigt.

Die angezeigten Namen hängen von der zuletzt ausgewerteten Statistikfunktion oder dem letzten Befehl ab.

Sie können einen Namen oder einen Wert kopieren und ihn an anderen Positionen einfügen.

Hinweis: Definieren Sie nach Möglichkeit keine Variablen, die

dieselben Namen haben wie die für die statistische Analyse verwendeten Variablen. In einigen Fällen kön nte ein Fehler auftreten. Namen von Variablen, die für die statistische Analyse verwendet werden, sind in der Tabelle unten aufgelistet.

Katalog

stat.a stat.AdjR² stat.b stat.b0 stat.b1 stat.b2 stat.b3 stat.b4 stat.b5 stat.b6 stat.b7 stat.b8 stat.b9 stat.b10 stat.bList stat.c² stat.c stat.CLower stat.CLowerList stat.CompList stat.CompMatrix stat.CookDist stat.CUpper stat.CUpperList stat.d

Hinweis: Immer, wenn die Applikation 'Lists & Spreadsheet' statistische Ergebnisse berechnet, kopiert sie die Gruppenvariablen

"stat." in eine "stat #."-Gruppe, wobei # eine automatisch inkrementierte Zahl ist. Damit können Sie vorherige Ergebnisse beibehalten, während mehrere Berechnungen ausgeführt werden.

stat.dfDenom stat.dfBlock stat.dfCol stat.dfError stat.dfInteract stat.dfReg stat.dfNumer stat.dfRow stat.DW stat.e stat.ExpMatrix stat.F stat.FBlock stat.Fcol

stat.FInteract stat.FreqReg stat.Frow stat.Leverage stat.LowerPred stat.LowerVal stat.m stat.MaxX stat.MaxY stat.ME stat.MedianX

stat.MedianY stat.MEPred stat.MinX stat.MinY stat.MS stat.MSBlock stat.MSCol stat.MSError stat.MSInteract stat.MSReg stat.MSRow stat.n stat.Ç

stat.Ç1 stat.Ç2 stat.ÇDiff stat.PList stat.PVal stat.PValBlock stat.PValCol

stat.PValInteract stat.PValRow stat.Q1X stat.Q1Y stat.Q3X

stat.Q3Y stat.r stat.r² stat.RegEqn stat.Resid stat.ResidTrans stat.sx

stat.sy stat.sx1 stat.sx2 stat.Gx stat.Gx² stat.Gxy stat.Gy stat.Gy² stat.s stat.SE

stat.SEList stat.SEPred stat.sResid stat.SEslope stat.sp stat.SS stat.SSBlock

stat.SSCol stat.SSX stat.SSY stat.SSError stat.SSInteract stat.SSReg stat.SSRow stat.tList stat.UpperPred stat.UpperVal stat.v stat.v1

stat.v2 stat.vDiff stat.vList stat.XReg stat.XVal stat.XValList stat.w

stat.y stat.yList

stat.YReg

86 TI-Nspire™ Referenzhandbuch

stat.values

Zeigt eine Matrix der Werte an, die für die zuletzt ausgewertete Statistikfunktion oder den letzten Befehl berechnet wurden.

Im Gegensatz zu zugeordneten Namen aus.

Sie können einen Wert kopieren und ihn an anderen Positionen einfügen.

stat.results lässt stat.values die den Werten

Siehe

stat.results.

Katalog

stDevPop() (Populations-Standardabweichung)

stDevPop(Liste[, Häufigkeitsliste]) ⇒ Ausdruck

Ergibt die Populations-Standardabweichung der Elemente in Liste. Jedes Häufigkeitsliste-Element gewichtet die Elemente von Liste in

der gegebenen Reihenfolge entsprechend.

Hinweis: Liste muss mindestens zwei Elemente haben. stDevPop(Matrix1[, Häufigkeitsmatrix]) ⇒ Matrix

Ergibt einen Zeilenvektor der Populations-Standa rdabweichungen der Spalten in Matrix1.

Jedes Häufigkeitsmatrix-Element gewichtet die Elemente von Matrix1 in der gegebenen Reihenfolge entsprechend.

Hinweis: Matrix1 muss mindestens zwei Zeilen haben.

stDevSamp() (Stichproben-Standardabweichung)

stDevSamp(Liste[, Häufigkeitsliste]) ⇒ Ausdruck

Ergibt die Stichproben-Standardabweichung der Elemente in Liste. Jedes Häufigkeitsliste-Element gewichtet die Elemente von Liste in

der gegebenen Reihenfolge entsprechend.

Hinweis: Liste muss mindestens zwei Elemente haben. stDevSamp(Matrix1[, Häufigkeitsmatrix]) ⇒ Matrix

Ergibt einen Zeilenvektor der Stichproben-Standardabweichunge n der Spalten in Matrix1.

Jedes Häufigkeitsmatrix-Element gewichtet die Elemente von Matrix1 in der gegebenen Reihenfolge entsprechend.

Hinweis: Matrix1 muss mindestens zwei Zeilen haben.

Im Bogenmaß- und automatischen Modus:

Katalog

TI-Nspire™ Referenzhandbuch 87

Stop (Stopp)

Stop

Programmierbefehl: Beendet das Programm.

Stop ist in Funktionen nicht zulässig. Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Katalog

Store (Speichern)

string() (String)

string(Ausdr) ⇒ St ring

Vereinfacht Ausdr und gibt das Ergebnis als Zeichenkette zurück.

subMat() (Untermatrix)

subMat(Matrix1[, vonZei] [, vonSpl] [, bisZei] [, bisSpl])

⇒ Matrix

Gibt die angegebene Untermatrix von Matrix1 zurück. Vorgaben: vonZei=1, vonSpl=1, bisZei=letzte Zeile, bisSpl=letzte

Spalte.

Summe (Sigma)

sum() (Summe)

sum(Liste[, Start[, Ende]]) ⇒ Ausdruck

Gibt die Summe der Elemente in Liste zurück. Start und Ende sind optional. Sie geben einen Elementebereich an.

Siehe

& (speichern)

, Seite 117.

Katalog

Siehe G(), Seite 113.

Katalog

88 TI-Nspire™ Referenzhandbuch

sum() (Summe)

sum(Matrix1[, Start[, Ende]]) ⇒ Matrix

Gibt einen Zeilenvektor zurück, der die Summen der Elemente aus den Spalten von Matrix1 enthält.

Start und Ende sind optional. Sie geben einen Zeilenbereich an.

Katalog

sumIf()

sumIf(Liste,Kriterien[, SummeListe]) ⇒ Wer t

Gibt die kumulierte Summe aller Elemente in Liste zurück, die die angegebenen Kriterien erfüllen. Optional können Sie eine Alternativliste, SummeListe, angeben, an die die Elemente zum Kumulieren weitergegeben werden sollen.

Liste kann ein Ausdruck, eine Liste oder eine Matrix sein. SummeListe muss, sofern sie verwendet wird, dieselben Dimension(en) haben wie Liste.

Kriterien können sein:

• Ein Wert, ein Ausdruck oder eine Zeichenfolge. So kumuliert beispielsweise 34 nur solche Elemente in Liste, die vereinfacht den Wert 34 ergeben.

• Ein Boolescher Ausdruck, der das Sonderzeichen ? als Platzhalter für jedes Element verwendet. Beispielsweise zählt ?<10 nur solche Elemente in Liste zusammen, die kleiner als 10 sind.

Wenn ein Element in Liste die Kriterien erfüllt, wird das Element zur Kumulationssumme hinzugerechnet. Wenn Sie SummeListe hinzufügen, wird stattdessen das entsprechende Element aus SummeListe zur Summe hinzugerechnet.

In der Lists & Spreadsheet Applikation können Sie anstelle von Liste und SummeListe auch einen Zellenbereich verwenden.

Hinweis: Siehe auch countIf(), Seite 19.

(Transponierte)

Matrix1

⇒ matrix

Gibt die komplex konjugierte, transponierte Matrix von Matrix1 zurück.

Katalog

TI-Nspire™ Referenzhandbuch 89

tan() (Tangens)

tan(We rt 1) ⇒ Wer t tan(Liste1) ⇒ Liste

tan(Wer t 1) gibt den Tangens des Arguments zurück. tan(Liste1) gibt in Form einer Liste für jedes Element in Liste1 den

Tangens zurück.

Hinweis: Das Argument wird entsprechend dem aktuellen

Winkelmodus als Winkel in Grad, Neugrad oder Bogenmaß interpretiert. Sie können ó,G oderôbenutzen, um die

Winkelmoduseinstellung temporär zu ändern.

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Taste

tan(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den Matrix-Tangens von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Tangens jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt

cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

tanê() (Arkustangens)

tanê(Wer t 1) ⇒ Wer t tanê(Liste1) ⇒ Liste

tanê(Wer t 1) gibt den Winkel zurück, dessen Tangens We rt 1 ist.

tanê(Liste1) gibt in Form einer Liste für jedes Element aus Liste1

den inversen Tangens zurück.

Hinweis: Das Ergebnis wird gemäß der aktuellen

Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben.

Im Bogenmaß-Modus:

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Tasten

90 TI-Nspire™ Referenzhandbuch

tanê() (Arkustangens)

tanê(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den inversen Matrix-Tangens von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des inversen Tangens jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

Im Bogenmaß-Modus:

Tasten

tanh() (Tangens hyperbolicus)

tanh(We rt 1) ⇒ Wer t tanh(Liste1) ⇒ Liste

tanh(Wer t1 ) gibt den Tangens hyperbolicus des Arguments zurück. tanh(Liste1) gibt in Form einer Liste für jedes Element aus Liste1

den Tangens hyperbolicus zurück.

tanh(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den Matrix-Tangens hyperbolicus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Tangens hyperbolicus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

tanhê() (Arkustangens hyperbolicus)

tanhê(Wer t 1) ⇒ Wer t tanhê(Liste1) ⇒ Liste

tanhê(Wer t 1) gibt den inversen Tangens hyperbolicus des

Arguments zurück.

tanhê(Liste1) gibt in Form einer Liste für jedes Element aus Liste1

den inversen Tangens hyperbolicus zurück.

tanhê(Quadratmatrix1) ⇒ Quadratmatrix

Gibt den inversen Matrix-Tangens hyperbolicus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des inversen Tangens hyperbolicus jedes einzelnen Eleme nts. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen.

Katalog

Im Bogenmaß-Modus:

Katalog

Im Komplex-Formatmodus “kartesisch”:

Um das ganze Ergebnis zu sehen, drücken Sie £ und verwenden dann ¡ und ¢, um den Cursor zu bewegen.

Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:

Um das ganze Ergebnis zu sehen, drücken Sie £ und verwenden dann ¡ und ¢, um den Cursor zu bewegen.

TI-Nspire™ Referenzhandbuch 91

tCdf()

tCdf(UntGrenze,ObGrenze,FreiGrad) ⇒ Zahl, wenn

UntGrenze und ObGrenze Zahlen sind, Liste, wenn UntGrenze

und

ObGrenze Listen sind

Berechnet für eine Student-t-Verteilung mit vorgegebenen Freiheitsgraden FreiGrad die Intervallwahrscheinlichkeit zwischen UntGrenze und ObGrenze.

Katalog

Für P(X  obereGrenze) setzen Sie untereGrenze = .9E999.

Then Siehe If, Seite 40.

tInterval

tInterval Liste[,Häuf[,KNiv]]

(Datenlisteneingabe)

tInterval v,sx,n[,KNiv]

(Zusammenfassende statistische Eingabe) Berechnet das Konfidenzintervall t. Eine Zusammenfassung

der Ergebnisse wird in der Variablen stat.results gespeichert. (Siehe Seite 86.)

Ausgabevariable Beschreibung

stat.CLower, stat.CUpper Konfidenzintervall für den unbekannten Populationsmittelwert

stat.x

Stichprobenmittelwert der Datenfolge aus der zufälligen Normalverteilung

stat.ME Fehlertoleranz

stat.df Freiheitsgrade

stat.sx

Stichproben-Standardabweichung

stat.n Länge der Datenfolge mit Stichprobenmittelwert

tInterval_2Samp (Zwei-Stichproben-tKonfidenzintervall)

tInterval_2Samp

Liste1,Liste2[,Häufigkeit1[,Häufigkeit2[,KStufe[,Verteilt]]]]

(Datenlisteneingabe)

tInterval_2Samp v1,sx1,n1,v2,sx2,n2[,KStufe[,Verteilt]]

(Zusammenfassende statistische Eingabe) Berechnet ein t-Konfidenzintervall für zwei Stichproben. Eine

Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (Siehe Seite 86.)

Ver t e i lt =1 verteilt Varianzen; Verteilt=0 verteilt keine Varianzen.

Katalog

Ausgabevariable Beschreibung

stat.CLower, stat.CUpper Konfidenzintervall mit dem Konfidenzniveau der Verteilungswahrscheinlichkeit

92 TI-Nspire™ Referenzhandbuch

Ausgabevariable Beschreibung

stat.x1-x2

stat.ME Fehlertoleranz

stat.df Freiheitsgrade

stat.

x1, stat.x2

stat.sx1, stat.sx2

stat.n1, stat.n2 Anzahl der Stichproben in Datenfolgen

stat.sp Die verteilte Standardabweichung. Wird berechnet, wenn Ve r te i l t =JA.

Stichprobenmittelwerte der Datenfolgen aus der zufälligen Normalverteilung

Stichproben-Standardabweichungen für Liste 1 und Liste 2

tPdf()

tPdf(XWert,FreiGrad) ⇒ Zahl, wenn XWert eine Zahl ist,

Liste, wenn XWert eine Liste ist

Berechnet die Wahrscheinlichkeitsdichtefunktion (Pdf) einer Studentt-Verteilung an einem bestimmten x-Wert für die vorgegebenen FreiheitsgradeFreiGrad.

trace()

trace(Quadratmatrix) ⇒ We rt

Gibt die Spur (Summe aller Elemente der Hauptdiagonalen) von Quadratmatrix zurück.

Katalog

TI-Nspire™ Referenzhandbuch 93

Try (Versuche)

Try

block1

Else

block2

EndTry

Führt Block1 aus, bis ein Fehler auftritt. Wenn in Block1 ein Fehler auftritt, wird die Programmausführung an Block2 übertragen. Die Systemvariable Fehlercode (errCode) enthält den Fehlercode, der es dem Programm ermöglicht, eine Fehlerwiederherstellung durchzuführen. Eine Liste der Fehlercodes finden Sie unter "Fehlercodes und -meldungen" auf Seite 119.

Block1 und Block2 können einzelne Anweisungen oder Reihen von Anweisungen sein, die durch das Zeichen “:” voneinander getrennt sind.

Hinweis zur Eingabe des Beispiels: In der Calculator-

Applikation des Handheld können Sie mehrzeilige Definitionen eingeben, indem Sie am Ende jeder Zeile @ statt · drücken.

Auf der Computertastatur halten Sie Alt gedrückt und drücken die

Eingabetaste.

Katalog

Beispiel 2

Um die Befehle Versuche (Try), LöFehler (ClrErr) und

ÜbgebFeh (PassErr) im Betrieb zu sehen, geben Sie das rechts

gezeigte Programm eigenvals() ein. Sie starten das Programm, indem Sie jeden der folgenden Ausdrücke eingeben.

Hinweis: Siehe auch LöFehler, Seite 14, und ÜbgebFeh, Seite 66.

tTest

tTest m0,Liste[,Häufigkeit[,Hypoth]]

(Datenlisteneingabe)

tTest m0,x,sx,n,[Hypoth]

(Zusammenfassende statistische Eingabe) Führt einen Hypothesen-Test für einen einzelnen, unbekannten

Populationsmittelwert m durch, wenn die PopulationsStandardabweichung s unbekannt ist. Eine Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (Siehe Seite 86.)

Getestet wird H0: m = m0 in Bezug auf eine der folgenden Alternativen:

Für Ha: m < m0 setzen Sie Hypoth<0 Für Ha: m ƒ m0 (Standard) setzen Sie Hypoth=0 Für Ha: m > m0 setzen Sie Hypoth>0

Disp "A= ",a Disp "B= ",b Disp " " Disp "Eigenwerte von A·B sind:",eigVl(a*b)

Else

If errCode=230 Then

Disp "Fehler: Produkt von A·B muss eine quadratische

Matrix sein"

ClrErr

Else

PassErr

EndIf EndTry EndPrgm

Katalog

94 TI-Nspire™ Referenzhandbuch

Texas Instruments TI-Nspire Reference Guide [de]

Specifications and Main Features

Frequently Asked Questions

User Manual

Wichtige Informationen

Inhaltsverzeichnis

Vorlagen für Ausdrücke

TI-Nspire™ Referenzhandbuch 1

Alphabetische Auflistung