Texas Instruments TI-Nspire Reference Guide [nl]

Referentiehandleiding

Deze handleiding heeft betrekking op TI-Nspire-software versie 1.4. Ga voor de nieuwste versie van de documentatie naar education.ti.com/guides.

Belangrijke informatie

Tenzij uitdrukkelijk anders vermeld in de bij een programma behorende Licentie, geeft Texas Instruments betreffende programma's of boekmateriaal geen uitdrukkelijke noch impliciete garantie, daaronder mede begrepen maar niet beperkt tot impliciete garanties met betrekking tot verkoopbaarheid en geschiktheid voor een bepaald doel, en maakt zulk materiaal uitsluitend beschikbaar op een “as-is” basis. In geen geval is Texas Instruments tegenover wie dan ook aansprakelijk voor enige speciale, indirecte, bijkomende of gevolgschade verband houdend met of voortvloeiend uit de aankoop of het gebruik van dit materiaal en, ongeacht de vorm van proces, zal de enige en uitsluitende aansprakelijkheid van Texas Instruments niet hoger zijn dan het in de bij een programma behorende licentie vermelde bedrag. Daarenboven wijst Texas Instruments elke aansprakelijkheid van de hand voor vorderingen van welke aard dan ook tegen het gebruik van dit materiaal door derden.

Licentie

Zie de complete licentie die is geïnstalleerd in C:\Program Files\TI Education\TI-Nspire.

Macintosh®, Windows®, Excel®, Vernier EasyLink®, EasyTemp®, Go!®Link, Go!®Motion, en Go!®Temp zijn handelsmerken van hun respectievelijke eigenaars.

Inhoud

Belangrijke informatie Uitdrukkingstemplates

Breukentemplate ......................................... 1

Exponent-template ......................................1

Worteltemplate ........................................... 1

N-de wortel-template ..................................1

e-macht-template ........................................2

Log-template ................................................ 2

Template voor stuksgewijs gedefinieerde

functies (2-stuks) .......................................... 2

Template voor stuksgewijs gedefinieerde

functies (N-stuks) ......................................... 2

Absolute waarde-template ......................... 2

dd°mm’ss.ss’’ template ................................3

Matrixtemplate (2 x 2) .................................3

Matrixtemplate (1 x 2) .................................3

Matrixtemplate (2 x 1) .................................3

Matrixtemplate (m x n) ............................... 3

Somtemplate (G) ..........................................3

Product-template (Π) ...................................4

Alfabetische lijst A

abs() ..............................................................5

amortTbl() .................................................... 5

and ................................................................5

angle() ..........................................................6

ANOVA .........................................................6

ANOVA2way ................................................ 7

Ans ................................................................9

approx() ........................................................9

approxRational() .......................................... 9

augment() .....................................................9

avgRC() ....................................................... 10

bal() .............................................................10

4Base2 (4Grondtal2) ....................................10

4Base10 (4Grondtal10) ................................11

4Base16 (4Grondtal16) ................................11

binomCdf() ................................................. 12

binomPdf() ................................................. 12

ceiling() .......................................................12

char() ...........................................................12

2way ........................................................12

Cdf() .........................................................13

GOF ......................................................... 13

Pdf() .........................................................13

ClearAZ .......................................................14

ClrErr ...........................................................14

colAugment() ............................................. 14

colDim() ......................................................14

colNorm() ....................................................14

conj() ...........................................................15

constructMat() ............................................ 15

CopyVar() ................................................... 15

corrMat() .................................................... 16

cos() ............................................................ 16

cosê() .......................................................... 17

cosh() .......................................................... 17

coshê() ........................................................ 17

cot() ............................................................ 18

cotê() .......................................................... 18

coth() .......................................................... 18

cothê() ........................................................ 18

count() ........................................................ 19

countif() ..................................................... 19

crossP() ....................................................... 19

csc() ............................................................. 20

cscê() ........................................................... 20

csch() ........................................................... 20

cschê() ......................................................... 20

CubicReg .................................................... 21

cumSum() ................................................... 21

Cycle ........................................................... 22

4Cylind ........................................................ 22

dbd() ........................................................... 22

4DD ............................................................. 23

4Decimal ..................................................... 23

Define (Definiëren) ................................... 23

Define LibPriv ............................................ 24

Define LibPub ............................................ 25

DelVar ........................................................ 25

det() ............................................................ 25

diag() .......................................................... 26

dim() ........................................................... 26

Disp ............................................................. 26

4DMS ........................................................... 27

dotP() .......................................................... 27

e^() ............................................................. 27

eff() ............................................................. 28

eigVc() ........................................................ 28

eigVl() ......................................................... 28

Else ............................................................. 28

ElseIf ........................................................... 29

EndFor ........................................................ 29

EndFunc ...................................................... 29

EndIf ........................................................... 29

EndLoop ..................................................... 29

EndPrgm ..................................................... 29

EndTry ........................................................ 29

EndWhile .................................................... 29

Exit .............................................................. 30

exp() ........................................................... 30

expr() .......................................................... 30

ExpReg ....................................................... 31

factor() ....................................................... 31

FCdf() ......................................................... 32

Fill ............................................................... 32

iii

FiveNumSummary ......................................32

floor() ..........................................................33

For ...............................................................33

format() ......................................................33

fPart() ..........................................................34

FPdf() ..........................................................34

freqTable4lijst() ...........................................34

frequency() .................................................34

Func .............................................................35

FTest_2Samp ..............................................35

gcd() ............................................................36

geomCdf() ...................................................36

geomPdf() ...................................................36

getDenom() ................................................36

getLangInfo() .............................................37

getMode() ...................................................37

getNum() ....................................................38

getVarInfo() ................................................38

Goto ............................................................39

4Grad ...........................................................39

identity() .....................................................39

If ..................................................................40

ifFn() ............................................................41

imag() ..........................................................41

Indirectie .....................................................41

inString() .....................................................41

int() .............................................................42

intDiv() ........................................................42

() .........................................................42

invc

invF() ...........................................................42

invNorm() ....................................................42

invt() ............................................................42

iPart() ..........................................................43

irr() ..............................................................43

isPrime() ......................................................43

Lbl ...............................................................44

lcm() ............................................................44

left() ............................................................44

libShortcut() ................................................45

LinRegBx .....................................................45

LinRegMx ....................................................46

LinRegtIntervals .........................................46

LinRegtTest .................................................48

@List() ..........................................................48

list4mat() .....................................................49

ln() ...............................................................49

LnReg ..........................................................49

Local ............................................................50

log() .............................................................51

Logistic ........................................................51

LogisticD .....................................................52

Loop ............................................................53

LU ................................................................53

mat4list() .....................................................53

max() ...........................................................54

mean() ........................................................ 54

median() ..................................................... 54

MedMed ..................................................... 55

mid() ........................................................... 55

min() ........................................................... 56

mirr() ........................................................... 56

mod() .......................................................... 56

mRow() ....................................................... 57

mRowAdd() ................................................ 57

MultReg ...................................................... 57

MultRegIntervals ....................................... 57

MultRegTests ............................................. 58

nCr() ............................................................ 59

nDeriv() ....................................................... 59

newList() ..................................................... 60

newMat() .................................................... 60

nfMax() ....................................................... 60

nfMin() ....................................................... 60

nInt() ........................................................... 60

nom() .......................................................... 61

norm() ......................................................... 61

normCdf() ................................................... 61

normPdf() ................................................... 61

not .............................................................. 61

nPr() ............................................................ 62

npv() ........................................................... 63

nSolve() ....................................................... 63

OneVar ....................................................... 64

or ................................................................ 65

ord() ............................................................ 65

P4Rx() .......................................................... 65

P4Ry() .......................................................... 66

PassErr ........................................................ 66

piecewise() .................................................66

poissCdf() .................................................... 66

poissPdf() .................................................... 66

4Polar .......................................................... 67

polyEval() .................................................... 67

PowerReg ................................................... 67

Prgm ........................................................... 68

Product (PI) ................................................. 68

product() .................................................... 68

propFrac() ................................................... 69

QR ............................................................... 70

QuadReg .................................................... 70

QuartReg .................................................... 71

R4Pq() .......................................................... 72

R4Pr() ........................................................... 72

4Rad ............................................................ 72

rand() .......................................................... 72

randBin() .................................................... 73

randInt() ..................................................... 73

randMat() ................................................... 73

randNorm() ................................................. 73

randPoly() ................................................... 73

randSamp() ................................................. 73

RandSeed .................................................... 74

real() ...........................................................74

4Rect ............................................................74

ref() .............................................................75

remain() ......................................................75

Return .........................................................75

right() ..........................................................75

root() ...........................................................76

rotate() .......................................................76

round() ........................................................77

rowAdd() ....................................................77

rowDim() ....................................................77

rowNorm() ..................................................77

rowSwap() .................................................. 77

rref() ............................................................78

sec() .............................................................78

sec/() ...........................................................78

sech() ...........................................................79

sechê() ......................................................... 79

seq() ............................................................79

setMode() ................................................... 80

shift() ..........................................................81

sign() ...........................................................81

simult() ........................................................82

sin() .............................................................82

sinê() ...........................................................83

sinh() ...........................................................83

sinhê() .........................................................84

SinReg .........................................................84

SortA ...........................................................85

SortD ...........................................................85

4Sphere ....................................................... 85

sqrt() ...........................................................86

stat.results (stat.resultaten) .......................86

stat.values ...................................................87

stDevPop() .................................................. 87

stDevSamp() ............................................... 87

Stop .............................................................88

Store ...........................................................88

string() ........................................................88

subMat() ..................................................... 88

Som (Sigma) ............................................... 88

sum() ...........................................................88

sumIf() .........................................................89

system() .......................................................89

T (transponeren) ........................................89

tan() ............................................................90

tanê() ..........................................................90

tanh() ..........................................................91

tanhê() ........................................................91

tCdf() ...........................................................92

Then ............................................................92

tInterval ......................................................92

tInterval_2Samp .........................................92

tPdf() ...........................................................93

trace() .........................................................93

Try ............................................................... 94

tTest ............................................................ 94

tTest_2Samp ............................................... 95

tvmFV() ....................................................... 95

tvmI() .......................................................... 96

tvmN() ........................................................ 96

tvmPmt() .................................................... 96

tvmPV() ....................................................... 96

TwoVar ....................................................... 97

unitV() ........................................................ 98

varPop() ...................................................... 98

varSamp() ................................................... 98

when() ........................................................ 99

While .......................................................... 99

“Met” ......................................................... 99

xor ............................................................ 100

zInterval ................................................... 100

zInterval_1Prop ........................................ 101

zInterval_2Prop ........................................ 101

zInterval_2Samp ...................................... 101

zTest ......................................................... 102

zTest_1Prop .............................................. 102

zTest_2Prop .............................................. 103

zTest_2Samp ............................................ 103

Symbolen

+ (optellen) .............................................. 105

N(aftrekken) ............................................. 105

·(vermenigvuldigen) .............................. 106

à (delen) ................................................... 106

^ (macht) .................................................. 107

(kwadraat) ........................................... 107

.+ (punt optellen) .................................... 108

.. (punt aftrekken) ................................... 108

·(punt vermenigvuldigen) .................... 108

. / (punt delen) ......................................... 108

.^ (punt machtsverheffen) ...................... 108

ë(negatief) ............................................... 109

% (percentage) ........................................ 109

= (is gelijk) ................................................ 110

ƒ (is niet gelijk) ........................................ 110

< (kleiner dan) ......................................... 111

{ (kleiner dan of gelijk aan) .................... 111

> (groter dan) .......................................... 111

| (groter dan of gelijk aan) ..................... 111

! (faculteit) ............................................... 112

& (toevoegen) .......................................... 112

‡() (wortel) ............................................... 112

Π() (product) ............................................ 112

G() (som) ................................................... 113

GInt() ......................................................... 113

GPrn() ........................................................ 114

# (indirectie) ............................................. 114

í (wetenschappelijke notatie) .................114

g (decimale graden) .................................115

ô(radialen) ................................................115

¡ (graden) ..................................................115

¡, ', '' (graad/minuut/seconde) .................115

 (hoek) ....................................................116

10^() ..........................................................116

^ê (omgekeerde) ......................................116

| (“met”) ....................................................117

& (opslaan) ...............................................117

:= (toewijzen) ...........................................117

0b, 0h ........................................................118

Foutcodes en meldingen Productinformatie, service en

garantie TI

TI-Nspire™

In deze handleiding worden de templates, functies, commando's en operatoren beschreven die beschikbaar zijn voor het uitwerken van wiskundige uitdrukkingen.

Referentiehandleiding

Uitdrukkingstemplates

Uitdrukkingstemplates bieden u een makkelijke manier om wiskundige uitdrukkingen in standaard wiskundige notatie in te voeren. Wanneer u een template invoegt, verschijnt deze op de invoerregel met kleine blokjes op de posities waarop u elementen kunt invoeren. Een cursor geeft aan welk element u kunt invoeren.

Gebruik de pijltoetsen of druk op

element, en typ een waarde of uitdrukking voor het element in. Druk op om de uitdrukking uit te werken.

Breukentemplate

Opmerking: zie ook / (delen), pag. 106.

e om de cursor te verplaatsen naar de positie van elk

· of /·

/p-toetsen

Voorbeeld:

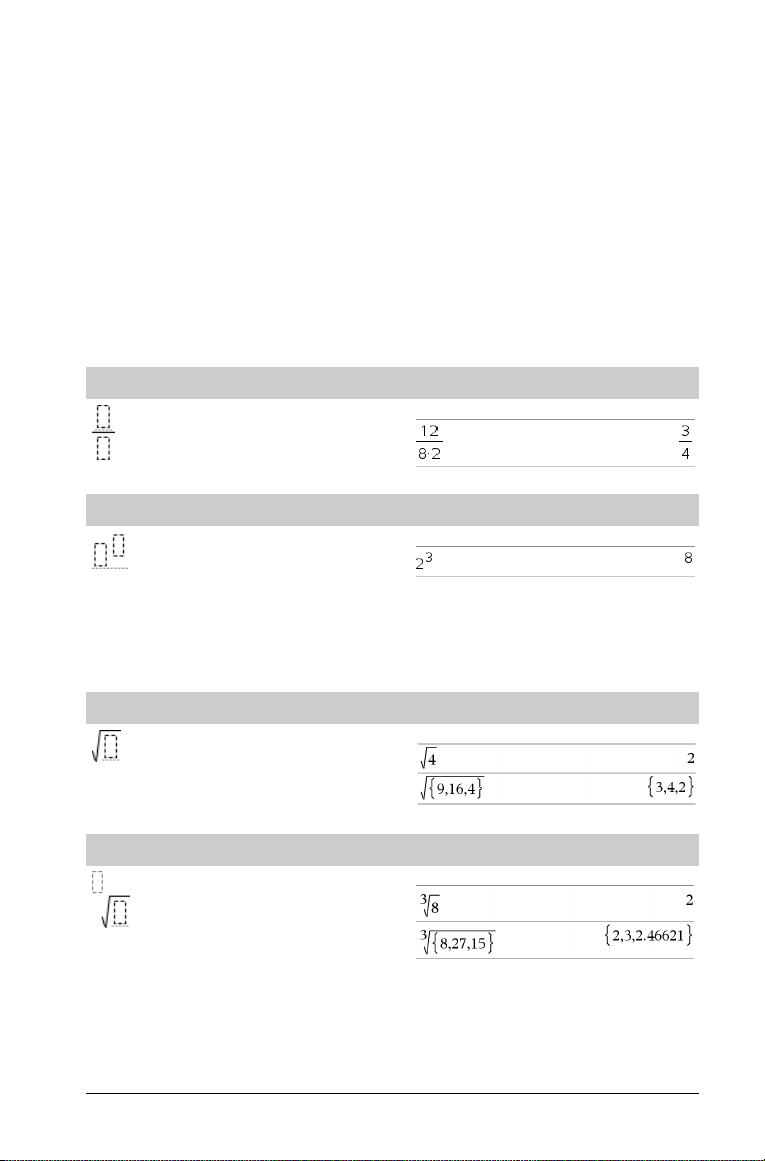
Exponent-template

Opmerking: typ de eerste waarde, typ op l en typ dan de

exponent. Om de cursor terug te brengen naar de basisregel drukt u op de pijl naar rechts (¢).

Opmerking: zie ook ^ (macht), pag. 107.

Worteltemplate

Opmerking: zie ook

N-de wortel-template

Opmerking: zie ook wortel (), pag. 76.

‡

() (wortel), pag. 112.

l-toets

Voorbeeld:

/q-toetsen

Voorbeeld:

/l-toetsen

Voorbeeld:

TI-Nspire™ Referentiehandleiding 1

e-macht-template

Het getal e verheven tot een macht

Opmerking: zie ook e^(), pag. 27.

u-toetsen

Voorbeeld:

Log-template

Berekent de log ten opzichte van een gespecificeerd grondtal. Voor het standaard grondtal 10 laat u het grondtal weg.

Opmerking: zie ook log(), pag. 51.

Template voor stuksgewijs gedefinieerde functies (2-stuks)

Hiermee kunt u uitdrukkingen en condities voor een in twee stukkenstuksgewijs gedefinieerde functie creëren. Om ee n stuk toe te voegen klikt u in de template en herhaalt u de template.

Opmerking: zie ook piecewise(), pag. 66.

Template voor stuksgewijs gedefinieerde functies (N-stuks)

Hiermee kunt u uitdrukkingen en condities voor een -stuksgewijs gedefinieerde functie in N stukken creëren. Vraagt om N.

/s-toets

Voorbeeld:

Catalogus >

Voorbeeld:

Catalogus >

Voorbeeld: Zie het voorbeeld bij Template voor stuksgewijs gedefinieerde functies (2-stuks).

Opmerking: zie ook piecewise(), pag. 66.

Absolute waarde-template

Voorbeeld:

Opmerking: zie ook abs(), pag. 5.

Catalogus >

2 TI-Nspire™ Referentiehandleiding

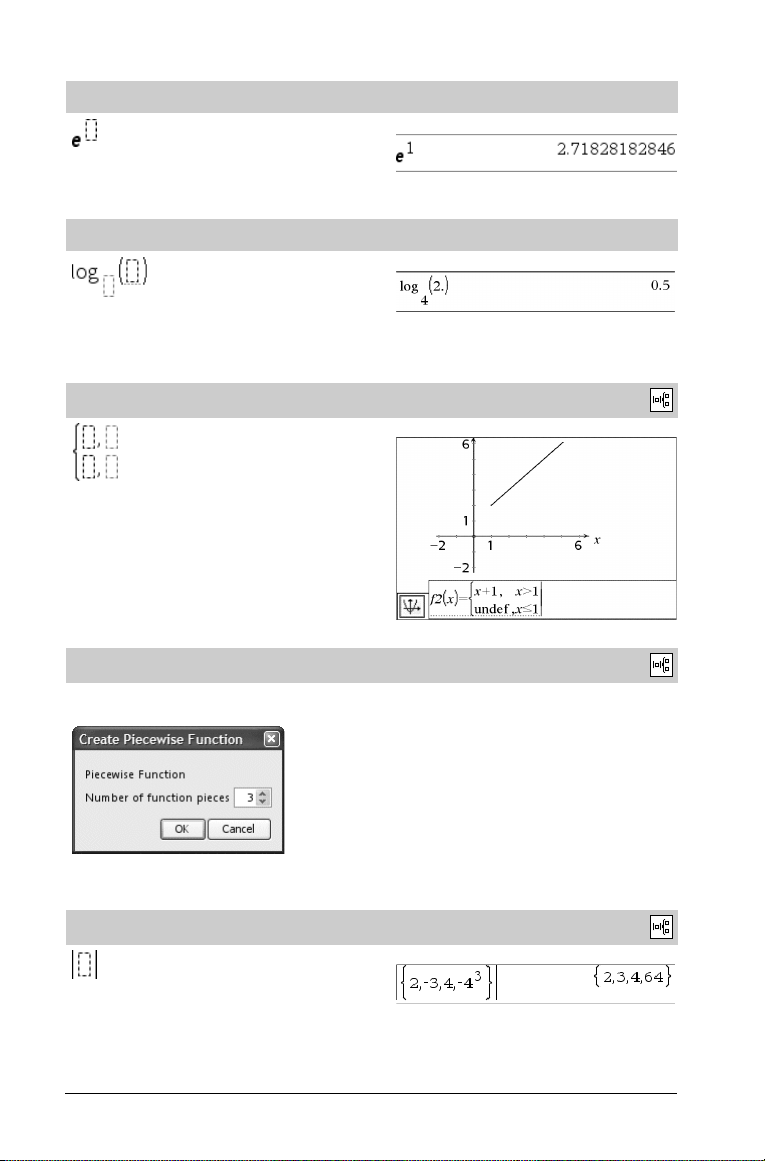
dd°mm’ss.ss’’ template

Hiermee kunt u hoeken in dd°mm’ss.ss’’-opmaak invoeren, waarbij

dd het aantal decimale graden, mm het aantal minuten en ss.ss het

aantal seconden is.

Catalogus >

Voorbeeld:

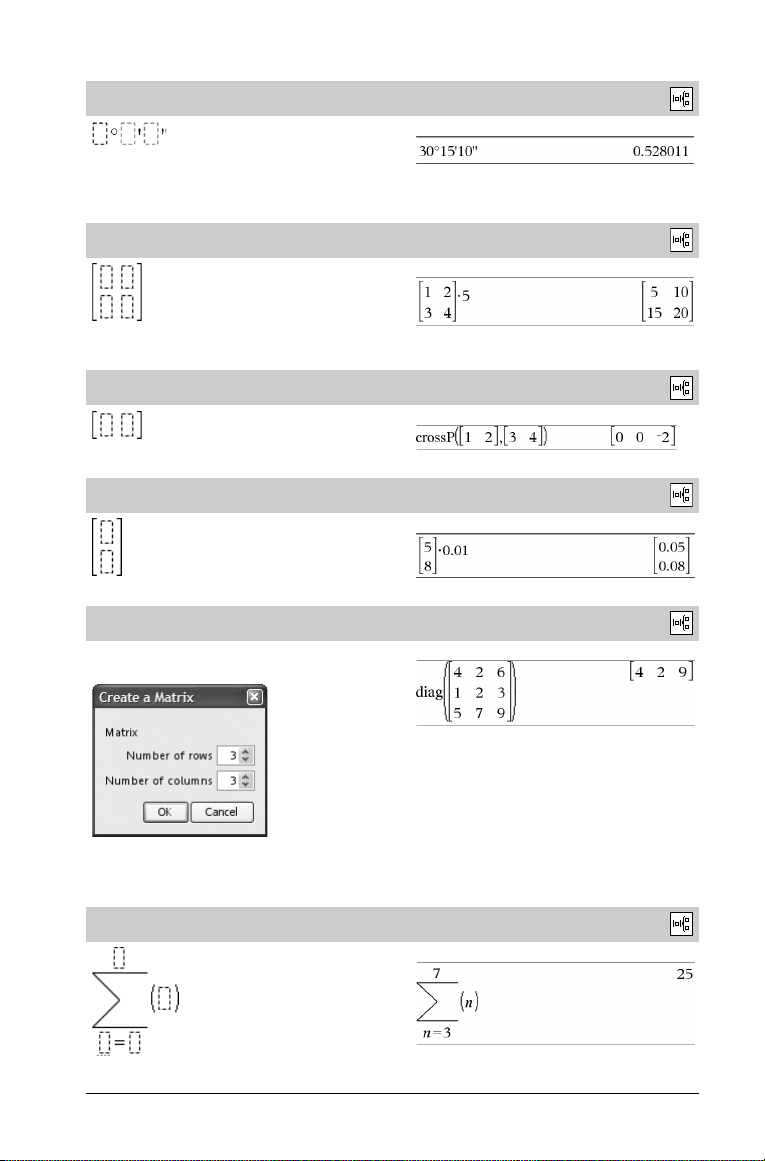
Matrixtemplate (2 x 2)

Creëert een 2 x 2 matrix.

Matrixtemplate (1 x 2)

Matrixtemplate (2 x 1)

Matrixtemplate (m x n)

De template verschijnt nadat u het aantal rijen en kolommen heeft ingevoerd.

Catalogus >

Voorbeeld:

Catalogus >

Voorbeeld:

Catalogus >

Voorbeeld:

Catalogus >

Voorbeeld:

Opmerking: als u een matrix creëert met een gro ot aantal rijen en kolommen, kan het even duren voordat deze verschijnt.

Somtemplate (G)

Voorbeeld:

Catalogus >

TI-Nspire™ Referentiehandleiding 3

Product-template (Π)

Opmerking: zie ook Π() (product), pag. 112.

Catalogus >

Voorbeeld:

4 TI-Nspire™ Referentiehandleiding

Alfabetische lijst

Elementen waarvan de namen niet alfabetische zijn (zoals +, ! en >) staan aan het eind van dit hoofdstuk, vanaf pag. 105. Tenzij anders gespecificeerd zijn alle voorbeelden in dit hoofdstuk uitgevoerd in de standaard reset-modus, en wordt van alle variabelen aangenomen dat ze onbepaald zijn.

abs()

abs(Waarde1) ⇒ waarde abs(

Lijst1) ⇒ lijst

abs(Matrix1) ⇒ matrix

Geeft de absolute waarde van het argument.

Opmerking: zie ook Absolute waarde-template, pag. 2.

Als het argument een complex getal is, dan wordt de modulus van dat getal gegeven.

Opmerking: alle onbepaalde variabelen worden behandeld als

reële variabelen.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],

[

afgerondeWaarde]) ⇒ matrix

Aflossingsfunctie die een matrix als aflossingstabel genereert voor een serie TVM-argumenten.

NPmt is het aantal betalingen dat in de tabel moet worden opgenomen. De tabel begint met de eerste betaling.

N, I, PV, Pmt, FV, PpY, CpY en PmtAt worden beschreven in de tabel met TVM-argumenten, pag. 96.

•Als u Pmt weglaat, dan wordt de standaardwaarde Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt) gebruikt.

•Als u FV weglaat, dan wordt de standaardwaarde FV=0 gebruikt.

• De standaardwaarden voor PpY, CpY en PmtAt zijn hetzelfde als voor de TVM-functies.

afgerondeWaarde specificeert het aantal decimalen voor afronding. Standaardwaarde=2.

De kolommen in de resulterende matrix zijn in de volgorde: Aantal betalingen, bedrag betaald aan rente, bedrag betaald aan de hoofdsom (aflossing) en balans.

De balans die getoond wordt in rij n is de balans na betaling n. U kunt de uitvoermatrix gebruiken als invoer voor de andere

aflossingsfuncties GInt() en GPrn(), pag. 113, en bal(), pag. 10.

Catalogus

and

BooleaanseUitdr1 and BooleaanseUitdr2 ⇒ Booleaanse uitdrukking BooleaanseLijst1 and BooleaanseLijst2 ⇒ Booleaanse lijst BooleaanseMatrix1 and BooleaanseMatrix2 ⇒ Booleaanse matrix

Geeft waar of onwaar of een vereenvoudigde vorm van de oorspronkelijke invoer.

Catalogus

TI-Nspire™ Referentiehandleiding 5

and

Geheel getal1 and Geheel getal2 ⇒ geheel getal

Vergelijkt twee reële gehele getallen bit-voor-bit met behulp van een

and-bewerking. Intern worden beide gehele getallen geconverteerd

naar 64-bits binaire getallen met een teken (positief of negatief). Wanneer overeenkomstige bits vergeleken worden, is het resultaat 1 als beide bits 1 zijn; anders is het resultaat 0. De geretourneerde waarde geeft de bitresultaten, en wordt weergegeven volgens de ingestelde grondtal-modus.

U kunt de gehele getallen invoeren in elk grondtal. Voor een binaire of hexadecimale invoer moet u respectievelijk het prefix 0b of 0h gebruiken. Zonder prefix worden gehele getallen behandeld als decimaal (grondtal 10).

Als u een decimaal geheel getal invoert dat te groot is voor een 64bits binaire vorm met een teken (positief of negatief), dan wordt er een symmetrische modulo-bewerking gebruikt om de waarde binnen het betreffende bereik te brengen.

Catalogus

In de Hex-grondtalmodus:

Belangrijk: nul, niet de letter O.

In de Bin-grondtalmodus:

In de Dec-grondtalmodus:

Opmerking: een binaire invoer kan maximaal 64 cijfers

hebben (het prefix 0b niet meegeteld). Een hexadecimale invoer kan maximaal 16 cijfers hebben.

angle()

angle(Waarde1) ⇒ waarde

Geeft de hoek van het argument, waarbij het argument als een complex getal wordt geïnterpreteerd.

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

angle(Lijst1) ⇒ lijst angle(Matrix1) ⇒ matrix

Geeft een lijst of matrix met de hoeken van de elementen in Lijst1 of Matrix1, waarbij elk element geïnterpreteerd wordt als een complex

getal dat een punt in een rechthoekig twee-dime nsionaal assenstelsel voorstelt.

ANOVA

ANOVA Lijst1,Lijst2[,Lijst3,...,Lijst20][,Vlag]

Voert een eenwegs-variantieanalyse uit voor het vergelijken van de gemiddelden van twee tot 20 populaties. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.results. (Zie pag. 86).

Vlag=0 voor gegevens, Vlag=1 voor statistieken

Uitvoervariabele Beschrijving

stat.F Waarde van de F-statistiek

stat.PVal Kleinste significantieniveau waarbij de nulhypothese verworpen kan worden

stat.df Vrijheidsgraden van de groepen

stat.SS Som van de kwadraten van de groepen

Catalogus

6 TI-Nspire™ Referentiehandleiding

Uitvoervariabele Beschrijving

stat.MS Gemiddelde van de kwadraten van de groepen

stat.dfError Vrijheidsgraden van de fouten

stat.SSError Som van de kwadraten van de fouten

stat.MSError Gemiddelde kwadraat van de fouten

stat.sp Gepoolde standaarddeviatie

stat.xbarlist Gemiddelde van de invoer van de lijsten

stat.CLowerList 95% betrouwbaarheidsintervallen voor het gemiddelde van elke invoerlijst

stat.CUpperList 95% betrouwbaarheidsintervallen voor het gemiddelde van elke invoerlijst

ANOVA2way

ANOVA2way Lijst1,Lijst2[,Lijst3,…,Lijst20][,NivRij]

Berekent een tweewegs variantieanalyse voor het vergelijken van de gemiddelden van twee tot 20 populaties. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.results. (Zie pag. 86).

NivRij=0 voor blok

NivRij=2,3,...,Len-1, voor tweeweg, waarbij Len=lengte(Lijst1)=lengte(Lijst2) = … = lengte(Lijst10) en Len / NivRij ∈ {2,3,…}

Uitvoer: Blokopmaak

Uitvoervariabele Beschrijving

stat.FF-statistiek van de kolomfactor

stat.PVal Kleinste significantieniveau waarbij de nulhypothese verworpen kan worden

stat.df Vrijheidsgraden van de kolomfactor

stat.SS Som van de kwadraten van de kolomfactor

stat.MS Gemiddelde van de kwadraten van de kolomfactor

stat.FBlock F-statistiek voor de factor

stat.PValBlock Kleinste kans waarbij de nulhypothese verworpen kan worden

stat.dfBlock Vrijheidsgraden van de factor

stat.SSBlock Som van de kwadraten van de factor

stat.MSBlock Gemiddelde van de kwadraten van de factor

stat.dfError Vrijheidsgraden van de fouten

stat.SSError Som van de kwadraten van de fouten

stat.MSError Gemiddelde van de kwadraten van de fouten

stat.s Standaarddeviatie van de fout

Catalogus

TI-Nspire™ Referentiehandleiding 7

Uitvoer van KOLOMFACTOR

Uitvoervariabele Beschrijving

stat.Fcol F-statistiek van de kolomfactor

stat.PValCol Kanswaarde van de kolomfactor

stat.dfCol Vrijheidsgraden van de kolomfactor

stat.SSCol Som van de kwadraten van de kolomfactor

stat.MSCol Gemiddelde van de kwadraten van de kolomfactor

Uitvoer van RIJFACTOR

Uitvoervariabele Beschrijving

stat.FRow F-statistiek van de rijfactor

stat.PValRow Kanswaarde van de rijfactor

stat.dfRow Vrijheidsgraden van de rijfactor

stat.SSRow Som van de kwadraten van de rijfactor

stat.MSRow Gemiddelde van de kwadraten van de rijfactor

Uitvoer van INTERACTIE

Uitvoervariabele Beschrijving

stat.FInteract F-statistiek van de interactie

stat.PValInteract Kanswaarde van de interactie

stat.dfInteract Vrijheidsgraden van de interactie

stat.SSInteract Som van de kwadraten van de interactie

stat.MSInteract Gemiddelde van de kwadraten van de interactie

Uitvoer van FOUT

Uitvoervariabele Beschrijving

stat.dfError Vrijheidsgraden van de fouten

stat.SSError Som van de kwadraten van de fouten

stat.MSError Gemiddelde van de kwadraten van de fouten

s Standaarddeviatie van de fout

8 TI-Nspire™ Referentiehandleiding

Ans

Ans ⇒ waarde

Geeft het resultaat van de meest recent uitgewerkte uitdrukking.

-toetsen

approx()

approx(Waarde1) ⇒ getal

Geeft de uitwerking van het argument als een uitdrukking met decimale waarden, indien mogelijk, ongeacht de huidige

Automatische of Benaderende modus.

Dit is hetzelfde als het argument invoeren en op drukken.

approx(Lijst1) ⇒ lijst approx(Matrix1) ⇒ matrix

Geeft een lijst of matrix waarin elk element uitgewerkt is naar een decimale waarde, indien mogelijk.

approxRational()

approxRational(Uitdr[, tol]) ⇒ uitdrukking approxRational(Lijst[, tol]) ⇒ lijst approxRational(Matrix[, tol]) ⇒ matrix

Geeft het argument als een breuk met een tolerantie van tol. Als tol wordt weggelaten, wordt er een tolerantie van 5.E-14 gebruikt.

augment()

augment(Lijst1, Lijst2) ⇒ lijst

Geeft een nieuwe lijst die bestaat uit Lijst2 aan het eind van Lijst1.

augment(Matrix1, Matrix2) ⇒ matrix

Geeft een nieuwe matrix die bestaat uit Matrix2 toevoegd aan Matrix1. Wanneer het teken “,” wordt gebruikt, moeten de matrices gelijke rijafmetingen hebben, en wordt Matrix2 toegevoegd aan Matrix1 als nieuwe kolommen. Augment verandert Matrix1 en Matrix2 niet.

Catalogus

TI-Nspire™ Referentiehandleiding 9

avgRC()

avgRC(Uitdr1, Var [=waarde] [, H]) ⇒ uitdrukking avgRC(Uitdr1, Var [=Waarde] [, Lijst1]) ⇒ lijst avgRC(Lijst1, Var [=Waarde] [, H]) ⇒ lijst avgRC(Matrix1, Var [=Waarde] [, H]) ⇒ matrix

Geeft het differentiequotiënt (gemiddelde veranderingssnelheid). Uitdr1 kan een door de gebruiker gedefinieerde functienaam zijn

(zie

Func).

Wanneer waarde gespecificeerd is, wordt elke eerdere variabeletoekenning of elke huidige “waarvoor geldt dat”-substitutie voor de variabele onderdrukt.

H is de stapgrootte. Als H wordt weggelaten, is de standaardwaarde 0,001.

Merk op dat de soortgelijke functie differentiequotiënt gebruikt.

nDeriv() het centraal-

Catalogus

bal()

bal(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],

afgerondeWaarde]) ⇒ waarde

[

bal(NPmt,amortTable) ⇒ waarde

Aflossingsfunctie die de geplande balans berekent na een gespecificeerde betaling.

N, I, PV, Pmt, FV, PpY, CpY en PmtAt worden beschreven in de tabel met TVM-argumenten, pag. 96.

NPmt specificeert het nummer van de betaling waarna u de gegevens berekend wilt hebben.

N, I, PV, Pmt, FV, PpY, CpY en PmtAt worden beschreven in de tabel met TVM-argumenten, pag. 96.

•Als u Pmt weglaat, dan wordt de standaardwaarde Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt) gebruikt.

•Als u FV weglaat, dan wordt de standaardwaarde FV=0 gebruikt.

• De standaardwaarden voor PpY, CpY en PmtAt zijn hetzelfde als voor de TVM-functies.

afgerondeWaarde specificeert het aantal decimalen voor afronding. Standaardwaarde=2.

bal(NPmt,amortTable) berekent de balans na het nummer van de

betaling NPmt, op basis van de aflossingstabel amortTable. Het argument amortTable moet een matrix zijn in de vorm die beschreven wordt onder amortTbl(), pag. 5.

Opmerking: zie ook GInt() en GPrn(), pag. 113.

Base2 (4Grondtal2)

Geheel getal1 4Base2 ⇒ geheel getal

Converteert Geheel getal1 naar een binair getal. Binaire of hexadecimale getallen hebben altijd respectievelijk het prefix 0b of 0h.

Catalogus

10 TI-Nspire™ Referentiehandleiding

Base2 (4Grondtal2)

0b binairGetal 0h hexadecimaalGetal

Nul, niet de letter O, gevolgd door b of h. Een binair getal kan maximaal 64 cijfers hebben. Een hexadecimaal

getal kan maximaal 16 cijfers hebben. Zonder prefix wordt Geheel getal1 behandeld als decimaal

(grondtal 10). Het resultaat wordt binair weergegeven, ongeacht de Grondtal-modus.

Base10 (4Grondtal10)

Geheel getal1 4Base10 ⇒ geheel getal

Converteert Geheel getal1 naar een decimaal (grondtal 10) getal. Een binair of hexadecimaal getal moet altijd respectievelijk het prefix 0b of 0h hebben.

0b binairGetal 0h hexadecimaalGetal

Nul, niet de letter O, gevolgd door b of h. Een binair getal kan maximaal 64 cijfers hebben. Een hexadecimaal

getal kan maximaal 16 cijfers hebben. Zonder prefix wordt Geheel getal1 behandeld als decimaal. Het

resultaat wordt als decimaal getal weergegeven, ongeacht de Grondtal-modus.

Base16 (4Grondtal16)

Geheel getal1 4Base16 ⇒ geheel getal

Converteert Geheel getal1 naar een hexadecimaal getal. Binaire of hexadecimale getallen hebben altijd respectievelijk het prefix 0b of 0h.

0b binairGetal 0h hexadecimaalGetal

Nul, niet de letter O, gevolgd door b of h. Een binair getal kan maximaal 64 cijfers hebben. Een hexadecimaal

getal kan maximaal 16 cijfers hebben. Zonder prefix wordt Geheel getal1 behandeld als decimaal

(grondtal 10). Het resultaat wordt als hexadecimaal getal weergegeven, ongeacht de Grondtal-modus.

Catalogus

TI-Nspire™ Referentiehandleiding 11

binomCdf()

binomCdf(n,p,ondergrens,bovengrens) ⇒ getal als

ondergrens en bovengrens getallen zijn, lijst als ondergrens en bovengrens lijsten zijn

binomCdf(n,p,bovengrens) ⇒ getal als bovengrens een getal is,

lijst als bovengrens een lijst is

Berekent de cumulatieve kans voor de discrete binomiale verdeling met aantal pogingen n en succeskans p bij iedere poging.

 bovengrens) stelt u ondergrens=0 in

Voor P(X

Catalogus

binomPdf()

binomPdf(n,p) ⇒ getal binomPdf(n,p,XWaarde) ⇒ getal als XWaarde een getal is,

lijst als XWaarde een lijst is

Berekent de kans voor de discrete binomiale verdeling met aantal pogingen n en succeskans p bij iedere poging.

ceiling()

ceiling(Waarde1) ⇒ waarde

Geeft het dichtstbijliggende gehele getal dat ‚ is aan het argument.

Het argument kan een reëel of complex getal zijn.

Opmerking: zie ook floor().

ceiling(Lijst1) ⇒ lijst ceiling(Matrix1) ⇒ matrix

Geeft een lijst of matrix met de 'plafondwaarde' van elk element.

char()

char(Geheel getal) ⇒ teken

Geeft een tekenreeks die het teken met het nummer Geheel getal van de tekenserie van de rekenmachine bevat. Het geldige bereik voor Geheel getal is 0–65535.

2way

2way obsMatrix

chi22way obsMatrix

Berekent een c2 -toets voor afhankelijkheid op de kruistabel van aantallen in de geobserveerde matrix ObsMatrix. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.results. (Zie pag. 86).

Catalogus

Uitvoervariabele Beschrijving

stat.c2 Chi-kwadraat-statistiek: som (geobserveerd - verwacht)2/verwacht.

12 TI-Nspire™ Referentiehandleiding

Uitvoervariabele Beschrijving

stat.PVal Kleinste significantieniveau waarbij de nulhypothese verworpen kan worden

stat.df Vrijheidsgraden van de chi-kwadraat-statistieken

stat.ExpMat Matrix van de verwachte tabel met aantallen elementen, waarbij wordt uitgegaan van de nulhypothese

stat.CompMat Matrix van chi-kwadraat-statistiekbijdragen van elementen

Cdf()

Cdf(ondergrens,bovengrens,df) ⇒ getal als ondergrens en

bovengrens getallen zijn, lijst als ondergrens en bovengrens

lijsten zijn

ondergrens,bovengrens,df) ⇒ getal als ondergrens en

chi2Cdf(

bovengrens getallen zijn, lijst als ondergrens en bovengrens

lijsten zijn

Berekent de c2 -verdelingskans tussen ondergrens en bovengrens voor de gespecificeerde vrijheidsgraden df.

Catalogus

Voor P(X  bovengrens) stelt u ondergrens = 0 in.

GOF

GOF obsLijst,expLijst,df

chi2GOF obsLijst,expLijst,df

Voert een toets uit om te bevestigen dat de steekproefgegevens afkomstig zijn uit een populatie met de gespecificeerde verdeling. obsLijst is een lijst met aantallen en moet gehele getallen bevatten. Een samenvatting van de resultaten wordt o pgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Catalogus

Uitvoervariabele Beschrijving

stat.c2 Chi-kwadraat-statistiek: som (geobserveerd - verwacht)2/verwacht

stat.PVal Kleinste significantieniveau waarbij de nulhypothese verworpen kan worden

stat.df Vrijheidsgraden van de chi-kwadraat-statistieken

stat.CompList Chi-kwadraat-statistiekbijdragen van elementen

Pdf()

Pdf(XWaarde,df) ⇒ getal als XWaarde een getal is, lijst als

XWaarde een lijst is

chi2Pdf(

XWaarde,df) ⇒ getal als XWaarde een getal is, lijst

XWaarde een lijst is

als

Berekent de kansdichtheidsfunctie (pdf) voor de c2-verdeling bij een gespecificeerde XWaarde voor de gespecificeerde vrijheidsgraden df.

Catalogus

TI-Nspire™ Referentiehandleiding 13

ClearAZ

Wist alle variabelen die bestaan uit één teken in de huidige opgave.

Catalogus

ClrErr

Wist de foutstatus en zet de systeemvariabele errCode op nul. De Else-bepaling van het Try...Else...EndTry-blok moet ClrErr of

PassErr gebruiken. Als de fout verwerkt of genegeerd moet worden,

gebruik dan ClrErr. Als onbekend is wat er met de fout gedaan moet worden, gebruik dan PassErr om hem te verzenden naar de volgende foutenafhandelaar. Als er geen onbesliste

Try...Else...EndTry-foutenafhandelaars meer zijn, wordt het

foutendialoogvenster weergegeven zoals normaal is.

Opmerking: zie ook PassErr, pag. 66 en Try , pag. 94. Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

colAugment()

colAugment(Matrix1, Matrix2) ⇒ matrix

Geeft een nieuwe matrix die bestaat uit Matrix2 toevoegd aan Matrix1. De matrices moeten evenveel kolommen hebben, en Matrix2 wordt toegevoegd aan Matrix1 als nieuwe rijen. Dit verandert Matrix1 of Matrix2 niet.

colDim()

colDim(Matrix) ⇒ uitdrukking

Geeft het aantal kolommen in Matrix.

Opmerking: zie ook rowDim().

Catalogus

Zie voor een voorbeeld van ClrErr Voorbeeld 2 onder het commando Try op pag. 94.

Catalogus

colNorm()

colNorm(Matrix) ⇒ uitdrukking

Geeft het maximum van de sommen van de absolute waarden van de elementen in de kolommen in Matrix.

Opmerking: onbepaalde matrixelementen zijn niet toegestaan. Zie

ook rowNorm().

Catalogus

14 TI-Nspire™ Referentiehandleiding

conj()

conj(Waarde1) ⇒ waarde conj(Lijst1) ⇒ lijst conj(Matrix1) ⇒ matrix

Geeft de complex geconjugeerde van het argument.

Opmerking: alle onbepaalde variabelen worden behandeld als

reële variabelen.

Catalogus

constructMat()

constructMat(Uitdr,Var 1 ,Va r2 ,aantalRijen,aantalKolommen)

⇒ matrix

Geeft een matrix op basis van de argumenten. Uitdr is een uitdrukking in de variabelen Va r 1 en Var 2 . Elementen in

de resulterende matrix worden gevormd door Uitdr uit te werken voor elke opgehoogde waarde van Va r 1 en Va r 2 .

Var 1 wordt automatisch verhoogd van 1 tot en met aantalRijen. Binnen elke rij wordt Va r 2 verhoogd van 1 tot en met

aantalKolommen.

CopyVar()

CopyVar Var 1 , Va r 2 CopyVar Var 1 ., Va r2 .

CopyVar Var 1 , Va r2 kopieert de waarde van variabele Va r1 naar

variabele Var 2, waar bij Var 2 indien nodig gecreëerd wordt. Variabele Var 1 moet een waarde hebben.

Als Va r1 de naam van een bestaande, door de gebruiker gedefinieerde functie is, kopieert CopyVar de definitie van die functie naar functie Va r2 . Functie Va r 1 moet gedefinieerd zijn.

Var 1 moet voldoen aan de naamgevingsvereisten of moet een indirecte uitdrukking zijn die vereenvoudigd wordt tot een variabelenaam die voldoet aan de vereisten.

CopyVar Var 1 ., Va r2 . kopieert alle leden van de variabelegroep

Var 1 . naar de groep Va r 2., waarbij Va r2 . indien nodig wordt gecreëerd.

Var 1 . moet de naam van een bestaande variabelegroep zijn, zoals de statistische stat.nn-resultaten, of van variabelen die gecreëerd zijn met de LibShortcut()-functie. Als Va r2 . reeds bestaat, dan vervangt deze opdracht alle leden die beide groepen

gemeenschappelijk hebben, en worden de leden die nog nie t bestaan toegevoegd. Als er een enkelvoudige (geen groep) variabele met de naam Va r2 bestaat, treedt er een fout op.

Catalogus

TI-Nspire™ Referentiehandleiding 15

corrMat()

corrMat(Lijst1,Lijst2[,…[,Lijst20]])

Berekent de correlatiematrix voor de matrix bestaande uit [Lijst1, Lijst2, ..., Lijst20].

Catalogus

cos()

cos(Waarde1) ⇒ waarde cos(Lijst1) ⇒ lijst

cos(Waarde1) geeft de cosinus van het argument als een waarde. cos(Lijst1) geeft een lijst van de cosinussen van alle elementen in

Lijst1.

Opmerking: het argument wordt geïnterpreteerd als een hoek in

graden, decimale graden of radialen volgens de huidige hoekmodusinstelling. U kunt ó,G of ôgebruiken om de hoekmodus tijdelijk te

onderdrukken.

cos(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de matrixcosinus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de cosinus van elk element.

Wanneer een scalaire functie f(A) werkt op vierkanteMatrix1 (A), dan wordt het resultaat berekend door het volgende algoritme:

Bereken de eigenwaarden (li) en de eigenvectoren (Vi) van A.

vierkanteMatrix1 moet diagonaliseerbaar zijn. Bovendien kan hij geen symbolische variabelen hebben die geen waarde toegekend hebben gekregen.

Vorm de matrices:

n-toets

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

Vervolgens A = X B Xêen f(A) = X f(B) Xê. Bijvoorbeeld cos(A) = X cos(B) Xê waarbij:

cos(B) =

Alle berekeningen worden uitgevoerd met behulp van drijvende komma-rekenkunde.

16 TI-Nspire™ Referentiehandleiding

cosê()

cosê(Waarde1) ⇒ waarde cosê(Lijst1) ⇒ lijst

/n-toetsen

In de hoekmodus Graden:

cosê(Waarde1) geeft de hoek waarvan de cosinus Waarde1 is.

cosê(Lijst1) geeft een lijst van de inverse cosinussen van elk

element van Lijst1.

Opmerking: de uitkomst wordt in graden, decimale graden of

radialen gegeven, volgens de ingestelde hoekmodus.

cosê(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de inverse matrixcosinus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de inverse cosinus van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

cosh()

cosh(Waarde1) ⇒ waarde cosh(Lijst1) ⇒ lijst

cosh(Waarde1) geeft de cosinus hyperbolicus van het argument. cosh(Lijst1) geeft een lijst van de cosinussen hyperbolicus van elk

element van Lijst1.

cosh(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de matrixcosinus hyperbolicus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de cosinus hyperbolicus van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

In de hoekmodus Radialen en rechthoekige complexe opmaak:

Om het hele resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.

Catalogus

In de hoekmodus Radialen:

coshê()

coshê(Waarde1) ⇒ waarde coshê(Lijst1) ⇒ lijst

cosh

(Waarde1) geeft de inverse cosinus hyperbolicus van het

argument.

cosh

(Lijst1) geeft een lijst van de inverse cosinussen hyperbolicus

van elk element van Lijst1.

Catalogus

TI-Nspire™ Referentiehandleiding 17

coshê()

coshê(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de inverse matrixcosinus hyperbolicus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de inverse cosinus hyperbolicus van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

Catalogus

In de hoekmodus Radialen en rechthoekige complexe opmaak:

Om het hele resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.

cot()

cot(Waarde1) ⇒ waarde cot(Lijst1) ⇒ lijst

Geeft de cotangens van Waarde1 of geeft een lijst van de cotangensen van alle elementen Lijst1.

Opmerking: het argument wordt geïnterpreteerd als een hoek in

graden, decimale graden of radialen volgens de huidige hoekmodusinstelling. U kunt ó,G ofôgebruiken om de hoekmodus tijdelijk te

onderdrukken.

cotê()

cotê(Waarde1) ⇒ waarde cotê(Lijst1) ⇒ lijst

Geeft de hoek waarvan de cotangens Waarde1 is of geeft een lijst met de inverse cotangens van elk element in Lijst1.

Opmerking: de uitkomst wordt in graden, decimale graden of

radialen gegeven, volgens de ingestelde hoekmodus.

coth()

coth(Waarde1) ⇒ waarde coth(Lijst1) ⇒ lijst

Geeft de cotangens hyperbolicus van Waarde1 of geeft een lijst van de cotangensen hyperbolicus van alle elementen in Lijst1.

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

Catalogus

cothê()

cothê(Waarde1) ⇒ waarde cothê(Lijst1) ⇒ lijst

Geeft de inverse cotangens hyperbolicus van Waarde1 of geeft een lijst met de inverse cotangensen hyperbolicus van elk element in Lijst1.

Catalogus

18 TI-Nspire™ Referentiehandleiding

count()

count(Waarde1ofLijst1 [,Waarde2ofLijst2 [,...]]) ⇒ waarde

Geeft het samengenomen aantal van alle elementen in de argumenten die uitgewerkt worden tot numerieke waarden.

Elk argument kan een uitdrukking, waarde, lijst of matrix zijn. U kunt gegevenstypen mengen en argumenten met verschillende afmetingen gebruiken.

Bij een lijst, matrix of reeks cellen wordt elk element uit gewerkt om te bepalen of het moet worden opgenomen in de telling.

In de toepassing Lijsten & Spreadsheet kunt u een reeks cellen op de plaats van elk argument gebruiken.

Catalogus

countif()

countif(Lijst,Criteria) ⇒ waarde

Geeft het samengenomen aantal van alle elementen in Lijst die voldoen aan de gespecificeerde Criteria.

Criteria kan zijn:

• Een waarde, uitdrukking of tekenreeks. Bijvoorbeeld: 3 telt alleen die elementen in Lijst die vereenvoudigd worden tot de waarde 3.

• Een Booleaanse uitdrukking met het symbool ? als tijdelijke plaatsaanduiding voor elk element. Bijvoorbeeld, ?<5 telt alleen die elementen in Lijst die kleiner zijn dan 5.

In de toepassing Lijsten & Spreadsheet kunt u een reeks cellen gebruiken op de plaats van Lijst.

Opmerking: zie ook sumIf(), pag. 89 en frequency(), pag. 34.

crossP()

crossP(Lijst1, Lijst2) ⇒ lijst

Geeft het uitwendige product van Lijst1 en Lijst2 als een lijst. Lijst1 en Lijst2 moeten gelijke afmetingen hebben, en de afmeting

moet 2 of 3 zijn.

crossP(Vector1, Vector2) ⇒ vector

Geeft een rij- of kolomvector (afhankelijk van de argumenten) die het uitwendig product is van Vector1 en Vec to r 2 .

Zowel Vector1 als Vector2 moeten rijvectoren zijn, of beide moeten kolomvectoren zijn. Beide vectoren moeten gelijke afmetingen hebben, en de afmeting moet 2 of 3 zijn.

Catalogus

Telt het aantal elementen dat gelijk is aan 3.

Telt het aantal elementen dat gelijk is aan "def".

Telt 1 en 3.

Telt 3, 5 en 7.

Telt 1, 3, 7 en 9.

Catalogus

TI-Nspire™ Referentiehandleiding 19

csc()

csc(Waarde1) ⇒ waarde csc(Lijst1) ⇒ lijst

Geeft de cosecans van Waarde1 of geeft een lijst met de cosencansen van alle elementen in Lijst1.

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

Catalogus

cscê()

cscê(Waarde1) ⇒ waarde cscê(Lijst1) ⇒ lijst

Geeft de hoek waarvan de cosecans Waarde1 is of geeft een lijst met de inverse cosecans van elk element in Lijst1.

Opmerking: de uitkomst wordt in graden, decimale graden of

radialen gegeven, volgens de ingestelde hoekmodus.

csch()

csch(Waarde1) ⇒ waarde csch(Lijst1) ⇒ lijst

Geeft de cosecans hyperbolicus van Waarde1 of geeft een lijst van de cosecansen hyperbolicus van alle elementen in Lijst1.

cschê()

cschê(Waarde) ⇒ waarde cschê(Lijst1) ⇒ lijst

Geeft de inverse cosecans hyperbolicus van Waarde1 of geeft een lijst met de inverse cosecans hyperbolicus van elk element in Lijst1.

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

Catalogus

20 TI-Nspire™ Referentiehandleiding

CubicReg

CubicReg X, Y[, [Freq] [, Categorie, Opnemen]]

Catalogus

Berekent de derdegraads veeltermregressie y = a·x3+b· x2+c·x+d op de lijsten X en Y met frequentie Freq. Een

samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen.

X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

punt voorkomt. De standaardwaarde is 1. Alle elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Uitvoervariabele Beschrijving

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.R

Regressievergelijking: a·x3+b·x2+c·x+d

Regressiecoëfficiënten

Determinatiecoëfficiënt

stat.Resid Residuen uit de regressie

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

beperkingen van Freq, Categorielijst en Categorieën opnemen

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

cumSum()

cumSum(Lijst1) ⇒ lijst

Geeft een lijst met de cumulatieve sommen van de elementen in Lijst1, beginnend bij element 1.

cumSum(Matrix1) ⇒ matrix

Geeft een matrix van de cumulatieve sommen van de elementen van Matrix1. Elk element is de cumulatieve som van de kolom, van boven naar beneden.

Catalogus

TI-Nspire™ Referentiehandleiding 21

Cycle

Brengt de besturing onmiddellijk naar de volgende iteratie van de

For, While of Loop).

huidige lus (

Cycle is niet toegestaan buiten de drie lusstructuren (For, While of Loop).

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Cylind

Vec t o r 4Cylind

Geeft de rij- of kolomvector in cilindrische vorm weer [r,q, z].

Vec t o r moet exact drie elementen hebben. De vector kan een rij of een kolom zijn.

@ te drukken in plaats van op ·

Catalogus

Functies die de gehele getallen van 1 tot 100 optelt, waarbij 50 wordt overgeslagen.

Catalogus

dbd()

dbd(datum1,datum2) ⇒ waarde

Geeft het aantal dagen tussen datum1 en datum2 met behulp van de actuele-dag-telmethode.

datum1 en datum2 kunnen getallen of lijsten met getallen zijn binnen het bereik van de datums op de standaard kalender. Als zowel datum1 als datum2 lijsten zijn, dan moeten deze dezelfde lengte hebben.

datum1 en datum2 moeten tussen de jaren 1950 tot en met 2049 liggen.

U kunt de datums in twee notaties invoeren. De plaatsing van de decimale punt onderscheidt de datumnotaties.

MM.DDJJ (algemeen gebruikte notatie in de Verenigde Staten) DDMM.JJ (algemeen gebruikte notatie in Europa)

Catalogus

22 TI-Nspire™ Referentiehandleiding

4DD ⇒ waarde

Uitdr1 Lijst1 4DD ⇒ lijst Matrix1

4DD ⇒ matrix

Geeft het decimale equivalent van het argument, uitgedrukt in graden. Het argument is een getal, lijst of matrix die op basis van de hoekmodus-instelling geïnterpreteerd wordt als decimale graden, radialen of graden.

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

Catalogus

4Decimal

Getal1

4Decimal

Lijst1 Matrix1

Geeft het argument in decimale vorm weer. Deze operator kan alleen op het eind van de invoerregel gebruikt worden.

Define (Definiëren)

Define Var = Uitdrukking Define Functie(Param1, Param2, ...) = Uitdrukking

Definieert de variabele Va r of de door de gebruiker gedefinieerde functie Functie.

Parameters, zoals Param1, vormen de plaats voor het doorgeven van argumenten aan de functie. Bij het oproepen van een door de gebruiker gedefinieerde functie moet u argumenten opgeven (bijvoorbeeld waarden of variabelen) die overeenkomen met de parameters. De functie werkt, wanneer deze wordt aangeroepen,

Uitdrukking uit met de opgegeven argumenten. Var en Functie kunnen niet de naam van een systeemvariabele of

van een ingebouwde functie of commando zijn.

Opmerking: deze vorm van Define staat gelijk aan het uitvoeren

van de uitdrukking: uitdrukking & Functie(Param1,Param2).

Decimal

⇒ waarde

Catalogus

TI-Nspire™ Referentiehandleiding 23

Define (Definiëren)

Define Functie(Param1, Param2, ...) = Func

Blok

EndFunc

Programma(Param1, Param2, ...) = Prgm

Define

Blok

EndPrgm

In deze vorm kan de door de gebruiker gedefinieerde functie of programma een blok van meerdere beweringen uitvoeren.

Blok kan zowel een enkele bewering als een serie beweringen op aparte regels zijn. Blok kan ook uitdrukkingen en instructies (zoals If,

Then, Else en For) bevatten. Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Opmerking: Zie ook Define LibPriv, pag. 24 en Define LibPub

, pag. 25.

Catalogus

Define LibPriv

Define LibPriv Var = Uitdrukking Define LibPriv Functie(Param1, Param2, ...) = Uitdrukking

Define LibPriv Functie(Param1, Param2, ...) = Func

Blok

EndFunc Define LibPriv

Blok

EndPrgm

Werkt hetzelfde als Define, behalve dat er een persoonlijke bibliotheekvariabele, -functie of -programma wordt gecreëerd. Persoonlijke functies en programma's verschijnen niet in de Catalogus.

Opmerking: Zie ook Define, pag. 23 en Define LibPub,

pag. 25.

Programma(Param1, Param2, ...) = Prgm

Catalogus

24 TI-Nspire™ Referentiehandleiding

Define LibPub

Define LibPub Var = Uitdrukking Define LibPub Functie(Param1, Param2, ...) = Uitdrukking

Define LibPub Functie(Param1, Param2, ...) = Func

Blok

EndFunc Define LibPub

Blok

EndPrgm

Werkt hetzelfde als Define, behalve dat er een openbare bibliotheekvariabele, -functie of -programma wordt gecreëerd. Openbare functies en programma verschijnen in de Catalogus nadat de bibliotheek is opgeslagen en vernieuwd.

Opmerking: Zie ook Define, pag. 23 en Define LibPriv,

pag. 24.

Programma(Param1, Param2, ...) = Prgm

Catalogus

DelVar

DelVar Var 1 [, Va r 2] [, Va r 3 ] ... DelVar

Var .

Wist de gespecificeerde variabele of variabelegroep uit het geheugen.

DelVar Var . wist alle leden van de variabelegroep Va r . (zoals de

statistische stat.nn-resultaten of variabelen die gecreëerd zijn met de

LibShortcut()-functie). De punt (.) in deze vorm van het

commando DelVar beperkt dit tot het wissen van een variabelegroep; de enkelvoudige variabele Va r wordt niet gewist.

det()

det(vierkanteMatrix[, Tolerantie]) ⇒ uitdrukking

Geeft de determinant van vierkanteMatrix. Optioneel wordt elk matrixelement behandeld als nul als de absolute

waarde ervan minder dan Tolerantie is. Deze tolerantie wordt alleen gebruikt als de matrix gegevens met een drijvende komma heeft, en geen symbolische variabelen bevat die geen waarde toegekend hebben gekregen. Anders wordt Tolerantie genegeerd.

•Als u

•Als Tolerantie wordt weggelaten of niet wordt gebruikt, dan

gebruikt of de modus Automatisch of

Benaderend

met behulp van de drijvende komma uitgevoerd.

wordt de standaardtolerantie berekend als:

5EM14 ·max(dim(vierkanteMatrix))·

rowNorm(vierkanteMatrix)

instelt op Benaderend, dan worden berekeningen

Catalogus

TI-Nspire™ Referentiehandleiding 25

diag()

diag(Lijst) ⇒ matrix diag(rijMatrix) ⇒ matrix diag(kolomMatrix) ⇒ matrix

Geeft een matrix met de waarden in de argumentenlijst of de argumentenmatrix op zijn hoofddiagonaal.

diag(vierkanteMatrix) ⇒ rijMatrix

Geeft een rijmatrix met de elementen uit de hoofddiagonaal van

vierkanteMatrix. vierkanteMatrix moet vierkant zijn.

Catalogus

dim()

dim(Lijst) ⇒ geheel getal

Geeft de afmeting van Lijst.

dim(Matrix) ⇒ lijst

Geeft de afmetingen van matrix als een lijst met twee elementen {rijen, kolommen}.

dim(Strin g) ⇒ geheel getal

Geeft het aantal tekens in de tekenreeks St ring.

Disp

Disp [uitdrOfString1] [, uitdrOfString2] ...

Geeft de argumenten in de geschiedenis van de Rekenmachine. De argumenten worden achter elkaar weergegeven, met smalle spaties als scheiding.

Vooral handig in programma's en functies om de weergave van tussenberekeningen te verzekeren.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Catalogus

26 TI-Nspire™ Referentiehandleiding

DMS

4DMS

Waarde Lijst 4DMS Matrix 4DMS

Interpreteert het argument als een hoek en geeft de equivalente DMS (DDDDDD¡MM'SS.ss'')-waarde weer. Zie ¡, ', '' op pag. 115 voor de

DMS (graden, minuten, seconden)-notatie.

Opmerking: 4DMS converteert van radialen naar graden als hij

wordt gebruikt in de radialenmodus. Als de invoer gevolgd wordt door een gradensymbool

4DMS alleen op het eind van een invoerregel gebruiken.

¡, treedt er geen conversie op. U kunt

In de hoekmodus Graden:

Catalogus

dotP()

dotP(Lijst1, Lijst2) ⇒ uitdrukking

Geeft het inwendige product van twee lijsten.

dotP(Vector1, Vector2) ⇒ uitdrukking

Geeft het inwendige product van twee vectoren. Beide moeten rijvectoren zijn, of beide moeten kolomvectoren zijn.

e^()

e^(Waarde1) ⇒ waarde

Geeft e tot de macht Waarde1.

Opmerking: zie ook e macht-template, pag. 2. Opmerking: op u drukken om

hetzelfde als drukken op het teken E op het toetsenbord.

U kunt een complex getal in re vorm echter alleen in de hoekmodus Radialen; hij veroorzaakt een domeinfout in de hoekmodi Graden en Decimale graden.

e^(Lijst1) ⇒ lijst

Geeft e tot de macht van elk element in Lijst1.

e^(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de 'e tot de macht van vierkanteMatrix1'. Dit is niet hetzelfde als het berekenen van e tot de macht van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

^( weer te geven is niet

polaire vorm invoeren. Gebruik deze

Catalogus

u-toets

TI-Nspire™ Referentiehandleiding 27

eff()

eff(nominaalPercentage,CpY) ⇒ waarde

Financiële functie die het nominale rentepercentage nominaalPercentage converteert naar een jaarlijks effectief percentage, waarbij CpY het aantal samengestelde periodes per jaar is.

nominaalPercentage moet een reëel getal zijn, en CpY moet een reëel getal > 0 zijn.

Opmerking: zie ook nom(), pag. 61.

Catalogus

eigVc()

eigVc(vierkanteMatrix) ⇒ matrix

Geeft een matrix met de eigenvectoren voor een reële of complexe vierkanteMatrix, waarbij elke kolom in het resultaat overeenkomt met een eigenwaarde. Merk op dat een eigenvector niet uniek is; hij kan geschaald worden door een willekeurige constante factor. De eigenvectoren worden genormaliseerd, wat betekent: als V = [x1,x2, …, xn], dan:

+ … + x

= 1

vierkanteMatrix wordt eerst gebalanceerd met gelijkheidstransformaties tot de rij- en kolomnormen zo dicht mogelijk bij dezelfde waarde liggen. vierkanteMatrix wordt vervolgens gereduceerd tot de upper-Hessenberg-vorm en de eigenvectoren worden berekend via een Schur-factorisatie.

eigVl()

eigVl(vierkanteMatrix) ⇒ lijst

Geeft een lijst van de eigenwaarden van een reële of complexe

vierkanteMatrix. vierkanteMatrix wordt eerst gebalanceerd met

gelijkheidstransformaties tot de rij- en kolomnormen zo dicht mogelijk bij dezelfde waarde liggen. vierkanteMatrix wordt vervolgens gereduceerd tot de upper-Hessenberg-vorm en de eigenwaarden worden berekend uit de upper-Hessenberg-matrix.

In rechthoekige complexe opmaak:

Om het hele resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.

In de rechthoekige complexe opmaak-modus:

Catalogus

Om het hele resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.

Else Zie If, pag. 40.

28 TI-Nspire™ Referentiehandleiding

ElseIf

Als BooleaanseUitdr1 Then

Blok1

ElseIf BooleaanseUitdr2 Then

Blok2

BooleaanseUitdrN Then

ElseIf

BlokN

EndIf

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

EndFor Zie For, pag. 33.

EndFunc Zie Func, pag. 35.

EndIf Zie If, pag. 40.

EndLoop Zie Loop, pag. 53.

EndPrgm Zie Prgm, pag. 68.

Catalogus

EndTry Zie Try, pag. 94.

EndWhile Zie While, pag. 99.

TI-Nspire™ Referentiehandleiding 29

Exit

Sluit het huidige For, While of Loop-blok af.

Exit is niet toegestaan buiten de drie lusstructuren (For, While of Loop).

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Functielijst:

Catalogus

exp()

exp(Waarde1) ⇒ waarde

Geeft e tot de macht Waarde1.

Opmerking: zie ook e exponent-template, pag. 2.

U kunt een complex getal in re vorm echter alleen in de hoekmodus Radialen; hij veroorzaakt een domeinfout in de hoekmodi Graden en Decimale graden.

exp(Lijst1) ⇒ lijst

Geeft e tot de macht van elk element in Lijst1.

exp(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de 'e tot de macht van vierkanteMatrix1'. Dit is niet hetzelfde als het berekenen van e tot de macht van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

expr()

expr(Stri ng) ⇒ uitdrukking

Geeft de tekenreeks in Str ing als een uitdrukking en voert deze onmiddellijk uit.

polaire vorm invoeren. Gebruik deze

u-toets

Catalogus

30 TI-Nspire™ Referentiehandleiding

ExpReg

ExpReg X, Y [, [Freq] [, Categorie, Opnemen]]

Berekent de exponentiële regressie y = a·(b)xop de lijsten X en Y met frequentie Freq. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen.

X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Uitvoervariabele Beschrijving

stat.RegEqn

stat.a, stat.b Regressiecoëfficiënten

stat.r

stat.r Correlatiecoëfficiënt voor getransformeerde gegevens (x, ln(y))

stat.Resid Residuen die geassocieerd zijn met het exponentiële model

stat.ResidTrans Residuen die geassocieerd zijn met de lineaire regressie van getransformeerde gegevens

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

Regressievergelijking: a·(b)

Coëfficiënt van lineaire verband voor getransformeerde gegevens

beperkingen van Freq, Categorielijst en Categorieën opnemen

Catalogus

factor()

factor(rationaalGetal) geeft het rationale getal ontbonden in

priemfactoren. Bij samengestelde getallen neemt de berekeningstijd exponentieel toe met het aantal cijfers in de op één na grootste factor. Het ontbinden van een geheel getal van 30 cijfers kan bijvoorbeeld langer dan een dag duren, en het ontbinden van een geheel getal van 100 cijfers kan meer dan een eeuw duren.

Opmerking: druk op w om een berekening te stoppen (af te

breken). Als u alleen wilt bepalen of een getal een priemgetal is, gebruik dan

liever isPrime(). Dat is veel sneller, vooral als rationaalGetal geen priemgetal is en als de op één na grootste factor meer dan vijf cijfers heeft.

TI-Nspire™ Referentiehandleiding 31

Catalogus

FCdf()

FCdf(ondergrens,bovengrens,dfTeller,dfNoemer) ⇒ getal als

ondergrens en bovengrens getallen zijn, lijst als ondergrens en bovengrens lijsten zijn

FCdf(onde rgrens,bovengrens,dfTeller,dfNoemer) ⇒ getal als

ondergrens en bovengrens getallen zijn, lijst als ondergrens en bovengrens lijsten zijn

Berekent de kans voor de F-verdeling tussen ondergrens en bovengrens voor de gespecificeerde dfTeller (vrijheidsgraden) en dfNoemer.

 bovengrens) stelt u ondergrens = 0 in.

Voor P(X

Catalogus

Fill

Fill Waarde, matrixVar ⇒ matrix

Vervangt ieder element in variabele matrixVar door Waarde. matrixVar moet al bestaan.

Fill Waarde, lijstVar ⇒ lijst

Vervang ieder element in variabele lijstVar door Waarde. lijstVar moet al bestaan.

FiveNumSummary

FiveNumSummary X[,[Freq][,Categorie,Opnemen]]

Levert een verkorte versie van de statistieken voor 1 variabele van lijst X. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

X representeert een lijst met de gegevens. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elke overeenkomstige X-

waarde voorkomt. De standaardwaarde is 1. Alle elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X-waarden.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Catalogus

Uitvoervariabele Beschrijving

stat.MinX Minimum van de x-waarden

stat.Q1X 1ste kwartiel van x

stat.MedianX Mediaan van x

stat.Q3X 3de kwartiel van x

stat.MaxX Maximum van de x-waarden

32 TI-Nspire™ Referentiehandleiding

floor()

floor(Waarde1) ⇒ geheel getal

Geeft het grootste gehele getal dat { dan het argument. Deze functie is hetzelfde als int().

Het argument kan een reëel of complex getal zijn.

floor(Lijst1) ⇒ lijst floor(Matrix1) ⇒ matrix

Geeft een lijst of matrix van de floor-waarde van elk element.

Opmerking: zie ook ceiling() en int().

Catalogus

For

For Var , Laag, Hoog [, St ap]

Blok

EndFor

Voert de beweringen in Blok iteratief uit voor elke waarde van Va r , van Laag naar Hoog, in stappen van Stap .

Var mag geen systeemvariabele zijn. Stap kan positief of negatief zijn. De standaardwaarde is 1. Blok kan een enkele bewering of een serie beweringen zijn die

gescheiden worden door het teken “:”.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

format()

format(Waarde[, opmaakString]) ⇒ string

Geeft Waarde als een tekenreeks op basis van de opmaaktemplate. opmaakString is een string die de volgende vorm moet hebben:

“F[n]”, “S[n]”, “E[n]”, “G[n][c]”, waarbij [ ] optionele gedeeltes aangeeft.

F[n]: Vaste opmaak. n is het aantal cijfers dat weergegeven moet worden achter de decimale punt.

S[n]: Wetenschappelijke opmaak. n is het aantal cijfers dat weergegeven moet worden achter de decimale punt.

E[n]: Ingenieursopmaak. n is het aantal cijfers na het eerste significante cijfer. De exponent wordt aangepast naar een veelvoud van drie, en de decimale punt wordt met nul, één of twee cijfers naar rechts verplaatst.

G[n][c]: Zelfde als de vaste opmaak, maar scheidt de cijfers links van de radix (decimale scheidingsteken) tevens in groepen van drie. c specificeert het groep-scheidingsteken; de standaardinstelling is een komma. Als c een punt is, wordt de radix weergegeven als een komma.

[Rc]: Elk van bovengenoemde specificatietekens kan als suffix de Rc radix-vlag krijgen, waarbij c een enkel teken is dat specificeert wat er gesubstitueerd moet worden voor het radixpunt.

Catalogus

TI-Nspire™ Referentiehandleiding 33

fPart()

fPart(Uitdr1) ⇒ uitdrukking fPart(Lijst1) ⇒ lijst fPart(Matrix1) ⇒ matrix

Geeft de breuk van het argument. Geeft bij een lijst of matrix de breuk van de elementen. Het argument kan een reëel of complex getal zijn.

Catalogus

FPdf()

FPdf(XWaarde,dfTeller,dfNoemer) ⇒ getal als XWaarde een

getal is,

lijst als XWaarde een lijst is

Berekent de kans voor de F-verdeling bij XWaarde voor de gespecificeerde dfTeller (vrijheidsgraden) en dfNoemer.

freqTable4lijst()

freqTable4list(Lijst1,freqGeheelGetalLijst) ⇒ lijst

Geeft een lijst met de elementen uit Lijst1 uitgebreid volgens de frequenties in freqGeheelGetalLijst. Deze functie kan gebruikt worden om een frequentietabel voor de Gegevensverwerking & Statistiek-toepassing samen te stellen.

Lijst1 kan elke geldige lijst zijn. freqGeheelGetalLijst moet dezelfde afmeting als Lijst1 hebben en

mag alleen niet-negatieve gehele getallen bevatten. Elk element specificeert het aantal keer dat het overeenkomstige element uit Lijst1 wordt herhaald in de resulterende lijst. Een waarde van nul sluit het overeenkomstige Lijst1-element uit.

frequency()

frequency(Lijst1,klassenLijst) ⇒ lijst

Geeft een lijst met de aantallen elemente n in Lijst1. De aantallen zijn gebaseerd op klassen die u definieert in klassenLijst.

Als klassenLijst {b(1), b(2), …, b(n)} is, dan zijn de gespecificeerde klassen {?{b(1), b(1)<?{b(2),…,b(n-1)<?{b(n), b(n)>?}. De resulterende lijst is één element langer dan klassenLijst.

Elk element van het resultaat komt over een met het aantal elementen in Lijst1 die binnen die klasse liggen. Uitgedrukt in termen van de

countIf()-functie is het resultaat { countIf(list, ?{b(1)), countIf(list,

b(1)<?{b(2)), …, countIf(list, b(n-1)<?{b(n)), countIf(list, b(n)>?)}.

Elementen van Lijst1 die niet “in een klasse geplaatst kunnen worden” worden genegeerd.

In de toepassing Lijsten & Spreadsheet kunt u een reeks cellen op de plaats van beide argumenten gebruiken.

Opmerking: zie ook countIf(), pag. 19.

Catalogus

Uitleg van het resultaat:

2 elementen van Datalist zijn {2,5 4 elementen van Datalist zijn >2,5 en {4,5 3 elementen van Datalist zijn >4,5

Het element "hello" is een string en kan niet in een van de gedefinieerde klassen geplaatst worden.

34 TI-Nspire™ Referentiehandleiding

FTest_2Samp

FTest_2Samp Lijst1,Lijst2[,Freq1[,Freq2[,Hypoth]]]

FTest_2Samp

(Invoer van een gegevenslijst)

Lijst1,Lijst2[,Freq1[,Freq2[,Hypoth]]]

FTest_2Samp sx1,n1,sx2,n2[,Hypoth]

FTest_2Samp

(Invoer van samenvattingsstatistieken)

Voert een F -toet s met twee steekproeven uit. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.results. (Zie pag.

86).

Voor H1: s1 > s2 stelt u Hypoth>0 in Voor H1: s1 ƒ s2 (standaardinstelling) stelt u Hypoth = 0 in Voor H1: s1 < s2 stelt u Hypoth<0 in

Uitvoervariabele Beschrijving

stat.F

stat.PVal Kleinste significantieniveau waarbij de nulhypothese verworpen kan worden

stat.dfNumer teller vrijheidsgraden = n1-1

stat.dfDenom noemer vrijheidsgraden = n2-1

stat.sx1, stat.sx2 Steekproefstandaarddeviatie van de gegevensverzamelingen in Lijst 1 en Lijst 2

stat.x1_bar stat.x2_bar

stat.n1, stat.n2 Grootte van de steekproeven

sx1,n1,sx2,n2[,Hypoth]

Berekende ó-statistiek voor de gegevensverzameling

Steekproefgemiddelde van de gegevensverzamelingen in Lijst 1 en Lijst 2

Catalogus

Func

Blok

EndFunc

Template voor het creëren van een door de gebruiker gedefinieerde functie.

Blok kan een enkele bewering of een serie beweringen zijn die gescheiden worden door het teken “:”, of een serie beweringen op aparte regels. De functie kan de instructie Return gebruiken om een specifiek resultaat te retourneren.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Een stuksgewijs gedefinieerde functie definiëren:

Resultaat grafiek g(x)

Catalogus

TI-Nspire™ Referentiehandleiding 35

gcd()

gcd(Waarde1, Waarde2) ⇒ uitdrukking

Geeft de grootste gemene deler van de twee argumenten. De van twee breuken is de gcd van hun tellers gedeeld door de lcm van hun noemers.

In de Automatische of Benaderende modus is de gcd van breuken met een drijvende komma 1,0.

gcd(Lijst1, Lijst2) ⇒ lijst

Geeft de grootste gemene delers van de overeenkomstige elementen in Lijst1 en Lijst2.

gcd(Matrix1, Matrix2) ⇒ matrix

Geeft de grootste gemene delers van de overeenkomstige elementen in Matrix1 en Matrix2.

geomCdf()

geomCdf(p,ondergrens,bovengrens) ⇒ getal als ondergrens

bovengrens getallen zijn, lijst als ondergrens en bovengrens

en lijsten zijn

geomCdf(

p,bovengrens) ⇒ getal als bovengrens een getal is,

lijst als bovengrens een lijst is Berekent een cumulatieve geometrische kans van ondergrens naar

bovengrens met de gespecificeerde succeskans p.

Voor P(X  bovengrens) stelt u ondergrens = 1 in.

geomPdf()

geomPdf(p,XWaarde) ⇒ getal als XWaarde een getal is, lijst

XWaarde een lijst is

als

Berekent de kans op XWaarde, het nummer van de poging waarbij het eerste succes optreedt, voor de discrete geometrische verdeling met de gespecificeerde succeskans p.

gcd

Catalogus

getDenom( )

getDenom(Breuk1) ⇒ waarde

Transformeert het argument in een uitdrukking met een vereenvoudigde gemeenschappelijke noemer, en geeft vervolgens de noemer ervan.

Catalogus

36 TI-Nspire™ Referentiehandleiding

getLangInfo( )

getLangInfo() ⇒ string

Geeft een string die overeenkomt met de korte naam van de actieve taal. U kunt deze functie bijvoorbeeld gebruiken in een progr amma of functie om de huidige taal te bepalen.

Engels = "en" Deens = "da" Duits = "de" Fins = "fi" Frans = "fr" Italiaans = "it" Nederlands = "nl" Vlaams = "nl_BE" Noors = "no" Portugees = "pt" Spaans = "es" Zweeds = "sv"

Catalogus

getMode()

getMode(ModeNaamGeheel getal) ⇒ waarde getMode(0) ⇒ lijst

getMode(ModeNaamGeheel getal) geeft een waarde die de

huidige instelling van de modus ModeNaamGeheel getal representeert.

getMode(0) geeft een lijst met getallenparen. Elk paar bestaat uit

een modusnummer en een instellingsnummer. Zie onderstaande tabel voor een lijst met de modi en de bijbehorende

instellingen.

Als u de instellingen opslaat met getMode(0) & var, dan kunt u

setMode(var) gebruiken in een functie of programma om de

instellingen tijdelijk te herstellen, alleen binnen de uitvoering van de functie of het programma. Zie setMode(), pag. 80.

Modusnaam

Cijfers weergeven

Hoek

Exponentiële opmaak

Reëel of complex

Automatisch of benaderend

Vectoropmaak

Grondtal

Modus nummer Instellingsnummers

=Drijvend, 2=Drijvend1, 3=Drijvend2, 4=Drijvend3, 5=Drijvend4, 6=Drijvend5,

1 7=Drijvend6, 8=Drijvend7, 9=Drijvend8, 10=Drijvend9, 11=Drijvend10, 12=Drijvend11, 13=Drijvend12, 14=Vast0, 15=Vast1, 16=Vast2, 17=Vast3, 18=Vast4, 19=Vast5, 20=Vast6, 21=Vast7, 22=Vast8, 23=Vast9, 24=Vast10, 25=Vast11, 26=Vast12

=Radialen, 2=Graden, 3=Decimale graden

=Normaal, 2=Wetenschappelijk, 3=Ingenieursnotatie

=Reëel, 2=Rechthoekig, 3=Polair

=Automatisch, 2=Benaderend

=Rechthoekig, 2=Cilindrisch, 3=Bolvormig

=Decimaal, 2=Hexadecimaal, 3=Binair

Catalogus

TI-Nspire™ Referentiehandleiding 37

getNum()

getNum(Breuk1) ⇒ waarde

Transformeert het argument naar een uitdrukking met een vereenvoudigde gemeenschappelijke noemer, en geeft vervolgens de teller ervan.

Catalogus

getVarInfo()

getVarInfo() ⇒ matrix of string getVarInfo(BibliotheekNaamString) ⇒ matrix of string

getVarInfo() geeft een matrix met informatie (variabelenaam, type

en bibliotheektoegankelijkheid) voor alle variabelen en bibliotheekobjecten die gedefinieerd zijn in de huidige opgave.

Als er geen variabelen gedefinieerd zijn, geeft getVarInfo() de string "NONE".

getVarInfo(BibliotheekNaamString) geeft een matrix met

informatie voor alle bibliotheekobjecten die gedefinieerd zijn in bibliotheek BibliotheekNaamString. BibliotheekNaamString moet een string zijn (tekst tussen aanhalingstekens) of een stringvariabele.

Als de bibliotheek BibliotheekNaamString niet bestaat, treedt er een fout op.

Zie het voorbeeld links, waarin het resultaat van getVarInfo() wordt toegekend aan variabele vs. Als u probeert rij 2 of rij 3 van vs weer te geven, krijgt u de foutmelding “Ongeldige lijst of matrix” omdat minimaal één van de elementen in deze rijen (variabele b bijvoorbeeld) opnieuw wordt uitgewerkt naar een matrix.

Deze fout kan ook optreden wanneer u Ans gebruikt om een

getVarInfo()-resultaat opnieuw uit te werken.

Het systeem geeft bovengenoemde foutmelding omdat de huidige versie van de software geen gegeneraliseerde matrixstructuur ondersteunt waarbij een element van een matrix een matrix of een lijst kan zijn.

Catalogus

38 TI-Nspire™ Referentiehandleiding

Goto

Goto labelNaam

Brengt de besturing over naar het label labelNaam. labelNaam moet in dezelfde functie gedefinieerd worden met behulp

Lbl-instructie.

van een

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Grad

Uitdr1 4 Grad ⇒ uitdrukking

Converteert Uitdr1 naar een hoek in decimale graden.

In de hoekmodus Graden:

In de hoekmodus Radialen:

Catalogus

identity()

identity(Geheel getal) ⇒ matrix

Geeft de eenheidsmatrix met de afmeting Geheel getal. Geheel getal moet een positief geheel getal zijn.

Catalogus

TI-Nspire™ Referentiehandleiding 39

If BooleaanseUitdr Bewering If BooleaanseUitdr Then

Blok

EndIf

Voert, als BooleaanseUitdr wordt uitgewerkt naar waar, de enkele bewering Bewering of het blok beweringen Blok uit alvorens door te gaan met de uitvoering.

Gaat, als BooleaanseUitdr wordt uitgewerkt naar onwaar, door met de uitvoering zonder de bewering of het blok beweringen uit te voeren.

Blok kan een enkele bewering of een reeks beweringen zijn die gescheiden worden door het teken “:”.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

If BooleaanseUitdr Then

Blok1

Else

Blok2

EndIf

Als BooleaanseUitdr wordt uitgewerkt naar waar, wordt Blok1 uitgevoerd en wordt Blok2 vervolgens overgeslagen.

Als BooleaanseUitdr wordt uitgewerkt naar onwaar, wordt Blok1 overgeslagen maar wordt Blok2 wel uitgevoerd.

Blok1 en Blok2 kunnen een enkele bewering zijn.

If BooleaanseUitdr1 Then

Blok1

ElseIf

BooleaanseUitdr2 Then

Blok2

BooleaanseUitdrN Then

ElseIf

BlokN

EndIf

Hiermee kunnen vertakkingen gemaakt worden. Als BooleaanseUitdr1 wordt uitgewerkt naar waar, wordt Blok1 uitgevoerd. Als BooleaanseUitdr1 wordt uitgewerkt naar onwaar, wordt BooleaanseUitdr2 uitgevoerd enz.

Catalogus

40 TI-Nspire™ Referentiehandleiding

ifFn()

ifFn(BooleaanseUitdr,Waarde_Indien_waar [,Waarde_Indien_onwaar [,

Waarde_Indien_onbekend]]) ⇒ uitdrukking, lijst of matrix

Werkt de Booleaanse uitdrukking BooleaanseUitdr (of ieder element uit BooleaanseUitdr ) uit en geeft een resultaat op basis van de volgende regels:

• BooleaanseUitdr kan een enkele waarde, een lijst of e en matrix toetsen.

• Als een element van BooleaanseUitdr wordt uitgewerkt naar waar, wordt het overeenkomstige element uit Waarde_Indien_waar gegeven.

• Als een element van BooleaanseUitdr wordt uitgewerkt naar onwaar, wordt het overeenkomstige element uit

Waarde_Indien_onwaar gegeven. Als u Waarde_Indien_onwaar weglaat, wordt undef gegeven.

• Als een element van BooleaanseUitdr niet waar en niet onwaar is, wordt het overeenkomstige element

Waarde_Indien_onbekend gegeven. Als u Waarde_Indien_onbekend weglaat, wordt undef gegeven.

• Als het tweede, derde of vierde argument van de ifFn()-functie een enkele uitdrukking is, dan wordt de Booleaanse toets toegepast op elke positie in BooleaanseUitdr.

Opmerking: als de vereenvoudigde BooleaanseUitdr-bewering

een lijst of een matrix bevat, dan moeten alle andere lijst- of matrixargumenten dezelfde afmeting(en) hebben, en heeft het resultaat dezelfde afmeting(en).

Catalogus

De toetswaarde 1 is kleiner dan 2,5, dus het overeenkomstige Waarde_Indien_Waar-element 5 wordt gekopieerd naar de resultatenlijst.

De toetswaarde 2 is kleiner dan 2,5, dus het overeenkomstige Waarde_Indien_Waar-element 6 wordt gekopieerd naar de resultatenlijst.

De toetswaarde 3 is niet kleiner dan 2,5, dus het overeenkomstige Waarde_Indien_Onwaar-element 10 wordt gekopieerd naar de resultatenlijst.

Waarde_Indien_waar is een enkele waarde en komt overeen met elke willekeurige geselecteerde positie.

Waarde_Indien_onwaar is niet gespecificeerd. Undef (onbepaald) wordt gebruikt.

Eén element geselecteerd uit Waarde_Indien_waar. Eén element geselecteerd uit Waarde_Indien_onbekend.

imag()

imag(Waarde1) ⇒ waarde

Catalogus

Geeft het imaginaire deel van het argument.

Opmerking: alle onbepaalde variabelen worden behandeld als

reële variabelen. Zie ook real(), pag. 74

imag(Lijst1) ⇒ lijst

Geeft een lijst met de imaginaire delen van de elementen.

imag(Matrix1) ⇒ matrix

Geeft een matrix met de imaginaire delen van de elementen.

Indirectie Zie

inString()

inString(bronString, subString[, Start]) ⇒ geheel getal

Geeft de tekenpositie in string bronString waarop string subString voor de eerste keer begint.

Start specificeert, indien opgenomen, de tekenpositie binnen bronString waarop de zoekactie begint. Standaardinstelling = 1 (het

eerste teken van bronString). Als bronString niet subString bevat of als Start > is dan de lengte

van bronString, dan wordt er een nul gegeven.

, pag. 114.

#()

Catalogus

TI-Nspire™ Referentiehandleiding 41

int()

int(Waarde) ⇒ geheel getal int(Lijst1) ⇒ lijst int(Matrix1) ⇒ matrix

Geeft het grootste gehele getal dat kleiner dan of gelijk is aan het argument. Deze functie is hetzelfde als

floor().

Het argument kan een reëel of complex getal zijn. Geeft bij een lijst of matrix het grootste gehele getal van elk van de

elementen.

Catalogus

intDiv()

intDiv(Getal1, Getal2) ⇒ geheel getal intDiv(Lijst1, Lijst2) ⇒ lijst intDiv(Matrix1, Matrix2) ⇒ matrix

Geeft het grootste gehele getal met een plus- of minteken dat kleiner of gelijk is aan (Getal1 ÷ Getal2).

Geeft bij lijsten en matrices dit getal (argument 1 ÷ argument 2) voor elk paar elementen.

invc2()

invc2(Oppervlakte,df)

Oppervlakte,df)

invChi2(

Berekent de inverse cumulatieve c2 (chi-kwadraat) kansfunctie die gespecificeerd wordt door de vrijheidsgraad, df voor een gegeven Oppervlakte onder de kromme.

invF()

invF(Oppervlakte,dfTeller,dfNoemer)

Oppervlakte,dfTeller,dfNoemer)

invF(

Berekent de inverse cumulatieve F verdelingsfunctie die gespecificeerd wordt door dfTeller en dfNoemer voor een gegeven Oppervlakte onder de kromme.

invNorm()

invNorm(Oppervlakte[,m,s])

Berekent de inverse cumulatieve normale verdelingsfunctie voor een gegeven Oppervlakte onder de normale verdelingskromme die gespecificeerd wordt door m en s.

Catalogus

invt()

invt(Oppervlakte,df)

Berekent de inverse cumulatieve student-t-kansfunctie die gespecificeerd wordt door de vrijheidsgraad, df voor een gegeven Oppervlakte onder de kromme.

Catalogus

42 TI-Nspire™ Referentiehandleiding

iPart()

iPart(Getal) ⇒ geheel getal iPart(Lijst1) ⇒ lijst iPart(Matrix1) ⇒ matrix

Geeft het gehele deel van het argument. Geeft bij lijsten en matrices het gehele deel van elk element. Het argument kan een reëel of complex getal zijn.

Catalogus

irr()

irr(CF0,CFLijst [,CFFreq]) ⇒ waarde

Financiële functie die de interne rentabiliteit van een investering berekent.

CF0 is de begin-cashflow op tijdstip 0; dit moet een reëel getal zijn. CFLijst is een lijst met cashflow-bedragen na de begin-cashflow CF0. CFFreq is een optionele lijst waarin elk element de frequentie

waarmee een gegroepeerde (opeenvolgend) cashflow-bedrag voorkomt specificeert; dit is het overeenkomstige element van CFLijst. De standaardwaarde is 1; als u waarden invoert, dan moeten dit positieve gehele getallen < 10.000 zijn.

Opmerking: zie ook mirr(), pag. 56.

isPrime()

isPrime(Getal) ⇒ Booleaanse constante uitdrukking

Geeft waar of onwaar om aan te geven of getal een geheel getal ‚ 2 is, dat alleen deelbaar is door zichzelf en door 1.

Als Getal groter is dan 306 cijfers en geen factoren {1021 heeft, dan geeft isPrime(Getal) een foutmelding weer.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Catalogus

Functie om het volgende priemgetal na een gespecificeerd getal te vinden:

TI-Nspire™ Referentiehandleiding 43

Lbl

Lbl labelNaam

Definieert een label met de naam labelNaam binnen een functie. U kunt een Goto labelNaam-instructie gebruiken om de besturing

naar de instructie onmiddellijk na het label te brengen. labelNaam moet aan dezelfde naamgevingsvereisten voldoen als een

variabelenaam.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

lcm()

lcm(Getal1, Getal2) ⇒ uitdrukking lcm(Lijst1, Lijst2) ⇒ lijst lcm(Matrix1, Matrix2) ⇒ matrix

Geeft het kleinste gemene veelvoud van de twee argumenten. De

lcm van twee breuken is de lcm van hun tellers gedeeld door de gcd (grootste gemene veelvoud) van hun noemers. De lcm van

breukgetallen met een drijvende komma is hun product. Geeft bij twee lijsten of matrices de kleinste gemene veelvouden van

de overeenkomstige elementen.

left()

left(bronString[, Aantal]) ⇒ string

Geeft het meest linkse Aantal tekens in tekenreeks bronString. Als u Aantal weglaat, wordt de hele bronString gegeven.

left(Lijst1[, Aantal]) ⇒ lijst

Geeft het meest linkse Aantal elementen in Lijst1. Als u Aantal weglaat, wordt de hele Lijst1 gegeven.

left(Vergelijken) ⇒ uitdrukking

Geeft het linkerlid van een vergelijking of ongelijkheid.

Catalogus

44 TI-Nspire™ Referentiehandleiding

libShortcut()

libShortcut(BibliotheekNaamString, SnelNaamString [, LibPrivVlag]) ⇒ lijst met variabelen

Creëert een variabelegroep in de huidige opgave die verwijzingen naar alle objecten in het gespecificeerde bibliotheekdocument BibliotheekNaamString bevat. Voegt de groepsleden tevens toe aan het Variabelen-menu. U kunt vervolgens naar elk object verwijzen met behulp van zijn SnelNaamString.

Stel LibPrivVlag= sluiten (standaardinstelling) Stel LibPrivVlag=1 om persoonlijke bibliotheekobjecten op te nemen

Zie voor het kopiëren van een variabelegroep CopyVar op pag. 15. Zie voor het wissen van een variabelegroep DelVar op pag. 25.

0 om persoonlijke bibliotheekobjecten uit te

Catalogus

In dit voorbeeld wordt uitgegaan van een op de juiste manier opgeslagen en vernieuwd bibliotheekdocument met de naam

linalg2 dat de gedefinieerde objecten clearmat, gauss1 en

gauss2 bevat.

LinRegBx

LinRegBx X,Y[,[Freq][,Categorie,Opnemen]]

Berekent de lineaire regressie y = a+b·x op de lijsten X en Y met frequentie Freq. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Catalogus

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen. X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Uitvoervariabele Beschrijving

stat.RegEqn

Regressievergelijking: a+b·x

stat.a, stat.b Regressiecoëfficiënten

stat.r

Determinatiecoëfficiënt

stat.r Correlatiecoëfficiënt

stat.Resid Residuen uit de regressie

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

beperkingen van Freq, Categorielijst en Categorieën opnemen

stat.FreqReg Lijst van frequenties die corresponderen met stat.FreqReg en stat.YReg

TI-Nspire™ Referentiehandleiding 45

LinRegMx

LinRegMx X,Y[,[Freq][,Categorie,Opnemen]]

Berekent de lineaire regressie y = m·x+b op de lijsten X en Y met frequentie Freq. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Catalogus

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen. X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Uitvoervariabele Beschrijving

stat.RegEqn

Regressievergelijking: m·x+b

stat.m, stat.b Regressiecoëfficiënten

stat.r

Determinatiecoëfficiënt

stat.r Correlatiecoëfficiënt

stat.Resid Residuen uit de regressie

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

beperkingen van Freq, Categorielijst en Categorieën opnemen

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

LinRegtIntervals

LinRegtIntervals X,Y[,Freq[,0[,CNiv]]]

Voor helling. Berekent een niveau C betrouwbaarheidsinterval voor de helling.

LinRegtIntervals X,Y[,Freq[,1,Xwaarde[,CNiv]]]

Voor respons. Berekent een voorspelde y-waarde, een niveau C voorspellingsinterval voor één observatie en een niveau C betrouwbaarheidsinterval voor de gemiddelde respons.

Een samenvatting van de resultaten wordt o pgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Catalogus

Alle lijsten moeten gelijke afmetingen hebben.

X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

46 TI-Nspire™ Referentiehandleiding

Uitvoervariabele Beschrijving

stat.RegEqn

stat.a, stat.b Regressiecoëfficiënten

stat.df Vrijheidsgraden

stat.r

stat.r Correlatiecoëfficiënt

stat.Resid Residuen uit de regressie

Alleen voor het type Hellling

Uitvoervariabele Beschrijving

[stat.CLower, stat.CUpper]

stat.ME Foutmarge betrouwbaarheidsinterval

stat.SESlope Standaardfout van helling

stat.s Standaardfout van de lijn

Alleen voor het type Respons

Uitvoervariabele Beschrijving

[stat.CLower, stat.CUpper]

stat.ME Foutmarge betrouwbaarheidsinterval

stat.SE Standaardfout van de gemiddelde respons

[stat.LowerPred , stat.UpperPred]

stat.MEPred Foutmarge voor voorspellingsinterval

stat.SEPred Standaardfout voor voorspelling

stat.y

Regressievergelijking: a+b·x

Determinatiecoëfficiënt

Betrouwbaarheidsinterval voor de helling

Betrouwbaarheidsinterval voor de gemiddelde respons

Voorspellingsinterval voor één observatie

a + b·XWaarde

TI-Nspire™ Referentiehandleiding 47

LinRegtTest

LinRegtTest X,Y[,Freq[,Hypoth]]

Berekent een lineaire regressie op de X- en Y-lijsten en een t-toets op de waarde van helling b en de correlatiecoëfficiënt r voor de vergelijking y=a+bx. Hij toetst de nulhypothese H0:b=0 (equivalent

r=0) tegen één van de drie alternatieve hypothesen.

Alle lijsten moeten gelijke afmetingen hebben.

X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Hypoth is een optionele waarde die één van de drie alternatieve hypothesen specificeert, waartegen de nulhypothese (H0:b=r=0) wordt getoetst.

Voor H1: bƒ0 en rƒ0 (standaard) stelt u Hypoth=0 in Voor H1: b<0 en r<0 stelt u Hypoth<0 in Voor H1: b>0 en r>0 stelt u Hypoth>0 in

Een samenvatting van de resultaten wordt o pgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Uitvoervariabele Beschrijving

stat.RegEqn

stat.t t-statistiek voor significantietoets

stat.PVal Kleinste significantieniveau waarbij de nulhypothese verworpen kan worden

stat.df Vrijheidsgraden

stat.a, stat.b Regressiecoëfficiënten

stat.s Standaardfout van de lijn

stat.SESlope Standaardfout van helling

stat.r

stat.r Correlatiecoëfficiënt

stat.Resid Residuen uit de regressie

Regressievergelijking: a + b·x

Determinatiecoëfficiënt

Catalogus

List()

Catalogus

@List(Lijst1) ⇒ lijst

Geeft een lijst met de verschillen tussen opeenvolgende elementen in Lijst1. Ieder element van Lijst1 wordt afgetrokken van het volgende

element van Lijst1. De resulterende lijst is altijd één element korter dan de oorspronkelijke Lijst1.

48 TI-Nspire™ Referentiehandleiding

list4mat()

list4mat(Lijst [, elementenPerRij]) ⇒ matrix

Geeft een matrix die rij voor rij gevuld wordt met de elementen uit

Lijst. elementenPerRij specificeert, indien opgenomen, het aantal

elementen per rij. De standaardwaarde is het aantal element in Lijst (één rij).

Als Lijst de resulterende matrix niet vult, dan worden er nullen toegevoegd.

Catalogus

ln()

ln(Waarde1) ⇒ waarde ln(Lijst1) ⇒ lijst

Geeft de natuurlijke logaritme van het argument. Geeft bij een lijst de natuurlijke logaritme van de elementen.

ln(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de natuurlijke logaritme van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de natuurlijke logaritme van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

LnReg

LnReg X, Y[, [Freq] [, Categorie, Opnemen]]

Berekent de logaritmische regressie y = a+b·ln(x) op de lijsten X en Y met frequentie Freq. Een samenvatting van de resultaten wordt

opgeslagen in de variabele stat.resultaten. (Zie pag. 86). Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen.

X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Catalogus

-toetsen

Als de complexe opmaak-modus Reëel is:

Als de complexe opmaak-modus Rechthoekig is:

In de hoekmodus Radialen en rechthoekige complexe opmaak:

Om het hele resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.

TI-Nspire™ Referentiehandleiding 49

Uitvoervariabele Beschrijving

stat.RegEqn

Regressievergelijking: a+b·ln(x)

stat.a, stat.b Regressiecoëfficiënten

stat.r

Coëfficiënt van lineaire determinatie voor getransformeerde gegevens

stat.r Correlatiecoëfficiënt voor getransformeerde gegevens (ln(x), y)

stat.Resid Residuen die geassocieerd zijn met het logaritmische model

stat.ResidTrans Residuen die geassocieerd zijn met de lineaire regressie van getransformeerde gegevens

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

beperkingen van Freq, Categorielijst en Categorieën opnemen

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

Local

Local Var 1 [, Va r 2] [, Va r 3 ] ...

Maakt de gespecificeerde vars bekend als lokale variabelen. Die variabelen bestaan alleen tijdens de uitwerking van een functie, en worden gewist wanneer de functie uitgevoerd is.

Opmerking: lokale variabelen besparen geheugen omdat ze

slechts tijdelijk bestaan. Bovendien storen ze eventuele bestaande algemene variabelen niet. Lokale variabelen moeten gebruikt worden voor For-lussen en voor het tijdelijk opslaan van waarden in een functie van meerdere regels, aangezien wijzigingen van algemene variabelen niet zijn toegestaan in een functie.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Catalogus

50 TI-Nspire™ Referentiehandleiding

log()

log(Waarde1[,Waarde2]) ⇒ waarde log(Lijst1[,Waarde2]) ⇒ lijst

Geeft de logaritme met grondtal-Waarde2- van het eerste argument.

Opmerking: zie ook Log-template, pag. 2.

Geeft bij een lijst de logaritme met grondtal-Waarde2- van de elementen.

Als het tweede argument wordt weggelaten, dan wordt 10 als grondtal gebruikt.

Als de complexe opmaak-modus Reëel is:

Als de complexe opmaak-modus Rechthoekig is:

-toetsen

log(vierkanteMatrix1[,Waarde]) ⇒ vierkanteMatrix

Geeft de logaritme met grondtal-Waarde- van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de logaritme met grondtalWaarde- van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

Als het grondtal-argument wordt weggelaten, dan wordt 10 als grondtal gebruikt.

Logistic

Logistic X, Y[, [Freq] [, Categorie, Opnemen]]

Berekent de logistische regressie y = (c/(1+a·e en Y met frequentie Freq. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen.

X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

-bx

)) op de lijsten X

In de hoekmodus Radialen en rechthoekige complexe opmaak:

Om het hele resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.

Catalogus

TI-Nspire™ Referentiehandleiding 51

Uitvoervariabele Beschrijving

stat.RegEqn

Regressievergelijking: c/(1+a·e

-bx

)

stat.a, stat.b, stat.c Regressiecoëfficiënten

stat.Resid Residuen uit de regressie

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

beperkingen van Freq, Categorielijst en Categorieën opnemen

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

LogisticD

LogisticD X, Y [, [Iteraties], [Freq] [, Categorie, Opnemen] ]

Berekent de logistische regressie y = (c/(1+a·e en Y met frequentie Freq, met behulp van een gespecificeerd aantal Iteraties. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

-bx

)+d) op de lijsten X

Catalogus

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen. X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Iteraties is een optionele waarde die het maximaal aantal keer

specificeert dat een oplossing wordt geprobeerd. Als deze wordt weggelaten, wordt 64 gebruikt. Doorgaans leiden grotere waarden tot een hogere nauwkeurigheid maar een langere berekeningstijd, en andersom.

Freq is een optionele lijst met frequentiewaarden. Elk element in Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Uitvoervariabele Beschrijving

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

Regressievergelijking: c/(1+a·e

Regressiecoëfficiënten

-bx

)+d)

stat.Resid Residuen uit de regressie

stat.XReg Lijst van gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

beperkingen van Freq, Categorielijst en Categorieën opnemen

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

52 TI-Nspire™ Referentiehandleiding

Loop

Blok

EndLoop

Voert de beweringen in Blok herhaaldelijk uit. Merk op dat de lus eindeloos wordt uitgevoerd, tenzij er een wordt uitgevoerd binnen Blok.

Blok is een reeks beweringen die gescheiden worden door het teken “:”.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Goto- of Exit-instructie

Catalogus

LU Matrix, lMatNaam, uMatNaam, pMatNaam[, Tol ]

Berekent de Doolittle LU (beneden-boven)-decompositie van een reële of complexe matrix. De benedendriehoeksmatrix wordt opgeslagen in lMatNaam, de bovendriehoeksmatrix in uMatNaam en de permutatiematrix (die de rijverwisselingen tijdens de berekening beschrijft) in pMatNaam.

lMatNaam · uMatNaam = pMatNaam · matrix

Optioneel wordt elk matrixelement behandeld als nul als de absolute waarde ervan minder dan To l is. Deze tolerantie wordt alleen gebruikt als de matrix gegevens met een drijvende komma heeft, en geen symbolische variabelen bevat die geen waarde toegekend hebben gekregen. Anders wordt To l genegeerd.

•Als u

Benaderend

met behulp van de drijvende komma uitgevoerd.

•Als Tol wordt weggelaten of niet wordt gebruikt, dan wordt de standaardtolerantie berekend als:

5EM14 ·max(dim(Matrix)) ·rowNorm(Matrix)

Het LU ontbindingsalgoritme gebruikt gedeeltelijke pivoting met rijverwisselingen.

· gebruikt of de modus Automatisch of

instelt op Benaderend, dan worden berekeningen

mat4list()

mat4list(Matrix) ⇒ lijst

Geeft een lijst die gevuld is met de elementen in Matrix. De elementen worden rij voor rij gekopieerd uit Matrix.

Catalogus

TI-Nspire™ Referentiehandleiding 53

max()

max(Waarde1, Waarde2) ⇒ uitdrukking max(Lijst1, Lijst2) ⇒ lijst max(Matrix1, Matrix2) ⇒ matrix

Geeft het maximum van de twee argumenten. Als de argumenten twee lijsten of matrices zijn, dan wordt een lijst of matrix met de maximumwaarde van elk paar corresponderende gegevens gegeven.

max(Lijst) ⇒ uitdrukking

Geeft het maximumelement in lijst.

max(Matrix1) ⇒ matrix

Geeft een rijvector met het maximumelement van elke kolom in Matrix1.

Opmerking: zie ook min().

Catalogus

mean()

mean(Lijst[, freqLijst]) ⇒ uitdrukking

Geeft het gemiddelde van de elementen in Lijst. Elk element uit freqLijst telt het aantal malen dat het

overeenkomstige element in Lijst achter elkaar voorkomt.

mean(Matrix1[, freqMatrix]) ⇒ matrix

Geeft een rijvector van de gemiddelden van alle kolommen in

Matrix1.

Elk element uit freqMatrix telt het aantal malen dat het overeenkomstige element in Matrix1 achter elkaar voorkomt.

median()

median(Lijst) ⇒ uitdrukking

Geeft de mediaan van de elementen in Lijst.

median(Matrix1) ⇒ matrix

Geeft een rijvector met de medianen van de kolommen in Matrix1.

Opmerking: alle gegevens in de lijst of matrix moeten

vereenvoudigen tot getallen.

In de rechthoekige vectoropmaak:

Catalogus

54 TI-Nspire™ Referentiehandleiding

MedMed

MedMed X,Y [, Freq] [, Categorie, Opnemen]]

Berekent de mediaan-mediaan-lijn y = (m·x+b) op de lijsten X en Y met frequentie Freq. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen.

X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Uitvoervariabele Beschrijving

stat.RegEqn

stat.m, stat.b Modelcoëfficiënten

stat.Resid Residuen uit de mediaan-mediaan-lijn

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

Mediaan-mediaan-lijnvergelijking: m·x+b

beperkingen van Freq, Categorielijst en Categorieën opnemen

Catalogus

mid()

mid(bronString, Start[, Aantal]) ⇒ string

Geeft Aantal tekens uit de tekenreeks bronString, beginnend met teken nummer Start.

Als Aantal wordt weggelaten of groter is dan de afmeting van bronString, dan worden alle tekens van bronString gegeven, beginnend met het teken nummer Start.

Aantal moet ‚ 0 zijn. Als Aantal = 0, dan wordt een lege string gegeven.

mid(bronLijst, Start [, Aantal]) ⇒ lijst

Geeft Aantal elementen uit bronLijst, beginnend met element nummer Start.

Als Aantal wordt weggelaten of groter is dan de afmeting van bronLijst, dan worden alle elementen uit bronLijst gegeven, beginnend met element nummer Start.

Aantal moet ‚ 0 zijn. Als Aantal = 0, dan wordt er een lege lijst gegeven.

mid(bronStringLijst, Start[, Aantal]) ⇒ lijst

Geeft Aantal strings uit de lijst met strings bronStringLijst, beginnend met element nummer Start.

Catalogus

TI-Nspire™ Referentiehandleiding 55

min()

min(Waarde1, Waarde2) ⇒ uitdrukking min(Lijst1, Lijst2) ⇒ lijst min(Matrix1, Matrix2) ⇒ matrix

Geeft het minimum van de twee argumenten. Als de argumenten twee lijsten of matrices zijn, dan wordt een lijst of matrix met de minimumwaarde van elk paar corresponderende gegevens gegeven.

min(Lijst) ⇒ uitdrukking

Geeft het minimumelement van Lijst.

min(Matrix1) ⇒ matrix

Geeft een rijvector met het minimumelement van elke kolom in Matrix1.

Opmerking: zie ook max().

Catalogus

mirr()

mirr(financPercentage,herinvestPercentage,CF0,CFLijst[,CFFr

eq])

Financiële functie die de gewijzigde interne rentabiliteit van een investering geeft.

financPercentage is het rentepercentage dat u betaalt over de cashflow-bedragen.

herinvestPercentage is het rentepercentage waarop de cashflows opnieuw geïnvesteerd worden.

Opmerking: zie ook irr(), pag. 43.

mod()

mod(Waarde1, Waarde2) ⇒ uitdrukking mod(Lijst1, Lijst2) ⇒ lijst mod(Matrix1, Matrix2) ⇒ matrix

Geeft het eerste argument modulus het tweede argument zoals gedefinieerd wordt door de identiteiten:

mod(x,0) = x mod(x,y) = x -ìy floor(x/y)

Wanneer het tweede argument niet-nul is, dan is het resultaat periodiek in dat argument. Het resultaat is nul of heeft hetzelfde teken als het tweede argument.

Als de argumenten twee lijsten of twee matrices zijn, dan wordt een lijst of matrix met de modulus van elk paar corresponderende elementen gegeven.

Opmerking: zie ook remain(), pag. 75

Catalogus

56 TI-Nspire™ Referentiehandleiding

mRow()

mRow(Waarde, Matrix1, Index) ⇒ matrix

Geeft een kopie van Matrix1 met elk element in rij Index van Matrix1 vermenigvuldigd met Waarde.

Catalogus

mRowAdd()

mRowAdd(Waarde, Matrix1, Index1, Index2) ⇒ matrix

Geeft een kopie van Matrix1 met elk element in rij Index2 van Matrix1 vervangen door:

Waarde · rij Index1 + rij Index2

MultReg

MultReg Y, X1[,X2[,X3,…[,X10]]]

Berekent een meervoudige lineaire regressie van lijst Y op de lijsten X1, X2, …, X10. Een samenvatting van de resultaten wordt

opgeslagen in de variabele stat.resultaten. (Zie pag. 86). Alle lijsten moeten gelijke afmetingen hebben.

Uitvoervariabele Beschrijving

stat.RegEqn

Regressievergelijking: b0+b1·x1+b2·x2+ ...

stat.b0, stat.b1, ... Regressiecoëfficiënten

stat.R

Coëfficiënt van meervoudige determinatie

stat.yLijst yLijst = b0+b1·x1+ ...

stat.Resid Residuen uit de regressie

MultRegIntervals

MultRegIntervals Y,

X1[,X2[,X3,…[,X10]]],XWaardeLijst[,CNiveau]

Berekent een voorspelde y-waarde, een niveau C voorspellingsinterval voor één observatie en een niveau C betrouwbaarheidsinterval voor de gemiddelde respons.

Een samenvatting van de resultaten wordt o pgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Alle lijsten moeten gelijke afmetingen hebben.

Catalogus

Uitvoervariabele Beschrijving

stat.RegEqn

Regressievergelijking: b0+b1·x1+b2·x2+ ...

stat.y Een puntschatting: y = b0 + b1 · xl + ... voor XWaardeLijst

stat.dfError Vrijheidsgraden van de fouten

stat.CLower, stat.CUpper Betrouwbaarheidsinterval voor een gemiddelde respons

TI-Nspire™ Referentiehandleiding 57

Uitvoervariabele Beschrijving

stat.ME Foutmarge betrouwbaarheidsinterval

stat.SE Standaardfout van de gemiddelde respons

stat.LowerPred, stat.UpperPred

Voorspellingsinterval voor één observatie

stat.MEPred Foutmarge voor voorspellingsinterval

stat.SEPred Standaardfout voor voorspelling

stat.bList Lijst van regressiecoëfficiënten, {b0,b1,b2,...}

stat.Resid Residuen uit de regressie

MultRegTests

MultRegTests Y, X1[,X2[,X3,…[,X10]]]

Meervoudige lineaire regressietoets berekent een meervoudige lineaire regressie op de gegevens, en biedt de globale F-toets- statistiek en t-toets-statistieken voor de coëfficiënten.

Een samenvatting van de resultaten wordt o pgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Catalogus

Uitvoer

Uitvoervariabele Beschrijving

stat.RegEqn

Regressievergelijking: b0+b1·x1+b2·x2+ ...

stat.F Globale F-toets-statistiek

stat.PVal P-waarde geassocieerd met de globale F-statistiek

stat.R

stat.AdjR

Coëfficiënt van meervoudige determinatie

Aangepaste coëfficiënt van meervoudige determinatie

stat.s Standaarddeviatie van de fout

stat.DW Durbin-Watson-statistiek; wordt gebruikt om te bepalen of er automatische correlatie van de eerste orde

aanwezig is in het model

stat.dfReg Vrijheidsgraden van de regressie

stat.SSReg Som van de kwadraten van de regressies

stat.MSReg Gemiddelde kwadraat van de regressies

stat.dfError Vrijheidsgraden van de fouten

stat.SSError Som van de kwadraten van de fouten

stat.MSError Gemiddelde kwadraat van de fouten

stat.bList {b0,b1,...} Lijst van coëfficiënten

stat.tList Lijst van t-statistieken, één voor elke coëfficiënt in de bLijst

stat.PList Lijst van P-waarden voor elke t-statistiek

stat.SEList Lijst van standaardfouten voor coëfficiënten in bLijst

58 TI-Nspire™ Referentiehandleiding

Uitvoervariabele Beschrijving

stat.yLijst yLijst = b0+b1·x1+...

stat.Resid Residuen uit de regressie

stat.sResid Gestandaardiseerde residuen; verkregen door een residu te delen door zijn standaarddeviatie

stat.CookDist Afstand van Cook; maat voor de invloed van een observatie op basis van het residue en de invloed

stat.Leverage Maat voor hoever de waarden van de onafhankelijke variabelen van hun gemiddelde waarden af liggen

nCr()

nCr(Waarde1, Waarde2) ⇒ uitdrukking

Voor geheel getal Waarde1 en Waarde2 met Waarde1 ‚ Waarde2 ‚ 0, is nCr() het aantal combinaties van Waarde1 dingen die met Waarde2 keer tegelijk genomen zijn. (Dit is ook bekend als een binomiale coëfficiënt.)

nCr(Waarde, 0) ⇒ 1

Waarde, negGeheel getal) ⇒ 0

nCr(

Waarde, posGeheel getal) ⇒ Waarde·(WaardeN1)...

nCr(

(WaardeNposGeheel getal+1)/ posGeheel getal!

Waarde, nietGeheel getal) ⇒ uitdrukking!/

nCr(

((WaardeNnietGeheel getal)!·nietGeheel getal!)

nCr(

Lijst1, Lijst2) ⇒ lijst

Geeft een lijst met combinaties op basis van de overeenkomstige elementparen in de twee lijsten. De argumenten moeten lijsten van dezelfde afmeting zijn.

nCr(Matrix1, Matrix2) ⇒ matrix

Geeft een matrix met combinaties op basis van de overeenkomstige elementparen in de twee matrices. De argumenten moeten matrices van dezelfde afmeting zijn.

nDeriv()

nDeriv(Uitdr1, Va r [=Waarde] [, H]) ⇒ uitdrukking nDeriv(Uitdr1, Va r [, H] | Var=Waarde) ⇒ uitdrukking

nDeriv(Uitdr1, Va r [=Waarde], Lijst) ⇒ lijst nDeriv(Lijst1, Va r [=Waarde] [, H]) ⇒ lijst nDeriv(Matrix1, Va r [=Waarde] [, H]) ⇒ matrix

Geeft de numerieke afgeleide als een uitdrukking. Gebruikt de centraal-differentiequotiënt-formule.

Wanneer waarde gespecificeerd is, wordt elke eerdere variabeletoekenning of elke huidige “waarvoor g eldt dat”-substitutie voor de variabele onderdrukt.

H is de stapwaarde. Als H wordt weggelaten, is de standaardwaarde 0,001.

Wanneer u Lijst1 of Matrix1 gebruikt, dan wordt de bewerking toegepast op de waarden in de lijst of op de elementen in de matrix.

Opmerking: zie ook avgRC().

Catalogus

TI-Nspire™ Referentiehandleiding 59

newList()

newList(aantalElementen) ⇒ lijst

Geeft een lijst met de afmeting aantalElementen. Elk element is nul.

Catalogus

newMat()

newMat(aantalRijen, aantalKolommen) ⇒ matrix

Geeft een matrix met nullen met de afmeting aantalRijen bij aantalKolommen.

nfMax()

nfMax(Uitdr, Va r ) ⇒ waarde nfMax(Uitdr, Va r , ondergrens) ⇒ waarde

nfMax(Uitdr, Va r , ondergrens, bovengrens) ⇒ waarde nfMax(Uitdr, Var) | ondergrens<Var <bovengrens ⇒ waarde

Geeft een mogelijke numerieke waarde van variabele Var waarvoor het lokale maximum van Uitdr optreedt.

Als u ondergrens en bovengrens opgeeft, zoekt de functie tussen deze waarden naar het lokale maximum.

nfMin()

nfMin(Uitdr, Var ) ⇒ waarde nfMin(Uitdr, Var , ondergrens) ⇒ waarde nfMin(Uitdr, Var , ondergrens, bovengrens) ⇒ waarde nfMin(Uitdr, Var) | ondergrens<Var <bovengrens ⇒ waarde

Geeft een mogelijke numerieke waarde van variabele Var waarvoor het lokale minimum van Uitdr optreedt.

Als u ondergrens en bovengrens opgeeft, zoekt de functie tussen die waarden naar het lokale minimum.

nInt()

nInt(Uitdr1, Var, Onder, Boven) ⇒ uitdrukking

Als de integrand Uitdr1 geen andere variabele dan Va r bevat, en als Onder en Boven constanten, positief ˆ of negatief ˆ zijn, dan geeft

nInt() een benadering van ‰(Uitdr1, Va r, Onder, Boven). Deze

benadering is een gewogen gemiddelde van enkele steekproefwaarden van de integrand in het interval

Onder<Va r<Boven. Het doel is zes significante cijfers. Het adaptieve algoritme eindigt

wanneer het waarschijnlijk lijkt dat het doel is bere ikt, of wanneer het onwaarschijnlijk lijkt dat extra steekproeven een lonende verbetering zullen opleveren.

Er wordt een waarschuwing weergegeven (“Twijfelachtige nauwkeurigheid”) wanneer het erop lijkt dat het doel niet is bereikt.

Nest nInt() om meervoudige numerieke integratie uit te voeren. Integratiegrenzen kunnen afhangen van integratievariabelen erbuiten.

Catalogus

60 TI-Nspire™ Referentiehandleiding

nom()

nom(effectiefPercentage,CpY) ⇒ waarde

Financiële functie die het jaarlijkse effectieve rentepercentage effectiefPercentage naar een nominaal percentage converteert, waarbij CpY het aantal rentetermijnen per jaar is.

effectiefPercentage moet een reëel getal zijn en CpY moet een reëel getal > 0 zijn.

Opmerking: zie ook eff(), pag. 28.

Catalogus

norm()

norm(Matrix) ⇒ uitdrukking norm(Ve c to r ) ⇒ uitdrukking

Geeft de Frobenius-norm.

normCdf()

normCdf(ondergrens,bovengrens[,m[,s]]) ⇒ getal als

ondergrens en bovengrens getallen zijn, lijst als ondergrens en bovengrens lijsten zijn

Berekent de normale verdelingskans tussen ondergrens en bovengrens voor de gespecificeerde m (standaard=0) en s

(standaard=1). Voor P(X  bovengrens) stelt u ondergrens = in.9E999.

normPdf()

normPdf(XWaarde[,m[,s]]) ⇒ getal als XWaarde een getal is,

lijst als XWaarde een lijst is

Berekent de kansdichtheidsfunctie voor de normale verdeling bij een gespecificeerde XWaarde voor de gespecificeerde m en s.

not

not BooleaanseUitdr ⇒ Booleaanse uitdrukking

Geeft waar, onwaar of een vereenvoudigde vorm van het argument.

Catalogus

TI-Nspire™ Referentiehandleiding 61

not

not Geheel getal1 ⇒ geheel getal

Geeft het één-complement van een reëel geheel getal. Intern wordt Geheel getal1 geconverteerd naar een 64-bits binair getal met een plus- of min-teken. De waarde van elke bit wordt omgewisseld (0 wordt 1 en andersom) voor het één-complement. Resultaten worden weergegeven volgens de grondtal-modus.

U kunt het gehele getal in elk grondtal invoeren. Voor een binaire of hexadecimale invoer moet u respectievelijk het prefix 0b of 0h gebruiken. Zonder prefix wordt het gehele getal behandeld als decimaal (grondtal 10).

Als u een decimaal geheel getal invoert dat te groot is voor een 64-bits binaire vorm met een plus- of min-teken, dan wordt er een symmetrische modulo-bewerking gebruikt om de waarde binnen het betreffende bereik te brengen.

Catalogus

In de Hex-grondtalmodus:

Belangrijk: nul, niet de letter O.

In de Bin-grondtalmodus:

Om het hele resultaat te zien drukt u op vervolgens ¡ en ¢ om de cursor te verplaatsen.

Opmerking: een binaire invoer kan maximaal 64 cijfers

hebben (het prefix 0b niet meegeteld). Een hexadecimale invoer kan maximaal 16 cijfers hebben.

£ en gebruikt u

nPr()

nPr(Waarde1, Waarde2) ⇒ uitdrukking

Voor geheel getal Waarde1 en Waarde2 met Waarde1 ‚ Waarde2 ‚ 0, is nPr() het aantal permutaties van Waarde1 dingen die met Waarde2 tegelijk genomen zijn.

nPr(Waarde, 0) ⇒ 1

Waarde, negGeheel getal) ⇒ 1/

nPr( ((

Waarde+1)·(Waarde+2)... (WaardeNnegGeheel getal))

Waarde, posGeheel getal) ⇒

nPr(

Waarde·(WaardeN1)... (WaardeNposGeheel getal+1)

Waarde, nietGeheel getal) ⇒

nPr(

Waarde! / (WaardeNnietGeheel getal)!

Lijst1, Lijst2) ⇒ lijst

nPr(

Geeft een lijst met permutaties op basis van de overeenkomstige elementparen in de twee lijsten. De argumenten moeten lijsten van dezelfde afmeting zijn.

nPr(Matrix1, Matrix2) ⇒ matrix

Geeft een matrix met permutaties op basis van de overeenkomstige elementparen in de twee matrices. De argumenten moeten matrices van dezelfde afmeting zijn.

Catalogus

62 TI-Nspire™ Referentiehandleiding

npv()

npv(RentePercentage,CFO,CFLijst[,CFFreq])

Financiële functie die de netto contante waarde berekent; de som van de contante waarden voor de kasinstromen en -uitstromen. Een positief resultaat voor npv duidt op een winstgevende investering.

RentePercentage is de rente waarmee de cashflows verdisconteerd moeten worden (de kosten van het geld) over één periode.

CF0 is de begin-cashflow op tijdstip 0; dit moet een reëel getal zijn. CFLijst is een lijst met cashflow-bedragen na de begin-cashflow

CF0. CFFreq is een lijst waarin elk element de frequentie waarmee een

gegroepeerde (opeenvolgend) cashflow-bedrag voorkomt specificeert; dit is het overeenkomstige element vanCFLijst. De standaardwaarde is 1; als u waarden invoert, dan moeten dit positieve gehele getallen < 10.000 zijn.

Catalogus

nSolve()

nSolve(Vergelijking,Var [=Gok]) ⇒ getal of fout_string nSolve(Vergelijking,Var [=Gok],ondergrens)

⇒ getal of fout_string

nSolve(Vergelijking,Var [=Gok],ondergrens,bovengrens)

⇒ getal of fout_string

nSolve(Vergelijking,Var [=Gok]) | ondergrens<Var <bovengrens

⇒ getal of fout_string

Zoekt iteratief naar één benaderende numerieke oplossing van Vergelijking, voor de ene variabele ervan. Specificeer de variabele als:

variabele

– of – variabele = reëel getal

Bijvoorbeeld: x is geldig en x=3 ook.

nSolve() probeert één punt te bepalen waarop het residu nul is, of

twee relatief dicht bij elkaar liggende punten waarop het residu tegenovergestelde tekens heeft, en de grootte van het residu niet overdreven is. Als dit niet bereikt kan worden met behulp van een bescheiden aantal steekproefpunten, dan wordt de string “geen oplossing gevonden” gegeven.

Catalogus

Opmerking: als er meerdere oplossingen zijn, dan kunt u een

gok gebruiken om een bepaalde oplossing te helpen vinden.

TI-Nspire™ Referentiehandleiding 63

OneVar

OneVar [1,]X[,[Freq][,Categorie,Opnemen]] OneVar [

n,]X1,X2[X3[,…[,X20]]]

Berekent statistieken voor één variabele op maximaal 20 lijsten. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.results. (Zie pag. 86).

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen.

De X-argumenten zijn gegevenslijsten. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elke overeenkomstige X-

waarde voorkomt. De standaardwaarde is 1. Alle elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X-waarden.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Uitvoervariabele Beschrijving

stat.v

stat.Gx

stat.sx Steekproef-standaarddeviatie van x

stat.ssssx Populatie-standaarddeviatie van x

stat.n Aantal gegevens

stat.MinX Minimum van de x-waarden

stat.Q1X 1ste kwartiel van x

stat.MedianX Mediaan van x

stat.Q3X 3de kwartiel van x

stat.MaxX Maximum van de x-waarden

stat.SSX Som van de kwadraten van de afwijkingen ten opzichte van het gemiddelde van x

Gemiddelde van de x-waarden

Som van de x-waarden

Som van de x2-waarden

Catalogus

64 TI-Nspire™ Referentiehandleiding

BooleaanseUitdr1 or BooleaanseUitdr2

⇒ Booleaanse uitdrukking

Geeft waar of onwaar of een vereenvoudigde vorm van de oorspronkelijke invoer.

Geeft waar als een van beide of beide uitdrukkingen uitgewerkt worden tot waar. Geeft alleen onwaar als beide uitdrukkingen uitgewerkt worden tot onwaar.

Opmerking: zie xor. Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Geheel getal1 or Geheel getal2 ⇒ geheel getal

Vergelijkt twee reële gehele getallen bit voor bit met behulp van een or-bewerking. Intern worden beide gehele getallen geconverteerd naar 64-bits binaire getallen met een plus- of min-teken. Wanneer overeenkomstige bits vergeleken worden, is het resultaat 1 als een van beide of beide bits 1 zijn; het resultaat is alleen 0 als beide bits 0 zijn. De geretourneerde waarde geeft de bitresultaten, en wordt weergegeven volgens de grondtal-modus.

Opmerking: zie xor.

Catalogus

In de Hex-grondtalmodus:

Belangrijk: nul, niet de letter O.

In de Bin-grondtalmodus:

Opmerking: een binaire invoer kan maximaal 64 cijfers

hebben (het prefix 0b niet meegeteld). Een hexadecimale invoer kan maximaal 16 cijfers hebben.

ord()

ord(Str ing) ⇒ geheel getal ord(Lijst1) ⇒ lijst

Geeft de numerieke code van het eerste teken in tekenreeks Strin g, of een lijst van de eerste tekens van elk lijstelement.

Catalogus

P4Rx()

P4Rx(rUitdr, qUitdr) ⇒ uitdrukking P4Rx(rLijst, qLijst) ⇒ lijst P4Rx(rMatrix, qMatrix) ⇒ matrix

Geeft de equivalente x-coördinaat van het (r, q)-paar.

Opmerking: het q-argument wordt geïnterpreteerd als een hoek in

graden, decimale graden of radialen, volgens de ingestelde hoekmodus. Als het argument een uitdrukking is, dan kunt u ó,G of ôgebruiken om de hoekmodusinstelling tijdelijk te onderdrukken.

In de hoekmodus Radialen:

TI-Nspire™ Referentiehandleiding 65

Catalogus

P4Ry()

P4Ry(rWaarde, qWaarde) ⇒ waarde P4Ry(rLijst, qLijst) ⇒ lijst P4Ry(rMatrix, qMatrix) ⇒ matrix

Geeft het equivalente y-coördinaat van het (r,q)-paar.

Opmerking: het q-argument wordt geïnterpreteerd als een hoek in

graden, decimale graden of radialen, volgens de ingestelde hoekmodus.

In de hoekmodus Radialen:

Catalogus

PassErr

Brengt een fout naar het volgende niveau. Als systeemvariabele errCode nul is, dan doet PassErr niets. De Else-zin van het Try...Else...EndTry-blok moet ClrErr of

PassErr gebruiken. Als de fout verwerkt of genegeerd moet worden,

gebruik dan ClrErr. Als onbekend is wat er met de fout gedaan moet worden, gebruik dan PassErr om hem te verzenden naar de volgende foutenafhandelaar. Als er geen onbesliste

Try...Else...EndTry-foutenafhandelaars meer zijn, wordt het

foutendialoogvenster weergegeven zoals normaal is.

Opmerking: zie ook ClrErr, pag. 14 en Try, pag. 94. Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

piecewise()

piecewise(Uitdr1 [, Cond1 [, Uitdr2 [, Cond2 [, … ]]]])

Geeft definities van een stuksgewijs gedefinieerde functie in de vorm van een lijst. U kunt ook stuksgewijs gedefinieerde functies creëren met behulp van een template.

Opmerking: zie ook Stuksgewijs gedefinieerde functietemplate

, page 2.

poissCdf()

poissCdf(l,ondergrens,bovengrens) ⇒ getal als ondergrens

bovengrens getallen zijn, lijst als ondergrens en bovengrens

lijsten zijn

poissCdf(

l,bovengrens) (voor P(0Xbovengrens) ⇒ getal

als

bovengrens een getal is, lijst als bovengrens een lijst is

Berekent een cumulatieve kans voor de discrete Poisson-verdeling met het gespecificeerde gemiddelde l.

Voor P(X  bovengrens) stelt u ondergrens=0 in

Catalogus

Zie voor een voorbeeld van PassErr Voorbeeld 2 onder het commando Try op pag. 94.

Catalogus

poissPdf()

poissPdf(l,XWaarde) ⇒ getal als XWaarde een getal is, lijst

als

XWaarde een lijst is

Berekent een kans voor de discrete Poisson-verdeling met het gespecificeerde gemiddelde l.

Catalogus

66 TI-Nspire™ Referentiehandleiding

Polar

4Polar

Vec t o r

Geeft vector weer in polaire vorm [r q]. De vector moet de afmeting 2 hebben en kan een rij of een kolom zijn.

Opmerking: 4Polar is een weergave-opmaakinstructie, geen

conversiefunctie. U kunt dit commando alleen gebruiken op het eind van een invoerregel, en ans wordt niet bijgewerkt.

Opmerking: zie ook 4Rect, pag. 74.

complexeWaarde 4Polar

Geeft complexeWaarde in polaire vorm weer.

• De hoekmodus Graden geeft (rq).

• De hoekmodus Radialen geeft re

complexeWaarde kan elke complexe vorm hebben. Een re veroorzaakt echter een fout in de hoekmodus Graden.

Opmerking: u moet haakjes gebruiken voor een (rq) polaire

invoer.

-invoer

In de hoekmodus Radialen:

In de hoekmodus Decimale graden:

In de hoekmodus Graden

Catalogus

polyEval()

polyEval(Lijst1, Uitdr1) ⇒ uitdrukking polyEval(Lijst1, Lijst2) ⇒ uitdrukking

Interpreteert het eerste argument als de coëfficiënt van een veelterm met aflopende machten, en geeft de veelterm uitgewerkt voor de waarde van het tweede argument.

PowerReg

PowerReg X,Y [, Freq] [, Categorie, Opnemen]]

Berekent de machtsregressie y = (a·(x)b) op de lijsten X en Y met frequentie Freq. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen.

X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Uitvoervariabele Beschrijving

stat.RegEqn

Regressievergelijking: a·(x)

stat.a, stat.b Regressiecoëfficiënten

Catalogus

TI-Nspire™ Referentiehandleiding 67

Uitvoervariabele Beschrijving

stat.r

Coëfficiënt van lineaire determinatie voor getransformeerde gegevens

stat.r Correlatiecoëfficiënt voor getransformeerde gegevens (ln(x), ln(y))

stat.Resid Residuen die geassocieerd zijn met het machtsmodel

stat.ResidTrans Residuen die geassocieerd zijn met de lineaire regressie van getransformeerde gegevens

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

beperkingen van Freq, Categorielijst en Categorieën opnemen

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

Prgm

Blok

EndPrgm

Template voor het creëren van een door de gebruiker gedefinieerd programma. Moet gebruikt worden met het commando Define,

Define LibPub of Define LibPriv.

Blok kan een enkele bewering of een serie beweringen zijn die gescheiden worden door het teken “:”, of een serie beweringen op aparte regels.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Product (PI)

product()

product(Lijst[, Start[, Eind]]) ⇒ uitdrukking

Geeft het product van de elementen in Lijst. Start en Eind zijn optioneel. Ze specificeren een bereik van elementen.

Catalogus

Bereken GCD (grootste gemene deler) en geef tussenresultaten weer.

Zie Π(), pag. 112.

Catalogus

68 TI-Nspire™ Referentiehandleiding

product()

product(Matrix1[, Start[, Eind]]) ⇒ matrix

Geeft een rijvector met de producten van de elementen in de kolommen van Matrix1. Start en Eind zijn optioneel. Ze specificeren een bereik van rijen.

Catalogus

propFrac()

propFrac(Waarde1[, Var ]) ⇒ waarde

propFrac(rationaal_getal) geeft rationaal_getal als de som van

een geheel getal en een breuk die hetzelfde t eken hebben, en waarbij de noemer groter is dan de teller.

propFrac(rationale_uitdrukking,Var ) geeft de som van echte

breuken en een veelterm ten opzichte van Var . De graad van Va r in de noemer is groter dan de graad van Va r in de teller in elke echte breuk. Gelijke machten van Va r worden samengenomen. De termen en hun factoren worden gesorteerd met Va r als de hoofdvariabele.

Als Va r wordt weggelaten, dan wordt een uitbreiding naar een echte breuk uitgevoerd ten opzichte van de belangrijkste hoofdvariabele. De coëfficiënten van het veeltermdeel worden vervolgens eerst echt gemaakt ten opzichte van hun belangrijkste hoofdvariabele, en zo verder.

U kunt de functie propFrac() gebruiken om gemengde breuken te representeren en om het optellen en aftrekken van gemengde breuken te demonstreren.

Catalogus

TI-Nspire™ Referentiehandleiding 69

QR Matrix, qMatrix, rMatrix[, Tol ]

Berekent de Householder QR-ontbinding van een reële of complexe matrix. De resulterende Q- en R-matrices worden opgeslagen in de gespecificeerde Matrix. De Q-matrix is unitair. De R-matrix is bovendriehoeks.

•Als u

Benaderend

met behulp van de drijvende komma uitgevoerd.

•Als Tol wordt weggelaten of niet wordt gebruikt, dan wordt de standaardtolerantie berekend als:

5Eë14 ·max(dim(Matrix)) ·rowNorm(Matrix)

De QR-ontbinding wordt numeriek berekend met behulp van Householder-transformaties. De symbolische oplossing wordt berekend met behulp van Gram-Schmidt. De kolommen in qMatNaam zijn de orthonormale basisvectoren die de ruimte die gedefinieerd wordt door matrix omspannen.

QuadReg

QuadReg X,Y [, Freq] [, Categorie, Opnemen]]

Berekent de kwadratische veeltermregressie y = a·x2+b·x+c op de lijsten X en Y met frequentie Freq. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag.

86).

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen.

X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

· gebruikt of de modus Automatisch of

instelt op Benaderend, dan worden berekeningen

Catalogus

Het getal met drijvende komma (9.) in m1 zorgt ervoor dat de resultaten worden berekend in drijvende-kommavorm.

Catalogus

Uitvoervariabele Beschrijving

stat.RegEqn

stat.a, stat.b, stat.c Regressiecoëfficiënten

stat.R

stat.Resid Residuen uit de regressie

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

Regressievergelijking: a·x2+b·x+c

Determinatiecoëfficiënt

beperkingen van Freq, Categorielijst en Categorieën opnemen

70 TI-Nspire™ Referentiehandleiding

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

beperkingen van Freq, Categorielijst en Categorieën opnemen

QuartReg

QuartReg X,Y [, Freq] [, Categorie, Opnemen]]

Berekent de vierdegraads veeltermregressie y = a·x4+b·x3+c· x2+d·x+e op de lijsten X en Y met frequentie

Freq. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen.

X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in

Freq specificeert de frequentie waarmee elk overeenkomsti g X- en Y-

gegeven voorkomt. De standaardwaarde is 1. All e elementen moeten gehele getallen | 0 zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

Uitvoervariabele Beschrijving

stat.RegEqn

stat.a, stat.b, stat.c, stat.d, stat.e

stat.R

stat.Resid Residuen uit de regressie

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

Regressievergelijking: a·x4+b·x3+c· x2+d·x+e

Regressiecoëfficiënten

Determinatiecoëfficiënt

beperkingen van Freq, Categorielijst en Categorieën opnemen

Catalogus

TI-Nspire™ Referentiehandleiding 71

R4Pq()

R4Pq (xWaarde, yWaarde) ⇒ waarde R4Pq (xLijst, yLijst) ⇒ lijst R4Pq (xMatrix, yMatrix) ⇒ matrix

Geeft de equivalente q-coördinaat van het (x,y)-paar argumenten.

Opmerking: de uitkomst wordt in graden, decimale graden of

radialen gegeven, volgens de ingestelde hoekmodus.

R4Pr()

R4Pr (xWaarde, yWaarde) ⇒ waarde R4Pr (xLijst, yLijst) ⇒ lijst R4Pr (xMatrix, yMatrix) ⇒ matrix

Geeft de equivalente r-coördinaat van het (x,y)-paar argumenten.

4Rad

Waarde14Rad ⇒ waarde

Converteert het argument naar radialen.

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

In de hoekmodus Graden:

Catalogus

In de hoekmodus Decimale graden:

rand()

rand() ⇒ uitdrukking rand(#Pogingen) ⇒ lijst

rand() geeft een toevalsgetal tussen 0 en 1. rand(#Pogingen) geeft een lijst met #Pogingen toevalsgetallen

tussen 0 en 1.

Stelt de seed van het toevalsgetal in.

Catalogus

72 TI-Nspire™ Referentiehandleiding

randBin()

randBin(n, p) ⇒ uitdrukking randBin(n, p, #Pogingen) ⇒ lijst

randBin(n, p) geeft een reëel toevalsgetal uit een gespecificeerde

binomiale verdeling.

randBin(n, p, #Pogingen) geeft een lijst met #Pogingen reële

toevalsgetallen uit een gespecificeerde binomiale verdeling.

Catalogus

randInt()

randInt(ondergrens,bovengrens) ⇒ uitdrukking randInt(ondergrens,bovengrens,#Pogingen) ⇒ lijst

randInt(ondergrens,bovengrens) geeft een geheel toevalsgetal

binnen het bereik dat gespecificeerd is door ondergrens en bovengrens.

randInt(ondergrens,bovengrens,#Pogingen) geeft een lijst met

#Pogingen gehele toevalsgetallen binnen het gespecificeerde bereik.

randMat()

randMat(aantalRijen, aantalKolommen) ⇒ matrix

Geeft een matrix met gehele getallen tussen -9 en 9 met de gespecificeerde afmeting.

Beide argumenten moeten vereenvoudigen tot gehele getallen.

randNorm()

randNorm(m, s [,aantalPogingen]) ⇒ uitdrukking

Geeft een decimaal getal uit de gespecificeerde normale verdeling. Dit kan elk reëel getal zijn, maar het zal sterk geconcentreerd zijn in

het interval [mN3·s, m+3·s].

randPoly()

randPoly(Va r , Orde) ⇒ uitdrukking

Geeft een veelterm in Va r van de gespecificeerde Orde. De coëfficiënten zijn gehele toevalsgetallen in het bereik ë9 tot en met

9. De leidende coëfficiënt is niet nul. Orde moet 0–99 zijn.

Catalogus

Opmerking: de waarden in deze matrix veranderen elke keer

dat u op · drukt.

Catalogus

randSamp()

randSamp(Lijst,#Pogingen[,geenTerugl]) ⇒ lijst

Geeft een lijst met een willekeurige steekproef van #Pogingen uit Lijst met teruglegging (geenTerugl=0), of zonder teruglegging (geenTerugl=1). De standaardinstelling is met teruglegging.

Catalogus

TI-Nspire™ Referentiehandleiding 73

RandSeed

RandSeed Getal

Als Getal = 0, dan worden de seeds op de fabrieksinstellingen voor de generator van toevalsgetallen ingesteld. Als Getal commando gebruikt om twee seeds te genereren, die opgeslagen worden in systeemvariabelen seed1 en seed2.

ƒ 0, wordt dit

Catalogus

real()

real(Waarde1) ⇒ waarde

Geeft het reële deel van het argument.

Opmerking: alle onbepaalde variabelen worden behandeld als

reële variabelen. Zie ook imag(), pag. 41.

real(Lijst1) ⇒ lijst

Geeft de reële delen van alle elementen.

real(Matrix1) ⇒ matrix

Geeft de reële delen van alle elementen.

Rect

Vec t o r 4Rect

Geeft Ve ct o r in rechthoekige vorm [x, y, z]. De vector moet de afmeting 2 of 3 hebben en kan een rij of een kolom zijn.

Opmerking: 4Rect is een weergave-opmaakinstructie, geen

conversiefunctie. U kunt dit commando alleen gebruiken op het eind van een invoerregel, en ans wordt niet bijgewerkt.

Opmerking: zie ook 4Polar, pag. 67.

complexeWaarde 4Rect

Geeft complexeWaarde in rechthoekige vorm a+bi weer. De complexeWaarde kan elke complexe vorm hebben. Een re

veroorzaakt echter een fout in de hoekmodus Graden.

Opmerking: u moet haakjes gebruiken voor een (rq) polaire

invoer.

-invoer

In de hoekmodus Radialen:

In de hoekmodus Decimale graden:

Catalogus

In de hoekmodus Graden:

Opmerking: om  te typen selecteert u dit uit de

symbolenlijst in de Catalogus.

74 TI-Nspire™ Referentiehandleiding

ref()

ref(Matrix1[, To l]) ⇒ matrix

Geeft de rij-echelon-vorm van Matrix1. Optioneel wordt elk matrixelement behandeld als nul als de absolute

waarde ervan minder dan To l is. Deze tolerantie wordt alleen gebruikt als de matrix gegevens met een drijvende komma heeft, en geen symbolische variabelen bevat die geen waarde toegekend hebben gekregen. Anders wordt To l genegeerd.

•Als u

Benaderend

met behulp van de drijvende komma uitgevoerd.

•Als Tol wordt weggelaten of niet wordt gebruikt, dan wordt de standaardtolerantie berekend als:

5Eë14 ·max(dim(Matrix1)) ·rowNorm(Matrix1)

Opmerking: zie ook rref(), pag. 78.

· gebruikt of de modus Automatisch of

instelt op Benaderend, dan worden berekeningen

Catalogus

remain()

remain(Waarde1, Waarde2) ⇒ waarde remain(Lijst1, Lijst2) ⇒ lijst remain(Matrix1, Matrix2) ⇒ matrix

Geeft de rest van het eerste argument ten opzichte van het tweede argument zoals gedefinieerd wordt door de identiteiten:

remain(x,0)  x remain(x,y)  xNy·iPart(x/y)

Merk op dat dientengevolge geldt: remain(Nx,y)  Nremain(x,y). Het resultaat is nul of heeft hetzelfde teken als het eerste argument.

Opmerking: zie ook mod(), pag. 56.

Return

Return [Uitdr]

Geeft Uitdr als het resultaat van de functie. Gebruik dit commando binnen een Func...EndFunc-blok.

Opmerking: Gebruik Return zonder argument binnen een Prgm...EndPrgm-blok om een programma te verlaten.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

right()

right(Lijst1[, Aantal]) ⇒ lijst

Geeft het meest rechtse Aantal elementen in Lijst1. Als u Aantal weglaat, wordt de hele Lijst1 gegeven.

Catalogus

TI-Nspire™ Referentiehandleiding 75

right()

right(bronString[, Aantal]) ⇒ string

Geeft het meest rechtse Aantal tekens in tekenreeks bronString. Als u Aantal weglaat, wordt de hele bronString gegeven.

right(Ver g e li j k en ) ⇒ uitdrukking

Geeft het rechterlid van een vergelijking of ongelijkheid.

Catalogus

root()

root(Waarde) ⇒ wortel root(Waarde1, Waarde2) ⇒ wortel

root(Waarde) geeft de wortel van Waarde. root(Waarde1, Waarde2) geeft de Waarde2-wortel van Waarde1.

Waarde1 kan een reël e of complexe constante met drijvende komma, een geheel getal of een complexe rationale constante zijn.

Opmerking: zie ook N-de wortel-template, pag. 1.

rotate()

rotate(Geheel getal1[,#Rotaties]) ⇒ geheel getal

Roteert de bits in een binair geheel getal. U kunt Geheel getal1 in elk grondtal invoeren; het wordt automatisch geconverteerd naar een 64bits binaire vorm met een teken. Als de grootte van Geheel getal1 te groot is voor deze vorm, dan wordt een symmetrische modulobewerking gebruikt om het binnen het bereik te brengen.

Als #Rotaties positief is, dan is de rotatie naar links. Als #Rotaties negatief is, dan is de rotatie naar rechts. De standaardinstelling is ë1 (één bit naar rechts roteren).

Bijvoorbeeld in een rotatie naar rechts:

Elk bit roteert naar rechts. 0b00000000000001111010110000110101 Het meest rechtse bit roteert naar het meest linkse. Dit levert op: 0b10000000000000111101011000011010 Het resultaat wordt weergegeven volgens de grondtal-modus.

rotate(Lijst1[,#Rotaties]) ⇒ lijst

Geeft een kopie van Lijst1 die met #Rotaties elementen naar rechts of links is geroteerd. Verandert Lijst1 niet.

Als #Rotaties positief is, dan is de rotatie naar links. Als #Rotaties negatief is, dan is de rotatie naar rechts. De standaardinstelling is ë1 (één element naar rechts roteren).

rotate(String1[,#Rotaties]) ⇒ string

Geeft een kopie van String1 die met #Rotaties tekens naar rechts of links is geroteerd. Verandert String1 niet.

Als #Rotaties positief is, dan is de rotatie naar links. Als #Rotaties negatief is, dan is de rotatie naar rechts. De standaardinstelling is ë1 (één teken naar rechts roteren).

Catalogus

In de Bin-grondtalmodus:

Om het hele resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.

In de Hex-grondtalmodus:

Belangrijk: om een binair of hexadecimaal getal in te voeren moet u altijd het prefix 0b of 0h gebruiken (nul, niet de letter O).

In de Dec-grondtalmodus:

76 TI-Nspire™ Referentiehandleiding

round()

round(Waarde1[, cijfers]) ⇒ waarde

Geeft het argument, afgerond op het gespecificeerde aantal cijfers achter de komma.

cijfers moet een geheel getal van 0–12 zijn. Als cijfers niet opgenomen wordt, dan wordt het argument afgerond op 12 significante cijfers.

Opmerking: de cijferweergavemodus kan invloed hebben op hoe

dit wordt weergegeven.

round(Lijst1[, cijfers]) ⇒ lijst

Geeft een lijst van een elementen, afgerond op het gespecificeerde aantal cijfers.

round(Matrix1[, cijfers]) ⇒ matrix

Geeft een matrix met de elementen, afgerond op het gespecificeerde aantal cijfers.

Catalogus

rowAdd()

rowAdd(Matrix1, rIndex1, rIndex2) ⇒ matrix

Geeft een kopie van Matrix1 met rij rIndex2 vervangen door de som van rijen rIndex1 en rIndex2.

rowDim()

rowDim(Matrix) ⇒ uitdrukking

Geeft het aantal rijen in Matrix.

Opmerking: zie ook colDim(), pag. 14.

rowNorm()

rowNorm(Matrix) ⇒ uitdrukking

Geeft het maximum van de sommen van de absolute waarden van de elementen in de rijen in Matrix.

Opmerking: alle matrixelementen moeten vereenvoudigen tot

getallen. Zie ook colNorm(), pag. 14.

rowSwap()

rowSwap(Matrix1, rIndex1, rIndex2) ⇒ matrix

Geeft Matrix1 met rijen rIndex1 en rIndex2 omgewisseld.

Catalogus

TI-Nspire™ Referentiehandleiding 77

rref()

rref(Matrix1[, To l]) ⇒ matrix

Geeft de gereduceerde rij-echelon-vorm van Matrix1.

•Als u

Benaderend

met behulp van de drijvende komma uitgevoerd.

•Als Tol wordt weggelaten of niet wordt gebruikt, dan wordt de standaardtolerantie berekend als:

5Eë14 ·max(dim(Matrix1)) ·rowNorm(Matrix1)

Opmerking: zie ook ref(), page 75.

· gebruikt of de modus Automatisch of

instelt op Benaderend, dan worden berekeningen

Catalogus

sec()

sec(Waarde1) ⇒ waarde sec(Lijst1) ⇒ lijst

Geeft de secans van Waarde1 of geeft een lijst met de secansen van alle elementen in Lijst1.

Opmerking: het argument wordt geïnterpreteerd als een hoek in

graden, decimale graden of radialen volgens de huidige hoekmodusinstelling. U kunt ó,G ofôgebruiken om de hoekmodus tijdelijk te

onderdrukken.

sec/()

sec/(Waarde1) ⇒ waarde sec/(Lijst1) ⇒ lijst

Geeft de hoek waarvan de secans Waarde1 is of geeft een lijst met de inverse secans van elk element in Lijst1.

Opmerking: de uitkomst wordt in graden, decimale graden of

radialen gegeven, volgens de ingestelde hoekmodus.

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

Catalogus

78 TI-Nspire™ Referentiehandleiding

sech()

sech(Waarde1) ⇒ waarde sech(Lijst1) ⇒ lijst

Geeft de secans hyperbolicus van Waarde1 of geeft een lijst met de secansen hyperbolicus van de elementen in Lijst1.

Catalogus

sechê()

sechê(Waarde1) ⇒ waarde sechê (Lijst1) ⇒ lijst

Geeft de inverse secans hyperbolicus van Waarde1 of geeft een lijst met de inverse secans hyperbolicus van elk element in Lijst1.

seq()

seq(Uitdr, Var , Laag, Hoog[, Sta p]) ⇒ lijst

Verhoogt Va r van Laag naar Hoog met een stapgrootte van Stap , werkt Uitdr uit en geeft de resultaten in een lijst. De oorspronkelijke inhoud van Va r is er nog steeds nadat seq() is uitgevoerd.

Var kan geen systeemvariabele zijn. De standaardwaarde voor Sta p = 1.

Catalogus

In de hoekmodus Radialen en rechthoekige complexe opmaak:

Catalogus

Druk op Ctrl+Enter /· om dit uit te werken:

TI-Nspire™ Referentiehandleiding 79

setMode()

setMode(modeNaamGeheel getal, instellingGeheel getal)

⇒ geheel getal

setMode(lijst) ⇒ lijst met gehele getallen

Alleen geldig binnen een functie of programma.

setMode(modeNaamGeheel getal, instellingGeheel getal)

stelt de modus modeNaamGeheel getal tijdelijk in op de nieuwe instelling instellingGeheel getal, een geeft een geheel getal dat correspondeert met de oorspronkelijke instelling van die modus. De verandering is beperkt tot de duur van de uitvoering van het programma/de functie.

modeNaamGeheel getal specificeert welke modus u wilt instellen. Dit moet één van de gehele getallen voor modi in onderstaande tabel zijn.

instellingGeheel getal specificeert de nieuwe instelling voor de modus. Dit moet één van de gehele getallen voor instellingen in onderstaande tabel zijn, voor de specifieke modus die u instelt.

setMode(lijst) stelt u in staat meerdere instellingen te

veranderen. lijst bevat paren van gehele getallen voor modi en instellingen. setMode(lijst) geeft een vergelijkbare lijst waarvan de paren gehele getallen de oorspronkelijke modi en instellingen representeren.

Als u alle modusinstellingen hebt opgeslagen met getMode(0)

& var, dan kunt u setMode(var) gebruiken om die

instellingen te herstellen tot de functie of het programma wordt afgesloten. Zie getMode(), pag. 37.

Opmerking: de huidige modusinstellingen worden

doorgegeven aan opgeroepen subroutines. Als een subroutine een modusinstelling verandert, dan gaat de modusverandering verloren als de besturing terugkeert naar de oproeproutine.

Opmerking voor het invoeren van het voorbeeld:

In de Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats

van op · aan het eind van elke regel. Op het toetsenbord v an de computer houdt u Alt ingedrukt en drukt u op Enter.

Catalogus

Geef de benaderde waarde van p weer met behulp van de standaardinstelling voor Cijfers weergeven, en geef p vervolgens weer met een instelling van Vast2. Controleer om te zien of de

standaardinstelling hersteld wordt nadat het programma is uitgevoerd.

Modusnaam

Cijfers weergeven

Hoek

Exponentiële opmaak

Reëel of complex

Automatisch of benaderend

Vectoropmaak

Grondtal

Modus nummer Instellingsnummers

=Drijvend, 2=Drijvend1, 3=Drijvend2, 4=Drijvend3, 5=Drijvend4, 6=Drijvend5,

7=Drijvend6, 8=Drijvend7, 9=Drijvend8, 10=Drijvend9, 11=Drijvend10, 12=Drijvend11, 13=Drijvend12, 14=Vast0, 15=Vast1, 16=Vast2, 17=Vast3, 18=Vast4, 19=Vast5, 20=Vast6, 21=Vast7, 22=Vast8, 23=Vast9, 24=Vast10, 25=Vast11, 26=Vast12

=Radialen, 2=Graden, 3=Decimale graden

=Normaal, 2=Wetenschappelijk, 3=Ingenieursnotatie

=Reëel, 2=Rechthoekig, 3=Polair

=Automatisch, 2=Benaderend

=Rechthoekig, 2=Cilindrisch, 3=Bolvormig

=Decimaal, 2=Hexadecimaal, 3=Binair

80 TI-Nspire™ Referentiehandleiding

shift()

shift(Geheel getal1[,#Verschuivingen]) ⇒ geheel getal

Verschuift de bits in een binair geheel getal. U kunt Geheel getal1 in elk grondtal invoeren; het wordt automatisch geconverte erd naar een 64-bits binaire vorm met een teken. Als de groott e van Geheel getal1 te groot is voor deze vorm, dan wordt een symmetrische modulobewerking gebruikt om het binnen het bereik te brengen.

Als #Verschuivingen p ositief is, dan is de verschuiving naar links. Als #Verschuivingen negatief is, dan is de verschuiving naar rechts. De standaardinstelling is ë1 (één bit naar rechts verschuiven).

In een verschuiving naar rechts vervalt de meest rechtse bit en wordt 0 of 1 ingevoegd om overeen te komen met de meest linkse bit. In een verschuiving naar links vervalt de meest linkse bit en wordt 0 ingevoegd als de meest rechtse bit.

Bijvoorbeeld in een verschuiving naar rechts: Elke bit schuift naar rechts. 0b0000000000000111101011000011010 Voegt 0 in als de meest linkse bit 0 is,

of 1 als de meest linkse bit 1 is. Dit levert op: 0b0000000000000011110101100001101-0 Het resultaat wordt weergegeven volgens de grondtal-modus. Nullen

aan het begin worden niet weergegeven.

shift(Lijst1 [,#Verschuivingen]) ⇒ lijst

Geeft een kopie van Lijst1 die met #Verschuivingen elementen naar rechts of links is verschoven. Verandert Lijst1 niet.

Als #Verschuivingen positief is, dan is de verschuiving naar links. Als #Verschuivingen negatief is, dan is de verschuiving naar rechts. De standaardinstelling is ë1 (één element naar rechts verschuiven).

Elementen die aan het begin of eind van lijst ingevoegd worden door de verschuiving, worden ingesteld op het symbool “undef”.

shift(String1 [,#Verschuivingen]) ⇒ string

Geeft een kopie van String1 die met #Verschuivingen tekens naar rechts of links is verschoven. Verandert String1 niet.

Als #Verschuivingen positief is, dan is de verschuiving naar links. Als #Verschuivingen negatief is, dan is de verschuiving naar rechts. De standaardinstelling is ë1 (één teken naar rechts verschuiven).

Tekens die aan het begin of eind van string ingevoegd worden door de verschuiving, worden ingesteld op een spatie.

Catalogus

In de Bin-grondtalmodus:

In de Hex-grondtalmodus:

Belangrijk: om een binair of hexadecimaal getal in te voeren

moet u altijd het prefix 0b of 0h gebruiken (nul, niet de letter O).

In de Dec-grondtalmodus:

sign()

sign(Waarde1) ⇒ waarde sign(Lijst1) ⇒ lijst sign(Matrix1) ⇒ matrix

Geeft, bij reële en complexe Waarde1, Waarde1 / abs(Waarde1) wanneer Waarde1ƒ 0.

Als de complexe opmaak-modus Reëel is:

Catalogus

Geeft 1 als Waarde1 positief is. Geeft ë1 als Waarde1 negatief is.

sign(0) geeft „1 als de complexe opmaak-modus Reëel is; anders

geeft hij zichzelf.

sign(0) representeert de eenheidscirkel in het complexe vlak.

Geeft bij een lijst of matrix de tekens van alle elementen.

TI-Nspire™ Referentiehandleiding 81

simult()

simult(coëffMatrix, constVector[, Tol ]) ⇒ matrix

Geeft een kolomvector die de oplossingen voor een stelsel lineaire vergelijkingen bevat.

coëffMatrix moet een vierkante matrix zijn die de coëfficiënten van de vergelijkingen bevat.

constVector moet hetzelfde aantal rijen (dezelfde afmeting) als coëffMatrix hebben en de constanten bevatten.

Optioneel wordt elk matrixelement behandeld als nul als de absolute waarde ervan minder dan To l is. Deze tolera ntie wordt alleen gebruikt als de matrix gegevens met een drijvende komma heeft, en geen symbolische variabelen bevat die geen waarde toegekend hebben gekregen. Anders wordt To l genegeerd.

• Als u de modus Automatisch of Benaderend instelt op Benaderend, dan worden berekeningen met behulp van de drijvende komma uitgevoerd.

•Als Tol wordt weggelaten of niet wordt gebruikt, dan wordt de standaardtolerantie berekend als:

5Eë14 ·max(dim(coëffMatrix)) ·rowNorm(coëffMatrix)

simult(coëffMatrix, constMatrix[, To l]) ⇒ matrix

Lost meerdere stelsels lineaire vergelijkingen op, waarbij elk stelsel dezelfde vergelijkingscoëfficiënten, maar verschillende constanten heeft.

Elke kolom in constMatrix moet de constanten voor een stelsel vergelijkingen bevatten. Elke kolom in de resulterende matrix bevat de oplossing voor het corresponderende stelsel.

Catalogus

Los op naar x en y: x + 2y = 1 3x + 4y = ë1

De oplossing is x=ë3 en y=2.

Los op: ax + by = 1 cx + dy = 2

Los op:

x + 2y = 1

3x + 4y = ë1

x + 2y = 2

3x + 4y = ë3

Voor het eerste stelsel: x=ë3 en y=2. Voor het tweede stelsel: x=ë7 en y=9/2.

sin()

sin(Waarde1) ⇒ waarde sin(Lijst1) ⇒ lijst

sin(Waarde1) geeft de sinus van het argument. sin(Lijst1) geeft een lijst van de sinussen van alle elementen in

Lijst1.

Opmerking: het argument wordt geïnterpreteerd als een hoek in

graden, in decimale graden of in radialen, volgens de ingestelde hoekmodus. U kunt ó,G of ô gebruiken om de hoekmodusinstelling

tijdelijk te onderdrukken.

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

-toets

82 TI-Nspire™ Referentiehandleiding

sin()

sin(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de matrixsinus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de sinus van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

In de hoekmodus Radialen:

-toets

sinê()

sinê(Waarde1) ⇒ waarde sinê(Lijst1) ⇒ lijst

sinê(Waarde1) geeft de hoek waarvan de waarde Waarde1 is.

sinê(Lijst1) geeft een lijst van de inverse sinussen van elk element

in Lijst1.

Opmerking: de uitkomst wordt in graden, decimale graden of

radialen gegeven, volgens de ingestelde hoekmodus.

sinê(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de inverse matrixsinus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de inverse sinus van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

sinh()

sinh(Getal1) ⇒ waarde sinh(Lijst1) ⇒ lijst

sinh (Waarde1) geeft de sinus hyperbolicus van het argument. sinh (Lijst1) geeft een lijst met de sinus hyperbolicus van elk

element in Lijst1.

sinh(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de matrixsinus hyperbolicus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de sinus hyperbolicus van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

In de hoekmodus Radialen en rechthoekige complexe opmaakmodus:

Om het hele resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.

In de hoekmodus Radialen:

Catalogus

-toetsen

TI-Nspire™ Referentiehandleiding 83

sinhê()

sinhê(Waarde1) ⇒ waarde sinhê(Lijst1) ⇒ lijst

sinhê(Waarde1) geeft de inverse sinus hyperbolicus van het

argument.

sinhê(Lijst1) geeft een lijst met de inverse sinus hyperbolicus van

elk element in Lijst1.

sinhê(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de inverse matrixsinus hyperbolicus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de inverse sinus hyperbolicus van elk element. Zie voor informatie over de berekeningsmethode

cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

In de hoekmodus Radialen:

Catalogus

SinReg

SinReg X, Y [, [Iteraties], [ Periode] [, Categorie, Opnemen] ]

Berekent de sinusoïde regressie op de lijsten X en Y. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Catalogus

Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen. X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Iteraties is een waarde die het maximaal aantal keer (1 tot en met

16) specificeert dat een oplossing wordt geprobeerd. Als dit wordt

weggelaten, wordt 8 gebruikt. Doorgaans leiden grotere waarden tot een hogere nauwkeurigheid maar een langere berekeningstijd, en andersom.

Periode specificeert een geschatte periode. Als deze wordt weggelaten, dan moet het verschil tussen waarden in X gelijk zijn en in volgorde. Als u Periode specificeert, kunnen de verschillen tussen x-waarden ongelijk zijn.

Categorie is een lijst met numerieke categoriecodes voor de overeenkomstige X- en Y-gegevens.

Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening.

De uitvoer van SinReg is altijd in radialen, ongeacht de instelling van de hoekmodus.

Uitvoervariabele Beschrijving

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

Regressievergelijking: a·sin(bx+c)+d

Regressiecoëfficiënten

stat.Resid Residuen uit de regressie

stat.XReg Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van

stat.YReg Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van

beperkingen van Freq, Categorielijst en Categorieën opnemen

84 TI-Nspire™ Referentiehandleiding

Uitvoervariabele Beschrijving

stat.FreqReg Lijst van frequenties die corresponderen met stat.XReg en stat.YReg

SortA

SortA Lijst1[, Lijst2] [, Lijst3] ... SortA

Vector1[, Vector2] [, Vector3] ...

Sorteert de elementen van het eerste argument in oplopende volgorde.

Als u extra argumenten opneemt, dan worden de elementen van elk daarvan gesorteerd, zodat de nieuwe posities overeenkomen met de nieuwe posities van de elementen in het eerste argument.

Alle argumenten moeten namen van lijsten of vectoren zijn. Alle argumenten moeten gelijke afmetingen hebben.

SortD

SortD Lijst1[, Lijst2] [, Lijst3] ... SortD

Vector1[,Vector2] [,Vector3] ...

Identiek aan SortA, behalve dat SortD de elementen in aflopende volgorde sorteert.

Sphere

Vec t o r 4Sphere

Geeft de rij- of de kolomvector in bolvorm weer [r q f].

Vec t o r moet de afmeting 3 hebben en kan een rij- of een kolomvector zijn.

Opmerking: 4Sphere is een weergave-opmaakinstructie, geen

conversiefunctie. U kunt dit commando alleen op het eind van een invoerregel gebruiken.

Catalogus

(ρ,θ,φ)

TI-Nspire™ Referentiehandleiding 85

sqrt()

sqrt(Waarde1) ⇒ waarde sqrt(Lijst1) ⇒ lijst

Geeft de wortel van het argument. Geeft bij een lijst de wortel van alle elementen in Lijst1.

Opmerking: zie ook

Wortel

-template

, pag. 1.

stat.results (stat.resultaten)

stat.results

Geeft resultaten van een statistische berekening weer. De resultaten worden weergegeven als een serie naam-waarde-

paren. De weergegeven specifieke namen zijn afhankelijk van de meest recent uitgewerkte statistiekfunctie of -commando.

U kunt een naam of waarde kopiëren en hem in andere locaties plakken.

Opmerking: vermijd het om variabelen te definiëren die dezelfde

namen hebben als de variabelen die gebruikt worden bij statistische analyse. In bepaalde gevallen zou er dan een fout kunnen optreden. Variabelenamen die gebruikt worden voor statistische analyse staan in onderstaande tabel vermeld.

Catalogus

stat.a stat.AdjR² stat.b stat.b0 stat.b1 stat.b2 stat.b3 stat.b4 stat.b5 stat.b6 stat.b7 stat.b8 stat.b9 stat.b10 stat.bList stat.c² stat.c stat.CLower stat.CLowerList stat.CompList stat.CompMatrix stat.CookDist stat.CUpper stat.CUpperList stat.d

stat.dfDenom stat.dfBlock stat.dfCol stat.dfError stat.dfInteract stat.dfReg stat.dfNumer stat.dfRow stat.DW stat.e stat.ExpMatrix stat.F

stat.FBlock stat.Fcol stat.FInteract stat.FreqReg stat.Frow stat.Leverage

stat.LowerPred stat.LowerVal stat.m stat.MaxX stat.MaxY stat.ME stat.MedianX

stat.MedianY stat.MEPred stat.MinX stat.MinY stat.MS stat.MSBlock stat.MSCol stat.MSError stat.MSInteract stat.MSReg stat.MSRow stat.n stat.Ç stat.Ç1

stat.Ç2 stat.ÇDiff stat.PList stat.PVal stat.PValBlock

stat.PValCol stat.PValInteract stat.PValRow stat.Q1X stat.Q1Y stat.Q3X

stat.Q3Y stat.r stat.r² stat.RegEqn stat.Resid stat.ResidTrans stat.sx stat.sy

stat.sx1 stat.sx2 stat.Gx stat.Gx² stat.Gxy stat.Gy stat.Gy² stat.s stat.SE

stat.SEList stat.SEPred stat.sResid stat.SEslope stat.sp stat.SS stat.SSBlock

stat.SSCol stat.SSX stat.SSY stat.SSError stat.SSInteract stat.SSReg stat.SSRow stat.tList stat.UpperPred stat.UpperVal stat.v stat.v1 stat.v2

stat.vDiff stat.vList stat.XReg stat.XVal stat.XValList

stat.w stat.y

stat.yList stat.YReg

86 TI-Nspire™ Referentiehandleiding

Opmerking: telkens wanneer de Lijsten & Spreadsheet-toepassing stat istische resultaten berekent, kopieert deze de variabelen uit

de "stat groep ." naar een groep "stat #.", waarbij # een getal is dat automatisch toeneemt. Hierdoor kunt u eerdere resultaten behouden terwijl u meerdere berekeningen uitvoert.

stat.values

Geeft een matrix met de waarden die berekend zijn voor de meest recent uitgewerkte statistiekfunctie of -commando.

In tegenstelling tot geassocieerd zijn met de waarden weg.

stat.results laat stat.values de namen die

U kunt een waarde kopiëren en deze op andere locaties plakken.

stDevPop()

stDevPop(Lijst[, freqLijst]) ⇒ uitdrukking

Geeft de populatiestandaarddeviatie van de elementen in Lijst. Elk element uit freqLijst telt het aantal malen dat het

overeenkomstige element in Lijst achter elkaar voorkomt.

Opmerking: Lijst moet tenminste twee elementen hebben. stDevPop(Matrix1[, freqMatrix]) ⇒ matrix

Geeft een rijvector met de populatiestandaarddeviaties van de kolommen in Matrix1.

Elk element van freqMatrix telt het aantal opeenvolgende malen dat het overeenkomstige element voorkomt in Matrix1.

Opmerking: Matrix1 moet tenminste twee rijen hebben.

stDevSamp()

stDevSamp(Lijst[, freqLijst]) ⇒ uitdrukking

Geeft de steekproefstandaarddeviatie van de elementen in Lijst. Elk element uit freqLijst telt het aantal malen dat het

overeenkomstige element in Lijst achter elkaar voorkomt.

Opmerking: Lijst moet tenminste twee elementen hebben. stDevSamp(Matrix1[, freqMatrix]) ⇒ matrix

Geeft een rijvector met de steekproefstandaarddeviaties van de kolommen in Matrix1.

Elk element van freqMatrix telt het aantal opeenvolgende malen dat het overeenkomstige element voorkomt in Matrix1.

Opmerking: Matrix1 moet tenminste twee rijen hebben.

Catalogus

Zie het voorbeeld

stat.results.

Catalogus

In de hoekmodus Radialen en de automatisch modus:

Catalogus

TI-Nspire™ Referentiehandleiding 87

Stop

Programmeringscommando: beëindigt het programma.

Stop is niet toegestaan in functies. Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Catalogus

Store

string()

string(Uitdr) ⇒ string

Vereenvoudigt Uitdr en geeft het resultaat als een tekenreeks.

subMat()

subMat(Matrix1[, startRij] [, startKol] [, eindRij] [, eindKol])

⇒ matrix

Geeft de gespecificeerde submatrix van Matrix1. Standaardinstellingen: startRij=1, startKol=1, eindRij=laatste rij,

eindKol=laatste kolom.

Som (Sigma)

sum()

sum(Lijst[, Star t[, Eind]]) ⇒ uitdrukking

Geeft de som van de elementen in Lijst. Start en Eind zijn optioneel. Ze specificeren een bereik van

elementen.

zie

& (store)

Catalogus

Zie G(), pag. 113.

Catalogus

, pag. 117.

88 TI-Nspire™ Referentiehandleiding

sum()

sum(Matrix1[, Start[, Eind]]) ⇒ matrix

Geeft een rijvector met de sommen van de elementen in de kolommen van Matrix1.

Start en Eind zijn optioneel. Ze specificeren een bereik van rijen.

Catalogus

sumIf()

sumIf(Lijst,Criteria[, SomLijst]) ⇒ waarde

Geeft de cumulatieve som van alle elementen in Lijst die vol doen aan de gespecificeerde Criteria. Optioneel kunt u een alternatieve lijst specificeren, somLijst, om de elementen te leveren die opgeteld moeten worden.

Lijst kan een uitdrukking, een lijst of een matrix zijn. SomLijst, indien gespecificeerd, moet dezelfde afmeting(en) hebben als Lijst.

Criteria kan zijn:

• Een waarde, uitdrukking of tekenreeks. Bijvoorbeeld: 34 telt alleen die elementen in Lijst op die vereenvoudigd worden tot de waarde 34.

• Een Booleaanse uitdrukking met het symbool ? als plaatsaanduiding voor elk element. Bijvoorbeeld, ?<10 telt alleen die elementen in Lijst op die kleiner zijn dan 10.

Als een Lijst-element voldoet aan de Criteria, dan wordt het element opgeteld bij de cumulatieve som. Als u somLijst opneemt, dan wordt in plaats daarvan het overeenkomstige element van somLijst bij de som opgeteld.

In de toepassing Lijsten & Spreadsheet kunt u een reeks cellen gebruiken op de plaats van Lijst en somLijst.

Opmerking: zie ook countIf(), pag. 19.

system()

system(Waarde1 [, Waarde2 [, Waarde3 [, ...]]])

Geeft een stelsel vergelijkingen, in de vorm van een lijst. U kunt ook een stelsel creëren met behulp van een template.

Opmerking: zie ook Stelsel van vergelijkingen, pag. 1.

Catalogus

(transponeren)

Matrix1

⇒ matrix

Geeft de complex geconjugeerde transponering van Matrix1.

Catalogus

TI-Nspire™ Referentiehandleiding 89

tan()

tan(Waarde1) ⇒ waarde tan(Lijst1) ⇒ lijst

tan(Waarde1) geeft de tangens van het argument. tan(Lijst1) geeft een lijst met de tangensen van alle elementen in

Lijst1.

Opmerking: het argument wordt geïnterpreteerd als een hoek in

graden, in decimale graden of in radialen, volgens de ingestelde hoekmodus. U kunt ó,G ofôgebruiken om de instelling van de

hoekmodus tijdelijk te onderdrukken.

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

-toets

tan(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de matrixtangens van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de tangens van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

tanê()

tanê(Waarde1) ⇒ waarde tanê(Lijst1) ⇒ lijst

tanê(Waarde1) geeft de hoek waarvan de tangens Waarde1 is.

tanê(Lijst1) geeft een lijst met de inverse tangens van elk element

in Lijst1.

Opmerking: de uitkomst wordt in graden, decimale graden of

radialen gegeven, volgens de ingestelde hoekmodus.

In de hoekmodus Radialen:

In de hoekmodus Graden:

In de hoekmodus Decimale graden:

In de hoekmodus Radialen:

-toetsen

90 TI-Nspire™ Referentiehandleiding

tanê()

tanê(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de inverse matrixtangens van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de inverse tangens van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

In de hoekmodus Radialen:

-toetsen

tanh()

tanh(Waarde1) ⇒ waarde tanh(Lijst1) ⇒ lijst

tanh(Waarde1) geeft de tangens hyperbolicus van het argument. tanh(Lijst1) geeft een lijst met de tangens hyperbolicus van elk

element in Lijst1.

tanh(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de matrixtangens hyperbolicus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de tangens hyperbolicus van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

tanhê()

tanhê(Waarde1) ⇒ waarde tanhê(Lijst1) ⇒ lijst

tanhê(Waarde1) geeft de inverse tangens hyperbolicus van het

argument.

tanhê(Lijst1) geeft een lijst van de inverse tangens hyperbolicus

van elk element in Lijst1.

tanhê(vierkanteMatrix1) ⇒ vierkanteMatrix

Geeft de inverse matrixtangens hyperbolicus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de inverse tangens hyperbolicus van elk element. Zie voor informatie over de berekeningsmethode cos().

vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma.

Catalogus

In de hoekmodus Radialen:

Catalogus

In rechthoekige complexe opmaak:

Om het hele resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.

In de hoekmodus Radialen en rechthoekige complexe opmaak:

Om het hele resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.

TI-Nspire™ Referentiehandleiding 91

tCdf()

tCdf(ondergrens,bovengrens,df) ⇒ getal als ondergrens en

bovengrens getallen zijn, lijst als ondergrens en bovengrens

lijsten zijn

Berekent de Student-t-verdelingskans tussen ondergrens en bovengrens bij de gespecificeerde vrijheidsgraden df.

 bovengrens) stelt u ondergrens = in.9E999.

Voor P(X

Then Zie If, pag. 40.

Catalogus

tInterval

TInterval Lijst[,Freq[,CNiveau]]

(Invoer van een gegevenslijst)

TInterval v,Sx,n[,CNiveau]

(Invoer van samenvattingsstatistieken) Berekent een t-betrouwbaarheidsinterval. Een samenvatting van

de resultaten wordt opgeslagen in de variabele stat.resultaten. (Zie pag. 86).

Uitvoervariabele Beschrijving

stat.CLower, stat.CUpper Betrouwbaarheidsinterval voor een onbekend populatiegemiddelde

stat.x

stat.ME Foutmarge

stat.df Vrijheidsgraden

stat.sx

stat.n Lengte van de gegevensverzameling met het steekproefgemiddelde

tInterval_2Samp

Lijst1,Lijst2[,Freq1[,Freq2[,CNiveau[,Gepoold]]]]

(Invoer van een gegevenslijst)

tInterval_2Samp v1,sx1,n1,v2,sx2,n2[,CNiveau[,Gepoold]]

(Invoer van samenvattingsstatistieken) Berekent een t-betrouwbaarheidsinterval met twee steekproeven. Een

samenvatting van de resultaten wordt opgeslagen in de variabele

stat.results. (Zie pag. 86). Gepoold=1 poolt de varianties; Gepoold=0 poolt de varianties niet.

Steekproefgemiddelde van de gegevensverzameling uit een normale willekeurige verdeling

Standaarddeviatie steekproef

Catalogus

Uitvoervariabele Beschrijving

stat.CLower, stat.CUpper Betrouwbaarheidsinterval met de betrouwbaarheidskans gebaseerd op de verdeling

92 TI-Nspire™ Referentiehandleiding

Uitvoervariabele Beschrijving

stat.x1-x2

stat.ME Foutmarge

stat.df Vrijheidsgraden

stat.

x1, stat.x2

stat.sx1, stat.sx2

stat.n1, stat.n2 Aantal steekproeven in de gegevensverzamelingen

stat.sp De gepoolde standaarddeviatie. Berekend wanneer Gepoold =JA.

Steekproefgemiddelden van de gegevensverzameling uit de willekeurige normale verdeling

Steekproefstandaarddeviaties voor Lijst 1 en Lijst 2

tPdf()

tPdf(XWaarde,df) ⇒ getal als XWaarde een getal is, lijst als

XWaarde een lijst is

Berekent de kansdichtheidsfunctie (pdf) voor de Student-t-verdeling bij een gespecificeerde x-waarde met de gespecificeerde vrijheidsgraden df.

trace()

trace(vierkanteMatrix) ⇒ waarde

Geeft het spoor (som van alle elementen van de hoofddiagonaal) van vierkanteMatrix.

Catalogus

TI-Nspire™ Referentiehandleiding 93

Try

blok1

Else

blok2

EndTry

Voert blok1 uit tenzij er een fout optreedt. De uitvoering van het programma gaat over naar blok2 als er een fout optreedt in blok1. Systeemvariabele errCode bevat de foutcode zodat het programma foutherstel kan uitvoeren. Zie "Foutcodes en meldingen", pag. 119 voor een lijst met foutcodes.

blok1 en blok2 kunnen een enkele bewering of een serie beweringe n zijn die gescheiden worden door het teken “:”.

Opmerking voor het invoeren van het voorbeeld: In de

Rekenmachine-toepassing op de rekenmachine kunt u meerregelige definities invoeren door op @ te drukken in plaats van op ·

aan het eind van elke regel. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.

Catalogus

Voorbeeld 2

Om de commando's Try , ClrErr en PassErr in werking te zien, voert u het eigenvals() programma in dat rechts wordt weergegeven. Voer het programma uit door elk van de volgende uitdrukkingen uit te voeren.

Opmerking: zie ook ClrErr, pag. 14 en PassErr, pag. 66.

tTest

tTest m0,Lijst[,Freq[,Hypoth]]

(Invoer van een gegevenslijst)

tTest m0,x,sx,n,[Hypoth]

(Invoer van samenvattingsstatistieken) Voert een hypothesetoets uit voor één onbekend

populatiegemiddelde, m, wanneer de populatiestandaarddeviate, s, onbekend is. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.results. (Zie pag. 86).

Toets H0: m = m0 tegen één van de volgende alternatieven:

Voor H1: m < m0 stelt u Hypoth<0 in Voor H1: m ƒ m0 (standaardinstelling) stelt u Hypoth=0 in Voor H1: m > m0 stelt u Hypoth>0 in

Disp "A= ",a Disp "B= ",b Disp " " Disp "Eigenwaarden van A·B zijn:",eigVl(a*b)

Else

If errCode=230 Then

Disp "Fout: Product van A·B moet een vierkante matrix

zijn"

ClrErr

Else

PassErr

EndIf EndTry EndPrgm

Catalogus

94 TI-Nspire™ Referentiehandleiding

Texas Instruments TI-Nspire Reference Guide [nl]

Specifications and Main Features

Frequently Asked Questions

User Manual

Belangrijke informatie

Inhoud

Uitdrukkingstemplates

TI-Nspire™ Referentiehandleiding 1

Alfabetische lijst