Texas Instruments TI-Nspire Reference Guide [fi]

Page 1

sovelluksen käsikirja

Tämä opas koskee TI-Nspire-ohjelmiston versiota 1.4. Uusin versio asiakirjoista on saatavilla Internet-sivustolta education.ti.com/guides.

Page 2

Tärkeitä tietoja

Ellei muuten ilmoiteta ohjelman mukaan liitetyssä käyttöluvassa, Texas Instruments ei anna minkäänlaista suoraa tai välillistä takuuta mukaan lukien, mutta ei näihin rajoittuen, kaikki välilliset takuut, jotka koskevat kaikkien ohjelmien ja kirjojen myyntikelpoisuutta tai erityiseen tarkoitukseen sopivuutta, ja tarjoaa kyseisiä materiaaleja ainoastaan “sellaisina kuin ne ovat” -pohjalla. Texas Instruments ei ole missään tapauksessa vastuussa kenellekään mistään erityisistä, rinnakkaisista, tahattomista tai seurauksellisista vaurioista näiden materiaalien hankinnan tai käytön aiheuttamana, ja Texas Instruments:n yksinomainen ja eksklusiivinen vastuu toimintamuodosta riippumatta ei ylitä määrää, joka on asetettu käyttöluvassa ohjelmaa varten. Texas Instruments ei myöskään vastaa mistään vaateista, joita toinen osapuoli voi esittää aiheutuen näiden materiaalien käytöstä.

Lisenssi

Katso täydellinen lisenssi osoitteesta C:\Program Files\TI Education\TI-Nspire.

Macintosh®, Windows®, Excel®, Vernier EasyLink®, EasyTemp®, Go!®Link, Go!®Motion, ja Go!®Temp ovat vastaavien omistajiensa tuotemerkkejä.

Page 3

Sisällys

Tärkeitä tietoja Lausekemallit

Murtolukumalli ............................................ 1

Eksponenttimalli .......................................... 1

Neliöjuurimalli ............................................. 1

N:s juuri -malli .............................................. 1

e eksponenttimalli ....................................... 2

Logaritmimalli .............................................. 2

Paloittain määritellyn funktion malli (2-

osainen) ........................................................2

Paloittain määritellyn funktion malli (N-

osainen) ........................................................2

Itseisarvon malli ...........................................2

dd°mm’ss.ss’’ -malli ...................................... 3

Matriisimalli (2 x 2) ...................................... 3

Matriisimalli (1 x 2) ...................................... 3

Matriisimalli (2 x 1) ...................................... 3

Matriisimalli (m x n) .....................................3

Summan malli (G) ......................................... 3

Tulon malli (Π) ............................................. 4

Luettelo aakkosjärjestyksessä A

abs() ..............................................................5

amortTbl() .................................................... 5

and ................................................................5

angle() ..........................................................6

ANOVA ......................................................... 6

ANOVA2way ................................................ 7

ans .................................................................8

approx() ........................................................9

approxRational() .......................................... 9

augment() ..................................................... 9

avgRC() ....................................................... 10

bal() .............................................................10

4Base2 (4Kantaluku2) ................................. 10

4Base10 (4Kantaluku10) .............................11

4Base16 (4Kantaluku16) .............................11

binomCdf() ................................................. 11

binomPdf() ................................................. 12

ceiling() .......................................................12

char() ...........................................................12

2way ........................................................12

Cdf() .........................................................13

GOF ......................................................... 13

Pdf() .........................................................13

clearAZ ........................................................13

ClrErr ...........................................................14

colAugment() ............................................. 14

colDim() ......................................................14

colNorm() .................................................... 14

conj() ...........................................................14

constructMat() ............................................ 15

CopyVar ...................................................... 15

corrMat() .................................................... 15

cos() ............................................................ 16

cosê() .......................................................... 17

cosh() .......................................................... 17

coshê() ........................................................ 17

cot() ............................................................ 18

cotê() .......................................................... 18

coth() .......................................................... 18

cothê() ........................................................ 18

count() ........................................................ 19

countif() ..................................................... 19

crossP() ....................................................... 19

csc() ............................................................. 20

cscê() ........................................................... 20

csch() ........................................................... 20

cschê() ......................................................... 20

CubicReg .................................................... 21

cumSum() ................................................... 21

Cycle ........................................................... 22

4Cylind ........................................................ 22

dbd() ........................................................... 22

4DD ............................................................. 23

4Decimal ..................................................... 23

Define (Määritä) ........................................ 23

Define LibPriv (Määritä LibPriv) ................24

Define LibPub (Määritä LibPub) ............... 25

DelVar ........................................................ 25

det() ............................................................ 26

diag() .......................................................... 26

dim() ........................................................... 26

Disp ............................................................. 27

4DMS ........................................................... 27

dotP() .......................................................... 27

e^() ............................................................. 28

eff() ............................................................. 28

eigVc() ........................................................ 28

eigVl() ......................................................... 29

Else ............................................................. 29

ElseIf ........................................................... 29

EndFor ........................................................ 29

EndFunc ...................................................... 29

EndIf ........................................................... 29

EndLoop ..................................................... 29

EndPrgm ..................................................... 29

EndTry ........................................................ 29

EndWhile .................................................... 30

Exit .............................................................. 30

exp() ........................................................... 30

expr() .......................................................... 30

ExpReg ....................................................... 31

factor() ....................................................... 31

FCdf() ......................................................... 32

Fill ............................................................... 32

iii

Page 4

FiveNumSummary ......................................32

floor() ..........................................................33

For ...............................................................33

format() ......................................................33

fPart() ..........................................................34

FPdf() ..........................................................34

freqTable4list() ............................................34

frequency() .................................................34

Func .............................................................35

FTest_2Samp ..............................................35

gcd() ............................................................36

geomCdf() ...................................................36

geomPdf() ...................................................36

getDenom() ................................................36

getLangInfo() .............................................37

getMode() ...................................................37

getNum() ....................................................38

getVarInfo() ................................................38

Goto ............................................................39

4Grad ...........................................................39

identity() .....................................................39

If ..................................................................39

ifFn() ............................................................41

imag() ..........................................................41

Epäsuora operaattori .................................41

inString() .....................................................41

int() .............................................................42

intDiv() ........................................................42

() .........................................................42

invc

invF() ...........................................................42

invNorm() ....................................................42

invt() ............................................................42

iPart() ..........................................................43

irr() ..............................................................43

isPrime() ......................................................43

Lbl ...............................................................44

lcm() ............................................................44

left() ............................................................44

libShortcut() ................................................45

LinRegBx .....................................................45

LinRegMx ....................................................46

LinRegtIntervals .........................................46

LinRegtTest .................................................48

@List() ..........................................................48

list4mat() .....................................................49

ln() ...............................................................49

LnReg ..........................................................49

Local ............................................................50

log() .............................................................51

Logistic ........................................................51

LogisticD .....................................................52

Loop (Silmukka) .........................................53

LU ................................................................53

mat4list() .....................................................53

max() ...........................................................54

mean() ........................................................ 54

median() ..................................................... 54

MedMed ..................................................... 55

mid() ........................................................... 55

min() ........................................................... 56

mirr() ........................................................... 56

mod() .......................................................... 56

mRow() ....................................................... 57

mRowAdd() ................................................ 57

MultReg ...................................................... 57

MultRegIntervals ....................................... 57

MultRegTests ............................................. 58

nCr() ............................................................ 59

nDeriv() ....................................................... 59

newList() ..................................................... 60

newMat() .................................................... 60

nfMax() ....................................................... 60

nfMin() ....................................................... 60

nInt() ........................................................... 60

nom() .......................................................... 61

norm() ......................................................... 61

normCdf() ................................................... 61

normPdf() ................................................... 61

not .............................................................. 61

nPr() ............................................................ 62

npv() ........................................................... 63

nSolve() ....................................................... 63

OneVar ....................................................... 64

or ................................................................ 65

ord() ............................................................ 65

P4Rx() .......................................................... 65

P4Ry() .......................................................... 66

PassErr ........................................................ 66

piecewise() .................................................66

poissCdf() .................................................... 66

poissPdf() .................................................... 66

4Polar (4Polaarinen) .................................... 67

polyEval() .................................................... 67

PowerReg ................................................... 67

Prgm ........................................................... 68

Product (PI) ................................................. 68

product() .................................................... 68

propFrac() ................................................... 69

QR ............................................................... 70

QuadReg .................................................... 70

QuartReg .................................................... 71

R4Pq() .......................................................... 72

R4Pr() ........................................................... 72

4Rad ............................................................ 72

rand() .......................................................... 72

randBin() .................................................... 73

randInt() ..................................................... 73

randMat() ................................................... 73

Page 5

randNorm() ................................................. 73

randPoly() ................................................... 73

randSamp() ................................................. 73

RandSeed .................................................... 74

real() (reaali) ............................................... 74

4Rect ............................................................74

ref() .............................................................75

remain() ...................................................... 75

Return ......................................................... 75

right() ..........................................................75

root() ........................................................... 76

rotate() ....................................................... 76

round() ........................................................ 77

rowAdd() .................................................... 77

rowDim() .................................................... 77

rowNorm() .................................................. 77

rowSwap() .................................................. 78

rref() ............................................................78

sec() .............................................................78

sec/() ...........................................................79

sech() ...........................................................79

sechê() ......................................................... 79

seq() (sekv) .................................................. 79

setMode() ................................................... 80

shift() .......................................................... 81

sign() (etumerkki) ...................................... 82

simult() ........................................................82

sin() .............................................................83

sinê() ...........................................................83

sinh() ...........................................................84

sinhê() .........................................................84

SinReg .........................................................85

SortA ........................................................... 85

SortD ........................................................... 86

4Sphere ....................................................... 86

sqrt() ...........................................................86

stat.results .................................................. 87

stat.values ................................................... 88

stDevPop() .................................................. 88

stDevSamp() ............................................... 88

Stop .............................................................89

Store ...........................................................89

string() (merkkijono) ..................................89

subMat() ..................................................... 89

Sum (Sigma) ............................................... 89

sum() ...........................................................89

sumIf() .........................................................90

system() .......................................................90

T (transponoi) ............................................. 90

tan() ............................................................91

tanê() ..........................................................91

tanh() .......................................................... 92

tanhê() ........................................................92

tCdf() ........................................................... 93

Then ............................................................93

TInterval ..................................................... 93

TInterval_2Samp ........................................ 93

tPdf() ...........................................................94

trace() .........................................................94

Try (Kokeile) ............................................... 94

tTest ............................................................ 95

tTest_2Samp ............................................... 96

tvmFV() ....................................................... 96

tvmI() .......................................................... 96

tvmN() ........................................................ 97

tvmPmt() .................................................... 97

tvmPV() ....................................................... 97

TwoVar ....................................................... 98

unitV() ........................................................ 99

varPop() ...................................................... 99

varSamp() ................................................... 99

when() ...................................................... 100

While ........................................................ 100

“With” ...................................................... 100

xor ............................................................ 101

zInterval ................................................... 101

zInterval_1Prop ........................................ 102

zInterval_2Prop ........................................ 102

zInterval_2Samp ...................................... 102

zTest ......................................................... 103

zTest_1Prop .............................................. 103

zTest_2Prop .............................................. 104

zTest_2Samp ............................................ 104

Symbolit

+ (yhteenlasku) ........................................ 106

N(vähennyslasku) ..................................... 106

·(kertolasku) ........................................... 107

à (jakolasku) ............................................. 107

^ (potenssi) ............................................... 108

(neliö) ................................................... 109

.+ (piste lisää) ........................................... 109

.. (piste-erotus) ........................................ 109

·(pistetulo) ............................................. 109

. / (pisteosamäärä) ................................... 109

.^ (pistepotenssi) ...................................... 110

ë(negaatio) .............................................. 110

% (prosentti) ............................................ 110

= (on yhtä kuin) ....................................... 111

ƒ (ei yhtä kuin) ......................................... 111

< (pienempi kuin) .................................... 112

{ (pienempi tai yhtä suuri kuin) ............. 112

> (suurempi kuin) .................................... 112

| (suurempi tai yhtä suuri kuin) .............. 112

! (kertoma) ............................................... 113

& (liitä) ..................................................... 113

‡() (neliöjuuri) ......................................... 113

Π() (tulo) ................................................... 113

G() (summa) .............................................. 114

GInt() ......................................................... 114

GPrn() ........................................................ 115

# (epäsuora operaattori) ......................... 115

Page 6

í (kymmenpotenssimuoto) ......................115

g (graadi) ..................................................116

ô(radiaani) ................................................116

¡ (aste) .......................................................116

¡, ', '' (astetta/minuuttia/sekuntia) ..........116

 (kulma) ..................................................117

10^() ..........................................................117

^ê (käänteisluku) ......................................117

| (“with”) ...................................................118

& (tallenna) ..............................................118

:= (määritä) ...............................................118

0b, 0h ........................................................119

Virhekoodit ja viestit TI-tuotteiden huolto- ja

takuutietoa

Page 7

TI-Nspire™

Tämä opas sisältää matemaattisten lausekkeiden sieventämisessä käytettävät mallit, funktiot, komennot ja operaattorit.

-sovelluksen käsikirja

Lausekemallit

Lausekemallien avulla voit syöttää matemaattisia lausekkeita normaalissa matemaattisessa muodossa. Lisätessäsi mallin se näkyy syöterivillä siten, että elementtien syöttökohdissa on pienet ruudut. Kohdistin on syötettävän elementin kohdalla.

Voit siirtää kohdistimen kunkin elementin kohdalle nuolipainikkeilla tai painikkeella jonka jälkeen voit kirjoittaa elementin arvon tai lausekkeen. Lauseke sievennetään painamalla

painikkeita

Murtolukumalli

· tai /·.

/p painikkeet

Esimerkki:

Huomaa: Katso myös / (jakolasku), sivu 107.

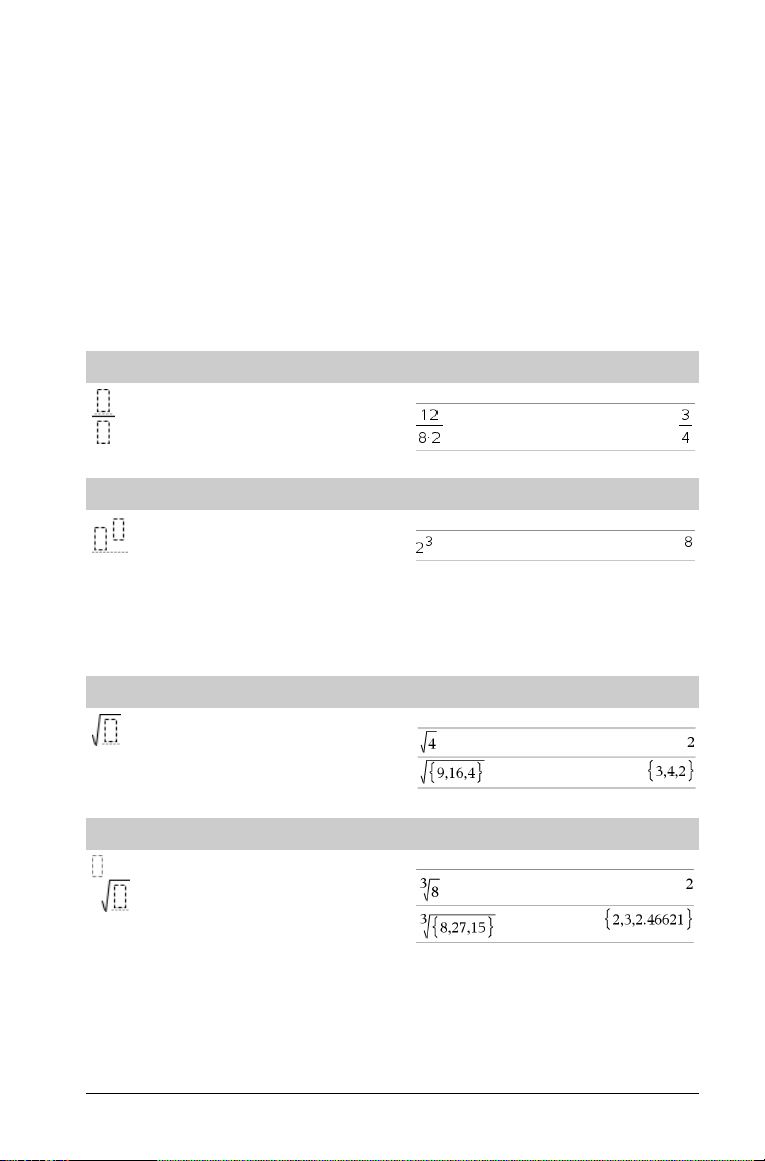
Eksponenttimalli

Huomaa: Syötä ensimmäinen arvo, paina l ja syötä sen

jälkeen eksponentti. Voit palauttaa kohdistimen perusviivalle painamalla oikealle osoittavaa nuolta (¢).

Huomaa: Katso myös ^ (potenssi), sivu 108.

Neliöjuurimalli

Huomaa: Katso myös

N:s juuri -malli

Huomaa: Katso myös root(), sivu 76.

‡

() (neliöjuuri), sivu 113.

l painike

Esimerkki:

/q painikkeet

Esimerkki:

/l painikkeet

Esimerkki:

TI-Nspire™ -sovelluksen käsikirja 1

Page 8

e eksponenttimalli

e-kantainen eksponenttifunktio korotettuna potenssiin

Huomaa: Katso myös e^(), sivu 28.

u painikkeet

Esimerkki:

Logaritmimalli

Laskee määritetyn kantaisen logaritmin. 10-kantaista logaritmia laskettaessa kantaluku jätetään pois.

Huomaa: Katso myös log(), sivu 51.

Paloittain määritellyn funktion malli (2-osainen)

Voit luoda lausekkeita ja ehtoja 2-osaiselle paloittain määritellylle funktiolle. Lisää osa napsauttamalla mallia ja toista malli.

Huomaa: Katso myös piecewise(), sivu 66.

Paloittain määritellyn funktion malli (N-osainen)

Voit luoda lausekkeita ja ehtoja N--osaiselle paloittain määritellylle funktiolle. Laskin pyytää N:n arvoa.

/s painike

Esimerkki:

Katalogi >

Esimerkki:

Katalogi >

Esimerkki: Katso paloittain määritellyn funktion (2-osaisen) mallin esimerkki.

Huomaa: Katso myös piecewise(), sivu 66.

Itseisarvon malli

Esimerkki:

Huomaa: Katso myös abs(), sivu 5.

Katalogi >

2 TI-Nspire™ -sovelluksen käsikirja

Page 9

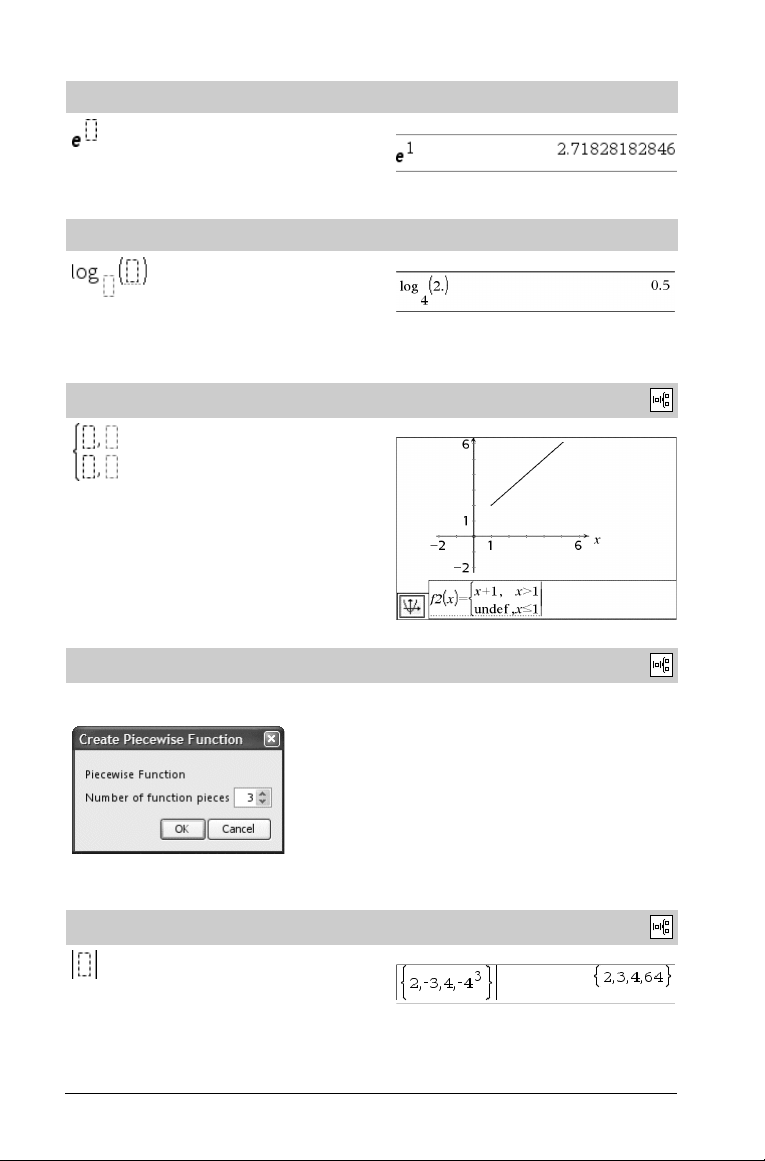
dd°mm’ss.ss’’ -malli

Voit syöttää kulmia muodossa dd°mm’ss.ss’’, jossa dd on desimaaliasteiden lukumäärä, mm on minuuttimäärä, ja ss.ss on sekuntimäärä.

Katalogi >

Esimerkki:

Matriisimalli (2 x 2)

Luo 2 x 2 -matriisin.

Matriisimalli (1 x 2)

Matriisimalli (2 x 1)

Matriisimalli (m x n)

Malli tulee näkyviin määritettyäsi rivien ja sarakkeiden lukumäärän syöttöruutuun.

Katalogi >

Esimerkki:

Katalogi >

Esimerkki:

Katalogi >

Esimerkki:

Katalogi >

Esimerkki:

Huomaa: Jos luot paljon rivejä ja sarakkeita sisältävän matriisin, voi kestää jonkin aikaa, ennen kuin matriisi tulee näkyviin.

Summan malli (G)

Esimerkki:

Katalogi >

TI-Nspire™ -sovelluksen käsikirja 3

Page 10

Tulon malli (Π)

Huomaa: Katso myös Π() (tulo), sivu 113.

Katalogi >

Esimerkki:

4 TI-Nspire™ -sovelluksen käsikirja

Page 11

Luettelo aakkosjärjestyksessä

Komennot, joiden nimiä ei voi järjestää aakkosjärjestykseen (esimerkiksi +, ! ja >), on esitetty tämän kappaleen lopussa alkaen sivulta 106. Ellei toisin ole mainittu, kaikki tämän kappaleen esimerkit on suoritettu laskimen oletustilassa, eikä mitään muuttujia ole määritetty.

abs()

abs(Arvo1) ⇒ arvo abs(

Lista1) ⇒ lista

abs(Matriisi1) ⇒ matriisi

Laskee argumentin itseisarvon.

Huomaa: Katso myös Itseisarvon malli, sivu 2.

Jos argumentti on kompleksiluku, määrittää luvun moduulin.

Huomaa: Kaikkia määrittämättömiä muuttujia käsitellään

reaalimuuttujina.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],

[

pyörArvo]) ⇒ matriisi

Lainan lyhennysfunktio, joka laskee lyhennystaulukon tiettyjen TVMargumenttien perusteella.

NPmt on taulukon maksuerien lukumäärä. Taulukko alkaa ensimmäisestä maksuerästä.

N, I, PV, Pmt, FV, PpY, CpY ja PmtAt on kuvattu TVMargumenttien taulukossa, sivulla 97.

• Jos jätät argumentin Pmt pois, sen oletusarvoksi tulee Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Jos jätät argumentin FV pois, sen oletusarvoksi tulee FV=0.

• Argumenttien PpY, CpY ja PmtAt oletusarvot ovat samat kuin TVM-funktioilla.

pyörArvo määrittää pyöristyksessä käytettävien desimaalien mä ärän. Oletusarvo=2.

Tulosmatriisin sarakkeet ovat seuraavassa järjestyksessä: maksuerän numero, koron määrä, pääoman lyhennysmäärä ja velkasaldo.

Rivillä n näkyvä saldo on maksuerän n jälkeen jäljellä oleva velkasaldo.

Voit käyttää tulosmatriisia syötteenä muissa lyhennyslaskutoimituksissa GInt() ja GPrn(), sivu 114, sekä bal(), sivu 10.

Katalogi

and

BoolenLaus1 and BoolenLaus2 ⇒ Boolen lauseke BoolenLista1 and BoolenLista2 ⇒ Boolen lista BoolenMatriisi1 and BoolenMatriisi2 ⇒ Boolen matriisi

Määrittää totuusarvon tosi tai epätosi tai antaa vastauksena sievennetyn muodon alkuperäisestä syötteestä.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 5

Page 12

and

Kokonaisluku1 and Kokonaisluku2 ⇒ kokonaisluku

Vertaa kahta reaalikokonaislukua bitti bitiltä Sisäisesti kumpikin kokonaisluku muunnetaan etumerkilliseksi, 64 bitin binaariluvuksi. Kun vastaavia bittejä verrataan, tulos on 1, jos kumpikin bitti on 1. Muussa tapauksessa tulos on 0. Laskettu arvo edustaa bittituloksia, ja se näkyy kantalukutilan mukaisesti.

Kokonaisluvut voi syöttää minkä tahansa luvun kantalukuna. Binaarisen syötteen edelle tulee merkitä etumerkki 0b ja heksadesimaalisen syötteen edelle 0h. Jos etumerkkiä ei ole, kokonaislukuja käsitellään desimaalilukuina (kantaluku 10).

Jos syötät desimaalikokonaisluvun, joka on liian suuri etume rkilliselle, 64 bitin binaarimuodolle, laskin käyttää symmetristä modulooperaatiota, jotta arvo saadaan oikealle alueelle.

and-operaation avulla.

Katalogi

Heksadesimaalisessa kantalukutilassa:

Tärkeää: Nolla, ei O-kirjain.

Binaarisessa kantalukutilassa:

Desimaalisessa kantalukutilassa:

Huomaa: Binaarisessa syötteessä voi olla korkeintaan 64

numeroa (etuliitettä 0b ei lasketa). Heksadesimaalisessa syötteessä voi olla korkeintaan 16 numeroa.

angle()

angle(Arvo1) ⇒ arvo

Astekulmatilassa:

Laskee argumentin kulman tulkiten argumentin kompleksiluvuksi.

Graadikulmatilassa:

Radiaanikulmatilassa:

angle(Lista1) ⇒ lista angle(Matriisi1) ⇒ matriisi

Laskee listan tai matriisin Lista1:n tai Matriisi1:n elementtien kulmista tulkiten jokaisen elementin kompleksiluvuksi, joka edustaa kaksiulotteista suorakulmakoordinaattipistettä.

ANOVA

ANOVA Lista1,Lista2[,Lista3,...,Lista20][,Lippu]

Suorittaa yksisuuntaisen varianssianalyysin 2-20 perusjoukon keskiarvon vertailua varten. Tulosten yhteenveto tallentuu

stat.results-muuttujaan. (Katso sivu 87.) Lippu=0 datalle, Lippu=1 tilastoille

Tulosmuuttuja Kuvaus

stat.FF-tilaston arvo

stat.PVal Alin merkitsevyystaso, jolla nollahypoteesi voidaan hylätä

stat.df Ryhmien vapausasteet

stat.SS Ryhmien neliöiden summa

stat.MS Ryhmien keskineliöt

stat.dfError Virheiden vapausasteet

Katalogi

6 TI-Nspire™ -sovelluksen käsikirja

Page 13

Tulosmuuttuja Kuvaus

stat.SSError Virheiden neliöiden summa

stat.MSError Virheiden keskineliö

stat.sp Poolattu keskihajonta

stat.xbarlist Listojen syötteiden keskiarvo

stat.CLowerList 95 %:n luottamusvälit jokaisen syötelistan keskiarvolle

stat.CUpperList 95 %:n luottamusvälit jokaisen syötelistan keskiarvolle

ANOVA2way

ANOVA2way Lista1,Lista2[,Lista3,…,Lista20][,Ta so Ri vi ]

Laskee kaksisuuntaisen varianssianalyysin 2-20 perusjoukon keskiarvojen vertaamiseksi. Tulosten yhteenveto tallentuu

stat.results-muuttujaan. (Katso sivu 87.) Tas o Ri v i=0 lohkolle

Tas o Ri v i=2,3,...,Len-1, kahdelle tekijälle, jossa Len=pituus(Lista1)=pituus(Lista2) = … = pituus(Lista10) ja Len / Tas oR iv i ∈ {2,3,…}

Tulokset: Lohkomuoto

Tulosmuuttuja Kuvaus

stat.FF-tilasto, saraketekijän F-tilasto

stat.PVal Alin merkitsevyystaso, jolla nollahypoteesi voidaan hylätä

stat.df Saraketekijän vapausasteet

stat.SS Saraketekijän neliöiden summa

stat.MS Saraketekijän keskineliöt

stat.FBlock F-tilasto, tekijän F-tilasto

stat.PValBlock Pienin todennäköisyys, jolla nollahypoteesi voidaan hylätä

stat.dfBlock Tekijän vapausasteet

stat.SSBlock Tekijän neliöiden summa

stat.MSBlock Tekijän keskineliöt

stat.dfError Virheiden vapausasteet

stat.SSError Virheiden neliöiden summa

stat.MSError Virheiden keskineliöt

stat.s Virheen keskihajonta

Katalogi

SARAKETEKIJÄN tulokset

Tulosmuuttuja Kuvaus

stat.Fcol F-tilasto, saraketekijän F-tilasto

TI-Nspire™ -sovelluksen käsikirja 7

Page 14

Tulosmuuttuja Kuvaus

stat.PValCol Saraketekijän todennäköisyysarvo

stat.dfCol Saraketekijän vapausasteet

stat.SSCol Saraketekijän neliöiden summa

stat.MSCol Saraketekijän keskineliöt

RIVITEKIJÄN tulokset

Tulosmuuttuja Kuvaus

stat.FRow F-tilasto, rivitekijän F-tilasto

stat.PValRow Rivitekijän todennäköisyysarvo

stat.dfRow Rivitekijän vapausasteet

stat.SSRow Rivitekijän neliöiden summa

stat.MSRow Rivitekijän keskineliöt

VUOROVAIKUTUKSEN tulokset

Tulosmuuttuja Kuvaus

stat.FInteract F-tilasto, vuorovaikutuksen F-tilasto

stat.PValInteract Vuorovaikutuksen todennäköisyysarvo

stat.dfInteract Vuorovaikutuksen vapausasteet

stat.SSInteract Vuorovaikutuksen neliöiden summa

stat.MSInteract Vuorovaikutuksen keskineliöt

VIRHEIDEN tulokset

Tulosmuuttuja Kuvaus

stat.dfError Virheiden vapausasteet

stat.SSError Virheiden neliöiden summa

stat.MSError Virheiden keskineliöt

s Virheen keskihajonta

ans

ans ⇒ arvo

Näyttää viimeksi sievennetyn lausekkeen tuloksen.

painikkeet

8 TI-Nspire™ -sovelluksen käsikirja

Page 15

approx()

approx(Arvo1) ⇒ luku

Määrittää argumentin sievennetyn arvon lausekkeena, joka sisältää desimaaliarvoja, mikäli mahdollista, riippumatta nykyise stä Auto or

Approximate (Automaattinen tai likimääräinen)

Tämä vastaa argumentin syöttämistä ja painikkeen painamista.

approx(Lista1) ⇒ lista approx(Matriisi1) ⇒ matriisi

Määrittää listan tai matriisin, jossa jokainen elementti on laskettu desimaaliarvoksi, mikäli mahdollista.

-tilasta.

Katalogi

approxRational()

approxRational(Laus[, tol]) ⇒ lauseke approxRational(Lista[, tol]) ⇒ lista approxRational(Matriisi[, tol]) ⇒ matriisi

Laskee argumentin murtolukuna käyttäen toleranssia tol. Jos operaattori tol jätetään pois, laskin käyttää toleranssia 5.E-14.

augment()

augment(Lista1, Lista2) ⇒ lista

Luo uuden listan, joka on Lista2 liitettynä Lista1:n loppuun.

augment(Matriisi1, Matriisi2) ⇒ matriisi

Luo uuden matriisin, joka on Matriisi2 liitettynä Matriisi1:een. Kun käytetään merkkiä “,”, matriiseiden rivimäärien on oltava samat, ja

Matriisi2 liitetään Matriisi1:een uusina sarakkeina. Ei muuta Matriisi1:ä eikä Matriisi2:a.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 9

Page 16

avgRC()

avgRC(Laus1, Muutt [=Arvo] [, H]) ⇒ lauseke avgRC(Laus1, Muutt [=Arvo] [, Lista1]) ⇒ lista avgRC(Lista1, Muutt [=Arvo] [, H]) ⇒ lista avgRC(Matriisi1, Muutt [=Arvo] [, H]) ⇒ matriisi

Laskee erotusosamäärän eteenpäin (keskimääräisen muutosnopeuden).

Laus1 voi olla käyttäjän määrittämä funktionimi (katso Kun Arvo määritetään, se ohittaa mahdolliset aikaisemmat

muuttujamääritykset tai mahdolliset muuttujan nykyiset “such that” substituutiot.

H on askelarvo. Jos H jätetään pois, sen oletusarvo on 0.001. Huomaa, että samankaltaisessa funktiossa

keskeiserotusosamäärää.

Func).

nDeriv() käytetään

Katalogi

bal()

bal(NPmt,N,I,PV ,[Pmt], [FV], [PpY], [CpY], [PmtAt],

pyörArvo]) ⇒ arvo

[

bal(NPmt,amortTable) ⇒ arvo

Lyhennysfunktio, joka laskee määritetyn maksuerän jälkeen jäljellä olevan velkasaldon.

N, I, PV, Pmt, FV, PpY, CpY ja PmtAt on kuvattu TVMargumenttien taulukossa, sivulla 97.

NPmt määrittää sen maksuerän numeron, jonka jälkeen velkasaldo halutaan laskea.

N, I, PV, Pmt, FV, PpY, CpY ja PmtAt on kuvattu TVMargumenttien taulukossa, sivulla 97.

• Jos jätät argumentin Pmt pois, sen oletusarvoksi tulee Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Jos jätät argumentin FV pois, sen oletusarvoksi tulee FV=0.

• Argumenttien PpY, CpY ja PmtAt oletusarvot ovat samat kuin TVM-funktioilla.

pyörArvo määrittää pyöristyksessä käytettävien desimaalien mä ärän. Oletusarvo=2.

bal(NPmt,amortTable) laskee maksueränumeron NPmt jälkeen

jäljellä olevan velkasaldon lyhennystaulukon amortTable perusteella. amortTable-argumentin on oltava matriisi, joka on kohdassa

amortTbl() kuvatun muotoinen, katso sivu 5.

Huomaa: Katso myös GInt() ja GPrn(), sivu 114.

Base2

Kantaluku2)

Kokonaisluku1 4Base2 ⇒ kokonaisluku

Muuttaa Kokonaisluku1:n binaariluvuksi. Binaariluvuissa on aina etuliite 0b ja heksadesimaaliluvuissa etuliite 0h.

Katalogi

10 TI-Nspire™ -sovelluksen käsikirja

Page 17

Base2

Kantaluku2)

0b binaariluku 0h heksadesimaaliluku

Nolla, ei O-kirjain, jonka perässä on b tai h. Binaariluvussa voi olla enintään 64 numeroa. Heksadesimaaliluvussa

voi olla enintään 16 numeroa. Ilman etuliitettä Kokonaisluku1:ä käsitellään desimaalilukuna

(kantaluku 10). Vastaus näkyy binaarilukuna kantalukutilasta riippumatta.

Jos syötät desimaalikokonaisluvun, joka on liian suuri etume rkilliselle, 64 bitin binaarimuodolle, laskin käyttää symmetristä modulooperaatiota, jotta arvo saadaan oikealle alueelle.

Base10

Base16

Kantaluku10)

Kantaluku16)

Kokonaisluku1 4Base10 ⇒ kokonaisluku

Muuttaa Kokonaisluku1:n desimaaliluvuksi (kantaluku 10). Binaarisen syötteen edellä tulee aina olla etumerkki 0b ja heksadesimaalisen syötteen edellä 0h.

0b binaariluku 0h heksadesimaaliluku

Nolla, ei O-kirjain, jonka perässä on b tai h. Binaariluvussa voi olla enintään 64 numeroa. Heksadesimaaliluvussa

voi olla enintään 16 numeroa. Ilman etuliitettä Kokonaisluku1:ä käsitellään desimaalilukuna.

Vastaus näkyy desimaalilukuna kantalukutilasta riippumatta.

Kokonaisluku1 4Base16 ⇒ kokonaisluku

Muuttaa Kokonaisluku1:n heksadesimaaliluvuksi. Binaariluvuissa on aina etuliite 0b ja heksadesimaaliluvuissa etuliite 0h.

0b binaariluku 0h heksadesimaaliluku

Nolla, ei O-kirjain, jonka perässä on b tai h. Binaariluvussa voi olla enintään 64 numeroa. Heksadesimaaliluvussa

voi olla enintään 16 numeroa. Ilman etuliitettä Kokonaisluku1:ä käsitellään desimaalilukuna

(kantaluku 10). Vastaus näkyy heksadesimaal ilukuna kantalukutilasta riippumatta.

Jos syötät desimaalikokonaisluvun, joka on liian suuri etume rkilliselle, 64 bitin binaarimuodolle, laskin käyttää symmetristä modulooperaatiota, jotta arvo saadaan oikealle alueelle.

Katalogi

binomCdf()

binomCdf(n,p,alaraja,yläraja) ⇒ luku, jos alaraja ja yläraja

ovat lukuja,

binomCdf(

yläraja on lista

Laskee kumulatiivisen todennäköisyyden diskreetille binomiselle jakaumalle, jossa toistojen määrä on n ja jokaisen toiston onnistumistodennäköisyys on p.

Kun P(X  yläraja), aseta alaraja=0

lista, jos alaraja ja yläraja ovat listoja n,p,yläraja) ⇒ luku, jos yläraja on luku, lista, jos

Katalogi

TI-Nspire™ -sovelluksen käsikirja 11

Page 18

binomPdf()

binomPdf(n,p) ⇒ luku binomPdf(n,p,XVal) ⇒ luku, jos XVal on luku, lista, jos XVal

on lista

Laskee todennäköisyyden diskreetille binomiselle jakaumalle, jossa toistojen määrä on n ja jokaisen toiston onnistumistodennäköisyys on p.

Katalogi

ceiling()

ceiling(Arvo1) ⇒ arvo

Laskee lähimmän kokonaisluvun, joka on ‚ argumentti.

Argumentti voi olla reaali- tai kompleksiluku.

Huomaa: Katso myös floor().

ceiling(Lista1) ⇒ lista ceiling(Matriisi1) ⇒ matriisi

Laskee listan tai matriisin jokaisen elementin ylärajasta.

char()

char(Kokonaisluku) ⇒ merkki

Näyttää vastauksena merkkijonon, joka sisältää kämmenlaitteen merkkisarjasta olevan merkin, jonka tunnusnumero on Kokonaisluku. Kokonaisluvun Kokonaisluku sallittu alue on 0–

65535.

2way

2way ObsMatriisi

chi22way ObsMatriisi

Laskee c2-testin tarkasteltavan matriisin ObsMatriisi sisältämän kaksisuuntaisen lukemataulukon arvojen välisestä assosiaatiosta. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu

87.)

Tulosmuuttuja Kuvaus

stat.c2 Khin neliö -tilasto: summa (tarkasteltava - odotettu)2/odotettu

stat.PVal Alin merkitsevyystaso, jolla nollahypoteesi voidaan hylätä

stat.df Khin neliö -tilastojen vapausasteet

stat.ExpMat Odotetun elementtilukemataulukon matriisi, oletuksena nollahypoteesi

stat.CompMat Elementtien Khin neliö -tilastokontribuutioiden matriisi

Katalogi

12 TI-Nspire™ -sovelluksen käsikirja

Page 19

Cdf()

Cdf(alaraja,yläraja,df) ⇒ luku, jos alaraja ja yläraja ovat

lista, jos alaraja ja yläraja ovat listoja

lukuja,

chi2Cdf(

alaraja,yläraja,df) ⇒ luku, jos alaraja ja yläraja ovat

lukuja,

lista, jos alaraja ja yläraja ovat listoja

Laskee c2-jakauman todennäköisyyden alarajan ja ylärajan väliltä määritetylle vapausasteelle df.

 yläraja), aseta alaraja= 0.

Kun P(X

GOF

GOF obsLista,expLista,df

chi2GOF obsLista,expLista,df

Suorittaa testin, jolla varmistetaan, että otoksen data on tiettyä jakaumaa vastaavasta perusjoukosta. obsList on lukemalista, ja sen tulee sisältää kokonaislukuja. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 87.)

Tulosmuuttuja Kuvaus

stat.c2 Khin neliö -tilasto: sum((tarkasteltava - odotettu)2/odotettu

stat.PVal Alin merkitsevyystaso, jolla nollahypoteesi voidaan hylätä

stat.df Khin neliö -tilastojen vapausasteet

stat.CompList Elementtien Khin neliö -tilastokontribuutiot

Pdf()

Pdf(XArvo,df) ⇒ luku, jos XArvo on luku, lista, jos XArvo

on lista

chi2Pdf(

XArvo,df) ⇒ luku, jos XArvo on luku, lista, jos XArvo

on lista

Laskee c2-jakauman todennäköisyystiheysfunktion (pdf) määritetyllä XArvon arvolla määritetylle vapausasteelle df.

Katalogi

clearAZ

Katalogi

Poistaa kaikki yksikirjaimiset muuttujat nykyiseltä tehtäväalueelta.

TI-Nspire™ -sovelluksen käsikirja 13

Page 20

ClrErr

Poistaa virhetilan ja nollaa järjestelmän muuttujan errCode .

Else-lauseessa lohkossa Try...Else...EndTry tulee käyttää

komentoa

ClrErr tai PassErr. Jos virhe on tarkoitus käsitellä tai

jättää huomiotta, käytä komentoa virheen suhteen, lähetä se seuraavaan virheenkäsittelijään käyttämällä komentoa virheenkäsittelijöitä ei ole enää, virheen valintaikkuna tulee näkyviin normaalisti.

Huomaa: Katso myös PassErr, sivu 66, ja Try , sivu 94. Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa

ClrErr. Jos et tiedä, mitä tehdä

PassErr. Jos odottavia Try...Else...EndTry-

painiketta @ painikkeen · sijaan. Tietokoneen näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Esimerkki

ClrErr-komennosta, katso esimerkki 2 Try-

komennon kohdalla, sivu 95.

Katalogi

colAugment()

colAugment(Matriisi1, Matriisi2) ⇒ matriisi

Luo uuden matriisin, joka on Matriisi2 liitettynä Matriisi1:een. Matriiseiden sarakemäärän on oltava sama, ja Matriisi2 liitetään Matriisi1:een uusina riveinä. Ei muuta Matriisi1:ä eikä Matriisi2:a.

colDim()

colDim(Matriisi) ⇒ lauseke

Laskee Matriisin sisältämien sarakkeiden lukumäärän.

Huomaa: Katso myös rowDim().

colNorm()

colNorm(Matriisi) ⇒ lauseke

Laskee maksimiarvon Matriisin sarakkeissa olevien elementtien itseisarvojen summista.

Huomaa: Määrittämättömät matriisielementit eivät ole sallittuja.

Katso myös rowNorm().

conj()

conj(Arvo1) ⇒ arvo conj(Lista1) ⇒ lista conj(Matriisi1) ⇒ matriisi

Laskee argumentin liittokompleksiluvun.

Huomaa: Kaikkia määrittämättömiä muuttujia käsitellään

reaalimuuttujina.

Katalogi

14 TI-Nspire™ -sovelluksen käsikirja

Page 21

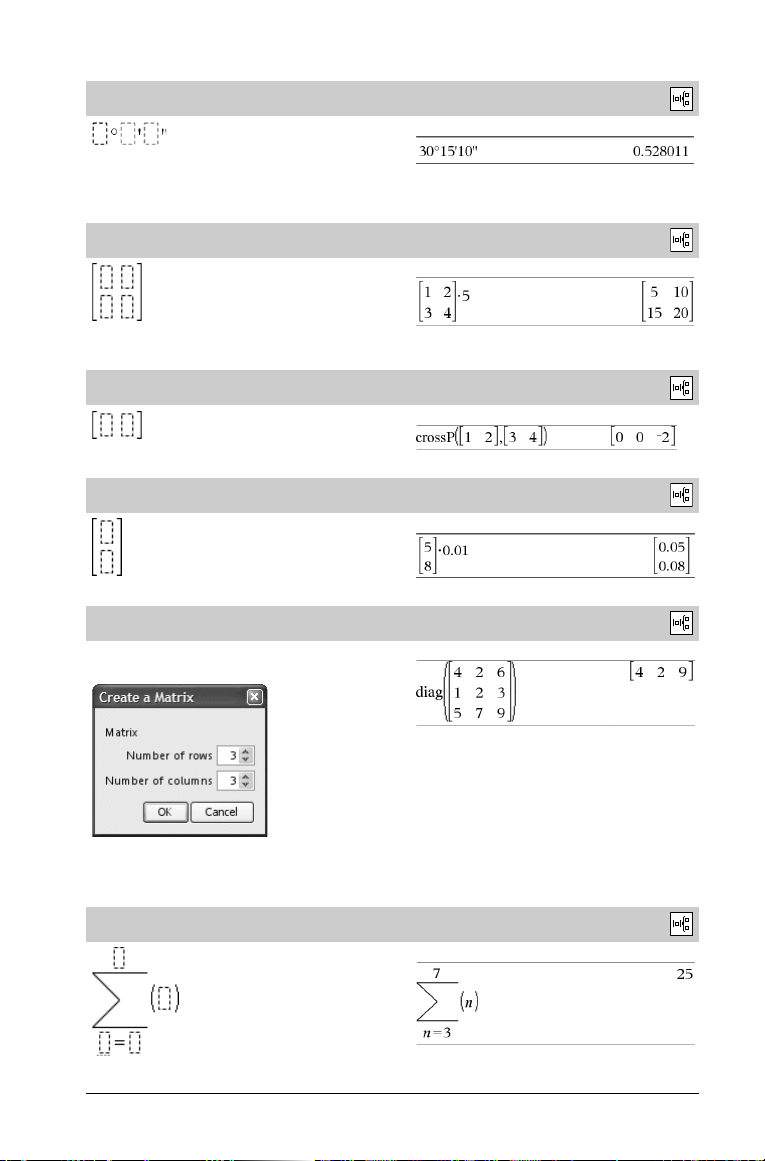
constructMat()

constructMat(Laus,Muutt1,Muutt2,numRivit,numSarakkeet)

⇒ matriisi

Laskee matriisin argumentteihin perustuen. Laus on lauseke muuttujissa Muutt1 ja Muutt2. Tuloksena olevan

matriisin elementit muodostetaan sieventämällä Laus jokaisella

Muutt1:n ja Muutt2:n lisätyllä arvolla. Muutt1:ä lisätään automaattisesti välillä

Muutt2:a lisätään välillä 1 - numSarakkeet.

1 - numRivit. Kullakin rivillä

Katalogi

CopyVar

CopyVar Muutt1, Muutt2 CopyVar Muutt1., Muutt2.

CopyVar Muutt1, Muutt2 kopioi muuttujan Muutt1 arvon

muuttujaan Muutt2 ja luo tarvittaessa Muutt2:n. Muuttujalla Muutt1 on oltava arvo.

Jos Muutt1 on olemassa olevan käyttäjän määrittämän funktion nimi, kopioi kyseisen funktion määrityksen funktioon Muutt2. Funktio

Muutt1 on määritettävä. Muutt1:n on oltava muuttujien nimeämissääntöjen mukainen tai

epäsuora lauseke, joka sieventyy näitä vaatimuksia vastaavaksi muuttujan nimeksi.

CopyVar Muutt1., Muutt2. kopioi kaikki Muutt1:n jäsenet.

muuttujaryhmä Va r 2:een. ryhmä, Muutt2:n luominen. tarvittaessa. Muutt1. on oltava olemassa olevan muuttujaryhmän nimi, kuten

tilastollinen stat.nn tulosta tai muuttujaa, jotka on luotu funktiolla

LibShortcut(). Jos Muutt2. on jo olemassa, komento korvaa kaikki

jäsenet, jotka ovat yhteisiä kummallekin ryhmälle, ja lisää jäsenet, joita ei vielä ole olemassa. Jos yksinkertainen (ei ryhmä) muuttuja nimeltä Muutt2 on olemassa, tapahtuu virhe.

corrMat()

corrMat(Lista1,Lista2[,…[,Lista20]])

Laskee korrelaatiomatriisin laajennetulle matriisille [Lista1, Lista2, ..., Lista20].

Katalogi

TI-Nspire™ -sovelluksen käsikirja 15

Page 22

cos()

cos(Arvo1) ⇒ arvo cos(Lista1) ⇒ lista

cos(Arvo1) määrittää argumentin kosinin arvona. cos(Lista1) määrittää listan kaikkien Lista1:n sisältämien

elementtien kosineista.

Huomaa: Argumentti tulkitaan aste-, graadi- tai radiaanikulmaksi

käytössä olevan kulmatila-asetuksen mukaisesti. Voit ohittaa kulmatilan väliaikaisesti painikkeilla ó,G tai ô.

n painike

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

cos(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisikosinin. Tämä ei ole sama kuin kunkin elementin kosinin laskeminen.

Kun skaalarista funktiota f(A) käytetään neliömatriisi1:een (A), tulos lasketaan algoritmilla:

Laske A:n ominaisarvot (li) ja ominaisvektorit (Vi).

neliömatriisi1:n on oltava diagonalisoitavissa. Lisäksi siinä ei voi olla symbolisia muuttujia, joille ei ole määritetty arvoa.

Matriiseista:

Tällöin A = X B Xêja f(A) = X f(B) Xê. Esimerkiksi, cos(A) = X cos(B) Xê, jossa:

cos(B) =

Kaikki laskut suoritetaan liukulukuaritmetiikalla.

Radiaanikulmatilassa:

16 TI-Nspire™ -sovelluksen käsikirja

Page 23

cosê()

cosê(Arvo1) ⇒ arvo cosê(Lista1) ⇒ lista

/n painikkeet

Astekulmatilassa:

cosê(Arvo1) laskee kulman, jonka kosini on Arvo1.

cosê(Lista1) laskee listan Lista1:n jokaisen elementin

käänteiskosineista.

Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana

käytössä olevan kulmatila-asetuksen mukaisesti.

cosê(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisin käänteiskosinin. Tämä ei ole sama kuin kunkin elementin käänteiskosinin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

cosh()

cosh(Arvo1) ⇒ arvo cosh(Lista1) ⇒ lista

cosh(Arvo1) laskee argumentin hyperbolisen kosinin. cosh(Lista1) määrittää listan Lista1:n kunkin elementin

hyperbolisista kosineista.

cosh(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisin hyperbolisen kosinin. Tämä ei ole sama kuin kunkin elementin hyperbolisen kosinin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

Graadikulmatilassa:

Radiaanikulmatilassa:

Radiaanikulmatilassa ja suorakulmakompleksimuodossa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeen kohdistinta painikkeilla ¡ ja ¢.

Katalogi

Radiaanikulmatilassa:

coshê()

coshê(Arvo1) ⇒ arvo coshê(Lista1) ⇒ lista

cosh

(Arvo1) laskee argumentin käänteisen hyperbolisen kosinin.

cosh

(Lista1) määrittää listan Lista1:n kunkin elementin

käänteisistä hyperbolisista kosineista.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 17

Page 24

coshê()

coshê(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisin käänteisen hyperbolisen kosinin. Tämä ei ole sama kuin kunkin elementin käänteisen hyperbolisen kosinin laskeminen. Laskentamenetelmä on kuvattu kohdassa

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

cos().

Katalogi

Radiaanikulmatilassa ja suorakulmakompleksimuodossa:

cot()

cot(Arvo1) ⇒ arvo cot(Lista1) ⇒ lista

Laskee Arvo1:n kotangentin tai määrittää listan Lista1:n kaikkien elementtien kotangenteista.

Huomaa: Argumentti tulkitaan aste-, graadi- tai radiaanikulmaksi

käytössä olevan kulmatila-asetuksen mukaisesti. Voit ohittaa kulmatilan väliaikaisesti painikkeilla ó,G tai ô.

cotê()

cotê(Arvo1) ⇒ arvo cotê(Lista1) ⇒ lista

Laskee kulman, jonka kotangentti on Arvo1, tai määritt ää listan, joka sisältää Lista1:n kunkin elementin käänteiskotangentit.

Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana

käytössä olevan kulmatila-asetuksen mukaisesti.

coth()

coth(Arvo1) ⇒ arvo coth(Lista1) ⇒ lista

Laskee Arvo1:n hyperbolisen kotangentin tai määrittää listan Lista1:n kaikkien elementtien hyperbolisista kotangenteista.

Jos haluat nähdä koko vastauksen, paina jälkeen kohdistinta painikkeilla ¡ ja ¢.

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

£ ja siirrä sen

Katalogi

cothê()

cothê(Arvo1) ⇒ arvo cothê(Lista1) ⇒ lista

Laskee Arvo1:n käänteisen hyperbolisen kotangentin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien käänteiset hyperboliset kotangentit.

Katalogi

18 TI-Nspire™ -sovelluksen käsikirja

Page 25

count()

count(Arvo1taiLista1 [,Arvo2taiLista2 [,...]]) ⇒ arvo

Laskee elementtien kokonaismäärän argumenteille, jotka sieventyvät numeroarvoiksi.

Argumentit voivat olla lausekkeita, arvoja, listoja tai matriiseja. Argumenttien datatyypit voivat olla erilaisia, ja argumentit voiva t olla erikokoisia.

Listan, matriisin tai solualueen jokainen elementti sievennetään, jot ta voidaan määrittää, kuuluuko se laskettavaan lukumäärään.

Listat & Taulukot -sovelluksessa voit käyttää solualueita argumenttien tilalla.

Katalogi

countif()

countif(Lista,Kriteerit) ⇒ arvo

Laskee niiden Listan sisältämien elementtien kokonaismäärän, jotka vastaavat määritettyjä kriteereitä Kriteerit.

Kriteeri voi olla:

• Arvo, lauseke tai merkkijono. Jos kriteerinä käytetään esimerkiksi lukua 3, laskee lukumäärään vain ne Listan elementit, jotka sieventyvät arvoksi 3.

• Boolen lauseke, joka sisältää symbolin ? kunkin elementin paikanpitäjänä. Esimerkiksi lauseke ?<5 laskee lukumäärään vain ne Listan elementit, jotka ovat alle 5.

Listat & Taulukot -sovelluksessa voit käyttää solualueita Listan tilalla.

Huomaa: Katso myös sumIf(), sivu 90, ja frequency(), sivu 34.

crossP()

crossP(Lista1, Lista2) ⇒ lista

Määrittää listan Lista1:n ja Lista2:n ristitulosta. Lista1:n ja Lista2:n on oltava samankokoiset, ja koon on oltava joko

2 tai 3.

crossP(Vek t o r i1 , Ve k t or i 2 ) ⇒ vektori

Laskee rivi- tai sarakevektorin (argumenteista riippuen), joka on Vek t o r i1 :n ja Ve k t or i 2 :n ristitulo.

Sekä Ve k t o ri 1 :n että Vektori2:n on oltava rivivektoreita tai sarakevektoreita. Vektoreiden on oltava samankokoiset , ja koon tulee olla joko 2 tai 3.

Katalogi

Laskee niiden elementtien lukumäärän, jotka ovat yhtä kuin 3.

Laskee niiden elementtien lukumäärän, jotka ovat yhtä kuin "def".

Laskee lukumäärään 1:n ja 3:n.

Laskee lukumäärään 3:n, 5:n ja 7:n.

Laskee lukumäärään 1:n, 3:n, 7:n ja 9:n.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 19

Page 26

csc()

csc(Arvo1) ⇒ arvo csc(Lista1) ⇒ lista

Laskee Arvo1:n kosekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien kosekantit.

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

Katalogi

cscê()

cscê(Arvo1) ⇒ arvo cscê(Lista1) ⇒ lista

Laskee kulman, jonka kosekantti on Arvo1, tai määrittää listan, joka sisältää Lista1:n kunkin elementin käänteiskosekantit.

Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana

käytössä olevan kulmatila-asetuksen mukaisesti.

csch()

csch(Arvo1) ⇒ arvo csch(Lista1) ⇒ lista

Laskee Arvo1:n hyperbolisen kosekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien hyperboliset kosekantit.

cschê()

cschê(Arvo) ⇒ arvo cschê(Lista1) ⇒ lista

Laskee Arvo1:n käänteisen hyperbolisen kosekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien käänteiset hyperboliset kosekantit.

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

Katalogi

20 TI-Nspire™ -sovelluksen käsikirja

Page 27

CubicReg

CubicReg X, Y[, [Frekv] [, Luokka, Sisällytä]]

Katalogi

Laskee 3. asteen polynomiregression y = a·x3+b· x2+c·x+d listoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto

tallentuu stat.results-muuttujaan. (Katso sivu 87.) Kaikkien listojen on oltava samankokoisia Sisällytä-listaa

lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja | 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tulosmuuttuja Kuvaus

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.R

Regressioyhtälö: a·x3+b·x2+c·x+d.

Regressiokertoimet.

Määrityskerroin.

stat.Resid Regressioyhtälön jäännökset

stat.XReg Muokatun X Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti.

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista.

cumSum()

cumSum(Lista1) ⇒ lista

Laskee listan Lista1:n sisältämien elementtien kumulatiivisista summista alkaen elementistä 1.

cumSum(Matriisi1) ⇒ matriisi

Laskee matriisin Matriisi1:n sisältämien elementtien kumulatiivisista summista. Jokainen elementti on ylhäältä alas ulottuvan sarakkeen kumulatiivinen summa.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 21

Page 28

Cycle

Siirtää ohjauksen välittömästi nykyisen silmukan (For, While tai

Loop) seuraavaan iteraatioon. Cycle ei ole sallittu näiden kolmen silmukkarakenteen (For, While

Loop) ulkopuolella.

tai

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa

@ painikkeen · sijaan. Tietokoneen

painiketta näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Cylind

Vektori 4Cylind

Näyttää rivi- tai sarakevektorin sylinterin muodossa [r,q, z].

Vektorissa on oltava täsmälleen kolme elementtiä. Se voi olla joko rivi tai sarake.

Katalogi

Funktio, joka laskee yhteen kokonaisluvut väliltä 1-100 ohittaen luvun 50.

Katalogi

dbd()

dbd(pvm1,pvm2) ⇒ arvo

Laskee pvm1:n ja pvm2:n välissä olevien päivien lukumäärän käyttäen todellisten päivien laskentamenetelmää.

pvm1 ja pvm2 voivat olla lukuja tai lukulistoja, jotka ovat vakiokalenterin päivämääräalueen sisällä. Jos sekä pvm1 että pvm2 ovat listoja, niiden on oltava samanpituiset.

pvm1:n ja pvm2:n on oltava vuosien 1950 ja 2049 välillä. Voit syöttää päivämäärät kahdessa eri muodossa. Desimaalipisteen

paikka on erilainen näissä päivämäärien esitystavoissa. MM.DDYY (Yhdysvalloissa yleisesti käytetty esitystapa)

DDMM.YY (Euroopassa yleisesti käytetty esitystapa)

Katalogi

22 TI-Nspire™ -sovelluksen käsikirja

Page 29

4DD ⇒ arvo

Laus1 Lista1 4DD ⇒ lista Matriisi1

4DD ⇒ matriisi

Laskee vastaavan desimaaliluvun asteina ilmaistulle argumentille. Argumentti on luku, lista tai matriisi, jonka kulmatila-asetus tulkitsee graadeina, radiaaneina tai asteina.

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

Katalogi

4Decimal

Luku1 Lista1 Matriisi1

Näyttää argumentin desimaalimuodossa. Tätä operaattoria voi käyttää ainoastaan syöterivin lopussa.

Define (Määritä)

Define Muutt = Lauseke Define Funktio(Param1, Param2, ...) = Lauseke

Määrittää muuttujan Muutt tai käyttäjän määrittämän funktion Funktio.

Parametrit, kuten Param1, toimivat paikanpitäjinä argumenttien syöttämiseksi funktioon. Kun haet käyttäjän määrittämän funktion, sinun on annettava parametreja vastaavat argumentit (esimerkiksi arvoja tai muuttujia). Kun funktio haetaan, se sieventää Lausekkeen annettujen argumenttien perusteella.

Muutt ja Funktio eivät voi olla järjestelmän muuttujan tai sisäänrakennetun funktion tai komennon nimenä.

Huomaa: Seuraava Define-funktion muoto on vastaava kuin

lausekkeen sieventäminen: lauseke & Funktio(Param1,Param2).

4Decimal

Decimal

⇒ arvo

Katalogi

TI-Nspire™ -sovelluksen käsikirja 23

Page 30

Define (Määritä)

Define Funktio(Param1, Param2, ...) = Func

Lohko

EndFunc

Ohjelma(Param1, Param2, ...) = Prgm

Define

Lohko

EndPrgm

Tässä muodossa käyttäjän määrittämä funktio tai ohjelma voi suorittaa useista lausekkeista koostuvan lohkon.

Lohko voi olla joko yksi lauseke tai eri riveillä olevien lausekkeiden sarja. Lohko voi sisältää myös lausekkeita ja ohjeita (kuten If, Then,

Else ja For). Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Huomaa: Katso myös Define LibPriv, sivu 24, ja Define LibPub

, sivu 25.

Katalogi

Define LibPriv (Määritä LibPriv)

Define LibPriv Muutt = Lauseke Define LibPriv Funktio(Param1, Param2, ...) = Lauseke

Define LibPriv Funktio(Param1, Param2, ...) = Func

Lohko

EndFunc Define LibPriv

Lohko

EndPrgm

Tämä komento toimii muuten samalla tavalla kuin Define paitsi, että se määrittää yksityisen kirjastomuuttujan, -funktion tai ohjelman. Yksityiset funktiot ja ohjelmat eivät ole katalogissa.

Huomaa: Katso myös Define, sivu 23, ja Define LibPub, sivu

25.

Ohjelma(Param1, Param2, ...) = Prgm

Katalogi

24 TI-Nspire™ -sovelluksen käsikirja

Page 31

Define LibPub (Määritä LibPub)

Define LibPub Muutt = Lauseke Define LibPub Funktio(Param1, Param2, ...) = Lauseke

Define LibPub Funktio(Param1, Param2, ...) = Func

Lohko

EndFunc Define LibPub

Lohko

EndPrgm

Tämä komento toimii muuten samalla tavalla kuin Define paitsi, että se määrittää julkisen kirjastomuuttujan, -funktion tai -ohjelman. Julkiset funktiot ja ohjelmat näkyvät katalogissa sen jälkeen, kun kirjasto on tallennettu ja näyttö on päivitetty.

Huomaa: Katso myös Define, sivu 23, ja Define LibPriv, sivu

24.

Ohjelma (Param1, Param2, ...) = Prgm

Katalogi

DelVar

DelVar Muutt1[, Muutt2] [, Muutt3] ... DelVar

Muutt.

Poistaa määritetyn muuttujan tai muuttujaryhmän muistista.

DelVar Muutt. poistaa kaikki Muutt:n jäsenet. muuttujaryhmä

(kuten tilastollinen stat.nn tulosta tai muuttujaa, jotka on luotu funktiolla LibShortcut()). Piste (.) tässä DelVar-komennon muodossa rajoittaa funktion muuttujaryhmän poistamiseen; komento

ei vaikuta yksinkertaiseen muuttujaan Muutt.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 25

Page 32

det()

det(neliömatriisi[, Toleranssi]) ⇒ lauseke

Laskee neliömatriisin determinantin. Valinnaisesti kaikkia matriisielementtejä käsitellään nollana, jos

niiden itseisarvo on pienempi kuin Toleranssi. Tätä toleranssia käytetään vain, jos matriisissa on liukulukusyötteitä eikä se sisällä symbolisia muuttujia, joille ei ole määritetty arvoa. Muussa tapauksessa Tolerassia ei huomioida.

• Jos käytät painikkeita

Approximate (Automaattinen tai likimääräinen)

tilan valintaa Approximate (Likimääräinen), laskut suoritetaan liukulukuaritmetiikalla.

•Jos Toleranssi jätetään pois tai sitä ei käytetä, oletusarvoinen toleranssi lasketaan seuraavasti:

5EM14 ·max(dim(neliömatriisi))·

rowNorm(neliömatriisi)

tai Auto or

Katalogi

diag()

diag(Lista) ⇒ matriisi diag(rivimatriisi) ⇒ matriisi diag(sarakematriisi) ⇒ matriisi

Laskee matriisin, joka sisältää arvot argumenttilistassa tai matriisin sen päälävistäjässä.

diag(neliömatriisi) ⇒ rivimatriisi

Laskee rivimatriisin, joka sisältää elementit neliömatriisin päälävistäjästä.

neliömatriisi:n on oltava neliö.

dim()

dim(Lista) ⇒ kokonaisluku

Laskee Listan mitat.

dim(Matriisi) ⇒ lista

Laskee matriisin mitat kahden elementin listana {rivit, sarakkeet}.

dim(Merkkijono) ⇒ kokonaisluku

Laskee merkkijonon Merkkijono sisältämien merkkien lukumäärän.

Katalogi

26 TI-Nspire™ -sovelluksen käsikirja

Page 33

Disp

Disp [lausTaiMerkkijono1] [, lausTaiMerkkijono2] ...

Näyttää Laskin-sovelluksen historiatietojen sisältämät argumentit. Argumentit näytetään peräkkäin, ja erotinmerkkeinä käytetään ohuita välilyöntejä.

Käyttökelpoisia pääasiassa ohjelmissa ja funktioissa, jotta välilaskutoimitusten näyttäminen voidaan varmistaa.

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa

@ painikkeen · sijaan. Tietokoneen

painiketta näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

DMS

Arvo 4DMS Lista 4DMS Matriisi 4DMS

Tulkitsee argumentin kulmana ja näyttää vastaavan DMS-luvun (DDDDDD¡MM'SS.ss''). DMS-muoto (asteet, minuutit, sekunnit) on

kuvattu kohdissa ¡, ', '' sivulla 116 .

Huomaa: 4DMS muuntaa radiaanit asteiksi, kun sitä käytetään

radiaanitilassa. Jos syötteen perässä on asteen merkki ¡, muunnosta ei suoriteta. Voit käyttää komentoa 4DMS ainoastaan syöterivin lopussa.

Astekulmatilassa:

Katalogi

dotP()

dotP(Lista1, Lista2) ⇒ lauseke

Laskee kahden listan “pistetulon”.

dotP(Ve k t or i 1 , Vektori2) ⇒ lauseke

Laskee kahden vektorin “pistetulon”. Kummankin on oltava rivivektoreita, tai kummankin on oltava

sarakevektoreita.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 27

Page 34

e^()

e^(Arvo1) ⇒ arvo

Laskee e:n arvon korotettuna Arvo1:n potenssiin.

Huomaa: Katso myös e eksponenttimalli, sivu 2. Huomaa: Painikkeen u painaminen, jotta näkyviin saadaan

^(, on eri asia kuin näppäimistön merkin E painaminen.

Voit syöttää kompleksiluvun re muotoa kuitenkin vain radiaanikulmatilassa; aste- tai graadikulmatilassa se aiheuttaa määritysjoukkovirheen (Domain).

e^(Lista1) ⇒ lista

Laskee e:n arvon korotettuna Lista1:n jokaisen elementin potenssiin.

e^(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisieksponentin. Tämä ei ole sama kuin laskettaessa e korotettuna kunkin elementin mukaiseen potenssiin. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

eff()

eff(nimelliskorko,CpY) ⇒ arvo

Talouslaskentatoiminto, joka muuntaa nimelliskorkokannan nimelliskorko efektiiviseksi vuosikoroksi, kun CpY määritetään korkojaksojen lukumääräksi vuodessa.

nimelliskoron on oltava reaaliluku, ja CpY:n on oltava reaaliluku >

Huomaa: Katso myös nom(), sivu 61.

eigVc()

eigVc(neliömatriisi) ⇒ matriisi

Laskee matriisin, joka sisältää ominaisvektorit reaaliselle tai kompleksiselle neliömatriisille, jossa jokainen vastauksen sarake vastaa ominaisarvoa. Huomaa, että ominaisvektori ei ole yksilöllinen; sitä voidaan skaalata millä tahansa vakiokertoimella. Ominaisvek torit ovat normaalimuotoisia, mikä tarkoittaa, että, jos V = [x1, x2, … ,

xn], tällöin:

+ … + x

neliömatriisia tasapainotetaan ensin similaarimuunnoksilla, kunnes rivi- ja sarakenormit ovat mahdollisimman lähellä samaa arvoa. Sen jälkeen neliömatriisi sievennetään Hessenbergin ylämatriisimuotoon ja ominaisvektorit lasketaan Schurin tekijöihin jaon menetelmällä.

polaarisessa muodossa. Käytä tätä

= 1

u painike

Katalogi

Suorakulmakompleksimuodossa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeen kohdistinta painikkeilla ¡ ja ¢.

28 TI-Nspire™ -sovelluksen käsikirja

Page 35

eigVl()

eigVl(neliömatriisi) ⇒ lista

Laskee listan reaalisen tai kompleksisen neliömatriisin ominaisarvoista.

Else Katso If, sivu 39.

Suorakulmakompleksimuodossa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeen kohdistinta painikkeilla ¡ ja ¢.

Katalogi

ElseIf

If BoolenLaus1 Then

Lohko1

ElseIf BoolenLaus2 Then

Lohko2

LohkoN

EndIf

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

EndFor Katso For, sivu 33.

EndFunc Katso Func, sivu 35.

EndIf Katso If, sivu 39.

EndLoop Katso Loop, sivu 53.

EndPrgm Katso Prgm, sivu 68.

Katalogi

EndTry Katso Try, sivu 94.

TI-Nspire™ -sovelluksen käsikirja 29

Page 36

EndWhile Katso While, sivu 100.

Exit

Poistuu nykyisestä For-, While- tai Loop-lohkosta.

Exit-komento ei ole sallittu näiden kolmen silmukkarakenteen (For, While tai Loop) ulkopuolella.

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

exp()

exp(Arvo1) ⇒ arvo

Laskee e:n arvon korotettuna Arvo1:n potenssiin.

Huomaa: Katso myös e eksponenttimalli, sivu 2.

Voit syöttää kompleksiluvun re muotoa kuitenkin vain radiaanikulmatilassa; aste- tai graadikulmatilassa se aiheuttaa määritysjoukkovirheen (Domain).

exp(Lista1) ⇒ lista

Laskee e:n arvon korotettuna Lista1:n jokaisen elementin potenssiin.

exp(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisieksponentin. Tämä ei ole sama kuin laskettaessa e korotettuna kunkin elementin mukaiseen potenssiin. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

polaarisessa muodossa. Käytä tätä

Funktion listaus:

Katalogi

u painike

expr()

expr(Merkkijono) ⇒ lauseke

Määrittää Merkkijonon sisältämän merkkijonon lausekkeena ja suorittaa toimenpiteen välittömästi.

Katalogi

30 TI-Nspire™ -sovelluksen käsikirja

Page 37

ExpReg

ExpReg X, Y [, [Frekv] [, Luokka, Sisällytä]]

Laskee eksponentiaalisen regression y = a·(b)xlistoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.resultsmuuttujaan. (Katso sivu 87.)

Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja | 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tulosmuuttuja Kuvaus

stat.RegEqn

stat.a, stat.b Regressiokertoimet

stat.r

stat.r Muunnettujen tietojen korrelaatiokerroin (x, ln(y))

stat.Resid Eksponentiaalimalliin liittyvät jäännökset

stat.ResidTrans Muunnettujen tietojen lineaariseen sovitukseen liittyvät jäännökset

stat.XReg Muokatun X Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

Regressioyhtälö: a·(b)

Muunnettujen tietojen lineaarimäärittelyn kerroin

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

Katalogi

factor()

factor(rationaaliluku) laskee rationaaliluvun, joka on jaettu

jaottomiin tekijöihin. Sekalukujen kohdalla laskenta-aika pitenee eksponentiaalisesti toiseksi suurimman tekijän sisältämien numeroiden määrän suhteen. Esimerkiksi 30-numeroisen kokonaisluvun tekijöihin jakaminen voi kestää pitempään kuin vuorokauden ja 100-numeroisen luvun pitempään kuin vuosisadan.

Huomaa: Voit pysäyttää (keskeyttää) laskutoimituksen painamalla

Katalogi

Jos haluat pelkästään määrittää, onko jokin luku jaoton, käytä sen sijaan komentoa isPrime(). Se on paljon nopeampi, erityisesti jos rationaaliluku ei ole jaoton, ja jos toiseksi suurimmassa tekijässä on enemmän kuin viisi numeroa.

TI-Nspire™ -sovelluksen käsikirja 31

Page 38

FCdf()

FCdf(alaraja,yläraja,dfOsoitt,dfNimitt) ⇒ luku, jos alaraja ja

yläraja ovat lukuja, lista, jos alaraja ja yläraja ovat listoja

FCdf(

alaraja,yläraja,dfOsoitt,dfNimitt) ⇒ luku, jos alaraja ja

yläraja ovat lukuja, lista, jos alaraja ja yläraja ovat listoja

Laskee F-jakauman todennäköisyyden alarajan ja yläraja n välillä määritetylle dfOsoittajalle (vapausaste) ja dfNimittäjälle.

Kun P(X  yläraja), aseta alaraja= 0.

Katalogi

Fill

Fill Arvo, matriisiMuutt ⇒ matriisi

Korvaa muuttujan matriisiMuutt jokaisen elementin Arvolla. matriisiMuuttujan on oltava valmiiksi olemassa.

Fill Arvo, listaMuutt ⇒ lista

Korvaa muuttujan listaMuutt jokaisen elementin Arvolla. listaMuuttujan on oltava valmiiksi olemassa.

FiveNumSummary

FiveNumSummary X[,[Frekv][,Luokka,Sisällytä]]

Antaa lyhennetyn version 1 muuttujan tilastoista listalle X. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu

87.)

X edustaa datan sisältävää listaa. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan X:n arvon esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaaville X:n arvoille. Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne

datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tulosmuuttuja Kuvaus

stat.MinX x:n arvojen minimi

stat.Q1X x:n ensimmäinen neljännes

stat.MedianX x:n mediaani

stat.Q3X x:n kolmas neljännes

stat.MaxX x:n arvojen maksimi

Katalogi

32 TI-Nspire™ -sovelluksen käsikirja

Page 39

floor()

floor(Arvo1) ⇒ kokonaisluku

Laskee suurimman kokonaisluvun, joka on { argumentti. Tämä funktio on identtinen funktion int() kanssa.

Argumentti voi olla reaali- tai kompleksiluku.

floor(Lista1) ⇒ lista floor(Matriisi1) ⇒ matriisi

Määrittää listan tai matriisin jokaisen elementin alarajasta.

Huomaa: Katso myös ceiling() ja int().

Katalogi

For

For Muutt, Matala, Korkea [, Askel]

Lohko

EndFor

Suorittaa Lohkon sisältämät lausekkeet iteratiivisesti jokaiselle muuttujan Muutt arvolle, Matalasta Korkeaaan kohdassa Askel määritetyin portain.

Muutt ei saa olla järjestelmän muuttuja. Askel voi olla positiivinen tai negatiivinen. Oletusarvo on 1. Lohko voi olla joko yksi lauseke tai sarja lausekkeita, jotka on

erotettu toisistaan kaksoispisteellä (:).

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

format()

format(Arvo[, muotoMerkkijono]) ⇒ merkkijono

Määrittää Arvon merkkijonona muotoilumallin perusteella. muotoMerkkijono on merkkijono, ja sen tulee olla muodossa: “F[n]”,

“S[n]”, “E[n]”, “G[n][c]”, jossa [ ] ilmaisevat valinnaisia osia. F[n]: Kiinteä muoto. n on desimaalipisteen jälkeen näytettävien

numeroiden lukumäärä. S[n]: Kymmenpotenssimuoto. n on desimaalipisteen jälkeen

näytettävien numeroiden lukumäärä. E[n]: Tekninen esitystapa. n on ensimmäisen merkitsevän numeron

jälkeen näytettävien numeroiden lukumäärä. Eksponentti säätyy kolmella kerrolliseksi, ja desimaalipiste siirtyy 0, 1 tai 2 numeroa oikealle.

G[n][c]: Muuten sama kuin kiinteä muoto, mutta erotta a myös juuren vasemmalla puolella olevat numerot kolmen ryhmiin. c määrittää ryhmän erotusmerkin, ja sen oletusarvo on pilkku. Jos c on piste, juuri näytetään pilkkuna.

[Rc]: Mihin tahansa edellä mainituista määrittäjistä voidaan liittää Rc-juurilippu, jossa c on yksi merkki, joka määrittää korvauksen kohteen juuripisteestä.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 33

Page 40

fPart()

fPart(Laus1) ⇒ lauseke fPart(Lista1) ⇒ lista fPart(Matriisi1) ⇒ matriisi

Laskee argumentin murtolukuosan. Kun kyseessä on lista tai matriisi, laskee elementtien murtolukuosat. Argumentti voi olla reaali- tai kompleksiluku.

Katalogi

FPdf()

FPdf(XArvo,dfOsoitt,dfNimitt) ⇒ luku, jos XArvo on luku,

lista, jos XArvo on lista

Laskee F-jakauman todennäköisyyden XArvon kohdalle määritetyille dfOsoittajalle (vapausasteet) ja dfNimittäjälle.

freqTable4list()

freqTable4list

Laskee listan, joka sisältää Lista1:n elementit lavennettuina frekvKokonaislukuListan määrittämien frekvenssien mukaisesti.

Tätä funktiota voidaan käyttää laadittaessa frekve nssitaulukkoa Data & Tilastot -sovelluksessa.

Lista1 voi olla mikä tahansa kelvollinen lista. frekvKokonaislukuListan on oltava samankokoinen kuin Lista1 ja

sen tulee sisältää ainoastaan ei-negatiivisia ko konaislukuelementtejä. Jokainen elementti määrittää kuinka monta kertaa Lista1-elementti toistetaan tuloslistassa. Nolla-arvo sulkee pois vastaavan Lista1- elementin.

frequency()

frequency(Lista1,lokerotLista) ⇒ lista

Luo listan, joka sisältää Lista1:n elementtien lukumäärät. Lukumäärät perustuvat alueisiin (lokeroihin), jotka määritetään kohtaan lokerotLista.

Jos lokerotLista on {b(1), b(2), …, b(n)}, määritetyt alueet ovat {?{b(1), b(1)<?{b(2),…,b(n-1)<?{b(n), b(n)>?}. Tuloksena oleva lista on yhden elementin pitempi kuin lokerotLista.

Jokainen vastauksen elementti vastaa niiden Lista1:n elementtien lukumäärää, jotka ovat kyseisen lokeron alueella. Funktion

countIf() termeillä ilmaistuna vastaus on { countIf(list, ?{b(1)),

countIf(list, b(1)<?{b(2)), …, countIf(list, b(n-1)<?{b(n)), countIf(list, b(n)>?)}.

Niitä Lista1:n elementtejä, joita ei voi “lokeroida”, ei huomioida. Listat & Taulukot -sovelluksessa voit käyttää solualueita kummankin

argumentin tilalla.

Huomaa: Katso myös countIf(), sivu 19.

(Lista1,frekvKokonaislukuLista) ⇒ lista

Katalogi

Vastauksen selitys:

2 Datalistan elementtiä on {2.5 4 Datalistan elementtiä on >2.5 ja {4.5 3 Datalistan elementtiä on >4.5

Elementti "hei" on merkkijono, jota ei voi sijoittaa mihinkään määritetyistä lokeroista.

34 TI-Nspire™ -sovelluksen käsikirja

Page 41

FTest_2Samp

FTest_2Samp Lista1,Lista2[,Frekv1[,Frekv2[,Hypot]]]

FTest_2Samp

(Datalistan syöte)

Lista1,Lista2[,Frekv1[,Frekv2[,Hypot]]]

FTest_2Samp sx1,n1,sx2,n2[,Hypot]

FTest_2Samp

(Yhteenvetotilaston syöte)

Suorittaa kahden otoksen F -testin. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 87.)

Kun Ha: s1 > s2, aseta Hypot>0 Kun Ha: s1 ƒ s2 (oletus), aseta Hypot =0 Kun Ha: s1 < s2, aseta Hypot<0

Tulosmuuttuja Kuvaus

stat.F

stat.PVal Alin merkitsevyystaso, jolla nollahypoteesi voidaan hylätä

stat.dfNumer osoittajan vapausasteet = n1-1

stat.dfDenom nimittäjän vapausasteet = n2-1

stat.sx1, stat.sx2 Otoksen keskihajonnat Lista 1:n ja Lista 2:n sisältämille datasekvensseille

stat.x1_bar stat.x2_bar

stat.n1, stat.n2 Otosten koko

sx1,n1,sx2,n2[,Hypot]

Laskettu ó-tilasto datasekvenssille

Otoksen keskiarvot Lista 1:n ja Lista 2:n sisältämille datasekvensseille

Katalogi

Func

Lohko

EndFunc

Malli käyttäjän määrittämän funktion luomista varten. Lohko voi olla yksi lauseke tai sarja lausekkeita, jotka on erotettu

toisistaan kaksoispisteellä (:), tai sarja eri riveillä olevia lausekkeita. Funktio voi käyttää Return-ohjetta tietyn vastauksen laskemiseen.

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Määritä paloittain määritelty funktio:

Funktion g(x) kuvaajan piirtämisen tulos

Katalogi

TI-Nspire™ -sovelluksen käsikirja 35

Page 42

gcd()

gcd(Arvo1, Arvo2) ⇒ lauseke

Laskee kahden argumentin suurimman yhteisen jakajan. Kahden

gcd on niiden osoittajien gcd jaettuna nimittäjien

murtoluvun

lcm:llä.

Auto or Approximate (Automaattinen tai likimääräinen) -tilassa murtoluvun liukulukujen

gcd(Lista1, Lista2) ⇒ lista

Laskee Lista1:n ja Lista2:n toisiaan vastaavien elementtien suurimmat yhteiset jakajat.

gcd(Matriisi1, Matriisi2) ⇒ matriisi

Laskee Matriisi1 :n ja Matriisi2:n toisiaan vastaavien elementtien suurimmat yhteiset jakajat.

geomCdf()

geomCdf(p,alaraja,yläraja) ⇒ luku, jos alaraja ja yläraja

ovat lukuja,

geomCdf(

yläraja on lista Laskee kumulatiivisen geometrisen todennäköisyyden alarajalta

ylärajalle määritetyllä onnistumistodennäköisyydellä p.

Kun P(X  yläraja), aseta alaraja = 1.

geomPdf()

geomPdf(p,XArvo) ⇒ luku, jos XArvo on luku, lista, jos

XArvo on lista

Laskee diskreetin jakauman todennäköisyyden XArvo:n, eli ensimmäisen onnistuneen kokeen järjestysnumeron kohdalla, määritetyllä onnistumistodennäköisyyllä p.

gcd on 1.0.

lista, jos alaraja ja yläraja ovat listoja

p,yläraja) ⇒ luku, jos yläraja on luku, lista, jos

Katalogi

getDenom( )

getDenom(Murtoluku1) ⇒ arvo

Muuttaa argumentin lausekkeeksi, jolla on sievennetty yhteinen nimittäjä, ja laskee sen jälkeen lausekkeen nimittäjän.

Katalogi

36 TI-Nspire™ -sovelluksen käsikirja

Page 43

getLangInfo( )

getLangInfo() ⇒ merkkijono

Antaa merkkijonon, joka vastaa parhaillaan käytössä olevan kielen lyhyttä nimeä. Voit käyttää sitä esimerkiksi ohjelmassa tai funktiossa nykyisen kielen määrittämiseen.

englanti = "en" tanska = "da" saksa = "de" suomi = "fi" ranska = "fr" italia = "it" hollanti = "nl" flaami = "nl_BE" norja = "no" portugali = "pt" espanja = "es" ruotsi = "sv"

Katalogi

getMode()

getMode(TilanNimiKokonaisluku) ⇒ arvo getMode(0) ⇒ lista

getMode(TilanNimiKokonaisluku) laskee arvon, joka vastaa

TilanNimiKokonaisluku-tilan nykyistä asetusta.

getMode(0) laskee listan, joka sisältää lukupareja. Jokainen pari

koostuu tilaa kuvaavasta kokonaisluvusta ja asetusta kuvaavasta kokonaisluvusta.

Tilat ja niiden asetukset on esitetty alla olevassa taulukossa.

Jos tallennat asetukset komennolla getMode(0) & muutt, voit käyttää komentoa setMode(muutt) funktiossa tai ohjelmassa ja tallentaa asetukset näin väliaikaisesti pelkästään funktion tai ohjelman suorituksen ajaksi. Katso setMode(), sivu 80.

Tilan nimi

Näytettävät numerot

Kulma

Eksponenttimuoto

Reaali- tai kompleksiluku

Automaattinen tai likimääräinen.

Vektorimuoto

Kantaluku

Tilaa vastaa va kokon aisluk u

Asetuksia vastaavat kokonaisluvut

=Liukuva, 2=Liukuva1, 3=Liukuva2, 4=Liukuva3, 5=Liukuva4, 6=Liukuva5, 7=Liukuva6,

8=Liukuva7, 9=Liukuva8, 10=Liukuva9, 11=Liukuva10, 12=Liukuva11, 13=Liukuva12, 14=Kiinteä0, 15=Kiinteä1, 16=Kiinteä2, 17=Kiinteä3, 18=Kiinteä4, 19=Kiinteä5, 20=Kiinteä6, 21=Kiinteä7, 22=Kiinteä8, 23=Kiinteä9, 24=Kiinteä10, 25=Kiinteä11, 26=Kiinteä12

=Radiaani, 2=Aste, 3=Graadi

=Normaali, 2=Kymmenpotenssi, 3=Tekninen

=Reaali, 2=Suorakulma, 3=Polaarinen

=Automaattinen, 2=Likimääräinen

=Suorakulma, 2=Sylinteri, 3=Pallo

=Desimaali, 2=Heksagonaalinen, 3=Binaarinen

Katalogi

TI-Nspire™ -sovelluksen käsikirja 37

Page 44

getNum()

getNum(Murtoluku1) ⇒ arvo

Muuttaa argumentin lausekkeeksi, jolla on sievennetty yhteinen nimittäjä, ja laskee sen jälkeen lausekkeen osoittajan.

Katalogi

getVarInfo()

getVarInfo() ⇒ matriisi tai merkkijono getVarInfo(LibNameString) ⇒ matriisi tai merkkijono

getVarInfo() antaa tuloksena tietomatriisin (muuttujan nimi,

tyyppi ja kirjaston käytettävyys) kaikille nykyisessä tehtävässä määritetyille muuttujille ja kirjasto-objekteille.

Jos yhtään muuttujaa ei ole määritetty, getVarInfo() antaa vastauksena merkkijonon "NONE".

getVarInfo(KirjNimiMerkkijono) antaa tuloksena tietomatriisin

kaikista kirjastossa KirjNimiMerkkijono määritetyistä kirjastoobjekteista. KirjNimiMerkkijonon on oltava merkkijono (lainausmerkkien sisällä oleva teksti) tai merkkijonomuuttuja.

Jos kirjastoa KirjNimiMerkkijono ei ole olemassa, esiintyy virhe.

Huomaa vasemmanpuoleinen esimerkki, jossa funktion

getVarInfo() vastaus on määritetty muuttujaan vs. Jos muuttujan

vs riviä 2 tai riviä 3 yritetään näyttää, tuloksena on “Kelpaamaton

lista tai matriisi” -virhe, koska vähintään yksi näiden rivien elementeistä (esimerkiksi muuttuja b) sieventyy uudelleen matriisiksi.

Tämä virhe voi esiintyä myös käytettäessä Ans-muuttujaa funktion

getVarInfo() tuloksen uudelleenlaskennassa.

Järjestelmä antaa edellä mainitun virheen, koska ohjelmiston nykyinen versio ei tue yleistettyä matriisirakennetta, jossa matriisin elementti voi olla joko matriisi tai lista.

Katalogi

38 TI-Nspire™ -sovelluksen käsikirja

Page 45

Goto

Goto tunnusnimi

Siirtää ohjauksen tunnukseen tunnusnimi. tunnusnimi on määritettävä samassa funktiossa käyttäen

ohjetta.

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Grad

Laus1 4 Grad ⇒ lauseke

Muuttaa Laus1:n graadikulmaan.

Lbl-

Astekulmatilassa:

Radiaanikulmatilassa:

Katalogi

identity()

identity(Kokonaisluku) ⇒ matriisi

Laskee identiteettimatriisin, jonka koko on Kokonaisluku. Kokonaisluvun on oltava positiivinen kokonaisluku.

If BoolenLaus lauseke If BoolenLaus Then

Lohko

EndIf

Jos BoolenLaus on tosi, suorittaa yhden lausekkeen Lauseke tai lausekkeiden lohkon Lohko ennen suorituksen jatkamista.

Jos BoolenLaus on epätosi, jatkaa suoritusta suorittamatta lauseketta tai lausekkeiden lohkoa.

Lohko voi olla joko yksi lauseke tai sarja lausekkeita, jotka on erotettu toisistaan kaksoispisteellä (:).

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 39

Page 46

If BoolenLaus Then

Lohko1

Else

Lohko2

EndIf

Jos BoolenLaus on tosi, suorittaaLohko1:n ja ohittaa sen jälkeen Lohko2:n.

Jos BoolenLaus on epätosi, ohittaa Lohko1:n, mutta suorittaa Lohko2:n.

Lohko1 ja Lohko2 voivat olla yksi lauseke.

If BoolenLaus1 Then

Lohko1

ElseIf

BoolenLaus2 Then

Lohko2

BoolenLausN Then

ElseIf

LohkoN

EndIf

Sallii hypyt. Jos BoolenLaus1 on tosi, suorittaa Lohko1:n. Jos BoolenLaus1 on epätosi, laskee BoolenLaus2:n jne.

Katalogi

40 TI-Nspire™ -sovelluksen käsikirja

Page 47

ifFn()

ifFn(BoolenLaus,Arvo_Jos_tosi [,Arvo_Jos_epätosi

Arvo_Jos_tuntematon]]) ⇒ lauseke, lista tai matriisi

Laskee Boolen lausekkeen BoolenLaus (kaikille BoolenLaus:n elementeille) ja laskee tuloksen noudattaen seuraavia sääntöjä:

• BoolenLaus voi testata yhtä arvoa, listaa tai matriisia.

• Jos jokin BoolenLaus:n elementti on tosi, laskee vastaavan elementin lausekkeesta Arvo_Jos_tosi.

• Jos jokin BoolenLaus:n elementti on epätosi, laskee vastaavan elementin lausekkeesta Arvo_Jos_epätosi. Jos jätät pois lausekkeen Arvo_Jos_epätosi, antaa vastauksen undef.

•Jos BoolenLaus:n elementti ei ole tosi eikä epätosi, laskee vastaavan elementin Arvo_Jos_tuntematon. Jos jätät pois lausekkeen Arvo_Jos_tuntematon, antaa vastauksen undef.

• Jos funktion

Huomaa: Jos sievennetty BoolenLaus-lauseke sisältää listan tai

matriisin, kaikkien muiden lista- tai matriisiargumenttien on oltava samankokoisia, ja myös vastaus on samankokoinen.

ifFn() toinen, kolmas tai neljäs argumentti on yksi

lauseke, Boolen testiä sovelletaan jokaiseen BoolenLaus:n positioon.

Katalogi

1:n testiarvo on alle 2.5, joten se vastaa

Arvo_Jos_Tosi-elementti arvolle 5 kopioidaan vastauslistaan.

2:n testiarvo on alle 2.5, joten se vastaa

Arvo_Jos_Tosi-elementti arvolle 6 kopioidaan vastauslistaan.

3:n testiarvo ei ole alle 2.5, joten se vastaa Arvo_Jos_Epätosi-

elementti arvolle 10 kopioidaan vastauslistaan.

Arvo_Jos_tosi on yksi arvo ja vastaa mitä tahansa valittua paikkaa.

Arvo_Jos_epätosi-elementtiä ei ole määritetty. Käytetään merkintää Undef.

Yksi elementti valittu lausekkeesta Arvo_Jos_tosi. Yksi elementti valittu lausekkeesta Arvo_Jos_epätosi.

imag()

imag(Arvo1) ⇒ arvo

Katalogi

Laskee argumentin imaginaarisen osan.

Huomaa: Kaikkia määrittämättömiä muuttujia käsitellään

reaalimuuttujina. Katso myös real(), sivu 74

imag(Lista1) ⇒ lista

Laskee listan elementtien imaginaarisista osista.

imag(Matriisi1) ⇒ matriisi

Laskee matriisin elementtien imaginaarisista osista.

Epäsuora operaattori Katso

inString()

inString(srcMerkkijono, alaMerkkijono[,

Alku]) ⇒ kokonaisluku

Määrittää merkin paikan merkkijonossa srcMerkkijono, jonka kohdalla merkkijonon alaMerkkijono ensimmäinen esiintyminen alkaa.

Alku, mikäli se on mukana, määrittää merkin paika n sen merkkijonon srcMerkkijonosisällä, josta haku alkaa. Oletusarvo = 1

(srcMerkkijonon ensimmäinen merkki). Jos srcMerkkijono ei sisällä alaMerkkijonoa tai Alku on >

srcMerkkijonon pituus, vastaus on nolla.

#()

Katalogi

, sivu 115.

TI-Nspire™ -sovelluksen käsikirja 41

Page 48

int()

int(Arvo) ⇒ kokonaisluku int(Lista1) ⇒ lista int(Matriisi1) ⇒ matriisi

Laskee suurimman kokonaisluvun, joka on pienempi tai yhtä suuri kuin argumentti. Tämä funktio on identtinen funktion kanssa.

floor()

Argumentti voi olla reaali- tai kompleksiluku. Kun kyseessä on lista tai matriisi, laskee kunkin elementin suu rimman

kokonaisluvun.

Katalogi

intDiv()

intDiv(Luku1, Luku2) ⇒ kokonaisluku intDiv(Lista1, Lista2) ⇒ lista intDiv(Matriisi1, Matriisi2) ⇒ matriisi

Määrittää lausekkeen (Luku1 ÷ Luku2) etumerkillisen kokonaislukuosan.

Listojen ja matriisien kohdalla, laskee lausekkeen (argumentti 1 ÷ argumentti 2) etumerkillisen kokonaislukuosan kullekin elementtiparille.

invc2()

invc2(Ala,df)

Ala,df)

invchi2(

Laskee käänteisen kumulatiivisen c2 (chi-neliö) todennäköisyysfunktion, joka on määritetty vapausasteella df tietylle käyrän alapuoliselle alueelle Ala.

invF()

invF(Ala,dfOsoitt,dfNimitt)

Ala,dfOsoitt,dfNimitt)

invF(

Laskee käänteisen kumulatiivisen F-jakaumafunktion, jolle on määritetty dfOsoitt ja dfNimitt, tietylle käyrän alapuoliselle alueelle Ala.

invNorm()

invNorm(Ala[,m,s])

Laskee käänteisen kumulatiivisen normaalijakaumafunktion tietylle normaalijakaumakäyrän alapuolella olevalle Alalle , jolle on määritetty m ja s.

Katalogi

invt()

invt(Ala,df)

Laskee käänteisen kumulatiivisen Studentin ttodennäköisyysfunktion, jolle on määritetty vapausaste, df, tietylle käyrän alapuoliselle Alalle.

Katalogi

42 TI-Nspire™ -sovelluksen käsikirja

Page 49

iPart()

iPart(Luku) ⇒ kokonaisluku iPart(Lista1) ⇒ lista iPart(Matriisi1) ⇒ matriisi

Laskee argumentin kokonaisosan. Listojen ja matriisien kohdalla, laskee jokaisen elementin

kokonaisosan. Argumentti voi olla reaali- tai kompleksiluku.

Katalogi

irr()

irr(CF0,CFLista [,CFFrekv]) ⇒ arvo

Talouslaskentatoiminto, joka laskee investoinnin sisäisen korkokannan.

CF0 on alkuperäinen kassavirta aikana 0; arvon on oltava kokonaisluku.

CFLista on lista kassavirtamääristä ensimmäisen kassavirran CF0 jälkeen.

CFFrekv on valinnainen lista, jossa jokainen elementti määrittää esiintymisfrekvenssin ryhmitetylle (peräkkäiselle) kassavirtamäärälle, joka on CFListan vastaava elementti. Oletusarvo on 1; jos syötät arvoja, niiden on oltava positiivisia kokonaislukuja < 10,000.

Huomaa: Katso myös mirr(), sivu 56.

isPrime()

isPrime(Luku) ⇒ Boolen vakiolauseke

Määrittää totuusarvon tosi tai epätosi ilmaisten, onko luku kokonaisluku ‚ 2, joka on tasan jaollinen vain itsellään ja ykkösellä (1).

Jos Luku on pitempi kuin 306 numeroa, eikä siinä ole tekijöitä

{1021, kaava isPrime(Luku) näyttää virheilmoituksen.

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Katalogi

Funktio, jolla etsitään seuraava jaoton luku määritetyn luvun jälkeen:

TI-Nspire™ -sovelluksen käsikirja 43

Page 50

Lbl

Lbl tunnusnimi

Määrittää funktion sisällä tunnuksen, jonka nimi on tunnusnimi. Ohjeella Siirry tunnusnimi voit siirtää ohjauksen kyseistä tunnusta

välittömästi seuraavaan ohjaukseen. tunnusnimellä on samat nimeämissäännöt kuin muuttujan nimellä.

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

lcm()

lcm(Luku1, Luku2) ⇒ lauseke lcm(Lista1, Lista2) ⇒ lista lcm(Matriisi1, Matriisi2) ⇒ matriisi

Laskee kahden argumentin pienimmän yhteisen jaettavan. Kahden murtoluvun lcm on niiden osoittajien lcm jaettuna niiden nimittäjien

gcd:llä. Murtoluvun liukulukujen lcm on niiden tulo.

Kun kyseessä on kaksi listaa tai matriisia, laskee vastaavien elementtien pienimmät yhteiset jakajat.

left()

left(lähdemerkkijono[, Num]) ⇒ merkkijono

Määrittää vasemmanpuoleisimmat Num-merkit, jotka sisältyvät merkkijonoon lähdemerkkijono.

Jos jätät pois komennon Num, määrittää kaiken merkkijonosta lähdemerkkijono.

left(Lista1[, Num]) ⇒ lista

Määrittää vasemmanpuoleisimmat Num-elementit, jotka sisältyvät listaan Lista1.

Jos jätät pois komennon Num, määrittää kaiken listasta Lista1.

left(Vertailu) ⇒ lauseke

Laskee yhtälön tai epäyhtälön vasemman puolen.

Katalogi

44 TI-Nspire™ -sovelluksen käsikirja

Page 51

libShortcut()

libShortcut(KirjNimiMerkkijono, PikavalNimiMerkkijono [, KirjYksitLippu]) ⇒ muuttujalista

Luo muuttujaryhmän nykyiseen ongelmaan, joka sisältää viittauksia kaikkiin määritetyn kirjastoasiakirjan kirjNimiMerkkijono sisältämiin objekteihin. Lisää myös ryhmän jäsenet Muuttujat-valikkoon. Tällöin voit viitata kuhunkin objektiin käyttäen sen komentoa PikavalNimimerkkijono.

Aseta KirjYksitLippu= objektit (oletusarvo) Aseta KirjYksitLippu=1, kun haluat sisällyttää yksityiset kirjastoobjektit

Muuttujaryhmän kopioiminen, katso CopyVar sivulla 15. Muuttujaryhmän poistaminen, katso DelVar sivulla 25.

0, kun haluat sulkea pois yksityiset kirjasto-

Katalogi

Tässä esimerkissä edellytetään asianmukaisesti tallennettua ja päivitettyä kirjastoasiakirjaa nimeltä linalg2, joka sisältää objektit clearmat, gauss1 ja gauss2.

LinRegBx

LinRegBx X,Y[,[Frekv][,Luokka,Sisällytä]]

Laskee lineaarisen regression y = a+b·x listoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.resultsmuuttujaan. (Katso sivu 87.)

Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta.

Katalogi

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tulosmuuttuja Kuvaus

stat.RegEqn

Regressioyhtälö: a+b·x

stat.a, stat.b Regressiokertoimet

stat.r

Määrityskerroin

stat.r Korrelaatiokerroin

stat.Resid Regressioyhtälön jäännökset

stat.XReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

stat.FreqReg Komentoja stat.FreqReg ja stat.YReg vastaava frekvenssilista

TI-Nspire™ -sovelluksen käsikirja 45

Page 52

LinRegMx

LinRegMx X,Y[,[Frekv][,Luokka,Sisällytä]]

Laskee lineaarisen regression y = m·x+b listoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.results-muuttujaan.

(Katso sivu 87.) Kaikkien listojen on oltava samankokoisia Sisällytä-listaa

lukuunottamatta.

Katalogi

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tulosmuuttuja Kuvaus

stat.RegEqn

Regressioyhtälö: m·x+b

stat.m, stat.b Regressiokertoimet

stat.r

Määrityskerroin

stat.r Korrelaatiokerroin

stat.Resid Regressioyhtälön jäännökset

stat.XReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

LinRegtIntervals

LinRegtIntervals X,Y[,Frekv[,0[,CTaso]]]

Katalogi

Kulmakerroin. Laskee tason C luottamusvälin kulmakertoimelle.

LinRegtIntervals X,Y[,Frekv[,1,Xarvo[,CTaso]]]

Vaste. Laskee ennustetun y:n arvon, tason C ennustevälin yhdelle havainnolle ja tason C luottamusvälin keskiarvovasteelle.

Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 87.)

Kaikkien listojen on oltava samankokoisia.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

46 TI-Nspire™ -sovelluksen käsikirja

Page 53

Tulosmuuttuja Kuvaus

stat.RegEqn

stat.a, stat.b Regressiokertoimet

stat.df Vapausasteet

stat.r

stat.r Korrelaatiokerroin

stat.Resid Regressioyhtälön jäännökset

Vain Kulmakerroin-tyyppi

Tulosmuuttuja Kuvaus

[stat.CLower, stat.CUpper]

stat.ME Luottamusvälin virhemarginaali

stat.SESlope Kulmakertoimen keskivirhe

stat.s Keskivirhe suoran ympärillä

Vain Vaste-tyyppi

Tulosmuuttuja Kuvaus

[stat.CLower, stat.CUpper]

stat.ME Luottamusvälin virhemarginaali

stat.SE Keskiarvovasteen keskivirhe

[stat.LowerPred , stat.UpperPred]

stat.MEPred Ennustevälin virhemarginaali

stat.SEPred Ennusteen keskivirhe

stat.y

Regressioyhtälö: a+b·x

Määrityskerroin

Kulmakertoimen luottamusväli

Keskiarvovasteen luottamusväli

Yhden havainnon ennusteväli

a + b·XArvo

TI-Nspire™ -sovelluksen käsikirja 47

Page 54

LinRegtTest

LinRegtTest X,Y[,Frekv[,Hypot]]

Laskee lineaarisen regression X- ja Y-listoista ja suorittaa t-testin kulmakertoimen b ja korrelaatiokertoimen r arvosta yhtälölle y=a+bx. Testaa nollahypoteesia H0:b=0 (vastaavasti, r=0) johonkin kolmesta vaihtoehtoisesta hypoteesista.

Kaikkien listojen on oltava samankokoisia.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Hypot on valinnainen arvo, joka määrittää yhden kolmesta hypoteesista, johon nollahypoteesia (H0:b=r=0) testataan.

Kun Ha: bƒ0 ja rƒ0 (oletus), aseta Hypot=0 Kun Ha: b<0 ja r<0, aseta Hypot<0 Kun Ha: b>0 ja r>0, aseta Hypot>0

Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 87.)

Tulosmuuttuja Kuvaus

stat.RegEqn

stat.t t-tilasto merkitsevyystestille

stat.PVal Alin merkitsevyystaso, jolla nollahypoteesi voidaan hylätä

stat.df Vapausasteet

stat.a, stat.b Regressiokertoimet

stat.s Keskivirhe suoran ympärillä

stat.SESlope Kulmakertoimen keskivirhe

stat.r

stat.r Korrelaatiokerroin

stat.Resid Regressioyhtälön jäännökset

Regressioyhtälö: a + b·x

Määrityskerroin

Katalogi

List()

Katalogi

@List(Lista1) ⇒ lista

Määrittää listan, joka sisältää Lista1:n peräkkäisten elementtien väliset erotukset. Jokainen Lista1:n elementti vähennetään Lista1:n seuraavasta elementistä. Tuloksena oleva lista on aina yhden elementin lyhyempi kuin alkuperäinen Lista1.

48 TI-Nspire™ -sovelluksen käsikirja

Page 55

list4mat()

list4mat(Lista [, elementtiäRivillä]) ⇒ matriisi

Laskee matriisin, joka on täytetty rivi riviltä Listan elementeillä. elementtiäRivillä, mikäli sisällytetään, määrittää elementtien

määrän rivillä. Oletusarvo on Listan elementtien määrä (yksi rivi). Jos Lista ei täytä tulosmatriisia, siihen lisätään nollia.

Katalogi

ln()

ln(Arvo1) ⇒ arvo ln(Lista1) ⇒ lista

Määrittää argumentin luonnollisen logaritmin. Jos kyseessä on lista, määrittää elementtien luonnolliset logaritmit.

ln(neliömatriisi1) ⇒ neliömatriisi

Määrittää neliömatriisi1:n matriisin luonnollisen logaritmin. Tämä ei ole sama kuin kunkin elementin luonnollisen logaritmin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

LnReg

LnReg X, Y[, [Frekv] [, Luokka, Sisällytä]]

Laskee logaritmisen regression y = a+b·ln(x) listoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.resultsmuuttujaan. (Katso sivu 87.)

Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Jos kompleksilukumuodon tila on Reaali:

Jos kompleksilukumuodon tila on Suorakulma:

Radiaanikulmatilassa ja suorakulmakompleksimuodossa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeen kohdistinta painikkeilla ¡ ja ¢.

painikkeet

Katalogi

TI-Nspire™ -sovelluksen käsikirja 49

Page 56

Tulosmuuttuja Kuvaus

stat.RegEqn

Regressioyhtälö: a+b·ln(x)

stat.a, stat.b Regressiokertoimet

stat.r

Muunnettujen tietojen lineaarimäärittelyn kerroin

stat.r Muunnettujen tietojen korrelaatiokerroin (ln(x), y)

stat.Resid Logaritmimalliin liittyvät jäännökset

stat.ResidTrans Muunnettujen tietojen lineaariseen sovitukseen liittyvät jäännökset

stat.XReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

Local

Local Muutt1[, Muutt2] [, Muutt3] ...

Määrittää määritetyt muuttujat paikallisina muuttujina. Nämä muuttujat ovat olemassa vain funktion sievennyksen aikana, ja ne poistetaan, kun funktion suoritus päättyy.

Huomaa: Paikalliset muuttujat säästävät muistia, koska ne ovat

olemassa vain väliaikaisesti. Lisäksi ne eivät häiritse mitään olemassa olevia globaalien muuttujien arvoja. Paikallisia muuttujia on käytettävä For-silmukoissa sekä tallennettaessa arvoja väliaikaisesti monirivisessä funktiossa, sillä globaalien muuttujien modifiointeja ei sallita funktiossa.

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Katalogi

50 TI-Nspire™ -sovelluksen käsikirja

Page 57

log()

log(Arvo1[,Arvo2]) ⇒ arvo log(Lista1[,Arvo2]) ⇒ lista

Laskee ensimmäisen argumentin kantaluku--Arvo2:n logaritmin.

Huomaa: Katso myös Logaritmimalli, sivu 2.

Kun kyseessä on lista, laskee elementtien kantaluku--Arvo2:n logaritmin.

Jos toinen argumentti jätetään pois, kantalukuna käytetään lukua 10.

Jos kompleksilukumuodon tila on Reaali:

Jos kompleksilukumuodon tila on Suorakulma:

painikkeet

log(neliömatriisi1[,Arvo]) ⇒ neliömatriisi

Laskee matriisin kantaluku-Arvo:n logaritmin neliömatriisi1:lle. Tämä ei ole sama kuin kunkin elementin kantaluku-Arvo-logaritmin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

Jos kantalukuargumentti jätetään pois, kantalukuna käytetään lukua 10.

Logistic

Logistic X, Y[, [Frekv] [, Luokka, Sisällytä]]

Laskee logistisen regression y = (c/(1+a·e frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.resultsmuuttujaan. (Katso sivu 87.)

Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

-bx

)) listoista X ja Y

Radiaanikulmatilassa ja suorakulmakompleksimuodossa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeen kohdistinta painikkeilla ¡ ja ¢.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 51

Page 58

Tulosmuuttuja Kuvaus

stat.RegEqn

Regressioyhtälö: c/(1+a·e

-bx

)

stat.a, stat.b, stat.c Regressiokertoimet

stat.Resid Regressioyhtälön jäännökset

stat.XReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

LogisticD

LogisticD X, Y [ , [Iteraatiot] , [Frekv] [, Luokka, Sisällytä] ]

Laskee logistisen regression y = (c/(1+a·e frekvenssillä Frekv käyttäen tiettyä Iteraatioiden määrää. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 87.)

Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta.

-bx

)+d) listoista X ja Y

Katalogi

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Iteraatiot on valinnainen arvo, joka määrittää ratkaisun

yrityskertojen enimmäismäärän. Mikäli se jätetään pois, käytetään arvoa 64. Suuremmilla arvoilla saadaan tyypillisesti parempi tarkkuus, mutta suoritusaika on pitempi ja päin vastoin.

Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tulosmuuttuja Kuvaus

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

Regressioyhtälö: c/(1+a·e

Regressiokertoimet

-bx

)+d)

stat.Resid Regressioyhtälön jäännökset

stat.XReg Muokatun X Listan sisältämä datapisteiden lista, jota käytetään todellisesti regressiossa komentojen

stat.YReg Muokatun Y Listan sisältämä datapisteiden lista, jota käytetään todellisesti regressiossa komentojen

Frekv, Luokka Lista ja Sisällytä Luokat rajoitusten mukaisesti

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

52 TI-Nspire™ -sovelluksen käsikirja

Page 59

Loop (Silmukka)

Loop

Lohko

EndLoop

Suorittaa toistuvasti Lohkon sisältämät lausekkeet. Huomaa, että silmukkaa suoritetaan loputtomasti, ellei suoriteta Lohkon sisällä.

Lohko on lausekkeiden sarja, jotka on erotettu toisistaan kaksoispisteellä (:).

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Goto- tai Exit-ohjetta

Katalogi

LU Matriisi, lMatNimi, uMatNimi, pMatNimi[, Tol ]

Laskee Doolittlen LU (ala-ylä)-dekomponoinnin reaali- tai kompleksimatriisista. Alakolmiomatriisi tallentuu muuttujaan lMatNimi, yläkolmiomatriisi muuttujaan uMatNimi ja permutaatiomatriisi (joka kuvaa laskennan aikana tehdyt rivien vaihdot) muuttujaan pMatNimi.

lMatName · uMatName = pMatName · matriisi

Valinnaisesti kaikkia matriisielementtejä käsitellään nollana, jos niiden itseisarvo on pienempi kuin To l. Tätä toleranssia käytetään vain, jos matriisissa on liukulukusyötteitä eikä se sisällä symbolisia muuttujia, joille ei ole määritetty arvoa. Muussa tapauksessa To l - komentoa ei huomioida.

• Jos käytät painikkeita

Approximate (Automaattinen tai likimääräinen)

tilan valintaa Approximate (Likimääräinen), laskut suoritetaan liukulukuaritmetiikalla.

•Jos Tol jätetään pois tai sitä ei käytetä, oletusarvoinen toleranssi lasketaan seuraavasti:

5EM14 ·max(dim(Matriisi)) ·riviNorm(Matriisi)

LU-dekomponointialgoritmi käyttää osittaista rivien vaihtoa

(pivoting).

· tai Auto or

mat4list()

mat4list(Matriisi) ⇒ lista

Luo listan, joka on täytetty Matriisin elementeillä. Elementit kopioidaan Matriisista rivi riviltä.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 53

Page 60

max()

max(Arvo1, Arvo2) ⇒ lauseke max(Lista1, Lista2) ⇒ lista max(Matriisi1, Matriisi2) ⇒ matriisi

Laskee kahden argumentin maksimiarvon. Jos argumentteina on kaksi listaa tai matriisia, laskee listan tai matriisin, joka sisältää vastaavien elementtien kunkin parin maksimiarvon.

max(Lista) ⇒ lauseke

Laskee lista:n maksimielementin.

max(Matriisi1) ⇒ matriisi

Luo rivivektorin, joka sisältää Matriisi1:n jokaisen sarakkeen maksimielementin.

Huomaa: Katso myös min().

Katalogi

mean()

mean(Lista[, frekvLista]) ⇒ lauseke

Laskee Listan sisältämien elementtien keskiarvon. Jokainen frekvListan elementti näyttää Listan vastaavien

elementtien peräkkäisten esiintymien lukumäärän.

mean(Matriisi1[, frekvMatriisi]) ⇒ matriisi

Luo rivivektorin kaikkien Matriisi1:n sarakkeiden keskiarvoista. Jokainen frekvMatriisin elementti näyttää Matriisi1:n vastaavien

elementtien peräkkäisten esiintymien lukumäärän.

median()

median(Lista) ⇒ lauseke

Laskee Listan elementtien mediaanin.

median(Matriisi1) ⇒ matriisi

Luo rivivektorin, joka sisältää Matriisi1:n sarakkeiden mediaanit.

Huomaa: Kaikkien listan tai matriisien syötteiden tulee sieventyä

luvuiksi.

Suorakulmavektorimuodossa:

Katalogi

54 TI-Nspire™ -sovelluksen käsikirja

Page 61

MedMed

MedMed X,Y [, Frekv] [, Luokka, Sisällytä]]

Laskee mediaani-mediaani-suoran y = (m·x+b) listoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.resultsmuuttujaan. (Katso sivu 87.)

Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tulosmuuttuja Kuvaus

stat.RegEqn

stat.m, stat.b Mallin kertoimet

stat.Resid Mediaani-mediaani-suoran jäännökset

stat.XReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

Mediaani-mediaani-suoran yhtälö: m·x+b

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

Katalogi

mid()

mid(lähdemerkkijono, Alku[, Count]) ⇒ merkkijono

Laskee Count:n merkit merkkijonosta lähdemerkkijono aloittaen merkistä numero Alku.

Jos Count jätetään pois, tai jos se on suurempi kuin lähdemerkkijono, laskee kaikki merkit lähdemerkkijonosta aloittaen merkistä numero Alku.

Count:n on oltava ‚ 0. Jos Count = 0, antaa vastauksena tyhjän merkkijonon.

mid(lähdelista, Alku [, Count]) ⇒ lista

Laskee Count:n elementit lähdelistasta aloittaen elementistä numero Alku.

Jos Count jätetään pois, tai jos se on suurempi kuin lähdelista, laskee kaikki elementit lähdelistasta aloittaen elementistä numero

Alku.

Count:n on oltava ‚ 0. Jos Count = 0, antaa vastauksena tyhjän

listan.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 55

Page 62

mid()

mid(lähdeMerkkijonoLista, Alku[, Count]) ⇒ lista

Laskee Count:n merkkijonot merkkijonolistasta lähdeMerkkijonoLista aloittaen elementistä numero Alku.

min()

min(Arvo1, Arvo2) ⇒ lauseke min(Lista1, Lista2) ⇒ lista min(Matriisi1, Matriisi2) ⇒ matriisi

Laskee kahden argumentin minimiarvon. Jos argumentteina on kaksi listaa tai matriisia, laskee listan tai matriisin, joka sisältää vastaavien elementtien kunkin parin minimiarvon.

min(Lista) ⇒ lauseke

Laskee Listan minimielementin.

min(Matriisi1) ⇒ matriisi

Luo rivivektorin, joka sisältää Matriisi1:n jokaisen sarakkeen minimielementin.

Huomaa: Katso myös max().

Katalogi

mirr()

mirr(tal.arvo,uud.invest.arvo,CF0,CFLista[,CFFrekv])

Talouslaskentatoiminto, joka laskee investoinnin modifioidun sisä isen korkokannan.

tal.arvo on kassavirtamääristä maksettava korkoprosentti. uud.invest.arvo on korkokanta, jolla kassavirrat investoidaan

uudelleen. CF0 on alkuperäinen kassavirta aikana 0; arvon on oltava

kokonaisluku. CFLista on lista kassavirtamääristä ensimmäisen kassavirran CF0

jälkeen. CFFrekv on valinnainen lista, jossa jokainen elementti määrittää

esiintymisfrekvenssin ryhmitetylle (peräkkäiselle) kassavirtamäärälle, joka on CFListan vastaava elementti. Oletusarvo on 1; jos syötät arvoja, niiden on oltava positiivisia kokonaislukuja < 10,000.

Huomaa: Katso myös irr(), sivu 43.

mod()

mod(Arvo1, Arvo2) ⇒ lauseke mod(Lista1, Lista2) ⇒ lista mod(Matriisi1, Matriisi2) ⇒ matriisi

Laskee ensimmäisen argumentin modulo toinen argumentti identtisten yhtälöiden määrittelyn mukaisesti:

mod(x,0) = x mod(x,y) = x -ìy floor(x/y)

Kun toinen argumentti on ei-nolla, vastaus on periodinen tässä argumentissa. Vastaus on joko nolla tai samanmerkkinen kuin toinen argumentti.

Jos argumentteina on kaksi listaa tai matriisia, laskee listan tai matriisin, joka sisältää vastaavien elementtien kunkin parin modulon (jakojäännöksen).

Huomaa: Katso myös remain(), sivu 75

Katalogi

56 TI-Nspire™ -sovelluksen käsikirja

Page 63

mRow()

mRow(Arvo, Matriisi1, Indeksi) ⇒ matriisi

Luo kopion Matriisi1:stä, jossa jokainen rivin Indeksi elementti Matriisi1:ssä on kerrottu arvolla Arvo.

Katalogi

mRowAdd()

mRowAdd(Arvo, Matriisi1, Indeksi1, Indeksi2) ⇒ matriisi

Luo kopion Matriisi1:stä, jossa jokainen rivin Indeksi2 elementti Matriisi1:ssä on korvattu seuraavasti:

Arvo · rivi Indeksi1 + rivi Indeksi2

MultReg

MultReg Y, X1[,X2[,X3,…[,X10]]]

Laskee listan Y moninkertaisen lineaarisen regression listojen X1, X2,

…, X10 suhteen. Tulosten yhteenveto tallentuu stat.results-

muuttujaan. (Katso sivu 87.) Kaikkien listojen on oltava samankokoisia.

Tulosmuuttuja Kuvaus

stat.RegEqn

Regressioyhtälö: b0+b1·x1+b2·x2+ ...

stat.b0, stat.b1, ... Regressiokertoimet

stat.R

Moninkertaisen määrityksen kerroin

stat.yLista yLista = b0+b1·x1+ ...

stat.Resid Regressioyhtälön jäännökset

MultRegIntervals

MultRegIntervals Y,

X1[,X2[,X3,…[,X10]]],XArvoLista[,CTaso]

Laskee ennustetun y:n arvon, tason C ennustevälin yhdelle havainnolle ja tason C luottamusvälin keskiarvovasteelle.

Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu

87.)

Kaikkien listojen on oltava samankokoisia.

Katalogi

Tulosmuuttuja Kuvaus

stat.RegEqn

Regressioyhtälö: b0+b1·x1+b2·x2+ ...

stat.y Pisteen A arvio: y = b0 + b1 · xl + ... XArvoListalle

stat.dfError Virheen vapausasteet

stat.CLower, stat.CUpper Keskiarvovasteen luottamusväli

TI-Nspire™ -sovelluksen käsikirja 57

Page 64

Tulosmuuttuja Kuvaus

stat.ME Luottamusvälin virhemarginaali

stat.SE Keskiarvovasteen keskivirhe

stat.LowerPred, stat.UpperrPred

Yhden havainnon ennusteväli

stat.MEPred Ennustevälin virhemarginaali

stat.SEPred Ennusteen keskivirhe

stat.bList Regressiokertoimien lista, {b0,b1,b3,...}

stat.Resid Regressioyhtälön jäännökset

MultRegTests

MultRegTests Y, X1[,X2[,X3,…[,X10]]]

Moninkertaisen lineaarisen regression testi laskee lineaarisen regression tietystä datasta ja määrittää kertoimille globaalin F-testin tilastot sekä t-testin tilastot.

Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 87.)

Katalogi

Tulokset

Tulosmuuttuja Kuvaus

stat.RegEqn

Regressioyhtälö: b0+b1·x1+b2·x2+ ...

stat.F Globaalin F-testin tilasto

stat.PVal Globaaliin F-tilastoon liittyvä P-arvo

stat.R

stat.AdjR

Moninkertaisen määrityksen kerroin

Moninkertaisen määrityksen säädetty kerroin

stat.s Virheen keskihajonta

stat.DW Durbin-Watsonin tilasto; käytetään määritettäessä, esiintyykö mallissa ensimmäisen asteen automaattista

korrelaatiota

stat.dfReg Regression vapausasteet

stat.SSReg Regression neliöiden summa

stat.MSReg Regression keskineliö

stat.dfError Virheen vapausasteet

stat.SSError Virheen neliöiden summa

stat.MSError Virheen keskineliö

stat.bList {b0,b1,...} Kertoimien lista

stat.tList t-tilastojen lista, yksi kullekin bListan sisältämälle kertoimelle

stat.PList P-arvojen lista kullekin t-tilastolle

stat.SEList Keskivirheiden lista bListan sisältämille kertoimille

58 TI-Nspire™ -sovelluksen käsikirja

Page 65

Tulosmuuttuja Kuvaus

stat.yLista yLista = b0+b1·x1+...

stat.Resid Regressioyhtälön jäännökset

stat.sResid Standardoidut jäännökset; saadaan jakamalla jäännös keskihajonnalla

stat.CookDist Cookin etäisyys; jäännökseen ja tuottosuhteeseen perustuvan havainnon vaikutus

stat.Leverage Miten kaukana riippumattoman muuttujan arvot ovat niiden keskiarvoista

nCr()

nCr(Arvo1, Arvo2) ⇒ lauseke

Kokonaisluvulle Arvo1 ja Arvo2 sekä Arvo1 ‚ Arvo2 ‚ 0, nCr() on Arvo1:n asioiden kombinaatioiden lukumäärä, joita otetaan Arvo2:n

verran kerrallaan. (Tästä käytetään myös nimitystä binomikerroin.)

nCr(Arvo, 0) ⇒ 1

Arvo, negKokonaisluku) ⇒ 0

nCr(

Arvo, posKokonaisluku) ⇒

nCr(

Arvo·(ArvoN1)... (ArvoNposKokonaisluku+1)/ posKokonaisluku!

nCr(

Arvo, eiKokonaisluku) ⇒ lauseke!/

((ArvoNeiKokonaisluku)!·eiKokonaisluku!)

nCr(

Lista1, Lista2) ⇒ lista

Laskee listan kombinaatioista kahden listan sisältämiin vastaaviin elementtipareihin perustuen. Argumenttien on oltava samankokoisia listoja.

nCr(Matriisi1, Matriisi2) ⇒ matriisi

Laskee matriisin kombinaatioista kahden matriisin sisältämiin vastaaviin elementtipareihin perustuen. Argumenttien on oltava samankokoisia matriiseja.

nDeriv()

nDeriv(Laus1, Muutt[=Arvo] [, H]) ⇒ lauseke nDeriv(Laus1, Muutt[, H] Muutt=Arvo) ⇒ lauseke

nDeriv(Laus1, Muutt[=Arvo], Lista) ⇒ lista nDeriv(Lista1, Muutt[=Arvo] [, H]) ⇒ lista nDeriv(Matriisi1, Muutt[=Arvo] [, H]) ⇒ matriisi

Laskee numeerisen derivaatan lausekkeena. Käyttää keskeiserotusosamäärän kaavaa.

Kun Arvo määritetään, se ohittaa mahdolliset aikaisemmat muuttujamääritykset tai mahdolliset muuttujan nykyiset “such that ” substituutiot.

H on askelarvo. Jos H jätetään pois, sen oletusarvo on 0.001. Lista1:ä tai Matriisi1:ä käytettäessä operaatio mapataan listan

arvojen tai matriisin elementtien suhteen.

Huomaa: Katso myös avgRC().

Katalogi

TI-Nspire™ -sovelluksen käsikirja 59

Page 66

newList()

newList(numElementit) ⇒ lista

Antaa tuloksena listan, jonka koko on numElementit. Jokainen elementti on nolla.

Katalogi

newMat()

newMat(numRivit, numSarakkeet) ⇒ matriisi

Antaa tuloksena nollamatriisin, jonka koko on numRivit ja numSarakkeet.

nfMax()

nfMax(Laus, Muutt) ⇒ arvo nfMax(Laus, Muutt, alaraja) ⇒ arvo nfMax(Laus, Muutt, alaraja, yläraja) ⇒ arvo nfMax(Laus, Muutt) alaraja<Muutt<yläraja ⇒ arvo

Laskee muuttujan Muutt numeerisen ehdotusarvon, jossa lausekkeen Laus paikallinen maksimi esiintyy.

Jos annat alarajan ja ylärajan, funktio etsii paikallista maksimia näiden arvojen väliltä.

nfMin()

nfMin(Laus, Muutt) ⇒ arvo nfMin(Laus, Muutt, alaraja) ⇒ arvo

nfMin(Laus, Muutt, alaraja, yläraja) ⇒ arvo nfMin(Laus, Muutt) alaraja<Muutt<yläraja ⇒ arvo

Laskee muuttujan Muutt numeerisen ehdotusarvon, jossa lausekkeen Laus paikallinen minimi esiintyy.

Jos annat alarajan ja ylärajan, funktio etsii paikallista minimiä näiden arvojen väliltä.

nInt()

nInt(Laus1, Muutt, Ala, Ylä) ⇒ lauseke

Jos integroitava funktio Laus1 ei sisällä muita muuttujia kuin Muutt, ja jos Ala ja Ylä ovat vakioita, positiivinen ˆ tai negatiivinen ˆ,

tällöin nInt() laskee likiarvon lausekkeesta ‰(Laus1, Va r, Ala, Ylä). Tämä likiarvo on integrandin välillä Ala<Muutt<Ylä olevien

joidenkin otosarvojen painotettu keskiarvo. Tavoitteena on kuusi merkitsevää numeroa. Adaptiivinen algoritmi

päättyy, kun näyttää todennäköiseltä, että tavoite on saavutettu, tai kun näyttää epätodennäköiseltä, että lisäotokset tuottaisivat merkittävää parannusta.

Näkyviin tulee viesti (Questionable accuracy (Kyseenalainen tarkkuus)), kun näyttää siltä, että tavoitetta ei ole saavutettu.

Sijoita nInt()-komentoa sisäkkäin, jos haluat suorittaa moninkertaisen numeerisen integroinnin. Integroinnin raja-arvot voivat riippua niiden ulkopuolella olevista integrointimuuttujista.

Katalogi

60 TI-Nspire™ -sovelluksen käsikirja

Page 67

nom()

nom(efektiivinenKorko,CpY) ⇒ arvo

Talouslaskentatoiminto, joka muuntaa efektiivisen vuosikoron efektiivinenKorko nimelliskoroksi, kun CpY määritetään korkojaksojen lukumääräksi vuodessa.

efektiivinenKorko on oltava reaaliluku, ja CpY:n on oltava reaaliluku > 0.

Huomaa: Katso myös eff(), sivu 28.

Katalogi

norm()

norm(Matriisi) ⇒ lauseke norm(Vektori) ⇒ lauseke

Laskee Frobeniusin normin.

normCdf()

normCdf(alaraja,yläraja[,m[,s]]) ⇒ luku, jos yläraja ja

alaraja ovat lukuja, lista, jos alaraja ja yläraja ovat listoja

Laskee normaalijakauman todennäköisyyden alarajan ja ylärajan välillä määritetylle m:lle (oletus=0) ja s:lle (oletus=1).

Kun P(X  yläraja), aseta alaraja = .9E999.

normPdf()

normPdf(XArvo[,m,s]) ⇒ luku, jos XArvo on luku, lista, jos

XArvo on lista

Laskee normaalijakauman pistetodennäköisyysfunktion määritetyssä XArvossa määritetylle m:lle ja s:lle.

not

not BoolenLaus ⇒ Boolen lauseke

Määrittää totuusarvon tosi, epätosi tai argumentin sievennetyn muodon.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 61

Page 68

not

not Kokonaisluku1 ⇒ kokonaisluku

Laskee reaalikokonaisluvun ykkösen komplementin. Sisäisesti Kokonaisluku1 muunnetaan etumerkilliseksi, 64-bittiseksi binaariluvuksi. Jokaisen bitin arvo vaihtuu (0:sta tulee 1 ja päin vastoin) ykkösen komplementille. Tulokset näytetään kantalukutilan mukaisesti.

Voit syöttää kokonaisluvun minkä tahansa luvun kantalukuna. Binaarisen syötteen edelle tulee merkitä etumerkki 0b ja heksadesimaalisen syötteen edelle 0h. Ilman etuliitettä kokonaislukua käsitellään desimaalilukuna (kantaluku 10).

Jos syötät desimaalikokonaisluvun, joka on liian suuri etume rkilliselle, 64 bitin binaarimuodolle, laskin käyttää symmetristä modulooperaatiota, jotta arvo saadaan oikealle alueelle.

Heksadesimaalisessa kantalukutilassa:

Tärkeää: Nolla, ei O-kirjain.

Binaarisessa kantalukutilassa:

Katalogi

nPr()

nPr(Arvo1, Arvo2) ⇒ lauseke

Kokonaisluvulle Arvo1 ja Arvo2 sekä Arvo1 ‚ Arvo2 ‚ 0, nPr() on Arvo1:n asioiden permutaatioiden lukumäärä, joita otetaan Arvo2:n

verran kerrallaan.

nPr(Arvo, 0) ⇒ 1

Arvo, negKokonaisluku)

nPr(

⇒ 1/((Arvo+1)·(Arvo+2)... (ArvoNnegKokonaisluku))

Arvo, posKokonaisluku)

nPr(

⇒ Arvo·(ArvoN1)... (ArvoNposKokonaisluku+1)

nPr(

Arvo, eiKokonaisluku)

⇒ Arvo! / (ArvoNeiKokonaisluku)!

Lista1, List2) ⇒ lista

nPr(

Luo listan permutaatioista kahden listan sisältämiin vastaaviin elementtipareihin perustuen. Argumenttien on oltava samankokoisia listoja.

nPr(Matriisi1, Matriisi2) ⇒ matriisi

Luo matriisin permutaatioista kahden matriisin sisältämiin vastaaviin elementtipareihin perustuen. Argumenttien on oltava samankokoisia matriiseja.

Jos haluat nähdä koko vastauksen, paina jälkeen kohdistinta painikkeilla ¡ ja ¢.

Huomaa: Binaarisessa syötteessä voi olla korkeintaan 64

numeroa (etuliitettä 0b ei lasketa). Heksadesimaalisessa syötteessä voi olla korkeintaan 16 numeroa.

£ ja siirrä sen

Katalogi

62 TI-Nspire™ -sovelluksen käsikirja

Page 69

npv()

npv(Korkoprosentti,CFO,CFLista[,CFFrekv])

Talouslaskentatoiminto, joka laskee nettonykyarvon; tulevien ja poistuvien kassavirtojen nykyisten arvojen summan. Jos npv:n tulos on positiivinen, investointi on kannattava.

Korkoprosentti on prosentti, jolla kassavirtoja (rahan kustannusta) vähennetään yhden jakson aikana.

CF0 on alkuperäinen kassavirta aikana 0; arvon on oltava kokonaisluku.

CFLista on lista kassavirtamääristä ensimmäisen kassavirran CF0 jälkeen.

CFFrekv on lista, jossa jokainen elementti määrittää esiintymisfrekvenssin ryhmitetylle (peräkkäiselle) kassavirtamäärälle, joka on CFListan vastaava elementti. Oletusarvo on 1; jos syötät arvoja, niiden on oltava positiivisia kokonaislukuja < 10,000.

Katalogi

nSolve()

nSolve(Yhtälö,Muutt[=Arvaus]) ⇒ luku tai virhe_merkkijono nSolve(Yhtälö,Muutt[=Arvaus],alaraja)

⇒ luku tai virhe_merkkijono

nSolve(Yhtälö,Muutt[=Arvaus],alaraja,yläraja) ⇒ luku tai

virhe_merkkijono

nSolve(Yhtälö,Muutt[=Arvaus]) | alaraja<Muutt<yläraja

⇒ luku tai virhe_merkkijono

Etsii iteratiivisesti yhtä likimääräistä numeerista ratkaisua Yhtälön yhdelle muuttujalle. Määritä muuttuja seuraavasti:

muuttuja

– tai – muuttuja = reaaliluku

Esimerkiksi x kelpaa ja samoin x=3.

nSolve() yrittää määrittää joko yhden pisteen, jossa jäännös on

nolla, tai kaksi toisiaan suhteellisen lähellä olevaa pistettä, jossa jäännöksen etumerkki on vastakkainen ja jäännöksen magnitudi ei ole liian suuri. Jos funktio ei pysty määrittämään tätä kohtuullisella otospisteiden määrällä, se antaa vastauksena merkkijonon “no solution found" (yhtään ratkaisua ei löydy).

Katalogi

Huomaa: Jos ratkaisuja on useita, voit yrittää löytää tietyn

ratkaisun käyttämällä apuna arvausta.

TI-Nspire™ -sovelluksen käsikirja 63

Page 70

OneVar

OneVar [1,]X[,[Frekv][,Luokka,Sisällytä]] OneVar [

n,]X1,X2[X3[,…[,X20]]]

Laskee yhden muuttujan tilaston enintään 20 listasta. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 87.)

Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta.

X-argumentit ovat datalistoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan X:n arvon esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaaville X:n arvoille. Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne

datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tulosmuuttuja Kuvaus

stat.v

stat.Gx

stat.sx x:n otoksen keskihajonta

stat.ssssx x:n perusjoukon keskihajonta

stat.n Datapisteiden lukumäärä

stat.MinX x:n arvojen minimi

stat.Q1X x:n ensimmäinen neljännes

stat.MedianX x:n mediaani

stat.Q3X x:n kolmas neljännes

stat.MaxX x:n arvojen maksimi

stat.SSX x:n keskiarvon poikkeamien neliöiden summa

x:n arvojen keskiarvo

x:n arvojen summa

x2:n arvojen summa

Katalogi

64 TI-Nspire™ -sovelluksen käsikirja

Page 71

BoolenLaus1 or BoolenLaus2

⇒ Boolen lauseke

Määrittää totuusarvon tosi tai epätosi tai antaa vastauksena sievennetyn muodon alkuperäisestä syötteestä.

Antaa vastauksen tosi, jos jompikumpi tai molemmat lause kkeet ovat tosia. Antaa vastauksen epätosi, jos kumpikin lauseke on epätosi.

Huomaa: Katso xor. Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Kokonaisluku1 or Kokonaisluku2 ⇒ kokonaisluku

Vertaa kahta reaalikokonaislukua bitti bitiltä or-operaation avulla. Sisäisesti kumpikin kokonaisluku muunnetaan etumerkilliseksi, 64 bitin binaariluvuksi. Kun vastaavia bittejä verrataan, tulos on 1, jos jompikumpi bitti on 1; tulos on 0 vain, jos kumpikin bitti on 0. Laskettu arvo edustaa bittituloksia, ja se näkyy kantalukutilan mukaisesti.

Jos syötät desimaalikokonaisluvun, joka on liian suuri etume rkilliselle, 64 bitin binaarimuodolle, laskin käyttää symmetristä modulooperaatiota, jotta arvo saadaan oikealle alueelle.

Huomaa: Katso xor.

Katalogi

Heksadesimaalisessa kantalukutilassa:

Tärkeää: Nolla, ei O-kirjain.

Binaarisessa kantalukutilassa:

Huomaa: Binaarisessa syötteessä voi olla korkeintaan 64

numeroa (etuliitettä 0b ei lasketa). Heksadesimaalisessa syötteessä voi olla korkeintaan 16 numeroa.

ord()

ord(Merkkijono) ⇒ kokonaisluku ord(Lista1) ⇒ lista

Määrittää merkkijonon Merkkijono ensimmäisen merkin numerokoodin tai luo listan jokaisen listaelementin ensimmäisistä merkeistä.

Katalogi

P4Rx()

P4Rx(rLaus, qLaus) ⇒ lauseke P4Rx(rLista, qLista) ⇒ lista P4Rx(rMatriisi, qMatriisi) ⇒ matriisi

Määrittää paria (r, q) vastaavan x-koordinaatin.

Huomaa: Argumentti q tulkitaan joko aste-, graadi- tai

radiaanikulmaksi valittuna olevan kulmatilan mukaisesti. Jos argumentti on lauseke, voit ohittaa kulmatila-ase tuksen väliaikaisesti

käyttämällä merkintää ó,G tai ô.

Radiaanikulmatilassa:

TI-Nspire™ -sovelluksen käsikirja 65

Katalogi

Page 72

P4Ry()

P4Ry(rArvo, qArvo) ⇒ arvo P4Ry(rLista, qLista) ⇒ lista P4Ry(rMatriisi, qMatriisi) ⇒ matriisi

Määrittää paria (r, q) vastaavan y-koordinaatin.

Huomaa: Argumentti q tulkitaan joko aste-, radiaani- tai

graadikulmaksi valittuna olevan kulmatilan mukaisesti.

Radiaanikulmatilassa:

Katalogi

PassErr

Ohittaa virheen siirtyen seuraavalle tasolle. Jos järjestelmän muuttuja errCode on nolla, PassErr ei tee mitään.

Else-lauseessa lohkossa Try...Else...EndTry tulee käyttää

komentoa ClrErr tai PassErr. Jos virhe on tarkoitus käsitellä tai jättää huomiotta, käytä komentoa ClrErr. Jos et tiedä, mitä tehdä virheen suhteen, lähetä se seuraavaan virheenkäsittelijään käyttämällä komentoa PassErr. Jos odottavia Try...Else...EndTry- virheenkäsittelijöitä ei ole enää, virheen valintaikkuna tulee näkyviin normaalisti.

Huomaa: Katso myös ClrErr, sivu 14, ja Try, sivu 94. Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

piecewise()

piecewise(Laus1 [, Ehto1 [, Laus2 [, Ehto2 [, … ]]]])

Laatii määritelmät paloittain määritellylle funktiolle listan muodossa. Voit luoda paloittain määriteltyjen funktioiden määrityksiä myös mallin avulla.

Huomaa: Katso myös Paloittain määritellyn funktion malli

, sivu 2.

poissCdf()

poissCdf(l,alaraja,yläraja) ⇒ luku, jos alaraja ja yläraja

ovat lukuja,

poissCdf(

on luku, lista, jos

Laskee kumulatiivisen todennäköisyyden diskreetille Poissonin jakaumalle, jolla on määritetty keskiarvo l.

lista, jos alaraja ja yläraja ovat listoja

l,yläraja) (kun P(0Xyläraja) ⇒ luku, jo s yläraja

yläraja on lista

Kun P(X  yläraja), aseta alaraja=0

Katalogi

Esimerkki PassErr-komennosta, katso esimerkki 2 Try komennon kohdalla, sivu 95.

Katalogi

poissPdf()

poissPdf(l,XArvo) ⇒ luku, jos XArvo on luku, lista, jos

XArvo on lista

Laskee todennäköisyyden diskreetille Poissonin jakaumalle, jolla on määritetty keskiarvo l.

Katalogi

66 TI-Nspire™ -sovelluksen käsikirja

Page 73

Polar

Polaarinen)

4Polar

Vektori

Näyttää vektorin polaarisessa muodossa [r q]. Vektorin on oltava kooltaan 2, ja se voi olla rivi tai sarake.

Huomaa: 4Polar on näyttömuodon ohje, ei muunnosfunktio.

Voit käyttää komentoa ainoastaan syöterivin lopussa, eikä se päivitä ans:n arvoa.

Huomaa: Katso myös 4Rect, sivu 74.

kompleksiArvo 4Polaarinen

Näyttää kompleksiVektorin polaarisessa muodossa.

• Astekulmatilassa vastauksena on (rq).

• Radiaanikulmatilassa vastauksena on re

kompleksiArvolla voi olla mikä tahansa kompleksilukumuoto. Syöte

aiheuttaa kuitenkin virheen astekulmatilassa.

Huomaa: Polaarisessa syötteessä (rq) on käytettävä sulkeita.

Radiaanikulmatilassa:

Graadikulmatilassa:

Astekulmatilassa:

Katalogi

polyEval()

polyEval(Lista1, Laus1) ⇒ lauseke polyEval(Lista1, Lista2) ⇒ lauseke

Tulkitsee ensimmäisen argumentin laskeva-asteisen polynomin kertoimeksi ja antaa vastauksena polynomin, josta on laskettu toisen argumentin arvo.

PowerReg

PowerReg X,Y [, Frekv] [, Luokka, Sisällytä]]

Laskee potenssiregression y = (a·(x)b) listoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso

sivu 87.) Kaikkien listojen on oltava samankokoisia Sisällytä-listaa

lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tulosmuuttuja Kuvaus

stat.RegEqn

Regressioyhtälö: a·(x)

Katalogi

TI-Nspire™ -sovelluksen käsikirja 67

Page 74

Tulosmuuttuja Kuvaus

stat.a, stat.b Regressiokertoimet

stat.r

Muunnettujen tietojen lineaarimäärittelyn kerroin

stat.r Muunnettujen tietojen korrelaatiokerroin (ln(x), ln(y))

stat.Resid Potenssimalliin liittyvät jäännökset

stat.ResidTrans Muunnettujen tietojen lineaariseen sovitukseen liittyvät jäännökset

stat.XReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

Prgm

Lohko

EndPrgm

Malli käyttäjän määrittämän ohjelman luomista varten. Käytetään komennon Define, Define LibPub tai Define LibPriv kanssa.

Lohko voi olla yksi lauseke tai sarja lausekkeita, jotka on erotettu toisistaan kaksoispisteellä (:), tai sarja eri riveillä olevia lausekkeita.

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Product (PI)

product()

product(Lista[, Alku[, loppu]]) ⇒ lauseke

Laskee Listan sisältämien elementtien tulon. Alku ja Loppu ovat valinnaisia. Ne määrittävät elementtien alueen.

Laske GCD ja näytä välitulokset.

Katalogi

Katso Π(), sivu 113.

Katalogi

68 TI-Nspire™ -sovelluksen käsikirja

Page 75

product()

product(Matriisi1[, Alku[, loppu]]) ⇒ matriisi

Laskee rivivektorin, joka sisältää Matriisi1:n sarakkeiden elementtien tulot. Alku ja Loppu ovat valinnaisia. Ne määrittävät rivialueen.

Katalogi

propFrac()

propFrac(Arvo1[, Muutt]) ⇒ arvo

propFrac(rationaali_luku) laskee rationaali_luvun kokonaisluvun

summana ja murtolukuna, jolla on sama etumerkki ja suurempi nimittäjä kuin osoittaja.

propFrac(rationaali_lauseke,Muutt) laskee aitojen suhdelukujen

summan ja polynomin muuttujan Muutt suhteen. Muuttujan Muutt aste nimittäjässä on suurempi kuin muuttujan Muutt aste osoittajassa kussakin aidossa suhdeluvussa. Muuttujan Muutt samanlaiset potenssit kerätään. Termit ja niiden tekijät lajitellaan siten, että Muutt on päämuuttuja.

Jos Muutt jätetään pois, varsinaisen murtoluvun lavennus tehdään pääasiallisimmalla muuttujalla. Polynomiosan kertoimet tehdään sen jälkeen aidoiksi ensin niiden pääasiallisimman muuttujan suhteen ja niin edelleen.

propFrac()-funktion avulla voit esittää sekalukuja ja suorittaa

sekalukujen yhteen- ja vähennyslaskua.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 69

Page 76

QR Matriisi, qMatNimi, rMatNimi[, Tol ]

Suorittaa Householderin QR-dekomponoinnin reaaliluku- tai kompleksilukumatriisista. Tuloksena olevat Q- ja R-matriisit tallentuvat määritettyihin MatNimi-muuttujiin. Q-matriisi on jakamaton. R-matriisi on yläkolmiomatriisi.

• Jos käytät painikkeita

Approximate (Automaattinen tai likimääräinen)

tilan valintaa Approximate (Likimääräinen), laskut suoritetaan liukulukuaritmetiikalla.

•Jos Tol jätetään pois tai sitä ei käytetä, oletusarvoinen toleranssi lasketaan seuraavasti:

5Eë14 ·max(dim(Matriisi)) ·rowNorm(Matriisi)

QR-hajotus lasketaan numeerisesti Householderin transformaatioiden avulla. Symbolinen ratkaisu lasketaan Gram-Schmidtin menete lmällä. Matriisin qMatNimi sarakkeet ovat ne ortonormitetut perusvektorit, jotka sijoittuvat matriisin määrittämään tilaan.

QuadReg

QuadReg X,Y [, Frekv] [, Luokka, Sisällytä]]

Laskee 2. asteen polynomiregression y = a·x2+b·x+c listoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.results-

muuttujaan. (Katso sivu 87.) Kaikkien listojen on oltava samankokoisia Sisällytä-listaa

lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

· tai Auto or

Katalogi

Liukuluku (9.) muuttujassa m1 aiheuttaa sen, että vastaukset lasketaan liukulukumuodossa.

Katalogi

Tulosmuuttuja Kuvaus

stat.RegEqn

stat.a, stat.b, stat.c Regressiokertoimet

stat.R

stat.Resid Regressioyhtälön jäännökset

stat.XReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

Regressioyhtälö: a·x2+b·x+c

Määrityskerroin

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

70 TI-Nspire™ -sovelluksen käsikirja

Page 77

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

QuartReg

QuartReg X,Y [, Frekv] [, Luokka, Sisällytä]]

Laskee 4. asteen polynomiregression y = a·x4+b·x3+c· x2+d·x+e listoista X ja Y frekvenssillä Frekv.

Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 87.)

Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n

elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tulosmuuttuja Kuvaus

stat.RegEqn

stat.a, stat.b, stat.c, stat.d, stat.e

stat.R

stat.Resid Regressioyhtälön jäännökset

stat.XReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

Regressioyhtälö: a·x4+b·x3+c· x2+d·x+e

Regressiokertoimet

Määrityskerroin

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

Katalogi

TI-Nspire™ -sovelluksen käsikirja 71

Page 78

R4Pq()

R4Pq (xArvo, yArvo) ⇒ arvo R4Pq (xLista, yLista) ⇒ lista R4Pq (xMatriisi, yMatriisi) ⇒ matriisi

Määrittää vastaavan q-koordinaatin (x,y)-parin argumenteille.

Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana

käytössä olevan kulmatila-asetuksen mukaisesti.

R4Pr()

R4Pr (xArvo, yArvo) ⇒ arvo R4Pr (xLista, yLista) ⇒ lista R4Pr (xMatriisi, yMatriisi) ⇒ matriisi

Määrittää (x,y)-parin argumenttien vastaavan r-koordinaatin.

4Rad

Arvo14Rad ⇒ arvo

Muuntaa argumentin radiaanikulmayksikköön.

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

Astekulmatilassa:

Katalogi

Graadikulmatilassa:

rand()

rand() ⇒ lauseke rand(Kokeiden lkm) ⇒ lista

rand() määrittää satunnaisluvun väliltä 0 ja 1. rand(Kokeiden lkm) määrittää listan, joka sisältää Kokeiden lkm

satunnaislukua väliltä 0 ja 1.

Asettaa satunnaisluvun siemenluvun.

Katalogi

72 TI-Nspire™ -sovelluksen käsikirja

Page 79

randBin()

randBin(n, p) ⇒ lauseke randBin(n, p, Kokeiden lkm) ⇒ lista

randBin(n, p) määrittää satunnaisreaaliluvun määritetystä

binomijakaumasta.

randBin(n, p, Kokeiden lkm) luo listan, joka sisältää Kokeiden

lkm satunnaisreaalilukua määritetystä binomijakaumasta.

Katalogi

randInt()

randInt(alaraja,yläraja) ⇒ lauseke randInt(alaraja,yläraja,Kokeiden lkm) ⇒ lista

randInt(alaraja,yläraja) määrittää satunnaiskokonaisluvun, joka

on kokonaislukujen alarajan ja ylärajan välissä.

randInt(alaraja,yläraja,Kokeiden lkm) luo listan, joka sisältää

Kokeiden lkm satunnaiskokonaislukua määritetyltä alueelta.

randMat()

randMat(numRivit, numSarakkeet) ⇒ matriisi

Laskee määrätynkokoisen kokonaislukumatriisin väliltä -9 ja 9. Kummankin argumentin tulee sieventyä kokonaisluvuksi.

randNorm()

randNorm(m, s [,kokeidenLkm]) ⇒ lauseke

Määrittää desimaaliluvun määritetystä normaalijakaumasta. Luku voi olla mikä tahansa reaaliluku, mutta se keskittyy voimakkaasti välille

[mN3·s, m+3·s].

randPoly()

randPoly(Muutt, Aste) ⇒ lauseke

Määrittää polynomin muuttujasta Muutt, joka on määritettyä Astetta. Kertoimet ovat satunnaisia kokonaislukuja väliltä ë9 ja 9.

Alussa oleva kertoin ei ole nolla. Asteen on oltava 0–99.

Katalogi

Huomaa: Tämän matriisin arvot muuttuvat aina, kun painat

·.

Katalogi

randSamp()

randSamp(Lista,Kokeiden lkm[,eiKorv]) ⇒ lista

Laskee listan, joka sisältää satunnaisotoksen Kokeiden lkm kokeesta, jotka on otettu Listasta, ja valinnaisena on otoksen korvaaminen (eiKorv=0) tai ei otoksen korvaamista (eiKorv=1). Oletusarvona on otoksen korvaaminen.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 73

Page 80

RandSeed

RandSeed Luku

Jos Luku = 0, asettaa siemenluvut satunnaislukugeneraattorin tehdasasetuksiin. Jos Luku jotka tallentuvat järjestelmän muuttujiin seed1 ja seed2.

ƒ 0, sillä luodaan kaksi siemenlukua,

Katalogi

real() (reaali)

real(Arvo1) ⇒ arvo

Määrittää argumentin reaalilukuosan.

Huomaa: Kaikkia määrittämättömiä muuttujia käsitellään

reaalimuuttujina. Katso myös imag(), sivu 41.

real(Lista1) ⇒ lista

Määrittää kaikkien elementtien reaaliosat.

real(Matriisi1) ⇒ matriisi

Määrittää kaikkien elementtien reaaliosat.

Rect

Vektori 4Rect

Näyttää Vektorin suorakulmamuodossa [x, y, z]. Vektorin koon on oltava 2 tai 3, ja se voi olla rivi tai sarake.

Huomaa: 4Rect on näyttömuodon ohje, ei muunnosfunktio. Voit

käyttää komentoa ainoastaan syöterivin lopussa, eikä se päivitä ans:n arvoa.

Huomaa: Katso myös 4Polar, sivu 67.

kompleksiArvo 4Rect

Näyttää kompleksiArvon suorakulmamuodossa a+bi. kompleksiArvon muoto voi olla mikä tahansa kompleksilukumuoto.

Syöte re

aiheuttaa kuitenkin virheen astekulmatilassa.

Huomaa: Polaarisessa syötteessä (rq) on käytettävä sulkeita.

Radiaanikulmatilassa:

Graadikulmatilassa:

Katalogi

Astekulmatilassa:

Huomaa: Voit syöttää merkin  valitsemalla sen Katalogin

symboliluettelosta.

74 TI-Nspire™ -sovelluksen käsikirja

Page 81

ref()

ref(Matriisi1[, To l]) ⇒ matriisi

Määrittää Matriisi1:n rivi-echelon-muodon. Valinnaisesti kaikkia matriisielementtejä käsitellään nollana, jos

niiden itseisarvo on pienempi kuin To l. Tätä toleranssia käytetään vain, jos matriisissa on liukulukusyötteitä eikä se sisällä symbolisia muuttujia, joille ei ole määritetty arvoa. Muussa tapauksessa To l - komentoa ei huomioida.

• Jos käytät painikkeita

Approximate (Automaattinen tai likimääräinen)

tilan valintaa Approximate (Likimääräinen), laskut suoritetaan liukulukuaritmetiikalla.

•Jos Tol jätetään pois tai sitä ei käytetä, oletusarvoinen toleranssi lasketaan seuraavasti:

5Eë14 ·max(dim(Matriisi1)) ·rowNorm(Matriisi1)

Huomaa: Katso myös rref(), sivu 78.

· tai Auto or

Katalogi

remain()

remain(Arvo1, Arvo2) ⇒ arvo remain(Lista1, Lista2) ⇒ lista remain(Matriisi1, Matriisi2) ⇒ matriisi

Laskee ensimmäisen argumentin jäännöksen toisen argumentin suhteen seuraavien identtisten yhtälöiden määrittelyn mukaisesti:

remain(x,0)  x remain(x,y)  xNy·iPart(x/y)

Huomaa, että seurauksena remain(Nx,y)  Nremain(x,y). Vastaus on joko nolla tai samanmerkkinen kuin ensimmäinen argumentti.

Huomaa: Katso myös mod(), sivu 56.

Return

Return [Laus]

Antaa lausekkeen Laus funktion tuloksena. Käytetään lohkon

Func...EndFunc sisällä. Huomaa: Voit poistua ohjelmasta käyttämällä Return-komentoa

ilman argumenttia lohkon Prgm...EndPrgm sisällä.

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

right()

right(Lista1[, Num]) ⇒ lista

Määrittää oikeanpuoleisimmat Num-elementit, jotka sisältyvät Lista1:een.

Jos jätät pois komennon Num, määrittää kaiken listasta Lista1.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 75

Page 82

right()

right(lähdemerkkijono[, Num]) ⇒ merkkijono

Määrittää oikeanpuoleisimmat Num-merkit, jotka sisältyvät merkkijonoon lähdemerkkijono.

Jos jätät pois komennon Num, määrittää kaiken merkkijonosta lähdemerkkijono.

right(Ver t a i lu ) ⇒ lauseke

Laskee yhtälön tai epäyhtälön oikean puolen.

Katalogi

root()

root(Arvo) ⇒ root root(Arvo1, Arvo2) ⇒ root

root(Arvo) laskee Arvon neliöjuuren. root(Arvo1, Arvo2) laskee Arvo1:n Arvo2-juuren. Arvo1 voi olla

reaalinen tai kompleksinen liukulukuvakio, kokonaisluku tai kompleksinen rationaalilukuvakio.

Huomaa: Katso myös N:s juuri -malli, sivu 1.

rotate()

rotate(Kokonaisluku1[,KiertojenLkm]) ⇒ kokonaisluku

Kiertää bittejä binaarisessa kokonaisluvussa. Voit syöttää Kokonaisluku1:n minä tahansa kantalukuna; se muunnetaan automaattisesti etumerkilliseen 64 bitin binaarimuotoon. Jos Kokonaisluku1 on liian suuri tälle muodolle, symmetrinen modulooperaatio sovittaa sen alueelle sopivaksi.

Jos KiertojenLkm on positiivinen, kierto tapahtuu vasemmalle. Jos KiertojenLkm on negatiivinen, kierto tapahtuu oikealle. Oletusarvo on ë1 (kierrä oikealle yksi bitti).

Esimerkki kierrosta oikealle:

Jokainen bitti kiertyy oikealle. 0b00000000000001111010110000110101 Oikeanpuoleisin bitti kiertyy eniten vasemmalle. tuottaa: 0b10000000000000111101011000011010 Vastaus näkyy kantalukutilan mukaisesti.

rotate(Lista1[,KiertojenLkm]) ⇒ lista

Luo Lista1:n kopion, jota on kierretty oikealle tai vasemmalle KiertojenLkm:n elementtien määrittämän määrän. Ei muuta Lista1:ä.

Jos KiertojenLkm on positiivinen, kierto tapahtuu vasemmalle. Jos KiertojenLkm on negatiivinen, kierto tapahtuu oikealle. Oletusarvo

on ë1 (kierrä oikealle yksi elementti).

Katalogi

Binaarisessa kantalukutilassa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeen kohdistinta painikkeilla ¡ ja ¢.

Heksadesimaalisessa kantalukutilassa:

Tärkeää: Binaariluvun edelle tulee aina merkitä etumerkki 0b ja heksadesimaaliluvun edelle 0h (nolla, ei O-kirjain).

Desimaalisessa kantalukutilassa:

76 TI-Nspire™ -sovelluksen käsikirja

Page 83

rotate()

rotate(Merkkijono1[,KiertojenLkm]) ⇒ merkkijono

Luo Merkkijono1:n kopion, jota on kierretty oikealle tai vasemmalle KiertojenLkm:n merkkien määrittämän määrän. Ei muuta Merkkijono1:ä.

Jos KiertojenLkm on positiivinen, kierto tapahtuu vasemmalle. Jos KiertojenLkm on negatiivinen, kierto tapahtuu oikealle. Oletusarvo

on ë1 (kierrä oikealle yksi merkki).

Katalogi

round()

round(Arvo1[, numerot]) ⇒ arvo

Pyöristää argumentin jättäen desimaalipisteen jälkeen määritetyn määrän numeroita.

numerot-ohjeen on oltava kokonaisluku väliltä 0–12. Jos numerotohjetta ei oteta mukaan, pyöristää argumentin 12 merkitsevän numeron tarkkuudelle.

Huomaa: Näytettävät numerot -tila voi vaikuttaa näyttöön.

round(Lista1[, numerot]) ⇒ lista

Pyöristää elementtien listan jättäen desimaalipisteen jälkeen määritetyn määrän numeroita.

round(Matriisi1[, numerot]) ⇒ matriisi

Pyöristää elementtien matriisin jättäen desimaalipisteen jälkeen määritetyn määrän numeroita.

rowAdd()

rowAdd(Matriisi1, rIndeksi1, rIndeksi2) ⇒ matriisi

Luo kopion Matriisi1:stä, jossa rivi rIndeksi2 on korvattu rivien rIndeksi1 ja rIndeksi2 summalla.

rowDim()

rowDim(Matriisi) ⇒ lauseke

Laskee Matriisin sisältämien rivien lukumäärän.

Huomaa: Katso myös colDim(), sivu 14.

Katalogi

rowNorm()

rowNorm(Matriisi) ⇒ lauseke

Laskee Matriisin riveillä olevien elementtien itseisarvojen summien maksimin.

Huomaa: Kaikkien matriisien elementtien tulee sieventyä luvuiksi.

Katso myös colNorm(), sivu 14.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 77

Page 84

rowSwap()

rowSwap(Matriisi1, rIndeksi1, rIndeksi2) ⇒ matriisi

Antaa tuloksena Matriisi1:n jossa rivien rIndeksi1 ja rIndeksi2 paikkoja on vaihdettu.

Katalogi

rref()

rref(Matriisi1[, Tol ]) ⇒ matriisi

Määrittää Matriisi1:n sievennetyn rivi-echelon-muodon.

• Jos käytät painikkeita

Approximate (Automaattinen tai likimääräinen)

tilan valintaa Approximate (Likimääräinen), laskut suoritetaan liukulukuaritmetiikalla.

•Jos Tol jätetään pois tai sitä ei käytetä, oletusarvoinen toleranssi lasketaan seuraavasti:

5Eë14 ·max(dim(Matriisi1)) ·rowNorm(Matriisi1)

Huomaa: Katso myös ref(), sivu 75.

· tai Auto or

sec()

sec(Arvo1) ⇒ arvo sec(Lista1) ⇒ lista

Laskee Arvo1:n sekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien sekantit.

Huomaa: Argumentti tulkitaan aste-, graadi- tai radiaanikulmaksi

käytössä olevan kulmatila-asetuksen mukaisesti. Voit ohittaa kulmatilan väliaikaisesti painikkeilla ó,G tai ô.

Astekulmatilassa:

Katalogi

78 TI-Nspire™ -sovelluksen käsikirja

Page 85

sec/()

sec/(Arvo1) ⇒ arvo sec/(Lista1) ⇒ lista

Määrittää kulman, jonka sekantti on Arvo1, tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien käänteissekantit.

Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana

käytössä olevan kulmatila-asetuksen mukaisesti.

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

Katalogi

sech()

sech(Arvo1) ⇒ arvo sech(Lista1) ⇒ lista

Laskee Arvo1:n hyperbolisen sekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien hyperboliset sekantit.

sechê()

sechê(Arvo1) ⇒ arvo sechê (Lista1) ⇒ lista

Laskee Arvo1:n käänteisen hyperbolisen sekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien käänteiset hyperboliset sekantit.

seq() (sekv)

seq(Laus, Muutt, Matala, Korkea[, Askel]) ⇒ lista

Lisää muuttujan Muutt arvoa arvosta Matala arvoon Korkea lisäysportaalla Askel, sieventää lausekkeen Laus ja antaa tulokset listana. Muuttujan Muutt alkuperäinen sisältö on edelleen tallessa sekvenssin seq() suorittamisen jälkeen.

Muutt ei voi olla järjestelmän muuttuja. Askeleen oletusarvo = 1.

Katalogi

Radiaanikulma- ja suorakulmakompleksitilassa:

Katalogi

Sievennä seuraava lauseke painamalla Ctrl+Enter /

TI-Nspire™ -sovelluksen käsikirja 79

Page 86

setMode()

setMode(tilaNimiKokonaisluku, asetusKokonaisluku)

⇒ kokonaisluku

setMode(lista) ⇒ kokonaislukulista

Toimii vain funktiossa tai ohjelmassa.

setMode(tilaNimiKokonaisluku, asetusKokonaislkuku)

asettaa tilan tilaNimiKokonaisluku väliaikaisesti uuteen asetukseen asetusKokonaisluku ja määrittää kokonaisluvun, joka vastaa kyseisen tilan alkuperäistä asetusta. Muutos on rajoitettu ohjelman/funktion suorittamisen ajalle.

tilaNimiKokonaisluku määrittää asetettavan tilan. Sen on oltava jokin alla olevan taulukon tilaa kuvaavista kokonaisluvuista.

asetusKokonaisluku määrittää tilan uuden asetuksen. Sen on oltava jokin seuraavista asetettavalle tilalle varatuista asetusta kuvaavista kokonaisluvuista.

setMode(lista)-komennolla voit muuttaa useita asetuksia. lista

sisältää tilaa ja asetusta kuvaavat kokonaislukuparit.

setMode(lista) luo samanlaisen listan, jonka kokonaislukuparit

kuvaavat alkuperäisiä tiloja ja asetuksia. Jos olet tallentanut kaikki tila-asetukset komennolla

getMode(0) & muutt, voit palauttaa nämä asetukset

komennolla setMode(muutt) aina funktion tai ohjelman sulkemiseen saakka. Katso getMode(), sivu 37.

Huomaa: Nykyiset tila-asetukset siirtyvät haettuihin

alarutiineihin. Jos jokin alarutiini muuttaa tila-asetusta, tilamuutos häviää, kun ohjaus palautuu hakurutiiniin.

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa

voit syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan

Enter.

Katalogi

Näytä p:n likiarvo käyttäen Näytettävät numerot -tilan oletusasetusta ja näytä sen jälkeen p asetuksella Kiinteä2. Tarkista, että oletusarvo palautuu ohjelman suorittamisen jälkeen.

Tilan nimi

Näytettävät numerot

Kulma

Eksponenttimuoto

Reaali- tai kompleksiluku

Automaattinen tai likimääräinen.

Vektorimuoto

Kantaluku

Tilaa vastaava kokonaisluku

Asetuksia vastaavat kokonaisluvut

=Liukuva, 2=Liukuva1, 3=Liukuva2, 4=Liukuva3, 5=Liukuva4, 6=Liukuva5,

1 7=Liukuva6, 8=Liukuva7, 9=Liukuva8, 10=Liukuva9, 11=Liukuva10, 12=Liukuva11, 13=Liukuva12, 14=Kiinteä0, 15=Kiinteä1, 16=Kiinteä2, 17=Kiinteä3, 18=Kiinteä4, 19=Kiinteä5, 20=Kiinteä6, 21=Kiinteä7, 22=Kiinteä8, 23=Kiinteä9, 24=Kiinteä10, 25=Kiinteä11, 26=Kiinteä12

=Radiaani, 2=Aste, 3=Graadi

=Normaali, 2=Kymmenpotenssi, 3=Tekninen

=Reaali, 2=Suorakulma, 3=Polaarinen

=Automaattinen, 2=Likimääräinen

=Suorakulma, 2=Sylinteri, 3=Pallo

=Desimaali, 2=Heksagonaalinen, 3=Binaarinen

80 TI-Nspire™ -sovelluksen käsikirja

Page 87

shift()

shift(Kokonaisluku1[,SiirtojenLkm]) ⇒ kokonaisluku

Siirtää binaarisen kokonaisluvun bittejä. Voit syöttää Kokonaisluku1:n minä tahansa kantalukuna; se muunnetaan automaattisesti etumerkilliseen 64 bitin binaarimuotoon. Jos Kokonaisluku1 on liian suuri tälle muodolle, symmetrinen modulooperaatio sovittaa sen alueelle sopivaksi.

Jos SiirtojenLkm on positiivinen, siirto tapahtuu vasemmalle. Jos SiirtojenLkm on negatiivinen, siirto tapahtuu oikealle. Oletusarv o on

ë1 (siirrä yksi bitti oikealle).

Oikealle tapahtuvassa siirrossa oikeanpuoleisin bitti pudotetaan, ja 0 ja 1 lisätään vastaamaan vasemmanpuoleista bittiä. Vasemmalle tapahtuvassa siirrossa vasemmanpuoleisin bitti pudotetaan, ja 0 lisätään vastaamaan oikeanpuoleisinta bittiä.

Esimerkki siirrosta oikealle: Jokainen bitti siirtyy oikealle. 0b0000000000000111101011000011010 Lisää 0:n, jos vasemmanpuoleisin bitti on 0,

tai 1:n, jos vasemmanpuoleisin bitti on 1. tuottaa: 0b00000000000000111101011000011010 Vastaus näkyy kantalukutilan mukaisesti. Alkunollia ei näytetä.

shift(Lista1 [,SiirtojenLkm]) ⇒ lista

Luo Lista1:n kopion, jota on siirretty oikealle tai vasemmalle SiirtojenLkm:n elementtien määrittämän määrän. Ei muuta Lista1:ä.

Jos SiirtojenLkm on positiivinen, siirto tapahtuu vasemmalle. Jos SiirtojenLkm on negatiivinen, siirto tapahtuu oikealle. Oletusarv o on

ë1 (siirrä yksi elementti oikealle).

Elementit, jotka siirto vie listan alkuun tai loppuun, asettuvat symboliksi “undef”.

shift(Merkkijono1 [,SiirtojenLkm]) ⇒ merkkijono

Luo Merkkijono1:n kopion, jota on siirretty oikealle tai vasemmalle SiirtojenLkm:n merkkien määrittämän määrän. Ei muuta Merkkijono1:ä.

Jos SiirtojenLkm on positiivinen, siirto tapahtuu vasemmalle. Jos SiirtojenLkm on negatiivinen, siirto tapahtuu oikealle. Oletusarv o on

ë1 (siirrä yksi merkki oikealle).

Merkit, jotka siirto vie merkkijonon alkuun tai loppuun, muuttuvat välilyönneiksi.

Katalogi

Binaarisessa kantalukutilassa:

Heksadesimaalisessa kantalukutilassa:

Tärkeää: Binaariluvun edelle tulee aina merkitä etumerkki 0b

ja heksadesimaaliluvun edelle 0h (nolla, ei O-kirjain).

Desimaalisessa kantalukutilassa:

TI-Nspire™ -sovelluksen käsikirja 81

Page 88

sign() (etumerkki)

sign(Arvo1) ⇒ arvo sign(Lista1) ⇒ lista sign(Matriisi1) ⇒ matriisi

Kun kyseessä on reaali- tai kompleksilukuarvo Arvo1, antaa vastauksena Arvo1 /

abs(Arvo1), kun Arvo1 ƒ 0.

Vastaus on 1, jos Arvo1 on positiivinen. Vastaus on ë1, jos Arvo1 on negatiivinen.

sign(0) antaa vastauksen „1, jos kompleksilukutilan asetus on

Reaali; muussa tapauksessa antaa vastauksena itsensä.

sign(0) edustaa kompleksialueen yksikköpiiriä.

Kun kyseessä on lista tai matriisi, määrittää kaikkien elementtien etumerkit.

Jos kompleksilukutila on Reaali:

Katalogi

simult()

simult(kerroinMatriisi, vakioVektori[, tol]) ⇒ matriisi

Määrittää sarakevektorin, joka sisältää lineaarisen yhtälöryhmän ratkaisut.

kerroinMatriisin on oltava neliömatriisi, joka sisältää yhtälöiden kertoimet.

vakioVektorissa on oltava sama rivimäärä (sama koko) kuin kerroinMatriisissa ja sen tulee sisältää vakiot.

• Jos asetat Auto or Approximate (Automaattinen tai

likimääräinen)

laskut suoritetaan liukulukuaritmetiikalla.

•Jos Tol jätetään pois tai sitä ei käytetä, oletusarvoinen toleranssi lasketaan seuraavasti:

-tilan valintaan Approximate (Likimääräinen),

5Eë14 ·max(dim(kerroinMatriisi))

·rowNorm(kerroinMatriisi)

simult(kerroinMatriisi, vakioMatriisi[, tol]) ⇒ matriisi

Ratkaisee lineaarisia yhtälöryhmiä, joissa jokaisessa ryhmässä on samat yhtälöiden kertoimet mutta eri vakiot.

Jokaisen vakioMatriisin sarakkeen tulee sisältää jonkin yhtälöryhmän vakiot. Jokainen tulosmatriisin sarake sisältää vastaavan ryhmän ratkaisun.

Katalogi

Ratkaise yhtälöstä x ja y: x + 2y = 1 3x + 4y = ë1

Ratkaisu on x=ë3 and y=2.

Ratkaise: ax + by = 1 cx + dy = 2

Ratkaise:

x + 2y = 1

3x + 4y = ë1

x + 2y = 2

3x + 4y = ë3

Ensimmäisessä ryhmässä x=ë3 ja y=2. Toisessa ryhmässä x=ë7 ja y=9/2.

82 TI-Nspire™ -sovelluksen käsikirja

Page 89

sin()

sin(Arvo1) ⇒ arvo sin(Lista1) ⇒ lista

sin(Arvo1) määrittää argumentin sinin. sin(Lista1) määrittää listan, joka sisältää Lista1:n kaikkien

elementin sinit.

Huomaa: Argumentti tulkitaan aste-, graadi- tai radiaanikulmaksi

käytössä olevan kulmatilan mukaisesti. Voit ohittaa kulmatilaasetuksen väliaikaisesti käyttämällä merkintää ó,G tai ô.

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

painike

sin(neliömatriisi1) ⇒ neliömatriisi

Määrittää neliömatriisi1:n matriisin sinin. Tämä ei ole sama kuin kunkin elementin sinin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

sinê()

sinê(Arvo1) ⇒ arvo sinê(Lista1) ⇒ lista

sinê(Arvo1) määrittää kulman, jonka sini on Arvo1.

sinê(Lista1) määrittää listan, joka sisältää Lista1:n kaikkien

elementtien käänteissinit.

Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana

käytössä olevan kulmatila-asetuksen mukaisesti.

sinê(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisin käänteissinin. Tämä ei ole sama kuin kunkin elementin käänteissinin laskeminen. Laskentamenetelm ä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

Radiaanikulmatilassa:

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

Radiaanikulmatilassa ja suorakulmakompleksimuodossa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeen kohdistinta painikkeilla ¡ ja ¢.

painikkeet

TI-Nspire™ -sovelluksen käsikirja 83

Page 90

sinh()

sinh(Numver1) ⇒ arvo sinh(Lista1) ⇒ lista

sinh (Arvo1) laskee argumentin hyperbolisen kosinin. sinh (Lista1) määrittää listan, joka sisältää Lista1:n jokaisen

elementin hyperbolisen sinin.

sinh(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisin hyperbolisen sinin. Tämä ei ole sama kuin kunkin elementin hyperbolisen sinin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

Radiaanikulmatilassa:

Katalogi

sinhê()

sinhê(Arvo1) ⇒ arvo sinhê(Lista1) ⇒ lista

sinhê(Arvo1) laskee argumentin käänteisen hyperbolisen sinin.

sinhê(Lista1) määrittää listan, joka sisältää Lista1:n jokaisen

elementin käänteiset hyperboliset sinit.

sinhê(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisin käänteisen hyperbolisen sinin. Tämä ei ole sama kuin kunkin elementin käänteisen hyperbolisen sinin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

Radiaanikulmatilassa:

Katalogi

84 TI-Nspire™ -sovelluksen käsikirja

Page 91

SinReg

SinReg X, Y [ , [Iteraatiot] ,[ Jakso] [, Luokka, Sisällytä] ]

Laskee siniregression listoista X ja Y. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 87.)

Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Iteraatiot on arvo, joka määrittää ratkaisun yrityskertojen (1-16)

enimmäismäärän. Mikäli sitä ei määritetä, oletuksena käytetään arvoa 8. Suuremmilla arvoilla saadaan tyypillisesti parempi tarkkuus, mutta suoritusaika on pitempi ja päin vastoin.

Jakso määrittää arvioidun jakson. Mikäli sitä ei käytetä, X:n arvojen välisen eron tulisi olla sama ja arvojen tulisi olla peräkkäisessä järjestyksessä. Jos määrität Jakson, x:n arvojen väliset erot voivat olla erisuuria.

Luokka on numeeristen luokkakoodien lista vastaavalle X- ja Ydatalle.

Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

SinReg:n tulos esitetään aina radiaaneina riippumatta kulmatilan

asetuksesta.

Tulosmuuttuja Kuvaus

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.Resid Regressioyhtälön jäännökset

stat.XReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.YReg Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv,

stat.FreqReg Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

Regressioyhtälö: a·sin(bx+c)+d

Regressiokertoimet

Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

Katalogi

SortA

SortA Lista1[, Lista2] [, Lista3] ... SortA

Vektori1[, Vek to r i 2 ] [, Ve kt o r i 3] ...

Lajittelee ensimmäisen argumentin elementit nousevaan järjestykseen.

Jos otat mukaan lisäargumentteja, lajittelee kunkin argumentin elementit siten, että niiden uudet paikat vastaavat ensimmäisen argumentin elementtien uusia paikkoja.

Kaikkien argumenttien on oltava lista- tai vektorinimiä. Kaikkien argumenttien on oltava samankokoisia.

Katalogi

TI-Nspire™ -sovelluksen käsikirja 85

Page 92

SortD

SortD Lista1[, Lista2] [, List3] ...

Vektori1[,Vek to r i 2 ] [,Vektori3] ...

SortD

Muuten samanlainen kuin SortA paitsi, että SortD lajittelee elementit laskevaan järjestykseen.

Sphere

Vektori 4Sphere

Näyttää rivi- tai sarakevektorin pallonmuotoisena [r q f].

Vektorin on oltava kooltaan 3, ja se voi olla rivi- tai sarakevektori.

Huomaa: 4Sphere on näyttömuodon ohje, ei muunnosfunktio.

Voit käyttää komentoa ainoastaan syöterivin lopussa.

Katalogi

(ρ,θ,φ)

sqrt()

sqrt(Arvo1) ⇒ arvo sqrt(Lista1) ⇒ lista

Laskee argumentin neliöjuuren. Kun kyseessä on lista, laskee kaikkien Lista1:n elementtien

Katalogi

neliöjuuret.

Huomaa: Katso myös

Neliöjuurimalli

, sivu 1.

86 TI-Nspire™ -sovelluksen käsikirja

Page 93

stat.results

Näyttää tilastollisen laskutoimituksen tulokset. Vastaukset näytetään nimiarvoparien sarjana. Näytetyt nimenomaiset

nimet riippuvat viimeksi sievennetystä tilastofunktiosta tai komennosta.

Voit kopioida nimen tai arvon ja liittää sen muihin paikkoihin.

Huomaa: Älä määritä muuttujia, joilla on sama nimi kuin

tilastoanalyyseissä käytettävillä muuttujilla. Joissakin tapauksissa tästä voi olla seurauksena virhetilanne. Tilastoanalyyseissä käytettävät muuttujanimet on esitetty alla olevassa taulukossa.

Katalogi

stat.a stat.AdjR² stat.b stat.b0 stat.b1 stat.b2 stat.b3 stat.b4 stat.b5 stat.b6 stat.b7 stat.b8 stat.b9 stat.b10 stat.bList stat.c² stat.c stat.CLower stat.CLowerList stat.CompList stat.CompMatrix stat.CookDist stat.CUpper stat.CUpperList stat.d

Huomaa: Aina kun Listat & Taulukot -sovellus laskee tilastolaskujen vastauksia, se kopioi "stat." -ryhmän muuttujat "stat#."

-ryhmään, jossa # on luku, jota lisätään automaattisesti. Tällä tavoin voit säilyttää aikaisemmat tulokset suorittaessasi useita laskutoimituksia.

stat.dfDenom stat.dfBlock stat.dfCol stat.dfError stat.dfInteract stat.dfReg stat.dfNumer stat.dfRow stat.DW stat.e stat.ExpMatrix stat.F stat.FBlock stat.Fcol

stat.FInteract stat.FreqReg stat.Frow stat.Leverage stat.LowerPred stat.LowerVal stat.m stat.MaxX stat.MaxY stat.ME stat.MedianX

stat.MedianY stat.MEPred stat.MinX stat.MinY stat.MS stat.MSBlock stat.MSCol stat.MSError stat.MSInteract stat.MSReg stat.MSRow stat.n stat.Ç

stat.Ç1 stat.Ç2 stat.ÇDiff stat.PList stat.PVal stat.PValBlock stat.PValCol

stat.PValInteract stat.PValRow stat.Q1X stat.Q1Y stat.Q3X

stat.Q3Y stat.r stat.r² stat.RegEqn stat.Resid stat.ResidTrans stat.sx

stat.sy stat.sx1 stat.sx2 stat.Gx stat.Gx² stat.Gxy stat.Gy stat.Gy² stat.s stat.SE

stat.SEList stat.SEPred stat.sResid stat.SEslope stat.sp stat.SS stat.SSBlock

stat.SSCol stat.SSX stat.SSY stat.SSError stat.SSInteract stat.SSReg stat.SSRow stat.tList stat.UpperPred stat.UpperVal stat.v stat.v1

stat.v2 stat.vDiff stat.vList stat.XReg stat.XVal stat.XValList stat.w

stat.y stat.yList

stat.YReg

TI-Nspire™ -sovelluksen käsikirja 87

Page 94

stat.values

Näyttää matriisin viimeksi sievennetylle tilastofunktiolle tai komennolle lasketuista arvoista.

stat.results, stat.values jättää pois arvoihin liittyvät

Toisin kuin nimet.

Voit kopioida arvon ja liittää sen muihin paikkoihin.

Katso esimerkki kohdassa

Katalogi

stat.results.

stDevPop()

stDevPop(Lista[, frekvLista]) ⇒ lauseke

Laskee Lista:n sisältämien elementtien perusjoukon keskihajonnan. Jokainen frekvListan elementti näyttää Listan vastaavien

elementtien peräkkäisten esiintymien lukumäärän.

Huomaa: Listassa tulee olla vähintään kaksi elementtiä. stDevPop(Matriisi1[, frekvMatriisi]) ⇒ matriisi

Laskee rivivektorin Matriisi1:n sarakkeiden perusjoukon keskihajonnoista.

Jokainen frekvMatriisin elementti näyttää Matriisi1:n vastaavien elementtien peräkkäisten esiintymien lukumäärän.

Huomaa: Matriisi1 :ssä on oltava vähintään kaksi riviä.

stDevSamp()

stDevSamp(Lista[, frekvLista]) ⇒ lauseke

Laskee Listan sisältämien elementtien otoksen keskihajonnan. Jokainen frekvListan elementti näyttää Listan vastaavien

elementtien peräkkäisten esiintymien lukumäärän.

Huomaa: Listassa tulee olla vähintään kaksi elementtiä. stDevSamp(Matriisi1[, frekvMatriisi]) ⇒ matriisi

Laskee rivivektorin Matriisi1:n sarakkeiden otosten keskihajonnoista.

Jokainen frekvMatriisin elementti näyttää Matriisi1:n vastaavien elementtien peräkkäisten esiintymien lukumäärän.

Huomaa: Matriisi1 :ssä on oltava vähintään kaksi riviä.

Radiaanikulma- ja automaattisissa tiloissa:

Katalogi

88 TI-Nspire™ -sovelluksen käsikirja

Page 95

Stop

Ohjelmointikomento: Pysäyttää ohjelman.

Stop ei ole sallittu funktioissa. Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Katalogi

Store

string() (merkkijono)

string(Laus) ⇒ merkkijono

Sieventää lausekkeen Laus ja antaa vastauksen merkkijonona.

subMat()

subMat(Matriisi1[, alkurivi] [, alkusarake] [, loppurivi] [,

loppusarake])

⇒ matriisi

Laskee Matriisi1:n määritetyn alimatriisin. Oletusarvot: alkurivi=1, alkusarake=1, loppurivi=viimeinen rivi,

endCol=viimeinen sarake.

Sum (Sigma)

sum()

sum(Lista[, Alku[, Loppu]]) ⇒ lauseke

Laskee Listan elementtien summan. Alku ja Loppu ovat valinnaisia. Ne määrittävät elementtien alueen.

Katso

& (tallenna)

Katalogi

Katso G(), sivu 114.

Katalogi

, sivu 118.

TI-Nspire™ -sovelluksen käsikirja 89

Page 96

sum()

sum(Matriisi1[, Alku[, Loppu]]) ⇒ matriisi

Laskee rivivektorin, joka sisältää Matriisi1:n sarakkeiden elementtien summat.

Alku ja Loppu ovat valinnaisia. Ne määrittävät rivialueen.

Katalogi

sumIf()

sumIf(Lista,Kriteerit[, SummaLista]) ⇒ arvo

Laskee kaikkien niiden Listan sisältämien elementti en kumuloituneen summan, jotka vastaavat määritettyjä kriteereitä Kriteerit. Voit halutessasi antaa kumuloivat elementit määrittämäll ä vaihtoehtoisen listan, summaLista.

Lista voi olla lauseke, lista tai matriisi. SummaListalla, mikäli se määritetään, on oltava samat mitat kuin Listalla.

Kriteeri voi olla:

• Arvo, lauseke tai merkkijono. Esimerkiksi 34 kumuloi vain niitä Listan elementtejä, jotka sieventyvät arvoon 34.

• Boolen lauseke, joka sisältää symbolin ? kunkin elementin paikanpitäjänä. Esimerkiksi lauseke ?<10 kumuloi vain niitä Listan elementtejä, jotka ovat alle 10.

Kun jokin Listan elementti vastaa kriteereitä Kriteerit, elementti lisätään kumuloituvaan summaan. Jos sisällytät funktioon

summaListan, summaan lisätäänkin sen sijaan vastaava summaListan elementti.

Listat & Taulukot -sovelluksessa voit käyttää solualueita Listan ja summaListan tilalla.

Huomaa: Katso myös countIf(), sivu 19.

system()

system(Arvo1 [, Arvo2 [, Arvo3 [, ...]]])

Laskee yhtälöryhmän listaksi muotoiltuna. Voit luoda yhtälöryhmän myös mallin avulla.

Huomaa: Katso myös Yhtälöryhmä, sivu 1.

(transponoi)

Matriisi1

⇒ matriisi

Laskee Matriisi1:n transponoidun liittokompleksimatriisin.

Katalogi

90 TI-Nspire™ -sovelluksen käsikirja

Page 97

tan()

tan(Arvo1) ⇒ arvo tan(Lista1) ⇒ lista

tan(Arvo1) laskee argumentin tangentin. tan(Lista1) määrittää Lista1:n kaikkien elementtien tangenttien

listan.

Huomaa: Argumentti tulkitaan aste-, graadi- tai radiaanikulmaksi

käytössä olevan kulmatilan mukaisesti. Voit ohittaa kulmatilaasetuksen väliaikaisesti käyttämällä merkintää ó,G tai ô.

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

painike

tan(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisin tangentin. Tämä ei ole sama kuin kunkin elementin tangentin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

tanê()

tanê(Arvo1) ⇒ arvo tanê(Lista1) ⇒ lista

tanê(Arvo1) laskee kulman, jonka tangentti on Arvo1.

tanê(Lista1) luo listan Lista1:n jokaisen elementin

käänteistangenteista.

Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana

käytössä olevan kulmatila-asetuksen mukaisesti.

Radiaanikulmatilassa:

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

painikkeet

TI-Nspire™ -sovelluksen käsikirja 91

Page 98

tanê()

tanê(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisin käänteistangentin. Tämä ei ole sama kuin kunkin elementin käänteisen tangentin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

Radiaanikulmatilassa:

painikkeet

tanh()

tanh(Arvo1) ⇒ arvo tanh(Lista1) ⇒ lista

tanh(Arvo1) laskee argumentin hyperbolisen tangentin. tanh(Lista1) luo listan Lista1:n jokaisen elementin hyperbolisista

tangenteista.

tanh(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisin hyperbolisen tangentin. Tämä ei ole sama kuin kunkin elementin hyperbolisen tangentin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

tanhê()

tanhê(Arvo1) ⇒ arvo tanhê(Lista1) ⇒ lista

tanhê(Arvo1) laskee argumentin käänteisen hyperbolisen

tangentin.

tanhê(Lista1) luo listan Lista1:n jokaisen elementin käänteisistä

hyperbolisista tangenteista.

tanhê(neliömatriisi1) ⇒ neliömatriisi

Laskee neliömatriisi1:n matriisin käänteisen hyperbolisen tangentin. Tämä ei ole sama kuin kunkin elementin käänteisen hyperbolisen tangentin laskeminen. Laskentamenetelmä on kuvattu kohdassa

cos().

neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

Katalogi

Radiaanikulmatilassa:

Katalogi

Suorakulmakompleksimuodossa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeen kohdistinta painikkeilla ¡ ja ¢.

Radiaanikulmatilassa ja suorakulmakompleksimuodossa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeen kohdistinta painikkeilla ¡ ja ¢.

92 TI-Nspire™ -sovelluksen käsikirja

Page 99

tCdf()

tCdf(alaraja,yläraja,df) ⇒ luku, jos alaraja ja yläraja ovat

lista, jos alaraja ja yläraja ovat listoja

lukuja,

Laskee Studentin t-todennäköisyysjakauman alarajan ja ylärajan välillä määritetylle vapausasteelle df.

Katalogi

Kun P(X  yläraja), aseta alaraja = .9E999.

Then Katso If, sivu 39.

TInterval

TInterval Lista[,Frekv[,CTaso]]

(Datalistan syöte)

TInterval v,Sx,n[,CTaso]

(Yhteenvetotilaston syöte) Laskee t-luottamusvälin. Tulosten yhteenveto tallentuu stat.results-

muuttujaan. (Katso sivu 87.)

Tulosmuuttuja Kuvaus

stat.CLower, stat.CUpper Tuntemattoman perusjoukon keskiarvon luottamusväli

stat.x

Satunnaisesta normaalijakaumasta olevan datasekvenssin otoksen keskiarvo

stat.ME Virhemarginaali

stat.df Vapausasteet

stat.sx

Otoksen keskihajonta

stat.n Otoksen keskiarvon sisältävän datasekvenssin pituus

TInterval_2Samp

Lista1,Lista2[,Frekv1[,Frekv2[,CTaso[,Poolaus]]]]

(Datalistan syöte)

TInterval_2Samp v1,Sx1,n1,v2,Sx2,n2[,CTaso[,Poolaus]]

(Yhteenvetotilaston syöte) Laskee kahden otoksen t-luottamusvälin. Tulosten yhteenveto

tallentuu stat.results-muuttujaan. (Katso sivu 87.) Poolaus=1 poolaa varianssit; Poolaus=0 ei poolaa variansseja.

Katalogi

Tulosmuuttuja Kuvaus

stat.CLower, stat.CUpper Luottamusväli, joka sisältää jakauman luottamusvälin todennäköisyyden

stat.x1-x2

Satunnaisesta normaalijakaumasta olevien datasekvenssien otosten keskiarvot

stat.ME Virhemarginaali

TI-Nspire™ -sovelluksen käsikirja 93

Page 100

Tulosmuuttuja Kuvaus

stat.df Vapausasteet

stat.x1, stat.x2

stat.sx1, stat.sx2

Satunnaisesta normaalijakaumasta olevien datasekvenssien otosten keskiarvot

Lista 1:n ja Lista 2:n otosten keskihajonnat

stat.n1, stat.n2 Otosten lukumäärä datasekvensseissä

stat.sp Poolattu keskihajonta. Laskettu, kun Poolaus = KYLLÄ

tPdf()

tPdf(XArvo,df) ⇒ luku, jos XArvo on luku, lista, jos XArvo on

lista

Laskee todennäköisyystiheysfunktion (pdf) Studentin t-jakaumalle määritetyllä x:n arvolla ja määritetyillä vapausasteilla df.

trace()

trace(neliömatriisi) ⇒ arvo

Laskee neliömatriisin jäljityksen (päälävistäjän kaikkien elementtien summan).

Try (Kokeile)

Try

lohko1

Else

lohko2

EndTry

Suorittaa lohko1:n, ellei virhettä esiinny. Ohjelman suoritus siirtyy lohko2:een, jos lohko1:ssä esiintyy virhe. Järjestelmän muuttuja errCode sisältää virhekoodin, jotta ohjelma voi korjata virheen.

Virhekoodien luettelo on esitetty kohdassa Virhekoodit ja viestit, sivulla 120.

lohko1 ja lohko2 voivat olla joko yksi lauseke tai sarja lausekkeita, jotka on erotettu toisistaan kaksoispisteellä (:).

Huomaa esimerkkiä syöttäessäsi: Laskin-sovelluksessa voit

syöttää monirivisiä määritelmiä painamalla jokaisen rivin lopussa painiketta @ painikkeen · sijaan. Tietokoneen

näppäimistöllä Alt-näppäintä pidetään alhaalla ja painetaan Enter.

Katalogi

94 TI-Nspire™ -sovelluksen käsikirja

Texas Instruments TI-Nspire Reference Guide [fi]

Specifications and Main Features

Frequently Asked Questions

User Manual

Tärkeitä tietoja

Sisällys

Lausekemallit

TI-Nspire™ -sovelluksen käsikirja 1

Luettelo aakkosjärjestyksessä