Texas Instruments TI-Nspire Reference Guide [es]

Guía de Referencia

Este manual de instrucciones es válido para el software TI-Nspire versión

1.4. Para obtener la versión más reciente de la documentación, vaya a education.ti.com/guides.

Información importante

A menos que la licencia que acompaña a este programa recoja expresamente lo contrario, Texas Instruments no otorga ningún tipo de garantía, ya sea implícita o explícita, con carácter enunciativo mas no limitativo, a ninguna garantía implícita de comerciabilidad o idoneidad para ningún propósito determinado, en relación con ningún programa o material impreso, y pone a disposición esos materiales únicamente tal y como están. Texas Instruments queda eximida de toda responsabilidad por daños especiales, colaterales, accidentales o derivados en relación con o a causa de la adquisición o el uso de estos materiales. La responsabilidad única de Texas Instruments independientemente de la acción legal adoptada, no podrá exceder la cantidad señalada en la licencia del programa. Además, Texas Instruments quedará exenta de toda responsabilidad frente a cualquier reclamación, independientemente de la clase que sea, en referencia al uso de estos materiales por un tercero.

Licencia

Sírvase ver la licencia completa instalada en C:\Program Files\TI Education\TI-Nspire.

Macintosh®, Windows®, Excel®, Vernier EasyLink®, EasyTemp®, Go!®Link, Go!®Motion, y Go!®Temp son marcas comerciales de sus propietarios respectivos.

Índice

Información importante Plantillas de expresión

Plantilla de fracción .....................................1

Plantilla de exponente ................................1

Plantilla de raíz cuadrada ............................1

Plantilla de raíz enésima ............................. 1

Plantilla de base e ........................................2

Plantilla de logaritmo ..................................2

Plantilla de función definida a trozos

(2 partes) ...................................................... 2

Plantilla de función definida a trozos

(N partes) ......................................................2

Plantilla de valor absoluto .......................... 2

Plantilla de gg°mm’ss.ss’’ .............................3

Plantilla de matriz (2 x 2) ............................3

Plantilla de matriz (1 x 2) ............................3

Plantilla de matriz (2 x 1) ............................3

Plantilla de matriz (m x n) ........................... 3

Plantilla de suma (G) .................................... 3

Plantilla de producto (Π) ............................. 4

Listado alfabético A

abs() ..............................................................5

amortTbl() .................................................... 5

and ................................................................5

angle() ..........................................................6

ANOVA .........................................................6

ANOVA de 2 variables .................................7

Ans ................................................................9

approx() ........................................................9

approxRational() .......................................... 9

augment() .....................................................9

avgRC() ....................................................... 10

bal() .............................................................10

4Base2 .........................................................10

4Base10 .......................................................11

4Base16 .......................................................11

binomCdf() ................................................. 11

binomPdf() ................................................. 12

ceiling() .......................................................12

char() ...........................................................12

de 2 elementos ...................................... 12

Cdf() .........................................................13

GOF ......................................................... 13

Pdf() .........................................................13

ClearAZ .......................................................13

ClrErr ...........................................................14

colAugment() ............................................. 14

colDim() ......................................................14

colNorm() ....................................................14

conj() ...........................................................14

constructMat() ............................................ 15

CopyVar ...................................................... 15

corrMat() .................................................... 15

cos() ............................................................ 16

cosê() .......................................................... 17

cosh() .......................................................... 17

coshê() ........................................................ 17

cot() ............................................................ 18

cotê() .......................................................... 18

coth() .......................................................... 18

cothê() ........................................................ 18

count() ........................................................ 19

countif() ..................................................... 19

crossP() ....................................................... 19

csc() ............................................................. 20

cscê() ........................................................... 20

csch() ........................................................... 20

cschê() ......................................................... 20

CubicReg .................................................... 21

cumSum() ................................................... 21

Cycle ........................................................... 22

4Cylind ........................................................ 22

dbd() ........................................................... 22

4DD ............................................................. 23

4Decimal ..................................................... 23

Define (Definir) .......................................... 23

Define LibPriv ............................................ 24

Define LibPub ............................................ 25

DelVar ........................................................ 25

det() ............................................................ 25

diag() .......................................................... 26

dim() ........................................................... 26

Disp ............................................................. 26

4GMS ........................................................... 27

dotP() .......................................................... 27

e^() ............................................................. 27

eff() ............................................................. 28

eigVc() ........................................................ 28

eigVl() ......................................................... 28

Else ............................................................. 28

ElseIf ........................................................... 29

EndFor ........................................................ 29

EndFunc ...................................................... 29

EndIf ........................................................... 29

EndLoop ..................................................... 29

EndPrgm ..................................................... 29

EndTry ........................................................ 29

EndWhile .................................................... 29

Exit .............................................................. 30

exp() ........................................................... 30

expr() .......................................................... 30

ExpReg ....................................................... 31

factor() ....................................................... 31

FCdf() ......................................................... 32

Fill ............................................................... 32

iii

FiveNumSummary ......................................32

floor() ..........................................................33

For ...............................................................33

format() ......................................................33

fPart() ..........................................................34

FPdf() ..........................................................34

freqTable4lista() ..........................................34

frequency() .................................................34

Func .............................................................35

FTest_2Samp ..............................................35

gcd() ............................................................36

geomCdf() ...................................................36

geomPdf() ...................................................36

getDenom() ................................................36

getLangInfo() .............................................37

getMode() ...................................................37

getNum() ....................................................38

getVarInfo() ................................................38

Goto ............................................................39

4Grad ...........................................................39

identity() .....................................................39

If ..................................................................40

ifFn() ............................................................41

imag() ..........................................................41

Indirection ..................................................41

inString() .....................................................41

int() .............................................................42

intDiv() ........................................................42

() .........................................................42

invc

invF() ...........................................................42

invNorm() ....................................................42

invt() ............................................................42

iPart() ..........................................................43

irr() ..............................................................43

isPrime() ......................................................43

Lbl ...............................................................44

lcm() ............................................................44

left() ............................................................44

libShortcut() ................................................45

LinRegBx .....................................................45

LinRegMx ....................................................46

LinRegtIntervals .........................................47

LinRegTTest (Test t de regresión lineal) ...48

@List() ..........................................................49

list4mat() .....................................................49

ln() ...............................................................49

LnReg ..........................................................50

Local ............................................................51

log() .............................................................51

Logistic ........................................................52

LogisticD .....................................................53

Loop ............................................................54

LU ................................................................54

mat4list() .....................................................54

max() ...........................................................55

mean() ........................................................ 55

median() ..................................................... 55

MedMed ..................................................... 56

mid() ........................................................... 56

min() ........................................................... 57

mirr() ........................................................... 57

mod() .......................................................... 57

mRow() ....................................................... 58

mRowAdd() ................................................ 58

MultReg ...................................................... 58

MultRegIntervals ....................................... 58

MultRegTests ............................................. 59

nCr() ............................................................ 60

nDeriv() ....................................................... 60

newList() ..................................................... 61

newMat() .................................................... 61

nfMax() ....................................................... 61

nfMin() ....................................................... 61

nInt() ........................................................... 61

nom() .......................................................... 62

norm() ......................................................... 62

normCdf() ................................................... 62

normPdf() ................................................... 62

not .............................................................. 62

nPr() ............................................................ 63

npv() ........................................................... 64

nSolve() ....................................................... 64

OneVar ....................................................... 65

or ................................................................ 66

ord() ............................................................ 66

P4Rx() .......................................................... 66

P4Ry() .......................................................... 67

PassErr ........................................................ 67

piecewise() .................................................67

poissCdf() .................................................... 67

poissPdf() .................................................... 67

4Polar .......................................................... 68

polyEval() .................................................... 68

PowerReg ................................................... 68

Prgm ........................................................... 69

Product (PI) ................................................. 69

product() .................................................... 69

propFrac() ................................................... 70

QR ............................................................... 71

QuadReg .................................................... 71

QuartReg .................................................... 72

R4Pq() .......................................................... 73

R4Pr() ........................................................... 73

4Rad ............................................................ 73

rand() .......................................................... 73

randBin() .................................................... 74

randInt() ..................................................... 74

randMat() ................................................... 74

randNorm() ................................................. 74

randPoly() ................................................... 74

randSamp() ................................................. 74

RandSeed .................................................... 75

real() ...........................................................75

4Rect ............................................................75

ref() .............................................................76

remain() ......................................................76

Return ......................................................... 76

right() ..........................................................76

root() ...........................................................77

rotate() .......................................................77

round() ........................................................78

rowAdd() ....................................................78

rowDim() ....................................................78

rowNorm() .................................................. 78

rowSwap() .................................................. 79

rref() ............................................................79

sec() .............................................................79

sec/() ...........................................................80

sech() ...........................................................80

sechê() ......................................................... 80

seq() ............................................................80

setMode() ................................................... 81

shift() ..........................................................82

sign() ...........................................................83

simult() ........................................................83

sin() .............................................................84

sinê() ...........................................................84

sinh() ...........................................................85

sinhê() .........................................................85

SinReg .........................................................86

SortA ...........................................................86

SortD ...........................................................87

4Sphere ....................................................... 87

sqrt() ...........................................................87

stat.results .................................................. 88

stat.values ...................................................89

stDevPop() .................................................. 89

stDevSamp() ............................................... 89

Stop .............................................................90

Store ...........................................................90

string() ........................................................90

subMat() ..................................................... 90

Sum (Sigma) ............................................... 90

sum() ...........................................................90

sumIf() .........................................................91

system() .......................................................91

T (transponer) ............................................91

tan() ............................................................92

tanê() ..........................................................92

tanh() ..........................................................93

tanhê() ........................................................93

tCdf() ...........................................................94

Then ............................................................94

tInterval ......................................................94

tInterval_2Samp .........................................94

tPdf() ...........................................................95

trace() .........................................................95

Try ............................................................... 96

tTest ............................................................ 96

tTest_2Samp ............................................... 97

tvmFV() ....................................................... 97

tvmI() .......................................................... 98

tvmN() ........................................................ 98

tvmPmt() .................................................... 98

tvmPV() ....................................................... 98

TwoVar ....................................................... 99

unitV() ...................................................... 100

varPop() .................................................... 100

varSamp() ................................................. 100

when() ...................................................... 101

While ........................................................ 101

“With” ...................................................... 101

xor ............................................................ 102

zInterval ................................................... 102

zInterval_1Prop ........................................ 103

zInterval_2Prop ........................................ 103

zInterval_2Samp ...................................... 103

zTest ......................................................... 104

zTest_1Prop .............................................. 104

zTest_2Prop .............................................. 105

zTest_2Samp ............................................ 105

Símbolos

+ (suma) .................................................... 107

N(resta) ..................................................... 107

·(multiplicación) ..................................... 108

à (división) ................................................ 108

^ (potencia) .............................................. 109

(cuadrado) ........................................... 109

.+ (punto suma) ....................................... 110

.. (punto resta) ......................................... 110

·(punto multiplic.) ................................. 110

. / (punto división) .................................... 110

.^ (punto de potencia) ............................ 110

ë(negación) .............................................. 111

% (porcentaje) ......................................... 111

= (igual) .................................................... 112

ƒ (no igual) ............................................... 112

< (menor que) .......................................... 113

{ (menor o igual que) .............................. 113

> (mayor que) .......................................... 113

| (mayor o igual que) .............................. 113

! (factorial) ............................................... 114

& (añadir) ................................................. 114

‡() (raíz cuadrada) ................................... 114

Π() (producto) .......................................... 114

G() (suma) ................................................. 115

GInt() ......................................................... 115

GPrn() ........................................................ 116

# (dirección) ............................................. 116

í (notación científica) ..............................116

g (grado centesimal) ................................117

ô(radián) ...................................................117

¡ (grado) ....................................................117

¡, ', '' (grados/minutos/segundos) ............118

 (ángulo) ................................................118

10^() ..........................................................118

^ê (inverso de un valor) ...........................119

| (“with”) ...................................................119

& (almacenar) ..........................................119

:= (asignar) ................................................120

0b, 0h ........................................................120

Códigos y mensajes de error Información sobre productos,

servicios y garantías de TI

Guía de referencia de TI-Nspire™

En esta guía se describen las plantillas, funciones, órdenes y operadores que podrá utilizar para calcular expresiones matemáticas.

Plantillas de expresión

Las plantillas de expresión son un medio fácil de introducir expresiones matemáticas en notación estándar. Cada plantilla que se inserta aparece en la línea de entrada y presenta bloques pequeños para indicar los elementos que se pueden introducir. Los elementos se indican por medio de un cursor.

Utilice las teclas de flecha o pulse

y escriba un valor o una expresión. Pulse

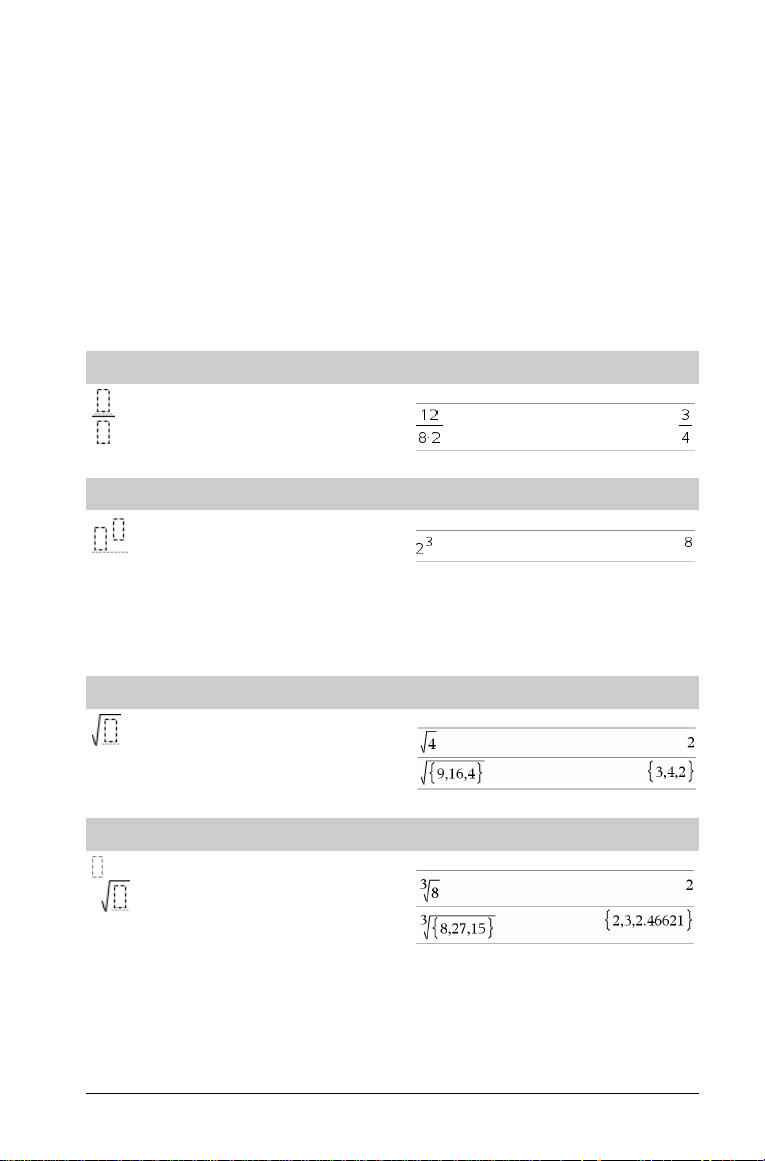
Plantilla de fracción

Nota: Consulte también / (división), en la página 108.

e para desplazar el cursor a cada posición del elemento,

· o /· para calcular la expresión.

Teclas

Ejemplo:

Plantilla de exponente

Nota: Escriba el primer valor, pulse l, y escriba el exponente.

Para desplazar el cursor hasta la línea de base, pulse la tecla de flecha (¢).

Nota: Consulte también ^ (potencia), en la página 109.

Plantilla de raíz cuadrada

Nota: Consulte también

página 114.

Plantilla de raíz enésima

Nota: Consulte también root(), en la página 77.

‡

() (raíz cuadrada), en la

Ejemplo:

Teclas

Tecla l

Guía de referencia de TI-Nspire™ 1

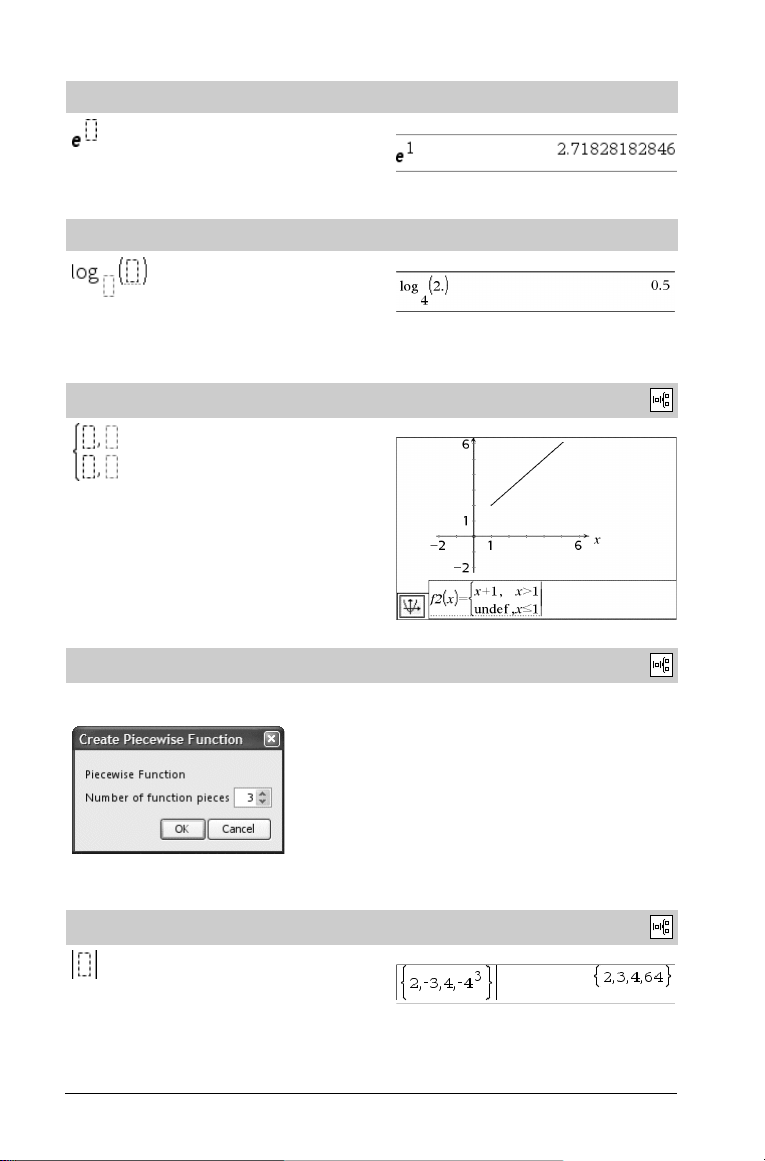
Plantilla de base e

Base el número e y exponente cualquiera

Nota: Consulte también e^(), en la página 27.

Teclas u

Ejemplo:

Plantilla de logaritmo

Calcula el logaritmo de la base que se indique. En el caso de la base por defecto, 10, no hay que indicar la base.

Nota: Consulte también log(), en la página 51.

Plantilla de función definida a trozos (2 partes)

Permite crear expresiones y condiciones para una función definida a trozos -con dos partes. Para añadir un trozo, haga clic en la plantilla y repita los pasos.

Nota: Consulte también piecewise(), en la página 67.

Plantilla de función definida a trozos (N partes)

Permite crear expresiones y condiciones para una función definida a trozos con N-partes. Solicita la introducción del número de partes, N.

Tecla /s

Ejemplo:

Catálogo >

Ejemplo:

Catálogo >

Ejemplo: Consulte el ejemplo de la plantilla definida a trozos (2 partes).

Nota: Consulte también piecewise(), en la página 67.

Plantilla de valor absoluto

Ejemplo:

Nota: Consulte también abs(), en la página 5.

Catálogo >

2 Guía de referencia de TI-Nspire™

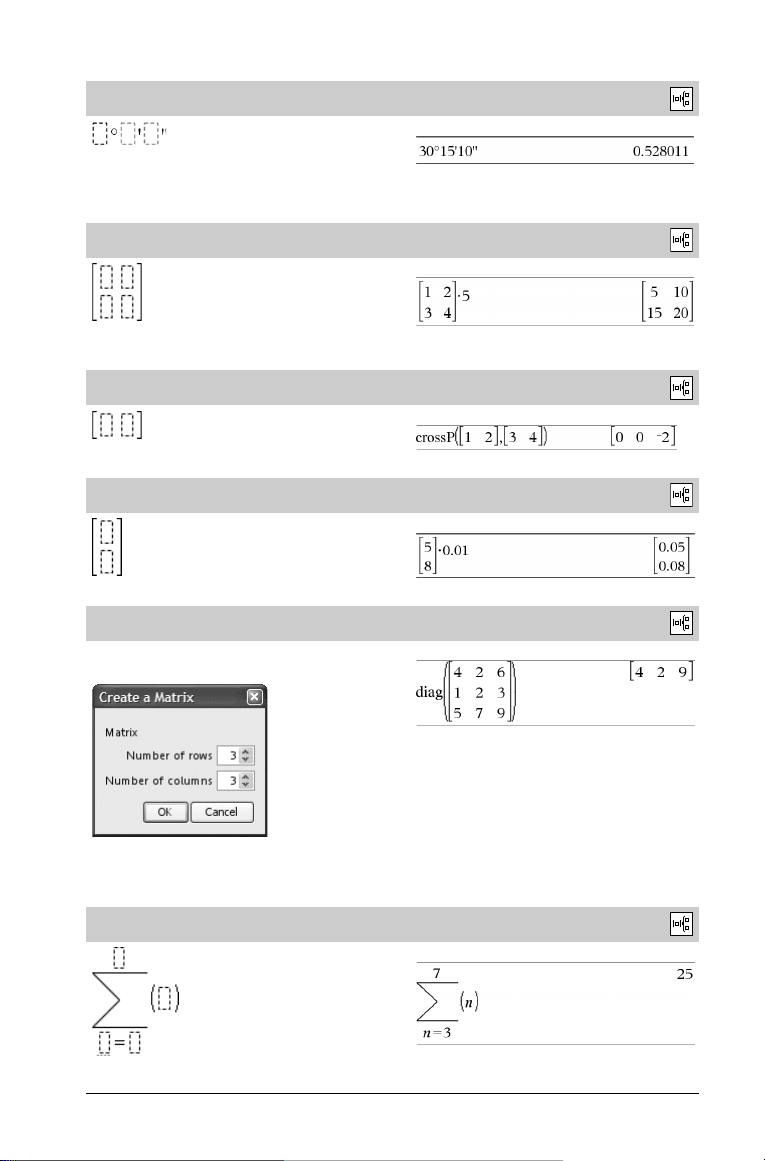
Plantilla de gg°mm’ss.ss’’

Permite introducir ángulos en formato gg°mm’ss.ss’’, donde gg es el número de grados sexagesimales, mm corresponde al número de minutos y ss.ss al de segundos.

Catálogo >

Ejemplo:

Plantilla de matriz (2 x 2)

Crea una matriz de 2 por 2.

Plantilla de matriz (1 x 2)

Plantilla de matriz (2 x 1)

Plantilla de matriz (m x n)

La plantilla aparece tras la solicitud para especificar el número de filas y columnas.

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

Nota: Si la matriz que ha creado tiene gran cantidad de filas y columnas puede tardar unos minutos en aparecer.

Plantilla de suma (G)

Ejemplo:

Catálogo >

Guía de referencia de TI-Nspire™ 3

Plantilla de producto (Π)

Nota: Consulte también Π() (producto), en la página 114.

Catálogo >

Ejemplo:

4 Guía de referencia de TI-Nspire™

Listado alfabético

Los elementos con nombres no alfabéticos (por ejemplo, +, ! y >) se incluyen al final de esta sección, en una lista que comienza en la página 107. A menos que se especifique lo contrario, todos los ejemplos de esta sección se han realizado en el modo de restablecimiento predeterminado y suponiendo que todas las variables están sin definir.

abs()

abs(Val o r 1 ) ⇒ valor abs(

Lista1) ⇒ lista

abs(Matriz1) ⇒ matriz

Calcula el valor absoluto de un argumento.

Nota: Consulte también Plantilla de valor absoluto, en la

página 2. Si el argumento es un número complejo, el r esultado es el módulo del

número.

Nota: Se considera que todas las variables no definidas son variables

reales.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],

redondValor]) ⇒ matriz

[

Función de amortización que genera una matriz como una tabla de amortización para un conjunto de argumentos de TVM (valor temporal del dinero).

NPmt es el número de pagos que se han de incluir en la tabla. La tabla se inicia con el primer pago.

N, I, PV, Pmt, FV, PpY, CpY y PmtAt se describen en la tabla de argumentos para TVM, en la página 98.

• Si se omite el valor de Pmt, se aplica de forma predeterminada Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Si se omite el valor de FV, se aplica de forma predeterminada FV=0.

• Los valores predeterminados para PpY, CpY y PmtAt son los mismos que los de las funciones de TVM.

redondValor especifica el número de decimales de redondeo. Valor predeterminado = 2.

Las columnas de la matriz de resultados siguen este orden: Número de pago, interés pagado, principal amortizado y principal que resta por pagar.

El principal que resta por pagar n corresponde al principal que resta por pagar tras el pago n.

La matriz de salida se puede utilizar como entrada de las otras funciones de amortización, GInt() y GPrn(), en la página 115, y

bal(), en la página 10.

Catálogo

and

ExprBooleana1 and ExprBooleana2 ⇒ Expresión booleana ListaBooleana1 and ListaBooleana2 ⇒ Lista booleana MatrizBooleana1 and MatrizBooleana2 ⇒ Matriz booleana

Muestra el resultado verdadero o falso o una forma simplificada de la entrada original.

Catálogo

Guía de referencia de TI-Nspire™ 5

and

Entero1 and Entero2 ⇒ entero

Compara bit a bit dos números enteros reales mediante una

and. Internamente, ambos enteros se convierten en

operación números binarios con signo de 64 bits. Cuando se comparan los bits correspondientes, el resultado es 1 si ambos bits son 1; en caso contrario, el resultado será 0. El valor obtenido representa el resultado de los bits, y aparece conforme al modo base especificado.

Los números enteros se pueden introducir en cualquier base. Para una entrada binaria o hexadecimal es necesario utilizar el prefijo 0b o 0h, respectivamente. Si no se indica un prefijo, los enteros se consideran decimales (base 10).

Si el entero decimal que se introduce es demasiado largo para un formato binario con signo de 64 bits, se utiliza una operación de módulo simétrico para llevar el valor al rango apropiado.

Catálogo

En modo base Hex:

Importante: Cero, no la letra O.

En modo base Bin:

En modo base Dec:

Nota: Una entrada binaria puede tener hasta 64 dígitos (sin

contar el prefijo 0b). Una entrada hexadecimal puede tener hasta 16 dígitos.

angle()

angle(Val o r 1 ) ⇒ valor

Devuelve el ángulo del argumento, interpretando el argumento como un número complejo.

En el modo de ángulo en grados:

En el modo de ángulo en grados centesimales:

En el modo de ángulo en radianes:

angle(Lista1) ⇒ lista angle(Matriz1) ⇒ matriz

Devuelve una lista o matriz de ángulos de los elementos en Lista1 o Matriz1, interpretando cada elemento como un número complejo

que representa las coordenadas de un punto del plano.

ANOVA

ANOVA Lista1,Lista2[,Lista3,...,Lista20][,Etiqueta]

Realiza un análisis de varianza de un factor para comparar la media de 2 a 20 poblaciones. El resumen de los resultados se guarda en la variable stat.results. (Consulte la página 88.)

Etiqueta = 0 para Datos, Etiqueta = 1 para Estadística

Vari able de salida

Descripción

stat.F Valor de la estadística F

stat.PVal Nivel de significancia mínimo al que se puede rechazar la hipótesis nula

stat.df Grados de libertad de los grupos

stat.SS Suma de los cuadrados de los grupos

stat.MS Media de los cuadrados de los grupos

Catálogo

6 Guía de referencia de TI-Nspire™

Vari able de salida

stat.dfError Grados de libertad de los errores

stat.SSError Suma de los cuadrados de los errores

stat.MSError Media de los cuadrados de los errores

stat.sp Desviación estándar sondeada

stat.xbarlist Media de las entradas de las listas

stat.CLowerList 95% de los intervalos de confianza para la media de cada lista de entrada

stat.CUpperList 95% de los intervalos de confianza para la media de cada lista de entrada

Descripción

ANOVA de 2 variables

ANOVA2way Lista1,Lista2[,Lista3,…,Lista20][,nivelFila]

Realiza un análisis de varianza de dos factores comparando las medias de 2 a 20 poblaciones. El resumen de los resultados se guarda en la variable stat.results. (Consulte la página 88.)

nivelFila = 0 para Bloque

nivelFila=2,3,...,Len-1, para Dos Factor, donde Len=lenght(Lista1)=length(Lista2) = … = length(Lista10) y Len / nivelFila ∈ {2,3,…}

Salidas: Estudio conjunto

Vari able de salida

stat.F Estadístico F de la variable columna

stat.PVal Nivel de significancia mínimo al que se puede rechazar la hipótesis nula

stat.df Grados de libertad de la variable columna

stat.SS Suma de los cuadrados de la variable columna

stat.MS Media de los cuadrados de la variable columna

stat.FBlock Estadístico F de la variable

stat.PValBlock Probabilidad mínima a la que se puede rechazar la hipótesis nula

stat.dfBlock Grados de libertad de la variable

stat.SSBlock Suma de los cuadrados de la variable

stat.MSBlock Media de los cuadrados de la variable

stat.dfError Grados de libertad de los errores

stat.SSError Suma de los cuadrados de los errores

stat.MSError Media de los cuadrados de los errores

stat.s Desviación estándar del error

Descripción

Catálogo

Guía de referencia de TI-Nspire™ 7

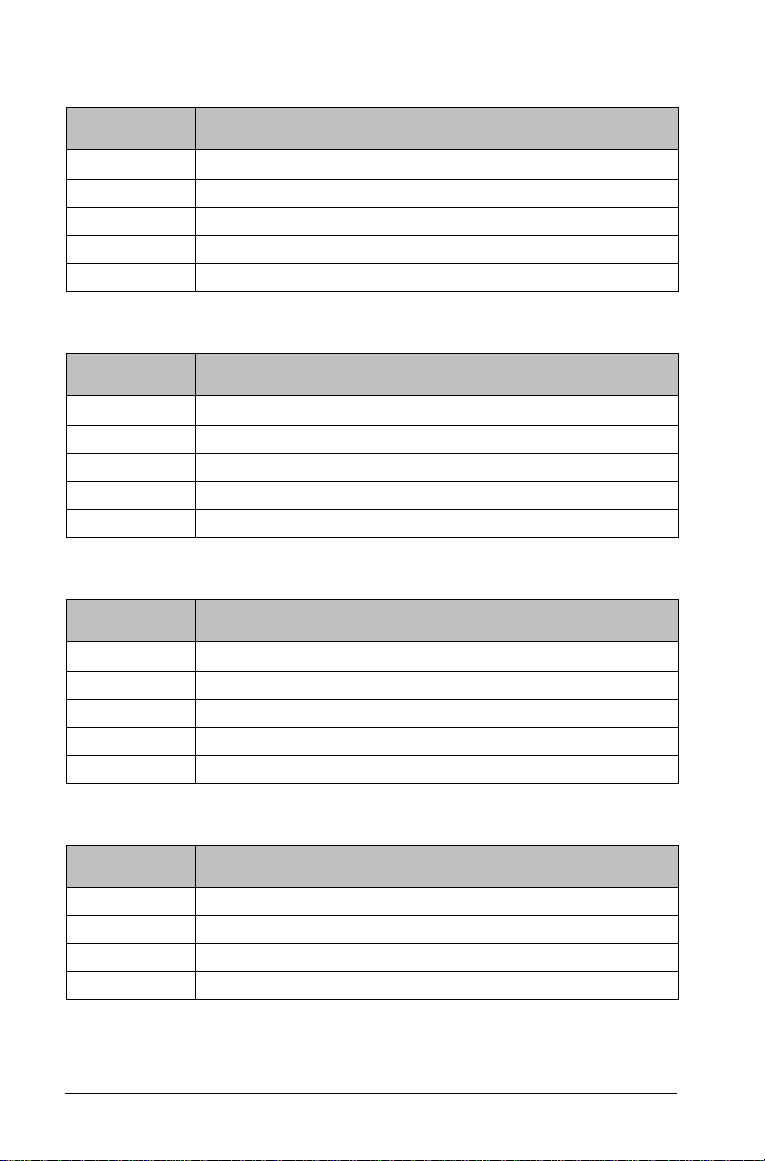
Salidas para la variable COLUMNA

Vari able de salida

stat.

Fcol Estadístico F de la variable columna

stat.PValCol Valor de probabilidad de la variable columna

stat.dfCol Grados de libertad de la variable columna

stat.SSCol Suma de los cuadrados de la variable columna

stat.MSCol Media de los cuadrados de la variable columna

Salidas para la variable FILA

Vari able de salida

stat.FRow Estadístico F de la variable fila

stat.PValRow Valor de probabilidad de la variable fila

stat.dfRow Grados de libertad de la variable fila

stat.SSRow Suma de los cuadrados de la variable fila

stat.MSRow Media de los cuadrados de la variable fila

Salidas para INTERACCIÓN

Vari able de salida

stat.FInteract Estadístico F de la interacción

stat.PValInteract Probabilidad de la interacción

stat.dfInteract Grados de libertad de la interacción

stat.SSInteract Suma de los cuadrados de la interacción

stat.MSInteract Media de los cuadrados de la interacción

Descripción

Salida para ERROR

Vari able de salida

stat.dfError Grados de libertad de los errores

stat.SSError Suma de los cuadrados de los errores

stat.MSError Media de los cuadrados de los errores

s Desviación estándar del error

Descripción

8 Guía de referencia de TI-Nspire™

Ans

Ans ⇒ valor

Devuelve el resultado de la expresión calculada en último lugar.

Teclas

approx()

approx(Val o r 1 ) ⇒ número

Devuelve el cálculo del argumento como una expresión que contiene cifras decimales, siempre que sea posible, sin tener en cuenta el modo actual, Auto or Approximate (Auto o Aproximado).

Equivale a introducir el argumento y pulsar

approx(Lista1) ⇒ lista approx(Matriz1) ⇒ matriz

Devuelve una lista o una matriz en donde cada elemento se ha calculado hasta un valor decimal, siempre que sea posible.

approxRational()

approxRational(Expr[, tol]) ⇒ expresión approxRational(Lista[, tol]) ⇒ lista approxRational(Matriz[, tol]) ⇒ matriz

Muestra el argumento como una fracción que utiliza la toler ancia tol. Si se omite el valor de tol, se utiliza una tolerancia de 5.E-14.

augment()

augment(Lista1, Lista2) ⇒ lista

Devuelve una nueva lista que es Lista2 añadida al final de Lista1.

augment(Matriz1, Matriz2) ⇒ matriz

Devuelve una nueva matriz que es Matriz2 añadida a Matriz1. Cuando se utiliza el carácter “,”, las matrices deben tener el mismo número de filas, y Matriz2 se añade a Matriz1 como si fueran nuevas columnas. No se altera el contenido de Matriz1 ni Matriz2.

·.

Catálogo

Guía de referencia de TI-Nspire™ 9

avgRC()

avgRC(Expr1, Va r [=Valor] [, H]) ⇒ expresión avgRC(Expr1, Va r [=Valor] [, Lista1]) ⇒ lista avgRC(Lista1, Va r [=Valor] [, H]) ⇒ lista avgRC(Matriz1, Var [=Valor] [, H]) ⇒ matriz

Devuelve el cociente incremental positivo (tasa media de cambio). Expr1 se puede utilizar como un nombre de función definido por el

usuario (consulte Cuando se especifica, valor sobrescribe cualquier otra asignación de

variable anterior o cualquier sustitución “tal como” actual de la variable.

H es el valor de paso. Si se omite, H adopta el valor predeterminado 0,001.

Observe que la función similar diferencia central.

Func).

nDeriv() utiliza el cociente de

Catálogo

bal()

bal(NPmt,N,I,PV ,[Pmt], [FV], [PpY], [CpY], [PmtAt],

[

redondValor]) ⇒ valor

bal(NPmt,amortTable) ⇒ valor

Función de amortización que calcula el principal que resta por pagar tras un pago especificado.

N, I, PV, Pmt, FV, PpY, CpY y PmtAt se describen en la tabla de argumentos para TVM, en la página 98.

NPmt especifica el número de pagos tras el cual se desean calcular los datos.

N, I, PV, Pmt, FV, PpY, CpY y PmtAt se describen en la tabla de argumentos para TVM, en la página 98.

• Si se omite el valor de Pmt, se aplica de forma predeterminada Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Si se omite el valor de FV, se aplica de forma predeterminada FV=0.

• Los valores predeterminados para PpY, CpY y PmtAt son los mismos que los de las funciones de TVM.

redondValor especifica el número de decimales de redondeo. Valor predeterminado = 2.

bal(NPmt,amortTable) calcula el principal que resta por pagar tras

el número de pago NPmt, según una tabla de amortización amortTable. El argumento amortTable debe ser una matriz en la forma descrita en la sección amortTbl(), en la página 5.

Nota: Consulte también GInt() y GPrn(), en la página 115.

Base2

Entero1 4Base2 ⇒ entero

Convierte Entero1 en un número binario. Los números binarios o hexadecimales llevan siempre un prefijo 0b o 0h, respectivamente.

Catálogo

10 Guía de referencia de TI-Nspire™

Base2

0b NúmeroBinario 0h NúmeroHexadecimal

Cero, no la letra O, seguido de b o h. Un número binario puede tener hasta 64 dígitos. Un número

hexadecimal puede tener hasta 16 dígitos. Si no se indica un prefijo, Entero1 se considera decimal (base 10).

El resultado aparece en formato binario, sea cual sea el modo de la base.

Si el entero decimal que se introduce es demasiado largo para un formato binario con signo de 64 bits, se utiliza una operación de módulo simétrico para llevar el valor al rango apropiado.

Base10

Entero1 4Base10 ⇒ entero

Convierte Entero1 en un número decimal (base 10). Una entrada binaria o hexadecimal debe llevar siempre el prefijo 0b o 0h, respectivamente.

0b NúmeroBinario 0h NúmeroHexadecimal

Cero, no la letra O, seguido de b o h. Un número binario puede tener hasta 64 dígitos. Un número

hexadecimal puede tener hasta 16 dígitos. Si no se indica un prefijo, Entero1 se considera decimal. El resultado

aparece en formato decimal, sea cual sea el modo de la base.

Base16

Entero1 4Base16 ⇒ entero

Convierte Entero1 en un número hexadecimal. Los números binarios o hexadecimales llevan siempre un prefijo 0b o 0h, respectivamente.

0b NúmeroBinario 0h NúmeroHexadecimal

Cero, no la letra O, seguido de b o h. Un número binario puede tener hasta 64 dígitos. Un número

hexadecimal puede tener hasta 16 dígitos. Si no se indica un prefijo, Entero1 se considera decimal (base 10).

El resultado aparece en formato hexadecimal, sea cual sea el modo de la base.

Si el entero decimal que se introduce es demasiado largo para un formato binario con signo de 64 bits, se utiliza una operación de módulo simétrico para llevar el valor al rango apropiado.

Catálogo

binomCdf()

binomCdf(n,p,Extremoinferior,Extremosuperior) ⇒ número si

Extremoinferior y Extremosuperior son números, lista si Extremoinferior y Extremosuperior son listas

binomCdf(

Extremosuperior es un número, lista si Extremosuperior es una

lista

Calcula una probabilidad acumulada para la distribución binomial discreta para un número de pruebas n y probabilidad de éxito p en cada prueba.

Para P(X  Extremosuperior), defina Extremoinferior=0

n,p,Extremosuperior) ⇒ número si

Catálogo

Guía de referencia de TI-Nspire™ 11

binomPdf()

binomPdf(n,p) ⇒ número binomPdf(n,p,XVal) ⇒ número si XVal es un número, lista si

XVal es una lista

Calcula una probabilidad para la distribución binomial discreta para un número de pruebas n y probabilidad de éxito p en cada prueba.

Catálogo

ceiling()

ceiling(Val o r 1 ) ⇒ valor

Devuelve el menor entero que sea ‚ el argumento.

El argumento puede ser un número real o complejo.

Nota: Consulte también floor().

ceiling(Lista1) ⇒ lista ceiling(Matriz1) ⇒ matriz

Devuelve una lista o una matriz con los correspondientes menores enteros.

char()

char(Entero) ⇒ carácter

Devuelve una cadena de caracteres que contiene el carácter dado por el número Entero del juego de caracteres de la unidad portátil. El rango válido para Entero es 0–65535.

de 2 elementos

2way ObsMatriz

chi22way ObsMatriz

Calcula un test de c2 para determinar si hay asociación con la tabla de recuentos de dos elementos incluida en la matriz observada

ObsMatriz. El resumen de los resultados se guarda en la variable stat.results. (Consulte la página 88.)

Vari able de salida

stat.c2 Estadística de chi cuadrado: suma (observada - esperada)2/esperada

stat.PVal Nivel de significancia mínimo al que se puede rechazar la hipótesis nula

stat.df Grados de libertad para la estadística de chi cuadrado

stat.ExpMat Matriz de tabla de recuentos de elementos esperada, suponiendo una hipótesis nula

stat.CompMat Matriz de contribuciones para estadística de chi cuadrado de los elementos

Descripción

Catálogo

12 Guía de referencia de TI-Nspire™

Cdf()

Cdf(Extremoinferior,Extremosuperior,gl) ⇒ número si

Extremoinferior y Extremosuperior son números, lista si Extremoinferior y Extremosuperior son listas

chi2Cdf(

Extremoinferior,Extremosuperior,gl) ⇒ número si Extremoinferior y Extremosuperior son números, lista si Extremoinferior y Extremosuperior son listas

Calcula la probabilidad de distribución de c2 entre el Extremoinferior y el Extremosuperior para los grados de libertad gl especificados.

Para P(X Extremosuperior), defina Extremoinferior=0.

GOF

GOF obsLista,expLista,gl

chi2GOF obsLista,expLista,gl

Lleva a cabo un test para confirmar que los datos de la muestra son de una población que cumple una distribución especificada. obsList es una lista de recuentos y debe contener números enteros. El resumen de los resultados se guarda en la variable stat.results. (Consulte la página 88).

Catálogo

Vari able de salida

Descripción

stat.c2 Estadística de chi cuadrado: suma (observada - esperada)2/esperada

stat.PVal Nivel de significancia mínimo al que se puede rechazar la hipótesis nula

stat.df Grados de libertad para la estadística de chi cuadrado

stat.CompList Contribuciones para estadística de chi cuadrado de los elementos

Pdf()

Pdf(XVal,gl) ⇒ número si XVal es un número, lista si XVal

es una lista

chi2Pdf(

XVal,gl) ⇒ número si XVal es un número, lista si XVal es una lista

Calcula la función de densidad de probabilidad (pdf) para la distribución de c2 para un valor XVal especificado para los grados de

libertad gl especificados.

ClearAZ

Borra todas las variables cuyo nombre esté compuesto por un único carácter del espacio del problema actual.

Catálogo

Guía de referencia de TI-Nspire™ 13

ClrErr

Borra el estado de error y define la variable del sistema errCode en cero.

La cláusula Else del bloque Try...Else...EndTry debería utilizar

ClrErr o PassErr. Si va a procesar o ignorar el error, utilice ClrErr.

Si desconoce el tratamiento que se va a dar al error, utilice PassErr para enviarlo al siguiente gestor de errores. Si no hay más gestores de errores de tipo Try...Else...EndTry, el cuadro de diálogo de errores aparecerá en su forma normal.

Nota: Consulte también PassErr, en la página 67, y Try , en la

página 96.

Nota para introducir el ejemplo: En la aplicación Calculadora

de la unidad portátil, puede introducir definiciones formadas por varias líneas si pulsa @ en lugar de · al final de cada línea.

En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse

Enter (Intro).

Para ver un ejemplo de

Try, en la página 96.

orden

Catálogo

ClrErr, consulte el ejemplo 2 de la

colAugment()

colAugment(Matriz1, Matriz2) ⇒ matriz

Devuelve una nueva matriz que es Matriz2 añadida a Matriz1. Las dos matrices han de tener el mismo número de columnas, y Matriz2 se añade a Matriz1 como si fueran nuevas filas. No se altera el contenido de Matriz1 ni Matriz2.

colDim()

colDim(Matriz) ⇒ expresión

Devuelve el número de columnas de Matriz.

Nota: Consulte también rowDim().

colNorm()

colNorm(Matriz) ⇒ expresión

Devuelve el máximo de las sumas de los valores absolutos de los elementos de las columnas de MatriZ.

Nota: No se admiten elementos de matriz sin definir. Consulte

también rowNorm().

conj()

conj(Val o r 1 ) ⇒ valor conj(Lista1) ⇒ lista conj(Matriz1) ⇒ matriz

Muestra el complejo conjugado del argumento.

Nota: Se considera que todas las variables no definidas son variables

reales.

Catálogo

14 Guía de referencia de TI-Nspire™

constructMat()

constructMat(Expr,Var 1 ,Var 2 ,númeroFilas,númeroColumnas)

⇒ matriz

Devuelve una matriz basada en los argumentos. Expr es una expresión en las variables Va r 1 y Var 2 . Los elementos de

la matriz resultante se forman calculando Expr para cada valor incrementado de Va r1 y Va r 2 .

Var 1 se incrementa automáticamente desde En cada fila, Va r2 se incrementa desde 1 hasta númeroColumnas.

1 hasta númeroFilas.

Catálogo

CopyVar

CopyVar Var 1 , Va r 2 CopyVar Var 1 ., Va r2 .

CopyVar Var 1 , Va r2 copia el valor de la variable Va r 1 hasta la

variable Var 2 , creando Va r2 si es necesario. La variable Va r 1 debe tener un valor.

Si Va r1 es el nombre de una función definida por el usuario, copia su definición en la función Va r2 . La función Va r 1 debe estar definida.

Var 1 debe cumplir los requisitos de nomenclatura aplicables a las variables o ser una expresión que pueda convertirse en un nombre de variable que cumpla dichos requisitos.

CopyVar Var 1 ., Va r2 . copia todos los miembros del grupo de

variables Var 1 . en el grupo Va r 2. creando Va r 2 . si es necesario. Var 1 . debe ser el nombre de un grupo de var iables existente, como el

resultado estadístico stat.nn, o bien variables creadas con la función

LibShortcut(). Si Var 2 . ya existe, la orden sustituye todos los

miembros que son comunes a ambos grupos y añade los que no existen. Si ya existe una variable sencilla (no un grupo) con el nombre Var 2 , devuelve un error.

corrMat()

corrMat(Lista1,Lista2[,…[,Lista20]])

Calcula la matriz de correlación de la matriz aumentada [Lista1, Lista2, ..., Lista20].

Catálogo

Guía de referencia de TI-Nspire™ 15

cos()

cos(Val o r 1 ) ⇒ valor cos(Lista1) ⇒ lista

cos(Val o r 1 ) devuelve el coseno del argumento en forma de valor. cos(Lista1) devuelve una lista de los cosenos de todos los elementos

de Lista1.

Nota: El argumento se interpreta como un ángulo en grad os, grados

centesimales o radianes, según el modo de ángulo actual. Puede utilizar ó,G o ôpara sobrescribir el modo de ángulo temporalmente.

Tecla n

En el modo de ángulo en grados:

En el modo de ángulo en grados centesimales:

En el modo de ángulo en radianes:

cos(Matrizcuadrada1) ⇒ Matrizcuadrada

Devuelve el coseno de la matriz Matrizcuadrada1. El resultado no es igual que calcular el coseno de cada elemento.

Cuando la función escalar f(A) actúa sobre Matrizcuadrada1 (A), el resultado se calcula mediante el algoritmo:

Calcula los valores propios (li) y los vectores propios (Vi) de A.

Matrizcuadrada1 debe ser diagonizable. Además, no puede tener variables simbólicas que no tengan un valor asignado.

Escriba las matrices:

A continuación, A = X B Xêy f(A) = X f(B) Xê. Por ejemplo, cos(A) = X cos(B) Xê donde:

cos(B) =

Todos los cálculos se realizan utlizando la coma aritmética flotante.

En el modo de ángulo en radianes:

16 Guía de referencia de TI-Nspire™

cosê()

cosê(Va lo r 1 ) ⇒ valor cosê(Lista1) ⇒ lista

En el modo de ángulo en grados:

Teclas

cosê(Va lo r 1 ) devuelve el ángulo cuyo coseno es Va lo r 1 .

cosê(Lista1) devuelve una lista de los cosenos inversos de cada

elemento de Lista1.

Nota: El resultado se muestra como un ángulo en grados, grados

centesimales o radianes, según el modo de ángulo actual.

cosê(Matrizcuadrada1) ⇒ Matrizcuadrada

Devuelve el coseno inverso de la matriz Matrizcuadrada1. El resultado no es igual que calcular el coseno inverso de cada elemento. Para obtener más información sobre el método de cálculo, consulte cos().

Matrizcuadrada1 debe ser diagonizable. El resultado contiene siempre números con coma flotante.

cosh()

cosh(Va lo r 1 ) ⇒ valor cosh(Lista1) ⇒ lista

cosh(Va lo r 1 ) devuelve el coseno hiperbólico del argumento. cosh(Lista1) devuelve una lista de cosenos hiperbólicos de cada

elemento de Lista1.

cosh(Matrizcuadrada1) ⇒ Matrizcuadrada

Devuelve el coseno hiperbólico de la matriz Matrizcuadrada1. El resultado no es igual que calcular el coseno hiperbólico de cada elemento. Para obtener más información sobre el método de cálculo, consulte cos().

Matrizcuadrada1 debe ser diagonizable. El resultado contiene siempre números con coma flotante.

En el modo de ángulo en grados centesimales:

En el modo de ángulo en radianes:

En el modo de ángulo en radianes y formato complejo rectangular:

Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para mover el cursor.

Catálogo

En el modo de ángulo en radianes:

coshê()

coshê(Va lo r 1 ) ⇒ valor coshê(Lista1) ⇒ lista

cosh

(Va lo r 1 ) devuelve el coseno hiperbólico inverso del

argumento.

cosh

(Lista1) devuelve una lista de cosenos hiperbólicos inversos

de cada elemento de Lista1.

Catálogo

Guía de referencia de TI-Nspire™ 17

coshê()

coshê(Matrizcuadrada1) ⇒ Matrizcuadrada

Devuelve el coseno hiperbólico inverso de la matriz Matrizcuadrada1. El resultado no es igual que calcular el coseno hiperbólico inverso de cada elemento. Para obtener más información sobre el método de cálculo, consulte cos().

Matrizcuadrada1 debe ser diagonizable. El resultado contiene siempre números con coma flotante.

Catálogo

En el modo de ángulo en radianes y formato complejo rectangular:

Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para mover el cursor.

cot()

cot(Val o r 1 ) ⇒ valor cot(Lista1) ⇒ lista

Devuelve la cotangente de Va l or 1 o una lista de las cotangentes de todos los elementos de Lista1.

Nota: El argumento se interpreta como un ángulo en grad os, grados

centesimales o radianes, según el modo de ángulo actual. Puede utilizar ó,G oôpara sobrescribir el modo de ángulo temporalmente.

cotê()

cotê(Va lo r 1 ) ⇒ valor cotê(Lista1) ⇒ lista

Devuelve el ángulo cuya cotangente es Va l o r1 o una lista de las cotangentes inversas de cada elemento de Lista1.

Nota: El resultado se muestra como un ángulo en grados, radianes o

grados centesimales, según el modo de ángulo actual.

coth()

coth(Val o r 1 ) ⇒ valor coth(Lista1) ⇒ lista

Devuelve la cotangente hiperbólica de Va l o r1 o una lista de las cotangentes hiperbólicas de todos los elementos de Lista1.

Catálogo

En el modo de ángulo en grados:

En el modo de ángulo en grados centesimales:

En el modo de ángulo en radianes:

Catálogo

En el modo de ángulo en grados:

En el modo de ángulo en grados centesimales:

En el modo de ángulo en radianes:

Catálogo

cothê()

cothê(Va lo r 1 ) ⇒ valor cothê(Lista1) ⇒ lista

Devuelve la cotangente hiperbólica inversa de Va l o r 1 o una lista de las cotangentes hiperbólicas inversas de todos los elementos de Lista1.

Catálogo

18 Guía de referencia de TI-Nspire™

count()

count(Valor1 o Lista1 [,Valor2 o Lista2 [,...]]) ⇒ valor

Devuelve el recuento acumulado de todos los elementos de los argumentos que sirven para calcular valores numéricos.

Cada argumento puede ser una expresión, valor, lista o matriz. Es posible mezclar tipos de datos y utilizar argumentos con distintas dimensiones.

En listas, matrices o rangos de celdas, se calcula cada elemento para determinar si debe incluirse en el recuento.

En la aplicación Listas y Hojas de cálculo, puede utilizarse un rango de celdas en lugar de cualquier argumento.

Catálogo

countif()

countif(Lista,Criterios) ⇒ valor

Devuelve el recuento acumulado de todos los elementos de Lista que cumplen los Criterios especificados.

Los criterios pueden ser:

• Un valor, una expresión o una cadena. Por ejemplo, 3 cuenta sólo

los elementos de Lista que se simplifican al valor 3.

• Una expresión booleana que contenga el símbolo ? como lugar

donde introducir cada elemento. Por ejemplo, ?<5 cuenta sólo los elementos de Lista que son menores de 5.

En la aplicación Listas y Hojas de cálculo, puede utilizarse un rango de celdas en lugar de Lista.

Nota: Consulte también sumIf(), en la página 91, y frequency(),

en la página 34.

crossP()

crossP(Lista1, Lista2) ⇒ lista

Devuelve el producto vectorial de Lista1 y Lista2 en forma de lista. Lista1 y Lista2 deben tener la misma dimensión, que deberá ser 2 o

crossP(Vector1, Vector2) ⇒ vector

Devuelve un vector fila o columna (depende del argument o) que es el producto vectorial de Vector1 y Vector2.

Tanto Vector1 como Vector2 deben ser vectores fila, o vectores columna. Los dos vectores deben tener la misma dimensión, que deberá ser 2 o 3.

Catálogo

Cuenta el número de elementos que son iguales a 3.

Cuenta el número de elementos que son iguales a “def”.

Cuenta 1 y 3.

Cuenta 3, 5 y 7.

Cuenta 1, 3, 7 y 9.

Catálogo

Guía de referencia de TI-Nspire™ 19

csc()

csc(Val o r 1 ) ⇒ valor csc(Lista1) ⇒ lista

Devuelve la cosecante de Va l or 1 o una lista de las cosecantes de todos los elementos de Lista1.

Catálogo

En el modo de ángulo en grados:

En el modo de ángulo en grados centesimales:

En el modo de ángulo en radianes:

cscê()

cscê(Va l or 1 ) ⇒ valor cscê(Lista1) ⇒ lista

Devuelve el ángulo cuya cosecante es Va l or 1 o una lista de las cosecantes inversas de todos los elementos de Lista1.

Nota: El resultado se muestra como un ángulo en grados, grados

centesimales o radianes, según el modo de ángulo actual.

csch()

csch(Val o r 1 ) ⇒ valor csch(Lista1) ⇒ lista

Devuelve la cosecante hiperbólica de Va l o r1 o una lista de las cosecantes hiperbólicas de todos los elementos de Lista1.

cschê()

cschê(Val o r ) ⇒ valor cschê(Lista1) ⇒ lista

Devuelve la cosecante hiperbólica inversa de Va l o r1 o una lista de las cosecantes hiperbólicas inversas de todos los elementos de Lista1.

Catálogo

En el modo de ángulo en grados:

En el modo de ángulo en grados centesimales:

En el modo de ángulo en radianes:

Catálogo

20 Guía de referencia de TI-Nspire™

CubicReg

CubicReg X, Y[, [Frec] [, Categoría, Incluir]]

Calcula la regresión polinómica cúbica y = a·x3+b· x2+c·x+d de las listas X e Y con la frecuencia Frec. El resumen de los resultados se guarda en la variable stat.results. (Consulte la página 88).

Todas las listas, salvo Incluir, deben tener la misma dimensión. X e Y son listas que contienen, respectivamente, la variable

independiente y la variable dependiente. Frec es una lista opcional de valores de frecuencia. Cada elemento

de Frec especifica la frecuencia de ocurrencia de cada punto de datos en X e Y. El valor predeterminado es 1. Todos los elementos deben ser enteros | 0.

Categoría es una lista de códigos numéricos de categoría para los datos de X e Y.

Incluir es una lista de uno o varios códigos de categoría. En el cálculo sólo se incluyen los elementos de datos cuyo código de categoría se encuentre en la lista.

Catálogo

Vari able de salida

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.R

Descripción

Ecuación de regresión: a·x3+b·x2+c·x+d

Coeficientes de regresión

Coeficiente de determinación

stat.Resid Residuos de la regresión

stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en

stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las

restricciones de Frec, Lista Categoría e Incluir Categoría

stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg

cumSum()

cumSum(Lista1) ⇒ lista

Devuelve una lista de las sumas acumuladas de los elementos de Lista1, a partir del elemento 1.

cumSum(Matriz1) ⇒ matriz

Devuelve una matriz de las sumas acumuladas de los elementos de Matriz1. Cada elemento es la suma acumulada de los elementos de la columna desde arriba hacia abajo.

Catálogo

Guía de referencia de TI-Nspire™ 21

Cycle

Transfiere el control de forma inmediata a la siguiente iteración del bucle actual (

Cycle no está admitido fuera de las tres estructuras de bucle (For, While o Loop).

Nota para introducir el ejemplo: En la aplicación Calculadora

de la unidad portátil, puede introducir definiciones formadas por varias líneas si pulsa

En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse

Enter (Intro).

Vec t o r 4Cylind

Muestra el vector de la fila o la columna en formato cilíndrico [r,q, z].

Vec t o r debe tener tres elementos exactamente. Puede ser una fila o una columna.

For, While o Loop).

@ en lugar de · al final de cada línea.

Cylind

Catálogo

Listado de función que suma los enteros de 1 a 100 omitiendo

50.

Catálogo

dbd()

dbd(fecha1,fecha2) ⇒ valor

Devuelve el número de días entre fecha1 y fecha2 utilizando el método de recuento de días reales.

fecha1 y fecha2 pueden ser números o listas de números comprendidos en el rango de fechas del calendario estándar. Si tanto

fecha1 como fecha2 son listas, deben tener la misma longitud. fecha1 y fecha2 deben estar comprendidas en los años 1950 y 2049.

Puede introducir las fechas en cualquiera de los dos formatos. El separador decimal permite diferenciar los formatos de fecha.

MM.DDAA (es el formato de uso más frecuente en EE. UU.) DDMM.AA (es el formato de uso más frecuente en Europa)

Catálogo

22 Guía de referencia de TI-Nspire™

4DD ⇒ valor

Expr1 Lista1 4DD ⇒ list Matriz1

4DD ⇒ matriz

Devuelve el equivalente decimal del argumento expresado en grados. El argumento es un número, lista o matriz que se interpreta en grados, radianes o grados centesimales según el modo de ángulo actual.

Catálogo

En el modo de ángulo en grados:

En el modo de ángulo en grados centesimales:

En el modo de ángulo en radianes:

4Decimal

Número1

4Decimal

Lista1

Decimal

Matriz1

Muestra el argumento en formato decimal. El operador sólo se puede utilizar al final de la línea de entrada.

Define (Definir)

Define Var = Expresión Define Function(Param1, Param2, ...) = Expresión

Define la variable Va r o la función definida por el usuario Function. Los parámetros, como Param1, son lugares donde insertar los

argumentos que pasan a la función. Al designar una función definida por el usuario es necesario facilitar los argumentos (por ejemplo, valores o variables) correspondientes a los parámetros. Cuando se activa, la función calcula el valor de Expresión con los argumentos facilitados.

Var y Function no pueden ser el nombre de una variable del sistema ni de una orden o función integrada.

Nota: Esta forma de la orden Define equivale a ejecutar la

expresión: expresión & Function(Param1,Param2).

⇒ valor

Catálogo

Guía de referencia de TI-Nspire™ 23

Define (Definir)

Define Function(Param1, Param2, ...) = Func

Bloque

EndFunc

Program(Param1, Param2, ...) = Prgm

Define

Bloque

EndPrgm

De esta forma, la función o programa definidos por el usuario pueden ejecutar un bloque de varias sentencias.

Bloque puede ser una sentencia sencilla o una serie de sentencias escritas en varias líneas. Bloque puede incluir también expresiones e instrucciones (como If, Then, Else y For).

Nota para introducir el ejemplo: En la aplicación Calculadora

de la unidad portátil, puede introducir definiciones formadas por varias líneas si pulsa @ en lugar de · al final de cada línea.

En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse

Enter (Intro). Nota: Consulte también Define LibPriv, en la página 24 y

Define LibPub, en la página 25.

Catálogo

Define LibPriv

Define LibPriv Var = Expresión Define LibPriv Function(Param1, Param2, ...) = Expresión

Define LibPriv Function(Param1, Param2, ...) = Func

Bloque

EndFunc Define LibPriv

Bloque

EndPrgm

Funciona igual que Define, salvo en que define una variable de biblioteca, función o programa privados. Las funciones y los programas privados no aparecen en el Catálogo.

Nota: Consulte también Define, en la página 23 y Define LibPub

Program(Param1, Param2, ...) = Prgm

, en la página 25.

Catálogo

24 Guía de referencia de TI-Nspire™

+ 116 hidden pages