Texas Instruments TI-Nspire Reference Guide [da]

Opslagsvejledning

Denne vejledning gælder TI-Nspire softwareversion 1.4. Du kan få den nyeste version af dokumentationen ved at gå til education.ti.com/guides.

Vigtige oplysninger

Medmindre andet udtrykkeligt angives i den Licens, der følger med et program, stiller Texas Instruments ingen garantier, hverken udtrykkeligt eller underforstået, herunder men ikke begrænset til underforståede garantier om salgbarhed og egnethed til et bestemt formål, for programmer eller skriftligt materiale, og Texas Instruments stiller udelukkende sådant materiale til rådighed, som det foreligger. Texas Instruments kan under ingen omstændigheder holdes ansvarlig for særlige, indirekte, hændelige eller følgeskader i forbindelse med eller som følge af køb eller brug af dette materiale, og hele Texas Instruments' erstatningsansvar kan, uanset søgsmålets art, ikke overstige det beløb, der fremgår af programlicensen. Derudover kan Texas Instruments ikke holdes ansvarlig for nogen form for krav som følge af en anden parts brug af dette materiale.

Licens

Se hele licensen der er installeret i C:\Program Files\TI Education\TI-

Nspire

Macintosh®, Windows®, Excel®, Vernier EasyLink®, EasyTemp®, Go!®Link, Go!®Motion, og Go!®Temp er varemærker, der tilhører deres respektive ejere.

Indholdsfortegnelse

Vigtige oplysninger Udtryksskabeloner

Brøkskabelon ............................................... 1

Eksponentskabelon ......................................1

Kvadratrodsskabelon ................................... 1

Nte rod-skabelon .........................................1

e ekponentskabelon ....................................2

Log-skabelon ................................................ 2

Stykkevis-skabelon (2 stykker) ....................2

Stykkevis-skabelon (N stykker) .................... 2

Absolut værdi-skabelon ..............................2

dd°mm’ss.ss’’-skabelon ................................ 3

Matrix-skabelon (2 x 2) ................................3

Matrix-skabelon (1 x 2) ................................3

Matrix-skabelon (2 x 1) ................................3

Matrix-skabelon (m x n) .............................. 3

Sum-skabelon (G) .........................................3

Produkt-skabelon (Π) ...................................4

Alfabetisk oversigt A

abs() ..............................................................5

amortTbl() .................................................... 5

and ................................................................5

angle() ..........................................................6

ANOVA ......................................................... 6

ANOVA2-way ............................................... 7

Ans ................................................................9

approx() ........................................................9

approxRational() .......................................... 9

augment() .....................................................9

avgRC() ....................................................... 10

bal() .............................................................10

4Base2 .........................................................10

4Base10 .......................................................11

4Base16 .......................................................11

binomCdf() ................................................. 11

binomPdf() ................................................. 12

ceiling() .......................................................12

char() ...........................................................12

2way ........................................................12

Cdf() .........................................................13

GOF ......................................................... 13

Pdf() .........................................................13

ClearAZ ....................................................... 13

ClrErr ...........................................................14

colAugment() ............................................. 14

colDim() ......................................................14

colNorm() ....................................................14

conj() ...........................................................14

constructMat() ............................................ 15

CopyVar ...................................................... 15

corrMat() ....................................................15

cos() ............................................................ 16

cosê() .......................................................... 17

cosh() .......................................................... 17

coshê() ........................................................ 17

cot() ............................................................ 18

cotê() .......................................................... 18

coth() .......................................................... 18

cothê() ........................................................ 18

count() ........................................................ 19

countif() ..................................................... 19

crossP() ....................................................... 19

csc() ............................................................. 20

cscê() ........................................................... 20

csch() ........................................................... 20

cschê() ......................................................... 20

CubicReg .................................................... 21

cumSum() ................................................... 21

Cycle ........................................................... 22

4Cylind ........................................................ 22

dbd() ........................................................... 22

4DD ............................................................. 23

4Decimal ..................................................... 23

Define ......................................................... 23

Define LibPriv ............................................ 24

Define LibPub ............................................ 25

DelVar ........................................................ 25

det() ............................................................ 25

diag() .......................................................... 26

dim() ........................................................... 26

Disp ............................................................. 26

4DMS ........................................................... 27

dotP() .......................................................... 27

e^() ............................................................. 27

eff() ............................................................. 28

eigVc() ........................................................ 28

eigVl() ......................................................... 28

Else ............................................................. 28

ElseIf ........................................................... 29

EndFor ........................................................ 29

EndFunc ...................................................... 29

EndIf ........................................................... 29

EndLoop ..................................................... 29

EndPrgm ..................................................... 29

EndTry ........................................................ 29

EndWhile .................................................... 29

Exit .............................................................. 30

exp() ........................................................... 30

expr() .......................................................... 30

ExpReg ....................................................... 31

factor() ....................................................... 31

Fill ............................................................... 32

FiveNumSammendrag ............................... 32

FCdf() ......................................................... 32

floor() ......................................................... 33

iii

For ...............................................................33

format() ......................................................33

fPart() ..........................................................34

FPdf() ..........................................................34

freqTable4list() ............................................34

frequency() .................................................34

FTest_2Samp ..............................................35

Func .............................................................35

gcd() ............................................................36

geomCdf() ...................................................36

geomPdf() ...................................................36

getDenom() ................................................36

getLangInfo() .............................................37

getMode() ...................................................37

getNum() ....................................................38

getVarInfo() ................................................38

Goto ............................................................39

4Grad ...........................................................39

identity() .....................................................39

If ..................................................................39

ifFn() ............................................................41

imag() ..........................................................41

Indirection ..................................................41

inString() .....................................................41

int() .............................................................42

intDiv() ........................................................42

() .........................................................42

invc

invF() ...........................................................42

invNorm() ....................................................42

invt() ............................................................42

iPart() ..........................................................43

irr() ..............................................................43

isPrime() ......................................................43

Lbl ...............................................................44

lcm() ............................................................44

left() ............................................................44

libShortcut() ................................................45

LinRegBx .....................................................45

LinRegMx ....................................................46

LinRegtIntervaller ......................................46

LinRegtTest .................................................48

@list() ...........................................................48

list4mat() .....................................................49

ln() ...............................................................49

LnReg ..........................................................49

Local ............................................................50

log() .............................................................51

Logistic ........................................................51

LogisticD .....................................................52

Loop ............................................................53

LU ................................................................53

mat4list() .....................................................53

max() ...........................................................54

mean() .........................................................54

median() .....................................................54

MedMed ..................................................... 55

mid() ........................................................... 55

min() ........................................................... 56

mirr() ........................................................... 56

mod() .......................................................... 56

mRow() ....................................................... 57

mRowAdd() ................................................ 57

MultReg ...................................................... 57

MultRegIntervals ....................................... 57

MultRegTests ............................................. 58

nCr() ............................................................ 59

nDeriv() ....................................................... 59

newList() ..................................................... 60

newMat() .................................................... 60

nfMax() ....................................................... 60

nfMin() ....................................................... 60

nInt() ........................................................... 60

nom() .......................................................... 61

norm() ......................................................... 61

normCdf() ................................................... 61

normPdf() ................................................... 61

not .............................................................. 61

nPr() ............................................................ 62

npv() ........................................................... 63

nSolve() ....................................................... 63

OneVar ....................................................... 64

or ................................................................ 65

ord() ............................................................ 65

P4Rx() .......................................................... 65

P4Ry() .......................................................... 66

PassErr ........................................................ 66

piecewise() .................................................66

poissCdf() .................................................... 66

poissPdf() .................................................... 66

4Polar .......................................................... 67

polyEval() .................................................... 67

PowerReg ................................................... 67

Prgm ........................................................... 68

Product (PI) ................................................. 68

product() .................................................... 68

propFrac() ................................................... 69

QR ............................................................... 69

QuadReg .................................................... 70

QuartReg .................................................... 70

R4Pq() .......................................................... 71

R4Pr() ........................................................... 71

4Rad ............................................................ 72

rand() .......................................................... 72

randBin() .................................................... 72

randInt() ..................................................... 72

randMat() ................................................... 72

randNorm() ................................................ 72

randPoly() ................................................... 73

randSamp() ................................................. 73

RandSeed .................................................... 73

real() ...........................................................73

4Rect ............................................................73

ref() .............................................................74

remain() ......................................................74

Return ......................................................... 75

right() ..........................................................75

root() ...........................................................75

rotate() .......................................................75

round() ........................................................ 76

rowAdd() .................................................... 76

rowDim() ....................................................76

rowNorm() .................................................. 77

rowSwap() .................................................. 77

rref() ............................................................77

sec() .............................................................77

sec/() ...........................................................78

sech() ...........................................................78

sechê() ......................................................... 78

seq() ............................................................78

setMode() ................................................... 79

shift() ..........................................................80

sign() ...........................................................80

simult() ........................................................81

sin() .............................................................81

sinê() ...........................................................82

sinh() ...........................................................82

sinhê() .........................................................83

SinReg .........................................................83

SortA ...........................................................84

SortD ...........................................................84

4Sphere ....................................................... 84

sqrt() ...........................................................84

stat.results .................................................. 85

stDevPop() .................................................. 86

stDevSamp() ............................................... 86

stat.values ................................................... 86

Stop .............................................................87

Store ...........................................................87

string() ........................................................87

subMat() ..................................................... 87

Sum (Sigma) ............................................... 87

sum() ...........................................................87

sumIf() .........................................................88

system() .......................................................88

T (transponere) ..........................................88

tan() ............................................................89

tanê() ..........................................................89

tanh() ..........................................................90

tanhê() ........................................................90

tCdf() ...........................................................91

Then ............................................................91

tInterval ......................................................91

tInterval_2Samp ......................................... 91

tPdf() ...........................................................92

trace() .........................................................92

Try ...............................................................92

tTest ............................................................93

tTest_2Samp ............................................... 94

tvmFV() ....................................................... 94

tvmI() .......................................................... 94

tvmN() ........................................................ 95

tvmPmt() .................................................... 95

tvmPV() ....................................................... 95

TwoVar ....................................................... 96

unitV() ........................................................ 97

varPop() ...................................................... 97

varSamp() ................................................... 97

when() ........................................................ 98

While .......................................................... 98

“With” ........................................................ 98

xor .............................................................. 99

zInterval ..................................................... 99

zInterval_1Prop ........................................ 100

zInterval_2Prop ........................................ 100

zInterval_2Samp ...................................... 100

zTest ......................................................... 101

zTest_1Prop .............................................. 101

zTest_2Prop .............................................. 102

zTest_2Samp ............................................ 102

Symboler

+ (adder) ................................................... 104

N(subtraher) ............................................. 104

·(multiplicer) ........................................... 105

à (divider) ................................................. 105

^ (potens) ................................................. 106

(kvadrat) .............................................. 106

.+ (punktum plustegn) ............................ 107

.. (punktum minus.) ................................. 107

·(punktum mult.) ................................... 107

. / (punktum divider) ................................ 107

.^ (punktum potens) ................................ 107

ë(neger) .................................................... 108

% (procent) .............................................. 108

= (lig med) ................................................ 109

ƒ (forskellig fra) ....................................... 109

< (mindre end) ......................................... 110

{ (mindre end eller lig med) ................... 110

> (større end) ........................................... 110

| (større end eller lig med) ..................... 110

! (fakultet) ................................................ 111

& (tilføj) .................................................... 111

‡() (kvadratrod) ....................................... 111

Π() (produkt) ............................................ 111

G() (sum) ................................................... 112

GInt() ......................................................... 112

GPrn() ........................................................ 113

# (henvisning) .......................................... 113

í (videnskabelig notation) ...................... 113

G (nygrader) ............................................. 114

ô(radian) ...................................................114

¡ (grader) ..................................................114

¡, ', '' (grader/minutter/sekunder) ...........114

 (vinkel) ..................................................115

' (mærke) ..................................................115

_ (lavtstillet linje) ......................................115

10^() ..........................................................115

^ê (reciprok) .............................................116

| (“with”) ...................................................116

& (lagring) ................................................116

:= (tildel) ...................................................117

0b, 0h ........................................................117

Fejlkoder og fejlmeddelelser Oplysninger om TI-

produktservice og garanti

TI-Nspire™

Denne vejledning indeholder lister over de skabeloner, funktioner, kommandoer og operatorer, der er tilgængelige til beregning af matematiske udtryk.

Opslagsvejledning

Udtryksskabeloner

Udtryksskabeloner er en nem metode til at indsætte matematiske udtryk i matematisk standardnotation. Når du indsætter en skabelon, optræder den i indtastningslinjen med små blokke på positioner, hvor du kan indsætte elementer. En markør viser, hvilket element, du kan indsætte.

Anvend piletasten eller tryk på

en værdi eller et udtryk for hvert element. Tryk på udtrykket.

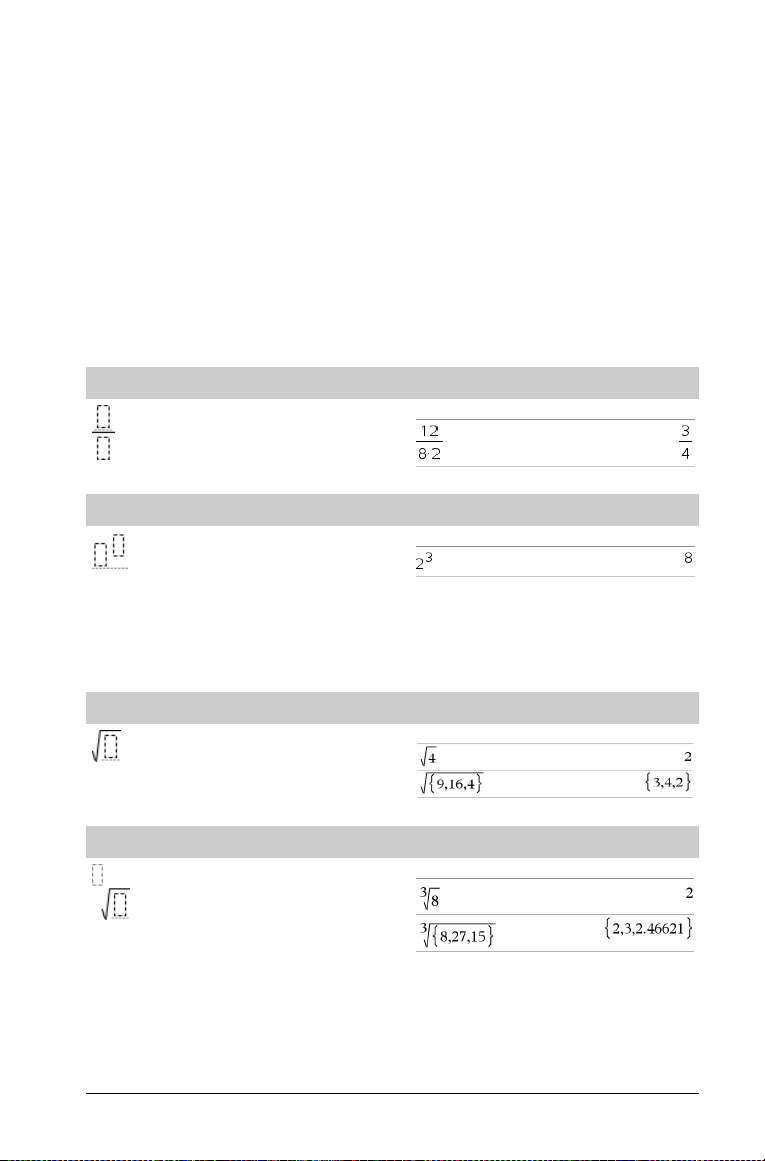
Brøkskabelon

Bemærk: Se også / (divider), side 104.

e for at flytte markøren til hvert elements position, og skriv

· eller /· for at beregne

/p-taster

Eksempel:

Eksponentskabelon

Bemærk: Skriv første værdi, tryk på l, og skriv derefter

eksponenten. Tryk på højrepilen (¢) for at hente markøren tilbage til basislinjen

Bemærk: Se også ^ (potens), side 105.

Kvadratrodsskabelon

Bemærk: Se også

Nte rod-skabelon

Bemærk: Se også root(), side 75.

‡

() (kvadratrod), side 110.

l-tast

Eksempel:

/q-taster

Eksempel:

/l-taster

Eksempel:

TI-Nspire™ Opslagsvejledning 1

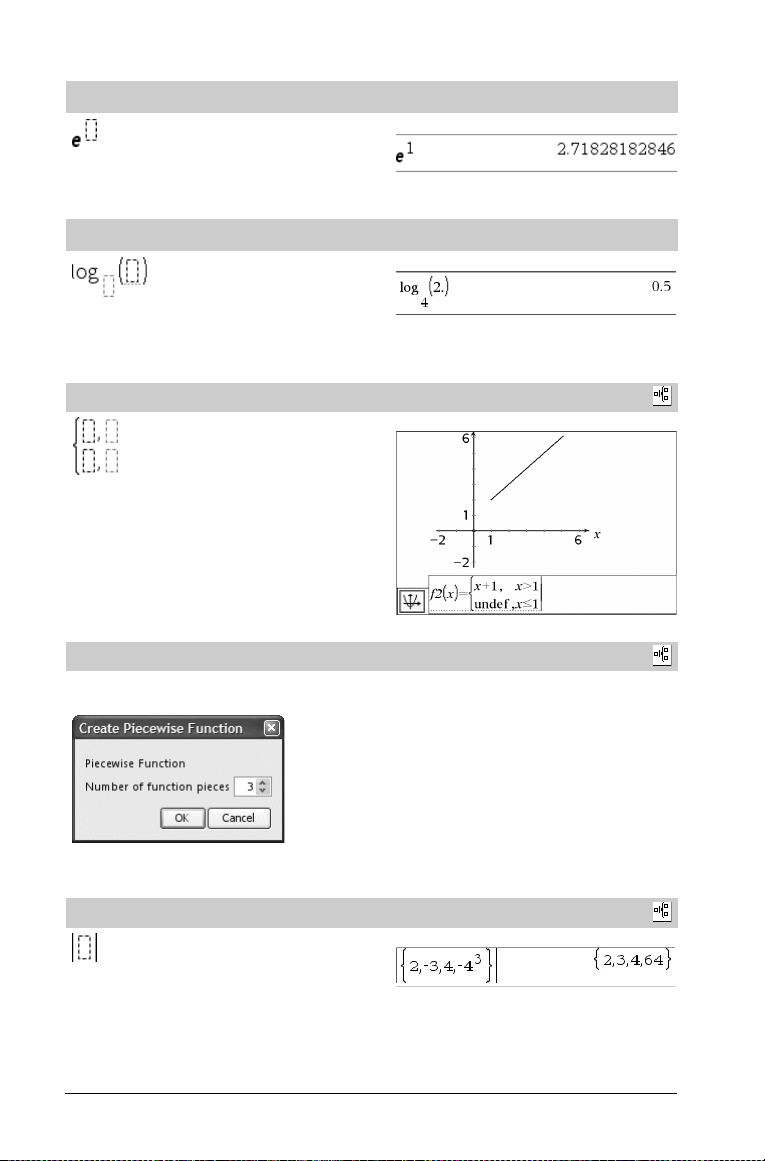
e ekponentskabelon

Den naturlige eksponentialfunktion e opløftet til en potens

Bemærk: Se også e^(), side 27.

u-taster

Eksempel:

Log-skabelon

Beregner logaritmen med et angivet grundtal. Ved 10-talslogarit men, der er standard, udelades grundtallet.

Bemærk: Se også log(), side 51.

Stykkevis-skabelon (2 stykker)

Gør det muligt at oprette udtryk og betingelser for en stykkevis funktion med to stykker.- Du kan tilføje et stykke ved at klikke på skabelonen og gentage skabelonen.

Bemærk: Se også piecewise(), side 66.

Stykkevis-skabelon (N stykker)

Gør det muligt at oprette udtryk og betingelser for en stykkevis funktion med N- stykker. Beder om N.

/s-tasten

Eksempel:

Katalog >

Eksempel:

Katalog >

Eksempel: Se eksemplet med stykkevis-skabelonen (2 stykker).

Bemærk: Se også piecewise(), side 66.

Absolut værdi-skabelon

Eksempel:

Bemærk: Se også abs(), side 5.

Katalog >

2 TI-Nspire™ Opslagsvejledning

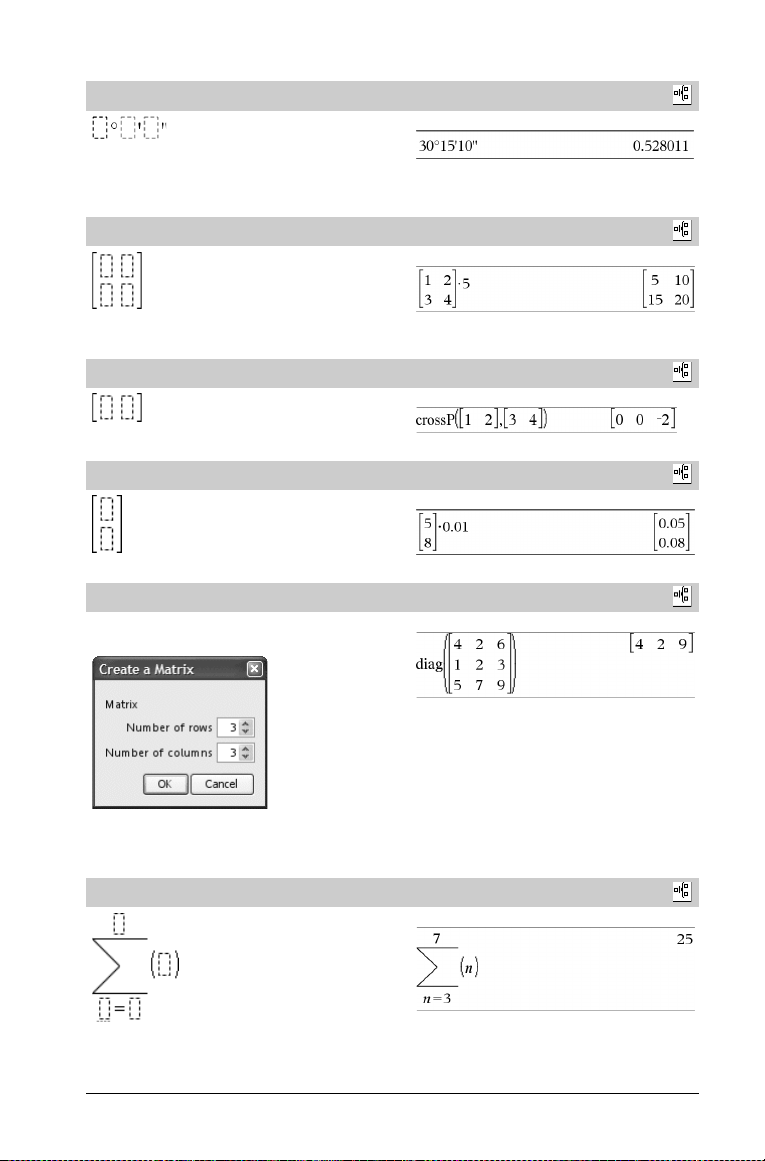
dd°mm’ss.ss’’-skabelon

Her kan du indtaste vinkler i gg°mm’ss.ss’’ format, hvor gg er antallet af decimalgrader, mm er antallet af minutter, og ss.ss antallet af sekunder.

Katalog >

Eksempel:

Matrix-skabelon (2 x 2)

Opretter en matrix 2 x 2.

Matrix-skabelon (1 x 2)

Matrix-skabelon (2 x 1)

Matrix-skabelon (m x n)

Skabelonen vises, efter at du er blevet bedt om at angive antallet af rækker og kolonner.

Katalog >

Eksempel:

Katalog >

Eksempel:

Katalog >

Eksempel:

Katalog >

Eksempel:

Bemærk: Hvis du opretter en matrix med mange rækker og kolonner, kan det tage et øjeblik, før den kommer frem.

Sum-skabelon (G)

Eksempel:

Katalog >

TI-Nspire™ Opslagsvejledning 3

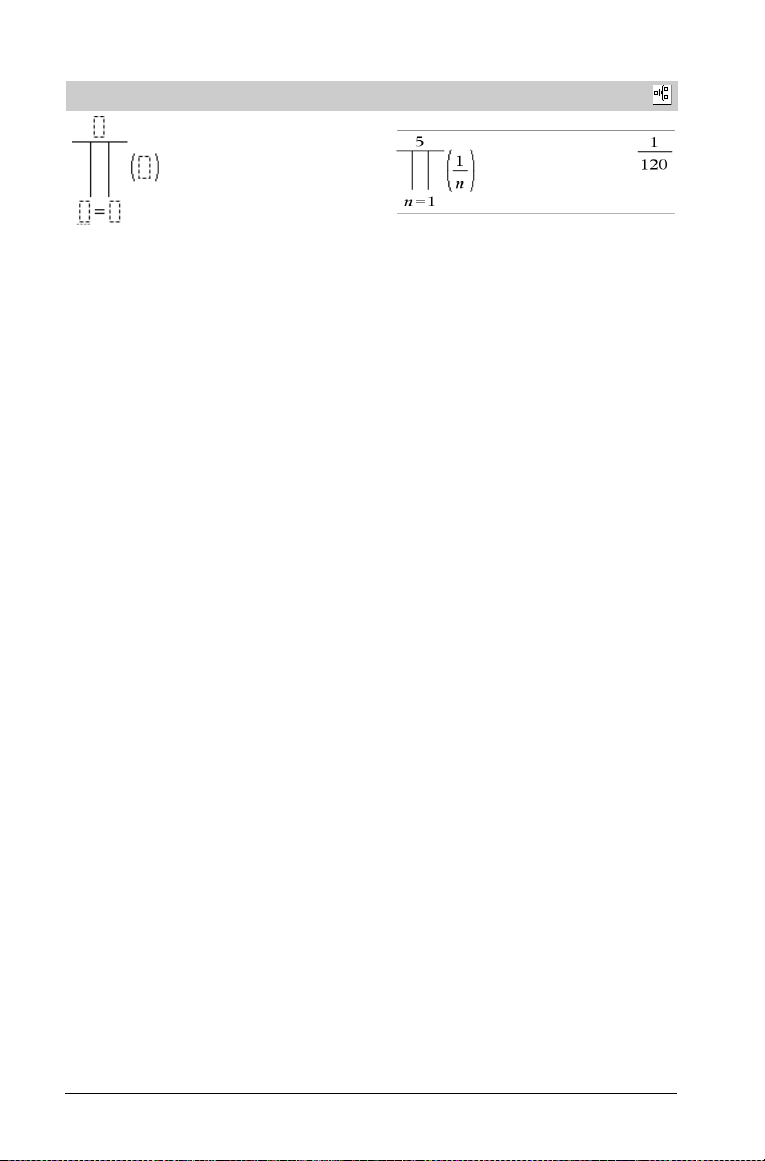
Produkt-skabelon (Π)

Bemærk: Se også Π() (produkt), side 110.

Katalog >

Eksempel:

4 TI-Nspire™ Opslagsvejledning

Alfabetisk oversigt

Elementer, hvis navne ikke er alfabetiske (som f.eks. +, ! og >), er anført sidst i dette afsnit, startende på side 103. Medmindre andet er angivet, udføres alle eksempler i dette afsnit i standard nulstillingstilstand, og alle variable antages at være ikke-defineret.

abs()

abs(Værdi1) ⇒ værdi abs(

Liste1) ⇒ liste

abs(Matrix1) ⇒ matrix

Returnerer den absolutte værdi af argumentet.

Bemærk: Se også Absolut værdi-skabelon, side 2.

Hvis argumentet er et komplekst tal, returneres tallets modulus.

Bemærk: Alle udefinerede variable behandles som reelle variable.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],

afrundVærdi]) ⇒ matrix

[

Amortiseringsfunktion, der returnerer en matrix som en amortiseringstabel for et sæt af TVM-argumenter.

NPmt er antallet af betalinger, der skal inkluderes i tabellen. Tabellen starter med den første betaling.

N, I, PV, Pmt, FV, PpY, CpY og PmtAt er beskrevet i tabellen over TVM-argumenter på side 95.

• Hvis du udelader Pmt, sættes den som standard til Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Hvis du udelader FV, sættes FV=0 som standard.

• Standardværdierne for PpY, CpY og PmtAt er de samme som for TVM-funktionerne.

afrundVærdi angiver antallet af decimaler til afrunding. Standardværdi=2.

Kolonnerne i resultatmatricen er i denne rækkefølge: Betalingsnummer, beløb betalt til renter, beløb betalt til hovedstol og saldo.

Saldoen, der vises i række n, er saldoen efter betaling n. Du kan bruge outputmatricen som input for de andre

amortiseringsfunktioner GInt() og GPrn(), side 111 og bal(), side

10.

Katalog

and

Boolsk Udtr1 and Boolsk Udtr2

⇒ Boolsk udtryk

Boolsk Liste1 and Boolsk Liste2 ⇒ Boolsk liste Boolsk Matrix1 and Boolsk Matrix2 ⇒ Boolsk matrix

Returnerer true eller false eller en forenklet form af den oprindelige indtastning.

Katalog

TI-Nspire™ Opslagsvejledning 5

and

Heltal1 and Heltal2 ⇒ heltal

Sammenligner to heltal bit for bit med en konverteres begge heltal til 64-bit binære tal med fortegn. Når de tilsvarende bits sammenlignes, er resultatet 1, hvis begge bits er 1. Ellers er resultatet 0. Den returnerede værdi repræsenterer bitresultaterne og vises i overensstemmelse med den valgte talsystemtilstand.

Du kan indtaste heltallene i ethvert talsystem. Til binære eller hexadecimale indtastninger skal du som præfiks benytte henholdsvis 0b eller 0h. Uden præfiks behandles heltallene som decimaltal (10 talssystem).

Hvis du indtaster et decimalt heltal, der er for stort til en 64-bit binær form med fortegn, anvendes en symmetrisk modulooperation til at bringe værdien ind i det korrekte område.

and-operation. Internt

Katalog

I hexadecimal tilstand:

Vigtigt: Tallet nul, ikke bogstavet O.

I binær tilstand:

I decimal tilstand:

Bemærk: En binær indtastning kan have op til 64 cifre

(præfikset 0b ikke medregnet). En hexadecimal indtastning kan have op til 16 cifre.

angle()

angle(Værdi1) ⇒ værdi

Returnerer vinklen på argumentet og fortolker argumentet som et komplekst tal.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

angle(Liste1) ⇒ liste angle(Matrix1) ⇒ matrix

Returnerer en liste eller matrix med vinkler af elementerne i Liste1 eller matrix1, hvor hvert element fortolkes som et komplekst tal, der repræsenterer et todimensionalt rektangulært koordinatpunkt.

ANOVA

ANOVA Liste1,Liste2[,Liste3,...,Liste20][,Flag]

Udfører envejsanalyse af varians til sammenligning af middelværdier for to til 20 populationer. En sammenfatning af resultaterne lagres i variablen stat.results. (Se side 85.)

Flag=0 for data, Flag=1 for statistik

Output-variabel Beskrivelse

stat.F Værdien for F-statistik

stat.PVal Mindste signifikansniveau, ved hvilket nul-hypotesen kan forkastes

stat.df Frihedsgrader i grupperne

stat.SS Kvadratsum i grupperne

stat.MS Middelkvadrat for grupperne

stat.dfError Frihedsgrader for fejl

Katalog

6 TI-Nspire™ Opslagsvejledning

Output-variabel Beskrivelse

stat.SSError Kvadratsum for fejlene

stat.MSError Middelkvadrat for fejlene

stat.sp Puljet standardafvigelse

stat.xbarlist Gennemsnit af input for listerne

stat.CLowerList 95% konfidensintervaller for middelværdien for hver inputliste

stat.CUpperList 95% konfidensintervaller for middelværdien for hver inputliste

ANOVA2-way

ANOVA2way Liste1,Liste2[,Liste3…,Liste20][,levRow]

Beregner en tovejsanalyse af varians til sammenligning af middelværdier for to til tyve populationer. En sammenfatning af resultaterne lagres i variablen stat.results. (Se side 85.)

levRow=0 for Blok

levRow=2,3,...,Læn-1, for Tofaktor, hvor Læn=længde(Liste1)=længde(Liste2) = … = længde(Liste10) og Læn / levRow ∈ {2,3,…}

Output: Blokdesign

Output-variabel Beskrivelse

stat.FF statistik for kolonnefaktor

stat.PVal Mindste signifikansniveau, ved hvilket nul-hypotesen kan forkastes

stat.df Frihedsgrader i kolonnefaktoren

stat.SS Kvadratsum for kolonnefaktoren

stat.MS Middelkvadrat for kolonnefaktoren

stat.FBlok F statistik for faktor

stat.PValBlock Mindste sandsynlighed, ved hvilken nul-hypotesen kan forkastes

stat.dfBlock Frihedsgrader for faktoren

stat.SSBlock Kvadratsum for faktoren

stat.MSBlock Middelkvadrat for faktoren

stat.dfError Frihedsgrader for fejl

stat.SSError Kvadratsum for fejlene

stat.MSError Middelkvadrat for fejlene

stat.s Standardafvigelse for fejlen

Katalog

TI-Nspire™ Opslagsvejledning 7

KOLONNEFAKTOR Output

Output-variabel Beskrivelse

stat.Fcol F statistik for kolonnefaktor

stat.PValCol Sandsynlighedsværdi for kolonnefaktoren

stat.dfCol Frihedsgrader i kolonnefaktoren

stat.SSCol Kvadratsum for kolonnefaktoren

stat.MSCol Middelkvadrat for kolonnefaktoren

RÆKKEFAKTOR Output

Output-variabel Beskrivelse

stat.Frow F statistik for rækkefaktoren

stat.PValRow Sandsynlighedsværdi for rækkefaktoren

stat.dfRow Frihedsgrader for rækkefaktoren

stat.SSRow Kvadratsum for rækkefaktoren

stat.MSRow Kvadraternes middelværdi for rækkefaktoren

INTERAKTION-output

Output-variabel Beskrivelse

stat.FInteract F statistik for interaktionen

stat.PValInteract Sandsynlighedsværdi for interaktionen

stat.dfInteract Frihedsgrader for interaktionen

stat.SSInteract Kvadratsum for interaktionen

stat.MSInteract Middelkvadrat for interaktionen

FEJL-output

Output-variabel Beskrivelse

stat.dfError Frihedsgrader for fejl

stat.SSError Kvadratsum for fejlene

stat.MSError Middelkvadrat for fejlene

s Standardafvigelse for fejlen

8 TI-Nspire™ Opslagsvejledning

Ans

Ans ⇒ værdi

Returnerer resultatet af de sidst beregnede udtryk.

-tasten

approx()

approx(Værdi1) ⇒ tal

Returnerer beregningen af argumentet som et udtryk med decimale værdier, når det er muligt, uanset den aktuelle indstilling af Auto/

approks

Dette svarer til at indtaste argumentet og trykke på

approx(Liste1) ⇒ liste approx(Matrix1) ⇒ matrix

Returnerer en liste eller matrix, hvor hvert element er beregnet til en decimalværdi, hvor det er muligt.

approxRational()

approxRational(Udtr[, tol]) ⇒ udtryk approxRational(Liste[, tol]) ⇒ liste approxRational(Matrix[, tol]) ⇒ matrix

Returnerer argumentet som en brøk med en tolerance på tol. Hvis tol udelades, anvendes en tolerance på 5.E-14.

augment()

augment(Liste1, Liste2) ⇒ liste

Returnerer en ny liste, der er liste2 føjet til enden af Liste1.

augment(Matrix1, Matrix2) ⇒ matrix

Returnerer en ny matrix, der er Matrix2 føjet til Matrix1. Når tegnet “,” anvendes, skal matricerne have lige store rækkedimensioner, og Matrix2 føjes til Matrix1 som nye kolonner. Ændrer ikke Matrix1 eller Matrix2.

·.

Katalog

TI-Nspire™ Opslagsvejledning 9

avgRC()

avgRC(Udtr1, Var [=Værdi] [, H]) ⇒ udtryk avgRC(Udtr1, Var [=Værdi] [, Liste1]) ⇒ liste avgRC(Liste1, Va r [=Værdi] [, H]) ⇒ liste avgRC(Matrix1, Var [=Værdi] [, H]) ⇒ matrix

Returnerer den fremadrettede differenskvotient (gennemsnitlig ændringshastighed).

Udtr1 kan være et brugerdefineret funktionsnavn (se Når værdi er angivet, tilsidesætter den alle forudgående

variabeltildelinger eller alle “således at” substitutioner for variablen. H er trinværdien. Hvis H udelades, er standardværdien 0,001. Bemærk, at den lignende funktion

differenskvotient.

nDeriv() anvender den centrale

Func).

Katalog

bal()

bal(NPmt,N,I,PV,[Pmt], [FV], [PpY], [CpY], [PmtAt],

afrundVærdi]) ⇒ værdi

[

bal(NPmt,amortTabel) ⇒ værdi

Amortiseringsfunktion, der beregner saldo efter en angivet betaling. N, I, PV, Pmt, FV, PpY, CpY og PmtAt er beskrevet i tabellen over

TVM-argumenter på side 95. NPmt angiver betalingsnummeret, hvorefter du vil have dataene

beregnet. N, I, PV, Pmt, FV, PpY, CpY og PmtAt er beskrevet i tabellen over

TVM-argumenter på side 95.

• Hvis du udelader Pmt, bliver den som standard Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Hvis du udelader FV, bliver den som standard FV=0.

• Standardværdierne for PpY, CpY og PmtAt er de samme som for TVM-funktionerne.

afrundVærdi angiver antallet af decimaler til afrunding. Standardværdi=2.

bal(NPmt,amortTabel) beregner saldoen efter betaling nummer

NPmt, baseret på amortiseringstabel amortTabel. amortTabelargumentet skal være en matrix i formen beskrevet under

amortTbl(), side 5.

Bemærk: Se også GInt() og GPrn(), side 111.

Base2

Heltal1 4Base2 ⇒ heltal

Konverterer Heltal1 til et binært tal. Binære eller hexadecimale tal har altid henholdsvis 0b eller 0h som præfiks.

Katalog

10 TI-Nspire™ Opslagsvejledning

Base2

0b binærtTal 0h hexadecimaltTal

Tallet nul, ikke bogstavet O, efterfulgt af b eller h. Et binært tal kan have op til 64 cifre. Et hexadecimalt tal kan have op

til 16. Uden præfiks behandles Heltal1 som decimaltal (10 talssystem).

Resultatet vises som binært uanset tilstanden for talsystem. Hvis du indtaster et decimalt heltal, der er for stort til en 64-bit binær

form med fortegn, anvendes en symmetrisk modulo-operation til at bringe værdien ind i det korrekte område.

Base10

Heltal1 4Base10 ⇒ heltal

Konverterer Heltal1 til et decimaltal (i titalssystemet). Binære eller hexadecimale indtastninger skal altid have hhv. 0b eller 0h som præfiks.

0b binærtTal 0h hexadecimaltTal

Tallet nul, ikke bogstavet O, efterfulgt af b eller h. Et binært tal kan have op til 64 cifre. Et hexadecimalt tal kan have op

til 16. Uden præfiks behandles Heltal1 som decimaltal. Resultatet vises

som decimaltal uanset tilstanden for talsystem.

Base16

Heltal1 4Base16 ⇒ heltal

Konverterer Heltal1 til et hexadecimalt tal. Binære eller hexadecimale tal har altid henholdsvis 0b eller 0h som præfiks.

0b binærtTal 0h hexadecimaltTal

Tallet nul, ikke bogstavet O, efterfulgt af b eller h. Et binært tal kan have op til 64 cifre. Et hexadecimalt tal kan have op

til 16. Uden præfiks behandles Heltal1 som decimaltal (10-talssystem).

Resultatet vises som hexadecimalt uanset tilstanden for talsystem. Hvis du indtaster et decimalt heltal, der er for stort til en 64-bit binær

form med fortegn, anvendes en symmetrisk modulo-operation til at bringe værdien ind i det korrekte område.

Katalog

binomCdf()

binomCdf(n,p,nedreGrænse,øvreGrænse) ⇒ tal hvis

nedreGrænse og øvreGrænse er tal, liste if nedreGrænse og øvreGrænse er lister

binomCdf(

liste hvis øvreGrænse er en liste

Beregner den kumulerede sandsynlighed for den diskrete binomialfordeling med n antal forsøg og sandsynligheden p for succes ved hvert forsøg.

For P(X  øvreGrænse), sæt nedreGrænse=0

n,p,øvreGrænse) ⇒ tal hvis øvreGrænse er et tal,

Katalog

TI-Nspire™ Opslagsvejledning 11

binomPdf()

binomPdf(n,p[,XVærdi]) ⇒ tal binomPdf(n,p) ⇒ tal binomPdf(n,p,XVal) ⇒ tal hvis XVærdi er et tal, liste hvis

XVærdi er en liste

Beregner en sandsynlighed ved XVærdi for den diskrete binomialfordeling med n antal forsøg og sandsynligheden p for succes ved hvert forsøg.

Katalog

ceiling()

ceiling(Værdi1) ⇒ værdi

Returnerer det nærmeste heltal, der er ‚ argumentet.

Argumentet kan være et reelt eller komplekst tal.

Bemærk: Se også floor().

ceiling(Liste) ⇒ liste ceiling(Matrix1) ⇒ matrix

Returnerer en liste eller matrix med oprunding anvendt på hvert element.

char()

char(Heltal) ⇒ tegn

Returnerer en tegnstreng med tegnet nummereret Heltal fra grafregnerens tegnsæt. Det gyldige område for Heltal er 0–65535.

2way

2way obsMatrix

chi22way obsMatrix

Beregner en c2 test til association på tovejstabellen med tællinger i den observerede matrix obsMatrix. En sammenfatning af resultaterne lagres i variablen stat.results. (Se side 85.)

Output-variabel Beskrivelse

stat.c2 Chi-kvadrat stat: sum (observeret - forventet)2/forventet

stat.PVal Mindste signifikansniveau, ved hvilket nul-hypotesen kan forkastes

stat.df Frihedsgrader for Chi-kvadrat stat

stat.ExpMat Matrix med forventet elementtællingstabel, der antager nulhypotese

stat.CompMat Matrix med bidrag til chi-kvadrat elementbidrag

Katalog

12 TI-Nspire™ Opslagsvejledning

Cdf()

Cdf(nedreGrænse,øvreGrænse,df) ⇒ tal hvis nedreGrænse

øvreGrænse er tal, liste hvis nedreGrænse og øvreGrænse er

og lister

chi2Cdf(

nedreGrænse,øvreGrænse,df) ⇒ tal hvis nedreGrænse og øvreGrænse er tal, liste hvis nedreGrænse og øvreGrænse er lister

Beregn c2 sandsynlighedsfordelingen mellem nedreGrænse og øvreGrænse for de angivne frihedsgrader df.

 øvreGrænse), sæt nedreGrænse=0.

For P(X

GOF

GOF obsListe,forvListe,fg

chi2GOF obsListe,forvListe,fg

Udfører en test for at bekræfte, at måledataene er fra en population, der er i overensstemmelse med en angivet distribution. obsList er en liste med antal, og skal indeholde heltal. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Output-variabel Beskrivelse

stat.c2 Chi-kvadrat stat: sum((observeret - forventet)2/forventet

stat.PVal Mindste signifikansniveau, ved hvilket nul-hypotesen kan forkastes

stat.df Frihedsgrader for Chi-kvadrat stat

stat.CompList Bidrag til chi-kvadrat elementbidrag

Pdf()

Pdf(XVal,df) ⇒ tal hvis XVal er et tal, liste hvis XVal er en

liste

chi2Pdf(

XVal,df) ⇒ tal hvis XVal er et tal, liste, hvis XVal er

en liste

Beregner tæthedsfunktionen (pdf) for c2 fordelingen ved en angivet XVal-værdi for den angivne frihedsgrad df.

Katalog

ClearAZ

Katalog

Sletter alle enkelttegnsvariable i det aktuelle opgaverum.

TI-Nspire™ Opslagsvejledning 13

ClrErr Katalog

ClrErr

Sletter fejlstatus og indstiller systemvariabel errCode til nul.

Else betingelsen i Try...Else...EndTry-blokken bør anvende ClrErr eller PassErr. Brug ClrErr, hvis fejlen skal behandles eller

ignoreres. Brug PassErr, hvis det ikke er kendt, hvad der skal gøres ved fejlen, for at sende den til den næste fejlhåndtering. Hvis der ikke er flere ventende Try...Else...EndTry-fejlhåndteringer, vises fejldialogboksen som normalt.

Bemærk: Se også PassErr, side 66, og Try, side 92. Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at

Se et eksempel på ClrErr, i Eksempel 2 under Try- kommandoen, side 93.

trykke på @ i stedet for · ved slutningen af hver linje. På computerens tastatur skal du holde Alt nede og trykke på Enter.

colAugment()

colAugment(Matrix1, Matrix2) ⇒ matrix

Returnerer en ny matrix, der er Matrix2 føjet til Matrix1. Matricerne skal have lige store kolonnedimensioner, og Matrix2 føjes til Matrix1 som nye rækker. Ændrer ikke Matrix1 eller Matrix2.

colDim()

colDim(Matrix) ⇒ udtryk

Returnerer antallet af kolonner i Matrix.

Bemærk: Se også rowDim().

colNorm()

colNorm(Matrix) ⇒ udtryk

Returnerer maksimum for summerne af de absolutte værdier for elementerne i kolonnerne i Matrix.

Bemærk: Udefinerede matrixelementer er ikke tilladt. Se også rowNorm().

conj()

conj(Værdi1) ⇒ værdi conj(Liste1) ⇒ liste conj(Matrix1) ⇒ matrix

Returnerer kompleks konjugerede af argumentet.

Bemærk: Alle udefinerede variable behandles som reelle variable.

Katalog

14 TI-Nspire™ Opslagsvejledning

constructMat()

constructMat(Udtr,Var 1 ,Va r2 ,antalRækker,antalKol)

⇒ matrix

Returnerer en matrix baseret på argumenter. Udtr er et udtryk i variablerne Var 1 og Va r 2 . Elementer i den

resulterende matrix er dannet ved beregning af Udtr for hver forøget værdi af Var 1 og Va r2 .

Var 1 er automatisk forøget fra række, Va r2 er forøget fra 1 til antalKol.

1 til antalRækker. Inden for hver

Katalog

CopyVar

CopyVar Var 1 , Va r 2 CopyVar Var 1 ., Va r2 .

CopyVar Var 1 , Va r2 kopierer værdien af variablen Var 1 til

variabelen Var 2 , og opretter Var 2 hvis nødvendigt. Variablen Va r 1 skal have en værdi

Hvis Va r1 er navnet på en eksisterende brugerdefineret funktion, kopieres definitionen af denne funktion til funktionen Va r 2 . Funktionen Va r1 skal defineres.

Var 1 skal opfylde kravene til navngivning af variable, eller være et indirekte udtryk, der kan reduceres til et variabelnavn, der opfylder betingelserne.

CopyVar Var 1 ., Va r2 . kopierer alle elementer af Va r1 .

variabelgruppen til Va r 2. gruppen, og opretter Va r2 . hvis nødvendigt.

Var 1 . skal være navnet på en eksisterende variabelgruppe, så som statistikken stat.nn resultater, eller variable dannet ved brug af

LibShortcut()-funktionen. Hvis Va r2 . allerede eksisterer, vil denne

kommando udskifte alle elementer, der er fælles i begge grupper, og tilføje de elementer, som ikke allerede eksisterer. Hvis en simpel (ikke-gruppe) variabel med navnet Va r 2 eksisterer, vil der opstå en fejl.

corrMat()

corrMat(Liste1,Liste2[,…[,Liste20]])

Beregner korrelationsmatricen for den udvidede matrix [Liste1 Liste2 . . . Liste20].

Katalog

TI-Nspire™ Opslagsvejledning 15

cos()

cos(Værdi1) ⇒ værdi cos(Liste1) ⇒ list

cos(Værdi1) returnerer cosinus af argumentet som en værdi. cos(Liste1) returnerer en liste med cosinus til alle elem enter i Liste1. Bemærk: Argumentet fortolkes som en vinkel målt i grader,

nygrader eller radianer afhængigt af den aktuelt indstillede vinkeltilstand. Du kan bruge ó,G ellerôtil midlertidigt at ignorere

vinkeltilstanden.

n-tast

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

cos(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer matrixcosinus af kvadratMatrix1. Dette er ikke det samme som at beregne cosinus for hvert element.

Når en skalær funktion f(A) opererer på kvadratMatrix1 (A), beregnes resultatet efter algoritmen:

Beregn egenværdierne (li) og egenvektorer (Vi) af A.

KvadratMatrix1 skal være diagonaliserbar. Den må heller ikke have symbolske variable, der ikke er tildelt en værdi.

Dan matricerne:

Derefter A = X B Xêog f(A) = X f(B) Xê. For eksempel cos(A) = X cos(B) Xê, hvor:

cos (B) =

Alle beregninger udføres aritmetisk med flydende komma.

I vinkeltilstanden Radian:

16 TI-Nspire™ Opslagsvejledning

cosê()

cosê(Værdi1) ⇒ værdi cosê(Liste1) ⇒ liste

/n-taster

I vinkeltilstanden Grader:

cosê(Værdi1) returnerer den vinkel, hvis cosinus er Værdi1.

cosê(Liste1) returnerer en liste med de inverse cosinusværdier for

hvert element af Liste1.

Bemærk: Resultatet returneres som en vinkel i grader eller radianer

afhængigt af den aktuelle vinkeltilstand.

cosê(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer den matrixinverse cosinus af kvadratMatrix1. Dette er ikke det samme som at beregne den inverse cosinus for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

cosh()

cosh(Værdi1) ⇒ værdi cosh(Liste1) ⇒ liste

cosh(Værdi1) returnerer den hyperperbolske cosinus af argumentet. cosh(Liste1) returnerer en liste med hyperbolsk cosinus for hvert

element i Liste1.

cosh(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer matrix hyperbolsk cosinus af kvadratMatrix1. Dette er ikke det samme som at beregne den hyperbolske cosinus for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

I vinkeltilstanden radian og rektangulært komplekst format:

Du kan se hele resultatet ved at trykke på £ og derefter anvende ¡ og ¢ til at bevæge markøren.

Katalog

I vinkeltilstanden Radian:

coshê()

coshê(Værdi1) ⇒ værdi coshê(Liste1) ⇒ liste

cosh

(Værdi1) returnerer den inverse hyperbolske cosinus af

argument.

cosh

(Liste1) returnerer en liste med de inverse hyperbolske

cosinusværdier for hvert element i Liste1.

Katalog

TI-Nspire™ Opslagsvejledning 17

coshê()

coshê(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer den matrixinverse hyperbolske cosinus af kvadratMatrix1. Dette er ikke det samme som at beregne den inverse hyperbolske cosinus for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

Katalog

I vinkeltilstanden Radian og i rektangulært komplekst format:

Du kan se hele resultatet ved at trykke på £ og derefter anvende ¡ og ¢ til at bevæge markøren.

cot()

cot(Værdi1) ⇒ værdi cot(Liste1) ⇒ liste

Returnerer cotangens af Værdi1 eller returnerer en liste med cotangens til alle elementer i Liste1.

Bemærk: Argumentet fortolkes som en vinkel målt i grader,

nygrader eller radianer afhængigt af den aktuelt indstillede vinkeltilstand. Du kan bruge ó,G ellerôtil midlertidigt at ignorere

vinkeltilstanden.

cotê()

cotê(Værdi1) ⇒ værdi cotê(Liste1) ⇒ liste

Returnerer den vinkel, hvis cotangens er Værdi1 eller returnerer en liste med den inverse cotangens til hvert element i Liste1.

Bemærk: Resultatet returneres som en vinkel i grader eller radianer

afhængigt af den aktuelle vinkeltilstand.

coth()

coth(Værdi1) ⇒ værdi coth(Liste1) ⇒ liste

Returnerer den hyperbolske cotangens til Udtr1 eller returnerer en liste med den hyperbolske cotangens til alle elementer i Liste1.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

Katalog

cothê()

cothê(Værdi1) ⇒ værdi cothê(Liste1) ⇒ liste

Returnerer den inverse hyperbolske cotangens til Værdi1 eller returnerer en liste med den inverse hyperbolske cotangens til hvert element i Liste1.

Katalog

18 TI-Nspire™ Opslagsvejledning

count()

count(Værdi1ellerListe1 [,Værdi2ellerListe2 [,...]]) ⇒ værdi

Returnerer det akkumulerede antal af alle elementer i argumenterne, der evalueres til numeriske værdier.

Hvert argument kan være et udtryk, en værdi, en liste eller en matrix. Du kan blande datatyper og anvende argumenter med forskellige dimensioner.

For lister, matricer eller celleområder evalueres hvert element for at bestemme, om det skal inkluderes i tællingen.

I applikationen Lister og regneark kan du anvende et celleområde i stedet for ethvert argument.

Katalog

countif()

countif(Liste,Kriterie) ⇒ værdi

Returnerer det akkumulerede antal af alle elementer i Liste, der opfylder de angivne Kriterie.

Kriterie kan være:

• En værdi, et udtryk eller en streng. For eksempel tæller 3 kun de

elementer i Liste, der reduceres til værdien 3.

• Et Boolsk udtryk, der indeholder symbolet ? som pladsholder for

hvert element. For eksempel ?<5 tæller kun de elementer i Liste, der er mindre end 5.

I applikationen Lister og regneark kan du anvende et celleområde i stedet for Liste.

Bemærk: Se også sumIf(), side 88, og frequency(), side 34.

crossP()

crossP(Liste1, Liste2) ⇒ liste

Returnerer vektorproduktet af Liste1 og liste2 som en liste. Liste1 og Liste2 skal have ens dimension, og dimensionen skal være

2 eller 3.

crossP(Vektor1, Vektor2) ⇒ vektor

Returnerer en række eller kolonnevektor (afhængigt af argumenterne), der er vektorproduktet af Vektor1 og Vektor2.

Både Vektor1 og Vektor2 skal være rækkevektorer, eller begge skal være kolonnevektorer. Begge vektorer skal have ens dimension, og dimensionen skal være enten 2 eller 3.

Tæller antallet af elementer lig med 3.

Tæller antallet af elementer lig med “def.”

Tæller 1 og 3.

Tæller 3, 5 og 7.

Tæller 1, 3, 7 og 9.

Katalog

TI-Nspire™ Opslagsvejledning 19

csc()

csc(Værdi1) ⇒ værdi csc(Liste1) ⇒ liste

Returner cosecansen til Værdi1 eller returnerer en liste med cosecansen til alle elementer i Liste1.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

Katalog

cscê()

cscê(Værdi1) ⇒ værdi cscê(Liste1) ⇒ liste

Returnerer den vinkel, hvis cosecans er Værdi1 eller returnerer en liste med den inverse cosecans til hvert element i Liste1.

Bemærk: Resultatet returneres som en vinkel i nygrader eller

radianer afhængigt af den aktuelle vinkeltilstand.

csch()

csch(Værdi1) ⇒ værdi csch(Liste1) ⇒ liste

Returnerer den hyperbolic cosecans til Værdi1 eller returnerer en liste med de hyperbolske cosecanser til alle elementer i Liste1.

cschê()

cschê(Tal ) ⇒ værdi cschê(Liste1) ⇒ liste

Returnerer den inverse hyperbolske cosecans til Værdi1 eller returnerer en liste med den inverse hyperbolske cosecans til hvert element i Liste1.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

Katalog

20 TI-Nspire™ Opslagsvejledning

CubicReg

CubicReg X, Y[, [Frekv] [, Kategori, Medtag]]

Katalog

Beregner polynomiel tredjegradsregression y = a·x3+b· x2+c·x+d på listerne X og Y med frekvens Frekv. En

sammenfatning af resultaterne lagres i stat.resultat variable. (Se side 85.)

Alle lister skal have samme dimension med undtagelse af Medtag.

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i Frekv

angiver hyppigheden af hvert tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output-variabel Beskrivelse

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.r

Regressionsligning: a·x3+b·x2+c·x+d

Regressionskoefficienter

Forklaringsgraden

stat.Resid Residualer fra regressionen

stat.XReg Liste af datapunkter i den modificerede X-liste, der faktisk bruges i regressionen ud fra begrænsninger af

stat.YReg Liste af datapunkter i den modificerede Y- li st e, der faktisk bruges i regressionen ud fra begrænsninger af

Hyppighed, Kategoriliste, og Medtag kategorier

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

cumSum()

cumSum(Liste1) ⇒ liste

Returnerer en liste med de kumulerede summer af elementerne i Liste1, startende ved element 1.

cumSum(Matrix1) ⇒ matrix

Returnerer en matrix af de kumulerede summer af elementerne i Matrix1. Hvert element er den kumulerede sum af kolonnen fra top til bund.

Katalog

TI-Nspire™ Opslagsvejledning 21

Cycle

Cyklus

Overfører kontrol direkte til næste iterat ion i den aktuelle løkke (For,

While eller Loop). Cycle må ikke ikke benyttes uden for (For, While eller Loop). Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

Cylind

Vek t o r 4Cylind

Viser række- eller kolonnevektoren i cylindrisk form [rq, z].

Vek t o r skal have nøjagtig tre elementer. Det kan væ re en række eller en kolonne.

Katalog

Funktionsliste, der adderer heltallene fra 1 til 100 og udelader

50.

Katalog

dbd()

dbd(dato1,dato2) ⇒ værdi

Returnerer antallet af dage mellem dato1 og dato2 med tælling af faktiske dage.

dato1 og dato2 kan være tal eller lister med tal inden for området af datoer i en standardkalender. Hvis både dato1 og dato2 er lister, skal de have samme længde.

dato1 og dato2 skal ligge mellem årene 1950 til 2049. Du kan indtaste datoerne i to formater. Placeringen af decimaler er

forskellen mellem datoformaterne. MM.DDÅÅ (almindeligt format i USA)

DDMM.ÅÅ (almindeligt format i Europa)

Katalog

22 TI-Nspire™ Opslagsvejledning

4DD ⇒ værdi

Tal Liste1 4DD ⇒ liste Matrix1

4DD ⇒ matrix

Returnerer den decimale ækvivalent til argumentet udtrykt i grader. Argumentet er et tal, en liste eller matrix, som efter den indstillede tilstand af Vinkel tolkes i grader, nygrader eller radianer.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

Katalog

4Decimal

Værdi1

4Decimal

Liste1 Matrix1

Viser argumentet i decimal form. Denne operator kan kun anvendes ved slutningen af indtastningslinjen.

Define

Define Var = Udtryk Define Funktion(Param1, Param2, ...) = Udtryk

Definerer variablen Var eller den brugerdefinerede funktion Funktion.

Parametre som Param1 er pladsholdere til at sætte argumenter ind i funktionen. Ved kald af en brugerdefineret funktion skal du angive argumenter (for eksempel værdier eller variable), der svarer til parametrene. Når den kaldes, evaluerer funktionen Udtryk med de angivne argumenter.

Var og Funktion kan ikke være navnet på en systemvariabel eller en integreret funktion eller kommando.

Bemærk: Denne form for Define svarer til at eksekvere udtrykket:

udtryk & Funktion(Param1,Param2).

Decimal

⇒ værdi

Katalog

TI-Nspire™ Opslagsvejledning 23

Define

Define Funktion(Param1, Param2, ...) = Func

Blok

EndFunc

Program(Param1, Param2, ...) = Prgm

Define

Blok

EndPrgm

I denne form kan den brugerdefinerede funktion eller programmet eksekvere en blok med flere sætninger.

Blok kan en være en enkelt sætning eller en række sætninger på separate linjer. Blok kan også rumme udtryk og kommandoer (som f.eks. If, Then, Else og For).

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

Bemærk: Se også Define LibPriv, side 24 og Define LibPub,

side 25.

Katalog

Define LibPriv

Define LibPriv Var = Udtryk Define LibPriv Funktion(Param1, Param2, ...) = Udtryk

Define LibPriv Funktion(Param1, Param2, ...) = Func

Blok

EndFunc Define LibPriv

Blok

EndPrgm

Fungerer på samme måde som Define med den undtagelse, at den definerer en privat biblioteksvariabel, funktion, eller et program. Private funktioner og programmer optræder ikke i Katalog.

Bemærk: Se også Define, side 23, og Define LibPub, side 25.

Program(Param1, Param2, ...) = Prgm

Katalog

24 TI-Nspire™ Opslagsvejledning

Define LibPub

Define LibPub Var = Udtryk Define LibPub Funktion(Param1, Param2, ...) = Udtryk

Define LibPub Funktion(Param1, Param2, ...) = Func

Blok

EndFunc Define LibPub

Blok

EndPrgm

Fungerer på samme måde som Define med den undtagelse, at den definerer en offentlig biblioteksvariabel, funktion, eller et program. Offentlige funktioner og programmer optræder i Katalog, når biblioteket er gemt eller opdateret.

Bemærk: Se også Define, side 23 og Define LibPriv, side 24.

Program(Param1, Param2, ...) = Prgm

Katalog

DelVar

DelVar Var 1 [, Va r 2] [, Va r 3 ] ... DelVar

Var .

Sletter de angivne variable, eller variabelgruppe fra hukommelse.

DelVar Var . sletter alle elementer i Var . variabelgruppe(så som

statistikken stat.nn resultater, eller variable dannet ved brug af

LibShortcut()-funktionen). Punktummet (.) i denne form af DelVar -kommandoen begrænser den til at slette en variabelgruppe:

den simple variabel Va r berøres ikke.

det()

det(kvadratMatrix[, Tolerance]) ⇒ udtryk

Returnerer determinanten af kvadratMatrix. Ethvert matrixelement kan valgfrit behandles som nul, hvis den

absolutte værdi er mindre end Tolerance. Denne tolerance anvendes kun, hvis matricen har elementer med flydende decimaler og ikke indeholder symbolske variable, der ikke er tildelt en værdi. Ellers, Tol e ra n ce ignoreres.

• Hvis du anvender

Approximate

beregningerne med aritmetik med flydende komma.

•Hvis Tolerance udelades eller ikke anvendes, beregnes

standardtolerancen som:

5EM14 ·max(dim(kvadratMatrix))?

rowNorm(kvadratMatrix)

-tilstanden til Approximate, foretages

eller indstiller Auto or

Katalog

TI-Nspire™ Opslagsvejledning 25

diag()

diag(List) ⇒ matrix diag(rækkeMatrix) ⇒ matrix diag(kolonneMatrix) ⇒ matrix

Returnerer en matrix med værdierne i argumentlisten eller matricen i hoveddiagonalen.

diag(kvadratMatrix) ⇒ rækkeMatrix

Returnerer en rækkematrix, der indeholder elementerne fra hoveddiagonalen i kvadratMatrix.

kvadratMatrix skal være kvadratisk.

Katalog

dim()

dim(Liste) ⇒ heltal

Returnerer dimensionen af liste.

dim(matrix) ⇒ liste

Returnerer dimensionerne af matricen som en liste med to elementer {rækker, kolonner}.

dim(Streng ) ⇒ heltal

Returnerer det antal tegn, der er indeholdt i tegnstrengen Streng.

Disp

Disp [udtrykEllerStreng1] [, udtrykEllerStreng2] ...

Viser argumenterne i Calculator historikken. Argumenter ne vises efter hinanden med små mellemrum som separator.

Anvendes hovedsagelig i programmer og funktioner til at sikre at mellemregninger vises.

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

Katalog

26 TI-Nspire™ Opslagsvejledning

DMS

4DMS

Tal List 4DMS Matrix 4DMS

Tolker argumentet som en vinkel og viser tilsvarende tal for grader (D), minutter (M) og sekunder (S/s) (DDDDDD¡MM'SS.ss''). Se mere om DMS-formatet for grader, minutter og sekunder

113.

Bemærk: 4DMS konverterer fra radianer til grader ved anvendelse i

radiantilstanden. Hvis inputtet følges af et grader-symbol ¡, sker der ingen konvertering. Du kan kun anvende 4DMS ved slutningen af en indtastningslinje.

¡, ', '' på side

I vinkeltilstanden Grader:

Katalog

dotP()

dotP(Liste1, Liste2) ⇒ udtryk

Returnerer “prik”produktet af to lister.

dotP(Vektor1, Vektor2) ⇒ udtryk

Returner “prik”produktet af to vektorer. Begge skal være rækkevektorer, eller begge skal være

kolonnevektorer.

e^()

e^(Værdi1) ⇒ værdi

Returnerer e opløftet til potensen Værdi1.

Bemærk: Se også e Eksponentskabelon, side 2. Bemærk: At trykke /u for at vise

som at trykke på tegnet E på tastaturet.

Du kan indtaste et komplekst tal i re denne form i vinkeltilstanden Radian. Den forårsager e n domænefejl i vinkeltilstandene Grader eller Nygrader.

e^(Liste1) ⇒ liste

Returnerer e opløftet til potensen af hvert element i Liste1.

e^(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer matrix eksponentialfunktion af kvadratMatrix1. Dette er ikke det samme som at beregne e opløftet til potensen af hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

^(er ikke det samme

i q

polær form. Anvend dog kun

Katalog

u-tast

TI-Nspire™ Opslagsvejledning 27

eff()

eff(nominelRente,CpY) ⇒ værdi

Finansfunktion, der omregner den nominelle rente nominelRente til en effektiv årlig rente, hvor CpY er antallet af rentetilskrivninger per år.

nominelRente skal være et reelt tal, og CpY skal være et reelt tal >

Bemærk: Se også nom(), side 61.

Katalog

eigVc()

eigVc(kvadratMatrix) ⇒ matrix

Returnerer en matrix med egenvektorerne for en reel eller kompleks kvadratMatrix, hvor hver kolonne i resultatet svarer til en egenværdi. Bemærk, at en egenvektor ikke er unik. Den kan skaleres af enhver konstantfaktor. Egenvektorerne er normaliseret, dvs. at hvi s V = [x1, x2, …, xn], så:

+ … + x

= 1

kvadratMatrix balanceres først med similaritetstransformationer, til række- og kolonnenormer er så tæt som muligt på samme værdi. KvadratMatrix reduceres derefter til øvre Hessenberg form, og egenvektorerne beregnes via en Schur faktorisering.

I rektangulært komplekst format:

Du kan se hele resultatet ved at trykke på £ og derefter

Katalog

anvende ¡ og ¢ til at bevæge markøren.

eigVl()

eigVl(kvadratMatrix) ⇒ liste

Returnerer en liste med egenværdier af en reel eller kompleks

kvadratMatrix. kvadratMatrix balanceres først med similaritetstransformationer, til

række- og kolonnenormer er så tæt som muligt på samme værdi. KvadratMatrix reduceres derefter til øvre Hessenberg form, og egenværdierne beregnes fra øvre Hessenberg-matricen.

I rektangulær kompleks formattilstand:

Katalog

Du kan se hele resultatet ved at trykke på £ og derefter anvende ¡ og ¢ til at bevæge markøren.

Else Se If, side 39.

28 TI-Nspire™ Opslagsvejledning

ElseIf

If Boolsk Udtr1 Then

Blok1

ElseIf Boolsk Udtr2 Then

Blok2

Boolsk UdtrN Then

ElseIf

BlokN

EndIf

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

EndFor Se For, side 33.

EndFunc Se Func, side 35.

EndIf Se If, side 39.

EndLoop Se Loop, side 53.

EndPrgm Se Prgm, side 68.

Katalog

EndTry Se Try, side 92.

EndWhile Se While, side 98.

TI-Nspire™ Opslagsvejledning 29

Exit

Afslutter den aktuelle For, While, eller Loop-blok.

Exit er ikke tilladt uden for de tre løkkestrukturer (For, While, eller Loop).

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at

@ i stedet for · ved slutningen af hver linje. På

trykke på computerens tastatur skal du holde Alt nede og trykke på Enter.

Funktionsliste:

Katalog

exp()

exp(Værdi1) ⇒ værdi

Returnerer e opløftet til potensen Udtr1. Returnerer e opløftet til potensen Værdi1.

Bemærk: Se også e eksponentskabelon, side 2.

Du kan indtaste et komplekst tal i reI denne form i vinkeltilstanden Radian. Den forårsager e n domænefejl i vinkeltilstandene Grader eller Nygrader.

exp(Liste1) ⇒ liste

Returnerer e opløftet til potensen af hvert element i Liste1.

exp(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer matrix eksponentialfunktion af kvadratMatrix1. Dette er ikke det samme som at beregne e opløftet til potensen af hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

expr()

expr(Stren g) ⇒ udtryk

Returnerer den tegnstreng, der er indeholdt i Stre ng som et udtryk og og eksekverer den straks.

q polær form. Anvend dog kun

u-tast

Katalog

30 TI-Nspire™ Opslagsvejledning

ExpReg

ExpReg X, Y [, [Frekv] [, Kategori, Medtag]]

Beregner the polynomielle tredjegradsregression y = a·(b)xpå listerne X og Y med hyppighed Frekv. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have ens dimensioner med undtagelse af Medtag.

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiver hyppigheden af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer, hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output-variabel Beskrivelse

stat.RegEqn

stat.a, stat.b Regressionskoefficienter

stat.r

stat.r Korrelationskoefficient til transformerede data (x, ln(y))

stat.Resid

stat.ResidTrans Residualer associeret med lineær tilpasning af transformerede data

stat.XReg Liste af datapunkter i den modificerede X-liste, der faktisk bruges i regressionen ud fra begrænsninger af

stat.YReg Liste af datapunkter i den modificerede Y- li st e, der faktisk bruges i regressionen ud fra begrænsninger af

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

Regressionsligning: a·(b)

Koefficient af en lineær forklaringsgrad til transformerede data

Residualer af kurvetilpasningen = y - a·(b)

Hyppighed, Kategoriliste og Medtag kategorier

Katalog

factor()

factor(rationaltTal) returnerer det rationale tal opløst i primtal. Ved

sammensatte tal øges beregningstiden eksponentielt med antallet af cifre i den næststørste faktor. Opløsning af et 30-cifret heltal kan for eksempel vare længere end en dag, og opløsning af et 100-cifret tal kan vare længere end et århundrede.

Bemærk: Du kan standse (afbryde) en beregning ved at trykke

på u.

Hvis du kun vil bestemme, om et tal er et primtal, skal du anvende

isPrime() i stedet. Det er meget hurtigere, især hvis RationaltTal

ikke er et primtal, og den næststørste faktor har mere end fem cifre.

TI-Nspire™ Opslagsvejledning 31

Katalog

FCdf()

FCdf(nedreGrænse,øvreGrænse,fgTæller,fgNævner) ⇒ tal

nedreGrænse og øvreGrænse er tal, liste hvis nedreGrænse

hvis

øvreGrænse er lister

FCdf(

nedreGrænse,øvreGrænse,fgTæller,fgNævner) ⇒ tal hvis nedreGrænse og øvreGrænse er tal, liste hvis nedreGrænse og øvreGrænse er lister

Beregner F sandsynlighedsfordelingen mellem nedreGrænsed og øvreGrænse for den angivne dfTæller (frihedsgrader) og dfNævner.

For P(X  øvreGrænse), sæt nedreGrænse=0.

Katalog

Fill

Fill Tal, matrixVar ⇒ matrix

Erstatter hvert element i variablen matrixVar med Udtr. matrixVar skal eksistere i forvejen.

Fill Tal, listVar ⇒ liste

Erstatter hvert element i variablen Listevar med Udtr. Listevar skal eksistere i forvejen.

FiveNumSammendrag

FiveNumSummary X[, [Frekvv][ Kategori,Medtag]]

Frembringer en forkortet version af 1-variabelstatistikken på listen X. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

X repræsenterer en liste med dataene. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekv¨angiver hyppigheden af hver tilsvarende X værdi.

Standardværdien er 1. Alle elementer skal være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X værdier.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer, hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output-variabel Beskrivelse

stat.MinX Minimum af x-værdier

stat.Q1X 1. kvartil af x

stat.MedianX Median af x

stat.Q3X 3. kvartil af x

stat.MaxX Maksimum af x-værdier

Katalog

32 TI-Nspire™ Opslagsvejledning

floor()

floor(Værdi1) ⇒ heltal

Returnerer det største heltal, der er { argumentet. Denne funktion er identisk med int().

Argumentet kan være et reelt eller komplekst tal.

floor(Liste1) ⇒ liste floor(Matrix1) ⇒ matrix

Returnerer en liste eller matrix med nedrunding af hvert element.

Bemærk: Se også ceiling() og int().

Katalog

For

For Var , Lav, Høj [, Tr in]

Blok

EndFor

Eksekverer sætningerne i blok iterativt for hver værdi af Var fra Lav til Høj i intervaller på Tri n.

Var må ikke være en systemvariabel. Tri n kan være positiv eller negativ. Standardværdien er 1. Blok kan enten være en enkelt sætning eller en serie sætninger

adskilt med kolon.

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

format()

format(Tal [, formatStreng]) ⇒ streng

Returnerer Tal som en tegnstreng baseret på formatskabelonen. formatStreng er en streng og skal være på formen: “F[n]”, “S[n]”,

“E[n]”, “G[n][c]”, hvor [ ] angiver valgfrie dele. F[n]: Fast format. n er det antal cifre, der vises efter decimalpunktet. S[n]: Videnskabeligt format. n er det antal cifre, der vises efter

decimalpunktet. E[n]: Teknisk format. n er antallet af cifre efter det betydende ciffer.

Eksponenter er justeret til et multiplum af tre, og decimalpunktet flyttes til højre med nul, en eller to pladser.

G[n][c]: Samme som fast format men skiller også cifrene til ve nstre for decimalpunktet i grupper på tre. c angiver gruppeskilletegnet og er som standard et komma. Hvis c er et punktum, vises grundtallet som et komma.

[Rc]: Alle ovennævnte angivelser kan udvides med Rc-grundtalflaget, hvor c er et enkelt tegn, der angiver, hvad der skal substitueres for grundtalspunktet.

Katalog

TI-Nspire™ Opslagsvejledning 33

fPart()

fPart(Udtr1) ⇒ udtryk fPart(Liste1) ⇒ liste fPart(Matrix1) ⇒ matrix

Returnerer decimaldelen af argumentet. For en liste eller matrix returneres decimaldelen af elementerne. Argumentet kan være et reelt eller komplekst tal.

Katalog

FPdf()

FPdf(XVærdi,dfTæller,dfNævner)

XVærdi,dfTæller,dfNævner)

FPdf(

Beregner F sandsynlighedsfordelingen på XVal for den angivne dfTæller (frihedsgrader i tælleren) og dfNævner (frihedsgrader i nævneren).

freqTable4list()

freqTable4liste(Liste1,frekvHeltalListe) ⇒ liste

Returnerer en liste indeholdende elementerne fra Liste1 udvidet i henhold til hyppighederne i frekvHeltalListe. Denne funktion kan anvendes til at danne en frekvenstabel for Data- & Statistikapplikationerne.

Liste1 kan være enhver gyldig liste. frekvHeltalListe skal have den samme dimension som Liste1 og må

kun indeholde ikke-negative heltalselementer. Hvert element angiver det antal gange det tilsvarende Liste1 element vil blive gentaget i resultatlisten. En nul-værdi udelukker det tilsvarende Liste1 element.

frequency()

frequency(Liste1,binsListe) ⇒ liste

Returnerer en liste, der indeholder optælling af elementerne i Liste1. Antallene er baseret på områder (bins), som du definerer i binsListe.

Hvis binsListe er {b(1), b(2), …, b(n)}, er de specificerede områder {?{b(1), b(1)<?{b(2),…,b(n-1)<?{b(n), b(n)>?}. Den resulterende liste er et element længere end binsListe.

Hvert element af resultatet svarer til antallet af elementer fra Liste1, der er i dette område. Udtrykt med countIf()-funktionen er resultatet { countIf(liste, ?{b(1)), countIf(liste, b(1)<?{b(2)), …,

countIf(liste, b(n-1)<?{b(n)), countIf(liste, b(n)>?)}.

Elementer i Liste1, der ikke kan “placeres i et område” ignoreres. I applikationen Lister og regneark kan du anvende et celleområde i

stedet for begge argumenter.

Bemærk: Se også countIf(), side 19.

Katalog

Forklaring af resultatet:

2 elementer fra Dataliste er {2.5 4 elementer fra Dataliste er >2,5 og {4,5 3 elementer fra Dataliste er >4,5

Elementet "hello" er en streng og kan ikke placeres i nogen af de definerede områder.

34 TI-Nspire™ Opslagsvejledning

FTest_2Samp

Liste1,Liste2[,Hyppighed1[,Hyppighed2[,Hypot]]]

FTest_2Samp

Liste1,Liste2[,Hyppighed1[,Hyppighed2[,Hypot]]]

(Datalisteinput)

FTest_2Samp sx1,n1,sx2,n2[,Hypot]

FTest_2Samp

(Sammenfatning, stat input) Udfører en F test med to målinger. En sammenfatning af resultaterne

lagres i variablen stat.results. (Se side 85.)

eller Ha: s1 > s2, sæt Hypot>0 Til Ha: s1 ƒ s2 (standard), sæt Hypot =0 Til Ha: s1 < s2, sæt Hypot<0

Output-variabel Beskrivelse

stat.F

stat.PVal Mindste signifikansniveau, ved hvilket nul-hypotesen kan forkastes

stat.dfTæller frihedsgrader for tæller = n1-1

stat.dfNævner tæller, frihedsgrader = n2-1

stat.sx1, stat.sx2 Stikprøve standardafvigelse for datasekvenserne i Liste 1 og Liste 2

stat.x1_bar stat.x2_bar

stat.n1, stat.n2 Størrelse på stikprøverne

sx1,n1,sx2,n2[,Hypot]

Beregnet ó statistik for datasekvensen

Middelværdi af stikprøver for datasekvenserne i Liste 1 og Liste 2

Katalog

Func

Blok

EndFunc

Skabelon til oprettelse af en brugerdefineret funktion. Blok kan være en enkelt sætning, en serie sætninger adskilt med

kolon eller en serie sætninger på separate linjer. Funktionen kan anvende Return-instruktionen til at returnere et specifikt resultat.

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

Definition af en stykvis funktion:

Tegnet resultat af grafen g(x)

Katalog

TI-Nspire™ Opslagsvejledning 35

gcd()

gcd(Værdi1, V ærdi2) ⇒ udtryk

Returnerer den største fælles divisor af to argumenter. brøker er gcd af deres tællere divideret med lcm af deres nævnere.

I Auto- eller Approks- tilstand er gcd af flydende decimalbrøker 1.0.

gcd(Liste1, Liste2) ⇒ liste

Returnerer de største fælles divisorer af de tilsvarende elementer i Liste1 og Liste2.

gcd(Matrix1, Matrix2) ⇒ matrix

Returnerer de største fælles divisorer af de tilsvarende elementer i Matrix1 og Matrix2.

geomCdf()

geomCdf(p,nedreGrænse,øvreGrænse) ⇒ tal, hvis

nedreGrænse og øvreGrænse er tal, liste, hvis nedreGrænse og øvreGrænse er lister

geomCdf(

p,øvreGrænse) ⇒ tal hvis øvreGrænse er et tal,

liste, hvis øvreGrænse er en liste

Beregner den kumulerede geometriske sandsynlighed fra nedreGrænse til øvreGrænse med den angivne sandsynlighed for succes p.

For P(X  øvreGrænse), sæt nedreGrænse= 1.

geomPdf()

geomPdf(p,XVærdi) ⇒ tal hvis XVærdi er et tal, liste hvis

XVærdi er en liste

Beregner sandsynligheden i XVærdi, nummeret på den forsøgsgang hvor den første succes forekommer, for den diskrete geometrisk distribution med den angivne sandsynlighed for succes, p.

Gcd for to

Katalog

getDenom( )

getDenom(Brøk1) ⇒ værdi

Transformerer argumentet til et udtryk med en forkortet fællesnævner og returnerer derefter dens nævner.

Katalog

36 TI-Nspire™ Opslagsvejledning

getLangInfo( )

getLangInfo() ⇒ streng

Returnerer en streng, som svarer til det korte navn af det aktuelle aktive sprog. Man kan, for eksempel, bruge det i et program eller funktion til at bestemme det aktuelle sprog.

Engelsk = "en" Dansk = "da" Tysk = "de" Finsk = "fi" Fransk = "fr" Italiensk = "den" Hollandsk = "nl" Belgisk Hollandsk = "nl_BE" Norsk = "no" Portugisisk = "pt" Spansk = "es" Svensk = "sv"

Katalog

getMode()

getMode(TilstandNavnHeltal) ⇒ værdi getMode(0) ⇒ liste

getMode(TilstandNavnHeltal) returnerer en værdi, der

repræsenterer den aktuelle indstilling for tilstanden TilstandNavnHeltal.

getMode(0) returnerer en liste, der indeholder talpar. Hvert par

består af et tilstandsheltal og et indstillingsheltal. Se tabellen nedenfor for en oversigt over tilstande og deres

indstillinger.

Hvis du gemmer indstillingerne med getMode(0) & var, kan du anvende setMode(var) i en funktion eller et program for midlertidigt at gendanne indstillingerne under eksekveringen af funktionen eller programmet. Se setMode(), side 79.

Tilstandsnavn

Viste cifre

Vinkel

Eksponentielt format

Reel eller kompleks

Auto eller tilnærmet

Vektorformat

Talsystem

Tilstandsheltal Indstillingsheltal

=Float, 2=Float1, 3=Float2, 4=Float3, 5=Float4, 6=Float5, 7=Float6, 8=Float7,

1 9=Float8, 10=Float9, 11=Float10, 12=Float11, 13=Float12, 14=Fix0, 15=Fix1, 16=Fix2, 17=Fix3, 18=Fix4, 19=Fix5, 20=Fix6, 21=Fix7, 22=Fix8, 23=Fix9, 24=Fix10, 25=Fix11, 26=Fix12

=Radian, 2=Grader, 3=Gradian

=Normal, 2=Videnskabelig, 3=Teknisk

=Reel, 2=Rektangulær, 3=Polær

=Auto, 2=Tilnærmet

=Rektangulær, 2=Cylindrisk, 3=Sfærisk

=Decimal, 2=Hex, 3=Binær

Katalog

TI-Nspire™ Opslagsvejledning 37

getNum()

getNum(Brøk1) ⇒ værdi

Transformerer argumentet til et udtryk med en forkortet fællesnævner og returnerer derefter dens tæller.

Katalog

getVarInfo()

getVarInfo() ⇒ matrix eller streng getVarInfo(BibNavnStreng) ⇒ matrix eller streng

getVarInfo() returnerer en matrix med oplysninger (variabelnavn,

type og biblioteksadgang) for alle variable og biblot eksobjeker, der er defineret i den aktuelle opgave.

Hvis der ikke er defineret nogen variable, returnerer getVarInfo() strengen "NONE"

getVarInfo(Biblioteksnavnestreng) returnerer en matrix med

oplysninger for alle biblioteksobjekter, der er defineret i biblioteket BibNavnStreng. BibNavnStreng skal være en streng (tekst omsluttet af citationstegn) eller en strengvariabel.

Hvis biblioteket BibNavnStreng ikke findes, opstår der en fejl.

Bemærk eksemplet til venstre, i hvilket resultatet af getVarInfo() er tilknyttet til variabel vs. Forsøg på at vise række 2 eller række 3 af vs returnerer en “ugyldig liste eller matrix” fejl, fordi mindst et af elementerne i disse rækker (variable b, f.eks) reevaluerer til en matrix.

Denne fejl kan også opstå, når Ans bruges til at evaluere et

getVarInfo() resultat.

Systemet giver den ovenfor nævnte fejl, fordi den aktuelle version af softwaren ikke understøtter en generaliseret matrixstruktur, hvor et element i en matrix enten kan være en matrix eller en liste.

Katalog

38 TI-Nspire™ Opslagsvejledning

Goto

Goto etiketnavn

Overfører kontrol til etiketten etiketnavn. Etiketnavn skal defineres i den samme funktion med en

kommando.

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

Grad

Udtr1 4 Grad ⇒ udtryk

Konverterer Udtr1 til vinkelmål i nygrader.

Lbl-

I vinkeltilstanden Grader:

I vinkeltilstanden Radian:

Katalog

identity()

identity(Heltal) ⇒ matrix

Returnerer identitetsmatricen med en dimension Heltal. Heltal skal være et positivt heltal.

If Boolsk udtryk Sætning If Boolsk udtryk Then

Blok

EndIf

Hvis Boolsk udtryk evalueres som true, eksekveres enkeltsætningen sætning eller sætningsblokken Blok, før eksekveringen fortsættes.

Hvis Boolsk udtryk evalueres som false, fortsættes eksekveringen uden eksekvering af sætningen eller sætningsblokken.

Blok kan enten være en enkelt sætning eller en serie sætninger adskilt med kolon.

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

Katalog

TI-Nspire™ Opslagsvejledning 39

If Boolsk udtryk Then

Blok1

Else

Blok2

EndIf

Hvis Boolsk udtryk evalueres som true, eksekveres Blok1 og Blok2 springes over.

Hvis Boolsk udtryk evalueres som false, springes over Blok1, men

Blok2 eksekveres. Blok1 og Blok2 kan være en enkelt sætning.

If Boolsk Udtr1 Then

Blok1

ElseIf

Boolsk Udtr2 Then

Blok2

Boolsk UdtrN Then

ElseIf

BlokN

EndIf

Muliggør en forgrening. Hvis Boolsk Udtr1 evalueres som true, eksekveres Blok1. Hvis Boolsk Udtr1 evalueres som false, evalueres Boolsk Udtr2, osv.

Katalog

40 TI-Nspire™ Opslagsvejledning

ifFn()

ifFn(BoolskUdtryk,Værdi_Hvis_sand [,Værdi_Hvis_falsk

Værdi_Hvis_ukendt]]) ⇒ udtryk, liste eller matrix

Beregner det boolske udtryk BoolskUdtryk (eller hvert element i BoolskUdtryk) og giver et resultat baseret på følgende regler:

• BoolskUdtryk kan teste en enkelt værdi, en liste eller en matrix.

• Hvis et element i BoolskUdtryk evaluerer sandt, returneres det tilsvarende element fra Værdi_Hvis_sandt.

• Hvis et element i BoolskUdtryk evaluerer falsk, returneres det tilsvarende element fra Værdi_Hvis_falsk. Hvis du udelader Værdi_Hvis_falsk, returneres undef.

• Hvis et element i BoolskUdtryk hverken er sandt eller falsk, returneres det tilsvarende element Værdi_Hvis_ukendt. Hvis du udelader Værdi_Hvis_ukendt, returneres undef.

• Hvis det andet, tredje eller fjerde argument i er et enkelt udtryk, udføres den Boolske test på hver position i BoolskUdtryk.

Bemærk: Hvis den reducerede BoolskUdtryk-sætning indeholder

en liste eller matrix, skal alle andre liste- eller matrixargumenter have de samme dimensioner, eller resultatet have de samme dimensioner.

ifFn()-funktionen

Katalog

Testværdien for 1 er mindre end 2,5, så dens tilsvarende Værdi_Hvis_Sandt-element på 5 kopieres til resultatlisten.

Testværdien for 2 er mindre end 2,5, så dens tilsvarende Værdi_Hvis_Sandt-element på 6 kopieres til resultatlisten.

Testværdien for 3 er ikke mindre end 2,5, så den tilhørende

Værdi_Hvis_Falsk element på 10 kopieres til resultatlisten.

Værdi_Hvis_sandt er en enkelt værdi og svarer til enhver valgt

position.

Værdi_Hvis_falsk er ikke specificeret. Undef anvendes.

Et element valgt fra Værdi_Hvis_sandt. Et element valgt fra Værdi_Hvis_ukendt.

imag()

imag(Værdi1) ⇒ værdi

Katalog

Returnerer imaginærdelen af argumentet.

Bemærk: Alle udefinerede variable behandles som reelle variable.

Se også real(), side 73

imag(Liste1) ⇒ liste

Returnerer en liste med imaginærdelen af elementerne.

imag(Matrix1) ⇒ matrix

Returnerer en matrix med imaginærdelene af elementerne.

Indirection Se

inString()

inString(Søgestreng, Delstreng[, Start]) ⇒ heltal

Returnerer tegnpositionen i strengen Søgestreng, hvor første forekomst af strengen Delstreng begynder.

Start, hvis medtaget, angiver den position i Søgestreng, hvor søgningen begynder. Standard = 1 (første tegn i Søgestreng).

Hvis Søgestreng ikke indeholder Delstreng, eller Start, er > længden på Søgestreng, returneres nul.

#()

Katalog

, side 112.

TI-Nspire™ Opslagsvejledning 41

int()

int(Ta l) ⇒ heltal int(Liste1) ⇒ liste int(Matrix1) ⇒ matrix

Returnerer det største heltal, der er mindre end eller lig med argumentet. Denne funktion identisk med

floor().

Argumentet kan være et reelt eller komplekst tal. For lister og matricer returneres det største heltal mindre end eller lig

med hvert element.

Katalog

intDiv()

intDiv(Værdi1, Værdi2) ⇒ heltal intDiv(Liste1, Liste2) ⇒ liste intDiv(Matrix1, Matrix2) ⇒ matrix

Returnerer det heltal med fortegn, der er en del af (Værdi1 ÷ Værdi2).

Returnerer ved lister og matricer heltalsdelen med fortegn af (argument 1 ÷ argument 2) for hvert elementpar.

invc2()

invc2(Område,fg)

Område,fg)

invChi2(

Beregner den inverse kufgTæller c2 (chi-kvadrat) sandsynlighedsfunktion angivet ved frihedsgrad, fg for et givet Område under kurven.

invF()

invF(område,fgTæller,fgNævner)

område,fgTæller,fgNævner)

invF(

Beregner den inverse kumulerede F distributi onsfunktion angivet ved fgTæller og fgNævner for et givet område under kurven.

invNorm()

invNorm(område[,m,s])

Beregner den inverse kumulerede normalfordelingsfunktion for et givet område under normalfordelingskurven angivet ved m og s.

invt()

invt(område,fg)

Beregner den inverse kumulerede student-t sandsynlighedsfunktion angivet ved frihedsgrad, fg for et givet område under kurven.

Katalog

42 TI-Nspire™ Opslagsvejledning

iPart()

iPart(Værdi1) ⇒ heltal iPart(Liste1) ⇒ liste iPart(Matrix1) ⇒ matrix

Returnerer heltalsdelen af argumentet. Returnerer heltalsdelen af hvert element ved lister og matricer. Argumentet kan være et reelt eller komplekst tal.

Katalog

irr()

irr(CF0,CFListe [,CFFrekv]) ⇒ værdi

Finansfunktion, der beregner den interne rente af en investering. CF0 er startpengestrømmen på tidspunkt 0; den skal være et reelt

tal. CFListe er en liste over pengestrømsbeløb efter startpengestrømmen

CF0. CFFrekv er en valgfri liste, hvor hvert element angiver hyppigheden

for et grupperet (fortløbende) pengestrømsbeløb, som er det tilsvarende element i CFListe. Standardværdien er 1; Hvis du indtaster værdier, skal de være positive heltal < 10.000.

Bemærk: Se også mirr(), side 56.

isPrime()

isPrime(Tal ) ⇒ Boolsk konstantudtryk

Returnerer true eller false for at vise, om Tal er et helt tal ‚ 2, der kun kan divideres med sig selv og 1.

Hvis Tal har flere end ca. 306 cifre og ikke har nogen faktorer {1021, viser isPrime(Ta l) en fejlmeddelelse.Note til indtastning af

eksemplet:

indtaste definitioner over flere linjer ved at trykke på @ i stedet for

I Regner-applikationen på den håndholdte kan du

· ved slutningen af hver linje. På computerens tastatur skal du

holde Alt nede og trykke på Enter.

Katalog

Funktion til søgning af det næste primtal efter det angivne tal:

TI-Nspire™ Opslagsvejledning 43

Lbl

Lbl etiketNavn

Definerer en etiket med navnet etiketNavn i en funktion. Du kan anvende en Goto etiketNavn-kommando til at videregive

kontrollen til kommandoen lige efter etiketten. EtiketNavn skal opfylde de samme navngivningskrav som et

variabelnavn.

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

lcm()

lcm(Værdi1, Værdi2) ⇒ udtryk lcm(Liste1, Liste2) ⇒ liste lcm(Matrix1, Matrix2) ⇒ matrix

Returnerer det mindste fælles multiplum af to argumenter. lcm af to brøker er lcm af deres tællere divideret med gcd af deres nævnere.

lcm af brøker med flydende komma er deres produkt.

For to lister eller matricer returneres det mindste fælles multiplum af deres tilsvarende elementer.

left()

left(kildeStreng[, Tal ]) ⇒ streng

Returnerer Antal-tegn fra venstre i tegnstrengen kildeStreng. Hvis du udelader Antal, returneres alle kildeStreng-variable.

left(Liste1[, Antal]) ⇒ liste

Returnerer Antal-elementer til venstre i Liste1. Hvis du udelader Antal, returneres hele Liste1.

left(Sammenligning) ⇒ udtryk

Returnerer venstre side af en ligning eller ulighed.

Katalog

44 TI-Nspire™ Opslagsvejledning

libShortcut()

libShortcut(BibNavneStreng, GenvejNavneStreng [, BibPrivFlag]) ⇒ liste med variable

Opretter en variabelgruppe i den aktuelle opgave, som indeholder referencer til alle objekter i det specificerede biblioteksdokument bibNavneStreng. Tilføjer også gruppemedlemmerne til variabelmenuen. Du kan henvise til hvert objekt ved brug af GenvejNavneStreng.

Sæt BibPrivFlag = (standard) Sæt BibPrivFlag = 1 for at medtage private biblioteksobjekter

For at kopiere en variabelgruppe, se CopyVar på side 15. For at slette en variabelgruppe, se DelVar på side 25.

0 for at udelukke private biblioteksobjekter

Katalog

Dette eksempel forudsætter et korrekt gemt og opdateret biblioteksdokument med navnet, linalg2, som indeholder objekter defineret som clearmat, gauss1, og gauss2.

LinRegBx

LinRegBx X, Y[, [Frekv][ Kategori, Medtag]]

Beregner den lineære regression y = a+b·x på listerne X og Y med hyppigheder Frekv. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have ens dimensioner med med undtagelse af undtagelse af Medtag.

Katalog

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiver hyppigheden af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output-variabel Beskrivelse

stat.RegEqn

Regressionsligning: a+b·x

stat.a, stat.b Regressionskoefficienter

stat.r

Forklaringsgraden

stat.r Korrelationskoefficient

stat.Resid Residualer fra regressionen

stat.XReg Liste af datapunkter i den modificerede X-liste der faktisk bruges i regressionen ud fra begrænsninger i

stat.YReg Liste af datapunkter i den modificerede Y- li st e der faktisk bruges i regressionen ud fra begrænsninger i

Frekv, kategoriliste,og Medtag kategorier

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

TI-Nspire™ Opslagsvejledning 45

LinRegMx

LinRegMx X, Y[, [Frekv][ Kategori, Medtag]]

Beregner den lineære regression y = m· x+b på listerne X og Y med hyppighed Frekv. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have ens dimensioner med med undtagelse af undtagelse af Medtag.

Katalog

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiver hyppigheden af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output-variabel Beskrivelse

stat.RegEqn

Regressionsligning: m·x+b

stat.m, stat.b Regressionskoefficienter

stat.r

Forklaringsgraden

stat.r Korrelationskoefficient

stat.Resid Residualer fra regressionen

stat.XReg Liste af datapunkter i den modificerede X-liste der faktisk bruges i regressionen ud fra begrænsninger i

stat.YReg Liste af datapunkter i den modificerede Y- li st e der faktisk bruges i regressionen ud fra begrænsninger i

Frekv, kategoriliste,og Medtag kategorier

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

LinRegtIntervaller

LinRegtIntervals X,Y[,Frekv[,0[,CNiveau]]]

Katalog

Til hældning. Beregner et niveau C konfidensinterval for hældningen.

LinRegtIntervals X,Y[,Frekv[,1, Xval [, CNiveau]]]

Åbent svar Beregner en forudset y-værdi, et niveau C forudsigelsesinterval for enkle observationer, og et niveau C konfidensinterval til gennemsnits-responsen.

En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have samme dimension.

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiver hyppigheden af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

46 TI-Nspire™ Opslagsvejledning

Output-variabel Beskrivelse

stat.RegEqn

stat.a, stat.b Regressionskoefficienter

stat.fg Frihedsgrader

stat.r

stat.r Korrelationskoefficient

stat.Resid Residualer fra regressionen

Kun for hældningstypen

Output-variabel Beskrivelse

[stat.CLower, stat.CUpper]

stat.ME Konfidensinterval, fejlmargen

stat.SESlope Standarfejl for hældning

stat.s Standardfejl for linjen

Kun for svartype

Output-variabel Beskrivelse

[stat.CLower, stat.CUpper]

stat.ME Konfidensinterval, fejlmargen

stat.SE Standardfejl for middelværdi

[stat.LowerPred , stat.UpperPred]

stat.MEPred Prædiktionsintervalsmargin for fejl

stat.SEPred standardfejl for prædiktion

Statistik.y

Regressionsligning: a+b·x

Forklaringsgraden

Konfidensinterval for hældningen

Konfidensinterval for en middelværdi

Prædiktionsinterval for en enkelt observation

a + b·XVærdi

TI-Nspire™ Opslagsvejledning 47

LinRegtTest

LinRegtTest X,Y[,Frekv[,Hypot]]

Beregner en lineær regression ud fra X og Y listerne og en t test på værdien af hældningen b og korrelationskoefficienten r for ligningen y=a+bx. Den tester nulhypotesen H0:b=0 (ækvivalent, r=0) mod en af tre alternative hypoteser.

Alle lister skal have samme dimension.

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiver hyppigheden af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Hypot er en valgfri værdi, som angiver en af tre alternative hypoteser, mod hvilken nul-hypotesen (H0:b=r=0) vil blive testet.

Til Ha: bƒ0 og rƒ0 (standard), sæt Hypot=0 Til Ha: b<0 og r<0, sæt Hypot<=0 Til Ha: b>0 og r>0, sæt Hypot> 0

En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Output-variabel Beskrivelse

stat.RegEqn

stat.t t-Statistik for signifikanstest

stat.PVal Mindste signifikansniveau, ved hvilket nul-hypotesen kan forkastes

stat.fg Frihedsgrader

stat.a, stat.b Regressionskoefficienter

stat.s Standardfejl for linjen

stat.SESlope Standarfejl for hældning

stat.r

stat.r Korrelationskoefficient

stat.Resid Residualer fra regressionen

Regressionsligning: a + b·x

Forklaringsgraden

katalog

list()

Katalog

@list(Liste1) ⇒ liste

Returnerer en liste med differenserne mellem konsekutive elementer i Liste1. Hvert element i Liste1 er subtraheret fra det næste element i Liste1. Den resulterende liste er altid et element kortere end den oprindelige Liste1.

48 TI-Nspire™ Opslagsvejledning

list4mat()

list4mat(Liste [, elementerPrRække]) ⇒ matrix

Returnerer en matrix fyldt rækkevis med elementerne fra Liste. ElementerPrRække angiver antallet af elementer pr. række, hvis den

er medtaget. Standard er antallet af elementer i Liste (en række). Hvis Liste ikke udfylder den resulterende matrix, tilføjes nuller.

Katalog

ln()

ln(Værdi1) ⇒ værdi ln(Liste1) ⇒ liste

Returnerer den naturlige logaritme til argumentet. Til en liste returneres de naturlige logaritmer af elementerne.

ln(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer den naturlige matrixlogaritme af kvadratMatrix1. Dette er ikke det samme som at beregne den naturlige logaritme af hvert element. Oplysninger om beregningsmetoden findes under cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

LnReg

LnReg X, Y[, [Frekv] [, Kategori, Medtag]]

Beregner den lineære regression y = a+b· ln(x)på liste X og Y med hyppighed Frekv. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have ens dimensioner med undtagelse af Medtag.

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiver hyppigheden af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer, hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Katalog

-taster

Hvis kompleks formattilstand er reel:

Hvis kompleks formattilstand er rektangulær:

I vinkeltilstanden radian og rektangulært komplekst format:

Du kan se hele resultatet ved at trykke på £ og derefter anvende ¡ og ¢ til at bevæge markøren.

TI-Nspire™ Opslagsvejledning 49

Output-variabel Beskrivelse

stat.RegEqn

Regressionsligning: a+b· ln(x)

stat.a, stat.b Regressionskoefficienter

stat.r

Koefficient af en lineær forklaringsgrad til transformerede data

stat.r Korrelationskoefficient til transformerede data (ln(x), y)

stat.Resid Residualer forbundet med eksponentielmodellen

stat.ResidTrans Residualer associeret med lineær tilpasning af transformerede data

stat.XReg Liste af datapunkter i den modificerede X-liste der faktisk bruges i regressionen ud fra begrænsninger i

stat.YReg Liste af datapunkter i den modificerede Y- li st e der faktisk bruges i regressionen ud fra begrænsninger i

Frekv, kategoriliste,og Medtag kategorier

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

Local

Local Var 1 [, Va r 2] [, Va r 3 ] ...

Erklærer de angivne var som lokale variable. Disse variable eksisterer kun under beregning af en funktion og slettes, når eksekveringen af funktionen afsluttes.

Bemærk: Lokale variable sparer hukommelse, fordi kun eksisterer

midlertidigt. De forstyrrer heller ikke de eksisterende globale variabelværdier. Lokale variable skal anvendes til For-løkker og midlertidig lagring af variabelværdier i en flerlinjefunktion da modifikationer af globale ikke er tilladt i en funktion.

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje.

På computerens tastatur skal du holde Alt nede og trykke på Enter.

Katalog

50 TI-Nspire™ Opslagsvejledning

log()

log(Værdi1[,Værdi2]) ⇒ værdi log(Liste1[,Værdi2]) ⇒ list

Returner -Udtr2-talslogaritmen til argumentet.

Bemærk: Se også Log-skabelon, side 2.

Ved en liste returneres Udtr2-talslogaritmen til elementerne. Hvis Udtr2 udelades, anvendes 10-talslogaritmen.

Hvis kompleks formattilstand er reel:

Hvis kompleks formattilstand er rektangulær:

-taster

log(kvadratMatrix1[,Værdi2]) ⇒ kvadratMatrix

Returnerer matrix Værdi2-logaritmen til kvadratMatrix1. Dette er ikke det samme som at beregne Værdi2-talslogaritmen til hvert element Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

Hvis tal-argumentet udelades, anvendes 10-talslogaritmen.

Logistic

Logistik X, Y[, [Frekv] [, Kategori, Medtag]]

Beregner den logistiske regression y = (c/(1+a·e og Y med hyppighed Frekv. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have ens dimensioner med undtagelse af Medtag.

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiver hyppigheden af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

-bx

)) på listerne X

I vinkeltilstanden radian og rektangulært komplekst format:

Du kan se hele resultatet ved at trykke på £ og derefter anvende ¡ og ¢ til at bevæge markøren.

Katalog

TI-Nspire™ Opslagsvejledning 51

Output-variabel Beskrivelse

stat.RegEqn

Regressionsligning: c/(1+a·e

-bx

)

stat.a, stat.b, stat.c Regressionskoefficienter

stat.Resid Residualer fra regressionen

stat.XReg Liste af datapunkter i den modificerede X-liste der faktisk bruges i regressionen ud fra begrænsninger i

stat.YReg Liste af datapunkter i den modificerede Y- li st e der faktisk bruges i regressionen ud fra begrænsninger i

Frekv, kategoriliste,og Medtag kategorier

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

LogisticD

LogisticD X, Y [, [Iterationer], [Frekv] [, Kategori, Medtag] ]

Beregner den logistiske regression y = (c/(1+a·e og Y med hyppighed Frekv, ved brug af et angivet tal fra Iterationer. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

-bx

)+d) på listerne X

Katalog

Alle lister skal have ens dimensioner med undtagelse af Medtag. X og Y er lister med uafhængige og afhængige variable. Iterationer er en valgfri værdi, som angiver det maksimale antal

gange en løsning vil forsøges. Hvis udeladt, anvendes 64. Typisk resulterer større værdier i større nøjagtighed men længere eksekveringstider og omvendt.

Frekv er en valgfri liste med hyppigheder. Hvert element i Frekvangiver hyppigheden af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output-variabel Beskrivelse

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

Regressionsligning: c/(1+a·e

Regressionskoefficienter

-bx

) +d)

stat.Resid Residualer fra regressionen

stat.XReg Liste af datapunkter i den modificerede X-liste der faktisk bruges i regressionen ud fra begrænsninger i

stat.YReg Liste af datapunkter i den modificerede Y- li st e der faktisk bruges i regressionen ud fra begrænsninger i

Frekv, Kategori liste og Medtag Kategorier

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

52 TI-Nspire™ Opslagsvejledning

Loop

Blok

EndLoop

Eksekverer gentagne gange sætningerne i Blok. Bemærk, at løkken eksekveres uendeligt, medmindre en eksekveres i Blok.

Blok er en sekvens af sætninger adskilt med kolon.

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at

@ i stedet for · ved slutningen af hver linje.

trykke på På computerens tastatur skal du holde Alt nede og trykke på Enter.

Goto eller Exit-kommando

Katalog

LU Matrix, lMatNavn, uMatNavn, pMatNavn[, Tol ]

Beregner Doolittle LU (nedre-øvre) opløsningen af en reel eller kompleks matrix. Den nedre triangulære matrix lagres i lMatNavn, den øvre triangulære matrix i uMatNavn, og permutationsmatricen (der beskriver, de foretagne rækkeombytninger under beregningen) i

pMatNavn. lMatNavn · uMatNavn = pMatNavn · matrix

Ethvert matricelement kan valgfrit behandles som nul, hvis dets absolutte værdi er mindre end To l. Denne tolerance anvendes kun, hvis matricen har elementer med flydende decimaler og ikke indeholder symbolske variable, der ikke er tildelt en værdi. Ellers ignoreres To l.

• Hvis du anvender

approks

med aritmetik med flydende komma.

•Hvis Tol udelades eller ikke anvendes, beregnes standardtolerancen som:

5EM14 ·max(dim(Matrix)) ·rækkeNorm(Matrix)

LU-algoritmen til faktoropløsning anvender partiel pivotering med

rækkeombytninger.

-tilstanden til Approximate, foretages beregningerne

· eller indstiller Auto/

mat4list()

mat4list(Matrix) ⇒ liste

Returner en liste bestående af elementerne i Matrix. Elementerne kopieres fra Matrix række for række.

Katalog

TI-Nspire™ Opslagsvejledning 53

max()

max(Værdi1, Værdi2) ⇒ udtryk max(Liste1, Liste2) ⇒ liste max(Matrix1, Matrix2) ⇒ matrix

Returnerer maksimum af de to argumenter. Hvis argumenterne er to lister eller matricer, returneres en liste eller matrix med maksimumsværdier for hvert sammenhørende elementpar.

max(List) ⇒ udtryk

Returnerer det største element i liste.

max(Matrix1) ⇒ matrix

Returnerer en rækkevektor med det største element i hver kolonne i Matrix1.

Bemærk: Se også min().

Katalog

mean()

mean(Liste[, hyppighedsliste]) ⇒ udtryk

Returnerer middelværdien for elementerne i Liste. Hvert hyppighedsliste-element tæller antallet af konsekutive

forekomster de tilsvarende elementer i Liste.

mean(Matrix1[, Hyppighedsmatrix])

⇒ matrix

Returnerer en rækkevektor af middelværdierne af alle kolonner i

Matrix1.

Hvert Hyppighedsmatrix-element tæller antallet af konsekutive forekomster af det tilsvarende element iMatrix1.

median()

median(Liste) ⇒ udtryk

Returnerer medianen af elementerne i Liste.

median(Matrix1) ⇒ matrix

Returnerer en rækkevektor med medianerne af kolonnerne i Matrix1.

Bemærk: Alle elementer i listen eller matricen skal kunne omregnes

til tal.

I rektangulært vektorformat:

Katalog

54 TI-Nspire™ Opslagsvejledning

MedMed

MedMed X, Y [, Frekv] [, Kategori, Medtag]]

Beregner median-median linje y = (m·x+b) på listerne X og Y med hyppighed Frekv. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have ens dimensioner med undtagelse af Medtag.

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiver hyppigheden af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer, hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output-variabel Beskrivelse

stat.RegEqn

stat.m, stat.b Modelkoeifficienter

stat.Resid Residualer fra median-median-linjen

stat.XReg Liste af datapunkter i den modificerede X-liste der faktisk bruges i regressionen ud fra begrænsninger i

stat.YReg Liste af datapunkter i den modificerede Y- li st e der faktisk bruges i regressionen ud fra begrænsninger i

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

Median-median-linjeligning: m·x+b

Frekv, kategoriliste,og Medtag Kategorier

Katalog

mid()

mid(kildeStreng, Start[, Antal]) ⇒ streng

Returnerer Antal tegn fra tegnstrengen kildeStreng, startende med tegn nummer Start.

Hvis Antal udelades eller er større end dimension på kildeStreng, returneres alle tegn fra kildeStreng, begyndende med tegn nummer

Start.

Antal skal være ‚ 0. Hvis Antal = 0, returneres en tom streng.

mid(kildeListe, Start [, Antal]) ⇒ liste

Returnerer Antal elementer fra kildeListe, begyndende med element nummer Start.

Hvis Antal udelades eller er større end dimensionen på kildeListe, returneres alle elementer fra kildeListe, begyndende med element nummer Start.

Antal skal være ‚ 0. Hvis antal = 0, returneres en tom liste.

mid(kildeStrengListe, Start [, Antal]) ⇒ liste

Returnerer Antal strenge fra listen med strenge kildeStrengListe begyndende med element nummer Start.

Katalog

TI-Nspire™ Opslagsvejledning 55

min()

min(Værdi1, Værdi2) ⇒ udtryk min(Liste1, Liste2) ⇒ liste min(Matrix1, Matrix2) ⇒ matrix

Returnerer minimum af de to argumenter. Hvis argumenterne er to lister eller matricer, returneres en liste eller matrix med minimumværdi af hvert sammenhørende elementpar.

min(Liste) ⇒ udtryk

Returnerer det mindste element af Liste.

min(Matrix1) ⇒ matrix

Returnerer en rækkevektor med det mindste element i hver kolonne i Matrix1.

Bemærk: Se også max().

Katalog

mirr()

mirr(finansRente,geninvestRente,CF0,CFListe[,CFFrekv])

Finansfunktion, der returnerer den modificerede interne rente af en investering.

finansRente er rentesatsen, du betaler for pengestrømsbeløbene. geninvestRente er rentesatsen, som pengestrømmen geninvesteres

til. CF0 er startpengestrømmen på tidspunkt 0. Den skal være et reelt

tal. CFListe er en liste over pengestrømsbeløb efter startpengestrømmen

CF0. CFFrekv er en valgfri liste, hvor hvert element angiver hyppigheden

for et grupperet (fortløbende) pengestrømsbeløb, som er det tilsvarende element i CFListe. Standardværdien er 1. Hvis du indtaster værdier, skal de være positive heltal < 10.000.

Bemærk: Se også irr(), side 43.

mod()

mod(Værdi1, Værdi2) ⇒ udtryk mod(Liste1, Liste2) ⇒ liste mod(Matrix1, Matrix2) ⇒ matrix

Returnerer det første argument modulo andet argument som defineret efter definitionen:

mod(x,0) = x mod(x,y) = x -ìy floor(x/y)

Når det andet argument er ikke-nul, er resultatet periodisk i det pågældende argument. Resultatet er enten nul eller har samme fortegn som det andet argument.

Hvis argumenterne er to lister eller to matricer, returneres en liste eller matrix med modulo af hvert par af sammenhørende elementer.

Bemærk: Se også remain(), side 74

Katalog

56 TI-Nspire™ Opslagsvejledning

mRow()

mRow(Ta l, Matrix1, Index) ⇒ matrix

Returnerer en kopi af Matrix1 med hvert element i rækken Indeks af Matrix1 ganget med Tal .

Katalog

mRowAdd()

mRowAdd(Tal , Matrix1, Indeks1, Indeks2) ⇒ matrix

Returnerer en kopi af Matrix1 med hvert element i rækken Indeks2 af Matrix1 erstattet med:

Tal × række Indeks1 + række Indeks2

MultReg

MultReg Y, X1[,X2[,X3,…[,X10]]]

Beregner multiple lineære regressioner af listen Y på listerne X1, X2,

…, X10. En sammenfatning af resultaterne lagres i stat.results

variable. (Se side 85.) Alle lister skal have samme dimension.

Output-variabel Beskrivelse

stat.RegEqn

Regressionsligning: b0+b1·x1+b2·x2+ ...

stat.b0, stat.b1, ... Regressionskoefficienter

stat.r

Koefficient af multipel forklaringsgrad

stati.yList yListe = b0+b1·x1+ ...

stat.Resid Residualer fra regressionen

MultRegIntervals

MultRegIntervals Y,

X1[,X2[,X3,…[,X10]]],XValListe[,CNiveau]

Beregner en forudset y-værdi, et niveau C forudsigelsesinterval for enkle observationer, og et niveau C konfidensinterva l til gennemsnitsresponsen.

En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have samme dimension.

Katalog

Output-variabel Beskrivelse

stat.RegEqn

Regressionsligning: b0+b1·x1+b2·x2+ ...

Statistik.y Et punktestimat: y = b0 + b1 · xl + ... for XValListe

stat.dfFejl (stat.dfError) Frihedsgrader for fejl

stat.CLower, stat.CUpper Konfidensinterval for en middelværdi

TI-Nspire™ Opslagsvejledning 57

Output-variabel Beskrivelse

stat.ME Konfidensinterval, fejlmargen

stat.SE Standardfejl for middelværdi

stat.LowerPred, stat.UpperPred

Prædiktionsinterval for en enkelt observation

stat.MEPred Prædiktionsintervalsmargin for fejl

stat.SEPred Standardfejl for prædiktion

stat.bList Liste med regressionskoefficienter, {b0,b1,b2,...}

stat.Resid Residualer fra regressionen

MultRegTests

MultRegTests Y, X1[,X2[,X3,…[,X10]]]

Multipel lineær regressionstest beregner en multipel lineær regression fra de givne data, og danner den globale F teststatistik og t teststatistikker for koefficienterne.

En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Katalog

Output

Output-variabel Beskrivelse

stat.RegEqn

Regressionsligning: b0+b1·x1+b2·x2+ ...

stat.F Global F teststatistik

stat.PVal P-værdi tilknyttet global F statistik

stat.r

stat.AdjR

Koefficient af multipel forklaringsgrad

Justeret koefficient af multipel forklaringsgrad

stat.s Standardafvigelse for fejlen

stat.DW Durbin-Watson-statistik; Anvendes til at bestemme, om første-ordens auto-korrelationen er tilstede i

modellen

stat.dfReg Frihedsgrader i regressionen

stat.SSReg Kvadraternes regressionsum

stat.MSReg Middelkvadrat af regression

stat.dfFejl Frihedsgrader for fejl

stat.SSError fejl, kvadratsum

stat.MSError fejl, middelkvadrat

stat.bList {b0,b1,...} Liste med koefficienter

stat.tList Liste med t statistikker for hver koefficient i bListen

stat.PList Liste P-værdier for hver t-statistik

stat.SEList Liste med standardfejl for koefficienter i bListe

58 TI-Nspire™ Opslagsvejledning

Output-variabel Beskrivelse

stat.yList yListe = b0+b1·x1+...

stat.Resid Residualer fra regressionen

stat.sResid Standardiserede residualer; Værdi opnået ved at dividere en residual med dens standardafvigelse

stat.CookDist Cooks distance; Mål for påvirkningen af en observation baseret på residual og udnyttelse

stat.Leverage Mål for, hvor langt værdierne for de uafhængige variable er fra deres middelværdier

nCr()

nCr(Værdi1, Værdi2) ⇒ udtryk

For heltal Værdi1 og Værdi2 med Værdi1 ‚ Værdi2 ‚ 0, nCr() er antallet af kombinationer af Værdi1 ting taget Værdi2 ad gangen. (Dette kendes også som en binomial koefficient).

nCr(Tal , 0) ⇒ 1

Tal , negHeltal) ⇒ 0

nCr(

Tal , posHeltal) ⇒ Tal ·(Tal N1)...

nCr( (Tal NposHeltal+1)/posHeltal!

Tal , ikkeHeltal) ⇒ udtryk!/

nCr( ((Tal NikkeHeltal)!·ikkeHeltal!)

nCr(

Liste1, Liste2) ⇒ liste

Returnerer en liste med kombinationer baseret på de sammenhørende elementpar i de to lister. Argumenterne skal være lister af samme størrelse.

nCr(Matrix1, Matrix2) ⇒ matrix

Returnerer en matrix af kombinationer ba seret på de sammenhørende elementpar i de to matricer. Argumenterne skal være matricer af samme størrelse.

nDeriv()

nDeriv(Udtr1, Va r [=Værdi] [, H]) ⇒ udtryk nDeriv(Udtr1, Va r [, H] | Var = V æ rd i ) ⇒ udtryk

nDeriv(Udtr1, Va r [=Værdi], List) ⇒ liste nDeriv(Liste1, Va r [=Værdi] [, H]) ⇒ liste nDeriv(Matrix1, Va r [=Værdi] [, H]) ⇒ matrix

Returnerer den numeriske differentialkvotient som et udtryk. Anvender den centrale differenskvotientformel.

Når Værdi er angivet, tilsidesætter den alle forudgående variabeltildelinger eller alle “således at” substitutioner for variablen.

H er trinværdien. Hvis H udelades, er standardværdien 0,001. Ved anvendelse af Liste1 eller Matrix1 bliver oper ationen mappet på

tværs af værdierne i listen eller på tværs af matricelementerne.

Bemærk: Se også avgRC().

Katalog

TI-Nspire™ Opslagsvejledning 59

newList()

newList(antalElementer) ⇒ liste

Returnerer en liste med en dimension af antalElementer. Hvert element er nul.

Katalog

newMat()

newMat(antalRækker, antalKolonner) ⇒ matrix

Returnerer en matrix med nulpunkter af dimensionen antalRækker gange antalKolonner.

nfMax()

nfMax(Udtr, Var ) ⇒ værdi nfMax(Udtr, Var , nedreGrænse) ⇒ værdi nfMax(Udtr, Var , nedreGrænse, øvreGrænse) ⇒ værdi nfMax(Udtr, Var) | nedreGrænse<Var <øvreGrænse ⇒ værdi

Returnerer mulig numerisk værdi for variablen Va r , hvor det lokale maksimum for Udtr optræder.

Hvis du angiver nedreGrænse og øvreGrænse, søger funktionen mellem disse værdier efter det lokale maksimum.

nfMin()

nfMin(Udtr, Var ) ⇒ værdi nfMin(

Udtr, Var , nedreGrænse) ⇒ værdi

nfMin(

Udtr, Var , nedreGrænse, øvreGrænse) ⇒ værdi

nfMin(

Udtr, Var) | nedreGrænse<Var <øvreGrænse ⇒ værdi

Returnerer mulig numerisk værdi for variablen Va r , hvor det lokale minimum for Udtr optræder.

Hvis du angiver nedreGrænseog øvreGrænse, søger funktionen mellem disse værdier efter det lokale minimum.

nInt()

nInt(Udtr1, Var, nedre, øvre) ⇒ udtryk

Hvis integranden Udtr1 ikke indeholder andre variable end Va r , og hvis Nedre og Øvre er konstante, + ˆ eller - ˆ, så returnerer nInt()

en tilnærmet værdi af ‰(Udtr1, Va r , Nedre, Øvre). Denne tilnærmede værdi er et vægtet gennemsnit af nogle ek sempelværdier af integranden i intervallet Nedre<Va r <Øvre.

Målet er seks betydende cifre. Algoritmen, der kan tilpasses, afsluttes hvis det virker sandsynligt, at målet er nået, eller når det virker usandsynligt, at ydeligere eksempler vil give en væsentlig forbedring.

Der vises en advarsel (“Tvivl om nøjagtighed“) når målet ikke ser ud til at være nået.

Indskyd flere nInt(), for at foretage numerisk integration i flere variable. Integrationsgrænser kan afhænge af integrationsvariable uden for dem.

Katalog

60 TI-Nspire™ Opslagsvejledning

nom()

nom(effektivRente,CpY) ⇒ værdi

Finansfunktion, der omregner den effektive årlige rent e effektivRente til en nominel rente, hvor CpY er antallet af rentetilskrivninger per år.

effektivRente skal være et reelt tal, og CpY skal være et reelt tal > 0.

Bemærk: Se også eff(), side 28.

Katalog

norm()

norm(Matrix) ⇒ udtryk norm(Ve k to r ) ⇒ udtryk

Returnerer Frobenius-normen.

normCdf()

normCdf(nedreGrænse,øvreGrænse[,m[,s]]) ⇒ tal hvis

nedreGrænse og øvreGrænse er tal, liste hvis nedreGrænse

og øvreGrænse er lister

Beregner normalfordelingenssandsynligheden mellem nedreGrænse og øvreGrænse for de angivne m (standard=0) og s (standard=1).

For P(X  øvreGrænse), sæt nedreGrænse= .9E999.

normPdf()

normPdf(XVærdi[,m,s]) ⇒ tal hvis XVærdi er et tal, liste hvis

XVærdi er en liste

Beregner tæthedsfunktionen for normalfordelingen i en angivet XVærdi for de angivne m og s.

not

not Boolsk udtr1 ⇒ Boolsk udtryk

Returnerer true eller false eller en forenklet form af argumentet.

Katalog

TI-Nspire™ Opslagsvejledning 61

not

not Heltal1 ⇒ heltal

Returnerer 1's komplement til et reelt heltal. Internt konverteres Heltal1 til et 64-bit binært tal med fortegn. Værdien af hver bit vendes (0 bliver 1, og omvendt) for 1's komplement. Resultatet vises i den valgte tilstand for talsystem.

Du kan indtaste heltallet i ethvert talsystem. Til binære eller hexadecimale indtastninger skal du som præfiks benytte henholdsvis 0b eller 0h. Uden præfiks behandles heltallet som decimaltal (10talssystem).

Hvis du indtaster et decimalt heltal, der er for stort til en 64-bit binær form med fortegn, anvendes en symmetrisk modulooperation til at bringe værdien ind i det korrekte område.

I hexadecimal tilstand:

Vigtigt: Tallet nul, ikke bogstavet O.

I binær tilstand:

Katalog

nPr()

nPr(Værdi1, Værdi2) ⇒ udtryk

For heltal er Værdi1 og Værdi2 med Værdi1 ‚ Værdi2 ‚ 0, nPr() antallet af permutationer af Værdi1 ting taget Værdi2 ad gangen.

nPr(Tal , 0) ⇒ 1

Tal , negHeltal)

nPr(

⇒ 1/((Tal +1)·(Ta l+2)... (Ta l NnegHeltal))

Tal , posHeltal)

nPr(

⇒ Tal ·(Ta lN1)... (Ta lNposHeltal+1)

nPr(

Tal , ikke-Heltal)

⇒ Tal ! / (Tal Nikke-Heltal)!

Liste1, Liste2) ⇒ liste

nPr(

Returnerer en liste med permutationer baser et på de sammenhørende elementpar i de to lister. Argumenterne skal være lister af samme størrelse.

nPr(Matrix1, Matrix2) ⇒ matrix

Returnerer en matrix med permutationer baseret på de sammenhørende elementpar i de to matricer. Argumenterne skal være matricer af samme størrelse.

Du kan se hele resultatet ved at trykke på anvende ¡ og ¢ til at bevæge markøren.

Bemærk: En binær indtastning kan have op til 64 cifre

(præfikset 0b ikke medregnet). En hexadecimal indtastning kan have op til 16 cifre.

£ og derefter

Katalog

62 TI-Nspire™ Opslagsvejledning

npv()

npv(RenteSats,CFO,CFListe[,CFFrekv])

Finansfunktion, der beregner nettonutidsværdien. Summen af de aktuelle værdier for indkommende og udgående pengestrømme. Et positivt resultat for npv indikerer en profitabel investering.

RenteSats er renten, som pengestrømmen skal reduceres med over en periode (pengenes pris).

CF0 er startpengestrømmen på tidspunkt 0. Den skal være et reelt tal.

CFListe er en liste over pengestrømsbeløb efter startpengestrømmen CF0.

CFFrekv er en liste, hvor hvert element angiver

hyppighedsfrekvensen for et grupperet (fortløbende) pengestrømsbeløb, som er det tilsvarende element i CFListe. Standardværdien er 1. Hvis du indtaster værdier, skal de være positive heltal < 10.000.

Katalog

nSolve()

nSolve(Ligning,Var [=Gæt]) ⇒ tal eller fejlstreng nSolve(Ligning,Var [=Gæt],nedreGrænse)

⇒ tal eller fejlstreng

nSolve(Ligning,Var [=Guess],nedreGrænse,øvreGrænse)

⇒ tal eller fejlstreng

nSolve(Ligning,Var [=Guess]) | nedreGrænse<Va r<øvreGrænse

⇒ tal eller fejlstreng

Søger iterativt efter en approksimeret reel numerisk løsning af

Ligning for dens ene variabel. Angiv variablen som:

variabel

– eller – variabel = reelt tal

For eksempel er x gyldig, og det er x=3 også.

nSolve() forsøger at bestemme enten et punkt, hvor residualen er

nul, eller to forholdsvis tætte punkter, hvor r esidualerne har modsatte fortegn, og residualen ikke er for stor. Hvis dette ikke kan opnås med et beskedent antal datapunkter, returneres strengen “Ingen løsning blev fundet.”

Katalog

Bemærk: Hvis der er flere løsninger, kan du anvende et gæt til

at finde en partikulær løsning.

TI-Nspire™ Opslagsvejledning 63

OneVar

OneVar [1,]X[,[Hyppighed][,Kategori,Medtag]] OneVar [

n,]X1,X2[X3[,…[,X20]]]

Beregner statistik med en variabel på op til 20 lister. En sammenfatning af resultaterne lagres i variablen stat.results. (Se side 85.)

Alle lister skal have ens dimensioner med undtagelse af Medtag.

X argumenterne er datalister. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiver hyppigheden af hændelse for hver tilsvarende X værdi.

Standardværdien er 1. Alle elementer skal være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X værdier.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output-variabel Beskrivelse

stat.v

stat.Gx

stat.sx Standardafvigelse for målingen for x

stat.ssssx Populations standardafvigelse for x

stat.n Antal datapunkter

stat.MinX Minimum af x-værdier

stat.Q1X 1. kvartil af x

stat.MedianX Median af x.

stat.Q3X 3. kvartil af x.

stat.MaxX Maksimum af x-værdier.

stat.SSX Summen af kvadraterne på afvigelser fra middelværdien for x.

Gennemsnit af x-værdier

Summen af x-værdier

Summen af x2 værdier

Katalog

64 TI-Nspire™ Opslagsvejledning

Boolsk Udtr1 or Boolsk Udtr2

⇒ Boolsk udtryk

Returnerer true eller false eller en forenklet form af den oprindelige indtastning.

Returnerer true, hvis enten et eller begge udtryk kan reduceres til true. Returnerer kun false, hvis begge udtryk evalueres til false.

Bemærk: Se xor. Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

Heltal1 or Heltal2 ⇒ heltal

Sammenligner to reelle heltal bit for bit med en or-operation. Internt konverteres begge heltal til 64-bit binære tal med fortegn. Når de tilsvarede bits sammenlignes, er resultatet 1, hvis en af bittene er 1. Resultatet er kun 0, hvis begge bits er 0. Den returnerede værdi repræsenterer bit-resultaterne og vises i overensstemmelse med den valgte talsystemstilstand.

Hvis du indtaster et decimalt heltal, der er for stort til en 64-bit binær form med fortegn, anvendes en symmetrisk modulooperation til at bringe værdien ind i det korrekte område.

Bemærk: Se xor.

Katalog

I hexadecimal tilstand:

Vigtigt: Tallet nul, ikke bogstavet O.

I binær tilstand:

Bemærk: En binær indtastning kan have op til 64 cifre

(præfikset 0b ikke medregnet). En hexadecimal indtastning kan have op til 16 cifre.

ord()

ord(Stren g) ⇒ heltal ord(Liste1) ⇒ liste

Returnerer den numeriske kode til første tegn i tegnstrengen Streng, eller en liste med de første tegn i hvert listeelement.

Katalog

P4Rx()

P4Rx(rUdtr, qUdtr) ⇒ udtryk

P4Rx(rListe, qListe) ⇒ liste P4Rx(rMatrix, qMatrix) ⇒ matrix

Returnerer den ækvivalente x-koordinat til parret (r, q).

Bemærk: Argumentet q tolkes i grader, nygrader eller radianer

afhængigt af den aktuelle vinkeltilstand. Hvis argumentet er et udtryk, kan du anvende ó,G eller ôtil midlertidigt at tilsidesætte den

indstillede vinkeltilstand.

I vinkeltilstanden Radian:

TI-Nspire™ Opslagsvejledning 65

Katalog

P4Ry()

P4Ry(rTal, qTal ) ⇒ værdi P4Ry(rListe, qListe) ⇒ liste P4Ry(rMatrix, qMatrix) ⇒ matrix

Returnerer den ækvivalente y-koordinat til parret (r, q).

Bemærk: Argumentet q tolkes i grader, nygrader eller radianer

afhængigt af den aktuelle vinkeltilstand.

I vinkeltilstanden Radian:

Katalog

PassErr

Videresender en fejl til næste niveau. Hvis systemvariabel errCode er nul, gør PassErr ingenting.

Else betingelsen i Try...Else...EndTry-blokken bør anvende ClrErr eller PassErr. Brug ClrErr, hvis fejlen skal behandles eller

Bemærk: Se også ClrErr, side 14, og Try, side 92. Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

piecewise()

piecewise(Udtr1 [, Betingelse1 [, Udtr2 [, Betingelse2 [, … ]]]])

Returnerer definitioner for en stykkevis funktion i form af en liste. Du kan også oprette stykkevise definitioner ved hjælp af en skabelon.

Bemærk: Se også Stykkevis skabelon, side 2.

poissCdf()

poissCdf(l,nedreGrænse,øvreGrænse) ⇒ tal hvis

nedreGrænse og øvreGrænse er tal, liste hvis nedreGrænse

øvregrænse er lister

poissCdf(

l,øvreGrænse) (for P(0XøvreGrænse) ⇒ tal hvis

øvreGrænse er et tal, liste hvis øvreGrænse er en liste

Beregner den kumulerede sandsynlighed for den diskrete Poissondistribution med en angivet middelværdi l.

For P(X  øvreGrænse), sæt nedreGrænse=0

Katalog

Se et eksempel på PassErr i Eksempel2 under Trykommandoen, side 93.

Katalog

poissPdf()

poissPdf(l,XVærdi) ⇒ tal hvis XVærdi er et tal, liste hvis

XVærdi er en liste

Beregner en sandsynlighed for den diskrete Poisson-distribution med den angivne middelværdi l.

Katalog

66 TI-Nspire™ Opslagsvejledning

Polar

4Polar

Vek t o r

Viser vektor i polær form [r q]. Vektoren skal være af dimensionen 2 og kan være en række eller kolonne.

Bemærk: 4Polar er en displayformat-kommando, ikke en

konverteringsfunktion. Du kan kun anvende den i slutningen af en indtastningslinje, og den opdaterer ikke ans.

Bemærk: Se også 4Rect, side 73.

kompleksVærdi 4Polar

Viser kompleksVærdi i polær form.

• Vinkeltilstanden Grader returnerer (rq).

• Vinkeltilstanden Radian returnerer reiq.

compleksVærdi kan have enhver kompleks form. Men en reiq- indtastning udløser en fejl i vinkeltilstanden Grader.

Bemærk: Du skal anvende parenteser til en (rq) polær

indtastning.

I vinkeltilstanden Radian:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Grader:

Katalog

polyEval()

polyEval(Liste1, Udtr1) ⇒ udtryk polyEval(Liste1, Liste2) ⇒ udtryk

Fortolker første argument som koefficienten til et polynomium i faldende grad og returnerer polynomiet beregnet for værdien af det andet argument.

PowerReg

PowerReg X, Y [, Frekv] [, Kategori, Medtag]]

Beregner den lineære regression y = (a·(x)b) på liste X og Y med hyppighed Frekv. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have ens dimensioner med undtagelse af Medtag.

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiver hyppigheden af hændelse for hvert tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output-variabel Beskrivelse

stat.RegEqn

Regressionsligning: a·(x)

Katalog

TI-Nspire™ Opslagsvejledning 67

Output-variabel Beskrivelse

stat.a, stat.b Regressionskoefficienter

stat.r

Koefficient af en lineær forklaringsgrad til transformerede data

stat.r Korrelationskoefficient til transformerede data (ln(x), ln(y))

stat.Resid Residualer forbundet med eksponentielmodellen

stat.ResidTrans Residualer associeret med lineær tilpasning af transformerede data

stat.XReg Liste af datapunkter i den modificerede X-liste der faktisk bruges i regressionen ud fra begrænsninger i

stat.YReg Liste af datapunkter i den modificerede Y- li st e der faktisk bruges i regressionen ud fra begrænsninger i

Frekv, kategoriliste,og Medtag Kategorier

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

Prgm

Blok

EndPrgm

Skabelon til oprettelse af et brugerdefineret program. Skal anvendes sammen med Define, Define LibPub, eller Define LibPrivkommandoen.

Blok kan være en enkelt sætning, en række sætninger adskilt med kolon eller en række sætninger på separate linjer.

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

Product (PI)

product()

product(Liste[, Start[, slut]]) ⇒ udtryk

Returnerer produktet af elementerne indeholdt i Liste. Start og Slut er valgfri De angiver en serie af elementer.

Beregn GCD og vis mellemresultater.

Katalog

Se Π(), side 110.

Katalog

68 TI-Nspire™ Opslagsvejledning

product()

product(Matrix1[, Start[, slut]]) ⇒ matrix

Returnerer en rækkevektor med produkterne af elementerne i kolonnerne i Matrix1. Start og slut er valgfri. De angiver en serie af rækker.

Katalog

propFrac()

propFrac(Værdi1[, Va r]) ⇒ værdi

propFrac(rationalt_tal) returnerer rationalt_tal som summen af et

heltal og en brøk med samme fortegn og en større nævner end tæller.

propFrac(rationalt_Udtryk,Var ) returnerer summen af ægte

brøker og et polynomium med hensyn til Va r . Graden af Var i nævneren overstiger graden af Va r i tælleren i hver enkelt ægte brøk. Ens potenser af Va r samles. Leddene og deres faktorer sorteres med Var som hovedvariabel.

Hvis Va r udelades, foretages en udvikling i ægte brøker med hensyn til den hyppigst forekommende variabel. Koefficienterne af polynomiumdelen gøres derefter ægte med hensyn til deres hyppigst forekommende variabel osv.

QR Matrix, qmatNavn, rmatNavn[, To l]

Beregner Householder QR faktoropløsningen af en reel eller kompleks matrix. De resulterende Q og R-matricer lagres i de angivne matNavne. Q matrix er unitær. R matrix er øvre-triangulær.

• Hvis du anvender

approks

aritmetik med flydende komma.

•Hvis Tol udelades eller ikke anvendes, beregnes standardtolerancen som:

5Eë14 ·max(dim(Matrix)) ·rowNorm(Matrix)

-tilstanden til Approks, foretages beregningerne med

· eller indstiller Auto/

Katalog

Tallet med flydende komma (9). i m1 får resultaterne beregnet med flydende komma.

QR faktoropløsningen beregnes numerisk med Householdertransformationer. Den symbolske løsning beregnes med GramSchmidt. Kolonnerne i qmatNavn er ortonormale vektorer, der udspænder rummet defineret ved matrix.

TI-Nspire™ Opslagsvejledning 69

QuadReg

QuadReg X, Y [, Frekv] [, Kategori, Medtag]]

Beregner andengrads polynomiel regression y = a· x2 +b·x+c på listerne X og Y med hyppighed Frekv. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have ens dimensioner med undtagelse af Medtag.

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiverr frekvensen af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output-variabel Beskrivelse

stat.RegEqn

stat.a, stat.b, stat.c Regressionskoefficienter

stat.r

stat.Resid Residualer fra regressionen

stat.XReg Liste af datapunkter i den modificerede X-liste der faktisk bruges i regressionen ud fra begrænsninger i

stat.YReg Liste af datapunkter i den modificerede Y- li st e der faktisk bruges i regressionen ud fra begrænsninger i

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

Regressionsligning: a·x2+b·x+c

Forklaringsgraden

Frekv, kategoriliste,og Medtag Kategorier

Katalog

QuartReg

QuartReg X, Y [, Frekv] [, Kategori, Medtag]]

Beregner the den polynomielle tredjegradsregression y = a·x4+b·x3+c· x2+d·x+e på listerne X og Y med frekvens

Frekv. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Alle lister skal have ens dimensioner med undtagelse af Medtag.

X og Y er lister med uafhængige og afhængige variable. Frekv er en valgfri liste med hyppigheder. Hvert element i

Frekvangiverr frekvensen af hændelse for hver tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal

være heltal | 0.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Katalog

70 TI-Nspire™ Opslagsvejledning

Output-variabel Beskrivelse

stat.RegEqn

stat.a, stat.b, stat.c, stat.d, stat.e

stat.r

stat.Resid Residualer fra regressionen

stat.XReg Liste af datapunkter i den modificerede X-liste der faktisk bruges i regressionen ud fra begrænsninger i

stat.YReg Liste af datapunkter i den modificerede Y- li st e der faktisk bruges i regressionen ud fra begrænsninger i

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

Regressionsligning: a·x4+b·x3+c· x2+d·x+e

Regressionskoefficienter

Forklaringsgraden

Frekv, kategoriliste,og Medtag Kategorier

R4Pq()

R4Pq (xTal, yTal) ⇒ værdi R4Pq (xListe, yListe) ⇒ liste R4Pq (xMatrix, yMatrix) ⇒ matrix

Returnerer den ækvivalente q-koordinat for (x,y) argumentparret.

Bemærk: Resultatet returneres som en vinkel i grader eller radianer

afhængigt af den aktuelle vinkeltilstand.

R4Pr()

R4Pr (xTal, yTal) ⇒ værdi R4Pr (xListe, yList) ⇒ liste R4Pr (xMatrix, yMatrix) ⇒ matrix

Returnerer den ækvivalente r-koordinat for (x,y) argumentparret.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

Katalog

TI-Nspire™ Opslagsvejledning 71

4Rad

4Rad ⇒ værdi

Værdi1

Konverterer argumentet til vinkelmåling i radianer.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

Katalog

rand()

rand() ⇒ udtryk rand(AntalForsøg) ⇒ liste

rand() returnerer en tilfældig værdi mellem 0 og 1. rand(antalForsøg) returnerer en liste med antalForsøg tilfældige

værdier mellem 0 og 1.

randBin()

randBin(n, p) ⇒ udtryk randBin(n, p, antalForsøg) ⇒ liste

randBin(n, p) returnerer et tilfældigt reelt tal fra en angivet

binomial fordeling.

randBin(n, p, antalForsøg) returnerer en liste med antalForsøg

tilfældige, reelle tal fra en angivet binomial fordeling.

randInt()

randInt(lavGrænse,højGrænse) ⇒ udtryk randInt(lavGrænse,højGrænse,antalForsøg) ⇒ liste

randInt(lavGrænse,højGrænse) returnerer et tilfældigt heltal i det

område, der angives af heltalsgrænserne lavGrænse og højGrænse.

randInt(lavGrænse,højGrænse,antalForsøg) returnerer en liste

med antalForsøg tilfældige heltal i det angivne område.

randMat()

randMat(antalRækker, antalKolonner) ⇒ matrix

Returnerer en matrix med heltal mellem -9 og 9 af den angivne dimension.

Begge argumenter skal kunne reduceres til heltal.

Katalog

Angiver seed-værdien for et tilfældigt tal.

Katalog

Bemærk: Værdierne i denne matrix ændres, hver gang du

trykker på ·.

randNorm()

randNorm(m, s [,antalForsøg]) ⇒ udtryk

Returnerer et decimalt tal fra den angivne normalfordeling. Det kan være ethvert reelt tal men vil være kraftigt koncentreret i intervallet

Katalog

[mN3·s, m+3·s].

randNorm(m, s, #Trials) returns a list containing #Trials decimal

numbers from the specified normal distribution.

72 TI-Nspire™ Opslagsvejledning

randPoly()

randPoly(Va r , Orden) ⇒ udtryk

Returnerer et polynomium i Va r af den angivne Orden. Koefficienterne er vilkårlige heltal i området foranstillede koefficient vil ikke være nul.

ë9 til og med 9. Den

Orden skal være 0–99.

Katalog

randSamp()

randSamp(Liste,antalMålinger[,ingenUdskiftning]) ⇒ liste

Returnerer en liste med tilfældige tal for antalMålinger målinger fra Liste med mulighed for udskiftning af måleantal

(ingenUdskiftning=0), eller ingen udskiftning af måleantal (ingenUdskiftning=1). Standardindstillingen er med udskiftning af målingsantal.

RandSeed

RandSeed tal

Hvis Tal = 0, indstilles seeds til fabriksindstillingerne for tilfældig-tal generatoren. Hvis Ta l ƒ 0, anvendes det til at generere to seeds, der lagres i systemvariablene seed1 og seed2.

real()

real(Værdi1) ⇒ værdi

Returnerer den reelle del af argumentet.

Bemærk: Alle udefinerede variable behandles som reelle variable.

Se også imag(), side 41.

real(Liste1) ⇒ liste

Returnerer realdelen af alle elementer.

real(Matrix1) ⇒ matrix

Returnerer realdelen af alle elementer.

Rect

Vek t o r 4Rect

Viser Vek t o r i rektangulær form [x, y, z]. Vektoren skal være af dimensionen 2 eller 3 og kan være en række eller kolonne.

Bemærk: 4Rect er en displayformatkommando, ikke en

konverteringsfunktion. Du kan kun anvende den i slutningen af en indtastningslinje, og den opdaterer ikke ans.

Bemærk: Se også 4Polar, side 67.

Katalog

TI-Nspire™ Opslagsvejledning 73

Rect

kompleksVærdi 4Rect

Viser komplexVærdi i rektangulær form a+bi. kompleksVærdi kan have enhver kompleks form. Men en reiq-indtastning udløser en fejl i vinkeltilstanden Grader.

Bemærk: Du skal anvende parenteser til en (rq) polær

indtastning.

Katalog

I vinkeltilstanden Radian:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Grader:

Bemærk: Du kan skrive  ved at vælge det i symbollisten i

Katalog.

ref()

ref(Matrix1[, To l]) ⇒ matrix

Returnerer række-echelonformen af Matrix1. Ethvert matricelement kan valgfrit behandles som nul, hvis dets

absolutte værdi er mindre end To l. Denne tolerance anvendes kun, hvis matricen har elementer med flydende decimaler og ikke indeholder symbolske variable, der ikke er tildelt en værdi. Ellers ignoreres To l.

• Hvis du anvender

approks

med aritmetik med flydende komma.

•Hvis Tol udelades eller ikke anvendes, beregnes standardtolerancen som:

5Eë14 ·max(dim(Matrix1)) ·rowNorm(Matrix1)

Bemærk: Se også rref(), side 77.

remain()

remain(Værdi1, Værdi2) ⇒ værdi remain(Liste1, Liste2) ⇒ liste remain(Matrix1, Matrix2) ⇒ matrix

Returnerer resten af det første argument med hensyn til det andet argument som defineret af identiteterne:

remain(x,0)  x remain(x,y)  xNy·iPart(x/y)

Bemærk som følge heraf, at remain(Nx,y)  Nremain(x,y). Resultatet er enten nul, eller det har samme fortegn som det første argument.

Bemærk: Se også mod(), side 56.

-tilstanden til Approximate, foretages beregningerne

· eller indstiller Auto/

Katalog

74 TI-Nspire™ Opslagsvejledning

Return

Return [Udtr]

Returner Udtr som resultat af funktionen. Anvendes i en

Func...EndFunc-blok. Bemærk: Du kan afslutte et program ved anvende Return uden et

argument i en

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at

Prgm...EndPrgm-blok.

trykke på @ i stedet for · ved slutningen af hver linje. På computerens tastatur skal du holde Alt nede og trykke på Enter.

Katalog

right()

right(Liste1[, Antal]) ⇒ liste

Returnerer Antal elementer fra højre i Liste1. Hvis du udelader Antal, returneres hele Liste1.

right(kildeStreng[, Antal]) ⇒ streng

Returnerer Antal tegn længst til højre i tegnstrengen kildeStreng. Hvis du udelader Antal, returneres hele kildeStreng.

right(Sammenligning) ⇒ udtryk

Returnerer højre side af en ligning eller ulighed.

root()

root(Værdi) ⇒ rod root(Værdi1, Værdi2) ⇒ rod

root(Værdi) returnerer kvadratroden af Værdi. root(Værdi1, Værdi2) returnerer Værdi2roden af Værdi1. Værdi1

kan være en reel eller kompleks konstant med flydende decimaler eller et heltal eller en kompleks rationel konstant.

Bemærk: Se også Nte rod-skabelon, side 1.

rotate()

rotate(Heltal1[,antalRotationer]) ⇒ heltal

Roterer bittene i et binært heltal. Du kan indtaste Heltal1 i ethvert talsystem. Det konverteres automatisk til en 64-bit binær form med fortegn. Hvis Heltal1 er for stort til denne form, bringer en symmetrisk modulooperation værdien ind i det korrekte område.

Hvis antalRotationer er positivt, kører rotationen mod venstre. Hvis antalRotationer er negativt, kører rotationen mod højre. Standardindstillingen er ë1 (roter en bit til højre).

For eksempel i en højrerotation:

Katalog

I binær tilstand:

Du kan se hele resultatet ved at trykke på £ og derefter anvende ¡ og ¢ til at bevæge markøren.

I hexadecimal tilstand:

TI-Nspire™ Opslagsvejledning 75

rotate()

Hver bit roterer til højre. 0b00000000000001111010110000110101 Bitten længst til højre roterer længst mod venstre. giver: 0b10000000000000111101011000011010 Resultatet vises i den valgte tilstand for talsystem.

rotate(Liste1[,antalRotationer]) ⇒ liste

Returnerer en kopi af Liste1 roteret til højre eller venstre med antalRotationer elementer. Ændrer ikke Liste1.

Hvis antalRotationer er positivt, kører rotationen mod venstre. Hvis antalRotationer er negativt, kører rotationen mod højre.

Standardindstillingen er ë1 (roter en bit til højre).

rotate(Streng1[,antalRotationer]) ⇒ streng

Returnerer en kopi af Streng1 roteret til højre eller venstre med antalRotationer tegn. Ændrer ikke Streng1.

Hvis antalRotationer er positivt, kører rotationen mod venstre. Hvis antalRotationer er negativt, kører rotationen mod højre.

Standardindstillingen er ë1 (roter en bit til højre).

Katalog

Vigtigt: Til binære eller hexa decimale indtastninger skal du som præfiks altid benytte henholdsvis 0b eller 0h (nul, ikke bogstavet O).

I decimal tilstand:

round()

round(Værdi1[, cifre]) ⇒ værdi

Returnerer argumentet afrundet til det angivne antal cifre efter decimalpunktet.

cifre skal være et heltal i området 0–12. Hvis cifre ikke er medtaget, returneres argumentet afrundet til 12 betydende cifre.

Bemærk: Vis cifre-tilstanden kan påvirke den måde, dette vises på.

round(Liste1[, cifre]) ⇒ liste

Returnerer en liste med elementerne afrundet til det angivne antal cifre.

round(Matrix1[, cifre]) ⇒ matrix

Returnerer en matrix med elementerne afrundet til det angivne antal cifre.

rowAdd()

rowAdd(Matrix1, rIndeks1, rIndeks2) ⇒ matrix

Returnerer en kopi af Matrix1 med række rIndeks2 erstattet af rækkesummen rIndeks1 og rIndeks2.

rowDim()

rowDim(Matrix) ⇒ udtryk

Returnerer antallet af rækker i Matrix.

Bemærk: Se også colDim(), side 14.

Katalog

76 TI-Nspire™ Opslagsvejledning

rowNorm()

rowNorm(Matrix) ⇒ udtryk

Returnerer maksimum for summerne af de absolutte værdier for elementerne i Matrix-rækkerne.

Bemærk: Alle matricelementer skal kunne reduceres til tal. Se også colNorm(), side 14.

Katalog

rowSwap()

rowSwap(Matrix1, rIndeks1, rIndeks2) ⇒ matrix

Returnerer Matrix1 med rækker rIndeks1 og rIndeks2 byttet.

rref()

rref(Matrix1[, To l]) ⇒ matrix

Returnerer den reducerede række-echelonform af Matrix1.

• Hvis du anvender tilstanden til Approx, foretages beregningerne med aritmetik

med flydende komma.

•Hvis Tol udelades eller ikke anvendes, beregnes standardtolerancen som:

5Eë14 ·max(dim(Matrix1)) ·rowNorm(Matrix1)

Bemærk: Se også ref(), side 74.

· eller sætter Auto/approks-

Katalog

sec()

sec(Værdi1) ⇒ værdi sec(Liste1) ⇒ list

Returnerer sekans til Værdi1 eller returnerer en liste med sekansen til alle elementer i Liste1.

Bemærk: Argumentet fortolkes som en vinkel målt i grader,

nygrader eller radianer afhængigt af den aktuelt indstillede vinkeltilstand. Du kan bruge ó,G ellerôtil midlertidigt at ignorere

vinkeltilstanden.

I vinkeltilstanden Grader:

TI-Nspire™ Opslagsvejledning 77

Katalog

sec/()

sec/(Værdi1) ⇒ værdi sec/(Liste1) ⇒ liste

Returnerer den vinkel, hvis sekans er Værdi1 eller returnerer en liste med de inverse sekanser til de enkelte elementer på Liste1.

Bemærk: Resultatet returneres som en vinkel i grader eller radianer

afhængigt af den aktuelle vinkeltilstand.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

Katalog

sech()

sech(Værdi1) ⇒ værdi sech(Liste1) ⇒ list

Returnerer den hyperbolske sekans til Værdi1 eller returnerer en liste med den hyperbolske sekans til elementerne Liste1.

sechê()

sechê(Værdi1) ⇒ værdi sechê (Liste1) ⇒ liste

Returnerer den inverse hyperbolske sekans til Værdi1 eller returnerer en liste med den inverse hyperbolske sekans til de en kelte elementer i

Liste1

seq()

seq(Udtr, Var , Lav, Høj[, Tr in]) ⇒ liste

Øger Va r med trin fra Lav til Høj i trin på Tri n, beregner Udtr, og returnerer resultaterne som en liste. Det oprinde lige indhold af Var er der stadigvæk, når seq() er gennemført.

Var kan ikke være en systemvariabel. Standardværdien for Trin = 1.

Katalog

I vinkeltilstanden radian og tilstanden rektangulært kompleks:

Katalog

Tryk Ctrl+Enter /· for at evaluere:

78 TI-Nspire™ Opslagsvejledning

setMode()

setMode(tilstandNavnHeltal, indstilHeltal) ⇒ heltal setMode(liste) ⇒ heltalsliste

Kun gyldig i en funktion eller et program.

setMode(tilstandNavnHeltal, indstilHeltal) indstiller

midlertidigt tilstanden tilstandNavnHeltal til den nye indstilling indstilHeltal og returnerer et heltal, der svarer til denne tilstands

oprindelige indstilling. Ændringen er begrænset til varigheden af eksekveringen af programmet/funktionen.

tilstandNavnHeltal angiver hvilken tilstand, du vil indstille. Det skal være et af tilstandsheltallene fra nedenstående tabel.

indstilHeltal angiver den nye indstilling for tilstanden. Det skal være et af indstillingsheltallene for den tilstand, du indstiller.

setMode(liste) lader dig ændre flere indstillinger. liste

indeholder et par af tilstandsheltal og indstillingsheltal.

setMode(liste) returnerer en tilsvarende liste, hvis heltalspar

repræsenterer de oprindelige tilstande og indstillinger.

Hvis du har gemt alle tilstandsindstillinger med getMode(0) & var, kan du anvende setMode(var) til at gendanne disse indstillinger, indtil funktionen eller programmet afsluttes. Se

getMode(), side 37. Bemærk: De aktuelle tilstandsindstillinger videresendes til

kaldte underrutiner. Hvis en underrutine ændrer en tilstandsindstilling, mistes tilstandsændringen, når kontrollen returnerer til den kaldende rutine.

Note til indtastning af eksemplet: I Regner-applikationen

på den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver

linje. På computerens tastatur skal du holde Alt nede og trykke på Enter.

Katalog

Viser en tilnærmet værdi af p med standardindstillingen for Viste cifre, og viser derefter p med en indstilling på Fix2. Sørg for, at standardindstillingen gendannes efter programmet er eksekveret.

Tilstandsnavn

Viste cifre

Vinkel

Eksponentielt format

Reel eller kompleks

Auto eller tilnærmet

Vektorformat

Talsystem

Tilstandsheltal Indstillingsheltal

=Float, 2=Float1, 3=Float2, 4=Float3, 5=Float4, 6=Float5, 7=Float6, 8=Float7,

9=Float8, 10=Float9, 11=Float10, 12=Float11, 13=Float12, 14=Fix0, 15=Fix1, 16=Fix2, 17=Fix3, 18=Fix4, 19=Fix5, 20=Fix6, 21=Fix7, 22=Fix8, 23=Fix9, 24=Fix10, 25=Fix11, 26=Fix12

=Radian, 2=Grader, 3=Gradian

=Normal, 2=Videnskabelig, 3=Teknisk

=Reel, 2=Rektangulær, 3=Polær

=Auto, 2=Tilnærmet

=Rektangulær, 2=Cylindrisk, 3=Sfærisk

=Decimal, 2=Hex, 3=Binær

TI-Nspire™ Opslagsvejledning 79

shift()

shift(Heltal1[,antalFlyt]) ⇒ heltal

Flytter bittene i et binært heltal. Du kan indtaste Heltal1 i ethvert talsystem. Det konverteres automatisk til en 64-bit binær form med fortegn. Hvis Heltal1 er for stort til denne form, bringer en symmetrisk modulooperation værdien ind i det korrekte område.

Hvis antalFlytninger er positivt, kører flytningen mod venstre. Hvis antalFlytninger er negativt, kører flytningen mod højre. Standardindstillingen er

I en flytning til højre droppes bitten længst mod højre, og 0 eller 1 indsættes for at matche bitten længst til venstre. I en flytning til venstre droppes bitten længst mod venstre, og 0 indsættes som bitten længst til højre.

ë1 (flytter en bit til højre).

For eksempel i en højreflytning: Hver bit flytter til højre. 0b0000000000000111101011000011010 Indsætter 0, hvis bitten længst til venstre er 0,

eller 1, hvis bitten længst til venstre er 1. giver: 00b0000000000000011110101100001101 Resultatet vises i den valgte tilstand for talsystem. Der vises ikke

foranstillede nuller.

shift(Liste1 [,antalFlytninger]) ⇒ liste

Returnerer en kopi af Liste1 flyttet til højre eller venstre med antalflytninger elementer. Ændrer ikke Liste1.

Hvis antalFlytninger er positivt, kører flytningen mod venstre. Hvis antalFlytninger er negativt, kører flytningen mod højre.

Standardindstillingen er ë1 (flyt en bit til højre).

Elementer indført i starten eller slutningen af liste af flytningen, indstilles til symbol “undef”.

shift(Streng1 [,antalFlytninger]) ⇒ streng

Returnerer en kopi af Streng1 flyttet til højre eller venstre med antalflytninger tegn. Ændrer ikke Streng1.

Hvis antalFlytninger er positivt, kører flytningen mod venstre. Hvis antalFlytninger er negativt, kører flytningen mod højre.

Standardindstillingen er ë1 (flyt et tegn til højre).

Tegn indført i starten eller slutningen af streng af flytningen, indstilles til et mellemrum.

Katalog

I binær tilstand:

I hexadecimal tilstand:

Vigtigt: Til binære eller hexadecimale indtastninger skal du

som præfiks altid benytte henholdsvis 0b eller 0h (nul, ikke bogstavet O).

I decimal tilstand:

sign()

sign(Værdi1) ⇒ værdi sign(Liste1) ⇒ liste sign(Matrix1) ⇒ matrix

For det reelle eller komplekse Værdi1, returneres Værdi1 /

abs(Værdi1) når Værdi1 ƒ 0.

Hvis kompleks formattilstand er real:

Katalog

Returnerer 1, hvisVærdi1 er positivt. Returnerer ë1 hvis Værdi1 er negativt.

sign(0) returnerer „1, hvis det komplekse format er reel. Ellers

returnerer det sig selv.

sign(0) repræsenterer enhedscirklen i det komplekse domæne.

For en liste eller matrix returneres fortegnene af elementerne.

80 TI-Nspire™ Opslagsvejledning

simult()

simult(koeffMatrix, konstVektor[, Tol ]) ⇒ matrix

Returnerer en kolonnevektor, der indeholder løsni ngerne til et system af lineære ligninger.

koeffMatrix skal være en kvadratisk matrix, der indeholder kofficienterne til ligningerne.

konstVektor skal have samme antal rækker (samme dimension) som koeffMatrix og indeholde konstanterne.

Ethvert matricelement kan valgfrit behandles som nul, hvis den absolutte værdi er mindre end To l. Denne tolerance anvendes kun, hvis matricen har elementer med flydende decimaler og ikke indeholder symbolske variable, der ikke er tildelt en værdi. Ellers ignoreres To l.

• Hvis du sætter tilstanden Auto/approkstil Approks, foretages beregningerne med aritmetik med flydende komma.

•Hvis tol udelades eller ikke anvendes, beregnes standardtolerancen som:

5Eë14 ·max(dim(koeffMatrix)) ·rækkeNorm(koeffMatrix)

simult(koeffMatrix, konstMatrix[, tol]) ⇒ matrix

Løser flere systemer af lineære ligninger, hvor hvert system har de samme ligningskoefficienter men forskellige konstanter.

Hver kolonne i konstMatrix skal indeholde konstanterne for et ligningssystem. Hver kolonne i den resulterende indeholder løsningen for det tilsvarende system.

Katalog

Løs for x og y: x + 2y = 1 3x + 4y = ë1

Løsningen er x=ë3 og y=2.

Løs: ax + by = 1 cx + dy = 2

Løs:

x + 2y = 1

3x + 4y = ë1

x + 2y = 2

3x + 4y = ë3

For det første system er x=ë3 og y=2. For det andet system er x=ë7 og y=9/2.

sin()

sin(Værdi1) ⇒ værdi sin(Liste1) ⇒ liste

sin(Værdi1) returnerer sinus til argumentet. sin(Liste1) returnerer en liste med sinus til alle elementer i Liste1. Bemærk: Argumentet fortolkes som en vinkel i enten grader eller

radianer afhængigt af den aktuelle vinkeltilstand. Du kan bruge ó,G, eller ô til midlertidigt at tilsidesætte den indstillede vinkeltilstand.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

-tast

TI-Nspire™ Opslagsvejledning 81

sin()

sin(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer matrixsinus af kvadratMatrix1. Dette er ikke det samme som at beregne sinus for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

I vinkeltilstanden Radian:

-tast

sinê()

sinê(Værdi1) ⇒ værdi sinê(Liste1) ⇒ liste

sinê(Værdi1) Returnerer den vinkel, hvis sinus er Værdi1.

sinê(Liste1) returnerer en liste med de inverse sinusværdier for

hvert element af Liste1.

Bemærk: Resultatet returneres som en vinkel i grader eller radianer

afhængigt af den aktuelle vinkeltilstand.

sinê(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer den matrixinverse sinus af kvadratMatrix1. Dette er ikke det samme som at beregne den inverse sinus for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

sinh()

sinh(Ta lv e r1 ) ⇒ værdi sinh(Liste1) ⇒ liste

sinh (Værdi1) returnerer den hyperbolske sinus til argumentet. sinh (Liste1) returnerer en liste af de hyperbolske sinuser af hvert

element af Liste1.

sinh(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer den matrixhyperbolske sinus af kvadratMatrix1. Dette er ikke det samme som at beregne den hyperbolske sinus for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

I vinkeltilstanden radian og tilstanden rektangulært komplekst format:

Du kan se hele resultatet ved at trykke på £ og derefter anvende ¡ og ¢ til at bevæge markøren.

I vinkeltilstanden Radian:

Katalog

-taster

82 TI-Nspire™ Opslagsvejledning

sinhê()

sinhê(Værdi1) ⇒ værdi sinhê(Liste1) ⇒ liste

sinhê(Værdi1) returnerer den inverse hyperbolske sinus af

argumentet.

sinhê(Liste1) returnerer den inverse hyperbolske sinus til hvert

element i Liste1.

sinhê(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer den matrixinverse hyperbolske sinus af kvadratMatrix1. Dette er ikke det samme som at beregne den inverse hyperbolske sinus for hvert element. Oplysninger om beregningsmetoden findes i

cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

I vinkeltilstanden Radian:

Katalog

SinReg

SinReg X, Y [, [Iterationer],[ Periode] [, Kategori, Medtag] ]

Beregner sinusregressionen på listerne X og Y. En sammenfatning af resultaterne lagres i stat.results variable. (Se side 85.)

Katalog

Alle lister skal have ens dimensioner med undtagelse af Medtag. X og Y er lister med uafhængige og afhængige variable. Iterationer er en valgfri værdi, som angiver det maksimale antal

gange (1 til 16) en løsning vil forsøges. Hvis udeladt, anvendes 8. Typisk resulterer større værdier i større nøjagtighed men længere eksekveringstider og omvendt.

Periode angiver en estimeret periode. Hvis den udelades, skal forskellen mellem værdierne i X være lige store og i sekvent iel orden. Hvis du angiver Periode, kan forskellen mellem x-værdierne være forskellig.

Kategori er en liste med numeriske kategorikoder for tilsvarende X og Y data.

Medtag er en liste med en eller flere af kategorikoderne. Kun de

dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Output af SinReg er altid i radianer, uanset vinkelindstillingen.

Output-variabel Beskrivelse

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

Regressionsligning: a·sin(bx+c)+d

Regressionskoefficienter

stat.Resid Residualer fra regressionen

stat.XReg Liste af datapunkter i den modificerede X-liste der faktisk bruges i regressionen ud fra begrænsninger i

stat.YReg Liste af datapunkter i den modificerede Y- li st e der faktisk bruges i regressionen ud fra begrænsninger i

Frekv, kategoriliste,og Medtag Kategorier

stat.FreqReg Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

TI-Nspire™ Opslagsvejledning 83

SortA

SortA Liste1[, Liste2] [, Liste3] ...

Vektor1[, Vektor2] [, Vektor3] ...

SortA

Sorterer elementerne i første argument i stigende rækkefølge. Hvis du medtager yderligere argumenter, sorteres elementerne i hvert

argument således, at deres nye positioner passer til de nye positioner for elementerne i det første argument.

Alle argumenter skal være navne på lister eller vektorer. Alle argumenterne skal have ens dimensioner.

Katalog

SortD

SortD Liste1[, Liste2] [, Liste3] ... SortD

Vektor1[,Vektor2] [,Vektor3] ...

Identisk med SortA, med den undtagelse, at SortD sorterer elementerne i faldende rækkefølge.

Sphere

Vek t o r 4Sphere

Viser række- eller kolonnevektoren i sfærisk form [r q f].

Vek t o r skal have dimensionen 3 og kan være enten en række- eller kolonnevektor.

Bemærk: 4Sphere er en displayformat-kommando, ikke en

konverteringsfunktion. Du kan kun anvende den i slutningen af en indtastningslinje.

Katalog

(ρ,θ,φ)

sqrt()

sqrt(Værdi1) ⇒ værdi sqrt(Liste1) ⇒ liste

Katalog

Returnerer kvadratroden af argumentet. For en liste returneres kvadratrødderne af alle elementer i Liste1.

Bemærk: Se også

vadratrodsskabelon

, side 1.

84 TI-Nspire™ Opslagsvejledning

stat.results

Viser resultater fra en statistikberegning. Resultaterne vises som en mængde af navn-værdi-par. De viste

specifikke navne afhænger af den senest beregnede statistiske funktion eller kommando.

Du kan kopiere et navn eller en værdi og sætte den ind andre steder.

Bemærk: Undgå at definere variable, der anvender samme navne

som dem, der anvendes til statistisk analyse. I visse tilfælde kan der opstå en fejl. Variabelnavne, der anvendes til statisti sk analyse, vises i nedenstående tabel.

Katalog

stat.a stat.AdjR² stat.b stat.b0 stat.b1 stat.b2 stat.b3 stat.b4 stat.b5 stat.b6 stat.b7 stat.b8 stat.b9 stat.b10 stat.bList stat.c² stat.c stat.CLower stat.CLowerList stat.CompList stat.CompMatrix stat.CookDist stat.CUpper stat.CUpperList stat.d

Bemærk: Hver gang en liste- & regneark-funktion beregner statistiske resultater, kopierer den "stat .”gruppevariable til en”

stat#.”gruppe, hvor # er et tal der automatisk sammenlignes. Dette gør, at man kan bevare tidligere resultater, mens man udfører flere beregninger.

stat.dfDenom stat.dfBlock stat.dfCol stat.dfError stat.dfInteract stat.dfReg stat.dfNumer stat.dfRow stat.DW stat.e stat.ExpMatrix stat.F stat.FBlock stat.Fcol

stat.FInteract stat.FreqReg stat.Frow stat.Leverage stat.LowerPred stat.LowerVal stat.m stat.MaxX stat.MaxY stat.ME stat.MedianX

stat.MedianY stat.MEPred stat.MinX stat.MinY stat.MS stat.MSBlock stat.MSCol stat.MSError stat.MSInteract stat.MSReg stat.MSRow stat.n stat.Ç

stat.Ç1 stat.Ç2 stat.ÇDiff stat.PList stat.PVal stat.PValBlock stat.PValCol

stat.PValInteract stat.PValRow stat.Q1X stat.Q1Y stat.Q3X

stat.Q3Y stat.r stat.r² stat.RegEqn stat.Resid stat.ResidTrans stat.sx

stat.sy stat.sx1 stat.sx2 stat.Gx stat.Gx² stat.Gxy stat.Gy stat.Gy² stat.s stat.SE

stat.SEList stat.SEPred stat.sResid stat.SEslope stat.sp stat.SS stat.SSBlock

stat.SSCol stat.SSX stat.SSY stat.SSError stat.SSInteract stat.SSReg stat.SSRow stat.tList stat.UpperPred stat.UpperVal stat.v stat.v1

stat.v2 stat.vDiff stat.vList stat.XReg stat.XVal stat.XValList stat.w

stat.y stat.yList

stat.YReg

TI-Nspire™ Opslagsvejledning 85

stat.values

Viser en matrix med de beregnede værdier for den senest beregnede statistiske funktion eller kommando.

I modsætning til er knyttet til værdierne.

stat.results udelader stat.values de navne, der

Du kan kopiere en værdi og sætte den ind andre steder.

Se eksemplet med

stat.results.

Katalog

stDevPop()

stDevPop(Liste[, Hyppighedsliste]) ⇒ udtryk

Returnerer population standardafvigelsen af elementerne i Liste. Hvert hyppighedsliste-element tæller antallet af konsekutive

forekomster de tilsvarende elementer i Liste.

Bemærk: Liste skal have mindst to elementer. stDevPop(Matrix1[, Hyppighedsmatrix]) ⇒ matrix

Returnerer en rækkevektor af populationsstandardafvigelser for kolonnerne i Matrix1.

Hvert Hyppighedsmatrix-element tæller antallet af konsekutive forekomster af det tilsvarende element iMatrix1.

Bemærk: Matrix1 skal have mindst to rækker.

stDevSamp()

stDevSamp(Liste[, Hyppighedsliste]) ⇒ udtryk

Returnerer stikprøvestandardafvigelsen af elementerne i liste. Hvert hyppighedsliste-element tæller antallet af konsekutive

forekomster de tilsvarende elementer i Liste.

Bemærk: Liste skal have mindst to elementer. stDevSamp(Matrix1[, Hyppighedsmatrix]) ⇒ matrix

Returnerer en rækkevektor af standardafvigelser for målingerne i kolonnerne i Matrix1.

Hvert Hyppighedsmatrix-element tæller antallet af konsekutive forekomster af det tilsvarende element iMatrix1.

Bemærk: Matrix1 skal have mindst to rækker.

I vinkeltilstanden Radian og tilstanden Auto:

Katalog

86 TI-Nspire™ Opslagsvejledning

Stop

Programmeringskommando: Afslutter programmet.

Stop er ikke tilladt i funktioner. Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

Katalog

Store

string()

string(Udtr) ⇒ streng

Reducerer Udtr og returnerer resultatet som en tegnstreng.

subMat()

subMat(Matrix1[, Startrække] [, Startkolonne] [, Slutrække] [,

Slutkolonne])

⇒ matrix

Returnerer den angivne delmatrix af Matrix1. Standardindstillinger: Star trække=1, Startkolonne=1,

Slutrække=sidste række, Slutkolonne=sidste kolonne.

Sum (Sigma) Se G(), side 111.

sum()

sum(Liste[, Start[, Slut]]) ⇒ udtryk

Returnerer summen af elementer i Liste. Start og Slut er valgfri. De angiver en serie af elementer.

& (store)

Katalog

, side 115.

TI-Nspire™ Opslagsvejledning 87

sum()

sum(Matrix1[, Start[, Slut]]) ⇒ matrix

Returnerer en rækkevektor med summerne af elementerne i kolonnerne i Matrix1.

Start og Slut er valgfri. De angiver en serie af rækker.

Katalog

sumIf()

sumIf(Liste,Kriterie[, SumListe]) ⇒ værdi

Returnerer den akkumulerede sum af alle elementerne i Liste, der opfylder det angivne Kriterie. Du kan også vælge at angive en alternativ liste, sumListe, for at levere de elementer, der skal akkumuleres.

Liste kan være et udtryk, en liste eller en matrix. SumListe skal, hvis den er angivet, have samme dimensioner som Liste.

Kriterie kan være:

• En værdi, et udtryk eller en streng. For eksempel akkumulerer 34 kun de elementer i Liste, der reduceres til værdien 34.

• Et Boolsk udtryk, der indeholder symbolet ? som pladsholder for hvert element. For eksempel akkumulerer ?<10 kun de elementer i Liste, der er mindre end 10.

Når et element i Liste opfylder Kriterie, føjes elementet til den akkumulerede sum. Hvis du inkluderer sumListe, tilføjes det tilsvarende element fra sumListe til summen i stedet.

I applikationen Lister og regneark kan du anvende et celleområde i stedet for Liste og sumListe.

Bemærk: Se også countIf(), side 19.

system()

system(Værdi1 [, Værdi2 [, Værdi3 [, ...]]])

Returnerer et system af ligninger formateret som en liste. Du kan også oprette et system ved hjælp af en skabelon.

Bemærk: Se også System af Ligninger, side 1.

(transponere)

Matrix1

⇒ matrix

Returnerer den kompleks konjugerede transponerede Matrix1.

Katalog

88 TI-Nspire™ Opslagsvejledning

tan()

tan(Værdi1) ⇒ værdi tan(Liste1) ⇒ liste

tan(Værdi1) returnerer tangens til argumentet. tan(Liste1) returnerer en liste med tangens til alle elementer i

Liste1.

Bemærk: Argumentet fortolkes som en vinkel i enten grader eller

radianer afhængigt af den aktuelle vinkel tilstand. Du kan bruge ó,G, eller ô til midlertidigt at tilsidesætte den indstillede vinkeltilstand.

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

-tast

tan(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer matrixtangens til kvadratMatrix1. Dette er ikke det samme som at beregne tangens for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

tanê()

tanê(Værdi1) ⇒ værdi tanê(Liste1) ⇒ list

tanê(Værdi1) Returnerer den vinkel, hvis tangent is Værdi1.

tanê(Liste1) returnerer en liste med den inverse tangens til hvert

element af Liste1.

Bemærk: Resultatet returneres som en vinkel i grader eller radianer

afhængigt af den aktuelle vinkeltilstand.

I vinkeltilstanden Radian:

I vinkeltilstanden Grader:

I vinkeltilstanden Nygrader:

I vinkeltilstanden Radian:

-taster

TI-Nspire™ Opslagsvejledning 89

tanê()

tanê(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer den matrixinverse tangens af kvadratMatrix1. Dette er ikke det samme som at beregne den inverse tangens for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

I vinkeltilstanden Radian:

-taster

tanh()

tanh(Værdi1) ⇒ værdi tanh(Liste1) ⇒ liste

tanh(Værdi1) returnerer den hyperbolske tangens til argumentet. tanh(Liste1) returnerer en liste med den hyperbolske tangens til

hvert enkelt element i Liste1.

tanh(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer den matrixhyperbolske tangens af kvadratMatrix1. Dette er ikke det samme som at beregne den hyperbolske tangens for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

tanhê()

tanhê(Værdi1) ⇒ værdi tanhê(Liste1) ⇒ liste

tanhê(Værdi1) returnerer den inverse hyperbolske tangens til

argumentet.

tanhê(Liste1) returnerer en liste med den inverse hyperbolske

tangens til alle elementer i Liste1.

tanhê(kvadratMatrix1) ⇒ kvadratMatrix

Returnerer den matrixinverse hyperbolske tangens af kvadratMatrix1. Dette er ikke det samme som at beregne den inverse hyperbolske tangens for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler.

Katalog

I vinkeltilstanden Radian:

Katalog

I rektangulært komplekst format:

Du kan se hele resultatet ved at trykke på £ og derefter anvende ¡ og ¢ til at bevæge markøren.

I vinkeltilstanden Radian og rektangulært komplekst format:

Du kan se hele resultatet ved at trykke på £ og derefter anvende ¡ og ¢ til at bevæge markøren.

90 TI-Nspire™ Opslagsvejledning

tCdf()

tCdf(nedreGrænse,øvreGrænse,fg) ⇒ tal hvis nedreGrænse og

øvreGrænse er tal, liste hvis nedreGrænse og øvreGrænse er

lister

Beregner Student-t sandsynlighedsfordelingen mellem nedreGrænse og øvreGrænse for de angivne frihedsgrader fg.

 øvreGrænse), sæt nedreGrænse= .9E999.

For P(X

Then Se If, side 39.

Katalog

tInterval

tInterval Liste[,Frekv[,CNiveau]]

(Datalisteinput)

tInterval v,sx,n[,CNiveau]

(Sammenfatning, stat input) Beregner et t konfidensinterval En sammenfatning af resultaterne

lagres i stat.results variable. (Se side 85.)

Output-variabel Beskrivelse

stat.CLower, stat.CUpper Konfidensinterval for et ukendt populationsgennemsnit

stat.x

stat.ME Fejlmargen

stat.fg Frihedsgrader

stat.sx

stat.n Længde på datasekvensen med målingsgennemsnit

tInterval_2Samp

Listet1,Liste2[,Hyppighed1[,Hyppighed12[,CNiveau[,Puljet]]]]

(Datalisteinput)

tInterval_2Samp v1,sx1,n1,v2,sx2,n2[,CNiveau[,Puljet]]

(Sammenfatning, stat input) Beregner et t konfidensinterval med to målinger. En sammenfatning

af resultaterne lagres i variablen stat.results. (Se side 85.) Puljet=1 puljer varianser. Puljet=0 puljer ikke varianser.

Middelværdi af stikprøven fra den uniforme fordeling

Stikprøve standardafvigelse

Katalog

Output-variabel Beskrivelse

stat.CLower, stat.CUpper Konfidensinterval med et konfidensniveau for fordelingssandsynlighed

stat.x1-x2

Middelværdi stikprøver i i datasekvenserne fra den vilkårlige normalfordeling

TI-Nspire™ Opslagsvejledning 91

Output-variabel Beskrivelse

stat.ME Fejlmargen

stat.df Frihedsgrader

stat.

x1, stat.x2

stat.sx1, stat.sx2

Middelværdi stikprøver i i datasekvenserne fra den vilkårlige normalfordeling

Stikprøve standardafvigelser for Liste 1 og Liste 2

stat.n1, stat.n2 Antal målinger i datasekvenserne

stat.sp Den puljede standardafvigelse. Beregnes, når Puljet = 1.

tPdf()

tPdf(XVærdi,fg) ⇒ tal hvis XVærdi er et tal, liste hvis XVærdi

er en liste

Beregner tæthedsfunktionen (pdf) for Student-t fordelingen ved en angivet x værdi med angivne frihedsgrader fg.

trace()

trace(kvadratMatrix) ⇒ værdi

Returner sporet (sum af alle elementer på hoveddiagonalen) af kvadratMatrix.

Try

blok1

Else

blok2

EndTry

Eksekverer blok1, med mindre der opstår en fejl. Programmets eksekvering fortsætter til blok2, hvis der opstår en fejl i blok1. Systemvariablen errCode indeholder fejlkoden, der gør det muligt for programmet at udføre fejlretning. En liste med fejlkoder findes i "Fejlkoder og fejlmeddelelser," side 117.

blok1 og blok2 kan enten være en enkelt sætning eller en række sætninger adskilt med kolon.

Note til indtastning af eksemplet: I Regner-applikationen på

den håndholdte kan du indtaste definitioner over flere linjer ved at trykke på @ i stedet for · ved slutningen af hver linje. På

computerens tastatur skal du holde Alt nede og trykke på Enter.

Katalog

92 TI-Nspire™ Opslagsvejledning

Try

Eksempel 2

Du kan se kommandoerne Try , ClrErr og PassErr i funktion ved at indtaste programmet eigenvals() vist til højre. Kør programmet ved at eksekvere hvert af de følgende udtryk.

Bemærk: Se også ClrErr, side 14, og PassErr, side 66.

Katalog

Disp "A= ",a Disp "B= ",b Disp " " Disp "Eigenværdier for A·B er:",eigVl(a*b)

Else

If errCode=230 Then

Disp "Error: Produktet af A·B skal være en kvadratisk

matrix"

ClrErr

Else

PassErr

EndIf EndTry EndPrgm

tTest

tTest m0,Liste[,Hyppighed[,Hypot]]

(Datalisteinput)

tTest m0,x,sx,n,[Hypot]

(Sammenfatning, stat input) Udfører en hypotesetest for et enkelt ubekendt

populationsgennemsnit m, når populationens standardafvigelses er ubekendt. En sammenfatning af resultaterne lagres i variablen stat.results. (Se side 85.)

Test H0: m = m0, mod en af de følgende:

Til Ha: m < m0, sæt Hypot<0 til Ha: m ƒ m0 (standard), sæt Hypot=0 til Ha: m > m0, sæt Hypot>0

Output-variabel Beskrivelse

stat.t

stat.PVal Mindste signifikansniveau, ved hvilket nul-hypotesen kan forkastes

stat.fg Frihedsgrader

stat.x

stat.sx Standardmåleafvigelse for datasekvensen

stat.n Stikprøvens størrelse

(x N m0) / (stdafvigelse / kvr(n))

Middelværdi af stikprøver af datasekvensen i Liste

Katalog

TI-Nspire™ Opslagsvejledning 93

tTest_2Samp

Liste1,Liste2[,Hyppighed1[,Hyppighed2[,Hypot[,Puljet]]]]

(Datalisteinput)

tTest_2Samp v1,sx1,n1,v2,sx2,n2[,Hypot[,Puljet]]

(Sammenfatning, stat input) Beregner en to-prøvers t test. En sammenfatning af resultaterne

lagres i variablen stat.results. (Se side 85.)

: m1 = m2, mod en af de følgende:

Test H

Til Ha: m1< m2, sæt Hypot<0 til Ha: m1ƒ m2 (standard), sæt Hypot=0 til Ha: m1> m2, sæt Hypot>0

Puljet=1 puljer varianser Puljet=0 puljer ikke varianser

Output-variabel Beskrivelse

stat.t Standardnormalværdi beregnet som differens af gennemsnit

stat.PVal Mindste signifikansniveau, ved hvilket nul-hypotesen kan forkastes

stat.df Frihedsgrader for t-statistik

stat.x1, stat.x2

Middelværdi af stikprøver for datasekvenserne i Liste 1 og Liste 2

stat.sx1, stat.sx2 Stikprøve standardafvigelse for datasekvenserne i Liste 1 og Liste 2

stat.n1, stat.n2 Størrelse på stikprøverne

stat.sp Den puljede standardafvigelse. Beregnes, når Puljet=1.

Katalog

tvmFV()

tvmFV(N,I,PV,Pmt,[PpY],[CpY],[PmtAt]) ⇒ værdi

Katalog

Finansfunktion, der beregner penges fremtidige værdi.

Bemærk: Argumenter, der bruges i TVM-funktionerne er beskrevet

i tabellen over TVM-argumenter, side 95. Se også amortTbl(), side 5.

tvmI()

tvmI(N,PV,Pmt,FV,[PpY],[CpY],[PmtAt]) ⇒ værdi

Katalog

Finansfunktion, der beregner den årlige rente.

Bemærk: Argumenter, der bruges i TVM-funktionerne er beskrevet

i tabellen over TVM-argumenter, side 95. Se også amortTbl(), side 5.

94 TI-Nspire™ Opslagsvejledning

Texas Instruments TI-Nspire Reference Guide [da]

Specifications and Main Features

Frequently Asked Questions

User Manual

Vigtige oplysninger

Indholdsfortegnelse

Udtryksskabeloner

TI-Nspire™ Opslagsvejledning 1

Alfabetisk oversigt