Lexibook SC500, SC500FR User Manual

Manuel d’instruction

SC500FR

3

INTRODUCTION

Avant la première utilisation

1.FONCTIONS USUELLES

Mise en marche et arrêt de la calculatrice

Afchage et symboles utilisés

Touches usuelles Fonctions secondes et fonctions ALPHA

Notations utilisées dans le manuel

Modes de calcul

Modication d’un calcul Notation scientique et ingénieur

Choix de la notation Fixation de la position de la virgule

Priorités de calcul

Calculs de pourcentage

2. UTILISATION DES MEMOIRES

Rappel du dernier résultat (ANS) Répétition du dernier calcul (K) Mémoire indépendante (M) Mémoires temporaires (A-D, X, Y)

3. FONCTIONS ARITHMETIQUES

Inverse, carré et exposants

Racines Fractions Logarithmes et exponentielles

Hyperboliques

4. CALCULS TRIGONOMETRIQUES

Nombre π

Unités d’angles Choix de l’unité d’angle et conversions Conversion sexagésimale (degrés / minutes /secondes)

Calculs horaires

Cosinus, sinus, tangente Arccosinus, arcsinus, arctangente Coordonnées polaires

Nombres complexes

5. CALCULS EN BASE-N

Pour mémoire

Changements de base

Les opérateurs logiques

Notations Commandes du mode Base N et conversions Calculs en Base N

Opérateurs logiques en Base N

6. STATISTIQUES

Commentaires préliminaires Touches de fonctions statistiques Statistiques à 1 variable – exemple pratique Statistiques à 2 variables – exemple pratique Régression non linéaire

7. AUTRES FONCTIONS

Factorielle n!, permutation, combinaison Génération de nombre aléatoire (fonction Random)

8. MESSAGES D’ERREUR

Causes possibles d’erreurs

Valeurs admissibles

9. PRECAUTIONS D’EMPLOI

Utilisation de RESET

Remplacement des piles

10. INDEX

11. GARANTIE

4 4 6 6 6 8 8 9 9

9 11 11 13 13 14 15 15 16 16 17 20 20 20 20 22 22 23 23 23 23 24 25 25 26 27 29 31 31 31 31 32 32 33 34 35 35 36 37 37 42 43 43 44 45 45 45 47 47 47 49 50

Calculatrice scientique à deux lignes, fonctions trigonométriques,

statistiques à une et deux variables, probabilités .

SOMMAIRE

CALCULATRICE SCIENTIFIQUE LEXIBOOK

®

SC500FR

4

5

3. Localisez le trou du RESET au dos de l’appareil. Insérez une pointe ne (un trombone par exemple) et appuyez doucement. Si les piles ont été correctement installées, l’icône DEG et le chiffre 0 seront afchés, ainsi qu’un curseur clignotant. Si ce n’est pas le cas, retirez et réinstallez à

nouveau la pile.

Pour plus d’informations concernant la pile, voir le chapitre « Précautions d’emploi ».

4. Faites coulisser la calculatrice dans le couvercle pour accéder au clavier.

5. Retirez la pellicule statique protectrice de l’écran LCD.

6. Appuyez sur la touche [ON/C] pour mettre la calculatrice en marche. Si la pile a été correctement installée, l’icône DEG et le chiffre 0 seront afchés. Si ce n’est pas le cas, retirez et réinstallez à nouveau la pile.

Nous sommes heureux de vous compter aujourd’hui parmi les nombreux

utilisateurs des produits Lexibook® et nous vous remercions de votre

conance. Depuis plus de 15 ans, la société française Lexibook conçoit, développe, fabrique et distribue à travers le monde des produits électroniques pour tous, reconnus pour leur valeur technologique et leur qualité de fabrication. Calculatrices, dictionnaires et traducteurs électroniques, stations météo, multimédia, horlogerie, téléphonie… Nos produits accompagnent votre quotidien. Pour apprécier pleinement les capacités de la calculatrice scientique SC500FR, nous vous invitons à lire attentivement ce mode d’emploi.

INTRODUCTION

Avant la première utilisation

Avant de démarrer, veuillez suivre attentivement les étapes suivantes :

1. Retirez avec précaution la languette de protection du compartiment à pile en tirant sur l’extrémité de la languette.

2. Si la languette reste coincée, dévissez le compartiment à piles à l’aide d’un tournevis et retirez la pile, puis la languette. Replacez ensuite la pile CR2025 en respectant la polarité comme indiqué dans le compartiment de l’appareil (côté + au-dessus). Remettez ensuite en place le couvercle

du compartiment et la vis.

DEG

0.

6

7

1. FONCTIONS USUELLES

Mise en marche et arrêt de la calculatrice

Signe moins pour indiquer que le nombre afché est négatif.

S’afche pour indiquer que le calcul en cours est trop long pour être afché en entier. Dans ce cas appuyer sur [ ] ou [ ] pour afcher le reste du calcul.

Indique que plusieurs lignes de calculs sont en mémoire. Si vous voulez vérier ou modier ces lignes de calcul, appuyez sur [ ], [ ].

Mémoire activée.

S’afche quand le calcul excède les limites permises ou qu’une erreur est détectée. Ex : division par 0. D’autres cas d’erreurs sont détaillés dans le chapitre correspondant, « Messages d’erreur ».

S’afche quand la fonction seconde est activée (pour une fonction imprimée en orange sur le clavier).

S’afche quand la fonction hyperbolique est activée.

S’afche quand la fonction hyperbolique inverse est activée.

S’afche pour indiquer que la fonction ALPHA est activée (une fonction imprimée en rouge sur le clavier, ou [STO], [RCL]). Ce sont toutes des fonctions liées à la mise en mémoire ou au rappel de données.

Indique que le résultat sera afché avec un nombre déterminé de chiffres après la virgule.

Indique que le résultat sera afché en notation scientique.

Indique que le résultat sera afché en notation ingénieur.

S’afche en mode degré ou quand la mesure d’angle afchée est en degrés.

S’afche en mode radian ou quand la mesure d’angle afchée est en radians.

S’afche en mode grade ou quand la mesure d’angle afchée est en grades.

S’afche en mode statistiques.

S’afche en mode complexes.

-

ou

, ou les deux ensemble

M

Error 1, 2, 3 ou 4

2ndF

HYP

2ndF HYP

ALPHA

FIX

SCI

ENG

DEG

RAD

GRAD

STAT

CPLX

[ON/C]

[2ndF] [OFF]

Mise en marche de la calculatrice.

Mise à zéro.

Note : quand votre calculatrice se remet en marche après avoir été éteinte, elle est réglée par défaut en mode décimal (DEC), avec virgule ottante et des mesures d’angles en degrés (DEG).

Arrêt.

Après 10 minutes environ de non-utilisation, la calculatrice s’éteindra automatiquement.

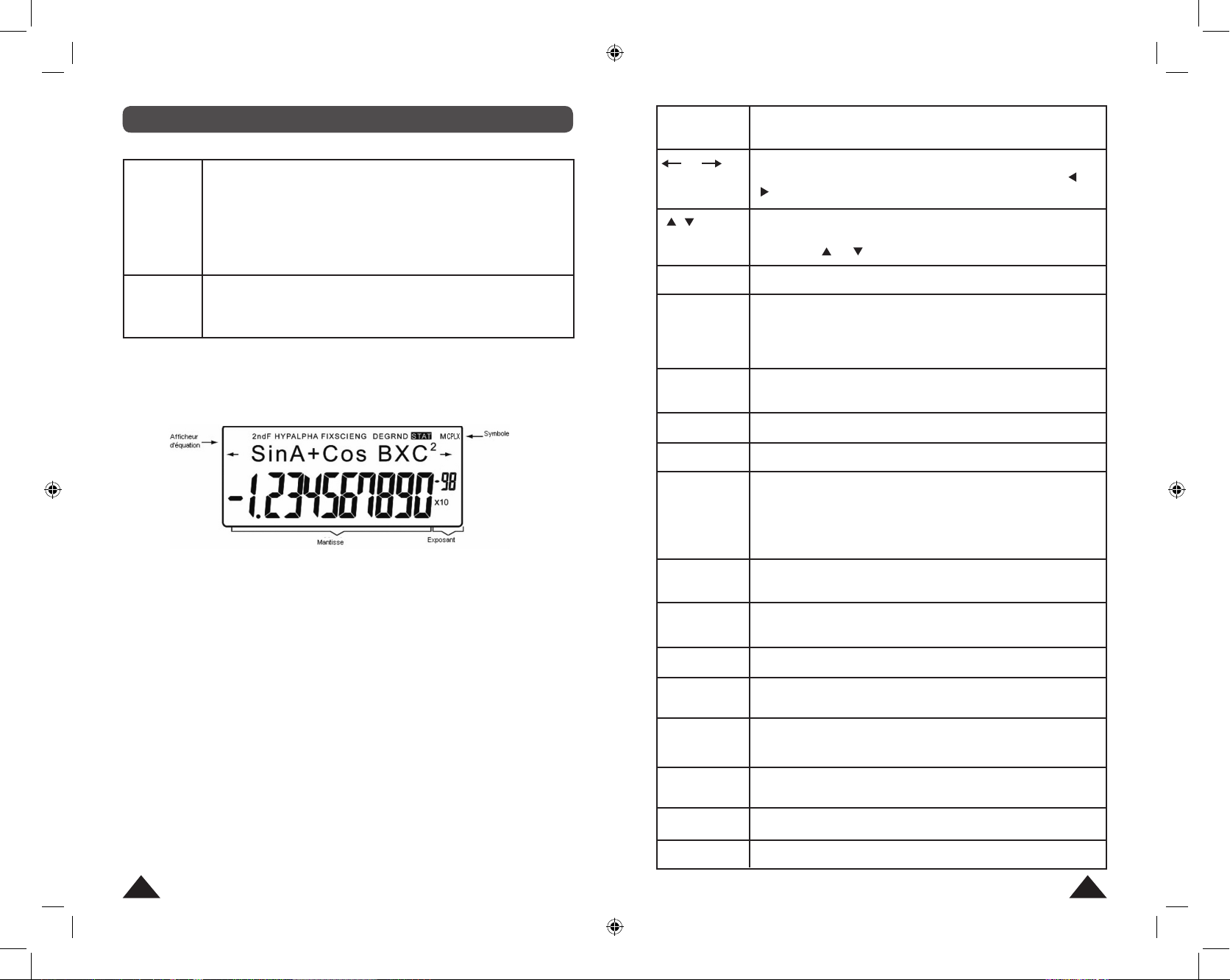
Afchage et symboles utilisés

Votre calculatrice dispose d’un afchage à deux lignes comme suit :

Sur la ligne du bas les valeurs et les résultats s’afchent avec 10 chiffres signicatifs, plus deux, sur la droite, de notation scientique (voir paragraphe “Notation scientique”).

La ligne immédiatement au dessus, est une ligne alphanumérique sur laquelle vous pouvez visualiser le calcul saisi, et le modier, même après avoir obtenu le résultat (voir paragraphe “Modication d’un calcul”).

Enn sur la ligne tout en haut et sur les côtés on trouve divers symboles. En utilisation réelle, ils ne s’allument pas tous en même temps, mais ceux qui sont allumés vous donnent des indications qui permettent une meilleure lisibilité des opérations en cours :

8

9

Modication d’un calcul

Pour déplacer le curseur sur la ligne alphanumérique.

Si on appuie sur une touche le texte/chiffre correspondant sera inséré immédiatement à gauche

du curseur.

Efface le caractère situé à l’endroit où se trouve le

curseur.

Passer au calcul précédent / suivant.

Aller au premier calcul / au dernier calcul.

Initie une nouvelle ligne de calcul.

[ ], [ ]

[DEL]

[ ], [ ]

[2ndF] [ ],[2ndF] [ ]

[2ndF] [CA]

Touches usuelles

0 - 9

[+]

[-]

[x]

[÷]

[=]

[.]

[+/-]

[ ( ], [ ) ]

Touches de chiffres.

Les touches de [0] a [9] seront notées 0 a 9 (Sans crochets)

pour faciliter la lecture.

Addition.

Soustraction.

Multiplication.

Division.

Donne le résultat.

Insertion de la virgule pour un nombre décimal.

Ex : pour écrire 12,3 -> 12[.]3

Change le signe du nombre qui sera rentré immédiatement

après.

42 [x] [+/-] 5 [+] 120 [=]

Ouvre / ferme une parenthèse.

Ex : [ ( ] 4 [+] 1 [ ) ] [x] 5 [=]

De nombreuses touches donnent accès à une deuxième fonction, voire à

une troisième.

Cette seconde fonction est afchée en orange au dessus de la touche. On y accède en tapant [2ndF] et la touche concernée.

La troisième fonction, une fonction relative à la mémoire et indiquée par une lettre, est imprimée en rouge au-dessus de la fonction principale. On y accède en tapant [2ndF], [ALPHA], puis la touche concernée.

Dans ce manuel les fonctions seront indiquées comme suit : principale [ln] seconde [2ndF] [ex ] Alpha [2ndF][ALPHA][X]

Les touches [0] à [9] seront notées 0 à 9 (sans crochets) pour faciliter la

lecture.

Les calculs et les résultats seront présentés comme suit :

description saisie -> ligne alphanumérique | ligne résultat

Ex :

Le calcul représenté par cet écran sera noté ainsi : [(] 4 [+] 1 [)] [x] 5 [=] -> (4+1)x5= | 25.

Lorsque cela ne nuira pas à la compréhension d’un exemple, la partie concernant la ligne alphanumérique pourra être omise.

Fonctions secondes et fonctions ALPHA

Accès aux fonctions secondes.

Accès aux fonctions ALPHA.

[2ndF]

[2ndF][ALPHA]

Note : la touche [ALPHA] se trouve au dessus de la touche principale [RCL].

Notations utilisées dans le manuel

DEG

42x-5+120=

-90.

DEG

( 4+1) x 5 =

25.

DEG

( 4+1) x 5 =

25.

Modes de calcul

Mode de calcul ordinaire (mode arithmétique).

Mode de calcul statistique à 1 variable (symbole STAT afché).

Mode de calcul statistique à 2 variables (symbole STAT afché).

[2ndF] [MODE] 0

[2ndF] [MODE] 1

[2ndF] [MODE] 2

Avant de commencer un nouveau calcul non statistique, vériez que vous êtes en mode normal et appuyez sur [ON/C] pour bien mettre à zéro.

fonction principale

fonction seconde

fonction ALPHA

10

11

FRANÇAIS

Grâce à sa ligne alphanumérique, votre calculatrice vous permet non seulement de visualiser le calcul en cours, mais aussi de revoir et modier vos calculs après en avoir obtenu les résultats. Le nombre de calculs ainsi conservés dépend de la longueur des calculs considérés, votre calculatrice pouvant conserver en mémoire jusqu’à 142 caractères.

Cette mémoire s’efface pour toutes les lignes dans les cas suivants :

• si vous appuyez sur [2ndF] [OFF].

• si la calculatrice s’éteint d’elle-même.

• lors des changements de modes (mode statistiques).

Note : les lignes de conversion (angles, coordonnées) ne sont pas mémorisées.

Ex : Vous avez effectué les saisies suivantes : [2ndF] [OFF] [ON/C] 34 [+] 57 [=] 45 [+] 17 [=] 68 [x] 25 [=] [(] 18 [+] 6 [)] [÷] [(] 15 [-] 8 [)] [=]

Les symboles , (non représentés ci-dessous) vous indiquent qu’il y a plusieurs lignes de calcul en mémoire.

L’afchage indique :

Si vous appuyez plusieurs fois sur [ ], il se décale sur la droite, le symbole

disparaît et le symbole apparaît.

Si vous appuyez sur [ ] vous allez au calcul précédent :

Si vous appuyez sur [2ndF] [ ] vous allez directement au premier calcul mémorisé:

Si vous appuyez sur [ ], vous allez au second calcul mémorisé et ainsi de suite:

• Vous voulez modier 45+17= en 45+57=

Vous positionnez le curseur à l’aide de la touche [ ] pour vous placer immédiatement sur l’endroit de correction.

Appuyez sur [DEL] pour effacer le 1.

Insérez le 5 à gauche de l’emplacement du curseur en appuyant tout simplement sur la touche 5, et ensuite appuyez sur [ = ] :

DEG

(18+6) (15-8

3.428571429

DEG

68x25 =

1700.

DEG

34+57 =

91.

DEG

18+6) (15-8)

0.

DEG

45+17 =

62.

DEG

45+17 =

62.

DEG

45+7 =

62.

DEG

45+57 =

102.

Notation scientique et ingénieur

La SC500FR afche directement le résultat d’un calcul (x) en mode décimal normal si x appartient à l’intervalle suivant :

0.000000001≤ | x | ≤ 9999999999

Note : |x| est la valeur absolue de x, soit |x|= -x si x≤0 et |x|=x si x≥0.

En dehors de ces limites la calculatrice afchera automatiquement le résultat d’un calcul selon le système de notation scientique, les deux chiffres à droite représentant l’exposant du facteur 10.

Choix de la notation

Passage en notation virgule xe / notation scientique / notation ingénieur / mode normal.

Saisie d’une valeur en notation scientique.

[2ndF][FSE]

[EXP]

12

13

Pour un nombre qui se situe dans l’intervalle précédent, votre calculatrice vous donne le choix de l’exprimer en notation normale, en notation scientique ou ingénieur, selon votre préférence.

• appuyez une fois sur [2ndF][FSE] pour passer en mode notation virgule xe (nombre déterminé de chiffres après la virgule). Le symbole FIX s’allume sur l’afchage.

• appuyer une seconde fois sur [2ndF][FSE] pour passer en mode notation scientique. Le symbole SCI s’allume sur l’afchage.

• appuyer une troisième fois sur [2ndF][FSE] pour passer en mode notation ingénieur. Le symbole ENG s’allume sur l’afchage.

• appuyer une fois sur [2ndF][FSE] pour passer en afchage normal.

Ex :

283100 [=] -> 283100. résultat avec virgule ottante

[2ndF][FSE] -> 283100.00000 mode FIX, résultat avec virgule

xe

[2ndF][FSE] -> 2.831000000

05

mode SCI, résultat en mode

scientique

[2ndF][FSE] -> 283.1000000 03 mode ENG, résultat en mode ingénieur

[2ndF][FSE] -> 283100. mode normal, résultat avec

virgule ottante

Pour saisir un nombre directement en notation scientique, utilisez la touche [EXP]:

retour virgule ottante

Avec un exposant négatif : 2 [.] 831 [EXP] [+/-] 5 [=] -> 2.831E-5= | 0.000020831

FIX SCI ENG

appuyez sur [2ndF][FSE]

Afchage normal

Fixation de la position de la virgule

Choix du nombre de chiffres après la virgule, accessible uniquement en mode FIX

Annulation du réglage du nombre de chiffres après la virgule, accessible uniquement en mode FIX

[2ndF][TAB]

[2ndF][TAB][.]

100000 [÷] 3 [=] -> 33333.33333 mode virgule ottante

[2ndF][FSE] -> 33333.33333 mode FIX [2ndF][TAB] 2 -> 33333.33 mode FIX, 2 chiffres après la virgule [2ndF][TAB] 3 -> 33333.333 mode FIX, 3 chiffres après la virgule

Fixer la position de la virgule est compatible avec la notation scientique et

ingénieur : [2ndF][FSE] -> 3.333 04 mode SCI [2ndF][FSE] -> 33.333 03 mode ENG

[2ndF][FSE] -> 33333.33333 afchage normal

[2ndF][FSE] -> 33333.333

On voit que le réglage n’avait pas été annulé par le passage en afchage

normal. [2ndF][TAB][.] -> 33333.33333 annulation en mode FIX

Priorités de calcul

Quand il y a plusieurs opérations à réaliser dans un calcul, votre calculatrice les évalue et détermine l’ordre dans lequel les effectuer, en fonction des règles arithmétiques. Cet ordre de priorités est le suivant :

1. Les opérations entre parenthèses, et, en cas de plusieurs niveaux de parenthèses, la dernière parenthèse ouverte.

2. Les fonctions utilisant un type d’exposant telles que X

-1

, X2 , √, xy et x√,

ainsi que le changement de signe [(-)].

3. Les fonctions de type cos, sin, ln, ex…

4. Les fonctions de saisie d’une donnée, telles que [Dº M’S] et [a b/c].

5. Les multiplications et divisions (la multiplication peut être implicite, par

exemple 2cosπ).

6. Les additions et soustractions.

7. Les fonctions qui signalent la n d’un calcul ou convertissent un résultat : [=], [STO], [M+], [SHIFT][DRG ], [SHIFT][ rθ], etc.

Lorsque les opérateurs sont de même niveau de priorité la calculatrice les effectue tout simplement par ordre d’apparition de gauche à droite. Au sein de parenthèses l’ordre des priorités suit les mêmes règles.

14

15

Ex: 24 [÷] [(] 4[+]6 [)] [=]

Le résultat (2,4) est automatiquement mémorisé dans la mémoire ANS.

On peut alors calculer 3 x ANS + 60 ÷ ANS 3 [x] [2ndF][ANS] [+] 60 [÷][2ndF][ANS] [=]

Calculs en chaîne

Il s’agit de calculs pour lesquels le résultat du calcul précédent sert de premier opérande du calcul suivant. Vous pouvez notamment utiliser dans ces calculs les fonctions [√], [x2], [sin],...

Ex : [ON/C] 6 [+] 4 [=] -> 6+4= | 10. [+] 71 [=] -> ANS+71= | 81.

[√] [=]

2. UTILISATION DES MEMOIRES

Rappel du dernier résultat (ANS)

[2ndF][ANS]

[2ndF][CA]

Rappelle le résultat du calcul précédent.

Efface le contenu de la mémoire ANS.

Ex :

1 [+] 3 [x] 5 [=] -> 1+3x5 = | 16. [(] 1 [+] 4 [)] [x] 5 [=] -> (1+4)x5 = | 25. 10 [-] 3 [x2] [=] -> 10-32 = | 1. 5 [yx] [ln] 2 [=] -> 5 ln 2= | 3.05132936 soit 5

ln2

Votre calculatrice fait la différence entre les différents niveaux priorités et, au besoin, mémorise les données et les opérateurs jusqu’à la bonne résolution du calcul, et ce jusqu’à six niveaux différents pour un calcul en

cours.

Calculs de pourcentage

Calcule le pourcentage, l’augmentation ou la diminution exprimée en pourcentage.

[2ndF] [%]

Ex :

Il y a 618 élèves au Lycée Gambetta. 49,5% sont des garçons. Combien y

a-t-il de garçons ? et de lles ?

618 [x] 49 [.] 5 [2ndF] [%] -> 305.91 soit 306 garçons

618 [-] 49 [.] 5 [2ndF] [%] -> 312.09 soit 312 lles

Article à 180 Euros, rabais de 20%, calcul du prix nal.

180 [-] 20 [2ndF] [%] -> 144.

DEG

24 (4+6)=

2.4

DEG

3xANS+60 ANS-

32.2

DEG

ANS+71

81.

DEG

ANS

9.

16

17

Dans certains cas, si l’on saisit une valeur et que l’on appuie sur [=] sans saisir d’opérateur, la calculatrice effectue un calcul et donne un résultat. En effet la calculatrice reprend la nouvelle valeur saisie, l’opérateur du dernier calcul et un de ses opérandes, et effectue une nouvelle opération. Cet opérande est noté K.

Attention : pour l’addition, la soustraction et la division, la calculatrice reprend l’opérande de droite, pour la multiplication la calculatrice reprend l’opérande de gauche.

Ex :

5 [x] 2 [=] -> 5x2 = | 10. 4 [=] -> Kx4= | 20. multiplication par 5 6 [=] -> Kx6= | 30.

8 [+] 6 [=] -> 8+6= | 14. 5 [=] -> 5+K= | 11. addition de 6 2 [=] -> 2+K= | 8.

32 [÷] 2 [=] -> 16. 8[=] -> 8÷K= | 4.

S’il y a plusieurs opérateurs dans le calcul l’opérateur retenu est celui qui a

été saisi en dernier.

Ex :

100 [-] 3 [x] 5 [=] -> 100-3x5= | 85. 25 [=] -> Kx25= | 75. (3x25) 25 [÷] 5 [+] 6 [=] -> 25÷5+6= | 11. 4 [=] -> 4+K= | 10.

Répétition du dernier calcul (K)

Répète le dernier calcul sur la valeur saisie. Fonctionne avec [+], [-], [÷] et [x].

[=]

[STO] [M]

[RCL] [M]

[M+]

[2ndF] [M-]

0 (zéro) [STO] [M]

ou [ON/C] [STO] [M]

Remplace le contenu de la mémoire M par le nombre afché.

Afche le contenu de la mémoire M.

Ajoute le nombre afché au contenu de la mémoire.

Soustrait le nombre afché au contenu de la mémoire.

Pour remettre à zéro la mémoire M. Dans ce cas le symbole M disparaît de l’écran.

Mémoire indépendante (M)

Ex :

On souhaite réaliser l’opération suivante :

Articles en stock le matin = 200 Articles livrés dans la journée : 5 boîtes de 12 et 9 boîtes de 6 Articles vendus dans la journée : 2 boîtes de 24

Quantité de pièces en stock à la n de la journée ? Valeur du stock si chaque pièce coûte 3,50€ ?

Le calcul s’effectue ainsi : 200 [STO] [M] -> 200.

5 [x] 12 [M+] -> 60.

9 [x] 6 [=] [M+] -> 54. 2 [x] 24 [=][2ndF] [M-] -> 48.

[RCL] [M] -> 266. nombre de pièces en stock

3 [.] 5 [x] [RCL] [M] [=] -> 931. valeur du stock

DEG M

200

->

M

200.

DEG M

5x12M+

60.

DEG M

M=

266.

DEG M

3.5xM=

931.

[STO] [Y]

[RCL] [Y] ou [2ndF][ALPHA][Y]

[2ndF][CA]

Remplace le contenu de la mémoire Y par le nombre afché.

Rappelle le contenu de la mémoire Y pour utilisation dans un calcul. La valeur de Y s’afche directement sur la ligne alphanumérique.

Efface le contenu des mémoires A-D, X, Y et ANS.

Mémoires temporaires (A-D, X, Y)

18

19

Votre calculatrice dispose de 8 mémoires temporaires, A, B, C, D, E, F, X et Y. Ces mémoires temporaires vous permettent de stocker des données pour

rappel et utilisation dans des calculs futurs.

Vous pouvez employer [STO], [RCL] et [2ndF] [ALPHA] pour chacune des touches [A], [B], [C], [D], [E], [F], [X] et [Y].

Note : les mémoires [E], [F], [X] et [Y] sont utilisées par d’autres fonctions, qui ont trait à la génération de nombres aléatoires et à la conversion des coordonnées cartésiennes / polaires. Il est bon de le savoir an d’éviter des interférences possibles entre calculs. Pour plus de détails sur ces fonctions, vous pouvez vous référer aux paragraphes correspondants.

Ex :

1 € = 140 Yens, combien valent 33 775 Yens en Euros ? Combien valent 2750 € en Yens ?

140 [STO] [Y]

33775 [÷][RCL][Y][=]

2750 [x] [RCL][Y][=]

Calcul de la surface d’un cercle de rayon r=3 3 [STO] [Y]

[π] [2ndF] [ALPHA] [Y] [x2][=]

A chaque utilisation de [STO], [RCL] et [2ndF] [ALPHA], le symbole ALPHA s’allumera sur l’afchage pour vous indiquer que la fonction est activée.

DEG

140

->Y

140.

DEG

33775 Y=

241.25

DEG

2750xY

385000.

DEG

3

->Y

3.

DEG

πY2=

28.27433388

Cette fonction de programmation vous permet d’effectuer toutes sortes de calculs répétitifs. Vous pouvez ainsi mettre en mémoire des expressions à une ou plusieurs inconnues et gagner du temps dans la saisie et l’exécution de vos calculs récurrents. Pour cela vous utilisez les mémoires indépendantes en tant que variables. Pendant l’exécution le programme les identiera et vous demandera leur valeur dans leur ordre d’apparition dans l’expression.

Ex : Pour effectuer le calcul suivant avec plusieurs valeurs différentes :

y= 5a + 2 √x

5 [RCL][A] [+] 2 [√] [RCL][X][LRN] -> 5A+2√X [COMP] -> A? | 0. 2 [=] -> X? | 0.

25[=] -> 5A+2√X= | 20.

[=] -> A? | 2. l’exécution reprend [ON/C] interruption de l’exécution

Remarques :

- Lorsque l’exécution commence, votre calculatrice vous propose une valeur de variable qui peut être non nulle, puisque c’est le contenu de la mémoire correspondante. Si cette valeur vous convient, il suft d’appuyer sur [=] pour conrmer.

- Vous pouvez rentrer un calcul à la place d’une valeur, par exemple 3ln 2

pour la valeur A.

- Vous pouvez utiliser les mémoires M, A-F, X, Y et Ans dans la formule (la calculatrice ne vous demandera pas la valeur de Ans !)

[LRN]

[COMP]

Mise en mémoire d’une formule de calcul.

Exécution d’un calcul mémorisé.

Mémorisation d’une formule de calcul

20

21

3. FONCTIONS ARITHMETIQUES

[2ndF] [x-1]

[X2]

[yx]

[2ndF][10x]

Calcule l’inverse de la valeur saisie immédiatement avant.

Calcule le carré de la valeur saisie immédiatement avant.

Elève la valeur y (saisie avant) à la puissance x (saisie après).

Calcule la puissance 10 du nombre saisi immédiatement

après.

Inverse, carré et exposants

Ex : 8 [2ndF] [x-1] [=] -> 8-1 = | 0.125 3 [x2][=] -> 32 = | 9. 5 [yx]3 [=] -> 5 3 | 125. 2 [yx]5 [=] -> 2 5 | 32. [2ndF][10x] [+/-] 3 [=] -> 10 -3 | 0.001

[√]

[2ndF] [3√]

[

2ndF] [x√]

Calcule la racine carrée du nombre saisi immédiatement

après.

Calcule la racine cubique du nombre saisi immédiatement

après.

Calcule la Xième racine du nombre saisi immédiatement

après.

Racines

En reprenant les exemples précédents :

[√] 9 [=] -> √9= | 3.

[2ndF] [ 3√]125 [=] ->

3

√125= | 5.

5 [2ndF] [ x√] 32 [=] -> 5 x√ 32= | 2.

[a b/c]

[2ndF] [d/c]

Permet de saisir une fraction de numérateur b et de dénominateur c, et une partie entière a (facultative).

Convertit un nombre décimal en un nombre entier plus une fraction irréductible, et vice-versa.

Fractions

Votre calculatrice vous permet d’effectuer un certain nombre d’opérations arithmétiques exprimées ou converties en fractions.

a, b et c peuvent être remplacés par un calcul entre parenthèses. Cependant dans certains cas on pourra obtenir un résultat décimal mais pas un résultat

en fractions.

Ex :

3 [a b/c] 1 [a b/c] 2 [+] 4 [a b/c] 3 [=] -> 3 1 2 + 4 3 = | 4 5 6

soit

[a b/c] -> 3 1 2 + 4 3 = | 4.833333333

[2ndF] [d/c] -> 3 1 2 + 4 3 = | 29 6.

1.25 [+] 2 [a b/c] 5 [=] -> 1.25+2 5= | 1.65 [a b/c] -> 1.25+2 5= | 1 13 20. [2ndF] [d/c] -> 1.25+2 5= | 33 20.

On peut utiliser une fraction en tant qu’exposant : 10

[2ndF] [10x] 2[a b/c]3 [=] -> 10 2 3= | 4.641588834

Notes :

• pour effectuer un calcul tel que + , on peut aussi utiliser [2ndF] [x-1] :

6 [2ndF] [x-1] + 7 [2ndF] [x-1] [=] -> 6-1+7-1 = | 0.309523809 [2ndF] [d/c] -> 6-1+7-1 = | 13 42.

• pour une fraction telle que :

On peut utiliser la notation a b/c. Il faut saisir le calcul comme suit : 24 [a b/c] [(] 4 [+] 6 [)] [=] -> 24 (4+6)= | 2 2 5 [a b/c] -> 24 (4+6)= | 2.4

DEG

3 1 2 + 4 3= 4 5 6

3

1

2

4 3

+ =

DEG

3 1 2 + 4 3=

4.833333333

DEG

3 1 2 + 4 3= 29 6

Signication des notations a b/c et d/c :

a = 3, b=1 et c=2. a est la partie entière de x, c’est-à-dire x= 3 + = 3,5

x = 3

1

2

En fait x=

En notation d/c, d=7 et c=2.

7

2

1

2

161

7

24

4+6

2 3

4

5 6

22

23

Ex :

[ HYP] [sin] 0 [=] -> sinh0= | 0. [ HYP] [cos] 0 [=] -> cosh0= | 1. [2ndF] [arc hyp] [tan] 0[=] -> tanh-10= | 0. [2ndF] [arc hyp] [cos] 1 [=] -> cosh-1 1= | 0.

Calcul de (cosh 1.5 + sinh 1.5)

2

[(] [HYP][cos] 1 [.] 5 [+] [HYP][sin] 1 [.]5 [)][x2][=]

Note : les saisies [2ndF] [archyp] [sin] et [HYP] [2ndF] [sin-1] sont équivalentes.

[ln]

[log]

[2ndF] [ex]

Touche de logarithme népérien.

Touche de logarithme décimal.

Touche de fonction exponentielle.

Logarithmes et exponentielles

A partir de ces touches s’obtiennent les différentes fonctions hyperboliques :

[ hyp ] [cos]

[ hyp ] [sin]

[ hyp ] [tan]

[2ndF] [archyp] [cos]

[2ndF] [archyp] [sin]

[2ndF] [archyp] [tan]

ch(x)

sh(x)

th(x)

cosh-1 (x)

sinh-1 (x)

tanh-1(x)

Cosinus hyperbolique.

Sinus hyperbolique.

Tangente hyperbolique.

Argument cosinus hyperbolique.

Argument sinus hyperbolique.

Argument tangente hyperbolique.

Ex : [ ln ] 20 [=] -> ln 20 = | 2.995732274 [ log ] [.] 01 [=] -> log .01= | -2. [2ndF] [ex] 3 [=] -> e 3= | 20.08553692

[HYP]

[2ndF] [archyp]

Touche de fonction hyperbolique.

Argument hyperbolique.

Hyperboliques

DEG

(cosh1.5+

20.08553692

4. CALCULS TRIGONOMETRIQUES

Nombre π

[π]

Afche la valeur approchée de la constante π, avec dix chiffres signicatifs, soit 3,141592654

Note : pour une meilleure précision la calculatrice utilise dans ses calculs une valeur de π à 12 chiffres signicatifs, soit 3,14159265359.

Ex :

Périmètre et surface maximales d’une roue de Formule 1, le diamètre

maximal étant de 660mm. On calcule le rayon (diamètre divisé par 2) exprimé en mètres, puis on applique les formules 2π r et π r2: 660 [÷] 2 [÷] 1000 [=] -> 660÷2÷1000 | 0.33

[STO][Y] mise en mémoire de la valeur du rayon

2 [π] [x] [RCL][Y] [=] -> 2πxY= | 2.073451151 [π] [RCL][Y] [x2] [=] -> πY 2= | 0.34211944 Le périmètre est donc de 2,1 m et la surface de 0,34 m2.

Remarque : la multiplication est implicite, nous n’avons pas eu besoin d’appuyer sur la touche [x].

[DRG]

[2ndF] [DRG ]

Touche de sélection des unités d’angle.

Convertit la valeur d’angle afchée dans l’unité

suivante.

Chaque fois que l’on appuie sur [DRG] ou [2ndF] [DRG ] l’unité active change selon le schéma suivant :

DEG RAD GRAD

L’unité active choisie est indiquée à l’écran par un symbole, DEG, GRAD ou RAD. Les calculs s’effectueront et les résultats apparaîtront alors dans l’unité choisie.

Unités d’angles

Choix de l’unité d’angle et conversions

24

25

Ex : Départ mode DEG (mode par défaut)

Par exemple, si on appuie sur [DRG] une fois l’écran devient :

On appuie encore deux fois sur [DRG] pour retourner en mode DEG, et on saisit un angle de 90 degrés à convertir :

90 [2ndF] [DRG ]

soit π/2 radians.

[2ndF] [DRG ]

DEG

0.

RAD

0.

RAD

90 RAD

1.570796327

GRAD

ANS GRAD

100.

DEG

ANS DEG

90.

[Dº M’S]

[2ndF] [ DEG]

Effectue la saisie des degrés, minutes, secondes et centièmes de seconde (facultatif).

Convertit les degrés sexagésimaux en degrés décimaux, et vice-versa.

Conversion sexagésimale (degrés / minutes /secondes)

Ex :

Conversion de la latitude 12º39’18”05 en degrés décimaux : 12 [Dº M’S] 39 [Dº M’S] 18.05 [Dº M’S] [=]-> 12º39º18.05º | 12’39’18.05

[2ndF] [ DEG] -> 12º39º18.05º | 12.65501389

Conversion de la latitude de Paris (48º51’44”Nord) en degrés décimaux : 48 [Dº M’S] 51 [Dº M’S] 44 [Dº M’S] [2ndF] [ DEG]

-> 48º51º44º= | 48.86222222

Conversion de 123.678 en degrés sexagésimaux :

123.678 [2ndF] [ DEG]

Calculs horaires

La fonction de conversion sexagésimale peut être également utilisée pour des calculs directs sur des heures / minutes / secondes :

Ex : 3h 30 min 45s + 6h 45min 36s

3 [Dº M’S] 30 [Dº M’S] 45 [Dº M’S] [+] 6 [Dº M’S] 45 [Dº M’S] 36 [Dº M’S] [=]

soit 10h 16 min 21 secondes.

3h 45 min – 1,69h =

3 [Dº M’S] 45 [D°M’S] – 1[.] 69 [=] -> 3º45º– 1.69 = | 2.06 [2ndF] [ DEG] -> 3º45º– 1.69 = | 2’03’36.00 Soit 2h 03min et 36 secondes.

DEG

12º39º18.05º

12.65501389

DEG

123.678 123º40’40.80

DEG

3º30º15º+6º4 10º16’21.00

[cos]

[sin]

[tan]

cos(x)

sin(x)

tan(x)

Cosinus, sinus, tangente

26

27

Ex :

Mode DEG

[cos] 90 [=] -> 0. [tan] 60 [=] -> 1.732050808

sin230 =

[(] [sin] 30 [)][x2] [=]

Mode RAD

[sin] [π][=] -> 0. [cos] [(] [π] [÷] 4 [)] [=] -> 0.707106781

Avec les degrés sexagésimaux :

Mode DEG

sin (62º12’24”)= [sin] 62 [Dº M’S] 12 [Dº M’S] 24 [D°M’S] [=] -> 0.884635235

DEG

(sin30)2=

0.25

DEG

cos(π÷4)=

0.707106781

DEG

SIN62º12º24º

0.884635235

Arccosinus, arcsinus, arctangente

[2ndF] [cos-1]

[2ndF] [sin-1]

[2ndF] [tan-1]

arccos(x)

arcsin(x)

arctan(x)

Pour les fonctions sin-1, tan-1 et cos-1 les résultats de mesure angulaire

seront donnés dans les intervalles suivants :

DEG

RAD

GRAD

-90≤ θ ≤90

-100≤ θ ≤100

θ=sin-1 x , θ=tan-1 x θ=cos-1 x

0≤ θ ≤180

0≤ θ ≤

π

0≤ θ ≤ 200

Ex :

Mode GRAD

[2ndF] [tan-1] 1 [=] -> 50

Un panneau routier indique une pente à 5%. Donnez la mesure de l’angle en degrés et en radians. Si la pente est à 5% l’altitude augmente de 5m tous les 100m. Le sinus de l’angle à trouver est de 5 divisé par 100, soit 0,05.

Mode DEG

[2ndF] [sin-1] [.] 0 5 [=] -> 2.865983983 (DEG) [2ndF] [DRG ] -> 0.050020857 (RAD)

GRAD

tan-11=

50.

x [2ndF] [ ] y ou

r [2ndF] [ ] θ

[2ndF] [ . ]

[2ndF] [ rθ]

[2ndF] [ xy]

Permet la saisie des coordonnées cartésiennes ou

polaires.

Afche l’autre coordonnée.

Convertit les coordonnés cartésiennes en coordonnées

polaires.

Convertit les coordonnés polaires en coordonnées cartésiennes.

Coordonnées polaires

Pour mémoire :

x = r cos θ y = r sin θ

r = x 2 + y

2

et

θ = tan-1 (y/x)

On appelle x et y les coordonnées cartésiennes, ou rectangulaires, r et θ sont les coordonnées polaires.

Note : l’angle θ sera calculé dans l’intervalle [-180º,+180º] (degrés décimaux) ; la mesure d’angle θ sera donnée dans l’unité d’angle qui a été présélectionnée sur la calculatrice : en degrés si la calculatrice est en mode Degré, en radians si la calculatrice est en mode Radian, etc.

28

29

Ex : En mode degrés (DEG afché) :

• conversion de x = 6 et y = 4 6 [2ndF] [ ] 4

[2ndF] [ rθ] calcule r, θ, et afche r

[2ndF] [ . ] afche l’autre coordonnée (θ puisque r est à l’écran)

[2ndF] [ . ] afche l’autre coordonnée (r puisque θ est à l’écran)

• conversion de r= 14 et θ= 36 degrés 14 [2ndF] [ ] 36

[2ndF] [ xy] calcule x, y, et afche x

[2ndF] [ . ] afche l’autre coordonnée (y puisque x est à l’écran)

[2ndF] [ . ] afche l’autre coordonnée (x puisque y est à l’écran)

DEG

6,4

0.

DEG

r=

7.211102551

DEG

θ=

33.69006753

DEG

r=

7.211102551

DEG

14,36

0.

DEG

x=

11.32623792

DEG

y=

8.228993532

DEG

x=

11.32623792

[2ndF] et [CMPLX]

[i]

[|R|]

[2ndF] [ARG]

[Re Im]

[2ndF] et [CMPLX]

Passage en mode de gestion des nombres

complexes, CPLX s’afche à l’écran.

Saisie de l’inconnu imaginaire i

i2=-1

(accès en touche principale au niveau de la touche CMPLX)

Calcule le module du nombre complexe saisi.

S’utilise après [=].

Calcule l’argument du nombre complexe saisi. S’utilise après [=].

Donne le résultat du calcul pour la partie imaginaire

du nombre complexe.

Si on appuie une deuxième fois la partie réelle est afchée, et ainsi de suite.

(accès en touche principale au niveau de la touche DEL)

Retour au mode normal (COMP).

Nombres complexes

Votre calculatrice vous permet de réaliser additions, soustractions, multiplications et divisions de nombres complexes. A noter cependant que ne sont disponibles en mode complexe que les mémoires temporaires A, B, C et M, les autres étant nécessaires au fonctionnement des calculs dans ce

mode.

On rappelle que les nombres complexes et les coordonnées polaires / cartésiennes sont très liés. Si x= a+ib, on a x= rcosθ +i rsinθ où r est le module de x, r= √(a2+b2) et θ l’argument, soit tan-1 y/x. La valeur de l’argument sera afchée dans l’unité de mesure d’angle présélectionnée.

Le mode complexe est compatible avec les touches [X2], [ab/c] notamment, et on peut convertir l’argument en degrés minutes secondes avec [2ndF] [ DEG].

Ex : x= 1 + 3i y= 5 - 2i

[2ndF] puis [CPLX] : on passe en mode complexe (CPLX afché)

argument de y

[(] 5 [-] 2 [i] [)] [=] -> 5-2i= | 5. afchage partie réelle [2ndF][ARG] -> ARG= | -21.80140949 en mode DEG arg y = tan-1(-2/5) en degrés décimaux. [2ndF][ DEG] -> ARG= | -21º48’05.07

30

31

module de x et carré [(] 1 [+] 3 [i] [)] [=] -> 1+3i= | 1. afchage partie réelle [|R|] -> |R| = | 3.16227766 [X2][=] -> Ans2 | -8.

Attention si on fait Ans2 on calcule le carré de x et non celui du module, soit

x au carré est égal à 12-32=-8.

calcul de x+y [(]1 [+] 3 [i][)] [+] [(] 5 [-] 2 [i][)] [=] -> 6. soit la partie réelle de x+y [Re Im] -> 1. soit la partie imaginaire [Re Im] -> 6. afchage de la partie réelle donc x+y=6+i

calcul de x-y [(]1 [+] 3 [i][)] [-] [(] 5 [-] 2 [i][)] [=] -> -4. soit la partie réelle de x-y [Re Im] -> 5. soit la partie imaginaire [Re Im] -> -4. afchage de la partie réelle donc x-y=-4+5i

calcul de xy

[(]1 [+] 3 [i] [)] [x] [(] 5 [-] 2 [i] [)][=] -> 11. [Re Im] -> 13. donc x.y=11+13i

calcul de x/y [(]1 [+] 3 [i][)] [÷] [(] 5 [-] 2 [i][)] [=] -> -0.034482758 [Re Im] -> 0.586206896

5. CALCULS EN BASE-N

Pour mémoire

Changements de base

Nous effectuons nos calculs de façon courante en base 10. Par exemple : 1675 = (1675)10 = 1x103 + 6x102 + 7x10 + 5

En mode binaire, un nombre est exprimé en base 2. 1 s’écrit 1, 2 s’écrit 10, 3 s’écrit 11, etc. Le nombre binaire 11101 est équivalent à : (11101)2= 1x24 + 1x23 + 1x22 + 0x2 +1 = (29)10

En mode octal, un nombre est exprimé en base 8. 7 s’écrit 7, 8 s’écrit 10, 9 s’écrit 11, etc. Le nombre octal 1675 est égal à : (1675)8= 1x83 + 6x82 + 7x81 + 5= (957)10

En mode hexadécimal, un nombre est exprimé en base 16, les chiffres au-delà du 9 étant remplacés par des lettres : 0123456789ABCDEF 9 s’écrit 9, 10 s’écrit A, 15 s’écrit F, 16 s’écrit 10, etc. Le nombre hexadécimal 5FA13 est égal à : (5FA13)16= 5x164 + 15x163 + 10x162 + 1x161 + 3= (391699)10

Pour récapituler :

déc 0 1 2 3 4 5 6 7 8

bin 0 1 10 11 100 101 110 111 1000 oct 0 1 2 3 4 5 6 7 10 hex 0 1 2 3 4 5 6 7 8

déc 9 10 11 12 13 14 15 16

bin 1001 1010 1011 1100 1101 1110 1111 10000 oct 11 12 13 14 15 16 17 20 hex 9 A B C D E F 10

Les opérateurs logiques

Outre les fonctions arithmétiques +, -, x, ÷, +/-, on utilise en base N des opérateurs logiques qui sont des fonctions à une ou deux variables A et B, notées :

• Not A (NON A ou inverse de A)

• And (ET)

• Or (OU)

• Xor (OU exclusif)

• Xnor (NON OU exclusif)

32

33

Les résultats des fonctions ci-dessus sont les suivantes en fonctions de A et B:

A B Not A A and B A or B A xor B A xnor B 0 1 1 0 0 0 1 0 0 0 1 0 1 1 0 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1

Pour A et B plus grands que 0 ou 1, le résultat se calcule bit par bit sur les valeurs exprimées en binaire. Par exemple si A=(19)16=(11001)2 et B=(1A)16=(11010)2 :

A 0 0 0 0 0 0 0 1 1 0 0 1 B 0 0 0 0 0 0 0 1 1 0 1 0 A and B 0 0 0 0 0 0 0 1 1 0 0 0 A xnor B 1 1 1 1 1 1 1 1 1 1 0 0

A and B = (11000)2 = (18)16 = (24)10 A xnor B = (111111111100)2 = (FFFFFFFC)16 = (-4)10

Notations

Lorsque la calculatrice est en Base N, un indicateur de base s’afche à droite :

• d pour décimal.

• b pour binaire.

• o pour octal.

• H pour hexadécimal.

Remarques sur le mode Base N :

• les touches de fonctions correspondant au mode Base N sont indiquées en orange et rouge en haut des touches principales. Le mode est conservé même si la calculatrice est éteinte et rallumée.

• Si vous entrez une valeur incompatible avec la base choisie (ex : [BIN] 3 [=] , la calculatrice afchera Error 1. Voir le chapitre « Messages d’erreurs » pour plus de détails sur les valeurs admissibles en mode Base N.

• La plupart des fonctions générales ne peuvent pas être utilisées en Base N. Les paragraphes suivants détaillent les opérateurs admissibles.

• Vous pouvez utiliser les mémoires et les touches de mise en mémoire et de rappel associées : [Ans], [STO], [RCL] (voir chapitre “ Utilisation des mémoires” .

[2ndF] puis [Base-N]

[DEC]

[BIN]

[OCT]

[HEX]

Passe en mode Base N

Annule le mode Base N quand celui-ci est actif.

Sélectionne la base 10 comme base active, d s’afche.

Sélectionne la base 2 comme base active, b s’afche.

Sélectionne la base 8 comme base active, o s’afche.

Sélectionne la base 16 comme base active, H s’afche.

Commandes du mode Base N et conversions

[2ndF] puis [Base-N] : nous passons en Base N.

A partir de maintenant tous les exemples donnés dans ce chapitre sont

en Base N.

Pour convertir une valeur d’une base dans une autre, une fois en Base N vous choisissez la base de la valeur à convertir. Vous saisissez la valeur,

puis vous changez la base.

Ex : Conversion de (11101)2 en base 10 : [BIN] -> | 0000000000 b 11101 [=] -> 11101 = | 0000011101 b [DEC] -> 11101 = | 29 d

Autres exemples de conversion (les deux méthodes sont utilisées) :

Conversion de (5FA13)16 en base 8 puis 10 : [ON/C] [HEX] -> | 00000000 H 5 [F] [A] 13 [=] -> 5FA13 | 0005FA13 H [OCT] -> | 0001375023 o [DEC] -> | 391699 d

[+]

[-]

[x]

[÷]

[NEG]

[(], [)]

Addition.

Soustraction.

Multiplication.

Division.

Change le signe de la valeur saisie immédiatement après, équivalent de la touche arithmétique [(-)].

Parenthèses.

Calculs en Base N

Votre calculatrice vous permet de réaliser des opérations usuelles (addition, soustraction, multiplication, division et parenthèses) en Base N. A noter qu’en Base N on ne manipule que des nombres entiers ; si une opération génère un résultat décimal, seule la partie entière de la valeur sera conservée.

Ex : Si, en mode hexadécimal on soustrait 5A7 à 5FA13, cela donne : [HEX] -> | 00000000 H 5 [F] [A] 13 [-] 5 [A] 7 [=] -> 5FA13-5A7= | 0005F46C H

On multiplie ce résultat par 12 : [x] 12 [=] -> Ansx12= | 006b2F98 H ou 12 [x] [2ndF][Ans][=] -> 12xAns= | 006b2F98 H

34

35

Lorsqu’on a deux variables on essaie de déduire des données une relation entre x et y. On étudie la solution la plus simple : une relation de type y=a+bx.

cov(x,y) est la covariance : La validité de cette hypothèse est vériée par le calcul suivant :

appelé coefcient de corrélation linéaire. Le résultat est toujours entre –1 et +1 et on considère bon un résultat supérieur ou égal à √3/2 en valeur

absolue.

Pour mémoire

On dispose de n données sur un échantillon de mesures, résultats, personnes, objets... Chaque donnée est constituée d’un nombre (une variable x) ou deux (deux variables x et y). On cherche à calculer la moyenne de ces données et la répartition de ces données autour de la moyenne, l’écart-type.

Ces données se calculent à partir de sommes que l’on notera :

∑x = x1+x2+x3+....xn-1+xn

∑x2= x12+x22+x32+....xn-12+xn

2

∑xy = x1y1+x2y2+x3y3+....xn-1yn-1+xnyn

Moyenne

écart type / déviation standard de l’échantillon pour x :

écart type / déviation standard de la population pour x :

variance = s2 ou

2

6. STATISTIQUES

En mode binaire on effectue (11010 + 1110) ÷10 et on convertit en mode décimal :

[BIN] -> | 0000000000 b [(] 11010+1110 [)] [÷] 10 [=]-> (11010+1110)÷10= | 0000010100 b

[DEC] ->(11010+1110)÷10= | 20 d Toujours en mode décimal on divise ce résultat par 12 [÷] 12 [=] -> Ans÷12= | 1 d Seule la partie entière du résultat de la division est conservée.

En mode hexadécimal on calcul le négatif de 1C6 :

[HEX] -> | 00000000 H [NEG] 1 [C] 6 [=] -> NEG 1C6 | FFFFFE3A H [+] 1 [C] 6 [=] -> Ans+1C6= | 00000000 H

[AND]

[OR]

[XOR]

[XNOR]

[NOT]

Fonction ET.

Fonction OU.

Fonction OU exclusif.

Fonction NON OU exclusif.

NON (inverse) de la valeur saisie immédiatement après.

Opérateurs logiques en Base N

Votre calculatrice effectue ces calculs à partir des valeurs que vous avez saisies, quelle qu’en soit la base initiale et les exprime directement dans la base que vous avez présélectionnée. Le type de saisie effectuée suit la même méthode que pour les opérateurs arithmétiques vus au paragraphe précédent.

Ex : (19)16 OR (1A)16 en base 16 [HEX] [ON/C] -> | 00000000 H 19 [OR] 1 [A] [=] -> 19or1A | 0000001b H

Commentaires préliminaires

cov(x,y)

(xi - x) (yi - y)=

1

n

cov(x,y)

i=1

1

n

xy-xy

y

cov(x,y)

V(x)

(x - x) + y

36

37

Votre calculatrice vous permet d’obtenir aisément ces résultats, en suivant les étapes suivantes :

• Choisissez votre mode statistique (une ou deux variables).

• Saisissez les données.

• Vériez que la valeur de n correspond bien au nombre de données théoriquement saisies.

• Calculez la moyenne et l’écart type (ou déviation standard) de l’échantillon ou de la population, ainsi que les autres calculs intermédiaires si nécessaire (∑ x , ∑ x2) à l’aide des touches correspondantes.

• S’il y a deux variables, procédez aux mêmes calculs pour y (moyenne, écart type), puis calculez la régression linéaire (a et b dans y=a+bx) et le coefcient de régression linéaire.

• Si la régression linéaire est jugée valide, on peut alors calculer la valeur estimée de y pour un x donné, ou la valeur estimée de x pour un y donné, de par la relation y=a+bx.

[RCL] [∑x2] , [∑y2]

[RCL] [∑xy]

[RCL] [Sx]

[RCL] [ x]

[RCL] [Sy]

[RCL] [ y]

[RCL] [a], [b]

[RCL] [r]

[2ndF] [Y ]

[2ndF] [X ]

Calcule la somme des carrés des données rentrées ∑x2, ∑y2.

Afche la somme des produits des données rentrées ∑xy

Afche l’écart-type (ou déviation standard) de l’échantillon pour la variable x.

Afche l’écart-type (ou déviation standard) de la

population pour la variable x.

Afche l’écart-type (ou déviation standard) de l’échantillon pour la variable y.

Afche l’écart-type (ou déviation standard) de la

population pour la variable y.

Afche la valeur du coefcient a, b pour la régression linéaire y=a+bx.

Afche la valeur du coefcient de régression linéaire r.

Donne la valeur de y estimée par régression linéaire

pour la valeur x saisie.

Donne la valeur de y estimée par régression linéaire

pour la valeur x saisie.

[2ndF] [MODE] 1

[2ndF] [MODE] 2

[2ndF] [MODE] 0

[2ndF] [CA]

[DATA CD]

[(x,y)]

[,]

[ON/C]

[2ndF] [DATA CD]

[RCL] [n]

[RCL] [ x ], [ y ]

[RCL] [∑x] , [∑y]

Passage en mode statistique à 1 variable. Initialise toutes les données en mémoire.

Passage en mode statistique à 2 variables. Initialise toutes les données en mémoire.

Retour au mode arithmétique. Initialise toutes les données en mémoire.

Initialise toutes les données en mémoire sans

changer de mode.

Enregistre les données : donnée1 [DATA CD] donnée2 [DATA CD] etc. Pour entrer la même donnée plusieurs fois, appuyer sur [DATA CD] plusieurs fois à la suite.

Pour saisir y après x lorsqu’il y a deux variables : x1 [(x,y)] y1 [DATA CD] x2 [(x,y)] y2 [DATA] etc.

Permet d’enregistrer plusieurs données identiques en une seule saisie : donnée1 [,] 3 [DATA CD] enregistre 3 fois la même valeur en mémoire.

Permet de corriger une saisie avant d’avoir appuyé sur [DATA CD].

Permet de corriger les erreurs de saisie après avoir

appuyé sur [DATA CD].

Indique le nombre d’échantillons rentrés (n), c’est-à-dire le nombre des données.

Afche la moyenne de x ou de y.

Afche la somme des données rentrées ∑x , ∑y.

Touches de fonctions statistiques

Statistiques à 1 variable – exemple pratique

Benjamin et ses amis ont obtenu les résultats suivants à la composition de Français :

Elève A B C D E F G H I J note 8 9.5 10 10 10.5 11 13 13.5 14.5 15

Moyenne et écart-type (de l’échantillon) pour les notes de Benjamin et ses

amis ?

[2ndF] [MODE] 1 -> remise à zéro et STAT s’afche

8 [DATA CD] -> début de saisie des données

DEG STAT

Stat x

0.

DEG STAT

n=

1.

38

39

9 [.] 5 [DATA CD]

10 [DATA CD] [DATA CD] ou 10 [ , ] 2 [DATA CD] pour saisir deux fois la même valeur :

Et ainsi de suite : 10 [.] 5 [DATA CD] 11 [DATA CD] 13 [DATA CD] 13 [.] 5 [DATA CD] 14 [.] 5 [DATA CD] 15 [DATA CD]

On vérie que le n afché correspond au nombre de valeurs saisies. Si on le souhaite on pourra le faire plus tard de nouveau avec [RCL] [n]. [RCL] [ x ] -> 11.5 : leur moyenne est de 11,5

[RCL] [sx] -> 2.34520788 soit l’écart type recherché.

Si on veut calculer la variance on appuie sur [x2][=]

On reprend l’expérience avec la composition de maths, à laquelle ils ont obtenu les notes suivantes :

DEG STAT

n=

2.

DEG STAT

n=

4.

DEG STAT

n=

10.

DEG STAT

x=

11.5

DEG STAT

sx=

2.34520788

DEG STAT

ANS2=

5.5

Elève A B C D E F G H I J note 4 7.5 12 8 8 8 14.5 17 18 18

[2ndF] [CA] -> remise à zéro, STAT est toujours afché On peut vérier en faisant : [RCL] [n] -> n=0 4 [DATA CD] -> début de saisie des données 7 [. ] 6 [ON/C] 7 [.] 5 [DATA CD] -> erreur de saisie avant [DATA CD]

et correction.

13 [DATA CD] [2ndF] [DATA CD] 12 [DATA CD]

-> erreur de saisie après [DATA CD] et correction 8 [,] 3 [DATA CD] -> on saisit 8 trois fois ou 8 [DATA CD] [DATA CD] [DATA CD] 14 [.] 5 [DATA CD]

Et ainsi de suite jusqu’à 18 [DATA CD] [DATA CD]

[RCL] [ x ] -> 11.5 leur moyenne est de 11,5 également [RCL] [sx] -> 5.088112507 soit l’écart type recherché.

On constate que la moyenne est la même mais que l’écart type est plus grand cette fois-ci : on peut en conclure qu’il y a plus d’écart entre les notes des élèves, leur niveau est donc moins homogène en maths qu’en français.

A titre d’exercice, dans cet exemple (les notes de maths) on obtient les valeurs suivantes pour ∑x et ∑x2 : [RCL] [∑x] -> 115.

[RCL] [∑x2] -> 1555.5

DEG STAT

n=

10.

DEG STAT

∑x=

115.

DEG STAT

∑x2=

1555.5.

40

41

On passe en mode statistiques à deux variables : [2ndF] [MODE] 2

On commence la saisie : 2 [(x,y)] 5 [DATA CD]

[DATA CD] pour saisir la même valeur une deuxième fois :

12 [(x,y)] 24 [DATA CD]

21 [(x,y)] 40 [,] 3 [DATA CD] pour entrer trois fois la même valeur :

16 [(x,y)] 25 [ON/C] erreur de saisie avant [DATA CD] 15 [(x,y)] 24 [DATA CD] [2ndF] [DATA CD] erreur de saisie après [DATA CD] 15 [(x,y)] 25 [DATA CD]

DEG STAT

Stat x y

0.

DEG STAT

n=

1.

DEG STAT

n=

2.

DEG STAT

n=

3.

DEG STAT

n=

6.

DEG STAT

n=

7.

On afche les résultats de la régression linéaire : [RCL] [a]

[RCL] [b]

[RCL] [r]

r est supérieur à √3/2 = 0.866 environ, la validité de la régression est vériée.

Grâce à la régression linéaire on estime y à partir de x=3 : 3 [2ndF] [ Y ]

On estime x à partir de y=46 : 46 [2ndF] [ X ]

Avec les touches statistiques de votre calculatrice vous pouvez afcher facilement et de façon claire tous les résultats intermédiaires, comme par exemple : [RCL] [sy]

[RCL] [ y]

Statistiques à 2 variables – exemple pratique

On a le tableau suivant où x est la longueur en mm et y le poids en mg d’une chenille de papillon à différents stades de son développement.

X 2 2 12 21 21 21 15 Y 5 5 24 40 40 40 25

DEG STAT

a=

1.050261097

DEG STAT

b=

1.826044386

DEG STAT

r=

0.995176343

DEG STAT

3y

6.528394256

DEG STAT

46x

24.61590706

DEG STAT

Sy=

15.67223812

DEG STAT

y=

14.50967306

42

43

7. AUTRES FONCTIONS

Régression non linéaire

Vous trouverez ci-dessous les types de régressions linéaires avec les valeurs que vous devez rentrer pour x et y :

Linéaire Logarithmique

Exponentielle

Puissance

Nom Formule Remplacez x par Remplacez y par a =

y=a + bx x y y=a + b ln x ln x y y=a’ ebx x ln y e

a

y=a’ xb ln x ln y e

a

Ex :

x 0,5 1 1,5 2

y 1,4 2 2,4 2,9

On soupçonne que x et y sont liés par une relation du type y=a xb et on cherche à conrmer l’hypothèse en procédant de la façon suivante : On saisit les valeurs en ajoutant les logarithmes de n=1 à n=4, par exemple pour la première saisie : [ln] 0[.]5 [(x,y)] [ln] 1[.]4 [DATA CD] Une fois les valeurs saisies, on obtient les valeurs de a, b et r suivantes : a = 0,690213912 b = 0,515317442 r = 0,998473288 La régression de type puissance est vériée puisque r=0,998. On obtient a’ en calculant l’exponentielle de a : [2ndF][ex][RCL][a][=] -> e^a= 1.994142059 Par approximation on peut dire que y ≈ 2x

1/2

= 2√x.

[2ndF] [n!]

[2ndF] [nCr]

[2ndF] [nPr]

Calcul de la factorielle n!

Votre calculatrice permet de calculer la factorielle n! jusqu’à n=69 (voir chapitre des “Messages d’erreur”).

Calcul du nombre de combinaisons (voir ci-dessous).

Calcul du nombre de permutations (voir ci-dessous).

Factorielle n!, permutation, combinaison

Pour mémoire

On appelle factorielle de n! ou factorielle n! le nombre suivant :

n! = 1 x 2 x 3 x.....x (n-2) x (n-1) x n

n! représente le nombre de façons différentes d’arranger n objets distincts (n! permutations). Lorsqu’on choisit r éléments parmi ces n objets :

• le nombre combinaisons, c’est-à-dire de façons différentes de choisir r éléments parmi ces n objets est de :

• si on peut les arranger de r façons, le nombre de permutations distinctes possibles est :

n!

nCr =

r!(n - r)!

n!

nPr =

(n - r)!

Ex :

8 chevaux sont au départ d’une course hippique. Combien de combinaisons y a-t-il de leur ordre d’arrivée ?

Combien de tiercés possibles dans le désordre ?

Combien de tiercé possibles dans l’ordre ?

Quelles sont mes chances de trouver le tiercé dans le désordre,

dans l’ordre ?

Nombre de permutations de leur ordre d’arrivée = n! avec n = 8. 8 [2ndF] [n!] [=] -> 40320.

Nombre de tiercés : on sélectionne 3 chevaux parmi 8. On calcule nCr avec n=8 et r=3

8 [2ndF] [nCr] 3 [=] -> 8C3= | 56.

Mes chances de gagner le tiercé dans le désordre : si je ne joue qu’une

seule combinaison mes chances de gagner le tiercé dans le désordre sont de 1 sur 56 : [2ndF][x-1] [=] -> ANS-1= | 0.017857142 Soit 1,8%.

44

45

Nombre de tiercés possibles avec un ordre donné. Non seulement on

sélectionne 3 chevaux parmi 8, mais on s’intéresse à l’ordre dans lequel ils

arrivent. On calcule nPr suivante avec n=8 et r=3

8 [2ndF] [nPr] 3 [=] -> 8P3= | 336.

Mes chances de gagner le tiercé dans l’ordre : si je ne joue qu’une seule combinaison mes chances de gagner le tiercé dans l’ordre sont de 1 sur

336. [2ndF][x-1] [=] -> ANS-1= | 0.00297619 soit 0,03%

[2ndF] [RANDOM]

Génère un nombre aléatoire ≥ 0 et <1, avec trois chiffres signicatifs. Pour générer le chiffre suivant appuyez sur [=].

Génération de nombre aléatoire (fonction Random)

Ex : [2ndF] [RANDOM][=] -> RANDOM= | 0.256 [=] -> RANDOM= | 0.84 [=] -> RANDOM= | 0.511 ... etc.

Note : il s’agit de générer une valeur aléatoire, donc en faisant la même manipulation vous ne trouverez pas les mêmes résultats que dans ce manuel !

Pour tirer les chiffres du Loto (entre 1 et 49)

[2ndF] [FSE] [2ndF] [TAB] 0 (mode FIX, avec 0 chiffres après la virgule, on

veut afcher des nombres entiers)

[2ndF] [RANDOM] [x] 48 [+] 1 [=] génère, compte tenu des arrondis, un nombre compris entre 1 et 49. [2ndF] [RANDOM] [x] 48 [+] 1 [=] -> RANDOMx48+1= | 39. [=] -> RANDOMx48+1= | 32. [=] -> RANDOMx48+1= | 17. [=] -> RANDOMx48+1= | 2.

Note : il s’agit d’une génération pseudo-aléatoire calculée sur la base de la valeur stockée dans la mémoire Y.

8. MESSAGES D’ERREUR

Causes possibles d’erreurs

Lorsque l’écran afche un message d’erreur, les raisons peuvent être :

• Error 1 : erreur de syntaxe ou l’opération n’est pas valide. Ex : 2 [2ndF][ rθ], 61 [2ndF][%].

• Error 2 : la valeur utilisée est en dehors des valeurs admissibles (voir tableau plus loin). Ex : division par 0, cos-1 (5), √(-2). Il se peut aussi que lors du calcul effectué à partir des valeurs saisies, une valeur intermédiaire est en dehors des valeurs admissibles, trop grande ou trop petite. Une valeur très petite (inférieure à 10

-99

) sera arrondie en un 0, ce

qui peut créer une situation de division par 0.

• Error 3 : dépassement de la capacité mémoire de la calculatrice. Celle-ci comporte 8 mémoires tampon pour les valeurs numériques, ainsi que 16 mémoires tampon pour les opérateurs en mode normal, et 4 mémoires tampon en mode statistique.

• Error 4 : équation trop longue. Une équation peut comporter un maximum de 96 caractères. Dans ce cas, découpez le calcul à effectuer en plusieurs étapes distinctes.

Pour sortir de l’écran d’afchage de l’erreur, appuyez sur [ON/C] ou utilisez les èches et pour corriger l’équation.

Valeurs admissibles

De manière générale les valeurs utilisées dans les calculs doivent vérier :

-9,999999999 x 1099 ≤ x ≤ 9,999999999 x 1099 soit |x| <10

100

Note : |x| est la valeur absolue de x, soit |x|= –x si x≤0 et |x|=x si x≥0.

46

47

Fonction

x

-1

x

2

y

x

√

y

10

x

ln x, log x

√

x

e

x

sinh x, cosh x, tanh x

sinh-1x

cosh-1x

tanh-1x

sin x , cos x

tan x

sin–1x, cos–1x

RAD GRAD

degrés décimaux et sexagésimaux

coordonnées polaires

nombres complexes

a=x+y

statistiques

n !

nPr

nCr

Base 10

Base 2

Base 8

Base 16

Conditions supplémentaires

|x| ≥ 10

-99

|x| < 10

50

si y > 0, x.logy ≤ 100 si y=0, x >0 si y < 0, x.log|y| ≤ 100 et x est impair ou 1/x est un entier (x≠ 0) si y > 0, 1/x.log y ≤ 100 si y=0, x >0 si y < 0, 1/x.log|y| ≤ 100 et 1/x est impair ou x est un entier (x≠ 0) x < 100 x ≥ 10

-99

x ≥ 0 x ≤ 230.2585092 |x| ≤ 230.2585092 |x| < 5 x 10

99

1 ≤|x| < 5 x 10

99

|x|<1 DEG |x| < 9 x 10

9

RAD |x| ≤ 5π x 10

7

GRAD |x| < 1 x 10

10

comme sin x, et : (avec n entier positif ou négatif) DEG x≠ (2n-1)x90 RAD x ≠ (2n-1)/2 x π GRAD x ≠ (2n-1)x100 |x| ≤ 1 |x| ≤ π/2 x 10

98

|x|<10

10

x, y < 1050

et x2+y2 < 10

100

r≥0, θ comme le x pour sin x et cos x. n entier, 0<n<10

10

0 ≤ DATA < 1050 pour s, n>1 valeurs intermédiaires de calcul (∑x, ∑y, ∑x2, ∑y, ∑xy)

dans les limites admissibles.

0 ≤ n ≤ 69 ; n entier 0 ≤ r ≤ n < 1010 ; n, r entiers nPr < 10

100

0 ≤ r ≤ n < 1010 et r ≤ 69 ; n, r entiers nCr < 10

100

-231 ≤ (x)10 < 2

31

nombres entiers binaires de 10 chiffres maximum 0≤ x ≤ 0111111111 ou 1000000000 ≤ x ≤ 1111111111 soit –29 ≤ (x)10 < 2

9

nombres entiers octaux de 10 chiffres maximum 0≤ x ≤ 3777777777 ou 4000000000 ≤ x ≤ 7777777777 soit -229 ≤ (x)10 < 229 nombres entiers hexadécimaux de 8 chiffres maximum 0≤ x ≤ 7FFFFFFF ou 80000000≤ x ≤ FFFFFFFF Soit -231 ≤ (x)10 < 2

31

9. PRECAUTIONS D’EMPLOI

Utilisation de RESET

N’appuyez sur la touche de réinitialisation du système (RESET) que dans les cas suivants:

• Lors de la première utilisation.

• Après le remplacement des piles.

• Pour effacer le contenu de toutes les mémoires.

• En cas de blocage général, toutes les touches étant inopérantes. Par exemple, si vous exposez la calculatrice à un champ électrique, ou à une décharge électrique pendant l’utilisation, il peut se produire des phénomènes anormaux qui peuvent neutraliser le fonctionnement de certaines touches y compris la touche [ON/C].

Pour appuyer sur le bouton Reset, utilisez un objet n et pointu tel qu’un trombone déplié, et appuyez doucement. Puis, appuyez sur [ON/C] pour remettre la calculatrice en marche. L’icône DEG et le chiffre 0 seront afchés.

Remplacement des piles

Dès que l’afchage faiblit nous vous conseillons de remplacer la pile, avec une pile neuve de type CR2025. La pile ayant été installée en usine avant expédition, il se peut dans certains cas qu’elle subisse une usure prématurée par rapport à la durée d’utilisation prévue.

1. Eteignez la calculatrice en appuyant sur [2ndF] [OFF].

2. Retirez la vis du compartiment à pile au dos de l’appareil.

3. Remplacez la pile en respectant la polarité (côté + au-dessus).

4. Remettez la trappe.

7. Appuyez doucement sur RESET avec un objet n et pointu pour réinitialiser la calculatrice.

8. Appuyez sur [ON/C] pour remettre la calculatrice en marche. Si la pile a été correctement installée, l’icône DEG et le chiffre 0 seront afchés. Si ce n’est pas le cas, retirez et réinstallez à nouveau la pile.

Une mauvaise utilisation de la pile peut causer une fuite de liquide électrolytique ou même la faire exploser, et peut endommager l’intérieur de votre calculatrice. Lisez donc bien les recommandations suivantes :

• S’assurer que la pile soit du modèle recommandé avant de l’installer.

• Bien respecter la polarité indiquée.

• Ne pas laisser une pile usagée dans la calculatrice, elle peut fuir et l’endommager irrémédiablement.

• Ne pas laisser une pile neuve ou usagée à la portée des enfants.

• Ne jamais jeter de pile au feu, elle pourrait exploser.

• Ne pas jeter la pile dans les ordures ménagères mais dans un lieu de collecte adapté pour son recyclage, dans la mesure du possible.

Pour certaines fonctions les intervalles sont nécessairement plus petits :

48

49

CMPLX 29 RESET 47 [ ] 27 [( DEG] 23 [(] 8 [(r(] 37

[(x,y)] 36

[%] 14

[∑x] 36 [∑x2] 37 [∑xy] 37 [∑y] 36 [∑y2] 37

[=] 8

[√] 20

[10x] 20 [2ndF] 8

[3√] 20

[a b/c] 20 [a] 37 [ALPHA] 8 [AND] 34 [ANS] 15

[archyp] 22

[b] 37 [Base-N] 31 [BIN] 31 [CA] 9 [COMP] 19 [cos-1] 26 [cos] 25 [d/c] 20 [DATA CD] 36 [DEC] 31 [DEL] 9 [Dº M’S] 24 [DRG] 23 [EXP] 11 [FSE] 11

Conditions extrêmes

Si vous exposez la calculatrice à un champ électrique, ou à une décharge électrique pendant l’utilisation, il peut se produire des phénomènes anormaux qui peuvent neutraliser le fonctionnement de certaines touches y compris la touche ON/C. Dans ce cas réinitialisez la calculatrice en retirant et insérant la pile à nouveau. Attention, le contenu de la mémoire sera complètement effacé si vous réalisez cette opération. Ne réinitialisez la calculatrice que dans les cas suivants:

• Pour effacer tout le contenu de la mémoire.

• Quand survient une condition extrême, et que les touches ne répondent plus.

Précautions d’emploi

- N’essayez jamais de démonter votre calculatrice, elle contient des pièces de précision.

- Evitez de faire tomber votre calculatrice ou qu’elle subisse tout autre choc.

- Ne la transportez pas dans la poche arrière d’un pantalon.

- Evitez que votre calculatrice soit en contact avec l’humidité, avec des impuretés, des poussières ou de fortes températures. Dans un

environnement froid la calculatrice peut ralentir ou même suspendre son

fonctionnement. Elle retrouvera un fonctionnement normal dès que la température redeviendra plus clémente.

- Evitez tout contact de la calculatrice avec de l’eau ou autres substances liquides car cela pourrait provoquer des courts-circuits et des risques d’incendie. Ne provoquez pas d’éclaboussures sur la calculatrice.

- Evitez d’utiliser des liquides chimiques ou de l’essence pour nettoyer la machine. Essuyez avec un linge doux et sec, ou avec un linge légèrement humidié avec de l’eau et un détergent neutre.

- En aucune circonstance le fabricant et ses fournisseurs ne seront responsables pour vous ou pour une autre personne de tout dommage, dépense, perte de prot, perte d’argent ou tout autre préjudice provenant d’une perte de données et/ou formules causée par un mauvais fonctionnement, des réparations ou le remplacement des piles. L’utilisateur doit prévoir des copies des dossiers et données an de se protéger contre

toute perte.

- Ne vous débarrassez jamais des piles, de l’écran à cristaux liquides ou des

autres pièces en les brûlant.

- Si la calculatrice est exposée à une forte décharge électrostatique, son contenu mémorisé pourra être endommagé ou les touches pourraient arrêter

de fonctionner.

- Si un dysfonctionnement potentiel est détecté, relisez bien ce manuel et vériez l’état des piles pour vérier que le problème ne vient pas d’une

mauvaise utilisation ou de piles trop faibles.

10. INDEX

[HEX] 31

[hyp] 22

[i] 29 [ln] 22

[log] 22

[LRN] 19 [M-] 16 [M+] 16 [MODE] 9 [MODE] 1 36 [MODE] 2 36 [n!] 43 [n] 36 [nCr] 43 [NOT] 34 [nPr] 43 [OCT] 31 [OFF] 6 [ON/C] 6 [OR] 34 [Pi] 23 [r] 37 [RANDOM] 44 [RCL] 17 [Re Im] 29 [sin-1] 26 [sin] 25 [STO] 17 [Sx] 37

[Sy] 37

[TAB] 13 [tan-1] 26 [tan] 25 [x-1] 20

[x√] 20

[x2] 20 [XNOR] 34 [XOR] 34 [ x] 37 [ y] 37

50

Ce produit est couvert par la garantie Lexibook de trois ans.

Pour toute mise en œuvre de la garantie ou de service après-vente, vous devez vous adresser à votre revendeur muni de votre preuve d’achat. Notre garantie couvre les vices de matériel ou de montage imputables au constructeur à l’exclusion de toute détérioration provenant du non-respect de la notice d’utilisation ou de toute intervention intempestive sur l’article (telle que démontage, exposition à la chaleur ou à l’humidité…).

LEXIBOOK SA 2, av de Scandinavie 91953 COURTABOEUF CEDEX

France

Assistance technique : 0 892 23 27 26 (0.34€ / min)

www.lexibook.com

Informations sur la protection de l’environnement. Tout appareil électrique usé est

une matière recyclable et ne devrait

pas faire partie des ordures ménagères! Nous vous demandons de bien vouloir

nous soutenir en contribuant activement

à la gestion des ressources et à la protection de l’environnement en déposant cet appareil dans des lieux de collecte adaptés (si existants).

Reproduction partielle ou intégrale de ce manuel interdite, sous quelque forme que ce soit, sauf avec autorisation

expresse écrite du fabricant.

Le fabricant et ses fournisseurs déclinent toute responsabilité quant aux conséquences de l’utilisation ou de la mauvaise utilisation de cette calculatrice ou de ce manuel d’utilisation. De même le fabricant et ses fournisseurs déclinent toute responsabilité concernant tous dommages, pertes nancières, manques à gagner ou autres préjudices liés à des pertes de données ou de calculs lors de l’utilisation

de cette calculatrice ou de ce manuel.

Du fait de certaines limitations techniques lors de l’édition et de l’impression de ce manuel, l’apparence de certaines touches ou afchages indiqués dans les textes peuvent présenter de légères différences avec l’apparence réelle. Le fabricant se réserve le droit de modier le contenu de ce manuel sans préavis.

11. GARANTIE

SC500FRIM0097

Lexibook SC500, SC500FR User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual