Lexibook GC700Z_01, GC700_01 Instructions Manual

Instruction Manual

GC700_01/GC700Z_01

GC700_01_GC700Z_01IM0108.indd 1 6/3/08 17:33:07

2

FRANÇAIS

ESPAÑOL

ITALIANO

PORTUGUÊS

----------

FR

ES

IT

PT

GC700_01_GC700Z_01IM0108.indd 2 6/3/08 17:33:08

3

Calculatrice scientique graphique programmable, fonctions base N,

statistiques à une et deux variables, probabilités, fonctions arithmétiques et

trigonométriques, programmation.

SOMMAIRE

INTRODUCTION 5

Avant la première utilisation 5

1. PRISE EN MAIN DE VOTRE CALCULATRICE 6

Mise en marche et arrêt de la calculatrice 6 Afchage et symboles utilisés 6 Réglage du contraste de l’écran 8 Fonctions secondes et fonctions alphanumériques (SHIFT et ALPHA) 8 Notations utilisées dans le manuel 10 Touches usuelles 10 Saisie et modication d’un calcul (Replay) 11 Calculs successifs sur une ligne 12 Notation scientique et ingénieur 13 Choix de la notation 14 Fixation de la position de la virgule 14 Choix du nombre de chiffres signicatifs 15 Priorités de calcul 16

2. Utilisation DES MEMOIRES 17

Rappel du dernier résultat (Ans) 17 Calculs en chaîne 17 Calculs successifs 17 Mémoires temporaires (A - Z) 18

3. FONCTIONS ARITHMETIQUES 20

Partie entière (Int), partie décimale (Frac) 20 Inverse, carré et exposants 20 Racines 21 Fractions 21 Logarithmes et exponentielles 23 Hyperboliques 23 Factorielle n!, permutation, combinaison 24 Génération de nombre aléatoire (fonction Random) 25

4. CALCULS TRIGONOMETRIQUES 26

Nombre π 26 Unités d’angles 26 Choix de l’unité d’angle et conversions 26 Conversion sexagésimale (degrés / minutes /secondes) 27

Calculs horaires 28

Cosinus, sinus, tangente 28 Arccosinus, arcsinus, arctangente 29 Coordonnées polaires 30

CALCULATRICE GRAPHIQUE LEXIBOOK®GC700_01/GC700Z_01

Français

GC700_01_GC700Z_01IM0108.indd 3 6/3/08 17:33:08

Français

4

Français

5. CALCULS EN BASE-N 32

Pour mémoire 32 Changements de base 32 Les opérateurs logiques 32 Notations 33 Commandes du mode Base N et conversions 34 Calculs en Base N 35 Opérateurs logiques en Base N 37

6. STATISTIQUES 38

Commentaires préliminaires 38 Touches de fonctions statistiques 40 Statistiques à 1 variable – exemple pratique 41 Statistiques à 2 variables – exemple pratique 43 Régression non linéaire 44

7. FONCTIONS GRAPHIQUES 46

Dénitions et notations 46 Tracer une courbe 47 Courbes préprogrammées 47 Courbes utilisateur 48 Fonction Zoom 50 Fonction Trace 52 Fonctions Plot et Line 53

8. PROGRAMMATION 55

Premiers pas en programmation 55 Ecrire un programme 55 Exécuter un programme 56 Modier un programme 57 Effacer des programmes 58 Programmation avancée 59 Insertion de messages 59 Saut inconditionnel 60 Saut conditionnel 62 Compteurs 64 Sous-programmes 64 Exemple récapitulatif : le jeu du nombre mystère 65 Programmation et graphiques 66 Programmation en Base-N 67 Utilisation des mémoires 68 Augmentation / diminution du nombre des mémoires 68 Mémoires tableau 70

9. MESSAGES D’ERREUR 71

Causes possibles d’erreurs 71

10. PRECAUTIONS D’EMPLOI 74

IMPORTANT : sauvegarde de vos données 74 Utilisation de RESET 74 Remplacement des piles 75 Entretien de votre calculatrice 76

11. INDEX 77

12. GARANTIE 79

GC700_01_GC700Z_01IM0108.indd 4 6/3/08 17:33:09

Français

5

Nous sommes heureux de vous compter aujourd’hui parmi les nombreux utilisateurs des produits Lexibook® et nous vous remercions de votre conance. Depuis plus de 15 ans, la société française Lexibook conçoit, développe, fabrique et distribue à travers le monde des produits électroniques pour tous, reconnus pour leur valeur technologique et leur qualité de fabrication. Calculatrices, dictionnaires et traducteurs électroniques, stations météo, multimédia, horlogerie, téléphonie… Nos produits accompagnent votre quotidien. Pour apprécier pleinement les capacités de la calculatrice graphique GC700_01/ GC700Z_01, nous vous invitons à lire attentivement ce mode d’emploi.

INTRODUCTION

AVANT LA PREMIÈRE UTILISATION

Avant de démarrer, veuillez suivre attentivement les étapes suivantes :

1. Retirez avec précaution les deux languettes de protection du compartiment à piles en tirant sur l’extrémité des languettes.

2. Si une languette reste coincée, dévissez le compartiment à piles à l’aide d’un tournevis et retirez les piles, puis la languette. Replacez ensuite 2 piles CR2025 en respectant la polarité comme indiqué dans le compartiment de l’appareil (côté + au-dessus). Remettez ensuite en place le couvercle du compartiment et la vis.

3. Faites coulisser la calculatrice dans le couvercle pour accéder au clavier.

GC700_01_GC700Z_01IM0108.indd 5 6/3/08 17:33:09

Français

6

Français

1. PRISE EN MAIN DE VOTRE CALCULATRICE

Mise en marche et arrêt de la calculatrice

[AC]

Mise en marche de la calculatrice. Mise à zéro.

Note : quand votre calculatrice se remet en marche après avoir été éteinte, elle est réglée par défaut en mode

décimal (DEC), avec virgule ottante et des mesures

d’angles en degrés (DEG).

[SHIFT]

[OFF]

Arrêt. Après 6 minutes environ de non-utilisation, la calculatrice s’éteindra automatiquement.

Votre calculatrice est une calculatrice scientique, graphique et programmable. Il y a un type d’écran correspondant à chacune de ces applications. Pour tout

ce qui concerne les applications graphiques et la programmation, se référer aux chapitres correspondants.

L’afchage correspondant aux fonctions usuelles est le suivant :

4. Retirez la pellicule statique protectrice de l’écran LCD.

5. Appuyez sur la touche [AC] pour mettre la calculatrice en marche. Vous verrez alors la lettre D et un curseur clignotant apparaître sur l’écran. Si ce n’est pas le cas, vériez l’état des piles et recommencez l’opération (voir si nécessaire le chapitre « Précautions d’emploi »).

6. Localisez le trou du RESET au dos de l’appareil. Insérez une pointe ne (un trombone par exemple) et appuyez doucement.

Pour plus d’informations concernant les piles, l’importance de RESET et de la sauvegarde de vos données, voir le chapitre « Précautions d’emploi ».

Afchage et symboles utilisés

D

5+In 2

saisie alphanumérique

GC700_01_GC700Z_01IM0108.indd 6 6/3/08 17:33:10

Français

7

-

Signe moins pour indiquer que le nombre afché est

négatif.

ou

S’afche pour indiquer que le calcul en cours est trop long pour être afché en entier. Dans ce cas appuyer sur [ ] ou [ ] pour afcher le reste du calcul.

Disp

Indique que la valeur afchée est un résultat intermédiaire,

voir le paragraphe « Calculs successifs » sur une ligne, ou le chapitre « Programmation ».

M

La fonction MODE est activée.

S

La fonction SHIFT est activée.

A

La fonction ALPHA est activée.

……

ERROR

S’afche quand le calcul excède les limites permises

ou qu’une erreur est détectée. Les différents messages d’erreur, leurs causes et leurs remèdes sont détaillés dans le chapitre correspondant, « Messages d’erreur ».

hyp

S’afche quand la fonction hyperbolique est activée.

Sur la ligne du bas vous pouvez visualiser en alphanumérique les opérations saisies. Puis, une fois que vous appuyez sur [EXE] :

Note : cette valeur est donnée pour exemple et ne correspond pas au calcul 5+ln2

La ligne du bas afche un résultat numérique avec 10 chiffres signicatifs, ou bien 10 chiffres signicatifs plus 2, en haut sur la droite, de notation scientique (voir paragraphe “Notation scientique”).

A noter que, si votre résultat apparaît en 10 ou 10+2 chiffres signicatifs, les calculs internes sont réalisés avec 24 chiffres signicatifs et deux d’exposant, ce qui vous donne un niveau de précision des calculs particulièrement performant.

A l’écran vous trouverez un certain nombre de symboles (ici seul D est afché). Ces symboles vous donnent des indications qui vous permettent une meilleure lisibilité des opérations en cours :

D

2.05 2631

-11

Exposant

Mantisse

GC700_01_GC700Z_01IM0108.indd 7 6/3/08 17:33:10

Français

8

Français

Fix

Indique que le résultat sera afché avec un nombre

déterminé de chiffres après la virgule.

Sci

Indique que le résultat sera afché avec un nombre déterminé de chiffres signicatifs.

D

S’afche en mode degré ou quand la mesure d’angle afchée est en degrés.

R

S’afche en mode radian ou quand la mesure d’angle afchée est en radians.

G

S’afche en mode grade ou quand la mesure d’angle afchée est en grades.

Réglage du contraste de l’écran

[MODE] [ ] , [ ]

Réglage du contraste de l’écran.

A droite de l’écran vous trouverez un cercle marqué REPLAY sur lequel vous trouverez les èches [ ] , [ ] , [ ] et [ ]. Pour l’instant nous nous intéresserons à [ ] et [ ].

Pour régler le contraste, appuyez une fois sur [MODE] et ensuite appuyez sur [ ] de façon continue ou répétée pour baisser le contraste, ou sur [ ] pour l’augmenter. Si le contraste n’augmente pas lors de cette manœuvre c’est probablement que le niveau de piles est faible et qu’il faut les changer ; référez-vous aux conseils et aux instructions sur le changement des piles en n de manuel.

Fonctions secondes et fonctions alphanumériques (SHIFT et ALPHA)

[SHIFT]

Accès aux fonctions secondes, signalées en bleu

turquoise au-dessus de la touche concernée.

[ALPHA]

Accès aux fonctions alphanumériques, signalées en

Orange/Jaune au-dessous à droite de la touche concernée.

[SHIFT]

[A-LOCK]

Accès en continu aux fonctions alphanumériques

(verrouillage de la fonction ALPHA), annulation en

appuyant sur [ALPHA] de nouveau, ou sur [EXE].

Le plus souvent les touches de votre calculatrice comportent au moins deux fonctions, voire trois ou quatre. Elles sont repérées par des couleurs et par leur position autour de la touche qui sert à y accéder.

GC700_01_GC700Z_01IM0108.indd 8 6/3/08 17:33:11

Français

9

Par exemple :

l X-1 est la fonction principale, en accès direct par pression de la touche.

l n ! est la fonction seconde, il faut appuyer sur [SHIFT] puis sur la touche

concernée (S apparaît brièvement à l’afchage).

l A est la fonction alphanumérique, il faut appuyer sur [ALPHA] puis sur la touche concernée (A apparaît brièvement à l’afchage). Il s’agit principalement de touches pour les mémoires ou la saisie de texte.

l /A et les autres fonctions indiquées en bas à gauche sont des fonctions accessibles uniquement lors des calculs en Base N, vous trouverez les détails de cette fonction au chapitre correspondant.

De même, les fonctions signalées entre sont des fonctions relatives aux fonctions statistiques qui seront détaillées dans le chapitre correspondant.

Si vous appuyez une fois sur la touche [SHIFT], le symbole S s’afche sur l’écran pour indiquer que [SHIFT] est activée et que vous pouvez accéder aux fonctions secondes. Le symbole s’éteint dès que vous appuyez sur une autre touche ou que vous appuyez une nouvelle fois sur [SHIFT].

De même si vous appuyez une fois sur la touche [ALPHA], le symbole A s’afche sur l’écran pour indiquer que [ALPHA] est activée et que vous pouvez accéder aux fonctions alphanumériques. Le symbole s’éteint dès que vous appuyez sur une autre touche ou que vous appuyez une nouvelle fois sur [ALPHA].

Si vous souhaitez utiliser plusieurs fois de suite des fonctions alphanumériques sans que ce soit fastidieux vous pouvez utiliser [SHIFT] [A-LOCK]. Le symbole A reste allumé et vous accédez en continu aux fonctions alphanumériques tant que vous n’aurez pas appuyé sur [ALPHA] pour annuler le réglage, ou [SHIFT] si vous voulez passer directement à une fonction seconde.

GC700_01_GC700Z_01IM0108.indd 9 6/3/08 17:33:11

Français

10

Français

Notations utilisées dans le manuel

Dans ce manuel les fonctions seront indiquées comme suit (en reprenant l’exemple précédent): principale [X

-1

] seconde [SHIFT] [n!] alpha [ALPHA][A]

0 - 9

[+]

[-]

[x]

[÷]

[=]

[.]

[SHIFT]

[(-)]

[(], [)]

Touches de chiffres.

Addition.

Soustraction.

Multiplication.

Division.

Donne le résultat.

Insertion de la virgule pour un nombre décimal.

Ex : pour écrire 12,3 -> 12[.]3

Change le signe du nombre qui sera rentré immédiatement après.

5 [x] [SHIFT] [(-)] [5] [EXE] -> -25.

Ouvre / ferme une parenthèse.

Ex : [(] 4 [+] 1 [)] [x] 5 [EXE] -> 25.

Les touches [0] à [9] seront notées 0 à 9 (sans crochets) pour faciliter la lecture.

Les calculs et les résultats seront présentés comme suit :

description saisie -> afchage alphanumérique | ligne résultat

Ex :

Pour effectuer le calcul (4+1)x5= le processus sera noté ainsi : [(] 4 [+] 1 [)] [x] 5 [EXE] -> (4+1)x5 | 25.

Lorsque cela ne nuira pas à la compréhension d’un exemple, la partie la plus à gauche pourra être omise.

Touches usuelles

GC700_01_GC700Z_01IM0108.indd 10 6/3/08 17:33:11

Français

11

Saisie et modication d’un calcul (Replay)

[ ] [ ]

Pour déplacer le curseur et éditer un calcul.

[ ] pressé une fois alors que le résultat numérique est

afché fait apparaître la ligne de calcul alphanumérique et

place le curseur en bout de ligne.

[ ] pressé une fois alors que le résultat numérique est

afché fait apparaître la ligne de calcul alphanumérique et

place le curseur en tête de ligne.

[DEL]

Efface le caractère à l’endroit où se trouve le curseur.

[SHIFT] [INS]

Insère un caractère immédiatement à gauche du curseur d’insertion.

Vous pouvez saisir dans votre calculatrice vos calculs et ceux-ci s’inscrivent en bas à gauche dans un style alphanumérique facile à lire et à corriger.

Une fois le calcul saisi et le résultat obtenu en appuyant sur [EXE], il est facile de revoir et modier votre calcul grâce aux èches [ ], [ ].

Remarques sur [SHIFT] [INS] :

l La fonction est située sur la touche [ ] . l Le curseur change tant que l’insertion est activée . l On peut utiliser [DEL] pendant que l’insertion est activée, cela efface le

caractère situé à gauche du curseur. l L’insertion est désactivée lorsqu’on appuie sur [ ] ou [ ].

Remarques sur la saisie de calculs : Vous pouvez saisir en une seule fois un calcul jusqu’à une longueur de 127 caractères ; à noter que même si une fonction telle que sin-1 nécessite de

taper sur 2 touches et qu’elle s’afche à l´écran en plusieurs lettres, elle

n’est comptée que pour un caractère par la calculatrice. Si vous arrivez à 121 caractères la calculatrice vous préviendra en changeant la forme du curseur de _ à .

Si votre calcul est excessivement long, mieux vaut le découper en plusieurs

parties.

GC700_01_GC700Z_01IM0108.indd 11 6/3/08 17:33:12

Français

12

Français

Ex :

Vous avez effectué la saisie suivante : 34 [+] 57 [-] 27 [x] 78 +5 [EXE] -> 34+57-27x78+5 | -2010.

Si vous appuyez sur [ ] vous retrouvez l’afchage alphanumérique de votre calcul et le symbole vous indique que le calcul est trop long pour pouvoir être afché entièrement.

l Vous voulez modier 27 en 7 dans le calcul:

Vous positionnez le curseur à l’aide de la touche [ ] pour vous placer sur l’endroit de correction, c’est-à-dire le 2.

Appuyez sur [DEL] pour supprimer le 2. Si vous appuyez sur [EXE],

le résultat devient -450.

l Vous voulez modier 34 en 3684 dans le calcul

Vous positionnez le curseur à l’aide de la touche [ ] une fois pour vous placer au début de la ligne de calcul puis une autre fois pour vous placer sur l’endroit de correction, c’est-à-dire le 4.

Appuyez sur [SHIFT] [INS] et tapez 6 puis 8 à l’endroit d’insertion. Si vous appuyez sur [EXE], le résultat devient 3200.

[ALPHA] [ ]

Marque de séparation entre deux calculs consécutifs saisis

sur une même ligne.

[AC]

Interrompt l’exécution de calculs consécutifs.

Calculs successifs sur une ligne

Votre calculatrice vous permet, si vous le souhaitez, de saisir plusieurs

calculs à réaliser successivement sur une seule ligne, puis de les exécuter en appuyant sur [EXE]. La calculatrice effectue alors le premier calcul saisi ; elle afche le résultat intermédiaire et le symbole Disp pour vous indiquer que l’exécution des calculs n’est pas terminée. Si vous appuyez sur [EXE] la calculatrice passe au deuxième calcul et ainsi de suite jusqu’au dernier, pour

lequel Disp s’éteint.

GC700_01_GC700Z_01IM0108.indd 12 6/3/08 17:33:12

Français

13

Ex :

Vous effectuez le calcul suivant : 54+39= 9-18= 4x6-2= 50x12= Vous pouvez le saisir comme suit : 54 [+] 39 [ALPHA] [ ] 9 [-] 18 [ALPHA] [ ] 4 [x] 6 [-] 2 [ALPHA] [ ] 50 [x] 12 [EXE]

-> 54+39 9-18 4x6-2 50x12 | 93. Disp [EXE] -> | -9. Disp [EXE] -> | 22. Disp [EXE] -> | 600.

Notes : l On ne peut pas éditer les calculs tant que Disp est afché et que le dernier calcul n’est pas atteint, sauf si on appuie sur [AC] pour les interrompre.

l Dans l’exemple précédent, si on appuie une fois de plus sur [EXE] le calcul recommence (l’écran afche 93. et Disp).

l Voir aussi pour ces calculs comment effectuer le rappel du résultat précédent, fonction Ans dans le chapitre suivant.

Notation scientique et ingénieur

La GC700 afche directement le résultat d’un calcul (x) en mode décimal normal si x appartient à l’intervalle suivant :

0.000000001≤ | x |≤ 9999999999

Note : |x| est la valeur absolue de x, soit |x|= -x si x<0 et |x|=x si x≥0.

En dehors de ces limites la calculatrice afchera automatiquement le résultat d’un calcul selon le système de notation scientique, les deux chiffres en haut à droite représentant l’exposant du facteur 10.

Ex :

carré de 2 500 000 et son inverse 2500000 [X2][EXE] -> 25000002 | 6.25 12 soit 6,25 x 1012 [X-1][EXE] -> 6.25E12-1 | 1.6

–13

soit 1,6 x 10

-13

La notation dite ingénieur découle du même principe, mais pour cette notation il faut que la puissance de 10 soit un multiple de 3 (103, 106,109 etc.). En reprenant l’exemple précédent : 6,25 x 1012 s’écrit aussi 6.25

12

en notation ingénieur, mais 1,6 x 10

-13

s’écrira 160.

–15

GC700_01_GC700Z_01IM0108.indd 13 6/3/08 17:33:12

Français

14

Français

Choix de la notation

Pour un nombre qui se situe dans l’intervalle précédent, votre calculatrice vous permet de le saisir directement en notation scientique, an d’éviter la saisie répétitive de zéros.

[EXP]

Saisie d’une valeur en notation scientique.

[ENG] Ou [SHIFT] [ ]

Flèche au-dessus de la touche [ENG]

Passage en notation ingénieur:

• Chaque fois que l’on appuie sur [ENG] l’exposant diminue de 3.

• Chaque fois que l’on appuie sur [SHIFT] [ ]

l’exposant augmente de 3.

Ex :

Pour entrer 2 500 000 soit 2,5 x 106 en notation scientique : 2 [.] 5 [EXP] 6 [EXE] -> 2.5E6 | 2500000.

Pour entrer 2 500 0002 soit (2,5 x 106 )2 en notation scientique : 2 [.] 5 [EXP] 6 [X2] [EXE] -> 2.5E62 | 6.25

12

Pour entrer 0.016 soit 1,6 x 10-2 en notation scientique : 1 [.] 6 [EXP] [SHIFT] [(-)] 2 [EXE] -> 1.6E-2 | 0.016.

Pour passer à la notation ingénieur, en reprenant les exemples précédents : 2 [.] 5 [EXP] 6 [EXE] -> 2.5E6 | 2500000. [ENG] -> 2.5

06

[ENG] -> 2500.

03

[ENG] -> 2500000.

00

[ENG] -> 2500000000.

-03

[.] 016 [EXE] -> .016 0.016 [SHIFT] [ ] -> 0.016

00

[ENG] -> 16.

-03

[ENG] -> 16000.

-06

[SHIFT] [ ] -> 16.

-03

[MODE]

7 + chiffre entre

0 et 9

Choix du nombre de chiffres après la virgule, le symbole

Fix s’afche.

[SHIFT] [Rnd]

Arrondit la valeur afchée en fonction du réglage Fix.

[MODE] 9

Annulation du réglage du nombre de chiffres après la virgule.

Fixation de la position de la virgule

GC700_01_GC700Z_01IM0108.indd 14 6/3/08 17:33:13

Français

15

Ex :

100000 [÷] 3 [EXE] -> 100000÷3 | 33333.33333 [MODE][7] 3 [EXE] -> Fix 3 | 33333.333

Fix

[MODE][7] 2 [EXE] -> Fix 2 | 33333.33

Fix

[x]10 [EXE] ->33333.33333x10 | 333333.33

Fix

[MODE][9] [EXE] -> Norm | 333333.3333

Choix du nombre de chiffres signicatifs

[MODE] 8 + chiffre

entre 0 et 9

Choix du nombre de chiffres signicatifs, le symbole

Sci s’afche.

[SHIFT] [Rnd]

Arrondit la valeur afchée en fonction du réglage

Sci.

[MODE] 9

Annulation du réglage du nombre de chiffres

signicatifs.

Lorsque vous xez le nombre de chiffres après la virgule d’une valeur par un réglage FIX, vous ne modiez que l’afchage de cette valeur et non la valeur mémorisée par la calculatrice, qui comporte 24 chiffres signicatifs. Si vous le souhaitez vous pouvez modier la valeur mémorisée pour continuer vos calculs avec une valeur arrondie, selon le nombre de chiffres après la virgule demandé. En reprenant l’exemple précédent :

100000 [÷] 3 [EXE] -> 100000÷3 | 33333.33333 [MODE][7] 2 [EXE] -> Fix 2 | 33333.33

Fix

[SHIFT] [Rnd] [EXE] -> Rnd | 33333.33

Fix

[x]10 [EXE] -> 33333.33x10 | 333333.30

Fix

Ex :

100000 [÷] 3 [EXE] -> 100000÷3 | 33333.33333 [MODE][8] 5 [EXE] -> Sci 5 | 3.3333

04

Sci

[MODE][8] 3 [EXE] -> Sci 3 | 3.33

04

Sci

[MODE][9] [EXE] -> Norm | 33333.33333

Lorsque vous xez le nombre de chiffres signicatifs d’une valeur par un réglage Sci, vous ne modiez que l’afchage de cette valeur et non la valeur mémorisée par la calculatrice, qui comporte 24 chiffres signicatifs. Si vous le souhaitez vous pouvez modier la valeur mémorisée pour continuer vos calculs avec une valeur arrondie, selon le nombre de chiffres signicatifs demandé. En reprenant l’exemple précédent :

GC700_01_GC700Z_01IM0108.indd 15 6/3/08 17:33:13

Français

16

Français

Ex :

100000 [÷] 3 [EXE] -> 100000÷3 | 33333.33333 [MODE][8] 3 [EXE] -> Sci 3 | 3.33

04

Sci

[SHIFT] [Rnd] [EXE] -> Rnd | 3.33

04

Sci

[x]10 [EXE] -> 33300.x10 | 3.33

05

Sci

[MODE][9] [EXE] -> Norm | 333000.

Note : ce mode d’afchage est compatible avec [ENG] :

100000 [÷] 3 [EXE] -> 100000÷3 | 33333.33333 [MODE][8] 5 [EXE] -> Sci 5 | 3.3333

04

Sci

[ENG] -> 33.333

03

Sci

Priorités de calcul

Quand il y a plusieurs opérations à réaliser dans un calcul, votre calculatrice les évalue et détermine l’ordre dans lequel les effectuer, en fonction des règles arithmétiques. Cet ordre de priorité est le suivant :

1. Les opérations entre parenthèses, et, en cas de plusieurs niveaux de parenthèses, la dernière parenthèse ouverte.

2. Les fonctions utilisant un type d’exposant telles que X-1, X2 , √, Xy et x√, ainsi que le changement de signe [(-)].

3. Les fonctions de type cos, sin, ln, ex…

4. Les fonctions de saisie d’une donnée, telles que

‘ ‘ ‘

[º ]

et [a b/c].

5. Les multiplications et divisions (la multiplication peut être implicite, par exemple 2cosπ).

6. Les additions et soustractions.

7. Les fonctions qui signalent la n d’un calcul ou mettent en mémoire une valeur : [EXE], [ ], [DT], etc.

Lorsque les opérateurs sont de même niveau de priorité la calculatrice les effectue tout simplement par ordre d’apparition de gauche à droite. Au sein des parenthèses l’ordre des priorités est conservé.

Ex :

1 [+] 3 [x] 5 [EXE] -> 1+3x5 | 16. [(] 1 [+] 4 [)] [x] 5 [EXE] -> (1+4)x5 | 25. 10 [-] 3 [X2] [EXE] -> 10-32 | 1. 5 [xy] [ln] 2 [EXE] -> 5xyln 2 | 3.05132936 soit 5

ln2

Votre calculatrice fait la différence entre les différents niveaux de priorité et, au besoin, mémorise les données et les opérateurs jusqu’à la bonne résolution du calcul, et ce jusqu’à 24 niveaux différents d’opérateurs et 10 niveaux de valeurs numériques intermédiaires pour un calcul en cours. Ces niveaux sont appelés ¨stacks¨ en anglais ; si votre calcul est très compliqué et dépasse les possibilités pourtant étendues de votre machine vous verrez apparaître le message suivant Stk ERROR (dépassement de la capacité ¨stacks¨).

GC700_01_GC700Z_01IM0108.indd 16 6/3/08 17:33:14

Français

17

2. UTILISATION DES MEMOIRES

Rappel du dernier résultat (Ans)

[Ans]

Rappelle le résultat du calcul précédent.

Ex:

24 [÷] [(] 4[+]6 [)] [EXE] -> 24÷(4+6) | 2.4 Le résultat (2,4) est automatiquement mémorisé dans la mémoire Ans.

On peut alors calculer 3x ANS + 60÷ANS 3 [x] [ANS] [+] 60 [÷][ANS] [EXE] -> 3xANS+60÷ANS | 32.2

Calculs en chaîne

Il s’agit de calculs pour lesquels le résultat du calcul précédent sert de premier opérande du calcul suivant. Vous pouvez notamment utiliser dans

ces calculs les fonctions [√], [X2], [sin],...

Ex :

[AC] 6 [+] 4 [EXE] -> 6+4 | 10. [+] 71 [EXE] -> 10.+71 | 81.

[√] [Ans] [EXE] -> √Ans | 9.

Calculs successifs

L’utilisation de Ans est impérative pour les calculs successifs écrits sur une ligne : 54 [+] 39 [ALPHA][ ] [Ans] [-] 18 [EXE] -> 93. puis en appuyant sur [EXE] : 75 54 [+] 39 [ALPHA] [ ] [-] 18 [EXE] ->93. puis en appuyant sur [EXE] : -18

GC700_01_GC700Z_01IM0108.indd 17 6/3/08 17:33:14

Français

18

Français

Mémoires temporaires (A - Z)

[ALPHA][A]

Rappelle le contenu de la mémoire A pour utilisation dans un calcul.

[ ][ALPHA][A]

Stocke la valeur afchée ou à calculer dans la mémoire

A.

[ALPHA] [~]

Permet d’accéder au contenu de plusieurs mémoires en même temps.

Ex : 5 [ ] [SHIFT] [A-LOCK] [A][~][D] [EXE] assigne la valeur 5 aux mémoires A, B, C et D.

Rappel : [SHIFT] [A-LOCK]=[SHIFT][ALPHA], verrouillage de [ALPHA]

0 [ ] [ALPHA][A] (zéro)

Mise à zéro de la mémoire A.

[SHIFT][Mcl]

Efface le contenu de toutes les mémoires temporaires.

Ex :

5 [ ] [ALPHA] [X] [EXE] -> 5 X | 5. [-] 3 [ ] [ALPHA] [X] [EXE] -> 5.-3 X | 2. 6 [x] [ALPHA] [X] [EXE] -> 6xX | 12. [ALPHA] [X][EXE] -> X | 2.

Les deux premières lignes de calcul modient la valeur de X (X=5 puis 2), le calcul 6xX utilise la valeur de X mais ne la modie pas.

Votre calculatrice dispose de 26 mémoires temporaires, A, B, C, D, E… ,Y, et Z. Ces mémoires temporaires vous permettent de stocker des données pour rappel et utilisation dans des calculs futurs.

Vous pouvez employer [ ], [ALPHA] pour chacune des touches [A], [B], [C], [D], …. [Y] et [Z]. Rappel : la lettre accessible via [ALPHA] est inscrite en orange et se trouve en bas à droite de la touche concernée. Ex : A se trouve en bas à droite de la touche [X-1].

Note : il est possible de modier le réglage de la calculatrice pour disposer de plus de 26 mémoires temporaires. La procédure à suivre est expliquée dans le chapitre « Programmation ».

GC700_01_GC700Z_01IM0108.indd 18 6/3/08 17:33:14

Français

19

5 [ ] [SHIFT] [A-LOCK] [A] [~][E] [EXE] -> 5 A~E | 5. A,B, C, D et E contiennent maintenant toutes la même valeur, 5. [ALPHA] [B] [x] [ALPHA] [C] [EXE] -> BxC | 25. [SHIFT][Mcl] [EXE] -> Mcl | 25. [ALPHA] [D] [EXE] -> D | 0. L’utilisation de [SHIFT][Mcl] a annulé le contenu de toutes les mémoires.

1 € = 140 Yens, combien valent 33 775 Yens en Euros ? Combien valent 2 750 € en Yens ? 140 [ ] [ALPHA] [A] [EXE] -> 140 A | 140. 33775 [÷] [ALPHA] [A][EXE] -> 33775÷A | 241.25 2750 [x] [ALPHA] [A] [EXE] -> 2750xA | 385000.

On souhaite réaliser l’opération suivante : Articles en stock le matin = 200 Articles livrés dans la journée : 5 boîtes de 12 et 9 boîtes de 6 Articles vendus dans la journée : 2 boîtes de 24 Quantité de pièces en stock à la n de la journée ? Si chaque pièce coûte 3,50€, valeur du stock.

On met en mémoire le nombre de pièces en stock au départ : 200 [ ] [ALPHA] [A] [EXE] -> 200 A | 200.

On rajoute les pièces livrées et on retranche les pièces vendues : [+] 5 [x] 12 [+] 9 [x] 6 [-] 2 [x] 24 [ ] [ALPHA] [A] [EXE]

-> 200.+5x12+9x6-2x24 A | 266. Le stock est de 266 pièces.

Et pour calculer la valeur du stock on fait : 3 [.] 5 [x] [ALPHA] [A] [EXE] -> 3.5xA | 931.

GC700_01_GC700Z_01IM0108.indd 19 6/3/08 17:33:15

Français

20

Français

Partie entière (Int), partie décimale (Frac)

3. FONCTIONS ARITHMETIQUES

[SHIFT] [Int]

Donne la partie entière de la valeur saisie immédiatement après.

[SHIFT] [Frac]

Donne la partie décimale de la valeur saisie immédiatement après.

[SHIFT] [Int] 9 [.] 256 [EXE] -> Int 9.256 | 9. [SHIFT] [Frac] 9 [.] 256 [EXE] -> Frac 9.256 | 0.256

Inverse, carré et exposants

[X-1]

Calcule l’inverse de la valeur saisie immédiatement avant.

[X2]

Calcule le carré de la valeur saisie immédiatement avant.

[xy]

Elève la valeur x (saisie avant) à la puissance y

(saisie après).

[SHIFT][10x]

Calcule la puissance 10 du nombre saisi immédiatement après.

Ex :

-03

GC700_01_GC700Z_01IM0108.indd 20 6/3/08 17:33:15

Français

21

Racines

[√]

Calcule la racine carrée du nombre saisi immédiatement après.

[SHIFT] [3√]

Calcule la racine cubique du nombre saisi immédiatement après.

[x√]

Calcule la Xième racine du nombre saisi

immédiatement après.

En reprenant les exemples précédents : [√] 9 [EXE] -> √9 | 3. [SHIFT] [3√] 125 [EXE] ->

3

√125 | 5.

5 [x√] 32 [EXE] -> 5 x√ 32 | 2.

Fractions

[a b/c]

Permet de saisir une fraction de numérateur b et de dénominateur c, et une partie entière a (facultative).

Change l’afchage d’une fraction de type nombre entier

+ fraction irréductible en nombre décimal, et vice-versa.

[SHIFT] [d/c]

Convertit une fraction de type nombre entier + fraction

irréductible en une fraction irréductible, et vice-versa.

Signication des notations a b/c et d/c :

Ex :

a = 3, b=1 et c=2. a est la partie entière de x, c’est-à-dire x= 3 + 1/2 = 3,5

En fait

En notation d/c, d=7 et c=2.

3

1

2

X=

7

2

X=

GC700_01_GC700Z_01IM0108.indd 21 6/3/08 17:33:15

Français

22

Français

Votre calculatrice vous permet d’effectuer un certain nombre d’opérations arithmétiques exprimées ou converties en fractions.

a, b et c peuvent être remplacés par un calcul entre parenthèses. Cependant dans certains cas on pourra obtenir un résultat décimal mais pas un résultat en fractions.

Ex :

3 [a b/c] 1 [a b/c] 2 [+] 4 [a b/c] 3 [EXE] -> 3 1 2 + 4 3 | 4 5 6. [a b/c] | 4.833333333 [a b/c] | 4 5 6. [SHIFT] [d/c] | 29 6.

1.25 [+] 2 [a b/c] 5 [EXE] -> 1.25+2 5 | 1.65 La somme d’une fraction et d’un nombre décimal (à partie décimale non nulle) aura pour résultat un nombre décimal et ne peut pas être reconvertie en fraction.

On peut utiliser une fraction en tant qu’exposant :

[SHIFT] [10x] 2[a b/c]3 [EXE] -> 102 3 | 4.641588834

Notes : l pour effectuer un calcul tel que + , si on utilise [SHIFT] [X-1] on

n’obtiendra qu’un résultat décimal et non exprimable en fractions.

6 [X-1] + 7 [X-1] [EXE] -> 6-1+7

-1

| 0.3095238095

l pour une fraction

On peut utiliser la notation a b/c pour obtenir un résultat en fractions. Il faut saisir le calcul comme suit :

24 [a b/c] [(] 4 [+] 6 [)] [EXE] -> 24 (4+6) | 2 2 5 [a b/c] -> 24 (4+6) | 2.4

3

1

2

+

4

3

LLLL

L

10

2

3

1 6

1 7

L

24 4 + 6

L L

L

GC700_01_GC700Z_01IM0108.indd 22 6/3/08 17:33:16

Français

23

Logarithmes et exponentielles

[ln]

Touche de logarithme népérien.

[log] Touche de logarithme décimal.

[SHIFT] [ex]

Touche de fonction exponentielle.

Ex :

[ln] 20 [EXE] -> ln 20 | 2.995732274 [log] [.] 01 [EXE] -> log .01 | -2. [SHIFT] [ex] 3 [EXE] -> e3 | 20.08553692

Hyperboliques

[hyp]

Touche de fonction hyperbolique.

A partir de cette touche s’obtiennent les différentes fonctions hyperboliques :

[ hyp ] [cos] cosh(x)

Cosinus hyperbolique.

[ hyp ] [sin]

sinh(x)

Sinus hyperbolique.

[ hyp ] [tan]

tanh(x)

Tangente hyperbolique.

[SHIFT] [ hyp ] [cos-1]

cosh-1 (x)

Argument cosinus hyperbolique.

[SHIFT] [ hyp ] [sin-1]

sinh-1 (x)

Argument sinus hyperbolique.

[SHIFT] [ hyp ] [tan-1]

tanh-1(x)

Argument tangente hyperbolique.

Note : On peut saisir [SHIFT] [ hyp ] [cos-1] ou [ hyp ] [SHIFT] [cos-1], les deux sont équivalents.

GC700_01_GC700Z_01IM0108.indd 23 6/3/08 17:33:16

Français

24

Français

Ex :

[ hyp ] [sin] 0 [EXE] -> sinh 0 | 0. [ hyp ] [cos] 0 [EXE] -> cosh 0 | 1. [SHIFT] [ hyp ] [tan-1] 0 [EXE] -> tanh

-1

0 | 0.

[SHIFT] [ hyp ] [cos-1] 1 [EXE] -> cosh-1 1 | 0.

Calcul de (cosh 1.5 + sinh 1.5)

2

[(] [hyp][cos] 1 [.] 5 [+] [hyp][sin] 1 [.]5 [)][X2][EXE]

-> (cosh 1.5 + sinh 1.5)2 | 20.08553692

Factorielle n!, permutation, combinaison

On appelle factorielle de n! ou factorielle n! le nombre suivant :

n! = 1 x 2 x 3 x.....x (n-2) x (n-1) x n

n! représente le nombre de façons différentes d’arranger n objets distincts (n! permutations).

[SHIFT] [n!]

Calcul de la factorielle n!

Votre calculatrice permet de calculer la factorielle n! jusqu’à n=69 (voir chapitre des Messages d’erreur).

Ex :

8 chevaux sont au départ d’une course hippique. Combien de combinaisons y a-t-il de leur ordre d’arrivée ?

Nombre de permutations de leur ordre d’arrivée = n! avec n = 8. 8 [SHIFT] [n!] [EXE] -> 40320.

GC700_01_GC700Z_01IM0108.indd 24 6/3/08 17:33:16

Français

25

Ex :

[SHIFT] [Ran #] [EXE] -> Ran # | 0.256 [EXE] -> 0.84 [EXE] -> 0.511 ... etc. Note : il s’agit de générer une valeur aléatoire, donc en faisant la même manipulation vous ne trouverez pas les mêmes résultats que dans ce manuel !

Pour tirer les chiffres du Loto (entre 1 et 49)

[MODE] [7] 0 [EXE] mode Fix, avec 0 chiffres après la virgule, on veut afcher des nombres entiers. [SHIFT] [Ran #] [x] 48 [+] 1 [EXE] génère, compte tenu des arrondis, un nombre compris entre 1 et 49. [SHIFT] [Ran#] [x] 48 [+] 1 [EXE] -> RAN#x48+1 | 39. [EXE] -> 32. [EXE] -> 17. [EXE] -> 2.

Génération de nombre aléatoire (fonction Random)

[SHIFT] [Ran#] [EXE]

Génère un nombre aléatoire 0 et <1, avec trois chiffres signicatifs. Pour générer le chiffre suivant appuyez sur [EXE].

≤

GC700_01_GC700Z_01IM0108.indd 25 6/3/08 17:33:17

Français

26

Français

4. CALCULS TRIGONOMETRIQUES ET COMPLEXES

Nombre π

Ex :

Périmètre et surface maximaux d’une roue de Formule 1, le diamètre maximal étant de 660mm. On calcule le rayon (diamètre divisé par 2) exprimé en mètres, puis on

applique les formules 2πr et πr2 :

660 [÷] 2 [÷] 1000 [EXE] -> 660÷2÷1000 | 0.33 [ ] [ALPHA] [Y] [EXE] -> 0.33 Y | 0.33 Mise en mémoire de la valeur du rayon

2 [SHIFT] [π] [ALPHA] [Y] [EXE] -> 2πY | 2.073451151 [SHIFT] [π] [ALPHA] [Y] [X2] [EXE] -> πY 2 | 0.34211944

Le périmètre est donc de 2,1 m et la surface de 0,34 m2. Remarque : la multiplication est implicite, nous n’avons pas eu besoin d’appuyer sur la touche [x].

[SHIFT][π] [EXE]

Afche la valeur approchée de la constante π, avec dix chiffres signicatifs,

soit 3,141592654.

Unités d’angles

Choix de l’unité d’angle et conversions

[MODE] 4

Sélectionne les degrés comme unité d’angle

active. Le symbole D s’afche à l’écran.

[MODE] 5

Sélectionne les radians comme unité d’angle

active. Le symbole R s’afche à l’écran.

[MODE] 6

Sélectionne les grades comme unité d’angle

active. Le symbole G s’afche à l’écran.

[SHIFT] [MODE] 4 (ou 5 ou 6)

Convertit la mesure d’angle introduite en degrés (ou radians ou grades) dans l’unité active.

GC700_01_GC700Z_01IM0108.indd 26 6/3/08 17:33:17

Français

27

Note : le réglage se conserve lorsque la calculatrice est éteinte et rallumée. Vériez bien l’unité active avant d’effectuer votre calcul !

Ex :

[MODE] [6] [EXE] -> Gra | 0.

G afché

Pour convertir 90 degrés en radians : [MODE] [5] [EXE] -> Rad | 0.

R afché

90 [SHIFT] [MODE] 4 [EXE] -> 90o | 1.570796327 soit π/2 radians

Pour convertir 100 grades en degrés : [MODE] [4] [EXE] -> Deg | 0.

D afché

100 [SHIFT] [MODE] 6 [EXE] -> 100

g

| 90.

Pour ajouter 36,9 degrés et 41,2 radians et obtenir le résultat en grades : [MODE] [6] [EXE] -> Gra | 0.

G afché

36[.]9 [SHIFT] [MODE] 4 [+] 41[.]2 [SHIFT] [MODE] 5 [EXE]

-> 36.9º + 41.2

r

| 2663.873462

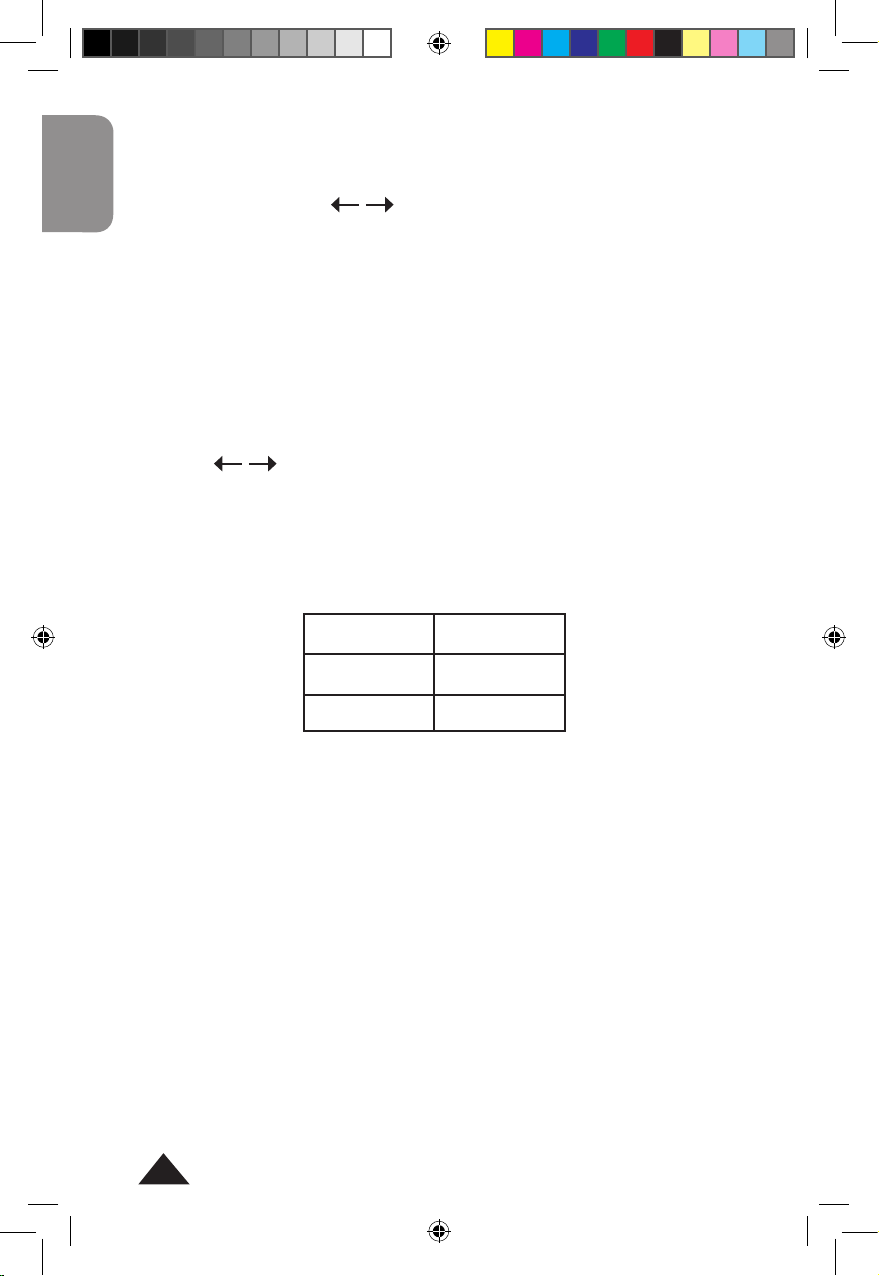
Conversion sexagésimale (degrés / minutes /secondes)

[º ]

Effectue la saisie des degrés, minutes, secondes et centièmes de seconde (facultatif).

[SHIFT] [ ]

Flèche au-dessus de

la touche

‘ ‘ ‘

[º ]

Convertit les degrés sexagésimaux en degrés décimaux, et vice-versa.

Ex :

Conversion de la latitude 12º39’18”05 en degrés décimaux :

12

‘ ‘ ‘

[º ]

39

‘ ‘ ‘

[º ]

18[.] 05

‘ ‘ ‘

[º ]

[EXE]

DEG

12º39º18.05

º

12.65501389

‘ ‘ ‘

GC700_01_GC700Z_01IM0108.indd 27 6/3/08 17:33:18

Français

28

Français

Conversion de la latitude de Paris (48º51’44”Nord) en degrés décimaux 48

‘ ‘ ‘

[º ]

51

‘ ‘ ‘

[º ]

44

‘ ‘ ‘

[º ]

[EXE] -> 48.86222222

Conversion de 123.678 en degrés sexagésimaux :

123.678 [EXE] [SHIFT][ ] ->123º 40’ 40.80’’

Calculs horaires

La fonction de conversion sexagésimale peut être également utilisée pour des calculs directs sur des heures / minutes /secondes :

Ex :

3h 30 min 45s + 6h 45min 36s 3

‘ ‘ ‘

[º ]

30

‘ ‘ ‘

[º ]

45

‘ ‘ ‘

[º ]

[+] 6

‘ ‘ ‘

[º ]

45

‘ ‘ ‘

[º ]

36

‘ ‘ ‘

[º ]

[EXE]

-> 10.2725 [SHIFT] [ ] -> 10°16’21’’ soit 10h 16 min 21 secondes.

Cosinus, sinus, tangente

[cos]

cos(x)

[sin]

sin(x)

[tan]

tan(x)

Ex :

Mode 4 [EXE] [cos] 90 [EXE] -> cos 90 | 0. [tan] 60 [EXE] -> tan 60 | 1.732050808

sin230 = [(] [sin] 30 [)][X2] [EXE] -> (sin30)2 | 0.25

Mode 5 [EXE] [sin] [SHIFT] [π][EXE] -> sin π | 0. [cos] [(] [SHIFT][π] [÷] 4 [)] [EXE] -> cos (π÷4) | 0.7071067812

GC700_01_GC700Z_01IM0108.indd 28 6/3/08 17:33:18

Français

29

Avec les degrés sexagésimaux : En mode degrés Mode 4 [EXE] sin (62º12’24”)= [sin] 62

‘ ‘ ‘

[º ]

12

‘ ‘ ‘

[º ]

24

‘ ‘ ‘

[º ]

[EXE] -> 0.8846352358

[SHIFT] [cos-1]

arccos(x)

[SHIFT] [sin-1]

arcsin(x)

[SHIFT] [tan-1]

arctan(x)

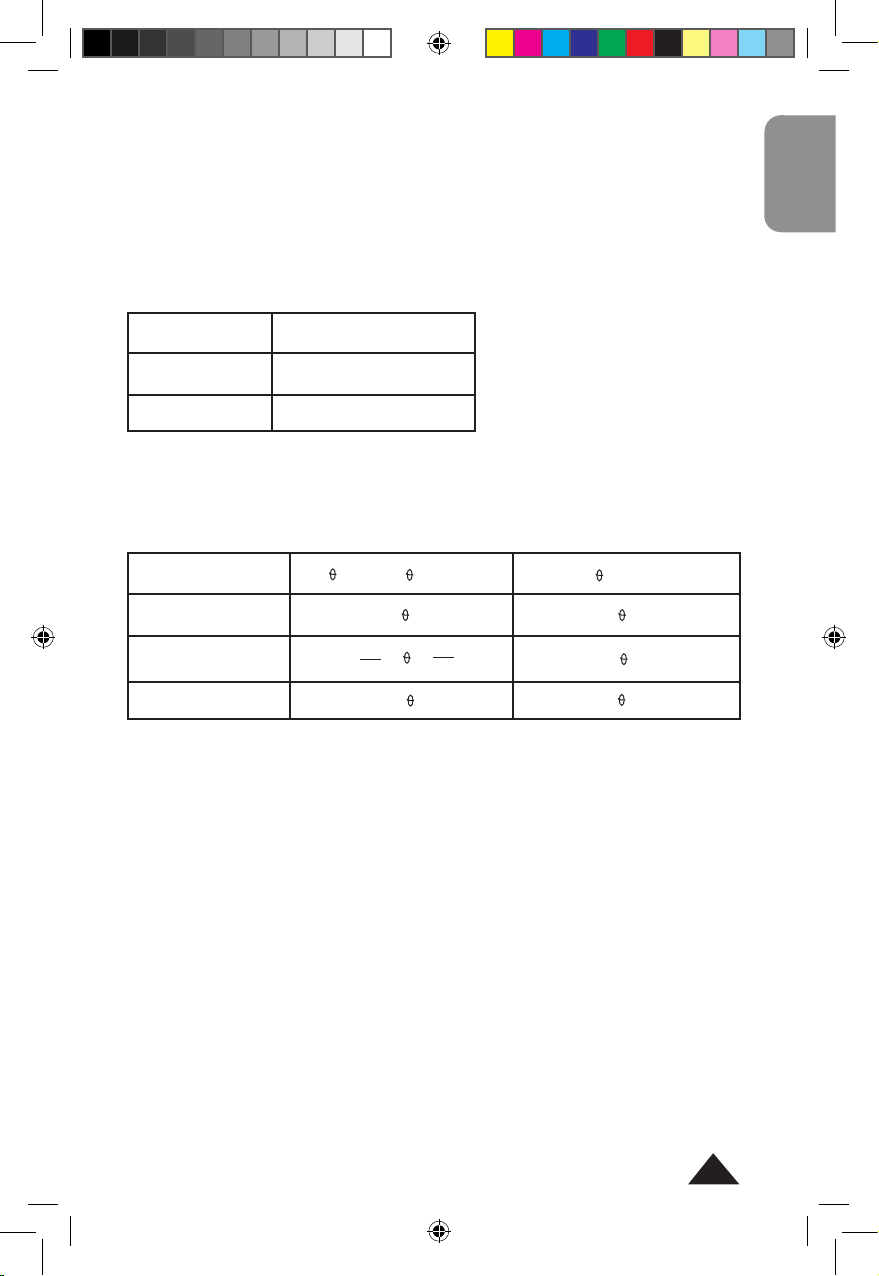
Pour les fonctions sin-1, tan-1 et cos-1 les résultats de mesure angulaire seront donnés dans les intervalles suivants :

=sin-1 x, =tan-1 x =cos

-1

x

DEG

-90≤ ≤90 0≤ ≤180

RAD

0≤ ≤

GRAD

-100≤ ≤100 0≤ ≤200

-

2

π

≤ ≤

2

π

Ex :

Mode 6 [EXE] [SHIFT] [tan-1] 1 [EXE] -> tan-1 1 | 50.

Un panneau routier indique une pente à 5%. Donner la mesure de l’angle en degrés et en radians. Si la pente est à 5% l’altitude augmente de 5m tous les 100m. Le sinus de l’angle à trouver est de 5 divisé par 100, soit 0,05.

Mode 4 [EXE] [SHIFT] [sin-1] [.] 0 5 [EXE]-> sin-1 .05 | 2.865983983 D [MODE] 5 [EXE] -> Rad | 2.865983983

R

[SHIFT] [MODE] 4 [EXE] -> 2.865983983º | 0.0500208568 radians

Arccosinus, arcsinus, arctangente

GC700_01_GC700Z_01IM0108.indd 29 6/3/08 17:33:19

Français

30

Français

[SHIFT] [Pol(]

Initie la saisie des coordonnées cartésiennes pour conversion en coordonnées polaires.

[SHIFT] [Rec(]

Initie la saisie des coordonnées polaires pour conversion en coordonnées cartésiennes.

[SHIFT] [,]

Utilisé avec [SHIFT] [Pol(] ou [SHIFT] [Rec(], se place entre x et y, ou r et pour signaler la saisie de la 2

ème

coordonnée.

[)]

Parenthèse terminant la saisie du couple de coordonnées.

[ALPHA] [I]

Afche la première coordonnée après conversion, x ou r.

[ALPHA] [J]

Afche la deuxième coordonnée après conversion, y ou .

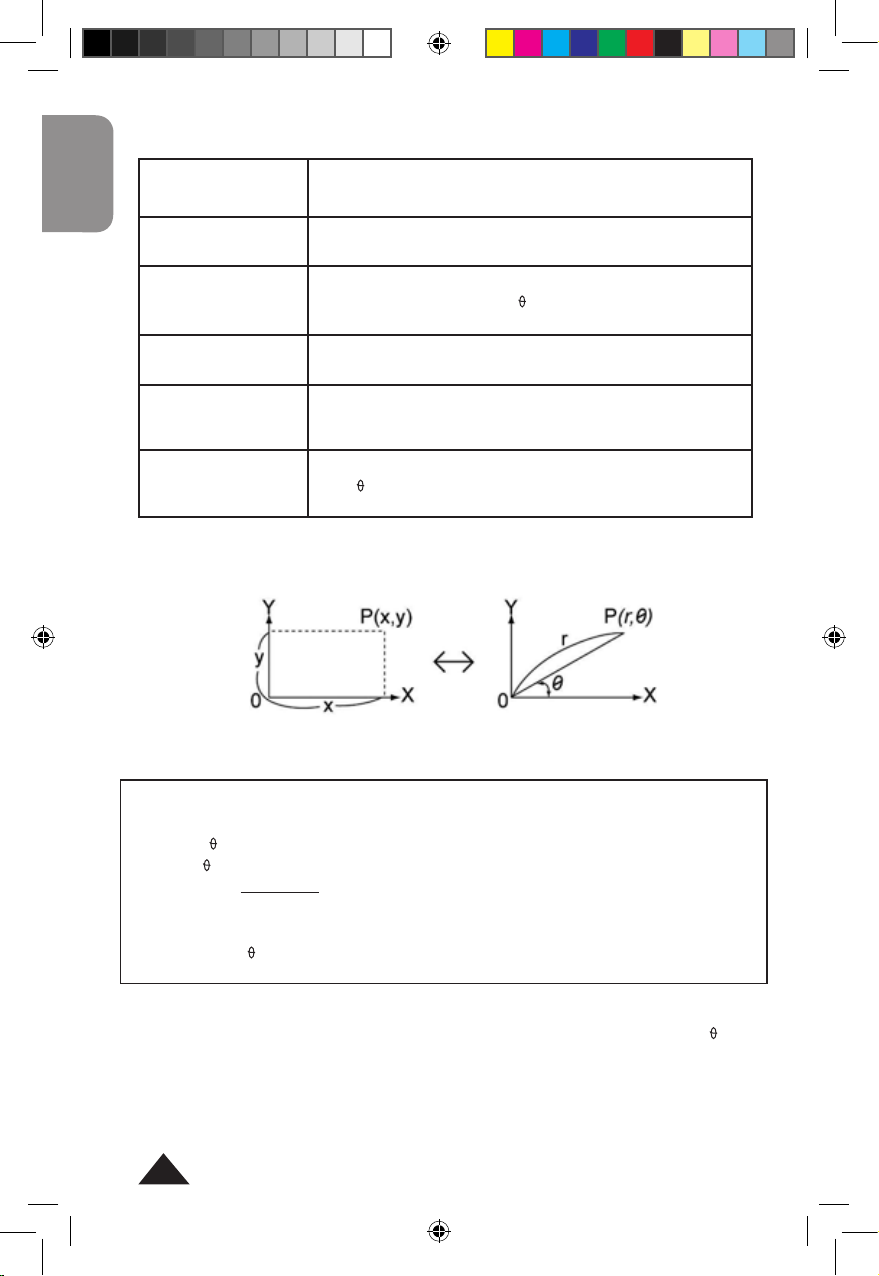
Coordonnées polaires

Pour mémoire :

x = rcos y = rsin

et

r= x2+y2

= tan-1 (y/x)

√

On appelle x et y les coordonnées cartésiennes, ou rectangulaires, r et sont les coordonnées polaires.

GC700_01_GC700Z_01IM0108.indd 30 6/3/08 17:33:19

Français

31

Note : l’angle sera calculé dans l’intervalle [-180º,+180º] (degrés décimaux) ; la mesure d’angle sera donnée dans l’unité d’angle qui a été présélectionnée sur la calculatrice : en degrés si la calculatrice est en mode D, en radians si la calculatrice est en mode R, etc.

Ex :

En mode degrés (D afché) :

l conversion de x= 6 et y= 4

[SHIFT] [Pol(]6 [SHIFT] [,] 4 [)] [EXE] -> Pol (6,4) | 7.211102551

La calculatrice afche directement le résultat pour la première coordonnée,

r= 7.211102551

[ALPHA] [J] [EXE] -> J | 33.69006753 J représente la valeur de , soit 33.69 degrés.

Si on souhaite revoir la valeur de r : [ALPHA] [I] [EXE] -> I | 7.211102551

l conversion de r= 14 et = 36 degrés [SHIFT] [Rec(] 14 [SHIFT] [,] 36 [)] [EXE] -> Rec(14,36) | 11.32623792

La calculatrice afche directement le résultat pour la première coordonnée,

x= 11.32623792.

[ALPHA] [J] [EXE] -> J | 8.228993532 [ALPHA] [I] [EXE] -> I | 11.32623792

Les coordonnées sont stockées dans les mémoires temporaires I et J après conversion ; comme les autres mémoires temporaires elles peuvent être rappelées à tout moment et utilisées dans d’autres calculs.

GC700_01_GC700Z_01IM0108.indd 31 6/3/08 17:33:20

Français

32

Français

5. CALCULS EN BASE-N

Pour mémoire

Changements de base

Nous effectuons nos calculs de façon courante en base 10. Par exemple :

1675 = (1675)10 = 1x103 + 6x102 + 7x10 + 5

En mode binaire, un nombre est exprimé en base 2. 1 s’écrit 1, 2 s’écrit 10, 3 s’écrit 11, etc. Le nombre binaire 11101 est équivalent à : (11101)2= 1x24 + 1x23 + 1x22 + 0x2 +1 = (29)

10

En mode octal, un nombre est exprimé en base 8.

7 s’écrit 7, 8 s’écrit 10, 9 s’écrit 11, etc.

Le nombre octal 1675 est égal à : (1675)8= 1x83 + 6x82 + 7x81 + 5= (957)

10

En mode hexadécimal, un nombre est exprimé en base 16, les chiffres

au-delà du 9 étant remplacés par des lettres : 0123456789ABCDEF 9 s’écrit 9, 10 s’écrit A, 15 s’écrit F, 16 s’écrit 10, etc. Le nombre hexadécimal 5FA13 est égal à :

(5FA13)16= 5x164 + 15x163 + 10x162 + 1x161 + 3= (391699)

10

Pour récapituler :

déc

0 1 2 3 4 5 6 7 8

bin

0 1 10 11 100 101 110 111 1000

oct

0 1 2 3 4 5 6 7 10

hex

0 1 2 3 4 5 6 7 8

déc

9 10 11 12 13 14 15 16

bin

1001 1010 1011 1100 1101 1110 1111 10000

oct

11 12 13 14 15 16 17 20

hex

9 A B C D E F 10

Les opérateurs logiques

Outre les fonctions arithmétiques +, -, x, ÷, (-), on utilise en base N des opérateurs logiques qui sont des fonctions à une ou deux variables A et B,

notées :

l Not A (NON A ou inverse de A) l And (ET) l Or (OU) l Xor (OU exclusif) l Xnor (NON OU exclusif)

GC700_01_GC700Z_01IM0108.indd 32 6/3/08 17:33:20

Français

33

Les résultats des fonctions ci-dessus sont les suivantes en fonctions de A et B:

A B Not A A and B A or B A xor B A xnor B

0 1 1 0 0 0 1 0 0 0 1 0 1 1 0 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1

A 0 0 0 0 0 0 0 1 1 0 0 1

B 0 0 0 0 0 0 0 1 1 0 1 0 A and B 0 0 0 0 0 0 0 1 1 0 0 0 A xnor B 1 1 1 1 1 1 1 1 1 1 0 0

Pour A et B plus grands que 0 ou 1, le résultat se calcule bit par bit sur les valeurs exprimées en binaire. Par exemple si A=25=(19)16=(11001)2 et B=(1A)16=(11010)2 :

A and B = (11000)2 = (18)16 = (24)

10

A xnor B = (111111111100)2 = (FFFFFFFC)16 = (-4)

10

Notations

Lorsque la calculatrice est en Base N, le message BASE-N reste afché en haut de l’écran, et un indicateur de base s’afche à droite :

l d pour décimal l b pour binaire l o pour octal l h pour hexadécimal

Pour éviter les confusions avec les noms des mémoires temporaires, les

chiffres hexadécimaux sont notés ainsi sur les touches de votre calculatrice :

A |A

B |B

C |C D |D E |E F |F

GC700_01_GC700Z_01IM0108.indd 33 6/3/08 17:33:21

Français

34

Français

Remarques sur le mode Base N :

l les touches de fonctions correspondant au mode Base N sont indiquées

en bas à gauche des touches concernées. Elles se trouvent sur les 3e, 4e et 5e lignes de touches à partir du haut.

l le mode est conservé même si la calculatrice est éteinte et rallumée. l Si vous entrez une valeur incompatible avec la base choisie (ex : [SHIFT]

[Bin] 3, la calculatrice afchera Syn ERROR. Voir le chapitre « Messages d’erreurs » pour plus de détails sur les valeurs admissibles en mode Base N. l La plupart des fonctions générales ne peuvent pas être utilisées en Base

N. Les paragraphes suivants détaillent les opérateurs admissibles. l Vous pouvez utiliser les mémoires et les touches de mise en mémoire et de rappel associées : [Ans], [ALPHA] [A]-[Z], [ ], [ALPHA] [~], [SHIFT][Mcl] (voir chapitre « Utilisation des mémoires »).

[MODE] [-]

Passe en mode Base N, BASE-N reste afché en haut

de l’écran.

[MODE] [+]

Annulation du mode Base N, retour en mode normal.

[Dec]

Sélectionne la base 10 comme base active, d s’afche.

[Bin]

Sélectionne la base 2 comme base active, b s’afche.

[Oct]

Sélectionne la base 8 comme base active, o s’afche.

[Hex]

Sélectionne la base 16 comme base active, h s’afche.

[SHIFT] [d] ou [b]

ou [o] ou [h]

Spécie que la valeur saisie immédiatement après est en base 10 ou 2 ou 8 ou 16, lorsque la base active est

différente.

Commandes du mode Base N et conversions

A partir de maintenant tous les exemples donnés dans ce chapitre sont en Base N.

Il y a deux façons de convertir une valeur d’une base dans une autre :

Méthode 1 :

Une fois en Base N vous choisissez la base de la valeur à convertir. Vous saisissez la valeur, puis vous changez la base.

Ex :

Conversion de (11101)2 en base 10 : [Bin] [EXE] -> Bin | 000000000000

b

11101 [EXE] -> 11101 | 000000011101

b

[Dec] [EXE] -> Dec | 29

d

GC700_01_GC700Z_01IM0108.indd 34 6/3/08 17:33:21

Français

35

Méthode 2 :

Une fois en Base N vous choisissez la base dans laquelle vous voulez convertir une valeur. Ensuite vous spéciez la base d’origine et vous

saisissez cette valeur.

Ex :

Conversion de (11101)2 en base 10 : [MODE] [-] [Dec] [EXE] -> Dec | 0

d

[SHIFT] [b] 11101 [EXE] -> b11101 | 29

d

Autres exemples de conversion (les deux méthodes sont utilisées) :

Conversion de (5FA13)16 en base 8 puis 10 : [Hex] [EXE] -> Hex | 00000000

h

5 [|F] [/A] 13 [EXE] -> 5FA13 | 0005FA13

h

[Oct] [EXE] -> Oct | 00001375023

o

[Dec] [EXE] -> Dec | 391699

d

Conversion de (1675)8 en base 10 : [Dec] [EXE] -> Dec | 0

d

[SHIFT] [o] 1675 [EXE] -> o1675 | 957

d

Calculs en Base N

[+]

Addition.

[-]

Soustraction.

[x]

Multiplication.

[÷]

Division.

[Neg]

Change le signe de la valeur saisie immédiatement après, équivalent de la touche arithmétique [(-)].

[(], [)]

Parenthèses.

GC700_01_GC700Z_01IM0108.indd 35 6/3/08 17:33:22

Français

36

Français

Votre calculatrice vous permet de réaliser des opérations usuelles (addition,

soustraction, multiplication, division et parenthèses) en Base N. A noter qu’en Base N on ne manipule que des nombres entiers ; si une opération génère un

résultat décimal, seule la partie entière de la valeur sera conservée.

Vous pouvez, sur une même ligne de calcul, utiliser des nombres exprimés

en bases différentes. Le résultat sera donné dans la base active qui a été présélectionnée.

Ex :

Si, en mode hexadécimal on soustrait 5A7 à 5FA13, cela donne : [Hex] [EXE] -> Hex | 00000000

h

5 [|F] [/A] 13 [-] 5 [/A] 7 [EXE] -> 5FA13-5A7 | 0005F46C

h

On multiplie ce résultat par 12 : [x] 12 -> 0005F46Cx12 | 006B2F98

h

ou 12 [x] [Ans] -> 12xAns | 006B2F98

h

En mode binaire on effectue (11010 + 1110) ÷10 : [Bin] [EXE] -> Bin | 000000000000

b

[(] 11010+1110 [)] [÷] 10 [EXE]

-> (11010+1110) ÷10 | 000000010100

b

On ajoute (101)2 et le chiffre octal (12)8 et on veut un résultat en base 10 : [Dec] [EXE] -> Dec | 0

d

[SHIFT] [b] 101 + [SHIFT] [o] 12 [EXE]

-> b101+o12 | 15

d

On divise ce résultat par 12 [÷] 12 [EXE] -> 15÷12 | 1

d

Seule la partie entière du résultat de la division est conservé. En mode hexadécimal on calcul le négatif de 1C6 : [Hex] [EXE] -> Hex | 00000000

h

[Neg] 1 [|C] 6 [EXE] -> Neg 1C6 | FFFFFE3A

h

[+]1 [|C] 6 [EXE] -> FFFFFE3A+1C6 | 00000000

h

[+]1 [C] 6 [=] -> Ans+1C6 | 000001C6

h

GC700_01_GC700Z_01IM0108.indd 36 6/3/08 17:33:22

Français

37

Opérateurs logiques en Base N

[SHIFT] [and]

Fonction ET.

[SHIFT] [or]

Fonction OU.

[SHIFT] [xor]

Fonction OU exclusif.

[SHIFT] [xnor]

Fonction NON OU exclusif.

[Not]

NON (inverse) de la valeur saisie immédiatement après.

Votre calculatrice effectue ces calculs à partir des valeurs que vous avez

saisies, quelles qu’en soit la base initiale et les exprime directement dans la base que vous avez présélectionnée. Le type de saisie effectuée suit la même

méthode que pour les opérateurs arithmétiques vus au paragraphe précédent.

Ex :

(19)16 OR (1A)16 en base 16 [Hex] [EXE] -> Hex | 00000000

h

19 [or] 1 [/A] [EXE] -> 19or1A | 0000001B

h

(120)16 XOR (1101)2 en décimal [Dec] [EXE] -> Dec | 0

d

[SHIFT] [h] 120 [SHIFT] [xor] [SHIFT] [b] 1101 [EXE]

-> h120xorb1101 | 301

d

NON de (1234)8 en base 8 puis 10, mise en mémoire dans la mémoire temporaire G, et comparaison avec Neg (1234)

8

[Oct] [EXE] -> Oct | 00000000000 o [Not] 1234 [EXE] -> Not 1234 | 37777776543

o

[Dec] [EXE] -> Dec | -669

d

[ ] [ALPHA] [G] [EXE] -> -669 G | -669

d

[Oct] [EXE] -> Oct | 37777776543

o

[Neg] 1234 [EXE] -> Neg 1234 | 37777776544

o

[-] [ALPHA] [G] [EXE] -> 37777776544-G | 00000000001

o

[Dec] [EXE] -> Dec | 1

d

GC700_01_GC700Z_01IM0108.indd 37 6/3/08 17:33:22

Français

38

Français

Pour mémoire

On dispose de n données sur un échantillon de mesures, résultats, personnes, objets... Chaque donnée est constituée d’un nombre (une variable

x) ou deux (deux variables x et y). On cherche à calculer la moyenne de ces données et la répartition de ces données autour de la moyenne, l’écart-type.

Ces données se calculent à partir de sommes que l’on notera :

∑x = x1+x2+x3+....x

n-1+xn

∑x2= x

1

2

+x

2

+x

3

2

+....x

n-1

2

+x

n

2

∑xy = x1y1+x2y2+x3y3+....x

n-1yn-1+xnyn

Moyenne x=

écart type / déviation standard de l’échantillon pour x :

écart type / déviation standard de la population pour x :

variance V = s2 ou

2

=

∑(x1-x)2

√

i=1

n

6. STATISTIQUES

Commentaires préliminaires

σ

s =

∑(x1-x)2

√

i=1

n

n - 1

=

∑x2 - (∑x)2 / n

√

n - 1

=

∑x2 - (∑x)2 / n

√

n

σ

n

∑x

GC700_01_GC700Z_01IM0108.indd 38 6/3/08 17:33:23

Français

39

Votre calculatrice vous permet d’obtenir aisément ces résultats, en suivant les étapes suivantes :

l Choisissez votre mode statistique (une ou deux variables).

l Saisissez les données.

l Vériez que la valeur de n correspond bien au nombre de données

théoriquement saisies.

l Calculez la moyenne x et l’écart type (ou déviation standard) de

l’échantillon ou de la population, ainsi que les autres calculs intermédiaires si

nécessaire ([∑x], [2ndF] [∑x2]) à l’aide des touches correspondantes.

l S’il y a deux variables, procédez aux mêmes calculs pour y (moyenne, écart type), puis calculez la régression linéaire (a et b dans y=a+bx) et le coefcient

de corrélation linéaire.

l Si la corrélation linéaire est jugée valide, on peut alors calculer la valeur

estimée de y pour un x donné, ou la valeur estimée de x pour un y donné, de par la relation y=a+bx.

Lorsqu’on a deux variables on essaie de déduire des données une relation entre x et y. On étudie la solution la plus simple : une relation de type y=a+bx. cov(x,y) est la covariance :

La validité de cette hypothèse est vériée par le calcul suivant :

appelé coefcient de corrélation linéaire. Le résultat est toujours entre –1 et +1 et on considère bon un résultat supérieur ou égal à √3/2 en valeur

absolue.

∑(x1-x)(y1-y) =

i=1

n

cov(x,y) =

n

1

n

1

∑x y-x y

cov(x,y)

x y

σ σ

GC700_01_GC700Z_01IM0108.indd 39 6/3/08 17:33:23

Français

40

Français

Touches de fonctions statistiques

[MODE] [x]

Passage en mode statistique à 1 variable. SD1 est

indiqué sur l’afchage.

[MODE] [÷]

Passage en mode statistique à 2 variables. LR1 est

indiqué sur l’afchage.

[MODE] [+]

Retour au mode normal.

[SHIFT] [Mcl]

Remet à zéro toutes les données statistiques.

[DT]

Enregistre les données : donnée1 [DT] donnée2 [DT] etc.

Pour entrer la même donnée plusieurs fois, appuyer

sur [DT] plusieurs fois à la suite.

[SHIFT] [,]

Pour saisir y après x lorsqu’il y a deux variables : x1 [,] y1 [DT] x2 [,] y2 [DT] etc.

[SHIFT] [;]

Permet d’enregistrer plusieurs données identiques en une seule saisie :

donnée1 [;] 3 [DT] ou x1 [,] y1 [;] 3 [DT] enregistre 3 fois

la même valeur en mémoire.

[AC]

Permet de corriger une saisie avant d’avoir appuyé

sur [DT].

[CL]

Permet de corriger les erreurs de saisie après avoir

appuyé sur [DT]:

- soit en appuyant sur [CL] [EXE] immédiatement

après la saisie erronée.

- soit en saisissant la valeur erronée saisie plus tôt et

en appuyant sur [CL].

[ALPHA] [W]

Afche le nombre d’échantillons rentrés (n),

c’est-à-dire le nombre des données.

[SHIFT] [x], [y]

Afche la moyenne de x ou de y.

[ALPHA] [V] , [Q]

Afche la somme des données rentrées ∑x , ∑y.

[ALPHA] [U] , [P]

Calcule la somme des carrés des données rentrées

∑x2, ∑y2.

[ALPHA] [R]

Calcule la somme du produit des données rentrées

∑xy.

[SHIFT] [xσn], [yσn]

Afche l’écart-type (ou déviation standard) de la

population

GC700_01_GC700Z_01IM0108.indd 40 6/3/08 17:33:24

Français

41

[SHIFT] [xσ

n-1

], [yσ

n-1

]

Afche l’écart-type (ou déviation standard) de

l’échantillon.

[SHIFT] [A], [B]

Afche la valeur du coefcient a, b pour la régression linéaire y=a+bx.

[SHIFT] [r]

Afche la valeur du coefcient de corrélation

linéaire r.

[SHIFT] [ y ]

Donne la valeur de y estimée par régression linéaire pour la valeur x saisie.

[SHIFT] [ x ]

Donne la valeur de x estimée par régression linéaire pour la valeur y saisie

Statistiques à 1 variable – exemple pratique

Benjamin et ses amis ont obtenu les résultats suivants à la composition de Français :

Elève A B C D E F G H I J note 8 9.5 10 10 10.5 11 13 13.5 14.5 15

Moyenne et écart-type (de l’échantillon) pour les notes de Benjamin et ses

amis ?

[MODE] [x] -> SD1 s’afche. [SHIFT] [Mcl] [EXE] -> Scl mise à zéro.

8 [DT] -> 8. début de saisie des données. 9 [.] 5 [DT] -> 9.5 10 [DT] [DT] -> 10. ou 10 [SHIFT] [;] 2 [DT] pour saisir deux fois la même valeur.

Et ainsi de suite : 10 [.]5 [DT] 11 [DT] 13 [DT] 13[.]5 [DT] 14 [.]5 [DT] 15 [DT]

^

GC700_01_GC700Z_01IM0108.indd 41 6/3/08 17:33:24

Français

42

Français

On reprend l’expérience avec la composition de maths, à laquelle ils ont

obtenu les notes suivantes :

On afche n et on vérie que le nombre afché correspond aux nombres de

valeurs saisies :

[ALPHA][W] [EXE] -> W | 10. [SHIFT] [x] [EXE] -> x | 11.5 Leur moyenne est de 11,5.

[SHIFT] [xσ

n-1

] [EXE] -> xσn-1 | 2.34520788

soit l’écart type recherché.

Si on veut calculer la variance on appuie sur

[x2][EXE] -> 2.34520788

2

| 5.5 c’est la variance.

Si on veut changer la première valeur, 8 en 14 : 8 [CL]

14 [DT]

On voit que n reste égal à 10 mais que la moyenne a été modiée : [ALPHA][W] [EXE] -> W | 10. [SHIFT] [ x] [EXE] -> x | 12.1

Elève A B C D E F G H I J note 4 7.5 12 8 8 8 14.5 17 18 18

[SHIFT] [Mcl] [EXE] -> Scl mise à zéro.

On peut vérier en faisant : [ALPHA][W] [EXE] -> W | 0.

Début de saisie des données :

4 [DT] -> 4 | 4.

7 [. ] 6 [AC] 7 [.] 5 [DT] -> erreur de saisie avant [DT] et correction. 13 [DT] [CL] [EXE] 12 [DT] -> erreur de saisie après [DT] et correction. 8 [SHIFT] [;] 3 [DT] -> on saisit 8 trois fois

ou

8 [DT] [DT] [DT]

14 [.] 5 [DT]

Et ainsi de suite jusqu’à 18 [DT] [DT]

GC700_01_GC700Z_01IM0108.indd 42 6/3/08 17:33:24

Français

43

[ALPHA][W] [EXE] -> W | 10. [SHIFT] [x] [EXE] -> x | 11.5 Leur moyenne est de 11,5 également.

[SHIFT] [xσ

n-1

] [EXE] -> xσn-1 | 5.088112507

soit l’écart

type recherché.

On constate que la moyenne est la même mais que l’écart type est plus grand cette fois-ci : on peut en conclure qu’il y a plus d’écart entre les notes

des élèves, leur niveau est donc moins homogène en maths qu’en français.

A titre d’exercice, dans cet exemple (les notes de maths) on obtient les valeurs suivantes pour ∑x et ∑x2 : [ALPHA] [V] [EXE] -> 115. soit ∑x [ALPHA] [U] [EXE] -> 1555.5 soit ∑x

2

Statistiques à 2 variables – exemple pratique

On a le tableau suivant où x est la longueur en mm et y le poids en mg d’une

chenille de papillon à différents stades de son développement.

X 2 2 12 15 21 21 21 Y 5 5 25 25 40 40 40

On passe en mode statistiques à deux variables : [MODE] [÷] -> LR1 afché [SHIFT] [Mcl] [EXE] -> Scl mise à zéro

On commence la saisie :

2 [SHIFT] [,] 5 [DT] -> 2.

[DT] pour saisir la même valeur une deuxième fois : [DT] -> 2.

12 [SHIFT] [,] 24 [DT] -> 12.

16 [SHIFT] [,] 25 [AC] erreur de saisie avant [DT].

15 [SHIFT] [,] 24 [DT] [CL] [EXE] erreur de saisie après [DT].

15 [SHIFT] [,] 25 [DT] correction.

21 [SHIFT] [,] 40 [SHIFT] [;] 3 [DT] pour entrer trois fois la même valeur

-> 21.

GC700_01_GC700Z_01IM0108.indd 43 6/3/08 17:33:25

Français

44

Français

On vérie n : [ALPHA][W] [EXE] -> W | 7.

On afche les résultats de la régression linéaire : [SHIFT] [A] [EXE] -> A | 1.050261097 [SHIFT] [B][EXE] -> B | 1.826044386 [SHIFT] [r] [EXE] -> r | 0.9951763432

r est supérieur à √3/2 = 0.866 environ, la validité de la régression est vériée.

Grâce à la régression linéaire on estime y à partir de x=3 : 3 [SHIFT] [ y ] [EXE] -> 3y | 6.528394256

On estime x à partir de y=46 : 46 [SHIFT] [ x ] [EXE] -> 3x | 24.61590706

Avec les touches statistiques de votre calculatrice vous pouvez afcher facilement tous les résultats intermédiaires, comme par exemple :

∑xy : [ALPHA] [R] [EXE] -> 3203. [SHIFT] [yσn] [EXE] -> 14.50967306

Nom

Formule Remplacez x par Remplacez y par a’ =

Linéaire y=a + bx x y

Logarithmique y=a + b ln x ln x y

Exponentielle y=a’ e

bx

x ln y e

a

Puissance y=a’ x

b

ln x ln y e

a

^

Régression non linéaire

Vous trouverez ci-dessous les types de régressions linéaires que vous pouvez

rechercher avec votre calculatrice, et les valeurs correspondantes que vous

devez rentrer pour x et y :

GC700_01_GC700Z_01IM0108.indd 44 6/3/08 17:33:25

Français

45

On soupçonne que x et y sont liés par une relation du type y=a’ xb et on cherche à conrmer l’hypothèse en procédant de la façon suivante. On saisit les valeurs en ajoutant les logarithmes de n=1 à n=4, par exemple pour la première saisie (en n’oubliant pas de faire [SHIFT][Mcl][EXE] avant !):

[ln] 0[.]5 [SHIFT] [,] [ln] 1[.]4 [DT]

Une fois les valeurs saisies, on obtient les valeurs de A, B et r suivantes : A = 0,6902139123 B = 0,5153174423 r = 0,9984732884 La régression de type puissance est vériée puisque r=0,998. On obtient A’ en calculant l’exponentielle de A :

[SHIFT][ex][SHIFT][A][EXE] -> eA= 1.994142059

Par approximation on peut dire que y ≈ 2x

1/2

= 2√x.

Ex :

x

0,5 1 1,5 2

y 1,4 2 2,4 2,9

GC700_01_GC700Z_01IM0108.indd 45 6/3/08 17:33:25

Français

46

Français

Dénitions et notations

Une courbe est la représentation graphique d’une fonction f, y=f(x), x étant l’abscisse, sur l’axe horizontal, et y l’ordonnée, sur l’axe vertical.

Pour représenter une fonction graphiquement il est nécessaire de décider d’une échelle, c’est-à-dire entre quelles valeurs on souhaite voir cette fonction

et comment on veut graduer les axes. Par exemple pour la fonction y=x2 il n’est pas très intéressant de représenter la courbe pour y=-100… La graduation des axes sera représentée par des points sur les axes et permettent de mieux repérer les valeurs de x ou de y intéressantes : par exemple pour y=ln x, graduation de 1, on voit facilement que y=0 pour x=1.

L’échelle sera dénie par les valeurs suivantes : X min, X max, et la graduation sur l’axe des X, Xscl. Y min, Y max et la graduation sur l’axe des Y, Yscl.

7. FONCTIONS GRAPHIQUES

Votre calculatrice comporte un certain nombre de courbes préprogrammées,

pour les fonctions sin, cos, x-1, ln, √… : pour celles-ci les échelles sont prédénies et non modiables.

GC700_01_GC700Z_01IM0108.indd 46 6/3/08 17:33:26

Français

47

Tracer une courbe

[MODE] [+]

Passe au mode normal & mode graphique.

[Graph]

Initie le traçage d’une courbe :

- [Graph] fonction ou [Graph] fonction [Alpha] [X] pour les

fonctions préenregistrées.

- [Graph] suivi d’une expression de variable x.

[Range]

Permet de saisir les valeurs d’échelle (Xmin, Xmax, Xscl, Ymin, Ymax, Yscl).

[G T]

Passe de l’afchage graphique à l’afchage normal et

vice versa.

[SHIFT] [Cls]

Efface toutes les courbes.

[SHIFT] [Mcl]

Remet les valeurs d’échelle à leur valeur par défaut :

Xmin=-3,8 Xmax= 3,8 Xscl= 1

Ymin= -2,2

Ymax= 2,2

Yscl= 1

[ ][ ][ ][ ]

Change la position des axes pour afcher la partie de la courbe située dans la direction de la èche.

Courbes préprogrammées

Pour tracer une courbe préprogrammée, il suft de faire : [Graph] fonction [EXE]. Pour tracer une deuxième courbe préprogrammée, il y a deux possibilités :

- soit on souhaite tracer une courbe seule sur un nouvel écran, alors on

appuie de nouveau sur [Graph] fonction [EXE].

- soit on souhaite tracer la deuxième courbe sur le même écran que la première, alors on appuie sur [Graph] fonction [ALPHA][X][EXE]. L’échelle

utilisée sera celle de la première courbe.

GC700_01_GC700Z_01IM0108.indd 47 6/3/08 17:33:26

Français

48

Français

Ex :

Tracez la courbe y=sin x Si vous n’êtes pas en mode normal appuyez sur [MODE][+]. [Graph] [sin] [EXE] Tracez la courbe y=tan x en remarquant bien le changement d’échelle : [Graph] [tan] [EXE] Maintenant, tracez les deux sur le même graphique : [Graph] [sin] [EXE] [Graph] [tan] [ALPHA][X] [EXE] Appuyez sur les touches [ ], [ ], [ ] ou [ ] pour visualiser les différentes parties de la dernière courbe tracée et le déplacement des axes.

Courbes utilisateur

Vous pouvez tracer votre propre courbe en saisissant simplement l’expression d’inconnue x que vous souhaitez représenter et l’échelle de représentation.

Ex :

Courbe y=x2+2x-3 Echelle : x entre –5 et +5, graduation de 2 en 2 y entre –10 et +10, graduation de 4 en 4 Et intersection avec la courbe y=1-x.

[SHIFT] [Cls] -> Cls [EXE] -> done (« done » = terminé). Effacement des courbes précédentes [Range] -> Xmin ? [SHIFT] [(-)] 5 [EXE] -> Xmax ? 5 [EXE] -> Xscl ? 2 [EXE] -> Ymin ? [SHIFT] [(-)] 10 [EXE] -> Ymax ? 10 [EXE] -> Yscl ? 4 [EXE] -> done [Graph] -> Graph Y= [ALPHA][X][X2][+] 2 [ALPHA][X][-]3

-> Graph Y=X

2

+2X-3 [EXE] -> La courbe se trace et on obtient l’écran suivant :

GC700_01_GC700Z_01IM0108.indd 48 6/3/08 17:33:26

Français

49

Appuyez sur les touches [ ], [ ], [ ] ou [ ] pour visualiser les différentes parties de la courbe et le déplacement des axes.

Notes :

La multiplication est implicite, pas besoin d’appuyer sur la touche multiplication [x] pour saisir 2X.

Pour faire réapparaître l’expression après avoir tracé la courbe, pour la vérier par exemple, appuyez sur : [G T] -> done [ ] -> Graph Y=X

2

+2X-3

Ensuite on trace y =1-x sur le même graphique : [Graph] -> Graph Y= 1[-] [ALPHA][X] -> Graph Y= 1-X [EXE]

On voit sur le graphique qu’il y deux solutions à l’équation, x2+2x-3=1-x, dont une évidente avec y=0 et x=1.

Pour tracer directement les deux courbes vous pouvez utiliser l’instruction [ALPHA][ ] : Graph Y=X2+2X-3 Graph Y= 1-X

GC700_01_GC700Z_01IM0108.indd 49 6/3/08 17:33:27

Français

50

Français

Fonction Zoom

[SHIFT] [Factor]

Permet de régler les paramètres de l’agrandissement.

[SHIFT] [Zoomxf] Agrandit la courbe selon les paramètres spéciés.

[SHIFT] [Zoomxf/f]

Réduit la taille de la courbe selon les paramètres

spéciés.

[SHIFT] [ZoomOrg]

Afche la courbe dans sa taille initiale.

Cette fonction permet de visualiser une courbe sous divers

agrandissements ou réductions, ce qui vous permet de mieux étudier ses caractéristiques : forme générale, points d’intersection… Il est intéressant de noter comment dans l’exemple suivant que l’utilisation de [Range] avec les fonctions Zoom permet de vérier les points

d’intersection.

Ex :

Nous reprenons la courbe y=x2+ 2x-3 sans modier l’échelle. Echelle : x entre –5 et +5, graduation de 2 en 2. y entre –10 et +10, graduation de 4 en 4.

Une fois la courbe tracée on spécie des paramètres de l’agrandissement :

[SHIFT] [Factor] -> Xfact ? 2 [EXE] -> Yfact ? 4 [EXE] -> done.

[EXE] ou [G T] -> la courbe s’afche sans modications.

[SHIFT] [Zoomxf/f]

La courbe s’afche en plus petit.

GC700_01_GC700Z_01IM0108.indd 50 6/3/08 17:33:27

Français

51

[SHIFT] [ZoomOrg] ou [SHIFT][Zoomxf] : retour à la taille d’origine.

[SHIFT][Zoomxf] -> la courbe s’afche agrandie.

Si on appuie sur [Range] on voit que les valeurs Xmin, Xmax, Ymin et Ymax ont changé. On modie Xscl et Yscl pour mieux voir l’échelle et vérier visuellement x=1 et y=0. [Range] -> Xmin ? | -2.5 [EXE] -> Xmax ? | 2.5 [EXE] -> Xscl ? | 2. 0 [.] 5 [EXE] -> Ymin ? | -2.5 [EXE] -> Ymax ? | 2.5 [EXE] -> Yscl ? | 4. 1 [EXE] -> done

On a donc gradué l’axe des x de 0,5 en 0,5 et l’axe des y de 1 en 1.

On peut donc voir vérier le point d’intersection entre la courbe et l’axe des x.

GC700_01_GC700Z_01IM0108.indd 51 6/3/08 17:33:27

Français

52

Français

A noter qu’une fois l’échelle modiée manuellement avec [Range], celle-ci est dénitivement modiée et [ZoomOrg] afchera la courbe

selon ces paramètres.

[Trace]

Place le curseur sur la courbe et afche la valeur de x

à la position du curseur.

[ ], [ ]

Déplace le curseur sur la courbe.

[SHIFT] [X Y]

Afche la valeur de y au lieu de celle de x à

l’emplacement du curseur, et vice versa.

Fonction Trace

Cette fonction vous permet de déplacer le curseur sur la courbe avec

les èches et de visualiser la valeur de x ou y à l’emplacement du

curseur.

Quelques points à retenir concernant cette fonction :

l le curseur se déplace de façon irrégulière, les valeurs de x et y sont

des valeurs approchées.

l La fonction Trace ne peut être utilisée que lorsque la courbe vient

d’être tracée. Elle peut cependant tout de même être utilisée après Range, G T et Factor.

l La fonction Trace ne peut pas être incluse dans un programme,

cependant on peut l’utiliser pendant une phase d’arrêt temporaire d’un programme (Disp afché). Voir pour plus de détails le chapitre “Programmation” .

Ex :

En reprenant l’exemple précédent : Courbe y=x2+2x-3 Echelle : x entre –5 et +5, graduation de 2 en 2 y entre –10 et +10, graduation de 4 en 4

Une fois la courbe afchée on appuie sur [Trace] :

[Trace] -> un curseur clignotant apparaît sur la courbe tout à fait sur la gauche de l’écran et la valeur de x s’inscrit. X= -4.73684.

[ ] -> on appuie sur la èche et on observe que les

valeurs de x croissent et que le curseur se déplace sur la courbe.

On positionne le curseur sur x=0 et on appuie sur [X Y]: [SHIFT][X Y] -> la valeur correspondante de y s’afche, Y=-3

GC700_01_GC700Z_01IM0108.indd 52 6/3/08 17:33:28

Français

53

Fonctions Plot et Line

[SHIFT][Plot]

Place le curseur à l’endroit spécié.

x [SHIFT] [,] y Sépare les coordonnées x et y pour la saisie.

[ ][ ][ ][ ]

Permet de déplacer le curseur à l’endroit souhaité.

[SHIFT] [Value] à côté de INS

Afche la valeur de x à la position du curseur.

[SHIFT] [X Y]

Afche la valeur de y au lieu de celle de x à

l’emplacement du curseur, et vice versa.

[SHIFT] [Line]

Trace un segment entre le curseur et le point marqué par Plot.

Plot permet de placer un point sur l’écran, on peut ensuite se

déplacer à l’aide des èches à partir de cette position. La fonction Line vous permet ensuite de tracer un segment entre ces deux points. L’opération peut être répétée plusieurs fois an de déterminer

notamment des positions de points sur la courbe avec une meilleure

précision par projection sur les axes.

Si les valeurs proposées pour la fonction Plot sont situées en dehors

des valeurs Xmin/Xmax et/ou Ymin/Ymax, l’instruction sera ignorée.

Ex :

Avec la même échelle que précédemment.

[SHIFT][Plot] 2 [SHIFT][,] 4 [EXE] -> X= 2.105263

Le curseur apparaît et une valeur approchée de x est afchée.

GC700_01_GC700Z_01IM0108.indd 53 6/3/08 17:33:28

Français

54

Français

On appuie sur [EXE] pour « xer » le point, puis on se déplace en appuyant 7 fois sur [ ] et 5 fois sur [ ] : [EXE] 7 fois [ ], 5 fois [ ] -> x= 3.947368 [SHIFT][X Y] -> y= 8,181818 On voit que le point d’origine xé par Plot est toujours afché par un point xe, et que le curseur clignote.

Si on appuie sur [SHIFT][Value] on obtient des valeurs plus précises

de x et y : [SHIFT][Value] -> Y=

8.181818182 [SHIFT][X Y] -> X=

3.947368421 [SHIFT][Line] [EXE] -> done.

-> un segment est tracé entre les deux points.

GC700_01_GC700Z_01IM0108.indd 54 6/3/08 17:33:28

Français

55

Premiers pas en programmation

Ecrire un programme

[MODE] [2]

Passage en mode d’écriture de programme.

Le symbole WRT s’afche.

[ALPHA] [?] Demande la saisie d’une valeur pendant l’exécution

d’un programme.

[:]

Sépare deux instructions dans un programme.

[ALPHA] [ ]

Donne le résultat intermédiaire ou nal. S’il s’agit d’un résultat intermédiaire, Disp est afché.

le peut être omis à la n d’un programme, sauf si le programme se déroule en Base N

(voir « programmation avancée »).

La programmation vous permet d’effectuer toutes sortes de calculs répétitifs.

Appuyez sur [MODE] 2.

Sur la ligne du bas vous voyez P suivi de numéros, cela indique que vous pouvez mémoriser jusqu’à 10 programmes différents, appelés P0, P1, … P8, et P9.

Si un programme a déjà été mis en mémoire, le chiffre est remplacé par un

tiret, ex : P012_45_789, si P3 et P6 existent déjà.

Sur la droite vous avez un nombre à trois chiffres : celui-ci vous indique le nombre de pas restants disponibles pour votre programmation. Un pas

correspond à un caractère ou une fonction (A, 1, +, cos, xy…), à part quelques

fonctions qui utilisent 2 pas (Prog et Lbl que nous verrons plus tard). Il est facile de suivre l’évolution du nombre de pas :

- Lorsque vous écrivez un programme le nombre de pas utilisés par ce

programme s’afche.

- En suivant le déplacement du curseur avec les èches [ ], [ ].

Le chiffre 0 clignote car le curseur se trouve à cet endroit. Appuyez sur [EXE]

pour commencer la saisie du programme P0.

8. PROGRAMMATION

GC700_01_GC700Z_01IM0108.indd 55 6/3/08 17:33:29

Français

56

Français

Ex :

Vous souhaitez calculer le périmètre 2πr et la surface d’un cercle πr2 pour différentes valeurs du rayon.

Ce programme va comporter les étapes suivantes : [ALPHA] [?] Demande d’une valeur de rayon. [ ][ALPHA] [R] Stockage dans la mémoire temporaire R. [:] Passage à l’instruction suivante. 2 [SHIFT] [ π ] [ALPHA] [R] Calcul du périmètre. [ALPHA] [ ] Obtention du résultat intermédiaire. [SHIFT] [ π ] [ALPHA] [R] [X2] Calcul de la surface.

[ALPHA] [ ] Résultat nal et n de l’exécution (facultatif).

On l’omettra dans les autres exemples.

La saisie s’inscrit ainsi sur votre écran : ? R:2 π R πR2

Et l’afchage indique un total de 12 pas.

Exécuter un programme

[MODE] [1]

Passage en mode exécution de programme.

[MODE] [1] et [MODE] [2] permettent d’arrêter un

programme en cours d’exécution.

[Prog] 0-9

Démarre l’exécution du programme spécié.

En reprenant l’exemple ci-dessus : [Prog] 0 [EXE] -> ? attente de saisie. 5 [EXE] -> 31.41592654 c’est le périmètre ;

Disp afché. [EXE] -> 78.53981634 c’est la surface ; n de l’exécution. Si vous appuyez de nouveau sur [EXE] l’exécution du programme

recommence :

[EXE] -> ? attente de saisie. 0 [.] 33 [EXE] -> 2.073451151 c’est le périmètre ;

Disp afché. [EXE] -> 0.34211944 c’est la surface ; n de l’exécution.

GC700_01_GC700Z_01IM0108.indd 56 6/3/08 17:33:29

Français

57

Modier un programme

[MODE] [2]

Passage en mode d’écriture de programme. Le

symbole WRT s’afche.

[ ], [ ]

Pour déplacer le curseur.

[DEL]

Efface le caractère à l’endroit où se trouve le curseur.

[SHIFT] [INS]

Insère un caractère immédiatement à gauche du curseur d’insertion.

Lorsque vous appuyez sur [MODE] [2] vous revenez à la liste des

programmes. Sélectionnez le programme concerné à l’aide des

èches et appuyez sur [EXE] pour faire apparaître son contenu.

Ex :

Reprenons l’exemple précédent et modions le programme pour

calculer la surface 4 πr2 et le volume 4πr3/3 d’une sphère de rayon r.

[MODE] [2] -> P _ 123456789

588

( _ = position du curseur)

[EXE] -> ? :2 π R πR2

000

[ ][ ][ ][ ] -> ? :2 π R πR2

004

4 -> ? :4 π R πR2

005

[ ][ ] -> ? :4 π R πR2

007

[SHIFT] [INS] [X2] [ ] -> ? :4 π R2 πR2

009

[SHIFT] [INS] 4 [÷]3[x] [ ][ ] -> ? :4 π R2 4÷3xπR2

015

[Xy] 3 -> ? :4 π R2 4÷3xπRxy3

017

[MODE] [1] [Prog] 0 [EXE] -> ? attente de saisie. 5 [EXE] -> 314.1592654 c’est la surface; Disp afché.

[EXE] -> 523.5987756 c’est le volume ; n de

l’exécution.

GC700_01_GC700Z_01IM0108.indd 57 6/3/08 17:33:30

Français

58

Français

Messages d’erreur

Il est possible que lors de l’exécution d’un programme, un message du type P0 Syn ERROR apparaisse sur votre écran à la place du résultat attendu ! Ce message vous informe à la fois sur le type d’erreur (syntaxe) rencontré et

sur son emplacement, P0. Il ne vous reste alors plus qu’à suivre la procédure

de modication d’un programme pour le relire, identier et corriger l’erreur en question… Vous pouvez vous référez au chapitre « Messages d’erreur » pour vous y aider.

Message d’erreur ou pas, une fois que vous avez écrit un programme, il est

recommandé de vérier qu’il fonctionne comme il devrait. Pour cela testez-le avec des valeurs simples et vériez que vous obtenez les mêmes résultats en

faisant le calcul à la main.

Effacer des programmes

[MODE] [3]

Passage en mode effacement de programme. Le

symbole PCL s’afche.

[AC]

Efface le programme sur le numéro duquel se trouve le curseur.

[SHIFT] [Mcl] Efface tous les programmes.

Note : lorsqu’on appuie sur [SHIFT] [Mcl] en mode PCL seuls les programmes sont effacés, pas le contenu des mémoires temporaires.

Ex :

Si deux programmes, P0, P2 et P6 sont en mémoire, on veut effacer P2 puis tous les programmes : [MODE] [3] -> P _1_345 _789 572 PCL afché. [ ][ ] -> P _1_345 _789 572 ( _ = curseur). [AC] -> P _12345 _789 580 P2 effacé. [SHIFT] [Mcl] -> P 0123456789 600 P0, P6 effacés.

GC700_01_GC700Z_01IM0108.indd 58 6/3/08 17:33:30

Français

59

Programmation avancée

Insertion de messages

[ALPHA] [“] texte [ALPHA] [“]

Pour afcher un texte entre 2 guillemets pendant l’exécution d’un programme.

[SHIFT] [A-LOCK] ([SHIFT][ALPHA])

Verrouillage de la fonction ALPHA, pour taper plusieurs lettres à la suite.

[ALPHA][SPACE]

Permet de saisir un espace dans un message. Vous pouvez en fait utiliser dans vos messages toutes les touches alphanumériques (signalées en orange sur

votre calculatrice notamment k, m, p, f, ~, m, ], […).

Dans un programme il est parfois utile de pouvoir afcher des messages, en particulier lorsqu’il y a plusieurs “?” pour saisir des données, ou pour clarier lorsqu’il y a plusieurs résultats intermédiaires.

Le 2eme guillemet doit être suivi par [ALPHA] [ ] ou [ALPHA] [?] : ainsi le

texte reste afché tant qu’on ne rentre pas une valeur ou qu’on appuie pas sur [EXE].

Ex :

En reprenant le premier exemple (périmètre et surface d’un cercle de rayon r) “R =”, “P =” pour le périmètre et “S =” pour la surface :

? R:2 π R πR2

010

On transforme le programme en : “R=” ? R : “P=” 2 π R “S=” πR2

025

La saisie à effectuer est la suivante : Note : la touche [SHIFT] [=] se trouve sur le [8].

[ALPHA] [“] [ALPHA] [R] [SHIFT] [=] [ALPHA] [“] [ALPHA] [?] [ ][ALPHA] [R] [:] -> “R=” ? :

[ALPHA] [“] [ALPHA] [P] [SHIFT] [=] [ALPHA] [“] [ALPHA] [ ] -> “P=”

2 [SHIFT] [π] [ALPHA] [R] [ALPHA] [ ] -> 2 π R

[SHIFT] [ALPHA] [“] [S] [SHIFT] [=] utilisation de [A-LOCK]

GC700_01_GC700Z_01IM0108.indd 59 6/3/08 17:33:30

Français

60

Français

[SHIFT] [ALPHA] [“] [ ] -> “S=”

[SHIFT] [π] [ALPHA] [R] [X2] -> πR

2

Lorsqu’on exécute le programme, cela donne : [MODE] [1] [PROG] 0 [EXE] -> R=? attente de saisie. 5 [EXE] -> P=

Disp afché.

[EXE] -> 31.41592654

Disp afché.

[EXE] -> S=

Disp afché.

[EXE] -> 78.53981634 c’est la surface; n de

l’exécution. Si on veut rajouter [ALPHA] [SPACE] après R cela s’écrit : [ALPHA] [“] [ALPHA] [R] [ALPHA] [SPACE] [SHIFT] [=] [ALPHA] [“] Et à l’exécution un espace est inséré entre le R et le signe = :

-> “R =” ? R :

Saut inconditionnel

[SHIFT] [Lbl] 0-9

Assigne une adresse à un emplacement dans un programme.

La touche Lbl se trouve au niveau de la èche [ ]

[SHIFT] [Goto] 0-9

Ordonne au programme de continuer son exécution

à l’endroit indiqué par [Lbl].

[MODE] 1, ou [AC] Interrompt l’exécution du programme.

Lorsque le programme rencontre l’instruction Goto, il se dirige vers l’adresse

indiquée par Lbl. Il y a alors deux cas de gure possibles :

- si Lbl est placé après le Goto correspondant, l’exécution « saute » une partie

du programme.

- si Lbl est placé avant le Goto correspondant, l’exécution se répète indéniment vu que cet ordre n’est pas soumis à condition : on parle alors de boucle sans n. Vous aurez alors besoin d’interrompre vous-même l’exécution

du programme.

GC700_01_GC700Z_01IM0108.indd 60 6/3/08 17:33:31

Français

61

Ex :

Reprenons notre programme sur le calcul du périmètre et de la surface d’un cercle de rayon r. “R=” ? R : “P=” 2 π R “S=” πR2

025

Nous voulons simplement obtenir la surface, sans effacer la partie sur le

périmètre, et répéter l’exécution indéniment. Nous modions le programme

ainsi (rappel : on effectue l’insertion avec [SHIFT][Ins]):

Lbl 0 : rajout de [SHIFT] [Lbl] 0 [ :] “R=” ? R: Goto 1 : rajout de [SHIFT] [Goto] 1 [:] “P=” 2 π R Lbl 1 : rajout de [SHIFT] [Lbl] 1 [ :] “S=” πR

2

: Goto 0 rajout de [ALPHA] [ ][Goto] 0

Lbl 0 :”R=” ? R :Goto 1 :”P=” 2 π R Lbl 1 :”S=” πR2 Goto 0

037

A l’exécution cela donne : [MODE] 1 [Prog] 0 [EXE] -> R = ? 5 [EXE] -> S=

Disp

[EXE] -> 78.53981634

Disp

[EXE] -> R = ? 2 [EXE] -> S=

Disp

[EXE] -> 12.56637061

Disp

On voit que lorsqu’on rentre la valeur de R, le programme passe directement au calcul de la surface car il a rencontré l’instruction Goto 1, Lbl 1 étant positionné devant « S= ». Ensuite une fois qu’on a obtenu le résultat pour S, le programme retourne au début parce qu’il a rencontré l’instruction Goto 0 et que Lbl 0 se trouve tout au début du programme ; le résultat S pour la calculatrice est alors un résultat

intermédiaire et pas le résultat nal, c’est pour cela que Disp reste afché.

Si on écrit : “R=” ? R : Lbl 0 :Goto 1 :”P=” 2 π R Lbl 1 :”S=” πR2 Goto 0

037

On ne peut rentrer la valeur de R qu’une seule fois et la calculatrice calcule en

boucle S= 78,53981634 … Heureusement les sauts conditionnels que nous

allons voir maintenant permettent d’aboutir à des résultats plus passionnants

qu’une boucle sans n.

GC700_01_GC700Z_01IM0108.indd 61 6/3/08 17:33:31

Français

62

Français

Saut conditionnel

[SHIFT] [ ]

Sépare l’énoncé d’une condition et celui de l’action à

effectuer si cette condition est vériée.

Condition Action si condition vraie.

Pour l’énoncé de la condition on utilisera les opérateurs logiques accessibles

avec [SHIFT] : =, ≠, ≤, ≥, >, >.

Ex :

On saisit une valeur A, si elle n’est pas négative on en calcule la racine carrée. Le saut conditionnel s’écrit ainsi :

A ≥ 0 √A

On saisit le programme : ? A: A≥0 √A “FIN” 016

[ALPHA] [?] [ ][ALPHA] [A] [:] -> ? A:

[ALPHA][A][SHIFT][≥] 0 [SHIFT][ ] [√][ALPHA][A][ALPHA][ ]

-> A≥0

√A

[SHIFT][ALPHA] [“] [F] [I] [N] [“] -> “FIN”

Lorsqu’on exécute le programme on obtient :

-> ? 4 [EXE] -> 2. [EXE] -> FIN [EXE] -> ? [SHIFT][(-)]4 [EXE] -> FIN

Remarque : pourquoi utilise-t-on souvent des Goto après un saut

conditionnel ?

l Souvent lorsqu’une condition est vériée, on a plusieurs actions à effectuer, alors que la syntaxe du saut conditionnel n’en permet qu’une. Le Goto permet d’aller à un endroit du programme et d’y écrire toutes les actions à effectuer.

l Parfois on veut effectuer une action si la condition est vraie et une AUTRE

action si la condition n’est pas vériée. Le Goto permet de sauter la partie qui

concerne cette autre action.

GC700_01_GC700Z_01IM0108.indd 62 6/3/08 17:33:31

Français

63

Ex :

A=B action si A=B : action suivante.

A=B Goto x : action suivante effectuée seulement si A≠B.

On a une équation y=ax2+bx+c qu’on veut résoudre pour y=0, en utilisant les formules =b2-4ac et x=(-b±√ )/2a si ≥0. On utilise Goto pour que les actions soient différentes selon que soit supérieur ou non à 0.

“A=”? A:”B=”? B:”C=”? C:B2-4AC D:D≥0 Goto 1:”D<0” Goto 2: Lbl 1:(√D-B)÷2÷A (-√D-B)÷2÷A Lbl 2:”FIN” 083

Pour saisir le programme :

[ALPHA] [“] [ALPHA] [A] [SHIFT] [=] [ALPHA] [“] [ALPHA] [?] [ ][ALPHA] [A] [:] -> “A=” ? A:

[ALPHA] [“] [ALPHA] [B] [SHIFT] [=] [ALPHA] [“] [ALPHA] [?] [ ][ALPHA] [B] [:] -> “B=” ? B:

[ALPHA] [“] [ALPHA] [C] [SHIFT] [=] [ALPHA] [“] [ALPHA] [?] [ ][ALPHA] [C] [:] -> “C=” ? C:

[ALPHA][B][X2][-]4 [ALPHA][A][ALPHA][C] [ ][ALPHA][D] [:]

-> B

2

-4AC D:

[ALPHA][D][SHIFT][≥]0 [SHIFT][ [SHIFT][Goto]1 [:] -> D≥ Goto 1:

[ALPHA][“][ALPHA][D][SHIFT][<] 0 [ALPHA][“][ALPHA][ ][SHIFT][Gotto] 2 [:]

-> “D”< 0” Goto 2:

[SHIFT] [Lbl] 1 [:] -> Lbl 1:

[(] [√][ALPHA][D] [-][ALPHA][B][)][÷]2[÷][ALPHA][A][ ]

-> (√D-B)÷2÷A [(] [SHIFT] [(-)][√][ALPHA][D] [-][ALPHA][B][)][÷]2[÷][ALPHA][A][ ]

-> (-√D-B)÷2÷A

[SHIFT] [Lbl] 2 [:] -> Lbl 2: [SHIFT][ALPHA] [“] [F] [I] [N] [“] -> “FIN”

GC700_01_GC700Z_01IM0108.indd 63 6/3/08 17:33:32

Français

64

Français

Compteurs

[SHIFT] [Dsz]

S’utilise suivi d’un nom de mémoire temporaire et d’une instruction : Dsz A : Instruction.

Diminue la valeur de A d’une unité et exécute l’instruction si A≠0.

[SHIFT] [Isz]

S’utilise suivi d’un nom de mémoire temporaire et d’une instruction : Isz A : Instruction.

Augmente la valeur de A d’une unité et exécute l’instruction si A≠0.

Associé à Goto et Lbl, le compteur permet de créer une boucle qui s’arrête

au bout d’un nombre de fois prévu à l’avance. Par exemple, dans le jeu du nombre mystère qui gure en n de ce chapitre, le compteur permet de donner dix chances au joueur de trouver la solution avant d’afcher « perdu ! » .

Ex :

On part de A=10 et on met le programme en boucle jusqu’à A=0. On afche

A à chaque début de boucle. 10 A:Lbl 1:A Dsz A:Goto 1 ”FIN”

Même chose avec A=-10 et avec [Isz].

-10 A:Lbl 1:A Isz A:Goto 1 ”FIN”

Si on veut que A augmente de 1 à 10, c’est possible en utilisant un saut conditionnel juste après Isz : 1 A:Lbl 1:A Isz A:A<10 Goto 1 A-1 A:”FIN”

La valeur de A peut être xée par le programme lui-même. Ici on utilise

la fonction Random (Ran#) pour déterminer une valeur entre 1 et 15. Int (Ran#x15+1) A:Lbl 1:A Dsz A:Goto 1 ”FIN”

Sous-programmes

[Prog] 0-9

Inséré dans un programme, déclenche l’exécution du sous-programme spécié.

GC700_01_GC700Z_01IM0108.indd 64 6/3/08 17:33:32

Français

65

Vous pouvez utiliser [Prog] en tant qu’instruction dans un programme an de déclencher l’exécution d’un programme écrit à un autre emplacement. On appelle sous-programme un programme qui s’exécute au sein d’un

autre. Faire appel à un sous-programme est utile notamment dans les cas suivants :

l pour utiliser un programme déjà écrit dans un programme nouveau. l pour des raisons de clarté, lorsque le sous-programme représente un

calcul long ou compliqué, qu’il vaut mieux séparer du reste.

l Lorsque la même procédure/calcul est utilisé plusieurs fois au sein d’un programme.

Attention : si vous avez des instructions Goto dans un programme ou dans

un sous-programme, vériez bien qu’elles s’adressent à des Lbl situés dans

le même programme ou sous-programme.

Ex :

On a un programme Prog 0 qui calcule une valeur X à partir de divers paramètres. Dans le programme 1 on a les instructions suivantes : Prog 0 : X+1 A Lorsque le programme rencontre l’instruction Prog 0, il exécute le programme Prog 0 dans son intégralité, puis il revient à Prog 1 chercher l’instruction suivante : il met alors la valeur de X+1 dans la mémoire temporaire A.

Exemple récapitulatif : le jeu du nombre mystère

Le principe du jeu est le suivant : la calculatrice génère un nombre entre 1 et

999 et vous avez 12 tentatives pour le découvrir.

Nous allons programmer ce jeu dans Prog 0 en utilisant un sous-programme, Prog 1, pour tous les préparatifs du jeu. On utilisera les variables suivantes :

l A pour le compteur des 12 tentatives. l N le nombre à découvrir. l X la valeur proposée par l’utilisateur.

Pour chaque valeur de A non nulle on demande une valeur de X.

l Si X=N, c’est gagné et on propose de rejouer. l Si X>N, on afche « Trop grand » et on demande une nouvelle valeur de X.

Sinon c’est que X est trop petit, et on redemande aussi une nouvelle valeur de X.

Si A=0, vous avez perdu et on vous propose de rejouer.

GC700_01_GC700Z_01IM0108.indd 65 6/3/08 17:33:32

Français

66

Français

Prog 1 assigne la valeur 12 à A et génère un nombre entier compris entre

0 et 999 à l’aide de Ran# (nombre aléatoire entre 0 et 0,999) et de Int

(partie entière). On écrit Prog 1 :

12 A:Int (Ran# x 999+1) N

Et Prog 0 :

Prog 1: exécution du sous-programme Prog 1.

Lbl 0: début de la boucle principale.

“X=”? X saisie de X. Dsz A Goto 1: compteur, si A≠0 on va à Lbl 1. “PERDU, N=” N Goto 4: A=0, on afche perdu et on va en n de

programme (Lbl 4).

Lbl 1 : A≠0, on va tester X. X=N Goto 2: Si X=N on va à Lbl 2. X> N Goto 3: Si X>N on va à Lbl 3. “TROP PETIT”:Goto 0: Si on arrive ici c’est que X<N, on repart au

début de la boucle pour demander une autre

valeur de X. Lbl 2:”GAGNE !” Goto 4: N trouvé, on sort de la boucle et on va en n

de programme. Lbl 3:”TROP GRAND” Goto 0: N n’est pas trouvé, on repart en début de boucle . Lbl 4:”JOUE ENCORE”

121

Fin du jeu.

Note : le ! s’obtient en appuyant sur [SHIFT][n!]

Programmation et graphiques

Vous pouvez utiliser toutes les fonctions graphiques, à part [Trace], sans

modications dans un programme. A noter que pour la fonction [Range] il suft

de rentrer les données dans l’ordre séparées par des virgules.

Ex :

Pour trouver graphiquement le nombre de solutions des équations : y=x2 +2x-3 y=1-x Avec les valeurs d’échelle suivantes : Xmin = -5 Xmax = 5 Xscl = 2 Ymin = -10 Ymax = 10 Yscl = 4

GC700_01_GC700Z_01IM0108.indd 66 6/3/08 17:33:32

Français

67

Le programme est le suivant :

Range –5,5,2,-10,10,4:Graph Y=X2+2X-3 Graph Y=1-X

030

On voit sur le graphique qu’il y deux solutions à l’équation, x2+2x-3=1-x, dont une évidente avec y=0 et x=1.

Note : le [ ] permet d’arrêter l’exécution une fois tracée la première courbe,

si on ne veut pas de pause on peut le remplacer par [:].

Programmation en Base-N

Il est possible de programmer des calculs à effectuer en Base N, avec les

adaptations suivantes :

≠ Pour spécier le mode Base N pour un programme, par exemple P3 : [MODE] 2 -> Passage en mode WRT. [MODE] [-] -> Passage en mode Base N pour le programme qui sera spécié immédiatement ensuite. [ ][ ][ ] [EXE] -> Sélection Prog 3.

• A la n du programme il ne faut pas omettre le tout dernier [ ] ou [:].

Note : la calculatrice n’a pas besoin d’être en mode Base N lorsqu’on lance l’exécution pour exécuter le programme en Base N.

Ex :

On écrit un programme qui demande une valeur A, la multiplie par (101)2 et donne le résultat en binaire, hexadécimal et décimal. ? A:Bin:Ax101 Hex Dec:

016

La base dans laquelle est entrée la valeur de A dépend du mode de la calculatrice au lancement de l’exécution (décimal si mode normal ou Base-N d, binaire si Base-N b, etc.). Si on souhaite une base précise pour A il faut le préciser dans le programme : Bin:? A:Ax101 Hex Dec:

016

GC700_01_GC700Z_01IM0108.indd 67 6/3/08 17:33:33

Français

68

Français

Programmation et statistiques

Il est possible de programmer des calculs statistiques à une ou deux

variables, avec les adaptations suivantes :

• Pour spécier le mode statistiques à une ou deux variables pour un programme, par exemple P3 : [MODE] 2 -> Passage en mode WRT. [MODE] [x] ou [÷] -> Passage en mode SD1 ou LR1 pour le programme qui sera spécié immédiatement ensuite. [ ][ ][ ] [EXE] -> Sélection Prog 3.

- Il y a un certain nombre de fonctions ou signes que l’on ne peut pas utiliser pour cause de touches assignées aux fonctions statistiques : Abs, 3√, Dsz, >, <, en mode une et deux variables ; =, ≠, ≤, ≥, Isz et en mode deux

variables.

Note : la calculatrice n’a pas besoin d’être en mode statistique lorsqu’on

lance l’exécution pour exécuter le programme.

Utilisation des mémoires

Augmentation / diminution du nombre des mémoires

[MODE] [.]

Augmente le nombre de mémoires. Diminue le nombre de pas de programme.

Ex : [MODE] [.] 10 [EXE] -> augmente le nombre de mémoires à 36 au lieu de 26, diminue le nombre de pas de 120.

[ALPHA][ [ ] et [ALPHA][ ] ]

S’utilisent pour le nom des mémoires supplémentaires :

Z[1], Z[2], …

GC700_01_GC700Z_01IM0108.indd 68 6/3/08 17:33:33

Français

69

Votre calculatrice dispose de 26 mémoires temporaires dans lesquelles vous pouvez stocker des valeurs numériques.

WRT

P012 3456 7 89

600

nombre de pas

Sur cet écran vous voyez que s’il n’y a aucun programme en mémoire, vous disposez en outre d’un maximum de 600 pas de programme.

Vous pouvez rajouter jusqu’à 50 mémoires supplémentaires, si vous n’avez aucun programme actif, car chaque fois que vous rajoutez une mémoire vous perdez 12 pas de programmes :

nb mémoires 26 27 28 … 72 73 74 75 76 nb pas 600 588 576 … 48 36 24 12 0

Ces mémoires s’utilisent en programmation ou en calcul direct comme des

mémoires temporaires normales, par exemple :

5 Z[4]

30xZ[4] [EXE] -> 150.

Si vous avez déjà des programmes en mémoire et que vous essayez

d’obtenir un nombre de mémoires trop grand vous obtiendrez le message Mem ERROR. De même si vous avez 3 mémoires supplémentaires et que

vous essayez d’utiliser une mémoire appelée Z[4].

Ex :

Si on fait [MODE] 2 on a l’écran suivant (pour exemple) :

P _ _2_34567_9 395

Il reste dans ce cas de gure, compte tenu des programmes existants,

395 pas de programme disponibles, soit un maximum de 32 mémoires supplémentaires. Pour rajouter 3 mémoires on fait : [MODE] [.] 3 -> Defm 3 [EXE] -> M-29 S-395 M représente le nouveau nombre de mémoires disponibles (26+3) et S le nombre de pas disponibles restants (395-3x12=359). Vous pouvez alors utiliser des mémoires temporaires supplémentaires Z[1], Z[2] et Z[3].

GC700_01_GC700Z_01IM0108.indd 69 6/3/08 17:33:33

Français

70

Français

Mémoires tableau

[ALPHA][ [ ] et [ALPHA][ ] ]

S’utilisent pour le nom des mémoires tableau : A[1], A[2],

…

Les mémoires tableau sont très utiles lorsqu’il s’agit de mettre en mémoire des valeurs de façon répétitive. Votre calculatrice vous offre cette fonctionnalité d’une manière simple, à partir des mémoires temporaires A-Z.

Lorsqu’on écrit par exemple S[n], n est un entier qui peut être négatif, nul ou positif, et S[n] correspond à une mémoire temporaire existante,T si n=1, U si

n=2, R si n=-1 et ainsi de suite. On peut visualiser cela par un tableau d’équivalence :

mém temp A B C D … Y Z

A tableau A[0] A[1] A[2] A[3] … A[25] A[26] B tableau B[-1] B[0] B[1] B[2] … B[24] B[25] C tableau C[-2] C[-1] C[0] C[1] … C[23] C[24]

… … … … … … … … Y tableau Y[-25] Y[-24] Y[-23] Y[-22] … Y[0] Y[1] Z tableau Z[-26] Z[-25] Z[-24] Z[-23] … Z[-1] Z[0]

Remarques :

l A tout moment C[23] est égale à la mémoire temporaire Y, attention de ne

pas les faire entrer en conit par mégarde en utilisant les deux dans le même

programme pour des applications différentes.

l A[-1] n’existe pas, pour n négatif A[n] provoque un message Mem ERROR. l A[27], B[26],…, Z[1] existent si le nombre de mémoires a été étendu comme

expliqué dans le paragraphe précédent.

Ex :

On veut mettre en mémoire les valeurs 1 à 10 dans les mémoires C à L. Sans mémoires tableau c’est fastidieux : 1 C:2 D:3 E:4 F:5 G:6 H:7 I:8 J:9 K:10 L

040

Avec les mémoires tableau c’est plus rapide et le résultat est exactement le même puisque les mémoires C[0]-C[9] sont les mémoires C-L.

0 Z:Lbl 1: Z+1 C[Z]:Isz Z: Z<10 Goto 1

026

C’est aussi beaucoup plus facile à modier. Par exemple on repart du même

programme pour rentrer les puissances de 2 (21, 22, 23… 210) dans les mémoires D à M : 0 Z:Lbl 1: 2xy(Z+1) D[Z]:Isz Z: Z<10 Goto 1

030

GC700_01_GC700Z_01IM0108.indd 70 6/3/08 17:33:34

Français

71

9. MESSAGES D’ERREUR

Causes possibles d’erreurs

Lorsque l’écran afche un message d’erreur, les raisons peuvent être :

l Syn ERROR : erreur de syntaxe. Ex : [sin] 3 [+] [EXE].

l Ma ERROR : la valeur utilisée est en dehors des valeurs admissibles (voir

tableau plus loin). Ex : division par 0, cos-1 (5), √(-2). Il se peut aussi que lors

du calcul effectué à partir des valeurs saisies, une valeur intermédiaire se retrouve en dehors des valeurs admissibles, trop grande ou trop petite. Une

valeur très petite (inférieure à 10-99) sera arrondie en un 0, ce qui peut créer

une situation de division par 0.

l Go ERROR : en programmation, indique qu’il manque une instruction [Lbl]

pour une commande [Goto] ou qu’il n’y a pas de programme à l’endroit

indiqué par une commande [Prog].

l Stk ERROR : dépassement de la capacité mémoire de la calculatrice. Votre

calcul est trop long, mieux vaut le découper en deux parties ou plus (voir

paragraphe « Priorités de calcul » dans le premier chapitre).

l Mem ERROR : erreur dans l’utilisation des mémoires, soit lors de

l’expansion du nombre de mémoires, soit dans l’utilisation des mémoires

tableau. Voir les paragraphes correspondants dans le chapitre « Programmation ».

l Arg ERROR : erreur d’argument sur une commande de type [MODE], [Goto] … Ex : Fix 11 [EXE]. Vériez que la valeur employée est entre 0 et 9.

l Ne ERROR : erreur concernant les sous-programmes. Vériez bien qu’il n’y a aucune instruction Prog n où n désigne le programme principal.

Pour sortir de l’écran d’afchage de l’erreur, appuyez sur [AC] ou utilisez les èches et pour corriger l’équation.

Valeurs admissibles

De manière générale les valeurs utilisées dans les calculs doivent vérier :

-9,999999999 x 1099 ≤ x ≤ 9,999999999 x 1099 soit |x| <10

100

Note : |x| est la valeur absolue de x, soit |x|= –x si x<0 et |x|=x si x≥0.

Pour certaines fonctions les intervalles sont nécessairement plus petits :

GC700_01_GC700Z_01IM0108.indd 71 6/3/08 17:33:34

Français

72

Français

|x| ≥ 10

-99

Fonction Conditions supplémentaires

x2x

-1

|x| < 10

50

x

2

|x| < 10

50

x

y

si x > 0, y.ln|x| ≤ 230.2585092 si x=0, y >0 si x < 0, y.ln|x| ≤ 230.2585092 et y est impair ou 1/y est un entier (y≠ 0)

x

√y

si y > 0, 1/x.ln|y| ≤ 230.2585092 si y=0, x >0 si y < 0, 1/x.ln|y| ≤ 230.2585092 et 1/x est impair ou x est un entier (x≠ 0)

10

x

x < 100

√x x ≥ 0

ln x, log x x ≥ 10

-99

e

x

x ≤ 230.2585092

sinh x, cosh x |x| ≤ 230.2585092

sinh-1x |x| < 5 x 10

99

cosh-1x 1 ≤|x| < 5 x 10

99

tanh-1x |x|<1

sin x

DEG |x| < 4.5 x 10

10

RAD |x| < π/4x10

9

GRAD |x| < 5.10

10

cos x

DEG |x| < 4.5x 10

10

RAD |x| < π/4x10

9

GRAD |x| < 5.10

10

tan x

comme sin x et : (avec n entier positif ou négatif) DEG x≠ (2n+1)x90 RAD x ≠ (2n+1)/2 x π GRAD x ≠ (2n+1)x100

sin –1x, cos –1x |x| ≤ 1

GC700_01_GC700Z_01IM0108.indd 72 6/3/08 17:33:35

Français

73

degrés décimaux et

sexagésimaux

|x|<10

10

coordonnées polaires x, y < 1050 et x2+y2 < 10

100

r≥0, θ comme le x pour sin x et cos x.

x ! 0 ≤ x≤ 69 (x entier )

Base 10 -231 ≤ (x)10 < 2

31

Base 2

nombres entiers binaires de 10 chiffres maximum 0≤ x ≤ 111111111 ou 1000000000 ≤ x ≤ 1111111111 soit –29 ≤ (x)10 < 2

9

Base 8

nombres entiers octaux de 10 chiffres maximum 0≤ x ≤ 37777777777 ou 4000000000 ≤ x ≤

7777777777 soit -229 ≤ (x)10 < 2

29

Base 16

nombres entiers hexadécimaux de 8 chiffres maximum 0≤ x ≤ 7FFFFFFF ou 80000000≤ x ≤ FFFFFFFF

Soit -231 ≤ (x)10 < 2

31

statistiques

n entier, 0<n<10

100

0 ≤ x, y < 1050 au minimum pour σ

n-1

, n>1 valeurs intermédiaires de calcul (∑x, ∑y, ∑x2, ∑y, ∑xy et ∑x4, ∑x3,∑x2y) dans les limites admissibles.

GC700_01_GC700Z_01IM0108.indd 73 6/3/08 17:33:35

Français

74

Français

10. PRECAUTIONS D’EMPLOI

IMPORTANT : sauvegarde de vos données

Votre calculatrice comporte une mémoire électronique capable de conserver une grande quantité d’informations. Ces informations sont gardées en

mémoire de manière able tant que les piles fournissent l’énergie nécessaire et sufsante à leur bonne conservation. Si vous laissez les piles

devenir trop faibles, lorsque vous changez les piles ou si l’alimentation électrique s’interrompt pour une autre raison, les informations stockées en mémoire seront être irrémédiablement perdues. Un choc électrostatique

important ou des conditions d’environnement extrêmes peuvent aussi causer

la perte des informations. Une fois les informations perdues elles ne peuvent pas être récupérées de quelque manière que ce soit, c’est pourquoi nous vous conseillons fortement

de garder systématiquement une sauvegarde de vos données (valeurs,

programmes) dans un lieu sûr.

Utilisation de RESET

N’appuyez sur la touche de réinitialisation du système (RESET) que dans les

cas suivants:

• Lors de la première utilisation.

• Après le remplacement des piles.

• Pour effacer le contenu de toutes les mémoires.

• En cas de blocage général, toutes les touches étant inopérantes. Par

exemple, si vous exposez la calculatrice à un champ électrique, ou à une

décharge électrique pendant l’utilisation, il peut se produire des phénomènes

anormaux qui peuvent neutraliser le fonctionnement de certaines touches y

compris la touche [AC].

ATTENTION : ne pas appuyer sur RESET lorsque vous pensez qu’un calcul ou opération interne est en cours, cela pourrait endommager irrémédiablement votre calculatrice.

Pour appuyer sur le bouton Reset, appuyez sur [AC] pour remettre la calculatrice en marche puis utilisez un objet n et pointu tel qu’un trombone déplié, et appuyez doucement.

GC700_01_GC700Z_01IM0108.indd 74 6/3/08 17:33:35

Français

75

Remplacement des piles

Dès que l’afchage faiblit et qu’un réglage de contraste n’améliore pas la

lisibilité, nous vous conseillons de remplacer les piles. Votre calculatrice utilise

deux piles lithium de type CR2025.

1. Effectuez une sauvegarde de toutes les données et programmes dont vous aurez besoin ultérieurement.

2. Eteignez la calculatrice en appuyant sur [SHIFT] [OFF].

3. Retirez la vis du compartiment à piles au dos de l’appareil à l’aide d’un tournevis.

4. Remplacez les piles en respectant la polarité (côté + au-dessus).

5. Remettez la trappe.

6. Appuyez sur [AC] pour remettre la calculatrice en marche. Si les piles ont

été correctement installées, l’icône D et le curseur clignotant seront afchés. Si ce n’est pas le cas, retirez et réinstallez à nouveau les piles.

7. Appuyez doucement sur RESET avec un objet n et pointu pour réinitialiser

la calculatrice (important).

GC700_01_GC700Z_01IM0108.indd 75 6/3/08 17:33:35

Français

76

Français

Une mauvaise utilisation des piles peut causer une fuite de liquide

électrolytique ou même les faire exploser, et peut endommager l’intérieur de

votre calculatrice. Lisez donc bien les recommandations suivantes :

- Toujours remplacer les deux piles en même temps.

- S’assurer qu’elles sont du modèle recommandé avant de les installer.

- Bien respecter les polarités indiquées.

- Ne pas laisser des piles usagées dans la calculatrice, elles peuvent fuir et l’endommager irrémédiablement.

- Ne pas laisser les piles neuves ou usagées à la portée des enfants.

- Ne jamais jeter des piles au feu, elles pourraient exploser.

- Ne pas jeter les piles dans les ordures ménagères mais dans un lieu de

collecte adapté pour leur recyclage, dans la mesure du possible.

Entretien de votre calculatrice

- Votre calculatrice est un instrument de précision. Ne pas essayer de la

démonter.

- Evitez de la faire tomber ou de lui faire subir des chocs violents.

- Ne la transportez pas dans la poche arrière d’un pantalon.

- Ne la rangez pas dans un endroit anormalement humide, chaud ou

poussiéreux. Dans un environnement froid la calculatrice peut ralentir ou

même suspendre son fonctionnement. Elle retrouvera un fonctionnement normal dès que la température redeviendra plus clémente.

- N’utilisez pas de solvant ou de pétrole pour nettoyer votre calculatrice, mais

simplement un chiffon sec, ou encore un chiffon trempé dans une solution d’eau et d’un peu de détergent neutre, bien essoré.

- Ne provoquez pas d’éclaboussures sur la calculatrice.

- Si un dysfonctionnement potentiel est détecté, relisez bien ce manuel et vériez l’état des piles pour vérier que le problème ne vient pas d’une

mauvaise utilisation ou de piles trop faibles.

GC700_01_GC700Z_01IM0108.indd 76 6/3/08 17:33:36

Français

77

RESET 74 [ [ ] 70

[ èches gauche

et droite] 11

[ èches haut et bas] 8

[ x ] 41 [,] 30 [(-)] 10 [(] 10 [~] 18

[√] 21

[10x] 20

[3√] 21 [a b/c] 21

[A-LOCK] 8 [A]-[Z] 18 [A], [B] régression linéaire 41 [AC] 6 [ALPHA] 8 [and] 32 [Ans] 17 [Bin] 34 [CL] 40 [Cls] 47 [cos-1] 29 [cos] 28 [d/c] 21 [Dec] 32 [DEL] 11 [Dsz] 64 [DT] 40 [ENG] 14 [ex] 23 [EXP] 14 [Factor] 50 [Frac] 20 [G T] 47 [Goto] 60 [Graph] 47 [Hex] 32

[hyp] 23

[I], [J] 30 [INS] 11 [Int] 20 [Isz] 64

11. INDEX

[Lbl] 60

[Line] 53 [ln] 23 [log] 23 [Mcl] 18 [MODE] 8 [MODE] [-] 34 [MODE] [.] 68 [MODE] [+] 34 [MODE] [÷] 40 [MODE] [x] 40 [MODE] 4 26 [MODE] 5 26 [MODE] 6 26 [MODE] 7 14 [MODE] 8 15 [MODE] 9 14 [Not] 32

‘ ‘ ‘

[º ]

27 [Oct] 32 [OFF] 6 [or] 32 [Pi] 26 [Plot] 53 [Pol(] 30 [Prog] 64 [r] 41 [R] 40 [Ran#] 25 [Range] 47 [Rec(] 30 [Rnd] 15 [SHIFT] 8 [SHIFT] [MODE] 26 [sin-1] 29 [sin] 28 [SPACE] 59 [tan-1] 29 [tan] 28 [Trace] 52 [U] 40 [V] 40 [Value] 53 [W] 40 [X Y] 53 [x-1] 20 [n!] 24

^

GC700_01_GC700Z_01IM0108.indd 77 6/3/08 17:33:36

Français

78

Français

[x√] 21

[x2] 20 [xnor] 32 [xor] 32

[xσn-1] 41 [xσn] 41

[y] 41 [yσn-1] 41 [yσn] 41

[ZoomOrg] 50 [Zoomxf] 50 [Zoomxf/f] 50 [ ] au-dessus touche [ENG] 14 [ ] au-dessus touche

‘ ‘ ‘

[º ]

27

^

GC700_01_GC700Z_01IM0108.indd 78 6/3/08 17:33:36

Français

79

Ce produit est couvert par notre garantie de trois ans. Pour toute mise en œuvre de la garantie ou de service après-vente, vous devez vous adresser à votre revendeur muni de votre preuve d’achat. Notre garantie couvre les vices de matériel ou de montage imputables au constructeur à l’exclusion de toute détérioration provenant du non-respect de la notice d’utilisation ou de toute intervention intempestive sur l’article (telle que démontage, exposition à la chaleur ou à l’humidité…).

LEXIBOOK SA 2, av de Scandinavie 91953 COURTABOEUF CEDEX

France

Assistance technique : 0 892 23 27 26 (0.34€ / min) www.lexibook.com

Informations sur la protection de l’environnement. Tout appareil électrique

usé est une matière recyclable et ne devrait pas faire partie des ordures ménagères! Nous vous demandons de bien vouloir nous soutenir en contribuant activement à la gestion des ressources et à la protection de

l’environnement en déposant cet appareil dans des lieux de collecte adaptés (si existants).

Reproduction partielle ou intégrale de ce manuel interdite, sous quelque forme que ce soit, sauf avec autorisation expresse écrite du fabricant. Le fabricant et ses fournisseurs déclinent toute responsabilité quant aux conséquences de l’utilisation ou de la mauvaise utilisation de cette calculatrice ou de ce manuel d’utilisation. De même le fabricant et ses fournisseurs déclinent toute responsabilité concernant tous dommages, pertes nancières, manques à gagner ou autres préjudices liés à des pertes de données ou de calculs lors de l’utilisation de cette calculatrice ou de ce manuel. Du fait de certaines limitations techniques lors de l’édition et de l’impression de ce manuel, l’apparence de certaines touches ou afchages indiqués dans les textes peuvent présenter de légères différences avec l’apparence réelle. Le fabricant se réserve le droit de modier le contenu de ce manuel sans préavis.

12. GARANTIE

GC700_01_GC700Z_01IM0108.indd 79 6/3/08 17:33:37

Español

80

Calculadora cientíca gráca programable, funciones en base N,

estadísticas con 1 ó 2 variables, probabilidades, funciones aritméticas,

trigonométricas y de programación.

ÍNDICE

INTRODUCCIÓN 82

Instrucciones previas a la primera utilización del aparato 82

1. GUÍA DE UTILIZACIÓN DE SU CALCULADORA

83

Cómo encender y apagar la calculadora 83 Pantalla y símbolos utilizados 83 Ajuste del contraste de la pantalla 85 Funciones secundarias y alfanuméricas (teclas SHIFT y ALPHA) 85 Notaciones utilizadas en este manual 87 Teclas básicas 87 Introducción y modicación de una operación (Replay) 88 Operaciones sucesivas sobre una misma línea 89 Notación cientíca y de ingeniería 90 Selección del tipo de notación 91 Selección de la posición de la coma (punto) decimal 91 Selección del número de cifras signicativas 92 Prioridades de cálculo 93

2. UTILIZACIÓN DE LAS FUNCIONES DE MEMORIA 94

Recuperación del último resultado obtenido (Ans) 94 Cálculos en cadena 94 Operaciones sucesivas 94 Memorias temporales (A - Z) 95

3. FUNCIONES ARITMÉTICAS 97

Parte entera (Int), Parte decimal (Frac) 97 Funciones inversas, raíces cuadradas y exponentes 97 Raíces 98 Fracciones 98 Funciones logarítmicas y exponenciales 100 Funciones hiperbólicas 100 Funciones factorial n!, permutación y combinación 101 Generación de número aleatorio (función Random) 102

4. CÁLCULOS TRIGONOMÉTRICOS 103

Número π 103 Unidades de ángulos 103 Selección de la unidad de ángulo y del tipo de conversión 103 Conversión sexagesimal (grados / minutos /segundos) 104 Cálculos horarios 105 Coseno, seno, tangente 105 Funciones de arcocoseno, arcoseno y arcotangente 106 Coordenadas polares 107

CALCULADORA GRÁFICA LEXIBOOK®GC700_01/GC700Z_01

GC700_01_GC700Z_01IM0108.indd 80 6/3/08 17:33:37

Español

81

5. CÁLCULOS EN BASE N 109

Recordatorio 109 Cambio de base 109 Operadores lógicos 109 Notaciones 110 Comandos del modo de Base N y conversiones 111 Cálculos en Base N 112 Operadores lógicos en Base N 114

6. FUNCIONES ESTADÍSTICAS 115

Notas preliminares 115 Teclas de funciones estadísticas 117 Estadísticas con una variable: ejemplo práctico 118 Estadísticas con 2 variables: ejemplo práctico 120 Regresión no lineal 121

7. FUNCIONES GRÁFICAS 123

Deniciones y notaciones 123 Como trazar una curva 124 Curvas predeterminadas 124 Curvas denidas por el usuario 125 Función de ampliación y reducción de la representación gráca 127 Función “Trace” (rastreo) 129 Funciones “Plot” (representación gráca) y “Line” (línea) 130

8. FUNCIÓN DE PROGRAMACIÓN 132

Primeros pasos en programación 132 Cómo escribir un programa 132 Cómo ejecutar un programa 133 Cómo modicar un programa 134 Cómo borrar programas 135 Programación avanzada 136 Inserción de mensajes 136 Salto incondicional 137 Salto condicional 139 Contadores 141 Subprogramas 141 Ejemplo a modo de recapitulación: Juego del “número escondido” 142 Programación y grácos 143 Programación en Base N 144 Utilización de las funciones de memoria 145 Incremento/reducción del número de memorias 145 Tablas de memoria 147

9. MENSAJES DE ERROR 148

Causas posibles de error 148

10. PRECAUCIONES DURANTE LA UTILIZACIÓN DEL APARATO 151

IMPORTANTE: cómo salvaguardar sus datos 151 Utilización de la función RESET (restablecimiento) 151 Sustitución de las pilas 152 Mantenimiento de su calculadora 153

11. ÍNDICE 154

12. GARANTÍA 156

GC700_01_GC700Z_01IM0108.indd 81 6/3/08 17:33:37

Español

82

Tenemos el placer de poder contarle entre los numerosos usuarios de productos LEXIBOOK® y le agradecemos la conanza depositada en nuestros productos. Desde hace más de 15 años, la empresa francesa Lexibook diseña, desarrolla, fabrica y distribuye por todo el mundo productos electrónicos dirigidos a todos los públicos. Dichos productos gozan de una reputación impecable gracias a su valor tecnológico y a su calidad de fabricación. Calculadoras, diccionarios y productos electrónicos, estaciones meteorológicas, aparatos multimedia, relojes y despertadores, sistemas de telefonía… Nuestros productos forman parte de su vida diaria. Para poder apreciar al máximo las capacidades de la calculadora gráca GC700_01/GC700Z_01, le invitamos a que lea detenidamente este manual de instrucciones.

INTRODUCCIÓN

INSTRUCCIONES PREVIAS A LA PRIMERA UTILIZACIÓN DEL APARATO

Antes de encender el aparato siga atentamente los pasos que se indican a continuación:

1. Retire con precaución las dos lengüetas de protección del compartimiento de las pilas tirando de los extremos de las lengüetas.

2. Si alguna de las lengüetas permanece trabada, retire los tornillos que jan el compartimiento de las pilas, extraiga la pila y, a continuación, retire la lengüeta. Instale 2 pilas de tipo CR2025 observando la polaridad indicada en el interior del compartimento (el polo positivo + orientado hacia arriba). A continuación, vuelva a colocar la tapa del compartimento y apriete los tornillos.

3. Deslice la calculadora en su tapa para acceder al teclado.

Tornillo

Botón “Reset”

GC700_01_GC700Z_01IM0108.indd 82 6/3/08 17:33:38

Español

83

1. GUÍA DE UTILIZACIÓN DE SU CALCULADORA

Cómo encender y apagar la calculadora

[AC]

Enciende la calculadora. Pone a cero la pantalla de la calculadora.

Nota: cuando se vuelve a encenderse la calculadora después de haberla apagado, el aparato estará

congurado por defecto en modo decimal (DEC), con la función de punto decimal otante activada y las medidas de ángulo expresadas en grados (DEG).

[SHIFT]

[OFF]

Apagado. Tras 6 minutos de inactividad, la calculadora se apagará de forma automática.

Esta calculadora es de tipo cientíco, gráco y programable. Cada una de estas aplicaciones posee un tipo de pantalla diferente. Para cualquier

información relacionada con las aplicaciones grácas y de

programación, consulte los capítulos que correspondan.

La pantalla que corresponde a las funciones básicas es la siguiente:

4. Retire la película estática de protección de la pantalla LCD.

5. Pulse la tecla [AC] para encender la calculadora. Observará que en la pantalla aparecen la letra D y un cursor que parpadea. De no ser así, verique el estado de las pilas y vuelva a comenzar desde el principio (en caso necesario, consulte el capítulo “Precauciones durante la utilización del aparato”).

6. Localice el oricio identicado con la palabra RESET (restablecer) situado en la parte trasera del aparato. Inserte un objeto de punta na (un clip para papeles por ejemplo) y presione suavemente.

Se desea obtener más información con referencia a las pilas, la importancia del botón “RESET”, o sobre cómo salvaguardar sus datos, consulte el capítulo “Precauciones durante utilización del aparato”.

Pantalla y símbolos utilizados

D

5+In 2

Introducción

automática

GC700_01_GC700Z_01IM0108.indd 83 6/3/08 17:33:38

Español

84

-

Signo negativo que indica que el número visualizado es negativo.

ou

Aparece para indicar que la operación en curso es

demasiado larga para que pueda visualizarse totalmente en la pantalla. En este caso, pulse las teclas [ ] o [ ] para mostrar el resto del cálculo.

Disp

Indica que el valor mostrado en la pantalla es un resultado intermedio, véase el párrafo “Operaciones sucesivas

sobre una misma línea”, o bien el capítulo “Programación”.

M

Indica que la tecla MODE (modo) está activada.

S

Indica que la tecla SHIFT (funciones secundarias) está activada.

A

Indica que la tecla ALPHA (alfanumérica) está activada.

……

ERROR

Se muestra cuando el cálculo excede la capacidad de visualización permitida o se detecta un error. Los diferentes mensajes de error, así como sus causas y posibles soluciones se describen en la sección

correspondiente del capítulo “Mensajes de error”.

hyp

Se muestra cuando la función hiperbólica está activada.

En la línea inferior se visualizarán las operaciones introducidas en caracteres alfanuméricos. Seguidamente, una vez que se pulse [EXE], aparecerá lo siguiente:

Nota: este valor se proporciona únicamente a título de ejemplo y no corresponde en absoluto a la operación 5+ln2

La línea inferior muestra un resultado numérico de 10 cifras signicativas, o bien 10 cifras signicativas más otras 2 cifras de notación cientíca en la parte superior derecha (véase el párrafo “Notación cientíca”).

Deberá tenerse en cuenta que si el resultado mostrado aparece en formato de 10 ó 10 más 2 cifras signicativas, los cálculos internos se realizan con 24 cifras signicativas y dos exponentes, lo cual le proporciona un nivel de precisión bastante alto durante la ejecución de las operaciones.

La línea superior mostrará un cierto número de símbolos (en este caso, sólo se muestra D). Estos símbolos le proporcionan indicaciones que permiten una mejor lectura de las operaciones en curso:

D

2.05 2631

-11

Exponente

Mantisa

GC700_01_GC700Z_01IM0108.indd 84 6/3/08 17:33:38

Español

85

Fix

Indica que el resultado se mostrará con un número determinado de cifras detrás de la coma (punto) decimal.

Sci

Indica que el resultado se mostrará con un número

determinado de cifras signicativas.

D

Se muestra cuando la calculadora está en modo de

representación angular en grados, o cuando la unidad de

medida del ángulo mostrado está en grados.

R

Se muestra cuando la calculadora está en modo de

representación angular en radianes, o cuando la unidad

de medida del ángulo mostrado está en radianes.

G

Se muestra cuando la calculadora está en modo de

representación angular en gradientes, o cuando la unidad

de medida del ángulo mostrado está en gradientes.

Ajuste del contraste de la pantalla

[MODE] [ ] , [ ] Ajuste del contraste de la pantalla.

A la derecha de la pantalla encontrará un círculo señalado con la palabra “REPLAY” y sobre el que observará las echas direccionales [ ] , [ ], [ ] y [ ]. De momento, sólo estaremos interesados en [ ] y [ ].

Para ajustar el contraste de la pantalla, pulse una vez la tecla [MODE] y, a continuación, pulse [ ] reiteradamente para reducir el nivel de contraste, o sobre [ ] para aumentarlo. Si no se logra aumentar el nivel de contraste mediante este procedimiento, se deberá seguramente a que las pilas están bajas de carga y será necesario sustituirlas ; consulte los consejos e instrucciones referentes a la sustitución de las pilas que se indican al nal de este manual.

Funciones secundarias y alfanuméricas (teclas SHIFT y ALPHA)

[SHIFT]

Permite acceder a las funciones secundarias, las cuales están indicadas en azul turquesa justo encima de la tecla que corresponda.

[ALPHA]

Permite acceder a las funciones alfanuméricas, las cuales están indicadas. En naranja/amarillo encima y a la derecha de la tecla que corresponda.

[SHIFT]

[A-LOCK]

Permite acceder continuamente a las funciones

alfanuméricas (bloqueo de la función ALFA), cancelación pulsando de nuevo la tecla [ALPHA], o sobre [EXE].

La mayoría de las veces, las teclas de su calculadora incorporan al menos dos funciones. No obstante es posible que incorporen tres o incluso cuatro funciones. Éstas están indicadas mediante colores y conforme a su posición alrededor de la tecla que sirve para acceder a las mismas.

GC700_01_GC700Z_01IM0108.indd 85 6/3/08 17:33:39

Español

86

Por ejemplo:

l X-1 es la función principal y se accede a ella directamente pulsando la tecla.

l n ! es la función secundaria, para acceder a ella, será necesario pulsar primero la tecla [SHIFT] y, a continuación, la tecla correspondiente (la pantalla mostrará brevemente la letra S).

l A es la función alfanumérica, para acceder a ella, será necesario pulsar primero la tecla [ALPHA] y, a continuación, la tecla correspondiente (la pantalla mostrará brevemente la letra A). Se trata principalmente de teclas para las funciones de memoria o de introducción de texto.

l /A y las otras funciones indicadas en azul oscuro sólo pueden accederse durante las operaciones en Base N. Encontrará más información sobre esta función en el capítulo correspondiente.

Asimismo, las funciones indicadas entre las echas son funciones relacionadas con el modo de operaciones estadísticas que se describen en el capítulo correspondiente.

Si pulsa una sola vez la tecla [SHIFT], el símbolo S aparecerá en la pantalla para indicar que la tecla [SHIFT] está activada y que es posible acceder las funciones secundarias. El símbolo se apagará en cuanto pulse cualquier otra tecla o vuelva pulsar la tecla [SHIFT].

Asimismo, si pulsa una sola vez la tecla [ALPHA], el símbolo A aparecerá en la pantalla para indicar que la tecla [ALPHA] está activada y que es posible acceder a las funciones alfanuméricas. El símbolo se apagará en cuanto pulse cualquier otra tecla o vuelva pulsar la tecla [ALPHA].

Si desea utilizar varias veces seguidas las funciones alfanuméricas sin que por ello suponga una tarea tediosa, podrá utilizar las teclas [SHIFT] [A-LOCK]. El símbolo A permanecerá indicado y podrá acceder de forma continua a las funciones alfanuméricas en tanto no pulse la tecla [ALPHA] para anular la selección, o bien la tecla [SHIFT] si desea pasar directamente a una función secundaria.

GC700_01_GC700Z_01IM0108.indd 86 6/3/08 17:33:39

Español

87

Notaciones utilizadas en este manual

En este manual, las funciones estarán indicadas de la manera siguiente (volviendo a utilizar el ejemplo anterior): Principal [X

-1

] Secundaria [SHIFT] [n!] Alfanumérica [ALPHA][A]

0 - 9

[+]

[-]

[x]

[÷]

[EXE]

[.]

[SHIFT]

[(-)]

[(], [)]

Teclas numéricas.

Suma.

Resta.

Multiplicación.

División.

Proporciona el resultado de las operaciones.

Inserción del punto (coma decimal) para números decimales. p. ej.: para escribir 12,3 se introduce 12[.]3

Cambiar el signo del número que se va introducir inmediatamente después. 5 [x] [SHIFT] [(-)] [5] [EXE] -> -25.

Abre/cierra un paréntesis.

p. ej.: [(] 4 [+] 1 [)] [x] 5 [EXE] -> 25.

Las teclas [0] a [9] se escribirán 0 a 9 (sin corchetes) para facilitar la lectura.

Los cálculos y los resultados se mostrarán de la manera siguiente:

descripción de los datos -> representación alfanumérica | línea de resultado

p. ej.:

Para efectuar el cálculo (4+1)x5= el proceso se indicará de la manera siguiente: [(] 4 [+] 1 [)] [x] 5 [EXE] -> (4+1)x5 | 25.

Una vez que esta representación no impida comprender el ejemplo, podrá omitirse la parte situada más a la izquierda de la pantalla.

Teclas básicas

GC700_01_GC700Z_01IM0108.indd 87 6/3/08 17:33:39

Español

88

Introducción y modicación de una operación (Replay)

[ ] [ ]

Se utiliza para desplazar el cursor y modicar una operación.

Si se pulsa una sola vez [ ] mientras que se muestra el resultado numérico, aparecerá la línea de cálculo

alfanumérico y el cursor se situará al nal de la línea.

Si se pulsa una sola vez [ ] mientras que se muestra el resultado numérico, aparecerá la línea de cálculo alfanumérico y el cursor se situará al principio de la línea.

[DEL]

Se borra el carácter situado en el lugar donde se encuentra el cursor.

[SHIFT] [INS]

Inserta un carácter inmediatamente a la izquierda del

cursor de inserción.

Será posible introducir en su calculadora las operaciones que desee y éstas aparecerán abajo a la izquierda en un estilo alfanumérico fácil de leer y de corregir.

Una vez que haya introducido el cálculo y obtenido el resultado pulsando la tecla [EXE], será bastante fácil revisar y modicar la operación utilizando las echas direccionales [ ], [ ].

Observaciones con respecto a las teclas [SHIFT] [INS]:

l La función está situada encima de la tecla [ ]. l El cursor cambiará en tanto el modo de inserción esté activado . l Es posible utilizar la tecla [DEL] mientras que el modo de inserción está

activado.

l El modo de inserción se desactiva en cuanto se pulsa la tecla [ ] o [ ].

Observaciones con respecto a la introducción de cálculos:

Esta calculadora le permite introducir de una sola vez un cálculo de hasta 127 caracteres. No obstante, deberá tenerse en cuenta que si incluso una

función (como por ejemplo sin-1) requiere que se pulsen 2 teclas y que la pantalla la muestre con varias letras, dicha función sólo será contabilizada por la calculadora para un sólo carácter. En cuanto se alcancen los 121

caracteres, la calculadora le avisará cambiando la forma del cursor de _ a .

En caso de que la operación a efectuar sea demasiado larga, será

conveniente dividirla en varias etapas.

GC700_01_GC700Z_01IM0108.indd 88 6/3/08 17:33:40

Español

89

p. ej.:

Se han introducido los siguientes datos: 34 [+] 57 [-] 27 [x] 78 +5 [EXE] -> 34+57-27x78+5 | -2010.

Si pulsa la tecla [ ], se mostrará la representación alfanumérica del cálculo efectuado y el símbolo le indicará que la operación es demasiado larga para que pueda mostrarse en su totalidad.

l Se desea sustituir 27 por 7 en su operación, proceda como sigue:

Posicione el cursor utilizando la tecla [ ] para desplazarse hasta el lugar

exacto donde desea efectuar la corrección, es decir, delante del número 2. Pulse la tecla [DEL] para suprimir el 2. Si, a continuación, pulsa la tecla [EXE], el resultado cambiará a -450.

l Se desea sustituir 34 por 3684 en su operación, proceda como sigue:

Posicione el cursor pulsando una vez la tecla [ ] para desplazarse hasta el

principio de la línea de cálculo. A continuación, pulse la tecla de nuevo para desplazarse al lugar donde desea efectuar la corrección, es decir, delante

del número 4.

Pulse las teclas [SHIFT] [INS] e introduzca los números 6 y 8 en su lugar correspondiente. Si pulsa la tecla [EXE], el resultado cambiará a 3200.

[ALPHA] [ ]

Marca de separación entre dos operaciones consecutivas

introducidas en una misma línea.

[AC]

Interrumpe la ejecución de operaciones consecutivas.

Operaciones sucesivas sobre una misma línea

Si así lo desea, su calculadora le permite introducir varias operaciones de

manera sucesiva sobre una misma línea y, a continuación, ejecutarlas expulsando la tecla [EXE]. De esta manera, la calculadora efectua la primera operación introducida y, a continuación muestra el resultado intermedio y el símbolo Disp para indicarle que la ejecución de las operaciones no ha nalizado. Si pulsa la tecla [EXE], la calculadora saltará a la segunda operación y así seguidamente hasta llegar a la última, tras lo

cual el símbolo Disp desaparecerá de la pantalla.

GC700_01_GC700Z_01IM0108.indd 89 6/3/08 17:33:40

Español

90

p. ej.:

Si desea efectuar la operación siguiente, proceda como sigue: 54+39= 9-18= 4x6-2= 50x12= Podrá introducir estas operaciones de la manera siguiente: 54 [+] 39 [ALPHA] [ ] 9 [-] 18 [ALPHA] [ ] 4 [x] 6 [-] 2 [ALPHA] [ ] 50 [x] 12 [EXE]

-> 54+39 9-18 4x6-2 50x12 | 93.

Disp

[EXE] -> | -9. Disp [EXE] -> | 22.

Disp

[EXE] -> | 600.

Notas:

l No podrán modicarse las operaciones en tanto que el símbolo Disp aparezca en la pantalla y no se haya alcanzado la última operación, a menos que se pulse [AC] para interrumpir la ejecución de las mismas.

l En el ejemplo anterior, si se pulsa una vez más de la cuenta la tecla

[EXE], volverá a iniciarse la operación (la pantalla mostrará 93. y Disp).

l Véase también para este tipo de cálculos, la manera de recuperar el

resultado anterior (función Ans) que se describe en el siguiente capítulo.

Notación cientíca y de ingeniería

El modelo GC700 muestra directamente el resultado de un cálculo (x) en modo decimal normal cuando x está dentro del intervalo siguiente:

0.000000001≤ | x |≤ 9999999999

Más allá de estos límites, la calculadora mostrará automáticamente el resultado de una operación según el sistema de notación cientíca, en el que las dos cifras situadas arriba y la derecha representan el exponente del factor 10.

p. ej.:

Cómo calcular el cuadrado de 2.500.000 y su función inversa 2500000 [X2][EXE] -> 25000002 | 6.25 12 es decir : 6,25 x 1012 [X-1][EXE] -> 6.25E12-1 | 1.6

–13

es decir : 1,6 x 10

-13

La notación denominada de ingeniería funciona siguiendo el mismo principio, sólo que en este caso es necesario que la potencia de 10 sea un múltiplo de 3 (103, 106, 109 etc.). Volviendo a utilizar el ejemplo anterior: 6,25 x 1012 se escribe también 6.25 12 en notación de ingeniería, sin embargo, 1,6 x 10

-13

se escribirá 160.

–15

GC700_01_GC700Z_01IM0108.indd 90 6/3/08 17:33:40

Español

91

Selección del tipo de notación

Para cualquier número comprendido dentro del intervalo mencionado anteriormente, su calculadora le permitirá introducirlos directamente en notación cientíca para evitar así una introducción reiterada de ceros.

[EXP]

Permite introducir un valor en notación cientíca.

[ENG] O [SHIFT] [ ]

Flecha situada encima de la tecla [ENG]

Permite pasar a notación de ingeniería:

• Cada vez que se pulsa la tecla [ENG], el exponente disminuye en 3.

• Cada vez que se pulsa las teclas [SHIFT] [ ],

el exponente aumenta en 3.

p. ej.:

Si desea introducir 2.500.000 (es decir: 2,5 x 106) en notación cientíca, proceda como sigue: 2 [.] 5 [EXP] 6 [EXE] -> 2.5E6 | 2500000.

Si desea introducir 2.500.0002, es decir: (2,5 x 106)2 en notación cientíca, proceda como sigue: 2 [.] 5 [EXP] 6 [X2] [EXE] -> 2.5E62 | 6.25

12

Si desea introducir 0.016 (es decir: 1,6 x 10-2) en notación cientíca, proceda como sigue: 1 [.] 6 [EXP] [SHIFT] [(-)] 2 [EXE] -> 1.6E-2 | 0.016.

Para pasar a notación de ingeniería utilizando los ejemplos anteriores, proceda como sigue: 2 [.] 5 [EXP] 6 [EXE] -> 2.5E6 | 2500000. [ENG] -> 2.5

06

[ENG] -> 2500.

03

[ENG] -> 2500000.

00

[ENG] -> 2500000000.

-03

[.] 016 [EXE] -> .016 0.016 [SHIFT] [ ] -> 0.016

00

[ENG] -> 16.

-03

[ENG] -> 16000.

-06

[SHIFT] [ ] -> 16.

-03

[MODE] 7 +

cifra entre 0 y 9

Permite seleccionar el número de cifras que aparecen detrás de la coma decimal. La pantalla muestra el símbolo FIX.

[SHIFT] [Rnd]

Redondea el valor mostrado en la pantalla en función del modo FIX seleccionado.

[MODE] 9

Cancela el modo de selección del número de cifras

después de la coma (punto) decimal.

Selección de la posición de la coma (punto) decimal

GC700_01_GC700Z_01IM0108.indd 91 6/3/08 17:33:41

Español

92

p. ej.:

100000 [÷] 3 [EXE] -> 100000÷3 | 33333.33333 [MODE][7] 3 [EXE] -> Fix 3 | 33333.333

Fix

[MODE][7] 2 [EXE] -> Fix 2 | 33333.33

Fix

[x]10 [EXE] ->33333.33333x10 | 333333.33

Fix

[MODE][9] [EXE] -> Norm | 333333.3333

Selección del número de cifras signicativas

[MODE] 8 + cifra

entre 0 y 9

Permite seleccionar el número de cifras signicativas.

La pantalla muestra el símbolo SCI.

[SHIFT] [Rnd]

Redondea el valor mostrado en la pantalla en

función del modo SCI seleccionado.

[MODE] 9

Cancela el modo de selección del número de cifras signicativas.

Cuando se ja el número de cifras después de la coma (punto) decimal a un valor determinado mediante el modo FIX, tan sólo se modica el modo de visualización de dicho valor y no así el valor memorizado por la calculadora, el cual incorpora 24 cifras signicativas. Si así lo desea, podrá modicar el valor memorizado para seguir ejecutando sus cálculos con un valor redondeado en función del número de cifras después de la coma (punto) decimal que se haya seleccionado. Volviendo a utilizar el ejemplo anterior:

100000 [÷] 3 [EXE] -> 100000÷3 | 33333.33333 [MODE][7] 2 [EXE] -> Fix 2 | 33333.33

Fix

[SHIFT] [Rnd] [EXE] -> Rnd | 33333.33

Fix

[x]10 [EXE] -> 33333.33x10 | 333333.30

Fix

p. ej.:

100000 [÷] 3 [EXE] -> 100000÷3 | 33333.33333 [MODE][8] 5 [EXE] -> Sci 5 | 3.3333

04

SCI

[MODE][8] 3 [EXE] -> Sci 3 | 3.33

04

SCI

[MODE][9] [EXE] -> Norm | 33333.33333

Cuando se ja el número de cifras signicativas a un valor determinado mediante el modo SCI, tan sólo se modica el modo de visualización de dicho valor y no así el valor memorizado por la calculadora, el cual incorpora 24 cifras signicativas. Si así lo desea, podrá modicar el valor memorizado para seguir ejecutando sus cálculos con un valor redondeado en función del número de cifras signicativas que se haya seleccionado. Volviendo a utilizar el ejemplo anterior:

GC700_01_GC700Z_01IM0108.indd 92 6/3/08 17:33:41

Español

93

100000 [÷] 3 [EXE] -> 100000÷3 | 33333.33333 [MODE][8] 3 [EXE] -> Sci 3 | 3.33

04

SCI

[SHIFT] [Rnd] [EXE] -> Rnd | 3.33

04

SCI

[x]10 [EXE] -> 33300.x10 | 3.33

05

SCI

[MODE][9] [EXE] -> Norm | 333000.

Nota: este modo de visualización es compatible con la notación [ENG]:

100000 [÷] 3 [EXE] -> 100000÷3 | 33333.33333 [MODE][8] 5 [EXE] -> Sci 5 | 3.3333

04

SCI

[ENG] -> 33.333

03

SCI

Prioridades de cálculo

Cuando se efectúen varias operaciones en un mismo cálculo, su calculadora los evaluará y determinará el orden en que han de completarse conforme a las reglas aritméticas establecidas. Este orden de prioridad es el siguiente:

1. Las operaciones entre paréntesis y, en caso de diferentes niveles de paréntesis, el último paréntesis abierto.

2. Las funciones que utilicen un tipo de exponente como X

-1

, X2, √, Xy y x√,

así como el cambio de signo [(-)].

3. Las funciones de tipo cos, sin, ln, ex…

4. Las funciones de introducción de datos como por ejemplo

‘ ‘ ‘

[º ]

y [a b/c].

5. Las multiplicaciones y divisiones (la multiplicación puede estar implícita, como por ejemplo 2cosπ).

6. Las sumas y restas.

7. Las funciones que denotan el n de una operación o que almacenan un valor en la memoria: [EXE], [ ], [DT], etc.

Cuando todos los operadores poseen el mismo nivel de prioridad, la calculadora los resuelve siguiendo simplemente el orden en el que aparecen de izquierda a derecha. En el interior de los paréntesis, se mantiene el orden de prioridad.

p. ej.:

1 [+] 3 [x] 5 [EXE] -> 1+3x5 | 16. [(] 1 [+] 4 [)] [x] 5 [EXE] -> (1+4)x5 | 25. 10 [-] 3 [X2] [EXE] -> 10-32 | 1. 5 [xy] [ln] 2 [EXE] -> 5xyln 2 | 3.05132936 o bien 5

ln2

Su calculadora establece la diferencia entre los diferentes niveles de prioridad y, según sea necesario, memoriza los datos y los operadores de cálculo hasta proporcionar el resultado correcto de la operación, teniendo en cuenta hasta un máximo de 24 niveles diferentes de operadores y 10 niveles de valores numéricos intermedios para la operación en curso. Dichos niveles se denominan en inglés “stacks”; si la operación realizada es demasiado complicada y sobrepasa la amplia capacidad de su calculadora, aparecerán el mensaje “Stk ERROR” (se ha excedido la capacidad de “stacks”).

GC700_01_GC700Z_01IM0108.indd 93 6/3/08 17:33:41

Español

94

2. UTILIZACIÓN DE LAS FUNCIONES DE MEMORIA

Recuperación del último resultado obtenido (Ans)

[Ans]

Recupera el resultado del cálculo anterior.

p. ej.:

24 [÷] [(] 4[+]6 [)] [EXE] -> 24÷(4+6) | 2.4 El resultado (2,4) queda automáticamente almacenado en la memoria Ans.

Esto nos permite calcular 3x ANS + 60÷ANS 3 [x] [ANS] [+] 60 [÷][ANS] [EXE] -> 3xANS+60÷ANS | 32.2

Cálculos en cadena

Se trata de cálculos para los que el resultado del cálculo anterior sirve de primer operando del cálculo siguiente. Es posible utilizar principalmente

en estos cálculos las funciones [√], [X2], [sin],...

p. ej.:

[AC] 6 [+] 4 [EXE] -> 6+4 | 10. [+] 71 [EXE] -> 10.+71 | 81.

[√] [Ans] [EXE] -> √Ans | 9.

Operaciones sucesivas

La utilización de la función Ans es esencial para la ejecución de operaciones sucesivas escritas sobre una misma línea: 54 [+] 39 [ALPHA][ ] [Ans] [-] 18 [EXE] -> 93. Al pulsar la tecla [EXE] se obtiene lo siguiente: 75 54 [+] 39 [ALPHA] [ ] [-] 18 [EXE] ->93. Al pulsar la tecla [EXE] se obtiene lo siguiente: -18

GC700_01_GC700Z_01IM0108.indd 94 6/3/08 17:33:42

Español

95

Memorias temporales (A - Z)

[ALPHA][A]

Recupera el contenido de la memoria A para utilizarlo en un cálculo.

[ ][ALPHA][A]

Almacena en la memoria “A” el valor mostrado en la pantalla o el valor que se desea calcular.

[ALPHA] [~]

Permite acceder simultáneamente al contenido de varias memorias. p. ej.:

5 [ ] [SHIFT] [A-LOCK] [A][~][D] [EXE] asigna el valor 5 a las memorias A, B, C y D.

Recordatorio: [SHIFT] [A-LOCK]=[SHIFT][ALPHA], bloqueo de [ALPHA]

0 [ ] [ALPHA][A] (cero)

Puesta a cero de la memoria A.

[SHIFT][Mcl]

Borra el contenido de todas las memorias temporales.

p. ej.:

5 [ ] [ALPHA] [X] [EXE] -> 5 X | 5. [-] 3 [ ] [ALPHA] [X] [EXE] -> 5.-3 X | 2. 6 [x] [ALPHA] [X] [EXE] -> 6xX | 12. [ALPHA] [X][EXE] -> X | 2.

Las 2 primeras líneas de cálculo modican el valor de X (X=5 y después 2), el cálculo 6xX utiliza el valor de X pero no lo modica.

Su calculadora dispone de 26 memorias temporales (A, B, C, D, E…, Y y Z). Dichas memorias le permiten almacenar datos y recuperarlos para utilizarlos en cálculos futuros.

Podrá utilizar las funciones [ ], [ALPHA] para cada una de las teclas [A], [B], [C], [D], ... [Y] y [Z]. Recordatorio: la letra a la que puede accederse mediante la función [ALPHA] está indicada en naranja y se encuentra en la parte inferior derecha de la tecla que corresponda. p. ej.: “A” se encuentra en la parte inferior derecha de la tecla [X-1].

Nota: es posible modicar la conguración de la calculadora para poder disponer de un número superior a las 26 memorias temporales existentes. El proceso a seguir se describe en el capítulo “Programación”.

GC700_01_GC700Z_01IM0108.indd 95 6/3/08 17:33:42

Español

96

5 [ ] [SHIFT] [A-LOCK] [A] [~][E] [EXE] -> 5 A~E | 5. A, B, C, D y E contienen ahora todas el mismo valor, 5. [ALPHA] [B] [x] [ALPHA] [C] [EXE] -> BxC | 25. [SHIFT][Mcl] [EXE] -> Mcl | 25. [ALPHA] [D] [EXE] -> D | 0. La utilización de las teclas [SHIFT][Mcl] ha borrado el contenido de todas memorias.

1 € = 140 Yenes, ¿cuánto hacen son 33.775 Yenes en Euros? ¿Cuanto valen 2.750 € en Yenes? 140 [ ] [ALPHA] [A] [EXE] -> 140 A | 140. 33775 [÷] [ALPHA] [A][EXE] -> 33775÷A | 241.25 2750 [x] [ALPHA] [A] [EXE] -> 2750xA | 385000.

Supongamos que deseamos efectuar la operación siguiente: Artículos disponibles en almacén por la mañana = 200 Artículos suministrados durante el día: 5 cajas de 12 unidades y 9 cajas de 6 unidades Artículos vendidos durante el día: 2 cajas de 24 unidades ¿Cuántos artículos quedan en el almacén al nal del día? Si cada artículo cuesta 3,50€, ¿Cuál es el valor total de los artículos existentes en almacén?

Se introduce en la memoria el número de artículos existentes al principio en el almacén: 200 [ ] [ALPHA] [A] [EXE] -> 200 A | 200.

Se añaden los artículos suministrados y se descuentan los artículos vendidos: [+] 5 [x] 12 [+] 9 [x] 6 [-] 2 [x] 24 [ ] [ALPHA] [A] [EXE]

-> 200.+5x12+9x6-2x24 A | 266. Las existencias en almacén cuentan con 266 artículos.

Asimismo, para calcular el valor de las existencias se procede de la manera siguiente: 3 [.] 5 [x] [ALPHA] [A] [EXE] -> 3.5xA | 931.

GC700_01_GC700Z_01IM0108.indd 96 6/3/08 17:33:42

Español

97

Parte entera (Int), Parte decimal (Frac)

3. FUNCIONES ARITMÉTICAS

[SHIFT] [Int]

Proporciona la parte entera del valor introducido inmediatamente después.

[SHIFT] [Frac]

Proporciona la parte decimal del valor introducido inmediatamente después.

[SHIFT] [Int] 9 [.] 256 [EXE] -> Int 9.256 | 9. [SHIFT] [Frac] 9 [.] 256 [EXE] -> Frac 9.256 | 0.256

Funciones inversas, raíces cuadradas y exponentes

[X-1]

Calcula la función inversa del valor introducido

inmediatamente antes.

[X2]

Calcula el cuadrado del valor introducido inmediatamente antes.

[xy]

Eleva el valor x (introducido anteriormente) a la potencia de y (introducida después).

[SHIFT][10x]

Calcula la potencia en base 10 del número introducido inmediatamente después.

p. ej.:

-03

GC700_01_GC700Z_01IM0108.indd 97 6/3/08 17:33:42

Español

98

Raíces

[√]

Calcula la raíz cuadrada del número introducido inmediatamente después.

[SHIFT] [3√]

Calcula la raíz cúbica del número introducido inmediatamente después.

[x√]

Calcula la raíz Xn del número introducido

inmediatamente después.

Utilizando de nuevo los ejemplos anteriores: [√] 9 [EXE] -> √9 | 3. [SHIFT] [3√] 125 [EXE] ->

3

√125 | 5.

5 [x√] 32 [EXE] -> 5 x√ 32 | 2.

Fracciones

[a b/c]

Permite introducir una fracción con numerador “b” y denominador “c”, así como una parte entera “a” (opción

facultativa)

Cambia la visualización de una fracción de tipo número entero + fracción irreducible en número decimal y

viceversa.

[SHIFT] [d/c]

Convierte una fracción del tipo número entero + fracción irreducible en una fracción irreducible y viceversa.

Signicado de las notaciones a b/c y d/c:

p. ej.:

a = 3, b=1 y c=2. “a” es la parte entera de x, es decir, x= 3 + 1/2 = 3,5

De hecho:

En notación d/c, d=7 y c=2.

3

1

2

X=

7

2

X=

GC700_01_GC700Z_01IM0108.indd 98 6/3/08 17:33:43

Español

99

Su calculadora le permite efectuar un cierto número de operaciones aritméticas expresadas o convertidas en fracciones.

Es posible sustituir a, b y c por un cálculo colocado entre paréntesis. Sin embargo, en algunos casos se podrá obtener un resultado expresado de forma decimal pero no así un resultado expresado como una fracción.

p. ej.:

3 [a b/c] 1 [a b/c] 2 [+] 4 [a b/c] 3 [EXE] -> 3 1 2 + 4 3 | 4 5 6. [a b/c] | 4.833333333 [a b/c] | 4 5 6. [SHIFT] [d/c] | 29 6.

1.25 [+] 2 [a b/c] 5 [EXE] -> 1.25+2 5 | 1.65 La suma de una fracción y de un número decimal (cuyo parte decimal no sea nula) tendrá como resultado un número decimal y no podrá convertirse en fracción.

Es posible utilizar una fracción como exponente:

[SHIFT] [10x] 2[a b/c]3 [EXE] -> 102 3 | 4.641588834

Notas: l Para efectuar una operación como por ejemplo + , si utilizamos [SHIFT] [X-1], tan sólo obtendremos un resultado decimal que no puede expresarse como fracción.

6 [X-1] + 7 [X-1] [EXE] -> 6-1+7

-1

| 0.3095238095

l Para una fracción como por ejemplo:

Podremos utilizar la notación a b/c para obtener un resultado expresado en fracciones. Para ello, será necesario introducir el cálculo de la manera siguiente:

24 [a b/c] [(] 4 [+] 6 [)] [EXE] -> 24 (4+6) | 2 2 5 [a b/c] -> 24 (4+6) | 2.4

3

1

2

+

4

3

LLLL

L

10

2

3

1 6

1 7

L

24 4 + 6

L L

L

GC700_01_GC700Z_01IM0108.indd 99 6/3/08 17:33:43

Español

100

Funciones logarítmicas y exponenciales

[ln]

Tecla de logaritmo neperiano.

[log] Tecla de logaritmo decimal.

[SHIFT] [ex]

Tecla de función exponencial.

p. ej.:

[ln] 20 [EXE] -> ln 20 | 2.995732274 [log] [.] 01 [EXE] -> log .01 | -2. [SHIFT] [ex] 3 [EXE] -> e3 | 20.08553692

Funciones hiperbólicas

[hyp]

Tecla de función hiperbólica.

Utilizando esta tecla se obtienen las diferentes funciones hiperbólicas:

[ hyp ] [cos] cosh(x)

Coseno hiperbólico.

[ hyp ] [sin]

sinh(x)

Seno hiperbólico.

[ hyp ] [tan]

tanh(x)

Tangente hiperbólica.

[SHIFT] [ hyp ] [cos-1]

cosh-1 (x)

Argumento del coseno hiperbólico.

[SHIFT] [ hyp ] [sin-1]

sinh-1 (x)

Argumento del seno hiperbólico.

[SHIFT] [ hyp ] [tan-1]

tanh-1(x)

Argumento de la tangente

hiperbólica.

Nota: se puede introducir [SHIFT] [ hyp ] [cos-1] o [ hyp ] [SHIFT] [cos-1], ya que las dos son equivalentes.

GC700_01_GC700Z_01IM0108.indd 100 6/3/08 17:33:43

Lexibook GC700Z_01, GC700_01 Instructions Manual

Specifications and Main Features

Frequently Asked Questions

User Manual