LEXIBOOK GC2210FR User Manual

Manuel d’instruction

GC2210FR

2

CALCULATRICE GRAPHIQUE LEXIBOOK® GC2210FR

Calculatrice scientique graphique, fonctions base N, fonctions statistiques

avancées à une et deux variables (interprétation graphique, 6 types de

régression), fonctions arithmétiques, trigonométriques et complexes,

intégrales et programmation d’équation.

SOMMAIRE

INTRODUCTION

Avant la première utilisation

1. PRISE EN MAIN DE VOTRE CALCULATRICE

Mise en marche et arrêt de la calculatrice Afchage et symboles utilisés

Disposition des touches

Fonctions secondes et fonctions alphanumériques (SHIFT et ALPHA) Notations utilisées dans le manuel Touches usuelles Priorités de calcul Saisie et modication d’un calcul Calculs successifs sur une ligne

Rappel du dernier résultat (Ans) Calculs en chaîne

Calculs successifs

Calculs en boucle Menus de la calculatrice

Notation scientique et ingénieur

Choix de la notation Fixation de la position de la virgule

Choix du nombre de chiffres signicatifs

Utilisation de Rnd Calculs de pourcentage

2. MEMOIRES Rappel du dernier résultat (Ans)

Utilisation de la mémoire M Mémoires temporaires (A - F)

3. FONCTIONS ARITHMETIQUES

Inverse, carré et exposants

Racines Fractions

Logarithmes et exponentielles Hyperboliques

Factorielle

Génération de nombre aléatoire (fonction Random)

4. CALCULS TRIGONOMETRIQUES ET COMPLEXES

Nombre π Unités d’angles Choix de l’unité d’angle Cosinus, sinus, tangente Arccosinus, arcsinus, arctangente Conversion sexagésimale (degrés / minutes /secondes)

Calculs horaires Coordonnées polaires

Nombres complexes

5 5 6 6 6 8

9 10 10 11 11 13 14 14 14 14 15 16 16 17 18 19 19 21 21 21 22 23 23 23 23 25 25 26 26 27 27 27 27 28 28 29 29 30 31

3

5. CALCULS EN BASE-N

Changements de base Les opérateurs logiques Notations Commandes du mode Base N et conversions Calculs en Base N Opérateurs logiques en Base N

6. FONCTIONS AVANCEES

Calculs d’intégrales Commentaires préliminaires Saisie d’intégrale Programmation d’une équation

7. FONCTIONS GRAPHIQUES

Dénitions et notations Tracer une courbe Courbes préprogrammées

Courbes utilisateur

Courbes paramétrées Effacer une courbe Fonction Zoom Résolution graphique Fonction Trace Fonctions Sketch Fonction Plot

Fonction Line

Fonction Tangente Fonction Horizontale

Fonction Verticale

8. STATISTIQUES

Commentaires préliminaires Statistiques à une variable Saisie des données Correction et/ou effacement des données saisies Calcul de moyenne et écart-type Représentation graphique Statistiques à deux variables

Choix du type de régression

Saisie des données Correction et/ou effacement des données saisies Calcul de moyenne et écart-type

Calculs de régression

Représentation graphique

9. MESSAGES D’ERREUR

Causes possibles d’erreurs Valeurs admissibles

10. PRECAUTIONS D’EMPLOI

IMPORTANT : sauvegarde de vos données Utilisation de RESET Remplacement des piles

Entretien de votre calculatrice

11. INDEX

12. ANNEXE : DETAIL DES FORMULES DE REGRESSION

13. GARANTIE

33 33 33 34 35 36 37 38 38 38 38 39 41 41 41 42 42 44 45 45 47 48 49 49 50 50 51 51 52 52 53 53 54 54 56 57 57 59 59 59 60 62 64 64 64 66 66 66 67 69 70 72 74

4

INTRODUCTION

Nous sommes heureux de vous compter aujourd’hui parmi les nombreux utilisateurs des produits Lexibook® et nous vous remercions de votre

conance.

Depuis plus de 15 ans, la société française Lexibook conçoit, développe, fabrique et distribue à travers le monde des produits électroniques pour tous, reconnus pour leur valeur technologique et leur qualité de

fabrication.

Calculatrices, dictionnaires et traducteurs électroniques, stations météo, multimédia, horlogerie, téléphonie… Nos produits accompagnent votre

quotidien.

Pour apprécier pleinement les capacités de la calculatrice graphique

GC2210FR, nous vous invitons à lire attentivement ce mode d’emploi.

Avant la première utilisation

Avant de démarrer, veuillez suivre attentivement les étapes suivantes :

• Retirez avec précaution la languette plastique de protection du compartiment à piles .

• Faites coulisser la calculatrice dans le couvercle pour accéder au clavier.

• Retirez la pellicule statique protectrice de l’écran LCD.

• Appuyez sur la touche [AC/ON] pour mettre la calculatrice en marche.

Vous verrez alors la lettre D et un curseur clignotant apparaître sur

l’écran. Si ce n’est pas le cas, vériez l’état des piles et recommencez l’opération (voir si nécessaire le chapitre « Précautions d’emploi »).

• Localisez le trou du RESET au dos de l’appareil dans le compartiment à piles. Insérez une pointe ne (un trombone par exemple) et appuyez doucement.

Pour plus d’informations concernant les piles, l’importance de RESET et

de la sauvegarde de vos données, voir le chapitre « Précautions

d’emploi ».

5

1. PRISE EN MAIN DE VOTRE CALCULATRICE

Mise en marche et arrêt de la calculatrice

[AC/ON]

Arrêt automatique :

La calculatrice s’éteint automatiquement si vous n’effectuez aucune opération durant environ six minutes.

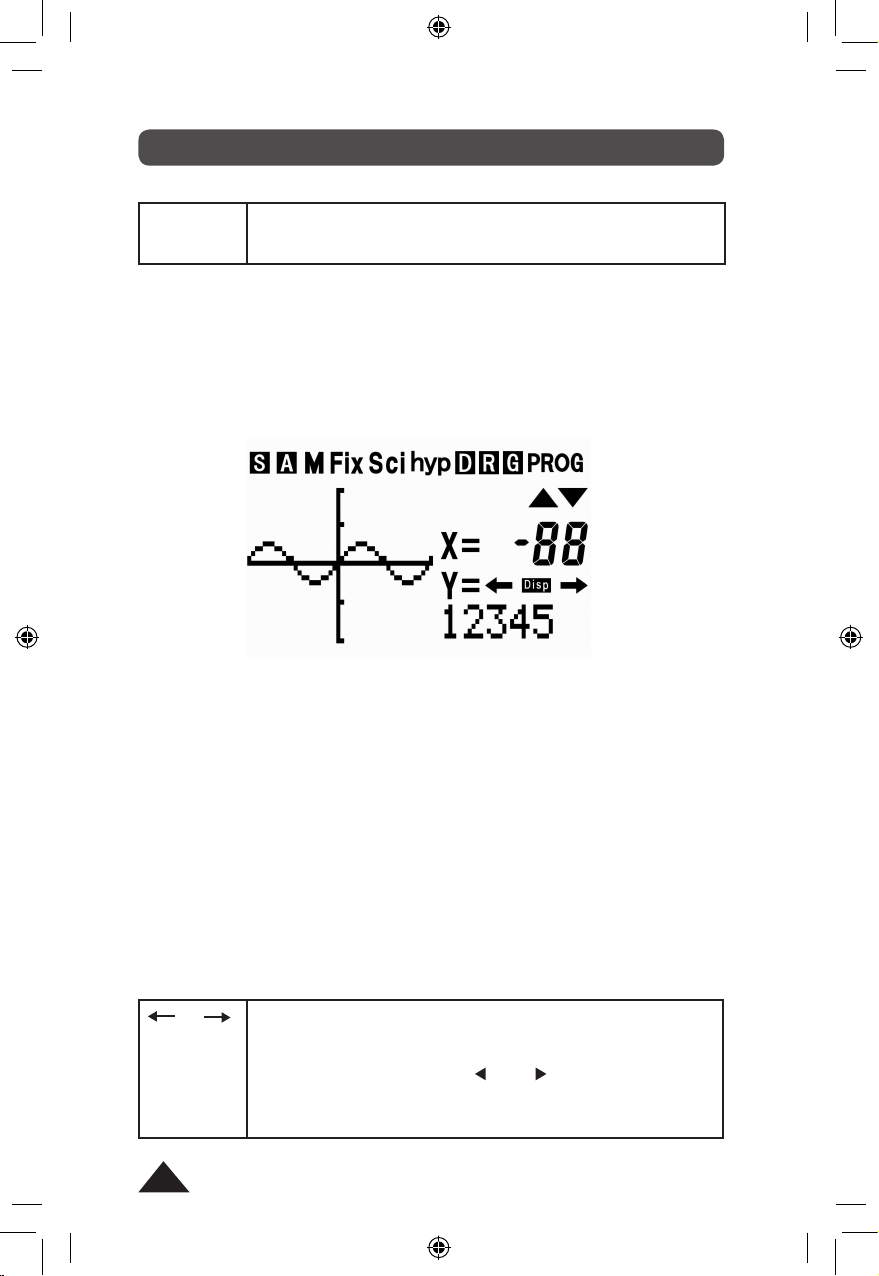
Afchage et symboles utilisés

L’afchage correspondant aux fonctions usuelles est le suivant :

Sur la ligne du bas vous pouvez visualiser en alphanumérique les opérations saisies. Puis, une fois que vous appuyez sur [=] cette ligne afche à partir de la droite un résultat numérique, avec 10 chiffres signicatifs, ou bien 10 chiffres signicatifs plus 2, en haut sur la droite, de notation scientique (voir paragraphe “Notation scientique”).

Mise en marche de la calculatrice. Mise à zéro.

A noter que, si votre résultat apparaît en 10 ou 10+2 chiffres signicatifs, les calculs internes sont réalisés avec 12 chiffres signicatifs et deux d’exposant.

Sur la ligne du haut vous trouverez un certain nombre de symboles (ici ils sont tous afchés mais ce n’est pas le cas au cours du fonctionnement normal). Ces symboles vous donnent des indications qui vous permettent une meilleure lisibilité des opérations en cours :

ou

S’afche pour indiquer que le calcul en cours est trop long pour être afché en entier, ou que le menu comporte d’autres options sur la gauche ou sur la droite. Dans ce cas appuyer sur [ ] ou [ ] pour afcher le reste du calcul ou du menu.

6

, ou les deux

ensemble

Indique que plusieurs lignes de calculs sont en mémoire. Si vous voulez vérier ou modier ces lignes de calcul, appuyez sur [ ], [ ].

Disp

CMPLX

i

SD

REG

S

A

…… ERROR

hyp

Fix

Sci

Indique que la valeur afchée est un résultat intermédiaire, voir le paragraphe « Calculs successifs » sur une ligne, ou le chapitre « Programmation ».

Indique que la calculatrice est en mode Nombres complexes.

En mode complexe, indique que la valeur afchée est la partie imaginaire d’un nombre complexe.

Indique que la calculatrice est en mode statistique à une variable.

Indique que la calculatrice est en mode statistique à deux variables.

La touche SHIFT est activée.

La touche ALPHA est activée.

S’afche quand le calcul excède les limites permises ou qu’une erreur est détectée. Les différents messages d’erreur, leurs causes et leurs remèdes sont détaillés dans le chapitre correspondant, « Messages d’erreur ».

S’afche quand la fonction hyperbolique est activée.

Indique que le résultat sera afché avec un nombre déterminé de chiffres après la virgule.

Indique que le mode notation scientique est activé.

Eng

D

Indique que le mode notation ingénieur est activé.

S’afche en mode degré ou quand la mesure d’angle afchée est en degrés.

R

S’afche en mode radian ou quand la mesure d’angle afchée est en radians.

G

S’afche en mode grade ou quand la mesure d’angle afchée est en grades.

M

X= ou Y=

S’afche quand la mémoire indépendante M est non nulle.

S’afche lorsque la fonction STO ou RCL (fonctions concernant les mémoires temporaires) est activée.

PROG

S’afche pendant la saisie d’une équation dans la mémoire programmable.

7

Disposition des touches

8

Fonctions secondes et fonctions alphanumériques (SHIFT et ALPHA)

[SHIFT]

Accès aux fonctions secondes, signalées en bleu en haut à gauche de la touche concernée.

[ALPHA]

Accès aux fonctions alphanumériques, signalées en orange en haut à droite de la touche concernée.

Le plus souvent les touches de votre calculatrice comportent au moins deux fonctions, voire trois ou quatre. Elles sont repérées par des couleurs et par leur position autour de la touche qui sert à y accéder. Certaines ne sont accessibles que dans des modes bien précis et seront détaillées dans les chapitres correspondants (Base N, statistiques).

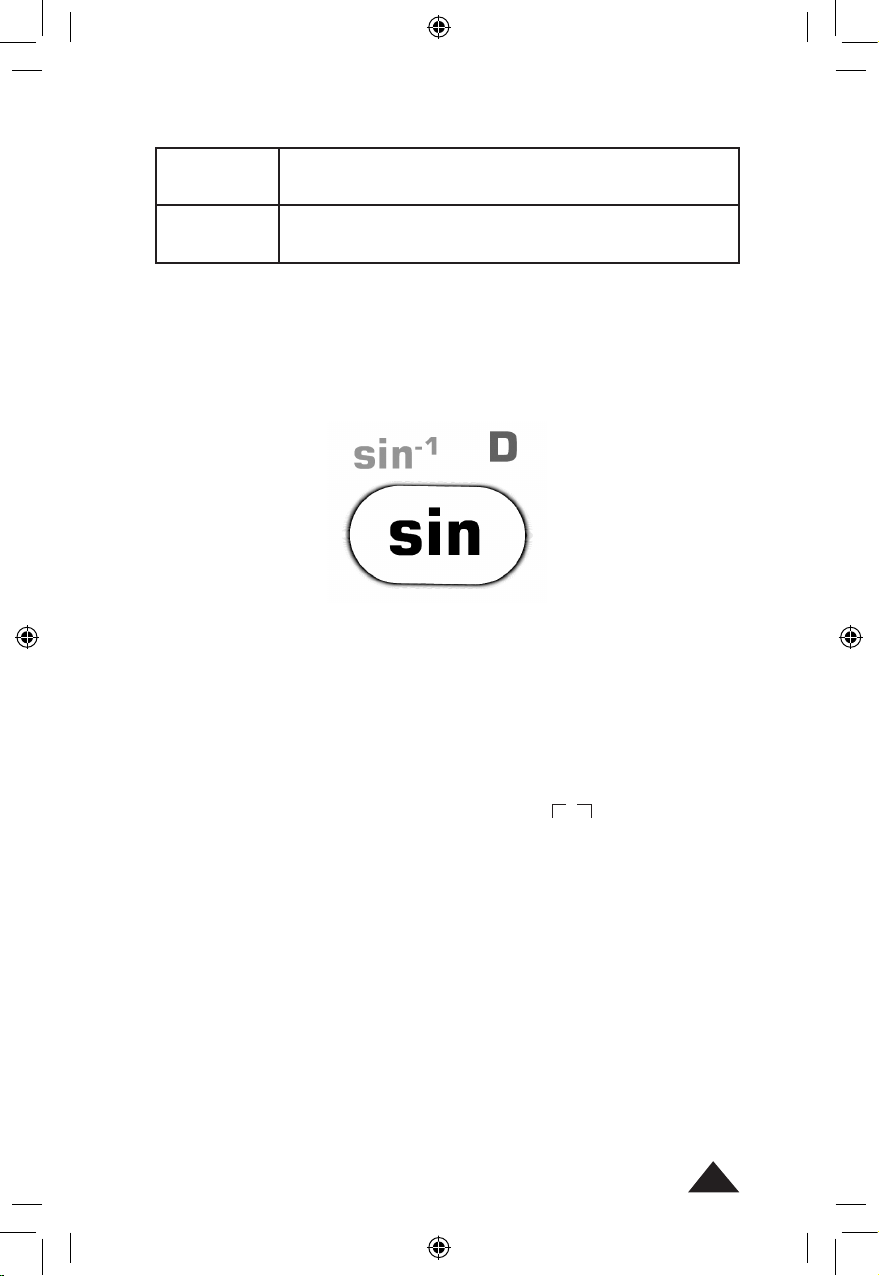
Par exemple :

• sin est la fonction principale, en accès direct par pression de la touche.

• sin-1 est la fonction seconde, il faut appuyer sur [SHIFT] puis sur la touche concernée (S apparaît brièvement à l’afchage).

• D est la fonction alphanumérique, il faut appuyer sur [ALPHA] puis sur la touche concernée (A apparaît brièvement à l’afchage). Il s’agit principalement de touches pour les mémoires ou la saisie de texte.

Les autres fonctions indiquées en jaune ou entre sont des fonctions relatives aux nombres complexes, aux fonctions Base N ou statistiques qui seront détaillées dans les chapitres correspondants.

Si vous appuyez une fois sur la touche [SHIFT], le symbole S s’afche sur l’écran pour indiquer que [SHIFT] est activée et que vous pouvez accéder aux fonctions secondes. Le symbole s’éteint dès que vous appuyez sur une autre touche ou que vous appuyez une nouvelle fois sur [SHIFT].

De même si vous appuyez une fois sur la touche [ALPHA], le symbole A s’afche sur l’écran pour indiquer que [ALPHA] est activée et que vous pouvez accéder aux fonctions alphanumériques. Le symbole s’éteint dès que vous appuyez sur une autre touche ou que vous appuyez une nouvelle fois sur [ALPHA].

9

Notations utilisées dans le manuel

Dans ce manuel les fonctions seront indiquées comme suit (en reprenant l’exemple précédent): principale [sin]

FRANÇAIS

seconde [SHIFT][sin-1] alpha [ALPHA][D]

Les touches [0] à [9] seront notées 0 à 9 (sans crochets) pour faciliter la lecture.

Les calculs et les résultats seront présentés comme suit :

description saisie -> afchage alphanumérique | ligne résultat

Ex : Pour effectuer le calcul (4+1)x5= le processus sera noté ainsi : [(] 4 [+] 1 [)] [x] 5 [=] -> (4+1)x5 | 25.

Lorsque cela ne nuira pas à la compréhension d’un exemple, une partie de cet afchage pourra être omise.

Touches usuelles

[0]-[9]

Touches de chiffres.

[+]

[-]

[x]

[÷]

[=]

[.]

[(-)]

[(], [)]

[AC/ON]

10

Addition.

Soustraction.

Multiplication. Le signe peut être omis devant les parenthèses, des constantes ou des noms de variables, par exemple : 2(5+6), 3π, 4B, 5ln 2 ou 2sin 30.

Division.

Donne le résultat.

Insertion de la virgule pour un nombre décimal.

Ex : pour écrire 12,3 -> 12[.]3

Change le signe du nombre qui sera rentré immédiatement après. 5 [x] [(-)] [5] [=] -> -25.

Ouvre / ferme une parenthèse.

Ex : [(] 4 [+] 1 [)] [x] 5 [=] -> 25.

Efface l’écran.

Priorités de calcul

Quand il y a plusieurs opérations à réaliser dans un calcul, votre calculatrice les évalue et détermine l’ordre dans lequel les effectuer, en fonction des règles arithmétiques. Cet ordre de priorité est le suivant :

1. Les opérations entre parenthèses, et, en cas de plusieurs niveaux de parenthèses, la dernière parenthèse ouverte.

2. Les fonctions utilisant un type d’exposant telles que x-1, x2 , √, xy et x√, ainsi que le changement de signe [(-)].

3. Les fonctions de type cos, sin, ln, ex…

4. Les fonctions de saisie d’une donnée, telles que [º ’’’] et [a b/c].

5. Les multiplications et divisions (la multiplication peut être implicite, par exemple 2cosπ).

6. Les additions et soustractions.

7. Les fonctions qui signalent la n d’un calcul ou enregistrent un résultat : [=], [STO], [M+], [DT] etc.

Lorsque les opérateurs sont de même niveau de priorité la calculatrice les effectue tout simplement par ordre d’apparition de gauche à droite. Au sein des parenthèses l’ordre des priorités est conservé.

Ex :

1 [+] 3 [x] 5 [=] -> 1+3x5 | 16. [(] 1 [+] 3 [)] [x] 5 [=] -> (1+3)x5 | 20. 10 [-] 3 [X2] [=] -> 10-32 | 1. 5 [Xy] [ln] 2 [=] -> 5 ^ ln 2 | 3.05132936 soit 5

ln2

Votre calculatrice fait la différence entre les différents niveaux de priorité et, au besoin, mémorise les données et les opérateurs jusqu’à la bonne résolution du calcul, et ce jusqu’à 24 niveaux différents pour un calcul en cours et 9 niveaux pour les valeurs numériques. Ces niveaux sont appelés “stacks” en anglais ; si votre calcul est très compliqué et dépasse les possibilités pourtant étendues de votre machine vous verrez apparaître le message suivant Stk ERROR (dépassement de la capacité “stacks”).

FRANÇAIS

Saisie et modication d’un calcul

[ ], [ ]

Pour déplacer le curseur sur la ligne alphanumérique et éditer un calcul.

[DEL]

Efface le caractère à l’endroit où se trouve le curseur.

[SHIFT] [INS]

Insère un caractère immédiatement à gauche du curseur d’insertion.

[ ], [ ]

Pour passer au calcul précédent / suivant.

11

Grâce à sa ligne alphanumérique, votre calculatrice vous permet non seulement de visualiser le calcul en cours, mais aussi de revoir et modier vos calculs après en avoir obtenu les résultats. Votre calculatrice pouvant conserver en mémoire jusqu’à 79 caractères sur une ligne, jusqu’à 20 lignes et 500 caractères en tout ! Vous pouvez saisir dans votre calculatrice vos calculs et ceux-ci s’inscrivent sur la ligne du haut à partir de la gauche dans un style alphanumérique facile à lire et à corriger.

Une fois le calcul saisi et le résultat obtenu en appuyant sur [=], il est facile de revoir et modier votre calcul grâce aux èches [ ], [ ]. Pour revoir un calcul précédent, et faire déler les lignes de calcul, utilisez [ ] et [ ].

Remarques sur [SHIFT] [INS] :

• Le curseur change tant que l’insertion est activée .

• On peut utiliser [DEL] pendant que l’insertion est activée, cela efface le caractère situé à gauche du curseur.

• L’insertion est désactivée lorsqu’on appuie sur [ ] ou [ ], sur [SHIFT][INS], ou sur [=] si on souhaite obtenir tout de suite le résultat.

Remarques sur la saisie de calculs :

Vous pouvez saisir en une seule fois un calcul jusqu’à une longueur de 79 caractères ; à noter que même si une fonction telle que sin-1 nécessite de taper sur 2 touches et qu’elle s’afche à l´écran en plusieurs lettres, elle n’est comptée que pour un caractère par la calculatrice. Vous pouvez vérier cela en observant le déplacement du curseur. Si votre calcul est excessivement long, mieux vaut le découper en plusieurs parties.

Note sur la position du curseur :

Une fois un résultat obtenu, si vous appuyez sur [ ] ou [ ], le curseur se positionne au début du calcul. Si vous appuyez sur [ ], le curseur se positionne à droite à la n du calcul.

Ex : Vous avez effectué la saisie suivante : 34 [+] 57 [-] 27 [x] 78 [+] 5 [=] -> 34+57-27x78+5 | - 2010.

Si vous appuyez sur [ ] vous retrouvez l’afchage alphanumérique de

votre calcul. Le carré gris indique la position du curseur clignotant.

• Vous voulez modier 27 en 7 dans le calcul [ ] -> 34+57-27x78+5

Vous positionnez le curseur à l’aide de la touche [ ] pour vous placer immédiatement sur l’endroit de correction, c’est-à-dire le 2 (le carré gris indique la position du curseur).

12

[ ]six fois -> 34+57-27x78+5 [DEL] -> 34+57-7x78+5 [=] -> 34+57-7x78+5 | -450.

• Vous voulez modier 34 en 3684 dans le calcul Vous positionnez le curseur à l’aide de la touche [ ] pour vous placer à l’endroit de correction, c’est-à-dire le 4.

[ ] -> 34+57-7x78+5 [ ] -> 34+57-7x78+5

[SHIFT] [INS] 6 -> 364+57-7x78+5 8 -> 3684+57-7x78+5 [=] -> 3684+57-7x78+5 | 3200.

• Vous avez effectué la saisie suivante : 4 [+] 5 [=] 5 [-] 2[=] Et vous voulez modier 4+5 en 4x5 [ ] deux fois -> 4+5 | 9. [ ] -> 4+5 [x] -> 4x5 [=] -> 4x5 | 20.

Calculs successifs sur une ligne

[ALPHA] [ ]

Marque de séparation entre deux calculs consécutifs saisis sur une même ligne.

[AC/ON]

Interrompt l’exécution de calculs consécutifs.

Votre calculatrice vous permet, si vous le souhaitez, de saisir plusieurs calculs à réaliser successivement sur une seule ligne, puis de les exécuter en appuyant sur [=]. La calculatrice effectue alors le premier calcul saisi ; elle afche le résultat intermédiaire et le symbole Disp pour vous indiquer que l’exécution des calculs n’est pas terminée. Si vous appuyez sur [=] la calculatrice passe au deuxième calcul et ainsi de suite jusqu’au dernier, pour lequel Disp s’éteint.

Ex : Vous effectuez le calcul suivant : 54+39= 9-18= 4x6-2= 50x12=

Vous pouvez le saisir comme suit : 54 [+] 39 [ALPHA][ ] 9 [-] 18 [ALPHA][ ] 4 [x] 6 [-] 2 [ALPHA][ ] 50 [x] 12 [=]

-> 54+39 9-18 4x6-2 50x12=

-> 54+39 | 93. Disp [=] -> 9-18 | -9. Disp [=] -> 4x6-2 | 22. Disp [=] -> 50x12 | 600.

13

Notes :

• On ne peut pas éditer les calculs tant que Disp est afché et que le dernier calcul n’est pas atteint, sauf si on appuie sur [AC/ON] pour les interrompre.

• Dans l’exemple précédent, si on appuie une fois de plus sur [=] le calcul recommence (l’écran afche 93. et Disp).

• Voir aussi pour ces calculs comment effectuer le rappel du dernier résultat.

Rappel du dernier résultat (Ans)

Rappelle le résultat du calcul précédent.[SHIFT][Ans]

Chaque fois que vous effectuez un calcul, son résultat est automatiquement stocké dans la mémoire Ans, dont vous pouvez rappeler le contenu pour le calcul suivant.

Ex: 24 [÷] [(] 4[+]6 [)] [=] -> 24÷(4+6) | 2.4 On peut alors calculer 3x ANS + 60÷ANS 3 [x] [SHIFT][Ans] [+] 60 [÷][SHIFT][Ans] [=]

-> 3xAns+60÷Ans | 32.2

Calculs en chaîne

Il s’agit de calculs pour lesquels le résultat du calcul précédent sert de premier opérande du calcul suivant. Vous pouvez notamment utiliser dans ces calculs les fonctions [√], [X2], [sin],... [AC/ON] 6 [+] 4 [=] -> 6+4 | 10. [+] 71 [=] -> Ans+71 | 81. [√][=] -> √ | 9.

Calculs successifs

L’utilisation de Ans est impérative pour les calculs successifs écrits sur une ligne : 54 [+] 39 [ALPHA][ ] [SHIFT][Ans] [-] 18 [=] -> 93. puis 75. 54 [+] 39 [ALPHA][ ] [-] 18 [=] -> 93. puis -18.

Calculs en boucle

Le même calcul se répète chaque fois que l’on appuie sur [=], la valeur du résultat étant modiée chaque fois : 9 [+] 1 [=] -> 9+1 | 10. [SHIFT][Ans][-]1 [=] -> Ans-1 | 9. [=] -> | 8. [=] -> | 7. [=] -> | 6. Pour ce genre d’expressions il faut être attentif à ne pas appuyer deux fois sur [=] par mégarde sous peine de recopier le mauvais résultat.

14

Menus de la calculatrice

[MENU]

Touche d’accès aux menus.

[ ], [ ]

[=]

Pour sélectionner une option.

Valide l’option choisie.

Votre calculatrice possède un système de menu convivial pour vous aider à sélectionner les modes de fonctionnement qui conviennent pour vos calculs et autres opérations. Il y a cinq modes de fonctionnement indépendants : COMP mode normal, pour tous les calculs habituels. CMPLX mode nombres complexes. SD mode statistique à une variable. REG mode statistique à deux variables. BASE-N mode Base N. Il y a aussi un certain nombre de menus, qui vous offrent des options de fonctionnement supplémentaires. Ceux-ci apparaîtront ou non selon qu’ils sont disponibles ou pas dans le mode choisi. Si une èche apparaît sur la droite de l’écran, elle indique qu’un même menu comporte plusieurs écrans, utilisez les èches gauche et droite pour visualiser toutes les options disponibles.

Pour sélectionner une option, déplacez le surlignement noir sur la fonction ou le mode que vous voulez sélectionner, et appuyez sur [=].

Si on presse une fois [MENU], cela donne:

MODE?

COMP CMPLX

MODE?

SD REG BASE-N

Si on presse [MENU] une seconde fois :

GRAPH? FUNCT PARAM

On presse [MENU] une troisième fois, et ainsi de suite :

ANGLE?

Deg Rad Gra

[MENU]

FORMAT? Fix Sci Norm

[MENU]

retour à l’afchage normal.

_

15

Pour :

CMPLX voir en n du chapitre les calculs trigonométriques. SD, REG voir le chapitre les fonctions statistiques. BASE-N voir le chapitre les calculs en Base N. Deg, Rad, Gra voir le chapitre les calculs trigonométriques. FUNCT, PARAM voir le chapitre les fonctions graphiques.

Sauf indication contraire dans ce manuel votre calculatrice est en

mode normal, et nous allons détailler ci-après les différentes

options Fix, Sci et Norm.

Notation scientique et ingénieur

La GC2210FR afche directement le résultat d’un calcul (x) en mode décimal normal si x appartient à l’intervalle suivant :

0.000000001≤ | x | ≤ 9999999999

Note : |x| est la valeur absolue de x, soit |x|= –x si x≤0 et |x|=x si x≥0.

En dehors de ces limites la calculatrice afchera automatiquement le résultat d’un calcul selon le système de notation scientique, les deux chiffres en haut à droite représentant l’exposant du facteur 10.

Ex :

Carré de 2 500 000 et son inverse

2500000 [X2][=] -> 25000002 | 6.2512 soit 6,25 x 10 [SHIFT][X-1][=] ->Ans -1 | 1.6

–13

soit 1,6 x 10

12

-13

La notation dite ingénieur découle du même principe, mais pour cette notation il faut que la puissance de 10 soit un multiple de 3 (103, 106,109 etc.). En reprenant l’exemple précédent : 6,25 x 1012 s’écrit aussi 6.25 s’écrira 160.

–15

12

en notation ingénieur, mais 1,6 x 10

-13

Choix de la notation

[EXP]

Saisie d’une valeur en notation scientique.

[ENG] Ou [SHIFT] [ ]

Flèche au-dessus de la

touche [ENG]

[MENU] [MENU] [MENU] [MENU] [ ][ ][=] suivi de 1 ou 2

16

Passage en notation ingénieur. Chaque fois que l’on appuie sur [ENG] l’exposant diminue de 3. Chaque fois que l’on appuie sur [SHIFT] [ ] l’exposant augmente de 3.

Réglage des paramètres de notation scientique. Cette fonction donne le choix entre deux options : Norm 1 : afchage normal pour 10-2≤|x|<1010, afchage en notation scientique au-delà. Norm 2 : afchage normal pour 10-9≤|x|<1010, afchage en notation scientique au-delà.

Pour un nombre qui se situe dans l’intervalle précédent, votre calculatrice vous permet de le saisir directement en notation scientique, an d’éviter la saisie répétitive de zéros.

Ex : Pour entrer 2 500 000 soit 2,5 x 106 en notation scientique : 2 [.] 5 [EXP] 6 [=] -> 2.5E6 | 2500000.

Pour entrer 2 500 0002 soit (2,5 x 106 )2 en notation scientique : 2 [.] 5 [EXP] 6 [X2] [=] -> 2.5E62 | 6.25

12

Pour entrer 0.00016 soit 1,6 x 10-4 en notation scientique : 1 [.] 6 [EXP] [(-)] 4 [=] -> 1.6E-4 | 0.00016

Avec cette valeur on peut expérimenter la différence entre les options Norm1 et Norm 2 :

1 [.] 6 [EXP] [(-)] 4 [=] -> 1.6E-4 | 0.00016 [MENU][MENU][MENU][MENU]

-> Norm 1~2? | 1

-> 1.6E-4 | 1.6 [MENU][MENU][MENU][MENU] [ ] [ ] [=]-

[ ][ ][=]

-04

>Norm 1~2? | 2

-> 1.6E-4 | 0.00016

Pour passer à la notation ingénieur, en reprenant les exemples précédents :

2 [.] 5 [EXP] 6 [=] -> 2.5E6 | 2500000. [ENG] -> 2.5 [ENG] -> 2500. [ENG] -> 2500000. [ENG] -> 2500000000. [SHIFT] [ ] -> 2500000.

[.] 00016 [=] -> 0.00016 [SHIFT] [ ] -> 0.16 [ENG] -> 160 [ENG] -> 160000. [SHIFT] [ ] -> 160.

06

03

00

-03

00

-03

-06

-09

-06

Fixation de la position de la virgule

[MENU][MENU] [MENU][MENU][=]

+ chiffre entre 0 et 9

[MENU][MENU] [MENU][MENU] [ ][ ][=]

suivi de 1 ou 2

Choix du nombre de chiffres après la virgule, le symbole Fix s’afche.

Annulation de la xation du nombre de chiffres après

la

virgule. Cette fonction donne le choix entre deux

options :

Norm 1 : afchage normal pour 10-2≤|x|<1010, afchage en notation scientique au-delà. Norm 2 : afchage normal pour 10-9≤|x|<1010, afchage en notation scientique au-delà.

[SHIFT] [Rnd]

Arrondit une valeur décimale innie selon le format déterminé par Fix.

17

Lorsque vous xez le nombre de chiffres après la virgule d’une valeur par un réglage Fix, vous ne modiez que l’afchage de cette valeur et non la valeur mémorisée par la calculatrice, qui comporte 12 chiffres signicatifs.

Si vous le souhaitez vous pouvez modier la valeur mémorisée pour

continuer

vos calculs avec une valeur arrondie, selon le nombre de chiffres après la virgule demandé, avec la fonction [Rnd]. Ainsi la valeur utilisée par la calculatrice pour ses calculs correspondra exactement à la valeur afchée.

Ex : 100000 [÷] 3 [=] -> 100000÷3 | 33333.33333 [MODE] [MENU][MENU][MENU] [=]

-> Fix 0~9? |

2 -> | 33333.33 Fix [x] 10 [=] -> Ansx10 | 333333.33 Fix [MENU][MENU][MENU][MENU] [ ][ ][=]

-> Norm 1~2? |

1 -> | 333333.3333

Utilisation de Rnd :

100000 [÷] 3 [=] -> 100000÷3 | 33333.33333 [MENU][MENU][MENU][MENU][=]

-> Fix 0~9? |

2 -> | 33333.33

[SHIFT] [Rnd] -> Rnd | 33333.33

[x] 10 [=] -> Ansx10 | 333333.30

Note : [Rnd] n’arrondit qu’une valeur décimale innie. Par exemple si vous saisissez 12,345 en mode Fix 2:

12[.]345 [=] -> 12.345 | 12.35 Fix

[SHIFT] [Rnd][=] -> Rnd | 12.35 Fix [MENU][MENU][MENU][MENU][ ][ ][=] 1 retour en mode normal

| 12.345

La valeur initiale n’a pas été modiée.

Choix du nombre de chiffres signicatifs

[MENU][MENU] [MENU][MENU]

[=] + chiffre entre 0 et 9

[MENU][MENU] [MENU][MENU] [ ] [ ] [=]

suivi de 1 ou 2

Choix du nombre de chiffres signicatifs, le symbole

[ ]

Sci s’afche.

Annulation de la xation du nombre de chiffres après la virgule. Cette fonction donne le choix entre deux options : Norm 1 : afchage normal pour 10-2≤|x|<1010, afchage en notation scientique au-delà. Norm 2 : afchage normal pour 10-9≤|x|<1010, afchage en notation scientique au-delà.

[SHIFT] [Rnd]

Arrondit une valeur décimale innie selon le format déterminé par Fix.

18

Lorsque vous xez le nombre de chiffres signicatifs d’une valeur par un réglage Sci, vous ne modiez que l’afchage de cette valeur et non la valeur mémorisée par la calculatrice, qui comporte 12 chiffres signicatifs. Si vous le souhaitez vous pouvez modier la valeur mémorisée avec la fonction [Rnd] pour continuer vos calculs avec une valeur arrondie, selon le nombre de chiffres signicatifs demandé.

Ex :

100000 [÷] 3 [=] -> 100000÷3 | 33333.33333 [MENU] [MENU] [MENU] [MENU] [ ][=]

-> Sci 0~9? |

3 -> | 3.33 04 Sci [x] 10 [=] -> Ansx10 | 3.33 05 Sci [MENU] [MENU] [MENU] [MENU] [ ][ ][=]

-> Norm 1~2? |

1 -> | 333333.3333

Utilisation de Rnd

100000 [÷] 3 [=] -> 100000÷3 | 33333.33333 [MENU][MENU][MENU][MENU] [ ][=]

-> Sci 0~9? |

3 -> | 3.33 04 Sci

[SHIFT] [Rnd] -> Rnd | 3.33 04 Sci

[x] 10 [=] -> Ansx10 | 3.33 05 Sci [MENU][MENU][MENU][MENU] [ ][ ][=]

-> Norm 1~2? |

1 -> | 333000.

Calculs de pourcentage

[SHIFT] [%]

Calcule un pourcentage, l’augmentation ou la diminution exprimée en pourcentage.

19

[÷][SHIFT] [%] calcule un pourcentage à partir de deux valeurs. [-] [SHIFT] [%] calcule le pourcentage à la hausse ou à la baisse.

[x] [SHIFT] [%] calcule une quantité à partir d’un pourcentage. [x] [SHIFT] [%] [-] calcule la diminution à partir d’un pourcentage. [x] [SHIFT] [%] [+] calcule l’augmentation à partir d’un pourcentage.

Ex :

Il y a 312 lles sur 618 élèves au lycée, pourcentage de lles ?

312 [÷] 618 [SHIFT] [%] | 50.48543689 soit 50,5%

Prix original 200 Euros, quel pourcentage de variation si le prix change

pour 220 Euros ou 180 Euros :

220 [-] 200 [SHIFT] [%] ->220-200 | 10. soit 10% de hausse 180 [-] 200 [SHIFT] [%] ->80-200 | -10. soit 10% de baiss

Il y a 618 élèves au lycée. 49,5% sont des garçons. Combien y a-t-il de garçons ? et de lles ? 618 [x] 49 [.] 5 [SHIFT] [%] | 305.91 soit 306 garçons 618 [x] 49 [.] 5 [SHIFT] [%][-] | 312.09 soit 312 lles

Article à 180 Euros, rabais de 20%, calcul du prix nal.

180 [x] 20 [SHIFT] [%] [-] -> 180x20 | 144.

Augmentation de 10%

10 [x] 10 [SHIFT] [%][+] -> 10x10 | 11.

Division par 10% 5 [÷] 10 [SHIFT] [%] -> 5÷10 | 50. (50÷0.1)

Article à 180 Euros après rabais de 10%, quel était le prix original.

180 [÷] 90 [SHIFT] [%] -> 180÷90 | 200.

20

2. MEMOIRES

Rappel du dernier résultat (Ans)

[SHIFT][Ans]

Rappelle le résultat du calcul précédent.

Chaque fois que vous effectuez un calcul, son résultat est automatiquement stocké dans la mémoire Ans, dont vous pouvez rappeler le contenu pour le calcul suivant. Voir les exemples donnés au chapitre précédent.

Utilisation de la mémoire M

[STO] [M]

Remplace le contenu de la mémoire indépendante M par le nombre afché.

(M orange en haut à droite de la touche M+)

Pour remettre à zéro la mémoire appuyez sur 0 (zéro) puis sur [STO] [M].

[SHIFT][RCL] [M]

[M+]

Afche le contenu de la mémoire.

Ajoute le nombre afché au contenu de la mémoire.

[SHIFT][M-]

Soustrait le nombre afché au contenu de la mémoire.

Le symbole M reste afché tant que la mémoire M n’est pas vide (contient une valeur non nulle).

On remarque qu’avant STO, RCL, M- et M+, appuyer sur [=] est facultatif. La valeur de M est conservée même si on éteint et on rallume la calculatrice.

Ex :

On souhaite réaliser l’opération suivante : Articles en stock le matin = 200 Articles livrés dans la journée : 5 boîtes de 12 et 9 boîtes de 6 Articles vendus dans la journée : 2 boîtes de 24 Quantité en stock en pièces à la n de la journée ? Si chaque pièce coûte 3,50€, valeur du stock.

Le calcul s’effectue ainsi : 200 [STO][M] -> M= | 200. 5 [x] 12 [M+] -> 5x12 | 60. 9 [x] 6 [M+] -> 9x6 | 54. 2 [x] 24 [SHIFT] [M-] -> 2x24 | 48.

Le nombre de pièces en stock s’obtient en appuyant sur [SHIFT][RCL][M]

[SHIFT][RCL][M] -> M= | 266. 3 [.] 5 [x] [SHIFT][RCL][M] [=]

-> 3.5xM | 931.

21

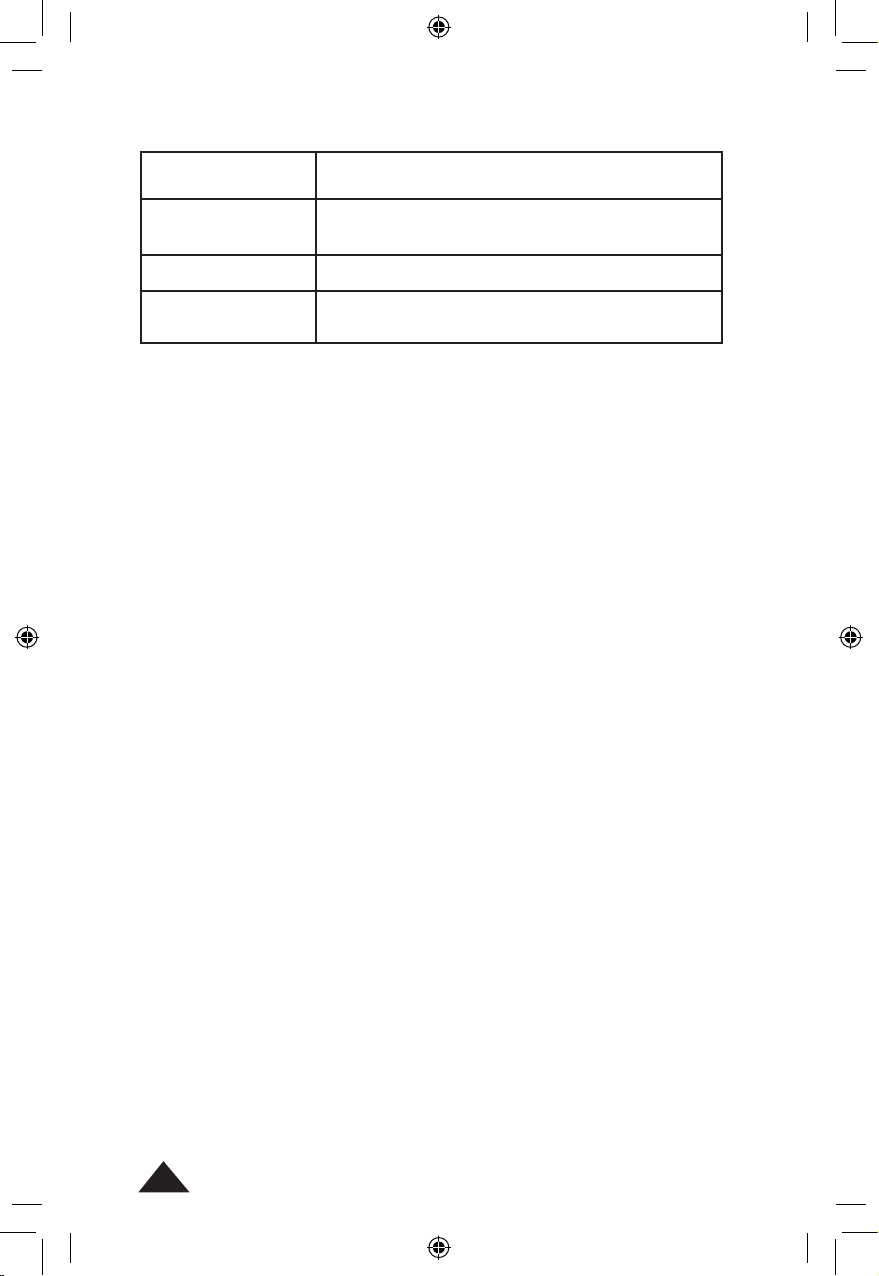
Mémoires temporaires (A - F)

[SHIFT][RCL][A] ou [ALPHA][A]

Rappelle le contenu de la mémoire A pour utilisation dans un calcul.

[STO][A]

Stocke la valeur afchée ou à calculer dans la mémoire A.

0 [STO][A] (zéro)

[SHIFT][Mcl] [=]

Mise à zéro de la mémoire A.

Efface le contenu de toutes les mémoires temporaires, y compris Ans et M.

En plus de M et Ans, votre calculatrice dispose de 8 mémoires temporaires, A, B, C, D, E, F, X, et Y. Ces mémoires temporaires vous permettent de stocker des données pour rappel et utilisation dans des calculs futurs. Les valeurs stockées dans ces mémoires temporaires sont conservées même si on éteint et on rallume la calculatrice.

Vous pouvez employer [STO], [RCL] pour chacune des touches [A], [B], [C], [D], …. [X] et [Y]. Rappel : la lettre accessible via [ALPHA] est inscrite en orange et se trouve en haut à droite de la touche concernée. Ex : A se trouve en haut à droite de la touche [X,T].

Ex : 5 [STO] [X] -> X= | 5. [-] 3 -> Ans-3 [STO] [X] -> X= | 2. 6 [x] [ALPHA] [X] [=] -> 6xX | 12. [SHIFT][RCL] [X] -> X= | 2.

Les deux premières lignes de calcul modient la valeur de X (X=5 puis

2), le calcul 6xX utilise la valeur de X mais ne la modie pas.

7 [STO] B -> B= | 7. [SHIFT][Mcl][=] -> Mcl | 0. [ALPHA] [B] [=] -> B | 0. [SHIFT][RCL][X] [=] -> X= | 0.

L’utilisation de Mcl a annulé le contenu de toutes les mémoires.

1 € = 140 Yens, combien valent 33 775 Yens en Euros ? Combien valent 2750 € en Yens ? 140 [STO] [A] -> A= | 140. 33775 [÷] [SHIFT][RCL] [A][=]-> 33775÷A | 241.25 2750 [x] [ALPHA] [A] [=] -> 2750xA | 385000.

22

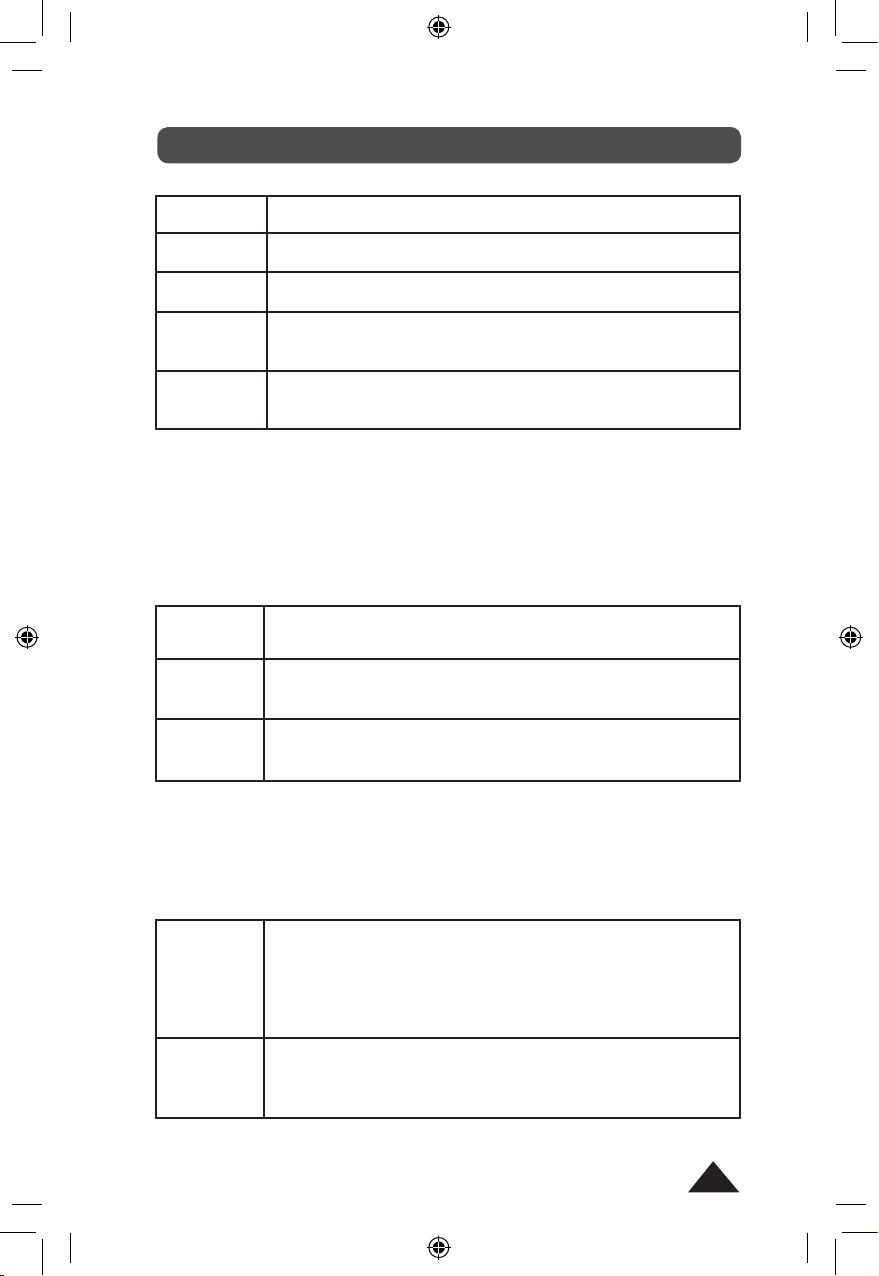
3. FONCTIONS ARITHMETIQUES

Inverse, carré et exposants

[SHIFT][X-1]

Calcule l’inverse de la valeur saisie immédiatement avant.

[X2]

[X3]

[Xy]

Calcule le carré de la valeur saisie immédiatement avant.

Calcule le cube de la valeur saisie immédiatement avant.

Elève la valeur x (saisie avant) à la puissance y (saisie après).

[SHIFT][10x]

Calcule la puissance 10 du nombre saisi immédiatement après.

Ex : 8 [SHIFT] [X-1][=] -> 8-1 | 0.125 3 [X2][=] -> 32 | 9. 5 [X3] [=] -> 53 | 125. 2 [Xy]5 [=] -> 2^5 | 32. [SHIFT][10x] [(-)] 3 [=] -> 10-3 | 1.

–03

ou 0.001 (selon le

mode Norm choisi, voir chapitre précédent).

Racines

[√]

Calcule la racine carrée du nombre saisi immédiatement après.

[SHIFT] [3√]

Calcule la racine cubique du nombre saisi immédiatement après.

[SHIFT] [x√]

Calcule la Xième racine du nombre saisi immédiatement après.

En reprenant les exemples précédents : [√] 9 [=] -> √9= | 3.

[SHIFT] [ 3√]125 [=] ->

3

√125= | 5.

5 [SHIFT] [ x√] 32 [=] -> 5 x√ 32= | 2.

Fractions

[a b/c]

Permet de saisir une fraction de numérateur b et de dénominateur c, et une partie entière a (facultative).

Change l’afchage d’une fraction de type nombre entier + fraction irréductible en nombre décimal, et vice-versa.

[d/c]

Convertit un nombre décimal en une fraction irréductible, et vice-versa.

23

Signication des notations a b/c et d/c :

1

x=

3

2

a = 3, b=1 et c=2. a est la partie entière de x, c’est-à-dire x= 3 + = 3,5

En fait x=

7 2

1

2

En notation d/c, d=7 et c=2.

Votre calculatrice vous permet d’effectuer un certain nombre d’opérations arithmétiques exprimées ou converties en fractions. a, b et c peuvent être remplacés par un calcul entre parenthèses, et on peut ajouter à une fraction un nombre décimal. Cependant dans certains cas on pourra obtenir un résultat décimal mais pas un résultat en fraction.

1

Ex :

3

+ =

2

4 3

3 [a b/c] 1 [a b/c] 2 [+] 4 [a b/c] 3 [=] -> 3 1 2 + 4 3 | 4 5 6. [a b/c] | 4.833333333 [a b/c] | 4 5 6. [SHIFT] [d/c] | 29 6.

1.25 [+] 2 [a b/c] 5 [=] -> 1.25+2 5 | 1.65 [a b /c] | 1 13 20

On peut utiliser une fraction en tant qu’exposant :

10

2 3

[SHIFT] [10x] 2[a b/c]3 [=] ->10 2 3 | 4.641588834

Notes :

• pour effectuer un calcul tel que + , on peut utiliser [SHIFT] [X-1] et convertir ensuite en fractions.

161

7

6 [SHIFT][X-1] + 7 [SHIFT][X-1] [=] -> 6-1+7-1 | 0.309523809 [a b/c] | 13 42.

• pour une fraction telle que :

24

4+6

On peut utiliser la notation a b/c pour obtenir un résultat en fractions. Il faut saisir le calcul comme suit : 24 [a b/c] [(] 4 [+] 6 [)] [=] -> 24 (4+6) | 2 2 5 [a b/c] -> | 2.4

24

Logarithmes et exponentielles

[ln]

[log]

[SHIFT] [ex]

Touche de logarithme népérien.

Touche de logarithme décimal.

Touche de fonction exponentielle.

Ex : [ ln ] 20 [=] -> ln 20 = | 2.995732274

[ log ] [.] 01 [=] -> log .01= | -2.

[SHIFT][ex] 3 [=] -> e 3= | 20.08553692

Hyperboliques

[ hyp ]

Touche de fonction hyperbolique.

A partir de ces touches s’obtiennent les différentes fonctions hyperboliques :

[ hyp ] [cos]

[ hyp ] [sin]

[ hyp ] [tan]

[ hyp ] [ SHIFT ] [cos-1]

[ hyp ] [ SHIFT ] [sin-1]

[ hyp ] [ SHIFT ] [tan-1]

cosh(x)

sinh(x)

tanh(x)

cosh-1 (x)

sinh-1 (x)

tanh-1(x)

Cosinus hyperbolique.

Sinus hyperbolique.

Tangente hyperbolique.

Argument cosinus hyperbolique.

Argument sinus hyperbolique.

Argument tangente hyperbolique.

Ex :

[ hyp ] [sin] 0 [=] -> sinh0= | 0. [ hyp ] [cos] 0 [=] -> cosh0= | 1. [ hyp ] [SHIFT] [tan-1] 0 [=] -> tanh-10= | 0. [ hyp ] [SHIFT] [cos-1] 1 [=] -> cosh-1 1= | 0.

Calcul de (cosh 1.5 + sinh 1.5)

2

[(] [hyp][cos] 1 [.] 5 [+] [hyp][sin] 1 [.]5 [)][X2][=]

-> (cosh 1.5 + sinh 1.5)2 | 20.08553692

25

Factorielle

[SHIFT] [x!]

Calcul de la factorielle n!

Votre calculatrice permet de calculer la factorielle n! jusqu’à n=69 (voir chapitre des “Messages d’erreur”).

On appelle factorielle de n! ou factorielle n! le nombre suivant :

n! = 1 x 2 x 3 x.....x (n-2) x (n-1) x n

n! représente le nombre de façons différentes d’arranger n objets distincts (n! permutations).

Ex :

8 chevaux sont au départ d’une course hippique. Combien de combinaisons y a-t-il de leur ordre d’arrivée ?

Nombre de permutations de leur ordre d’arrivée = n! avec n = 8. 8 [SHIFT] [x!][=] -> 8! | 40320.

Génération de nombre aléatoire (fonction Random)

[SHIFT] [Ran#]

Génère un nombre aléatoire ≥ 0 et <1, avec trois

chiffres après la virgule. Pour générer le chiffre suivant appuyez sur [=]

Ex : [SHIFT] [Ran#] [=] -> Ran # | 0.256 [=] -> 0.845 [=] -> 0.511 ... etc.

Note : il s’agit de générer une valeur aléatoire, donc en faisant la même manipulation vous ne trouverez pas les mêmes résultats que dans ce manuel !

Pour tirer les chiffres du Loto (entre 1 et 49)

[MENU] [MENU] [MENU] [MENU] [=] 0 : mode Fix, avec 0 chiffres après la virgule, on veut afcher des nombres entiers. [SHIFT] [Ran#] [x] 48 [+] 1 [=] génère, compte tenu des arrondis, un nombre compris entre 1 et 49. [SHIFT] [Ran#] [x] 48 [+] 1 [=] -> RAN#x48+1 | 39. [=] -> 32. [=] -> 17. [=] -> 2.

26

4. CALCULS TRIGONOMETRIQUES ET COMPLEXES

Nombre π

[SHIFT] [π]

A noter que votre calculatrice utilise pour ses calculs une valeur de Pi à 12 chiffres signicatifs et non 10, pour une précision encore meilleure.

Ex :

Périmètre et surface maximales d’une roue de Formule 1, le diamètre maximal étant de 660mm. On calcule le rayon (diamètre divisé par 2) exprimé en mètres, puis on applique les formules 2π r et π r2:

660 [÷] 2 [÷] 1000 [=] -> 660÷2÷1000 | 0.33

[STO][Y] -> Y= Mise en mémoire de la valeur du rayon

2[SHIFT][π][SHIFT][RCL][Y][=] -> 2πY= | 2.073451151 [SHIFT][π][SHIFT][RCL][Y] [x2][=]-> πY 2= | 0.34211944

Le périmètre est donc de 2,1 m et la surface de 0,34 m2.

Remarque : la multiplication est implicite, nous n’avons pas eu besoin d’appuyer sur la touche [x].

Unités d’angles

Choix de l’unité d’angle

[MENU][MENU] [MENU][=]

Afche la valeur approchée de la constante π, avec dix chiffres signicatifs, soit 3,141592654.

Sélectionne les degrés comme unité d’angle active. Le symbole D s’afche à l’écran.

[MENU][MENU] [MENU] [ ][=]

[MENU][MENU] [MENU][ ][ ][=]

Sélectionne les radians comme unité d’angle active. Le symbole R s’afche à l’écran.

Sélectionne les grades comme unité d’angle active. Le symbole G s’afche à l’écran.

Les écrans conviviaux vous aident à choisir la bonne unité, lorsqu’on appuie sur [MENU] [MENU] [MENU] :

ANGLE?

Deg Rad Gra

Le réglage se conserve lorsque la calculatrice est éteinte et rallumée. Vériez bien l’unité active avant d’effectuer votre calcul !

27

Ex : [MENU] [MENU] [MENU] [ ][ ][=] -> | 0. G afché

Note : Pour mémoire, 180º = π radians = 200 grades

Pour convertir : degrés en radians : diviser par 180 et multiplier par π. radians en grades : diviser par π et multiplier par 200.

grades en degrés : diviser par 200 et multiplier par 180.

Cosinus, sinus, tangente

[cos] cos(x).

[sin] sin(x).

[tan] tan(x).

Ex : [MENU] [MENU] [MENU] [=] [cos] 90 [=] -> cos 90 | 0. [tan] 60 [=] -> tan 60 | 1.732050808

sin230 = [(] [sin] 30 [)][X2] [=] -> (sin30)2 | 0.25

[MENU] [MENU] [MENU][ ][=]

[sin] [SHIFT] [π][=] -> sin π | 0. [cos] [(][SHIFT] [π] [÷] 4 [)] [=]-> cos (π÷4) | 0.707106781

Arccosinus, arcsinus, arctangente

[SHIFT] [cos-1]

[SHIFT] [sin-1]

[SHIFT] [tan-1]

arccos(x)

arcsin(x)

arctan(x)

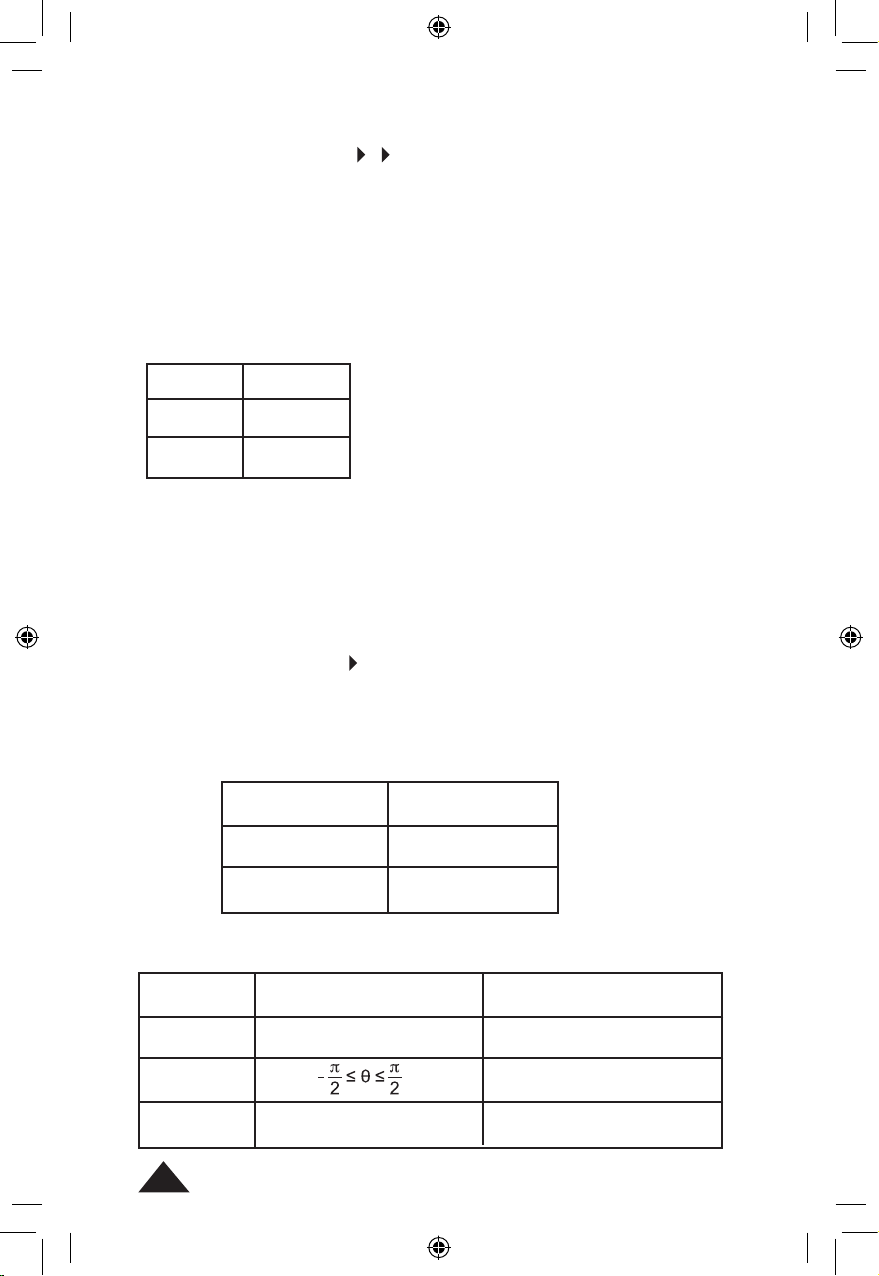
Pour les fonctions sin-1, tan-1 et cos-1 les résultats de mesure angulaire seront donnés dans les intervalles suivants :

θ=sin-1 x , θ=tan-1 x θ=cos-1 x

DEG

-90≤ θ ≤90

0≤ θ ≤180

RAD

GRAD

28

-100≤ θ ≤100

0≤ θ ≤ 200

0≤ θ ≤

π

Ex : [MENU] [MENU] [MENU] [ ][ ] [=] [SHIFT] [tan-1] 1 [=] -> tan-1 1 | 50.

Un panneau routier indique une pente à 5%. Donner la mesure de l’angle en degrés et en radians. Si la pente est à 5% l’altitude augmente de 5m tous les 100m. Le sinus de l’angle à trouver est de 5 divisé par 100, soit 0,05.

[MENU] [MENU] [MENU][=] [SHIFT] [sin-1] [.] 0 5 [=] -> sin-1 .05 | 2.865983983 D afché [MENU][MENU][MENU][ ][=] | 0.050020856 R afché

Conversion sexagésimale (degrés / minutes /secondes)

[º ’’’]

Effectue la saisie des degrés, minutes, secondes et centièmes de seconde (facultatif).

[SHIFT][ ]

Flèche au-dessus de la touche [º ’’’]

Utilisé après [=], convertit les degrés sexagésimaux en degrés décimaux, et vice-versa.

Ex :

En mode degrés (D afché) : Conversion de la latitude 12º39’18”05 en degrés décimaux : 12 [º ’’’] 39 [º ’’’] 18 [.] 05 [º ’’’] [=] -> 12º39º18.05º | 12º39’18.05’’ [SHIFT] [ ] -> 12º39º18.05º | 12.65513889

Conversion de la latitude de Paris (48º51’44”Nord) en degrés décimaux 48 [º ’’’] 51 [º ’’’] 44 [º ’’’] [=] -> 48º51º44º | 48º51’44’’ [SHIFT] [ ] -> 48º51º44º | 48.86222222

Conversion de 123.678 en degrés sexagésimaux :

123.678 [=] [SHIFT] [ ] -> 123.678 | 123º 40’40.8’’

Avec les fonctions trigonométriques : sin (62º12’24”)= [sin] 62 [º’’’] 12 [º’’’] 24 [º’’’] [=] -> sin 62º12º24 | 0.884635235

Calculs horaires

La fonction de conversion sexagésimale peut être également utilisée pour des calculs directs sur des heures / minutes /secondes :

Ex :

3h 30 min 45s + 6h 45min 36s 3 [º ’’’] 30 [º ’’’] 45 [º’’’] [+] 6 [º’’’] 45 [º’’’] 36[º ’’’] [=]

-> 3º30º45+6º45º36 | 10º16’21’’ soit 10h 16 min 21 secondes. 3h 45 min – 1,69h = 3 [º ’’’] 45 [°’’’] [–] 1[.] 69 [=] -> 3º45º – 1.69 | 2.06 [SHIFT] [ ] 3º45º – 1.69 | 2º3’36’’ Soit 2h 03min et 36 secondes.

29

Coordonnées polaires

[SHIFT] [Pol(]

Initie la saisie des coordonnées cartésiennes pour conversion en coordonnées polaires.

[SHIFT] [Rec(]

[SHIFT][,]

Initie la saisie des coordonnées polaires pour conversion en coordonnées cartésiennes.

Utilisé avec [SHIFT] [Pol(] ou [SHIFT] [Rec(], se place entre x et y, ou r et θ pour signaler la saisie de la 2 coordonnée.

[)]

Parenthèse terminant la saisie du couple de coordonnées.

[SHIFT][RCL] [E] ou[ALPHA][E][=]

[SHIFT][RCL][F] ou[ALPHA][F][=]

Afche la première coordonnée après conversion, x ou r.

Afche la deuxième coordonnée après conversion, y ou θ.

Pour mémoire :

x = rcos θ y = rsin θ et r= √(x2+y2) θ = tan-1 (y/x) On appelle x et y les coordonnées cartésiennes, ou rectangulaires, r et θ sont les coordonnées polaires.

ème

Note : l’angle θ sera calculé dans l’intervalle [-180º,+180º] (degrés décimaux) ; la mesure d’angle θ sera donnée dans l’unité d’angle qui a été présélectionnée sur la calculatrice : en degrés si la calculatrice est en mode Degrés, en radians si la calculatrice est en mode Radians, etc.

Les coordonnées sont stockées dans les mémoires temporaires E et F après conversion ; comme les autres mémoires temporaires elles peuvent être rappelées à tout moment et utilisées dans d’autres calculs.

30

Ex :

En mode degrés (D afché) :

• conversion de x= 6 et y= 4

[SHIFT] [Pol(]6 [SHIFT][,] 4 [)] [=] -> Pol (6,4) | 7.211102551

La calculatrice afche directement le résultat pour la première coordonnée, r= 7.211102551

[SHIFT][RCL] [F] -> F= | 33.69006753

F représente la valeur de θ, soit 33.69 degrés.

Si on souhaite revoir la valeur de r :

[ALPHA] [E] [=] ou [SHIFT][RCL][E] -> E= | 7.211102551

• conversion de r= 14 et θ= 36 degrés

[SHIFT] [Rec(] 14 [SHIFT][,] 36 [)] [=] -> Rec (14,36) | 11.32623792

La calculatrice afche directement le résultat pour la première coordonnée, x= 11.32623792.

[SHIFT][RCL] [F] -> F= | 8.228993532 [ALPHA] [E] [=] -> E | 11.32623792

Nombres complexes

[MENU][ ][=]

Passage en mode de gestion des nombres complexes, CMPLX s’afche à l’écran.

[i]

Saisie de l’inconnu imaginaire i.

i2=-1

(accès en touche principale au niveau de la touche ENG)

[SHIFT][Abs]

Calcule le module du nombre complexe saisi immédiatement après entre parenthèses.

[SHIFT] [arg]

[SHIFT] [Re Im]

Calcule l’argument du nombre complexe.

Donne le résultat du calcul pour la partie

imaginaire du nombre complexe, et afche le symbole i en bas à droite. Si on appuie une deuxième fois la partie réelle est afchée, et i disparaît.

[MENU][=]

Retour au mode normal (COMP).

Votre calculatrice vous permet de réaliser additions, soustractions, multiplications et divisions de nombres complexes. A noter cependant que ne sont disponibles en mode complexe que les mémoires temporaires A, B, C et M, les autres étant nécessaires au fonctionnement des calculs dans ce mode. On rappelle que nombres complexes et coordonnées polaires / cartésiennes sont très liés. Si x= a+ib, on a x= rcosθ +i rsinθ où r est le module de x, r= √(a2+b2) et θ l’argument, soit tan-1 y/x. θ sera donné dans l’unité angulaire active. Le mode complexe est compatible avec les touches [X2], [ab/c] notamment, et on peut convertir l’argument en degrés minutes secondes avec [º’’’ ].

31

Ex : x= 1 + 3i y= 5 - 2i

[MENU] [ ][=] : on passe en mode complexe (CMPLX afché)

• argument de y calculé en mode Degrés [SHIFT][arg] [(] 5 [-] 2 [i] [)] [=] -> arg (5-2i) | -21.80140949 arg y = tan-1(-2/5) en degrés décimaux.

• module de x et son carré

[SHIFT][Abs] [(] 1 [+] 3 [i] [)] [=] -> Abs (1+3i) | 3.16227766 [X2][=] -> Ans2 | 10.

Le module de x au carré est égal à 12+32.

• calcul de x+y

[(]1 [+] 3 [i][)] [+] [(] 5 [-] 2 [i][)] [=] -> (1+3i)+(5-2i)= | 6. soit la partie

réelle de x+y

[SHIFT][Re Im]->(1+3i)+(5-2i)= | 1. soit la partie imaginaire i [SHIFT][Re Im]->(1+3i)+(5-2i)= | 6. afchage de la partie réelle

donc x+y=6+i

• calcul de x-y [(]1 [+] 3 [i][)] [-] [(] 5 [-] 2 [i][)] [=] -> -4. soit la partie réelle de x-y

[SHIFT][Re Im] -> 5. soit la partie imaginaire [SHIFT][Re Im] -> -4. afchage de la partie réelle

donc x-y=-4+5i

• calcul de xy

[(]1 [+] 3 [i][)] [x] [(] 5 [-] 2 [i][)] [=] -> 11. [SHIFT][Re Im] -> 13. i

donc x.y=11+13i

• calcul de x/y

[(]1 [+] 3 [i][)] [÷] [(] 5 [-] 2 [i][)] [=] -> -0.034482758 [SHIFT][Re Im] -> 0.586206896 i

32

5. CALCULS EN BASE-N

Pour mémoire

Changements de base

Nous effectuons nos calculs de façon courante en base 10. Par exemple : 1675 = (1675)10 = 1x103 + 6x102 + 7x10 + 5

En mode binaire, un nombre est exprimé en base 2. 1 s’écrit 1, 2 s’écrit 10, 3 s’écrit 11, etc. Le nombre binaire 11101 est équivalent à : (11101)2= 1x24 + 1x23 + 1x22 + 0x2 +1 = (29)10

En mode octal, un nombre est exprimé en base 8. 7 s’écrit 7, 8 s’écrit 10, 9 s’écrit 11, etc. Le nombre octal 1675 est égal à : (1675)8= 1x83 + 6x82 + 7x81 + 5= (957)10

En mode hexadécimal, un nombre est exprimé en base 16, les chiffres au-delà du 9 étant remplacés par des lettres : 0123456789ABCDEF 9 s’écrit 9, 10 s’écrit A, 15 s’écrit F, 16 s’écrit 10, etc. Le nombre hexadécimal 5FA13 est égal à :

(5FA13)16= 5x164 + 15x163 + 10x162 + 1x161 + 3= (391699)10

Pour récapituler :

déc 0 1 2 3 4 5 6 7 8 bin 0 1 10 11 100 101 110 111 1000

oct 0 1 2 3 4 5 6 7 10 hex 0 1 2 3 4 5 6 7 8

déc 9 10 11 12 13 14 15 16 bin 1001 1010 1011 1100 1101 1110 1111 10000

oct 11 12 13 14 15 16 17 20 hex 9 A B C D E F 10

Les opérateurs logiques

Outre les fonctions arithmétiques +, -, x, ÷, +/-, on utilise en base N des opérateurs logiques qui sont des fonctions à une ou deux variables A et B, notées :

• Not A (NON A ou inverse de A)

• And (ET)

• Or (OU)

• Xor (OU exclusif)

• Xnor (NON OU exclusif)

33

Les résultats des fonctions ci-dessus sont les suivantes en fonctions de A et B:

A B Not A A and B A or B A xor B A xnor B 0 1 1 0 0 0 1 0 0 0 1 0 1 1 0 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1

Pour A et B plus grands que 0 ou 1, le résultat se calcule bit par bit sur les valeurs exprimées en binaire. Par exemple si A=(19)16=(11001)2 et B=(1A)16=(11010)2 :

A 0 0 0 0 0 0 0 1 1 0 0 1 B 0 0 0 0 0 0 0 1 1 0 1 0 A and B 0 0 0 0 0 0 0 1 1 0 0 0 A xnor B 1 1 1 1 1 1 1 1 1 1 0 0

A and B = (11000)2 = (18)16 = (24)10 A xnor B = (111111111100)2 = (FFFFFFFC)16 = (-4)10 Not A =(111111100110)2 = (FFFFFFE6)16 = (-26)10 Neg A=(111111100111)2 = (FFFFFFE7)16 = (-25)10

Notations

Lorsque la calculatrice est en Base N, un indicateur de base s’afche à droite :

• d pour décimal.

• b pour binaire.

• o pour octal.

• h pour hexadécimal.

Remarques sur le mode Base N :

• Comme pour les autres réglages de mode le mode Base N est conservé même si la calculatrice est éteinte et rallumée. On y accède en appuyant sur [MENU] [ ][ ][ ][ ][=]

MODE?

COMP CMPLX

• Les touches spéciques du mode Base N, DEC, HEX, BIN, OCT, sont indiquées en jaune et sont accessibles en touche principale (sans appuyer sur SHIFT). Pour la saisie des lettres A, B, … F pour la base hexadécimale, utilisez les lettres inscrites en orange qui servent aussi pour les mémoires temporaires.

• La touche [LOGIC] (accès en touche principale à partir de la touche X3) vous permet d’accéder à un menu convivial pour le choix des opérateurs logiques / Neg.

[LOGIC]

34

LOGIC? And Or Xnor

LOGIC? Xor Not Neg

• La notation se fait sur 10 chiffres en base 2, 8 et 10, et sur 8 chiffres en base 16. Si vous entrez une valeur incompatible avec la base choisie (ex : 3 en binaire, la calculatrice afchera Syn ERROR. Voir le chapitre « Messages d’erreurs » pour plus de détails sur les valeurs admissibles en mode Base N.

• La plupart des fonctions générales ne peuvent pas être utilisées en Base N. Les paragraphes suivants détailleront les opérateurs admissibles.

• Vous pouvez utiliser les mémoires et les touches de mise en mémoire et de rappel associées : [SHIFT][Ans], [ALPHA], [STO], [SHIFT][RCL], [A]-[F], [M], [X], [Y], [SHIFT][Mcl] (voir chapitre « Utilisation des mémoires »).

Commandes du mode Base N et conversions

Passe en mode Base N, BASE-N est afché en

[MENU] [ ][ ][ ][ ][=]

permanence en haut de l’écran et un indicateur de la base active est également afché sur la droite de l’écran.

[MENU][=]

Annulation du mode Base N, retour en mode normal (mode COMP).

[DEC ]

[BIN]

[OCT]

[HEX]

[SHIFT][DEC]

ou [BIN] ou [OCT]

ou [HEX]

Sélectionne la base 10 comme base active, d s’afche.

Sélectionne la base 2 comme base active, b s’afche.

Sélectionne la base 8 comme base active, o s’afche.

Sélectionne la base 16 comme base active, h s’afche.

Spécie que la valeur saisie immédiatement après est en base 10 ou 2 ou 8 ou 16, lorsque la base active est différente.

A partir de maintenant tous les exemples donnés dans ce chapitre

sont en Base N.

Il y a deux façons de convertir une valeur d’une base dans une autre :

Méthode 1 : Une fois en Base N vous choisissez la base de la valeur à convertir. Vous saisissez la valeur, puis vous changez la base.

Ex :

Conversion de (11101)2 en base 10 :

[BIN] -> | b 11101 [=] -> 11101 = | 11101 b [DEC] -> 11101 = | 29 d

Méthode 2 : Une fois en Base N vous choisissez la base dans laquelle vous voulez convertir une valeur. Ensuite vous spéciez la base d’origine et vous saisissez cette valeur.

35

Ex :

Conversion de (11101)2 en base 10 :

[DEC] -> | d [SHIFT] [BIN] -> b | d 11101 [=] -> b11101 | 29 d

Autres exemples de conversion (les deux méthodes sont utilisées) :

Conversion de (5FA13)16 en base 8 puis 10 :

[AC/ON] [HEX] -> | h 5 [F] [A] 13 [=] -> 5FA13 | 5FA13 h [OCT] -> 5FA13 | 1375023 o

Conversion de (1675)8 en base 10 :

[DEC] -> | d [SHIFT][OCT] 1675 [=] -> o1675 | 957 d

Calculs en Base N

[+]

Addition.

[-]

[x]

[÷]

[LOGIC] [ ][ ][ ][ ][=]

Soustraction.

Multiplication.

Division.

Fonction Neg : change le signe de la valeur saisie immédiatement après, équivalent de la touche arithmétique [(-)].

[(], [)]

Parenthèses.

Votre calculatrice vous permet de réaliser des opérations usuelles (addition, soustraction, multiplication, division et parenthèses) en Base N. A noter qu’en Base N on ne manipule que des nombres entiers ; si une opération génère un résultat décimal, seule la partie entière de la valeur sera conservée. Vous pouvez, sur une même ligne de calcul, utiliser des nombres exprimés en bases différentes. Le résultat sera donné dans la base active qui a été présélectionnée.

Ex :

Si, en mode hexadécimal on soustrait 5A7 à 5FA13, cela donne : [HEX] -> | h 5 [F][A] 13 [-] 5 [A] 7 [=] ->5FA13-5A7 | 5F46C h

On multiplie ce résultat par 12 : [x] 12 [=] -> Ansx12 | 6B2F98 h

ou

12 [x] [SHIFT][Ans] [=] -> 12xAns | 6B2F98 h

En mode binaire on effectue (11010 + 1110) ÷10

[AC/ON][BIN] -> | b [(] 11010+1110 [)] [÷] 10 [=] -> (11010+1110) ÷10 | 10100 b

36

On ajoute (101)2 au chiffre octal (12)8 et on veut un résultat en base 10 :

[DEC] -> | 0 d [SHIFT][BIN] 101 + [SHIFT][OCT]12 [=]

-> b101+o12 | 15 d

On divise ce résultat par 12

[÷] 12 [=] -> Ans÷12 | 1 d

Seule la partie entière du résultat de la division est conservée.

En mode hexadécimal on calcule le négatif de 1C6 :

[HEX] -> | h [LOGIC]

[ ][ ][ ][ ][ ]

[=] 1[C] 6 [=]

-> Neg 1C6 | FFFFFE3A h

[+]1 [C] 6 [=] -> Ans+1C6 | 0 h

Opérateurs logiques en Base N

[LOGIC]

Accès au menu des fonctions logiques.

[LOGIC][=]

Fonction And (ET).

[LOGIC]

[ ]

[=]

Fonction Or (OU).

[LOGIC]

[ ][ ]

[ ][ ][ ]

[LOGIC] [ ][ ][ ][ ]

[=]

Fonction Xnor (NON OU exclusif).

Fonction Xor (OU exclusif).

[[=]

Fonction Not (NON) : inverse de la valeur saisie immédiatement après.

Votre calculatrice effectue ces calculs à partir des valeurs que vous avez saisies, quelles qu’en soit la base initiale et les exprime directement dans la base que vous avez présélectionnée.

Ex : (19)16 Or (1A)16 en base 16 [HEX] -> | h 19 [LOGIC][ ][=] 1 [A] [=] ->19or1A | 1B h

(120)16 XOR (1101)2 en décimal [AC/ON][DEC] -> | 0 d [SHIFT][HEX] 120 [LOGIC] [ ][ ][ ][=] [SHIFT][BIN] 1101 [=]

-> h120xorb1101 | 301 d

NON de (1234)8 en base 8 puis 10, mise en mémoire dans la mémoire temporaire F, et comparaison avec Neg (1234)8

[ ][ ][ ][ ][ ]

[=]1234[=] -> Neg 1234 | 7777776544 o

[-] [SHIFT][RCL] [F][=] -> Ans-F | 1 o [DEC] -> Ans-F | 1 d

37

6. FONCTIONS AVANCEES

Calculs d’intégrales

Commentaires préliminaires

Votre calculatrice peut réaliser pour vous des calculs d’intégration sous le format suivant ∫f(x)dx avec les paramètres suivants : a valeur initiale. b valeur nale. n nombre entre 0 et 9 xant le nombre de divisions N=2n.

Le calcul d’intégrale est réalisé à l’aide de la loi de Simpson pour déterminer la fonction f(x). Pour cela il est nécessaire de partitionner la surface servant au calcul d’intégration. Si vous ne spéciez pas de valeur n, la calculatrice décidera elle-même de la valeur N à utiliser.

Saisie d’intégrale

[SHIFT][∫dx]

Initie la saisie d’une intégrale.

[SHIFT][,]

Sépare les paramètres d’intégrale : formule d’inconnue x , a, b , n.

[)]

Termine la saisie d’une intégrale.

Pour votre expression f(x) vous devez absolument utiliser la mémoire X en tant que variable. Si vous utilisez d’autres noms de mémoires temporaires (A-F, Y) elles seront considérées comme des constantes et la valeur en mémoire sera utilisée. Si votre expression commence par une parenthèse, par exemple (x+1)2, vous devez saisir cette parenthèse de départ : l’écran afchera ∫((x+1 ... La saisie de n et de la parenthèse nale sont facultatives. Dans le cas où vous choisissez de ne pas entrer de valeur n, la calculatrice choisira elle-même le nombre de divisions N. ATTENTION le calcul peut prendre entre quelques secondes et plusieurs minutes. Pour l’interrompre vous pouvez appuyer sur [AC/ON].

38

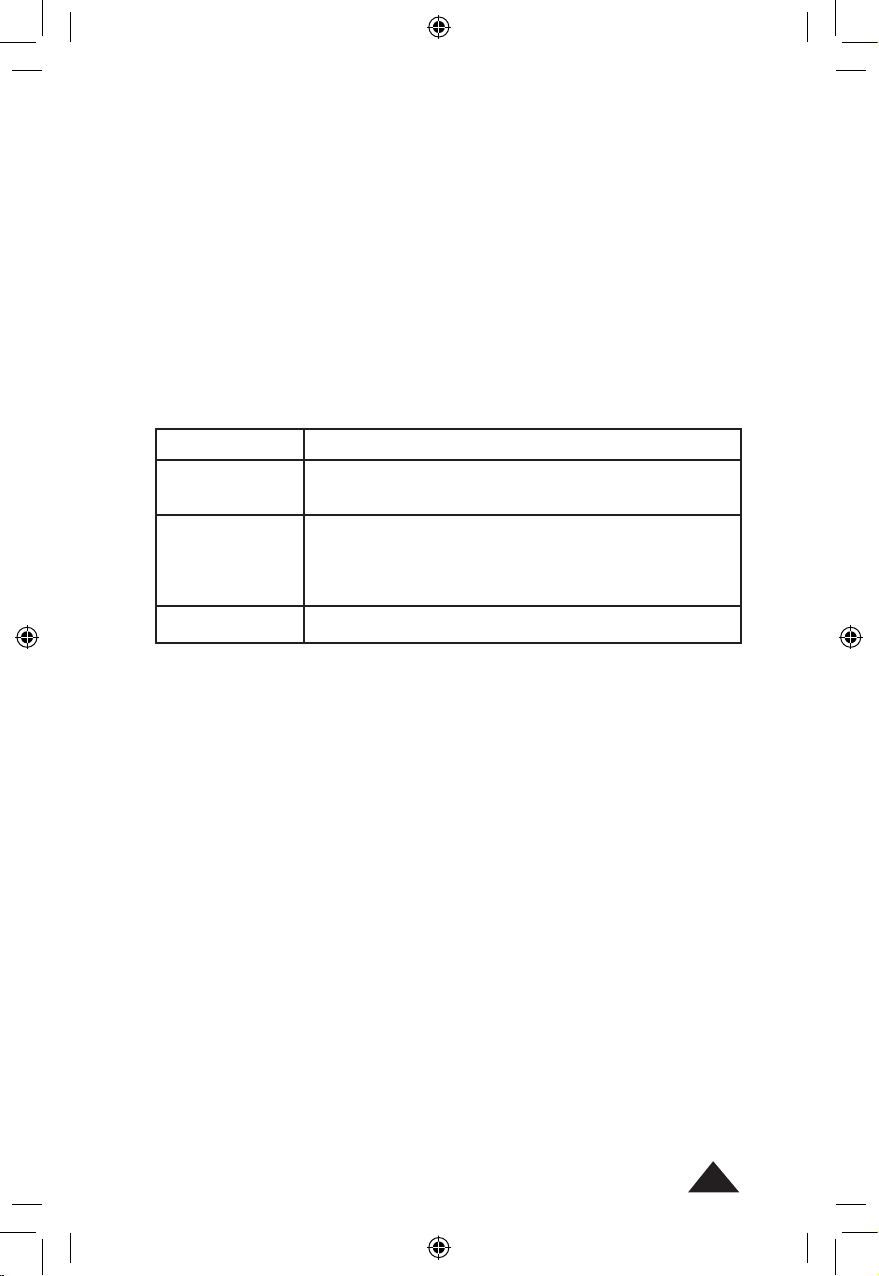
Ex :

Intégrale de f(x) = 3x2+2x+5 entre 1 et 5. [SHIFT][∫dx] -> ∫(

3 [ALPHA][X][X2][+] 2 [ALPHA][X] [+] 5 [SHIFT] [,]

-> ∫(3X2+2X+5, saisie de la formule 1[SHIFT][,]5 -> ∫(3X2+2X+5,1,5 saisie de a et b [=] -> ∫(3X2+2X+5,1,5 | 168. n omis ou [SHIFT][,]6[)][=]-> ∫(3X2+2X+5,1,6) | 168.

n xé (N=26 divisions)

On peut vérier le résultat manuellement, la primitive de f(x) = 3x2+2x+5

étant F(x) = x3+x2+5x + C, l’intégrale entre 1 et 5 est égale à F(5)-F(1)= 175-7=168.

Programmation d’une équation

[SHIFT][PROG]

Mise en mémoire d’une équation.

[ALPHA][=]

en haut de la touche X

[X,T]

Saisie du signe = dans une équation.

y

Saisie de la variable X dans les équations. Pour les autres mémoires temporaires, et X également, on peut utiliser [ALPHA] puis le nom de la mémoire temporaire.

[CALC]

Exécution d’un calcul mémorisé.

Cette fonction de programmation vous permet d’effectuer toutes sortes de calculs répétitifs. Vous pouvez ainsi mettre en mémoire des expressions à une ou plusieurs inconnues et gagner du temps dans la saisie et l’exécution de vos calculs récurrents. Pour cela vous utilisez les mémoires indépendantes en tant que variables. Pendant l’exécution le programme les identiera et vous demandera leur valeur dans leur ordre d’apparition dans l’expression.

39

Ex :

Pour effectuer le calcul suivant avec plusieurs valeurs différentes :

y= 5a + 2√x

[ALPHA][Y] [ALPHA][=] 5[ALPHA][A] [+] 2 [√] [X,T] -> Y=5A+2√X [SHIFT][PROG] -> _

[CALC] -> A? | 0. 4 [=] -> X? | 0.

9[=] -> | 26.

[=] -> A? | 4. l’exécution reprend [AC/ON] interruption de

l’exécution

Remarques :

- Lorsque l’exécution commence, votre calculatrice vous propose une valeur de variable qui peut être non nulle, puisque c’est le contenu de la mémoire correspondante. Si cette valeur vous convient, il suft d’appuyer sur [=] pour conrmer.

- Vous pouvez rentrer un calcul à la place d’une valeur, par exemple 3ln 2 pour la valeur A.

- Vous pouvez utiliser les mémoires M, A-F, X, Y et Ans dans la formule (la calculatrice ne vous demandera pas la valeur de Ans !).

40

7. FONCTIONS GRAPHIQUES

Dénitions et notations

Une courbe est la représentation graphique d’une fonction f, y=f(x), x étant l’abscisse, sur l’axe horizontal, et y l’ordonnée, sur l’axe vertical. On peut aussi exprimer cette courbe en fonction d’une autre variable, t, avec x=f1(t) et y=f2(t). On appelle cela une courbe paramétrée. Par exemple x=2t et y= 3 cos t, ce qui est équivalent à y= 3 cos x/2.

Pour représenter une fonction graphiquement il est nécessaire de décider d’une échelle, c’est-à-dire entre quelles valeurs on souhaite voir cette fonction et comment on veut graduer les axes. Par exemple pour la fonction y=x2 il n’est pas très intéressant de représenter la courbe pour y=-100…

La graduation des axes sera représentée par des points sur les axes et

permettent de mieux repérer les valeurs de x ou de y intéressantes : par exemple pour y=ln x, graduation de 1, on voit facilement que y=0 pour x=1.

L’échelle sera dénie par les valeurs suivantes : X min, X max, et la graduation sur l’axe des X, Xscl. Y min, Y max et la graduation sur l’axe des Y, Yscl. Tmin et Tmax et l’incrément choisi pour T (pitch).

Tracer une courbe

[MENU] [MENU] [=]

Passe au mode graphique pour tracer une fonction y=f(x) (FUNCT).

[SHIFT][Funct]

[X,T] ou [ALPHA] [X]

[Draw]

[Range]

[SHIFT][G T]

[SHIFT] [CLS]

[ ][ ][ ][ ]

Initie la saisie d’une fonction à tracer, Y1 ou Y2.

Saisie X pour l’écriture des fonctions.

Trace les graphes.

Permet de saisir les valeurs d’échelle (Xmin, Xmax, Xscl, Ymin, Ymax, Yscl, Tmin, Tmax, pitch). Pour sortir de la fonction RANGE, appuyez sur [RANGE] à nouveau ou sur [AC/ON].

Passe de l’afchage graphique à l’afchage normal et vice versa. On peut aussi utiliser [AC/ON] pour passer de l’afchage graphique à l’afchage normal.

Efface toutes les courbes du graphe.

Change la position des axes pour afcher la partie de la courbe située dans la direction de la èche.

41

Quand on appuie sur [MENU][MENU] on voit l’écran suivant :

GRAPH? FUNCT PARAM

On sélectionne FUNCT avec [=] et lorsque vous appuyez sur [SHIFT][Funct] :

FUNCT? Y1 Y2

Vous pouvez tracer 2 courbes sur le même écran. Appuyez sur [=] pour sélectionner Y1.

Courbes préprogrammées

Votre calculatrice comporte un certain nombre de courbes préprogrammées, pour les fonctions sin, cos, x-1, ln, √… : pour celles-ci les échelles sont prédénies et non modiables. Pour tracer une courbe préprogrammée, il suft de d’appuyer sur la touche de fonction après avoir sélectionné Y1 (ou Y2).

Ex :

[SHIFT][FUNCT][=] -> Y1= [sin] -> Y1= | sin [Draw]

La courbe se trace. Appuyez sur les touches [ ], [ ], [ ] ou [ ] pour visualiser les différentes parties de la courbe et le déplacement des axes.

On peut éventuellement tracer une deuxième courbe préprogrammée sur

le

même graphe, dans le cas où les échelles prédéterminées sont compatibles : par exemple sin et cos. Dans ce cas il faut saisir la variable x (en faisant ALPHA X).

Courbes utilisateur

Vous pouvez tracer votre propre courbe en saisissant simplement l’expression d’inconnue x que vous souhaitez représenter et l’échelle de représentation.

Ex : Courbe y=x2+2x-3

Echelle : x entre –5 et +5, graduation de 2 en 2 y entre –10 et +10, graduation de 4 en 4

Et intersection avec la courbe y=1-x.

42

[SHIFT] [CLS] -> Cls [=] -> done (« done » = terminé). Effacement des

courbes précédentes

[Range] -> Xmin ? [(-)] 5 [=] -> Xmax ? 5 [=] -> Xscl ? 2 [=] -> Ymin ? [(-)] 10 [=] -> Ymax ? 10 [=] -> Yscl ? 4 [=] -> Tmin ? [=] -> Tmax ? on accepte les valeurs pour T quelles [=] -> pitch ? qu’elles soient car T n’est pas utilisé [=] -> Xmin ? [AC/ON] [SHIFT][Funct][=] -> Y1= [ALPHA][X][X2][+] 2 [ALPHA][X][-]3

-> Y1= | X2+2X-3 [=] [DRAW] ->

La courbe se trace et on obtient l’écran suivant :

Appuyez sur les touches [ ], [ ], [ ] ou [ ] pour visualiser les différentes parties de la courbe et le déplacement des axes. Si vous appuyez sur [RANGE] vous verrez que les valeurs de x et y min et max on été mises à jour.

Notes :

• La multiplication est implicite, pas besoin d’appuyer sur la touche multiplication [x] pour saisir 2X.

• Astuce : si vous avez appuyé un peu trop sur les èches et que vous avez « perdu » un des axes de référence et/ou votre courbe, appuyez sur [RANGE] et modiez un ou plusieurs paramètres.

Pour faire réapparaître l’écran normal après avoir tracé la courbe, appuyez sur [SHIFT][G T].

Ensuite on trace y =1-x sur le même graphique : [SHIFT][Funct][ ][=] -> Y2= 1[-] [ALPHA][X] -> Y2= | 1-X [=][DRAW]

On voit sur le graphique qu’il y deux solutions à l’équation, x2+2x-3=1-x, dont une évidente avec y=0 et x=1.

43

Courbes paramétrées

[MENU] [MENU][ ][=]

Passe au mode graphique pour tracer une fonction y=f(T), x=f(T) (PARAM).

[X,T]

Saisie de T pour l’écriture des fonctions.

On réafche le menu graphique mais cette fois-ci on sélectionne PARAM : [MENU][MENU][ ][=]

GRAPH? FUNCT PARAM

[SHIFT][Funct]

PARAM?

X(t) Y(t)

Vous devez saisir X(t) et Y(t), sinon aucune courbe ne se tracera.

Exemple 1 :

On trace la courbe suivante : x(T)= 30Tcos25 y(T)= 30Tsin 25-4.9T

2

Avec les valeurs suivantes d’échelle : x entre –1 et +100, graduation de 5 en 5 y entre –10 et +15, graduation de 5 en 5 t entre 0 et 10, incrément 0,1

(unité angulaire = degrés) [SHIFT] [CLS] -> Cls [=] -> done [MENU][MENU][ ][=][SHIFT][Funct] [=]-> X(t)= 30 [X,T] [cos] 25 -> X(t)= | 30Tcos 25 [=][ ][=] -> Y(t)= 30 [X,T] [sin] 25 –4[.]9 [X,T][X2] -> Y(t)= | 30Tsin 25-4.9T

2

[=][AC/ON] [Range] -> Xmin ? [(-)] 1 [=] -> Xmax ? 100 [=] -> Xscl ? 5 [=] -> Ymin ? [(-)] 10 [=] -> Ymax ? 15 [=] -> Yscl ? 5 [=] -> Tmin ? 0[=] -> Tmax ? on accepte les valeurs pour T quelles 10[=] -> pitch ? qu’elles soient car T n’est pas utilisé 0[.]1[=] -> Xmin ? [AC/ON] [DRAW]

44

La courbe se trace et on obtient l’écran suivant :

Exemple 2 :

Tracez y=4 sin T et x= 4 cos T, avec x et y entre –5 et +5. avec T entre 0 et 360, incrément (pitch) 5 : on obtient un cercle. Si on prend Tmax = 180, on obtient un demi-cercle. Si on prend y=2 sinT on obtient une ellipse.

Effacer une courbe

[DEL]

Efface la formule d’une courbe.

[SHIFT][Funct][ ] -> FUNCT ? | Y1 Y2 [DEL] -> Y2 | DELETE? [=] -> Y2 effacé

Si on presse [DRAW] juste après il y a de grandes chances que la courbe Y2 soit toujours représentée à l’écran. Pour ne plus voir que la courbe Y1, appuyez sur [SHIFT][CLS] puis [DRAW], ou bien appuyez sur une des èches an que le graphique se recalcule.

Fonction Zoom

[SHIFT] [Factor]

Permet de régler les paramètres de l’agrandissement.

[SHIFT] [Zoomxf]

Agrandit la courbe selon les paramètres spéciés.

[SHIFT] [Zoomx 1/f]

Réduit la taille de la courbe selon les

paramètres spéciés.

[SHIFT] [ZoomOrg]

Remet la courbe à sa taille initiale.

Cette fonction permet de visualiser une courbe sous divers agrandissements ou réductions, ce qui vous permet de mieux étudier ses caractéristiques : forme générale, points d’intersection… Il est intéressant de noter comment dans l’exemple suivant que l’utilisation de [Range] avec les fonctions Zoom permet de vérier les points d’intersection.

45

Ex : Nous reprenons la courbe y=x2+ 2x-3 sans modier l’échelle.

Echelle : x entre –5 et +5, graduation de 2 en 2. y entre –10 et +10, graduation de 4 en 4.

Une fois la courbe tracée on spécie des paramètres de l’agrandissement :

[SHIFT] [Factor] -> Xfact ? 4 [=] -> Yfact ? 2 [=] -> Xfact ? [AC/ON][SHIFT][G T] -> la courbe s’afche sans modications. [SHIFT] [Zoomx1/f]

La courbe s’afche en plus petit.

[SHIFT] [ZoomOrg] ou [SHIFT][Zoomxf] : retour à la taille d’origine.

[SHIFT][Zoomxf] -> la courbe s’afche agrandie.

Si on appuie sur [Range] on voit que les valeurs Xmin, Xmax, Ymin et Ymax ont changé. On modie Xscl et Yscl pour mieux voir l’échelle et vérier visuellement x=1 et y=0. [Range] -> Xmin ? | -2.5 [=] -> Xmax ? | 2.5 [=] -> Xscl ? | 2. 0 [.] 5 [=] -> Ymin ? | -2.5 [=] -> Ymax ? | 2.5 [=] -> Yscl ? | 4. 1 [=] -> Tmin ? [AC/ON] [Draw]

On a donc gradué l’axe des x de 0,5 en 0,5 et l’axe des y de 1 en 1.

On peut donc voir vérier le point d’intersection entre la courbe et l’axe des x.

46

Résolution graphique

[G-solve]

Fonction résolution graphique, initie la saisie de l’équation y=f(x).

Votre calculatrice permet de résoudre graphiquement et de façon conviviale une équation de type y=f(x)=a. On obtient une ou plusieurs valeurs Il faut pour cela :

- choisir avec soin l’échelle avec Range.

- appuyer sur [G-solve] et saisir l’équation d’inconnue X.

- saisir la valeur de y, a.

- obtenir une ou plusieurs valeurs de x (utilisez les èches [ ] et [ ] pour naviguer entre les différentes solutions). Votre calculatrice afche la valeur de x.

- répétez éventuellement l’opération avec une échelle plus petite pour obtenir une meilleure précision sur les valeurs.

Ex :

on cherche les solutions de y= x3-5,25x-2,5 pour y=0. Appuyez sur [Range] et saisissez les valeurs d’échelle suivantes : Xmin=-3,5 ; Xmax= 3,5 ; Xscl= 1 Ymin=-10 ; Ymax= 10 ; Yscl= 0.5

[G-solve] -> Solve | Graph Y= [X,T][X3] [-]5[.]25[X,T][-]2[.]5 -> Solve | Graph Y= X3-5.25X-2.5 [=] -> La courbe se trace et a? s’afche

on saisit a : 0 [=]

Si on appuie sur [ ], on passe à la deuxième solution :

[ ] -> x= 2.58695652, troisième solution approchée. Si on répète l’opération avec une nouvelle échelle : Xmin=-2.1 ; Xmax= 2.6 Ymin=-2 ; Ymax= 2 On obtient les valeurs approchées suivantes : x1= -1,997826 x2= -0,4652173 x3= 2,49782608 En fait y= x3-5,25x-2,5 = (x+2)(2x+1)(2x-5)

1 4

Vu sous cet angle, il est facile de voir que les solutions exactes de y=0 sont –2, -0,5 et –2,5.

47

Fonction Trace

[Trace]

Place le curseur sur la courbe et afche la valeur de x à la position du curseur.

[ ], [ ]

[ ][ ]

Déplace le curseur sur la courbe.

Dans le cas où il y a deux courbes, passe la position du curseur d’une courbe à l’autre.

[SHIFT] [X Y]

Afche la valeur de y au lieu de celle de x à l’emplacement du curseur, et vice versa.

[SHIFT] [Value]

Afche la valeur détaillée de x ou y à la position du curseur. Annulation avec [SHIFT][Value].

Cette fonction vous permet de déplacer le curseur sur la courbe avec les èches et de visualiser la valeur de x ou y à l’emplacement du curseur.

Attention : le curseur se déplace de façon irrégulière, les valeurs de x et y sont des valeurs approchées.

Ex :

En reprenant l’exemple précédent :

Courbe y=x2+2x-3

Echelle : x entre –5 et +5, graduation de 2 en 2 y entre –10 et +10, graduation de 4 en 4

Une fois la courbe afchée on appuie sur [Trace] :

[Trace] -> un curseur clignotant apparaît sur la courbe tout à fait sur la gauche de l’écran et la valeur de x s’inscrit. X= -4.7826086. [SHIFT][Value] -> Afchage d’une valeur plus précise de X :

-4.782608696

[ ] -> on appuie sur la èche et on observe que les valeurs de x décroissent et que le curseur se déplace sur la courbe.

On positionne le curseur sur x=0 et on utilise [X Y]: [SHIFT][X Y] -> la valeur correspondante de y s’afche, Y=-3

Dans le cas où il y a deux courbes, les èches vous permettent de passer d’une courbe à une autre. Pour cela observez bien la position du point clignotant. Vous pouvez ainsi obtenir une valeur approchée des coordonnées du point d’intersection pour x négatif.

On peut ainsi se positionner à l’intersection des deux courbes et trouver : x= -3,9130434 et y= 4,91304347, les valeurs réelles étant x=-4 et y=-5.

48

Fonctions Sketch

[SHIFT][Sketch]

Accès au menu des fonctions Sketch : Plot, Line, Tangent, Horiz, Vert.

x [SHIFT] [,] y

[ ][ ][ ][ ]

[SHIFT] [Value]

[SHIFT] [X Y]

Sépare les coordonnées x et y pour la saisie.

Permet de déplacer le curseur à l’endroit souhaité.

Afche la valeur détaillée de x ou y à la position du curseur. Annulation avec [SHIFT][Value].

Afche la valeur de y au lieu de celle de x à l’emplacement du curseur, et vice versa.

Lorsqu’on ouvre le menu Sketch avec [SHIFT][Sketch] :

SKETCH? Plot Line

SKETCH? Tangent Horiz

SKETCH?

Vert

Voyons chaque fonction en détail : Fonction Plot

Plot permet de placer un point sur l’écran, on peut ensuite se déplacer à l’aide des èches à partir de cette position. L’opération peut être répétée plusieurs fois an de déterminer notamment des positions de points sur la courbe avec une meilleure précision par projection sur les axes.

Si les valeurs proposées pour la fonction Plot sont situées en dehors des valeurs Xmin/Xmax et/ou Ymin/Ymax, l’instruction sera ignorée.

Ex :

Avec la même échelle que précédemment. x entre –5 et +5, graduation de 2 en 2 y entre –10 et +10, graduation de 4 en 4

[SHIFT][Sketch][=] -> Plot 2 [SHIFT][,] 4 [=] -> X= 1.95652173 Le curseur apparaît et une valeur approchée de x est afchée. [SHIFT][X Y] -> Y= 4.

On appuie sur [=] pour « xer » le point, puis on se déplace en appuyant 7 fois sur [ ] et 6 fois sur [ ] : [=] 7 fois [ ], 6 fois [ ] -> x= 3.347826086 [SHIFT][X Y] -> y= 8. On voit que le point d’origine xé par Plot est toujours afché par un point xe, et que le curseur clignote. Vous pouvez marquer plusieurs points de cette manière, chaque fois que vous appuyez sur [=] le point clignotant se transforme en point xe et vous repartez de l’endroit xé par les coordonnées rentrées pour Plot.

49

Fonction Line

La fonction Line vous permet de tracer un segment entre deux points déterminés par la fonction Plot.

Ex :

En reprenant l’exemple précédent : On est parti du point x=2 et y=4, appuyé sur [=] pour xer le point, puis on a déplacé le curseur jusqu’à la position x= 3.47826086 et y= 8.

Ensuite on exécute la fonction Line :

[SHIFT][Sketch][ ][=] -> Line [=] -> done (terminé) [DRAW] -> le segment est tracé

Fonction Tangente La fonction Tangent permet de tracer une tangente au point de la courbe repérée par la fonction Trace.

Ex : On trace la courbe Y=x2-3 avec l’échelle suivante :

x entre –3,5 et +3,5, graduation de 1 en 1 y entre –3,5 et +3,5, graduation de 1 en 1 (c’est une courbe y=f(x) donc les valeurs pour t importent peu).

Une fois la courbe afchée, on appuie sur [TRACE] puis sur [ ] jusqu’à ce que x=-1.3695652.

Puis on exécute la fonction Tangente : [SHIFT][Sketch][ ][ ][=]

On remarque que si on utilise les èches le graphique se recalcule et seules les courbes programmées Y1 et Y2 restent à l’écran.

50

Fonction Horizontale Permet de tracer une droite horizontale, à partir d’un point déterminé par Plot.

Ex :

En reprenant l’exemple précédent :

On se place avec Plot avec x=1 et y=2.

[SHIFT][Sketch][=] -> Plot

1 [SHIFT][,] 2 -> Plot 1,2 [=] -> X= 1.06521739

[SHIFT][Sketch][ ][ ][ ]-> Horiz

[=] La droite se trace, parallèle à l’axe des x. On remarque que si on utilise les èches, le graphique se recalcule et seules les courbes programmées Y1 et Y2 restent à l’écran.

Fonction Verticale

Permet de tracer une droite verticale, à partir d’un point déterminé par Plot.

Ex :

En reprenant l’exemple précédent :

On se place avec Plot avec x=1 et y=2.

[SHIFT][Sketch][=] 1 [SHIFT][,] 2 -> Plot 1,2 [=] -> X= 1.06521739

[SHIFT][Sketch][ ][ ][ ][ ] -> Vert [=] La droite se trace, parallèle à l’axe des y.

On remarque que si on utilise les èches, le graphique se recalcule et seules les courbes programmées Y1 et Y2 restent à l’écran.

51

8. STATISTIQUES

Commentaires préliminaires

Pour mémoire

On dispose de n données sur un échantillon de mesures, résultats,

personnes, objets... Chaque donnée est constituée d’un nombre

(une variable x) ou deux (deux variables x et y). On cherche à

calculer la moyenne de ces données et la répartition de ces

données autour de la moyenne, l’écart-type.

Ces données se calculent à partir de sommes que l’on notera :

∑x = x1+x2+x3+....xn-1+xn

∑x2= x12+x22+x32+....xn-12+xn

∑xy = x1y1+x2y2+x3y3+....xn-1yn-1+xnyn

Moyenne

écart type / déviation standard de l’échantillon pour x :

écart type / déviation standard de la population pour x :

2

variance = s2 ou

2

Lorsqu’on a deux variables on essaie de déduire des données une relation entre x et y. On étudie la solution la plus simple : une relation de type y=a+bx.

La validité de cette hypothèse est vériée par le calcul d’une donnée r appelée coefcient de corrélation linéaire. Le résultat est toujours entre –1 et +1 et on considère bon un résultat supérieur ou égal à √3/2 en valeur absolue. Si la régression linéaire n’est pas vériée on peut étudier d’autres types de relation entre x et y, en particulier : logarithmique : y = A + Blnx exponentielle : y = A e puissance : y = A x inverse : y = A + B/x quadratique : y = A + Bx +Cx

52

Bx

B

2

Votre calculatrice vous permet d’obtenir aisément ces résultats, en suivant les étapes suivantes :

• Choisissez votre mode statistique (une ou deux variables).

• Saisissez les données;

• Vériez que la valeur de n correspond bien au nombre de données théoriquement saisies;

• Calculez la moyenne X et l’écart type (ou déviation standard) de l’échantillon ou de la population, ainsi que les autres calculs intermédiaires si nécessaire (∑ x , ∑ x2) à l’aide des touches correspondantes.

• S’il y a deux variables, procédez aux mêmes calculs pour y (moyenne, écart type), puis calculez la régression linéaire (a et b dans y=a+bx) et le coefcient de régression linéaire.

• Si la régression linéaire est jugée valide, on peut alors calculer la valeur estimée de y pour un x donné, ou la valeur estimée de x pour un y donné, de par la relation y=a+bx.

Statistiques à une variable

Saisie des données

[MENU][ ][ ][=]

Passage en mode statistique à 1 variable. SD est indiqué sur l’afchage.

[MENU][=]

[SHIFT] [Scl]

[DT]

Retour au mode normal (COMP).

Remet à zéro toutes les données.

Enregistre les données : donnée1 [DT] donnée2 [DT] etc. Pour entrer la même donnée plusieurs fois, appuyer sur [DT] plusieurs fois à la suite.

[SHIFT] [;]

Permet d’enregistrer plusieurs données identiques en une seule saisie : x1 [SHIFT][;] 3 [DT] enregistre 3 fois la même valeur x1 en mémoire.

[ALPHA][n]

Afche le nombre d’échantillons rentrés (n), c’est-à-dire le nombre des données.

Dans une certaine mesure vous pouvez vérier les données saisies avec les èches [ ] et [ ]. Ex : On veut saisir les données 10, 20, 20, 30, 30, 30, 60 ln2, 45. [MENU] [ ][ ][=] -> SD est afché

MODE?

SD REG BASE-N

[SHIFT][Scl] [=] -> Scl remise à zéro 10 [DT] -> 10. 20 [DT][DT] -> 20. la valeur est enregistrée 2 fois 30 [SHIFT][;]3 [DT] -> 30. la valeur est enregistrée 3 fois 60ln2 [DT] -> 41.58883083 45 [DT] -> 45 [ALPHA][n][=] -> n = 8.

53

Correction et/ou effacement des données saisies

[AC/ON]

Permet de corriger une saisie avant d’avoir appuyé sur [DT].

[SHIFT][CL]

Permet de corriger les erreurs de saisie après avoir appuyé sur [DT].

- soit en appuyant sur [SHIFT][CL] immédiatement après la saisie erronée.

- soit en saisissant la valeur erronée saisie plus tôt et en appuyant sur [SHIFT][CL].

Ex :

On saisit les données 10, 20, 20, 30, 30, 30, 60 ln2, 48.

• En cours de saisie, tant que vous n’avez pas appuyé sur [DT], utilisez

[AC/ON] : 30 [AC/ON] 30 [SHIFT][;] [AC/ON] En cours de saisie, si vous voulez effacer la dernière valeur saisie et pour laquelle vous avez appuyé sur [DT], utilisez [SHIFT][CL] : juste après [48] [DT], [SHIFT][CL] efface la saisie de 48

• Pour effacer une valeur saisie précédemment, il faut saisir la valeur puis appuyer sur [SHIFT][CL] : 10 [SHIFT][CL] 20 [SHIFT][;] 2 [SHIFT][CL] efface les deux saisies de valeur 20 30 [SHIFT][CL] efface l’un des trois 30 60ln2 [SHIFT][CL] efface la saisie de valeur calculée

Calcul de moyenne et écart-type

[SHIFT] [ x ]

[ALPHA] [∑x2]

[ALPHA] [∑x]

[SHIFT][x n]

Calcule la moyenne de x.

Afche la somme des carrés des données rentrées ∑x2.

Afche la somme des données rentrées ∑x.

Calcule l’écart-type (ou déviation standard) de la population.

[SHIFT] [x n-1]

Calcule l’écart-type (ou déviation standard) de l’échantillon.

Exemple pratique

Benjamin et ses amis ont obtenu les résultats suivants à la composition de Français :

Elève A B C D E F G H I J note 8 9.5 10 10 10.5 11 13 13.5 14.5 15

54

Moyenne et écart-type (de l’échantillon) pour les notes de Benjamin et ses amis ?

[MENU][ ][ ][=] -> SD est afché [SHIFT][Scl][=] -> remise à zéro

8 [DT] -> 8. début de saisie des données 9 [.] 5 [DT] -> 9.5 10 [DT] [DT] -> 10. ou 10 [SHIFT] [;] 2 [DT] pour saisir deux fois la même valeur.

Et ainsi de suite : 10 [.]5 [DT] 11 [DT] 13 [DT] 13[.]5 [DT] 14 [.]5 [DT] 15 [DT] On afche n et on vérie que le nombre afché correspond aux nombres de valeurs saisies : [ALPHA][n][=] -> n = | 10. [SHIFT] [ ] [=] -> = | 11.5 Leur moyenne est de 11,5.

[SHIFT] [x n-1][=] -> x n-1 | 2.34520788 soit l’écart type recherché.

Si on veut calculer la variance on appuie sur [x2][=] -> Ans2 | 5.5 c’est la variance.

Si on veut changer la première valeur, 8 en 14 : 8 [SHIFT][CL] 14 [DT] On voit que n reste égal à 10 mais que la moyenne a été modiée : [ALPHA][n][=] -> n = | 10. [SHIFT] [ ] [=] -> | 12.1

On reprend l’expérience avec la composition de maths, à laquelle ils ont obtenu les notes suivantes :

Elève A B C D E F G H I J note 4 7.5 12 8 8 8 14.5 17 18 18

[SHIFT][Scl] [=] -> remise à zéro

On peut vérier en faisant : [ALPHA][n][=] -> n = | 0. Début de saisie des données : 4 [DT] -> 4 | 4. … Et ainsi de suite jusqu’à 18 [DT]

55

[ALPHA][n][=] -> n = | 10. [SHIFT] [ ] [=] -> | 11.5 Leur moyenne est de 11,5 également. [SHIFT] [x n-1][=]-> x n-1 | 5.088112507 soit l’écart type recherché. On constate que la moyenne est la même mais que l’écart type est plus grand cette fois-ci : on peut en conclure qu’il y a plus d’écart entre les notes des élèves, leur niveau est donc moins homogène en maths qu’en français.

A titre d’exercice, dans cet exemple (les notes de maths) on obtient les valeurs suivantes pour ∑x et ∑x2 : [ALPHA][ ∑x] [=] -> 115. [ALPHA] [∑x2] [=] -> 1555.5

Représentation graphique

[DRAW]

Représente graphiquement une fonction sous forme de graphiques à barres ou de courbe.

On peut choisir entre ces fonctions lorsqu’on appuie sur [DRAW] :

SD DRAW? Bar Line

Si on choisi un graphique à barres, on xe dans [Range]:

• une nouvelle échelle pour y, entre 0 et 20 graduation en 2.

• un nombre de barres « Bar 1~20 ? ». On choisit 10, qui est par ailleurs

la valeur par défaut.

Ex :

groupe

0 10 20 30 40 50

60

70 80 90

100

nombre

1 3 2 2 3 5

6

8

15

9 1

[MENU][ ][ ][=] -> SD est afché. [SHIFT][Scl][=] -> remise à zéro. 0 [DT] -> 0. début de saisie des données. 10[SHIFT] [;] 3 [DT] -> 10.

--[ALPHA][n][=] -> n = | 55.

56

En traçant [DRAW][=] on obtient l’écran suivant :

Note : les paramètres d’échelles sont à choisir soigneusement pour que votre graphique à barres s’afche correctement.

On xe les paramètres d’échelle pour une courbe “Line” : x entre 0 et 110, graduation de 10 y entre 0 et 0.05, graduation de 0.01

[DRAW][ ][=] La courbe s’afche selon la formule :

- xr

2

- ( x - u )

y =

i

2 π

-e

Il s’agit d’une belle courbe de Gauss, en « forme de cloche ».

Statistiques à deux variables

Choix du type de régression

[MENU][ ][ ][ ][=]

Passage en mode statistique à 2 variables et choix parmi 6 types de régression. REG est indiqué sur l’afchage.

[MENU][=]

Retour au mode normal (COMP).

Après avoir choisi le mode REG vous avez les choix suivants :

MODE? Lin Log Exp

MODE?

Pwr Inv Quad

Votre calculatrice vous permet de saisir les données de la même façon quelle que soit le type de régression choisi au départ. En fait votre calculatrice effectue elle-même pendant la saisie les modications nécessaires comme suit :

57

Régression

Linéaire

Logarithmique

Exponentielle

Puissance Inverse Quadratique

Formule

y=A + Bx

y=A + B ln x

Bx

y=A e

B

y=A x

y=A+B/x

y=A+Bx+Cx

x est remplacé par

x

ln x

x

ln x

1/x

2

x

y est remplacé par

y

y ln y ln y

y

Vous n’avez besoin de prendre en compte ces modications que lorsque vous afchez les différentes sommes. Par exemple pour la régression inverse ∑xy devient ∑y/x, ou pour la régression de type exponentielle ∑y2=∑(lny)2. Voir les tableaux récapitulatifs en annexe.

Saisie des données

[SHIFT] [Scl]

Remet à zéro toutes les données statistiques (et du contenu des mémoires).

[SHIFT][,] [DT]

Sépare les données x et y pour la saisie. Enregistre les données : x1 [SHIFT][,] y1 [DT] x2 [SHIFT][,] y2 [DT] etc. Pour entrer la même saisie plusieurs fois, appuyer sur [DT] plusieurs fois à la suite.

[SHIFT][;]

Permet d’enregistrer plusieurs données identiques en une seule saisie : x1 [SHIFT][,] y1 [SHIFT][;] 3 [DT] enregistre 3 fois la même saisie x1 et y1 en mémoire.

On peut rentrer un calcul au lieu d’une valeur de variable, et la calculatrice met en mémoire le résultat. Dans une certaine mesure vous pouvez vérier les données saisies avec les èches [ ] et [ ].

Note : lorsque vous appuyez sur [DT], les points entrés sont automatiquement afchés sur l’écran graphique. Cependant, si les valeurs d’échelle préenregistrées par Range ne correspondent pas aux valeurs saisies le point ne s’afchera pas. Voir plus loin le paragraphe “Représentation graphique”.

Ex :

On veut saisir les données 10/5, 20/8, 20/8, 30/11, 30/11, 30/11, 60

ln2/40ln3, 45/13.

En mode régression linéaire :

[MENU][ ][ ][ ][=][=]

[SHIFT][Scl] [=] -> remise à zéro

10 [SHIFT][,] 5 [DT] -> 10. 20 [SHIFT][,] 8 [DT][DT] -> 20. la valeur est

enregistrée 2 fois 30 [SHIFT][,] 11 [SHIFT][;]3 [DT] -> 30. la valeur est enregistrée 3 fois

60ln 2[SHIFT][,] 40ln 3 [DT] -> 41.58883083 45 [SHIFT][,]13 [DT] -> 45 [ALPHA][n][=] -> n = | 8.

58

Correction et/ou effacement des données saisies

[AC/ON]

Permet de corriger une saisie avant d’avoir appuyé sur [DT].

[SHIFT][CL]

Permet de corriger les erreurs de saisie après avoir appuyé sur [DT]:

- soit en appuyant sur [SHIFT][CL] immédiatement après la saisie erronée.

- soit en saisissant la valeur erronée saisie plus tôt et en appuyant sur [SHIFT][CL].

Ex :

On veut saisir les données 10/5, 20/8, 20/8, 30/11, 30/11, 30/11, 60 ln2/40ln3, 45/13 (on note 10/5 la première saisie soit x1=10 et y1=5)

• En cours de saisie, tant que vous n’avez pas appuyé sur [DT], utilisez

[AC/ON] : 30 [AC/ON] 30 [SHIFT][,] 11

30 [SHIFT][,] 11 [SHIFT][;] [AC/ON]

• En cours de saisie, si vous voulez effacer la dernière valeur saisie et pour laquelle vous avez appuyé sur [DT], utilisez [SHIFT][CL] :

juste après 45 [SHIFT] [;] 13 [DT], [SHIFT][CL] efface la saisie de 45/13.

• Pour effacer une valeur saisie précédemment, il faut saisir la valeur

puis appuyer sur [SHIFT][CL] :

10 [SHIFT][,] 5 [SHIFT][CL] efface la saisie de 10/5 20 [SHIFT][,] 8 [SHIFT][;] 2 [SHIFT][CL] efface les deux saisies de

valeur 20/8.

30 [SHIFT][,] 11 [SHIFT][CL] efface l’un des trois 30/11. 60ln2 [SHIFT][,] 40ln 3 [DT] [SHIFT][CL] efface la saisie de valeur

calculée.

Calcul de moyenne et écart-type

[SHIFT] [

[ALPHA] [∑x2] , [∑y2]

], [

]

x

y

Calcule la moyenne de x ou de y.

Afche la somme des carrés des données rentrées ∑x2, ∑y2.

[ALPHA] [∑x] , [∑y]

[ALPHA] [∑xy]

Afche la somme des données rentrées ∑x , ∑y.

Afche la somme du produit des données rentrées ∑xy.

Pour la régression quadratique:

[ALPHA][ ∑x2y]

Afche la somme ∑x2y.

[ALPHA][ ∑x4]

[ALPHA][ ∑x3]

[SHIFT][x n], [y n]

Afche la somme ∑x4.

Afche la somme du produit des données rentrées ∑x3.

Calcule l’écart-type (ou déviation standard) de la population.

[SHIFT] [x n-1],

[y n-1]

Calcule l’écart-type (ou déviation standard) de l’échantillon.

59

Votre calculatrice vous permet de saisir les données de la même façon quelle que soit le type de régression choisi au départ. On rappelle que les sommes ∑x2, ∑y2, ∑xy subissent des modications pour certaines régressions, comme expliqué au paragraphe sur le choix du type de régression. Le détail complet de ces variations est aussi donné en annexe de ce manuel.

Ex :

On saisit les données 10/5, 20/8, 20/8, 30/11, 30/11, 30/11, 60 ln2/40ln3, 45/13 (on note 10/5 la première saisie soit x1=10 et y1=5).

On obtient les résultats suivants pour une régression linéaire : [SHIFT] [ x ][=] -> [SHIFT] [ y ][=] ->

| 28.32360385

x

| 13.86806144

y

Calculs de régression

[SHIFT] [ A ]

Calcule la valeur du coefcient A.

[SHIFT] [ B ]

[SHIFT] [ C ]

Calcule la valeur du coefcient B.

Calcule la valeur du coefcient C (en cas de régression quadratique).

[SHIFT] [ r ]

Calcule la valeur du coefcient de corrélation r (ne s’afche pas pour la régression quadratique).

[SHIFT] [ y ]

Afche la valeur de y estimée par régression pour la valeur x saisie.

[SHIFT] [ x ]

Afche la valeur de x estimée par régression pour la valeur y saisie. Pour une régression quadratique on peut obtenir

deux valeurs de x (voir détail et conditions en

annexe) : valeur de y [SHIFT] [ x ] afche x1, puis de nouveau [SHIFT] [ x ] afche x2.

Exemples pratiques

Régression linéaire :

On a le tableau suivant où x est la longueur en mm et y le poids en mg d’une chenille de papillon à différents stades de son développement.

X 2 2 12 15 21 21 21 Y 5 5 24 25 40 40 40

60

Régression non linéaire

On passe en mode statistiques à deux variables et régression linéaire : [MENU][ ][ ][ ][=] -> choix du type de régression. [=] -> choix de Lin, REG est afché. [SHIFT][Scl][=] -> remise à zéro.

On commence la saisie : 2 [SHIFT][,] 5 [DT] [DT] -> 2. … 21 [SHIFT][,] 40 [ ;] 3 [DT] -> 15. On vérie n : [ALPHA][n] [=] -> n= | 7.

On afche les résultats de la régression linéaire : [SHIFT] [ A ][=] -> A | 1.050261097 [SHIFT] [ B ][=] -> B | 1.826044386 [SHIFT] [ r ][=] -> r | 0.9951763432

r est supérieur à √3/2 = 0.866 environ, la validité de la régression est vériée.

Grâce à la régression linéaire on estime y à partir de x=3 : 3 [SHIFT] [ ] -> | 6.528394256

On estime x à partir de y=46 : 46 [SHIFT] [ x ] -> x | 24.61590706

Avec les touches statistiques de votre calculatrice vous pouvez afcher facilement tous les résultats intermédiaires, comme par exemple : [ALPHA] [∑xy] [=] -> 3203. [SHIFT] [y n] [=] -> 14.50967306

Régression de type puissance :

On soupçonne que x et y sont liés par une relation du type y=A xB et on cherche à conrmer l’hypothèse :

x 0,5 1 1,5 2 y 1,4 2 2,4 2,9

On passe en mode statistiques à deux variables et régression puissance : [MENU][ ][ ][ ][=] -> choix du type de régression. [ ][ ][ ][=] -> REG est afché, choix de Pwr. [SHIFT][Scl] [=] -> remise à zéro. Début de saisie : [.]5 [SHIFT][,] 1[.]4 [DT] 1 [SHIFT][,] 2 [DT] … etc. [ALPHA][n] -> n= | 4.

61

On obtient les valeurs de A, B et r suivantes : [SHIFT] [ A ][=] -> A | 1.994142059 [SHIFT] [ B ][=] -> B | 0.515317442 [SHIFT] [ r ] [=] -> r | 0.998473288 La régression de type puissance est vériée puisque r=0,998. Par approximation on peut dire que y ≈ 2x

1/2

= 2√x. 4 [SHIFT] [ ] -> | 4.073878837 6 [SHIFT] [ ] -> | 8.479112672

Régression quadratique :

On soupçonne que x et y sont liés par une relation du type y= A+Bx+Cx2 et on cherche à conrmer l’hypothèse :

x 29 50 74 103 118

y 1,6 23,5 38 46,4 48

On passe en mode statistiques à deux variables et régression quadratique : [MENU][ ][ ][ ][=] -> choix du type de régression [ ][ ][ ][ ][ ][=] -> REG est afché, choix de Quad [SHIFT][Scl] [=] -> remise à zéro Début de saisie : 29 [SHIFT][,] 1[.]6 [DT] 50 [SHIFT][,] 23[.]5 [DT] … etc. [ALPHA][n][=] -> n= | 5.

On obtient les valeurs de A, B, et C suivantes : [SHIFT] [ A ][=] -> A | -35.59856934 [SHIFT] [ B ][=] -> B | 1.495939413 [SHIFT] [ C ][=] -> C | -0.006716296

Pour x= 16 on obtient une seule valeur de y estimé : 16 [SHIFT] [ ] -> | -13.38291067 Mais pour y=20 on obtient deux valeurs possibles de x : 20 [SHIFT] [ ] -> 1 | 47.14556728 [SHIFT] [ ] -> 2 | 175.5872105

Si la valeur de y proposée n’a pas de solution x réelle, par exemple y=56, votre calculatrice afchera Ma ERROR.

Représentation graphique

Votre calculatrice représente graphiquement les données au fur et à mesure que vous procédez à leur saisie. Il suft pour cela :

- de choisir des paramètres d’échelle compatibles avant de saisir vos données.

- d’appuyer sur [DRAW] à la n de la saisie pour visualiser la courbe.

62

Ex :

On soupçonne que x et y sont liés par une relation du type y=A xB et on cherche à conrmer l’hypothèse :

x 0,5 1 1,5 2 y 1,4 2 2,4 2,9

On entre en premier les paramètres d’échelle avec [Range] : xmin = 0 xmax = 2,5 xscl = 0,5 ymin = 0 ymax = 3 yscl = 1

Ensuite on choisit le mode de régression puissance (Pwr), et on saisit les données. Les points s’afchent au fur et à mesure :

Et lorsqu’on appuie sur [DRAW], la courbe s’afche, ainsi que la formule de régression utilisée.

63

9. MESSAGES D’ERREUR

Causes possibles d’erreurs

Lorsque l’écran afche un message d’erreur, les raisons peuvent être :

• Syn ERROR : erreur de syntaxe. Ex : [sin] 3 [+] [=].

• Ma ERROR : la valeur utilisée est en dehors des valeurs admissibles (voir tableau plus loin). Ex : division par 0, cos-1 (5), √(-2). Il se peut aussi que lors du calcul effectué à partir des valeurs saisies, une valeur intermédiaire se retrouve en dehors des valeurs admissibles, trop grande ou trop petite. Une valeur très petite (inférieure à 10 un 0, ce qui peut créer une situation de division par 0.

• Stk ERROR : dépassement de la capacité mémoire de la calculatrice. Votre calcul est trop long, mieux vaut le découper en deux parties ou plus (voir paragraphe Priorités de calcul dans le premier chapitre).

Pour sortir de l’écran d’afchage de l’erreur, appuyez sur [AC/ON] et utilisez les èches [ ] et [ ] pour corriger l’équation.

Valeurs admissibles

De manière générale les valeurs utilisées dans les calculs doivent vérier :

-9,999999999 x 1099 ≤ x ≤ 9,999999999 x 1099 soit |x| <10

-99

) sera arrondie en

100

Note : |x| est la valeur absolue de x, soit |x|= –x si x≤0 et |x|=x si x≥0.

64

Pour certaines fonctions les intervalles sont nécessairement plus petits :

Fonction

-1

x

2

x

y

Conditions supplémentaires

-99

|x| ≥ 10

50

|x| < 10 si x > 0, y.ln|x| ≤ 230.2585092 si x=0, y >0 si x < 0, y.ln|x| ≤ 230.2585092 et

x

y

√

y est impair ou 1/y est un entier (y≠ 0) si y > 0, 1/x.ln|y| ≤ 230.2585092 si y=0, x >0 si y < 0, 1/x.ln|y| ≤ 230.2585092 et

x

10

x

√

ln x, log x

x

e

sinh x, cosh x

sinh-1x

cosh-1x

tanh-1x

sin x

cos x

sin–1x, cos–1x

degrés décimaux et sexagésimaux

coordonnées polaires

nombres complexes

a=x+iy

x !

Base 10

1/x est impair ou x est un entier (x≠ 0) x < 100 x ≥ 0

-99

x ≥ 10 x ≤ 230.2585092 |x| ≤ 230.2585092 |x| < 5 x 10 1 ≤|x| < 5 x 10 |x|<1 DEG |x| < 4.5 x 10 RAD |x| ≤ π/4 x 10 GRAD |x| < 5.10 DEG |x| < 4.5 x 10 RAD |x| ≤ π/4 x 10 GRAD |x| < 5.10 |x| ≤ 1 |x|<10 x, y < 1050

et x2+y2 < 10

99

10

9

10

9

10

100

r≥0, θ comme le x pour sin x et cos x. 0 ≤ x ≤ 69 ; (x entier)

-231 ≤ (X)10 < 2

31

nombres entiers binaires de 10 chiffres maximum

Base 2

Base 8

0≤ x ≤ 0111111111 ou 1000000000 ≤ x ≤ 1111111111

soit –29 ≤ (x)10 < 2

9

nombres entiers octaux de 10 chiffres maximum 0≤ x ≤ 3777777777 ou 4000000000 ≤ x ≤ 7777777777 soit -229 ≤ (x)10 < 229

Base 16

statistiques

nombres entiers hexadécimaux de 8 chiffres maximum 0≤ x ≤ 7FFFFFFF ou 80000000≤ x ≤ FFFFFFFF Soit -231 ≤ (x)10 < 2 n entier, 0<n<10 0 °‹ x, y < 1050 au minimumpour

100

31

n-1

, n>1

valeurs intermédiaires de calcul (∑x, ∑y, ∑x2, ∑y,

∑

xy et ∑x4, ∑x3,∑x2y) dans les limites admissibles.

65

10. PRECAUTIONS D’EMPLOI

IMPORTANT : sauvegarde de vos données

Votre calculatrice comporte une mémoire électronique capable de conserver une grande quantité d’informations. Ces informations sont gardées en mémoire de manière able tant que les piles fournissent l’énergie nécessaire et sufsante à leur bonne conservation. Si vous laissez les piles devenir trop faibles, lorsque vous changez les piles ou si l’alimentation électrique s’interrompt pour une autre raison, les informations stockées en mémoire seront irrémédiablement perdues. Un choc électrostatique important ou des conditions d’environnement extrêmes peuvent aussi causer la perte des informations. Une fois les informations perdues elles ne peuvent pas être récupérées de quelque manière que ce soit, c’est pourquoi nous vous conseillons fortement de garder systématiquement une sauvegarde de vos données (valeurs, programmes) dans un lieu sûr.

Utilisation de RESET

N’appuyez sur la touche de réinitialisation du système (RESET) que dans les cas suivants:

• Lors de la première utilisation.

• Après le remplacement des piles.

• Pour effacer le contenu de toutes les mémoires.

• En cas de blocage général, toutes les touches étant inopérantes. Par exemple, si vous exposez la calculatrice à un champ électrique, ou à une décharge électrique pendant l’utilisation, il peut se produire des phénomènes anormaux qui peuvent neutraliser le fonctionnement de certaines touches y compris la touche [AC/ON].

ATTENTION : ne pas appuyer sur RESET lorsque vous pensez qu’un calcul ou opération interne est en cours, cela pourrait endommager irrémédiablement votre calculatrice.

Pour appuyer sur le bouton Reset, appuyez sur [AC/ON] pour remettre la calculatrice en marche puis utilisez un objet n et pointu tel qu’un trombone déplié, et appuyez doucement.

66

Remplacement des piles

Dès que l’afchage faiblit et qu’un réglage de contraste n’améliore pas la lisibilité, nous vous conseillons de remplacer les piles. Votre calculatrice utilise deux piles de type 1,5V AAA (fournies) pour l’alimentation principale et une pile de type 3V (+DC voltage symbol) CR2032 comme alimentation de secours.

• Effectuez une sauvegarde de toutes les données et programmes dont vous aurez besoin ultérieurement.

• Attendez que votre calculatrice soit éteinte, après quelques minutes d’inactivité.

• Appuyez sur [AC/ON] pour remettre la calculatrice en marche. Si les piles ont été correctement installées, l’icône D et le curseur clignotant seront afchés. Si ce n’est pas le cas, retirez et réinstallez à nouveau les piles.

• Appuyez doucement sur RESET avec un objet n et pointu pour réinitialiser la calculatrice (important).

Ne pas recharger les piles non rechargeables. Retirer les accumulateurs du produit avant de les recharger. Ne charger les accumulateurs que sous la surveillance d’un adulte. Ne pas mélanger différents types de piles ou accumulateurs, ou des piles et accumulateurs neufs et usagés. Les piles et accumulateurs doivent être mis en place en respectant la polarité. Les piles et accumulateurs usagés doivent être enlevés du produit. Les bornes d’une pile ou d’un accumulateur ne doivent pas être mises en court circuit. Ne pas jeter les piles au feu. Retirer les piles en cas de non utilisation prolongée. Ce produit doit être alimenté avec les piles spéciées seulement.

67

ATTENTION : D’importantes interférences électromagnétiques ou des décharges électrostatiques peuvent provoquer un dysfonctionnement ou une perte de données. Si l’appareil ne fonctionne pas correctement, enlevez puis remettez la pile.

Une mauvaise utilisation des piles peut causer une fuite de liquide électrolytique ou même les faire exploser, et peut endommager l’intérieur de votre calculatrice. Lisez donc bien les recommandations suivantes :

• Toujours remplacer les deux piles en même temps.

• S’assurer qu’elles sont du modèle recommandé avant de les installer.

• Bien respecter les polarités indiquées.

• Ne pas laisser des piles usagées dans la calculatrice, elles peuvent fuir et l’endommager irrémédiablement.

• Ne pas laisser les piles neuves ou usagées à la portée des enfants.

• Ne jamais jeter des piles au feu, elles pourraient exploser.

• Ne pas jeter les piles dans les ordures ménagères mais dans un lieu de collecte adapté pour leur recyclage, dans la mesure du possible.

Conditions extrêmes

Si vous exposez la calculatrice à un champ électrique, ou à une décharge électrique pendant l’utilisation, il peut se produire des phénomènes anormaux qui peuvent neutraliser le fonctionnement de certaines touches y compris la touche ON. Dans ce cas, réinitialisez la calculatrice en retirant et insérant la pile à nouveau. Attention, le contenu de la mémoire sera complètement effacé si vous réalisez cette opération. Réinitialisez la calculatrice que dans les cas suivants:

• Pour effacer tout le contenu de la mémoire.

• Quand survient une condition extrême, et que les touches ne répondent plus.

68

Entretien de votre calculatrice

• N’essayez jamais de démonter votre calculatrice, elle contient des pièces de précision.

• Evitez de faire tomber votre calculatrice et protégez-la des chocs.

• Ne la transportez pas dans la poche arrière d’un pantalon.

• Evitez que votre calculatrice soit en contact avec l’humidité, avec des impuretés, des poussières ou de fortes températures. Dans un environnement froid la calculatrice peut ralentir ou même suspendre son fonctionnement. Elle retrouvera un fonctionnement normal dès que la température redeviendra plus clémente.

• Evitez tout contact de la calculatrice avec de l’eau ou autres substances liquides car cela pourrait provoquer des courts-circuits et des risques d’incendie. Ne provoquez pas d’éclaboussures sur la calculatrice.

• Evitez d’utiliser des liquides chimiques ou essence pour nettoyer la machine. Essuyez-la avec un linge doux et sec, ou avec un linge légèrement humidié avec de l’eau et un détergent neutre.

• En aucune circonstance le fabricant et ses fournisseurs ne seront

responsables envers vous ou toute une autre personne de tout

dommage, dépense, perte de prot, perte d’argent ou tout autre préjudice provenant d’une perte de données et/ou de formules causée par un mauvais fonctionnement, des réparations ou le remplacement des piles. L’utilisateur doit prévoir des copies des dossiers et données an de se protéger contre toute perte.

• Ne vous débarrassez jamais des piles, de l’écran à cristaux liquides ou des autres pièces en les brûlant.

• Si la calculatrice est exposée à une forte décharge électrostatique, son contenu mémorisé pourra être endommagé ou les touches pourraient arrêter de fonctionner.

• L’afchage disparaît et les touches du clavier sont inopérantes pendant que la calculatrice effectue des calculs. Surveillez bien votre écran an de vérier que votre saisie est enregistrée correctement.

• Si un dysfonctionnement potentiel est détecté, relisez bien ce manuel et vériez l’état des piles pour vérier que le problème ne vient pas d’une mauvaise utilisation ou de piles trop faibles.

• Avant de présumer un dysfonctionnement de la machine, assurez-vous encore d’avoir bien lu ce mode d’emploi et vériez que le problème n’est pas dû à une insufsance des piles ou à cause d’une erreur opérationnelle.

69

10. INDEX

A, B, C, r calculs de

régression 62

And 33 BASE 34 CMPLX 31

Deg 27

Disp 13 Fix 17 FUNCT 41 Gra 27

Horiz 49

Line 59

Neg 36

Norm 16 Not 37 Or 37 PARAM 44 Plot 49 Rad 27 REG 59 RESET 68 Sci 18 SD 55 Shift (fonction graphique) 41

Tangent 49

Vert 49 Xnor 37 Xor 37

[ èches gauche et droite]

11

[ èches haut et bas] 11

[ ] 62 [,] 30

[,] intégrales 38 [(-)] 10 [(] 10

[ ] au dessus touche [ENG] 16 [ ] au dessus touche [º ‘ ‘ ‘] 29

[(]-[)] 10 [)] intégrales 38

[%] 19

[∑x] 56 [∑x2] 56 [∑x2y] 61

[∑x3] 61 [∑x4] 61 [∑xy] 61 [∑y] 61 [∑y2] 61 [=] saisie d’une équation 41 [√] 23 [∫dx] 38

[10x] 23

[3√] 23 [a b/c] 23 [A]-[F] hexadécimal 33

[A]-[F], [X],[Y] 22

[Abs] nombre complexe 31

[AC/ON] 6 [ALPHA] 9 [Ans] 21

[arg] 31 [b] 34

[CALC] 39 [CL] 56 [CLS] 41 [cos-1] 28 [cos] 28

[cos] hyperbolique 25

[d] 34 [d/c] 23 [DEL] 11 [DRAW] 41 [DT] 55

[E] [F] coordonnées

polaires 30 [ENG] 16 [ex] 25 [EXP] 16 [Factor] 45 [Func] 41 [G T] 41 [G-SOLVE] 47 [h] 34 [HEX] 34

[hyp] 25

[i] 31

70

[INS] 11 [ln] 25

[log] 25

[LOGIC] 36 [M-] 21 [M] 21 [M+] 21 [Mcl] 22 [MODE] 15 [n] 55 [º’’’] 29 [o] 34 [OFF] 6 [AC/ON] 6 [Pi] 27

[point virgule] 55 [Pol(] 30

[PROG] 39 [Ran#] 26

[Range] 41

[RCL] 21 [Re Im] 31

[Rec(] 30

[Rnd] 17 [Scl] 55 [SHIFT] 9 [sin-1] 28 [sin] 28

[sin] hyperbolique 25

[Sketch] 49 [STO] 22 [tan-1] 28 [tan] 28

[tan] hyperbolique 25

[Trace] 48 [Value] 48 [X Y] 48 [X-1] 23 [X,T] 41 [n!] 26

[x√] 23

[X2] 23 [X3] 23

[Xy] 23

[x n-1] 56 [x n] 56 [ ] 62

[y n] 61 [ZoomOrg] 45

[Zoomx 1/f] 45 [Zoomxf] 45

71

12. ANNEXE : DETAIL DES FORMULES DE REGRESSION

Linéaire

Formule

x = f(y)

saisie de x

saisie de y ∑x ∑y

2

∑x

2

∑y ∑xy

coeff A coeff B r

Logarithmique

Formule

x = f(y)

saisie de x

saisie de y ∑x ∑y

2

∑x

2

∑y ∑xy

coeff A coeff B r

y=A + Bx x = (y-A)/B

x y

∑x ∑y

2

∑x

2

∑y ∑xy

(∑y-∑x)/n (n∑xy-∑x∑y)/(n∑x2-(∑x)2) (n∑xy-∑x∑y)/÷((n∑x2-(∑x)2) (n∑y2-(∑y)2)

y=A + Bln x lnx = (y-A)/B

ln x y

∑ln x ∑y ∑ln2x

2

∑y ∑yln x

(∑y-∑ln x)/n (n∑yln x-∑lnx∑y)/(n∑ln2x-(∑lnx)2) (n∑ylnx-∑lnx∑y)/÷((n∑ln2x-(∑lnx)2) (n∑y2-(∑y)2)

Exponentielle

Formule

x = f(y)

saisie de x

saisie de y

∑x ∑y

2

∑x

2

∑y ∑xy

coeff A coeff B r

72

Bx

y=A e x = (ln(y/A))/B

x ln y

∑x ∑lny

2

∑x ∑ln2y ∑xln y

(∑lny-∑x)/n (n∑xlny-∑x∑lny)/(n∑x-(∑x)2) (n∑xlny-∑x∑lny)/÷((n∑x2-(∑x)2) (n∑ln2y-(∑lny)2)

Puissance

Formule

x = f(y)

saisie de x

saisie de y ∑x ∑y

2

∑x

2

∑y ∑xy

coeff A coeff B r

y=A x ln x = (ln(y/A))/B

ln x ln y

∑ln x ∑lny ∑ln2x ∑ln2y ∑xln y

(∑lny-∑lnx)/n (n∑xlny-∑x∑lny)/(n∑lnx-(∑lnx)2) (n∑xlny-∑x∑lny)/÷((n∑ln2x-(∑lnx)2) (n∑ln2y-(∑lny)2)

Inverse

Formule

x = f(y)

saisie de x

saisie de y ∑x ∑y

2

∑x

2

∑y ∑xy

coeff A coeff B r

y=A + B/x x =B/(y-A) 1/x

y

∑1/x ∑y ∑1/x ∑y2 ∑y/x

(∑y-∑1/x)/n (n∑y/x-∑1/x ∑y)/(n∑1/x2-(∑1/x)2) (n∑y/x-∑1/x∑y)/÷((n∑1/x2-(∑17x)2) (n∑y2-(∑y)2)

Quadratique

Formule

x = f(y)

saisie de x

saisie de y ∑x ∑y

2

∑x

2

∑y

4

∑x

3

∑x ∑x2y ∑xy

coeff A coeff B coeff C

y=A+Bx+Cx x = -B/2C ± ÷(y/C-A/C+B2/4C2) pour Cy ≥AC-B2/4

x y

∑x ∑y

2

∑x

2

∑y

4

∑x

3

∑x ∑x2y

∑xy (∑y-B∑x-C∑x2)/n (n∑xy-∑x∑y-C(n∑x3-∑x2∑x))/(n∑x2-(∑x)2) ((n∑x2(∑x)2)(n∑x2y-∑x2Sy)-(n∑x3-∑x2∑x)(n∑xy-∑x∑y)) / ((n∑x2-(∑x)2) (n∑x4-(∑x2)2)-( n∑x3-Sx2Sx)2)

B

2

73

13. GARANTIE

Ce produit est couvert par notre garantie de trois ans. Pour toute mise en œuvre de la garantie ou de service après-vente, vous devez vous adresser à votre revendeur muni de votre preuve d’achat. Notre garantie couvre les vices de matériel ou de montage imputables au constructeur à l’exclusion de toute détérioration provenant du non-respect de la notice d’utilisation ou de toute intervention intempestive sur l’article (telle que démontage, exposition à la chaleur ou à l’humidité…).

Note : Veuillez garder ce mode d’emploi, il contient d’importantes informations.

Lexibook S.A, 2, Avenue de Scandinavie, 91953 Courtaboeuf Cedex, France. Service consommateurs : 0892 23 27 26 (0.34€ TTC/min), www.lexibook.com

Informations sur la protection de l’environnement

Tout appareil électrique usé est une matière recyclable et ne devrait pas faire partie des ordures ménagères! Nous vous demandons de bien vouloir nous soutenir en contribuant activement au ménagement des ressources et à la protection de l’environnement en déposant cet appareil dans des sites de collecte (si existants).

Reproduction partielle ou intégrale de ce manuel interdite, sous quelque forme que ce soit, sauf avec autorisation expresse écrite du fabricant. Le fabricant et ses fournisseurs déclinent toute responsabilité quant aux conséquences de l’utilisation ou de la mauvaise utilisation de cette calculatrice ou de ce manuel d’utilisation. De même le fabricant et ses fournisseurs déclinent toute responsabilité concernant tous dommages, pertes nancières, manques à gagner ou autres préjudices liés à des pertes de données ou de calculs lors de l’utilisation de cette calculatrice ou de ce manuel. Du fait de certaines limitations techniques lors de l’édition et de l’impression de ce manuel, l’apparence de certaines touches ou afchages indiqués dans les textes peuvent présenter de légères différences avec

l’apparence réelle.

Le fabricant se réserve le droit de modier le contenu de ce manuel sans préavis.

IM code : GC2210FRIM1110

74

LEXIBOOK GC2210FR User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual