HP 11729C-2 User Manual

Product Note 11729C-2

Phase Noise Characterization of
Microwave Oscillators

Frequency Discriminator Method

Ol S L1BRAR

>)2./a

<^$f,

4y>

sj

V

*J

\

\

Kr

v

*4&

>j **

fr»

/■

HEWLETT
PACKARD

Phase Noise Characterization of Microwave Oscillators

Frequency Discriminator Method

Table of Contents Page

Chapter 1: Introduction 3

Chapter 2: Phase Noise and its Effect on Microwave Systems 4

What is Phase Noise 4
Two-port and Absolute Noise 7
Why Phase Noise is Important 7

Digital Communications Systems 8
Analog Microwave Communications Systems 8
Doppler Radar System 8

Chapter 3: Phase Noise Measurements — Frequency

Discriminator Method 10

Common Measurement Techniques 10

Direct Measurement 10
Heterodyne/Counter Measurement 10
Carrier Removal/Demodulation 10

Measurement with a Phase Detector 11
Measurement with a Frequency Discriminator 12

The Delay Line/Mixer Frequency Discriminator Method 12

Basic Theory 12
The Discriminator Transfer Response 12

System Sensitivity 13
Optimum Sensitivity 14

Making A Measurement 15

System Setup 15
System Calibration 15
The Phase Noise Measurement 16

Chapter 4: HP 11729C Carrier Noise Test Set Theory of Operation

and Measurement Considerations 18
General Operation 18
Multiplier Chain 18
Demodulating and Bandpass Signal Processing 20

First Down Conversion 20
IF Processing and the Frequency Discriminator 20
Baseband Signal Processing 20

Phase Locked Loop/Quadrature Section 21

Chapter 5: Making Frequency (Phase) Noise Measurements

with the HP 11729C 22

System Setup 22

The Source 22
The 640 MHz Drive Signal 22
The Delay Line 23
System Operation 24

System Calibration 24

The Calibration Signal 24
System Response 25
The Discriminator Constant (Kd) 26

Measuring the Frequency (Phase) Noise 26

Measurement Corrections 27
Conversion to Other Units 27

Table of Contents (cont'd) Page

Chapter 6: Considerations in System Accuracy 29

Spectrum Analyzer 29

Relative Amplitude Accuracy 29

Resolution Bandwidth Accuracy 29
The IF Gain Accuracy 29
Spectrum Analyzer Frequency Response 29

System Parameters of the HP 11729C 30

Frequency Discriminator Flatness 30

Baseband Signal Processing Section Flatness 30

System Noise Floor 30

Measurement Procedure 31

Quadrature Maintenance 31

System Calibration 31

The Randomness of Noise 31

Overall Accuracy 31
Accuracy Without Error Correction 32
Accuracy With Error Correction 32

Appendix A: The Delay Line/Mixer Frequency

Discriminator Transfer Response 34

Appendix
Appendix C: System Sensitivity 38
Appendix D: Calibration and the Discriminator Constant Kd 40
Appendix E: The Importance of Quadrature 41
Appendix F: HP 11729C Programming Codes 42
Appendix G: References 43

B:

The Double-Balanced Mixer as a Phase Detector 36

As the performance of microwave radar and communication systems advances,
certain system parameters take on increased

importance.

One of these parameters that

must be measured is the spectral purity of microwave signal sources.

In the past, many techniques for measuring spectral purity have used complex,
dedicated instrumentation, often cumbersome in both size and operation and often
limited to narrow bands of operating frequency. The broadening focus on spectral
purity has created a need for measurement techniques that provide the high perform­ance necessary for R&D requirements, and that can be automated for production
environments. Also, service applications require a versatile system with a broad
frequency and performance range.

The Hewlett-Packard 11729C Carrier Noise Test Set

is

a key element of a system that
provides convenient manual or automatic phase noise measurements. With appro­priate companion instrumentation, phase noise measurements can be made on a
broad range of

This product
in Chapter
the phase noise of

sources,

note discusses

2.

Chapter 3 describes a frequency discriminator technique for measuring

from 10 MHz to 18 GHz.

phase noise and

sources.

The implementation of

its

effects on modern microwave systems

this

technique with the HP 11729C
is shown in Chapter 4. (See HP product note PN 11729B-1 for phase detector
method.) Chapter 5 outlines the measurement steps needed to make a phase noise
measurement, and the resultant measurement accuracy is derived in Chapter 6.

3

L Phase Noise and its Effect on Microwave Systems

WHAT IS PHASE NOISE? Frequency stability can be defined as the degree to which an oscillating source

produces the same frequency throughout a specified period of
microwave source exhibits some amount of frequency
be broken down into two components—long-term and short-term stability.

Long-term stability describes the frequency variations that occur over long time
periods, expressed in parts per million per hour, day, month, or year. Short-term
frequency stability contains all elements causing frequency changes about the nomi­nal frequency of less than a few seconds duration. This product note deals with
short-term frequency stability.

Mathematically, an ideal sinewave can be described by

V(t) = VoSin (27rfot)

where V0 = nominal amplitude,

27rf0t = linearly growing phase component,

and f0 = nominal frequency.

But an actual signal is better modeled by

instability.

time.

Every RF and

This

stability

can

be

V(t) = [v0+e(t)] sin [27rf0t + A<ftt)]

where e(t) = amplitude fluctuations,

and A</>(t) = randomly fluctuating phase term or phase noise.

This randomly fluctuating phase term
analyzer (one which had no sideband noise of
two types of fluctuating phase terms. The first, deterministic, are discrete signals
appearing as distinct components in the spectral density plot. These signals, com­monly called

as power line frequency, vibration frequencies, or mixer products.

The second type of phase instability is random in nature, and is commonly called
phase noise. The sources of random sideband noise in an oscillator include thermal

noise, shot noise, and flicker noise.

Many terms exist to quantify the characteristic randomness of phase noise. Essen­tially, all methods measure the frequency or phase deviations of the source under test
in either the frequency or time
other, all of the terms that characterize phase noise are also related.

One fundamental description of phase instability or phase noise
of phase fluctuations on a per-Hertz basis. The term spectral density describes the
energy distribution

unit bandwidth. Thus

spurious,

as a

can be related to known phenomena in the signal source such

continuous function, expressed in units of phase variance per

S^fj,,)

(Figure 2.1b) may be considered as

domain.

A<£(t)

could be observed on an ideal spectrum

its

own) as in Figure 2.1a. There are

Since frequency and phase are related to each

is the

spectral density

A4>L(fm) rad

BW used to measure Ac/^ Hz

where BW (bandwidth) is negligible with respect to any changes in S^ versus the

fourier frequency or offset frequency fm.

4

2

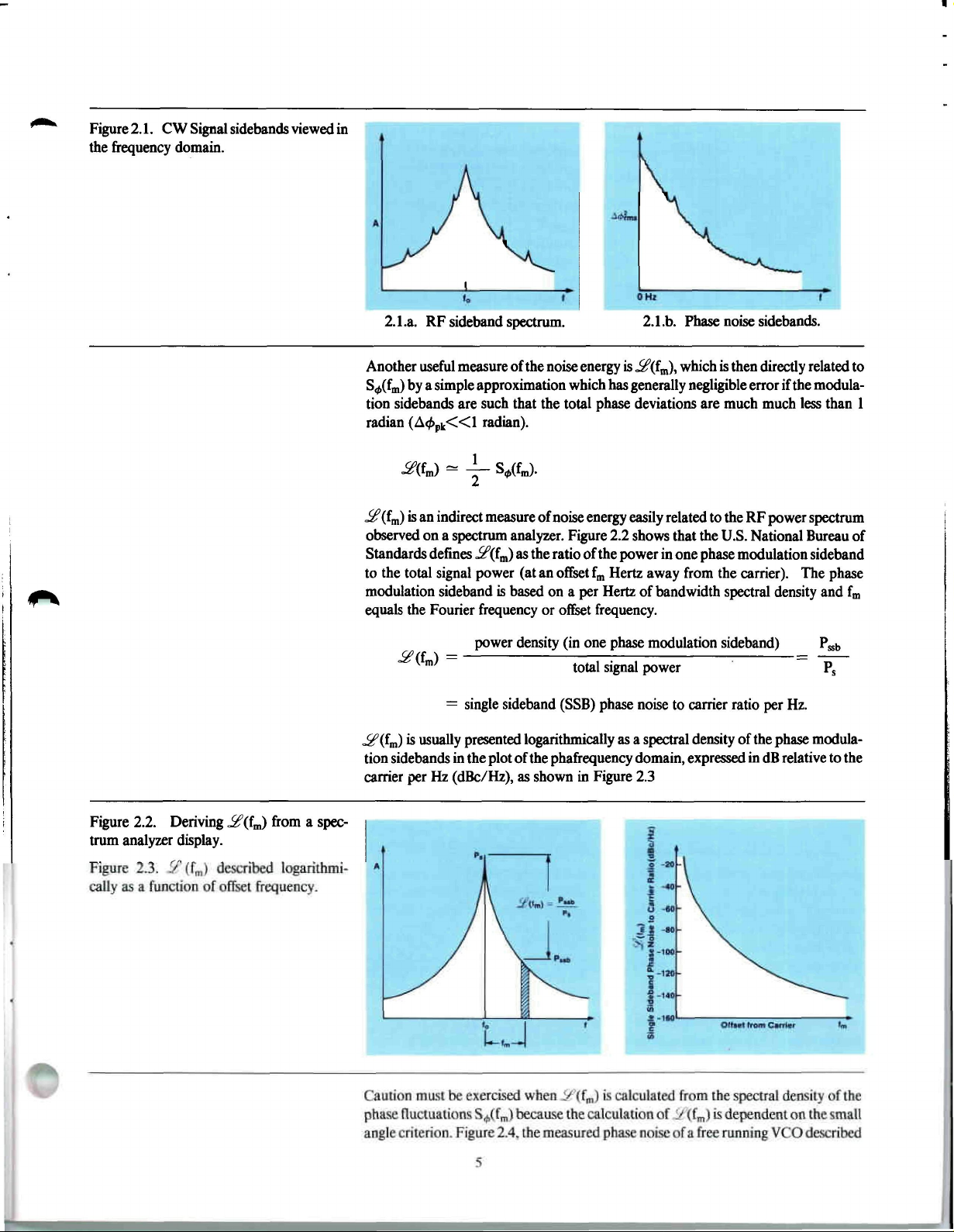
Figure

2.1.

CW Signal sidebands viewed in

the frequency domain.

A.

2.1.a.

RF sideband spectrum. 2.1.b. Phase noise sidebands.

Another useful measure of the noise energy
S^(fm)

by

a simple
tion sidebands are such that the total phase deviations are much much less than 1
radian (A$pk«l radian).

J^(fm)

is

an indirect measure of
observed on a spectrum analyzer. Figure 2.2 shows that the
Standards defines

to the total signal power (at an offset fm Hertz away from the carrier). The phase

modulation sideband is based on a per Hertz of bandwidth spectral density and f
equals the Fourier frequency or offset frequency.

■S?(U

J?f (fm) is usually presented logarithmically as a spectral density of

tion sidebands in the plot of the phafrequency domain, expressed
carrier per Hz (dBc/Hz), as shown in Figure 2.3

approximation which

noise

J^(fm)

as

the ratio of the power in one phase modulation sideband

power density (in one phase modulation sideband)

total signal power P

= single sideband (SSB) phase noise to carrier ratio per Hz.

is

J?(fm), which

has

generally negligible error if the modula-

energy easily related to the RF power spectrum

is

then directly related to

U.S.

National Bureau of

r

ssb

the phase

in dB

modula-

relative to the

m

s

Figure 2.2. Deriving i?(fm) from a spec­trum analyzer display.

Figure 2.3. ¥ (im) described logarithmi­cally as a function of offset frequency.

Caution must be exercised when :/'(fm) is calculated from the spectral density of the

phase fluctuations
angle

criterion.

S,^(fm)

Figure

5

because

2.4.

the

calculation of

the measured phase noise of a free running

.'J

(fm)

is

dependent on

VCO

the

small

described

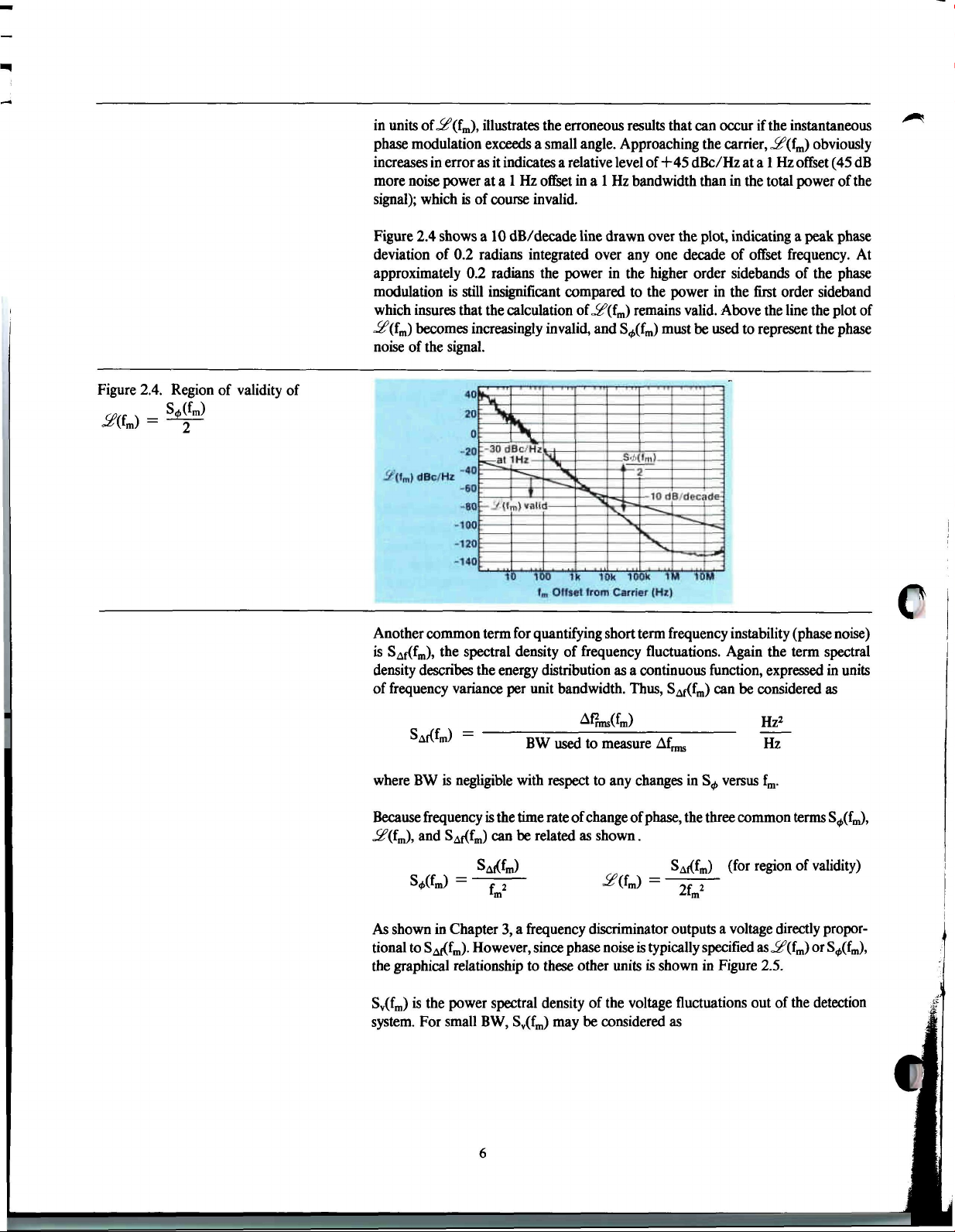
Figure 2.4. Region of validity of

in units of jSf

(fm),

illustrates the erroneous results that can occur if

the

instantaneous
phase modulation exceeds a small angle. Approaching the carrier, =^(fm) obviously
increases in error

as

it indicates a relative level of+45 dBc/Hz at a 1 Hz

offset (45 dB
more noise power at a 1 Hz offset in a 1 Hz bandwidth than in the total power of the
signal); which is of course invalid.

Figure 2.4 shows a 10 dB/decade line drawn over the plot, indicating a peak phase
deviation of 0.2 radians integrated over any one decade of offset frequency. At
approximately 0.2 radians the power in the higher order sidebands of the phase
modulation is still insignificant compared to the power in the first order sideband
which insures that the calculation of -5?(fm) remains valid. Above the line the plot of
Jz?(fm) becomes increasingly invalid, and

S^(fm)

must be used to represent the phase

noise of the signal.

^[!m)dBc^Hi

l„,

01 (set

from Carrier (Hi)

Another common term for quantifying short term frequency instability (phase noise)
is SAf(fm), the spectral density of frequency fluctuations. Again the term spectral
density describes the energy distribution as a continuous function, expressed in units
of frequency variance per unit bandwidth. Thus,

AfUU

SAKU

BW used to measure AL

SAf(fm)

can be considered as

Hz

Hz

2

where BW is negligible with respect to any changes in S^, versus fm.

Because frequency

J£(fm),

and

SAf(fm)

is

the time rate of

change

can be related as shown.

of

phase,

the

three

common terms S0(fm),

SAf(fm) (for region of validity)

S^(lm) — f 2

As shown in Chapter
tional to SAf(fm)- However, since phase noise

3,

a frequency discriminator outputs a voltage directly propor-

is

typically specified

as

<£(fm)

or S0(fm),

the graphical relationship to these other units is shown in Figure 2.5.

Sv(fm)

is the power spectral density of the voltage fluctuations out of the detection

system. For small BW,

Sv(fm)

may be considered as

6

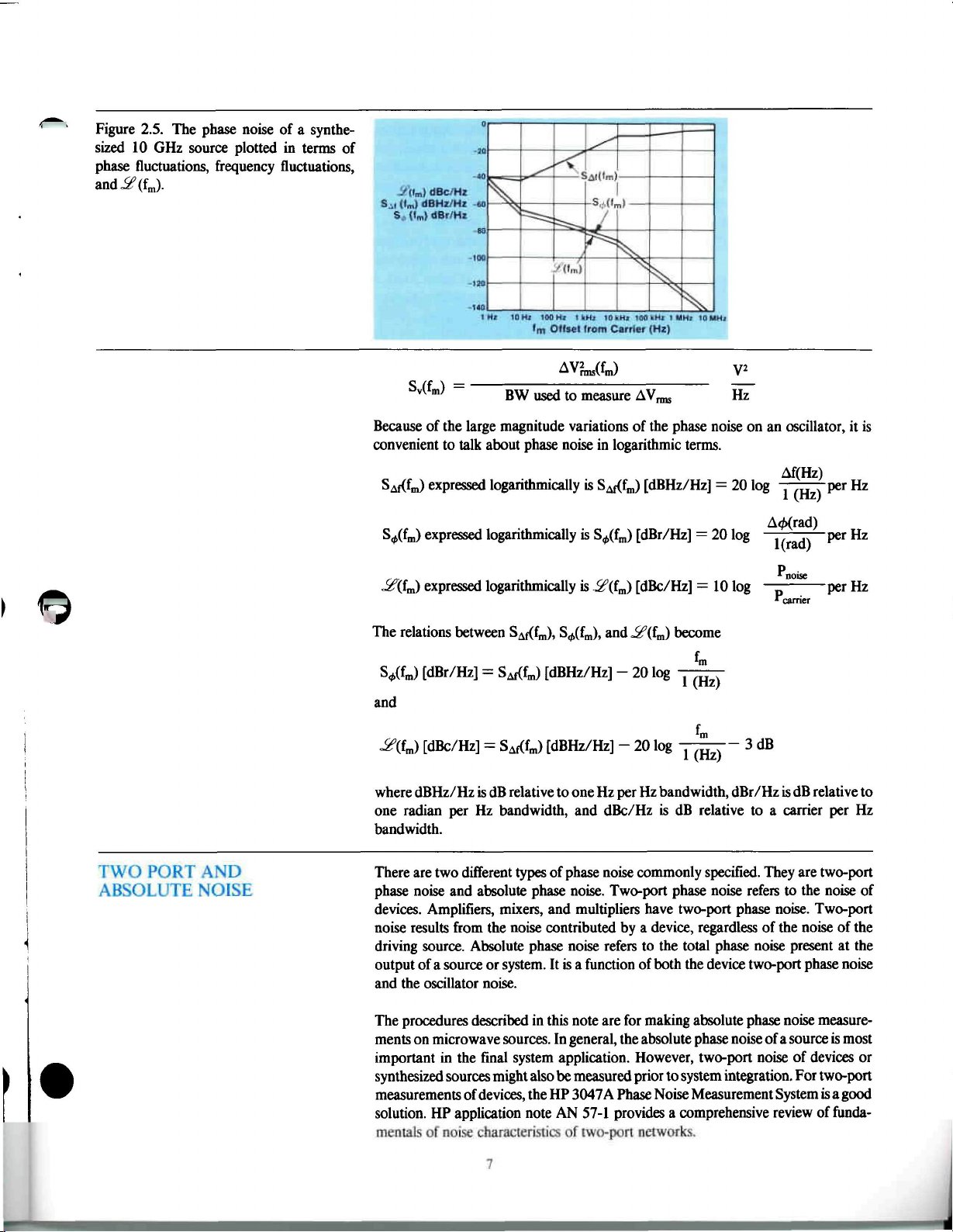
Figure 2.5. The phase noise
sized

10

GHz source plotted

of a

in

synthe-

terms

of
phase fluctuations, frequency fluctuations,
andi?(fm).

Sii ((„,) dBHi/Hi -10

S.,

(W dBr/Hz

r Hi ill HI

IOOHI

I hHj 10 tHj 10(! kHi 1 MHi

'm Oltsel from Carrier

(Hz)

lOMHl

AVUU

Sv(fm)

=

Because

of

the large magnitude variations

convenient to talk about phase noise in logarithmic terms.

SAKW

expressed logarithmically is

S^(fm)

expressed logarithmically is

i?(fm) expressed logarithmically is i?(fm) [dBc/Hz] = 10 log

The relations between

S^(fm)

[dBr/Hz] = SAKU

and

&(fj [dBc/Hz]

BW used to measure AV

S^f,,,)

S^f,,,),

S^(fm), and^f(fm) become

[dBHz/Hz] - 20 log

= S^U

[dBHz/Hz] - 20 log

n

of

the phase noise on an oscillator,

S^Q

[dBHz/Hz] = 20 log

[dBr/Hz] = 20 log . .,—per Hz

l(Hz)

l(Hz)

2

V

H7

-3dB

Af(Hz)

. ,„ .

1 (Hz)

A<Krad)

it is

per Hz

-per Hz

TWO PORT AND

ABSOLUTE NOISE

where dBHz/Hz
one radian

is dB

per Hz

relative to one Hz per

bandwidth,

and

dBc/Hz

Hz

bandwidth, dBr/Hz

is dB

relative

to a

is dB

relative to

carrier

per Hz

bandwidth.

There are two different types of
phase noise and absolute phase noise. Two-port phase noise refers

phase

noise commonly specified. They are two-port

to

the noise of
devices. Amplifiers, mixers, and multipliers have two-port phase noise. Two-port
noise results from the noise contributed by a device, regardless of the noise of the
driving source. Absolute phase noise refers

to

the total phase noise present

at

the
output of a source or system. It is a function of both the device two-port phase noise
and the oscillator noise.

The procedures described in this note are for making absolute phase noise measure­ments on microwave
important
synthesized

in

sources

measurements of

sources.

In

general,

the absolute phase noise of a source

the final system application. However, two-port noise

might

also

be

devices,

measured prior

the HP 3047 A Phase Noise Measurement System

to

system integration. For two-port

of

is

most

devices

is a

good

or

solution. HP application note AN 57-1 provides a comprehensive review of funda-

mentals

of

noise characteristics of iwo-ptin networks.

7

WHY PHASE NOISE
IS IMPORTANT

Phase noise on signal sources
signal levels span a wide dynamic range. The frequency offset of concern and the
tolerable level of noise at this offset vary greatly for different microwave systems.
Sideband phase
system sensitivity.

noise

is

a concern in frequency conversion applications where

can convert

into the

information passband and limit

the

overall

Figure

2.6.

Effect of LO noise

conversion application.

in

frequency

This general
input to the frequency conversion system, where they are to be mixed with a local
oscillator signal fLO (Figure 2.6a) down to an intermediate frequency (IF) for
processing. The phase noise of
mixer products (Figure 2.6b). Note that though the system's IF filtering may be
sufficient to resolve the larger signal's mixing product (fpfLo). the smaller signal's
mixing product (f2-fLo) is
noise.
its selectivity. Three specific examples of frequency conversion applications where
phase noise is important follow.

2.6.a. Inputs to mixer.

case is

illustrated in Figure

the

no

longer recoverable due to the translated local oscillator

The noise on the local oscillator thus degrades the system's sensitivity

2.6.

Suppose two desired signals f ] and f2 are

local oscillator will be directly translated onto the

as

well as

Digital Communications System

Analog Microwave
Communications System

2.6.b. IF output.

In digital communications, phase noise very close to the carrier (less than 1 kHz) is
important. Close-in phase noise (or phase jitter in the time domain) on the system
local oscillator (LO) affects the system bit-error rate.

In many analog communications systems, modulation information exists at least
several hundred kHz away from the carrier. Initially, the signal-to-noise ratio is
sufficiently high. However, in each repeater station, the incoming signal
usually with a down &
on the carrier. If the signal passes through several repeater stations, the level of this
broadband noise induced by the
Too high a level of broadband noise on each system local oscillator will affect the
signal-to-noise (or system sensitivity) at the receiving end of a multiple repeater
system.

up

conversion method, increasing the

L.O.

can increase and start to mask the information.

level

is

amplified,

of broadband noise

Doppler Radar System

Figure

2.7.

Effect of carrier phase noise

Doppler radar system.

Doppler radars determine the velocity of a target by measuring the small shifts in
frequency that the return echoes have undergone. In actual systems, however, the
return signal is much more than just the target echo. The return includes a large
'clutter' signal from the large, stationary earth (Figure 2.7). If this clutter return is
decorrelated by the delay time difference, the phase noise from
partially or even totally mask the target signal. Thus, phase noise on the local
oscillator can set the minimum signal level that must be returned by a target in order
to be detectable.

in i

the local

oscillator can

9

3 Phase Noise Measurements—Frequency Discriminator Method

COMMON MEASUREMENT
TECHNIQUES

Direct Spectrum Measurement

Heterodyne/Counter Measurement

There

are several
of advantages and disadvantages. This brief summary of
methods also adds a few comments about their applicability.

The most straightforward method of
into a spectrum analyzer, directly measuring the power spectral density of the
oscillator. However, this method may be significantly limited by the spectrum
analyzer's dynamic range, resolution, and its own LO phase noise.

Though this direct measurement is not useful for measurements close-in to a drifting
carrier, it provides a convenient method for qualitative, quick evaluation on sources
with relatively high noise. The following conditions make the measurement valid:

A. the spectrum analyzer

the noise of the Device Under Test (DUT);

B.

since the

the DUT must be significantly below its own phase

suffice.)

This time domain method down-converts the signal under test to an intermediate
frequency. The down-converting signal must be of greater stability than the signal to

be measured. Then a high resolution frequency counter repeatedly counts the IF

signal frequency, with the time period between each measurement held
allows several calculations of the fractional frequency difference, y, over the time
period

used.

in the time domain corresponds to

methods of making phase

SSB

phase noise at the offset of interest must

spectrum analyzer

From

these values

will

for

noise

measurements, each with

some

of

the

phase

noise measurement inputs the test signal

measure total noise power, the amphtude noise

noise.

(Typically 10 dB will

y,

the Allan variance, oy(r) can

Sy(fm)

in the frequency domain.

its

own set

most common

be

lower than

constant.

be

computer. ay(r)

of

This

Figure

3.1.

Heterodyne frequency measure-

ment.

Carrier Removal/Demodulation

This method gives particularly useful results for short-term frequency instabilities
occurring over periods of time greater than 10 ms (less than 100 Hz offset from the
carrier in the frequency domain), where the phase noise is increasing rapidly. Using
the heterodyne/counter method is ideal for close-in measurements on frequency
standards. However, it
carrier greater than 10 kHz (Figure 3.1), or for measuring noise which is flat or
decreasing slowly vs. offset frequency fm (as a function having a frequency domain
slope of l/fm or less).

DUT

is

not well suited for measurements of noise at offsets from the

©■

Mosi of the techniques for phase noise measurements fall into this class. Increased

sensitivity results

ing the noise on the resultant baseband signal. Most common of this class are

1) measurements with a phase detector and 2) measurements with a frequency

discriminator. Figure 3.2 compares

heterodyne/counter measurement.

by

nulling

the

carrier, or demodulating the carrier and then measur-

some

typical sensitivities of these methods and

the

It.)

Figure 3.2. Comparison of typical system
sensitivities at 10 GHz.

10 100 Ik 10k 100k

tm Otlsalfrom Carrier (Hi)

Measurement with a Phase Detector

Figure 3.3. Basic phase detector method.

The basic phase detector or two-source method (Figure 3.3) uses a double-balanced
mixer

to

convert phase fluctuations
the same frequency (f0) are input into the
with a low-pass filter

(LPF)
out of phase (phase quadrature) the difference frequency will
output voltage of

0V.

Riding on this dc signal are ac voltage fluctuations that are

leaving

into

baseband

mixer.

the

difference frequency. If

voltage

The sum

fluctuations. Two

frequency

(2^)

the two signals

be 0 Hz

with an average

signals

is

filtered

at

off

are 90°

linearly proportional to the phase noise of both sources.

S,;,ffm}

Saieband

Analyzer

As mentioned above, for the mixer to act as a phase detector, the two signals need to
be 90°

out of

phase.

Usually

this

quadrature condition

is

maintained by

phase

locking

the two signals. Phase locking requires that at least one of the sources be

electronically tunable and requires some type of circuitry

to drive

the tunable source.
The quadrature condition is indicated by zero volts dc at the output of the phase
detector and can be monitored with an oscilloscope or a dc volt meter.

Figure 3.2 indicates that the phase detector method

yields

the best overall sensitivity.
However, because the two signals must be phase locked, the phase detector method
works optimally with fairly stable sources. The reference source must have lower
phase noise than the DUT, and measurements made inside the loop bandwidth
(bandwidth used to phase lock the two sources) require correction, increasing the
complexity of the phase detector method. See HP product note PN 11729B-1 for a
complete discussion of the phase detector method.

11

Measurement with a Frequency
Discriminator

THE DELAY LINE/MIXER

FREQUENCY DISCRIMINATOR

METHOD
Basic Theory

Unlike the phase detector method, the frequency discriminator method does not
require a second reference source phase locked to the source under test (Figure 3.4).
This makes the frequency discriminator method extremely useful for measuring
sources that are difficult to phase lock, including sources that are microphonic or
drifting

quickly.

It

can

also be

used to measure

sources

with

high-level,

low-rate phase
noise, or high close-in spurious sidebands, conditions which can pose serious prob­lems

for the phase detector

method.

Frequency discriminators can

be

implemented in
several common ways including cavity resonators, RF bridges, and a delay line/
mixer. A wide band delay line/mixer frequency discriminator is easy to implement
using the HP 11729C Carrier Noise Test Set and common coaxial cable. This
wide-band approach will be discussed in detail in this and subsequent chapters.

The delay line/mixer implementation of a frequency discriminator (Figure 3.4)
converts the short-term frequency fluctuations of a source into voltage fluctuations
that can be measured

by a

baseband spectrum analyzer. The conversion

is

a two part
process, first converting the frequency fluctuations into phase fluctuations, and then
converting the phase fluctuations to voltage fluctuations.

The frequency fluctuation to phase fluctuation transformation (Af—-A<£) takes place
in the delay line. The nominal frequency arrives at the double-balanced mixer at a
particular phase. As the frequency changes slightly, the phase shift incurred in the
fixed delay time will change proportionally. The delay line converts the frequency
change at the line input to a phase change at the line output when compared to the

undelayed signal arriving at the mixer in the second path.

Figure 3.4. Basic delay line/mixer fre­quency discriminator method.

The Discriminator
Transfer Response

The double-balanced mixer, acting as a phase detector, transforms the instantaneous

phase fluctuations into voltage fluctuations (A#->AV). With the two input signals
90°

out of phase

(phase

quadrature),

the voltage out

is

proportional to the input phase
fluctuations. The voltage fluctuations can then be measured by a baseband spectrum
analyzer and converted to phase noise units.

DUT

KV,V*)

N—**SpHlltr

tuieclor

Phase

Shllter

Appendix A develops the complete transformation from frequency fluctuations
(phase

noise)

to voltage fluctuations by the delay line/mixer frequency discriminator.

The important equation is the final magnitude of the transfer response.

AV(fm) = K^27rrdAf(fm)

sin(7rfmrd)

Where AV(fm) represents the voltage fluctuations out of the discriminator and Af(fm)
represents the frequency fluctuations of the device under test

(DUT).

K^,

is

the phase

12

detector constant (phase to voltage translation)

as

developed in Appendix

B.

rd is

the
amount of delay provided by the delay line and fm is the frequency offset from the
carrier that the phase noise measurement is made.

Ti

System Sensitivity

Figure 3.5. Nulls in sensitivity of delay line
discriminator.

A frequency discriminator's system sensitivity

is

determined by the transfer response.

As shown below, it is desirable to make both the phase detector constant K0 and the

amount of delay rd large so that the voltage fluctuations AV out of a frequency
discriminator will be measurable for even small frequency fluctuations Af.

sin(7rfmrd)

AV(fJ = K

27TT

0

d

(TrfmTd)

Af(fm)

NOTE: The system sensitivity is independent of carrier frequency f0.

The magnitude of the sinusoidal output term of the frequency discriminator is
proportional to sin(7rfmrd)/(7rfmrd). This implies that the output response will have
peaks and nulls, with the first null occurring at fm = l/rd. Increasing the rate of a
modulation signal applied to the system will cause nulls to appear at frequency
multiples of l/rd (Figure 3.5).

Delay rd lOOni

0

to

FM Input \

DUT

20 MH* /C\AJ

Magnitude

ol Trans lor

Response

Measurement Limit WMhoiil

Correction

Quad

"V

Q<-

ftirj-d lm " 10 MHz lm 20 MHi

t„.

OIIHI

Irom Carrier (Hi)

To

avoid having

made at offset frequencies (fm) much

to

compensate for

the sin

less

(x)/x

response,

than l/rd. It

measurements

is

possible to measure at offset

are

typically

frequencies out to and beyond the null by scaling the measured results using the
transfer

equation.

The transfer function shows that increasing rd increases the sensitivity of
However, increasing rd also decreases the
without compensating for the sin(x)/x

However, the sensitivity of the system

offset frequencies (fm) that can

response.

For example a 200

gets very

poor near

the

be

ns

delay

the

nulls.

system.

measured

line

will
have better sensitivity close to the carrier than a 50 ns line, but will not be usable
beyond 2.5 MHz offsets without compensating for the sin(x)/x response; the 50 ns
line is usable to offsets of 10 MHz.

Increasing the delay, rd, also increases the attenuation of the
direct effect on the sensitivity provided by the delay

line,

line.

While this has no

it

does

reduce the signal into

the phase detector and can result in decreased K^ and decreased system sensitivity.

13

As developed in Appendix B the phase detector constant
mixer sine wave output at the zero
K^ equals KLVR where KL is

crossings.

When the mixer is not in compression,

the mixer efficiency and VR is

K^,

equals the slope of the

the voltage into the R port

of the mixer. VR is also the voltage available at the output of the delay line.

Optimum Sensitivity If measurements are made such that the offset frequency of interest (fm) is < 1 /2

the sin(x)/x term can be ignored and the transfer response can be reduced to

AV(fm) =

Y^M(fm)

= K*7rrdAf(fm)

where Kj is the discriminator constant.
The reduced transfer equation implies that a frequency discriminator's system sensi-

tivity can be increased simply by increasing the delay rd, or by increasing the phase
detector constant K^. This assumption is not completely correct. K^

is

dependent on
the signal level provided by the delay line and cannot exceed a device dependent
maximum. This maximum is achieved when the phase detector is operating in
compression. Increasing the delay Td will reduce the signal level out of the coaxial
delay line often reducing the sensitivity of the phase detector. Optimum system
sensitivity is obtained in a trade-off between delay and attenuation.

Appendix C develops this trade off in terms of coaxial delay line length L

Sensitivity = KLVinLXClO)-^

where KL is the phase detector efficiency,

20

V„,

is

the signal voltage into the delay line,

LX (dB) is the sensitivity provided by the delay line and LZ is the attenuation of the

delay

line.

Taking the derivative with respect to lenght L to

find

the maximum of this

equation results in

7rrd,

LZ = 8.7 dB of attenuation.

The optimum sensitivity for a system with the phase detector operating out of results
from using a length of coaxial line that has 8.7 dB of attenuation.

One way to increase
of compression is to increase the signal into the delay
with an RF amplifier before
degrade the measurement if the two-port noise of the amplifier
noise

of the

DUT.

local oscillator port of

the

sensitivity of

the signal

the

discriminator when the

splitter.

The noise of the RF amplifier will not

However, some attenuation may

the

double-balanced mixer (phase detector) to protect it from

phase

detector

line.

This can be accomplished

is

much

be

needed in the signal path

less

is

out

than the

to

the

excessive power levels.

If the amplified signal puts the

and system sensitivity

is

sensitivity more delay can be added until the signal level out of

phase

detector into compression, K^

now only dependent

is

at

its

maximum

on

the length of delay rd. For maximum

the

delay

line is

8.7

dB

below the phase detector compression point.

The following example illustrates how to choose a delay line that provides optimum
sensitivity given certain system parameters.

14

Parameters

Source signal level
Mixer compression point

+7dBm

+3dBm

Delay line attenuation at

source carrier frequency

30dBper 100 ns of delay

Highest offset frequency

of interest

5 MHz

1) To avoid having to correct for the sin(x)/x response choose the delay such that
rd < . A delay rd of

2TT-5-W

32

ns or less can be used for offset frequencies

out to 5 MHz.

Making a Measurement

System Setup

Figure 3.6. Delay line/mixer frequency
discriminator.

2) The attenuation for

attenuation through the splitter and the delay line is 15.6

32 ns

of delay

is

30

dB-32

ns/100

ns

or 9.6

dB.

dB.

The signal level out

The total signal

of the delay line is —8.6 dBm which is 11.6 dB below the phase detector
compression point. Improved sensitivity can
the delay or by using a more efficient line

be

achieved by reducing

so

that the signal level out

the

length

is —5.7

of

dBm

or 8.7 dB below the mixer compression point.

Careful delay line selection is crucial for good system sensitivity. In cases where the
phase detector
lower

loss

is

operating out of compression, sensitivity can be increased by using

delay

line,

or

by

amplifying the signal from the

DUT.

Because attenuation

a

in coaxial lines is frequency dependent, optimum system sensitivity will be achieved
with different lengths of

Making a phase noise measurement with the delay line/mixer implementation of
frequency discriminator can

line

for different carrier frequencies.

be

broken into

3 simple

steps:

1)

system

setup;

2)

a

system

calibration; and 3) noise measurement.

Figure 3.6 shows a delay line/mixer frequency discriminator implementation. Details
to check during the setup are the signal level out of

the

delay line and the ability to
obtain quadrature. If the level is more than 8.7 dB below the phase detector
compression point delay line attenuation

is

too great and maximum sensitivity is not

being achieved.

Delay Llna.'d

Low

Nolle

DUT Amplifier

©HL^HS

Low Low

PHI

Noise

Fitter Amplifier

■|>~

Sjltlm)

Baleband

Analyzef

System Calibration

The calibration procedure determines the discriminator constant Kd to use in the

transfer response .iV = KjAf =
K^ and ru individually, and 2) measuring

K^,2TTTJ

Af. Kj can be determined by )) measuring

the

overall Kd by measuring the response

of

the system lo a known input.

The delay

r^

is a

function of both the length and type of delay line used. For example,

for coaxial cables with a polyethelcne dielectric the delay is approximately 1.5

15

ns/foot. An accurate measure of the delay can be made by setting up a delay line
discriminator and varying the input signal carrier frequency through two zero
crossings on the quadrature monitor (an oscilloscope or dc volt
will equal 1/(2 Af0) where Af0 is the change in the carrier frequency needed to pass
through the two consecutive quadrature points.

meter).

The delay r

d

Figure 3.7. Carrier with single FM tone.

K^ the phase detector constant
phase detector as indicated in Appendix

generate the beat note. The signal level of the second source must match the signal

level out of the delay line for accurate calibration.

Usually the easiest way to determine the discriminator constant Kd is by measuring
the system response to a known FM signal. The signal depicted in Figure 3.7
represents a carrier with
rad, the power in the higher order sidebands is negligible. Note the system must be
operating in quadrature during calibration.
equation as developed in Appendix D.

Kd [dB] = P^ [dB] - (ASB^ [dBc/Hz] + 20 tog^ [dBHz] + 3 [dB])

Pcai is

the system
analyzer.
the rate of the FM signal.

1

zl

d-

w

fT

V~

ASB^,

/

/

/

/

/

response to

is

the

\

t

\

/

/

(

\j

V

first

can be

determined

B.

a single

\

\

-■m

FM

tone.

If the modulation index

the known FM signal and

sideband

\

\

\

V

cil"*"

to

carrier ratio of the calibration signal and f^ is

AS

tell

/

r^

/

\

/

\

\

%

j

T

!F

by

developing a beat

This method requires a second source to

K<j [dB]

is calculated from the following

is

measured with the spectrum

note

/? is

kept below 0.2

out of the

The Phase Noise Measurement

Ctnlw 5110.000 MHi SPAN 5.00 kHz

Once Kd [dB] is determined it can be used to convert the detected output of the
discriminator
source

in a 1 Hz bandwidth. Since K

rithmic form

SJtJ [dBHz/Hz] =

Since phase noise
must be converted to 1 Hz noise bandwidth data. This is a simple power normaliza­tion process, where the noise bandwidth correction, NBW(dB), is simply

Sv(fm)

[dB] into the spectral density of frequency fluctuations of the

SAf(fm)

[dBHz/Hz] (source phase noise). By definition

is

typically defined for

NBW [dB] = 10 log

16

2

=

d

Sv(fm)

[dBm] - Kd [dBm]

B„

1Hz

SAf(fm)

AV2 AV

AP

a 1 Hz

,then SAf =

n

bandwidth, the measured

= AP

or in loga-

2

noise

rms(fm

power

2

K,

)

where Bm is the actual measurement bandwidth.

The correction NBW [dB] is subtracted from the measured data to convert the

measured phase noise to a 1 Hz noise bandwidth. The power spectral density of
frequency fluctuations is then given by

SAf(fm)

[dBHz/Hz] =

Sv(fm)

- Kd - NBW

or, using the relations developed in Chapter 2, the power spectral density of phase
fluctuations is given by

S<»(fm) [dBr/Hz] =

Sv(fm)

- Kd - NBW - 20

logf

m

For peak phase deviations «1 radian, the single sideband phase noise to carrier
ratio is given by,

^(fm) [dBc/Hz] =

Sv(fm)

- Kd - NBW - 20

logfm - 3 dB.

For HP analog spectrum analyzers the noise bandwidth is 10 log (1.2-RBW) where
RWB is the resolution bandwidth indicated on the front panel.

T

i

4 HP 11729C Theory of Operation and Measurement Considerations

The HP 11729C Carrier Noise Test Set implements the delay line/mixer frequency
discriminator for phase noise measurement on sources from 10 MHz to 18 GHz. It
can also be used for the phase detector method (see HP Product Note PN 11729B-1,

HP Lit. #5952-8286). This chapter explains how the HP 11729C makes measure­ments using

sensitivity of better than —140 dBc/Hz at a 1 MHz offset from a 10 GHz source.

the

delay line/mixer frequency discriminator and provides typical system

GENERAL OPERATION

Figure 4.1. HP 11729C simplified block
diagram.

The HP 11729C Carrier Noise Test Set uses an internal low noise microwave

reference signal to down-convert the test signal to an IF frequency. The resulting IF

signal is amplified and then applied to a delay line/mixer frequency discriminator

where the phase noise is demodulated and made available for analysis.

The HP 11729C supplies everything needed for a delay line discriminator measure­ment except the delay line and the spectrum analyzer. The Carrier Noise Test Set
includes the phase detector, the quadrature monitor, and both the low noise IF and
baseband amplifiers. Because the discriminator operates at an IF frequency below

1.28

GHz,

common coaxial cable such
because the output of the discriminator is amplified, almost any available low
frequency spectrum analyzer can be used. The HP 11729C provides all this in a
compact package that is HP-IB controllable, making automatic phase noise meas­urements easy.

The HP 11729C features a major new contribution with its improved low noise
microwave signal needed for the down conversion to the IF frequency. Remember
from Chapter 2 that the noise on this reference signal
on the

IF

signal.

This means that the signal used for down-conversion must have very

low phase noise or its noise will mask the noise of the source under test. The
generation of this signal leads to the first n of the HP 11729C. See Figure 4.1 for a
simplified block diagram of the HP 11729C. For a more complete block diagram see

Figure 4.4.

DUT

r

Demodulation and Baseband Signal Processing

as

RG223 can be used for the delay

is

down-converted and appears

~\

line.

Also

MULTIPLIER CHAIN

0

10MHI-

leGHi

MO

I

To obtain a low noise microwave signal, the HP 11729C requires a fixed frequency
640 MHz drive signal for multiplication to microwave.

There are two ways to obtain the 640 MHz signal. One is to use the auxiliary 640

MHz fixed frequency output of the HP 8662/8663 Synthesized Signal Generator.

I

r

■-T!

i L
I

I

I

{>-

$

**>

i_'_ _-rr_ i

Multiplier Chain

18

Oulpu

£Ln_nj-|_r

Out

i |j

i

i

i

i

Guides lure

Section

5-128Q MHz

J

Input

Figure 4.2. HP 11729C cable hookup for
640 MHz self-generation.

(The HP 8662/8663 are used with the HP 11729C to make phase noise measure­ments using the phase detector method, see PN 11729B-1.) If an HP 8662/8663 is
part of the measurement system, the auxiliary 640 MHz output is an excellent low
noise drive signal for the HP 11729C.

However, for a low-cost, stand-alone system, the HP 11729C can be configured to
generate its own 640 MHz signal internally. A Surface Acoustic Wave (SAW)
oscillator can be created
two rear panel connectors of
Figure 4.2. (Do not substitute cables as the physical length affects the oscillating
frequency.)

The 640 MHz reference signal determines the HP 11729C system noise floor. Figure

4.3 shows the noise floor of the HP 11729C at 10 GHz when in the SAW oscillator
mode or when using the signal from the HP
the SAW oscillator mode is lower from 70 kHz to 10 MHz, and the noise floor
provided by the HP 8662/8663 is lower from 70 kHz and closer.

by

connecting the 640 MHz output to the 640 MHz input on

the

HP 11729C with the included cable as indicated in

8662/8663.

Note that the noise

floor

for

I

Z>

I 9

Figure 4.3. Noise floor of HP 11729C
phase noise test system.

i

s

I

s

I

\

I

i

9C «<ih HP

s

i

1

i

The standard HP 11729C uses 8 microwave transfer switches with 7 bandpass filters
installed (Figure
GHz and to switch from band-to-band under computer control for automatic testing.
For test frequencies less than 1.28 GHz, one switch bypasses the microwave mixer
and applies the test signal directly to the IF amplifier. A single filter version of the HP

11729C, for narrowband or single test frequency applications, retains the bypass

switch for low frequencies and one user-defined bandpass filter, at lower cost.

HP 1173

-1IO

-140

160

rt* 10 Hi 1WH1 1*HI m*H* 1M

iflO MHi jil

1

4.4).

\

\

\

j'Otclllitnj

\

">f ll

10

GHl

OGHl

t„ OttHl Worn

This allows it to down-convert test signals from

C*rri*r

■H

%

(Hi)

^

s^_

^***>

"""^

VKJ 1MKI

—

10

HHi

10

MHz to 18

19

DEMODULATING AND
BANDPASS SIGNAL
PROCESSING SECTION

Once the HP 11729C
DUT frequency, the microwave test signal is down-converted and processed.

has

generated the very low

noise signal

within

1280 MHz

of the

First Down-conversion The selected harmonic of the 640 MHz
(Microwave mixer) under test in the input mixer, yielding an IF frequency between 10 to 1280 MHz.

Because of
test must provide the local oscillator (LO) drive
and +20 dBm (for input signals >1.28 GHz) is appropriate. For DUT frequencies
between 10 MHz and 1.28 GHz, the signal is input directly into the IF amplifier and
should have a signal level of between —5 and +10 dBm.

IF Processing and the The resultant IF signal is amplified and then split into two paths. One of the signals

Frequency Discriminator supplies

the phase detector. The other signal
monitoring or in this case to be connected to the external delay line. After passing
through the delay line, the signal returns to the R port of the RF mixer (5 to 1280
MHz input).

Typical values of
dBm, depending on the IF frequency. The minimum specified value for
dBm. A high level IF signal is important as it allows the use of longer delay lines for
improved sensitivity.

The resultant IF signal phase correlates against a delayed version of
signals are 90° out-of-phase (phase quadrature), the RF mixer operates
phase detector. If

ing baseband signal represents the frequency noise of the microwave test source.

the

low signal level of

the local

oscillator drive to the RF double-balanced mixer that

the

the

IF signal level out of

frequency discriminator has the required sensitivity, the result-

drive

signal mixes with the microwave source

the

higher frequency comb

power.

is

output to the front panel of the HP 11729C for

the

front panel are between +9 and +14

lines,

the source under

A signal level of between +7

will be

all

IF

itself.

If

as

the system

used as

es is

the

two

+7

Baseband Signal Processing A 15 MHz (3 dB BW) Low-Pass Filter (LPF) processes the baseband signal to

remove the mixer sum products and the LO feedthrough. The baseband signal is
further processed through a Low Noise Amplifier (LNA), and then applied to the
<10 MHz Noise Spectrum Output for viewing with a spectrum analyzer.

The amplifier
of about 10 Hz to 30 MHz. Typical flatness is less than 1 dB and the noise
<2.0

dB.

standard lab spectrum analyzer at the <I0 MHz output.

If the IF frequency is less than 20 MHz, additional low-pass filtering is needed to

remove the unwanted mixer products and LO feedthrough. The HP 11729C provides
a L5 MHz low-pass filler thai allows IF frequencies of 10 MHz or greater to be
processed. The resulting noise signal is available at the <1 MHz Noise Spectrum
Output for viewing on a low frequency spectrum analyzer. The < I MHz
amplified by the LNA. If a lower IF Frequency
can be user added.

The IF amplifier of
problem as the comb line fitters are chosen such that the IF frequency is never more

than 1280 MHz. For example the 9.6 GHz filter covers test frequencies from 8.32
GHz to 10.88 GHz (excluding ±

has

approximately 40

The LNA permits the HP 11729C detected noise output to be viewed on a

the

HP 11729C

:n

dB

of gain (coupled into 50O

is

critical,

is

bandwidth limited to 1500 MHz. This

10 MHz

centered on 9.6

additional low-pass filtering

GHz).

I,

and a bandwidth

figure

signal is

The frequency of the

is

not

not a

is

Figure 4.4. HP 11729C Carrier Noise Test
Set.

selected comb line, as well as the range of input signals that can be down-converted

with each comb line, are indicated on the front panel of the HP 11729C.

OUT

AM Hoar Option

■""1

&><>J

J^>_(^

OomotfuteMan A Signal Protesting

Pufxd

Baseband

11

Output

. i

Input

Ourtdraturr

Indicator

Spectrum

Outputs

■*■ tOMHtSO!!

-»-•

1 MHz 600i

-*- AVX 600 It

i

PHASE-LOCK LOOP/
QUADRATURE SECTION

LqjpJ

The inputs to the

phase

S-ISBOMHi
Input

detector must

be

maintained

in

quadrature for the duration of
the measurement. Quadrature can be observed on the red and green LED display of
the front panel of the HP 11729C or can be monitored over the HP-IB bus during
automated

measurements.

The

phase-lock

loop

circuitry

is

not used when implement­ing the frequency discriminator because the DUT signal is phase detected against
itself.

However the quadrature indicator remains active and can

be

used to insure that

quadrature is maintained.

21

J Making Frequency (Phase) Noise Measurements with

This chapter integrates the theory of the delay line/mixer frequency discriminator
(Chapter 3) and its implementation in the HP 11729C (Chapter 4) into procedures
for making phase noise measurements on microwave sources. The measurement
procedure breaks down into three easy
and 3) noise measurement. Specific instrument operation instructions are given for
the HP 11729C Carrier Noise Test Set.

steps:

1)

system

the

HP11729C

set-up;

2) system calibration,

SYSTEM SET-UP

Figure 5.1. System set-up for making a
delay line/mixer frequency discrimination
phase noise measurement.

The Source

The delay line/mixer implementation of a frequency discriminator with the HP

11729C is shown in Figure
required to obtain quadrature if the source frequency

5.1.

Note that a phase shifter or a line stretcher may be

is

not adjustable. The maximum

frequency adjustment Af„ required of the source can be determined from the follow-

ing equation

Af0 =

l/4r

d

MO MH*

Horn

_t 1

r

I HP 8662/3 I
I I

Microwave

Ts»t

G>

IOMHl-18 GHl

The frequency of

Microwavn Tell

Signal In

the

test source determines the filter band of

eao MHz Out

HP11729C

MOMHi

C

-.5-1280 MH*
In

1OMH1
Out

H=

Spectrum

Anilywr

the

HP 11729C to be
used. Because the source must provide the local oscillator drive signal (LO) to the
microwave mixer for frequencies above 1.28

GHz,

the source output power should be
between +7 dBm and +20 dBm. For frequencies below 1.28 GHz the microwave
mixer

is

bypassed and

dBm (with an optimal

the source

level

from

output power should
—2

to +3

dBm).

Power

be

between — 5 dBm and +10

levels

below +7 dBm (—5
dBm <1.28 GHz) can be used with a degradation in the system noise floor. Keep the
cable length from the source under test to the HP 11729C short to reduce cable
attenuation. This will help provide the necessary LO level and also help prevent
system noise floor degradation.

The 640 MHz Drive Signal

The 640 MHz drive signal required by the HP 11729C can be self-generated or
obtained from an HP 8662/8663 Synthesized Signal Generator. By using the self
generated 640 MHz drive

signal, a lower system noise floor results from 70 kHz to 10
MHz. (Typically the phase detector method is used if close-in sensitivity is needed.
See HP product note PN 11729B-1 Phase Noise Characterization of Microwave
Sources—Phase Detector Method.) To use the self-generated 640 MHz drive signal,
connect the supplied cable between the rear panel 640 MHz output and 640 MHz
input

ports.

To

use

the 640 MHz drive signal from an HP 8662/8663 connect
MHz output from the rear of
rear panel of the HP

11729C.

the

HP 8662/8663 to the 640 MHz input port on the

Then

cap

the

640

MHz output port on the HP 11729C

the

640

with the 50O SMA termination provided.

22

<?~>,

The Delay Line

As developed in Chapter 3, system sensitivity depends on both the length and
attenuation of the delay
signal to
or semi-rigid

an

IF

cable.

frequency of

line.

Because the HP 11729C down-converts the microwave

less

than 1.28

Coaxial cable such

as

GHz,

RG

the delay

223

line

provides about 1.5

can

be

common coaxial

ns

delay per foot

of cable.

Because a discriminator is typically used only to offsets of less than 1/2 rd, the

maximum delay to be used is determined by the highest offset frequency of interest.
For example, if measurements are desired of an offset frequency (fm) of
delay must be less than 1/2 fm =

1/2(10

MHz) = 50 ns.

10

MHz,

the

n

Figure 5.2. Optimum system sensitivity/
delay line length vs. IF frequency.

An easy way to determine the delay r for an unknown length of

cable is

to tune the
source frequency so that phase quadrature occurs, then continue tuning the source
until quadrature is again established. The delay rd is equal to l/2(Af0) where Af0 is
the frequency difference between the two quadrature points.

After choosing a cable length, measure the signal power out of the HP 11729C IF
output through the length of cable with a spectrum analyzer. As developed in
Appendix C, optimum sensitivity results if the power out of the delay is approxi­mately

—5

dBm. If

too great and system sensitivity

the

power out goes below

degrades.

—5

dBm, the delay line attenuation is

Either use a delay line with

less

attenuation
or shorten the delay line until the signal power equals —5 dBm. This increases the
system sensitivity and also increases the offset frequency to which measurements can
be made without corrections to the discriminator transfer response.

Because cable
by reducing the IF frequency out of

attenuation

is

frequency dependent, system sensitivity

the

HP 11729C. This technique is only possible

can be

improved

by tuning the source under test. The reduction of delay line attenuation translates
directly into increased system sensitivity. Figure 5.2 shows typical lengths of RG 223

coaxial cable versus HP 11729C IF frequencies that provide optimum sensitivity.
Figure 5.3 shows the sensitivity of the HP 11729C implementation of the delay line
frequency discriminator using a 100 ns RG 223 delay line.

x

400

E

• 300
il

o
gaoo
a

E

100

\

\

\

\

-HP11729C

—-

1P1172S

a\

+7

dB

m

0

200 400 GOO 800 1000 1200

HP 117Z9C IF Frequency (MHl)

OG 223 Cable used as delay lino

°-~i

1

450

f

300 «

a

_

'

150

f)

23

Figure

5.3.

Typical HP 11729C sensitivity

with a 100 ns delay line.

SSa Phase Noise

to Carrier Hallo

^■(WldBe/Hi] -100

-120

-160

,SAW

Oscillator

•V~at10GHi

HP 11729C with HP B662/3

S40MHia110GHz

1Hz 10Hz 100Hz 1kHz 10kHz 100kHz 1MHz 10

L Oflsel Irorn Carrier (Hi)

MHz

System Operation

SYSTEM CALIBRATION

The Calibration Signal

Make the following tests to insure that the HP 11729C system is operating as
expected. Disconnect the delay line from the IF output port on the HP 11729C and
measure the IF frequency and the IF power with an RF spectrum analyzer. The IF
frequency should be equal to the source under test frequency minus the filter center
frequency.

IF= f(source) - f(filter)

The IF output power should
signal is obtained, reconnect the delay line between the IF output and the
MHz input ports on the HP 11729C. Check to

be

greater than or equal to +7

see

that quadrature can

dBm.

After

the

proper IF

5-1280

be

established
by adjusting the source frequency, the phase shifter or the line stretcher. The green
LED in the PHASE LOCK display on the HP 11729C front panel indicates phase
quadrature. After obtaining quadrature the system is ready to be calibrated.

Usually the easiest way to calibrate the frequency discriminator is to measure the
system response to a known signal. This establishes a reference for subsequent
measurements. System calibration consists of the following:

a) generation and measurement of the calibration signal.
b) measuring system response to the calibration signal.
c) calculating the discriminator constant Kj.

A

signal with a single FM tone will be used

under test itself can be modulated to produce

as

the calibration

this

signal.

signal.

Often the source

If not, an alternate source can

be substituted for the test source. The substitution method can be made either with a

microwave source or at the IF frequency (see Figures 5.4 and 5.5).

f*

Figure 5.4. Calibrating the HP 11729C
delay line/mixer frequency discriminator
with a microwave source.

Microwave

Carrier

with known

FM

Modulation

1,28-18

GHz T

r

Filter Band

I Filler tsa

_(2-<M

24

IF Output

5-12S0

IF

AMP

MH2

Delay

Lin*

5-1280

] Input

MH*

HP11723C

System

Response

c

Figure 5.5. Calibrating the HP 11729C
delay line/mixer frequency discriminator

with an RF source.

OF Carrier

with known

FM

Modulation

IF Oulpul

5-12SD MHi

IF

AMP

Daisy Line

Pcil

t

M2S0MHII I I

Filler Bund

(11

System

Retponi*

The modulation index on the calibration signal should be set to <0.2 radians (to
satisfy the small angle criterion and the relation between

SAf(fm)

and =^(fm) as

developed in Chapter 2). The modulation index /? is the peak FM deviation (Afpk)
divided by the FM rate (fm).

Af,

k

P = modulation index = —

P

Remember:

^(fm) =

sAf(fm)

2P

m

2P

(for m <0.2 rad)

m

An FM rate of 1 kHz with a peak deviation of 0.1 kHz yields a modulation index of

0.1 radian which should result in a sideband to carrier ratio of

—26

dBc.

Record the
FM rate used in the calibration signal (f,^ = ). See Appendix D for a more
complete discussion of the calibration theory.

If the source under test cannot be modulated, the system can still be calibrated by
substituting a modulated microwave source at the same level and frequency. The HP
8683/8684 Signal Generator and the HP 8672/8673 Synthesized Signal Generator
are all good microwave sources that could be used.

System Response

If a modulated microwave source is not available, then calibration can still be
accomplished

by

using a modulated RF

source

substituted at

the

IF frequency. Set the
RF calibration source to the HP 11729C IF frequency, at a level of—10 dBm with
FM modulation applied (/3 <0.2 radians). Setting the signal level to —10 dBm
improves the calibration accuracy by closely matching the signal level of
converted microwave test

signal.

A signal level between

—3

and +2 dBm gives best

the

down-

results for test sources that use the <1280 MHz filter band directly. The HP
8662/8663,

8640, 8642, 8656, and 8660 all have internal modulation capabilities

and can be used as the RF calibration source.

Measure the sideband to carrier level of the calibration signal with a spectrum
analyzer, and record this ratio (ASB,^ = — dBc).

The second step in calibrating the system measures its response to the signal created
previously. Connect
the HP 11729C and select
the 0.01-1.28 GHz
indicates phase quadrature by

the

calibration signal to the Microwave Test Signal input port on

the

appropriate filter

band.

Before measuring the response, check to

the

green LED in the Phase Lock Indicator on the front

band.

If RF calibration

is

used, select

see

that the system

panel of the HP 11729C. Set auadrature bv adjusting the calibration source fre-

quency, adjusting the phase shifter, or adjusting the line stretcher.

25

Once quadrature has been obtained, measure the system response to the calibration
signal.

The demodulated calibration signal will have
frequency corresponding to the FM
the power
so

that the spike
help improve measurement accuracy, by avoiding extra corrections for display
attenuation steps.

level,

P^ = If possible, adjust
is

at

the top

of the

rate,

as

display.

shown in Figure

Leave the input sensitivity at

a sharp

response at

5.6.

the

spectrum analyzer input sensitivity

the

baseband

Measure and record

this setting

to

Figure 5.6.

signal.

System response to calibration

r

P

JS

"l

T

4

\

* nicai "*

BHi Frequency Hi 5,00

Discriminator Constant (Kd)

MEASURING THE FREQUENCY After completing calibration, the source frequency noise can be measured by:

(rHAab) NUlbt

a

To complete the calibration procedure, calculate the discriminator constant Kd. As
explained in Appendix D,

K<j

[dBm] = P^ [dBm] - [3 dB + 20 log ^ + ASB^]

Calculate and record the discriminator constant.

Kd [dBm] =

) Measuring the frequency noise.

b) Applying measurement corrections.

c) Converting to other phase noise units if desired.

™

(LHJ

Measuring the Frequency Noise

If an alternate source was used for calibration, reconnect the test source to the HP
11729C Microwave Test Signal input. If an RF source was used, select the appro­priate filter band on the HP 11729C
itself

was

used for calibration, remove the FM modulation from it. Adjust the source
frequency, phase shifter, or line stretcher as necessary to re-establish phase quadra­ture.

Quadrature should be maintained throughout the measurement procedure.

Set

up

the spectrum analyzer span
sensitivity of the spectrum analyzer should not be changed from the calibration
procedure if possible. Select a resolution bandwidth RBW that
chosen frequency

10 kHz to 100 kHz, or 10 kHz for 100 kHz to 10 MHz.

Because noise
digital averaging can be selected or some analog averaging can be done by reducing
the video BW on the spectrum analyzer. The HP 8566 Spectrum Analyzer
suited.

span.

For

example, a good choice of RBW is 1 kHz

is

a random quantity, some sort of averaging

26

to

down-con ven the test

to

cover the offset frequencies of interest. The input

source.

If the test source

is

in keeping with the

for

a span from

is

desirable. If available,

is

ideally

After averaging, take a reading from the spectrum analyzer in dBm at the offset
frequency of interest, noting the resolution bandwidth setting. Set other frequency
spans and make measurements as desired. Record the values from the spectrum
analyzer display (Pnoise)>

tne

offset frequencies they were taken at (fm), and the

resolution bandwidths (RBW) used to measure the value.

P

= [dBm] fm [Hz] RBW = [Hz]

noise

Noise levels measured within 10 dB of

can degrade the measurement accuracy. If

the

bottom of the spectrum analyzer's display

possible,

increase the spectrum analyzer
input sensitivity and repeat the measurement. This should not be a problem if the
calibration signal P^i

is

brought to the top of

the

CRT as discussed in the calibration

procedure.

Measurement Corrections Because the spectrum analyzer responds differently to sine waves than to random

noise, two corrections must be made to the measured data. The first correction

accounts for the log-shaping and detection circuitry of

an

analog spectrum analyzer.

This correction (SA) is +2.5 dB for HP analog spectrum analyzers (see HP applica-

tion note AN 150-4).

The second correction normalizes the measurement to a 1 Hz noise bandwidth

(NBW) and accounts for the spectrum analyzer resolution bandwidth used during

the noise measurements. This correction (NBW) is 10 log (1.2 • RBW) to the first
approximation for HP spectrum analyzers, where RBW is the indicated resolution
bandwidth on the analyzer.

As developed in Chapter 3,

SAf(fm)

equals the spectrum analyzer display Pnoise(fm)
minus the discriminator constant Kd. Including the measurement corrections to the
original equation yields:

SAf(fm)

[dBHz/Hz] = P

(fJ [dBm] - Kd [dBm] + SA [dB] - NBW [dB]

noise

where from Appendix D

IC [dBm] = P,*, [dBm] - (ASB^, + 20 log L . + 3) [dB].

Conversion to Other Units To convert

Chapter 2 and the two previous equations. J^(fm) and

£({J [dBc/Hz] =

P

noise

[dBm]

- P^,

[dBm]

+ ASBcal

= SAKfm)-201ogfm-3dB

S^(fm)

[dBr/Hz] =

P

[dBm] - P^, [dBm] + ASB^, [dBc] - 20logy12— NBW [dB] + SA [dB] + 3 dB

noise

=

SAf(fm)-201ogf

m

Figures 5.7, 5.8, and 5.9 show example calculations required to obtain SAf(fm),
S^d'n,},

and J (fm) using data from a free running

I kHz tone (fm ,) with a modulation index of 0.2 rad (ASBCB] = — 20 dBc). The
system response P^i was
MHz offset was —71.5 dBm. The resolution bandwidth (RBW) of the spectrum
analyzer used during the measurement was 300
ently different represents the phase noise for the same VCO expressed in different

units.

SAf(fm)

[dBc]

to other phase noise units, use the relationships developed in

S,j(fm)

can be derived as

f

- 20

27

m

log

-z NBW [dB] + SA [dB]

■"cal

m

cal

VCO.

—54.6 dBm

and the

lest source

H/..

Calibration

frequency

was

made with a

noise (P

nulM

.) ai a 1

Note each result though appar-

Figure 5.7. Computing

SAf(fm)

[dBHz/Hz] 1) Establish known sideband/carrier ratio

from the spectrum analyzer display.

2) Record

f

mca|

f

mcal

ASB^fJ = -20 dBc

=lkHz

Figure 5.8. Computing

S^(fm)

[dBr/Hz] 1) Establish known sideband/carrier ratio

from the spectrum analyzer display.

3) Measure system response

4) Determine discriminator constant
Kd[dBm] = P^tdBm] - (ASB^,^20 log f

5) Measure

P

(in known RBW)

noise

mcal

6) Noise Bandwidth correction
NBW [dB] = 10 log RBW • 1.2

7) Spectrum Analyzer correction

8) SAf (UtdB] = (P

noise

-

Kd +

S/R - NBW)

SAf (U[dB] = (-71.5) - (-97.6) + 2.5 - 25.5

2) Record

f

,

^

mca

L

1 kHz

3) Measure system response

4) Measure Pnoise (m known RBW)

5) Offset frequency

Wse, = 1

MHZ

6.) Noise Bandwidth correction

NBW [dB] = 10 log RBW • 1.2

Pcai = "54.6 dBm

+3)[dB] Kd =

Pnoise = -71.5 dBm

NBW = 25.5 dBHz

S/A = 2.5 dB*

SAftfm) = 3.1 dBHz/Hz**

ASBcal(fm) = -20 dBc

Peal = -54.6 dBm

Pnoise = -71.5 dBm

NBW = 25.5 dBHz

-97.6 dBm

7) Spectrum Analyzer correction

8) S^fJ = Pn0iSe - Peal + ASB^i - 20 log

(-71.5) - (-54.6) + (-20) - 20 log IPL - 25.5 + 2.5 +3

Figure 5.9. Computing i?(fm) [dBc/Hz] 1) Establish known sideband/carrier ratio
from the spectrum analyzer display.

2) Record

f

,

mca

f

,= lkHz

mca

3) Measure system response

4) Measure Pnoise (m known RBW)

5) Offset frequency

f

=

m

1 MHz

6) Noise Bandwidth correction
NBW [dB] = 10 log RBW • 1.2

7) Spectrum Analyzer correction

8) S£(tJ = Pnoise " Peal + ASB^i - 20 log^

(-71.5) - (-54.6) + (-20) - 20 log 15L- 25.5 + 2.5

S/A = 2.5 dB*

f,

■"offset

103

S0(fm) = -116.9 dBr/Hz**

- NBW + S/A + 3 dB

m

cal

ASB^fJ = -20 dBc

Peal = -54.6 dBm

Pnoise = -71-5 dBm

NBW = 25.5 dBHz

S/A = 2.5 dB*

m

offset

- NBW + S/A

m

cal

103

i?(fm) = -119.9 dBc/Hz**

♦Correction for HP analog spectrum analyzers.

**Phase noise measured at a 1 MHz offset from the carrier.

28

O Considerations in System Accuracy

After configuring a phase noise measurement system, it may be necessary to deter­mine the accuracy of
that can affect overall system accuracy. With careful system design, phase noise
measurements can be made to typical overall accuracies of
without extensive correction routines, typical accuracies between ±3 to ±5 dB can
be expected. The overall accuracy is a function of 1) the instrumentation used to
measure the source

measurement procedure. Looking at the individual contributions to system accuracy

isolates the areas where accuracy can be improved.

THE SPECTRUM ANALYZER The spectrum analyzer measures both the source phase noise and the calibration

signal. There are several areas within the spectrum analyzer that can affect system
accuracy, including:

a) the relative amplitude accuracy;
b) the resolution bandwidth of the spectrum analyzer used to measure
c) the relative IF bandwidth gain accuracy;
d) the spectrum analyzer frequency response (flatness).

the

measurement. This chapter discusses some of the elements

less

than ±2.5

noise,

2) certain system parameters of the HP 11729C, and 3) the

dB.

the

Even

noise;

tr ,

Relative Amplitude Accuracy The overall level accuracy of a spectrum analyzer

by using the analyzer in a relative mode and by limiting the number of analyzer

parameters changed between calibration and measurement, the accuracy can be
improved to between ±0.4 and ±1.5 dB. See HP application note AN 150-8
"Spectrum Analysis Accuracy Improvement" (HP Lit. #5952-1147) for more
information.

Resolution Bandwidth Accuracy Because phase noise

the bandwidth used during the measurement
depends on the resolution bandwidth (RBW) of the particular spectrum analyzer
used during the phase noise measurement.

There are 3 methods of determining the noise bandwidth for HP analog spectrum
analyzers. The least accurate
multiply it by 1.2. (RBW on an HP spectrum analyzer typically exhibit accuracy of
±10%.) A more accurate estimation of the noise bandwidth could be obtained by
measuring the 3 dB resolution bandwidth and multiplying it by 1.2.

The most accurate method of determining the noise bandwidth would be to actually
characterize the resolution bandwidth response to random noise
The accuracy of such a measured
3 dB resolution bandwidth of the spectrum analyzer is measured.

The IF Gain Accuracy The relative IF gain accuracy results from changes in the resolution bandwidth gain

and depends on the particular spectrum analyzer. Typically its contribution remains
small (±0.05 dB) and time should not be spent trying to reduce it.

is

typically specified on a per hertz

is

to take the displayed resolution bandwidth

noise

bandwidth can be typically ±0.2

is

needed.

can be as

basis,

This noise

large

as ± 6

dB.

However,

an accurate measure

bandwidth (NBW)

setting

(see HP

AN 150-4).

dB

of

and

when the

Spectrum Analyzer Frequency Typicallytheamplituderesponseofthespectrumanalyzercanvary±0.5to±1.5dB
Response over its entire frequency

the error will be
inaccuracy. The frequency response for
over the 100
only a narrow portion of this range is used (100 Hz to 10 MHz).

Hz

range.

However, by using only a small portion of

less.

Check the specifications of

to 2.5 GHz

29

range.

The actual error will be closer to ±0.3

the

analyzer to determine the actual

an

HP 8566A Spectrum Analyzer

the

range,

is

±0.6 dB

dB

because

SYSTEM PARAMETERS of
the HP U729C

The system parameters of the HP 11729C that can affect measurement accuracy are:

a) the frequency discriminator flatness;
b) baseband signal processing;
c) the system noise floor.

Frequency Discriminator Flatness The frequency discriminator

delay

line

attenuation slope over the input frequency
HP 11729C introduces typical error of ±1.0 dB (10 MHz to 1.28 GHz range). Over
the same range the attenuation of a 50 ns delay line (34 ft. of RG 223) can vary as
much as ±2.5 dB.

However, the error is actually much less because both the phase detector and the
delay line must only operate over a ±10 MHz range centered around the IF
frequency. By recalibrating the system for each new test frequency that yields a
different IF frequency into the HP 11729C phase detector, the error can
less than ±0.2 dB. Much of this inaccuracy results from the variation in delay line

Baseband Signal
Processing Flatness

attenuation and can
recalibrating the system with different FM tones (keeping the modulation index
constant) for the offset frequencies of interest.

The HP 11729C signal processing section typically provides flatness to within ±1.0
dB (1 Hz to 10 MHz). If a very flat spectrum analyzer or other measurement
instrument is available, this inaccuracy can be reduced by one of
noise measurement at only a few offset frequencies
be done at each offset frequency of interest.

For a more complete error correction, the HP 11729C signal processing section can
be swept-characterized. This swept characterization as a function of frequency may
be done by applying a varying frequency into the signal processing section and

measuring the resultant output

Output ports. Note the source used for this characterization must be flatter than the

filters and low noise amplifier in the HP 11729C.

be

further reduced by

flatness

signals

results from the phase detector

range.

The phase detector

using

delay

lines

with

less

two

is

desired, a calibration

at the <1

MHz

and <10 MHz Noise Spectrum

flatness

attenuation or by

and the

in

the

be

reduced to

methods. If a

step

could

System Noise Floor

The noise measured at the output of the frequency discriminator comes from the noise
on the source being tested, the noise of the 640 MHz source used by the HP 11729C
to down convert the test source, and the two-port noise of

J^HP

) 1729C

equal the total HP 11729C system noise (two-port and contribution from

the 640 MHz signal) the error is given by

error (dB) = 10 log (1 + antilog

<£

The following table lists this error for several values of noise power differences.

1

-^DUT ™^HP 11729C (dB)

correction (dB)

This error can be corrected by actually characterizing the noise of the HP 11729C

system, and then using

shown in the table.

30

this

known value of noise to correct for the measured value as

0

3.0

2.5 2 2.1

OUT

X

10

1.8 4 1.5

HP11729C

3

the

HP 11729C. Letting

10

0.4

15

0.2

5

1.2

ME ASUREM ENT PROCEDURE

The care

used when actually making a measurement with the frequency discriminator
has a direct effect on the measurement accuracy. The areas that can affect the
measurement include:

a) quadrature maintenance;
b) system calibration;
c) the randomness of noise.

Quadrature Maintenance Because the discriminator method

maintained for most

sources.

The HP 11729C provides a monitor to allow constant
quadrature verification. As developed in Appendix E, close phase quadrature main­tenance can result in uncertainties of

System Calibration The accuracy of

the

signal used for calibration also contributes to the uncertainty of
the phase noise measurement. Because the spectrum analyzer measures the calibra­tion

signal,

its uncertainty

is the same as
and ±1.5 dB). Since measurement of
ment and is viewed in a small portion of the available spectrum analyzer dynamic
range, the error is typically closer to ±0.4 dB.

If calibration uses an alternate source, additional error is introduced because the
carrier frequency and power level cannot be matched exactly. Because the signal of
the test source before the splitter is not directly accessible in the HP 11729C, the
power levels must be matched before they enter the HP 11729C or at the IF output.
Typical accuracies of ±0.2 dB can be obtained if only minor attempts are made to

match the source and calibration signal levels.

This relatively small error results from the high gain RF amplifier before the signal
splitter in the HP 11729C. This amplifier operates in compression for signals of
dBm or greater with a very flat output (±0.2 dB) for signals above

error can be further reduced to ±0.05
the

test source

and calibration source at the IF output of the HP 11729C with a power

meter.

is

a single oscillator

less

than ±0.05 dB.

technique,

quadrature

indicated previously (typically between ±0.4

the

calibration signal gives a relative measure-

—5

dB

by accurately matching the power

is

easily

—20

dBm. This

levels of

Because the
carrier

calibration information comes from a relative measurement (sideband to

ratio),

mismatch has no effect on system accuracy when an alternate source is

used.

The Randomness of Noise A phase noise measurement

has

an inherrent amount of error

because we are

trying to
quantize a random quantity. This error can be reduced by averaging through analog
or digital means at the spectrum analyzer. A typical uncertainty of ±0.5 dB can be
achieved with averaging.

OVERALL ACCURACY The overall accuracy for a phase noise measurement can be calculated using the

individual uncertainties.
extra effort

11729C

is

made

is > 15 dB

First,

examine the typical accuracy that

to

calibrate out system

below the noise of

errors.

the source

can be

Assume that system

under

test,

and that the discriminator

obtained if no

noise

of the HP

flatness doesn't contribute error because the calibration is performed at the IF of
interest. Also assume that an alternate signal source will be used for calibration. The
total resultant errors tabulate as follows:

31

Typical Uncertainty ^^

l)Spectrum Analyzer (±dB)

Relative Amplitude Accuracy 1.5
Resolution Bandwidth Accuracy 0.2

IF Gain Accuracy 0.05

Spectrum Analyzer Frequency Response 1.5

2) System Parameters of the HP 11729C
Frequency Discriminator Flatness 0.2
Baseband Signal Processing 1.0
System Noise Floor 0.0

(assuming test system noise >15 dB below source)

3) Measurement Procedure

Quadrature Maintenance 0.05
Calibration Signal 1.5

Alternate Source (additional error) 0.2

Random Error Due to Randomness of Noise 0.5

Total Worst Case Uncertainty ±6.7

Accuracy Without Error Correction The typical system accuracy without extra error correction is ±6.7 dB. Potentially,

some of these errors would occur in the opposite direction and
error or correction factor due to system noise varies with the relative

cancel.

noise

Of course, the

level of the

test source and the system.

These numbers are worst case assuming that all errors add in the worst case way. A

more realistic approximation can be obtained by examining each inaccuracy and its

cause to determine if it is random or systematic. Often, this results in relative

measurements having errors that partially cancel out. For a probabilistic error
estimate, some errors are often combined by a root sum-of-the-squares (RSS)
method, instead of

simple

addition. Taking the RSS of

the

above errors gives a total

inaccuracy of ±2.85 dB.

Also remember that phase noise is a random quantity of which any measurement is
only an estimate. Averaging, whether video or digital, significantly improves the
accuracy and repeatability of a random measurement. Though a single sweep can be

measured with summation of the accuracies given above, this single sweep does not
characterize the statistical randomness of the signal.

Accuracy With Error Correction Careful measurement procedures, characterization of the HP 11729C baseband

signal processing section, a very low loss delay line, and careful spectrum analyzer
operation (as discussed before) can reduce measurement error as indicated below.

Typical Uncertainty

1) Spectrum Analyzer (±dB)
Relative Amplitude Accuracy 0.4
Resolution Bandwidth Accuracy 0.2
IF Gain Accuracy 0.05
Spectrum Analyzer Frequency Response 0.5

2) System Parameters of the HP 11729C
Frequency Discriminator Flatness 0.1
Baseband Signal Processing Flatness 0.5
System Noise Floor 0.0

(assuming test system noise >15 dB below source)

32

3) Measurement Procedure
Quadrature Maintenance 0.05
Calibration Signal 0.4
Alternate Source 0.05

Random Error Due to Randomness of Noise 0.5

Total Worst Case Uncertainty ±2.75

Phase Noise Measurement Linear Summation RSS
Total Uncertainty (±dB) of Typical Uncertainty of Typical Uncertainty

Overall Accuracy

(No effort) 6.70 2.85

Overall Accuracy

(Extra Effort) 2.75 1.06

33

UMMna

A Frequency Discriminator Transfer Response

START of signal through delay line/mixer frequency discriminator (Figure A.1).

Vs(t) = V0 cos (2TT f0t +~r~ cos

Af

THROUGH SPLITTER

Vd(t) = VL(t) = v cos (2TT fot +

INTRODUCTION OF DELAY

VR(t) = v cos [2TT f0 (t - rd) + ~r— cos 2n fm (t - rd) ]

VL(t) = v cos [2TT f0t + —— cos

Af

THROUGH MIXER

cos [2n f0 (t — rd) + ——cos 2n fm (t — rd) — 2n f0t — ——cos 2ir fmt] +

Vm(t) = K*

cos

[2TT

f0 (t - rd) + -7— cos

i Sum Frequency '

THROUGH FILTER

V(t) = K. cos [2TT f0 (t - Td) +

V(t) = K,,, cos [2?r f0 (t - T„ - t) + -7- (cos 2w fm (t - rd) - cos 2TT fmt) ]

V(t) = K^ cos [- 2 n f0Td + 2 —— sin

2jr f

mt)

Af

-j—

cos

2TT

fmt)

Af

Mil

2TT

fmt]

(Delayed Signal)

(Non-Delayed Signal)

-Difference Frequency-

Af Af

Af

2JT

m ni

fm (t - rd) +

2TT

Af

f0t + -r—

cos

Af Af

-j—

cos

2TT

fm (t - rd) -

2TT

f0t - -7— cos 2w fmt]

Af

'm

Af

(TT

fm Td) sin

2TT

fm (t - rd/2) ]

2TT

fmt] + HARMONICS

QUADRATURE ASSUMPTION (2n

V(t) =

K^

cos [- TT/2 + 2 -r— sin

Af

cos (- 7r/2) cos [2 —— sin (n fm rd) sin 27r fm (t - rd/2) ] -

V(t) = K*

in (- TT/2) sin [2 -7— sin

sin

1

V(t) =

K^,

Af

sin [2 —— sin

Mil

(TT

fm rd) sin

f0rd = (2K + 1)

(TT

fm rd) sin

Af

Af

f,

(TT

2TT

fm (t - rd/2) ]

TT/2)

K = 0, 1, 2, 3, 4,

2TT

fm (t - rd/2) ]

fm rd) sin 2?r fm (t - rd/2) ]

Af (Af) Af

SMALL SIGNAL ASSUMPTION

V(t) = K0 2-r- sin

Af

Mil

(TT

fm rd) sin 2n fm (t - rd/2)

For —— <0.2 rad , sin

Im

f f

TRANSFER RESPONSE

Af sin (n fm rd) 1

AV=K,2—sin(.fmrd) = K,27rrdAf ^ ^ ^ (For fm < —
AV

=»

K^

2TT

rd Af

AV — KdAf Kd = K^lnTi [V/Hz] Frequency Discriminator Constant

sin (TT fm rd)

-1)

34

Vs(t) = DUT SIGNAL (with frequency fluctuations)
Vd(t) = SIGNAL TO R PORT

VL(t) = SIGNAL TO L.O. PORT
VR(t) = DELAYED SIGNAL INTO R PORT
Vm(t) = SIGNAL OUT

V(t) = SIGNAL OUT

OF
OF

OF

OF

MIXER
FILTER

MIXER (phase detector)

MIXER (drives mixer)

OF

MIXER

f0 =

fm =FMRate

f(t) = f0 +

Af sin

Carrier Frequency

Af = FM Peak Deviation

rd = Delay

KJ.

= Phase detector constant

2TT

fmt

35

13 A Doubled-balanced Mixer Operating as a Phase Detector

Figure

B.

1.

Typical double-balanced mixer

phase detector characteristic.

Figure B.l shows a typical mixer-phase detector characteristic. When operated as a
phase detector, the mixer outputs a voltage
difference between the two input signals $LO —
sensitivity (the greatest voltage change per degree of phase change) and the center of
the region of most linear operation occur where the phase difference between the two
inputs is equal to 90 degrees, or phase quadrature.

To understand how a mixer operates as a phase detector, let's
mixer output (Figure B.2).

20 40 fill 80/100 120 140 160 ISO

too

-*RF)

V(t)

proportional to the fluctuating phase

</>RF.

The point of maximum phase

first

examine a normal

^

Figure B.2. Mixer operation.

Figure

B.3.

Filtered mixer output.

Let the L port

+

<£(t)].

VIF(t)

The low-pass
components, leaving V(t), as shown in Figure B.3.

signal be

Then the output of the mixer

= KLVR cos [a*-

filter

described by

a>L)

t +

in the block diagram of Figure B.2 removes the higher frequency

VL cos

toLt,

and the R port

V|F(t)

is the product of the two signals:

<*>(t)]

+ KLVR cos [o>R + cuL) t + 0(t)] +...

signal

by VR [cos wRt

[B.1]

36

V(t) = KLVR cos

[OIR

- coL) t + <K0] [B.2]

Let the peak amplitude of

V(t)

be defined as

Vb ^ (peak voltage of

the

beat signal),

equal to KLVR, where KL = mixer efficiency.

Vbpeak = K:LVR. [B.3]

Then,

V(t) = ± Vb ^ cos [a* - wL) t + etft)] [B.4]

When operating the mixer
is,

frequency and 90° out-of-phase. That quadrature,

as a

phase detector, the input

signals

must

be

at the

same

at

o>L = wR, and c#t) = (k + 1) 90° + A<ftt) [B.5]

Therefore, substituting in equation B.4, the output of the mixer at quadrature is
described by

AV(t) = ±V

sinA</>(t), [B.6]

bpeak

where AV(t) = instantaneous voltage fluctuations around 0V, and A</>(t) = instan­taneous phase fluctuations.

For A^pejit «1 radian, sin A#(t) = A#(t), and equation B.6 becomes

AV(t) = ±V

A<Kt) [B.7]

bpeak

Note that

this yields a

direct linear relationship between the voltage fluctuations at the

mixer output and the phase fluctuations of the input signals, or

AV = K0A0

where K^ =

Vb p^ = phase detector constant (volts/radian), which is equal to the

slope of the mixer sine wave output at the zero crossings.

To determine this phase detector constant, K^, the mixer is operated not in quadra­ture,

but with the inputs at two different frequencies, resulting in V(t) as described in

equation

value of the signal (Vb „). The phase detector constant K^,, equal to V
measured value V

B.4.

The IF output

bmi

signal

x ^2

measured on a spectrum analyzer provides the rms

is the

b peak

When the mixer is again operated as a phase detector (input signals in quadrature),
the voltage output of the mixer

as a

function of frequency

will be

directly proportional

to the input phase deviations from equation B.7.

AV(fm) = K^AtfQ [B.8]

AV(fm) = x/2V

Then A(/>

rms(fm

A0(fm) [B.9]

brms

) as measured on the spectrum analyzer is

A</>

) =-^-AV

rms(fm

(fJ = ~j^- AV

rms

* V2V

37

)

rms(fm

brms [B1()]

. ■■

\^s System Sensitivity

Sensitivity Factor Provided by
the Coaxial Delay Line

Phase Detector Sensitivity Factor

The transfer response of the delay line/mixer frequency discriminator

as

developed

in

Appendix A is

AV(fm) = KdAf(fm)

assuming that the offset frequency (fm) of interest is less than 1/2 7rrd. Kd the
discriminator constant is equal to K^27rrd, where K^ is the phase detector constant
and rd is the delay provided by the coaxial line.

Because the
both.

sensitivity of

K^,

is

dependent on the signal level out of the delay

the

system depends on both K^ and rd we

want

to

line,

which in turn depends

maximize

on the length of coaxial line while attenuation is proportional to length for a given
frequency. Thus we can only maximize the total function.

The sensitivity factor provided by the coaxial delay line increases directly propor­tional to the coaxial line length. For this reason the sensitivity can be expressed as

where

Srd = LX

L is

the length of the coaxial

line

and X represents the sensitivity per unit length.

[C.1]

Srd represents the sensitivity factor provided by the delay line.

As developed in Appendix
is

the mixer efficiency and VR is

B,

the phase detector constant K^ equals KLVR where K

the signal level into the R port of the phase detector.
VR depends on the input signal power and the attenuation of the delay line.
Attenuation of a coaxial delay line increases linearly with length when attenuation is
expressed in logarithmic terms [dB].

L

Attenuation [dB] = 10 log — = LZ

* in

[C.2]

Again L represents the length of the delay line and, Z represents a constant of
attenuation
the delay

with the negative sign on the exponent because V

The voltage out of the delay line (Vout) enters the R port of the phase detector

[dB]

per unit

line.

Solving for the voltage out of the coaxial delay

P V

r

out

10 log— =10 log— = LZ[dB]

"

r

in " in

-LZ/20

length.

P

2

out

and Pj„ refer to the signal power into and out of

out

v0u, = vinio

line gives

is less than V;,

0lU

the following.

[C.3]

[C.4]

VR,

so

K^, becomes

K„ =

KLKR = KLVin(10)-

LZ/20

[C.5]

Thus the sensitivity factor provided by the phase detector SK^, is

SK*

= KLVin(10r

LZ/2

°

[C.6]

The system sensitivity is a product of the delay line sensitivity factor Srd, and the

phase detector sensitivity factor

S

.

K<t>

38

S — Sr

SR^

d

S = KLVinLX(10)

Taking the derivative of
equal to zero allows the maximum to be found.

S = KLVinLX(10)

JC

— = [1 - (LZ/20) In 10] * [KLVinX(10)-

Setting equal to zero and rearranging terms

0 = [1 - (LZ/20) In 10] * [KLVinX(10) "

0 = [1 - (LZ/20) In 10]

1 = (LZ/20) In 10

LZ =

Finally the maximum sensitivity occurs at an attenuation, LZ, of

LZ = 8.7 dB.

20

In 10

_LZ/20

this

equation with respect to length L and setting the result

-LZ/20

LZ/20

]

LZ/20

[C.7]

[C.8]

[C.9]

Figure C.l. System sensitivity

attenuation.

vs.

delay line

The maximum
to note because the attenuation of a given coaxial line will change depending on the
carrier frequency passing through it. Figure C.l shows a plot of sensitivity versus
attenuation and indicates the maximum sensitivity at an attenuation of 8.7 dB.

1

L

I

i

t

i

( S 10 15 JO 25 JO 35 40 45 50

The maximum determined above assumed that the phase detector sensitivity was
being affected by the delay
in compression, K^
Any signal power above the phase detector compression point can be attenuated in
the delay line (increased length for increased sensitivity). Thus as soon as the phase
detector comes out of compression, the 8.7 dB trade off applies.

is

u

?

not specified

A

tttn

nation of

is

constant and the equation developed above

in

length,

but

OB

lay Lint idB)

line

attenuation. However,

in

terms of attenuation.

as

This is

long

as

the phase detector is

does

important

not hold true.

The phase detector compression point for
means for optimum sensitivity the signal level out of the delay line should be
approximately -5 dBm (3.5 dBm - 8.7 dB = -5.2 dBm).

39

the

HP

11729C is

typically +3.5

dBm.

This

D

Calibration and the Discriminator Constant (Kd)

The discriminator constant

(Kj)

is

the

constant

of

proportionality between

the
frequency fluctuations of a source and the voltage fluctuations out of the frequency
discriminator.

As

shown in Appendix

A,

Kd is

equal to AV/Af with units of

volts

per

hertz (V/Hz).

An easy
response P^j to a known signal

way

to

determine

the

discriminator constant

ASB,^

(see Figure

is to

measure

D.

1).

From modulation theory for

the

system

small modulation index (m<0.2rad)

[dB]

2

ASB

-

f^,

is the FM rate of

the

calibration signal.

[D.l]

[D.2]

m2 1_

4

~ 4 (f^ "

Where

Af,^

is the peak deviation and

By rearranging equation

2

(AW)

(.'"calniisJ

4f2

=

2

=

2*^10

nca.

(AW)

D.l

ASB^dB]

10 10

ASBc,

io

By definition

AV?™

1

Kr

— "

Aft. f°

,fm

"2,

d

[D.3]

Figure

D.

1.

Determining the discriminator

constant by measuring system response.

Substitution of equation D.2 into D.3 yields

2

AV

2P

mcal

"-1* rms

ASB^,

10

10

[dB]

K2a

=

Or in logarithmic terms

Kd [dB] = P^

[dB] - (ASB,*, [dB] + 20 log

t^, + 3

where P^i equals the measured system response (AV2^)

Frequency

Olscriminilor

Known FM Modulation

in

[dB])

dB.

\JCL

'ma

System Response

P«l

40

lli The Importance of Quadrature

As shown in Figure E.l, phase quadrature is the point of maximum phase sensitivity
and the region of most linear
in a measurement error given by

££t —

error (dB) = 20 log [cos (magnitude of the phase deviation from quadrature]

operation.

Any deviation,

(A<£),

from quadrature results

Figure E.
phase detector characteristic.

1.

Typical double-balanced

where error

error in dB is always negative,

The
in the table below.

Even though the error for small deviation around quadrature is small, in a user­designed noise measurement
monitored. The HP 11729C's quadrature maintenance section provides the monitor­ing capability.

is

defined

error contribution

Offset from quadrature

1°

3°

10°

as

=^(fm)

measured—„^(fm) at A0 = 0 in

since

J^(fm)

measured is always < Jz?(fm) at

is very

small for small deviations around quadrature,

Error

-0.001 dB

-0.01 dB

-0.13 dB

system,

this

deviation from quadrature would have

dB.

Notice that the

A</>

as

= 0.

shown

to

be

41

MPINUOI

F HP 11729C HP-IB Programming Codes

The Hewlett-Packard Interface Bus (HP-IB) is a general purpose digital interface ^^
which simplifies the design and integration of instruments and computers into
systems. The following commands can be used to control the HP 11729C by
computer.

AM Selects AM Noise Measurement Mode
PH Selects Phase Noise Meausrement Mode
PU Selects Pulsed Carrier Measurement Mode

FT1 Selects first filter band (10 to 1280 MHz)

FT2 Selects second filter band (1.28 to 3.2 GHz)
FT3 Selects third filter band (3.2 to 5.76 GHz)
FT4 Selects fourth filter band (5.76 to 8.32 GHz)
FT5 Selects fifth filter band (8.32 to 10.88 GHz)
FT6 Selects sixth filter band (10.88 to 13.44 GHz)
FT7 Selects seventh filter band (13.44 to 16 GHz)
FT8 Selects eighth filter band (16 to 18.56 GHz)

LK1 Selects Lock Bandwidth Factor of 1
LK2 Selects Lock Bandwidth Factor of 10
LK3 Selects Lock Bandwidth Factor of 100
LK4 Selects Lock Bandwidth Factor of Ik
LK5 Selects Lock Bandwidth Factor of 10k

CA1 Enables Capture
CA0 Disables Capture

LP Learn Front Panel
RO Read Option List
RM Read RSQ
@ Accept RSQ
CS Clear Status Byte
?ID Read Instrument Type

42

tffflMD)

Cj References

References

Other References

Hewlett-Packard Application Notes

AN 150-4 Spectrum Analysis ..
AN 150-8 Spectrum Analysis ..

Hewlett-Packard Product Notes

PN 11729B-1 Phase Noise Characterization of Microwave Oscillators Phase

Detector Method (HP Lit #5952-8286)

Scherer, D. (HP) "The 'Art' of Phase Noise Measurements", HP RF Microwave
Measurement Symposium, October, 1984.

"Phase Noise" RF & Microwave Phase Noise Measurement Seminar, Hewlett­Packard.

.. Noise Measurements (HP

Accuracy Improvement

(HP Lit

Lit

#5952-1147)

#5952-9210)

■0

43

HEWLETT

m

For more information, call your local HP sales office listed in the telephone directory white pages. Ask for the Electronic Instrument Department, or write to
Hewlett-Packard: U.S.A. ­Drive, Mississauga, L4V 1M8, Ontario. Japan - Yokogawa-Hewlett-Packard Ltd., 3-29-21, Takaido-Higashi, Suginami-ku, Tokyo 168. Elsewhere in the world,
write to Hewlett-Packard Intercontinental, 3495 Deer Creek Road, Palo Alto, CA 94304.

P.O.

Box

10301,

Palo

Alto,

CA 94303-0890. Europe - P.O. Box 999,1180 AZ Amstelveen, The Netherlands. Canada - 6877 Goreway

PACKARD

5953-6497

September 1985

Printed in U.S.A.