Casio Algebra FX 2.0 PLUS, FX 2.0 - Algebra FX 2.0 Graphing Calculator, Algebra FX 1.0 PLUS User Manual

Download

ALGEBRA FX 2.0 PLUS

FX 1.0 PLUS

User’s Guide

http://world.casio.com/edu_e/

GUIDELINES LAID DOWN BY FCC RULES FOR USE OF THE UNIT IN THE U.S.A. (not applicable to other areas).

NOTICE

This equipment has been tested and found to comply with the limits for a Class B digital device, pursuant to Part 15 of the FCC Rules. These limits are designed to provide reasonable protection against harmful interference in a residential installation. This equipment generates, uses and can radiate radio frequency energy and, if not installed and used in accordance with the instructions, may cause harmful interference to radio communications. However, there is no guarantee that interference will not occur in a particular installation. If this equipment does cause harmful interference to radio or television reception, which can be determined by turning the equipment off and on, the user is encouraged to try to correct the interference by one or more of the following measures:

•Reorient or relocate the receiving antenna.

•Increase the separation between the equipment and receiver.

•Connect the equipment into an outlet on a circuit different from that to which the receiver is connected.

•Consult the dealer or an experienced radio/TV technician for help.

FCC WARNING

Changes or modifications not expressly approved by the party responsible for compliance could void the user’s authority to operate the equipment. Proper connectors must be used for connection to host computer and/or peripherals in order to meet FCC emission limits.

Connector SB-62 Power Graphic Unit to Power Graphic Unit Connector FA-123 Power Graphic Unit to PC for IBM/Macintosh Machine

IBM is a registered trademark of International Business Machines Corporation. Macintosh is a registered trademark of Apple Computer, Inc.

Declaration of Conformity

Model Number: ALGEBRA FX 2.0 PLUS / FX 1.0 PLUS Trade Name: CASIO COMPUTER CO., LTD. Responsible party: CASIO, INC. Address: 570 MT. PLEASANT AVENUE, DOVER, NEW JERSEY 07801 Telephone number: 973-361-5400

This device complies with Part 15 of the FCC Rules. Operation is subject to the following two conditions: (1) This device may not cause harmful interference, and (2) this device must accept any interference received, including interference that may cause undesired operation.

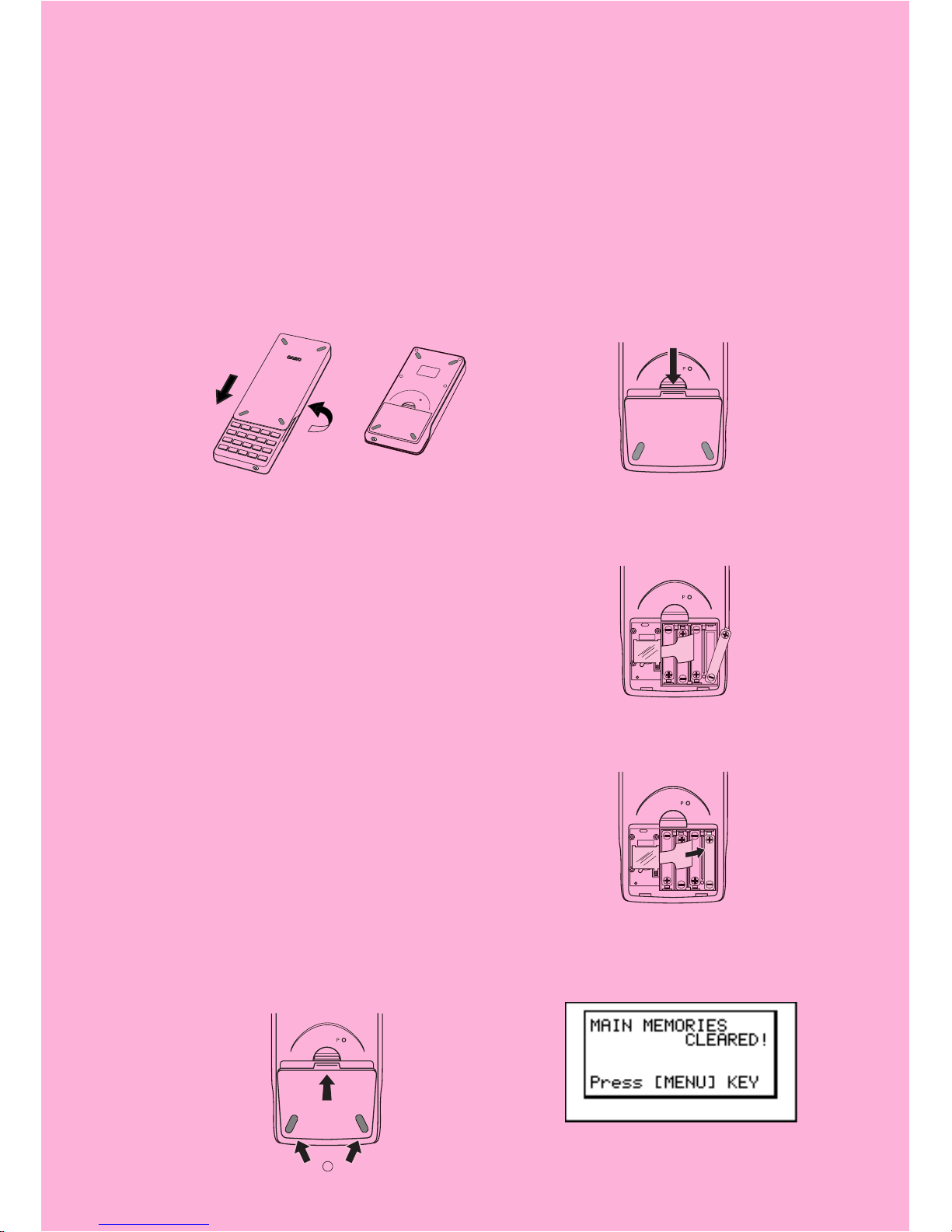
BEFORE USING THE CALCULATOR FOR THE FIRST TIME...

This calculator does not contain any main batteries when you purchase it. Be sure to perform the following procedure to load batteries, reset the calculator, and adjust the contrast before trying to use the calculator for the first time.

1. Making sure that you do not accidently press the o key, slide the case onto the

calculator and then turn the calculator over. Remove the back cover from the calculator by pulling with your finger at the point marked

2. Load the four batteries that come with calculator.

• Make sure that the positive (+) and negative (–) ends of the batteries are facing correctly.

3. Remove the insulating sheet at the location marked “BACK UP” by pulling in the direction indicated by the arrow.

4. Replace the back cover, making sure that its tabs enter the holes marked 2 and turn the calculator front side up. The calculator should automatically turn on power and perform the memory reset operation.

BACK UP

19990401

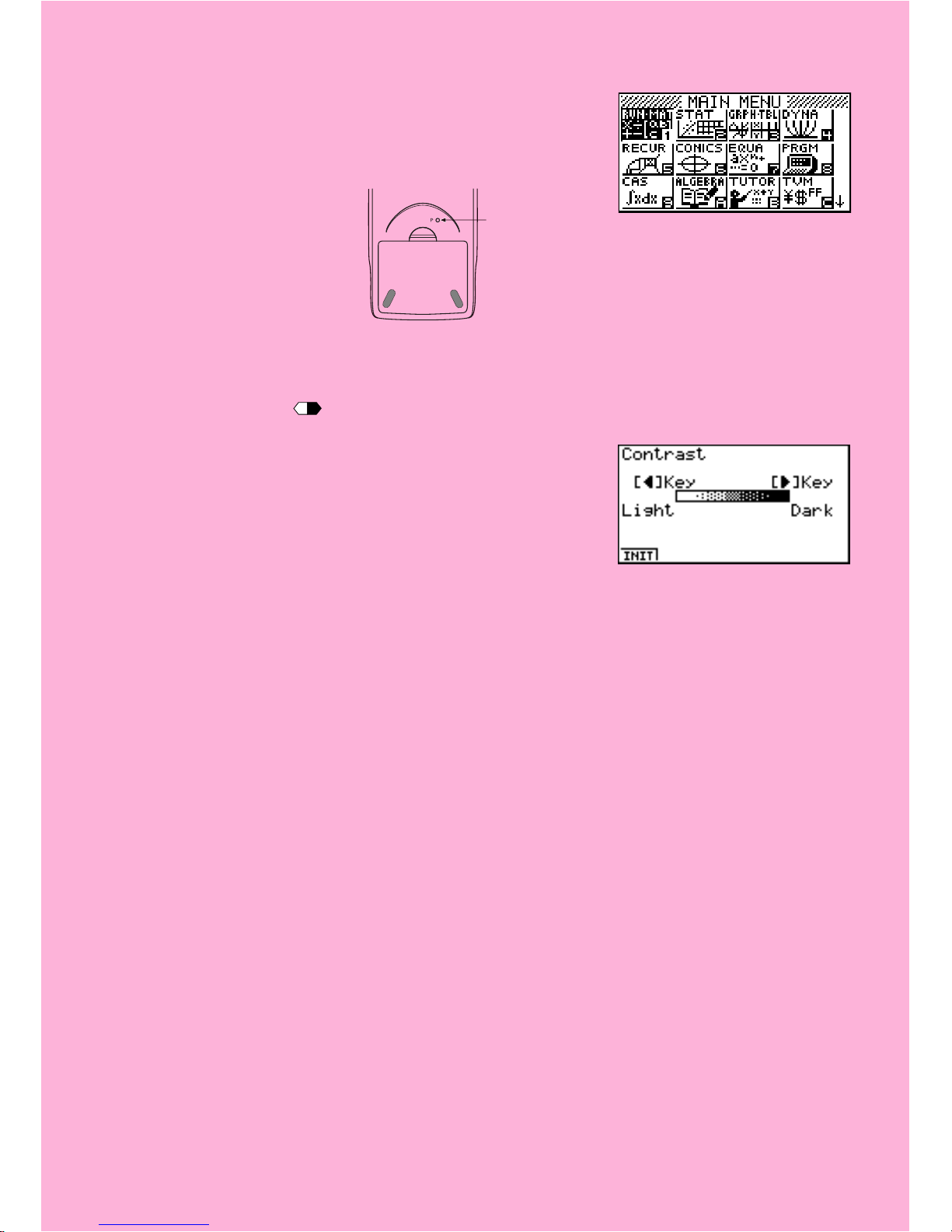
P button

5. Press m.

• If the Main Menu shown to the right is not on the display, press the P button on the back of the calculator to perform memory reset.

6. Use the cursor keys (f, c, d, e) to select the SYSTEM icon and press w, then press 2(

) to display the contrast adjustment screen.

7. Adjust the contrast.

• The e cursor key makes display contrast darker.

• The d cursor key makes display contrast lighter.

• 1(INIT) returns display contrast to its initial default.

8. To exit display contrast adjustment, press m.

* The above shows the ALGEBRA

FX 2.0 PLUS screen.

20010102

19990401

Turning Power On And Off

Using Modes

Basic Calculations Replay Feature

Fraction Calculations

Exponents Graph Functions

Dual Graph

Box Zoom

Dynamic Graph Table Function

Quick-Start

19990401

Quick-Start

Welcome to the world of graphing calculators.

Quick-Start is not a complete tutorial, but it takes you through many of the most common functions, from turning the power on, and on to graphing complex equations. When you’re done, you’ll have mastered the basic operation of this calculator and will be ready to proceed with the rest of this user’s guide to learn the entire spectrum of functions available.

Each step of the examples in Quick-Start is shown graphically to help you follow along quickly and easily. When you need to enter the number 57, for example, we’ve indicated it as follows:

Press

Whenever necessary, we’ve included samples of what your screen should look like. If you find that your screen doesn’t match the sample, you can restart from the beginning by pressing the “All Clear” button

TURNING POWER ON AND OFF

To turn power on, press o.

To turn power off, press

OFF

Calculator power turns off automatically if you do not perform any operation within the Auto Power Off trigger time you specify. You can specify either six minutes or 60 minutes as the trigger time.

USING MODES

This calculator makes it easy to perform a wide range of calculations by simply selecting the appropriate mode. Before getting into actual calculations and operation examples, let’s take a look at how to navigate around the modes.

To select the RUN

•

MAT Mode

1. Press m to display the Main Menu.

Quick-Start

* The above shows the ALGEBRA

FX 2.0 PLUS screen.

20010102

19990401

2. Use defc to highlight RUN

•

MAT

and then press w.

This is the initial screen of the RUN

•

MAT Mode,

where you can perform manual calculations, matrix calculations, and run programs.

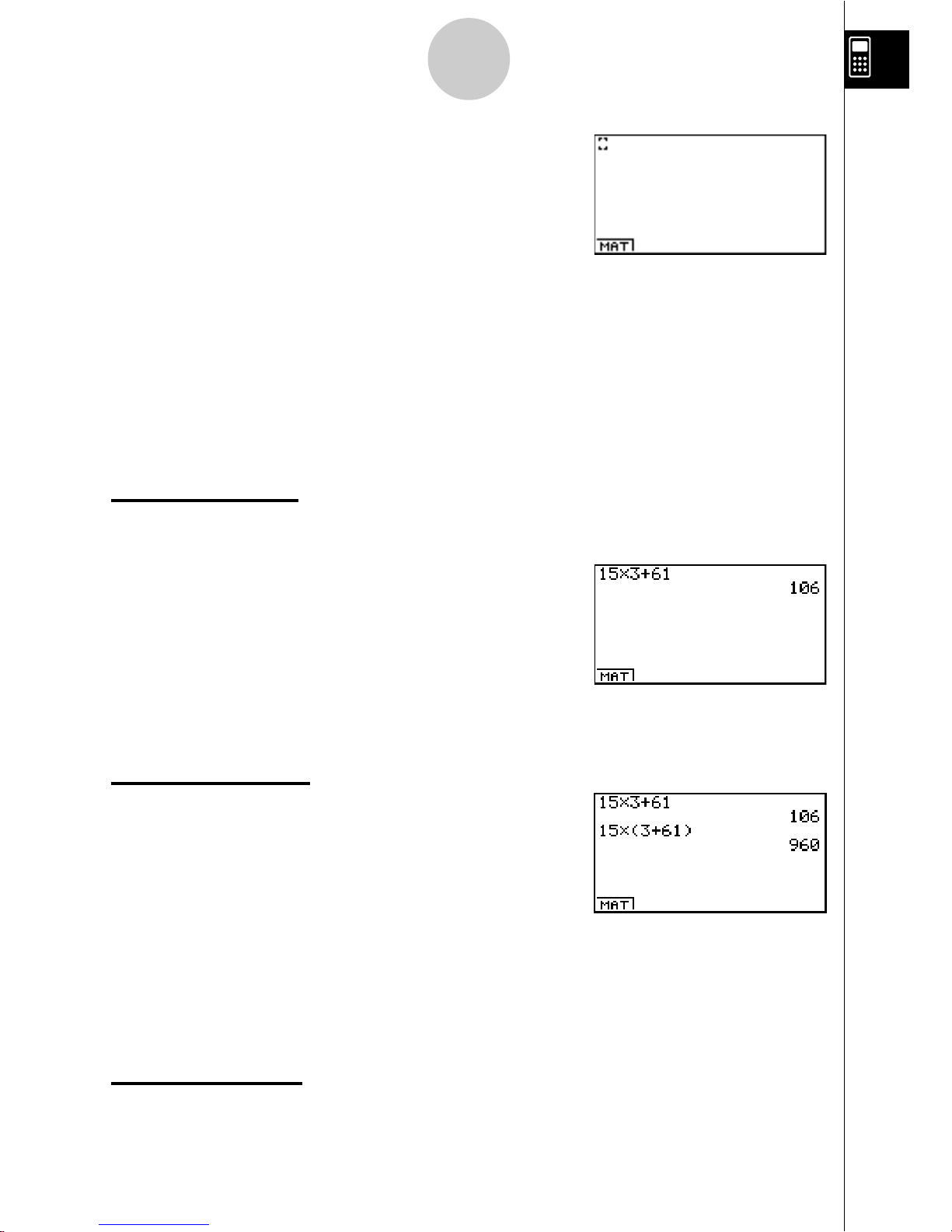
BASIC CALCULATIONS

With manual calculations, you input formulas from left to right, just as they are written on paper. With formulas that include mixed arithmetic operators and parentheses, the calculator automatically applies true algebraic logic to calculate the result.

Example:

15 × 3 + 61

1. Press

o to clear the calculator.

2. Press

bf*d+gbw.

Parentheses Calculations

Example:

15 × (3 + 61)

1. Press

bf*(d +gb)w.

Built-In Functions

This calculator includes a number of built-in scientific functions, including trigonometric and logarithmic functions.

Example:

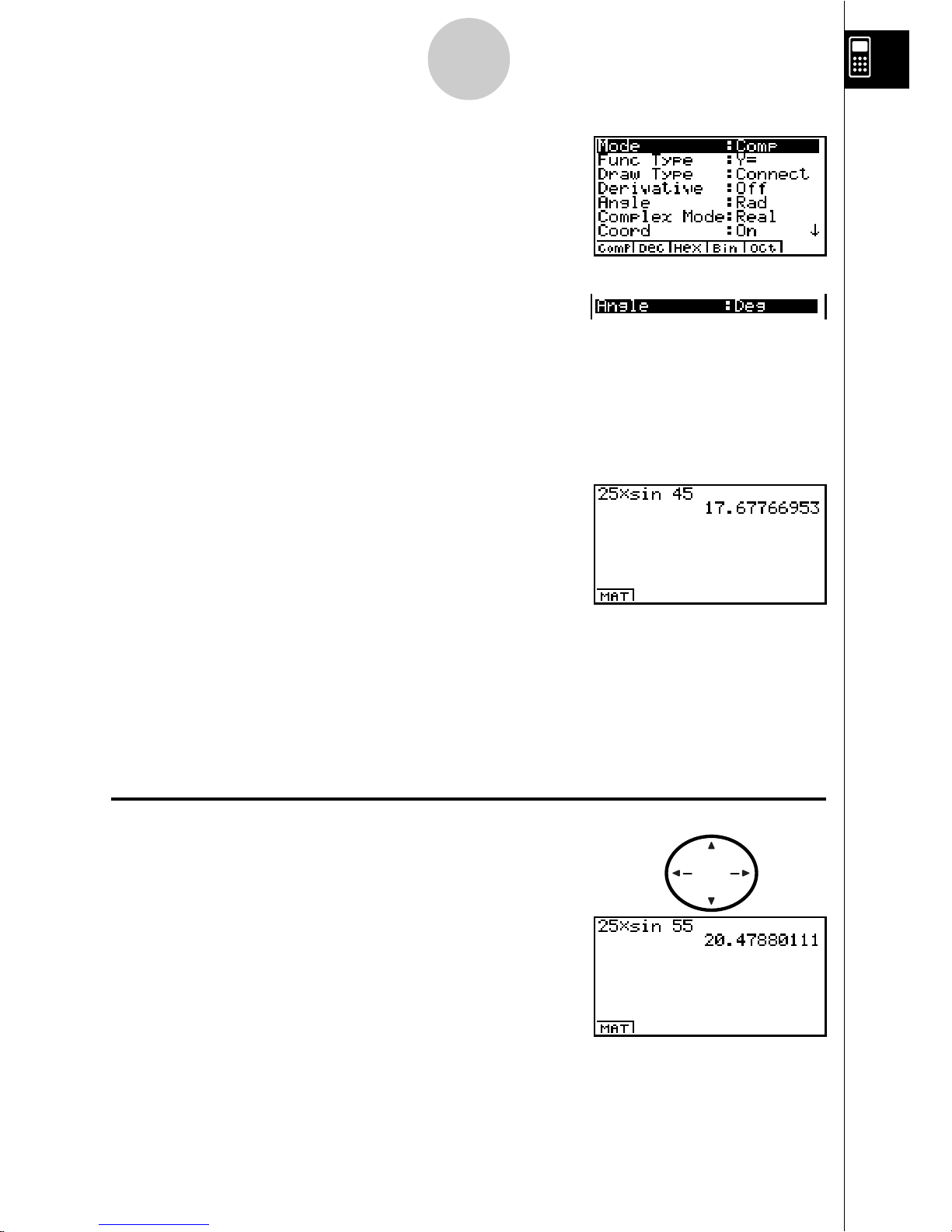
25 × sin 45˚

Important!

Be sure that you specify Deg (degrees) as the angle unit before you try this example.

Quick-Start

19990401

1. Pressu

SET UP

to display the SET UP screen.

2. Press cccc1 (Deg) to specify

degrees as the angle unit.

3. Press

i to clear the menu.

4. Press

o to clear the unit.

5. Press

cf*sefw.

REPLAY FEATURE

With the replay feature, simply press d or e to recall the last calculation that

was performed so you can make changes or re-execute it as it is.

Example:

To change the calculation in the last example from (25 × sin 45˚) to (25 × sin 55˚)

1. Press

d to display the last calculation.

2. Press

d twice to move the cursor (t) to 4.

3. Press

D to delete 4.

4. Press f.

5. Press

w to execute the calculation again.

Quick-Start

REPLAY

19990401

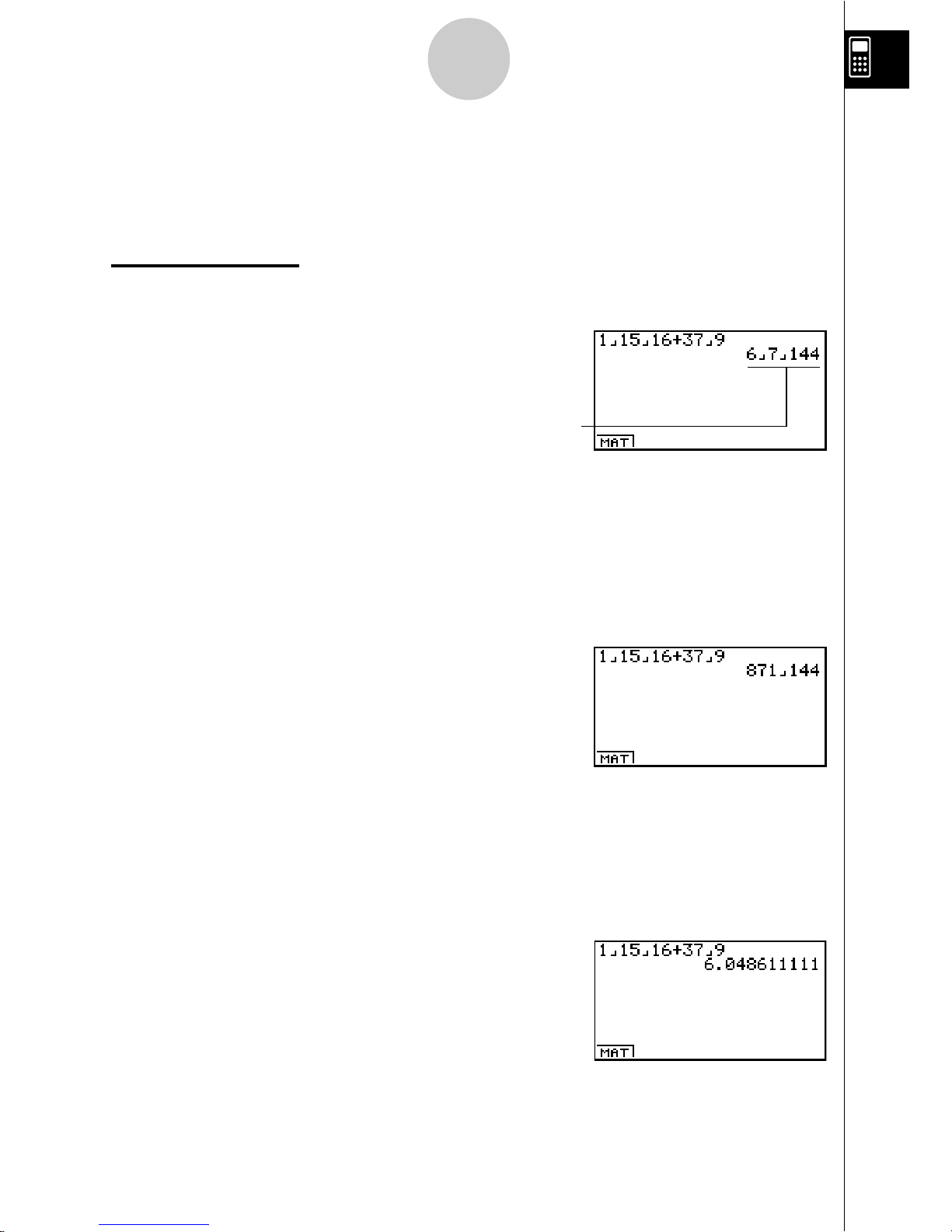
FRACTION CALCULATIONS

You can use the $ key to input fractions into calculations. The symbol “ { ” is used

to separate the various parts of a fraction.

Example:

1 15/16 + 37/

1. Press o.

2. Press

b$bf$ bg+dh$ jw

Converting a Mixed Fraction to an Improper Fraction

While a mixed fraction is shown on the display, press !

d/c

to convert it to an

improper fraction.

Press

d/c

again to convert back to a mixed fraction.

Converting a Fraction to Its Decimal Equivalent

While a fraction is shown on the display, press $ to convert it to its decimal

equivalent.

Press

$ again to convert back to a fraction.

Indicates 6 7/

144

Quick-Start

19990401

EXPONENTS

Example:

1250 × 2.06

1. Press o.

2. Press

bcfa*c.ag.

3. Press

M and the ^ indicator appears on the display.

4. Press

f. The ^5 on the display indicates that 5 is an exponent.

5. Press

Quick-Start

19990401

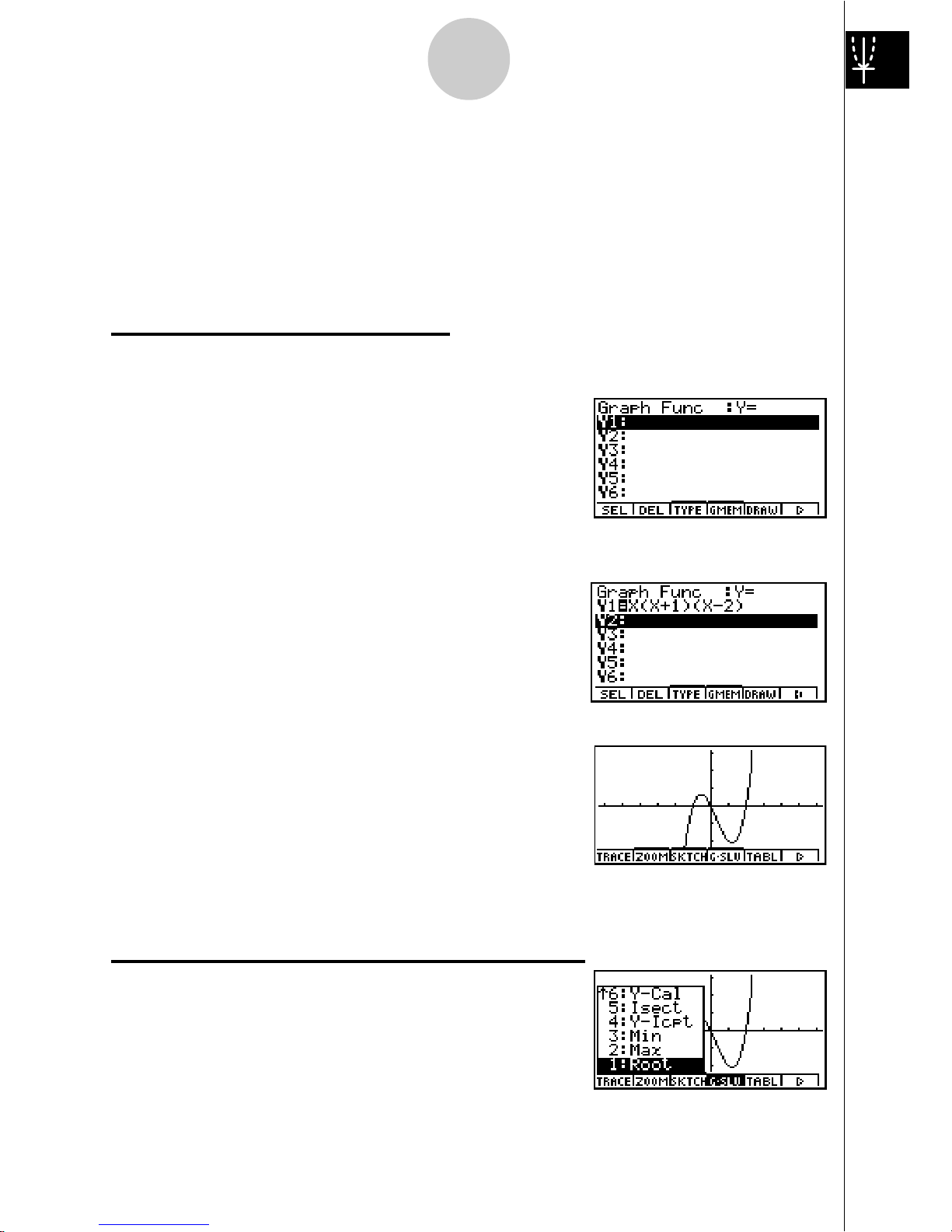
GRAPH FUNCTIONS

The graphing capabilities of this calculator makes it possible to draw complex graphs using either rectangular coordinates (horizontal axis: x ; vertical axis: y) or polar coordinates (angle:

; distance from origin: r). All of the following graphing examples are performed starting from the calculator setup in effect immediately following a reset operation.

Example

1: To graph Y = X(X + 1)(X – 2)

1. Press

2. Use

defc to highlight

GRPH

•

TBL, and then press w.

3. Input the formula.

v(v+b)

(v -c)w

4. Press 5(DRAW) or w to draw the graph.

Example

2: To determine the roots of Y = X(X + 1)(X – 2)

1. Press

4(G-SLV) to display the pull-up menu.

Quick-Start

19990401

2. Press b(Root).

Press e for other roots.

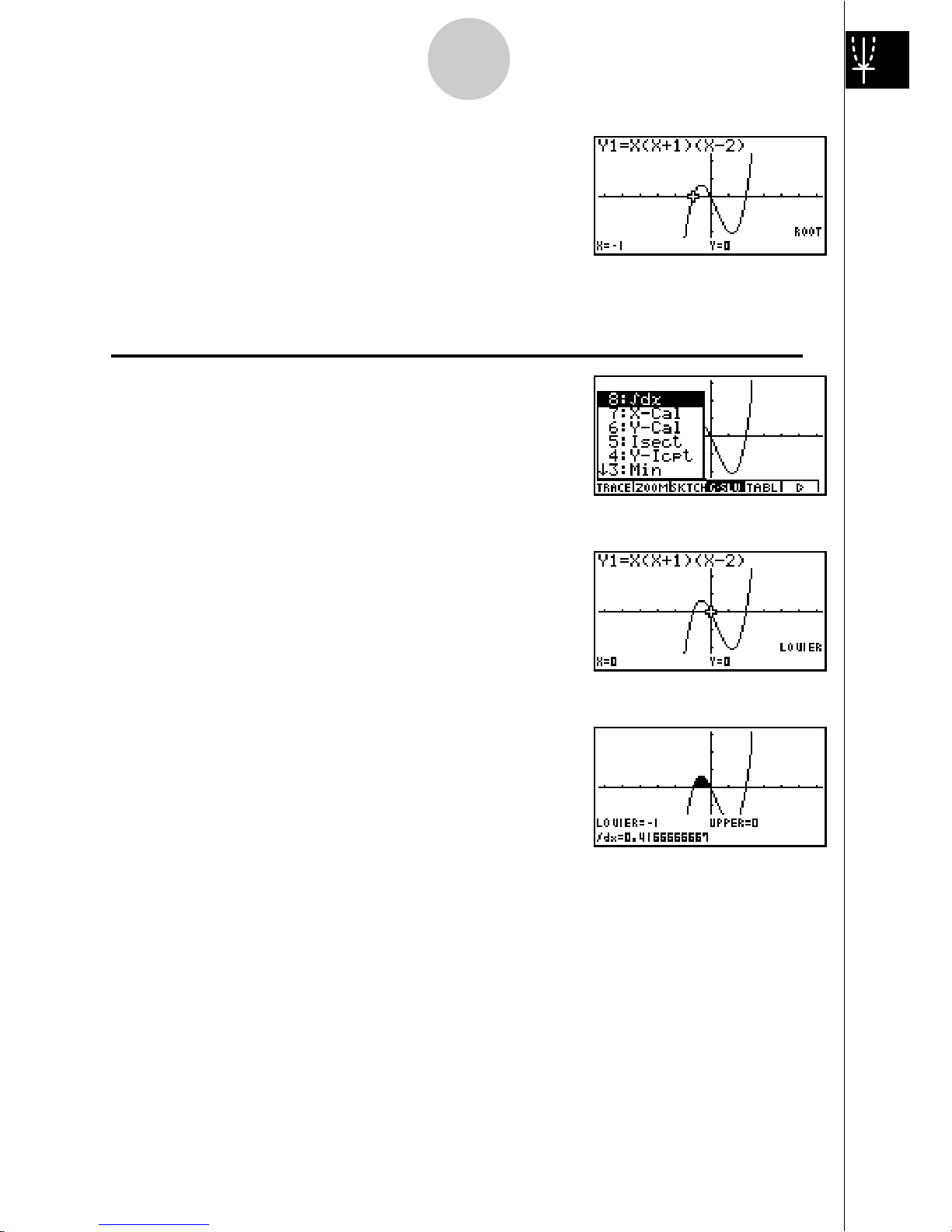
Example

3: Determine the area bounded by the origin and the X = –1 root obtained

for Y = X(X + 1)(X – 2)

1. Press

i4(G-SLV)c.

2. Press i(∫dx).

3. Use d to move the pointer to the location where

X = –1, and then press w. Next, use e to

move the pointer to the location where X = 0, and

then press

to input the integration range,

which becomes shaded on the display.

Quick-Start

19990401

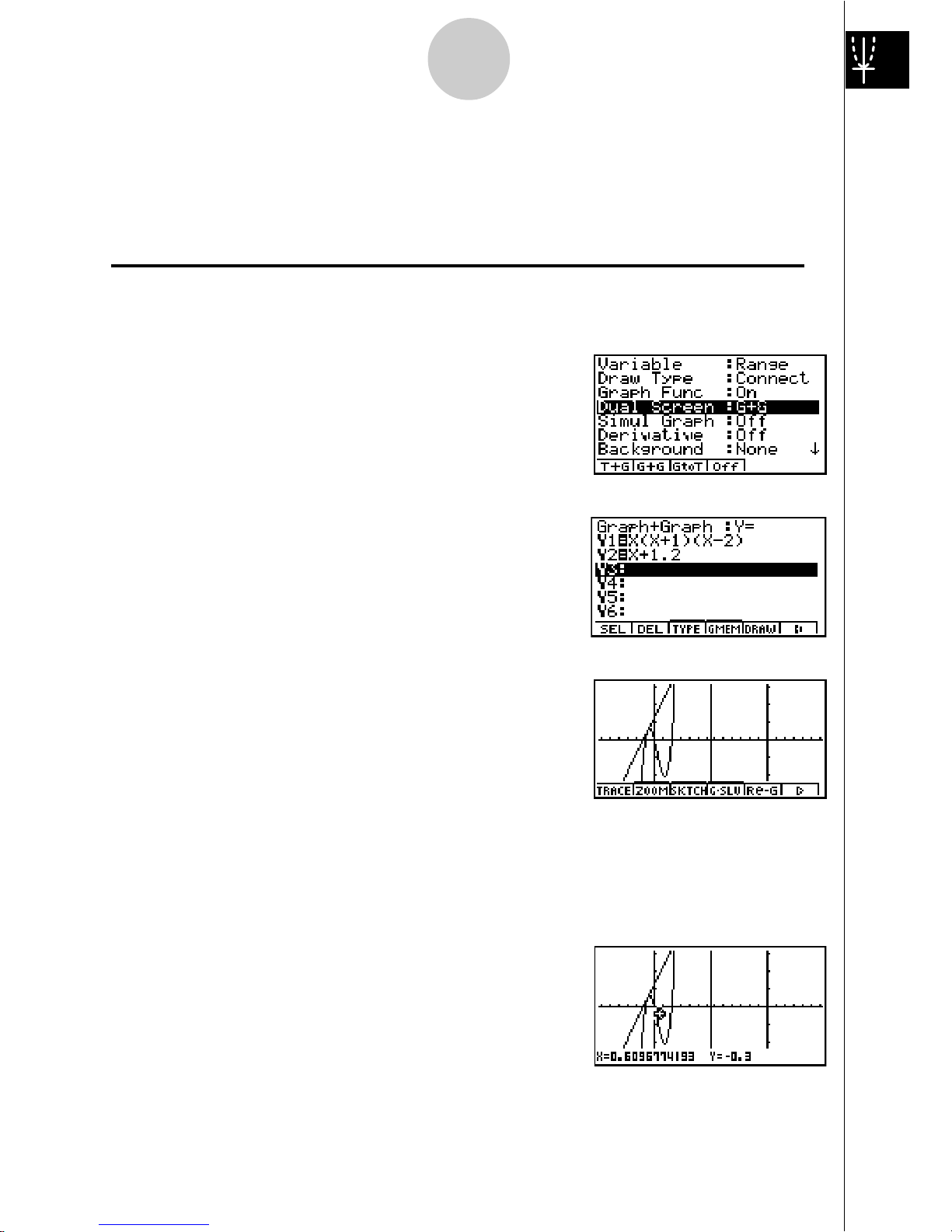
DUAL GRAPH

With this function you can split the display between two areas and display two graphs on the same screen.

Example:

To draw the following two graphs and determine the points of intersection

Y1 = X(X + 1)(X – 2) Y2 = X + 1.2

1. Press u

SET UP

ccc2(G+G)

to specify “G+G” for the Dual Screen setting.

2. Press

i, and then input the two functions.

v(v+b) (v-c)w v+b.cw

3. Press 5(DRAW) or w to draw the graphs.

BOX ZOOM

Use the Box Zoom function to specify areas of a graph for enlargement.

1. Press

2(ZOOM) b(Box).

2. Use

d e f c to move the pointer

to one corner of the area you want to specify and then press

Quick-Start

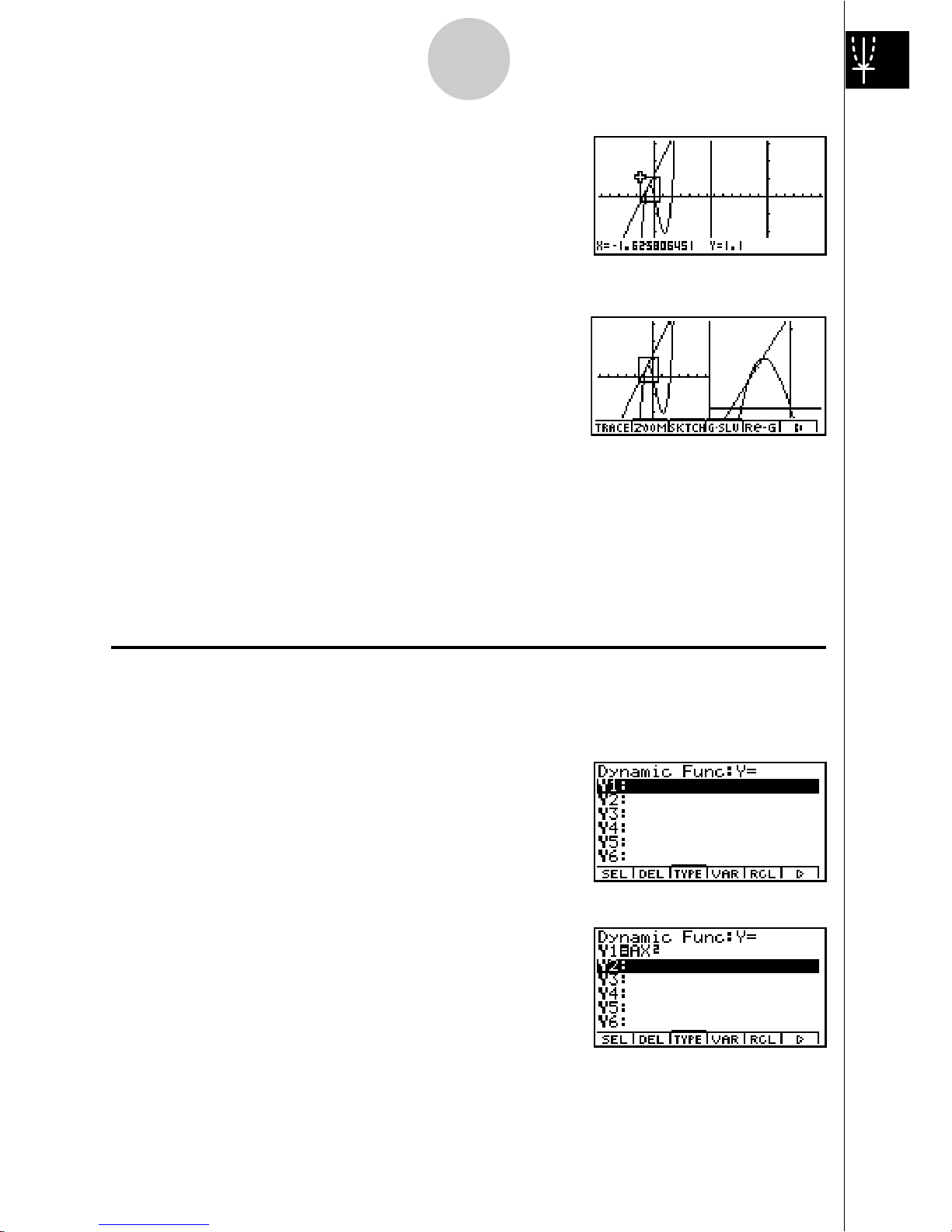
19990401

3. Use d e f c to move the pointer

again. As you do, a box appears on the display. Move the pointer so the box encloses the area you want to enlarge.

4. Press

w, and the enlarged area appears in the

inactive (right side) screen.

DYNAMIC GRAPH

Dynamic Graph lets you see how the shape of a graph is affected as the value assigned to one of the coefficients of its function changes.

Example:

To draw graphs as the value of coefficient A in the following function changes from 1 to 3

Y = AX

1. Press m.

2. Use

d e f c to highlight DYNA,

and then press w.

3. Input the formula.

vxw

12356

Quick-Start

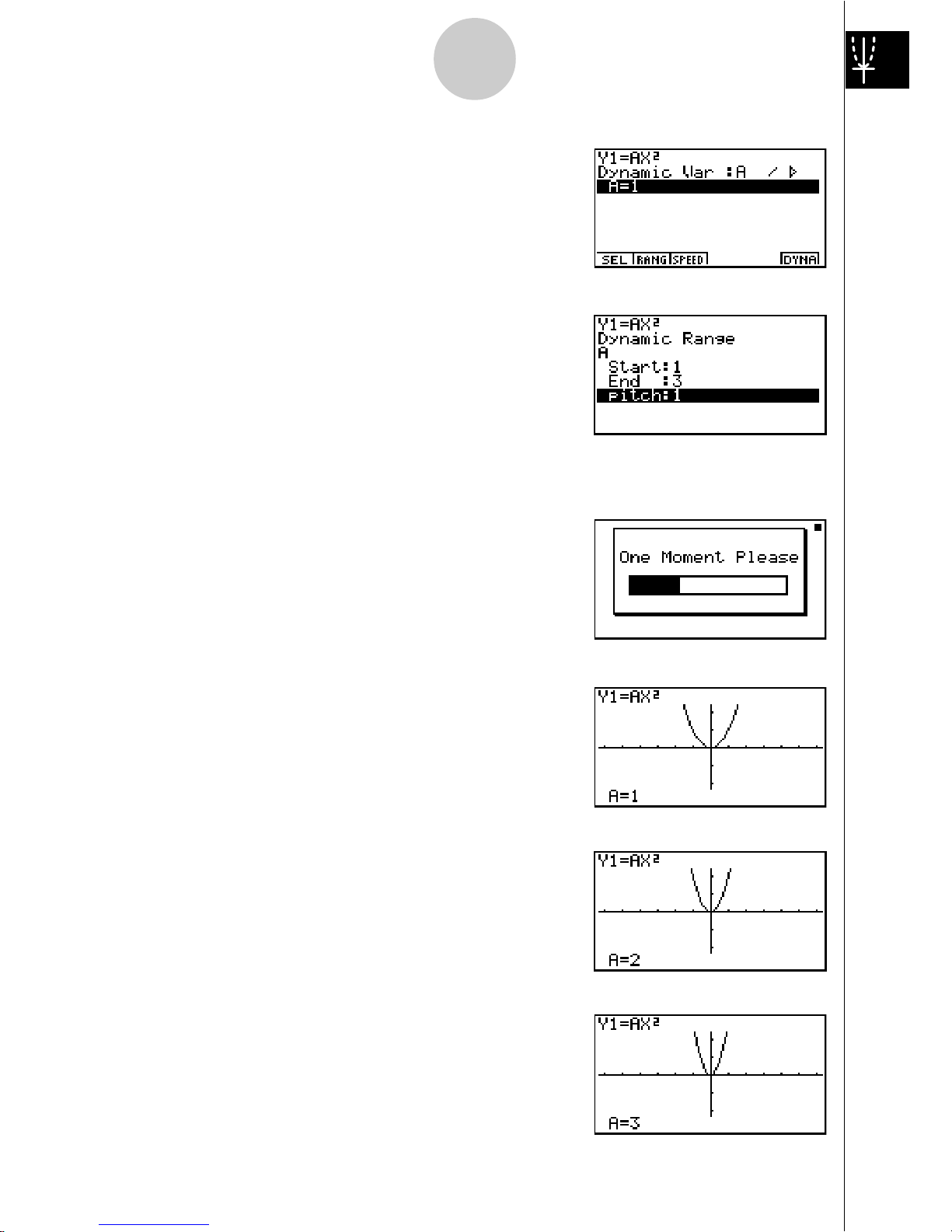
19990401

4. Press 4(VAR) bw to assign an initial value

of 1 to coefficient A.

5. Press

2(RANG) bwdw b

wto specify the range and increment of change

in coefficient A.

6. Press

7. Press

6(DYNA) to start Dynamic Graph drawing.

The graphs are drawn 10 times.

↓

↓↑

Quick-Start

19990401

TABLE FUNCTION

The Table Function makes it possible to generate a table of solutions as different values are assigned to the variables of a function.

Example:

To create a number table for the following function

Y = X (X+1) (X–2)

1. Press m.

2. Use

defc to highlight

GRPH

•

TBL, and then press w.

3. Input the formula.

v(v+b)

(v-c)w

4. Press 6(g)5(TABL) to generate the number

table.

To learn all about the many powerful features of this calculator, read on and explore!

Quick-Start

19990401

Handling Precautions

•Your calculator is made up of precision components. Never try to take it apart.

•Avoid dropping your calculator and subjecting it to strong impact.

•Do not store the calculator or leave it in areas exposed to high temperatures or humidity, or

large amounts of dust. When exposed to low temperatures, the calculator may require more time to display results and may even fail to operate. Correct operation will resume once the calculator is brought back to normal temperature.

• The display will go blank and keys will not operate during calculations. When you are operating

the keyboard, be sure to watch the display to make sure that all your key operations are being performed correctly.

•Replace the main batteries once every 2 years regardless of how much the calculator is used

during that period. Never leave dead batteries in the battery compartment. They can leak and damage the unit.

•Keep batteries out of the reach of small children. If swallowed, consult a physician immediately.

•Avoid using volatile liquids such as thinner or benzine to clean the unit. Wipe it with a soft, dry

cloth, or with a cloth that has been moistened with a solution of water and a neutral detergent and wrung out.

•Always be gentle when wiping dust off the display to avoid scratching it.

•In no event will the manufacturer and its suppliers be liable to you or any other person for any

damages, expenses, lost profits, lost savings or any other damages arising out of loss of data and/or formulas arising out of malfunction, repairs, or battery replacement. It is up to you to prepare physical records of data to protect against such data loss.

•Never dispose of batteries, the liquid crystal panel, or other components by burning them.

•When the “Low Main Batteries!” message or the “Low Backup Battery!” message appears on the

display, replace the main power supply batteries or the back up battery as soon as possible.

•Be sure that the power switch is set to OFF when replacing batteries.

• If the calculator is exposed to a strong electrostatic charge, its memory contents may be

damaged or the keys may stop working. In such a case, perform the Reset operation to clear the memory and restore normal key operation.

• If the calculator stops operating correctly for some reason, use a thin, pointed object to press

the P button on the back of the calculator. Note, however, that this clears all the data in calculator memory.

•Note that strong vibration or impact during program execution can cause execution to stop or

can damage the calculator’s memory contents.

•Using the calculator near a television or radio can cause interference with TV or radio reception.

•Before assuming malfunction of the unit, be sure to carefully reread this user’s guide and ensure

that the problem is not due to insufficient battery power, programming or operational errors.

19990401

Be sure to keep physical records of all important data!

Low battery power or incorrect replacement of the batteries that power the unit can cause the data stored in memory to be corrupted or even lost entirely. Stored data can also be affected by strong electrostatic charge or strong impact. It is up to you to keep back up copies of data to protect against its loss.

In no event shall CASIO Computer Co., Ltd. be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the purchase or use of these materials. Moreover, CASIO Computer Co., Ltd. shall not be liable for any claim of any kind whatsoever against the use of these materials by any other party.

• The contents of this user’s guide are subject to change without notice.

•No part of this user’s guide may be reproduced in any form without the express written consent of the manufacturer.

• The options described in Chapter 10 of this user’s guide may not be available in certain geographic areas. For full details on availability in your area, contact your nearest CASIO dealer or distributor.

19990401

• • • • • • • • • • • • • • • • • • •

ALGEBRA FX 2.0 PLUS

FX 1.0 PLUS

20010102

19990401

Contents

Getting Acquainted — Read This First!

Chapter 1 Basic Operation

1-1 Keys ................................................................................................. 1-1-1

1-2 Display.............................................................................................. 1-2-1

1-3 Inputting and Editing Calculations .................................................... 1-3-1

1-4 Option (OPTN) Menu ....................................................................... 1-4-1

1-5 Variable Data (VARS) Menu ............................................................. 1-5-1

1-6 Program (PRGM) Menu ................................................................... 1-6-1

1-7 Using the Set Up Screen .................................................................. 1-7-1

1-8 When you keep having problems… ................................................. 1-8-1

Chapter 2 Manual Calculations

2-1 Basic Calculations ............................................................................ 2-1-1

2-2 Special Functions ............................................................................. 2-2-1

2-3 Specifying the Angle Unit and Display Format ................................. 2-3-1

2-4 Function Calculations ....................................................................... 2-4-1

2-5 Numerical Calculations..................................................................... 2-5-1

2-6 Complex Number Calculations ......................................................... 2-6-1

2-7 Binary, Octal, Decimal, and Hexadecimal Calculations

with Integers ..................................................................................... 2-7-1

2-8 Matrix Calculations ........................................................................... 2-8-1

Chapter 3 List Function

3-1 Inputting and Editing a List ............................................................... 3-1-1

3-2 Manipulating List Data ...................................................................... 3-2-1

3-3 Arithmetic Calculations Using Lists .................................................. 3-3-1

3-4 Switching Between List Files ............................................................ 3-4-1

Chapter 4 Equation Calculations

4-1 Simultaneous Linear Equations ........................................................ 4-1-1

4-2 Higher Degree Equations ................................................................. 4-2-1

4-3 Solve Calculations ............................................................................ 4-3-1

4-4 What to Do When an Error Occurs ................................................... 4-4-1

Contents

20011101

19990401

Chapter 5 Graphing

5-1 Sample Graphs ................................................................................ 5-1-1

5-2 Controlling What Appears on a Graph Screen ................................. 5-2-1

5-3 Drawing a Graph .............................................................................. 5-3-1

5-4 Storing a Graph in Picture Memory .................................................. 5-4-1

5-5 Drawing Two Graphs on the Same Screen ...................................... 5-5-1

5-6 Manual Graphing .............................................................................. 5-6-1

5-7 Using Tables ..................................................................................... 5-7-1

5-8 Dynamic Graphing............................................................................ 5-8-1

5-9 Graphing a Recursion Formula ........................................................ 5-9-1

5-10 Changing the Appearance of a Graph ............................................ 5-10-1

5-11 Function Analysis ........................................................................... 5-11-1

Chapter 6 Statistical Graphs and Calculations

6-1 Before Performing Statistical Calculations ....................................... 6-1-1

6-2 Calculating and Graphing Single-Variable Statistical Data ............... 6-2-1

6-3 Calculating and Graphing Paired-Variable Statistical Data .............. 6-3-1

6-4 Performing Statistical Calculations ................................................... 6-4-1

Chapter 7 Computer Algebra System and Tutorial Modes

(ALGEBRA FX 2.0 PLUS only)

7-1 Using the CAS (Computer Algebra System) Mode .......................... 7-1-1

7-2 Algebra Mode ................................................................................... 7-2-1

7-3 Tutorial Mode.................................................................................... 7-3-1

7-4 Algebra System Precautions ............................................................ 7-4-1

Chapter 8 Programming

8-1 Basic Programming Steps ................................................................ 8-1-1

8-2 Program Mode Function Keys .......................................................... 8-2-1

8-3 Editing Program Contents ................................................................ 8-3-1

8-4 File Management.............................................................................. 8-4-1

8-5 Command Reference ....................................................................... 8-5-1

8-6 Using Calculator Functions in Programs .......................................... 8-6-1

8-7 Program Mode Command List ......................................................... 8-7-1

8-8 Program Library................................................................................ 8-8-1

Chapter 9 System Settings Menu

9-1 Using the System Settings Menu ..................................................... 9-1-1

9-2 Memory Operations .......................................................................... 9-2-1

9-3 System Settings ............................................................................... 9-3-1

9-4 Reset ................................................................................................ 9-4-1

9-5 Tutorial Lock (ALGEBRA FX 2.0 PLUS only) ................................... 9-5-1

Contents

20010102

19990401

Contents

Chapter 10 Data Communications

10-1 Connecting Two Units .................................................................. 10-1-1

10-2 Connecting the Unit with a CASIO Label Printer .......................... 10-2-1

10-3 Connecting the Unit to a Personal Computer ............................... 10-3-1

10-4 Performing a Data Communication Operation ............................. 10-4-1

10-5 Data Communications Precautions .............................................. 10-5-1

10-6 Sending a Screen Shot ................................................................ 10-6-1

10-7 Add-ins ......................................................................................... 10-7-1

10-8 MEMORY Mode ........................................................................... 10-8-1

Appendix

1Error Message Table ...........................................................................α-1-1

2Input Ranges .......................................................................................

-2-1

3 Specifications.......................................................................................

-3-1

4Index ....................................................................................................

-4-1

5 Key Index .............................................................................................

-5-1

6P Button (In case of hang up) .............................................................

-6-1

7 Power Supply.......................................................................................

-7-1

19990401

Getting Acquainted

— Read This First!

About this User’s Guide

u! x( )

The above indicates you should press ! and then x, which will input a symbol. All multiple-key input operations are indicated like this. Key cap markings are shown, followed by the input character or command in parentheses.

uFunction Keys and Menus

•Many of the operations performed by this calculator can be executed by pressing function

keys 1 through 6. The operation assigned to each function key changes according to the mode the calculator is in, and current operation assignments are indicated by function menus that appear at the bottom of the display.

• This user’s guide shows the current operation assigned to a function key in parentheses

following the key cap for that key. 1(Comp), for example, indicates that pressing 1 selects {Comp}, which is also indicated in the function menu.

•When (g) is indicated in the function menu for key 6, it means that pressing 6 displays

the next page or previous page of menu options.

uMenu Titles

•Menu titles in this user’s guide include the key operation required to display the menu

being explained. The key operation for a menu that is displayed by pressing K and then {MAT} would be shown as: [OPTN]-[MAT].

• 6(g) key operations to change to another menu page are not shown in menu title key

operations.

19990401

0-1-1

Getting Acquainted

uGraphs

As a general rule, graph operations are shown on facing pages, with actual graph examples on the right hand page. You can produce the same graph on your calculator by performing the steps under the Procedure above the graph. Look for the type of graph you want on the right hand page, and then go to the page indicated for that graph. The steps under “Procedure” always use initial RESET settings.

The step numbers in the “SET UP” and “Execution” sections on the left hand page correspond to the “Procedure” step numbers on the right hand page.

Example:

Left hand page Right hand page

3. Draw the graph. 3 5(DRAW)(or w)

uCommand List

The Program Mode Command List (page 8-7) provides a graphic flowchart of the various function key menus and shows how to maneuver to the menu of commands you need.

Example: The following operation displays Xfct: [VARS]-[FACT]-[Xfct]

uPage Contents

Three-part page numbers are centered at the top of each page. The page number “1-2-3”, for example, indicates Chapter 1, Section 2, page 3.

uSupplementary Information

Supplementary information is shown at the bottom of each page in a “ (Notes)” block.

indicates a note about a term that appears in the same page as the note.

# indicates a note that provides general information about topic covered in the same section

as the note.

1-2-2

Display

1-2-3

Display

19981001 19981001

Use this mode for arithmetic calculations and function calculations, and for calculations involving binary, octal, decimal, and hexadecimal values and matrices.

Use this mode to perform single-variable (standard deviation) and paired-variable (regression) statistical calculations, to perform tests, to analyze data and to draw statistical graphs.

Use this mode to store functions, to generate a numeric table of different solutions as the values assigned to variables in a function change, and to draw graphs.

Use this mode to store graph functions and to draw multiple versions of a graph by changing the values assigned to the variables in a function.

Use this mode to store recursion formulas, to generate a numeric table of different solutions as the values assigned to variables in a function change, and to draw graphs.

Use this mode to draw graphs of implicit functions.

Use this mode to solve linear equations with two through six unknowns, quadratic equations, and cubic equations.

Use this mode to store programs in th program area and to run programs.

Use this mode to perform algebraic calculations.

Use this mode for step-by-step solution of expressions.

Use this mode to determine the expression type and solve mode, and for interactive equation solutions.

Use this mode for step-by-step solution of expressions.

Use this mode to manage data stored in memory.

Use this mode to initialize memory, adjust contrast, and to make other system settings.

The following explains the meaning of each icon.

Description

Icon

Mode Name

RUN

STATistics

GRaPH-TaBLe

DYNAmic graph

RECURsion

CONICS

EQUAtion

PRoGraM

Computer Algebra Syetem

ALGEBRA

TUTORial

LINK

MEMORY

SYSTEM

k About the Function Menu

Use the function keys (1 to 6) to access the menus and commands in the menu bar along the bottom of the display screen. You can tell whether a menu bar item is a menu or a command by its appearance.

• Command (Example: )

Pressing a function key that corresponds to a menu bar command executes the command.

• Pull-up Menu (Example: )

Pressing a function key that corresponds to a pull-up menu opens the menu.

You can use either of the following two methods to select a command from a pull-up menu.

k About Display Screens

This calculator uses two types of display screens: a text screen and a graphic screen. The text screen can show 21 columns and 8 lines of characters, with the bottom line used for the function key menu. The graph screen uses an area that measures 127 (W) × 63 (H) dots.

• Input the key to the left of the command on the pull-up menu.

• Use the f and c cursor keys to move the highlighting to the command you want, and then press w. The symbol ' to the right of a command indicates that executing the command displays a submenu. To cancel the pull-up menu without inputting the command, press i.

Text Screen

Graph Screen

The contents of each type of screen are stored in independent memory areas. The contents of each type of screen are stored in independent memory areas.

#The contents of each type of screen are stored in independent memory areas.

#The contents of each type of screen are stored in independent memory

5-1-1

Sample Graphs

5-1-2

Sample Graphs

Set Up

1. From the Main Menu, enter the GRPH • TBL Mode.

Execution

2.Input the function you want to graph. Here you would use the V-Window to specify the range and other parameters of the graph. See 5-3-1.

3.Draw the graph.

k How to draw a simple graph (1)

Description

To draw a graph, simply input the applicable function.

Procedure

1 m GRPH-TBL

2 dvxw

35(DRAW) (or w)

Example To graph y = 3x2

Result Screen

19990401 19990401

5-1 Sample Graphs

19990401

Basic Operation

1-1 Keys

1-2 Display

1-3 Inputting and Editing Calculations 1-4 Option (OPTN) Menu

1-5 Variable Data (VARS) Menu

1-6 Program (PRGM) Menu 1-7 Using the Set Up Screen

1-8 When you keep having problems…

Chapter

19990401

1-1 Keys

1-1-1 Keys

REPLAY

COPY

PASTE CAT/CAL

H-COPY

PRGM

List

Mat

19990401

Page Page Page Page Page Page

1-3-5

Page Page Page Page Page

1-3-5 1-7-1

1-6-1 2-4-4

1-1-3 1-5-1 2-4-4

1-3-5 5-3-6 10-6-1

5-2-1

1-1-3 1-3-4 1-4-1 1-2-1

2-4-4 2-4-4

2-4-3 2-4-3

1-3-3

1-3-1

2-1-1

2-2-5

2-1-12-1-1

2-4-6

2-1-1

2-4-10

3-1-2 2-8-11

2-4-3

2-4-6 2-4-6

2-1-1

2-4-3

2-2-1

2-4-6

COPY

PASTE

CAT/CAL

H-COPY

PRGM

List

Mat

REPLAY

1-1-2 Keys

k Key Table

20010102

19990401

1-1-3 Keys

k Key Markings

Many of the calculator’s keys are used to perform more than one function. The functions marked on the keyboard are color coded to help you find the one you need quickly and easily.

Function Key Operation

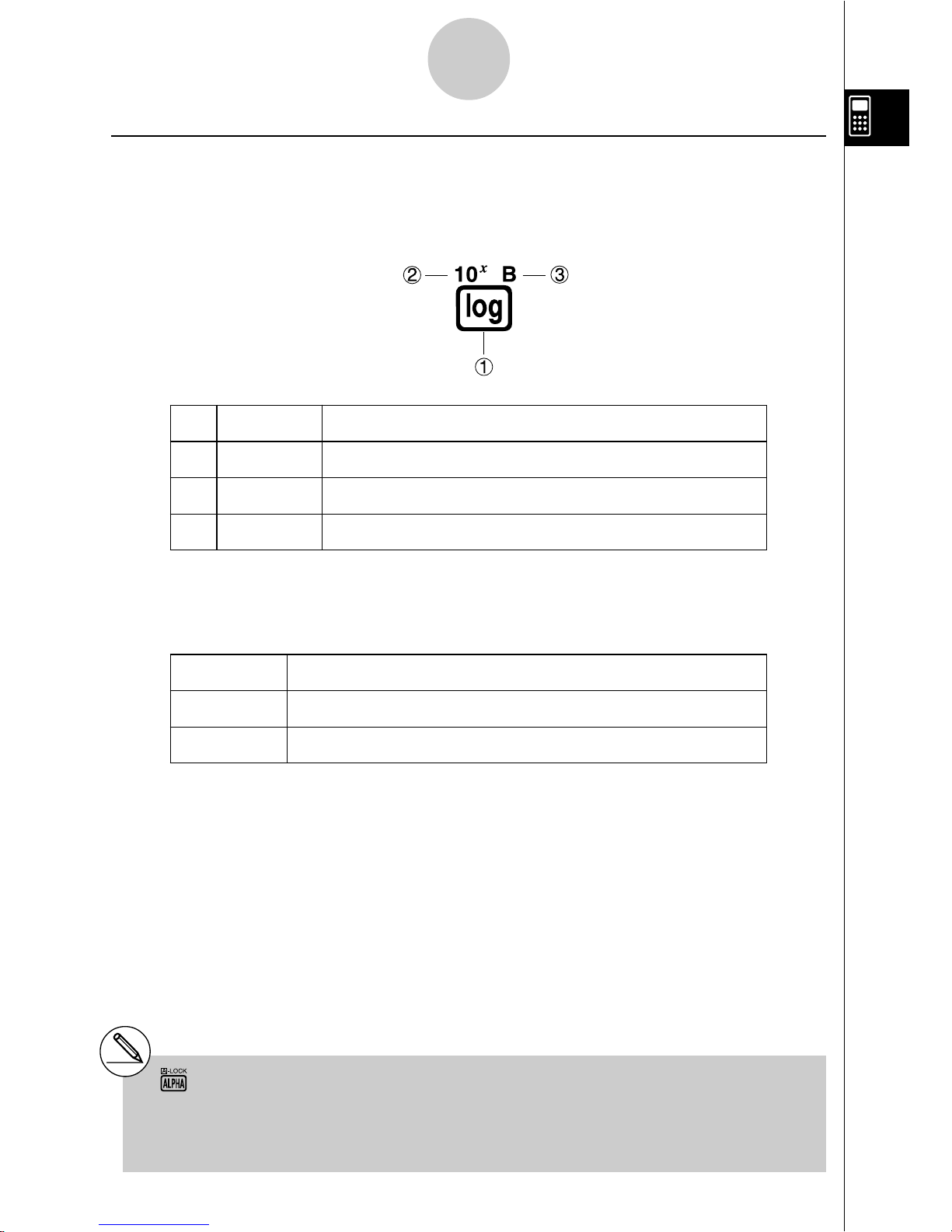
1 log l

2 10

3 B al

The following describes the color coding used for key markings.

Color Key Operation

Orange Press ! and then the key to perform the marked function.

Red Press a and then the key to perform the marked function.

# Alpha Lock

Normally, once you press a and then a key to input an alphabetic character, the keyboard reverts to its primary functions immediately.

If you press ! and then a, the keyboard locks in alpha input until you press a again.

19990401

1-2-1

Display

1-2 Display

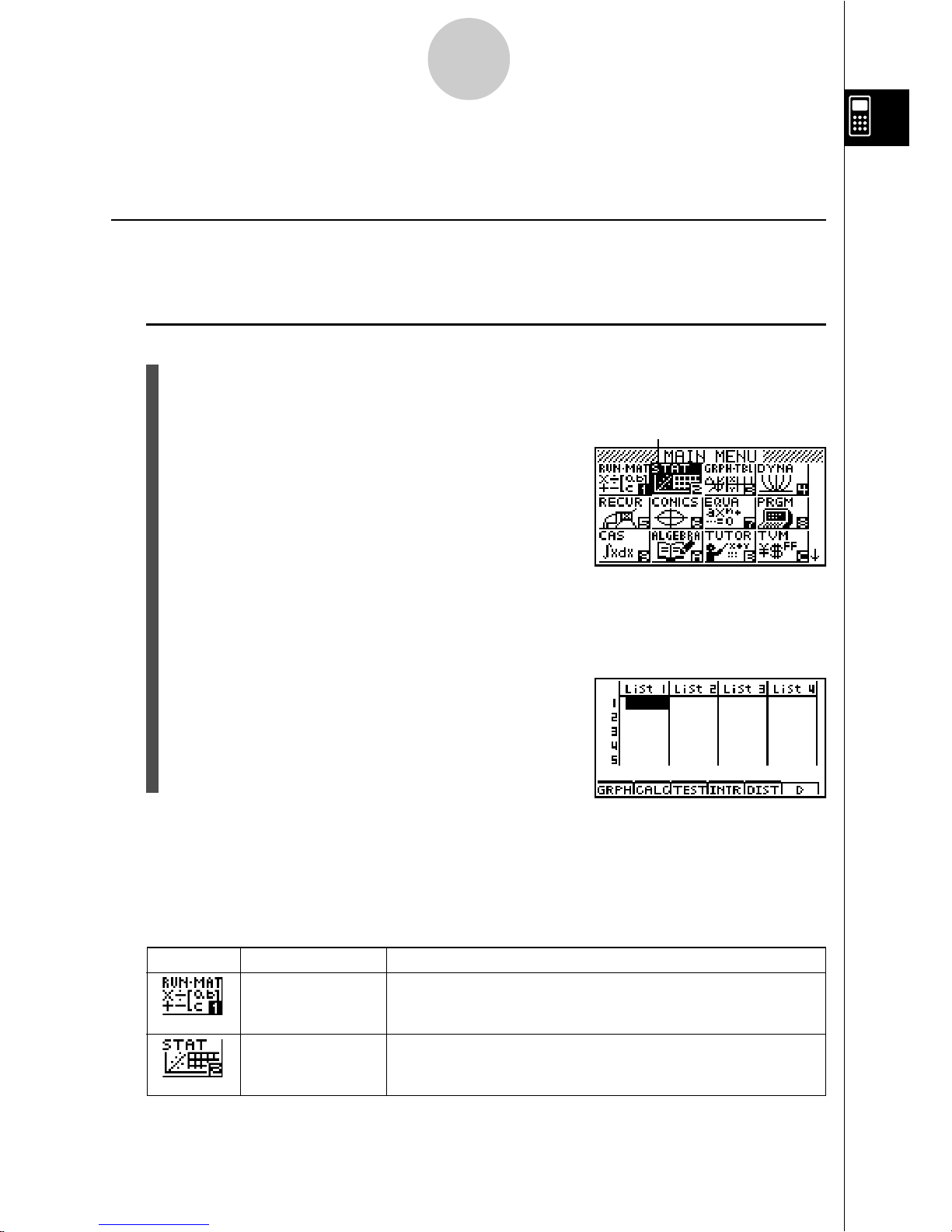
k Selecting Icons

This section describes how to select an icon in the Main Menu to enter the mode you want.

uTo select an icon

1. Press m to display the Main Menu.

2. Use the cursor keys (d, e, f, c) to move the highlighting to the icon you want.

3. Press w to display the initial screen of the mode whose icon you selected.

Here we will enter the STAT Mode.

•You can also enter a mode without highlighting an icon in the Main Menu by inputting the number or letter marked in the lower right corner of the icon.

Currently selected icon

* The above shows the ALGEBRA

FX 2.0 PLUS screen.

Icon Mode Name Description

RUN

•

MATrix Use this mode for arithmetic calculations and function

calculations, and for calculations involving binary, octal, decimal, and hexadecimal values and matrices.

STATistics Use this mode to perform single-variable (standard deviation)

and paired-variable (regression) statistical calculations, to analyze data and to draw statistical graphs.

The following explains the meaning of each icon.

20010102

19990401

1-2-2

Display

Icon Mode Name Description

GRaPH-TaBLe Use this mode to store functions, to generate a numeric table

of different solutions as the values assigned to variables in a function change, and to draw graphs.

DYNAmic graph Use this mode to store graph functions and to draw multiple

versions of a graph by changing the values assigned to the variables in a function.

RECURsion Use this mode to store recursion formulas, to generate a

numeric table of different solutions as the values assigned to variables in a function change, and to draw graphs.

CONICS Use this mode to draw graphs of conic sections.

EQUAtion Use this mode to solve linear equations with 2 to 30

unknowns, and higmh degree (2 to 30) equations.

PRoGraM Use this mode to store programs in th program area and to

run programs.

Computer Algebra Use this mode to perform algebraic calculations. System (ALGEBRA FX 2.0 PLUS only)

ALGEBRA Use this mode for step-by-step solution of expressions.

(ALGEBRA FX 2.0 PLUS only)

TUTORial Use this mode to determine the expression type and solve

mode, and for interactive equation solutions. (ALGEBRA FX 2.0 PLUS only)

TVM Use this mode to perform financial calculations. (Financial) (On the FX 1.0 PLUS menu, the icon has the number 9 in the

lower right corner.) to make other system settings.

DIFFerential Use this mode to solve differential equations. EQuation (On the FX 1.0 PLUS menu, the icon has the letter A in the

lower right corner.)

E-CON Use this mode when you want to control a CASIO EA-100

unit from this calculator. (On the FX 1.0 PLUS menu, the icon has the letter B in the lower right corner.)

LINK Use this mode to transfer memory contents or back-up data

to another unit. (On the FX 1.0 PLUS menu, the icon has the letter C in the lower right corner.)

MEMORYUse this mode to manage data stored in memory.

(On the FX 1.0 PLUS menu, the icon has the letter D in the lower right corner.)

SYSTEM Use this mode to initialize memory, adjust contrast, and to

make other system settings. (On the FX 1.0 PLUS menu, the icon has the letter E in the lower right corner.)

20011101

19990401

k About the Function Menu

Use the function keys (1 to 6) to access the menus and commands in the menu bar along the bottom of the display screen. You can tell whether a menu bar item is a menu or a command by its appearance.

• Command (Example: )

Pressing a function key that corresponds to a menu bar command executes the command.

• Pull-up Menu (Example: )

Pressing a function key that corresponds to a pull-up menu opens the menu.

You can use either of the following two methods to select a command from a pull-up menu.

•Input the key to the left of the command on the pull-up menu.

•Use the f and c cursor keys to move the highlighting to the command you want, and

then press w.

The symbol ' to the right of a command indicates that executing the command displays a submenu.

To cancel the pull-up menu without inputting the command, press i.

k About Display Screens

Text Screen Graph Screen

The contents of each type of screen are stored in independent memory areas.

Press u5(G↔T) to switch between the graphic screen and text screen.

1-2-3

Display

# The symbol ↑ in the upper left corner of a pull-

up menu indicates that there are more commands running off the top of the menu.

Use the cursor keys to scroll the menu contents to view the commands running off the top.

19990401

k Normal Display

The calculator normally displays values up to 10 digits long. Values that exceed this limit are automatically converted to and displayed in exponential format.

u How to interpret exponential format

1.2E+12 indicates that the result is equivalent to 1.2 × 1012. This means that you should move

the decimal point in 1.2 twelve places to the right, because the exponent is positive. This results in the value 1,200,000,000,000.

1.2E–03 indicates that the result is equivalent to 1.2 × 10–3. This means that you should move

the decimal point in 1.2 three places to the left, because the exponent is negative. This results in the value 0.0012.

You can specify one of two different ranges for automatic changeover to normal display.

Norm 1 .................. 10–2 (0.01) > |x|, |x| > 10

Norm 2 .................. 10–9 (0.000000001) > |x|, |x| > 10

All of the examples in this manual show calculation results using Norm 1.

See page 2-3-2 for details on switching between Norm 1 and Norm 2.

1-2-4

Display

19990401

k Special Display Formats

This calculator uses special display formats to indicate fractions, hexadecimal values, and degrees/minutes/seconds values.

u Fractions

................. Indicates: 456

u Hexadecimal Values

................. Indicates: ABCDEF12(16), which

equals –1412567278(10)

u Degrees/Minutes/Seconds

................. Indicates: 12° 34’ 56.78”

•In addition to the above, this calculator also uses other indicators or symbols, which are described in each applicable section of this manual as they come up.

k Calculation Execution Indicator

Whenever the calculator is busy drawing a graph or executing a long, complex calculation or program, a black box “k” flashes in the upper right corner of the display. This black box tells you that the calculator is performing an internal operation.

1-2-5

Display

––––

19990401

1-3 Inputting and Editing Calculations

k Inputting Calculations

When you are ready to input a calculation, first press A to clear the display. Next, input your calculation formulas exactly as they are written, from left to right, and press w to obtain the result.

Example 1 2 + 3 – 4 + 10 =

Ac+d-e+baw

Example 2 2(5 + 4) ÷ (23 × 5) =

Ac(f+e)/ (cd*f)w

k Editing Calculations

Use the d and e keys to move the cursor to the position you want to change, and then perform one of the operations described below. After you edit the calculation, you can execute it by pressing w. Or you can use e to move to the end of the calculation and input more.

u To change a step

Example To change cos60 to sin60

Acga

ddd

1-3-1

Inputting and Editing Calculations

19990401

u To delete a step

Example To change 369 × × 2 to 369 × 2

Adgj**c

ddD

u To insert a step

Example To change 2.362 to sin2.36

Ac.dgx

ddddd

u To change the last step you input

Example To change 396 × 3 to 396 × 2

Adgj*d

1-3-2

Inputting and Editing Calculations

19990401

k Using Replay Memory

The last calculation performed is always stored into replay memory. You can recall the contents of the replay memory by pressing d or e. If you press e, the calculation appears with the cursor at the beginning. Pressing d causes the calculation to appear with the cursor at the end. You can make changes in the calculation as you wish and then execute it again.

Example 1 To perform the following two calculations

4.12 × 6.4 = 26.368

4.12 × 7.1 = 29.252

Ae.bc*g.ew

dddd

!D(INS)

h.b

After you press A, you can press f or c to recall previous calculations, in sequence from the newest to the oldest (Multi-Replay Function). Once you recall a calculation, you can use e and d to move the cursor around the calculation and make changes in it to create a new calculation.

Example 2

Abcd+efgw cde-fghw

f (One calculation back)

f (Two calculations back)

1-3-3

Inputting and Editing Calculations

#Pressing !D(INS) changes the cursor to

‘‘_’’. The next function or value you input is overwritten at the location of ‘‘_’’. To abort this operation, press !D(INS) again.

# A calculation remains stored in replay memory

until you perform another calculation or change modes.

# The contents of replay memory are not cleared

when you press the A key, so you can recall a calculation and execute it even after performing the all clear operation.

19990401

1-3-4

Inputting and Editing Calculations

k Making Corrections in the Original Calculation

Example 14 ÷ 0 × 2.3 entered by mistake for 14 ÷ 10 × 2.3

Abe/a*c.d

Press i.

Make necessary changes.

Execute again.

k Copy and Paste

You can temporarily copy commands, programs, and other text data you input to a memory area called “the clipboard,” and then paste it to another location on the display.

u To specify the copy range

1. Move the cursor (t) the beginning or end of the range of text you want to copy and

then press u. This changes the cursor to “ ”.

2. Use the cursor keys to move the cursor and highlight the range of text you want to copy.

3. Press u1 (COPY) to copy the highlighted text to the clipboard, and exit the copy

Cursor is positioned automatically at the location of the cause of the error.

19990401

range specification mode.

To cancel text highlighting without performing a copy operation, press i.

u Pasting Text

Move the cursor to the location where you want to paste the text, and then press u

2(PASTE). The contents of the clipboard are pasted at the cursor position.

u2(PASTE)

k Catalog Function

The Catalog is an alphabetic list of all the commands available on this calculator. You can input a command by calling up the Catalog and then selecting the command you want.

u To use the Catalog to input a command

1. Press u4(CAT/CAL) to display the Catalog at

the bottom of the screen.

2. Press the function key that matches the first letter of the command you want to input.

3. Select the command from the pull-up menu.

Example 1 To use the Catalog to input the ClrGraph command

Au4(CAT/CAL)3(C~)h(CLR)

b(Graph)

1-3-5

Inputting and Editing Calculations

19990401

Example 2 To use the Catalog to input the Prog command

Au4(CAT/CAL)6(g)6(g) 5(P)I(Prog)

Pressing i or !i(QUIT) closes the Catalog.

1-3-6

Inputting and Editing Calculations

19990401

1-4 Option (OPTN) Menu

The option menu gives you access to scientific functions and features that are not marked on the calculator’s keyboard. The contents of the option menu differ according to the mode you are in when you press the K key.

See “8-7 Program Mode Command List” for details on the option (OPTN) menu.

u Option Menu in the RUN

•

MAT or PRGM Mode

•{LIST} ... {list function menu}

•{MAT} ... {matrix operation menu}

•{CPLX} ... {complex number calculation menu}

•{CALC} ... {functional analysis menu}

•{NUM} ... {numeric calculation menu}

•{PROB} ... {probability/distribution calculation menu}

•{HYP} ... {hyperbolic calculation menu}

•{ANGL} ... {menu for angle/coordinate conversion, DMS input/conversion}

•{STAT} ... {paired-variable statistical estimated value menu}

•{FMEM} ... {function memory menu}

•{ZOOM} ... {zoom function menu}

•{SKTCH} ... {sketch function menu}

•{PICT} ... {picture memory menu}

•{SYBL} ... {symbol menu}

•{° ’ ”} … {DMS}

•{ ° ’ ”} … {DMS conversion}

•{ENG}/{ ENG} … {ENG conversion}

1-4-1

Option (OPTN) Menu

# The option (OPTN) menu does not appear

during binary, octal, decimal, and hexadecimal calculations.

19990401

The following shows the function menus that appear under other conditions.

u Option Menu when a number table value is displayed in the GRPH • TBL or

RECUR Mode

•{LMEM} … {list memory menu}

•{ ° ’ ”}/{ENG}/{ ENG}

u Option Menu in the CAS or ALGEBRA or TUTOR Mode

(ALGEBRA FX 2.0 PLUS only) t

•{∞} … {infinity}

•{Abs} … {absolute value}

•{x!} … {factorial}

•{sign} … {signum function}

•{HYP}/{FMEM}

The meanings of the option menu items are described in the sections that cover each mode.

1-4-2

Option (OPTN) Menu

1999120120010102

19990401

1-5 Variable Data (VARS) Menu

To recall variable data, press J to display the variable data menu.

{V-WIN}/{FACT}/{STAT}/{GRPH}/{DYNA}/

{TABL}/{RECR}/{EQUA*1}

See “8-7 Program Mode Command List” for details on the variable data (VARS) menu.

u V- WIN — Recalling View Window values

•{Xmin}/{Xmax}/{Xscale}/{Xdot}

…X-axis {minimum value}/{maximum value}/{scale}/{dot value*2}

•{Ymin}/{Ymax}/{Yscale}

…Y-axis {minimum value}/{maximum value}/{scale}

•{T

min}/{T

max}/{T

ptch}

…T, θ {minimum value}/{maximum value}/{pitch}

•{R-Xmin}/{R-Xmax}/{R-Xscl}/{R-Xdot}

…Dual Graph right graph X-axis {minimum value}/{maximum value}/{scale}/

{dot value*2}

•{R-Ymin}/{R-Ymax}/{R-Yscl}

…Dual Graph right graph Y-axis {minimum value}/{maximum value}/{scale}

•{R-Tmin}/{R-Tmax}/{R-Tpch}

…Dual Graph right graph T,θ {minimum value}/{maximum value}/{pitch}

u FACT — Recalling zoom factors

•{Xfact}/{Yfact}

... {x-axis factor}/{y-axis factor}

1-5-1

Variable Data (VARS) Menu

*1The EQUA item appears only when you

access the variable data menu from the RUN

•

MAT or PRGM Mode.

# The variable data menu does not appear if

you press J while binary, octal, decimal, or hexadecimal is set as the default number system.

The dot value indicates the display range (Xmax value – Xmin value) divided by the screen dot pitch (126). The dot value is normally calculated automatically from the minimum and maximum values. Changing the dot value causes the maximum to be calculated automatically.

19990401

u STAT — Recalling statistical data

• {n} … {number of data}

• {X} … {single-variable, paired-variable x-data}

•{

o}/{Σx}/{Σx

}/{x

n}/{xσn–1}/{minX}/{maxX}

…{mean}/{sum}/{sum of squares}/{population standard deviation}/{sample

standard deviation}/{minimum value}/{maximum value}

• {Y} ... {paired-variable y-data}

•{

}/{Σ

y}/{Σ y

}/{Σ

xy}/{ y

n}/{

n–1}/{minY}/{maxY}

…{mean}/{sum}/{sum of squares}/{sum of products of x-data and y-data}/

{population standard deviation}/{sample standard deviation}/{minimum value}/ {maximum value}

•{GRAPH} ... {graph data menu}

•{a}/{b}/{c}/{d}/{e}

... {regression coefficient and polynomial coefficients}

•{r}/{r2}

... {correlation coefficient}

•{Q1}/{Q3}

... {first quartile}/{third quartile}

•{Med}/{Mod}

... {median}/{mode} of input data

•{H-Strt}/{H-ptch}

... histogram {start division}/{pitch}

•{PTS} ... {summary point data menu}

•{x1}/{y1}/{x2}/{y2}/{x3}/{y3} ... {coordinates of summary points}

1-5-2

Variable Data (VARS) Menu

20011101

19990401

u GRPH — Recalling Graph Functions

•{Yn}/{rn}

... {rectangular coordinate or inequality function}/{polar coordinate function}

•{Xtn}/{Ytn}

... parametric graph function {Xt}/{Yt}

•{Xn} ... {X=constant graph function}

(Press these keys before inputting a value to specify a storage area.)

u DYNA — Recalling Dynamic Graph Set Up Data

•{Start}/{End} /{Pitch}

... {coefficient range start value}/{coefficient range end value}/{coefficient value

increment}

u TABL — Recalling Table & Graph Set Up and Content Data

•{Start}/{End} /{Pitch}

... {table range start value}/{table range end value}/{table value increment}

•{Result*1}

... {matrix of table contents}

1-5-3

Variable Data (VARS) Menu

The Result item appears only when the TABL menu is displayed in the RUN

•

MAT or PRGM

Mode.

19990401

u RECR — Recalling Recursion Formula

, Table Range, and Table Content Data

• {FORM}

... {recursion formula data menu}

• {an}/{an+1}/{an+2}/{bn}/{bn+1}/{bn+2}/{cn}/{cn+1}/{cn+2}

... {an}/{an+1}/{an+2}/{bn}/{bn+1}/{bn+2}/{cn}/{cn+1}/{cn+2} expressions

• {RANGE} ... {table range data menu}

• {R-Strt}/{R-End}

... table range {start value}/{end value}

• {a0}/{a1}/{a2}/{b0}/{b1}/{b2}/{c0}/{c1}/{c2}

... {a0}/{a1}/{a2} {b0}/{b1}/{b2}/{c0}/{c1}/{c2} value

• {anStrt}/{bnStrt}/{cnStrt}

... origin of {an }/{bn}/{cn} recursion formula convergence/divergence graph (WEB

graph)

• {Result*2} ... {matrix of table contents

}

u EQUA — Recalling Equation Coefficients and Solutions

*4 *

•{S-Rslt}/{S-Coef}

... matrix of {solutions}/{coefficients} for linear equations

•{P-Rslt}/{P-Coef}

... matrix of {solution}/{coefficients} for a high degree equation

1-5-4

Variable Data (VARS) Menu

An error occurs when there is no function or recursion formula numeric table in memory.

“Result” is available only in the RUN

•

MAT and

PRGM Modes.

Ta ble contents are stored automatically in Matrix Answer Memory (MatAns).

Coefficients and solutions are stored automatically in Matrix Answer Memory (MatAns).

The following conditions cause an error. —When there are no coefficients input for the

equation

—When there are no solutions obtained for the

equation

Coefficient and solution memory data for a linear equation cannot be recalled at the same time.

19990401

1-6 Program (PRGM) Menu

To display the program (PRGM) menu, first enter the RUN

•

MAT or PRGM Mode from the

Main Menu and then press !J(PRGM). The following are the selections available in the program (PRGM) menu.

• {Prog } ........ {program recall}

• {JUMP} ...... {jump command menu}

• {?} .............. {input prompt}

• {^} ............. {output command}

• {I/O} ............ {I/O control/transfer command menu}

• {IF } ............. {conditional jump command menu}

• {FOR} ......... {loop control command menu}

• {WHLE} ...... {conditional loop control command menu}

• {CTRL} ....... {program control command menu}

• {LOGIC} ..... {logical operation command menu}

• {CLR} ......... {clear command menu}

• {DISP} ........ {display command menu}

• {:} ............... {multistatement connector}

The following function key menu appears if you press !J(PRGM) in the RUN

•

MAT

Mode or the PRGM Mode while binary, octal, decimal, or hexadecimal is set as the default number system.

• {Prog}/{JUMP}/{?}/{^}/{:}

• {=

G <} ....... {relational operator menu}

The functions assigned to the function keys are the same as those in the Comp Mode.

For details on the commands that are available in the various menus you can access from the program menu, see “8. Programming”.

1-6-1

Program (PRGM) Menu

19990401

1-7 Using the Set Up Screen

The mode’s set up screen shows the current status of mode settings and lets you make any changes you want. The following procedure shows how to change a set up.

u To change a mode set up

1. Select the icon you want and press w to enter a mode and display its initial screen.

Here we will enter the RUN

•

MAT Mode.

2. Press u3(SET UP) to display the mode’s

SET UP screen.

• This SET UP screen is just one possible example. Actual SET UP screen contents will differ according to the mode you are in and that mode’s current settings.

3. Use the f and c cursor keys to move the highlighting to the item whose setting you want to change.

4. Press the function key (1 to 6) that is marked with the setting you want to make.

5. After you are finished making any changes you want, press i to return to the initial screen of the mode.

k SET UP Screen Function Key Menus

This section details the settings you can make using the function keys in the SET UP display.

indicates default setting.

u Mode (calculation/binary, octal, decimal, hexadecimal mode)

•{Comp} ... {arithmetic calculation mode}

•{Dec}/{Hex}/{Bin}/{Oct} ... {decimal}/{hexadecimal}/{binary}/{octal}

1-7-1

Using the Set Up Screen

...

20011101

19990401

u Func Type (graph function type)

Pressing one of the following function keys also switches the function of the v key.

•{Y=}/{r=}/{Parm}/{X=c}

... {rectangular coordinate}/{polar coordinate}/{parametric coordinate}/

{X = constant} graph

•{Y>}/{Y<}/{Yt}/{Ys}

... {y>f(x)}/{y<f(x)}/{y≥f(x)}/{y≤f(x)} inequality graph

u Draw Type (graph drawing method)

•{Con}/{Plot}

... {connected points}/{unconnected points}

u Derivative (derivative value display)

•{On}/{Off}

... {display on}/{display off} while Graph-to-Table, Table & Graph, and Trace are

being used

u Angle (default angle unit)

•{Deg}/{Rad}/{Gra}

... {degrees}/{radians}/{grads}

u Complex Mode

•{Real} ... {calculation in real number range only}

•{a + bi}/{r · e^θi}

... {rectangular format}/{polar format} display of a complex calculation

u Coord (graph pointer coordinate display)

•{On}/{Off}

... {display on}/{display off}

u Grid (graph gridline display)

•{On}/{Off}

... {display on}/{display off}

u Axes (graph axis display)

•{On}/{Off}

... {display on}/{display off}

u Label (graph axis label display)

•{On}/{Off}

... {display on}/{display off}

1-7-2

Using the Set Up Screen

19990401

u Display (display format)

•{Fix}/{Sci}/{Norm}/{Eng}

... {fixed number of decimal places specification}/{number of significant digits

specification}/{normal display setting}/{Engineering Mode}

u Stat Wind (statistical graph view window setting method)

•{Auto}/{Man}

... {automatic}/{manual}

u Reside List (residual calculation)

•{None}/{LIST}

... {no calculation}/{list specification for the calculated residual data}

u List File (list file display settings)

•{FILE} ... {settings of list file on the display}

u Va riable (table generation and graph draw settings)

•{Rang}/{LIST}

... {use table range}/{use list data}

u Graph Func (function display during graph drawing and trace)

•{On}/{Off}

... {display on}/{display off}

u Dual Screen (Dual Screen Mode status)

•{T+G}/{G+G}/{GtoT}/{Off}

... {graph on one side and numeric table on the other side of Dual Screen}/

{graphing on both sides of Dual Screen}/{graph on one side and numeric table on the other side of Dual Screen}/{Dual Screen off}

u Simul Graph (simultaneous graphing mode)

•{On}/{Off}

... {simultaneous graphing on (all graphs drawn simultaneously)}/{simultaneous

graphing off (graphs drawn in area numeric sequence)}

u Background (graph display background)

•{None}/{PICT}

... {no background}/{graph background picture specification}

1-7-3

Using the Set Up Screen

19990401

u Dynamic Type (Dynamic Graph locus setting)

•{Cnt}/{Stop}

... {non-stop (continuous)}/{automatic stop after 10 draws}

u Σ Display (Σ value display in recursion table)

•{On}/{Off}

... {display on}/{display off}

u Slope (display of derivative at current pointer location in conic section

graph)

•{On}/{Off}

... {display on}/{display off}

u Answer Type (result range specification) (ALGEBRA FX 2.0 PLUS only)

•{Real}/{Cplx}

... {real number}/{complex number} range result

u H-Copy (screen shot settings)

•{Dirct}/{Mem}

... {direct send}/{store in memory}

1-7-4

Using the Set Up Screen

20011101

19990401

1-8 When you keep having problems…

If you keep having problems when you are trying to perform operations, try the following before assuming that there is something wrong with the calculator.

k Getting the Calculator Back to its Original Mode Settings

1. From the Main Menu, enter the SYSTEM Mode.

2. Press 5(Reset).

3. Press 1(S/U), and then press w(Yes).

4. Press m to return to the Main Menu.

Now enter the correct mode and perform your calculation again, monitoring the results on the display.

k In Case of Hang Up

•Should the unit hang up and stop responding to input from the keyboard, press the P button on the back of the calculator to reset the calculator to its initial defaults (see page α-6-1). Note, however, that this may clear all the data in calculator memory.

1-8-1

When you keep having problems…

19990401

k Low Battery Message

If either of the following messages appears on the display, immediately turn off the calculator and replace main batteries or the back up battery as instructed.

If you continue using the calculator without replacing main batteries, power will automatically turn off to protect memory contents. Once this happens, you will not be able to turn power back on, and there is the danger that memory contents will be corrupted or lost entirely.

#You will not be able to perform data

communications operations after the low battery message appears.

1-8-2

When you keep having problems…

#If main batteries and the back up battery go

low at the same time (indicated when both of the messages described above appear), replace the back up battery first and then replace the main batteries.

20010101

Manual Calculations

2-1 Basic Calculations

2-2 Special Functions 2-3 Specifying the Angle Unit and Display Format

2-4 Function Calculations

2-5 Numerical Calculations 2-6 Complex Number Calculations

2-7 Binary, Octal, Decimal, and Hexadecimal Calculations

2-8 Matrix Calculations

Chapter

19990401

2-1-1

Basic Calculations

2-1 Basic Calculations

k Arithmetic Calculations

•Enter arithmetic calculations as they are written, from left to right.

•Use the - key to input the minus sign before a negative value.

•Calculations are performed internally with a 15-digit mantissa. The result is rounded to a 10-digit mantissa before it is displayed.

•For mixed arithmetic calculations, multiplication and division are given priority over addition and subtraction.

Example Operation

23 + 4.5 – 53 = –25.5 23+4.5-53w

56 × (–12) ÷ (–2.5) = 268.8 56*-12/-2.5w

(2 + 3) × 102 = 500 (2+3)*1E2w*

1 + 2 – 3 × 4 ÷ 5 + 6 = 6.6 1+2-3*4/5+6w

100 – (2 + 3) × 4 = 80 100-(2+3)*4w

2 + 3 × (4 + 5) = 29 2+3*(4+5w*

(7 – 2) × (8 + 5) = 65 (7-2)( 8+5)w*

= 0.3 6 /(4*5)w*

4 × 5

(1 + 2i) + (2 + 3i) = 3 + 5i (b+c!a(i))+(c+

d!a(i))w

(2 + i) × (2 – i) = 5 (c+!a(i))*(c-!a(i)

*1(2+3)E2 does not produce the correct

result. Be sure to enter this calculation as shown.

Final closed parentheses (immediately before operation of the w key) may be omitted, no matter how many are required.

A multiplication sign immediately before an open parenthesis may be omitted.

*4This is identical to 6 / 4 / 5 w.

19990401

2-1-2

Basic Calculations

*1Displayed values are rounded off to the place

you specify.

k Number of Decimal Places, Number of Significant Digits, Normal

Display Range

[SET UP]- [Display] -[Fix] / [Sci] / [Norm]

•Even after you specify the number of decimal places or the number of significant digits, internal calculations are still performed using a 15-digit mantissa, and displayed values are stored with a 10-digit mantissa. Use Rnd of the Numeric Calculation Menu (NUM) (page 2-4-1) to round the displayed value off to the number of decimal place and significant digit settings.

•Number of decimal place (Fix) and significant digit (Sci) settings normally remain in effect until you change them or until you change the normal display range (Norm) setting.

Example 100 ÷ 6 = 16.66666666...

Condition Operation Display

100/6w 16.66666667

4 decimal places u3(SET UP)

cccccccccc

1(Fix)ewiw 16.6667

5 significant digits u3(SET UP)

cccccccccc

2(Sci)fwiw 1.6667E+01

Cancels specification u3(SET UP)

cccccccccc

3(Norm)iw 16.66666667

20011101

1999040120011101

2-1-3

Basic Calculations

Example 200 ÷ 7 × 14 = 400

Condition Operation Display

200/7*14w 400

3 decimal places u3(SET UP)

cccccccccc

1(Fix)dwiw 400.000

Calculation continues 200/7w 28.571 using display capacity * Ans × of 10 digits 14w 400.000

• If the same calculation is performed using the specified number of digits:

200/7w 28.571

The value stored K5(NUM)e(Rnd)w 28.571 internally is rounded * Ans × off to the number of 14w 399.994 decimal places you specify.

k Calculation Priority Sequence

This calculator employs true algebraic logic to calculate the parts of a formula in the following order:

1 Coordinate transformation Pol (x, y), Rec (r, θ)

Differentials, quadratic differentials, integrations, Σ calculations

d/dx, d

/dx2, ∫dx, Σ, Mat, Solve, FMin, FMax, List→Mat, Seq, Min, Max, Median, Mean,

Augment, Mat →List, P(, Q(, R(, t(, List

Composite functions*1 fn, Yn, rn, Xtn, Ytn, Xn

2 Type A functions

With these functions, the value is entered and then the function key is pressed.

, x–1, x !, ° ’ ”, ENG symbols, angle unit o, r,

*1You can combine the contents of multiple

function memory (fn) locations or graph memory (Yn, rn, Xtn, Ytn, Xn) locations into composite functions. Specifying fn1(fn2),

for example, results in the composite function fn1°fn2 (see page 5-3-3). A composite function can consist of up to five functions.

1999040120011101

2-1-4

Basic Calculations

3 Power/root ^(xy),

4 Fractions a

5 Abbreviated multiplication format in front of π, memory name, or variable name.

2π, 5A, Xmin, F Start, etc.

6 Type B functions

With these functions, the function key is pressed and then the value is entered.

, 3, log, In, ex, 10x, sin, cos, tan, sin–1, cos–1, tan–1, sinh, cosh, tanh, sinh–1, cosh–1, tanh–1, (–), d, h, b, o, Neg, Not, Det, Trn, Dim, Identity, Sum, Prod, Cuml, Percent, AList, Abs, Int, Frac, Intg, Arg, Conjg, ReP, ImP

7 Abbreviated multiplication format in front of Type B functions

2 , A log2, etc.3

8 Permutation, combination nPr, nCr 9 × , ÷

0 +, – ! Relational operators >, <, ≥, ≤ @ Relational operators =,

# and (bitwise operation)

$ xnor, xor (bitwise operations)

% or (bitwise operation) ^ And (logical operation)

Or (logical operation)

Example 2 + 3 × (log sin2π2 + 6.8) = 22.07101691 (angle unit = Rad)

#When functions with the same priority are used

in series, execution is performed from right to left.

In → ex{In( )}

120 120

Otherwise, execution is from left to right.

#Compound functions are executed from right to

left.

#Anything contained within parentheses receives

highest priority.

19990401

2-1-5

Basic Calculations

# Other errors can occur during program

execution. Most of the calculator’s keys are inoperative while an error message is displayed.

Press i to clear the error and display the error position (see page 1-3-4).

# See the “Error Message Table” on page α-1-1

for information on other errors.

k Multiplication Operations without a Multiplication Sign

You can omit the multiplication sign (×) in any of the following operations.

•Before coordinate transformation and Type B functions (1 on page 2-1-3 and 6 on page

2-1-4), except for negative signs

Example 2sin30, 10log1.2, 2 , 2Pol(5, 12), etc.

•Before constants, variable names, memory names

Example 2π, 2AB, 3Ans, 3Y1, etc.

•Before an open parenthesis

Example 3(5 + 6), (A + 1)(B – 1), etc.

k Overflow and Errors

Exceeding a specified input or calculation range, or attempting an illegal input causes an error message to appear on the display. Further operation of the calculator is impossible while an error message is displayed. The following events cause an error message to appear on the display.

•When any result, whether intermediate or final, or any value in memory exceeds

±9.999999999 × 1099 (Ma ERROR).

•When an attempt is made to perform a function calculation that exceeds the input range (Ma ERROR).

•When an illegal operation is attempted during statistical calculations (Ma ERROR). For example, attempting to obtain 1VAR without data input.

• When an improper data type is specified for the argument of a function calculation

(Ma ERROR).

•When the capacity of the numeric value stack or command stack is exceeded (Stack ERROR). For example, entering 25 successive ( followed by 2 + 3 * 4 w.

•When an attempt is made to perform a calculation using an illegal formula (Syntax ERROR). For example, 5 ** 3 w.

20010102

19990401

•When you try to perform a calculation that causes memory capacity to be exceeded (Memory ERROR).

•When you use a command that requires an argument, without providing a valid argument (Argument ERROR).

•When an attempt is made to use an illegal dimension during matrix calculations (Dimension ERROR).

• When you are in the real mode and an attempt is made to perform a calculation that produces a complex number solution. Note that “Real” is selected for the Complex Mode setting on the SET UP Screen (Non-Real ERROR).

k Memory Capacity

Each time you press a key, either one byte or two bytes is used. Some of the functions that require one byte are: b, c, d, sin, cos, tan, log, In, , and π. Some of the functions that take up two bytes are d/dx(, Mat, Xmin, If, For, Return, DrawGraph, SortA(, PxIOn, Sum, and

an+1.

2-1-6

Basic Calculations

#As you input numeric values or commands,

they appear flush left on the display. Calculation results, on the other hand, are displayed flush right.

# The allowable range for both input and output

values is 15 digits for the mantissa and two digits for the exponent. Internal calculations are also performed using a 15-digit mantissa and two-digit exponent.

20011101

19990401

2-2 Special Functions

k Calculations Using Variables

Example Operation Display

193.2aav(A)w 193.2

193.2 ÷ 23 = 8.4 av(A)/23w 8.4

193.2 ÷ 28 = 6.9 av(A)/28w 6.9

k Memory

uVariables

This calculator comes with 28 variables as standard. You can use variables to store values you want to use inside of calculations. Variables are identified by single-letter names, which are made up of the 26 letters of the alphabet, plus r and θ. The maximum size of values that you can assign to variables is 15 digits for the mantissa and 2 digits for the exponent.

u To assign a value to a variable

[value] a [variable name] w

Example To assign 123 to variable A

Abcdaav(A)w

Example To add 456 to variable A and store the result in variable B

Aav(A)+efgaa l(B)w

2-2-1

Special Functions

# Variable contents are retained even when

you turn power off.

19990401

u To display the contents of a variable

Example To display the contents of variable A

Aav(A)w

u To clear a variable

Example To clear variable A

Aaaav(A)w

u To assign the same value to more than one variable

[value]a [first variable name*1]K6(g)6(g)4(SYBL)d(~) [last variable name*1]w

Example To assign a value of 10 to variables A through F

Abaaav(A)

K6(g)6(g)4(SYBL)d(~)

at(F)w

uFunction Memory [OPTN]-[FMEM]

Function memory (f1~f20) is convenient for temporary storage of often-used expressions. For longer term storage, we recommend that you use the GRPH

•

TBL Mode for expressions and

the PRGM Mode for programs.

•{Store}/{Recall}/{fn}/{SEE} ... {function store}/{function recall}/{function area specification as a variable name inside an expression}/{function list}

2-2-2

Special Functions

You cannot use “r” or “θ” as a variable name.

19990401

u To store a function

Example To store the function (A+B) (A–B) as function memory number 1

(av(A)+al(B)) (av(A)-al(B))

K6(g)5(FMEM)

b(Store)bw

u To recall a function

Example To recall the contents of function memory number 1

K6(g)5(FMEM)

c(Recall)bw

u To display a list of available functions

K6(g)5(FMEM)

e(SEE)

2-2-3

Special Functions

# If the function memory number to which you

store a function already contains a function, the previous function is replaced with the new one.

# The recalled function appears at the current

location of the cursor on the display.

19990401

2-2-4

Special Functions

u To delete a function

Example To delete the contents of function memory number 1

AK6(g)5(FMEM)

b(Store)bw

•Executing the store operation while the display is blank deletes the function in the

function memory you specify.

u To use stored functions

Example To store x3 + 1, x2 + x into function memory, and then graph:

y = x

+ x2 + x + 1

Use the following View Window settings.

Xmin = – 4, Xmax = 4, Xscale = 1

Ymin = –10, Ymax = 10, Yscale = 1

u3(SET UP)c1(Y=)i

AvMd+bK6(g)5(FMEM)b(Store)bw(stores (x3 + 1))

iAvx+v5(FMEM)b(Store)cw(stores (x2 + x))

iAK6(g)6(g)2(SKTCH)b(Cls)w

2(SKTCH)e(GRAPH)b(Y=) K6(g)5(FMEM)d(fn)b+

5(FMEM)d(fn)cw

•For full details about graphing, see “5. Graphing”.

#You can also use a to store a function in

function memory in a program. In this case, you must enclose the function inside of double quotation marks. The maximum size of the function you can store is 255 bytes.

19990401

k Answer Function

The Answer Function automatically stores the last result you calculated by pressing w(unless the w key operation results in an error). The result is stored in the answer memory.

u To use the contents of the answer memory in a calculation

Example 123 + 456 = 579

789 – 579 = 210

Abcd+efgw hij-!-(Ans)w

k Performing Continuous Calculations

Answer memory also lets you use the result of one calculation as one of the arguments in the next calculation.

Example 1 1 ÷ 3 =

1 ÷ 3 × 3 =

Ab/dw

(Continuing)*dw

Continuous calculations can also be used with Type A functions (x2, x-1, x!, page 2-1-3), +, –, ^(xy), x, ° ’ ”, etc.

2-2-5

Special Functions

# The largest value that the answer memory

can hold is 15 digits for the mantissa and 2 digits for the exponent.

# Only numeric values and calculation results

can be stored in answer memory.

# Answer memory contents are not cleared

when you press the A key or when you switch power off.

#Answer memory contents are not changed

by an operation that assigns values to value memory (such as: faav(A)w).

19990401

k Stacks

The unit employs memory blocks, called

stacks

, for storage of low priority values and

commands. There is a 10-level

numeric value stack

, a 26-level

command stack

, and a 10-

level

program subroutine stack

. An error occurs if you perform a calculation so complex that it exceeds the capacity of available numeric value stack or command stack space, or if execution of a program subroutine exceeds the capacity of the subroutine stack.

Example

2-2-6

Special Functions

( (

(

...

Numeric Value Stack Command Stack

#Calculations are performed according to the pri-

ority sequence. Once a calculation is executed, it is cleared from the stack.

# Storing a complex number takes up two numeric

value stack levels.

#Storing a two-byte function takes up two

command stack levels.

19990401

k Using Multistatements

Multistatements are formed by connecting a number of individual statements for sequential execution. You can use multistatements in manual calculations and in programmed calculations. There are two different ways that you can use to connect statements to form multistatements.

• Colon (:)

Statements that are connected with colons are executed from left to right, without stopping.

•Display Result Command (

When execution reaches the end of a statement followed by a display result command, execution stops and the result up to that point appears on the display. You can resume execution by pressing the w key.

Example 6.9 × 123 = 848.7

123 ÷ 3.2 = 38.4375

Abcdaav(A) !J(PRGM)6(g)6(g)3(:)g.j

*av(A)!J(PRGM)4(^)

av(A)/d.cw

2-2-7

Special Functions

# The final result of a multistatement is always

displayed, regardless of whether the calculation ends with a display result command.

Example : 123 × 456: × 5

Invalid

#You cannot construct a multistatement in

which one statement directly uses the result of the previous statement.

19990401

2-3 Specifying the Angle Unit and Display

Format

Before performing a calculation for the first time, you should use the SET UP screen to specify the angle unit and display format.

k Setting the Angle Unit [SET UP]- [Angle]

1. On the Set Up screen, highlight “Angle”.

2. Press the function key for the angle unit you want to specify, then press i.

•{Deg}/{Rad}/{Gra} ... {degrees}/{radians}{grads}

• The relationship between degrees, grads, and radians is shown below.

360° = 2π radians = 400 grads 90° = π/2 radians = 100 grads

k Setting the Display Format [SET UP]- [Display]

1. On the Set Up screen, highlight “Display”.

2. Press the function key for the item you want to set, then press i.

•{Fix}/{Sci}/{Norm}/{Eng} ... {fixed number of decimal places specification}/ {number of significant digits specification}/{normal display}/{Engineering Mode}

u To specify the number of decimal places (Fix)

Example To specify two decimal places

1(Fix) cw

Press the function key that corresponds to the number of decimal places you want to specify (

= 0 to 9).

2-3-1

Specifying the Angle Unit and Display Format

#Displayed values are rounded off to the

number of decimal places you specify.

19990401

u To specify the number of significant digits (Sci)

Example To specify three significant digits

2(Sci) dw

Press the function key that corresponds to the number of significant digits you want to specify (

= 0 to 9).

u To specify the normal display (Norm 1/Norm 2)

Press 3(Norm) to switch between Norm 1 and Norm 2.

Norm 1: 10

–2

(0.01)>|x|, |x| >10

Norm 2: 10

–9

(0.000000001)>|x|, |x| >10

Ab/caaw (Norm 1)

(Norm 2)

u To specify the engineering notation display (Eng Mode)

Press 4(Eng) to switch between engineering notation and standard notation. The indicator “/E” is on the display while engineering notation is in effect.

You can use the following symbols to convert values to engineering notation, such as 2,000 (= 2 × 103) → 2k.

E (Exa) × 10

m (milli) × 10

–3

P (Peta) × 10

µ (micro) × 10

–6

T (Tera) × 10

n (nano) × 10

–9

G (Giga) × 10

p (pico) × 10

–12

M (Mega) × 10

f (femto) × 10

–15

k (kilo) × 10

2-3-2

Specifying the Angle Unit and Display Format

#Displayed values are rounded off to the number

of significant digits you specify.

#Specifying 0 makes the number of significant

digits 10.

# The engineering symbol that makes the

mantissa a value from 1 to 1000 is automatically selected by the calculator when engineering notation is in effect.

20010101

2-4 Function Calculations

k Function Menus

This calculator includes five function menus that give you access to scientific functions not printed on the key panel.

• The contents of the function menu differ according to the mode you entered from the Main

Menu before you pressed the K key. The following examples show function menus that appear in the RUN

•

MAT Mode.

u Numeric Calculations (NUM) [OPTN]-[NUM]

•{Abs} ... {select this item and input a value to obtain the absolute value of the value.}

•{Int}/{Frac} ... select the item and input a value to extract the {integer}/{fraction} part.

•{Rnd} ... {rounds off the value used for internal calculations to 10 significant digits (to match the value in the Answer Memory), or to the number of decimal places (Fix) and number of significant digits (Sci) specified by you.}

•{Intg} ... {select this item and input a value to obtain the largest integer that is not greater than the value.}

•{E-SYM} ... {engineering symbol}

•{m}/{µ}/{n}/{p}/{f} ... {milli (10–3)}/{micro (10–6)}/{nano (10–9)}/{pico (10

–12

)}/{femto

(10

–15

)}

•{k}/{M}/{G}/{T}/{P}/{E} ... {kilo (103)}/{mega (106)}/{giga (109)}/{tera (1012)}/{peta (1015)}/{exa (1018)}

u Probability/Distribution Calculations (PROB) [OPTN]-[PROB]

•{x!} ... {press after inputting a value to obtain the factorial of the value.}

•{nPr}/{nCr} ... {permutation}/{combination}

•{Ran#}... {pseudo random number generation (0 to 1)}

•{P(}/{Q(}/{R(} ... normal probability {P(t)}/{Q(t)}/{R(t)}

•{t(} ... {value of normalized variate t(x)}

2-4-1

Function Calculations

20011101

20010101

u Hyperbolic Calculations (HYP) [OPTN]-[HYP]

•{sinh}/{cosh}/{tanh} ... hyperbolic {sine}/{cosine}/{tangent}

•{sinh–1}/{cosh–1}/{tanh–1} ... inverse hyperbolic {sine}/{cosine}/{tangent}

u Angle Units, Coordinate Conversion, Sexagesimal Operations (ANGL)

[OPTN]-[ANGL]

•{°}/{r}/{g} ... {degrees}/{radians}/{grads} for a specific input value

•{° ’ ”} ... {specifies degrees (hours), minutes, seconds when inputting a degrees/minutes/

seconds value}

•{'DMS} ... {converts decimal value to sexagesimal value}

•{Pol(}/{Rec(} ... {rectangular-to-polar}/{polar-to-rectangular} coordinate conversion

u Instant Functions

•{ ° ’ ”} ... {converts decimal value to degrees/minutes/seconds value}

•{ENG}/{ ENG} ... shifts the decimal place of the displayed value three digits to the {left}/{right} and {decreases}/{increases} the exponent by three. When you are using engineering notation, the engineering symbol is also changed accordingly.

• The { ° ’ ” }, {ENG} and { ENG} menu operations are available only when there is a

calculation result on the display.

k Angle Units

To change the angle unit of an input value, first press K3(ANGL). On the pull-up menu that appears, select “°”, “r”, or “g”.

•Be sure to specify Comp for Mode in the SET UP screen.

Example Operation

To convert 4.25 rad to degrees:

u3(SET UP)cccc1(Deg)i

243.5070629 4.25K6(g)3(ANGL)c(r)w

47.3° + 82.5rad = 4774.20181°

47.3+82.5K6(g)3(ANGL)c(r)w

2-4-2

Function Calculations

# Once you specify an angle unit, it remains

in effect until you specify a different one.

The specification is retained even if you turn power off.

20010101

k Trigonometric and Inverse Trigonometric Functions

•Be sure to set the angle unit before performing trigonometric function and inverse

trigonometric function calculations.

•Be sure to specify Comp for Mode in the SET UP screen.

Example Operation

sin 63° = 0.8910065242 u3(SET UP)cccc1(Deg)i

s63w

cos (–– rad) = 0.5 u3(SET UP)cccc2(Rad)i

c(!E(π)/d)w

tan (– 35gra) = – 0.6128007881

u3(SET UP)cccc3(Gra)i t-35w

2 • sin 45° × cos 65° = 0.5976724775

u3(SET UP)cccc1(Deg)i 2*s45*c65w*

cosec 30° =

= 2 1/s30w

sin30°

sin-10.5 = 30° !s(sin–1)0.5*2w (x when sinx = 0.5)

2-4-3

Function Calculations

*1* can be omitted. *2Input of leading zero is not necessary.

(90° = ––– radians = 100 grads)

20010101

k Logarithmic and Exponential Functions

•Be sure to specify Comp for Mode in the SET UP screen.

Example Operation

log 1.23 (log101.23) = 8.990511144 × 10

–2

l1.23w

In 90 (loge90) = 4.49980967 I90w

1.23

= 16.98243652

(To obtain the antilogarithm of common !l(10x)1.23w logarithm 1.23)

4.5

= 90.0171313

(To obtain the antilogarithm of natural !I(ex)4.5w logarithm 4.5)

(–3)4 = (–3) × (–3) × (–3) × (–3) = 81 (-3)M4w

–34 = –(3 × 3 × 3 × 3) = –81 -3M4w

(= 1237) = 1.988647795 7!M(x )123w

2 + 3 ×

– 4 = 10 2+3*3!M(x )64-4w*

2-4-4

Function Calculations

123

*1^ (xy) and x take precedence over

multiplication and division.

20011101

20010101

k Hyperbolic and Inverse Hyperbolic Functions

•Be sure to specify Comp for Mode in the SET UP screen.

Example Operation

sinh 3.6 = 18.28545536 K6(g)2(HYP)b(sinh)3.6w

cosh 1.5 – sinh 1.5 K6(g)2(HYP)c(cosh)1.5- = 0.2231301601 2(HYP)b(sinh)1.5w = e

–1.5

(Display: –1.5) I!-(Ans)w

(Proof of cosh x ± sinh x = e±x)

cosh–1

= 0.7953654612

K6(g)2(HYP)f(cosh–1)(20/15)w

Determine the value of x when tanh 4 x = 0.88

x =

tanh

–1

0.88

K6(g)2(HYP)g(tanh–1)0.88/4w

= 0.3439419141

2-4-5

Function Calculations

20010101

k Other Functions

•Be sure to specify Comp for Mode in the SET UP screen.

Example Operation

+ =

3.65028154 !x( )2+!x( )5w

1.755317302

!x( )(d+!a(i))w

(3 + i)

+0.2848487846i

(–3)2 = (–3) × (–3) = 9 (-3)xw

–32 = –(3 × 3) = –9 -3xw

(3!)(x

–1

)-4!)(x–1))!)(x–1)w

8! (= 1 × 2 × 3 × .... × 8) 8K6(g)1(PROB)b(x!)w

= 40320

= 42

(

)

(36*42*49

)w36 × 42 × 49

What is the absolute value of

the common logarithm of

log | = 0.1249387366

K5(NUM)b(Abs)l(3/4)w

What is the integer part of K5(NUM)c(Int)-3.5w – 3.5? – 3

What is the decimal part of K5(NUM)d(Frac)-3.5w – 3.5? – 0.5

What is the nearest integer K5(NUM)f(Intg)-3.5w not exceeding – 3.5? – 4

2-4-6

Function Calculations

3 4

–––––– = 12

–– – ––

20010101

k Random Number Generation (Ran#)

This function generates a 10-digit truly random or sequentially random number that is greater than zero and less than 1.

•A truly random number is generated if you do not specify anything for the argument.

Example Operation

Ran # (Generates a random number.) K6(g)1(PROB)e(Ran#)w

(Each press of w generates a new random w number.) w

•Specifying an argument from 1 to 9 generates random numbers based on that sequence.

•Specifying an argument of 0 initializes the sequence.*

Example Operation

Ran# 1 (Generates the first random number in sequence 1.) 1(PROB)e(Ran#)bw (Generates the second random number in sequence 1.) w

Ran# 0 (Initializes the sequence.) 1(PROB)e(Ran#)aw Ran# 1 (Generates the first random number in sequence 1.) 1(PROB)e(Ran#)bw

2-4-7

Function Calculations

*1Changing to a different sequence or

generating a totally random number (without an argument) initializes the sequence.

20010101

2-4-8

Function Calculations

k Coordinate Conversion

u Rectangular Coordinates

u Polar Coordinates

•With polar coordinates, θ can be calculated and displayed within a range of

–180°< θ < 180° (radians and grads have same range).

•Be sure to specify Comp for Mode in the SET UP screen.

Example Operation

Calculate r and θ° when x = 14 and y = 20.7 u3(SET UP)cccc1(Deg)i

K6(g)3(ANGL)g(Pol()

14,20.7)w

Calculate x and y when r = 25 and θ = 56° u3(SET UP)cccc1(Deg)i

K6(g)3(ANGL)h(Rec()

25,56)w

1 24.989 → 24.98979792 (r) 2 55.928 → 55.92839019 (θ)

1 13.979 → 13.97982259 (x) 2 20.725 → 20.72593931 (y)

20010101

2-4-9

Function Calculations

n! n!

nPr = ––––– nCr = –––––––

(n – r)! r! (n – r)!

k Permutation and Combination

u Permutation

u Combination

•Be sure to specify Comp for Mode in the SET UP screen.

Example To calculate the possible number of different arrangements using 4

items selected from among 10 items

Formula Operation

10P4 = 5040 10K6(g)1(PROB)c(nPr)4w

Example To calculate the possible number of different combinations of 4 items

that can be selected from among 10 items

Formula Operation

10C4 = 210 10K6(g)1(PROB)d(nCr)4w

20010101

k Fractions

•Fractional values are displayed with the integer first, followed by the numerator and then

the denominator.

•Be sure to specify Comp for Mode in the SET UP screen.

Example Operation

(Display: 3{13{20) 2$5+3$1$4w

= 3.65 $(Conversion to decimal)

$(Conversion to fraction)

1$2578+1$4572w

1$2*.5w

1.5+2.3!a(i)w $$*

1$(1$3+1$4)w*

2-4-10

Function Calculations

2 1 13

–– + 3 –– = 3 –––

5 4 20

––––– + –––––

2578 4572

= 6.066202547 × 10

–4

–– × 0.5 = 0.25*

(Display: )

6.066202547E–04*

(Norm 1 display format)

= ––

(Display: 1{5{7)

–––––– = 1––

1 1 7

–– + ––

*1When the total number of characters,

including integer, numerator, denominator and delimiter marks exceeds 10, the input fraction is automatically displayed in decimal format.

Calculations containing both fractions and decimals are calculated in decimal format.

Pressing $ once when converting the decimal part of a complex number to a fraction first displays the real part and imaginary part on separate lines.

You can include fractions within the numerator or denominator of a fraction by putting the numerator or denominator in parentheses.

1.5 + 2.3i = 1–– + 2––i 2 10

Display: 1{1{2

+2{3{10i

20010101

2-4-11

Function Calculations

k Engineering Notation Calculations

Input engineering symbols using the engineering notation menu.

•Be sure to specify Comp for Mode in the SET UP screen.

Example Operation

u3(SET UP)cccccccccc 4(Eng)i

999k (kilo) + 25k (kilo) 999K5(NUM)g(E-SYM)g(k)+255(NUM) = 1.024M (mega) g(E-SYM)g(k)w

9 ÷ 10 = 0.9 = 900m (milli) 9/10w

= 0.9 K6(g)6(g)6(g)3( ENG)*

= 0.0009k (kilo) 3( ENG)*

= 0.9 2(ENG)*

= 900m 2(ENG)*

*1Converts the displayed value to the next higher

engineering unit, by shifting the decimal point three places to the right.

Converts the displayed value to the next lower engineering unit, by shifting the decimal point three places to the left.

20010101

2-5 Numerical Calculations

The following describes the items that are available in the menus you use when performing differential/ quadratic differential, integration, Σ, maximum/minimum value, and Solve calculations.

When the option menu is on the display, press 4(CALC) to display the function analysis menu. The items of this menu are used when performing specific types of calculations.

•{d/dx}/{d2/dx2}/{∫dx}/{Σ}/{FMin}/{FMax}/{Solve} ... {differential}/{quadratic differential}/

{integration}/{Σ (sigma)}/{minimum value}/{maximum value}/{solve} calculations

Solve calculations

The following is the syntax for using the Solve function in a program.

Solve( f(x), n, a, b) (a: lower limit, b: upper limit, n: initial estimated value)

• There are two different input methods that can be used for Solve calculations: direct assignment and variable table input.

With the direct assignment method (the one described here), you assign values directly to variables. This type of input is identical to that used with the Solve command used in the PRGM Mode.

Variable table input is used with the Solve function in the EQUA Mode. This input method is recommend for most normal Solve function input.

An Error (Iteration ERROR) occurs when there is no convergence of the solution.

2-5-1

Numerical Calculations

20010101

k Differential Calculations [OPTN]-[CALC]-[d

/dx]

To perform differential calculations, first display the function analysis menu, and then input the values shown in the formula below.

K4(CALC)b(d/dx) f(x),a,tol)

The differentiation for this type of calculation is defined as:

In this definition,

infinitesimal

is replaced by a

sufficiently small

Ax, with the value in the

neighborhood of f ' (a) calculated as:

In order to provide the best precision possible, this unit employs central difference to perform differential calculations.

Using Differential Calculation in a Graph Function

• Omitting the tolerance (tol) value when using the differential command inside of a graph

function simplifies the calculation for drawing the graph. In such a case, precision is sacrificed for the sake of faster drawing. The tolerance value is specified, the graph is drawn with the same precision obtained when you normally perform a differential calculation.

• You can also omit input of the derivative point by using the following format for the

differential graph: Y2=d/dx(Y1). In this case, the value of the X variable is used as the derivative point.

2-5-2

Numerical Calculations

d/dx ( f (x), a) ⇒ ––– f (a)

f (a + Ax) – f (a)

f '(a) = lim –––––––––––––

Ax→0

f (a + Ax) – f (a)

f '(a) –––––––––––––

(a: point for which you want to determine the

derivative, tol: tolerance)

20010101

Example To determine the derivative at point x = 3 for the function

y = x

+ 4x2 + x – 6, with a tolerance of “tol” = 1E – 5

Input the function f(x).

AK4(CALC)b(d/dx)vMd+evx+v-g,

Input point x = a for which you want to determine the derivative.

Input the tolerance value.

bE-f)

# In the function f(x), only X can be used as a

variable in expressions. Other variables (A through Z, r,

) are treated as constants, and the value currently assigned to that variable is applied during the calculation.

# Input of the tolerance (tol) value and the

closing parenthesis can be omitted. If you omit tolerance (tol) value, the calculator automatically uses a value for tol as 1

E-10.

# Specify tolerance (tol) value of 1

E-14 or less.

An error (Iteration ERROR) occurs whenever no solution that satisfies the tolerance value can be obtained.

#Discontinuous points or sections with drastic

fluctuation can adversely affect precision or even cause an error.

2-5-3

Numerical Calculations

20010101

u Applications of Differential Calculations

•Differentials can be added, subtracted, multiplied or divided with each other.

Therefore:

•Differential results can be used in addition, subtraction, multiplication, and division, and in functions.

2 × f '(a), log ( f '(a)), etc.

• Functions can be used in any of the terms ( f (x), a, tol) of a differential.

2-5-4

Numerical Calculations

#You cannot use a differential, quadratic

differential, integration, Σ, maximum/minimum value or solve calculation expression inside a differential calculation term.

#Pressing A during calculation of a differential

(while the cursor is not shown on the display) interrupts the calculation.

#Always use radians (Rad Mode) as the angle

unit when performing trigonometric differentials.

––– f (a) = f '(a), ––– g (a) = g'(a)

dx dx

f '(a) + g'(a), f '(a) × g'(a), etc.

––– (sinx + cosx, sin0.5, 1E - 8), etc.

20011101

20010101

k Quadratic Differential Calculations [OPTN]-[CALC]-[d

/dx2]

After displaying the function analysis menu, you can input quadratic differentials using either of the two following formats.

K4(CALC)c(d2/dx2) f(x),a,tol)

Quadratic differential calculations produce an approximate differential value using the following second order differential formula, which is based on Newton’s polynomial interpretation.

2 f(a + 3h) – 27 f(a + 2h) + 270 f (a + h) – 490 f(a)+270 f(a – h) – 27 f(a – 2h) +2 f(a – 3h)

f''(a)

= –––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

180h

In this expression, values for “sufficiently small increments of h” are used to obtain a value that approximates f ”(a).

Example To determine the quadratic differential coefficient at the point where

x = 3 for the function y = x

+ 4x2 + x – 6

Here we will use a tolerance tol = 1E – 5

Input the function f(x).

AK4(CALC)c(d2/dx2) vMd+

evx+v-g,

Input 3 as point a, which is the differential coefficient point.

Input the tolerance value.

bE-f) w

2-5-5

Numerical Calculations

# In the function f(x), only X can be used as a

variable in expressions. Other variables (A through Z, r,

) are treated as constants, and the value currently assigned to that variable is applied during the calculation.

#Input of the tolerance (tol) value and the closing

parenthesis can be omitted.

#Discontinuous points or sections with drastic

fluctuation can adversely affect precision or even cause an error.

(a: differential coefficient point , tol: tolerance)

––– (f (x), a) ⇒ ––– f (a)

20011101

20010101

u Quadratic Differential Applications

•Arithmetic operations can be performed using two quadratic differentials.

Therefore:

f ''(a) + g''(a), f ''(a) × g''(a), etc.

• The result of a quadratic differential calculation can be used in a subsequent arithmetic or function calculation.

2 × f ''(a), log ( f ''(a) ), etc.

• Functions can be used within the terms ( f(x), a, tol ) of a quadratic differential expression.

2-5-6

Numerical Calculations

––– f (a) = f ''(a), ––– g (a) = g''(a)

––– (sin x + cos x, sin 0.5, 1E - 8), etc.

#You cannot use a differential, quadratic

differential, integration, Σ, maximum/minimum value or Solve calculation expression inside of a quadratic differential calculation term.

# Specify tolerance (tol) value of 1

E-14 or less.

An error (Iteration ERROR) occurs whenever no solution that satisfies the tolerance value can be obtained.

#You can interrupt an ongoing quadratic

differential calculation by pressing the A key.

#Always use radians (Rad Mode) as the angle

unit when performing trigonometric quadratic differentials.

# Using Quadratic Differential Calculation in a

Graph Function (see page 2-5-2)

20010101

k Integration Calculations [OPTN]-[CALC]-[

∫

dx]

To perform integration calculations, first display the function analysis menu and then input the values in the formula shown below.

K4(CALC)d (∫dx) f(x) , a , b , tol )

∫

( f(x), a, b, tol) ⇒

∫

f(x)dx

As shown in the illustration above, integration calculations are performed by calculating integral values from a through b for the function y = f (x) where a < x < b, and f (x) > 0. This in effect calculates the surface area of the shaded area in the illustration.

2-5-7

Numerical Calculations

Area of

∫

f(x)dx is calculated

(a: start point, b: end point, tol: tolerance)

# If f (x) < 0 where a a < x < b, the surface area

calculation produces negative values (surface area × – 1).

20010101

Example To perform the integration calculation for the function shown

below, with a tolerance of “tol” = 1E - 4

∫

(2x2 + 3x + 4) dx

Input the function f (x).

AK4(CALC)d(∫dx)cvx+dv+e,

Input the start point and end point.

b,f,

Input the tolerance value.

bE-e) w

u Application of Integration Calculation

•Integrals can be used in addition, subtraction, multiplication or division.

∫

f(x) dx +

∫

g(x) dx, etc.

•Integration results can be used in addition, subtraction, multiplication or division, in functions.

2 ×

∫

f(x) dx, etc. log (

∫

f(x) dx), etc.

• Functions can be used in any of the terms ( f(x), a, b, tol) of an integral.

∫

cos 0.5

(sin x + cos x) dx = ∫(sin x + cos x, sin 0.5, cos 0.5, 1E - 4)

sin 0.5

2-5-8

Numerical Calculations

#In the function f(x), only X can be used as a

variable in expressions. Other variables (A through Z,

) are treated as constants, and the value currently assigned to that variable is applied during the calculation.

#Input of “tol” and closing parenthesis can be

omitted. If you omit “tol,” the calculator automatically uses a default value of 1

E-5.

# Integration calculations can take a long time to

complete.

#You cannot use a differential, quadratic

differential, integration, Σ, maximum/minimum value or Solve calculation expression inside of an integration calculation term.

20011101

20010101

Note the following points to ensure correct integration values.

(1) When cyclical functions for integration values become positive or negative for different

divisions, perform the calculation for single cycles, or divide between negative and positive, and then add the results together.

∫

f(x)dx =

∫

f(x)dx + (–

∫

f(x)dx)

Positive part (S)Negative part (S)

(2) When minute fluctuations in integration divisions produce large fluctuations in integration

values, calculate the integration divisions separately (divide the large fluctuation areas into smaller divisions), and then add the results together.

∫

f(x)dx =

∫

f(x)dx +

∫

f(x)dx +.....+

∫

f(x)dx

2-5-9

Numerical Calculations

Negative part (S)

Positive part (S)

#Pressing A during calculation of an integral

(while the cursor is not shown on the display) interrupts the calculation.

#Always use radians (Rad Mode) as the angle

unit when performing trigonometric integrations.

# An error (Iteration ERROR) occurs whenever

no solution that satisfies the tolerance value can be obtained.

20010101

k Σ Calculations [OPTN]-[CALC]-[Σ ]

To perform Σ calculations, first display the function analysis menu, and then input the values shown in the formula below.

K4(CALC)e(Σ) ak , k , α , β , n )

Example To calculate the following:

Use n = 1 as the distance between partitions.

AK4(CALC)e(Σ)a,(K)x

-da,(K)+f,

a,(K),c,g,b)w

2-5-10

Numerical Calculations

(k2 – 3k + 5)

k = 2

#You can use only one variable in the function for

input sequence

ak.

#Input integers only for the initial ter m (

) of

sequence

ak and last term (

) of sequence ak .

#Input of

n and the closing parentheses can be

omitted. If you omit

n, the calculator automati-

cally uses

n = 1.

(ak, k, α, β, n) = Σ ak = aα + a

+........+ a

k = α

(n: distance between partitions)

20010101

u Σ Calculation Applications

•Arithmetic operations using Σ calculation expressions

Expressions:

Possible operations: Sn + Tn, Sn – Tn, etc.

•Arithmetic and function operations using Σ calculation results

2 × Sn, log (Sn), etc.

• Function operations using Σ calculation terms (ak , k)

Σ (sink, k, 1, 5), etc.

2-5-11

Numerical Calculations

Sn = Σ ak, Tn = Σ bk

k = 1 k = 1

#You cannot use a differential, quadratic

differential, integration, Σ, maximum/minimum value or Solve calculation expression inside of a Σ calculation term.

#Make sure that the value used as the final term

is greater than the value used as the initial

term

. Otherwise, an error will occur.

#To interrupt an ongoing Σ calculation (indicated

when the cursor is not on the display), press the A key.

20010101

2-5-12

Numerical Calculations

k Maximum/Minimum Value Calculations [OPTN]-[CALC]-[FMin]/[FMax]

After displaying the function analysis menu, you can input maximum/minimum calculations using the formats below, and solve for the maximum and minimum of a function within interval a < x < b. (a: start point of interval, b: end point of interval, n: precision (n = 1 to 9))

uMinimum Value

K4(CALC)f(FMin) f(x) , a , b , n )

uMaximum Value

K4(CALC)g(FMax) f(x), a , b , n )

Example 1 To determine the minimum value for the interval defined by start

point a = 0 and end point b = 3, with a precision of n = 6 for the function y = x

– 4x + 9

Input f(x).

AK4(CALC)f(FMin) vx-ev+j,

Input the interval a = 0, b = 3.

a,d,

Input the precision n = 6.

20010101

2-5-13

Numerical Calculations

#In the function f(x), only X can be used as a

variable in expressions. Other variables (A through Z,

) are treated as constants, and the value currently assigned to that variable is applied during the calculation.

#Input of

n and the closing parenthesis can be

omitted.

#Discontinuous points or sections with drastic

fluctuation can adversely affect precision or even cause an error.

#You cannot use a differential, quadratic

differential, integration, Σ, maximum/minimum value or Solve calculation expression inside of a maximum/minimum calculation term.

#Inputting a larger value for

n increases the

precision of the calculation, but it also increases the amount of time required to perform the calculation.

# The value you input for the end point of the

interval (

b) must be greater than the value you

input for the start point (

a). Otherwise an error

occurs.

#You can interrupt an ongoing maximum/

minimum calculation by pressing the A key.

#You can input an integer in the range of 1 to 9

for the value of

n. Using any value outside this

range causes an error.

Example 2 To determine the maximum value for the interval defined by start

point a = 0 and end point b = 3, with a precision of n = 6 for the function y = –x

+ 2x + 2

Input f(x).

AK4(CALC)g(FMax) -vx+cv+c,

Input the interval a = 0, b = 3.

a,d,

Input the precision n = 6.

20010101

2-6 Complex Number Calculations

You can perform addition, subtraction, multiplication, division, parentheses calculations, function calculations, and memory calculations with complex numbers just as you do with the manual calculations described on pages 2-1-1 and 2-4-6.

You can select the complex number calculation mode by changing the Complex Mode item on the SET UP screen to one of the following settings.

• {Real} ... Calculation in the real number range only*

• {a+bi} ... Performs complex number calculation and displays results in rectangular

form

• {re^

i} ... Performs complex number calculation and displays results in polar form*

Press K3(CPLX) to display the complex calculation number menu, which contains the following items.

• {Abs}/{Arg} ... obtains {absolute value}/{argument}

• {Conjg} ... {obtains conjugate}

• {ReP}/{ImP} ... {real}/{imaginary} part extraction

• {'re^

i}/{'a+bi} ... converts the result to {polar}/{linear}

2-6-1

Complex Number Calculations

*1 When there is an imaginary number in the

argument, however, complex number calculation is performed and the result is displayed using rectangular form.

Examples: ln 2i = 0.6931471806 + 1.570796327i ln 2i + ln (- 2 ) = (Non-Real ERROR)

The display range of θ depends on the angle

unit set for the Angle item on the SET UP screen.

• Deg ... –180 <

< 180

• Rad ... – π <

< π

• Gra ... –200 <

< 200

# Solutions obtained by the Real and a+bi

/ re^

modes are different for power root (x

) calculations when x < 0 and y = m/n when n is an odd number.

Example:

(- 8) = – 2 (Real)

= 1 + 1.732050808i(a+bi

/ re^θ i)

20011101

20010101

2-6-2

Complex Number Calculations

k Absolute Value and Argument [OPTN]-[CPLX]-[Abs]/[Arg]

The unit regards a complex number in the form a + bi as a coordinate on a Gaussian plane, and calculates absolute value Z and argument (arg).

ExampleTo calculate absolute value (r) and argument (θ) for the complex

number 3 + 4i, with the angle unit set for degrees

AK3(CPLX)b(Abs) (d+e!a(i))w

(Calculation of absolute value)

AK3(CPLX)c(Arg) (d+e!a(i))w

(Calculation of argument)

# The result of the argument calculation differs

in accordance with the current angle unit setting (degrees, radians, grads).

Imaginary axis

Real axis

20011101

20010101

k Conjugate Complex Numbers [OPTN]-[CPLX]-[Conjg]

A complex number of the form a + bi becomes a conjugate complex number of the form

a – bi.

Example To calculate the conjugate complex number for the complex number 2

+ 4i

AK3(CPLX)d(Conjg)

(c+e!a(i))w

k Extraction of Real and Imaginary Parts [OPTN]-[CPLX]-[ReP]/[lmP]

Use the following procedure to extract the real part a and the imaginary part b from a complex number of the form a + bi.

Example To extract the real and imaginary parts of the complex number 2 + 5i

AK3(CPLX)e(ReP)

(c+f!a(i))w

(Real part extraction)

AK3(CPLX)f(ImP) (c+f!a(i))w

(Imaginary par t extraction)

2-6-3

Complex Number Calculations

# The input/output range of complex numbers is

normally 10 digits for the mantissa and two digits for the exponent.

#When a complex number has more than 21

digits, the real part and imaginary part are displayed on separate lines.

#When either the real part or imaginary part of

a complex number equals zero, that part is not displayed in rectangular form.

# 18 bytes of memory are used whenever you

assign a complex number to a variable.

# The following functions can be used with

complex numbers.

, x2, x–1, ^(x

, x, In, log, 10x, ex, sin,

cos, tan, sin

–1

, cos–1, tan–1, sinh, cosh, tanh,

sinh

–1

, cosh–1, tanh

–1

Int, Frac, Rnd, Intg, Fix, Sci, ENG, ENG, ° ’ ”,

° ’ ”, a b/c, d/c

20011101

20010101

k Polar Form and Rectangular Transformation [OPTN]-[CPLX]-[

re^

Use the following procedure to transform a complex number displayed in rectangular form to polar form, and vice versa.

Example To transform the rectangular form of complex number 1 + 3

i to its

polar form

Ab+(!x( )d)! a(i)

K3(CPLX)g('re^θi)w

2-6-4

Complex Number Calculations

20010101

2-7 Binary, Octal, Decimal, and Hexadecimal

Calculations with Integers

You can use the RUN • MAT Mode and binary, octal, decimal, and hexadecimal settings to perform calculations that involve binary, octal, decimal and hexadecimal values. You can also convert between number systems and perform bitwise operations.

•You cannot use scientific functions in binary, octal, decimal, and hexadecimal calculations.

•You can use only integers in binary, octal, decimal, and hexadecimal calculations, which means that fractional values are not allowed. If you input a value that includes a decimal part, the unit automatically cuts off the decimal part.

• If you attempt to enter a value that is invalid for the number system (binary, octal, decimal, hexadecimal) you are using, the calculator displays an error message. The following shows the numerals that can be used in each number system.

Binary: 0, 1

Octal: 0, 1, 2, 3, 4, 5, 6, 7

Decimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Hexadecimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

•Negative binary, octal, and hexadecimal values are produced using the two’s complement of the original value.

• The following are the display capacities for each of the number systems.

Number System Display Capacity

Binary 16 digits

Octal 11 digits

Decimal 10 digits

Hexadecimal 8 digits

2-7-1

Binary, Octal, Decimal, and Hexadecimal Calculations with Integers

# The alphabetic characters used in the

hexadecimal number appear differently on the display to distinguish them from text characters.

Normal Text

Hexadecimal Values

Keys

A B C D E F

u v w x y z

20011101

20010101

• The following are the calculation ranges for each of the number systems.

Binary Values

Positive: 0 < x < 111111111111111

Negative: 1000000000000000 < x < 1111111111111111

Octal Values

Positive: 0 < x < 17777777777

Negative: 20000000000 < x < 37777777777

Decimal Values

Positive: 0 < x < 2147483647

Negative: –2147483648 < x < –1

Hexadecimal Values

Positive: 0 < x < 7FFFFFFF

Negative: 80000000 < x < FFFFFFFF

u To perform a binary, octal, decimal, or hexadecimal calculation

1. In the main menu, select RUN • MAT.

[SET UP]- [Mode] -[Dec]/[Hex]/[Bin]/[Oct]

2. Press u3(SET UP) and then specify the default number system by pressing 2(Dec), 3(Hex), 4(Bin), or 5(Oct).

3. Press i to change to the screen for calculation input. This causes a function menu with the following items to appear.

•{d~o}/{LOGIC}/{DISP}/{SYBL} ... {number system specification}/{bitwise operation}/ {decimal/hexadecimal/binary/octal conversion}/{symbol} menu

2-7-2

Binary, Octal, Decimal, and Hexadecimal Calculations with Integers

20011101

20010101

k Selecting a Number System

You can specify decimal, hexadecimal, binary, or octal as the default number system using the set up screen. After you press the function key that corresponds to the system you want to use, press w.

u To specify a number system for an input value

You can specify a number system for each individual value you input. Press 1(d~o) to display a menu of number system symbols. Press the function key that corresponds to the symbol you want to select and then input the value.

•{d}/{h}/{b}/{o} ... {decimal}/{hexadecimal}/{binary}/{octal}

u To input values of mixed number systems

Example To input 12310 or 10102, when the default number system is

hexadecimal

u3(SET UP)3(Hex)i

A1(d~o)b(d)bcdw

1(d~o)d(b)babaw

k Arithmetic Operations

Example 1 To calculate 101112 + 110102

u3(SET UP)4(Bin)i

Ababbb+ bbabaw

2-7-3

Binary, Octal, Decimal, and Hexadecimal Calculations with Integers

20011101

20010101

Example 2 To input and execute 1238 × ABC16, when the default number system is

decimal or hexadecimal

u3(SET UP)2(Dec)i

A1(d~o)e(o)bcd*

1(d~o)c(h)ABC*1w

3(DISP)c(Hex)w

k Negative Values and Bitwise Operations

Press 2(LOGIC) to display a menu of negation and bitwise operators.

•{Neg} ... {negation}*

•{Not}/{and}/{or}/{xor}/{xnor} ... {NOT}*3/{AND}/{OR}/{XOR}/{XNOR}*

u Negative Values

Example To determine the negative of 1100102

u3(SET UP)4(Bin)i A2(LOGIC)b(Neg)

bbaabaw

uBitwise Operations

Example 1 To input and execute “12016 and AD16”

u3(SET UP)3(Hex)i

Abca2(LOGIC)

d(and)AD*1w

2-7-4

Binary, Octal, Decimal, and Hexadecimal Calculations with Integers

*1See page 2-7-1. *

two’s complement

one’s complement (bitwise complement)

20011101

*4bitwise AND, bitwise OR, bitwise XOR,

bitwise XNOR

Casio Algebra FX 2.0 PLUS, FX 2.0 - Algebra FX 2.0 Graphing Calculator, Algebra FX 1.0 PLUS User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual