Page 1

Capítulo
Cálculos e gráficos
estatísticos
Este capítulo descreve como introduzir dados estatísticos em
listas e como calcular a média, máximo e outros valores
estatísticos, assim como realizar cálculos de regressão.
6-1 Antes de realizar cálculos estatísticos
6-2 Cálculos e gráficos estatísticos com uma variável
6-3 Cálculos e gráficos estatísticos com duas variáveis
6-4 Realizar cálculos estatísticos
6-5 Distribution
6
Importante!
• Este capítulo contem um conjunto de imagens do ecrã. Em cada caso,
foram introduzidos novos valores de modo a realçar caracteristicas
particulares do respectivo gráfico. Por isso, quando tenta desenhar um
gráfico semelhante, a calculadora usa dados que introduziu utilizando a lista
de funções. Por isso, os gráficos que surgem no ecrã quando realiza uma
operação gráfica podem ser diferentes dos gráficos deste manual.
20000501
Page 2
Antes de realizar cálculos estatísticos
6-1-1
6-1 Antes de realizar cálculos estatísticos
A partir do menu principal, entre o modo STAT e visualize as listas de dados estatísticos.
Utilize as listas de dados estatísticos para introduzirdados e para realizar os cálculos.
Utilize
f, c, d
mover a selecção pelas listas.
e e para
Uma vez introduzidos os dados pode utilizad-los para produzir um gráfico e verificar as
tendências. Pode também utilizar diversos cálculos de regressão para análise de dados.
k Introduzir dados em listas
○○○○○
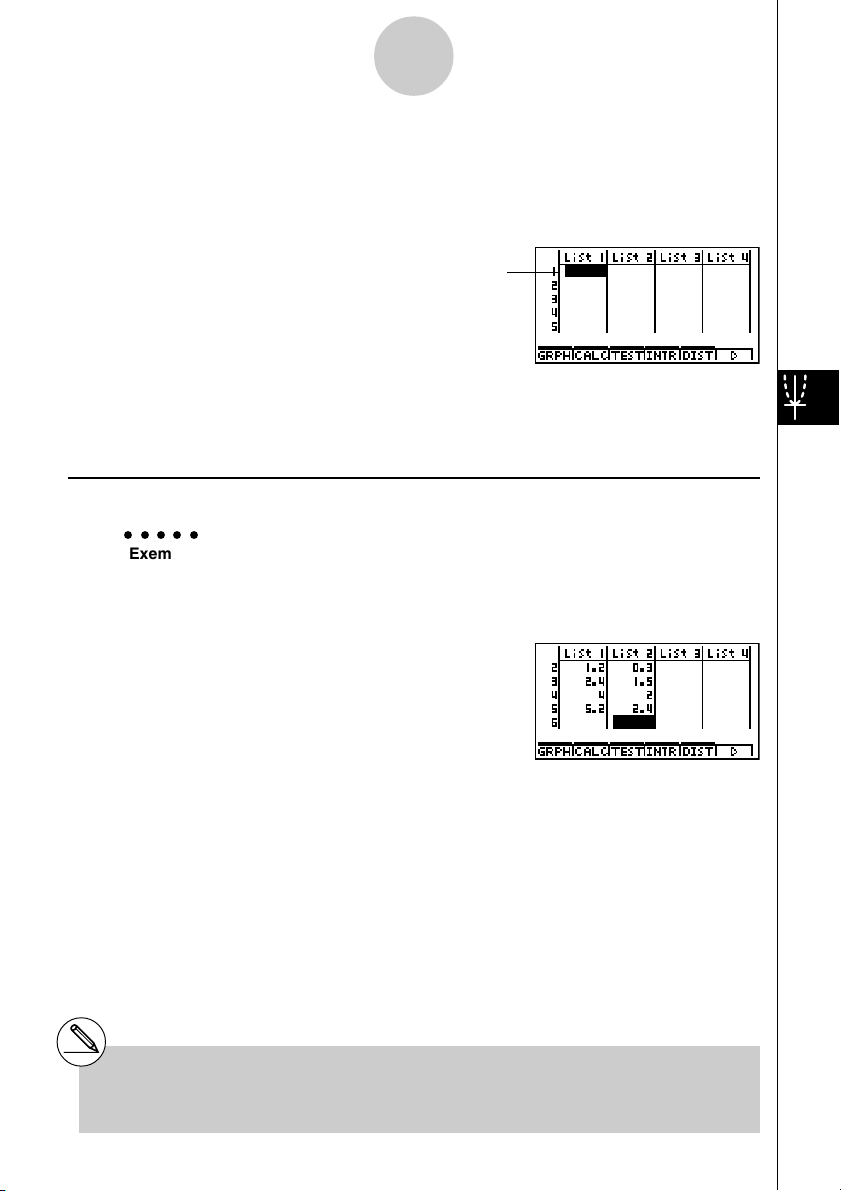
Exemplo Introduzir os dois conjuntos de dados
0.5, 1.2, 2.4, 4.0, 5.2
–2.1, 0.3, 1.5, 2.0, 2.4
a.fwb.cw
c.ewewf.cw
e
-c.bwa.dw
b.fwcwc.ew
Uma vez introduzidos os dados, pode utiliza-los para realizar gráficos ou cálculos
estatísticos.
# O resultado dos cálculos podem ser
introduzidos como dados estatísticos com
excepção dos números complexos.
# Pode utilizar as teclas f, c, d e e
para mover a selecção para qualquer celula
da lista para introdução de dados.
20010102
Page 3

Antes de realizar cálculos estatísticos
6-1-2
k Modificar parâmetros gráficos
Utilize os seguintes procediemntos para especificar o estado desenhar/não desenhar de um
gráfico, o tipo de gráfico e outros ajustes gerais para cada gráfico no menu gráfico (GPH1,
GPH2, GPH3).
Com a lista de dados estatísticos no ecrã, pressione 1(GRPH) para visualizar o menu
gráfico que contem os seguintes items:
•{S-Gph1}/{S-Gph2}/{S-Gph3} ... desenho do gráfico{1}/{2}/{3}
*1
•{Select} ... {selecção de gráfico simultâneo(GPH1, GPH2, GPH3)} (pode especificar
múltiplos gráficos.)
•{Set} ... {ajustes gráficos (tipo de gráfico, lista de tarefas)}
1. Ajustes gráficos gerais [GRPH]-[Set]
Esta secção descreve como utilizar o ecrã de ajustes gráficos gerais para realizar os
seguintes ajustes para cada gráfico(GPH1, GPH2, GPH3).
• Tipo de gráfico
O gráfico inicial por defeito é o gráfico de dispersão. pode seleccionar um dos vários tipos
de gráficos estatísticos para cada um dos gráficos.
• Lista
Os dados estatísticos iniciais por defeito são a lista 1 para dados de uma variável e lista 1 e
2 para dados de dupla variável. Pode especificar a lista de dados estatísticos que pretende
para os dados de x e y.
• Frequência
Normalmente cada dado ou par de dados na lista de dados estatisticos é representado no
gráfico como um ponto. No entanto, quando trabalha com um grande número de dados,
podem ocorrer alguns problemas devido ao número de pontos do gráfico. Quando isto
acontecer, especifique uma lista de frequência que contenha valores que indiquem o
número de incidências (a frequência) dos dados nas celulas correspondentes ás listas que
está a utilizar para os dados x e y. Quando o fizer, apenas um ponto é desenhado para os
múltiplos dados, tornando o gráfico mais fácil de ler.
*1
O tipo de gráfico inicial por defeito para todos
os gráficos (do Graph 1 ao Graph 3) é o
diagrama de dispersão,mas pode mudar
cada um deles para qualquer outro tipo.
# Pode especificar a condição desenhar/não
desenhar do gráfico, o tipo de gráfico e outros
ajustes gerais para cada um dos gráficos no
menu de gráficos(GPH1, GPH2, GPH3).
20000501
Page 4

Antes de realizar cálculos estatísticos
6-1-3
Tipo de marca
Esta função permite especificar a forma dos pontos do gráfico.
u Visualizar o ecrã de ajustes gráficos gerais [GRPH]-[Set]
Pressione 1(GRPH)f(Set) para visualizar o ecrã de ajustes gráficos gerais.
• Os ajustes demonstrados aqui são apenas exemplos. Os ajustes no ecrã de ajustes
gráficos gerais podem ser diferentes.
• StatGraph (especificação do gráfico estatístico)
•{GPH1}/{GPH2}/{GPH3} ... gráfico{1}/{2}/{3}
• Graph Type (especificação do tipo de gráfico)
•{Scat}/{xy}/{NPP} ... {diagrama de dispersão}/{ gráfico linear xy}/{pontos de probalidade
normal}
•{Hist}/{Box}/{ModB}/{N·Dis}/{Brkn} ... {histograma}/{gráfico Med-box}/{gráfico de caixa
modificado}/{curva de distribuição normal}/{gráfico linear}
•{X}/{Med}/{X^2}/{X^3}/{X^4} ... {gráfico de regressão linear}/{gráfico Med-Med}/{gráfico
de regressão quadrática}/{gráfico de regressão cúbica}/{gráfico de regressão cuártica}
•{Log}/{Exp}/{Pwr}/{Sin}/{Lgst} ...{gráfico de regressão logarítmica }/{gráfico de
regressão exponêncial}/{gráfico de regressão de potência}/{gráfico de regressão
sonusoidal}/{gráfico de regressão logística}
• XList (lista de dados do eixo x)
•{LIST} ... {Lista de 1 a 20}
• YList (lista de dados do eixo y)
•{LIST} ... {Lista de 1 a 20}
• Frequência (número de vezes que um valor ocorre)
•{1} ... {ponto 1 a 1}
•{LIST} ... o conteúdo desta lista indica a frequência dos dados da XList e da YList
• Mark Type (tipo de marcação de pontos)
•{ }/{×}/{•} ... pontos do diagrama de dispersão
20000501
Page 5

Antes de realizar cálculos estatísticos
6-1-4
2. Condição desenhar/não desenhar [GRPH]-[Select]
O procedimento seguinte pode ser utilizado para especificar a condição desenhar (On)/não
desenhar (Off) de cada um dos gráficos do menu gráfico.
u Especificar a condição desenhar/não desenhar de um gráfico
1. Pressionar 1(GRPH) e(Select) para visualizar o ecrã de activação/desactivação do
gráfico.
•Tenha em conta que o ajuste StatGraph 1 é para o Graph 1 (GPH 1 do menu gráfico,
StatGraph2 é para o Graph 2 e StatGraph3 para o Graph 3.
2.Utilize as teclas de cursor para mover a selecção para o gráfico que pretende modificar
e pressione a tecla de função correspondente para mudar a condição.
•{On}/{Off} ... {Activado (desenhar)}/{Desactivado (não desenhar)}
•{DRAW} ... {desenha todos os gráficos activados}
3.Para regressar ao menu gráfico, pressione i.
# Os parâmetros do ecrã de visualização são
configurados automáticamente para os
gráficos estatísticos. Se os pretender
configurar manualmente, deve mudar o item
"Stat Wind" para "Manual".
Com a lista de dados estatísticos no ecrã,
realize o seguinte procediemnto:
u3(SET UP)2(Man)
i(Regressa ao ecrã anterior.)
# Os ajustes por defeito utilizam automáticamente
os dados da lista 1 como os valores do eixo
(horizontal) e os dados da lista 2 como os
valores do eixo
diagrama de dispersão.
#Pressionar uanão esconde o menu se
estiver no ecrã um gráfico estatístico.
20000501
y (vertical) é um ponto no
x
Page 6

Cálculos e gráficos estatísticos com uma variável
6-2-1
6-2 Cálculos e gráficos estatísticos com uma
variável
Os dados de uma variável são os que apenas apresentam uma única variável. Se calcular,
por exemplo, a altura média dos alunos de uma classe, existe apenas uma variável (altura).
As estatísticas de uma variável incluem a distribuição e a soma. Os tipos de gráficos
disponíveis para estatísticas de uma variável são apresentados a seguir.
Também pode utilizar os procedimentos da página 6-1-2 para realizar os ajustes que quer
antes de desenhar cada gráfico.
kk
k Pontos de probabilidade normal (NPP)
kk
Este ponto compara a relação dos dados acumulados com uma distribuição normal de
relações acumuladas. A XList especifica a lista onde os dados são introduzidos, enquanto
que o Mark Type é utilizado para seleccionar as marcas { / × / • } que pretende desenhar.
Pressione i ou !i(QUIT) para a lista de dados estatísticos.
kk
k Histograma (Gráfico de barras) (Hist)
kk
XList especifica a lista onde se introduz os dados e Freq a lista onde é introduzida a
frequência dos dados. Quando não se especifica um valor para Freq, esse valor é 1.
⇒
w(Draw)
O ecrã tem a aparência do exemplo anterior antes do gráfico ser desenhado. Neste ponto,
pode modificar os valores de inicio (start) e de intervalo (pitch).
20010102
Page 7
Cálculos e gráficos estatísticos com uma variável
6-2-2
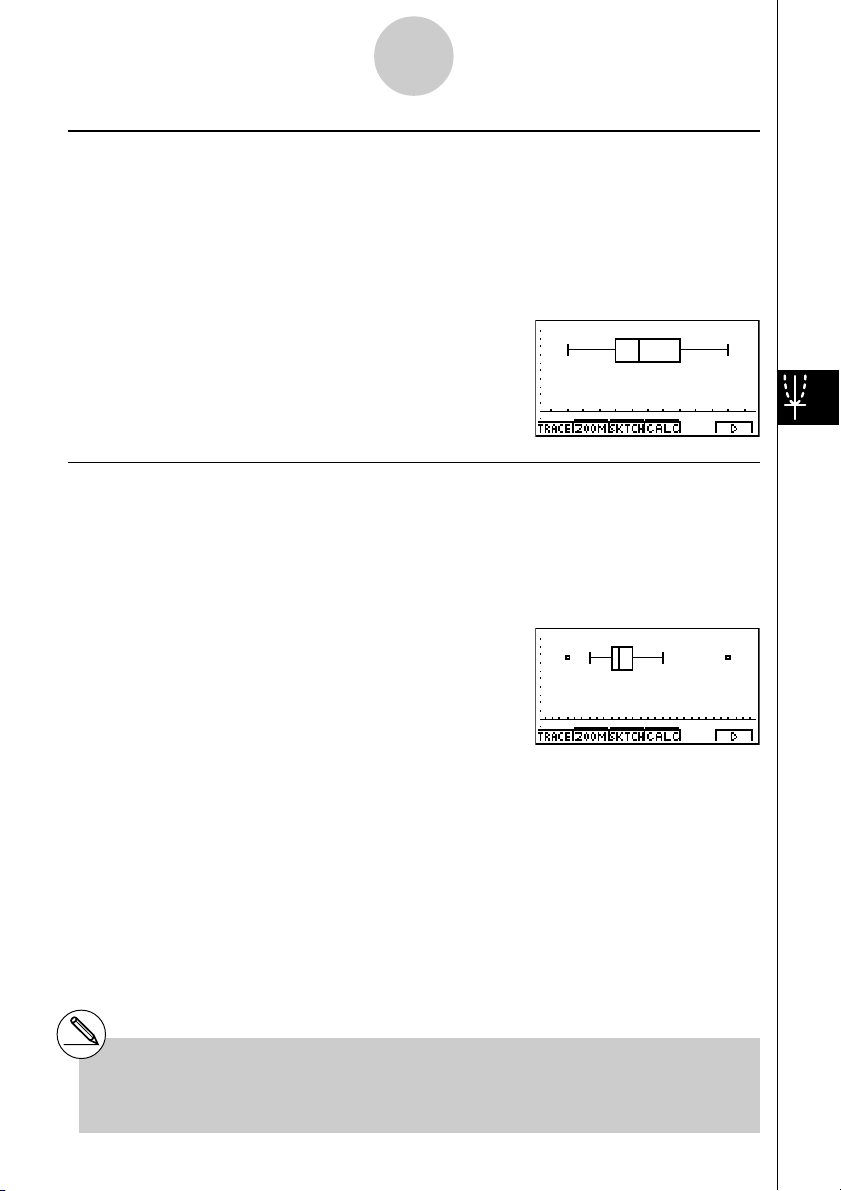
k Gráfico Med-box (Box)
Este tipo de gráfico permite ver como um grande número de items de dados se agrupam
dentro de um dado limite. Uma caixa enquadra todos os dados numa área desde o 25º ao
75º percentil, com uma linha desenhada no 50º percentil. As linhas (filamentos) extendemse de qualquer um dos extremos da caixa até ao minimo e máximo dos dados.
A XList especifica a lista onde se introduz os dados e Freq a lista onde se introduz a
frequência. Quando não se especifica um valor para Freq, esse valor é 1.
k Gráfico de caixa modificado (ModB)
O gráfico de caixa modificado omite tudo o que passa do limite 1.5 × IQR (IQR = Q3 – Q1,
Q3: 3rd quartil, Q1: 1st quartil) até ao 4 quartil em caixa e desenha os filamentos.
Os dados atípicos são visualizados como pontos de marcação.
XList especifica a lista onde se introduz os dados e Freq a lista onde é introduzida a
frequência dos dados. Quando não se especifica um valor para Freq, esse valor é 1.
#Introduza um inteiro positivo para os dados de
frequência. Outros tipos de valores (décimais,
por exemplo) produzem um erro.
20000501
Page 8
y
Cálculos e gráficos estatísticos com uma variável
6-2-3
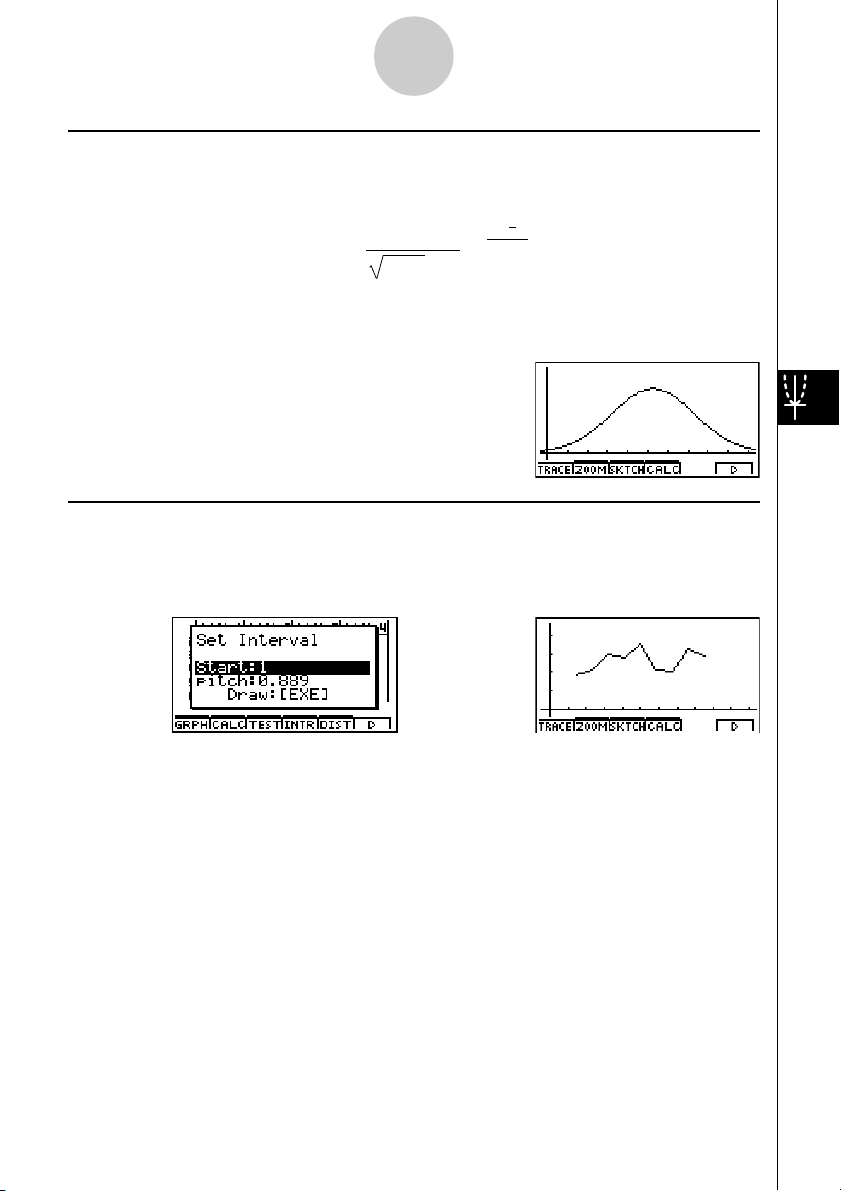
kCurva de distribuição normal (N
•
Dis)
A curva de distribuição normal é representada gráficamente utilizando a seguinte função de
distribuição:
2
(
)
x–
x
–
2
2x σ
n
e
=
1
(2 π) xσ
n
A XList especifica a lista onde se introduz os dados e Freq a lista onde se introduz a
frequência. Quando não se especifica um valor para Freq, esse valor é 1.
kGráfico linear (Brkn)
As linhas ligam pontos centrais de um historigrama de barras.
A XList especifica a lista onde se introduz os dados e Freq a lista onde se introduz a
frequência. Quando não se especifica um valor para Freq, esse valor é 1.
⇒
w(Draw)
O ecrã tem a aparência do exemplo anterior antes do gráfico ser desenhado. Neste ponto,
pode modificar os valores de inicio (start) e de intervalo (pitch).
20010102
Page 9

Cálculos e gráficos estatísticos com uma variável
6-2-4
k Visualizar os resultados de um cálculo de um gráfico de uma variável
desenhadas
As estatísticas de uma variável podem ser expressas quer como gráficos, quer como
valores de parâmetros. Quando estes gráficos são visualizados, o resultado do cálculo de
uma variável surge como no exemplo seguinte quando pressiona 4(CALC)b(1VAR).
• Utilizec para navegar pela lista de modo a poder ver os items que se encontram fora
do ecrã.
A seguir descreve-se o significado de cada um dos parâmetros.
o ............. media
Σx ........... soma
Σx2.......... soma dos quadrados
xσn .......... desvio standart da população
xσn–1 ........ desvio standart da amostra
n ............. número de items de dados
minX ....... mínimo
Q1 .......... primeiro quartil
Med ........ mediana
Q3 .......... treceiro quartil
maxX ...... máximo
Mod ........ modo
Mod : n ... número de items de modo de dados
Mod : F ... frequência do modo de dados
• Pressione 6(DRAW) para regressar ao gráfico estatístico de uma variável original.
# Quando o Mod tem várias soluções, elas são
todas visualizadas.
20000501
Page 10

Cálculos e gráficos estatísticos com duas variáveis
6-3-1
6-3 Cálculos e gráficos estatísticos com duas
variáveis
k Desenhar um diagrama de dispersão e um gráfico linear xy
Descrição
O procedimento seguinte desenha um diagrama de dispersão e ligaos pontos para realizar
um gráfico linear xy.
Ajustes básicos
1.A partir do menu principal, entre o modo STAT.
Execução
2. Introduza os dados numa lista.
3. Especifique Scat (diagrama de dispersão) ou xy (gráfico linear xy) como o tipo de
gráfico e execute de seguida a operação gráfica.
Pressione i ou !i(QUIT) para regressar à lista de dados estatísticos.
20000501
Page 11

Cálculos e gráficos estatísticos com duas variáveis
6-3-2
○○○○○
Exemplo Introduza os dois conjuntos de dados seguintes. A seguir marque os
pontos num diagrama de dispersão e ligue os pontos para produzir
um gráfico linear xy.
0.5, 1.2, 2.4, 4.0, 5.2,
–2.1, 0.3, 1.5, 2.0, 2.4
Procedimento
1 m STAT
2 a.fwb.cw
c.ewewf.cw
e
-c.bwa.dw
b.fwcwc.ew
3 (Diagrama de dispersão)1(GRPH)f(Set)c1(Scat)i
1(GRPH)b(S-Gph1)
3 (gráfico linear xy)1(GRPH)f(Set)c2(xy)i
1(GRPH)b(S-Gph1)
Ecrã de resultados
(Diagrama de dispersão)
(gráfico linear xy)
20000501
Page 12

Cálculos e gráficos estatísticos com duas variáveis
6-3-3
k Desenhar um gráfico de regressão
Descrição
Utilize o procedimento seguinte para introduzir dados estatísticos de duas variáveis, realizar
cálculos de regressão e representar gráficamente os resultados.
Ajustes básicos
1. A partir do menu principal, entre o modo STAT.
Execução
2. Introduza os dados numa lista e marque os pontos do diagrama de dispersão.
3. Escolha o tipo de regressão, execute o cálculo e visualize os parâmetros de
regressão.
4. Desenhe o gráfico de regressão.
# Pode realizar a função de traçar num gráfico
de regressão, mas não a função de traçar
navegando no ecrã.
20000501
Page 13

Cálculos e gráficos estatísticos com duas variáveis
6-3-4
○○○○○
Exemplo Introduza os dois conjuntos de dados seguintes e marque os pontos
num diagrama de regressão. A seguir, realize a regressão logoritmica
nos dados para visualizar os parâmetros de regressão e desenhe o
gráfico de regressão correspondente.
0.5, 1.2, 2.4, 4.0, 5.2,
–2.1, 0.3, 1.5, 2.0, 2.4
Procedimento
1 m STAT
2 a.fwb.cw
c.ewewf.cw
e
-c.bwa.dw
b.fwcwc.ew
1(GRPH)f(Set)c1(Scat)i
1(GRPH)b(S-Gph1)
3 4(CALC)h(Log)
4 6(DRAW)
Ecrã de resultados
20010102
Page 14

Cálculos e gráficos estatísticos com duas variáveis
kk
k Seleccionar o tipo de regressão
kk
Após representar gráficamente os dados estatísticos de duas variáveis, pressione
4(CALC). Assim, pode utilizar o menu de funções que se encontra no fundo do ecrã para
seleccionar diversos tipos de regressão.
•{2VAR} ... {resultados estatísticos de duas variáveis}
•{Linear}/{MedMed}/{Quad}/{Cubic}/{Quart}/{Log}/{Exp}/{Power}/{Sin}/{Lgstic}
... cálculos e representações gráficas de {regressão linear}/{Med-Med}/{regressão
quadrática}/{regressão cúbica}/{regressão quartica}/{regressão logaritmica}/
{regressão exponêncial}/{regressão de potência}/{regressão sinusoidal}/{regressão
logística}
kk
k Visualizar resultados de cálculos estatísticos
kk
Quando realiza um cálculo de regressão, o cálculo dos parâmetro da fórmula de regressão
(tal como a e b na regressão linear y = ax + b) surgêm no ecrã. Pode utilizá-los para obter
resultados de cálculos estatísticos.
Os parâmetros de regressão são cálculados assimque pressiona uma tecla de função para
seleccionar um tipo de regressão quando o gráfico está no ecrã.
6-3-5
kk
kRepresentar gráficamente resultados de cálculos estatísticos
kk
Com os resultados dos cálculos dos parâmetros no ecrã, pode representar gráficamente a
fórmula de regressão visualizada, pressionando 6(DRAW).
20000501
Page 15

Cálculos e gráficos estatísticos com duas variáveis
kk
k Gráfico de regressão linear
kk
A regressão linear utiliza o método de mínimo quadrático para desenhar um linha recta que
passa perto do maior número de pontos possivel e retoma os valores para apendente e
intercepção y (coordenada y quando x = 0) da linha.
A representação gráfica desta relação é um gráfico linear de regressão.
4(CALC)c(Linear)
6(DRAW)
O fórmula modelo da regressão linear é o seguinte:
6-3-6
y = ax + b
a
............. coeficiente de regressão (pendenete)
b ............. termo de constante de regressão (intercepção)
r ............. coeficiente de correlação
2
r
............ coeficiente de determinação
MSe ........ quadrados médios de erro
kk
k Gráfico Med-Med
kk
Quando se suspeita que existam numeros valores extremos, pode se utilizar um gráfico
Med-Med em vez do método do mínimo quadrático, que é semelhante à regressão linear
mas minimiza os efeitos dos valores extremos.
4(CALC)d(MedMed)
6(DRAW)
A fórmula modelo do gráfico Med-Med é o seguinte:
y = ax + b
a .............
pendente do gráfico Med-Med
b ............. intersecção do gráfico Med-Med
# Introduza um inteiro positivo para os dados de
frequência. Outros tipos de valores (décimais,
por exemplo) originam um erro.
20010102
Page 16

Cálculos e gráficos estatísticos com duas variáveis
kk
k Gráfico de regressão quadrática/cúbica /quártica
kk
Um gráfico de regressão quadrática, cúbica/quártica representa a ligação entre pontos de
dados de um diagrama de dispersão. Utiliza o método de mínimo quadrático para desenhar
um linha curva que passa perto do maior número de pontos de dados possivel. A fórmula
que representa isto é a regressão quadrática, cúbica/quártica.
Ex. Regressão quadrática
4(CALC)e(Quad)
6(DRAW)
Regressão quadrática
Fórmula ............... y = ax2 + bx + c
a .............
coeficiente de segunda regressão
6-3-7
b ............. coeficiente de primeira regressão
c ............. termo constante de regressão (intercepção)
2
r
............ coeficiente de determinação
MSe ........ quadrados médios de erro
Regressão cúbica
Fórmula ............... y = ax3 + bx2 + cx + d
a .............
coeficiente de terceira regressão
b ............. coeficiente de segunda regressão
c ............. coeficiente de primeira regressão
d ............. termo constante de regressão (intercepção)
2
r
............ coeficiente de determinação
MSe ........ quadrados médios de erro
Regressão quártica
Fórmula ............... y = ax4 + bx3 + cx2 + dx + e
a .............
coeficiente de quarta regressão
b ............. coeficiente de terceira regressão
c ............. coeficiente de segunda regressão
d ............. coeficiente de primeira regressão
e ............. termo constante de regressão (intercepção)
2
r
............ coeficiente de determinação
MSe ........ quadrados médios de erro
20010102
Page 17

Cálculos e gráficos estatísticos com duas variáveis
6-3-8
k Gráfico de regressão logarítmica
A regressão logarítmica expressa y como a função logarítmica de x. A fórmula de regressão
logarítmica standart é y = a + b × In x, assim, se X = In x, a fórmula corresponde à fórmula
de regressão linear y = a + bX.
4(CALC)h(Log)
6(DRAW)
A fórmula modelo da regressão logarítmica é:
y = a + b
•
ln x
a .............
termo constsnte de regressão
b ............. coeficiente de regressão
r .............. coeficiente de correlação
2
r
............ coeficiente de determinação
MSe ........ quadrados médios de erro
k Gráfico de regressão exponêncial
A regressão exponêncial expressa y como uma proporção da função exponêncial de x. A
fórmula de regressão exponêncial standart é y = a × ebx, assim se tirarmos os logarítmos de
ambos os lados, temos In y = In a + bx. A seguir, se tivermos Y = In y e a = In a, ta fórmula
corresponde à fórmula de regressão linear Y = a + bx.
4(CALC)i(Exp)
6(DRAW)
A fórmula modelo da regressão exponêncial é:
bx
y = a • e
a ............. coeficiente de regressão
b ............. termo constsnte de regressão
r .............. coeficiente de correlação
2
r
............ coeficiente de determinação
MSe ........ quadrados médios de erro
20010102
Page 18

Cálculos e gráficos estatísticos com duas variáveis
kk
k Gráfico de regressão de potência
kk
A regressão de potência expressa y como uma proporção da potência de x. A fórmula de
regressão de potência standart é y = a × xb, se tirarmos os logarítmos de ambos os lados,
temos In y = In a + b × In x. A seguir, se X = In x, Y = In y e a = In a a fórmula corresponde à
fórmula de regressão linear Y = a + bX.
4(CALC)j(Power)
6(DRAW)
6-3-9
A fórmula modelo da regressão de potência é:
y = a • x
b
a ............. coeficiente de regressão
b ............. regressão de potência
r .............. coeficiente de correlação
r2............. coeficiente de determinação
MSe ........ quadrados médios de erro
kk
kGráfico de regressão sinusoidal
kk
A regressão sinusoidal aplica-se melhor para dados cíclicos.
A fórmula modelo da regressão sinusoidal é:
y = a·sin(bx + c) + d
Com a lista de dados estatísticos no ecrã, realize a seguinte operação:
4(CALC)v(Sin)
6(DRAW)
Desenhar um gráfico de regressão sinusoidal faz com que o juste da unidade angular da
calculadora mude automáticamente para Rad (radiais) A unidade angular não muda quando
realiza um cálculo de regressão sinusoidal sem desenhar o gráfico.
• Alguns tipos de dados podem levar algum tempo a serem calculados, o que não quer dizer
mau funcionamento da calculadora.
20010102
Page 19

Cálculos e gráficos estatísticos com duas variáveis
6-3-10
kk
k Gráfico de regressão logística
kk
A regressão logística aplica-se melhor a fenómenos baseados no tempo em que existe um
aumento contínuo até se alcançar o ponto de saturação.
A fórmula modelo da regressãologística é:
y =
4(CALC)l(Lgstic)
6(DRAW)
• Alguns tipos de dados podem levar algum tempo a serem calculados, o que não quer dizer
mau funcionamento da calculadora.
kk
k Cálculo residual
kk
Os pontos de marcação actuais (coordenadas y) e a distância do modelo de regressão
podem ser calculados durante cálculos de regressão.
Com a lista de dados estatístico no ecrã, chame o ecrã de ajustes básicos e especifique
LIST ("List 1" a "List 20") para “Resid List”. Os dados do cálculo residual são armazenados
na lista específica.
A distância vertical dos pontos de marcação até ao modelo de regressão serão
armazenados na lista.
Os pontos maiores que o modelo de regressão são positivos, enquanto que os menores são
negativos.
O cálculo residual pode realizar-se e armazenar-se para todos os modelos de regressão.
c
1 + ae
–bx
# Qualquer dado que exista na lista
seleccionada é apagado. O resto de cada
ponto é armazenado na mesma precedência
dos dados utilizados como modelo.
20000501
Page 20

Cálculos e gráficos estatísticos com duas variáveis
kk
k Visualizar os resultados de um cálculo de um gráfico de duas
kk
6-3-11
variáveis desenhadas
As estatísticas de duas variáveis podem ser expressas quer como gráficos quer como
valores de parâmetro. Quando este gráficos são visualizados os resultados dos cálculos de
duas variáveis surgem como a seguir se demonstra quando pressiona
4(CALC)b(2VAR).
• Utilize c para vizualizar os items que não surgem no ecrã.
o ............... média dos dados
armazenados na xList
Σx ............. soma dos dados
armazenados na xList
Σx2........... soma dos quadrados dos
dados armazenados na
xList
xσn ............ desvio standart da
população dos dados
armazenados na xList
xσn-1 .......... desvio standart da amostra
dos dados armazenados
na xList
n ............... número de dados
p ............... média dos dados
armazenados na yList
Σy ............. soma dos dados
armazenados na
yList
Σy2...... soma dos quadrados dos
dados armazenados na yList
yσn ...... desvio standart da
população dos dados
armazenados na yList
yσn-1 .... desvio standart da amostra
dos dados armazenados
na yList
Σxy ..... soma de dados armazenados na
xList e yList
minX ... mínimo de dados armazenados na
xList
maxX .. máximo de dados armazenados na
xList
minY ... mínimo de dados armazenados na
yList
maxY .. máximo de dados armazenados na
yList
kk
k Copiar uma fórmula de gráfico de regressão para o modo GRPH
kk
Pode copiar os resultados dos cálculos da fórmula de regressão para a área de fórmula
gráfica do modo GRPH
1. Pressione 5(COPY) para copiar a fórmula de regressão que produziu os dados
visualizados para a área de fórmula gráfica*1 do modo GRPH
2. Pressione w para salvar a fórmula gráfica copiada e regressar ao ecrã anterior.
*1Não pode editar fórmulas de regressão para
fórmulas de gráfico no modo GRPH
•
TBL armazená-lo e compará-lo.
•
TBL.
20000501
•
TBL.
•
TBL
Page 21

Cálculos e gráficos estatísticos com duas variáveis
6-3-12
kk
k Gráficos múltiplos
kk
Pode desenhar mais do que um gráfico no mesmo ecrã, utilizando o procedimento da
secção "Modificar parâmetros de Gráfico" para especificar a condição desenhar (On)/não
desenhar (Off) dos dois ou dos três gráficos para desenhar On e de seguida pressionar
6(DRAW)(consultar página 6-1-4). Depois de desenhar os gráficos, pode seleccionar qual
a fórmula gráfica a utilizar quando realiza istatísticas de uma variável ou cálculos de
regressão.
4(CALC)
c(Linear)
•O texto no topo do ecrã indica o gráfico seleccionado (StatGraph1 = gráfico 1,
StatGraph2 = gráfico 2, StatGraph3 = gráfico 3).
1. Pressione c. O nome do gráfico no topo do ecrã muda.
2. Quando o gráfico que pretende estiver seleccionado, pressione w.
Agora pode utilizar o procedimento na secção "Visualizar o resultado dos cálculos de um
gráfico de duas variáveis desenhadas" da página 6-3-11 para realizar cálculos estatísticos.
20010102
Page 22

Cálculos e gráficos estatísticos com duas variáveis
6-3-13
k Sobrepor uma função gráfica a um gráfico estatístico
Descrição
Pode sobrepor um gráfico estatístico de duas variáveis com qualquer outra função gráfica
que queira.
Ajustes básicos
1. A partir dos menu principal, entre o modo STAT.
Execução
2. Introduza os dados numa lista e desenhe o gráfico estatístico.
3. Visualize o menu de funções gráficas e introduza a função que pretende sobrepor ao
gráfico estatístico.
4. Represente gráficamente a função.
20000501
Page 23

Cálculos e gráficos estatísticos com duas variáveis
6-3-14
○○○○○
Exemplo Introduza os dois conjuntos de dados seguintes. A seguir, desenhe os
pontos dos dados num diagrama de dispersão e sobreponha a função
gráfica y = 2ln x.
0.5, 1.2, 2.4, 4.0, 5.2,
–2.1, 0.3, 1.5, 2.0, 2.4
Procedimento
1 m STAT
2 a.fwb.cw
c.ewewf.cw
e
-c.bwa.dw
b.fwcwc.ew
1(GRPH)b(S-Gph1)
3 5(DefG)
cIvw(Registo Y1 = 2In x)
4 6(DRAW)
Ecrã de reultados
# Também pode utilizar a função traçar, etc.
para desenhar gráficos de funções.
# Gráficos que não sejam de coordenada
rectangular não podem ser desenhados.
# Se pressionar i enquanto estiver a introduzir
uma função, regressa a expressão á sua
condição anterior.
Pressionar!i(QUIT) apaga a expressão
introduzida e regressa à lista de dados
estatísticos.
20000501
Page 24

Realizar cálculos estatísticos
6-4-1
6-4 Realizar cálculos estatísticos
Todos os cálculos estatísticos até agora foram realizados depois de visualizar-se um
gráfico. Os procedimentos seguintes podem ser utilizados apenas para realizar cálculos
estatísticos.
uu
u Especificar listas de dados de cálculos estatísticos
uu
Tem de introduzir os dados estatísticos para o cálculo que pretende realizar e especificar
onde se encontra localizado antes de iniciar o cálculo. Visualize os dados estatísticos e de
seguida pressione 2(CALC)e(Set).
O significado de cada item é o seguinte:
1Var XList............ Localização dos valores x de estatísticas de uma variável
(XList)
1Var Freq ............ Localização dos valores de frequência de estatísticas de uma
2Var XList............ Localização dos valores x de estatísticas de duas variáveis
2Var YList ............ Localização dos valores y e estatísticas de duas variáveis
2Var Freq ............ Localização dos valores de frequência de estatísticas de duas
variável (Frequency)
(XList)
(YList)
variáveis (Frequency)
• Os cálculos nesta secção são realizados com base nas especificações anteriores.
20000501
Page 25

Realizar cálculos estatísticos
kk
kCálculos estatísticos de uma variável
kk
No exemplos anteriores os resultados dos cálculos estatísticos eram visualizados depois de
sererm desenhados os gráficos. Estes eram expressões numéricas das caracteristicas das
variáveis utilizadas no ecrã gráfico.
Estes valores também podem ser obtidos directamente visualizando a lista de dados
estatísticos, pressionando 2(CALC)b(1VAR).
A seguir, pressione f ou cpara visualizar o ecrã de resultados de cálculos estatísticos
de modo a ver as características das variáveis.
Para mais detalhes sobre o significado destes valores estatísticos, consulte a secção
"Visualizar os resultados de um cálculo de um gráfico de uma variável desenhadas" (página
6-2-4).
kk
k Cálculos estatísticos de duas varíáveis
kk
Nos exemplos anteriores desde "Gráfico de regressão linear" até "Gráfico de regressão
logística", o resultados dos cálculos esatísticos eram visualizados depois de serem
desenhados os gráficos. Estes eram expressões numéricas das características das
variáveis utilizadas no ecrã gráfico.
Estes valores também podem ser obtidos directamente visualizando a lista de dados
estatísticos, pressionando 2(CALC)c(2VAR).
6-4-2
A seguir, pressione f ou cpara visualizar o ecrã de resultados de cálculos estatísticos
de modo a ver as características das variáveis.
Para mais detalhes sobre o significado destes valores estatísticos, consulte a secção
"Visualizar os resultados de um cálculo de um gráfico de duas variáveis desenhadas"
(página 6-3-11).
20000501
Page 26

Realizar cálculos estatísticos
6-4-3
kCálculo de regressão
Nas explicações desde "Gráfico de regressão linear" até "Gráfico de regressão logística", os
resultados dos cálculos de regressão eram visualizados depois de serem desenhados os
gráficos. Aqui, cada valor de coeficiente da linha e da curva de regressão é expresso como
um número.
Pode determinar directamente a mesma expressão a partir do ecrã de introdução de dados.
Pressione 2(CALC)d(REG) para visualizar o menu de opções que contem os seguintes
items:
•{Linear}/{MedMed}/{Quad}/{Cubic}/{Quart}/{Log}/{Exp}/{Power}/{Sin}/{Lgstic} ...
parâmetros de {regressão linear}/{Med-Med}/{regressão quadrática}/{regressão cúbica}/
{regressão quártica}/{regressão logarítmica}/{regressão exponêncial}/
{regressão de potência}/{regressão sinusoidal}/ {regressão logística}
○○○○○
Exemplo Visualizar parâmetro de regressão de uma variável
2(CALC)d(REG)b(Linear)
Os significados dos parâmetros que surgem neste ecrã são os mesmos do "Gráfico de
regressão linear" e "Gráfico de regressão logística".
20010102
Page 27

Realizar cálculos estatísticos
6-4-4
k Cálculo de valor estimado ( , )
Depois de desenhar um gráfico de regressão com o modo STAT, pode utilizar o modo RUN
MAT para calcular os valores estimados para os parâmetros x e y do gráfico de regressão
○○○○○
Exemplo Realizar a regressão de potência utilizando os
dados ao lado e estimar os valores de e quando
xi = 20 e yi = 1000
1. A partir do menu principal, entre o modo STAT.
2. Introduza os dados na lista e desenhe o gráfico de regressão linear.
xi yi
10 1003
15 1005
20 1010
25 1011
30 1014
•
3. A partir do menu principal, entre o modo RUN
4. Pressione as teclas na seguinte sequência:
ca(valor de xi)
K6(g)4(STAT)c( )w
O valor estimado de é visualizado para xi = 20.
baaa(valor de yi)
4(STAT)b( )w
O valor estimado de é visualizado para yi = 1000.
# Não pode obter valores estimados para Med-
Med, regressão quadrática, regressão cúbica,
20000501
•
MAT.
regressão cúbicam regressão sinusoidal ou
gráfico de regressão logísitca.
Page 28

Realizar cálculos estatísticos
6-4-5
k Cálculo de distribuição de probabilidades
Pode calcular distribuições de probabilidade para estatísticas de uma variável com o modo
•
RUN
MAT.
Pressione K6(g)1(PROB) para visualizar o menu de funções que contem os
seguintes items:
•{P(}/{Q(}/{R(} ... obtem o valor {P(t)}/{Q(t)}/{R(t)} da probabilidade
•{t(} ... {obtem o valor da variável normalizada t(x)}
•A probabilidade P(t), Q(t) e R(t) e a variável normalizada t(x) são cálculadas utilizando
as seguintes fórmulas:
P (t)Q
○○○○○
(t)R
(t)
Exemplo A tabela seguinte contem os resultados das medições da altura de 20
estudantes universitários. determine qual a percentagem de
estudantes que se encontram no limite entre 160.5 cm e 175.5 cm. E
ainda qual a percentagem de estudantes que medem 175.5 cm?
Nº de classe
Altura (cm) Frequência
1 158.5 1
2 160.5 1
3 163.3 2
4 167.5 2
5 170.2 3
6 173.3 4
7 175.5 2
8 178.6 2
9 180.4 2
10 186.7 1
20000501
Page 29

Realizar cálculos estatísticos
6-4-6
1.Introduza os dados da altura na lista 1 e os dados de frequência na lista 2.
2. Realize os cálculos estatísticos de uma variável
*1
2(CALC)e(Set)
c2(LIST)cwi
2(CALC)b(1VAR)
3. Pressione m, seleccione o modo RUN
•
MAT, pressione K6(g)1(PROB) e
chame o menu de cálculo de probabilidades (PROB).
1(PROB)i(t() bga.f)w
(variável normalizada t para 160.5cm) Resultado:–1.633855948
( –1.634)
1(PROB)i(t() bhf.f)w
(variável normalizada t para 175.5cm) Resultado: 0.4963343361
( 0.496)
1(PROB)f(P()a.ejg)-
1(PROB)f(P()-b.gde)w
(Percentagem do total) Resultado: 0.638921
(63.9% do total)
1(PROB)h(R()a.ejg)w
(Percentil) Resultado: 0.30995
(31.0 percentil)
*1
Apenas pode obter a variável normalizada
imediatamente após realizar cálculos
estatísticos de uma variável.
20000501
Page 30

Realizar cálculos estatísticos
6-4-7
kDesenhar um gráfico de distribuição de probabilidades
Descrição
Pode desenhar um gráfico de distribuição de probabilidades utilizando gráficos manuais com o
modo RUN
Ajustes básicos
Execução
•
MAT.
1. A partir do menu principal entre o modo RUN
•
MAT.
2. Introduza os comandos para desenhar o gráfico de coordenada rectangulares.
3. Introduza o valor de probabilidade.
20000501
Page 31

Realizar cálculos estatísticos
6-4-8
○○○○○
Exemplo Desenhar o gráfico de probabilidades P (0.5) graph.
Procedimento
1 m RUN
2 K6(g)6(g)2(SKTCH)b(Cls)w
2(SKTCH)e(GRPH)b(Y=)
3 K6(g)1(PROB)f(P()a.fw
•
MAT
Ecrã de resultados
20000501
 Loading...
Loading...