
Engineer-to-Engineer Note EE-263
a
Technical notes on using Analog Devices DSPs, processors and development tools
Contact our technical support at dsp.support@analog.com and at dsptools.support@analog.com
Or vi sit our o n-li ne r esou rces htt p:/ /www.analog.com/ee-notes and http://www.analog.com/processors
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors
Contributed by Boris Lerner Rev 1 – February 3, 2005
Introduction
The advance of modern highly paralleled
processors, such as the Analog Devices
TigerSHARC® family of processors, requires
finding efficient ways to parallel
implementations of many standard algorithms.
This applications note not only explains how the
fastest 16-bit FFT implementation on the
TigerSHARC works, but also provides guidance
about algorithm development, so you can apply
similar techniques to other algorithms.
Generally, most algorithms have several levels of
optimization, which are discussed in detail in this
note. The first and most straightforward level of
optimization is the paralleling of instructions, as
permitted by the processor's architecture. This is
simple and boring. The second level of
optimization is loop unrolling and software
pipelining to achieve maximum parallelism and
to avoid pipeline stalls. Although more complex
than the simple parallelism of level one, this can
be done in prescribed steps without a firm
understanding of the algorithm and, thus,
requires little ingenuity. The third level is
restructuring the math of the algorithm to still
produce valid results, but fit the processor’s
architecture better. This requires a thorough
understanding of the algorithm and, unlike
software pipelining, there are no prescribed steps
that lead to the optimal solution. This is where
most of the fun in writing optimized code lies.
In practical applications, it is often unnecessary
to go through all of these levels. When all of the
levels are required, it is best to perform these
levels of optimization in reverse order. By the
time the code is fully pipelined, it is too late to
try to change the fundamental underlying
algorithm. Thus, a programmer would have to
think about the algorithm structure first and
organize the code accordingly. Then, levels one
and two (paralleling, unrolling, and pipelining)
are usually done at the same time.
The code to which this note refers is supplied by
Analog Devices. A 256-point FFT is used as the
specific example, but the mathematics and ideas
apply equally to other sizes (no smaller than 16
points).
As we will see, the restructured algorithm breaks
down the FFT into much smaller parts that can
then be paralleled. In the case of the 256-point
FFT (its code listing is at the end of this
applications note), the FFT is split into 16 FFTs
of 16 points each and each, 16-point FFT is done
in radix-4 fashion (i.e., each has only two
stages). If we were to do a 512=point FFT, we
would have to do 16 FFTs of 32 points each
(and, also, 32 FFTs of 16 points each), each 32point FFT would have the first two stages done
in radix-4 and the last stage in radix-2. These
differences imply that it would be difficult to
write the code that is FFT size-generic. Although
the implemented algorithm is generic and applies
equally well to all sizes, the code is not, and it
must be hand-tuned to each point size to be able
to take full advantage of its optimization.
Copyright 2005, Analog Devices, Inc. All rights reserved. Analog Devices assumes no responsibility for customer product design or the use or application of
customers’ products or for any infringements of patents or rights of others which may result from Analog Devices assistance. All trademarks and logos are property
of their respective holders. Information furnished by Analog Devices Applications and Development Tools Engineers is believed to be accurate and reliable, however
no responsibility is assumed by Analog Devices regarding technical accuracy and topicality of the content provided in Analog Devices’ Engineer-to-Engineer Notes.
a
With all this in mind, let us dive into the
fascinating world of fixed-point FFTs in the land
of the TigerSHARC.
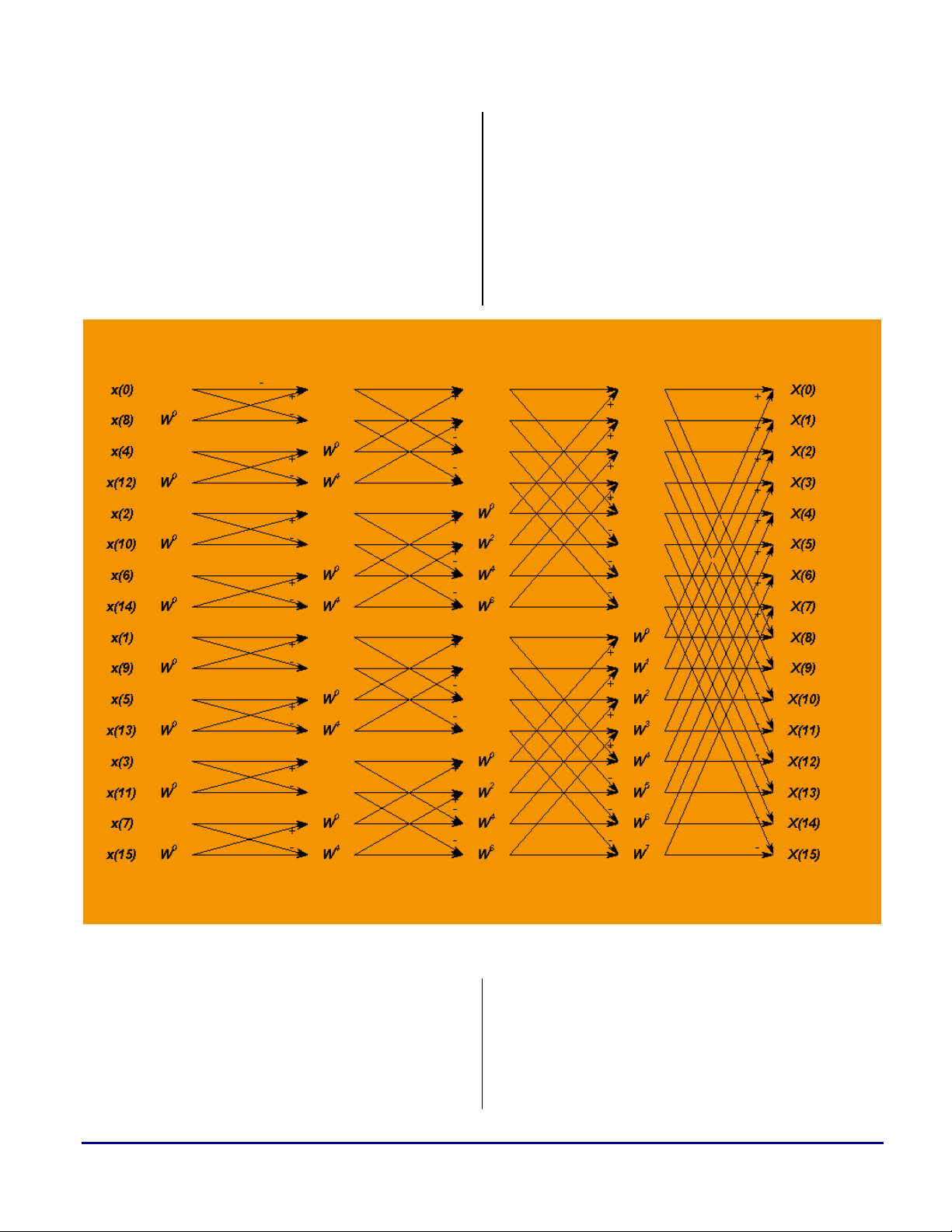
Standard Radix-2 FFT Algorithm
Figure 1 shows a standard 16-point radix-2 FFT
implementation, after the input has been bitreversed. Traditionally, in this algorithm, stages
1 and 2 are combined with the required bit
reversing into a single optimized loop (since
these two stages require no multiplies, only adds
and subtracts). Each of the remaining stages is
usually done by combining the butterflies that
share the same twiddle factors together into
groups (so the twiddles need only to be fetched
once for each group).
Figure 1. Standard Structure of the 16-Point FFT
Since TigerSHARC processors offer vectorized
16-bit processing on packed data, we would like
to parallel this algorithm into at least as many
parallel processes as the TigerSHARC can
handle. An add/subtract instruction of the
TigerSHARC (which is instrumental in
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 2 of 12
computing a fundamental butterfly) can be
paralleled to be performed on eight 16-bit values
per cycle (four in each compute block of the
TigerSHARC processor). Since data is complex,
this equates to four add/subtracts of data per
cycle. Thus, we would like to break the FFT into

+
=
a
at least four parallel processes. Looking at the
diagram of Figure 1, it is clear that we can do
this by simply combining the data into blocks,
four points at a time, i.e.:
1st block = {x(0), x(8), x(4), x(12)}
2nd block = {x(2), x(10), x(6), x(14)}
3rd block = {x(1), x(9), x(5), x(13)}
4th block = {x(3), x(11), x(7), x(15)}
These groups have no interdependencies and will
parallel very nicely for the first two stages of the
FFT. After that we are in trouble and the
parallelism is gone. At this point, however, we
could re-arrange the data into different blocks to
ensure that the rest of the way the new blocks do
not crosstalk to each other and, thus, can be
paralleled. A careful examination shows that the
required re-arrangement is an operation of
interleaving (or de-interleaving), with new
blocks given by:
1st block = {x(0), x(2), x(1), x(3)}
comes from this is that N must be a perfect
square. As it turns out, we can dispose of this
requirement, but that will be discussed later. At
this time we are concerned with the 256-point
FFT and, as luck would have it,
2
16256 = .
So, which shall we parallel, the rows or the
columns? The answer lies in the TigerSHARC
processor’s vector architecture. When the
TigerSHARC processor fetches data from
memory, it fetches it in chunks of 128 bits at a
time (i.e., four 16-bit complex data points) and
packs it into quad or paired (for SIMD fetches)
registers. Then it vectorizes processing across the
register quad or pair. Thus, it is the columns of
the matrix that we want to parallel (i.e., we
would like to structure our math so that all the
columns of the matrix are independent from one
another).
Now that we know what we would like the math
to give us, it is time to do this rigorously in the
language of mathematics.
2nd block = {x(8), x(10), x(9), x(11)}
3rd block = {x(4), x(6), x(5), x(7)}
4th block = {x(12), x(14), x(13), x(15)}
Another way to look at these new blocks is as the
4x4 matrix transpose (where blocks define the
matrix rows). Of course, there is a significant
side effect—after the data re-arrangement the last
stages will parallel, but will not produce data in
the correct order. Maybe we can compensate for
this by starting with an order other than the bitreverse we had started with, but let us leave this
detail for the rigorous mathematical analysis that
comes later.
At this time, the analysis of the 16 point FFT
seems to suggest that, in general, given an N
point FFT, we would like to view it in two
dimensions as a
NN × matrix of data and
parallel-process the rows or columns, then
transpose the matrix and parallel-process the
rows or columns again. Another requirement that
Mathematics of the Algorithm
The following notation will be used:
N = Number of points in the original FFT (256 in
our example),
NM = ,
∧
x will stand for the Discrete Fourier Transform
(henceforth abbreviated as DFT) of
Now, given signal x,
−
2
ink
−
1
∧
M
m
N
=
0
k
−
2
inm
π
−
1
=
0
M
N
=
l
N
−
1
0
−=−
101
MmM
∑∑∑
−
2
=
0
l
inl
π
M
=+
where:
mMlxlx
(1)
m
)(:)(
x.
+−
)(2
mMlin
ππ
N
)()()(
emMlxekxnx
−
2
inm
π
−
1
M
∑∑∑
=
0
m
∧
N
m
=+==
)()(
nxeemMlxe
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 3 of 12

∧
≤
and
x is this function’s M–point DFT. Now, we
m
view the output index n as arranged in an M x M
matrix (i.e., 1,0 , −<
−
∧
M
∑
=
m
−
2
π
ism
itm
N
∧
m
−
1
M
∑
m
=
0
since
−
2
π
M
x , being an M–point DFT, is periodic
+= MtstMsn ) Thus,
π
+−
)(2
1
0
∧
m
mtMsi
N
)(
txee
∧
m
)()(
tMsxetMsx
=+=+
with period = M. Thus,
ism
−
π
2
M
−
∑
m
1
=
0
*
M
t
∧
∧
*
)( )()(
sxmxetMsx
==+
t
, (2)
where:
itm
−
2
π
*
=
t
∧
*
x is this function’s M–point DFT.
and
t
∧
N
m
)(:)(
txemx
(3)
a
L
xxxx
)0()0()0()0(
⎡
⎢
⎢
⎢
L
L
xxxx
⎢
⎢
⎢
⎣
3.
We now compute parallel FFTs on columns
L
xxxx
(as mentioned before, TigerSHARC
processors do this very efficiently) obtaining:
⎡
⎢
⎢
⎢
⎢
L
L
L
xxxx
xxxx
⎢
⎢
⎢
⎣
4.
We point-wise multiply this by matrix
2≤≤−
itm
π
⎡
256
e
⎢
⎣
L
xxxx
⎤
⎥
⎦
15,0
mt
⎤
15210
⎥
xxxx
)1()1()1()1(
15210
⎥
⎥
)2()2()2()2(
15210
⎥
MMMMM
⎥
⎥
)15()15()15()15(
15210
⎦
∧∧∧∧
⎤
)0()0()0()0(
15210
⎥
∧∧∧∧
⎥
)1()1()1()1(
xxxx
15210
⎥
∧∧∧∧
15210
∧∧∧∧
15210
⎥
)2()2()2()2(
⎥
MMMMM
⎥
⎥
)15()15()15()15(
⎦
Implementation of the Algorithm
Equations (1), (2), and (3) show how to compute
the DFT of x using the following steps (here we
go back to our specific example of N=256,
M=16):
1.
Arrange the 256 points of the input data x(n)
linearly, but think of it as a 16x16 matrix:
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
2.
Using equation (1), re-write as:
L
L
L
L
)15()2()1()0(
xxxx
⎤
⎥
)31()18()17()16(
xxxx
⎥
⎥
)47()34()33()32(
xxxx
⎥
MMMMM
⎥
⎥
)255()242()241()240(
xxxx
⎦
to obtain
−
∧
⎡
⎢
0
∧
⎢
⎢
0
⎢
∧
⎢
0
⎢
⎢
∧
⎢
0
⎣
02
256
−
02
256
−
02
256
−
02
256
−
∧
1
∧
∧
1
∧
1
02
256
−
12
256
1
−
22
256
−
152
256
−
∧
2
∧
2
∧
2
∧
2
02
256
−
22
256
−
42
256
−
302
256
L
L
L
L
∧
15
∧
15
∧
15
∧
15
which, according to equation (3) is precisely
*
⎡
0
⎢
*
1
⎢
*
⎢
2
⎢
*
0
*
1
*
2
*
0
*
1
*
2
⎢
*
⎢
15
⎣
Now we would like to compute the 16-point
5.
FFTs of
*
15
t
*
15
)(*mx
, but these are arranged to be
L
L
L
L
*
xxxx
xxxx
xxxx
xxxx
⎤
)15()2()1()0(
0
⎥
*
)15()2()1()0(
1
⎥
*
⎥
)15()2()1()0(
2
⎥
MMMMM
⎥
*
⎥
)15()2()1()0(
15
⎦
paralleled in rows instead of columns. Thus,
we have to transpose to obtain
−
iiii
ππππ
02
⎤
256
)0()0()0()0(
exexexex
⎥
−
152
iiii
ππππ
⎥
256
)1()1()1()1(
exexexex
⎥
−
302
iiii
ππππ
⎥
256
)2()2()2()2(
exexexex
⎥
⎥
MMMMM
⎥
−
2252
iiii
ππππ
⎥
256
)15()15()15()15(
exexexex
⎦
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 4 of 12

*
⎡
0
⎢
*
0
⎢
*
⎢
0
⎢
*
1
*
1
*
1
*
2
*
2
*
2
L
L
L
⎢
*
⎢
0
⎣
We compute parallel FFTs on the columns
6.
*
1
*
2
L
*
⎤
xxxx
)0()0()0()0(
15
⎥
*
xxxx
)1()1()1()1(
15
⎥
*
⎥
xxxx
15
*
xxxx
15
)2()2()2()2(
⎥
MMMMM
⎥
⎥
)15()15()15()15(
⎦
and use equation (2) to obtain
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
L
L
L
L
∧∧∧∧
⎤
)15()2()1()0(
xxxx
⎥
∧∧∧∧
⎥
xxxx
)31()18()17()16(
⎥
∧∧∧∧
xxxx
⎥
)47()34()33()32(
⎥
MMMMM
∧∧∧∧
xxxx
⎥
⎥
)255()242()241()240(
⎦
This is the FFT result that we want, and it is in
the correct order! The math is done, and we are
ready to consider the programming
implementation. In the following discussion, we
will refer to the steps outlined above as Steps 1
through 6.
a
for each of the four sets of the four FFTs (instead
of doing both stages for each set).
Step 4 is a point-wise complex multiply (256
multiplies in total), and Step 5 is a matrix
transpose. These two steps can be combined—
while multiplying the data points we can store
them in a transposed fashion.
Step 6 is identical to Step 3—we have to
compute 16 parallel 16-point FFTs on the
columns of our new input matrix. This part need
not need be written. We can simply branch to the
code of Step 3, remembering to exit the routine
once the FFTs are finished (instead of going on
to the Step 4, as before).
Figure 2 represent buffers containing the data,
and arrows correspond to transformations of data
between buffers.
Programming Implementation
We will go through the steps of the previous
section, one step at a time.
Steps 1 and 2 do not need to be programmed.
The input data is already arranged in the proper
order.
Step 3 requires us to compute 16 parallel 16point FFTs on the columns of the input matrix.
As mentioned before, the TigerSHARC can
easily parallel four FFTs at a time, thanks to its
vector processing, so we can do four FFTs at a
time and repeat this process four times to
compute all 16 FFTs. 16-point FFTs can be done
very efficiently in radix-4, resulting in two
stages, at four butterflies per stage. To minimize
overhead, it is more efficient to compute only the
first stage for each of the four sets of the four
FFTs, followed by computing the second stage
Figure 2. Block Diagram of the Code
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 5 of 12

a
Pipelining the Algorithm - Stage 1
Let us concentrate on Step 3 first.
Mnemonic Operation
F1
F2
F3
F4
AS1 F1+/-F2
AS2 F3+/-F4
MPY1
M1 Move MPY1 into compute block register
MPY2
Fetch 4 complex Input1 of the 4
butterflies=4 32-bit values
Fetch 4 complex Input2 of the 4
butterflies=4 32-bit values
Fetch 4 complex Input3 of the 4
butterflies=4 32-bit values
Fetch 4 complex Input4 of the 4
butterflies=4 32-bit values
1st half of (F1-F2)*(-i)
Note that we can do only 2 complex
mpys per cycle
2nd half of (F1-F2)*(-i)
Note that we can do only 2 complex
mpys per cycle
Table 1 lists the operations necessary to perform
four parallel radix-4 complex butterflies of stage
1 in vector fashion of the TigerSHARC
processor. Actually, this portion is the same for
stages other than first, except that the other
stages also require a complex twiddle multiply at
the beginning of the butterfly. This makes other
stages more complicated, and they will be dealt
with in the next section.
Cycle/
Operat
JALU
ion
1 F1 S4--- AS3--
2 F2 S1-- MPY1- AS2-
3 F3 S2-- M1-, MPY2- AS4--
4 F4 S3-- M2- AS1
5 F1+ S4-- AS3-
6 F2+ S1- MPY1 AS2
7 F3+ S2- M1, MPY2 AS4-
KA
LU
MAC ALU
M2 Move MPY2 into compute block register
AS3
AS4
S1
S2
S3
S4
Table 1. Single Butterfly of Stage 1 Done Linearly –
Logical Implementation
(F3 + F4)+/-(F1+F2) =Output1 and
Output3 of the 4 butterflies
(F3 – F4)+/-(F1-F2)*(-i) =Output2 and
Output 4 of the 4 butterflies
Store (Output1) of the 4 butterflies=4 32-
bit values
Store (Output2) of the 4 butterflies=4 32-
bit values
Store (Output3) of the 4 butterflies=4 32-
bit values
Store (Output4) of the 4 butterflies=4 32-
bit values
8 F4+ S3- M2 AS1+
9 F1++ S4- AS3
10 F2++ S1 MPY1+ AS2+
11 F3++ S2 M1+, MPY2+ AS4
12 F4++ S3 M2+ AS1++
13 F1+++ S4 AS3+
14 F2+++ S1+ MPY1++ AS2++
15 F3+++ S2+ M1++, MPY2++ AS4+
16 F4+++ S3+ M2++
Table 2. Pipelined Butterflies – Stage 1
AS1++
+
Table 2 shows the butterflies pipelined. A “+” in
the operation indicates the operation that
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 6 of 12

a
corresponds to the next set of the butterflies and
a “-” corresponds to the operation in the previous
set of butterflies. All instructions are paralleled,
and there are no stalls.
Pipelining the Algorithm - Stage 2
To do a butterfly for stage 2, one must perform
the same computations as for stage 1, except for
an additional complex multiply of each of the 16
(4 paralleled x 4 points) inputs at the beginning.
This creates a problem. The original butterfly has
two SIMD complex multiplies in it already.
Adding 8 more makes 10 complex multiplies,
while ALU, fetch, and store remain at 4. This
would make the algorithm unbalanced—too
many multiplies and too few other compute units
will not parallel well. The best that can be done
this way is 10 cycles per vector of butterflies.
It turns out that each of the two original
multiplies (being multiplies by -i) can be
replaced by one short ALU (negate) and one long
rotate. In addition, two register moves are
required to ensure that the data is back to being
packed in long registers for the parallel
add/subtracts that follow. For the vectored
butterfly, this would leave a total of 8 multiplies,
6 ALUs (4 add/subtracts and 2 negates), and 2
shifts (rotates)—perfectly balanced for an 8cycle execution. Also, 4 fetches and 4 stores
leave plenty of room for register moves.
Table 3 lists the operations necessary to perform
vectored (i.e., four parallel) radix-4 complex
butterflies of stage 2 on the TigerSHARC
processor. Things have gotten significantly more
complex!
Mnemonic Operation
F1
F2
F3
F4
MPY1 1st half of F1*twiddle
M1 Move MPY1 into compute block register
MPY2 2nd half of F1*twiddle
M2 Move MPY2 into compute block register
MPY3 1st half of F2*twiddle
M3 Move MPY3 into compute block register
MPY4 2nd half of F2*twiddle
M4 Move MPY4 into compute block register
MPY5 1st half of F3*twiddle
M5 Move MPY5 into compute block register
MPY6 2nd half of F3*twiddle
M6 Move MPY6 into compute block register
MPY7 1st half of F4*twiddle
M7 Move MPY7 into compute block register
MPY8 2nd half of F4*twiddle
M8 Move MPY8 into compute block register
Fetch 4 complex Input1 of the 4
butterflies=4 32-bit values
Fetch 4 complex Input2 of the 4
butterflies=4 32-bit values
Fetch 4 complex Input3 of the 4
butterflies=4 32-bit values
Fetch 4 complex Input4 of the 4
butterflies=4 32-bit values
Table 4 shows the butterflies pipelined. A “+” in
the operation indicates the operation that
corresponds to the next set of the butterflies, and
a “-” corresponds to the operation in the previous
AS1 M1,M2+/-M3,M4
AS2 M5,M6+/-M7,M8
A1 Negate (M1-M3)
set of the butterflies.
MV1
Move (M1-M3) into a pair of the register
that contains A1
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 7 of 12

a
R1
A2 Negate (M2-M4)
MV2
R2
AS3 (F3 + F4)+/-(F1+F2)
AS4
S1 Store 1 of the 4 butterflies=4 32-bit values
S2 Store 2 of the 4 butterflies=4 32-bit values
S3 Store 3 of the 4 butterflies=4 32-bit values
S4 Store 4 of the 4 butterflies=4 32-bit values
Table 3. Single Butterfly of Stage 2 Done Linearly –
Logical Implementation
Rotate the long result of A1,MV1 – now
the low register contains (M1-M3)*(-i)
Move (M2-M4) into a pair of the register
that contains A2
Rotate the long result of A2,MV2 – now
the low register contains (M2-M4)*(-i)
(F3 – F4)+/-(F1-F2)*(-i)
Here (F1-F2)*(-i) was obtained by R1
and R2
7 S1-- M1, MPY2 AS4--
8 S2-- M2, MPY3 AS2-
9 F1+ MV1- M3, MPY4 A1-
10 F2+ M4, MPY5 A2-
11 S3-- M5, MPY6 R1-
12 S4-- M6, MPY7 R2-
13 F3+ MV2- M7, MPY8 AS3-
14 F4+ M8, MPY1+ AS1
15 S1- M1+, MPY2+ AS4-
16 S2- M2+, MPY3+ AS2
17 F1++ MV1 M3+, MPY4+ A1
18 F2++ M4+, MPY5+ A2
19 S3- M5+, MPY6+ R1
All instructions are paralleled, and there are no
stalls. There is still a question of twiddle fetch
which was not addressed, but there are so many
JALU and KALU instruction slots still available
that scheduling twiddle fetches will not cause
any problems (they are actually the same value
per vector, so broadcast reads will bring them in
efficiently).
Cycle/
Operat
JALU KALU MAC ALU
ion
1 F1 MV1-- M3-, MPY4- A1--
2 F2 M4-, MPY5- A2--
3 S3--- M5-, MPY6- R1--
4 S4--- M6-, MPY7- R2--
5 F3 MV2-- M7-, MPY8- AS3--
6 F4 M8-, MPY1 AS1-
20 S4- M6+, MPY7+ R2
21 F3++ MV2 M7+, MPY8+ AS3
22 F4++ M8+, MPY1++ AS1+
23 S1 M1++, MPY2++ AS4
24 S2 M2++, MPY3++ AS2+
25 F1+++ MV1+ M3++, MPY4++ A1+
26 F2+++ M4++, MPY5++ A2+
27 S3 M5++, MPY6++ R1+
28 S4 M6++, MPY7++ R2+
Table 4. Pipelined Butterflies – Stage 2
The multiplies and transpose of Steps 4 and 5 are
very simple to pipeline. They involve only
fetches, multiplies, and stores, so the pipelining
of these parts of the algorithm is not discussed in
detail here.
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 8 of 12

a
The Code
Now, writing the code is trivial. The ADSPTS201 TigerSHARC processor is so flexible that
it takes all the challenge right out of it. Just
follow the pipelines of Table 2 and Table 4 and
the code is done. The resulting code is shown in
Listing 1.
Now, for the bottom line—how much did the
cycle count improve? Table 5 lists cycle counts
for the old and new implementations of the 16bit complex input FFTs. As shown, the cycle
counts have improved considerably.
Points
N
64 302 147
256 886 585
1024 3758 2725
2048 7839 5776
4096 16600 12546
Table 5. Core Clock Cycles for N-Point 16-bit
Complex FFT
Old
Implementation
New
Implementation
Usage Rules
The C-callable complex FFT routine is called as
fft256pt(&(input), &(ping_pong_buffer1),
&(ping_pong_buffer2), &(output));
where:
input -> FFT input buffer,
output -> FFT output buffer,
ping_pong_bufferx are the ping pong buffers.
All buffers are packed complex values in normal
(not bit-reversed) order.
ping_pong_buffer1 and ping_pong_buffer2 must
be two distinct buffers. However, depending on
the routine’s user requirements, some memory
optimization is possible. ping_pong_buffer1 can
be made the same as input if input does not need
to be preserved. Also, output can be made the
same as ping_pong_buffer2. Below is an
example of the routine usage with minimal use of
memory:
fft256pt (&(input), &( input),
&( output), &(output));
To eliminate memory block access conflicts,
input and ping_pong_buffer1 must reside in a
different memory block than ping_pong_buffer2
and output, and the twiddle factors must reside in
a different memory block than the ping-pong
buffers. Of course, all code must reside in a
block that is different from all the data buffers, as
well.
Remarks
The example examined here is that of a 256point FFT. At the time of writing this note, 64point, 1024-point, 2048-point and 4096-point
FFT examples using the algorithm described
above have also been written. In those cases, the
FFTs were viewed as 8x8, 32x32, 32x64, and
64x64 matrices, respectively. The 32-point FFTs
were done in radix-4 (all the way to the last
stage) and the last stage was done in the
traditional radix-2.
The 2048-point FFT was arranged in a matrix of
32 columns and 64 rows. 32 FFTs of 64 points
each are done in parallel on the columns.
Applying a point-wise multiply and transpose
gives a matrix of 64 columns and 32 rows. Doing
64 FFTs of 32 points each in parallel on the
columns completes the algorithm. The only side
effect is that the parallel FFT portion of the code
cannot be re-used (remember, the algorithm
needs it twice) because the number of rows and
columns is no longer the same. This results in
longer source code, but the cycle count
efficiency is just as good.
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 9 of 12

a
Appendix
Complete Source Code of the Optimized FFT
/******************************************************************************************************************************************
fft256pt.asm
Prelim rev. August 10, 2004 BL
This is assembly routine for the complex C-callable 256-point 16-bit FFT on
TigerSHARC family of DSPs.
I. Description of Calling.
1. Inputs:
j4 -> input
j5 -> ping_pong_buffer1
j6 -> ping_pong_buffer2
j7 -> output
2. C-Calling Example:
Fft256pt(&(input), &(ping_pong_buffer1), &(ping_pong_buffer2), &(output));
3. Limitations:
a. All buffers must be aligned on memory boundary which is a multiple of 4.
b. Buffers input.and ping_pong_buffer2 must be aligned on memory boundary
which is a multiple of 256.
c. If memory space savings are required and input does not have to be
preserved, ping_pong_buffer1 can be the same buffer as input with no
degradation in performance.
d. If memory space savings are required, output can be the same buffer
as ping_pong_buffer2 with no degradation in performance.
4. For the code to yield optimal performance, the following must be observed:
a. Buffer input must have been cached previously. This is reasonable to
assume since any engine that would have brought the data into internal
memory, such as a DMA, would also have cached it.
b. input and ping_pong_buffer2 must be located in different memory blocks.
c. ping_pong_buffer1 and ping_pong_buffer2 must be located in different
memory blocks.
d. ping_pong_buffer1 and output must be located in different memory blocks.
e. twiddles and input must be located in different memory blocks.
f. AdjustMatrix and ping_pong_buffer1 must be located in different memory
blocks.
II. Description of the FFT algorithm.
1. All data is treated as complex packed data.
2. An application note will be provided for the description of the math of
the algorithm.
******************************************************************************************************************************************/
//************************* Includes ******************************************************************************************************
#include <defTS201.h>
//*****************************************************************************************************************************************
.section data6a;
.align 4; // allign to quad
.var _AdjustMatrix[256] = "MatrixCoeffs.dat";
.align 4; // allign to quad
.var _twiddles16[32] = "Twiddles16.dat";
//*****************************************************************************************************************************************
.section program;
.global _fft256pt;
//************************************** Start of code ************************************************************************************
_fft256pt:
j2=j4+64;;
j0=j4+0; k1=j6;;
j3=j4+(128+64); LC1=2;; // -----------------------------------r5:4 =br Q[j2+=32]; k3=k31+(_twiddles16+2);; //|F1-- | | | | |
j1=j4+128;; // ------------------------------------
.align_code 4;
_VerticalLoop:
//*************************************** Stage 1 *****************************************************************************************
// 1st time: From j0,j1,j2,j3->_input to k1->_ping_pong_buffer2
// 2nd time: From _ping_pong_buffer2 to _ping_pong_buffer1
// -----------------------------------r7:6 =br Q[j3+=32]; kL1=k31+252;; //|F2-- | | | | |
r1:0 =br Q[j0+=32]; r31=0x80000000;; //|F3-- | | | | |
r3:2 =br Q[j1+=32]; kB3=k31+_twiddles16; sr13:12=r5:4+r7:6, sr15:14=r5:4-r7:6;; //|F4-- | | |AS1-- | |
r5:4 =br Q[j2+=32]; kB1=k1+4;; //|F1- | | | | |
// -----------------------------------r7:6 =br Q[j3+=32]; jL0=252; mr1:0+=r14**r31(C); sr9:8=r1:0+r3:2, sr11:10=r1:0-r3:2;; //|F2- |MPY1-- | |AS2-- | |
r1:0 =br Q[j0+=32]; kL3=k31+32; r24=mr1:0, mr1:0+=r15**r31(C);; //|F3- |MPY2-- |M1-- | | |
r3:2 =br Q[j1+=32]; LC0=4; r25=mr1:0, mr1:0+=r15**r31(C); sr29:28=r5:4+r7:6, sr15:14=r5:4-r7:6;; //|F4- | |M2-- |AS1- | |
r5:4 =br Q[j2+=32]; jB0=kB1; sr17:16=r9:8+r13:12, sr21:20=r9:8-r13:12;; //|F1 | | |AS3-- | |
// -----------------------------------.align_code 4;
_VerFFTStage1: // -----------------------------------r7:6 =br Q[j3+=32]; cb Q[k1+=32]=r17:16; mr1:0+=r14**r31(C); sr9:8=r1:0+r3:2, sr27:26=r1:0-r3:2;; //|F2 |MPY1- | |AS2- |S1-- |
r1:0 =br Q[j0+=32]; cb Q[k1+=-16]=r21:20; r24=mr1:0, mr1:0+=r15**r31(C); sr19:18=r11:10+r25:24, sr23:22=r11:10-r25:24;; //|F3 |MPY2- |M1- |AS4-- |S2-- |
r3:2 =br Q[j1+=32]; cb Q[k1+=32]=r19:18; r25=mr1:0, mr1:0+=r15**r31(C); sr13:12=r5:4+r7:6, sr15:14=r5:4-r7:6;; //|F4 | |M2- |AS1 |S3-- |
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 10 of 12

r5:4 = Q[j2+=-44]; cb Q[k1+=16]=r23:22; sr17:16=r9:8+r29:28, sr21:20=r9:8-r29:28;; //|F1+ | | |AS3- |S4-- |
// ------------------------------------
r7:6 = Q[j3+=-44]; cb Q[k1+=32]=r17:16; mr1:0+=r14**r31(C); sr9:8=r1:0+r3:2, sr11:10=r1:0-r3:2;; //|F2+ |MPY1 | |AS2 |S1- |
r1:0 = Q[j0+=-44]; cb Q[k1+=-16]=r21:20; r24=mr1:0, mr1:0+=r15**r31(C); sr19:18=r27:26+r25:24, sr23:22=r27:26-r25:24;; //|F3+ |MPY2 |M1 |AS4- |S2- |
r3:2 = Q[j1+=-44]; cb Q[k1+=32]=r19:18; r25=mr1:0, mr1:0+=r15**r31(C); sr29:28=r5:4+r7:6, sr15:14=r5:4-r7:6;; //|F4+ | |M2 |AS1+ |S3- |
r5:4 =br Q[j2+=32]; cb Q[k1+=16]=r23:22; sr17:16=r9:8+r13:12, sr21:20=r9:8-r13:12;; //|F1++ | | |AS3 |S4- |
// -----------------------------------r7:6 =br Q[j3+=32]; cb Q[k1+=32]=r17:16; mr1:0+=r14**r31(C); sr9:8=r1:0+r3:2, sr27:26=r1:0-r3:2;; //|F2++ |MPY1+ | |AS2+ |S1 |
r1:0 =br Q[j0+=32]; cb Q[k1+=-16]=r21:20; r24=mr1:0, mr1:0+=r15**r31(C); sr19:18=r11:10+r25:24, sr23:22=r11:10-r25:24;; //|F3++ |MPY2+ |M1+ |AS4 |S2 |
r3:2 =br Q[j1+=32]; cb Q[k1+=32]=r19:18; r25=mr1:0, mr1:0+=r15**r31(C); sr13:12=r5:4+r7:6, sr15:14=r5:4-r7:6;; //|F4++ | |M2+ |AS1++ |S3 |
r5:4 =br Q[j2+=32]; cb Q[k1+=16]=r23:22; sr17:16=r9:8+r29:28, sr21:20=r9:8-r29:28;; //|F1+++ | | |AS3+ |S4 |
// -----------------------------------r7:6 =br Q[j3+=32]; cb Q[k1+=32]=r17:16; mr1:0+=r14**r31(C); sr9:8=r1:0+r3:2, sr11:10=r1:0-r3:2;; //|F2+++ |MPY1++ | |AS2++ |S1+ |
r1:0 =br Q[j0+=32]; cb Q[k1+=-16]=r21:20; r24=mr1:0, mr1:0+=r15**r31(C); sr19:18=r27:26+r25:24, sr23:22=r27:26-r25:24;; //|F3+++ |MPY2++ |M1++ |AS4+ |S2+ |
r3:2 =br Q[j1+=32]; cb Q[k1+=32]=r19:18; r25=mr1:0, mr1:0+=r15**r31(C); sr29:28=r5:4+r7:6, sr15:14=r5:4-r7:6;; //|F4+++ | |M2++ |AS1+++ |S3+ |
// -----------------------------------.align_code 4;
if NLC0E, jump _VerFFTStage1; // -----------------------------------r5:4 =br Q[j2+=32]; cb Q[k1+=16]=r23:22; sr17:16=r9:8+r13:12, sr21:20=r9:8-r13:12;; //|F1++++ | | |AS3++ |S4+ |
// ------------------------------------
//*************************************** Stage 2 *****************************************************************************************
// 1st time: From j0->_ping_pong_buffer2 to k1->_ping_pong_buffer1
// 2nd time: From j0->_ping_pong_buffer1 to k1->_output
.align_code 4;
j0=j6+12*16; j1=-4*16;; // -----------------------------------r7:6 = Q[j0+=-4*16]; r31:30= L[k3+=-2];; //| F1-- | | | | |
r5:4 =cb Q[j0+=-4*16]; r29:28=cb L[k3+=6]; mr1:0+=r7**r31(C);; //| F2-- |MPY1-- | | | |
r3:2 = Q[j0+=-4*16]; LC0=7; r15=mr1:0, mr1:0+=r6**r31(C);; //| F3-- |MPY2-- |M1-- | | |
r1:0 =cb Q[j0+=28*16]; j2=28*16; r14=mr1:0, mr1:0+=r5**r30(C);; //| F4-- |MPY3-- |M2-- | | |
// -----------------------------------r7:6 =cb Q[j0+=-4*16]; k1=j5; r13=mr1:0, mr1:0+=r4**r30(C);; //| F1- |MPY4-- |M3-- | | |
r5:4 =cb Q[j0+=j1]; r12=mr1:0, mr1:0+=r3**r29(C);; //| F2- |MPY5-- |M4-- | | |
r11=mr1:0, mr1:0+=r2**r29(C);; //| |MPY6-- |M5-- | | |
r10=mr1:0, mr1:0+=r1**r28(C);; //| |MPY7-- |M6-- | | |
// -----------------------------------r3:2 = Q[j0+=j1]; r9=mr1:0, mr1:0+=r0**r28(C);; //| F3- |MPY8-- |M7-- | | |
r1:0 =cb Q[j0+=28*16]; r8=mr1:0, mr1:0+=r7**r31(C); sr21:20=r13:12+r15:14, sr23:22=r13:12-r15:14;; //| F4- |MPY1- |M8-- |AS1-- | |
r15=mr1:0, mr1:0+=r6**r31(C);; //| |MPY2- |M1- | | |
kB1=k1+4; r14=mr1:0, mr1:0+=r5**r30(C); sr17:16=r9:8 +r11:10, sr19:18=r9:8 -r11:10;; //| |MPY3- |M2- |AS2-- | |
r7:6 =cb Q[j0+=j1]; r8=r23; r13=mr1:0, mr1:0+=r4**r30(C); sr9=-r23;; //| F1 |MPY4- |M3- |A1-- |MV1-- |
r5:4 =cb Q[j0+=j1]; r31:30=cb L[k3+=-2]; r12=mr1:0, mr1:0+=r3**r29(C); sr23=-r22;; //| F2 |MPY5- |M4- |A2-- | |
r11=mr1:0, mr1:0+=r2**r29(C); lr9:8=rot r9:8 by -16;; //| |MPY6- |M5- |R1-- | |
k5=k31+4*16; r10=mr1:0, mr1:0+=r1**r28(C); lr23:22=rot r23:22 by -16;; //| |MPY7- |M6- |R2-- | |
// -----------------------------------.align_code 4;
_VerFFTStage2: // -----------------------------------r3:2 = Q[j0+=j1]; r23=r8; r9=mr1:0, mr1:0+=r0**r28(C); sr17:16=r17:16+r21:20, sr21:20=r17:16-r21:20;; //| F3 |MPY8- |M7- |AS3-- |MV2-- |
r1:0 =cb Q[j0+=j2]; r29:28=cb L[k3+=6]; r8=mr1:0, mr1:0+=r7**r31(C); sr25:24=r13:12+r15:14, sr27:26=r13:12-r15:14;; //| F4 |MPY1 |M8- |AS1- | |
cb Q[k1+=k5]=r17:16; r15=mr1:0, mr1:0+=r6**r31(C); sr19:18=r19:18+r23:22, sr23:22=r19:18-r23:22;; //| S1-- |MPY2 |M1 |AS4-- | |
cb Q[k1+=k5]=r19:18; r14=mr1:0, mr1:0+=r5**r30(C); sr17:16=r9:8 +r11:10, sr19:18=r9:8 -r11:10;; //| S2-- |MPY3 |M2 |AS2- | |
r7:6 =cb Q[j0+=j1]; r8=r27; r13=mr1:0, mr1:0+=r4**r30(C); sr9=-r27;; //| F1+ |MPY4 |M3 |A1- |MV1- |
r5:4 =cb Q[j0+=j1]; r12=mr1:0, mr1:0+=r3**r29(C); sr27=-r26;; //| F2+ |MPY5 |M4 |A2- | |
cb Q[k1+=k5]=r21:20; r11=mr1:0, mr1:0+=r2**r29(C); lr9:8=rot r9:8 by -16;; //| S3-- |MPY6 |M5 |R1- | |
cb Q[k1+=k5]=r23:22; r10=mr1:0, mr1:0+=r1**r28(C); lr27:26=rot r27:26 by -16;; //| S4-- |MPY7 |M6 |R2- | |
// -----------------------------------r3:2 = Q[j0+=j1]; r27=r8; r9=mr1:0, mr1:0+=r0**r28(C); sr17:16=r17:16+r25:24, sr25:24=r17:16-r25:24;; //| F3+ |MPY8 |M7 |AS3- |MV2- |
r1:0 =cb Q[j0+=j2]; r8=mr1:0, mr1:0+=r7**r31(C); sr21:20=r13:12+r15:14, sr23:22=r13:12-r15:14;; //| F4+ |MPY1+ |M8 |AS1 | |
cb Q[k1+=k5]=r17:16; r15=mr1:0, mr1:0+=r6**r31(C); sr19:18=r19:18+r27:26, sr27:26=r19:18-r27:26;; //| S1- |MPY2+ |M1+ |AS4- | |
cb Q[k1+=k5]=r19:18; r14=mr1:0, mr1:0+=r5**r30(C); sr17:16=r9:8 +r11:10, sr19:18=r9:8 -r11:10;; //| S2- |MPY3+ |M2+ |AS2 | |
r7:6 =cb Q[j0+=j1]; r8=r23; r13=mr1:0, mr1:0+=r4**r30(C); sr9=-r23;; //| F1++ |MPY4+ |M3+ |A1 |MV1 |
r5:4 =cb Q[j0+=j1]; r31:30=cb L[k3+=-2]; r12=mr1:0, mr1:0+=r3**r29(C); sr23=-r22;; //| F2++ |MPY5+ |M4+ |A2 | |
cb Q[k1+=k5]=r25:24; r11=mr1:0, mr1:0+=r2**r29(C); lr9:8=rot r9:8 by -16;; //| S3- |MPY6+ |M5+ |R1 | |
.align_code 4; // -----------------------------------if NLC0E, jump _VerFFTStage2; // -----------------------------------cb Q[k1+=k5]=r27:26; r10=mr1:0, mr1:0+=r1**r28(C); lr23:22=rot r23:22 by -16;; //| S4- |MPY7+ |M6+ |R2 | |
// -----------------------------------.align_code 4; // ----------------------------------- r23=r8; r9=mr1:0, mr1:0+=r0**r28(C); sr17:16=r17:16+r21:20, sr21:20=r17:16-r21:20;; //| |MPY8+ |M7+ |AS3 |MV2 |
k3=k31+_AdjustMatrix; r8=mr1:0, mr1:0+=r7**r31(C); sr25:24=r13:12+r15:14, sr27:26=r13:12-r15:14;; //| | |M8+ |AS1+ | |
// -----------------------------------cb Q[k1+=k5]=r17:16; k2=-236; sr19:18=r19:18+r23:22, sr23:22=r19:18-r23:22;; //| S1 | | |AS4 | |
cb Q[k1+=k5]=r19:18; j10=j31+j6; sr17:16=r9:8 +r11:10, sr19:18=r9:8 -r11:10;; //| S2 | | |AS2+ | |
// -----------------------------------cb Q[k1+=k5]=r21:20; j9=j31+j5;;
//*************************************** MPY/Xpose ***************************************************************************************
// 1st time: From _ping_pong_buffer1 to _ping_pong_buffer2
// ----------------------------------r29:28=Q[k3+=16]; r8=r27; sr9=-r27;; //| | | | |TF1-- |
r1:0= Q[j9+=16]; cb Q[k1+=k5]=r23:22; sr27=-r26;; //|F1-- | | | | |
r3:2= Q[j9+=16]; r31:30=Q[k3+=16]; lr9:8=rot r9:8 by -16;; //|F2-- | | | |TF2-- |
r5:4= Q[j9+=16]; r21:20=Q[k3+=16]; lr27:26=rot r27:26 by -16;; //|F3-- | | | |TF3-- |
j4=j31+j6; r27=r8; mr1:0+=r2**r28(C); sr17:16=r17:16+r25:24, sr25:24=r17:16-r25:24;; //| |MPY1-- | | | |
// ----------------------------------r7:6= Q[j9+=16]; r23:22=Q[k3+=16]; r8=mr1:0, mr1:0+=r3**r29(C);; //|F4-- |MPY2-- |M1-- | |TF4-- |
cb Q[k1+=k5]=r17:16; LC0=4; r12=mr1:0, mr1:0+=r0**r30(C); sr19:18=r19:18+r27:26, sr27:26=r19:18-r27:26;; //| |MPY3-- |M2-- | | |
cb Q[k1+=k5]=r19:18; j6=j5; r9=mr1:0, mr1:0+=r1**r31(C);; //| |MPY4-- |M3-- | | |
cb Q[k1+=k5]=r25:24; k8=j4; r13=mr1:0, mr1:0+=r4**r20(C);; //| |MPY5-- |M4-- | | |
// ----------------------------------.align_code 4;
if LC1E, CJMP(ABS); // ----------------------------------cb Q[k1+=k5]=r27:26; j5=j7; r10=mr1:0, mr1:0+=r5**r21(C);; //| |MPY6-- |M5-- | | |
// ----------------------------------.align_code 4;
_MultXposeLoop: // ----------------------------------r1:0= Q[j9+=16]; r17:16=Q[k3+=16]; r14=mr1:0, mr1:0+=r6**r22(C);; //|F1- |MPY7-- |M6-- | |TF1- |
r3:2= Q[j9+=16]; r19:18=Q[k3+=16]; r11=mr1:0, mr1:0+=r7**r23(C);; //|F2- |MPY8-- |M7-- | |TF2- |
r5:4= Q[j9+=16]; r21:20=Q[k3+=16]; r15=mr1:0, mr1:0+=r0**r16(C);; //|F3- |MPY1- |M8-- | |TF3- |
r7:6= Q[j9+=16]; r23:22=Q[k3+=16]; r24=mr1:0, mr1:0+=r1**r17(C);; //|F4- |MPY2- |M1- | |TF4- |
Q[j10+=16]=yr11:8; j0=k8; r28=mr1:0, mr1:0+=r2**r18(C);; //|S1-- |MPY3- |M2- | | |
Q[j10+=16]=yr15:12; k9=k8+128; r25=mr1:0, mr1:0+=r3**r19(C);; //|S2-- |MPY4- |M3- | | |
Q[j10+=16]=xr11:8; j1=k9; r29=mr1:0, mr1:0+=r4**r20(C);; //|S3-- |MPY5- |M4- | | |
Q[j10+=-44]=xr15:12; k1=j6; r26=mr1:0, mr1:0+=r5**r21(C);; //|S4-- |MPY6- |M5- | | |
// ----------------------------------r1:0= Q[j9+=16]; r17:16=Q[k3+=16]; r30=mr1:0, mr1:0+=r6**r22(C);; //|F1 |MPY7- |M6- | |TF1 |
a
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 11 of 12

r3:2= Q[j9+=16]; r19:18=Q[k3+=16]; r27=mr1:0, mr1:0+=r7**r23(C);; //|F2 |MPY8- |M7- | |TF2 |
r5:4= Q[j9+=16]; r21:20=Q[k3+=16]; r31=mr1:0, mr1:0+=r0**r16(C);; //|F3 |MPY1 |M8- | |TF3 |
r7:6= Q[j9+=16]; r23:22=Q[k3+=16]; r8=mr1:0, mr1:0+=r1**r17(C);; //|F4 |MPY2 |M1 | |TF4 |
Q[j10+=16]=yr27:24; k9=k8+64; r12=mr1:0, mr1:0+=r2**r18(C);; //|S1- |MPY3 |M2 | | |
Q[j10+=16]=yr31:28; j2=k9; r9=mr1:0, mr1:0+=r3**r19(C);; //|S2- |MPY4 |M3 | | |
Q[j10+=16]=xr27:24; k9=k8+(128+64); r13=mr1:0, mr1:0+=r4**r20(C);; //|S3- |MPY5 |M4 | | |
Q[j10+=-44]=xr31:28; j3=k9; r10=mr1:0, mr1:0+=r5**r21(C);; //|S4- |MPY6 |M5 | | |
// ----------------------------------r1:0= Q[j9+=16]; r17:16=Q[k3+=16]; r14=mr1:0, mr1:0+=r6**r22(C);; //|F1+ |MPY7 |M6 | |TF1+ |
r3:2= Q[j9+=16]; r19:18=Q[k3+=16]; r11=mr1:0, mr1:0+=r7**r23(C);; //|F2+ |MPY8 |M7 | |TF2+ |
r5:4= Q[j9+=16]; r21:20=Q[k3+=16]; r15=mr1:0, mr1:0+=r0**r16(C);; //|F3+ |MPY1+ |M8 | |TF3+ |
r7:6= Q[j9+=-236]; r23:22=Q[k3+=k2]; r24=mr1:0, mr1:0+=r1**r17(C);; //|F4+ |MPY2+ |M1+ | |TF4+ |
Q[j10+=16]=yr11:8; r28=mr1:0, mr1:0+=r2**r18(C);; //|S1 |MPY3+ |M2+ | | |
Q[j10+=16]=yr15:12; r25=mr1:0, mr1:0+=r3**r19(C);; //|S2 |MPY4+ |M3+ | | |
Q[j10+=16]=xr11:8; r29=mr1:0, mr1:0+=r4**r20(C);; //|S3 |MPY5+ |M4+ | | |
Q[j10+=-44]=xr15:12; r26=mr1:0, mr1:0+=r5**r21(C);; //|S4 |MPY6+ |M5+ | | |
// ----------------------------------r1:0= Q[j9+=16]; r17:16=Q[k3+=16]; r30=mr1:0, mr1:0+=r6**r22(C);; //|F1++ |MPY7+ |M6+ | |TF1++ |
r3:2= Q[j9+=16]; r19:18=Q[k3+=16]; r27=mr1:0, mr1:0+=r7**r23(C);; //|F2++ |MPY8+ |M7+ | |TF2++ |
r5:4= Q[j9+=16]; r21:20=Q[k3+=16]; r31=mr1:0, mr1:0+=r0**r16(C);; //|F3++ |MPY1++ |M8+ | |TF3++ |
r7:6= Q[j9+=16]; r23:22=Q[k3+=16]; r8=mr1:0, mr1:0+=r1**r17(C);; //|F4++ |MPY2++ |M1++ | |TF4++ |
Q[j10+=16]=yr27:24; r12=mr1:0, mr1:0+=r2**r18(C);; //|S1+ |MPY3++ |M2++ | | |
Q[j10+=16]=yr31:28; r9=mr1:0, mr1:0+=r3**r19(C);; //|S2+ |MPY4++ |M3++ | | |
Q[j10+=16]=xr27:24; r13=mr1:0, mr1:0+=r4**r20(C);; //|S3+ |MPY5++ |M4++ | | |
.align_code 4; // ----------------------------------if NLC0E, jump _MultXposeLoop; // ----------------------------------Q[j10+=4]=xr31:28; r10=mr1:0, mr1:0+=r5**r21(C);; //|S4+ |MPY6++ |M5++ | | |
// ----------------------------------.align_code 4;
jump _VerticalLoop; // Repeat the vertical loop
r5:4=br Q[j2+=32]; k3=k31+(_twiddles16+2);; // with swapped pointers
//******************************************* Done ****************************************************************************************
_fft256pt.end:
a
Listing 1. fft256pt.asm
References
[1] ADSP-TS201 TigerSHARC Processor Programming Reference. Revision 1.0, August 2004. Analog Devices, Inc.
Document History
Revision Description
Rev 1 – February 03, 2005
by Boris Lerner
Initial Release
Parallel Implementation of Fixed-Point FFTs on TigerSHARC® Processors (EE-263) Page 12 of 12
 Loading...
Loading...