Agilent Technologies Network Analyzer 8510-58 User Manual
Agilent
Specifying Calibration
Standards for the Agilent 8510
Network Analyzer
Product Note 8510-5B
2
3
3
3
4
5
5
7
7
8
9
9
9
11
12
12
12
14
14
15
16
16
17
17
17
18
18
18
18
19
19
19
19
19
20
20
20
21
21
22
22
22
23
23
26
29
Introduction
Measurement errors
Measurement calibration
Calibration kit
Standard definition
Class assignment
Modification procedure
Select standards
Define standards
Standard number
Standard type
Open circuit capacitance: C0, C1, C2and C
3
Short circuit inductance: L0, L1, L2and L
3
Fixed or sliding
Terminal impedance
Offset delay
Offset Z
0
Offset loss
Lower/minimum frequency
Upper/maximum frequency
Coax or waveguide
Standard labels
Assign classes
Standard classes
S11A,B,C and S22A,B,C
Forward transmission match/thru
Reverse transmission match/thru
Isolation
Frequency response
TRL Thru
TRL Reflect
TRL Line
Adapter
Standard class labels
TRL options
Calibration kit label
Enter standards/classes
Verify performance
User modified cal kits and Agilent 8510 specifications
Modification examples
Modeling a thru adapter
Modeling an arbitrary impedance
Appendix A
Calibration kit entry procedure
Appendix B
Dimensional considerations in coaxial connectors
Appendix C
Cal coefficients model
Table of contents
Known devices called calibration standards
provide the measurement reference for network analyzer error-correction. This note
covers methods for specifying these standards and describes the procedures for their
use with the Agilent Technologies 8510 network analyzer.
The 8510 network analyzer system has the
capability to make real-time error-corrected
measurements of components and devices
in a variety of transmission media.
Fundamentally, all that is required is a set
of known devices (standards) that can be
defined physically or electrically and used
to provide a reference for the physical interface of the test devices.
Agilent Technologies supplies full calibration
kits in 1.0-mm, 1.85-mm, 2.4-mm, 3.5-mm,
7-mm, and Type-N coaxial interfaces. The
8510 system can be calibrated in other interfaces such as other coaxial types, waveguide
and microstrip, given good quality standards that can be defined.
The 8510’s built-in f lexibility for calibration
kit definition allows the user to derive a
precise set of definitions for a particular set
of calibration standards from precise physical measurements. For example, the characteristic impedance of a matched impedance
airline can be defined from its actual physical dimensions (diameter of outer and inner
conductors) and electrical characteristics
(skin depth). Although the airline is
designed to provide perfect signal transmission at the connection interface, the dimensions of individual airlines will vary
somewhat—resulting in some ref lection due
to the change in impedance between the test
port and the airline. By defining the actual
impedance of the airline, the resultant
reflection is characterized and can be
removed through measurement calibration.
The scope of this product note includes a
general description of the capabilities of the
8510 to accept new cal kit descriptions via
the MODIFY CAL KIT function found in the
8510 CAL menu. It does not, however,
describe how to design a set of physical
standards. The selection and fabrication of
appropriate calibration standards is as varied as the transmission media of the particular application and is beyond the scope of
this note.
3
Introduction
This product note covers measurement calibration
requirements for the Agilent 8510B/C network
analyzer. All of the capabilities described in this
note also apply to the Agilent 8510A with the
following exceptions: response & isolation calibration; short circuit inductance; class assignments
for forward/reverse isolation, TRL thru, reflect,
line and options; and adapter removal.
Measurement errors
Measurement errors in network analysis can be
separated into two categories: random and systematic errors. Both random and systematic errors are
vector quantities. Random errors are non-repeatable measurement variations and are usually
unpredictable. Systematic errors are repeatable
measurement variations in the test setup.
Systematic errors include mismatch and leakage
signals in the test setup, isolation characteristics
between the reference and test signal paths, and
system frequency response. In most microwave
measurements, systematic errors are the most significant source of measurement uncertainty. The
source of these errors can be attributed to the signal separation scheme used.
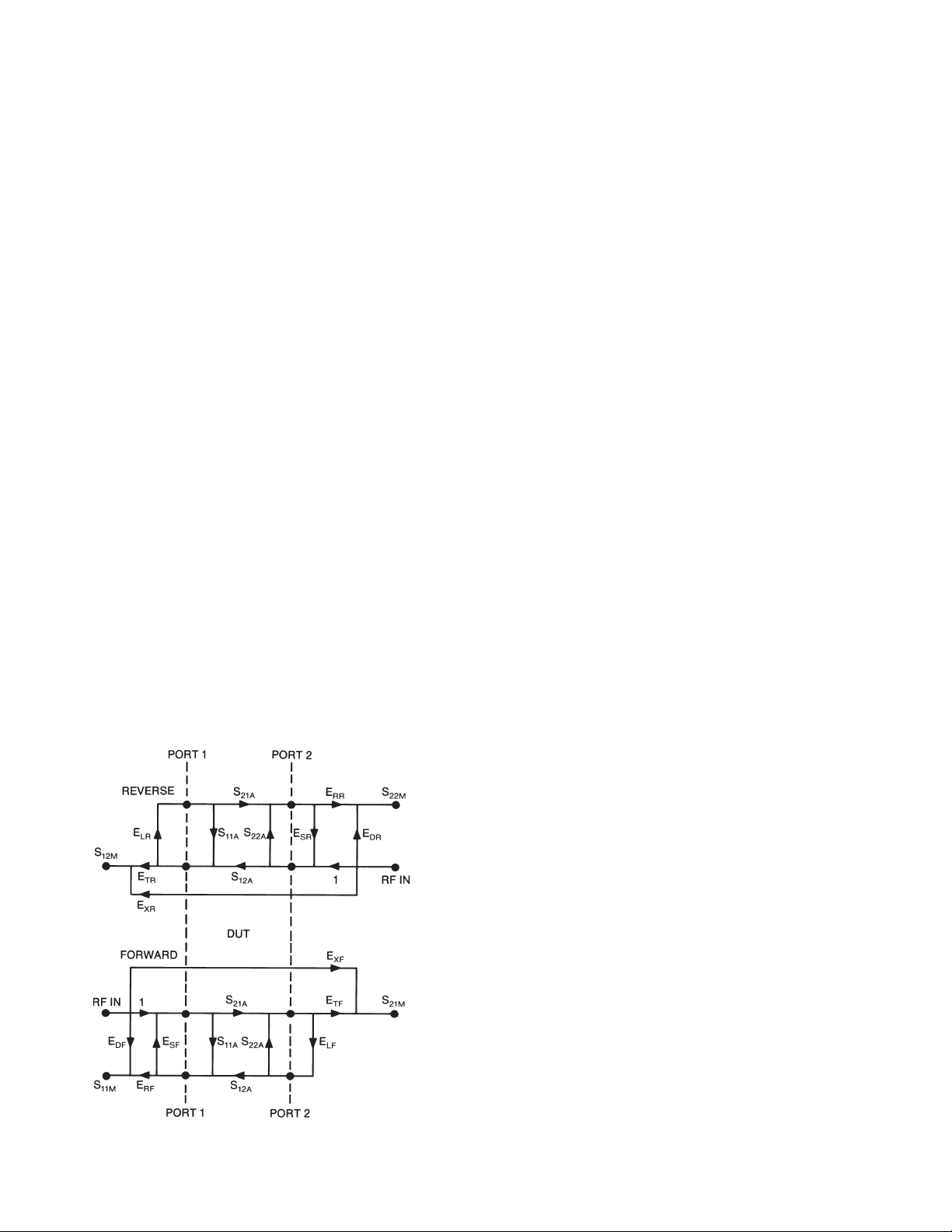
The systematic errors present in an S-parameter
measurement can be modeled with a signal f lowgraph. The flowgraph model, which is used for error
correction in the 8510 for the errors associated with
measuring the S-parameters of a two port device, is
shown in the figure below.
The six systematic errors in the forward direction
are directivity, source match, reflection tracking,
load match, transmission tracking, and isolation.
The reverse error model is a mirror image, giving a
total of 12 errors for two-port measurements. The
process of removing these systematic errors from
the network analyzer S-parameter measurement is
called measurement calibration.
E
DF
, EDR-Directivity ELF, ELR-Load Match
ESF, ESR-Source Match ETF, ETR-Trans. Tracking
ERF, ERR-Refl. Tracking EXF, EXR-Isolation
Measurement calibration
A more complete definition of measurement calibration using the 8510, and a description of the
error models is included in the 8510 operating and
programming manual. The basic ideas are summarized here.
A measurement calibration is a process which
mathematically derives the error model for the
8510. This error model is an array of vector coefficients used to establish a fixed reference plane of
zero phase shift, zero magnitude and known
impedance. The array coefficients are computed by
measuring a set of “known” devices connected at a
fixed point and solving as the vector difference
between the modeled and measured response.
Figure 1. Agilent 8510 full 2-port error model
4
The array coefficients are computed by measuring
a set of “known” devices connected at a fixed point
and solving as the vector difference between the
modeled and measured response.
The full 2-port error model shown in Figure 1 is
an example of only one of the measurement calibrations available with the 8510. The measurement
calibration process for the 8510 must be one of
seven types: RESPONSE, RESPONSE & ISOLATION,
Sll1-PORT, S221-PORT, ONE PATH 2-PORT, FULL
2-PORT, and TRL 2-PORT. Each of these calibration
types solves for a different set of the systematic
measurement errors. A RESPONSE calibration
solves for the systematic error term for reflection or transmission tracking depending on the
S-parameter which is activated on the 8510 at the
time. RESPONSE & ISOLATION adds correction
for crosstalk to a simple RESPONSE calibration.
An S11l-PORT calibration solves for the forward
error terms, directivity, source match and ref lection tracking. Likewise, the S221-PORT calibration
solves for the same error terms in the reverse
direction. A ONE PATH 2-PORT calibration solves
for all the forward error terms. FULL 2-PORT and
TRL 2-PORT calibrations include both forward and
reverse error terms.
The type of measurement calibration selected by
the user depends on the device to be measured
(i.e., 1-port or 2-port device) and the extent of
accuracy enhancement desired. Further, a combination of calibrations can be used in the measurement of a particular device.
The accuracy of subsequent test device measurements is dependent on the accuracy of the test
equipment, how well the “known” devices are modeled and the exactness of the error correction
model.
Calibration kit
A calibration kit is a set of physical devices called
standards. Each standard has a precisely known or
predictable magnitude and phase response as a
function of frequency. In order for the 8510 to use
the standards of a calibration kit, the response of
each standard must be mathematically defined and
then organized into standard classes which correspond to the error models used by the 8510.
Agilent currently supplies calibration kits with
1.0-mm (85059A), 1.85-mm (85058D), 2.4-mm
(85056A/D/K), 3.5-mm (85052A/B/C/D/E), 7-mm
(85050B/C/D) and Type-N (85054B) coaxial connectors. To be able to use a particular calibration
kit, the known characteristics from each standard
in the kit must be entered into the 8510 nonvolatile memory. The operating and service manuals for each of the Agilent calibration kits contain
the physical characteristics for each standard in
the kit and mathematical definitions in the format
required by the 8510.
Waveguide calibration using the 8510 is possible.
Calibration in microstrip and other non-coaxial
media is described in Agilent Product Note 8510-8A.
5
Standard definition
Standard definition is the process of mathematically modeling the electrical characteristics (delay,
attenuation and impedance) of each calibration
standard. These electrical characteristics can be
mathematically derived from the physical dimensions and material of each calibration standards or
from its actual measured response. A standard
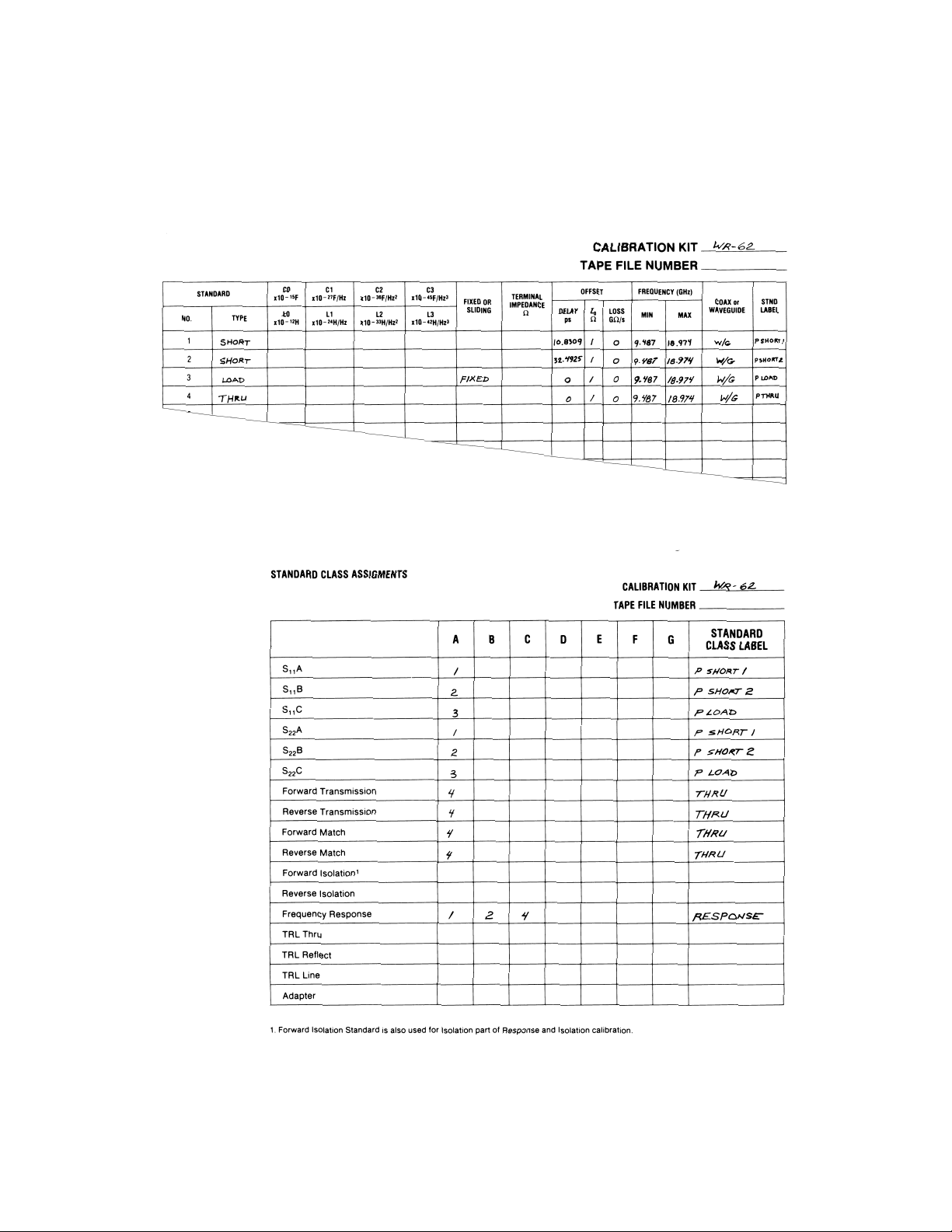
definition table (see Table 1) lists the parameters
that are used by the 8510 to specify the mathematical model.
Class assignment
Class assignment is the process of organizing calibration standards into a format which is compatible with the error models used in measurement
calibration. A class or group of classes correspond
to the seven calibration types used in the 8510.
The 17 available classes are identified later in this
note (see Assign classes).
6
Table 1. Standard definitions table
Table 2. Standard class assignments
7
Modification procedure
Calibration kit modification provides the capability
to adapt to measurement calibrations in other connector types or to generate more precise error
models from existing kits. Provided the appropriate standards are available, cal kit modification
can be used to establish a reference plane in the
same transmission media as the test devices and at
a specified point, generally the point of device connection/insertion. After calibration, the resultant
measurement system, including any adapters
which would reduce system directivity, is fully corrected and the systematic measurement errors are
mathematically removed. Additionally, the modification function allows the user to input more precise physical definitions for the standards in a
given cal kit. The process to modify or create a cal
kit consists of the following steps:
1. Select standards
2. Define standards
3. Assign classes
4. Enter standards/classes
5. Verify performance
To further illustrate, an example waveguide calibration kit is developed as the general descriptions
in MODIFY CAL KIT process are presented.
Select standards
Determine what standards are necessary for calibration and are available in the transmission
media of the test devices.
Calibration standards are chosen based on the following criteria:
• A well defined response which is mechanically
repeatable and stable over typical ambient temperatures and conditions. The most common
coaxial standards are zero-electrical-length
short, shielded open and matched load terminations which ideally have fixed magnitude and
broadband phase response. Since waveguide
open circuits are generally not modelable, the
types of standards typically used for waveguide
calibration are a pair of offset shorts and a fixed
or sliding load.
• A unique and distinct frequency response. To
fully calibrate each test port (that is to provide
the standards necessary for S
11
or S221-PORT
calibration), three standards are required that
exhibit distinct phase and/or magnitude at each
particular frequency within the calibration
band. For example, in coax, a zero-length short
and a perfect shielded open exhibit 180 degree
phase separation while a matched load will provide 40 to 50 dB magnitude separation from
both the short and the open. In waveguide, a
pair of offset shorts of correct length provide
phase separation.
• Broadband frequency coverage. In broadband
applications, it is often difficult to find standards that exhibit a known, suitable response
over the entire band. A set of frequency-banded
standards of the same type can be selected in
order to characterize the full measurement
band.
• The TRL 2-PORT calibration requires only a single precision impedance standard—a transmission line. An unknown high reflection device
and a thru connection are sufficient to complete
this technique.
8
Define standards
A glossary of standard definition parameters used
with the Agilent 8510 is included in this section.
Each parameter is described and appropriate conversions are listed for implementation with the
8510. To illustrate, a calibration kit for WR-62 rectangular waveguide (operating frequency range
12.4 to 18 GHz) will be defined as shown in Table
1. Subsequent sections will continue to develop
this waveguide example.
The mathematical models are developed for each
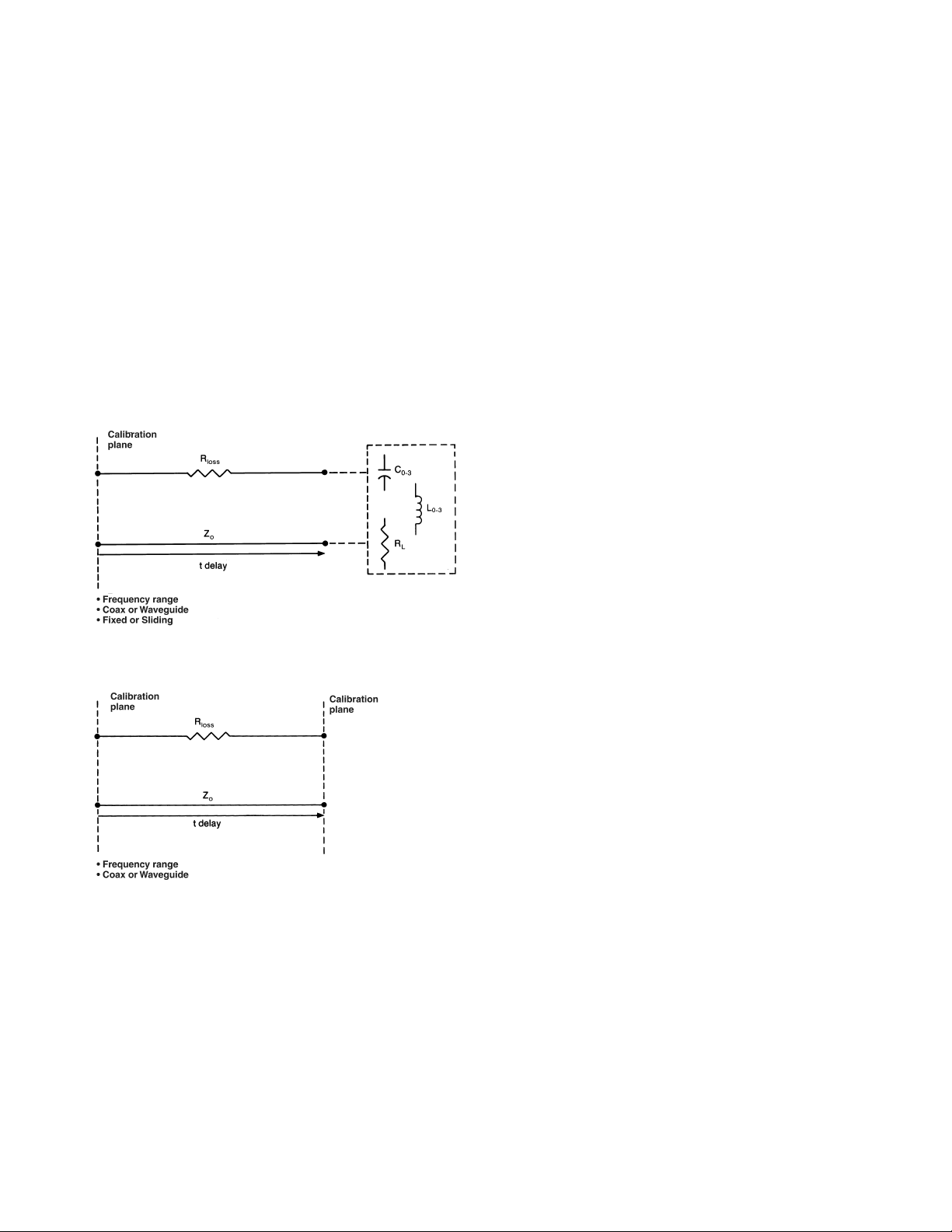
standard in accordance with the standard definition parameters provided by the 8510. These standard definition parameters are shown in Figure 2.
Figure 2. Standard definition models
Model for reflection standard
(short, open, load or arbitrary
impedance)
Model for transmission
standard (Thru)
9
Each standard is described using the Standard
Definition Table in accordance with the 1- or 2port model. The Standard Definition table for a
waveguide calibration kit is shown in Table 1. Each
standard type (short, open, load, thru, and arbitrary impedance) may be defined by the parameters as specified below.
• Standard number and standard type
• Fringing capacitance of an open, or inductance
of a short, specified by a third order polynomial
• Load/arbitrary impedance, which is specified as
fixed or sliding
• Terminal resistance of an arbitrary impedance
• Offsets which are specified by delay, Z0, R
loss
• Frequency range
• Connector type: coaxial or waveguide
• Label (up to 10 alphanumeric characters)
Standard number
A calibration kit may contain up to 21 standards
(See Table 1). The required number of standards
will depend on frequency coverage and whether
thru adapters are needed for sexed connectors.
For the WR-62 waveguide example, four standards
will be sufficient to perform the FULL 2-PORT calibration. Three reflection standards are required,
and one transmission standard (a thru) will be sufficient to complete this calibration kit.
Standard type
A standard type must be classified as a “short”
“open,” “load”, “thru,” or “arbitrary impedance.”
The associated models for reflection standards
(short, open, load, and arbitrary impedance) and
transmission standards (thru) are shown in Figure 1.
For the WR-62 waveguide calibration kit, the four
standards are a
1
/8λλ and 3/8λ λ offset short, a fixed
matched load, and a thru. Standard types are
entered into the Standard Definition table under
STANDARD NUMBERS 1 through 4 as short, short,
load, and thru respectively.
Open circuit capacitance: C0, C1, C2and C
3
If the standard type selected is an “open,” the C
0
through C3coefficients are specified and then used
to mathematically model the phase shift caused by
fringing capacitance as a function of frequency.
As a reflection standard, an “open” offers the
advantage of broadband frequency coverage, while
offset shorts cannot be used over more than an
octave. The reflection coefficient ( = pe-je) of a
perfect zero-length-open is 1 at 0° for all frequencies. At microwave frequencies however, the magnitude and phase of an “open” are affected by the
radiation loss and capacitive “fringing” fields,
respectively. In coaxial transmission media, shielding techniques are effective in reducing the radiation loss. The magnitude (p) of a zero-length
“open” is assigned to be 1 (zero radiation loss) for
all frequencies when using the Agilent 8510
Standard Type “open.”
10
It is not possible to remove fringing capacitance,
but the resultant phase shift can be modeled as a
function of frequency using C0through C3(C0+C
l
f + C2 f2+ C3 f3,with units of F(Hz), C0(fF),
C1(10
-27
F/Hz), C2(10
-36
F/Hz2) and C3(10
-45
F/Hz3),
which are the coefficients for a cubic polynomial
that best fits the actual capacitance of the “open.”
A number of methods can be used to determine the
fringing capacitance of an “open.” Three techniques, described here, involve a calibrated reflection coefficient measurement of an open standard
and subsequent calculation of the effective capacitance. The value of fringing capacitance can be calculated from the measured phase or reactance as a
function of frequency as follows.
C
eff
– effective capacitance
∆∅ – measured phase shift
f – measurement frequency
F – farad
Z0 – characteristic impedance
X – measured reactance
This equation assumes a zero-length open. When
using an offset open the offset delay must be
backed-out of the measured phase shift to obtain
good C0through C3coefficients.
This capacitance can then be modeled by choosing
coefficients to best fit the measured response
when measured by either method 3 or 4 below.
1. Fully calibrated 1-Port–Establish a calibrated
reference plane using three independent standards
(that is, 2 sets of banded offset shorts and load).
Measure the phase response of the open and solve
for the capacitance function.
2. TRL 2-PORT–When transmission lines standards
are available, this method can be used for a complete 2-port calibration. With error-correction
applied the capacitance of the open can be measured directly.
3. Gating–Use time domain gating to correct the
measured response of the open by isolating the
reflection due to the open from the source match
reflection and signal path leakage (directivity).
Figure 3 shows the time domain response of the
open at the end of an airline. Measure the gated
phase response of the open at the end of an airline
and again solve for the capacitance function.
tan( )
∆∅
2
2πfZ
0
1
2πfX
C
eff
==
Loading...