Agilent Technologies 8510 User Manual

Agilent Specifying Calibration Standards for the Agilent 8510 Network Analyzer

Application Note 8510-5B

Discontinued Product Information

— For Support Reference Only —

Information herein, may refer to products/services no longer supported. We regret any inconvenience caused by obsolete information. For the latest information on Agilent’s test and measurement products go to:

www.agilent.com/find/products

In the US, call Agilent Technologies at 1-800-829-4444

(any weekday between 8am–5pm in any U.S. time zone)

World-wide Agilent sales office contact information is available at:

www.agilent.com/find/contactus

3 3 4 5 5

7 8 9 9

9 11 12 12 12 14 14 15 16 16 17 17 17 18 18 18 18 19 19 19 19 19 20 20 20 21 21

22 22

22 23

Introduction

Measurement errors Measurement calibration Calibration kit Standard definition Class assignment

Modification procedure

Select standards Define standards Standard number Standard type

Open circuit capacitance: C0, C1, C2and C

Short circuit inductance: L0, L1, L2and L

Fixed or sliding Terminal impedance Offset delay Offset Z

Offset loss Lower/minimum frequency Upper/maximum frequency Coax or waveguide Standard labels

Assign classes

Standard classes S11A,B,C and S22A,B,C Forward transmission match/thru Reverse transmission match/thru Isolation Frequency response TRL Thru TRL Reflect TRL Line Adapter Standard class labels TRL options

Calibration kit label Enter standards/classes Verify performance

User modified cal kits and Agilent 8510 specifications Modification examples

Modeling a thru adapter Modeling an arbitrary impedance

Appendix A

Calibration kit entry procedure

Appendix B

Dimensional considerations in coaxial connectors

Appendix C

Cal coefficients model

Table of contents

Known devices called calibration standards provide the measurement reference for network analyzer error-correction. This note covers methods for specifying these standards and describes the procedures for their use with the Agilent Technologies 8510 network analyzer.

The 8510 network analyzer system has the capability to make real-time error-corrected measurements of components and devices in a variety of transmission media. Fundamentally, all that is required is a set of known devices (standards) that can be defined physically or electrically and used to provide a reference for the physical interface of the test devices.

Agilent Technologies supplies full calibration kits in 1.0-mm, 1.85-mm, 2.4-mm, 3.5-mm, 7-mm, and Type-N coaxial interfaces. The 8510 system can be calibrated in other interfaces such as other coaxial types, waveguide and microstrip, given good quality standards that can be defined.

The 8510’s built-in flexibility for calibration kit definition allows the user to derive a precise set of definitions for a particular set of calibration standards from precise physical measurements. For example, the characteristic impedance of a matched impedance airline can be defined from its actual physical dimensions (diameter of outer and inner conductors) and electrical characteristics (skin depth). Although the airline is designed to provide perfect signal transmission at the connection interface, the dimensions of individual airlines will vary somewhat—resulting in some reflection due to the change in impedance between the test port and the airline. By defining the actual impedance of the airline, the resultant reflection is characterized and can be removed through measurement calibration.

The scope of this product note includes a general description of the capabilities of the 8510 to accept new cal kit descriptions via the MODIFY CAL KIT function found in the 8510 CAL menu. It does not, however, describe how to design a set of physical standards. The selection and fabrication of appropriate calibration standards is as varied as the transmission media of the particular application and is beyond the scope of this note.

Introduction

This product note covers measurement calibration requirements for the Agilent 8510B/C network analyzer. All of the capabilities described in this note also apply to the Agilent 8510A with the following exceptions: response & isolation calibration; short circuit inductance; class assignments for forward/reverse isolation, TRL thru, reflect, line and options; and adapter removal.

Measurement errors

Measurement errors in network analysis can be separated into two categories: random and systematic errors. Both random and systematic errors are vector quantities. Random errors are non-repeatable measurement variations and are usually unpredictable. Systematic errors are repeatable measurement variations in the test setup.

Systematic errors include mismatch and leakage signals in the test setup, isolation characteristics between the reference and test signal paths, and system frequency response. In most microwave measurements, systematic errors are the most significant source of measurement uncertainty. The source of these errors can be attributed to the signal separation scheme used.

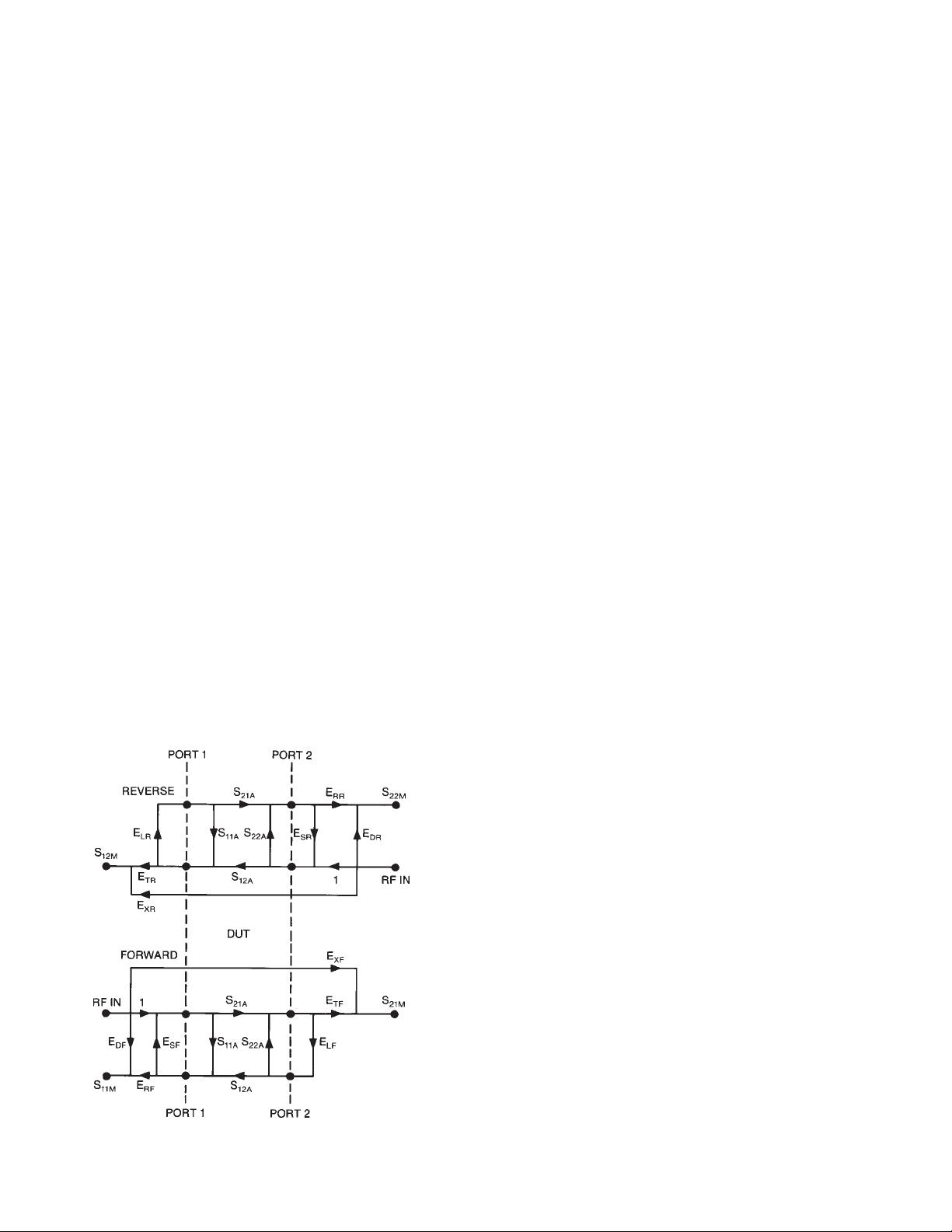
The systematic errors present in an S-parameter measurement can be modeled with a signal flowgraph. The flowgraph model, which is used for error correction in the 8510 for the errors associated with measuring the S-parameters of a two port device, is shown in the figure below.

The six systematic errors in the forward direction are directivity, source match, reflection tracking, load match, transmission tracking, and isolation. The reverse error model is a mirror image, giving a total of 12 errors for two-port measurements. The process of removing these systematic errors from the network analyzer S-parameter measurement is called measurement calibration.

, EDR-Directivity ELF, ELR-Load Match ESF, ESR-Source Match ETF, ETR-Trans. Tracking ERF, ERR-Refl. Tracking EXF, EXR-Isolation

Measurement calibration

A more complete definition of measurement calibration using the 8510, and a description of the error models is included in the 8510 operating and programming manual. The basic ideas are summarized here.

A measurement calibration is a process which mathematically derives the error model for the

8510. This error model is an array of vector coefficients used to establish a fixed reference plane of zero phase shift, zero magnitude and known impedance. The array coefficients are computed by measuring a set of “known” devices connected at a fixed point and solving as the vector difference between the modeled and measured response.

Figure 1. Agilent 8510 full 2-port error model

The array coefficients are computed by measuring a set of “known” devices connected at a fixed point and solving as the vector difference between the modeled and measured response.

The full 2-port error model shown in Figure 1 is an example of only one of the measurement calibrations available with the 8510. The measurement calibration process for the 8510 must be one of seven types: RESPONSE, RESPONSE & ISOLATION, Sll1-PORT, S221-PORT, ONE PATH 2-PORT, FULL 2-PORT, and TRL 2-PORT. Each of these calibration types solves for a different set of the systematic measurement errors. A RESPONSE calibration solves for the systematic error term for reflection or transmission tracking depending on the S-parameter which is activated on the 8510 at the time. RESPONSE & ISOLATION adds correction for crosstalk to a simple RESPONSE calibration. An S11l-PORT calibration solves for the forward error terms, directivity, source match and reflection tracking. Likewise, the S221-PORT calibration solves for the same error terms in the reverse direction. A ONE PATH 2-PORT calibration solves for all the forward error terms. FULL 2-PORT and TRL 2-PORT calibrations include both forward and reverse error terms.

The type of measurement calibration selected by the user depends on the device to be measured (i.e., 1-port or 2-port device) and the extent of accuracy enhancement desired. Further, a combination of calibrations can be used in the measurement of a particular device.

The accuracy of subsequent test device measurements is dependent on the accuracy of the test equipment, how well the “known” devices are modeled and the exactness of the error correction model.

Calibration kit

A calibration kit is a set of physical devices called standards. Each standard has a precisely known or predictable magnitude and phase response as a function of frequency. In order for the 8510 to use the standards of a calibration kit, the response of each standard must be mathematically defined and then organized into standard classes which correspond to the error models used by the 8510. Agilent currently supplies calibration kits with

1.0-mm (85059A), 1.85-mm (85058D), 2.4-mm (85056A/D/K), 3.5-mm (85052A/B/C/D/E), 7-mm (85050B/C/D) and Type-N (85054B) coaxial connectors. To be able to use a particular calibration kit, the known characteristics from each standard in the kit must be entered into the 8510 nonvolatile memory. The operating and service manuals for each of the Agilent calibration kits contain the physical characteristics for each standard in the kit and mathematical definitions in the format required by the 8510.

Waveguide calibration using the 8510 is possible. Calibration in microstrip and other non-coaxial media is described in Agilent Product Note 8510-8A.

Standard definition

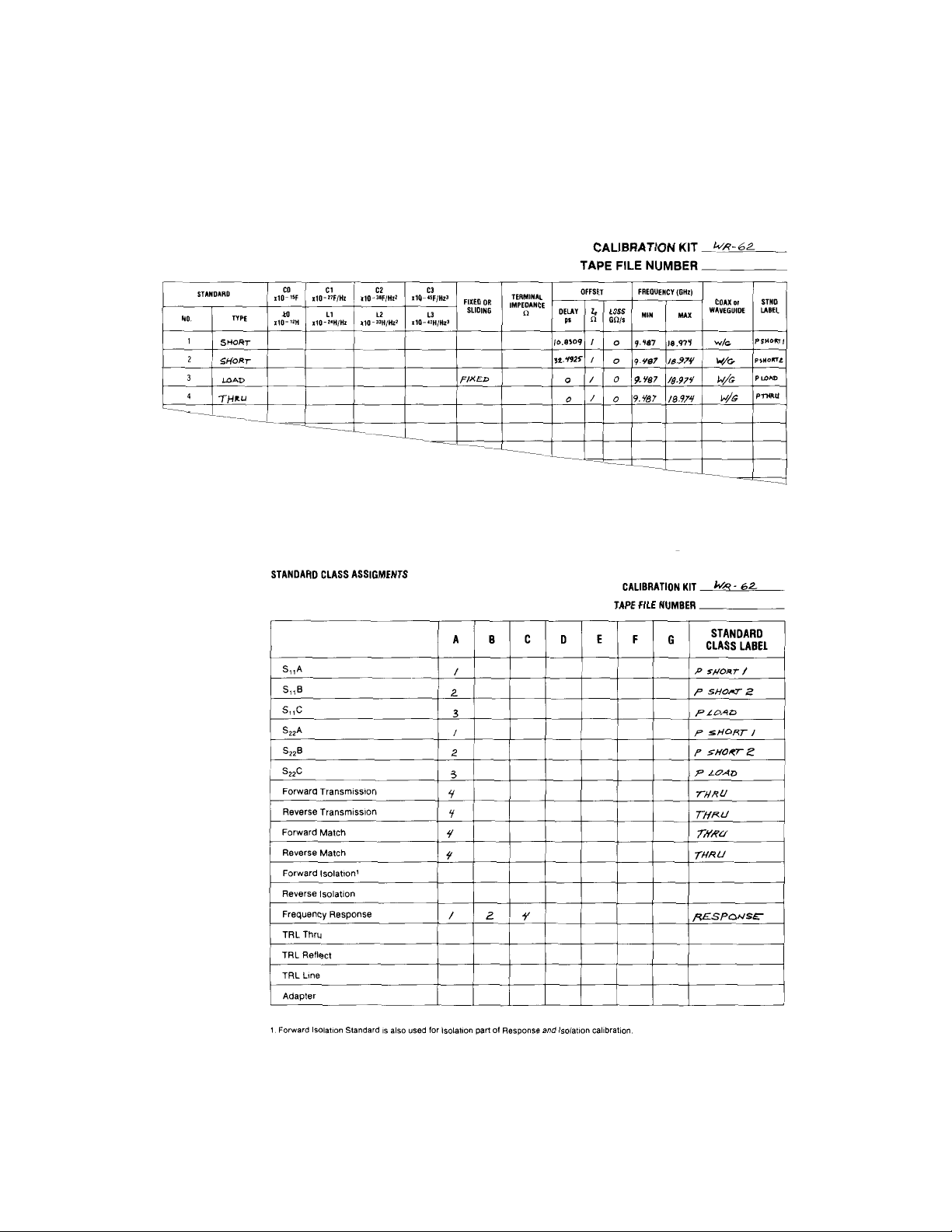
Standard definition is the process of mathematically modeling the electrical characteristics (delay, attenuation and impedance) of each calibration standard. These electrical characteristics can be mathematically derived from the physical dimensions and material of each calibration standards or from its actual measured response. A standard definition table (see Table 1) lists the parameters that are used by the 8510 to specify the mathematical model.

Class assignment

Class assignment is the process of organizing calibration standards into a format which is compatible with the error models used in measurement calibration. A class or group of classes correspond to the seven calibration types used in the 8510. The 17 available classes are identified later in this note (see Assign classes).

Table 1. Standard definitions table

Table 2. Standard class assignments

Modification procedure

Calibration kit modification provides the capability to adapt to measurement calibrations in other connector types or to generate more precise error models from existing kits. Provided the appropriate standards are available, cal kit modification can be used to establish a reference plane in the same transmission media as the test devices and at a specified point, generally the point of device connection/insertion. After calibration, the resultant measurement system, including any adapters which would reduce system directivity, is fully corrected and the systematic measurement errors are mathematically removed. Additionally, the modification function allows the user to input more precise physical definitions for the standards in a given cal kit. The process to modify or create a cal kit consists of the following steps:

1. Select standards

2. Define standards

3. Assign classes

4. Enter standards/classes

5. Verify performance

To further illustrate, an example waveguide calibration kit is developed as the general descriptions in MODIFY CAL KIT process are presented.

Select standards

Determine what standards are necessary for calibration and are available in the transmission media of the test devices.

Calibration standards are chosen based on the following criteria:

• A well defined response which is mechanically

repeatable and stable over typical ambient temperatures and conditions. The most common coaxial standards are zero-electrical-length short, shielded open and matched load terminations which ideally have fixed magnitude and broadband phase response. Since waveguide open circuits are generally not modelable, the types of standards typically used for waveguide calibration are a pair of offset shorts and a fixed or sliding load.

• A unique and distinct frequency response. To

fully calibrate each test port (that is to provide the standards necessary for S

or S221-PORT calibration), three standards are required that exhibit distinct phase and/or magnitude at each particular frequency within the calibration band. For example, in coax, a zero-length short and a perfect shielded open exhibit 180 degree phase separation while a matched load will provide 40 to 50 dB magnitude separation from both the short and the open. In waveguide, a pair of offset shorts of correct length provide phase separation.

• Broadband frequency coverage. In broadband applications, it is often difficult to find standards that exhibit a known, suitable response over the entire band. A set of frequency-banded standards of the same type can be selected in order to characterize the full measurement band.

• The TRL 2-PORT calibration requires only a single precision impedance standard—a transmission line. An unknown high reflection device and a thru connection are sufficient to complete this technique.

Define standards

A glossary of standard definition parameters used with the Agilent 8510 is included in this section. Each parameter is described and appropriate conversions are listed for implementation with the

8510. To illustrate, a calibration kit for WR-62 rectangular waveguide (operating frequency range

12.4 to 18 GHz) will be defined as shown in Table

1. Subsequent sections will continue to develop this waveguide example.

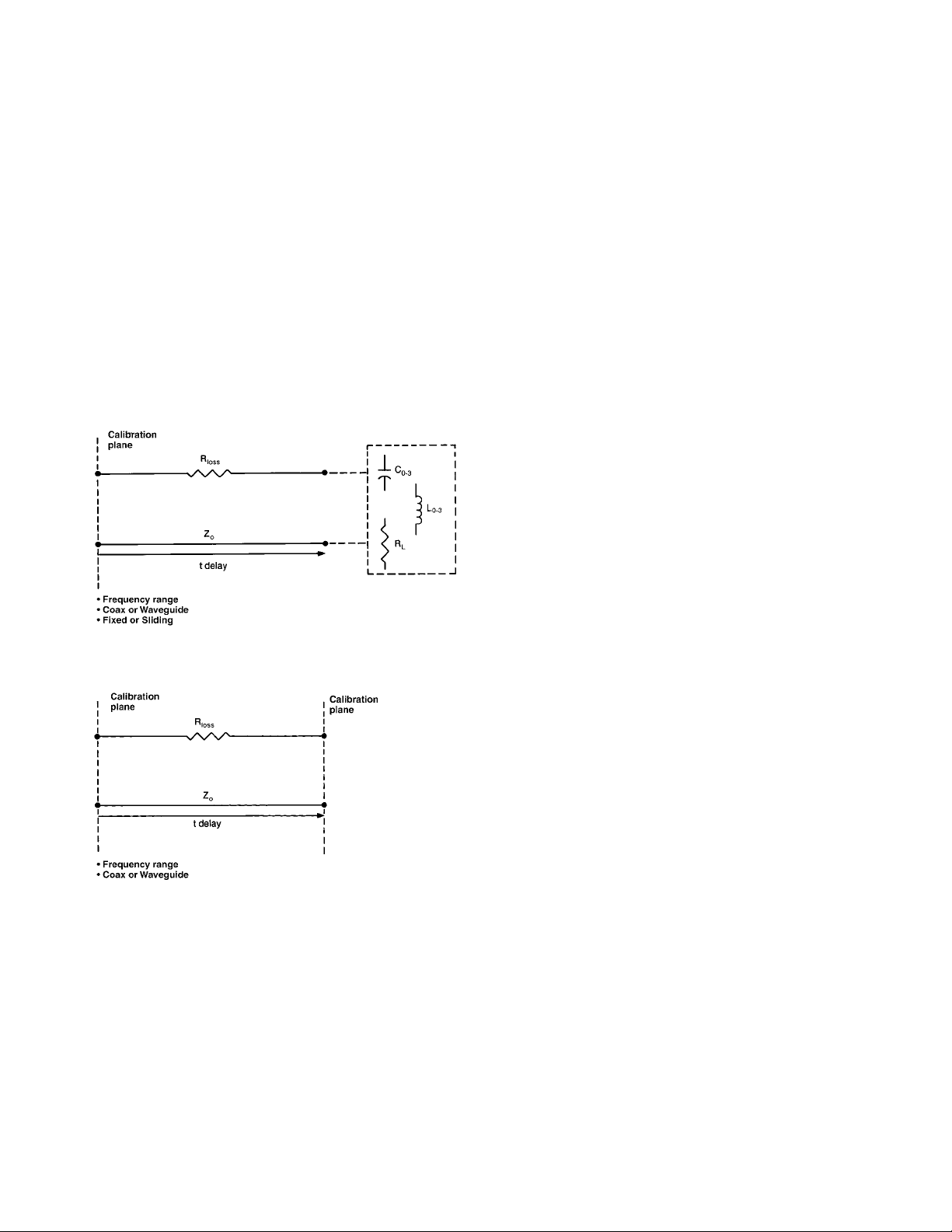
The mathematical models are developed for each standard in accordance with the standard definition parameters provided by the 8510. These standard definition parameters are shown in Figure 2.

Figure 2. Standard definition models

Model for reflection standard (short, open, load or arbitrary impedance)

Model for transmission standard (Thru)

Each standard is described using the Standard Definition Table in accordance with the 1- or 2port model. The Standard Definition table for a waveguide calibration kit is shown in Table 1. Each standard type (short, open, load, thru, and arbitrary impedance) may be defined by the parameters as specified below.

• Standard number and standard type

• Fringing capacitance of an open, or inductance of a short, specified by a third order polynomial

• Load/arbitrary impedance, which is specified as fixed or sliding

• Terminal resistance of an arbitrary impedance

• Offsets which are specified by delay, Z0, R

loss

• Frequency range

• Connector type: coaxial or waveguide

• Label (up to 10 alphanumeric characters)

Standard number

A calibration kit may contain up to 21 standards (See Table 1). The required number of standards will depend on frequency coverage and whether thru adapters are needed for sexed connectors.

For the WR-62 waveguide example, four standards will be sufficient to perform the FULL 2-PORT calibration. Three reflection standards are required, and one transmission standard (a thru) will be sufficient to complete this calibration kit.

Standard type

A standard type must be classified as a “short” “open,” “load”, “thru,” or “arbitrary impedance.” The associated models for reflection standards (short, open, load, and arbitrary impedance) and transmission standards (thru) are shown in Figure 1.

For the WR-62 waveguide calibration kit, the four standards are a

/8λλ and 3/8λ λ offset short, a fixed matched load, and a thru. Standard types are entered into the Standard Definition table under STANDARD NUMBERS 1 through 4 as short, short, load, and thru respectively.

Open circuit capacitance: C0, C1, C2and C

If the standard type selected is an “open,” the C

through C3coefficients are specified and then used to mathematically model the phase shift caused by fringing capacitance as a function of frequency.

As a reflection standard, an “open” offers the advantage of broadband frequency coverage, while offset shorts cannot be used over more than an octave. The reflection coefficient (Γ = pe-je) of a perfect zero-length-open is 1 at 0° for all frequencies. At microwave frequencies however, the magnitude and phase of an “open” are affected by the radiation loss and capacitive “fringing” fields, respectively. In coaxial transmission media, shielding techniques are effective in reducing the radiation loss. The magnitude (p) of a zero-length “open” is assigned to be 1 (zero radiation loss) for all frequencies when using the Agilent 8510 Standard Type “open.”

It is not possible to remove fringing capacitance, but the resultant phase shift can be modeled as a function of frequency using C

through C3(C0+C

f + C

f2+ C

f3,with units of F(Hz), C0(fF),

C1(10

-27

F/Hz), C2(10

-36

F/Hz2) and C3(10

-45

F/Hz3), which are the coefficients for a cubic polynomial that best fits the actual capacitance of the “open.”

A number of methods can be used to determine the fringing capacitance of an “open.” Three techniques, described here, involve a calibrated reflection coefficient measurement of an open standard and subsequent calculation of the effective capacitance. The value of fringing capacitance can be calculated from the measured phase or reactance as a function of frequency as follows.

eff

– effective capacitance

∆∅ – measured phase shift f – measurement frequency F – farad Z0 – characteristic impedance X – measured reactance

This equation assumes a zero-length open. When using an offset open the offset delay must be backed-out of the measured phase shift to obtain good C0through C3coefficients.

This capacitance can then be modeled by choosing coefficients to best fit the measured response when measured by either method 3 or 4 below.

1. Fully calibrated 1-Port–Establish a calibrated reference plane using three independent standards (that is, 2 sets of banded offset shorts and load). Measure the phase response of the open and solve for the capacitance function.

2. TRL 2-PORT–When transmission lines standards are available, this method can be used for a complete 2-port calibration. With error-correction applied the capacitance of the open can be measured directly.

3. Gating–Use time domain gating to correct the measured response of the open by isolating the reflection due to the open from the source match reflection and signal path leakage (directivity). Figure 3 shows the time domain response of the open at the end of an airline. Measure the gated phase response of the open at the end of an airline and again solve for the capacitance function.

tan( )

∆∅

2πfZ

2πfX

eff

+ 22 hidden pages