Page 1

3B SCIENTIFIC
Set of Five Blocks of Various Densities U8404556
Instruction Sheet
04/08 ALF
®
PHYSICS
1 Sample block - copper
2 Sample block - iron
3 Sample block - aluminium
4 Sample block - brass
5 Sample block - wood
6 Hollow body
1. Description
The set of five blocks of various densities is used to
determine the densities of different materials and
to demonstrate Archimedes’ principle.
The set consists of five sample blocks of different
materials with identical dimensions plus a
transparent hollow body with internal volume
equal to that of the sample blocks and a loop
attached for suspending it. The sample blocks are
provided with 2 mm holes for suspending them.
2. Technical data
Materials: Wood, aluminium,
iron, brass, copper
Dimensions of each block: 10 × 20 × 45 mm
3. Experiment procedure
3.1 Determining densities of solid bodies
The following additional equipment is needed for
determining the densities:
1 Electronic balance, 200 g (230 V, 50/60 Hz)
U42048-230
3
or
1 Electronic balance, 200 g (115 V, 50/60 Hz)
U42048-115
1 Vernier calliper, 150mm U10071
1 Beaker, low shape, from set U14210
3.1.1 Determining density by weighing and
calculating the volume
• Measure the dimensions of the blocks using
the Vernier calliper and calculate the volume.
• Determine the mass m by weighing.
• Calculate the densities of the samples
according to the formula:
m
.
=ρ
V
Note:
The 2 mm holes introduce an error and for precise
determination that must be taken into account in
the calculation.
3.1.2 Determining density by measuring the
buoyant force
• Push about 20 cm of nylon thread through a
hole in the sample block and tie the ends to
make a loop.
1
Page 2
Place the sample block on the balance and
•
note the weight.
• Fill the beaker with water.
• Hang the sample block on the hook below the
scale-pan of the balance.
• Immerse the sample block completely in the
water and note the weight reading.
The block shows an apparent loss of weight caused
by the buoyant force, which is equal to the weight
of the volume of liquid that it displaces.
• Note the weight difference and from it
determine the volume of the sample block,
using the fact that the density of water is
3
1 g/cm
.
• Calculate the density of the sample according
to the formula:
m
.
=ρ
V
• Repeat the measurement with the other
sample blocks and compare the results with
those from Experiment 3.1.1.
Note:
For the wooden sample block the density can only
be determined by the method of Experiment 3.1.1.
3.2 Confirming Archimedes’ principle
Archimedes’ principle states that the buoyant force
F
on a body immersed in a medium is exactly
A
equal to the weight (force due to gravity) F
of that
G
volume of the medium which is displaced by the
body; F
= FG.
A
Archimedes’ principle applies to both liquids and
gases.
Additional equipment needed:
1 Precision dynamometer, 1 N U20032
1 Beaker from set U14210
1 Vernier caliper, 150 mm U10071
1 Stand base, A-shape, 200mm U8611160
1 Stand rod, 750mm U15003
1 Clamp with hook U13252
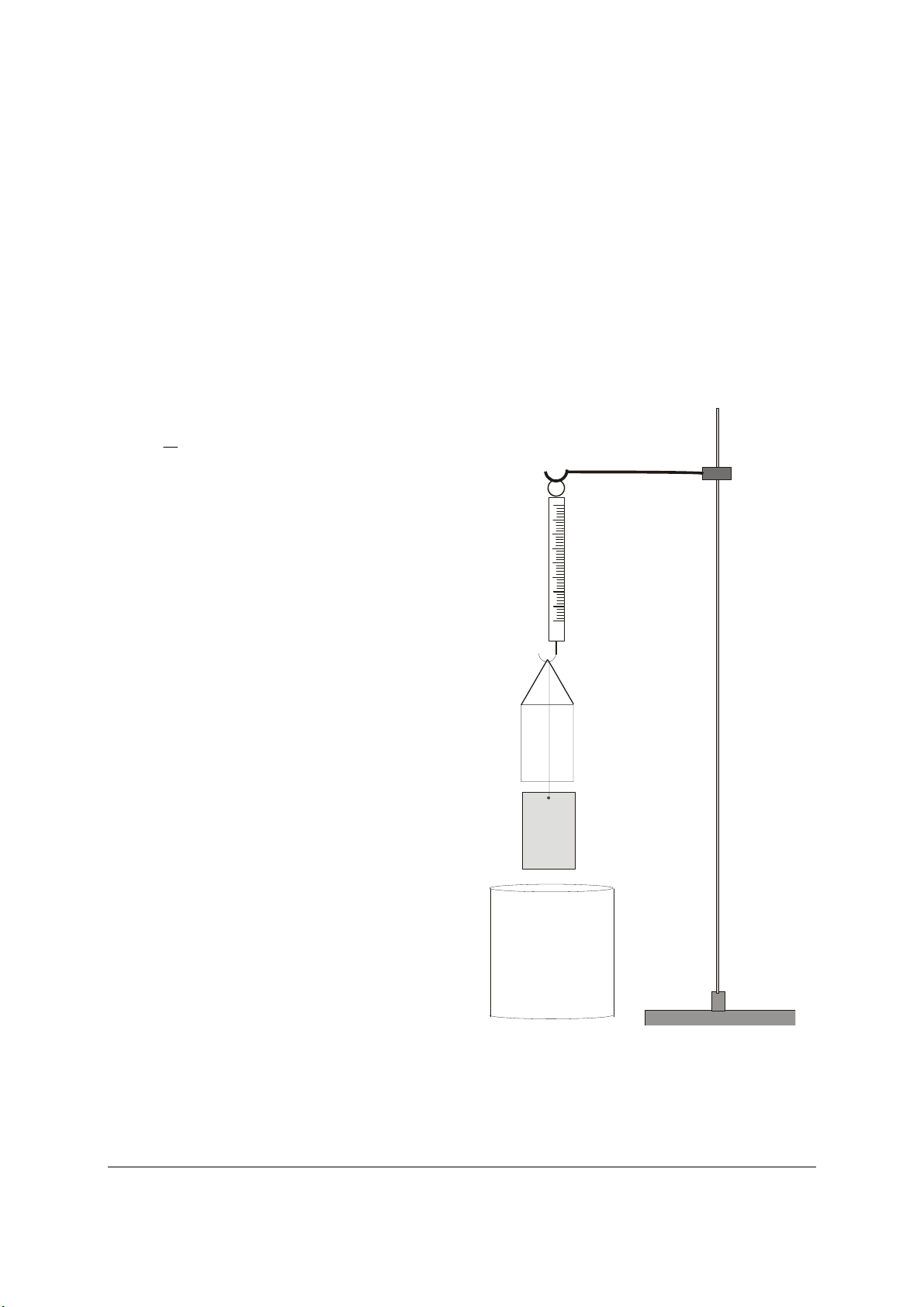
• Set up the stand and clamp and hang the
dynamometer on the hook (Fig. 1).
• Fit the sample block into the sample holder to
confirm that its volume is equal to the internal
volume of the hollow body.
• Calculate the volume of the sample block from
its dimensions.
• Suspend the hollow body and the sample block
on the dynamometer.
• Note the weight reading on the dynamometer.
• Place the beaker underneath and fill it with
water.
• Lower the dynamometer until the sample
block is completely immersed in the water.
• Note the new dynamometer reading.
The difference between the two readings is the
buoyant force F
• Fill the hollow body with water.
on the sample block.
A
As the internal volume of the hollow body is equal
to the volume of the sample block, the quantity of
water in it is equal to the quantity of water
displaced by the sample block.
The dynamometer now shows the same reading as
at the beginning. This confirms Archimedes’
principle.
Fig. 1 Experiment setup
Elwe Didactic GmbH ▪ Steinfelsstr. 6 ▪ 08248 Klingenthal ▪ Germany ▪ www.elwedidactic.com
3B Scientific GmbH ▪ Rudorffweg 8 ▪ 21031 Hamburg ▪ Germany ▪ www.3bscientific.com
Subject to technical amendments
© Copyright 2008 3B Scientific GmbH
 Loading...
Loading...