Page 1

3B SCIENTIFIC
Satz 5 Dichtekörper U8404556
Bedienungsanleitung
04/08 ALF
®
PHYSICS
1 Probekörper Kupfer
2 Probekörper Eisen
3 Probekörper Aluminium
4 Probekörper Messing
5 Probekörper Holz
6 Hohlkörper
1. Beschreibung
Der Satz 5 Dichtekörper dient zur Dichtebestimmung unterschiedlicher Materialien und zum
Nachweis des archimedischen Prinzips.
Der Satz besteht aus fünf Probekörpern unterschiedlichen Materials und gleichen Abmessungen
sowie einem transparenten Hohlkörper mit Haltebügel gleichen Innenvolumens. Die Probekörper
sind mit 2-mm-Bohrungen zur Aufhängung versehen.
2. Technische Daten
Materialien: Holz, Aluminium,
Eisen, Messing,
Kupfer
Abmessungen eines Quaders: 10 x 20 x 45 mm
3. Bedienung
3.1 Dichtebestimmung fester Körper
Zur Bestimmung der Dichte sind folgende Geräte
zusätzlich erforderlich:
3
1 Elektronische Waage 200 g (230 V, 50/60 Hz)
U42048-230
oder
1 Elektronische Waage 200 g (115 V, 50/60 Hz)
U42048-115
1 Messschieber U10071
1 Becherglas aus U14210
3.1.1 Dichtebestimmung durch Wägung und Vo-
lumenberechnung
• Abmessungen der Körper mittels Messschieber
bestimmen und daraus Volumen berechnen,
• Gewicht durch Wägung bestimmen.
• Dichte der Probekörper nach der Formel
m
=ρ
V
berechnen.
Anmerkung:
Durch die 2-mm-Bohrung entsteht ein Fehler, der
für genaue Berechnungen berücksichtigt werden
muss.
1
Page 2
3.1.2 Dichtebestimmung durch Auftriebsmessung
• Ca. 20 cm Perlonfaden durch die Bohrung in
den Probekörpern führen und zu einer Schlaufe zusammen binden.
• Probekörper auf die Waage stellen und das
Gewicht notieren.
• Becherglas mit Wasser füllen.
• Probekörper an den Unterflurwägehaken der
Waage hängen.
• Probekörper vollkommen in das Wasser tau-
chen und das Gewicht ablesen.
Durch den Auftrieb verliert der Körper scheinbar
soviel an Gewicht wie das von ihm verdrängte Flüssigkeitsvolumen besitzt.
• Gewichtsdifferenz bilden und daraus das Volu-
men des Probekörpers bestimmen. (Dichte von
Wasser 1 g/cm
• Dichte des Probekörpers nach der Formel
m
=ρ
V
3
)
berechnen.
• Messung mit den anderen Probekörpern wie-
derholen und mit den Ergebnissen aus Experiment 3.1.1 vergleichen.
Anmerkung:
Für den Probenkörper Holz ist die Dichte wie unter
Punkt 3.1.1 beschrieben zu bestimmen.
3.2 Bestätigung des archimedischen Prinzips
Das archimedische Prinzip lautet:
Die Auftriebskraft F
um ist genau so groß wie die Gewichtskraft F
vom Körper verdrängten Mediums; F
eines Körpers in einem Medi-
A
= FG.
A
des
G
Das archimedische Prinzip gilt in Flüssigkeiten und
Gasen.
Zusätzlich benötigte Geräte:
1 Präzisionskraftmesser 1 N U20032
1 Becherglas aus U14210
1 Messschieber U10071
1 Stativfuß U8611160
1 Stativstange, 750 mm U15003
1 Muffe mit Haken U13252
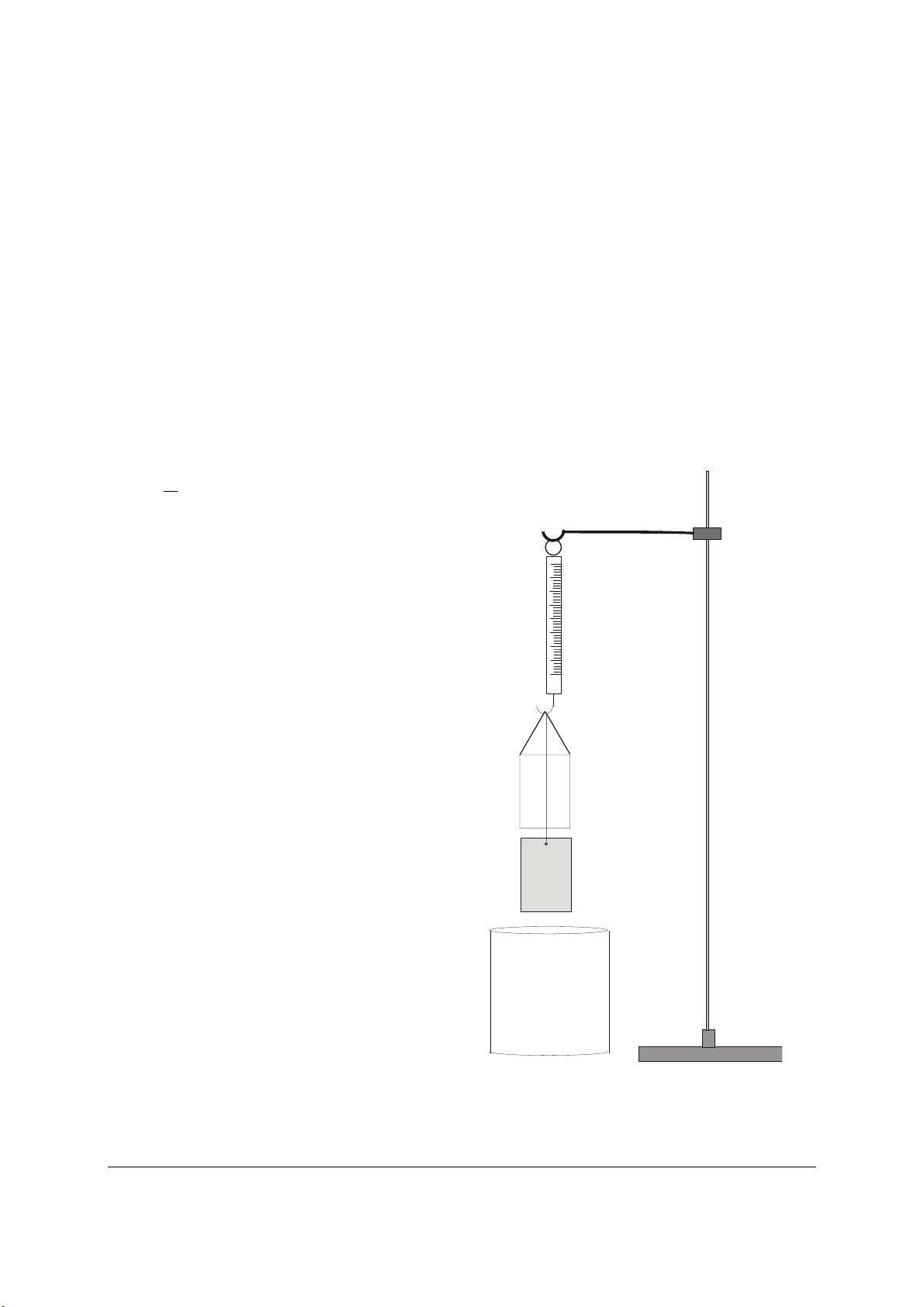
• Stativ aufbauen und Kraftmesser an den Haken
hängen (Fig. 1).
• Probekörper in den Hohlkörper stecken, um zu
demonstrieren, dass sein Volumen gleich dem
Innenvolumen des Hohlkörpers ist.
• Volumen des Probekörpers aus seinen Abmes-
sungen berechnen.
• Hohlkörper und Probekörper an den Kraftmes-
ser hängen.
• Gewicht ablesen und notieren.
• Becherglas darunter stellen und mit Wasser
befüllen.
• Kraftmesser soweit absenken, dass der Probe-
körper vollständig im Wasser eingetaucht ist.
• Neuen Wert am Kraftmesser ablesen.
Die Differenz zwischen beiden Ablesungen entspricht der Auftriebskraft F
• Hohlkörper mit Wasser füllen.
auf den Probekörper.
A
Da das Innenvolumen des Hohlkörpers gleich dem
Volumen des Probekörpers ist, entspricht die eingefüllte Menge Wasser der durch den Probekörper
verdrängten Menge Wasser.
Der Kraftmesser zeigt wieder den ursprünglichen
Wert an. Das Archimedische Prinzip ist damit bestätigt.
Fig. 1 Experimenteller Aufbau
Elwe Didactic GmbH ▪ Steinfelsstr. 6 ▪ 08248 Klingenthal ▪ Deutschland ▪ www.elwedidactic.com
3B Scientific GmbH ▪ Rudorffweg 8 ▪ 21031 Hamburg ▪ Deutschland ▪ www.3bscientific.com
Technische Änderungen vorbehalten
© Copyright 2008 3B Scientific GmbH
Page 3

3B SCIENTIFIC
Set of Five Blocks of Various Densities U8404556
Instruction Sheet
04/08 ALF
®
PHYSICS
1 Sample block - copper
2 Sample block - iron
3 Sample block - aluminium
4 Sample block - brass
5 Sample block - wood
6 Hollow body
1. Description
The set of five blocks of various densities is used to
determine the densities of different materials and
to demonstrate Archimedes’ principle.
The set consists of five sample blocks of different
materials with identical dimensions plus a
transparent hollow body with internal volume
equal to that of the sample blocks and a loop
attached for suspending it. The sample blocks are
provided with 2 mm holes for suspending them.
2. Technical data
Materials: Wood, aluminium,
iron, brass, copper
Dimensions of each block: 10 × 20 × 45 mm
3. Experiment procedure
3.1 Determining densities of solid bodies
The following additional equipment is needed for
determining the densities:
1 Electronic balance, 200 g (230 V, 50/60 Hz)
U42048-230
3
or
1 Electronic balance, 200 g (115 V, 50/60 Hz)
U42048-115
1 Vernier calliper, 150mm U10071
1 Beaker, low shape, from set U14210
3.1.1 Determining density by weighing and
calculating the volume
• Measure the dimensions of the blocks using
the Vernier calliper and calculate the volume.
• Determine the mass m by weighing.
• Calculate the densities of the samples
according to the formula:
m
.
=ρ
V
Note:
The 2 mm holes introduce an error and for precise
determination that must be taken into account in
the calculation.
3.1.2 Determining density by measuring the
buoyant force
• Push about 20 cm of nylon thread through a
hole in the sample block and tie the ends to
make a loop.
1
Page 4

Place the sample block on the balance and
•
note the weight.
• Fill the beaker with water.
• Hang the sample block on the hook below the
scale-pan of the balance.
• Immerse the sample block completely in the
water and note the weight reading.
The block shows an apparent loss of weight caused
by the buoyant force, which is equal to the weight
of the volume of liquid that it displaces.
• Note the weight difference and from it
determine the volume of the sample block,
using the fact that the density of water is
3
1 g/cm
.
• Calculate the density of the sample according
to the formula:
m
.
=ρ
V
• Repeat the measurement with the other
sample blocks and compare the results with
those from Experiment 3.1.1.
Note:
For the wooden sample block the density can only
be determined by the method of Experiment 3.1.1.
3.2 Confirming Archimedes’ principle
Archimedes’ principle states that the buoyant force
F
on a body immersed in a medium is exactly
A
equal to the weight (force due to gravity) F
of that
G
volume of the medium which is displaced by the
body; F
= FG.
A
Archimedes’ principle applies to both liquids and
gases.
Additional equipment needed:
1 Precision dynamometer, 1 N U20032
1 Beaker from set U14210
1 Vernier caliper, 150 mm U10071
1 Stand base, A-shape, 200mm U8611160
1 Stand rod, 750mm U15003
1 Clamp with hook U13252
• Set up the stand and clamp and hang the
dynamometer on the hook (Fig. 1).
• Fit the sample block into the sample holder to
confirm that its volume is equal to the internal
volume of the hollow body.
• Calculate the volume of the sample block from
its dimensions.
• Suspend the hollow body and the sample block
on the dynamometer.
• Note the weight reading on the dynamometer.
• Place the beaker underneath and fill it with
water.
• Lower the dynamometer until the sample
block is completely immersed in the water.
• Note the new dynamometer reading.
The difference between the two readings is the
buoyant force F
• Fill the hollow body with water.
on the sample block.
A
As the internal volume of the hollow body is equal
to the volume of the sample block, the quantity of
water in it is equal to the quantity of water
displaced by the sample block.
The dynamometer now shows the same reading as
at the beginning. This confirms Archimedes’
principle.
Fig. 1 Experiment setup
Elwe Didactic GmbH ▪ Steinfelsstr. 6 ▪ 08248 Klingenthal ▪ Germany ▪ www.elwedidactic.com
3B Scientific GmbH ▪ Rudorffweg 8 ▪ 21031 Hamburg ▪ Germany ▪ www.3bscientific.com
Subject to technical amendments
© Copyright 2008 3B Scientific GmbH
Page 5

3B SCIENTIFIC
Jeu de 5 corps de densité U8404556
Instructions d'utilisation
04/08 ALF
®
PHYSICS
1 Échantillon de cuivre
2 Échantillon de fer
3 Échantillon d'aluminium
4 Échantillon de laiton
5 Échantillon de bois
6 Corps creux
1. Description
Le jeu de 5 corps de densité permet de déterminer
la densité de différents matériaux et de démontrer
le principe d'Archimède.
Le jeu est constitué de cinq échantillons de
différents matériaux et de mêmes dimensions ainsi
que d'un corps creux transparent avec arceau de
même volume intérieur. Les échantillons
présentent des alésages de 2 mm servant à leur
suspension.
Matériaux : bois, aluminium,
Dimensions d'un parallélépipède : 10 x 20 x
3.1 Déterminer la densité de solides
Pour déterminer la densité, vous nécessitez le
matériel supplémentaire suivant :
2. Caractéristiques techniques
fer, laiton, cuivre
3
45 mm
3. Manipulation
1 balance électronique 200 g (230 V, 50/60 Hz)
U42048-230
ou
1 balance électronique 200 g (115 V, 50/60 Hz)
U42048-115
1 pied à coulisse U10071
1 bécher de U14210
3.1.1 Détermination de la densité par pesage et
calcul du volume
• Déterminez les dimensions des corps à l'aide
du pied à coulisse, puis calculez leur volume.
• Déterminez le poids en pesant les corps.
• Calculez la densité des échantillons en vous
servant de la formule suivante :
m
=ρ
V
Remarque :
L'alésage de 2 mm entraîne une erreur dont il
faudra tenir compte pour obtenir des résultats
exacts.
1
Page 6

3.1.2 Détermination de la densité par mesure de
la poussée verticale
• Faites passer environ 20 cm de fil en perlon à
travers l'alésage dans les échantillons et nouezle en formant une boucle.
• Placez l'échantillon sur la balance et notez son
poids.
• Remplissez le bécher d'eau.
• Accrochez l'échantillon au crochet de pesée.
•
Plongez complètement l'échantillon dans l'eau
et lisez son poids.
Par la poussée verticale, le corps semble perdre
autant de poids que le volume de liquide repoussé.
• Calculez la différence de poids, puis le volume
de l'échantillon (densité de l'eau = 1 g/cm
•
Calculez la densité de l'échantillon en vous
servant de la formule suivante :
m
=ρ
V
• Répétez la mesure avec les autres échantillons
3
).
et comparez les résultats avec ceux de
l'expérience 3.1.1.
Remarque :
Déterminez la densité de l'échantillon en bois en
suivant la description du point 4.1.1.
3.2 Confirmation du principe d'Archimède
Que dit le principe d'Archimède ?
La force verticale F
fluide correspond à la force F
déplacé par le corps ; F
d'un corps plongé dans un
A
= FG.
A
du poids de fluide
G
Le principe d'Archimède s'applique aux liquides et
aux gaz.
Matériel supplémentaire requis :
1 dynamomètre de précision, 1 N U20032
1 bécher de U14210
1 pied à coulisse U10071
1 tige statif U8611160
1 tige statif, 750 mm U15003
1 noix de serrage avec crochet U13252
• Montez la tige statif et suspendez le
dynamomètre au crochet (fig. 1).
• Insérez l'échantillon dans le corps creux pour
démontrer que son volume est le même que
celui du volume intérieur du corps creux.
• Calculez le volume de l'échantillon à partir de
ses dimensions.
• Accrochez le corps creux et l'échantillon au
dynamomètre.
• Lisez et notez le poids.
• Placez le bécher par-dessous et remplissez-le
d'eau.
• Abaissez le dynamomètre de manière à ce que
l'échantillon plonge entièrement dans l'eau.
• Lisez la nouvelle valeur sur le dynamomètre.
La différence entre les deux valeurs correspond à la
poussée verticale F
• Remplissez le corps creux d'eau.
exercée sur l'échantillon.
A
Comme le volume intérieur du corps creux est
identique au volume de l'échantillon, la quantité
d'eau remplie correspond à la quantité d'eau
déplacée par l'échantillon.
Le dynamomètre reprend sa valeur d'origine. Le
principe d'Archimède est confirmé.
Fig. 1 Montage expérimental
Elwe Didactic GmbH ▪ Steinfelsstr. 6 ▪ 08248 Klingenthal ▪ Allemagne ▪ www.elwedidactic.com
3B Scientific GmbH ▪ Rudorffweg 8 ▪ 21031 Hamburg ▪ Allemagne ▪ www.3bscientific.com
Sous réserve de modifications techniques
© Copyright 2008 3B Scientific GmbH
Page 7

3B SCIENTIFIC
Set di 5 corpi da immersione U8404556
Istruzioni per l'uso
04/08 ALF
®
PHYSICS
1 Corpo campione in rame
2 Corpo campione in ferro
3 Corpo campione in alluminio
4 Corpo campione in ottone
5 Corpo campione in legno
6 Corpo cavo
1. Descrizione
Il set composto da 5 corpi da immersione viene
utilizzato per determinare la densità di diversi
materiali e per dimostrare il principio di
Archimede.
Il set è costituito da cinque corpi di prova di
materiale diverso e con le stesse misure, nonché da
un corpo cavo trasparente con staffa e uguale
volume interno. I corpi di prova sono provvisti di
fori da 2 mm per la sospensione.
2. Dati tecnici
Materiali: legno, alluminio,
Dimensioni di un
parallelepipedo: 10 x 20 x 45 mm
3. Utilizzo
3.1 Determinazione della densità di corpi solidi
Per determinare la densità sono inoltre necessari i
seguenti apparecchi:
ferro, ottone,
rame
3
1 bilancia elettronica 200 g (230 V, 50/60 Hz)
U42048-230
oppure
1 bilancia elettronica 200 g (115 V, 50/60 Hz)
U42048-115
1 calibro a corsoio U10071
1 bicchiere di vetro U14210
3.1.1 Determinazione della densità mediante
pesata e calcolo del volume
• Definire le dimensioni dei corpi tramite il
calibro a corsoio e calcolare il volume.
• Determinare il peso tramite pesata.
• Calcolare la densità dei corpi di prova secondo
la formula
m
=ρ
V
• .
Nota:
Il foro da 2 mm determina un errore, che deve
essere tenuto in considerazione per eseguire calcoli
precisi.
1
Page 8

3.1.2 Determinazione della densità mediante
misura della spinta statica
• Infilare ca. 20 cm di filo Perlon attraverso il
foro nei corpi di prova e unire le estremità per
formare un occhiello.
• Collocare il corpo di prova sulla bilancia e
annotare il peso.
• Riempire il bicchiere con acqua.
• Appendere il corpo di prova al gancio di pesata
sotto la bilancia.
• Immergere completamente il corpo di prova
nell’acqua e leggere il peso.
A causa della spinta statica il corpo perde
apparentemente un peso corrispondente a quello
del volume del liquido da lui spostato.
• Ricavare la differenza di peso e in base ad essa
determinare il volume del corpo di prova
(densità dell’acqua 1 g/cm
• Calcolare la densità del corpo di prova secondo
la formula
=ρ
• Ripetere la misurazione con gli altri corpi di
m
V
3
).
prova e confrontare con i risultati ottenuti
dall’esperimento 3.1.1.
Nota:
Per il corpo di prova in legno la densità deve essere
determinata secondo quanto indicato nel punto
3.1.1.
3.2 Conferma del principio di Archimede
Il principio di Archimede dice:
La spinta idrostatica F
pari alla forza peso F
corpo; F
= FG.
A
di un corpo in un liquido è
A
del liquido spostato dal
G
Il principio di Archimede vale per i liquidi e anche
per i gas.
Apparecchi ulteriormente necessari:
1 dinamometro di precisione 1 N U20032
1 bicchiere di vetro U14210
1 calibro a corsoio U10071
1 base di supporto U8611160
1 asta di supporto, 750 mm U15003
1 manicotto con gancio U13252
• Montare il supporto e appendere il
dinamometro al gancio (Fig. 1).
• Infilare il corpo di prova nel corpo cavo, per
dimostrare che il suo volume è pari al volume
interno del corpo cavo.
• Calcolare il volume del corpo di prova in base
alle sue dimensioni.
• Appendere il corpo cavo e il corpo di prova al
dinamometro.
• Leggere e annotare il peso.
• Posizionare un bicchiere sotto il dinamometro
e riempirlo con acqua.
• Abbassare il dinamometro fino a immergere
completamente il corpo di prova in acqua.
• Leggere il nuovo valore sul dinamometro.
La differenza tra le due letture corrisponde alla
spinta idrostatica F
• Riempire il corpo cavo con acqua.
sul corpo di prova.
A
Poiché il volume interno del corpo cavo è uguale al
volume del corpo di prova, la quantità di acqua
usata per il riempimento corrisponde a quella
spostata dal corpo di prova.
Il dinamometro indica di nuovo il valore originario.
Il principio di Archimede è quindi confermato.
Fig. 1 Struttura sperimentale
Elwe Didactic GmbH • Steinfelsstr. 6 • 08248 Klingenthal • Germania • www.elwedidactic.com
3B Scientific GmbH • Rudorffweg 8 • 21031 Amburgo • Germania • www.3bscientific.com
Con riserva di modifiche tecniche
© Copyright 2008 3B Scientific GmbH
Page 9

3B SCIENTIFIC® PHYSICS
Juego de 5 Cuerpos de densidad U8404556
Instrucciones de uso
04/08 ALF
2 Cuerpo de prueba: Hierro
3 Cuerpo de prueba: Aluminio
4 Cuerpo de prueba: Latón
5 Cuerpo de prueba: Madera
6 Cuerpo hueco
1 Cuerpo de prueba: Cobre
1. Descripción
El juego de 5 cuerpos de densidad sirve para la
determinación de la densidad de diferentes
materiales y para comprobar el principio de
Arquímedes.
El juego se compone de cinco cuerpos de prue ba
de diferentes materiales, de iguales dimensiones y
además de un cuerpo hueco con arco soporte y de
volumen interno igual al de los otros cuerpos. Cada
uno de los cuerpos de prueba está provisto de
adicionalmente los siguientes aparatos::
1 Balanza electrónica 200 g (230 V, 50/60 Hz)
U42048-230
o
1 Balanza electrónica 200 g (115 V, 50/60 Hz)
U42048-115
1 Pie de rey U10071
1 Vaso de precipitados de U14210
3.1.1 Determinación de la densidad por pesada y
orificio de 2 mm para poder ser colgado.
2. Datos técnicos
Materiales: Madera, Aluminio,
Hierro, Latón y Cobre
Dimensiones de un
paralelepípedo: 10 x 20 x 45 mm
3
3. Manejo
3.1 Determinación de la densidad de cuerpos
• Se determinan las dimensiones con el pie de
rey y se calcula el volumen,
• Se determina el volumen haciendo una pesa-
da.
• Con la siguiente fórmula
se calcula la densidad del cuerpo de prueba.
Onservación:
Debido al orificio de 2-mm se origina un error que
debe ser considerado para un cálculo exacto.
sólidos
Para la determinación de la densidad se requieren
cálculo del volumen
m
=ρ
V
1
Page 10

3.1.2 Determinación de la densidad por medición
del empuje ascensional
• Un hilo de perlón de 20 cm aprox. se pasa por
el orificio del cuerpo de prueba y se hace un
lazo.
• Se coloca el cuerpo en el platillo de la balanza
y se anota el peso.
• El vaso de precipitados se llena de agua.
• El cuerpo de prueba se cuelga del gancho bajo
el plato de la balanza.
• El cuerpo de prueba se sumerje
completamente en el agua.
Debido al empuje ascensional el cuerpo de prueba
pierde aparentemente tanto peso como el volumen
del líquido desplazado por el mismo.
• Se calcula la diferencia de peso y se determina
así el volumen del cuerpo de prueba.
(Densidad del agua 1 g/cm
• Con la fórmula siguiente
m
=ρ
V
3
)
se calcula la densidad del cuerpo de prueba.
• Se repita la medición con los otros cuerpos de
prueba y se comparan los resultados con los
del experimento 3.1.1.
Observación:
La densidad del cuerpo de madera se determina
como se describe en el punto 4.1.1.
3.2 Comprobación del principio de Arquímedes
El principio de Arquímedes dice que:
La fuerza de empuje ascensional F
que
A
experimenta un cuerpo en un medio es
exactamente igual al peso del volumen F
medio desplazado por el cuerpo; F
= FG.
A
del
G
El principio de Arquímedes se cumple tanto en
líquidos como en gases.
Aparatos requeridos adicionalmente:
1 Dinamómetro de precisión 1 N U20032
1 Vaso de precipitados de U14210
1 Pie de rey U10071
1 Pie soporte U8611160
1 Varilla soporte, 750 mm U15003
1 Nuez con gancho U13252
• Se monta el sistema de soporte y el dinamó-
metro se cuelga del gancho (Fig. 1).
• Se inserta el cuerpo de prueba en el cuerpo
hueco para demostrar que su volumen es igual
al volumen interno del cuerpo hueco.
• Se calcula el volumen del cuerpo de prueba
por medio de sus dimensiones.
• Se cuelgan en el dinamómetro el cuerpo de
prueba y el cuerpo hueco.
• Se lee y se anota el peso.
• Se coloca el vaso de precipitados por debajo y
se llena de agua.
• Se baja el dinamómetro hasta que el cuerpo de
prueba se encuentre totalmente sumergido en
el agua.
• Se lee el nuevo valor en el dinamómetro.
La diferencia entre las dos lecturas corresponden a
la fuerza ascensional F
que experimenta el cuerpo
A
de prueba.
• Se llena de agua el cuerpo hueco.
Como el volumen interno del cuerpo hueco es igual
al volumen del cuerpo de prueba, la cantidad de
agua llenada corresponde al volumen de agua
desplazado por el cuerpo de prueba.
El dinamómetro muestra ahora el valor original. En
esta forma se comprueba el principio de
Arquímedes.
Fig. 1 Montaje experimental
Elwe Didactic GmbH • Steinfelsstr. 6 • 08248 Klingenthal • Alemania • www.elwedidactic.com
3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburgo • Alemania • www.3bscientific.com
Se reservan las modificaciones técnicas
© Copyright 2008 3B Scientific GmbH
Page 11

3B SCIENTIFIC
Jogo de 5 Corpos de Densidade U8404556
Instruções de Operação
04/08 ALF
®
PHYSICS
1 Corpo-de-prova de cobre
2 Corpo-de-prova de ferro
3 Corpo-de-prova de alumínio
4 Corpo-de-prova de latão
5 Corpo-de-prova de madeira
6 Corpo vazio
1. Descrição
O jogo de 5 corpos de densidade serve para a
determinação da densidade de diversos materiais e
para a comprovação do princípio de Arquimedes.
O jogo é composto de cinco corpos-de-prova de
diversos materiais com as mesmas dimensões, bem
como de um corpo vazio ou oco transparente com
alças de sustentação e de igual volume interno. Os
corpos-de-prova são providos de furos de 2-mm
para serem pendurados.
2. Dados Técnicos
Materiais: madeira,
alumínio, ferro,
latão, cobre.
Medidas dos corpos-de-prova: 10 x 20 x 45 mm
3. Utilização
3.1 Determinação da densidade de corpos
sólidos
Para determinação da densidade são necessários os
seguintes aparelhos suplementares:
3
1 Balança eletrônica 200 g (230 V, 50/60 Hz)
U42048-230
ou
1 Balança eletrônica 200 g (115 V, 50/60 Hz)
U42048-115
1 Calibrador U10071
1 Copo do U14210
3.1.1 Determinação da densidade pela pesagem e
cálculo de volume
• Determinar as medidas dos corpos por meio do
calibrador para então calcular o volume.
• Determinar o peso por pesagem.
• Calcular a densidade dos corpos-de-prova pela
fórmula
m
=ρ
Nota:
Através do furo de 2-mm constitui-se um erro que
deve ser levado em conta para cálculos exatos.
V
1
Page 12

3.1.2 Determinação de densidade pela medição
da força ascensional.
• Passar aprox. 20 cm de cordão de nylon /
perlon pelo furo dos corpos-de-prova e
amarrar em forma de laço.
• Colocar os corpos-de-prova na balança e anotar
o peso.
• Encher o copo com água.
• Pendurar os corpos-de-prova no gancho da
balança.
• Mergulhar os corpos-de-prova completamente
na água e ler o peso.
Através da força ascensional o corpo
aparentemente perde tanto o peso quanto o
volume de líquido por ele deslocado.
• Verificar a diferença de peso e dela determinar
o volume dos corpos-de-prova. (Densidade da
água 1 g/cm
• Calcular a densidade dos corpos-de-prova pela
3
)
fórmula
m
=ρ
V
• Repetir a medição com os outros corpos-de-
prova e comparar com os resultados da
experiência 3.1.1.
Nota:
Para os corpos-de-prova de madeira deve ser
determinada a densidade como descrito no ponto
3.1.1.
3.2 Confirmação do Princípio de Arquimedes
O princípio de Arquimedes diz:
A força ascensional F
de um corpo dentro de um
A
meio tem exatamente a grandeza como a força do
peso F
do meio deslocado pelo corpo; FA = FG.
G
O princípio de Arquimedes vale tanto em líquidos
como em gases.
Aparelhos Suplementares Necessários:
1 Dinamômetro de precisão 1 N U20032
1 Copodo U14210
1 Calibrador U10071
1 Base de suporte U8611160
1 Barra de suporte, 750 mm U15003
1 Manga com gancho U13252
• Montar o suporte e pendurar o dinamômetro
no gancho (fig. 1).
• Encaixar os corpos-de-prova no corpo vazio
para demonstrar que o seu volume é igual ao
volume interno do corpo vazio.
• Calcular o volume dos corpos-de-prova pelas
suas dimensões.
• Pendurar o corpo vazio e os corpos-de-prova
no dinamômetro.
• Ler o peso e anotar.
• Colocar um copo embaixo e encher com água.
• Abaixar o dinamômetro até que os corpos-de-
prova estejam totalmente mergulhados na
água.
• Ler o novo valor no dinamômetro.
A diferença entre as duas leituras corresponde à
força F
atuante sobre os corpos-de-prova.
A
• Encher o corpo vazio com água.
Dessa forma o volume interno do corpo vazio é
igual ao volume dos corpos-de-prova a quantidade
de água colocada é igual à quantidade de água
deslocada pelos corpos-de-prova.
O dinamômetro mostra novamente o valor
original. Assim fica confirmado o princípio de
Arquimedes.
Fig. 1 Montagem Experimental
Elwe Didactic GmbH ▪ Steinfelsstr. 6 ▪ 08248 Klingenthal ▪ Alemanha ▪ www.elwedidactic.com
3B Scientific GmbH ▪ Rudorffweg 8 ▪ 21031 Hamburgo ▪ Alemanha ▪ www.3bscientific.com
Reservados Todos os Direitos de Modificações Técnicas
© Copyright 2008 3B Scientific GmbH
 Loading...
Loading...