Page 1

3B SCIENTIFIC
Instruction sheet
01/10 ALF
®
PHYSICS
Force Table U52004
1 Base
2 Clamps with pulleys
3 Centre rod
4 Mount for cords
5 Work disc
6 Weight holder with slotted
weights
1. Description
The force table serves to prove that force is a vector
quantity. It is also used for quantitative investigation of how forces combine and resolve.
The force table consists of a circular work disc on a
stable base with a dual angle scale. Weights are
attached to three pulleys with securing clamps. The
three sets of brass weights consist of 2x 5 g, 2x 10 g,
2x 20 g and 2x 50 g weights and weight holders
weighing 50 g.
2. Technical data
Dimensions: 300 mm x 390 mm dia. approx.
Scale: 0 to 360° with 1° resolution
Weight: 3 kg approx.
3. Principle
Forces are vector quantities. This means that the
resultant of two forces working at a single point is
not simply the sum of the forces but is dependent
1
Page 2
on the direction in which the forces act. The resul-
A
r
r
A
r
tant of two forces acting at the same point in a
single plane is defined as that force which, acting
alone in the same plane, would have the same
effect as the combination of the two forces. A force
of equal magnitude to the resultant but acting in
the opposite direction therefore maintains the
body in equilibrium. The resultant can be obtained
by analysis or by graphical means using various
laws (parallelogram of forces, triangle of forces,
polygon of forces).
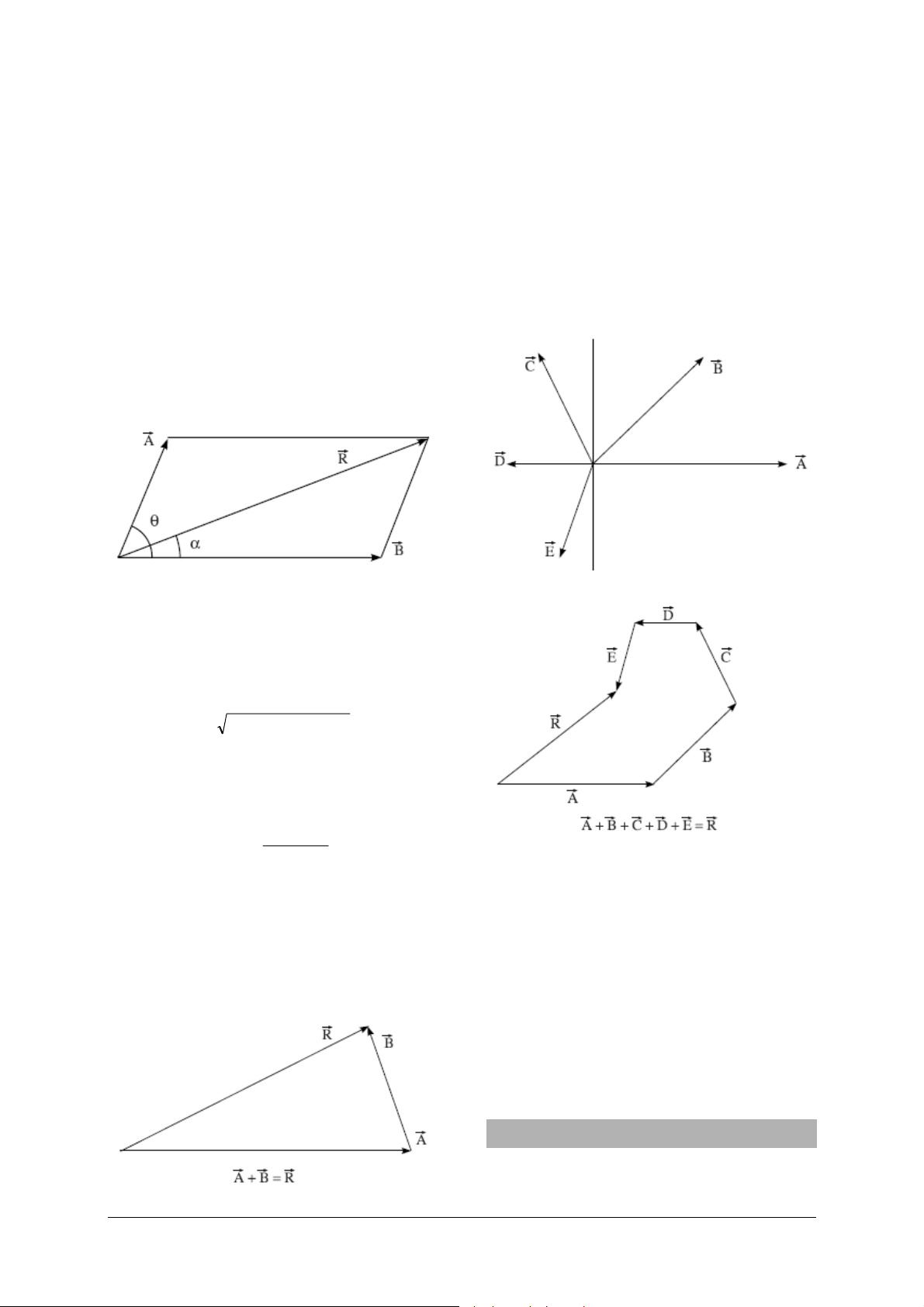
A parallelogram of forces represents two forces
acting simultaneously on a body as two adjacent
sides of a parallelogram. The magnitude and direction of their resultant is then given by the diagonal
originating from the same point.
From this it can be determined that a body is in
equilibrium if three forces are acting upon it,
which can be represented by the three sides of a
triangle.
If more than two forces act on a body at once, the
law of the polygon of forces is used. This represents
several forces acting at the same point as following
sides of a polygon where one side remains open. As
for the triangle, following the side that closes the
polygon in the opposite direction gives the resultant force.
This theorem can be expressed mathematically as
follows: When two forces
and Br acting on a
body with an angle θ between them, the resultant
R
is given by:
22
θ++= cosABBAR 2
If α is the angle between the resultant and force
then:
θ
sinB
tan
=α
θ+
cosBA
With the law of the triangle of forces, two forces
acting simultaneously on a body are represented in
terms of magnitude and direction by two following
sides of a triangle. The magnitude and direction of
the resultant is then given by following the third
side of the triangle in the opposite direction.
Therefore a body is in equilibrium when several
forces act upon it that can be represented as a
closed polygon. The vector sum of the individual
forces is equal to zero and so is the resultant force.
On closer observation, this law can be seen to be a
simple extension of the law of the triangle of
forces. The force table is suitable for demonstrating
vector addition and equilibrium of forces and for
confirming the graphic and analytical methods.
The equilibrium between two or three forces can
be demonstrated and the magnitude and direction
of each force easily determined.
4. Operation
4.1 Equipment Setup
• Place the base on an even surface.
• Screw the centre rod vertically into the base.
2
Page 3

• Press the work disc with force onto the centre
rod.
• Place the washer onto the central bore and
screw in the mount for cords.
• Attach the pulleys with clamps at the positions
on the work disc marked 0°, 120° and 240°.
• Place the ring above the mount in the centre of
the work disc.
• Run the cords over the pulleys, suspend the
weight holders and attach the slotted weights.
• The ring should be in a state of equilibrium.
4.2 Sample experiment: Vector Addition
• Set up the force table as above.
• Add a 20 g mass to one weight holder and a
50 g mass to another at 0° and 120°.
• By adding weights to a third weight holder and
selecting a suitable angle it is possible to establish equilibrium. To check the equilibrium, lift
the ring and let it drop. If it falls back to the
centre, equilibrium has been attained. If not,
then further adjustments are necessary.
• Calculate the magnitude and direction of the
forces required to attain equilibrium. Compare
the values obtained in the experiment to those
determined by the theory.
• Draw the forces to scale showing their magni-
tude and direction to confirm the law of the
triangle of forces.
• Repeat the experiment with different masses
and angles.
3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Germany • www.3bscientific.com
Subject to technical amendments
© Copyright 2010 3B Scientific GmbH
Page 4

 Loading...
Loading...